Назад Вперёд

2.4.    Равновесная концентрация СНЗ в примесных и беспримесных полупроводниках

2.4.1. Равновесная концентрация зарядов в собственном полупроводнике

Вероятность p нахождения свободного электрона в энергетическом состоянии W определяется статистической функцией Ферми— Дирака:

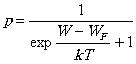                                                                                                (2.1)

где WF — уровень Ферми; kT— средняя энергия теплового движения микрочастицы при температуре Т К; k=1,38×10-23 Дж/К — постоянная Больцмана.

В интервале значений энергий от  W до W+dW  число энергетических  уровней, на которых могут находиться электроны проводимости, равно

                                                                             (2.2)

где mn- эффективная масса  электрона проводимости (в германии и кремнии, например, она составляет 0,22-0,33 от массы покоя электрона соответственно), h = 6,62×10-34 Дж×с - постоянная Планка

 Из соотношений (2.1), (2.2) можно определить концентрацию электронов проводимости для собственного полупроводника:

                                                                                                 (2.3)

При умеренных температурах, когда , концентрация электронов проводимости для собственного полупроводника

                                             (2.4)

где  nпр — эффективная  плотность  состояний   в   зоне   проводимости (Nпр=5×1019 см-3 для германия, Nпр=2×1020 см-3 для кремния), DW - ширина запрещенной зоны ( DW =0,66 эВ для германия, DW=1,12 эВ для кремния)

Число дырок в идеальной кристаллической решетке собственного полупроводника равно числу свободных электронов:

                                                      pi = ni.                                                 (2.5)

На основании приведенного соотношения можно сосчитать, что при комнатной температуре, т. е. при T=300 К, число свободных электронов в германии ni = 2,5×1013 см -3.

Поскольку в кристаллической решетке германия в каждом 1 см3 объема находится 4,4×1022 атомов, один свободный электрон приходится на 1 млрд. атомов вещества. В кремнии при той же температуре число свободных электронов на три порядка меньше вследствие более высокой энергии ионизации: ni = 1,4×1010 см-3.

Полученные величины концентраций электронов и дырок представляют собой результат динамического равновесия двух процессов — генерации и рекомбинации подвижных носителей заряда.

Скорость рекомбинации, т. е. число исчезающих в единицу времени электронно-дырочных пар, определяется свойствами полупроводника; кроме того, она пропорциональна концентрации электронов и дырок, так как чем больше число носителей заряда, тем вероятнее их встреча, завершающаяся рекомбинацией. Таким образом, скорость рекомбинации

vрек  = g i × ni × pi =g i × n2i

где g i — коэффициент рекомбинации, определяемый свойствами полупроводника.

Скорость генерации — число освобождающихся в единицу времени электронно-дырочных пар — зависит от температуры полупроводника и ширины его запрещенной зоны.

В стационарном режиме должно существовать динамическое равновесие — скорость генерации должна равняться скорости рекомбинации:

vген = g × ni2.

Отсюда

ni2  = vген /g .

Назад Вперёд