8.3. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ФУНКЦИОНИРОВАНИЯ СИСТЕМ

НА БАЗЕ N-CXEM

Особенности использования при моделировании систем сетевого подхода, реализуемого в виде N-схем, и основные понятия сетей Петри и их модификаций были даны в § 2.6. Рассмотрим возможности применения N-схем для формального описания процесса функционирования некоторой моделируемой системы S. Характерной особенностью N-схем является то, что с их помощью можно моделировать процессы в системах S, в которых происходит последовательная смена дискретных состояний, в том числе если эта смена происходит при выполнении разнообразных условий. Таким образом, с использованием N-схем могут быть описаны системы S, относящиеся к разным классам: аппаратные, физические, программные, экономические и т. д.

Структурный подход на базе N-схем. Применение аппарата N-схем позволяет осуществить структурный подход к построению имитационной модели системы S, при котором обеспечиваются наглядность модели, модульный принцип ее разработки (сборки), возможность перехода к автоматизированной интерактивной процедуре проектирования [30, 33, 54]. Рассмотрим особенности такого подхода, используя для общности и простоты понятия, введенные в § 8.2 для Q-схем, на следующих примерах.

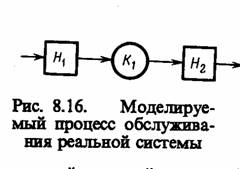
Пример 8.6. Пусть процесс функционирования некоторой реальной системы S (процессор ЭВМ, мультиплексный канал, станок в технологической цепочке н т. п.), являющийся по своей природе процессом обслуживания, представлен в виде двухфазной одноканальной Q-схемы (рис. 8.16). Тогда этот процесс можно представить N-схемой, структура, которой показана на рис. 8.17.

Чтобы маркировать эту структуру, нужно задать состояние системы. Пусть в накопителе H_t находятся две заявки, в Н₂, — заявок нет, канал обслуживания К₁ свободен. Такому состоянию соответствует маркировка, показанная на рис. 8.18. Процесс выполнения этой N-схемы моделирует процесс функционирования системы S, представленной в виде Q-схемы.

Через переход  d₁   эта N-схема может быть сведена с другой N-схемой, моделирующей процесс порождения заявок на обслуживание, аналогично — по переходу d_A — с системой потребления заявок.

Пример 8.7. Пусть имеется некоторая система S, например производственно-технологическая, процесс функционирования которой представлен в виде Q-схемы (рис. 8.19). По технологическому циклу для выполнения заказа необходимо выполнить две фазы обслуживания: сначала обслуживание в канале К_1; затем либо в К₂, либо в К,. Операторы F₁ и F₂ обслуживают (поддерживают в работоспособном состоянии) каналы, причем .F, обслуживает К₁ и К₂, z.F₂ — K_1и К₃.

Тогда в этой системе могут быть следующие состояния:

а — заказ пришел и ждет в накопителе H₁

б — заказ обработан К₁ и ждет в накопителе Н₂;

в — заказ выполнен и находится в накопителе Н₃;

г — канал K₁ не занят;

д — канал К₂ не занят;

е — канал К₃ не занят;

ж — оператор F₁ не занят;

з — оператор F₂ не занят;

и — канал К₁ выполняет заказ под управлением F₁;

к — канал К₂ выполняет заказ под управлением F₂;-

л — канал К₂ выполняет заказ под управлением F₁

м — канал К₃ выполняет заказ под управлением F₂ и могут происходить следующие события-переходы:

1 — поступление заказа;

2 — F₁ начинает   выполнение заказа на К₁;

3 — F₁ закончил   выполнение заказа на К₁;

4 —F₁   начинает   выполнение заказа на К₁

5 — F₂ закончил   выполнение заказа на K₁;

6 — F₁ начинает   выполнение заказа на К₂;

7 — F₁ закончил   выполнение заказа на К₂;

8 — F₂ начинает   выполнение заказа на К₃;

9 — F₂ закончил   выполнение заказа на К₃;

10 — заказ отправляется на доставку.

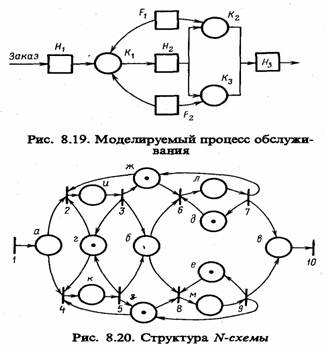
                   После этого построение N-cxeмы происходит формально: состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанесем маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов (рис. 8.20).

Синхронизация событии в N-схемах. Из приведенных примеров видно, что для выполнения каждого события (перехода) необходимо выполнение определенных условий. Эти условия в N-схемах (сетях Петри) называются предусловиями. Выполнение события может вызвать нарушение предусловий и привести к выполнению условий для совершения других событий — постусловий.

                   Для примера 8.7 построена таблица предусловий и постусловий (табл. 8.2). Эта таблица является описанием структуры N-схемы, удобным для ввода в ЭВМ. Кроме таблицы для выполнения процесса моделирования должна быть задана начальная маркировка в виде n-мерного вектора. Для примера 8.7:

Процесс моделирования заключается в последовательном вычислении маркировок, получающихся в результате выполнения событий (переходов). События, по которым нет предусловий, являются входами N-схемы. Каждый вход должен быть присоединен к модели, генерирующей запуск события в соответствии с условиями, определяемыми моделируемой реальностью. В частности, это может быть другая N-схема, моделирующая процесс появления этих событий.

В N-схемах два или несколько разрушенных невзаимодействующих событий могут происходить независимо друг от друга, т. е. N-схемам и их моделям свойствен параллелизм, или одновременность. Синхронизировать события, пока этого не требует моделируемая система, нет нужды. Таким образом, N-схемы удобны для моделирования системы с распределенным управлением, в которых несколько процессов выполняются одновременно.

Другая важная особенность N-схем — это их асинхронная природа. Внутри N-схемы отсутствует измерение времени. Для простоты обычно вводят следующее ограничение. Запуск перехода (и соответствующего события) рассматривается как мгновенное событие, занимающее нулевое время, а возникновение двух событий одновременно невозможно. Моделируемое таким образом событие называется примитивным (примитивные события мгновенны и неодновременны).

Непримитивными называются такие события, длительность которых отлична от нуля. Любое непримитивное событие может быть представлено в виде двух примитивных событий: «начало непримитивного события», «конец непримитивного события» — и состояния (условия) «непримитивное событие происходит».

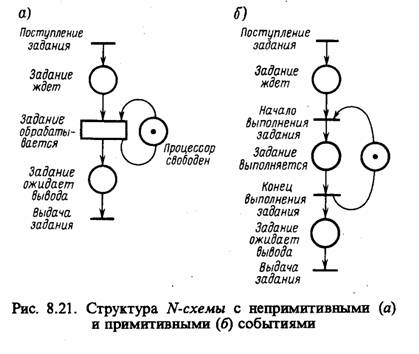
Пример 8.8. Рассмотрим особенности использования понятий примитивных и непримитивных событий на примере обработки заданий процессором ЭВМ. На рис. 8.21 представлены N-схемы (эквивалентные сети Петри) для моделирования обработки задания в процессоре с применением перехода, соответствующего непримитивному событию (рис. 8.21, а), и с применением только переходов — примитивных событий (рис. 8.21, б).

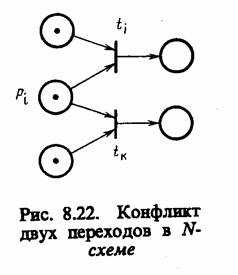
Ранее упоминалось, что в N-схемах все разрешенные переходы срабатывают одновременно и независимо. Однако с помощью N-схем можно моделировать и такие системы S, в которых   порядок запуска в разрешенных переходах имеет существенное значение. Ситуация, в которой невозможно одновременное выполнение двух разрешенных переходов,  изображена  на рис.  8.22,  где  два  разрешенных перехода dj и d_k находятся в конфликте. Может быть запущен только один из них, так как при запуске он удаляет метку из общего входа и запрещает другой переход.

Моделирование параллельных процессов. Возможность моделирования параллелизма и довольно простые процедуры объединения подсистем, представленных N-схемами, делают их весьма полезным инструментом моделирования сложных аппаратно-программных информационно-вычислительных комплексов и сетей, состоящих из большого количества одинаковых компонент. Поясним это следующим примером.

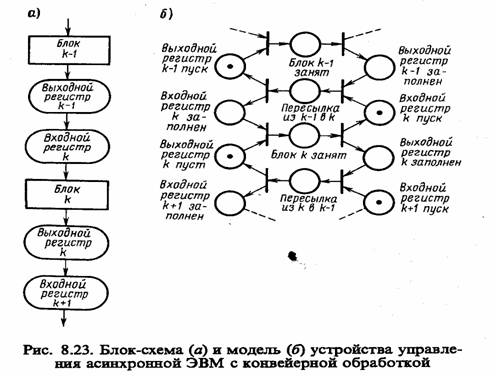
Пример 8.9. Рассмотрим процесс функционирования ЭВМ с конвейерной обработкой. При построении высокопроизводительных асинхронных ЭВМ широко применяют метод конвейерной обработки чисел. Этот метод обработки подобен функционированию сборочного конвейера и особенно удобен для работы с векторами и массивами. Конвейер состоит из набора операций, которые могут выполняться одновременно в разных блоках ЭВМ. Когда операция в k- м блоке завершается, ее результат передается в (к+ 1)-й блок, а k-й блок принимает результат операции(k— 1)-го блока. Если каждая операция запускается по завершении предыдущей, то имеем дело с асинхронным способом управления конвейером. Для управления k-м блоком такого конвейера необходима информация о выполнении следующих условий:

— входной регистр заполнен;

— входной регистр пуст;

— выходной регистр заполнен;

— выходной регистр пуст;

— блок к занят;

— блок к свободен;

— пересылка осуществляется.

На рис. 8.23, а показано, как строится N-схема для моделирования асинхронного конвейера такого типа, причем эта модель позволяет анализировать взаимодействия между блоками, игнорируя конкретные детали процессов, которые происходят внутри блоков. Эти процессы в свою очередь могут быть промоделированы N-схемами и соединены между собой в соответствии со схемой, показанной на рис. 8.23, б. Такая возможность построения иерархических моделей может быть весьма полезной при моделировании сложных систем S.

Особенности программирования N-схем. Как уже отмечалось, N-схема представляет собой формализованное описание процесса функционирования системы S, причем структура N-схем отражает причинно-следственные связи в системе S, а совместно с начальной маркировкой — процессы, которые в этой системе происходят. Таким образом, переход от N-схем к моделирующей программе может производиться формальным путем, т. е. автоматически, с использованием специального языка и транслятора. Такие языки и трансляторы созданы за рубежом и в нашей стране [4, 24, 28, 29, 30, 50, 54].

Рассмотрим особенности программирования N-схем, моделирующих процессы в системе S, на конкретных примерах.

Пример 8.10. Рассмотрим принципы программирования N-схем в языке MODAL, который предназначен для моделирования и реализации вычислительных алгоритмов на базе N-схем (сетей Петри). Он содержит семь операторов:

START — описание начальной маркировки;

STOP — описание конечной маркировки;

T(MOD) — описание структуры сети Петри;

TYPE — оператор промежуточного вывода на печать;

SOMMENT          -вспомогательные операторы

COMPLEKXITY

END — конец.

                      Операторы START и STOP представляют собой списки позиций, в которых устанавливаются метки в начале и должны оказаться в конце моделирования.

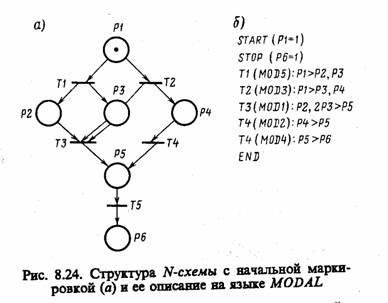
Оператор T(MOD) представляет собой таблицу пред- и постусловий для каждого

перехода N-схем.

Пусть задана N-схема с начальной маркировкой (рис. 8.24, а). Соответствующее ей описание на языке MODAL представлено на рис. 8.24, б.

Кроме описания структуры должны быть составлены программные модули — описания переходов (событий) MOD1 — MOD5, причем все модули должны содержать единую для данного набора COMMON-область, которая служит для передачи данных между модулями.

Естественно предположить, что для моделирования конкретных систем S в узкоспециализированной области количество возможных событий-переходов ограничено. Можно составить список стандартных событий и соответствующий ему набор программных модулей. Вместе со средствами описания структуры N-схемы, поясняющей взаимодействия, такой набор составит пакет моделирования систем в специализированной области. Известны системы, построенные по такому принципу для моделирования аппаратных и программных средств вычислительных систем, для моделирования протоколов связи. Известны также примеры успешного применения N-схем (сетей Петри) для исследования социальных_> экономических систем, сложных физических и химических процессов.

Расширение N-схем. Возможные расширения N-схем, заданных в виде сетей Петри, о которых говорилось в § 2.6, рассмотрим с точки зрения их прикладного использования, т. е. с ориентацией на увеличение моделирующих возможностей данного аппарата. Для моделирования процессов в информационных системах наибольший интерес представляют N-схемы в виде временных сетей и Е-сетей, являющихся наиболее мощным расширением сетей Петри

[28].

Задание временной сети, т. е. Ng-схемы, включает семь множеств

где В, D, I, О, М имеют тот же смысл, что и ранее (см. § 2.6); v=(t₁, ... ..., ti...) — возрастающая последовательность действительных чисел, называемая временной базой; v:Bx v=>v — функция временных задержек.

Фактор времени учитывается в Ng-схемах путем введения пассивного состояния метки в позиции. При поступлении метки в позицию bi она остается в пассивном состоянии (не может участвовать в возбуждении переходов) на время v (b_i,t_s)—t_s и только после этого переходит в активное состояние.

Подклассом временной сети является сеть Мерлина, где время пассивного состояния метки определяется как случайная величина, находящаяся в диапазоне между t* и t**(t*≤t_s ≤t**), которые задаются в описании N_s-cxeмы.

Пример 8.11. Построим в виде Ns-схемы модель микропроцессорного абонентского пункта (АП) информационно-вычислительной сети [30, 54,]. Структура этого АП показана на рис. 8.25, где обозначено: МП — микропроцессор; ОЗУ — оперативное запоминающее устройство; ПА — периферийный адаптер; ЭПМ — электрифицированная пишущая машинка; KC ₁и КС₂ — входной и выходной каналы связи.

Задание N _S-схемы в виде временной сети включает в себя задание структуры <В, D, I, О>, вектора разметок М_о и вектора задержек Z.

Структуру Ns-схемы зададим графически, так как именно графическое представление обладает наибольшей наглядностью и простотой соотношения со структурой объекта, т. е. в данном примере со структурой АП. На рис. 8.26 для наглядности пунктиром выделены элементы Ns-схемы, относящиеся к конкретным элементам структуры АП (рис. 8.25).

Вектор разметок имеет вид

М_о ==(010100001110000001Nb₀)

а вектор задержек

Z = (z_вх, 0, z_кс1,. 0, 0, z_мп1,. 0, z_лм1, 0, 0, 0, z_bx , z_пм2,. 0, z_кс, 0, 0).

С использованием N-схем осуществляется структурный подход к построению имитационной модели, при котором обеспечиваются наглядность модели, модульный принцип ее разработки (сборки), возможность перехода к автоматизированной интерактивной процедуре проектирования.

Еще большие возможности для моделирования сложных систем дают такие расширения N-схем, как Е-сети, которые обозначим как N_E-схемы. В отличие от временных сетей в Е-сетях определено дополнительно четыре типа переходов: разветвление, объединение, управляемое разветвление и приоритетное объединение. Важной особенностью N_Е-схем является также детализация представления метки. С каждой меткой в N_E-cxeмe связаны

n описателей. Каждый из описателей метки несет в себе определенную количественную информацию о моделируемом объекте, т. е. системе S.

Структурное задание модели элементов системы S в форме N_Е-схемы позволяет использовать модульный принцип разработки имитационной модели с применением библиотеки E-сетевых модулей и их параметрической настройки. В этом случае E-сетевая модель является основой для сборки имитационной программы из модулей, реализованных на некотором языке программирования

[30, 54].

Базой для построения программных модулей служит обобщенный алгоритм функционирования E-сетевого модуля, который рассмотрим на следующем примере.

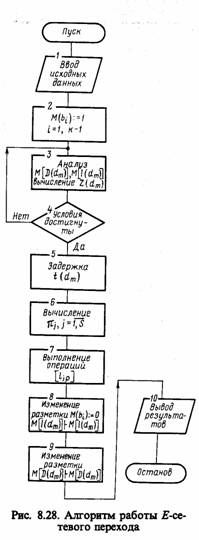Одним из основных вопросов, который надо решить разработчику имитационной модели процесса, формализуемого на базе N-схем, является выбор языка программирования. Реализация модулей N_Е-схем на машинно-ориентированном языке или же языках общего назначения позволяет снизить затраты машинного времени и оперативной памяти при моделировании систем, но при этом следует учитывать высокую трудоемкость разработки библиотеки моделирующих подпрограмм. Этот недостаток устраняется при использовании для моделирования системы S, формализованной на базе N-схем, языков имитационного моделирования.

Использование ЯИМ. Программная реализация моделей систем S на базе расширенных N-схем (N_s-, N_E-cxeм) более сложна по сравнению с программированием моделей на основе обычных сетей Петри. Для упрощения перехода к моделирующей программе рационально использовать языки имитационного моделирования (ЯИМ). Рассмотрим особенности использования ЯИМ для имитации на базе N_E-cxeм на примере применения системы моделирования GPSS, которая детально была рассмотрена ранее.

Таким образом, рассмотренное представление моделей элементов информационных систем в виде N_Е-схем позволяет упростить этап определения их базовой структуры. Задание модели в виде N_E -схем допускает достаточно простую программную реализацию имитационной модели на ЯОН или ЯИМ.

8.4. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ

ФУНКЦИОНИРОВАНИЯ СИСТЕМ НА БАЗЕ А -СХЕМ

Особенности использования при моделировании систем обобщенного агрегативного подхода, реализуемого с помощью А-схем, и основные понятия агрегативных систем были даны в § 2.7. Остановимся на возможностях использования А-схем для формализации процессов функционирования различных систем [4, 36, 37].

Формализация на базе А-схем. Рассмотрим частный случай А-схем в виде кусочно-линейных агрегатов (КЛА), позволяющих описать достаточно широкий класс процессов и дающих возможность построения на их основе не только имитационных, но и аналитических моделей. В отличие от общей постановки (см. § 2.7) полагаем, что на вход агрегата А не поступают управляющие сигналы и(0, т. е. агрегат рассматривается как объект, который в каждый момент времени характеризуется внутренними состояниями z(t) Z; в изолированные моменты времени на вход агрегата А могут поступать входные сигналы х (t) X, а с его выхода могут сниматься выходные  сигналы у {t) Y. Класс КЛА выделяется с помощью конкретизации

структуры множеств Z, X, Y, т. е. пространств состояний, входных и выходных сигналов соответственно,атакже операторов переходов V, U, W и выходов G.

Способы построения моделирующих алгоритмов А-схем. Основные преимущества агрегативного подхода состоят в том, что в руки разработчиков моделей и пользователей дается одна и та же формальная схема, т. е. А-схема. Это позволяет использовать результаты математических исследований процессов, описывающих функционирование агрегативных систем, при создании моделирующих алгоритмов и их программной реализации на ЭВМ. В настоящее время имеются разработки математического обеспечения, в основу которого положен агрегативный подход. Но при этом у пользователя всегда должна оставаться свобода в переходе от концептуальной к формальной модели. Таким образом, имеется возможность многовариантного представления процесса функционирования некоторой системы S в виде модели М, построенной на основе А-схем.

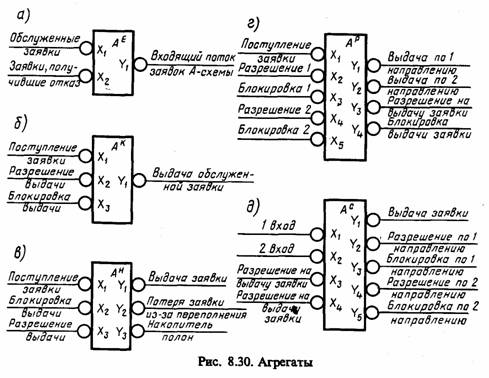
выдачи обслуженной каналом заявки; с выхода У^(k)₁ снимают сигнал выдачи обслуженной каналом заявки. Вектор состояний агрегата

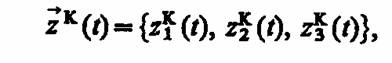
где z^k₁ (t) — время, оставшееся до окончания обслуживания заявки, которая находится в канале;

Таким образом, используя набор агрегатов А^Е, А^к, А^н, А^р и А^с, можно описать процесс функционирования рассматриваемой системы (см. рис. 8.6). Для возможности формализации более сложных систем требуется в пределах данного класса объектов (Q-схем) увеличение числа состояний перечисленных агрегатов, а для других классов систем — расширение набора агрегатов.

Моделирующий алгоритм А-схемы. Укрупненная схема моделирующего алгоритма такой системы, представленной в виде А-схемы, приведена на рис. 8.31. В основу моделирования положен принцип просмотра состояний модели в моменты скачков, т. е. «принцип δz» («принцип особых состояний»). Обработка каждого особого состояния выполняется блоками б и 12. Работа такого блока иллюстрируется схемой, представленной на рис. 8.32, и сводится к выбору типа агрегата (А^Е, А^к, А^н, А^Р и А^с), для которого реализуется дальнейшее «продвижение» при моделировании.

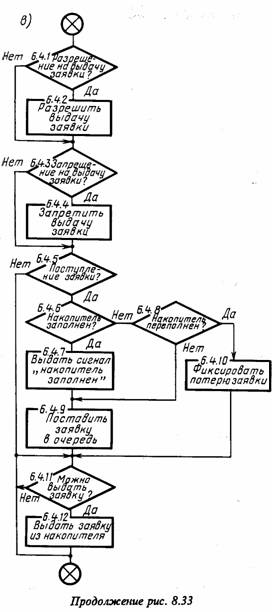
Схема моделирующего алгоритма, имитирующего воздействие на систему S внешней среды Е, показана на рис. 8.33, а. При этом определяется, какое событие имело место, поступление или выдача сигнала из внешней среды, т. е. заявки входного потока в А-схему (блок 6.2.1). При наступлении времени выдачи заявки она выдается в А-схему (блок 6.2.2) и генерируется интервал времени между моментом поступления новой заявки (блок 6.2.3).

      Схемы моделирующих алгоритмов, имитирующих работу агрегатов А^к и А^н, приведены на рис 8.33, б, в соответственно. Работа этих схем полностью соответствует описанию процесса функционирования агрегатов А^к и А^н, показанных на рис. 8.30, б, в.

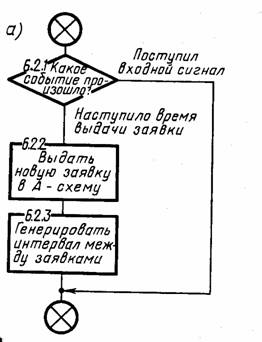
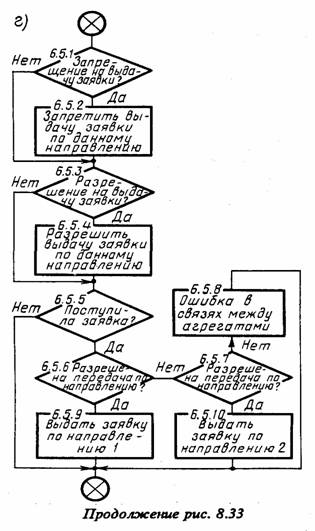
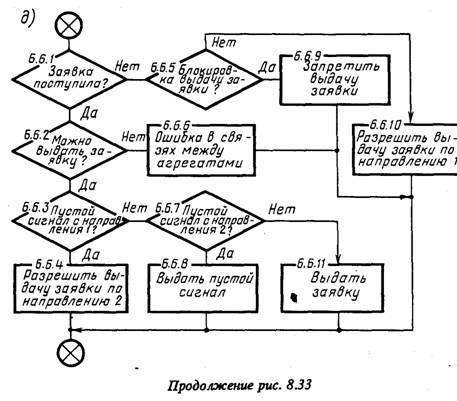
Схемы работы агрегатов А^p и А^с, выполняющих вспомогательные функции сопряжения агрегатов, показаны на рис. 8.33, г, д соответственно. Они реализуют взаимодействие основных агрегатов А^E, А^к и А^н, разрешая или запрещая передачу сигналов между ними в зависимости от ситуации с учетом правил обмена сигналами в А-схеме, описанных в § 2.7. При этом в схемах предусмотрено тестирование ошибок (блоки 6.5.8 и 6.6.6), связанных с нарушением при задании исходных данных этих правил обмена сигналами в А-схеме.

Из рассмотренного примера моделирования конкретной системы S (в данном случае заданной в виде Q-схемы) видно, что агрегативный подход является тем фундаментом, на котором базируется построение автоматизированной имитационной системы, разработка ее внутреннего и внешнего математического и программного обеспечений. При этом стандартная форма математической модели исследуемого объекта позволяет не только унифицировать моделирующие алгоритмы, но и применять также стандартные методы обработки и анализа результатов моделирования, реализованные в виде специальных  библиотек программ [7, 10, 12, 21].

Применение агрегативного подхода при моделировании систем дает ряд преимуществ по сравнению с другими, менее универсальными подходами. Так, агрегативный подход в силу модульной структуры модели и дискретного характера обмена сигналами дает возможность использовать внешнюю память ЭВМ для хранения сведений о моделируемых объектах, что в значительной степени снижает ограничения по сложности, возникающие при попытке представить процесс функционирования моделируемой системы S в целом как последовательность взаимосвязанных системных событий для записи его в виде моделирующего алгоритма или на языке имитационного моделирования. При этом объем программ имитации мало зависит от сложности моделируемого объекта, которая определяет лишь число операций, требуемых для реализации машинной модели М_м, и объем памяти, необходимой для хранения сведений об агрегатах и их связях.

Важно, что такие имитационные программы позволяют проводить их предварительную автономную отладку и являются программами многоразового использования, что повышает оперативность решения задач моделирования систем. При наличии таких отлаженных программных модулей время подготовки к моделированию практически совпадает со временем формализации моделируемой системы S в виде А-схемы и задания исходных данных.

       При агрегативном подходе возникают и некоторые трудности, например, связанные с организацией диалога пользователя с имитационной системой, так как представление моделируемой системы в виде А-схемы предполагает и структуризацию в соответствующем виде входных данных. Следовательно, пользователь, как и разработчик модели М_м, должен владеть языком агрегативных систем для решения своих залач.

В    перспективе  агрегативный подход создает основу для автоматизации машинных экспериментов. Такая автоматизация может полностью или частично охватывать этапы формализации процесса функционирования системы S, подготовки исходных данных для моделирования, планирования и проведения машинных экспериментов, обработки и интерпретации результатов моделирования. Процесс автоматизации моделирования будет постепенным и поэтапным. Решение задачи автоматизации создает перспективы применения моделирования в качестве инструмента для повседневной работы инженера-системотехника в сфере проектирования и эксплуатации информационных систем, систем сбора и обработки информации, систем автоматизации проектирования, систем автоматизации научных исследований и комплексных испытаний и т. д.

Таким образом, использование типовых математических схем, рассмотренных в данной главе на примере Q- и А-схем, позволяет формализовать процесс функционирования конкретной системы S,

т. е. переход от концептуальной модели системы М_м к ее машинной модели М_м. Типовые математические схемы при моделировании конкретных систем будут рассмотрены в гл.10.

Контрольные вопросы

8.1. Какие основные блоки выделяются при построении иерархической модели системы?

8.2. Какие существуют способы построения моделирующих алгоритмов Q- схем?

8.3. Чем отличаются синхронный и асинхронный моделирующие алгоритмы Q-систем

8.4. В чем суть структурного подхода при моделировании систем на базе N-схем?

8.5. Каковы особенности использования языков имитационного моделирования на базе N-схем?

8.6. В чем заключается особенности формализации процессов функционирования систем на бае Ф-систем?

8.7. каково преимущество использования типовых математических схем при имитационном моделировании?

ГЛАВА 9

МОДЕЛИРОВАНИЕ ДЛЯ ПРИНЯТИЯ РЕШЕНИЙ

 ПРИ УПРАВЛЕНИИ

Машинное моделирование является эффективным инструментом исследования характеристик процесса функционирования сложных систем на этапе их проектирования. Но этим возможности этого метода не ограничиваются: в современных системах управления машинное моделирование используется непосредственно в контуре управления, на его основе решаются задачи прогнозирования для принятия решений по управлению объектом, т. е. реализуются адаптивные системы управления. Построение таких адаптивных систем стало возможным, с одной стороны, после решения ряда вопросов информационного подхода к проблеме управления, а с другой стороны, после проработки задач моделирования в реальном масштабе времени на современных ЭВМ с учетом ограниченности ресурсов в системе управления объектом.

9.1. ГНОСЕОЛОГИЧЕСКИЕ И ИНФОРМАЦИОННЫЕ

 МОДЕЛИ ПРИ УПРАВЛЕНИИ

Создание системы управления (СУ) различными объектами требует наличия большого объема информации, как о самом объекте, так и о его входных и выходных переменных. Эта информация необходима для построения адекватной модели СУ, на основе которой может быть эффективно осуществлен процесс управления. При этом следует различать два вида информации, необходимой для построения и совершенствования модели и СУ: априорную и текущую. Априорная информация об объекте управления (ОУ), его входных и выходных переменных, внутренних состояниях необходима для построения модели, по которой будет создаваться СУ этим объектом: выбираться структура, алгоритмы и параметры СУ, критерий функционирования. Обычно для сложных вновь проектируемых ОУ отсутствует необходимая для создания СУ модель, и задача управления должна решаться в условиях недостаточной или вовсе отсутствующей априорной информации об o6ъектe. Речь идет об отсутствии информационной («управленческой») модели ОУ, устанавливающей взаимосвязь между выходными и входными переменными [41, 43, 54].

Особенности системы управления. Проблема создания СУ неизбежно возникает при разработке ОУ и при их модернизации. На первый взгляд может показаться, что в тех случаях, когда новая СУ разрабатывается для уже давно функционирующей системы S, длительное время находящейся в эксплуатации, положение с априорной информацией лучше и построение модели проще. Опыт показывает, что это не так, и получение информационной модели и в этом случае весьма трудоемко. Таким образом, как для случая вновь проектируемой системы S, так и для уже функционирующей возникает проблема получения дополнительной информации для создания СУ. Единственным эффективным путем получения такой информации в настоящее время является машинное моделирование.

В том случае, когда СУ создана и функционирует вместе с системой S, управляя ею, существует необходимость в получении текущей информации, вызванная в основном двумя причинами. Во-первых, это потребность в совершенствовании СУ, а во-вторых, необходимость уточнения поведения системы и возникающих в ней ситуаций с целью компенсации изменений характеристик системы S как ОУ. Процессы, с которыми связана текущая информация первого вида, являются достаточно медленными и для управления ими необходима подсистема эволюционного управления, а процессы второго типа являются более быстрыми и для управления ими необходима подсистема оперативного управления в реальном масштабе времени (РМВ).

Следует подчеркнуть, что по темпу принятия решений и месту решения задач подсистемы эволюционного и оперативного управления существенно отличаются друг от друга. Так, например, процессы оперативного управления могут быть на несколько порядков более быстрыми по сравнению с процессами эволюционного управления.

Важнейшей задачей современной теории и практики управления является построение модели ОУ, т. е. формализация закономерностей функционирования объекта. На основе этой модели определяются структура, алгоритмы и параметры СУ, выбираются аппаратно-программные средства реализации системы. Одним из эффективных методов построения модели сложного объекта является идентификация.

Широкое развитие в настоящее время работ по формализации процессов и построению их моделей во многих областях исследований (технике, экономике, социологии и т. д.) преследуют две основные цели. Первая из них связана со значительным увеличением возможностей изучения на базе ЭВМ сложных процессов функционирования различных объектов при помощи метода моделирования, для чего необходимо математическое описание исследуемого процесса. Не меньшее значение в технических системах имеют модели, используемые для достижения второй цели, т. е. применяемые непосредственно в контуре управления объектами.

Эволюционные и десиженсные модели. Невозможность ограничиться только одной универсальной моделью связана с тем, что, с одной стороны, перед этими моделями ставятся различные цели, а с другой стороны, они описывают процессы, протекающие в различных масштабах времени, причем степень полноты модели, ее соответствие реальному объекту зависят от целей, для которых эта модель используется. Модели первого типа имеют в основном гносеологический характер, от них требуется тесная связь с методами той конкретной области знаний, для которой они строятся. Модели такого типа являются достаточно «инерционными» в своем развитии, так как отражают эволюцию в конкретной области знаний. Такие модели будем называть эволюционными. Модели второго типа имеют информационный характер и должны соответствовать конкретным целям по принятию решений по управлению объектом, который они описывают. Такие модели будем называть десиженсными. Деление на гносеологические (эволюционные) и информационные (десиженсные) модели достаточно условно, но оно удобно для отражения целей моделирования.

В информационных моделях, используемых непосредственно для принятия решений в СУ, требование оперативности является одним из основных. Оно вызвано тем, что при каждом воздействии на ОУ необходимо в модели учесть действительные изменения, происшедшие в объекте, и внешние возмущения, на основе которых рассчитывается управление. Это требование оперативности, т. е. необходимость работы такой модели в РМВ, часто ведет к отказу от сложных и точных моделей, к разработке специальных, так называемых робастных, алгоритмов построения моделей, использование которых в СУ обычно ведет к поставленной цели [18, 21, 43, 54].

Появление идентификации в начале 60-х годов было связано с острой необходимостью разработки методов построения именно информационных моделей ОУ. Отсутствие таких моделей сдерживало процесс автоматизации этих объектов, использования ЭВМ в контуре управления. Объекты оказались неподготовленными к внедрению вычислительной техники из-за отсутствия их математического описания, их информационных моделей. Построение информационной модели методами идентификации должно быть направлено на ликвидацию этого разрыва и разработку методов оперативного получения модели ОУ. При этом методы идентификации должны предусматривать использование ЭВМ для решения задач построения информационной модели.

Элементы теории моделирования. Отсутствие формальных методов перехода от гносеологических моделей к информационным в современной теории управления не дает возможности получить по имеющейся информации адекватное описание, необходимое для создания СУ. Но учет сведений, содержащихся в гносеологических моделях, может значительно увеличить объем априорной информации о рассматриваемом ОУ. Поставив цель построения гносеологической модели процесса функционирования системы S для получения необходимой априорной информации для построения эффективной СУ и сузив класс объектов моделирования до конкретного, т. е. до поведения конкретной системы S, решим задачу-построения прикладной теории эволюционного и десиженсного моделирования, позволяющей эффективно (в реализационном аспекте) перейти от гносеологических («исследовательских») моделей к информационным («управленческим») моделям. Наиболее просто такой переход можно совершить, если оба этих класса моделей будут базироваться на единую концептуальную модель, использовать единую систему информации (базу знаний) и иметь единую критериальную систему. Рассмотрим сначала особенности гносеологических и информационных моделей.

Вопрос применимости некоторой математической модели к изучению рассматриваемого объекта не является чисто математическим вопросом и не может быть решен математическими методами. Только критерий практики позволяет сравнивать различные гипотетические модели и выбрать из них такую, которая является наиболее простой и в то же время правильно передает свойства изучаемого объекта, т. е. системы S.

Ориентируясь на общие вопросы методологии моделирования сложных технических систем, сформулируем требования к прикладной теории моделирования, а точнее — к элементам этой теории в ее приложении для решения конкретно поставленной задачи. Как уже отмечалось выше, эта задача ставится следующим образом. Необходимо сначала построить и реализовать на ЭВМ эволюционную модель процесса функционирования системы S, полученную в ходе стратегической идентификации ОУ, а затем на ее базе построить десиженсную модель, используемую для решения практических задач оперативного управления в адаптивной СУ сетью. Или, используя терминологию теории идентификации, необходимо построить конкретную дискретную адаптивную систему управления с идентификатором и предсказателем (комбинированную) в цепи обратной связи (ДАСК), т. е. реализовать сначала стратегический идентификатор, а затем на его базе тактический оперативный идентификатор и предсказатель, рассматривая в качестве ОУ не реальную систему S (ввиду ее отсутствия), а машинную модель процесса ее функционирования.

Таким образом, можно поставленную задачу трактовать и как задачу автоматизации исследования объекта (машинной модели М_м) для целей синтеза тактической и оперативной модели, используемой непосредственно в контуре управления системой S, а затем для проверки эффективности управления в целом.

Прежде чем переходить к изложению элементов теории моделирования процессов в системе S, дадим ряд определений. Напомним, что под моделированием будем понимать исследование объекта посредством изучения его модели, т. е. другого объекта, более удобного для этой цели. Под сложностью моделируемого объекта будем понимать фактически сложность сведений о нем (его описания), зависящую от целей моделирования и уровня, на котором выполняется описание. Таким образом, сложность возрастает нетолько при введении в рассмотрение новых качеств, но и при переходе к более детальному описанию процесса функционирования объекта моделирования, т. е. системы 5.

Задачу прикладной теории моделирования сформулируем, исходя из тех требований, которые будет предъявлять к ней пользователь (исследователь, разработчик системы 5), проводящий эксперименты с процессами функционирования S и ее элементов для решения конкретной прикладной задачи. В таком контексте основной задачей при решении проблем управления является выбор моделей на уровне оперативного управления, сохраняющих при этом существенные для СУ черты S с учетом ограничений реализации в РМВ (особенно при оперативном управлении). В дальнейшем модель, практически реализуемую с учетом ограниченности ресурсов, будем называть трактабельной. Таким образом, помимо теоретических вопросов построения модели вообще будем рассматривать вопросы трактабельности модели, связанные с формальным представлением ее описания, его упрощением, проверкой адекватности упрощенной модели и т. д.

Тот факт, что моделируемая система S существует лишь как замысел разработчика, вносит в проблему разработки такой теории значительные трудности. В частности, не удается непосредственно проверить адекватность модели процесса функционирования системы S с помощью реального объекта. Частично эта трудность устраняется путем проведения натурных экспериментов с элементами S. Ряд существенных трудностей возникает из-за неполноты исходной информации об объекте моделирования.

Большой объем знаний о системах и их элементах, накопленный к настоящему времени, подлежащий объединению в рамках теории моделирования и несоизмеримый с познавательными возможностями одного исследователя, выдвигает необходимость организации и детализации таких знаний (теории) в систему, затрагивающую лишь существенно ограниченное число объектов при сохранении общности подхода. При этом развитие отдельных методов статистического моделирования, языков моделирования, теории планирования машинных экспериментов и т. д. оказывается недостаточным.

Создание прикладной теории, обеспечивающей конкретные потребности разработчика модели и охватывающей весь процесс моделирования в широком смысле этого слова, требует системного подхода и прежде всего установления основ теории: понятий об объекте, предмете, содержании, структуре и логике теории.

Объект прикладной теории моделирования. Объектом разрабатываемой прикладной теории является непосредственно процесс моделирования поведения системы S, т. е. процесс перехода от моделируемого объекта (системы S) сначала к статической модели S^s, используемой при стратегической идентификации, а затем и к динамической модели D^s, непосредственно используемой при оперативном управлении с использованием методов и алгоритмов СУ. При этом ориентируются на критериальную систему К. Такой переход осуществляется через описание (концептуальную модель), фиксирующее сведения об объекте S в понятиях языка L (терминах типовых математических схем) [41, 54]. При выборе математической схемы моделирования М вводится также понятие среды S, позволяющее использовать информацию прикладного характера J о целях моделирования, законах функционирования системы S, имеющемся математическом аппарате и т. д. для исследования методов и алгоритмов управления системой А.

Таким образом, так как объектом данной прикладной теории моделирования является процесс моделирования, то возникает необходимость в построении и изучении «модели моделей», или репромодели RM (от англ. reproduce — воспроизводить, делать копию, порождать). Репромодель представляет собой упрощенный и наглядный прототип создаваемых моделей, используемых в СУ, и дает возможность эффективного приближения к таким моделям с максимальным использованием априорной и оперативной информации о поведении системы 5, поступающей в процессе ее функционирования. Для решения поставленной задачи разработки модели для СУ схема репромодели приведена на рис. 9.1. После того как сформулирована концептуальная модель С и введены понятия компонент сред S, основное содержание элементов прикладной теории моделирования для управления системой составят компоненты М, А, S^S и D^S (критерий К считается заданным), причем переход от М к S^S, следуя терминологии [29, 53], составит статику моделирования, а переход от М к множеству D^S привлечением информации из компонент S^S и А составит динамику моделирования. Такое разделение на статику и динамику условно показано на рис. 9.1 пунктирной и сплошной линиями соответственно.

Движение в пространстве статических моделей процесса функционирования системы S^S назовем эволюцией (или эволюционным моделированием), а движение в пространстве динамических (активных) моделей D^S, используемых в контуре управления,— самоорганизацией (или моделированием с самоорганизацией). Важно отметить, что компоненты объекта теории L, С, Е, М имеют искусственное происхождение, базирующееся на эвристических представлениях, и могут при необходимости изменяться (развиваться) в интересах самой прикладной теории. Это существенно отличает прикладную теорию моделирования от естественно-научных теорий.

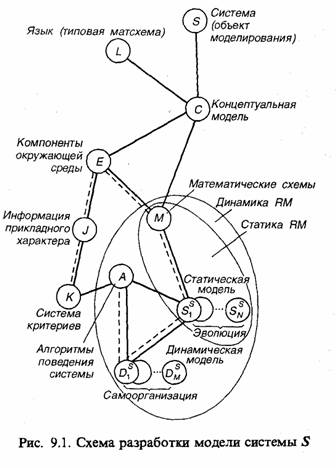
Предмет прикладной теории моделирования. Высказывания, составляющие любую теорию, формируются относительно предмета теории, а именно системы понятий, отображающих с той или иной степенью обобщения объект теории (репромодель). Таким образом, задание предмета прикладной теории моделирования процессов в системе S равносильно заданию репромоделей. Очевидно, что вообще различным репромоделям должны соответствовать различные аспекты теории. Применительно к СУ сужаем круг этих аспектов за счет конкретизации целей моделирования путем введения в репромодель компонент А, ограниченных методами и алгоритмами оперативного управления. Построение репромодели по схеме, приведенной на рис. 9.1, позволяет использовать как информацию общего характера о процессах моделирования и управления J, так и конкретную информацию о методах и алгоритмах управления системой S* с учетом выбранных критериев оценки эффективности К.

Содержание, структура и логика прикладной теории. Содержание прикладной теории моделирования охватывает две части: базис теории, включающей систему эвристических принципов, полученных при обобщении имеющегося опыта моделирования сложных объектов вообще, и тело теории, содержащее эвристические правила машинной реализации конкретных моделей процесса функционирования S (S^S и D^S), которые будут рассмотрены в § 10.1.

Предложения теории, относящиеся к компонентам М, А,S^S и D^s или возможным переходам между ними, содержат множество условий, позволяющих точно их сформулировать лишь для простейших случаев. В пределе предложения сводятся к описанию фактов, относящихся к отдельным реализациям процесса моделирования, которые назовем прецедентами Рr. Отметим, что Рr составляют эмпирическую основу прикладной теории моделирования, а множество {Рr}, классифицированное по условиям, может рассматриваться как обобщенное предложение теории, содержащее весь зафиксированный в {Рr} опыт моделирования сложных систем вообще.

Более определенные предложения теории могут быть получены на основе системного подхода с детализацией репромодели по этапам построения и реализации S^S и D^S, когда ставятся различные цели при моделировании процессов в системе S. В общем случае репромодель, т. е. ее базис, задается множеством принципов {Иr}, определяющих желаемые свойства моделей (S^s и D^s) и другие ограничения. Использование {Пr} регламентируется предложениями теории, относящимися к ограниченному множеству обобщенных ситуаций. Поиск этих ситуаций в множестве известных {Рr} позволяет накопить необходимые факты в количестве, достаточном для формулировки обобщенных предложений.

Говоря о прикладной теории моделирования с системных позиций, невозможно обойти ее реализационный аспект. В теории это отражено введением понятия трактабельности модели, т. е. ее реализуемости в рамках принятых ресурсных ограничений (например, на оперативную память и быстродействие ЭВМ). Особенно важна трактабельность десиженсных моделей, непосредственно используемых в СУ, так как часто от нее зависит эффективность конкретного метода и алгоритма управления (а иногда и возможность его использования вообще). Вопросы трактабельности модели ставятся во главу угла при проведении стратегического и тактического планирования машинных экспериментов (см. гл. 6). Поэтому не будем останавливаться на этих вопросах детально, отметим только, что трактабельность модели достигается выполнением набора практических правил реализации модели {Рr}, которые и составляют тело прикладной теории моделирования.

Таким образом, в конечном итоге множество прецедентов {Рr} выражается через меньшее число эвристических принципов {Пr} и практических правил реализации {Рr} (базис и тело теории). Это позволяет считать репромодель и систему [{Пr}, {Рr}] основой «системного» аспекта прикладной теории моделирования. При практическом применении неизбежно объединение «прецедентного» и «системного» аспектов теории моделирования на основе логического понятия дополнительности. В данном случае это способствует сужению общей проблемы моделирования за счет введения в прикладную теорию компоненты А. Для обеспечения возможности развития репромодель должна строиться как открытая система, т. е. с соблюдением принципов архитектуры открытых систем, что нашло свое отражение при машинной реализации моделей [41, 54].

Относительно логики прикладной теории моделирования отметим, что она опирается на индуктивный подход, т. е. обобщение и классификацию множества прецедентов {Рr}, оставляя место для дедуктивного подхода в рамках конкретных математических схем М.

Вопросы практического воплощения прикладной теории моделирования непосредственно связаны с реализацией соответствующих инструментальных средств моделирования (см. гл. 5) и возможностью ее использования для решения задач моделирования конкретных систем (см. гл. 10).

9.2. МОДЕЛИ В АДАПТИВНЫХ СИСТЕМАХ УПРАВЛЕНИЯ

Одной из центральных проблем современной теории управления является проблема управления динамическими объектами в условиях неопределенности, т. е. проблема построения адаптивных СУ. Принцип работы этих систем основан на изменении параметров и структуры в результате наблюдения и обработки текущей информации так, чтобы адаптивная или обучающая система с течением времени улучшила свое функционирование, достигая в конечном итоге оптимального состояния. В адаптивных СУ недостаток априорной информации компенсируется благодаря целенаправленной обработке текущей информации. Рассмотрим возможность и особенности использования машинных моделей М_M для решения основных задач построения адаптивных СУ.

Адаптация в системах управления. Под адаптацией понимается процесс изменения структуры, алгоритмов и параметров системы S на основе информации, получаемой в процессе управления с целью достижения оптимального (в смысле принятого критерия) состояния или поведения системы при начальной неопределенности и изменяющихся условиях работы системы во взаимодействии с внешней средой Е.

Адаптация использует обучение и самообучение для получения в условиях неопределенности информации о состояниях и характеристиках объекта, необходимой для оптимального управления. Обучение понимается как процесс выработки в некотором объекте тех или иных свойств его реакции на внешние воздействия путем многократных испытаний и корректировок. Самообучение отличается от обучения отсутствием внешней корректировки.

             Характерная черта адаптации — текущее накопление информации о процессе функционирования системы S и внешней среды Е и ее использование для улучшения избранного показателя качества. Процесс накопления информации связан с затратами времени, что в итоге приводит к запаздыванию в получении системой управления информации, необходимой для принятия решений. Это существенно снижает эффективность работы систем управления в реальном масштабе времени. Поэтому актуальной является задача прогнозирования состояний (ситуаций) системы S и внешней среды Е и характеристик (поведения) системы S для адаптивного управления. Такой прогноз может быть выполнен при использовании методов моделирования в системе управления в реальном масштабе времени (см. § 9.3).

Виды используемых моделей. Выделяются два направления в теории и практике построения адаптивных СУ — создание систем с эталонной моделью (АСЭМ) и с идентификацией объекта управления (АСИ). В АСИ сначала осуществляется идентификация объекта, а затем по оценкам его параметров определяются параметры управляющего устройства, а в АСЭМ осуществляется подстройка параметров управляющего устройства так чтобы замкнутая система была близка к эталонной модели. Авторы считают, что дальнейшее развитие АСЭМ и АСИ пойдет по пути взаимного проникновения методов, и результатов исследования, что позволит синтезировать алгоритмы, обладающие всеми достоинствами как того, так и другого направления. Широкое применение в СУ средств вычислительной техники вызвало особый интерес к дискретным адаптивным системам управления (ДАС), которым в последнее время посвящается большая часть публикаций по адаптивным системам [41, 43, 54].

Следует отметить, что выбор за классификационный признак наличия или отсутствия эталонной модели для современных ДАС не является, по сути дела, оправданным, так как эталонная модель в той или иной форме присутствует в любой ДАС. Сравнительно недавно предложена и развита более обоснованная классификация ДАС на прямые и непрямые и дана трактовка их общности, свойств и особенностей [37, 50]. Согласно этой классификации, все ДАС можно подразделить на два типа: непрямые ДАС, в которых параметры управляющего устройства определяются по оценкам параметров объекта с помощью некоторого вычислительного устройства, и прямые ДАС, в которых параметры управляющего устройства определяются непосредственно, без вычислительного устройства.

К непрямым ДАС относятся системы с идентификатором в контуре адаптации (ДАСИ), а к прямым — системы с предсказателем (ДАСП) в контуре. В соответствии с этой классификацией ДАС, используемые для управления процессами в таком сложном объекте, как информационная система S, можно отнести к непрямым комбинированным (ДАСК), так как в адаптивной системе управления S имеют место идентификатор и предсказатель, реализуемые с помощью вычислительных устройств, причем комбинирование понимается как в смысле использования ДАСИ и ДАСП, так и в смысле использования принципов АСИ и АСЭМ.

Создание и развитие теории ДАС обусловлено прежде всего неполнотой априорной информации о процессе функционирования исследуемого объекта (в нашем случае ИС и ее элементов). Именно от объема априорной информации зависит и математическая постановка задачи, а часто этим определяется не только подход, но и метод ее решения. Исходя из того, что элементы ИС часто являются мало изученными объектами, т. е. практически отсутствуют априорные сведения о них, напрашивается вывод о необходимости построения непараметрических ДАС. Но для такой сложной системы, как ИС, следует отметить возникающие существенные трудности при использовании непараметрической адаптации для всей системы, т. е. при практическом рассмотрении ОУ как «черного ящика» сложность методов и громоздкость алгоритмов адаптивного управления и, как следствие, их практическая  нереализуемость с учетом ограничений вычислительных ресурсов ИС, а часто и необходимости управления в РМВ.

В ряде случаев более перспективен параметрический подход к решению проблемы адаптивного управления при максимальном использовании априорной информации об ОУ и процессе его функционирования. Поэтому применительно к проблеме построения ДАС сложными объектами в ИС можно сделать следующий вывод. Нельзя использовать один и тот же подход к решению задач адаптивного управления на различных уровнях. На каждом из уровней необходимо использовать те методы адаптации, которые позволяют достичь наиболее эффективного управления в каждом конкретном случае.

Идентификация процессов. Как уже отмечалось, одно из важнейших направлений в области идентификации и управления связано с дискретными АС, содержащими в контуре управления идентификатор, т. е. ДАСИ. Процесс идентификации, осуществляемый в ДАСИ, условно разделяется на два этапа, на каждом из которых информация для решения задачи идентификации поступает непосредственно с ОУ в виде реализаций входных и выходных переменных.

Первый этап связан с решением задачи идентификации в широком смысле, или задачи стратегической идентификации. Сюда относятся построение концептуальной модели, выбор информативных переменных, оценка степени стационарности объекта, выбор структуры и параметров модели, оценка точности и достоверности модели реальному объекту.

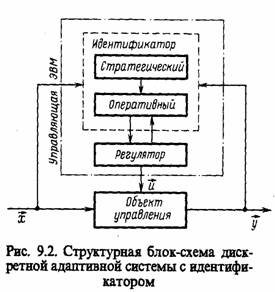            Второй этап предусматривает текущую идентификацию — уточнение модели в связи с текущими изменениями объекта и внешних воздействий; здесь обычно решаются задачи идентификации  в узком смысле, т. е. задачи оценки поведения объекта или его состояний. Структурная      блок-схема классической ДАСИ приведена

на рис. 9.2, где х, у, u — векторы входов, выходов и управления. Стратегический идентификатор осуществляет решение задач идентификации в широком смысле вне контура управления, а оперативный идентификатор — в узком смысле и «является составной частью замкнутого контура управления.

В целом ДАСИ обладают рядом важных практических достоинств: автоматизация идентификации, объединение процессов идентификации и управления, универсальность, высокая надежность. Для сложных объектов трудоемкость процесса идентификации соизмерима с трудоемкостью процесса проектирования системы. Объединение процессов идентификации и управления сокращает сроки создания и освоения системы в результате параллельного проведения работ и, кроме того, является, пожалуй, единственной возможностью оперативно компенсировать текущие изменения характеристик объекта и воздействий внешней среды в процессе функционирования. Из сказанного ясно, что одним из основных в ДАСИ является процесс идентификации. В ДАСИ реализуется принцип современной теории управления: «хорошая модель — залог успешного управления» [43, 54].

9.3. МОДЕЛИРОВАНИЕ В СИСТЕМАХ УПРАВЛЕНИЯ

В РЕАЛЬНОМ МАСШТАБЕ ВРЕМЕНИ

С ускорением темпов развития экономики и интенсификации производственных процессов все шире внедряется автоматизация на предприятиях: от организационного управления цехами и участками до управления технологическими процессами выпуска различных изделий. Наиболее перспективным направлением является создание гибких автоматизированных производств и производственных систем, позволяющих на базе использования современных робототехнических комплексов, станков с числовым программных управлением, средств вычислительной техники оперативно переходить на выпуск новейших изделий, отслеживая динамику потребностей и конъюнктуру мирового рынка. Управление в таких гибких системах наиболее эффективно может быть реализовано на базе локальных сетей ЭМВ, обеспечивающих взаимодействие и координацию всех информационно-вычислительных ресурсов для управления отдельными агрегатами в системе и дающих возможность проводить обработку информации в реальном масштабе времени.

Особенности управления в реальном масштабе времени. Прогресс развития национальной экономики в настоящее время все теснее связывается с тем, насколько эффективно происходит накопление, обмен и выдача информации различным пользователям (административному управленческому персоналу, проектировщикам и конструкторам, исследователям, работникам сферы обслуживания и т. д.). По сути дела, на базе современных средств вычислительной техники и техники связи создается настоящая «индустрия» производства и потребления информации, требующая больших информационно-вычислительных ресурсов и оперативного доступа к ним. Наиболее перспективно объединение всех информационно-вычислительных ресурсов с помощью цифровых сетей интегрального обслуживания, позволяющих в единой цифровой форме передавать различные виды информации (оперативные, диалоговые данные и файлы ЭВМ, речь, телевизионные сигналы и т. п.). Для эффективного удовлетворения требований различных пользователей к качеству и своевременности доставки информации управление сетями интегрального обслуживания должно быть реализовано в реальном масштабе времени.

Можно привести и другие примеры систем, управление которыми должно осуществляться в реальном масштабе времени. Все перечисленные системы объединяет то, что они относятся к классу больших систем (см. гл. 1), что усложняет решение задач управления ими. При разработке систем управления такими объектами обычно отсутствует априорная информация об условиях их работы. Это делает перспективным построение адаптивных систем управления (см. § 9.2).

В рассмотренных в предыдущих параграфах примерах метод моделирования применялся для целей исследования характеристик систем S во взаимодействии с внешней средой Е, проектирования (синтеза) структуры, алгоритмов и параметров системы и т. п. Во всех этих случаях, как правило, отсутствовали жесткие ограничения на время между началом моделирования и получением результата, в качестве технических средств предполагалось использование высокопроизводительных ЭВМ и ГВК.

Прогнозирование и принятие решений. Основной целью моделирования является прогнозирование в широком смысле этого слова. Моделирование позволяет сделать вывод о принципиальной работоспособности объекта (системы S), оценить его потенциально возможные характеристики, установить зависимость характеристик от различных параметров и переменных, определить оптимальные значения параметров и т. п. Машинные модели М_м, используемые в качестве имитаторов и тренажеров, дают возможность предсказать поведение системы S в условиях взаимодействия с внешней средой Е.

Использование метода моделирования для получения прогноза при принятии решений в системе управления в реальном масштабе времени выдвигает на первое место задачу выполнения ограничения на ресурс времени моделирования процесса функционирования системы S. Поэтому рассмотрим более подробно особенности прогнозирования на основе машинной модели М_м в реальном масштабе времени.

Для управления объектом может использоваться в системе либо информация о состояниях (ситуациях) системы S и внешней среды Е, либо информация о выходных характеристиках (поведении) системы S во взаимодействии с внешней средой Е. Это обстоятельство определяет, и цели моделирования В одном случае требуется

оценить изменения состояний z_keZ, k= 1, nz, за время прогнозирования τ_П (назовем такое моделирование ситуационным). В другом  случае требуется оценить выходные характеристики y_jeY,j=l, n_Y, на интервале времени (О, Т) (назовем такое моделирование бихеви-оральным).

Таким образом, цель ситуационного моделирования — получение прогноза вектора состояний z (t) (см. 2.3)), а цель бихевиорального моделирования — оценка вектора выходных характеристик у (t) [см. (2.2) и (2.5)]. Например, если в качестве концептуальной модели М_х процесса функционирования системы S используется Q-схема, то при ситуационном моделировании требуется прогнозировать такие состояния, как число заявок в накопителях, количество занятых каналов и т. д., а при бихевиоральном моделировании в этом случае необходимо оценивать такие характеристики, как вероятность потери заявки, среднее время задержки заявки в системе и т. д. Соответственно целям ситуационного и бихевиорального моделирования должен отличаться и подход к разработке и реализации моделирующих алгоритмов, хотя принципы их построения («принцип Δt» и «принцип δz») сохраняются.

Другой особенностью моделирования для принятия решений по управлению объектом в реальном масштабе времени является существенная ограниченность вычислительных ресурсов, так как такие системы управления, а следовательно, и машинные модели М_м, реализуются, как правило, на базе мини и микро ЭВМ или специализированных микропроцессорных наборов, когда имеется ограничение по быстродействию и объему памяти. Это требует тщательного подхода к минимизации затрат ресурсов по моделированию в реальном масштабе времени [12, 29, 52].

Кроме того, следует учитывать, что достоверность и точность решения задачи моделирования (прогнозирования ситуаций или поведения) системы существенно зависят от количества реализаций N, которые затрачены на получение статистического прогноза (см. гл. 7). Таким образом, возникает проблема поиска компромисса между необходимостью увеличения затрат времени на моделирование, т. е. числа реализаций N [на интервале (О, Т)] для повышения точности и достоверности результатов моделирования (прогнозирования), и необходимостью уменьшения затрат машинного времени из условий управления в реальном масштабе времени.

При использовании машинной модели М_м в контуре управления системой S в реальном масштабе времени возникает также проблема оперативного обновления информации как в базе данных об объекте, так и в базе данных об эксперименте, т. е. в данном случае о конкретном прогнозе.

Рассмотрим более подробно возможности построения моделирующих алгоритмов для ситуационных и бихевиоральных моделей. При ситуационном моделировании важно не потерять информацию о смене состояний системы S, так как от этого зависит эффективность управления. Поэтому построение детерминированных моделирующих алгоритмов, когда используется «принцип Δt», приводит либо к увеличению времени моделирования при уменьшении Δt, либо к снижению достоверности прогноза состояний при увеличении Δt. Это говорит в пользу использования стохастических алгоритмов, а именно тех вариантов, которые наиболее просто реализуются, т. е. асинхронных спорадических алгоритмов.

При бихевиоральном моделировании важно получить усредненную статистическую оценку характеристик системы S на интервале (О, Т). Поэтому при построении моделирующих алгоритмов важно при заданной точности и достоверности результатов моделирования выбрать наиболее просто реализуемый алгоритм, требующий минимальных затрат времени и оперативной памяти на его прогон. В этом случае эффективными могут оказаться как стохастические, так и детерминированные моделирующие алгоритмы. Выбор принципа построения моделирующего алгоритма для принятия решений в системе управления может быть проведен только с учетом особенностей конкретной S.

С точки зрения программирования моделей М_м при моделировании в реальном масштабе времени также имеется ряд особенностей. Это в первую очередь связано с отсутствием или невозможностью использования ЯОН и ЯИМ для программной реализации моделей исходя из возможностей программного обеспечения мини- и микро-ЭВМ и жестких ограничений на время счета по моделирующему алгоритму. В этом случае основное применение находят языки низкого уровня, что усложняет процесс разработки программного обеспечения моделирования в реальном масштабе времени, но

обычно позволяет получить достаточно эффективные рабочие программы моделирования. Для ускорения процесса разработки программного обеспечения моделирования в реальном масштабе времени и повышения его качества рационально разрабатывать соответствующие пакеты прикладных программ, которые с использованием ресурсов высокопроизводительных ЭВМ генерируют рабочие программы моделирования.

Таким образом, моделирование процесса функционирования систем для целей управления в реальном масштабе времени имеет ряд специфических особенностей, но методика моделирования и принципы реализации моделирующих алгоритмов сохраняются.

Контрольные вопросы

9.1. Что называется информационной моделью системы?

9.2. Каковы характерные черты эволюционных моделей систем?

9.3. Что называется трактабельностью модели системы?

9.4. в чем суть адаптации применительно к системам уравления различными объектами?

9.5. Какова роль эталонной модели  в контуре управления ?

9.6. Какие модели используется к для принятия решений?

9.7. Какие требования предъявляются к модели ,реализуемой в реальном масштабе времени?

ГЛАВА 10

ИСПОЛЬЗОВАНИЕ МЕТОДА МОДЕЛИРОВАНИЯ

ПРИ РАЗРАБОТКЕ АВТОМАТИЗИРОВАННЫХ СИСТЕМ

После изучения основ методологии моделирования, освоения технологии машинной имитации, рассмотрения вопросов реализации моделирующих алгоритмов и программ на ЭВМ необходимо, с одной стороны, подвести итоги, т. е. сформулировать, исходя из ранее рассмотренного, общие правила построения и способы реализации моделей систем, а с другой стороны, показать, как в целом работает инструмент моделирования в доступных приложениях. Поэтому в данной, заключительной, главе формулируются эвристические принципы и практические методы реализации машинных моделей, которые иллюстрируются приложениями к разработке организационно-производственных систем и информационно-вычислительных сетей, т. е. тех классов ИС, которые лежат в сфере будущей деятельности дипломированных специалистов.

10.1. ОБЩИЕ ПРАВИЛА ПОСТРОЕНИЯ И СПОСОБЫ

РЕАЛИЗАЦИИ МОДЕЛЕЙ СИСТЕМ

В настоящее время метод машинного моделирования широко применяется при разработке обеспечивающих и функциональных подсистем различных АСОИУ (интегрированных АСУ, автоматизированных систем научных исследований и комплексных испытаний, систем автоматизации проектирования и т. д.). При этом, как уже отмечалось, независимо от объекта можно выделить следующие основные этапы моделирования: 1) построение концептуальной модели системы S и ее формализация; 2) алгоритмизация модели системы S и ее машинная реализация; 3) получение результатов машинного моделирования и их интерпретация.

            Методология машинного моделирования. На первом этапе моделирования формулируется модель, строится ее формальная схема и решается вопрос об эффективности и целесообразности моделирования системы S (об аналитическом расчете или имитационном моделировании) на вычислительной машине (на ЭВМ, АВМ или ГВК). На втором этапе математическая модель, сформулированная на первом этапе, воплощается в машинную, т. е. решается проблема алгоритмизации модели, ее рационального разбиения на блоки и организации интерфейса между ними, а также задача получения необходимой точности и достоверности результатов при проведении машинных экспериментов. На третьем этапе ЭВМ используется для имитации процесса функционирования системы S, для сбора  необходимой информации, ее статистической обработки и интерпретации результатов моделирования.

При этом следует учитывать, что на всех этапах моделирования переход от описания к машинной модели М_м, разбиение модели на части, выбор основных и второстепенных параметров, переменных и характеристик системы являются неформальными операциями, построенными на эвристических принципах, охватывающих как механизм принятия решений, так и проверку соответствия принятого решения действительности. Обобщая полученные результаты в области методологии машинного моделирования, можно условно разделить эвристические принципы моделирования на совокупность основных правил построения моделей систем и способов их машинной реализации, причем правила определяют общие свойства, которыми должна обладать построенная машинная модель, а способы реализации дают конкретные приемы получения нужных свойств модели системы. Следует отметить, что правила построения и способы их реализации образуют единую систему, так что обособленное их рассмотрение не дает полного представления о методологии машинного моделирования [29, 36, 37, 53].

Иерархическая структура взаимосвязи эвристических правил построения и практических способов реализации машинных моделей М_м может быть условно представлена в виде схемы (рис. 10.1), которая задает цепь неформальных действий, выполняемых при моделировании систем в широком смысле этого слова. На рисунке  приняты следующие обозначения: правила: 1 — сопоставление точности и сложности модели; 2 — соразмерность погрешностей моделирования и описания; 3 — реализация блочного представления модели; 4 — специализация моделей для конкретных условий; 5 — достаточность набора элементов модели; 6 — наглядность модели для исследователя и пользователя; способы: 7 — минимальный  обмен  информацией   между    блоками;

8 — упрощение модели по критерию     интерпретации;     9 — удаление блоков с модификацией критерия; 10 — замена зависимых воздействий независимыми;   11 — проверка  точности на условных моделях; 12 — проверка точности по сходимости результатов; 13 — выбор эквивалента входных блоков; 14 — сравнение моделей различной сложности; 15 — параллельное моделирование вариантов системы.

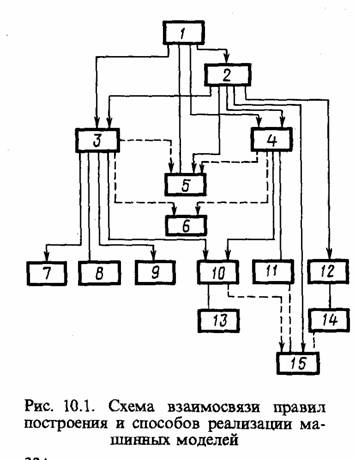
На схеме сплошными линиями показаны связи общих правил и способов с частными, пунктирными — возможность использования соответствующего правила или способа. Коротко рассмотрим основной смысл перечисленных правил и способов моделирования и их взаимосвязь.

Правила построения машинных моделей. Правило сопоставления точности и сложности модели (правило 1) характеризует компромисс между ожидаемой точностью и достоверностью результатов моделирования и сложностью модели системы S с точки зрения ее машинной реализации. Правило соразмерности погрешностей моделирования системы и ее описания (правило 2) представляет, по сути, «баланс точностей», определяемый соответствием систематической погрешности моделирования из-за неадекватности модели М_м описанию системы S с погрешностью в задании описания вследствие неопределенности исходных данных; взаимным соответствием точностей блоков модели; соответствием систематической погрешности моделирования на ЭВМ и случайной погрешности представления результатов моделирования.

Следует помнить, что сложность модели системы S характеризуется затратами времени на построение модели М_M, затратами машинного времени на ее реализацию и объемом памяти конкретной ЭВМ, используемой для моделирования, причем выигрыш в затратах машинного времени получают при сравнительной оценке вариантов разбиения модели М_M на блоки. Отсюда вытекает следующий способ реализации этих правил, а именно способ параллельного моделирования вариантов системы (способ 15), т. е. возможность параллельного моделирования конкурирующих вариантов исследуемой системы S с оценкой разностей соответствующих показателей качества функционирования.

Практическая реализация правил 1 и 2 возможна лишь при наличии гибкой системы, позволяющей создать достаточное разнообразие вариантов модели, т. е. необходимо выполнение правила достаточности набора элементов модели М_м (правило 5) — типовых процедур моделирования и оптимизации в математическом и программном обеспечении моделирования.

Построение моделей во многом — творческая задача, решаемая человеком, т. е. при ее решении должно быть соблюдено правило наглядности модели для исследователя (правило 6), выполнение которого дает возможность исследователю и пользователю (заказчику) оперировать с привычными представлениями об объекте моделирования, что позволяет избежать многих ошибок и упрощает трактовку полученных результатов. В частности, необходимость  блочной  конструкции модели М_м вызывается не только особенностями ее машинной реализации, но и удобствами сохранения понятий, которыми привык оперировать пользователь.

Переходить от описания системы 5 к ее машинной модели М_м наиболее рационально путем построения блочной модели, т. е. необходимо выполнение правила реализации блочного представления модели (правило 3), в соответствии с которым надо находить блоки, удобные для автономного моделирования (на ЭВМ, АВМ и ГВК), и блоки, допускающие исследования натурными методами; принимать решение о существенности или несущественности каждого блока для задачи исследования характеристик данной системы S с целью сохранения структуры описания в пределах этого блока, замены ее упрощенным описанием или удаления блока из модели.

Способы реализации машинных моделей. Разбиение на блоки с точки зрения дальнейшей реализации модели целесообразно проводить, по возможности минимизируя число связей между блоками модели, т. е. отсюда вытекает способ минимального обмена информацией между блоками (способ 7).

Кроме того, при решении вопроса о допустимости удаления блоков из модели целесообразно пользоваться способом упрощения модели М_м по критериям интерпретации (способ 8), т. е. несущественными считаются те блоки, которые мало влияют на критерий интерпретации результатов моделирования и в силу этого могут быть удалены из модели, в том числе и в процессе моделирования системы. Способы удаления блоков различаются в зависимости от характера взаимодействия этих блоков с оставшейся частью системы. Удаляя оконечные блоки, составляющие описание взаимодействия системы S с внешней средой Е, необходимо учесть это при формировании критерия интерпретации результатов моделирования, т. е. это соответствует способу удаления блоков с модификацией критерия (способ 9).

Рассмотрим теперь способ замены блока, осуществляющего воздействие на исследуемую часть системы S. Такой блок не является автономным и его нельзя заменить одним эквивалентным, не зависимым от исследуемой части системы. Но в ряде случаев удается указать диапазон изменения переменных, т. е. функционирование исследуемой части системы можно изучать путем многократного моделирования (по числу воздействий) при различных значениях переменных внутри заданного интервала. Эти предположения реализуются способом замены зависимых воздействий независимыми (способ 10).

При реализации модели М_м системы S необходимо решить путем сопоставления вопрос о способе выбора эквивалента входных воздействий (способ 13): упрощение замкнутого контура, образуемого входным блоком и исследуемой частью системы без разрыва обратной связи; построение вероятностного эквивалента на основе предварительного его исследования (частичного моделирования); замена входного блока наихудшим воздействием по отношению к исследуемой части системы.

До сих пор рассматривались только блоки, реализующие структурное разделение машинной модели на непересекающиеся части, но можно использовать и временное разделение на блоки (условные подмодели), которые отражают различные этапы или режимы функционирования системы S, т. е. в этом случае в них могут входить пересекающиеся части системы. В ряде случаев выделение условных подмоделей позволяет добиться упрощений при реализации машинной модели М_M, сузить разброс результатов моделирования и тем самым сократить требуемое количество прогонов. Обобщая схему условных подмоделей, можно сформулировать правило специализации для конкретных условий (правило 4), определяющее целесообразность использования набора частных условных подмоделей, предназначенных для анализа характеристик процесса функционирования системы S в конкретных условиях и дающих возможность судить о системе в целом по совокупности частных показателей, полученных на условных подмоделях, построенных с учетом особенностей планирования машинных экспериментов.

При этом специализация полной модели системы позволяет в отдельных случаях проверить точность ее упрощенного блочного представления, т. е. отсюда вытекает способ проверки точности на условных моделях (способ 11). Условные подмодели строятся независимо друг от друга, что позволяет ускорить исследование, выполняя параллельные машинные эксперименты со всеми подмоделями, например на нескольких ЭВМ.

Динамика моделирования системы S может быть определена как движение в некотором подпространстве моделей {М}. Причем при исследовании систем движение идет в сторону усложнения модели. Отсюда вытекает способ проверки точности по сходимости результатов (способ 12), т. е. проверки точности результатов моделирования, получаемых на моделях возрастающей сложности. Такой способ позволяет двигаться «снизу — вверх» в подпространстве моделей {М} от упрощенной модели, заведомо реализуемой на ЭВМ, в сторону ее развития и усложнения в пределах ограничений вычислительных ресурсов. В таком движении в подпространстве моделей {М} следует остановиться, когда различие моделей становится незначительным. Эти особенности и реализуются способом сравнения моделей с различной сложностью (способ 14).

Рассмотренные эвристические правила, и способы моделирования задают общую схему построения и реализации модели системы S, но не конкретные решения для каждого этапа машинного моделирования. Даже при работе с конкретным программно-техническим обеспечением для исследования определенного класса систем, например в виде пакета прикладных программ моделирования, необходимо   предварительно   решить   ряд   задач   формализации  объекта моделирования, планирования машинных экспериментов и других, которые были рассмотрены в предшествующих главах.

10.2. МОДЕЛИРОВАНИЕ ПРИ РАЗРАБОТКЕ РАСПРЕДЕЛЕННЫХ АВТОМАТИЗИРОВАННЫХ СИСТЕМ И ИНФОРМАЦИОННЫХ СЕТЕЙ

Рассматривая АСОИУ с точки зрения технологии обработки информации и принятия решений, можно выделить функциональную схему управления, состоящую из обеспечивающих подсистем, находящихся во взаимосвязи как между собой, так и с внешней средой. При проектировании АСОИУ различных уровней, исходя из общности решаемых задач, принято выделять информационное, математическое, программное, техническое и организационное обеспечение [2, 25, 34, 35, 52].

Объект моделирования. Техническое обеспечение — одна из основных составных частей АСОИУ, той материально-технической базы, с помощью которой реализуются экономико-математические методы управления. Комплекс технических средств включает в себя разнообразные средства вычислительной техники, сбора и передачи информации, обеспечивающие своевременную и качественную переработку управляющей информации, причем территориальная удаленность объектов управления в АСОИУ требует применения средств передачи информации, основная задача которых — обмен информацией между местом ее возникновения и информационно-вычислительным центром с необходимой скоростью и достоверностью.

Наиболее перспективным направлением в  области  создания технического обеспечения АСОИУ является построение информационно-вычислительных сетей, цифровых сетей интегрального обслуживания, позволяющих наиболее эффективно использовать ресурсы обработки и хранения информации [35, 38, 51, 54]. Структурная схема такой сети показана на рис. 10.2, где выделены уровни базовой (магистральной) сети, реализующей обмен информацией между центрами коллективного пользования, и терминальной (абонентской)  сетью,  обеспечивающей обмен информацией между пользователями и ЭВМ.   

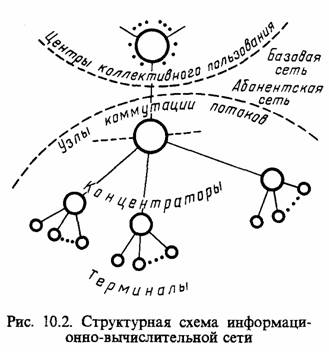
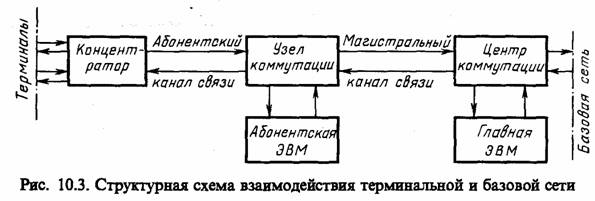
Основными структурными элементами сети являются: узлы (центры) коммутации потоков, осуществляющие все основные операции по управлению сетью, включая коммутацию и маршрутизацию потоков сообщений (пакетов); концентраторы, обеспечивающие сопряжение входных низкоскоростных каналов связи с выходным высокоскоростным каналом; терминалы, выполняющие функции организации доступа пользователя к ресурсам сети и функции по локальной обработке информации; каналы связи, реализующие обмен информацией между узлами сети (узлами коммутации, концентраторами, терминалами) с требуемым качеством.

Рассмотрим более подробно работу фрагмента такой информационно-вычислительной сети на уровне взаимодействия терминальной и базовой ее частей (рис. 10.3). Информация, требующая обработки, поступает с терминалов пользователей в виде сообщений длиной q бит с интенсивностью λ сообщений/с. Абонентская ЭВМ, подключенная к узлу коммутации, производительностью h бит/с обрабатывает поступающую от концентраторов информацию. Мультиплексные каналы ЭВМ обслуживают по к терминалов каждый, передавая данные к ЭВМ со скоростью В бит/с. При недостатке вычислительной мощности для обработки информации пользователей абонентская ЭВМ через узлы коммутации и магистральный канал связи с пропускной способностью С бит/с подключается посредством центра коммутации к ЭВМ верхнего уровня сети (главным ЭВМ), которые имеют суммарную производительность Н бит/с при наличии и мультиплексных каналов. При этом предполагается,   что   процессы   коммутации   выполняются   мгновенно. При проектировании АСОИУ необходимо оценить среднее время обработки информации Т₀ и вероятность отказа в выполнении работ Р_от в случае работы только с абонентской ЭВМ, т. е. в автономном режиме, и в случае подключения к одной из ЭВМ сети коллективного пользования.

Формализация процесса функционирования объекта моделирования. Процесс функционирования данного фрагмента информационно-вычислительной сети может быть представлен в виде Q-схемы, имеющей два параллельных канала обслуживания, а также связи, управляющей блокировкой. Структура такой Q-схемы, формализующей процесс работы фрагмента описанной сети, представлена на рис. 10.4. Здесь И — источник; К_х и К₂ — каналы обслуживания. В качестве выходного потока источника (И) рассматривается суммарный поток сообщений от терминалов, т. е. поток на выходе концентратора. Выходной поток Q-схемы составят обслуженные сообщения при работе каналов К₁ и К₂ и потерянные сообщения при отключении (блокировке) канала К₂. В такой постановке решение этой задачи аналитическим методом (в явном виде) с использованием теории массового обслуживания не представляется возможным из-за стохастического характера работы механизма блокировок, поэтому для оценки интересующих характеристик воспользуемся методом имитационного моделирования.

В этом случае можно записать: эндогенные переменные: Т₀ — среднее время обслуживания сообщений; Р_от — вероятность отказа в обслуживании; экзогенные переменные: λ_Σ  = knqλ — интенсивность входного потока сообщений; h — производительность абонентской ЭВМ; Н — суммарная производительность главных ЭВМ сети; В — пропускная способность селекторных каналов ЭВМ; С — пропускная способность магистрального канала связи; уравнения модели: а) при блокированном канале

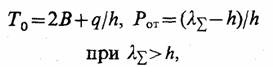
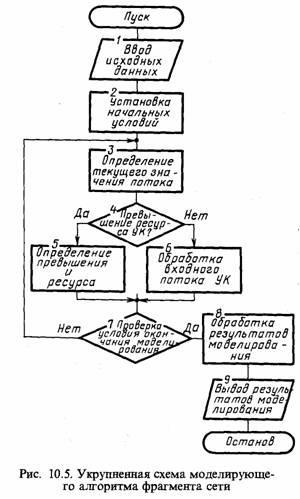
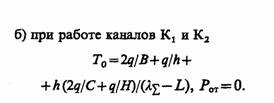
Моделирующий алгоритм. Укрупненная схема моделирующего алгоритма процесса функционирования фрагмента информационно-вычислительной сети представлена на рис. 10.5.

Примеры результатов моделирования в виде зависимости P_ot = ƒ(kn) приведены на рис. 10.6.

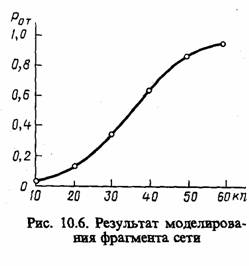
10.3. МОДЕЛИРОВАНИЕ ПРИ РАЗРАБОТКЕ ОРГАНИЗАЦИОННЫХ И ПРОИЗВОДСТВЕННЫХ СИСТЕМ

Эффективность работы АСОИУ существенно зависит от качества моделей, на базе которых реализуется процесс управления. В силу сложности объекта управления проводится его декомпозиция на отдельные части, т. е. выделяются функциональные подсистемы, включая такие, как технико-экономическое планирование, техническая подготовка производства, оперативное управление производством и т. д. [25, 29, 34, 52].

Объект моделирования. Рассмотрим одну из функциональных задач подсистемы оперативного управления основным производством. В качестве примера такой задачи можно привести задачу «Расчет плана сдачи и получения деталей в натуральном выражении».

Решение этой задачи на ЭВМ полностью позволяет автоматизировать получение информации по расчету планов сдачи и деталей в натуральном выражении по цехам на год с разбивкой по кварталам и месяцам на предприятиях с подметальной системой планирования. Планы сдачи и получения деталей рассчитываются для всех цехов-изготовителей и цехов-потребителей предприятия согласно технологическому маршруту. Основу этих планов составляет развернутый план потребности в деталях на товарный выпуск продукции, скорректированный с учетом величины плана изменения заделов и компенсации неизбежных внутрипроизводственных потерь.

На предприятиях с дискретным характером производства (например, крупносерийного и массового приборостроения и машиностроения) процесс движения изделий (деталей, узлов) состоит из заготовительной, механообрабатывающей и сборочной стадий (рис. 10.7). Обычно стадии заготовки и сборки представляют собой детерминированные

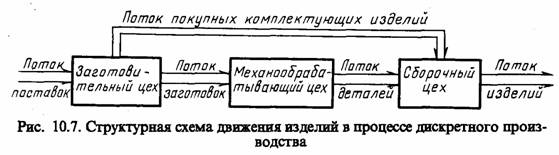
процессы, а механообрабатывающее производство имеет стохастическую природу. Фактически механообрабатывающие подразделения производства представляют собой некоторую кибернетическую систему типа «черног ящика», на вход которого поступает поток заготовок, а на выходе имеется поток партий готовых деталей. Количество стандартных деталей в партии и время выпуска — случайные величины. Для сглаживания стохастичности и придания потоку партий деталей, поступающих на сборку, ритмичного характера заранее до начала планового периода устанавливаются заделы деталей.

Под заделами (запасами) понимаются различного рода заготовки, покупные комплектующие изделия, готовые детали и т. д., находящиеся на разных стадиях производственного процесса в предназначенные для обеспечения бесперебойного хода работы на различных его стадиях. Обычно выделяют следующие заделы: оборотные, представляющие собой запасы деталей, комплексующих изделий и т. п., которые возникают из-за неполной согласованности времени выполнения работы на отдельных линиях или рабочих местах; страховые (резервные), представляющие собой запасы, предназначенные для локализации непредвиденных перебоев и неполадок с тем, чтобы не дать им распространиться далее по направлению технологического маршрута.

Для определения оптимального размера задела деталей в функциональной подсистеме оперативного управления основным производством АСУ предприятием решается соответствующая задача, в основе которой лежит модель, построенная на базе аналитического или имитационного подхода.

Фрагмент производственного процесса, показывающего взаимодействие цеха 1 (механообрабатывающего) и цеха 2 (сборочного) через оборотный и страховой заделы, представлен в виде структурной схемы (рис. 10.8). В процессе производства возможны следующие ситуации: а) нормальная, когда детали из цеха 1 поступают в оборотный задел (связь 1), а из оборотного задела — на сборку (связь 5); в страховом заделе имеется полный запас деталей; б) аварийная, когда детали из цеха 1 не поступают, оборотный задел израсходован, а сборка в цехе 2 обеспечивается только за счет страхового задела (связь 4); в) простойная, когда нет потока деталей

из цеха 1, а запасы деталей в оборотном и страховом заделах израсходованы, т. е. цех 2 простаивает; г) переходная, когда в оборотном заделе имеются детали и он пополняется из цеха 1 (связь 1), детали поступают на сборку (связь 3), а кроме того, идет комплектование страхового задела (связь 2).

Формализация процесса функционирования объекта моделирования. Процесс поступления и потребления деталей в цехе 2 можно формализовать в виде Q-схемы (рис. 10.9). Здесь И — источник; К — канал; Н — накопитель.

Таким образом, процесс заготовки изделий для сборки (деталей, покупных комплектующих изделий) можно представить в виде некоторого источника (И), выдающего детерминированный поток покупных комплектующих изделий и стохастический поток партий деталей для сборки. В дальнейшем будем предполагать, что детерминированный поток покупных комплектующих изделий отсутствует, так как в общем случае он может быть рассмотрен как частный случай стохастического потока. Тогда на выходе И будет иметь место поток деталей на обработку, который описывается как количество единиц деталей q в партии, каждая из которых поступает через Q часов.

Процесс обработки в механообрабатывающем цехе 1 при наличии оборотного и страхового заделов можно представить в виде канала К_х с временем обработки Qоб=const и временем межоперационного пролеживания Q_MП=var, т. е. время обслуживания каналом К_х составит Q₁ = Q_об + Q_мп, а также двух накопителей: H₁и Н₂, причем в результате потерь от брака qe количество выпускаемых деталей q₁ является случайным.

Детали после обработки поступают в накопитель Н₁, емкость которого L₁ соответствует номинальному значению деталей в оборотном заделе L₁ = Z_oб. При достижении номинального значения L₁ детали поступают в накопитель Н₂, соответствующий страховому заделу (если он нуждается в пополнении). При заполнении накопителя Н₂, т. е. достижении величины L₂, клапан на его входе блокируется, причем начальное значение L₁ в накопителе H₁ на планируемый период равно величине одной партии деталей, выпускаемых из канала К_1, а необходимое значение страхового задела L₂=Z_CT должно быть оценено в результате решения задачи.

Процесс сборки изделий в сборочном цехе 2 можно представить в   виде   канала   К₂,   потребляющего   q₂ = const   деталей   через

интервалы времени Q₂ = =const. При нехватке деталей в оборотном заделе (накопитель Н₁) потребность для сборки восполняется из страхового задела (накопитель Н₂) путем разблокировки соответствующего клапана на выходе Н₂.

При недостатке деталей в оборотном и страховом заделах сборочный участок, т. е. канал К₂, простаивает до момента поступления из канала К₁ необходимого числа деталей.

Для возможности выбора необходимого значения оборотного задела L₁ определим вероятность простоя сборочного участка (канала К₂) как функцию L₂, т. е. вероятность Р_пр.

Таким образом, данная модель является двухфазной Q-схемой с двумя параллельными очередями во второй фазе обслуживания и с наличием блокировок. При этом потоки поступления и обслуживания заявок имеют как детерминированный, так и стохастический характер. Учитывая сказанное, получение вероятности Рщ, аналитическим методом в явном виде невозможно, поэтому воспользуемся методом имитационного моделирования на ЭВМ.

Для рассматриваемой модели производственного процесса в виде Q-схемы имеют место два выходных потока: поток обработанных изделий q₂ и поток бракованных деталей q_б.

Представим переменные и уравнения модели в следующем виде: эндогенная переменная: Р_пр — вероятность простоя цеха 2; экзогенные переменные: Q — интервал времени между запуском партий деталей в цех 1; q — размер партий деталей, поступающих на обработку в цех 1; Q_t = Qоб +Q_{м .п}  — интервал   времени между моментами выпуска деталей из цеха 1, где Qоб — постоянное время обработки; Q_{м п} — время межоперационного пролеживания ; q₁ — q—q_б — число выпускаемых деталей цехом 1, где q_б=qF₆ — число бракованных деталей; F_б — доля бракованных деталей, которая считается равномерно распределенной в интервале (О, Fб); Q.2 — интервал времени

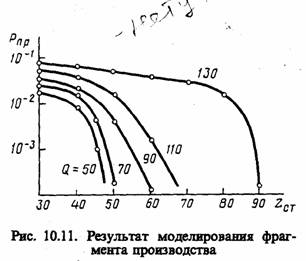
между запуском деталей в цех 2; q₂ — количество деталей в партии для цеха 2; Z_CT —страховой задел, значение которого на начало года Z_сто   Z_об  — оборотный задел, значение которого на начало года Z_обо, уравнение модели

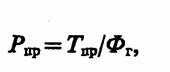
где Ф_г — годовой фонд времени; Т_пр, — время простоя цеха 2 из-за отсутствия деталей. За интервал моделирования (0, 7) примем годовой фонд времени Т=Ф_г=4080 ч.

Моделирующий алгоритм. Укрупненная схема моделирующего алгоритма фрагмента производства на уровне решения задачи определения страхового задела, т. е. взаимодействия механообрабатывающего (цех 1) и сборочного (цех 2) цехов, представлена на рис. 10.10.

Результаты моделирования в виде зависимости P_np=ƒ(Z_CT) для различных значений запуска приведены на рис. 10.11.

ЗАКЛЮЧЕНИЕ

ПЕРСПЕКТИВЫ ИСПОЛЬЗОВАНИЯ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ В ИНФОРМАЦИОННОМ ОБЩЕСТВЕ

Процесс проектирования информационных систем, реализующих новую информационную технологию, непрерывно совершенствуется. В центре внимания инженеров - системотехников оказываются все более сложные системы, что затрудняет использование физических моделей и повышает значимость математических моделей и машинного моделирования систем. Машинное моделирование стало эффективным инструментом исследования и проектирования сложных систем. Актуальность математических моделей непрерывно возрастает из-за их гибкости, адекватности реальным процессам, невысокой стоимости реализации на базе современных ЭВМ. Все большие возможности предоставляются пользователю, т. е. специалисту по моделированию систем средствами вычислительной техники. Особенно эффективно применение моделирования на ранних этапах проектирования автоматизированных систем, когда цена ошибочных решений наиболее значительна.

Современные вычислительные средства позволили существенно увеличить сложность используемых моделей при изучении систем, появилась возможность построения комбинированных, аналитико-имитационных моделей, учитывающих все многообразие факторов, имеющих место в реальных системах, т. е. использования моделей, более адекватных исследуемым явлениям. Поэтому в учебнике особое внимание уделено методологическим аспектам моделирования, типовым математическим схемам, методам и средствам их реализации в процессе моделирования на современных ЭВМ.

В целом в учебнике сделана попытка системного подхода к изложению научных основ моделирования систем. Реализация возможностей машинного моделирования освещается авторами в учебном пособии «Моделирование систем: Практикум», которое издается параллельно с данным учебником издательством «Высшая школа».

Перспективным и значимым для теории и практики системного моделирование является дальнейшее развитие научных основ моделирования с ориентацией на новые информационные технологии в научных исследованиях, проектировании, управлении и обучении.

            Одной из основных в настоящее и ближайшее время будет проблема информатизации образования в условиях перехода к информационному обществу. В конце текущего столетия, по определению Н. Винера [35], человечество переходит из века энергетики в век информатики, общество из индустриального превращается в информационное. В этих условиях информатизацию можно рассматривать как процесс перехода от индустриального общества к информационному. Начиная с 80-х годов сумма знаний в обществе возрастает вдвое за каждые два года. Происходит перераспределение трудовых ресурсов из материального производства в сферу информации. В ряде стран суммарные расходы на компьютерную технику, телекоммуникации, электронику превышают расходы на энергетику, т. е. в силу уверенно вступает век информатизации.

Для информационного общества характерно полное удовлетворение информационных потребностей при завершении формирования единой информационной среды, которая определяет и информационную культуру общества и каждого человека. Информационная культура не ограничивается системой знаний в области информационных процессов и должна включать активно-преобразовательный аспект отношения к миру. В создании информационной культуры лидирующая роль принадлежит образованию.

Достижениями информатики, в которой, как в научном направлении, можно выделить 3 уровня: физический — программно-аппаратные средства вычислительной техники и техники связи, т. е. средства телематики (телекоммуникаций и информатики); логический — информационные технологии; прикладной — пользовательские информационные системы. Исходя из этого, можно провести анализ мирового состояния и тенденций развития процесса информатизации и место компьютерного (машинного) моделирования в этом многогранном процессе. Моделирование вообще и компьютерное имитационное моделирование, в частности, получает применение в таких информационных технологиях как:

1.  Компьютерные программы, включающие в себя электронные учебники, тренажеры, тьюторы, лабораторные практикумы, тестовые системы, деловые игры, использующие машинные имитаторы.

2.  Системы на базе мультимедиа технологий, построенные с использованием персональных ЭВМ, видеотехники, накопителей на оптических дисках, включая системы виртуальной реальности.

3.  Интеллектуальные и обучающие экспертные системы, широко использующие имитационный подход в различных предметных областях.

4.  Распределение базы данных по отраслям знаний, электронные библиотеки, распределенные и централизованные издательские системы.

5.  Средства   телекоммуникации,   включающие   в  себя  электронную почту, телеконференции, локальные и региональные сети связи, цифровые сети интегрального обслуживания и т. д. с использованием новых интеллектуальных сетевых технологий.

            6.  Геоинформационные системы, базирующиеся на технологии, объединяющей компьютерную картографию и системы управления базами   данных,   и   реализующие   технологию   создания  многослойной электронной карты,  опорный слой которой описываетгеографию территории, а каждый из остальных слоев — один из аспектов состояния территории.

7. Технологии защиты информации, включая защиту от несанкционированного доступа в ПЭВМ, защиту от перехвата в сетях и т. п.

Важно отметить, что, говоря о совокупности средств информатизации, следует иметь в виду не только средства вычислительной техники и некоторую «сумму информационных технологий», но также и сумму общественных знаний и умений по использованию указанных средств, которая может быть определена как уровень общественного (или организационного) обучения. Очевидно, что ни одна предметная область, в том числе и машинное моделирование, не может перешагнуть через некоторые объективные стадии такого общественного обучения. Этот факт впервые был облечен в форму модели стадий роста Р. Ноланом в 1979 г. Эта модель показывает, как изменяются расходы на информатизацию, которые определяют уровень организационного обучения, в зависимости от степени проникновения информационной технологии в деятельность организации. Таким образом, наряду с психологической необходимо обеспечить и профессиональную подготовленность пользователей. Особенно это актуально в сфере использования ЭВМ для целей имитации широкого класса систем.

Таким образом, информатизация является объективной реальностью. Возникает вопрос, не может ли информатизация предотвратить глобальный кризис цивилизации и явиться основным механизмом свершения образовательной революции? Считается возможным становление новой системы непрерывного открытого гибкого дистанционного образования на базе перспективных информационных технологий. Это возможно, если вложить в информационные технологии необходимое гуманистическое содержание. В этом смысле цель информатизации общества — создание гибридного интегрального интеллекта всей цивилизации, способного предвидеть и управлять развитием человечества.

                  В настоящее время в образовании создано и внедрено достаточно большое количество программных и технических разработок, реализующих отдельные информационные технологии. Но при этом используются различные методические подходы, несовместимые технические и программые средства, что затрудняет тиражирование, становится преградой на пути общения с информационными ресурсами и компьютерной техникой, приводит к распылению сил и средств. Наряду с этим различный подход к информатизации на школьном и вузовском уровнях вызывает большие трудности у учащихся при переходе с одного уровня обучения на другой, приводит к необходимости расходования учебного времени на освоение элементарных основ современных компьютерных технологий. Выход может быть найден путем создания системы непрерывного образования «школа — вуз».

Переход к информационному обществу предполагает формирование информационной культуры, как свода правил поведения в информационном обществе, в коммуникационной среде, человеко-машинных системах, вписывающихся в мировую гуманистическую культуру человечества. Вхождение пользователя в мировую сеть (например, Internet) позволяет получать огромные потоки информации, в том числе и для целей моделирования. Например, имеются базы данных по различным версиям языка моделирования GPSS/PC, доступные пользователям Internet. Информационное пространство Российского образования должно отвечать национальным интересам и базироваться на традициях отечественной культуры. Проблема развития интеллекта учащихся может быть решена не только средствами информатики. Проблемы науки об образовании должны решаться с учетом перехода в информационное общество, в котором будет сформирована «инфоноосфера личности». Проблема развития интеллектуальных способностей личности смыкается уже сейчас с проблемой информатизацией образования.

Информатизация должна предусматривать эволюционное развитие методологии образования. Не отрицание, а последовательное эволюционное развитие сложившейся методологии образования за счет использования явных преимуществ компьютерных технологий, включая и имитационное моделирование (наглядность, возможность использования различных форм представления информации — звук, изображение, удаленный доступ, обработка и хранение больших объемов информации), должно стать основой опережающего развития образования. Информатизация может внести существенные изменения в структуру и организацию учебного процесса. Необходимо управлять ходом информатизации образования. И опять здесь существенные результаты могут быть получены специалистами по системному моделированию.

Использование персонального компьютера открывает принципиально новые возможности в организации изучения физических явлений с помощью машинной имитации. При традиционном подходе физическое понимание по существу вырабатывалось у учащихся (школьников, студентов и др.) в процессе выполнения ими необходимых математических преобразований и вычислений, что и представляет собой наибольшую трудность для указанной категории учащихся. Благодаря специально разработанным программам имитации физических процессов в реальных системах такую работу берет на себя компьютер, и на долю учащихся остается не само добывание результата, а выявление и усвоение его физических причин. Другими словами, теперь доминирует роль идей и качественных методов исследования, которые связаны с гораздо большей наглядностью и образностью мышления. При этом заметно возрастает эмоциональный фактор, и предмет изучения становится не только доступным, но и интересным.