6.3. ТАКТИЧЕСКОЕ ПЛАНИРОВАНИЕ МАШИННЫХ ЭКСПЕРИМЕНТОВ

С МОДЕЛЯМИ СИСТЕМ

Тактическое планирование эксперимента с машинной моделью М_м системы S связано с вопросами эффективного использования выделенных для эксперимента машинных ресурсов и определением конкретных способов проведения испытаний модели М_м, намеченных планом эксперимента, построенным при стратегическом планифровании. Тактическое планирование машинного эксперимента связано прежде всего с решением следующих проблем: 1) определения начальных условий и их влияния на достижение установившегося результата при моделировании; 2) обеспечения точности и достоверности результатов моделирования; 3) уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; 4) выбора правил автоматической остановки имитационного эксперимента с моделями систем [36, 37, 46].

Проблема определения начальных условий и их влияния на достижение установившегося результата при моделировании. Первая проблема при проведении машинного эксперимента возникает вследствие искусственного характера процесса функционирования модели М_м, которая в отличие от реальной системы S работает эпизодически, т. е. только когда экспериментатор запускает машинную модель и проводит наблюдения. Поэтому всякий раз, когда начинается очередной прогон модели процесса функционирования системы S, требуется определенное время для достижения условий равновесия, которые соответствуют условиям функционирования реальной системы. Таким образом, начальный период работы машинной модели М_ы искажается из-за влияния начальных условий запуска модели. Для решения этой проблемы либо исключается из рассмотрения информация о модели М_м, полученная в начальной части периода моделирования (0, 7), либо начальные условия выбираются так, чтобы сократить время достижения установившегося режима. Все эти приемы позволяют только уменьшить, но не свести к нулю время переходного процесса при проведении машинного эксперимента с моделью М_м.

Проблема обеспечения точности и достоверности результатов моделирования. Решение второй проблемы тактического планирования машинного эксперимента связано с оценкой точности и достоверности результатов моделирования (при конкретном методе реализации модели, например, методе статистического моделирования на ЭВМ) при заданном числе реализаций (объеме выборки) или с необходимостью оценки необходимого числа реализаций при заданных точности и достоверности результатов моделирования системы 5.

Как уже отмечалось, статистическое моделирование системы S — это эксперимент с машинной моделью М_ы. Обработка результатов подобного имитационного эксперимента принципиально не может дать точных значений показателя эффективности Е системы S; в лучшем случае можно получить только некоторую оценку Е такого показателя. При этом экономические вопросы затрат людских и машинных ресурсов, обосновывающие целесообразность статистического моделирования вообще, оказываются тесно связанными с вопросами точности и достоверности оценки показателя эффективности Е системы S на ее модели М_и [4,7,11,18,21,25].

Таким образом, количество реализаций N при статистическом моделировании системы S должно выбираться исходя из двух основных соображений: определения затрат ресурсов на машинный эксперимент с моделью М_м (включая построение модели и ее машинную реализацию) и оценки точности и достоверности результатов эксперимента с моделью системы S (при заданных ограничениях не ресурсы). Очевидно, что требования получения более хороших оценок и сокращения затрат ресурсов являются противоречивыми и при планировании машинных экспериментов на базе статистического моделирования необходимо решить задачу нахождения разумного компромисса между ними.

Из-за наличия стохастичности и ограниченности числа реализаций N в общем случае Ё≠Е. При этом величина Е называется точностью (абсолютной) оценки:

вероятность того, что неравенство

выполняется, называется достоверностью оценки

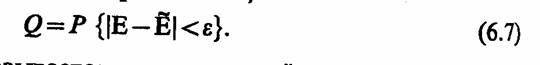
              Величина  ε_o = ε/E называется относительной точностью оценки, а достоверность оценки соответственно будет иметь вид

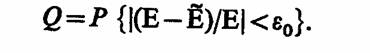
Для того чтобы при статистическом моделировании системы S по заданным Б (или Е_о) и Q определить количество реализаций N или, наоборот, при ограниченных ресурсах (известном N) найти необходимые Е и Q, следует детально изучить соотношение (6.7). Сделать это удается не во всех случаях, так как закон распределения вероятностей величины |Е—Ё| для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе S, либо из-за сложности вероятностных расчетов. Основным путем преодоления подобных трудностей является выдвижение предположений о характере законов распределения случайной величины Ё, т. е. оценки показателя эффективности системы S.

Рассмотрим взаимосвязь точности и достоверности результатов с количеством реализаций при машинном эксперименте, когда в качестве показателей эффективности Е выступают вероятность р, математическое ожидание а и дисперсия а².

Пусть цель машинного эксперимента с моделью М_м некоторой системы S — получение оценки р вероятности появления р=Р(А) некоторого события А, определяемого состояниями процесса функционирования исследуемой системы S. В качестве оценки вероятности р в данном случае выступает частость p=m/N, где т — число положительных исходов.

Тогда соотношение (6.7), связывающее точность и достоверюсть оценок с количеством реализаций, будет иметь вид

Для ответа на вопрос о законе распределения величины p=m/N представим эту частность в виде p=mlN=(1N) Σ х_i так как количество наступлений события А в данной реализации из N реализаций является случайной величиной ξ, принимающей значения x₁= 1 с вероятностью р и х₂=0 с дополнительной вероятностью 1—р. Математическое ожидание и дисперсия случайной величины ξ, будут

таковы:

В силу центральной предельной теоремы теории вероятностей [или ее частного случая — теоремы Лапласа, см. (4.8)] частность mN при достаточно больших N можно рассматривать как случайную величину, описываемую нормальным законом распределения вероятностей с математическим ожиданием р и дисперсией p(l —p)/N. Поэтому соотношение (6.8) с учетом (4.8) можно переписать так:

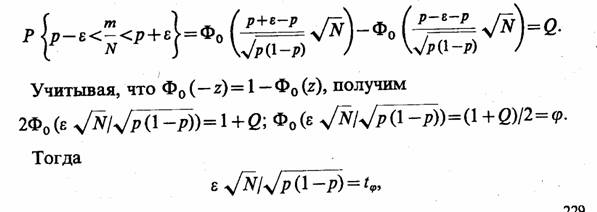
где    t_φ — квантиль    нормального    распределения    вероятностей порядка φ = (1 + Q/)2; находится из специальных таблиц [18, 21].

В результате точность оценки р вероятности р можно определить как

т.  е.  точность  оценки вероятностей обратно пропорциональна

Из соотношения для точности оценки е можно вычислить количество реализаций

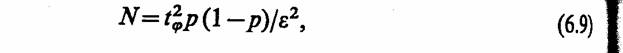
необходимых для получения оценки р с точностью е и достоверностью Q.

Пример 6.7. Необходимо рассчитать количество реализаций N при статистическом моделировании системы S, когда в качестве показателя эффективности используется вероятность р при достоверности 6=0,95 (/,, = 1,96) и точности е=0,01; 0,02; 0,05. Так как значения р до проведения статистического моделирования системы S неизвестны, то вычислим множество оценок N для диапазона возможных значений р, т. е. от 0 до 1, с дискретном 0,1. Результаты расчетов с использованием выражения (6.9) представлены в табл. 6.4. Из таблицы видно, что при переходе от p=0,1 (0,9) кp=0,5 количество реализаций N возрастает примерно в три раза, а при переходе от ε=0,05 к ε =0,01 количество реализаций N возрастает примерно в 25 раз [4].

При тактическом планировании машинного эксперимента, когда решается вопрос о выборе количества реализаций N, значение р неизвестно. Поэтому на практике проводят предварительное моделирование для произвольно выбранного значения N_o, определяют p_o=m/N_o, а затем по (6.9) вычисляют, используя вместо р значение р₀, необходимое количество реализаций N. Такая процедура оценки N может выполняться несколько раз в ходе машинного эксперимента с некоторой системой S.

           При отсутствии возможности получения каких-либо априорных сведений о вероятности р использование понятия абсолютной точности теряет смысл. Действительно, можно, например, предварительно задать точность результатов моделирования е=0,01, а искомая р в результате окажется хотя бы на порядок ниже, т. е. р≤ 0,001. В таких случаях целесообразно задавать относительную точность результатов моделирования ε₀. Тогда соотношение (6.9) примет вид

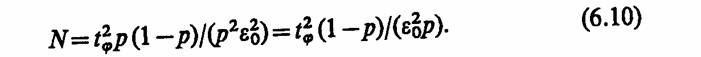
Соотношение (6.10) наглядно иллюстрирует специфику статистического моделирования систем, выражающуюся в том, что для оценивания малых вероятностей р с высокой точностью необходимо очень большое число реализаций N. В практических случаях для оценивания вероятностей порядка 10^-k целесообразно количество реализаций выбирать равным 10 ⁺ . Очевидно, что даже для сравнительно простых систем метод статистического моделирования приводит к большим затратам машинного времени.

Другим распространенным случаем в практике машинных экспериментов с моделью М_ы является необходимость оценки показателей эффективности Е системы S по результатам определения среднего значения некоторой случайной величины. Пусть случайная величина I; имеет математическое ожидание а и дисперсию а². В реализации с номером z она принимает значение х,. В качестве оценки математического ожидания а используется среднее арифметическое .

           В силу центральной предельной теоремы теории вероятностей при больших значениях N среднее арифметическое х будет иметь распределение, близкое к нормальному с математическим ожиданием а и дисперсией a²jN. Для математического ожидания а точность оценки а количество реализаций

      Аналогично, если в качестве показателя эффективности Е системы S выступает дисперсия с², а в качестве ее оценки используется величина S², то математическое ожидание и дисперсия соответственно будут

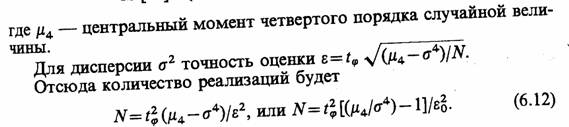
Для частного случая, когда случайная величина имеет нормальное распределение μ₄ = 3σ⁴, получим

Таким образом, на основании соотношений (6.9) — (6.12) можно  сделать вывод, что количество реализаций при статистическом моделировании существенно зависит от дисперсии оцениваемой случайной величины. Поэтому выгодно выбирать такие оцениваемые показатели эффективности Е системы S, которые имеют малые дисперсии.

Проблема уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем. Таким образом, с проблемой выбора количества реализаций при обеспечении необходимой точности и достоверности результатов машинного эксперимента тесно связана и третья проблема, а именно проблема уменьшения дисперсии. В настоящее время существуют методы, позволяющие при заданном числе реализаций увеличить точность оценок, полученных на машинной модели М_м, и, наоборот, при заданной точности оценок сократить необходимое число реализаций при статистическом моделировании. Эти методы используют априорную информацию о структуре и поведении моделируемой системы S и называются методами уменьшения дисперсии.

Рассмотрим в качестве иллюстрации метод коррелированных реализаций (выборок), используемый в задачах сравнения двух или более альтернатив. При исследовании и проектировании системы 5 всегда происходит сравнение вариантов S_h i= 1, к, отличающихся друг от друга структурой, алгоритмами поведения и параметрами.

Независимо от того, как организуется выбор наилучшего варианта системы S (простым перебором результатов моделирования системы Si или с помощью автоматизированной процедуры поиска), элементарной операцией при этом является равнение статистически усредненных критериев интерпретации [18, 21, 29, 33, 53].

Сравниваемые статистические показатели Е_i, вариантов моделируемой системы S_i, i = 1, k, полученные на машинной модели М_м, можно записать в виде средних значений Е_i = M [ q_i], i = 1, k, критериев η_i, характеризующих систему S_i или в виде средних значений функции этих критериев f_j (q_i), i = 1 -, k, j = 1, L. Например, если

то показатели Еi являются вероятностями нормальной работы системы Si Если

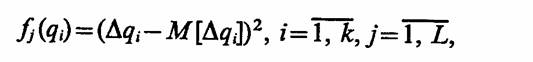
то показателиь Еi, является дисперсией значения контролируемой величины и т. д. Здесь Δq_i=q_i — q_ui — отклонение значения контролируемой для системы 5, величины q_t от истинной qиi

В дальнейшем, поскольку при сравнении характеристик, полученных на машинной модели М_м, всегда рассматриваются два конкурирующих варианта моделируемой системы, будем сопоставлять только две системы: 5_Х и S₂. Существенной особенностью операции сравнения вариантов систем S₁ и S₂ является повышение требований к точности статистических оценок Ё_х, Ё₂ показателей Ец Е₂ при уменьшении разности ДЕ=|Е₁—Е₂|. Это обстоятельство требует разработки специальных приемов получения статистически зависимых оценок для уменьшения дисперсии.

Рассмотрим наиболее характерные случаи, имеющие место при имитационных экспериментах, когда в качестве оценок выступают средние значения, вероятности и дисперсии [29, S3].

Если полученные в результате имитационного эксперимента с вариантами модели системы S_x и S₂ оценки а_х, а₂ средних значений критериев q_u q₂, a₁ = M[q₁], a₂=M[q₂] имеют дисперсии D[uj], D[a₂] и коэффициент корреляции оценок а_г, а₂ равен R[a_x, a_z], то дисперсию погрешности оценки й—а_у — а₂ разности d=a_l — a₂ можно найти из соотношения

Где — средние квадратические отклонения

оценок.

При независимом моделировании вариантов системы с использованием различных реализаций псевдослучайных последовательностей коэффициент корреляции оценок R = [ã₁, ã₂] = 0 и D_н [d̃] = D [ã₁] + D [ã₂].

При моделировании удается получить положительный коэффициент корреляции R [ã₁, ã₂] > 0, т. е. D [d̃] < D_н [d̃], когда при имитационных экспериментах с вариантами системы S₁ и S₂ используются, например, одни и те же псевдослучайные последовательности. Рассмотренные соотношения для дисперсии D [d̃] не связаны со специальными предположениями о способе получения оценок ã₁, ã₂.

Пример 6.8. Рассмотрим полученные при машинном моделировании реализации y₁(rΔt), y₂(rΔt), r = 0,N, критериев q₁, q₂ как выборку из двухмерного векторного стационарного процесса (t) = ||q₁(t), q₂(t)|| средним значением ||a₁, a₂|| и матричной корреляционной функцией

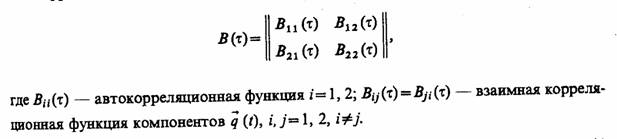
Эту формулу применяют для расчета точности оценки d при заданной матричной корреляционной функции В (т).

Вероятностир_1гр₂ событий А₁ А₂, характеризующих сравниваемые варианты модели Вероятности р₁, р₂ событий А₁, А₂, характеризующих сравниваемые варианты модели систем S₁ и S₂, можно представить как средние значения двоичных случайных величин q₁, q₂ с распределением вероятностей P {q₁ = 1} = p₁; P {q₁ = 0} = 1 - p₁; P {q₂ = 1} = p₂; P {q₂ = 0} = 1 - p₂.

Поэтому для оценки разности вероятностей Δp = p₁ - p₂ = M [q₁] - M [q₂] можно использовать все выражения, полученные ранее при сравнении средних значений, видоизменив в них обозначения с учетом того, что двухмерное распределение вектора (q₁, q₂), описывающее зависимость между событиями А₁, А₂, имеет вид P {q₁ = 1, q₂ = 1} = P (A₁, A₂) = p_A; P {q₁ = 0, q₂ = 0} = P (A₁, A₂) = p_B; P {q = 1, q₂ = 0} = P (A₁, A₂) = p_C; P {q₁ = 0, q₂ = 1} = P (A₁, A₂) = p_D, причем p_A + p_C = p₁, p_A + p_D = p₂. В частности, для повторной выборки объемом N получим, что оценка

где т₁, т₂ - количество наступлений событий А₁, А₂, полученных при независимых прогонах модели. Учитывая, что между q₁, q₂ ковариация B₁₂ = р_А - р₁р₂, найдем дисперсию оценки

что следует из (6.13).

Если в процессе проведения имитационных экспериментов с моделью фиксируются эмпирические частоты р̃_C, p̃_D событий С, D, то для дисперсии D [Δp̃] при достаточно большом N можно воспользоваться несмещенной оценкой

И наконец, рассмотрим случай, когда в качестве оценки вариан; тов систем S₁ и S₂ выступает дисперсия. В этом случае оценка ΔD̃ разности ΔD = D₁ - D₂ дисперсией критериев q₁, q₂ вычисляется по независимым реализациям вектора (q₁, q₂) с помощью формулы ΔD̃ = D̃₁ - D̃₂, где D̃₁, D̃₂ - эмпирические дисперсии критериев q₁, q₂, рассчитываемые по формуле

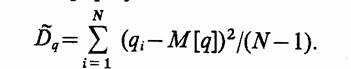
где В₁₂ — ковариация. Использование зависимых испытаний дает выигрыш в точности сравнения дисперсий (В₁₂ ≠0) независимо от знака корреляции. Воспользовавшись оценкой

можно организовать последовательную процедуру сравнения дисперсий для вариантов системы S₁ и S₂.

Таким образом, при таком подходе к уменьшению дисперсии задача состоит в специальном построении моделирующего алгоритма системы S, позволяющего получить положительную корреляцию, например, за счет управления генерацией случайных величин. Вопрос об эффективности использования метода уменьшения дисперсии может быть решен только с учетом необходимости дополнительных затрат машинных ресурсов (времени и памяти) на реализацию подхода, т. е. теоретическое уменьшение затрат машинного времени на моделирование вариантов системы (при той же точности результатов) должно быть проверено на сложность машинной реализации модели.

Проблема выбора правил автоматической остановки имитационного эксперимента с моделями системы. И наконец, последней из проблем, возникающих при тактическом планировании имитационных экспериментов, рассмотрим проблему выбора правил автоматической остановки имитационного эксперимента. Простейший способ решения проблемы — задание требуемого количества реализаций N (или длины интервала моделирования Т). Однако такой детерминированный подход неэффективен, так как в его основе лежат достаточно грубые предположения о распределении выходных переменных, которые на этапе тактического планирования являются неизвестными. Другой способ — задание доверительных интервалов для выходных переменных и остановка прогона машинной модели М_м при достижении заданного доверительного интервала, что позволяет теоретически приблизить время прогона к оптимальному. При практической реализации введение в модель М_м правил остановки и операций вычисления доверительных интервалов увеличивает машинное время, необходимое для получения одной выборочной точки при статистическом моделировании.

Правила автоматической остановки могут быть включены в машинную модель такими способами: 1) путем двухэтапного проведения прогона, когда сначала делается пробный прогон из N* реализаций, позволяющий оценить необходимое количество реализаций N (причем если N*≥N, то прогон можно закончить, в противном случае необходимо набрать еще N—N* реализаций); 2) путем использования последовательного анализа для определения минимально необходимого количества реализаций N, которое рассматривается при этом как случайная величина, зависящая от результатов N— 1 предыдущих реализаций (наблюдений, испытаний) машинного эксперимента.

Рассмотрим особенности последовательного планирования машинных экспериментов, построенных на последовательном анализе. В последовательном анализе объем выборки не фиксирован, а после i-го наблюдения принимается одно из следующих решений: принять данную гипотезу, отвергнуть гипотезу, продолжить испытания, т. е. повторить наблюдения еще раз. Благодаря такому подходу можно объем выборки существенно уменьшить по сравнению со способами остановки, использующими фиксированный объем выборки. Таким образом, последовательное планирование машинного эксперимента позволяет минимизировать объем выборки в эксперименте, необходимой для получения требуемой при исследовании системы S информации. Построив критерий, можно на каждом шаге решать вопрос либо о принятии нулевой гипотезы Н_о, либо о принятии альтернативной гипотезы Н₁ либо о продолжении машинного эксперимента. Последовательное планирование машинного эксперимента использует принцип максимального правдоподобия и последовательные проверки статистических гипотез [18, 21, 33].

Пусть распределение генеральной совокупности характеризуется функцией плотности вероятностей с неизвестным параметром Y = f(y, θ). Определяются нулевая и альтернативная гипотезы Н₀: θ = θ₀ и H₁: θ = θ₁. Гипотезы проверяют на основании выборки нарастающего объема т. Можно записать: вероятность получения данной выборки P_0m = f (y₁, θ₀) f (y₂, θ₀) ... f (y_m, θ₀) при условии, что верна гипотеза Н₀ (правдоподобная выборка); вероятность получения выборки P_1m = f (y₁, θ₁) f (y₂, θ₁) ... f (y_m, θ₁) при условии верности гипотезы H₁. Процедура проверки строится на отношении правдоподобия P_1m/P_0m.

Последовательный критерий отношения вероятностей строится следующим образом. На каждом шаге машинного эксперимента определяются P_1m и Р_0m, а также проверяется условие:

где 0 < B < 1, A > 1, m = 1, N.

Для сходимости критерия необходимо, чтобы А ≤ (1 - β)/α, B ≥ β/(1 - α), где α - вероятность ошибки первого рода; β - вероятность ошибки второго рода.

Данный метод позволяет снизить среднее число реализаций в машинных экспериментах по сравнению с использованием фиксированных объемов выборки (при одинаковых вероятностях ошибок). Примером применения метода может служить проверка гипотезы о среднем значении величины, распределенной по нормальному закону.

Пример 6.10. Пусть для случайной величины у известна дисперсия σ² и неизвестно среднее μ. При этом нулевая гипотеза Н₀: μ = θ₀, альтернативная Н₁: μ = θ₁. Если H₀ верна, то вероятность ее отвергнуть равна α. Если верна гипотеза Н₁, то вероятность принять ее равна β. В случае θ₀ < μ < θ₁ ни одна из гипотез не принимается.

Для нормального распределения

Можно упростить процедуру, если использовать логарифмическую функцию правдоподобия. В этом случае

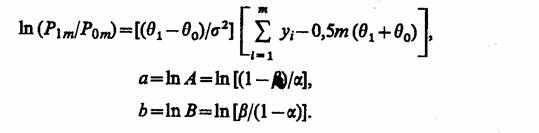
               Тогда на каждом шаге т проверяется выполнение неравенств: если

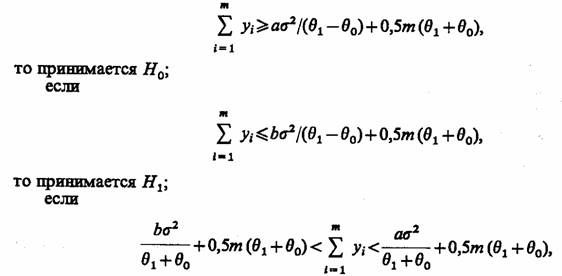
то машинный эксперимент продолжается.

       Для математического ожидания числа наблюдений при условии верности Н₁ и Н₂ соответственно можно записать

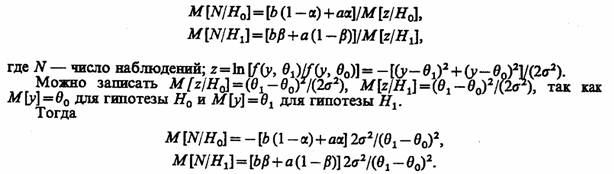
Применение данного метода по сравнению с фиксированным объемом выборки N дает уменьшение числа реализаций при статистическом моделировании более чем в два раза.

Для проверки гипотезы о среднем для случайных величин с нормальным законом распределения, неизвестным средним μ и неизвестной дисперсией σ можно использовать следующую процедуру. Проверяют гипотезы Н₀: μ < μ₀ и Н₁: μ > μ₀. Необходимо, чтобы вероятность отвергнуть Н₀ при μ ≤ μ₀ была Р ≤ α и вероятность принять Н₀ при μ > μ + Δ была P ≤ β.

На первом шаге берут выборку размером т и вычисляют выборочную дисперсию

 здесь число т выбрано таким, чтобы выполнялось условие

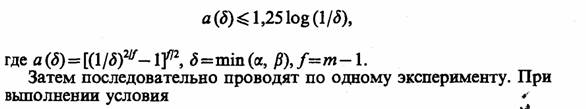
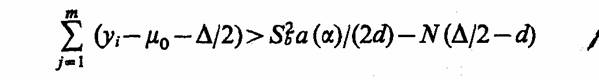
эксперимент прекращают и гипотезу Н_о отвергают. Гипотезу Н_о принимают, если

где d =ЗΔ/8.

Таким образом, чем сложнее машинная модель М_м, тем важнее этап тактического планирования машинного эксперимента, выполняемый непосредственно перед моделированием на ЭВМ системы 5. Процесс планирования машинных экспериментов с моделью М_м итерационен, т. е. при уточнении некоторых свойств моделируемой системы S этапы стратегического и тактического планирования экспериментов могут чередоваться.

Контрольные вопросы

6.1. Каковы характерные особенности машинного эксперимента по сравнению с другими видами экспериментов?

6.2. Какие виды факторов бывают в имитационном эксперименте с моделями систем?

6.3. Что называется полным факторным экспериментом?

6.4. Какова цель стратегического планирования машинных экспериментов?

6.5. Какие проблемы стратегического планирования машинных экспериментов с моделями систем являются основными?

6.6. Какова цель тактического планирования машинных экспериментов?

6.7. Что называется точностью и достоверностью результатов моделирования систем на ЭВМ?

6.8. Как повысить точность результатов статистического моделирования системы в условиях ограниченности ресурсов инструментальной ЭВМ?

ГЛАВА 7

ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ

 МОДЕЛИРОВАНИЯ СИСТЕМ

Концепция статистического моделирования систем в реализационном плане неразрывно связана с ограниченностью ресурсов инструментальных ЭВМ. Поэтому ори рассмотрении теоретических проблем машинной имитации, относящихся в основном к разделу математической статистики, необходимо учитывать особенности и возможности текущей обработки экспериментальной информации на ЭВМ. Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальной информации при использовании модели для целей автоматизации проектирования систем.

7.1. ОСОБЕННОСТИ ФИКСАЦИИ И СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ СИСТЕМ НА ЭВМ

После того как машинный эксперимент спланирован, необходимо предусмотреть меры по организации эффективной обработки и представления его результатов. Вообще, проблема статистической обработки результатов эксперимента с моделью тесно связана с рассмотренными в гл. 6 проблемами стратегического и тактического планирования. Но важность этой проблемы и наличие специфики в машинной обработке результатов моделирования выделяют ее в самостоятельную проблему. При этом надо иметь в виду, что применяемые на практике методы обработки результатов моделирования составляют только небольшую часть арсенала математической статистики [7, 11, 18, 21 25, 33].

Особенности машинных экспериментов. При выборе методов обработки существенную роль играют три особенности машинного эксперимента с моделью системы S.

          1. Возможность получать при моделировании системы S на ЭВМ большие выборки позволяет количественно оценить характеристики процесса функционирования системы, но превращает в серьезную проблему хранение промежуточных результатов моделирования. Эту проблему можно решить, используя рекуррентные алгоритмы обработки, когда оценки вычисляют по ходу моделирования, причем большой объем выборки дает возможность пользоваться при этом достаточно простыми для расчетов на ЭВМ асимптотическими формулами.

2.  Сложность исследуемой системы S при ее моделировании на ЭВМ часто приводит к тому, что априорное суждение о характеристиках процесса функционирования системы, например о типе ожидаемого распределения выходных переменных, является невозможным. Поэтому при моделировании систем широко используются непараметрические оценки и оценки моментов распределения.

3.  Блочность конструкции машинной модели М_м и раздельное исследование блоков связаны с программной имитацией входных переменных для одной частичной модели по оценкам выходных переменных, полученных на другой частичной модели. Если ЭВМ, используемая для моделирования, не позволяет воспользоваться переменными, записанными на внешние носители, то следует представить эти переменные в форме, удобной для построения алгоритма их имитации.

          Методы оценки. Рассмотрим наиболее удобные для программной реализации методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки (числе реализаций N). Математическое ожидание и дисперсия случайной величины I; соответственно имеют вид

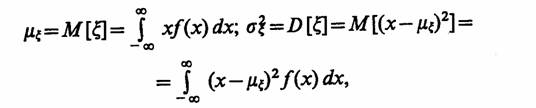
где ƒ (х) — плотность распределения случайной величины ξ, принимающей значения х.

          При проведении имитационного эксперимента со стохастической моделью системы S определить эти моменты нельзя, так как плотность распределения, как правило, априори неизвестна. Поэтому при обработке результатов моделирования приходится довольствоваться лишь некоторыми оценками моментов, полученными на конечном числе реализаций N. При независимых наблюдениях значений случайной величины £ в качестве таких оценок используются

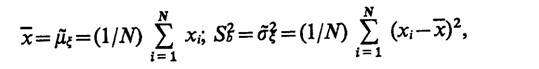
где х и Sb² — выборочное среднее и выборочная дисперсия соответственно. Знак ~ над μ_ξ и σ_ξ² означает, что эти выборочные моменты используются в качестве оценок математического ожидания μξ и дисперсии σ ².

К качеству оценок, полученных в результате статистической обработки результатов моделирования, предъявляются следующие требования [7, 11, 25]:

1) несмещенность оценки, т. е. равенство математического ожидания оценки определяемому параметру М [g̃] = g, где g̃ оценка переменной (параметра) g;

2) эффективность оценки, т. е. минимальность среднего квадрата ошибки данной оценка М [g̃₁ - g] ≤ M [(g̃_i - g)²], где g̃₁ - рассматриваемая оценка; g̃_i - любая другая оценка;

3) состоятельность оценки, т. е. сходимость по вероятности при N → ∞ к оцениваемому параметру

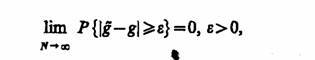
либо, учитывая неравенство Чебышева, достаточное (но не обязательно необходимое) условие   выполнения   этого   неравенства   заключается   в   том,   чтобы

lim M[(g-gf)]=0.

N → ∞

Рассмотрим оценку выборочного среднего значения х. Математическое ожидание выборочного среднего значения х составит

получим M[S_b²]=(Nσ²—σ²_ξ)/N=(N—l)σ²_ξ/N, т. е. оценка  σ²_ξ = S²_b является смещенной. Можно показать, что эта оценка состоятельна и эффективна.

         Несмещенную оценку дисперсии, σ² можно получить, вычисляя выборочную дисперсию вида

Эта оценка также удовлетворяет условиям эффективности и состоятельности.

           Статистические методы обработки. Рассмотрим некоторые особенности статистических методов, используемых для обработки результатов моделирования системы S. Для случая исследования сложных систем при большом числе реализаций N в результате моделирования на ЭВМ получается значительный объем информации о состояниях процесса функционирования системы. Поэтому необходимо так организовать в процессе вычислений фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались постепенно по ходу моделирования, т. е. без специального запоминания всей информации о состояниях процесса функционирования системы 5.

Если при моделировании процесса функционирования конкретной системы S учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т. д.

Пусть в качестве искомой величины фигурирует вероятность некоторого события А. В качестве оценки для искомой вероятности р=Р(А) используется частность наступления события m/N, где т — число случаев наступления события А; N — число реализаций. Такая оценка вероятности появления события А является состоятельной, несмещенной и э

            эффективной. В случае необходимости получения оценки вероятности в памяти ЭВМ при обработке результатов моделирования достаточно накапливать лишь число т (при условии, что N задано заранее).

Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, т. е. закона распределения. Область возможных значений случайной величины η разбивается на п интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы mк, k = l, n. Оценкой для вероятности попадания случайной величины в интервал с номером к служит величина mk/N. Таким образом, при этом достаточно фиксировать п значений т_к при обработке результатов моделирования на ЭВМ.

       Для оценки среднего значения случайной величины ц накапливается сумма возможных значений случайной величины у к, к=1, N, которые она принимает при различных реализациях. Тогда среднее

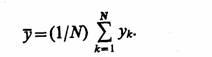
 При этом ввиду несмещенности и состоятельности оценки

         В качестве оценки дисперсии случайной величины η при обработке результатов моделирования можно использовать

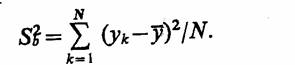
Непосредственное вычисление дисперсии по этой формуле нерационально, так как среднее значение у изменяется в процессе накопления значений у_k Это приводит к необходимости запоминания всех N значений у_k Поэтому более рационально организовать фиксацию результатов моделирования для оценки дисперсии с использованием следующей формулы:  

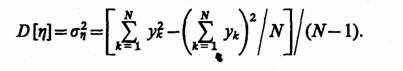
Тогда для вычисления дисперсии достаточно накапливать две суммы: значений ук и их квадратов у_k².

         Для случайных величин ξ и η с возможными значениями х_к и у_к корреляционный момент

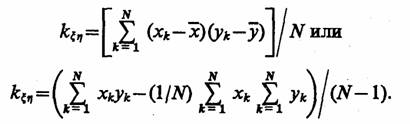
Последнее выражение вычисляется при запоминании в процессе моделирования небольшого числа значений.

Если при моделировании системы S искомыми характеристиками являются математическое ожидание и корреляционная функция случайного процесса y(t) [в интервале моделирования (О, Т)], то для нахождения оценок этих величин указанный интервал разбивают на отрезки с постоянным шагом At и накапливают значения процесса y_k(t) для фиксированных моментов времени t=t_m=mΔt.

           При обработке результатов моделирования математическое ожидание и корреляционную функцию запишем так:

где u и z пробегают все значения t_m.

                 Для уменьшения затрат машинных ресурсов на хранение промежуточных результатов последнее выражение также целесообразно привести к следующему виду:

Отметим особенности фиксации и обработки результатов моделирования, связанные с оценкой характеристик стационарных случайных процессов, обладающих эргодическим свойством. Пусть рассматривается процесс y{t). Тогда с учетом этих предположений поступают в соответствии с правилом: среднее по времени равно среднему по множеству. Это означает, что для оценки искомых характеристик выбирается одна достаточно продолжительная реализация процесса y(t), для которой целесообразно фиксировать результаты моделирования. Для рассматриваемого случая запишем математическое ожидание и корреляционную функцию процесса:

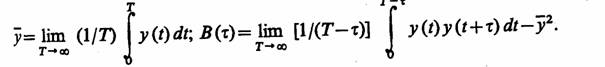
 На практике при моделировании на ЭВМ системы S интервал (О, Т) оказывается ограниченным и, кроме того, значения y(t) удается определить только для конечного набора моментов времени t_m. При обработке результатов моделирования для получения оценок у и В(х) используем приближенные формулы

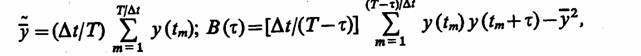
которые целесообразно преобразовать к виду, позволяющему эффективно организовать порядок фиксации и обработки результатов моделирования на ЭВМ [4].

Задачи обработки результатов моделирования. При обработке результатов машинного эксперимента с моделью М_ы наиболее часто возникают следующие задачи: определение эмпирического закона распределения случайной величины, проверка однородности распределений, сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т. д. Эти задачи с точки зрения математической статистики являются типовыми задачами по проверке статистических гипотез.

Задача определения эмпирического закона распределения случайной величины наиболее общая из перечисленных, но для правильного решения требует большого числа реализаций N. В этом случае по результатам машинного эксперимента находят значения выборочного закона распределения F_э(y) (или функции плотности ƒ_э y)) и выдвигают нулевую гипотезу Н_о, что полученное эмпирическое распределение согласуется с каким-либо теоретическим распределением. Проверяют эту гипотезу Н_о с помощью статистических критериев согласия Колмогорова, Пирсона, Смирнова и т. д., причем необходимую в этом случае статистическую обработку результатов ведут по возможности в процессе моделирования системы S на ЭВМ.

Для принятия или опровержения гипотезы выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения, связанную с недостаточностью статистического материала и другими случайными причинами. Закон распределения этой случайной величины зависит от закона распределения случайной величины η и числа реализаций N при статистическом моделировании системы S. Если вероятность расхождения теоретического и эмпирического распределений P{U_T ≥ U} велика в понятиях применяемого критерия согласия, то проверяемая гипотеза о виде распределения H₀    не опровергается. Выбор вида теоретического распределения F(y) (или  ƒ y) проводится по графикам (гистограммам) F_э(y) (или ƒ ₃(у)), выведенным на печать или на экран дисплея

. Рассмотрим особенности использования при обработке результатов моделирования системы S на ЭВМ ряда критериев согласия [7,11,18,21,25].

Критерий согласия Колмогорова. Основан на выборе в качестве меры расхождения U величины D = max [F_э(y) - F(y)].

Из теоремы Колмогорова следует, что δ = D √N при N → ∞ имеет функцию распределения

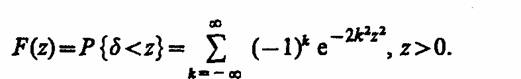
Если вычисленное на основе экспериментальных данных значение δ меньше, чем табличное значение при выбранном уровне значимости у, то гипотезу Н_о принимают, в противном случае расхождение между F₃(y) и F(y) считается неслучайным гипотеза Н_о отвергается.

Критерий Колмогорова для обработки результатов моделирования целесообразно применять в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования этого критерия связан с необходимостью фиксации в памяти ЭВМ для определения D всех статистических частот с целью их упорядочения в порядке возрастания.

         Критерий согласна Пирсона. Основан на определении в качестве меры расхождения U величины

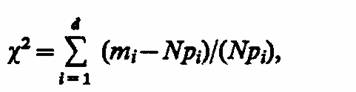
где mi,- — количество значений случайной величины ц, попавших в i-й. подынтервал; Pi — вероятность попадания случайной величины η  в i-й подынтервал, вычисленная из теоретического распределения; d — количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте.

При N→oo закон распределения величины U, являющейся мерой расхождения, зависит только от числа подынтервалов и приближается к закону распределения х (хи-квадрат) с (d—r—1) степенями свободы, где г — число параметров теоретического закона распределения.

Из теоремы Пирсона следует, что, какова бы не была функция распределения F(y) случайной величины η , при N →∞  распределение величины х² имеет вид

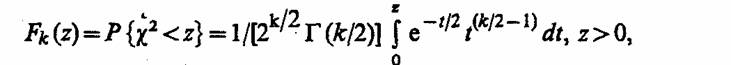
где Г(k/2)- гамма-функция; z - значение случайной величины χ²; k = d - r - 1 - число степеней свободы. Функции распределения F_k(z) табулированы.

По вычисленному значению U = χ² и числу степеней свободы k с помощью таблиц находится вероятность Р {χ² ≥ χ²}. Если эта вероятность превышает некоторый уровень значимости γ, то считается, что гипотеза H₀ о виде распределения не опровергается результатами машинного эксперимента.

Критерий согласия Смирнова. При оценке адекватности машинной модели М_м реальной системе S возникает необходимость проверки гипотезы Н₀, заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов v и ξ, то для проверки гипотезы Н₀ можно использовать критерий согласия Смирнова, применение которого сводится к следующему. По имеющимся результатам вычисляют эмпирические функции распределения F_э(и) и F_э(z) и определяют

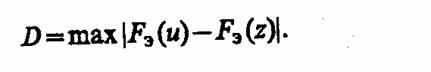
Затем при заданном уровне значимости у находят допустимое отклонение

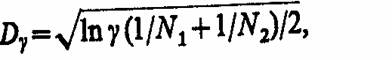
где N₁ и N₂ - объемы сравниваемых выборок для F_э(и) и F_э(z), и проводят сравнение значений D и D_γ,: если D > D_γ, то нулевую гипотезу H₀ о тождественности законов распределения F(u) и F(z) с доверительной вероятностью β = 1 - γ отвергают.

Критерий согласия Стьюдента. Сравнение средних значений двух независимых выборок, взятых из нормальных совокупностей с неизвестными, но равными дисперсиями D [v] = D [ξ], сводится к проверке нулевой гипотезы H₀: Δ = и - z = 0 на основании критерия согласия Стьюдента (t-критерия). Проверка по этому критерию сводится к выполнению следующих действий. Вычисляют оценку

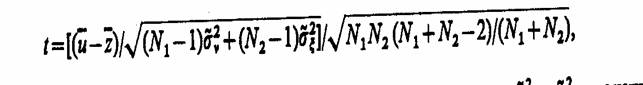
где N₁ и N₂ - объемы выборок для оценки и и z соответственно; σ̃²_v и σ̃²_ξ - оценки дисперсий соответствующих выборок.

Затем определяют число степеней свободы k = N₁ + N₂ - 2, выбирают уровень значимости γ и по таблицам находят значение t_γ. Расчетное значение t сравнивается с табличным t_γ и если |t| < t_γ, то гипотеза Н₀ не опровергается результатами машинного эксперимента.

Критерий согласна Фишера. Задача сравнения дисперсий сводится к проверке нулевой гипотезы Н₀, заключающейся в принадлежности двух выборок к одной и той же генеральной совокупности. Пусть необходимо сравнить две дисперсии σ̃²₁ и σ̃²₂, полученные при обработке результатов моделирования и имеющие k₁ и k₂ степеней свободы соответственно, причем σ̃²₁ > σ̃²₂. Для того чтобы опровергнуть нулевую гипотезу Н₀: σ̃²₁ = σ̃²₂, необходимо при уровне значимости у указать значимость расхождения между σ̃²₁ и σ̃²₂. При условии независимости выборок, взятых из нормальных совокупностей, в качестве критерия значимости используется распределение Фишера (F-критерий) F = σ²₁/σ²₂, которое зависит только от числа степеней свободы

объемы выборок для оценки σ²₁ и σ²₂ соответственно.

Алгоритм применения критерия Фишера следующий: 1) вычисляется выборочное отношение F = σ̃²₁/σ̃²₂; 2) определяется число степеней свободы k₁ = N₁ - 1 и k₂ = N₂ - 1; 3) при выбранном уровне значимости у по таблицам F-распределения находятся значения границ критической области F₁ = 1/[F_{1 - γ/2} (k₁, k₂)]; F₂ = F_{1 - γ/2} (k₁, k₂); 4) проверяется неравенство F₁ ≤ 1 ≤ F₂; если это неравенство выполняется, то с доверительной вероятностью β нулевая гипотеза Н₀: σ²₁ = σ²₂ может быть принята.

Хотя рассмотренные оценки искомых характеристик процесса функционирования системы S, полученные в результате машинного эксперимента с моделью М_м, являются простейшими, но охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы для целей ее исследования и проектирования.

7.2. АНАЛИЗ И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ

 МАШИННОГО МОДЕЛИРОВАНИЯ

Возможность фиксации при моделировании системы S на ЭВМ значений переменных (параметров) и их статистическая обработка для получения интересующих экспериментатора характеристик позволяют провести объективный анализ связей между этими величинами. Для решения этой задачи существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик. Рассмотрим особенности использования методов корреляционного, регрессионного и дисперсионного анализа для результатов моделирования систем [7, 11, 18, 21, 25, 46].

Корреляционный анализ результатов моделирования. С помощью корреляционного анализа исследователь может установить, насколько тесна связь между двумя (или более) случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы S. Корреляционный анализ результатов моделирования сводится к оценке разброса значений η относительно среднего значения у, т. е. к оценке силы корреляционной связи. Существование этих связей и их тесноту можно для схемы корреляционного анализа у=М[η 1ξ=х] выразить при наличии линейной связи между исследуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции

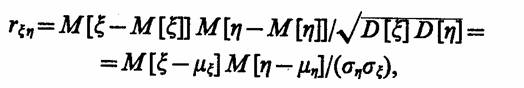
т. е. второй смешанный центральный момент делится на произведение средних квадратичных отклонений, чтобы иметь безразмерную величину, инвариантную относительно единиц измерения рассматриваемых случайных переменных.

Пример 7.1. Пусть результаты моделирования получены при N реализациях, а коэффициент корреляции

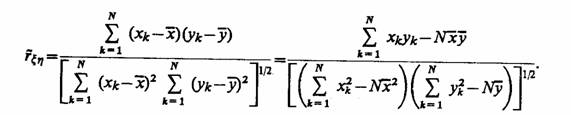
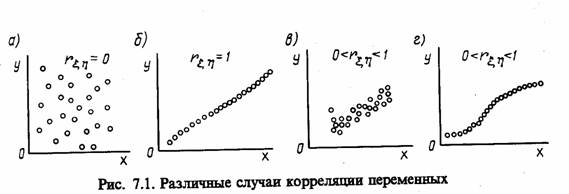
Очевидно, что данное соотношение требует минимальных затрат машинной памяти на обработку результатов моделирования. Получаемый при этом коэффициент корреляции |r ηξ≤|1. При сделанных предположениях r ηξ = 0 свидетельствует о взаимной независимости случайных переменных ξ и η исследуемых при моделировании (рис. 7.1, а). При |r ηξ | = 1 имеет место функциональная (т. е. нестохастическая) линейная зависимость вида у=b₀ + b1х, причем если r ηξ>0, то говорят о положительной корреляции, т. е. большие значения одной случайной величины соответствуют большим значениям другой (рис. 7.1, б). Случай 0<r ηξ <1 соответствует либо наличию линейной корреляции с рассеянием (рис. 7.1, в), либо наличию нелинейной корреляции результатов моделирования (рис. 7.1, г).

            Для того чтобы оценить точность полученной при обработке результатов моделирования системы 5 оценки rξ η целесообразно ввести в рассмотрение коэффициент w=ln[(l+r η )/(l —r η)]/2, причем w приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:

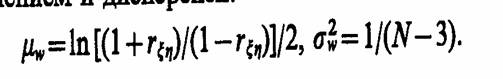
Из-за влияния числа реализаций при моделировании N на оценку 1 коэффициента   корреляции   необходимо   убедиться   в   том,   что 0 ≤ r η ≤ 1 действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели М_м. Это можно сделать проверкой гипотезы H_о: r η_ξ =0. Если гипотеза Н_о при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента w при  rξη,=0 является гауссовским с нулевым средним μ_w=0 и дисперсией σ²=(N— З)- ¹. Следовательно, область принятия гипотезы Н_о определяется неравенством

Где z_a2 подчиняется нормированному гауссовскому распределению. Если  rξη лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уровне значимости у.

При анализе результатов моделирования системы 5 важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные ξ и η стохастически зависимы, хотя причинно они являются для системы 5 независимы-: ми. При статистическом моделировании наличие такой зависимости может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имитации событий, положенных в основу вычисления значений х и у.

 Таким образом, корреляционный анализ устанавливает связь  между исследуемыми случайными переменными машинной модели и оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью зависимости, полученной после обработки результатов моделирования.

Регрессионный анализ результатов моделирования. Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой S. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок.

Пример 7.2. Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На рис. 7.2, а показаны точки x_i, y_i, i = 1, N, полученные в машинном эксперименте с моделью М_м системы S.

Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии

ŷ = φ (х) = b₀ + b₁ x,

где ŷ - величина, предсказываемая регрессионной моделью.

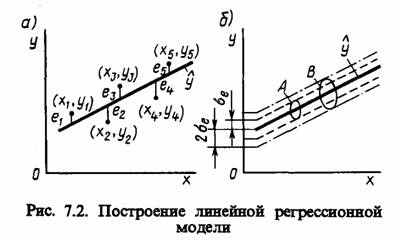
Требуется получить такие значения коэффициентов b₀ и b₁, при которых сумма квадратов ошибок является минимальной. На рисунке ошибка е₁, i = 1, N, для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии у = φ (х).

Обозначим ŷ_i = b₀ + b₁x_i, i = 1, N. Тогда выражение для ошибок будет иметь вид

Решая систему этих двух линейных алгебраических уравнений, можно получить значения b_а и b₁ В матричном представлении эти уравнения имеют вид

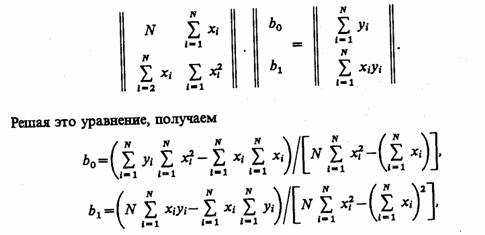
где N — число реализаций при моделировании системы.

Соотношения для вычисления b_о и b_х требуют минимального объема памяти ЭВМ для обработки результатов моделирования. Обычно мерой ошибки регрессионной модели служит среднее квадратичное отклонение

Для нормально распределенных процессов приблизительно 67% точек находится в пределах одного отклонения а_е от линии регрессии и 95% — в пределах 2 σ_е (трубки. А я В соответственно на рис. 7.2, б). Для проверки точности оценок b₀ и b₁, регрессионной модели могут быть использованы, например, критерии Фишера (F-распределенное) и Стьюдента ((-распределение). Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.

Дисперсионный анализ результатов моделирования. При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {у⁽¹⁾} , {у⁽²⁾}, ..., {y⁽ⁿ⁾} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели М_м, а следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ.

Пример 7.3. Рассмотрим решение задачи дисперсионного анализа при обработке результатов моделирования системы в следующей постановке. Пусть генеральные совокупности случайной величины {у⁽¹⁾}, {у⁽²⁾}, ..., {y⁽ⁿ⁾} имеют нормальное распределение и одинаковую дисперсию. Необходимо по выборочным средним значениям при некотором уровне значимости у проверить нулевую гипотезу Н₀ о равенстве математических ожиданий. Выявим влияние на результаты моделирования только одного фактора, т. е. рассмотрим однофакторный дисперсионный анализ.

Допустим, изучаемый фактор х привел к выборке значений неслучайной

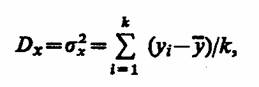
где y - среднее арифметическое значение величины Y.

Если генеральная дисперсия D[у] известна, то для оценки случайности разброса наблюдений необходимо сравнить D[y] с выборочной дисперсией S²_в, используя критерий Фишера (F-распределение). Если эмпирическое значение F_э попадает в критическую область, то влияние фактора х считается значимым, а разброс значений x - неслучайным. Если генеральная дисперсия D[х] до проведения машинного эксперимента с моделью М_м неизвестна, то необходимо при моделировании найти ее оценку.

Пусть серия наблюдений на уровне у_i, имеет вид у_i1, y_i2, ..., y_in, где n - число повторных наблюдений на i-м уровне. Тогда на i-м уровне среднее значение наблюдений

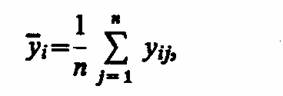
а среднее значение наблюдений по всем уровням

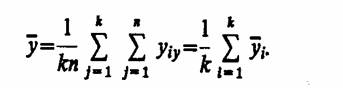
Общая выборочная дисперсия всех наблюдений

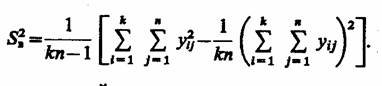
При этом разброс значений у определяется суммарным влиянием случайных причин и фактора х. Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D [у] на составляющие, связанные со случайными и неслучайными причинами.

Оценка генеральной дисперсии, связанной со случайными факторами,

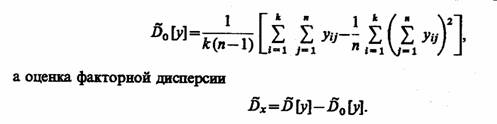
         Учитывая, что факторная дисперсия наиболее заметна при анализе средних значений на i-м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, найдем более точную оценку выборочной дисперсии:

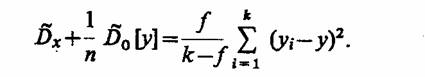
            Умножив обе части этого выражения на п, получим в правой части выборочную дисперсию S²_b, имеющую (k - 1)-ю степень свободы. Влияние фактора х будет значимым, если при заданном γ выполняется неравенство S̃²_b/D̃₀[y] > F_{1 - γ}. В противном случае влиянием фактора х на результаты моделирования можно пренебречь и считать нулевую гипотезу Н₀ о равенстве средних значений на различных уровнях справедливой.

Таким образом, дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсий.

Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы S.

7.3. ОБРАБОТКА РЕЗУЛЬТАТОВ МАШИННОГО

ЭКСПЕРИМЕНТА ПРИ СИНТЕЗЕ СИСТЕМ

При синтезе системы S на базе машинной модели М_м задача поиска оптимального варианта системы при выбранном критерии оценки эффективности и заданных ограничениях решается путем анализа характеристик процесса функционирования различных вариантов системы, их сравнительной оценки и выбора наилучшего варианта. Независимо от того, как организуется выбор наилучшего варианта системы — простым перебором всех проанализированных при машинных экспериментах результатов или с помощью специальных процедур поиска оптимального варианта, например методов математического программирования,— элементарной операцией является сравнение статистически усредненных критериев оценки эффективности вариантов систем [9, 29, 33, 53].

Особенности машинного синтеза. Учитывая то обстоятельство, что конкурирующие варианты системы S отличаются друг от друга структурой, алгоритмами поведения, параметрами, число таких вариантов достаточно велико. Поэтому при синтезе оптимального варианта системы Sopt особенно важно минимизировать затраты ресурсов на получение в результате моделирования характеристик каждого варианта системы. Исходя из этих особенностей, при синтезе системы S обработку и анализ результатов моделирования каждого варианта системы S следует рассматривать не автономно, а в их тесной взаимосвязи. Очевидно, что задача синтеза оптимального варианта моделируемой системы Sop_t должна быть уже поставлена при планировании машинного эксперимента с моделью М_м.

    В предыдущей главе было показано, что искусственная организация статистической зависимости между выходными характеристиками сравниваемых вариантов S₁ и S₂ системы дает выигрыш в точности оценки средних значений, вероятностей и дисперсий при положительно коррелированных критериях q₁ и q₂. Корреляция между критериями q₁ и q₂ возникает в силу того, что случайные векторыμμμ

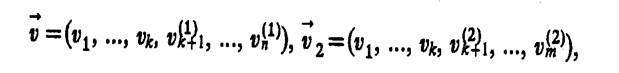
описывающие воздействие внешней среды Е на варианты S₁ и S₂ системы, имеют общие составляющие = (υ₁, ..., υ_k), в то время как составляющие (υ⁽¹⁾_{k + 1}, ..., υ⁽¹⁾_n) и (υ⁽²⁾_{k + 1}, ..., υ⁽²⁾_m)) статистически независимы.

Если через = (υ₁, ..., υ_k) обозначить фиксированные значения составляющих = (υ₁, ..., υ_k), то условные средние значения q₁ и q₂ будут такими:

т. е. являются функциями переменных v =(v_l ...,vk).

     Рассмотрим особенности обработки результатов моделирования, когда сравниваемые в ходе проведения имитационных экспериментов полные средние значения критериев q₁ и q₂ примут вид

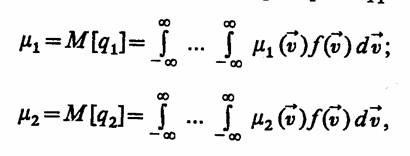
где d = dυ₁, ..., dυ_k; f () = f_k (υ, ..., υ_k) - совместная плотность вероятностей составляющих υ₁, ..., υ_k.

Ковариация

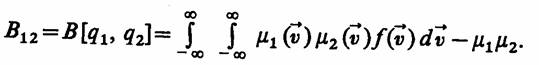
Достаточным условием неотрицательности ковариации, дающим выигрыш в оценке разности средних, является одинаковая упорядоченность условных средних μ₁ (v), μ₂(v) относительно векторного аргумента v=(v₁, ..., v₂), т. е. выполнение неравенства

            Так как f () ≥ 0 для всех, то при выполнении (7.1) имеем В₁₂ ≥ 0, что и требовалось доказать.

Когда в качестве результатов моделирования выступают вероятности событий A₁, A₂ для вариантов S₁ и S₂ системы, то условные значения

где P (A₁/) - условная вероятность, i= 1, 2.

Тогда достаточное условие неотрицательности ковариации запишется в виде

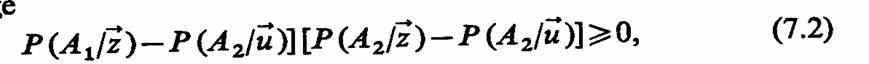
что соответствует одинаковой упорядоченности условных вероятностей P(A1v) и P(A₂/v) относительно векторного аргумента v.

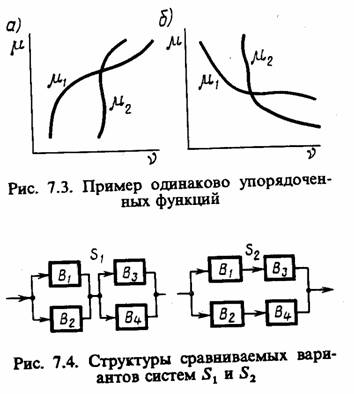
Одинаково упорядоченными являются монотонно возрастающие или монотонно убывающие функции μ (v) и μ ₂(v)   скалярного аргумента v, а также одинаковые функции μ ₁(v) = μ₂(v) независимо от их монотонности. Пример одинаково упорядоченных возрастающих (а) и убывающих (б) функций μ(v) показан на рис. 7.3.

Если положительные функции μ₁/(v), j = l, n, одинаково упорядочены, то произведение любой комбинации этих функций μ_k (v) μ(v)…μ_m (v) одинаково упорядочено с произведением      любой      комбинации μ (v) μ_q(v) …μ_p(v).   Это же можно сказать и об условных вероятностях Р(Aj/v), j= 1, n.      

Пример 7.4. Пусть методом статистического моделирования на ЭВМ необходимо сравнить результаты моделирования двух вариантов S_t и S₂ системы, составленных из одинаковых блоков В_х— В4 (структура системы показана на рис. 7.4) и сравниваемых по критерию надежности с учетом случайных изменений внешней температуры. События А_х и А₂ соответствуют безотказной работе вариантов S₁ и S₂ системы в течение заданного времени Т.

                       Вероятность   безотказной  работы  B_i  при  заданной   температуре   v=v можно определить как

где λ_i (v) - интенсивности отказов, являющиеся возрастающими функциями температуры.

Таким образом, функции P (B_i/v) являются одинаково упорядоченными убывающими функциями. Можно показать, что функции Р (А₁/v) = {1 - [1 - P (B₁/v)] [1 - P (B₂/v)]} {1 - [1 - P (B₃/v)] (1 - P (B₄/v)]}, P (A₂/v) = 1 - [1 - P (B₁/v) × P (B₃/v)] [1 - P (B₂/v) P (B₄/v)] также одинаково упорядочены и убывают с ростом температуры v. Поэтому, используя при машинном эксперименте с вариантами S₁ и S₂ системы одни и те же реализации v случайной температуры v, получим в результате моделирования большую точность сравнения вероятностей Р (A₁) и Р (А₂), чем при раздельном моделировании S₁ и S₂ системы с использованием независимых реализаций v.

Рассмотренный пример можно обобщить и на случай векторного аргумента, например для набора таких переменных, как температура, давление, ускорение и т. п.

Когда независимые компоненты в воздействиях внешней среды Е отсутствуют, т.е. v₁ = v₂ — v, условные средние μ ₁ ((v))=M[q₁v], / μ  ₂(v)=M q₂/v] преобразуются в детерминированные зависимости критериев от случайных воздействий q_{1 ƒ}(v),

При этом условия одинаковой упорядоченности становятся еще более жесткими. Так, например, условия (7.2) выполняются лишь тогда, когда для всех значений исключено одно из состояний: А_хА_г или A_XA₂. Другими словами, положительная корреляция В₁₂ и связанные с ней преимущества гарантируются лишь тогда, когда вариант системы S₁ равномерно лучше (хуже) варианта S₂. В принятых в § 6.3 обозначениях это соответствует р_с=0 или/>₀=О.

Состояния С = А₁А₂ или D = A₁A₂ вариантов систем S₁ и S₂ возможны лишь при наличии двух неисправных блоков В_i, i = 1, 4, состояние А = А₁А₂ возможно при отсутствии неисправностей или при одной неисправности, а состояние В = А₁А₂ - при трех или четырех неисправностях. Обозначив через B_iB_j ситуацию с неисправностями блоков В_i и B_j, находим соответствие между состояниями

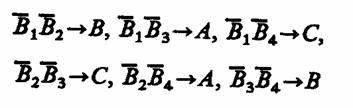
и убеждаемся в отсутствии состояния D.

Следует помнить, что условия одинаковой упорядоченности (7.1) и (7.2) являются достаточными, но не необходимыми и достаточными условиями неотрицательности корреляции. Поэтому, обнаружив в конкретной схеме проведения имитационного эксперимента нарушение этих условий при некоторых реализациях входных воздействий, следует более детально рассмотреть процедуру сравнения средних значений или вероятностей. Например, при сравнении вероятностей, задаваясь значениями Δp = p₁ - p₂, p_A и p_D, необходимо рассчитать значения р₂ = p_A + p_D, p₁ = p₂ + Δp, p_C = p_D + Δp и вычислить коэффициенты корреляции и "выигрыша" соответственно:

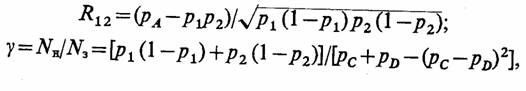
где Nn и N₃ — объемы выборки, необходимые для получения заданной точности оценки Ар при использовании независимых и зависимых реализаций.

Таким образом, использование зависимых испытаний дает возможность значительно сократить затраты машинного времени на моделирование. Рассмотренная методика сравнения характеристик вариантов при синтезе системы с учетом их корреляции является формальной. Однако основа для получения с помощью этой методики практических преимуществ — неформальная операция выбора такой схемы имитации, при которой искусственно создавалась бы

требуемая корреляция.

Оценка результатов моделирования системы. Рассмотрим возможность оценки при обработке результатов моделирования абсолютных значений характеристик процесса функционирования системы S. Пусть исследование одного из вариантов системы, например 5₂, выполнено аналитическим методом и определено среднее значение ц_г критерия q_z. Тогда оценка μ₁ = μ₂ —d среднего значения ц₁ имеет дисперсию

.

где γ_μ - коэффициент выигрыша, получаемого при оценке разности средних значений d = μ₂ - μ₁ за счет зависимости испытаний; α = D [μ̃₂]/D [μ̃₁]. Оценка μ̃'₁ точнее μ̃₁, если (1 + α)/γ_μ < 1.

Однако затраты машинного времени для получения оценки μ̃'₁, которые обозначим как t₁₂, превышают при заданном N затраты машинного времени t₁, необходимого для автономной оценки μ₁. Поэтому при заданной точности оценки среднего μ₁ оценка μ̃'₁ дает выигрыш по затратам машинного времени на имитацию только в том случае, если (1 + α) t₁₂/(γ_μt₁) < 1.

Для нормально распределенных критериев q₁ и q₂ оценка дисперсии D̃'₁ = D₂ + ΔD̃. Выигрыш в затратах машинного времени на имитационное моделирование по сравнению с автономной оценкой D̃₁ будет лишь при условии (1 + α)/t₁₂/γ_D t₁) < 1, где γ_D - коэффициент выигрыша, получаемого при оценке разности дисперсий ΔD̃ за счет зависимых испытаний.

Рассмотренные методы сравнения вариантов S₁ и S₂ моделируемой системы можно использовать в алгоритмах оптимизации на этапе проектирования системы S, т. е. при ее синтезе, по результатам имитационного эксперимента с ее машинной моделью M_м.

При синтезе системы S на основе проведения машинных экспериментов с моделью M_м возникает задача анализа чувствительности модели к вариациям ее параметров. Под анализом чувствительности машинной модели M_м понимают проверку устойчивости результатов моделирования, т. е. характеристик процесса функционирования системы S, полученных при проведении имитационного эксперимента, по отношению к возможным от клонениям параметров машинной модели Δ= (Δh₁, ..., Δh_n) от истинных их значений = (h₁, ..., h_n) [29, 33, 53].

Анализ чувствительности позволяет сравнивать методические погрешности, полученные при построении машинной модели M_м, с неточностями задания исходных данных, что особенно важно при практической реализации для целей синтеза системы S.

Малым отклонениям Δ будут соответствовать изменения характеристик q (), которые в практических расчетах можно оценить величиной Δq=q'() Δh+r_Q, где q'() =(dq ()/dh₁, ..., dq()/dh_n);

г₀ — остаточный член второго порядка малости относительно вариации, который используется для проверки точности решения.

Частная производная q'(h) определяется в точках, соответствующих номинальным значениям параметров h_ном. Если h_ном=h*, где

h * — оптимальные параметры системы по показателю q (h), то q (h ном) = 0 и необходимо проводить оценку с использованием второй производной q"(h_ном). Таким образом, частные производные

q'(h), q"(h) количественно характеризуют чувствительность машинной модели М_м к изменениям ее параметров.

Большие отклонения характеристик q(h) при малых вариациях Δh свидетельствуют о неустойчивости модели М_м по отношению

к этим вариациям. Для получения оценок q(h) показателя q(h) удобно рассматривать зависимые реализации внешних воздействий при различных h и проводить соответствующую обработку результатов машинного эксперимента с моделью М_м.

Чувствительность можно оценить и на более простой модели, чем модель для определения характеристик процесса функционирования системы S. Кроме того, универсальные оценки производных

q'(h) и q"(h), выполняемые при моделировании по зависимым испытаниям, в ряде частных случаев можно заменить более удобными непосредственными вычислениями.

Таким образом, результаты машинного эксперимента с моделью М_м обрабатываются с учетом целей моделирования системы S, которые находятся в тесной связи с вопросами, решаемыми при планировании экспериментов. При синтезе системы 5 на базе ее машинной модели М_м необходимо принять меры по организации зависимых испытаний анализируемых вариантов системы и оценке чувствительности модели к вариации ее параметров, что позволит упростить работу с моделью на каждом шаге оптимизации.

Контрольные вопросы

7.1. Каковы особенности имитационного эксперимента на ЭВМ с точки зрения обработки результатов?

7.2. В чем сущность методов фиксации и обработки результатов при статистическом моделировании систем на ЭВМ?

7.3. Какие методы математической статистики используются для анализа результатов имитационного моделирования систем?

7.4. Какое место занимают имитационные модели при машинном синтезе систем?

7.5. Какова цель организации зависимых испытаний модели системы на ЭВМ?

ГЛАВА 8

МОДЕЛИРОВАНИЕ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ТИПОВЫХ МАТЕМАТИЧЕСКИХ СХЕМ

Объекты информационных систем характеризуются сложностью структуры, алгоритмов поведения, многопараметричностью, что, естественно, приводит и к сложности их машинных моделей; это требует при их разработке построения иерархических модульных конструкций, а также использования формального описания внутрисистемных процессов. Типовые математические схемы являются связующим звеном в цепочке «концептуальная модель — машинная модель», позволяя эффективно решать при моделировании проблемы взаимодействия заказчика (постановщика задачи) и исполнителя (разработчика модели). Наиболее характерными для информационных систем являются объекты дискретного типа (дискретные производственные процессы, вычислительные комплексы, каналы передачи данных, информационные сети и т. д.), что предопределяет необходимость детального ознакомления с машинным моделированием на базе дискретных, вероятностных, а также универсальных типовых математических схем.

8.1. ИЕРАРХИЧЕСКИЕ МОДЕЛИ ПРОЦЕССОВ

ФУНКЦИОНИРОВАНИЯ СИСТЕМ

При машинной реализации любой из рассмотренных типовых математических схем (D, F, P, Q, N, А-схем) необходимо решить вопрос о взаимодействии блоков модели М_м при использовании аналитического, имитационного или комбинированного (аналитико-имитационного) подходов.

           Блочная конструкция модели. Рассмотрим машинную модель М_м системы S как совокупность блоков {m_i,}, i=1, n. Каждый блок модели можно охарактеризовать конечным набором возможных состояний {z₀}, в которых он может находиться. Пусть в течение рассматриваемого интервала времени (О, Т), т. е. времени прогона модели, блок изменяет состояния в моменты времени t_i^j ≤ T, где j — номер момента времени. Вообще моменты времени смены состояний блока /я, можно условно разделить на три группы: 1) случайные моменты, связанные с внутренними свойствами части системы S, соответствующей данному блоку; 2) случайные моменты, связанные с изменением состояний других блоков (включая блоки, имитирующие воздействия внешней среды Е); 3) детерминированные моменты, связанные с заданным расписанием функционирования блоков модели [29, 36, 37, 53].

Моментами смены состояний модели M_м в целом t^(k) ≤ Т будем считать все моменты изменения состояний блоков {m_i}, т. е. {t_i^(j)} ∈ {t^k}, i = 1, n. Пример для модели с тре мя блоками m₁, m₂ и m₃ показан на рис. 8.1.

При этом моменты t_i^(j) и t^k являются моментами системного времени, т. е. времени, в котором функционирует моделируемая система S, но не моментами машинного времени. Мгновенные изменения состояний модели во время дискретного события (особого состояния) возможны только при моделировании в системном времени.

При моделировании для каждого блока модели m_i, i = 1, п, необходимо фиксировать момент очередного перехода блока в новое состояние t_i^(j) и номер этого состояния s_i, образуя при этом массив состояний. Этот массив отражает динамику функционирования модели системы, так как в нем фиксируются все изменения в процессе функционирования моделируемой системы S по времени. В начале моделирования в массив состояний должны быть занесены исходные состояния, заданные начальными условиями.

При машинной реализации модели М_м ее блоки, имеющие аналогичные функции, могут быть представлены в виде отдельных программных модулей. Работа каждого такого модуля имитирует работу всех однотипных блоков. В общем случае при числе блоков модели п можно получить набор машинных модулей l ≤ п. Таким образом, каждому блоку или элементу модели будет соответствовать некоторый модуль или "стандартная подпрограмма", число которых не будет превосходить числа блоков модели.

Моделирующий алгоритм. Типовая укрупненная схема моделирующего алгоритма, построенного по блочному принципу, для систем с дискретными событиями приведена на рис. 8.2.

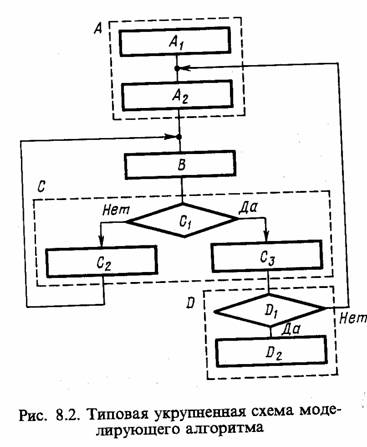
Эта схема содержит следующие укрупненные модули: А - модуль задания начальных значений состояний, содержащий два подмодуля (A₁ - для задания начальных состояний моделируемого варианта и А₂ - для задания начальных состояний для одного прогона модели); В - модуль определения очередного момента смены состояния, осуществляющий просмотр массива состояний и выбирающий блок модели m_i, i = 1, n, с минимальным временем смены состояния min t_i^(j); С - модуль логического переключения, содержащий три подмодуля (С₁ - для логического перехода по номеру блока модели i или по времени Т, т. е. для решения вопроса о завершении прогона; С₂ - для фиксации информации о состояниях, меняющихся при просмотре блока, а также для определения момента следующей смены состояния блока т_i и номера следующего особого состояния s₀; C₃ - для завершения прогона в случае, когда t_i^(j) ≥ T, фиксации и предварительной обработки результатов моделирования); D₁ - модуль управления и обработки, содержащий два подмодуля (D₁ - для проверки окончания исследования варианта модели М_м по заданному числу прогонов или по точности результатов моделирования; D₂ - для окончательной обработки информации, полученной на модели М_м и выдачи результатов моделирования).

Данная укрупненная схема моделирующего алгоритма соответствует статике моделирования. При необходимости организации моделирования последовательностей вариантов модели М_м и проведении оптимизации моделируемой системы S, например, на этапе ее проектирования, т. е. для решения вопросов, относящихся к динамике моделирования, следует добавить внешний цикл для варьирования структуры, алгоритмов и параметров модели М_м.

Пример 8.1. Рассмотрим модульный принцип реализации модели S, формализованной в виде Q-схемы. Пусть имеется L^Ф-фазная многоканальна Q-схема без потерь с L^И-входными потоками заявок. В каждой фазе имеется L_j^K, j = 1, L^Ф, каналов обслуживания. Определить распределения времени ожидания заявок в каждой фазе и времени простоя каждого обслуживающего канала.

В качестве блоков модели М_м будем рассматривать: т^И - блоки источников заявок, имитирующие L^И входных потоков; т^K - блоки каналов обслуживания, имитирующие функционирование каналов; т^B - блок взаимодействия, отражающий взаимосвязь всех блоков машинной модели М_м. При этом в массиве состояний будем фиксировать моменты поступления заявок, освобождения каналов и окончания моделирования, т. е. количество элементов этого массива будет равно

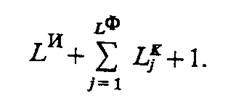
Схема моделирующего алгоритма для данного примера приведена на рис. 8.3. Как видно из схемы, в подмодуле С₂ предусмотрены три вида процедур: С'₂, С''₂ и C'''₂. Первая процедура С'₂ работает при поступлении заявки из любого входного потока, вторая процедура С''₂ работает в момент освобождения канала любой фазы обслуживания, кроме последней, третья процедура С'''₂ работает при освобождении канала последней фазы, т. е. при окончании обслуживания заявки Q-схемой.

Рассмотрим более подробно операторы процедур С'₂, C''₂ и C'''₂. Оператор С'₂₁ определяет принадлежность заявки к одному из L^И входных потоков, генерируемых модулем B. Оператор С'₂₂ проверяет, есть ли на первой фазе очередь свободных каналов обслуживания. Если очередь есть, то управление передается оператору С'₂₃, в противном случае - оператору С'₂₄. Оператор С'₂₃ фиксирует момент поступления заявки в массиве очереди заявок первой фазы. Оператор С'₂₄ выбирает номер канала из массива очереди канала первой фазы, уменьшая ее длину на единицу, вычисляет и фиксирует длительность простоя канала, определяет длительность обслуживания и засылает новый момент освобождения канала в массив состояний. Оператор С'₂₅ определяет новый момент поступления заявки и засылает его в соответствующую ячейку массива состояний.

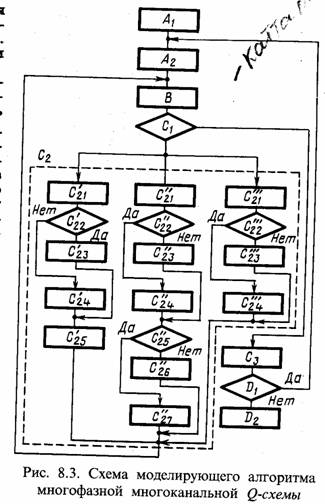
Оператор С''₂₁ служит для определения j-й фазы и k-гo канала, j = 2, L^Ф - 1, k = 1, L_j^K. Оператор C''₂₂ проверяет наличие очереди заявок на выбранной j-й фазе. При отсутствии очереди управление передается оператору С''₂₃, а при ее наличии - оператору C''₂₄. Оператор С''₂₃ засылает момент освобождения канала в массив очереди каналов j-й фазы, уменьшает длину очереди на единицу и фиксирует время ожидания выбранной заявкой начала ее обслуживания. Далее определяется длительность обслуживания этой заявки освободившимся каналом, вычисляется и засылается в массив состояний новый момент освобождения канала. Операторы С''₂₅, С''₂₆ и С''₂₇ выполняют те же действия с заявкой, обслуживаемой на j-й фазе, что и операторы С'₂₂, С'₂₃ и С'₂₄ с заявкой, которая поступила в первую фазу Q-схемы.

Оператор C'''₂₄ настраивает операторы этой процедуры С'''₂₂, С'''₂₃ и C'''₂₄ на выбранный канал обслуживания последней, L^Ф-й, фазы. Работа операторов С'''₂₂, С'''₂₃ и C'''₂₄ аналогична работе операторов С''₂₂, С''₂₃ и С''₂₄.

Назначение остальных подмодулей алгоритма не отличается от рассмотренного ранее для моделирующего алгоритма, приведенного на рис. 8.2.

Построение моделирующего алгоритма по блочному принципу позволяет за счет организации программных модулей уменьшить затраты времени на моделирование системы S, так как машинное время в этом случае не тратится на просмотр повторяющихся ситуаций. Кроме того, данная схема моделирующего алгоритма получается проще, чем в случае, когда модули не выделяются.

Автономность процедур подмодуля С₂ позволяет проводить их параллельное программирование и отладку, причем описанные процедуры могут быть стандартизованы, положены в основу разработки соответствующего математического обеспечения моделирования и использованы для автоматизации процесса моделирования систем. Если говорить о перспективах, то блочный подход создает хорошую основу для автоматизации имитационных экспериментов с моделями систем, которая может полностью или частично охватывать этапы формализации процесса функционирования системы S, подготовки исходных данных для моделирования, анализа свойств машинной модели М_м системы, планирования и проведения машинных экспериментов, обработки и интерпретации результатов моделирования системы. Такие машинные эксперименты должны носить научный, а не эмпирический характер, т. е. в результате должны предлагаться не только методы решения конкретной поставленной задачи, но и указываться границы эффективного использования этих методов, оцениваться их возможности. Лишь только автоматизация процесса моделирования создаст перспективы использования моделирования в качестве инструмента повседневной работы системного специалиста.

8.2. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ

ФУНКЦИОНИРОВАНИЯ СИСТЕМ НА БАЗЕ Q-CXEM

Особенности использования при моделировании систем непрерывно-стохастического подхода, реализуемого в виде Q-схем, и основные понятия массового обслуживания были даны в § 2.5. Рассмотрим возможности использования Q-схем для формального описания процесса функционирования некоторой системы S. Характерная ситуация в работе таких систем — появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирования. В общем случае моменты поступления заявок в систему S из внешней среды Е образуют входящий поток, а моменты окончания обслуживания образуют выходящий поток обслуженных заявок [6, 13, 39, 51, 53].

Формализация на базе Q-схем. Формализуя какую-либо реальную систему с помощью Q-схемы, необходимо построить структуру такой системы. В качестве элементов структуры Q-схем будем рассматривать элементы трех типов: И — источники; Н — накопители; К — каналы обслуживания заявок.

Пример структуры системы S, представленной в виде Q-схемы, приведен на рис. 8.4. Кроме связей, отражающих движение заявок в Q-схеме (сплошные линии), можно говорить о различных управляющих связях. Примером таких связей являются различные блокировки обслуживающих каналов (по входу и по выходу«клапаны» изображены в виде треугольников, а управляющие связи — пунктирными линиями. Блокировка канала по входу означает, что этот канал отключается от входящего потока заявок, а блокировка канала по выходу указывает, что заявка, уже  обслуженная  блокированным каналом, остается в этом канале до момента снятия блокировки (открытия «клапана»). В этом случае, если перед накопителем нет «клапана», при его переполнении будут иметь место потери заявок. Помимо выходящего потока обслуженных заявок можно говорить о потоке потерянных заявок.

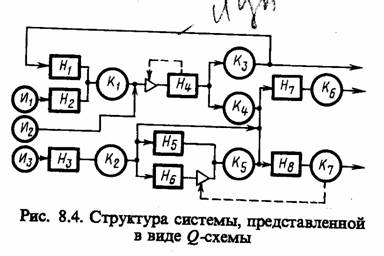
Как отмечалось выше, Q-схему можно считать заданной, если определены: потоки событий (входящие потоки заявок и потоки обслуживании для каждого Н и К); структура системы S (число фаз L^ф, число каналов обслуживания L^K, число накопителей L^H каждой из L^ф фаз обслуживания заявок и связи И, Н и К); алгоритмы функционирования системы (дисциплины ожидания заявок в Н и выбора на обслуживание К, правила ухода заявок из Ни К).

Рассмотрим возможности формализации воздействий внешней среды Е, представляемых в Q-схемах в виде источников (И). Формирование однородных потоков событий, заданных в общем виде многомерным интегральным законом или плотностью распределения вероятностей, т.е.-

сводится к рассмотренным ранее методам машинной имитации fc-мерных векторных величин, требующих больших затрат машинных ресурсов. При моделировании систем, формализуемых в виде Q-схем, часто возникают задачи имитации потоков заявок с некоторыми ограничениями, позволяющими упростить как математическое описание, так и программную реализацию генераторов потоков заявок.

Так, для ординарных потоков с ограниченным последействием интервалы между моментами поступления заявок являются независимыми и совместная плотность распределения может быть представлена в виде произведения частных законов распределения: f(y₁, y₂, ..., y_k) = f₁(y₁) f₂(y₂) ... f_k(y_k), где f_i(у_i), i = 1, k, при i > 1 являются условными функциями плотности величин y_i при условии, что в момент начала i-го интервала поступит заявка. Относительно начального момента времени t₀ никаких предположений не делается, поэтому функция f₁(y₁) - безусловная.

              Если поток с ограниченным последействием удовлетворяет условию стационарности, т.е. вероятность появления к событий на интервале (r₀, t₀ + ДО зависит только от длины интервала Δt, то при i>0 интервалы г, распределены одинаково, т. е.

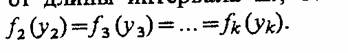
Плотность распределения первого интервала f₁ (у₁) может быть найдена с использованием соотношения Пальма

где λ— интенсивность потока событий.

     Порядок моделирования моментов появления заявок в стационарном потоке с ограниченным последействием следующий. Из последовательности случайных чисел, равномерно распределенных на интервале (0, 1), выбирается случайная величина и формируется первый интервал у_х в соответствии с (8.1) любым из рассмотренных выше способов формирования случайной величины. Момент наступления первого события t_x = t₀+y_lt следующие моменты появления событий определяются как

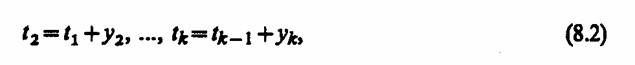
где y_k - случайная величина с плотностью f (у).

Пример 8.2. Пусть при моделировании некоторой системы необходимо сформировать на ЭВМ простейший поток заявок. Распределение длин интервалов между заявками является экспоненциальным, т. e. f(y) = λe^{- λy}, y > 0.

Используем формулу Пальма для определения первого интервала у, т. е.

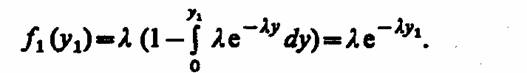
Из этого выражения следует, что ƒ i (y_t)=f (у), т. е. первый интервал распределен так же, как и остальные. Этого и следовало ожидать ввиду отсутствия последействия в простейшем потоке. Формируя на ЭВМ равновероятностные случайные числа х_i на интервале   (0,   1),   будем  преобразовывать   их  в  соответствии  с  выражением

∫ f(y)dy=Xi. Тогда длина интервала между (i—1)-м и i-m событиями yi= — (1/λ) lnх„

а моменты появления заявок в потоке определяются согласно (8.2).

Пример 83. Пусть при моделировании некоторой системы требуется сформировать на ЭВМ поток событий, равномерно распределенных на интервале (а, Ь.) Функция плотности интервалов между событиями f(y)=1/(b-a), а≤у≤b.

Распределение первого интервала между началом отсчета и первым событием

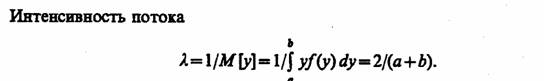
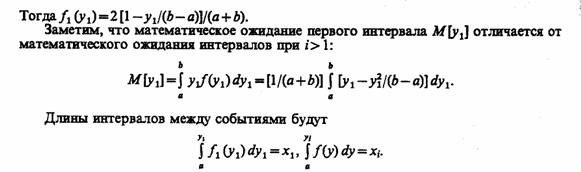
где Xi — случайная величина, равномерно распределенная на интервале (0,1).

       Пример 8.4. Рассмотрим формирование на ЭВМ потока Эрланга, в котором между последовательными событиями закон распределения интервалов

Пусть к=2 (поток Эрланга второго порядка). Тогда распределение первого интервала находится по формуле Пальма:

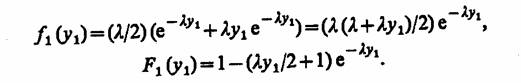
              Для определения у_х решают трансцендентное уравнение вида

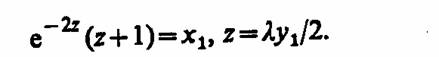
При i> 1 интервалы yi между последовательными событиями в потоке Эрланга второго порядка формируются с учетом того, что y_i представляет собой сумму двух случайных величин у_i', и у_i", одинаково распределенных по показательному закону с интенсивностью Я. Для нахождения yi необходимо определять у_i и у_i" и вычислить

сумму y'i+у_i"-

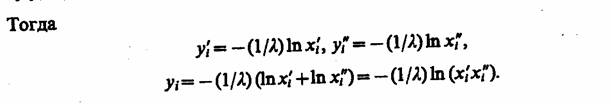
Если реализация моделируемого случайного процесса оказывается достаточно длинной, то можно положить/ƒ₁ (у₁)=ƒi;(у_i,-), i>1, т. е. считать, что все интервалы одинаково распределены. Влияние такого допущения на результаты моделирования системы S будет незначительным.

           Проведем анализ принципов формирования потока событий, описываемого нестационарным распределением Пуассона с мгновенной плотностью потока λ(t)

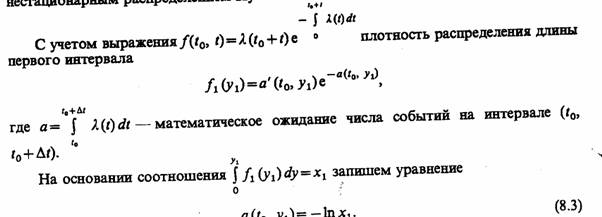
     Из (8.3) аналитически или любым приближенным способом определяется y_v Дальнейшая методика моделирования случайной величины уi при i>1 аналогична формированию yi с использованием условной функции распределения

где t_i_i — момент наступления (i—1)-го события.

Уравнение для нахождения очередного значения интервала имеет вид a(t_i,-_1, уi,)= —1nх₍.

Чтобы описать неординарные потоки событий, для которых limP_m(t₀, t_o+ Δt)≠ 0, кроме задания законов распределения моментов появления t_i необходимо определять распределение количества событий в рассматриваемый момент времени. Если количество событий, поступающих в систему S в момент времени Ц, не зависит от tj, то достаточно задать вероятность того, что в произвольный момент времени наступает ровно т событий, т. е. величину Р_т (t₀, t,).

Вопросы построения и машинной реализации программных генераторов, имитирующих потоки событий, были рассмотрены в гл. 4, поэтому более подробно остановимся на особенностях построения моделирующих алгоритмов процесса функционирования таких элементов Q-схем, как накопители (Н) и каналы (К).

Способы построения моделирующих алгоритмов Q-схем. Моделирующий алгоритм должен адекватно отражать процесс функционирования системы S и в то же время не создавать трудностей при машинной реализации модели М_м. При этом моделирующий алгоритм должен отвечать следующим основным требованиям: обладать универсальностью относительно структуры, алгоритмов функционирования и параметров системы S; обеспечивать одновременную (в один и тот же момент системного времени) и независимую работу необходимого числа элементов системы S; укладываться в приемлемые затраты ресурсов ЭВМ (машинного времени и памяти) для реализации машинного эксперимента; проводить разбиение на достаточно автономные логические части, т. е. возможность построения блочной структуры алгоритма; гарантировать выполнение рекуррентного правила — событие, происходящее в момент времени t_i, может моделироваться только после того, как промоделированы все события, произошедшие в момент времени

При этом необходимо иметь в виду, что появление одной заявки входящего потока в некоторый момент времени и может вызвать изменение состояния не более чем одного из элементов Q-схемы, а окончание обслуживания заявки в момент t_i в некотором канале (К) может привести в этот момент времени к последовательному изменению состояний нескольких элементов (Н и К), т. е. будет иметь место процесс распространения смены состояний в направлении, противоположном движению заявок в системе S.

Известно, что существует два основных принципа построения моделирующих алгоритмов: «принцип Δt» и «принцип δz». При построении моделирующего алгоритма Q-схемы по «принципу Δt », т. е. алгоритма с детерминированным шагом, необходимо для

построения адекватной модели М_м определить минимальный интервал времени между соседними событиями A'=min{u,} (во входящих потоках и потоках обслуживании) и принять, что шаг моделирования равен At'. В моделирующих алгоритмах, построенных по «принципу δz», т. е. в алгоритмах со случайным шагом, элементы Q-схемы просматриваются при моделировании только в моменты особыхсостояний (в моменты появления заявок из И или изменения состояний К). При этом длительность шага Δt =var зависит как от особенностей самой системы S, так и от воздействий внешней среды Е. Моделирующие алгоритмы со случайным шагом могут быть реализованы синхронным и асинхронным способами. При синхронном способе один из элементов Q-схемы (И, Н или К) выбирается в качестве ведущего и по нему «синхронизируется» весь процесс моделирования. При асинхронном способе построения моделирующего алгоритма ведущий (синхронизирующий) элемент не используется, а очередному шагу моделирования (просмотру элементов Q-схемы) может соответствовать любое особое состояние всего множества элементов И, Н и К. При этом просмотр элементов Q-схемы организован так, что при каждом особом состоянии либо циклически просматриваются все элементы, либо спорадически — только те, которые могут в этом случае изменить свое состояние (просмотр с прогнозированием) [4, 36, 37].

Классификация возможных способов построения моделирующих алгоритмов Q-схем приведена на рис. 8.5.

Более подробно особенности построения и реализации перечисленных разновидностей, моделирующих алгоритмов будут рассмотрены при моделировании конкретных вариантов систем.

Особенности моделирования на базе Q-схем. Математическое обеспечение и ресурсные возможности современных ЭВМ позволяют достаточно эффективно провести моделирование различных систем, формализуемых в виде Q-схем, используя либо пакеты прикладных программ, созданные на базе алгоритмических языков общего назначения, либо специализированные языки имитационного моделирования. Но прежде чем применять эти средства автоматизации моделирования, необходимо глубже вникнуть в суть процесса построения и реализации моделирующих алгоритмов [4, 7, 17, 23, 32, 46].

Пример 8.5. Для более детального ознакомления с технологией машинной имитации остановимся на рассмотрении Q-схемы достаточно общего вида, показанной на рис. 8.6. В частности, разберем на данном примере, какое влияние оказывает на

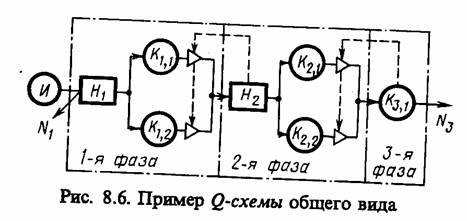
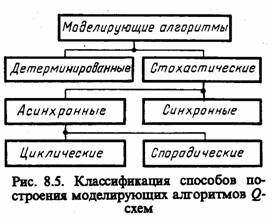особенности построения схемы моделирующего алгоритма принцип, положенный в основу его машинной реализации.

 На рисунке представлена трехфазная Q-схема (L^Ф=3) с блокировкой каналов по выходу в 1-й и 2-й фазах обслуживания (пунктирные линии на рисунке). В качестве выходящих потоков такой Q-схемы  могут быть рассмотрены поток , потерянных заявок го Н, и поток обслуженных  заявок из К₃, ₁ (N_l и N₃ на рис. 8.6).

Для имитационной модели рассматриваемой Q-схемы можно записать следующие переменные и уравнения: эндогенная переменная Р — вероятность потери заявок; экзогенные переменные: t_M—время появления очередной заявки из И; tk, j — время окончания обслуживания каналом Кk, j очередной заявки, к=1, 2, 3; j= 1, 2; вспомогательные переменные: z_i,- и Zk, j — состояния Н_i и Кк,j, i=l, 2 к=1, 2, 3;j =1, 2; параметры: L_i; — емкость i-гo H_IL^K_k — число каналов в к-й фазе; L^k=2, LI =2, L^k =1; переменные состояния: N₁ — число потерянных заявок в H1, N₃ — число обслуженных заявок, т. е. вышедших из 3-й фазы; уравнение модели: P=N₁(N₁+N₃)=N₁/N.

При имитации процесса функционирования Q-схемы на ЭВМ требуется организовать массив состояний. В этом массиве должны быть выделены: подмассив К для запоминания текущих значений Zk, j соответствующих каналов К_{k j} и времени окончания обслуживания очередной заявки tk,j,j=1, Lk^K, подмассив Н для записи текущего значения г, соответствующих накопителей Нi, i=l, 2; подмассив И, в который записывается время поступления очередной заявки t_m из источника (И).

Процедура моделирования процесса обслуживания каждым элементарным каналом К_k, сводится к следующему. Путем обращения к генератору случайных чисел с законом распределения, соответствующим обслуживанию данных К_k j, получается длительность времени обслуживания и вычисляется время окончания обслуживания t_k, j, а затем фиксируется состояние z_{k i7}=l; при освобождении Zk,j=0; в случае блокировки Kk,j записывается zk,j=2. При поступлении заявки в Н_i, к его содержимому добавляется единица, т. е. Zi=zi+l, а при уходе заявки из Нi, на обслуживание вычитается единица, т. е. z_i-=z_i,+ 1, i=l, 2.

Детерминированный моделирующий алгоритм. Укрупненная схема детерминированного моделирующего алгоритма Q-схемы, т. е. алгоритма, построенного по «принципу Δt », представлена на рис. 8.7. Специфика наличия постоянного шага Δt позволяет оформить «часы» системного времени в виде автономного блока 10. Этот блок служит для отсчетов системного времени, т. е. для вычисления t_n = t_n-i + Δt . Для определения момента остановки при моделировании Q-схемы (по числу реализаций N или по длине интервала времени моделирования Г) проводится проверка соответствующих условий (блок 3). Работа вспомогательных блоков — ввода     исходных данных 1, установки начальных условий 2, обработки 11 я вывода результатов моделирования 12 — не   отличается   по своей сути от аналогичных   блоков,   используемых в алгоритмах вычислений на ЭВМ. Поэтому остановимся более детально    на    рассмотрении работы той части моделирующего алгоритма, которая отражает специфику   детерминированного подхода (блоки 4 — 9). Детализированные     схемы     алгоритмов     этих блоков     приведены    на рис. 8.8, а — е. На этих и   последующих   схемах моделирующих   алгоритмов Q-схем приняты следующие        обозначения:

ZN(I)=Z_i   Z(K,   J)=z_k.j

 TM=t_m,     TN=t_n,     T(K,

.           J)≡ _{tk  j,}LO (I) ≡Li PO≡P

NO1≡N₁                     NO3≡N₃

NO≡N

Процедура обслуживания заявок каналами Kk,j оформлена   в   виде подпрограммы WORK [K(K, J)], позволяющей обратиться к генератору случайных чисел с соответствующим данному каналу К_{k j},; законом распределения, генерирующему длительность интервала обслуживания очередной заявки t_k j. Процедура генерации заявок источником (И) оформлена в виде подпрограммы D (тМ), которая определяет момент поступления очередной t_m в Q-схему.

Окончание обслуживания заявки в некотором канале К_k, j в момент времени t_n может вызвать процесс распространения изменений состояний элементов («особых состоянии») системы в направлении, противоположном движению заявок в системе, поэтому все Н и К  системы  должны просматриваться при моделировании

начиная с обслуживающего канала последней фазы по направлению к накопителю 1-й фазы (см. рис. 8.6).

После пуска, ввода исходных данных и установки начальных  условий  (блоки 1 и 2 на рис. 8.7) проверяется условие окончания моделирования системы (блок 3). Затем переходят к имитации обслуживания заявок каналом К_{3 1}, 1 3-й фазы Q-схемы «(рис.   8.8,   а).   Если   закончилось      обслуживание     в Кз, 1 (операторы 4.1 и 4.2), то фиксируется      выход      из системы   очередной   обслуженной   заявки    (оператор 4.3) и проводится освобождение канала К₃, i (оператор 4.4).

Далее реализуется переход к моделированию работы каналов 2-й фазы Q-схемы (рис. 8.8, б). При этом проводится   последовательный просмотр каналов этой фазы   (операторы   5.1,   5.9 и 5.10). Затем определяется,  имеются ли в каналах 2-й фазы   заявки,    ожидающие обслуживания     в     канале Кз, 1 (операторы 5.2 и 5.3). Если    в   момент   времени t_n имеются  заявки,   требующие обслуживания в К₃. ь и этот канал свободен (оператор   5.4),   то  выбирается в соответствии с дисциплиной обслуживания одна из заявок и имитируется ее обслуживание  Кз, 1  (оператор

5.6), фиксируются занятость канала 3-й фазы (оператор 5.7) и освобождение канала 2-й фазы (оператор 5.8). Если канал К₃, i занят (оператор 5.4), то фиксируется блокировка канала 2-й фазы (оператор 5.5).

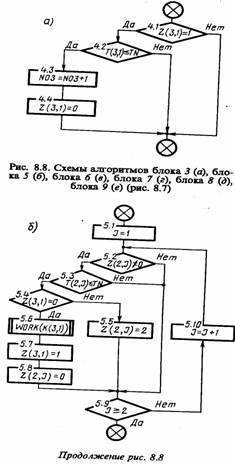
Затем имитируется взаимодействие в процессе обслуживания заявок в накопителе и каналов 2-й фазы последовательно для каждого из каналов (операторы 6.1, 6.7 и 6.8 на рис. 8.8, о). Далее, если в накопителе Н₂ имеются заявки (оператор 6.2) и свободные ка    налы 2-й фазы (оператор    И 6.3), то имитируется обслуживание заявки одним из     свободных каналов (операторы 6.4, 6.5) и освобождение места в накопителе Н₂ (оператор 6.6).

Потом  имитируется взаимодействие конкретного канала 1-й фазы и накопителя 2-й фазы Н, (операторы 7.1, 7.2, 7.13 — 7.16 на рис. 8.8, г). Для Ki, jпроверяется наличие в них заявок, требующих обслуживания в t_n (операторы 7.3 и 7.4). Если нет свободных каналов 2-й фазы (оператор 7.5), но в накопителе имеются свободные места (оператор 7.6), то моделируются запись заявки в Н₂ (оператор 7.7) и освобождение конкретного канала 1-й  фазы  (оператор  7.8). Если свободных мест в Н₂ нет, то фиксируется блокировка   канала   1-й   фазы (оператор 7.9). При наличии свободных каналов 2-й фазы   осуществляется   обслуживание заявки (оператор  7.10)  и  фиксируются занятость одного из каналов   2-й   фазы   (оператор 7.11) и  освобождение  одного из каналов 1-й фазы

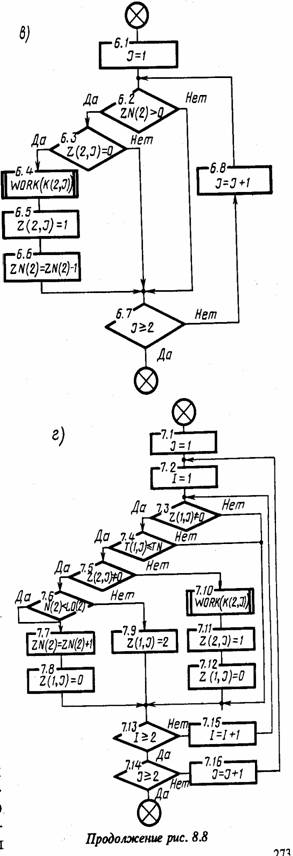
(оператор 7.12). Затем операторы 7.3 и 7.4 повторяются, так как одновременно из 1-й фазы во 2-ю могут переместиться две заявки. При третьем выполнении операторов 7.13 и 7.14 управление будет передано по условию «Да» следующему блоку 8 (см. рис. 8.7).

Затем имитируется взаимодействие в процессе обслуживания заявок в накопителе и каналов 1-й фазы (операторы 8.1, 8.7 и 8.8 на рис. 8.8, д). Проверяется необходимость    и    возможность обслуживания каналами К₁, j заявок из накопителя   Н_х   (операторы   8.2 и 8.3). Если в Н₁ имеются заявки и один из K_{1 j} свободен, то имитируется обслуживание  заявки в   1-й служившие  заявки  в   1-й

фазе (оператор 8.4), фиксируются, занятость конкретного канала (оператор 8.5) и освобождение одного места в Н_х (оператор 8.6).

Далее имитируется взаимодействие источника (И) и накопителя 1-й фазы H₁ с учетом занятости каналов этой фазы (рис. 8.8, е). В блоке 9 (см. рис. 8.7) вспомогательными операторами циклов являются операторы 9.2, 9.6 — 9.9 (рис. 8.8, ё). Если в t_n поступила заявка из И (оператор 9.1), то она при наличии свободного канала (оператор 9.3) может быть обслужена K_1j (операторы 9.4 и 9.5), при наличии места в H_t поставлена в очередь (операторы 9.10 и 9.11) либо при отсутствии места в Н_х (его переполнении) потеряна (оператор 9.12). После этого определяется время поступления в g-схему очередной заявки из источника t_m (оператор 9.13) и управление передается блоку 10, который определяет момент очередного шага t_n (см. рис. 8.7).

Затем управление снова передается блоку 3 (рис. 8.7), который при наборе необходимой статистики проводит обработку и выдачу результатов моделирования, а затем остановку моделирования (блоки 11 и 12).

Синхронный моделирующий алгоритм. Рассмотрим особенности построения моделирующих алгоритмов той же Q-схемы, структура

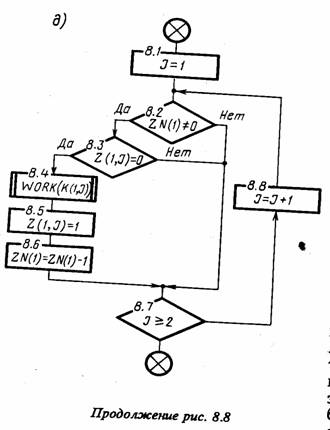
которой приведена на рис. 8.6, по «принципу δz ». Сначала построим синхронный моделирующий алгоритм, причем для определенности примем в качестве синхронизирующего элемента источник (И), т. е. t_n=t_m. В момент t_n, т. е. на n-м шаге моделирования, на вход 1-й фазы Q-схемы поступает очередная заявка из И. С момента t_n-1 до момента t_n в Q-схеме могли произойти изменения состояний Н₁ и K₁,_j , если в интервале (t _n-1 t_n) либо могло закончиться обслуживание в K_1j, либо могли освободиться Кг, j. Эти изменения необходимо промоделировать раньше, чем поступление заявок в эту фазу в t_n. Это справедливо и для остальных фаз Q-схемы: необходимо моделировать все изменения состояний к-й фазы до поступления в к-ю фазу заявок из (к— 1)-й фазы (в этом случае 0-я фаза эквивалентна И).

Каналом К*_k, _j имеющим  минимальное время окончания обслуживания, является тот, для которого

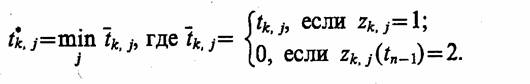
Укрупненная схема синхронного моделирующего алгоритма представлена на рис. 8.9. Работа большинства блоков этой схемы аналогична детально рассмотренной схеме детерминированного моделирующего алгоритма (см. рис. 8.7). Поэтому остановимся более подробно только на взаимодействии синхронизирующего элемента, т. е. источника И) с остальной частью Q-схемы, т. е. рассмотрим работу блока 6, имитирующего запись заявки из вход-

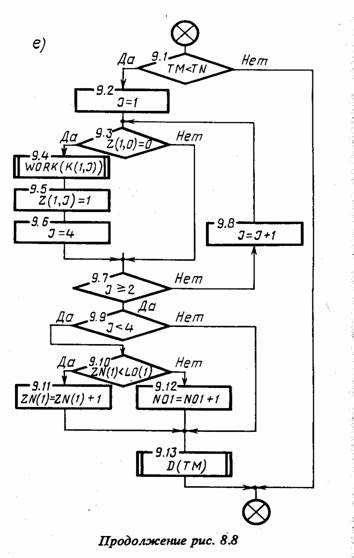
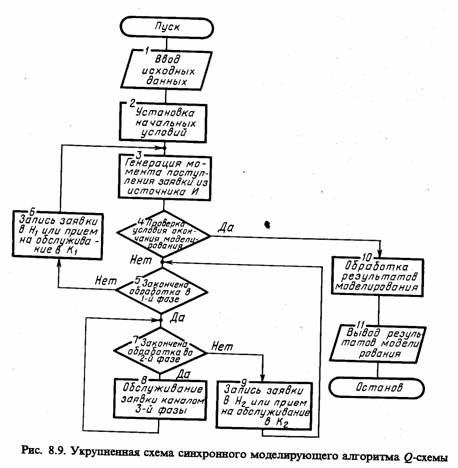
ного потока в накопитель Н₁ или прием на обслуживание в один из каналов 1-й фазы (рис. 8.10).

На этой схеме вспомогательными являются операторы 6.1, 6.5 — 6.8. Проверяется наличие свободных каналов 1-й фазы (оператор 6.2). Если среди каналов 1-й фазы Ki,, есть свободные, то выбирается один из них и имитируется обслуживание, т. е. определяется время окончания обслуживания в этом канале (оператор 6.3), затем фиксируется его новое состояние (оператор 6.4) и осуществляется переход к следующему шагу. Если же оба канала 1-й фазы заняты, то проверяется, есть ли свободные места в накопителе И₁ этой фазы (оператор 6.9). Если свободные места есть, то имитируется запись заявки в Н_х (оператор 6.10), а в противном случае фиксируется потеря заявки (оператор 6.11).

Асинхронный моделирующий алгоритм. Рассмотрим особенности построения асинхронного моделирующего алгоритма, который отличается

от синхронного отсутствием ведущего (синхронизирующего) элемента, причем очередному шагу моделирования соответствует особое состояние, т. е. момент окончания обслуживания одной из заявок любым каналом или момент поступления заявки из источника. При использовании такого принципа построения моделирующего алгоритма целесообразно процесс изменения состояний элементов Q-схемы рассматривать в направлении, противоположном направлению движения заявок в системе. Это можно сделать, циклически просматривая на каждом шаге моделирования все элементы Q-схемы и определяя, какие переходы заявок из одного элемента в другой могут иметь место в данный момент системного времени. Такой асинхронный циклический моделирующий алгоритм в плане просмотра состояний элементов Q-схемы тождествен детерминированному моделирующему алгоритму, который приведен на рис. 8.7. Отличие заключается лишь в том, что отсчет системного времени проводится следующим образом:

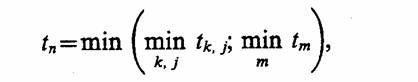
т. е. время очередного шага определяется как минимум из минимальных времен окончания начатого обслуживания всеми каналами всех фаз Q-схемы и минимального времени поступления очередных заявок из источника. В силу указанных причин не будем подробно останавливаться на рассмотрении асинхронного циклического моделирующего алгоритма Q-схемы, а рассмотрим только укрупненную схему, приведенную на рис. 8.11.

В асинхронных спорадических моделирующих алгоритмах в отличие от циклических для каждого момента системного времени t_n просматриваются только те элементы Q-схемы, которые изменяют свое состояние в этот момент времени. Для моделирования процесса распространения изменений состаяние элементов Q-схемы в направлении, противоположном направлению движения заявок в системе, необходимо прослеживать цепочку разблокирований в случае освобождения каналов, т. е. рассматривать, вызовет ли освобождение K_kJ разблокирование K_k -_1j , освобождение K_k -₂,j разблокирование К_k-2j и т. д. Рассмотрим случай, когда эта цепочка просматривается за один шаг моделирования.

       Укрупненная схема асинхронного спорадического моделирующего алгоритма, реализующего «принцип δz », показана на рис. 8.12. Рассмотрим подробно отсутствующий в предыдущих схемах блок 3 (рис. 8.13).

Блок 3 служит для определения временного интервала до ближайшего момента изменения состояния каким-либо элементом Q-схемы (И, Н или К). Системное время

— это минимальное время освобождения канала К_k, j или время до поступления новой заявки из И (операторы 3.13 и 3.14). Поиск минимального времени освобождения канала К_к, j реализуется с помощью операторов 3.1 — 3.12. В момент осуществления ближайшего события продвижение состояний реализуется операторами 3.15 и 3.16. Таким образом, в результате работы блока 3 t_m=0, если ближайшим событием является поступление из И, и _tk,j=0  определены к и j, если ближайшим событием является освобождение k-гo канала j-й фазы Q-схемы.

      Рассмотренные алгоритмы моделирования многофазовой многоканальной Q-схемы, конечно, по своей общности не охватывают всех тех разновидностей Q-схем, которые применяют в практике анализа и синтеза систем. Однако эти конкретные примеры моделирования позволяют детально ознакомиться с основными принципами построения моделирующих алгоритмов таких систем, причем эти принципы инвариантны к виду и сложности моделируемой системы S.

Возможности модификации моделирующих алгоритмов Q-схемы. В плане усложнения машинных моделей М_м при исследовании вариантов системы S можно рассмотреть следующие модификации:

1. Наличие потоков заявок нескольких типов. В этом случае необходимо иметь несколько источников (генераторов) заявок и фиксировать признак принадлежности заявки к тому или иному потоку тогда, когда накопители и каналы рассматриваемой Q-схемы критичны к этому признаку или требуется определить характеристики обслуживания заявок каждого из потоков в отдельности.

2. Наличие  редь в накопитель. В зависимости от класса приоритета заявок может быть рассмотрен случай, когда заявки одного класса имеют приоритет по записи в накопитель (при отсутствии свободных мест вытесняют из накопителя заявки с более низким классом приоритета, которые при этом считаются потерянными). Этот фактор может быть учтен в моделирующем алгоритме соответствующей Q-схемы путем фиксации для каждого накопителя признаков заявок, которые в нем находятся (путем организации соответствующего массива признаков).

3. Наличие приоритетов при выборе заявок на обслуживание каналов. По отношению к каналу могут быть рассмотрены заявки

с абсолютным и относительным приоритетами. Заявки с абсолютным приоритетом при выборе из очереди в накопитель вытесняют из канала заявки с более низким классом приоритета, которые при этом снова поступают в накопитель (в начало или конец очереди) или считаются потерянными, а заявки с относительным приоритетом дожидаются окончания обслуживания каналом предыдущей заявки. Эти особенности учитываются в моделирующих алгоритмах приоритетных Q-схем, при определении времени освобождения канала и выборе претендентов на его занятие. Если наличие абсолютных приоритетов приводит к потере заявок, то необходимо организовать фиксацию потерянных заявок.

4.  Ограничение по времени пребывания заявок в системе. В этом случае возможно ограничение как по времени ожидания заявок в накопителях, так и по времени обслуживания заявок каналами, а также ограничение по сумме этих времен, т. е. по времени пребывания заявок в обслуживающем приборе. Причем эти ограничения могут рассматриваться как применительно к каждой фазе, так и к Q-схеме в целом. При этом необходимо в качестве особых состояний Q-схемы рассматривать не только моменты поступления новых заявок и моменты окончания обслуживания заявок, но и моменты окончания допустимого времени пребывания (ожидания, обслуживания) заявок в Q-схеме.

5.  Выход элементов системы из строя и их дальнейшее восстановление. Такие события могут быть рассмотрены в Q-схеме, как потоки событий с абсолютными приоритетами, приводящими к потере заявок, находящихся в обслуживании в канале или ожидающих начала обслуживания в накопителе в момент выхода соответствующего элемента из строя. В этом случае в моделирующем алгоритме Q-схемы должны быть предусмотрены датчики (генераторы) отказов и восстановлений, а также должны присутствовать операторы для фиксации и обработки необходимой статистики.

Рассмотренные моделирующие алгоритмы и способы их модификации могут быть использованы для моделирования широкого класса систем. Однако эти алгоритмы будут отличаться по сложности реализации, затратам машинного времени и необходимого объема памяти ЭВМ.

Дадим краткую сравнительную оценку сложности различных моделирующих алгоритмов Q-схем, в основу построения которых положены перечисленные принципы. Детерминированный и асинхронный циклический алгоритмы наиболее просты с точки зрения логики их построения, так как при этом используется перебор всех элементов Q-схемы на каждом шаге. Трудности возникают с машинной реализацией этих алгоритмов вследствие увеличения затрат машинного времени на моделирование, так как просматриваются все состояния элементов Q-схемы (по «принципу Δt» или по «принципу δz»). Затраты машинного времени на моделирование  существенно  увеличиваются  при  построении

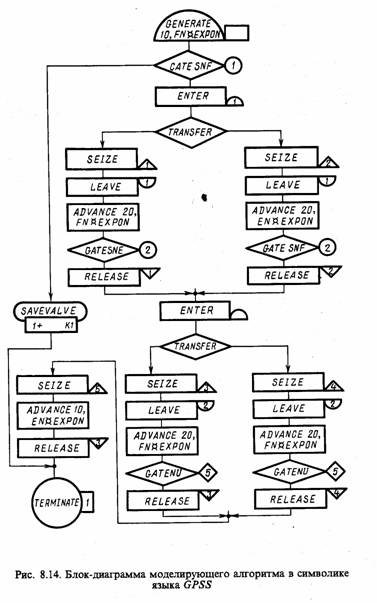
детерминированных моделирующих алгоритмов Q-схем, элементы которых функционируют в различных масштабах времени, например когда длительности обслуживания заявок каналами многоканальной Q-схемы значительно отличаются друг от друга.

В стохастическом синхронном алгоритме рассматриваются прошлые изменения состояний элементов Q-схемы, которые произошли с момента предыдущего просмотра состояний, что несколько усложняет логику этих алгоритмов.

Асинхронный спорадический алгоритм позволяет просматривать при моделировании только те элементы Q-схемы, изменения состояний которых могли иметь место на данном интервале системного времени, что приводит к некоторому упрощению этих моделирующих алгоритмов по сравнению с синхронными алгоритмами и существенному уменьшению затрат машинного времени по сравнению с детерминированными и циклическими алгоритмами.

Затраты необходимой оперативной памяти ЭВМ на проведение имитации могут быть значительно уменьшены при построении блочных моделей, когда отдельные блоки (модули) Q-схемы реализуются в виде процедур (подпрограмм).

К настоящему времени накоплен значительный опыт моделирования Q-схем (при их классическом рассмотрении или в различных приложениях). Рассмотренные моделирующие алгоритмы

позволяют практически отразить всевозможные варианты многофазных и многоканальных Q-схем, а также провести исследование всего спектра их вероятностно-временных характеристик, различных выходных характеристик, интересующих исследователя или разработчика системы S.

Рассмотрим особенности моделирования систем, формализуемых в виде Q-схем, с использованием языка имитационного моделирования GPSS. В этом случае отпадает необходимость выбора принципа построения моделирующего алгоритма, так как механизм системного времени и просмотра состояний уже заложен в систему имитации дискретных систем, т. е. в язык GPSS [33, 47].

         Пример 8.5. Использование языка GPSS рассмотрим при моделировании Q-схемы, схема которой приведена на рис. 8.6. Блок-диаграмма моделирующего алгоритма в символике языка GPSS представлена на рис. 8.14. Условные обозначения отдельных блоков были приведены в табл. 5.2. Как уже отмечалось, блок-диаграмма языка GPSS позволяет генерировать адекватные программы имитации. Пример программы на языке GPSS показан на рис. 8.IS. Действия операторов блок-диаграммы (и программы) GPSS для данного примера приведены в табл. 8.1. При этом приняты следующие обозначения: NAKI KANKI ≡H_I KANKJ≡K_k,j

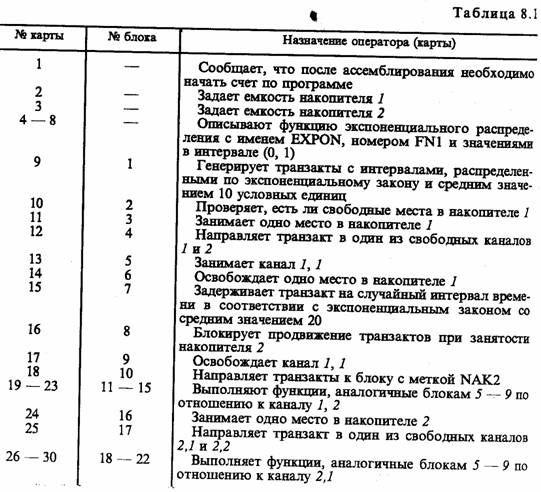
Из приведенных примеров моделирования системы S, формализуемой в виде Q-схемы, видно, что при использовании для реализации как универсального алгоритмического языка, так и языка имитационного моделирования GPSS возможности по оценке в процессе имитации вероятностно-временных характеристик исследуемых систем существенно расширяются по сравнению с применением аналитического подхода, когда получение оценок в явном виде ограничено результатами, полученными в теории массового обслуживания.