Глава 7.  Распространение УКВ над земной поверхностью

7.1   Электродинамические параметры различных видов поверхности Земли

 

Распространение земных радиоволн происходит непосредственно над полупроводящей сферической поверхностью Земли. Поэтому при рассмотрении этих вопросов совершенно необходимы знание электрических параметров различных видов поверхности Земли (т.е. её диэлектрической проницаемости и удельной электрической проводимости) и учет её неоднородностей.

 

Большая часть (71%) поверхности земного шара покрыта водой. С точки зрения электрических свойств следует отличать соленую воду океанов, морей и некоторых озер от пресной воды озер и рек. В то время как при отсутствии ветра поверхность небольших озер и водоемов может быть зеркально гладкой, поверхность океанов и морей подвержена более или менее значительному волнению.

Встречаются следующие разновидности суши: влажная почва в виде полей, лугов и вспаханной земли; та же почва, покрытая кустарником и лесом; сухая почва в виде песков (пустыня); холмистая местность, покрытая растительностью, и скалистые, лишенные растительности горы. Вот далеко не полный перечень различных видов поверхности Земли.

 

При изучении особенностей распространения земных волн приходится в какой-то мере идеализировать условия, в которых протекают процессы распространения. Например, не представляется возможным учитывать непрерывные изменения свойств почвы на пути распространения волны. При практических расчетах довольствуются тем, что принимают во внимание только резкие изменения, например, береговую линию, границу между полем и большим лесным массивом.

 

Встречающиеся разновидности поверхности земного шара можно разбить на 2 группы: к первой относятся те виды поверхности земного шара, которые характеризуются незначительными неровностями, поэтому их непосредственно можно заменить сглаженной поверхностью с теми же электрическими параметрами; ко второй группе относятся поверхности со значительными неровностями, которые должны быть заменены сглаженной поверхностью с эквивалентными электрическими параметрами. Эквивалентные электрические параметры почвы выбирают из тех соображений, чтобы вызываемое реальной неровной поверхностью поглощение земных радиоволн соответствовало поглощению, создаваемому эквивалентной сглаженной поверхностью в заданном диапазоне частот.

 

Например, типичными поверхностями второй группы являются лес и большой город. Распространяющаяся над лесом волна поглощается, главным образом, за счет токов, наводимых ею в стволах и ветвях деревьев, которые можно рассматривать как своеобразные заземленные антенны из полупроводящего материала. Разумеется, механизм поглощения энергии радиоволны лесом не имеет ничего общего с механизмом поглощения гладкой полупроводящей поверхностью. С другой стороны, можно подобрать электрические параметры гладкой полупроводящей почвы так, чтобы поглощение волн, распространяющихся над этой воображаемой почвой, было таким же, как и над лесом. Таким же способом можно подобрать параметры гладкой полупроводящей поверхности, эквивалентной по своему поглощающему действию городу (в определенном диапазоне частот).

 

 

В таблице 7.1 приведены средние значения действительных (для почв первой группы) и эквивалентных электрических параметров для различных видов поверхности Земли.

 

Таблица 7.1. Электродинамические параметры различных видов поверхности Земли.

 

Вид земного покрова	ε	σ, См/м
Морская вода	80	1...6
Пресная вода рек и озер	80	10-3…10-2
Влажная почва	10...30	3 × 10-3..3 × 10-2
Сухая почва	3...6	1 × 10-5…5 × 10-3
Мерзлая почва	3...6	10-3...10-2
Лед (t=-10°С)	4...5	10-2...10-1
Снег (t=-10°С)	1	10-6

 

 

Для проведения расчетов, относящихся к распространению земных волн, необходимо располагать данными о точных значениях электрических параметров почвы в различных районах страны. С этой целью в отдельных странах проводятся обширные работы по составлению карт проводимости почвы.

 

 

 

 

7.2   Распространение радиоволн над плоской поверхностью Земли

Распространение радиоволн при поднятых передающей и приемной антеннах

Изучение распространения земных радиоволн естественно надо на­чать с этого наиболее простого случая. При небольших расстояниях между передающей и приемной антеннами кривизной поверхности Земли можно пренебречь. Будем считать поверхность Земли гладкой и однородной на протяжении всей трассы. Задача формулируется так: заданы геометриче­ские параметры (расстояние между передающей и приемной антеннами, высоты подвеса передающей h₁ и приемной h₂ антенн) и электрические па­раметры (подводимая к передающей антенне мощность Р_1, коэффициенты усиления передающей и приемной антенн G₁ и G₂, длина волны λ, вид по­ляризации волны, относительная диэлектрическая проницаемость почвы ε и ее удельная проводимость σ). Требуется определить множитель ослабле­ния F и напряженность поля по формуле

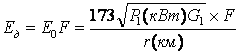                                                                          , мВ/м                                      (7.1)

Как впервые было показано еще в 1922 году академиком Б. А. Вве­денским электрическое поле радиоволны в месте расположения приемной антенны можно рассматривать как результат интерференции прямого луча 1 и луча 2, отраженного в точке С от поверхности Земли (Рис. 7.1).

                                                                                         

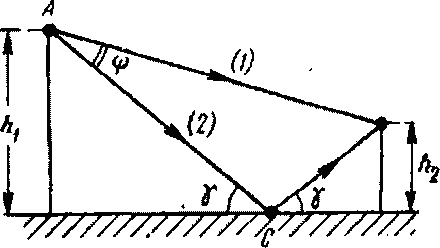
                                                                                       Рис.7.1. К расчету поля в точке приема

При решении задачи распро­странения радиоволн вдоль грани­цы воздух - земля существенное значение имеет абсолютная вели­чина комплексной диэлектриче­ской проницаемости почвы

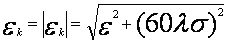                                                                                                                                        (7.2)

Земная волна, распространяясь вдоль границы раздела воздух-почва, возбуждает в воздухе и почве токи, которые являются источниками вторичного поля. В соответствии с принципом Гюйгенса-Кирхгофа поле земной волны можно считать результатом суперпозиции полей, наведен­ных воображаемыми вторичными источниками, которые возбуждаются первичным полем в воздухе и почве. В почве интенсивность вторичных источников ослаблена по сравнению со свободным пространством, за счет тепловых потерь, которые появляются из-за конечных значений проводимости σ. Почва экранирует проникновение поля в глубокие об­ласти земли (явление скин-эффекта), что препятствует оттоку энергии в нижнюю полусферу.

Напряженность поля в точке приема равна

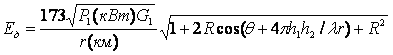                                                                 ,мВ/м.                   (7.3)

Формула показывает, что в месте расположения приемной антенны поле имеет интерференционную структуру. По мере удаления от передающей антенны будем на­блюдать такую картину (Рис.7.2). При изменении r косинус аргумен­та будет меняться. Когда косинус равен единице поле максимально.

 При       соs [θ + 4πh₁h₂ / (λr)] = 1        r_max = 4h₁h₂ / [λ (2N +1)], где   N = 0, 1, 2, … F_max = 1 + R.

Когда      косинус    равен     минус     единице    поле     минимально.                                        

                                                                                      

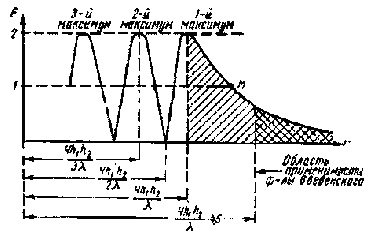
                                                                        Рис.7.2. Зависимость множителя ослабления от расстояния при R=1

При  cos [θ + 4πh₁h₂ / (λr)] = - 1,     r_min = 2h₁h₂ / [λ(N +1)], N = 0,1,2,…       F_min = 1 - R .Отсчет максимумов и минимумов ведется от конца радиотрассы. При r ≤ 4h₁h₂ / λ  наблюдаются    максимумы    и    минимумы    напряженности    поля,   а   при   r > 4h₁h₂ / λ наблюдается плавное уменьшение напряженности поля с увеличением расстояния.

 

Дальнейшее упрощение интерференционных формул. С увеличением рас­стояния значение R стремится к 1, а θ - к 180°, тогда

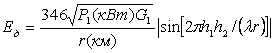                                                                      ,мВ/м                                           (7.4)

                                                                                                     или

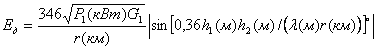                                                             , мВ/м                          (7.5)

 

При дальнейшем увеличении расстояния, когда 2πh₁h₂ / (λr) ≈ π / 9 ,то си­нус аргумента можно заменить его аргументом (при r ≥ 18h₁h₂ / λ)

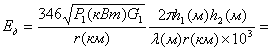
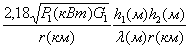                                                           .               (7.6)

 

Напряженность поля на расстояниях r ≥ 18h₁h₂ / λ убывает с квадратом расстояния. Надо твердо помнить, что в условиях применимости формулы Введенского, луч, отраженный от поверхности земли является вредным, т.к. он стремится скомпенсировать поле прямого луча.

7.3  Область пространства, эффективно участвующая в передаче энергии радиоволн. Зоны Френеля

 

Вопрос о форме пространства, эффективно участвующего в передаче энергии радиоволн, решается на основе принципа Гюйгенса и представлении о зонах Френеля.

 

Принцип Гюйгенса, в его наиболее элементарной формулировке, утверждает, что каждая точка фронта распространяющейся волны (созданной некоторым первичным источником) является источником новой вторичной сферической волны. Принцип Гюйгенса позволяет вычислить электромагнитное поле в любой точке пространства по известным значениям поля на некоторой поверхности.

 

Принцип Гюйгенса позволяет определить ту часть пространства, которая существенно участвует в процессе распространения волн. Проведем для этого из точки А, как из центра, сферу радиуса L1, которая будет представлять собой поверхность фронта волны (Рис. 7.3).

                                                                        

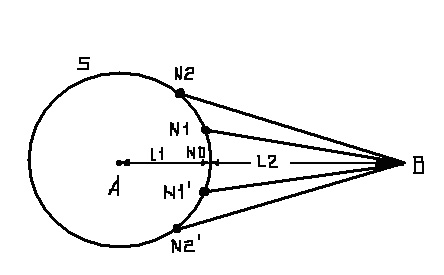
                                                                               Рис.7.3.  Построение зон Френеля на поверхности сферы

 

Обозначим через L2 расстояние, измеренное вдоль прямой АВ от пункта приема до поверхности сферы. Проведем из точки В семейство прямых, пересекающих сферу S. Это семейство образует коническую поверхность, пересекающую плоскость рисунка по прямым BN1 и BN1’. Аналогичным образом строятся конические поверхности высших порядков.

 

 

                                                                          

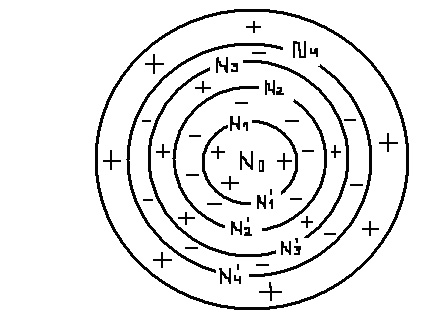
                                                                                Рис.7.4.  Зоны Френеля на поверхности сферы

 

Пересечения конических поверхностей со сферой образуют систему концентрических окружностей. Вид на эти окружности со стороны точки В показан на Рис.7.4. Участки, заключенные между соседними окружностями, получили название зон Френеля. Первая зона Френеля представляет собой часть сферы, ограниченную окружностью, а зоны высших порядков представляют собой кольцевые области на поверхности сферы.

 

Воображаемые источники вторичных волн (так называемые виртуальные источники), расположенные в пределах первой зоны, характеризуются тем, что создаваемые ими фазы колебаний в точке В отличаются от фазы, создаваемой виртуальным излучателем в точке N0, не более чем на 180°, так как разности хода в половину длины волны отвечает разность фаз в 180°. Фаза колебаний, создаваемых виртуальными излучателями, расположенными в пределах второй зоны, отличается от фазы колебаний источника N0  на величину от 180° до 360°. Можно сказать, что в целом колебания, создаваемые второй зоной, отличаются по фазе на 180° от колебаний, создаваемых первой зоной. На Рис.7.4  это обстоятельство условно отмечается тем, что последовательные зоны маркируются знаками “+” и “-“.

 

В курсах оптики показывается, что действия смежных зон высших порядков взаимно компенсируются, притом, чем больше порядковый номер зон, тем полнее осуществляется эта компенсация. В результате такой попарной нейтрализации смежных зон совокупное действие всех зон эквивалентно действию примерно половины первой зоны. Таким образом, первая зона Френеля (с известным “запасом”) и ограничивает область пространства, существенно участвующего в процессе распространения волн.

Для эффективной связи с помощью высокочастотных волн нужно обеспечить беспрепятственную линию прямой видимости между передатчиком и приемником. Возникает вопрос: сколько же пространства вокруг прямого тракта между передатчиком и приемником должно быть свободно от преград? При ответе на него удобно использовать такое понятие, как зоны Френеля.

Как уже говорилось выше, понятие зон Френеля основано на принципе Гюйгенса, согласно которому каждая точка среды, до которой доходит возмущение, сама становится источником вторичных волн, и поле излучения может рассматриваться как суперпозиция всех вторичных волн. На основе этого принципа можно показать, что объекты лежащие внутри концентрических окружностей, проведенных вокруг линии прямой видимости двух трансиверов, могут влиять на качество как положительно, так и отрицательно. Все препятствия, попадающие внутрь первой окружности, первой зоны Френеля, оказывают наиболее негативное влияние.

Рассмотрим точку, находящуюся на прямом тракте между передатчиком и приемником, причем расстояние от точки до передатчика равно S, а расстояние от точки до приемника равно D, т.е. расстояние между передатчиком и приемником равно S + D.

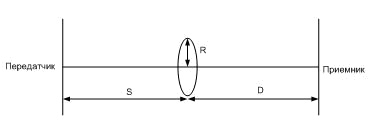
Рис.7.5.  К определению радиуса первой зоны Френеля

 

Вычислим радиус первой зоны Френеля в этой точке

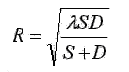                                                                                                                   (7.7)

где R, S и D измеряются в одних и тех же единицах, а λ обозначает длину волны сигнала вдоль тракта.

 Для удобства формулу можно переписать следующим образом

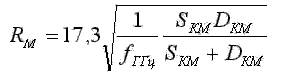                                                                             (7.8)

где R выражается в метрах, два остальных расстояния - в километрах, а частота сигнала - в гигагерцах.

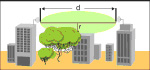
Рис.7.6. Естественные и искусственные препятствия на линии распространения волн

Например, для радиолинии диапазона 2,4 ГГц при расстоянии между станциями 1 км радиус первой зоны Френеля составит 5,5 м. То есть вдоль линии, соединяющей приемник и передатчик в ее средней части в радиусе 4,4 м (80%) (или хотя бы 3,3 м – 60%) не должно быть предметов, отражающих или рассеивающих радиоизлучение. Только обеспечив это условие, имеет смысл говорить о доминировании прямого луча и об ослаблении, связанном лишь с длиной радиотрассы. Для сравнения: при протяженности 500 м радиус этой зоны составит всего 3,9 м (80% – 3,2 м), а при расстоянии 100 м, исходя из этого принципа, следует разблокировать зону диаметром всего 2,8 м.

Немного подробнее о влиянии растительности. Как правило, избежать прохода через нее (например, через листву высоких деревьев) на всей радиотрассе не удается. В таком случае необходимо ориентироваться на следующие оценки: поглощение 12–20 дБ на одно дерево для лиственных пород и до 40 дБ – для группы из одного–трех хвойных деревьев, когда листва находится внутри 60% первой зоны Френеля. Основными многолучевыми эффектами, к которым приводит наличие лиственного покрова, являются дифракция и рассеяние. Присутствие деревьев вблизи месторасположения абонента может привести к замиранию сигнала вследствие многолучевого распространения. Отмечается также, что эффекты последнего сильно зависят от ветра.

 

7.4   Деление радиотрасс на зоны освещенности, тени и полутени

 

Для определения того, каким способом надлежит учесть влияние кривизны Земли на процессы распространения радиоволн при поднятых передающей и приемной антеннах, принято разбивать трассу линии радиосвязи на три участка: зону освещенности, зону тени и зону полутени.

 

Термин "Зона освещенности" имеет смысл только при поднятых антеннах. При низкорасположенных антеннах область, прилегающую к передающей антенне, называют зоной "приближения плоской Земли", поскольку в пределах этой зоны поверхность Земли можно приближенно считать плоской.

 

В зонах полутени и тени расчет напряженности поля как для поднятых, так и для низко расположенных антенн ведется по общим дифракционным формулам Фока.

 

В зоне освещенности (обозначенной на Рис.7.8 под номером I) передающая и приемная антенны находятся в условиях прямой видимости, а в зоне тени – вне пределов видимости. Центр зоны полутени находится на расстоянии прямой видимости.

 

                                                                                        

 

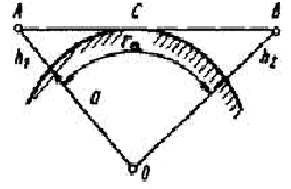
                                                                          Рис.7.7. К определению расстояния прямой видимости

 

 

Зона полутени (обозначенная на Рис.7.8 под номером II) разделяет две основные зоны. В первом приближении принято считать, что границы зоны полутени удалены

 

                           

                                                                             

 

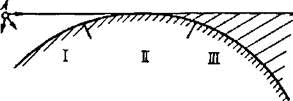
Рис.7.8.  Зоны освещенности, тени и полутени при дифракции радиоволн вокруг земного шара

 

 

от передающей антенны на расстоянии 0,8ro  и 1,2ro. Точнее, зоной освещенности называют ту область расстояний, в пределах которой можно применять интерференционные формулы. В области тени (Рис.7.8, III) поле можно рассчитать по наиболее простым, так называемым “одночленным дифракционным формулам”. Таким образом, внешняя граница полутени определяется возможностью применения одночленных формул. Понятно, что в область тени радиоволны проникают за счет дифракции вокруг земного шара.

7.5   Распространение УКВ в зонах освещенности, тени и полутени. Влияние тропосферы на РРВ. Учет атмосферной рефракции

 

 

Учет сферичности земной поверхности при расчете напряженности поля

 

Сферичность земной волны влияет на амплитуду за счет рассеивания от выпуклой поверхности Земли и фазу отраженной волны, т.к. выпуклость земной поверхности изменяет длину пути от­раженной волны. Если в точке отражения ра­диоволны от поверхности Земли (Рис.7.9) провести плоскость MN, касательную к по­верхности Земли и отсчитывать высоты под­веса антенн не от поверхности Земли, а от указанной плоскости, то, подставляя в интер­ференционные формулы вместо действитель­ных высот h₁ и h₂ «приведенные    высоты»    h’₁   и   h’₂, получим правильное  значение напряженности поля в месте приема, ибо угол скольже­ния луча относительно выпуклой  поверхности Земли тот же, что и угол скольжения над ка­сательной плоскостью. Учет кривизны Земли при пользовании интерференционными фор­мулами сводится к нахождению приведенных высот h₁’ и h₂’ по известным значениям r, h₁, h₂, a_э.

 

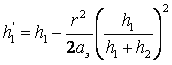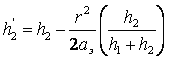                                               ;                                                              (7.9)

 

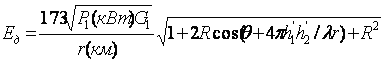                                              , мВ/м;                                      (7.10)

 

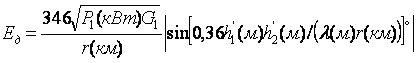                                                , мВ/м;                             (7.11)

 

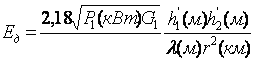                                              , мВ/м.                                                                           (7.12)

 

 

 

 

 

 

 

 

                                                                                                 

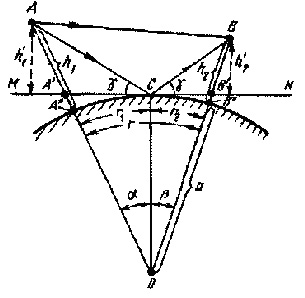
                                                                                           Рис.7.9. К учету сферичности поверхности Земли

 

 

 

Расчет напряженности поля в зонах полутени и тени

 

В. А. Фок получил выражение для функции ослабления пригод­ное для любых удалений от передатчика. На небольших расстояниях от передатчика оно переходило в интерференционную формулу. Наоборот, при больших расстоя­ниях, решение превращалось в одночлен­ную дифракционную формулу. Фок ввел понятия о "масштабе расстояний" L и о "масштабе высот" Н. Это позволяет длину трассы r и высоты подвеса

антенн h₁ и h₂ выразить в безразмерных единицах: приведенное расстояние x = r / L,  приведенные высоты подвеса антенн  y₁ = h₁ / H, y₂ = h₂  / H. Выражение для множителя ослабления одночленной дифракционной формулы (для расчета уровня поля в зоне тени) может быть представлено в виде произведения трех сомножителей F = U(х)V(y₁)V(у₂), первый из ко­торых зависит от расстояния, второй и третий от высот подвеса передаю­щей и

приемной антенн. Расчет напряженности поля в области тени в диа­пазонах СДВ, ДВ, СВ и большей части КВ значительно проще, т.к. F = U(х). Для расчета значения множителя ослаб­ления в зоне тени используются графи­ки (Рис.7.10 и 7.11) для определения зна­чений  U(x),V(y₁),V(y₂)   в    дБ,    тогда F = U(x) + V(y₁) + V(y₂),дБ. Из дБ в разы значение множителя ослабления можно пересчитать по формуле F = 10^FдБ/20. Зна­чение напряженности поля рассчитыва­ется   по   формуле   Е = Е₀F,   где   Е₀   -напряженность поля в свободном про­странстве.

                                                                                                                                               

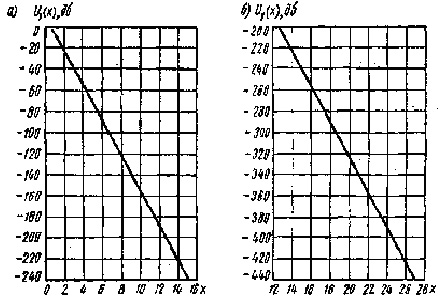
                                                                                          Рис.7.10. К определению величины U(x)                   

 

                            

 

                                

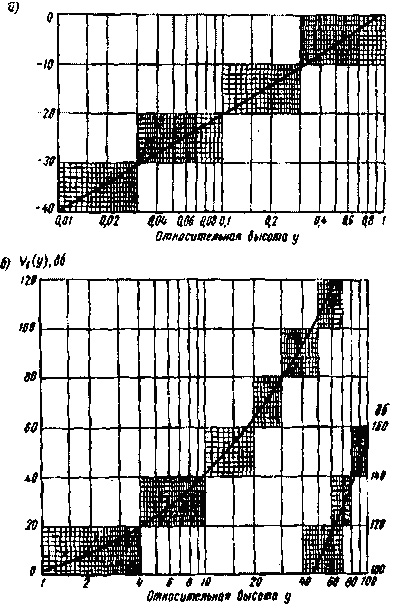
                                                                                         Рис.7.11. К определению величины V(y)

 

 

В зоне полутени для приближенной оценки уровня напряженности поля из­вестную пользу приносит способ опре­деления множителя ослабления на гра­нице прямой видимости, т.е. на таком расстоянии, где интерференционные формулы показывают уже нулевые значения поля. Метод разработан для горизонтально поляризованного излу­чения.

 

 

При вертикальной поляризации он дает менее точные результаты и используется для              λ < 50 см. Множитель ослабления на границе прямой ви­димости рассчитывается по формуле           F = (r₀ / L)F(y_1,y₂). Значение функции F(y₁,y₂)получено из многочленной дифракционной формулы и определя­ется графически из Рис.7.12 в дБ. Это значение пересчитывается в разы по формуле F = 10^{F(y1,y2)дБ/20}.  Напряженность поля рассчитывается по формуле  Е = Е₀F.

 

                                                    

 

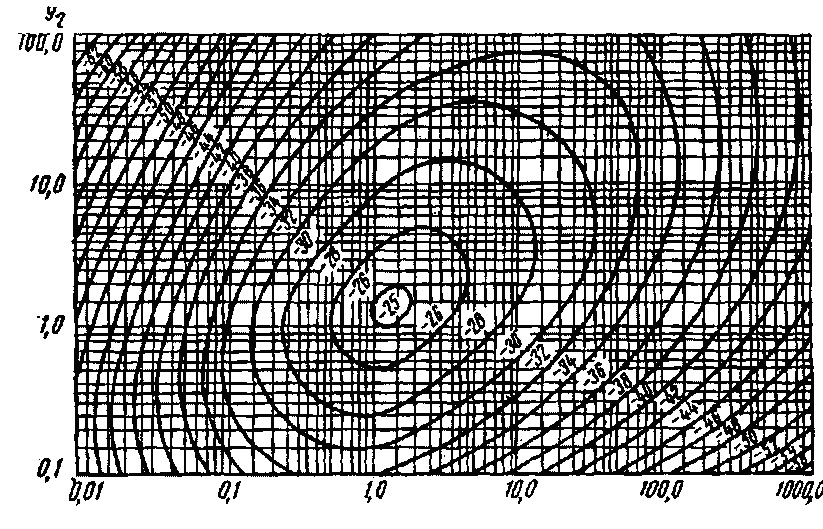
Рис.7.12. К определению величины V(y1,y2)

 

 

 

 

Влияние тропосферы на РРВ

 

Влияние неоднородностей тропосферы на условия распространения земных волн теснейшим образом связано с явлением атмосферной реф­ракции. Явление ат­мосферной рефракции, как известно, заключается в преломлении световых лучей (а, следовательно, и радиоволн), распространяющихся в земной ат­мосфере. Выражение для радиуса кривизны траектории радиоволны, рас­пространяющейся в тропосфере имеет вид R = n_т / [sinφ(-dn/dh)]. Известно, что в тропосфере n_т ≈ 1. Когда луч пологий sinφ =>1. Отсюда                               R = 10⁶ / (-dN/dh).

 

Это выражение показывает, что радиус кривизны луча в нижних слоях тропосферы определяется не абсолютным значением показателя преломления, а быстротой изменения показателя преломления с высотой. Знак минус у производной означает, что радиус кривизны будет положи­тельным, т.е. траектория будет обращена выпуклостью вверх только в том случае, если коэффициент преломления уменьшается с высотой.

 

При распространении в нормальной тропосфере, которая характери­зуется постоянством градиента - во всей толще тропосферы, траектории радиоволн получают форму дуг окружности радиуса R = 25000 км.

 

Следует отметить, что радиоволны испытывают в нормальной тро­посфере несколько большее преломление, чем световые лучи. Объясняется это тем, что обладающие постоянным дипольным моментом молекулы во­ды вследствие конечной массы не успевают под действием электромагнитного поля      весьма     высоких    частот,     свойственных видимому свету (4 × 10¹⁴Гц...7,5 × 10¹⁴Гц), менять свою ориентировку. Наоборот, в диапа­зоне радиоволн (f < 3 × 10¹¹ МГц) полярные молекулы в полной мере уча­ствуют в колебательном движении и вносят свои изменения в значение коэффициента преломления. Для световых лучей R ≈ 50000 км. Атмо­сферная рефракция, имеющая место в нормальной тропосфере, получила название нормальной рефракции.

 

Учёт атмосферной рефракции при распространении радиоволн в пределах прямой видимости

 

Рассмотрим учёт влияния атмосферной рефракции на распростране­ние радиоволн при поднятых передающей и приёмной антеннах в услови­ях применимости интерференционных формул. Как известно, подобные условия встречаются только в диапазоне ультракоротких волн. Необходимость такого учёта именно в диапазоне ультракоротких волн обусловлена тем, что в условиях приме­нимости интерференционных формул результирующее поле в месте приё­ма зависит от геометрической разности хода прямого и отражённого от земли лучей. Вывод интерференционных формул основывается на предположении, что волны распространяются по прямым, тогда как в дей­ствительности радиоволны распространяются по криволинейным траекто­риям, т.е. проходят более длинные пути, что, несомненно, влияет на гео­метрическую разность хода лучей. Кроме того, изменение диэлектриче­ской проницаемости с высотой влияет на скорость распространения ра­диоволн, а, следовательно, и на «оптическую разность хода лучей», как принято называть разность хода, вычисленную с учётом скорости распро­странения волн.

                                                

                                                                                                 

                                                                            Рис.7.13.  Траектории радиоволн в реальной атмосфере

На Рис.7.13 пунктирными линиями показаны прямоли­нейные траектории прямого и отражённого от земли лучей при распро­странении в однородной атмосфере. В нормальной тропосфере радиовол­ны распространяются по криволинейным траекториям, точнее, по дугам окружностей, показанных на рисунке сплошными линиями. Замена пря­молинейных  траекторий  дугами  окружностей  изменит  конечные  значения разности хода лучей. В 1933 г. Скиллинг, Берроуз и Феррел предложили упрощенный способ учета влияния атмосферной рефракции, заключающийся в том, что оба луча, как и прежде, распространяются по прямолинейным траекториям, однако не над поверхностью Земли радиуса а, а над воображаемой поверхностью с экви­валентным радиусом а_э. Значение эквивалентного радиуса определяется из условия сохранения постоянства относительной кривизны между лучом и поверхностью Земли в  действительных  условиях и  в эквивалентной схеме распространения (табл.7.2). Относительной кривизной в аналитической геометрии называют разность 1/а-1/R. Отсюда 1/а –1/R = 1 /а_э-1/∞. Из этого выражения получаем формулу для эквивалентного радиуса Земли

                                                                                                    а_э = а / (1 – a / R),         а_э = а / [1 + а(dN/dh) × 10^-6].                                    (7.13)

 

При нормальной тропосферной рефракции а_э = 8500 км. Представ­ление об эквивалентном радиусе земного шара позволяет учесть неодно­родную атмосферу путём замены в формулах действительного радиуса Земли а его эквивалентным значением. Так формула для определения рас­стояния прямой видимости принимает вид       

                           

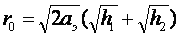                                                                                                                                                                                (7.14)

В табл.7.2 приведены значения эквивалентного радиуса Земли, ре­альные и эквивалентные траектории для различных видов тропосферной рефракции. В тех случаях, когда кривизна земли во внимание не принима­ется, что возможно при расчётах напряжённости поля на небольших уда­лениях от передатчика, можно не принимать во внимание и атмосферную рефракцию.

Таблица 7.2. Классификация различных видов атмосферной рефракции.

 

7.6  РРВ в пределах прямой видимости над шероховатой поверхностью Земли

Земная поверхность существенно влияет на напряженность поля в месте приема. Если антенны приподняты над гладкой плоской поверхностью земли, то последняя отражает радиоволны, подобно тому, как зеркало отражает свет. К приемной антенне приходят две волны – прямая и отраженная. Длина пути  этих волн различна и, следовательно, будут различны их фазы. Если волны приходят к приемной антенне в одной и той же фазе, то напряженность поля достигает наибольшего значения. Наименьшее значение получается в случае прихода волн в противоположных фазах (в противофазе). В результате по мере удаления от передатчика напряженность поля то возрастает, то резко падает, и лишь, начиная с некоторого расстояния, убывает плавно. На метровых волнах при небольшой высоте приемной антенны плавное спадание поля начинается уже на расстоянии нескольких километров от передатчика.

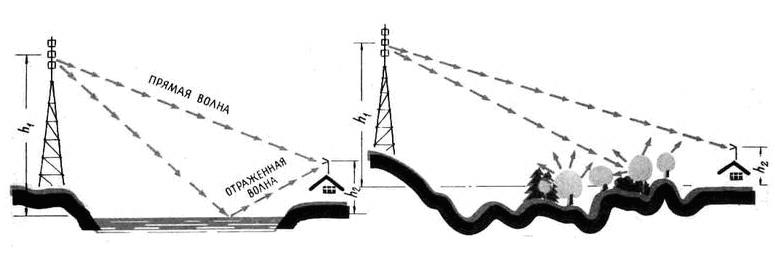
                                                                                   Рис.7.14.  Многолучевое распространение          

Наибольший интерес представляет распространение УКВ над неровной поверхностью (покрытой горами, оврагами, лесами, строениями и т.п.). Над такой местностью отраженный от земли луч будет в месте приема ослаблен, так как земная поверхность представляет собой уже «кривое зеркало». Помимо этого луча, в точку приема могут приходить волны, отраженные от соседних высоких зданий и гор. Над неровной местностью зависимость напряженности поля от расстояния и высоты неопределенна и почти не зависит от длины волны. На расстояниях до 30 – 40 км среднее значение множителя V (7.15) над обычной пересеченной местностью грубо можно оценить по формуле

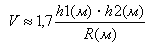                                                                                                          (7.15)

Если: h1=100 м, h2=10 м, R=10 км, то V=0,17.

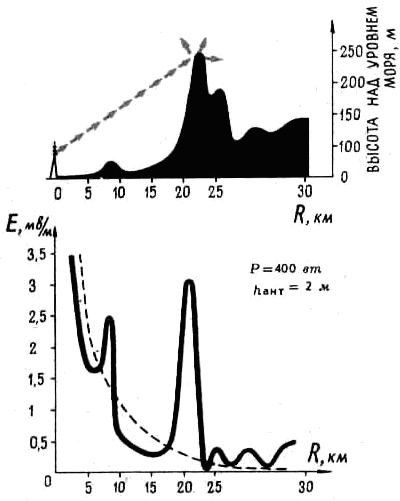
                                                                           Рис.7.15.  Влияние местности на напряженность поля

Характер влияния местности можно себе представить, глядя на Рис.7.15, где показан реальный профиль местности перед телецентром (верхний рисунок) и результат измерений напряженности поля на этой местности (жирная кривая на нижнем рисунке).    В начале трассы местность ровная и напряженность поля убывает плавно, так же как над плоской поверхностью (ср. жирную и пунктирную кривые). На расстоянии 8 км местность приподнята, и напряженность поля растет. За холмом напряженность резко падает, это – область тени. За последующим холмом напряженность поля немного выше, чем поле, которое должно быть над плоской поверхностью. Это  объясняется тем, что данный холм, благодаря своим определенным геометрическим размерам, «работает» как ретранслятор. Падающие на него волны он переизлучает во все стороны, в том числе и в область тени. Аналогичный эффект может наблюдаться в горах, причем может случиться так, что в приемную антенну попадут еще волны, отраженные от земли, на участках «передатчик – гора» и «гора – приемник». При благоприятном совпадении фаз волн напряженность поля может быть выше, чем на такой же трассе, но без горы. Этот эффект называется «усиление препятствием».

Земная поверхность никогда не бывает идеально гладкой. Даже равнинная местность покрыта большим числом хаотически расположенных неровностей. При интерфе­ренционной структуре поля земной волны на условия распространения оказывают влияние неровности местности, распределенные в пределах существенной зоны для отражения. При скользящем распространении не­обходимо учитывать неровности местности почти вдоль всей трассы. Если небольшие неровности земной поверхности в среднем распределены рав­номерно, то такую поверхность называют шероховатой. При распространении над шероховатой поверхностью происходит рассеяние поля земной волны, что является причиной ослабления плотно­сти потока энергии в заданном направлении. Существуют два метода учета этого ослабления.

В условиях открытых трасс при работе в диапазонах метровых, дециметровых и сантиметровых волн наличие земли проявляется в виде отра­женной волны. В этом случае ослабление поля в результате рассеяния ше­роховатой отражающей поверхностью учитывают с помощью эффектив­ного коэффициента отражения Rэфф. Величина Rэфф всегда меньше зер­кального коэффициента отражения R , который справедлив для гладкой отражающей поверхности. Степень неровности шероховатой поверхности оценивают с помощью критерия Рэлея. Пусть плоская волна падает под углом скольжения ∆ на плоскую поверхность с горизонтальной впадиной глубиной ∆h (Рис.7.16). ЛучА'С'В',
попавший во впадину и отразившийся под углом скольжения ∆, на плоскости S отличается по фазе от луча АСВ, отразившегося от плоской поверхности на величину
∆φ = (2π / λ)2∆hsin∆.

 

                                                                                       

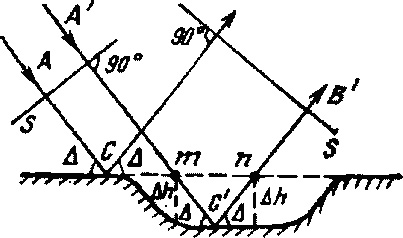
                                                                                 Рис.7.16. К определению критерия Рэлея

Обычно счита­ют, что возмущающим действием неровности можно пренебречь, если           ∆φ < (π/4…π/2). Обозначая через ∆hmах так называемую критическую высоту, которая соответствует критическим значениям ∆φmах, получим ∆hmax = λ / [(16…8)sin∆]. Для пологих траекторий, когда sin∆ ≈∆, и для обычно принимаемого критического значения ∆φmах = π/2 выражение упрощается   ∆hmах∆ ≈λ / (8∆). Если высота неровности ∆h ≤∆ hmах ≈λ /(8∆), то отражение можно считать зеркальным. Это условие называется критерием Рэлея, ко­торый показывает, что чем более полога траектория падающей волны, тем слабее возмущающее действие неровности. Так, на волне 10 см при ∆ = 5° критическая высота равна всего лишь 14 см, а при снижении угла до 0,5° допустимый размер неровности возрастает до 1,4 м. Критерий Рэлея носит приближенный характер, поскольку не учитывает формы неровности, по­ляризации поля и др. Однако измерения показывают, что качественно этот критерий правильно оценивает влияние шероховатости поверхности. Если на открытых трассах в пределах минимальной зоны для отражения высота неровностей ∆h > ∆hmах, то в интерференционных формулах используют эффективный коэффициент отражения Rэфф. Величины Rэфф для разных видов шероховатых поверхностей определяют по результатам статистиче­ской обработки экспериментальных данных.

7.7 Особенности РРВ в городе

 

Условия приема сигналов в диапазоне УКВ существенно зависят от расположения приемной антенны относительно окружающих ее предметов. В городских условиях такими предметами являются здания, деревья, заводские трубы, мачты и т.д. Близ­ко расположенные здания могут, в зависимости от их расположения, ока­заться затеняющими препятствиями или источниками местных отражен­ных волн. Затеняющее действие отдельного препятствия приводит к тому, что поле за препятствием появляется в результате двух процессов: ди­фракции и проникновения через препятствие. Дифракция в рассматривае­мом диапазоне волн протекает с большими потерями. Проникновение сквозь препятствия типа стен зданий также сопровождается большими по­терями за счет поглощения. Измерения показывают, что напряженность поля за отдельно стоящим кирпичным зданием на 20...30дБ ниже, чем пе­ред ним, а за железобетонным строением уровень сигнала падает на 30...40 дБ. В целом внутри городской застройки имеются многочисленные тене­вые зоны, где сигнал значительно ослаблен. Действие окружающих зда­ний, как источников отраженных волн, проявляется, как в виде неравно­мерного распределения амплитуды поля в пространстве из-за интерферен­ции многочисленных отраженных волн, так и в своеобразном подсвечивании теневых зон. В случае вертикальной поляризации первичного поля от­ражения наиболее интенсивны от предметов, протяженных по вертикали (стены зданий, деревья). Большое влияние местных предметов на условия приема вертикально-поляризованного поля является одной из причин преимущественного применения горизонтальной поляризации в системах те­левизионного вещания.

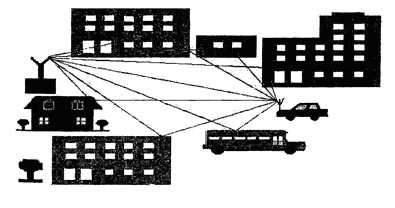
Рис.7.17. Многолучевое распространение радиоволн в городе

Сложность условий распространения УКВ в городе определяет ста­тистический характер, как теоретических, так и экспериментальных ис­следований. По условиям приема сигнала можно выделить три наиболее типичных ситуации: передающая и приемная антенны находятся над уровнем городской застройки, и между ними имеется прямая видимость; связь между подвижным объектом и базовой станцией; связь между двумя подвижными объектами. В первом случае, характерном для приема сигна­лов телевизионного вещания, расчет напряженности поля можно вести по формуле Введенского, умножая результат расчета на поправочный коэф­фициент (обычно 0,4...0,6). Во втором и третьем случаях между пунктами передачи и приема, как правило, нет прямой видимости, и основной вклад в формирование многолучевого поля вносят отражения от зданий в окре­стности подвижного пункта.

Рассмотрим закономер­ности изменения напряженно­сти поля в точке приема в го­родских условиях в зависимо­сти от расстояния, частоты вол­ны и высот установки антенн. На Рис.7.18 приведены зависи­мости среднего (медианного) значения мощности сигнала Р_с от расстояния r при различных высотах подвеса антенны базо­вой станции h₁, измеренные на частоте 922 МГц. Высота под­веса антенны на подвижном объекте  h₂ = 3 м. Штриховой линией показана зависимость Р_с от расстояния для условий свободного пространства.

Уровень 0 дБ соот­ветствует полю в свободном пространстве на расстоянии 1 км от базовой станции. Анализ приведенных зависимостей показывает, что при увеличе­нии расстояния до 15 км мощность сигнала убывает как r^-3 . Последующее увеличение г приводит к еще более быстрому уменьшению уровня сигна­ла. Ослабление сигнала в городе возрастает с увеличением его частоты. Эту зависимость можно представить в виде P_c = Af^-n, где А - коэффициент пропорциональности. С увеличением частоты от 100 до 2000 МГц значе­ние коэффициента п изменяется от 0,2 до 1. При r = 1...10 км зависимость уровня поля от частоты слабая, но при дальнейшем увеличении расстояния значение коэффициента п начинает зависеть от него и растет значительно быстрее.

                                                                                     

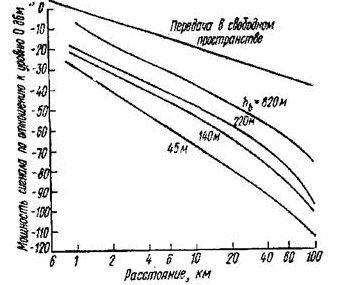
Рис.7.18. Зависимость медианного значения мощности сигнала в городских условиях при различных высотах подвеса антенны базовой станции

Зависи­мость среднего уровня поля от высоты расположения антенны базовой стан­ции можно проследить по Рис.7.18. Высота подвеса антенны сильно не влияет на скорость уменьшения уровня сигнала с расстоянием. Однако подъем антенны базовой станции приводит к увеличению абсолютного значения по­ля примерно пропорционально квадра­ту высоты (6дБ/октаву). На поле в точ­ке приема влияют не только рассмот­ренные факторы, но и многие другие. В частности, установлено, что уровень сигнала существенно зависит от распо­ложения улиц в городе, которые оказывают канализирующее действие на распространяющиеся волны. Вдоль радиально расположенных улиц уро­вень сигнала на 10...20 дБ выше, чем в перпендикулярных направлениях.

За счет переотражения волн от стен зданий и подстилающей по­верхности в городе наблюдается явление деполяризации - появление ор­тогональной (перпендикулярной) составляющей напряженности поля в которую переходит часть энергии волны. Коэффициент деполяризации представляет собой разницу в дБ между составляющей напряженности поля основной поляризации и ортогональной составляющей.

Установлено, что в г. Ташкенте значение коэффициентов деполяри­зации на радиальных (по отношению к передающей антенне) улицах в среднем на 2...4 дБ больше, чем на поперечных. Значения коэффициентов деполяризации в районах с большой плотностью застройки ниже, чем в районах с малой плотностью застройки. Наблюдается увеличение значе­ний коэффициентов деполяризации при увеличении высоты подвеса при­емной антенны. Значения горизонтальной и вертикальной составляющих напряженности поля в городе практически не коррелированны, что по­зволяет рекомендовать для приема и передачи кроссполяризованные ан­тенны (антенны с ортогональными поляризациями). Структура поля но­сит интерференционный характер. Архитектура города сильно влияет на величину квазипериода (усредненного расстояния между ближайшими минимумами) интерференционной картины напряженности поля. Так, в г. Ташкенте в районах с малой плотностью застройки величина квазипериода в среднем составляет 0,62λ, а для районов с большой плотностью застройки - 0,76λ. На поперечных улицах величина квазипериода в сред­нем составляет 0,81λ, а на радиальных улицах - 0,5λ.