7.3.     Пролетный режим работы

В иностранной литературе этот режим   называют режимом IМРАТТ (IМРасt Avalanche Transit Time — ударная ионизация и пролетное время). Пролетный режим  работы диода основан на использовании лавинного пробоя и эффекта времени пролета носителей в обедненной области различных полупроводниковых структур. Распределение поля в этой области, определяющее физические процессы в диоде, зависит от типа структуры и закона распределения концентрации примесей в областях структуры. Ниже будет рассмотрена структура типа n+—р—i—p+ (диод Рида) (рис. 7.2, a), в которой области лавинного умножения и дрейфа носителей пространственно разделены. Распределение концентрации примесей в областях структуры показано на рис. 7.2,б. Концентрация примеси в крайних областях p⁺, n⁺ много больше, чем в р-области, по концентрации носителей i-область близка к собственному полупроводнику.

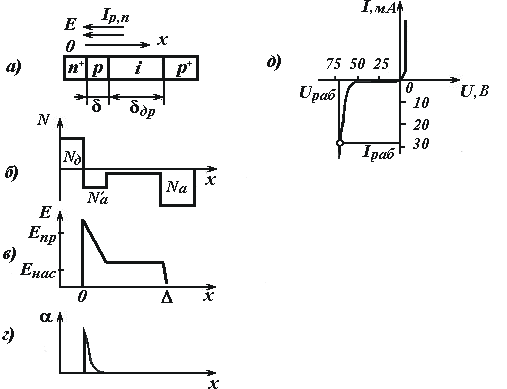
Рис.  7.2 Структура лавинно-пролетного диода (a) и распределение в нем концентрации примеси (6), электрического поля (в), коэффициента ударной ионизации (г), а также вoльт-aмпepнaя характеристика ЛПД (д)

 Максимальная напряженность электрического поля имеет место в области р⁺-n-пepexoдa (рис. 7.2. в). Электрическое  поле резко убывает в n-области и остается практически постоянным в i-cлoe, который полностью обеднен при больших обратных напряжениях. Если обратное напряжение увеличивать, то электрическое поле в переходе превысит значение пробивной напряженности E_пp, при которой коэффициент ударной ионизации α достигает больших значений (порядка 10⁵ cм^-1). поскольку α сильно зависит от E, то протяженность области ударной ионизации невелика (рис. 7.2, г). В ней происходит лавиннообpaзнoe нарастание количества свободных носителей заряда. Эту область называют областью лавинного умножения. Образующиеся дырки увлекаются внутренним электрическим полем перехода в p⁺-область, а электроны, попадая в i-cлoй, движутся к n-⁺области в постоянном электрическом поле. Если напряженность электрического поля в слаболегированной области велика и превышает несколько кB/cм, то скорость электронов остается почти постоянной и равной υ_нac = 10⁵ м/с. Происходит так называемое насыщение дрейфовой скорости носителей. Следовательно, носители заряда дрейфуют с конечной скоростью за конечный промежуток времени. Это предельное значение дрейфовой скорости называют скоростью насыщения. Обедненную область, в которой происходит движение электронов с постоянной скоростью, называют областью дрейфа. Поскольку при этом дифференциальная подвижность электронов близка к нулю, при движении электронов не происходит уменьшения объемной плотности заряда.

Принцип работы ЛПД поясним с помощью пространственно-временной диаграммы, показанной на рис. 7.3.

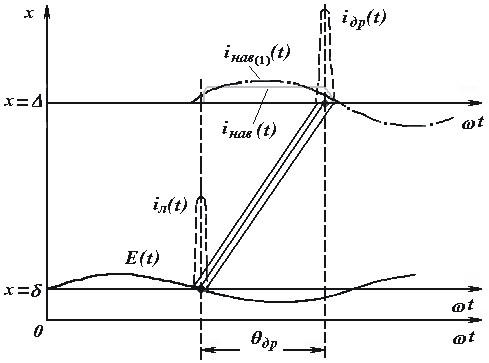
Рис. 7.3. Пространственно-временная диаграмма

 Предположим, что в слое умножения и дрейфа имеется одинаковая и достаточно большая напряженность электрического поля, изменяющаяся во времени по синусоидальному закону E(t). При большой амплитуде поля лавинный процесс приводит к образованию короткого сгустка носителей, запаздывающего на четверть периода от максимума поля. Этому сгустку соответствует короткий импульс лавинного тока i_л(t) на границе x=d между слоями умножения и дрейфа. Далее носители сгустка двигаются в электрическом поле слоя дрейфа, пока не достигнут его границы (х—D) при угле пролета θ_дp. Пространственно-временная диаграмма для слоя дрейфа изображена на рис. 7.3 прямыми линиями, так как дрейфовая скорость носителей постоянна.

Угол пролета при выбранной ширине слоя D зависит от частоты. Если θ_дp<π, то носители все время пролета находятся в тормозящем полупериоде поля и отдают свою энергию полю, вызывая увеличение этого поля. При θ_дp>π последнюю часть пути в области дрейфа носители летят в ускоряющем полупериоде поля, что ослабляет эффект предыдущего взаимодействия и приводит в целом к снижению энергии, передаваемой носителями полю за все время пролета. Если θ_дp—2π, то эффект взаимодействия носителей и поля исчезает.

На рис. 7.3.  при х—D показана зависимость дрейфового тока от времени i_др(t) в виде узкого импульса, повторяющего импульс i_л(t). Одновременно изображена кривая наведенного тока i_нaв(t). созданного движением короткого сгустка на пути от x=d до χ=D. В случае короткого сгустка форма кривой наведенного тока близка к прямоугольной. Разложением в ряд Фурье может быть определена первая гармоника i_нaв(1) этого тока. В идеальном случае она совпадает по фазе с полем, если θ_дp=π.