7.2.     Лавинное умножение носителей

Лавинно-пролетный диод (ЛПД)— это полупроводниковый СВЧ-диод, в котором для получения носителей заряда используется лавинное умножение (ударная ионизация) в области электрического перехода и взаимодействие этих носителей с переменным полем в переходе в течение времени пролета. Лавинно-пролетные диоды относятся к классу двухполюсников, обладающих отрицательным сопротивлением на зажимах, что позволяет использовать ЛПД для создания генераторов и усилителей. Отрицательное  сопротивление ЛПД проявляется только на достаточно высоких частотах и не проявляется в статическом режиме. Причиной этого является наличие фазового сдвига между током и напряжением на ЛПД.

 В иностранной литературе такие диоды часто называют диодами Рида по фамилии ученого, предложившего в 1958 г. структуру типа р—п—i—р и принципы работы устройства, однако эта структура была реализована только в 1965 г. Первый ЛПД создан в СССР А. С. Тагером с сотрудниками на основе обнаруженного в 1959 г. эффекта генерации СВЧ-колебаний при лавинном пробое германиевых диодов.

На рис. 7.1 показана схема  плавного p-n-перехода  ЛПД  и  распределение  электрического   поля  в переходе. На диод подается обратное напряжение такой величины, что рабочая точка смещается в область лавинного умножения (рис.7.2). В p-n-переходе начинается процесс ударной ионизации атомов кристаллической решетки подвижными носителями заряда и образование новых пар электронов и дырок.  С этим явлением связан резкий рост обратного тока перехода, называемый лавинным пробоем. Для количественной характеристики процесса ударной ионизации  вводят коэффициенты ионизации a_n и a_p для электронов и дырок — число электронно-дырочных пар, создаваемых на единице пути (1 см) электроном и дыркой соответственно.

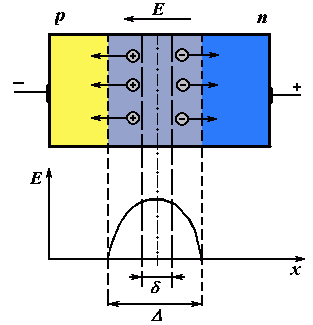
Рис. 7.1. Схема ЛПД и распределение   напряженности   электрического поля:

D — ширина  запирающего слоя;   d— ширина слоя умножения

 Лавинный пробой возникает, в результате ударной ионизации нейтральных атомов в р-n-переходе быстрыми электронами или дырками. В результате генерируются новые пары носителей заряда, которые, двигаясь в электрическом поле перехода, вновь при столкновении с атомами образуют новые пары носителей и т. д., т. е. носители в переходе лавинообразно размножаются. Параметром этого процесса является коэффициент умножения М, определяемый как отношение числа носителей, выходящих из p-n-перехода, к числу носителей того же типа, входящих в переход. Коэффициент М можно рассчитать по следующей эмпирической формуле:

                                                                                                   (7.1)

где U_пр- напряжение пробоя.

Показатель степени для кремния и германия n-типа b= 3; для германия p-типа b=5,5. Величина пробивного напряжения не зависит от типа носителей и растет с увеличением удельного сопротивления полупроводника; у кремния это напряжение выше, чем у германия при тех же значениях удельного сопротивления.

Принято считать, что лавинный пробой наступает при таком обратном напряжении на переходе, когда коэффициент лавинного умножения обращается в бесконечность. Если начало лавинного умножения вызвано дырками (I_P0>>I_n0), то условие лавинного пробоя будет выглядеть следующим образом:

                                                                                                                      (7.2)

Условие (7.2)  имеет простой физический смысл; для возникновения лавинного пробоя необходимо, чтобы каждый электрон и каждая дырка, вошедшие в переход и возникающие в переходе, создавали в среднем по одной электронно-дырочной паре. Если α_п¹α_р, то носители, имеющие больший коэффициент ионизации, должны создавать при прохождении перехода в среднем более одной пары, чтобы скомпенсировать уменьшение коэффициента ионизации носителей другого типа.

Напряженность  электрического поля максимальна на границе между р- и n-областями. Поэтому ударная ионизация происходит лишь в узком слое умножения δ, прилежащем к плоскости границы. Вновь созданные электроны и дырки под действием сильного поля дрейфуют через p- и n- пролетные участки запирающего слоя, расположенные по обе стороны от слоя умножения. Дырки дрейфуют через p-слой, а электроны через n-слой. При возрастании электрического поля скорость носителей заряда растет линейно. Но уже при напряженности поля, вызывающей лавинное умножение носителей (Е >> 10⁵ В/м), скорость носителей заряда становится практически постоянной.

Пролетное время носителей заряда пропорционально ширине области пролета D и это объясняет запаздывание лавинного тока от напряжения в ЛПД. Сдвиг фазы между изменением напряженности поля и изменением тока при определенной частоте составит π/2. Дрейфуя через пролетные участки, электроны и дырки частично компенсируют объемный заряд ионов примеси и снижают напряженность поля в слое умножения.