10.2.1. Квантовые переходы

В твердых телах взаимодействие частиц становится настолько сильным, что образуются зоны с очень близко расположенными уровнями, между этими зонами имеются зоны запрещенных значений энергии (запрещенные зоны). Уровень, соответствующий наименьшей допустимой энергии микрочастицы, называется основным, а остальные – возбужденными.

В атомах осуществляются только те переходы между энергетическими уровнями, которые удовлетворяют правилам отбора, устанавливающим допустимые различия квантовых чисел. Переходы, удовлетворяющие правилам отбора, называются разрешенными, а остальные — запрещенными.

Изменение  внутренней энергии называется переходом с  уровня  на уровень. При переходе с более высокого энергетического уровня W₂ на низкий W₁ выделяется энергия DW₂₁=W₂ - W₁. Переходы с излучением или поглощением квантов электромагнитной энергии (фотонов) называют излучательными, а переходы, в которых квант энергии выделяется в виде тепла в среде, — безызлучательными. Состояние, из которого запрещены все излучательные переходы в более низкие энергетические состояния, называется метастабильным. Эти состояния играют важную роль в квантовых приборах.

Переходы, которые совершаются в системах микрочастиц, классифицируются по различным признакам. Основными видами переходов являются спонтанные, вынужденные и релаксационные.

Спонтанные переходы - самопроизвольные излучательные квантовые переходы из верхнего энергетического состояния в нижнее. Электромагнитное поле спонтанного излучения характеризуется тремя параметрами: центральной частотой спектральной линии ν_π, спектральной плотностью излучения S(v) и мощностью излучения. Центральная частота излучения называется также частотой квантового перехода и частотой спектральной линии и определяется постулатом Бора:

,                                                                                                    (10.1)

где W₂ и W₁ - энергии верхнего и нижнего уровней соответственно; h -постоянная Планка.

Определим теперь мощность спонтанного излучения. Здесь и в дальнейшем будем рассматривать процессы в единице объема вещества.

Пусть в рассматриваемом объеме содержится N₂ частиц с энергией W₂ и N₁ частиц с энергией W₁. Число частиц в единице объема с данной энергией называется населенностью уровня. Спонтанные переходы носят случайный характер и оцениваются вероятностью перехода в единицу времени A₂₁, которая называется коэффициентом Эйнштейна для спонтанных переходов. Если населенность уровня Ν₂ остается неизменной во времени (или изменяется незначительно), то число переходов в единицу времени с уровня W₂ на уровень W₁ составит

n₂₁ = Ν₂×Α₂₁.                                                                                                                  (10.2)

При каждом переходе выделяется энергия W₂-W₁₌ hv₂₁ поэтому мощность излучения

Р₂₁ = n₂₁×(W₂ -W₁) = N₂×A₂₁×h×v₂₁.                                                                                  (10.3)

 Между коэффициентом Эйнштейна и средним временем жизни частицы на уровне (время, за которое при отсутствии внешнего возбуждения населенность уровня падает в е раз) существует простая связь:

A₂₁=1/t₂.                                                                                                                        (10.4)

В системе частиц, имеющих несколько энергетических уровней, возможны спонтанные переходы частиц с данного уровня на нижние (рис. 10.2). Полная вероятность a_j спонтанного перехода с уровня j на все нижние уровни i равна сумме вероятностей отдельных спонтанных переходов А_ji:

.                                                                       (10.5)

Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными.

Время жизни на уровне j в многоуровневой системе определяется аналогично (10.4) с учетом (10.5):

                                                                                                                       (10.6)

Среднее время жизни на уровне составляет величину в пределах от единицы до сотен наносекунд. На метастабильных уровнях время жизни составляет миллисекунды.

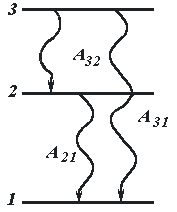
Рис. 10.2 Спонтанные переходы   частиц с одного уровня на другой

 Вынужденные переходы - это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня 2 на нижний 1 и с нижнего на верхний. В первом случае под действием внешнего электромагнитного поля с частотой v₂₁ происходит вынужденное испускание кванта энергии. Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внешнего поля. Вынужденное излучение имеет такие же частоту, фазу, направление распространения и поляризацию, как и вынуждающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода v₂₁. Это служит предпосылкой для создания квантовых усилителей и генераторов.

При каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля hv₂₁.

Вынужденные переходы (как и спонтанные) имеют статистический характер. Поэтому вводятся вероятностные коэффициенты: W₂₁ - вероятность вынужденного перехода сверху вниз и W₁₂ - снизу вверх в 1с. Эти вероятности пропорциональны объемной плотности энергии внешнего поля u_v в единичном спектральном интервале на частоте перехода и определяются соотношениями

W₂₁=B₂₁ × u_{v ,}      

W₁₂=B₁₂× u_{v ,}                                                                                                                   (10.7)

где B₂₁ и B₁₂ - коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно.

Коэффициенты B₂₁ и Β₁₂ имеют смысл вероятностей вынужденных переходов в 1 с при единичной объемной плотности энергии внешнего поля (u_v = 1 Дж см ^-3c ^-1).

Число вынужденных переходов сверху вниз с излучением энергии в единицу времени в единице объема пропорционально вероятности W₂₁ и населенности верхнего уровня n₂, т.е. с учетом (10.7)

n₂₁=W₂₁ ×N₂=B₂₁ × u_v  ×N_{2 .}                                                                                               (10.8)

Аналогично  при тех же условиях число вынужденных переходов снизу вверх с поглощением энергии

n₁₂=W₁₂ ×N₁=B₁₂ × u_v  ×N_{2 .}                                                                                               (10.9)

В приборах СВЧ-диапазона, работающих на «низкой» частоте, вероятность спонтанных переходов мала по сравнению с вероятностью вынужденных переходов и их роль невелика. В лазерах же, работающих на оптических частотах, пренебрегать спонтанными переходами нельзя.

Релаксационные переходы. Переход системы частиц в состояние термодинамического равновесия называется процессом релаксации, а квантовые переходы, которые способствуют установлению и поддержанию термодинамического равновесия, называются релаксационными переходами.

Релаксационные процессы происходят как в газах, так и в твердых телах. Переход кинетической энергии одной частицы во внутреннюю энергию другой при неупругих столкновениях молекул газа является примером релаксационных переходов. Релаксационные переходы носят статистический характер. Вероятности релаксационных переходов между уровнями W₁ и W₂ будем обозначать w₁₂, а обратных переходов w₂₁. В большинстве случаев, имеющих место в квантовых приборах, релаксационные переходы являются безызлучательными.

В состоянии термодинамического равновесия населенности уровней не изменяются во времени, поэтому число безызлучательных переходов с уровня 1 на уровень 2 в 1 с равно числу обратных безызлучательных переходов с уровня 2 на уровень 1:

Ν_1Б ×w₁₂ = Ν_2Б ×w₂₁                                                                             (10.10)

В состоянии термодинамического равновесия распределение населенностей определяется законом Больцмана. С учетом (10.10) получаем

w₂₁ / w₁₂ = ехр(hv₂₁ / kT)                                                                                            (10.11)

Из (10.11) следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх (w₂₁ > w₂₁) в отличие от вероятностей вынужденных переходов, которые одинаковы. Если hv₂₁ << kT, что обычно справедливо для квантовых приборов СВЧ-диапазона, то (10.11) можно заменить приближенным выражением

w₂₁/w₁₂ = 1 + hν₂₁/kΤ                                                                                                  (10.12)