ГЛАВА 12. ОБЕСПЕЧЕНИЕ БЕЗОПАСНОСТИ ПЛАТЕЖНЫХ СИСТЕМ НА ОСНОВЕ
СМАРТ-КАРТ И ПРОГРАММНО-АППАРАТНЫХ СРЕДСТВ
ФИРМЫ АНКАД

Одна из наиболее важных сфер применения средств серии КРИПТОН-обеспечение безопасности платежных систем. Эта задача имеет комплексный характер. Рассмотрим один из ее аспектов - защиту информации, циркулирующей в аппаратно-программных объектах платежной системы.

12.1. Технические объекты платежной системы

К техническим объектам платежной системы относятся:

• платежная смарт-карта (карточка с однокристальным специализированным процессором, имеющим долговременную защищенную память, стандартизированные размеры и интерфейс);

• устройство чтения/записи (отдельное интерфейсное устройство или устройство в составе терминала, в которое вставляется смарт-карта, и взаимодействующие с смарт - картой механические и электрические устройства);

• терминальное оборудование (торговые терминалы, кассовые аппараты, банкоматы и другое оборудование), предназначенное для непосредственных операций со смарт - картой и передачи
информации в центр обработки транзакций;

• автоматизированное рабочее место (АРМ) персонализации смарт-карт (персональный компьютер с устройством чтения/записи для записи на смарт-карты информации);

• АРМ операциониста банка (персональный компьютер с устройством чтения/записи);

• рабочая станция банка-эквайера, банка-эмитента, процессингового центра {персональный компьютер с устройством чтения/записи);

• сервер банка-эквайера, банка-эмитента, процессингового центра;

• каналы связи, объединяющие указанные выше компоненты.

На платежной смарт-карте обычно размещается следующая информация:

• ключи шифрования и подписи (может быть несколько наборов ключей: ключ аутентификации, ключи для связи с процессинговым центром, ключи для кредитования и дебетования и т.д);

• информация о наличии денег, о проведенных транзакциях и т. п.

12.2. Основные принципы обеспечения безопасности платежной системы

Идентификация и аутентификация субъектов платежной системы. До начала проведения любой операции устанавливаются: выпускающая смарт-карты организация, банк, торговая организация, владелец смарт-карты.

Данные выпускающей смарт-карты организации и номер смарт-карты записываются в однократно программируемую память и защищаются от изменения аппаратным способом.

Данные о банке и владельце смарт-карты могут быть изменены на смарт-карте в центре персонализации банка-эмитента при предъявлении соответствующих полномочий (ключей).

Данные о торговой организации вносятся непосредственно в терминал сервисной организации с соответствующих технологических смарт-карт вместе с ключами банков или со смарт-карт кассиров и продавцов.

Идентификация и аутентификация должна осуществляться на основе методов симметричной и асимметричной криптографии. Для решения этих задач фирма АНКАД предлагает библиотеки функций шифрования и вычисления имитовставки (ГОСТ 28147-89), хеширования (ГОСТ Р 34.11-94) и электронной цифровой подписи (ГОСТ Р 34.10-94), реализованные программным и аппаратным способами.

Проверка целостности данных. Система должна гарантировать, что данные в системе или на смарт-карте не будут изменены неправомочными пользователями неправомочным образом. Целостность данных в системе с шифрованием можно подтвердить имитовставкой, вычисленной на секретных ключах банков. Целостность информации о проведенных операциях (транзакциях) подтверждается имитовставками, вычисленными на секретных ключах участников операции (клиента, кассира и продавца). Для систем с
электронной подписью вместо имитовставки можно использовать ЭЦП с проверкой ее достоверности сертифицированными ранее открытыми ключами. Можно комбинировать оба способа в зависимости от возможностей используемых устройств.

Проверка целостности данных может осуществляться с помощью библиотек (см. табл.11.1).

Определение происхождения информации. Все сделки и данные системы должны сопровождаться информацией, идентифицирующей их происхождение и назначение. При выполнении каждой операции (фиксируются дата и время ее проведения, участвующие в ней субъекты и объекты. Информация об операции подтверждается сертификатами каждого участника (имитовставкой или электронной подписью). Действительность операции можно проверить на основании соответствующих ключей ее участников. Эти ключи знает участник и банк. Для проверки происхождения информации предназначены те же самые библиотеки.

Обеспечение секретности данных. Система должна гарантировать конфиденциальность данных. Только допущенный к системе пользователь имеет возможность просмотра данных. Секретность гарантируется применением шифрования как в каналах связи, так и внутри устройств.

Для ограничения доступа к оборудованию на базе ПК предлагаются системы защиты от несанкционированного доступа КРИПТОН-ВЕТО или КРИПТОН-ЗАМОК. Защита ПК со стороны
сети и каналов связи осуществляется с помощью "прозрачно" шифрующих коммуникационных программ или криптошлюзов и криптомаршрутизаторов.

Защита кредитных операций. Кредитные операции должны выполняться непосредственно в банке или в режиме on-line. Разрешается их проводить и в режиме off-line для определенных сумм кредита. Система должна защищать проведение кредитных операций (перевод денег со счета на смарт-карту) путем:

• проверки банком действительности смарт-карты;

• проверки действительности терминала банка;

• определения владельца карточки по PIN коду;

• создания подтверждающего электронного сертификата;

• подтверждения сертификатом проведенной операции;

• вывода смарт-карты из обращения при попытке мошенничества с возможностью восстановления.

Сумма кредита подписывается специальным ключом банка (создание сертификата), если терминалы, работающие в режиме off-line, умеют проверять электронную подпись. Иначе формируется имитовставка на все данные банка и клиента, включая и сумму кредита. Подтверждение сертификатом проведенной операции выполняется в виде электронной подписи работника банка.

Для решения приведенных выше задач предлагается использовать библиотеки криптографических функций фирмы АНКАД.

Защита дебитных операций. При приобретении товаров или услуг производятся:

• проверка терминалом торгового предприятия действительности смарт-карты;

• проверка картой действительности торгового терминала;

• определение владельца смарт-карты по PIN коду;

• проверка наличия средств на смарт-карте;

• создание подтверждающего электронного сертификата;

• подтверждение сертификатом проведенной операции;

• вывод смарт-карты из обращения при попытке мошенничества с возможностью восстановления.

Все проверки выполняются аналогично операции кредитования, только в качестве работника банка выступает кассир магазина. Проверка наличия средств на смарт-карте производится путем сравнения суммы услуг с остатком средств на смарт-карте. На смарт-карте записывается с нарастанием сумма истраченных средств. Она сравнивается с предоставленной суммой кредита. Последняя может быть изменена только банком-эмитентом.

Согласование проведенных операций. Все кредитные и дебетовые операции, проведенные в течение дня в каждом магазине, собираются, согласовываются и передаются в банк. При этом:

• удостоверяется действительность торгового терминала;

• проверяется подлинность сделки;

• проверяется целостность данных о сделке.

Проверки должны производиться на основе оценки сертификатов сделок с помощью библиотеки криптографических функций.

Обеспечение безопасности смарт-карты. Обеспечение безопасности смарт-карты должно осуществляться на всех этапах ее жизненного цикла - от производства кристалла, транспортировки,
персонализации до защиты информации на ней от самого владельца карты. При производстве и транспортировке могут быть искажены или модифицированы характеристики карты с целью последующего получения доступа к ресурсам платежной системы или нарушения ее функционирования.

Для определения качества карточки, выходящей из производства, используется выборочный контроль на соответствие топологии кристалла и содержимого ОС эталонным образцам. При этом
только применение отечественной смарт-карты в достаточной степени может гарантировать надежность контроля.

Основная опасность утечки конфиденциальной информации о владельце карты существует на этапе персонализации карты. Рабочее место для персонализации карт должно иметь надежную систему защиты от НСД, в качестве которой может быть использована система КРИПТОН-ВЕТО или КРИПТОН-ЗАМОК.

Защита конфиденциальной информации на карточке от ее владельца или постороннего злоумышленника (при краже карты) обеспечивается использованием физико-технологических методов
защиты от НСД к кристаллу и ОС, а также механизмом аутентификации владельца.

Защита оборудования и программного обеспечения. Все оборудование и программное обеспечение, используемое в системе, должно подвергаться проверке, с тем чтобы оно не могло быть
использовано в недобросовестных целях. Все терминалы должны быть защищены от несанкционированного доступа аппаратными и программными средствами. Терминалы не должны работать без загрузки определенных ключей. Следует вести журналы работы с фиксацией попыток несанкционированного доступа или использования устройств.

Эта задача также решается с помощью системы КРИПТОН- ВЕТО или КРИПТОН-ЗАМОК.

Защита устройств чтения/записи. Основные угрозы заключаются в перехвате, модификации, вторичном использовании информации, передаваемой по каналу связи, и считывании ключевой информации из устройства. Для смарт-карт с симметричными методами криптографии ситуация усложняется тем, что компрометация ключа в одном устройстве приводит к необходимости замены ключей во всех устройствах.

Безопасность устройства строится на закрытии канала связи с применением методов симметричной и асимметричной криптографии. В настоящее время имеется единственный отечественный
ридер SCAT-200 (разработки фирмы АНКАД) с шифрованием по ГОСТ28147-89 и библиотеками к нему для различных смарт-карт под управлением операционных систем DOS и Windows 95/98. Сохранность ключевой информации обеспечивается модулем безопасности устройства, в составе которого работает ридер. Фирма разрабатывает защищенное устройство чтения/записи (с модулем безопасности) по требованию заказчика.

Защита терминального оборудования. Для терминального оборудования имеют место те же угрозы, что и для считывающих устройств. Кроме того, существуют угрозы нарушения целостности
программного обеспечения и перехвата, модификации, уничтожения информации в канале терминал рабочая станция банка.

Для защиты терминального оборудования, реализованного на основе ПК, предлагается использовать:

• систему защиты от НСД КРИПТОН-ВЕТО или КРИПТОН-ЗАМОК;

• коммуникационные программы прозрачного шифрования IP-пакетов и ограничения доступа к компьютеру по сети;

• библиотеки функций шифрования и электронной цифровой подписи для различных операционных систем.

Персональные компьютеры, рабочие станции, серверы процессинговых центров и банков и каналы связи. Подробное описание угроз для этого оборудования и соответствующих методов защиты было приведено ранее. В качестве средств защиты можно использовать:

• систему КРИПТОН-ВЕТО или КРИПТОН-ЗАМОК;

• коммуникационные программы прозрачного шифрования IP-пакетов и ограничения доступа к компьютеру по сети;

• криптомаршрутизаторы (для защиты серверов и сегментов сетей);

• библиотеки функций шифрования и электронной цифровой подписи для различных операционных систем.

ПРИЛОЖЕНИЕ

ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ

Модулярная арифметика

Модулярная арифметика часто изучается в школе как "арифметика часов". Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:

3 + 14 = 5 (mod12)

или

(3+14) mod 12 = 5

Это арифметика по модулю 12.

Обычная запись в модулярной арифметике

a º b(mod n)

читается так: "а сравнимо с b по модулю n". Это соотношение справедливо для целых значений а, b и n ¹ 0, если, и только если

a = b + k * n

для некоторого целого k.

Отсюда, в частности, следует

n |(a – b)

Это читается как "n делит (а - b)".
Если

a º b(mod n)

то b называют вычетом числа а по модулю n.

Операцию нахождения вычета числа а по модулю n

a(mod n)

называют приведением числа а по модулю n или приведением по модулю.

В нашем примере

(3+ 14) mod 12 = 17 mod 12 = 5

или

17 º 5 (mod 12),

число 5 является вычетом числа 17 по модулю 12.

Набор целых чисел от 0 до (n-1) называют полным набором вычетов по модулю п. Это означает, что для любого целого а(а>0) его вычет г по модулю n есть некоторое целое число в интервале от 0 до (n-1), определяемое из соотношения

r = a – k * n,

где k-целое число.

Например, для n =12 полный набор вычетов:

{0,1,2, …,11}

Обычно предпочитают использовать вычеты

r Î {0,1,2,…,n-1}

но иногда полезны вычеты в диапазоне целых:

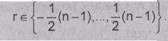
Заметим, что

-12(mod 7) º -5(mod 7) º 2(mod 7) º 9(mod 7) и т.д.

Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n
является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(a + b) mod n = [a(mod n) + b(mod n )] mod n,

(a - b) mod n = [a(mod n) - b(mod n )] mod n,

(a * b) mod n = [a(mod n) * b(mod n )] mod n,

[a * (b + c)] mod n = {[a * b(mod n)] + [a * c(mod n)]} mod n.

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.

Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа а по модулю n

a^x mod n

можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

a⁸ mod n,

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(a * a * a * a * a * a * a * a) mod n

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a² mod n)² mod n)² mod n.

Тем же способом вычисляют

a¹⁶ mod n = (((a² mod n)² mod n)²mod n)² mod n.

Вычисление

a^x mod n.

где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2:

x = 25₍₁₀₎ ® 1 1 0 0 1₍₂₎, поэтому 25 = 2⁴+ 2³ + 2⁰

Тогда

a²⁵ mod n = (a * a²⁴) mod n = (a * a⁸ * a¹⁶) mod n = a * ((a²)²)² * (((a²)²)²)² mod n = ((((a² * a)²)²)² * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n) * a) mod n)² mod n)² mod n)² mod n) * a) mod n

Этот метод уменьшает трудоемкость вычислений до 1,5xk операций в среднем, где k-длина числа в битах [123].

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.

Алгоритм Евклида для нахождения наибольшего общего делителя

Целое число а делит без остатка другое целое число b, если, и только если

b = k * a

для некоторого целого числа k. В этом случае число а называют делителем числа b или множителем в разложении числа b на множители.

Пусть а - целое число, большее 1. Тогда а является простым числом, если его единственными положительными делителями будут 1 и само а, в противном случае а называется составным.

Любое целое n >1 может быть представлено единственным образом с точностью до порядка сомножителей как произведение простых [45].

Существенный с точки зрения криптографии факт состоит в том, что не известно никакого эффективного алгоритма разложения чисел на множители; не было получено и никакой нетривиальной нижней оценки временной сложности разложения. Никаких эффективных методов не известно даже в таком простом случае, когда необходимо восстановить два простых числа р и q из их произведения:

n = p * q

Наибольший общий делитель чисел а и b, обозначаемый как ПОД (а, b) или просто (а, b),-это наибольшее целое, делящее одновременно числа а и b. В эквивалентной форме (а, b)-это то
единственное натуральное число, которое делит а и b и делится на любое целое, делящее и а и b. Если НОД (а, b)=1, то целые а и b- взаимно простые.

Наибольший общий делитель может быть вычислен с помощью алгоритма Евклида. Евклид описал этот алгоритм в своей книге "Начала", написанной около 300 лет до н.э. Он не изобрел его. Историки полагают, что этот алгоритм, возможно, старше еще на 200 лет. Это древнейший нетривиальный алгоритм, который просуществовал до настоящего времени и все еще хорош и сегодня.

Опишем алгоритм Евклида для нахождения НОД (а, b). Введем обозначения: q_i -частное; r_i-остаток. Тогда алгоритм можно представить в виде следующей цепочки равенств:

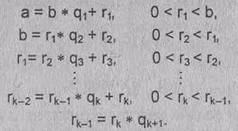
Остановка гарантируется, поскольку остатки r_i от делений образуют строго убывающую последовательность натуральных чисел. Из этой цепочки немедленно получаем, что r_k есть общий делитель чисел а и b и, более того, что любой общий делитель чисел а и b делит и r_k. Таким образом, r_k=HOД(a, b) или r_k =(a, b).

Алгоритм Евклида для вычисления наибольшего общего делителя

Вычисление обратных величин

В арифметике действительных чисел нетрудно вычислить мультипликативную обратную величину а~1 для ненулевого а:

a^-1 = 1/a или a * a^-1 =1

Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку

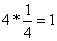
В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения

4 * x º 1(mod 7)

эквивалентно нахождению таких значений х и k, что

4 * x º 7 * k +1

где х и k-целые числа.

Общая формулировка этой задачи -нахождение такого целого числа х, что

a * x(mod n) = 1

Можно также записать

a^-1 º x(mod n)

Решение этой задачи иногда существует, а иногда его нет. Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку

5 * 3 = 15 º 1(mod 14).

С другой стороны, число 2 не имеет обратной величины по модулю 14.

Вообще сравнение

a^-1 º x(mod n)

имеет единственное решение, если а и n - взаимно простые числа.

Если числа а и n не являются взаимно простыми, тогда сравнение

не имеет решения [45].

a^-1º x(mod n)]

Сформулируем основные способы нахождения обратных величин. Пусть целое число а Î{0,1,2,..., n-1}. Если НОД(а, n)=1, то a * i (mod n) при 1 = 0,1,2,...,n-1 является перестановкой множества {0,1,2, ...,n-1}.

Например, если а=3 и n=7(НОД(3,7}=1), то

3 * i (mod 7) при i = 0,1,2,…,6

является последовательностью 0, 3, 6, 2, 5, 1, 4, т.е. перестановкой множества (0,1,2, ...,6).

Это становится неверным, когда НОД(а, n)¹1. Например, если а=2 и n= 6, то

Если НОД(а, n) = 1, тогда существует обратное число а^-1, 0<а^-1<n, такое, что

a * a^-1 º 1(mod n)

Действительно, a * i(mod n) является перестановкой 0,1,..., n-1, поэтому существует i, такое, что

a * i º 1(mod n).

Как уже отмечалось, набор целых чисел от 0 до n-1 называют полным набором вычетов по модулю п. Это означает, что для любого целого числа а(а>0) его вычет r = a(mod n)-это некоторое целое число в интервале от 0 до n-1.

Выделим из полного набора вычетов подмножество вычетов, взаимно простых с п. Такое подмножество называют приведенным набором вычетов.

Пример. Пусть модуль n=11- простое число. Полный набор вычетов по модулю 11.

(0,1,2,…,10)

При формировании приведенного набора вычетов из них удаляется только один элемент-0. Приведенный набор вычетов по модулю 11 имеет 11-1=10 элементов.

Вообще приведенный набор вычетов по модулю простого числа n имеет n-1 элементов.

Пример. Пусть модуль n=10. Полный набор вычетов по модулю n =10

{0,1,2,3,4,5,6,7,8,9}.

Из них только 1, 3, 7, 9 не имеют общего сомножителя с числом 10. Поэтому приведенный набор вычетов по модулю 10 равен {1, 3, 7, 9}. При формировании этого приведенного набора были исключены элементы:

0 (1 элемент),

кратные 2 (4 элемента),

кратные 5 (1 элемент),

т.е. всего шесть элементов. Вычитая их из 10, получаем 10-1-4-1=4. т.е. четыре элемента в приведенном наборе.

Для произведения простых чисел p*q = n приведенный набор вычетов имеет (p-1)(q-1) элементов. При n=p*q=2*5=10 число элементов в приведенном наборе

(p-1)(q-1) = (2-1)(5-1) = 4.

Пример. Приведенный набор вычетов по модулю 27=33 имеет 18 элементов:

{1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26}.

Из полного набора вычетов исключены элементы, кратные 3 (всего девять элементов).

Для модуля в виде простой степени n^r приведенный набор вычетов имеет n^r^-1(n-1) элементов.

При n=3, r=3 получаем 3^3-1(3-1)=3²*2=18.

Функция Эйлера j(n) характеризует число элементов в приведенном наборе вычетов (табл. П.1).

Таблица П.1

Иначе говоря, функция j(n) -это количество положительных целых, меньших n, которые взаимно просты с n [123].

Малая теорема Ферма: если n-простое и НОД(а, n)=1, то

a^n-1º 1(mod n)

Согласно обобщению Эйлером малой теоремы Ферма имеем: если НОД(а, n)=1, то

a^j⁽ⁿ⁾ º 1(mod n).

Если n-простое число, то предыдущий результат, учитывая, что j(n) = n-1, приводится к виду (малой теоремы Ферма)

a^n-1º 1(mod n)

Основные способы нахождения обратных величин

a^-1º 1(mod n)

1. Проверить поочередно значения 1,2,...,n-1, пока не будет найден a^-1º 1(mod n) такой, a*a^-1 (mod n) º 1.

2. Если известна функция Эйлера j(n), то можно вычислить используя алгоритм быстрого возведения в степень.

a^-1 (mod n) º a^j^(n)-1(mod n).

3. Если функция Эйлера j(n) не известна, можно использовать расширенный алгоритм Евклида.

Проиллюстрируем эти способы на числовых примерах.

1. Поочередная проверка значений 1,2,...,n-1, пока не будет найден х= a^-1 (mod n), такой что a * x º1(mod n).

Пусть n = 7, а = 5. Требуется найти x=a^-1(mod n).

a * x º 1(mod n) или 5 * x º 1(mod 7).

n -1= 7-1 = 6

Получаем x=5^-1(mod 7)=3.

Результаты проверки сведены в табл. П.2.

Таблица П.2

5 * х

5 * х (mod 7)

2. Нахождение a^-1(mod n), если известна функция Эйлера j(n).

Пусть n = 7, а = 5. Найти x=a^-l(mod n)=5^-1(mod 7). Модуль n=7-простое число. Поэтому функция Эйлера j(n) = j(7) = n-1 = 6. Обратная величина от 5 по mod 7

a^-1 (mod n) = a^j^(n)-1(mod n) =

5^6-1 mod 7 = 5⁵ mod 7 = (5²mod 7)(5³ mod 7) mod 7

=(25 mod 7)(125 mod 7) mod 7= (4*6 mod 7 =24 mod 7 = 3.

Итак, x = 5^-1(mod 7) =3

3. Нахождение обратной величины a-1(mod n) с помощью расширенного алгоритма Евклида.

Алгоритм Евклида можно обобщить способом, который имеет большое практическое значение. При этом способе во время вычисления НОД(а,b) можно попутно вычислить такие целые числа u₁ и u₂, что

a * u_{1 +}b * u₂ = НОД (a, b).

Это обобщение (расширение) алгоритма Евклида удобно описать, используя векторные обозначения [45].

Расширенный алгоритм Евклида

При заданных неотрицательных целых числах а и b этот алгоритм определяет вектор

(u₁, u₂, u₃),

такой, что

a * u_{1 +}b * u₂ = u₃ = НОД (a, b).

В процессе вычисления используются вспомогательные векторы (v₁, v₂, v₃), (t₁, t₂, t₃). Действия с векторами производятся таким образом, что в течение всего процесса вычисления выполняются соотношения

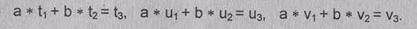
Для вычисления обратной величины a^-1(mod n) используется частный режим работы расширенного алгоритма Евклида, при котором b = n, НОД(а,n) = 1, и этот алгоритм определяет вектор

(u₁, u₂, u₃),

такой, что

Шаги алгоритма:

1. Начальная установка.
Установить (u₁,u₂,u₃):=(0,1, n),

(v_l, v_2, v₃) = (1, 0, a).

2. u₃ = 1?. Если u₃ = 1, то алгоритм заканчивается.

3. Разделить, вычесть.

Установить q:=[u₃/v₃].

Затем установить

(t₁, t₂, t₃) := (u₁,u₂,u₃) - (v₁, v₂, v₃) * q,

(u₁,u₂,u₃):= (v₁, v₂, v₃),

(v₁, v₂, v₃) := (t₁, t₂, t₃).

Возвратиться к шагу 2.

Пример. Заданы модуль n=23 и число а = 5. Найти обратное число a^-1 (mod 23), т.е. x=5^-1(mod23).

Используя расширенный алгоритм Евклида, выполним вычисления, записывая результаты отдельных шагов в табл. П.3.

Таблица П.З

u₁

u₂

u₃

v_l

v₂

v₃

4
1

0
1
-4
5
-9

0
1
-1
2

n = 23
5
3
2
1

-4
5
-9

0
1
-1
2

a = 5
3
2

При u₃ = 1, u₁ = -9, u₂= 2

(a * u₁ + n * u₂) mod n = (5 * (-9) + 23 * 2) mod 23 = 5* (-9) mod 23 º 1,

a^-1 (mod n) = 5^-1 (mod 23) = (-9) mod 23 = (-9 + 23) mod 23 = 14.

Итак, x = 5^-1 (mod 23) в 14 (mod 23) = 14.
Для решения более сложных сравнений

a * x = b(mod n), т. е. b¹1, x = ?

используется следующий прием. Сначала решают сравнение

а * у º (mod n),

т.е. определяют

у = a^-1(mod n),

а затем находят

х = a^-1b (mod n) = у * b (mod n).

Пример. Найти х для сравнения

5 * х = 9 (mod 23).

1 Сначала решаем сравнение

5*y º (mod 23).

Получаем у = 5^-1(mod 23) =14. Затем находим

х = 5^-1 * 9 (mod 23) =14 * 9 (mod 23) =126 (mod 23) =11(mod 23)

х = 11.

Китайская теорема об остатках

Любое неотрицательное целое число, не превосходящее произведения модулей, можно однозначно восстановить, если известны его вычеты по этим модулям. Этот результат был известен еще в древнем Китае и носит название китайской теоремы об остатках. Теорема была предложена китайским математиком первого века Сун Це. Китайская теорема об остатках является мощным криптографическим инструментом. Китайская теорема об остатках формулируется следующим образом.

Пусть m₁, m₂,.... m_i-модули (целые числа, большие 1), которые являются попарно взаимно простыми, т.е. HOД(m_i, m_j)=1 при i ¹ j.

Пусть а_1, а₂, ...,а_t -тоже целые числа, 0 <a_i< m_i.

Пусть М=m₁*m₂*…*m_i-произведение всех m_i. Обозначим M_i = M/m_i.

И пусть N_i будет обратным к M_i(mod m_i), i=1,2,...,t, т.е. М_i* N_i,º 1(mod m_i).

Так как НОД(М_i, m_i)=1, то обратный элемент N_i существует и легко находится из алгоритма Евклида из соотношения

M_i * N_i +m_i * n_i = 1, i = 1,2,…., t.

Сравнения x º a_i(mod mj), i=1,2,...,t, имеют в интервале [О, М-1] единственное общее решение

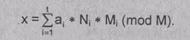
Рассмотрим частный случай. Пусть M=m₁*m₂, где m₁, m₂-взаимно простые числа. Тогда для произвольных целых a₁<m₁ и а₂<m₂ существует единственное число х, х<М, такое, что

x º a₁ (mod m₁) и x º a₂(mod m₂).

Чтобы найти значение решения х, сначала используют алгоритм Евклида для вычисления значений N₁ и N₂, таких, что

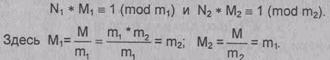
Затем вычисляют значение

x = a₁ *N₁*M₁+a₂ * N₂ * M₂)(mod M).

Алгоритм нахождения решения системы сравнений,

использующий Китайскую теорему об остатках

Пример. Решить систему из двух сравнений

x = 1(mod n)

x = 10 (mod 11)

и найти общее решение х по модулю 55. Здесь m₁ = 5; m₁=11; M=m₁*m₂=5*11 = 55; a₁=1; a₂=10; M₁=M/m₁=m₂=11; М₂=М/m₂=m₁=5.

Найдем значения N₁ и N₂, обратные к M₁ и М₂ соответственно по mod m₁ и mod m₂:

M₁ * N₁ = 1(mod m₁), 11* N₁ = 1(mod 5) Þ N₁ =1

M₂ * N₂ = 1(mod m₂), 5 * N₂ = 1(mod 11) Þ N₂ =9.

Вычисляем общее значение

Квадратичные вычеты

Рассмотрим некоторое простое р>2 и число а<р. Если число а сравнимо с квадратом некоторого числа х по модулю р, т.е. выполняется сравнение x²ºa (mod p), тогда а называют квадратичным вычетом по модулю р. В противном случае а называют квадратичным невычетом по модулю р.

Если а -квадратичный вычет, сравнение x²º a(mod p) имеет два решения: +х и -х, т.е. а имеет два квадратных корня по модулю р.

Все квадратичные вычеты находят возведением в квадрат элементов 1,2,3,...,(р-1)/2.

Не все значения а<р являются квадратичными вычетами. Например, при р=7 квадратичные вычеты это 1, 2. 4:

1² = 1 º 1(mod 7),

2² = 4 º 4(mod 7),

3² = 9 º 2 (mod 7),

4² = 16 º 2 (mod 7),

5² = 25 º 4 (mod 7),

6² = 36 º 1 (mod 7).

Заметим, что каждый квадратичный вычет появляется в этом списке дважды. Не существует никаких значений х, которые удовлетворяли бы любому из следующих уравнений:

x² º 3 (mod 7),

x² º 5 (mod 7),

x² º 6 (mod 7),

Числа 3, 5 и 6-квадратичные невычеты по модулю 7. Можно доказать, что существует точно (р-1)/2 квадратичных вычетов по модулю р и (р-1)/2 квадратичных невычетов по модулю р.

Если а - квадратичный вычет по модулю р, то а имеет точно два квадратных корня: один корень между 0 и (р-1)/2, другой корень между (р-1)/2 и (р-1).

Один из этих квадратных корней также является квадратичным вычетом по модулю р; он называется главным квадратным корнем.

Вычисление квадратных корней при р=7 представлено в табл. П.4.

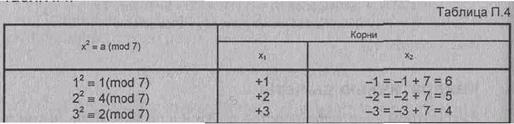
Если n - произведение двух простых р и q, т.е. n=p*q, то существуют точно

(p-1)(q-1)/4

квадратичных вычетов по модулю n, взаимно простых с п. Например, по модулю 35(р=5, а=7, n=5*7=35) существуют

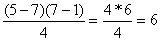
квадратичных вычетов: 1, 4, 9,11,16, 29, взаимно простых с 35.

Вычисления в конечных полях

Поле F есть множество, на котором определены операции сложения и умножения, удовлетворяющие требованиям: ассоциативности, коммутативности, дистрибутивности, существования аддитивного 0 и мультипликативной 1, аддитивных обратных и мультипликативных обратных для всех элементов за исключением 0.

Конечное поле F(p) с конечным числом р элементов играет важную роль в криптографии. В общем случае число элементов

p = qⁿ,

где q-некоторое простое число и n ³1. Такие конечные поля называют полями Галуа и обозначают GF(qⁿ) или GF(q) при n=1. (Эварист Галуа -французский математик начала XIX века.) Многие криптосистемы базируются на полях Галуа GF(q), где q-большое простое число.

Пример. Поле Галуа GF(5) имеет элементы 0,1, 2, 3, 4 и описывается таблицами сложения и умножения (табл. П.5):

Если q-простое число, то число a Î [1,q-1] является взаимно простым с q, и поэтому обратный элемент а^-1 имеет единственное значение. Тем самым однозначно определяется операция деления.

Обозначим через GF*(q) множество всех ненулевых элементов поля GF(q). Некоторый элемент g из GF*(q) называют образующим или порождающим элементом GF*(q), если для всех а из GF*(q) найдется такое целое х, что g^x = a mod q. Всего имеется j(q-1) образующих элементов g. Число х называют дискретным логарифмом элемента а по основанию g и модулю q. Вычисление дискретных логарифмов (когда заданы g, а и q) примерно такая же труднорешаемая задача, как и разложение на множители.

Еще один тип поля Галуа, используемый в криптографии, основывается на арифметике по модулю неприводимых многочленов степени n, чьи коэффициенты-целые числа по модулю q, где q-простое. Эти поля Галуа обозначают как GF(qn). Они имеют элементы, которые описываются многочленами степени не выше (n-1) в форме

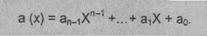
Каждый элемент а(Х) является вычетом по модулю р(Х), где р(Х)- неприводимый многочлен степени n (т.е. р(Х) нельзя разложить на сомножители-многочлены степени меньше n).

Арифметические действия над коэффициентами а, выполняются по модулю q, а наивысшая степень X равна (n-1), так как выполняется приведение по модулю многочлена р(Х), имеющего старшую степень п.

Особый интерес представляют поля GF(2ⁿ). Здесь коэффициентами а; являются 0 и 1. Поэтому многочлен а(Х) степени не выше (n-1) можно представить как вектор из n двоичных цифр:

a_n_-1a_n_-2 … a₁a₀

Каждый из n-битовых векторов соответствует конкретному элементу поля GF(2ⁿ).

Например, поле Галуа GF(2³) имеет элементы:

Организация вычислений в полях Галуа предполагает знание некоторых свойств многочленов и их корней в двоичном поле GF(2). Кратко приведем некоторые из них:

Свойство 1. Ненулевые элементы поля GF(2ⁿ) являются корнями обобщенного многочлена X²ⁿ^-1+1.

Свойство 2. Каждый многочлен р(Х) степени n, неприводимый над полем GF(2), является делителем двучлена X²^n-1+1, и каждый делитель двучлена X ²^n-1 +1, неприводимый над полем GF(2), имеет степень, равную n и менее.

Свойство 3. Все элементы поля GF(2ⁿ) можно получить как совокупность остатков от деления 100...00 на неприводимый многочлен р(Х), входящий в разложение двучлена (X²ⁿ^-1+1). Эти остатки -

корни двучлена (X^2n-1+1)р т.е. обращают его в нуль. Число остатков равно (2^п-1).

Свойство 4. В поле GF(2n) существует примитивный элемент а, такой, что каждый ненулевой элемент поля GF(2ⁿ) может быть представлен как некоторая степень а, т.е. мультипликативная группа GF(2ⁿ) является циклической.

Пример. Определение элементов а, поля GF(2⁴). Согласно свойству 1 ненулевые элементы поля GF(2⁴) являются корнями обобщенного двучлена (Х^24-1+1) = (Х¹⁵+1). Двучлен (Х¹⁵+1) можно представить в виде произведения неприводимых многочленов - сомножителей:

(X¹⁵+1) = P(X¹) * P(X²)* P₁(X⁴)* P₂(X⁴);

где

P(X¹) = (X+1), P(X²) = X² +X+1,

P₁(X⁴) = X⁴ +X+1, P₂(X⁴) = X⁴ +X³+1,

P₃(X⁴) = X⁴ +X³ +X²+X+1.

В соответствии со свойством 3 вычислим элементы a_i поля GF(2⁴) как совокупность остатков отделения 100...00 на неприводимый многочлен P₁(X⁴)=X⁴+X+1.

Процедура определения остатков

Делят на P₁(X⁴)=X⁴+X+1«10011 единицу с возрастающим числом нулей, т.е. делят одночлены Xⁱ,

где j=0,1,2.3,..., на многочлен (Х⁴+Х+1). Степени одночленов Х⁰, X¹, Х², X³ меньше степени многочлена P₁(X⁴), поэтому первые четыре остатка от деления на P₁(X₄) равны делимым, т.е. одночленам X⁰, X¹, X², X³. Для одночлена X⁴«10 000 получаем остаток

Вычисленные остатки и нулевые элементы a₀-a₁₄ поля Галуа GF(2⁴) сведены в табл. П. 6.

Таблица П.6

xⁱ

Остаток

a_i

Х⁰

0 0 0 1

a₀

X¹

0 0 1 0

a₁

X²

0 1 0 0

a₂

1 0 0 0

a₃

X₄

0 0 1 1

a₄

X₅

0 1 1 0

a₅

X₆

х.

1 1 0 0

a_б

X₇

1 0 1 1

a₇

X₈

0 1 0 1

a₈

X₉

1 0 1 0

a₉

X₁₀

0 1 1 1

a₁₀

X₁₁

1 1 1 0

a₁₁

X₁₂

1 1 1 1

a₁₂

X₁₃

1 1 0 1

a₁₃

X₁₄

1 0 0 1

a₁₄

Поле Галуа СР(2⁴) построено как поле многочленов с коэффициентами 0 и 1 по модулю неприводимого многочлена:

P₁(X⁴)=X⁴+X+1«1 0 0 1 1.

В поле Галуа GF(2ⁿ) определены четыре алгебраические операции. Операции сложения и вычитания выполняются как операции поразрядного сложения по модулю 2; операция умножения элементов поля выполняется как умножение соответствующих многочленов с приведением по модулю неприводимого многочлена Р(Х), т.е. многочлена, по модулю которого построены элементы поля GF(2ⁿ).

Чтобы выполнить деление элемента b на элемент а в поле GF(2ⁿ) по модулю Р(Х), сначала находят обратный элемент a^-1(mod P(X)), а затем вычисляют

b* a^-1(mod P(X)).

Каждый двоичный вектор длиной n, исключая 0, является взаимно простым с неприводимым многочленом Р(Х) независимо от значения Р(Х). Поэтому число вычетов, взаимно простых с Р(Х), равно j(Р(Х))=2ⁿ-1 (расширение функции Эйлера для многочленов). Поэтому

Достоинства вычислений в поле GF(2ⁿ):

1. Все элементы поля Галуа имеют конечный размер, деление элементов не имеет каких-либо ошибок округления.

2. Сложение и вычитание элементов поля GF(2ⁿ) не требует деления на модуль.

3. Алгоритмы вычислений в поле GF(2ⁿ) допускают параллельную реализацию.

4. Для поля GF(2ⁿ) обычно применяют в качестве модуля трехчлен Р(Хⁿ) =Хⁿ+Х+1.

Длинная строка нулей между коэффициентами при Хⁿ и X обеспечивает более простую реализацию быстрого умножения (с приведением по модулю). Трехчлен Р(Хⁿ) должен быть неприводимым и примитивным.

Трехчлен Р(Хⁿ)=Хⁿ+Х+1 является примитивным для следующих значений n(n<1000):

1, 3, 4, 6, 9, 15, 22, 28, 30, 46, 60, 63,
127, 153, 172, 303, 471, 532, 865, 900.
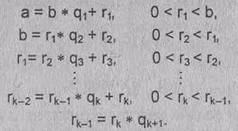
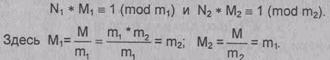