5.4. Протоколы идентификации с нулевой передачей знаний

Широкое распространение интеллектуальных карт (смарт-карт) для разнообразных коммерческих, гражданских и военных применений (кредитные карты, карты социального страхования, карты доступа в охраняемое помещение, компьютерные пароли и ключи, и т.п.) потребовало обеспечения безопасной идентификации таких карт и их владельцев. Во многих приложениях главная проблема заключается в том, чтобы при предъявлении интеллектуальней карты оперативно обнаружить обман и отказать обманщику в до пуске, ответе или обслуживании.

Для безопасного использования интеллектуальных карт разработаны протоколы идентификации с нулевой передачей знаний [121]. Секретный ключ владельца карты становится неотъемлемым признаком его личности. Доказательство знания этого секретного ключа с нулевой передачей этого знания служит доказательством подлинности личности владельца карты.

Упрощенная схема идентификации с нулевой передачей знаний

Схему идентификации с нулевой передачей знаний предложили в 1986 г. У. Фейге, А. Фиат и А. Шамир. Она является наиболее известным доказательством идентичности с нулевой передачей конфиденциальной информации.

Рассмотрим сначала упрощенный вариант схемы идентификации с нулевой передачей знаний для более четкого выявления ее основной концепции. Прежде всего выбирают случайное значение модуля n, который является произведением двух больших простых чисел. Модуль n должен иметь длину 512... 1024 бит. Это значение n может быть представлено группе пользователей, которым придется доказывать свою подлинность. В процессе идентификации участвуют две стороны:

• сторона А, доказывающая свою подлинность,

• сторона В,   проверяющая   представляемое  стороной А доказательство.

Для того чтобы сгенерировать открытый и секретный ключи для стороны А, доверенный арбитр (Центр) выбирает некоторое число V, которое является квадратичным, вычетом по модулю n. Иначе говоря, выбирается такое число V, что сравнение

x² º V(mod n)

имеет решение и существует целое число

V^-1mod n

Выбранное значение V является открытым ключом для А. Затем вычисляют наименьшее значение S, для которого

S º sqrt (V^-1)(mod n).

Это значение S является секретным ключом для А.

Теперь можно приступить к выполнению протокола идентификации.

1. Сторона А выбирает некоторое случайное число r, r < n. Затем она вычисляет

x = r² mod n

и отправляет х стороне В.

2. Сторона В посылает А случайный бит b.

3. Если b = 0, тогда А отправляет г стороне В. Если b = 1, то А отправляет стороне В

y = r * S mod n

4. Если b = 0, сторона В проверяет, что

x = r² mod n

чтобы убедиться, что А знает sqrt(x). Если b = 1, сторона В проверяет, что

x = y² * V mod n,

чтобы быть уверенной, что А знает sqrt(V^-1).

Эти шаги образуют один цикл протокола, называемый аккредитацией. Стороны А и В повторяют этот цикл t раз при разных случайных значениях г и b до тех пор, пока В не убедится, что А знает значение S.

Если сторона А не знает значения S, она может выбрать такое значение г, которое позволит ей обмануть сторону В, если В отправит ей b = 0, либо А может выбрать такое г, которое позволит
обмануть В, если В отправит ей b = 1. Но этого невозможно сделать в обоих случаях. Вероятность того, что А обманет В в одном цикле, составляет 1/2. Вероятность обмануть В в t циклах равна (1/2)^t,

Для того чтобы этот протокол работал, сторона А никогда не должна повторно использовать значение г. Если А поступила бы таким образом, а сторона В отправила бы стороне А на шаге 2
другой случайный бит b, то В имела бы оба ответа А. После этого В может вычислить значение S, и для А все закончено.

Параллельная схема идентификации с нулевой передачей знаний

Параллельная схема идентификации позволяет увеличить число аккредитаций, выполняемых за один цикл, и тем самым уменьшить длительность процесса идентификации.

Как и в предыдущем случае, сначала генерируется число n как произведение двух больших чисел. Для того, чтобы сгенерировать открытый и секретный ключи для стороны А, сначала выбирают К
различных чисел V_1, V₂, ...,V_K, где каждое Vi является квадратичным вычетом по модулю n. Иначе говоря, выбирают значение Vi таким, что сравнение

x² º Vi mod n

имеет решение и существует  Vi^-1 mod п. Полученная строка V₁, V₂, ..., V_K является открытым ключом.

Затем вычисляют такие наименьшие значения Si, что

S_i º sqrt (V_i ^-1)(mod n).

Эта строка S₁, S₂,.... S_K является секретным ключом стороны А.
Протокол процесса идентификации имеет следующий вид:

1. Сторона А выбирает некоторое случайное число r, r < n. Затем она вычисляет х= r² mod n и посылает х стороне В.

2. Сторона В отправляет стороне А некоторую случайную двоичную строку из. К бит: b₁, b₂,..., b_K.

3. Сторона А вычисляет

Перемножаются только те значения Si для которых b₁ = 1. Например, если b₁ = 1, то сомножитель S, входит в произведение, если же b₁ = 0, то S₁ не входит в произведение, и т.д. Вычисленное значение у отправляется стороне В.

4. Сторона В проверяет. Что

Фактически сторона В перемножает только те значения Vi для которых bi = 1. Стороны А и В повторяют этот протокол t раз, пока В не убедится, что А знает S_l, S₂,..., S_K

Вероятность того, что А может обмануть В, равна {1/2)^Kt. Авроры рекомендуют в качестве контрольного значения брать вероятность обмана В равной (1/2)²⁰ при К = 5 и t=4.

Пример. Рассмотрим работу этого протокола для небольших числовых значений [102]. Если n = 35 (n - произведение двух простых чисел 5 и 7), то возможные квадратичные вычеты будут следующими:

1:    х² º   1 (mod 35)         имеет решения: х = 1, 6. 29, 34;
4:    х² º   4 (mod 35)         имеет решения: х = 2, 12, 23, 33;

9:    х² º   9 (mod 35)         имеет решения: х= 3, 17, 18, 32;

11:    х² º 11 {mod 35)         имеет решения: х = 9, 16, 19. 26;

14:   х² º 14 (mod 35)       имеет решения: х = 7, 28;

15:   x²º15(mod35)           имеет решения: х = 15, 20;

16:   х² º 16 (mod 35)       имеет решения: х = 4, 11, 24, 31;

21:   х² º 21 (mod 35)       имеет решения: х = 14, 21;

25:    x²º25(mod35)         имеет решения: х = 5, 30;

29:    х² º 29 (mod 35)         имеет решения: х = 8, 13. 22, 27;
30:    х² º 30 (mod 35)         имеет решения: х = 10, 25.

Заметим, что 14, 15, 21, 25 и 30 не имеют обратных значений по модулю 35, потому что они не являются взаимно простыми с 35. Следует также отметить, что число квадратичных вычетов по модулю 35, взаимно простых с n = p*q = 5*7=35 (для которых НОД (х, 35) =1), равно

(p-1)(q-1)/4 = (5-1)(7-1)/4 = 6

Составим таблицу квадратичных вачетов по модулю 35, обратных к ним значений по модулю 35 и их квадратных корней.

V	V^-1	S = sqrt (V^-1)
1	1	1
4	9	3
9	4	2
11	16	4
16	11	9
29	29	8

            Итак, сторона А получает открытый ключ, состоящий из К=4 значений V:   

[4,11,16,29].  

            Соответствующий секретный ключ, состоящий из К= 4 значений S: 

[3 4 9 8].

            Рассмотрим один цикл протокола.           

1. Сторона А выбирает некоторое случайное число r = 16, вычисляет x=16²mod35=11и посылает это значение х стороне В.                                                                      

2. Сторона В отправляет стороне А некоторую случайную двоичную строку 

[1,1,0,1].        

3. Сторона А вычисляет значение

и отправляет это значение у стороне В.

4. Сторона В проверяет, что

            Cтороны А и В повторяют этот протокол t раз, каждый раз с разным случайным числом г, пока сторона В не будет удовлетворена.           ;

            При малых значениях величин, как в данном примере, не достигается настоящей безопасности. Но если n представляет собой число длиной 512 бит и более, сторона В не сможет узнать ничего о секретном ключе стороны А, кроме того факта, что сторона А знает этот ключ. 

В этот протокол можно включить идентификационную информацию [123].

Пусть I-некоторая двоичная строка, представляющая идентификационную, информацию о владельце карты (имя, адрес, персональный идентификационный номер, физическое описание) и о карте (дата окончания действия и т.п.). Эту информацию  формируют в Центре выдачи интеллектуальных карт по заявке пользователя А.

Далее используют одностороннюю функцию f(×) для вычисления f(l,j), где j-некоторое двоичное число, сцепляемое со строкой I. Вычисляют значения  

V_j = f(l, j)

для небольших значений j, отбирают К разных значений j, для которых Vj являются квадратичными вычетами по модулю n. Затем для отобранных квадратичных вычетов Vj вычисляют наименьшие
квадратные корни из Vj^-1(mod n). Совокупность из К значений Vj образует открытый ключ, а совокупность из К значений Sj- секретный ключ пользователя А.

Схема идентификации Гиллоу-Куискуотера

Алгоритм идентификации с нулевой передачей знания, разработанный Л. Гиллоу и Ж. Куискуотером [121], имеет несколько лучшие характеристики, чем предыдущая схема идентификации. В
этом алгоритме обмены между сторонами А и В и аккредитации в каждом обмене доведены до абсолютного минимума для каждого доказательства требуется только один обмен с одной аккредитацией. Однако объем требуемых вычислений для этого алгоритма больше, чем для схемы Фейге-Фиата-Шамира.

Пусть сторона А интеллектуальная карточка, которая должна доказать свою подлинность проверяющей стороне В. Идентификационная информация стороны А представляет собой битовую строку I, которая включает имя владельца карточки, срок действия, номер банковского счета и др. Фактически идентификационные данные могут занимать достаточно длинную строку, и тогда их хэшируют к значению I.

Строка I является аналогом открытого ключа. Другой открытой информацией, которую используют все карты, участвующие в данном приложении, являются модуль n и показатель степени V,
Модуль n является произведением двух секретных простых чисел.

Секретным ключом стороны А является величина G, выбираемая таким образом, чтобы выполнялось соотношение

I * G^V º 1(mod n)

Сторона А отправляет стороне В свои идентификационные данные I. Далее ей нужно доказать стороне В, что эти идентификационные данные принадлежат именно ей. Чтобы добиться этого,
сторона А должна убедить сторону В, что ей известно значение G.

Вот протокол доказательства подлинности А без передачи стороне В значения G:

1. Сторона А выбирает случайное целое г, такое, что 1<r£<n-1.
Она вычисляет

T = r^V mod n

и отправляет это значение стороне В.

2. Сторона В выбирает случайное целое d, такое, что 1<d£n-1, и отправляет это значение d стороне А.

3. Сторона А вычисляет

D = г * Gd mod n

и отправляет это значение стороне В.

4. Сторона В вычисляет значение

Т'= D^V I^dmod n.

Если

TºT'(mod n),

то проверка подлинности успешно завершена.

Математические выкладки, использованные в этом протоколе, не очень сложны:

Т’ = D^V I^d = (rG^d)^V I^d = r^V G^dvI^d = r^V(IG^V)^d= r^VºT (mod n)

поскольку G вычислялось таким образом, чтобы выполнялось соотношение

IG^Vº1(mod n).

ГЛАВА 6. ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ

6.1. Проблема аутентификации данных и электронная цифровая подпись

При обмене электронными документами по сети связи существенно снижаются затраты на обработку и хранение документов, убыстряется их поиск. Но при этом возникает проблема аутентификации автора документа и самого документа, т.е. установления подлинности автора и отсутствия изменений в полученном документе. В обычной (бумажной) информатике эти проблемы решаются за счет того, что информация в документе и рукописная подпись автора жестко связаны с физическим носителем (бумагой). В электронных документах на машинных носителях такой связи нет.

Целью аутентификации электронных документов является их защита от возможных видов злоумышленных действий, к которым относятся:

• активный перехват-нарушитель, подключившийся к сети, перехватывает документы (файлы) и изменяет их;

• маскарад-абонент С посылает документ абоненту B от имени абонента А;

• ренегатство - абонент А заявляет, что не посылал сообщения абоненту В, хотя на самом деле послал;

• подмена-абонент В изменяет или формирует новый документ и заявляет, что получил его от абонента А;

• повтор - абонент С повторяет ранее переданный документ, который абонент А посылал абоненту В.

Эти виды злоумышленных действий могут нанести существенный ущерб банковским и коммерческим структурам, государственным предприятиям и организациям, частным лицам, применяющим в своей деятельности компьютерные информационные технологии.

При обработке документов в электронной форме совершенно непригодны традиционные способы установления подлинности по рукописной подписи и оттиску печати на бумажном документе.
Принципиально новым решением является электронная цифровая подпись (ЭЦП).

            Электронная цифровая подпись используется для аутентификации текстов, передаваемых по телекоммуникационным каналам. Функционально она аналогична обычной рукописной подписи обладает ее основными достоинствами:      

• удостоверяет, что подписанный текст исходит от лица, поставившего подпись;  

• не дает самому этому лицу возможности отказаться от обязательств, связанных с подписанным текстом;

• гарантирует целостность подписанного текста.                     

            Цифровая подпись представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом.   

Система ЭЦП включает две процедуры: 1) процедуру постановки подписи; 2) процедуру проверки подписи. В процедуре постановки подписи используется секретный ключ отправителя сообщения, в процедуре проверки подписи - открытый ключ отправителя.

При формировании ЭЦП отправитель прежде всего вычисляет хэш-функцию h(M) подписываемого текста М. Вычисленное значение хэш-функции h(M) представляет собой один короткий блок информации т, характеризующий весь текст М в целом. Затем число m шифруется секретным ключом отправителя.  Получаемая при этом пара чисел представляет собой ЭЦП для данного текста М.

При проверке ЭЦП получатель сообщения снова вычисляет хэш-функцию m--h(M) принятого по каналу текста М, после чего при помощи открытого ключа отправителя проверяет, соответствует ли полученная подпись вычисленному значению m хэш-функции.

Принципиальным моментом в системе ЭЦП является невозможность подделки, ЭЦП пользователя без знания его секретного ключа подписывания.

В качестве подписываемого документа может быть использован любой файл. Подписанный файл создается из неподписанного путем добавления в него одной или более электронных подписей.

Каждая подпись содержит следующую информацию:

• дату подписи;

• срок окончания действия ключа данной подписи;

• информацию о лице,  подписавшем файл (Ф.И.О.. должность, краткое наименование фирмы);

• идентификатор подписавшего (имя открытого ключа);

• собственно цифровую подпись.

6.2. Однонаправленные хэш-функции

            Хэш-функция предназначена для сжатия подписываемого документа М до нескольких десятков или сотен бит. Хэш-функция h(×) принимает в качестве аргумента сообщение (документ) М произвольной длины и возвращает хэш-значение h(M)-H фиксированной длины. Обычно хэшированная информация является сжатым двоичным представлением основного сообщения произвольной длины. Следует отметить, что значение хэш-функции h(M) сложным образом зависит от документа М и не позволяет восстановить
сам документ М.

Хэш-функция должна удовлетворять целому ряду условий:

• хэш-функция должна быть чувствительна к всевозможным изменениям в тексте М, таким как вставки, выбросы, перестановки и т.п.;

• хэш-функция должна обладать свойством необратимости, то есть задача подбора документа М', который обладал бы требуемым значением хэш-функции, должна быть вычислительно неразрешима;

• вероятность того, что значения хэш-функции двух различных документов (вне зависимости от их длин) совпадут, должна быть ничтожно мала [123].

Большинство хзш-функций строится на основе однонаправленной функции f(-), которая образует выходное значение длиной n при задании двух входных значений длиной п. Этими входами являются блок исходного текста Мi и хэш-значение Нм предыдущего блока текста (рис. 6.1):

Hi = f(Mi, H_i-1).

Хэш-значение, вычисляемое при вводе последнего блока текста, становится хэш-значением всего сообщения М.

Рис. 6.1. Построение однонаправленной хэш-функции

В результате однонаправленная хэш-функция всегда формирует выход фиксированной длины n (независимо от длины входного текста).

Однонаправленные хэш-функции на основе симметричных блочных алгоритмов

Однонаправленную хэш-функцию можно построить, используя симметричный блочный алгоритм. Наиболее очевидный подход состоит в том, чтобы шифровать сообщение М посредством блочного алгоритма в режиме СВС или СРВ с помощью фиксированного ключа и некоторого вектора инициализации IV, Последний блок шифртекста можно рассматривать в качестве хэш-значения сообщения М. При таком подходе не всегда возможно построить безопасную однонаправленную хэш-функцию, но всегда можно получить код аутентификации сообщения MAC (Message Authentication Code).

Более безопасный вариант хэш-функции можно получить, используя блок сообщения в качестве ключа, предыдущее хэш-значение-в качестве входа, а текущее хэш-значение-в качестве выхода. Реальные хэш-функции проектируются еще более сложными. Длина блока обычно определяется длиной ключа, а длина хэш-значения совпадает с длиной блока.

Поскольку большинство блочных алгоритмов являются 64-битовыми, некоторые схемы хэширования проектируют так, чтобы хэш-значение имело длину, равную двойной длине блока.

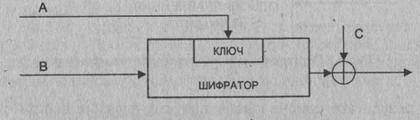
Если принять, что получаемая хэш-функция корректна, безопасность схемы хэширования базируется на безопасности лежащего в ее основе блочного алгоритма. Схема хэширования, у которой длина хэш-значения равна длине блока, показана на рис.6.2. Ее работа описывается выражениями:

H₀ = I_H,

H_i =E_A(B) Å C,

где 1Н-некоторое случайное начальное значение; А, В и С могут принимать значения M_i, Н_i-1, (M_i Å Н_i-1) или быть константами.

Рис. 6.2. Обобщенная схема формирования хэш-функции

Сообщение М разбивается на блоки Мi принятой длины, которые обрабатываются поочередно.

Три различные переменные А, В и С могут принимать одно из четырех возможных значений, поэтому в принципе можно получить 64 варианта общей схемы этого типа. Из них 52 варианта являются либо тривиально слабыми, либо небезопасными. Остальные 12 безопасных схем хэширования перечислены в табл.6.1 [121].

Первые четыре схемы хэширования, являющиеся безопасными при всех атаках, приведены на рис. 6

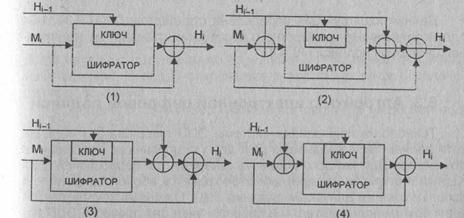
Рис. 6.3. Четыре схемы безопасного хэширования

Отечественный стандарт хэш-функции

Российский стандарт ГОСТ Р 34.11-94 определяет алгоритм и процедуру вычисления хэш-функции для любых последовательностей двоичных символов, применяемых в криптографических методах обработки и защиты информации. Этот стандарт базируется на блочном алгоритме шифрования ГОСТ 28147-89. хотя в принципе можно было бы использовать и другой блочный алгоритм шифрования с 64-битовым блоком и 256-битовым ключом.

Данная хэш-функция формирует 256-битовое хэш-значение. Функция сжатия Н_i = f(M_i, H_i-1) (оба операнда Мi и Н_i-1 являются 256-битовыми величинами) определяется следующим образом:

1. Генерируются 4 ключа шифрования Kj, j = 1,.. 4, путем линейного смешивания M_i, Н_i-1 и некоторых констант Cj.

2. Каждый ключ Kj, используют для шифрования 64-битовых подслое h_i слова Н_i-1 в режиме простой замены: S_j = E_K(h_j). Результирующая последовательность S₄, S₃, S₂, S₁ длиной 256 бит запоминается во временной переменной S.

3. Значение H_i является сложной, хотя и линейной функцией смешивания S, M_i и H_i-1.

При вычислении окончательного хэш-значения сообщения М учитываются значения трех связанных между собой переменных:

Н_n-хэш-значение последнего блока сообщения;

Z- значение контрольной суммы, получаемой при сложении по модулю 2 всех блоков сообщения;

L-длина сообщения.

Эти три переменные и дополненный последний блок М' сообщения объединяются в окончательное хэш-значение следующим образом:

H = f(Z Å M`, f(L, f(M`, H_n))).

Данная хэш-функция определена стандартом ГОСТ Р 34.11-94 для использования совместно с российским стандартом электронной цифровой подписи [40,41].

6.3. Алгоритмы электронной цифровой подписи

Технология применения системы ЭЦП предполагает наличие сети абонентов, посылающих друг другу подписанные электронные документы. Для каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ хранится абонентом в тайне и используется им для формирования ЭЦП. Открытый ключ известен всем другим пользователям и предназначен для проверки ЭЦП получателем подписанного электронного документа. Иначе говоря, открытый ключ является необходимым инструментом, позволяющим проверить подлинность электронного документа и автора подписи. Открытый ключ не позволяет вычислить секретный ключ.

Для генерации пары ключей (секретного и открытого) в алгоритмах ЭЦП, как и в асимметричных системах шифрования, используются разные математические схемы, основанные на применении однонаправленных функций. Эти схемы разделяются на две группы. В основе такого разделения лежат известные сложные вычислительные задачи:

· задача факторизации (разложения на множители) больших целых чисел;

· задача дискретного логарифмирования.

Алгоритм цифровой подписи RSA

Первой и наиболее известной во всем мире конкретной системой ЭЦП стала система RSA, математическая схема которой была разработана в 1977г. в Массачусетском технологическом
институте США.

Сначала необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель (автор) электронных документов вычисляет два больших простых числа Р и Q, затем находит их произведение 

N = P * Q

и значение функции

j(N) = (P-1)(Q-1)

Далее отправитель вычисляет число Е из условий:

E £ j(N), НОД(E, j(N))=1

и число D из условий:

D < N, E * D º 1(mod j(N)).

Пара чисел (Е,N) является открытым ключом. Эту пару чисел автор передает партнерам по переписке для проверки его цифровых подписей. Число D сохраняется автором как секретный ключ
для подписывания.

Обобщенная схема формирования и проверки цифровой подписи RSA показана на рис. 6.4.

Допустим, что отправитель хочет подписать сообщение М перед его отправкой. Сначала сообщение М (блок информации, файл, таблица) сжимают с помощью хэш-функции h(×) в целое число m:

M= h(M).

Затем вычисляют цифровую подпись S под электронным документом М, используя хэш-значение m и секретный ключ D:

S = m^D (mod N)

Пара (М, S) передается партнеру-получателю как электронный документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа D.

После приема пары (М, S) получатель вычисляет хэш-значение сообщения М двумя разными способами.

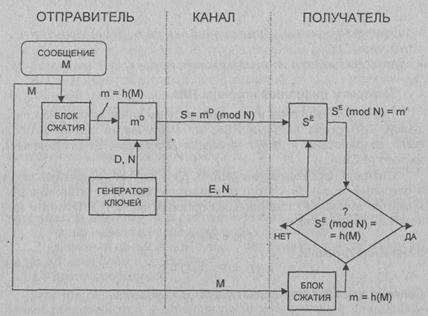
Рис. 6.4. Обобщенная схема цифровой подписи RSA.

Прежде всего он восстанавливает хэш-значение m', применяя криптографическое преобразование подписи S с использованием открытого ключа Е:

m` = S^E (mod N).

Кроме того, он находит результат хэширования принятого сообщения М с помощью такой же хэш-функции h(×):

m = h(M)

Если соблюдается равенство вычисленных значений, т.е.

S^E(mod N) = h(m)

то получатель признает пару (М, S) подлинной. Доказано, что только обладатель секретного ключа D может сформировать цифровую подпись S по документу М, а определить секретное число D по открытому числу Е не легче, чем разложить модуль N на множители.

Кроме того, можно строго математически доказать, что результат проверки цифровой подписи S будет положительным только в том случае, если при вычислении S был использован секретный ключ D, соответствующий открытому ключу Е. Поэтому открытый ключ Е иногда называют "идентификатором" подписавшего.

Недостатки алгоритма цифровой подписи RSA.

1. При вычислении модуля N, ключей Е и D для системы цифровой подписи RSA необходимо проверять большое количество дополнительных условий, что сделать практически трудно. Невыполнение любого из этих условий делает возможным фальсификацию цифровой подписи со стороны того, кто обнаружит такое
невыполнение. При подписании важных документов нельзя допускать такую возможность даже теоретически.

2. Для обеспечения криптостойкости цифровой подписи RSA по отношению к попыткам фальсификации на уровне, например, национального стандарта США на шифрование информации (алгоритм DES), т.е. 1018, необходимо использовать при вычислениях N, D и Е целые числа не менее 2512 (или около 10154) каждое, что требует больших вычислительных затрат, превышающих на 20...30% вычислительные затраты других алгоритмов цифровой подписи при сохранении того же уровня криптостойкости.

3. Цифровая подпись RSA уязвима к так называемой мультипликативной атаке. Иначе говоря, алгоритм цифровой подписи RSA позволяет злоумышленнику без знания секретного ключа D сформировать подписи под теми документами, у которых результат хэширования можно вычислить как произведение результатов хэширования уже подписанных документов.

Пример. Допустим, что злоумышленник может сконструировать три сообщения M₁, M₂ и М₃, у которых хэш-значения причем

m₁ = h(M₁), m₂ =  h(M₂), m₃ = h(M₃),

m₃ = m₁ * m₂ (mod N).

Допустим также, что для двух сообщений М₁ и М₂ получены законные подписи

S₁ = m₁^D (mod N) и S₂ = m₂^D (mod N).

Тогда злоумышленник может легко вычислить подпись S₃ для документа М₃, даже не зная секретного ключа D:

S₃ = S₁ * S₂ (mod N).

Действительно,

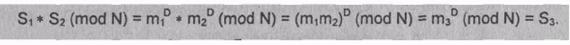
Более  надежный и удобный для реализации на персональных компьютерах алгоритм цифровой подписи был разработан в 1984г. американцем арабского происхождения Тахером Эль Гамалем. В 1991 г. НИСТ США обосновал перед комиссией Конгресса США выбор алгоритма цифровой подписи Эль Гамаля в качестве основы для национального стандарта.

Алгоритм цифровой подписи Эль Гамаля (EGSA)

Название EGSA происходит от слов El Gamai Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа, задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью
подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.

Рассмотрим подробнее алгоритм цифровой подписи Эль Гамаля. Для того чтобы генерировать пару ключей (открытый ключ секретный ключ), сначала выбирают некоторое большое простое целое число Р и большое целое число G, причем G<P. Отправитель и получатель подписанного документа используют при вычислениях одинаковые большие целые числа Р(~10³⁰⁸ или ~2¹⁰²⁴) и G(~10¹⁵⁴ или ~2⁵¹²), которые не являются секретными.

Отправитель выбирает случайное целое число Х,1<Х£ (Р-1), и вычисляет

Y = G^X mod P.

Число Y является открытым ключом, используемым для проверки подписи отправителя. Число Y открыто передается всем потенциальным получателям документов.

Число X является секретным ключом отправителя для подписывания документов и должно храниться в секрете.

Для того чтобы подписать сообщение М, сначала отправитель  хэширует его с помощью хэш-функции h(×) в целое число т:

m = h(M), 1 < m < (P-1)

и генерирует случайное целое число К, 1< К< (Р -1), такое, что К и (Р-1) являются взаимно простыми. Затем отправитель вычисляет целое число а:

a = G^K mod P

и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа X целое число b из уравнения

m = X* a + K * b (mod (P-1))

Пара чисел (а, b) образует цифровую подпись S:

S = (a, b)

проставляемую под документом М.

Тройка чисел (М, а, b) передается получателю, в то время как
пара чисел (Х,К) держится в секрете.

После приема подписанного сообщения (М, а, b) получатель должен проверить, соответствует ли подпись S = (a, b) сообщению М. Для этого получатель сначала вычисляет по принятому сообщению М число

m = h(M),

т.е. хэширует принятое сообщение М.

Затем получатель вычисляет значение

A = Y * a^b (mod P)

и признает сообщение М подлинным, если, и только если

A = G^m (mod P).

Иначе говоря, получатель проверяет справедливость соотношения

Y^aa^b (mod P) = G^m (mod P).

Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S = (a, b) под документом М получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправителем сообщения М был обладатель именно данного секретного ключа X, не раскрывая при этом сам ключ, и что отправитель подписал именно этот конкретный документ М.

Следует отметить, что выполнение каждой подписи по методу Эль Гамаля требует нового значения К, причем это значение должно выбираться случайным образом. Если нарушитель раскроет когда-либо значение К, повторно используемое отправителем, то он сможет раскрыть секретный ключ X отправителя.

Пример. Выберем: числа Р = 11, G = 2 и секретный ключ Х = 8. Вычисляем значение открытого ключа:

Y= G^X mod Р =Y= 2⁸ mod 11 = 3.

Предположим, что исходное сообщение М характеризуется хэш-значением m = 5.

Для того чтобы вычислить цифровую подпись для сообщения М, имеющего хэш-значение т = 5, сначала выберем случайное целое число К=9. Убедимся, что числа К и (Р-1) являются взаимно простыми.

Действительно,

НОД(9, 10)= 1

Далее вычисляем элементы а и b подписи:

a = G^K mod P* 2⁹ mod 11 = 6,

элемент   b определяем, используя расширенный алгоритм Евклида:

m = X * a + K * b (mod(P-1)).

При m = 5, а=6, Х=8, К=9, Р=11 получаем

5 = (6 * 8 + 9 * b)(mod 10)

или                                                                9 * b º -43(mod10).

Решение: b = 3. Цифровая подпись представляет собой пару: а=6, b=3.

Далее отправитель передает подписанное сообщение. Приняв подписанное сообщение и открытый ключ Y=3, получатель вычисляет хэш-значение для сообщения М:m=5, а затем вычисляет два числа:

1) Y^a a^b (mod Р) = 3⁶ * б³ (mod 11) = 10 (mod 11);

2) G^m (mod P) = 2⁵ (mod 11) =10 (mod 11).

Так как эти два целых числа равны, принятое получателем сообщение признается подлинным.

Следует отметить, что схема Эль Гамаля является характерным примером подхода, который допускает пересылку сообщения М в открытой форме вместе с присоединенным аутентификатором (а, b). В таких случаях процедура, установления подлинности принятого сообщения состоит в проверке соответствия аутентификатора сообщению.

Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой подписи RSA:

1.При заданном уровне стойкости алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись на 25 % короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти.

2. При выборе модуля Р достаточно проверить, что это число является простым и что у числа (Р-1) имеется большой простой множитель (т.е. всего два достаточно просто проверяемых условия).

3. Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSA).

Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по сравнению со схемой подписи RSA. В частности, длина цифровой подписи получается в 1,5 раза больше,
что, в свою очередь, увеличивает время ее вычисления.

Алгоритм цифровой подписи DSA

Алгоритм цифровой подписи DSA (Digital Signature Algorithm) предложен в 1991 г. в НИСТ США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Алгоритм DSA является развитием алгоритмов цифровой подписи Эль Гамаля и К. Шнорра [121].

Отправитель и получатель электронного документа используют при вычислении большие целые числа: G и Р - простые числа,  L бит каждое (512 £ L £ 1024); q-простое число длиной 160 бит (делитель числа (Р-1)). Числа G, P, q являются открытыми и могут быть общими для всех пользователей сети.

Отправитель выбирает случайное целое число X,1<X<q. Число X является секретным ключом отправителя для формирования электронной цифровой подписи.

Затем отправитель вычисляет значение

Y = G^X mod P.

Число Y является открытым ключом для проверки подписи отправителя. Число Y передается всем получателям документов. Этот алгоритм также предусматривает использование односторонней функции хэширования h(×). В стандарте DSS определен 3 алгоритм безопасного хэширования SHA (Secure Hash Algorithm).      

Для того чтобы подписать документ М, отправитель хэширует
его в целое хэш-значение m:

m = h(M), 1< m < q

затем генерирует случайное целое число K, 1<K<q, и вычисляет число r:

r = (G^K mod P) mod q

Затем отправитель вычисляет с помощью секретного ключа X целое число s:

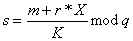
Пара чисел r и s образует цифровую подпись S = (r, s) под документом М.

Таким образом, подписанное сообщение представляет собой тройку чисел [М, r, s].

Получатель подписанного сообщения [М, r, s] проверяет выполнение условий

0 < r < q, 0 < s < q

и отвергает подпись, если хотя бы одно из этих условий не выполнено.

Затем получатель вычисляет значение

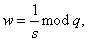
хэш-значение

m = h(m)

и числа

u₁ = (m * w) mod q,

u₂ = (r * w) mod q.

Далее получатель с помощью открытого ключа Y вычисляет значение

v = ((G^u1* Y^u2) mod P) mod q

и проверяет выполнение условия

v = r.

Если условие v = г выполняется, тогда подпись S = (r, s) под документом М признается получателем подлинной. Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S =  (r,s) под документом М получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправитель сообщения владеет именно данным секретным ключом X (не раскрывая при этом значения ключа X) и что отправитель подписал именно данный документ М.

По сравнению с алгоритмом цифровой подписи Эль Гамаля алгоритм DSA имеет следующие основные преимущества; 

1. При любом допустимом уровне стойкости, т.е. при любой паре чисел G и Р (от 512 до 1024 бит), числа q, X, r, s имеют длину по 160 бит, сокращая длину подписи до 320 бит.

2. Большинство операций с числами К, r, s, X при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.

3. При проверке подписи большинство операций с числами и u₁, u₂, v, w также производится по модулю числа q длиной 160 бит, что сокращает объем памяти и время вычисления.

Недостатком алгоритма DSA является то, что при подписывания и при проверке подписи приходится выполнять сложные операции деления по модулю q:

,

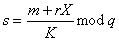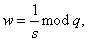
что не позволяет получать максимальное быстродействие.

Следует отметить, что реальное исполнение алгоритма DSA может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения М и его хэш-значения m. Можно заранее создать строку случайных значений К и затем для каждого из этих значений вычислить значения г. Можно также заранее вычислить обратные значения К^-1 для каждого из значений К. Затем, при поступлении сообщения М, можно вычислить значение s для данных значений r и К^-1. Эти предварительные вычисления значительно ускоряют работу алгоритма DSA.

Отечественный стандарт цифровой подписи

Отечественный стандарт цифровой подписи обозначается как ГОСТР 34.10-94 [40]. Алгоритм цифровой подписи, определяемый этим стандартом, концептуально близок к алгоритму DSA. В нем
используются следующие параметры:

р- большое простое число длиной от 509 до 512 бит либо от 1020 до 1024 бит;

q-простой   сомножитель   числа   (р-1),   имеющий   длину 254...256 бит.

а- любое число, меньшее (р-1), причем такое, что a^q mod p = 1;

х- некоторое число, меньшее q; y = a^x mod p.

Кроме того, этот алгоритм использует однонаправленную хэш-функцию Н(х). Стандарт ГОСТР34,11-94 определяет хэш-функцию, основанную на использовании стандартного симметричного алгоритма ГОСТ 28147-89.

Первые три параметра p,q и а являются открытыми и могут быть общими для всех пользователей сети. Число х является секретным ключом. Число у является открытым ключом.

Чтобы подписать некоторое сообщение m, а затем проверить подпись, выполняются следующие шаги.

1. Пользователь А генерирует случайное число k, причем k<q.

2. Пользователь А вычисляет значения

r = (a^k mod p) mod q,

s = (x * r + k(H(m))) mod q.

Если H(m) mod q = 0, то значение H(m)mod q принимают равным единице. Если r = 0, то выбирают другое значение k и начинают снова.

Цифровая подпись представляет собой два числа:

r mod 2²⁵⁶ и s mod 2²⁵⁶

Пользователь А отправляет эти числа пользователю В.

3. Пользователь В проверяет полученную подпись, вычисляя Если u = r, то подпись считается верной.

v = H(m)^q-2 mod q,

z₁ = (s * v) mod q,

z₂ = ((q – r) * v) mod q,

u = (( a^z1 * y^z2) mod p) mod q.

Различие между этим алгоритмом и алгоритмом DSA заключается в том, что в DSA

s = (k^-1(x * r + (H(m)))) mod q,

что приводит к другому уравнению верификации.

Следует также отметить, что в отечественном стандарте ЭЦП параметр q имеет длину 256 бит. Западных криптографов вполне устраивает q длиной примерно 160 бит. Различие в значениях параметра q является отражением стремления разработчиков отечественного стандарта к получению более безопасной подписи.

Этот стандарт вступил в действие с начала 1995 г.

6.4. Цифровые подписи с дополнительными функциональными свойствами

Рассматриваемые в этом разделе цифровые подписи обладают дополнительными функциональными возможностями, помимо обычных свойств аутентификации сообщения и невозможности отказа подписавшего лица от обязательств, связанных с подписанным текстом. В большинстве случаев они объединяют базовую схему цифровой подписи, например на основе алгоритма RSA, со специальным протоколом, обеспечивающим достижение тех дополнительных свойств, которыми базовая схема цифровой подписи не обладает [117,121].

К схемам цифровой подписи с дополнительными функциональными свойствами относятся:

• схемы слепой (blind) подписи,

• схемы неоспоримой (undeniable) подписи

Схемы слепой цифровой подписи

В отличие от обычных схем цифровой подписи, описанных в §6.3, схемы слепой подписи (иногда называемые схемами подписи вслепую) являются двусторонними протоколами между отправителем А и стороной В, подписывающей документ.

Основная идея этих схем заключается в следующем. Отправитель А посылает порцию информации стороне В, которую В подписывает и возвращает А. Используя полученную подпись, сторона А может вычислить подпись стороны В на более важном для себя сообщении т. По завершении этого протокола сторона В ничего не знает ни о сообщении т, ни о подписи под этим сообщением [108].

Цель слепой подписи состоит в том, чтобы воспрепятствовать подписывающему лицу В ознакомиться с сообщением стороны А, которое он подписывает, и с соответствующей подписью под этим
сообщением. Поэтому в дальнейшем подписанное сообщение невозможно связать со стороной А.

Приведем пример применения слепой подписи. Схема слепой подписи может найти применение в тех случаях, когда отправитель А (клиент банка) не хочет, чтобы подписывающая сторона В (банк) имела возможность в дальнейшем связать сообщение m и подпись s_B(m) с определенным шагом выполненного ранее протокола.

В частности, это может быть важно при организации анонимных безналичных расчетов, когда сообщение m могло бы представлять денежную сумму, которую А хочет потратить. Когда сообщение m с подписью s_B(m) предъявляется банку В для оплаты, банк В не может проследить, кто именно из клиентов предъявляет подписанный документ. Это позволяет пользователю А остаться анонимным. Принципы организации системы анонимных безналичных расчетов с использованием так называемой "электронной
наличности" ("цифровых денег") на базе протоколов слепой подписи рассмотрены в [49, 67].

Для построения протокола слепой подписи необходимы следующие компоненты [108,117]:

1. Механизм обычной цифровой подписи для подписывающей стороны В. Пусть s_B(X) обозначает подпись стороны В на документе X,

2. Функции f(×) и g(×) (известные только отправителю) такие, что

g(s_B(f(m)) = s_m (m),

где f(×) - маскирующая (blinding) функция; g(×)-демаскирующая (unblinding) функция; f(m)- замаскированное (blinded) сообщение m.

При выборе s_B, f и g существует ряд ограничений.

Выберем в качестве алгоритма подписи s_B для стороны В схему цифровой подписи RSA (см. §6.3) с открытым ключом (N,E) и секретным ключом D, причем N=Р * Q -произведение двух больших случайных простых чисел.

Пусть k - некоторое фиксированное целое число, взаимно простое с N, т.е. НОД (N, k) = 1.

Маскирующая функция f; Zn®  Zn определяется как f(m) = m* k^E mod N, а демаскирующая функция g:Zn-® Zn как g(m) = k^-1 m mod N. При таком выборе f, g и s получаем

g(s_B (f(m))) = g(s_B (mk^E mod N)) = g(m^D k mod N) = m^D mod N = s_B (m),

что соответствует требованию 2.

Согласно протоколу слепой подписи, который предложил Д. Чом [121], отправитель А сначала получает подпись стороны В на замаскированном сообщении m. Используя эту подпись, сторона А вычисляет подпись В на заранее выбранном сообщении m, где 0£ m £ N-1. При этом стороне В ничего неизвестно ни с значении m, ни о подписи, связанной с m.

Пусть сторона В имеет для подписи по схеме RSA открытый ключ (N,E) и секретный ключ D. Пусть k- случайное секретное целое число, выбранное стороной А и удовлетворяющее условиям 0£ m £ N-1  и НОД(N,k).

Протокол слепой подписи Д. Чома включает следующие шаги:

1. Отправитель А вычисляет замаскированное сообщение m = mk^E mod N и посылает его стороне В.

2. Подписывающая сторона В вычисляет подпись s = (m)^D mod N и отправляет эту подпись стороне А.

3. Сторона А вычисляет подпись s = k^-1 s mod N, которая является подписью В на сообщении m.
Нетрудно видеть  что

(m)^D º (mk^E)^D º m^D k (mod N),

поэтому

k^-1s º m^D k k^-1 º m^D (mod N)  -Л

Д. Чом разработал несколько алгоритмов слепой подписи для            создания системы анонимных безналичных электронных расчетов eCash [49,108].

Схемы неоспоримой подписи

            Неоспоримая подпись, как и обычная цифровая подпись, зависит от подписанного документа и секретного ключа. Однако в отличие от обычных цифровых подписей неоспоримая подпись не            может быть верифицирована без участия лица, поставившего эту подпись. Возможно, более подходящим названием для этих подписей было бы "подписи, не допускающие подлога".  

            Рассмотрим два возможных сценария применения неоспоримой подписи [107,117].

Сценарий 1. Сторона А (клиент) хочет получить доступ в защищенную зону, контролируемую стороной В (банком). Этой защищенной зоной может быть, например, депозитарий (хранилище ценностей клиентов). Сторона В требует от А поставить до предоставления клиенту доступа на заявке о допуске в защищенную зону подпись, время и дату. Если А применит неоспоримую подпись, тогда сторона В не сможет впоследствии доказать кому-либо, что А получил допуск без непосредственного участия А в процессе верификации подписи.

Сценарий 2. Предположим, что известная корпорация А разработала пакет программного обеспечения. Чтобы гарантировать подлинность пакета и отсутствие в нем вирусов, сторона А подписывает этот пакет неоспоримой подписью и продает его стороне В. Сторона В решает сделать копии этого пакета программного обеспечения и перепродать его третьей стороне С. При использовании стороной А неоспоримой подписи сторона С не сможет убедиться в подлинности этого пакета программного обеспечения и отсутствии в нем вирусов без участия стороны А.      

            Конечно, этот сценарий не препятствует стороне В поставить     на пакете свою подпись, но тогда для стороны В будут утрачены все маркетинговые преимущества, связанные с использованием торговой марки корпорации А. Кроме того, будет легче раскрыть мошенническую деятельность стороны В.

            Рассмотрим алгоритм неоспоримой цифровой подписи, разработанный Д. Чомом [107]. Сначала опишем алгоритм генерации ключей, с помощью которого каждая сторона А. Подписывающая документ, выбирает секретный ключ и соответствующий открытый ключ.        

            Каждая сторона А должна выполнить следующее:

1. Выбрать случайное простое число p = 2q+1, где q-также простое число,

2. Выбрать генераторное число а для подгруппы порядка q в циклической группе Zp*;     

            2.1.Выб6ать случайный элемент b Î Z_p*  и вычислить а =  b^(p-1)/q mod p.

            2.2. Если а = 1, тогда возвратиться к шагу 2.1.

3. Выбрать случайное целое xÎ{1,2,...,q-1} и вычислить у = a^X mod p.

4. Для стороны А открытый ключ равен (р,a,у), секретный ключ равен х.

Согласно алгоритму неоспоримой подписи Д. Чома, сторона А подписывает сообщение т, принадлежащее подгруппе порядка q в Zp*. Любая сторона В может проверить эту подпись при участии А.

В работе алгоритма неоспоримой подписи можно выделить два этапа:

• генерация подписи;

• верификация подписи.

На этапе генерации подписи сторона А вычисляет s=m^x mod p, где s-подпись стороны А на сообщении т. Сообщение т с подписью s отсылается стороне В.

             Этап верификации подписи выполняется стороной В с участием стороны А и включает следующие шаги:

1. В получает подлинный открытый ключ (р,a,у) стороны А.

2. В выбирает два  случайных  секретных  целых числа а, bÎ {1,2,....q-1}.

3. В вычисляет z = s^a y^D mod p и отправляет значение z стороне А.

4. А вычисляет w = (z)^1/X mod р, где xx^-1 º (mod q), и отправляет значение w стороне В.

5. В вычисляет w'=m^a a^b mod p и признает подпись s подлинной, если и только если w = W.

Убедимся, что проверка подписи s работает:

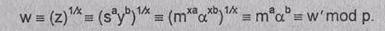
Можно показать, что с высокой степенью вероятности злоумышленник не сможет заставить В принять фальшивую подпись. Предположим, что s представляет собой подделку подписи стороны А на сообщении т, т.е. s ¹ m^x mod p. Тогда вероятность принятия стороной этой подписи в данном алгоритме составляет только Vq, причем эта вероятность не зависит от вычислительных ресурсов злоумышленника.

Подписавшая сторона А при некоторых обстоятельствах могла бы попытаться отказаться от своей подлинной подписи одним из трех способов:

(а) отказаться от участия в протоколе верификации;

(б) некорректно выполнить протокол верификации;

(в) объявить подпись фальшивой, даже если протокол верификации оказался успешным.

Отречение от подписи способом (а) рассматривалось бы как очевидная попытка неправомерного отказа. Против способов (б) и (в) бороться труднее, здесь требуется, специальный протокол дезавуирования. Этот протокол определяет, пытается ли подписавшая сторона А дезавуировать правильную подпись s или эта подпись является фальшивой. В этом протоколе по существу дважды применяется протокол верификации и затем производится проверка с целью убедиться, что сторона А выполняет этот протокол
корректно [107,117].

Протокол дезавуирования для схемы неоспоримой подписи Д. Чома включает следующие шаги:

1. В принимает от стороны А сообщение m с подписью s и получает подлинный открытый ключ (р,a,у) стороны А.

2. В выбирает случайные секретные целые числа а, b Î{1,2, .., q-1}, вычисляет z` = s^a y^b mod p и отправляет значение z стороне А,

3. А вычисляет w` = (z`)^1/Xmod р, где xx^-1 º 1(mod q), и отправляет значение w стороне В.

4. Если w = m^a a^b mod p, тогда В признает подпись s подлинной и выполнение протокола прекращается.

5. В выбирает случайные секретные целые числа а`, b` Î{1,2, ...,q-1}, вычисляет z' = s^a'y^b' mod р и отправляет значение t стороне А.

6. А вычисляет w' = (z')^1/X mod p и отправляет значение w` стороне В.

7. Если w'= m^a a^b mod р, тогда В принимает подпись s и выполнение протокола останавливается.

8. В вычисляет с = (wa^-b )^a` mod p, c'=(w'a^-b )^a mod p. Если с = с', тогда В заключает, что подпись s фальшивая; в противном случае В делает вывод, что подпись s подлинная, а сторона А пытается
дезавуировать подпись s.

Нетрудно убедиться в том, что этот протокол достигает поставленной цели. Пусть т-сообщение и предположим, что s- подпись стороны А под сообщением т. Если подпись s фальшивая, т.е. s¹m^x mod p, и если стороны А и В следуют протоколу должным образом, тогда w = w` (и поэтому справедливо заключение В, что подпись s фальшивая). Пусть s на самом деле является подписью стороны А под сообщением т, т.е. s = m^x mod p. Предположим, что В точно следует протоколу, а А не следует. Тогда вероятность того, что w = w' (и А преуспевает а дезавуировании подписи), составляет только 1/q.

Следует отметить, что третья сторона С никогда не должна принимать в качестве доказательства подлинности подписи s запись стороной В протокола верификации, поскольку сторона В может выдумать успешную запись шага 2 и последующих шагов протокола верификации без участия подписывающей стороны А.

Неоспоримая подпись может быть верифицирована только путем непосредственного взаимодействия с подписывающей стороной А.

Разработан также алгоритм для обратимой неоспоримой подписи [105], которая может быть верифицирована, дезавуирована, а также преобразована в обычную цифровую подпись. Этот алгоритм основан на использовании алгоритма цифровой подписи Эль Гамаля.

ГЛАВА 7. УПРАВЛЕНИЕ КРИПТОГРАФИЧЕСКИМИ КЛЮЧАМИ

Любая криптографическая система основана на использовании криптографических ключей. В симметричной криптосистеме отправитель и получатель сообщения используют один и тот же секретный ключ. Этот ключ должен быть неизвестен всем остальным и должен периодически обновляться одновременно у отправителя и получателя. Процесс распределения (рассылки) секретных ключей между участниками информационного обмена в симметричных криптосистемах имеет весьма сложный характер.

            Асимметричная криптосистема предполагает использование       двух ключей - открытого и личного (секретного). Открытый ключ можно разглашать, а личный надо хранить в тайне. При обмене сообщениями необходимо пересылать только открытый ключ. Важным требованием является обеспечение подлинности отправителя сообщения. Это достигается путем взаимной аутентификации участников информационного обмена.

            Под ключевой информацией понимают совокупность всех действующих в АСОИ ключей. Если не обеспечено достаточно надежное управление ключевой информацией, то, завладев ею, злоумышленник получает неограниченный доступ ко всей информации.          

            Управление ключами - информационный процесс, включающий реализацию следующих основных функций:

• генерация ключей;                                                                         

• хранение ключей;                                                                           

• распределение ключей.                                                                 

7.1. Генерация ключей

            Безопасность любого криптографического алгоритма определяется используемым криптографическим ключом. Добротные криптографические ключи должны иметь достаточную длину и случайные значения битов. В табл.4.3 приведены длины ключей симметричной и асимметричной криптосистем, обеспечивающие одинаковую стойкость к атаке полного перебора (атаке "грубой силы") [123].   

            Для получения ключей используются аппаратные и программные средства генерации случайных значений ключей. Как правило, применяют датчики псевдослучайных чисел (ПСЧ). Однако степень
случайности генерации чисел должна быть достаточно высокой. Идеальными генераторами являются устройства на основе "натуральных" случайных процессов, например на основе белого радиошума.

В АСОИ со средними требованиями защищенности вполне приемлемы программные генераторы ключей, которые вычисляют ПСЧ как сложную функцию от текущего времени и (или) числа, введенного пользователем.

Один из методов генерации сеансового ключа для симметричных криптосистем описан в стандарте ANSI X 9.17. Он предполагает использование криптографического алгоритма DES (хотя можно применить и другие симметричные алгоритмы шифрования).

Обозначения:

Е_К(Х)- результат шифрования алгоритмом DES значения X;

К- ключ, зарезервированный для генерации секретных ключей;

V₀ - секретное 64-битовое начальное число;

Т- временная отметка.

Схема генерации случайного сеансового ключа Rj в соответствии со стандартом ANSI X 9.17 показана на рис.7.1. Случайный ключ R, генерируют, вычисляя значение

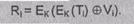
Следующее значение V_i+1 вычисляют так:

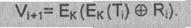
Если необходим 128-битовый случайный ключ, генерируют пару ключей R_i, R_i+1 и объединяют их вместе.

Если ключ не меняется регулярно, это может привести к его раскрытию и утечке информации. Регулярную замену ключа можно осуществить, используя процедуру модификации ключа.

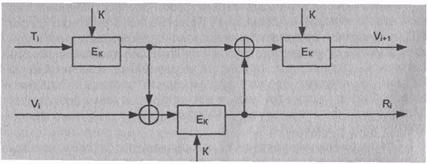
Рис.7.1. Схема генерации случайного ключа R, в соответствии
со стандартом ANSI X 9.17

Модификация ключа - это генерирование нового ключа из предыдущего значения ключа с помощью односторонней (однонаправленной) функции. Участники информационного обмена разделяют
один и тот же ключ и одновременно вводят его значение в качестве аргумента в одностороннюю функцию, получая один и тот же результат. Затем они берут определенные биты из этих результатов,
чтобы создать новое значение ключа.

Процедура модификации ключа работоспособна, но надо помнить, что новый ключ безопасен в той же мере, в какой был безопасен прежний ключ. Если злоумышленник сможет добыть прежний
ключ, то он сможет выполнить процедуру модификации ключа.

Генерация ключей для асимметричных криптосистем с открытыми ключами много сложнее, потому что эти ключи должны обладать определенными математическими свойствами (они должны
быть очень большими и простыми и т.д.).

7.2. Хранение ключей

Под функцией хранения ключей понимают организацию их безопасного хранения, учета и удаления. Ключ является самым привлекательным для злоумышленника объектом, открывающим
ему путь к конфиденциальной информации. Поэтому вопросам безопасного хранения ключей следует уделять особое внимание. Секретные ключи никогда не должны записываться в явном виде на носителе, который может быть считан или скопирован.

Носители ключевой информации

Ключевой носитель может быть технически реализован различным образом на разных носителях информации - магнитных дисках, устройствах хранения ключей типа Touch Memory, пластиковых картах и т. д.

Магнитные диски представляют собой распространенный тип носителя ключевой информации. Применение магнитного диска (МД) в качестве носителя ключа позволяет реализовать необходимое свойство отчуждаемости носителя ключа от защищенной компьютерной системы, т.е. осуществить временное изъятие МД из состава технических средств компьютерной системы. Особенно целесообразно использование в качестве ключевых носителей съемных накопителей - гибких магнитных дисков, съемных магнитооптических носителей и т.д. [73].

Основное преимущество МД по сравнению с другими носителями ключевой информации заключается в том, что оборудование для взаимодействия с МД (дисковод) входит в состав штатных

средств компьютера. Другая важная особенность, определяющая широкое распространение МД,-стандартный формат хранения информации на дисках и стандартные программные средства доступа к дискам. Кроме того, из всех средств хранения ключевой информации гибкие магнитные диски имеют самую низкую стоимость.

Для обеспечения надежного хранения ключевой информации на МД применяют как минимум двукратное резервирование объектов хранения. Это позволяет защитить ключевую информацию от
ошибок при считывании с МД и от сбоев программной и аппаратной части.

Для предотвращения возможности перехвата ключевой информации в процессе ее чтения с МД используют хранение ключевой информации на МД в зашифрованном виде.

Устройство хранения ключей типа Touch Memory является относительно новым носителем ключевой информации, предложенным американской компанией Dallas Semiconductor. Носитель
информации Touch Memory (TM) представляет собой энергонезависимую память, размещенную в металлическом корпусе, с одним сигнальным контактом и одним контактом земли. Корпус ТМ имеет
диаметр 16,25 мм и толщину 3,1 или 5,89 мм (в зависимости от модификации прибора).

В структуру ТМ входят следующие основные блоки [73]:

• Постоянное запоминающее устройство (ПЗУ) хранит 64-разрядный код, состоящий из байтового кода типа прибора, 48-битового уникального серийного номера и 8-битовой контрольной суммы. Содержимое ПЗУ уникально и не может быть изменено в течение всего срока службы прибора.

• Оперативное запоминающее устройство (ОЗУ) емкостью от 128 до 8192 байт содержат практически все модификации ТМ. В одной из модификаций оперативная память аппаратно защищена от несанкционированного доступа.

• Встроенная миниатюрная литиевая батарейка со сроком службы не менее 10 лет обеспечивает питанием все блоки устройства.

Особенностью технологии хранения и обмена ключевой информации между носителем ТМ и внешними устройствами является сравнительно низкая скорость (обусловленная последовательной передачей данных) и высокая вероятность сбоя в тракте чтения-записи, обусловленная тем, что контакт устройства ТМ с устройством чтения осуществляется пользователем вручную без дополнительной фиксации (простое касание, что и определило название прибора ТМ). В связи с этим особое значение приобретают вопросы надежного обмена между программами обработки ключевой информации пользователей и носителем ТМ.

В устройстве ТМ конструктивно отработаны вопросы надежности функционирования и вопросы интерфейса со считывающим устройством на основе одного, сигнального контакта. Для обеспечения достоверного чтения применяются корректирующие коды, для обеспечения достоверной записи в приборе предусмотрена технология буферизации. При проведении операции записи первоначально вектор передаваемой в ТМ информации помещается в буфер, далее выполняется операция чтения из буфера, затем прочтенная из буфера информация сравнивается с записываемой и в случае совпадения подается сигнал переноса информации из буфера в память долговременного хранения.

Таким образом, носитель ТМ является микроконтроллерным устройством без собственной вычислительной мощности и с ограниченным объемом хранения, но с достаточно высокими надежностными характеристиками. Поэтому применение ТМ вполне обосновано в случае повышенных требований к надежности носителя ключа и небольшого объема ключевой информации, хранимой в ТМ.

 Электронные пластиковые карты становятся в настоящее время наиболее распространенным и универсальным носителем конфиденциальной информации, который позволяет идентифицировать и аутентифицировать пользователей, хранить криптографические ключи, пароли и коды.

Интеллектуальные карты (смарт-карты), обладающие наибольшими возможностями, не только эффективно применяются для хранения ключевой информации, но и широко используются в электронных платежных системах, в комплексных решениях для медицины, транспорта, связи, образования и т.п. Более подробные сведения об электронных пластиковых картах приводятся в § 9.4.

Концепция иерархии ключей

Любая информация об используемых ключах должна быть защищена, в частности храниться в зашифрованном виде.

Необходимость в хранении и передаче ключей, зашифрованных с помощью других ключей, приводит к концепции иерархии ключей. В стандарте ISO 8532 (Banking-Key Management) подробно
изложен метод главных/сеансовых ключей (master/session keys).Суть метода состоит в том, что вводится иерархия ключей: главный ключ (ГК), ключ шифрования ключей (КК), ключ шифрования данных (КД).

Иерархия ключей может быть:

• двухуровневой (КК/КД);

• трехуровневой (ГК/КК/КД).

Самым нижним уровнем являются рабочие или сеансовые КД, которые применяются для шифрования данных, персональных идентификационных номеров (PIN) и аутентификации сообщений.

Когда эти ключи надо зашифровать с целью защиты при передаче или хранении, используют ключи следующего уровня - ключи шифрования ключей. Ключи шифрования ключей никогда не должны использоваться как сеансовые (рабочие) КД, и наоборот, Такое разделение функций необходимо для обеспечения максимальной безопасности. Фактически стандарт устанавливает, что различные типы рабочих ключей (например, для шифрования данных, для аутентификации и т.д.) должны всегда шифроваться с
помощью различных версий ключей шифрования ключей. В частности, ключи шифрования ключей, используемые для пересылки ключей между двумя узлами сети, известны также как ключи обмена между узлами сети (cross domain keys). Обычно в канале используются два ключа для обмена между узлами сети, по одному в каждом направлении. Поэтому каждый узел сети будет иметь ключ отправления для обмена с узлами сети и ключ получения для каждого канала, поддерживаемого другим узлом сети.

На верхнем уровне иерархии ключей располагается главный ключ, мастер-ключ. Этот ключ применяют для шифрования КК, когда требуется сохранить их на диске. Обычно в каждом компьютере используется только один мастер-ключ.

Мастер-ключ распространяется между участниками обмена неэлектронным способом - при личном контакте, чтобы исключить его перехват и/или компрометацию. Раскрытие противником значения мастер -ключа полностью уничтожает защиту компьютера.

Значение мастер - ключа фиксируется на длительное время (до нескольких недель или месяцев). Поэтому генерация и хранение мастер - ключей являются критическими вопросами криптографической защиты. На практике мастер-ключ компьютера создается истинно случайным выбором из всех возможных значений ключей.

Мастер-ключ помещают в защищенный от считывания и записи и от механических воздействий блок криптографической системы таким образом, чтобы раскрыть значение этого ключа было невозможно. Однако все же должен существовать способ проверки, является ли значение ключа правильным.

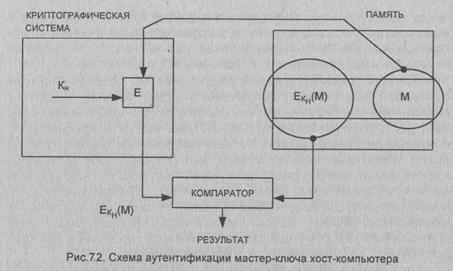
Проблема аутентификации мастер - ключа может быть решена различными путями. Один из способов аутентификации показан на рис.7.2 [123].

Администратор, получив новое значение мастер - ключа Кн хост - компьютера, шифрует некоторое сообщение М ключом Кн. Пара (криптограмма Е_Кн{М), сообщение М) помещается в память компьютера. Всякий раз, когда требуется аутентификация мастер - ключа хост - компьютера, берется сообщение М из памяти и подается в криптографическую систему. Получаемая криптограмма сравнивается с криптограммой, хранящейся в памяти. Если они совпадают, считается, что данный ключ является правильным.

Рабочие ключи (например, сеансовый) обычно создаются с помощью псевдослучайного генератора и могут храниться в незащищенном месте. Это возможно, поскольку такие ключи генерируются в форме соответствующих криптограмм, т.е. генератор ПСЧ выдает вместо ключа К3 его криптограмму Е_Kн(К3), получаемую с помощью мастер - ключа хост - компьютера. Расшифровывание такой криптограммы выполняется только перед использованием ключа Ks.

Схема защиты рабочего (сеансового) ключа показана на рис.7.3. Чтобы зашифровать сообщение М ключом Ks, на соответствующие входы криптографической системы подается криптограмма

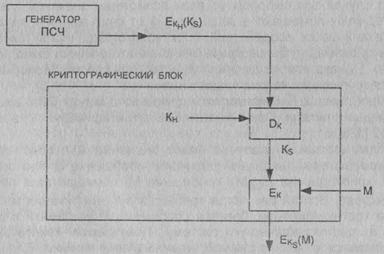
Рис.7.3. Схема защиты ключа K_S

E_KH и сообщение М. Криптографическая система сначала восстанавливает ключ Ks, а затем шифрует сообщение М, используя открытую форму сеансового ключа Ks.

Таким образом, безопасность сеансовых ключей зависит от безопасности криптографической системы. Криптографический блок может быть спроектирован как единая СБИС и помещен в физически защищенное место.

Очень важным условием безопасности информации является периодическое обновление ключевой информации в АСОИ. При этом должны переназначаться как рабочие ключи, так и мастер - ключи. В особо ответственных АСОИ обновление ключевой информации (сеансовых ключей) желательно делать  ежедневно. Вопрос обновления ключевой информации тесно связан с третьим элементом управления ключами - распределением ключей.