3.6. Блочные и поточные шифры

Проектирование алгоритмов шифрования данных основано на рациональном выборе функций, преобразующих исходные (незашифрованные) сообщения в шифртекст. Идея непосредственного
применения такой функции ко всему сообщению реализуется очень редко. Практически все применяемые криптографические методы связаны с разбиением сообщения на большое число фрагментов (или знаков) фиксированного размера, каждый из которых шифруется отдельно. Такой подход существенно упрощает задачу шифрования, так как сообщения обычно имеют различную длину.

Различают три основных способа шифрования: поточные шифры, блочные шифры и блочные шифры с обратной связью. Для классификации методов шифрования данных следует выбрать
некоторое количество характерных признаков, которые можно применить для установления различий между этими методами. Будем полагать, что каждая часть или каждый знак сообщения
шифруется отдельно в заданном порядке.

Можно выделить следующие характерные признаки методов шифрования данных [72].

• Выполнение операций с отдельными битами или блоками. Известно, что для некоторых методов шифрования знаком сообщения, над которым производят операции шифрования, является отдельный бит, тогда как другие методы оперируют конечным множеством битов, обычно называемым блоком.

• Зависимость или независимость функции шифрования от результатов шифрования предыдущих частей сообщения.

• Зависимость или независимость шифрования отдельных знаков от их положения в тексте. В некоторых методах знаки шифруются с использованием одной и той же функции независимо от их положения в сообщении, а в других методах, например при поточном шифровании, различные знаки сообщения шифруются с учетом их положения в сообщении. Это свойство называют позиционной зависимостью или независимостью шифра.

• Симметрия или асимметрия функции шифрования. Эта важная характеристика определяет существенное различие между обычными симметричными (одноключевыми) криптосистемами и асимметричными (двухключевыми) криптосистемами с открытым ключом. Основное различие между ними состоит в том, что в асимметричной криптосистеме знания ключа шифрования (или расшифрования) недостаточно для раскрытия соответствующего ключа расшифрования (или шифрования).

В табл.3.11 приведены типы криптосистем и их основные характеристики.

Таблица 3.11

Основные характеристики криптосистем

Тип криптосистемы	Операции с битами или блоками	Зависимость от предыдущих знаков	Позиционная зависимость	Наличие симметрии функции шифрования
Поточного шифрования	Биты	Не зависит	Зависит	Симметричная
Блочного шифрования	Блоки	Не зависит	Не зависит	Симметричная или несимметричная
С обратной связью от шифртекста	Биты или блоки	Зависит	Не зависит	Симметричная

Поточное шифрование состоит в том, что биты открытого текста складываются по модулю 2 с битами псевдослучайной последовательности. К достоинствам поточных шифров относятся
высокая скорость шифрования, относительная простота реализации и отсутствие размножения ошибок. Недостатком является необходимость передачи информации синхронизации перед заголовком сообщения, которая должна быть принята до расшифрования любого сообщения. Это обусловлено тем, что если два различных сообщения шифруются на одном и том же ключе, то для расшифрования этих сообщений требуется одна и та же псевдослучайная последовательность. Такое положение может создать угрозу криптостойкость системы. Поэтому часто используют дополнительный, случайно выбираемый ключ сообщения, который передается в начале сообщения и применяется для модификации ключа шифрования. В результате разные сообщения будут шифроваться с помощью различных последовательностей.

Поточные шифры широко применяются для шифрования преобразованных в цифровую форму речевых сигналов и цифровых данных, требующих оперативной доставки потребителю информации. До недавнего времени такие применения были преобладающими для данного метода шифрования. Это обусловлено, в частности, относительной простотой проектирования и реализации генераторов хороших шифрующих последовательностей. Но самым важным фактором, конечно, является отсутствие размножения ошибок в поточном шифре. Стандартным методом генерирования последовательностей для поточного шифрования является метод, применяемый в стандарте шифрования DES в режиме обратной
связи по выходу (режим OFB).

При блочном шифровании открытый текст сначала разбивается на равные по длине блоки, затем применяется зависящая от ключа функция шифрования для преобразования блока открытого
текста длиной m бит в блок шифртекста такой же длины. Достоинством блочного шифрования является то, что каждый бит блока шифртекста зависит от значений всех битов соответствующего блока открытого текста, и никакие два блока открытого текста не могут быть представлены одним и тем же блоком шифртекста. Алгоритм блочного шифрования может использоваться в различных режимах. Четыре режима шифрования алгоритма DES фактически применимы к любому блочному шифру: режим прямого шифрования или шифрования с использованием электронной книги кодов ЕСВ (Electronic code Book), шифрование со сцеплением блоков шифртекста СВС (Cipher block chaining), шифрование с обратной связью по шифртексту СFВ (Cipher feedback) и шифрование с обратной связью по выходу OFB (Output feedback).

Основным достоинством прямого блочного шифрования ЕСВ является то, что в хорошо спроектированной системе блочного шифрования небольшие изменения в шифртексте вызывают
большие и непредсказуемые изменения в соответствующем открытом тексте, и наоборот. Вместе с тем применение блочного шифра в данном режиме имеет серьезные недостатки. Первый из них заключается в том, что вследствие детерминированного характера шифрования при фиксированной длине блока 64 бита можно осуществить криптоанализ шифртекста "со словарем" в ограниченной форме. Это обусловлено тем, что идентичные блоки открытого текста длиной 64 бита в исходном сообщении представляются идентичными блоками шифртекста, что позволяет криптоаналитику сделать определенные выводы о содержании сообщения. Другой потенциальный недостаток этого шифра связан с размножением ошибок. Результатом изменения только одного бита в принятом блоке шифртекста будет неправильное расшифрование всего блока. Это, в свою очередь, приведет к появлению искаженных битов (от 1 до 64) в восстановленном блоке исходного текста.

Из-за отмеченных недостатков блочные шифры редко применяются в указанном режиме для шифрования длинных сообщений. Однако в финансовых учреждениях, где сообщения часто состоят
из одного или двух блоков, блочные шифры широко используют в режиме прямого шифрования. Такое применение обычно связано с возможностью частой смены ключа шифрования, поэтому вероятность шифрования двух идентичных блоков открытого текста на одном и том же ключе очень мала.

Криптосистема с открытым ключом также является системой блочного шифрования и должна оперировать блоками довольно большой длины. Это обусловлено тем, что криптоаналитик знает
открытый ключ шифрования и мог бы заранее вычислить и составить таблицу соответствия блоков открытого текста и шифртекста. Если длина блоков мала, например 30 бит, то число возможных
блоков не слишком большое (при длине 30 бит это 2³⁰ = ~10⁹), и может быть составлена полная таблица, позволяющая моментально расшифровать любое сообщение с использованием известного открытого ключа. Асимметричные криптосистемы с открытым ключом подробно разбираются в следующей главе.

Наиболее часто блочные шифры применяются в системах шифрования с обратной связью. Системы шифрования с обратной связью встречаются в различных практических вариантах. Как и при блочном шифровании, сообщения разбивают на ряд блоков, состоящих из m бит. Для преобразования этих блоков в блоки шифртекста, которые также состоят из m бит, используются специальные функции шифрования. Однако если в блочном шифре такая функция зависит только от ключа, то в блочных шифрах с обратной связью она зависит как от ключа, так и от одного или более предшествующих блоков шифртекста.

Практически важным шифром с обратной связью является шифр со сцеплением блоков шифртекста СВС. В этом случае   m  бит предыдущего шифртекста суммируются по модулю 2 со следующими   m  битами открытого текста, а затем применяется алгоритм блочного шифрования под управлением ключа для получения следующего блока шифртекста. Еще один вариант шифра с обратной связью получается из стандартного режима СFВ алгоритма DES, т.е. режима с обратной связью по шифртексту.

Достоинством криптосистем блочного шифрования с обратной связью является возможность применения их для обнаружения манипуляций сообщениями, производимых активными перехватчиками. При этом используется факт размножения ошибок в таких, шифрах, а также способность этих систем легко генерировать код аутентификации сообщений. Поэтому системы шифрования с обратной связью используют не только для шифрования сообщений, но и для их аутентификации. Криптосистемам блочного шифрования с обратной связью свойственны некоторые недостатки. Основным из них является размножение ошибок, так как один ошибочный бит при передаче может вызвать ряд ошибок в расшифрованном тексте. Другой недостаток связан с тем, что разработка и реализация систем шифрования с обратной связью часто оказываются более трудными, чем систем поточного шифрования.

На практике для шифрования длинных сообщений применяют поточные шифры или шифры с обратной связью. Выбор конкретного типа шифра зависит от назначения системы и предъявляемых к ней требований.

3.7. Криптосистема с депонированием ключа

Общие сведения

Криптосистема с депонированием ключа предназначена для шифрования пользовательского трафика (например, речевого или передачи данных) таким образом, чтобы сеансовые ключи, используемые для зашифрования и расшифрования трафика, были доступны при определенных чрезвычайных обстоятельствах авторизованной третьей стороне [97, 117, 121].

По существу, криптосистема с депонированием ключа реализует новый метод криптографической защиты информации, обеспечивающий высокий уровень информационной безопасности при
передаче по открытым каналам связи и отвечающий требованиям национальной безопасности. Этот метод основан на применении специальной шифрующей/дешифрующей микросхемы типа Clipper и процедуры депонирования ключа, определяющей дисциплину раскрытия уникального ключа этой микросхемы. Микросхема Clipper разработана по технологии TEMPEST, препятствующей считыванию информации с помощью внешних воздействий. Генерация и запись уникального ключа в микросхему выполняется до встраивания микросхемы в конечное устройство. Следует отметить, что не существует способа, позволяющего непосредственно считывать этот ключ как во время, так и по завершении технологического процесса производства и программирования данной микросхемы.

Ключ разделяется на два компонента, каждый из которых шифруется и затем передаётся на хранение доверенным Агентам Депозитной Службы, которые представляют собой правительственные организации, обеспечивающие надёжное хранение компонентов ключа в течение срока его действия. Агенты Депозитной Службы выдают эти компоненты ключа только по соответствующему запросу, подтверждённому решением Федерального Суда. Полученные компоненты ключа позволяют службам, отвечающим за национальную безопасность, восстановить уникальный ключ и выполнить расшифрование пользовательского трафика.

В 1994г. в США был введён новый стандарт шифрования с депонированием ключа EES (Escrowed Encryption Standard) [97]. Стандарт EES предназначен для защиты информации, передаваемой по коммутируемым телефонным линиям связи ISDN (Integrated Services Digital Network) и радиоканалам, включая голосовую информацию, факс и передачу данных со скоростями стандартных коммерческих модемов. Стандарт EES специфицирует алгоритм криптографического преобразования Skipjack с 80-битовым ключом и метод вычисления специального поля доступа LEAF (Law Enforcement Access Field), позволяющего впоследствии раскрыть секретный ключ в целях контроля трафика при условии соблюдения законности. Алгоритм Skipjack и метод вычисления поля LEAF должны быть реализованы на базе микросхемы типа Clipper. Этот стандарт специфицирует уникальный идентификатор (серийный номер) микросхемы UID (Device Unique Identifier), уникальный ключ микросхемы KU (Device Unique Key) и общий для семейства микросхем ключ KF (Family Key). Вся эта информация записывается в микросхему после её производства, но до встраивания в конкретное устройство. Хотя ключ KU не используется непосредственно для шифрования информационных потоков между отправителем и получателем, объединение его с полем доступа LEAF и ключом KF позволяет восстановить сеансовый ключ KS и выполнить дешифрование.

Криптоалгоритм SkipJack. Криптоалгоритм Skipjack преобразует 64-битовый входной блок в ,64-битовый выходной блок с помощью 80-битового секретного ключа. Поскольку один и тот же ключ используется для шифрования и расшифрования, этот алгоритм относится к классу симметричных криптосистем. Отметим, что размер блока в алгоритме Skipjack такой же, как и в DES, но при этом используется более длинный ключ.

Алгоритм Skipjack может функционировать в одном из четырёх режимов, введённых для стандарта DES:

• электронной кодовой книги (ЕСВ);

• сцепления блоков шифртекста (СВС);

• 64-битовой обратной связи по выходу (OFB);

• обратной связи по шифртексту (CFB) для 1-, 8-, 16-, 32- или 64-битовых блоков.

Алгоритм SpikJack был разработан непосредственно Агентством Национальной Безопасности (АНБ) США и засекречен, чтобы сделать невозможной разработку программной или аппаратной
реализации процедур шифрования и расшифрования отдельно от процедуры депонирования ключа. Практическая криптостойкость алгоритма Skipjack была подтверждена группой независимых экспертов -криптографов.

Метод вычисления поля LEAF. Поле доступа LEAF передаётся получателю в начале каждого сеанса связи и содержит секретный сеансовый ключ шифрования/расшифрования KS (Session Key). Только официальные лица, имеющие законное разрешение, могут получить сеансовый ключ КЗ и дешифровать все ранее зашифрованные на нём сообщения. Хотя ключ KS передаётся в поле LEAF, последнее используется исключительно для контроля над соблюдением законности и не предназначено для распределения ключей абонентам. Микросхема Clipper, установленная в принимающем устройстве, не позволяет извлечь ключ KS из информации в поле LEAF.

Поле доступа LEAF вычисляется как функция от сеансового ключа KS, вектора инициализации IV (Initialization Vector), идентификатора микросхемы DID и уникального ключа KU. Поле LEAF состоит из ключа KS, зашифрованного на Ключе KU (80 бит), идентификатора   UID   (32 бита)   и   16-битового   аутентификатора   ЕА (Escrow Authenticator). Формирование содержимого поля LEAF завершается шифрованием указанной информации на ключе семейства микросхем KF, т. е.

LEAF = E_KF(E_KU(KS), UID, ЕА).

Таким образом, сеансовый ключ KS закрыт двойным шифрованием (рис. 3.14) и может быть раскрыт в результате последовательного расшифрования на ключах KF и KU.           

Детали алгоритма вычисления LEAF засекречены, включая режим шифрования алгоритма Skipjack и метод вычисления ayтентификатора ЕА. Аутентификатор ЕА позволяет контролировать целостность и защищает поле LEAF от навязывания ложной информации.

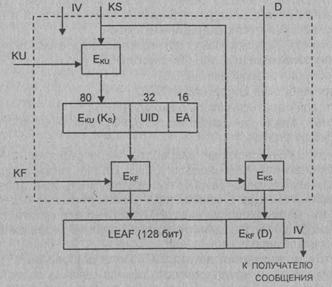
Обозначения:

KS       - сеансовый ключ

IV        - вектор инициализации

D         - передаваемые данные

KU      - уникальный ключ микросхемы

DID     - идентификатор микросхемы

ЕА       - аутентификатор поля LEAF

KF       - ключ семейства

Рис. 3.14. Вычисление LEAF и формирование зашифрованного сообщения

Способ применения. Для защиты телефонных переговоров каждый из абонентов должен иметь специальное криптографическое устройство, содержащее Clipper, Capstone или другую аналогичную микросхему (рис. 3.15). В этом устройстве должен быть реализован протокол, позволяющий абонентам обмениваться секретным сеансовым ключом KS, например, с помощью известного метода "цифрового конверта" (digital envelope).

Данный метод применяется в устройстве защиты телефонных  переговоров TSD (3600 Telephone Security Device) компании AT&T. Оно подключается встык между телефонной трубкой и основным блоком и активизируется нажатием кнопки. После установления ключевого синхронизма ключ KS вместе с вектором инициализации IV подаётся на вход микросхемы для вычисления LEAF. Затем LEAF вместе с IV передается принимающей стороне для проверки и синхронизации микросхем на передающем и приёмном концах. После синхронизации микросхем сеансовый ключ KS используется для шифрования и расшифрования данных (речь предварительно оцифровывается) в обоих направлениях.       

В дуплексном и полудуплексном режимах связи каждое криптографическое устройство передаёт свою уникальную пару IV и  LEAF. При этом оба устройства используют один и тот же сеансовый ключ КS для шифрования и расшифрования.

Первая партия микросхем для криптографических устройств с депонированием ключа была изготовлена компанией VLSI Technology Inc. и запрограммирована фирмой Mykotronx, В устройстве
TSD используется микросхема МУК-78Т (Mykotronx) с быстродействием 21 Мбит/с.

Рассмотрим подробнее функционирование криптосистемы с депонированием ключа и необходимую для её работы инфраструктуру.

Процедура генерации ключей

В процедуре генерации ключей участвуют Национальный Менеджер Программы; два Агента Депозитной Службы; два Агента KF-Службы, отвечающие за формирование и хранение ключа семейства KF; представитель Службы Программирования микросхем (Programming Facility) [97, 117].

До генерации уникального ключа микросхемы KU и соответствующих ему ключевых компонентов КС1 и КС2 необходимо сгенерировать вспомогательные ключи KN1 и KN2 и случайные числа RS1 и RS2 (Random Seeds). В процедуре генерации используется специальная смарт-карта, на которой в соответствии со стандартом Х9.17 (FIPS 171) реализован генератор псевдослучайных чисел. Начальное значение генератора формируется как результат вычисления хэш-функции от последовательности случайных символов, введённых с клавиатуры, временных интервалов между нажатиями при вводе символов с клавиатуры и текущего времени суток.

Описанная выше процедура используется Агентами Депозитной Службы для генерации ключевых чисел KN1, KN2 и случайных чисел RS1,. RS2. Назначение вспомогательных ключевых чисел и случайных чисел будет пояснено в последующих разделах.

Компоненты ключа семейства KF. Агенты KF-Службы, отвечающие за формирование ключа семейства KF, генерируют компоненты KFC1 и KFC2 на отдельных операционных пунктах.

По две копии каждого компонента записываются на магнитные носители. Каждый магнитный носитель помещают в специальный пронумерованный контейнер. Контейнер с копией каждого компонента на магнитном носителе помещается в отдельный сейф.

Ключевые и случайные числа. Каждый Агент Депозитной Службы генерирует и записывает на магнитные носители четыре копии ключевых чисел KN1 и KN2. Каждый магнитный носитель
помещается в специальный пронумерованный контейнер. Контейнер с копией каждого компонента на магнитном носителе помещают в отдельный сейф, установленный в операционном пункте
Агента. Кроме того, каждый Агент генерирует и записывает на магнитный носитель одно случайное число RS. Магнитный носитель в контейнере помещается в сейф.

Каждый Офицер Депозитной Службы (представитель Агента) доставляет в Службу  Программирования микросхем две копии ключевого числа (KN1 или KN2) и одну копию случайного числа (RS1 или RS2).

Программирование микросхемы

Программирование микросхемы осуществляется внутри специального бокса SCIF (Sensitive Compartmented Information Facility).

Операция программирования выполняется с санкции Национального Менеджера Программы и требует участия:

• Офицеров Депозитной Службы (по одному от каждого Агента);

• двух Офицеров, представляющих Агентов KF-Службы (далее -Офицеров KF-Службы);

• Представителя Службы Программирования микросхем [97].

Служба Программирования использует:

• автоматизированное рабочее место (под управлением ОС UNIX)
для генерации уникального ключа микросхемы KU и его компонентов КС1 и КС2;

• персональный компьютер для контроля процесса программирования микросхемы;

• устройство программирования микросхем IMS (Integrated Measurement System) с производительностью порядка 120 микросхем в час.

Инициализация. Подготовительные действия перед каждой процедурой включают передачу (секретной почтой) в Службу Программирования по одной копии каждого компонента (KFC1, KFC2)
ключа семейства KF. Контейнеры с магнитными носителями помещают в сейф с двойным замком Службы Программирования.

Офицеры Депозитной Службы доставляют в Службу Программирования свои контейнеры с ключевой информацией (KN1, KN2, RS1, RS2). Затем два Офицера Депозитной Службы (по одному от каждого Агента) отпирают сейф.

Представитель Службы Программирования, действующий по доверенности от Агентов KF-Службы, извлекает из сейфа магнитные носители с компонентами KFC1 и KFC2. Следуя установленной процедуре, магнитные носители с компонентами KFC1 и KFC2 вставляются в считывающее устройство автоматизированного рабочего места.

Ключ семейства KF вычисляется путем побитового сложения по модулю 2 компонент KFC1 и

KF = KFC1 Å KFC2,

Затем Офицеры Депозитной Службы вводят значения KN1, KN2, RS1, RS2 и произвольные последовательности символов АI1           и AI2 с клавиатуры.

Ключевые   числа   KN1   и   KN2   побитово   суммируются   по модулю 2 для вычисления ключа шифрования КСК (Key Component Enciphering Key):

KCK = KN1 Å KN2

Ключ КСК предназначен для шифрования компонентов КС1 и КС2 ключа KU.

Офицеры Депозитной Службы вводят также начальный серийный номер (Start DID) для формирования уникального идентификатора микросхемы DID. Процедура генерации и программирования микросхемы иллюстрируется на рис. 3.16.

Генерация ключа KU. Случайные числа RS1, RS2 и произвольные последовательности символов АI1, AI2 используются для вычисления пары значений. Одно из этих значений служит для формирования ключа KU, а другое - для формирования компоненты КС1.

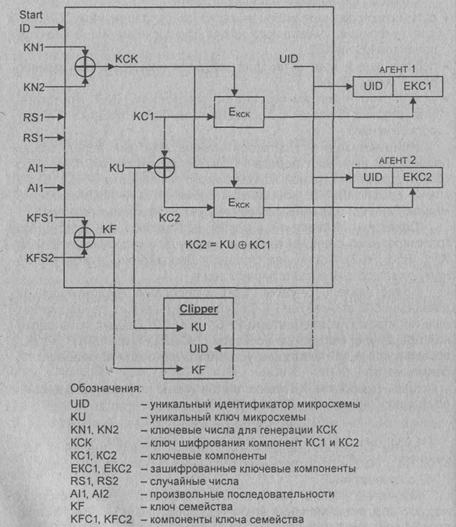
Рис. 3.16. Генерация ключа и программирование микросхемы

Далее ключ KU и компонента КС1 побитово суммируются по модулю 2 для вычисления компонента КС2:

KC2= KU Å KC1.

Таким образом, ключ KU может быть вычислен как сумма компонентов КС1 и КС2:

KU = KC1 Å KC2

Затем компоненты КС1 и КС2 шифруются на ключе КСК.

Пара KU/LJID подаётся на вход устройства программирования IMS и вместе с ключом KF записывается в микросхему.

Зашифрованные компоненты КС1 и КС2 (т.е. ЕКС1, ЕКС2) вместе с DID записываются на четыре магнитных носителя (по две копии каждого компонента), упаковываются в пронумерованные
контейнеры и помещаются в сейф с двойным замком до момента завершения процедуры программирования микросхемы.

Уничтожение и транспортировка ключевых компонентов. В обязанности Офицеров входит также активизация специальной программы, стирающей ключевую информацию с магнитных накопителей и оперативной памяти. По завершении этой процедуры Офицеры Депозитной Службы независимо друг от друга доставляют в депозитарий первого Агента контейнер с магнитным носителем, содержащим компонент ЕКС1 и DID, и в депозитарий второго Агента-компонент ЕКС2 и UID. До того как покинуть SCIF, Офицеры Депозитной Службы регистрируют свои действия в специальном журнале.

Обслуживание ключей

Агенты Депозитной Службы помещают копии ключевых компонентов в отдельный сейф с двойным замком. Для отпирания такого сейфа требуется участие двух лиц. Таким образом, надежность депозитария обеспечивается за счет двойного контроля, физической безопасности, криптографических средств и резервирования.

После доставки ключевых компонентов ЕКС1 и ЕКС2 в депозитарий каждый из двух Офицеров проверяет целостность контейнеров и их номеров. Если контейнеры не были скомпрометированы, Офицеры выполняют их регистрацию и помещают копию регистрационной записи вместе с контейнерами в сейф. Эти контейнеры с ключевыми компонентами хранятся в сейфах до тех пор, пока не будет получена санкция на их извлечение [97].

Процедура выдачи ключевых компонентов. Ключевые компоненты выдаются только с санкции Федерального Суда и в соответствии с процедурой, установленной Генеральным Прокурором. Эта процедура предполагает формирование специальных запросов и представление их Агентам Депозитной Службы. Назначение запроса заключается в установлении факта легальности расследования со стороны запрашивающего органа, законности расследования, определения сроков и т.д. Запрос включает также
идентификатор DID и серийный номер Процессора Дешифрования (Key Escrow Decryption Processor). В случае, если запрос принят, Агенты Депозитной Службы выдают ключевые компоненты, соответствующие заданному UID. Следует отметить, что должна  быть обеспечена гарантия того, что по истечении срока расследования эти ключевые компоненты не смогут быть повторно использованы
в тех же целях.

Извлечение и транспортировка ключевых компонентов. Получив официальное разрешение на выдачу ключевого компонента, соответствующего одному или более UID, Агент Депозитной Службы дает указание своим Офицерам открыть один из сейфов и извлечь ключевой компонент. Поскольку сейф имеет двойной замок, для его отпирания необходимо участие двух Офицеров. Помимо ключевого компонента (ЕКС1 или ЕКС2) из сейфа извлекаются ключевые числа (KN1, KN2), необходимые для формирования
ключа дешифрования КСК. Факт извлечения ключевого компонента регистрируется в журнале.

Офицеры извлекают магнитные носители из контейнеров и в соответствии с запросом Программы Извлечения Ключа (Key Extract Program) вставляют их в считывающее устройство персонального компьютера. Эта Программа идентифицирует ключевой компонент по заданному UID и копирует его на отдельный магнитный -носитель. По завершении процесса копирования все магнитные носители убираются в контейнеры. Все контейнеры, кроме контейнера с копией зашифрованного ключевого компонента и ключевым числом, помещаются в сейф.

В результате два Офицера от каждого Агента Депозитной Службы доставляют контейнеры с копией зашифрованного ключевого компонента и ключевыми числами на специальный операционный пункт Службы Дешифрования. Права доступа на операционный пункт Службы Дешифрования  подтверждаются процедурой авторизации.

Процедура дешифрования

Поставщики телекоммуникационных услуг обязаны предоставлять компетентным органам доступ к каналам связи в том случае, если необходимость этого подтверждается соответствующим судебным решением. Обычной практикой является предоставление выделенной линии связи для передачи перехваченных шифртекстов на операционный пункт Службы Дешифрования.

Дешифрующий Процессор, установленный на операционном пункте, представляет собой персональный компьютер со специально разработанной платой. Запуск этого компьютера выполняется только после ввода ключа с Touch Memory. Дешифрующий Процессор узко специализирован, функционально ограничен и предназначен для решения конкретных задач дешифрования
[97, 117].

При обработке речевой информации необходимо дополнительное оборудование для преобразования цифрового сигнала в аналоговый.

Инициализация дешифрующего процессора. Перед тем как Дешифрующий Процессор будет использован по назначению, необходимо выполнить его инициализацию – ввести ключ семейства
KF. Для этого два Офицера от каждого Агента KF-Службы доставляют компоненты ключа семейства на операционный пункт Службы Дешифрования. Далее компоненты KFC1 и KFC2 вводятся в
Дешифрующий Процессор для формирования ключа KF путём их суммирования по модулю 2:

KF= KFC1 Å KFC2.

Извлечение LEAF и UID. Процедура дешифрования информации отправителя иллюстрируется на рис. 3.17. Дешифрующий Процессор выделяет LEAF отправителя и получателя из зашифрованного информационного потока и. затем выполняет его дешифрование на ключе семейства KF с целью получения UID. Несмотря на то, что Дешифрующий Процессор выделяет два, возможно различных, идентификатора UID микросхем на приёмном и передающем концах, сеансовый ключ KS используется для шифрования/дешифрования в обоих направлениях.

Полученный в результате дешифрования UID вместе с запросом передаются Агентам Депозитной Службы с целью получения ключевых компонентов.

Загрузка ключевых компонентов и ключевых чисел. После доставки магнитных носителей с ключевыми числами (KN1, KN2) и копий зашифрованного ключевого компонента (ЕКС1, ЕКС2) Офицеры Депозитной Службы проверяют соответствие серийного номера Дешифрующего Процессора номеру, указанному в запросе (см. раздел "Процедура выдачи ключевых компонент"). Если номера идентичны, Офицеры извлекают магнитные носители из контейнеров и в соответствии с процедурой вставляют их в считывающее устройство Дешифрующего Процессора. Кроме того, в Дешифрующий Процессор вводится информация о временном интервале, в течение которого ключевой материал может быть использован на законном основании.

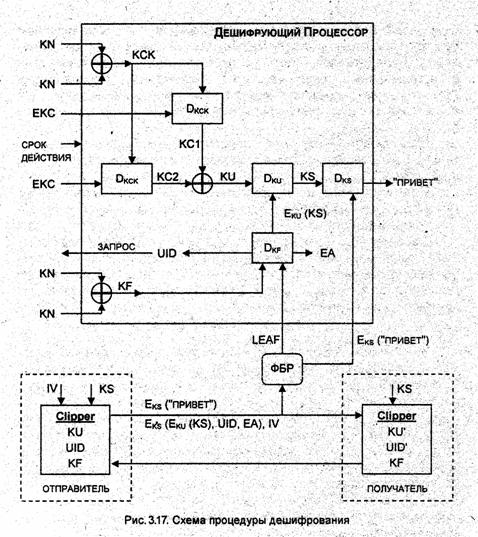
Дешифрующий Процессор выполняет суммирование по модулю 2 ключевых чисел KN1 и KN2 для вычисления значения ключа КСК. После дешифрования ЕКС1 и EKC2 на ключе КСК и получения компонентов КС1 и КС2 последние суммируются по модулю 2 для получения ключа KU.

После завершения процедуры загрузки копии ключевых компонентов, доставленные Офицерами Депозитной Службы, уничтожаются, а контейнер с ключевыми числами (KN1, KN2) доставляется обратно в депозитарий Агента.

Дешифрование. Раскрытие ключа KU конкретной микросхемы позволяет дешифровать любой шифртекст, полученный с помощью этой микросхемы. Для этого достаточно перехватить LEAF, передаваемое в начале каждого сеанса связи, затем дешифровать LEAF на ключе KF и получить DID и зашифрованный сеансовый ключ KS.      

Следующий шаг заключается в раскрытии сеансового ключа KS путём дешифрования на ключе KU и проверке аутентификатора ЕА. Правильность ЕА свидетельствует о том, что ключ KS восстановлен корректно и может быть использован для дешифрования информации в обоих направлениях.

Полученные в результате дешифрования речевые данные в цифровой форме преобразуются в сигнал тональной частоты с помощью цифроаналогового преобразователя. Ранее перехваченная зашифрованная информация (до раскрытия KU) также может быть дешифрована. Если ключ KU известен, быстродействие аппаратуры позволяет осуществлять прослушивание телефонных переговоров в реальном масштабе времени.

По истечении установленного срока действия выдаётся команда уничтожения ключа KU, хранящегося в памяти Дешифрующего Процессора. Уничтожение этого ключа подтверждается аутентичным сообщением, посылаемым каждому Агенту Депозитной Службы. Поэтому применение ключа после истечения срока будет обнаружено при аудиторской проверке.

Развитие этой криптосистемы заключается в автоматизации большинства ручных процедур, в первую очередь транспортировки ключей и регистрации.

ГЛАВА 4. АСИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ

4.1. Концепция криптосистемы с открытым ключом

Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования - другой ключ (отсюда и название асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.

Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.

Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рис.4.1. В этой криптосистеме применяют два различных ключа: К_B - открытый ключ отправителя А; k_B- секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ k_B по незащищенному каналу). Значения ключей К_B и k_B зависят от начального состояния генератора ключей. Раскрытие секретного ключа k_B по известному открытому ключу К_B должно быть вычислительно неразрешимой задачей.  

Характерные особенности асимметричных криптосистем:

1. Открытый ключ К_B и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны К_B и С.

2. Алгоритмы шифрования и расшифрования

Е_B: М ® С,

D_B: С ® М

являются открытыми.

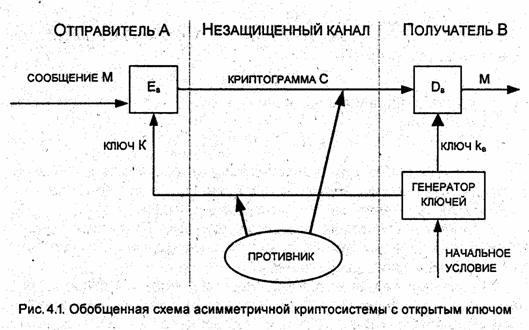
Защита информации в асимметричной криптосистеме основана на секретности ключа ka.

У. Диффи и М. Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:

1. Вычисление пары ключей (К_B, k_B) получателем В на основе начального условия должно быть простым.

2. Отправитель А, зная открытый ключ К_B и сообщение М, может легко вычислить криптограмму

(4.1)

3. Получатель В, используя секретный ключ k_B и криптограмму С, может легко восстановить исходное сообщение

M = D_kB(C) = D_B(C) =D_B[E_B(M)].                                                   (4.2)

4. Противник, зная открытый ключ К_B при попытке вычислить секретный ключ kB наталкивается на непреодолимую вычислительную проблему.

5. Противник, зная пару (К_B, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему [28].

4.2. Однонаправленные функции

Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Неформально однонаправленную функцию можно определить следующим образом. Пусть X и Y- некоторые произвольные множества. Функция     

f: X®Y

является однонаправленной, если для всех хÎХ можно легко вычислить функцию

y = f(x), где yÎY

И в то же время для большинства yÎY достаточно сложно получить значение хÎХ, такое, что f(x) = y (при этом полагают, что существует по крайней мере одно такое значение х).         

Основным критерием отнесения функции f к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования Y®X.

В качестве первого примера однонаправленной функции рассмотрим целочисленное умножение. Прямая задача-вычисление произведения двух очень больших целых чисел Р и Q, т.е. нахождение значения

N=P* Q,                                  (4.3)

является относительно несложной задачей для ЭВМ.

Обратная задача-разложение на множители большого целого числа, т.е. нахождение делителей Р и Q большого целого числа N = Р * Q, является практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел при целом N»2⁶⁶⁴ и Р » Q для разложения числа N потребуется около 10²³ операций, т.е. задача практически неразрешима на современных ЭВМ.    Т

Следующий характерный пример однонаправленной функции это модульная экспонента с фиксированными основанием и модулем. Пусть А и N-целые числа, такие, что 1 £ A £ N. Определим множество Z_N:

Z_N = {0,1,2,…, N-1}

Тогда модульная экспонента с основанием А по модулю N представляет собой функцию

F_A.N : Z_N ® Z_N

F_A.N(x) = A^x (mod N),                         (4.4)

Где X – целое число, 1 £ x £ N-1.

Существуют   эффективные алгоритмы,  позволяющие достаточно быстро вычислить значения функции f_A.N (х).       

Если у = А*, то естественно записать х = log_A(y).                      

Поэтому задачу обращения функции f_A.N(x) называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.

Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, у найти целое число х, такое, что

A^x mod N = y

Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.

По современным оценкам теории чисел при целых числах A » 2⁶⁶⁴ и N » 2⁶⁶⁴  решение задачи дискретного логарифмирования (нахождение показателя степени х для известного у) потребует
около 10²⁶ операций, т.е. эта задача имеет в 10³ раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач
возрастает.

Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.

Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с "потайным ходом" (с лазейкой). Дадим неформальное определение такой функции. Функция

f :X®Y

относится к классу однонаправленных функций с "потайным ходом" в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если
известен "потайной ход" (секретное число, строка или другая информация, ассоциирующаяся сданной функцией).

В качестве примера однонаправленной функции с "потайным ходом" можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для указания числового значения сообщения М либо криптограммы С (см. § 4.3.).

4.3. Криптосистема шифрования данных RSA

Алгоритм RSA предложили в 1978г. три автора: Р. Райвест (Rivest), А. Шамир (Shamir) и А. Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи [118].

Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.

В криптосистеме RSA открытый ключ К_B, секретный ключ К_B, сообщение М и криптограмма С принадлежат множеству целых   чисел   

Z_N = {0,1,2,…, N-1}

Где N-модуль

N = Р * Q

Здесь Р и Q-случайные большие простые числа. Для обеспечения максимальной безопасности выбирают Р и Q равной длины и хранят в секрете.        .

Множество Z_N с операциями сложения и умножения по модулю N образует арифметику по модулю N.

Открытый ключ К_B выбирают случайным образом так, чтобы выполнялись условия:

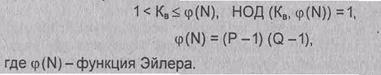                      (4.7)(4.8)

Функция Эйлера j(N) указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N.

Второе из указанных выше условий означает, что открытый ключ К_B и функция Эйлера j(N) должны быть взаимно простыми.

Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ k_B, такой, что

(4.9)

k_B * K_B º 1(mod j(N))                                  (4.9)

или

k_B * K_B^-1º (mod (P-1)(Q-1)).

Это можно осуществить, так как получатель В знает пару простых чисел (P.Q) и может легко найти j(N). Заметим, что k_B и N должны быть взаимно простыми.

Открытый ключ К_B используют для шифрования данных, а секретный ключ К_B -для расшифрования.

Преобразование шифрования определяет криптограмму С через пару (открытый ключ К_B, сообщение М) в соответствии со следующей формулой:

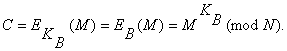                      (4.10)

В качестве алгоритма быстрого вычисления значения С используют ряд последовательных возведений в квадрат целого М и умножений на М с приведением по модулю N.

Обращение функции C=M ^К_B (mod N), т.е. определение значения М по известным значениям С, К_B  и N, практически не осуществимо при N»2⁵¹².

Однако обратную задачу, т.е. задачу расшифрования криптограммы С, можно решить, используя пару (секретный ключ k_B, криптограмма С) по следующей формуле:

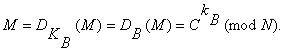           (4.11)

Процесс расшифрования  можно записать так:

D_B(E_B(M)) = M                                              (4.12)

Подставляя в (4.12)  значения (4.10) и (4.11), получаем:

(M^K_B)^k_B = M(mod N)

или

M^K_B^k_B = M(mod N)                (4.13)

 Величина j(N) играет важную роль в теореме Эйлера, которая утверждает, что если НОД (х, N) = 1, то

X^j(N) º 1(mod N),

или в несколько более общей форме

X^n×j(N)+1 º x(mod N).                  (4.14)

 Сопоставляя выражения (4.13) и (4.14), получаем

K_B* k_B = n * j(N) +1

или, что то же самое

K_B* k_B º 1(mod j(N)).

Именно поэтому для вычисления секретного ключа k_B используют соотношение (4.9).
Таким образом, если криптограмму

С = M^K_B (mod N)

возвести в степень k_B, то в результате восстанавливается исходный открытый текст М, так как

 Таким образом,        получатель В, который создает криптосистему, защищает два параметра: 1) секретный ключ k_B и 2) пару чисел  (P,Q), произведение которых дает значение модуля N. С другой

стороны, получатель  В открывает значение модуля N и открытый ключ К_B.

Противнику известны лишь значения K_B и N. Если бы он смог " разложить число N на множители Р и Q, то он узнал бы "потайной ход" тройку чисел {Р, Q, К_B}, вычислил значение функции Эйлера

j(N) = (P-1)(Q-1)

и определил значение секретного ключа k_B.

Однако, как уже отмечалось, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных Р и Q составляют не менее 100 десятичных знаков).

Процедуры шифрования и расшифрования   в криптосистеме RSA

Предположим, что пользователь А хочет передать пользователю В сообщение в зашифрованном виде, используя криптосистему RSA. В таком случае пользователь А выступает в роли отправителя сообщения, а пользователь В в роли получателя. Как  отмечалось выше, криптосистему RSA должен сформировать получатель сообщения, т.е. пользователь В. Рассмотрим последовательность действий пользователя В и пользователя А.

1. Пользователь В выбирает два произвольных больших простых числа Р и Q.

2. Пользователь В вычисляет значение модуля N = Р * Q.

3. Пользователь В вычисляет функцию Эйлера

j(N) = (P-1)(Q-1)

и выбирает случайным образом значение открытого ключа К_B с учетом выполнения условий:

1 < K_B £ j(N),   НОД(K_B, j(N))=1

4. Пользователь В вычисляет значение секретного ключа k_B,  используя  расширенный алгоритм  Евклида при  решении сравнения

k_B º K_B^-1(mod j(N)).

5. Пользователь В пересылает   пользователю А пару   чисел   (N, К_B) по незащищенному каналу.

Если  пользователь А хочет передать  пользователю В сообщение М, он выполняет следующие шаги.

6. Пользователь А разбивает исходный открытый текст М на  блоки, каждый из которых может быть представлен в виде числа     

M_i = 0,1,2,…,N-1

7. Пользователь А    шифрует текст,   представленный   в   виде последовательности чисел M_i по формуле

C_i = M_i^K_B (mod N)

и отправляет криптограмму

C₁, C₂, C₃,…,C_i,…

пользователю В.
8. Пользователь В расшифровывает принятую криптограмму

C₁, C₂, C₃,…,C_i,…

используя секретный ключ kB, по формуле

M_i = C_i^K_B (mod N)

В результате будет получена последовательность чисел M_i, которые представляют собой исходное сообщение М. Чтобы алгоритм RSA имел практическую ценность, необходимо иметь возможность без существенных затрат генерировать большие простые числа, уметь оперативно вычислять значения ключей К_B и k_B.

Пример. Шифрование сообщения CAB. Для простоты вычислений будут использоваться небольшие числа. На практике применяются очень большие числа (см. следующий раздел).

Действия пользователя В.

1. Выбирает Р = 3 и Q=11.

2. Вычисляет модуль N = P*Q = 3*11 = 33.

3. Вычисляет значение функции Эйлера для N = 33:

j(N) = j(33) = (P-1)(Q-1) = 2*10 = 20

Выбирает в качестве открытого ключа K_B произвольное число с учетом выполнения условий:

1 < K_B £ 20,   НОД(K_B, 20)=1

Пусть К_B = 7.

4. Вычисляет значение секретного ключа К_B, используя расширенный алгоритм Евклида (см. приложение) при решении сравнения

k_B º 7^-1(mod  20).

Решение дает k_B = 3.

5. Пересылает пользователю А пару чисел (N = 33. К_B =7).
Действия пользователя А.  

6. Представляет шифруемое сообщение как последовательность целых чисел в диапазоне 0...32. Пусть буква А представляется как число 1, буква В - как число 2, буква С - как число 3. Тогда сообщение CAB можно представить как последовательность чисел 312, т. е. M₁ = 3, М₂ = 1, М₃ = 2.

7. Шифрует текст, представленный в виде последовательности чисел М_1, М₂ и М₃, используя ключ К_B=7 и N =33, по формуле

Отправляет пользователю В криптограмму

Действия пользователя B.

8. Расшифровывает принятую криптограмму C₁, С₂, С₃, используя секретный ключ k_B= 3, по формуле

Безопасность и быстродействие криптосистемы RSA        

            Безопасность алгоритма RSA базируется на трудности решения задачи факторизации больших чисел, являющихся произведениями двух больших простых чисел. Действительно, криптостойкость алгоритма RSA определяется тем, что после формирования секретного ключа k_B и открытого ключа К_B "стираются" значения простых чисел Р и Q, и тогда исключительно трудно определить секретный ключ К_B по открытому ключу К_B, поскольку для этого необходимо решить задачу нахождения делителей Р и Q модуля N.

            Разложение величины N на простые множители Р и Q позволяет вычислить   функцию j(N) = (P-1)(Q-1) и затем определить секретное значение k_B, используя уравнение

K_B * k_B º 1(mod j(N)).

            Другим возможным способом криптоанализа алгоритма RSA является непосредственное вычисление или подбор значения функции j(N) = (P-1)(Q-1). Если установлено значение j(N), то сомножители Р и Q вычисляются достаточно просто. В самом деле, пусть  

x = P + Q = N + 1 -j(N),

y = (P - Q)² = (P + Q)²  – 4 * N

            Зная j(N), можно определить х и затем у; зная х и у, можно определить числа Р и Q из следующих соотношений:           

Однако эта атака не проще задачи факторизации модуля N [28]. Задача факторизации является трудно разрешимой задачей для больших значений модуля N.

Сначала авторы алгоритма RSA предлагали для вычисления модуля N выбирать простые числа Р и Q случайным образом, по 50 десятичных разрядов каждое. Считалось, что такие большие  числа N очень трудно разложить на простые множители. Один из авторов алгоритма RSA, Р. Райвест, полагал, что разложение на простые множители числа из почти 130 десятичных цифр, приведенного в их публикации, потребует более 40 квадриллионов лет машинного времени.  Однако этот прогноз не оправдался из-за
сравнительно быстрого прогресса компьютеров и их вычислительной мощности, а также улучшения алгоритмов факторизации.

            Ряд алгоритмов факторизации приведен в [45]. Один из наиболее быстрых алгоритмов, известных в настоящее время, алгоритм NFS (Number Field Sieve) может выполнить факторизацию  большого числа N (с числом десятичных разрядов больше 120) за  число шагов, оцениваемых величиной

В 1994 г. было факторизовано число со 129 десятичными цифрами. Это удалось осуществить математикам А. Ленстра и М. Манасси посредством организации распределенных вычислений на
1600 компьютерах, объединенных сетью, в течение восьми месяцев. По мнению А. Ленстра и М. Манасси, их работа компрометирует криптосистемы RSA и создает большую угрозу их дальнейшим применениям. Теперь разработчикам криптоалгоритмов с открытым ключом на базе RSA приходится избегать применения
чисел длиной менее 200 десятичных разрядов. Самые последние публикации предлагают применять для этого числа длиной не менее 250-300 десятичных разрядов.

В [121] сделана попытка расчета оценок безопасных длин ключей асимметричных криптосистем на ближайшие 20 лет исходя из прогноза развития компьютеров и их вычислительной мощности, а также возможного совершенствования алгоритмов факторизации. Эти оценки (табл.4.1) даны для трех групп пользователей (индивидуальных пользователей, корпораций и государственных организаций), в соответствии с различием требований к их информационной безопасности. Конечно, данные оценки следует рассматривать как сугубо приблизительные, как возможную тенденцию изменений безопасных длин ключей асимметричных криптосистем со временем.

Таблица 4.1

Оценки длин ключей для асимметричных криптосистем, бит

Год	Отдельные пользователи	Корпорации	Государственные организации
1995	768	1280	1536
2000	1024	1280	1536
2005	1280	1536	2048
2010	1280	1536	2048
2015	1536	2048	2048

Криптосистемы RSA реализуются как аппаратным, так и программным путем.

Для аппаратной реализации операций зашифрования и расшифрования RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах
(СБИС), позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время. И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.

Одна из самых быстрых аппаратных реализаций RSA с модулем 512 бит на сверхбольшой интегральной схеме имеет быстродействие 64 Кбит/с. Лучшими из серийно выпускаемых СБИС являются процессоры фирмы CYLINK, выполняющие 1024-битовое шифрование RSA.

Программная реализация RSA примерно в 100 раз медленнее программной реализации DES. С развитием технологии эти оценки могут несколько изменяться, но асимметричная криптосистема RSA никогда не достигнет быстродействия симметричных криптосистем.

Следует отметить, что малое быстродействие криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.

4.4. Схема шифрования Полига-Хеллмана

Схема шифрования Полига-Хеллмана [121] сходна со схемой шифрования RSA. Она представляет собой несимметричный алгоритм, поскольку используются различные ключи для шифрования
и расшифрования. В то же время эту схему нельзя отнести к классу криптосистем с открытым ключом, так как ключи шифрования и расшифрования легко выводятся один из другого. Оба ключа (шифрования и расшифрования) нужно держать в секрете.

Аналогично схеме RSA криптограмма С и открытый текст Р определяются из соотношений:

C = P^e mod n,

P = C^d mod n,

где e*d º1 (по модулю некоторого составного числа).

В отличие от алгоритма RSA в этой схеме число n не определяется через два больших простых числа; число n должно оставаться частью секретного ключа. Если кто-либо узнает значения e
и n, он сможет вычислить значение d.

Не зная значений e или d, противник будет вынужден вычислять значение

e = log_P C (mod n)

Известно, что это является трудной задачей.
Схема шифрования Полига-Хеллмана запатентована в США и Канаде.

4.5. Схема шифрования Эль Гамаля

Схема Эль Гамаля, предложенная в 1985г., может быть использована как для шифрования, так и для цифровых подписей. Безопасность схемы Эль Гамаля обусловлена сложностью вычисления дискретных логарифмов в конечном поле.

Для того чтобы генерировать пару ключей (открытый ключ - секретный ключ), сначала выбирают некоторое большое простое число Р и большое целое число G, причем G<P. Числа Р и G могут быть распространены среди группы пользователей.

Затем выбирают случайное целое число X, причем Х<Р. Число X является секретном ключом и должно храниться в секрете.

            Далее вычисляют Y=G^X mod P. Число Y является открытым ключом.

Для того чтобы зашифровать сообщение М, выбирают случайное целое число К, 1<К<Р-1, такое, что числа К и (Р-1) являются взаимно простыми.

Затем вычисляют числа

a = G^K mod P,

b = Y^K M mod P.

Пара чисел (а, b) является шифртекстом. Заметим, что длина шифртекста вдвое больше длины исходного открытого текста М.

Для того чтобы расшифровать шифртекст (а, b), вычисляют

M = b/a^X mod P. (*)

Поскольку

a^X º G^KX mod P,

b/a^X º Y^KM/a^X º G^KXM/G^GXº M (mod P),

то соотношение (*) справедливо.

Пример. Выберем Р=11, G = 2, секретный ключ X = 8.
Вычисляем

Y = G^X mod P = 2⁸ mod 11 = 256 mod 11 = 3

Итак, открытый ключ Y= 3.

Пусть сообщение М=5. Выберем некоторое случайное число К=9. Убедимся, что НОД (К, Р-1) =1. Действительно, НОД (9,10) =1. Вычисляем пару чисел а и b:

a = G^K mod P = 2⁹ mod 11 = 512 mod 11= 6,

b = Y^K M mod P = 3⁹ * 5 mod 11 = 19683 * 5 mod 11 = 9

Получим шифртекст (а, b) = (6, 9).

Выполним расшифрование этого шифртекста. Вычисляем сообщение М, используя секретный ключ X:

M = b/a^X mod P = 9/6⁸ mod 11.

Выражение M = 9/6amod11 можно представить в виде

6⁸ * M º9 mod 11

или 1679616 * M º 9 mod 11.

Решая данное сравнение, находим М = 5.

В реальных схемах шифрования необходимо использовать в качестве модуля Р большое целое простое число, имеющее в двоичном представлении длину 512... 1024 бит.

При программной реализации схемы Эль Гамаля [123] скорость ее работы {на SPARC-M) в режимах шифрования и расшифрования при 160-битовом показателе степени для различных длин
модуля Р определяется значениями, приведенными в табл. 4.2.

Таблица 4.2

Скорости работы схемы Эль. Гамаля

Режим работы	Длина модуля, бит
	512	768	1024
Шифрование	0,33с	0,80с	1.09с
Расшифрование	0,24с	0,58с	0,77 С

4.6. Комбинированный метод шифрования

Главным достоинством криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому бы то ни было значения секретных ключей, ни убеждаться в их подлинности. В симметричных криптосистемах существует опасность раскрытия секретного ключа во время передачи.

Однако алгоритмы, лежащие в основе криптосистем с открытым ключом, имеют следующие недостатки:

• генерация новых секретных и открытых ключей основана на генерации новых больших простых чисел, а проверка простоты чисел занимает много процессорного времени;

• процедуры шифрования и расшифрования, связанные с возведением в степень многозначного числа, достаточно громоздки.

Поэтому быстродействие криптосистем с открытым ключом обычно в сотни и более раз меньше быстродействия симметричных криптосистем с секретным ключом.

Комбинированный (гибридный) метод шифрования позволяет сочетать преимущества высокой секретности, предоставляемые асимметричными криптосистемами с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом. При таком подходе криптосистема с открытым ключом применяется для шифрования, передачи и последующего расшифрования только секретного ключа симметричной криптосистемы. А симметричная криптосистема применяется для шифрования и передачи исходного открытого текста. В результате криптосистема с открытым ключом не заменяет симметричную криптосистему с секретным ключом, а лишь дополняет ее, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного цифрового конверта.

Если пользователь А хочет передать зашифрованное комбинированным методом сообщение М пользователю В, то порядок его действий будет таков.

1. Создать (например, сгенерировать случайным образом) симметричный ключ, называемый в этом методе сеансовым ключом Ks.

2. Зашифровать сообщение М на сеансовом ключе Ks.

3. Зашифровать сеансовый ключ Ks на открытом ключе К_B  пользователя В.

4. Передать по открытому каналу связи в адрес пользователя В зашифрованное сообщение вместе с зашифрованным сеансовым ключом.

Действия пользователя В при получении зашифрованного сообщения и зашифрованного сеансового ключа должны быть обратными:

5. Расшифровать на своем секретном ключе k_B сеансовый ключ Ks.

6. С помощью полученного сеансового ключа Ks расшифровать и прочитать - сообщение М.

При использовании комбинированного метода шифрования можно быть уверенным в том, что только пользователь В сможет правильно расшифровать ключ К₃ и прочитать сообщение М.

Таким образом, при комбинированном методе шифрования применяются криптографические ключи как симметричных, так и асимметричных криптосистем. Очевидно, выбор длин ключей для
каждого типа криптосистемы следует осуществлять таким образом, чтобы злоумышленнику было одинаково трудно атаковать любой механизм защиты комбинированной криптосистемы.

В табл.4.3. приведены распространенные длины ключей симметричных и асимметричных криптосистем, для которых трудность атаки полного перебора примерно равна трудности факторизации
соответствующих модулей асимметричных криптосистем [121].

Таблица 4.3

Длины ключей для симметричных и асимметричных криптосистем
при одинаковой их криптостойкости

Длина ключа симметричной криптосистемы, бит	Длина ключа асимметричной криптосистемы бит
56	384
64	512
80	768
112	1792
128	2304

Комбинированный метод допускает возможность выполнения процедуры аутентификации, т.е. проверки подлинности передаваемого сообщения. Для этого пользователь А на основе функции
хэширования сообщения и своего секретного ключа k_A с помощью известного алгоритма электронной цифровой подписи (ЭЦП) генерирует свою подпись и записывает ее, например, в конец передаваемого файла.

Пользователь В, прочитав принятое сообщение, может убедиться в подлинности цифровой подписи абонента А. Используя тот же алгоритм ЭЦП и результат хэширования принятого сообщения, пользователь В проверяет полученную подпись (см. гл.6). Комбинированный метод шифрования является наиболее рациональным, объединяя в себе высокое быстродействие симметричного шифрования и высокую криптостойкость, гарантируемую системами с открытым ключом.

ГЛАВА 5. ИДЕНТИФИКАЦИЯ И ПРОВЕРКА ПОДЛИННОСТИ

5.1. Основные понятия и концепции

С каждым объектом компьютерной системы (КС) связана некоторая информация, однозначно идентифицирующая его. Это может быть число, строка символов, алгоритм, определяющий данный
объект. Эту информацию называют идентификатором объекта. Если объект имеет некоторый идентификатор, зарегистрированный в сети, он называется законным (легальным) объектом; остальные
объекты относятся к незаконным (нелегальным).

Идентификация объекта - одна из функций подсистемы защиты. Эта функция выполняется в первую очередь, когда объект делает попытку войти в сеть. Если процедура идентификации завершается успешно, данный объект считается законным для данной сети.

Следующий шаг-аутентификация объекта (проверка подлинности объекта). Эта процедура устанавливает, является ли данный объект именно таким, каким он себя объявляет.

После того как объект идентифицирован и подтверждена его подлинность, можно установить сферу его действия и доступные ему ресурсы КС. Такую процедуру называют предоставлением
полномочий (авторизацией).

Перечисленные три процедуры инициализации являются процедурами защиты и относятся к одному объекту КС [55].

При защите каналов передачи данных подтверждение подлинности (аутентификация) объектов означает взаимное установление подлинности объектов, связывающихся между собой по линиям связи. Процедура подтверждения подлинности выполняется обычно в начале сеанса в процессе установления соединения абонентов. (Термин "соединение" указывает на логическую связь (потенциально двустороннюю) между двумя объектами сети. Цель данной процедуры - обеспечить уверенность, что соединение установлено с законным объектом и вся информация дойдет до места назначения.

После того как соединение установлено, необходимо обеспечить выполнение требований защиты при обмене сообщениями:

(а) получатель должен быть уверен в подлинности источника данных;

(б) получатель должен быть уверен в подлинности передаваемых данных;

(в) отправитель должен быть уверен в доставке данных получателю;

(г) отправитель должен быть уверен в подлинности доставленных данных.

Для выполнения требований (а) и (б) средством защиты является цифровая подпись. Для выполнения требований (в) и (г) отправитель должен получить уведомление о вручении с помощью

•удостоверяющей почты (certified mail). Средством защиты в такой процедуре является цифровая подпись подтверждающего ответного сообщения, которое в свою очередь является доказательством пересылки исходного сообщения.

Если эти четыре требования реализованы в КС, то гарантируется защита данных при их передаче по каналу связи и обеспечивается функция защиты, называемая функцией подтверждения (неоспоримости) передачи. В этом случае отправитель не может отрицать ни факта посылки сообщения, ни его содержания, а получатель не может отрицать ни факта получения сообщения, ни подлинности его содержания.

5.2. Идентификация и аутентификация пользователя

Прежде чем получить доступ к ресурсам компьютерной системы, пользователь должен пройти процесс представления компьютерной системе, который включает две стадии:

• идентификацию - пользователь сообщает системе по ее запросу свое имя (идентификатор);

• аутентификацию - пользователь подтверждает идентификацию, вводя в систему уникальную, не известную другим пользователям информацию о себе (например, пароль).

Для проведения процедур идентификации и аутентификации пользователя необходимы:

• наличие соответствующего субъекта (модуля) аутентификации

• наличие аутентифицирующего объекта, хранящего уникальную информацию для аутентификации пользователя.

Различают две формы представления объектов, аутентифицирующих пользователя:

• внешний аутентифицирующий объект, не принадлежащий системе;

• внутренний объект, принадлежащий системе, в который переносится информация из внешнего объекта..

Внешние объекты могут быть технически реализованы на различных носителях информации- магнитных дисках, пластиковых картах и т.п. Естественно, что внешняя и внутренняя формы представления аутентифицирующего объекта должны быть семантически тождественны.

Типовые схемы идентификации и аутентификации пользователя

Рассмотрим структуры данных и протоколы идентификации и аутентификации пользователя [73]. Допустим, что в компьютерной системе зарегистрировано n пользователей. Пусть i-й аутентифицирующий объект i-гo пользователя содержит два информационных поля:

IDi-неизменный идентификатор i-гo пользователя, который является аналогом имени и используется для идентификации пользователя;

K_i-аутентифицирующая информация пользователя, которая может изменяться и служит для аутентификации (например, пароль Pi-Ki).

Описанная структура соответствует практически любому ключевому носителю информации, используемому для опознания пользователя. Например, для носителей типа пластиковых карт выделяется
неизменяемая информация ID_i первичной персонализации пользователя и объект в файловой структуре карты, содержащий К_i.

Совокупную информацию в ключевом носителе можно назвать первичной аутентифицирующей информацией i-гo пользователя. Очевидно, что внутренний аутентифицирующий объект не должен
существовать в системе длительное время (больше времени работы конкретного пользователя). Для длительного хранения следует использовать данные в защищенной форме.

Рассмотрим две типовые схемы идентификации и аутентификации [73].

Схема 1. В компьютерной системе выделяется объект-эталон для идентификации и аутентификации пользователей. Структура объекта-эталона для схемы 1 показана в табл. 5.1. Здесь Ei = F(lDi, K_i), где F-функция, которая обладает свойством "невосстановимости" значения K_i по E_i и ID_i. “Невосстановимость" K_i  оценивается некоторой пороговой трудоемкостью Т₀ решения задачи восстановления аутентифицирующей информации K_i по E_i и ID_i. Кроме того, для пары К_i и K_j возможно совпадение соответствующих значений Е. В связи с этим вероятность ложной аутентификации пользователя не должна быть больше некоторого порогового значения Р₀. На практике задают Т₀ = 10²⁰…10³⁰, P₀ = 10^-7 …10^-9 [73]

Таблица 5.1

Структура объекта-эталона для схемы 1

Номер пользователя	Информация для идентификации	Информация для аутентификации
1	ID1	E1
2	ID2	Е2
…	…	…
N	IDn	Еn

Протокол идентификации и аутентификации (для схемы 1).

1. Пользователь предъявляет свой идентификатор ID.

2. Если ID не совпадает ни с одним ID_i, зарегистрированным в компьютерной системе, то идентификация отвергается - пользователь не допускается к работе, иначе (существует IDi-ID) устанавливается, что пользователь, назвавшийся пользователем i, прошел идентификацию.

3. Субъект аутентификации запрашивает у пользователя его аутентификатор К.

4. Субъект аутентификации вычисляет значение Y=F(ID_i, К).

5. Субъект аутентификации производит сравнение значений У и E_i. При совпадении этих значений устанавливается, что данный пользователь успешно аутентифицирован в системе: Информация об этом пользователе передается в программные модули, использующие ключи пользователей (т.е. в систему шифрования, разграничения доступа и т.д.). В противном случае аутентификация отвергается - пользователь не допускается к работе.

Данная схема идентификации и аутентификации пользователя может быть модифицирована. Модифицированная схема 2 обладает лучшими характеристиками по сравнению со схемой 1.

Схема 2. В компьютерной системе выделяется модифицированный объект-эталон, структура которого показана в табл. 5.2.

Таблица 5.2

Структура модифицированного объекта-эталона

Номер пользователи	Информация для идентификации	Информация для аутентификации
1	ID1, S1	Е1
2	ID2, S2	Е2
N	IDn, Sn	Еn

В отличие от схемы 1, в схеме 2 значение Ei равно F(Si, Кi), где Si-случайный вектор, задаваемый при создании идентификатора пользователя, т.е. при создании строки, необходимой для идентификации и аутентификации пользователя; F-функция, которая обладает свойством "невосстановимости" значения Кi по Ei и Si.

Протокол идентификации и аутентификации (для схемы 2).

1. Пользователь предъявляет свой идентификатор ID.

2. Если ID не совпадает ни с одним IDi, зарегистрированным в компьютерной системе, то идентификация отвергается - пользователь не допускается к работе, иначе (существует IDi = ID) устанавливается, что пользователь, называвшийся пользователем i, прошел идентификацию.

3. По идентификатору IDi выделяется вектор Si.

4. Субъект аутентификации запрашивает у пользователя аутентификатор К.

5. Субъект аутентификации вычисляет значение Y= F(Si, К).

6. Субъект аутентификации производит сравнение значений Y и Ei. При совпадении этих значений устанавливается, что данный пользователь успешно аутентифицирован в системе. В противном
случае аутентификация отвергается - пользователь не допускается к работе.

Вторая схема аутентификации применяется в ОС UNIX. В качестве идентификатора ID используется имя пользователя (запрошенное по Loqin), в качестве аутентификатора Ki-пароль пользователя (запрошенный по Password), функция F представляет собой алгоритм шифрования DES. Эталоны для идентификации и аутентификации содержатся в файле Etc/passwd.

Следует отметить, что необходимым требованием устойчивости схем аутентификации к восстановлению информации Кi является случайный равновероятный выбор Ki из множества возможных
значений.

Системы парольной аутентификации имеют пониженную стойкость, поскольку в них выбор аутентифицирующей информации происходит из относительно небольшого множества осмысленных
слов. Мощность этого множества определяется энтропией соответствующего языка.

Особенности применения пароля для аутентификации пользователя

Традиционно каждый законный пользователь компьютерной системы получает идентификатор и/или пароль. В начале сеанса работы пользователь предъявляет свой идентификатор системе,
которая затем запрашивает у пользователя пароль.

Простейший метод подтверждения подлинности с использованием пароля основан на сравнении представляемого пользователем пароля Р_A' с исходным значением Р_А', хранящимся в компьютерном центре (рис. 5.1). Поскольку пароль должен храниться в тайне, он должен шифроваться перед пересылкой по незащищенному каналу. Если значения Р_А и Р_A’ совпадают, то пароль Р_А считается подлинным, а пользователь - законным [123].

Рис. 5.1. Схема простой аутентификации с помощью пароля

Если кто-нибудь, не имеющий полномочий для входа в систему, узнает каким-либо образом пароль и идентификационный номер законного пользователя, он получает доступ в систему.

Иногда получатель не должен раскрывать исходную открытую форму пароля. В этом случае отправитель должен пересылать вместо открытой формы пароля отображение пароля, получаемое
с использованием односторонней функции a(×) пароля. Это преобразование должно гарантировать невозможность раскрытия противником пароля по его отображению, так как противник наталкивается на неразрешимую числовую задачу.

Например, функция a(×) может быть определена следующим образом:

a(P) = E_P(ID)

где Р - пароль отправителя; ID-идентификатор отправителя; Е_Р- процедура шифрования, выполняемая с использованием пароля Р в качестве ключа.

Такие функции особенно удобны, если длина пароля и ключа одинаковы. В этом случае подтверждение подлинности с помощью пароля состоит из пересылки получателю отображения а(Р) и
сравнения его с предварительно вычисленным и хранимым эквивалентом a(Р).

На практике пароли состоят только из нескольких букв, чтобы дать возможность пользователям запомнить их. Короткие пароли уязвимы к атаке полного перебора всех вариантов. Для того чтобы
предотвратить такую атаку, функцию a(Р) определяют иначе, а именно:

a(P) = E_{P Å K} (ID)

где К и ID-соответственно ключ и идентификатор отправителя.

Очевидно, значение a(Р) вычисляется заранее и хранится в виде a(Р) в идентификационной таблице у получателя (рис. 5.2). Подтверждение подлинности состоит из сравнения двух отображений пароля a(Р_А) и a’(Р_A) и признания пароля Р_А, если эти отображения равны.

Рис. 5.2. Схема аутентификации с помощью пароля с использованием
идентификационной таблицы

Конечно, любой, кто получит доступ к идентификационной таблице, может незаконно изменить ее содержимое, не опасаясь, что эти действия будут обнаружены.

Применение для целей идентификации и аутентификации персонального идентификационного номера PIN рассматривается в гл. 9.

Биометрическая идентификация и аутентификация пользователя

Процедуры идентификации и аутентификации пользователя могут базироваться не только на секретной информации, которой обладает пользователь (пароль, секретный ключ, персональный
идентификатор и т.п.). В последнее время все большее распространение получает биометрическая идентификация и аутентификация пользователя, позволяющая уверенно идентифицировать потенциального пользователя путем измерения физиологических параметров и характеристик человека, особенностей его поведения.

Отметим основные достоинства биометрических методов идентификации и аутентификации пользователя по сравнению с традиционными [73]:

• высокая степень достоверности идентификации по биометрическим признакам из-за их уникальности;
•  неотделимость   биометрических   признаков   от   дееспособной личности;
• трудность фальсификации биометрических признаков.

В качестве биометрических признаков, которые могут быть использованы при идентификации потенциального пользователя, можно выделить следующие:

• узор радужной оболочки и сетчатки глаз;

• отпечатки пальцев;

• геометрическая форма руки;

• форма и размеры лица;

• особенности голоса;

• биомеханические характеристики рукописной подписи;

• биомеханические характеристики "клавиатурного почерка".

При регистрации пользователь должен продемонстрировать один или несколько раз свои характерные биометрические признаки. Эти признаки (известные как подлинные) регистрируются системой как контрольный "образ" законного пользователя. Этот образ пользователя хранится в электронной форме и используется для проверки идентичности каждого, кто выдает себя за соответствующего законного пользователя. В зависимости от совпадения или несовпадения совокупности предъявленных признаков с зарегистрированными в контрольном образе их предъявивший признается
законным пользователем (при совпадении) или нет (при несовпадении).

Системы идентификации по узору радужной оболочки и сетчатки глаз могут быть разделены на два класса:

• использующие рисунок радужной оболочки глаза;

» использующие рисунок кровеносных сосудов сетчатки глаза.

Поскольку вероятность повторения данных параметров равна 10^-78, эти системы являются наиболее надежными среди всех биометрических систем. Такие средства идентификации применяются
там, где требуется высокий уровень безопасности (например, в США в зонах военных и оборонных объектов).

Системы идентификации по отпечаткам пальцев являются  самыми распространенными. Одна из основных причин широкого распространения таких систем заключается в наличии больших банков данных по отпечаткам пальцев. Основными пользователями подобных систем во всем мире являются полиция, различные государственные и некоторые банковские организации.

Системы идентификации по геометрической форме руки используют сканеры формы руки, обычно устанавливаемые на стенах. Следует отметить, что подавляющее большинство пользователей предпочитают системы именно этого типа, а не описанные выше.

Системы идентификации по лицу и голосу являются наиболее доступными из-за их дешевизны, поскольку большинство современных компьютеров имеют видео- и аудиосредства. Системы данного класса широко применяются при удаленной идентификации субъекта доступа в телекоммуникационных сетях.

Системы идентификации личностей по динамике рукописной подписи учитывают интенсивность каждого усилия подписывающего, частотные характеристики написания каждого элемента подписи и начертание подписи в целом.

Системы идентификации по биомеханическим характеристикам "клавиатурного почерка" основываются на том, что моменты нажатия и отпускания клавиш при наборе текста на клавиатуре существенно различаются у разных пользователей. Этот динамический ритм набора ("клавиатурный почерк") позволяет построить достаточно надежные средства идентификации. В случае обнаружения изменения клавиатурного почерка пользователя ему автоматически запрещается работа на ЭВМ.

Следует отметить, что применение биометрических параметров при идентификации субъектов доступа автоматизированных систем пока не получило надлежащего нормативно-правового обеспечения,
в частности в виде стандартов. Поэтому применение систем биометрической идентификации допускается только в автоматизированных системах, обрабатывающих и хранящих персональные данные, составляющие коммерческую и служебную тайну [73].

5.3. Взаимная проверка подлинности пользователей

           Обычно   стороны,   вступающие   в   информационный   обмен, нуждаются во взаимной проверке подлинности (аутентификации) друг друга. Этот процесс взаимной аутентификации выполняют в начале сеанса связи.

           Для проверки подлинности применяют следующие способы [55]:

· механизм запроса-ответа;

· механизм отметки времени ("временной штемпель").

Механизм запроса-ответа состоит в следующем. Если пользователь А хочет быть уверенным, что сообщения, получаемые им  от пользователя В, не являются ложными, он включает в посылаемое для В сообщение  непредсказуемый  элемент-запрос X (например, некоторое случайное число). При ответе пользователь В должен выполнить над этим элементом некоторую операцию (например, вычислить некоторую функцию f(X}). Это невозможно осуществить заранее, так как пользователю В неизвестно, какое случайное число X придет в запросе, Получив ответ с результатом действий В, пользователь может быть уверен, что В - подлинный. Недостаток этого метода-возможность установления закономерности между запросом и ответом.

Механизм отметки времени подразумевает регистрацию времени для каждого сообщения. В этом случае каждый пользователь сети может определить, насколько "устарело" пришедшее сообщение, и решить не принимать его, поскольку оно может быть ложным.

В обоих случаях для защиты механизма контроля следует применять шифрование, чтобы быть уверенным, что ответ послан не злоумышленником.

При использовании отметок времени возникает проблема допустимого временного интервала задержки для подтверждения подлинности сеанса. Ведь сообщение с "временным штемпелем" в принципе не может быть передано мгновенно. Кроме того, компьютерные часы получателя и отправителя не могут быть абсолютно синхронизированы. Какое запаздывание "штемпеля" является подозрительным?

Для взаимной проверки подлинности обычно используют процедуру "рукопожатия" [55,123]. Эта процедура базируется на указанных выше механизмах контроля и заключается во взаимной проверке ключей, используемых сторонами. Иначе говоря, стороны признают друг друга законными партнерами, если докажут друг другу, что обладают правильными ключами. Процедуру рукопожатия обычно применяют в компьютерных сетях при организации сеанса связи между пользователями, пользователем и хост - компьютером, между хост-компьютерами и т.д.

Рассмотрим в качестве примера процедуру рукопожатия для двух пользователей А и В. (Это допущение не влияет на общность

Рис. 5.3. Схема процедуры рукопожатия (пользователь А проверяет
подлинность пользователя В)

рассмотрения. Такая же процедура используется, когда вступающие в связь стороны не являются пользователями). Пусть применяется симметричная криптосистема. Пользователи А и В разделяют один и тот же секретный ключ КАВ. Вся процедура показана на рис. 5.3.

• Пусть пользователь А инициирует процедуру рукопожатия, отправляя пользователю В свой идентификатор ID_А в открытой форме.

• Пользователь В, получив идентификатор ID_A, находит в базе данных секретный ключ КАВ и вводит его в свою криптосистему.

• Тем временем пользователь А генерирует случайную последовательность S с помощью псевдослучайного генератора PG и отправляет ее пользователю В в виде криптограммы

• Пользователь В расшифровывает эту криптограмму и раскрывает исходный вид последовательности S.

• Затем оба пользователя А и В преобразуют последовательность S, используя открытую одностороннюю функцию a(×).

• Пользователь В шифрует сообщение a(S) и отправляет эту криптограмму пользователю А.

• Наконец, пользователь А расшифровывает эту криптограмму и сравнивает полученное сообщение a'(S) с исходным a(S). Если эти сообщения равны, пользователь А признает подлинность пользователя В.

Очевидно, пользователь В проверяет подлинность пользователя А таким же способом. Обе эти процедуры образуют процедуру рукопожатия, которая обычно выполняется в самом начале любого сеанса связи между любыми двумя сторонами в компьютерных сетях.

Достоинством модели рукопожатия является то, что ни один из участников сеанса связи не получает никакой секретной информации во время процедуры подтверждения подлинности.

Иногда пользователи хотят иметь непрерывную проверку подлинности отправителей в течение всего сеанса связи. Один из простейших способов непрерывной проверки подлинности показан на
рис. 5.4 [123]. Передаваемая криптограмма имеет вид

E_K(ID_A, M),

где ID_A-идентификатор отправителя А; М-сообщение.

Получатель В, принявший эту криптограмму, расшифровывает ее и раскрывает пару (ID_А, М). Если принятый идентификатор ID_А совпадает с хранимым значением ID’_A получатель В признает эту криптограмму.

Рис. 5.4. Схема непрерывной проверки подлинности отправителя

Другой вариант непрерывной проверки подлинности использует вместо идентификатора отправителя его секретный пароль. Заранее подготовленные пароли известны обеим сторонам. Пусть Р_А
и Р_B-пароли пользователей А и В соответственно. Тогда пользователь А создает криптограмму

C= E_K(P_A, M).

Получатель криптограммы расшифровывает ее и сравнивает пароль, извлеченный из этой криптограммы, с исходным значением. Если они равны, получатель признает эту криптограмму.

Процедура рукопожатия была рассмотрена в предположении, что пользователи А и В уже имеют общий секретный сеансовый ключ. Реальные процедуры предназначены для распределения ключей между подлинными партнерами и включает как этап распределения ключей, так и этап собственно подтверждения подлинности партнеров по информационному обмену. Такие процедуры будут рассмотрены а гл.7.