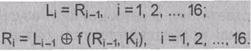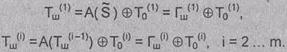ГЛАВА 3. СОВРЕМЕННЫЕ СИММЕТРИЧНЫЕ КРИПТОСИСТЕМЫ

По мнению К. Шеннона [101], в практических шифрах необходимо использовать два общих принципа: рассеивание и перемешивание.

Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста.

Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе.

Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, т.е. такого шифра, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.

В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановке просто перемешивают символы открытого текста, причем
конкретный вид перемешивания определяется секретным ключом. При подстановке каждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки
также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно
длиной 64 бита. В принципе каждый блок может принимать 2⁶⁴ значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 2⁶⁴ »10¹⁹ "символов".

При многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить очень стойкий шифр с хорошим рассеиванием и перемешиванием. Рассмотренные ниже криптоалгоритмы DES, IDEA и отечественный стандарт шифрования данных построены в полном соответствии с указанной методологией.

3.1. Американский стандарт шифрования данных DES

Стандарт шифрования данных DES (Data Encryption Standard) опубликован в 1977г. Национальным бюро стандартов США. Стандарт DES предназначен для защиты от  несанкционированного доступа к важной, но несекретной информации в государственных и коммерческих организациях США. Алгоритм, положенный в основу стандарта, распространялся достаточно быстро, и уже в 1980 г. был одобрен Национальным институтом стандартов и технологий США (НИСТ). С этого момента DES превращается в стандарт не только  по названию (Data Encryption Standard), но и фактически. Появляются программное обеспечение и специализированные микроЭВМ,
предназначенные для шифрования и расшифрования информации в сетях передачи данных.

К настоящему времени DES является наиболее распространенным алгоритмом, используемым в системах защиты коммерческой информации. Более того, реализация алгоритма DES в таких
системах становится признаком хорошего тона.

Основные достоинства алгоритма DES:

• используется только один ключ длиной 56 бит;

• зашифровав сообщение с помощью одного пакета программ, для расшифровки можно использовать любой другой пакет программ, соответствующий стандарту DES;

• относительная простота алгоритма обеспечивает высокую скорость обработки;
• достаточно высокая стойкость алгоритма.

Первоначально метод, лежащий в основе стандарта DES, был разработан фирмой IBM для своих целей и реализован в виде сиcтемы "Люцифер". Система "Люцифер" основана на комбинировании методов подстановки и перестановки и состоит из чередующейся последовательности блоков перестановки и подстановки. В ней использовался ключ длиной 128 бит, управлявший состояниями блоков перестановки и подстановки. Система "Люцифер" оказалась весьма сложной для практической реализации из-за относительно алой скорости шифрования (2190 байт/с-программная реализация, 96970 байт/с аппаратная реализация).

Алгоритм DES также использует комбинацию подстановок и перестановок. DES осуществляет шифрование 64-битовых блоков данных с помощью 64-битового ключа, в котором значащими являются 56 бит (остальные 8 бит-проверочные биты для контроля на четность). Дешифрование в DES является операцией, обратной шифрованию, и выполняется путем повторения операций шифрования в обратной последовательности. Обобщенная схема процесса шифрования в алгоритме DES показана на рис.3.1. Процесс шифрования заключается в начальной перестановке битов 64-битового блока, шестнадцати циклах шифрования и, наконец, в конечной перестановке битов.

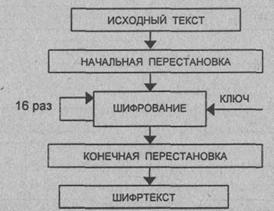
Рис. 3.1. Обобщенная схема шифрования в алгоритме DES

Следует сразу отметить, что все приводимые таблицы являются стандартными и должны включаться в реализацию алгоритма DES в неизменном виде.

Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путем подбора ключа. При описании алгоритма DES
(рис. 3.2) применены следующие обозначения:

L и R - последовательности битов (левая (left) и правая (right));

LR - конкатенация последовательностей L и R, т.е. такая последовательность битов, длина которой равна сумме длин L и R; в последовательности LR биты последовательности R следуют за
битами последовательности L;

Å - операция побитового сложения по модулю 2.

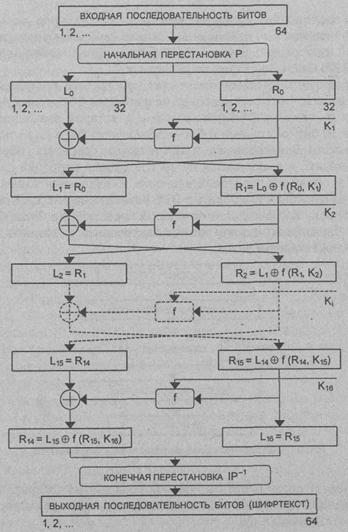
Рис. 3.2. Структура алгоритма DES

Пусть из файла исходного текста считан очередной 64-битовый (8-байтовый) блок Т. Этот блок Т преобразуется с помощью матрицы начальной перестановки IP (табл. 3.1).

Биты входного блока Т (64 бита) переставляются в соответствии с матрицей IP: бит 58 входного блока Т становится битом 1, бит 50-битом 2 и т.д. Эту перестановку можно описать выражением
Т₀=IР(Т). Полученная последовательность битов Т₀ разделяется на две последовательности: L₀-левые или старшие биты, R₀-правые или младшие биты, каждая из которых содержит 32 бита.

58	50	42	34	26	18	10	2
60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6
64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1
59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5
63	55	47	39	31	23	15	7

Таблица 3.1. Матрица начальной перестановки IР

Таблица 3.2. Матрица обратной перестановки IP^-1

	8	48	16	56	24	64	32
39	7	47	15	55	23	63	31
38	6	46	14	54	22	62	30
37	5	45	13	53	21	61	29
36	4	44	12	52	20	60	28
35	3	43	11	51	19	59	27
34	2	42	10	50	18	58	26
33	1	41	9	49	17	57	25

Затем выполняется итеративный процесс шифрования, состоящий из 16 шагов (циклов). Пусть Ti- результат i-й итерации:

T_i = L_iR_i

Где L_i = t₁t₂…t₃₂ (первые 32 бита); R_i = t₃₃t₃₄…t₆₄ (последние 32 бита).
Тогда результат i-й итерации описывается следующими формулами:

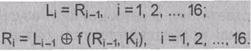
Функция f называется функцией шифрования. Ее аргументами являются последовательность R_i-1, получаемая на предыдущем шаге итерации, и 48-битовый ключ К_i который является результатом преобразования 64-битового ключа шифра К. (Подробнее функция шифрования f и алгоритм получения ключа K_i описаны ниже.)

На последнем шаге итерации получают последовательности R₁₆ и L₁₆ (без перестановки местами), которые конкатенируются в 64-битовую последовательность R₁₆L₁₆.

По окончании шифрования осуществляется восстановление позиций битов с помощью матрицы обратной перестановки IP^-1 (табл. 3.2).

Пример того, как соотносятся элементы первой строки матрицы IР-1 с элементами матрицы IP приведен в табл. 3.3.

Таблица 3.3

                        Связь элементов матриц

Элемент матрицы IP^-1	Элемент матрицы IP
40	01
8	02
48	03
16	04
56	05

Процесс расшифрования данных является инверсным по отношению к процессу шифрования. Все действия должны быть выполнены в обратном порядке. Это означает, что расшифровываемые данные сначала переставляются в соответствии с матрицей IР^-1, а затем над последовательностью битов R¹⁶L¹⁶ выполняются те же действия, что и в процессе шифрования, но в обратном порядке.

Итеративный процесс расшифрования может быть описан следующими формулами:

Таким образом, для процесса расшифрования с переставленным входным блоком R¹⁶L¹⁶ на первой итерации используется ключ К₁₆, на второй итерации-K₁₆ и т.д. На 16-й итерации используется ключ K₁. На последнем шаге итерации будут получены последовательности L₀ и r₀, которые конкатенируются в 64-битовую последовательность L0R0. Затем в этой последовательности 64 бита переставляются в соответствии с матрицей IP. Результат такого преобразования - исходная последовательность битов (расшифрованное 64-битовое значение).

Теперь рассмотрим, что скрывается под преобразованием, обозначенным буквой f. Схема вычисления функции шифрования f(R_i-1,K_i) показана на рис. 3.3.

Рис 3.3. Схема вычисления функции шифрования f

Для вычисления значения функции f используются:

• функция Е (расширение 32 бит до 48);

• функция S₁ S₂,..., S₈ (преобразование 6-битового числа в 4-битовое);

• функция Р (перестановка битов в 32-битовой последовательности).

Приведем определения этих функций.

Аргументами функции шифрования f являются R_i-1 (32 бита) и K_i (48 бит). Результат функции E(R_i-1) есть 48-битовое число. Функция расширения Е, выполняющая расширение 32 бит до 48 (принимает блок из 32 бит и порождает блок из 48 бит), определяется табл. 3.4.

В соответствии с табл.3.4 первые три бита E(R_i-1)-это биты 32,1 и 2, а последние -31, 32,1. Полученный результат (обозначим его E(R_i-1)) складывается по модулю 2 (операция XOR) с текущим
значением ключа Kj и затем разбивается на восемь 6-битовых блоков B_1,В₂,..., В₈:

Таблица 3.4

Функция расширения Е

32  1  2  3  4  5
4   5  6  7  8  9
8   9 10 11 12  13
12 13  14  15  16  17
16  17  18  19  20  21
20  21  22  23  24  25
24  25  26  27  28  29
28 29 30 31  32  1

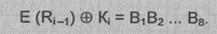
Далее каждый из этих блоков используется как номер элемента в функциях-матрицах S₁, S₂,..., S₈, содержащих 4-битовые значения (табл. 3.5).

Следует отметить, что выбор элемента в матрице Sj осуществляется достаточно оригинальным образом. Пусть на вход матрицы Sj поступает 6-битовый блок Bj = b1b₂b₃b₄b₅b₆, тогда двухбитовое число b₁b₂ указывает номер строки матрицы, а четырехбитовое число b₂b₃b₄b₅-номер столбца. Например, если на вход матрицы S₁ поступает 6-битовый блок В₁=b₁b₂b₃b₄b₅b₆ = 100110, то 2-битовое число b₁b₆ = 10_{( 2)} = 2₍₁₀₎ указывает строку с номером 2 матрицы S_1, а 4-битовое число b₂b₃b₄ b₅ = 0011₍₂₎ = 3₍₁₀₎ указывает столбец с номером 3 матрицы S₁. Это означает, что в матрице S₁ блок В₁ = 100110 выбирает элемент на пересечении строки с номером 2 и столбца с номером 3, т.е. элемент 8₍₁₀₎ = 1000_(2). Совокупность 6-битовых блоков b₁, b₂,..., b₈ обеспечивает выбор четырехбитового элемента в каждой из матриц S₁, S₂,..., S₈.

В результате получаем S₁(В₁)S₂(В₂)S₃(В₃)... S₈(B₈), т.е. 32-битовый блок (поскольку матрицы Sj содержат 4-битовые элементы).

Этот 32-битовый блок преобразуется с помощью функции перестановки битов Р (табл. 3.6).

Таким образом, функция шифрования

F(R_i-1, K_i) = P(S₁(B₁),…, S₈(B₈)).

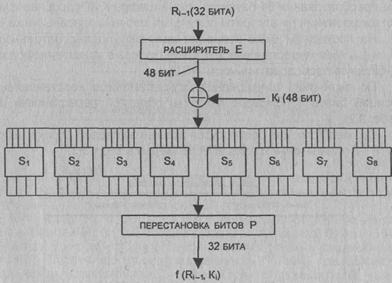
Как нетрудно заметить, на каждой итерации используется новое значение ключа Ki (длиной 48 бит). Новое значение ключа Ki вычисляется из начального ключа К (рис. 3.4). Ключ К представляет собой 64-битовый блок с 8 битами контроля по четности, расположенными в позициях 8,16, 24, 32, 40, 48, 56, 64. Для удаления контрольных битов и подготовки ключа к работе используется функция G первоначальной подготовки ключа (табл. 3.7).

Табл. 3.7 разделена на две части. Результат преобразования G(K) разбивается на две половины С₀ и D₀ по 28 бит каждая. Первые четыре строки матрицы G определяют, как выбираются биты последовательности С₀ (первым битом С₀ будет бит 57 ключа шифра, затем бит 49 и т.д., а последними битами - биты 44 и 36 ключа).

Рис. 3.4. Схема алгоритма вычисления ключей Ki

Следующие четыре строки матрицы G определяют, как выбираются биты последовательности D₀ (т.е. последовательность D₀ будет состоять из битов 63, 55, 47, ...,12, 4 ключа шифра).

Как видно из табл. 3.7, для генерации последовательностей С₀ и D₀ не используются биты 8,16, 24, 32, 40, 48, 56 и 64 ключа шифра. Эти биты не влияют на шифрование и могут служить для других
целей (например, для контроля по четности). Таким образом, в действительности ключ шифра является 56-битовым.

После определения С₀ и D₀ рекурсивно определяются Ci и Di, i = 1,2, ...,16. Для этого применяются операции циклического сдвига влево на один или два бита в зависимости от номера шага итерации, как показано в табл. 3.8.

Операции сдвига выполняются для последовательностей Сi и Di, независимо. Например, последовательность С₃ получается посредством циклического сдвига влево на две позиции последовательности С₂, а последовательность D₃ - посредством сдвига влево на две позиции последовательности D₂, C₁₆ и D₁₆ получаются из С₁₅ и D₁₅ посредством сдвига влево на одну позицию.

Таблица 3.8

Таблица сдвигов Si для вычисления ключа

Номер итерации	Количество Si сдвигов влево, бит	Номер итерации	Количество Si сдвигов влево, бит
1	1	9	1
2	1	10	2
3	2	11	2
4	2	12	2
5	2	13	2
6	2	14	2
7	2	15	2
8	2	16	1

Ключ Ki, определяемый на каждом шаге итерации, есть результат выбора конкретных битов из 56-битовой последовательности Ci Di и их перестановки. Другими словами, ключ Ki = H(CiDi), где
функция Н определяется матрицей, завершающей обработку ключа (табл. 3.9).

Как следует из табл. 3.9, первым битом ключа Кi будет 14-й бит последовательности CiDi, вторым-17-й бит, 47-м битом ключа К_i будет 29-й бит СiDi, а 48-м битом - 32-й бит CiDi.

Таблица 3.9

Функция Н завершающей обработки ключа
(переставленная выборка 2)

14    17   11   24    1    5
      3     28   15    6   21   10
23    19   12    4   26    8

16     7   27   20   13    2
41   52   31   37   47   55
30   40   51   45   33   48
44   49   39   56   34   53
46   42   50   36   29   32

3.2.Основные режимы работы алгоритма DES

Алгоритм DES вполне подходит как для шифрования, так и для аутентификации данных. Он позволяет непосредственно преобразовывать 64-битовый входной открытый текст в 64-битовый
выходной шифрованный текст, однако данные редко ограничиваются 64 разрядами.

Чтобы воспользоваться алгоритмом DES для решения разнообразных криптографических задач, разработаны четыре рабочих режима:

• электронная кодовая книга ЕСВ (Electronic Code Book);

• сцепление блоков шифра СВС (Cipher Block Chaining);

• обратная связь по шифртексту СFВ (Cipher Feed Back);

• обратная связь по выходу OFB (Output Feed Back).

Режим "Электронная кодовая книга"

Длинный файл разбивают на 64-битовые отрезки (блоки) по 8 байтов. Каждый из этих блоков шифруют независимо с использованием одного и того же ключа шифрования (рис.3.5).

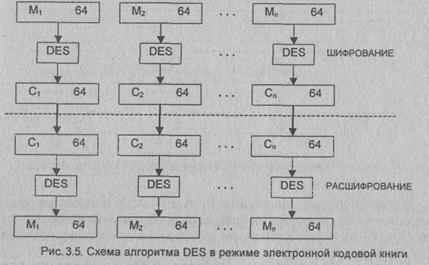
Основное достоинство - простота реализации. Недостаток относительно слабая устойчивость против квалифицированных криптоаналитиков. Из-за фиксированного характера шифрования
при ограниченной длине блока 64 бита возможно проведение криптоанализа "со словарем". Блок такого размера может повториться в сообщении вследствие большой избыточности в тексте на естественном языке. Это приводит к тому, что идентичные блоки открытого текста в сообщении будут представлены идентичными блоками шифртекста, что дает криптоаналитику некоторую информацию о содержании сообщения.

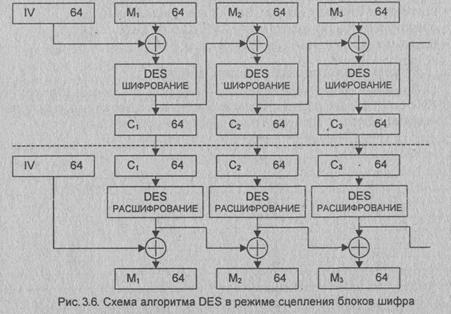
Режим "Сцепление блоков шифра"

В этом режиме исходный файл М разбивается на 64-битовые блоки: М = М₁М₂... М_n. Первый блок m1 складывается по модулю 2 с 64-битовым начальным вектором IV, который меняется ежедневно
и держится в секрете (рис. 3.6). Полученная сумма затем шифруется с использованием ключа DES, известного и отправителю, и получателю информации. Полученный 64-битовый шифр С₁ складывается по модулю 2 со вторым блоком текста, результат шифруется и получается второй 64-битовый шифр С₂, и т.д. Процедура повторяется до тех пор, пока не будут обработаны все блоки текста.

Таким образом, для всех i = 1... n (n-число блоков) результат шифрования Ci определяется следующим образом: C_i = DES(M_i Å C_i-1), где С₀ = IV-начальное значение шифра, равное начальному вектору (вектору инициализации).

Очевидно, что последний 64-битовый блок шифртекста является функцией секретного ключа, начального вектора и каждого бита открытого текста независимо от его длины. Этот блок шифртекста называют кодом аутентификации сообщения (КАС).

Код КАС может быть легко проверен получателем, владеющим секретным ключом и начальным вектором, путем повторения процедуры, выполненной отправителем. Посторонний, однако, не может осуществить генерацию КАС, который воспринялся бы получателем как подлинный, чтобы добавить его к ложному сообщению, либо отделить КАС от истинного сообщения для использования его с измененным или ложным сообщением.

Достоинство данного режима в том, что он не позволяет накапливаться ошибкам при передаче.

Блок M_i является функцией только С_i-1 и C_i. Поэтому ошибка при передаче приведет к потере только двух блоков исходного текста.

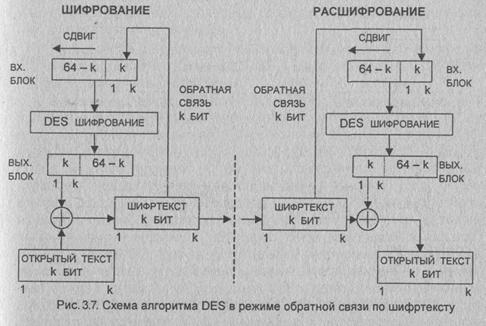
Режим "Обратная связь по шифру"

В этом режиме размер блока может отличаться от 64 бит (рис. 3.7). Файл, подлежащий шифрованию (расшифрованию), считывается последовательными блоками длиной k битов (k =1... 64).

Входной блок (64-битовый регистр сдвига) вначале содержит вектор инициализации, выровненный по правому краю.

Предположим, что в результате разбиения на блоки мы получили n блоков длиной k битов каждый (остаток дописывается нулями или пробелами). Тогда для любого i = 1... n блок шифртекста

C_i = M_i Å P_i-1,

где P_i-1, обозначает k старших битов предыдущего зашифрованного блока.

Обновление сдвигового регистра осуществляется путем удаления его старших k битов и записи Сi в регистр. Восстановление зашифрованных данных также выполняется относительно просто:
P_i-1 и Ci вычисляются аналогичным образом и

M_i = C_i Å P_i-1,

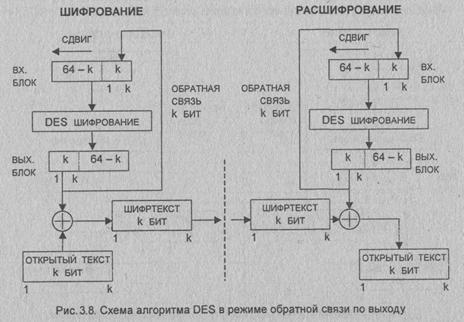
Режим "Обратная связь по выходу"

Этот режим тоже использует переменный размер блока и сдвиговый регистр, инициализируемый так же, как в режиме СFВ, а именно-входной блок вначале содержит вектор инициализации IV, выровненный по правому краю (рис. 3.8). При этом для каждого сеанса шифрования данных необходимо использовать новое начальное состояние регистра, которое должно пересылаться по каналу открытым текстом.

Положим

M=M₁M₂…M₃

Для всех i =1... n

C_i = M_i Å P_i,

где Pi-старшие k битов операции DES (С_i-1).

Отличие от режима обратной связи по шифртексту состоит в методе обновления сдвигового регистра.

Это осуществляется путем отбрасывания старших k битов и дописывания справа Р_i.

Области применения алгоритма DES

Каждому из рассмотренных режимов (ЕСВ, СВС, СFВ, OFB) свойственны свои достоинства и недостатки, что обусловливает области их применения.

Режим ЕСВ хорошо подходит для шифрования ключей: режим СFВ, как правило, предназначается для шифрования отдельных символов, а режим OFB нередко применяется для шифрования в спутниковых системах связи.

Режимы СВС И СFВ пригодны для аутентификации данных. Эти режимы позволяют использовать алгоритм DES для:

• интерактивного шифрования при обмене данными между терминалом и главной ЭВМ;

• шифрования криптографического ключа в практике автоматизированного распространения ключей;

• шифрования файлов, почтовых отправлений, данных спутников и других практических задач.

Первоначально стандарт DES предназначался для шифрования и расшифрования данных ЭВМ. Однако его применение было обобщено и на аутентификацию.

В системах автоматической обработки данных человек не в состоянии просмотреть данные, чтобы установить, не внесены ли в них какие-либо изменения. При огромных объемах данных, проходящих в современных системах обработки, просмотр занял бы слишком много времени. К тому же избыточность данных может оказаться недостаточной для обнаружения ошибок.  Даже в тех случаях, когда просмотр человеком возможен, данные могут быть изменены таким образом, что обнаружить эти изменения человеку очень трудно. Например, "do" может быть заменено на "do not", "$1900"-на "$9100". Без дополнительной информации человек при просмотре может легко принять измененные данные за подлинные. Такие опасности могут существовать даже при использовании шифрования данных. Поэтому желательно иметь автоматическое средство обнаружения преднамеренных и непреднамеренных изменений данных.

Обыкновенные коды, обнаруживающие ошибки, непригодны, так как если алгоритм образования кода известен, противник может выработать правильный код после внесения изменений в данные. Однако с помощью алгоритма DES можно образовать криптографическую контрольную сумму, которая может защитить как от случайных, так и преднамеренных, но несанкционированных изменений данных.

Этот процесс описывает стандарт для аутентификации данных ЭВМ (FIPS 113). Суть стандарта состоит в том, что данные зашифровываются в режиме обратной связи по шифртексту (режим СFВ) или в режиме сцепления блоков шифра (режим СВС), в результате чего получается окончательный блок шифра, представляющий собой функцию всех разрядов открытого текста. После этого сообщение, которое содержит открытый текст, может быть передано с использованием вычисленного окончательного блока шифра, служащего в качестве криптографической контрольной суммы.

Одни и те же данные можно защитить, пользуясь как шифрованием, так и аутентификацией. Данные защищаются от ознакомления шифрованием, а изменения обнаруживаются посредством
аутентификации. Алгоритм аутентификации можно применить как к открытому, так и к зашифрованному тексту. При финансовых операциях, когда в большинстве случаев реализуются и шифрование, и аутентификация, последняя применяется и к открытому тексту.

Шифрование и аутентификацию используют для защиты данных, хранящихся в ЭВМ. Во многих ЭВМ пароли зашифровывают необратимым образом и хранят в памяти машины. Когда пользователь обращается к ЭВМ и вводит пароль, последний зашифровывается и сравнивается с хранящимся значением. Если обе зашифрованные величины одинаковы, пользователь получает доступ к машине, в противном случае следует отказ.

            Нередко зашифрованный пароль вырабатывают с помощью алгоритма DES, причем ключ полагается равным паролю, а открытый текст-коду идентификации пользователя.

            С помощью алгоритма DES можно также зашифровать файлы ЭВМ для их хранения [82].

Одним из наиболее важных применений алгоритма DES является защита сообщений электронной системы платежей (ЭСП) при операциях с широкой клиентурой и между банками.   

            Алгоритм DES реализуется в банковских автоматах, терминалах в торговых точках,  автоматизированных рабочих местах и  главных ЭВМ. Диапазон защищаемых им данных весьма широк от оплат $50 до переводов на многие миллионы долларов. Гибкость основного алгоритма DES позволяет использовать его в самых разнообразных областях применения электронной системы платежей.           

3.3. Комбинирование блочных алгоритмов

В настоящее время блочный алгоритм DES считается относительно  безопасным  алгоритмом   шифрования.   Он  подвергался тщательному криптоанализу в течение 20 лет, и самым практичным способом его взламывания является метод перебора всех  возможных вариантов ключа. Ключ DES имеет длину 56 бит, поэтому существует 256 возможных вариантов такого ключа. Если предположить, что суперкомпьютер может испытать миллион вариантов ключа за секунду, то потребуется 2285 лет для нахождения правильного ключа. Если бы ключ имел длину 128 бит, то потребовалось бы 1025 лет (для сравнения: возраст Вселенной около 1010лет).

Нетрудно представить себе, что при постоянном прогрессе возможностей компьютерной техники недалеко то время, когда машины поиска ключа DES методом полного перебора станут экономичными для мощных в финансовом отношении государственных и коммерческих организаций.

Возникает естественный вопрос: нельзя ли использовать DES в качестве строительного блока для создания другого алгоритма с более длинным ключом?

           В принципе существует много способов комбинирования блочных алгоритмов для получения новых алгоритмов. Одним из таких способов  комбинирования  является  многократное  шифрование,
т.е. использование блочного алгоритма несколько раз с разными ключами для шифрования одного и того же блока открытого текста. Двухкратное шифрование блока открытого текста одним и тем
 же ключом не приводит к положительному результату. При использовании одного и того же алгоритма такое шифрование не влияет на сложность криптоаналитической атаки полного перебора.
           Рассмотрим эффективность двухкратного шифрования блока  открытого текста с помощью двух разных ключей. Сначала шифруют блок Р ключом K₁ а затем получившийся шифртекст E_K1(P)
 шифруют ключом К₂. В результате двухкратного шифрования получают криптограмму

C = E_K2(EK1(P)).

         Расшифрование является обратным процессом:

P = D_K1(D_K2(C)).

         Если блочный алгоритм обладает свойствами группы [125], то всегда найдется такой ключ К₃, что

С = Е_K2(Е_K1(Р))=Е_K3(Р).

         Если же блочный алгоритм не является группой, то результирующий двухкратно шифрованный блок текста окажется намного сложнее для взламывания методом полного перебора вариантов.

Вместо 2ⁿ попыток, где n-длина ключа в битах, потребуется 2²ⁿ . попыток. В частности, если n = 64, то двухкратно зашифрованный  блок текста потребует 2¹²⁸ попыток для нахождения ключа.
            Однако Р. Меркль и М. Хеллман показали на примере DES,  что, используя метод "обмена времени на память" и криптоаналитическую атаку "встреча посредине", можно взломать такую схему
 двухкратного шифрования за 2ⁿ⁺¹ попыток [34]. Хотя эта атака потребует очень большого объема памяти (для алгоритма с 56-битовым ключом потребуется 256 64-битовых блоков или 1017 бит

памяти).

Более привлекательную идею предложил У. Тачмен [125]. Суть этой идеи состоит в том, чтобы шифровать блок открытого текста Р три раза с помощью двух ключей K₁ и К₂ (рис. 3.9). Процедура
шифрования:

C = E_K1(D_K2(E_K1(P))),

т.е. блок открытого текста Р сначала шифруется ключом K₁, затем расшифровывается ключом К₂ и окончательно зашифровывается ключом K₁

.

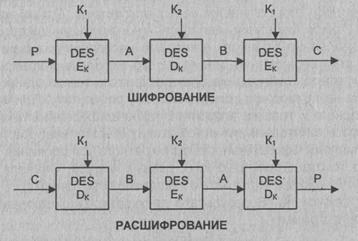
Рис. 3.9. Схемы трехкратного применения алгоритма DES
с двумя разными ключами

Этот режим иногда называют режимом EDE (encrypt-decrypt- encrypt). Введение в данную схему операции расшифрования D_K2 позволяет обеспечить совместимость этой схемы со схемой однократного использования алгоритма DES. Если в схеме трехкратного использования DES выбрать все ключи одинаковыми, то эта схема превращается в схему однократного использования DES. Процедура расшифрования выполняется в обратном порядке:

Р = D_K1(Е_K2(D_К1(С))),

т.е. блок шифртекста С сначала расшифровывается ключом K₁, затем зашифровывается ключом К₂ и окончательно расшифровывается ключом K₁.

Если исходный блочный алгоритм имеет n-битовый ключ, то схема трехкратного шифрования имеет 2n-битовый ключ. Чередование ключей K₁ и К₂ позволяет предотвратить криптоаналитическую атаку "встреча посредине". Данная схема приводится в стандартах Х9.17 и ISO 8732 в качестве средства улучшения характеристик алгоритма DES.

При трехкратном шифровании можно применить три различных ключа. При этом возрастает общая длина результирующего ключа. Процедуры шифрования и расшифрования описываются выражениями:

С = Е_K3(D_К2(Е_К1(Р))),

Р = D_К1(Е_К2(D_К3(С))).

Трехключевой вариант имеет еще большую стойкость. Очевидно, что если требуется повысить безопасность большого парка оборудования, использующего DES, то гораздо дешевле переключиться на схемы трехкратных DES, чем переходить на другой тип криптосхем.

3.4. Алгоритм шифрования данных IDEA

Алгоритм IDEA (International Data Encryption Algorithm) является блочным шифром. Он оперирует 64-битовыми блоками открытого текста. Несомненным достоинством алгоритма IDEA является то, что его ключ имеет длину 128 бит. Один и тот же алгоритм используется и для шифрования, и для расшифрования.

Первая версия алгоритма IDEA была предложена в 1990г., ее авторы -X. Лей и Дж. Мэсси. Первоначальное название алгоритма PES (Proposed Encryption Standard). Улучшенный вариант этого
алгоритма, разработанный в 1991г., получил название IPES (Improved Proposed Encryption Standard). В 1992г. IPES изменил свое имя на IDEA. Как и большинство других блочных шифров, алгоритм IDEA использует при шифровании процессы смешивания и рассеивания, причем все процессы легко реализуются аппаратными и программными средствами.

В алгоритме IDEA используются следующие математические операции:

• поразрядное сложение по модулю 2 (операция "исключающее ИЛИ"); операция обозначается как Å

• сложение беззнаковых целых по модулю 2¹⁶ (модуль 65536); операция обозначается как;

• умножение целых по модулю (2¹⁶ + 1) (модуль 65537), рассматриваемых как беззнаковые целые, за исключением того, что "блок из 16 нулей рассматривается как 2¹⁶; операция обозначается как

Все операции выполняются над 16-битовыми субблоками.

Эти три операции несовместимы в том смысле, что:

• никакая пара из этих трех операций не удовлетворяет ассоциативному закону, например

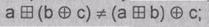
• никакая пара из этих трех операций не удовлетворяет дистрибутивному закону, например

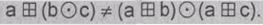
Комбинирование этих трех операций обеспечивает комплексное преобразование входа, существенно затрудняя криптоанализ IDEA по сравнению с DES, который базируется исключительно на операции "исключающее ИЛИ".          

Общая схема алгоритма IDEA приведена на рис.3.10. 64-битовый блок данных делится на четыре 16-битовых субблока. Эти четыре субблока становятся входом в первый цикл алгоритма. Всего выполняется восемь циклов. Между циклами второй и третий субблоки меняются местами. В каждом цикле имеет место следующая последовательность операций:

(1) (×) - умножение субблока X₁ и первого подключа.                      

(2) Ä - сложение субблока Х₂ и второго подключа.

(3) Ä- сложение субблока Х₃ и третьего подключа.

(4) (×) - умножение субблока Х₄ и четвертого подключа.

(5) Å- сложение результатов шагов (1) и (3).

(6) Å - сложение результатов шагов (2) и (4).                                   

(7) (×) - умножение результата шага (5) и пятого подключа.            

(8) Ä- сложение результатов шагов (6) и (7).

(9) (×)- умножение результата шага (8) с шестым подключим.

(10) Ä - сложение результатов шагов (7) и (9).                                

(11) Å - сложение результатов шагов (1) и (9).

(12) Å - сложение результатов шагов (3) и (9).

(13) Å - сложение результатов шагов (2) и (10).

(14) Å - сложение результатов шагов (4) и (10).

            Выходом цикла являются четыре субблока, которые получают  как результаты выполнения шагов (11), (12), (13) и (14). В завершение цикла переставляют местами два внутренних субблока (за исключением последнего цикла), и в результате формируется вход  для следующего цикла.           I

После восьмого цикла осуществляют заключительное преобразование выхода:

(1) (×)- умножение субблока X₁ и первого подключа.                      

(2) Ä- сложение субблока Х₂ и второго подключа.

(3) Ä- сложение субблока Х₃ и третьего подключа.

(4) (×) - умножение субблока Х4 и четвертого подключа.

Наконец, эти результирующие четыре субблока Y₁...Y₄ вновь объединяют для получения блока шифртекста.

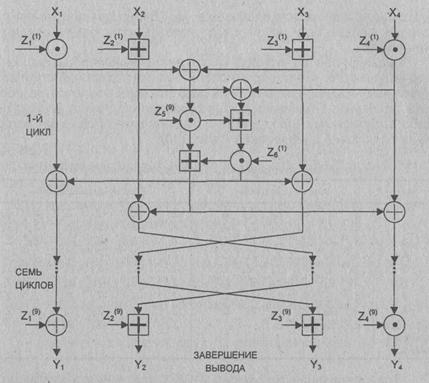
Обозначения:

Xi -16-битовый субблок открытого текста, i = 1... 4

yi  -16-битовый субблок шифртекста, i = 1... 4

Zj(r)-16-битовый подключ (субблок ключа), j =1...6, r=1...8

 - поразрядное суммирование по модулю 2 16-битовых субблоков

 - сложение по модулю 2¹⁶ 16-битовых целых -умножение по модулю 2¹⁶ 16-битовых целых (с нулевым субблоком,  соответствующим 2¹⁶)

Рис. 3.10. Схема алгоритма IDEA (режим шифрования)

Создание подключен Zj также относительно несложно. Алгоритм использует всего 52 подключа (по шесть для каждого из восьми циклов и еще четыре для преобразования выхода). Сначала 128-битовый ключ делят на восемь 16-битовых подключей. Это- первые восемь подключей для алгоритма (шесть подключей – для первого цикла и первые два подключа - для второго цикла). Затем 128-битовый ключ циклически сдвигается влево на 25 бит и снова делится на восемь подключей. Первые четыре из них используют во втором цикле; последние четыре - в третьем цикле. Ключ снова циклически сдвигается влево еще на 25 бит для получения следующих восьми подключей и т.д., пока выполнение алгоритма не завершится.           

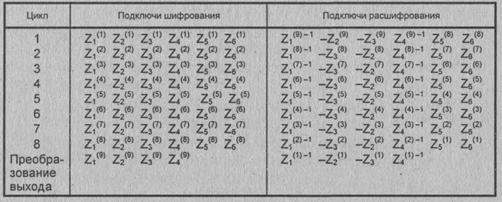
            Расшифрование осуществляют аналогичным образом, за исключением того, что порядок использования подключей становится обратным, причем ряд значений подключен заменяется на обратные значения.  Подключи расшифрования являются в основном либо аддитивными, либо мультипликативными обратными величинами подключей шифрования (табл. 3.10).

Таблица 3.10           

Подключи шифрования и расшифрования алгоритма IDEA

Для реализации алгоритма IDEA было  принято предположение, что нулевой субблок равен 2¹⁶= -1; при этом мультипликативная обратная величина от 0 равна 0 [121]. Вычисление значений
мультипликативных обратных величин требует некоторых затрат, но это приходится делать только один раз для каждого ключа расшифрования.

Алгоритм IDEA может работать в любом режиме блочного шифра, предусмотренном для алгоритма DES. Алгоритм IDEA обладает рядом преимуществ перед алгоритмом DES. Он значительно безопаснее алгоритма DES, поскольку 128-битовый ключ алгоритма IDEA вдвое больше ключа DES. Внутренняя структура алгоритма IDEA обеспечивает лучшую устойчивость к криптоанализу. Существующие программные реализации алгоритма IDEA примерно вдвое быстрее реализаций алгоритма DES. Алгоритм IDEA шифрует данные на IBM PC/486 со скоростью 2,4 Мбит/с.
Реализация IDEA на СБИС шифрует данные со скоростью 177 Мбит/с при частоте 25 Мгц. Алгоритм IDEA запатентован в Европе и США.

3.5. Отечественный стандарт шифрования данных

В нашей стране установлен единый алгоритм криптографического преобразования данных для систем обработки информации в сетях ЭВМ, отдельных вычислительных комплексах и ЭВМ, который определяется ГОСТ 28147-89 [81]. Стандарт обязателен для организаций, предприятий и учреждений, применяющих криптографическую защиту данных, хранимых и передаваемых в сетях ЭВМ, в отдельных вычислительных комплексах и ЭВМ.

Этот алгоритм криптографического преобразования данных предназначен для аппаратной и программной реализации, удовлетворяет криптографическим требованиям и не накладывает ограничений на степень секретности защищаемой информации. Алгоритм шифрования данных представляет собой 64-битовый блочный алгоритм с 256-битовым ключом.

При описании алгоритма используются следующие обозначения:

L и R - последовательности битов;

LR - конкатенация последовательностей L и R, в которой биты последовательности R следуют за битами последовательности L;

 - операция побитового сложения по модулю 2;

 -операция сложения по модулю 232 двух 32-разрядных двоичных чисел;

 -операция сложения двух 32-разрядных чисел по модулю 2³²-1.

Два целых числа а, b, где 0 £ а,b£ 2³²-1,

а = (а₃₂а₃₁... а₂а₁),   b = (b₃₂, b₃₁, ..., b₂, b₁),

представленные в двоичном виде, т.е.

а = а₃₂-2³¹ + а₃₁2³⁰ +...+ а₂-21 + а₁,

b = b₃₂*2³¹ + b₃₁*2³⁰+...+ b₂*21 + b₁,

суммируются по модулю 2³² (операция) по следующему правилу:

Правила суммирования чисел по модулю 2³²-1:

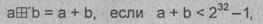
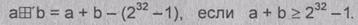
Алгоритм предусматривает четыре режима работы:

• шифрование данных в режиме простой замены;

• шифрование данных в режиме гаммирования;

• шифрование данных в режиме гаммирования с обратной связью;

• выработка имитовставки.

Режим простой замены    

Для реализации алгоритма шифрования данных в режиме простой замены используется только часть блоков общей криптосистемы (рис. 3.11). Обозначения на схеме:      

N₁, N₂-32-разрядные накопители;                                                 

СM₁- 32-разрядный сумматор по модулю 2³² (Ä);

СМ²-32-разрядный сумматор по модулю 2 (Å);                           

R-32-разрядный регистр циклического сдвига;                           

КЗУ - ключевое запоминающее устройство на 256 бит, состоящее из восьми 32-разрядных накопителей Х₀, X₁, Х₂, ..., Х₇;                                                                                    

S-блок подстановки, состоящий из восьми узлов замены (S-блоков замены) S₁, S₂, S₃, ..., S₇, S₈;  

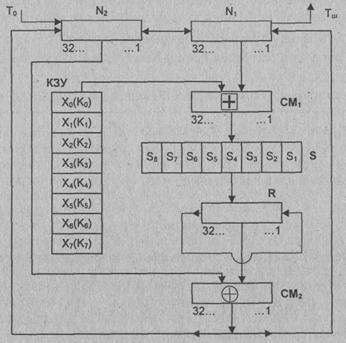
Рис. 3.11. Схема реализации режима простой замены

             Зашифрование открытых данных в режиме простой замены. Открытые данные, подлежащие зашифрованию, разбивают на 64-разрядные блоки Т₀. Процедура зашифрования 64-разрядного блока Т₀ в режиме простой замены включает 32 цикла (j = 1... 32). В ключевое запоминающее устройство вводят 256 бит ключа К в виде восьми 32-разрядных подключей (чисел) Ki:       

К= K₇K₆K₅K₄K₃K₂K₁K₀.

Последовательность битов блока

Т₀= (а₁(0), а₂(0), ..., а₃₁(0), а₃₂(0),   b₁(0), b₂(0), ..., b₃₁(0), b₃₂(0))

разбивают на две последовательности по 32 бита: b(0) а(0), где b(0)-левые или старшие биты, а(0)- правые или младшие биты.

Эти последовательности вводят в накопители N₁ и N₂ перед началом первого цикла зашифрования. В результате начальное заполнение накопителя n₁

а(0) = (а₃₂(0), а₃₁(0), ..., а₂(0), a₁(0)),

                                                   32,      31,   ...    2,          1       ¬номер разряда N₁

начальное заполнение накопителя N₂

b(0) = (b₃₂(0),b₃₁(0),...,b₂(0),b₁(0)).

                                                    32,    31,    ...    2,          1       ¬ номер разряда N₂

Первый цикл (j = 1) процедуры зашифрования 64-разрядного блока открытых данных можно описать уравнениями:

Здесь а (1)-заполнение N₁ после 1-го цикла зашифрования; b(1)-заполнение N₂ после 1-го цикла зашифрования; f-функция шифрования.

Аргументом функции f является сумма по модулю 2³² числа а(0) (начального заполнения накопителя N₁) и числа К₀-подключа, считываемого из накопителя Х₀ КЗУ. Каждое из этих чисел равно
32 битам.

Функция f включает две операции над полученной 32-разрядной суммой (a(0)ÄK₀).

Первая операция называется подстановкой (заменой) и выполняется блоком подстановки S. Блок подстановки S состоит из восьми узлов замены (S-блоков замены) S₁, S₂, ...,S₈ с памятью
64 бит каждый. Поступающий из CM₁ на блок подстановки S₃₂-разрядный вектор разбивают на восемь последовательно идущих 4-разрядных векторов, каждый из которых преобразуется в четырехразрядный вектор соответствующим узлом замены. Каждый узел замены можно представить в виде таблицы-перестановки шестнадцати четырехразрядных двоичных чисел в диапазоне 0000...1111. Входной вектор указывает адрес строки в таблице, а число в этой строке является выходным вектором. Затем четырехразрядные выходные векторы последовательно объединяют в 32-разрядный вектор. Узлы замены (таблицы-перестановки), представляют собой ключевые элементы, которые являются общими
для сети ЭВМ и редко изменяются. Эти узлы замены должны сохраняться в секрете.

Вторая операция - циклический сдвиг влево (на 11 разрядов) 32-разрядного вектора, полученного с выхода блока подстановки S. Циклический сдвиг выполняется регистром сдвига R.

Далее результат работы функции шифрования f суммируют поразрядно па модулю 2 в сумматоре СМ₂ с 32-разрядным начальным заполнением b(0) накопителя N₂. Затем полученный на выходе СМ₂ результат (значение а(1)) записывают в накопитель N₁, а старое значение N₁ (значение а(0)) переписывают в накопитель N₂ (значение b(1) = а(0)). Первый цикл завершен.

Последующие циклы осуществляются аналогично, при этом во втором цикле из КЗУ считывают заполнение X₁-подключ K₁, в третьем цикле - подключ К₂ и т.д., в восьмом цикле - подключ К₇. В
циклах с 9-го по 16-й, а также в циклах с 17-го по 24-й подключи из КЗУ считываются в том же порядке: К₀, К₁, К₂,.... К₆, К₇. В последних восьми циклах с 25-го по 32-й порядок считывания подключей из
КЗУ обратный: К₇, К₆, ..., К₂, К₁, К₀. Таким образом, при зашифровании в 32 циклах осуществляется следующий порядок выборки из КЗУ подключей:

K₀, K₁, K₂, К₃, К₄, K₅, K₆, К₇, К₀, К₁, К₂, К₃, К₄, K₅, K₆, K₇,

K₀, K₁, К₂, К₃, К₄, K₅, К₆, К₇, K₇, K₆, K₅, К₄, К₃, К₂, K₁, K₀.

В 32-м цикле результат из сумматора СМ₂ вводится в накопитель N₂, а в накопителе N₁ сохраняется прежнее заполнение. Полученные после 32-го цикла зашифрования заполнения накопителей N₁ и N₂ являются блоком зашифрованных данных Т_ш, соответствующим блоку открытых данных Т₀.       

Уравнения зашифрования в режиме простой замены имеют вид:

где  a(j) = (a₃₂ (i),  a₃₁(j),...., а₁( j ))-заполнение  N₁ после j-гo   цикла зашифрования;   b(j) = (b₃₂(j), b₃₁(j), …,b₁(j))-заполнение   N₂ после j- гo цикла зашифрования, j = 1... 32.  

            Блок зашифрованных данных Тш (64 разряда) выводится из накопителей N_l N₂ в следующем  порядке: из разрядов 1...32 накопителя N₁, затем из разрядов 1... 32 накопителя N₂, т.е. начиная      c младших-разрядов:                                 

Тш= (а₁ (32), а₂(32), ..., а₃₂(32), b₁(32), b₂(32), .... b₃₂(32)).

Остальные блоки открытых данных зашифровываются в режиме простой замены аналогично.

Расшифрование в режиме простой замены. Криптосхема, реализующая алгоритм расшифрования в режиме простой замены, имеет тот же вид, что и при зашифровании (см. рис. 3.11).

В КЗУ вводят 256 бит ключа, на котором осуществлялось зашифрование. Зашифрованные данные, подлежащие расшифрованию, разбиты на блоки Тш по 64 бита в каждом. Ввод любого блока

Тш = (a₁ (32), а₂(32),.... а₃₂(32), b₁(32), b₂(32),.... b₃₂(32))

в накопители N₁ и N₂ производят так, чтобы начальное значение накопителя N₁ имело вид

(а₃₂(32),а₃₁(32), ...,а₂(32),а₁(32)),
    32,     31,     ...,    2,       1          ¬ номер разряда N₁

а начальное заполнение накопителя N₂ – вид

(b₃₂(32)b₃₁(32), ..., b₂(32)b₁(32)).

    32       31,        ...,  2,       1          ¬ номер разряда N₂

Расшифрование осуществляется по тому же алгоритму, что и зашифрование, с тем изменением, что заполнения накопителей Х₀, X_l ,..., Х₇ считываются из КЗУ в циклах расшифрования в следующем порядке:

K₀, K₁, К₂, К₃, К₄, K₅, K₆, К₇, К₇, K₆, K₅, K₄, К₃, К₂, K₁, K₀,

K₇, K₆, K₅, К₄, K₃, К₂, K₁, K₀, K₇, K₆, K₅, K₄, K₃, K₂, K₁, K₀.

Уравнения расшифрования имеют вид:

Полученные после 32 циклов работы заполнения накопителей N₁ и N₂ образуют блок открытых данных

Т₀ = (a₁(0), а₂(0), .... а₃₂(0), b₁(0), b₂(0), ..., b₃₂(0)),

соответствующий блоку зашифрованных данных Тш. При этом состояние накопителя N₁

(а₃₂(0),а₃₁(0),..,а₂(0),а₁(0)),

                                      32,     31,  ...,  2,     1         ¬ номер разряда N₁

состояние накопителя N₂

(b₃₂(0)b₃₁(0), ..., b₂(0)b₁(0)).

                                    32,     31, ...,  2,     1          ¬ номер разряда N₂

Аналогично расшифровываются остальные блоки зашифрованных данных.

Если алгоритм зашифрования в режиме простой замены 64-битового блока Т₀ обозначить через А, то

А (Т₀) = А (а(0), b(0)) = (а (32), b (32)) =Т_Ш.

Следует иметь в виду, что режим простой замены допустимо использовать для шифрования данных только в ограниченных случаях - при выработке ключа и зашифровании его с обеспечением имитозащиты для передачи по каналам связи или для хранения в памяти ЭВМ.

Режим гаммирования

Зашифрование открытых данных в режиме гаммирования. Криптосхема, реализующая алгоритм зашифрования в режиме гаммирования, показана на рис. 3.12. Открытые данные разбивают на 64-разрядные блоки

T₀⁽¹⁾, T₀⁽²⁾,…, T₀⁽ⁱ⁾,…,T₀^(m)

где T₀⁽ⁱ⁾ -i-й 64-разрядный блок открытых данных, i = 1... m, m определяется объемом шифруемых данных.

Эти блоки поочередно зашифровываются в режиме гаммирования путем поразрядного сложения по модулю 2 в сумматоре СМ₅ с гаммой шифра Г_ш, которая вырабатывается блоками по 64 бита, т.е.

Г_ш = (Г_ш⁽¹⁾, Г_ш⁽²⁾,…., Г_ш⁽ⁱ⁾, Г_ш^(m)),

где Г_ш⁽ⁱ⁾ - i-й 64-разрядный блок, i = 1... m.

Число двоичных разрядов в блоке Т₀^(m) может быть меньше 64, при этом неиспользованная для зашифрования часть гаммы шифра из блока Г_ш^(m) отбрасывается.

Уравнение зашифрования данных в режиме гаммирования имеет вид

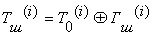
где 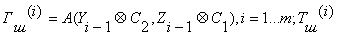    -i-й блок 64-разрядного блока зашифрованного текста; А(.)- функция зашифрования в режиме простой замены; C₁, С₂-32-разрядные двоичные константы; Y_i, Z_i- 32-разрядные двоичные последовательности.

Величины Y_i, Z_i определяются итерационно по мере формирования гаммы Г_ш следующим образом:

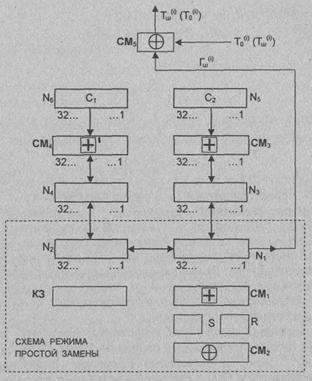
Рис. 3.12. Схема реализации режима гаммирования

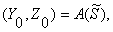
где 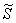- синхропосылка (64-разрядная двоичная последовательность),

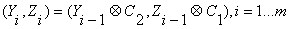
Рассмотрим реализацию процедуры зашифрования в режиме гаммирования. В накопители N₆ и N₅ заранее записаны 32-разрядные двоичные константы С₁ и С₂, имеющие следующие значения (в шестнадцатеричной форме):

С₁ = 01010104₍₁₆₎,  С₂ = 01010101₍₁₆₎

В КЗУ вводится 256 бит ключа; в накопители N₁ и N₂-64-разрядная двоичная последовательность (синхропосылка)

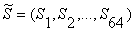
Синхропосылка 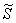 является исходным заполнением накопителей N₁ и N₂ для последовательной выработки m блоков гаммы шифра.

Исходное заполнение накопителя N₁:

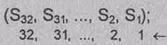 номер разряда N₁

исходное заполнение накопителя N₂:

¬ номер разряда N₂

Исходное заполнение N₁ и N₂ (синхропосылка S) зашифровывается в режиме простой замены. Результат зашифрования

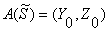
переписывается в 32-разрядные накопители N₃ и N₄ так, что заполнение N₁ переписывается в N₃, а заполнение N₂ – N₄

Заполнение накопителя N₄ суммируют по модулю (2³²-1) в сумматоре СМ₄ с 32-разрядной константой C₁ из накопителя N₆. Результат записывается в N₄. Заполнение накопителя N₃ суммируется по модулю 2³² в сумматоре СМ₃ с 32-разрядной константой С₂ из накопителя N₅. Результат записывается в N₃. Заполнение N₃ переписывают в N₁ а заполнение N₄-в N₂, при этом заполнения N₃, N₄ сохраняются. Заполнение накопителей N₁ и N₂ зашифровывается в режиме простой замены.

            Полученное в результате зашифрования заполнение накопителей N₁, N₂ образует первый 64-разрядный блок гаммы шифра 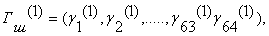, который суммируют поразрядно по модулю 2 в сумматоре СМ₅ с первым 64-разрядным блоком открытых данных

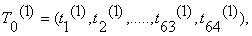
В результате суммирования по модулю 2 значений Г_ш⁽¹⁾ и Т₀⁽¹⁾ получают первый 64-разрядный блок зашифрованных данных:

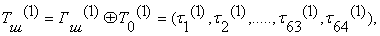
где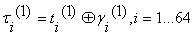

Для получения следующего 64-разрядного блока гаммы шифра Гш⁽²⁾ заполнение N₄ суммируется по модулю (2³²-1) в сумматоре СМ₄ с константой С₁ из N₆. Результат записывается в N₄. Заполнение N₃ суммируется по модулю 2³² в сумматоре СМ₃ с константой С₂ из N₅. Результат записывается в N₃.          Новое заполнение N₃ переписывают в N₁, а новое заполнение N₄-в N₂, при этом заполнения
N₃ и N₄ сохраняют. Заполнения  N₁, N₂ зашифровывают в режиме простой замены.

Полученное в результате зашифрования заполнение накопителей N₁ и N₂ образует второй 64-разрядный блок гаммы шифра Г_ш⁽²⁾, который суммируется поразрядно по модулю 2 в сумматоре
СМ₅ со вторым блоком открытых данных Т₀⁽²⁾:

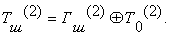
Аналогично вырабатываются блоки гаммы шифра Г_ш⁽³⁾, Г_ш⁽⁴⁾, .... Г_ш^(m) и зашифровываются блоки открытых данных Т₀⁽³⁾, Т₀⁽⁴⁾, …, Т₀^(m).

В канал связи или память ЭВМ передаются синхропосылка S и блоки зашифрованных данных

T_ш⁽¹⁾, Т_ш⁽²⁾,…, Т_ш^(m)

Расшифрование в режиме гаммирования. При расшифровании криптосхема имеет тот же вид, что и при зашифровании (см. рис. 3.12).

Уравнение расшифрования:

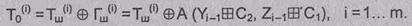
Следует отметить, что расшифрование данных возможно только при наличии синхропосылки, которая не является секретным элементом шифра и может храниться в памяти ЭВМ или передаваться по каналам связи вместе с зашифрованными данными.

            Рассмотрим реализацию процедуры расшифрования. В КЗУ вводят 256 бит ключа, с помощью которого осуществляется зашифрование данных T₀⁽¹⁾, Т₀⁽²⁾,…, Т₀^(m)       В накопители N₁ и N₂ вводится синхропосылка. и осуществляется процесс выработки m блоков гаммы шифра Г_ш⁽¹⁾, Г_ш⁽²⁾,…, Г_ш^(m) Блоки зашифрованных данных T_ш⁽¹⁾, Т_ш⁽²⁾,…, Т_ш^(m) суммируются поразрядно по модулю 2 в сумматоре СМ₅ с блоками гаммы шифра Г_ш⁽¹⁾,..., Г_ш^(m). В результате получаются блоки открытых данных

T₀⁽¹⁾, Т₀⁽²⁾,…, Т₀^(m)

при этом T₀^(m) может содержать меньше 64 разрядов.

Режим гаммирования с обратной связью

Зашифрование открытых данных в режиме гаммирования с обратной связью. Криптосхема, реализующая алгоритм зашифрования в режиме гаммирования с обратной связью, имеет вид, показанный на рис.3.13.

Открытые данные, разбитые на 64-разрядные блоки T₀⁽¹⁾, Т₀⁽²⁾,…, Т₀^(m), зашифровываются в режиме гаммирования с обратной связью путем поразрядного сложения по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бита:

Г_ш = (Г_ш⁽¹⁾, Г_ш⁽²⁾,…, Г_ш^(m))

Число двоичных разрядов в блоке Т₀^(m) может быть меньше 64, при этом неиспользованная для шифрования часть гаммы шифра из блока Г_ш^(m) отбрасывается.

Уравнения зашифрования в режиме гаммирования с обратной связью имеют вид:

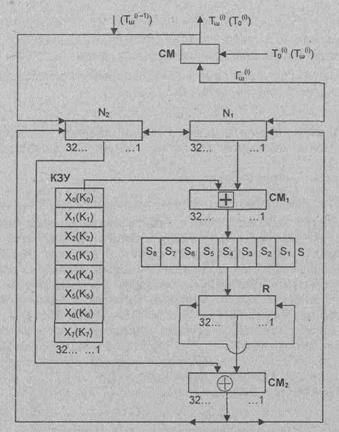
Рис. 3.13. Схема реализации режима гаммирования с обратной связью

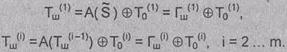
Здесь Т_ш⁽ⁱ⁾ -i-й 64-разрядный блок зашифрованного текста; А(.)- функция зашифрования  в режиме простой замены; m-определяется объемом открытых данных.

Аргументом функции А(.) на первом шаге итеративного алгоритма является 64-разрядная синхропосылка 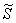, а на всех последующих шагах - предыдущий блок зашифрованных данных Т_ш^(i-1).

Процедура зашифрования данных в режиме гаммирования с обратной связью реализуется следующим образом. В КЗУ вводятся 256 бит ключа. В накопители N₁ и N₂ вводится синхропосылка

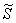= (S₁, S₂,…,S₆₄) из 64 бит. Исходное заполнение накопителей N₁ и N₂ зашифровывается в режиме простой замены. Полученное в результате зашифрования заполнение накопителей N₁ и N₂ образует первый 64-разрядный блок гаммы шифра Г_ш⁽ⁱ⁾ =A(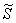), который суммируется поразрядно по модулю 2 в сумматоре СМ₅ с первым 64-разрядным блоком открытых данных

T₀⁽¹⁾= (t₁⁽¹⁾, t₂⁽¹⁾,…,t₆₄⁽¹⁾).

В результате получают первый 64-разрядный блок зашифрованных данных

T_ш⁽¹⁾ = Г_ш⁽¹⁾ Å T₀⁽¹⁾

где T_ш⁽¹⁾= (t_ш⁽¹⁾, t_ш⁽¹⁾,…,t_ш⁽¹⁾).

Блок зашифрованных данных Т_ш⁽¹⁾ одновременно является также исходным состоянием накопителей N₁, N₂ для выработки второго блока гаммы шифра Тш⁽²⁾, и поэтому по обратной связи Т_ш⁽¹⁾
записывается в указанные накопители N₁ и N₂.

Заполнение накопителя N₁

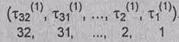¬номер разряда N₁

Заполнение накопителя N₂

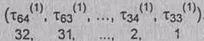¬ номер разряда N₂

Заполнение накопителей N₁ и N₂ зашифровывается в режиме простой замены. Полученное в результате зашифрования заполнение накопителей N₁ и N₂ образует второй 64-разрядный блок
гаммы шифра Г_ш⁽²⁾, который суммируется поразрядно по модулю 2 в сумматоре СМ₅ со вторым блоком открытых данных Т₀⁽²⁾:

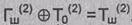
Выработка последующих блоков гаммы шифра Гш⁽ⁱ⁾ и зашифрование соответствующих блоков открытых данных T₀⁽ⁱ⁾ (i=3…m) производится аналогично.

Если длина последнего m-го блока открытых данных Т₀^(m) меньше 64 разрядов, то из Г_ш^(m) используется только соответствующее число разрядов гаммы шифра, остальные разряды отбрасываются.

В канал связи или память ЭВМ передаются синхропосылка 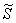 и блоки зашифрованных данных T_ш⁽¹⁾, T_ш⁽²⁾,…,T_ш^(m).

Расшифрование в режиме гаммирования с обратной связью. При расшифровании криптосхема имеет тот же вид, что и при зашифровании (см. рис.3.13).

Уравнения расшифрования:

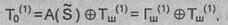
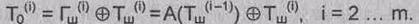
Реализация процедуры расшифрования зашифрованных данных в режиме гаммирования с обратной связью происходит следующим образом. В КЗУ вводят 256 бит того же ключа нa котором
осуществлялось зашифрование открытых блоков T₀⁽¹⁾, T₀⁽²⁾,…,T₀^(m).

В накопители N₁ и N₂ вводится синхропосылка S. Исходное заполнение накопителей N₁ и N₂ (синхропосылка 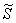) зашифровывается в режиме простой замены. Полученное в результате зашифрования заполнение N₁ и N₂ образует первый блок гаммы шифра

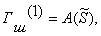
который суммируется поразрядно по модулю 2 в сумматоре СМ₅ с блоком зашифрованных данных Т_ш⁽¹⁾.

В результате получается первый блок открытых данных

T₀⁽¹⁾=Г_ш⁽¹⁾ Å T_ш⁽¹⁾

            Блок зашифрованных данных Т_ш⁽¹⁾ является исходным заполнением накопителей N₁ и N₂ для выработки второго блока гаммы шифра Г_ш⁽²⁾ : Г_ш⁽²⁾= А(Т_ш⁽¹⁾). Полученное заполнение накопителей N₁
и N₂ зашифровывается в режиме простой замены. Образованный в результате зашифрования блок Гш⁽²⁾ суммируется поразрядно по модулю 2 в сумматоре СМ₅ со вторым блоком зашифрованных
данных Т_ш⁽²⁾. В результате получают второй блок открытых данных. Аналогично в N₁ N₂ последовательно записывают блоки зашифрованных данных T_ш⁽²⁾, T_ш⁽³⁾,…,T_ш^(m) из которых в режиме простой замены вырабатываются блоки гаммы шифра Г_ш⁽²⁾, Г_ш⁽³⁾,…,Г_ш^(m).

Блоки гаммы шифра суммируются поразрядно по модулю 2 в сумматоре СМ₅ с блоками зашифрованных данных T_ш⁽³⁾, T_ш⁽⁴⁾,…,T_ш^(m).

В результате получают блоки открытых данных

T₀⁽³⁾, T₀⁽⁴⁾,…,T₀^(m).

при этом последний блок открытых данных T₀^(m) может содержать меньше 64 разрядов.

Режим выработки имитовставки

Имитовставка - это блок из Р бит, который вырабатывают по определенному правилу из открытых данных с использованием ключа и затем добавляют к зашифрованным данным для обеспечения их имитозащиты.

Имитозащита - это защита системы шифрованной связи от навязывания ложных данных.

В стандарте ГОСТ 28147-89 определяется процесс выработки имитовставки, который единообразен для любого из режимов  шифрования данных. Имитовставка Ир вырабатывается из блоков
открытых данных либо перед шифрованием всего сообщения, либо параллельно с шифрованием по блокам. Первые блоки открытых данных, которые участвуют в выработке имитовставки, могут
содержать служебную информацию (например, адресную часть, время, синхропосылку) и не зашифровываются.

Значение параметра Р (число двоичных разрядов в имитовставке) определяется криптографическими требованиями с учетом того, что вероятность навязывания ложных помех равна 1/2^р.

Для выработки имитовставки открытые данные представляют в виде последовательности 64-разрядных блоков Т₀⁽ⁱ⁾, i =1…m.

Первый блок открытых данных Т₀⁽¹⁾ подвергают преобразованию А(.), соответствующему первым 16 циклам алгоритма зашифрования в режиме простой замены, В качестве ключа для выработки имитовставки используют ключ длиной 256 бит, по которому шифруют данные.

Полученное после 16 циклов 64-разрядное числе 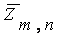      суммируют по модулю 2 со вторым блоком открытых данных T₀^(2). Результат суммирования 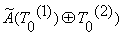 снова подвергают преобразованию А(.).

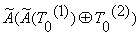Полученное 64-разрядное число    суммируют по модулю 2 с третьим блоком Т₀⁽³⁾ и снова подвергают преобразованию А(.), получая 64-разрядное число

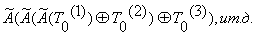
Последний блок T₀^(m) (при необходимости дополненный нулями до полного 64-разрядного блока) суммируют по модулю 2 с результатом вычислений на шаге (m-1), после чего зашифровывают
в режиме простой замены, используя преобразование А(.).

Из полученного 64-разрядного числа выбирают отрезок И_Р (имитовставку) длиной Р бит:

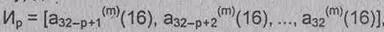
Где a_i^(m) -i-й бит 64-разрядного числа, полученного после 16-го цикла последнего преобразования,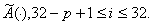

Имитовставка Ир передается по каналу связи или в память ЭВМ в конце зашифрованных данных, т.е.

T_ш⁽¹⁾, T_ш⁽²⁾,…, T_ш^(m), И_р.

 Поступившие к получателю зашифрованные данные

T_ш⁽¹⁾, T_ш⁽²⁾,…, T_ш^(m)

расшифровываются, и из полученных блоков открытых данных  T₀⁽¹⁾, T₀⁽²⁾,…, T₀^(m),  аналогичным образом вырабатывается имитовставка Ир. Эта Имитовставка Ир сравнивается с имитовставкой Ир,
полученной вместе с зашифрованными данными из канала связи или из памяти ЭВМ. В случае несовпадения имитовставок полученные при расшифровании блоки открытых данных Т₀^(1), T₀⁽²⁾, ....
T₀^(m) считают ложными.