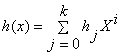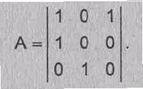2.3. Шифры простой
замены
При
шифровании заменой (подстановкой) символы шифруемого текста заменяются
символами того же или другого алфавита с заранее установленным правилом замены.
В шифре простой замены каждый символ исходного текста заменяется символами того
же алфавита одинаково на всем протяжении текста. Часто шифры простой замены
называют шифрами одноалфавитной подстановки.
Система шифрования Цезаря
Шифр Цезаря является частным случаем шифра
простой замены (одноалфавитной подстановки). Свое название этот шифр получил по
имени римского императора Гая Юлия Цезаря, который использовал этот шифр при
переписке с Цицероном (около 50 г. до н.э.).
При шифровании исходного текста каждая буква
заменялась на другую букву того же алфавита по следующему правилу. Заменяющая
буква определялась путем смещения по алфавиту от исходной буквы на К букв. При
достижении конца алфавита выполнялся циклический переход к его началу. Цезарь
использовал шифр замены при смещении К= 3. Такой шифр замены можно задать
таблицей подстановок, содержащей соответствующие пары букв открытого текста и
шифртекста. Совокупность возможных подстановок для К= 3 показана в табл. 2.3.
Например, послание Цезаря
VENI VIDI VICI
(в переводе на русский означает "Пришел,
Увидел, Победил"), направленное его другу Аминтию после победы над
понтийским царем Фарнаком, сыном Митридата, выглядело бы в зашифрованном
виде так:
YHQL YLGL YLFL
Таблица 2.3
Одноалфавитные
подстановки (К = 3, m = 26)
|
А
® D J ® М S®V
В ® Е К ® N T®W
С® F L
® 0 U ®X
D ® G M ®P V ®Y
E ®H N ®Q W®Z
F ®I О ® R X ® A
G->J P -> S Y -> В
H->K Q -> Т Z -> С
I -> L R -> U
|
Выполним математический анализ шифра простой
замены (подстановки) на основе понятий, введенных в начале гл.2 [113].
Подстановка в алфавите 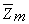 является взаимно
однозначным отображением p из
является взаимно
однозначным отображением p из 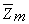 на
на 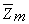
p : t ® p(t),
которое
заменяет букву t открытого текста на букву p(t)
шифртекста. Множество всех подстановок на 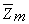 называется симметричной группой
называется симметричной группой 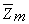 и обозначается
и обозначается 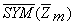
Симметричная группе 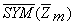 обладает следующими свойствами:
обладает следующими свойствами:
1. Замкнутость.
Произведение подстановок p1p2 является подстановкой:
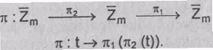
2. Ассоциативность. Оба способа заключения в
скобки произведения подстановок p1p2
p3
p1(p2 p3 ) = (p1p2) p3
дают
одинаковый результат.
3. Существование единичного элемента.
Подстановка d, определенная как
d(t) = t, 0 £ t < m,
является
единственным единичным элементом группы 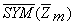 по умножению:
по умножению:
dp = dp
для всех p Î 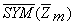
4. Существование обратных элементов. Для каждой
подстановки и имеется взаимно однозначно определенная обратная подстановка,
обозначаемая p-1 которая удовлетворяет
соотношению:
pp-1 = d
Указанные свойства являются аксиомами группы.
Ключ К подстановки для алфавита 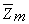 представляет собой
последовательность элементов симметричной группы из
представляет собой
последовательность элементов симметричной группы из 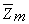 :
:

Подстановка, определяемая ключом К, является
криптографическим преобразованием ЕK, которое шифрует
n-грамму (х0, x1,х2, ...,хn-1) открытого текста в
n-грамму (y0, y1,y2, ..., yn-1) шифртекста, где
yi
= pi(xi),
0 £ i < n,
для
каждого n, n = 1,2,3,....
Криптографическое преобразование ЕK называется одноалфавитной
подстановкой, если значение pi одинаково для каждого i, i = 0,1,2,...; в
противном случае преобразование ЕK называется
многоалфавитной подстановкой.
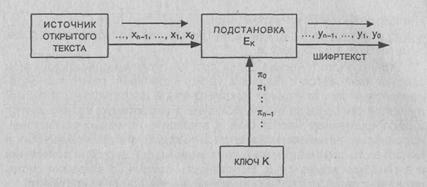
Рис. 2.5. Схема
подстановки Ек
Отметим характерные особенности подстановки Ек:
•
открытый текст шифруется побуквенно (буква за буквой);
•
i-я буква уi шифртекста является функцией только i-й компоненты pi ключа К и i-й буквы xi
открытого текста;
•
шифрование n-граммы (x0, x1, х2, ...,хn-1) производится в
соответствии с формулой
(y0, y1, y2, ...,yn-1) = EK (x0, x1,
х2, ...,хn-1)
Система Цезаря представляет собой одноалфавитную
подстановку, которая шифрует n-грамму (x0,x1, х2,
...,хn-1) открытого текста в
n-грамму (y0, y1, y2, ...,yn-1) шифртекста согласно
следующему правилу:
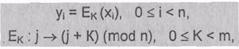 (2.3)
(2.3)
где
j-числовой код буквы открытого текста; j +К-числовой код соответствующей буквы
шифртекста.
В отличие от шифра Цезаря, описанного в начале
этого подраздела, система шифрования Цезаря образует по существу семейство
одноалфавитных подстановок для выбираемых значений ключа К, причем 0 £ К <m.
Достоинством системы шифрования Цезаря является
простота шифрования и расшифрования. К недостаткам системы Цезаря следует
отнести следующие:
•
подстановки, выполняемые в соответствии с системой Цезаря, не маскируют частот
появления различных букв исходного открытого текста;
•
сохраняется алфавитный порядок в последовательности заменяющих букв; при
изменении значения К изменяются только начальные позиции такой
последовательности;
•
число возможных ключей К мало;
•
шифр Цезаря легко вскрывается на основе анализа частот появления букв в
шифртексте.
Криптоаналитическая атака против системы
одноалфавитной замены начинается с подсчета частот появления символов:
определяется число появлений каждой буквы в шифртексте. Затем полученное распределение
частот букв в шифртексте сравнивается с распределением частот букв в алфавите
исходных сообщений, например в английском. Буква с наивысшей частотой появления
в
шифртексте заменяется на букву с наивысшей частотой появления в английском
языке и т.д. Вероятность успешного вскрытия системы шифрования повышается с
увеличением длины шифртекста.
Концепция, заложенная в систему шифрования
Цезаря, оказалась весьма плодотворной, о чем свидетельствуют ее многочисленные
модификации. Несколько таких модификаций будут рассмотрены ниже.
Аффинная система подстановок Цезаря
В системе шифрования Цезаря использовались
только аддитивные свойства множества целых 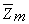 . Однако символы множества
. Однако символы множества 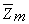 можно также умножать по
модулю т. Применяя одновременно операции сложения и умножения по модулю над
элементами множества
можно также умножать по
модулю т. Применяя одновременно операции сложения и умножения по модулю над
элементами множества 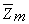 , можно получить систему подстановок, которую
называют аффинной системой подстановок Цезаря.
, можно получить систему подстановок, которую
называют аффинной системой подстановок Цезаря.
Определим преобразование в такой системе:
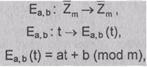 (2.4)
(2.4)
где
a, b - целые числа, 0£ a, b < m, НОД (a, m) =1
В данном преобразовании буква, соответствующая
числу t, заменяется на букву, соответствующую числовому значению (at + b) по
модулю m.
Следует заметить, что преобразование Ea,b (t)
является взаимно однозначным отображением на множестве Zm только в том случае,
если наибольший общий делитель чисел а и т, обозначаемый как НОД (а, m), равен
единице, т.е. а и m должны быть взаимно простыми числами.
Например, пусть m = 26, а = 3, b = 5. Тогда,
очевидно, НОД (3,26) = 1, и мы получаем следующее соответствие между числовыми
кодами букв:
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
3t+5
|
5
|
8
|
11
|
14
|
17
|
20
|
23
|
0
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
1
|
4
|
7
|
10
|
13
|
16
|
19
|
22
|
25
|
2
|
Преобразуя числа в буквы английского языка,
получаем следующее соответствие для букв открытого текста и шифртекста:
|
A
|
В
|
С
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
К
|
L
|
M
|
N
|
О
|
P
|
Q
|
R
|
S
|
T
|
U
|
V
|
W
|
X
|
Y
|
Z
|
|
F
|
I
|
L
|
О
|
R
|
U
|
X
|
A
|
D
|
G
|
J
|
M
|
P
|
S
|
V
|
Y
|
В
|
E
|
H
|
к
|
N
|
Q
|
T
|
W
|
2
|
С
|
Исходное сообщение НОРЕ
преобразуется
в шифртекст AVYR
Достоинством аффинной системы является удобное
управление ключами - ключи шифрования и расшифрования представляются в
компактной форме в виде пары чисел (а, b). Недостатки аффинной системы
аналогичны недостаткам системы шифрования Цезаря.
Аффинная система использовалась на практике
несколько веков назад, а сегодня ее применение ограничивается большей частью
иллюстрациями основных криптологических положений.
Система Цезаря с ключевым словом
Система шифрования Цезаря с ключевым словом
является одноалфавитной системой подстановки. Особенностью этой системы
является использование ключевого слова для смещения и
изменения порядка символов в алфавите подстановки [79].
Выберем некоторое число k, 0 £ k < 25, и слово или
короткую фразу в качестве ключевого слова. Желательно, чтобы все буквы
ключевого слова были различными. Пусть выбраны слово
DIPLOMAT в качестве ключевого слова и число k = 5.
Ключевое слово записывается под буквами
алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом k:

Оставшиеся
буквы алфавита подстановки записываются после ключевого слова в алфавитном
порядке:

Теперь мы имеем подстановку для каждой буквы
произвольного сообщения.
Исходное сообщение SEND MORE MONEY
шифруется как HZBY
TCGZ TCBZS
Следует отметить, что требование о различии всех
букв ключевого слова не обязательно. Можно просто записать ключевое слово (или
фразу) без повторения одинаковых букв. Например, ключевая фраза
КАК ДЫМ ОТЕЧЕСТВА НАМ СЛАДОК И ПРИЯТЕН
и
число k = 3 порождают следующую таблицу подстановок:
0
3
АБВ ГДЕЖЗ
ИЙКЛМНОПРСТУФХЦЧШЩЬЫЪЭЮЯ
ЪЭЮКАДЫМОТЕЧСВНЛИПРЯБГЖЗЙУФХЦШЩЬ
Несомненным достоинством системы Цезаря с
ключевым словом является то, что количество возможных ключевых слов практически
неисчерпаемо. Недостатком этой системы является возможность взлома шифртекста
на основе анализа частот появления букв.
Шифрующие
таблицы Трисемуса
В 1508г. аббат из Германии Иоганн Трисемус
написал печатную работу по криптологии под названием "Полиграфия". В
этой книге он впервые систематически описал применение шифрующих
таблиц, заполненных алфавитом в случайном порядке [32]. Для получения такого
шифра замены обычно использовались таблица для записи букв алфавита и ключевое
слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово,
причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не
вошедшими в нее буквами алфавита по порядку. Поскольку ключевое слово или фразу
легко хранить в памяти, то такой подход упрощал процессы шифрования и
расшифрования.
Поясним этот метод шифрования на примере. Для
русского алфавита шифрующая таблица может иметь размер 4x8. Выберем в качестве
ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рис. 2.6.
|
Б
|
А
|
Н
|
Д
|
Е
|
Р
|
О
|
Л
|
|
Ь
|
В
|
Г
|
Ж
|
3
|
И
|
Й
|
К
|
|
М
|
П
|
С
|
Т
|
У
|
Ф
|
X
|
Ц
|
|
Ч
|
Ш
|
Щ
|
Ы
|
Ъ
|
Э
|
Ю
|
Я
|
Рис. 2.6. Шифрующая таблица с
ключевым словом БАНДЕРОЛЬ
Как и в случае полибианского квадрата, при
шифровании находят в этой таблице очередную букву открытого текста и записывают
в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста
оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю
букву из того же столбца.
Например, при шифровании с помощью этой таблицы
сообщения
ВЫЛЕТАЕМПЯТОГО
получаем
шифртекст
ПДКЗЫВЗЧШЛЫЙСЙ
Такие табличные шифры называются монограммными,
так как шифрование выполняется по одной букве. Трисемус первым заметил, что
шифрующие таблицы позволяют шифровать сразу по две
буквы. Такие шифры называются биграммными.
Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854г., является
наиболее известным биграммным шифром замены. Он применялся Великобританией во
время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица
со случайно расположенными буквами алфавита исходных сообщений.
Для
удобства запоминания шифрующей таблицы отправителем и получателем сообщений
можно использовать ключевое слово (или фразу) при заполнении начальных строк
таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью
аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения
процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей
таблицей Трисемуса из предыдущего раздела (см. рис. 2.6).
Процедура шифрования включает следующие шаги.
1.
Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст
должен иметь четное количество букв и в нем не должно быть биграмм, содержащих
две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется
даже из-за незначительных орфографических ошибок.
2.
Последовательность биграмм открытого текста преобразуется с помощью шифрующей
таблицы в последовательность биграмм шифртекста по следующим правилам:
2а.Если обе буквы биграммы открытого текста не
попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.
2.6), тогда находят буквы в углах прямоугольника, определяемого данной парой
букв. (В нашем примере это буквы АЙОВ. Пара букв АЙ отображается в пару ОВ.
Последовательность букв в биграмме шифртекста должна быть зеркально
расположенной по отношению к последовательности букв в биграмме открытого
текста.)
2б.Если обе буквы биграммы открытого текста
принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы,
которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.)
Если при этом буква открытого текста находится в нижней строке, то для
шифртекста берется соответствующая буква из верхней строки того же столбца.
(Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в.Если обе буквы биграммы открытого текста
принадлежат одной строке таблицы, то буквами шифртекста считаются буквы,
которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста
ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце,
то для
шифра берут соответствующую букву из левого столбца в той же строке. (Например,
биграмма ФЦ дает биграмму шифртекста ХМ.)
Зашифруем текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Разбиение этого текста на биграммы дает
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого
текста преобразуется с помощью шифрующей таблицы (см. рис.2.6) в следующую
последовательность биграмм шифртекста:
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА
ЧТ
При расшифровании применяется обратный порядок
действий. Следует отметить, что шифрование биграммами резко повышает стойкость
шифров к вскрытию. Хотя книга И. Трисемуса "Полиграфия" была
относительно доступной, описанные в ней идеи получили признание лишь спустя три
столетия. По всей вероятности, это было обусловлено плохой осведомленностью
криптографов о работах богослова и библиофила Трисемуса в области криптографии
[32].
Криптосистема
Хилла
Алгебраический метод, обобщающий аффинную
подстановку Цезаря
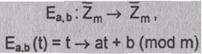
для
определения n-грамм, был сформулирован Лестером С. Хиллом [79].
Множество целых 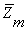 , для которого определены операции сложения,
вычитания и умножения по модулю m, является примером кольца. Кольцо R
представляет собой алгебраическую систему, в которой определены операции
сложения, вычитания и умножения пар элементов. Эта алгебраическая система
обладает рядом свойств:
, для которого определены операции сложения,
вычитания и умножения по модулю m, является примером кольца. Кольцо R
представляет собой алгебраическую систему, в которой определены операции
сложения, вычитания и умножения пар элементов. Эта алгебраическая система
обладает рядом свойств:
•
элементы кольца R образуют коммутативную группу относительно операции сложения;
кроме того, существуют единичный и обратный элементы относительно операции
сложения;
•
умножение и сложение удовлетворяют ассоциативному и дистрибутивному законам.
Мультипликативное обратное a-1 элемента а кольца может
существовать не всегда. Например, если модуль m = 26, то значения 2-1(mod
26) и 13-1(mod 26) не могут существовать.
Если
модуль m является простым числом р, то существует обратная величина любого ненулевого
элемента t из 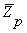 (при m = р), поскольку значения
(при m = р), поскольку значения
t
(mod m), 2t (mod m), 3t (mod m),..., (p -1) t (mod m)
различаются,
если 1 £ t £ p -1.
Множество 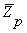 , где р - простое число, является примером
алгебраической системы, называемой конечным полем. Ненулевые элементы
, где р - простое число, является примером
алгебраической системы, называемой конечным полем. Ненулевые элементы 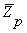 образуют мультипликативную группу.
образуют мультипликативную группу.
Множество всех n-грамм 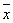 = (х0, х1, х2,...,
x n-1) с компонентами из кольца
= (х0, х1, х2,...,
x n-1) с компонентами из кольца 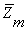 образует векторное пространство
образует векторное пространство 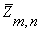 над кольцом
над кольцом 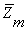 . Каждая n-грамма х называется вектором. В
векторном пространстве
. Каждая n-грамма х называется вектором. В
векторном пространстве 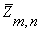 для векторов х
определены операции сложения и вычитания по модулю n, а также скалярное
умножение вектора на элемент t кольца
для векторов х
определены операции сложения и вычитания по модулю n, а также скалярное
умножение вектора на элемент t кольца 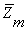 . Сложение и скалярное умножение являются
. Сложение и скалярное умножение являются
операциями, удовлетворяющими коммутативному, ассоциативному и дистрибутивному
законам. Вектор 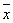 является линейной
комбинацией векторов
является линейной
комбинацией векторов
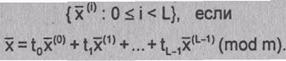 (2.5)
(2.5)
Линейное
преобразование 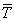 является отображением:
является отображением:
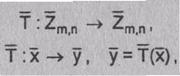 (2.6)
(2.6)
которое
удовлетворяет условию линейности

для
всех s, t в
 Линейное преобразование Т может быть
представлено матрицей размером nхn вида
Линейное преобразование Т может быть
представлено матрицей размером nхn вида
 (2.7)
(2.7)
причем
или 
Базисом для векторного пространства 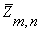 является набор векторов из
является набор векторов из 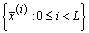 которые линейно независимы и порождают
которые линейно независимы и порождают 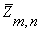 . Каждый базис для
. Каждый базис для 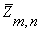 содержит n линейно независимых векторов. Любой
набор из n векторов, которые линейно независимы над
содержит n линейно независимых векторов. Любой
набор из n векторов, которые линейно независимы над 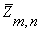 является базисом.
является базисом.
Пусть 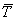 является линейным преобразованием, описываемым
матрицей (2.7), причем
является линейным преобразованием, описываемым
матрицей (2.7), причем
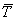 :
: 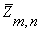 ®
® 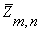
Если векторы 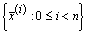 линейно независимы над
линейно независимы над 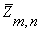 , тогда их образы
линейно
, тогда их образы
линейно 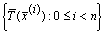 независимы над
независимы над 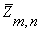 только в том случае, если определитель матрицы
только в том случае, если определитель матрицы
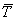 , обозначаемый как det (
, обозначаемый как det (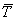 ), не делится на любое простое р, которое делит m. В этом случае
преобразование
), не делится на любое простое р, которое делит m. В этом случае
преобразование 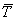 называется обратимым
(или невырожденным) линейным преобразованием, имеющим обратное преобразование
называется обратимым
(или невырожденным) линейным преобразованием, имеющим обратное преобразование 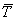 -1:
-1:
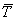 -1 :
-1 : 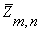 ®
® 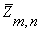 ,
,
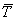
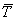 -1 =
-1 = 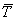 -1T =
-1T = 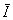 (2.8)
(2.8)
где
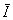 -единичная матрица.
Кроме того,
-единичная матрица.
Кроме того, 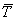 -1 также является линейным преобразованием.
-1 также является линейным преобразованием.
Например, когда m = 26 и матрица преобразования
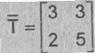
то
определитель этой матрицы
det(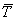 ) = 9 = 1(mod
2),
) = 9 = 1(mod
2),
det(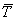 ) = 9 = 9
(mod 13)
) = 9 = 9
(mod 13)
Поэтому
существует обратное преобразование 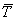 -1. Нетрудно убедиться, что
-1. Нетрудно убедиться, что
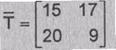
удовлетворяет
соотношению
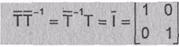
Пусть 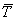 является линейным
преобразованием на Z26.2 c матрицей
является линейным
преобразованием на Z26.2 c матрицей
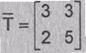
Используем это преобразование 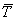 для определения
биграммной подстановки в английском алфавите {ABCDEFGH..XYZ}. Сначала разобьем
n-грамму открытого текста на биграммы, причем
для определения
биграммной подстановки в английском алфавите {ABCDEFGH..XYZ}. Сначала разобьем
n-грамму открытого текста на биграммы, причем
выберем n кратным 2. Например, 12-грамма PAYMOREMONEY делится на шесть биграмм:
PA YM OR EM ON EY
Затем в каждой биграмме открытого текста заменим
каждую букву ее числовым эквивалентом из таблицы:

Преобразование биграмм xj открытого
текста в биграммы, уi шифртекста осуществляется в соответствии с
уравнением
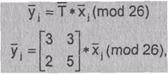
где
хj и уi – вектор - столбцы биграмм шифртекста и открытого
текста соответственно.
Получаем
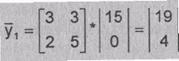
букву
исходного текста и в левом столбце очередное значение ключа. Очередная буква
шифртекста находится на пересечении столбца, определяемого шифруемой буквой, и
строки, определяемой числовым значением ключа.
Пусть ключевая последовательность имеет
длину r, тогда ключ r-алфавитной подстановки есть r-строка
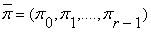 (2.9)
(2.9)
Система шифрования Вижинера преобразует открытый
текст x = (x0, x1 , ...,xn-1) в шифртекст у = (у0,
у1 , ...,yn-1) с помощью ключа 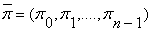 согласно правилу
согласно правилу
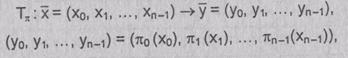 (2.10)
(2.10)
где pi = p(i mod r).
Рассмотрим
пример получения шифртекста с помощью таблицы Вижинера. Пусть выбрано ключевое
слово АМБРОЗИЯ. Необходимо зашифровать сообщение ПРИЛЕТАЮ СЕДЬМОГО.
Выпишем исходное сообщение в строку и запишем
под ним ключевое слово с повторением. В третью строку будем выписывать буквы
шифртекста, определяемые из таблицы Вижинера.
Сообщение П Р И Л Е Т А Ю С Е Д Ь М О Г О
Ключ А М Б Р О З И Я А М Б Р О З И Я
Шифртекст П Ъ Й Ы У Щ И Э С С Е К Ь Х Л Н
Шифр
"двойной квадрат" Уитстона
В 1854г. англичанин Чарльз Уитстон разработал
новый метод шифрования биграммами, который называют "двойным
квадратом". Свое название этот шифр получил по аналогии с полибианским
квадратом. Шифр Уитстона открыл новый этап в истории развития криптографии. В
отличие от полибианского шифр "двойной квадрат" использует сразу две
таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в
шифре Плейфейра. Эти не столь сложные модификации привели к появлению на свет
качественно новой криптографической системы ручного
шифрования. Шифр "двойной квадрат" оказался очень надежным и удобным
и применялся Германией даже в годы второй мировой войны.
Поясним процедуру шифрования этим шифром на
примере. Пусть имеются две таблицы со случайно расположенными в них русскими
алфавитами (рис.2.10). Перед шифрованием исходное
сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую
букву биграммы находят в левой таблице, а вторую букву - в правой таблице.
Затем мысленно строят прямоугольник так, чтобы буквы биграммы лежали в его
противоположных вершинах. Другие две вершины этого прямоугольника дают буквы
биграммы шифртекста.
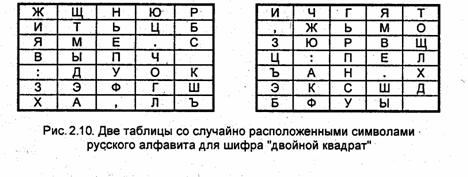
Предположим, что шифруется биграмма исходного
текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква И
находится в столбце 5 и строке 4 правой таблицы. Это означает, что
прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5
правой таблицы. Следовательно, в биграмму шифртекста входят буква О,
расположенная в столбце 5 и строке 2
правой таблицы, и буква В, расположенная в столбце 1 и строке 4 левой таблицы,
т.е. получаем биграмму шифртекста ОВ.
Если
обе буквы биграммы сообщения лежат в одной строке, то и буквы шифртекста берут
из этой же строки. Первую букву биграммы шифртекста берут из левой таблицы в
столбце, соответствующем второй букве биграммы сообщения. Вторая же буква
биграммы шифртекста берется из правой таблицы в столбце, соответствующем первой
букве биграммы сообщения. Поэтому биграмма сообщения ТО превращается в биграмму
шифртекста ЖБ. Аналогичным образом шифруются все биграммы сообщения:
Сообщение
ПР ИЛ ЕТ АЮ _Ш ЕС ТО ГО
Шифртекст ПЕ ОВ ЩН ФМ ЕШ РФ БЖ ДЦ
Шифрование методом "двойного квадрата"
дает весьма устойчивый к вскрытию и простой в применении шифр. Взламывание
шифртекста "двойного квадрата" требует больших усилий, при
этом длина сообщения должна быть не менее тридцати строк.
Одноразовая система шифрования
Почти все применяемые на практике шифры
характеризуются как условно надежные, поскольку они могут быть в принципе
раскрыты при наличии неограниченных вычислительных возможностей. Абсолютно надежные
шифры нельзя разрушить даже при использовании неограниченных вычислительных
возможностей. Существует единственный такой шифр, применяемый на практике,
одноразовая система шифрования. Характерной особенностью одноразовой системы
шифрования является одноразовое использование ключевой последовательности.
Одноразовая система
шифрует исходный открытый текст
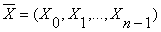
в
шифртекст
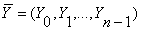
посредством
подстановки Цезаря
Yi = (Xi + Ki)mod m, 0£ i <n, (2.11)
где
Ki-i-й элемент случайной ключевой последовательности.
Ключевое пространство 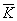 одноразовой системы представляет собой набор
дискретных случайных величин из
одноразовой системы представляет собой набор
дискретных случайных величин из 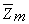 и содержит mn значений.
и содержит mn значений.
Процедура расшифрования описывается
соотношением
Yi = (Xi
- Ki)mod m, (2.12)
где
Ki-i-й элемент той же самой случайной ключевой последовательности.
Одноразовая система изобретена в 1917г.
американцами Дж. Моборном и Г. Вернамом [113]. Для реализации этой системы
подстановки иногда используют одноразовый блокнот. Этот блокнот составлен из
отрывных страниц, на каждой из которых напечатана таблица со случайными числами
(ключами) Ki. Блокнот выполняется в двух экземплярах: один
используется отправителем, а другой - получателем. Для каждого символа Xi
сообщения используется свой ключ Ki из таблицы только один раз. После того как
таблица использована, она должна быть удалена из блокнота и уничтожена.
Шифрование нового сообщения начинается с новой страницы.
Этот
шифр абсолютно надежен, если набор ключей Ki действительно случаен и
непредсказуем. Если криптоаналитик попытается использовать для заданного
шифртекста все возможные наборы ключей и восстановить все возможные варианты
исходного текста, то они все окажутся равновероятными. Не существует способа выбрать
исходный текст, который был действительно послан. Теоретически доказано, что
одноразовые системы являются нераскрываемыми системами, поскольку их шифртекст
не содержит
достаточной информации для восстановления открытого текста.
Казалось бы, что благодаря данному достоинству
одноразовые системы следует применять во всех случаях, требующих абсолютной
информационной безопасности. Однако возможности применения одноразовой системы
ограничены чисто практическими аспектами. Существенным моментом является требование
одноразового использования случайной ключевой последовательности. Ключевая
последовательность с длиной, не меньшей длины сообщения, должна передаваться
получателю сообщения заранее или отдельно по некоторому секретному каналу. Это
требование не будет слишком обременительным для передачи действительно важных
одноразовых сообщений, например, по горячей линии Вашингтон-Москва. Однако
такое требование практически неосуществимо для современных систем обработки
информации, где требуется шифровать многие миллионы символов.
В некоторых вариантах одноразового блокнота
прибегают к более простому управлению ключевой последовательностью, но это
приводит к некоторому снижению надежности шифра. Например, ключ определяется
указанием места в книге, известной отправителю и получателю сообщения. Ключевая
последовательность начинается с указанного места этой книги и используется
таким же образом, как в системе Вижинера. Иногда такой шифр называют шифром с
бегущим ключом. Управление ключевой последовательностью в таком варианте шифра
намного проще, так как длинная ключевая последовательность может быть
представлена в компактной форме. Но с другой стороны, эти ключи не будут
случайными. Поэтому у криптоаналитика появляется возможность использовать
информацию о частотах букв исходного естественного языка.
Шифрование
методом Вернама
Система шифрования Вернама является в сущности
частным случаем системы шифрования Вижинера при значении модуля m = 2.
Конкретная версия этого шифра, предложенная в 1926г.
Гилбертом Вернамом, сотрудником фирмы AT&T США, использует двоичное
представление символов исходного текста.
Каждый символ исходного открытого текста из
английского алфавита {А, В, С, D, ..., Z}, расширенного шестью вспомогательными
символами (пробел, возврат каретки и т.п.), сначала кодировался в 5-битовый
блок (b0, b1,..., b4) телеграфного кода
Бодо.
Случайная последовательность двоичных ключей k0,
k1, k2,... заранее записывалась на бумажной ленте.
Схема
передачи сообщений с использованием шифрования методом Вернама показана на рис.
2.11. Шифрование исходного текста, предварительно преобразованного в
последовательность двоичных символов х, осуществлялось путем сложения по модулю
2 символов х с последовательностью двоичных ключей k.
Символы
шифртекста
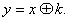
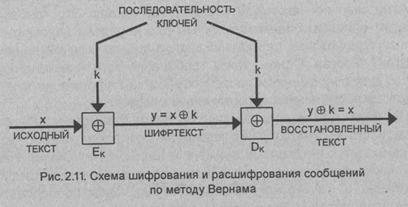 (2.13)
(2.13)
Расшифрование состоит в сложении по модулю 2
символов у шифртекста с той же последовательностью ключей k:
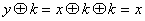 (2.14)
(2.14)
При этом последовательности ключей,
использованные при шифровании и расшифровании, компенсируют друг друга (при
сложении по модулю 2), и в результате восстанавливаются символы х исходного
текста.
При разработке своей системы Вернам проверял ее
с помощью закольцованных лент, установленных на передатчике и приемнике для
того, чтобы использовалась одна и та же последовательность ключей.
Следует
отметить, что метод Вернама не зависит от длины последовательности ключей и,
кроме того, он позволяет использовать случайную последовательность ключей.
Однако при реализации метода Вернама возникают серьезные проблемы, связанные с
необходимостью доставки получателю такой же последовательности ключей, как у
отправителя, либо с необходимостью безопасного хранения идентичных
последовательностей ключей у отправителя и получателя. Эти недостатки системы
шифрования Вернама
преодолены при шифровании методом гаммирования.
2.5. Шифрование методом
гаммирования
Под гаммированием понимают процесс наложения по
определенному закону гаммы шифра на открытые данные. Гамма шифра - это
псевдослучайная последовательность, выработанная по заданному алгоритму для
зашифрования открытых данных и расшифрования зашифрованных данных.
Процесс зашифрования заключается в генерации
гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым
образом, например с использованием операции сложения по модулю 2.
Следует отметить, что перед зашифрованием
открытые данные разбивают на блоки 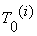 одинаковой длины, обычно по 64 бита. Гамма шифра
вырабатывается в виде последовательности блоков
одинаковой длины, обычно по 64 бита. Гамма шифра
вырабатывается в виде последовательности блоков
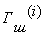 аналогичной длины.
аналогичной длины.
Уравнение
зашифрования можно записать в виде
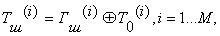 (2.15)
(2.15)
где 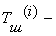 i –й шифртекста;
i –й шифртекста; 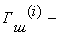 i – й блок гаммы шифра;
i – й блок гаммы шифра; 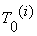 - i – й блок открытого текста; М - количество
блоков открытого текста.
- i – й блок открытого текста; М - количество
блоков открытого текста.
Процесс расшифрования сводится к повторной
генерации гаммы шифра и наложению этой гаммы на зашифрованные данные. Уравнение
расшифрования имеет вид
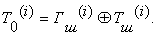 (2.16)
(2.16)
Получаемый этим методом шифртекст достаточно труден
для раскрытия, поскольку теперь ключ является переменным. По сути дела гамма
шифра должна изменяться случайным образом для каждого шифруемого блока. Если
период гаммы превышает длину всего шифруемого текста и злоумышленнику
неизвестна никакая часть исходного текста, то такой шифр можно раскрыть только
прямым перебором всех вариантов ключа. В этом случае криптостойкость шифра
определяется длиной ключа.
Методы генерации псевдослучайных
последовательностей чисел
При шифровании методом гаммирования в качестве
ключа используется случайная строка битов, которая объединяется с открытым
текстом, также представленным в двоичном виде (например, А= 00000, В = 00001, С
= 00010 и т.д.), с помощью побитового сложения по модулю 2, и в результате
получается шифрованный текст. Генерирование непредсказуемых двоичных
последовательностей большой длины является одной из важных проблем классической
криптографии. Для решения этой проблемы широко используются генераторы двоичных
псевдослучайных последовательностей.
Генерируемые псевдослучайные ряды чисел часто
называют гаммой шифра или просто гаммой (по названию буквы g греческого алфавита, часто используемой
в математических формулах для обозначения случайных величин). Обычно для
генерации последовательности псевдослучайных чисел применяют компьютерные
программы, которые, хотя и называются генераторами случайных чисел, на самом
деле выдают детерминированные числовые последовательности, которые по своим
свойствам очень похожи на случайные [32].
К криптографически стойкому генератору
псевдослучайной последовательности чисел (гаммы шифра) предъявляются три
основных требования:
•
период гаммы должен быть достаточно большим для шифрования сообщений различной
длины;
•
гамма должна быть практически непредсказуемой, что означает невозможность
предсказать следующий бит гаммы, даже если известны тип генератора и
предшествующий кусок гаммы;
•
генерирование гаммы не должно вызывать больших технических сложностей.
Длина периода гаммы является самой важной
характеристикой генератора псевдослучайных чисел. По окончании периода числа
начнут повторяться, и их можно будет предсказать. Требуемая длина периода гаммы
определяется степенью закрытости данных. Чем длиннее ключ, тем труднее его
подобрать. Длина периода гаммы зависит от выбранного алгоритма получения
псевдослучайных чисел.
Второе требование связано со следующей
проблемой: как можно достоверно убедиться, что псевдослучайная гамма
конкретного генератора является действительно непредсказуемой? Пока не
существуют такие универсальные и практически проверяемые критерии и методики.
Чтобы гамма считалась непредсказуемой, т.е. истинно случайной, необходимо,
чтобы ее период был очень большим, а различные комбинации битов определенной
длины были равномерно распределены по всей ее длине.
Третье требование обусловливает возможность
практической реализации генератора программным или аппаратным путем с
обеспечением необходимого быстродействия.
Один из первых способов генерации
псевдослучайных чисел на ЭВМ предложил в 1946 г. Джон фон Нейман. Суть этого
способа состоит в том, что каждое последующее случайное число образуется
возведением в квадрат предыдущего числа с отбрасыванием цифр младших и старших
разрядов. Однако этот способ оказался ненадежным и от него вскоре отказались.
Из известных процедур генерации
последовательности псевдослучайных целых чисел наиболее часто применяется так
называемый линейный конгруэнтный генератор. Этот генератор вырабатывает
последовательность псевдослучайных чисел Y1, Y2,…,Yi-1, Yi .... используя
соотношение
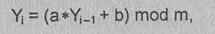 (2.17)
(2.17)
где
Yi - i-e (текущее) число последовательности; Yi-1 –предыдущее
число последовательности; а,b и m-константы; m-модуль; а- множитель
(коэффициент); b-приращение; Y0- порождающее число (исходное
значение).
Текущее
псевдослучайное число Yi получают из предыдущего числа Yi-1
умножением его на коэффициент а, сложением с приращением b и вычислением
остатка от деления на модуль m. Данное уравнение генерирует псевдослучайные
числа с периодом повторения, который зависит от выбираемых значений параметров
а, b и m и может достигать значения m. Значение модуля т берется равным 2n
либо равным простому числу, например m = 231-1. Приращение b должно
быть взаимно простым с т, коэффициент а должен быть нечетным числом.
Конгруэнтные
генераторы, работающие по алгоритму, предложенному Национальным бюро стандартов
США, используются, в частности, в системах программирования. Эти генераторы
имеют
длину периода 224 и обладают хорошими статистическими свойствами. Однако такая
длина периода мала для криптографических применений. Кроме того, доказано, что
последовательности, генерируемые конгруэнтными генераторами, не являются
криптографически стойкими.
Существует
способ генерации последовательностей псевдослучайных чисел на основе линейных
рекуррентных соотношений [69].
Рассмотрим
рекуррентные соотношения и их разностные уравнения:
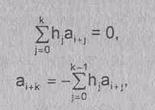 (2.18)
(2.18)
где
h0 ¹ 0, hk = 1 каждое hi принадлежит полю GF(q).
Решением этих уравнений является
последовательность элементов а0,a1,a2,... поля
GF(q) (см. Приложение). Соотношение (2.18) определяет правило вычисления ak
по известным значениям
величин а0,a1,a2,... ,аk-1. Затем
по известным значениям а0, а1,a2,.... аk находят ak+1 и
т.д. В результате по начальным значениям a0, a1, a2,...,
аk-1 можно построить бесконечную последовательность, причем каждый
ее последующий член определяется из k предыдущих. Последовательности такого
вида легко реализуются на компьютере, при этом реализация получается особенно
простой, если все hi и аi принимают значения 0 и 1 из
поля GF(2).
На рис. 2.12 показана линейная последовательная
переключательная схема, которая может быть использована для вычисления суммы
(2.18) и, следовательно, для вычисления значения ak по
значениям k предыдущих членов последовательности. Исходные величины a0,
a1, a2,..., аk-1 помещаются в разряды
сдвигового регистра, последовательные сдвиги содержимого которого соответствуют
вычислению последовательных символов, при этом
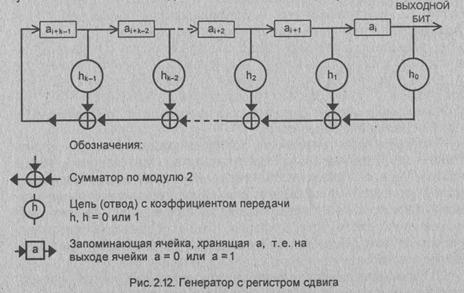
выход после
i-го сдвига равен аi. Данное устройство называют генератором
последовательности чисел, построенным на базе сдвигового регистра с линейной
обратной связью.
Решения линейных рекуррентных соотношений,
реализуемые генератором с регистром сдвига, описываются следующей теоремой.
Пусть многочлен
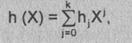
где
Х-формальная переменная; hj- коэффициент при Xj,
принимающий значение 0 или 1; h0 ¹ 0, hk = 1
пусть
n - наименьшее целое положительное число, для которого многочлен Хn-1 делится
на h(X). Кроме того, многочлен
g(X) = (Xn –1)/h(X)
Тогда
решения рекуррентных соотношений
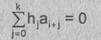
в
виде последовательности элементов а0, а1, аi,...,
an-1 периодичны с периодом n
и совокупность, составленная из первых периодов всех возможных решений,
рассматриваемых как многочлены по
модулю (Хn-1), т.е.
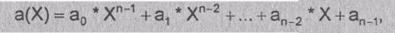
совпадает с
идеалом, порожденным многочленом g(Х) в алгебре многочленов по модулю (Хn-1). Доказательство этой теоремы можно
найти в [69].
Заметим, что если при таком определении
многочлена а(Х) элементы а0, а1, а2,...
вычисляются в порядке возрастания номеров, то коэффициенты многочлена а(Х)
вычисляются, начиная с коэффициентов при степенях высших порядков. Следует
также отметить, что вид многочлена 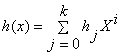 определяет конфигурацию обратных связей
(отводов) hj в генераторе со сдвиговым регистром. Другими словами,
если у многочлена h(X) коэффициент hj = 1, это означает, что отвод hj
в схеме генератора присутствует, если же у многочлена h(X) коэффициент hj
= 0, то отвод hj в схеме генератора отсутствует. В [58] показано,
что в качестве h(X) необходимо выбирать неприводимый примитивный многочлен (см.
также приложение). При таком выборе многочлена h(X) со старшей степенью m
генератор обеспечивает выдачу псевдослучайной последовательности двоичных чисел
с максимально возможным периодом 2m-1.
определяет конфигурацию обратных связей
(отводов) hj в генераторе со сдвиговым регистром. Другими словами,
если у многочлена h(X) коэффициент hj = 1, это означает, что отвод hj
в схеме генератора присутствует, если же у многочлена h(X) коэффициент hj
= 0, то отвод hj в схеме генератора отсутствует. В [58] показано,
что в качестве h(X) необходимо выбирать неприводимый примитивный многочлен (см.
также приложение). При таком выборе многочлена h(X) со старшей степенью m
генератор обеспечивает выдачу псевдослучайной последовательности двоичных чисел
с максимально возможным периодом 2m-1.
Рассмотрим в качестве примера трехразрядный
сдвиговый регистр с линейной обратной связью (рис. 2.13), построенный в
соответствии с неприводимым примитивным многочленом
h(X) = X3
+X2 +1
где
коэффициенты h3 = 1, h2 = 1, h1=0, h0
= 1.
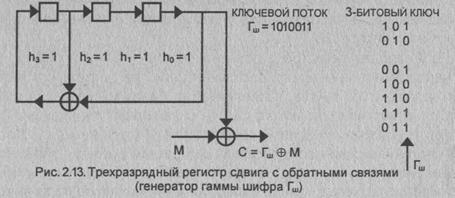
Пусть ключом является 101. Регистр начинает
работать с этого состояния; последовательность состояний регистра приведена на
рис. 2.13. Регистр проходит через все семь ненулевых состояний и снова
возвращается в свое исходное состояние 101. Это наиболее длинный период данного
регистра с линейной обратной связью. Такая последовательность называется
последовательностью максимальной длины для сдвигового регистра (Maximal Lenght
Shift Register Sequence -MLSRS). Питерсон и Уэлдон [69]
показали, что при любом целом m существует m-битовая последовательность MLSRS с
периодом 2m-1. В частности, при m = 100 последовательность будет
иметь период 2100-1 и не повторится 1016 лет при передаче ее по линии связи со
скоростью 1 Мбит/с.
В нашем примере выходной последовательностью
(гаммой шифра) Гш сдвигового регистра с обратной связью является
последовательность 1010011, которая циклически повторяется. В этой
последовательности имеется четыре единицы и три нуля, и их распределение
настолько близко к равномерному, насколько это возможно в последовательности,
имеющей длину 7. Если рассмотреть пары последовательных битов, то пары 10 и 01
появляются по два раза, а пары 00 и 11-один раз, что опять оказывается
настолько близким к равномерному распределению, насколько это возможно. В
случае последовательности максимальной длины для m-разрядного регистра это
свойство равнораспределенности распространяется на тройки, четверки и т.д.
битов, вплоть до m-битовых групп. Благодаря такой близости к равномерному
распределению последовательности максимальной длины часто используются в
качестве псевдослучайных последовательностей в криптографических системах,
которые имитируют работу криптостойкой системы одноразового шифрования.
Хотя такая криптографическая система
осуществляет имитацию заведомо криптостойкой системы одноразового шифрования,
сама она не отличается стойкостью и может быть раскрыта за несколько секунд
работы компьютера при условии наличия известного открытого текста [29].
Если отводы регистра с обратной связью
зафиксированы, то для нахождения начального состояния регистра достаточно знать
m битов открытого текста. Чтобы найти m битов ключевого потока, m битов
известного открытого текста складывают по модулю 2 с соответствующими m битами
шифртекста. Полученные m битов дают состояние сдвигового регистра с обратной
связью в обратном направлении на некоторый момент времени. Затем, моделируя
работу регистра назад, можно определить его исходное состояние.
Если отводы регистра с обратной связью не
фиксированы, а являются частью ключа, то достаточно 2m битов известного
открытого текста, чтобы сравнительно быстро определить расположение отводов
регистра и его начальное состояние. Пусть S(i)- вектор-столбец, состоящий из m
символов 0 и 1, который определяет состояние регистра в i-й момент времени.
Тогда

где
А-матрица размером mxm, определяющая положение отводов регистра с обратной
связью.
Для
трехразрядного регистра (рис. 2.13)
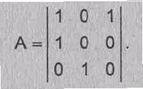
Матрица А всегда имеет следующую структуру: в ее
первой строке отражена последовательность отводов в регистре, непосредственно
под главной диагональю располагаются единицы, а в остальных позициях располагаются
нули.
2m битов известного открытого текста позволяют
вычислить 2m последовательных битов ключевого потока. Для упрощения обозначений
предположим, что это первые 2m битов ключевого потока. Следовательно,
•
S(1)-первая группа m известных битов ключевого потока;
•
S(2) - следующая группа (начиная с номера 2) из m известных битов ключевого
потока;
•
S(m + 1)-последняя группа из m известных битов ключевого потока.
Далее можно образовать две матрицы размером mxm:
X(1)=[S(1),
S(2),…,S(m)],
X(2) = [S(2), S(3),…,S(m+1)],
которые
связаны соотношением
X(2) = A * X(1) mod 2.
Можно
показать, что для любой последовательности максимальной длины матрица Х(1)
всегда несингулярна, поэтому матрицу А можно вычислить как
A=X(2) [X(1)]-1
mod 2.
Обращение матрицы Х(1) требует (самое большее)
порядка m3 операций, поэтому легко выполняется при любом разумном
значении m.
Для
криптографии последовательности максимальной длины MLSRS можно сделать более
криптостойкими, используя нелинейную логику. В частности, предложен вариант
[29], в котором в качестве ключевого потока используется нелинейно
"фильтрованное" содержимое сдвигового регистра, а для получения
последовательности максимальной длины - линейная обратная связь, как
показано на рис. 2.14.
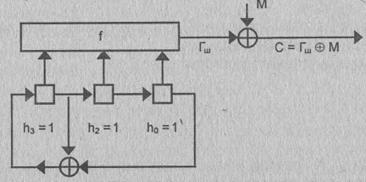
Рис. 2.14.
Линейный сдвиговый регистр с нелинейными
логическими цепями на выходе
Функция f должна выбираться так, чтобы
обеспечить хороший баланс между нулями и единицами, а фильтрованная
последовательность имела распределение, близкое к равномерному. Необходимо
также, чтобы фильтрованная последовательность имела большой период. Если (2m-1)
является простым числом (как в примере: при m = 3 имеем 23-1 = 7),
то фильтрованная последовательность может иметь период (2m-1) (при
выборе структуры сдвигового регистра в соответствии с неприводимым примитивным
многочленом h(Х) степени m).
К таким значениям m относятся, в частности,
следующие:
2,
3, 5, 7. 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, а
полученные таким образом простые числа называются простыми числами Мерсенна.
Несмотря на то, что фильтрованную выходную
последовательность обычно нельзя получить с помощью m-разрядного сдвигового
регистра с линейной обратной связью, ее всегда можно получить с помощью
сдвигового регистра большей длины с линейной обратной связью [59]. Регистр
длиной (2m-1) всегда позволит это сделать, а иногда пригоден и более
короткий регистр.
Еще более привлекательно использование в цепи
обратной связи нелинейной логики, однако теория таких схем недостаточно хорошо
освещена (в открытой литературе).
![]() является взаимно
однозначным отображением p из
является взаимно
однозначным отображением p из ![]() на
на ![]()
![]() называется симметричной группой
называется симметричной группой ![]() и обозначается
и обозначается ![]()
![]() обладает следующими свойствами:
обладает следующими свойствами: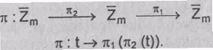
![]() по умножению:
по умножению:![]()
![]() представляет собой
последовательность элементов симметричной группы из
представляет собой
последовательность элементов симметричной группы из ![]() :
:![]()

![]() (2.3)
(2.3)![]() . Однако символы множества
. Однако символы множества ![]() можно также умножать по
модулю т. Применяя одновременно операции сложения и умножения по модулю над
элементами множества
можно также умножать по
модулю т. Применяя одновременно операции сложения и умножения по модулю над
элементами множества ![]() , можно получить систему подстановок, которую
называют аффинной системой подстановок Цезаря.
, можно получить систему подстановок, которую
называют аффинной системой подстановок Цезаря.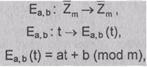 (2.4)
(2.4)
![]()
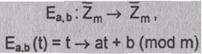
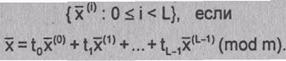 (2.5)
(2.5)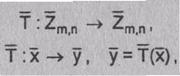 (2.6)
(2.6) (2.7)
(2.7)
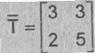

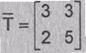

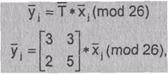
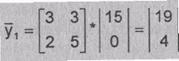



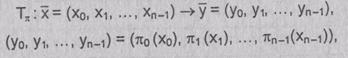

 (2.13)
(2.13)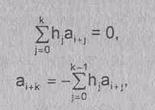 (2.18)
(2.18)