Глава 11

ОБЪЕМНЫЕ РЕЗОНАТОРЫ

11.1. ОБЩИЕ СВОЙСТВА ОБЪЕМНЫХ РЕЗОНАТОРОВ

11.1.1. Общие сведения

На низких частотах в качестве колебательного контура (резонатора) широко применяется параллельное соединение сосредоточенных индуктивности и емкости. Колебательный процесс в такой системе возникает, как известно, в результате непрерывного обмена энергией между электрическим полем, сосредоточивающимся в конденсаторе, и магнитным полем, сосредоточивающимся в индуктивности. В диапазоне СВЧ создание контуров из сосредоточенных элементов с малыми потерями и соответственно высокой добротностью практически невозможно. Поэтому в этом диапазоне применяют преимущественно колебательные системы из элементов с распределенными параметрами (отрезки двухпроводной, коаксиальной линий, волноводов и др.).

Возможность построения таких систем вытекает из уравнений Максвелла. Действительно, согласно этим уравнениям переменное электрическое поле является источником переменного магнитного поля, а переменное магнитное поле, в свою очередь, возбуждает переменное электрическое поле, и т.д., т.е. обмен энергией между электрическим и магнитным полями происходит непрерывно в любой области пространства. Если каким-либо образом устранить излучение электромагнитных волн из некоторой области пространства и добиться отсутствия тепловых потерь, то обмен энергиями должен протекать сколь угодно долго. Это означает, что в изолированном от внешнего пространства объеме, заполненном средой без потерь, может существовать, как и в обычном резонансном контуре без потерь, незатухающий колебательный процесс. Подобные резонансные системы получили название объемных резонаторов.

Простейшие типы объемных резонаторов представляют собой часть пространства, ограниченную со всех сторон металлической оболочкой. Сюда, в частности, относятся резонаторы в виде короткозамкнутых отрезков коаксиальной линии, полых металлических

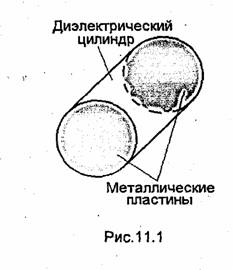
Волноводов и др. По аналогии с направляющими системами резонаторы этого типа называют закрытыми. Можно также почти полностью устранить излучение в окружающее пространство, используя явление полного отражения от границы раздела двух диэлектриков с различными диэлектрическими проницаемостями. В качестве примера на рис.11.1 показан объемный резонатор этого типа, представляющий собой отрезок диэлектрического волновода, торцы которого металлизированы. По аналогии с направляющими системами резонаторы, в которых отсутствует замкнутая металлическая оболочка, называют открытыми.

11.1.2. Свободные гармонические колебания в объемных резонаторах

Предположим, что в объеме V_o (в произвольном резонаторе) тепловые потери равны нулю и, кроме того, отсутствует обмен энергией между внешним пространством и внутренним объемом резонатора. Уравнение баланса (1.126) при этих условиях имеет вид

Р^ст =dWldt.                                (11.1)

Под влиянием источника в объеме V_o возникнут электромагнитные колебания. Пусть через некоторое время сторонний источник отключается. При этом за счет запасенной в резонаторе энергии колебательный процесс будет продолжаться сколь угодно долго и при отсутствии источников. В резонаторе возникнут свободные или, другими словами, не связанные со сторонним источником электромагнитные колебания. При Р^ст = 0 из (11.1) получаем

dWdf = O,                                       (11.2)

т.е. в соответствии с законом сохранения энергии полная энергия, запасенная в изолированном от внешнего пространства объеме, при отсутствии потерь в любой момент времени остается постоянной. Однако соотношение величин электрической и магнитной энергий в общей неизменной сумме непрерывно меняется ввиду обмена энергией между переменными электрическим и магнитным полями. В общем случае изменение во времени напряженности электрических и магнитных полей в резонаторе носит негармонический характер. Особый интерес представляет случай, когда свободные колебания являются гармоническими. Пусть, например, Е = Ei sin ω_ot, где E₁ - функция, зависящая от пространственных координат, а ω_о - угловая частота свободных колебаний. В момент t = 0 напряженность электрического поля равна нулю. Равна нулю в этот момент и энергия, запасенная в электрическом поле. Но полная энергия в объеме V_o резонатора, как следует из (11.2), не зависит от времени. Следовательно, в момент t = 0 у рассматриваемого свободного колебания вся энергия сосредоточена в магнитном поле, что при гармонических колебаниях означает наличие фазового сдвига, равного π/2, между векторами Е и Н, т.е. Н = H₁ cos ω_ot, где Н₁ - функция пространственных координат. Переписывая (11.2) для гармонических колебаний с учетом формул (1.130)-( 1.132), получаем

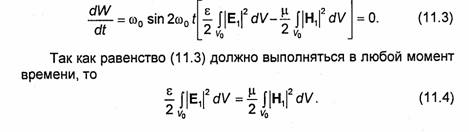
11.1.3. Резонансные частоты свободных колебаний

В рассматриваемом случае уравнения Максвелла (1.33) и (1.39) можно переписать в виде

Слева в (11.6) стоит квадрат резонансной угловой частоты объемного резонатора, а справа - всегда положительная величина, равная отношению двух объемных интегралов. Численное значение каждого из этих интегралов зависит от формы объема Vo и его размеров, а также от характера подынтегральной функции. Поэтому резонансная частота резонатора зависит от структуры попей в резонаторе, его формы и размеров.

Структура полей в резонаторе, как и в направляющих системах, определяется путем решения уравнений Максвелла при определенных граничных условиях на поверхности, окружающей объем V_o. В случае закрытых резонаторов без потерь задача сводится к решению трехмерного векторного волнового уравнения:

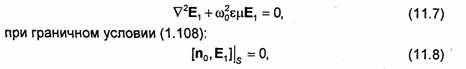
где S - внутренняя поверхность металлической оболочки резонатора, а n₀ - орт нормали к этой поверхности.

Можно доказать, что уравнение (11.7) при граничном условии (11.8), как и аналогичные уравнения теории направляющих систем, имеет бесконечное число различных решений, каждому из которых согласно (11.6) соответствует определенное значение резонансной угловой частоты ω₀, т.е. объемные резонаторы, в отличие от обычных контуров из сосредоточенных элементов, резонируют не на одной частоте, а на бесконечном множестве дискретных частот ωo₁, ω₀₂.....ω_0p.....То колебание, которому при данных размерах резонатора соответствует минимальная резонансная частота ω_О1, называют низшим колебанием. Отметим, что каждой резонансной частоте соответствует определенная структура электромагнитного поля в резонаторе.

Не исключено, что в объемном резонаторе резонансные частоты двух или большего числа колебаний с различной структурой полей совпадут. Обладающие этим свойством колебания принято называть вырожденными.

11.1.4. Добротность объемных резонаторов

Добротность резонаторов описывается равенствами (1.154) и (1.155). Сравнивая эти выражения с известными выражениями для добротности обычных колебательных контуров, можно убедиться в их тождественности.

Потери электромагнитной энергии в резонаторе складываются из потерь в среде, заполняющей резонатор, и потерь в металлической оболочке резонатора. Кроме того, часть энергии из резонатора передается через элементы связи в устройства, связанные с резонатором. Элементы связи объемных резонаторов с внешними устройствами, идентичные элементам связи в направляющих системах, во-первых, необходимы для возбуждения и поддержания незатухающих колебаний и, во-вторых, позволяют часть энергии из резонатора передать другим элементам аппаратуры (усилителю, линии передачи и др.). В открытых резонаторах дополнительно часть энергии теряется на излучение. Поэтому общие потери энергии в резонаторе

Строгий расчет величины каждого из видов потерь в объемном резонаторе встречает большие трудности, ибо, как правило, не удается найти решение уравнения (11.7), если не пренебречь потерями в оболочке, через элементы связи и т.д. Поэтому при анализе резонаторов обычно исходят из предположения, что небольшие общие потери, которые имеют место в резонаторе, не сказываются существенно на структуре полей в нем, т.е. предполагают, что в первом приближении структура поля в резонаторе с потерями и без них одинакова. В указанном приближении энергия, запасенная в резонаторе с малыми потерями и без потерь, практически одинакова. При этом потери в металле, среде, на излучение и потери, вызываемые передачей части энергии через элементы связи, можно рассчитывать независимо друг от друга. Исключением является случай, когда в резонаторе возбуждаются вырожденные колебания. При вырождении в резонаторе без потерь могут одновременно существовать на одной частоте два или несколько колебаний с различной структурой электрических и магнитных полей и соответственно с различной структурой токов проводимости на оболочке резонатора. Естественно, что величина потерь энергии для каждого колебания будет различна. Различие в величине потерь может вызвать некоторое различие в резонансных частотах, т.е. вырождение может исчезнуть. Соответственно изменится структура поля в резонаторе.

11.1.5. Собственная добротность закрытых резонаторов

Собственная добротность произвольного резонатора, как следует из (11.12), зависит от Q_мет, Q_Д и О_рад. В закрытых резонаторах радиационные потери отсутствуют, поэтому

то из (11.11) следует, что

Аналогично можно показать, что добротность, обусловленная

магнитными потерями, равна отношению μ'/μ". Добротность Q_A

резонатора, заполненного веществом с параметрами ε = ε'-iε" и

μ= μ- iμ", находится из формулы

11.1.6. Связь между добротностью объемного резонатора и длительностью процесса свободных колебаний в нем

При наличии потерь свободные электромагнитные колебания в резонаторах должны быть затухающими. Чем выше собственная добротность резонатора, тем меньше потери в нем и тем дольше свободные колебания сохраняют заметную амплитуду. В соответствии с формулой (1.120) для закрытого резонатора при наличии джоулевых потерь должно выполняться соотношение

dW/dt=-PП.                                 (11.19)

Очевидно, что в случае монохроматических колебаний мгновенные значения РП и W связаны, как и средние значения этих величин, равенством

P_П=ω_QW/Q.                                  (11.20)

Подставляя (11.20) в (11.19) и интегрируя, получаем

W=W_oexp(-ω_Qt/Q),                           (11.21)

где W_o - начальный запас энергии в резонаторе при t = 0.

Как видно из (11.21), запас энергии в резонаторе с потерями экспоненциально убывает. За время, равное t≈ 0,75 Q/f_Oi энергия, запасенная в резонаторе, уменьшится в 100 раз. Если Q= 10⁴ и fo= 1000 МГц, то t = 7,5 мкс, что свидетельствует о весьма быстром затухании свободных колебаний даже в высокодобротных резонаторах. Поэтому для поддержания незатухающих колебаний в резонаторы вводят постоянно восполняющие потери сторонние источники. При этом резонатор уже работает в режиме вынужденных, а не свободных колебаний.

В момент подключения стороннего источника резонатору сообщается некоторый начальный запас энергии, что влечет за собой возникновение свободных колебаний, рассмотренных в 11.1.2. Свободные колебания, как было показано выше, при наличии потерь в резонаторе весьма быстро затухают, а электромагнитные колебания с частотой источника, т.е. вынужденные колебания, поддерживаются за счет энергии последнего. Поэтому уже через небольшой интервал времени после включения стороннего источника частота электромагнитных колебаний в резонаторе практически не отличается от частоты электромагнитных колебаний стороннего источника. Согласно (11.21) длительность периода установления стационарного режима тем больше, чем выше добротность объемного резонатора и ниже частота электромагнитных колебаний.

Возбуждение электромагнитных колебаний в объемных резонаторах и вывод энергии из них основаны на тех же принципах, что и в линиях передачи (см.. гл.12).

11.2. РЕЗОНАТОРЫ В ВИДЕ ОТРЕЗКОВ РЕГУЛЯРНЫХ ЛИНИЙ ПЕРЕДАЧИ

11.2.1. Общие сведения

Теоретическое исследование структуры электромагнитных полей и других свойств объемных резонаторов, ограниченных сложной по форме оболочкой, встречает весьма значительные математические трудности, связанные с необходимостью нахождения решений трехмерного уравнения Гельмгольца, удовлетворяющих - граничному условию (11.8). Задача существенно упрощается, если резонатор образован из отрезка линии передачи с известной структурой электромагнитного поля. Рассмотрим, например, отрезок закрытой линии передачи, в котором возбуждена волна одного типа, распространяющаяся в направлении, указанном на рис.11.2 сплошной стрелкой. Конец линии, удаленный от точки питания, замкнем накоротко с помощью идеально проводящей металлической пластины, перпендикулярной продольной оси линии (режим короткого замыкания). Начало координат совместим с короткозамыкающей плоскостью, ориентировав ось z параллельно продольной оси линии (см. рис.11.2).

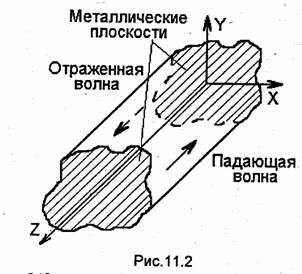
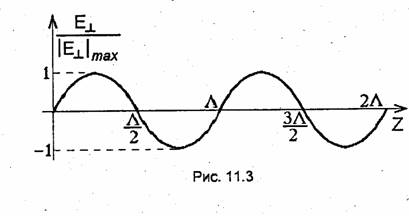
Так как коэффициент отражения от идеально проводящей плоскости для касательной к ней (т.е. перпендикулярной оси Z) составляющей вектора напряженности электрического поля равен -1, то комплексная амплитуда этой составляющей в произвольном сечении рассматриваемого отрезка линии определяется выражением

На рис.11.3 построена описываемая выражением (зд зависимость поперечной составляющей вектора Е от координаты z. На расстоянии l = рΛ/2 от точки z = 0, где Λ-длина волны в линии, а р- произвольное натуральное число, модуль поперечной составляющей, как это следует из (11.22) и видно из рис.11.3, обращается в нуль. Поэтому, не нарушая структуры поля в направляющей системе, в любое из сечений, где поперечная составляющая напряженности электрического поля равна нулю, можно ввести еще одну короткозамыкающую металлическую плоскость, перпендикулярную оси Z. Но отрезок линии между двумя короткозамыкающими пластинами представляет собой объем V_o, окруженный со всех сторон металлической оболочкой, т.е. является объемным резонатором закрытого типа. Если направляющая система открытого типа, то короткозамкнутый с двух сторон отрезок линии является открытым резонатором.

Таким образом, длина объемного резонатора равна целому числу полуволн колебания, распространяющегося в линии:

l = р(Λ/2),  р = 1,2.....                        (11.23)

После подстановки (9.17) в (11.23) и решения полученного уравнения относительно X находим резонансную длину волны резонатора:

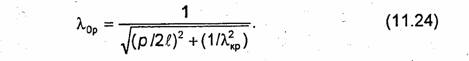
Классификация колебаний в объемных резонаторах, представляющих собой короткозамкнутый отрезок направляющей системы, осуществляется в соответствии с типом волны, стоячая волна которого образуется в резонаторе. Чтобы различать колебания с различным числом полуволн, укладывающихся вдоль оси Z резонатора, в указатель типа волны вводят дополнительный индекс р, равный числу полуволн в стоячей волне. Например, если в прямоугольном резонаторе колебание представляет собой стоячую волну, образованную в результате полного отражения волны Н_ю, причем вдоль оси Z уложилось четыре полуволны, то такая структура поля обозначается Н₁₀4- Аналогичный смысл имеют обозначения Н_тпр, Е_тпр, ТЕМ_Р, НЕ_тпр.

Так как у ТЕМ-волн критическая длина волны равна бесконечности, то в случае колебаний ТЕМ_Р выражение (11.24) упрощается и принимает вид

Вывод формул (11.22) и (11.24) основан на предположении, что у волны, распространяющейся в линии передачи, обязательно существуют поперечные составляющие электрического поля, обращающиеся в нуль на короткозамыкающих пластинах. Для волн Н_тп и ТЕМ это условие, очевидно, выполняется всегда, так как у этих волн вектор электрического поля лежит в плоскости, перпендикулярной направлению распространения волны. У волн Е, как следует из выражений (9.14) и (9.19), при поперечные составляющие вектора напряженности электрического поля равны нулю в любом сечении линии передачи. В то же время продольная составляющая напряженности электрического поля и поперечный вектор магнитного поля отличны от нуля. Поэтому при короткозамыкающие пластины можно вводить в произвольные сечения линии с волной Е_тп, т.е. резонансная частота такого резонатора не зависит от его длины. Можно заметить, что данный результат есть частный случай (11.24), так как при р = 0.Следовательно, у колебаний Е_тпр p≥O, тогда как у волн Н_тпр, ТЕМ_Р всегда р ≥1.

Отметим, что в линиях с ТЕМ- и квази-ГЕМ-волнами полное отражение от конца линии возможно не только в режиме короткого замыкания. Если поперечные размеры линии малы по сравнению с длиной волны, то распространяющаяся по линии волна ТЕМ (квази-ТЕМ) практически полностью отражается от ее свободно оборванного (незагруженного) конца (режим холостого хода (XX)). При этом коэффициент отражения для поперечных составляющих вектора Е равен +1, и вместо (11.22) выполняется соотношение

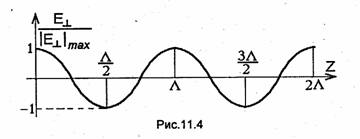
Зависимость поперечной составляющей вектора Е от координаты z показана на рис.11.4. Образуя второй обрыв рассматриваемой линии  на расстоянии l = рΛ2, р =1, 2.....  от ее конца, получаем объемный резонатор.

11.2.2. Коаксиальный резонатор

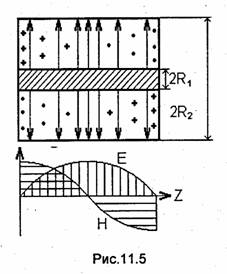
Коаксиальный резонатор представляет собой отрезок коаксиальной линии, замкнутый с обоих концов проводящими пластинками. Поперечные размеры коаксиального резонатора, так же как и поперечные размеры коаксиальной линии, выбираются в соответствии с (10.55), что обеспечивает отсутствие резонансов высших типов волн. Резонансная длина волны определяется выражением (11.25), откуда следует, что длина коаксиального резонатора l = рλ_Ор/2. Структура электрического и магнитного полей, а также эпюры, показывающие распределение этих полей вдоль полуволнового резонатора, изображены на рис.11.5.

Как уже отмечалось (см. 11.1.2), векторы Е и Н в объемном резонаторе сдвинуты по фазе на π/2. Если в какой-то момент времени, например t=0, электрическое поле обращается в нуль, то магнитное поле в этот момент времени имеет экстремум. Через четверть периода (t= T/4) электрическое поле достигает экстремума, а магнитное обращается в нуль. Структура поля, показанная на рис.11.5, соответствует некоторому промежуточному моменту времени, когда отличны от нуля и электрическое, и магнитное поля.

Определим собственную добротность коаксиального резонатора, предполагая, что он заполнен диэлектриком без потерь. Вектор напряженности магнитного поля в резонаторе, как и в коаксиальной линии, имеет одну φ-ю составляющую, равную

Как показывает численный расчет по формуле (11.27), у коаксиальных резонаторов из меди собственная добротность на волнах до 10 см может достигать нескольких тысяч и быстро падает по мере уменьшения резонансной длины волны.

Коаксиальные резонаторы широко применяют в качестве волномеров, колебательных контуров в радиопередающих устройствах, в фильтрах и других приборах.

11.2.3. Резонатор в виде отрезка коаксиальной линии, нагруженной на емкость

Для уменьшения геометрической длины коаксиального резонатора, что особенно важно на волнах длиной порядка  1 м и более,   между  центральным  проводником  коаксиальной  линии резонатора и одной из короткозамыкающих пластин оставляют зазор (рис.11.6). Ширина зазора выбирается значительно меньше длины волны, что обеспечивает повышенную концентрацию электрического поля в зазоре, т.е. зазор эквивалентен конденсатору, подключенному к линии. Эквивалентная схема такого резонатора (рис.11.7) может быть представлена в виде короткозамкнутого с одной стороны отрезка длиной h коаксиальной линии,  второй конец которой нагружен на сосредоточенную емкость. Резонанс в данной системе возможен, если только входное сопротивление короткозамкнутого отрезка линии длиной h имеет индуктивный характер в точках подсоединения к емкости С. Как известно из курса теории линейных электрических цепей и будет также показано в гл.12, короткозамкнутый отрезок линии обладает индуктивным

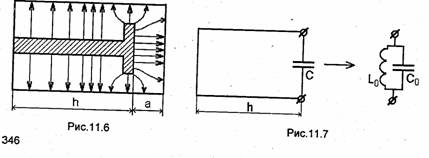
тивным входным сопротивлением при h < λ₀/A. Поэтому общая длина такого резонатора Не превышает четверти длины волны. Отметим, что добротность резонаторов с емкостной нагрузкой несколько ниже, чем у полуволнового резонатора.

11.2.4. Прямоугольный резонатор

Прямоугольный резонатор представляет собой отрезок прямоугольного волновода, замкнутый с обоих концов проводящими пластинами (рис.11.8). Резонансная длина волны колебаний Е_тпр и Н_тпр, в таком резонаторе определяется из формулы (11.24), которая после подстановки в нее выражения (10.12) принимает вид

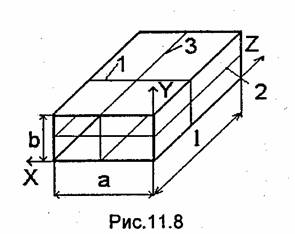
У волны Е_тпр ни индекс т, ни индекс п не может быть равен нулю, поскольку существование волн Е_о„ и Е_т0 в прямоугольном волноводе невозможно. У волн Н_тпр только один из индексов т или п может быть нулевым. Значение индекса р, равное нулю, допустимо для волн Е_тпр и невозможно для волн Н_тпр (см. выше).Следовательно, в формуле (11.28) независимо от типа волны только один из трех индексов т, п или р может обращаться в нуль.

Низшее (основное) колебание имеет наибольшую резонансную длину волны. В прямоугольном резонаторе основным колебанием при b < а и b < l является H₁₀₁, при а < b и а < l – H₀₁₁, a при l<a и l<b- Е₁₁₀. Обычно наименьшим размером является b.

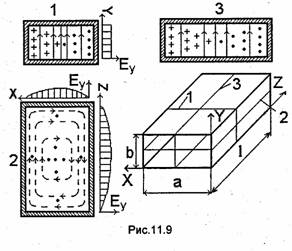
Поэтому наиболее часто используется колебание Н₁₀₁. Структура электромагнитного поля этого колебания в некоторый момент времени 0 < t <T/4 показана на рис.11.9.

Собственная добротность резонатора с колебанием Н_ш может быть определена из формулы (11.16). Выполнив необходимые преобразования, получаем

Как показывает расчет, собственная добротность, прямоугольного резонатора достигает десятков тысяч в сантиметровом диапазоне волн.

11.2.5. Цилиндрический резонатор

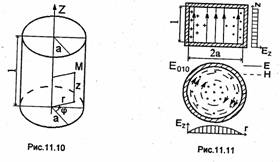
Цилиндрический резонатор представляет собой отрезок круглого волновода, замкнутый с обоих концов проводящими пластинами (рис.11.10). Резонансная длина волны колебаний в цилиндрическом резонаторе определяется из формулы (11.24) и равна для волн Е_тпр (р ≥ 0)

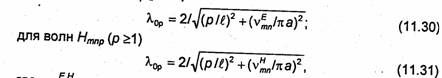
 - корни функций Бесселя и их производных (см. 10.3).

Как видно из формул (11.30) и (11.31), основным колебанием в цилиндрическом резонаторе в зависимости от отношения l/а может быть либо Е₀₁₀, либо H₁₁₁. У колебания E₀₁₀ резонансная длина волны не зависит от l и равна  У колебания

Так как  не зависит от l, то резонатор, рассчитанный на это колебание, может иметь весьма небольшие габариты.

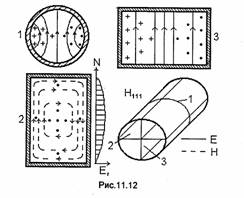
При анализе распространения волны Н₀₁в круглом волноводе было показано, что при достаточно большом диаметре волновода можно добиться весьма малых потерь. Поэтому резонатор, в котором укладывается одна или несколько полуволн колебания Н₀₁, должен обладать чрезвычайно высокой добротностью. Действительно ,

как показывает расчет по формуле (11.34), собственная добротность резонатора с волной H_ori достигает сотен тысяч. При столь высокой добротности полоса пропускания резонатора на частоте 10000 МГц не превышает 100 кГц. Это позволяет использовать резонатор с волной H₀₁₁ в качестве высокоточного волномера.

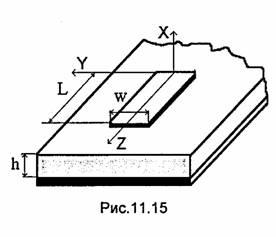
Чтобы иметь возможность перестраивать резонатор с одной частоты на другую, одна из короткозамыкающих металлических пластин выполняется в виде подвижного поршня (рис.11.14). По мере движения поршня меняется длина резонатора, что влечет за собой изменение его резонансной длины волны. Как видно из рис.11.14, поршень не касается стенок резонатора, т.е. электрический контакт между поршнем и стенками резонатора отсутствует. Объясняется это стремлением подавить колебание Е₁₁₁, у которого та же резонансная длина волны, что и у Н_о11. Волна Но₁, в круглом волноводе и, следовательно, колебание Н₀₁₁ в резонаторе возбуждают на стенках только поперечные токи (j_z=O). Поэтому небольшой зазор между поршнем и стенками резонатора вполне допустим и практически не влияет на электрические характеристики резонатора. В то же время зазор является препятствием для продольных токов волны E₁₁₁ и делает невозможным резонанс этого колебания.

Следует отметить, что реальные значения Qo несколько меньше расчетных.

11.2.6. Полосковые резонаторы

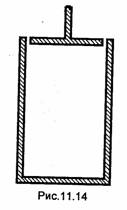
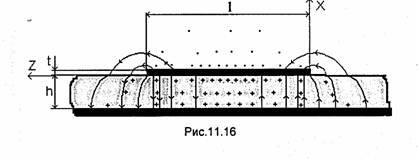
Полосковый резонатор представляет собой отрезок полосковой линии, на обоих концах которого осуществлен режим XX. На рис.11.15 показан полосковый резонатор, выполненный на МПЛ. Его поперечные размеры так же, как поперечные размеры полосковой линии, выбираются из условия отсутствия высших типов волн и излучения из линии. Так как у волн ТЕМ и квази-ТЕМλ_кр=∞, то резонансная длина волны колебания ТЕМ_Р и квази-TEMp равна λ_0р=2l/р, р = = 1,2,.... Следовательно, длина резонатора l = рλ_Ор12. Продольное сечение полуволнового резонатора на МПЛ и структура силовых линий электрического поля показаны на рис.11.16. Как видно, вблизи концов отрезка МПЛ наблюдается концентрация электрического поля, что эквивалентно включению некоторых емкостей между концами полоски и экраном. Из-за этого длина резонатора I выбирается несколько меньше λ_0р12.

11.3. ПРОХОДНОЙ РЕЗОНАТОР

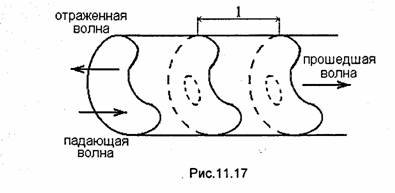
Рассмотрим резонатор в виде короткозамкнутого отрезка линии передачи, включенного в линию, в торцевых металлических стенках которого прорезаны одинаковые отверстия (рис.11.17). Отверстие на входе резонатора обеспечивает возбуждение колебаний в резонаторе, а отверстие на его выходе служит для передачи энергии в нагрузку. Резонатор рассматриваемого типа получил название "проходнойрезонатор" и широко применяется в технике СВЧ.

Нагруженную добротность подобного резонатора проще определить не из общего формулы (11.10), а из адекватного ей при

Q>>1 выражения

где Δf_o,₅- расстройка, при которой мощность на выходе резонатора уменьшается в 2 раза.

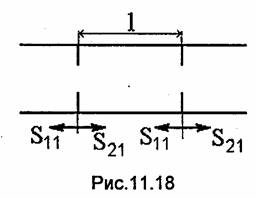
Перейдем к определению зависимости коэффициента передачи резонатора т от частоты, что позволит рассчитать добротность по формуле (11.35). Торцевые металлические плоскости резонатора, в которых прорезаны отверстия, можно рассматривать как две диафрагмы, одна из которых находится на входе, а другая -на выходе резонатора. Поток энергии, соответствующий падающей электромагнитной волне, частично отражается от первой диафрагмы, а оставшаяся часть проходит в резонатор. Дойдя до второй диафрагмы, этот поток частично проходит через диафрагму и поглощается в нагрузке. Оставшаяся часть отражается от второй диафрагмы и распространяется в направлении к первой. Напряженность полного электрического поля за резонатором (при z = l) равна сумме напряженностей полей, соответствующих всем волнам, прошедшим через вторую диафрагму. Обозначим коэффициент отражения от диафрагмы через S₁₁ (см. гл.12), а коэффициент прохождения - через S₂₁ (рис.11.18). Если пренебречь мощностью джоулевых потерь в диафрагмах, должно выполняться равенство

После взаимодействия падающей волны с первой диафрагмой комплексная амплитуда напряженности электрического поля прошедшей через диафрагму волны равна  Прошедшая волна на пути от первой диафрагмы цр второй приобретает фазовый сдвиг βl. Она частично отражается от второй диафрагмы и частично проходит за нее. Комплексная амплитуда напряженности электрического поля волны, прошедшей за вторую диафрагму при  Волна, отразившаяся от второй диафрагмы, распространяется по направлению к первой диафрагме и приобретает фазовый сдвиг βl.

Она частично проходит через первую диафрагму и частично отражается от нее. Отраженная волна доходит до второй диафрагмы, частично проходит за нее и частично отражается, и т.д. Комплексная амплитуда напряженности электрического поля  волны, прошедшей вэтом случае через вторую диафрагму при z=l,  равна  

Комплексная амплитуда напряженности полного электрического поля за второй диафрагмой при z = e равна

Так как то ряд в (11.37) представляет собой бесконечно убывающую геометрическую прогрессию. Производя суммирование, определяем коэффициент передачи проходного резонатора:

Вычисляя абсолютное значение коэффициента т и используя (11.36), получаем

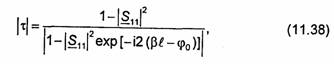
гдеφо=аrgs₁₁. Как видно, при правая часть

выражения (11.38) равна единице (|τ|=1), т.е. вся мощность падающей волны поступает на выход резонатора. Такой режим называют резонансным. Найдем длину резонатора l, соответствующую данному случаю. Так как β = 2π/Λ, где Λ - длина волны в линии передачи, то

Зависимость Λ от длины волны λ = c/f для каждого типа волны определяется из соотношения (9.17). Длина волны λ_Ор, и соответствующая ей частота f_Op, на которой выполняется равенство (11.39), называется резонансной.

Как следует из (11.39), только при φ_О=О длина резонатора точно кратна целому числу полуволн. При φ_О<О (диафрагма индуктивная) длина резонатора меньше рΛ/2. При емкостной диафрагме (φ₀ > 0) длина резонатора больше рΛ/2.

На частотах, отличных от резонансной, равенство (11.39) не удовлетворяется, и поэтому амплитуда прошедшей волны уменьшается.

Изменение величины |τ| от частоты определяется зависимостью β и φ₀ от частоты. При малых изменениях частоты величину φ₀ обычно можно считать постоянной. Зависимость величины β от частоты согласно (9.14) имеет вид

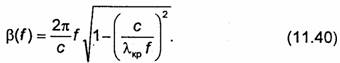
Аналогичная зависимость коэффициента передачи от частоты имеет место у параллельного контура, включенного параллельно в линию. Таким образом, эквивалентная схема линии передачи с включенным в нее проходным резонатором имеет вид, показанный на рис.11.19.

При выводе формулы (11.38) мы пренебрегли тепловыми потерями в диафрагмах и линии передачи. Поэтому найденная величина фактически является внешней добротностью резонатора. Если тепловыми потерями в резонаторе пренебречь нельзя, то нагруженную добротность можно рассчитывать по формуле (11.13), предварительно определив собственную добротность из (11.14), а внешнюю-из (11.42).

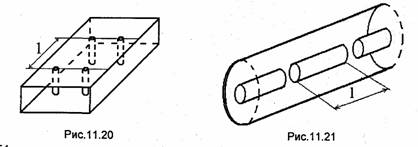
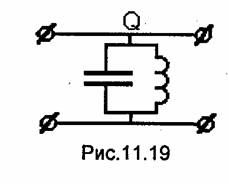
Отметим, что вывод формулы (11.38) и получаемый результат не изменяются, если вместо диафрагм на вход и выход резонатора включить любые другие неоднородности без потерь. Например, в прямоугольных резонаторах широко применяются неоднородности, состоящие из нескольких штырей (рис.11.20). Подбором количества стержней, их диаметра и расстояний между ними можно получить значения коэффициента отражения, соответствующие заданным значениям нагруженной добротности резонатора [57]. В полосковых и коаксиальных линиях роль неоднородности может выполнять зазор (щель) в центральном проводнике (рис.11.21).

11.4. КВАЗИСТАЦИОНАРНЫЕ РЕЗОНАТОРЫ

Характерным признаком квазистационарных резонаторов является весьма четко выраженное пространственное разделение электрического и магнитного полей у колебания с наименьшей резонансной частотой, т.е. энергия электрического и магнитного полей концентрируется преимущественно в различных частях объема резонатора. Это позволяет рассматривать квазистационарные резонаторы, в которых возбуждается колебание с низшей резонансной частотой, как обычные колебательные контуры с сосредоточенными постоянными, причем те части объема, где концентрируется энергия электрического и магнитного полей, эквивалентны соответственно емкостному и индуктивному элементам контора. Если величина индуктивного и емкостного сопротивлений элементов известна, то резонансная частота квазистационарного   резонатора   может  быть   рассчитана   по   формуле

   На рис.11.22 и 11.23 изображены тороидальный резонатор, применяемый в клистронах, и резонатор магнетрона соответственно.

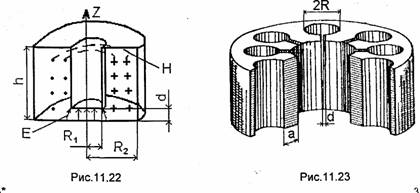
В случае тороидального резонатора электрическое поле почти полностью сосредоточено в зазоре шириной d (рис.11.22). Емкость эквивалентного резонансного контура равна емкости зазора между параллельными пластинами резонатора, которая рассчитывается по формуле Эта формула является приближенной, так как не учитывает искажение поля на краях конденсатора. Магнитное поле концентрируется преимущественно в боковых полостях резонатора. Если пренебречь неравномерностью распределения магнитного поля вдоль оси Z, можно считать, что вектор Н имеет только азимутальную составляющую  где /-ток, текущий по боковой поверхности внутреннего цилиндра, а r-расстояние от оси Z до рассматриваемой точки. Магнитный поток, проходящий через боковые полости резонатора,

где S_┴ - площадь половины поперечного сечения резонатора, пронизываемая магнитными силовыми линиями. Индуктивность резонатора вычисляется по формуле  Зная С_о и Lо, находим угловую резонансную частоту тороидального резонатора:

Аналогично для ячейки магнетронного резонатора {рис.11.23) получаем

Глава 12

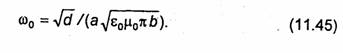
ОБЩАЯ ТЕОРИЯ ЦЕПЕЙ СВЧ

12.1. ПОНЯТИЕ ОБ ЭКВИВАЛЕНТНОЙ СХЕМЕ ЦЕПИ СВЧ. КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ

12.1.1. Цепь СВЧ (тракт СВЧ)

Радиосистемы, работающие в диапазоне 30 МГц <f<3000 ГГц, обычно можно представить в виде некоторых устройств, соединенных отрезками линий передачи. Часть такой системы, расположенную между начальным и оконечным устройствами (например, между антенной и радиопередающим или радиоприемным устройством), называют трактом СВЧ или цепью СВЧ. Подобный тракт осуществляет передачу электромагнитной энергии от передатчика к антенне или от антенны к приемнику, обеспечивает требуемый режим работы выходных или входных цепей передатчика или приемника, выполняет частотное и поляризационное разделение и объединение передаваемых сигналов и ряд других функций. Отметим, что цепью СВЧ называют также и отдельные части тракта СВЧ. Наиболее распространенными элементами СВЧ цепей являются отрезки линий передачи, переходные и стыковочные узлы между линиями разных типов, согласующие и настроечные элементы, сумматоры, делители и ответвители мощности, поляризационные устройства, фильтры, фазовращатели, коммутаторы и переключатели, невзаимные устройства с намагниченными ферритами и др. Перечисленные и некоторые другие элементы СВЧ рассмотрены в последующих главах.

Процессы передачи электромагнитных сигналов в цепях СВЧ и в образующих их элементах являются весьма сложными. Их можно было бы проанализировать на основе решения соответствующих краевых задач электродинамики. Однако строгая постановка и решение таких задач даже для сравнительно простых элементов цепей СВЧ возможны далеко не всегда. А для применяемых на практике цепей СВЧ из-за их конфигурационной сложности решение краевых задач в строгой постановке в настоящее время практически невозможно. На практике при анализе сложных цепей СВЧ применяют метод декомпозиции (разбиения): цепь СВЧ разбивается на ряд элементов, которые анализируются независимо. При этом каждый такой элемент рассматривается как независимая электродинамическая система.

Постановка и решение краевых задач, соответствующих отдельным элементам, существенно проще, чем для всего устройства в целом. Используя или решение электродинамической задачи или результаты экспериментального исследования, если подобное решение получить не удается, для каждого выделенного элемента строят такое описание, которое позволяет находить влияние этого элемента на передаваемые электромагнитные сигналы. Обычно описание элементов цепи представляют либо в виде одной из матриц (матрицы рассеяния, матрицы передачи и др.), либо в виде эквивалентной схемы, состоящей из отрезков эквивалентной линии передачи, в которую тем или иным способом включены сосредоточенные элементы L, С, R и трансформаторы. Имея подобные универсальные описания всех элементов цепи СВЧ, можно определить все требуемые характеристики цепи (см. 12.3).

Обычно при построении математической модели цепи СВЧ для упрощения анализа отрезки линий передачи, соединяющие входящие в эту цепь устройства, заменяют отрезками эквивалентной линии, а устройства рассматриваются как некоторые многополюсники. Электромагнитные процессы в эквивалентной линии описываются скалярными функциями (напряжением 0_т и током i_т), зависящими лишь от продольной координаты z. Эти функции строятся на основе векторных функций Ё_т и Н_т, определяемых для каждой линии из решения соответствующей электродинамической задачи (см. гл.10). Отметим, что указанную упрощенную модель отрезка линии передачи можно использовать лишь в диапазоне частот, где соблюдается одноволновый режим работы линии. Кроме того, эта модель непригодна для определения ряда характеристик цепи СВЧ, например таких, как максимальная мощность, передаваемая по цепи СВЧ, или величина взаимной связи между элементами цепи СВЧ, построенной на отрезках линий передачи открытого типа, и некоторых других.

Рассмотрим переход к эквивалентной линии. Для TЕМ-волн в линиях передачи, структура поля которых в поперечной плоскости имеет потенциальный характер, можно, используя векторы Ё_т и Н_т, однозначно определить соответствующие им напряжение 0_т и ток i_т. При этом для волны, распространяющейся по линии без потерь вдоль оси Z, можно записать

где k- коэффициент фазы рассматриваемой волны.

В гл.10 были определены U_m(z) и l_m(z) для TЕМ-волн в двухпроводной и коаксиальной линиях. Зная функции (12.1), можно вычислить волновое сопротивление линии Z_B = U_m(z)/i_m{z) и среднюю за период мощность, переносимую волной по линии:

Для линии передачи, в которой распространяются Е-, Н- или смешанные волны, напряжение и ток в эквивалентной линии могут быть выражены через контурные интегралы от функций E_m┴ и Н_т┴ соответственно; указанные функции описывают поперечные составляющие полей в рассматриваемой линии передачи. В отличие от случая TЕМ-волн у Е-, Н- и смешанных волн поле, описываемое функциями Ё_т┴ и Н_т┴ не является потенциальным. Поэтому значения функций U_m(z) и i_m(z) определяются неоднозначно: они зависят от выбора контуров интегрирования. Для устранения этой трудности при переходе к эквивалентной линии заранее оговаривают форму указанных контуров. Рассмотрим, как вычисляются напряжение, ток и волновое сопротивление для волны Н₁₀, бегущей вдоль оси Z прямоугольного волновода. Используя выражение (10.18) для составляющей Ё_ту волны Н₁₀, определяем комплексную амплитуду напряжения между точками, лежащими на средних линиях широких стенок при х = а/2:

Изменив форму контура либо методику определения напряжения и тока, можно получить другие выражения для Z_B. Однако во всех случаях формула для  имеет вид где А-числовой коэффициент, зависящий от способа вычисления величин Неопределенность в выборе этого коэффициента существенного значения не имеет, так как при инженерном проектировании цепей СВЧ важно знать отношение волновых сопротивлений соединяемых отрезков линий, а не конкретные значения каждого из них.

На основе изложенного любую линию передачи можно заменить эквивалентной длинной линией, в которой распространяются соответствующие волны напряжения и тока. Отметим, что математическую модель в виде эквивалентной линии можно использовать и для линии передачи, в которой могут распространяться несколько типов волн. В этом случае для каждого распространяющегося по линии типа волны с помощью формул, аналогичных (12.3)—(12.5), строится своя эквивалентная линия, т.е. математическая модель образуется несколькими (по числу распространяющихся типов волн) эквивалентными линиями.

12.1.2. Линии передачи конечной длины. Неоднородности в линиях передачи

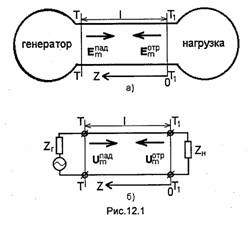
Пусть отрезок произвольной  регулярной линии  (рис.12.1) включен между генератором И оконечным устройством, которое в дальнейшем будем называть нагрузкой. Предположим, что линия работает в одноволновом  режиме  и  по ней  может распространяться волна основного типа, электрическое поле которой описывается векторной функцией .  Поскольку в конце линии в месте подключения нагрузки появляются новые границы раздела сред, то по сравнению с бесконечной линией в рассматриваемом случае изменяются краевые условия для векторов электромагнитного поля.

В результате этого на конце линии возникает новая, соответствующая изменившимся краевым условиям структура поля.  Поскольку в регулярной линии в общем случае может существовать бесконечное число типов волн, отличающихся друг от друга структурой полей, то образовавшееся после подключения нагрузки поле должно быть суперпозицией этих волн. Однако, если линия работает в одноволновом режиме, амплитуды векторов поля всех типов волн, кроме основного, экспоненциально убывают в линии по мере удаления от нагрузки. Поэтому, если плоскость Т₁ (рис.12.1,а), перпендикулярная оси Z, расположена на таком расстоянии от нагрузки, при котором в этой плоскости можно пренебречь амплитудами векторов поля всех высших типов волн, то во всех точках линии, находящихся левее плоскости Т₁ кроме падающей будет распространяться лишь отраженная волна основного типа, электрическое поле которой описывается функцией Если в месте подключения нагрузки образуется такая структура поля, при которой в ее составе отсутствует волна основного типа, то отраженная волна в линии не появится. При этом, если отсутствуют потери в линии, вся переносимая падающей волной энергия поглощается в нагрузке, что следует из закона сохранения энергии. В этом случае говорят, что линия идеально согласована с нагрузкой или что линия работает в режиме бегущей волны. Аналогичные процессы происходят и в месте подключения генератора к линии.

Рассмотрим еще один случай, часто встречающийся при анализе цепей СВЧ. Пусть в регулярной линии передачи расположена какая-либо неоднородность (рис.12.2,а), например в прямоугольный волновод помещен некоторый объект, электродинамические параметры которого отличаются от параметров среды, заполняющей волновод (металлическая перегородка или штырь, диэлектрический цилиндр и др.)

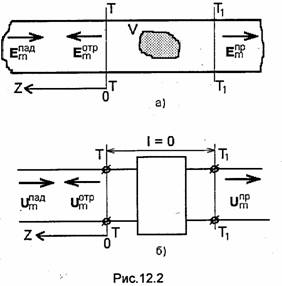
К этому же случаю можно отнести и соединение (стык) двух линий передачи с разной формой или разными размерами поперечного сечения. Во всех случаях в месте расположения неоднородности изменяется структура поля по сравнению с полем в регулярной линии.  Вблизи неоднородности поле имеет сложную структуру, обусловленную суперпозицией волн, которые могут существовать в данной линии. Если линия работает в одноволновом режиме, то, располагая перпендикулярно оси Z плоскости Т и Т₁ на таком расстоянии от неоднородности, при котором в этих плоскостях можно пренебречь амплитудами векторов поля всех высших типов волн, можно утверждать, что во всех точках линии, находящихся левее плоскости Т, появится (в общем случае) отраженная волна основного типа, напряженность электрического поля которой  а во всех точках линии правее плоскости Т₁ появится прошедшая волна основного типа  Поэтому обычно при рассмотрении процессов передачи энергии от генератора к нагрузке (см. рис.12.1, а) и исследовании влияния неоднородности на распространение энергии   по  линии   (рис. 12.2, а)   переходят   к  эквивалентной   схеме (рис.12.1,6 и  12.2,6).  При этом участки линии, где существуют лишь падающие и отраженные волны низшего типа, представляют эквивалентной линией. Участок линии, находящийся левее плоскости Т (рис.12.1,а) с подключенным генератором и участок линии, находящийся  правее  плоскости   Т₁ с подключенной  нагрузкой, представляют в виде эквивалентных двухполюсников (устройство с одним входом). Участок линии, содержащий неоднородность и находящийся между плоскостями Т и Т₁ (рис. 12.2, а), представляют в виде эквивалентного четырехполюсника (устройства, имеющего вход и выход). Из теории линейных электрических цепей [28] известно, что двухполюсники и четырехполюсники могут быть представлены в виде эквивалентных схем (схем замещения), состоящих   из   сосредоточенных   элементов   L, С, R.    Например,   на рис.12.1,6" двухполюсник, представляющий отрезок линии с подключенной   нагрузкой,   изображен  в  виде  комплексного  сопротивления Z_H, а отрезок с подключенным генератором - в виде генератора напряжения с внутренним сопротивлением Z_r.

Отметим, что поскольку амплитуда и фаза векторов электромагнитного поля как отраженной волны, так и прошедшей зависят от конструкции неоднородности в линии или конструкции оконечного устройства, то параметры эквивалентных схем или элементы матриц, описывающих двухполюсники или четырехполюсники, могут быть определены либо с помощью решения соответствующей электродинамической задачи, либо с помощью эксперимента.

Рассмотрим передачу энергии от генератора к нагрузке по линии (рис.12.1,а). На рис.12.1,6 показана эквивалентная схема для этого случая. Пусть отрезок эквивалентной линии без потерь (α = 0) длиной l, имеющий волновое сопротивление Z_B, возбуждается генератором напряжения с внутренним сопротивлением Z_r= Z_B. К концу отрезка подключена нагрузка Z_H. Генератор создает в линии падающую волну,  описываемую функциями   и Комплексную  амплитуду  напряжения   падающей   волны можно записать в виде

где -модуль и начальная фаза функции  в начале координат (при z= 0). Начало оси Z совпадает с плоскостью Т₁ а ее положительное направление указано на рис. 12.1. В общем случае подключение к линии произвольной нагрузки вызывает появление в линии  отраженной  волны,  описываемой функциями

Комплексную амплитуду напряжения отраженной волны можно записать в виде

Отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны в произвольном поперечном сечении линии передачи называют коэффициентом отражения по напряжению в указанном сечении:

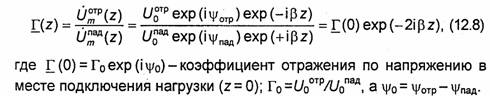
Полное напряжение U_m(z) и полный ток i_m(z), возникающей

в произвольном поперечном сечении линии, являются суммой напряжений и токов падающей и отраженной волн соответственно в; этом сечении:

Из  формулы  (12.9),   учитывая  формулу  (12.8),   определим модуль полного напряжения в произвольном сечении линии:

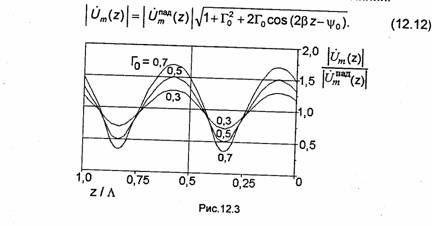
На рис. 12.3 показана зависимость величины   от координаты z, вычисленная по (12.12). Как видно, отраженная волна суммируется с падающей,  что приводит к образованию повторяющихся минимумов и максимумов. При этом минимумы, равные 1-Г₀, наблюдаются в сечениях линии, имеющих координату  а максимумы, равные 1 + Г₀-в сечениях с координатой   где n = 1, 2,3,.... Расстояние между ближайшими максимумами (или минимумами) всегда одно и то же и равно половине длины волны, соответствующей распространяющемуся типу волны в линии. В инженерной практике режим работы линии обычно характеризуют коэффициентом бегущей волны (КБВ)

где -минимальное и максимальное значения модуля полного напряжения.

Часто вместо КБВ используют обратную величину, называемую коэффициентом стоячей волны КСВ = 1/КБВ. В линии, идеально согласованной с нагрузкой, имеется только падающая волна (отраженная волна отсутствует) Г₀=0; КБВ = КСВ = 1. Такой режим работы линии называют режимом бегущей волны. При полном отражении падающей волны от нагрузки, когда Такой режим называют режимом стоячей волны.

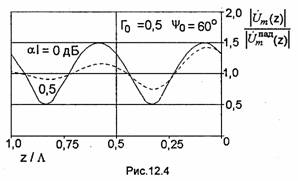
Следует отметить, что изображенная на рис. 12.3 зависимость получена в пренебрежении тепловыми потерями в линии. В этом случае как модуль коэффициента отражения |Г(z)|, так и величины КСВ и КБВ не изменяются вдоль линии. При учете тепловых потерь в линии (α≠0) в формулах (12.6)—(12.11) следует заменить (β на -iγ, где γ= α+ 1β₁-коэффициент распространения рассматриваемой волны в линии. При этом амплитуды напряжений, соответствующих падающей и отраженной волнам, экспоненциально убывают вдоль направления распространения волны в линии. Коэффициент отражения (12.8) вычисляется по формуле

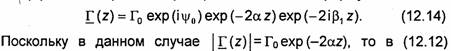
следует заменить Г_о на Г₀exp(-2αz) и β на β_1. Распределение модуля полного напряжения вдоль линии с учетом тепловых потерь построено на рис. 12.4 (пунктирная линия).

В линии с тепловыми потерями КБВ следует определять как отношение обязательно соседних минимального и максимального значений модуля полного напряжения. При удалении от нагрузки величина максимумов уменьшается, а минимумов возрастает, т.е. КБВ возрастает. Режим работы такой линии можно характеризовать двумя значениями КБВ: у нагрузки (КБВ_Н) и у генератора (КБВ_Г), которые связаны формулой [29]:

Еще одной важной характеристикой процесса передачи энергии от генератора в нагрузку с помощью линии является коэффициент полезного действия (КПД), равный отношению средней мощности P_cp^H, поступающей в нагрузку, к средней мощности Р_ср^паД, переносимой падающей волной в начале линии (при z=l). Если в линии отсутствует отраженная волна, то вся мощность, переносимая падающей волной в точках подключения нагрузки, поступает в нагрузку, т.е.

Согласно (12.11) появление отраженной от нагрузки волны приводит к дополнительному уменьшению средней мощности, поступающей в нагрузку, в 1/(1-Г₀²) раз. Используя (12.17), запишем формулу для КПД:

Определим среднюю мощность тепловых потерь в линии (см. рис.12.1,а):

где Р_ср^Вх-средняя мощность, поступающая от генератора на вход линии; она равна средней мощности, отдаваемой генератором падающей волне Р_ср^пад минус средняя мощность Р_ср^отр, переносимая отраженной волной при z=l (предполагается, что генератор идеально согласован с линией). Поэтому

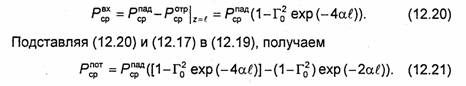
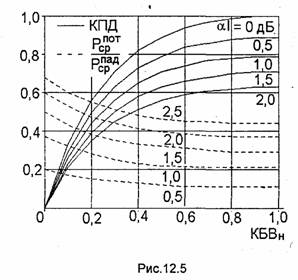
На рис. 12.5 показаны рассчитанные по (12.18) и (12.21) графики зависимости КПД и отношения Рср^ПОТ/Р_Ср^ПАД от КБВ_Н при разных значениях полного затухания линии аl [дБ]. Как видно, полная передача энергии от генератора в нагрузку (КПД=1) будет при идеальном согласовании нагрузки с линией (Г₀ = 0 и КБВ_Н = 1) и отсутствии  потерь в линии (αl=0). Отметим, что даже при отсутствии потерь в линии при КБВ_Н<1 КПД <1 из-за отражения части мощности от нагрузки.

Как уже отмечалось, максимальная величина мощности, которую может переносить падающая волна, ограничена тем значением, при котором в линии происходит электрический пробой или разрушение диэлектрического заполнения (тепловой пробой). При возникновении пробоя передача энергии по линии прекращается. Наличие отраженной волны в линии приводит к появлению в ней областей с повышенным значением напряжения (см. рис. 12.3) по отношению к напряжению падающей волны, что приводит к уменьшению электрической прочности линии. Например, при полном отражении от нагрузки (Г_о = 1) пробой в линии наступает при мощности падающей волны, составляющей 0,25 мощности падающей волны, приводящей к пробою в согласованной линии, когда Г_о = 0. Нередко волна, отраженная от нагрузки, оказывается причиной затягивания частоты генератора, питающего линию, при этом генератор начинает работать на частоте, несколько отличающейся от требуемой. Таким образом, при передаче энергии от генератора к нагрузке с помощью линии наиболее выгоден режим бегущей волны в линии, когда Г_о = 0 и КБВ_Н = 1. В этом случае отсутствуют потери энергии на отражение, КПД максимален и зависит только от потерь, в линии рассеивается наименьшая мощность, электрическая прочность максимальна, нагрузка на генератор активна и не зависит от длины линии.

12.1.3. Полное эквивалентное сопротивление линии передачи

Процесс распространения волн в линии передачи, нагруженной на произвольное сопротивление Z_H, может характеризоваться с помощью полного эквивалентного сопротивления линии Z_n(z), которое в заданном сечении линии равно отношению

комплексных амплитуд полного напряжения и полного тока в этом сечении. Используя (12.9) и (12.10), запишем формулу, связывающую полное сопротивление с коэффициентом отражения в произвольном сечении линии:

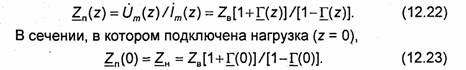
Из (12.23) следует формула, которая позволяет определить модуль Г_о и аргумент щ коэффициента отражения по известной величине Z_H:

Подставляя в (12.22) выражение (12.14) и учитывая равенство (12.24), запишем формулу для вычисления полного эквивалентного сопротивления в произвольном сечении линии:

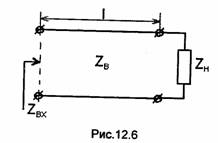
Отметим, что полное сопротивление в произвольном сечении линии называют эквивалентным, поскольку если линию рассечь в этом сечении, то входное сопротивление образовавшегося справа от сечения отрезка линии, нагруженного на Z_H (рис. 12.6), будет равно полному сопротивлению линии в этом сечении, т.е. Z_BX=Zn(z).

Часто при вычислении сопротивлений (полных, входных и т.д.) используют их нормированные значения, т.е. отнесенные к некоторому нормировочному сопротивлению Z_BH; например, нормированное полное сопротивление Z_n(z) = Z_n(z)/Z_eH, нормированное волновое сопротивление линии Z_B = Z_B/Z_BH, нормированное сопротивление нагрузки z_H=Z_H/Z_BH. Как правило, для рассматриваемой линии (см. рис.12.1,а) выбирают Z_BH=Z_B, при этом z_B = 1. Однако в некоторых случаях, например если цепь СВЧ включает каскадное соединение нескольких отрезков линий с разными волновыми сопротивлениями, в качестве Z_BH для всей цепи выбирают Z_B одного из них.

В ряде случаев удобно оперировать не полным эквивалентным сопротивлением в произвольном сечении линии, а полной эквивалентной проводимостью в этом сечении:

или нормированной полной эквивалентной проводимостью: y(z)=1/z_n(z).

Полное эквивалентное сопротивление в заданном сечении линии зависит от расстояния между этим сечением и нагрузкой. Поэтому отрезок линии длиной l (см.рис.12.6) можно использовать для трансформации (преобразования) величины сопротивления нагрузки Z_H. Например, при α = 0 входное сопротивление Z_BX отрезка линии длиной l равно полному сопротивлению, рассчитываемому по (12.26) при z=l Аналогично по (12.25) при z=l можно рассчитать входное сопротивление отрезка с учетом тепловых потерь в нем. Как следует из (12.26), при Z_H=Z_B входное сопротивление отрезка равно Z_B при любой его длине l и любой рабочей частоте.

Рассмотрим некоторые частные случаи трансформирующих отрезков.

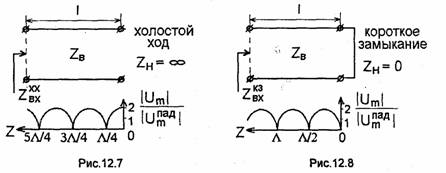
1. Короткозамкнутые и разомкнутые на конце отрезки линии (реактивные шлейфы). На рис.12.7 и 12.8 показаны отрезки эквивалентной линии, называемые реактивными шлейфами, на конце которых или режим холостого хода (XX) при Z_H = ∞

 (рис.12.7) или режим короткого замыкания (КЗ) при Z_H = 0 (рис. 12.8). Волновое сопротивление отрезков линии равно Z_B. Из (12.24) следует, что в случае XX на конце линии Г(0) ⁼ 1> т.е. Г_о = 1, ψ_о = О; а в случае КЗ Г(0)⁼-1. т.е. Г_о = 1, ψ_о = π. Падающая волна, распространяющаяся по реактивному шлейфу, полностью отражается от его конца; при этом в шлейфе устанавливается режим стоячей волны. Входное сопротивление шлейфов при а = 0 можно определить из (12.26), подставляя zl.

Как видно, входное сопротивление чисто реактивное, т.е. либо индуктивное либо емкостное, и зависит от длины отрезка и рабочей частоты.

Из формул (12.28) следует соотношение позволяющее по известным (например, измеренным) входным сопротивлениям отрезка в режимах КЗ и XX определить волновое сопротивление отрезка.

Отметим, что режим КЗ для отрезков реальных линий можно осуществить, поместив в конце металлическую пластину, расположенную перпендикулярно продольной оси линии и имеющей конконтакт с ее стенками.

В полосковых линиях режим, близкий к режиму короткого замыкания, можно обеспечить, соединяя полоску с экранирующими пластинами с помощью металлического проводника (перемычки). В случае линий с ТЕМ-волной, поперечные размеры которых достаточно малы по сравнению с длиной волны, режим, близкий к режиму XX, можно обеспечить путем обрыва линий. В линиях с волнами Е или Н такой режим обеспечить не удается.. Отрезок любого волновода, открытый на конце, при распространении по нему Е- или Н-волн имеет эквивалентную схему, показанную на рис.12.6, поскольку часть мощности, переносимая падающей волной, будет излучаться в открытое пространство, а оставшаяся часть будет отражаться от открытого конца отрезка обратно, т.е. в этом случае Г_о< 1.

2. Четвертьволновый отрезок линии передачи. Если длина отрезка l=Λ/4, величина βl=π/2, при этом входное сопротивление отрезка

Такой отрезок называют четвертьволновым трансформатором или инвертором сопротивления, поскольку его входное сопротивление пропорционально проводимости нагрузки, подключенной к его концу. Для четвертьволнового реактивного шлейфа из (12.28) следует, что  Поэтому в линиях с TЕМ-волнами режим КЗ в конце линии можно обеспечить либо закоротив проводники, либо подключив к концу линии четвертьволновый отрезок, разомкнутый на конце. Хотя второй способ выглядит менее привлекательно, при проектировании устройств на основе полосковых линий его применяют намного чаще. При этом не нарушается плоская форма конструкции и не требуются дополнительные технологические операции для установки металлической перемычки между полоской и экранами, как в первом случае.

3. Полуволновый отрезок линии  передачи. Для  отрезка линии длиной l=Λ/2 (см. рис.12.6),  называемого полуволновым трансформатором,  величина  βl=π;  его входное сопротивление Z_BX=Z_H, т.е. такой отрезок при любом Z_B на расчетной частоте трансформирует сопротивление нагрузки само в себя.

12.1.4. Круговая диаграмма полных сопротивлений

Основные параметры, характеризующие процессы передачи энергии по линии с волновым сопротивлением Z_B, нагруженной на произвольное сопротивление Z_H, можно определить по формулам  (12.14) и (12.25). Однако работа с комплексными числами, наличие гиперболических функций от комплексного аргумента в формуле (12.25) усложняют расчеты. Если требуемая точность вычислений не превышает двух значащих цифр, расчеты существенно упрощаются при использовании круговой диаграммы полных сопротивлений. Диаграмма основана на графическом представлении коэффициента отражения Г(z) и нормированного полного эквивалентного сопротивления z_n(z) = Z_n(z)/Z_B в произвольном сечении линии передачи. Эти параметры связаны вытекающим из (12.22) соотношением

Равенство (12.31) в прямоугольных координатах и, v определяет семейство ^окружностей с центрами в точках и=r/(1 +r), v= 0 и радиусами, равными 1/(1 +r). Эти окружности показаны на рис.12.9. Каждой окружности соответствует определенное значение активной части полного нормированного сопротивления (r= = const). Все окружности проходят через точку с координатами и = 1 и v= 0, а их центры лежат на оси переменной и.

Отметим, что в переводной литературе обычно ось U располагают горизонтально, а ось V вертикально, что соответствует повороту диаграммы полных сопротивлений, изображенной в данной главе, на 90° по часовой стрелке.

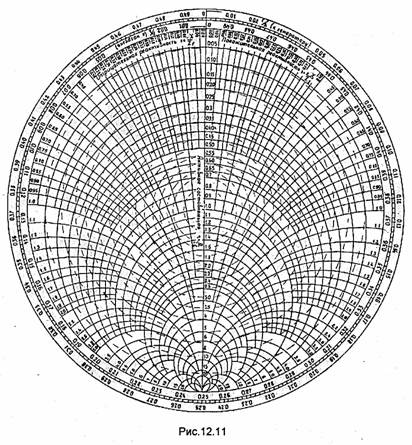
Равенство (12.32) в декартовых координатах и, v также определяет семейство окружностей с центрами в точках u = 1, v=1/x и с радиусами, равными 1/х (рис.12.10). Все окружности проходят через точку с координатами и =1, v=0, а их центры лежат на прямой линии, проходящей через эту точку параллельно оси переменной v. Каждой окружности (рис.12.10) соответствует определенное значение реактивной части полного нормированного сопротивления (х = const). Окружности, лежащие в полуплоскости v>0, соответствуют положительным (индуктивным) х, а в полуплоскости v<0-отрицательным (емкостным) х.

Диаграмма полных нормированных сопротивлений (рис.12.11) представляет собой круг единичного радиуса, центр которого расположен в начале координат и, v. В этом круге совмещены оба семейства окружностей (см. рис.12.9 и 12.10). Значения активного нормированного сопротивления r указаны на вертикальной оси, проходящей через центр диаграммы, значения реактивного нормированного сопротивления х (индуктивного или емкостного) указаны по периметру внешней окружности диаграммы. Отметим, что нанесенная координатная сетка в виде семейств окружностей позволяет изобразить на диаграмме все возможные значения полного нормированного сопротивления. При этом полное нормированное сопротивление на диаграмме отображается точкой пересечения двух окружностей. Одна из них принадлежит семейству, изображенному на рис.12.9 и соответствует активной части сопротивления, а другая - семейству, показанному на рис.12.10, и соответствует его реактивной части. Поскольку коэффициент отражения в любом сечении линии связан с полным нормированным сопротивлением в этом сечении равенством (12.30), то каждая точка диаграммы соответствует также определенному коэффициенту отражения. Для отсчета модуля (величины) и аргумента (фазового угла) коэффициента отражения на диаграмме используется полярная система координат с началом в центре диаграммы. Для отсчёта модуля коэффициента отражения используется радиальная шкала (рис. 12.12), на которую наносятся значения от 0 до 1. Поэтому расстояние от точки диаграммы до центра, отсчитанное по радиальной шкале, соответствует модулю коэффициента отражения, отображаемого данной точкой. Поскольку модуль | Г(2)| и КБВ связаны равенством (12.13), то на радиальную шкалу

наносят также значения КБВ от 1 в центре диаграммы до 0 на ее внешней окружности (см. дополнительные вертикальные оси на рис. 12.12). Иногда на диаграмму наносят семейство концентрических окружностей (рис. 12.12), каждая из которых является геометрическим местом точек, имеющих заданные значения модуля | Г(z) | или КБВ. Для отсчета аргумента коэффициента отражения используется азимутальная шкала (рис.12.12), на которую нанесены значения аргумента в пределах от -180° до +180°. Для определения значения аргумента, соответствующего данной точке диаграммы, следует из центра диаграммы провести через данную точку прямую до пересечения с азимутальной шкалой и по последней отсчитать значение аргумента.

Для точного вычисления коэффициента отражения Г(z) и полного нормированного сопротивления Zn(z) в произвольном сечении линии с координатой z=z₁ (см.рис.12.1,а) по известным

величинам в каком-либо сечении с координатой z=z₂ (например, на конце линии при z₂ = 0) для случая α= 0 можно воспользоваться формулами (12.30), (12.26), заменив в них z на l где l=z₁-z₂-расстояние между рассматриваемыми сечениями. В этом случае при перемещении по линии от сечения к сечению изменяется лишь аргумент коэффициента отражения, а его модуль остается неизменным. Анализ формул показывает, что величины Г(z) и Zn(z) при изменении расстояния l изменяются периодически с периодом Λ/2. Поэтому перемещение по линии передачи от одного сечения к другому отображается на диаграмме движением вокруг ее центра по окружности постоянного КБВ от одной точки к другой в ту или иную сторону. Для отсчета проходимого при этом расстояния используется еще одна азимутальная шкала, на которую нанесены значения нормированного расстояния l/Λ в пределах от 0 до 0,5 и указано направление перемещения - к генератору z₁>z₂) или нагрузке (z₁ <z₂) (рис.12.11). Например, пусть известно полное нормированное сопротивление z_A =r_А+iх_А в некотором сечении линии; этому сечению на диаграмме соответствует точка А (рис.12.13). Из центра диаграммы через точку А проводим пунктирную окружность и по радиальной шкале находим КБВ, в линии. Прямая из центра диаграммы через точку А пересечет азимутальную шкалу в точке В, что позволяет отсчитать (l/Λ)_А для заданного сечения линии. Чтобы определить полное нормированное сопротивление в сечении линии, отстоящем от заданного на расстояние Δl/Λ в сторону генератора, вычисляем для нового сечения нормированное расстояние  и, откладывая его на азимутальной шкале, получаем точку С. Проводим прямую, соединяющую С с центром диаграммы. При ее пересечении с пунктирной окружностью образуется точка D, соответствующая новому сечению линии. На диаграмме для точки D отсчитываем z_D =r_D+ix_D.

Как видно из диаграммы, перемещению вдоль линии передачи от заданного сечения (точка А на рис.12.13) на расстояние Δl/Λ=0,5 соответствует перемещение по диаграмме от точки А по пунктирной окружности на 360°, в результате чего мы снова попадаем в точку А, совершая один оборот вокруг центра диаграммы. Значит, точка А на диаграмме соответствует не одному, а многим сечениям

линии передачи, отстоящим друг от друга на расстояние, равное целому числу полуволн в линии. Причем в пределах длины отрезка, равной половине длины волны в линии, есть два сечения, в которых полное нормированное сопротивление чисто активно. Этим сечениям на диаграмме соответствуют точки М и N (рис. 12.13). В сечении линии, которому соответствует точка М, аргумент коэффициента отражения Г(z) равен ±180°, поэтому в этом сечении напряжения падающей и отраженной волн находятся в противофазе, вследствие чего в этом сечении формируется минимум полного напряжения (см. рис. 12.3). При этом полное нормированное сопротивление чисто активно: z_M=r_M, где r_м=КБВ₁, а х_м=0. В свою очередь в сечении, которому соответствует точка N, аргумент коэффициента отражения Г(z) равен 0°, поэтому в этом сечении напряжения падающей и отраженной волн находятся в фазе, вследствие чего в нем формируется максимум полного напряжения (см. рис.12.3). Полное нормированное сопротивление чисто активно и равноz_N=r_N, где r_N= KCB₁ =1/КБВ_и a x_nN= 0.

С помощью диаграммы полных сопротивлений можно определить не только полное нормированное сопротивление в произвольном сечении линии, но и полную нормированную проводимость. Как следует из (12.29), нормированное входное сопротивление четвертьволнового отрезка численно равно нормированной проводимости нагрузки, подключенной к его концу. В этом случае полная нормированная проводимость у__А =1/z_A =g_А+ib_А в некотором сечении (точка А на рис.12.13) равна полному нормированному сопротивлению z_F=r_F+ix_F в сечении (точка F на рис.12.13), отстоящем от исходного на расстояние Δl/Λ=0,25, т.е.  Это означает, что диаграмма полных нормированных сопротивлений может использоваться и как диаграмма полных нормированных проводимостей.

С помощью диаграммы полных нормированных сопротивлений можно проводить и более сложные расчеты, например определять Г(z) и z_n(z) в произвольном сечении линии с учетом потерь в линии передачи или использовать диаграмму при отрицательных значениях активной части комплексного сопротивления, например, если линия нагружена на активный полупроводниковый элемент (туннельный диод, диод Ганна, полевой транзистор и т.д.) при проектировании усилителей и генераторов. Более подробно о применении круговой диаграммы см. [30].

12.2. ПРОБЛЕМА СОГЛАСОВАНИЯ И МЕТОДЫ ЕЕ РЕШЕНИЯ

12.2.1. Методы согласования линии передачи с нагрузкой

Линия называется идеально согласованной с нагрузкой, если в ней отсутствуют отраженные волны. Однако при передаче по цепи СВЧ сигналов, занимающих определенную полосу частот, обеспечить идеальное согласование линии с нагрузкой во всей требуемой полосе частот практически невозможно. Поэтому при проектировании задают допустимый уровень рассогласования в требуемой полосе частот Δf=f₂-f_1, Этот уровень определяют величиной Г_доп или КБВ_Д0П так, чтобы при f₁≤f≤f₂ выполнялось соотношение | Г(z) | ≤ Г_доп или КБВ≥КБВ_ДОП. Линии, в которых выполняются эти неравенства, называются согласованными с нагрузкой. Интервал частот Δf называют полосой согласования. Иногда говорят об относительной полосе согласования Δf_omн=Δf/f₀, где  f_o = (f₁+f₂)/2.  Эту величину  можно  вычислять в  процентах:

Параметры Г_доп и КБВ_Д0П зависят от назначения и условий работы линии. Например, в линии передачи, соединяющей радиовещательный длинноволновый передатчик с передающей антенной, стараются обеспечить симметричную относительно несущей частоты амплитудно-частотную характеристику (АЧХ) коэффициента отражения в полосе Δf_OTH% = 10% при КБВ_ДОП«0,8...0,9. Нарушение этих требований приводит к недопустимым нелинейным искажениям передаваемого сигнала. В спутниковых системах связи, работающих в сантиметровом диапазоне волн, высокая степень согласования (КБВ_ДОП≈0,95) необходима для обеспечения электромагнитной совместимости одновременно работающих стволов (каналов).

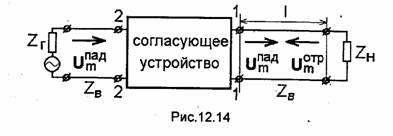
Рассмотрим схему согласования произвольной нагрузки Z_H с линией (рис. 12.14). Согласующее устройство должно устранить отраженную от нагрузки волну. Эту задачу можно решить двумя способами: либо поглотить отраженную волну в согласующем устройстве (при этом падающая волна должна проходить через устройство без заметного затухания), либо погасить (компенсировать) волну, отраженную от нагрузки, волной,

отраженной от согласующего устройства. Во втором случае нужно, чтобы амплитуды волн напряжений, отраженных от нагрузки и от согласующего устройства, были равны, а их фазы отличались на п. Первый метод согласования основан на применении либо мостовых схем, либо невзаимных ферритовых устройств: вентилей или циркуляторов (см. гл.14).

Отметим, что поглощение вентилем отраженной волны не зависит от характера нагрузки, вызвавшей эту волну. Поэтому создание вентилей и циркуляторов, работающих в широкой полосе частот, решает задачу широкополосного согласования произвольных нагрузок. Недостатком согласования с помощью вентилей и циркуляторов является более низкий КПД по сравнению с согласующими схемами, использующими второй метод

согласования, что связано с тем, что мощность, переносимая отраженной волной, полностью рассеивается в вентиле. Согласующие устройства, основанные на методе компенсации, состоят из реактивных элементов и при соответствующем выполнении практически не вносят потерь. При этом отраженная от нагрузки волна не поглощается, а отражается согласующим устройством обратно к нагрузке, где переносимая ею мощность частично поступает в нагрузку, а частично опять отражается в сторону согласующего устройства. В результате подобных многократных отражений вся мощность, переносимая падающей волной по линии, поступает в нагрузку.

Различают согласующие схемы, обеспечивающие узкополосное и широкополосное согласование нагрузки с линией передачи.

12.2.2. Узкополосное согласование с помощью реактивных элементов

Параметры схемы, обеспечивающей узкополосное согласование, определяют из условия обеспечения идеального согласования (Г_о=0, КБВ = 1) на заданной частоте. В данном случае полоса согласования не контролируется. Она определяется или из анализа синтезированной схемы или экспериментально. При этом относительная полоса согласования может находиться в очень широких пределах (от сотых долей процента до нескольких десятков процентов) и зависит от КБВ_Д0П и частотных свойств нагрузки. Как следует из (12.24), при подключении к линии с волновым сопротивлением Z_B нагрузки Z_H=Z_B, z_H = 1 величина Г₀ = 0, т.е. в линии отсутствует отраженная волна, при этом согласно (12.22) во всех сечениях линии полное нормированное сопротивление z_n (z) = 1  и полная нормированная проводимость y_П(z)=1

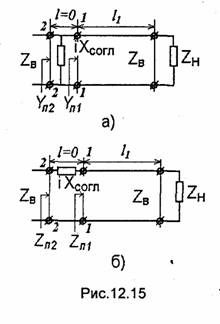
Одним из простейших устройств, обеспечиваюших узкополосное согласование нагрузки Z_H = R_H + iX_H с линией, имеющей волновое сопротивление Z_B, является неоднородность, помещенная в линию на некотором расстоянии l₁от нагрузки. Пренебрегая вносимыми потерями, неоднородность можно рассматривать как реактивное сопротивление iX_согл или реактивную проводимость На рис. 12.15, а показана эквивалентная схема с параллельным, а на рис.12.15,б-с последовательным включением в линию согласующей неоднородности. Введем нормированные значения для всех сопротивлений и прово- димостей, выбрав

Предполагаем, что расстояние между сечениями 1-1 и 2-2 много меньше длины волны в линии и можно считать 1=0. Рассмотрим согласующую схему, изображенную на рис.12.15,а. Поскольку согласующий элемент включается в линию параллельно, то удобнее оперировать с полной нормированной проводимостью в сечении линии. Пусть полная нормированная проводимость в сечении 1-1 равна тогда в сечении 2-2 полная нормированная проводимость будет равна

Волна, распространяющаяся по линии, не будет испытывать отражение в сечении 2-2 (Г₀=0), если в этом сечении Уп2=1; для этого необходимо, чтобы выполнялось равенство откуда получаем g₁=1 и b_согл=-b₁. На этом основании величина l₁ вычисляется с помощью (12.26) из условия, чтобы активная часть полной нормированной проводимости в сечении 1-1 была равна 1, а величина b_согл была равна взятой с обратным знаком реактивной части полной нормированной проводимости в сечении 1-1.

Рассмотрим расчет величин l₁ и b_согл (см. рис.12.15,а) с помощью диаграммы. Пусть точка А (рис. 12.16) соответствует сечению линии, в котором подключена нагрузка, а также сечениям линии, отстоящим от него на расстояние, равное целому числу полуволн в линии. Во всех этих сечениях полное нормированное сопротивление z_A = z_H=r_H+ix_H. Пунктирная окружность, проходящая через точку А, соответствует КБВ₁ (см. рис.12.13). Перейдем к диаграмме полных нормированных проводимостей. На этой диаграмме сечению, в котором подключена нагрузка, соответствует точка М, образующаяся перемещением из точки А по пунктирной окружности на расстояние Δl/Λ= 0,25. Отсчитаем полную нормированную проводимость в точке М, равную нормированной проводимости нагрузки 

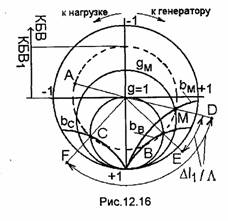
Проводим из центра прямую через точку М до пересечения с азимутальной шкалой (точка D). Перемещаясь по той же пунктирной окружности из точки М в сторону генератора, находим точки пересечения В и С этой окружности с окружностью, проходящей через центр диаграммы (ей соответствует активная нормированная проводимость g=1). Проводим из центра прямые через точки В и С до пересечения с азимутальный шкалой (точки Е и F). По азимутальной шкале определяем расстояния DE и DF, соответствующие двум значениям l₁/Λ .По найденным значениям l₁/Λ, предварительно вычислив Λ для заданной частоты, можно рассчитать расстояние U от нагрузки (или от сечения линии, в котором полное сопротивление равно сопротивлению нагрузки) до сечений линии, соответствующих точкам B и С, в которых следует параллельно подключить согласующий элемент. По диаграмме определяем величину полной нормированной проводимости, соответствующую точкам В и С: . причем поскольку точки Б и С расположены симметрично относительно горизонтальной прямой, проходящей через центр диаграммы, то b_в=-b_с- Реактивность согласующего элемента, подключаемого к линии, должна компенсировать реактивную часть полной проводимости в сечении подключения, т.е. для сечения, которому соответствует точка В, b_com=-b_B или

X _согл =Z_B/b_B< а для сечения, которому соответствует точка С, b_согл =-b_с или X_согл =Z_B/bc. Как следует из сказанного, в пределах полуволны от нагрузки (или от любого сечения, отстоящего от нагрузки на целое число полуволн в линии) вдоль линии имеются два сечения (точки В и С на диаграмме), в которых можно поместить согласующую неоднородность, причем требуемая для согласования эквивалентная реактивность неоднородности в этих сечениях имеет разный знак, т.е. если в одном сечении необходимо подключить индуктивный элемент, то в другом обязательно емкостной и наоборот.

Обычно стараются включить согласующую неоднородность как можно ближе к нагрузке, т.е. выбрать минимальное значение l₁ Этим преследуют две цели: во-первых, повышают КПД линии, поскольку при наличии тепловых потерь в линии чем меньше l₁, тем меньшее затухание испытывает отраженная от нагрузки волна; во-вторых, уменьшение l₁, приводит к увеличению полосы согласования при заданном КБВд_ОП. Последнее обстоятельство связано с тем, что отраженные волны от нагрузки и от неоднородности полностью компенсируют друг друга лишь на расчетной частоте, где они имеют сдвиг по фазе, равный π; при отклонении частоты от расчетной этот сдвиг будет отличаться от π, и отличие тем больше, чем больше величина l₁.

В согласующей схеме (см. рис. 12.15, б), где согласующий элемент, имеющий нормированное сопротивление z_corn = i х_СОГл, подключается последовательно к линии, длина отрезка l₁ вычисляется с помощью (12.26) или с помощью диаграммы из условия, чтобы активная часть полного нормированного сопротивления в сечении 1-1 была равна 1, в этом случае z₁ + ix₁. Величину Хсо_ГЛ выбирают из условия х_согп=-х₁. При этом в сечении 2-2 полное нормированное сопротивление равно 1, что и обеспечивает отсутствие отраженной волны на участке от сечения 2-2 до генератора.

В рассматриваемых схемах при использовании линий с ТЕМ-волнами на сравнительно низких частотах в качестве согласующих элементов используют элементы с сосредоточенными параметрами (конденсаторы или индуктивности). На более высоких частотах, где затруднено использование подобных элементов, применяют элементы с распределенными параметрами, например, реактивные шлейфы, позволяющие, как видно из (12.28), обеспечить любое значение индуктивного или емкостного входного сопротивления на расчетной частоте. На рис. 12.17 показаны эквивалентные согласующие схемы, использующие параллельное подключение шлейфов с режимами холостого хода и короткого замыкания на конце. Величины l₁,и Х_согл рассчитываются по рассмотренной выше методике для схемы (см. рис.12.15,а). Затем, выбрав волновое сопротивление шлейфа Z_Bшл, определяем или из (12.28) или с помощью диаграммы длину шлейфа l_шл, при которой величина входного сопротивления шлейфа равна Хсогл.

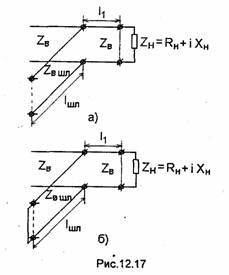
В волноводных линиях передачи в качестве согласующих элементов схем (см. рис.12.15) обычно используют малогабаритные неоднородности-реактивные штыри или реактивные диафрагмы (см. 12.5).

12.2.3. Согласование с помощью четвертьволнового трансформатора

Для согласования линии передачи с волновым сопротивлением Z_B с нагрузкой Z_H на ее конце между ними включается отрезок линии передачи длиной l_тр=Λ/4 с волновым сопротивлением Z_Tp (рис. 12.18, а), который называют четвертьволновым трансформатором. Пренебрегая тепловыми потерями в линии, входное сопротивление четвертьволнового трансформатора, нагруженного на Z_H, можно вычислить по (12.29). Если подобрать Z_Tp так, чтобы его входное сопротивление Z_BX=Z_B, а это

выполняется  при  Z_Tp = √Z_BZ_H,   то  в  линии   передачи  не  будет

отраженной волны. Поскольку Z_B и Z_Tp являются действительными числами, то четвертьволновый трансформатор может согласовывать лишь чисто активные сопротивления нагрузки Z_H.

При распространении падающей волны в линии (рис.12.18, а) в первом приближении будут возникать две отраженные волны: одна в месте соединения линии с трансформатором (сечение 1-1), вторая-в месте соединения трансформатора с нагрузкой (сечение 2-2), причем относительный сдвиг по фазе между отраженными волнами в линии равен тс, что достигается выбором длины l_тр=Λ/4. Выбирая Z_Tp = √Z_BZ_H, обеспечиваем равенство амплитуд отраженных волн, что приводит к их компенсации в линии, т.е. к согласованию линии с нагрузкой.

Четвертьволновый трансформатор можно использовать для согласования комплексной нагрузки Z_H=R_H +iX_H с линией пере-дачи. В этом случае трансформатор включают на некотором расстоянии l₁, от места подключения нагрузки к линии (рис. 12.18, б). Длину l₁, вычисляют или по (12.26), или с помощью диаграммы таким образом, чтобы полное сопротивление в сечении 2-2 было чисто активным: Z₂ = R2, а Х₂ = 0. Поскольку нагрузкой для трансформатора в этом случае является R₂, то его волновое сопротивление должно быть равно Z_Tp = √Z_BR₂.

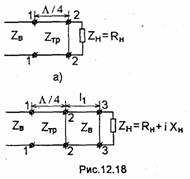
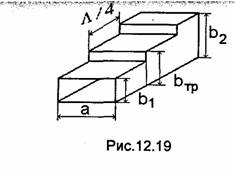
К недостаткам согласования с помощью четвертьволнового трансформатора можно отнести трудность подстройки трансформатора после изготовления, а также необходимость использования отрезка линии передачи с волновым сопротивлением, отличным от волнового сопротивления согласуемой линии. Последний недостаток несуществен при проектировании полосковых трактов, однако может вызвать определенные трудности при проектировании коаксиальных трактов, в которых желательно использовать выпускаемые промышленностью коаксиальные кабели.

Отметим, что при согласовании волноводов с помощью четвертьволнового трансформатора используются волновые сопротивления для соответствующих волн в волноводе. Например, для согласования двух прямоугольных волноводов, работающих в одноволновом режиме на волне Н₁₀ и имеющих одинаковые широкие стенки (а), но разные узкие (b₁ и b₂), используют четвертьволновый отрезок прямоугольного волновода с поперечными раз-

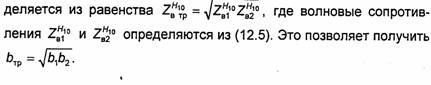
12.2.4. Широкополосное согласование нагрузки с линией

В отличие от ранее рассмотренных схем для узкополосного согласования, при синтезе которых полоса согласования не контролируется, при проектировании схем, обеспечивающих широкополосное согласование, задаются шириной полосы согласования Δf и величиной Гдоп или КБВ_ДОП. Синтез таких схем проводят исходя из условия, чтобы на всех частотах полосы Δf модуль коэффициента отражения в линии не превышал Г_доп. Если согласуемые сопротивления активны и не зависят от частоты (например, сочленение двух линий передачи с разными размерами поперечного сечения), между ними включают нерегулярный отрезок линии передачи, называемый переходом. На рис. 12.20 показана конструкция соединения двух МПЛ с разными волновыми сопротивлениями с помощью перехода. Различают плавные переходы, в которых размеры поперечного сечения изменяются непрерывно вдоль длины отрезка, и ступенчатые, образованные каскадным соединением регулярных отрезков линии с разными волновыми сопротивлениями.

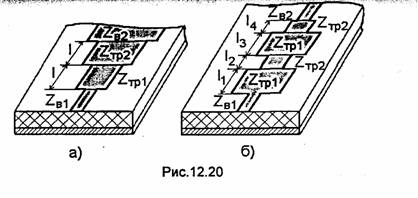
Ступенчатые переходы. Переходы бывают монотонные, когда поперечные размеры отдельных отрезков, образующих переход, или только увеличиваются или только уменьшаются вдоль перехода (рис. 12.20, а), и немонотонные (рис. 12.20, б), в которых отсутствует подобное ограничение. В первом случае электрические длины всех отрезков перехода выбирают одинаковыми и равными l/Λ=0,25, а их волновые сопротивления должны возрастать (убывать) вдоль перехода. Во втором случае обычно для построения перехода используют отрезки регулярной линии с фиксированными волновыми сопротивлениями Z_Tp1 и Z_Tp2 и разными длинами l₁, l₂, ... l_n, На практике немонотонные ступенчатые переходы находят ограниченное применение и в дальнейшем рассматриваться не будут. Вопросы проектирования таких переходов изложены в [37].

Рассмотрим монотонные ступенчатые переходы. Простейшим переходом является четвертьволновый трансформатор. Рассмотрим более подробно его принцип действия (см. рис.12.18,а), полагая, что трансформатор согласует линии передачи с волновыми сопротивлениями Z_B1 и Z_B2. Так как волновые сопротивления в схеме меняются дважды: сначала в сечении 1-1, а затем в сечении 2-2, то отраженная волна в линии является суперпозицией волн, отраженных от сечений 1-1 и 2-2. Коэффициент отражения падающей волны в сечении 1-1 согласно (12.24) имеет вид Г₁ = (Z_Tp-_ZB1 )/(_ZTp+Z_B1). Пройдя путь l_тр до сечения 2-2, волна получает сдвиг по фазе, равный β_тр lтр, где β_тр-коэффициент фазы волны в линии, образующей трансформатор. В сечении 2-2 коэффициент отражения падающей волны равен Г₂=(Z_B2-Z_Tp)/(Z _B2+Z_Tp). Пройдя путь l_Тр и получив фазовый сдвиг β_тр l_Тр> вторая отраженная волна возвращается на вход трансформатора (сечение 1-1). Если пренебречь повторным отражением части энергии этой волны при переходе из трансформатора в линию с Z_B1, то суммарный коэффициент отражения от входа трансформатора Согласование достигается, когда Г_вх = 0, т.е.

когда волны, отраженные от сечений 1-1 и 2-2, противофазны,  их амплитуды равны. Противофазность отраженных волн обеспечивают, выбирая l_ТР=Λ/4 (при этом 2β_тр l_тр = π). Волновое сопротивление Z_Tp находится из условия равенства амплитуд отраженных волн , что позволяет записать (Z_TP-Z_B1)/(Z_TP +Z_B1) = = (Z_B2-Z_tP )/(Z_b2+Z_Tp), откуда Это совпадает с результатом,  полученным в  12.2.3.  Полная  компенсация отраженных волн имеет место лишь на расчетной частоте, так как сдвиг фаз между ними зависит от частоты. При этом чем меньше отличаются величины Z_B1 и Z_B2, тем меньше| Г₁| и |Г₂| (меньше амплитуды векторов поля отраженных волн), а значит, и меньше  | Г_вх | при одном и том же отклонении частоты от расчетной. Если величины Z_B1 и Z_B2 отличаются друг от друга достаточно сильно и с помощью одного четвертьволнового трансформатора невозможно получить требуемое согласование в заданной полосе -частот, применяют несколько каскадно включенных четвертьволновых трансформаторов (рис. 12.20, а). Чем большее число трансформаторов включено, тем шире полоса согласования при фиксированных значениях Z_B1 и Z_B2. Чем больше отличаются друг от друга Z_B1 и Z_B2, тем большее число четвертьволновых трансформаторов необходимо включить в переход, чтобы не превышался заданный уровень отражений в полосе согласования.

Наибольшее распространение на практике получили ступенчатые переходы с чебышевской и максимально плоской амплитудно-частотными характеристиками (АЧХ) коэффициента отражения. В случае чебышевского ступенчатого перехода, содержащего п ступенек, АЧХ описывается формулой [34]

-полином Чебышева первого рода порядка Λ_Н длина волны в линии на нижней частоте полосы согласования.

Такой переход имеет оптимальные соотношения между полосой согласования, допуском на рассогласование и длиной перехода, т.е. позволяет получить минимальную длину перехода по сравнению с длиной перехода с иной АЧХ.

Максимально плоская АЧХ ступенчатого перехода, содержащего п ступенек, определяется формулой [34]:

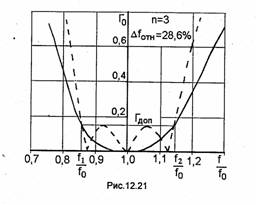
Такой переход не является оптимальным по длине, но в отличие от чебышевского перехода он не имеет осцилляции коэффициента отражения в полосе согласования и его фазочастотная характеристика (ФЧХ) коэффициента передачи более близка к линейной.

На рис.12.21 показаны АЧХ чебышевского (пунктирная линия) и максимально плоского (сплошная линия) ступенчатых переходов, имеющих три ступеньки.

Если известны Г_доп и относительная полоса согласования Δf oтн, то количество ступенек в переходе можно рассчитать по следующим формулам [33]:

для перехода с чебышевской АЧХ

На практике вычисленная по (12.36) или (12.37) величина округляется до ближайшего большего целого числа. Длина каждой ступеньки равна четверти длины волны в линии на центральной частоте полосы согласования. Если переход конструируется из отрезков линии с дисперсией, в которой фазовая скорость зависит от частоты, то приближенно длину ступеньки можно определить по формуле [33] -длины волн в линии на крайних частотах f, и f₂ полосы согласования соответственно (рис.12.21).

Строгие и приближенные методы расчета волновых сопротивлений ступенек для переходов с рассматриваемыми видами АЧХ описаны в [33]-[35]. Точные формулы для вычисления волновых сопротивлений отдельных ступенек в переходе получены лишь для переходов с п<4. Например, в случае двухступенчатого пере-

Для переходов с л>4 точное вычисление волновых сопротивлений ступенек достаточно сложно и, как правило, требует применения ЭВМ. На практике обычно в этом случае используют приближенные формулы из [33].

Следует отметить, что в местах стыка отрезков линий с разными волновыми сопротивлениями образуется неоднородность, которая может быть представлена в эквивалентной схеме перехода в виде параллельно подключаемой емкости [33] (рис.12.22). Как, будет показано ниже (см.12.5), короткий отрезок линии, последовательно подключаемый в линию передачи (при условии, что волновое сопротивление отрезка меньше волнового сопротивления линии), может быть эквивалентно представлен в виде параллельно подключаемой емкости. Поэтому из-за влияния неоднородностей стыков полоса согласования реального перехода оказывается смещенной относительно заданной при расчете полосы в сторону более низких частот из-за увеличения электрической длины каждой ступени. Для устранения этого явления ранее определенные длины ступенек уменьшают, пытаясь скомпенсировать влияние емкостей в эквивалентной схеме. Уменьшение длины каждой ступени зависит от величины эквивалентной емкости. Приближенные формулы для вычисления длины ступенек можно найти в [33]. Уточненное значение длины ступенек в переходе определяется или экспериментально или с помощью анализа схемы ступенчатого перехода с учетом неоднородностей, возникающих в местах стыка отрезков линии с разными волновыми сопротивлениями.

Плавные переходы. На рис. 12.23 показано согласование двух микрополосковых линий с разными волновыми сопротивлениями Z_B1 и Z_b2 с помощью плавного перехода длиной l, являющегося отрезком нерегулярной линии, поперечные размеры которой изменяются непрерывно вдоль длины. Обычно увеличение поперечных размеров линии приводит к уменьшению волнового сопротивления и наоборот. Меняя соответствующим образом волновое сопротивление вдоль согласующего отрезка, можно обеспечить достаточно плавное его изменение, что устраняет резкие

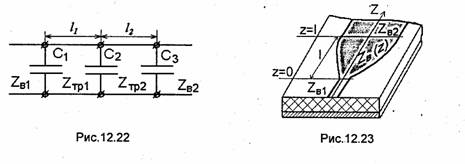
скачки волнового сопротивления при стыке соединяемых линий, уменьшает величины неоднородностей, а значит, и отражения от них. Монотонные плавные переходы (см. рис. 12.23) в отличие от ступенчатых обеспечивают требуемое согласование (|г_вх|≤Г_Д0П) . на частотах f≥f₁ где f₁,-граничная частота полосы согласования. На практике стремятся при заданной величине Г_доп обеспечить по возможности минимальную длину перехода. Эта задача решается  путем выбора функции изменения волнового сопротивления вдоль перехода. Одним из наиболее простых и часто используемых на практике является экспоненциальный плавный переход, для которого волновое сопротивление Z_B вдоль длины перехода изменяется по закону [30]

Данная формула получена с помощью соотношения (10.49).

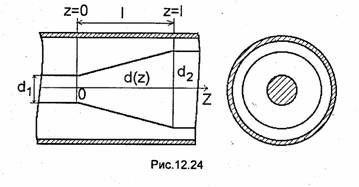
В [31] для вычисления модуля коэффициента отражения от входа экспоненциального перехода длиной l приведена следующая приближенная формула:

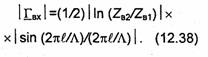
На практике применяют плавные переходы- и с иными законами изменения волнового сопротивления вдоль длины перехода: гиперболические, чебышевские и др. Например, чебышевский плавный переход получается как предельный случай чебышевского ступенчатого перехода, в котором неограниченно увеличивается число ступенек и одновременно стремится к бесконечности верхняя частота полосы согласования f₂, при этом длина каждой ступеньки стремится к нулю. Как и в случае ступенчатых переходов, чебышевский плавный переход является самым коротким из всех плавных переходов при заданных величинах Гдоп и Z_B2/Z_B1. Более подробная информация о плавных переходах имеется в [31, 33, 34].

Если сопоставить частотные характеристики плавных и ступенчатых переходов (см. рис.12.25 и 12.21), то легко заметить, что у плавных переходов коэффициент отражения на входе уменьшается по мере увеличения частоты. Следовательно, плавный переход обеспечивает хорошее согласование в значительно более широкой полосе частот, чем требуется. Поэтому плавный переход всегда длиннее, чем ступенчатый, при заданных величинах Z_доп, Z_B2/Z_B, и Δf.

12.3. МАТРИЧНОЕ ОПИСАНИЕ ЦЕПЕЙ СВЧ

При построении математических моделей сложных цепей СВЧ обычно используют характеристические матрицы. Достаточно общую конструкцию произвольной цепи СВЧ можно представить в виде сочленения, образованного N линиями передачи, которые могут быть как одного, так и разных типов. На рис. 12.26 показано такое устройство, содержащее четыре подводящих линии (N=4). Линии передачи используются либо для подвода энергии от генератора к устройству, либо для подключения к нему внешних оконечных устройств (полезных нагрузок, поглощающих нагрузок, короткозамыкающих поршней и т.д.). Для построения математической модели рассматриваемого сочленения в каждой подводящей линии выбираем поперечное сечение, расположенное на некотором расстоянии от места сочленения. Проводим через эти сечения плоскости Т₁,Т₂.....T_N (рис.12.26), которые в дальнейшем будем называть плоскостями отсчета фаз элементов характеристических матриц. Предположим, что расстояние от плоскостей отсчета до сочленения выбрано так, что в этих плоскостях можно пренебречь амплитудами нераспространяющихся волн, которые могут возникать в месте сочленения линий. Рассмотрим устройство, образовавшееся между плоскостями отсчета. Оно имеет N плеч, образованных отрезками линий передачи. Причем каждый свободный конец этих отрезков линии служит или входом, через который энергия вводится в устройство, или выходом, через который энергия выводится из него. Поскольку каждый отрезок линии может быть представлен отрезком эквивалентной линии, имеющей два входных зажима (полюса) на входе, то рассматриваемое устройство возможно представить эквивалентным многополюсником (рис.12.27). Причем если в каждом из N плеч устройства распространяется лишь один невырожденный тип волны, то эквивалентный многополюсник имеет 2N полюсов, обоз-

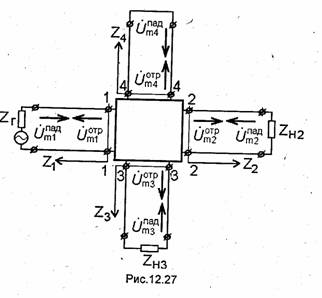
начаемых 1-1,2-2, ...,N-N. Рассмотрим случай, когда в одном или  в  нескольких  плечах  устройства  будут  распространяться несколько типов волн, т.е. линия, образующая такое плечо, работает в многоволновом режиме, или линия работает в одноволновом  режиме,  но по ней  распространяются  вырожденные волны (например, распространяющаяся по круглому волноводу волна H₁₁ с круговой поляризацией вектора Е в центре волновода может быть представлена суммой двух вырожденных распространяющихся волн H₁₁ с линейными взаимно перпендикулярными поляризациями векторов Е). При этом каждое плечо, в котором может распространяться несколько типов волн,  следует представить в эквивалентном многополюснике несколькими входами или выходами по числу распространяющихся волн в плече; при этом многополюсник будет иметь 2n полюсов, где п >N.

Заменив линии передачи эквивалентными линиями, а генераторы, оконечные нагрузки, короткозамыкающие поршни их эквивалентными представлениями, получаем для рассматриваемого устройства (рис. 12.26) эквивалентную схему (рис. 12.27), при этом в каждой эквивалентной линии могут распространяться соответствующие падающие и отраженные волны напряжений (токов). Поскольку мощность, переносимая волной напряжения (тока) по эквивалентной линии, зависит не только от амплитуды напряжения (тока) волны, но и от волнового сопротивления линии (12.2), обычно при рассмотрении свойств многополюсника, ко входам которого могут подключаться линии с разными значениями волнового сопротивления, вводят нормированные напряжение u(z) и ток i(z), распространяющиеся в каждой эквивалентной линии и связанные с напряжением U_m(z) и током i_m(z) с формулами

где Z_B - волновое сопротивление эквивалентной линии.

Величины u(z) и i(z) имеют одинаковую размерность √Вт, поэтому нормированное волновое сопротивление z_B эквивалентной линии, в которой распространяются нормированные напряжение и ток, будет безразмерной величиной, равной 1:

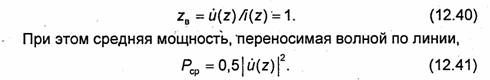
Введем в каждой линии передачи (см. рис. 12.26) соответствующую систему координат так, чтобы продольная ось была направлена от сочленения, а ее начало было расположено в плоскости отсчета фаз рассматриваемой линии. При этом начало

отсчета   продольных  осей  Z₁Z₂.....Z_N в  эквивалентной   схеме (рис.12.27) совмещено с соответствующими полюсами 1-1,2-2, ...,N-N. Будем называть волны, распространяющиеся в плечах в сторону многополюсника, падающими, а волны, распространяющиеся от многополюсника,-отраженными. Пусть генератор создает в линии 1, подключенной к плечу 1 многополюсника, падающую волну напряжения..Эта волна, дойдя до сочленения, будет частично отражаться, вызывая в линии 1 отраженную волну, а частично, пройдя через многополюсник, поступит на выходы остальных плеч, вызывая в подключенных к ним линиях отраженные волны напряжений. Эти волны, в свою очередь, распространяясь по линиям, подключенным к плечам 2, 3,..., N многополюсника, будут в общем случае частично поступать в оконечные нагрузки, а частично отражаться от них, вызывая в линиях падающие волны напряжения. В свою очередь, падающие волны в линиях, подключенных к плечам 2, 3.....N, будут на входах многополюсника частично отражаться от сочленения, а частично проходить через него, вызывая отраженные волны в линиях, подключенных к плечам многополюсника, и т.д. Таким образом, в каждой плоскости отсчета устройства (см. рис.12.26) или на входах каждой пары полюсов в эквивалентной схеме (см. рис.12.27) будут действовать  падающая   и   отраженная   волны,   которые  будем характеризовать нормированными функциями и_j^пад и u_j°^тр, где j=1, 2, ...,N(рис.12.28,а). Каждая из указанных волн представляет

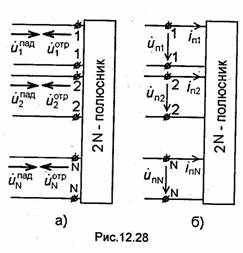
собой суперпозицию волн, созданных как непосредственно генератором, так и оконечными нагрузками линий, подключенных к выходам устройства. Согласно (12.9) и (12.10) в плоскостях отсчета или на полюсах многополюсника можно ввести полные нормированные напряжения   u_п1, u_п2, ..., u_nN и  токи  (рис. 12.28, б).

В общем случае режим работы каждого входа многополюсника можно описать с

помощью двух комплексных величин, например, для j-го входа это могут быть или

  Поэтому можно ввести несколько различных описаний многополюсника, считая в каждой выбранной паре одну из величин независимой, а вторую зависимой. Наибольшее применение в технике СВЧ при описании свойств многополюсников нашла волновая матрица рассеяния || S ||, устанавливающая связь между нормированными напряжениями отраженных и падающих волн во всех плоскостях отсчета устройства или на всех полюсах его эквивалентной схемы.

Если рассматриваемое N-плечное устройство является пассивным и линейным (содержит лишь линейные среды), то в силу линейности уравнений Максвелла нормированное напряжение отраженной волны u_j°^тр в плоскости отсчета j-го плеча (на полюсах j-j многополюсника) можно рассматривать как суперпозицию волн_, образовавшихся под воздействием падающих волн в плоскостях отсчета всех плеч устройства (на всех полюсах многополюсника при n = N):

где  безразмерные комплексные величины, не зависящие от нормированных напряжений падающих и отраженных волн. Систему из N уравнений (12.42), устанавливающую связь между напряжениями падающих и отраженных волн на входах многополюсника, удобно записать в матричном виде:

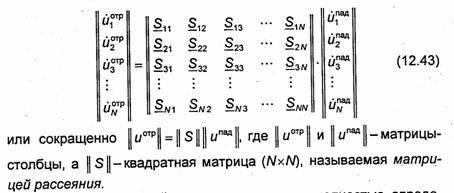
Передаточные свойства многополюсника полностью определены, если известна его матрица ||S ||, записанная для выбранной системы плоскостей отсчета в каждом плече на заданной частоте. Вид матрицы не зависит от подключаемых к многополюснику устройств. Определиим физический смысл элементов S_jq матрицы рассеяния. Для этого рассмотрим частный случай работы многополюсника (рис.12.28, а): пусть к полюсам j-j подключен генератор, а к полюсам всех остальных плеч подключены сог-

S_qj-коэффициент передачи по нормированному напряжению от полюсов j-j к полюсам q-q многополюсника (от плоскости отсчета в плече q к плоскости отсчета в плече q устройства) при заданных выше условиях.

Рассмотренная выше матрица рассеяния называется нормированной, поскольку она устанавливает связь между нормированными напряжениями. Иногда вводят [33] ненормированную матрицу || S||, связывающую ненормированные напряжения отраженных и падающих волн в плоскостях отсчета каждой линии. В дальнейшем будут рассматриваться лишь нормированные матрицы.   Для  таких  матриц  согласно  (12.44)   и   (12.41)     что совпадает с

коэффициентом передачи по мощности из плеча j в плечо q устройства при условии, что мощность (P_j^пад)_Cp подается на вход плеча  j ,а во всех остальных плечах падающие волны отсутствуют. Поэтому для всех элементов матрицы рессеяния выполняется условие  | S_qj| ≤1. Для ненормированной матрицы величина  | S_qj |зависит не только от отношения мощностей (P_q^отp)_cp и(Рj^пад)_ср, но и от волновых сопротивлений линий, подключенных к полюсам j-j и q-q многополюсника.

Кроме  матрицы   ||s|| в  технике  СВЧ   используют  матрицу *   сопротивлений и матрицу проводимостей. Матрица сопротивлений ||z|| устанавливает связь между полными нормированными напряжениями  и токами  на  всех входах многополюсника  (см. рис. 12.28, б):

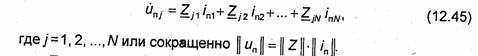
Последнее соотношение напоминает описание цепи с помощью матрицы сопротивлений в классической теории цепей [28]. Это позволяет с заданным многополюсником сопоставить некоторую цепь, называемую эквивалентной схемой, имеющую такую же матрицу сопротивлений. Следует отметить, что переход от многополюсника к эквивалентной схеме неоднозначен, так как имеется множество схем с одинаковыми матрицами сопротивлений. Эквивалентность между многополюсником и цепью, строго говоря, существует только на одной частоте, однако в некотором приближении можно рассматривать и узкую полосу частот вблизи этой частоты. Матрица проводимостей ||Y|| устанавливает связь между полными нормированными токами и напряжениями на всех входах многополюсника (рис. 12.28, б):

где j = 1,2,'...,N, или сокращенно || i_п || = || У || • || и_п ||. Хотя по аналогии с низкочастотными цепями можно определить физический смысл элементов матриц || Z|| и || У||, как сделано в [16], однако в общем случае в диапазоне СВЧ элементы этих матриц имеют формальный смысл, поскольку формальный смысл имеют и нормированные напряжения и токи в произвольной линии передачи. Напротив, элементы матрицы ||S||  имеют выясненный выше физический смысл в любом случае.

Матрицы ||Z|| и || У|| обычно более удобны при анализе последовательного или параллельного соединения многополюсников

[33].  Используя (12.9) и (12.10), легко установить связь между матрицами [34]:

где ||/|| -единичная квадратная матрица порядка N, а (|| Z|| +||/||)^-1-матрица, обратная матрице (|| Z|| + || /|).

Изменение положения плоскостей отсчета в плечах многополюсника. Характеристические матрицы многополюсника определяются для выбранного заранее положения плоскостей отсчета в каждом плече Т₁Т₂, ...,T_N (см. рис.12.26). На практике очень часто при экспериментальном определении элементов матриц многоплечных устройств бывает затруднительно, а иногда и невозможно измерить те или иные величины в поперечных сечениях линий, где расположены плоскости отсчета. Как правило, между измерительной аппаратурой и поперечным сечением, где расположена плоскость отсчета, оказывается включенным дополнительный отрезок линии передачи. Из-за этого измеренные величины относятся к новым плоскостям отсчета, сдвинутым в ту или иную сторону вдоль линии передачи относительно старых плоскостей отсчета. Поэтому возникает необходимость преобразования известной матрицы устройства относительно введенных новых плоскостей отсчета. Наиболее просто такое преобразование выполняется для элементов матрицы || S ||. Пусть в каждом плече j (j = 1,2.....N) на расстоянии ∆z_j, от старой плоскости отсчета Тj) (см. рис. 12.26) введена новая плоскость отсчета Tj, причем при ∆z_j>0 новая плоскость расположена дальше от сочленения, а при ∆z_j<0-ближе к сочленению относительно старой плоскости. Матрицу рассеяния устройства относительно новых плоскостей

Отсюда следует, что при смещении плоскостей отсчета изменяются аргументы элементов матрицы ||S ||из-за изменения

путей, проходимых падающими и отраженными волнами в плече устройства. Кроме того, из-за наличия затухания в линиях передачи изменяются и модули элементов матрицы. При малых ∆Zj можно пренебречь потерями в отрезках линий (α_j≈0) в этом случае смещение плоскостей отсчета в плечах устройства приводит лишь к изменению аргументов элементов матрицы || S ||.

Основные свойства характеристических матриц. 1. Пассивный многополюсник, выполненный на основе изотропных материалов, является взаимным; в этом случае  S_jq = S_qj для любых jи q. Для такого многополюсника матрица || S || будет симметрической, т.е. ||S| |= ||S|^T, где || S||^т-транспонированная матрица |S||. Матрицы ||Z|| и || У ||также будут симметрическими. Многополюсник, содержащий анизотропный материал (например, намагниченный постоянным магнитным полем феррит), является невзаимным, его характеристические матрицы не будут симметрическими (S_jq ≠S_qJ).

2. Матрица рассеяния || S || многополюсника без потерь (с изотропным или анизотропным заполнением) является унитарной, для нее справедливо || S* ||^т • || S || = || /1||, где || S* ||^т - комплексно-сопряженная транспонированная  матрица  || S ||;   это  равенство является следствием закона сохранения энергии. Действительно, на его основе можно записать

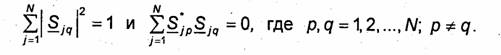
Элементы матриц ||Z|| и || У|| для многополюсника без потерь

будут чисто мнимыми величинами. Более подробно с характе-, ристическими матрицами можно ознакомиться в [32, .33].

12.4. МЕТОД ДЕКОМПОЗИЦИИ И МАТРИЧНОЕ ОПИСАНИЕ СЛОЖНЫХ ЦЕПЕЙ СВЧ

При анализе произвольной цепи СВЧ необходимо определить элементы ее матрицы рассеяния на любой частоте из требуемого диапазона, что позволяет найти электрические характеристики цепи. Элементы матрицы ||S|| находятся или из решения соответствующей электродинамической задачи или измеряются экспериментально. Предпочтение следует отдать первому, так как в этом случае объем и качество получаемой об объекте информации существенно выше, если решение задачи проведено с достаточной точностью. Однако нахождение решений уравнения Максвелла для сложных цепей СВЧ, когда граничные условия задаются на поверхностях сложной конфигурации, даже при использовании ЭВМ встречает серьезные трудности, связанные главным образом с огромным объемом вычислений. Как правило, необходимые решения удается получить для ограниченного числа достаточно простых элементов цепи СВЧ (индуктивные и емкостные диаграммы, реактивные штыри, несложные разветвления и т.д.). Поэтому одним из наиболее широко применяемых на практике методов расчета электрических характеристик сложных СВЧ цепей является декомпозиция (расчленение) сложного устройства на ряд более простых, поддающихся электродинамическому анализу. Эти простые устройства называют базовыми элементами. Матрицы рассеяния базовых элементов определяются без учета взаимодействия между ними. Затем, с помощью специальных алгоритмов рассчитывают элементы матрицы рассеяния для объединения двух и более базовых элементов, т.е. всей сложной цепи. Следует отметить, что структура цепей СВЧ, как правило, благоприятствует , подобному расчленению, так как обычно они состоят из отдельных относительно простых элементов, соединенных друг с другом отрезками линий передачи. При составлении библиотеки базовых элементов используют одну из двух возможностей.

В первом случае каждый элемент цепи заменяют эквивалентной схемой, состоящей, из сосредоточенных элементов L, С, R и отрезков эквивалентной линии. При этом решение электродинамической задачи для базового элемента представляется в виде эквивалентной схемы, в виде приближенных формул и справочных ' данных, определяющих связь величин элементов эквивалентной схемы с геометрическими размерами базового элемента,, длиной волны и параметрами диэлектрического заполнения. В этом случае большое количество базовых элементов цепей СВЧ может быть сведено к небольшому числу элементов эквивалентных схем. Преимуществами такого подхода является универсальность, возможность разумной идеализации эквивалентных схем, а недостатками - потеря точности при использовании упрощенных эквивалентных схем и трудности в количественной оценке погрешностей расчета.

Во втором случае на основе решения электродинамической задачи для каждого базового элемента аналитически или численно находится характеристическая матрица. При этом удается выполнять расчеты с любой требуемой точностью. Однако такой подход менее универсален и требует значительно большего объема вычислений. Отметим, что оба подхода не имеют глубоких принципиальных различий.

Анализ каскадного соединения четырехполюсников. Рассмотрим частный случай цепи СВЧ, достаточно часто встречающийся на практике,-каскадное соединение четырехполюсников, т.е. выход предшествующего элемента цепи соединяется со входом последующего и т.д. (рис. 12.29). Анализ каскадного соединения значительно упрощается, если описывать четырехполюсники не матрицей  || S ||,   а специальной матрицей передачи

|| А ||, которая связывает полные нормированные напряжения и токи на входе u_п1, i_п1 и на выходе u_п1, i_п1 четырехполюсника:

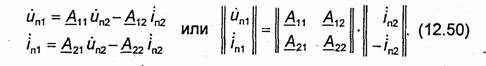
Для определения физического смысла элементов матрицы || A || рассмотрим некоторые частные случаи работы четырехполюсника. Пусть сигнал от генератора подается на вход четырехполюсника (полюса 1^1), а выходные полюса его (2-2) остаются разомкнутыми. При этом i_п2=0 и из (12.50) следует, что А₁₁= u_п1/ i_п1. А₁₁ обычно называют коэффициентом передачи четырехполюсника по полному напряжению при размыкании его выходных полюсов,  т.е. A₂₁-нормированная проводимость четырехполюсника при размыкании его выходных полюсов. Если подать сигнал от генератора на вход четырехполюсника, а его выходные полюсы замкнуть накоротко, то при этом u_п2 = 0 и из (12.50) следует, что  т.е. А₂₂-коэффициент передачи четырехполюсника по полному току при КЗ на его выходе, а  т.е. A₁₂ - нормированное сопротивление четырехполюсника при КЗ на его выходе.

Нетрудно показать с помощью (12.50), что матрица передачи ||А|| четырехполюсника , образованного каскадным соединением двух четырехполюсников, имеющих матрицы передачи ||A₁|| и ||А₂||,

вычисляется по формуле ||А|| = || А₁||∙|| А₂||(рис.12.29). Это свойство матрицы передачи распространяется на любое число каскадно соединенных четырехполюсников.

Из (12.50) и (12.42), используя (12.9), получаются формулы, связывающие элементы матриц || S| | и ||А||, для произвольного четырехполюсника: S_U=(A_U+A₁₂-A_2i-A₂₂)/D,   

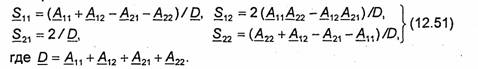
Итак, анализ каскадного соединения четырехполюсников сводится к вычислению на заданной частоте матрицы || А || для каждого элемента цепи, перемножению матриц отдельных элемен-тов, что определяет матрицу || А || всей цепи, нахождению элемен-тов

матрицы S всей цепи по формулам (12.51).

Характеристические матрицы эквивалентных схем некоторых базовых элементов. При декомпозиции цепей СВЧ наиболее часто встречаются базовые элементы, имеющие следующие эквивалентные схемы.

1. Отрезок эквивалентной линии передачи (рис.12.30) длиной l является двухплечным устройством и может быть представлен четырехполюсником. Матрица ||S || для него имеет вид (12.43) при N=2. Пренебрегая тепловыми потерями в отрезке линии и исходя из физического смысла элементов ||S||,  получаем Из (12.51) находим элементы матрицы А через элементы матрицы || S ||. На рис.12.30 выписаны матрицы ||S|| и ||А||. Для получения матриц ||S || и ||А || отрезка эквивалентной линии с учетом потерь следует в выражениях для элементов матриц (рис. 12.30) заменить

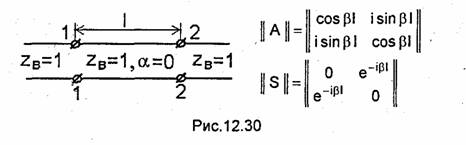
2. Стык двух линий передачи с разными волновыми сопротивлениями -двухплечное устройство (рис.12.31), которое можно представить четырехполюсником. Причем расстояние между плоскостями отсчета в плечах равно 0.

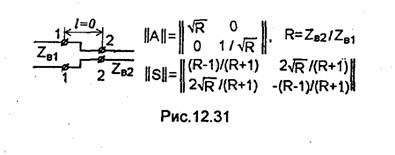
Матрица || S || имеет вид (12.43) при N=2. В плоскости стыка равны полные ненормированные напряжения и токи:U_п1 = U_п2 и i_п1 = -i_П2. Знак минус в последнем равенстве учитывает тот факт, что за положительные направления для тока на каждом входе выбраны направления внутрь четырехполюсника (см. рис. 12.28, б). Переходя в записанных равенствах к нормированным напряжениям и токам, согласно (12.39) получаем что позволяет найти элементы матрицы || А|| а по (12.51) и элементы || S|| (рис.12.31).

3. Четырехполюсник, образованный последовательно включенным сопротивлением Z в линию с волновым сопротивлением Z_B (рис. 12.32). Считаем расстояниеl между полюсами 1-1 и 2-2 равным нулю. В данном случае можно записать следующие выражения, связывающие нормированные напряжения и токи на входе и выходе: Сравнивая это с (12.50), получаем из (12.51) находим элементы матрицы ||S|| (рис.12.32).

4. Четырехполюсник, образованный параллельно включенной проводимостью У в линию передачи с волновым сопротивлением Z_B (рис.12.33). Считаем расстояние l между полюсами 1-1 и 2-2 равным нулю. Используя законы Кирхгофа для рассматриваемой цепи, запишем связь между нормированными напряжениями и токами на полюсах:  гдеэто позволяет определить элементы матрицы || А ||, а из (12.51) найти элементы матрицы || S || (рис.12.33).

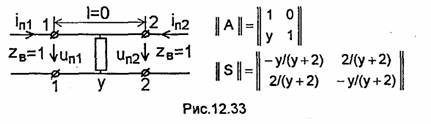
Анализ произвольной цепи СВЧ. В этом случае цепь расчленяется на базовые элементы, для которых заранее определены характеристические матрицы. Матрицы рассеяния некоторых часто встречающихся базовых элементов можно найти в [29,33]. Затем на ЭВМ с помощью специально составленной вычислительной программы рассчитывают матрицу рассеяния всего устройства. Основу алгоритмов для разработки таких программ составляют формулы для расчета элементов матрицы ||S||  соединения двух многополюсников с известными матрицами || S., || и || S₂||. Явные формулы для вычисления || S || через || S, || и || S₂||  приведены в [29,43]. Далее к полученному многополюснику присоединяется третий базовый элемент с матрицей || S₃ J и находится матрица рассеяния для нового соединения, и так далее до тех пор, пока не будут присоединены все базовые элементы рассматриваемой цепи. В результате последовательного применения описанной процедуры может быть построена матрица рассеяния любого сложного соединения произвольного числа базовых элементов. Варианты алгоритмов вычисления матриц рассеяния произвольных линейных и пассивных цепей СВЧ по известным матрицам рассеяния базовых элементов, отличающиеся организацией процесса вычисления ||S||  приведены в [36,43].

12.5. ПОСТРОЕНИЕ ЭКВИВАЛЕНТНЫХ СХЕМ ПРОСТЕЙШИХ ЦЕПЕЙ СВЧ. РЕАЛИЗАЦИЯ ЦЕПЕЙ ИЗ СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТОВ В ДИАПАЗОНЕ СВЧ

Применение метода декомпозиции для анализа сложной цепи СВЧ требует знания или характеристических матриц, или эквивалентных схем базовых элементов цепи. Кроме того, на практике решается и обратная задача: по заданным функциональным свойствам проектируемого устройства вначале выбирают его эквивалентную схему, состоящую из сосредоточенных элементов L, С, R и отрезков эквивалентной линии; затем на основе этой схемы строят конструкцию устройства, пытаясь реализовать сосредоточенные элементы с помощью элементов с распределенными параметрами.

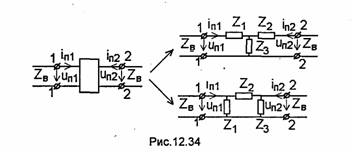
Это вызвано тем, что физические размеры сосредоточенных элементов L, С и R с повышением частоты уменьшаются и на частотах выше нескольких сотен мегагерц становятся настолько малыми, что их изготовление вызывает серьезные трудности. Кроме того, с повышением частоты на параметры сосредоточенных элементов все большее влияние оказывают тепловые потери в них и потери на излучение. Поэтому, как правило, в диапазоне СВЧ вместо подобных элементов используют элементы с распределенными параметрами, например отрезки линий передачи. Подбором длины и волнового сопротивления отрезков линии стараются смоделировать поведение сосредоточенных элементов в соответствующей эквивалентной схеме устройства.

Характеристические матрицы базовых элементов определяют или из решения электродинамической задачи, или экспериментально. На основе найденной матрицы строят эквивалентную схему элемента. Например, если для взаимного четырехполюсника (рис.12.34) известна матрица ||  Z || или || У||, то с ним обычно сопоставляют либо Т-образную {рис.12.34) либо П-образную (рис. 12.34) эквивалентные схемы; величины элементов эквивалентной схемы находят, приравнивая матрицы сопротивлений (для Т-схемы) или матрицы проводимостей (для П-схемы) на требуемой частоте [30]:

для Т-схемы

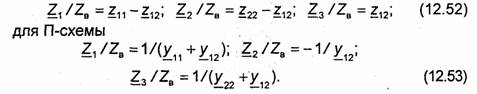
Рассмотрим эквивалентные схемы некоторых базовых элементов.

Эквивалентная схема однородного отрезка линии передачи. Такой отрезок может быть представлен четырехполюсником, и его эквивалентная схема выбирается или в виде Т-, или в виде П-схемы (рис.12.34). Величины элементов этих схем можно найти по (12.52) и (12.53), предварительно вычислив элементы матриц || Z || и || Y ||  по (12.48)-(12.48) по известной матрице || S ||  (рис.12.30):

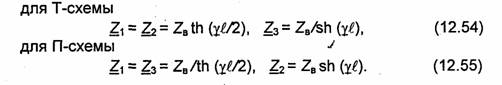
Если длина отрезка l мала, можно пренебречь тепловыми потерями в нем (α = 0 и γ.= iβ), при этом гиперболические функции в (12.54) и (12.55) перейдут в тригонометрические, эквивалентная схема отрезка будет состоять лишь из реактивных элементов (рис.12.35):

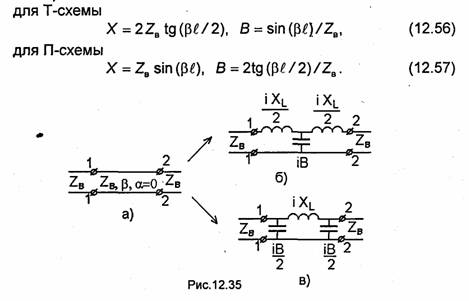
Формулы (12.56) и (12.57) позволяют связать параметры сосредоточенных элементов и элементов с распределенными параметрами. Например, для коротких отрезков линии (l<<Λ), учитывая, что при малых х можно считать tgx≈sinx≈x, получаем Поэтому, если в разрыв линии с волновым сопротивлением Z_B включить короткий отрезок с намного большим волновым сопротивлением Z_B1, то эквивалентной схемой такой цепи будет индуктивность, последовательно включенная в разрыв эквивалентной линии (при большой величине Z_B1 из (12.56)-(12.57) следует, что X>>B, т.е. С→0, (рис.12.35)). Аналогично можно показать, что если в разрыв линии включить отрезок с намного меньшим волновым сопротивлением, чем у линии, то эквивалентной схемой такой цепи будет емкость, параллельно подключаемая в эквивалентную линию. В табл.12.1 приведены некоторые базовые элементы цепей СВЧ, состоящие из отрезков полосковых линий передачи (на рисунках в таблице изображены конструкции

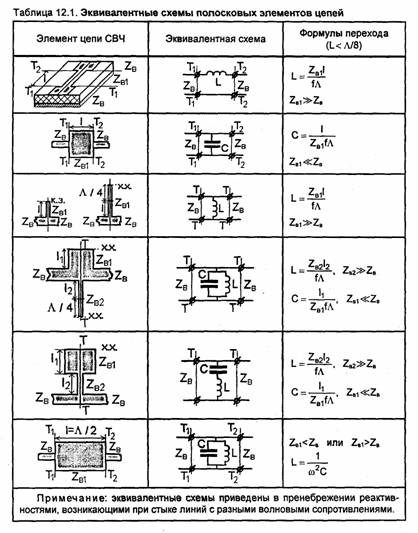
полоски для СПЛ или МПЛ), соответствующие им эквивалентные схемы и формулы перехода. По данным таблицы несложно изобразить конструкцию соответствующих элементов на основе коаксиальной или двухпроводной линии передачи.

Эквивалентные схемы отражающих неоднородностей в волноводных трактах. В таких трактах для реализации сосредоточенных элементов эквивалентных схем в волновод вводят специальные отражающие неоднородности.

Волноводные диафрагмы. Диафрагмой называют тонкую металлическую пластину, расположенную в поперечной плоскости волновода и частично перекрывающую его поперечное сечение. На рис. 12.36 показана диафрагма, уменьшающая лишь размер широкой  стенки  прямоугольного  волновода.   Считаем толщину диафрагмы пренебрежимо малой и не учитываем тепловые потери в ней. Волновод работает в одноволновом режиме. При построении эквивалентной схемы будем руководствоваться следующими физическими соображениями: свойства элемента, обладающего способностью концентрировать вблизи себя энергию электрического поля W_зл, близки к свойствам конденсатора, вследствие этого такой элемент можно эквивалентно представить в виде реактивности емкостного характера; если же элемент концентрирует вблизи себя энергию магнитного поля W_Maг, то его можно эквивалентно представить в виде реактивности индуктивного характера, а если вблизи элемента концентрируется и та и другая энергия, то при W_эл>W_маг элемент можно эквивалентно представить в виде реактивности емкостного характера, а при W_эл<W_маг-индуктивного

характера.

Рассмотрим диафрагму, изображенную на рис. 12.36. При взаимодействии распространяющейся по волноводу волны Н₁₀ с диафрагмой вблизи последней возникает структура магнитного поля, показанная на рис.12.36, т.е. в данном случае поперечные и продольные токи, текущие по широким стенкам волновода, частично замыкаются через пластины диафрагмы, с ними связано дополнительное магнитное поле, возникающее вблизи диафрагмы. Это приводит к увеличению концентрации энергии магнитного поля в области диафрагмы. Поэтому эквивалентной схемой рассматриваемой диафрагмы является индуктивность, подключаемая параллельно в эквивалентную линию (см. рис.12.36). Для тонкой диафрагмы можно считать расстояние между полюсами 1-1 и 2-2 равным нулю. Формулы для расчета величины X_L по заданным размерам диафрагмы d₁ и d₂ можно найти в [33]. Рассматриваемая диафрагма (рис.12.36) получила название индуктивная диафрагма.

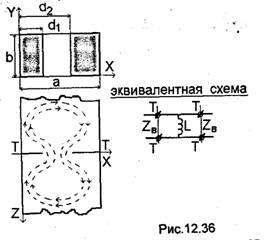
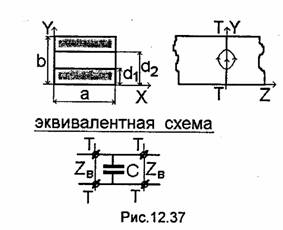
Диафрагма, изображенная на рис. 12.37, частично уменьшающая лишь размер узкой стенки прямоугольного волновода, называется емкостной диафрагмой. При распространении волны Н₁₀ по волноводу между кромками диафрагмы концентрируются силовые линии электрического поля, что приводит к увеличению концентрации энергии электрического поля в области диафрагмы. Поэтому эквивалентной схемой рассматриваемой диафрагмы является емкость, подключаемая параллельно в эквивалентную линию. Расчетные формулы для этого случая можно найти в [33].

Диафрагма, образованная совмещением в одной плоскости волновода индуктивной и емкостной диафрагм, называется резонансной диафрагмой (рис.12.38). Размеры отверстия а₁ и b₁ могут быть выбраны так, чтобы на заданной частоте коэффициент отражения волны Н₁₀ от диафрагмы был бы равен нулю [33] (это означает, что в эквивалентном контуре возникает резонанс, т.е. W_эл=W_маг в области диафрагмы).

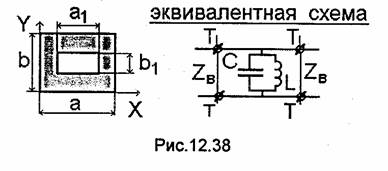
Реактивный стержень в прямоугольном волноводе -это металлический проводник, установленный параллельно вектору Е волны Н₁₀ и соединенный по крайней мере с одной стороны с широкой стенкой волновода (рис. 12.39). Иногда его называют реактивным штырем. Отметим, что аналогичные стержни (штыри) устанавливаются и в других линиях передачи. Эквивалентной схемой тонкого (d<<a) реактивного стержня является последовательный контур, включенный в эквивалентную линию параллельно. Индуктивность связана с токами проводимости, протекающими по стержню, а емкость-с концентрацией электрического поля в зазоре между торцом стержня и стенкой волновода. Формулы для расчета X_L и Х_с можно найти в [33]. Анализ стержня в волноводе, выполненный в [38], показывает, что при длине стержня l≈λ/4 величины X_L≈X_C, при этом сопротивление контура стремится к нулю

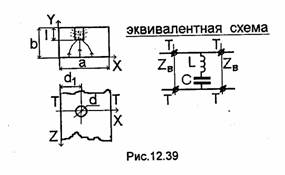
(резонанс), из-за чего вся энергия, переносимая падающей волной в волноводе, полностью отражается от стержня. На практике из-за конечной проводимости металла, модуль коэффициента отражения от стержня несколько меньше единицы. При l<λ/4 реактивное сопротивление контура становится емкостным, а при l>λ/4 - индуктивным.

В настоящее время существует большое число научных работ, посвященных построению эквивалентных схем как для разных неоднородностей в линиях передачи, так и для простейших конструкций элементов тракта СВЧ. Расчетные формулы и эквивалентные схемы для волноводных и коаксиальных элементов можно найти в [33,39]; сведения для полосковых элементов в [36, 40]; данные для элементов оптических трактов в [41,42]. При использовании тех или иных справочных данных особое внимание следует обращать на границы применимости и обеспечиваемую точность.

12.6. СТРУКТУРНЫЙ И ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ. АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ УСТРОЙСТВ СВЧ

Проектирование СВЧ трактов современных радиотехнических систем представляет достаточно сложную задачу, решение которой практически невозможно без ЭВМ. В результате проектирования должна быть получена конструкция устройства, частотные характеристики которой удовлетворяют заданным требованиям. В столь общей постановке данная задача не имеет единственного решения, так как различные по конструкции устройства могут иметь идентичные электрические характеристики. При проектировании СВЧ тракта выделяют два основных этапа. Первый этап, называемый конструктивным синтезом, состоит в выборе одного или нескольких допустимых вариантов разрабатываемого устройства. На этом этапе разработчик, основываясь на интуиции и инженерном опыте, используя некоторые общие приближенные представления о принципе работы устройств СВЧ, пользуясь специальными пособиями, где содержатся сведения об аналогичных устройствах и необходимые справочные материалы, определяет набор элементов, из которых состоит разрабатываемое устройство, и порядок их включения, т.е. предопределяет конструктивное выполнение элементов. Следует отметить, что для многих устройств СВЧ в настоящее время созданы приближенные методики синтеза, как правило, использующие приближение теории длинных линий, с помощью которых можно по заданным техническим требованиям приближенно определить конструктивные параметры элементов (см. гл.13 и 14).

Второй этап проектирования, называемый параметрическим синтезом, состоит в окончательном выборе варианта конструкции и уточнении параметров всех его элементов с целью получения требуемых частотных характеристик устройства. На этом этапе строят более точную эквивалентную схему проектируемого устройства и выполняют анализ схемы, вычисляют элементы матрицы рассеяния, что позволяет рассчитать частотные характеристики проектируемого устройства. Частотные характеристики, рассчитанные по уточненной эквивалентной схеме, могут существенно отличаться от заданных при проектировании. Это отличие будет тем больше, чем более грубые и приближенные методики синтеза использовались на первом этапе. Если найденные характеристики не удовлетворяют техническому заданию, возникает задача коррекции параметров базовых элементов, выбранных на первом этапе, с целью улучшения характеристик устройства.

Процесс улучшения характеристик устройства на основе какого-то исходного варианта называется оптимизацией. Он состоит в целенаправленном поиске таких параметров элементов устройства, которые обеспечивали бы минимальное значение некоторой целевой функции, оценивающей отклонение получающихся характеристик от требуемых техническим заданием. Как правило, оптимизация проводится численно, т.е. по определенному плану перебираются возможные значения параметров элементов. Для каждого сочетания параметров вычисляется матрица рассеяния и рассчитывается значение целевой функции. Отыскивается такое оптимальное сочетание параметров, при котором получается минимум целевой функции. По вопросам численной оптимизации существует обширная литература. Достаточно полное представление о методах численной оптимизации применительно к задачам проектирования радиосистем можно найти в [43, 45]. Чем сложнее устройство и жестче требования к его характеристикам, тем важнее роль оптимизации. Второй этап проектирования практически невозможно выполнить без ЭВМ.

Эффективность любого проектирования в большей степени зависит от того, в какой мере удается автоматизировать стандартные операции, не требующие принятия решений. Такими стандартными операциями при проектировании трактов СВЧ являются расчет частотных характеристик известной схемы и в определенной степени процесс оптимизации.

Структурный синтез, выполняемый на первом зтапе, где разработчик, используя свой опыт, принимает неформальное решение по выбору конструкции, очевидно, не может быть полностью автоматизирован. Поэтому при проектировании СВЧ трактов используют системы автоматизированного проектирования (САПР) устройств* СВЧ.  Ядром  САПР  является  библиотека  математических моделей базовых элементов, содержащая вычислительные программы для расчета их матриц рассеяния. От полноты библиотеки зависит возможность проектировать те или иные тракты СВЧ на основе САПР. В настоящее время созданы САПР для проектирования СВЧ трактов определенного класса:  например, САПР волноводных трактов или САПР полосковых плат [43] и т.д. В соответствии с назначением и формируется библиотека базовых элементов. Кроме этого, в САПР входит программа для вычисления матрицы рассеяния всего устройства по известным матрицам базовых элементов. И наконец, одним из основных блоков САПР является блок оптимизации. В качестве вспомогательных блоков, входящих в САПР, можно отметить блок ввода исходных данных на проектирование и блок выдачи конструкторской документации.

Возможны различные варианты САПР. Идеальная САПР предполагает полную автоматизацию, т.е. весь указанный объем работ, вплоть до выдачи конструкторской документации, осуществляется ЭВМ без участия человека, кроме тех случаев, когда из предложенных элементов ЭВМ не может синтезировать конструкцию с заданными характеристиками. В этом случае разработчик с учетом полученной от ЭВМ информации производит корректировку исходной конструкции (первый этап) либо требований к проектируемому устройству, и весь процесс повторяется на ЭВМ. Однако, как показывает практика, подобные системы чрезвычайно сложны. Поэтому, как правило, разрабатывают более простые и эффективные системы диалогового типа, когда конструкция устройства и начальный набор параметров базовых элементов, образующих ее, задаются разработчиком, а ее анализ, т.е. расчет электрических характеристик и частичная оптимизация, выполняется ЭВМ. Результаты анализа и оптимизации отображаются на экране дисплея или выдаются в виде графиков, таблиц и т.д. При значительном расхождении требуемых и полученных характеристик разработчик вносит определенные коррективы в исходные данные либо критерии оценок при оптимизации и дает указание повторить анализ и оптимизацию. Подобный диалог человека с машиной продолжается до тех пор, пока не достигаются с заданной точностью требуемые характеристики. Затем ЭВМ составляет и оформляет конструкторскую документацию. Как показывает практика, режим диалога позволяет активно использовать опыт и интуицию разработчика, что существенно упрощает вычислительные программы и ускоряет поиск оптимальной конструкции устройства. Более подробно ознакомиться с САПР устройств СВЧ можно в [43-45].