Глава 9

ОБЩИЕ СВОЙСТВА НАПРАВЛЯЕМЫХ ВОЛН

9.1. НАПРАВЛЯЮЩИЕ СИСТЕМЫ И НАПРАВЛЯЕМЫЕ

ВОЛНЫ

Кроме свободно распространяющихся волн, рассмотренных в предыдущих главах, существуют волны, распространение которых возможно только при наличии каких-либо направляющих элементов (границы раздела сред, металлических, диэлектрических или полупроводящих трубок, стержней и др.). Такие волны называют направляемыми. Совокупность направляемых элементов образует направляющую систему. Направляющие системы служат для передачи энергии электромагнитной волны от источника (генератора) к потребителю например от передатчика к антенне, от приемной антенны ко входу приемника и т.д. В связи с этим направляющие системы называют также линиями передачи энергии или, более коротко, линиями передачи. Направляющую систему, у которой поперечное сечение и другие параметры не меняются в продольном направлении, называют однородной. На рис. 9.1 изображены поперечные сечения некоторых используемых на практике однородных направляющих систем: двухпроводной (а), коаксиальной (б), экранированной двухпроводной (в), симметричной (г) и несимметричной (д) полосковых линий, диэлектрического волновода (е), световода (ж) и полых металлических волноводов: прямоугольного (з), круглого (и) и эллиптического (к).

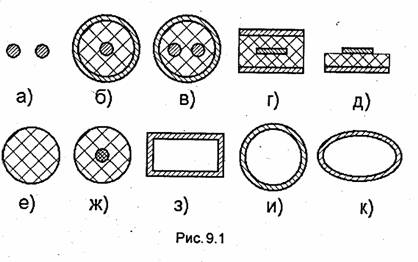
Все линии передачи можно разделить на два класса: линии открытого типа (см., например, рис.9.1,а,г,д,е,ж) и линии закрытого типа (см., например, рис.9.1,б,в,з,и,к). В линиях передачи закрытого типа вся передаваемая энергия сосредоточена в области, экранированной от внешней среды металлической оболочкой той или иной формы. В линиях открытого типа электромагнитное поле, строго говоря, распределено во всем пространстве, окружающем линию. Линии открытого типа обычно выполняют таким образом, чтобы подавляющая часть передаваемой энергии была сосредоточена в непосредственной близости к линии. Тем не менее линии открытого типа подвержены влиянию внешних воздействий. На волны в таких линиях влияют электромагнитные поля, созданные другими источниками, и внешние условия (например, метеорологические: дождь, снег, обледенение).

По структуре поля направляемые волны делятся на поперечные, электрические, магнитные и гибридные.

Поперечными волнами, или ТЕМ-волнами (Т- первая буква английского слова transvers, что означает поперечный), называют волны, у которых векторы Е и Н перпендикулярны направлению распространения волны, т.е. не имеют продольных составляющих. Отметим, что в соответствии с ГОСТ 18238-72 (Линии передачи сверхвысоких частот. Термины и определения) эти волны полагается называть 7-волнами. Однако это название практически не используется ни в зарубежной, ни в отечественной литературе. Поэтому в книге сохранен общепринятый термин ТЕМ-волны.

Электрическими волнами, или Е-волнами, называют волны, у которых вектор Е имеет как поперечные, так и продольную составляющие, а продольная составляющая вектора Н равна нулю. Е-волны иногда называют поперечными магнитными волнами или ТМ-волнами.

Магнитными волнами, или Н-волнами, называют волны, у которых вектор Н имеет как поперечные, так и продольную составляющую, а продольная составляющая вектора Е равна нулю. Н-волны иногда называют поперечными электрическими волнами или ГЕ-волнами.

Гибридными, или смешанными волнами называют волны, у которых и вектор Е, и вектор Н наряду с поперечными составляющими имеют и продольные составляющие.

9.2. СВЯЗЬ МЕЖДУ ПОПЕРЕЧНЫМИ И ПРОДОЛЬНЫМИ СОСТАВЛЯЮЩИМИ ВЕКТОРОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Рассмотрим произвольную бесконечно протяженную однородную направляющую систему, ориентированную вдоль оси Z Будем считать, что направляющая система не вносит потерь.

В области, где отсутствуют сторонние источники, комплексные амплитуды векторов Е и Н, соответствующие волне, бегущей вдоль однородной линии передачи, могут быть представлены в виде

где β = const (коэффициент фазы), а ξ и η - координаты, изменяющиеся в поперечном сечении рассматриваемой линии передачи. Выбор конкретной системы координат зависит от формы поперечного сечения линии. Множитель exp(-iβz) соответствует волне, бегущей в положительном направлении оси Z, а множитель exp (iβz)-волне, бегущей в обратном направлении. Для определенности будем считать, что волна распространяется в положительном направлении оси Z. Если потребуется рассмотреть волны, бегущие в обратном направлении, это всегда будет оговорено.

Векторы Ё_т и Н_т должны удовлетворять однородным уравнениям Гельмгольца (2.32) и (2.33) соответственно. С учетом формул (9.1) эти уравнения при могут быть переписаны в виде

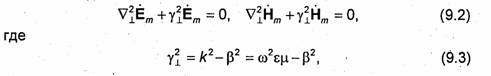
а оператор Величину γ_┴ называют поперечным волновым числом.

Покажем, что в тех случаях, когда векторы Ё_тиН_т (оба или

один из них) имеют продольные составляющие, нахождение поля направляемой волны может быть сведено к определению составляющих Ё_тz и H_mz, так как поперечное составляющие векторов

поля выражаются через продольные. Проецируя уравнения Максвелла (1.76) на оси X и У декартовой дистемы координат и учитывая, что в рассматриваемом случае дифференцирование по переменной z эквивалентно умножению на (- iβ), получаем

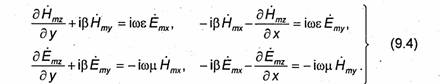
Система уравнений (9.4) позволяет выразить составляющие Ё_тх,Ё_ту,Н_тх и Н_ту через Ё_mz и Н_тz. После элементарных преобразований имеем .

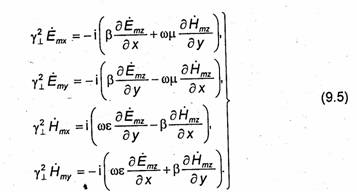
Система уравнений (9.5) связывает поперечные и продольные составляющие векторов поля в декартовой системе координат. Для выражения этой связи в произвольной системе координат перейдем к векторной форме уравнений (9.5). Введем векторы

вытекающим из (9.2).

Таким образом, для определения поля Е-, Н- и гибридных

волн достаточно найти составляющие E_mz и H_mz путем решения уравнений (9.10) с учетом краевых условий, соответствующих рассматриваемой направляющей системе, а для вычисления поперечных составляющих использовать равенства (9.5) или (9.8)

У ТЕМ-волн продольные составляющие векторов  Ё_т и Н_т

отсутствуют {Ё_тг = 0 и H_mz = 0). Однако, как будет видно из дальнейшего, соотношения (9.5) или эквивалентные им равенства (9.8) и (9.9) оказываются полезными и в этом случае.

9.3. ОБЩИЕ СВОЙСТВА И ПАРАМЕТРЫ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И ГИБРИДНЫХ ВОЛН

В случае электрических (E_mz ≠0, Н_тг = 0), магнитных (H_mz ≠ 0, E_mz = 0) и гибридных (Е_mz ≠ 0 и H_mz ≠ 0) волн постоянная γ_┴ отлична от нуля. Это следует, в частности, из равенств (9.8) и (9.9). Для каждой конкретной линии передачи она может быть определена в результате решения уравнений (9.10) и учета краевых условий, соответствующих этой линии. Постоянная γ_┴зависит от формы и размеров поперечного сечения линии передачи и от типа распространяющейся волны, но не зависит от частоты.

Выражая коэффициент фазы β из (9.3), получаем

Так как то в зависимости от частоты подкоренное

выражение в (9.11) может быть положительным (при k> γ_┴), равным нулю (при k = γ_┴) или отрицательным (при k < γ_┴).

В первом случае параметр β -действительное число и фазы составляющих векторов поля в фиксированный момент t= t_o= const линейно зависят от координаты z, что является признаком распространения волны вдоль оси Z с постоянной скоростью v_ф = ω/β. Как будет видно из дальнейшего, распространение волны в этом случае сопровождается переносом энергии вдоль оси Z.

В третьем случае к< γ_┴. Подкоренное выражение в (9.11) оказывается отрицательным, и  Знак в правой части последнего равенства выбран из физических соображений: при этом множитель ехр и амплитуды составляющих векторов Ё_т и Н_т экспоненциально убывают вдоль оси

Z. Если принять β= i | β|, то амплитуды векторов поля будут возрастать с удалением от источников, что в рассматриваемой задаче физически невозможно. Фазы составляющих векторов поля в данном случае не зависят от координат: поле имеет характер стоячей волны и экспоненциально уменьшается вдоль оси Z. Переноса энергии вдоль линии передачи в этом случае не происходит. Подчеркнем, что экспоненциальное убывание поля вдоль линии передачи не связано с потерями энергии: рассматривается идеальная направляющая система, в которой потери отсутствуют.

Во втором случае параметр β = 0. Такой режим называют критическим. Частота f = f_кp, определяемая из условия к = γ_┴, называется критической частотой:

Соответствующая этой частоте критическая длина волны

Выражая γ_┴ из (9.13) и подставляя в (9.11), получаем

Как видно, параметр β является действительной величиной, т.е. поле (9.1) представляет собой распространяющуюся волну, только при выполнении условия

Неравенство (9.15) можно переписать в виде

Таким образом, Е-, Н- и гибридные волны в идеальной линии передачи могут распространяться только на частотах, превышающих некоторую критическую частоту, определяемую формулой (9.12). Отметим, что значение f_кp зависит от формы и размеров поперечного сечения линии и типа волны.

Неравенство (9.15), а также (9.16) часто называют условием распространения волны в линии передачи.

По аналогии с обычным определением назовем длиной направляемой волны Λ, распространяющейся в линии передачи, расстояние между двумя поперечными сечениями, в которых в один и тот же момент времени фазы составляющих вектора Е (или Н) отличаются на 2π. Очевидно также, что длина волны Λ равна расстоянию, на которое поверхность равной фазы перемещается за период. Так как зависимость всех составляющих векторов поля от координаты z определяется множителем ехр (- iβz), то

а фазовая скорость вычисляется по формуле

Как видно,   при  λ < λ_кр длина  волны  в  линии  и  фазовая скорость Е-, Н- и гибридных волн больше соответственно длины волны λ = c/f и фазовой скорости v_ф=с волны, свободно распространяющейся в безграничной однородной среде без потерь с параметрами ε и μ .

Отметим, что у Е-, Н- и гибридных волн фазовая скорость зависит от частоты. Это явление называют дисперсией волн. При f = f_кp (λ = λ_кр) фазовая скорость равна бесконечности, при увеличении частоты v_ф приближается к скорости света (рис. 9.2).

Общие выражения для критической длины волны (9.13), критической частоты (9.12), коэффициента фазы (9.14), длины волны в линии (9.17) и фазовой скорости (9.18) одинаковы для Е-, Н- и гибридных волн. Однако из этого не следует, что значения перечисленных параметров будут одинаковыми для этих волн. Критическая длина волны зависит от поперечного волнового числа (λ_кр = 2π/ γ_┴). В свою очередь, значение γ_┴ зависит от формы и размеров поперечного сечения линии передачи и от структуры поля распространяющейся волны. Структура поля Е-, Н- и гибридных волн различна, поэтому в общем случае соответствующие данным волнам значения γ_┴ могут не совпадать. При этом для указанных волн не будут совпадать и значения параметров λ_кр, f_rp, β, \/_ф и Λ.

Перейдем к вычислению характеристических сопротивлений рассматриваемых волн. По определению характеристическое сопротивление волны равно отношению поперечных к направлению распространения составляющих векторов Ё_т и Н_т.

В случае Е-волн поперечные составляющие векторов Ё_т и Н_m определяются формулами

перпендикулярны. Из полученного соотношения вытекает следующее выражение для характеристического сопротивления Е-волн:

Как видно, в случае Н-волн векторы Ё_т┴ и Н_т┴ (и соответствующие им векторы , как и аналогичные им векторы в случае Е-волн, взаимно   перпендикулярны. Характеристическое сопротивление Н-волн зависит от частоты. При λ < λ _кроно всегда больше Z_c. При увеличении частоты от критической до бесконечности  убывает от бесконечности до Z_c (см. рис. 9.3).

В области волн длиннее критической (λ > λк_Р) характеристические сопротивления Е- и Н-волн являются чисто мнимыми величинами. Это означает,  что при λ >λ_кр поперечные составляющие векторов напряженностей электрического и магнитного полей Ё_{т ┴}и Н_т┴ сдвинуты по фазе на 90°. Очевидно, что при этом комплексный вектор Пойнтинга принимает чисто мнимые значения, т.е. вдоль линии не происходит переноса энергии. Поле в линии при λ > λк_Р является чисто реактивным. Напомним, что все формулы данного раздела получены в предположении, что линия является идеальной (не вносит потерь).

В случае гибридных волн (E_mz ≠ 0 и Н_mz # 0) поперечные составляющие векторов Ё_т и Н_т определяются общими формулами (9.8) и (9.9). Поэтому получить единое простое выражение для характеристического сопротивления не удается: его величина зависит и от линии передачи, и от структуры поля распространяющейся волны и при λ < λк_Р может быть как больше, так и меньше Z_c. На частотах, меньших критической (λ > λк_Р), характеристическое сопротивление гибридных волн также принимает чисто мнимые значения.

9.4. ОБЩИЕ СВОЙСТВА ПОПЕРЕЧНЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Соотношения (9.8) и (9.9) были получены непосредственно из уравнений Максвелла. Они должны выполняться для любых направляемых волн, включая ТЕМ-волны. Полагая в (9.8) и (9.9) Ё_тз = 0 и Н_тз = 0,  приходим к равенствам Так как  то эти равенства будут выполняться только при λ_┴= 0. При этом из (9.12) и (9.13) следует, что у ТЕМ-волн 4р = 0 и Х_кр=<х>. Следовательно, в тех направляющих системах, в которых возможно распространение ТЕМ-волн, эти волны могут существовать на любой частоте вплоть до f →0. Поэтому ТЕМ-волны могут распространяться только в тех линиях передачи, в которых может протекать постоянный ток. Этому требованию удовлетворяют направляющие системы, состоящие не менее чем из двух изолированных друг от друга металлических проводников (двухпроводная, коаксиальная, полосковая, экранированная двухпроводная линии и др.). В полых металлических трубах с любой формой поперечного сечения, диэлектрических волноводах и других аналогичных системах распространение ТЕМ-волн невозможно. Действительно, предположим, что внутри полой идеально проводящей трубы распространяется ТЕМ-волна. Линии магнитного поля в этом случае должны образовывать замкнутые кривые, лежащие в поперечных плоскостях. Из первого уравнения Максвелла следует, что они должны охватывать продольные линии токов проводимости и(или) смещения. Для существования продольного тока вектор Ё_т должен иметь продольную составляющую  Однако у ТЕМ-волн такой составляющей не может быть по определению.

Так как в случае ТЕМ-волн γ_┴= 0, то коэффициент фазы, фазовая скорость и длина волны будут совпадать с аналогичными параметрами волны, свободно распространяющейся в безграничной однородной изотропной среде:

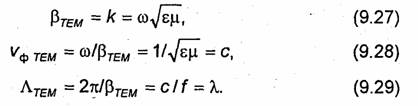
Характеристическое сопротивление  ТЕМ-волны легко находится из уравнений (9.4). Полагая в этих уравнениях Е_mz = 0  и H_mz = 0,   приходим к соотношениям, которые можно записать в виде векторного равенства

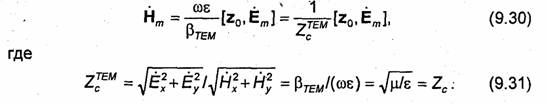
Как видно, Z_C^TEM совпадает с характеристическим сопротивлением волны, свободно распространяющейся в безграничной однородной среде с параметрами ε и μ.

Отметим, что равенства (9.22), (9.25) и (9.30) однотипны и отличаются только значениями характеристических сопротивлений. Эти равенства можно объединить в одну формулу:

Поле, удовлетворяющее таким уравнениям, является потенциальным. Это означает, что решения уравнений (9.33) могут быть представлены в виде градиентов от некоторых скалярных функций, например:

E⁰=-gradu⁰,                                   (9.34)

где функция и° зависит только от поперечных координат и удовлетворяет уравнению Лапласа ∆_┴²u°=0. Аналогичное представление для вектора Й°_т┴ можно не выписывать, так как векторы Ё°и Н°связаны соотношением, аналогичным (9.30): H°=(1/Z_c)x

x[z_o,E°].

В уравнения (9.33) не входит частота. Из этого следует, что функции Ё° и Н°, определяющие структуру поля в поперечных сечениях линии, не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при f→0. Для определения вектора Ё° достаточно решить двумерную электростатическую задачу для такой же линии. При этом во многих случаях целесообразно вначале определить функцию и⁰, которую можно трактовать как электростатический потенциал указанной электростатической задачи, а затем воспользоваться формулой (9.34).

Функция Н° совпадает с напряженностью магнитного поля, создаваемого постоянными токами, текущими по рассматриваемой линии при f→0. Поэтому она может быть найдена либо непосредственно,   если  известно  распределение токов,  либо  по

формуле, аналогичной (9.30), после определения вектора Ё°.

Подчеркнем, что аналогия с электростатическим полем и полем постоянных токов относится лишь к распределению поля в плоскости поперечного сечения. Закон распределения поля ТЕМ-волны вдоль оси Z существенно отличается от соответствующих постоянных полей. Вместо однородного распределения вдоль оси Z, характерного для случая электростатического поля и поля постоянных токов, распределение поля ТЕМ-волны имеет волновой характер. У ТЕМ-волны поля в поперечной плоскости, совпадая по конфигурации силовых линий с соответствующими постоянными полями, не остаются неизменными во времени, а непрерывно меняют свою величину по гармоническому закону.

При неидеальной проводимости металлических проводников, образующих линию, электромагнитное поле проникает в металл. В соответствии с граничным условием Леонтовича-Щукина (7.52) появляется отличная от нуля касательная составляющая напряженности электрического поля, параллельная оси Z, что делает невозможным существование ТЕМ-волны. Однако при достаточно высокой проводимости металла структура поля распространяю-, щейся волны настолько мало отличается от структуры поля ТЕМ-волны в идеально проводящей системе, что этим отличием во многих случаях можно пренебречь.

Очевидно, что структуры полей Е- и Н-волн при неидеальной проводимости металлических элементов линии передачи также будут несколько отличаться от структур соответствующих волн в случае идеальной проводимости указанных элементов. Эти отличия также будут незначительными, и, если речь не идет о вычислении потерь линии, ими обычно пренебрегают.

9.5. КОНЦЕПЦИЯ ПАРЦИАЛЬНЫХ ВОЛН

Свойства Е-, Н- и гибридных волн существенно отличаются от свойств ТЕМ-волн. Эти отличия легко объясняются, если предположить, что Е-, Н- и гибридные волны могут быть представлены в виде суперпозиции парциальных ТЕМ-волн, распространяющихся под некоторым углом к оси линии передачи (оси Z). Распространение парциальных волн в этом случае может происходить, например, вдоль ломаной линии путем многократных отражений от стенок (рис. 9.4) или других элементов направляющей системы. Если направляющая система заполнена неоднородной средой, характер распространения парциальной волны может быть более сложным.

У ТЕМ-волны, распространяющейся непосредственно вдоль оси Z (рис. 9.5), векторы Ё_т и Н_т лежат в поперечной плоскости (перпендикулярны оси 2). У парциальной ТЕМ-волны векторы Ё_т и Н_т  лежат в плоскостях, перпендикулярных отрезкам ломаной линии (рис. 9.4), вдоль которой распространяется парциальная волна. В данном случае по меньшей мере один из векторов (Ё_т или Н_т) будет не перпендикулярен оси Z. При этом либо вектор Ё_т (рис. 9.6), либо вектор Н_т (рис.9.7), либо оба вектора   (и Ё_т и Н_т) будут иметь продольные составляющие, что соответствует Е-, Н- и гибридной волнам, распространяющимся вдоль оси Z.

Используем представление о парциальных волнах для объяснения полученных выше результатов: длина волны в линии и фазовая скорость у Е-, Н- и гибридных волн больше соответствующих параметров ТЕМ-волны, характеристическое сопротивление у Е-волны меньше, а у Н-волны больше характеристического сопротивления ТЕМ-волны.

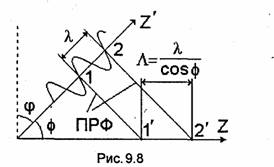
В случае Е-, Н- и гибридных волн парциальная ТЕМ-волна распространяется вдоль линии, образующей угол ф с осью Z (рис. 9.8). Поверхности равных фаз (ПРФ) этой волны перпендикулярны оси Z' и перемещаются вдоль нее с фазовой скоростью -период электромагнитных колебаний. За время Т каждая ПРФ, например ПРФ 1-1’ на рис. 9.8, переместится вдоль оси Z' на расстояние λ (расстояние 1-2 на рис. 9.8). Путь, пройденный этой же ПРФ за время Г вдоль оси Z, будет больше и равен расстоянию между точками 1' и 2'. Соответственно длина волны вдоль оси Z (длина волны в линии в случае Е-, Н- и гибридных волн) будет больше λ и равна Λ = λlcos ф. Отсюда фазовая скорость по оси Z равна у_ф=Λ/T= λ/(Тcos ф) = с/соsф, т.е. фазовые скорости Е-, Н- и гибридных волн больше скорости света в данной среде.

Из рис. 9.6, соответствующего Е-волне, видно, что амплитуда поперечной относительно оси Z составляющей напряженности электрического поля (Е_х на рис. 9.6) меньше амплитуды вектора Е парциальной волны, тогда как амплитуды напряженности магнитных полей у обеих волн совпадают (см. рис.9.6). Следовательно, у Е-волны, распространяющейся вдоль оси Z, отноше- ние поперечных составляющих на-пряженностей электрического и магнитного полей меньше, чем у парциальной ТЕМ-волны. Соответственно Z_C^E<Z_C^TEM. У Н-волн амплитуда поперечной составляющей напряженности магнитного поля (Н_у на рис. 9.7) меньше амплитуды поперечной составляющей напряженноети

магнитного поля парциальной ТЕМ-волны, тогда как амплитуды поперечных составляющих напряженностей электрических полей у обеих волн совпадают (см. рис. 9.7). Следовательно, характеристическое сопротивление /-/-волны больше, чем характеристическое сопротивление ТЕМ-волны (Z_C^H> Z_C^TEM).

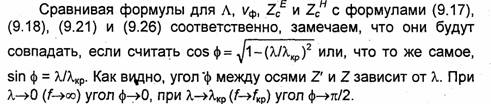
Концепция парциальных волн впервые была сформулирована Бриллюэном применительно к частному случаю распространения волны Ню (см. 10.1) в прямоугольном волноводе. В дальнейшем она была обобщена Г.З.Айзенбергом [25] на случай любых направляемых волн.

9.6. СКОРОСТЬ РАСПРОСТРАНЕНИЯ ЭНЕРГИИ И ГРУППОВАЯ СКОРОСТЬ

Скорость распространения энергии направляемой волны может быть вычислена по формуле (1.162). Трубка, по площади поперечного сечения ∆S которой ведется интегрирование в (1.162), должна выбираться так, чтобы отсутствовал поток энергии, перпендикулярный ее боковой поверхности. Например, в линиях передачи закрытого типа, ограниченных идеально проводящей металлической оболочкой, под ∆S следует понимать поперечное сечение линии передачи. Если металлическая оболочка не идеально проводящая, то появляется перпендикулярный к ней поток энергии (см.7.8.2). Поэтому поперечное сечение энергетической трубки ∆S строго говоря, должно простираться до бесконечности. Аналогично должно быть выбрано поперечное сечение энергетической трубки в случае линий передачи открытого типа.

До сих пор рассматривались исключительно монохроматические волны. Однако реальные электромагнитные сигналы являются немонохроматическими: они состоят из конечного либо бесконечного числа монохроматических колебаний с различными частотами. В системах, в которых имеет место дисперсия волн, например линии передачи с использованием Е-, Н- или гибридных волн, диэлектрическая среда с потерями и др., фазовая скорость монохроматической волны зависит от частоты; проходя один и тот же путь, монохроматические волны разной частоты получают разные фазовые сдвиги. В результате изменяется сдвиг по фазе между колебаниями, образующими сигнал. Соответственно изменяется форма сигнала - сигнал искажается. Чем уже спектр сигнала, тем меньше разница между фазовыми скоростями отдельных монохроматических волн, тем очевидно меньше эти искажения.

Для характеристики перемещения немонохроматических сигналов вводят понятие групповой скорости, обозначая этим термином скорость перемещения максимума огибающей группы монохроматических волн, близких между собой по частоте.

Пусть в диспергирующей системе распространяется эквивалентная некоторому сигналу в общем случае бесконечная сумма монохроматических волн. Мгновенное значение любой составляющей напряженности электрического поля £ (z, t), соответствующего этому сигналу, можно записать в виде интеграла

Следовательно, максимум сигнала непрерывно перемещается вдоль оси Z со скоростью

По определению эта величина и является групповой скоростью. Индекс ω = ω₀ в (9.40) опущен, поскольку центральная частота ω_о была выбрана произвольно. Так как. при выводе формулы (9.40) в разложении (9.37) были сохранены только два первых члена, то условием применимости формулы (9.40) являются медленное изменение коэффициента фазы β(ω) вблизи частоты ш₀ и узость спектра сигнала. При невыполнении этих условий влияние дисперсии становится весьма заметным, и сигнал в процессе распространения так сильно меняет свою форму, что само понятие групповой скорости теряет смысл.

В направляющих системах коэффициент фазы описывается выражением (9.14). Подставляя (9.14) в (9.40), находим групповую скорость направляемых волн:

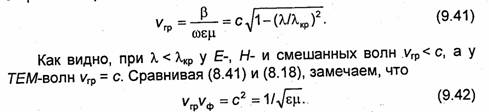
В окрестности максимума сигнала, очевидно, сосредоточена основная часть энергии. Поэтому скорость перемещения максимума сигнала, т.е. групповая скорость, характеризует скорость перемещения энергии электромагнитного поля сигнала по линии передачи. Так как сигнал предполагался узкополосным, то эта скорость должна мало отличаться от скорости распространения энергии v₃ монохроматической волны, т.е. v₃≈ v_гp. Как показывают расчеты по формуле (1.162), на которых не будем останавливаться, в линиях передачи закрытого типа и некоторых других направляющих системах без потерь v₃= v_гp. Поэтому скорость распространения энергии v₃ в идеальных линиях передачи можно определять по формуле (9.42) с учетом (9.41):

Как и следовало ожидать, v_э < с для Е-, Н- и гибридных волн, 1 v₃= с для ТЕМ-волн. Зависимость v₃ от частоты для Е-, И- и смешанных волн показана на рис. 9.2. При λ. = λ_кр скорость распространения энергии равна нулю и по мере повышения частоты приближается к скорости света в данной среде.

Этот же вывод о соотношении между v₃ и с для Е-, Н- и смешанных волн следует непосредственно из концепции парциальных волн. Как уже отмечалось, Е-, Н- и гибридные волны, распространяющиеся вдоль оси Z, могут быть представлены в виде суперпозиции парциальных ТЕМ-волн, распространяющихся по зигзагообразному (или криволинейному) пути под некоторым углом φ к оси Z. Скорость распространения энергии парциальных ТЕМ-волн совпадает со скоростью света в среде, заполняющей линию передачи. Так как зигзагообразный путь длиннее, чем прямой путь вдоль оси Z, то скорость распространения энергии Е-, И- и гибридных волн меньше скорости распространения энергии ТЕМ-волн и равна v₃ = v₃^TEM cos ф = с cos ф.

9.7. ЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ ЛИНИИ ПЕРЕДАЧИ

9.7.1. Мощность, переносимая электромагнитной волной по линии передачи

Средний за период поток энергии через элементарную площадку dS, расположенную в поперечном счении S_± линии передачи, равен dP_cp = Re П_z dS, где

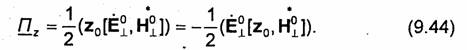
Перепишем соотношение (9.32) для комплексно сопряженных векторов и подставим его в (9.44). Раскрывая получающееся при этом двойное векторное произведение по формуле (П.31), приходим к равенству

где E₀ - максимальное значение напряженности электрического поля в линии передачи,   безразмерная функция, Зависящая только от поперечных координат (в общем случае ζ, η) и определяющая структуру электрического поля в поперечном сечении линии, a Z_c^л -характеристическое сопротивление распространяющейся волны. Напомним, что для ТЕМ-, Е- и W-волн Z_c^л равно Z_c> Zc ^Еи Z_C^H соответственно.

Таким образом, средний за период поток энергии Р_ср через поперечное сечение линии передачи или, что то же самое, средняя мощность, переносимая волной по линии передачи, определяется выражением

9.7.2. Предельная и допустимая мощности

Как видно из формулы (9.46), передаваемая по линии мощность Р_ср пропорциональна Е₀², т.е. чем больше Р_ср, тем больше максимальное значение напряженности электрического поля. Поэтому при увеличении передаваемой мощности в направляющей системе может возникнуть электрический разряд, те. наступит электрический пробой воздуха или диэлектрического заполнения. Плотность тока проводимости в разрядном промежутке достигает относительно больших значений (15 А/см² и более), что приводит к интенсивному выделению тепла и резкому повышению температуры в месте пробоя. Кроме того, активное сопротивление разрядного промежутка ввиду значительной плотности электронов в нем (до 10¹⁵ электрон/см³) мало, и пробой вызывает почти полное короткое замыкание линии передачи в том сечении, где происходит разряд. Поступление мощности в нагрузку практически прекращается, так как большая часть энергии падающей волны отражается от места, где произошел пробой. Это может привести, например, к выходу из строя генератора, либо к другим нежелательным эффектам.

Увеличение уровня передаваемой средней мощности по реальной линии передачи приводит к увеличению мощности потерь в металлических элементах линии и заполняющем диэлектрике, что сопровождается нагревом последних. Если при этом нагреве температура любого материала, из которого изготовлена линия, достигает некоторой предельной величины, происходит его разрушение (например, расплавление диэлектрика) и наступает так называемый тепловой пробой. Поэтому максимальное значение передаваемой по линии мощности ограничено как электрическим, так и тепловым пробоем.

Для определения максимальной передаваемой по линии мощности вводят понятия предельной и допустимой мощностей. Предельной (Р_пред) называют наименьшую мощность, при которой возникает либо электрический, либо тепловой пробой в режиме бегущей волны (см. гл.12). Допустимую мощность (Р_доп) принимают в несколько раз меньше предельной: Рд_0П⁼ (0,2...0,3) Р_пред. Это связано с тем, что появление отраженных волн в реальной линии (см. гл.12) приводит к увеличению напряженности электрического поля в отдельных сечениях линии, что может привести к электрическому или тепловому пробою при мощности существенно меньшей P_npeд.

Величина P_npeд, связанная с электрическим пробоем определяется предельной напряженностью электрического поля Е₀=Е_пред, при которой возникает электрический разряд. Для воздуха при нормальном  атмосферном давлении  и  нормальной  ионизации (=10элекг/(с•см³) Е_npeд =30кВ/см). В свою очередь Р_пред, связанную с тепловым пробоем, определяют по температуре, при которой возникает тепловое разрушение материалов, образующих линию.

Отметим, что в линиях передачи с воздушным заполнением и в случае, когда линия работает в импульсном режиме с высокой скважностью, более опасен электрический пробой. В линиях с диэлектрическим заполнением, отличным от воздуха, а также, если по линии передается большая мощность в непрерывном режиме, более опасен тепловой пробой.

При необходимости передачи по линии высокого уровня мощности избегают применения линий с диэлектрическими вставками или с твердым диэлектрическим заполнением, а используют  воздушное заполнение или заполнение специальными газами (элегаз) или жидкими диэлектриками (например, нонан, декан, гексан, гептан), которые имеют Е _пред >100 кВ/см. С такой же целью линии передачи заполняют воздухом или иным газом под давлением, в несколько раз превышающим атмосферное. При этом возрастает вероятность столкновения образующихся свободных электронов с положительно заряженными ионами газа, что снижает их концентрацию и увеличивает Е _пред. Величина Е_пред увеличивается и при существенном понижении давления газа, заполняющего линию, по сравнению с атмосферным давлением, поскольку вероятность столкновения свободных электронов с молекулами газа резко снижается:

Для увеличения Р_пред. связанной с тепловым пробоем в линиях с диэлектрическим заполнением, используют диэлектрики с более высокой предельной температурой (например, разные виды керамики).

9.8. ЗАТУХАНИЕ В ЛИНИЯХ ПЕРЕДАЧИ

9.8.1. Коэффициент ослабления

Проведенный анализ общих свойств направляемых волн был выполнен в предположении, что линия передачи является идеальной (не вносит потерь). Зависимость векторов поля от координаты z была принята в виде множителя ехр (- iβz), где постоянная β могла быть либо чисто действительным, либо чисто мнимым числом.

Распространение волны в реальной линии передачи сопровождается уменьшением переносимой мощности. Это связано: 1) с рассеянием части мощности в металлических проводниках линии; 2) с затуханием волны в заполняющем диэлектрике; 3) с излучением части мощности в окружающее пространство (в линиях передачи открытого типа).

В этом случае зависимость векторов поля от координаты z обычно принимают в виде exp(-γz), где γ = α + iβ – комплексная величина, называемая постоянной распространения. Параметры аир называют коэффициентом ослабления и коэффициентом фазы соответственно (α = Re γ, β = Im γ).

Отметим, что постоянную γ часто вводят в рассмотрение и при анализе волн, распространяющихся в безграничной однородной среде. В этом случае она связана с использованной в гл.6 комплексной постоянной k = β -iα соотношением γ = i k.

Зависимость комплексного вектора Пойнтинга от координаты z определяется множителем ехр (- 2 α z). Также зависит от z и мощность бегущей волны (средний за период поток энергии через поперечное сечение линии передачи, соответствующий рассматриваемой волне):

P_cp=P₀exp(-2 α z),                              (9.47)

где Р_о = Р_Ср(0)-средний за период поток энергии через сечение z = 0. Разность между потоками энергии P_cp{z) и P_cp(z + ∆z), проходящими через сечения с координатами z и z + ∆z соответственно, равна средней за период мощности джоулевых потерь ∆Р_пср на отрезке линии между указанными сечениями ∆Р_Пср= P_Cp(z) -P_Cp(z ⁺ ∆z). Разделив обе части этого равенства на ∆z и перейдя к пределу при ∆z→0, найдем среднюю за период мощность джоулевых потерь Р_пср, приходящуюся на единицу длины линии:

где α _м - коэффициент ослабления, обусловленный потерями энергии в металлических проводниках линии; α _д - коэффициент ослабления, обусловленный потерями энергии в заполняющем линию диэлектрике; α _Σ - коэффициент ослабления, обусловленный потерями энергии волны за счет излучения из линии.

Следует отметить, что в линиях передачи закрытого типа α _Σ = 0. При конструировании линий передачи открытого типа стараются как можно сильнее уменьшить излучение энергии из линии в окружающее пространство. Поэтому в реальных линиях, применяемых на практике, α _Σ <<α _м или α _Σ << α _д и α _Σ можно пренебречь по сравнению с α _м или α _д.

9.8.2. Затухание, обусловленное потерями в среде,

заполняющей линию

Если комплексная диэлектрическая проницаемость заполняющего линию диэлектрика равна ε = ε'-iε", то постоянная распространения в такой линии γ = i β, где β находят из (9.11) при замене ε на ε. При этом

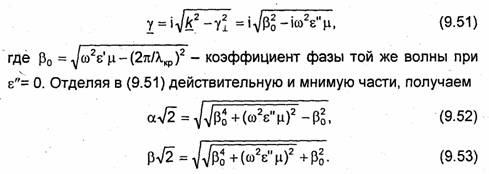
Отметим любопытный факт. Ранее было показано, что в линии без потерь Е-, Н- и гибридные волны на частотах f<f_кp не распространяются. Однако, как видно из (9.53), при наличии потерь эти волны могут распространяться при f=f_кр и даже на более низких частотах. Как видно из формулы (9.52), распространение волн в этом случае происходит со значительными потерями, независимо от того, что является причиной потерь.

При выводе формул (9.52) и (9.53) предполагалось, что учитываются потери, связанные с током проводимости и переменной поляризацией диэлектрика. Однако при распространении электромагнитной волны в слабо проводящих диэлектриках (воздух, стекло и др.) на достаточно высоких частотах (например, в оптическом диапазоне) затухание волны определяется также иными эффектами. На таких частотах величина кванта энергии становится соизмеримой с разностью энергий близко расположенных энергетических уровней атомов диэлектрика. Поэтому под влиянием электромагнитной волны может происходить переход электронов с более низкого энергетического уровня на более высокий, что сопровождается поглощением части энергии волны. Например, подобное поглощение наблюдается в парах воды на частотах 22...23 ГГц, а в молекулах кислорода на частотах, близких к 60 и 120 ГГц. В оптическом диапазоне возникает затухание волн, связанное с так называемым рэлеевским рассеянием [66].

9.8.3. Затухание, вызванное потерями в металлических элементах линии передачи

Анализ структуры поля в линиях передачи, сделанный в предположении идеальной проводимости ее металлических элементов, неточен для реальных линий с конечной проводимостью этих элементов. Однако так как проводимость металлических проводников весьма велика, то действительная структура поля волны мало отличается от структуры поля, полученной в предположении идеальной проводимости металлических элементов линии. Отличие в основном сводится к тому, что в соответствии с граничным условием Леонтовича-Щукина (7.52) у поверхности металлических частей линии передачи появляется весьма малая касательная составляющая вектора Е. Изменению структуры электрических силовых линий соответствует изменение структуры векторных линий магнитного поля. В частности, нормальная к поверхности металлических частей линии составляющая вектора Н не равна нулю. Однако, как уже отмечалось, эти изменения поля весьма малы, и обычно можно считать, что структура поля, найденная в приближении идеальной линии, практически не отличается от структуры поля в реальной линии. Изменение структуры токов в основном сводится к тому, что они в действительности текут не по поверхности, а проникают на некоторую глубину внутрь проводника.

Наличие отличных от нуля тангенциальных составляющих векторов Е и Н у поверхности металлических элементов линии передачи означает, что вектор Пойнтинга имеет составляющую, перпендикулярную этой поверхности, т.е. появляется поток энергии, направленный в металлические части линии передачи, и, следовательно, в них происходят джоулевы потери энергии (см.7.8.2).

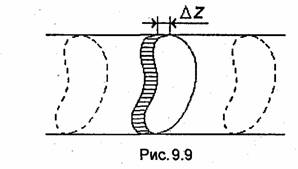
Выделим на поверхности металлических частей линии передачи участок длиной ∆z, как показано на рис. 9.9. Средняя за период мощность тепловых потерь на отрезке проводника длиной ∆z согласно (7.57)

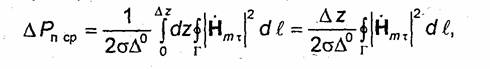
Подставляя (9.54) и (9.46) в (9.49), находим коэффициент ослабления, обусловленный потерями в металлических элементах линии передачи:

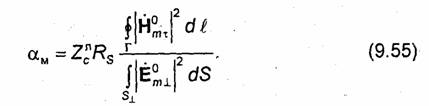
Как уже отмечалось, распределение векторов в линии передачи с металлическими элементами, обладающими конечной проводимостью, мало отличается от распределения тех же векторов в идеальной линии. Поэтому при вычислении α _м по формуле (9.55) можно использовать значения векторов  найденные при анализе идеальной линии передачи.

Гл а в а 10

НАПРАВЛЯЮЩИЕ СИСТЕМЫ

10.1. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД

10.1.1. Вывод формул для поля

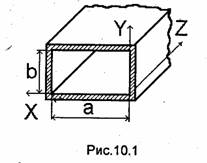
Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения (рис. 10.1). Предположим, что стенки волновода обладают бесконечной проводимостью, а заполняющая его среда - идеальный диэлектрик с параметрами ε и μ. В такой направляющей системе могут существовать волны Е и Н и не могут существовать TЕМ-волны (см. 9.4). На рис. 10.1 показаны используемая система координат и размеры а и b поперечного сечения волновода. Для определенности будем считать, что а ≥ b, а источники, создающие поле, расположены со стороны отрицательных значений переменной z за пределами рассматриваемой части линии передачи (созданная ими волна распространяется в положительном направлении оси Z). При а > b стенки с поперечными размерами а и b будем называть соответственно широкой и узкой стенками прямоугольного волновода.

Так как поперечные составляющие векторов поля выражаются через продольные (см. 9.2), то для вычисления поля волн Е и Н  достаточно определить составляющую Е_mz или Н_тг соответственно. Составляющие Ё_тz и Н_тz удовлетворяют уравнению Гельмгольца

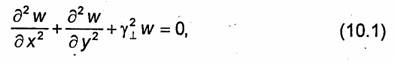
где функция w равна E_mz для Е-волн и H_mz- для H-волн,  - коэффициент фазы рассматриваемой волны. Правая часть уравнения (10.1) равна нулю, так как по предположению сторонние источники расположены за пределами рассматриваемой части волновода. Фактически задача состоит в нахождении так называемых собственных волн прямоугольного волновода.

Для решения уравнения (10.1) применим метод разделения переменных. Запишем функцию w в виде w= w(x, у, z, t) = = w°(x, y)exp[i(ωt- β z)]. Очевидно, что функция w°(x, y) также удовлетворяет уравнению (10.1). Представим ее в виде произведения двух функций, каждая из которых зависит только от одной переменной:

Отметим, что в случае Е-волн значения т = 0и n = 0 не годятся, так как при этом случае E_mz = 0 во всех точках внутри волновода.

Поперечные составляющие векторов поля выражаются через E_mz соотношениями (9.19) и (9.20). Введем обозначение А•С = = E_Oz и выпишем окончательные выражения для составляющих векторов поля Е-волн в прямоугольном волноводе:

Подчеркнем, что индекс т в формулах (10.10а) и (10.106) имеет совершенно разный смысл. В (10.10а) он указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в (10.106) индекс т - натуральное число, определяющее значение постоянной γ_х, как это следует из формулы (10.9).

Значение постоянной у_± находится из формул (10.4) и (10.9):

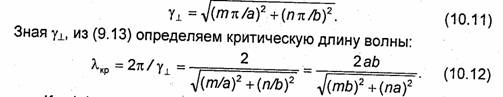
Коэффициент фазы р вычисляется по формуле (9.14).

Таким образом, все параметры, входящие в формулы для поля Е-волн, кроме постоянной Е_0z определены. При той постановке задачи, которая была здесь использована, постоянную E_Oz определить нельзя. Для ее нахождения требуются дополнительные данные: либо более конкретные сведения об источнике, создающем рассматриваемую волну, либо значение какой-нибудь составляющей векторов поля в точке, где эта составляющая отлична от нуля, либо задание мощности бегущей волны (т.е. задание среднего за период значения потока энергии через поперечное сечение волновода, соответствующего рассматриваемой волне). Для анализа вопросов, изучаемых в данной главе, конкретное значение постоянной E_Oz не требуется.

Прежде чем перейдем к анализу свойств поля Е-волн, описываемого выражениями (10.10), выведем формулы для поля Н-волн в прямоугольном волноводе. Волны Е и Н имеют много общих черт, и их свойства удобно анализировать совместно.

В случае Н-волн (H_z≠0, Ё_z=0) функция w = H_mz. Решение уравнения (10.1) строится так же, как для Е-волн. Изменяются только краевые условия. Требуя, чтобы касательные составляющие вектора Ё на стенках волновода обращались в нуль, имеем

Но искомой является функция w, поэтому выписанные краевые условия следует преобразовать в условия для функции w. Поперечные составляющие вектора Е_т выражаются через H_mz соотношением (9.14). Из этого соотношения и краевых условий (10.13) после перехода к функции w°(x, y) получаем

В отличие от (10.9) в случае Н-волн индексы т и п могут принимать нулевые значения. Однако они не могут равняться нулю одновременно: при этом составляющая Н_z не зависит от переменных х и у и вектор Ё будет тождественно равен нулю, что невозможно. Выпишем окончательные выражения для комплексных амплитуд составляющих векторов поля Н-волн в прямоугольном волноводе:

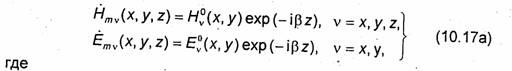
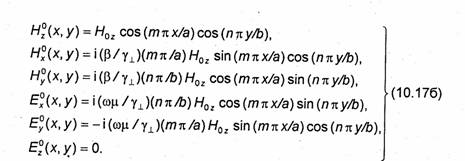
Аналогично случаю Е-волн в формулах (10.17а) индекс т указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в формулах (10.176) т связано с постоянной у_х соотношением (10.16).

Составляющие векторов поля Н-волн найдены с точностью до произвольного постоянного множителя H_oz , определение которого в рамках выбранной электродинамической модели невозможно (см. аналогичное замечание, сделанное при анализе Е-волн).

Легко показать, что поперечное волновое число γ_┴ и критическая длина волны λ_кр в случае Н-волн также определяются формулами (10.11) и (10.12) соответственно.

Перейдем к анализу свойств Е- и Н-волн в прямоугольном волноводе. Как видно из формул (10.10) и (10.17), в прямоугольном волноводе возможно существование различных Е- и Н-волн, структура поля которых зависит от значений индексов т и п. Каждая пара значений индексов т и п определяет свои волны, которые обозначают Е_тп (в случае Е-волн) или Н_тп (в случае Н-волн). При этом у Е-волн m≥1 и n≥ 1, а у Н-волн один из индексов может равняться нулю. Структура поля в поперечном сечении (при фиксированном значении   координаты z) аналогична структуре

стоячей волны, и ее можно характеризовать длинами волн λ_х = 2а/т и λу = 2b/п в направлениях осей X и У соответственно. Индекс m, таким образом, равен числу полуволн (λ_х /2), укладывающихся на поперечном размере а стенки, параллельной оси X. Аналогично индекс п равен числу полуволн (λ_х/2)- укладывающихся на поперечном размере b стенки, параллельной оси Y. Равенство нулю одного из индексов означает, что поле рассматриваемой волны не зависит от соответствующей координаты (при n = 0-от координаты х, а при n= 0-от координаты y). Изменение всех составляющих комплексных амплитуд векторов Ё и Н вдоль оси Z описывается множителем ехр (- iβz). Распространение волны происходит только при λ < λ_кр (предполагается, чтo в волноводе отсутствуют потери энергии). Критическая длина волны вычисляется по формуле (10.12). Она зависит от размеров а и b и от индексов т и п. При увеличении значений индексов т и n и фиксированных размерах а и b значение λ_кр уменьшается. Наибольшую λ_кр среди всех возможных волн при а > b имеет волна Н₁₀. Соответствующая ей λ_кр равна 2а. При а = b наибольшую λ_кр имеют две волны Н_ю и Н₀₁. Волну, имеющую наибольшую λ_кр,

называют основной волной рассматриваемой линии передачи (или волной низшего типа). Таким образом, при а > b основной волной прямоугольного волновода является волна Н₁₀.

Длина волны в волноводе Λ, фазовая скорость v_ф и скорость распространения энергии v_э вычисляются соответственно по формулам (9.17), (9.18) и (9.43), одинаковым для Е- и Н-волн. Характеристическое сопротивление Е-волн вычисляется по формуле (9.21), а Н-волн - по формуле (9.26).

Формулы (10.10) и (10.17) позволяют рассчитать и изобразить графически структуру поля (линии векторов Е и Н) любой из волн Е_тп или Н_тп, распространяющихся в волноводе. В качестве примера на рис. 10.2 и 10.3 показаны структуры полей волн Е₁₁ и Н₁₀ соответственно в некоторый фиксированный момент времени в

случае λ < λ_кр для трех сечений волновода. С течением времени картины, изображающие структуру полей в продольных сечениях (сечения 2 и 3 на рис. 10.2 и 10.3), перемещаются вдоль оси Z с фазовой скоростью соответствующей волны.

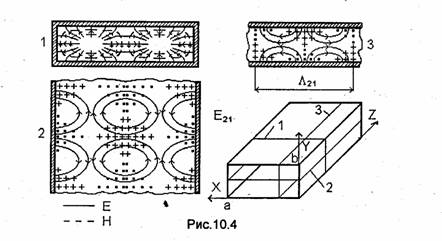
Отметим, что, зная структуру поля волны Е₁₁, легко построить структуру поля волны Е_тп при любых значениях индексов тип. Например, структура поля волны Е₂₁ представляет собой объединение структур двух волн Е₁₁ (рис. 10.4). Для построения структуры волны Е_тп нужно мысленно разделить волновод на т •п "волноводных секций". Структура поля в каждой секции будет соответствовать структуре поля волны Е₁₁, а линии векторов будут непрерывно переходить из одной "секции" в другую. Аналогично волну Н₂₀ можно представить как бы состоящей из двух волн Н₁₀.

Структура поля волны Н₂₀ в поперечном сечении показана на рис. 10.5.

При λ> λ_кр волна не распространяется: образуется стоячая волна, амплитуды составляющих векторов Е и Н которой экспоненциально убывают вдоль оси Z (в этом случае  Напомним, что анализ проводится в предположении отсутствия потерь.

10.1.2. Основная волна прямоугольного волновода

Свойства волны. Как уже отмечалось, при а> b основной волной прямоугольного волновода является волна Н₁₀. Она имеет наибольшую критическую длину волны, равную 2а. На заданной частоте размеры поперечного сечения волновода, при которых возможна передача энергии по прямоугольному волноводу, для этой волны можно выбрать наименьшими. При этом волновод будет иметь наименьшие массу, габариты и стоимость.

Полагая в (10.17) т=1 и n = 0 и учитывая формулы (10.16), получаем следующие выражения для составляющих комплексных амплитуд векторов Е и Н в случае волны Н₁₀:

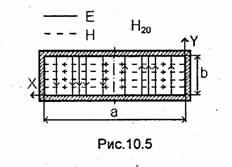
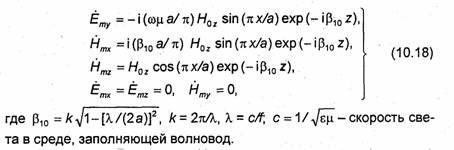
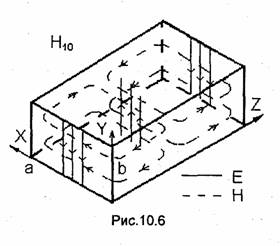
Структура поля волны H₁₀, построенная в соответствии с формулами (10.18), показана на рис.10.3 и 10.6. Остановимся на картине распределения поля волны H₁₀ в плоскостях, параллельных широким стенкам волновода.

Согласно уравнениям Максвелла замкнутые линии магнитного поля должны охватывать токи проводимости или токи смещения. В волноводе замкнутые линии магнитного поля пронизываются токами смещения. В случае волны Н₁₀ (см. рис. 10.6) линии магнитного поля охватывают токи смещения, текущие между широкими стенками параллельно оси Y. В распространяющейся волне максимальная плотность тока смещения получается в центре замкнутых магнитных силовых -линий, где напряженность электрического поля равна нулю.

Это следует из того, что вектор плотности тока смещения  и, следовательно, сдвинут по фазе относительно вектора напряженности электрического поля на угол π/2, т.е. расстояние между максимумом плотности тока смещения и максимумом напряженности электрического поля вдоль оси Z в фиксированный момент времени равно Λ/4.

Фазовая скорость V_ф, скорость распространения энергии V_Э, длина волны в волноводе Λ и характеристическое сопротивление Z_c в случае волны Н₁₀ вычисляются по формулам

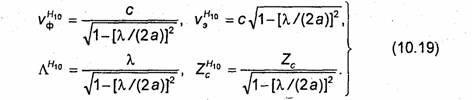
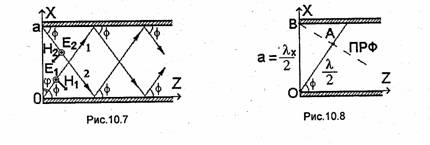
В соответствии с концепцией Бриллюэна (см. гл.9) представим волну Н₁₀ в виде суперпозиции парциальных ТЕМ-волн.

Поле волны Н₁₀ не зависит от переменной у. Следовательно, поля парциальных волн также не должны зависеть от у, т.е. парциальные ТЕМ-волны должны распространяться, отражаясь от боковых (х = 0 и х = а) стенок волновода.

Пусть парциальная волна распространяется под углом ф к оси Z (волна 1 на рис.10.7). Комплексная амплитуда вектора напряженности электрического поля этой волны Ё_т1 определяется выражением

где А - некоторая (в общем случае комплексная) постоянная. Электрическое поле волны Н₁₀ имеет пучность на плоскости х = а/2 и симметрично относительно этой плоскости. Поэтому кроме волны (10.20) должна существовать еще одна парциальная ТЕМ-волна (волна 2), распространяющаяся, как показано на рис.10.7. Комплексная амплитуда напряженности электрического поля этой волны равна Для образования пучности электрического поля в плоскости х = а/2 необходимо, чтобы векторы Ё_т1 и Ё_т2 при х = а/2 складывались синфазно. Для этого достаточно, например, чтобы фаза вектора Ё_т2 в точке (а, 0, 0) совпадала с фазой вектора Ё_т1 в точке (0, 0, 0). С учетом данного условия вектор

Для определения угла ф учтем, что на поперечном размере а широкой стенки волновода должна укладываться половина длины волны λ_х, а на отрезке ОА - половина длины волны ТЕМ (λI2). Из треугольника ОАВ (см. рис. 10.8) следует равенство

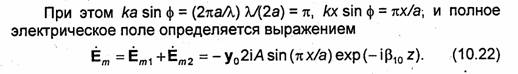
Полученный результат отличается от выражения для Ё_ту в формуле (10.17) лишь постоянным коэффициентом, что несущественно, так как формулы (10.17) были найдены с точностью до произвольного постоянного множителя. Аналогично вычисляются

составляющие Н_тх и Hmz.  Они отличаются от соответствующих выражений в (10.17) лишь тем же постоянным множителем.

      Из рис. 10.8 и формулы (10.21) видно, что по мере повышения частоты (уменьшения X) уменьшается угол ф и, следовательно, тем меньше    по   абсолютной    векличине   становится    продольная составляющая  H_mz по сравнению с поперечной составляющей

Н_тх, т.е. структура волны Н₁₀ начинает приближаться к структуре волны ТЕМ. Одновременно, как следует из (10.19), уменьшается разница между  и с. Аналогично можно интерпретировать и другие типы волн в прямоугольном волноводе.

10.1.3. Токи на стенках прямоугольного волновода

Каждому типу волны, распространяющейся в волноводе, соответствует определенная структура токов проводимости на его стенках. В случае идеально проводящих стенок токи проводимости являются поверхностными, а комплексная амплитуда их плотности

j_Sm вычисляется по формуле

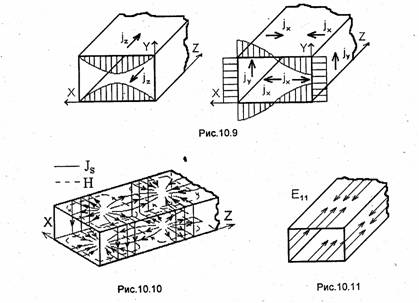
Распределение составляющих плотности токов проводимости по контуру Г и структура линий вектора j_s на стенках волновода для волны Н₁₀ показаны на рис. 10.9 и 10.10 соответственно. В случае волны Е₁₁ по стенкам волновода текут только продольные токи (рис. 10.11).

10.1.4.   Выбор   размеров   поперечного   сечения   прямоугольного волновода из условия одноволновой передачи

Как было показано выше, в прямоугольном волноводе возможно существование бесконечного числа типов волн, отличающихся друг от друга структурой электрического и магнитного полей, критическими частотами, фазовой скоростью и другими параметрами. Однако при конструировании линий передачи обычно принимают все меры к тому, чтобы энергия переносилась каким-либо одним типом волны. Объясняется это тем, что различным типам волн соответствуют различные групповые скорости. Поэтому при передаче сигнала несколькими типами волн один и тот же сигнал приходит в точку приема в виде нескольких смещенных во времени сигналов, что приводит к его искажению и увеличению уровня шумов. Характер искажений зависит от способа модуляции, вида и скорости передаваемой информации и других факторов.

Передачу энергии одним типом волны наиболее просто обеспечить, если в качестве этого типа использовать основную волну, имеющую наибольшую λ_кр. Для этого достаточно так выбрать поперечные размеры линии, чтобы на любой частоте рабочего диапазона длина волны электромагнитных колебаний не превышала критической длины основной волны (λ_{кр (1)}), но была больше критической длины волны первого высшего типа (λ_кр(2) ).Такой режим называют одноволновым. Полосу частот, в пределах которой сохраняется одноволновый режим, обычно характеризуют коэффициентом широкополосности

Частотный диапазон использования прямоугольных волноводов, охватывающий частоты от 400 МГц до 140 ГГц, в соответствии с рекомендацией Международной электротехнической комиссии разбит на 28 поддиапазонов, частично перекрывающих друг друга, и для каждого поддиапазона рекомендованы стандартные размеры волновода [33]. На частотах порядка 500 МГц и ниже прямоугольные волноводы применяются редко из-за значительных габаритов и массы. Например, отрезок волновода из алюминия длиной 1 м при размерах поперечного сечения 457x228,5 мм (λ_о= 60 см) и с толщиной стенок 3 мм имеет массу около 11 кг, а медный того же сечения и с той же толщиной стенок - около 36 кг.

10.1.5. Передача энергии по прямоугольному волноводу

Мощность бегущей волны (см.9.7.1) вычисляется по формуле (9.46). В случае волны /-/₁₀ из формул (9.46) и (10.17) получаем

где Е₀= (ωμa/π)Н_oz- амплитудное значение напряженности электрического поля волны Н₁₀. При выводе формулы (10.26) учтено, что ωμ = kZ_c.  При стандартных размерах волновода (а = 0,75λ, b = 0,5а), подставляя предельное значение Е_о= 30 кВ/см, находим, что предельная мощность волны Н₁₀ равна P_npeдH10 = 125λ²кВт, где длина волны выражена в сантиметрах. Например, при λ = 30 см предельная мощность Р_предН10 =112 МВт. Соответственно допустимая мощность (см.9.7.1) Р_допн₁₀ =28 МВт. Как видно, в дециметровом  диапазоне  по  прямоугольному  волноводу  стандартного сечения можно передавать весьма значительную мощность. Однако по мере повышения частоты допустимая мощность быстро уменьшается и при λ = 1 см не превышает 30...45 кВт.

Когда методы повышения электрической прочности, указанные в 9.7.2, почему-либо неприемлемы, то, как следует из формулы (10.26), предельную мощность можно существенно повысить, увеличив площадь поперечного сечения волновода по сравнению со стандартными.

Если размеры волновода увеличены настолько, что в части или во всем рабочем диапазоне волновод оказывается в многоволновом режиме, то необходимо принять специальные меры для предотвращения распространения всех типов волн, кроме Н₁₀ (см. 13.2).

Коэффициент ослабления α_м, обусловленный потерями энергии в металлических стенках волновода, вычисляется по формуле (9.49) с учетом (9.46) и (9.54). Ограничимся вычислением α_м для волны Н₁₀. Подставляя (10.18) в (9.46) и (9.54), находим значения Р_ср и Р_{п ср} соответственно. Подставляя затем полученные выражения в (9.49), после несложных преобразований имеем

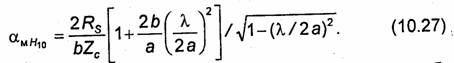
Аналогично выводятся формулы для коэффициентов ослабления, соответствующих другим типам волн. Расчеты показывают, что наименьшие потери в прямоугольном волноводе имеют место при передаче энергии волной Н₁₀. На рис.10.12 показаны графики зависимости коэффициента ослабления α_м (в дБ/км) от частоты для волн Н₁₀, Е₁₁ и Н₂₀ в случае медного волновода при а = 51 мм и b = 25 мм. Как видно из приведенных графиков, потери энергии в волноводе резко возрастают при приближении частоты к критической.

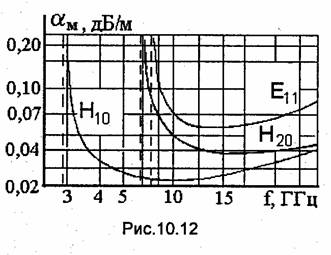
Это свойство, характерное для всех металлических волноводов, легко объясняется на основе концепции парциальных волн. Действительно, у Е- и Н-волн парциальные волны распространяются по ломаным линиям, многократно отражаясь от поверхности металлических стенок. На частотах, близких к критической, угол падения парциальных волн на металлическую поверхность мало отличается от нулевого (угол ф на рис. 10.7 близок к π/2). Но чем ближе угол падения к нулю, тем большее число отражений испытывают парциальные волны при своем движении на некотором отрезке линии. При каждом отражении часть энергии электромагнитной волны теряется из-за неидеальной проводимости металла (появляется преломленная волна). Поэтому потери в проводниках линии, перенос энергии по которым осуществляется Е- и Н-волнами, растут по мере приближения . к критической частоте. Вслед за резким падением затухания при удалении от критической частоты (рис.10.12) снова начинается его монотонное возрастание, вызванное увеличением поверхностного сопротивления металла R_s с ростом частоты.

Отметим, что, как следует из формулы (10.27), в. коротковолновой части сантиметрового диапазона потери в стандартных волноводах весьма велики. Например, при λ = λ₀=0,01 м в стандартном волноводе с медными стенками  = 0,55 дБ/м,

т.е. при длине линии всего 10 м потери энергии будут составлять 5,5 дБ (более 70 % входящей мощности). Объясняется это тем, что при заданной мощности уменьшение поперечных размеров волновода сопровождается возрастанием плотности поверхностного тока проводимости в его стенках и соответственно возрастают потери. Поэтому на волнах порядка 1 см и короче применение прямоугольных волноводов целесообразно только в виде коротких отрезков. В некоторых случаях, чтобы уменьшить потери, размеры поперечного сечения волновода увеличивают по сравнению со стандартными.

10.2. КРУГЛЫЙ ВОЛНОВОД

10.2.1. Вывод формул для поля

При анализе волн в круглом волноводе (рис. 10.13) будем считать, что заполняющая его среда - идеальный диэлектрик с параметрами ε и μ, а оболочка обладает бесконечной проводимостью. В таком волноводе возможно раздельное существование Е- и /-/-волн и невозможно существование ТЕМ-волн (см. 9.4). При анализе естественно использовать цилиндрическую систему координат, совместив ось Z с продольной

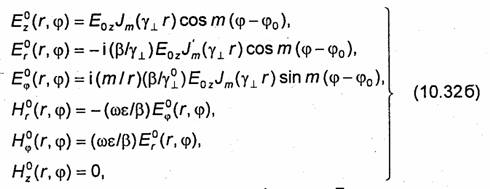
а штрих означает дифференцирование функции Бесселя по всему аргументу.

Так же как в формулах для поля в прямоугольном волноводе, индекс т в формулах (10.32а) и (10.326) имеет разный смысл. В (10.32а) он означает, что записана комплексная амплитуда рассматриваемой функции, а в (10.326) т- определяет порядок функции Бесселя.

Входящая в (10.326) постоянная ф₀ влияет только на начало отсчета угла φ, ее изменение соответствует повороту структуры поля вокруг оси Z. В рамках используемой физико-математической модели постоянные E_Oz и φ₀ определить нельзя. Для их нахождения требуются дополнительные данные об источнике, создающем поле в волноводе (о мощности бегущей волны, ориентации вектора γ_┴ и т.д.). Аналогичный вопрос обсуждался ранее при анализе формул (10.16) и (10.17).

Чтобы найти неизвестную постоянную у_х,  используем граничное условие (1.104). В рассматриваемом случае из него следует равенство

где а - радиус волновода (см. рис. 10.13). Подставляя выражение для Е_z°( r, φ,) из (10.326) в (10.33), получаем

J_m (γ_┴ a) =0                                             (10.34)

Имеется бесконечное множество значений аргумента, при которых функция Бесселя равна нулю. Эти значения называют корнями функции Бесселя. Обозначая n-й корень функции Бесселя m-го порядка через v_mn^E (см. рис.10.14), из (10.34) находим

Параметр β вычисляется по формуле (9.14).

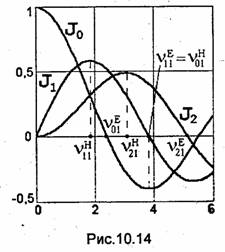
Как видно, в круглом волноводе возможно существование Е-волн различной структуры. Наименование этих волн производится в соответствии с обозначением корней уравнения {10.34). Например, корню соответствует волна Е₀₁ корню v₁₂^Е -волна Е₁₂, корню v_mn^Е - волна Е_тп.

Зависимость структуры поля волны от угла φ определяется индексом т.  Поперечное сечение волновода можно условно разделить на т секторов с одинаковой структурой поля в каждом секторе: поле волны периодично по углу φ с периодом 2π/m. Индекс т, таким образом, равен числу периодов структуры поля волны, укладывающихся на интервале [0, 2π] изменения угла φ. Равенство нулю индекса т означает, что структура поля волны обладает осевой симметрией (не зависит от угла φ).

На распределение составляющих векторов поля вдоль радиуса в интервале [0, а] влияют оба индекса т и п. При этом т определяет порядок функции Бесселя, а п-число вариаций составляющих векторов поля при изменении г от 0 до а: при /7=1 составляющие векторов поля не изменяют знак (одна вариация), при л = 2 они один раз изменяют знак (две вариации) и т.д.

Каждому типу волны соответствует своя критическая длина волны, связанная с постоянной у_х соотношением (10.33). В рассматриваемом случае

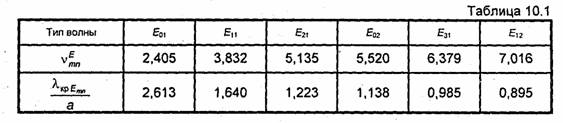
Несколько первых корней функций Бесселя v_mn^E в порядке их возрастания и соответствующие критические длины волн, рассчитанные по формуле (10.36), приведены в табл. 10.1. Низшим типом среди волн Е в круглом волноводе является волна Е₀1-

Фазовая скорость, скорость распространения энергии, длина волны в волноводе и характеристическое сопротивление рассчитываются по формулам (9.18), (9.43), (9.17) и (9.21) соответственно. На рис. 10.15 показана структура поля волны Е₀₁.

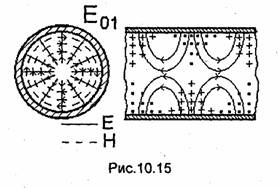
Как видно, в круглом волноводе возможно существование Н-волн различной структуры, которые принято обозначать Н_тп. Нумерация Н-волн аналогична нумерации волн Е_тп. Индекс т совпадает с порядком функции Бесселя, а n-с номером нуля первой производной функции Бесселя т-го порядка. Так же как и в случае E-волн, структура поля волны Н_тп периодична по углу ср с периодом 2π/m, т.е. индекс т равен числу периодов структуры поля волны Н_тп, укладывающихся на интервале [0, 2π] изменения угла φ. Равенство нулю индекса т означает, что поле волны не зависит от угла φ. Индекс л равен числу вариаций составляющих векторов поля вдоль радиуса волновода.

Несколько первых корней v_mn^H в порядке их возрастания и соответствующие им критические длины волн, рассчитанные по формуле

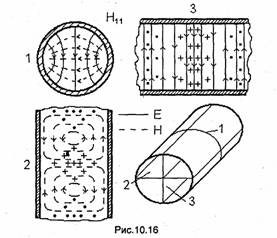
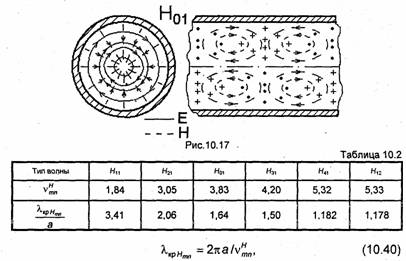
приведены в табл. 10.2. Низшим типом среди не только волн Н, но и всех волн в круглом волноводе, как следует из табл. 10.1 и 10.2, является волна Нц. Интересно отметить, что структура поля этой волны (рис. 10.16) близка к структуре поля волны Н₁₀ в прямоугольном волноводе (см. рис. 10.3), также имеющей наибольшую критическую длину волны. На рис. 10.17 показана структура поля волны Н₀₁.

Параметры H-волн β, v_ф, v_Э и Λ вычисляются по формулам (9.14), (9.18), (9.43) и (9.17) соответственно, а характеристическое сопротивление находится по формуле (9.26).

10.2.2. Токи на стенках круглого волновода

Плотность токов на стенках круглого волновода j_Sm  в соответствии с граничным условием (1.110) определяется формулой

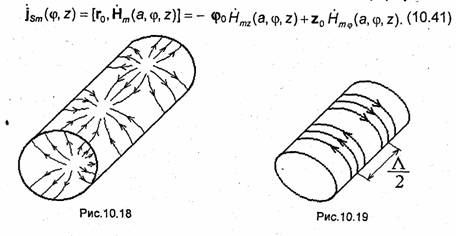
Из формул (10.41) и (10.37) следует, что при распространении по волноводу основной волны Н₁₁ на его стенках текут и поперечные, и продольные токи (рис.10.18), а волна Н₀₁ возбуждает только поперечные токи (рис. 10.19). В случае волны Е₀₁, как следует из формул (10.41) и (10.32), текут только продольные токи, равномерно распределенные по периметру волновода.

10.2.3. Передача энергии по круглому волноводу

Основной волной круглого волновода является волна Н₁₁, а первым высшим типом – Е₀₁ Поэтому в соответствии с данными табл.10.1 и 10.2 условие одноволновости имеет вид 2,61а<λ<3,41а

Коэффициент широкополосности, определяемый по формуле (10.24), ζ = 1,3, т.е. существенно ниже, чем у прямоугольного волновода.

Мощность, переносимая волной по круглому волноводу (мощность бегущей волны), рассчитывается по формуле (9.46). Вычисляя входящие в эту формулу интегралы, для волны Н„ получаем:

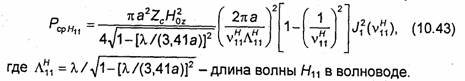
Коэффициент ослабления α _мсоответствующий волне Н₁₁, вычисляется по формуле

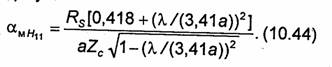
Формулы для коэффициента ослабления α_м, соответствующие другим типам волн, могут быть получены из (9.49). Окончательные выражения приведены, например, в [1]. Графики зависимости α_м (в дБ/м) от частоты для волн Н₁₁, Е₀₁ и H₀₁ в круглом   медном волноводе для случая а = 25,4 мм показаны на рис. 10.20. Как видно, для волн Н₁₁ и Еo₁ они аналогичны графикам, приведенным на рис.10.12 для случая  волн  в  прямоугольном  волноводе.   График,  характеризующий зависимость коэффициента, ослабления от частоты для волны Н₀₁ в круглом волноводе, имеет существенное отличие от графиков для  волн  Н₁₁ и  Е₀₁.   У этих  волн  коэффициент α_м неограниченно возрастает при f+f_Kp и f→∞. Указанные особенности поведения α_м объясняются так же, как в случае прямоугольного волновода.  Поведение коэффициента ослабления волны Н₀₁ в круглом волноводе при увеличении частоты имеет иной характер, а именно коэффициент α_м для этой волны монотонно убывает с ростом частоты. Эта особенность объясняется тем, что у волны Ho₁ в круглом волноводе вектор плотности поверхностного тока проводимости   не  имеет  продольной  составляющей   (j _Smz=0). Отличная от нуля составляющая j_Smφ) возбуждается продольной составляющей напряженности магнитного поля  H_mz(a, φ,z).   При повышении частоты в волноводе с фиксированными размерами поперечного сечения структура поля любой волны приближается к структуре поля ТЕМ-волны, у которой Н_z = 0.  Следовательно, у волны   Н₀₁   при   повышении   частоты   H_mz -> 0 и   одновременно стремится к нулю плотность поперечных токов проводимости. Но это означает, что потери должны непрерывно уменьшаться. Как показывает численный расчет, потери в круглом волноводе на волне Н₀₁ меньше потерь в волноводе того же радиуса на волне Н₁₁, если только а/λ>2, а существенный выигрыш достигается при а/λ>3...4.

10.3. ВОЛНОВОДЫ СЛОЖНОЙ ФОРМЫ

10.3.1. П-и Н-образные волноводы

Одноволновый режим в стандартном прямоугольном волноводе, как было показано в 10.1.4, сохраняется в двукратной полосе частот. Однако используемый на практике диапазон частот обычно не превышает полуторакратного, поскольку в области частот, близких к критической, велики тепловые потери и мала допустимая мощность.                                             

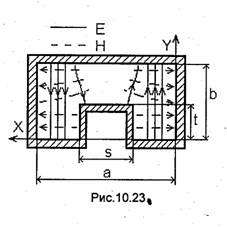
В значительно более широкой полосе частот можно сохранить одноволновый режим при использовании П- и Н-образных волноводов (см. рис.10.21 и 10.22), которые часто называют более коротко: П- и Н-волноводы. Если так подобрать поперечные размеры этих волноводов, чтобы коэффициент их широкополосное был равен коэффициенту широкополосности прямоугольного волновода, то П- и Н-волноводы будут иметь меньшие габариты, чем прямоугольный волновод. На рис.10.21 и 10.23 показана структура электрического поля соответственно волн Н₁₀ и Н₂₀ в поперечном сечении П-волновода. Эти волны условно названы Н₁₀ и Н₂₀. Основанием для этого является то, что при плавном уменьшении высоты прямоугольного выступа t (обычно его называют ребром) они постепенно преобразуются в волны /-/₁₀ и Н₂о прямоугольного волновода.

При равных размерах а и b расширение рабочей полосы частот у Н- и П-волноводов по сравнению с прямоугольным достигается за счет того, что они имеют практически равные критические частоты для волны Н₂₀, а критическая частота для волны Н_ю в Н- и П-волноводах существенно ниже, чем в прямоугольных. Сказанное можно объяснить следующим образом. Ребро (или ребра у /-/-волновода) находится в пучности напряженности электрического поля .волны Н₁₀, где концентрация электромагнитного  поля относительно велика. Наличие ребра

приводит к еще большей концентрации поля и энергии в этом месте. Поэтому свойства волны и, в частности, критическая частота определяются в основном структурой поля в зазоре. Пока отношение ширины ребра s (рис. 10.21) к ширине волновода а не превышает 0,2...0,3, энергия электрического и магнитного полей вблизи боковых стенок волновода мала и мала продольная составляющая H_z магнитного поля. Распространяющаяся в П-волноводе волна близка по структуре к ТЕМ-волне. Поэтому введение ребра приближает структуру волны Н₁₀ к структуре ТЕМ-волны и приводит к понижению критической частоты волны Н₁₀. (Напомним, что у ТЕМ-волны f_кp = 0 (см. 9.4)).

Чем больше высота t ребра, т.е. чем ближе отношение t/b к единице, тем выше концентрация поля в зазоре и тем, следовательно, ниже критическая частота волны Н10- В то же время влияние относительно узкого (s/a < 0,2...0,3) ребра (или ребер в Н-волноводе) на критическую частоту волны Н₂о незначительно, так как ребро вводится в сечение, где напряженность электрического поля волны Н₂о мала (рис.10.23). Поэтому при s/a ≤ 0,2...0,3 коэффициент широкополосности ζ Н- и П-волно-водов существенно выше, чем прямоугольного волновода с теми же размерами а и b. Дальнейшее увеличение отношения s/a приводит к уменьшению коэффициента широкополосности, так как боковые стенки волновода приближаются к краям ребер, возрастает концентрация энергии полей вблизи боковых стенок и увеличивается продольная составляющая Н_z напряженности магнитного поля, повышается критическая частота волны Н₁₀, уменьшается коэффициент широкополосности.

Недостатком Н- и П-волноводов являются повышенный по сравнению с прямоугольным волноводом уровень потерь и пониженная электрическая прочность. Чем больше высота ребра t, тем меньше предельная мощность и выше потери. Поэтому обычно применяют Н- и П-волноводы с ζ≤4.

10.3.2. Эллиптические волноводы

Волна Н₁₁ в круглом волноводе описывается формулами (10.37) при т=1 и n = 1. В эти формулы входит угол ф₀, изменение которого соответствует повороту структуры поля волны вокруг оси Z, т.е. к изменению ориентации (поляризации) вектора Е на оси волновода. Будем называть плоскостью поляризации волны диаметральное сечение волновода, содержащее вектор Е. У волны 1, показанной на рис.10.24,а, угол φ_О=О и входящая в выражение для Н°_zфункция cos (φ - φ₀) = cos φ, а плоскость поляризации совпадает с плоскостью XOZ. У волны 2 (рис.10.24, б) Фо = л/2 и cos (ф - ф₀) = sin ф, а плоскость поляризации совпадает с плоскостью YOZ. Волны 1 и 2 принято называть волнами Н₁₁^с и H₁₁^s соответственно. Критические частоты этих волн и параметры v_ф, v₃, Λ и др. совпадают. Это явление называют поляризационным вырождением.

Наличие в волноводе каких-либо нерегулярностей (несимметричное соединение отрезков волновода, дефекты изготовления и др.) может привести к частичному преобразованию одной волны в другую. При этом если на входе волновода была, например, одна волна Н₁₁^с, то на его выходе помимо волны Н₁₁^с появится волна Н₁₁^s Суммарный вектор Е на оси волновода будет иметь эллиптическую поляризацию, причем большая ось эллипса будет повернута на некоторый угол относительно оси X. Таким образом, при поляризационном вырождении плоскость поляризации оказывается неустойчивой. Этот эффект отсутствует в эллиптических волноводах (рис. 10.25).

Строгий анализ волн в эллиптическом волноводе требует решения уравнений Гельмгольца (9.2), записанных в эллиптической системе координат. Эти решения выражаются через функции Матье (см., например, [24]) и здесь не приводятся. Качественное представление о структуре поля волн в эллиптическом волноводе можно  получить, рассматривая его как деформацию

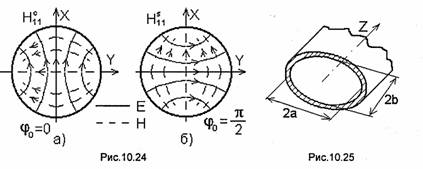
круглого волновода. При этом волны Н₁₁^с (рис.10.24,а) и Н₁₁^s (рис.10.24,б) круглого волновода преобразуются в волны Н₁₁^с рис.10.26,а) и Н₁₁^s (рис.10.26,б) эллиптического волновода. Критические длины этих волн зависят от эксцентриситета  e где а и b - большая и малая полуоси эллипса (рис.10.25). При небольшой эллиптичности    увеличением   эксцентриситета   различие  между    возрастает (рис. 10.27). Основной волной эллиптического волновода является волна Н₁₁^с. Ее критическая частота может быть рассчитана по приближенной формуле [64]

где f - частота, ГГц; а - большая полуось, см. Погрешность определения f к_Р по формуле (10.45) не превышает 1 %.

Обычно используют волноводы с отношением b/а = 0,5...0,6, при этом обеспечивается наибольшая полоса одномодового режима при относительно малом затухании. Например, при b/а = 0,5 критическая частота первого высшего типа (в этом случае им является волна Н₂₁^с, а не Н₁₁^s) в 1,82 раза превышает критическую частоту основной волны, а затухание на основной волне в эллиптическом волноводе оказывается меньше, чем в прямоугольном с таким же периметром.

В антенной технике нашли применение также гибкие гофрированные эллиптические волноводы. Они выпускаются промышленностью в виде отрезков длиной в несколько сотен метров, намотанных на кабельные барабаны.

10.4. КОАКСИАЛЬНАЯ ЛИНИЯ

10.4.1. TEМ-волна

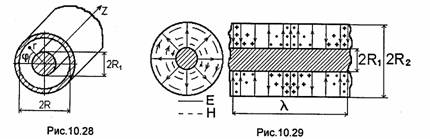
Коаксиальная линия (рис. 10.28) является направляющей системой закрытого типа, состоящей из двух соосных проводников, изолированных друг от друга. Как обычно, будем считать, что проводники обладают бесконечно большой проводимостью, а пространство между ними заполнено идеальным диэлектриком с параметрами ε и μ. При этих предположениях в коаксиальной линии могут распространяться волны ТЕМ, Е и Н. Так как то во всех линиях, в которых может распространяться ТЕМ-волна, эта волна является основной.

Совместим ось Z цилиндрической системы координат r, φ, z с осью внутреннего проводника коаксиальной линии (рис. 10.28). Векторы Е и Н ТЕМ-волны представим в виде

Формулы (10.46) справедливы в области R₁≤ r ≤R_2l где R₁-радиус центрального проводника, а R₂-внутренний радиус внешнего проводника. Структура поля ТЕМ-волны в коаксиальной линии показана на рис. 10.29. Как и у любой другой TЕМ-волны, фазовая скорость и скорость распространения энергии TЕМ-волны в коаксиальной линии равны скорости света в среде, заполняющей линию.

Так как поле в поперечном сечении линии (векторы Е° и Н°) у ТЕМ- волны имеет потенциальный характер, можно говорить о токе и напряжении в коаксиальной линии. Комплексные амплитуды тока и разности потенциалов между центральным и внешним проводниками равны соответственно i_m =/°exp(-ikz) и

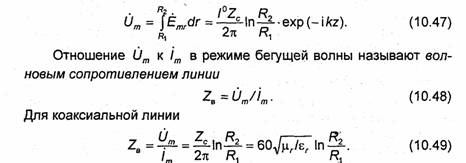
Отметим, что волновое сопротивление линии можно выразить через ее погонную емкость. В случае ТЕМ -волны в любой однородной идеальной линии текут только продольные поверхностные токи. Их плотность js связана с плотностью поверхностных зарядов p_s уравнением непрерывности divj_s=-дρ_s/дf, которое можно переписать в виде Интегрируя последнее равенство по контуру поперечного сечения проводника, по которому течет рассматриваемый ток, получаем  где Q_m-комплексная амплитуда заряда на единицу длины проводника. Учитывая формулу (3.72), получаем

где C₁ - погонная емкость линии. В случае коаксиальной линии С₁ определяется формулой (3.76), в которой нужно только положить  Подставляя затем (3.76) в (10.50), приходим к формуле (10.49).

Внутренний проводник коаксиальной линии может быть сплошным, сплетенным из отдельных проволочек, либо трубчатым. Обычно этот проводник выполняется из меди или с целью увеличения механической прочности из биметаллической проволоки (стальная проволока, покрытая слоем меди). Внешний проводник в зависимости от назначения линии представляет собой либо полую трубу (рис.10.30) - жесткая коаксиальная линия, либо выполняется в виде оплетки (рис.10.31) из медной проволоки или ленты - гибкий коаксиальный кабель.

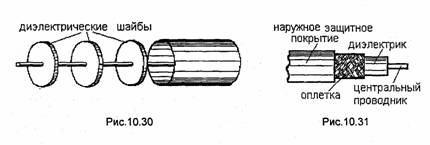
Изоляция гибких радиочастотных коаксиальных линий выполняется либо из сплошного диэлектрика (рис. 10.31) с малыми потерями (полиэтилен, фторопласт и др.), либо в виде диэлектрических шайб (рис.10.30). Более подробно конструкции коаксиальных линий описаны в [67] и [68].

10.4.2. Электрические и магнитные волны в коаксиальной линии

Формулы для поля Е- и Н-волн в коаксиальной линии выводятся так же, как в случае круглого волновода. Однако при анализе волн в коаксиальной линии постоянную D в формуле (10.31) нельзя считать равной нулю, так как в области R₁≤r≤R₂ функция Неймана является ограниченной. В случае Е-волн из условий E_z°(R₁,φ) = 0 и E_z°(R_2l, φ) = 0 приходим к трансцендентному уравнению:

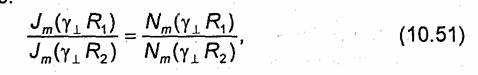
из которого находится величина  В случае Н-волн можно показать, что значения поперечного волнового числа являются корнями трансцендентного уравнения:

Корни уравнений (10.51) и (10.52) находятся численными методами.

Как показывает анализ уравнений (10.52) и (10.51), первым высшим типом волны в коаксиальной линии является при любом диаметре внутреннего проводника волна Н₁₁. Структура этой волны в поперечном сечении линии показана на рис. 10.32. Критическую частоту волны Н₁₁ в коаксиальной линии можно определить

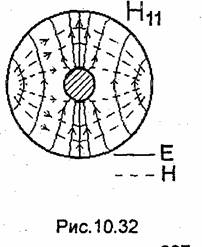
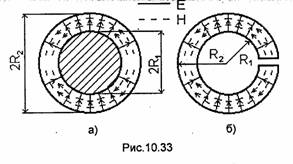
достаточно точно, не решая уравнения (10.52). Действительно, если Ri = 0, то коаксиальная линия превращается в круглый волновод, низшим типом волны в котором является волна Н₁₁. Введение вдоль оси круглого волновода тонкого металлического стержня, как это имеет место в коаксиальной линии, слабо влияет на распространение волны Н₁₁ ввиду отсутствия у нее продольных составляющих вектора Е. Поэтому при малых значениях R₁ критическая длина волны Н₁₁ в коаксиальной линии приближенно равна критической длине волны Н₁₁ в круглом волноводе, т.е.

Рассмотрим другой предельный случай, когда R₁ = R₂. Структура поля волны Н₁₁ в плоскости поперечного сечения такой коаксиальной линии изображена на рис. 10.33, а. Для сравнения рядом (рис. 10.33, б) построена структура поля волны Н₂₀ в прямоугольном волноводе, изогнутом по окружности большого радиуса

(R₁>>b, где b = R₂- R₁ - размер узкой стенки прямоугольного волновода). Почти полное совпадение этих структур позволяет считать, что критические частоты волны Н₁₁ в коаксиальной линии при R₁  →R₂ и волны Н₂₀ в прямоугольном волноводе также совпадают. Критическая длина волны Н₂₀ равна поперечному размеру широкой стенки а прямоугольного волновода. В изогнутом волноводе   можно   считать   а = π (R₁ + R₂).   Следовательно,   при R₁  →R₂

При R₁  <<R₂ формула (10.54) дает значение Х_крН11 =3,14R_2,

что менее чем на 10 % отличается от значения, вычисленного по формуле (10.53). Таким образом, можно без большой погрешности пользоваться формулой (10.54) не только при R₁ ≈R₂, но и при произвольных значениях R_{1  И} R_2.

10.4.3. Передача энергии по коаксиальной линии

В коаксиальной линии одноволновый режим сохраняется при  λ> λ_крН11 или с учетом формулы (10.54) при

Мощность, переносимая ТЕМ-волной по коаксиальной линии, в соответствии с (9.46) и

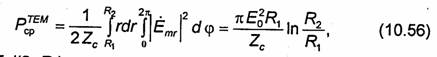
где Е_о = /°Z_с  (2 π R1)- амплитуда  напряженности электрического поля на поверхности внутреннего проводника (наибольшее значение составляющей Е_r). Пользуясь формулой (10.56), нетрудно найти условие, при котором величина Е₀² будет минимальной. Для этого выразим из (10.56) Е₀² через Р_ср^ТЕМ и, считая Р_ср^ТЕМ и Р_ср^ТЕМ постоянными, найдем значение R₂ соответствующее минимуму Е₀². В результате получим соотношение In (R₂/R1) = 0,5, из которого следует R₂ = √eR₁. При таком соотношении между радиусами проводников получается наибольшее значение предельной мощности Р_пред, а волновое сопротивление коаксиальной линии

При воздушном заполнении линии пробой возникает при Е_о = = 30 кВ/см. Подставляя это значение в (10.56) и учитывая, что в рассматриваемом случае Z_c= 120π, a In (R₂/Ri) = 0,5, получаем

где величина Ri выражена в сантиметрах.

Если пространство между центральным и внешним проводниками коаксиальной линии заполнено полностью или частично диэлектриком, то максимальная мощность, которую можно передать по линии, в несколько раз ниже, чем рaccчитанная по формуле (10.57). Объясняется это как возможностью теплового пробоя диэлектрика, так и увеличением напряженности электрического поля в небольших (около 10^-2... 10^{-3 см) воздушных зазорах между диэлектриком и центральным проводником коаксиальной линии, неизбежно возникающих даже при самом тщательном изготовлении линии. Можно показать, что напряженность электрического поля в зазоре в ε}_г раз выше, чем максимальная напряженность в диэлектрике. Для предотвращения пробоя воздушного зазора предельная мощность должна быть уменьшена в ε_r² раз.

В некоторых случаях представляет интерес определение отношения R₂/R₁ при котором разность потенциалов ∆U =│U_т│между внутренним и внешним  проводниками минимальна. Используя формулу (10.47), находим, что минимум  │U_т│ имеет место при

In (R₂/R₁) = 1.  что соответствует волновому сопротивлению Z_B =

Потери в коаксиальной линии складываются из потерь в диэлектрике, заполняющем линию, и потерь в металлических проводниках. Таким образом, коэффициент затухания α = α_д + α_м. При сплошном заполнении величина α_д находится из выражения (9.52). Если заполнение частичное, то коэффициент ослабления α_д', обусловленный потерями в диэлектрике, приближенно может быть определен по формуле

где V_Д - объем диэлектрического заполнения в коаксиальной линии единичной длины и V_Л- полный внутренний объем этой линии.

Определим затухание, обусловленное потерями в металлических проводниках. Амплитуда касательной составляющей магнитного поля, согласно (10.46), на поверхности центрального проводника равна E₀/Z_С , а на внутренней поверхности внешнего про-

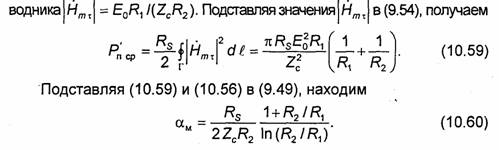
 Подчеркнем, что формула (10.60) выведена для случая резко выраженного поверхностного эффекта. На низких частотах поверхностный эффект в центральном проводнике проявляется слабо. В этом случае при определении потерь во внутреннем проводнике коаксиальной линии нужно учитывать результаты, полученные в 7.4.

Так как R, < R₂, то большая часть энергии теряется в центральном проводнике. Увеличение радиуса R₁ центрального проводника сопровождается уменьшением плотности тока проводимости в этом проводнике и соответствующим уменьшением потерь. Однако, с другой стороны, увеличение r₁ при неизменной величине R₂ влечет за собой понижение волнового сопротивления, что при заданной мощности приводит к увеличению тока в линии и соответствующему увеличению потерь. Поэтому следует ожидать существования оптимального соотношения между R, и R₂, при котором затухание, вызываемое потерями в металлических проводниках, минимально. Полагая da/dR₁ = 0, приходим к соотношению R₂/R₁ = 3,6, которому соответствует волновое сопротивление

Как видно, разным критериям соответствуют свои оптимальные значения Z_B. В соответствии с рекомендацией Международной электротехнической комиссии волновое сопротивление коаксиальной линии, предназначенной для передачи значительной мощности, выбирается равным 50 Ом (при ε_r= 1 и μ_r= 1), что приблизительно равно полусумме значений Z_B, оптимальных по предельной мощности и по затуханию. Широко используются также коаксиальные линии с номинальным волновым сопротивлением 75 Ом.

Как показывают расчеты, на волнах короче 10 см суммарный коэффициент ослабления в коаксиальной линии значительно превышает коэффициент ослабления в металлических волноводах. Поэтому на таких волнах применяют лишь короткие отрезки коаксиальной линии.

10.5. ДВУХПРОВОДНАЯ ЛИНИЯ

Двухпроводная линия, представляющая собой систему двух параллельных проводов, широко используется на практике. Строгий анализ основных собственных волн в такой линии при конечной проводимости проводов был проведен на основе решения уравнения Гельмгольца в биполярной системе координат [13]. Он является весьма сложным и здесь не приводится. Ограничимся рассмотрением идеальной двухпроводной линии, т.е. будем считать, что провода обладают бесконечной проводимостью и расположены в однородной изотропной среде без потерь. В такой линии возможно распространение ТЕМ-волн двух типов, которые принято называть однотактной и, двухтактной или соответственно четной и нечетной волнами, В любом поперечном сечении линии у однотактной волны токи в проводах синфазны, а у двухтактной -противофазны (имеют противоположное направление). Ограничимся рассмотрением двухтактной волны.

Поперечное сечение линии и используемая декартова система координат показаны на рис. 10.34. Расстояние между осями проводов dh = 2, радиусы проводов одинаковы и равны а. Комплексные амплитуды токов в первом (i_т1) и втором  (i_т2)  проводах (рис. 10.34) и векторы Ё и Н в соответствии с общей теорией   ТЕМ-волн (см.9.4) представим  в  виде 

При этом выполняется равенство Е°(х, у) =-grad u°(x, у), где функция и°(х, у) совпадает с электростатическим потенциалом в двумерной задаче о поле двух разноименно заряженных цилиндров, на одном из которых потенциал и°= V⁰ (первый провод), а на другом и°=- V° (второй провод). Эта задача рассматривалась в 3.6.3, и было показано, что электростатическое поле таких проводов эквивалентно полю двух разноименно заряженных нитей, проходящих через точки с координатами х = l, у = z = 0 (первая нить) и х =- l, у - z = 0 (вторая нить) параллельно оси Z. Погонные заряды первой и второй нитей обозначим через τ° и -τ° соответственно. Отметим, что по сравнению с формулами 3.6.3 здесь изменены обозначения (и⁰, V⁰ и τ° вместо и, V и τ т). Величины h,l и а связаны соотношением (3.56), аV°и τ°-формулой (3.57), в которой нужно только заменить Vна V° и τ°на τ°. В соответствии с формулой (3.49) имеем

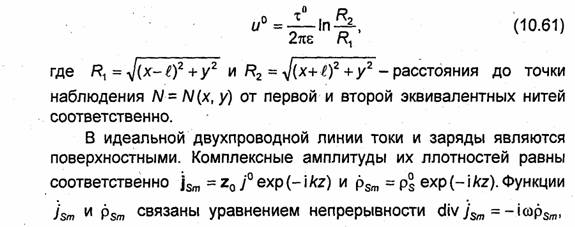
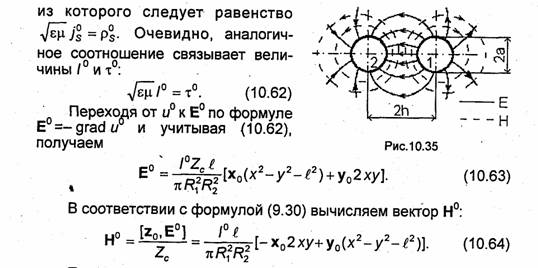
Подчеркнем, что формулы (10.63) и (10.64) являются строгими и справедливы при любом расстоянии d между проводами.

На рис.10.35 показана построенная на основе формул (10.63) и (10.64) структура поля двухтактной ТЕМ-волны в поперечном сечении симметричной двухпроводной линии.

Зная напряженность магнитного поля, нетрудно найти плотность токов, текущих по проводам. Рассмотрим, например, первый провод. Введем систему цилиндрических координат связанных с координатами х, у, z соотношениями

Из полученной формулы видно,  что ток в общем случае распределен по периметру провода неравномерно, величина  │j_Sm │возрастает при φ₁→π. При h>>а эта неравномерность проявляется

слабо, и   можно   считать,   что  распределение тока в каждом проводе   осесимметрично. При сближении проводов неравномерность распределения тока возрастает. Это приводит к увеличению потерь в линии. Указанное явление называют эффектом   близости.   На рис. 10.36 показана зависимость функции j_s° от угла ф, для нескольких   значений   отношения Л/а, указанных на соответствующих кривых. Коэффициенты ослабления (а) и фазы (Р) двухтактной волны в симметричной двухпроводной линии могут быть вычислены по приближенной формуле, полученной Зоммерфельдом [13]:

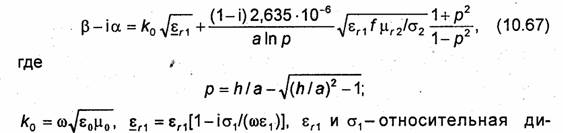
электрическая проницаемость и удельная проводимость среды, окружающей линию, а μ _r2 и σ₂ - относительная магнитная проницаемость и удельная проводимость проводов линии. При выводе формулы (10.67) предполагалось, что имеет место сильно выраженный поверхностный эффект (т.е. выполняется неравен-

При анализе волн в многопроводных линиях обычно используют методы, не учитывающие эффект близости. При близком расположении проводов эти методы могут привести к заметным погрешностям.

Представление о влиянии эффекта близости на затухание волн в двухпроводной линии дает рис. 10.37, на котором   показана   зависимость отношения истинных значений коэффициента ослабления α_м к его значениям   α_м °,   вычисленным в предположении осесимметричного распределения тока в каждом  проводе,  т.е.  без учета эффекта близости. Приведенный график рассчитан для случая двухтактной волны в симметричной    двухпроводной линии с алюминиевыми проводами при а =.3 мм и   f=1 МГц.   Как  видно, при  близком   расположении проводов неучет эффекта близости приводит к существенной погрешности. Волновое сопротивление  идеальной  двухпроводной  линии вычисляется по формуле Z_B= 2 V°//°. Для двухтактной волны

10.6. Полосковые линии

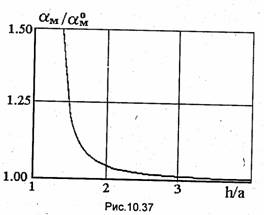
Будем называть полосковой пинией направляющую систему открытого типа, состоящую из двух или более изолированных друг от друга проводящих полос. Данное определение не претендует на полноту. В настоящее время этот термин используют для обозначения настолько разных линий передачи [23], что дать всеобъемлющее определение полосковых линий не представляется возможным. На практике наиболее часто используются следующие линии: симметричная полосковая линия, несимметричная полосковая линия, микрополосковая линия, щелевая полосковая линия и некоторые другие. Как правило, полосковые линии выполняются в виде тонких металлических слоев, нанесенных на листы диэлектрика. В качестве диэлектрика используют материалы с малыми потерями в диапазоне СВЧ (с малым tg δ): фторопласт, полиэтилен, керамика, поликор (двуокись алюминия), сапфир, кварц, ферриты и др. [23]. Иногда применяют воздушное запол^ нение линий. При изготовлении полосковых линий используют или фольгированные диэлектрики [23], или наносят металлические полоски на поверхность диэлектрика, применяя тонкопленочную или толстопленочную технологии [54].

Несмотря на относительно простую геометрию полосковых линий, их строгий анализ представляет достаточно сложную задачу, решаемую, как правило, с помощью численных методов. Так как полосковые линии относятся к линиям открытого типа, то при распространении вдоль них электромагнитных волн возникают радиационные потери (часть мощности излучается из линии во внешнее пространство). На практике используют полосковые линии, поперечные размеры которых малы по сравнению с длиной волны. Радиационные потери в таких линиях обычно незначительны, и при анализе структуры поля и параметров основных волн ими пренебрегают.

Основной волной в полосковых линиях, как правило, является TЕМ-волна или квази-TEM волна, по структуре поля и другим свойствам близкая к TЕМ-волне. Анализ таких волн обычно проводят на основе квазистатического приближения, как было сделано в случае коаксиальной и двухпроводной линий. Рассмотрим более подробно основные типы полосковых линий, широко используемые в технике СВЧ.

Симметричная полосковая линия (СПЛ) представляет собой трехпроводную полосковую линию, состоящую из полоски 1 шириной w и толщиной t, помещенной симметрично относительно экранирующих пластин, расположенных на расстоянии b друг от друга и имеющих ширину а (рис.10.39). Пространство между проводниками полностью заполнено однородным диэлектриком 2 с параметрами ε_r, μ_r=1, σ_д. Токонесущие элементы (полоска 1 и экранирующие пластины) выполнены из металла с удельной проводимостью  σ_м.При σ_д=0, σ_м=∞  и а=∞  основной волной в

СПЛ является ТЕМ-волна, для которой λКр =∞ Строгий анализ ТЕМ-волны в СПЛ при а=∞ может быть выполнен методами теории функций комплексного переменного с помощью конформных отображений [55]. Однако качественное представление о структуре поля ТЕМ-волны в СПЛ можно получить более просто, рассматривая СПЛ как линию, получающуюся в результате деформации коаксиальной линии (см. рис. 10.40, а,б,в).

Отметим, что основные характеристики ТЕМ-волны в СПЛ можно определять по формулам для плоских волн в однородной изотропной среде (см. гл.6). Важной характеристикой линии передачи с ТЕМ-волной является ее волновое сопротивление Z_B = = U_m/i_m, где U_m и /_m- комплексные амплитуды напряжения и тока в линии, соответствующие бегущей волне. Зная формулы для электрического и магнитного полей в СПЛ, можно найти для нее Z_B также, как это было сделано в случае коаксиальной линии. Однако обычно волновое сопротивление полосковых линий определяют иначе. В 10.4 было показано, что Z_B линии с ТЕМ-волной можно рассчитывать по формуле (10.50).

В случае СПЛ погонную емкость линии С₁ можно представить (рис. 10.41) в виде С₁ = 2С_пл + 4С_кр, где С_пл = ε2w/(b-t)-емкость плоского конденсатора с пластинами шириной w и длиной 1 м, расположенными на расстоянии (b-t)/2, рассчитанная без учета краевых эффектов, а С_кр - емкость, связанная с краевыми полями на концах полоски. Емкость С_кр зависит от ε, t и b линии и определяется методами конформных отображений [55]. Приведем

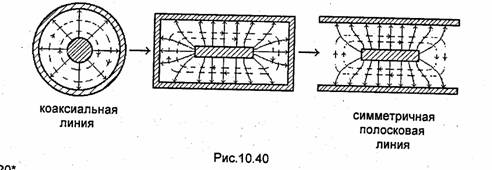
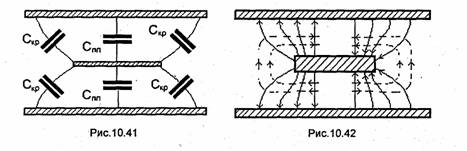
окончательные приближенные формулы для Z_B, позволяющие проводить расчеты с относительной погрешностью, не превышающей 1,24% [23]:

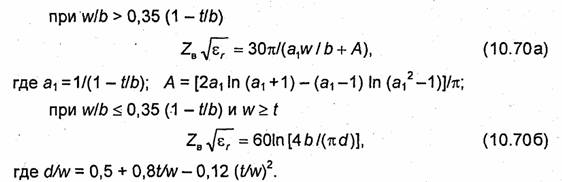
Как следует из (10.70), волновое сопротивление СПЛ уменьшается при увеличении ε_r заполняющего диэлектрика, увеличении w и t полоски и уменьшении величины 6, поскольку при указанных изменениях увеличивается емкость С_пл.

Расчетные и экспериментальные данные показывают [23], что в СПЛ с конечной шириной экранирующих пластин а (рис. 10.39) при a>w + 2b поле практически полностью сосредоточено в заполняющем диэлектрике, а на границе диэлектрик - воздух оно отсутствует; поэтому все характеристики СПЛ в этом случае можно рассчитывать по формулам, справедливым для а =∞.

Первым высшим типом в СПЛ является волна Н⁽¹⁾ [23]. Ее структуру (рис. 10.42) можно получить, последовательно деформируя (как на рис. 10.40) поперечное сечение коаксиальной линии, в которой распространяется первый высший тип Н₁₁(рис. 10.32). Поэтому приближенно можно считать, что  Условие одноволновой работы СПЛ можно приближенно записать в виде w<  Λ/2, где Λ - длина, ТЕМ-волны в СПЛ.

Если то при распространении ТЕМ-волны по СПЛ происходят потери энергии в заполняющем диэлектрике и проводниках линии. Кроме того, имеет место излучение энергии в окружающее пространство. При a>w+2b и b< Λ/2 затуханием волны за счет излучения можно пренебречь [23]. В этом случае коэффициент ослабления можно записать в виде (см. 9.8); α_д вычисляется по (9.52), формулы для вычисления а_м приведены в [23]. Расчеты показывают, что даже в самом благоприятном случае (при использовании высокочастотных диэлектриков с малым tg δи хорошо проводящих металлов, например меди) коэффициент ослабления α в СПЛ на частотах выше 1 ГГц имеет величину от нескольких десятых до нескольких единиц

децибел на метр. Причем а возрастает как с увеличением частоты, так и с увеличением ε_r. На одних и тех же частотах коэффициент ослабления   в   СПЛ   в   несколько   раз   больше   коэффициента

ослабления в металлических волноводах и коаксиальной линии, что объясняется весьма малыми поперечными размерами СПЛ и полным диэлектрическим заполнением линии. Несмотря на это, полосковые линии находят широкое применение в технике СВЧ: практически вся приемная аппаратура конструируется на их основе. При использовании полосковых линий удается получить весьма малые габариты и массу устройств. Отметим, что затухание электромагнитного сигнала, проходящего через то или иное устройство, зависит как от коэффициента ослабления в отрезках линии, образующих это устройство, так и от длины пути. Как будет показано ниже при рассмотрении вопросов конструирования различных устройств СВЧ, их длина пропорциональна длине волны в линии передачи, на основе которой строится устройство. Поэтому конструируя устройство на основе полосковых линий и увеличивая ε_r.  заполняющего диэлектрика, удается уменьшить длину волны в линии, а значит, и длину устройства.

С целью уменьшения затухания волны в СПЛ применяют несколько измененную конструкцию СПЛ, называемую высокодобротной полосковой линией (рис. 10.43). В этом случае проводящую полоску между экранами выполняют в виде двух полосок 1, нанесенных по разные стороны тонкой диэлектрической пластины 2. Обе полоски находятся под одним и тем же потенциалом. Пространство между полосками и экранами заполнено воздухом. Тонкая диэлектрическая пластина обеспечивает крепление и центрирование полосок между экранами. При этом ослабление волны в диэлектрической пластине весьма мало, поскольку из-за одинаковых  потенциалов полосок концентрация

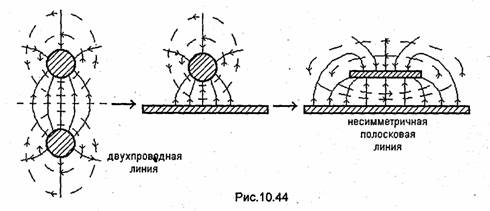
электромагнитного поля в. диэлектрике невелика. Симметричное расположение пластины 2 между экранирующими пластинами 3 обеспечивается, специальными диэлектрическими опорами 4.

Несимметричная полосковая (НПЛ) и микрополосковая (МПЛ) линии. НПЛ (рис. 10.44), представляет собой двухпроводную полосковую линию, состоящую из полоски шириной w и толщиной t, помещенной на расстоянии h от экранирующей пластины, имеющей ширину а. Пространство между проводниками и над полоской заполнено диэлектриком с параметрами . Токонесущие элементы (полоска и экран) выполнены из металла с удельной проводимостью σ_м. На практике, как правило, используют воздушное заполнение НПЛ. При σ_д=0, σ_м=∞ и а=∞ основной волной в НПЛ является ТЕМ-волна, для которой λ_кр=∞. В [55] выполнен анализ НПЛ и приведены формулы для расчета поля ТЕМ-волны. На рис. 10.44 показана структура поля ТЕМ-волны в НПЛ, построенная путем последовательных деформаций структуры поля симметричной двухпроводной линии.

Как и в случае СПЛ, волновое сопротивление НПЛ обычно рассчитывают по формуле (10.50), где  -погонная емкость плоского конденсатора, а С_кр-емкость, связанная с краевыми полями. Приведем окончательные приближенные формулы для Z_B, позволяющие проводить расчеты с относительной погрешностью, не превышающей 0,6 % при t = 0 [23]:

При конечной толщине полоски, в случае 0 <t/h< 0,1, сопротивление Z_B для НПЛ можно определять по (10.71), если вместо w/h подставить w'/h, где

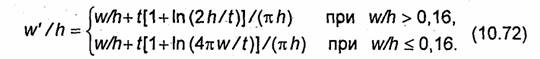
Как и в случае СПЛ, волновое сопротивление НПЛ уменьшается при увеличении ε_r. увеличении w и t и уменьшении h.

Как показывает анализ, характеристики НПЛ с конечной шириной экранирующей пластиньГпри условии a>(8...12)w практически полностью совпадают с аналогичными для НПЛ с а =∞.

Одноволновый режим работы НПЛ на ТЕМ -волне и отсутствие излучения из линии обеспечиваются соответствующим выбором поперечных размеров линии [23]:

где Λ -длина ТЕМ -волны в НПЛ.

На практике широкое применение находит несколько измененная конструкция (рис. 10.45), называемая микрополосковой линией. Она отличается от НПЛ тем, что между полоской 1 и экранирующей пластиной 2 помещается подложка из диэлектрика Зс параметрами   над полоской находится диэлектрик с параметрами  Как правило,, над полоской используют воздушное заполнение  Если сравнить передачу энергии по НПЛ и МПЛ, то в МПЛ уровень излучения энергии в окружающее пространство гораздо ниже, чем в НПЛ, что связано с увеличением концентрации электромагнитного поля в диэлектрике подложки, особенно при больших значениях ε_r2.

При передаче энергии по МПЛ электромагнитное поле существует не только в подложке, но и в воздухе. При этом появляются продольные составляющие векторов поля, т.е. по МПЛ в общем случае энергия переносится гибридными волнами (E_z≠ 0 и H_z≠ 0). Однако, как показывает анализ [55], при достаточно малых по сравнению с длиной волны размерах поперечного сечения МПЛ для основной волны величина продольных составляющих векторов поля оказывается на порядок меньше величины поперечных составляющих, и ими можно пренебречь. Поэтому приближенно можно считать, что структура основной волны в МПЛ (рис. 10.45),

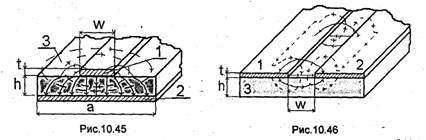
получившей название квази-ТЕМ, совпадает со структурой ТЕМ-волны. Волна Квази-ТЕМ, как и ТЕМ -волна, может распространяться на любых частотах, для нее λ_кр=∞. Причем, поскольку квази ТЕМ -волна переносит часть энергии в подложке, а часть в воздухе, ее фазовая скорость удовлетворяет неравенству

 Чем больше энергии переносится в подложке, тем ближе Vф к скорости света в подложке, и наоборот. Обычно при определении основных характеристик волн в линиях с поперечно неоднородным диэлектрическим заполнением вводят эффективную диэлектрическую проницаемость линии  связанную с фазовой Скоростью волны  причем

 эффективную проницаемость для волны квази- ТЕМ в МПЛ можно определить по формуле, справедливой для t = 0 [23]:

Из (10.74) следует, что фазовая скорость квази- ТЕМ волны зависит не только от параметров заполняющего диэлектрика, но и от геометрических размеров линии (Последнее свойство характерно для Н- и Е-волн в волноводах): при увеличении w и ε_r2 или уменьшении h фазовая скорость волны квази- ТЕМ в МПЛ уменьшается, поскольку при подобном изменении увеличивается количество энергии, переносимой волной в подложке, и наоборот. Все основные характеристики волны квази- ТЕМ рассчитываются по формулам для ТЕМ -волн путем замены ε_r. на ε_rэф. Например, длина

волны квази- ТЕМ в МПЛ на частоте f равна  Волновое сопротивление МПЛ рассчитывается по формулам (10.71), где ε_r. заменяется на вычисленную по (10.74) ε_rэ. Путем аналогичной замены в (10.73) получаются условия для одно-волнового режима работы и отсутствия излучения в МПЛ.

Отметим, что поскольку волна квази-ГЕМ является гибридной, ее характеристики  зависят от частоты, т.е. наблюдается дисперсия основной волны в МПЛ. Как показывают расчеты и эксперимент [23] для МПЛ, используемых на практике, дисперсия основной волны практически не проявляется при f<1 ГГц. На более высоких частотах характеристики основной волны в МПЛ следует определять с учетом дисперсии, используя формулы для ε_rэф из [23]. При  волна квази- ТЕМ испытывает затухание, которое можно рассчитать по формулам, приведенным в [23].

Отметим, что на основе МПЛ конструируется большинство интегральных схем, при этом в качестве подложки используют весьма тонкие диэлектрические пластины (доли миллиметра), имеющие достаточно высокое значение ε_r2. При этом удается значительно уменьшить длину волны в линии, а значит, и габариты интегральной схемы.

Щелевая полосковая линия (ЩПЛ). Это двухпроводная полосковая линия (рис. 10.46), в которой электромагнитная волна распространяется вдоль щели между проводящими поверхностями 1 и 2, нанесенными на одну сторону подложки 3 из диэлектрика с параметрами . На рис. 10.46 изображены линии электрического (сплошные) и магнитного (пунктирные) полей основной волны в ЩПЛ. Анализ ЩПЛ показывает [23], что основной волной в линии является H-волна, поскольку величина продольной составляющей напряженности электрического поля на порядок меньше величины поперечных составляющих, а все три составляющие магнитного поля сравнимы по величине. Как правила, основные характеристики ЩПЛ (V_ф, Z_B, Λ и т.д.) определяют численно. Результаты подобных расчетов можно найти в [23]. Одноволновый режим работы ЩПЛ, а также отсутствие заметного излучения из линии обеспечиваются при w < Λ/2 и h < Λ/2.

По сравнению с МПЛ в ЩПЛ: 1) более сильно проявляется дисперсия; 2) при одинаковых отношениях w/h и ε_r. подложки Z_B в ЩПЛ больше, чем в МПЛ; 3) значительно ниже потери, поскольку ток проводимости рассредоточен по большей поверхности, чем в МПЛ. Отметим, что при конструировании гибридных интегральных схем использование ЩПЛ, в отличие от СПЛ и МПЛ, позволяет более просто монтировать навесные элементы в схеме. Магнитное поле в ЩПЛ эллиптически поляризовано, поскольку в H-волнах продольная и поперечные составляющие напряженности магнитного поля сдвинуты по фазе на 90°. Это свойство основной волны в ЩПЛ используется при конструировании полосковых невзаимных устройств с намагниченными ферритами (см, гл.14).

Связанные полосковые линии. Рассмотрим две СПЛ (рис. 10.47, а) или две МПЛ (рис. 10.47, б), имеющие одинаковую ширину полосок, общие экранирующие пластины и общее диэлектрическое заполнение. Полоски линий расположены параллельно на расстоянии s друг от друга. Изображенные на рис. 10.47, а и 10.47,6 линии называют соответственно связанными СПЛ и связанными МПЛ с боковой связью полосок. При достаточно малом расстоянии s электромагнитная волна, распространяющаяся вдоль одной из полосок, будет возбуждать волну, распространяющуюся вдоль второй полоски. Благодаря возникающей между полосками электромагнитной связи часть энергии, переносимой волной вдоль одной из полосок, будет ответвляться и

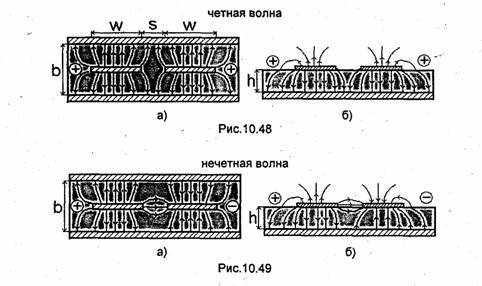
переноситься волной вдоль другой полоски и наоборот. Это явление используется в технике СВЧ при конструировании направленных ответвителей, фильтров и других устройств (см. гл.14).

Анализ связанных СПЛ и МПЛ, проведенный в [17], показал, что в таких линиях возможно существование двух независимых основных волн: четной (рис.10.48) и нечетной (рис. 10.49), соответствующих двум способам возбуждения полосок. У четной волны в произвольном поперечном сечении потенциалы полосок одинаковы по величине и знаку, а токи на полосках текут в одном направлении. У нечетной волны потенциалы одинаковы по величине, но противоположны по знаку, а токи текут в противоположных направлениях.

Как следует из общих свойств ТЕМ - волн, основные параметры четной и нечетной ТЕМ -волн в СПЛ совпадают и вычисляются по формулам, приведенным в 9.4. Волновые сопротивления для этих волн можно рассчитать по формуле (10.50), где полная погонная емкость

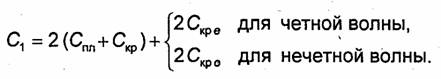
Входящие в эти выражения величины С_пл и С_кр были определены выше при анализе СПЛ, а С_кре и С_кро-погонные емкости, возникающие за счет краевых полей вблизи связанных краев полосок соответственно для четной и нечетной волн. Из физических соображений очевидно, что С_кре<С_Кр₀. Соответственно полная погонная емкость C1 = С_е для четной волны меньше полной погонной емкости С₁ = С_о' для нечетной волны (С_е < Со). Поэтому для волновых сопротивлений четной (Z_Be) и нечетной (Z_B0) волн выполняется неравенство Z_Be> Z_B0.

Аналогично с помощью формул, приведенных в 9.4 для ТЕМ-волн, можно определить основные характеристики четной и нечетной квази ТЕМ-волн в связанных микрополосковых линиях; заменив в них ε_r. на эффективные диэлектрические проницаемости (ε_rэф)_е для четной волны и (ε_rэф)₀ -для нечетной. Анализ показывает, что (ε_rэф)_е всегда больше (ε_rэф)₀, т.е. четная и нечетная квази ТЕМ-волны распространяются по линии с разными скоростями Vф₀ > V_фе. Формулы для расчета (ε_rэф)_е ,(ε_rэф)₀ а также волновых сопротивлений Z_ве и Z_B0 достаточно громоздки и здесь не выписываются, они имеются в [23] и [17]; там же можно найти и результаты численных расчетов этих величин.

10.7. ЛИНИИ ПОВЕРХНОСТНОЙ ВОЛНЫ. ЗАМЕДЛЯЮЩИЕ СИСТЕМЫ

10.7.1. Простейшие диэлектрические волноводы

Как было показано в 7.4, при падении плоской электромагнитной волны на плоскую границу раздела двух диэлектриков при определенных условиях происходит полное отражение волны. При этом как в первой, так и во второй средах возникает направляемая волна, распространяющаяся вдоль границы раздела. Во второй среде эта волна является поверхностной: ее поле экспоненциально убывает в направлении нормали к границе раздела. Поскольку фазовая скорость поверхностной волны меньше фазовой скорости ТЕМ -волны во второй среде, иногда эту волну называют медленной.

Рассмотрим некоторые линии передачи, в которых имеют место поверхностные волны.

Пусть на границу раздела двух диэлектриков, удовлетворяющих условию k₁ > k₂, падает под углом φ₁ > φ_кр плоская параллельно поляризованная волна (см.7.4). В результате полного отражения распределение амплитуд составляющих векторов поля

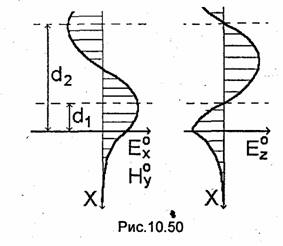
вдоль нормали к границе раздела (вдоль оси X) имеет характер стоячей волны (рис. 10.50). Как видно, имеется множество плоскостей х=х_п, n=1,2,3,... (их следы показаны пунктиром), на которых векторы Е и Н удовлетворяют условиям, аналогичным граничным условиям на поверхности идеального проводника. Если одну из плоскостей (х = х_n) металлизировать (сделать идеально проводящей), то структура поля в области х > х„ может быть сохранена. При этом прилегающий к плоскости х = х_п слой диэлектрика (х„<х<0) будет представлять собой направляющую систему открытого типа. В рассматриваемом случае в диэлектрическом слое распространяется Е-волна, распределение амплитуд составляющих векторов поля которой совпадает при х> х_n с приведенным на рис.10.50. Структура поля (линии векторов Е и Н) этой волны для случая, когда металлизирована плоскость x=x₁, показана на рис.10.51. Отметим, что волну, распространяющуюся в диэлектрическом слое, ограниченном металлической плоскостью, можно рассматривать как суперпозицию парциальных волн, возникающих при полном отражении первичной ТЕМ -волны от поверхности идеального проводника (х = х₁) и от границы раздела двух диэлектриков (х = 0), как показано на рис.10.52. Полное отражение от границы раздела (х = 0) возможно при углах падения При  условия полного отражения не выполняются, и слой диэлектрика перестает играть роль волновода. Для слоя фиксированной толщины d условие  выполняется при вполне определенном значении частоты f= f_Kp, называемом критической частотой. Поэтому волна в рассматриваемой системе может распространяться лишь при f > f_Kp.

При полном отражении нормально поляризованной плоской волны от плоской границы раздела двух диэлектриков образуется направляемая Н-волна (см.7.4). Рассуждая далее так же, как в случае параллельной поляризации, придем к аналогичной направляющей системе c волной типа Н.

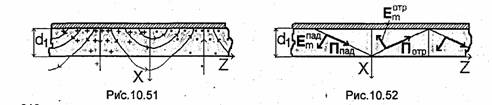
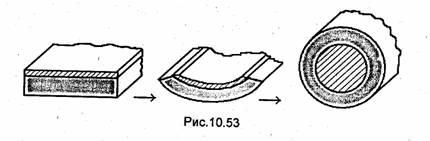
Таким образом, в системе, состоящей из металлической * пластины, покрытой слоем диэлектрика, при f>f_Kp могут распространяться направляемые Е- и H-волны. В общем случае (при конечной проводимости металлической пластины) будут распространяться гибридные волны. Отметим некоторые особенности волн в такой направляющей системе: электромагнитная энергия переносится как в диэлектрике, так и в прилегающей воздушной среде; амплитуды составляющих векторов поля в воздухе экспоненциально убывают по мере удаления от поверхности диэлектрика; средний за период поток энергии в направлении нормали к границе раздела "воздух-диэлектрик" равен нулю; фазовая скорость направляемых волн меньше фазовой скорости ТЕМ -волны в воздухе (поэтому, как уже отмечалось, такие волны называют медленными).

Свойство границы раздела двух диэлектриков направлять поток электромагнитной энергии сохраняется и при ее цилиндрическом искривлении (рис. 10.53), т.е. одиночный провод, покрытый слоем диэлектрика, является волноводом, по которому можно передавать электромагнитную энергию.

Можно выбрать толщину слоя диэлектрика таким образом, что он будет направлять волну и без ограничивающей его металлической пластины. Направляемую волну в этом случае можно представить в виде суперпозиции парциальных ТЕМ -волн, распространяющихся путем полного отражения от обеих границ раздела диэлектрика с менее плотной средой.

Как уже отмечалось, направляющие свойства границы раздела двух диэлектриков сохраняются и при ее цилиндрическом искривлении. Поэтому направляющей системой является не только диэлектрический слой, но и диэлектрическая трубка и сплошной диэлектрический цилиндр (рис. 10.54).

Рассмотрим более подробно некоторые из перечисленных направляющих систем.

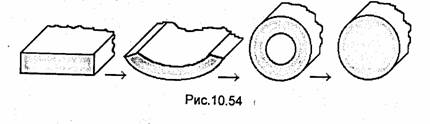
10.7.2. Металлическая плоскость, покрытая слоем диэлектрика

Пусть на идеально проводящей плоскости х = 0 расположен слой идеального диэлектрика (μ_г=1,σ = 0) толщиной d с относительно диэлектрической проницаемостью ε_r>1 (рис.10.55). В направлении осей Y и Z слой имеет неограниченные размеры. Среда при х > d- воздух  (ε_r2 = 1, μ_r2 = 1, σ₂ = 0). Предположим

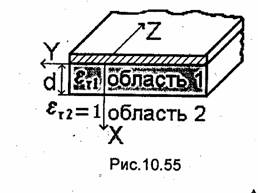
жим вначале, что по данной системе в направлении оси Z распространяется Е-волна (Е_z≠О, H_Z= 0). Поперечные составляющие векторов Е и Н выражаются через Е_z по формулам (9.19), (9.20). Предположим, что поле волны не зависит от переменной у, и, как обычно, выделим зависимость от координаты z в виде множителя exp (-iβz), где р - пока неизвестная постоянная. При этом продольная составляющая вектора Ё_т принимает вид E_mz = = E_mz(x,z) = Е°(х) exp (-iβz). Функция Е°_z(х) должна удовлетворять

уравнению Гельмгольца (9.2), которое в рассматриваемом случае имеет вид

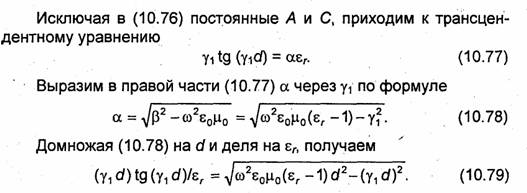
Решая (10.79), можно найти γ₁ и по (10.78) рассчитать α. После этого легко вычисляются параметр β и постоянные А и С.

Рассмотрим графическое решение трансцендентного уравнения (10.79). Поскольку для рассматриваемых волн α>0, то обе части (10.79) должны быть положительными. На рис. 10.56 построены значения левой и правой частей уравнения (10.79) в зависимости от величины γ₁d при ε_r= 2. Значения правой части (10.79) лежат на окружности с центром в начале координат и радиусом  зависящим как от рабочей частоты,

так и от толщины слоя диэлектрика и его диэлектрической проницаемости. Значения левой части уравнения (10.79) будут положительными   при   γ₁ > 0,   если   значения   γ₁d находятся   в интервалах , где п = 0,1, 2..... Точки пересечения

окружности, на которой лежат значения правой части уравнения (10.79), с кривыми, изображающими положительные значения левой части (10.79), соответствуют значениям γ₁d являющимся корнями уравнения (10.79). Как видно, при фиксированных f, d и ε_r

окружность пересекается с конечным числом кривых, изображающих левую часть уравнения, т.е. существует конечное число корней уравнения (10.79), каждому из которых соответствует определенное значение параметра β. Это означает, что в рассматриваемой линии может распространяться конечное число Е-волн, которые будем обозначать

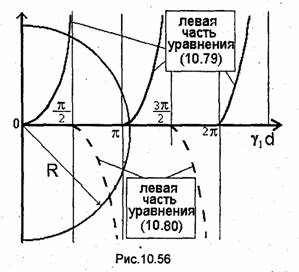
£^<п). При R<n существует лишь один корень уравнения (10.79) (одна точка пересечения кривых на рис.10.56), при этом в линии может распространяться лишь одна (основная) волна типа Е. Структура поля этой волны показана на рис.10.51. Так как данный корень существует при любых f и d, то для основной Е-волны 4_Р= 0, т.е. эта волна может распространяться в рассматриваемой линии при любой толщине диэлектрика и на любой частоте. При % < R < 2п в линии кроме основной сможет распространяться еще одна (высшая) Е-волна (существуют две точки пересечения кривых на рис.10.56). Чем больше R, тем большее количество волн типа Е может распространяться по линии. В общем случае может распространяться конечное число Е-волн, критические длины волн

которых определяются из условия R = nn, л =1, 2..... Подставляя

выражение для R, получаем к _£(n) = 2d^z_r-Vn.

Анализ магнитных волн, распространяющихся вдоль оси Z по рассматриваемой линии (рис. 10.55), проводится аналогично. В этом случае поперечное волновое число y_t является корнем следующего трансцендентного уравнения: y-i ctg (yid) =- s,a. Дом-ножим обе части этого уравнения на d и разделим на г_г. Подставляя затем значение а из (10.78), получаем

10.7.3. Плоский диэлектрический волновод

Плоская диэлектрическая пластина с диэлектрической проницаемостью ε_r >1, расположенная в однородной изотропной среде с меньшей диэлектрической проницаемостью (например, в воздухе),  также представляет собой  направляющую систему,   по которой могут распространяться Е- и H-волны, а при σ≠ 0 - гибридные. Такую направляющую систему (линию) обычно называют плоским диэлектрическим волноводом.

Введем декартову систему координат x,y,z, как показано на рис. 10.57. Толщина пластины равна 2d, а ее размеры вдоль осей У и Z неограниченны, диэлектрик считается идеальным (μ_r =1, σ = 0). Предполагаем, что волна распространяется вдоль оси Z.

Анализ волн в плоском диэлектрическом волноводе проводится так же, как для слоя диэлектрика на металлической плоскости. Анализ показывает, что в плоском диэлектрическом волноводе при фиксированных частоте и толщине пластины может распространяться конечное число медленных

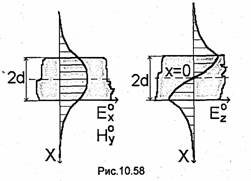
Е- и Н-волн. Основной волной является Е-волна низшего типа, у которой f_Kp= 0. Распределение амплитуд составляющих векторов поля этой волны вдоль оси X показано на рис.10.58, а структура поля изображена на рис. 10.59. Одноволновый режим выполняется при

10.7.4. Металлический цилиндр, покрытый слоем диэлектрика

Однопроводная линия в виде цилиндрического проводника, покрытого слоем диэлектрика, известна в литературе как линия Губо. Приближенный анализ волн в такой линии можно провести,

рассматривая ее как металлическую пластину, покрытую слоем диэлектрика и свернутую в цилиндр (рис. 10.53).

Основной волной в идеальной линии Губо является волна типа Е, структура поля которой показана на рис. 10.60. Затухание волны при распространении по линии определяется потерями энергии в металле и диэлектрическом слое. Чем толще слой диэлектрика и тоньше диаметр проводника, тем, очевидно, выше затухание волны. Поэтому, например, в сантиметровом диапазоне волн толщину слоя выбирают достаточно малой - порядка 0,05...0,1 мм, а диаметр проводника берут не менее 1 мм. При этом коэффициент ослабления для основной волны в такой линии с диэлектрическим слоем из полистирола оказывается в 2...3 раза меньше, чем в прямоугольном волноводе на тех же частотах. Однако существенная зависимость параметров распространяющейся волны в линии Губо от расположенных вблизи линии проводящих тел, а также от атмосферных условий приводит к ограниченному использованию ее на практике.

Следует отметить, что волна Е, изображенная на рис. 10.60, может распространяться вдоль проводника и при отсутствии диэлектрической оболочки, если на его поверхности из-за окисления образовалась тонкая пленка с относительно низкой проводимостью, играющая роль диэлектрического слоя.

10.7.5. Круглый диэлектрический волновод

Рассмотрим распространение электромагнитных волн вдоль бесконечно длинного диэлектрического цилиндра радиуса а, расположенного в безграничной однородной изотропной среде. Диэлектрик и окружающая среда считаются идеальными (σ = 0) и характеризуются параметрами ε,μ ₀ и ε _{0 ,}μ₀ соответственно.

Введем цилиндрическую систему координат r,φ ,z,  ось Z которой совместим с осью цилиндра. Как обычно, зависимость от координаты z выделим в виде множителя exp(-iβz), где β-подлежащая определению постоянная. При этом продольные составляющие векторов   Ё_т и Н_т   записываются  в виде   E_mz =

где т=1,2,3.....  а А, В, φ₀  и  ψ₀- некоторые  постоянные.   В области 2 поле должно представлять собой поверхностную волну, амплитуды составляющих векторов поля которой экспоненциально убывают с удалением от поверхности цилиндра. Поэтому должно выполняться соотношение и параметр γ₂ удобно представить в виде Решения уравнения (10.28), справедливые в области 2 и удовлетворяющие данному требованию, имеют вид

Поперечные составляющие векторов Е° и Н° вычисляются через E_z   и Н_z° по формулам (9.8) и (9.9). Подставляя явные

выражения для E_Xv° и Н_Ху°, где х = r,φ и v=1;2 в соотношения (10.83), приходим к системе четырех уравнений, содержащих неизвестные постоянные А, В, С, D, φ₀ и ψ₀. Анализируя эту систему, замечаем, что входящие в нее уравнения при т ≠ 0 будут совместными только при

 Для этого необходимо, чтобы выполнялось равенство

 Из данной системы видно, также, что при т ≠ 0 волна, распространяющаяся по круглому диэлектрическому волноводу, должна иметь продольные составляющие и у вектора Е, и у вектора Н, т.е. является гибридной. При т = 0 одна из составляющих E_z или Н_z может равняться нулю, т.е. возможно существование независимых Е- и Н-волн с осесимметричной структурой поля (такие волны часто называют симметричными).

Исключая в указанной системе уравнений, соответствующей т ≠ 0, постоянные А, В, С и D, приходим к трансцендентному уравнению

Решая (численно или графически) уравнение (10.84), находим параметр β и вычисляем постоянные γ₁и α. После этого расчет структуры поля и остальных параметров гибридной волны не вызывает затруднений.

В случае т = 0 правая часть уравнения (10.84) обращается в нуль, и оно распадается на два независимых уравнения

Убывание поля в радиальном направлении вне цилиндра определяется параметром а. Чем меньше а, тем медленнее убывает поле, тем меньшая часть мощности бегущей волны переносится непосредственно по диэлектрическому цилиндру. Значение а = 0 соответствует критической длине волны. Используя выписанные выше выражения параметров у-| и а через коэффициент фазы р, получаем соотношение

При f<f_Kp волны типа Е в диэлектрическом волноводе распространяться не могут.

Таким образом, свойства симметричных Е-волн в круглом диэлектрическом волноводе аналогичны свойствам Е-волн в диэлектрическом слое, расположенном в однородной среде (или в диэлектрическом слое, расположенном на металлической плоскости).

Анализ симметричных (т = 0) Н-волн проводится аналогично. В этом случае А = С= 0 и требуется найти корни уравнения (10.86), отличие которого от (10.85) несущественно.

При m≠0 в диэлектрическом волноводе могут распространяться только гибридные волны, у которых отличны от нуля

И E_Z, H_z.

Анализ гибридных волн несколько более сложен, так как требуется найти корни более сложного трансцендентного уравнения (10.84). Однако общие закономерности распространения гибридных волн сходны с описанными выше для симметричных Е-волн. Исключение составляет основная волна диэлектрического волновода ЕН₁₁ей соответствует значение m=1 и первый корень

уравнения (10.84), т.е. n=1). Структура поля этой волны показана на рйс.10.61. Так как критическая частота волны ЕH₁₁ равна нулю, то формально данная волна может существовать на любых частотах. Однако это не означает, что с помощью диэлектрического волновода можно передавать энергию на сколь угодно низкой частоте. Электромагнитная волна в диэлектрическом волноводе переносит энергию не только внутри стержня, но и в окружающем его пространстве. В качестве параметра, характеризующего протяженность поля волны в поперечном направлении, обычно используют так называемый граничный радиус поля r_о = 1/α. Расчеты показывают, что через площадь, ограниченную окружностью радиуса r₀, переносится 80-90% мощности бегущей волны. Поэтому для распространения волны по диэлектрическому волноводу необходимо иметь вокруг него свободное пространство в радиусе (2-3)r₀. Это обычно и вызывает трудности при использовании такого волновода. Как показывает анализ, при уменьшении частоты уменьшается а и, следовательно, увеличивается г₀, т.е. все меньшая часть энергии распространяется внутри стержня и все большая - в окружающем его пространстве. Поэтому, хотя критическая длина волны ЕH₁₁ равна нулю, существует нижняя граница рабочего диапазона при ^использовании этой волны, определяемая допустимым значением граничного радиуса, т.е. должно выполняться условие r₀<r_0доп. Со стороны верхних частот рабочий диапазон при использовании волны ЕН₁₁ должен быть ограничен критической частотой волны Е₀₁, определяемой из (10.88).

Отметим существенную особенность диэлектрического волновода: одноволновый режим работы для заданной рабочей частоты f(f< f_кp) можно обеспечить как выбором (уменьшением) радиуса стержня а, так и уменьшением разницы между относительными диэлектрическими проницаемостями материала стержня и окружающего пространства: выбрав ε_r мало отличающимся от 1, можно обеспечить одноволновый режим даже при a>>λ. Это свойство и используют при конструировании диэлектрических волноводов в оптическом диапазоне волн, где рабочие частoты вёсьма велики .Обычно диэлектрические волноводы, предназначенные для работы в оптическом диапазоне волн, называют световодами.

Диэлектрические волноводы применяют в качестве линий передачи в миллиметровом (КВЧ), субмиллиметровом (ГВЧ) и оптическом диапазонах волн, где они обеспечивают передачу, большей мощности с меньшими потерями, чем металлические волноводы.

10.7.6. Световоды

В настоящее время наибольшее применение на практике для передачи оптических сигналов находят пленочные и волоконные световоды. Основу пленочного световода (рис.10.62) составляет диэлектрическая пленка с параметрами ε_пл, μ_о, выращенная на диэлектрической подложке или сформированная методами интегральной технологии. Подложка имеет параметры ε₁, μ₀; параметры среды над пленкой ε₂, μ_о- Отметим, что чаще оптические немагнитные среды описываются с помощью коэффициента преломления п =√ε_r, при этом предполагается, что магнитная проницаемость у всех рассматриваемых сред одинакова и равна μ₀. Пленку можно рассматривать как плоский диэлектрический волновод (см.10.7.3). Для распространения волн по такому волноводу необходимо, чтобы n_пл>n₁ и п_пл>п₂. Подобные световоды используются для передачи света на небольшие расстояния, как правило, в пределах интегральной схемы оптического диапазона.

Волоконный световод состоит из диэлектрических сердечника и оболочки, диаметры которых равны d_c и d_oб соответственно (рис. 10.63). Коэффициенты преломления сердечника и оболочки равны п_с и n_о6, причем п_с>п_об. Для защиты от внешних воздействий и повышения механической прочности световода на наружную поверхность оболочки наносят полимерное покрытие (на рисунке покрытие не показано). В данном случае полное внутреннее отражение парциальных волн, распространяющихся в сердечнике, происходит на границе между сердечником  и оболочкой. Воз-

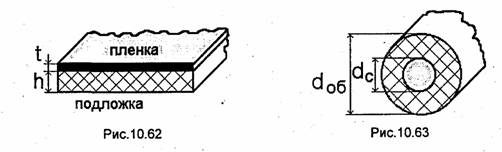
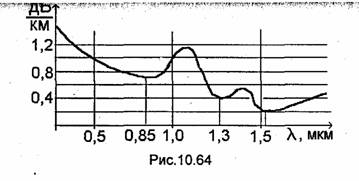
никающая при этом поверхностная волна распространяется в оболочке. Поэтому энергия, переносимая волнами по световоду, сосредоточена в сердечнике и оболочке. На оболочку можно наносить поглощающее покрытие, не влияющее на распространяющиеся по световоду волны и поглощающее энергию волн излучения, возникающих в световоде при его возбуждении источником (см. 15.2).

Обычно в качестве диэлектрика, из которого изготавливают сердечник световода, используют стекло, иногда для этой цели применяют различные полимеры. В качестве материала оболочки, как правило, также используют стекло, иногда полимеры [28]. Показатель преломления оболочки постоянен, а показатель преломления сердечника может быть как постоянной величиной, так и функцией поперечной координаты. В настоящее время получены волоконные световоды на основе кварцевого стекла, легированного германием, фосфором или бором, с достаточно малыми потерями в некоторых областях оптического спектра, называемых окнами прозрачности. На рис.10.64 показана типовая зависимость затухания в таком световоде, выраженная в дБ/км. Как видно из графика, существуют три окна прозрачности для распространяющихся по световоду сигналов λ≈0,85 мкм, λ≈1,3 мкм и λ≈1,5 мкм. Эти частотные диапазоны, как правило, и используют для передачи оптических сигналов по световодам.

По волоконному световоду, как по диэлектрическому волноводу, могут распространяться E-, Н- и гибридные волны. Поскольку критические частоты волн в диэлектрическом волноводе, как следует из результатов, полученных в 10.7.5, зависят не только от величины  d_c,   но  и  от  разницы  коэффициентов  преломления

то, выбирая достаточно близкие по величине п_с и n_об,

можно обеспечить одноволновый или близкий к нему режим работы световода при достаточно больших значениях d_c (много больших длины волны): Последнее обстоятельство весьма существенно из-за очень малой длины волны светового излучения

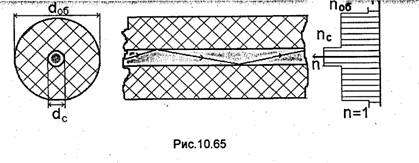
(λ≈1 мкм). Как правило, применяемые на практике одноволновые световоды или, как их называют в литературе, одномодовые световоды, работающие на основной волне диэлектрического волновода, имеют d_c≈ 3...5 мкм и d_Об≈50 мкм, при этом величины п_с и n_об отличаются не более чем на 3%. На рис. 10.65 показаны поперечное и продольное сечения такого световода; на продольном сечении изображены парциальные волны, соответствующие распространяющейся по световоду волне. На этом же рисунке изображено распределение вдоль радиуса коэффициента преломления сред, образующих световод. Одномодовый световод, как и любой диэлектрический волновод, обладает дисперсией, поскольку и фазовая скорость основной волны зависит от частоты и величина коэффициента преломления стекла является функцией частоты. Дисперсия ограничивает полосу передаваемых по световоду частот, т.е. вносит искажения в передаваемые сигналы. Если на вход световода подать сигнал в виде импульса, то по мере распространения этот импульс будет расширяться, причем величина расширения зависит как от степени дисперсии, так и от длины пути, проходимого сигналом по световоду. Расширение импульса эквивалентно сужению полосы пропускания световода и часто оценивается эквивалентной шириной полосы пропускания, выраженной в мегагерцах на километр [МГц/км]. При передаче импульсных сигналов обычно такое искажение сигналов оценивается величиной километрического уширения, выраженной в наносекундах на километр [Нс/км]. Расчеты и эксперименты показывают [28], что изготовленные на основе кварцевого стекла одномодовые световоды имеют минимальную дисперсию в области λ≈ «1,3...1,4 мкм. В этой области такие световоды имеют наибольшую полосу пропускания.

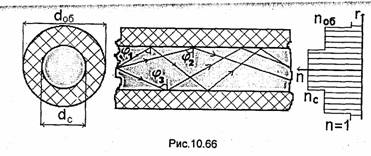
Весьма малые поперечные размеры сердечника одномодовых световодов вызывают достаточно серьезные трудности при их изготовлении, что сильно удорожает производство. Кроме того, малый диаметр сердечника затрудняет эффективный ввод мощности от источника в световод и предъявляет весьма жесткие требования к устройствам соединения таких световодов. Как правило, для возбуждения одномодовых световодов приходится использовать дорогостоящие полупроводниковые лазеры [23]. Поэтому одномодовые световоды применяют в случае, если требуется передавать значительные объемы информации на достаточно большие расстояния (более нескольких сотен или тысяч километров).

Для передачи небольших объемов информации на не очень большие расстояния (несколько десятков километров) используют многомодовые световоды, имеющие, как правило, d_c≈50 МКМ и d_cб ≈ 120MKM (рис.10.66). Изготовление таких волокон гораздо проще и дешевле. Увеличение диаметра сердечника по сравнению с диаметром сердечника одномодового световода обеспечивает два преимущества: возможность работы таких световодов с достаточно простыми и дешевыми некогерентными источниками излучения (светодиодами) и менее жесткие требования к устройствам соединения световодов. Из-за значительной величины d_c по многомодовому световоду может распространяться множество различных типов волн (порядка 1000), которые и переносят передаваемые по световоду сигналы. Каждую из распространяющихся волн можно представить парциальными волнами (лучами), движущимися под определенным углом к нормали к границе раздела сердечник - оболочка. На рис.10.66 показаны три луча, соответствующие трем волнам, распространяющимся по волокну,

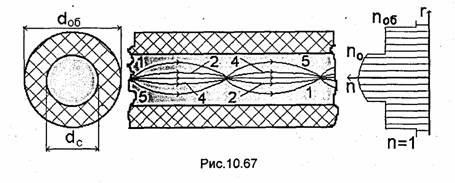
Для сохранения достаточно большого диаметра сердечника (как у многомодового волокна) и одновременного уменьшения величины модовой дисперсии на практике применяют так называемые градиентные световоды (рис. 10.67). Такие световоды имеют, как правило, d_c ≈50 мкм и d_Oб≈80 мкм. Сигнал по таким световодам передается многими типами волн. Для уменьшения величины модовой дисперсии используют сердечник, коэффициент преломления которого является функцией поперечной координаты r и, как правило, описывается формулой

где ∆ = (п₀-п_об)/п₀, п₀ - величина коэффициента преломления на оси сердечника, q- целое положительное число. Коэффициент преломления уменьшается от значения п₀ (на оси сердечника) до значения л_об на границе с оболочкой.

Как следует из законов Снеллиуса, если плоская волна падает на границу раздела двух сред из более плотной среды (n₁>n₂) под углом φ (или под углом 90°- φ к границе раздела), то направление распространения преломленной волны будет составлять с границей раздела угол меньший, чем 90°-φ, поскольку в этом случае θ > φ. Если же падающая плоская волна распространяется в менее плотной среде {п₁<п₂), то направление распространения преломленной волны будет составлять с границей раздела угол больший, чем 90°-φ. На этом основании можно утверждать, что если плоская волна движется в среде с плавно изменяющейся величиной коэффициента преломления под некоторым углом к направлению изменения величины п, то в общем случае направление распространения волны будет плавно искривляться. Поэтому в градиентном волокне траектории лучей, соответствующих различным типам  волн  и  направленных под разными углами  к оси сердечника, будут криволинейными (рис. 10.67): чем больший угол с осью составляет направление луча, тем  по более длинной траектории он перемещается, и наоборот. Однако луч, распространяющийся по самой длинной траектории, будет иметь самую высокую среднюю фазовую скорость, поскольку его траектория проходит через области сердечника с самым низким значением коэффициента преломления (вблизи оболочки).  Напомним, что фазовая скорость плоской волны обратно пропорциональна величине п среды. В свою очередь, луч, распространяющийся вдоль оси сердечника, имеет самую низкую фазовую скорость, поскольку его траектория проходит в области сердечника с самым высоким значением n.  Фазовый  сдвиг,  получаемый  каждым лучом  при прохождении конечного отрезка волокна, прямо пропорционален длине траектории и обратно пропорционален средней фазовой скорости луча. Поэтому выбором величины q в (10.89) можно в значительной   степени   уменьшить   разность   фазовых  сдвигов, получаемых разными лучами при прохождении конечного отрезка волокна, т.е. уменьшить разность фазовых скоростей различных волн в градиентном волокне.

Наиболее часто на практике применяют градиентные волокна с q = 2, которые называют параболическими. Такие волокна по сравнению с многомодовыми имеют значительно меньшую величину модовой дисперсии, что приближает их к одномодовым волокнам [23].

10.7.7. Замедляющие структуры

Поверхностная волна образуется при выполнении определенных условий на границе раздела сред. Одним из параметров, характеризующих поверхностную волну, является так называемый поверхностный импеданс (поверхностное сопротивление) Z_s, равный   отношению   комплексных   амплитуд   касательных   составляющих векторов Е и Н, вычисленных на границе раздела, вдоль которой   распространяется   поверхностная   волна.   Рассмотрим, например, поверхностную Е-волну, распространяющуюся в воздухе вдоль плоского диэлектрического волновода (рис. 10.57) или вдоль диэлектрического слоя,  ограниченного с одной стороны металлической пластиной (10.55). Как было показано в 10.7.2, комплексная амплитуда продольной составляющей напряженности электрического поля поверхностной волны при х≥ d определяется выражением         Применяя    формулу (9.20),   находим,   что    Это позволяет на поверхности структуры записать импедансное граничное условие (см. 2.2.2)

Величину Z_Sm часто называют поверхностным импедансом.

 Как видно, пока существует поверхностная волна, т.е. выполняется неравенство β² > ω²е_оμо или α > 0, поверхностный  импеданс Z_s является реактивным, индуктивным по характеру. Это означает, что у распространяющейся волны составляющие E_mz и Н_ту сдвинуты по фазе на π/2. При этом отсутствует средний за период поток энергии, переносимый волной вдоль нормали к границе раздела. Отсутствие активного потока энергии вдоль нормали к границе раздела является характерным признаком поверхностной волны. Поэтому поверхностная волна типа Е будет возникать во всех случаях, когда на границе раздела поверхностный импеданс будет чисто реактивным и индуктивным.

Существуют различные способы создания структур, имеющих чисто индуктивный поверхностный импеданс для распространяющихся вдоль них поверхностных (медленных) волн. Такие структуры получили название замедляющих [8]. Например, можно прорезать поперечные (по отношению к направлению распространения волны) канавки в металлической пластине, как показано на рис. 10.68. Канавки имеют ширину s и глубину h и отстоят друг от друга на расстояние t. При этом образуется гребенчатая структура. Каждую канавку такой гребенчатой структуры можно рассматривать как короткозамкнутый отрезок линии длиной h. Поэтому на частотах, для которых глубина канавки h не превышает четверти длины волны в линии, входное сопротивление канавки будет чисто реактивным (потери энергии в проводнике считаем пренебрежимо малыми) и индуктивным (см. гл.11). Если число канавок на отрезке, равном длине волны, достаточно велико, т.е. s + <<λ можно пренебречь влиянием тонких металлических перегородок в структуре и считать, что при x = h (рис.10.68) расположена плоскость, в любой точке которой поверхностный

импеданс Z_SM является чисто реактивным и имеет индуктивный характер. Поэтому на частотах, на которых h < λ/4, вдоль рассматриваемой гребенчатой структуры, как и вдоль металлической плоскости с диэлектрическим слоем, могут распространяться медленные Е-волны. Электромагнитное поле низшей Е-волны в гребенчатой структуре при х > h аналогично полю поверхностной волны, распространяющейся вдоль слоя диэлектрика при х > d, изображенному на рис.10.51. Путем изменения глубины канавок можно изменять фазовую скорость распространяющейся поверхностной волны, поскольку при изменении глубины канавки изменяется ее входное сопротивление, т.е. величина Z_Sи, а при этом согласно (10.90) изменяются коэффициенты α и βдля поверхностной волны.

Отметим, что для поверхностных Н-волн поверхностный импеданс также будет чисто реактивным, но имеет емкостной характер [8]. Это необходимо учитывать при построении замедляющих структур с поверхностными медленными Н-волнами.