Глава 3

ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

3.1 ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОСТАТИКИ

Электростатическое поле описывается системой дифференциальных уравнений (1.55), которая получается из системы уравнений Максвелла в предположении, что векторы поля не зависят от времени и отсутствует перемещение зарядов (j = 0). Аналогично находятся основные уравнения электростатики в интегральной форме:

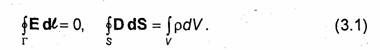
Электростатическое поле обладает рядом специфических свойств. В частности, непосредственно из уравнений (1.55) следует, что оно является потенциальным, а его векторные линии имеют истоки и стоки: они начинаются и заканчиваются на зарядах. В случае электростатического поля вектор Е можно представить в виде градиента скалярной функции и, называемой электростатическим потенциалом:

Соотношение (3.2) получается из формулы (2.36), если в последней положить dA/dt=O, а также непосредственно следует из первого уравнения системы (1.55). Оно определяет функцию и неоднозначно. Величина вектора Е не изменится, если вместо потенциала и ввести функцию и₁, отличающуюся от и на произвольную постоянную. При решении конкретных задач обычно вначале находят потенциал и, а затем вычисляют вектор Е. При этом, как правило, произвольную постоянную выбирают таким образом, чтобы, если это возможно, потенциал в бесконечно удаленных точках равнялся нулю.

Выясним физический смысл электростатического потенциала. Вычислим работу А, совершаемую при перемещении точечного заряда величины q из точки N₁ в точку N₂ по контуру Г (рис. 3.1). Так как напряженность Е электрического поля определяется как сила, с которой поле действует на единичный точечный положительный заряд, то

Знак минус в формуле (3.3) означает, что положительная работа совершается в том случае, когда заряд перемещается против сил поля. Подынтегральное выражение в формуле (3.3) можно представить в виде.

Edl=-grad u∙dl=-du. (3.4)

где du - полный дифференциал и. Второе равенство в формуле (3.4) представляет собой известное тождество векторного анализа. Для его доказательства достаточно grad и и дl разложить по ортам

декартовой системы  координат и вычислить скалярное произведение. Подставляя (3.4) в (3.3), получаем

A=q(u₂-u₁)                  (3.5)

где u₁ и и₂ - значения потенциала и в точках N_{1 И} N₂ соответственно. Полагая q = 1 Кл, получаем, что работа, совершаемая при перемещении единичного точечного положительного заряда в электростатическом поле, численно равна разности потенциалов в конечной и начальной точках пути. Она не зависит от формы пути, по которому перемещается заряд, и от абсолютного значения потенциала. Если потенциалы бесконечно удаленных точек считать равными нулю, то потенциал и в точке N можно определить как работу, которую нужно совершить для перемещения единичного точечного положительного заряда из бесконечности в точку N. Потенциал измеряется в вольтах, что легко устанавливается из (3.2).

Сравнивая формулы (3.3) и (3.5), находим связь между разностью потенциалов в точках N_{1 И} N₂ и напряженностью электростатического поля:

Если потенциалы бесконечно удаленных точек считаются равными нулю, то выражение (3.6) принимает вид

В (2.6) было показано, что в случае однородных сред (ε = = const) электростатический потенциал удовлетворяет уравнению Пуассона (2.45). Для упрощения записи в правой части равенства (2.45) у функции ρ^ст опустим индекс "ст", т.е. перепишем (2.45) в виде

Если в рассматриваемой части пространства заряды отсутствуют (ρ = 0), то (3.7) переходит в уравнение Лапласа

Δ² и = 0.                                           (3.8)

Решение уравнения (3.7) было получено в 2.6. В тех случаях, когда заряды распределены в ограниченной области V с плотностью ρ(ρ-функция координат), потенциал и в соответствии с формулой (2.44) определяется выражением

где R- расстояние от точки интегрирования M_ЄdV до точки наблюдения N = N (х, у, z) (см. рис.2.6).

В случае поверхностных зарядов, распределенных с плотностью ρ_s на поверхности S, нужно вместо равенства (3.9) использовать формулу

где R - расстояние от элемента dS до точки, в которой вычисляется потенциал (см. рис. 2.7).

Если поле создается заряженной нитью конечных размеров, т.е. зарядами, распределенными вдоль линии, то потенциал выражается формулой

где интегрирование осуществляется вдоль нити (контур Г); R-расстояние от элемента dl до точки, в которой вычисляется потенциал (рис. 2.8), а τ- линейная плотность заряда, определяемая выражением

Соотношения (3.9)—(3.11) позволяют определить потенциал, а следовательно, и векторы электростатического поля в однородном изотропном пространстве по заданному распределению зарядов. Однако во многих практически важных случаях распределение зарядов нельзя считать известным заранее. Вопрос о постановке и возможности решения такого рода задач будет рассмотрен отдельно.

Чтобы получить наглядное представление об электростатическом поле, его иногда изображают графически. При этом помимо силовых линий обычно рассматривают его эквипотенциальные поверхности, т.е. поверхности равного потенциала. Выясним связь между поверхностями равного потенциала и силовыми линиями электростатического поля. На эквипотенциальной поверхности потенциал и постоянен и, следовательно, du = 0. При этом согласно соотношению (3.4) должно выполняться равенство Edl - О, где вектор дl совпадает по направлению с касательной к эквипотенциальной поверхности. Это равенство означает, что поверхности равного потенциала и силовые линии электростатического поля пересекаются под прямым углом. Зная семейство эквипотенциальных поверхностей, можно построить силовые линии, и, наоборот, зная силовые линии, можно построить эквипотенциальные поверхности.

3.2. ГРАНИЧНЫЕ УСЛОВИЯ

До сих пор рассматривалось электростатическое поле в однородном пространстве. Если имеются две (или более) разнородные среды, то для определения поля необходимо знать граничные условия для составляющих векторов. Е и D и потенциала и на границе раздела. Электростатическое поле является частным случаем электромагнитного поля, общие свойства которого были рассмотрены в предыдущих главах. Поэтому граничные условия для векторов Е и D, выведенные в 1.7, должны выполняться и для электростатического поля-. Эти условия имеют вид:

Напомним, что при выводе граничных условий нормаль считалась направленной из второй среды в первую.

Так как при решении конкретных задач, как правило, оперируют с функцией и, то от условий для векторов Е и D нужно перейти к граничным условиям для потенциала и. Используя соотношение (3.2) и учитывая, что проекция grad и на произвольное направление l₀ равна производной функции и по этому направлению, поручаем из формулы (3.13) следующее равенство:

где оператор д/ дτ означает дифференцирование по любому направлению в плоскости, касательной к поверхности раздела в рассматриваемой точке. Интегрируя равенство (3.15) по τ, получаем

и₁= и₂  +b,                     (3.16)

где b - произвольная постоянная, а u₁ и u₂ - значения потенциала и на поверхности раздела в первой и второй средах соответственно. Постоянную b в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом из равенства (3.16) следует, что

u₁ = и₂.                                            (3.17)

Соотношение (3.17) нарушается, если на поверхности раздела имеется двойной заряженный слой. Этот слой можно представить следующим образом. Рассмотрим две параллельные поверхности S₁ и S₂, на одной из которых распределены поверхностные заряды с плотностью ρ_s, а на другой-такие же заряды, но противоположного знака. Расстояние между поверхностями S₁ и S₂ обозначим через l (рис. 3.2). Если считать, что поверхности неограниченно приближаются друг к другу, а плотность поверхностных зарядов при этом возрастает (причем произведение ρ_s l остается постоянным, то в пределе получим двойной заряженный слой. Параметр ρ_s l  называют мощностью слоя. При переходе через двойной заряженный слой потенциал претерпевает разрыв, величина которого зависит от мощности слоя. В дальнейшем будет предполагаться, что в рассматриваемой области отсутствуют двойные заряженные слои.

Переходя в формулах (3.14) к функции и, получаем второе граничное условие для электростатического потенциала:

где оператор д/дп означает дифференцирование по нормали к поверхности раздела, направленной из второй среды в первую.

Если одна из сред является проводником, то граничные условия принимают более простой вид. В самом деле, при анализе макроскопических свойств поля проводник можно рассматривать как замкнутую область, внутри которой возможно свободное перемещение зарядов. Плотность потока зарядов, т.е. плотность тока проводимости в проводнике, пропорциональна напряженности электрического поля: j = σЕ. В электростатике перемещение зарядов отсутствует: j = 0. Так как σ≠ 0, то напряженность электростатического поля внутри проводника должна быть равна нулю. Это - одна из особенностей электростатического поля. В 1.7 было показано, что переменное электромагнитное поле не проникает в идеальный металл. Электростатическое поле равно нулю внутри любого реального проводника.

Напряженность электростатического поля связана с потенциалом и соотношением (3.2). Полагая в (3.2) Е = 0, получаем, что внутри проводника grad и = 0. Откуда и = const. Следовательно, в электростатике все точки проводника имеют один и тот же потенциал. Это позволяет говорить о потенциале проводника. Потенциалы изолированных друг от друга проводников могут, конечно, иметь разные значения.

Граничные условия на поверхности проводника для составляющих векторов Е и D находятся из формул (3.13) и (3.14). Пусть первая среда - диэлектрик, а вторая - проводник. Тогда, полагая E₂ =0 и D₂=0 получаем

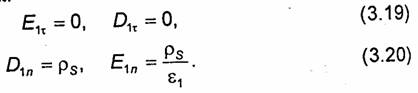
Условия (3.19) и (3.20)можно переписать в векторной форме:

Подчеркнем, что в случае переменного поля аналогичные условия выполняются лишь на поверхности идеального проводника, а в электростатике условия (3.19)—(3.21) справедливы при любой отличной от нуля удельной проводимости второй среды.

Граничные условия для потенциала и на поверхности проводника получаются из формул (3.19) и (3.20):

Нормаль  n₀. считается  внешней  по отношению  к проводящей

среде.

Из условия (3.22) следует, что поверхность проводника всегда

эквипотенциальна.

3.3. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Как известно из курса физики, энергия W^э электростатического поля, сосредоточенного в объеме V, определяется формулой (1.131). Эту формулу можно преобразовать таким образом, чтобы энергия W^э была выражена через заряды. Заменяя вектор Е через - grad и и используя тождество div (ψа) = ψ div а + a grad ψ, где а и ψ - произвольные векторная и скалярная функции, имеющие первые производные, получаем

Последний   интеграл  в  (3.24)   преобразуем   по  теореме Остроградского-Гаусса:

где S - поверхность, ограничивающая объем V.

Предположим, что заряды, создающие электростатическое поле, сосредоточены в ограниченной области V_o, и распространим интегрирование в формуле (3.25) на все пространство. При этом поверхность S будет удалена в бесконечность, и в пределе интеграл (3.25) окажется равным нулю. Действительно, из формулы (3.9) следует, что потенциал зарядов, распределенных в ограниченной области V_O на большом по сравнению с размерами области V_o расстоянии убывает пропорционально 1/r, где r- расстояние от некоторой точки внутри области V до точки наблюдения. Вектор электрического смещения D убывает как 1/r², a поверхность S возрастает пропорционально r². Таким образом, интеграл (3.25) при r →∞убывает как 1/r и в пределе равен нулю. Учитывая, что div D = ρ, получаем окончательное выражение для энергии электростатического поля:

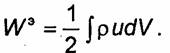                           (3.26)

Если электростатическое поле создается поверхностными зарядами, распределенными по поверхности S с плотностью ρ_s, то выражение для энергии электростатического поля принимает вид

В случае распределения зарядов вдоль контура Г_о с плотностью τ (заряженная нить):

В общем случае при наличии зарядов всех трех типов

Рассмотрим частный случай, когда электростатическое поле создается зарядами, расположенными на проводниках. Пусть имеется п проводников (рис. 3.3), потенциалы которых равны соответственно  u₁, и₂.....и_п.  Так  как  потенциал   проводника  имеет

одинаковые значения во всех его точках, а заряды распределены по его поверхности, то, применяя формулу (3.27), получаем

-полный  заряд m-гo  проводника,  a p⁽_s^m)-плотность поверхностных зарядов, с которой заряд Q_m распределен по поверхности S_m рассматриваемого проводника.

Выражение для энергии уединенного проводника, т.е. бесконечно удаленного от других тел и зарядов, находится из формулы (3.29) как частный случай. Полагая в (3.29) п = 1, получаем

На энергию электростатического поля не распространяется принцип суперпозиции. Поэтому энергия системы проводников не равна суммарной энергии уединенных проводников. Представим потенциал m-го проводника в виде суммы:

где и_т° - потенциал уединенного проводника, а и_т- потенциал, создаваемый действием всех остальных проводников. Подставляя (3.31) в (3.29), получаем

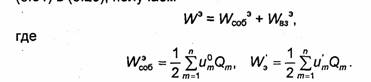
Величину  принято называть собственной энергией системы проводников, а  - взаимной энергией.

Можно показать, что заряды, находящиеся на системе заданных проводников, расположенных в диэлектрике, распределяются по поверхности этих проводников таким образом, что энергия получающегося в результате электростатического поля минимальна. Это важное утверждение известно под названием теоремы Томсона.

3.4. ЕМКОСТЬ

Потенциал уединенного проводника зависит от его размеров и формы, а также от величины имеющегося на нем заряда. При равных потенциалах уединенные тела разной формы или размеров обладают зарядами разной- величины. Отношение величины заряда к потенциалу при условии, что потенциалы бесконечно удаленных точек считаются равными нулю, называется емкостью уединенного проводника:

С = Q/u.                                          (3.32)

Емкость измеряют в фарадах (Ф = Кл/В). С учетом формулы (3.32) выражение для энергии электростатического поля уединенного заряженного проводника (3.30) принимает вид

W₃ = Си²/2 = Q²/2C.                                 (3.33)

Если проводник не уединен, то потенциал, приобретаемый им при сообщении ему какого-либо заряда, существенно зависит от формы и расположения других проводников. Заряженные тела создают электрическое поле, под действием которого заряды на всех соседних проводящих телах перераспределяются. Перераспределение продолжается до тех пор, пока суммарное электрическое поле внутри каждого проводника не станет равным нулю.

Рассмотрим   систему   из   n   проводников   с   зарядами   Q_1, Q₂.....Q_n соответственно. Потенциал каждого проводника линейно

зависит от величины зарядов Q₁, Q₂.....Q_n, т.е. должно выполняться л соотношений вида

где и_т - потенциал m-го проводника, a a_mk, k = 1, 2,..., n- некоторые постоянные, называемые потенциальными коэффициентами, зависящие от размеров, формы и взаимного расположения проводников. Коэффициент а_тk численно равен потенциалу л7-го проводника, наведенному зарядом k-го проводника при условии, что заряд последнего равен 1 Кл. а заряды остальных - нулю. Например, a₁₃ численно равен потенциалу проводника 1, наведенному единичным зарядом проводника 3 при отсутствии зарядов на остальных проводниках.

Система уравнений (3.34) определяет потенциалы проводников через заряды Q и потенциальные коэффициенты а_тк. Если потенциалы и_1, и₂.....и_п проводников и потенциальные коэффициенты а_тk известны, то система (3.34) позволяет однозначно определить заряды проводников

Постоянные коэффициенты с_тk, т= 1, 2,..., п; k= 1, 2,....n однозначно определяются потенциальными коэффициентами a_ip, i=1,2,..., n; р = 1, 2,..., n, и находятся при решении системы (3.34) относительно зарядов Q_1, Q₂....,Q_n. Из уравнений (3.35) следует, что коэффициент с_тk численно равен заряду m-го проводника, если потенциал k-го проводника равен единице, а потенциалы остальных проводников - нулю.

Отметим, что потенциальные коэффициенты а_тk и коэффициенты с_тk удовлетворяют правилу взаимности:

Обычно систему уравнений (3.35) записывают в несколько иной форме. Прибавим к правой части m-го уравнения системы равное нулю выражение В   результате   получим   следующую   систему  п

уравнений:

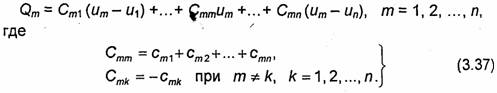
Коэффициенты С_тk называют частичными емкостями. Иногда вводят различные названия для коэффициентов с одинаковыми и разными индексами: коэффициент С_тт называют собственной емкостью т-го проводника, а С_тk - взаимной емкостью m-го и k-го проводников. Отметим, что собственные емкости уединенных проводников могут отличаться от коэффициентов С_тт. Аналогично взаимные емкости двух проводников, отделенных от остальных, могут отличаться от соответствующих коэффициентов С_тk, так как частичные емкости С_тk и С_тт определяются не только рассматриваемыми проводниками, но и всеми остальными проводниками системы.

Из формул (3.36) и (3.37) следует, что частичные емкости также удовлетворяют правилу взаимности: С_тk = С_kт.

3.5. ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЭЛЕКТРОСТАТИКИ

3.5.1. Определение поля, создаваемого известными источниками в безграничной однородной среде

Прямая задача электростатики заключается в определении векторов поля по заданному распределению зарядов. При этом область пространства, в которой требуется определить поле, может быть как ограниченной, так и неограниченной.

Наиболее просто такая задача решается в том случае, когда рассматриваемая область представляет собой неограниченное пространство, заполненное однородной изотропной средой, а заряды сосредоточены внутри некоторого объема конечных размеров (т.е. отсутствуют заряды в бесконечно удаленных точках). Математически она формулируется следующим образом. Задана объемная плотность заряда ρ как функция координат. Требуется найти функцию и, удовлетворяющую уравнению Пуассона (3.7) и обращающуюся в нуль в бесконечно удаленных точках. Эта задача была рассмотрена в 2.5.2 и 3.2. Ее решением является выражение (3.9). Если заряды распределены на поверхности конечных размеров S с плотностью ρ_s, то соответствующий им потенциал определяется формулой (3.10). Если же поле создается зарядами, распределенными с линейной плотностью τ вдоль контура конечных размеров Г, искомая функция и определяется выражением (3.11).

В тех случаях, когда система зарядов не может быть охвачена описанной вокруг начала координат сферой конечного радиуса, т.е. содержит заряды в бесконечно удаленных точках (например, бесконечно длинная заряженная нить), то формулы (3.9)—(3.11) могут оказаться непригодными. Это, в частности, имеет место при решении так называемых плоских задач электростатики, т.е. при одинаковом распределении зарядов (и поля) в любой плоскости, перпендикулярной к некоторой прямой линии, например к одной из осей декартовой системы координат. Такую систему зарядов можно представить как бы состоящей из тонких, равномерно заряженных по длине бесконечно протяженных прямолинейных нитей. Поэтому для определения поля, создаваемого подобной системой зарядов, нужно знать потенциал, создаваемый одной нитью.

Пусть имеется бесконечно тонкая равномерно заряженная с плотностью τ = const нить. Введем цилиндрическую систему координат τ, φ, z, ось Z которой совпадает с нитью, и рассмотрим поток вектора D через поверхность кругового цилиндра радиуса а и длиной Δl, ось которого совпадает с осью Z (рис. 3.4). Из условия задачи очевидно, что поле должно обладать осевой симметрией, а векторы Е и D должны быть перпендикулярны к боковой поверхности цилиндра. Поэтому поток вектора D через основания цилиндра отсутствует, а поток через боковую поверхность равен D∙2πrΔl. Используя теорему Гаусса (1.40) и учитывая, что полный заряд внутри рассматриваемого цилиндра равен  τΔl, получаем

где r₀-орт радиуса-вектора цилиндрической системы координат. Поскольку в рассматриваемом случае поле не зависит от переменных φ и z (производные потенциала и по переменным φ и z равны нулю), то из определения электростатического потенциала (3.2) и формулы (3.38) имеем

где В - произвольная постоянная. Обычно постоянную В полагают равной нулю и потенциал нити определяют выражением

Если вместо нити имеется тонкий бесконечно длинный цилиндр с площадью поперечного сечения ΔS, равномерно заряженный с объемной плотностью ρ, то соотношение (3.39) примет вид

где - расстояние от элемента ΔS, характеризуемого координатами ζ£, η, до точки N с координатами х, у, в которой вычисляется потенциал.

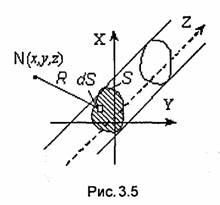
От формулы (3.41) нетрудно перейти к выражению для потенциала, созданного произвольным двумерным (не зависящим от z) распределением зарядов с плотностью ρ:

где S - площадь сечения данной системы зарядов плоскостью, перпендикулярной к оси Z (рис. 3.5).

Функцию и, определяемую соотношениями (3.39)-(3.42), принято называть логарифмическим потенциалом.

Если поле создается зарядами, распределенными по цилиндрической поверхности S, образующие которой параллельны оси Z, а плотность поверхностных зарядов не зависит от переменной z, то соответствующий логарифмический потенциал

где Г-линия пересечения поверхности S с плоскостью, перпендикулярной оси, Z, a R - расстояние от элемента dl до точки N, в которой вычисляется потенциал (рис. 2.9).

Из формул (3.39)-(3.43) следует, что логарифмический потенциал на бесконечности нельзя принять равным нулю не только в направлении оси Z, но и в перпендикулярных к ней плоскостях. Исключение составляет случай, когда полный заряд системы равен нулю.

Поле, соответствующее потенциалам (3.42) и (3.43), убывает на бесконечности пропорционально 1/r (или быстрее), если поверхность S (или контур Г) ограничена. Если S (или Г) не ограничена, то векторы Е и D на бесконечности могут иметь конечные значения (например, поле равномерно заряженной плоскости).

3.5.2. Примеры определения поля известных источников

В некоторых задачах напряженность электростатического поля, сoдаваемого в безграничной однородной изотропной среде заданным распределением зарядов, легко находится непосредственно без предварительного вычисления электростатического потенциала и, в других - введение потенциала и упрощает построение решения. Рассмотрим несколько примеров.

Поле равномерно заряженной сферы. Пусть заряд Q равномерно распределен по поверхности сферы радиуса а, находящейся в однородной изотропной безграничной среде с диэлектрической проницаемостью ε. Введем сферическую систему координат r, θ, φ, начало которой совпадает с центром сферы. Из симметрии задачи очевидно, что поле в этом случае может зависеть только от координаты r, причем векторы Е и D могут иметь только радиальную компоненту. Применяя закон Гаусса (1.40) к сфере радиуса r и учитывая, что заряды равномерно распределены по поверхности сферы радиуса а, получаем

Отсюда следует, что поле равномерно заряженной сферы в области r≥a совпадает с полем точечного заряда величины q= Q, расположенного в начале координат.

Электростатический потенциал в этом случае определяется выражениями:

Из определения емкости и формулы (3.44) находим

Поле равномерно заряженного цилиндра. Пусть заряд равномерно распределен по объему бесконечного кругового цилиндра радиуса а с плотностью ρ = const. Из соображений симметрии очевидно, что векторы Е и D в этом случае будут направлены перпендикулярно оси цилиндра. Рассмотрим поток вектора D через поверхность цилиндра длиной l и радиуса а, ось которого совпадает с осью основного цилиндра. Учитывая, что поток вектора D через основания этого цилиндра равен нулю, из закона Гаусса (1.40) получаем

где r₀ - координатный орт переменной r цилиндрической системы координат.

Если заряд распределен по бесконечно протяженной цилиндрической поверхности радиуса а с плотностью поверхностных зарядов p_s = const, то

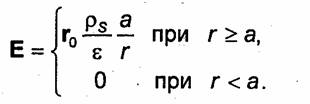
Отметим, что поля, создаваемые равномерно заряженными бесконечно протяженными цилиндром и цилиндрической поверхностью радиуса а в области r≥a совпадают с полем равномерно заряженной нити с линейной плотностью зарядов τ =πа²ρ и τ = 2πaρ_s соответственно.

Поле электростатического диполя. Электростатическим диполем называется система из двух близлежащих равных по величине постоянных точечных разноименных зарядов +q и -q (рис. 3.6). Диполи характеризуются дипольным моментом

где l- вектор, направленный от отрицательного заряда к положительному, по абсолютной величине равный расстоянию между зарядами l, а 1₀- орт, соответствующий вектору l(l=l_ol).

Если сближать заряды, одновременно увеличивая их значения так, чтобы вектор р оставался неизменным, то в пределе получится точечный или идеальный диполь с тем же моментом.

Вычислим поле электростатического диполя. Введем сферическую систему координат r, θ, φ так, чтобы полярная ось проходила через оба заряда, а начало координат находилось на равном расстоянии от них (рис. 3.6). Потенциал, создаваемый диполем, найдем

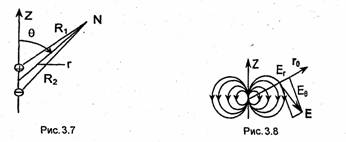
по принципу суперпозиции как сумму потенциалов, создаваемых зарядами +q и-q:

где R₁ и R₂ - расстояния соответственно от зарядов +q и -q до точки, в которой вычисляется потенциал (рис. 3.7):

При вычислении поля будем считать, что расстояние r от центра диполя до точки наблюдения велико по сравнению с расстоянием между зарядами l. При этом условии справедливы следующие приближенные равенства

При этом (3.46) принимает вид

где r_о - координатный орт переменной г. Для определения напряженности электрического поля воспользуемся соотношением (3.2). Выражение для grad и в сферической системе координат приведено в приложении (см. (П. 15)). Выполняя указанные в (П. 15) действия и учитывая, что в рассматриваемом случае ди/дφ = 0, получаем

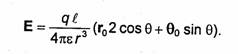
Направления единичных векторов r₀,θ₀ и φ₀ показаны на рис. 3.6. Как видно, вектор напряженности электрического поля, создаваемого электростатическим диполем, не зависит от угла φ (поле обладает осевой симметрией) и имеет две составляющие:

Силовые линии этого поля показаны на рис. 3.8.       

Поле параллельных противоположно заряженных нитей.

Вычислим поле двух параллельных бесконечно тонких равномерно заряженных нитей с линейной плотностью зарядов +τ и -τ соответственно, расположенных на расстоянии 2£ друг от друга (рис. 3.9). Введем декартову х, у, z систему координат, как показано на рис. 3.9. Потенциал системы нитей равен сумме потенциалов каждой и| них. Потенциал одной нити определяется формулой (3.39). Выбирая постоянную В так, чтобы на оси Z потенциал и был равен нулю, получаем

где R₁ и R₂ - расстояния от положительно и отрицательно заряженных нитей соответственно до точки N, в которой вычисляется потенциал (рис. 3.9).

Найдем  эквипотенциальные   поверхности   рассматриваемой системы зарядов. Потенциал (3.49) постоянен, если

R₂/R₁ = b = const.                                 (3.50)

Следовательно, эквипотенциальные поверхности представляют собой  поверхности  круговых цилиндров,  параллельных оси Z.Найдем их радиусы и положение осей. Так как , то из уравнения (3.50) следует соотношение

которое можно переписать в виде

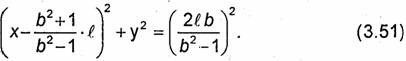
Уравнение (3.51) описывает семейство окружностей, образующихся при пересечении эквипотенциальных поверхностей с плоскостью XOY. Центры окружностей расположены на оси Х и имеют координаты:

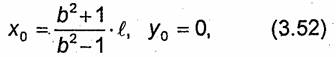
а их радиусы равны

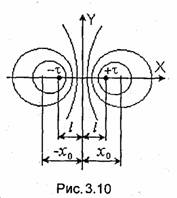
Значения параметра b у окружностей, расположенных симметрично относительно оси Y, выражаются обратными числами (например, Ь_о и 1/Ь₀). Величины r₀, l и х₀ связаны простым соотношением

являющимся следствием формул (3.52) и (3.53). Решая уравнение (3.53) относительно b и используя равенства (3.52) и (3.54), находим значения параметра b и потенциала и на соответствующей эквипотенциальной поверхности:

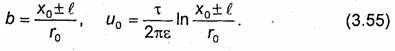
В формулах (3.55) знак "+" выбирают для точек, находящихся справа от оси У, а знак "-" для точек, лежащих слева от оси У. Структура эквипотенциальных поверхностей показана на рис. 3.10.

3.5.3. Краевые задачи электростатики

Выше был рассмотрен вопрос об определении поля в однородном изотропном пространстве по известному распределению зарядов. Однако на практике часто встречаются задачи другого типа, например: задано расположение и форма всех проводников, находящихся в однородном диэлектрике, требуется найти поле в этом диэлектрике, если известен потенциал каждого проводника (задача 1) или общий заряд каждого проводника (задача 2). Такие задачи называют краевыми задачами электростатики.

Область V, в которой требуется найти поле, либо ограничена поверхностями проводников (рис. 3.11), либо простирается до бесконечности. Во втором случае проводящие тела целиком лежат внутри области V (рис. 3.12). Потенциал в бесконечно удаленных точках считается равным нулю.

Доказано (см., например, [12]), что данные задачи имеют единственное решение. В задаче 1 и вектор Е электростатического поля и потенциал и определяются однозначно. Различные решения задачи 2 могут отличаться на постоянную величину в выражениях для электростатического потенциала. Однако это различие

несущественно при вычислении вектора Е. В задачах смешанного типа, когда на каком-либо проводнике (или нескольких проводниках) задан потенциал, а для других известен полный заряд, функция и определяется однозначно.

Отметим, что построение строгого аналитического решения краевой задачи электростатики во многих случаях сопряжено со значительными математическими трудностями. Практически его удается найти лишь при достаточно простой форме проводящих тел. Подробное изложение методов решения задач электростатики имеется в [15 и 16].

Рассмотрим несколько примеров с целью дать представление о некоторых методах решения задач электростатики.

Электростатическое поле двухпроводной линии. Вычислим электростатическое поле двухпроводной линии, т.е. поле двух параллельных противоположно заряженных бесконечных цилиндров (проводов) радиуса а, расстояние между осями которых равно 2Л (рис. 3.13). Потенциал одного из проводов равен -U, другого - соответственно +U. Заряды проводов на единицу длины равны по величине и противоположны по знаку.

Математически задачу можно сформулировать следующим образом. Требуется найти функцию и, которая во внешнем по отношению к цилиндрам пространстве удовлетворяет уравнению Лапласа (3.8), на поверхностях цилиндров принимает заданные

значения +U и -U, а в направлениях, перпендикулярных осям цилиндров, на бесконечности обращается в нуль. В силу теоремы единственности существует только одна функция и, удовлетворяющая указанным требованиям. Для построения функции и применим искусственный прием.

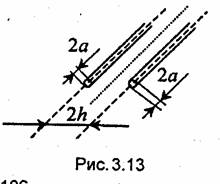
Выше было показано, что эквипотенциальные поверхности поля двух параллельных противоположно заряженных нитей образуют семейство поверхностей круговых цилиндров. Найдем расстояние между нитями, при котором две эквипотенциальные поверхности будут совпадать с поверхностями цилиндров, образующих двухпроводную линию. Полагая в (3.54) х_о = h и r_о = а, получаем

Потребуем, кроме того, чтобы потенциалы рассматриваемых цилиндров, расположенных справа и слева от оси Y (рис. 3.13), равнялись +U и -U соответственно. Подставляя х_о = h в формулу (3.55) и учитывая соотношение (3.56), определяем линейную плотность зарядов эквивалентных нитей:

Таким образом, определены и местоположение (х = ± h, у = 0), и плотности линейных зарядов (±τ) эквивалентных заряженных нитей (их называют электрическими осями проводов). Потенциал этих нитей, определяемый выражением (3.49), во внешнем по отношению к проводам линии пространстве отвечает всем поставленным требованиям, т.е. является решением задачи. Вектор Е вычисляется по формуле Е =- grad и.

Подчеркнем, что потенциал найденных таким образом эквивалентных заряженных нитей (электрических осей проводов) совпадает с искомым потенциалом только вне цилиндров, образующих двухпроводную линию. Внутри цилиндров истинный потенциал имеет постоянные значения (±U т.е. принципиально отличается от определяемого выражением (3.49).

Определим емкость С₁ на единицу длины рассматриваемой системы проводов как отношение заряда, приходящегося на единицу длины одного из проводов, к разности потенциалов между проводами:

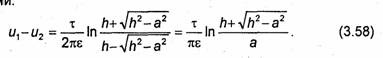
Из (3.57) и (3.58) получаем

В случае тонких проводов (а <<h) справедливо приближенное равенство

Поле точечного заряда,  расположенного над идеально проводящей   плоскостью.   Метод  зеркальных  отображений.

Рассмотрим еще раз поле двух разноименных зарядов +q и -q, расположенных на расстоянии 2h друг от друга. Создаваемый ими потенциал выражается формулой (3.46), если в последней положить l = 2h. Очевидно, плоскость А-В, расположенная симметрично относительно зарядов +q и -q (рис. 3.14), является эквипотенциальной поверхностью с нулевым потенциалом. На основании теоремы единственности можно утверждать, что поле над этой плоскостью не изменится, если ее заменить металлической плоскостью или заполнить нижнее (см. рис.3.14) полупространство проводящей средой. Иными словами, задача определения поля точечного заряда, расположенного над проводящей плоскостью, эквивалентна задаче определения поля, создаваемого в верхнем  полупространстве двумя зарядами:  заданным  и  некоторым дополнительным (фиктивным) зарядом противоположного знака, являющегося зеркальным отображением первого. При вычислении поля двух зарядов нужно считать, что никакой металлической плоскости нет и оба заряда расположены в безграничной среде,   такой  же,   как  среда,   заполняющая   верхнее   полупространство.

Пусть заряд q расположен на высоте h над металлической плоскостью А-В (см. рис. 3.14). Найдем величину и распределение заряда, индуцированного на плоскости А-В. Введем цилиндрическую систему координат R, φ, z, ось Z которой проходит через заряды +q и -q, а начало координат находится на плоскости А-В. В этой системе координат потенциал и в области z ≥ 0 выражается формулой (3.46), в которой нужно считать, что. В области z< 0 потенциал и = 0. Из граничного условия (3.18) получаем, что плотность поверхностных зарядов, наведенных на плоскости z = 0, определяется выражением

Интегрируя (3.60) по всей плоскости, получаем, что полный заряд, наведенный на плоскости, равен -q. Таким образом, введение фиктивного сосредоточенного заряда эквивалентно учету всех зарядов, наведенных на плоскости z = 0.

Отметим, что полученные выше формулы для поля электростатического диполя можно использовать для вычисления поля (вектора Е)

точечного заряда, расположенного над проводящей плоскостью, в области z ≥ 0 (в верхнем полупространстве), если в них положить l = 2Л.

Метод замены проводящей, поверхности фиктивным сосредоточенным зарядом получил название метода зеркальных отображений.

Очевидно, в силу принципа суперпозиции метод зеркальных отображений можно обобщить на случай произвольной системы зарядов, расположенных над проводящей плоскостью. Таким образом, если над бесконечной проводящей плоскостью заряды распределены по закону р = f (х, у, z) (рис. 3.15, а), то создаваемый ими потенциал (а следовательно, и напряженность электрического поля) в верхнем полупространстве будет равен потенциалу (напряженности электрического поля), создаваемому этими зарядами и системой зарядов, являющихся их зеркальным отображением (рис. 3.15, б).

Поле точечного заряда, расположенного в уголковой области. Пусть точечный заряд q расположен в уголковой области V, представляющей собой двугранный угол с проводящими стенками. Если соответствующий линейный угол (рис. 3.16) равен α = π/п где п - целое число, то для определения поля в этой области также можно использовать метод зеркальных отображений. Однако в этом случае нужно ввести уже не один фиктивный заряд, а 2n - 1 фиктивных зарядов. В качестве примера на рис.3.17 показана система зарядов для случая а =π /2, а на рис. 3.18- система зарядов для случая α= π/3.

Поле образованной таким образом системы зарядов в рассматриваемой уголковой области удовлетворяет всем необходимым требованиям (потенциал на стенках двугранного угла и в бесконечно удаленных точках равен нулю) и, следовательно, является решением исходной задачи.

Если угол между проводящими плоскостями не равен целой части от л, то метод зеркальных отображений требует введения бесчисленного множества фиктивных зарядов.

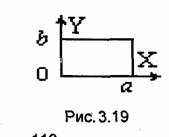
Задача Дирихле для прямоугольной области (метод Фурье). Найдем распределение электростатического потенциала и внутри бесконечно длинной металлической коробки прямоугольного сечения, боковые и нижняя стенки которой заземлены (и = 0), а потенциал верхней равен V_o = const (верхняя стенка изолирована от боковых). Ширина нижней и верхней стенок равна а, боковых - b. Введем декартову систему координат х, у, z, как показано на рис. 3.19. Пвперечное сечение коробки и функция и не зависят от переменной z. Потенциал и - и(х, у) должен удовлетворять уравнению Лапласа (3.8)

и следующим краевым условиям:

Условия, определяющие значения искомой функции на границе области, называют краевыми условиями первого рода. Условия, определяющие значения производной искомой функции по нормали к границе области, называют краевыми условиями второго рода. Задачу определения функции, удовлетворяющей уравнению Лапласа и краевым условиям первого рода, называют задачей Дирихле, а аналогичную задачу с граничными условиями второго рода - задачей Неймана.

Будем искать решение уравнения (3.61) методом разделения переменных. Представим и(х, у) в виде произведения двух функций, одна из которых зависит только от х, а другая - только от у.

Подставляя (3.66) в (3.61) и деля результат на произведение X(x)Y(y), получаем

Левая часть равенства (3.67) зависит только от х, правая - только от у. Переменные х и у являются независимыми, и соотношение (3.67) представляет собой равенство двух независимых функций, что возможно, только если они равны

одной и той же постоянной. Обозначая эту постоянную через v², приходим к двум дифференциальным уравнениям: X” + v²X=0 и У”-v²Y=0, решая которые получаем Х(х) = A sin vx + В cos vx, У(у) = = С sh vy + D ch vy. Из краевых условий (3.62) и (3.64) находим, что В = D = 0, а из (3.63) вытекает соотношение A sin va = 0, откуда следует, что v = nπ/a, где n =1,2,.... Таким образом, решение уравнения (3.61) можно представить в виде

где М_n= А·В - некоторые, пока неизвестные постоянные. Выражение (3.68) удовлетворяет уравнению (3.61) и трем краевым условиям (3.62)-(3.64). Чтобы удовлетворить последнему краевому условию (3.65), воспользуемся принципом суперпозиции и представим искомое решение в виде суммы всех возможных частных решений (3.68):

Подставим (3.69) в (3.65) и разложим постоянную V_o в ряд Фурье по функциям  Приравнивая  коэффициенты  при одинаковых п, приходим к соотношению

с учетом которого решение рассматриваемой задачи принимает вид

Метод сеток. Как уже отмечалось (см. 2.6), для решения краевых задач электродинамики, и в частности электростатики, широко используют численные методы. В случае внутренних задач часто применяют так называемый метод сеток. Изложим его основы на примере уже решенной методом Фурье двумерной задачи Дирихле для прямоугольной области, показанной на рис. 3.19. Задача состоит в определении электростатического потенциала и = и(х,у), удовлетворяющего при 0≤х≤а и 0≤у≤b уравнению Лапласа (3.61) и краевым условиям (3.62)-(3.65).

Предположим для простоты, что стороны а и b соизмеримы, т.е. рассматриваемая область может быть покрыта сеткой с квадратными ячейками (рис. 3.20), стороны которых Δx и Δy Δ

Уравнение (3.71) справедливо для каждого узла сетки. Для узлов, расположенных влизи границы рассматриваемой области, некоторые из функций, входящих в (3.71), являются известными. Совокупность уравнений вида (3.71), записанных для всех внутренних узлов сетки, образует систему линейных алгебраических уравнений (СЛАУ) относительно значений потенциала в этих узлах. Решив СЛАУ, найдем искомые значения потенциала во всех узловых точках.

Для решения СЛАУ, полученной на основе описанной конечно-разностной аппроксимации уравнения Лапласа, обычно применяют метод итераций. Уравнение (3.71) можно переписать в виде

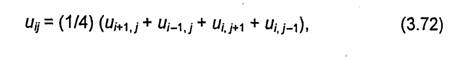
из чего следует, что значение искомой функции в узле сетки (х_j-, y_j) равно среднему арифметическому значению функции и(х, у) в четырех соседних узлах. Поэтому можно использовать следующую схему построения приближенного решения. Во всех внутренних узлах сетки задают произвольные значения функции и(х, у), а в узлах, расположенных на границе области, - значения, соответствующие краевым условиям задачи (нулевое приближение). Затем по формуле (3.72) находят новые значения функции и(х, у) во всех внутренних узлах (первое приближение). Используя первое приближение, опять рассчитывают значения u_ij по формуле (3.72), т.е. находят второе приближение, и т.д. Процесс заканчивают, когда отличие (v + 1)-го приближения от v-гo не превышает заданной величины. Доказано, что итерационный процесс сходится при любых начальных значениях u_ij .

Применение метода сеток для решения более общих краевых задач электростатики, в частности для случаев трехмерной области, неравномерной сетки, криволинейной границы области и др., описано в [16] и [30]. Доказано, что при уменьшении размеров ячеек (при т→∞ и n→∞) решение, полученное методом сеток, приближается к точному. Погрешность решения уравнения Лапласа методом сеток с шагом сетки Δ имеет порядок Δ², т.е. погрешность δ u_ij в любом внуреннем узле может быть представлена в виде g(x_i y_j) Δ², где функция g не зависит от Δ. Если известны приближенные численные решения конкретной электростатической задачи u_ij(2Δ)  и u_ij (Δ)полученные методом сеток с шагом 2Δ и Δ соответственно, то погрешность решения с шагом Δ может быть оценена по формуле .

Интегральные уравнения задач электростатики. Краевые задачи электростатики могут быть также сведены к интегральным уравнениям относительно плотности зарядов, наведенных на проводниках. Пусть, например, требуется найти потенциал или электростатическое поле вне проводящего объекта, потенциал которого равен U_o, а поверхность - S. Потенциал обусловлен поверхностными электрическими зарядами, распределенными по S с плотностью ps(M), M_Є S, и определяется формулой (3.10). Применяя (3.10) к точкам, лежащим на поверхности S, приходим к соотношению

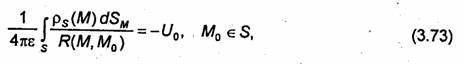
где R(M, Mo) - расстояние от точки истока М _Є S до точки наблюдения М_{о Є} S. Соотношение (3.73) представляет собой интегральное уравнение Фредгольма первого рода относительно функции p_s(M). В некоторых случаях (например, если S-полуплоскость; полоса, бесконечно тонкий диск, плоскость с круглым отверстием и некоторые другие поверхности) уравнение (3.73) может быть решено аналитически, однако в большинстве случаев его решение может быть найдено только численными методами. После определения функции ps(M) электростатический потенциал может быть вычислен по формуле (3.10) в любой точке пространства. Для вычисления поля следует воспользоваться формулой (3.2).

3.6. КОНДЕНСАТОРЫ

3.6.1. Емкость конденсатора

Конденсатором в электростатике называют систему двух проводников, изолированных от внешнего влияния. Идеальным является конденсатор, в котором один проводник образует замкнутую полость, а второй находится внутри этой полости. Если второму проводнику сообщен заряд Q, то на внутренней поверхности первого проводника возникнет заряд противоположного знака -Q. Абсолютную величину отношения заряда одного из проводников к разности потенциалов между проводниками U ₁ –U₂ называют емкостью конденсатора.

Рассмотрим конденсаторы простейших типов.

3.6.2. Плоский конденсатор

Две одинаковые проводящие плоские пластины, расположенные параллельно друг другу и имеющие равные по величине и противоположные по знаку заряды, образуют плоский конденсатор (рис. 3.22). Если размеры пластин велики по сравнению с расстоянием между ними, можно пренебречь искажением поля у краев пластин и считать, что оно такое же, как между двумя параллельными противоположно заряженными с плотностями p_s= ± Q/(εS), Q > 0, безграничными плоскостями

где  S- площадь  одной  пластины,   а  n₀- единичная   нормаль, направленная от положительно заряженной плоскости к отрицательно заряженной. Формула (3.75) легко получается с помощью закона Гаусса.

Разность потенциалов между пластинами (обкладками конденсатора) определяется формулой

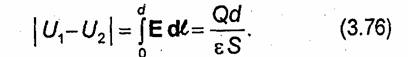
Подставляя (3.76) в (3.74),  находим емкость плоского конденсатора:

C = εS/d.                                        (3.77)

Если размеры пластин нельзя считать большими по сравнению с величиной d, то формула (3.77) становится неточной. Действительная емкость несколько больше емкости, рассчитанной по этой формуле.

3.6.3. Цилиндрический конденсатор

Цилиндрический конденсатор состоит из внутреннего провода радиуса а\ и коаксиальной с ним цилиндрической оболочки с внутренним радиусом а₂ (рис. 3.23). Пусть заряд внутреннего проводника на единицу длины равен τ > 0. Поле в пространстве между проводниками в цилиндрической системе координат r, φ, z, ось Z которой совпадает с осью внутреннего провода, описывается выражением

 где r_о- координатный орт переменной r. Разность потенциалов между внутренним проводом и оболочкой

Следовательно, емкость на единицу длины бесконечного цилиндрического конденсатора определяется формулой

Формула (3.78) достаточно точна для практических целей только в случае конденсаторов, длина проводников которых велика по сравнению с зазором между ними. В конденсаторах с короткими проводниками поле между ними нельзя считать равномерным, и формула (3.78) дает емкость, меньшую действительной.

Гл а в а 4

СТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

4.1. ОСНОВНЫЕ УРАВНЕНИЯ СТАЦИОНАРНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Стационарным называют неизменное во времени электромагнитное поле, создаваемое постоянным током. Оно описывается системой дифференциальных уравнений (1.57). Как уже отмечалось (см. 1.5.2), в системе (1.57) можно выделить две группы уравнений а и б, одна из которых (б) содержит только векторы электрического поля Е и D, а другая (а)-только магнитного поля В и Н. При наличии постоянного тока эти группы уравнений связаны соотношением j = σE. Из уравнений группы б следует, что электрическое поле постоянного тока, как и электростатическое, является потенциальным, а из уравнений группы а следует, что магнитное поле постоянного тока является вихревым.

Уравнения стационарного электромагнитного поля в интегральной форме получаются из уравнений (1.54), если входящие в них величины считать не зависящими от времени. При этом интегральные соотношения, соответствующие уравнениям группы б, совпадают с уравнениями электростатики в интегральной форме (3.1), а интегральные соотношения, соответствующие уравнениям группы а, имеют вид

Полагая в уравнении непрерывности (1.48) дρ/дt=0, получаем, что плотность постоянного тока удовлетворяет условию

divj = O.                                           (4.2)

Следовательно, в стационарном поле линии тока проводимости являются непрерывными.               

Вытекающая из (1.57) относительная независимость электрических и магнитных векторов позволяет рассматривать отдельно электрическое и магнитное поля, что существенно упрощает изучение стационарных электромагнитных процессов.

Отметим, что для существования постоянного тока в однородной проводящей среде недостаточно действия одного потенциального электрического поля,

удовлетворяющего соотношениям (3.1). В самом деле, рассмотрим замкнутый проводник длины l и постоянного сечения S, ось которого образует контур Г (рис. 4.1, а). Пусть по этому проводнику течет ток /, равномерно распределенный по сечению. Вектор плотности тока j=l//S, гдеl₀-орт касательной к линии тока. Предположим, что в проводнике действует только потенциальное электрическое поле. Тогда во всех точках проводника выполняется соотношение j = σЕ. Из (3.1) следует, что

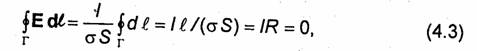
где R-сопротивление проводника.

Так как величина R=l/(σS) заведомо отлична от нуля, то равенство (4.3) возможно лишь при /=0. Действительно, при перемещении заряда по замкнутому контуру в потенциальном электрическом поле работа не совершается. Поэтому ток, представляющий собой упорядоченное движение заряженных частиц, не может расходовать энергию потенциального электрического поля Е Для создания тока в цепи должен действовать источник энергии так называемая сторонняя эдс. На рис. 4.1,6 этот источник условно показан кружком.

Пусть напряженность электрического поля, создаваемого сторонней эдс, равна Е. Закон Ома (1.9) в этом случае записывается в форме

С учетом формулы (4.4) соотношение (4.3) принимает вид

где е^ст- действующая в цепи сторонняя эдс.

Уравнение (4.5) представляет собой закон Ома для цепи постоянного тока. Сторонние эдс вызываются различными причинами, например они возникают на границе раздела проводящих сред, химически воздействующие друг на друга (гальванические эдс).

4.2. МАГНИТОСТАТИКА

Изучение магнитных явлений начнем с наиболее простого случая. Предположим, что в каждой точке рассматриваемой области плотность тока проводимости равна нулю (j = 0), а сама область не охватывает тока. Кольцевые области, сцепленные с током (рис.4.2), в данном разделе не анализируются.

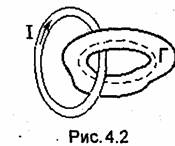
Уравнения группы а в (1.57), описывающие магнитное поле, в этом случае не зависят от уравнений группы б и переходят в уравнения (1.56). Как уже отмечалось, магнитное поле, определяемое уравнениями (1.56), принято называть магнитостатическим, а соответствующий раздел теории электромагнитного поля-  магнитостатикой. Интегральные соотношения магнитостатики получаются из уравнений (4.1), если в последних положить j = 0. При этом второе уравнение остается без изменений, а первое принимает вид

Так как в рассматриваемом случае rot Н = 0, то по аналогии с электростатикой можно ввести в рассмотрение скалярную функцию, и^M, называемую магнитостатическим потенциалом и связанную с вектором Н соотношением

Н =- grad u^M.                                     (4.7)

В однородной среде магнитостатический потенциал удовлетворяет уравнению Лапласа

Δ²u^M=0                        ( 4.8)

Разность значений магнитостатического потенциала между точками N₁ и N₂ можно по аналогии с (3.6) представить в виде

На границе раздела двух сред с разными магнитными проницаемостями (μ₁ и μ₂) должны выполняться общие граничные условия (см.1.7) для составляющих векторов В и Н:

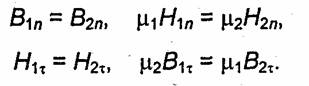
Таким образом, напряженность магнитостатического поля Н и напряженность электростатического поля Е в области без зарядов удовлетворяют одинаковым уравнениям и однотипным граничным условиям. Следовательно, решение задач магнитостатики можно получить из решений аналогичных задач электростатики простой заменой в них Е на Н и ε на μ.

4.3. МАГНИТНОЕ ПОЛЕ И ПОСТОЯННЫЙ ТОК

В тех случаях, когда в рассматриваемой области имеется ток( j ≠0) или область охватывает ток (рис. 4.2), магнитостатический потенциал и^M становится неоднозначной функцией. Разность его значений между точками N₁ и N₂ зависит от контура, по которому выполняется интегрирование в формуле (4.9), а именно при каждом обходе контура вокруг тока / в положительном направлении (так, чтобы контур образовывал с направлением, в котором течет ток, правовинтовую систему) значение интеграла в (4.9) возрастает на величину /.

Таким образом, магнитостатический потенциал и^M не позволяет установить связь между стационарным магнитным полем и создающим его постоянным током. Для определения стационарного поля обычно вводят векторный потенциал А (см. 2.6), связанный с векторами В и Н соотношениями

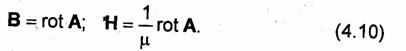
Основные формулы для вектора А, характеризующего стационарное магнитное поле, можно получить непосредственно из формул для электродинамического потенциала А, выведенных в 2.4.1, если в последних считать все величины не зависящими от времени.

            Векторный потенциал стационарного поля удовлетворяет уравнению

Δ²А=-μj                                           (4.11)

вытекающему из (2.40), и условию калибровки divA = 0, которое следует из (2.39). Для упрощения записи в правой части равенства (4.11) и в последующих формулах у функции j опущен индекс "ст".

Если токи  сосредоточены  в  ограниченной  области   V,  то решение уравнения (4.11) можно получить из формулы (2.50):

где R-расстояние от элемента dV до точки, в которой вычисляется потенциал.

Если токи распределены по поверхности S с плотностью j_S, равенство (4.12) следует заменить выражением

а в случае линейного тока  /,  протекающего по  контуру Г, -формулой

В (4.13) и (4.14) R- расстояние от элементов dS и dl. соответственно до точки, в которой вычисляется потенциал.

Перейдем от векторного потенциала А к напряженности магнитного поля Н. Предполагая, что пространство заполнено однородной изотропной средой, получаем

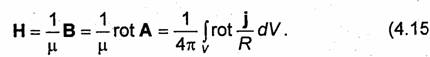
Учитывая, что плотность тока j не зависит от координат точки, в которой вычисляется поле, и используя тождество rot(ψ,a)-= ψ rot a + [grad ψ, а], преобразуем подынтегральное выражение в (4.15):

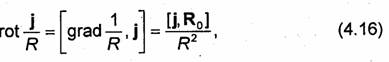
где R₀ = R/R-opт вектора R, проведенного из dV в точку наблюдения.

Подставляя (4.16) в (4.15), получаем

К аналогичным выражениям для вектора Н приводят формулы 4.13) и (4.14) в случае поверхностных и линейных токов:

Соотношения (4.17)-(4.19) представляют собой интегральные формы закона Био-Савара:

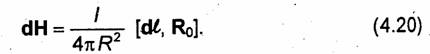
Закон Био-Савара характеризует магнитное поле dH, создаваемое элементом тока Idl. Связь формул (4.19) и (4.20) очевидна. Покажем, что поля, определяемые выражениями (4.17) и (4.18), также можно представить в виде суперпозиции элементарных полей dH, определяемых соотношением (4.20), от отдельных элементарных токов.  Преобразуем  подынтегральное выражение в (4.17). Выберем в качестве элемента dV элемент токовой трубки . длиной dl, ось которой, направлена по току, а сечение равно dS. Обозначив через /=jdS полный ток, протекающий по трубке, и  учитывая множитель 1/4π перед интегралом, получим выражение ;

полностью совпадающее с правой частью формулы (4.20). Связь формул (4.18) и (4.20) доказывается аналогично.

Часто при решении практических задач для упрощения расчета предполагается, что ток вдоль одной из координатных осей остается неизменным, т.е. что линии тока по этой координате уходят в бесконечность. Такие предположения обычно делаются при определении поля, создаваемого линейным током, который протекает вдоль длинной нити, или токами, протекающими вдоль длинного цилиндра. Предположение о бесконечной протяженности линий тока не позволяет использовать формулы (4.17)-(4.19). Рассмотрим эти особые случаи.

Найдем магнитное поле и векторный потенциал прямолинейной бесконечно-протяженной уединенной нити, обтекаемой постоянным током. Пусть эта нить совпадает с осью Z цилиндрической системы координат. Очевидно, что напряженность магнитного поля Н в этом случае имеет одну составляющую Н_φ и не зависит от переменных z и φ. Выбирая в качестве контура Г в (4.1) окружность радиуса r, лежащую в плоскости, перпендикулярной к оси Z, получаем напряженность магнитного поля нити

За направление тока в (4.21) принято направление оси Z.

Векторный потенциал рассматриваемой нити должен иметь только z-ю составляющую (A=z_oA), величина которой зависит от координаты r. Учитывая (4.10) и расписывая rot А в цилиндрической системе координат, получаем , откуда следует, что

Интегрируя выражение (4.22) по г, находим

Постоянную С в формуле (4.23) обычно полагают равной нулю. Тогда

От формулы (4.24) нетрудно перейти к выражению для потенциала, создаваемого токами, неизменными вдоль оси Z, которые протекают по цилиндру произвольного сечения S:

где  - расстояние от элемента dS, характеризуемого координатами ξ; η, До точки наблюдения N(х;у), dS = dξ,dη (см. рис. 3.5).

Если поле создано поверхностными токами, распределенными по некоторой цилиндрической поверхности S, образующие которой параллельны оси Z, а плотность поверхностных токов не зависит от координаты z, то векторный потенциал А выражается формулой

где Г-линия пересечения поверхности S с плоскостью, перпендикулярной к оси Z, a R- расстояние от элемента dl до точки N, в которой вычисляется потенциал (см. рис. 3.6).

4.4. ЭНЕРГИЯ СТАЦИОНАРНОГО МАГНИТНОГО ПОЛЯ

Общее (1.132) выражение для энергии магнитного поля, сосредоточенной в некотором объеме V, остается справедливым и в случае стационарных процессов:

Формулу (4.27) можно преобразовать таким образом, чтобы магнитная энергия была выражена через токи, создающие магнитное поле. Для этого заменим в (4.27) вектор В его представлением через векторный потенциал А. Используя тождество НВ = Н rot A = div [А, Н] + A rot H, получаем

Первый интеграл в уравнении (4.28) преобразуем в поверхностный интеграл, используя теорему Остроградского-Гаусса, а во втором интеграле выразим rot H через плотность токов j с помощью равенства rot Н = j. Тогда соотношение (4.28) примет вид

где S-поверхность, ограничивающая объем V.

Выберем в качестве поверхности S сферу радиуса r и устремим r к бесконечности, т.е. распространим интегрирование в (4.29) на все пространство.

Любая пространственно ограниченная система токов, как следует из формул (4.12)-(4.14) и (4.17)-(4.19), создает магнитное поле, напряженность Н и векторный потенциал А которого при r→∞ убывают пропорционально 1/r² и 1/r соответственно (или еще быстрее). При этом поверхность S возрастает пропорционально r². Следовательно, в пределе при r→∞ первый интеграл в правой части уравнения (4.29) будет равен нулю. В результате получим

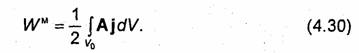
В отличие от исходного выражения (4.27) интегрирование в (4.30) распространяется лишь на ту область пространства V_o, в которой имеются токи. В формуле (4.30) можно исключить векторный потенциал А. Для этого нужно заменить вектор А его представлением в виде интеграла (4.12).

В случае линейных токов выражение для энергии магнитного поля упрощается. Рассмотрим вначале уединенный контур Г с током /. Формула (4.30) для этого контура принимает вид

Применим к интегралу в (4.31) теорему Стокса:

где Ф-магнитный поток через поверхность S, опирающуюся на контур Г. Подставляя (4.32) в (4.31), получаем

В случае N контуров (Г_1,Г₂,...,Г_N) выражение для W^M записывается следующим образом:

где Ф_n-магнитный поток, сцепленный с контуром Гn a /_n-ток в контуре Гn.

В формуле (4.34) векторный потенциал А и поток Фn обусловлены не только током /n но и токами в остальных контурах. В силу принципа суперпозиции можно записать следующее равенство:                                            

где А_k- векторный потенциал, создаваемый в рассматриваемой точке током 1_к, протекающим в контуре Г_k.

Выделим в сумме (4.35) векторный потенциал А_n соответствующий току 1_п:

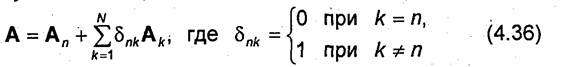
и подставим (4.36) в (4.34). В результате придем к выражению

Преобразовав интегралы в полученном выражении с помощью теоремы Стокса, перепишем его в виде

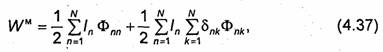
где Ф_nk -поток, сцепленный с контуром Г_n который обусловлен током 1_к контура Г_k.

Первое слагаемое в правой части формулы (4.37) определяет собственную энергию контуров системы, а второе -взаимную энергию.

4.5. ИНДУКТИВНОСТЬ

Поток Ф, пронизывающий уединенный контур Г, пропорционален току в этом контуре:

Ф = LI.                                         (4.38)

Коэффициент L зависит от конфигурации и размеров контура Г и называется его индуктивностью. Индуктивность измеряется в генри (Гн). Из закона индукции Фарадея (1.34) и формулы (4.38) следует, что индуктивность уединенного контура численно равна величине эдс, наводимой в этом контуре при линейном изменении его тока на 1 А за 1 с.

Подставляя (4.38) в (4.33), получаем

W^M = L1²I2.                                        (4.39)

В случае N контуров поток Ф_пk пропорционален току 1_к:

Ф_пк=М_пкI_к.                                        (4.40)

Коэффициент пропорциональности М_пk при к≠п называют взаимной индуктивностью контуров Г_k и Гn а коэффициент М_kk=L_k-собственной индуктивностью контура Г_k.

Коэффициент М_пk при к≠п можно определить следующим образом. Воспользовавшись формулами (4.32) и (4.14), представим выражение для потока Ф_пk в виде

где dl_n и dl_k-элементы контуров Г_n и Г_k соответственно, a R-расстояние между этими элементами.

Приравнивая правые части формул (4.41) и (4.40), получаем

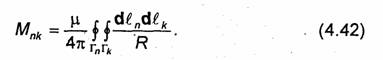
Как видно, взаимная индуктивность контуров Г_n и Г_k зависит только от их формы и взаимного расположения и не изменяется при перестановке индексов (свойство взаимности):

Из закона индукции Фарадея (1.34) и формулы (4.40) следует, что взаимная индуктивность двух контуров численно равна эдс, наводимой в одном из них при линейном изменении тока в другом на 1 А за 1 с.

Для определения собственной индуктивности контура выражение (4.42) непригодно. Обычно вместо него используют соотношения (4.38) и (4.39).

Перепишем выражение для энергии магнитного поля системы линейных токов (4.37) с учетом равенства (4.40):

Таким образом, для определения энергии магнитного поля системы линейных токов достаточно знать собственные и взаимные индуктивности контуров и токи в них.

4.6. ПРИМЕРЫ РАСЧЕТА МАГНИТНЫХ ПОЛЕЙ

Поле бесконечно длинного проводника. Вычислим магнитное поле бесконечно длинного цилиндрического проводника радиуса а. Будем считать для простоты, что ток / распределен равномерно по сечению проводника. Введем цилиндрическую систему координат r,φ, z, ось Z которой совпадает с осью проводника. Ввиду симметрии задачи поле не зависит от угла φ. Поле также не зависит от z, поэтому для определения вектора Н можно использовать  закон Ампера  (первое уравнение в (4.1)).

Выбирая в качестве контура Г окружность радиуса r≥a, лежащую в плоскости, перпендикулярной к оси Z с центром на оси Z, получаем

Для   определения   магнитного поля внутри провода выберем в   качестве контура   Г   окружность   радиуса   r<a.   Учитывая,   что   ток,   охватываемый   контуром Г, в  этом  случае  равен 1(r/а)², получаем

Таким образом, поле цилиндрического проводника в области  0≤ r ≤ a линейно возрастает от нуля до некоторого максимального значения (рис. 4.3), равногоI /(2πa), а при r≥а совпадает с полем прямолинейного тока величиной /, определяемого формулой (4.21).

Вычислим энергию магнитного поля сосредоточенного внутри проводника на участке единичной длины. Используя (4.27) и выражение (4.44), получаем

По аналогии с формулой (4.39) величину

называют внутренней индуктивностью на единицу длины цилиндрического проводника. Из формул (4.45) и (4.46) получаем

Таким образом, внутренняя индуктивность на единицу длины цилиндрического проводника при равномерном распределении тока по его сечению не зависит от диаметра проводника.

Поле коаксиального кабеля. Пусть ток, протекающий по внутреннему проводу коаксиального кабеля (рис. 4.4), равен /, а ток внешнего проводника -/. Распределение тока по сечениям проводников будем считать равномерным. Поступая так же, как и в случае уединенного проводника, придем к следующим выражениям для напряженности магнитного поля:

Радиусы проводников а_1,а₂ и а₃ указаны на рис. 4.4. Там же приведена кривая, характеризующая зависимость напряженности магнитного поля коаксиального кабеля от координаты r.

Для вычисления индуктивности L₁ на единицу длины коаксиального кабеля представим ее в виде суммы трех слагаемых:

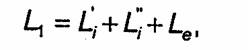
где L’_i и L’’_i-внутренние индуктивности на единицу длины центрального и наружного проводников соответственно, а L_е-так называемая внешняя индуктивность на единицу длины коаксиального кабеля, определяемая магнитным потоком между проводниками.

Величины  L’_i и L’’_i вычисляются по формуле (4.46). Опуская очевидные преобразования, выпишем окончательные результаты:

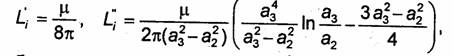
где μ- абсолютная магнитная проницаемость проводника. Как видно, внутренняя индуктивность на единицу длины центрального проводника коаксиального кабеля  (L’_i)   совпадает с внутренней индуктивностью на единицу длины уединенного цилиндрического проводника (4.47).

Внешнюю индуктивность L_e определим в соответствии с формулой (4.39) следующим образом:

где - энергия магнитного поля, сосредоточенного в зазоре между проводниками, приходящаяся на единицу длины коаксиального кабеля. Вычисляя энергию магнитного поля по формуле (4.27):

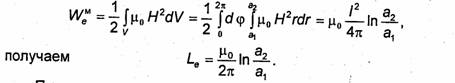
Предполагается, что магнитная проницаемость среды, заполняющей коаксиальный кабель, равна μ₀-

Поле двухпроводной линии. Рассмотрим вначале поле двух линейных противоположно направленных токов / и -/, т.е. токов, протекающих по бесконечно тонким прямолинейным нитям, расположенным на расстоянии 2l друг от друга (рис. 4.5). Магнитные силовые линии лежат в плоскостях, перпендикулярных оси Z, и определяются (см. 1.2.4) уравнением

Векторный потенциал имеет только продольную (параллельную оси Z составляющую и в силу принципа суперпозиции равен сумме потенциалов каждого из токов:

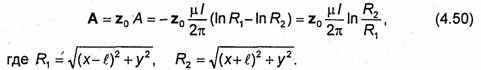
Учитывая равенство (4.10), из уравнения (4.49) получаем соотношение (дA/dx)dx + (dA/dy)dy = 0, которое может быть переписано в виде dA=0, где dA-полный дифференциал функции А. Следовательно, функция А не изменяется вдоль магнитной силовой линии. Это означает, что магнитные силовые линии совпадают с линиями пересечения плоскостей, перпендикулярных оси Z, с поверхностями, на которых А = const. Эти поверхности определяются из условия R₂/R₁ = b = const, которое совпадает с уравнением (3.50), определяющим эквипотенциальные поверхности системы двух параллельных противоположно заряженных нитей. Таким образом, поверхности, на которых величина векторного потенциала постоянна, представляют собой поверхности круговых цилиндров, параллельных оси Z, местоположение осей и радиусы которых определяются формулами (3.52) и (3.53) соответственно, а магнитные линии образуют семейство окружностей, возникающих при пересечении этих цилиндрических поверхностей с плоскостями, перпендикулярными оси Z (рис. 4.6).

В реальной двухпроводной линии проводники имеют круговые сечения конечных размеров. Однако, если магнитная проницаемость проводов равна магнитной проницаемости внешней среды, то в случае тонких проводов поле вне проводов практически не отличается от поля линейных токов, совпадающих с геометрическими осями проводов. Поэтому все сказанное применимо и к реальной линии из тонких проводов.

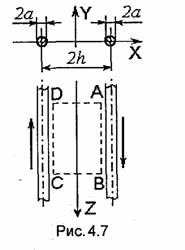
Вычислим индуктивность L₁ на единицу длины двухпроводной линии, образованной одинаковыми проводами, расстояние между осями которых (2ft) много больше их диаметров (2а). Величина L₁‘=2L_I‘ + L_e, где L_е- внешняя индуктивность двухпроводной линии на единицу длины. Значение L₁‘ вычисляется   по  формуле (4.47).   Для   определения   L_e воспользуемся   формулой   (4.38). Вычислим магнитный поток Ф через поверхность, охватываемую контуром   ABCD,   расположенным   в   плоскости   у=0   (рис.4.7). Стороны АВ и CD параллельны оси Z, имеют единичную длину и лежат на поверхности проводов (х = h - а на АВ и х = а - h на CD).

В рассматриваемом случае векторный потенциал А определяется выражением (4.50), в котором нужно только заменить l на h. Так как В = rot А, то

Интегрируя (4.51) по площади S_ABCD, ограниченной контуром А имеем                                                                                   

ABCD, имеем

Следовательно, внешняя индуктивность двухпроводной линии на единицу длины

Если абсолютные магнитные проницаемости проводов и окружающей среды равны |д₀, то полная погонная индуктивность двухпроводной линии в случае тонких проводов (h>>а) равна

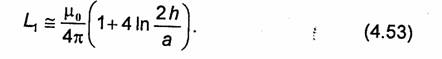
Поле кругового контура, обтекаемого постоянным электрическим током. Вычислим поле линейного тока /, образующего круговой виток радиуса а (рис. 4.8). Введем сферическую систему координат r, θ, φ, полярная ось которой совпадает с осью витка, а начало-с его центром. Так как рассматриваемое поле должно быть осесимметричным, то начало отсчета угла φ можно выбрать произвольно. Будем отсчитывать его от плоскости, проходящей чер полярную ось и точку наблюдения N( r, θ,0), в которой вычисляется поле. Для определения векторного потенциала воспользуемся выражением (4.14). Проецируя вектор dl на направления r₀,θ₀, φ_о, соответствующие точке наблюдения N(r, θ ,0), получаем

-полные эллиптические интегралы первого и второго рода соответственно.

Эллиптические интегралы не выражаются через элементарные функции, однако они подробно изучены, и имеются таблицы их значений в зависимости от величины b, называемой модулем этих интегралов.

Для вычисления вектора Н воспользуемся соотношением (4.10). Выражение для rot А в сферической системе координат определяется формулой (П. 17), приведенной в приложении 4. Так как векторный потенциал А имеет одну составляющую А=φ₀А не зависящую от угла φ, из формулы (П. 17) следует, что напряженность магнитного поля имеет две составляющие:

При дифференцировании  полных эллиптических интегралов  К(b)  и  E(b), входящих в формулу (4.55), удобно пользоваться формулами

где  Ь,=-\Л-й² -так называемый дополнительный модуль эллиптических интегралов.

Отметим, что выведенные формулы можно использовать и в случае кольцевого проводника конечной толщины, если радиус витка и расстояние до точки, в которой вычисляется поле, велики по сравнению с поперечными размерами сечения проводника.

Поле магнитного диполя. Рассмотрим поле кругового витка, считая, что точки наблюдения находятся на больших по сравнению

с радиусом витка расстояниях от его центра (r>>а). В этом случае выражение для векторного потенциала (4.54) существенно упрощается. Разложим входящую под знак интеграла величину 1/R в ряд по степеням отношения air и пренебрежем членами порядка (a/r)² по сравнению с единицей:

Напряженность магнитного поля имеет две составляющие Н_r и Н_θ, определяемые соотношениями (4.56). Выполняя дифференцирование, получаем

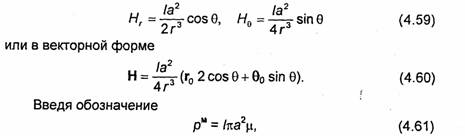
перепишем формулу (4.60) в виде

В области, где справедливо равенство (4.62), плотность тока проводимости равна нулю (j = 0), а любой принадлежащий ей контур не охватывает тока, т.е. выполняются уравнения (1.56). Следовательно, поле, определяемое формулой (4.62), можно считать магнитостатическим. С каждой магнитостатической задачей можно сопоставить некоторую электростатическую задачу, переход к которой может быть осуществлен, например, на основе принципа двойственности (см. 2.6). Заменим в формуле (4.62) Н на Е, μ на-ε, а р^м-на (-р), где p = ql- величина момента некоторого электростатического диполя системы двух зарядов q и -q, расположенных на расстоянии l. После этих преобразований формула (4.62) будет полностью совпадать с выражением (3.47) для напряженности электрического поля, создаваемого электростатическим диполем с моментом p = z_op. Следовательно, выражение (4.62) является магнитостатическим аналогом формулы (3.47). По аналогии с электростатическим диполем можно ввести понятие о магнитном диполе (т.е. о системе двух точечных магнитных зарядов +q^M и -q^M, расположенных на расстоянии l друг от друга), поле которого определяется выражением (4.62). При этом будет выполняться соотношение p^M = q^Ml. Момент магнитного диполя, как и момент электрического диполя р, является векторной величиной:

где l -вектор, направленный от отрицательного магнитного заряда (-q^M) к положительному (+q^M), по абсолютной величине равный расстоянию между зарядами l, a l₀-орт вектора l.

Соотношение (4.62) было получено из выражения (4.59) для магнитного поля кругового витка (рамки) с током. Следовательно, рамка с током /, расположенная в плоскости z = 0 симметрично относительно оси Z, создает на больших по сравнению с его радиусом расстояниях такое же поле, как магнитный диполь с моментом

помещенный в начале координат.

Выражение (4.64) можно представить в виде

                    (4.65)

где   S-площадь   рамки, а n₀-орт нормали к плоскости рамки (рис. 1.3).

Соотношение (4.65) справедливо для плоских рамок произвольной формы. Отметим, что вектор р^м связан с введенным ранее (см. 1.2) магнитным моментом рамки т соотношением

4.7. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

Электрическое поле в диэлектрике, окружающем проводники с постоянным током. Постоянный ток помимо магнитного поля создает также электрическое поле, которое описывается системой уравнений (1.576). Следовательно, оно является потенциальным, и для его характеристики можно ввести скалярный потенциал и, связанный с вектором Е соотношением (3.2). Если рассматриваемая среда является однородной (ε = const) и в ней отсутствуют свободные заряды (ρ = 0), то потенциал и удовлетворяет уравнению Лапласа (3.8), а система уравнений (1.576) принимает вид

rot Е = 0,    div D = О,    D = εE.

Как видно, уравнения, описывающие электрическое поле постоянного тока в идеальном диэлектрике, окружающем проводники, совпадают  с  уравнениями,   описывающими  электростатическое поле. Однако электрическое поле постоянного тока отличается от электростатического. Электрическое поле постоянного тока существует и в проводящей среде. Вектор Е связан с вектором плотности тока проводимости соотношением j = σE. Это приводит к изменению граничных условий  на  поверхности  проводника  по сравнению с граничными условиями в случае электростатики. Так как электрический ток в проводнике создает падение потенциала, то поверхность проводника уже не будет эквипотенциальной и на ней появится отличная от нуля касательная составляющая напряженности электрического поля. При определении поля в диэлектрике, окружающем проводники с постоянными токами, это в большинстве случаев несущественно, так как касательная составляющая вектора Е пренебрежимо мала по сравнению с нормальной составляющей.

Рассмотрим в качестве примера соотношение между нормальной и касательной составляющими вектора Е в воздухе у поверхности проводов двухпроводной линии передачи (см. рис.4.7). Пусть проводники расположены на расстоянии 2h = 10 см друг от друга при разности потенциалов между ними в 200 В и плотностью тока j=2А/мм². Проводники предполагаются выполненными  из  меди  (σ = 5,65-10⁷ См/м).   Касательную составляющую вектора Е определим из закона Ома: Еτ =j/σ = 0,035 В/м. Для оценки величины нормальной составляющей найдем отношение разности потенциалов между проводами к расстоянию 2/7 между ними: ∆u/(2h) = 2000 В/м. В действительности поле между проводами является неоднородным, причем наиболее сильное поле сосредоточено около проводов, поэтому истинное значение Е_п будет больше ∆u(2h). Отношение Е_n к Е_τ, таким образом, даже для рассматриваемого случая линии низкого напряжения имеет порядок 10⁵. Это позволяет в большинстве практически интересных случаев при вычислении электрического поля в диэлектрике, окружающем проводники с постоянными токами, пренебречь касательной составляющей, т.е. Читать, что граничные условия являются такими же, как в электростатике, и для определения поля использовать решения соответствующих электростатических задач.

Электрическое поле в проводящей среде. Если в рассматриваемой области отсутствуют сторонние эдс, то электрическое поле постоянного тока в проводящей среде описывается следующей системой дифференциальных уравнений:

rotE = 0,   j = aE,    div j = 0.                       (4.66)

Соответствующие интегральные соотношения имеют вид

Второе уравнение системы (4.67) является следствием закона сохранения заряда (1.50), так как в случае стационарного электромагнитного поля dQ/dt=O. Из этого уравнения следует, что на грайице раздела двух сред с различными удельными проводи-мостями нормальная составляющая вектора j является непрерывной:

а касательные составляющие связаны соотношением

Равенство (4.68) выводится так же, как граничное условие для нормальной составляющей вектора В (см. 1.7.1), а формула (4.69) является следствием соотношения Е_1τ = Е_2τ.

В ряде практически важных случаев требуется найти токи, которые возникают в среде, изолирующей проводники друг от друга (токи утечки). Удельная проводимость изоляции во много раз меньше удельной проводимости металла. Поэтому вектор плотности тока утечки можно считать перпендикулярным к поверхности проводников. Действительно, пусть угол между вектором j и нормалью к поверхности раздела в первой среде (в изоляции) равен θ₁ а во второй (в металле) -θ₂. Из равенства (4.68) и (4.69) получается следующее соотношение между углами θ₁ и θ₂:

Так как отношение σ₁ /σ₂ очень мало (например, для кабельной бумаги и меди оно равно около 1,7∙10^-21), угол θ₁ можно считать равным нулю при любом угле 9₂.

Аналогия между электрическим полем постоянного тока и электростатическим полем. Из уравнений (4.66) следует, что электрическое поле постоянного тока является потенциальным, т.е. вектор Е можно представить в виде E=-grad u.  В случае однородной проводящей среды (а = const) условие divj = O эквивалентно условию divE = 0. Следовательно, в однородной проводящей среде потенциал и электрического поля постоянного тока в области,  в которой отсутствуют сторонние эдс,  удовлетворяет уравнению Лапласа (divE=-div grad u = 0, т.е. ∆²u = 0). Если на границе рассматриваемой области значения потенциала и известны, то задача определения электрического поля постоянного тока в однородной проводящей среде сводится к нахождению потенциала и, удовлетворяющего уравнению Лапласа V²u = 0 и заданным  граничным  условиям.   К такой  же задаче  сводится задача   определения   электростатического   поля   в   однородном диэлектрике, когда внутри рассматриваемой области отсутствуют заряды. Как известно, такая задача имеет единственное решение. Следовательно,  электрическое поле постоянного тока в однородной проводящей среде аналогично электростатическому полю в однородном диэлектрике, если конфигурация рассматриваемых областей в обоих случаях одинакова и, кроме того, одинаковы граничные условия для  потенциалов.  Эта аналогия  позволяет использовать известные решения электростатических задач для нахождения электрического поля постоянного тока и наоборот.

В качестве примера применения указанной аналогии вычислим сопротивление R между электродами, находящимися в однородной проводящей среде. Пусть потенциалы электродов равны U₁ и U₂, причем U₁>U₂. Согласно закону Ома R=(U₁-U₂)/I, где /-ток между электродами. Очевидно, что ,   где S-замкнутая поверхность, охватывающая один из электродов. Учитывая, что j = σE, получаем          

Для определения величины рассмотрим другую задачу.

Пусть такие же электроды находятся в однородном идеальном диэлектрике, характеризуемом диэлектрической проницаемостью ε. Поток вектора Е через поверхность S при этом согласно закону Гаусса равен

где Q-заряд электрода, находящегося внутри поверхности S.

Если потенциалы электродов в этом случае также равны U₁ и U₂, то на основе указанной аналогии можно утверждать, что интеграл   в формулах (4.70) и (4.71) имеет одно и то же значение.   Так  как  из  определения  емкости   С  системы  двух проводников (см. формулу (3.72)) следует, что Q = C| U₁ -U₂, то

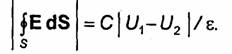
Подставляя (4.72) в (4.70), получаем

Используем формулу (4.73) для определения сопротивления утечки изоляции коаксиального кабеля. Емкость на единицу длины коаксиального кабеля или, что то же самое, емкость на единицу длины цилиндрического конденсатора (рис. 3.21) определяется выражением (3.76). Подставляя (3.76) в (4.73), находим, что сопротивление утечки на единицу длины коаксиального кабеля

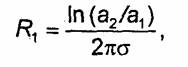
где σ-удельная проводимость изоляции кабеля; a₁- радиус внутреннего провода кабеля; а₂-внутренний радиус оболочки кабеля (рис. 4.4).

Глава 5

ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

5.1. ВВЕДЕНИЕ

Возможность излучения и распространения электромагнитной энергии в пространстве, по существу, непосредственно следует из положения Максвелла, согласно которому электрический ток может циркулировать в диэлектрике и свободном пространстве в виде тока смещения. При этом ток смещения, как и ток проводимости, создает вокруг себя магнитное поле. Своим предположением, основанным на опытах Фарадея, Максвелл как бы приписал диэлектрику и свободному пространству свойства проводника - проводника тока смещения. Так как электромагнитное поле является носителем электромагнитной энергии, то распространение в пространстве токов смещения сопровождается возникновением активного потока энергии (мощности излучения), распространяющегося от источника, создающего токи смещения, в окружающее пространство. Принципиальная возможность ответвления (излучения) электромагнитной энергии в пространство доказывается теоремой Пойнтинга (см. 1.8), являющейся прямым следствием уравнений Максвелла.

Таким образом, любая электрическая схема, способная создавать в пространстве токи смещения, является излучателем электромагнитной энергии или, как принято говорить, излучателем электромагнитных волн. Рассмотрим, например, конденсатор, питаемый источником переменной ЭДС (рис. 5.1). В пространстве между обкладками конденсатора циркулирует ток смещения. Так как пространство, окружающее конденсатор, обладает способностью проводить ток смещения, то последний должен ответвляться в него так же, как ответвлялся бы ток проводимости, если бы конденсатор находился в пространстве, обладающем проводимостью. Процесс ответвления токов смещения и, следовательно, излучения электромагнитной энергии в пространство, окружающее конденсатор, является с точки зрения теории Максвелла таким

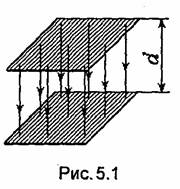
ким же естественным, как и процесс ответвления энергии в провода, присоединенные к какому-либо источнику эдс.

Практически в качестве излучателей электромагнитных волн (антенн) применяют схемы, удовлетворяющие определенным требованиям. Обычно стремятся уменьшить реактивную мощность, непосредственно связанную с антенной и не излучаемую в пространство. Показанная на рис. 5.1 схема излучателя в виде уединенного конденсатора из двух параллельных пластин в указанном смысле является неудачной. В этой схеме электромагнитное поле сосредоточено в основном в пространстве между пластинами, что приводит к большой реактивной мощности по сравнению с мощностью излучения. Реактивная мощность уменьшается при повороте пластин конденсатора и расположении их так, как показано на рис. 5.2.

Один из вариантов схемы, обеспечивающей интенсивное излучение, показан на рис. 5.3. Эта схема, в которой пластины заменены проводами с шарами на концах, была впервые осуществлена Генрихом Герцем и известна под названием диполя Герца.

Инициатива и практическое решение вопроса применения радиоволн в качестве средства связи принадлежит А.С. Попову, который впервые в мире осуществил сеанс радиосвязи. Им же были предложены и осуществлены передающие и приемные антенны в виде несимметричных вибраторов.

5.2. ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ВИБРАТОР

Элементарным электрическим вибратором (ЭЭВ) называют короткий по сравнению с длиной волны провод, обтекаемый электрическим током, амплитуда и фаза которого не изменяются вдоль провода. Этот вибратор является по существу идеализированной, удобной для анализа излучающей системой, так как практически создание вибратора с неизменными по всей длине амплитудой и фазой тока невозможно. Однако вибратор Герца (рис. 5.3) оказывается весьма близким по своим свойствам к ЭЭВ.

Благодаря имеющимся на его концах металлическим шарам, которые обладают значительной емкостью, амплитуда тока слабо изменяется вдоль вибратора. Неизменность фазы обеспечивается малыми по сравнению с длиной волны размерами вибратора.

Изучение поля ЭЭВ крайне важно для понимания процесса излучения электромагнитных волн антеннами. Любое проводящее тело, обтекаемое токами, можно считать как бы состоящим из множества элементарных электрических вибраторов, а при определении поля, создаваемого этими токами, можно воспользоваться принципом суперпозиции, т.е. рассматривать его как сумму полей элементарных вибраторов.

Перейдем к анализу поля ЭЭВ, расположенного в безграничной однородной изотропной среде, характеризуемой параметрами ε, μ. Ток в вибраторе будем считать известным, т.е. сторонним током, изменяющимся по закону /^CT = /_m^CTcos(ωt+ψ₀), где /_т^ст- его амплитуда, а ψ₀- начальная фаза (фаза в момент времени t = 0). Так как поле, создаваемое вибратором, в рассматриваемом случае является монохроматическим, удобно воспользоваться методом комплексных амплитуд.  Вместо тока /^ст

введем комплексную величину комплексная амплитуда стороннего тока. Ток /^ст связан с  /^cт_mобычным соотношением .

Таким образом, задача сводится к нахождению поля по заданному распределению тока. Сначала найдем векторный потенциал А. Введем сферическую систему координат r,θ,φ, ходится в его центре (рис. 5.4).

Комплексная амплитуда векторного потенциала в случае монохроматического поля при произвольном распределении токов в объеме V определяется формулой (2.58). Разобьем интегрирование по объему, занимаемому ЭЭВ, на интегрирование по площади

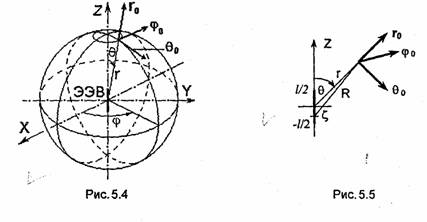
его поперечного сечения ∆S и по длине вибратора l. Для упрощения преобразований будем считать поперечный размер вибратора (диаметр) малым по сравнению с его длиной l. Учитывая, что представим формулу (2.58) в виде

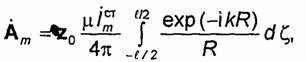
где  - значение координаты точки интегрирования (рис.5.5). При вычислении интеграла (5.1) ограничимся случаем, когда расстояние от вибратора до точек, в которых определяется поле, велико по сравнению с длиной вибратора (r>>l). Тогда в знаменателе подынтегрального выражения величину R можно считать равной r и вынести за знак интеграла. Так как то наибольшая относительная погрешность, возникающая при замене R на r, имеет порядок  Кроме того, по предположению Как известно из курса физики (это будет также показано ниже), отношение c/f равно длине волны λ в среде без потерь с параметрами ε и μ. Поэтому k = 2π/λ, и в (5.1) можно заменить ехр (- ikR) на ехр (- iкг). При такой замене погрешность определения фазы подынтегрального выражения равна  С учетом изложенного формула (5.1) принимает вид

Отметим, что сделанное предположение о малости диаметра вибратора d по сравнению с его длиной не является необходимым. Достаточно считать, что d«r.

Вектор Н_т связано А_m соотношением Н_т =(1/μ) rot A_m. Вектор Ё_т можно вычислить по формуле (2.57), однако несколько проще, найдя Н_m, определить Е_т из первого уравнения Максвелла:

В сферической системе координат  rotA_m   вычисляется по

формуле (П. 17). В рассматриваемом случае вектор А_m параллелен оси Z. Чтобы воспользоваться равенством (П. 17), нужно найти

Этот результат можно было предвидеть из физических соображений, так как прямолинейный ток вибратора может создать только кольцевые магнитные силовые линии, лежащие в плоскостях, перпендикулярных оси вибратора.

Произведя дифференцирование, получим

Для определения вектора Е_m подставим найденный вектор Н_mв (5.2). Учитывая, что Н_т = Н_θт = 0 и дН_φт/дφ =0, приходим к выражению

Полученные формулы определяют составляющие комплексных амплитуд векторов Е и Н. Для перехода к мгновенным значениям векторов Е и Н нужно полученные выражения умножить на exp(iωt). а затем отделить действительную часть (Е =

5.3. АНАЛИЗ СТРУКТУРЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ЭЛЕМЕНТАРНОГО ЭЛЕКТРИЧЕСКОГО ВИБРАТОРА

5.3.1. Деление пространства вокруг вибратора на зоны

Из полученных формул следует, что вектор напряженности электрического поля, создаваемого ЭЭВ, имеет две составляющие Е_r и Е_θ а вектор Н - одну Н_φ Таким образом, в любой точке пространства вектор Е лежит в меридианальной плоскости, т.е. в плоскости, проходящей через ось вибратора и рассматриваемую точку, а вектор Н - в азимутальной плоскости, т.е. в плоскости, перпендикулярной оси вибратора.

Из  выражений  (5.3),  (5.4)  и  (5.5)  видно,  что зависимость

амплитуд составляющих векторов Ё_т и Н_т от расстояния r определеляется величинами 1/(kr), 1 /( kr )² и 1/( kr)³. При больших значениях kr (kr >>1) величинами 1/( kr)² и 1 /(kr)³ можно пренебречь по сравнению с 1/( kr), и, наоборот, при малых значениях kr(kr<<1) основными будут величины 1/( kr)³ для составляющих вектора Ё и 1/( kr), ² - для вектора Н. Поэтому при анализе структуры электромагнитного поля вибратора пространство вокруг вибратора делят на три зоны: дальнюю или волновую ( kr>>1),  ближнюю (kr<<1) и промежуточную, где кг соизмеримо с единицей.

Величина kr зависит от соотношения между расстоянием от вибратора до точки, в которой вычисляется поле, и длиной волны.

Так как k=2π/λ, то условия kr>>1, kr<<1, kr=1, определяющие дальнюю, ближнюю и промежуточную зоны, эквивалентны условиям соответственно.

Перейдем к анализу свойств электромагнитного поля элементарного электрического вибратора в различных зонах.

5.3.2. Дальняя (волновая) зона

Дальняя или волновая зона, как уже указывалось, характеризуется условием k=2π/λ. Из сравнения формул (5.4) и (5.5) следует, что в этом случае можно пренебречь составляющей Е_r по сравнению с Ё_θ. Кроме того, в выражениях для E_θ и Н_φ можно в квадратных скобках пренебречь слагаемыми 1/( kr)³и I /( kr)², по сравнению с 1/( kr). Учитывая, что  получаем:

Таким образом, в дальней зоне напряженность электрического поля имеет только составляющую Е_θ, а напряженность магнитного

поля - составляющую Н_φ, которые изменяются синфазно.

Поверхность, во всех точках которой в один и тот же момент времени фаза рассматриваемой функции имеет одинаковые значения, называется поверхностью равных фаз (ПРФ). В случае монохроматического поля на ПРФ постоянна фаза комплексной амплитуды рассматриваемой функции. Соответственно поверхность, на которой постоянна амплитуда (модуль комплексной амплитуды) рассматриваемой функции, называют поверхностью равных амплитуд (ПРА).

В анализируемом случае ПРФ определяются уравнением r = = const, т.е. представляют собой концентрические сферы с центром в середине вибратора.

Выберем какую-либо поверхность равных фаз и проследим, что происходит с нею с течением времени. Фаза составляющей Ё_θ в точке с координатой r₀ в момент времени t₀ равна ψ₀ = ωto- kr₀ + π/2. Записывая выражение для фазы в точке с координатой r = r₀ + ∆r в момент t₁ = t₀ + ∆t и приравнивая это выражение ψо, получаем, что ω∆t=k∆r. Следовательно, за время ∆t поверхность равной фазы смещается на расстояние ∆r и в момент t₁ представляет собой сферу радиуса r_о + ∆r. Скорость перемещения поверхности равной фазы (фазовая скорость)

Как видно, поле (5.6) - электромагнитная волна, расходящаяся от вибратора.

Убедимся, что использованное выше соотношение λ =c/f действительно выполняется. Длиной волны называют кратчайшее расстояние между двумя ПРФ, на которых в один и тот же момент времени значения фазы рассматриваемой функции отличаются на 2π.

Пусть фаза составляющей Е_θ на сфере, соответствующей значению r = r₀ = const, в момент t= t_o = const равна ψ=ωt_o - kr₀ + π/2, а на сфере r= r₀ + λ равна ψ₁ =ωt₀-k(r₀+λ)+π/2. По определению длины волны должно выполняться соотношение ψ₀-ψ₁ == 2π. Подставляя значения ψо и ψ₁ получаем ωt_o - kr₀ + π/2 - [ωto - k (r₀ + λ) + π/2] = kλ= 2π. Следовательно, λ = 2π/k =  2πl(2nf√εμ) = c/f. Длина волны может быть определена также

как расстояние, на которое перемещается ПРФ за период. Так как период Т= 1/f,тоλ= v_фT= c/f.

Свободно распространяющиеся волны классифицируют по форме ПРФ. Волны, у которых поверхности равных фаз совпадают с поверхностями равных амплитуд, называют однородными. В нашем случае ПРА определяются уравнением sin θ/r= const и не совпадают с ПРФ. Таким образом, в дальней зоне поле ЭЭВ представляет собой неоднородную сферическую волну, распространяющуюся от вибратора со скоростью света с = 1/√εμ. Векторы Ё_т и Н_т этой волны взаимно перпендикулярны и перпендикулярны направлению распространения волны. Волны, обладающие таким свойством, называют поперечными.

Распространение волны сопровождается переносом энергии. Средняя за период плотность потока энергии равна П_ср = Re П. Комплексный вектор Пойнтинга в рассматриваемом случае является чисто вещественной величиной, поэтому

Из этого выражения следует, что излучение электромагнитной энергии максимально в направлениях, перпендикулярных оси вибратора (θ = π/2) и не зависит от угла φ. Вдоль своей оси (θ = 0 и θ = π) вибратор не излучает. Средняя за период скорость распространения энергии определяется по формуле (1.162). Подставляя в (1.162) выражение (5.7) и учитывая, что

получаем . Используя формулу (1.160), нетрудно

убедиться, что мгновенное значение скорости распространения энергии v₃ = v₃ cp = r_oc Таким образом, излучаемая вибратором электромагнитная энергия распространяется вдоль радиусов, проведенных из середины вибратора (т.е. перпендикулярно ПРФ) со скоростью света в данной среде.

Векторы Е и Н изменяются синфазно. На рис. 5.6 показано изменение векторов Е и Н вдоль радиуса r в некоторый момент

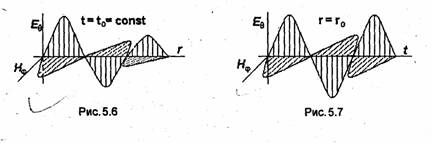
времени t = t₀, а на рис. 5.7 приведена зависимость значений Е и Н в точке r = r₀ от времени.

Важным параметром электромагнитной волны является ее характеристическое сопротивление Z_c, равное отношению поперечных к направлению распространения волны составляющих векторов Ё_т и Н_т. Так как рассматриваемая волна является поперечной, то

В теории антенн величину часто называют волновым сопротивлением среды. В случае вакуума и формулу (5.8) можно переписать в виде

Обобщая полученные результаты, перечислим еще раз основные свойства электромагнитного поля в дальней зоне в среде без потерь.

В дальней зоне поле ЭЭВ представляет собой расходящуюся неоднородную сферическую волну, векторы Е и Н которой взаимно перпендикулярны и перпендикулярны направлению распространения волны (вектору r₀). При этом вектор Е лежит в плоскостях, проходящих через ось вибратора, а Н-в плоскостях, перпендикулярных этой оси.  Векторы Е и Н изменяются синфазно.

Отношение составляющих Ё_θт и Н_φm равно характеристическому сопротивлению. Фазовая скорость и скорость распространения энергии равны скорости света. Комплексный вектор Пойнтинга является чисто действительной величиной и направлен вдоль радиуса-вектора, проведенного из середины вибратора в точку наблюдения, т.е. имеется только активный поток энергии. Плотность потока энергии максимальна в направлениях, перпендикулярных оси вибратора (θ = π/2), и равна нулю в направлениях, соответствующих оси вибратора (θ = 0 и π).

5.3.3. Ближняя зона

В ближней зоне . Однако, формулы для поля элементарного вибратора были выведены в предположении r»l. Поэтому ближняя зона характеризуется неравенствами В этом случае в квадратных скобках формулы (5.4) можно пренебречь величиной 1/(kr)², в формуле (5.5) - величинами 1/(kr) и i/(kr)² , а в (5.3) - величиной 1/(kr). Домножая окончательные выражения на exp (iωt), получаем

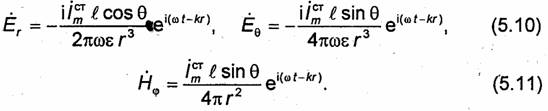
Рассмотрим выражение (5.11). Так как 2πr<<λ, можно считать,

что exp (-ikr)≈1. Переходя к мгновенным значениям вектора Н, получаем

Напомним, что ψ₀ - начальная фаза тока /^ст

Сравним выражение (5.12) с напряженностью магнитного пля Н, создаваемого элементом длины l постоянного линейного тока, расположенного так же, как ЭЭВ:

Формула (5.13) вытекает из закона Био-Савара (4.20).

Так как при выводе формул для поля, создаваемого ЭЭВ,

предполагалось, что ток вибратора равен то

выражение (5.12) аналогично выражению (5.13). Следовательно, напряженность магнитного поля вибратора в ближней зоне совпадает с напряженностью магнитного поля, вычисленной на основе закона Био-Савара, при условии, что постоянный ток / равен току вибратора в рассматриваемый момент времени.

Перейдем к анализу электрического поля вибратора в ближней зоне. Изменение тока в вибраторе приводит к изменению величины зарядов на его концах.

Суммарный заряд вибратора в любой момент времени равен нулю, а заряды на его концах равны по величине и противоположны по знаку. При этом для каждого из концов вибратора выполняется закон сохранения заряда / =- dq/dt. Следовательно, заряды изменяются по закону

Знак "+" соответствует верхнему (см. рис. 5.5) концу вибратора (z = =+l/2), а знак "-" - нижнему (z=-l/2). Так как в ближней зоне ехр (- ikr)≈1, то, заменяя в формулах (5.10) i_т на ωq_m и переходя затем к мгновенным значениям составляющих вектора Е, получаем

Таким образом, в ближней зоне ЭЭВ создает такое же электрическое поле, как и электростатический диполь с моментом р = z_oql (см. (3.48)), заряды которого равны зарядам, сосредоточенным на концах вибратора, в рассматриваемый момент времени.

Составляющие напряженности электрического и магнитного полей в ближней зоне, определяемые формулами (5.10) и (5.11), сдвинуты по фазе на 90°. Поэтому комплексный вектор Пойнтинга оказывается чисто мнимой величиной, а его среднее значение -равным нулю. Это не означает, конечно, что в ближней зоне отсутствует излучение. Как и в дальней зоне, здесь в выражениях для поля имеются слагаемые, пропорциональные 1/(kr), которые определяют излучаемую энергию. Однако их абсолютные величины малы по сравнению с абсолютными значениями составляющих Е_r, Е_θ и Е_φ, определяемых формулами (5.10) и (5.11). Это означает, что в ближней зоне имеется относительно большое реактивное поле. Подчеркнем, что в случае среды без потерь полные потоки энергии в ближней и дальней зонах одинаковы, а плотность потока энергии в ближней зоне значительно больше, чем в дальней.

5.3.4. Промежуточная зона

Промежуточная зона является переходной от ближней зоны к дальней. При анализе формул (5.3), (5.4) и (5.5) в этом случае нельзя пренебречь ни одним из слагаемых. Следовательно, в промежуточной зоне поле излучения и реактивное (связанное с вибратором) поле оказываются одного порядка.

Выражения (5.3), (5.4) и (5.5) позволяют исследовать структуру поля, создаваемого ЭЭВ в области,  соответствующей значениям r>> l

Линии распространяющегося электрического поля, соответствующие полю излучения, являются замкнутыми. Их структура в меридианальной плоскости в некоторый фиксированный момент времени показана на рис.5.8. Линии магнитного поля в плоскости, перпендикулярной оси вибратора (θ = π        /2), изображены на рис. 5.9.

Процесс образования структуры поля, изображенной на рис. 5.8 и 5.9, качественно можно представить по структуре силовых линий электрического поля в непосредственной близости к вибратору, построенной на основе общих физических представлений (рис.5.10).

Пусть в момент t=t₀ ток в вибраторе равен нулю, положительный заряд сосредоточен на верхнем конце вибратора, а отрицательный - на нижнем. Силовые линии электрического поля начинаются на верхнем конце вибратора и заканчиваются на нижнем (рис.5.10,а). Линии, возникшие до момента t=t₀, на рисунке не показаны.

В интервале t₀ < t < t₀ + T/4 абсолютные значения зарядов на концах вибратора уменьшаются, а абсолютное значение тока возрастает. Ток течет от верхнего конца вибратора к нижнему.

Начинается «отшнуровывание» линий поля (рис.5.10,б). В момент t = to+T/4 абсолютная величина тока максимальна, заряды на концах вибратора равны нулю, «отшнуровывание» линий поля закончено (рис.5.10, в).

К концу второй четверти периода (в момент t = t_o + Т/2) ток снова равен нулю, а заряды на концах вибратора максимальны по абсолютной величине. Положительные заряды сосредоточены на нижнем конце вибратора, отрицательные - на верхнем. Структура силовых линий электрического поля вблизи вибратора (рис.5.10, г) отличается от показанной на рис.5.10, а только тем, что линии имеют противоположные направления.

5.4. ДИАГРАММЫ НАПРАВЛЕННОСТИ ЭЛЕМЕНТАРНОГО V   ЭЛЕКТРИЧЕСКОГО ВИБРАТОРА

Рассмотрим более подробно выражение для амплитуды напряженности электрического поля, создаваемого в дальней зоне элементарным электрическим вибратором. Из (5.6) следует, что

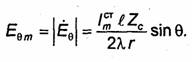
При заданных амплитуде тока и длине вибратора амплитуда напряженности его электрического поля зависит от двух переменных: расстояния г и угла Э. При одном и том же расстоянии от вибратора (r = const) поле будет различным в зависимости от угла θ. Как уже отмечалось, амплитуда напряженности поля максимальна в плоскости, проходящей через середину вибратора, перпендикулярно его оси (θ = π/2), и равна нулю в направлении последней, т.е. при θ = 0 и θ = π.

Для более наглядного представления о характере излучения (направленных свойствах) антенны строят графики зависимости амплитуды напряженности поля или амплитуд ее составляющих от направления в точку наблюдения При r = const. Такие графики называют амплитудными диаграммами направленности или просто диаграммами направленности (ДН). Обычно строят нормированные ДН. На них показывают не абсолютные значения амплитуды напряженности поля, а нормированные значения, отнесенные к ее максимальной величине. Если необходимо дать представление о фазовой структуре излученного поля, строят так называемые фазовые диаграммы направленности - графики зависимости фазы напряженности поля от направления в точку наблюдения.

Наиболее полную информацию о характере излучения дает пространственная диаграмма направленности. Она может быть построена, например, таким образом, чтобы расстояние от начала сферической системы координат до любой точки, характеризуемой углами θ и φ, было пропорционально отношению амплитуды напряженности электрического поля в данном направлении (θ, φ) к максимальной амплитуде для того же значения r. Во многих случаях построение такой диаграммы сложно, поэтому чаще пользуются диаграммами, показывающими зависимость амплитуды поля от одного из углов (θ или φ) при постоянном значении другого.

Диаграмма направленности, соответствующая φ = const, показывает изменение амплитуды напряженности поля в меридиональной плоскости. Очевидно, что для ее определения по

известной пространственной диаграмме достаточно рассмотреть сечение последней плоскостью φ = const. Аналогично кривая, образованная пересечением пространственной диаграммы с поверхностью конуса θ = const, дает диаграмму направленности, построенную при θ = const.

Пространственная ДН элементарного электрического вибратора совпадает с поверхностью тора, образованного вращением круга, радиус которого равен расстоянию от центра круга до оси вращения (рис. 5.11). Диаграмма направленности ЭЭВ в мери-дианальной плоскости, построенная в полярной системе координат, имеет вид восьмерки из двух окружностей. У нормированной ДН диаметры этих окружностей равны единице (рис. 5.12). Правая половина ДН соответствует некоторому значению угла φ = φ_о, а левая - значению φ = φ_о + π. На рис. 5.13 показана построенная в полярной системе координат нормированная ДН в экваториальной плоскости (θ= π/2). Эта ДН имеет вид окружности единичного радиуса. Указанная на рисунках функция

D.

Так как ДН на рис. 5.13 соответствует значению θ = π/2, то на этом рисунке D = 1.

Помимо полярной системы координат для построения диаграмм направленности используют также декартову систему координат. Нормированные диаграммы направленности ЭЭВ в меридианальной и экваториальной (θ = π/2) плоскостях, построенные в декартовой системе координат, изображены на рис. 5.14 и 5.15 соответственно.

Фаза напряженности электрического (магнитного) поля, создаваемого ЭЭВ, не зависит от углов 0 и ф. Поэтому вид фазовых диаграмм ЭЭВ очевиден, и они здесь не приводятся.

5.5. МОЩНОСТЬ ИЗЛУЧЕНИЯ ЭЛЕМЕНТАРНОГО ЭЛЕКТРИЧЕСКОГО ВИБРАТОРА

Средняя мощность, излучаемая в пространство ЭЭВ, находящимся в среде без потерь, равна среднему потоку энергии через любую замкнутую поверхность, окружающую вибратор, и может быть вычислена по формуле (1.144). Вычисление интеграла в (1.144) упрощается, если в качестве поверхности S, охватывающей вибратор, используется сфера с центром в начале координат и достаточно большим  радиусом  r,  чтобы выполнялось условие kr>>1. В сферической системе координат элемент поверхности . С учетом формулы (5.7) выражение (1.144) принимает вид

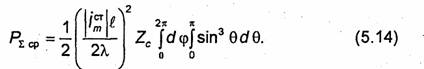
Входящий в (5.14) двойной интеграл легко вычисляется и равен 8π/3, следовательно,

По аналогии с обычным выражением для мощности,  расходуемой в среднем за период в электрической схеме на активном сопротивлении  (закон Джоуля-Ленца),  формулу (5.15) можно представить в виде

Коэффициент пропорциональности R_Σ между R_Σcp и измеряется в омах и называется сопротивлением излучения. В свободном пространстве

5.6. ЭЛЕМЕНТАРНЫЙ МАГНИТНЫЙ ВИБРАТОР

5.6.1. Физические модели элементарного магнитного вибратора

По аналогии с элементарным электрическим вибратором систему, эквивалентную короткому по сравнению с длиной волны элементу магнитного тока, амплитуда и фаза которого одинаковы во всех точках этого элемента, будем называть элементарным магнитным вибратором. Рассмотрим некоторые физические модели элементарного магнитного вибратора. Для этого вначале вернемся к элементарному электрическому вибратору.

Как уже отмечалось, одной из возможных моделей ЭЭВ является элемент прямолинейного провода (рис. 5.16). Для простоты изложения будем считать провод идеально проводящим. Тогда протекающий по вибратору ток окажется поверхностным с

плотностью j_s=i^ст/L, где L - периметр провода.

На поверхности S вибратора касательная составляющая вектора Н неизменна вдоль его длины и связана с плотностью тока

j_s соотношением j_s=[n₀,H]|_s. Комплексная амплитуда -электрического тока, обтекающего ЭЭВ, равна  комплексная амплитуда составляющей H_φ. На вибраторе линии вектора Н перпендикулярны линиям вектора j и имеют вид колец, охватывающих вибратор (рис. 5.16).

Таким образом, ЭЭВ можно представить в виде стержня, на поверхности которого задано распределение касательной составляющей вектора Н.   На концах вибратора ток проводимости переходит в ток смещения, которому соответствуют выходящие из торцов электрические силовые линии (рис. 5.16). Так как ток в ЭЭВ однозначно связан с касательной составляющей напряженности магнитного поля на его поверхности, то поле в пространстве вокруг вибратора можно выразить через значение .

Рассмотрим теперь систему, аналогичную описанной модели ЭЭВ, но отличающуюся от нее тем, что на поверхности стержня выполняется иное граничное условие, а именно касательная составляющая вектора Ё отлична от нуля и неизменна вдоль длины l, причем линии вектора Ё имеют вид колец, охватывающих поверхность S (рис. 5.17). Иными словами, данная система отличается от рассмотренной тем, что на поверхности S вместо замкнутых векторных линий магнитного поля задано распределение замкнутых линий электрического поля. Векторные линии магнитного поля второй системы совпадают по форме с векторными линиями электрического поля первой системы, но имеют противоположное направление. Различное направление магнитных и электрических линий системы следует из уравнений Максвелла (правые части первого и второго уравнений (1.75) имеют разные знаки). Задание касательной составляющей вектора Ё на поверхности стержня эквивалентно заданию плотности поверхностного магнитного тока . Так как по предположению значения E_φm одинаковы во всех точках поверхности S, то рассматриваемая система эквивалентна элементу длиной (. магнитного тока i^м, т.е. представляет собой элементарный магнитный вибратор.

Практически систему, близкую к данной модели элементарного магнитного вибратора, можно получить, если стержень выполнить из материала с магнитной проницаемостью μ₂. значительно большей магнитной проницаемости μ окружающей среды, например из феррита. В качестве возбуждающего устройства можно использовать рамку, обтекаемую током проводимости  (рис. 5.18).  Рамка  и стержень должны иметь общую ось.

Благодаря большой величине μ_r2 поток линий вектора В пронизывает стержень, почти не ответвляясь через его боковую поверхность, т.е. поток линий вектора В равномерен по длине стержня. Пронизывающим стержень линиям вектора В соответствуют

ветотвуют замкнутые линии вектора Е. Равномерность потока вектора В обусловливает равномерное распределение Е_φ на поверхности магнитного вибратора. Практически для того, чтобы распределение E_φ на поверхности магнитного вибратора было действительно равномерным, нужно аналогично тому, как это было сделано Герцем в случае электрического вибратора, использовать стержни с шарами или другими концевыми нагрузками (рис. 5.18). Элементарным магнитным вибратором можно считать также любой достаточно малый элемент длинного стержня, выполненного из соответствующего материала и возбужденного таким образом, что на его поверхности имеется отличная от нуля перпендикулярная оси стержня касательная составляющая напряженности электрического поля (Ё_φs ≠ 0), а другие составляющие вектора Е отсутствуют.

Следует отметить, что аналогия между физическими моделями элементарных электрического и магнитного вибраторов проявляется не только в распределении Н_φ на электрическом и Е_φ на магнитном вибраторах. Благодаря высокой проводимости материала электрического вибратора, на его поверхности выполняется условие Ё_τ Is→ 0. Точно так же при μ_r2»μ_r1 на поверхности магнитного вибратора Н_r |_s→ 0. Это следует из второго уравнения Максвелла  и условия непрерывности касательной составляющей вектора Н на границе раздела двух сред.

Если в схеме, изображенной на рис. 5.18, изъять стержень, оставив одну рамку, то характер структуры поля не изменится (рис. 5.19). Поэтому рамку достаточно малых размеров, обтекаемую электрическим током, также можно считать элементарным магнитным вибратором.

5.6.2. Поле элементарного магнитного вибратора

Выражения для комплексных амплитуд составляющих векторов поля, создаваемого элементарным магнитным вибратором, могут быть получены из формул (5.3), (5.4) и (5.5) для поля ЭЭВ, в которых нужно только в соответствии с принципом двойственности

заменить   на

(-μ) и μ на (-ε). Окончательные выражения очевидны, и мы не будем их здесь выписывать. Из формул для поля элементарного магнитного вибратора следует, что вектор Ё имеет одну составляющую  Ё_φ, а вектор  Н-две составляющие  Н_rи H _θт.е.

вектор Ё  в этом случае лежит в азимутальных плоскостях, а

вектор, Н - в меридиональных.

Подчеркнем, что найденные таким образом формулы соответствуют магнитному току, который при нулевой начальной фазе  в момент времени t=0 течет в направлении, противоположном полярной оси системы координат r, θ, φт.е. в направлении (-z₀).

Как и в случае ЭЭВ, в выражениях для поля элементарного магнитного вибратора (ЭМВ) имеются слагаемые, пропорциональные 1/(kr) в первой, второй и третьей степенях. Поэтому при анализе структуры поля элементарного магнитного вибратора окружающее его пространство также удобно разделить на три зоны:

ближнюю (kr<<1), дальнюю (kr>>1) и промежуточную, где kr соизмеримо с единицей.

Ограничимся анализом дальней зоны. Поступая так же, как и в случае элементарного электрического вибратора, получаем

Из формул (5.20) следует, что поле, создаваемое ЭМВ в дальней зоне, представляет собой неоднородную поперечную сферическую. волну, распространяющуюся от вибратора со скоростью света. Векторы Е и Н изменяются синфазно. На рис.5.20 показана ориентация векторов ЕиНв дальней зоне в случае ЭЭВ (рис. 5.20, а) и элементарного магнитного вибратора (рис. 5.20, б).

Распространение электромагнитной волны сопровождается переносом энергии. Энергия распространяется со скоростью света перпендикулярно поверхностями равных фаз, т.е. фазовая скорость и скорость распространения энергии совпадают. Отношение амплитуд напряженностей электрического и магнитного полей

Kак и элементарный электрический виоратор, элементарный магнитный вибратор обладает направленными свойствами. Его излучение максимально в экваториальной плоскости

Вдоль своей оси (оси Z) элементарный магнитный вибратор не излучает. Диаграммы направленности элементарного магнитного вибратора совпадают с диаграммами направленности элементарного электрического вибратора (рис. 5.11-5.15).

Как уже отмечалось, достаточно малая рамка (виток провода), обтекаемая постоянным по амплитуде электрическим током /_р = = /_pm cos (ωt + ψ₁), где ψ₁-начальная фаза тока, также может рассматриваться как элементарный магнитный вибратор. В этом случае вибратор характеризуется амплитудой тока (/_р) и площадью рамки S. Формулы для поля, создаваемого рамкой, могут быть получены независимо от формул для поля элементарного электрического вибратора. Для этого нужно записать выражение для

векторного потенциала кольцевого электрического тока А, вычислить входящий в это выражение интеграл в предположении, что расстояние от рамки до точки наблюдения велико по сравнению с размерами рамки, а затем перейти к векторам Ё и Н, как

это было сделано в случае элементарного электрического вибратора. Сравнение окончательных выражений для поля, создаваемого рамкой, с формулами для поля элементарного магнитного вибратора показывает, что они переходят друг в друга при замене вида

Длину ЭЭВ, при которой в случае одинаковых токов, обтекающих рамку и вибратор  мощность излучения ЭЭВ равна мощности излучения рамки, называют действующей высотой как видно той рамки. Она равна и из формул (5.22) и (5.6), рамка создает в дальней зоне такие же по величине (но не по ориентации векторов электрическое и магнитное поля, как и элементарный электрический вибратор.

Полученные выше результаты позволяют также выписать формулы для поля, создаваемого элементарным магнитным вибратором в виде короткого по сравнению с длиной волны стержня из материала с μ_r2>>1. на боковой поверхности которого задано распределение касательной  составляющей  вектора E(E_τm |_S=E°_φ = const). Для этого достаточно в формулах для поля элементарного магнитного вибратора в виде элемента магнитного тока заменить L - периметр поперечного сечения стержня).

5.6.3. Элементарный щелевой излучатель

Рассмотрим бесконечно протяженную идеально проводящую плоскость, по которой текут поверхностные электрические токи с плотностью j_s. Если в такой плоскости перпендикулярно j_s прорезать узкую щель, то эта щель пересечет линии вектора j_s (рис. 5.21), а на ее краях линии тока проводимости будут преобразовываться в линии тока смещения, т.е. в области щели касательная составляющая вектора Ё будет отлична от нуля: Ё_τm = E₀. Предположим, что длина щели l много меньше длины

волны, а значения амплитуды и фазы Ё_о не изменяются по всей длине щели (E₀ = const). Описанную систему будем называть элементарным щелевым излучателем или элементарным щелевым вибратором.

В случае реальной щели условие Ё_о = const не выполняется. Выровнять распределение E_τm  вдоль щели можно, если конфигурацию щели сделать аналогичной вибратору Герца (рис. 5.22).

Элементарным щелевым вибратором является также достаточно малый элемент щелевого вибратора конечных размеров.

В области щели имеется касательная составляющая напряженности электрического поля и отсутствует касательная составляющая  напряженности   магнитного  поля.  Последнее  следует, например, из того, что любое распределение поверхностных токов, текущих по плоскому экрану, создает вне его магнитное поле, имеющее в плоскости экрана только нормальную составляющую вектора Н. Таким образом, в щели выполняются такие же условия, как на поверхности элементарного магнитного вибратора. Отличие состоит только  в том,   что  электрические  силовые  линии  на поверхности ЭМВ являются замкнутыми (см. рис. 5.17), а в случае щели  они  оканчиваются  на ее  краях.  Аналогичными  будут и структуры полей, создаваемые ЭМВ и элементарным щелевым излучателем. Предположим для простоты, что ЭМВ представляет собой узкую бесконечно тонкую плоскую пластинку, выполненную из материала с бесконечно большой магнитной проницаемостью. Пластинка и щель имеют одинаковую конфигурацию, а значения составляющей E_τm  на них совпадают и равны E₀. Вообразим теперь бесконечную плоскость Q, проходящую через плоскость ЭМВ (рис. 5.23, а). Составляющая Ё_τm на этой плоскости обращается в нуль всюду, кроме участка, занимаемого ЭМВ, где она равна Е_о. На плоскости, в которой прорезана щель, выполняются такие же краевые условия: в области щели Ё _τm = E₀, на остальной части E_τm = 0. При рассмотрении поля в одном полупространстве можно считать,  что  металлическая  плоскость  в  случае  щелевого вибратора и воображаемая плоскость Q являются замкнутыми, предполагая, что они замыкаются в бесконечности. При этом

краевые условия получаются заданными на замкнутых поверхностях. Одинаковым краевым условиям на одинаковых замкнутых поверхностях соответствуют одинаковые поля во всем рассматриваемом пространстве. Поэтому можно утверждать, что поле, создаваемое в каждом полупространстве элементарным щелевым вибратором (см. рис. 5.23, б), будет таким же, как поле, создаваемое ЭМВ. В частности, в пространстве над плоскостью со щелью поле, создаваемое элементарным щелевым излучателем, будет определяться формулами (5.20), в которых надо считать i^M=LE₀, где L-периметр ЭМВ, равный 2а (а-ширина щели). Подставляя в (5.10)i^м =2аЁ₀, получаем

5.7. ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

При анализе конкретных излучающих систем часто возникают ситуации, когда распределение токов в системе либо неизвестно, либо имеет крайне сложный характер, но зато можно считать известным поле на некоторой замкнутой поверхности, охватывающей излучающую систему. В этих случаях поле, излучаемое системой, можно найти непосредственно по значениям векторов Ё и Н на этой поверхности.

Задача формулируется следующим образом. Пусть источники сосредоточены в ограниченной области V. Характер источников и их расположение неизвестны, но зато известны значения векторов Ё и Н на внешней по отношению к источникам стороне поверхности S, ограничивающей объем V. Поверхность S может быть как действительной поверхностью раздела различных сред, так и воображаемой, важно только, что на ней задано поле Ё,Н. Требуется найти поле вне области V. В силу теоремы единственности задача имеет единственное решение.

Среду, расположенную с внешней стороны поверхности S, будем называть первой средой, а внутри S- второй. Они характеризуются параметрами соответственно. Поля обозначаются аналогично: в первой среде-Ё ₁Н₁,   во второй-

Е₂,Н₂.

Предположим, что на S отсутствуют поверхностные токи и заряды. Тогда на S должны выполняться следующие условия:

поверхности S.

Для решения задачи применим искусственный прием. Предположим, что поле в облачи V отсутствует. Это заведомо неверное предположение. Однако если значения касательных составляющих векторов Ё и Н на внешней по отношению к V стороне поверхности S останутся прежними, то полученное с помощью такого предположения решение будет правильным вне области V. Так как при сделанном предположении , то при прежних значениях не будут выполняться граничные условия (5.24)-(5.27). Для того чтобы на поверхности S векторы  остались прежними и в то же время удовлетворяли граничным условиям, предположим, что на S распределены дополнительные источники (поверхностные заряды и токи), компенсирующие образовавшиеся разрывы составляющих векторов Ё и Н. Рассмотрим вначале нормальную компоненту вектора Ё. Если на S имеются

поверхностные электрические заряды с плотностью psskb. to вместо условия (5.24) должно выполняться условие, аналогичное (1.86):   .   Так как по предположению , то искомая плотность эквивалентных поверхностных зарядов

Аналогично компенсируется разрыв касательной составляющей вектора Н. При наличии поверхностных электрических токов с плотностью j_{s экв} на S вместо условия (5.27) должно выполняться условие, подобное (1.98):  Полагая в этом соотношении , получаем

Разрывы касательной составляющей вектора Ё и нормальной составляющей вектора В = μН можно компенсировать, введя эквивалентные поверхностные магнитные токи и заряды с плотностями  соответственно. При этом соотношения (5.25) и (5.26) следует заменить условиями, подобными (1.98) и (1.86) соответственно. Учитывая, что поле Ё₂,Н₂ считается равным нулю, приходим к равенствам

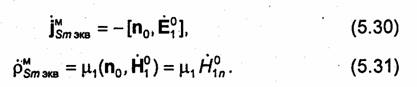
Подчеркнем еще раз: предполагается, что в природе нет свободных магнитных зарядов и токов. Их вводят формально для упрощения анализа. В рассматриваемом случае на S вообще может не быть источников, при этом фиктивными будут не только магнитные, но и электрические токи и заряды. Они были введены лишь для того, чтобы при произвольно сделанном предположении об отсутствии поля в области V, где находятся реальные источники, на внешней стороне поверхности S сохранились прежние

значения векторов Ё и Н. При этом в силу теоремы единственности поле в рассматриваемой области не изменится. В тех случаях, когда поверхность S совпадает (полностью или частично) с поверхностью идеального проводника, формулы (5.29) и (5.28) определяют на S (или на части поверхности S) реальные токи и заряды.

Электрические и магнитные поверхностные заряды и токи, определяемые соотношениями (5.28)-(5.31), называют эквивалентными источниками электромагнитного поля, а возможность перехода от значений векторов Е и Н на поверхности S к эквивалентным источникам-принципом эквивалентности (теоремой эквивалентности).

Зная распределение эквивалентных источников, можно найти создаваемое ими электромагнитное поле, например, с помощью векторных электродинамических потенциалов  которые были рассмотрены в 2.4. Векторный потенциал А_m в данном случае определяется выражением (2.61), в котором нужно только заменить Магнитный векторный потенциал  вычисляется по аналогичной формуле, вытекающей из (2.61) и перестановочной двойственности уравнений Максвелла:

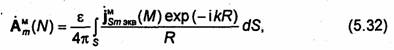
где N и М-точки наблюдения и интегрирования соответственно, а R - расстояние от точки М до N.

Поле, созданное эквивалентными источниками, выражается через векторные потенциалы  формулами (2.70).

Плотности эквивалентных поверхностных токов и зарядов связаны между собой уравнениями непрерывности,  которые в случае монохроматического поля имеют вид:  Следовательно, искомое электромагнитное поле однозначно определяется электрическими и магнитными токами,   т.е.   одними   касательными   составляющими   векторов

Ё и Н на поверхности S. Напомним, что для единственности решения рассматриваемой задачи (см.2.2) достаточно задать на поверхности S либо Ё_τ, либо Н_τ. Поэтому одновременное произвольное задание и  недопустимо.

5.8. ЭЛЕМЕНТ ГЮЙГЕНСА

 5.8.1. Принцип Гюйгенса

Гюйгенсом было сформулировано предположение, согласно которому каждая точка фронта волны, созданной каким-либо первичным источником, является вторичным источником сферической волны. Это предположение называют принципом Гюйгенса.

Под фронтом волны обычно понимают поверхность, отделяющую область, в которой в данный момент времени уже имеют место электромагнитные колебания, от области, в которую волна еще не успела распространиться. При описании распространяющихся монохроматических электромагнитных волн часто вместо термина поверхность равных фаз используют термин фронт волны, что, строго говоря, не совсем корректно.

Пусть известна поверхность Si (рис. 5.24), на которой фаза функции, характеризующей волну, в момент t=t₀ равна некоторому значению ψ₀. В следующий момент времени t = t₀ + ∆t поверхность, соответствующая значению фазы ψ₀., уже не будет совпадать с S₁. Для определения этой новой поверхности согласно принципу Гюйгенса нужно каждую точку поверхности S₁ принять за центр сферы радиуса r₀ = c∆t, где с-скорость распространения волны. Тогда поверхность S₂ (рис. 5.24), огибающая семейство построенных таким образом сфер,  проведенная-с учетом направления распространения волны, будет искомой поверхностью, на которой фаза в момент t = t_o + +At равна ψ₀.

Принцип Гюйгенса справедлив для любых волновых процессов и позволяет проследить за перемещением фронта волны или поверхности равных фаз, начиная с момента времени, в который являются известными фронт волны, или соответствен- но ПРФ. Математическая формулировка принципа Гюйгенса впервые была дана Кирхгофом. Поэтому указанный принцип обычно называют принципом Гюйгенса-Кирхгофа.

Принцип Гюйгенса-Кирхгофа позволяет находить поле и в том случае, когда поверхность, окружающая источники, не совпадает с поверхностью равных фаз. При этом, конечно, необходимо учитывать распределение фаз эквивалентных источников.

Принцип Гюйгенса-Кирхгофа широко применяется при расчете диаграмм направленности различных излучающих систем СВЧ диапазона. Основные типы антенн этого диапазона: щелевые, рупорные и зеркальные (схематически изображенные на рис. 5.25, а,б,в соответственно) можно представить в виде замкнутой поверхности; одна часть которой (S_o) является металлической, а другая (S_Σ) представляет собой поверхность раскрыва (через нее электромагнитная энергия излучается в окружающее пространство)., Поле йа S_Σ обычно известно с той или иной степенью точности, и его можно заменить распределением эквивалентных источников. Поверхности S_o можно считать идеально проводящей, тогда , что соответствует отсутствию магнитных токов . Кроме того, при приближенных расчетах часто пренебрегают затеканием электрических токов на внешнюю поверхность антенны, т.е. предполагают, что на поверхности S₀ отсутствуют

также электрические токи

В таком приближении поле в дальней зоне определяется только эквивалентными поверхностными электрическими и магнитными токами или, что то же самое, касательными составляющими векторов, Ё и Н на поверхности S_Σ.

При вычислении поля можно воспользоваться принципом суперпозиции: разбить поверхность S_Σ на элементарные площадки ∆S, найти поле, создаваемое эквивалентными токами каждой площадки, а затем просуммировать полученные результаты.

5.8.2. Поле элемента Гюйгенса

Практически элемент Гюйгенса можно представить как элемент фронта (или ПРФ) распространяющейся волны. Магнитное поле, действующее на этом элементе,

можно заменить эквивалентным электрическим током, а электрическое поле-эквивалентным магнитным током. Таким образом, элемент Гюйгенса можно рассматривать как элементарный излучатель, обтекаемый электрическими и магнитными токами. Определим его направленные свойства.

Так как векторы Е и Н свободно распространяющейся волны взаимно перпендикулярны, то эквивалентные им электрические и магнитные токи также будут взаимно перпендикулярны. Расположим прямоугольный элемент Гюйгенса (плоскую прямоугольную площадку ∆S = l₁l ₂) в плоскости ХОΥ так, чтобы начало координат совпадало с его центром. Ориентация касательных составляющих векторов Е и Н на площадке ∆S, соответствующая некоторому моменту времени t₀, показана на рис. 5.26, а ориентация электрических и магнитных токов, эквивалентных этим составляющим, в тот же момент времени t₀ - на рис. 5.27.

Полагая  ,   получаем, что комплекс-

ные амплитуды эквивалентных электрического  и магнитного

токов, текущих по ∆S, равны

Поле, создаваемое элементом Гюйгенса, равно сумме полей, создаваемых расположенными перпендикулярно друг другу элементарным электрическим вибратором длиной l₂ с током i³_т и элементарным магнитным вибратором длиной l₁ с током . Вычислим поле элемента Гюйгенса в дальней зоне. Рассмотрим, например, плоскость YOZ (плоскость E). Комплексная амплитуда напряженности электрического поля, создаваемого ЭЭВ, в системе

координат, полярная ось которой совпадает с осью У, определяется выражением

где θ₁° - координатный орт угла θ₁отсчитываемого от оси Υ (рис. 5.28). Соответственно комплексная амплитуда напряженности электрического поля, создаваемого элементарным магнитным вибратором, в рассматриваемой плоскости в системе координат, полярная ось которой совпадает с осью X, равна

где φ₂⁰ - координатный орт угла φ₂, отсчитываемого от плоскости XOY (рис. 5.29). В верхней части рассматриваемой плоскости (при z > 0)   орты θ₁° и φ₂⁰  совпадают,   а   в   нижней   (при   z < 0) –то в направлены противоположно. Если можно считать, что то в направлении оси Z вектор напряженности полного электрического поля  а в противоположном направлении (при φ₂ = Зπ/2) Ё_т = 0. Вдоль оси Υ (т.е. при φ₂ = 0 и φ₂ = π) ЭЭВ не излучает, и  Ё_т = Ё_2т.  При сделанном предположении диаграмма направленности элемента Гюйгенса в рассматриваемой плоскости (х = 0) имеет вид кардиоиды (рис. 5.30). Обычно поле элемента Гюйгенса записывают в системе координат r, θ, φ, показанной на рис. 5.26. Переходя в формулах (5.33) и (5.34) от единичных векторов  к орту θ₀ и от угла θ₁ к углу 0 (см. рис. 5.28 и 5.29), получаем следующее выражение для вектора

Ё_т = Ё_1т + Ё_2т в плоскости х = 0:

где знак «-» соответствует положительным значениям координаты Υ а знак «+»- отрицательным.

Нетрудно показать, что в произвольном направлении, характеризуемом координатами θи φ, комплексная амплитуда напряженности Электрического поля, создаваемого элементом Гюйгенса, имеет две составляющие:

Из формул (5.36) видно, что при выполнении условия диаграмма направленности элемента Гюйгенса одинакова во всех плоскостях, проходящих через ось Z, и имеет вид кардиоиды (см. рис. 5.30). Пространственная диаграмма направленности элемента Гюйгенса представляет собой поверхность, образующуюся при вращении кардиоиды вокруг ее оси симметрии (оси Z). Из диаграммы направленности видно, что излучение максимально в направлением оси Z, перпендикулярной к площадке ∆S.

Вектор напряженности магнитного поля, создаваемого элементом Гюйгенса, в дальней зоне при любых значениях углов θ и φ можно найти по формуле  где г₀-орт радиуса-вектора, проведенного из середины элемента Гюйгенса в точку наблюдения. Переходя к составляющим Н_θт и H_φm, получаем

5.9. Лемма Лоренца. Теорема взаимности

Пусть в линейной изотропной среде имеются две независимые группы источников, одна из которых характеризуется сторонними электрическими токами с плотностью  а вторая - токами с

Равенство (5.44) называют леммой Лоренца.

На основе леммы Лоренца доказывается теорема взаимности, имеющая фундаментальное значение. Предположим, что источники первой группы  сосредоточены в конечном объеме V₁ а источники второй группы  -в конечном объеме V₂. Области Vi и V₂ пространственно разделены (не пересекаются

друг с другом).

Интегрируя равенство (5.44) по произвольной области V, включающей в себя V₁ и V₂ (рис. 5.31), и применяя теорему Остроградского-Гаусса, получаем

где S - поверхность, ограничивающая объем V.

Соотношение (5.45) является интегральной формулировкой леммы Лоренца.

Распространим интегрирование в уравнении (5.45) на все пространство. При этом поверхность S уйдет в бесконечность. Не нарушая общностисти рассуждений, можно считать,   что   амплитуды   векторов Ё₁Н₁,  Ё₂ и Н₂ убывают с увеличением расстояния от источников быстрее, чем 1/r (см. теорему единственности, доказанную в 2.2). Тогда при r→∞ левая часть уравнения (5.45) обратится в нуль. Учитывая, кроме того, что по предположению вектор плотности сторонних токов отличен от нуля только в объеме V_b а вектор -только в объеме V₂, получаем

В полученном выражении Ё₁, - вектор напряженности электрического поля, создаваемого в точках объема V₂ токами  распределенными в объеме V₁ a E₂- напряженность электрического поля, создаваемого в точках объема V₁ токами, протекающими в объеме V₂.

Соотношение (5.46) является одной из наиболее общих математических формулировок теоремы взаимности.

Выясним некоторые следствия, вытекающие из этой теоремы. Предположим,   что  объемы   V₁   и   V₂ и   распределение  токов   в них совершенно одинаковы. Из равенства (5.44) следует, что в этом случае векторы Ё₁ и Ё₂ также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым, распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или неоднородным, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1.

На основе теоремы взаимности можно также доказать, что диаграмма направленности приемной антенны имеет такую же форму, какую она имела бы, если бы антенна работала в качестве передающей. Применение теоремы взаимности в ряде случаев позволяет существенно упростить решение электродинамических задач.

При доказательстве теоремы взаимности предполагалось, что среда, заполняющая рассматриваемое пространство, является линейной и изотропной. Предположим теперь, что среда, оставаясь линейной,  является  анизотропной.   В  этом  случае  параметры ε и μ (оба или по крайней мере один из них) будут тензорами.

Тогда вместо уравнения (5.44) получаем