ПРЕДИСЛОВИЕ

Настоящая книга является вторым существенно переработанным изданием учебника В.И. Вольмана, Ю.В. Пименова "Техническая электродинамика" под редакцией Г.З. Айзенберга (М.: Связь, 1971). Книга написана в соответствии с государственным образовательным стандартом высшего профессионального образования по специальностям: 201100 ("Радиосвязь, радиовещание и телевидение"), 201000 ("Многоканальные телекоммуникационные системы"), 200900 ("Системы связи с подвижными объектами"), 071700 ("Физика и техника оптической связи"), а также по специальности 200799 ("Радиотехника"). Книга может быть использована в качестве учебного пособия по общепрофессиональной дисциплине "Электромагнитные поля и волны", а также по дисциплинам "Антенно-фидерные устройства", "Электродинамика и распространение радиоволн", "Устройства СВЧ", "Спутниковые и радиорелейные системы передачи данных" и др. Предполагается, что студентами усвоены разделы курса физики, посвященные теории электромагнетизма, а также соответствующие разделы курсов высшей и вычислительной математики и теории линейных электрических цепей.

В пособии излагаются основные законы электродинамики. Статические и стационарные поля рассматриваются как частные случаи электромагнитного поля. Анализируются вопросы излучения, распространения и дифракции электромагнитных волн. Дается представление о постановке и некоторых строгих, асимптотических и численных методах решения задач электродинамики. Излагается теория и приводятся сведения о методах анализа, технических характеристиках и конструктивных особенностях элементов и устройств высокочастотных трактов, включая оптические. При подборе этого материала особое внимание уделялось элементам высокочастотных трактов, применяемых в современных многоканальных системах связи. Большое внимание уделено физической трактовке результатов анализа, что, по убеждению авторов, содействует лучшему усвоению материала и развитию научной инициативы студентов.

Авторы полагают, что учебное пособие может быть использовано не только в университетах и институтах связи Российской Федерации, но также на радиофакультетах других вузов.

В основу пособия положены лекции, читавшиеся авторами в Московском техническом университете связи и информатики.

Главы 1-8 и §10.5 написаны Ю.В. Пивеновым ,гл.9 и 11 –В.И. Вольманом §10.1-10.4-совместно В.И. Вольманом и Ю.В. Пи-меновым, гл.15 и §10.6 и 10.7-А.Д. Муравцовым, гл.12-14-А.Д. Муравцовым с частичным использованием материала соответствующих разделов первого издания, написанных В.И. Вольманом. Весь текст книги отредактирован Ю.В. Пименовым.

Авторы с искренней благодарностью вспоминают заслуженного деятеля науки и техники СССР, лауреата Государственных и Ленинской премий, докт. техн. наук, профессора Григория Захаровича Айзенберга, принявшего исключительно большое участие в определении содержания и методики изложения первого издания книги.

Авторы с благодарностью приняли и учли при окончательном редактировании рукописи ряд ценных замечаний профессора Э.А. Павловской.

Авторы выражают глубокую благодарность В.В. Калевичу, чьи многочисленные ценные замечания по первому изданию данной книги были учтены при ее переиздании.

Авторы весьма признательны заведующему кафедрой "Технической электродинамики и антенн" МТУСИ заслуженному деятелю науки и техники РФ, докт. техн. наук, профессору Г.А. Ерохину, сделавшему существенные замечания, которые позволили устранить ряд неточностей и улучшить изложение материала.

Авторы признательны всем приславшим отзывы и замечания по первому изданию книги и с благодарностью примут все замечания по данному изданию.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ

Указаны лишь величины, для которых в книгах по электродинамике используются разные обозначения.

i  - мнимая единица (i² =-1);

j  - плотность тока проводимости;

Р  - комплексная мощность;

x_о, y_о, z₀ - координатные орты соответствующих переменных

декартовой системы координат;

r_о, θ_о, φо - координатные орты соответствующих переменных

сферической системы координат;

Z_c - характеристическое сопротивление;

Z_B - волновое сопротивление линии передачи;

α - коэффициент ослабления;

β - коэффициент фазы;

 Δ⁰ - глубина проникновения;

ε и μ- абсолютные диэлектрическая и магнитная проницаемости среды;

ε _rи μ_r  - относительные диэлектрическая и магнитная проницаемости среды;

ε и μ - комплексные диэлектрическая и магнитная проницаемости среды;

Λ - длина волны в направляющей системе;

П  - вектор Пойнтинга;

П   - комплексный вектор Пойнтинга;

ρ - объемная плотность зарядов;

 ρ_s и j_s - плотности поверхностных зарядов и токов

ПРИМЕЧАНИЯ

1. Для обозначения комплексных мгновенных значений величин, являющихся гармоническими функциями времени, ставится точка над основным обозначением, например, вектору Е соответствует комплексный вектор É= É _mехр(iω t), где É _m- комплексная амплитуда вектора Е, причем Е = Re É.

Сопряженные комплексные величины обозначаются символом * над буквенным обозначением.

2. Комплексные величины, не являющиеся гармоническими функциями времени, обозначаются черточкой под соответствующим буквенным обозначением, например, Р _Σ - комплексный поток энергии.

3. Средние за период величины обозначаются нижним индексом «ср», например, П_ср- среднее за период значение вектора Пойнтинга.

4. Тензоры и матрицы обозначаются двойными вертикальными линиями, например, || S || - волновая матрица рассеяния, ||  ε || - тензор абсолютной диэлектрической проницаемости среды.

Глава  1

ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ

1.1. ОБЩИЕ СВЕДЕНИЯ

В современной физике при рассмотрении многих явлений наряду с понятием вещества вводится понятие поля: электромагнитное, гравитационное, поле ядерных сил и др. Иными словами, предполагается, что возможны две формы существования материи: вещество и поле. Несмотря на то, что вещество и электромагнитное поле являются различными формами существования материи, их свойства сходны во многих отношениях.

Вещество состоит из отдельных частиц: молекул, атомов, элементарных частиц (протонов, электронов, нейтронов и др.). Но и распространяющееся электромагнитное поле (электромагнитные волны) можно рассматривать как поток дискретных частиц-фотонов. Электромагнитное поле так же, как и вещество, характеризуется энергией, массой и импульсом. Правда, масса и импульс характерны только для распространяющегося электромагнитного поля (электромагнитных волн). В отличие от вещества электромагнитное поле не обладает массой покоя. Электромагнитные волны испытывают воздействие гравитационных сил. Известно, что путь распространения световых волн заметно искривляется под влиянием гравитационных сил больших масс вещества, например Солнца. Импульс электромагнитных волн проявляется в давлении, которое они оказывают на материальные тела. С другой стороны, такие характерные для электромагнитных волн свойства, как дифракция и интерференция, присущи также материальным частицам. Известны, например, явления дифракции и интерференции электронов.

Энергия электромагнитного поля может переходить в другие виды энергии. Фактически само существование жизни на Земле обусловлено преобразованием электромагнитной энергии (энергии солнечных лучей) в тепловую, химическую и другие виды энергии.

Классическая или максвелловская ,теория электромагнитного поля учитывает только макроскопические свойства вещества: предполагается, что размеры рассматриваемой области пространства и расстояние от источников поля до рассматриваемой точки велики по сравнению с размерами молекул, а характерное для изменения электромагнитного поля время (например, период колебаний) велико по сравнению со временем, характерным для внутримолекулярных колебательных процессов. На основе классической теории электромагнитного поля может быть изучен широкий круг вопросов, встречающихся в радиотехнике. Классическая теория поля не охватывает, однако, всех его свойств. За ее пределами остаются такие явления, как излучение и поглощение веществом электромагнитных волн очень высокой частоты (например, световых), фотоэффект и др. Строгий анализ подобных явлений должен учитывать микроструктуру вещества и, следовательно, должен базироваться на квантовой теории поля. В пределах данного курса изучается классическая теория электромагнитного поля, т.е. исследуются только его макроскопические свойства.

Электромагнитное поле обычно разделяют на два взаимосвязанных поля: электрическое и магнитное.

Источниками электромагнитного поля являются электрические заряды. Неподвижные заряды создают только электрическое поле. Движущиеся заряды создают и электрическое, и магнитное поля. Токи проводимости и конвекционные токи представляют собой упорядоченно движущиеся электрические заряды и также создают электромагнитное поле. Заряды взаимодействуют друг с другом, причем сила их взаимодействия определяется законом Кулона.

Разделение единого электромагнитного поля на электрическое и магнитное имеет относительный характер: оно зависит от выбранной системы отсчета. Например, движущийся прямолинейно с постоянной скоростью электрический заряд создает вокруг себя как электрическое, так и магнитное поле. Однако для наблюдателя, движущегося в том же направлении с той же скоростью, этот заряд является неподвижным и, следовательно, создает только электрическое поле.

Оба поля проявляются в виде механических или, как их принято называть, "пондеромоторных" сил. Если в электрическое поле внести пробный электрический заряд, то под действием этих сил он будет перемещаться. Аналогично магнитное поле изменяет направление движения пробного электрического заряда, а также ориентирует пробный постоянный магнит (магнитную стрелку). Электрическое поле действует и на неподвижные, и на движущиеся заряды, магнитное -только на движущиеся. Действие электромагнитного поля обладает определенной направленностью, поэтому для его описания вводят векторные величины. Рассмотрим основные векторы, характеризующие электромагнитное поле.

1.2. ВЕКТОРЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ И КЛАССИФИКАЦИЯ СРЕД

1.2.1. Векторы электрического поля

Напряженность электрического поля Е определяют как силу, с которой электрическое поле действует на точечный положительный единичный заряд. Следовательно, между вектором Е и силой F, действующей на точечный заряд q, существует простая связь: Е = F/q. Заряд q должен быть достаточно малым, чтобы можно было пренебречь изменением распределения зарядов, создающих исследуемое поле. Поэтому данное соотношение правильнее представить в виде

Символ q →0 означает, что уменьшается не только величина заряда, но и размеры объекта, на котором распределен заряд.

В системе СИ сила измеряется в ньютонах (Н), заряд-в кулонах (Кл), напряженность электрического поля-в вольтах на метр ([Е] = Н/Кл = В∙А∙с/(м∙А∙с) = В/м).

Сила взаимодействия зарядов, а следовательно, и напряженность электрического поля в различных средах различны. Физически это объясняется следующим образом. Под действием электрического поля вещество поляризуется. В результате появляется дополнительное электрическое поле, которое налагается на первичное. При этом суммарное электрическое поле оказывается отличным от того, каким оно было бы в вакууме.

Поляризация-сложный физический процесс, непосредственно связанный с атомной структурой вещества. Упрощенно этот процесс можно объяснить следующим образом. Каждый атом состоит из положительно заряженного ядра и окружающих его электронов. Суммарный заряд атома равен нулю. Соединения атомов образуют молекулы. Различают полярные и неполярные молекулы. В неполярных молекулах распределение положительных и отрицательных зарядов таково, что точка приложения равнодействующей сил поля, действующих на все электроны, совпадает с точкой приложения равнодействующей сил поля, действующих на все протоны. Это, как известно, возможно лишь при условии, что центр тяжести всех электронов молекулы совпадает с центром тяжести всех ее протонов. В полярных молекулах центр тяжести электронов сдвинут относительно центра тяжести протонов. Поэтому полярную молекулу можно уподобить крошечному электрическому диполю-системе из двух равных по величине и противоположных по знаку зарядов (+q и -q), расположенных на некотором малом расстоянии l друг от друга. Диполи обычно характеризуют дипольным моментом р. Дипольный момент-вектор, численно равный произведению величины заряда на расстояние между зарядами, направленный вдоль оси диполя от отрицательного заряда к положительному:  где l-орт вектора, соединяющего заряды -q и +q. Размерность дипольного момента-кулон, умноженный на метр (Кл∙м).

Суммарный дипольный момент объема  ΔV вещества равен геометрической сумме дипольных моментов р_i- молекул в этом объеме. Внешнее электрическое поле оказывает силовое воздействие на диполь, стремясь повернуть его таким образом, чтобы он был ориентирован по полю, причем момент приложенных к диполю сил К = [р,Е](рис.1.1).

Неполярные молекулы не обладают собственным дипольным моментом. Однако под действием внешнего электрического поля в такой молекуле перераспределяется отрицательный заряд, и она становится полярной: у нее появляется дипольный момент. Дипольные моменты отдельных молекул ориентируются по полю, и суммарный дипольный момент оказывается отличным от нуля. Этот процесс принято называть электронной поляризацией.

Полярные молекулы обладают собственными дипольными . моментами. В отсутствие внешнего электрического поля дипольные моменты отдельных молекул ориентированы хаотически, и суммарный дипольный момент равен нулю. Под действием внешнего электрического поля происходит ориентация дипольных моментов отдельных молекул, в результате чего появляется суммарный дипольный момент рассматриваемого объема. Этот процесс называют ориентационной поляризацией. Очевидно, что ориентационная поляризация всегда сопровождается электронной.

Указанные типы поляризаций являются основными в газообразных и жидких средах. Поляризация твердых сред имеет некоторые особенности, но сущность явления остается той же.

Для характеристики поляризации вводят вектор поляризованности Р; определяемый как предел отношения суммарного дипольного момента вещества в объеме  ΔV к величине этого объема при  ΔV→0:

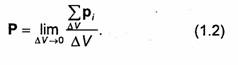
Вектор P измеряется в кулонах на квадратный метр (Кл/м²).

Как уже отмечалось, в классической электродинамике рассматриваемый объем всегда предполагается большим по сравнению с объемом отдельной молекулы. Это относится и к случаю элементарного объема dV. Поэтому выражение  Δ\/→0 нельзя рассматривать в строго математическом смысле: при любом уменьшении объема  ΔVero нужно считать достаточно большим по сравнению с объемом молекулы. Аналогичные предположения должны быть сделаны также относительно элементарной длины dl и элементарной площадки dS. В дальнейшем будем считать эти условия выполненными.

При не очень сильном внешнем поле величину индуцированного дипольного момента можно считать пропорциональной напряженности электрического поля:

Входящий в формулу (1.3) безразмерный параметр χ- характеризует среду и называется диэлектрической восприимчивостью среды. Постоянный коэффициент ε ₀ называется электрической постоянной. Его величина зависит от выбора системы единиц. В системе СИ ε ₀ = 10^-9/(36π), [Ф/M].

При рассмотрении многих процессов удобно ввести вектор D, связанный с вектором Р соотношением

D = ε ₀E + P.                                     (1.4)

С учетом (1.3) формулу (1.4) можно представить в виде

D = ε E,                                            (1.5)

где  ε = ε _о(1+χ) .Вектор D принято называть вектором электрического смещения, а параметр ε -абсолютной диэлектрической проницаемостью среды. Так как диэлектрическая восприимчивость вакуума считается равной нулю (χ= 0), то электрическую постоянную ε ₀ можно рассматривать как абсолютную диэлектрическую проницаемость вакуума. Электрическое смещение D измеряется в кулонах на квадратный метр (Кл/м²), диэлектрическая проницаемость -в фарадах на метр (Ф/м). Наряду с ε часто вводят относительную диэлектрическую проницаемость среды ε _r, связанную с  ε соотношением

ε  = ε₀ ε_r                                          (1.6)

Относительная диэлектрическая проницаемость может быть выражена через диэлектрическую восприимчивость: ε _r=1+ χ

Подчеркнем, что соотношения (1.3) и (1.5) являются приближенными. В большинстве, сред пропорциональность векторов Е и Р, а следовательно, и векторов Е и D нарушается в сильных электрических полях. В некоторых веществах это происходит даже при сравнительно слабых полях. Кроме того, параметры χ и ε зависят от скорости изменения вектора Е: молекулы имеют инерцию и требуется некоторое время, чтобы их дипольные моменты изменили ориентацию под действием поля. В исследуемых

в книге вопросах соотношение (1.5) можно считать справедливым.

Рассмотрим электрическое поле, создаваемое точечным зарядом Q, расположенным в безграничной среде, у которой ε -скалярная постоянная (ε  = const). Такую среду называют однородной и изотропной по отношению к электрическому полю. Определение этих терминов будет дано ниже (см. 1.2.3). Согласно закону Кулона сила, с которой точечный заряд Q в рассматриваемом случае действует на точечный заряд q,

где r- расстояние между зарядами Q и q, а r₀-единичный вектор, направленный вдоль гот Q к q (рис. 1.2). Из этой формулы и определения вектора Е (1.1) следует, что напряженность электрического поля, создаваемого точечным зарядом Q,

Переходя к вектору D на основе равенства (1.5), замечаем, что вектор D в однородных изотропных средах не зависит от ε .Следовательно, при ε  = const и одинаковом распределении свободных зарядов вектор D имеет одинаковые значения в разных средах, т.е. не зависит от "связанных" зарядов вещества. Эта особенность вектора D в однородных изотропных средах характерна не только для поля точечного заряда, но и для поля, созданного любым более сложным распределением зарядов.

Под действием электрического поля в среде, обладающей проводимостью, возникает электрический ток (ток проводимости), распределение которого удобно характеризовать вектором плотности тока проводимости

где i₀-единичный вектор, показывающий направление тока (направление движения положительных зарядов) в рассматриваемой точке М; ΔS-плоская площадка, содержащая точку М, расположенная перпендикулярно вектору i₀, а Δ/-ток проводимости, протекающий через ∆S.  Вектор j часто называют также вектором объемной плотности тока проводимости. Как видно из (1.8), вектор j измеряется в амперах на квадратный метр (А/м ²).

Вектор j связан с вектором Е соотношением

j = σE,                                          (1.9)

которое представляет собой закон Ома в дифференциальной форме. Коэффициент пропорциональности  σ называют удельной проводимостью среды и измеряют в сименсах на метр (См/м).

1.2.2. Векторы магнитного поля

Сила,  с  которой  электромагнитное  поле  воздействует  на

точечный  электрический  заряд,   зависит  не  только  от  местоположения и величины заряда, но и от скорости его движения. Эту силу обычно раскладывают на две: электрическую и магнитную.

Электрическая сила не зависит от движения заряда:

F_э = qE.                                        (1.10)

Магнитная сила F_M зависит от величины и направления скорости v движения заряда и всегда перпендикулярна ей:

F_M = q[v, В].                                     (1.11)

Здесь В-вектор магнитной индукции, характеризующий силовое воздействие магнитного поля. Как видно, магнитная индукция численно равна силе, с которой магнитное поле действует на единичный точечный положительный заряд, движущийся с единичной скоростью перпендикулярно линиям вектора В. Магнитная индукция измеряется в теслах (Тл) или, что то же самое, в веберах на квадратный метр (Вб/м²). Размерность следует, например, из формулы (1.11): [В] = [F]/([q] [v]) = Нс/(Клм) = = (В∙А∙с²/м)/(А∙с∙м) = В∙с/м² = Вб/м² = Тл.

Полная сила, действующая на точечный заряд q, находящийся в электромагнитном поле (лоренцова сила),

F = qE + q[v, В].                                 (1.12)

Магнитное поле действует, конечно, не только на отдельные движущиеся заряды, но и на проводники, по которым течет электрический ток. Например, сила F, с которой однородное магнитное поле действует на прямолинейный проводник длиной I с током /, определяется экспериментально установленным законом

F = /l[l_o,B],                                   (1.13)

где l_o-единичный вектор, направление которого совпадает с направлением тока, т.е. с направлением движения положительных зарядов в проводнике. Отметим, что формула (1.13) является следствием формулы (1.11).

Если в магнитное поле внести достаточно малую плоскую рамку, обтекаемую током /, то на нее будет действовать момент сил К, стремящийся повернуть рамку таким

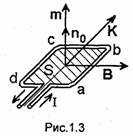
образом, чтобы ее плоскость была перпендикулярна вектору В (достаточная малость рамки определяется из требования, чтобы в ее пределах магнитное поле можно было считать однородным). Рассмотрим рамку, показанную на рис. 1.3. Токи, протекающие вдоль сторон ab и cd рамки, направлены противоположно друг другу. Поэтому силы, с которыми магнитное поле действует на элементы ab и cd рамки, будут согласно формуле (1.13) равны по величине и противоположны по направлению. Следовательно, на рамку abcd будет действовать пара сил, стремящихся ее повернуть. Момент сил, действующий на достаточно малую плоскую рамку с площадью S, находящуюся в магнитном поле, определяется выражением К = /S[n₀, В], где п₀-орт нормали к плоскости рамки, образующий с направлением тока, обтекающего рамку, правовинтовую систему. Рамки с током обычно характеризуют величиной m = n_o/S, называемой магнитным моментом рамки. Размерность вектора m-ампер, умноженный на квадратный метр (А∙м²). Выражая момент сил К через магнитный момент рамки, получаем К = [т, В]. Отметим, что данное выражение для К аналогично записанному выше выражению для момента сил, действующего на диполь, находящийся в электрическом поле. Как видно, момент сил, действующий на рамку, находящуюся в магнитном поле, стремится повернуть ее так, чтобы момент рамки совпадал с направлением вектора В. Величина вектора В зависит от свойств среды. Физически это объясняется следующим образом. Под действием магнитного поля вещество намагничивается. В результате появляется дополнительное магнитное поле, которое налагается на первичное. При этом суммарное магнитное поле оказывается отличным от того, каким оно было бы в вакууме.

Явление намагничивания - сложный физический процесс, непосредственно связанный с атомной структурой вещества. Упрощенно его можно представить следующим образом. Атомы и молекулы многих веществ обладают магнитным моментом и могут быть уподоблены маленьким рамкам с током. Каждая рамка с током, как известно, создает собственное магнитное поле, пропорциональное магнитному моменту. В отсутствие внешнего магнитного поля магнитные моменты молекул, как правило, направлены хаотически и суммарный магнитный момент рассматриваемого объема ΔV, представляющий собой геометрическую сумму магнитных моментов m,- отдельных молекул в объеме ΔV, равен нулю, т.е. магнитные поля отдельных молекул взаимно компенсируются. Под действием внешнего магнитного поля происходит ориентация магнитных моментов отдельных молекул, и суммарный магнитный момент оказывается отличным от нуля. Образующееся в результате намагничивания дополнительное магнитное поле может как ослаблять, так и усиливать первичное поле. Среды, в которых магнитное поле ослабляется, называют диамагнитными, среды, в которых поле незначительно усиливается, называют парамагнитными, а среды, в которых происходит существенное усиление магнитного поля,- ферромагнитными. Явление намагничивания и особенности свойств ферромагнитных сред более подробно рассмотрены в гл.14.

Намагниченность среды характеризуется вектором намагниченности М, который определяют как предел отношения суммарного магнитного момента вещества в объеме ΔV к величине этого объема при Δ\/→0:

Вектор М измеряется в амперах на метр (А/м).

 При рассмотрении многих процессов удобно вместо вектора М ввести вектор Н, связанный с М соотношением

где μ₀- постоянная величина, называемая магнитной постоянной, значение и размерность которой зависят от выбора системы единиц. В системе СИ μ₀ = 4-10^-7 Гн/м.

Вектор Н принято называть вектором напряженности магнитного поля. Он, как и вектор М, измеряется в амперах на метр (А/м).

При не очень сильном внешнем магнитном поле можно считать, что вектор М пропорционален вектору В. В силу линейности уравнения (1.15) можно также считать пропорциональными векторы М и Н:

Безразмерный коэффициент χ_т называют магнитной восприимчивостью среды. У диамагнитных сред параметр χ_т отрицательный, у парамагнитных и ферромагнитных-положительный. У диамагнитных и парамагнитных сред   у ферромагнитных χ_т значительно больше единицы.

Подставляя формулу (1.16) в (1.15), получаем

где Коэффициент пропорциональности р. между В и Н называют абсолютной магнитной проницаемостью среды. В системе СИ μ₀ измеряется в генри на метр (Гн/м). Магнитная восприимчивость вакуума считается равной нулю, поэтому магнитную постоянную μ₀ можно рассматривать как абсолютную магнитную проницаемость вакуума.

Наряду с абсолютной магнитной проницаемостью среды р вводят также относительную магнитную проницаемость μ_r связанную с μ соотношением

Очевидно, что

Отметим важное свойство вектора Н. В средах, в которых μ -скалярная постоянная (такие среды называют однородными и изотропными по отношению к магнитному полю; термины определены в 1.2.3), вектор Н не зависит от μ. Поэтому при одинаковых источниках магнитного поля значения вектора Н в разных однородных изотропных средах будут одинаковы.

Для большинства сред при не очень сильных полях уравнение (1.17) правильно передает взаимосвязь между векторами В и Н. При этом для диамагнитных и парамагнитных веществ μ_r обычно можно считать скалярной величиной, а для намагниченных ферромагнитных веществ μ_r является тензором. Однако необходимо помнить, что уравнения (1.16) и (1.17), как и аналогичные уравнения для электрического поля (1.3) и (1.5), являются приближенными. Магнитная восприимчивость, а следовательно, и магнитная проницаемость ферромагнитных сред существенно зависят от величины магнитного поля. Кроме того, в ферромагнитных материалах намагниченность среды зависит не только от величины магнитного поля в данный момент, но и от того, как оно изменялось раньше (явление магнитного гистерезиса).

Подчеркнем, что векторы электромагнитного поля были введены в результате обобщения огромного числа экспериментальных данных, выражением которых являются основные законы электромагнитного поля (закон Кулона, закон Фарадея и др.).

1.2.3. Классификация сред

Свойства среды по отношению к электромагнитному полю определяются параметрами ε, μ и σ. Различают следующие среды:

линейные ,в которых параметры ε, μ и σ не зависят от величины электрического и магнитного полей, и

нелинейные, в которых параметры ε, μ и σ (или хотя бы один из них) зависят от величины электрического или магнитного поля .

Все реальные среды, по существу, являются нелинейными с Однако при не очень сильных полях во многих случаях можно -пренебречь зависимостью параметров ε, μ,σ о от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна. В дальнейшем будут рассматриваться только линейные среды.                                                                                      

В свою очередь, линейные среды делятся на однородные иt неоднородные, изотропные и анизотропные.                                    

Однородными называют среды, параметры ε, μ и σ  которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров ε, μ  илиσ является функцией координат, называют неоднородными.

Если свойства среды одинаковы по разным направлениям, то среду называют изотропной.  Соответственно среды,  свойство которых различны по разным направлениям,  Называют анизотропными. В изотропных средах векторы Р и Е, D и Е, а также М и Н, В и Н параллельны, а в анизотропных средах они могут быть не параллельными. В изотропных средах ε, μ и σ  -скалярные величины. В анизотропных по крайней мере один из этих параметров ' является тензором. К анизотропным средам относятся, например, I кристаллические диэлектрики,  намагниченная  плазма  и  намагниченный феррит.  В кристаллическом диэлектрике и намагниченной  плазме тензором  является диэлектрическая  проницаемость ε.  При использовании декартовой системы координат в  общем случае тензор диэлектрической проницаемости может быть записан в виде матрицы

Величины   называют компонентами тензора ||ε|. В частных случаях некоторые из них могут равняться нулю. Форма уравнения (1.5) остается прежней:

Чтобы записать уравнение (1.20) в проекциях на оси декартовой системы координат х, у, z, нужно раскрыть правую часть уравнения (1.20) по обычным правилам умножения матриц. В результате получим:

Непараллельность векторов D и Е (а также Р и Е) в анизотропной среде объясняется тем, что в общем случае направление возникающего в результате поляризации анизотропной среды вторичного электрического поля, созданного связанными зарядами вещества, составляет некоторый угол (отличный от 0 и π) с направлением первичного электрического поля.

В намагниченной ферромагнитной среде тензором является магнитная проницаемость. В общем случае в декартовой системе координат тензор магнитной проницаемости может быть представлен в виде

При этом форма уравнения (1.17) сохраняется:

Записывая уравнение (1.23) в проекциях на оси декартовой системы координат х, у, z, приходим к формулам, аналогичным

(1.21).

Удельная проводимость а также может быть тензорной величиной. Для таких сред закон Ома в дифференциальной форме (1.9) принимает вид j = || σ  || ∙Е.

1.2.4. Графическое изображение полей

Векторное поле обычно изображают с помощью линий, которые в каждой точке касаются характеризующего его вектора (рис. 1.4). Их называют векторными линиями. Чтобы дать представление о величине поля, векторные линии проводят так, чтобы их число на единицу площади, расположенной перпендикулярно линиям, было пропорционально величине вектора. Там, где поле сильнее, линии проводят гуще, там, где оно слабее ,- реже. Линии

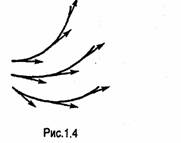
векторов, являющихся силовыми характеристиками поля, например, линии векторов Е и В, обычно называют силовыми линищ поля.

Пусть некоторое поле характеризуется вектором а и Г-одна из линий этого вектора (рис. 1.5).  Начало декартовой системы координат х, у, z расположено в точке  О.  Проведем  радиусы-векторы  r и r₁  = r + dr в точки  N и  N₁ соответственно,   расположенные   на   кривой   Г  достаточно   близко   друг   к  другу. Приращение радиуса-вектора dr можно записать в виде dr = x_odx + y_о dу + z_odz, где х₀, у₀ и z_o - координатные орты переменных х, у и z соответственно. Так как кривая Г-линия вектора а, то вектор dr должен быть параллелен вектору а, следовательно,

где a_x = a_x(x,y,z), a_y = a_y(x,y,z) и а_г = а_г (х, у, z) - проекции вектора а на оси X, Y и Z соответственно. Соотношение (1.24) представляет собой уравнение линий вектора а.

1.3. УРАВНЕНИЯ МАКСВЕЛЛА

1.3.1. Первое уравнение Максвелла

Для описания электромагнитного поля было введено шесть векторов Е, Р, D, В, М и Н. Так как векторы электрического поля Е, Р, D связаны соотношением (1.4), а векторы магнитного поля В, М, Н-соотношением (1.15), то для определения электромагнитного поля можно ограничиться нахождением четырех векторов. Обычно в качестве таких векторов используют векторы Е, D, В и Н. В линейных изотропных средах, для которых справедливы соотношения (1.5) и (1.17), электромагнитное поле может быть полностью определено двумя векторами (обычно Е и Н).

Все электромагнитные процессы, относящиеся к макроскопической электродинамике, подчиняются законам, впервые сформулированным в виде дифференциальных уравнений Дж.К. Максвеллом, которые были опубликованы им в 1873 г. Эти уравнения были получены в результате обобщения накопленных к тому времени экспериментальных данных и называются уравнениями Максвелла.

Первое уравнение Максвелла является обобщением закона полного тока (закона Ампера). В домаксвелловской формулировке это уравнение могло быть сформулировано следующим образом: циркуляция вектора напряженности Н магнитного поля по замкнутому контуру Г равна току /, пронизывающему данный контур:

где dl =τ_odl- элемент контура Г, направленный по касательной к Г; τ₀-орт этой касательной, положительное направление которого выбирается в соответствии с обходом контура Г. В качестве контура Г может быть взят любой одновитковый замкнутый контур.

До Максвелла под током / понимали только ток проводимости. В общем случае распределение тока / внутри контура Г может быть неравномерным. При этом

где j-вектор плотности тока проводимости; S-произвольная поверхность, опирающаяся на контур Г; dS = n_odS, a n₀ - орт нормали к поверхности S (рис.1.6). Направление вектора п₀ определяется направлением обхода контура Г. Пусть для определенности все точки поверхности S расположены с одной стороны относительно контура Г. Тогда, если смотреть вдоль вектора п₀, обход контура Г будет идти по часовой стрелке. Такую * взаимосвязь направлений вектора п₀ и обхода контура для краткости будем условно называть правовинтовоп системой. Подставляя (1.26) в (1.25), получаем

Уравнение (1.27), справедливое при постоянном токе, оказывается неверным в случае переменных процессов. Действительно, рассмотрим конденсатор, включенный в цепь переменного тока (рис. 1.7). Пусть Г-замкнутый контур, охватывающий провод, по которому течет переменный ток. Правая часть уравнения (1.27) представляет собой интеграл от плотности тока проводимости j по произвольной поверхности S, опирающейся на контур Г. Эту поверхность можно провести так, чтобы она либо пересекла провод (поверхность Si на рис. 1.7), либо прошла между обкладками конденсатора (поверхность S₂). Интеграл в правой части уравнения (1.27) в первом случае равен току /, а во втором обращается в нуль. В то же время циркуляция   напряженности магнитного поля по контуру Г (левая часть уравнения) не зависит от того, как проведена поверхность S. Это противоречие свидетельствует о непригодности уравнения (1.27) для описания переменных полей.

Максвелл дал  обобщенную  формулировку закона  полного тока. Он ввел фундаментальное понятие тока смещения и, основываясь   на   работах  Фарадея,   предположил,   что   в  случае переменных полей ток смещения с точки зрения образования магнитного поля равноценен току проводимости. Примером электрической   системы,   в   которой   преобладают  токи   смещения, может служить  рассмотренный  выше конденсатор в  цепи  переменного тока.  Переменный ток может циркулировать  между обкладками конденсатора даже в том случае, когда они разделены идеальным  диэлектриком  или  находятся  в  вакууме  и,  следовательно, образование тока проводимости невозможно.  Соединительный провод, по которому течет ток проводимости, окружен i кольцевыми линиями магнитного поля, которые как бы образуют  "оболочку" вокруг всего провода. Максвелл предположил, что эта.) "оболочка" не обрывается у пластин конденсатора, а образует непрерывную поверхность, т.е. изменяющееся электрическое поле 5 конденсатора также окружено кольцевыми линиями  магнитного поля. Таким образом, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля.Это дало основание ввести понятие о новом виде тока, получившем название тока смещения. Плотность тока смещения onределяется формулой                                                                              

Как и плотность тока проводимости, она измеряется в А/м².

Подчеркнем, что ток проводимости и ток смещения в вакууме имеют различную физическую сущность. Ток проводимости -это упорядоченное движение свободных электрических зарядов. Ток смещения в вакууме соответствует только изменению электрического поля и не сопровождается каким-либо движением электрических зарядов. В вакууме D = е₀Е и уравнение (1.28) принимает вид Ток смещения в вакууме не сопровождается выделением тепла.

Рассмотрим общий случай, когда ток смещения возникает в какой-либо среде. Вектор электрического смещения связан с векторами Е и Р соотношением (1.4). Подставляя это соотношение в (1.28), получаем

Первое слагаемое в правой части этой формулы совпадает с выражением для плотности тока смещения в вакууме, т.е. определяет как бы "чистый" ток смещения, не связанный непосредственно с движением зарядов. Второе слагаемое определяет ток смещения, обусловленный движением зарядов, связанных с атомами вещества, в результате действия переменного поля. Эту составляющую тока смещения можно рассматривать как своеобразный ток проводимости, так как она, по существу, обусловлена упорядоченным перемещением связанных зарядов. На ее поддержание в реальной среде затрачивается некоторая часть энергии электромагнитного поля.

Вернемся к закону полного тока. Как уже указывалось, Максвелл предположил, что уравнение (1.25) имеет частный характер, так как не учитывает токов смещения. Для того чтобы оно было справедливым и в случае переменных полей, нужно в его правую часть помимо тока проводимости / ввести ток смещения /^см:

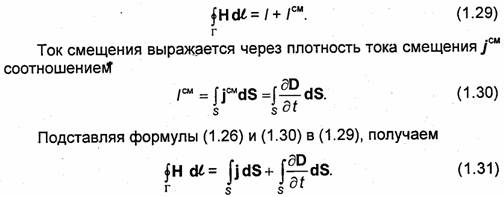
Уравнение (1.31) сформулировано применительно к контуру конечных размеров. Оно представляет собой первое уравнение Максвелла в интегральной форме.

Максвеллом этот закон был сформулирован также в дифференциальной форме. Для перехода к дифференциальной форме воспользуемся теоремой Стокса (П.20). Заменяя в уравнении (1.31) циркуляцию вектора Н интегралом от rot H по поверхности S, получаем

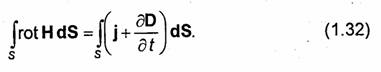
Так как S-произвольная поверхность, то равенство (1.32) возможно только в том случае, если

Равенство (1.33) называют первым уравнением Максвелла. Векторное уравнение (1.33) эквивалентно трем скалярным уравнениям, которые в декартовой системе координат х, у, z имеют вид

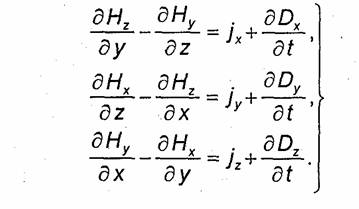
1.3.2. Второе уравнение Максвелла

Второе уравнение Максвелла является обобщением закона индукции Фарадея, который формулируется следующим образом: если замкнутый контур Г пронизывается переменным магнитным потоком Ф, то в контуре возникает ЭДС е, равная скорости изменения этого потока:

Знак минус в правой части формулы (1.34) означает, что возникающая в контуре ЭДС всегда как бы стремится воспрепятствовать изменению потока, пронизывающего данный контур. Это положение известно под названием "правило Ленца".

До Максвелла считалось, что уравнение (1.34) справедливо только в случае проводящего контура Г. Максвелл предположил, что это уравнение будет справедливо и в том случае, когда рассматриваемый контур представляет собой замкнутую линию, проведенную в непроводящей среде.

Пусть Г-произвольный одновитковый замкнутый контур, a S-произвольная поверхность, опирающаяся на контур Г (рис.1.6). Электродвижущая сила, наводимая в этом контуре

а магнитный поток Ф связан с вектором В соотношением

где dS = n_odS; п₀-орт нормали к поверхности S, образующий правовинтовую систему с обходом контура Г (рис.1.6). Подставляя (1.35) и (1.36) в (1.34), получаем

Соотношение (1.37) сформулировано для контура конечных размеров и называется вторым уравнением Максвелла в интегральной  форме.   Максвеллом  это  уравнение  было  сформулировано также в дифференциальной форме.

Предположим, что контур Г неподвижен и не изменяется со временем. В этом случае производную по времени в правой части уравнения (1.37) можно внести под знак интеграла. Преобразовывая левую часть равенства (1.37) по теореме Стокса, имеем

Так как S-произвольная поверхность,  соотношение (1.38) возможно только в том случае, если

Равенство (1.38) называют вторым уравнением Максвелла. Переходя к декартовой системе координат х, у, z, получаем три скалярных уравнения:

1.3.3. Третье и четвертое уравнения Максвелла

Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности:

где dS = n_odS; n₀ - орт внешней нормали к поверхности S.

До Максвелла уравнение (1.40) рассматривалось только в применении к постоянным полям. Максвелл предположил, что оно справедливо и в случае переменных полей.

Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае

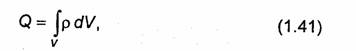
где  ρ-объемная  плотность  зарядов;   V- объем,   ограниченный поверхностью S. Объемная плотность зарядов

где  ΔQ - заряд, сосредоточенный в объеме ΔV. Размерность ρ-кулон на кубический метр (Кл/м³).

Подставляя (1.41) в (1.40), получаем

Уравнение (1.43) обычно называют третьим уравнением Максвелла в интегральной форме. Для перехода к дифференциальной форме преобразуем левую часть этого уравнения по теореме Остроградскогo—Гаусса (П. 19). В результате получим

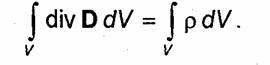
Это равенство должно выполняться при произвольном объеме V, что возможно только в том случае, если

Соотношение (1.44) принято называть третьим уравнением Максвелла. В декартовой системе координат оно записывается в виде

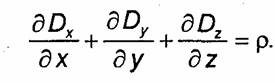
Из равенства (1.44) следует, что дивергенция вектора D отлична от нуля в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора D начинаются на положительных зарядах и заканчиваются - на отрицательных.

В отличие от вектора D истоками (стоками) вектора Е могут быть как свободные, так и связанные заряды. Чтобы показать это, перепишем уравнение (1.44) для вектора Е. Подставляя соотношение (1.4) в (1.44), получаем ε_o div E = ρ- div ρ. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов ρ_р, возникающих в результате неравномерной поляризации среды (такие заряды будем называть поляризационными):

divP=-ρ_P.                                                    (1.45)

Поясним возникновение поляризационных зарядов на следующем примере. Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем ΔV, ограниченный поверхностью ΔS. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8 объем ΔV показан пунктиром). Подчеркнем, что поляризационные заряды являются "связанными" и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из 24

определения вектора Р (см.1.2.1). Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к соотношению

 из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды.

Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора В через любую замкнутую поверхность S равен нулю, т.е.

Это означает, что не существует линий вектора В, которые только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S): они всегда пронизывают ее (рис. 1.9).

Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме уравнения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим

div В = 0,                                       (1.47)

Уравнение (1.47) представляет собой четвертое уравнение Максвелла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.

1.4. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ И ЗАКОН

СОХРАНЕНИЯ ЗАРЯДОВ

Из первого и третьего уравнений Максвелла вытекает важное соотношение, называемое уравнением непрерывности. Возьмем дивергенцию от обеих частей равенства (1.33). Учитывая, что дивергенция ротора любого вектора равна нулю, и используя уравнение (1.44), получаем

Правая часть уравнения (1.33) представляет собой сумму плотностей тока проводимости и тока смещения, т.е. плотность полного тока j_noлн = j ⁺ dD/dt, поэтому уравнение (1.48) эквивалентно условию divj_полн⁼0. Равенство нулю дивергенции какого-либо вектора означает непрерывность линий этого вектора. Следовательно, уравнение (1.48) показывает, что линии плотности полного тока являются непрерывными, в то время как линии плотностей токов проводимости и смещения могут иметь начало и конец. Например, линии плотности тока проводимости начинаются в тех точках пространства, где плотность зарядов уменьшается, и оканчиваются там, где плотность зарядов возрастает.

Уравнение (1.48) тесно связано с законом сохранения заряда и по существу является его дифференциальной формой. Закон сохранения заряда можно сформулировать следующим образом. Всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток /, втекающий в эту область или вытекающий из нее:

Покажем, что формулу (1.49) можно получить из уравнения (1.48). Проинтегрируем последнее по объему V. Преобразовывая левую часть получающегося равенства по теореме Остроград-ского-Гаусса, а в первой части меняя порядок интегрирования и дифференцирования, приходим к уравнению

совпадающему с (1.49). Ток   полажителен (т.е. вытекает из объема V), если заряд  уменьшается, и, наоборот, отрицателен (т.е. втекает в объем V), если заряд увеличивается.

Подчеркнем, что под током / в законе сохранения заряда понимается ток через всю поверхность S, ограничивающую объем V. Например, если в цилиндрическом проводнике мысленно выделить объем V, как показано на рис. 1.10, то ограничивающая этот

объем поверхность S будет состоять из трех частей: S = S₁ + S₂ + S_3l и при

определении / нужно учесть токи, протекающие через оба торца (S₁ и S₂) и боковую поверхность (S₃) рассматриваемого цилиндрического объема V.

Закон сохранения заряда (1.50) был получен из уравнения непрерывности. Очевидно, можно было бы поступить наоборот: постулировать закон сохранения заряда как экспериментальный закон   а из него независимо от уравнений Максвелла вывести

равнение непрерывности.

Используя уравнение непрерывности, можно обосновать постулированное ранее соотношение (1.28), определяющее вектор плотности  тока  смещения.   Действительно,   применяя  теорему Стокса  к  левой   части  уравнения  (1.27),   выражающего  закон

Ампера, приходим к равенству

Так как div rot H = 0, то из соотношения (1.51) следует, что div j = 0. Последнее равенство заведомо несправедливо для переменных процессов, так как в этом случае должно выполняться уравнение непрерывности (1.48), вытекающее из закона сохранения заряда (1.50). Чтобы уравнение (1.51) стало пригодным для переменных процессов, его надо видоизменить, добавив в его правую часть некоторую функцию, имеющую размерность плотности тока и удовлетворяющую условию, что ее дивергенция равна dp/dt. В качестве такой функции следует взять функцию дD/dt, так как указанное условие будет выполнено в силу третьего уравнения Максвелла (1.44). Получающееся при этом уравнение будет полностью совпадать с первым уравнением Максвелла (1.33).

Отметим, что уравнение (1.33) было получено Максвеллом на основе аналогичных рассуждений.

1.5. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА И КЛАССИФИКАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ЯВЛЕНИЙ

1.5.1. Физическая сущность уравнений Максвелла

Выше были рассмотрены основные уравнения электродинамики. Каждое из них описывает те или иные свойства электромагнитного поля. Анализ электромагнитных процессов возможен только на основе системы уравнений электродинамики. Такой системой являются уравнения Максвелла

совместно с уравнениями, связывающими векторы D и Е, В и Н, j и Е, которые в случае линейных изотропных сред имеют вид

Уравнения (1.53) часто называют уравнениями состояния, а также материальными уравнениями; они характеризуют среду. Напомним, что в случае линейных анизотропных сред уравнения (1.52) остаются без изменения, а в уравнениях (1.53) параметры ε, μ , σ  (по крайней мере один из них) будут тензорами (см. 1.2.3).

Наряду с уравнениями Максвелла в дифференциальной форме в ряде случаев удобно использовать уравнения Максвелла в интегральной форме:

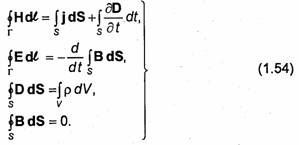
На основе уравнений Максвелла можно сделать следующие выводы относительно свойств электромагнитного поля. Электрическое и магнитное поля тесно связаны между собой. Всякое изменение одного из них вызывает изменение другого. Независимое существование одного поля без другого (например, электрического без магнитного, или магнитного без электрического) возможно только в статическом случае. Источниками электромагнитного поля являются заряды и токи. Магнитное поле всегда вихревое, электрическое поле может быть и вихревым, и потенциальным и в общем случае представляет собой суперпозицию таких полей. Чисто потенциальным электрическое поле может быть только в статическом случае. Векторные линии электрического поля могут иметь истоки и стоки. Векторные линии магнитного поля (и линии вихревого электрического поля) всегда непрерывны. Применяя уравнение (1.31) к достаточно малому контуру, можно показать, что замкнутая линия магнитного поля, расположенная в непосредственной близости к рассматриваемой точке, охватывает линию плотности полного тока, проходящую через эту точку, и образует с ней правовинтовую систему (рис. 1.11). в общем случае направление линии магнитного поля определяется знаком суммарного

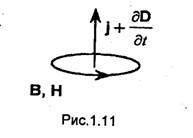
тока, сцепленного с этой линией. Аналогично из уравнения (1.37) следует, что замкнутая линия вихревого электрического поля, расположенная в непосредственной близости к рассматриваемой точке, охватывает проходящую через эту точку

линию вектора дВ/дt и образует с ней левовинтовую систему о рис. 1.12).

Уравнения, входящие в полную систему уравнений Максвелла 1(1.52) и (1.53), являются линейными уравнениями. Поэтому можно (утверждать, что электромагнитные поля удовлетворяют принципу (суперпозиции: поле, созданное несколькими источниками, можно (рассматривать как сумму полей, созданных каждым источником.

1.5.2. Классификация электромагнитных явлений

Система уравнений Максвелла охватывает всю совокупность электромагнитных явлений, относящихся к макроскопической электродинамике. В ряде частных случаев уравнения Максвелла упрощаются. Самым простым является случай, когда поле не зависит от времени и, кроме того, отсутствует перемещение заряженных частиц (j = 0). При этих условиях система уравнений [1.52) и (1.53) распадается на две независимые системы:

Уравнения (1.55) содержат только векторы электрического поля, а (1.56)-только векторы магнитного поля. Это означает, что в данном случае электрические и магнитные явления независимы.

Явления, описываемые системой уравнений (1.55), принято называть электростатическими. Электростатические поля-это поля, созданные неподвижными, неизменными по величине зарядами. Система уравнений (1.55) является полной системой дифференциальных уравнений электростатики.

Уравнения (1.56) характеризуют поля, создаваемые постоянными магнитами. Они также могут быть использованы для анализа свойств магнитного поля, созданного постоянными оками в области, в которой плотность тока проводимости равна нулю (j = 0) и которая не сцеплена с током (не охватывает его линий). Явления, описываемые системой (1.56), называют магнитостатическими, а соотношения (1.56) - уравнениями магнитостатики.

При наличии постоянного тока электрическое и магнитное поля уже нельзя считать независимыми. Электромагнитное поле, созданное постоянными токами, называют стационарным электромагнитным полем. Система уравнений Максвелла в этом случае принимает вид

В качестве самостоятельного класса выделяют также так называемые квазистационарные процессы, т.е. процессы, протекающие достаточно медленно. В этом случае в первом уравнении Максвелла при наличии тoка проводимости можно пренебречь током смещения: rot H = j. Однако в тех случаях, когда токов проводимости нет (например, емкость в цепи переменного тока), токи смещения необходимо учитывать, при этом rot H =.- dDldt. Второе уравнение Максвелла при анализе квазистационарных процессов записывается в обычной форме: rot H =- dD/dt.

В общем случае используют полную систему уравнений Максвелла (1.52) и (1.53).

В случае гармонических во времени колебаний систему (1.52) удается упростить с помощью искусственного приема, получившего название метода комплексных амплитуд.

1.6. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ

 МОНОХРОМАТИЧЕСКОГО ПОЛЯ

1.6.1. Метод комплексных амплитуд

Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических во времени электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют также монохроматическими. В буквальном переводе "монохроматический" означает "одноцветный". Название взято из оптики: как известно, каждому цвету соответствуют колебания определенной частоты.

Анализ гармонических процессов существенно упрощается при использовании метода комплексных амплитуд. В этом случае вместо любой скалярной функции, изменяющейся по закону

где ψ_m - амплитуда; φ - начальная фаза; ω = 2πf = 2π/T; a f и T-частота и период гармонического колебания, вводится в рассмотрение комплексная функция

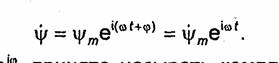
Величину  принято называть комплексной амплитудой функции ψ. Для перехода от комплексной функции ψ к исходной функции ψ нужно взять от ψ реальную часть

Аналогично вместо вектора

можно ввести в рассмотрение комплексный вектор

- комплексная амплитуда вектора а.

Для перехода от комплексной амплитуды а_м к мгновенному «значению исходной функции нужно вычислить реальную часть произведения а_м на exp (i ψt):

Отметим, что в общем случае вместо разложения вектора а по ортам декартовой системы координат (1.58) может оказаться необходимым разложение по каким-либо другим ортогональным векторам, что не вносит в рассмотрение никаких принципиальных изменений. Если функции а и ψ удовлетворяют линейным уравнениям, то таким же уравнениям будут удовлетворять соответствующие комплексные функции а и ψ. Однако определение комплексных функций во многих случаях оказывается проще определения исходных функций. Это объясняется тем, что дифференцирование комплексной функции по времени равносильно умножению ее на а интегрирование по времени -делению на

1.6.2. Уравнения Максвелла в комплексной форме

Уравнения   Максвелла  являются  линейными  дифференциальными уравнениями.   Поэтому при  изучении  монохроматических электромагнитных полей можно вместо векторов Е и Н рассматривать  комплексные  векторы 

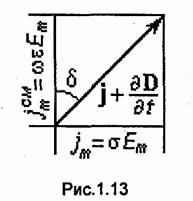
Уравнение (1.62) является первым уравнением Максвелла для монохроматического поля. Величина е, определяемая формулой

(1.61), характеризует электрические свойства среды и называется комплексной диэлектрической проницаемостью среды. Ее значение зависит от частоты. Входящая в (1.61) величина ст/(сое) равна отношению амплитуд плотностей тока проводимости и тока смещения (подробнее об этом - в 1.6.3) и называется тангенсом угла электрических потерь (рис. 1.13):

Отметим, что комплексная диэлектрическая проницаемость е определяется выражением (1.61) только в тех случаях, когда можно пренебречь поляризационными потерями, т.е. потерями энергии на периодическое изменение поляризации среды. Если этими потерями пренебречь нельзя, следует считать, что

 -вещественные числа, отношение которых определяет фазовый  сдвиг   между векторами D и Е. При этом входящая в (1.62) комплексная диэлектрическая проницаемость

где  Для перехода от общей формулы (1.65) к

(1.61) достаточно положить  

В случае анизотропной по отношению к электрическому полю &реды комплексная диэлектрическая проницаемость является Гензором. Конкретный вид тензора || ε || зависит от свойства среды.

Рассмотрим второе уравнение Максвелла для изотропной среды. Переходя в (1.39) к комплексным векторам и учитывая соотношение (1.17), получаем

При вещественных значениях μ- векторы В и Н изменяются сεεинфазно, что эквивалентно предположению об отсутствии магнитных потерь (затрат энергии на поддержание периодически изменяющейся намагниченности среды). Несинфазность векторов

ВиН в случае гармонических во времени электромагнитных процессов можно учесть, введя комплексную магнитную проницаемость

Рассмотрим третье уравнение Максвелла. Переходя в (1.44) к комплексным функциям и учитывая соотношение (1.5), получаем

Если требуется учесть поляризационные потери, то в уравнении (1.69) следует ε заменить на ε  (см. формулы (1.64) и (1.65)).

Четвертое уравнение Максвелла в комплексной форме имеет вид

Если среда характеризуется комплексной магнитной проницаемостью, в уравнении (1.70) следует заменить μ на μ

Выпишем также уравнение непрерывности для монохроматического поля. Переходя в (1.48) к комплексным функциям,

получаем

Преобразуем равенство (1.69) с учетом уравнения непрерывности. Из (1.71) следует, что  Подставляя это равенство в (1.69), имеем

Третье уравнение Максвелла в комплексной форме (1.72) является следствием первого уравнения Максвелла. Действительно, беря дивергенцию от обеих частей равенства (1.62) и учитывая, что div rot H=О, приходим к уравнению (1.72). Аналогично уравнение (1.70) является следствием второго уравнения

Максвелла.

Рассмотрим третье и четвертое уравнения Максвелла для частного случая однородной изотропной среды. Так как параметры  такой среды не зависят от координат, то уравнения (1.72) и (1.70) упрощаются и принимают вид

и

Таким образом, в качестве полной системы уравнений Максвелла для монохроматического поля можно использовать систему двух уравнений  

Переходя в (1.75) к комплексным амплитудам векторов Е и Н, получаем

Напомним, что при анализе поля в среде без потерь в уравнениях (1.75) и (1.76) следует заменить соответственно.

Уравнение непрерывности (1.71) также можно записать для комплексных амплитуд

                                      (1.77)

1.6.3. Уточнение понятий о проводниках и диэлектриках

Среды могут сильно отличаться друг от друга по величине удельной проводимости, поэтому электромагнитные поля в таких средах могут обладать разными свойствами. Чем больше величина а, тем больше плотность тока проводимости в среде при той же напряженности электрического поля. Часто для упрощения анализа вводят понятия идеального проводника и идеального диэлектрика. Идеальный проводник-это среда с бесконечно большой удельной проводимостью  . В идеальном диэлектрике вещественные скалярные функции или постоянные. В идеальном проводнике может существовать только ток проводимости, а в идеальном диэлектрике

только ток смещения. В реальных средах имеется как ток проводимости, так и ток смещения. Поэтому проводниками принято называть среды, в которых ток проводимости намного превосходит ток смещения, а диэлектриками - среды, в которых основным является ток смещения. Такое деление сред на проводники и диэлектрики имеет относительный характер, так как существенно зависит от скорости изменения электромагнитного поля.

В случае монохроматического поля комплексные амплитуды векторов плотности тока проводимости и плотности тока смещения равны соответственно . Отношение

и является критерием деления сред на проводники и диэлектрики.

Если tgδ»1, среду называют проводником, если tg δ«1 —диэлектриком. Из соотношения (1.78) следует, что диэлектрические свойства сильнее проявляются при более высоких частотах.

Металлы имеют большую удельную проводимость. Например, у холоднотянутой  меди ст = 5,65-10⁷ См/м,  у железа σ=1,0-10⁷ См/м. Поэтому у металлов tgδ»1 на всех частотах, используемых в радиотехнике. У типичных диэлектриков, наоборот, удельная проводимость очень мала, например у кварца σ = 2-10^-17См/м; у стекла σ = 10 ^-12 См/м.

Существует ряд сред, занимающих промежуточное положение между проводниками и диэлектриками, например вода, почва и др. (у морской воды σ = 3...5 См/м, у влажной почвы σ = 10^-3 …10^-5 См/м, у дистиллированной воды σ = 2-10^-4 См/м). Такие среды (их называют полупроводящими) на одних частотах являются проводниками (σ »εω), а на других – диэлектриками (σ >>εω).

1.6.4. Понятие о времени релаксации

Из уравнения непрерывности (1.48) вытекает важное следствие. Рассмотрим безграничную однородную изотропную среду, обладающую отличной от нуля проводимостью (σ ≠ 0). Так как в этом случае  то соотношение (1.48) принимает вид Решая это уравнение, получаем

где - объемная плотность заряда в начальный момент времени t=0. Таким образом, при σ ≠ О объемная плотность зарядов в каждой точке, где экспоненциально убывает со временем. Промежуток времени τ, в течение которого заряд в каком-либо малом элементе объема уменьшается в е раз, называется временем релаксации. Приравнивая единице показатель степени в формуле (1.79), получаем выражение . Время релаксации для хорошо проводящих сред очень мало. Например, для металлов τ имеет порядок 10^-18с; для морской воды-2·10^-10 с. Даже при σ =2·10^-4 См/м (дистиллированная вода) τ не превышает 10^-6 с.

То, что объемная плотность заряда в каждой точке внутри проводящей области, например внутри металлического объекта, экспоненциально убывает со временем, не означает, конечно, что заряды исчезают. Если рассматриваемая область окружена непроводящей средой, заряды задерживаются на границе области (например, на внешней поверхности металлического объекта), образуя весьма тонкий заряженный слой. Однако этот процесс не сопровождается появлением зарядов во внутренних точках проводящей области, в которых в начальный момент они отсутствовали.

1.7. ГРАНИЧНЫЕ УСЛОВИЯ

1.7.1. Граничные условия для нормальных составляющих векторов электрического и магнитного полей

Уравнениями Максвелла в дифференциальной форме удобно пользоваться при анализе электромагнитных полей в средах, параметры ε, μ и σ а которых - непрерывные функции координат (или не зависят от координат). На практике, однако, рассматриваемая область может состоять из двух (и более) разнородных сред. При анализе макроскопических свойств поля обычно считают, что параметры ε, μ и σ (или по крайней мере один из них) на границе раздела сред меняются скачком. При этом пользоваться уравнениями Максвелла в дифференциальной форме на границе раздела неудобно, и для изучения поведения векторов поля при переходе из одной среды в другую следует исходить из уравнений Максвелла в интегральной форме (1.54).

Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными условиями.

Граничные условия для нормальных составляющих векторов электрического и магнитного полей могут быть получены соответственно из третьего (1.43) и четвертого (1.46) уравнений Максвелла в интегральной форме. Сравнивая эти уравнения, замечаем, что равенство (1.46) может быть формально получено из уравнения (1.43), если в последнем заменить D на В и положить ρ = 0. Поэтому ограничимся выводом граничного условия для нормальной составляющей вектора D, а из него указанными преобразованиями получим граничное условие для нормальной составляющей вектора В.

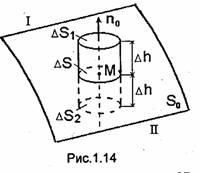
На поверхности раздела S_o двух изотропных сред, характеризуемых параметрами  соответственно, в. окрестности произвольно выбранной точки М выделим достаточно малый элемент . Элемент ΔS должен быть достаточно мал, чтобы, во-первых, его можно было считать плоским, а, во- вторых, чтобы в обеих средах распределение нормальной компоненты вектора D можно было считать равномерным в пределах ΔS.

Построим на элементе ΔS прямой цилиндр высотой 2Δ/h так, чтобы его основания находились в разных средах (рис.1.14), и применим к нему третье уравнение Максвелла в интегральной форме (1.43):

Если заряд  не сосредоточен на поверхности раздела,

т.е. не является поверхностным, то при любой конечной величине объемной плотности заряда р правая часть формулы (1.82) равна нулю, а нормальная компонента вектора D непрерывна при переходе из одной среды в другую:

Особый интерес представляет случай, когда заряды распределены вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие заряды называют поверхностными и характеризуют плотностью поверхностных зарядов p_s (ее часто называют также поверхностной плотностью зарядов), определяемой соотношением

где ∆Q - заряд на элементе поверхности ∆S. Как видно из (1.84), ρ_s измеряется в кулонах на квадратный метр (Кл/м²).

Пусть теперь на границе раздела имеются поверхностные заряды с плотностью ρ_s. В этом случае правая часть уравнения (1.82) уже не будет равна нулю. Считая распределение заряда на площадке ΔS равномерным (в противном случае нельзя считать равномерным распределение D_1n и D_2n), разделим обе части уравнения (1.82) на ΔS. В результате получим

D_1n-D_2n=ρ_s.                                (1.85)

Соотношение (1.85) показывает, что при переходе из одной среды в другую нормальная компонента вектора D претерпевает разрыв (скачок), равный плотности поверхностных зарядов, распределенных по границе раздела. Выражая в этом соотношении D_1n и D_2n через Е_1n и Е_2п с помощью равенства D = εE, получаем граничное условие для нормальных компонент вектора Е:

Если на границе раздела отсутствуют поверхностные заряды, то условие (1.86) можно представить в виде

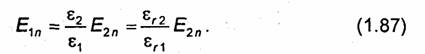
Соотношение (1.87) показывает, что нормальная составляющая вектора Е при переходе через незаряженную поверхность раздела двух сред имеет разрыв, величина которого определяется отношением диэлектрических проницаемостей этих сред. Наличие плотности поверхностных зарядов ρ_s в рассматриваемой точке приводит к изменению величины разрыва, увеличивая или уменьшая его. При определенном значении ρ_s нормальная составляющая вектора Е может даже оказаться непрерывной.

Отметим, что поверхностные заряды обычно вводят для упрощения расчетов вместо реального тонкого слоя зарядов, когда не интересуются распределением поля внутри слоя. В каждой точке внутри реального заряженного слоя составляющая D_n непрерывна, но ее значения по разные стороны слоя отличаются на конечную величину. Поэтому при замене реального слоя зарядов бесконечно тонким (т.е. поверхностными зарядами) приходится считать, что D_n изменяется скачком.

Граничное условие для нормальной составляющей вектора В, как уже отмечалось, формально может быть получено из (1.85), если положить ρ_s=0 и заменить D_1n и D_2n на В_1л и В_2n соответственно. При этом придем к соотношению

Из (1.88) следует, что составляющая В_n непрерывна при переходе через границу раздела двух сред. В свою очередь, нормальная составляющая вектора Н имеет разрыв, величина которого определяется отношением магнитных проницаемостей. Выражая в равенстве (1.88) B_1n и В_2n через H_1п и Н_2п, получаем

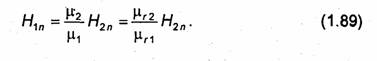
1.7.2. Граничные условия для касательных составляющих векторов электрического и магнитного полей

Граничные условия для касательных составляющих векторов электрического и магнитного полей могут быть получены соответственно из второго (1.37) и первого (1.31) уравнений Максвелла в интегральной форме. В рассматриваемом случае можно считать, что контур Г в уравнении (1.37) не зависит от времени. Поэтому, внося производную по t под знак интеграла, получаем

Сравнивая (1.90) с первым уравнением Максвелла (1.31), замечаем, что равенство (1.90) формально может быть получено . из уравнения (1.31), если в последнем положить j = 0 и заменить Н на Е и D на В. Следовательно, можно ограничиться выводом граничного условия для касательной составляющей вектора Н из (1.31), а затем с помощью указанных преобразований получить граничное условие для касательной составляющей вектора Е.

Пусть S_o - граница раздела двух изотропных сред, характеризуемых параметрами  соответственно. Из произвольной точки M_ЄS проведем единичную нормаль n₀, направленную из второй среды в первую (рис. 1.15). Через n₀ проведем плоскость Р. На линии пересечения поверхности раздела S_o с плоскостью Р выделим достаточно малый отрезок Δl содержащий точку М. Размеры отрезка должны быть такими, чтобы, во-первых, его можно было считать прямолинейным, а во-вторых, чтобы распределение касательной составляющей вектора Н в пределах Δl в обеих средах можно было считать равномерным. В плоскости Р построим прямоугольный контур ABCD, как показано на рис. 1.15.

Стороны АВ и CD параллельны Δl и находятся в разных средах.    -Кроме того, в точке М проведем единичную касательную τ₀ к линии пересечения поверхности раздела S с плоскостью Р и единичную нормаль N_o к плоскости Р так, чтобы орты п₀, τ₀ и N_o составляли правую тройку векторов:

а обход контура ABCD образовывал правовинтовую систему с вектором N_o- Применим к контуру ABCD первое уравнение Максвелла (1.31):

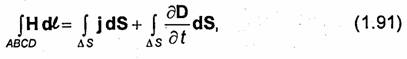
где ΔS - площадь, охватываемая контуром ABCD, a dS = N_odS. Левую часть этого равенства можно представить в виде суммы четырех интегралов:

Отметим, что стороны ВС и DA параллельны и равны 2 Δh, а направление элемента dl определяется выбранным обходом контура:

Устремляя Δh к нулю (при этом стороны АВ и CD рассматриваемого контура совпадут с Δl) и учитывая, что функции Н и dDldt являются ограниченными, приходим к соотношениям

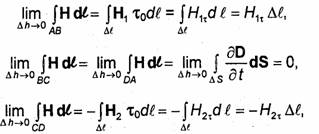
где Н₁ и Н₂ - значения вектора Н на границе раздела S в первой и второй средах соответственно, а Н_1τ и H_2τ- проекции векторов Н₁ и Н₂ на касательную τ₀. Используя эти соотношения при переходе к пределу при Δh→0 в уравнении (1.92), получаем

Если на границе раздела отсутствуют поверхностные токи, правая часть равенства (1.93) равна нулю. В этом случае касательная составляющая вектора Н оказывается непрерывной:

Касательная составляющая вектора В,    наоборот,  претерпевает разрыв,  величина которого определяется отношением магнитных проницаемостей:       

Особый интерес представляет случай, когда токи распределены вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие токи называют поверхностными. Плотность поверхностных токов (ее часто называют также поверхностной плотностью) определяется соотношением

где i₀- единичный вектор, указывающий направление движения положительных зарядов в данной точке; ΔL-элемент линии, перпендикулярный вектору i₀; Δ/-ток, протекающий через ΔL (рис.1.16). Плотность поверхностных токов измеряется в амперах на метр (А/м). В этом случае правая часть равенства (1.95) уже не будет равна нулю. Считая распределение поверхностного тока на отрезке ΔL равномерным (если это не выполняется, нельзя считать равномерным распределение касательной составляющей вектора Н), преобразуем правую часть указанного равенства следующим образом:

где j_sn - проекция вектора j_s на направление N_o. Подставляя это выражение в (1.93) и деля обе части получающегося равенства на Δl, приходим к соотношению

Уравнение (1.97) справедливо для любого направления касательной τ_o, и его можно переписать в векторной форме

где Н₁ и Н₂ - значения вектора Н у границы раздела в первой и во второй средах соответственно.

Уравнения (1.97) и (1.98) показывают, что при переходе через границу раздела, по которой текут поверхностные токи, касательная составляющая вектора Н претерпевает разрыв, величина которого определяется значением плотности поверхностных токов в рассматриваемой точке. Переходя в уравнении (1.97) к касательным составляющим вектора В, получаем

Отметим, что поверхностные токи, как и поверхностные заряды, обычно вводят для упрощения расчетов вместо реального тонкого слоя токов, когда не интересуются распределением поля внутри слоя. В каждой точке внутри реального токового слоя касательная составляющая вектора Н непрерывна, но ее значения по разные стороны слоя отличаются на конечную величину. Поэтому при замене реального токового слоя бесконечно тонким (т.е. поверхностными токами) приходится считать, что H_τ изменяется скачком.

Граничное условие для касательной составляющей вектора Е может быть формально получено из равенства (1.97) на основе i указанных выше изменений. Полагая в (1.97)j_SN = О и заменяя касательные составляющие вектора Н на соответствующие касательные составляющие вектора Е, приходим к соотношению:

Равенство (1.99) показывает, что касательная составляющая вектора Е непрерывна при переходе через границу раздела двух сред. Касательная составляющая вектора D, наоборот, претерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями. Выражая E_1τ и Е_2τ в равенстве (1.99) через D_1τ и D_2τ, получаем

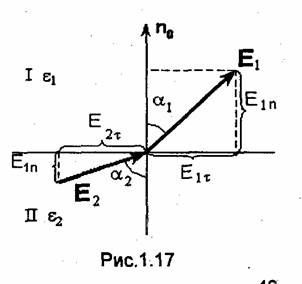
Граничные условия, полученные для составляющих векторов электрического поля, показывают, что на границе раздела векторы Е и D преломляются. Обозначим углы между нормалью п₀ к поверхности раздела и векторами Е₁ и Е₂ соответственно через си и α₂ (рис. 1.17). Так как то, используя граничные условия (1.86) и (1.99), получаем, что при отсутствии поверхностных зарядов на границе раздела справедливо следующее соотношение:

В изотропных средах векторы Е и D направлены одинаково. Поэтому соотношение (1.100) определяет также преломление вектора D. Очевидно, аналогичное соотношение может быть получено и для векторов магнитного поля. Пусть α₁ и α₂- углы между нормалью п₀ и векторами H₁ и Н₂. Тогда, как следует из уравнений (1.89) и (1.94), имеет место соотношение

 В случае изотропных сред это равенство определяет также изменение ориентации вектора В.

1.7.3.  Граничные условия   на  поверхности  идеального

проводника

Таким образом, на поверхности раздела любых двух изотропных сред должны выполняться следующие граничные условия:

Уравнения (1.1.01) составляют полную систему граничных условий. Они справедливы для любых электромагнитных процессов, рассматриваемых в макроскопической электродинамике. Не включенные в систему (1.101) граничные условия для составляющих D_τ, Е_п, В_τ и Н_п являются следствиями соотношений (1.101) и уравнений состояния (1.53). Граничные условия (1.101) можно записать также в векторной форме:

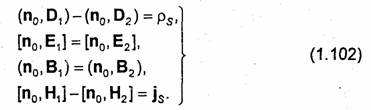
При изучении переменных электромагнитных полей вблизи поверхности металлических тел часто предполагают, что рассматриваемое тело является идеально проводящим. При этом граничные условия упрощаются, так как в среде с σ = ∞ поле отсутствует. Действительно, плотность тока проводимости j должна быть ограниченной величиной. Поэтому из закона Ома в дифференциальной форме (1.9) следует, что напряженность электрического поля внутри идеального проводника должна быть равна нулю. Полагая во втором уравнении Максвелла Е = 0, получаем dB/dt= 0. Так как поле считается переменным, то последнее равенство выполняется только при В = 0.

Пусть идеально проводящей является вторая среда. Тогда D₂= E₂= В₂= Н₂= 0 и условия (1.101) принимают вид

1.7.4. Физическая сущность граничных условий

Выше было показано, что граничные условия для нормальных и касательных составляющих векторов электромагнитного поля имеют существенные различия. Выясним физические причины этого явления. Рассмотрим вначале граничные условия для составляющих вектора Е. Пусть имеются две изотропные среды с общей границей раздела, характеризуемые диэлектрическими проницаемостями ε ₁и ε ₂. Предположим вначале, что на границе раздела сред отсутствуют свободные поверхностные заряды (p_s = 0). Под воздействием внешнего электрического поля обе среды поляризуются, причем вектор Р, характеризующий поляризацию, будет иметь разные значения в этих средах, так как - Если вектор Е, а следовательно, и вектор Р перпендикулярны поверхности раздела (рис.1.18), то на ней появятся некомпенсированные поверхностные заряды, связанные с молекулами вещества. На рис.1.18 показан случай, когда ε₂> ε₁  и соответственно вторая среда поляризуется легче, чем первая. Это символически отображено на рис. 1.18, а тем, что во второй среде больше молекулярных диполей, ориентированных параллельно вектору Е. Образующиеся на границе раздела нескомпенсированные поверхностные заряды в рассматриваемом примере являются положительными (рис.1.18,6). Если векторы Е и Р параллельны поверхности раздела, то такие заряды не возникают (рис. 1.19). Очевидно, что при произвольной ориентации вектора Е

(или Р) у границы раздела величина появляющихся на ней не-скомпенсированных поверхностных зарядов определяется изменением значений нормальной составляющей вектора Р при переходе через границу раздела.

Выберем на поверхности раздела сред некоторую точку М и рассмотрим поведение составляющих вектора Е при переходе через границу раздела. Электрическое поле в рассматриваемой точке складывается из первичного поля, вызвавшего поляризацию сред, и вторичного поля, создаваемого поляризационными зарядами. Все заряды, кроме расположенных в непосредственной близости к рассматриваемой точке, создают в этой точке в соответствии с законом Кулона непрерывное поле. Исключение составляет поле, создаваемое некомпенсированными "связанными" поверхностными зарядами, расположенными в непосредственной близости к точке М. Эти заряды создают в точке М дополнительное электрическое поле ΔЕ, нормальные к границе раздела составляющие которого по разные стороны от этой границы (ΔЕ_1п и ΔЕ_2п) равны по величине и противоположны по направлению (рис. 1.20), а касательные - равны по величине и направлению (аналогично полю точечного заряда, расположенного в точке М). Это означает, что касательная составляющая напряженности дополнительного электрического поля ΔЕ непрерывна, а нормальная имеет разрыв. Складывая дополнительное поле с первичным полем и полем всех остальных поляризационных зарядов, получаем, что у полного поля в точке М нормальная составляющая вектора Е имеет разрыв (Е_1n≠Е_2п), а касательная - непрерывна (Е_1τ= Е_2τ).

Очевидно, что наличие на границе раздела в точке М плотности свободных поверхностных зарядов (ps≠0) не может нарушить непрерывность касательной составляющей вектора Е, но приводит к изменению величины разрыва его нормальной составляющей.

Рассмотрим теперь граничные условия для составляющих вектора В. Пусть имеются две изотропные среды с общей границей раздела, характеризуемые магнитными проницаемостями  μ ₁ и μ₂. Предположим вначале, что на границе раздела отсутствуют поверхностные токи, обусловленные движением свободных зарядов (j_s= 0). Под воздействием внешнего магнитного поля обе среды намагничиваются. На рис. 1.21, а показана система кольцевых электрических токов, эквивалентных ориентированным по полю магнитным моментам молекул, которую в средах I и II можно заменить противоположно направленными поверхностными токами (РИС. 1.21, б) c плотностями

ответственно. Так как намагниченность сред различна (μ_1≠ μ₂), то эти эквивалентные поверхностные токи не компенсируют друг друга и суммарный поверхностный ток на границе раздела не равен нулю. Каждый элемент поверхностного тока создает вокруг себя замкнутые линии вектора В. Их структура показана на рис. 1.22 (плоскость, показанная на рис. 1.22, перпендикулярна плоскости, изображенной на рис.1.21). Нормальные к поверхности раздела составляющие этих элементарных полей попарно компенсируются, а касательные складываются. В результате у поверхности раздела в средах I и II появляются противоположно направленные магнитные поля В⁽¹⁾ и В⁽²⁾ (см. рис.1.22). Поэтому касательные составляющие суммарного вектора В, определяемого суммой первичного и вторичного полей, имеют разные значения по разные стороны от границы раздела, т.е. B_1τ ≠B_{2 τ}. Нормальная составляющая суммарного вектора В остается непрерывной

(В_1n = В_2n).

Пусть теперь j_s ≠ 0. Из изложенного очевидно, что поверхностные токи не приводят к разрыву нормальной составляющей вектора В, т.е. граничное условие для этой составляющей остается прежним (В_1п = В_2п). Однако поверхностные токи изменяют величину разрыва касательной составляющей вектора В.

На основе аналогичных рассуждений нетрудно дать физическое объяснение и граничным условиям для составляющих векторов D и Н (см. [1]).

1.8. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

1.8.1. Сторонние токи и заряды

При рассмотрении уравнений Максвелла (1.52) под вектором j подразумевалась плотность тока проводимости, возникающего в проводящей среде под воздействием электромагнитного поля. Этот вектор удовлетворяет закону Ома в дифференциальной форме (1.9).Для упрощения реальной электродинамической задачи обычно вместо имеющейся на самом деле системы рассматривают некоторую модель. При этом часть системы вообще исключается из рассмотрения. Для учета влияния этой части системы во многих случаях ее заменяют введением некоторых токов, которые рассматриваются как первопричина возникновения электромагнитного поля и считаются заданными. Эти токи принято называть сторонними. Например, в гл.5 будет рассмотрено излучение электромагнитных волн элементарным электрическим вибратором. Ток в вибраторе обусловлен подведением к нему энергии от генератора. При анализе этот ток будет считаться известным, что позволит исключить из рассмотрения процессы, протекающие в генераторе, прохождение энергии по линии, соединяющей генератор с вибратором, и т.д., т.е. существенно упростит задачу. Если этого не делать и каждую проблему рассматривать во всей ее полноте, то любая конкретная задача становится трудноразрешимой.

Для учета сторонних токов следует первое уравнение Максвелла представить в виде

где j^ст - плотность сторонних токов в рассматриваемой точке пространства, a j - как и прежде, плотность тока проводимости, вызванного электромагнитным полем: j = σЕ.

Аналогично сторонним токам вводится понятие сторонних зарядов. Они учитываются в третьем уравнении Максвелла:

где ρ^ст - объемная плотность сторонних зарядов.

Второе и четвертое уравнения Максвелла остаются без изменений. В случае переменных полей функции j^ст ρ^ст связаны уравнением непрерывности

При анализе многих вопросов вместо сторонних токов задаются сторонней напряженностью электрического поля Е^ст. В большинстве случаев при исследовании электродинамических явлений, под Е^ст подразумевается напряженность электрического поля, создаваемого зарядами и токами, расположенными за пределами рассматриваемой области. При изучении постоянного электрического поля под Е^ст иногда понимают напряженность поля  сторонних электродвижущих сил неэлектрического происхождения (химических, диффузионных и др.). Введение Е^ст является таким же упрощением задачи, как и введение j^ст .Фактически оно исключает детальный анализ процессов, происходящих в какой-либо части пространства.

Выпишем также уравнения Максвелла для монохроматического поля в однородной среде, учитывающие сторонние источники:

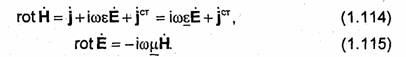
Уравнение непрерывности для сторонних токов (1.113) в этом случае имеет вид

Третье уравнение Максвелла в комплексной форме

является следствием уравнений (1.114) и (1.116), а четвертое

(div H = 0)- следствием уравнения (1.115).

Систему уравнений Максвелла в комплексной форме (1.114)-(1.115) можно переписать также для комплексных амплитуд:

1.8.2. Уравнение баланса мгновенных значений мощности

Как уже отмечалось в 1.1, электромагнитное поле является одной из форм материи. Как и любая другая форма материи, оно обладает энергией. Эта энергия может распространяться в пространстве и преобразовываться в другие формы энергии.

Сформулируем уравнение баланса для мгновенных значений мощности применительно к некоторому объему V, ограниченному поверхностью S (рис.1.23). Пусть в объеме V, заполненном однородной изотропной средой, находятся сторонние источники. Из общих физических представлений очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на джоулевы потери и на изменение энергии электромагнитного поля внутри V, а также может частично рассеиваться, уходя в окружающее пространство через поверхность S. При этом должно выполняться равенство

где Р^ст-мощность сторонних источников; Р_П-мощность джоулевых потерь внутри объема V; Р_Σ -мощность, проходящая через поверхность S; W-энергия электромагнитного поля, сосредоточенного в объеме V, a dW/dt- мощность, расходуемая на изменение энергии в объеме V.

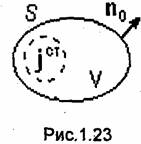
В данном разделе будут использованы уравнения состояния (1.53). Эти уравнения не позволяют учесть потери энергии при поляризации и намагничивании среды. Поэтому слагаемое Р_п в равенстве (1.120) фактически определяет мощность джоулевых потерь в объеме V, обусловленных током проводимости.

Уравнение (1.120) дает только качественное представление об энергетических соотношениях. Чтобы получить количественные соотношения, нужно воспользоваться уравнениями Максвелла. Рассмотрим первое уравнение Максвелла с учетом сторонних токов (1.111). Все члены этого уравнения - векторные величины, имеющие размерность А/м².

Чтобы получить уравнение, аналогичное (1.120), нужно видоизменить первое уравнение Максвелла (1.111) так, чтобы его члены стали скалярными величинами, измеряющимися в ваттах. Для этого достаточно все члены указанного равенства скалярно умножить на вектор Е, а затем проинтегрировать полученное выражение по объему V. После скалярного умножения на вектор Е получаем

Используя известную из векторного анализа формулу div[E,H]= = Н rot Е - Е rot H, преобразуем левую часть соотношения (1.121) и заменим rot E его значением из второго уравнения Максвелла (1.39):

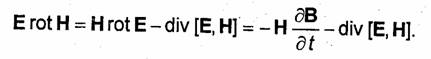
Подставляя это выражение в (1.121), получаем

В последнем слагаемом в правой части (1.122) изменен порядок сомножителей в скалярном произведении векторов dB/dt и Н. Это допустимо, так как Н dB/dt = дВ/дt· H. Данное изменение не является принципиальным и не дает никаких преимуществ при выводе рассматриваемого здесь уравнения баланса для мгновенных значений мощности. Однако при такой записи во всех членах уравнения (1.122) второй сомножитель (векторы j^ст, j, BDIdt и Н) является вектором, входившим ранее в первое уравнение Максвелла. Это обстоятельство позволит в дальнейшем (см. 1.8.4) несколько упростить вывод уравнения баланса в случае монохроматического поля (уравнения баланса комплексной мощности). Интегрируя почленно уравнение (1.122) по объему V, получаем

где направление элемента dS совпадает с направлением внешней нормали к поверхности S. При переходе от.(1.122) к (1.123) использована теорема Остроградского-Гаусса для перевода объемного интеграла от div[E, H] в поверхностный интеграл от векторного произведения [Е, Н]. Введем обозначение

и    преобразуем    подынтегральное   выражение   в   последнем слагаемом в правой части (1.123):

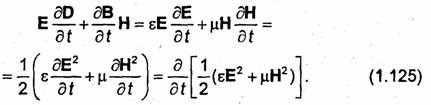
Подставляя (1.124) и (1.125) в (1.123) и меняя порядок интегрирования и дифференцирования, получаем

Выясним физический смысл выражений, входящих в уравнение (1.126).

Рассмотрим первое слагаемое в правой части (1.126). Представим объем V в виде суммы бесконечно малых цилиндров длиной dl, торцы которых (dS) перпендикулярны направлению тока (вектору j). Тогда EjdV = EjdV=(Edl)(jdS) = dUdl = dP_n, где dl =jdS - ток, протекающий по рассматриваемому бесконечно малому цилиндру; dU = Edl - изменение потенциала на длине dl, a dP_n -мощность джоулевых потерь в объеме dV. Следовательно, рассматриваемое слагаемое представляет собой мощность джоулевых потерь Р_п в объеме V. Используя соотношение j = σЕ, для Р_п можно получить и другие представления:

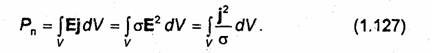
Формулы (1.127) можно рассматривать как обобщенный закон Джоуля-Ленца, справедливый для проводящего объема V произвольной формы.

Интеграл в левой части (1.126) отличается от первого слагаемого в правой части только тем, что в подынтегральное выражение вместо j входит j^cт. Поэтому он должен определять мощность сторонних источников. Будем считать положительной мощность, отдаваемую сторонними токами электромагнитному полю. Электрический ток представляет собой упорядоченное движение заряженных частиц. Положительным направлением тока считается направление движения положительных зарядов. Ток отдает энергию электромагнитному полю при торможении образующих его заряженных частиц. Для этого необходимо, чтобы вектор напряженности электрического поля Е имел составляющую, ориентированную противоположно направлению тока, т.е. чтобы скалярное произведение векторов Е и j^ст было отрицательным (E j^ст <0). При этом левая часть равенства (1.126) будет положительной величиной. Таким образом, мгновенное значение мощности, отдаваемой сторонними токами электромагнитному полю в объеме V, определяется выражением

Для уяснения физического смысла последнего слагаемого в правой части уравнения (1.126) рассмотрим частный случай. Предположим, что объем V окружен идеально проводящей оболочкой, совпадающей с поверхностью S. Тогда касательная составляющая вектора Е на поверхности S будет равна нулю. Элемент поверхности dS совпадает по направлению с внешней нормалью n₀. Следовательно, поверхностный интеграл в уравнении (1.126) будет равен нулю, так как нормальная компонента векторного произведения [Е, Н] определяется касательными составляющими входящих в него Векторов. Кроме того, предположим, что среда в пределах объема V не обладает проводимостью ( σ = 0). При этом в рассматриваемой области не будет джоулевых потерь, и первый интеграл в правой части уравнения (1.126) также будет равен нулю. В результате получим

Очевидно, что в рассматриваемом случае мощность сторонних источников может расходоваться только на изменение энергии электромагнитного поля. Таким образом, правая часть равенства (1.129) представляет собой скорость изменения энергии электромагнитного поля, запасенной в объеме V, т.е. соответствует слагаемому dW/dt в уравнении (1.126). Естественно предположить, что интеграл в правой части (1.129) равен энергии электромагнитного поля, сосредоточенного в объеме V:

Строго говоря, этот интеграл может отличаться от W на некоторую функцию g = g(х, у, z), не зависящую от времени. Нетрудно убедиться, что функция д равна нулю. Перепишем (1.130) в виде W=W^Э+W^М, где

Предположим, что электрическое и магнитное поля являются постоянными (не зависят от времени). В этом случае, как известно из курса физики (см. также гл.З и 4), выражения (1.131) и (1.132) определяют энергию соответственно электрического и магнитного полей в объеме V. Но это означает, что g = 0 и указанные выражения определяют мгновенные значения энергии электрического и магнитного полей в объеме V при любой зависимости от временила их сумма, определяемая формулой (1.130), действительно равна мгновенному значению энергии электромагнитного поля в объеме V.

Осталось выяснить физическую сущность поверхностного интеграла в уравнении (1.126). Предположим, что в объеме V отсутствуют потери и, кроме того, величина электромагнитной энергии остается постоянной (W= const). При этом уравнение (1.126) принимает вид

В то же время из физических представлений очевидно, что в данном частном случае вся мощность сторонних источников должна уходить в окружающее пространство (Р^ст = Р_Σ). Следовательно, правая часть уравнения (1.133) равна потоку энергии через поверхность S (пределу отношения количества энергии, проходящей через S за время Δt при Δt→0), т.е.

Естественно предположить, что вектор П представляет собой плотность потока энергии (предел отношения потока энергии через площадку ΔS, расположенную перпендикулярно направлению распространения энергии, к ΔS  при ΔS →0). Формально математически это предположение не очевидно, так как замена вектора П на П₁ = П + rot а, где а - произвольный вектор, не изменяет величину Р_Σ. Однако оно является верным и в частности, непосредственно вытекает из релятивистской теории электромагнитного поля [11].

Таким образом, равенство (1.126) аналогично (1.120) и представляет собой уравнение баланса мгновенных значений мощности электромагнитного поля. Оно было получено Пойнтингом в 1884 г. и называется теоремой Пойнтинга. Соответственно вектор П называют вектором Пойнтинга. Часто используют также названия "теорема Умова-Пойнтинга" и "вектор Умова-Пойн-тинга" с целью подчеркнуть тот факт, что формулировка закона сохранения энергии в общей форме с введением понятия потока энергии и вектора, характеризующего его плотность, впервые была дана Н.А. Умовым в 1874 г.

Отметим, что энергия может поступать в объем V не только от сторонних источников. Например, поток энергии через поверхность S может быть направлен из окружающего пространства в объем V. При этом мощность P_Σ будет отрицательной, так как положительным считается поток энергии, выходящий из объема V в окружающее пространство (направление элемента dS совпадает с направлением внешней нормали к поверхности S).

Сторонние источники могут не только отдавать энергию, но и получать ее от электромагнитного поля. При этом мощность сторонних источников будет отрицательной. Действительно, электромагнитное поле отдает энергию току проводимости, если оно ускоряет движение заряженных частиц, образующих ток. Для этого вектор напряженности электрического поля Е должен иметь составляющую, ориентированную вдоль линий тока, т.е. чтобы скалярное произведение векторов Е и j^ст было больше нуля.

Рассмотрим более подробно формулы, определяющие энергию   электромагнитного   поля.   Подынтегральные   выражения   в

 можно интерпретировать как мгновенные значения объемных плотностей энергии электрического и магнитного полей соответственно, а их сумму

- как объемную плотность полной энергии электромагнитного поля.

Подчеркнем, что принцип суперпозиции, которому удовлетворяют векторы напряженностей электрического и магнитного полей, не распространяется на энергию. Действительно, пусть энергии полей E₁, H₁ и Е₂, Н₂, существующих по отдельности в области V, равны соответственно W₁ и W₂. Тогда энергия суммарного поля Е = Е₁ + Е₂, Н = Н₁ + Н₂ определится выражением

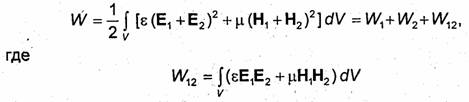
- взаимная энергия полей. Взаимная энергия W₁₂ может быть как положительной, так и отрицательной. Если векторы Е₁ и Е₂, а также H₁ и Н₂ взаимно перпендикулярны, то W₁₂ = 0.

В случае переменных процессов распределение электромагнитной энергии непрерывно изменяется. Это изменение в каждой данной точке можно определить на основе уравнения (1.122), которое удобно представить в виде

где p^ст =-E j^ст и p_n = Ej-мгновенные значения плотностей мощности сторонних источников и мощности джоулевых потерь соответственно. При переходе от соотношения (1.122) к уравнению (1.136) учтены формулы (1.125) и (1.135). Уравнение (1.136) является дифференциальной формой теоремы Пойнтинга.

1.8.3. Активная, реактивная и комплексная мощности

Рассмотрим выражение для мгновенных значений мощности Р в электрической цепи, в которой напряжение и ток равны соответственно  -начальные фазы напряжения и тока. По закону Джоуля-Ленца . После элементарных тригонометрических преобразований представим Р в виде суммы двух слагаемых:

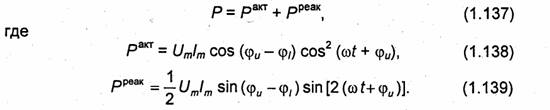
Составляющую Р^АКТ называют активной мощностью. Так как в любой цепи  то активная мощность не может быть

отрицательной . Среднее за период значение активной мощности

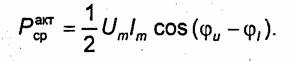
Составляющую Р^реак называют реактивной мощностью.

 Как видно из (1.139), она изменяется с частотой 2ώ и в течение периода Т= 1/f дважды изменяет знак. Среднее за период значение реактивной мощности равно нулю. Поэтому среднее за период значение мощности Р совпадает со средним за период значением активной мощности:

При анализе гармонических колебаний в электрических цепях широко используют метод комплексных амплитуд. При этом    вместо мгновенных значений напряжения U и тока / вводят в рассмотрение комплексные функции Ủ и Ỉ соответствующие им комплексные амплитуды Ủ  и Ỉ_m ,  связанные обычными (см.1.6)

соотношениями:  Для перехода от мгновенных значений напряжения и тока к их комплексным функциям Ủ и Ỉ достаточно заменить . Однако метод комплексных амплитуд непосредственно применим только в случае линейных соотношений. Поэтому переходить в выражениях для мгновенных значений мощности к комплексным функциям обычными заменами U на Ủ и / на Ỉ не имеет смысла. В то же время можно ввести понятие комплексной мощности, удобное для практического использования. Назовем комплексной мощностью функцию

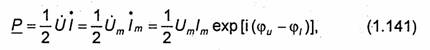
где символ * означает, что взята комплексно-сопряженная величина: функции Ỉ и Ỉ_m являются комплексно сопряженными Ỉ и Ỉ_m соответственно. Как видно из (1.141), комплексная мощность не зависит от времени. Отделяя в (1.141) действительную и мнимую части, замечаем, что действительная часть комплексной мощности совпадает со средним за период значением мощности

а мнимая часть равна  амплитуде реактивной мощности  Аналогично может быть введена комплексная мощность и в любом другом случае. Рассмотрим, например, мощности, входящие в уравнение (1.126).

Заменяя в (1.128) вектор Е комплексным вектором Ё, aj^ст-

вектором j^ст, комплексно сопряженным с j_ст, и умножая результат

на 1/2, приходим к выражению для комплексной мощности сторонних источников:

где  - вектор, комплексно сопряженный с комплексной амплитудой плотности сторонних токов   Векторы связаны соотношением    Действительная часть комплексной мощности сторонних источников (ReP^ст) равна средней за

период мощности сторонних источников, которая в свою очередь равна средней за период активной мощности сторонних источников:

Мнимая часть комплексной мощности сторонних источников

равна амплитуде реактивной мощности сторонних источников.

Преобразовывая аналогичным образом формулу (1.127) для мгновенных значений мощности джоулевых потерь Р_п, получаем вещественную величину, равную среднему за период значению мощности джоулевых потерь в объеме V:

Рассмотрим выражение для потока энергии через поверхность

S. Переходя в (1.134) к комплексным векторам Е и Н, получаем выражение для комплексного потока энергии через поверхность S:

- комплексный вектор Пойнтинга.

Действительная и мнимая части Р_Е равны соответственно среднему за период потоку энергии через поверхность S и амплитуде реактивного потока энергии через S. Аналогично действительная и мнимая части комплексного вектора Пойнтинга представляют собой среднюю за период плотность потока энергии в рассматриваемой точке пространства и амплитуду плотности реактивного потока энергии в той же точке соответственно.

1.8.4. Уравнение баланса комплексной мощности

Уравнение баланса комплексной мощности может быть получено либо из уравнений Максвелла в комплексной форме, либо непосредственно из теоремы Пойнтинга. Второй путь короче. При этом вывод упрощается, если в качестве исходного использовать уравнение баланса мгновенных значений мощности в форме (1.123). Перейдем от мгновенных значений мощностей, входящих в (1.123), к комплексным мощностям на основе приема, описанного в 1.8.3. Все подынтегральные выражения в (1.123) содержат произведения двух векторов. Заменим в этих произведениях первый вектор соответствующим ему комплексным вектором (например,

вектор Е - на Ё), а второй вектор - соответствующим ему комплексно-сопряженным вектором (например, j^ст-нa j^ст). Умножая обе части получающегося при этом равенства на 1/2, приходим к соотношению     

Вычисляя  производные  по  t и  учитывая  обозначение  (1.145), получаем уравнение баланса комплексной мощности:

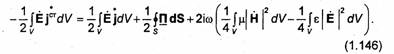
Проанализируем это уравнение. Используя формулы (1.142)—(1.144),

перепишем его в виде

-соответственно средние за период значения энергий электрического и магнитного полей в объеме V. Из равенства комплексных величин следуют отдельные равенства для их действительных и мнимых частей. Отделяя в (1.147) действительные части, получаем

Левая часть равенства (1.148) представляет собой среднюю за период мощность сторонних источников, которая равна также средней за период активной мощности сторонних источников. Второе слагаемое в правой части (1.148) равно среднему за период потоку энергии через поверхность S и соответственно среднему за период активному потоку энергии через ту же поверхность:

Поэтому равенство (1.148) эквивалентно соотношению

Таким образом, уравнение (1.148) представляет собой уравнение баланса средних за период мощностей. Уравнение (1.148) иногда называют также уравнением баланса активных мощностей.

Из (1.149) видно, что в тех случаях, когда  поток энергии в среднем за период выходит из рассматриваемого объема в окружающее пространство. При  средний поток энергии отрицателен, т.е. направлен из окружающего пространства в объем V.

Отделяя в (1.147) мнимые части, получаем

Входящие в (1.150) величины 1тР^ст и ImP_Σ; равны соответственно амплитуде реактивной мощности сторонних источников и амплитуде реактивного потока энергии через поверхность S. Поэтому уравнение (1.150) иногда называют уравнением баланса реактивных мощностей.

Реактивный поток энергии изменяется со временем по гармоническому закону с удвоенной круговой частотой 2ω. В течение периода он половину времени имеет положительное значение, т.е. энергия поступает в окружающее пространство, а другую половину - отрицательное, т.е. энергия поступает из окружающего пространства, в объем V. Среднее за период значение реактивного потока энергии равно нулю. Таким образом, из (1.150) следует, что разность между амплитудами реактивной мощности сторонних источников и реактивного потока энергии через ограничивающую этот объем поверхность S равна умноженной на 2ω разности между средними за период значениями энергий магнитного и электрического полей в объеме V.

Предположим, что объем V представляет собой изолированную систему (например, ограничен идеально проводящей поверхностью). Тогда поток комплексного вектора Пойнтинга через S будет равен нулю, и уравнения (1.149) и (1.150) примут вид

В этом случае в объеме V энергия электрического поля будет периодически преобразовываться в энергию магнитного поля и обратно. Если средние за период значения энергий электрического и магнитного полей равны, т.е.

то этот процесс протекает без участия источников, и мощность сторонних источников оказывается чисто активной (ImР^ст = 0). Если же, то периодическое преобразование энергии электрического поля в энергию магнитного поля и обратно возможно только при участии сторонних источников. При этом реактивная мощность сторонних источников будет отлична от нуля . Если в изолированной области мощность сторонних источников является чисто активной, то имеет место резонанс. Из изложенного следует, что для резонанса необходимо выполнение условия (1.153). Отношение

где, называют добротностью изолированной системы. Выражение (1.154) можно переписать в иной форме. Заменяя со на 2π/Т, получаем

где ΔW - изменение энергии электромагнитного поля системы за период. Таким образом, добротность изолированной системы - это увеличенное в 2π раз отношение запаса энергии системы W_CP к энергии ΔW, расходуемой за период Т.

Уравнение (1.146) было выведено в предположении, что ε  Отметим, что в общем случае, когда.ε уравнение баланса комплексных мощностей также имеет вид (1.147), однако при этом входящие в него величины  определяются выражениями

1.8.5. Скорость распространения электромагнитной энергии

Как уже отмечалось, из теоремы Пойнтинга (1.126) следует возможность распространения в пространстве энергии электромагнитного поля. Вычислим скорость, с которой происходит это распространение. Выделим в рассматриваемой части пространства так называемую энергетическую трубку, т.е. трубку на боковой поверхности которой перпендикулярная к ней составляющая вектора Пойнтинга (П_п) тождественно равна нулю (рис.1.24). При этом условии средний за период поток энергии через поперечное сечение трубки при отсутствии джоулевых потерь не изменяется вдоль трубки.

Энергия электромагнитного поля ΔW, прошедшая за время Δt через поперечное сечение трубки ΔS, будет распределена с плотностью w в объеме ΔV, ограниченном боковой поверхностью трубки и поперечными сечениями ΔS и ΔS₁ находящимися на расстоянии Δl друг от друга (рис.1.24). Эта энергия может быть вычислена по формуле

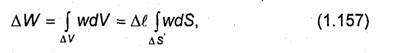
где ΔS' - некоторое поперечное сечение трубки, расположенное между сечениями ΔS и ΔS₁.

Будем называть скоростью распространения энергии v₃ предел отношения Δ l кΔt при Δt→O.

При достаточно малых значениях Δt можно считать, что в пределах Δt вектор Пойнтинга не изменяется. Поэтому наряду с (1.157) должно выполняться соотношение

где dS=l₀dS, а l₀ - единичный вектор, перпендикулярный к ΔS и направленный в сторону ΔS₁. Приравнивая правые части выражений (1.157) и (1.158) и переходя к пределу при Δt→0, находим

При выводе формулы (1.159) учтено, что в пределе при Δt→0сечение ΔS' совпадает с ΔS. Если Е и Н, а следовательно, П и w не изменяются вдоль сечения ΔS, формула (1.159) упрощается. Так как в этом случае направление вектора Пойнтинга совпадает с направлением распространения энергии, то

Нетрудно показать, что в случае монохроматического поля среднее за период значение скорости распространения энергии v_3cp определяется формулой

Если значения вектора П и функции w_cp одинаковы во всех точках сечения AS, выражение (1.161) может быть записано в виде

Таким образом, в данной главе рассмотрены основные уравнения электродинамики. Перейдем к рассмотрению вопроса о применении этих уравнений к решению конкретных задач.

Глава 2

ПОСТАНОВКА ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

2.1. КЛАССИФИКАЦИЯ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

При решении многих проблем радиотехники, электро- и радиосвязи, радиофизики и других научно-технических отраслей необходимо знать структуру электромагнитного поля в рассматриваемой части пространства. К таким проблемам относятся, например, разработка излучающих систем (антенн) и повышение их помехозащищенности, обеспечение электромагнитной совместимости радиотехнических устройств и систем, разработка различных линий передачи энергии и многие другие. Для расчета электромагнитного поля в каждом конкретном случае требуется решить соответствующую электродинамическую задачу.

Выделяют два класса задач электродинамики, которые называют прямыми и обратными задачами. Прямые задачи электродинамики (их часто называют также задачами анализа) состоят в определении электромагнитного поля, которое создается в рассматриваемой части пространства под воздействием известных (заданных) источников. Обратные задачи электродинамики (обычно их называют задачами синтеза) состоят в определении системы источников, которые создают электромагнитное поле, обладающее требуемой (заданной) структурой. Прямые задачи электродинамики часто формулируют как краевые задачи, состоящие в нахождении электромагнитного поля, удовлетворяющего определенным (краевым) условиям на границе рассматриваемой части пространства. Различают внутренние и внешние краевые задачи .Пусть задана некоторая область V, ограниченная замкнутой поверхностью S (см. рис. 1.23). Определение поля внутри области V называют внутренней задачей. Соответственно определение поля во всем пространстве, внешнем по отношению к области V (рис. 2.1), называют внешней задачей.

Возникающие на практике электродинамические задачи обычно весьма сложны,

и их решение удается получить лишь после введения ряда упрощающих предположений. Поэтому практически всегда вместо реальной задачи рассматривают некоторую модельную задачу, которая в той или иной степени отражает реальную ситуацию. Часто исходную задачу удается разбить на ряд более простых, каждая из которых позволяет учесть один или несколько влияющих факторов.

2.2. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

2.2.1. Вводные Замечания

Уравнения Максвелла являются дифференциальными уравнениями в частных производных. Такие уравнения допускают множество решений. Однако из общих физических представлений очевидно, что при полном повторении условий эксперимента распределение поля должно быть одинаковым. Следовательно, в каждом конкретном случае электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но и некоторым дополнительным условиям. Эти дополнительные условия определяются специальными теоремами, называемыми теоремами единственности решения задач электродинамики. Ограничимся доказательством этих теорем для краевых задач в случае монохроматического поля, причем будем считать, что в рассматриваемой части пространства происходит (хотя бы и очень слабое) поглощение энергии, т.е. что Рпср ≠ О.

2.2.2. Единственность решения внутренних задач электродинамики

Покажем, что внутренняя задача электродинамики имеет единственное решение, если на граничной поверхности S (см. рис.1.23) выполняется одно из следующих четырех условий:

в каждой точке М поверхности S задана проекция вектора Е на плоскость Р[М), касательную к S в точке М (Е-задача):

в каждой точке М поверхности S задана проекция вектора Н на плоскость Р(М) (Н-задача):

на одной части поверхности S (обозначим ее S₁) задана проекция Е_τ вектора Ё, а на другой части (S₂) - проекция Н_τ вектора Н на плоскость Р{М), причем S₁ + S₂ = S (ЕН-задача):

в каждой точке М поверхности S проекции векторов Ё и Н на оскость Р(М) связаны соотношением

Условие (2.4) часто называют импедансным краевым условием. Очевидно, что векторы E_t и H_t., образующиеся при проецировании Ё_τ и Н_τ на плоскость Р(М), имеют различное направление -единичные векторы, лежащие в плоскости Р(М).

В формулах (2.1)-(2.5) через f(M), g(M), F,{M), F₂{M) и Z(M) обозначены известные (заданные) функции точки M_ЄS.

Предположим, что существуют два различных решения поставленной задачи и рассмотрим их разность:

Векторы удовлетворяют уравнениям Максвелла

и одинаковым краевым условиям на поверхности S. Уравнения Максвелла для поля Ё₃,Н₃ получаются почленным вычитанием уравнения (2.8) из (2.7). При этом векторы j^CT сокращаются, и уравнения Максвелла для поля Ё₃, Н₃ принимают вид

На поверхности S поле Ё₃, Н₃ должно удовлетворять следующим краевым условиям:

в случае Е-задачи

в случае Н-задачи

в случае Е-задачи

в случае импедансного краевого условия (2.4)

Составим уравнение баланса для средней за период мощности разностного поля Ё₃, Н₃. Так как векторы Ё₃, Н₃ удовлетворяют уравнениям Максвелла (2.9), то мощность сторонних источников разностного поля  равна нулю, и уравнение (1.148) принимает вид

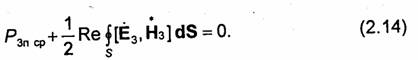
Так как dS = n_odS, где п₀-орт внешней нормали к поверхности S, то произведение [Ё₃, H3]dS определяется только касательными составляющими векторов Ё₃ и Нз. В случае выполнения условий (2.10)—(2.12) произведение на поверхности S обращается в нуль. При этом из (2.14) следует, что

Предположим вначале, что потери энергии в объеме V обусловлены только наличием проводимости .   В этом случае уравнение (2.15) принимает вид

Так как  то из равенства (2.16) следует, что Ё₃ = 0. Используя второе уравнение Максвелла, записанное относительно векторов Ё₃ и Н₃, получаем Н₃ = 0. Следовательно, Ё₂ = Ё₁ и Н₂ = Н₁, т.е. задача имеет единственное решение.

Рассмотрим теперь краевое условие (2.4). В этом случае подынтегральное  выражение во  втором  слагаемом  в уравнении (2.14) может быть преобразовано следующим образом: При этом из (2.14) получаем соотношение

Так как  и, кроме того, выполняется условие (2.5),

то равенство (2.17) возможно только при Ё₃ = 0. Таким образом, и в этом случае задача имеет единственное решение.

Единственность решения в более общем случае, когда доказывается аналогично на основе анализа уравнения (2.14). При этом выражение для средней за период мощности потерь в объеме V для поля Ё₃,Н₃ должно быть записано на основе равенства (1.156).

2.2.3. Единственность решения внешних задач электродинамики

В случае внешней задачи электродинамики поверхность S не охватывает рассматриваемую часть пространства, простирающуюся до бесконечности. Поэтому для единственности решения кроме одного из условий (2.1)-(2.4) требуется задать дополнительное условие, характеризующее поведение векторов Е и Н в точках, бесконечно удаленных от поверхности S. Выясним, каким должно быть это дополнительное условие.

Пусть на S выполняется одно из условий (2.1)-(2.4). Предположим, что имеется два решения задачи E_1, H₁ и Е₂, Н₂, и введем в рассмотрение разностное поле Е₃, Н₃ по формулам (2.6). Как и  в случае внутренней  задачи  электродинамики,  векторы

Ё₃ и Н₃ удовлетворяют уравнениям Максвелла (2.9) и одному из условий (2.10)—(2.13) на поверхности S. Из произвольной точки 0 внутри области V мысленно проведем сферу радиуса г так, чтобы вся область V и все сторонние источники оказались внутри этой сферы. Объем, заключенный между поверхностями S и S', обозначим через V (рис.2.1). Составим уравнение баланса для средних за период значений мощности поля Ё₃,Н₃ в объеме V:

Перейдем в уравнении (2.18) к пределу при r→ ∞. Тогда область V распространится на все пространство, внешнее по отношению к области V. Если в пределе третье слагаемое в левой части уравнения (2.18) окажется равным нулю, то получающееся при этом соотношение

не будет иметь принципиальных отличий от аналогичного уравнения (2.14) для внутренней задачи электродинамики, и, следовательно, рассматриваемая задача также будет иметь единственное решение. Действительно, при выполнении условий (2.1)-(2.3), второе слагаемое в левой части (2.19) обращается в нуль, и это уравнение принимает вид

В частном случае, когда потери в среде обусловлены только наличием проводимости, т.е. когда уравнение (2.20) записывается в форме

Так как а то из (2.21) получаем Ё₃ =0, а из второго

уравнения Максвелла - Н₃ = 0. Следовательно, Ё₂ = Ё₁ и Н₂ = Н₁.

Если на поверхности S выполняется условие (2.4), то из уравнений (2.19) и (2.13) имеем

откуда также следует единственность решения.

В более общем случае, когда единственность решения доказывается также на основе формулы (2.20) для краевых условий (2.1)-(2.3) и на основе уравнения (2.19) в случае краевого условия (2.4). При этом должно быть использовано соотношение (1.156).

Найдем условие, при котором

и, следовательно, проведенное выше доказательство справедливо. При r→ ∞ поверхность S' возрастает пропорционально r². Поэтому для выполнения условия (2.22) необходимо, чтобы абсолютная величина произведения [Ё₃,Нз] при r→ ∞ убывала быстрее r^-2. Для этого достаточно потребовать, чтобы искомые векторы Е и Н убывали быстрее, чем 1/r.

Таким образом, внешняя задача электродинамики имеет единственное решение, если на поверхности S, ограничивающей объем V, выполняется одно из условий (2.1)-(2.4) и, кроме того, при r→ ∞ векторы Е и Н убывают быстрее, чем 1/r. Последнее всегда имеет место, так как в любых реальных средах имеются потери энергии.

Отметим, что теорему единственности для внешней задачи электродинамики можно доказать и в случае среды без потерь, если вместо условия убывания векторов Е и Н при r→ ∞ быстрее 1/г потребовать выполнения следующих условий:

Предельные соотношения (2.23) называются условиями излучения. Они были сформулированы Зоммерфельдом. Физически эти условия эквивалентны требованию, чтобы при r→ ∞ поле имело характер поперечных волн, распространяющихся вдоль направления r₀ (предполагается, что источники поля находятся на конечном расстоянии от поверхности S). Использованный здесь термин "поперечная волна" определен в гл.5.

Отметим, что в тех случаях, когда поверхность S имеет особенности типа изломов, острых кромок и др., для единственности решения краевой задачи электродинамики перечисленных условий недостаточно. Необходимо выполнение дополнительных условий, определяющих поведение составляющих векторов Е и Н вблизи этих особенностей.

К таким условиям относятся, в частности, "условия на ребре", сформулированные Мейкснером для случая идеально проводящих тел. Рассмотрим эти условия. Пусть контур Со представляет собой ребро (острую кромку) идеально проводящей поверхности S. Введем систему координат (рис. 2.2), связанную с контуром Со, где s - длина дуги, отсчитываемая вдоль контура Со от некоторой точки О _Є Со, а  - полярные координаты в плоскости, перпендикулярной Со. Условия на ребре записываются в виде

Соотношения (2.24) должны выполняться равномерно по

Условия на ребре (2.24) обеспечивают существование интеграла

где V_r - объем кольцевой области радиуса r, охватывающей контур Со. Существование этого интеграла эквивалентно выполнению требования ограниченности энергии электромагнитного поля в любом конечном объеме, охватывающем контур С_о (рис.2.3). Анализируя соотношения (2.24) совместно с уравнениями Максвелла,

можно показать, что касательные к ребру (контуру Со) составляющие  должны быть ограниченными, а нормальные к ребру составляющие  могут иметь

особенности вида г^-x, где 0<х < 1. Для определения параметра и нужно знать внутренний угол так называемого эквивалентного клина, который строится следующим образом. Через произвольную точку М на рассматриваемом ребре С_о проводится касательная l к С_о и две полуплоскости, касательные к S в точке М, так, чтобы их ребра совпали с l Клин, образованный этими полуплоскостями, и называют эквивалентным клином (на рис. 2.4 показано сечение поверхности S плоскостью, перпендикулярной ребру эквивалентного клина в точке М; касательная l перпендикулярна плоскости рисунка, а ее след совпадает с точкой М). Пусть внутренний угол эквивалентного клина равен Ω. (предполагается, что Ω< π). Анализируя структуры полей вблизи ребра идеально проводящего клина, найденные на основе

решения соответствующих краевых задач, получили, что x = (π - Ω)/(2π - Ω). В частном случае, когда поверхность S имеет острую кромку (например, на краю бесконечно тонкого экрана), Ω = 0 и х = 1/2. На таком ребре составляющие имеют

особенность вида  const,   а составляющие  обращаются в нуль как

Из приведенного выше доказательства единственности решения краевых задач электродинамики следует, что при отсутствии потерь энергии в области V решение внутренней задачи может быть неединственным. Физически это означает, что в такой системе помимо полей, созданных непрерывно действующими сторонними источниками, могут существовать незатухающие поля, созданные когда-то действовавшими сторонними источниками (но в рассматриваемое время переставшими действовать). Эти поля из-за отсутствия потерь в среде могут существовать сколь угодно долго (например, собственные колебания идеального объемного резонатора).

2.3. ВОЛНОВЫЕ УРАВНЕНИЯ

2.3.1. Общий случай

При решении прямых задач электродинамики требуется найти векторы Е и Н по известным (заданным) сторонним источникам. Предположим, что сторонние источники расположены в безграничной однородной изотропной среде. Для упрощения преобразований будем считать, что σ= 0. Записывая уравнения Максвелла для данного частного случая, получаем

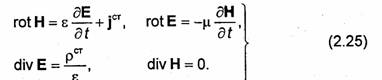
Определение векторов Е и Н непосредственно из системы уравнений (2.25) затруднительно. Поэтому целесообразно преобразовать ее, исключив либо вектор Е, либо вектор Н, т.е. получить из нее такое дифференциальное уравнение, в которое входил бы только один из векторов Е или Н. Для этого возьмем ротор от обеих частей второго уравнения системы (2.25) и изменим порядок дифференцирования по времени и по пространственным координатам. Учитывая известное из векторного анализа равенство

где Δ²≡Δ-оператор Лапласа, и третье равенство рассматриваемой системы, приходим к уравнению

Аналогично выводится и уравнение для вектора Н:

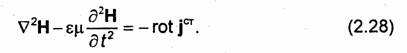
Каждое из векторных уравнений (2.27) и (2.28) эквивалентно трем скалярным уравнениям, получающимся при проецировании векторного уравнения на оси X, Y и Z декартовой системы координат. Эти скалярные уравнения относятся к уравнениям вида

где w и f(x, у, z, f)-искомая и заданная (известная) функции соответственно. Как известно, уравнения вида (2.29) описывают волновые процессы, причем параметр v равен скорости этого процесса. Такие уравнения принято называть неоднородными уравнениями Даламбера или неоднородными волновыми уравнениями. Уравнения (2.27) и (2.28) отличаются от (2.29) только тем, что входящие в них функции являются векторными. Уравнения такого типа называют неоднородными векторными уравнениями Даламбера или неоднородными векторными волновыми уравнениями. Аналогичные уравнения, правые части которых равны нулю, называют однородными векторными уравнениями Даламбера (однородными векторными волновыми уравнениями).

В дальнейшем будет показано, что входящий в уравнения

(2.27) и (2.28) параметр являющийся аналогом параметра v в (2.29), в случае среды без потерь также представляет собой скорость распространения электромагнитного поля и равен скорости света ев рассматриваемой среде. Этот результат не является неожиданным, так как свет - это электромагнитные волны определенного диапазона частот.

Без затруднений записываются аналогичные уравнения для векторов Е и Н и в том случае, когда σ≠ 0 (см., напр., [1]).

2.3.2. Монохроматическое поле

В случае монохроматического поля полная система уравнений Максвелла в комплексной форме, учитывающая сторонние электрические источники, имеет вид

Предположим, что среда, заполняющая рассматриваемую часть пространства, является однородной и изотропной. Возьмем ротор от обеих частей второго уравнения системы (2.30) и исключим вектор Н, используя первое уравнение. Учитывая формулу (2.26) и равенство справедливое для однородной изотропной среды, придем к уравнению

где Для вектора Н получаем аналогично

Очевидно, что такие же уравнения связывают между собой комплексные амплитуды

Если   в  рассматриваемой  области   отсутствуют  сторонние источники, уравнения (2.31) и (2.32) упрощаются:

Для перехода к случаю среды без потерь в уравнениях (2.30)-(2.34) нужно положить .  Каждое

из векторных уравнений (2.33) и (2.34) эквивалентно трем однотипным скалярным уравнениям для декартовых составляющих соответствующего вектора: ∆²w+k²w = 0, где w-любая из составляющих

2.4. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

2.4.1. Общий случай

Выведенные в предыдущем разделе дифференциальные уравнения позволяют в принципе определить векторы Е и Н через функции j^ст и ρ^ст. Однако наличие в их правых частях выражений grad ρ^ст и rot j^ст в ряде случаев несколько затрудняет получение

удобных расчетных формул. Поэтому указанные уравнения обычно используют в тех случаях, когда сторонние источники расположены за пределами рассматриваемой области, т.е. когда уравнения (2.27) и (2.28) становятся однородными и соответственно уравнения (2.31) и (2.32) переходят в (2.33) и (2.34).

В общем случае для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы Е и Н. Эти вспомогательные функции можно ввести различным образом в зависимости от специфических особенностей анализируемой задачи. Для упрощения решения многих задач вводят так называемые электродинамические потенциалы. Рассмотрим систему уравнений Максвелла (2.25). Последнее уравнение этой системы представляет собой четвертое уравнение Максвелла div В = 0, записанное для случая однородной изотропной среды. Так как дивергенция ротора любого вектора равна нулю (div rot a = 0), то из уравнения div В = 0 следует, что вектор В можно представить в виде В = rot А. При этом вектор

При известном векторе А уравнение (2.35) позволяет однозначно найти вектор Н. Однако оно допускает некоторый произвол в определении вектора А. Действительно, если вместо А взять вектор A₁= А + grad ψ, где ψ - произвольная скалярная функция, то значение вектора Н не изменится, так как

Неоднозначность определения вектора А будет использована при выводе дифференциального уравнения для А.

Подставим выражение (2.35) во второе уравнение системы (2.25) и изменим порядок дифференцирования по времени и пространственным координатам. Объединив затем векторы Е и дА/дt под знаком ротора, получим rot(E + дА/дt) = 0. Учитывая тождество (2.36), можно положить, что стоящее под знаком ротора выражение равно - grad и, где и- некоторая скалярная функция, или

Знак минус перед grad и в формуле (2.37) введен, чтобы в случае электростатического поля функция и совпадала с обычным электростатическим потенциалом.

Таким образом, все векторы, определяющие электромагнитное поле, выражаются через две функции: векторный потенциал А и скалярный потенциал и. Следовательно, задача состоит теперь в том, чтобы найти функции А и и. Подставляя (2.35) и (2.37) в первое уравнение системы (2.25) и преобразовывая левую часть получающегося при этом соотношения с помощью тождества (2.26), приходим к равенству

Упростим уравнение (2.38). Как уже отмечалось, вектор А определен с точностью до градиента произвольной скалярной функции. Следовательно, можно потребовать, чтобы вектор А удовлетворял добавочному условию. Потребуем, чтобы

Соотношение (2.39) принято называть условием калибровки. учетом (2.39) уравнение (2.38) принимает вид

Аналогичное уравнение получается и для скалярного потенциала и. Подставляя (2.37) в третье уравнение системы (2.25), получаем

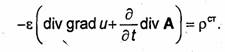
Используя условие калибровки (2.39) и тождество div grad и =Δ²u, приходим к уравнению

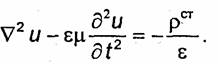(2.41)

Таким образом, векторный и скалярный потенциалы, как и векторы Е и Н, удовлетворяют неоднородным уравнениям Даламбера. Однако правые части уравнений для потенциалов имеют более простой вид. Поэтому уравнения (2.40) и (2.41) оказываются более удобными при решении многих конкретных задач.

Найдем частные решения уравнений (2.40) и (2.41), считая функции j^ст и ρ^ст. известными. Вначале рассмотрим уравнение (2.41). Предположим, что электрическое поле создается точечным неподвижным зарядом постоянной величины Q = const, расположенным в начале координат, вектор Е в этом случае определяется выражением (1.7). Так как поле не должно зависеть от времени, то dA/дt = 0 и соотношение (2.37) принимает вид Е =- grad и. Расписывая grad и в сферической системе координат r,θ,φ (см. приложение 4) и учитывая, что вектор Е в рассматриваемом случае может зависеть только от координаты r (от расстояния от заряда Q до точки наблюдения), получаем

где r₀ - координатный орт переменной r. Подставляя выражение (2.42) в (1.7) и выполняя интегрирование по переменной r, находим функцию и:

Постоянная интегрирования в (2.43) принята равной нулю, чтобы при r→ ∞ функция и обращалась в нуль. Формула (2.43) полностью совпадает с известным из курса общей физики выражением для электростатического потенциала точечного заряда (см. замечание по поводу выбора знака перед grad и в выражении (2.37)). Если заряд сосредоточен в малом элементе объема dV с плотностью ρ^ст, то и =ρ^стdV/(4πεR), где R- расстояние от элемента dV до точки наблюдения. От этой формулы легко перейти к выражению для электростатического потенциала, создаваемого произвольным распределением зарядов в объеме V. В соответствии с принципом суперпозиции получаем

Значение и, определяемое формулой (2.44), можно рассматривать как решение уравнения

получающегося из равенства (2.41), если в последнем положить д²u/дt²=0. Уравнение (2.45) называют уравнением Пуассона.

Предположим теперь, что поле также создается точечным зарядом, расположенным в начале координат, но величина этого заряда изменяется со временем Q = Q (t). Тогда в любой точке, кроме начала координат, потенциал и будет удовлетворять однородному уравнению Даламбера

Для решения уравнения (2.46) удобно использовать сферическую систему координат r, θ, φ (рис.2.5). Оператор Лапласа Δ² в этой системе координат определяется формулой (П. 18). Так как лоле создается точечным зарядом, расположенным в начале координат, то потенциал и не должен зависеть от углов θ и φ. Поэтому уравнение (2.45) можно переписать в виде

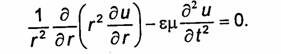
Учитывая, что  и переходя от и к функции и₁, связанной с и соотношением u₁ = rи, получаем

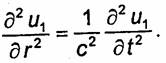
Общее решение уравнения (2.47) имеет вид - произвольные дважды дифференцируемые функции аргументов t-rlc и t+rlc соответственно. В том, что функции f₁(t-r/c) и f₂(t+r/c) удовлетворяют (2.47), можно убедиться непосредственной подстановкой их в это уравнение. Таким образом, скалярный потенциал и можно представить в виде

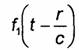Первое слагаемое в выражении (2.48) представляет собой волну, распространяющуюся из начала координат вдоль радиусов r со скоростью света    Действительно, функция в фиксированный момент времени t имеет одинаковые значения на сфере радиуса r = const. В момент времени t + Δt функция принимает то же значение на сфере радиуса r+cΔt, так как t+ Δt-(r+ cΔt)/c= t-r/c. Волны типа принято называть расходящимися сферическими волнами. Соответственно второе слагаемое в выражении (2.48) представляет собой сферическую волну, распространяющуюся из бесконечности со скоростью света с и сходящуюся к началу координат. Отметим существенную особенность функций, описывающих волновые процессы. Они всегда содержат множители вида f(t±r/v), характер зависимости которых от расстояния вдоль направления распространения волны в фиксированный момент времени повторяет характер их зависимости от времени в фиксированной точке пространства, а v-скорость распространения волны.

Если источники поля сосредоточены в ограниченной области, то сходящаяся сферическая волна может возникнуть только в результате отражения расходящейся сферической волны. Так как пространство считается однородным, то отраженной волны не может быть, и функцию f₂(t +r/с) нужно считать равной нулю. Следовательно, и = f₁(t- r/c)/r. Значения потенциала и должны быть связаны с интенсивностью источников поля. В рассматриваемом случае источником поля является точечный заряд Q(t). Полученное выражение для и должно быть справедливым при любом законе изменения функции Q(t). Так как в статическом случае потенциал и определяется формулой (2.43), естественно предположить, что f₁-r/c) = Q(t-r/c)/(4πε). Тогда u=Q(t-R/c)/(4πεr). Если заряд сосредоточен в малом элементе объема dV с плотностью ρ^ст = ρ^ст(t), то скалярный потенциал и = p^СТ(t-R/c)dV/(4πεR), где R-как и ранее, расстояние от элемента dV до точки наблюдения. От этой формулы легко перейти к выражению для скалярного потенциала, обусловленного произвольным распределением сторонних зарядов в объеме V:

декартовы координаты элемента dV; x, у, z -декартовы координаты точки наблюдения N; элемент объема  (рис.2.6).                                           

Выражение (2.49) является частным решением неоднородного уравнения Даламбера (2.41). Отметим, что приведенный здесь вывод не является строгим, он имеет лишь наводящий характер. Строгий вывод формулы (2.49) можно найти, например, в [12].

Аналогично можно записать и решение уравнения (2.40). Для этого нужно в (2.49) заменить и на А, ρ^ст на j^СТ и ε на 1/μ. В результате получим

Из (2.49) и (2.50) следует, что для вычисления электродинамических потенциалов и и А в произвольной точке пространства N=N(х, у, z) в момент времени t нужно брать значения токов и зарядов в каждом элементе dV в более ранний по сравнению с t момент времени t’= t-R/c, определяемый расстоянием R от элемента dV до точки наблюдения N(х, у, z) (рис.2.6). Иными словами, влияние источников электромагнитного поля проявляется не мгновенно: требуется некоторое время Δt = Rlc, за которое электромагнитные колебания, вызванные зарядами и токами в элементе dV, успеют распространиться от элемента dV до точки наблюдения. Поэтому функции А и и в форме (2.50) и (2.49) часто называют запаздывающими потенциалами.

2.4.2. Монохроматическое поле

Рассмотрим систему уравнений Максвелла для монохроматического поля, записанную для комплексных амплитуд векторов Е и Н:

Используя равенство div(μH_m) = O,  являющееся следствием второго уравнения системы (2.51), представим вектор Н_m в виде

где  А_m-комплексная амплитуда некоторого, пока неизвестного,

вектора А. Подставляя (2.52) во второе уравнение системы (2.51) и учитывая тождество (2.36), получаем

где   Ă_т - комплексная  амплитуда  некоторой,  пока  неизвестной,

скалярной функции и. Подставляя (2.52) и (2.53) в первое уравнение системы (2.51) и учитывая (2.26), имеем

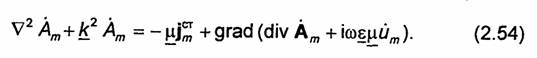
Соотношение (2.52) допускает некоторую свободу в определении вектора А_m (см. замечание к формуле (2.37)). Поэтому с целью упрощения  уравнения  (2.54)   потребуем   выполнения  дополнительного условия

которое обычно называют условием калибровки Лоренца. При этом равенство (2.54) переходит в неоднородное векторное уравнение Гельмгольца

Отметим, что условие калибровки (2.55) позволяет выразить через один векторный потенциал не только вектор Н_m, но и вектор

Ё_m. Действительно, выражая й_т из (2.55) и подставляя в (2.53), получаем

Предположим вначале, что среда, в которой ищется поле, является идеальным диэлектриком  В этом случае выражение для А_т может быть получено из формулы (2.50) заменой функции -комплексная амплитуда  плотности  сторонних электрических токов. Так как ,

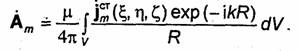
Для перехода к случаю среды с потерями достаточно в (2.58) заменить μ на μ и k на

Подставляя (2.53) в равенство являющееся следствием первого уравнения системы (2.51), и учитывая условие калибровки (2.55) и тождество (П.ЗО), приходим к уравнению Гельмгольца для скалярного потенциала:

В случае однородной среды без потерь (ε =ε,μ = μ, k = к) решение уравнения (2.59) может быть получено из (2.58) заменой функции  . При этом имеем

Для перехода к случаю среды с потерями нужно в (2.60) заменить ε на ε и k на

Полученные формулы соответствуют распределению сторонних источников в некотором объеме V. Если сторонние электрические токи являются поверхностными и распределены по некоторой поверхности S, то

где M-точка на поверхности S, принадлежащая элементу dS, a R-расстояние от точки М до точки наблюдения N=N(х, у, z) (рис. 2.7).

В случае линейного стороннего тока  j^ст,   распределенного

вдоль контура Г, комплексная амплитуда векторного потенциала определяется выражением

где t_o(M) - орт касательной к контуру Г в точке М, направление которой совпадает с направлением тока; dl - элемент контура Г, содержащий точку М; R-расстояние от точки М_Є Г до точки наблюдения N (рис. 2.8).

Аналогично видоизменяется формула (2.60) для скалярного потенциала и в случае поверхностных и линейных зарядов.

2.4.3. Плоские задачи электродинамики

При построении электродинамических моделей реальных задач часто считают, что поле, созданное сторонними источниками, и поперечное сечение рассматриваемой области не зависят от одной из декартовых координат, например от z. Такие модели называют плоскими (двумерными) задачами. Простейшим сторонним источником в этом частном случае является синфазная токовая нить- линейный электрический ток, текущий параллельно оси Z, амплитуда и фаза которого не зависят от z. Вычислим соответствующий ему векторный потенциал.

Предположим, что линейный электрический ток течет вдоль

оси Z. То/да, полагая в (2.62)   получаем

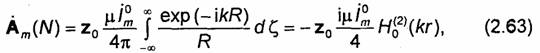
где -расстояние от точки интегрирования М =  М(0, О, ζ ), лежащей на оси Z, до точки наблюдения N(х, у, z);  - расстояние от точки N(х, у, z) до оси Z, a H ⁽²⁾₀ (kR)-функция Ханкеля второго рода нулевого порядка от аргумента кг, связанная с функциями Бесселя Jo(kr) и Неймана N₀(kr) нулевого порядка соотношением

При r→0 функция

имеет логарифмическую особенность, а при r→0 справедливо асимптотическое соотношение Как видно, на больших расстояниях от источника (kr>>1) поверхности, на которых фаза функции А_m одинакова во всех точках, описываются уравнением r = const и представляют собой поверхности соосных круговых цилиндров, бесконечно протяженных вдоль оси z. С учетом знака в показателе степени множителя ехр [— i (kr—π/4)] поле, создаваемое синфазной токовой нитью, может быть названо цилиндрической волной, распространяющейся от источника к бесконечности.

Так как в рассматриваемом случае поле не зависит от z, a

вектор A_m=z_QA_m, то divA_m=0 и выполняется простое соотношение Ёm = -iωA_m.

Отметим, что хотя до сих пор при записи формул (2.50), (2.58) и (2.61)-(2.63) для векторного потенциала речь шла о поле, создаваемом сторонними источниками, аналогичные формулы имеют место и для векторного потенциала, создаваемого другими токами, например токами, возникающими на металлическом объекте под воздействием поля сторонних источников.

Выпишем в качестве примера векторный потенциал, соответствующий поверхностным токам, текущим по идеально проводящей бесконечно протяженной вдоль оси Z цилиндрической поверхности S, поперечное сечение которой - контур Г (рис. 2.9). Рассмотрим случай, когда токи текут вдоль образующих поверхности S. Комплексная амплитуда плотности этих токов равна . Контур Г может быть как замкнутым (в этом случае поверхность S эквивалентна сплошному идеально проводящему цилиндру), так и незамкнутым (поверхность S представляет собой бесконечно тонкий идеально проводящий незамкнутый экран). В случае незамкнутого контура Г под j_sm(M) следует понимать сумму комплексных амплитуд плотностей поверхностных токов, текущих по обеим сторонам поверхности S в точке М. Ток, протекающий через элемент dl. контура Г, можно рассматривать как токовую нить, параллельную оси Z и проходящую через точку М. Комплексная амплитуда этого тока равна dj_m = j_Sm(M)dl, M_Єdl В соответствии с принципом суперпозиции комплексная амплитуда векторного потенциала, создаваемого всеми токами, текущими по S, определяется выражением

где R(M, N) - расстояние от точки МеГ до точки наблюдения N = (х, у); контур Г и точка N лежат в одном поперечном сечении поверхности S.

2.5. СТОРОННИЕ МАГНИТНЫЕ ТОКИ И ЗАРЯДЫ

Понятия сторонних электрических токов и зарядов, распределенных в некотором объеме с плотностями j^ст и ρ^ст соответственно, были введены в §1.8. Если сторонние токи и заряды заданы в тонком слое, то при постановке электродинамической задачи часто считают, что этот слой является бесконечно тонким, т.е. может быть аппроксимирован некоторой поверхностью S, а вместо j^ст и ρ^ст задают плотности сторонних поверхностных электрических токов  и зарядов . Назовем одну из сторон поверхности S первой, а другую- второй. Значения функций, вычисленные в точках, принадлежащих определенной стороне поверхности, будем обозначать соответствующим индексом 1 или 2.

Наличие на S поверхностных электрических токов обязательно приводит (см.1.7.2) к разрыву при переходе через S касательной составляющей вектора Н:

где п₀ - орт нормали к первой стороне поверхности S.

Аналогично сторонние поверхностные электрические заряды, распределенные по S, вызывают появление разрыва при переходе через S нормальной составляющей вектора D = εЕ:

где ε₁ и ε₂ - абсолютные диэлектрические проницаемости сред, расположенных с соответствующих сторон поверхности S. В общем случае поверхность S может частично или полностью совпадать с границей раздела сред. Поэтому параметры ε₁ и ε₂ могут быть как одинаковыми, так и разными. Таким образом, задание сторонних поверхностных электрических токов и зарядов эквивалентно заданию разрыва касательной составляющей вектора Н и нормальной составляющей вектора D (вектора Е) соответственно.

Для упрощения электродинамической модели, заменяющей реальную систему, в ряде случаев вводят так называемые сторонние магнитные токи и заряды.

Задание сторонних поверхностных магнитных токов эквивалентно заданию разрыва касательной составляющей вектора Е при переходе через рассматриваемую поверхность S:

где индексы 1 и 2, как и прежде, означают, что функция вычислена соответственно на первой или на второй стороне поверхности S. Выбор знака в правой части равенства (2.67) будет пояснен ниже. Задание  на поверхности S обязательно приведет к разрыву на

S нормальной составляющей вектора В = μН. Величину этого разрыва можно трактовать как плотность сторонних поверхностных магнитных зарядов:

Подчеркнем, что введенные таким образом магнитные токи и заряды являются фиктивными, однако в ряде случаев они позволяют существенно упростить электродинамическую модель реальной системы.

Зная плотности , можно вычислить величины магнитных токов и зарядов , сосредоточенных на S или какой-либо части поверхности S. По аналогии с обычным током проводимости магнитный ток можно рассматривать как упорядоченное движение магнитных зарядов, а в качестве положительного направления магнитного тока принять направление движения положительных магнитных зарядов. Магнитные токи измеряются в вольтах, магнитные заряды - в веберах. Плотность поверхностных магнитных зарядов измеряется в веберах на квадратный метр, плотность поверхностных магнитных токов - в вольтах на метр.

При построении электродинамических моделей реальных систем иногда удобно, считать, что магнитные токи и заряды распределены в некотором объеме с плотностями j^м и ρ^м соответственно. Функции j^м и ρ^м определяются формулами, аналогичными (1.8) и (1.42) соответственно. Плотность магнитных токов j^м измеряется в В/м² , об%емная плотность магнитных зарядов-в Вб/м³ . Магнитные токи /^м выражаются через их плотность j^м формулой, аналогичной (1.26), магнитные заряды Q^м - через ρ^м формулой, аналогичной (1.41).

Сторонние магнитные источники можно учесть в уравнениях Максвелла так же, как были учтены сторонние электрические источники (см. 1.8.1). Из первого уравнения Максвелла (1.111) видно, чо плотность сторонних электрических токов j^ст входит в правую часть этого уравнения со знаком "+" так же, как плотность тока смещения dD/dt. Плотность сторонних магнитных токов должна быть введена во второе уравнение Максвелла (1.39). В правой части этого уравнения стоит функция dB/dt. Формально, по аналогии с dD/dt, ее можно назвать плотностью магнитного тока смещения. Так как перед dB/dt стоит знак минус, то и функцию j^м целесообразно ввести с таким же знаком. При этом второе уравнение Максвелла примет вид

Из уравнения (2.69) следует, что сторонние магнитные токи, так же, как переменное во времени магнитное поле, создают вихревое электрическое поле, силовые линии которого, расположенные в непосредственной близости к рассматриваемой точке, охватывают линии вектора  образуя с ним левовинтовую систему (рис. 2.10).

Вернемся к соотношению (2.67), определяющему плотность сторонних поверхностных магнитных токов  . Как видно, выбор

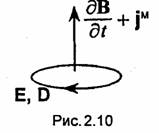
знака в правой части формулы (2.67) соответствует выбору знака перед j^м во втором уравнении Максвелла (2.69).

Сторонние магнитные заряды учитываются в четвертом уравнении Максвелла:

div В = ρ^м.                           (2.70)

Из (2.69) и (2.70) следует соотношение

аналогичное уравнению непрерывности (1.48). Интегрируя (2.71) по объему V, приходим к закону сохранения магнитных зарядов:

где S-замкнутая поверхность, ограничивающая объем  V, dS = n_odS, n₀ - орт внешней нормали к поверхности S.

Таким образом, система уравнений Максвелла, учитывающая сторонние электрические и магнитные источники, имеет вид

Полная  система  уравнений   Максвелла  для  монохроматического поля состоит из двух уравнений:

так как третье и четвертое уравнения Максвелла в этом случае могут быть получены из (2.74), уравнения непрерывности (1.116) и соотношения div j^м + iωρ^м = 0, вытекающего из (2.71).

2.6. ПРИНЦИП ДВОЙСТВЕННОСТИ

Рассмотрим систему уравнений Максвелла для монохроматического поля (2.74). Если в этих уравнениях формально заменить

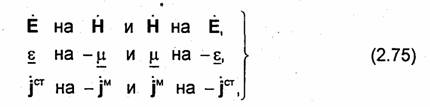
то первое уравнение системы (2.74) превратится во второе, а второе -в первое. В целом система уравнений (2.74) не изменится. Эту особенность уравнений (2.74) называют перестановочной двойственностью уравнений Максвелла.

Из перестановочной двойственности уравнений Максвелла вытекает важное следствие. Пусть две краевые электродинамические задачи сформулированы для геометрически одинаковых областей таким образом, что все условия, которым должны удовлетворять векторы Ё и Н в первой задаче, при заменах (2.75)переходят соответственно в условия для векторов Н и Ё второй задачи. Иными словами, при заменах (2.75) первая задача превращается во вторую, а вторая -в первую. Тогда нет необходимости решать обе задачи, достаточно найти решение одной из них. Произведя в найденном решении замены (2.75), получим решение другой задачи. Возможность применения перестановочной двойственности уравнений Максвелла для решения краевых задач электродинамики будем называть принципом двойственности.

В качестве примера применения перестановочной двойственности уравнений Максвелла рассмотрим вопрос о вычислении поля, создаваемого Сторонними магнитными источниками в однородной изотропной среде. Это поле удовлетворяет уравнениям

Система уравнений (2.76) может быть получена из (2.51), если в последней произвести замены (2.75). Поэтому и формулы для поля, создаваемого магнитными источниками, могут быть получены на основе замен (2.75) в окончательных формулах для поля, создаваемого сторонними электрическими источниками. При этом

удобно ввести в рассмотрение векторный (А^м) и скалярный (й^м) магнитные потенциалы, связанные условием калибровки  При использовании этого условия поле, создаваемое сторонними магнитными источниками, может быть выражено через один векторный магнитный потенциал:

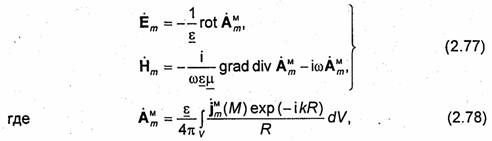
a R - расстояние от точки интегрирования M_ЄdV до точки наблюдения.

В случае поверхностных и линейных магнитных токов формулы для  могут быть получены аналогично из (2.61) и (2.62) соответственно. Окончательные выражения очевидны и здесь не выписываются.

Если электромагнитное поле создается и электрическими, и магнитными сторонними источниками, т.е. удовлетворяет системе

уравнений (2.74), то векторы  определяются соотношениями

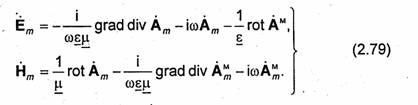
2.7. ПОСТАНОВКА И НЕКОТОРЫЕ ПОДХОДЫ К РЕШЕНИЮ

КРАЕВЫХ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

С учетом изложенного в данной главе остановимся более подробно на вопросе о постановке краевых задач электродинамики.

Вначале анализируется реальная электродинамическая проблема и определяется, на какие вопросы требуется получить ответ, что необходимо учесть, чем можно пренебречь. Затем от реальной задачи переходят к ее электродинамической модели (одной или нескольким). Выбранная модель должна быть такой, чтобы, во-первых, соответствующая ей электродинамическая задача могла быть решена, а во-вторых, чтобы полученное решение дало ответ на интересующие вопросы. Указанную задачу обычно формулируют как краевую задачу электродинамики. Она состоит в нахождении такого электромагнитного поля, которое в рассматриваемой части пространства удовлетворяет уравнениям Максвелла, а на границе области - одному из краевых условий, при которых может быть доказана теорема единственности. В случае внешней задачи полученное решение должно, кроме того, удовлетворять условиям излучения (2.23). Если граница области (поверхность S) имеет изломы, решение должно удовлетворять условиям на ребре. При выполнении перечисленных требований решение краевой задачи, соответствующей выбранной электродинамической модели, будет единственным.

Получить аналитическое решение непосредственно из уравнений Максвелла обычно не удается. Поэтому часто краевую задачу сводят к решению уравнения Гельмгольца либо для векторов поля, либо для электродинамических (или других) потенциалов. Полученное при указанном подходе аналитическое решение электродинамической задачи обычно- выражается в виде бесконечных рядов по специальным функциям. Примеры таких решений приведены в гл.З и 8 (см.3.6.2 и 8.2).

Интенсивное развитие вычислительной техники позволило разработать ряд эффективных численных методов решения краевых задач электродинамики.

В случае внутренних задач широко используется так называемый метод сеток. При его применении рассматриваемая область разбивается на ячейки. В случае плоских (двумерных) задач эти ячейки образуют плоскую сетку. Значения неизвестных функций ищутся в узлах сетки или в серединах ячеек, а их производные определяются по обычным формулам численного дифференцирования. Пример применения метода сеток для решения внутренних задач приведен в гл.З.

Внешние задачи электродинамики часто сводят к решению интегральных уравнений, т.е. уравнений, в которых искомая функция входит под знак интеграла. Если рассматриваемое тело (граница области V, вне которой требуется найти поле) является  идеально проводящем, в качестве искомой функции обычно выбирают комплексную амплитуду плотности поверхностных токов

j_sm, текущих по поверхности тела S.

Комплексная амплитуда напряженности вторичного электрического поля Ё_m выражается по формуле (2.57) через комплексную амплитуду векторного потенциала А_m, которая связана с функцией j_sm соотношением (2.61). Это позволяет представить вектор Ё_m в виде интеграла от j_Sm. Используя затем граничное условие  комплексная амплитуда касательной к поверхности S составляющей вектора напряженности первичного электрического поля в точке М_о, получаем   соотношение,   содержащее   одну   неизвестную   функцию

j_sm(M), M_ЄS, стоящую под знаком интеграла. Это соотношение можно рассматривать как, интегральное (в общем случае интегро-дифференциальное)  уравнение  относительно  функции   j_sm (М).

Вывод интегрального уравнения для частной задачи и один из возможных способов построения его численного решения приведены в 8.3.

Если размеры области V велики по сравнению с длиной волны, для решения электродинамических задач обычно используют различные приближенные методы (см. гл.8).