7.5. Коды Хемминга

К этому типу кодов обычно относят систематические коды с расстоянием d = 3, которые позволяют исправить все одиночные ошибки (7.3).

Рассмотрим построение семизначного кода Хемминга, каждая комбинация которого содержит четыре информационных и три контрольных символа. Такой код удовлетворяет неравенству (7.11) и имеет избыточность:

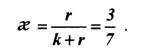
Если информационные символы занимают в комбинации первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:

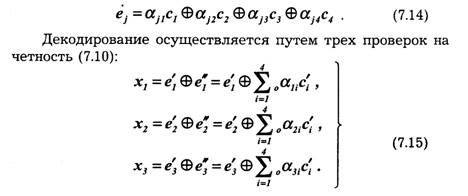
Так как х равно  0 или 1, то всего может быть восемь контрольных чисел   X = х_гх₂х₃: 000,100,010,001,011,101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами и искаженными символами. Если искажен один из контрольных символов е'_1,е'₂ или е'₃, то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах. Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1.

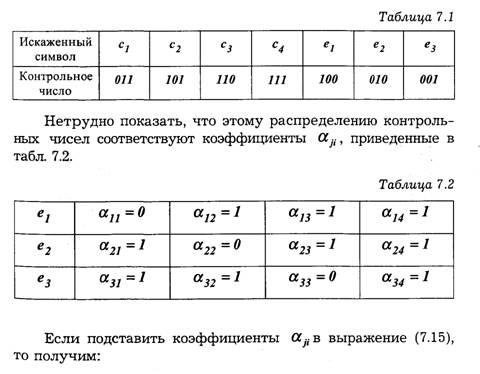
При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число Х = х₁х₂х₃ согласуется с табл. 7.1. Нетрудно заметить, что первые четыре контрольные числа табл. 7.1. совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов α_ji. Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1. определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 7 на 0. В качестве примера рассмотрим передачу комбинации, в которой информационными символами являются c₁c₂c₃c₄ = 1011. Используя формулу (7.14) и табл. 7.2., вычислим контрольные символы:

Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблицей. Вместе с тем существует более простой метод отыскания одиночных ошибок, предложенный впервые самим Хеммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Символы в комбинациях должны размещаться в следующем порядке: c₁c₂c₃c₄c₅c₆c₇, а контрольное число вычисляться по формулам:

Так, если произошла ошибка в информационном символе с'₅, то контрольное число X = x₁x₂x₃=101, что соответствует числу 5 в двоичной системе.

В заключение отметим, что при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.

7.6. Циклические коды

Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации A_i дает другую кодовую комбинацию A_j также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносит-

Помимо цикличности кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени r = п-k, где k — значность первичного кода без избыточности, а n — значность циклического кода.

Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A* (z) на порождающий полином G(z)

Умножение производится по модулю zⁿ и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.

В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа r нулей, что эквивалентно повышению полинома A*(z) на r разрядов, т. е. умножению его на z^r. Затем произведение z^r • A*(z) делится на порождающий полином. В общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда:

В A(z) высшие четыре разряда занимают информационные символы, а остальные три — контрольные.

Контрольные символы в циклическом коде могут быть вычислены и по общим формулам (7.9), однако здесь определение коэффициентов α_ji. затрудняется необходимостью выполнять требование делимости A(z) на порождающий полином G(z).

Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z) . Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.

Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают, сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигналов.

7.7. Коды с постоянным весом

В теории кодирования весом кодовых комбинаций принято называть количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5 Примером комбинаций кода   3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной кратности и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:

В этом коде из общего числа комбинаций М = 2⁷ = 128 разрешенными являются лишь М₀ =с³₇ = 35, поэтому коэффициент избыточности:

Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.

7.8. Непрерывные коды

Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка — Хагелъбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:

Расстояние между информационными символами L = k — i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода æ =0,5. Процесс образования последовательности контрольных символов показан на рис. 7.2а.

Полученные контрольные символы размещаются между информационными символами с задержкой на два шага сложения.

При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов   е'' , которая сравнивается с принятой последовательностью контрольных символов е'   (рис. 7.26). Если произошла ошибка в информационном символе, например,   с'_k, то это вызовет искажения сразу двух символов: е"_ik и е"_kт, что и обнаружится в результате их сравнения с е'_ik и е'_kт. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с'_k. Ошибка в принятом контрольном символе, например, e'_ik, приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление такой ошибки не требуется.

Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но и группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2L, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2L при интервале между пакетами не менее 6L+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения L, а следовательно, и с усложнением кодирующих и декодирующих устройств.

7.9. Обобщение теории кодирования на недвоичные коды

До сих пор мы рассматривали только двоичные коды. Однако это делалось лишь для простоты. На самом деле теория линейных кодов обычно излагается сразу для m-ичных кодов, где т= р^L , р — простое число, L — натуральное число, т. е. для случая, когда над символами кода могут быть осуществлены все арифметические действия, которые существуют над вещественными или комплексными числами. Для таких т -ичных кодов могут быть определены и доказаны все свойства, известные для двоичных кодов. Наиболее важным классом т -ичных кодов являются коды Рида—Соломона (кратко — PC-коды). Они могут быть построены как систематические циклические (п,к)-коды при n = q — l, n—k = 2t, где t — число исправляемых ошибок. Коды PC являются частью стандарта цифровой записи на компакт-дисках.

Можно показать, что никакой линейный систематический т -ичный (т≥2) код не может иметь d>n — k +1. Действительно, если выбрать значение k минус одного информационного символа равным нулю, то это даст ненулевое кодовое слово веса не более, чем п—k + 1, что по свойству линейного кода и определяет верхнюю границу для d как п — k + 1. Поскольку PC-код реализует верхнюю границу для минимального кодового расстояния, то он оказывается оптимальным среди всех т -ичных (п, к) -кодов в смысле исправления и обнаружения ошибок гарантированной кратности.

Выбор длины кода n = q-1 является достаточно сильным ограничением, поэтому можно строить так называемые укороченные коды PC, имеющие произвольную длину n≤q — 1. Их можно получить из полных PC-кодов, имеющих длину п = q — 1, если положить часть информационных символов равными нулю и выбросить их из кодовых блоков. Легко видеть, что укорочение кода не может уменьшить кодовогорасстояния, и поэтому (п,k)-код, при n≤q — 1 будет по-прежнему иметь d = n - k +1.

Такого типа коды совместно с двоичными кодами могут быть использованы для построения каскадных кодов.

7.10. Итеративные и каскадные коды

Мощные коды (т. е. коды с длинными блоками и большим кодовым расстоянием d ) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код из двух линейных систематических кодов (n₁,k₁) и (п_2,k₂) — см. табл. 7.3. Вначале сообщение кодируется кодом первой ступени (n₁,k₁) Пусть k₂ блоков кода 1-й ступени записаны в виде строк матрицы. Ее столбцы содержат по k₂ символов, которые будем считать информационными для кода 2-й ступени (п₂,k₂), и подпишем к ним п₂—k₂ проверочных символов. В результате получится блок (матрица n₂xn₂), содержащий n₁п₂ символов, из которых k₁k₂ являются информационными. Процесс построения кода можно продолжить в 3-м измерении и т. д.

При декодировании каждого блока 1-й ступени обнаруживают и исправляют ошибки. После того, как принят весь двумерный блок, вновь исправляют ошибки и стирания, но уже по столбцам, кодом 2-й ступени, причем приходится исправлять только те ошибки, которые не были исправлены (или были ложно "исправлены") кодом 1-й ступени. Легко убедиться, что минимальное кодовое расстояние для двухмерного итеративного кода d = d₁d₂, где d₁d₂ и— соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступени.

Весьма эффективная разновидность мощных кодов — каскадные коды.

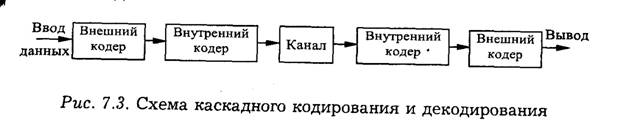
Двухкаскадный код (рис. 7.3) строится следующим образом: сначала k₁, двоичных символов источника рассматривается как укрупненный символ многопозиционного кода с основанием   т=2^k1. Затем к последовательности из   k₂ таких укрупненных символов добавляется п₂ -k₂ проверочных символов   m-ичного кода (каждый проверочный символ — это последовательность из k₁ проверочных символов). На этом завершается образование внешнего кода. После этого формируется внутренний код с кодовым расстоянием  d₁: к каждым k₁ элементарным двоичным символам внешнего кода прибавляется  n₁-k₁ проверочных двоичных символов, из которых k₁-k₂ являются информационными. Этим каскадный код похож на итеративный. Однако декодирование каскадного кода выполняется следующим образом: сначала последовательно осуществляется декодирование всех блоков внутреннего кода (с обнаружением или исправлением ошибок), затем декодируется блок внешнего m-ичного кода (п₂,k₂), причем исправляются ошибки и стирания, оставшиеся после декодирования внутреннего кода. Внутренний код обычно рассчитан на исправление одиночных ошибок, внешний — на исправление пачек ошибок (которые являются одиночными ошибками в укрупненных т -ичных символах — рис. 7.3). В качестве внешнего кода используется обычно т -ичный код Рида—Соломона, обеспечивающий наибольшее возможное   d₂ при заданных значениях п₂ и k₂, если п₂<т.

Построенный каскадный код эквивалентен линейному двоичному коду с минимальным расстоянием d > d_td₂ Фактически рассмотренный выше алгоритм декодирования каскадного кода оказывается достаточно эффективным и простым.

Использование каскадных кодов позволяет сделать скорость передачи сколь угодно близкой к пропускной способности канала. Процесс наращивания ступеней каскадного кода можно продолжить. Каскадные коды во многих случаях наиболее перспективны среди известных блоковых помехоустойчивых кодов.

7.11. Адаптивные корректирующие коды

Существенным недостатком многих корректирующих кодов является их слабая приспособленность к изменяющимся условиям передачи информации. Избыточность таких кодов постоянна и выбирается обычно из соображений обеспечения требуемой верности при наихудших условиях передачи. Если избыточность кода привести в соответствие с реальным состоянием канала в контролируемом интервале времени (по результатам анализа группирования ошибок), можно существенно повысить эффективность использования каналов без снижения достоверности. Эта идея лежит в основе адаптивных корректирующих кодов.

Различают методы адаптивного декодирования, когда в зависимости от числа ошибок в принимаемых кодовых комбинациях изменяют структуру или параметры алгоритмов декодирования и функции схем декодеров, и методы адаптивно-

го кодирования, когда наряду с этим изменяют структуру или параметры кодов, алгоритмов кодирования и схем кодеров. Функции адаптивных декодеров в значительной степени зависят от возможностей организации обратного канала, характера искажений сигналов и помех в канале, показателя группирования ошибок и других факторов. Для построения систем адаптивного кодирования требуется канал обратной связи, по которому на передающую сторону направляют информацию о качестве канала и об условиях приема.

Обнаружение ошибок адаптивными кодами систем без обратной связи позволяет обеспечить практически любую заданную достоверность при относительно невысокой сложности оборудования, но часть информации теряется, так как комбинации с обнаруженными ошибками потребителю не выдаются. Исправление ошибок также позволяет обеспечить достоверность передачи, но при отсутствии потерь информации. Платой за это является значительное увеличение длины кодовых комбинаций, до десятков тысяч разрядов, а также существенное усложнение аппаратуры. Недостатком систем без обратной связи является и то, что передатчик не получает никаких подтверждений о том, как принята информация приемником. Поэтому предъявляют очень высокие требования к надежности систем. Системы без обратной связи находят применение в случаях, когда канал обратной связи невозможно организовать или когда недопустимы задержки при передаче информации. К таким системам относятся, например, некоторые системы спутниковой связи.

Наиболее широкое применение получили системы с обратной связью, в которых повышение достоверности достигается обнаружением ошибок на приемном конце и повторением только неправильно принятых комбинаций. Адаптивное управление повторением информации существенно приближает избыточность кода к информационному пределу. Избыточность оптимальна при отсутствии ошибок и растет с увеличением числа ошибок. Основными задачами, которые решают при построении систем с адаптивными алгоритмами кодирования и декодирования, являются: разработка методов и аппаратуры контроля состояния каналов, оптимизация использования полученной информации о состоянии канала для изменения способа кодирования, параметров элементов сигнала, процедуры принятия решений и т. п.; разработка стратегий принятия оптимальных решений в приемнике в зависимости от состояния канала и характера группирования ошибок; отыскание таких алгоритмов кодирования и декодирования, при которых системы становятся инвариантными относительно статистических особенностей реальных каналов и позволяют добиться оптимальной избыточности; построение методов и аппаратуры контроля канала, которые не зависят от того, какие сигналы передаются в моменты контроля.

Теория адаптивного корректирующего кодирования интенсивно развивается, так как позволяет более полно учесть реальные условия передачи информации.

Контрольные вопросы и задания

1. Как могут быть классифицированы корректирующие коды?

2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?

3. В чем состоят основные принципы корректирования ошибок?

4. Дайте определение кодового расстояния.

5.  При каких условиях код может обнаруживать или исправлять ошибки?

6. Как используется корректирующий код в системах со стиранием?

7. Какие характеристики определяют корректирующие способности кода?

8. Как осуществляется построение кодовых комбинаций в систематических кодах?

9. На чем основан принцип корректирования ошибок с использованием контрольного числа?

10. Объясните метод построения кода с четным числом единиц.

11. Как осуществляется процедура кодирования в семизначном коде Хемминга?

12. Почему семизначный код ³/₄ не обнаруживает ошибки смещения?

13. Каким образом производится непрерывное кодирование?

14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?

15. Объясните принцип построения каскадного кода.

16.  Для каких целей используются адаптивные корректирующие коды?

ГЛАВА 8

ЭЛЕМЕНТЫ ТЕОРИИ ПРИЕМА И ОБРАБОТКИ ИНФОРМАЦИИ

8.1. Общие сведения о приеме сигналов

На приемной стороне о передаваемых сигналах обычно имеются некоторые предварительные (априорные) сведения. Могут быть известными, например, частота несущей, вид модуляции и т. п. Сигнал, о котором заранее все известно, не несет информации, а абсолютно неизвестный сигнал нельзя было бы принять.

Известные параметры сигнала используются в приемнике для лучшего отделения сигналов от помех. Чем больше мы знаем о сигнале, тем совершеннее могут быть методы приема.

Параметры, в изменениях которых заключена переносимая информация, называются информационными (см. гл. 2,3). Изменения этих параметров на приемной стороне заранее

неизвестны.

В зависимости от вида и назначения системы передачи информации при приеме сигналов возникают следующие основные задачи:

• обнаружение сигналов;

• различение сигналов;

• восстановление сигналов.

При обнаружении сигналов задача сводится к получению ответа на вопрос, имеется на входе приемника сигнал или нет, точнее, имеется ли на входе сигнал плюс шум или только шум.

С такой задачей мы обычно встречаемся в радиолокации, она также имеет место и в системах передачи дискретной информации. Если мы в состоянии обнаружить сигнал, то появляется возможность передачи информации при помощи двоичного кода. Наличие сигнала (посылка) будет соответствовать символу 1, отсутствие сигнала (пауза) — символу 0. Этот принцип используется в системах с пассивной паузой.

При передаче двух сигналов s₁ и s₂ возникает задача не обнаружения, а различения сигналов. Здесь необходимо дать ответ на вопрос: имеется ли на входе приемника сигнал s₁ или сигнал s₂ ? Ответ на этот вопрос определяется уже не свойствами каждого сигнала в отдельности, а их различием. Сигналы могут отличаться один от другого своими параметрами. Очевидно, нужно стремиться к тому, чтобы различие было наибольшим и устойчивым к воздействию помех. Случай обнаружения может рассматриваться как вырожденный случай различия двух сигналов, когда один из них тождественно равен нулю.

Передача двоичным кодом, в котором каждому символу (1 и 0) соответствует определенный сигнал (s₁ и s₂), не равный нулю, называется передачей с активной паузой. Случай различения многих сигналов принципиально мало отличается от случая различения двух сигналов.

Задача восстановления сообщения принципиально отличается от задач обнаружения и различения сигналов. Она состоит в том, чтобы получить выходной видеосигнал v(t), наименее отличающийся от переданного сообщения u(t). При этом сообщение u(t) заранее неизвестно: известно лишь, что оно принадлежит к некоторому множеству или является реализацией некоторого случайного процесса.

На рис. 8.1 приведена функциональная схема обработки дискретных сигналов. Принятый сигнал, искаженный помехой, в приемнике подвергается определенной обработке, детектируется и для опознавания поступает на решающее устройство. Очевидно, что вероятность правильного опознавания сигналов существенно зависит от отношения сигнала к помехе на входе решающего устройства. В связи с этим основной задачей обработки сигналов в приемнике является увеличение отношения сигнал/шум. Обработка сигналов, как правило, сводится к тем или иным методам фильтрации.

В каскадах обработки производится также усиление сигналов до величин, при которых могут нормально работать детектор и решающее устройство.

В обычном приемнике непрерывных сигналов детекторная обработка сигналов осуществляется с помощью резонансных усилителей, обеспечивающих необходимую частотную избирательность. Функции последетекторной обработки при этом выполняются видеоусилителем (или усилителем низкой частоты). Решающее устройство в таких приемниках отсутствует. Вместо него на выходе имеется устройство, воспроизводящее или записывающее (регистрирующее) принятое сообщение.

В системах передачи дискретных сообщений основными видами обработки сигналов в приемнике являются фильтрация со стробированием, интегрирование и корреляционная обработка.

Стробирование сигнала является простейшим видом обработки. Оно давно известно и широко применяется в практике. Обработку сигналов стробированием часто называют приемом по методу укороченных контактов. При стробировании данного элемента сигнала производится отсчет его текущего значения (напряжения или тока) в определенный момент времени. Последний выбирается в той части элемента, которая в наименьшей степени подвержена искажениям. Так как статистические характеристики помех мало зависят от выбора момента времени, то момент стробирования необходимо выбирать тогда, когда полезный сигнал имеет максимальное значение. Вследствие переходных процессов в фильтрах границы элементов сигнала в значительной степени искажены, и поэтому максимальное значение сигнала, как правило, соответствует средней части элемента. Стробирование производится при помощи специальных сигналов, поступающих от системы синхронизации.

Фильтрация принимаемых сигналов может выполняться как до, так и после детектора. При использовании синхронного детектора фильтрация до и после детектора принципиально может дать один и тот же результат. Практически же обычно производят фильтрацию сигнала дважды: как до, так и после детектора.

Операция интегрирования может рассматриваться либо как процесс накопления (суммирования), либо как определение среднего значения сигнала. Любой фильтр в той или иной мере производит интегрирование поступающего на его вход колебания. При определенных условиях операция интегрирования эквивалентна фильтрации. Интегрирование, так же как и фильтрация, может осуществляться либо до, либо после детектора.

Методы приема можно классифицировать по видам применяемых детекторов, по способам додетекторной и последетекторной обработки. Различают следующие основные методы приема:

•   когерентный;

•   некогерентный;

•   корреляционный;

•   автокорреляционный.

8.2. Методы накопления

Одним из эффективных и широко применяемых в различных вариантах методов борьбы с помехами является метод накопления. Сущность метода состоит в том, что сигнал или его элементы многократно повторяются. На приеме отдельные образцы сигнала сличаются (обычно суммируются), и так как различные образцы по разному искажаются помехой, в силу независимости последних, то можно восстановить переданный сигнал с большой достоверностью.

В простейшей форме метод накопления часто применяется при телефонном разговоре в условиях плохой слышимости, когда переспрашивают и повторяют одно и то же слово по несколько раз.                                                                       

В случае двоичного кода каждая кодовая комбинация передается по несколько раз. Если вероятность сбоя символов 1 и 0 одинакова, то на приеме решение выносится "по большинству", т. е. воспроизводится символ 1 на данной позиции, когда их число на этой позиции больше числа символов 0, и, наоборот, воспроизводится 0, когда число "нулей" больше числа "единиц". Пример:

Переданная комбинация                               01001

1-я принятая комбинация                             00001

2-я принятая комбинация                             11010

3-я принятая комбинация                             01101

Воспроизведенная комбинация                   01001

Заметим, что можно было бы получить n образцов сигнала не путем их повторения во времени, а путем передачи по независимым каналам, разделенным по частоте, или каким-либо другим способом.

Существуют и другие разновидности метода накопления. К ним, в частности, относится метод синхронного накопления, когда на протяжении посылки берется не один отсчет, а несколько. На приеме эти отсчеты суммируются в накопителе. Пусть отдельные отсчеты принятого сигнала:

Таким образом, при описанных условиях накопление отсчетов сигнала позволяет увеличить отношение сигнала к помехе на выходе приемника в п раз. Суть дела сводится к тому, что мощность сигнала при суммировании растет пропорционально п₂ (складываются напряжения), а мощность помехи — пропорционально п (суммируются мощности). Поэтому отношение сигнала к помехе увеличивается в п раз, если помехи независимы. При наличии корреляции между значениями помехи этот выигрыш будет меньше.

коррелированна с сигналом). Описанный способ приема называется интегральным.

Практическая реализация метода интегрирования осуществляется проще, чем суммирование дискретных значений. Так, при приеме двоичных сигналов широко используется цепочка RC, разряжаемая синхронно по окончании каждой элементарной посылки (рис. 8.2.)

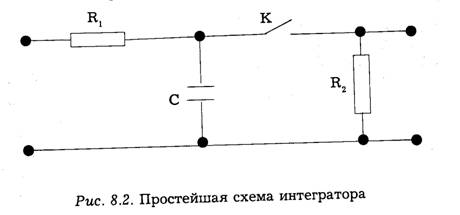
В конце каждой посылки заряд на емкости приблизительно пропорционален интегралу входного сигнала. Додетекторное интегрирование можно осуществить с помощью резонатора большой добротности. В простейшем случае таким резонатором может быть колебательный контур.

8.3. Когерентный и некогерентный приемы

Для оптимального когерентного приема необходимо выполнение следующих условий: передаваемые сигналы полностью известны и могут быть точно воспроизведены в приемном устройстве; канал связи гауссов с постоянными параметрами, искажения сигналов в канале отсутствуют; спектральная плотность аддитивной помехи известна; синхронизация принимаемых и опорных сигналов является идеальной.

Функциональная схема когерентного приемника приведена на рис. 8.3. Она состоит из перемножителя П, генератора опорного колебания Г и фильтра нижних частот ФНЧ.

Опорное колебание s₀(t) при когерентном приеме представляет собой точную копию переданного сигнала s(t). Если сигналом s(t) является колебание с известной частотой и фазой, то в приемнике используется синхронный детектор, в котором опорное колебание синхронно с колебанием несущей частоты. При синхронном детектировании на нелинейный элемент (см. п. 3.6) подается сумма двух сигналов:

На выходе синхронного детектора выделяется передаваемое сообщение, причем по соотношению к входному сигналу такая обработка практически является линейной.

Фильтр нижних частот выполняет роль интегратора, он выделяет на выходе напряжение, практически совпадающее с огибающей входного (высокочастотного) сигнала.

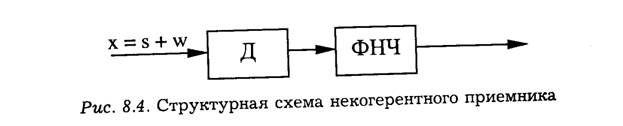
При некогерентном приеме априорные сведения о начальной фазе принятого сигнала не учитываются, поэтому в схеме можно применять не синхронный, а амплитудный детектор (Рис. 8.4).

8.4. Корреляционный и автокорреляционный методы приема

При корреляционном приеме некоторый момент времени Т измеряется значением функции взаимной корреляции у(Т) принятого сигнала x(t) = s(t) + w(t) и опорного колебания s_g(t). Структурная схема корреляционного приемника приведена на рис. 8.5. Она состоит из перемножителя П, генератора колебания Г и интегратора И.

В зависимости от метода регистрации сигнала на выходе корреляционный прием может быть когерентным и некогерентным.

Отношение сигнала к помехе на выходе корреляционного приемника при когерентном приеме будет равно:

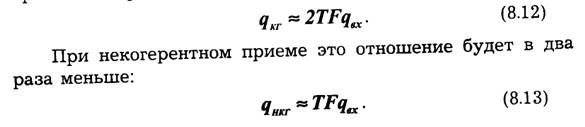
Корреляционный способ приема можно рассматривать как обобщение метода накопления на сигналы произвольной формы.

В схеме автокорреляционного приемника отсутствует специальный генератор опорных колебаний (рис. 8.6).

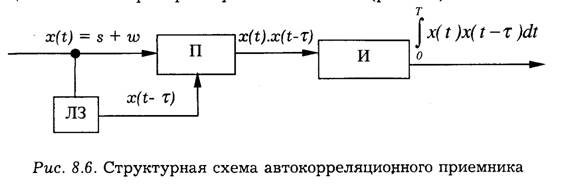
В данной схеме имеется линия задержки ЛЗ, осуществляющая задержку принимаемого сигнала на время τ. Задержанное колебание x(t-τ) используется в качестве опорного.

При большом уровне помех (qвx<<1) автокорреляционный приемник по помехоустойчивости приближается к приемнику с квадратичным детектором. Более низкая помехоустойчивость автокорреляционного приемника по сравнению с корреляционным при любых значениях q_ex обусловлена наличием помехи в тракте опорного напряжения. Автокорреляционный прием возможен и в том случае, когда отсутствуют сведения не только о фазе сигнала, но и о частоте. Это возможно благодаря тому, что опорное колебание порождается самим принимаемым сигналом, а не создается специальным генератором в месте приема.

8.5. Прием на согласованный фильтр

Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна. К таким сигналам, в первую очередь, относятся дискретные двоичные сигналы. В этих случаях важным параметром, характеризующим качество обнаружения, является отношение сигнала к помехе. Линейный фильтр, максимизирующий это отношение, называется оптимальным согласованным фильтром.

Пусть на входе фильтра действует сумма сигнала s(t) и помех w(t), т. е. колебание:

из которых следует, что амплитудно-частотная характеристика согласованного фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнала, а фазо-частотная характеристика определяется фазовым спектром сигнала φ(ω) и линейной функцией частоты ωt_о. Таким образом, частотная характеристика оптимального фильтра полностью определяется спектром сигнала, "согласована" с ним. Отсюда и название — согласованный фильтр.

Фаза сигнала на выходе согласованного фильтра равна:

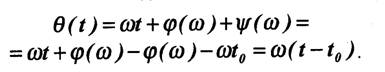
При t = t₀, и = 0, т. е. в момент t₀, все гармонические составляющие сигнала имеют одинаковую фазу и складываются арифметически, образуя в этот момент пик сигнала на выходе фильтра. Спектральные же составляющие помехи на выходе фильтра имеют случайную фазу. Этим и объясняется доказанное выше положение о том, что согласованный фильтр максимизирует отношение сигнала к помехе на выходе.

В качестве примера рассмотрим построение согласованного фильтра для прямоугольного видеоимпульса, заданного в виде:

В ряде случаев согласованные фильтры оказываются практически труднореализуемыми. Поэтому часто применяют фильтры, которые согласованы с сигналом только по полосе (квазиоптимальные фильтры). Оптимальная полоса для различных импульсов различна и может быть вычислена без особых трудностей. Так, для фильтра с прямоугольной частотной характеристикой, на который воздействует радиоимпульс прямоугольной формы длительностью τ₀, оптимальная

Можно показать, что отношение сигнала к помехе на выходе квазиоптимального фильтра по сравнению с согласованным фильтром уменьшается на величину порядка.

8.6. Прием сигналов как статистическая задача

Обычно задан способ передачи (способ кодирования и модуляции) и нужно определить помехоустойчивость, которую обеспечивают различные способы приема. Эти вопросы являются предметом теории помехоустойчивости, основы которой разработаны В. А. Котельниковым.

Помехоустойчивостью системы передачи информации называется способность системы различать (восстанавливать) сигналы с заданной достоверностью.

Задача определения помехоустойчивости всей системы в целом весьма сложная. Поэтому часто определяют помехоустойчивость отдельных звеньев системы: приемника при заданном способе передачи, системы кодирования или системы модуляции при заданном способе приема и т. д.

Предельно достижимая помехоустойчивость называется, по Котельникову, потенциальной помехоустойчивостью. Сравнение потенциальной и реальной помехоустойчивости устройства позволяет дать оценку качества реального устройства и найти еще неиспользованные резервы. Зная, например, потенциальную помехоустойчивость приемника, можно судить, насколько близка к ней реальная помехоустойчивость существующих способов приема и насколько целесообразно их дальнейшее усовершенствование при заданном способе передачи.

Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнить эти способы передачи между собой и указать, какие из них в этом отношении являются наиболее совершенными.

При отсутствии помех каждому принятому сигналу х соответствует вполне определенный сигнал s. При наличии помех это однозначное соответствие нарушается. Помеха, воздействуя на передаваемый сигнал, вносит неопределенность относительно того, какое из возможных сообщений было передано, и по принятому сигналу х только с некоторой вероятностью можно судить о том, что был передан тот или иной сигнал s' . Эта неопределенность описывается апостериорным распределением вероятностей P(s/x).

Если известны статистические свойства сигнала s и помехи w, то можно создать приемник, который на основании анализа сигнала х будет находить апостериорное распределение P(s/ х). Затем по виду этого распределения принимается решение о том, какое из возможных сообщений было передано. Решение принимается оператором или самим приемником по правилу, которое определяется заданным критерием.

Задача состоит в том, чтобы воспроизвести передаваемое сообщение наилучшим образом в смысле выбранного критерия. Такой приемник называется оптимальным, а его помехоустойчивость будет максимальной при заданном способе передачи.

Несмотря на случайный характер сигналов х, в большинстве случаев имеется возможность выделить множество наиболее вероятных сигналов {х_i}, соответствующих передаче некоторого сигнала s_i Геометрическое представление позволяет множество сигналов заменить областью многомерного пространства.

Пусть область X принимаемых сигналов разбита на непрерывающиеся областиX_j(j= 1,2,...,т), причем каждому сигналу s_i соответствует область Х_i. Если принятый сигнал попал в эту область, то приемник принимает решение о том, что передавался сигнал s_i. С некоторой вероятностью сигнал x_i сможет попасть в любую другую область Xj(j≠i), и тогда принимается ошибочное решение: вместо сигнала s_j. воспроизводится сигнал sj. Вероятность того, что переданный сигнал принят правильно, равна  P(x_j/s_i), а вероятность того,

где P(s_i) — априорные вероятности передаваемых сигналов. В случае двоичного канала область принимаемых сигналов разбивается на две области: Х₁ и Х₂. Если сигнал х попадает в область Х₁ то воспроизводится сигнал s₁ а если в область Х₂, то — s_2.

В канале последовательность элементов входного сообщения u(t) преобразуется в последовательность элементов выходного сообщения v(t). В геометрическом представлении это означает преобразование пространства входных сообщений U в пространство выходных сообщений V. При изучении каналов иногда удобно рассматривать вместо элементов исходного сообщения последовательность кодовых символов (а_i).

Канал называется дискретным, если входные и выходные пространства (сообщения) дискретны и непрерывны, если эти пространства непрерывны. Если одно из пространств дискретно, а другое — непрерывно, то канал называется дискретно-непрерывным или непрерывно-дискретным.

Свойства дискретного канала определены, если заданы: алфавиты входных кодовых символов а'_i(i=1,2,...,т) и выходных a'j(j = 1,2,...,т), скорость передачи символов V и вероятности переходов P_ji = P(a'j /a_i)(i = 1,2,...,m;j = 1,2,...,т' ) , т. е. вероятность того, что принят символ а'_j, когда был передан символ а_i. В общем случае т≠т и символы a_i могут отличаться по своей природе от символов а≠_j. Например, звуки речи, составляющие входной алфавит при телефонной передаче, могут воспроизводиться на приемном конце не только в виде звука, но и в виде текста.

Если вероятности P(a'j/a_i) переходов для каждой пары i, j не зависят от времени и от того, какие символы передавались и принимались ранее, то такой канал называется однородным без памяти. Если эти вероятности зависят от времени, то канал называется неоднородным, а если они зависят от того, какие символы передавались и принимались ранее, то канал называется каналом с памятью.

Если в однородном канале алфавиты кодовых символов на входе и выходе одинаковы и для любой пары i ' j вероятности переходов постоянны P(a'j /a_i) = P₀= const, то такой канал называется симметричным (рис. 8.8а).

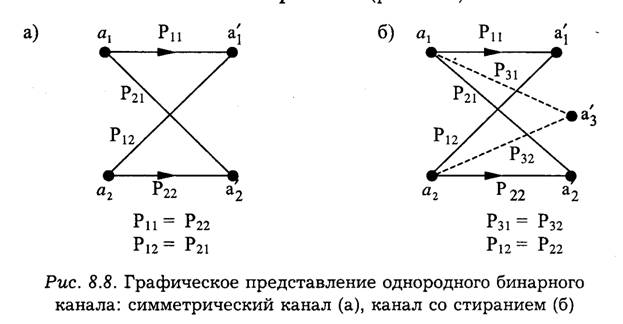
Среди каналов, в которых алфавиты на входе неодинаковы, представляет интерес так называемый стирающий канал, в котором т '=т + 1. В таком канале выходной алфавит содержит дополнительный символ а'_т+1, обозначающий "стирание". Появление этого символа на выходе означает, что переданный символ искажен помехами и не может быть опознан. Введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации. Геометрическое представление стирающего канала дано на рис. 8.86. В канале без помех каждому входному символу a_к однозначно соответствует символ а'_k на выходе (вероятности неправильных переходов равны нулю).

8.7. Критерий оптимального приема сигналов

Для того чтобы определить, какая из решающих схем является оптимальной, необходимо прежде всего установить, в каком смысле понимается оптимальность. Выбор критерия оптимальности не является универсальным, он зависит от поставленной задачи и условий работы системы.

Пусть на вход приемника поступает сумма сигнала и помехи:

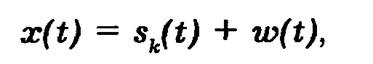
где s_k(t) — сигнал, которому соответствует кодовый символ а_к, w(t) — аддитивная помеха с известным законом распределения. Сигнал s_k в месте приема является случайным с априорным распределением P(s_k ). На основании анализа колебания x(t) приемник воспроизводит сигнал s_r При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение P(s_i/x), содержащее все сведения, которые можно извлечь из принятой реализации сигнала x(t). Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения P(s_i/x) решения относительно переданного сигнала s_k.

При передаче дискретных сообщений широко используется критерий Котелъникова (критерий идеального наблюдения). Согласно этому критерию принимается решение, что передан сигнал s_i, для которого апостериорная вероятность P(si/x) имеет наибольшее значение, т. е. регистрируется сигнал s_i, если выполняются неравенства:

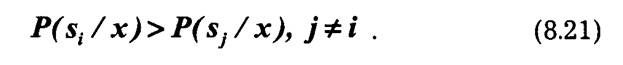
При использовании такого критерия полная вероятность ошибочного решения будет минимальной. Действительно, если по сигналу х принимается решение о том, что был передан сигнал s_i, то, очевидно, вероятность правильного решения будет равна P(s_i/x), а вероятность ошибки — [1 — P(s_i/x)]. Отсюда следует, что максимуму апостериорной вероятности P(s_i/x) соответствует минимум полной вероятности ошибки (8.20).

Таким образом, критерий идеального наблюдателя сводится к сравнению отношений правдоподобия (8.26). Этот критерий является более общим и называется  критерием максимального правдоподобия.

Рассмотрим бинарную систему, в которой передача сообщений осуществляется с помощью двух сигналов s₁(t) и s₂(t), соответствующих двум кодовым символам а₁ и а₂ Решение принимается по результату обработки принятого колебания x(t) пороговым методом: регистрируется s₁ если х<х₀, и s₂, если х>х₀, где х₀ — некоторый пороговый уровень х. Здесь могут быть ошибки двух видов: воспроизводится s₁ когда передавался s₂, и s₂, когда передавался s₁ Условные вероятности этих ошибок (вероятности переходов) будут равны:

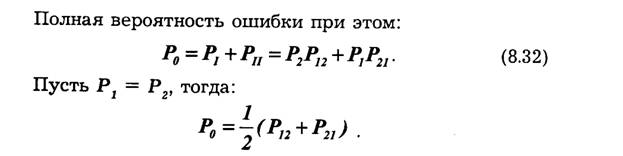
Несмотря на естественность и простоту, критерий Котель-никова имеет недостатки. Первый заключается в том, что для построения решающей схемы, как это следует из соотношения (8.23), необходимо знать априорные вероятности передачи различных символов кода. Вторым недостатком этого критерия является то, что все ошибки считаются одинаково нежелательными (имеют одинаковый вес). В некоторых случаях такое допущение не является правильным. Например, при передаче чисел ошибка в первых значащих цифрах более опасна, чем ошибка в последних цифрах.

Следовательно, в общем случае при выборе критерия оптимального приема необходимо учитывать те потери, которые несет получатель сообщений при различных видах ошибок. Эти потери можно выразить некоторыми весовыми коэффициентами, приписываемыми каждому из ошибочных решений.

Обозначим потери ошибочных решений первого и второго видов соответственно L₁₂ и L₂₁. Тогда можно определить средние ожидаемые потери или средний риск:

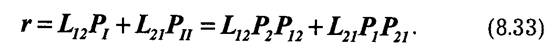
Оптимальной решающей схемой будет такая, которая обеспечивает минимум среднего риска. Критерий минимального риска относится к классу так называемых байесовых критериев.

8.8. Оптимальный прием дискретных сигналов

Источник дискретных сообщений характеризуется совокупностью возможных элементов сообщения u_1,и₂,..., и_т и вероятностями появления этих элементов на выходе источника P(u₁),P(u₂),...,P(u_m).

В передающем устройстве сообщение преобразовывается в сигнал таким образом, что каждому элементу соответствует определенный сигнал. Обозначим эти сигналы через s₁, s₂,..., s_m, а их вероятности на выходе передатчиков (априорные вероятности) соответственно через P(s₁),P(s₂) ,...,P(s_m),Очевидно, априорные вероятности сигналов P(s_i)равны априорным вероятностям Р(и_i) соответствующих сообщений P(s )= Р(u ). В процессе передачи на сигнал накладывается помеха. Пусть эта помеха имеет равномерный спектр мощности с интенсивностью

Отсюда следует, что при равновероятных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала.

Если все возможные сигналы равновероятны и имеют одинаковую энергию, оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, взаимная корреляция которого с принятым сигналом максимальна.

8.9. Вероятность ошибки при когерентном приеме двоичных сигналов

Определим вероятность ошибки в системе передачи двоичных сигналов при приеме на оптимальный приемник. Эта вероятность, очевидно, будет минимально возможной и будет характеризовать потенциальную помехоустойчивость при данном способе передачи. При приеме на реальный приемник помехоустойчивость может быть равна потенциальной, но не может быть больше нее.

Введем следующие понятия:

Сравнение полученных формул показывает, что из всех систем передачи бинарных сигналов наибольшую потенциальную помехоустойчивость обеспечивает система с фазовой манипуляцией. По сравнению с ЧМ она позволяет получить двухкратный, а по сравнению с AM — четырехкратный выигрыш по мощности.

В системах передачи информации сигнал обычно составляется из последовательности простых сигналов. Так, в телеграфии каждой букве соответствует кодовая комбинация, состоящая из пяти элементарных посылок. Возможны и более сложные комбинации. Если элементарные сигналы, составляющие кодовую комбинацию, независимы, то вероятность ошибочного приема кодовой комбинации определяется следующей формулой:

где Р₀— вероятность ошибки элементарного сигнала; п — число элементарных сигналов в кодовой комбинации (значность кода).

Следует заметить, что вероятность ошибки в рассмотренных выше случаях полностью определяется отношением энергии сигнала к спектральной плотности помехи и не зависит от формы сигнала.

Контрольные вопросы и задания

1. Какие задачи рассматриваются при приеме сигналов?

2.  Нарисуйте функциональную схему обработки дискретных сигналов и поясните основные виды обработки сигналов.

3. Поясните сущность метода накопления.

4. Нарисуйте структурную схему когерентного и некогерентного приемников. Как вводится понятие потенциальной помехоустойчивости?

5. Поясните сущность корреляционного и автокорреляционного методов приема.

6. Какими характеристиками обладает согласованный фильтр?

7. Что такое квазиоптимальный фильтр?

8. Поясните графическое представление однородного бинарного канала.

9. Как формируется критерий оптимального приема сигналов?

10.  Сформулируйте и поясните критерий Котельникова при приеме дискретных сигналов.

11. Как определяется вероятность ошибки при когерентном приеме дискретных сигналов?

ГЛАВА 9

ПРИНЦИПЫ

МНОГОКАНАЛЬНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ

9.1. Элементы теории разделения сигналов

Практика построения современных систем передачи информации показывает, что наиболее дорогостоящими звеньями трактов передачи являются линии связи (кабельные, волоконно-оптические, сотовой мобильной радиосвязи, радиорелейной и спутниковой связи и т. д.).

Поскольку экономически нецелесообразно использовать дорогостоящую линию связи для передачи информации единственной паре абонентов, то возникает необходимость построения многоканальных систем передачи, обеспечивающих передачу большого числа сообщений различных источников информации по общей линии связи. Многоканальная передача возможна в тех случаях, когда пропускная способность линии С' не меньше суммарной производительности источников информации:

где R'_uк — производительность k-гo источника, а N — число каналов (независимых источников информации). Многоканальные системы, так же как и одноканальные, могут быть аналоговыми и цифровыми. Для унификации аналоговых многоканальных систем за основной или стандартный канал принимают канал тональной частоты, обеспечивающий передачу сообщений с эффективно передаваемой полосой частот 300÷3400 Гц, соответствующей основному спектру телефонного сигнала. В цифровых системах передачи наибольшее распространение получили основные цифровые каналы со скоростью 64 Кбит/с. Многоканальные аналоговые системы формируются путем объединения каналов тональной частоты в группы, обычно кратные 12 каналам. Цифровые системы передачи, используемые на сетях связи, формируются в соответствии с принятыми иерархическими структурами.

Общий принцип построения системы многоканальной передачи поясняется с помощью структурной схемы рис. 9.1.

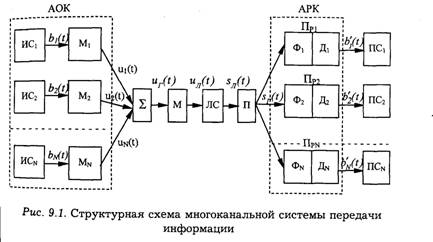
Наконец, с учетом частотного диапазона направляющей системы (линии связи) сигнал u_г(t) с помощью группового передатчика М преобразуется в линейный сигнал u_л(t), который и поступает в линию связи (ЛС). Сначала будем считать, что помеха в канале отсутствует, а канал не вносит искажения в сигнал, т. е. принимаемый линейный сигнал s_л(t) = γu_л(t), где γ— коэффициент передачи канала, который можно считать равным единице. Тогда на приемном конце линии связи (ЛС) линейный сигнал s_л(t) с помощью группового приемника Пр может быть вновь преобразован в групповой сигнал s_г(t)= γuⁱ(t). Канальными, или индивидуальными, приемниками Пp₁,Пp_2,.... ,Пр_к,.. .,Пp_N из группового сигнала выделяются соответствующие канальные сигналы s_i(t) = γu_i(t), (i = 1,..., N), которые посредством детектирования преобразуются в предназначенные     индивидуальным     получателям     сигналы b'₁(t),b'₂(t),...,b'_i(t),...,b'_N(t).

Канальные передатчики вместе с устройствами объединения образуют аппаратуру объединения (уплотнения) каналов АОК.

Групповой передатчик, линия связи ЛС и групповой приемник Пр составляют групповой тракт передачи, который вместе с аппаратурой объединения и разделения каналов составляет систему многоканальной связи.

Индивидуальные приемники Пр_i системы наряду с выполнением обычной операции преобразования канальных сигналов s_i(t) в соответствующие первичные сигналы b'_i(t) должны обеспечить выделение сигналов s_i(t) из группового сигнала с допустимыми искажениями. Аппаратуру индивидуальных приемников, обеспечивающую эту операцию, называют аппаратурой разделения каналов (АРК).

Рассмотрим теперь основные свойства сигналов, пригодных для независимой передачи информации в системах многоканальной связи. Чтобы разделяющие устройства были в состоянии различать сигналы отдельных каналов, должны существовать определенные признаки, присущие только сигналу данного канала. Такими признаками в общем случае могут быть параметры переносчика, например, амплитуда, частота или фаза в случае модуляции синусоидального переносчика, временное положение, длительность или форма сигнала при модуляции импульсных переносчиков. Соответственно будут различаться и способы разделения сигналов: частотный, временной, фазовый, разделение по форме сигналов и др.

Пусть необходимо организовать одновременно работу N индивидуальных каналов по общему групповому тракту. Будем считать, что групповой тракт пригоден для передачи сигналов любого i-го канала u_i(t). Предполагаем, что сигнал i-гo канала:

После преобразования группового сигнала в линейный и_л(t) последний поступает в тракт передачи. На приемном конце s_i (t) вновь преобразуется в групповой s_г (t;

Для разделения N канальных сигналов на приемной стороне потребуется соответствующее число N разделяющих устройств, причем каждое k-e разделяющее устройство должно выполнять операцию выделения k-гo сигнала. Действие приемного устройства k-гo канала будем обозначать оператором разделения П_к. В идеальном случае k-e приемное устройство должно реагировать ("откликаться") только на сигнал s_k(t) и давать нулевые отклики на сигналы всех других каналов. Дополнительным требованием к оператору будем считать его линейность, т. е. он должен удовлетворять принципу независимости действия (суперпозиция):

Полученные результаты могут быть обобщены также на случай, когда отклик разделяющего устройства на сигнал s_k(t) будет иметь иную форму; важно, чтобы величина отклика была однозначно связана с передаваемым сигналом. В частном случае откликом на сигнал s_k(t) может быть просто некоторое число γk, однозначно связанное с коэффициентом с_k:

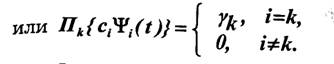
Физический смысл полученных выражений (9.6) и (9.8) сводится к тому, что приемник Пр_к обладает избирательными свойствами по отношению к сигналам s_k(t). Поскольку действие приемников Пр_к в (9.6) и (9.8) описывается линейным оператором П_к, то соответствующие устройства разделения являются линейными, а теорию разделения называют линейной.

Мы рассмотрели случай идеального разделения. В реальных условиях при разделении сигналов возникают переходные помехи.

Условие линейного разделения (9.6) будет выполняться лишь тогда, когда канальные сигналы линейно независимы. Частным случаем линейно независимых сигналов являются ортогональные сигналы, для которых выполняется условие (на отрезке [а,b]).

Типичными ортогональными сигналами являются сигналы с неперекрывающимися спектрами, а также неперекрывающиеся во времени сигналы.

9.2. Частотное, временное и фазовое разделение сигналов

1. Частотное разделение сигналов

Рассмотрим основные этапы преобразования сигналов, спектры которых занимают неперекрывающиеся полосы частот (рис. 9.2).

Сначала в соответствии с передаваемыми сообщениями первичные индивидуальные сигналы b₁(t), b₂(t),…,b_N(t) со спектрами S₁(f),S₂(f),...S_N(ƒ)модулируют переносчики — поднесущие частоты f_k каждого канала. Эта операция выполняется с помощью модуляторов M₁, M₂,...,M_N канальных передатчиков. Полученные на выходе частотных фильтров Ф₁, Ф₂,..., Ф_N спектры S_k(f) канальных сигналов занимают соответственно полосы частот Δƒ₁, Δƒ₂,…, Δƒ_N которые для упрощения будем считать равными ширине спектра сообщения Δf_k = F (используется однополосная модуляция). Тогда можно выбрать поднесущие частоты f _k так, что полосы Δf₁,Δf_2,…, Δƒ_N перекрываются. При этом условии сигналы s_k(t) (k=1,2,...,N) взаимно ортогональны. Спектры S₁(f),S₂(f ),..S_N(ƒ)суммируются 1-м устройстве объединения сигналов, и их совокупность S_г(f) поступает на 2-й групповой модулятор М. Суммарная полоса частот группового сигнала Δf_г =NF. В групповом модуляторе спектр S (f) с помощью колебания несущей частоты f₀ переносится в область частот, отведенную для передачи данной группы каналов, таким образом, групповой сигнал s_r(t) преобразуется в линейный сигнал sjt). При этом может использоваться любой вид модуляции, обеспечивающий необходимую помехоустойчивость передачи.

На приемной стороне тракта линейный сигнал поступает на групповой демодулятор (приемник Пр), который преобразует спектр линейного сигнала в спектр группового сигнала S_r(f)- Спектр группового сигнала затем с помощью канальных приемников Пр_к и входящих в них частотных фильтров Ф_к вновь разделяется на отдельные полосы Af_k и затем с помощью демодуляторов Д_к преобразуется в спектры сообщений S_bk(f), предназначенные получателям (рис. 9.3).

кать без ослабления лишь те частоты, которые принадлежат сигналу данного канала; частоты сигналов всех других каналов фильтр должен подавлять. Для идеального выделения сигналов при частотном разделении необходимо выполнение двух условий: полное сосредоточение энергии сигналов s_k(f) в пределах отведенных полос ∆ƒ_k и идеальность характеристик разделительных фильтров. Однако ни одно из этих условий принципиально не выполнимо. Результатом этого является возникновение взаимных помех при разделении каналов. Для снижения взаимных переходных помех между каналами до допустимого уровня приходится вводить защитные частотные интервалы ∆ƒ_защ (рис. 9.4).

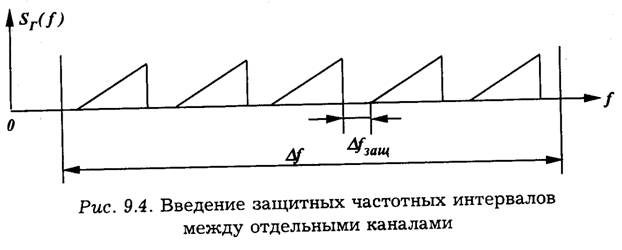
В современных системах многоканальной телефонной связи каждому каналу выделяется полоса частот 4 кГц, хотя частотный спектр передаваемых речевых сигналов ограничивается полосой от 300 до 3400 Гц, т. е. ширина спектра составляет 3,1 кГц.

Между полосами частот соседних каналов предусмотрены интервалы шириной по 0,9 кГц, предназначенные для снижения уровня взаимных помех при расфильтровке сигналов. Это означает, что в многоканальных системах с частотным разделением каналов эффективно используется лишь около 80% полосы пропускания тракта передачи. Кроме того, необходимо обеспечить очень высокую степень линейности всего тракта группового сигнала.

2. Временной способ разделения каналов

При временном разделении каналов групповой тракт с помощью коммутатора К_пер предоставляется поочередно для передачи сигналов каждого канала многоканальной системы (рис. 9.5).

Сначала передается сигнал 1-го канала, затем следующего и так далее до последнего канала с номером N, после чего опять подключается 1 канал, и процесс периодически повторяется с частотой дискретизации f₁. Возможность такого временного уплотнения сигналов уже обсуждалась в главе 4. На приемном конце устанавливается аналогичный коммутатор К_пр, который подключает групповой канал поочередно к приемникам различных каналов. Приемник i-го канала подключается только на время передачи i-го сигнала и отключается на все остальное время, пока передаются сигналы других каналов. Для нормальной работы системы необходимо обеспечить синхронное и синфазное переключение каналов на передающей и приемной сторонах. Часто для синхронизации занимают один из информационных каналов.

В качестве канальных сигналов в системах с временным разделением каналов используются неперекрывающиеся во времени последовательности модулированных импульсов (например, по амплитуде) s₁(t), s₂(t),..., s_N(t). Совокупность канальных сигналов образует групповой сигнал s_г (t. На рис. 9.6 для упрощения представлены только сигналы 1-го и 2-го каналов.

Групповой сигнал s_r (t_y поступает на коммутатор К_пр, действие которого можно отождествлять с "временным фильтром" (и ключом), передаточный коэффициент которого (рис. 9.66) равен единице только на интервалах действия импульсов избираемого канала:

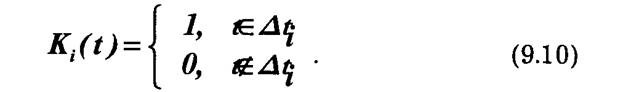
В результате временной фильтрации на выходе i-го приемника выделяются лишь импульсы i-го канала (рис. 9.6в). Полученные после демодуляции сообщения b_i(t) поступают к i-му получателю.

При временном разделении взаимные помехи в основном обусловлены двумя причинами. Первая состоит в том, что линейные искажения, возникающие за счет ограничения полосы частот и неидеальности АЧХ и ФЧХ всякой физически осуществимой системы передачи информации, нарушают форму импульсов сигналов. Действительно, если при передаче модулированных импульсов конечной длительности ограничить спектр, то импульсы "расплывутся", и вместо импульсов конечной длительности получим процессы, бесконечно протяженные во времени. При временном разделении каналов это приведет к тому, что импульсы одного канала будут накладываться на импульсы других каналов (рис. 9.7). Иначе говоря, между каналами возникают переходные помехи. Возможны такие помехи и за счет нарушения синхронизации.

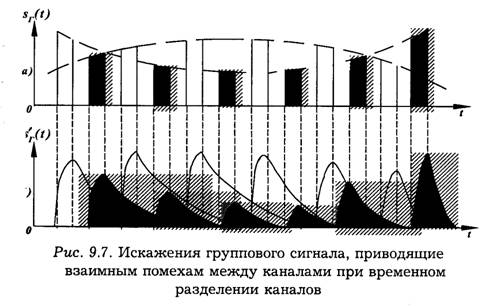
Для снижения уровня взаимных помех приходится вводить "защитные" временные интервалы. Это требует уменьшения длительности импульса каждого канала и, как следствие, расширения спектра сигналов. Так, например, в многоканальных системах телефонии полоса эффективно используемых частот — F_B— 3100 Гц; в соответствии с теоремой отсчетов минимальное значение частоты дискретизации

= 6200 Гц . Однако в реальных системах частоту следования импульсов выбирают несколько большей (с некоторым запасом): ƒ_д= 8 кГц. Для передачи таких импульсов в однока-нальном режиме потребуется полоса частот не менее F_B = 4кГц. При временном разделении каналов сигнал каждого канала занимает одинаковый интервал времени, определяемый в идеальных условиях согласно теореме отсчетов из соотношения (без учета канала синхронизации).

где F_общ = NF_B равно общей полосе частот системы с частотным разделением каналов. Хотя теоретически системы с временным и частотным разделением позволяют получить одинаковую эффективность использования частотного спектра, тем не менее в реальных условиях системы с временным разделением несколько уступают системам с частотным разделением каналов по этому показателю.

Однако системы с временным разделением каналов имеют ряд преимуществ, связанных с тем, что благодаря разновременности передачи сигналов различных каналов в них отсутствуют переходные помехи нелинейного происхождения, кроме того, аппаратура таких систем значительно проще. Системы с временным разделением каналов находят широкое применение при передаче непрерывных сообщений с помощью аналоговых видов импульсной модуляции (ФИМ, ШИМ), но особенно в цифровых системах с ИКМ.

3. Разделение сигналов по фазе

Рассмотрим множество сигналов:

где A_i — коэффициенты, отображающие передаваемые сообщения; разность фаз между сигналами соседних каналов.

Сигналы (9.12) различаются по фазе и, казалось бы, могут быть использованы для построения многоканальной передачи на одной несущей частоте ω₀ нескольких сообщений. Однако из множества различающихся по фазе сигналов (9.12) линейно независимы только любые два сигнала. Поэтому на одной несущей частоте ω₀, при произвольных значениях амплитуд A_i и A_k и фаз φ_i и φ_k, можно обеспечить лишь двухканальную передачу, причем разность фаз переносчиков — Δφ = π/₂.

9.3. Разделение сигналов по форме.

Системы передачи с шумоподобными сигналами

1. Разделение линейно независимых сигналов

Для разделения сигналов могут использоваться не только такие очевидные признаки, как частота и время. Наиболее общим признаком может служить форма сигналов. Различающиеся по форме сигналы могут передаваться одновременно, иметь перекрывающиеся частотные спектры, и тем не менее такие сигналы можно разделить, если выполняется условие их линейной независимости или условие ортогональности.

Сущность селекции сигналов по форме заключается в следующем. Определяют взаимную энергию принятого сигнала x(t) и передаваемых сигналов s_i(t), i =1,2,...,N. (Д_ля случайных переносчиков взаимная энергия пропорциональна взаимокорреляционной функции.) Принимают решение, что передавался тот сигнал, взаимная энергия которого с принятым  максимальна. Например, если:

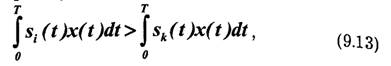
принимается решение о том, что передавался сигнал s_i (t) w практике используют слабокоррелированные сигналы, взаимная энергия которых намного меньше энергии каждого сигнала.

В качестве переносчиков при формировании различающихся по форме сигналов находят применение различные ортогональные функции, полученные на основе ортогонализации степенного ряда либо на основе дискретных ортогональных последовательностей в виде функций Уолша.

2. Системы передачи с шумоподобными сигналами

Рассмотренные выше системы многоканальной передачи с ортогональными и линейно независимыми сигналами требуют для нормальной работы той или иной синхронизации: точного совпадения спектра сигнала с полосой пропускания при частотном разделении каналов; точного совпадения временных интервалов передачи сигналов отдельных каналов при временном разделении каналов; точного определения моментов начала и конца тактового интервала в системах с разделением сигналов по форме активными фильтрами; точной установки момента отсчета в системах с согласованными фильтрами.

В ряде случаев осуществить точную синхронизацию затруднительно. С подобными ситуациями приходится сталкиваться, например, при организации оперативной связи между подвижными объектами (автомобилями, самолетами).Такая задача возникает при организации оперативной связи с использованием искусственных спутников Земли в качестве ретрансляторов. Во всех этих случаях могут быть использованы системы асинхронной многоканальной связи, когда сигналы всех абонентов передаются в общей полосе частот, а каналы синхронизированы между собой во времени. Поскольку в не таких системах за каналами не закреплены ни частотные полосы, ни временные интервалы и время работы каждого канала произвольно, то такие системы называют системами со свободным доступом к линии связи пли системами с незакрепленными каналами.

В системах со свободным доступом каждому каналу (абоненту) присваивается определенная форма сигнала, которая и является отличительным признаком, "адресом" данного абонента. В отличие от обычного разделения по форме, где условие ортогональности сигналов выполняется лишь тогда, когда тактовые интервалы всех каналов жестко синхронизированы, для возможности полного линейного разделения сигналов в системах со свободным доступом ортогональность или линейная независимость должны сохраняться при любых временных сдвигах сигналов. Это значит, что для любой пары сигналов s_i(t) и s_k(t) должно выполняться условие (волнистая черта означает усреднение во времени):

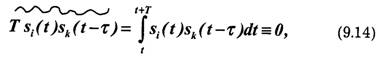
При 0≤τ≤Т, где T — длительность элементарного сигнала, а интегрирование производится на любом интервале от t до t+T условие (9.14) выполняется только в том случае, когда сигналы s_k(t) представляют собой белый шум, т.е. имеют неограниченную ширину спектра и бесконечную дисперсию; Для реальных сигналов оно невыполнимо. Вместе с тем можно сформировать такие сигналы, для которых (9.14) выполняется приближенно в том смысле, что

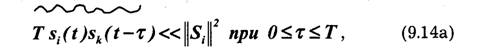
т. е. скалярные произведения сигналов при любом сдвиге по времени много меньше энергии элементарного сигнала. Такие сигналы можно назвать почти ортогональными. По своим свойствам почти ортогональные сигналы приближаются к белому шуму, поэтому их часто называют шумоподобными: их корреляционные функции и спектры плотности мощности близки к аналогичным характеристикам квазибелого шума. Шумоподобные сигналы не являются случайными, они относятся к классу сложных сигналов, база которых В = 2FT>>1.

Наиболее распространенным примером технической реализации почти ортогональных шумоподобных сигналов могут служить определенным образом сформированные псевдослучайные последовательности дискретных, в частности, двоичных радиоимпульсов. База сигналов при этом определяется числом импульсов в последовательности. Каждому каналу присваивается одна из множества почти ортогональных двоичных последовательностей, которая служит "адресом" канала. Это приводит к названию "асинхронные адресные системы связи" (ААСС).

Важным достоинством ААСС является то, что нет необходимости в центральной коммутационной станции; все абоненты имеют прямой доступ друг к другу без частотной перестройки приемных и передающих устройств (рис. 9.8). Здесь достаточно набрать "адрес" вызываемого абонента, т. е. изменить "форму" импульсной адресной последовательности.

В системах с закрепленными каналами (частотное и временное разделение каналов) добавление хотя бы одного нового абонента оказывается возможным лишь при исключении одного из имевшихся в системе. Значительно проще эта задача решается в системах ААСС. Здесь вследствие свободного доступа к линии связи могут вести передачу любые N_a активных абонентов из общего числа N абонентов системы передачи информации. При определении числа N_a нужно учитывать, что вследствие неполной ортогональности сигналов в ААСС неизбежны переходные помехи ("шумы неортогональности"), уровень которых растет по мере увеличения N_а . Поэтому число одновременно работающих абонентов должно" быть ограничено. Допустимое значение N_a возрастает по мере увеличения базы сигнала.

В зависимости от времени активности абонентов (т. е. от доли времени, занимаемого k-м каналом для передачи сообщений) можно организовать, например 1000-канальную систему связи, в которой одновременно ведут передачу любые 50 абонентов из тысячи. В таких системах легко реализуются резервы пропускной способности, возникающие за счет малоактивных абонентов. Изучив статистику сообщений, передаваемых по каждому каналу, можно установить допустимоечисло каналов в системе N, при котором обеспечивается нормальная работа N_a активных каналов.

В настоящее время усиленно разрабатываются методы синтеза сигналов с заданными автокорреляционными и взаимно корреляционными свойствами. В качестве адресных сигналов используются последовательности Баркера, линейные рекуррентные М-последовательности и т. д. Один из способов формирования шумоподобных сигналов для асинхронно-адресных систем связи состоит в использовании частотно-временной матрицы. Уже отмечалось, что в системах с ортогональными сигналами энергия каждого сигнала отделяется от энергии других сигналов. Это положение становится наиболее отчетливым, если обратиться к частотно-временным диаграммам системы связи при частотном разделении (рис. 9.9а) и при временном разделении каналов (рис. 9.96).

Здесь каждому каналу отводится определенная область частотно-временного пространства; положение площадки можно рассматривать как "адрес" абонента. Однако частотно-временную область FxT можно разделить на площадки иным способом: адрес каждого канала можно сформировать из набора "элементарных площадок" частотно-временной плоскости (рис. 9.10а). Каждый двоичный информационный символ (рис. 9.10а) передается за время Т и отображается определенной последовательностью импульсов, имеющих разные частоты (рис. 9.106) в общей полосе F.

Двоичную информацию в последовательность можно заложить, меняя один из параметров элементарного радиоимпульса. Эти адресные наборы импульсов составляются на основе их представления в виде частотно-временной матрицы (рис. 9.10в); к ним предъявляются обычные требования хороших автокорреляционных функций и малых значений взаимной корреляции. Изменение временного положения импульсов и различие в их частотах позволяют сравнительно простыми техническими средствами получить несколько тысяч частотно-временных колебаний (адресов). Разумеется, не все комбинации частотно-временной матрицы используют в качестве адресных сигналов; среди них встречаются и такие, которые не обладают необходимыми корреляционными свойствами.

Максимальное количество адресов приближается к FT. Сигналы частотно-временной матрицы являются разновидностью сигналов, различающихся по форме, их можно разделить согласованными фильтрами или корреляторами.

Отметим в заключение, что в технической литературе имеются описания большого числа различных систем связи со свободным доступом. Наиболее характерными из них являются системы на 1000—1500 каналов с 50—100 активными абонентами.

9.4. Комбинационное разделение сигналов

При многоканальной передаче дискретной информации используется также комбинационный способ формирования группового сигнала. Сущность этого способа состоит в следующем.

Пусть необходимо организовать передачу N независимых дискретных сообщений по общему групповому тракту. Если элемент i-го сообщения может принимать одно из т. возможных значений (i = 1,2,...,N), то общее число значений, которое может принимать элемент N-канального источника, объединяющего исходные N источников, будет равноПри одинаковых значениях m_i = m имеем:

Таким образом, при комбинационном уплотнении каждое сочетание канальных сообщений отображается элементом группового сообщения с основанием кода (9.15), т. е. используя основание кода М = m^N, можно одновременно передавать информацию от N индивидуальных источников, работающих с основанием кода т. Если, в частности, m = 2 (двоичные коды), а число каналов N = 2, то групповое сообщение b_г может принимать четыре возможных значения, соответствующих различным комбинациям нулей и единиц в обоих каналах, при N = 2 число различных комбинаций будет равно М = 8 и т. д. Задача теперь сводится к передаче некоторых чисел b_г, определяющих номер комбинации.

Эти числа могут передаваться посредством сигналов дискретной модуляции любого вида. Разделение сигналов b_г, основанное на различии в комбинациях сигналов разных каналов, называется комбинационным. Структурная схема многоканальной системы с комбинационным (кодовым) разделением (уплотнением) представлена на рис. 9.11.

Здесь первичные сообщения b₁(t),b₂(t),...b_N(t) от N источников поступают на вход кодера, выполняющего функции устройства объединения каналов (УОК). Полученное групповое сообщение b_г(t) преобразуется с помощью группового модулятора М в групповой сигнал u_г(t), поступающий в групповой тракт. На приемной стороне после демодуляции и декодирования формируются канальные сообщения, соответствую ющие N первичным сообщениям.

Типичным примером комбинационного уплотнения является система двукратной частотной модуляции (ДЧМ), в которой для передачи четырех комбинаций сигналов двух источников (каналов) используют четыре различия частоты: f₁ ƒ₂, f₃, f₄. При двукратной фазовой модуляции (ДФМ) каждой комбинации сообщений 1-го и 2-го источника соответствует определенное значение фазы группового сигнала φ₁,φ₂,φ_3,φ₄ (табл. 9.1).

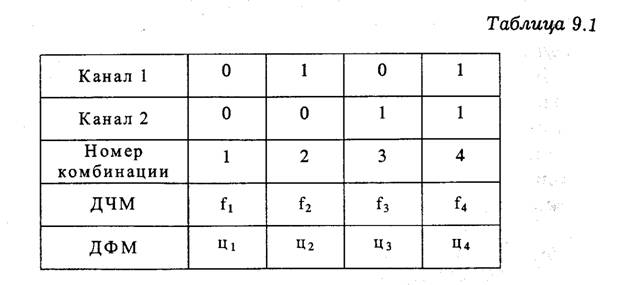
Сравнение системы с ДЧМ с обычной двухканальной ЧМ-системой с частотным разделением каналов показывает, что обе системы занимают практически одинаковую полосу частот, однако мощность сигнала, требуемая для обеспечения заданной вероятности ошибки при ДЧМ, почти вдвое меньше. Существенно меньше оказывается и пиковая мощность при ДЧМ. Поэтому в системах с ограниченной энергетикой комбинационное уплотнение по методу ДЧМ находит широкое применение.

Аналогично можно формировать сигналы комбинационного уплотнения для большого числа каналов — многократную частотную модуляцию (МЧМ), многократную относительную фазовую модуляцию (МОФМ) и др. При МЧМ получаем многочастотные сигналы, а при МФМ — многофазные. Вместе с тем можно модулировать одновременно несколько параметров переносчика, например, амплитуду и частоту, частоту и фазу и др.

В последнее время большой интерес проявляется к сигналам амплитудно-фазовой модуляции (АФМ), которые можно реализовать схемой квадратурной модуляции. В системах АФМ в течение интервала передачи одного элементарного сигнала его фаза и амплитуда принимают значения, выбранные из ряда возможных дискретных значений амплитуд и фаз. Каждая комбинация значений амплитуды и фазы отображает один из многопозиционных сигналов группового сигнала с основанием кода M=2^N. Сигналы АФМ можно формировать, например, путем многоуровневой амплитудной и фазовой модуляции двух квадратурных (сдвинутых по фазе на ) колебаний несущей частоты.

В последние годы успешно развивается теория сигналь-но-кодовых конструкций (СКК), направленная на повышение скорости передачи и помехоустойчивости при существенных ограничениях на энергетику и занимаемую полосу частот.

9.5. Пропускная способность многоканальных систем передачи информации

Предельная пропускная способность системы передачи (бит/с) с равномерной АЧХ и линейной ФЧХ в пределах полосы пропускания тракта передачи при наличии стационарного гауссовского шума со средней мощностью Р_ш и сигналов со средней мощностью Р_с определяется по формуле Шеннона:

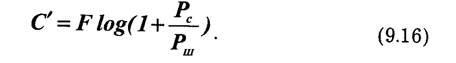
При многоканальной передаче, как уже отмечалось, возникают специфические переходные помехи между каналами, обусловленные неидеальностью разделяющих устройств на приемной стороне и устройств формирования сигналов на передающей стороне, линейными и нелинейными искажениями в групповом тракте передачи. Качество многоканальной системы с точки зрения переходных помех можно охарактеризовать величиной затухания (дБ) между влияющим i -м каналом и подверженным влиянию k-м каналом:

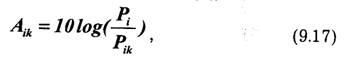
где Рi и Р_ik — мощности на входе влияющего и выходе подверженного влиянию каналов; затухание A_ik называют также защищенностью канала от переходных помех. При большом числе каналов можно считать, что плотность вероятности помех подчиняется нормальному закону, а спектральная плотность мощности является равномерной. Иначе говоря, результирующую помеху, обусловленную действием шумов и переходных помех, можно считать гауссовской и квазибелой.

В соответствии с (9.17) для мощности помех, наводимых 1-м каналом на выходе i-м канала, имеем:

Если формулу Шеннона (9.16) переписать с учетом действия переходных помех (9.18), то:

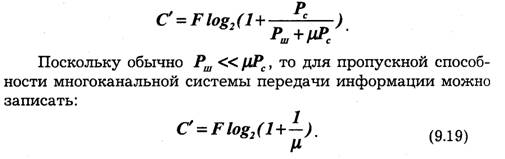
Из (9.19) следует, что переходные помехи ограничивают пропускную способность многоканальной системы. Расчеты показывают, что при увеличение мощности сигнала Р_с приводит к повышению пропускной способности, если. При дальнейшем увеличении мощности

сигнала пропускная способность практически не возрастает и определяется соотношением (9.19). Практика проектирования аппаратуры многоканальной связи показывает, что для снижения уровня взаимных помех в системах с частотным разделением каналов приходится вводить защитные частотные интервалы между каналами, занимающие до 20% общей полосы пропускания системы передачи информации.

Контрольные вопросы и задания

1.  Нарисуйте структурную схему системы многоканальной передачи информации и поясните назначение ее элементов.

2. Каким образом происходит преобразование сигналов в многоканальной системе передачи?

3. Поясните принципы частотного разделения сигналов.

4. Нарисуйте структурную схему многоканальной передачи информации с временным разделением каналов.

5.  Как возникают искажения группового сигнала при временном разделении каналов?

6. Каким образом происходит разделение сигналов по форме?

7.  Нарисуйте структурную схему многоканальной асинхронно-адресной системы связи.

8. Поясните принципы формирования широкополосного сигнала с помощью частотно-временной матрицы.

9.  Нарисуйте структурную схему многоканальной системы с комбинационным уплотнением.

10.  Как определяется пропускная способность многоканальных систем передачи информации?

ГЛАВА   10

ПРОБЛЕМЫ ПОСТРОЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ

Под вычислительной системой в общем случае понимается совокупность взаимосвязанных и согласованно действующих процессоров (ЭВМ), периферийного оборудования и математического обеспечения, предназначенная для автоматизации процессов приема исходной информации, ее обработки и выдачи результатов обработки потребителям или на аппаратуру регистрации и документации.

Вычислительные системы как сложные комплексы взаимосвязанных и взаимодействующих аппаратных средств и программного обеспечения различаются между собой, прежде всего степенью использования общего оборудования. Наибольшая степень использования общих средств достигается тогда, когда каждая из комплексируемых ЭВМ разбирается на отдельные устройства, которые затем собираются в многопроцессорную систему с большим набором устройств. Такое комплексирование означает, по существу, создание новой, более мощной системы второго порядка с радикальной перестройкой всего математического обеспечения исходных ЭВМ и поэтому встречается довольно редко.

Меньшая степень использования общего оборудования предусматривает обобществление части модулей основной оперативной памяти при сохранении центральными частями комплексируемых ЭВМ своих модулей оперативной памяти. Возможно и такое комплексирование, при котором объединяется лишь периферийное оборудование (все или часть). В современных вычислительных системах такое комплексирование осуществляется относительно просто, поскольку они имеют стандартный интерфейс с периферией и допускают подсоединение периферийного оборудования к нескольким различным каналам.

Возможна и такая организация комплексирования, когда общие аппаратные модули в чистом виде отсутствуют. В таких комплексах отдельные ЭВМ выступают в полной системной конфигурации как элементарные модули, а задачей комплексирования является организация обмена сообщениями между ними.

Для обеспечения согласованной работы комплексируемые в систему вычислительные средства должны быть совместимыми. Возможности согласованной работы вычислительных средств определяются программной, информационно-логической и аппаратной совместимостью.

10.1. Связь компьютера с периферийными устройствами

Для обмена данными между компьютером и периферийным устройством (ПУ) в компьютере предусмотрен внешний интерфейс (рис. 10.1), т. е. набор проводов, соединяющих компьютер и периферийное устройство, а также набор правил обмена информацией по этим проводам (иногда вместо термина "интерфейс" употребляется термин "протокол"). Примерами интерфейсов, используемых в компьютерах, являются: параллельный интерфейс Centroniks, предназначенный, как правило, для подключения принтеров, и последовательный интерфейс RS-232C, через который подключаются мышь, модем и много других устройств. Интерфейс реализуется со стороны компьютера совокупностью аппаратных и программных средств: контроллером ПУ и специальной программой, управляющей этим контроллером, которую часто называют драйвером соответствующего периферийного устройства. Со стороны ПУ интерфейс чаще всего реализуется аппаратным устройством управления, хотя встречаются и программно-управляемые периферийные устройства.

Программа, выполняемая процессором, может обмениваться данными с помощью команд ввода/вывода с любыми модулями, подключенными к внутренней шине компьютера, в том числе и с контроллерами ПУ.

Периферийные устройства могут принимать от компьютера как данные в виде байтов информации, которую нужно распечатать на бумаге, так и команды управления, в ответ на которые ПУ может выполнить специальные действия, например, перевести головку диска на требуемую дорожку или же вытолкнуть лист бумаги из принтера. Периферийное устройство использует внешний интерфейс компьютера не только для приема информации, но и для передачи информации в компьютер, т. е. обмен данными по внешнему интерфейсу, как правило, является двунаправленным. Так, например, даже принтер, который по своей природе является устройством вывода информации, возвращает в компьютер данные о своем состоянии.

Контроллеры ПУ принимают команды и данные от процессора в свой внутренний буфер, который часто называется регистром или портом, затем выполняют необходимые преобразования этих данных и команд в соответствии с форматами, понятными ПУ, и выдают их на внешний интерфейс.

Распределение обязанностей между контроллером и драйвером ПУ может быть разным, но обычно контроллер выполняет набор простых команд по управлению ПУ, а драйвер использует эти команды, чтобы заставить устройство совершать более сложные действия по некоторому алгоритму. Например, контроллер принтера может поддерживать такие элементарные команды, как "Печать символа", "Перевод строки", "Возврат каретки" и т. п. Драйвер же принтера с помощью этих команд организует печать строк символов, разделение документа на страницы и другие более высокоуровневые операции. Для одного и того же контроллера можно разработать различные драйверы, которые будут управлять данным ПУ по-разному: одни лучше, а другие хуже — в зависимости от опыта и способностей программистов, их разработавших.

Рассмотрим схему передачи одного байта информации от прикладной программы на периферийное устройство. Программа, которой потребовалось выполнить обмен данными с ПУ, обращается к драйверу этого устройства, сообщая ему в качестве параметра адрес байта памяти, который нужно передать. Драйвер загружает значение этого байта в буфер контроллера ПУ, который начинает последовательно передавать биты в линию связи, представляя каждый бит соответствующим электрическим сигналом. Чтобы устройству управления ПУ стало понятно, что начинается передача байта, перед передачей первого бита информации контроллер ПУ формирует стартовый сигнал специфической формы, а после передачи последнего информационного бита — стоповый сигнал. Эти сигналы синхронизируют передачу байта.

Кроме информационных бит контроллер может передавать бит контроля четности для повышения достоверности обмена. Устройство управления, обнаружив на соответствующей линии стартовый бит, выполняет подготовительные действия и начинает принимать информационные биты, формируя из них байт в своем приемном буфере. Если передача сопровождается битом четности, то выполняется проверка правильности передачи: при правильно выполненной передаче в соответствующем регистре устройства управления устанавливается признак завершения приема информации.

Обычно на драйвер возлагаются наиболее сложные функции протокола (например, подсчет контрольной суммы последовательности передаваемых байтов, анализ состояния периферийного устройства, проверка правильности выполнения команды). Но даже самый примитивный драйвер контроллера должен поддерживать, как минимум, две операции: "Взять данные из контроллера в оперативную память" и "Передать данные из оперативной памяти в контроллер".

10.2. Простейший случай взаимодействия двух компьютеров

В самом простом случае взаимодействие компьютеров может быть реализовано с помощью тех же самых средств, которые используются для взаимодействия компьютера с периферией, например, через последовательный интерфейс RS-232C. В отличие от взаимодействия компьютера с периферийным устройством, когда программа работает, как правило, только с одной стороны — со стороны компьютера, в этом случае происходит взаимодействие двух программ, работающих на каждом из компьютеров.

Программа, работающая на одном компьютере, не может получить непосредственный доступ к ресурсам другого компьютера — его дискам, файлам, принтеру. Она может только "попросить" об этом программу, работающую на том компьютере, которому принадлежат эти ресурсы. Эти "просьбы" выражаются в виде сообщений, передаваемых по каналам связи между компьютерами. Сообщения могут содержать не только команды на выполнение некоторых действий, но и собственно информационные данные (например, содержимое некоторого файла).

Рассмотрим случай, когда пользователю, работающему с текстовым редактором на персональном компьютере А, нужно прочитать часть некоторого файла, расположенного на диске персонального компьютера В (рис. 10.2). Предположим, что мы связали эти компьютеры по кабелю связи через СОМ — порты, которые, как известно, реализуют интерфейс RS-232C (такое соединение часто называют нуль-модемным). Пусть для определенности компьютеры работают под управлением MS-DOS, хотя принципиального значения в данном случае это не имеет.

Драйвер СОМ-порта вместе с контроллером СОМ-порта работают примерно так же, как и в описанном выше случае взаимодействия ПУ с компьютером. Однако при этом роль устройства управления ПУ выполняют контроллер и драйвер СОМ-порта другого компьютера. Вместе они обеспечивают передачу по кабелю между компьютерами одного байта информации. (В "настоящих" локальных сетях подобные функции передачи данных в линию связи выполняются сетевыми адаптерами и их драйверами.)

Драйвер компьютера В периодически запрашивает признак завершения приема, устанавливаемый контроллером при правильно выполненной передаче данных, и при его появлении считывает принятый байт из буфера контроллера в оперативную память, делая его тем самым доступным для программ компьютера В. В некоторых случаях драйвер вызывается асинхронно, по прерываниям от контроллера.

Таким образом, в распоряжении программ компьютеров А и В имеется средство для передачи одного байта информации. Но рассматриваемая в нашем примере задача значительно сложнее, так как нужно передать не один байт, а определенную часть заданного файла. Все связанные с этим дополнительные проблемы должны решить программы более высокого уровня, чем драйверы СОМ-портов. Для определенности назовем такие программы компьютеров А и В приложением А и приложением В соответственно. Итак, приложение А должно сформировать сообщение-запрос для приложения В. В запросе необходимо указать имя файла, тип операции (в данном случае — чтение), смещение и размер области файла, содержащей нужные данные.

Чтобы передать это сообщение компьютеру В, приложение А обращается к драйверу СОМ-порта, сообщая ему адрес в оперативной памяти, по которому драйвер находит сообщение и затем передает его байт за байтом приложению В. Приложение В, приняв запрос, выполняет его, т. е. считывает требуемую область файла с диска с помощью средств локальной ОС в буферную область своей оперативной памяти, а далее с помощью драйвера СОМ-порта передает считанные данные по каналу связи в компьютер А, где они и попадают к приложению  А. Описанные функции приложения   А могла бы выполнить сама программа текстового редактора, но включать эти функции в состав каждого приложения — текстовых редакторов, графических редакторов, систем управления базами данных и других приложений, которым нужен доступ к файлам, — не очень рационально (хотя существует большое количество программ, которые действительно самостоятельно решают все задачи по межмашинному обмену данными. Гораздо выгоднее создать специальный программный модуль, который будет выполнять функции формирования сообщений-запросов и приема результатов для всех приложений   компьютера.   Такой   служебный   модуль   называется клиентом. На стороне же компьютера  В должен работать другой модуль — сервер, постоянно ожидающий прихода запросов на удаленный доступ к файлам, расположенным на диске этого компьютера. Сервер, приняв запрос из сети, обращается к локальному файлу и выполняет с ним заданные действия, возможно, с участием локальной ОС.

Программные клиент и сервер выполняют системные функции по обслуживанию запросов приложений компьютера А на удаленный доступ к файлам компьютера В. Чтобы приложения компьютера В могли пользоваться файлами компьютера А, описанную схему нужно симметрично дополнить клиентом для компьютера В и сервером для компьютера А.

Схема взаимодействия клиента и сервера с приложениями и операционной системой приведена на рис. 10.3. Несмотря на то, что мы рассмотрели очень простую схему аппаратной связи компьютеров, функции программ, обеспечивающих доступ к удаленным файлам, очень похожи на функции модулей сетевой операционной системы, работающей в сети с более сложными аппаратными связями компьютеров.

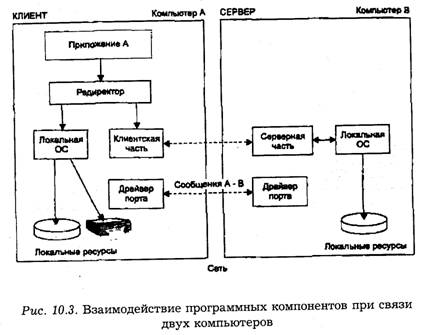
Очень удобной и полезной функцией клиентской программы является способность отличить запрос к удаленному файлу от запроса к локальному файлу. Если клиентская программа умеет это делать, то приложения не должны заботиться о том, с каким файлом они работают (локальным или удаленным), клиентская программа сама распознает и перенаправляет (redirect) запрос к удаленной машине. Отсюда и название, часто используемое для клиентской части сетевой ОС, — редиректор. Иногда функции распознавания выделяются в отдельный программный модуль, в этом случае редиректором называют не всю клиентскую часть, а только этот модуль.

10.3. Проблемы физической передачи данных по линиям связи

Даже при рассмотрении простейшей сети, состоящей всего из двух машин, можно увидеть многие проблемы, присущие любой вычислительной сети, в том числе проблемы, связанные с физической передачей сигналов по линиям связи, без решения которой невозможен любой вид связи.

В вычислительной технике для представления данных используется двоичный код. Внутри компьютера единицам и нулям данных соответствуют дискретные электрические сигналы. Представление данных в виде электрических или оптических сигналов называется кодированием. Существуют различные способы кодирования двоичных цифр 1 и 0, например, потенциальный способ, при котором единице соответствует один уровень напряжения, а нулю — другой, или импульсный способ, когда для представления цифр используются импульсы различной или одной полярности.

Аналогичные подходы могут быть использованы для кодирования данных и при передаче их между двумя компьютерами по линиям связи. Однако эти линии связи отличаются по своим электрическим характеристикам от тех, которые существуют внутри компьютера. Главное отличие внешних линий связи от внутренних состоит в их гораздо большей протяженности, а также в том, что они проходят вне экранированного корпуса по пространствам, зачастую подверженным воздействию сильных электромагнитных помех. Все это приводит к значительно большим искажениям прямоугольных импульсов (например, "заваливанию" фронтов), чем внутри компьютера. Поэтому для надежного распознавания импульсов на приемном конце линии связи при передаче данных внутри и вне компьютера не всегда можно использовать одни и те же скорости и способы кодирования. Например, медленное на-растание фронта импульса из-за высокой емкостной нагрузки линии требует передачи импульсов с меньшей скоростью (чтобы передний и задний фронты соседних импульсов не перекрывались и импульс успел дорасти до требуемого уровня).

В вычислительных сетях применяют как потенциальное, так и импульсное кодирование дискретных данных, а также различные способы модуляции, которые никогда не используются внутри компьютера (рис. 10.4).

Потенциальное или импульсное кодирование применяется на каналах высокого качества, а модуляция на основе синусоидальных сигналов предпочтительнее в том случае, когда канал вносит сильные искажения в передаваемые сигналы. Обычно модуляция используется в глобальных сетях при передаче данных через аналоговые телефонные каналы связи, которые были разработаны для передачи голоса в аналоговой форме и поэтому плохо подходят для непосредственной передачи импульсов.

На способ передачи сигналов влияет и количество проводов в линиях связи между компьютерами. Для сокращения стоимости линий связи в сетях обычно стремятся к сокращению количества проводов и из-за этого используют не параллельную передачу всех бит одного байта или даже нескольких байт, как это делается внутри компьютера, а последовательную, побитную передачу, требующую всего одной пары проводов.

Еще одной проблемой, которую нужно решать при передаче сигналов, является проблема взаимной синхронизации передатчика одного компьютера с приемником другого. При организации взаимодействия модулей внутри компьютера эта проблема решается очень просто, так как в этом случае все модули синхронизируются от общего тактового генератора. Проблема синхронизации при связи компьютеров может решаться разными способами, как с помощью обмена специальными тактовыми синхроимпульсами по отдельной линии, так и с помощью периодической синхронизации заранее обусловленными кодами или импульсами характерной формы, отличающейся от формы импульсов данных.

Несмотря на предпринимаемые меры — выбор соответствующей скорости обмена данными, линий связи с определенными характеристиками, способа синхронизации приемника и передатчика, — существует вероятность искажения некоторых бит передаваемых данных. Для повышения надежности передачи данных между компьютерами часто используется стандартный прием — подсчет контрольной суммы и передача ее по линиям связи после каждого байта или после некоторого блока байтов. Часто в протокол обмена данными включается как обязательный элемент сигнал-квитанция, который подтверждает правильность приема данных и посылается от получателя отправителю.

Задачи надежного обмена двоичными сигналами, представленными соответствующими электромагнитными сигналами, в вычислительных сетях решает определенный класс оборудования. В локальных сетях это сетевые адаптеры, а в глобальных сетях — аппаратура передачи данных, к которой относятся, например, устройства, выполняющие модуляцию и демодуляцию дискретных сигналов, — модемы. Это оборудование кодирует и декодирует каждый информационный бит, синхронизирует передачу электромагнитных сигналов по линиям связи, проверяет правильность передачи поконтрольной сумме и может выполнять некоторые другие операции. Сетевые адаптеры рассчитаны, как правило, на работу с определенной передающей средой — коаксиальным кабелем, витой парой, оптоволокном и т. п. Каждый тип передающей среды обладает определенными электрическими характеристиками, влияющими на способ использования данной среды, и определяет скорость передачи сигналов, способ их кодирования и некоторые другие параметры.

10.4. Проблемы объединения нескольких компьютеров

До сих пор мы рассматривали вырожденную сеть, состоящую всего из двух машин. При объединении в сеть большего числа компьютеров возникает целый комплекс новых проблем.

1. Топология физических связей

В первую очередь необходимо выбрать способ организации физических связей, т. е. топологию. Под топологией вычислительной сети понимается конфигурация графа, вершинам которого соответствуют компьютеры сети (иногда и другое оборудование, например, концентраторы), а ребрам — физические связи между ними. Компьютеры, подключенные к сети, часто называют станциями или узлами сети.

Заметим, что конфигурация физических связей определяется электрическими соединениями компьютеров между собой и может отличаться от конфигурации логических связей между узлами сети. Логические связи представляют собой маршруты передачи данных между узлами сети и образуются путем соответствующей настройки коммуникационного оборудования.

Выбор топологии электрических связей существенно влияет на многие характеристики сети. Например, наличие резервных связей повышает надежность сети и делает возможным балансирование загрузки отдельных каналов. Простота присоединения новых узлов, свойственная некоторым топологиям, делает сеть легкорасширяемой. Экономические соображения часто приводят к выбору топологий, для которых характерна минимальная суммарная длина линий связи.

Рассмотрим некоторые, наиболее часто встречающиеся топологии.

Полносвязная топология (рис. 10.5а) соответствует сети, в которой каждый компьютер сети связан со всеми остальными. Несмотря на логическую простоту, этот вариант оказывается громоздким и неэффективным. Действительно, каждый компьютер в сети должен иметь большое количество коммуникационных портов, достаточное для связи с каждым из остальных компьютеров сети. Для каждой пары компьютеров должна быть выделена отдельная электрическая линия связи. Полносвязные топологии применяются редко, так как не удовлетворяют ни одному из приведенных выше требований. Чаще этот вид топологии используется в многомашинных комплексах или глобальных сетях при небольшом количестве компьютеров.

Все другие варианты основаны на неполносвязных топологиях, когда для обмена данными между двумя компьютерами может потребоваться промежуточная передача данных через другие узлы сети. Ячеистая топология (mesh) получается из полносвязной путем удаления некоторых возможных связей (рис. 10.56). В сети с ячеистой топологией непосредственно связываются только те компьютеры, между которыми происходит интенсивный обмен данными, а для обмена данными между компьютерами, не соединенными прямыми связями, используются транзитные передачи через промежуточные узлы. Ячеистая топология допускает соединение большого количества компьютеров и характерна, как правило, для глобальных сетей.

Общая шина (рис. 10.5в) является очень распространенной (а до недавнего времени самой распространенной) топологией для локальных сетей. В этом случае компьютеры подключаются к одному коаксиальному кабелю по схеме "монтажного ИЛИ". Передаваемая информация может распространяться в обе стороны. Применение общей шины снижает стоимость проводки, унифицирует подключение различных модулей, обеспечивает возможность почти мгновенного широковещательного обращения ко всем станциям сети. Таким образом, основными преимуществами такой схемы являются дешевизна и простота разводки кабеля по помещениям. Самый серьезный недостаток общей шины заключается в ее низкой надежности: любой дефект кабеля или какого-нибудь из многочисленных разъемов полностью парализует всю сеть. К сожалению, дефект коаксиального разъема редкостью не является. Другим недостатком общей шины является ее невысокая производительность, так как при таком способе подключения в каждый момент времени только один компьютер может передавать данные в сеть. Поэтому пропускная способность канала связи всегда делится здесь между всеми узлами сети.

Топология звезда (рис. 10.5г). В этом случае каждый компьютер подключается отдельным кабелем к общему устройству, называемому концентратором, который находится в центре сети. В функции концентратора входит направление передаваемой компьютером информации одному или всем остальным компьютерам сети. Главное преимущество этой топологии перед общей шиной — существенно большая надежность. Любые неприятности с кабелем касаются лишь того компьютера, к которому этот кабель присоединен, и только неисправность концентратора может вывести из строя всю сеть. Кроме того, концентратор может играть роль интеллектуального фильтра информации, поступающей от узлов в сеть, и при необходимости блокировать запрещенные администратором передачи.

К недостаткам топологии типа "звезда" относится более высокая стоимость сетевого оборудования из-за необходимости приобретения концентратора. Кроме того, возможности по наращиванию количества узлов в сети ограничиваются количеством портов концентратора. Иногда имеет смысл строить сеть с использованием нескольких концентраторов, иерархически соединенных между собой связями типа "звезда" (рис. 10.5д). В настоящее время иерархическая звезда является самым распространенным типом топологии связей как в локальных, так и глобальных сетях.

В сетях с кольцевой конфигурацией (рис. 10.5е) данные передаются по кольцу от одного компьютера к другому, как правило, в одном направлении. Если компьютер распознает данные как "свои", то он копирует их себе во внутренний буфер. В сети с кольцевой топологией необходимо принимать специальные меры, чтобы в случае выхода из строя или отключения какой-либо станции не прервался канал связи между остальными станциями. Кольцо представляет собой очень удобную конфигурацию для организации обратной связи — данные, сделав полный оборот, возвращаются к узлу-источнику. Поэтому этот узел может контролировать процесс доставки данных адресату. Часто это свойство кольца используется для тестирования связности сети и поиска узла, работающего некорректно. Для этого в сеть посылаются специальные тестовые сообщения.

В то время как небольшие сети, как правило, имеют типовую топологию — "звезда", "кольцо" или "общая шина", для крупных сетей характерно наличие произвольных связей между компьютерами. В таких сетях можно выделить отдельные произвольно связанные фрагменты (подсети), имеющие типовую топологию, поэтому их называют сетями со смешанной топологией (рис. 106).

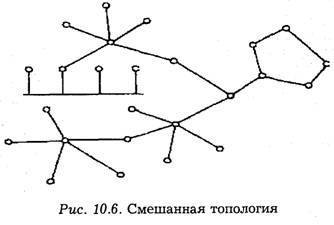
2. Организация совместного использования линий связи

Только в сети с полносвязной топологией для соединения каждой пары компьютеров имеется отдельная линия связи. Во всех остальных случаях неизбежно возникает вопрос о том, как организовать совместное использование линий связи несколькими компьютерами сети. Как и всегда при разделении ресурсов, главной целью здесь является удешевление сети.

В вычислительных сетях используют как индивидуальные линии связи между компьютерами, так и разделяемые (shared), когда одна линия связи попеременно используется несколькими компьютерами. В случае применения разделяемых линий связи (часто используется также термин "разделяемая среда передачи данных" — "shared media") возникает комплекс проблем, связанных с их совместным использованием, который включает как чисто электрические проблемы обеспечения нужного качества сигналов при подключении к одному и тому же проводу нескольких приемников и передатчиков, так и логические проблемы разделения во времени доступа к этим линиям.

Классическим примером сети с разделяемыми линиями связи являются сети с топологией "общая шина", в которых один кабель совместно используется всеми компьютерами сети. Ни один из компьютеров сети в принципе не может индивидуально, независимо от всех других компьютеров сети, использовать кабель, так как при одновременной передаче данных сразу несколькими узлами сигналы смешиваются и искажаются. В топологиях "кольцо" или "звезда" индивидуальное использование линий связи, соединяющих компьютеры, принципиально возможно, но эти кабели часто также рассматривают как разделяемые для всех компьютеров сети, так что, например, только один компьютер кольца имеет право в данный момент времени отправлять по кольцу пакеты другим компьютерам.

Существуют различные способы решения задачи организации совместного доступа к разделяемым линиям связи. Внутри компьютера проблемы разделения линий связи между различными модулями также существуют — примером является доступ к системной шине, которым управляет либо процессор, либо специальный арбитр шины. В сетях организация совместного доступа к линиям связи имеет свою специфику из-за существенно большего времени распространения сигналов по длинным проводам, к тому же это время для различных пар компьютеров может быть различным. Из-за этого процедуры согласования доступа к линии связи могут занимать слишком большой промежуток времени и приводить к значительным потерям производительности сети.

Несмотря на все эти сложности, в локальных сетях разделяемые линии связи используются очень часто. Этот подход, в частности, реализован в широко распространенных классических технологиях Ethernet и Token Ring. Однако в последние годы наметилась тенденция отказа от разделяемых сред передачи данных и в локальных сетях. Это связано с тем, что за достигаемое таким образом удешевление сети приходится расплачиваться производительностью.

Сеть с разделяемой средой при большом количестве узлов будет работать всегда медленнее, чем аналогичная сеть с индивидуальными линиями связи, так как пропускная способность индивидуальной линии связи достается одному компьютеру, а при ее совместном использовании — делится на все компьютеры сети. Часто с такой потерей производительности мирятся ради увеличения экономической эффективности сети. Не только в классических, но и в совсем новых технологиях, разработанных для локальных сетей, сохраняется режим разделяемых линий связи. Например, разработчики технологии Gigabit Ethernet, принятой в 1998 г. в качестве нового стандарта, включили режим разделения передающей среды в свои спецификации наряду с режимом работы по индивидуальным линиям связи.

При использовании индивидуальных линий связи в полносвязных топологиях конечные узлы должны иметь по одному порту на каждую линию связи. В звездообразных топологиях конечные узлы могут подключаться индивидуальными линиями связи к специальному устройству — коммутатору. В глобальных сетях коммутаторы использовались уже на начальном этапе, а в локальных сетях — с начала 90-х годов. Коммутаторы приводят к существенному удорожанию локальной сети, поэтому пока их применение ограничено, но по мере снижения стоимости коммутации этот подход, возможно, вытеснит применение разделяемых линий связи. Необходимо подчеркнуть, что индивидуальными в таких сетях являются только линии связи между конечными узлами и коммутаторами сети, а связи между коммутаторами остаются разделяемыми, так как по ним передаются сообщения разных конечных узлов (рис. 10.7).

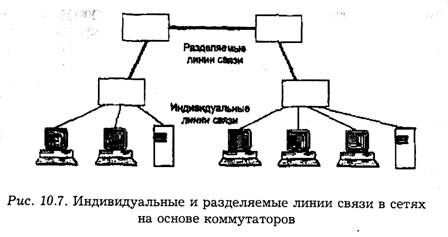
В глобальных сетях отказ от разделяемых линий связи объясняется техническими причинами. Здесь большие временные задержки распространения сигналов принципиально ограничивают применимость техники разделения линии связи. Компьютеры могут затратить больше времени на переговоры о том, кому сейчас можно использовать линию связи, чем непосредственно на передачу данных по этой линии связи. Однако это не относится к линиям связи типа "коммутатор — коммутатор". В этом случае только два коммутатора борются за доступ к линии связи, и это существенно упрощает задачу организации совместного использования линии.

3. Адресация компьютеров

Еще одной новой проблемой, которую нужно учитывать при объединении трех и более компьютеров, является проблема их адресации. К адресу узла сети и схеме его назначения можно предъявить несколько требований.

•  Адрес должен уникально идентифицировать компьютер в сети любого масштаба.

• Схема назначения адресов должна сводить к минимуму ручной труд администратора и вероятность дублирования адресов.

•  Адрес должен иметь иерархическую структуру, удобную для построения больших сетей. Эту проблему хорошо иллюстрируют международные почтовые адреса, которые позволяют почтовой службе, организующей доставку писем между странами, пользоваться только названием страны адресата и не учитывать название его города, а тем более улицы. В больших сетях, состоящих из многих тысяч узлов, отсутствие иерархии адреса может привести к большим издержкам — конечным узлам и коммуникационному оборудованию придется оперировать таблицами адресов, состоящими из тысяч записей.

•  Адрес должен быть удобен для пользователей сети, а это значит, что он должен иметь символьное представление, например, Server3 или www.cisco.com.

•  Адрес должен иметь по возможности компактное представление, чтобы не перегружать память коммуникационной аппаратуры — сетевых адаптеров, маршрутизаторов и т. п.

Нетрудно заметить, что эти требования противоречивы — например, адрес, имеющий иерархическую структуру, скорее всего будет менее компактным, чем неиерархический (такой адрес часто называют "плоским", т. е. не имеющим структуры). Символьный же адрес скорее всего потребует больше памяти, чем адрес-число.

Так как все перечисленные требования трудно совместить в рамках какой-либо одной схемы адресации, то на практике обычно используется сразу несколько схем, так что компьютер одновременно имеет несколько адресов-имен. Каждый адрес используется в той ситуации, когда соответствующий вид адресации наиболее удобен. А чтобы не возникало путаницы и компьютер всегда однозначно определялся своим адресом, используются специальные вспомогательные протоколы, которые по адресу одного типа могут определить адреса других типов.

Наибольшее распространение получили три схемы адресации узлов.

• Аппаратные (hardware) адреса. Эти адреса предназначены для сети небольшого или среднего размера, поэтому они не имеют иерархической структуры. Типичным представителем адреса такого типа является адрес сетевого адаптера локальной сети. Такой адрес обычно используется только аппаратурой, поэтому его стараются сделать по возможности компактным и записывают в виде двоичного или шестнадцатиричного значения, например, 0081005е24а8. При задании аппаратных адресов обычно не требуется выполнение ручной работы, так как они либо встраиваются в аппаратуру компанией-изготовителем, либо генерируются автоматически при каждом новом запуске оборудования, причем уникальность адреса в пределах сети обеспечивает оборудование. Помимо отсутствия иерархии использование аппаратных адресов связано с еще одним недостатком — при замене аппаратуры, например, сетевого адаптера, изменяется и адрес компьютера. Более того, при установке нескольких сетевых адаптеров у компьютера появляется несколько адресов, что не очень удобно для пользователей сети.

•  Символьные адреса или имена. Эти адреса предназначены для запоминания людьми и поэтому обычно несут смысловую нагрузку. Символьные адреса легко использовать как в небольших, так и в крупных сетях. Для работы в больших сетях символьное имя может иметь сложную иерархическую структуру, например, ftp-archl.ucl.ac.uk. Этот адрес говорит о том, что данный компьютер поддерживает ftp-архив в сети одного из колледжей Лондонского университета (University College London-itcZ) и эта сеть относится к академической ветви (ас) Internet Великобритании (United Kingdom). При работе в пределах сети Лондонского университета такое длинное символьное имя явно избыточно и вместо него удобно пользоваться кратким символьным именем, на роль которого хорошо подходит самая младшая составляющая полного имени, т. е. имя ftp-arch1.

• Числовые составные адреса. Символьные имена удобны для людей, но из-за переменного формата и потенциальнобольшой длины их передача по сети не очень экономична. Поэтому во многих случаях для работы в больших сетях в качестве адресов узлов используют числовые составные адреса фиксированного и компактного форматов. Типичным представителями адресов этого типа являются IP- и IPX-адреса. В них поддерживается двухуровневая иерархия, адрес делится на старшую часть — номер сети и младшую — номер узла. Такое деление позволяет передавать сообщения между сетями только на основании номера сети, а номер узла используется только после доставки сообщения в нужную сеть, точно так же, как название улицы используется почтальоном только после того, как письмо доставлено в нужный город. В последнее время, чтобы сделать маршрутизацию в крупных сетях более эффективной, предлагаются более сложные варианты числовой адресации, в соответствии с которыми адрес имеет три и более составляющих. Такой подход, в частности, реализован в новой версии протокола IPv6, предназначенного для работы в сети Internet.

В современных сетях для адресации узлов применяются, как правило, одновременно все три приведенные выше схемы. Пользователи адресуют компьютеры символьными именами, которые автоматически заменяются в сообщениях, передаваемых по сети, на числовые номера. С помощью этих числовых номеров сообщения передаются из одной сети в другую, а после доставки сообщения в сеть назначения вместо числового номера используется аппаратный адрес компьютера. Сегодня такая схема характерна даже для небольших автономных сетей, где, казалось бы, она явно избыточна — это делается для того, чтобы при включении этой сети в большую сеть не нужно было менять состав операционной системы.

Проблема установления соответствия между адресами различных типов, которой занимается служба разрешения имен, может решаться как полностью централизованными, так и распределенными средствами. В случае централизованного подхода в сети выделяется один компьютер (сервер имен), в котором хранится таблица соответствия друг другу имен различных типов, например, символьных имен и числовых номеров. Все остальные компьютеры обращаются к серверу имен, чтобы по символьному имени найти числовой номер компьютера, с которым необходимо обменяться данными.

При другом, распределенном, подходе каждый компьютер сам решает задачу установления соответствия между именами. Например, если пользователь указал для узла назначения числовой номер, то перед началом передачи данных компьютер-отправитель посылает всем компьютерам сети сообщение (такое сообщение называется широковещательным) с просьбой опознать это числовое имя. Все компьютеры, получив это сообщение, сравнивают заданный номер со своим собственным. Тот компьютер, у которого обнаружилось совпадение, посылает ответ, содержащий его аппаратный адрес, после чего становится возможным отправка сообщений по локальной сети.

Распределенный подход хорош тем, что не предполагает выделения специального компьютера, который к тому же часто требует ручного задания таблицы соответствия имен. Недостатком распределенного подхода является необходимость широковещательных сообщений — такие сообщения перегружают сеть, так как они требуют обязательной обработки всеми узлами, а не только узлом назначения. Поэтому распределенный подход используется только в небольших локальных сетях. В крупных сетях распространение широковещательных сообщений по всем ее сегментам становится практически нереальным, поэтому для них характерен централизованный подход. Наиболее известной службой централизованного разрешения имен является служба Domain Name System (DNS) сети Internet.

10.5. Ethernet — пример стандартного построения сетей

Рассмотрим, каким образом описанные выше общие подходы к решению наиболее важных проблем построения сетей воплощены в наиболее известной сетевой технологии —Ethernet.

Сетевая технология — это согласованный набор стандартных протоколов и реализующих их программно-аппаратных средств (например, сетевых адаптеров, драйверов, кабелей и разъемов), достаточный для построения вычислительной сети. Определение "достаточный" подчеркивает то обстоятельство, что этот набор представляет собой минимальный набор средств, с помощью которых можно построить работоспособную сеть. Возможно, эту сеть можно улучшить, например, за счет выделения в ней подсетей, что сразу потребует кроме протоколов стандарта Ethernet применения протокола IP, а также специальных коммуникационных устройств — маршрутизаторов. Улучшенная сеть будет, скорее всего, более надежной и быстродействующей, но за счет надстроек над средствами технологии Ethernet, которая составила базис сети.

Термин "сетевая технология" чаще всего используется в описанном выше узком смысле, но иногда применяется и его расширенное толкование как любого набора средств и правил для построения сети, например, "технология сквозной маршрутизации", "технология создания защищенного канала", "технология IP-сетей".

Протоколы, на основе которых строится сеть определенной технологии (в узком смысле), специально разрабатывались для совместной работы, поэтому от разработчика сети не требуется дополнительных усилий по организации их взаимодействия. Иногда сетевые технологии называют базовыми технологиями, имея в виду то, что на их основе строится базис любой сети. Примерами базовых сетевых технологий могут служить наряду с Ethernet такие известные технологии локальных сетей, как Token Ring и FDDI, или же технологии территориальных сетей Х.25 и frame relay. Для получения работоспособной сети в этом случае достаточно приобрести программные и аппаратные средства, относящиеся к одной базовой технологии — сетевые адаптеры с драйверами, концентраторы, коммутаторы, кабельную систему и т. п., — и

соединить их в соответствии с требованиями стандарта на данную технологию.

Стандарт Ethernet был принят в 1980 г. Число сетей, построенных на основе этой технологии, к настоящему моменту оценивается в 5 млн, а количество компьютеров, работающих в таких сетях, — в 50 млн.

Основной принцип, положенный в основу Ethernet, — случайный метод доступа к разделяемой среде передачи данных. В качестве такой среды может использоваться толстый или тонкий коаксиальный кабель, витая пара, оптоволокно или радиоволны (кстати, первой сетью, построенной на принципе случайного доступа к разделяемой среде, была радиосеть Aloha Гавайского университета).

В стандарте Ethernet строго зафиксирована топология электрических связей. Компьютеры подключаются к разделяемой среде в соответствии с типовой структурой "общая шина" (рис. 10.8). С помощью разделяемой во времени шины любые два компьютера могут обмениваться данными. Управление доступом к линии связи осуществляется специальными контроллерами — сетевыми адаптерами Ethernet. Каждый компьютер, а более точно, каждый сетевой адаптер, имеет уникальный адрес. Передача данных происходит со скоростью 10 Мбит/с. Эта величина является пропускной способностью сети Ethernet .

Суть случайного метода доступа состоит в следующем. Компьютер в сети Ethernet может передавать данные по сети, только если сеть свободна, т. е. если никакой другой компьютер в данный момент не занимается обменом. Поэтому важной частью технологии Ethernet является процедура определения доступности среды.

После того как компьютер убедился, что сеть свободна, он начинает передачу, при этом "захватывает" среду. Время монопольного использования разделяемой среды одним узлом ограничивается временем передачи одного кадра. Кадр — это единица данных, которыми обмениваются компьютеры в сети Ethernet. Кадр имеет фиксированный формат и наряду с полем данных содержит различную служебную информацию, например, адрес получателя и адрес отправителя.

Сеть Ethernet устроена так, что при попадании кадра в разделяемую среду передачи данных все сетевые адаптеры одновременно начинают принимать этот кадр. Все они анализируют адрес назначения, располагающийся в одном из начальных полей кадра, и, если этот адрес совпадает с их собственным адресом, кадр помещается во внутренний буфер сетевого адаптера. Таким образом компьютер-адресат получает предназначенные ему данные.

Иногда может возникать ситуация, когда одновременно два или более компьютера решают, что сеть свободна, и начинают передавать информацию. Такая ситуация, называемая коллизией, препятствует правильной передаче данных по сети. В стандарте Ethernet предусмотрен алгоритм обнаружения и корректной обработки коллизий. Вероятность возникновения коллизии зависит от интенсивности сетевого трафика.

После обнаружения коллизии сетевые адаптеры, которые пытались передать свои кадры, прекращают передачу и после паузы случайной длительности пытаются снова получить доступ к среде и передать тот кадр, который вызвал коллизию.

Главным достоинством сетей Ethernet, благодаря которому они стали такими распространенными, является их экономичность. Для построения сети достаточно иметь по одному сетевому адаптеру для каждого компьютера плюс один физический сегмент коаксиального кабеля нужной длины. Другие базовые технологии, например, Token Ring, для создания даже небольшой сети требуют наличия дополнительного устройства — концентратора.

Кроме того, в сетях Ethernet реализованы достаточно простые алгоритмы доступа к среде, адресации и передачи данных. Простота логики работы сети ведет к упрощению и, соответственно, удешевлению сетевых адаптеров и их драйверов. По той же причине адаптеры сети Ethernet обладают высокой надежностью.

И, наконец, еще одним замечательным свойством сетей Ethernet является их хорошая расширяемость, т. е. легкость подключения новых узлов.

Другие базовые сетевые технологии — Token Ring, FDDI, WOVGAny-LAN, хотя и обладают многими индивидуальными чертами, в то же время имеют много общих свойств с Ethernet. В первую очередь — это применение регулярных фиксированных топологий (иерархическая звезда и кольцо), а также разделяемых сред передачи данных. Существенные отличия одной технологии от другой связаны с особенностями используемого метода доступа к разделяемой среде. Так, отличия технологии Ethernet от технологии Token Ring во многом определяются спецификой заложенных в них методов разделения среды — случайного алгоритма доступа в Ethernet и метода доступа путем передачи маркера в Token Ring.

10.6. Структуризация как средство построения больших сетей

В сетях с небольшим (10—30) количеством компьютеров чаще всего используется одна из типовых топологий — "общая шина", "кольцо", "звезда" или "полносвязная сеть". Все перечисленные топологии обладают свойством однородности, т. е. все компьютеры в такой сети имеют одинаковые права в отношении доступа к другим компьютерам (за исключениемцентрального компьютера при соединении "звезда"). Такая однородность структуры делает простой процедуру наращивания числа компьютеров, облегчает обслуживание и эксплуатацию сети.

Однако при построении больших сетей однородная структура связей превращается из преимущества в недостаток. В таких сетях использование типовых структур порождает различные ограничения, важнейшими из которых являются:

•  ограничения на длину связи между узлами;

•  ограничения на количество узлов в сети;

•  ограничения на интенсивность трафика, порождаемого узлами сети.

Например, технология Ethernet на тонком коаксиальном кабеле позволяет использовать кабель длиной не более 185 м, к которому можно подключить не более 30 компьютеров. Однако, если компьютеры интенсивно обмениваются информацией между собой, иногда приходится снижать число подключенных к кабелю компьютеров до 20, а то и до 10, чтобы каждому компьютеру доставалась приемлемая доля общей пропускной способности сети.

Для снятия этих ограничений используются специальные методы структуризации сети и специальное структурообразующее оборудование — повторители, концентраторы, мосты, коммутаторы, маршрутизаторы. Оборудование такого рода также называют коммуникационным, имея в виду, что с помощью него отдельные сегменты сети взаимодействуют между собой.

1. Физическая структуризация сети

Простейшее из коммуникационных устройств — повторитель (repeator) — используется для физического соединения различных сегментов кабеля локальной сети с целью увеличения общей длины сети. Повторитель передает сигналы, приходящие из одного сегмента сети в другие ее сегменты (рис. 10.9). Повторитель (широкополосный усилитель) позволяет преодолеть ограничения на длину линий связи за счет улучшения качества передаваемого сигнала — восстановления его мощности и амплитуды, улучшения фронтов и т. п.

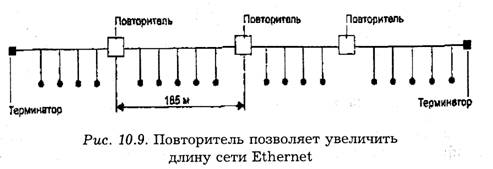
Повторитель, который имеет несколько портов и соединяет несколько физических сегментов, часто называют концентратором (concentrator), или хабом (hub). Эти названия (hub — основа, центр деятельности) отражают тот факт, что в данном устройстве сосредоточиваются все связи между сегментами сети.

Концентраторы характерны практически для всех базовых технологий локальных сетей — Ethernet, ArcNet, Token Ring, FDDI, Fast Ethernet, Gigabit Ethernet, WOVG-AnyLAN.

Нужно подчеркнуть, что в работе концентраторов любых технологий много общего — они повторяют сигналы, пришедшие с одного из своих портов, на других своих портах. Разница состоит в том, на каких именно портах повторяются входные сигналы. Так, концентратор Ethernet повторяет входные сигналы на всех своих портах, кроме того, с которого сигналы поступают (рис. 10.10а). А концентратор Token Ring (рис. 10.106) повторяет входные сигналы, поступающие с некоторого порта, только на одном порту — на том, к которому подключен следующий в кольце компьютер.

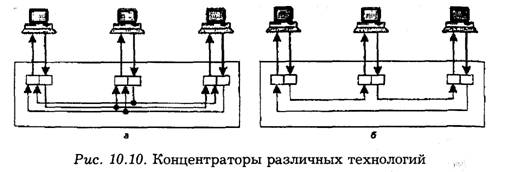
Напомним, что под физической топологией понимается конфигурация связей, образованных отдельными частями кабеля, а под логической — конфигурация информационных потоков между компьютерами сети. Во многих случаях физическая и логическая топологии сети совпадают. Например, сеть, представленная на рис. 10.11а, имеет физическую топологию "кольцо". Компьютеры этой сети получают доступ к кабелям кольца за счет передачи друг другу специального кадра — маркера, причем этот маркер также передается последовательно от компьютера к компьютеру в том же порядке, в котором компьютеры образуют физическое кольцо, т. е. компьютер А передает маркер компьютеру В, компьютер В — компьютеру С и т. д.

Сеть, показанная на рис. 10.116, демонстрирует пример несовпадения физической и логической топологии. Физически компьютеры соединены по топологии "общая шина". Доступ же к шине происходит не по алгоритму случайного доступа, применяемому в технологии Ethernet, а путем передачи маркера в кольцевом порядке: от компьютера А — компьютеру В, от компьютера В — компьютеру С и т. д. Здесь порядок передачи маркера уже не повторяет физические связи, а определяется логическим конфигурированием драйверов сетевых адаптеров. Ничто не мешает настроить сетевые адаптеры и их драйверы так, чтобы компьютеры образовали кольцо в другом порядке, например: В, А, С... При этом физическая структура сети никак не изменяется.

Другим примером несовпадения физической и логической топологий сети является уже рассмотренная сеть на рис. 10.10а. Концентратор Ethernet поддерживает в сети физическую топологию "звезда". Однако логическая топология сети осталась без изменений — это "общая шина". Так как концентратор повторяет данные, пришедшие с любого порта, на всех остальных портах, то они появляются одновременно на всех физических сегментах сети, как и в сети с физической общей шиной. Логика доступа к сети совершенно не меняется: все компоненты алгоритма случайного доступа — определение незанятости среды, захват среды, распознавание и отработка коллизий — остаются в силе.

Физическая структуризация сети с помощью концентраторов полезна не только для увеличения расстояния между узлами сети, но и для повышения ее надежности. Например, если какой-либо компьютер сети Ethernet с физической общей шиной из-за сбоя начинает непрерывно передавать данные по общему кабелю, то вся сеть выходит из строя, и для решения этой проблемы остается только один выход — вручную отсоединить сетевой адаптер этого компьютера от кабеля. В сети Ethernet, построенной с использованием концентратора, эта проблема может быть решена автоматически — концентратор отключает свой порт, если обнаруживает, что присоединенный к нему узел слишком долго монопольно занимает сеть. Концентратор может блокировать некорректно работающий узел и в других случаях, выполняя роль некоторого управляющего узла.

2. Логическая структуризация сети

Физическая структуризация сети полезна во многих отношениях, однако в ряде случаев, обычно относящихся к сетям большого и среднего размера, невозможно обойтись без логической структуризации сети. Наиболее важной проблемой, не решаемой путем физической структуризации, остается проблема перераспределения передаваемого трафика между различными физическими сегментами сети.

В большой сети естественным образом возникает неоднородность информационных потоков: сеть состоит из множества подсетей рабочих групп, отделов, филиалов предприятия и других административных образований. Очень часто наиболее интенсивный обмен данными наблюдается между компьютерами, принадлежащими к одной подсети, и только небольшая часть обращений происходит к ресурсам компьютеров, находящихся вне локальных рабочих групп. (До недавнего времени такое соотношение трафиков не подвергалось сомнению, и был даже сформулирован эмпирический закон "80/20", в соответствии с которым в каждой подсети 80% трафика является внутренним и только 20% — внешним.) Сейчас характер нагрузки сетей во многом изменился, широко внедряется технология intranet, на многих предприятиях имеются централизованные хранилища корпоративных данных, активно используемые всеми сотрудниками предприятия. Все это не могло не повлиять на распределение информационных потоков. И теперь нередки ситуации, когда интенсивность внешних обращений выше интенсивности обмена между "соседними" машинами. Но независимо от того, в какой пропорции распределяются внешний и внутренний трафик, для повышения эффективности работы сети неоднородность информационных потоков необходимо учитывать.

Сеть с типовой топологией (шина, кольцо, звезда), в которой все физические сегменты рассматриваются в качестве одной разделяемой среды, оказывается неадекватной структуре информационных потоков в большой сети. Например, в сети с общей шиной взаимодействие любой пары компьютеров занимает ее на все время обмена, поэтому при увеличении числа компьютеров в сети шина становится узким местом. Компьютеры одного отдела вынуждены ждать, когда окончит обмен пара компьютеров другого отдела, и это при том, что необходимость в связи между компьютерами двух разных отделов возникает гораздо реже и требует совсем небольшой пропускной способности.

Этот случай иллюстрирует рис. 10.12а. Здесь показана сеть, построенная с использованием концентраторов. Пусть компьютер А, находящийся в одной подсети с компьютером В, посылает ему данные. Несмотря на разветвленную физическую структуру сети, концентраторы распространяют любой кадр по всем ее сегментам. Поэтому кадр, посылаемый компьютером А компьютеру В, хотя и не нужен компьютерам отделов 2 и 3, в соответствии с логикой работы концентраторов поступает на эти сегменты тоже. И до тех пор, пока компьютер В не получит адресованный ему кадр, ни один из компьютеров этой сети не сможет передавать данные.

Такая ситуация возникает из-за того, что логическая структура данной сети осталась однородной — она никак не учитывает увеличение интенсивности трафика внутри отдела и предоставляет всем парам компьютеров равные возможности по обмену информацией (рис. 10.126).

Решение проблемы состоит в отказе от идеи единой однородной разделяемой среды. Например, в рассмотренном выше примере желательно было бы сделать так, чтобы кадры, которые передают компьютеры отдела 1, выходили бы за пределы этой части сети в том и только в том случае, если эти кадры направлены какому-либо компьютеру из других отделов. С другой стороны, в сеть каждого из отделов должны попадать те и только те кадры, которые адресованы узлам этой сети. При такой организации работы сети ее производительность существенно повысится, так как компьютеры одного отдела не будут простаивать в то время, когда обмениваются данными компьютеры других отделов.

Нетрудно заметить, что в предложенном решении приходится отказаться от идеи общей разделяемой среды в пределах всей сети, хотя она остается в пределах каждого отдела. Пропускная способность линий связи между отделами не должна совпадать с пропускной способностью среды внутри отделов. Если трафик между отделами составляет только 20% трафика внутри отдела (как уже отмечалось, эта величина может быть другой), то и пропускная способность линий связи и коммуникационного оборудования, соединяющего отделы, может быть значительно ниже внутреннего трафика сети i отдела.

    Для логической структуризации сети используются такие коммуникационные устройства, как мосты, коммутаторы, ; маршрутизаторы и шлюзы.

Мост (bridge) делит разделяемую среду передачи сети на части (часто называемые логическими сегментами), передавая информацию из одного сегмента в другой только в том случае, если такая передача действительно необходима, т. е. если адрес компьютера назначения принадлежит другой подсети. Тем самым мост изолирует трафик одной подсети от трафика другой, повышая общую производительность передачи данных в сети. Локализация трафика не только экономит пропускную способность, но и уменьшает возможность несанкционированного доступа к данным, так как кадры не выходят за пределы своего сегмента и их сложнее перехватить злоумышленнику.

На рис. 10.13 показана сеть, которая была получена из сети с центральным концентратором (см. рис. 10.12.) путем его замены на мост. Сети 1-го и 2-го отделов состоят из отдельных логических сегментов, а сеть отдела 3 — из двух логических сегментов. Каждый логический сегмент построен на базе концентратора и имеет простейшую физическую структуру, образованную отрезками кабеля, связывающими компьютеры с портами концентратора.

Мосты используют для локализации трафика аппаратные адреса компьютеров. Это затрудняет распознавание принадлежности того или иного компьютера к определенному логическому сегменту — сам адрес не содержит никакой информации по этому поводу. Поэтому мост достаточно упрощенно представляет деление сети на сегменты — он запоминает, через какой порт на него поступил кадр данных от каждого компьютера сети, и в дальнейшем передает кадры, предназначенные для этого компьютера, на этот порт. Точной топологии связей между логическими сегментами мост не знает. Из-за этого применение мостов приводит к значительным ограничениям на конфигурацию связей сети — сегменты должны быть соединены таким образом, чтобы в сети не образовывались замкнутые контуры.

Коммутатор (switch, switching hub) по принципу обработки кадров ничем не отличается от моста. Основное его отличие от моста состоит в том, что он является своего рода коммуникационным мультипроцессором, так как каждый его порт оснащен специализированным процессором, который обрабатывает кадры по алгоритму моста независимо от процессоров других портов. За счет этого общая производительность коммутатора обычно намного выше производительности традиционного моста, имеющего один процессорный блок. Можно сказать, что коммутаторы — это мосты нового поколения, которые обрабатывают кадры в параллельном режиме.

Ограничения, связанные с применением мостов и коммутаторов — по топологии связей, а также ряд других, — привели к тому, что в ряду коммуникационных устройств появился еще один тип оборудования — маршрутизатор (router). Маршрутизаторы более надежно и более эффективно, чем мосты, изолируют трафик отдельных частей сети друг от друга. Маршрутизаторы образуют логические сегменты посредством явной адресации, поскольку используют не плоские аппаратные, а составные числовые адреса. В этих адресах имеется поле номера сети, так что все компьютеры, у которых значение этого поля одинаково, принадлежат к одному сегменту, называемому в данном случае подсетью (subnet).

Кроме локализации трафика маршрутизаторы выполняют еще много других полезных функций. Так, маршрутизаторы могут работать в сети с замкнутыми контурами, при этом они осуществляют выбор наиболее рационального маршрута из нескольких возможных. Сеть, представленная на рис. 10.14, отличается от своей предшественницы (см. рис. 10.13) тем, что между подсетями отделов 1 и 2 проложена дополнительная связь, которая может использоваться как для повышения производительности сети, так и для повышения ее надежности.

Другой очень важной функцией маршрутизаторов является их способность связывать в единую сеть подсети, построенные с использованием разных сетевых технологий, например, Ethernet и Х.25.

Кроме перечисленных устройств отдельные части сети может соединять шлюз (gateway). Обычно основной причиной, по которой в сети используют шлюз, является необходимость объединить сети с разными типами системного и прикладного программного обеспечения, а не желание локализовать трафик. Тем не менее шлюз обеспечивает и локализацию трафика в качестве некоторого побочного эффекта.

Крупные сети практически никогда не строятся без логической структуризации. Для отдельных сегментов и подсетей характерны типовые однородные топологии базовых технологий, и для их объединения всегда используется оборудование, обеспечивающее локализацию трафика, — мосты, коммутаторы, маршрутизаторы и шлюзы.

10.7. Программная совместимость различных систем

Различают три уровня программной совместимости:

•  уровень машинных команд;

• уровень символических команд или интерпретирующих программ;

•  уровень программирующих программ.

Существует несколько типов совместимости на уровне машинных команд: полная совместимость, совместимость типа "общей наименьшей машины", совместимость иерархического типа и частичная совместимость с имитацией недостающих команд.

Обозначим через A={A₁, А₂, ..., A_N} множество программ, выполняемых одним вычислителем системы, и через В={В_1г, В₂, -..,В_М} множество программ, выполняемых другим вычислителем (N и М — соответственно количество различных про-

грамм, выполняемых на первом и втором вычислителях). Если для пересечения множеств А и В справедливо соотношение:

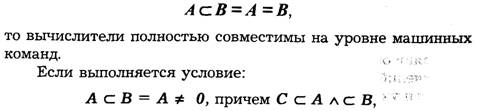
то множество программ С соответствует возможностям некоторой символической "общей наименьшей машины". При организации обмена программами по этому типу совместимости аппаратные средства системы, выходящие за пределы "общей наименьшей машины", используются не полностью, особенно если задачи, решаемые системой, неоднородны по объему и содержанию.

Если множество программ А есть подмножество множества программ В или наоборот, т. е.:

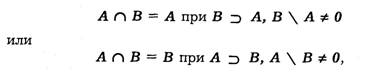
то такая совместимость вычислителей называется иерархической. Для нее характерно, что все программы, составленные для первого вычислителя, могут быть использованы на втором вычислителе, но не наоборот. При такой совместимости возможен без ограничений только односторонний обмен программами — от вычислителя с меньшими возможностями к вычислителю с большими возможностями.

Частичная совместимость имеет место тогда, когда часть программы (части нескольких программ), составленной для одного вычислителя, пригодна для другого, хотя в целом вся программа (программы) непригодна. В этом случае справедливо:

Для увеличения степени частичной совместимости отсутствующие в малом вычислителе команды можно имитировать специальными программами (экстракодами). Этот же прием позволяет обеспечить двусторонний обмен программами (без ограничений) при иерархической совместимости.

Если у сопрягаемых вычислителей для реализуемых программ на уровне машинных команд справедливо:

то они несовместимы на этом уровне. Совместная работа таких вычислителей осуществляется путем эмуляции — автоматического преобразования программы, записанной на машинном языке одного вычислителя, в программу, записанную на машинном языке другого вычислителя.

В целом совместимость на уровне машинных команд имеет ряд недостатков, в частности, требуются значительные дополнительные затраты, связанные с имитацией недостающих у менее мощных вычислителей команд, а также в связи с разработкой программно-аппаратных эмулирующих средств.

В связи с этим желательным является второй уровень совместимости, при котором программы составляются в символической форме с использованием псевдокоманд.

Наиболее высокая степень программной совместимости характера для третьего уровня, когда обмен программами, по существу, заменяется обменом алгоритмами. Последние записываются на одном из универсальных алгоритмических языков и преобразуются каждым вычислителем в программы, составленные на машинном языке данного вычислителя .

10.8 Оценка эффективности

вычислительных систем.

Для оценки эффективности различных комплексирования вычислительных средств в системе  с заданным составом аппаратуры можно использовать следующие показатели эффективности комплексирования.

Коэффициент снижения реальной производительности системы, характеризующий затраты производительности вычислительных средств на организацию совместной работы комплексируемых ЭВМ (процессоров):

где V_эi — эффективная производительность i-гo вычислительного средства при индивидуальном функционировании и решении определенного класса задач; П_э — то же для системы в целом; N — количество комплексируемых ЭВМ (процессоров).

Возможность непосредственного доступа к информации, хранящейся в памяти системы, которая характеризуется коэффициентами доступа вычислительных средств к различным блокам данных:

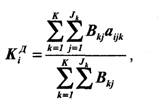
где К — количество уровней памяти системы (оперативная память, память на жестких дисках, память на флоппи-дисках, память на магнитных лентах и т. д.): J_k — количество модулей в запоминающих устройствах k-гo уровня; В_kj. — объем информации, хранящейся в j-м модуле k уровня памяти;

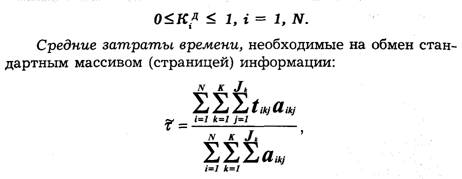
где t_ikj — время, затрачиваемое i-й ЭВМ (процессором) на запись стандартного массива информации, хранящегося в j-м модуле k-гo уровня памяти, в доступную ей область оперативной памяти.

Коэффициент увеличения цикла обращения к оперативной памяти системы для 1-го комплексируемого вычислительного средства:

где t₀ — время цикла обращения к модулю оперативной памяти; τ_k — задержка обращения за счет обработки запроса в аппаратуре комплексирования и устройстве управления памятью; t^-ож _i^. — среднее значение времени ожидания обслуживания запросов i-й ЭВМ (процессора) оперативной памятью, обусловленное конфликтными ситуациями при одновременном обращении более одного вычислительного средства к одному и тому же модулю памяти.

Коэффициент увеличения надежности функционирования вычислительной системы:

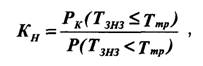
где Р_k и Р — соответственно вероятности реализации типового набора задач за требуемый промежуток времени Т_тp для комплексированных и раздельно работающих ЭВМ.

Кроме рассмотренных показателей оценку эффективности организации комплексирования вычислительных средств можно проводить по затратам на разработку, создание и ввод в эксплуатацию аппаратно-программных средств, обеспечивающих комплексирование ЭВМ.

Известно, что эффективность реализации некоторого алгоритма или класса алгоритмов на ЭВМ практически целиком определяется соотношением структуры выбранного алгоритма и структуры ЭВМ. Все сказанное в полной мере относится и к вычислительным системам. При практическом применении вычислительных систем гибкость логической структуры алгоритма, ее способность к преобразованию приобретает особо важное значение.

Для определения эффективности реализации алгоритмов на вычислительных системах необходимо проанализировать возможные структуры алгоритмов. Условно можно разделить все алгоритмы на три большие группы: последовательные, параллельные и последовательно-параллельные. Естественно, что наиболее эффективно реализуются на вычислительных системах параллельные алгоритмы.

Следует отметить, что приведенное деление алгоритмов на последовательные, параллельные и последовательно-параллельные является весьма условным, поскольку детерминированность структуры вычислительной системы дает возможность производить необходимые преобразования структур алгоритмов, если, конечно, такое преобразование в принципе возможно.

Представляется целесообразным иметь количественную меру эффективности преобразования алгоритма к параллельному или параллельно-последовательному виду. Допустим, что общее и минимальное число обобщенных операций вычислительного алгоритма равно М. Это число принято называть минимальной длиной алгоритма. Если общее число операций, составляющих вычислительный алгоритм, равно N, то:

Если заданы величины N и М, то возможна количественная оценка эффективности преобразования структуры вычислительного алгоритма.

При такой постановке возникает задача об оценке минимальной длины алгоритма:

Эта же задача возникает и при определении оптимального числа машин объединения.

Для получения минимальной длины алгоритма вычислительной системы, состоящей из nⁿ машин одинаковой производительности, достаточно разделить длину последовательного алгоритма на п. Таким образом:

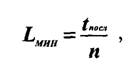
где L_мин — минимальная длина алгоритма вычислительной системы; L_посл — длина последовательного алгоритма.

Конечно, эта оценка является идеализированной, так как она не учитывает структурных особенностей алгоритма или только частично учитывает структурные особенности системы. Тем не менее она позволяет производить оценку различных вариантов преобразования структур алгоритмов вычислительных систем. Такой подход справедлив и при определении минимальной длины алгоритма для систем, состоящих из вычислительных машин различной производительности.

10.9. Качество функционирования вычислительной системы

Под качеством (эффективностью) вычислительной системы понимается совокупность технических характеристик или параметров, отражающих динамику ее функционирования. В общем случае качество можно характеризовать вектором качества:

где Р_1, Р₂,..., P_j — составляющие вектора Ê или показатели качества функционирования вычислительной системы.

Все многообразие вопросов, связанных с построением вычислительных систем, правильностью их функционирования, синтезом оптимальных структур таких систем и т. д., можно практически, в конце концов, свести к рассмотрению показателей качества.

Производительность вычислительной системы ПВС

Эта характеристика, включающая в себя комплекс параметров, зависящих от логической структуры вычислительной системы и от предполагаемого класса решаемых задач. Комплекс должен включать в себя параметры, отражающие чистое машинное время решения задачи, сложность составления и отладки программы для данной вычислительной системы, организацию счета, степень сложности конструкции и т. д.

Для вычислительной системы решающим параметром оценки производительности является параметр, отражающий чистое машинное время решения задачи. Обычно под производительностью понимают чистое время, затрачиваемое системой на решение некоторой задачи.

Кратность повышения производительности вычислительной системы λ _вс

В том случае, если структура объединения однотипна, λ_вс  может быть выражена отношением:

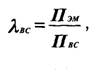
где П_вс — производительность вычислительной системы; П_эм — производительность элементарной машины объединения.

Если система включает в свой состав разнотипные машины, то соответствующий показатель имеет вид:

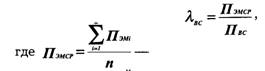усредненное значение производительности элементарной машины.

Данный показатель дает возможность судить о получаемом выигрыше в производительности при применении вычислительной системы. Сущность этого показателя становится более очевидной тогда, когда необходимая производительность не может быть технически обеспечена одной вычислительной машиной.

Показатель, характеризующий степень соответствия структуры реализуемого алгоритма структуре вычислительной системы γ

Известно, что эффективность реализации данного алгоритма на данной ЭВМ в первую очередь зависит от того, насколько согласованы между собой структура алгоритма и структура ЭВМ. Последнее справедливо и для случая реализации алгоритмов, и в вычислительной системе.

Соответствие структуры реализуемого алгоритма структуре системы может быть формализовано в следующем виде:

где L_мин     — минимальная длина реализуемого алгоритма (программы); L_реальн — реальная длина алгоритма (программы).

Эта характеристика показывает, во-первых, насколько правильно произведено преобразование структуры вычислительного алгоритма, и, во-вторых, указывает, целесообразна или нет реализация выбранного класса алгоритмов на данной системе.

Загруженность вычислительной системы ξ

Введение этого обобщенного показателя позволяет судить о степени загруженности системы или об эффективности использования машин системы. Выражение для показателя загруженности может быть представлено в следующем виде:

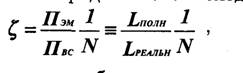
где N — количество машин объединения.

По самой сущности комплексирования производительность системы должна в идеальном случае увеличиваться в N раз. Следовательно, в идеальном случае показатель ξ принимает значение, равное единице. Однако в реальных условиях вследствие неполного соответствия структур алгоритма и системы, а также в силу необходимости обмена информацией между машинами и вынужденного простоя машин значение этого показателя оказывается меньше единицы. Естественно, что эффективность реализации определенного алгоритма на данной системе будет тем выше, чем ближе к единице приближается показатель ξ.

Сложность или экономичность вычислительной системы  μ_с с точки зрения эффективности повышения производительности

Этот обобщенный показатель позволяет судить о том, какой "ценой" достигнуто повышение производительности. Выразим μ_с системы через показатель сложности одной элементарной машины объединения:

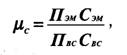
где С_эм    — коэффициент, учитывающий сложность элементарной машины объединения;

— коэффициент, учитывающий сложность системы;

С_кс — коэффициент, учитывающий сложность каналов связи между машинами.

Таким образом, по степени приближения данного коэффициента к своему предельному значению (единице — для однородных структур) можно судить об экономичности системы при реализации алгоритмов определенного класса. Этот показатель можно трактовать и как количество затраченного оборудования на получение единицы производительности.

Контрольные вопросы и задания

1. Каким образом осуществляется связь компьютера с периферийным устройством?

2. Поясните процесс взаимодействия двух компьютеров.

3. Как осуществляется передача данных по линиям связи?

4.  Нарисуйте и объясните особенности различных топологий вычислительных сетей.

5.  Каким образом осуществляется совместное использование линий связи?

6. Какие требования предъявляются к адресу компьютера в сети и какие существуют схемы адресации узлов?

7.  Что такое сетевая технология и как она реализуется в различных сетях?

8. Поясните процесс физической структуризации сети.

9. Как осуществляется логическая структуризация сети?

10.  Поясните уровни программной совместимости различных систем.

11.  Перечислите основные показатели эффективности вычислительных систем.

СПИСОК ЛИТЕРАТУРЫ

1. Артюшенко В.М., Бреусов К.В. Системы сотовой подвижной радиосвязи: Учебное пособие для вузов. — М.: Российский университет сервиса, 1997. — 175 с.

2. Варакин Л.Е. Системы связи с шумоподобными сигналами. — М.: Радио и связь, 1985. — 384 с.

3.  Варламов И.В.,. Душин В.К., Феоктистов Н.А.  Оптоэлек-тронные элементы информационных систем: Учебное пособие для вузов. — М.: МГУС, 2001. — 75 с.

4. Васильев В.И., Горшков Л.Ф., Свириденко В.А. Методы и средства организации каналов передачи данных. — М.: Радио и связь, 1982. — 152 с.

5.  Герасименко В.А. Основы информационной грамоты. — М.: Энергоатомиздат, 1996. — 320 с.

6.  Голдман С.  Теория информации / Пер. с англ. — М.: ИЛ, 1957. — 446 с.

7.  Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. — М.: Радио и связь, 1986. — 512 с.

8. Давыдов Г.В. Информация и сети связи. — М.: Наука, 1984. — 128 с.

9.  Душин В.К., Кернов Ю.П. Устройства приема и обработки сигналов: Учеб. пособие для вузов. — М.: МГУС, 2000. — 140 с.

10. Душин В.К., Князев И.И. Проектирование информационных систем, их модификация и эксплуатация: Учеб. пособие для вузов. — М.: МГУС, 2001. — 82 с.

11. Зиновьев А.А., Филиппов Л.И. Введение в теорию сигналов и цепей: Учеб. пособие для вузов. — М.: Высшая школа, 1968. — 280 с.

12.  Зюко А.Г., Коробов Ю.Ф. Теория передачи сигналов: Учебник для вузов. — М.: Связь, 1972. — 282 с.

13. Зюко А.Г. Помехоустойчивость и эффективность систем связи. — М.: Связь, 1963 — 319 с.

14. Игнатов В.А. Теория информации и передачи сигналов: Учебник для вузов. — М.: Сов. радио, 1979. — 280 с.

15. Информатика: Учебник. — 3-е изд. / Под ред. Н.В. Макаровой. — М.: Финансы и статистика, 2000. — 768 с.

16.   Колесниченко О.В., Шишигин И.В.  Аппаратные средства PC. — СПб.: БХВ — Санкт-Петербург, 1999. — 800 с.

17.  Колмогоров А.Н.  Теория информации и теория алгоритмов. — М.: Наука, 1987. — 304 с.

18. Миловзоров В.П. Элементы информационных систем: Учебник для вузов. — М.: Высшая школа, 1989. — 440 с.

19.  Нанс Б. Компьютерные сети / Пер. с англ. — М.: БИНОМ, 1996. — 400 с.

20.  Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы. — СПб.: Питер, 2001. — 672 с.

21.  Пилипчук Н.И., Яковлев В.П. Адаптивная импульсно-кодо-вая модуляция. — М.: Радио и связь, 1986. — 296 с.

22.  Прокис Дж. Цифровая связь / Пер. с англ. — М.: Радио и связь, 2000. — 800 с.

23. Помехоустойчивость и эффективность систем передачи информации / Под ред. А.Г. Зюко. — М.: Радио и связь, 1985. — 272 с.

24. Справочник по теоретическим основам радиоэлектроники / Под ред. Б.Х. Кривицкого. — М.: Энергия, 1977. — 472 с.

25. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники: Учеб. пособие для вузов. — М.: Энергия, 1979. — 512 с.

26. Теория электрической связи / Под ред. Д.Д. Кловского: Учебник для вузов. — М.: Радио и связь, 1998. — 432 с.

27.  Финк Л.М. Сигналы, помехи, ошибки. — М.: Радио и связь, 1984. — 256 с.

28. Харатишвили Н.Г. Цифровое кодирование с предсказанием непрерывных сигналов. — М.: Радио и связь, 1986. — 140 с.

29. Чернега B.C., Василенко В.А., Бондарев В.Н. Расчет и проектирование технических средств обмена и передачи информации: Учеб. пособие для вузов. — М.: Высшая школа, 1990. — 224 с.

30. Шелухин О.И., Лукъянцев Н.Ф. Цифровая обработка и передача речи. — М.: Радио и связь, 2000. — 456 с.

31. Шехтман Л.И. Системы телекоммуникаций: проблемы и перспективы. — М.: Радио и связь, 1998. — 280 с.

32. Яглом A.M., Яглом И.М. Вероятность и информация. — М.: Наука, 1973. — 512 с.