3.7. Детектирование амплитудно-модулированных сигналов

Детекторы АМ-сигналов предназначаются для преобразования модулированного электрического колебания высокой частоты в напряжение (ток), изменяющееся по закону модуляции. Детекторы на нелинейных элементах строятся по структурной схеме, показанной на рис. 3.14.

Детектируемое напряжение описывается уравнением:

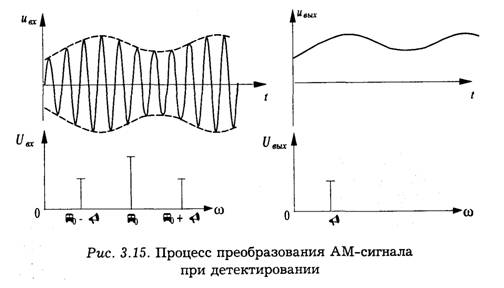
Простейшим и широко используемым является нелинейный диодный детектор, имеющий последовательную или параллельную схему включения диода (рис. 3.16).

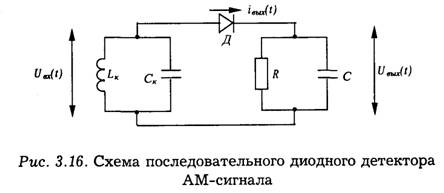
Рассмотрим качественно явление, происходящее при детектировании. Предположим, что нелинейный элемент обладает вольтамперной характеристикой:

При воздействии на детектор амплитудно-модулированного напряжения в его выходной цепи протекает ток в виде высокочастотных импульсов с огибающей модулированного колебания (рис. 3.17).

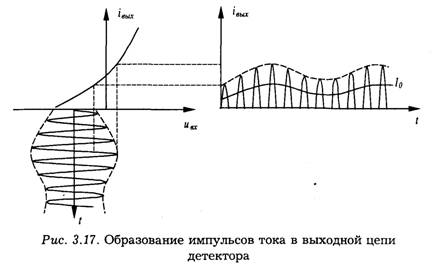
В спектре тока имеются колебания несущей частоты и ее гармоники, постоянная составляющая и составляющая с частотой модуляции. Среднее значение тока нелинейного элемента за период высокочастотного напряжения прямо пропорционально площади импульса тока, протекающего через нелинейный элемент в данный период. Площадь синусоидального импульса прямо пропорциональна его максимальному значению, а огибающая импульсов по своей форме соответствует огибающей входного модулированного колебания. Поэтому и усредненное по периоду высокой частоты значение тока нелинейного элемента изменяется по закону модуляции. Таким образом, для выделения сигнала, изменяющегося по закону модуляции, достаточно произвести усреднение выходного тока (или напряжения) детектора.

Усреднение (или фильтрация) выходного напряжения детектора осуществляется с помощью нагрузки в виде фильтра, составленного из резистора R и емкости С. Постоянная времени этой цепи обычно выбирается из условия

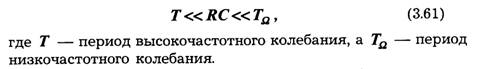
При выполнении условия (3.61) детектор безынерционен по отношению к модулирующему напряжению и поэтому называется безынерционным. При нарушении неравенства RС << Т_Ω детектор становится инерционным, в результате модулирующий сигнал воспроизводится в искаженном виде. Обычно условие безынерционности детектора предполагается выполненным.

Для детектирования импульсных радиосигналов применяются схемы обычных амплитудных детекторов, которые отличаются параметрами элементов.

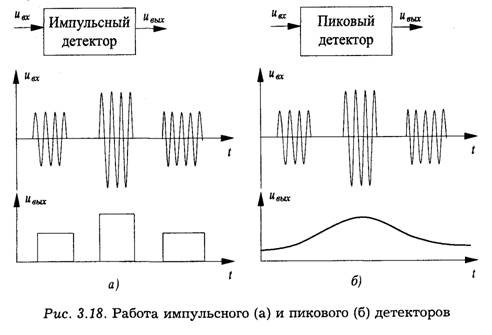
Детектор импульсных радиосигналов осуществляет либо выделение огибающей каждого входного радиоимпульса, либо выделение последовательности входных радиоимпульсов. В первом случае на выходе детектора формируются импульсы

различной амплитуды (видеоимпульсы). Такой детектор называют импульсным (рис. 3.18а). Во втором случае последовательность импульсов высокой частоты преобразуется в напряжение, форма которого повторяет форму огибающей последовательности. Поскольку выходное напряжение в этом случае пропорционально максимальному (пиковому) значению амплитуды импульсов последовательности, детектор называют пиковым (рис. 3.186). Так как частота изменения огибающей последовательности импульсов существенно меньше частоты следования импульсов, то фактически импульсный и пиковый детекторы различаются только величиной постоянной времени цепи нагрузки.

3.8. Частотные и фазовые детекторы

Частотным детектором называют устройство, в котором осуществляется преобразование входного частотно-модулированного радиосигнала в выходное напряжение (или ток), меняющееся по закону модуляции (рис. 3.19).

В настоящее время для частотного детектирования используют два наиболее распространенных метода.

Первый заключается в частотном детектировании напряжения, амплитуда которого изменяется по закону изменения частоты входного сигнала. Второй метод заключается в преобразовании синусоидального ЧМ-сигнала в импульсный с временной модуляцией (ВИМ). Преобразование импульсного сигнала ВИМ в низкочастотный осуществляется с помощью преобразователя "код — напряжение". Частотные детекторы первого типа можно условно назвать частотно-амплитудными, а второго — частотно-импульсными.

Рассмотрим детектор частотно-амплитудного типа.

Структурная схема состоит из двух элементов: преобразователя сигнала ЧМ в сигнал с амплитудой, изменяющейся соответственно изменению частоты, и амплитудного детектора.

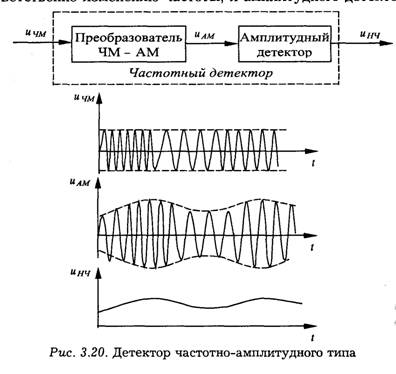
Первый элемент является линейным устройством, поэтому используемый здесь и далее термин "преобразователь ЧМ в AM" не означает замену частотной модуляции амплитудной. Это лишь означает, что в результате зависимости коэффициента передачи от частоты напряжение на выходе преобразователя изменяется по амплитуде. Причем изменение амплитуды достаточно точно повторяет закон изменения частоты входного сигнала. Обычно сохраняется и изменение частоты. Но на дальнейшее преобразование высокочастотного сигнала в низкочастотный с помощью амплитудного детектора это изменение частоты не влияет.

При анализе частотного детектора предполагается, что радиосигнал ЧМ на входе частотного детектора имеет постоянную амплитуду. Однако в реальных условиях амплитуда входного ЧМ-радиосигнала оказывается переменной вследствие возникновения сопутствующей амплитудной модуляции в передатчике и приемнике и воздействия помех в линии связи. В частотном детекторе частотно-амплитудного типа выходное напряжение преобразователя ЧМ в AM и, тем более, амплитудного детектора будет зависеть не только от частоты, но и от амплитуды входного сигнала. В результате на выходе частотного детектора сигнал будет искажен за счет паразитной AM. Устранение паразитной AM осуществляется с помощью амплитудного ограничителя, включенного на входе частотного детектора, или благодаря физическим процессам, происходящим в самом детекторе.

Простейшим вариантом частотного детектора является однотактная схема с одиночным расстроенным контуром. Схема внешне совпадает со схемой амплитудного детектора (рис. 3.16). Отличие в том, что контур L_kC_k расстроен относительно средней частоты ω₀ радиосигнала на ∆ω₀. Этот контур и используется в качестве преобразователя радиосигнала с ЧМ в напряжение с изменяющейся амплитудой (рис. 3.21).

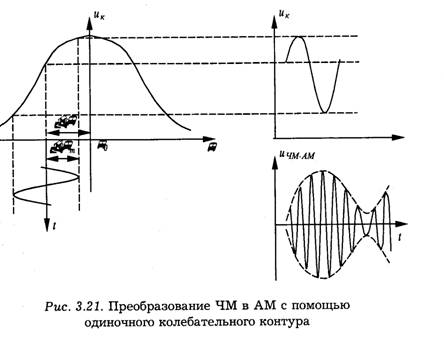
Амплитуда напряжения на контуре меняется по закону изменения частоты модулированного сигнала. Напряжение с контура подается на диодный амплитудный детектор. Вследствие того, что скаты резонансной характеристики не являются прямолинейными, в процессе преобразования сигнала ЧМ в сигнал с изменяющейся амплитудой возникают различные несимметричные нелинейные искажения. На практике обычно применяются более сложные схемы частотных детекторов (дифференциальный частотный детектор, дробный детектор и т. д.).

Фазовым детектором называют устройство, в котором входной фазомодулированный сигнал преобразуется в напряжение (или ток), изменяющееся по закону модуляции фазы. Для определения изменения фазы входного сигнала на фазовый детектор подается второй опорный сигнал с постоянной фазой.

Принцип действия фазового детектора заключается в амплитудном детектировании результирующего колебания, амплитуда которого зависит от разности фаз слагаемых колебаний:

Эта зависимость представляет собой характеристику простейшего фазового детектора, содержащего один нелинейный элемент (рис. 2.226). В таком однотактном детекторе характеристика имеет малый линейный участок, кроме того, напряжение не меняет знака при изменении фазы. На практике широкое применение получил двухтактный балансный фазовый детектор.

Контрольные вопросы и задания

1. Поясните основные методы модуляции различных носителей

информации.

2. Как определяется коэффициент модуляции?

3. Нарисуйте спектр амплитудно-модулированного колебания при гармонической и сложной модулирующих функциях.

4. Для чего применяется однополосная модуляция?

5.  Покажите общность двух разновидностей угловой модуляции — частотной и фазовой.

6.  Что называется девиацией частоты и индексом угловой модуляции?

7.  Как определяется спектр сигнала при угловой модуляции и каким образом он зависит от индекса угловой модуляции?

8. Поясните особенности спектров частотно-модулированного и фазомодулированного колебаний.

9. В чем особенность модуляции импульсных носителей?

10. Нарисуйте и поясните спектр АИМ-сигнала.

11. Для чего вводится понятие узкополосного сигнала?

12. Что такое аналитический сигнал?

13. Для чего применяется аппроксимация характеристик нелинейного элемента? В чем смысл аппроксимации степенным рядом и кусочно-линейной аппроксимации?

14. Как проявляется нелинейность вольтамперной характеристики при гармоническом воздействии?

15. Нарисуйте и поясните спектр тока при гармоническом воздействии на резистивный элемент и при частотной модуляции.

16.  К каким результатам приводит воздействие суммы гармонических сигналов на безынерционный нелинейный элемент?

17.  Нарисуйте структурную схему устройства для преобразования спектра сигналов.

18.  Нарисуйте простейший амплитудный детектор и поясните

принцип его работы.

19. Чем различаются импульсный и пиковый детекторы?

20. Поясните принцип работы частотного детектора.

21. Какие сигналы подаются на фазовый детектор?

ГЛАВА 4

ДИСКРЕТИЗАЦИЯ И КВАНТОВАНИЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ

4.1. Основные понятия и определения

Переход от аналогового представления сигнала к цифровому, который дает в ряде случаев значительные преимущества при передаче, хранении и обработке информации, связан с дискретизацией сигнала x(t) по времени и с квантованием по уровню.

Рассмотрим разновидности сигналов, которые описываются функцией x(t).

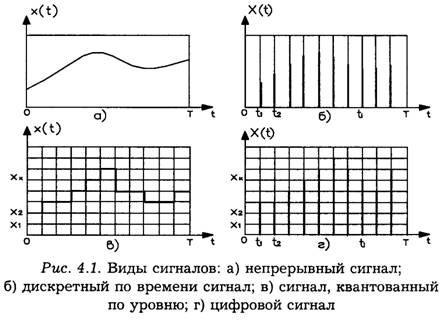
Непрерывная функция непрерывного аргумента (непрерывный сигнал, рис. 4.1а). В этом случае значения, которые может принимать функция x(t) и аргумент t, заполняют конечные (или бесконечные) промежутки [0,Х] и [0,Т] соответственно.

Непрерывная функция дискретного аргумента (дискретный во времени сигнал, рис. 4.16). Здесь значения функции x(t) определяются лишь на дискретном множестве значений аргумента t.,i= 0,1,2,...,(0<t< T).

Дискретная функция непрерывного аргумента (квантованный по уровню сигнал, рис. 4.1в). В этом случае значения, которые может принимать функция x(t), образуют дискретный ряд чисел x_l,x₂…x_k..., т. е. такой конечный или бесконечный ряд, в котором каждому числу можно поставить в соответствие интервал (а_k, b_k ), внутри которого других чисел данного ряда нет. Значение аргумента t может быть любым на отрезке [0,Т].

Дискретная функция дискретного аргумента (цифровой сигнал, рис. 4.1г). Значения, которые могут принимать функция x(t) и аргумент t, образуют дискретные ряды чисел x₁,x₂,...,х_k...и t_o,t₁,t₂,...,t_i,..., заполняющие отрезки [0,Х] и [0,Т] соответственно.

Дискретизация состоит в преобразовании сигнала x(t) непрерывного аргумента t в сигнал x(t.) дискретного аргумента t_i.

Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала x (t_i) в дискретное множество значений x_k,k = 0,l,2,...,m-1.

Совместное применение операций дискретизации и квантования позволяет преобразовывать непрерывный сигнал x(t) в дискретный по координатам х ut.

Применительно к детерминированной функции рассмотрим сущность понятия дискретизации сигнала x(t).

Дискретизация реализации сигнала x(t) связана с заменой промежутка изменения независимой переменной некоторым множеством точек, т. е. операции дискретизации соответствует отображение:

 (4.1)

где x(t) — функция, описывающая сигнал;

x(t) — функция, описывающая сигнал в результате дискретизации.

Следовательно, в результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(f)

По значениям функции x(f) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функцию, полученную по результатам восстановления (интерполяции) по значениям x(t), будем называть воспроизводящей и обозначим через V(t)

Воспроизводящая функция V(t) строится как взвешенная сумма некоторого ряда функций f(t-t_k):

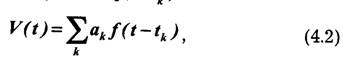
причем коэффициенты а_k зависят от отсчетов x(t ),х(t-₁)...

При обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям х (t) можно было получить воспроизводящую функцию V(t, которая с заданной точностью отображает исходную функцию x(t).

При дискретизации сигналов приходится решать вопрос о том, как часто следует производить отсчеты функции, т. е. каков должен быть шаг дискретизации ∆t_i =t_i-t_i-₁.

При малых шагах дискретизации ∆t_i количество отсчетов функции на отрезке обработки будет большим и точность воспроизведения — высокой. При больших ∆t_i количество отсчетов уменьшится, но при этом, как правило, снижается точность восстановления.

Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборок. В этом случае все отсчеты существенны для восстановления исходного сигнала. При неоптимальной дискретизации кроме существенных отсчетов имеются и избыточные отсчеты.

Избыточные отсчеты не нужны для восстановления сигнала с заданной точностью. Они загружают тракт передачи информации, отрицательно сказываются на производительности обработки данных ЭВМ, вызывают дополнительные расходы на хранение и регистрацию данных. В связи с этим актуальна задача сокращения избыточных данных. Сокращение избыточной для получателя информации может производиться в процессе дискретизации сигналов. В более общем плане задача сокращения избыточных отсчетов может рассматриваться как задача описания непрерывных сигналов с заданной точностью минимальным числом дискретных характеристик.

4.2. Методы дискретизации сигналов

Методы дискретизации и восстановления сигналов можно разделить на несколько групп в зависимости от принятых признаков классификации. Выберем для классификации следующие признаки:

регулярность отсчетов;

критерий оценки точности дискретизации и восстановления;

базисные функции;

принцип приближения.

1. Регулярность отсчетов

В процессе дискретизации отрезок обработки сигнала x(t) разбивается на ряд не перекрывающихся интервалов ∆t₁, ∆t₂, ∆t₃,...

В соответствии с признаком регулярности отсчетов можно выделить две основные группы методов: равномерную инеравномерную дискретизацию (соответственно и восстановление).

Дискретизацию будем называть равномерной, если длительность интервалов

на всем отрезке обработки [0,Т] сигнала.

Шаг дискретизации ∆t, или частота отсчетов F_o= 1/ ∆t, выбираются на основе априорных сведений о характеристиках сигнала x(t). При использовании методов равномерной дискретизации приходится решать в числе основных вопрос о выборе частоты отсчетов (шага дискретизации) и способа восстановления сигналов.

Методы равномерной дискретизации нашли широкое применение. Это объясняется тем, что алгоритм дискретизации и восстановления сигналов и соответствующая аппаратура достаточно просты. Однако из-за несоответствия априорных характеристик сигнала характеристикам обрабатываемой реализации возможна значительная избыточность отсчетов.

Дискретизацию будем называть неравномерной, если длительность интервалов между отсчетами различна.

Выделяют две группы неравномерных методов: адаптивные и программируемые.

При адаптивных методах интервал изменяется в зависимости от текущего изменения параметров реализации сигналов.

Такие способы передачи информации очень перспективны, так как позволяют существенно уменьшить избыточность сигнала и тем самым увеличить фактическую пропускную способность. В настоящее время разработаны системы с адаптивной импульсно-кодовой модуляцией.

При программируемых методах изменение интервалов (частоты опроса) производится либо оператором на основе анализа поступающей информации, либо в соответствии с заранее установленной программой работы.

2. Критерий оценки точности

Разность между истинными значениями сигнала x(t) и приближающей P(t_, или воспроизводящей V(t)-функцией, представляет собой текущую погрешность дискретизации или соответственно восстановления:

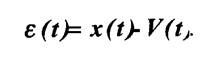
Выбор критерия оценки погрешности дискретизации (и восстановления) сигнала осуществляется получателем информации и зависит от целевого использования дискретизированного сигнала и возможностей аппаратной (программой) реализации. Оценка погрешности может проводиться как для отдельных, так и для множества реализаций сигнала.

Чаще других отклонение воспроизводимой функции V(t) от сигнала x(t) на интервале дискретизации ∆t_i=t_i—t_i-₁ оценивается следующими критериями.

а) Критерий наибольшего отклонения:

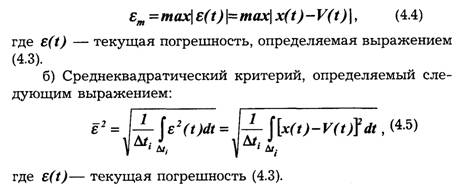
где ε(t)— текущая погрешность (4.3).

Черта сверху означает усреднение по вероятностному множеству.

в) Интегральный критерий как мера отклонения x(t) от V(t) имеет вид:

3. Базисные функции

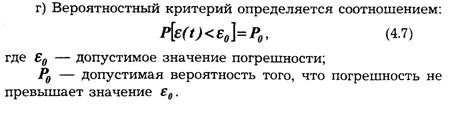
Задачи дискретизации сигналов, особенно адаптивной, в математическом плане достаточно близки к задачам равномерных и среднеквадратических приближений функций. Формулировка задачи дискретизации может быть следующей.

Для данной функции x(t), определенной на отрезке [a,в], найти функцию Р(t,(или V(t)), для которой число точек разбиения t_i отрезка минимально и ε(t )≤ ε₀. Здесь ε₀ — допустимое значение погрешности, ε (t ) — оценка отклонения x(t) от P(t) (или V(t) в  соответствии с принятым критерием.

Функции P(t) называют приближающими.

На практике при решении задач дискретизации сигналов выбор типа базисных (приближающих, воспроизводящих) функций в основном определяется требованиями ограничения сложности устройств (программ) дискретизации и восстановления сигналов.

Задачи восстановления дискретизированных сигналов в общем случае аналогичны задачам интерполирования функций. При восстановлении исходного сигнала x(t) совокупность выборок x(t) ставится в соответствии с некоторым обобщенным многочленом:

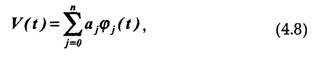
значения которого в точках отсчета t- совпадают со значениями функции x(t).

Иногда, кроме того, требуют совпадения производных до n-го порядка, n = 1,2,3...

Воспроизводящие функции V(t) обычно совпадают с приближающимися P(t,, хотя в общем случае они могут и отличаться от них.

Основные типы функций, применяемые в задачах дискретизации и восстановления сигналов, следующие: ряд Фурье, ряд Котельникова, полиномы Чебышева, полиномы Ле-жандра, степенные полиномы, функции Уолша и др.

4. Принцип приближения

По принципу приближения можно выделить три группы методов:

•   интерполяционные;

•   экстраполяционные;

•    комбинированные (интерполяционно-экстраполяцион-ные).

Экстраполяционные методы не требуют задержки сигнала при проведении дискретизации. Следовательно, они могут использоваться в системах, которые работают в реальном времени.

Для обработки сигналов более эффективны интерполяционные методы, обеспечивающие меньшую избыточность отсчетов по сравнению с экстраполяционными методами. Однако использование интерполяционных методов связано с задержкой сигнала на интервал интерполяции.

Интерполяционно-экстраполяционные методы обладают положительными качествами первых двух методов. Адаптивная дискретизация непрерывного сигнала x(t) связана с подбором приближающих функций Р(t для каждого из интервалов дискретизации ∆t_i. При интерполяционно-экстраполяционных методах процедура нахождения приближающихся функций разбивается на два этапа. На первом этапе методами интерполяции находится приближающая функция P(t, для начальной части интервала ∆t′_i дискретизации ∆t_i.

На втором этапе найденная функция экстраполируется для значений t>t_i-₁ + ∆t′i и проверяется отклонение сигнала от этой функции.

При выборе шага адаптивной дискретизации рассматриваются различные модели сигналов и вводятся соответствующие критерии отбора отсчетов.

Можно отметить некоторые из них:

а)  частотный критерий, при котором интервалы между отсчетами выбираются с учетом частотного спектра дискретизируемого сигнала;

б) корреляционный критерий отсчетов, устанавливающий связь интервалов между отсчетами с интервалами корреляции сигнала;

в)  квантовый критерий отсчетов, предложенный для детерминированной модели сигнала и устанавливающий зависимость интервалов между отсчетами от значения ступени квантования и крутизны (первой производной) сигнала.

4.3. Равномерная дискретизация. Теорема Котельникова

При равномерной дискретизации шаг ∆t и частота отсчетов являются постоянными величинами. Точки отсчетов в этом случае равномерно размещены по оси t.

Устройства, с помощью которых проводится дискретизация сигналов, носят название дискретизаторов. На рис. 4.2. изображена функциональная схема дискретизатора.

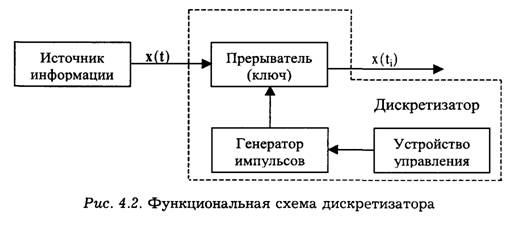
Дискретизатор можно рассматривать как прерыватель исходного сигнала x(t). Генератор импульсов выдает на вход прерывателя некоторую последовательность импульсов, в результате чего входной сигнал x(t) преобразуется в последовательность дискретных выборок сигнала x(t). Работа генератора импульсов определяется устройством управления. В случае равномерной дискретизации частота импульсов, поступающих от генератора, является неизменной.

В. А. Котельниковым доказана теорема для функций с ограниченным (финитным) спектром (теорема отсчетов), которая формулируется следующим образом: если наивысшая частота в спектре функции x(t) меньше, чемƒ_m, то функция x(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на секунд.

Интерполяционный ряд вида (4.9) носит название ряда Котельникова. (В иностранной литературе этот ряд связывают с именами Найквиста и Шеннона.)

Пусть сигнал, описываемый непрерывной функцией времени x(t), имеет ограниченный спектр, т. е. преобразование Фурье:

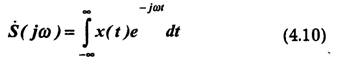
Подставим выражение (4.14) в формулу (4.11), изменив при этом знак при п с учетом, что суммирование проводится по всем отрицательным и положительным значениям п. Кроме того, учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и суммирования:

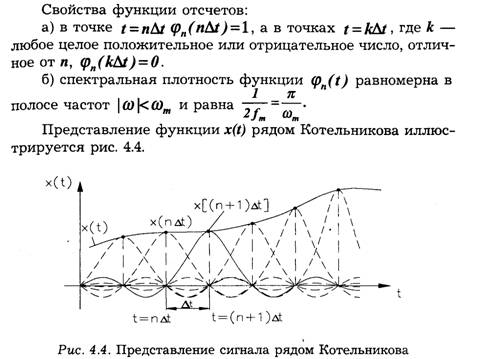
При выводе (4.9) предполагалось, что x(t) удовлетворяет условиям Дирихле. Это не дает возможности использовать полученный результат для функций, не стремящихся к нулю при t →∞, или для функций, не интегрируемых на интервале (а, в).

Теорема Котельникова относится к сигналам с ограниченным спектром. Реальные сообщения имеют конечную длительность. Спектр таких сигналов не ограничен, т. е. реальные сигналы не соответствуют модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов по формуле (4.9) и неопределенностью выбора шага дискретизации (4.16) или частоты отсчетов F₀=2f_m.

Приведенные соображения свидетельствуют, что применение теоремы Котельникова к реальным сигналам вызывает определенные трудности в том случае, если теорема рассматривается как точное утверждение. Для практических условий, однако, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром.

Практически всегда можно определить наивысшую частоту спектра f_m так, чтобы "хвосты" функции времени, обусловленные отсеканием частот, превышающих f_m, содержали пренебрежимо малую долю энергии по сравнению с энергией исходного сигнала x(t). При таком допущении для сигнала длительностью Т с полосой частот общее число независимых параметров [т. е. значений x(n∆t) ], которое необходимо для полного задания сигнала, очевидно, будет:

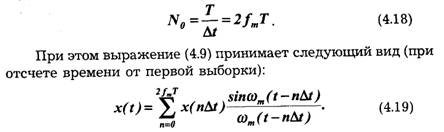
Величина N₀ представляет собой число степеней свободы сигнала x(t), так как даже при произвольном выборе значений x(r∆t) сумма вида (4.19) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала.

Параметр B=N₀, который широко применяется в системах передачи информации, называют базой сигнала.

Представление сигналов в виде ряда Котельникова положено в основу построения систем передачи информации с временным уплотнением. Смысл временного уплотнения состоит в том, что в интервале времени между двумя соседними отсчетами одного сигнала можно передавать отсчеты других сигналов. Формирование такого группового сигнала показано на рис. 4.5.

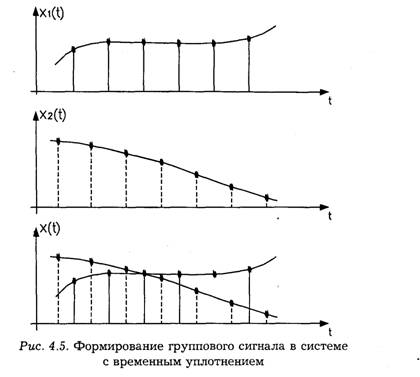
В заключение данного параграфа заметим, что хотя теорема Котельникова базируется на модели сигнала с ограниченным спектром, она имеет большую теоретическую и практическую ценность. Поэтому представление сигналов рядом Котельникова наиболее широко применяется в технике преобразования, передачи и обработки информации.

4.4. Адаптивная дискретизация

При адаптивной дискретизации отсчетные точки t_i в отличие от равномерной выборки не образуют периодической последовательности. В процессе обработки сигнала отбираются лишь те точки t_i (минимально необходимое число) и соответствующие выборки x(f), на основании которых можно восстановить исходный сигнал   с заданной точностью ε₀.

Таким образом, в процессе адаптивной дискретизации выделяется минимальное число выборок x(t), называемых существенными, которые с заданной точностью отображают непрерывный сигнал.

В связи с тем, что отсчетные точки при адаптивной дискретизации в общем случае произвольно размещены на временной оси, необходимо иметь информацию о значении моментов опроса t_i или о длинах соответствующих отрезков ∆t_i.

В настоящее время существует значительное число способов и алгоритмов адаптивной дискретизации. Среди них можно выделить две группы:

•  способы, при которых производится сравнение сигнала x(t) с приближающей функцией P(t, формируемой в процессе обработки сигнала x(t) с учетом его характеристик;

•  способы, при которых осуществляется сравнение сигнала с некоторыми эталонными фиксированными функциями

Значительный интерес представляют способы и алгоритмы адаптивной дискретизации, относящиеся к первой группе, так как при этом обеспечивается наиболее эффективное устранение избыточности отсчетов и соответственно минимизация описания исходного сигнала. В общем виде процедура адаптивной дискретизации в этом случае сводится к поиску на каждом из отрезков (t_i, t_i+1) некоторой функции принятого типа, наилучшим образом представляющей исходную функцию x(t) в соответствии с заданным критерием уклонения.

Адаптивная дискретизация может быть организована таким образом, что на отрезках (t_i t_i+1) постоянной длины могут меняться тип и порядок (степень) приближающих функций или при неизменном типе и порядке приближающей функции изменяется длина отрезка. Возможна адаптация и по двум этим показателям.

В практических применениях наибольшее распространение нашли алгоритмы адаптивной дискретизации с адаптацией по длинам отрезков (t, t_i+1) , использующие алгебраические полиномы нулевой и первой степени. Рассмотрим простейшие алгоритмы адаптивной дискретизации при оценке точности приближения (воспроизведения) по критерию наибольшего отклонения.

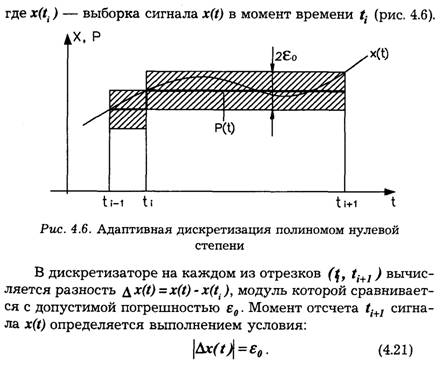
Экстраполяционные способы адаптивной дискретизации полиномом нулевой степени относительно t содержат операцию сравнения текущего значения сигнала x(t) со значением предшествующей выборки x(t_i) сигнала.

Пусть приближающая функция P(t_, на отрезке (t_i, t_i+1) выбирается следующим образом:

В устройствах адаптивной дискретизации с полиномами нулевой степени этот способ применяется наиболее часто.

При использовании адаптивной дискретизации с полиномами первой степени приближающая функция P(t, на отрезке (t_i, t_i+1) может иметь вид:

В устройстве дискретизации на каждом из отрезков (t_i, t_i+1) генерируется приближающая функция вида (4.22) и вычисляется ∆x(t). Моменты отсчета определяются выполнением условия:

В данном случае определение приближающих функций на отрезках (t_i, t_i+1) связано с дифференцированием сигнала.

Следует заметить, что аппаратная реализация алгоритмов адаптивной дискретизации с полиномами первой степени достаточно сложна.

При адаптивной дискретизации с эталонными приближающими функциями исходный сигнал x(t) сравнивается с набором эталонных сигналов {f_k(t)}, поступающих от специального генератора. По результатам сравнения определяются моменты отсчетов сигнала.

4.5. Квантование по уровню

Квантование сигнала x(t) по уровню состоит в преобразовании непрерывных значений сигнала x(t) в моменты отсчета t_i в дискретные. В результате квантования по уровню непрерывное множество значений сигнала x(t) разбивается на т одинаковых частей — интервалов квантования. Под шагом (интервалом) квантования δ_k понимается разность:

где х_k-1, х_k — соседние уровни квантования.

Шкала х значений сигнала x(t) может быть разбита на отдельные участки различным образом: с привязкой уровней квантования x_k точке x(t) = 0, к границам x_min, x_max диапазона изменения сигнала и т. д.

Обычно применяются следующие способы отнесения значений сигнала x(f)K соответствующему уровню квантования:

а)  сигнал   x(t) отождествляется с ближайшим уровнем квантования;

б)  сигнал  x(t) отождествляется с ближайшим меньшим (или большим) уровнем квантования.

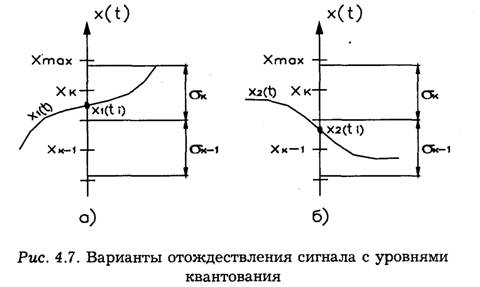
Для сигнала x₁(t) показанного на рис. 4.7а, по первому способу отождествления x₁(f) →х_k, а по второму х₁(1) →х_k-1. Для второго сигнала в обоих случаях х₂(t) →x_k-1 (рис. 4.76).

Так как в процессе квантования по уровню значение сигнала jc отображается уровнем квантования х_k, а каждому уровню х_k может быть поставлен в соответствие свой номер (число), то при передаче или хранении можно вместо истинного значения уровня квантования х_k использовать соответствующее число k. Истинное значение уровня квантования легко восстановить, зная масштаб по шкале x.

Устройство для квантования сигналов по уровню, называемое квантизатором (рис. 4.8а), представляет собой нелинейный элемент с амплитудной характеристикой типа приведенной на рис. 4.86 при отождествлении сигнала с ближайшим меньшим уровнем квантования или типа приведенной на рис. 4.8 в в случае отождествления сигнала с ближайшим уровнем.

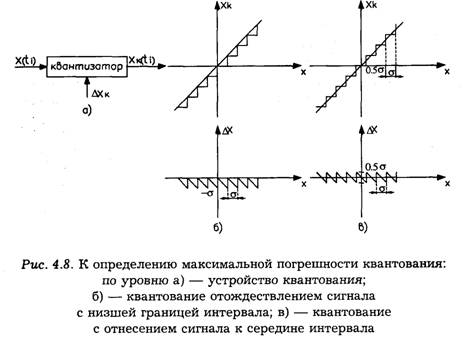
Квантование по уровню сопровождается шумами квантования, или погрешностью квантования. Погрешность квантования Δx_k = x(t)-x_k связана с заменой истинного значения сигнала x(t) уровнем квантования х_k. Максимальная погрешность квантования зависит от способа отождествления сигнала с уровнем квантования. Для первого из рассмотренных способов она равна (рис. 4.86):

При отождествлении сигнала с ближайшим уровнем квантования максимальная погрешность (рис. 4.8в) не превышает 0.5δ_k, т. е. способ квантования по уровню, отождествляющий сигнал с ближайшим квантованным уровнем, приводит к снижению максимальной погрешности квантования.

В заключение можно сказать, что преобразование непрерывного сообщения в цифровое состоит из трех операций: сначала непрерывное сообщение подвергается дискретизации по времени через интерва Δt; полученные отсчеты мгновенных значений x(n Δ t) квантуются с шагом δ ; наконец, последовательность квантованных значений передаваемого сообщения представляется посредством кодирования в виде последовательности типичных кодовых комбинаций.

Такое преобразование называется импулъсно-кодовой модуляцией (ИКМ).

Контрольные вопросы и задания

1. Какими функциями описываются разновидности сигналов?

2. Дайте определение понятиям дискретизации и квантования.

3. Что называется воспроизводящей функцией?

4. По каким признакам классифицируются методы дискретизации сигналов?

5. Как формулируются критерии оценки точности восстановления сигналов?

6.  Как подразделяются принципы приближения при проведении дискретизации сигналов?

7. Поясните функциональную схему дискретизации сигналов.

8. Сформулируйте теорему Котельникова.

9. Перечислите основные свойства функции отсчетов.

10. Для каких сигналов применима теорема Котельникова?

11. Дайте определение понятиям числа степеней свободы и базы сигнала.

12. Поясните процесс формирования группового сигнала в системах с временным уплотнением.

13. Поясните основные способы адаптивной дискретизации сигналов.

14. Как определяется шаг квантования по уровню?

15. Какими характеристиками должен обладать квантизатор?

16. Что такое "шум" квантования?

ГЛАВА 5 ХАРАКТЕРИСТИКИ И МОДЕЛИ КАНАЛОВ ПЕРЕДАЧИ ИНФОРМАЦИИ

5.1. Общие сведения о каналах передачи

Информации

Во введении канал связи (передачи информации) определен как совокупность средств, предназначенных для передачи сигналов (сообщений) между различными точками системы передачи информации (информационной системы).

Под "средством" понимают и технические устройства, и линию связи — физическую среду, в которой распространяется сигнал между пунктами связи. Канал связи можно представить как последовательное соединение устройств (блоков), выполняющих различные функции в общей системе передачи информации.

Классификация каналов передачи информации возможна с использованием различных признаков. В зависимости от назначения информационной системы каналы делят на телеграфные, фототелеграфные, телефонные, звукового вещания, передачи данных, телевизионные, телеметрические, смешанные и т. д. В зависимости от характера физической среды, в которой распространяются сигналы, выделяют: радиоканалы (в частности, космические каналы) и каналы проводной связи (воздушные, кабельные, волоконно-оптические линии связи, волноводные СВЧ-тракты и т. д.). В технике передачи информации находят применение также механические и акустические каналы. В зависимости от характера связи между сигналами на входе и выходе канала различают каналы линейные и нелинейные.

Различают каналы чисто временные (с сосредоточенными параметрами), в которых сигналы на входе и выходе описываются функциями одного скалярного параметра (времени t), и пространственно-временные каналы (с распределенными параметрами), в которых сигналы на входе и (или) выходе описываются функциями более одного скалярного параметра (например, времени t и пространственных координат х, у,z). Такие сигналы называют полями.

При использовании электрических сигналов для передачи информации более существенна классификация каналов по диапазону рабочих частот, так как именно этот фактор определяет пропускную способность канала. На современных симметричных кабельных линиях связи применяют сигналы, занимающие полосы частот в диапазоне, ограниченном сверху частотой в несколько сотен килогерц.

Коаксиальные кабели, являющиеся основой сетей магистральной связи, пропускают в настоящее время диапазон частот до сотни мегагерц. На воздушных проводных линиях используют частоты не выше 150 кГц, так как на более высоких частотах в этих линиях сильно сказывается мешающее действие аддитивных помех и резко возрастает затухание в линии.

При передаче сигналов по радиоканалам применяют частоты от 3·10³ до 3·10¹² Гц. Этот диапазон принято в соответствии с десятичной классификацией подразделять следующим образом (см. табл. 5.1).

В таблице в скобках указаны нестандартные, но используемые названия диапазонов волн. Диапазон децимиллиметровых волн уже вплотную подходит к диапазону инфракрасных волн. В настоящее время благодаря созданию и широкому внедрению оптических квантовых генераторов (лазеров)

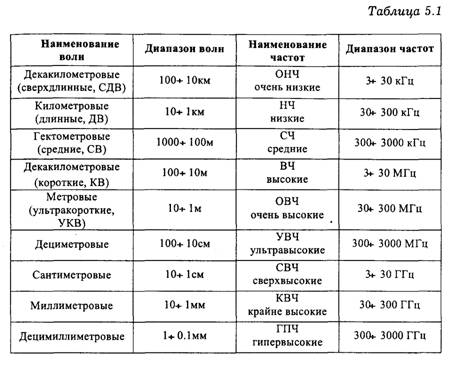
освоен оптический диапазон. В волоконно-оптических линиях связи (ВОЛС) используются частоты порядка 10¹⁴Гц (длины волн 1.55÷0.85 мкм).

Для современного этапа развития техники передачи ин-L формации характерна тенденция к переходу на все более I высокие частоты. Это вызвано рядом причин, в частности, необходимостью повышать скорость передачи сообщений (увеличивать быстродействие систем), возможностью получить остронаправленное излучение при небольших размерах излучателей, меньшей интенсивностью атмосферных и многих видов промышленных помех в более высокочастотных диапазонах, возможностью применения помехоустойчивых широкополосных систем модуляции и т. п.

Для теории передачи информации большой интерес представляет классификация каналов связи по характеру сигналов на входе и выходе канала. Различают каналы:

а)  непрерывные (по уровням), на входе и выходе которых сигнал непрерывен.

Примером может служить канал, заданный между выходом модулятора и входом демодулятора в любой системе передачи информации;

б) дискретные (по уровням), на входе и выходе которых сигналы дискретны. Примером такого канала является канал, заданный от входа кодирующего устройства до выхода декодера;

в) дискретные со стороны входа и непрерывные со стороны выхода или наоборот. Такие каналы называются дискретно-непрерывными, или полунепрерывными (например, каналы, заданные между входом модулятора и входом демодулятора или между выходом модулятора и выходом декодера).

Структурная схема канала передачи информации приведена на рис. 5.1.

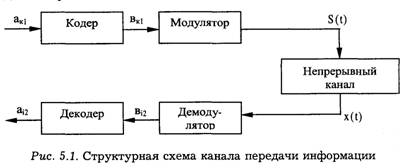
Всякий дискретный или полунепрерывный канал содержит внутри себя непрерывный канал. Следует помнить, что дискретность и непрерывность канала не связана с характером сообщений: можно передавать дискретные сообщения по непрерывному каналу и непрерывные сообщения — по дискретному.

5.2. Анализ непрерывных каналов

Методы и модели анализа непрерывных каналов разрабатываются на основе изучения физических и статистических характеристик реальных каналов. Так как непрерывные каналы являются основной составной частью всех других каналов, результаты анализа непрерывных каналов широко используются для решения задач анализа и синтеза систем передачи информации. Основными задачами анализа непрерывных каналов являются анализ линейных и нелинейных искажений сигналов в каналах и анализ влияния помех в каналах.

Для анализа искажений сигналов в каналах необходимо располагать сведениями о характеристиках входных сигналов, структуре и параметрах операторов преобразования сигналов в канале и изучать характеристики выходных сигналов. Характеристики входных сигналов определяют как характеристики модулированных сигналов (см. гл. 3).

Структуру и параметры операторов преобразования сигналов в канале определяют на основе построения математических моделей каналов.

При строгом рассмотрении реальные непрерывные каналы являются нелинейными инерционными системами со случайными параметрами (стохастические системы). В них реакция на выходе не может предшествовать воздействию на входе, поэтому такие системы часто называют динамическими. Анализ таких систем представляет сложную задачу. Ее решение еще более усложняется, когда в роли входных воздействий выступают случайные модулированные сигналы.

Передача сигналов по реальным каналам всегда сопровождается изменениями (преобразованиями) этих сигналов. С точки зрения передачи информации по каналу важно подразделение преобразований сигнала на обратимые и необратимые. Обратимые преобразования не влекут за собой потери информации. При необратимых преобразованиях потери информации неизбежны. Поэтому для обратимых преобразований сигнала также часто используется термин "искажение", а необратимые преобразования называют "помехами".

Линейные искажения сигналов появляются в линейном инерционном четырехполюснике с постоянными параметрами из-за наличия в нем реактивных элементов. При линейных искажениях нарушаются существующие частотные и фазовые соотношения между отдельными составляющими сигнала и форма сигналов. Для отсутствия искажений необходимо, чтобы модуль коэффициента передачи и времени запаздывания для всех составляющих были одинаковы (гл. 2). Нелинейными называют искажения сигналов, которые возникают в нелинейных безынерционных четырехполюсниках с постоянными параметрами из-за нелинейности характеристик активных элементов: транзисторов, диодов и др. В результате нелинейных искажений спектр сигналов расширяется, в них появляются дополнительные компоненты, растут уровни взаимных помех в каналах.

Для рассмотрения помех в непрерывных каналах выходной сигнал представляют в виде:

где S(t) — входной сигнал; μ(t) и τ (t) — соответственно мультипликативная и аддитивная помехи; τ (t) — задержка сигнала в канале.

Мультипликативные помехи обусловлены случайными изменениями коэффициента передачи канала из-за изменения характеристик среды, в которой распространяются сигналы, и коэффициентом усиления схем при изменении питающих напряжений, из-за замираний сигналов в результате интерференции и различного затухания сигналов при многолучевом распространении радиоволн. К мультипликативным помехам следует отнести и "квантовый шум" лазеров, применяемых в оптических системах передачи и обработки информации. "Квантовый шум" лазера вызван дискретной природой светового излучения и зависит от интенсивности излучения, т. е. от самого полезного сигнала. Мультипликативные помехи бывают "медленные", когда:

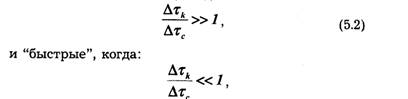
где Δτ_k — интервал корреляции случайного процесса μ(t), Δ τ _с — интервал корреляции или длительность сигнала, если он рассматривается как детерминированный.

Аддитивные помехи обусловлены флуктуационными явлениями (случайными колебаниями тока и напряжения), связанными с тепловыми процессами в проводах, резисторах, транзисторах и других элементах схем, наводками под действием атмосферных явлений (грозовые разряды и т. д.) и индустриальных процессов (работа промышленных установок, других линий связи и т. д.).

Аддитивные помехи делят на сосредоточенные и флуктуационные. Сосредоточенные аддитивные помехи отличаются сосредоточенностью энергии помех в полосе частот (узкополосные помехи) или на отрезке времени (импульсные помехи).

Узкополосные помехи в основном обусловлены действием посторонних источников — ширина спектра этих помех сравнима или значительно меньше ширины спектра полезных сигналов. Узкополосные помехи как помехи от соседних станций характерны для передачи информации по радиоканалам. Борьба с узкополосными аддитивными помехами ведется методами улучшения технических характеристик устройств приема и обработки сигналов.

Импульсные помехи — это случайные последовательности импульсов, создаваемые промышленными установками и атмосферными источниками сигналов. Эти помехи характеризуются широким энергетическим спектром. Ширина их спектра, как известно, обратно пропорциональна длительности импульсов. Энергия спектральных составляющих импульсных помех падает в области сверхнизких и сверхвысоких частот.

Флуктуационная аддитивная помеха характеризуется "размытостью" энергии спектра в широком диапазоне частот. Она обусловлена главным образом внутренними шумами элементов аппаратуры (тепловой шум, дробовой эффект и т. д.). Средняя мощность теплового шума в полосе частот ΔF полезного сигнала определяется по формуле:

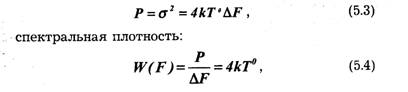
где k = 1,38 · 10 ^-23 Дж/град — постоянная Больцмана, Т° — абсолютная температура. Флуктуационную помеху из-за "внутренней" природы невозможно устранить, можно лишь учесть ее характеристики при синтезе такой оптимальной системы, в которой наличие флуктуационной помехи меньше всего сказывается на качестве передачи информации.

Математическими моделями сосредоточенных аддитивных помех являются узкополосные случайные сигналы и случайные последовательности импульсов. Математической моделью флуктуационной аддитивной помехи служит гауссовский "белый шум" (гл. 2).

В настоящее время разработано большое количество моделей непрерывных каналов, различных по сложности математического описания, требуемым исходным данным и погрешностям описания реальных каналов. Наиболее распространены следующие модели: идеальный канал, гауссовский канал, гауссовский канал с неопределенной фазой, гауссовский однолучевой канал с замираниями и сосредоточенными помехами. Для анализа реальных каналов в конкретных условиях

обычно выбирают такую модель, которая приводит к не слишком трудоемким решениям задач и в то же время обладает погрешностями, допустимыми в инженерных расчетах.

Идеальный канал можно применять как модель реального непрерывного канала, если соблюдаются следующие условия: помехи любого вида отсутствуют, преобразование сигналов в канале является детерминированным, мощность и полоса сигналов ограниченны.

Для анализа выходных сигналов с помощью этой модели необходимо знать характеристики входных сигналов и операторов преобразования. Модель идеального канала слабо отражает реальные условия, ее применяют чаще всего для анализа линейных и нелинейных искажений модулированных сигналов в многоканальных системах проводной связи.

Гауссовский канал. Основные допущения при построении такой модели следующие: коэффициент передачи и время задержки сигналов в канале не зависят от времени и являются детерминированными величинами, известными в месте приема сигналов; в канале действует аддитивная флуктуа-ционная помеха — гауссовский "белый шум" (гауссовский процесс). Гауссовский канал применяют как модель реальных каналов проводной связи и однолучевых каналов без замираний или с медленными замираниями. При этом замирания представляют собой неконтролируемые случайные изменения амплитуды сигнала. Такая модель позволяет анализировать амплитудные и фазовые искажения сигналов и влияние флуктуационной помехи.

Гауссовский канал с неопределенной фазой сигнала. В этой модели время задержки сигнала в канале рассматривают как случайную величину, поэтому фаза выходного сигнала также случайна. Для анализа выходных сигналов канала необходимо знать закон распределения времени задержки или фазы сигнала.

Гауссовский однолучевой канал с замираниями. В этой модели коэффициент передачи канала и фазовую характеристику канала рассматривают как случайные величины или процессы. В этом случае спектр выходного сигнала канала шире спектра входного даже при отсутствии помехи из-за паразитных амплитудной и фазовой модуляций. Такие модели достаточно хорошо описывают свойства радиоканалов различных диапазонов и проводных каналов со случайными, в том числе и переменными параметрами.

Гауссовский многолучевой канал с замираниями. Эта модель описывает радиоканалы, распространение сигналов от передатчика к приемнику в которых происходит по различным "каналам" — путям. Длительность прохождения сигналов и коэффициенты передачи различных "каналов" являются неодинаковыми и случайными. Принимаемый сигнал образуется в результате интерференции сигналов, пришедших по разным путям. В общем случае частотная и фазовая характеристики канала зависят от времени и частоты. Для описания многолучевых каналов с замираниями необходимо задавать в п раз больше (n — число путей распространения радиоволн) статистических характеристик по сравнению с однолучевым. В то же время характеристика многолучевого канала с замираниями является одной из наиболее общих и пригодна для описания свойств большинства радиоканалов и проводных каналов.

Гауссовский многолучевой канал с замираниями и аддитивными сосредоточенными помехами. В этой модели наряду с флуктуационной помехой учитывают и различного вида сосредоточенные помехи. Она является наиболее общей и достаточно полно отражает свойства многих реальных каналов. Однако ее использование порождает сложность и трудоемкость задач анализа, а также необходимость сбора и обработки большого объема исходных статистических данных.

В настоящее время для решения задач анализа непрерывных и дискретных каналов используются, как правило, модель гауссовского канала и модель гауссовского однолучевого канала с замираниями.

5.3. Анализ дискретных каналов

Для анализа дискретных каналов разрабатывают специальные математические модели и методы. Рассмотрим основные из них и на примере двоичного канала покажем, как определяют характеристики дискретных каналов: условные вероятности появления ошибок, полные вероятности появления ошибки и правильного приема, вероятности появления различных символов на выходе дискретного канала и др.

Дискретный канал образуют устройства тракта "вход кодера — выход декодера" (рис. 5.1). На вход канала поступают символы а_к1, а с выхода — а_к2. Математическая модель дискретного канала определена, если известны следующие характеристики: алфавит и априорные вероятности Р(а_к1) появления символов а_к1 сообщений (к = 1,...,т₂, т₂ — объем алфавита); скорость передачи символов W_1, алфавит символов а_i2 копии сообщений (i = 1,...,т₂, т₂ — объем алфавита); априорная условная вероятность Р(а_i2 /а_k1) появления символа а.₂ при условии, что был передан а_k1.

Первые две характеристики определяются свойствами источника сообщений и полосой пропускания непрерывного канала. Объем выходного алфавита т₂ определяется способом построения системы передачи информации. Условная вероятность Р(а_i1 /а_k1) определяется в основном свойствами непрерывного канала и его характеристиками. Если в системе используется канал обратной связи и "стирание" символов, то т₂ > m_1. Стирание символов вводят тогда, когда из-за искажений и помех неясно, какой символ передавался. Решающее устройство декодера выдает символ стирания, если символ а_{2 настолько отличается от символов источника сообщений, что его нельзя с большой вероятностью отождествить ни с одним из передаваемых. Стирание символов позволяет уменьшить вероятность появления ошибки, но приводит к уменьшению вероятности правильного приема. Определены условия, при которых стирание символов целесообразно. Обычно вводят один символ стирания.

Результатом анализа дискретного канала является определение апостериорной условной вероятности Р(а_к1 /a_i2) того, что при получении символа a_i2 передавался символ а_к1.

С помощью этих апостериорных вероятностей и априорных вероятностей Р(а_к1) рассчитывают полную вероятность появления ошибки в канале, полную вероятность правильного приема, вероятность появления символов на выходе канала, информационные характеристики дискретного канала (скорость передачи информации, пропускную способность, количество принятой информации и др.).

Апостериорная вероятность рассчитывается по формуле Байеса:

то канал называют каналом без памяти. Если условие (5.8) не выполняется, канал обладает памятью на i символов. Выполнение условий (5.7) и (5.8) зависит от того, на каком непрерывном канале построен дискретный канал. Например, еслк непрерывный канал является гауссовым, то условия (5.7) у (5.8) выполняются, и построенный на нем дискретный канал является однородным и без памяти.

Реальные дискретные каналы являются неоднородными и с памятью. Это обусловлено следующими причинами: искажением сигналов и влиянием помех в непрерывном канале, задержкой во времени выходной последовательности сигнала по отношению к входной, нарушением тактовой синхронизации передаваемых и принимаемых импульсов, ошибками решающих схем. Однако модель дискретного однородного канала без памяти как модель первого приближения находит широкое применение. Она позволяет упростить методы анализа и получения исходных данных.

Для математического описания дискретных однородных каналов без памяти необходимо использовать матрицы типа:

элементами которых являются условные вероятности p_ik = P(a_i2/a_kl). Совместно с априорными вероятностями Р(а_к1) эти вероятности р_iк перехода i-госимвола в k-й полностью определяют вероятностные характеристики дискретных каналов.

Математическим аппаратом, который позволяет использовать дискретные каналы, является теория марковских цепей. Она предназначена для описания случайных дискретных последовательностей. Рассмотрим те элементы этой теории, которые используются в дальнейшем.

Если случайная последовательность получена дискретизацией стационарного и эргодического процесса, она также обладает этими свойствами. Числовые характеристики такой последовательности получают использованием операций усреднения по множеству и по времени (гл. 2).

Оценка математического ожидания последовательности:

где при усреднении по множеству: п — количество реализаций, измеренных в один момент времени t_i; х_ik — k-е значение случайной величины X_i; при усреднении по времени: n — количество моментов времени, рассматриваемых для одной реализации.

Если все значения Х_i стационарной последовательности непрерывны и независимы, то полной характеристикой является одномерная плотность распределения ƒ(x_i). Плотности распределения большей размерности определяют как произведение одномерных плотностей. Если X_i являются дискретными независимыми символами, что имеет место при определенных условиях передачи дискретных сообщений, полной характеристикой является распределение вероятностей р_i появления символа Xi ,i= 1,...,n. Так как X_i образует полную группу сообщений, то:

Равенство (5.11) называют условием нормировки.

Если символы последовательности взаимозависимы (коррелированны), помимо вероятности появления отдельных символов необходимо задавать условные вероятности Р(Х_i/ Х_i-1, X_i-2,…X _i-i), появление в последовательности символа X_i при, что перед ним появилась группа символов Х_i-1,X_{i- 2},...Х_i-i.. Последовательности, в которых существуют статистические свя-|зи между символами, называют цепями Маркова, или марковскими цепями. Если статистическая связь существует только между двумя символами i-м и (i-1)-м, то марковскую цепь называют простой, ее поведение полностью описывается матрицей (5.9) при заданные начальных вероятностях P(a_kl) ⁼ p_k. Для эргодической марковской цепи вероятности р. появление символов X_j в установившемся режиме находят из системы алгебраических уравнений:

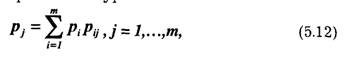
с использованием условия нормировки (5.11).

Для математического описания дискретных однородных каналов без памяти используют методы теории марковских простых однородных цепей.

Используя эти результаты, найдем вероятностные характеристики двоичного дискретного однородного канала без памяти.

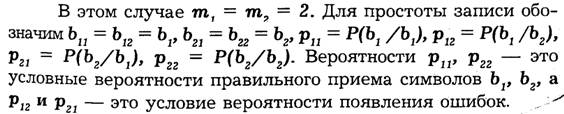
Рассмотрим работу решающей схемы реализации сигналов s₁(t) = s(t) на выходе модулятора и s₂(t) — x(t) на входе демодулятора (показаны на рис. 5.2). Положительные импульсы соответствуют передаче символа b₁ отрицательные — передаче b₂. Можно заметить, что прохождение сигнала через канал привело к изменению его формы.

Если искажения сигналов в канале отсутствуют и непрерывный канал является гауссовым, то изменение формы сигнала обусловлено лишь действием флуктуационной помехи ξ(t). Сигнал на входе решающей схемы можно представить в виде s₂(t) = s₁(t) + ξ(t).

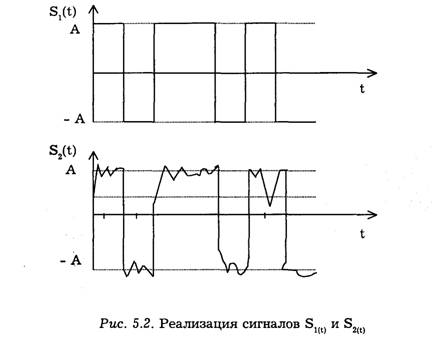
На основании отсчетов напряжения принятого сигнала s_2(t) в моменты времени t₁,t₂,...,t_k,..., решающая схема демодулятора должна определить: был принят импульс с амплитудой +А или импульс с амплитудой -А. Так как |А| является детерминированной величиной, то распределение суммы |А| + ξ(t_k) полностью определяется одномерным распределением помехи ƒ(ξ)

Вероятность ошибок и правильного приема определяется не только характеристиками помех, но и порогом о принятия решения. Если s₂(t_k) < а, то принимается решение о том, что пришел отрицательный импульс. Правильные решения принимаются тогда, когда выполняются следующие неравенства:

Ошибки происходят тогда, когда неравенства (5.13) и (5.14) не выполняются из-за выбросов, обусловленных помехой. Условные вероятности ошибок — это вероятности выполнения противоположных неравенств, поэтому:

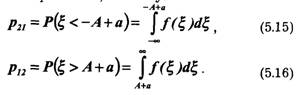
Из-за симметрии двоичного канала полная вероятность ошибки совпадает с условной вероятностью. Это удобное свойство симметричного канала, так как значение р₀ (одного параметра) полностью определяет свойства двоичного однородного симметричного канала без памяти. Полная вероятность правильного приема сигналов:

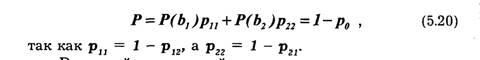
Реальный дискретный канал можно рассматривать как функциональный преобразователь распределения вероятностей появления символов входного алфавита в распределение вероятностей появления символов выходного алфавита.

Идеальный дискретный канал не является преобразователем, поскольку оставляет распределение символов неизменным, и оригиналы и копии дискретных сообщений совпадают.

Так как символы дискретных сообщений кодируют кодовыми комбинациями, которые включают п элементарных кодовых сигналов, представляет интерес определение вероятности того, что в кодовой комбинации будет q ошибочно принятых элементарных сигналов. Величину называют кратностью ошибок. Если все элементарные сигналы в кодовой комбинации независимы, эта вероятность определяется биномиальным распределением и формулой Бернулли:

Поэтому в первую очередь обращают внимание на обнаружение и исправление ошибок малой кратности.

В заключение данной главы отметим, что для решения задачи прохождения сигналов через реальные каналы в общей постановке необходимо изучать прохождение случайных сигналов через нелинейные стохастические инерционные нестационарные системы. Работа таких систем описывается нелинейными дифференциальными уравнениями со случайными переменными коэффициентами и случайной правой частью. Поэтому решение таких задач является сложным, для многих реальных каналов оно является предметом современных научных исследований. Характерные особенности задач анализа прохождения случайных сигналов через каналы обычно рассматривают с помощью более простых приближенных моделей каналов.

Контрольные вопросы и задания

1.  Приведите классификацию каналов по различным признакам.

2. Нарисуйте структурную схему канала передачи информации и поясните ее назначение ее элементов.

3. Поясните разницу между помехами и искажениями.

4. Объясните причины возникновения различных видов помех.

5. Каковы особенности различных моделей каналов?

6. Каким образом осуществляется анализ дискретных каналов?

7.  Поясните разницу между каналом без памяти и каналом с памятью.

8. Как определяются вероятностные характеристики двоичного дискретного однородного канала без памяти?

ГЛАВА  6

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЕ ТЕОРИИ ИНФОРМАЦИИ

6.1. Мера количества информации

В теории информации изучаются количественные закономерности передачи, хранения и обработки информации.

Основное внимание в теории информации уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования. Предельные соотношения теории информации позволяют оценить эффективность различных систем связи и установить условия согласования в информационном отношении источника с каналом и канала с потребителем.

Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам событии, очевидно, никакой информации не несет. Напротив, сообщение о малоизвестном событии несет много информации.

Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятности этого события. Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать монотонно убывающую функцию вероятности F[P(a)] , где Р(а) — вероятность сообщения. Простейшей из них является функция которая характеризует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации в логарифмических единицах, т. е. определять количество информации в отдельно взятом сообщении как:

что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифма k может быть любым. Чаще всего принимают k = 2, и тогда количество информации выражается в двоичных единицах:

Двоичную единицу называют бит. Слово "бит" произошло от выражения binary digit (двоичная цифра). В двоичных системах передачи информации используется два символа, условно обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда Р(0) = Р(1) - ₁/₂, каждый из них несет одну двоичную единицу информации:

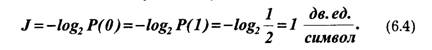
Формула (6.1) позволяет вычислять количество информации в сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограниченно. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:

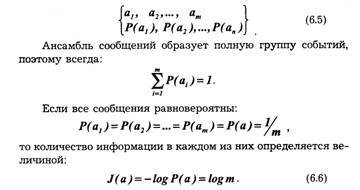
Отсюда следует, что количество информации в сообщении зависит от ансамбля, из которого оно выбрано. До передачи сообщения имеется неопределенность относительно того, какое из т -сообщений ансамбля будет передано. После приема сообщения эта неопределенность снижается. Очевидно, чем больше т, тем больше неопределенность и тем большее количество информации содержится в переданном сообщении.

Рассмотрим пример. Пусть ансамбль возможных сообщений представляет собой алфавит, состоящий из т различных букв. Необходимо определить, какое количество информации содержится в передаваемом слове длиной п букв, если вероятности появления букв одинаковы, а сами буквы следуют независимо друг от друга. Количество информации при передаче одной буквы:

В общем случае при передаче сообщений неопределенность снимается не полностью. Так, в канале с шумами возможны ошибки. По принятому сигналу v только с некоторой вероятностью P(a/v) < 1 можно судить о том, что было передано сообщение а. Поэтому после получения сообщения остается некоторая неопределенность, характеризуемая величиной апостериорной вероятности  P(a/v), а количество информации, содержащееся в сигнале v, определяется степенью уменьшения неопределенности при его приеме. Если Р(а)— априорная вероятность, то количество информации в принятом сигнале относительно переданного сообщения а, очевидно, будет равно:

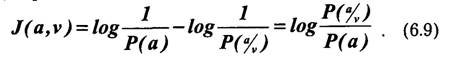
Это выражение можно рассматривать также как разность между количеством информации, поступившим от источника сообщений, и тем количеством информации, которое потеряно в канале за счет действия шумов.

6.2. Энтропия источника дискретных сообщений

1. Энтропия источника независимых сообщений

До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во многих случаях, когда требуется согласовать канал с источником сообщений, таких сведений оказывается недостаточно. Возникает потребность в характеристиках, которые позволяли бы оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и определяется выражением:

При этом среднее количество информации равно  log m. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле т.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ — редко. Поэтому знание числа сообщений т в ансамбле является недостаточным, необходимо иметь сведения о вероятности каждого сообщения: P(a₁), Р(а₂),...,Р(а_т).

Так как вероятности сообщений неодинаковы, то они несут различное количество информации: J(a_i) = -logP(a_i). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a_i):

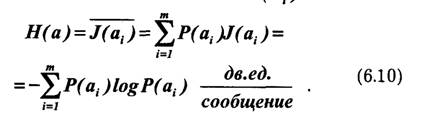
Величина Н(а) называется энтропией. Этот термин заимствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность состояния физической системы. В теории информации энтропия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Для нас самым существенным является то, что чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений а₁и а₂ с вероятностями Р(а₁) = р и Р(а₂) = 1 — р. На основании (6.10) энтропия такого источника будет равна:

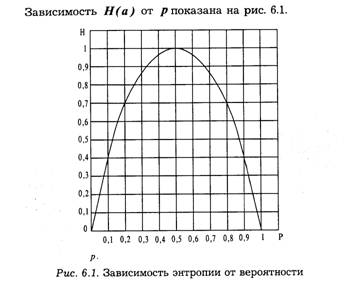
Максимум энтропии имеет место при р= ¹/₂, т. е. когда ситуация является наиболее неопределенной. При р = 1 или р = 0, что соответствует передаче одного из сообщений а₁ или а₂, неопределенности отсутствуют. В этих случаях энтропия Н(а) равна нулю.

Среднее количество информации, содержащееся в последовательности из п -сообщений, равно:

Отсюда следует, что количество передаваемой информации можно увеличить не только за счет числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.

Обобщая эти результаты, можно сформулировать основные свойства энтропии источника независимых сообщений (6.10):

2. Энтропия источника зависимых сообщений

Рассмотренные выше источники независимых сообщений являются простейшим типом источников. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примером может быть обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных букв О, Е, И больше, чем согласных.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью Р(а_k,а_I)или условной вероятностью P(a_L/a_k), которая выражает вероятность появления сообщения a_k при условии, что известно предыдущее сообщение а_k. Количество информации, содержащейся в сообщении при условии, что известно предыдущее сообщение а_k согласно (6.1), будет равно:

Среднее количество информации при этом определяется условной энтропией

H(a_L /a_k), которая вычисляется как математическое ожидание информации J(a_L/a_k)no всем возможным сообщениям а_k и a_L.

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В сооответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства:

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящейся в среднем на одно сообщение.

6.3. Избыточность источника сообщений

Уменьшение энтропии источника с увеличением статистической взаимосвязи (6.14) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличии взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них. Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются при чтении телеграммы на основании известных правил построения фраз и слов.

Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количе-

называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устранить избыточность. Источник, обладающий избыточностью, передает излишнее количество сообщений. Это увеличивает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осуществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, информационная емкость которых используется наиболее полно. Этому условию удовлетворяют равновероятные и независимые сообщения.

Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.

6.4. Статистические свойства источников сообщений

Использование энтропии в качестве усредненной величины, количественно характеризующей информационные свойства источника, выдающего последовательности дискретных сообщений, является целесообразным при условии, что вероятностные соотношения для этих последовательностей сохраняются неизменными. Источник называют стационарным, когда распределение вероятностей сообщений не зависит от их места в последовательности сообщений, создаваемых этим источником, т. е.:

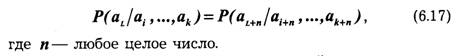
По аналогии со стационарным случайным процессом статистические характеристики последовательности сообщений стационарного источника не зависят от выбора начала отсчета.

Среди стационарных источников сообщений важное место занимают эргодические источники, которые отличаются тем, что с вероятностью, близкой к единице, любая достаточно длинная последовательность сообщений такого источника полностью характеризует его статистические свойства. Важной особенностью эргодических источников является то, что статистическая связь между сообщениями всегда распространяется только на конечное число предыдущих сообщений.

Существуют стационарные источники, которые могут работать в различных режимах, отличающихся друг от друга своими статистическими характеристиками. В этом случае источник не является эргодическим, так как при работе в одном режиме даже продолжительная последовательность сообщений уже не может в целом характеризовать свойства источника.

Подобного рода случайные последовательности (обладающие эргодическими свойствами) известны в математике как дискретные цепи А. А. Маркова (см. гл. 5).

В марковском эргодическом источнике вероятность передачи того или иного сообщения однозначно определяется состоянием источника. После передачи сообщения источник переходит в новое состояние, которое зависит от предыдущего состояния и переданного сообщения.

Достаточно длинные эргодические последовательности сообщений, с высокой степенью вероятности содержащие все сведения о статистических характеристиках источника, называются типичными. Чем длиннее последовательность, тем больше вероятность того, что она является типичной. В типичных последовательностях частота появления отдельных сообщений сколь угодно мало отличается от их вероятности. Отсюда вытекает важное свойство типичных последовательностей, состоящее в том, что типичные последовательности одинаковой длины примерно равновероятны.

Что касается нетипичных последовательностей, то вследствие их малой вероятности при большом числе сообщений они во многих случаях вообще не учитываются.

6.5. Скорость передачи информации и пропускная способность дискретного канала без помех

`Передача информации происходит во времени, поэтому можно ввести понятие скорости передачи как количество информации, передаваемой в среднем за единицу времени. Для эргодических последовательностей сообщений, где допускается усреднение во времени, скорость передачи равна:

Выданная источником информация в виде отдельных сообщений поступает в канал связи, где осуществляются кодирование и ряд других преобразований, в результате которых информация переносится уже сигналами и, имеющими другую природу и в общем случае обладающими другими статистическими характеристиками. Для сигналов также может быть найдена скорость передачи по каналу связи:

Высокая скорость передачи является одним из основных требований, предъявляемых к системам передачи информации. Однако в реальных условиях существует ряд причин, ведущих к ее ограничению. Остановимся на некоторых из них.

В реальном канале число используемых сигналов всегда конечно, поэтому энтропия в соответствии с (6.12) есть величина ограниченная:

С другой стороны, уменьшение длительности сигналов приводит, как известно, красширению спектра, что ограничивается полосой пропускания канала. Это в конечном счете ставит предел уменьшению и средней длительности τ. Таким образом, существуют, по крайней мере, две причины: конечное число сигналов и конечная длительность сигналов, которые не позволяют беспредельно повышать скорость передачи информации по каналу связи.

Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется пропускной способностью канала:

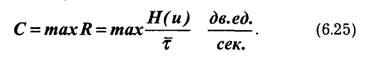
Пропускная способность канала характеризует его предельные возможности в отношении передачи среднего количества информации за единицу времени. Максимум скорости R в выражении (6.25) ищется по всем возможным ансамблям сигналов и.

Определим пропускную способность канала, в котором существуют два ограничения: число используемых сигналов не должно превышать т, а длительность их не может быть меньше τ сек. Так как Н(и) и τ независимы, то, согласно выражению (6.25), следует искать максимум Н(и) и минимум τ.

Тогда :

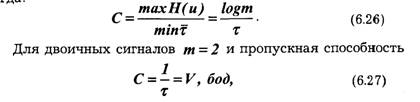
т. е. совпадает со скоростью телеграфирования в бодах. При передаче информации простейшими двоичными сигналами — телеграфными посылками — необходимая полоса пропускания канала зависит от частоты манипуляции F_m =¹/_{2 τ}, которая по определению равна частоте первой гармоники спектра сигнала, представляющего собой периодическую последовательность посылок и пауз. Очевидно, минимальная полоса пропускания канала, при которой еще возможна передача сигналов, F = F_m. Отсюда максимальная скорость передачи двоичных сигналов по каналу без помех равна:

Понятие пропускной способности применимо не только ко всему каналу в целом, но и к отдельным его звеньям. Существенным здесь является то, что пропускная способность С' какого-нибудь звена не превышает пропускной способности С'' второго звена, если оно расположено внутри первого. Соотношение С' ≤ С'' обусловлено возможностью дополнительных ограничений, накладываемых на участок канала при его расширении и снижающих пропускную способность.

6.6. Оптимальное статистическое кодирование сообщений

Для дискретных каналов без помех Шенноном была доказана следующая теорема: если производительность источника R_И =С— ε, где ε — сколь угодно малая величина, то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника. Передачу всех сообщений при R_И>C осуществить невозможно.

Смысл теоремы сводится к тому, что как бы ни была велика избыточность источника, все его сообщения могут быть переданы по каналу, если R_H ≤ C- ε. Обратное утверждение теоремы легко доказывается от противного. Допустим, R _И>С, но для передачи всех сообщений источника по каналу необходимо, чтобы скорость передачи информации R была не меньше R_И. Тогда имеем R ≥ R_И>C, что невозможно, так как, по определению, пропускная способность C = R_max.

Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений. Статистическим, или оптимальным, называется кодирование, при котором наилучшим образом используется пропускная способность канала без помех. При оптимальном кодировании фактическая скорость передачи информации по каналу R приближается к пропускной способности С, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответствовали ограничениям, которые накладываются на сигналы, передаваемые по каналу связи. Поэтому структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.

Рассмотрим основные принципы оптимального кодирования на примере источника независимых сообщений, который необходимо согласовать с двоичным каналом без помех. При этих условиях процесс кодирования заключается в преобразовании сообщений источника в двоичные кодовые комбинации. Поскольку имеет место однозначное соответствие между сообщениями источника и комбинациями кода, то энтропия кодовых комбинаций равна энтропии источника:

Одним из кодов, удовлетворяющих условию (6.33), является код Шеннона-Фано. Для ознакомления с принципами его построения рассмотрим в качестве примера источник сообщений, вырабатывающий четыре сообщения а₁ а₂ , а₃, и а₄ с вероятностями .

Все сообщения выписываются в кодовую таблицу (табл. 6.1) в порядке убывания их вероятностей. Затем они разделяются на две группы так, чтобы суммы их вероятностей по возможности были одинаковыми. В данном примере в первую группу входит сообщение а_; с вероятностью и во вторую Р(а₁) = 0,5 — сообщения а₂, и с суммарной вероятностью, также равной 0,5.

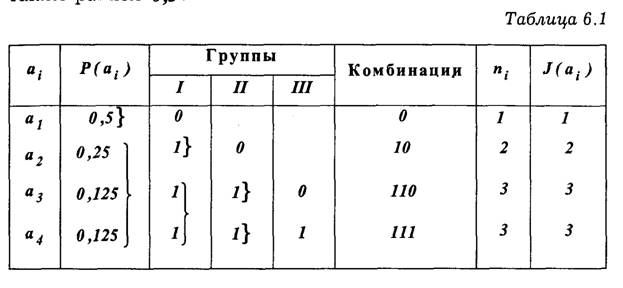
Комбинациям, которые соответствуют сообщениям первой группы, присваивается в качестве первого символа кода — 0 , а комбинациям второй группы — 1. Каждая из двух групп опять делится на две группы с применением того же правила присвоения символов 0 и 1. В идеальном случае после первого деления вероятности каждой группы должны быть равны 0,5, после второго деления — 0,25 и т. д. Процесс деления продолжается до тех пор, пока в группах не останется по одному сообщению.

При заданном распределении вероятностей сообщений код получается неравномерным, его комбинации имеют различное число элементов n_i. Причем, как нетрудно заметить, такой способ кодирования обеспечивает выполнение условия (6.33) полностью для всех сообщений.

В неравномерных кодах при декодировании возникает трудность в определении границ между комбинациями. Для устранения возможных ошибок обычно применяются специальные разделительные знаки. Так, в коде Морзе между буквами передается разделительный знак в виде паузы длительностью в одно тире. Передача разделительных знаков занимает дополнительное время, что снижает скорость передачи информации.

Важным свойством кода Шеннона-Фано является то, что, несмотря на его неравномерность, здесь не требуются разделительные знаки. Это обусловлено тем, что короткие комбинации не являются началом более длинных. Указанное свойство легко проверить на примере любой последовательности:

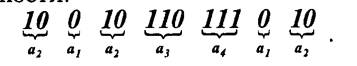
Таким образом, все элементы закодированного сообщения несут полезную информацию, что при выполнении условия (6.33) позволяет получить максимальную скорость передачи. Она может быть найдена путем непосредственного вычисления по формуле (6.32):

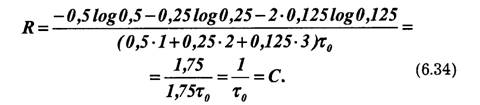
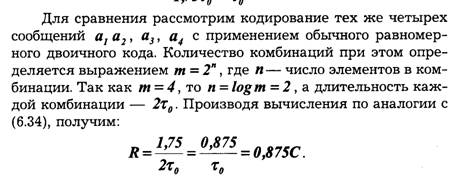
Пропускная способность в этом случае используется только частично. Из выражения (6.33) вытекает основной принцип оптимального кодирования. Он сводится к тому, что наиболее вероятным сообщениям должны присваиваться более короткие комбинации, а сообщениям с малой вероятностью — более длинные комбинации.

Одним из способов оптимального кодирования зависимых сообщений является применение так называемых "скользящих" кодов, основная идея которых состоит в том, что присвоение кодовых комбинаций по правилу Шеннона-Фано производится с учетом условных, а не априорных вероятностей сообщений. Число элементов в кодовой комбинации выбирается как n_S=—logP(a_sa_i,...,i_r), т. е. текущему сообщению присваивается та или иная комбинация в зависимости от того, какие сообщения ему предшествовали.

Необходимо подчеркнуть, что при оптимальном способе кодирования в сигналах, передающих сообщения источника, совершенно отсутствует какая-либо избыточность. Устранение избыточности приводит к тому, что процесс декодирования становится весьма чувствительным к воздействию помех. Это особенно сильно проявляется при оптимальном кодировании зависимых сообщений. Например, в "скользящих" кодах одна-единственная ошибка может вызывать неправильное декодирование всех последующих сигналов. Поэтому оптимальные коды применимы только для каналов, в которых влияние помех незначительно.

6.7. Скорость передачи информации и пропускная способность дискретных каналов с помехами

Отличительной особенностью рассмотренных ранее каналов без помех является то, что при выполнении условия теоремы Шеннона количество принятой

информации на выходе канала всегда равно количеству информации, переданной от источника сообщений.

При этом, если на вход канала поступил сигнал u_i, то на выходе возникает сигнал v_i, вполне однозначно определяющий переданный сигнал u_i. Количество информации, прошедшее по каналу без помех в случае передачи ui. и приема v_i., равно количеству информации, содержащейся в сигнале u_i :

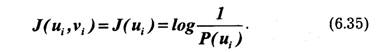
Здесь величина вероятности Р(и_i) характеризует ту неопределенность в отношении сигнала u_i, которая существовала до его передачи. После приема v_i, в силу однозначного соответствия между u_i и v_i, неопределенность полностью устраняется.

Иное положение имеет место в каналах, где присутствуют различного рода помехи. Воздействие помех на передаваемый сигнал приводит к разрушению и необратимой потере части информации, поступающей от источника сообщения. Поскольку v_i канале с помехами принятому сигналу u может соответствовать передача одного из нескольких сигналов и, то после приема v_i. остается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие между u и v носит случайный характер, поэтому степень неопределенности характеризуется условной апостериорной вероятностью P(u_i/v_i), причем всегда P(u_i/v_i)<1. Количество информации, необходимое для устранения оставшейся неопределенностиочевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда в соответствии с формулой (6.9) количество принятой информации определяется как разность:

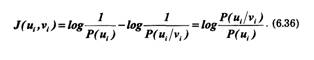
Для оценки среднего качества принятой информации при передаче одного сообщения выражение (6.36) необходимо усреднить по всему ансамблю и и v:

Соотношение (6.38) показывают, что среднее количество принятой информации равно среднему количеству переданной информации Н(и) минус среднее количество информации H(u/v), потерянное в канале вследствие воздействия помех.

Вторая форма записи средней взаимной информации может быть получена, если в (6.37) подставить выражение для условной вероятности. После соответствующих преобразований получим:

здесь H(v)— энтропия выхода канала, H(v/u)— условная энтропия, равная энтропии шума. Она определяет бесполезную часть информации, которая содержится в принятых сигналах за счет действия помех.

Понятия скорости передачи информации и пропускной способности, введенные для каналов без помех, могут быть использованы и в каналах с помехами. В этом случае скорость передачи информации по каналу определяется как

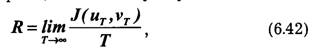
где и_T и v_T — соответственно последовательности передаваемых и принимаемых сигналов длительностью .

Необходимым условием применимости формулы (6.42) является соблюдение свойства эргодичности как для последовательности и_T, так и последовательности v_T, Последнее означает, что помехи, действующие в канале, также должны быть эргодическими.

Выражение для скорости передачи можно представить в более удобных формах:

Пропускная способность канала с помехами определяется как максимально возможная скорость передачи при заданных ограничениях, накладываемых на передаваемые сигналы:

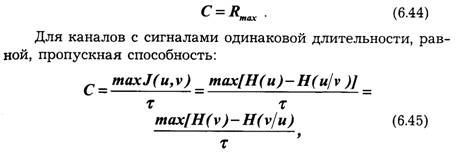
где максимум ищется по всем возможным ансамблям сигналов и.

Рассмотрим двоичный канал с помехами, по которому передаются дискретные сигналы, выбранные из ансамбля, содержащего два независимых сигнала u и и₂ с априорными вероятностями Р(и₁) и Р(и₂). На выходе канала образуются сигналы v₁ и v₂, при правильном приеме отражающие сигналы u₁ и и_2. В результате действия помех возможны ошибки, которые характеризуются при передаче u₁ условной вероятностью P(v₁/u₁), при передачи u₂ – условной вероятностью P(v₂/u₂)

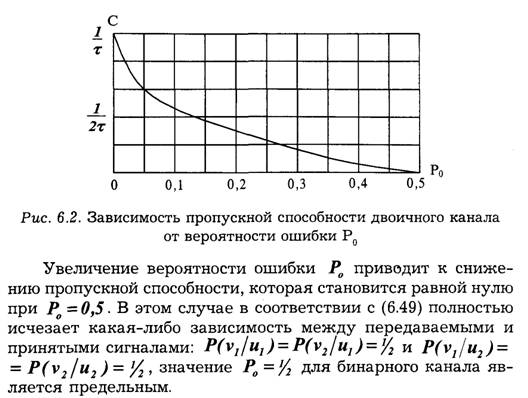
6.8. Теорема Шеннона для дискретного канала с помехами

Для дискретных каналов с помехами Шеннон доказал теорему, имеющую фундаментальное значение в теории передачи информации. Эта теорема может быть сформулирована следующим образом.

Если производительность источника R_И ≤C — ε, где ε — сколь угодно малая величина, то существует способ кодирования, позволяющий передавать все сообщения источника со сколь угодно малой вероятностью ошибки. При R_H>C такая передача невозможна.

Предположим, что на вход канала поступают сигналы и, которые вызывают на его выходе сигналы v. Предварительно будем полагать, что по каналу могут передаваться исключительно типичные последовательности, состоящие из и сигналов и: U₁,U₂,...,U_M. Соответственно на выходе канала сигналы при достаточно большом — образуют типичные последовательности: V₁,V₂,...,V_N, содержащие типичные последовательности ошибок. Общее число типичных последовательностей и равно:

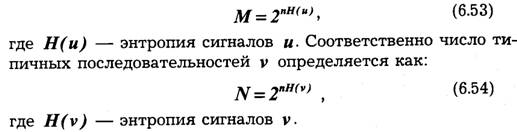
Действие помех проявляется в том, что нарушается однозначное соответствие между последовательностями U и V, т. е. при передаче некоторой последовательности U_i возможно появление на выходе канала одной из нескольких последовательностей у. Процесс передачи в этих условиях можно представить так, как показано на рис. 6.3, где стрелками отмечены переходы от типичных последовательностей V к типичным последовательностям V.

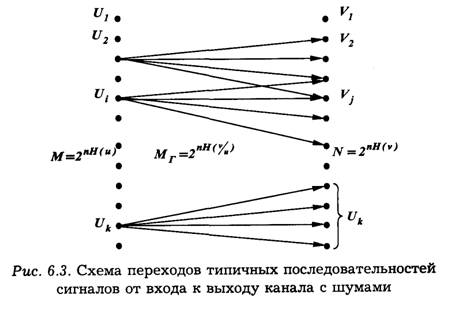
Так как последовательности ошибок типичные, то и переходы от U к V также являются типичными. Каждой последовательности U соответствует группа типичных переходов, которая характеризует неопределенность, возникающую при передаче U. Количественно указанная неопределенность описывается произведением n ·H(v/u), где H(v/u) —условная энтропия (энтропия шума). Тогда количество типичных (переходов в каждой группе:

В общем случае переходы перекрещиваются, т. е. одна и та же последовательность Vj может образоваться в результате передачи одной из нескольких последовательностей U. Для того, чтобы иметь возможность с высокой точностью однозначно определить принадлежность принятой последовательности V переданной последовательности U (на рис. 6.3 этому условию удовлетворяет U_k), очевидно, необходимо между группами последовательностей V установить достаточный интервал. Поэтому из всего набора последовательностей U только часть может использоваться для передачи информации.

Обозначим последовательности, выбранные для переноса информации, через U_и, а их число — буквой М_и. Выясним взаимосвязь М_и с вероятностью ошибки при декодировании принятых сигналов. Вероятности всех типичных переходов от U_и к V одинаковы, поэтому полная вероятность ошибки равна вероятности перекрещивания переходов Р_пер. Для вычисления P_пер необходимо знать ансамбль последовательностей U_и Иными словами, нужно знать конкретный способ кодирования. Решение вопроса об оптимальном выборе последовательностей U_и в общем случае представляет собой чрезвычайно сложную задачу, требующую отдельного рассмотрения. С целью ее упрощения будем полагать, что последовательности U_и выбираются из последовательностей и случайным образом. При этом условии вероятность того, что случайный переход от U_и к V будет перекрещиваться с другими переходами, приближенно равна отношению общего числа переходов ко всему количеству типичных последовательностей у. Следовательно, вероятность ошибки декодирования:

Эта оценка вероятности ошибки является грубым приближением, однако она правильно указывает на характер зависимости Р_од от М_и.

При согласовании канала с источником каждой типичной последовательности источника присваивается одна из последовательностей U_и, поэтому их число М_н выбирается равным количеству типичных последовательностей источника. Если энтропия источника равна Н_и, то можно записать:

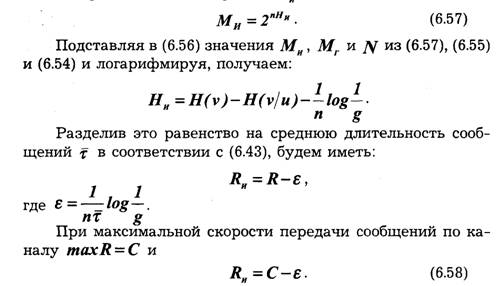
Из выражения (6.56) следует, что вероятность ошибки декодирования Р_oд может быть сколь угодно малой при неограниченном уменьшении g. Для того чтобы при этих условиях сохранить достаточно малой величину g, необходимо увеличивать количество сообщений п в типичных последовательностях. Что касается всех остальных нетипичных последовательностей из n-сообщений, которые до сих пор не рассматривались, то их можно закодировать весьма сложными сигналами, обладающими высокой помехоустойчивостью, не заботясь о длительности таких сигналов, поскольку суммарная вероятность нетипичных последовательностей весьма мала, и они не вызовут существенного уменьшения скорости передачи информации.

Таким образом, возможность одновременного установления сколь угодно малой вероятности ошибки декодирования Р_од и малой величины ε доказывает справедливость теоремы Шеннона.

 Обратное утверждение теоремы о том, что при R_И >С декодирование со сколь угодно малой ошибкой невозможно, следует из того факта, что в этих условиях М_иМ_г > N и, следовательно, всегда будут иметь место перекрещивания переводов от U к V, создающие неопределенность в установлении принадлежности V.

      На первый взгляд может показаться, что, поскольку вероятность ошибки в канале Р_о монотонно уменьшается с увеличением длительности сигналов, то сколь угодно высокая достоверность при декодировании достигается только при неограниченном уменьшении скорости передачи. Теорема Шеннона доказывает, что наличие помех и ошибок в канале само по себе не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок декодирования  Р_од, а лишь ограничивает максимальную скорость передачи информации С.Высокая достоверность декодирования и конечная скорость передачи не исключают друг друга. В этом состоит чрезвычайно важное значение теоремы для теории и техники передачи информации. Вместе с тем следует подчеркнуть, что из теоремы не вытекает конкретный способ наилучшего кодирования.

Применение на практике рассмотренного в теореме Шеннона общего метода, основанного на укрупнении кодируемых (Последовательностей, сильно усложняет кодирующие устройства и увеличивает задержку сигналов. Поэтому с инженерной точки зрения такой метод неэффективен. Однако теорема не утверждает, что укрупнение кодируемых сообщений является единственным способом. Поэтому в настоящее время продолжаются интенсивные поиски способов кодирования, которые бы позволяли с аппаратурой приемлемой сложности достигать предельных возможностей, указанных теоремой Шеннона.

Для обеспечения высокой достоверности передачи сообщений необходимо применять коды с избыточностью. Если R = С, то в соответствии с (6.43) средняя взаимная информация:

Иными словами, теорема утверждает, что для передачи сообщений со сколь угодно малой вероятностью ошибки декодирования  P_од могут быть найдены коды с минимальной избыточностью, равной æ . При передаче бинарных сигналов минимальная избыточность равна:

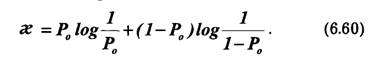
6.9. Энтропия непрерывных сообщений

При передаче непрерывных сообщений переданные сигналы  s(t) являются функциями времени, принадлежащими некоторому множеству, а принятые сигналы будут x(t) их искаженными вариантами. Все реальные сигналы имеют спектры, основная энергия которых сосредоточена в ограниченной полосе F. Согласно теореме Котельникова такие сигналы определяются своими значениями в точках отсчета, выбираемых через интервалы

В канале на сигнал накладываются помехи, вследствие чего количество различных уровней сигнала в точках отсчета будет конечным. Следовательно, совокупность значений непрерывного сигнала эквивалентна некоторой дискретной конечной совокупности. Это позволяет нам определить необходимое количество информации и пропускную способность канала при передаче непрерывных сообщений на основании результатов, полученных для дискретных сообщений.

Определим количество информации, которое содержится в одном отсчете сигнала х_i, относительно переданного сигнала s_i. Это можно сделать на основании соотношения (6.36), если в последней вероятности выразить через соответствующие плотности вероятности и взять предел при Δs →0 :

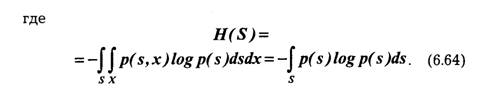
Величина Н( s ) характеризует информационные свойства сигналов и по форме записи аналогична энтропии дискретных сообщений. Так как в выражение (6.64) входит дифференциальное распределение вероятностей p(s), то Н(х) называют дифференциальной энтропией сигнала s.

Выражение H(s/x) представляет собой условную дифференциальную энтропию сигнала s:

H(x,s) — условная дифференциальная энтропия сигнала х, называемая также энтропией шума.

Многие свойства энтропии непрерывного распределения аналогичны свойствам энтропии дискретного распределения. Если непрерывный сигнал s ограничен интервалом s₁ ≤ s ≤ s₂, то энтропия H(s) максимальна и равна log(s₂ —s₁), когда сигнал имеет равномерное распределение:

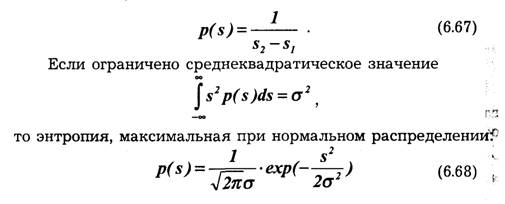
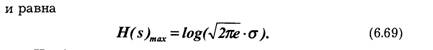
Необходимо отметить, что, в отличие от энтропии дискретных сигналов, величина дифференциальной энтропии зависит от размерности непрерывного сигнала. По этой причине она не является мерой количества информации, хотя и характеризует степень неопределенности, присущую источнику.

Только разность дифференциальных энтропии (6.66) количественно определяет среднюю информацию J(s,x).

6.10. Скорость передачи и пропускная способность непрерывного канала.

Формула Шеннона

 Для того чтобы найти среднее количество информации J_T(s,x), передаваемое сигналом на интервале Т, необходимо рассмотреть п = 2FT отсчетов непрерывного сигнала на входе канала: s_1,s₂,...,s_n и на выходе канала: x₁,x₂,...,x_n. В этом случае по аналогии с выражениями (6.63) и (6.69) можно записать:

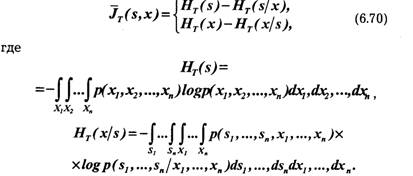
Энтропия H_T(s) и H_T(s/x) описывается аналогичными выражениями, только всюду необходимо поменять местами переменные s и х. Скорость передачи информации по непрерывному каналу находится как предел:

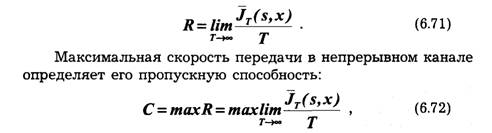
где максимум определяется по всем возможным ансамблям входных сигналов s.

Вычислим пропускную способность непрерывного канала, в котором помехой является аддитивный глум w(t), представляющий собой случайный эргодический процесс с нормальным и равномерным спектром.

Средние мощности сигнала и шума ограничены величинами Р_с и Р_ш, а ширина их спектра равна F.

Согласно выражениям (6.70) и (6.72) имеем:

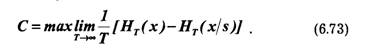
Прежде всего найдем величину H_T(x/s). С этой целью рассмотрим энтропию шума для одного отсчета, которая, с учетом соотношения p(s,x) = p(s) ·p(x/s), может быть представлена в виде:

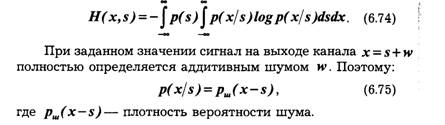
Значения шума с равномерным спектром некоррелированы между собой в моменты отсчетов, разделенные интервалом . Отсутствие статистической взаимосвязи между отсчетами шума позволяет представить энтропию суммы отсчетов шума (6.76) как сумму п энтропии отдельных отсчетов, которые вследствие стационарности шума равны между собой. С учетом этих соображений можно записать:

где вместо σ подставлено √P_ш .

       При данной величине H_T(x/s) = H_T(w) пропускная способность (6.73) отыскивается путем максимизации   Н_т(х). I Максимум Н_т(х), очевидно, имеет место, когда сигнал х, так же, как и шум, характеризуется нормальным распределением и равномерным спектром.

Отсюда:

Здесь предполагается, что сигнал s и помеха w независимы, поэтому мощность сигнала х равна сумме мощностей Р_с+Р_ш. Подставляя (6.78) в (6.73), окончательно получаем:

Так как х и w имеют нормальное распределение, то сигнал s = x-w также должен иметь нормальное распределение. Отсюда следует важный вывод: для того чтобы получить максимальную скорость передачи информации, необходимо применять сигналы с нормальным распределением и равномерным спектром.

Формула (6.79), впервые выведенная Шенноном, играет важную роль в теории и технике передачи информации. Она показывает те предельные возможности, к которым следует стремиться при разработке современных систем передачи информации.

Так как при равномерном спектре мощность шума определяется произведением P_ш = N₀F, то формулу (6.79) можно записать в другом виде:

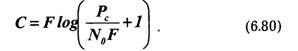
С увеличением F пропускная способность монотонно возрастает и стремится к величине:

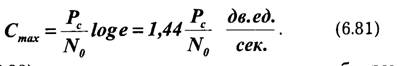
Формулу (6.80) можно рассматривать и таким образом, что при фиксированных значениях пропускной способности С и энергетического спектра шума N_o существует обратная зависимость Р_с и F . Иными словами, допускается уменьшение мощности сигнала за счет расширения его спектра.

Формулу (6.79), выведенную для равномерных спектров сигнала и шума, можно распространить и на случай неравномерных спектров. Можно показать, что при заданных спектрах шума G_ш(f) и сигнала G_c(f) максимум пропускной способности С имеет место в случае выполнения условия:

т. е. мощность сигнала должна возрастать на тех частотах, где уменьшается мощность шума, и наоборот. Можно также поставить вопрос: если выполняется условие (6.82), то при каком спектре шума получается минимальная пропускная способность? Оказывается, что этому условию удовлетворяет равномерный спектр, т. е. спектр "белого шума". Таким образом, белый шум, уменьшающий в наибольшей степени пропускную способность, является самым опасным видом помех.

Рассмотрим теперь вопрос о производительности источника непрерывных сообщений и о влиянии на качество их передачи помех, действующих в канале связи. При отсутствии каких-либо ограничений, накладываемых на непрерывные сообщения, количество содержащейся в них информации согласно (6.1) равно бесконечности:

Поэтому источник таких сообщений обладает бесконечной производительностью. Для того чтобы количество информации и производительность источника приобрели определенный смысл и стали конечными величинами, необходимо рассматривать непрерывное сообщение u(t) с учетом точности его оценки. Последняя, в частности, определяется погрешностью приборов, с помощью которых измеряется или регистрируется непрерывное сообщение. Обычно погрешность количественно оценивается среднеквадратическим отклонением приближенного непрерывного сообщения u*(t) от его точного значения u(t):

Нетрудно понять, что чем меньше ε²₀ , тем большее количество информации в среднем содержится в u*(t) относительно u(t) и тем выше производительность источника.

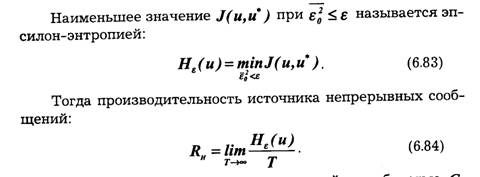
Для непрерывного канала с пропускной способностью С , на вход которого подключается источник, обладающий производительностью R_и, Шенноном была доказана следующая теорема.

Если при заданной погрешности оценки сообщений источника ε²_в его производительность R_и<C, то существует способ кодирования, позволяющий передавать все непрерывные сообщения источника с ошибкой в воспроизведении на_выходе канала, сколь угодно мало отличающейся от ε²₀ •

Иначе говоря, дополнительная неточность в воспроизведении сообщения v(t) на выходе канала, обусловленная воздействием помех, может быть сделана весьма незначительной.

Скорость передачи информации по каналу в конечном счете определяется скоростью потока информации на выходе приемника. Если считать, что сообщение v(t) и помеха w* (t) на выходе приемника имеют нормальное распределение и равномерный спектр, то:

Здесь F_m — ширина спектра частот принимаемого сообщения, обычно равная полосе пропускания приемника по низкой частоте; Р* _с— средняя мощность принятого сообщения v(t); Р*_ш— средняя мощность шума на выходе приемника.

6.11. Эффективность систем передачи информации

Пропускная способность канала связи С определяет максимальную скорость передачи информации, т. е. является тем пределом, которого можно достигнуть при идеальном кодировании. Естественно, что в реальных каналах скорость передачи всегда будет меньше С. Степень отличия R от С зависит от того, насколько рационально выбрана и эффективно используется та или иная система передачи информации. Наиболее общей оценкой эффективности системы передачи информации является коэффициент использования канала:

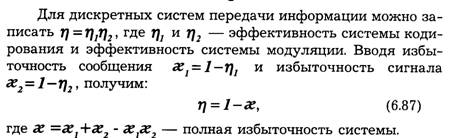
В ряде практических случаев удобными оценками эффективности системы является  коэффициент использования мощности сигнала:

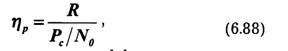
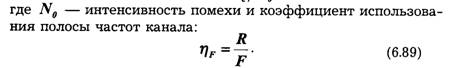
Согласно выражению (6.87) для коэффициента использования канала эффективность системы полностью определяется величиной ее избыточности, т. е. задача повышения эффективности системы передачи информации сводится

Согласно выражению (6.87) для коэффициента использования канала эффективность системы полностью определяется величиной ее избыточности, т. е. задача повышения эффективности системы передачи информации сводится к задаче уменьшения избыточности сообщения и сигнала.

Избыточность сообщения обусловлена тем, что элементы сообщения не являются равновероятными, и между ними имеется статистическая связь. При кодировании можно перераспределить вероятности исходного сообщения так, чтобы распределение вероятностей символов кода приближалось к оптимальному (к равномерному в дискретном случае или к нормальному при передаче непрерывных сообщений). Такое перераспределение позволяет устранить избыточность, зависящую от распределения вероятностей элементов сообщения. Примером подобного кодирования является код Шеннона-Фано. Если перейти от кодирования отдельных символов сообщения к кодированию целых групп символов, то можно устранить взаимосвязь между ними и тем самым еще уменьшить избыточность. Общая идея такого кодирования, который называют методом укрупнения, состоит в следующем. Исходное сообщение разбивается на отрезки по k символов в каждом. Такие отрезки могут рассматриваться как укрупненные элементы сообщения. Можно показать, что вероятностные связи между такими укрупненными элементами слабее, чем между элементами исходного сообщения. Очевидно, чем больше   k (крупнее отрезки), тем слабее будет связь между ними. Далее укрупненные элементы кодируются с учетом их распределения вероятностей.

Следует заметить, что при укрупнении элементов происходит преобразование, состоящее в переходе к коду с более высоким основанием т₁=т^k, где т — первоначальное основание.

Своеобразным примером метода укрупнения сообщений является стенографический текст. Каждый стенографический знак в этом тексте выражает целое слово или даже группу слов.

Что касается сигнала, то его избыточность зависит от способа модуляции и от вида переносчика. Процесс модуляции обычно сопровождается расширением полосы частот сигнала по сравнению с полосой частот передаваемого сообщения. Это расширение полосы и является избыточным. Частотная избыточность также увеличивается при переходе от синусоидального переносчика к переносчику импульсному или шумо-подобному. С точки зрения повышения эффективности передачи следовало бы выбирать такие способы модуляции, которые имеют малую избыточность. К таким системам, в частности, относится однополосная передача, в которой передаваемые сигналы не содержат частотной избыточности, — они являются просто копиями передаваемых сообщений.

Однако, говоря об эффективности системы передачи информации, нельзя забывать об ее помехоустойчивости. Устранение избыточности повышает эффективность передачи, но снижает при этом достоверность (помехоустойчивость), и, наоборот, сохранение или введение избыточности позволяет обеспечить высокую достоверность передачи. Например, при телеграфной передаче текста устранение избыточности приводит к тому, что становится труднее исправлять ошибки в сообщении, и в конечном счете снижается помехоустойчивость. При сохранении избыточности в тексте помехоустойчивость будет выше.

При кодировании в ряде случаев избыточность специально вводится с целью повышения достоверности передачи. Примером такого кодирования являются корректирующие коды, которые будут рассмотрены ниже.

Аналогичная ситуация имеет место и в отношении избыточности сигнала. Частотная избыточность при различных видах модуляции используется по-разному. При частотной модуляции, например, мы можем получить больший выигрыш в помехоустойчивости, чем при амплитудной модуляции, а при кодовой импульсной модуляции этот выигрыш будет еще больше. Частотная избыточность шумового переносчика позволяет снизить влияние замираний и сосредоточенных помех.

Следовательно, при оценке систем передачи информации необходимо учитывать по крайней мере два показателя: эффективность и помехоустойчивость; совокупность этих двухпоказателей составляет достаточно полную характеристику системы.

Наиболее совершенной системой передачи информации считается такая, которая обеспечивает наибольшую эффективность при заданной помехоустойчивости или, наоборот, обеспечивает наибольшую помехоустойчивость при заданной эффективности.

Контрольные вопросы и задания

1.  Как вводится логарифмическая мера информации и какими свойствами она обладает?

2. Дайте определение понятию ансамбля сообщений.

3.  Что называется энтропией и как она определяется для источников независимых и зависимых сообщений?

4. Каковы причины появления избыточности в сообщении?

5.  Какие источники сообщения называются стационарными и эргодическими?

6.  Что называется пропускной способностью канала? Чему она равна для двоичного канала без помех?                                            ,

7.  Поясните принцип оптимального статистического кодировав ния.

8.  Как определяется скорость передачи и пропускная способность канала с помехами?

9. Какие выводы следуют из теоремы Шеннона для дискретного канала с помехами?

10.  Как определяется количество передаваемой информации в непрерывных каналах?

11.  Проанализируйте формулу Шеннона для пропускной способности непрерывного канала.

12. Сформулируйте теорему Шеннона для непрерывного канала и поясните ее смысл.

13. Что называется эффективностью системы передачи информации и как она определяется количественно?

14.  Поясните зависимость между помехоустойчивостью и эффективностью системы передачи информации.

ГЛАВА  7

ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

7.1. Классификация корректирующих Кодов

В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны такие коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы код обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.

В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов.

Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. В неразделимых кодах такое разделение провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую к этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими.

7.2. Принципы помехоустойчивого кодирования

В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности .для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные коды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно М = 2ⁿ , где п - значность кода.

В обычном некорректирующем коде без избыточности, например, в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М_о, и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число комбинаций источника М₀. Однако в этом случае лишь М_о комбинаций из общего числа используются для передачи информации. Эти комбинации называются разрешенными, а остальные М — М_о комбинации носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие — запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях — исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.

Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d_tj между двумя комбинациями Ai и Aj определяется количеством единиц в сумме этих комбинаций по модулю два.

 Например:

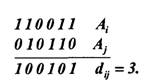
Для любого кода d_ij ≤n. Минимальное различие между разрешенными комбинациями в данном коде называется кодовым расстоянием d.

Расстояние между комбинациями A_i и Aj условно обозначено на рис. 7.1а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. В общем случае некоторая пара разрешенных комбинаций А_р1 и А_р2, разделенных кодовым расстоянием d, изображается на прямой рис. 7.16, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация А_р1 преобразовалась в другую разрешенную комбинацию А_р2, должно исказиться d символов. При искажении меньшего числа символов комбинация А_р1 перейдет в запрещенную комбинацию, и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации:

Если g <d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация в этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d = 2.

Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d₀ равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g -символов в п -значной комбинации будет равна:

где Р_о — вероятность искажения одного символа. Так как обычно Р_о<<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d₀. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация А_о (см. рис. 7.16), тогда принимается решение, что была принята комбинация А₁. Это правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального количества ошибок. (В общем случае оптимальное правило декодирования зависит от распределения ошибок.)

Аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который в наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности:

Минимальное значение d , при котором еще возможно исправление любых одиночных ошибок, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.1в ошибки кратности g ≤d_и исправляются, а ошибки, кратность которых лежит в пределах d_и ≤ g ≤d — d_и, только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах d -d ≤ g ≤d ,то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А_р2 вместо А_р1, или наоборот.

Существуют двоичные системы передачи информации, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще и так называемый символ стирания θ. Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов θ оказалось равным g_c, причем                                                         

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов θ необходимо перебрать всевозможные сочетания из g_c символов типа 0 и 1. Естественно, что

все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок g ≤g_c ≤d — 1, то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из g_c -символов совместно с правильно принятыми символами образуют запрещенные комбинации, и только одно сочетание стертых символов дает разрешенную комбинацию, которую и следует считать как правильно восстановленную.

Если g_c > d — 1, то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.

Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие коды обычно используются для корректирования ошибок малой кратности.

Корректирующая способность кода возрастает с увеличением d . При фиксированном числе разрешенных комбинаций М_о увеличение d возможно лишь за счет роста количества запрещенных комбинаций:

что, в свою очередь, требует избыточного числа символов r = п —k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить, как:

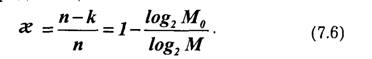
При независимых ошибках вероятность определенного сочетания g ошибочных символов в п -значной кодовой комбинации выражается формулой (7.2), а количество всевозможных сочетаний ошибочных g-символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний:

Анализ формулы (7.8) показывает, что при малой величине Р₀ и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.

Вероятность Р_ош, избыточность æ и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретной информации и какой ценой это достигается.

Общая задача, которая ставится при создании кода, заключается в достижении наименьших значений Р_ош и æ. Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.

В соответствии с общими принципами корректирования ошибок, основанных на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках.

7.3. Систематические коды

Систематические коды относятся к блочным разделимым кодам, т. е. к кодам, где операция кодирования осуществляется независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.

Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:

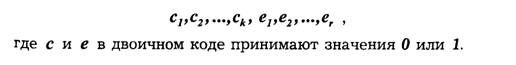
Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы xj = é_jΘе''_j, а следовательно, и контрольное число X будет равным нулю. При появлении ошибок некоторые значения x могут оказаться равными 1. В этом случае X ≠ 0, что и позволяет обнаруживать ошибки. Таким образом, контрольное число X определяется путем г проверок на четность.

Для исправления ошибок знание одного факта их возникновения является недостаточным, необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить местоположение ошибок и исправить их.

Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно 2' —1. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно k + r. В этом случае должно выполняться условие:

Формула (7.11) позволяет при заданном количестве информационных символов к определить необходимое число контрольных символов г , с помощью которых исправляются все одиночные ошибки.

7.4. Код с четным числом единиц. Инверсный код

Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит помимо информационных символов один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на основании (7.9) в следующей форме:

Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и, в общем случае, ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются.

На основании (7.8) вероятность необнаруженной ошибки равна:

К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую избыточность æ =1/(1 +k), однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.

Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000,11000 и 01101,10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными. Если количество единиц в информационных символах четное, т. е. сумма этих символов:

равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольный символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид:

При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е.:

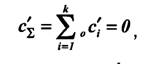
то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда с'_∑ = 1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность:

Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.

Анализ показывает, что при k ≥5 наименьшая кратность не обнаруживаемой ошибки g = 4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100,10100, а принята 10111,10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения x_j равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением:

Для g > 4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов Р_о можно полагать, что полная вероятность необнаруженных ошибок Р_ош ≈Р_ош4.

Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину æ= 0,5 .