Бурное развитие науки и промышленности в XX веке, неудержимый рост объемов поступающей информации привели к тому, что человек оказался не в состоянии воспринимать и перерабатывать все, ему предназначенное. Возникла необходимость классифицировать поступления по темам, организовать их хранение и доступ к ним, понять закономерности движения информации и т. д.
Это обстоятельство накладывает определенный отпечаток на всю информатику как науку об организации компьютерных информационных систем — такие системы могут использоваться в самых разных предметных областях, привнося в них свои "правила игры", свои закономерности и ограничения и, вместе с тем, новые возможности организации бизнеса, которые были бы немыслимы без информатики и связанного с ней компьютера. В этом плане невозможно переоценить такие свойства информации, как доступность, своевременность получения, коммерческая ценность, надежность.
Информационные ресурсы в современном обществе играют не меньшую, а нередко и большую роль, чем ресурсы материальные. Знание о том, кому, когда и где продать товар, может цениться не меньше, чем собственно товар. В этом плане динамика развития общества свидетельствует о том, что на "весах" материальных и информационных ресурсов последние начинают преобладать, причем тем сильнее, чем более открыто общество, чем более развиты в нем средства коммуникаций, чем большей информацией оно располагает.
С позиций рынка информация давно уже стала товаром, и это обстоятельство требует интенсивного развития теориии практики компьютеризации общества. Компьютер как информационная среда не только позволил совершить качественный скачок в области промышленности, науки и рынка, но он и определил новые, самостоятельные области производства: вычислительную технику, телекоммуникации, программные продукты.
Тенденции компьютеризации общества связаны с появлением новых профессий, связанных с вычислительной техникой, и различных категорий пользователей ЭВМ. Если в 60—70-е годы в этой среде доминировали специалисты по вы-, числительной технике (инженеры и программисты), создававшие новые средства вычислительной техники и новые пакеты прикладных программ, то сегодня интенсивно расширяется категория пользователей ЭВМ — представителей самых разных областей знаний, не являющихся специалистами по компьютерам в узком смысле, но умеющих использовать их для решения своих специфических задач.
Пользователь ЭВМ (или конечный пользователь) должен знать общие принципы организации информационных процессов в компьютерной среде, уметь выбирать нужные ему информационные системы и технические средства и быстро осваивать их применительно к своей предметной области. Учитывая интенсивное развитие вычислительной техники и во многом насыщенность рынка программных продуктов, два последних качества приобретают особое значение.
Минимум знаний по организации компьютерных систем обычно называют компьютерной грамотностью. Не существует строго ограниченных рамок, определяющих это понятие, — каждый пользователь определяет их для себя сам, но вместе с тем отсутствие такой грамотности делает сегодня невозможным доступ ко многим профессиям, на первый взгляд, весьма далеким от компьютера.
Целью настоящего учебника является изложение основных фундаментальных вопросов теории передачи и обработки информации, построения информационных систем, необходимых для того, чтобы "...достичь заветной цели — слияния технологий не только локальных и глобальных сетей, но и технологий любых информационных сетей — вычислительных, телефонных, телевизионных и т. п."1
В основу учебника положены лекционные курсы, которые прочитаны автором в течение последних семи лет на кафедре "Электроника и электронные информационные системы" Московского государственного университета сервиса для студентов специальностей и специализаций "Информационные системы и технологии", "Информационный сервис".
Материалы учебника могут быть использованы при изучении "'последующих специальных дисциплин: "Информационные сети", "Проектирование информационных систем", "Электронные информационные системы и организация каналов связи", "Офисная техника" и т. д.
Автор выражает благодарность доктору технических наук, проф. Н. А. Феоктистову и кандидату технических наук, доц. И. И. Князеву за помощь и ценные советы, высказанные при обсуждении рукописи данной книги, а также благодарит всех сотрудников кафедры, принимавших участие в оформлении и подготовке учебника к изданию.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные задачи изучения дисциплины
Объектом изучения теории информационных систем является информация — понятие во многом абстрактное, существующее "само по себе", вне связи с конкретной областью знания, в которой она используется.
Вообще, существует несколько взглядов на то, что принято считать информацией. Один взгляд, и его, по-видимому, придерживается большая часть специалистов и неспециалистов, сводится к тому, что существует как бы два сорта информации:
1. Информация техническая, которая передается по каналам связи и отображается на экранах дисплеев. Количество такой информации может быть точно вычислено, и процессы, происходящие с такой информацией, подчиняются физическим законам.
2. Информация семантическая, т. е. смысловая. Это та самая информация, которая содержится, к примеру, в литературном произведении. Для такой оценки информации предлагаются различные количественные оценки и даже строятся математические теории. Но общее мнение скорее сводится к тому, что оценки здесь весьма условны и приблизительны, и алгеброй гармонию все-таки не проверишь.
Второй взгляд состоит в том, что информация — это физическая величина, такая же, как, например, температура или скорость. Определенным образом и в определенных условиях информация равным образом описывает как процессы, происходящие в естественных физических системах, так и процессы в системах, искусственно созданных.
Как всегда, при наличии двух резко противоположных мнений существует и третье, примиряющее. Сторонники третьего подхода считают, что информация едина, но вот количественные оценки должны быть разными. Отдельно нужно измерять количество информации, причем количество информации — строгая оценка, относительно которой можно развивать единую строгую теорию. Кроме количества информации следует измерять еще и ценность. А вот с ценностью информации происходит то же самое, что и с понятием семантической информации. С одной стороны, вроде, ее можно вычислить, а с другой стороны, все эти вычисления справедливы лишь в ограниченном числе случаев. И, вообще, кто может точно вычислить, скажем, ценность крупного научного открытия?
Введем основные определения:
1. Информационный процесс — это любой процесс, в котором присутствует хотя бы один из элементов: передача информации, ее прием, хранение, обработка, выдача пользователю.
2. Информационная система — это любая система, реализующая или поддерживающая информационный процесс.
При таком подходе становится очевидным, что теория информационных систем является естественным развитием общей теории связи, которая включает в себя следующие основные разделы: теорию сигналов, теорию помехоустойчивости и теорию информации.
Начало общей теории связи было заложено в работе В. А. Котельникова "О пропускной способности "эфира" и проволоки" (1933 г.), в которой была сформулирована и доказана теорема отсчетов, и в работе Р. Хартли "Передача информации" (1928 г.), где была введена логарифмическая мера информации. Следующим шагом явились работы В. А. Котельникова по потенциальной помехоустойчивости (1946 г.) и К. Шеннона по теории информации (1948 г.).
Дальнейшее развитие теория получила в трудах А. А. Харкевича, А. Н. Колмогорова, Н. Винера, Р. Фано, Л. М. Финка и многих других отечественных и зарубежных ученых.
1.2. Система передачи и обработки информации
Объектом передачи в любой системе передачи информации является сообщение, несущее какую-либо информацию. Каждый из нас неоднократно употреблял выражение "масса информации", однако немногие знают, что можно измерять информацию количественно. Прежде чем вводить систему формул и чисел, рассмотрим пример. Пусть 10 июня мы услышали сообщение бюро прогнозов: "Осадков в виде снега завтра в Москве не будет". За последние 100 лет 10 июля в Москве снега, вероятно, ни разу не было; поэтому услышанное нами сообщение содержит в себе очень мало нового — мало информации. Если бы, однако, мы, зная, что работа бюро прогнозов надежна, услышали, что "завтра будут осадки в виде снега", то в этом сообщении для нас содержалось бы гораздо больше информации, чем в предыдущем. Таким образом, сообщение о том, что произойдет событие, которое должно произойти почти наверняка, содержит в себе очень мало информации. Напротив, сообщение о том, что произойдет событие, которое почти наверняка произойти не должно, содержит много информации. Сообщение о некотором событии содержит тем больше информации, чем больше изменяется вероятность этого события после приема сообщения о нем, по сравнению с вероятностью того же события до того, как было принято соответствующее сообщение. В общем случае мерой количества информации в сообщениях должна служить величина, измеряющая изменение вероятности события под действием сообщения.
Любое сообщение может быть непрерывным (речь, музыка) или дискретным (письменный текст, цифровые данные).
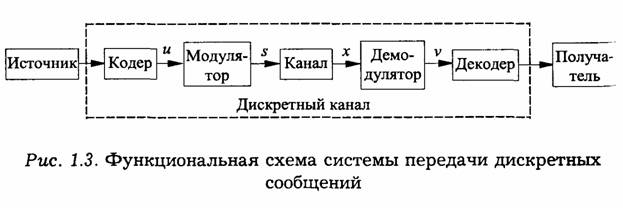
Функциональная схема системы передачи информации представлена на рис. 1.1.

Источником информации является отправитель сообщения, а потребителем — ее получатель. В одних системах передачи информации источником и потребителем информации может быть человек, а в других — различного рода автоматические устройства, ЭВМ и т. д.
Поступающее от источника сообщение u(t) в передатчике обрабатывается определенным образом, и формируется сигнал s(t), удобный для передачи по линии связи.
В телефонии, например, эта операция сводится просто к преобразованию звукового давления в пропорционально изменяющийся электрический ток микрофона. В телеграфии производится кодирование, в результате которого последовательность элементов сообщения (букв, цифр) преобразовывается в последовательность кодовых символов (0, 1, точка, тире).
Линией связи называется среда, используемая для передачи сигналов от передатчика к приемнику. В системах электрической связи — это пара проводов, кабель или волновод; в системах радиосвязи — область пространства, в которой распространяются электромагнитные волны от передатчика к приемнику; в системах оптической связи — оптическое волокно (ВОЛС). При передаче сигнал может искажаться, и на него могут воздействовать помехи w(t). Приемник обрабатывает принятый сигнал x(t), искаженный помехой, и восстанавливает по нему переданное сообщение u(t). Обычно в приемнике выполняются операции, обратные тем, которые были осуществлены в передатчике.
Каналом связи принято называть совокупность технических средств, служащих для передачи сообщения от источника к потребителю. Этими средствами являются передатчик, линия связи и приемник.
Канал связи вместе с источником и потребителем образуют систему передачи и обработки информации. Различают системы передачи дискретных сообщений (напри-. мер, система телеграфной связи, система передачи цифровых данных) и системы передачи непрерывных сообщений (системы радиовещания, телевидения и т. д.).
Система передачи информации называется многоканальной, если она обеспечивает взаимонезависимую передачу нескольких сообщений по одному общему каналу связи.
1.3. Сообщение и сигнал. Канал связи
Под информацией понимают сведения о каком-либо явлении, событии, объекте. Информация, выраженная в определенной форме, представляет собой сообщение, иначе говоря, сообщение — это то, что подлежит передаче. Сигнал является материальным носителем сообщения.
В качестве сигнала можно использовать любой физический процесс, изменяющийся в соответствии с передаваемым сообщением. Существенно то, что сигналом является не сам физический процесс, а изменение отдельных параметров этого процесса. Указанные изменения определяются тем сообщением, которое несет данный сигнал. Правила этих изменений — код — обычно задаются
заранее. В системах передачи и обработки информации сигнал предназначен для передачи информации от отправителя к получателю. Код полностью известен как на передающей, так и на приемной сторонах — он устанавливается заранее.
Сообщения и соответствующие им сигналы бывают дискретными и непрерывными. Дискретное сообщение представляет собой последовательность отдельных элементов. Сигнал также представляет собой дискретную последовательность отдельных элементов, соответствующих элементам передаваемого сообщения. С такими сигналами мы имеем дело в вычислительной технике, в телеграфии. Так, при передаче телеграммы сообщением является текст телеграммы, элементами сообщения — буквы, сигналами — кодовые комбинации, соответствующие этим буквам.
Непрерывное сообщение — это некоторая физическая величина (звуковое давление, температура и т. п.), принимающая любые значения в заданном интервале. Сообщение с помощью датчиков преобразовывается в непрерывно изменяющуюся электрическую величину u(t) — видеосигнал или аналоговый сигнал. В большинстве случаев видеосигнал является низкочастотным колебанием, которое отображает передаваемое сообщение. Для удобства анализа видеосигнал часто условно рассматривают как сообщение, которое необходимо передать по каналу связи.
Для передачи на большое расстояние видеосигнал преобразовывается в высокочастотный сигнал (радиосигнал).
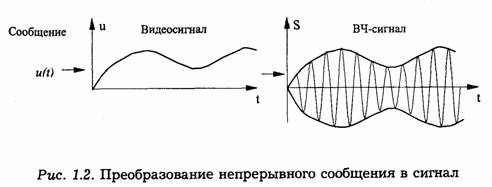
Во многих случаях сигнал отображает временные процессы, происходящие в некоторой системе.
Поэтому описанием конкретного сигнала может быть некоторая функция времени. Определив так или иначе эту функцию, мы определяем и сигнал. Однако такое полное описание сигнала требуется не всегда. Для решения ряда вопросов достаточно более общего описания в виде нескольких обобщенных параметров, характеризующих основные свойства сигнала, подобно тому, как это делается в системах транспортирования. Указывая габариты и вес, мы характеризуем основные свойства предмета с точки зрения условий его транспортирования; другие свойства (например, цвет) с этой точки зрения являются несущественными.
Сигнал есть также объект транспортирования, а техника передачи информации есть, по существу, техника транспортирования (передачи) сигналов по каналам связи. Поэтому целесообразно определить параметры сигнала, которые являются основными с точки зрения его передачи. Такими параметрами являются длительность сигнала, динамический диапазон и ширина спектра.
Всякий сигнал, рассматриваемый как временной процесс, имеет начало и конец. Поэтому длительность сигнала Ò является естественным его параметром, определяющим интервал времени, в пределах которого сигнал существует.
Характеристиками сигнала внутри интервала его существования являются динамический диапазон и скорость изменения сигнала.
Динамический диапазон определяется как отношение наибольшей мгновенной мощности сигнала к наименьшей:
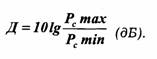
Динамический диапазон речи диктора равен 25÷30 дБ, вокального ансамбля — 45÷55 дБ, симфонического оркестра — 65÷75 дБ.
В реальных условиях всегда имеют место помехи. Для удовлетворительной передачи требуется, чтобы наименьшая мощность сигнала превышала мощность помех. Отношение сигнала к помехе характеризует относительный уровень сигнала. Обычно определяется логарифм этого отношения, который называется превышением сигнала над помехой. Это превышение и принимается в качестве второго параметра сигнала. Третьим параметром является ширина спектра сигнала F. Эта величина дает представление о скорости изменения сигнала внутри интервала его существования. Спектр сигнала может простираться в пределах очень большой полосы частот. Однако для большинства сигналов можно указать полосу частот, в пределах которой сосредоточена его основная энергия. Этой полосой и определяется ширина спектра сигнала.
Канал связи можно охарактеризовать так же, как и сигнал, тремя параметрами: временем, в течение которого по каналу ведется передача, динамическим диапазоном и полосой пропускания канала.
Общими признаками различных каналов являются следующие. Во-первых, большинство каналов можно считать линейными. В таких каналах выходной сигнал представляет собой просто сумму входных сигналов (принцип суперпозиции). Во-вторых, на выходе канала, даже при отсутствии полезного сигнала, всегда имеются помехи. В-третьих, сигнал при передаче по каналу претерпевает задержку по времени и затухание по уровню. И, наконец, в реальных каналах всегда имеют место искажения сигнала, обусловленные несовершенством канала.
Сигнал на выходе канала можно записать в следующем виде:
![]()
где s(t) — сигнал на входе канала; w(t) — помеха; μ и τ — величины, характеризующие затухание и время задержки сигнала.
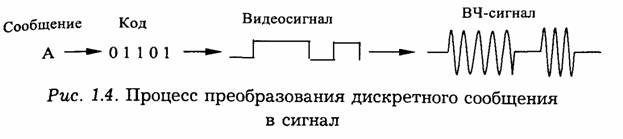
Преобразование дискретного сообщения в сигнал состоит из двух операций: кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция — вид формируемого сигнала, который должен передаваться по каналу связи.
Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Для европейских языков число элементов колеблется от 52 до 55, для восточных языков оно может исчисляться сотнями и даже тысячами. Так как число элементов в дискретном сообщении конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел.
Так, для передачи букв русского алфавита (их 32) необходимо передавать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача десяти цифр от 0 до 9. Практически для этого нужно передавать по каналу связи десять сигналов, соответствующих различным цифрам. Систему передачи дискретных сообщений можно существенно упростить, если воспользоваться при кодировании двоичной системой счисления.
В десятичной системе основанием счисления является число N. Поэтому любое число N можно представить в виде:
![]()
где ао,а1,...,аn— коэффициенты, принимающие значения от 0 до 9. Так, число 265 можно записать как:

Очевидно, в качестве основания счисления можно принять любое целое число т и представить число N как:

где à0, à 1,..., à n— коэффициенты, принимающие значения от 0 до т-1- Задаваясь величиной т, можно построить любую систему счисления. При т=2 получим двоичную систему, в которой числа записываются при помощи всего лишь двух цифр: 0 и 1:
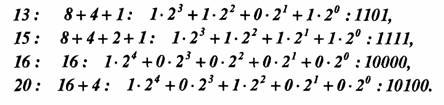
Арифметические действия в двоичной системе весьма простые. Так, сложение осуществляется по следующим правилам:
![]()
Различают еще символическое поразрядное сложение без переноса в высший разряд, так называемое "сложение по модулю два". Правила этого сложения следующие:
![]()
Если преобразовать последовательность элементов сообщения в последовательность двоичных чисел, то для передачи последних по каналу связи достаточно передавать всего лишь два кодовых символа: 0 и 1. Практическая реализация такой передачи очень проста: символы 0 и 1 могут передаваться колебаниями с различными частотами или посылками постоянного тока разной полярности.
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией.
Совокупность кодовых комбинаций, обозначающих дискретные сообщения, называется кодом. Правило кодирования обычно выражается кодовой таблицей, в которой приводятсяалфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество — основанием кода. В общем случае при основании кода т правила кодирования N элементов сообщения сводятся к правилам записи различных чисел в m-ичной системе счисления. Число символов и, образующих кодовую комбинацию, называется значностъю кода или длиной кодовой комбинации.
В зависимости от системы счисления, используемой при кодировании, различают двухпозиционные и многопозиционные коды. К первым относятся все коды, в которых используется двоичная система счисления. Часто эти коды называют двоичными. К многопозиционным кодам относятся все коды, в которых число позиций (основание кода) больше двух. Различают коды равномерные и неравномерные.
Равномерными называют такие коды, у которых все кодовые комбинации имеют одинаковую длину. Для равномерного кода число возможных кодовых комбинаций равно mn. Примером такого кода является пятизначный код Бодо. Этот код содержит пять двоичных элементов (т=2; п=5). Число возможных кодовых комбинаций равно 25 = 32, что достаточно для кодирования букв алфавита.
Кодовая таблица представлена в табл. 1.1.
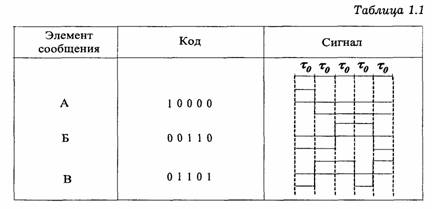
Символ 1 передается положительным импульсом длительности т, а символ 0 — отрицательным импульсом той же длительности. Время передачи любой кодовой комбинации равно 5 τ0 . Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями
Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов 0 и 1, но и их количеством. Это приводит к тому, что различные кодовые комбинации имеют разную длительность.
Типичным примером неравномерных кодов является код Морзе,хв котором символы 0 и 1 используются только в двух сочетаниях: как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам — тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями.
Кодовая таблица представлена в табл. 1.2.
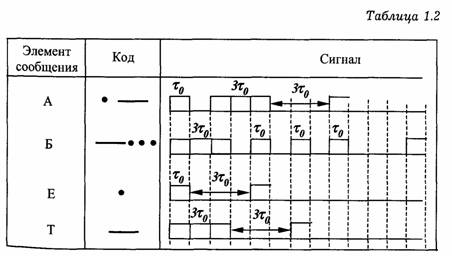
Время передачи различных кодовых комбинаций различно. Самая короткая кодовая комбинация (буква "Å") по длительности равна 4τ0, а самая длинная (цифра 0) — 22τ0(при передаче однополярными импульсами). Средняя длительность кодовой комбинации при передаче текста на русском языке равна примерно 9,5 τ 0. По сравнению с пятизначным равномерным кодом Бодо это почти в два раза больше.
По помехоустойчивости коды делятся на обыкновенные и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются обыкновенными, или кодами без избыточности. В обыкновенных равномерных кодах превращение одного символа комбинации в другой, например, 1 в 0 или 0 в 1, приводит к появлению новой возможной комбинации, т. е. к ошибке. Корректирующие коды строятся так, что для передачи сообщения используются не все возможные кодовые комбинации, а лишь некоторая их часть. Тем самым создается возможность обнаружить и исправлять ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются ценой введения в кодовые комбинации дополнительных (избыточных) символов.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называются соответственно кодером и декодером. Как правило, это нелинейные логические устройства. Устройства, преобразующие код в сигнал (модулятор) и сигнал в код (демодулятор), принято называть модемами.
Передача сообщений по каналу связи осуществляется с помощью некоторого физического процесса, который называется переносчиком. В системах передачи информации переносчиком является электрическое колебание.
Всякий сигнал получается путем модуляции. Немодулированный переносчик не несет информации — он подобен чистому листу бумаги, в то время как модулированный переносчик можно сравнить с листом бумаги, на котором написаны буквы и знаки, отображающие информацию.
Модуляция состоит в том, что один из параметров переносчика f(a,b,c,...) изменяется во времени в соответствии с передаваемым сообщением u(t).
Например:
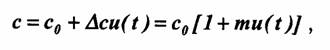
где т=Δс/с0 —коэффициент модуляции.
Если изменяется (модулируется) параметр с, то получается с-модуляция, если изменяется параметр b, то получается b-модуляция, и т. д. Модулированные сигналы различаются переносчиками и модулируемыми параметрами. Число возможных видов модуляции при данном виде переносчика определяется числом его параметров.
1.5. Демодуляция и декодирование
Восстановление переданного сообщения в приемнике обычно осуществляется в такой последовательности. Сначала производится детектирование сигнала. Цель этой операции состоит в извлечении из модулированного сигнала модулирующего
сигнала. При этом производятся действия, обратные операции модуляции, поэтому детектирование называют демодуляцией.
В системах передачи непрерывных сообщений в результате демодуляции выделяется видеосигнал, отображающий переданное сообщение. Этот сигнал поступает затем на воспроизводящее или записывающее устройство.
В системах передачи дискретных сообщений в результате демодуляции последовательность элементов сигнала превращается в последовательность кодовых символов, после чего эта последовательность преобразовывается в последовательность элементов сообщения, выдаваемую получателю (рис. 1.5). Это преобразование называется декодированием.

Иногда операции демодуляции и декодирования объединяются в одном устройстве, которое приходящую последовательность элементов сигнала преобразовывает сразу в последовательность букв сообщения. Такой метод приема называют "приемом в целом", в отличие от метода "поэлементного приема". В первом случае анализируется целиком отрезок сигнала, соответствующий кодовой комбинации, и на основании того или иного критерия восстанавливается переданный элемент сообщения (буква). Во втором случае сначала анализируются отдельные элементы сигнала, соответствующие кодовым символам, а затем восстановленная кодовая комбинация декодируется, т. е. преобразовывается в элемент (букву) сообщения
Строго говоря, по принятому сигналу можно судить лишь с некоторой степенью точности о том, что был передан тот или иной сигнал из множества возможных для данной системы сигналов. При этом необходимо решить, какому переданному сигналу соответствует принятый сигнал. В некоторых случаях это решение принимает сам человек. Так, например, при приеме телеграфных сигналов на слух оператор решает, какой сигнал ("точка" или "тире") был передан. Он же выполняет и операцию декодирования.
В приемниках дискретных сообщений, предназначенных для записи информации, все эти операции выполняются автоматически. В этих случаях приемник принимает решение, какому переданному сигналу соответствует принятый искаженный сигнал. Для этой цели сигнал сначала детектируется, а затем опознается с помощью решающей схемы. Демодулятор при этом состоит из детектора и решающего устройства.
В простейшем случае решающая схема представляет собой пороговое устройство в форме реле или триггера, работающих по принципу "да" или "нет". Если принятый элемент сигнала имеет значение выше порогового, выдается один символ кода, например, (1), если ниже — другой (0). Высота порога, очевидно, должна выбираться с учетом вероятности появления элементов сигнала и относительной важности положительного и отрицательного решений.
В более ответственных случаях применяются решающие схемы с двумя порогами. В этом случае при попадании уровня сигнала между двумя порогами решение не принимается — вместо сомнительного элемента сигнала выдается специальный символ стирания. Введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации.
1.6. Дискретизация и кодирование непрерывных сообщений
Под дискретизацией понимается преобразование непрерывных сообщений (сигналов) в дискретные. При этом используется дискретизация по времени и по уровню.
Дискретизация по времени выполняется путем взятия отсчетов функции u(t) в определенные дискретные моменты времени tk.
В результате непрерывная функция u(t) заменяется совокупностью мгновенных значений uk = {u(tk )}. Обычно моменты отсчетов выбираются на оси времени равномерно, т. е. tk = к Δt,
Выбор интервала At производится на основании теоремы Котельникова, согласно
которой функция с ограниченным спектром полностью определяется своими
значениями, отсчитываемыми через интервалы ![]() где F— ширина спектра.
где F— ширина спектра.
Дискретизация значений функции (уровня) носит название квантования. Операция квантования сводится к тому, что вместо данного мгновенного значения сообщения u(t) передаются ближайшие значения по установленной шкале дискретных уровней.
Дискретные значения по шкале уровней чаще всего выбираются равномерно: иk = kΔ и. При квантовании вносится погрешность (искажение), так как истинные значения функции заменяются округленными значениями иk. Величина этой погрешности ε = и-иk не превосходит половины шага квантования Δ и и может быть сведена до допустимого значения. Погрешность ε является случайной функцией и проявляется на выходе как дополнительный шум ("шум квантования"), наложенный на передаваемое сообщение.
Дискретизация одновременно по времени и уровню позволяет непрерывное сообщение преобразовать в дискретное (аналоговый сигнал в цифровую форму), которое затем может быть закодировано и передано методами дискретной (цифровой) техники.
В реальном канале сигнал при передаче искажается, и сообщение воспроизводится с некоторой ошибкой. Причиной таких ошибок являются искажения, вносимые самим каналом, и помехи, воздействующие на сигнал.
Частотные и временные характеристики канала определяют линейные и нелинейные искажения. Как правило, эти искажения обусловлены известными характеристиками канала и могут быть устранены или уменьшены путем коррекции.
Следует четко отделить искажения от помех, имеющих случайный характер. Помехи заранее неизвестны и поэтому не могут быть полностью устранены.
Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющее его прием. Помехи разнообразны по своему происхождению: грозы, помехи электротранспорта, электрических моторов, систем зажигания двигателей, соседних радиостанций, коммутации реле и т. д.
Практически в любом диапазоне частот имеют место внутренние шумы аппаратуры, обусловленные хаотическим движением носителей заряда в усилительных приборах, так называемый тепловой шум. Квадрат эффективного напряжения теплового шума определяется формулой Найквиста:
![]()
где k — постоянная Больцмана, Т — абсолютная температура, R — сопротивление, Δ f — полоса частот.
В общем случае действие помехи w на передаваемый сигнал s можно выразить оператором:
![]()
В частном случае, когда оператор ψ вырождается в сумму:
x=s+w
помеха называется аддитивной.
Если же оператор может быть представлен в виде произведения:
![]()
то помеху называют мультипликативной.
В реальных каналах обычно имеют место и аддитивные, и мультипликативные помехи, поэтому:
![]()
Виды помех: флуктпуационные — случайный процесс с нормальным распределением, импульсные, сосредоточенные по спектру.
1.8 Достоверность и скорость передачи информации
Когда мы оцениваем работу системы передачи информации, то прежде всего интересуемся, какую достоверность передачи сообщений обеспечивает система и сколько информации при этом передается. Первое определяет качество передачи, второе — количество.
В реальной системе передачи информации достоверность определяется степенью искажения сигнала. Эти искажения зависят от свойств и технического состояния системы, а также от интенсивности и характера помех. В правильно спроектированной и технически исправной системе передачи информации искажения сигналов обусловлены лишь воздействием помех. В этом случае достоверность передачи сообщений полностью определяется помехоустойчивостью системы.
Под помехоустойчивостью системы обычно понимают способность системы противостоять вредному влиянию помехи на передачу сообщений. Так как действие помехи проявляется в том, что принятое сообщение отличается от переданного, то количественно помехоустойчивость при заданной помехе можно характеризовать степенью соответствия принятого сообщения переданному. Назовем эту величину общим термином — достоверность. Количественную меру достоверности приходится выбирать по-разному, в зависимости от характера сообщения.
Пусть сообщение представляет собой дискретную последовательность элементов из некоторого конечного множества возможных элементов. Влияние помехи на передачу такого сообщения проявляется в том, что вместо фактически переданного элемента может быть принят какой-либо другой. Такое событие называется ошибкой. В качестве количественной меры достоверности можно принять вероятность ошибки Ро или любую возрастающую функцию этой вероятности.
При передаче непрерывных сообщений степенью соответствия принятого сообщения v(t) переданному u(t) может служить некоторая величина ε , представляющая собой отклонение v от u. Часто принимается критерий квадратичного уклонения, выражающийся соотношением:
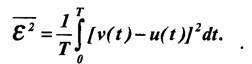
Количественную меру достоверности можно также определить как вероятность того, что уклонение не превзойдет некоторой заранее заданной величины ε 0:
![]()
Следует отметить, что достоверность передачи зависит от отношения мощностей сигнал/помеха. Чем больше это отношение, тем меньше вероятность ошибки (больше — достоверность).
При данной интенсивности помехи вероятность ошибки тем меньше, чем сильнее различаются между собой сигналы, соответствующие разным элементам сообщения. Задача состоит в том, чтобы выбрать для передачи сигналы с большим различием. Так, при фазовой манипуляции различие между сигналами больше, чем при амплитудной или частотной манипуляции. Поэтому следует ожидать, что достоверность передачи при ФМ будет выше, чем при AM иЧМ.
Наконец, достоверность зависит и от способа приема. Нужно выбрать такой способ приема, который наилучшим образом реализует различие между сигналами при данном отношении сигнал/помеха. Правильно спроектированный приемник может увеличивать отношение сигнал/помеха.
Необходимо обратить внимание на существенное различие между системами передачи дискретных и непрерывных сообщений. В системах передачи непрерывных сообщений всякое, даже сколь угодно малое, мешающее воздействие на сигнал, вызывающее искажение модулируемого параметра, всегда влечет за собой внесение соответствующей ошибки в передаваемое сообщение. В системах передачи дискретных сообщений ошибка возникает только тогда, когда сигнал воспроизводится (опознается) неправильно, а это происходит лишь при сравнительно больших искажениях. Свойство систем передачи дискретных сообщений правильно регистрировать искаженные (в некоторых пределах) сигналы называется исправляющей способностью.
В теории помехоустойчивости, разработанной В. А. Котельниковым, показывается, что при заданном методе кодирования и модуляции существует предельная (потенциальная) помехоустойчивость, которая в реальном приемнике может быть достигнута, но не может быть превзойдена. Приемное устройство, реализующее потенциальную помехоустойчивость, называется оптимальным приемником.
Наряду с достоверностью (помехоустойчивостью) важнейшим показателем работы системы передачи информации является скорость передачи.
В системах передачи дискретных сообщений скорость измеряется числом передаваемых двоичных символов в секунду R. Для одного канала двоичная скорость передачи определяется соотношением:
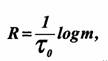
где τ 0 — длительность элементарной посылки сигнала, т — основание кода. При т = 2:
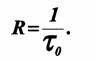
Для любого канала при заданных ограничениях существует предельная скорость передачи, которая называется пропускной способностью канала Ñ.
В реальных системах скорость передачи всегда меньше пропускной способности канала Ñ.
Современная теория показывает, что при R≤C можно найти такие способы передачи и соответствующие им способы приема, при которых достоверность передачи может быть сделана сколь угодно большой.
1. Нарисуйте функциональную схему системы передачи информации.
2. Что такое информация, сообщение, сигнал?
3. Как происходит преобразование непрерывного сообщения в сигнал?
4. Дайте определение основным характеристикам сигнала.
5. Поясните процесс кодирования сигнала.
6. Как происходит процесс преобразования дискретного сообщения в сигнал?
7. Что такое модуляция?
8. Каким образом восстанавливается переданное сообщение в приемнике?
9. Для чего применяется дискретизация по времени и по уровню?
10. Что такое аддитивная и мультипликативная помехи?
11. Какими параметрами определяется качество передачи информации и количество переданной информации?
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
СИГНАЛОВ, СООБЩЕНИЙ И ПОМЕХ
2.1. Определение и классификация сигналов
Передача и хранение информации, т. е. перенос информации в пространстве и времени, осуществляется сигналами.
Сигналами называются физические процессы, параметры которых содержат информацию, т. е. сигналы являются материальными носителями информации. В исходном состоянии любой носитель информации представляет собой как бы чистую поверхность, подготовленную к нанесению необходимых данных — модуляции. Последняя состоит в том, что изменяется один или несколько (сложная модуляция) параметров носителя в соответствии с передаваемой информацией. Эти параметры будем называть информационными.
В информационных системах в качестве носителей используются электрические сигналы, т. е. ток или напряжение, значения которых меняются по закону, отображающему передаваемое сообщение. Сигналы можно классифицировать по ряду признаков. Как уже отмечено в главе 1, различают дискретные и непрерывные сигналы, которые, в свою очередь, могут быть детерминированными или случайными. Дискретный сигнал представляет собой дискретную последовательность определенных элементов, соответствующую элементам
передаваемого сообщения. Непрерывный сигнал может принимать любые значения в заданном интервале времени.
Сигнал называется детерминированным или регулярным, если его математическим представлением является заданная функция времени. С информационной точки зрения это означает, что под регулярным сигналом понимается такой сигнал, который соответствует известному сообщению. Такие сигналы не несут информации.
Сигналы, несущие информацию, на приемном конце заранее будут неизвестными. Сигналы, и тем более помехи для получателя являются случайными (недетерминированными).
Необходимо подчеркнуть относительность понятия недетерминированности. Сигнал для отправителя на передающем конце детерминирован, так как при заданном способе передачи он определяется известным сообщением. Для получателя тот же сигнал недетерминирован, так как передаваемое сообщение на приемном конце неизвестно. Реальные сигналы, передаваемые в информационных системах, как правило, обладают сочетанием свойств детерминированных и недетерминированных сигналов: некоторые параметры сигнала получателю известны заранее, а некоторые для него являются случайными.
Между сигналами и помехами нет принципиальной разницы. Помеха — это тоже сигнал, но нежелательный для данной системы. В ряде случаев один и тот же сигнал для одной системы является полезным носителем информации, а для другой — помехой. Например, повторное использование частот в системах сотовой связи приводит к тому, что для одной соты сигнал является полезным, а для другой — помехой (со-канальные помехи).
Случайным сигналом мы будем называть сигнал, математическим описанием которого является случайная Функция времени.
Для образования сигналов используются в основном три типа носителей (рис. 2.1).
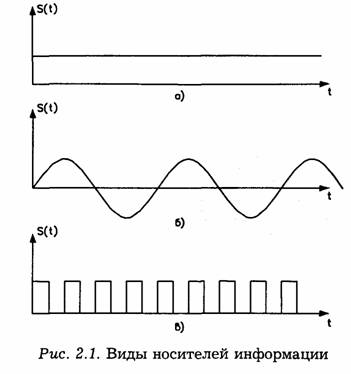
Первый тип носителя s(t) — постоянное состояние (рис, 2.1а), например, постоянное напряжение имеет только один информационный параметр; это в данном случае — значение напряжения, причем модуляция сводится к такому изменению напряжения, чтобы оно в определенном представляло передаваемые данные. При этом может меняться и полярность напряжения.
Второй тип носителя — гармоническое колебание (рис. 2.16), например, переменное напряжение содержит три таких параметра: амплитуду, частоту и фазу.
Третий тип носителя — последовательность импульсов (рис. 2.1 в) предоставляет еще большие возможности. Здесь параметрами модуляции могут быть: амплитуда импульсов, фаза импульсов, частота импульсов, длительность импульсов или пауз, число импульсов и комбинация импульсов и пауз, определяющая код.
Простейшим периодическим сигналом является гармоническое колебание (тока, напряжения, заряда, напряженности поля), определяемое законом:
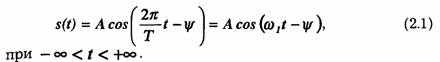
Здесь А, Т, ω1, ψ — постоянные амплитуда, период, частота и фаза.
Реальные сигналы имеют начало и конец. В дальнейшем под гармоническим сигналом будет подразумеваться сигнал, определяемый функцией, совпадающей с выражением (2.1) в конечном интервале времени.
Гармоническое колебание, определяемое выражением (2.1), иногда удобно представлять в одной из следующих форм:
![]()
Первой из этих форм соответствует векторное представление, изображенное на рис. (2.2а), а второй форме — на рис. (2.26).
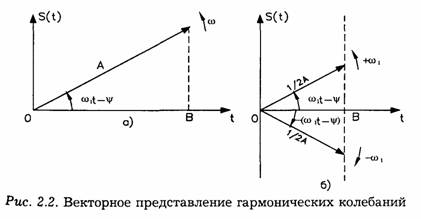
В первом случае действительная функция s(t) получается как проекция ОВ вектора на его горизонтальную ось, а во втором — как сумма проекций ОВ на ту же ось двух векторов с амплитудами 1/2À , вращающимися с угловой частотой во взаимно противоположных направлениях.
Гармонический сигнал находит широкое применение на практике, в частности, при регулировке устройств обработки информации и снятии их амплитудных и частотных характеристик.
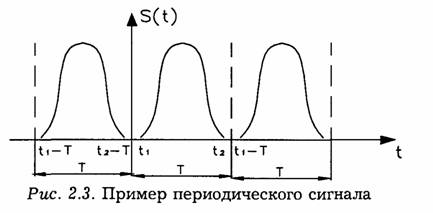
Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов, действующих - ∞ <t<+∞. Это представление осуществляется с помощью ряда Фурье.
Пусть заданная в интервале t1<t<t2 функция s(t) периодически
повторяется с частотой, ![]() где Т — период
повторения (рис. 2.3), причем выполняются следующие условия (условия Дирихле):
где Т — период
повторения (рис. 2.3), причем выполняются следующие условия (условия Дирихле):
1) в любом конечном интервале функция s(t) должна быть непрерывна или должна иметь конечное число разрывов первого рода;
2) в пределах одного периода функция s(t) должна иметь конечное число максимумов и минимумов.
Подобная функция может быть представлена рядом Фурье, который записывается в тригонометрической или комплексной формах:

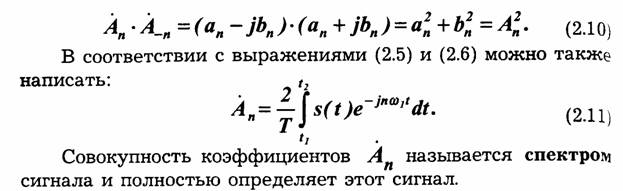
Сопоставление формул (2.2) и (2.3) показывает, что фигурирующие в последней "отрицательные" частоты (при отрицательных и) имеют формальный характер и связаны с применением комплексной формы для представления действительной функции времени. Таким образом, при использовании удобной для анализа формулы (2.3) всегда можно освободиться от отрицательных частот путем перехода к тригонометрической форме.
Следует отметить, что приведенным выше условиям Дирихле удовлетворяют все физически осуществимые сигналы, Поэтому при представлении периодических сигналов в виде рядов Фурье эти условия в практике не приходится специально оговаривать.
В тех случаях, когда сигнал представляет собой функцию, четную относительно t, т. е. s(t) = s(-t), в тригонометрической записи остаются только косинусоидальные члены, так как коэффициенты b в соответствии с формулой (2.6) обращаются в нуль. Для нечетной относительно t функции s(t), наоборот, в нуль обращаются коэффициенты ап [формула (2.5)], и ряд состоит только из синусоидальных членов.
Структура частотного спектра периодического сигнала полностью определяется двумя характеристиками — амплитудной и фазовой, т. е. модулем и аргументом комплексной амплитуды [формулы (2.7) и (2.8)]. Наглядное представление о "ширине" спектра и относительной величине отдельных его составляющих дает графическое изображение спектра (рис. 2.4) Здесь по оси ординат отложены модули амплитуд, по оси абсцисс — частоты гармоник. Для исчерпывающей характераcтики спектра подобное изображение должно быть дополнено заданием фаз отдельных гармоник.

Спектр периодической функции состоит из отдельных "линий", соответствующих дискретным частотам: 0, ω1,2ω1 ... nω1. Отсюда и название — линейчатый, или дискретный, спектр.
Значение рядов Фурье в современной технике очень велико. Основанный на формулах (2.2) и (2.3) гармонический анализ сложных периодических сигналов в сочетании с принципом наложения (суперпозиции) представляет собой эффективное средство для изучения влияния линейных систем на прохождение сигналов.
Если на входе линейной системы, характеристики которой известны, существует сигнал e(t) (электродвижущая сила), то для нахождения выходного сигнала достаточно учесть амплитудные и фазовые изменения, претерпеваемые каждой из гармонических составляющих сигнала при прохождении через рассматриваемую систему. Условие линейности системы позволяет рассматривать прохождение каждой из гармоник сигнала независимо от всех остальных гармоник.
Пусть коэффициент передачи системы (линейного четырехполюсника), представляющий собой отношение комплексной амплитуды напряжения на выходе к комплексной амплитуде на входе, задан в форме:
![]()
Тогда для учета амплитудных и фазовых изменений комплексная амплитуда каждой из гармоник входного сигнала должна быть умножена на Ќ(ω).
Поэтому, если сигнал e(t) на входе линейной системы передачи записан в форме:
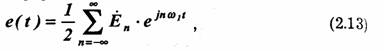
то сигнал u(t) на выходе в соответствии с принципом суперпозиции может быть найден с помощью следующего выражения:

представляют собой соответственно комплексные амплитуды n-й гармоники сигнала на входе и выходе системы передачи. Таким образом, для получения решения задачи о прохождении сигнала через систему необходимо только умножить Ėп на комплексный коэффициент передачи Ќ (пω 1).
Следует иметь в виду, что такое решение имеет практическую ценность при условии быстрой сходимости рядов Фурье. Между тем наиболее распространенные сигналы этому условию не отвечают, и для удовлетворительного воспроизведения формы сигналов обычно необходимо суммировать большое число гармоник.
2.3. Спектры некоторых периодических cигналов
Рассмотрим спектры некоторых часто встречающихся сигналов.
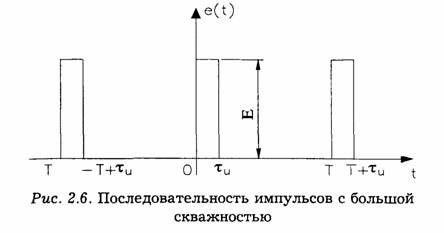
1. Переодическая последовательность прямоугольных импульсов.

Для периодической последовательности импульсов (рис. 2.5а) с амплитудой À и длительностью τ и, применяя формулы (2.4), (2.5) и (2.6), находим среднее значение ("постоянную составляющую"):


В системах передачи информации очень часто
используются последовательности импульсов, которые характеризуются очень
малым отношением длительности импульса к периоду повторения, т. е. ![]() Величина, обратная
этому отношению
Величина, обратная
этому отношению ![]() называется скважностью
импульсной последовательности.
называется скважностью
импульсной последовательности.
Большая по сравнению с длительностью импульса величина периода повторения приводит к необходимости учитывать очень большое число гармоник. Спектр в этом случае имеет вид, показанный на рис. 2.7.
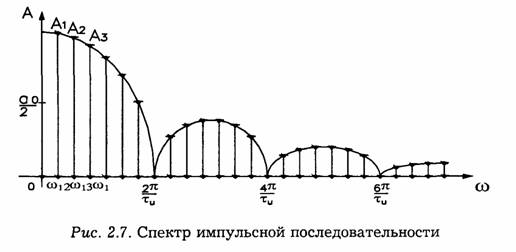
Расстояние между спектральными линиями очень
мало![]() а амплитуды
соседних гармоник близки по величине.
а амплитуды
соседних гармоник близки по величине.
Это наглядно видно из формулы (2.18), которую в данном случае удобно записать в несколько видоизмененном виде:
![]()
Ввиду малой величины отношения аргумент синуса с ростом и изменяется медленно. При малых значениях и приблизительно можно считать:
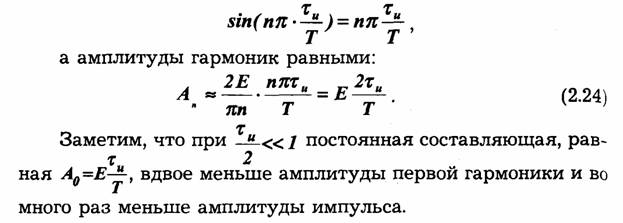
2. Последовательность пилообразных импульсов
Подобные функции часто встречаются на практике в устройствах для развертки изображения на экране кинескопа
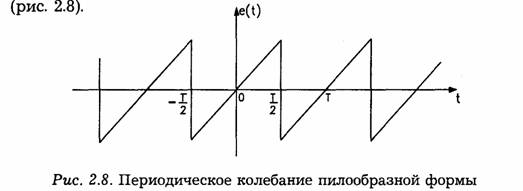
Так как эта функция является нечетной, ряд Фурье для нее содержит только синусоидальные члены. С помощью формул (2.5) — (2.7) нетрудно определить коэффициенты ряда Фурье. Опуская эти выкладки, напишем окончательное выражение для ряда:
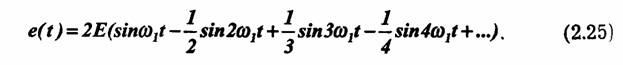
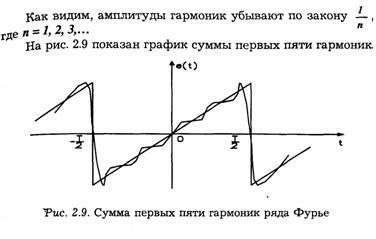
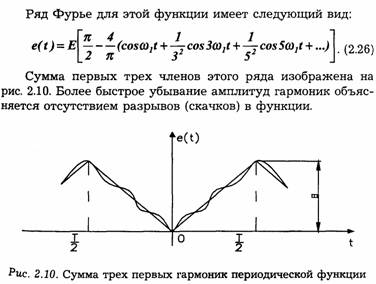
3. Последовательность треугольных импульсов
2.4. Распределение мощности в спектре периодического сигнала
Пусть сигнал s(t) представляет собой сложную периодическую функцию времени с периодом Ó. Средней за период мощностью будем называть величину:
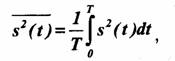
где черта над функцией обозначает операцию усреднения по времени.
Разложим сигнал s(t) в ряд Фурье:
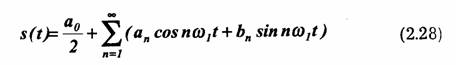
и подставим этот ряд под интеграл в выражении (2.27). После преобразований выражение (2.27) принимает следующий простой вид:

![]()
При использовании комплексного ряда Фурье этот результат в соответствии с формулой (2.10) может быть представлен в форме:
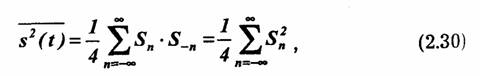
Если s(t) = i(t) представляет собой электрический ток, то при прохождении через омическое сопротивление г выделяется мощность (средняя за период Ó):

Как видим, полная мощность является суммой средних мощностей, выделяемых по отдельности постоянной составляющей I0 и гармониками (с амплитудами I1,I2 и т. д.).
Важно отметить, что эта мощность не зависит от фазировки отдельных гармоник. Это означает, что изменение формы сигнала, получающееся при изменении фазовых соотношений между отдельными гармониками внутри спектра, не оказывает влияния на величину средней мощности сигнала.
Итак, можно считать, что в энергетическом отношении отдельные спектральные составляющие сложного периодического сигнала аддитивны, т. е. суммарную среднюю мощность сигнала можно определить как сумму мощностей отдельных компонент спектра сигнала.
По виду функции, представляющей собой огибающую величину, можно судить о распределении мощности в спектре периодического сигнала. Это позволяет выбирать полосу пропускания системы передачи информации, обеспечивающую достаточно полное использование мощности сигнала. Подробнее этот вопрос рассматривается ниже в п. 2.9 (применительно к непериодическим сигналам).
В реальных системах передачи всегда действуют непериодические сигналы, так как все сигналы имеют конечную длительность.
Пусть задан сигнал в виде функции времени, удовлетворяющей условиям Дирихле (п. 2.2) во всяком конечном интервале и, кроме того, абсолютно интегрируемой.
Последнее условие означает, что интеграл:

где |s(t)| — абсолютное значение функции s(t), должен сходиться.
Для удобства рассуждений примем пока, что сигнал s(t) действует в конечном интервале t1 <t < t2 Из дальнейшего будет видно, что это допущение не ограничивает общности
рассмотрения.
Для
проведения гармонического анализа непериодической функции поступим следующим
образом. Превратим эту функцию в периодическую путем повторения ее с произвольным
периодом Т > t2 — t1 .Тогда для этой новой функции применимо разложение в ряд
Фурье, причем входящие в выражение (2.2) коэффициенты , ![]() в соответствии с формулами
(2.4) — (2.6) будут тем меньше, чем больше интервал Ó , выбранный в качестве периода. Устремляя Ó к бесконечности, в
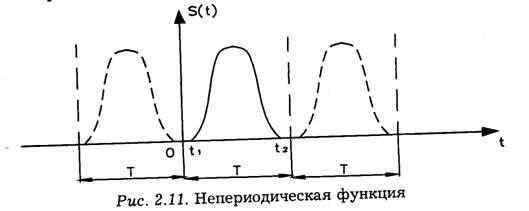
пределе получим бесконечно малые амплитуды гармонических составляющих, сумма
которых изображает исходную непериодическую функцию s(t), заданную в интервале t1<t<t2(рис. 2.11).
в соответствии с формулами
(2.4) — (2.6) будут тем меньше, чем больше интервал Ó , выбранный в качестве периода. Устремляя Ó к бесконечности, в
пределе получим бесконечно малые амплитуды гармонических составляющих, сумма
которых изображает исходную непериодическую функцию s(t), заданную в интервале t1<t<t2(рис. 2.11).
Количество гармонических составляющих, входящих
в ряд Фурье, будет при этом бесконечно большим, так как при  основная частота функции
основная частота функции![]() . Иными словами, расстояние между
спектральными линиями (рис. 2.4), равное основной частоте ω1,
становится бесконечно малым, а спектр — сплошным.
. Иными словами, расстояние между
спектральными линиями (рис. 2.4), равное основной частоте ω1,
становится бесконечно малым, а спектр — сплошным.
Отсюда следует, что при гармоническом анализе непериодической функции получается сплошной спектр, состоящий из бесконечно большого количества гармоник с бесконечно малыми амплитудами.
Математически это можно выразить следующим образом. Подставив формулы (2.5) и (2.6) в формулу (2.9), получаем:

S(ω) называется спектральной плотностью, или спектральной характеристикой функции s(t).
В общем виде, когда не уточнены пределы t1 и t2, спектральную плотность представляют выражением:
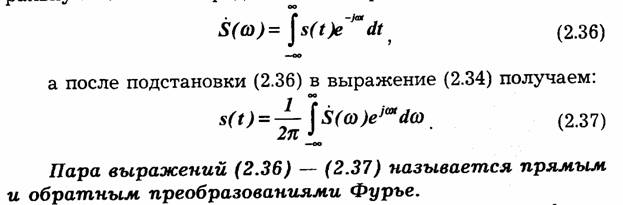
Выражение (2.37) представляет непериодическую
функцию в виде суммы (интеграла) гармонических колебаний с бесконечно малыми
амплитудами. Из сравнения выражения (2.37) с рядом Фурье (2.3) видно, что
амплитуды этих составляющих равны![]()
Сравнение (2.36) с выражением (2.11) для комплексной амплитуды соответствующей гармоники периодической функции позволяет в наглядной форме пояснить смысл спектральной плотности S(ω).
Именно, выделив какую-либо дискретную частоту ωn =nω1, соответствующую в случае периодической функции n-й гармонике, получим для амплитуды этой гармоники выражение:

В случае же непериодической функции, совпадающей с s(t) в интервале t1<t<t2, получим для спектральной плотности, соответствующей той же частоте ω = ω п, следующее выражение:
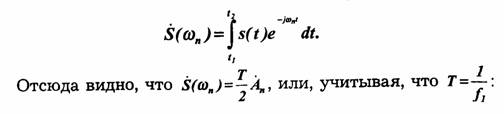
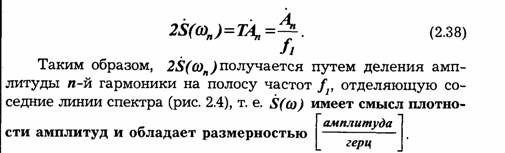
Из выражения (2.38) вытекает следующее важное положение: огибающая сплошного спектра (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции (полученной из непериодической путем продолжения ее с периодом Т) совпадают по форме и отличаются только масштабом.
Итак:

Спектральная плотность S(ω) обладает всеми основными свойствами комплексной амплитуды Аn.
По аналогии в выражение (2.9) можно написать следующее соотношение:
![]()
где А(ω) èВ(ω) — соответственно действительная и мнимая части спектральной плотности;
S(ω) èψ (ω) — амплитудно-частотная (АЧХ) и фазо-частотная (ФЧХ) характеристики спектральной плотности.
Непосредственно из формулы (2.36) вытекают следующие выражения для А(ω) и В(ω), аналогичные формулам (2.5) и (2.6):

Как и в случае ряда Фурье, модуль спектральной плотности есть функция четная, а фаза — нечетная относительно частоты ω.
На основании формулы (2.40) нетрудно привести интегральное преобразование к тригонометрической форме.
Имеем:
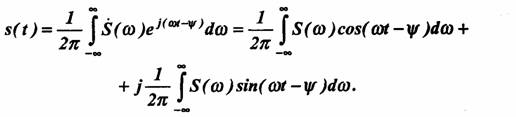
Из упомянутых выше свойств модуля и фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором интеграле — нечетной относительно ω. Следовательно, второй интеграл равен нулю, и окончательно
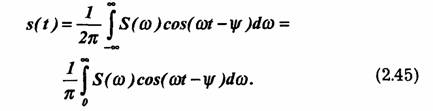
Как видим, при переходе от комплексной формы (2.37) к тригонометрической (2.45) отпадет необходимость интегрирования в области отрицательных значений ω. Обычно этот переход целесообразен в конце анализа; все промежуточные выкладки при применении интеграла Фурье удобнее и проще производить на основе комплексной формы (2.37).
Интегральные преобразования (2.36) — (2.37) очень удобны для исследования прохождения непериодических сигналов через линейные системы передачи. По аналогии с выражениями (2.13) — (2.14) можно написать следующие очевидные соотношения для сигнала e(t) на входе и сигнала u(t) на выходе линейной системы передачи:

Прикладное значение интегральных преобразований (2.36) — (2.37), позволяющих осуществить гармонический анализ непериодических сигналов, еще более велико, чем значение рядов Фурье, так как в практике непериодические сигналы встречаются чаще, чем периодические.
Большим облегчением при использовании интеграла Фурье является возможность получения выражения для выходного сигнала в замкнутой форме, а не в виде медленно сходящегося ряда.
2.6. Свойства преобразования Фурье
Между сигналом s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований сигнала рассмотрим наиболее важные и часто встречающиеся.
Пусть сигнал s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω) При задержке этого сигнала на время t0 (при сохранении его формы) получим новую функцию времени:
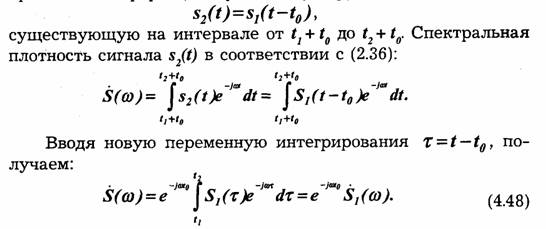
Из этого соотношения видно, что сдвиг во времени функции s(t) на ± t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ± ω t0. Очевидно и обратное положение: если всем составляющим спектра функции s(t) дать фазовый сдвиг φ= ±ωt0, линейно связанный с частотой ± ωt0 , то функция сдвигается на время ± t0.
Амплитудно-частотная характеристика спектра (т. е. модуль спектральной плотности) от положения сигнала на оси времени не зависит.
Указанные свойства преобразования Фурье позволяют сформулировать требования к линейным системам, выполнение которых необходимо для неискаженной передачи сигналов: амплитудно-частотная характеристика системы должна быть равномерна, а фазо-частотная характеристика (ω) — линейна в пределах всего спектра сигнала (или, по крайней мере, той части спектра, в которой сосредоточена основная доля общей энергии сигнала). Действительно, пусть в выражении (2.12) модуль коэффициента передачи системы не зависит от частоты и является постоянной величиной К(ω) = K0, а фаза — линейной функции частоты φ(ω) = -t0.
Тогда, если на входе системы передачи действует сигнал s(t) со спектром S(ω), то на выходе будет сигнал:
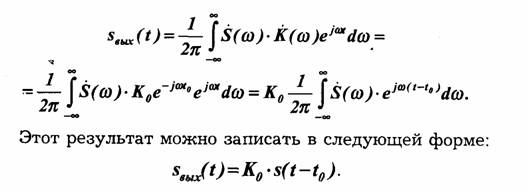
Отсюда видно, что при прохождении через систему с равномерной амплитудно-частотной и фазо-частотной характеристиками (рис. 2.12) сигнал полностью сохраняет свою форму: изменяется лишь величина сигнала (в Ео раз), и появляется запаздывание ("время пробега"), равное t0, т. е. равное наклону фазовой характеристики системы:
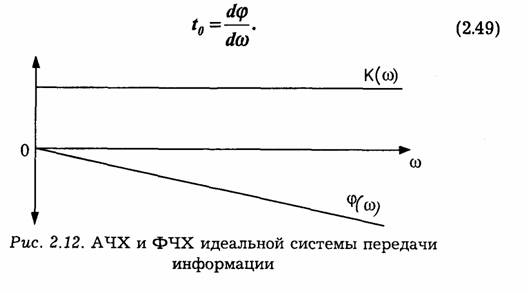
Отметим, что в физически выполнимых (реальных) системах передачи наклон фазовой характеристики φ(ω) всегда отрицателен в полосе пропускания, так как сигнал на выходе не может опережать сигнал на входе системы.
Другие свойства преобразования Фурье приведем без доказательства.
Пусть сигнал s(t), изображенный на рис. 2.13 сплошной линией, подвергся сжатию во времени.
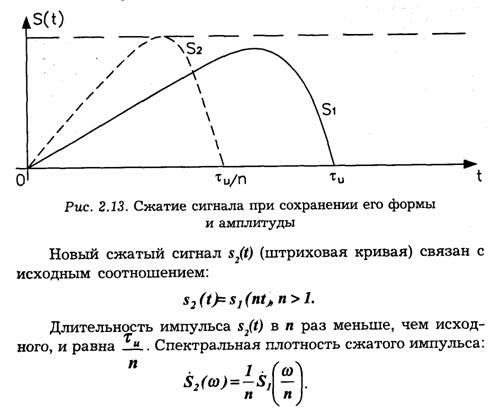
Итак, при сжатии сигнала в п раз во временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в п раз. Очевидно, что при растягивании сигнала во времени (т. е. при п < 1) имеют место сужение спектра и увеличение модуля спектральной плотности.
Отсюда важный практический вывод: увеличение скорости передачи информации путем сжатия во времени неизбежно ведет к необходимости расширения полосы пропускания системы передачи.
Из выражения (2.50) следует, что расщепление спектра S(ω) на две части, смещенные соответственно на + ω0 и – ω0, эквивалентно умножению функции s(t) на гармоническое колебание cos(ω0t) (при ψ0 = 0). Более подробно это положение рассматривается в главе 3 при изучении модулированных колебаний.
4. Дифференцирование и интегрирование
Сигналов
Дифференцирование сигнала s1(t) можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции eJωt равна jωeJωt , из чего непосредственно вытекают следующие соответствия:
![]()
Аналогичным образом можно показать, что сигналу
Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным, очевидно, что при сложении сигналов s1(t), s2(t),..., обладающих спектрами S1(ω),S2(ω),..., суммарному сигналу
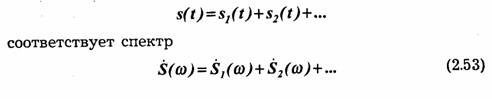
Пусть рассматриваемый сигнал s(t) является произведением двух функций времени f(t) и g(t), причем имеют место следующие соответствия:
![]()
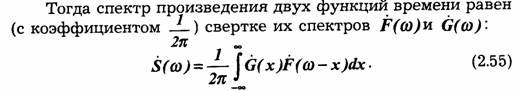
Аналогично можно показать, что произведению двух спектров F(ω)xG(ω) = S(ω)соответствует функция времени s(t), являющаяся сверткой функций (*) и g(t):
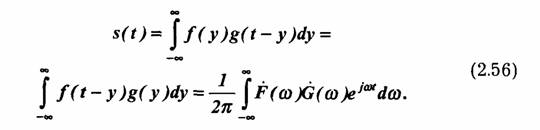
Последнее выражение особенно широко используется при анализе передачи сигналов через линейные системы. В этом случае функции времени ƒ(t) и g(t) имеют смысл соответственно входного сигнала и импульсной характеристики системы передачи, a F(ω)и G(ω) — спектральной плотности сигнала и передаточной функции системы.
2.7 Спектры непериодических сигналов
Как уже отмечалось, структура частотного спектра сигнала полностью определяется двумя характеристиками: амплитудно-частотной и фазо-частотной, т. е. модулем и аргументом спектральной плотности S(ω).
Определение указанных характеристик для функций s(t), отвечающих условию абсолютной интегрируемости, легко производится с помощью формул (2.36), (2.43), (2.44) и не требует дополнительных пояснений. Остановимся лишь на некоторых частных случаях, существенных для практического применения.
1. Сигнал в виде единичного скачка
Рассмотрим прежде всего единичный скачок (функцию включения), т. е. функцию, определяемую условиями (рис. 2.14):
![]()
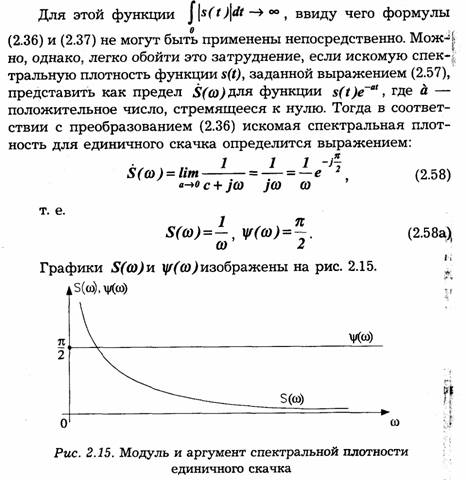
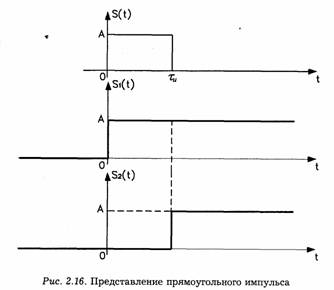
Вместо прямого использования общего выражения (2.36) для нахождения спектра прямоугольного импульса мы воспользуемся принципом суперпозиции, позволяющим находить спектр суммы или разности функций времени в виде суммы или разности соответствующих этим функциям спектров. Представим прямоугольный импульс, действующий на протяжении отрезка времени от 0 до τu, в виде разности двух скачков: одного в момент t = 0 и другого в момент t=τu (рис. 2.16).
Для первого скачка в соответствии с выражением (2.58) получим спектральную плотность:

Таким образом, для нулевой частоты спектральная плотность прямоугольного импульса равна площади импульса. Этот вывод можно распространить на импульс произвольной формы.
Зависимость модуля S(ω) изображена на рис. 2.17. Появление нулей в спектре прямоугольного импульса является результатом взаимной компенсации гармонических составляющих скачков S1(t) и S2(t), для которых сдвиг фаз равен целому числу 2π. Такие сдвиги получаются на частотах со , отвечающих условию ωτи — п2π, где n — любое целое число. Отметим, что график модуля спектральной плотности совпадает
с графиком огибающей спектра последовательности прямоугольных импульсов (рис. 2.17).

3. Треугольный импульс
Представленный на рис. 2.19а треугольный импульс определяется выражением:
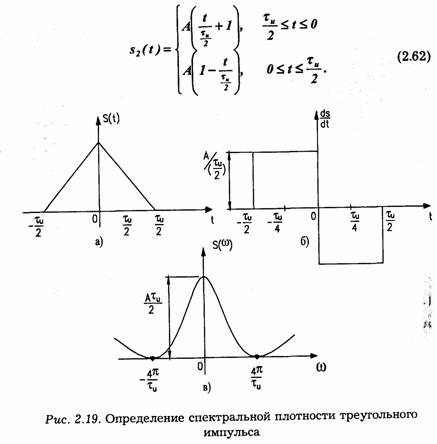
Прямое вычисление спектральной плотности треугольного импульса по формуле (2.35) несложно, но достаточно громоздко.

4. Бесконечно короткий импульс с единичной площадью (дельта-функция)
Рассмотрим импульс, у которого амплитуда обратно пропорциональна длительности (рис. 2.20). При стремлении длительности к нулю амплитуда обращается в бесконечность, а площадь импульса остается неизменной и равна единице.

Функция δ (х), обладающая указанными свойствами, называется единичным импульсом, импульсной функцией или дельта-функцией (а также функцией Дирака).
При сдвиге импульса по оси ŏ на вершину определения (2.65) и (2.66) должны быть записаны в более общей форме:
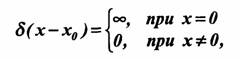

Функция δ (х) обладает важными свойствами, благодаря которым она получила широкое распространение. Из определений (2.67) и (2.68) вытекает основное соотношение:
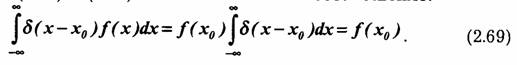
Так как по определению функция δ (х-х0) равна нулю на всей оси ŏ, кроме точки где она бесконечно велика, то промежуток интегрирования можно сделать сколь угодно малым, лишь бы он включал в себя точку х0. В этом промежутке функция ƒ(x) принимает постоянное значение f(x0), которое можно вынести за знак интеграла. Таким образом, умножение любой подынтегральной функции ƒ(х)на δ(х—х0) позволяет приравнять интеграл произведения значению f(x)в точке х=х0. В математике соотношение (2.69) называется фильтрующим свойством дельта-функции.
В теории передачи информации иногда говорят о стробирующем свойстве дельта-функции.
В теории сигналов приходится иметь дело с дельта-функциями от аргументов t или ω, в зависимости от того, в какой области рассматривается функция во временной или частотной.
Спектральная плотность дельта-функции определяется с помощью преобразования Фурье, с учетом свойства (2.69), следующим образом:
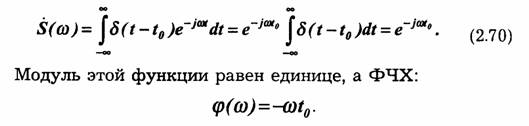
Понятие единичного импульса широко применяется при исследовании линейных систем передачи. При этом не обязательно, чтобы амплитуда реального импульса была бесконечно велика, а длительность — бесконечно мала. Достаточно, чтобы длительность импульса была мала по сравнению с постоянной времени исследуемой цепи.
Все, что ранее было сказано относительно δ (t), можно распространить на δ (ω) при замене t на ω и ω на t, т. е.:
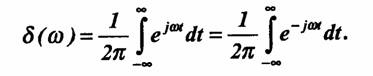
Перемена знака в показателе степени в данном случае не влияет на значение интеграла.
2.8 Распределение энергии в спектре непериодического сигнала
Пусть задан сигнал s(t), обладающий конечной энергией. Это означает, что интеграл:

пропорциональный величине энергии сигнала, является сходящимся.
В дальнейшем мы будем называть Л энергией сигнала, не уточняя размерности s(t) (ток, напряжение, напряженность
поля и т. д.).
Выразим À через модуль спектральной плотности сигнала S(t). С этой целью рассмотрим периодическую функцию snep(t), образованную путем повторения исходной функции с выбранным периодом Ó.
По отношению к этой непериодической функции может быть применена формула (2.30) для средней за период мощности сигнала:
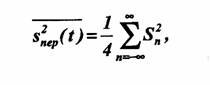

Это выражение называется равенством Парсеваля.
В отличие от выражения (2.30) формула (2.73) определяет не среднюю мощность (которая для любой непериодической, абсолютно интегрируемой функции равна нулю), а полную энергию, выделяемую сигналом s(t) за все время его действия.
По виду функции [S(ω)]2можно судить о распределении энергии в спектре непериодической функции, и потому формула (2.73) может быть использована для выбора полосы пропускания системы передачи информации, обеспечивающей достаточно полное использование энергии сигнала. В частности, при прохождении сигнала s(t) через систему передачи с полосой пропускания от 0 до ω7, энергия на выходе будет равна:
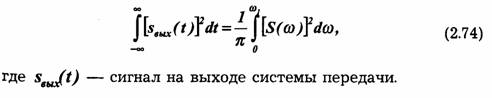
2.9. Связь между временными и спектральными характеристиками Сигнала
Основной вывод, который можно сделать из рассмотрения свойств непериодического сигнала, сводится к следующему: чем короче сигнал, тем шире его частотный спектр.
Такая формулировка не является строгой, так как теоретически любой сигнал конечной длительности обладает бесконечно широким спектром.
В практике под шириной спектра сигнала обычно подразумевают полосу частот, в которой сосредоточена основная доля энергии сигнала. При таком определении полосы обычно обеспечивается и достаточно удовлетворительное воспроизведение формы сигнала, хотя в некоторых случаях последнее требование заставляет сохранять в спектре более высокие частоты, чем это диктуется энергетическими соображениями.
При грубых оценках в технике широко принято считать, что произведение соответствующим образом определенной длительности сигнала на "техническую" ширину спектра близко к единице.
Таким образом:

Однако это соотношение относится только к управляющему сигналу (сообщению). Как будет видно из дальнейшего, спектр модулированного сигнала может быть во много раз шире.
Вычисление, которое нетрудно провести с помощью
формулы (2.74) для прямоугольного импульса, показывает, что в полосе частот ![]() сосредоточено несколько более 90% полной
энергии импульса.
сосредоточено несколько более 90% полной
энергии импульса.
Следующее важное свойство частотного спектра сигнала конечной длины заключается в том, что в области достаточно низких частот спектральная плотность равна площади сигнала независимо от его формы. Этот вывод легко сделать из общего выражения (2.35), устремив в нем ω к нулю. Очевидно:

Правая часть этого выражения есть не что иное, как площадь импульса s(t). Под "импульсом" здесь подразумевается любой сигнал конечной длительности.
Отметим, что задание модуля S(ω), т. е. амплитудно-частотного спектра, однозначно определяет распределение энергии сигнала по частотам [это следует из равенства Парсеваля (2.73)], но ничего не говорит о форме сигнала. Совместно же с фазо-частотной характеристикой φ(ω) задание S(ω) полностью определяет сигнал: как форму, так и положение его на оси времени.
2.10. Случайные сигналы и их аналитическое описание
В реальных условиях при передаче информации сигнал в месте приема заранее неизвестен и потому не может быть описан определенной функцией времени. То же самое можно сказать и о помехах, появление которых обусловлено самыми различными и чаще всего неизвестными причинами.
Таким образом, реальные сигналы и помехи представляют собой случайные процессы. Случайный процесс описывается случайной функцией, значения которой при любом значении аргумента являются случайными величинами. В отличие от детерминированной функции, однозначно определяющей и, таким образом, достоверно предсказывающей значение описываемой величины в любой заданный момент времени,
ход случайной функции предсказан быть не может. Самое большое, что можно сказать заранее о поведении случайной функции — это вероятность, с которой она в будущем может принять тот или иной вид из множества возможных.
В ряде практически важных задач случайный процесс наряду с вероятностным описанием можно описать совокупностью неслучайных числовых характеристик, постоянных или меняющихся во времени. От этих характеристик требуется, чтобы в условиях конкретно поставленной задачи они отражали самое существенное случайного процесса.
1. Одномерный закон распределения мгновенных значений случайной функции и связанные с ним основные характеристики
Случайный процесс обозначим случайной функцией X(t), значения которой в любой заданный момент времени не могут быть точно предсказаны, т. е. являются случайными величинами. Определенный вид x(t), принятый случайной функцией X(t)в результате опыта, называют реализацией случайной функции или процесса (рис. 2.21).
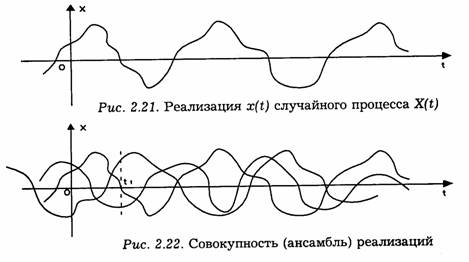
Под опытом или испытанием понимается, например, однократное включение источника случайного процесса на некоторое определенное время с соответствующей записью колебания. В результате многократного повторения опыта с данным источником можно получить множество реализаций процесса, внешне совершенно не похожих одна на другую. Для получения реализаций процесса таким путем необходима повторяемость условий испытаний. Во многих случаях повторяемость условий испытаний единственного источника не может быть соблюдена, так как параметры источника необратимо меняются во времени. В этих условиях следует оперировать понятием не единственного источника, а их множества. В результате опыта, предусматривающего параллельную работу источников, получаем множество реализаций. При этом источники могут быть неидентичными, их параметры имеют разброс и меняются во времени.
Случайный процесс полностью характеризуется бесконечным множеством реализаций, образующих ансамбль. Понятием ансамбля, состоящего из бесконечно большого или конечного, но достаточно большого числа реализаций (рис. 2.22), удобно пользоваться при установлении статистических закономерностей, свойственных случайным процессам. Совокупность мгновенных значений случайного процесса, заданного ансамблем, в произвольный момент времени называют сечением случайного процесса.
Если зафиксировать произвольный момент времени t1(рис. 2.22), т. е. получить сечение случайного процесса, то для этого сечения может быть вычислено распределение вероятности Ð(ŏ) непрерывной случайной величины Õ(t1):
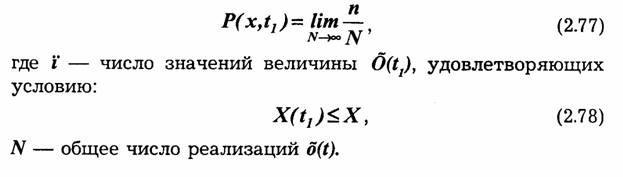

и является производной по õ функции (2.77). Выражения (2.77) или (2.79) статистически полностью характеризуют значения случайной функции Õ(t) в заданный момент времени tt и выражают ее одномерный закон распределения. Если момент tt выбирать произвольно, то в соответствии с (2.77) и (2.79) можно получить одномерный закон распределения в виде зависимости от времени P(x,t) или p(x,t).
Если закон распределения зависит от рассматриваемого момента времени t, то говорят о нестационарности случайного процесса, о неоднородности его протекания во времени. Необходимым условием стационарности процесса является независимость одномерного закона распределения от времени, т. е. выполнение одного из равенств:
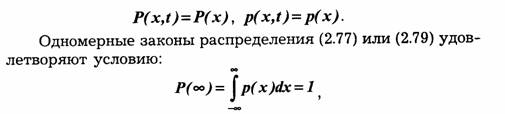
отражающему достоверность того, что величина X(tt) обязательно примет одно из значений, находящихся в пределах от
— ∞ ДО + ∞•
Наряду с вероятностными характеристиками Р(х) и случайной величины могут рассматриваться ее числовые характеристики, или моменты случайной величины.


2 Многомерный закон распределения мгновенных значений случайной функции и связанные с ним основные характеристики
Одномерная плотность вероятности недостаточна для полного описания процесса, так как она дает вероятностное представление о случайном процессе X(t1) только в отдельные фиксированные моменты времени. Более полной характеристикой является двумерная плотность вероятности p(x1,x2;t1,t2), позволяющая учитывать связь значений õ1 и õ 2, принимаемых случайной функцией в произвольно выбранные моменты времени t1 И t2
Исчерпывающей вероятностной характеристикой случайного процесса является ï -мерная плотность вероятности при достаточно больших ï. Однако большое число задач, связанных с описанием случайных процессов, удается решать на основе двумерной плотности вероятности.
Задание двумерной плотности вероятности p(xl,x2;t1,t2) позволяет, в частности, определить важную характеристику случайного процесса — ковариационную функцию:
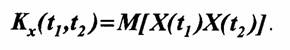
Согласно этому определению ковариационная функция случайного процесса X(t) представляет собой статистически усредненное произведение значений случайной функции X(t) в моменты времени t1 и t2.
Для каждой реализации случайного процесса произведение x(t1) ∙ x(t2) является некоторым числом совокупность реализаций образует множество случайных чисел, распределение которых характеризуется двумерной плотностью вероятности p(x],x2;t],t2). При заданной функции p(x1,x2;t1,t2) операция усреднения по множеству осуществляется по формуле
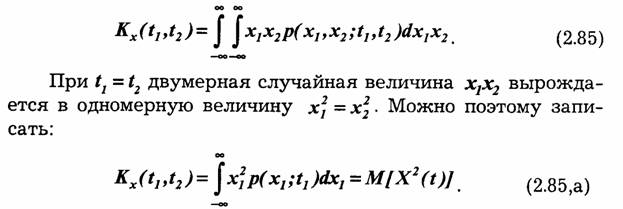
Таким образом, при нулевом интервале между моментами t1 и t2 ковариационная функция определяет величину среднего квадрата случайного процесса в момент t = t1.
Как уже говорилось, частичное описание свойств случайного процесса может быть дано при помощи неслучайных функций времени M1(t) и σ 2(t). Недостаточность только таких характеристик хорошо видна из сопоставления двух процессов, заданных ансамблями их реализаций и представленных на рис. 2.23.
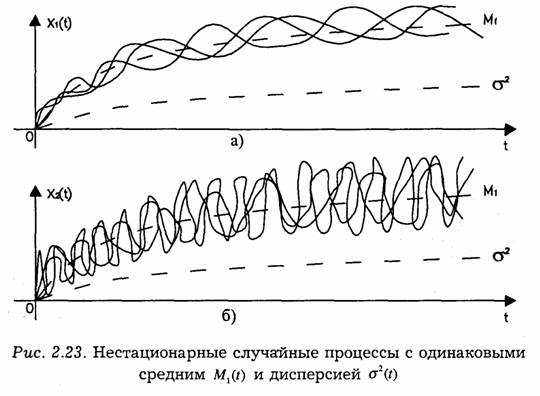
Из рис. 2.23 а и б видно, что процессы имеют приблизительно одинаковые средние значения M1(t) и дисперсии σ 2(t). Однако характеры протекания этих процессов во времени и их внутренние структуры существенно различны. В первом преобладают медленные изменения во времени, во втором — более быстрые. Таким образом, среднее значение и дисперсия не отражают структуры случайного процесса, быстроты его протекания. Быстрота изменения случайной функции может характеризоваться степенью статистической связи мгновенных значений, взятых в различные моменты времени.
Количественно эта связь устанавливается корреляционным моментом:
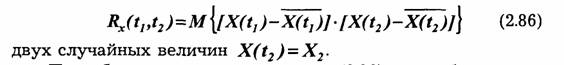
Подробнее символическая запись (2.86) может быть представлена в виде:
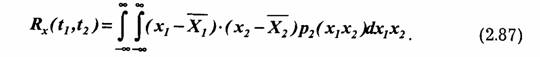
Выражения (2.86) и (2.87) являются функциями двух переменных tt и t2 и поэтому называются корреляционными или автокорреляционными функциями.
В теории вероятностей доказывается, что величина корреляционного момента двух случайных величин не зависит от последовательности, в которой эти величины рассматриваются. Вследствие этого корреляционная функция симметрична относительно tt и t2, т. е.:
![]()
Это же свойство вытекает из определения корреляционной функции по формуле (2.86).
Поскольку корреляционная функция отражает статистическую связь между значениями одной и той же случайной функции, взятыми в моменты t1 и t2 она убывает с ростом интервала τ = t1-t2. Корреляционная функция является более полной характеристикой случайного процесса, чем дисперсия, включающая ее как частный случай.
При анализе случайных процессов часто вводится понятие нормированной функции автокорреляции:
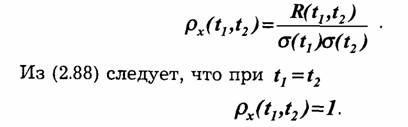
Функция корреляции позволяет ввести понятие интервала корреляции. Под интервалом корреляции понимают такое значение τ k=t1-t2, при котором
![]()
где α<1— некоторая заданная величина. Величина α может зависеть от конкретно поставленной задачи. Введение этого понятия позволяет приближенно считать мгновенные значения случайного процесса X(t1) и X(t2) при t1-t2> τ k некоррелированными.
В приложении к многомерным законам распределения можно сказать, что случайный процесс называется строго стационарным, если его плотность вероятности p(x1,x2,...xn;t1,t2,...tn) произвольного порядка ï зависит только от интервалов t2—t1, t3—t1,...tn—t1 и не зависит от положения этих интервалов в области изменения аргумента t.
В теории сигналов условие стационарности обычно ограничивается требованием независимости от времени только одномерной и двумерной плотностей вероятности. Выполнение этого условия позволяет считать, что математическое ожидание, средний квадрат и дисперсия случайного процесса не зависят от времени, а корреляционная функция зависит не от самих моментов времени tt и t2, а только от интервала между ними τ = t1-t2.
Дальнейшее упрощение анализа случайных сигналов достигается при использовании условия эргодичности случайного процесса. Стационарный случайный процесс называется эргодическим, если при определении любых статистических характеристик усреднение по множеству реализаций эквивалентно усреднению по времени одной теоретически бесконечно длинной реализации.
Определение статистической связи между мгновенными значениями случайного сигнала (корреляционный анализ) и свойство эргодичности широко используются в современных системах приема и обработки сигналов.
3. Гауссовский случайный процесс
Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом. Одномерная плотность вероятности нормального процесса определяется выражением:
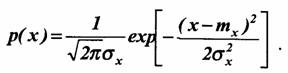
В данном случае будет рассматриваться стационарный и эргодический гауссовский процесс. Поэтому под тх и σ х можно подразумевать соответственно постоянную составляющую и среднюю мощность флуктуационной составляющей одной (достаточно длительной) реализации случайного процесса.
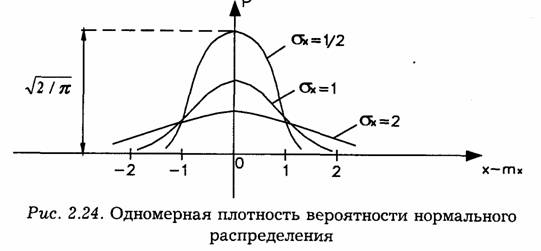
Графики плотности вероятности при нормальном законе для некоторых значений
σ х изображены на рис. 2.24. Функция р(х) симметрична относительно среднего значения. Чем больше σ х, меньше максимум, а кривая становится более пологой [площадь под кривой р(х) равна единице при любых значениях σ х]
Широкое распространение нормального закона распределения в природе объясняется тем, что при суммировании достаточно большого числа независимых или слабо зависимых случайных величин распределение суммы близко к нормальному при любом распределении отдельных слагаемых.
Это положение, сформулированное в 1901 г. А. М. Ляпуновым, получило название центральной предельной теоремы. Наглядными физическими примерами случайного процесса с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Не только шумы и помехи, но и полезные сигналы, являющиеся суммой большого числа независимых случайных элементарных сигналов, например, гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гауссовские случайные процессы.
На основе функции р(х) можно найти относительное время пребывания сигнала x(t) в определенном интервале уровней, отношение максимальных значений к среднеквадратическому (пик фактора) и ряд других важных для практики параметров случайного сигнала.
Отношение времени пребывания x(t) в заданном интервале к общему времени наблюдения можно трактовать как вероятность попадания x(t) в указанный интервал. При этом следует заметить, что данные о распределении вероятностей не дают никаких представлений о поведении функции x(t) во времени.
4. Спектральная плотность мощности случайного процесса
Подразумевая под случайным процессом множество (ансамбль) функций времени, необходимо иметь в виду, что функциям, имеющим различную форму, соответствуют различные спектральные характеристики. Усреднение комплексной спектральной плотности, введенной в п. 2.5, по всем функциям приводит к нулевому спектру процесса (при M[x(t)]=0) из-за случайности и независимости фаз спектральных составляющих в различных реализациях. Можно, однако, ввести понятие спектральной плотности среднего квадрата случайной функции, поскольку значение среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случайной функцией x(t) подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощность, выделяемую сопротивлением 1Ом. Эта мощность распределена по частотам в некоторой полосе, зависящей от механизма образования случайного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1Гц при заданной частоте ω . Размерность функции W(ω), являющейся отношением мощности к полосе частот, есть:

Спектральную плотность случайного процесса можно найти, если известен механизм образования случайного процесса. Здесь мы приведем только определение общего характера.
Выделив из ансамбля какую-нибудь реализацию xk (t) и ограничив ее длительность конечным интервалом у, можно применить к ней обычное преобразование Фурье и найти спектральную плотность ХКТ(ω). Тогда энергию рассматриваемого отрезка реализации можно вычислить с помощью формулы (2.73):

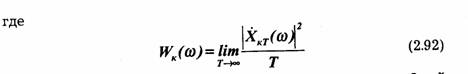
представляет собой спектральную плотность средней мощности ê-й. реализации.
В общем случае величина Wk(ω) должна быть усреднена по множеству реализаций. Ограничиваясь в данном случае рассмотрением стационарного и эргодического процесса, можно считать, что найденная усредненная по одной реализации функция Wk (ω) характеризует весь процесс в целом. Опуская индекс к, получаем окончательное выражение для средней мощности случайного процесса:
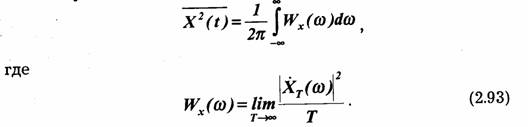
Энергетический спектр, естественно, не несет в себе сведений о фазовых соотношениях. Восстановить реализации процесса как функции времени по энергетическому спектру нельзя.
5. Соотношение между спектральной плотностью и ковариационной функцией случайного процесса. Белый шум
С одной стороны, скорость изменения x(t) во времени определяет ширину спектра. С другой стороны, скорость изменения x(t) определяет ход ковариационной функции. Очевидно, что между Wx(ω) и Кх(τ) имеется взаимно однозначная связь.
Теорема Винера-Хинчина утверждает, что Кх(τ) и WX(ω) связаны между собой преобразованиями Фурье:
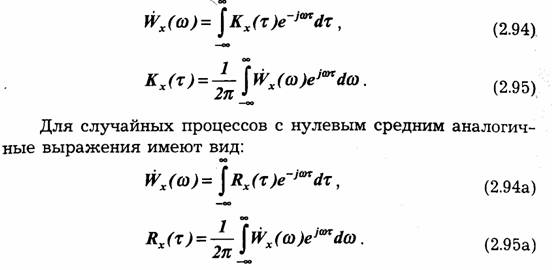
Из этих выражений вытекает свойство, аналогичное свойствам преобразований Фурье, установленным в п. 2.9 для детерминированных сигналов: чем шире спектр случайного процесса, тем меньше интервал корреляции и, соответственно, чем больше интервал корреляции, тем уже спектр процесса.

Для белого шума с бесконечным и равномерным спектром корреляционная функция равна нулю для всех значений τ, кроме τ = 0, при котором Rx(0) обращается в бесконечность. Подобный шум, имеющий игольчатую структуру с бесконечно тонкими случайными выбросами, иногда называют дельта-коррелированным процессом. Дисперсия белого шума бесконечно велика. Если спектр Wx(ω) ограничен сверху частотой ω в, то такой процесс называется квазибелым шумом.
1. Дайте определение дискретного, непрерывного, детерминированного и случайного сигналов.
2. Какие виды носителей информации используются для передачи сообщений?
3. В чем состоят условия Дирихле для периодических сигналов?
4. Поясните смысл величин, входящих в тригонометрическую и комплексную формы записи ряда Фурье?
5. Какой вид имеет спектр периодического сигнала?
6. Какова практическая ценность спектрального представления при решении задачи о прохождении сигнала через линейную систему передачи информации?
7. Нарисуйте спектр периодической последовательности прямоугольных импульсов, дайте определение скважности импульсной последовательности.
8. Запишите выражения для ряда Фурье последовательностей пилообразных и треугольных импульсов.
9. Дайте определение понятию средней мощности периодического сигнала.
10. Каким образом вводится понятие спектра для непериодических сигналов?
11. Запишите выражения для прямого и обратного преобразований Фурье, дайте определение понятия спектральной плотности и ее размерности.
12. Каким образом преобразование Фурье используется для исследования прохождения непериодических сигналов через линейные системы передачи?
13. Дайте определение основным свойствам преобразования Фурье (сдвиг сигналов во времени, изменение масштаба, дифференцирование и интегрирование сигналов, сложение сигналов).
14. Как формулируются условия неискаженной передачи сигналов и физической реализуемости линейных систем передачи информации?
15. Нарисуйте и поясните графики модулей спектральных плотностей прямоугольного и треугольного импульсов.
16. Дайте определение дельта-функции и укажите основные ее свойства.
17. Каким образом оценивается в технике практическая ширина спектра сигнала, и какие характеристики полностью определяют сигнал?
18. Дайте определение понятий реализации и ансамбля реализаций случайного процесса.
19. Какой случайный процесс называется стационарным?
20. Дайте определение основных характеристик случайного процесса.
21. Какие характеристики связаны с многомерным законом распределения и какие параметры отражают структуру случайного процесса?
22. Дайте определение функции корреляции и интервала корреляции.
23. Нарисуйте графики одномерной плотности вероятности нормального распределения и сформулируйте основное положение центральной предельной теоремы.
24. Что нужно знать для определения спектральной плотности мощности случайного процесса?
25. Укажите основные свойства белого шума.
МОДУЛЯЦИЯ И ДЕМОДУЛЯЦИЯ НОСИТЕЛЕЙ ИНФОРМАЦИИ
3.1. Классификация методов модуляции
Исследование различных видов модуляции необходимо для определения требуемых свойств каналов, сокращения избыточности модулированных сигналов и улучшения использования мощности передающих устройств, определения потенциальной помехоустойчивости, помех соседним каналам и решения проблем электромагнитной совместимости различных систем передачи информации.
Общий принцип модуляции состоит в изменении параметров носителя информации s(t,a,b,c...) в соответствии с передаваемым сообщением (а,b,с... — информационные параметры). Если в качестве переносчика выбрано гармоническое колебание
![]()
то можно образовать три вида модуляции: амплитудную (AM), частотную (ЧМ), фазовую (ФМ).
Если переносчиком является периодическая последовательность импульсов, то при заданной форме импульсов можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную (АИМ), широтно-импулъсную (ШИМ), время-импульсную (ВИМ, ФИМ) и частотно-импульсную (ЧИМ).
При дискретной (цифровой) модуляции закодированное сообщение аi, представляющее собой последовательность кодовых символов {bi}, преобразуется в последовательность элементов (посылок) сигнала {si(t)} путем воздействия кодовых символов на переносчик s(t). Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление тока. Обычно в качестве переносчика, как и в непрерывной модуляции, используют переменный ток (гармоническое колебание).
На рис. 3.1 приведены формы сигнала при двоичном коде для различных видов дискретной или цифровой модуляции (манипуляции). При AM символу 1 соответствует передача несущего колебания в течение времени T (посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой ƒ1 соответствует символу 1, а передача колебания с частотой f0 соответствует 0. При двоичной ФМ меняется фаза несущей на π при каждом переходе от 1 к 0 и от 0 к 1.
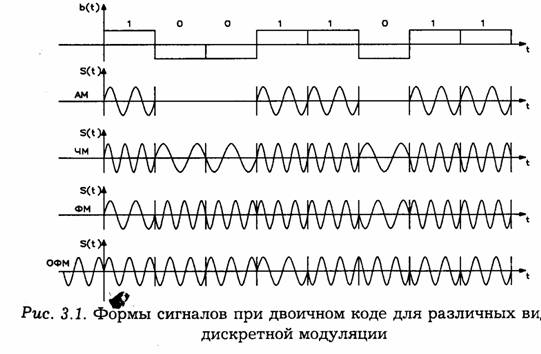
На практике применяют систему относительной фазовой модуляции (ОФМ). В отличие от ФМ при ОФМ фазу сигналов отсчитывают не от некоторого эталона, а от фазы предыдущего элемента сигнала. Например, символ 0 передается отрезком синусоиды с начальной фазой предшествующего элемента сигнала, а символ 1 — таким же отрезком с начальной фазой, отличающейся от начальной фазы предшествующего элемента сигнала на π. При ОФМ передача начинается с посылки одного не несущего информации элемента, который служит опорным сигналом для сравнения фазы последующего элемента.
В более общем случае дискретную модуляцию следует рассматривать как преобразование кодовых символов 0,1,..., m-1 определенные отрезки сигнала si(t), где i = 0,1,...m—1 — передаваемый символ. При этом вид сигнала si(t), в принципе, может быть произволен. В действительности его выбирают так, чтобы удовлетворить требованиям, предъявляемым к системе передачи информации (в частности, по скорости передачи и по занимаемой полосе частот), и чтобы сигналы хорошо различались с учетом воздействующих помех.
Длительность посылки первичного сигнала bn(t) при дискретной передаче определяет скорость передачи посылок (техническую скорость или скорость модуляции). Эта скорость выражается числом посылок, передаваемых за единицу времени. Измеряется техническая скорость в Бодах. Один Бод —это скорость, при которой за 1с передается одна посылка.
Для классификации видов модуляции удобно использовать следующие признаки: характер полезного сигнала и переносчика (детерминированный процесс, случайный стационарный процесс, случайный нестационарный процесс); вид сигналов (аналоговые, дискретные); вид информационного параметра (амплитуда, частота, фаза, форма, длительность, период и т. п.) и др.
В теории информации и передачи сигналов основное внимание уделяется тем классам модуляции, в которых полезные сигналы рассматривают как случайные. Это обусловлено тем, что детерминированные сигналы не несут информации. Использование способов передачи информации в цифровой форме порождает необходимость изучения модулирующих сигналов в виде дискретных случайных стационарных и нестационарных последовательностей. При этом в качестве переносчика используется, как правило, детерминированный непрерывный сигнал.
Амплитудная модуляция (AM) является наиболее простым и распространенным способом изменения параметров носителя информации. При AM огибающая амплитуда гармонического колебания (переносчика) изменяется по закону, совпадающему с законом изменения передаваемого сообщения, частота же и начальная фаза колебания поддерживаются неизменными. Поэтому для амплитудно-модулированного колебания выражение (3.1) можно заменить следующим:
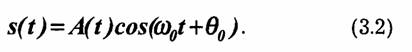
Характер огибающей A(t) определяется видом передаваемого сообщения.
Основным параметром амплитудно-модулированного колебания является коэффициент модуляции, когда модулирующая функция является гармоническим колебанием:
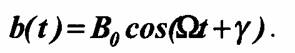
Огибающую модулированного колебания при этом можно представить в виде:
![]()
где Ω — частота модуляции; γ — начальная фаза огибающей; kAм — коэффициент пропорциональности; ΔAm= kАМ • В0 — амплитуда знаменения огибающей (рис. 3.2).
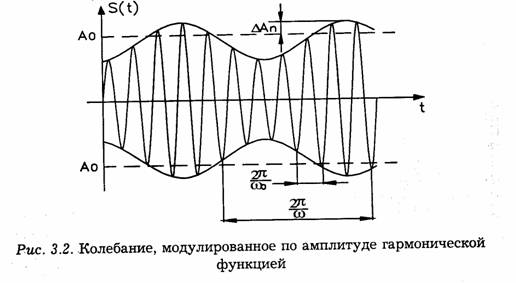

При неискаженной модуляции (М ≤ 1) амплитуда колебания изменяется в пределах от минимальной Amin = А0( 1—М) до максимальной Атах=А0(1+М). При передаче дискретных сообщений амплитудно-модулированное колебание имеет вид последовательности радиоимпульсов (рис. 3.1).
Для определения технических характеристик канала связи необходимо знать спектр модулированного колебания, т. е. установить связь между спектром модулированного колебания и спектром модулирующей функции (спектром исходного сообщения b(t)). Проще и наглядней это можно сделать для тональной (гармонической) модуляции, когда огибающая:
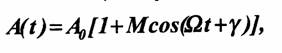
а модулированное колебание определяется выражением (3.4).
Перепишем выражение (3.4) в форме:
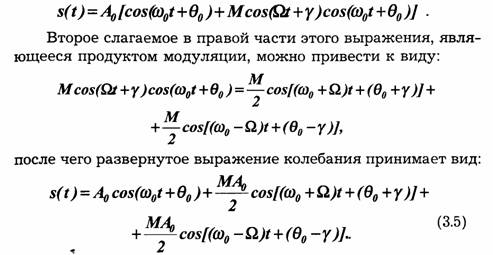
Первое слагаемое в правой части представляет собой исходное немодулированное колебание с частотой ω0. Второе и третье слагаемые соответствуют новым колебаниям (гармоническим), появляющимся в процессе модуляции амплитуды. Частоты этих колебаний ω o+ Ω и ω 0— Ω называются верхней и нижней боковыми частотами модуляции.
Спектральная диаграмма колебаний при тональной модуляции показана на рис. 3.3. Ширина спектра в этом случае равна удвоенной частоте модуляции 2 ω, а амплитуды колебаний боковых частот не могут превышать половины амплитуды смодулированного колебания (при М ≤ 1).
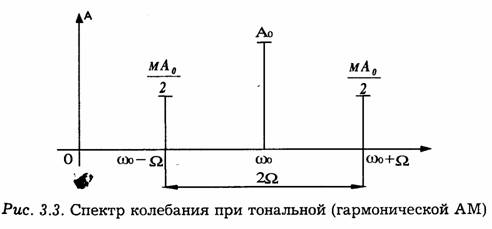
Если управляющий сигнал b(t) обладает более сложным спектром, картина не изменяется: каждая составляющая спектра b(t) дает свою пару боковых частот. В результате получается спектр, состоящий из двух полос, симметричных относительно несущей частоты ω 0, причем с увеличением числа составляющих в спектре b(t) снижается значение коэффициента модуляции, приходящееся на каждую из этих составляющих.
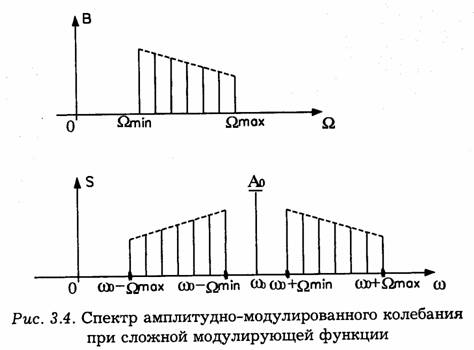
Построение амплитудного спектра модулированного колебания по заданному спектру передаваемого сообщения b(t) поясняется на рис. 3.4. В верхней части этого рисунка изображен спектр управляющего сигнала, а в нижней части — спектр модулированного сигнала.
Перейдем к общему случаю, когда спектр сообщения b(t) не обязательно дискретный. Передаваемое сообщение b(t) содержится в законе изменения огибающей A(t). He определяя вида функции b(t), составляем выражение для спектральной плотности S(ω) модулированного по амплитуде колебания s(t), рассматриваемого как произведение огибающей A(t) на гармоническое колебание cos(ω 0t+Ө0). Используя соотношение (2.50), получаем:
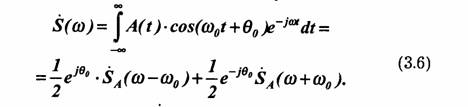
В этом выражении SA(ω) означает спектральную плотность огибающей, т. е. модулирующей функции.
Следует подчеркнуть, что спектр огибающей A(t), как правило, концентрируется в области относительно низких частот. Поэтому функция SA(ω — ω 0) существенно отличается от нуля лишь при частотах ω, близких к ω 0, т. е. когда разность ω - ω 0= Ω, относительно мала. Аналогичное слагаемое существует при частотах, близких к - ω 0. Таким образом, спектральная плотность модулированного колебания S(ω) образует два всплеска: вблизи ω = ω0 и вблизи ω = - ω 0. Спектральные плотности огибающей SA (Ω) и модулированного сигнала S(ω) представлены на рис. 3.5, причем в реальной системе передачи информации рассматривается только область положительных частот.
В современных системах передачи информации широко применяется однополосная модуляция, при которой передача ведется только на одной боковой полосе частот (ОБП).

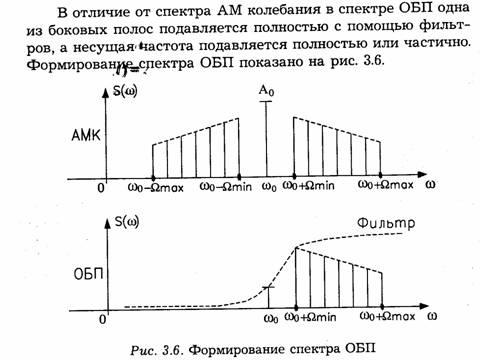
Спектр частот при передаче ОБП уменьшается по сравнению с AM в два раза, что позволяет сузить полосу пропускания приемного устройства и канала связи. Выигрыш по мощности при передаче ОБП по сравнению с AM составляет 8 раз. Такой способ передачи в настоящее время используется в телевизионном вещании. Отметим, что передача ОБП положена в основу построения многоканальных систем с частотным уплотнением, которые будут рассматриваться ниже.
В заключение следует отметить, что идеальная амплитудная модуляция представляет собой перенос спектра передаваемого сообщения в область более высоких частот без нелинейных, частотных и фазовых искажений. Реально модуляция сопровождается искажениями, что приводит к увеличению ширины спектра модулированных сигналов, изменению законов распределения огибающей и фазы и т. д.
3.3. Угловая модуляция
Рассмотрим теперь частотную и фазовую модуляции гармонического носителя информации. При изменении частоты всегда меняется фаза колебаний, а при изменении фазы меняется частота. Этим определяется общий характер частотной (ЧМ) и фазовой (ФМ) модуляции. Поэтому их часто объединяют под общим названием угловой модуляции.
Для простого гармонического колебания:
![]()
набег фазы (изменение фазы) за какой-либо конечный промежуток времени от t = t1 до t = t2 равен:
![]()
Отсюда видно, что при постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка.
С другой стороны, если известно, что набег фазы за время ![]()
то угловую частоту можно определить как отношение:
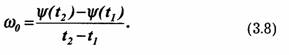
Отсюда видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.
В случае сложного колебания, частота которого меняется во времени, равенства (3.7) и (3.8) следует заменить интегральными и дифференциальными соотношениями:
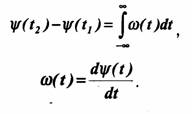
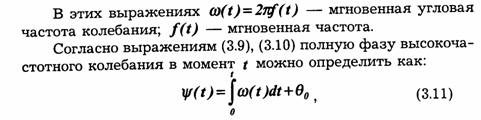
где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемого момента t; Ө0 — начальная фаза колебания (в момент t = 0).
Полную фазу колебания можно представить в виде:
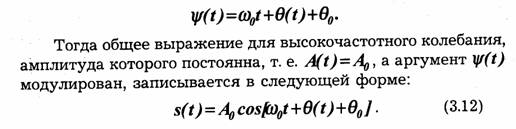
Соотношения (3.10), (3.11), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции — частотной и фазовой.
Поясним эти соотношения на примере простейшей гармонической ЧМ, когда мгновенная частота колебания определяется выражением:


Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω 0, а определяется исключительно девиацией ω д и модулирующей частотой Ω.
Рассмотрим теперь противоположный случай, когда стабильное по частоте и фазе колебание пропускается через устройство, осуществляющее периодическую модуляцию фазы по закону Ө(t) = Өmaxsini Ωt, так что колебание на выходе устройства имеет вид:

чить, с какой модуляцией мы имеем дело — с частотной или фазовой. Иное положение при негармонической модулирующей функции. В этом случае вид модуляции — частотной или фазовой — можно установить непосредственно по характеру изменения частоты и фазы во времени.
При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции.
При ЧМ девиация ω д пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции. Это означает, что индекс модуляции т (3.16) прямо пропорционален амплитуде модулирующего колебания и обратно пропорционален его частоте.
При ФМ величина Өтах пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции. Таким образом, при фазовой модуляции девиация частоты пропорциональна т (или амплитуде модулирующего колебания) и частоте модуляции.
Рассмотрим спектр колебания при гармонической угловой модуляции, используя выражение:
![]()
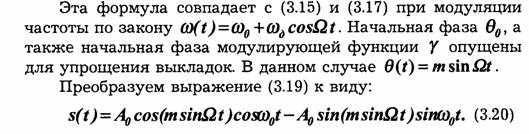
Отсюда сразу видно, что модулирующая функция подвергается нелинейному преобразованию (cosӨ(t) и sinӨ(t)). Это означает, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем спектр амплитудно-модулированного колебания. При угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на ве-
личину несущей частоты ω 0, как это имеет место при AM. При угловой модуляции связь между спектрами сообщения и модулированного колебания оказывается более сложной.

Таким образом, при частотной и фазовой модуляциях спектр колебания состоит из бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты ω0 и отличающихся от последней на nΩ, где n — любое целое число. Амплитуда п -й боковой составляющей An=Jn(m) ∙ A0, где А0 — амплитуда немодулированного колебания, а т — индекс модуляции. Спектры колебаний при различных индексах модуляции приведены на рис. 3.7.
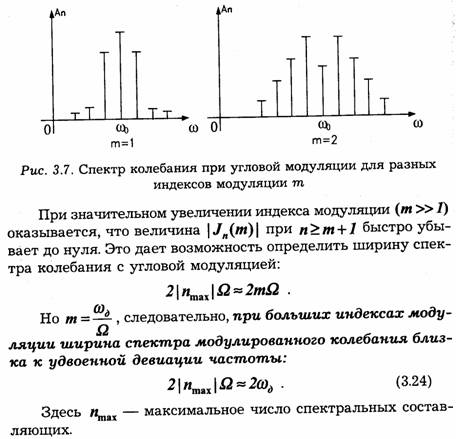
В заключение отметим одно важное для практических приложений
следствие. Особенностью спектра частотно-модулированного колебания, в отличие
от фазо-модулированного, является практическая независимость его ширины
от частоты модуляции. При увеличении Ω индекс
модуляции уменьшается пропорционально Ω, а ширина спектра при этом
остается постоянной. Причем спектральные составляющие на рис. 3.7
"раздвигаются", а учитываемое их количество![]()
уменьшается. Для фазо-модулированного колебания индекс модуляции не зависит от Ω. Поэтому с увеличением Ω ширина спектра увеличивается, а спектральные составляющие, не изменяясь по амплитуде и количеству (амплитуды равны A0 ∙ Jn(m), a т = const), "раздвигаются" по частоте.
3.4. Модуляция импульсных носителей
Для периодической последовательности импульсов (импульсного носителя) спектр является дискретным, и все расчетные соотношения для такого сигнала приведены в п. 2.3.
Временные диаграммы для основных видов импульсной модуляции приведены на рис. 3.8.
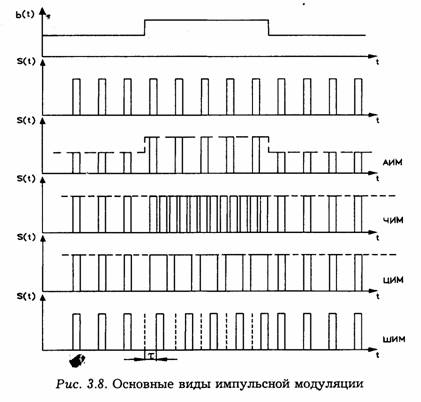
Амплитуды спектральных составляющих периодической последовательности определяются в соответствии с формулой (2.21):
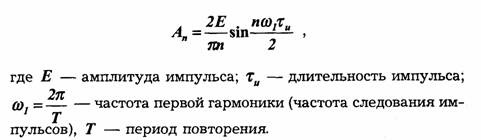
Расстояние между спектральными составляющими (рис. 2.7) равно частоте следования импульсов ω1. Отсюда следует, что изменение периода Т следования импульсов приводит к изменению плотности дискретных составляющих, а изменение
скважности ![]() при неизменном периоде (т. е. изменение
τи) вызывает сужение или расширение
огибающей с сохранением ее формы, оставляя неизменным расстояние между линиями
дискретного спектра.
при неизменном периоде (т. е. изменение
τи) вызывает сужение или расширение
огибающей с сохранением ее формы, оставляя неизменным расстояние между линиями
дискретного спектра.
Следует отметить, что периодической последовательности импульсов в чистом виде в природе не существует, поскольку любая последовательность имеет начало и конец. Степень приближения зависит от числа импульсов в последовательности. Поэтому для строгого описания импульсного носителя последний должен рассматриваться как одиночный импульс, представляющий собой пакет элементарных импульсов определенной формы. Такой сигнал имеет непрерывный спектр. Однако по мере накопления числа импульсов в последовательности ее спектр дробится и деформируется таким образом, что все более приближается к решетчатому. Составляющие на частотах дискретного спектра сужаются и быстро растут, остальные составляющие подавляются.
Покажем, как меняется спектр при амплитудно-импульсной модуляции (АИМ). При любой форме импульсов импульсный носитель описывается рядом Фурье:

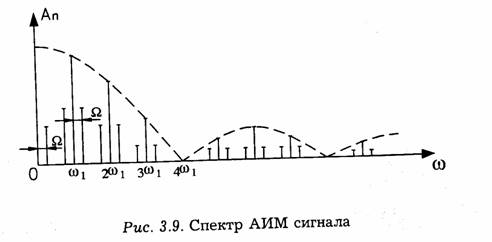
При более сложной модулирующей функции по обе стороны от каждой основной линии располагается полоса дополнительных составляющих, которая определяется полосой частот модулирующей функции.
При время-импульсной и частотно-импульсной модуляции, даже при элементарной модулирующей функции с одной гармоникой, вокруг каждой линии спектра носителя располагается бесконечно большое число дополнительных гармоник, которые, однако, быстро убывают.
Из сказанного следует важный вывод: несмотря на то, что характер спектра при модуляции носителя изменяется, его ширина практически остается такой же, как и для отдельного импульса. Она определяется главным образом шириной этого импульса и может быть оценена на основании (2.75) следующим образом:

Эта величина берется за основу при определении полосы пропускания системы передачи информации с импульсным носителем.
Современное состояние техники характеризуется непрерывным совершенствованием способов передачи информации. Изыскиваются новые виды сигналов и новые способы их обработки.
Рассмотренные в предыдущих параграфах модулированные колебания являются лишь простейшими видами сигналов. В настоящее время широко применяются сигналы, полученные в результате модуляции амплитуды и частоты (или фазы) колебания по очень сложному закону.
В любом случае предполагается, что заданный сигнал s(t) представляет собой узкополосный процесс. Это означает, что все спектральные составляющие сигнала группируются в относительно узкой, по сравнению с некоторой центральной частотой 0)д, полосе.
При представлении подобных сигналов в форме:

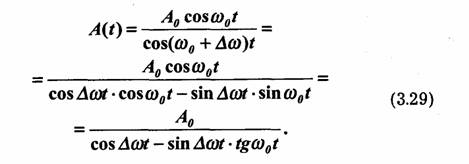
Из этого примера видно, что при нерациональном выборе ψ (t) (ω t вместо ω 0t) очень усложнилось выражение для A(t), причем эта новая функция A(t) по существу не является "огибающей" в общепринятом смысле, так как она может пересекать кривую s(t) (вместо касания в точках, где s(t) имеет максимальное значение). Оперирование подобной "огибающей" не имеет смысла, а в некоторых случаях и недопустимо, так как может привести к ошибочным практическим выводам.
Неопределенности можно избежать при представлении A(t) и ψ (t) с помощью следующих соотношений:


В данном случае получается "простейшая" огибающая в виде линии, касательной к исходной функции в точках ее максимума и соединяющей эти точки кратчайшим путем. Это свойство выражения (3.30) сохраняется и для сложного сигнала, если выполняется условие медленности изменения огибающей, т. е. если речь идет об узкополосном сигнале.
Если исходный сигнал представляет собой сумму спектральных составляющих

Нетрудно установить связь между спектрами функций s(t) и s1(t). Так как при преобразовании гармонического колебания по Гильберту его амплитуда остается неизменной, то очевидно, что по модулю спектральная плотность S1(ω) сопряженной функции s1(t) не может отличаться от исходной функции s(t). Фазовая же характеристика спектра S1(ω) отличается от ФЧХ спектра S(ω). Из сопоставления (3.36) и (3.37) непосредственно вытекает:

Вследствие изменения ФЧХ сопряженная функция s1(t) по своей форме может сильно отличаться от исходной функции s(t).
После того как найдена сопряженная функция s1(t), можно с помощью выражений (3.30), (3.31) найти огибающую A(t), полную фазу ψ (t) и мгновенную частоту узкополосного сигнала:
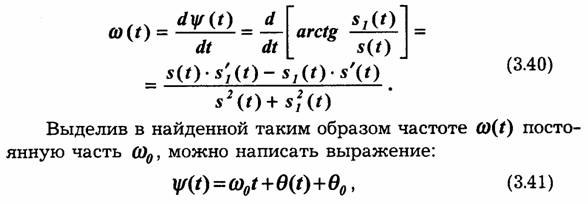
в котором Ө(t) не содержит слагаемого, линейно меняющегося от времени. Тем самым устраняется произвол в выборе "средней частоты" сигнала ω 0 и соответственно функции Ө(t). Характерный вид такого узкополосного сигнала приведен на рис. 3.10.

В заключение данного параграфа рассмотрим еще один способ представления сигналов, который в настоящее время достаточно широко применяется в теории передачи информации.
Если задан физический сигнал s(t) в виде действительной функции, то соответствующий ему комплексный сигнал представляется в форме:

Комплексный сигнал, определяемый выражениями (3.42) и (3.43), называется аналитическим сигналом.
В теории электрических цепей принято представлять гармонические колебания в комплексной форме записи. Аналитический сигнал является обобщением такой формы записи на негармонические колебания. Пусть задан физический сигнал:
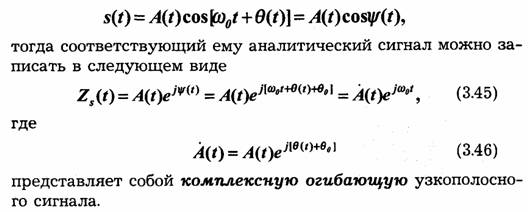
Модуль комплексной огибающей, равный A(t), содержит информацию только об амплитудной модуляции колебания, а фазовый множитель ejө(t) — только об угловой модуляции. В целом же произведение A(t)ejө(t) содержит полную информацию о сигнале s(t) (за исключением несущей частоты ω 0, которая предполагается известной).
Это свойство комплексной огибающей, позволяющее при анализе узкополосных сигналов исключить из рассмотрения частоту ω 0, придает важное значение понятию "аналитический сигнал". В некоторых устройствах обработки сигналов приходится иметь дело с совокупностью двух функций времени, сопряженных по Гильберту, т. е. с аналитическим сигналом как с физическим процессом.
3.6. Воздействие сигналов на нелинейные элементы
`Основные преобразования сигналов осуществляются с помощью либо нелинейных электрических цепей, либо линейных цепей с переменными параметрами. Однако последние реализуются тоже с помощью нелинейных элементов (например, емкость p-n-перехода в полупроводниковом диоде).
Следует различать резистивные (сопротивления) и реактивные (индуктивности, емкости) нелинейные элементы.
Наиболее характерными и распространенными резистивными нелинейными элементами являются полупроводниковые, ламповые и любые другие приборы, используемые для усиления или преобразования сигналов и имеющие нелинейную вольтамперную характеристику. Важным параметром резистивного нелинейного элемента является крутизна его характеристики. На рис. 3.11 приведены различные режимы работы нелинейного элемента.
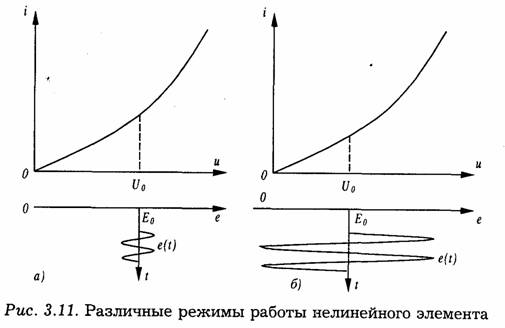
На рис. 3.11а в рассматриваемой рабочей точке Uo действует слабый сигнал e(t). Это соответствует линейному режиму работы нелинейного элемента, который характеризуется дифференциальной крутизной:
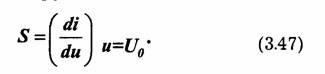
При воздействии сильного сигнала (рис. 3.116), что соответствует существенно нелинейному режиму работы элемента, вводится понятие средней крутизны. Средняя крутизна определяется с учетом формы вольтамперной характеристики нелинейного элемента в широких пределах, зависящих от амплитуды входного сигнала.
Примером нелинейной емкости может служить любое устройство с нелинейной вольткулонной характеристикой q(u) или вольтфарадной характеристикой с(и) = q(u)/u. В качестве нелинейной индуктивности L(i) может быть использована катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения.
Для анализа нелинейных цепей необходимо задать вольт-амперные или иные аналогичные характеристики нелинейных элементов в аналитической форме. Реальные характеристики обычно имеют сложный вид, что затрудняет точное их описание с помощью достаточно простого аналитического выражения.
Широкое распространение получили способы представления характеристик относительно простыми функциями, лишь приближенно отображающими истинные характеристики. Замена истинной характеристики приближенно представляющей ее функцией называется аппроксимацией характеристики.
Оптимальный выбор способа аппроксимации зависит от вида нелинейной характеристики, а также от режима работы нелинейного элемента. Одним из наиболее распространенных способов является аппроксимация степенным полиномом.
Запишем аппроксимирующий степенной полином в форме:

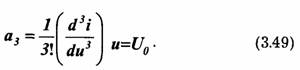
Нетрудно видеть, что а; представляет собой крутизну характеристики в точке u = U0, а2 — первую производную крутизны (с коэффициентом 1/2!), а3 — вторую производную крутизны (с коэффициентом 1/3!) и т. д. При заданной форме вольт-амперной характеристики коэффициенты a1,a2,a3,... существенно зависят от U0, т. е. от положения рабочей точки на характеристике.
При очень больших амплитудах сигнала часто удобнее заменять реальную характеристику идеализированной, линейно-ломаной, составленной из отрезков прямых линий. Такое представление характеристики называется кусочно-линейной аппроксимацией (см. рис. 3.12).

Следует особо подчеркнуть, что замена реальной нелинейной характеристики линейными отрезками не означает линеаризации цепи. Например, несмотря на то, что на участке b-с (рис. 3.12) характеристика линейна по отношению к сигналу, захватывающему область изменения à-ñ, система в целом является существенно нелинейной.
Рассмотрим воздействие узкополосного радиосигнала на безынерционный нелинейный элемент. Под безынерционным нелинейным элементом подразумевается любой электронный прибор с нелинейной вольтамперной характеристикой при использовании его в диапазоне частот, на которых можно пренебречь влиянием паразитных параметров (внутренних емкостей и индуктивностей).
Рассмотрим режим работы, при котором вольтамперная характеристика i(u) удовлетворительно аппроксимируется степенным полиномом (3.48).
Сигнал e(t) зададим в форме гармонического колебания:


Выражения (3.51) — (3.54) полностью сохраняют свою структуру при замене постоянной начальной фазы 0} модулированной фазой Ө1 (t)=Ө1max ∙ s(t). Из этого следует, что сформулированные выше положения можно распространить также и на воздействие частотно-модулированного сигнала на резынерционный нелинейный элемент (при постоянной амплитуде). Необходимо лишь каждую из гармоник тока с амплитудой Iп трактовать как несущее колебание, модулированное по углу. Это объясняется тем, что при угловой модуляции амплитуда колебания, несмотря на возникновение спектра боковых частот, остается неизменной.
Для первой (основной) гармоники индекс угловой модуляции совпадает с Өlmax =m1, а для высших гармоник индекс пӨ1тах=пт1. Соответственно в n раз увеличивается и девиация частоты.
Сказанное иллюстрируется рис. 3.13, где частота модуляции Ω<< ω1. С увеличением номера гармоники ширина спек-тра боковых частот возрастает, но, как отмечалось выше, амплитуда суммарного колебания остается равной In.
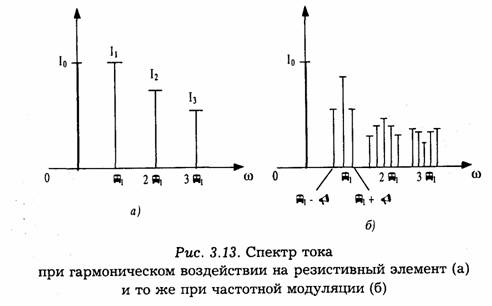
Для амплитудно-модулированного колебания, когда Е = E(t), нелинейность характеристики может коренным образом исказить форму передаваемого сигнала (нелинейное резонансное усиление, амплитудное ограничение и т. д.).
Рассмотрим воздействие суммы гармонических сигналов на нелинейный резистивный элемент.
Представим колебание в виде суммы:
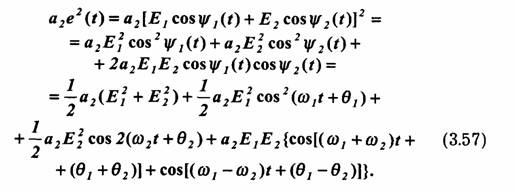
Первое слагаемое, не зависящее от времени, определяет приращение постоянного тока. Слагаемые с частотами 2ω1 и 2ω2 представляют собой вторые гармоники от соответствующих компонентов входного сигнала. Слагаемые же с частотами ω1+ ω2 и ω1- ω 2 представляют комбинационные колебания.
Частоты, образуемые квадратичным слагаемым a2e2(t), можно записать в форме:
![]()

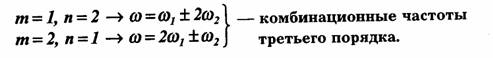
Приведенных выражений достаточно для установления закономерности образования частот гармоник и комбинационных колебаний при воздействии двух гармонических составляющих на нелинейный элемент:
• слагаемые ряда (3.48) четной степени вносят в спектр тока гармоники и комбинационные частоты четных порядков;
• слагаемые ряда (3.48) нечетной степени вносят в спектр тока гармоники и комбинационные частоты нечетных порядков;
• число р = т + п определяет порядок колебаний, причем максимально возможный порядок ртлх= k, где k — степень полинома, аппроксимирующего нелинейную характеристику.
Полученные результаты могут быть обобщены и на случай воздействия суммы большого числа гармонических составляющих на нелинейный элемент.
Содержание настоящего параграфа показывает, что нелинейная цепь преобразует спектр входного сигнала: возникают гармоники на кратных частотах и различные комбинационные колебания.
Принцип работы многих устройств преобразования сигналов основан на использовании тех или иных составляющих спектра тока на выходе безынерционного нелинейного элемента. Обобщенную структурную схему подобных устройств можно представить в виде сочетания нелинейной цепи и линейного фильтра (рис. 3.14).
На рис. 3.14 изображена схема, соответствующая "развязанным" нелинейному и линейному элементам, когда отсутствует обратная реакция выходного сигнала на ток в нелинейной цепи. Нелинейная функция f(e), описывающая характеристику нелинейного элемента, зависит от его устройства и от режима работы. Через z(ω) обозначено сопротивление (комплексное) линейной частотно-избирательной цепи. Структура этой цепи, частотная характеристика и полоса пропускания выбираются в зависимости от назначения устройства.