Г Л А В А 10

ЗАЩИТА ИНФОРМАЦИИ И КАНАЛОВ СВЯЗИ ПРИ ПЕРЕДАЧЕ

СООБЩЕНИЙ В УСЛОВИЯХ РАДИОЭЛЕКТРОННОЙ БОРЬБЫ (РЭБ)

Сценарий РЭБ определяет следующие четыре основных требования к радиотелекоммуникационной системе:

1. Безопасность передачи сообщений с целью обеспечения невозможности             раскрытия противником содержания передаваемой информации (обеспечение конфиденциальности или криптозащиты передаваемых сообщений).

            2. Защита каналов связи от доступа к ним противника, который может навязывать            нам ложные сообщения для дезорганизации работы телекоммуникационной         системы или перехвата управления нашей технической системой. Защита каналов    связи от поддельных сообщений называется имитозащитой каналов связи. В       гражданских телекоммуникационных системах к этой задаче также относятся             защита подписей на документах от подделок, защита электронных паролей доступа           в систему, защита кредитных карточек, охранных сигнализаций и др.

3. Обеспечение энергетической скрытности излучаемых радиосигналов с целью предотвратить обнаружение противником факта работы радиолинии и возможность           пеленгации наших радиоизлучающих средств с целью их огневого уничтожения.

4. Защита радиолиний от радиоэлектронного подавления помехами от станций     помех противника.

10.1. Конфиденциальность (криптозащита) передаваемых сообщений

В Российской Федерации установлен единый стандарт криптографического преобразования данных по ГОСТ 28147—89 при передаче информации для всех государственных органов, организаций и предприятий. Согласно этому ГОСТ режим шифрования, называемый режимом гаммирования, состоит в поразрядном сложении по модулю два передаваемых двоичных сообщений с двоичной шифрпоследователъностью (гаммой), которая вырабатывается шифратором. Тактовые частоты передаваемых сообщений и шифрпоследовательности одинаковы и синхронны.

Шифратор представляет собой некоторый цифровой автомат, имеющий 2^m возможных состояний. Выбор конкретного состояния шифратора производится выбором ключа. Общее число возможных ключей равно 2^т, где т называется длиной ключа. Для выбранного ключа шифратор преобразует входную открытую синхропосле-довательность S в шифрпоследовательность Г («бегущий шифр») со свойствами абсолютно случайной двоичной последовательности.

Предполагаем, что противник знает о нашем шифраторе все и даже физически имеет его. Единственно, что он не знает — это конкретно выбранного ключа, который оперативно должен меняться в системе. Шифратор должен быть так разработан, чтобы противнику для раскрытия сообщений пришлось бы угадывать ключ методом перебора всех ключей, на что потребуется несколько лет работы перспективной вычислительной техники.

Функциональная схема передачи сообщений с крип-тозащитой по линии связи представлена на рис. 38. Особенностью этой схемы является выбор синхропоследова-тельности S с большим периодом повторения (год и более), способ уплотнения ее с информационной последовательностью и способ формирования синхропоследо-

вательности S в приемнике для различных условий передачи: непрерывная передача, пакетная передача, учет помехоустойчивого кодирования информационной последовательности и др.

Инженерная задача заключается в организации канала передачи синхропоследовательности шифратора с помехоустойчивостью существенно выше помехоустойчивости канала информационного сообщения.

10.2. Имитозащита передаваемых сообщений

Имитозащита передаваемых сообщений осуществляется криптографическим способом. Для этого к передаваемому сообщению добавляются избыточные биты для обнаружения ошибок в приемном устройстве. Каждый избыточный бит должен зависеть от значений всех информационных бит. На информационные и избыточные биты накладывается шифр последовательность. В этом случае для создания ложного сообщения противник должен передать некие k информационные биты и правильно угадать необходимые для этих k бит значения r избыточных бит. Вероятность этого события есть Р_л = (1/2)^r .

10.3. Помехозащита радиолиний

            Способность радиолинии работать в условиях воздействия естественных помех называется помехоустойчивостью. Способность радиолинии работать в условиях воздействия организованных помех называется помехозащищенностью .

            Помехозащита разделяется на два класса: 1) пространственная помехозащита (за счет низкого уровня боковых лепестков приемной антенны, по которым действует помеха формирование «нулей» диаграммы направленности Приемной антенны в направлении на источник помех); 2) сигнальная помехозащита за счет широкополосных методов модуляции.

            При сигнальной помехозащите спектр излучаемого сигнала искусственно расширяется за счет применения фазоманипулированных псевдошумовых сигналов (ПШС) или псевдослучайной перестройки рабочей частоты (ППРЧ), либо за счет комбинированного метода модуляции ПШС-ППРЧ.

            Если противник ставит заградительную шумовую помеху во всей полосе частот нашего сигнала, так что на входе приемной антенны нашей радиостанции спектральная плотность шумовой заградительной помехи есть N_oп, то вероятность ошибки на бит в нашем приемнике будет определяться величиной

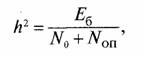
где Е_б — энергия бита полезного принимаемого сигнала на выходе приемной антенны, N₀ — спектральная плотность аддитивных шумов приемной системы.

            Из теории потенциальной помехоустойчивости еле- _; дует, что вероятность ошибки на бит определяется только энергией бита и не зависит от формы сигнала (с широкополосной модуляцией, узкополосной модуляцией и пг>Л

где Р_п — мощность помехи на выходе приемной антенны, Δƒ — полоса частот широкополосного сигнала.

            При N_oп >> N_o для порогового значения h² = h²_пор получим

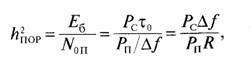
где τ₀ = 1/R длительность информационного бита, R — скорость передачи информации.

            Обозначим через базу широкополосного сигнала В отношение В = Δf/R = Δƒτ₀ >>1. Тогда сигнальная помехозащита, определяемая как такое отношение помеха-сигнал (Р_П/Р_С), при котором обеспечивается работа радиолинии с заданным качеством (обеспечивается требуемое отношение h²_п0Р), равна Р_п/Р_с = В/h²_пор.

Отсюда следует, что помехозащита радиолинии повышается при уменьшении скорости передачи информации Р, расширении полосы частот широкополосного сигнала Δƒ и уменьшении величины h²_пор. В помехозащищенных радиолиниях критерий оптимальности помехоустойчивого кода — максимальный энергетический выигрыш кода.

Уравнение помехозащиты

Радиолиния должна быть работоспособной при ЭИИМ станции помех P_ПХG_ПХ где Р_ПХ — мощность помехового сигнала на входе передающей антенны станции помех, G_пx — коэффициент усиления передающей антенны станции помех. Величина Р_пхG_пх задается моделью РЭБ. Тогда ЭИИМ нашей станции P_CG_C в радиолиниях без замираний сигнала определяется из уравнения помехозащиты

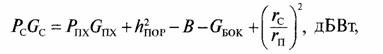
где G_БОК — относительный уровень бокового лепестка (или «нуля» диаграммы направленности приемной антенны) в направлении на помеху, r_с — дальность связи, r_п — расстояние от станции помех до приемника нашей радиостанции.

На рис. 39 представлена функциональная схема помехозащищенной радиолинии. Смена рабочей частоты при ППРЧ или формы ТТШС в радиолинии должна происходить по закону, неизвестному противнику, т. е. этот закон должен определяться устройством криптозащиты (шифратором). На рис. 40 показан вид радиосигнала с ППРЧ.

Противнику выгодно ставить не заградительную шумовую помеху, а более энергетически выгодные помехи, к которым относятся:

1) узкополосные помехи;

2) ретранслированные помехи;

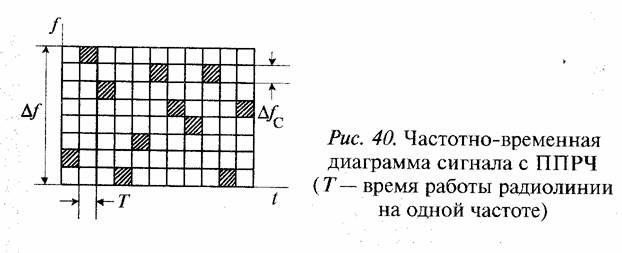
3) несущая, модулированная по частоте шумовым сигналом в части или во всей полосе сигнала Δƒ;

4) хаотическая, импульсная шумовая помеха с большой скважностью.

В разрабатываемой радиолинии должны бытъ предусмотрены меры, парирующие вышеуказанные помехи, чтобы вынудить противника ставить наименее энергетически выгодную для него заградительную шумовую помеху во всей полосе частот широкополосного сигнала. При этом противник создает помехи и своим собственным радиосредствам в максимально широкой полосе частоaт.

Узкополосные помехи должны быть подавлены в приемнике режекторными фильтрами. Ретранслированные помехи могут быть полностью подавлены при быстрой ПГТРЧ. Хаотические импульсные помехи могут быть сделаны малоэффективными при перемежении символов и использовании мощного кода с исправлением ошибок.

Задача 117. В качестве генератора синхропоследовательности шифратора в схеме рис. 38 можно использовать генератор m-последовательности на регистре сдвига с обратными связями. Определить период m-последовательности, если длина регистра сдвига т = 64, а частота следования символов m-последовательности равна 2,048 Мбит/с.

Задача 118. При передаче команд управления полетом летательного аппарата требуется обеспечить имитозащиту передаваемых команд с вероятностью ложного формирования команды не более 10^-9.

При криптографическом способе обеспечения ими-тозащиты определить число избыточных бит кода с обнаружением ошибок, которое нужно передавать с каждой командой.

Какие дополнительные кодовые методы защиты передаваемых команд можно предложить для стирания наших команд, принятых противником и ретранслированных им через некоторое время для дезорганизации работы командной радиолинии?

Задача 119. При передаче засекреченного телефонного сигнала нужно ли обеспечивать имитозащиту передаваемых сигналов. Если нет, объяснить почему.

Задача 120. Станция помех находится на расстоянии 30 км от нашей станции спутниковой связи, работающей в режиме ППРЧ. Каково допустимое максимальное время передачи сообщений на одной частоте, чтобы исключить воздействие ретранслированных помех на радиолинию?

Задача 121. Перевозимая станция помех системе спутниковой связи в диапазоне частот 8 ГГц для постановки помех спутниковому ретранслятору имеет антенну диаметром 5 м и мощность излучения 10 кВт. Определите ЭИИМ станции помех.

Задача 122. Станция помех спутниковому ретранслятору в диапазоне частот 8 ГГц имеет ЭИИМ 90дБВт. Используя уравнение помехозащиты радиолиний, определить требуемую ЭИИМ нашей станции спутниковой связи при следующих условиях:

• скорость передачи информации R = 2,4 кбит/с;

•  полоса частот используемого псевдошумового сигнала в радиолинии 36 МГц (полоса частот одного ствола спутникового ретранслятора);

• r_c=r_n;

•  пространственная помехозащита спутникового ретранслятора не используется;

•  требуемая величина E₆/N_o на выходе приемной антенны ретранслятора составляет величину 8 дБ. При излучаемой станцией спутниковой связи мощности радиосигнала 50 Вт определить необходимый диаметр передающей антенны станции спутниковой связи, при котором обеспечивается помехозащита радиолинии.

Задача 123. Для дополнительной защиты радиолинии от узкополосньгх помех при использовании ПШС предложите свои варианты построения устройства, вырезающего узкополосные помехи из спектра псевдошумового сигнала.

10.4. Отбор мощности спутникового ретранслятора помехой

Если на входе приемника ствола спутникового ретранслятора с прямой ретрансляцией сигналов возникла преднамеренная помеха, то она будет переизучаться ретранслятором, затрачивая некоторую мощность ретранслятора на ее переизлучение. Этот эффект называется отбором мощности ретранслятора помехой. Воздействие преднамеренной помехи наиболее разрушительно, когда напряжение сигнала плюс помеха переводят усилитель мощности в режим насыщения. Чтобы не допустить работу усилителя мощности в режиме насыщения, а обеспечить его работу в линейном режиме, в состав усилительных трактов вводят АРУ.

Задача 124. Пусть на входе приемника ствола ретранслятора прямой ретрансляцией сигналов действует многоканальный сигнал с результирующей мощностью P_C и помеха мощностью Р_П. Ретранслятор имеет коэффициент усиления k, который меняется таким образом, чтобы выполнялось условие к²(Р_с+Р_п) = Р₀ = const, где Р₀ — номинальная выходная мощность усилителя мощности в линейном режиме.

Требуется определить мощность полезного сигнала к²Р_с на выходе усилителя мощности и поведение коэффициента усиления ствола ретранслятора k в зависимости от входного отношения мощностей помеха—сигнал.

10.5. Скрытность работы радиолиний.

Стего-системы

Скрытная передача сообщений подразумевает, что противник в условиях РЭБ не может в течение сеанса связи обнаружить факт передачи сообщений. Скрытная передача сообщений возможна двумя путями:

1) передачей сигналов таким образом, что противник не может обнаружить излучения радиопередающих средств радиолинии. Такая скрытность называется энергетической;

2) передача полезных сигналов производится на фоне мощных маскирующих сигналов. Такой способ передачи сигналов называют стеганографическим, а системы связи — стего-системами.

Энергетическая скрытность радиолиний.

Энергетическая скрытность работы радиолиний является наиболее важным параметром радиолиний в условиях РЭБ. После обнаружения факта работы радиолинии следует пеленгация радиоизлучающих средств, определение их координат и, как правило, их огневое уничтожение, если радиоизлучающие средства находятся в пределах досягаемости артиллерии или авиации.

Теоретически за достаточно длительный промежуток времени всегда возможно обнаружить излучение радио-передающих средств. Поэтому скрытную работу радиолинии будем определять временем скрытной работы Т_ОБН, т. е. временем, которое необходимо разведывательному приемнику для обнаружения факта работы радиолинии. При этом следует принять, что разведывательный приемник использует самые быстрые методы поиска и обнаружения сигнала, включая параллельные поиск сигнала по частоте (параллельный спектроанализатор) и параллельный поиск по пространству (многолучевая приемная антенна).

Также примем, что в нашей радиолинии используются широкополосные сигналы типа ПШС или ППРЧ, параметры которых меняются по закону, неизвестному противнику, так что разведывательный приемник вынужден использовать некогерентную обработку широкополосного радиосигнала, т.е. для обнаружения сигнала должен измерять мощность принимаемого сигнала. Такой приемник называется энергетическим и проектируется как радиометр. Типовая схема радиометра представлена на рис. 41.

Схема работает следующим образом. Ключ КлА поочередно с некоторой тактовой частотой F_T подключает к малошумящему усилителю (МШУ) либо антенну, либо шумящее сопротивление R_ш с шумовой температурой, равной шумовой температуре антенны, которые складываются из космических шумов, шумов атмосферы и Земли. В отсутствие излучения передатчика радиолинии мощности шумов от антенны и шумящего сопротивления одинаковы.

На выходе усилительно-преобрзовательных каскадов на некоторой промежуточной частоте включены анализирующие фильтры (с полосой каждого фильтра Δƒ_ф) параллельного спектроанализатора. Напряжения с выходов анализирующих фильтров поступают на квадратичные детекторы и последующие фильтры нижних частот для выделения сигнала в области видеочастот. Напряжения с выходов фильтров нижних частот поступают на ключи

Кл1... Клп, которые работают синхронно с ключом КлА, в результате на входе интегратора возникает биполярный сигнал вида, показанного на рис. 42.

Напряжение положительной полярности соответствует сигналу, принятому антенной (обнаруживаемый сигнал плюс шумы антенны), напряжение отрицательной полярности соответствует напряжению шумов шумящего сопротивления R_ш. Величина U_o соответствует мощности обнаруживаемого сигнала, которая должна быть измерена путем дальнейшей фильтрации шумов интегратором со сбросом в конце интервала интегрирования (видеофильтром) с узкой полосой ΔF (что соответствует времени интегрирования сигнала Т_ОБН = 1/2ΔF) и последующего сравнения с порогом U_п для принятия решения о наличии или отсутствии излучения передатчика в полосе измерительного фильтра.

Скрытность работы радиолинии как и помехозащищенность радиолинии можно разбить на две составляющие: 1) сигнальную скрытность, обусловленную применением широкополосной модуляции (ПШС, ППРЧ и их комбинации) и 2) пространственную скрытность, обусловленную низким уровнем боковых лепестков передающей антенны радиолинии. Мы вначале рассмотрим сигнальную скрытность для некоторого эталонного сравнительного сценария геометрического расположения радиосредств радиолинии и разведывательного приемника на поверхности Земли, показанного на рис. 43.

Расстояние между передатчиком и приемником радиолинии г положим равному расстоянию между передатчиком и разведывательным приемником r_р, т. е. r = r_р. Все антенны передатчика и приемников положим всенаправленными. Определим время скрытной работы радиолинии Т_о для сигнальной скрытности и разведывательного приемника типа радиометра, представленного на рис. 41.

Принимаем, что выбранный нами широкополосный сигнал с полосой сигнала Δƒ_с, появляющийся на выходе измерительного фильтра в полосе Δƒ_ф<<P_c/Δƒ_с, будет представлять собой гауссовский процесс со спектральной плотностью N_ос = Р_с /Δf_c, где Р_с — мощность сигнала на выходе приемной антенны радиометра. Спектральная плотность аддитивного шума на выходе антенны радиометра (и на выходе ключа КлА) есть N_o. Полагаем, что для обеспечения скрытности радиолинии обеспечивается N_oc <<N₀ за счет широкополосной модуляции.

На выходе приемной антенны телекоммуникационной радиолинии мощность принимаемого сигнала также равна Р_с, а спектральная плотность аддитивного шума есть N₀.

Найдем отношение мощностей сигнал-шум на выходе квадратичного детектора одного частотного канала радиометра, считая для удобства, что на его входе действует шум со спектральной плотностью N_o + N_oc, либо N_o. Спектр шумов на выходе квадратичного детектора в видеополосе при воздействии на его входе гауссовского шума определен в решении задачи № 12 и представлен на рис. 44 для обозначений рис. 41 для случая, когда к МШУ постоянно подключена антенна.

Для положения KлA, когда к МШУ постоянно подключено шумящее сопротивление, на рис. 44 необходимо положить N_oc = 0. Мощность постоянной составляющей на выходе квадратичного детектора равна (N₍₎ +N_ос)²Δƒ²ф, а амплитуда постоянной составляющей есть (N_o +N_ОС) Δƒ_Ф при подключенной к МШУ антенне.

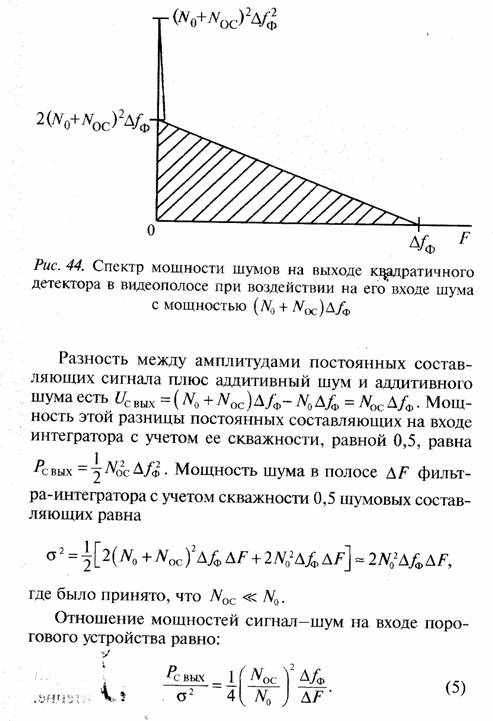
Положим вероятность пропуска сигнала Р_ПРОП = 10^-2 (требуемую вероятность обнаружения сигнала 0,99). Тогда

Если все измерительные фильтры используются для обнаружения сигнала, так что пА/_ф = А/_с или А/_ф = Д/_с, то получим окончательно для сигнальной скрытности, что время скрытной работы радиолинии равно

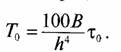   (7)

Требуемая величина h² должна быть обеспечена на выходе антенны приемника нашей радиолиний для получения заданной вероятности ошибки на бит. Поскольку в эталонной модели r = r_р и антенны, и приемники радиолинии и радиометра идентичны это же величина h² будет наблюдаться и на выходе антенны радиометра. Поэтому в выражении (7) необходимо подставлять значение h², получаемое в приемнике нашей радиолинии.

Проанализируем выражение (7).  Увеличить время скрытной работы можно за счет:

• уменьшения величины h² в нашей радиолинии за счет помехоустойчивого кодирования и, следовательно, за счет уменьшения излучаемой мощности передатчика;

• увеличения базы В широкополосного сигнала. Базу можно увеличивать двумя путями: 1) увеличением полосы излучаемого сигнала без изменения скорости передачи информации. В этом случае время скрытной работы увеличивается прямо пропорционально базе сигнала; 2) уменьшением скорости передачи информации с пропорциональным увеличением длительности информационного символа τ₀. В этом случае время скрытной работы увеличивается пропорционально В².

Важно отметить, что согласно выражениям (5) и (7) время скрытной работы увеличивается пропорционально квадрату уменьшения принимаемой мощности перехватываемого сигнала.

Уменьшить излучаемую мощность полезного сигнала можно, например, уменьшив расстояние r между передатчиком и приемником радиолинии. Тогда без учета замираний радиосигнала (и других особенностей распространения радиосигнала) для эталонной модели рис. 43 можно получить выражение для времени скрытной работы при r≠r_р в следующем виде T_ОБН =Т₀(r_р/r)⁴, где было принято, что принимаемая мощность сигнала меняется обратно пропорционально квадрату расстояния между передатчиком и приемником.

Рассмотрим пространственную скрытность работы радиолиний за счет направленных антенн телекоммуникационной радиолинии. Для условий свободного пространства принимаемая мощность полезного сигнала на выходе антенны приемного устройства нашей радиолинии равна

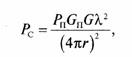
где Р_п — мощность, подводимая к передающей антенне, G_п — коэффициент усиления передающей антенны, G — коэффициент усиления приемной антенны, λ — длина волны.

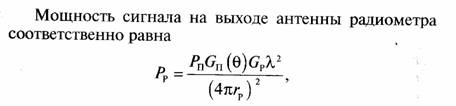
где G_п (Ө) — коэффициент усиления передающей антенны в направлении на радиометр; G_р — коэффициент усиления антенны радиометра.

Считаем, что максимум диаграммы направленности приемной антенны радиометра направлен на передатчик.

По сравнению с эталонной моделью рис. 43 мощность перехватываемого радиометром сигнала будет меньше в число раз, равное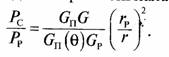

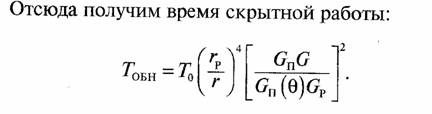
Будем считать, что для повышения скрытности работы радиолинии в ней используются передающая и приемная антенны с высокой направленностью, так что G_п (Ө) описывает боковые лепестки диаграммы направленности передающей антенны.

Огибающая боковых лепестков диаграммы направленности антенны должна быть равна или менее величины, определяемой выражением (относительно изотропного излучателя) в дБ:

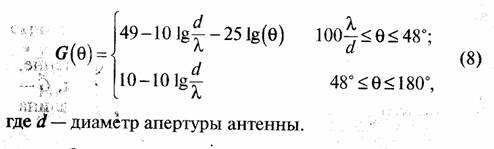
где h²_пop — пороговое отношение энергии бита к спектральной плотности шумов на выходе приемной антенны телекоммуникационной радиолинии.

Полученное соотношение показывает, что для скрытной работы радиолиний необходимо использовать наиболее высокочастотные диапазоны частот, дающие максимум отношения d_П/λ.

Задача 125. Определить время скрытной работы радиорелейной линии связи с параметрами:

•  диаметр антенны 1,5 м;

•  рабочая частота 6 ГГц;

•  скорость передачи информации 2,048 Мбит/с;

•  полоса псевдошумового сигнала 262 МГц;

дальность связи r_p — 30 км;

•  расстояние от передатчика до разведывательного приемника на самолете r_р=100 км;

•  коэффициент усиления антенны разведывательного приемника 30 дБ.

Определить во сколько раз увеличится время скрытной работы радиолинии при использовании специальной передающей антенны с уровнем боковых лепестков на 10 дБ меньшим по отношению к уровню боковых лепестков, определенных соотношением (8).

Задача 126. Определить время скрытной работы наземной станции спутниковой связи со следующими параметрами:

•  диаметр антенны 1,2 м;

•  рабочая частота 8 ГГц;

•  скорость передачи информации 2,4 кбит/с;

•  ширина спектра широкополосного сигнала с ППРЧ 500 МГц;

•  дальность связи 40 000 км;

•  h²_п0Р на ретрансляторе равно 10 дБ;

•  коэффициент усиления приемной антенны ретранслятора 30 д Б;

•  расстояние от станции спутниковой связи до разведывательного приемника на самолете r_p = 100 км;

•  коэффициент усиления антенны разведывательного приемника 30 дБ.

Определить во сколько раз увеличится время скрытной работы радиолинии при использовании специальной передающей антенны с уровнем боковых лепестков на 10 дБ меньшим по отношению к уровню боковых лепестков, определенных соотношением (8).

Задала 127. Пусть широкополосный псевдошумовой сигнал с полосой Δƒ представляет собой гармоническое колебание, манипулированное по фазе на 180° по

закону псевдослучайной двоичной последовательности. Для обнаружения такого сигнала используется тот факт, что после удвоителя частоты на удвоенной несущей частоте образуется смодулированное синусоидальное колебание, которое можно выделить узкополосным полосовым фильтром для последующего его обнаружения с помощью детектора и порогового устройства.

Требуется определить время скрытной работы радиолинии, в которой используется фазоманипулированный псевдошумовой сигнал с манипуляцией фазы на 180° по псевдослучайному закону. Обнаружитель сигнала состоит из полосового фильтра с полосой Δƒ на некоторой промежуточной частоте, умножителя частоты на два (квадратичного детектора) и узкополосного полосового фильтра с полосой Δƒ_у на удвоенной промежуточной частоте, после которого стоит детектор и пороговое устройство. Принять, что несущая частота фазоманипулированного сигнала и его полоса частот Δƒ известны на стороне разведывательного приемника. При этом считать, что псевдошумовой сигнал обнаружен, если в полосе Δƒ_у отношение мощностей сигнал—шум равно или более 50. Время скрытной работы принять равным T_0БН = 1/Δƒ_у.

Стего-системы

Стеганография — это направление техники связи, которое решает задачи защиты документов и другой информации от несанкционированного копирования, а также подтверждения подлинности информации на основе скрытного встраивания меток («водяных знаков») в передаваемое сообщение. В более широком смысле стего-системы обеспечивают создание скрытных каналов связи на фоне мощных маскирующих сигналов, которые представляют собой изображение, звук, видео, компьютерные файлы и др. Скрытный стего-канал связи может создаваться на основе известных методов уплотнения по времени, частоте и коду и нелинейных методов уплотнения с основным информационным каналом (видео, звук и др.). Также стего-канал связи должен иметь криптографическую защиту передаваемых сообщений. Например, при передаче оцифрованных выборок изображений к каждой выборке сигнала добавляется один дополнительный бит стего-канала. Поскольку человеческий глаз различает не более 8—10 градаций яркости этот дополнительный бит практически не искажает передаваемое изображение и не заметен при приеме изображения.

Задача 128. Требуется организовать скрытный стего-канал связи через существующие работающие стволы коммерческого телекоммуникационного КА-ретранслятора с прямой ретрансляцией сигналов путем использования псевдошумовых сигналов (ПШС) в станциях военной сети связи при следующих условиях:

•  полоса частот ствола ретранслятора равна 36 МГц;

•  излучаемый псевдошумовой сигнал создает помеху передаваемым коммерческим телекоммуникационным сигналам, которая не должна увеличивать спектральную плотность шумов приемника ретранслятора более чем на 10%.

В составной радиолинии «Терминал-КА-базовая станция», в которой базовая станция имеет диаметр антенны существенно больше, чем диаметр антенны терминала, принять превышение сигнала над шумом в ретрансляторе h²_ст = h²+Δ, где Δ= 1 дБ, h² — требуемое отношение энергии бита к спектральной плотности шумов в составном стего-канале, а в радиолинии «Базовая станция—КА—терминал» h²_cт = h² + Δ, где Δ = ЗдБ.

Требуется определить возможную скорость передачи информации в прямом и обратном стего-канале связи для одного ствола ретранслятора для величины h² = 6 дБ.

ОТВЕТЫ И РЕШЕНИЯ ЗАДАЧ

Глава 1

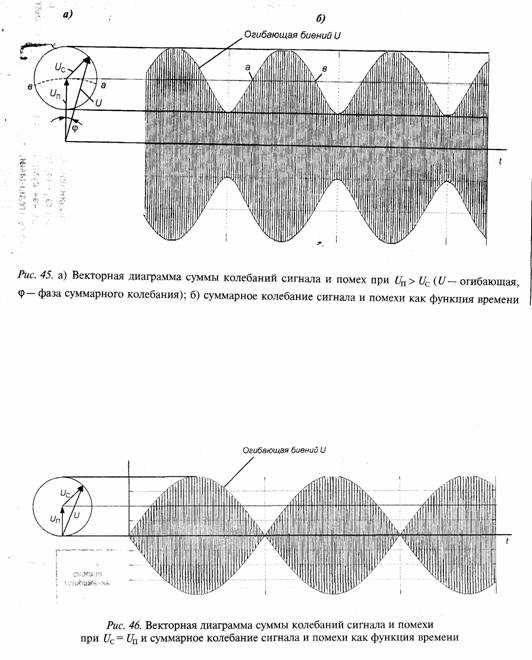
Задача 1. Вектор сигнала U_c равномерно вращается относительно вектора помехи с разностной частотой Δω на векторной диаграмме сигнала плюс помеха. Через равные интервалы времени определяется положение вектора U_c на векторной диаграмме рис. 45 и находится величина огибающей суммы сигнала и помехи U (длина вектора U). На рис. 45, б через равные интервалы времени на оси ординат откладывается значение полученной огибающей U и далее отображается высокочастотное заполнение суммарного колебания.

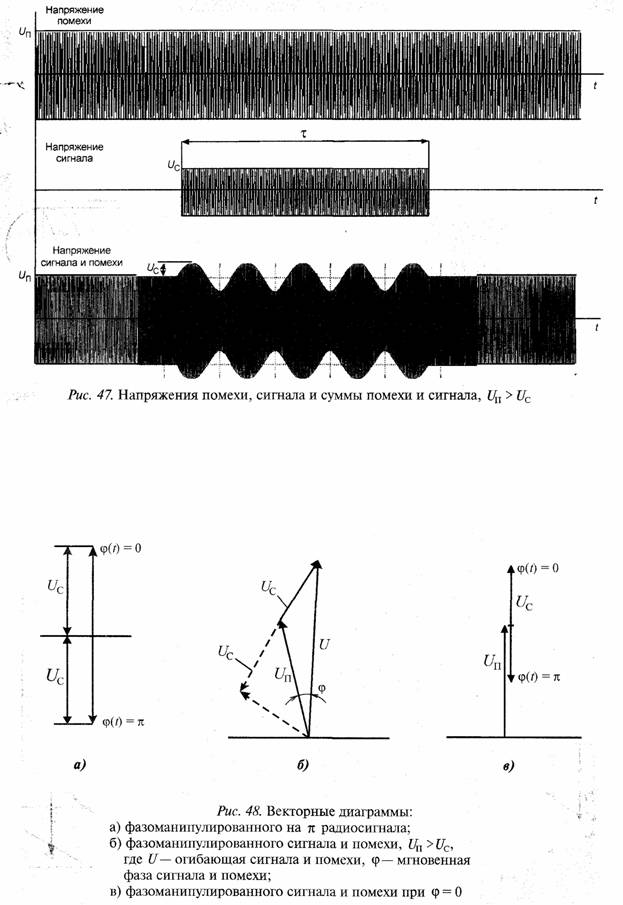
Задача 2. См. рис. 47.

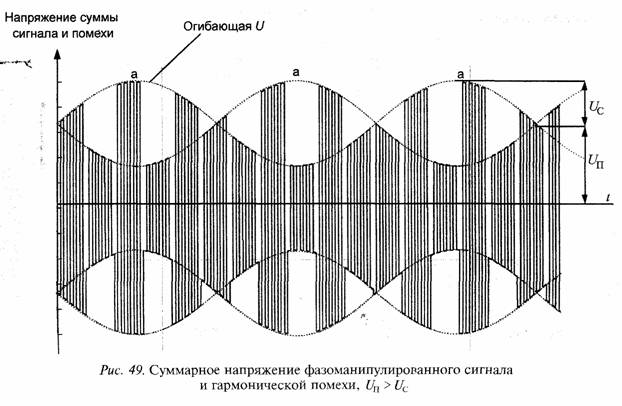
Задача 3. При наложении помехи на фазоманипулированный сигнал информация о манипуляции сигнала содержится в амплитуде (рис. 49) суммарного сигнала и в фазе φ (рис. 48, б) результирующего колебания. При ограничении результирующего колебания амплитудные изменения колебания устраняются и информация о фазоманипулированном колебании сохраняется в фазе (р результирующего колебания.

В отдельные моменты времени, фаза результирующего колебания близка к нулю (φ≈0), что соответствует векторной диаграмме, показанной на рис. 48, в для U_п>U_c. В эти моменты времени (показаны буквами «а» на рис. 49) сигнал вызывает только амплитудные изменения результирующего колебания, которые устраняются ограничителем, в результате чего полезный сигнал будет полностью подавлен. Если разность несущих частот помехи и сигнала ω_п - ω_с мала (ω_п - ω_с = 0), пропадания сигнала в точках «а» суммарного колебания могут быть весьма продолжительными.

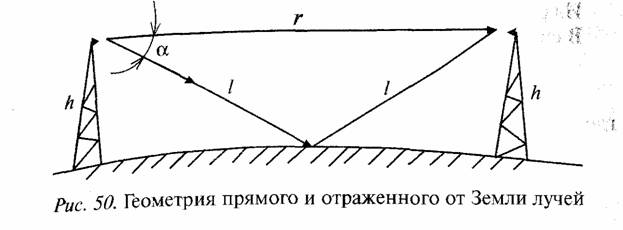
Задача 4. Рассмотрим рис. 50. Амплитуду прямого луча  на входе  приемной  антенны  обозначим  через U_csinω_ct. Амплитуда отраженного от поверхности Земли луча есть ρ U_c sin(ω_ct+φ), где ρ ≤1 есть коэффициент отражения, φ — набег фазы за счет разности хода лучей Δr  плюс π. Из векторной диаграммы рис. 51 амплитуда разности прямого и отраженного лучей равна

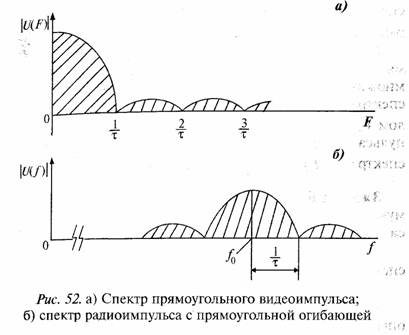
Спектр прямоугольного видеоимпульса для положительных частот показан на рис. 52, а.

На рис. 53 показана схема формирования радиоимпульса длительностью τ.

На входе перемножителя действует прямоугольный видеоимпульс длительностью τ и с амплитудой U_c. На второй вход перемножителя поступает гармонический

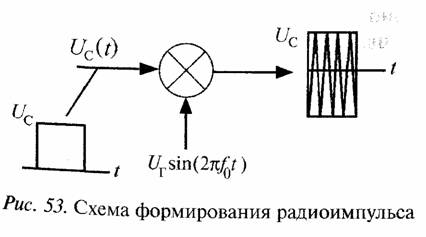
сигнал на частоте f₀. Выходной сигнал перемножителя

Представляя входной видеоимпульс U_c (t) в виде суммы бесконечно-близких частот получим на выходе перемножителя суммарные и разностные частоты между спектральными составляющими U_c (t) и опорным сигналом U_Гsin(2πf₀t). При U_г = 2 получим спектр радиоимпульса, показанный на рис. 52,6, как два зеркальных спектра U_c (F) относительно частоты f_Q.

Задача 6. Нормированный относительно максимума спектр мощности прямоугольного видеоимпульса сигнала длительностью т как квадрат амплитудного

спектра равен ,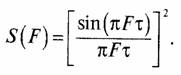

Ширина нормированного спектра мощности S(F) определяется как его площадь и равна

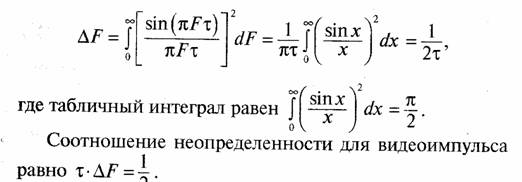
Для радиоимпульса длительностью т с прямоугольной огибающей спектр сигнала повторяет форму спектра видеоимпульса слева и справа относительно несущей частоты f₀ (см. рис. 52), так что ширина спектра радиоимпульса равна Δƒ= 2ΔF и соотношение неопределенности для радиоимпульса равно τ • ΔF = 1.

Полоса пропускания радиоприемного устройства как согласованного фильтра должна быть равна ширине спектра радиоимпульса сигнала Δƒ= 1/τ.

Задача 7. Этот спектр является линейчатым со спектральным линиями, вписанными вогибающую спектра одиночного импульса сигнала с расстоянием

между линиями

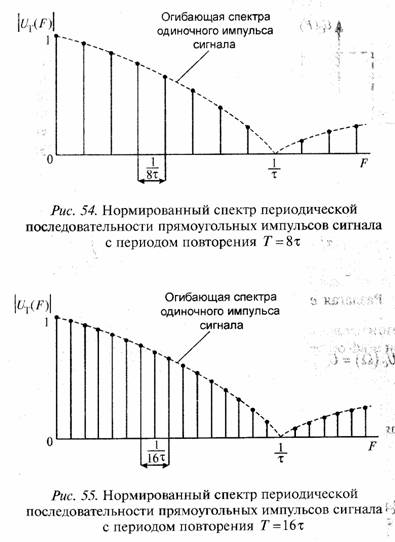
Задача 8. Мы знаем, что импульс сигнала как функция времени и его спектр связаны друг с другом преобразованием Фурье. Прямоугольный импульс сигнал имеет преобразование Фурье (спектр импульса) вида функции (sinx)/x.На основании этого можно заключить, что преобразование Фурье от функции вида (sinх)/х (функция времени, показанная на рис. 3) будет иметь форму прямоугольника, показанного на рис. 56 (отрицательные частоты показаны пунктиром).Для строгости анализа дополнительно дадим математическое вычисление спектра импульса сигнала

Задача 9. Огибающая спектра радиочастотного гармонического сигнала, манипулированного по фазе на 180°  меандровым  сигналом будет повторять форму спектра меандра слева и справа от частоты несущей ƒ₀.

На рис. 57 показан меандр, а на рис. 58 его линейчатый спектр.

Постоянная составляющая меандра равна нулю.

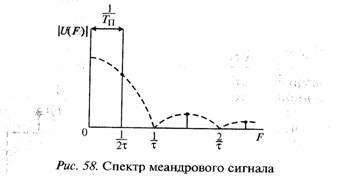
Спектр меандра линейчатый с расстоянием между спектральными составляющими

Огибающая спектральных составляющих меандра (пунктирная линия на рис. 58) описывается огибающей спектра одиночного прямоугольного импульса сигнала длительностью τ.

Отсюда получаем спектр радиосигнала, модулированного по фазе на 180° меандровым сигналом, показанный на рис. 59.

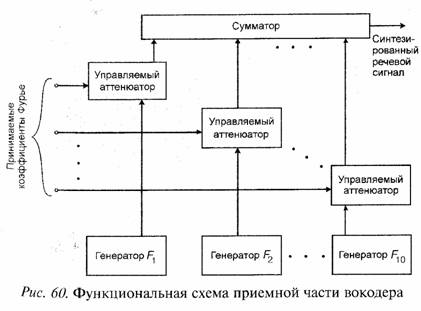
Задача 10. Приемная часть вокодера состоит из 10 генераторов тональных частот (гармонических колебаний). Частоты десяти генераторов совпадают с десятью центральными частотами полосовых фильтров анализатора спектра в передающей части вокодера. Колебание от каждого генератора поступает на управляемый принимаемым коэффициентом Фурье аттенюатор и далее в сумматор.

В итоге на вход сумматора будут поступать гармонические колебания десяти частот, амплитуды которых соответствуют текущим коэффициентам Фурье, полученным в передающей части вокодера. Сумма гармонических колебаний на выходе сумматора дает речевой сигнал как функцию времени. Экспериментально установлено, что синтезированный в приемнике речевой сигнал с числом гармонических колебаний равному 10 обладает высокой разборчивостью.

Скорость передачи речевого сигнала через вокодер составляет 30 бит за время 30 мс или около 1 кбит/с, что

по сравнению со скоростью 64 кбит/с сигнала с ИКМ означает уменьшение скорости передачи речевого сигнала в 64 раза.

Задача 11. На выходе перемножителя схемы синхронного детектора схемы рис. 5 получаем напряжение, равное

и опущены члены с суммарными частотами 2/_с и f_c+f\, поскольку колебания с этими частотами не проходят на выход фильтра нижних частот. Полагая U_T/2 = 1, получим

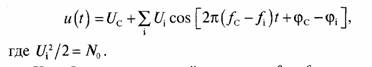
Колебание разностной частоты ƒ_с - ƒi создают две компоненты входного спектра шума, отстоящие от частоты /_с слева и справа на величину разностной частоты. Эти компоненты шума имеют случайные фазы по отношению друг к другу и после перемножителя суммируются по мощности, давая значение спектральной плотности мощности шумов 2N₀.

Максимальное значение разностной частоты ƒ_с – f_i, как следует из рис. 6, равно Δƒ/2 . Спектр мощности шумов на выходе перемножителя будет иметь вид, показанный на рис. 61.

На выходе фильтра нижних частот с полосой ΔF = Δƒ/2 мощность шума равна P_ш= 2N₀ΔF = N₀Δf , мощность сигнала равна Р_свык=U²_c=2Р_с, где Р_С=U²_c/2 есть мощность полезного сигнала на входе перемножителя.

Отношение мощностей сигнал-шум на выходе фильтра нижних частот равно:

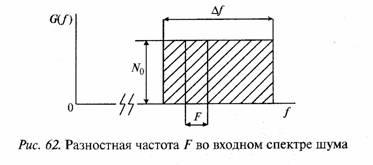
квадратичного детектора стоит видеофильтр, который подавляет высокие частоты 2ƒ_i и f_i +ƒj.

Из рис. 62 следует, что разностные частоты F на выходе квадратичного детектора лежат диапазоне от F= 0 до F - Δƒ, а число компонент пар частот fi, ƒj в спектре входного шума, которые создают разностную частоту F, равно Af-F.

Запишем для постоянной составляющей и разностных частот выходное напряжение квадратичного детектора]

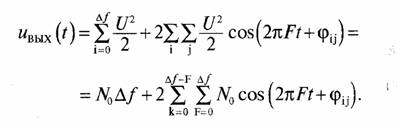
Найдем выходной спектр мощности. Мощность постоянной составляющей (первый член вышенаписанного выражения) на единичном сопротивлении есть

(N₀Δƒ)²

Мощность спектральной компоненты на частоте F под знаком двойной суммы равна (2N₀)² /2=2N₀² .  Все компоненты спектра входного шума, находящиеся на расстоянии F друг от друга имеют случайные фазы и под знаком двойной суммы должны суммироваться по мощности. Проведя это суммирование, получим спектр

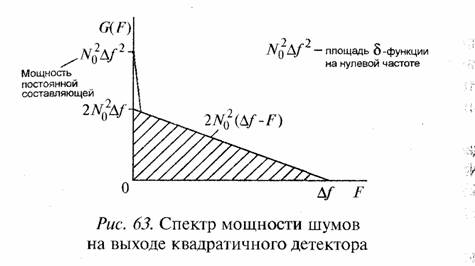
мощности на выходе квадратичного детектора в области видеочастот, показанный на рис. 63.

Задача 13. Эта задача является наиболее сложной в задачнике и предлагается будущим магистрам.

Рассмотрим вначале спектр суммы гармонического сигнала и шума на выходе квадратичного детектора в области видеочастот.

Входное колебание имеет вид

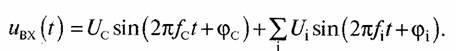
Первое слагаемое дает выходной полезный сигнал (постоянную составляющую). Амплитуда постоянной составляющей есть U²_C/2 = Р_с, где Р_с — мощность полезного сигнала на входе квадратичного детектора. Мощность сигнала на выходе квадратичного детектора равна Р_с².

Второе слагаемое, называемое биениями шум-шум, дает треугольный спектр шума, рассмотренный в задаче № 12 и представленный на рис. 63. Третье слагаемое — биения сигнал—шум — дает равномерный спектр шума в полосе от нуля до Δƒ/2, рассмотренный в задаче №11.

В третьем слагаемом мощность спектральной компоненты биений сигнал—шум на разностной частоте ƒ_с - f_x на единичном сопротивлении равна U²_CU²/2 = U²_C U₀ = 2P_CN_O.

Компоненту биений сигнал—шум на частоте F = f_c-fi создают две компоненты входного шума, отстоящие слева и справа от ƒ_с на величину F, поэтому на выходе детектора спектральная плотность мощности биений сигнал—шум будет равна 4P_cN₀.

Результирующая форма спектра мощности шума на выходе квадратичного детектора представлена на рис. 64 в виде суммы двух спектров: спектра биений сигнал—шум

(рис. 64, а) и спектра биений шум—шум (рис. 64,6). На рисунке также указаны мощности постоянной составляющей для полезного сигнала Р²_C и шума N²₀Δf².

Отношение мощностей сигнал—шум на входе квадратичного детектора есть

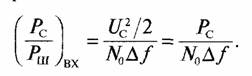
Отношение мощностей сигнал—шум на выходе квадратичного детектора в полосе частот от нуля до Δƒ/2 равно

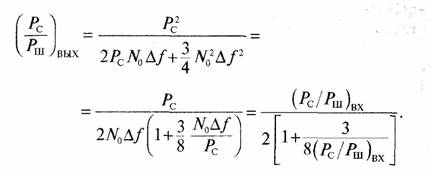
Определим вначале спектр шумов на выходе квадратичного детектора в отсутствие сигнала в окрестности удвоенной частоты

Рассмотрим двойную сумму и компоненту спектра шума на некоторой суммарной частоте 2ƒ_к на выходе квадратичного детектора. Суммарную частоту 2ƒ_к образуют все компоненты шума на частотах f_i= f_k-F и fi⁼ƒ_k + F где F принимает значения от нуля до Δƒ/2-(ƒ₀ -ƒ_к) (см. рис. 65, а), если ƒ_к <ƒ₀ и от нуля до Δƒ/2 -(ƒ_к - ƒ₀) см. рис. 65, б), где ƒ₀ — центральная частота входного спектра шума.

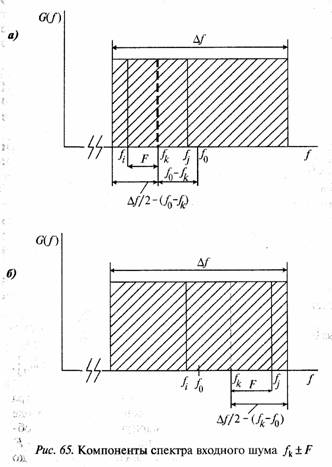
Рассмотрим спектр мощности выходного шума. Первый член дает равномерный спектр мощности со спектральной плотностью N²₀/2 в полосе частот Δƒ. Эта спектральная плотность ничтожно мала по отношению к спектральной плотности выходного шума, создаваемой компонентами шума под знаками двойной суммы.

Максимальное значение спектральной плотности шумов образуется на частоте 2ƒ_k = 2f₀ которое равно

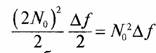Спектр мощности линейно убывает по обе стороны от частоты 2/₀ и имеет вид, показанный на рис. 66.

Спектр сигнала и шумов на выходе квадратического детектора в области удвоенных частот определяется из

выражения (опуская члены, дающие постоянную составляющую и видеочастоты):

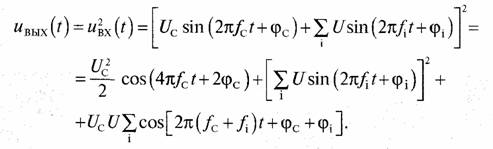
Первое слагаемое дает полезный сигнал с амплитудой U²_c/2=P_C и мощностью Р²₀/2,где Р_с есть мощность полезного сигнала на входе квадратичного детектора.

Второе слагаемое (биения шум—шум) дает треугольный спектр шума, изображенный на рис. 66.

Третье слагаемое дает равномерный спектр шума в полосе Δƒ (биения сигнал—шум). Мощность спектральной компоненты на частоте ƒ_с+ƒ_i есть U²_CU²/2 = U²_CN₀ = 2P_cN₀.  Спектр сигнала и шумов на выходе

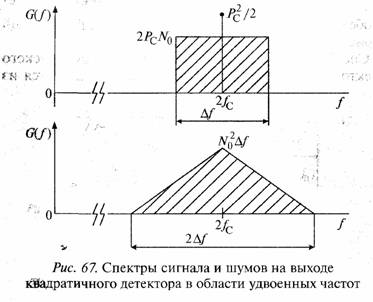
квадратичного детектора в области удвоенных частот показан на рис. 67.

Обозначим отношение мощностей сигнал—шум на входе квадратичного детектора как

Отношение мощностей сигнал—шум на выходе квадратичного детектора в некоторой узкой полосе частот Δƒ_у <<Δƒ на центральной частоте 2ƒ_с равно

Глава  2

Задача 16. Теория информации устанавливает, что в канале связи с шумами возможна передача информации без ошибок. Шумы ограничивают скорость передачи информации без ошибок, которая для некоторого идеального помехоустойчивого кодирования определяется формулой Шеннона

где ΔF — полоса канала связи; Р_с/Р_ш — отношение мощностей сигнал—шум в канале связи.

Задача 17. Пусть W(x) есть плотность распределения вероятностей амплитуд х шумов квантования внутри интервала ±Δ/2. Из условия нормировки плотности

Задача 18

а) При увеличении k на один разряд отношение сигнал-шум квантования увеличится по амплитуде в 2 раза или в децибелах на 20lg2 = 6 дБ;

б) на 12 дБ.

Задача 19. Число уровней квантования аналогового сигнала определяем из уравнения

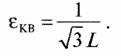
Отсюда L = 1/√3ε_KB • При ε_кв = 0,5% = 0,005 1 = 116. Число разрядов k АЦП определяется из соотношения 2^k >> L, откуда k = 7.

Задача 20. Из уравнения √3L = U_c/ε_KB, где U_c /ε_КВ, есть отношение сигнал—шум квантования, запишем в децибелах 20 lg(√3L,) = 50 дБ. Отсюда L=182. Требуемое

число разрядов АЦП к определяется из условия 2^k >> L. Отсюда k= 8.

Задача 21. Скорость передачи телефонного сигнала равна R = F_дlog₂L бит/с, где L — требуемое число уравнений квантования по амплитуде выборок телефонного сигнала и L = 2^k при их оцифровке.

Из исходных данных следует, что при отношении средней мощности телефонного сигнача к мощности шумов квантования 23 дБ, отношение пикового значения телефонного сигнала к мощности шумов квантования должно быть равно 23 + 15 = 38 дБ.

С учетом возможности уменьшения среднего значения телефонного сигнала на 10 дБ отношение пикового значения амплитуды телефонного сигнала к среднеквадратическому значению шумов квантования должно быть не менее 48 дБ.

Из уравнения 20 (lg√3L) = 48 дБ получаем L≥145 и при двоичном представлении оцифрованных выборок L ≤ 2^к получаем k = 8 и R = Fд·8 = 64 кбит/с.

Задача 22

а) Число градаций яркости или уровней квантования телевизионного сигнала L в дБ составляет 30 + 10 = 40 дБ. Отсюда L определяется из уравнения 20logL = 40 или

L = 100. Число разрядов k при оцифровке выборки сигнала яркости (2^k ≥ L = 100) равно 7. Отсюда скорость передачи телевизионного сигнала R = F_дk = 105 Мбит/с.

б) До сжатия телевизионного сигнала необходимо просуммировать требуемые скорости передачи сигнала яркости и сигналов цветности.

Для сигнала яркости число разрядов при его оцифровке (2^k≥L = 126) равно 7. Аналогично получаем, что для каждого из двух сигналов цветности при оцифровке требуется 4 разряда. Итого, для оцифровки по одной выборке сигналов яркости и двух сигналов цветности требуется 15 двоичных разрядов, что дает скорость передачи несжатого телевизионного сигнала R = 13,5 Мгц х 15 = 202,5 Мбит/с.

После сжатия телевизионного сигнала в 50 раз требуемая скорость передачи информации R ≈4 Мбит/с.

Задача 23. Число бит, формируемых в одном кадре цифрового фотоаппарата, равно 16-10⁶ log₂ 256 = 128 10⁶ бит или 128 Мбит.

Требуемая скорость передачи информации равна 128 Мбит • 5 = 640 Мбит/с.

Задача 24. Ширина полосы захвата земной поверхности равна числу пикселей в строке 12 000, умноженной на разрешающую способность на поверхности Земли и составляет:

•  12 км для разрешающей способности 1 м;

•  36 км для разрешающей способности 3 м;

•  120 км для разрешающей способности 10м.

За одну секунду в направлении движения КА просматривается участок Земли в 8 км, что создает число пикселей в направлении движения КА:

•  8000 при разрешающей способности 1 м;

•  2667 при разрешающей способности 3 м;

•  800 при разрешающей способности 10м.     

Итого за 1 секунду на борту КА формируется число пикселей для одного участка спектра наблюдения:

•  12 000-8000 = 96 • 10⁶ при разрешающей способности 1 м;

•  12 000 • 2667 = 32 • 10⁶ при разрешающей способности Зм;

•  12 000 • 800 = 9,6 • 10⁶ при разрешающей способности 10м.

При оцифровке амплитуды каждого пикселя 8-ю разрядами для несжатого изображения при формировании изображения в трех участках оптического спектра формируются информационные потоки со скоростями:

•  96 • 10⁶ • 3 • 8 = 2,3 Гбит/с при разрешающей способности 1 м;

•  32-10⁶-3 -8 = 768 Мбит/с при разрешающей способности 3 м;

•  9,6 • 10⁶- 3• 8 = 230 Мбит/с при разрешающей способности 10м.

Задача 25.  T_п =0,156 с.

Задача 26

1. Длительность сверхцикла NT_ц = 45мс.

2.  Период появления стаффинг-бита T_ст =156 мс. Требуемое условие NTц < Т_ст выполняется.

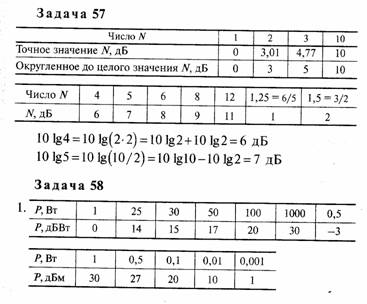
Задача 27

1. Число потерянных пакетов из-за переполнения буферного запоминающего устройства за время 1 секунда равно v -1. Отношение числа потерянных пакетов к числу поступивших пакетов за 1с есть (v-l)/v. Процент потерянных пакетов есть 100(v-l)/v.

2. Процент пустых пакетов есть 100(1 —v).

Задача 28. Пиковая мощность передатчика наземной станции спутниковой связи при МДВР должна быть больше непрерывной мощности передатчика наземной станции при МДЧР:

1) в п = 256 раз;

2) в 16 раз.

Задача 30. В телефонной сотовой сети мобильной связи число возможных телефонных каналов на одну соту при h² = 6 дБ для направления связи «Терминал-базовая   станция»  для   асинхронного   МДКР   равно

Глава 3

            Задача 31. Кодовые слова двоичного циклического систематического (п, к) кода по определению состоят из k информационных бит, которые всегда стоят в начале кодового слова, и последующих r = п — к проверочных бит. Эти k бит записываются в регистр сдвига с обратными связями, как это показано рис. 68.

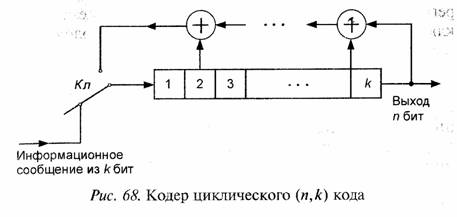
После этого ключ Кл перекидывается в верхнее положение и на вход регистра сдвига начинают поступать с тактовой частотой проверочные биты. Одновременно с выхода регистра сдвига начинают поступать биты циклического (u, k) кода. После п тактов схема рис. 68 возвращается в исходное состояние.

По аналогичному принципу строится схема декодера (и, k) кода в режиме обнаружения ошибок, которая представлена на рис. 69.

В исходном состоянии, показанном на рис. 69, к информационных бит с выхода приемника заполняют

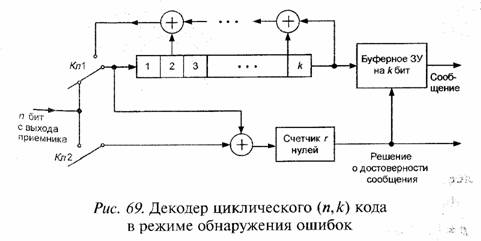
регистр сдвига, содержащего k ячеек. После приема k бит ключи Кл.1 и Кл.2 перекидываются в верхнее положение и регистр сдвига начинает формировать проверочные биты, которые сравниваются с проверочными битами с выхода приемника в сумматоре по модулю 2. Если все информационные и проверочные биты приняты приемником правильно, на выходе счетчика нулей появится r нулей. В этом случае принимается решение о считывании с буферного запоминающего устройства k информационных бит. Если на выходе счетчика число нулей менее r, то принимаемое сообщение стирается как недостоверное.

Задача 32. Вероятность того, что в слове из п бит будут искажены не менее чем из n бит равна

Задача 41

1. Из выражения для эффективности телекоммуникационной системы

получим для систем с закрепленными каналами η = α:

•  η = 0,01 для мобильной связи;

•  η = 0,1 для фиксированной связи.

2. Полагая α = 1, допустимое число абонентов N определяется по графику рис. 8 или по графику рис. 9, полагая N =ηn. Получим N= 8.

Задача 42. Принимаем оптимистический сценарий, при котором ретранслятор КА загружен круглосуточно. Из рис. 9 при п = 100 величина η = 0,8, т. е. эффективно на ретрансляторе загружено 80 каналов.

В году содержится 0,5 млн. минут. Каждый телефонный канал приносит владельцу космического сегмента доход за год, равный 1,25 млн долларов, а 80 работающих каналов принесут доход за год 100 млн долларов. Таким образом, за два года доход оператора космического сегмента будет равен его первоначальным затратам.

Задача 43. Вначале определим доход оператора станции спутниковой связи.

По графику рис. 9 находим, что при 12 каналах связи в среднем будет занято 6 каналов. Годовой доход равен 6 • 2,4 • 60 · 365 -0,5 = 150 000 долл. Примем следующий примерный сценарий годовых расходов:

•  Аренда емкости ретранслятора КА — 10 тыс. долл.

•  Оплата наземных линий связи (20% от дохода) — 30 тыс. долл.

•  Заработная плата персонала — 30 тыс. долл.

•  Накладные расходы — 30 тыс. долл.

•  Налоги (36% от заработной платы) — 10 тыс. долл._____________________________

Итого, 110 тыс. долл.

Принимаем, что покупка станции спутниковой связи окупится менее чем за 2 года.

Задача 44. Суммарная допустимая нагрузка для одного 10 канального коммутатора Nα = ηn = 10η = 4,2 (см. рис.9), где N=42 абонента, которые могут быть подключены к коммутатору. Для десяти коммутаторов суммарная нагрузка равна 42 Эрл.

Для 100-канального коммутатора допустимая нагрузка Wcc = 82 Эрл, что почти в два раза выше чем для десяти 10-канальных коммутаторов.

Задача 45. Форма диаграммы направленности антенны с круглой апертурой описывается выражением

диаграммы направленности определяются нулями функции Бесселя первого рода первого порядка J₁(πdӨ/λ). Первый нуль имеет место при Ө= 1,22λ/d. Отсюда диаметр антенны определяется из уравнения 1,22 λ/d = 0,1, где 0,1 радиан равен 6°. Для частоты 12 ГГц длина волны λ = 2,5 см и d = 30 см. Также возможны диаметры антенн, в целое число раз превышающие апертуру 30см, т.е. диаметры антенн 30 см, 60 см, 90 см, 120 см обеспечат подавление сигналов от других спутников телевизионного вещания.

Задача 46. Методика расчета электромагнитной совместимости спутниковых систем связи основана на расчете помехи от одной другой системы спутниковой связи с КА, имеющего ближайший угловой разнос на геостационарной орбите относительно рассматриваемого КА. Схема возникновения помехи в приемнике станции № 2 °т излучений станции № 1 другой спутниковой системы связи показана на рис. 70.

Станции № 1 и № 2 двух спутниковых систем связи Работают на одних и тех же рабочих частотах. Сигнал

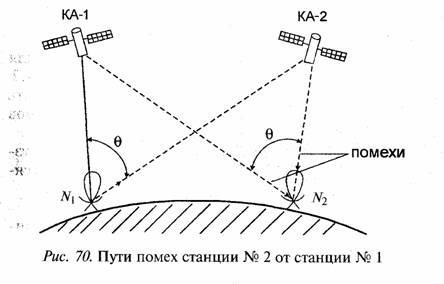
от мешающей станции № 1 приходит в приемник станции № 2 по двум путям. Первый путь: станция №1— КА2—станция № 2. Второй путь: станция № 1—КА1 — станция № 2.

По условиям задачи для идентичных станций спутниковой связи и одинаковых дальностей от станций спутниковой связи до КА при расчетах отношений сигнал-помеха достаточно учитывать только коэффициенты усиления приемных и передающих антенн наземных станций по основному и боковым лепесткам диаграмм направленностей. Диаграмму направленности антенн КА принимаем достаточно широкой, так что ее коэффициент усиления одинаков для направлений на станцию № 1 и №2.

Мощность полезного сигнала на выходе приемной антенны станции № 2 пропорциональна величине G_пG_пр, где G_п = G_п (0) и G_пр = G_пр (0) коэффициенты усиления передающей и приемной антенны наземной станции в основном лепестке диаграммы направленности антенн. Мощность помехи по первому пути пропорциональна G_п(Ө)G_пр, по второму пути— G_пG_пр(Ө), где G_п(Ө) и Gпр(Ө) коэффициенты усиления передающей и приемной антенны наземных станций в направлении 9 (по боковым лепесткам диаграммы направленности антенн). Тогда для защитного отношения сигнал—помеха справедливо соотношение

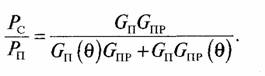
В частности, если помеха по пути № 1 отсутствует, что соответствует случаю непосредственного спутникового телевещания, защитное отношение сигнал—помеха имеет простой вид Р_с/Р_п =G_пр/G_np(Ө). Для нашего случая, телекоммуникационной спутниковой системы выражение для защитного отношения сигнал—помеха целесообразно привести к аналогичному виду.

Обозначим частоту приема наземной станции через f_np, частоту передачи — через ƒ_п.

Тогда G_пр/G_п = (f_пр/f_п)   и можно записать

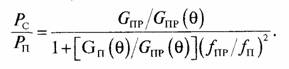
Из выражения (2) для уровня боковых лепестков можно определить, что отношение G_п(Ө)/G_пр(Ө) зависит от отношения длин волн (частот) на передачу и прием при одном и том же значении  Ө, так что G_П(Ө)/G_П(Ө) =ƒ _пр/ƒ_п и получим

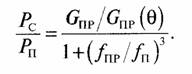
Для диапазона частот 11/14 ГГц, где 11 ГГц есть частота приема наземной станции, 14 ГГц — частота передачи наземной станции, можно записать: 

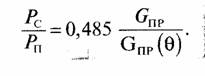
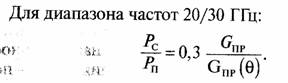
Из этих уравнений для защитного отношения P_С/ Р_П - 20 дБ необходимо определить диаметры антенн наземных станций, которые обеспечивают это заданное защитное отношение. Выразим коэффициент усиления приемной антенны с круглой апертурой через ее диаметр d. Имеем G_пр = k_ипπ² (d/λ)² где k_ип — коэффициент использования поверхности антенны. Для типового значения k_ип = 0,6 получим в дБ: G_ПР = 7,7 + 20 lg(d/λ).

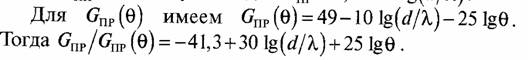
Можно принять, что угол Ө между двумя КА относительно наземной станции близок к углу Δφ между двумя КА относительно центра Земли, так что в вышенаписан-ном выражении можно записать по условиям задачи Ө = 2,5°. Окончательно найдем

Глава 4

Задача 47. Если скорость распространения электромагнитных колебаний (света в том числе) есть с =  300 000 км/с, то за время одного периода колебания Т электромагнитная волна пробегает расстояние, равное длине волны λ, т.е. сТ = λ. Частота колебаний f =1/T. Отсюда получаем λ = с/ f. Если λ выразить в см, а частоту ƒ в ГГц, то λ_Гсм] = 30/ƒ_{[ ГГц1}.

Задача 49. Скорость   самолета   составляет    V= 800 км/ч = 222,2 м/с. Частоте радиосигнала 300 МГц соответствует длина волны λ= 1 м. Отсюда доплеровское смещение частоты составляет Δƒ_д = V/λ= 222,2 Гц.

На частоте 11 ГГц максимальный доплеровский сдвиг частоты равен 264 Гц.

Задача 51. Максимальная радиальная скорость КА по отношению к наземной станции достигается, когда угол места КА равен нулю. В этом случае V= 8 км/с. При нулевом угле места КА расстояние между КА и наземной станцией равно r = 3,57√H, км, где H =700 000 м есть высота орбиты КА. Получим r = 3000 км. Это расстояние КА пролетает за 6 минут.

Частоте радиосигнала 2 ГГц соответствует длина волны λ = 15 см и максимальный доплеровский сдвиг частоты равен Δƒ_дМАКС = V/λ ~≈53 кГц.

Примерный ход изменения частоты Доплера во времени показан на рис. 72.

Доплеровское смещение частоты уменьшается в два раза при угле 60°, что наблюдается в моменты времени + 1 минута.

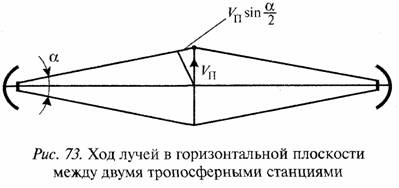
Задача 52. Отражатели (неоднородности тропосферы) при движении вдоль трассы распространения радиосигнала при переизлучении радиосигнала не создают доплеровского смещения частоты. Доплеровское смещение частоты создают только отражатели, имеющие компоненту вектора скорости в направлении поперек трассы распространения радиосигнала.

Рассеиватель с поперечной скоростью V_n создает доплеровское смещение частоты (см. рис. 73):

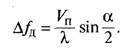
Задача 53. При замене кварца частота кварцевого генератора может изменится на величину долговременной нестабильности частоты кварцевого резонатора.

Задача 54. При относительной нестабильности кварцевого резонатора 10^-6 на градус Цельсия, относительная нестабильность частоты кварцевого генератора в интервале температур от -50 ⁰С до +50 °С будет равна 10^-4

Задача 55. Обозначим тактовую частоту передаваемых символов как F_T = 1/τ, тактовую частоту генератора тактовой частоты в несинхронизированном режиме как

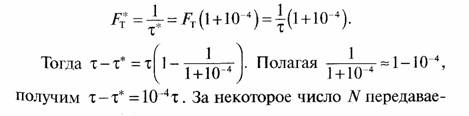
мых символов изменение длительности N символов будет равно N(τ-τ*) = 10^-4Nτ = τ/2. Отсюда N= 5000. При тактовой частоте передаваемых символов F_T=1МГц, длительность символа τ = 1/F_T = 1 мкс. Время, через которое начнется неправильная демодуляция символов равно T = Nτ = 5000 мкс = 5 мс.

Задача 56. Для частоты радиосигнала ω средне-квадратическое значение флюктуации фазы сигнала есть Δφ_Эф=ωΔτ_ЭФ, для удвоенной частоты Δφ_эф = 2ωΔτ_ЭФ, а при умножении частоты в п раз Δφ_эф =nωΔτ_Эф, поскольку при умножении частоты величина Δτ (моменты перехода гармонических колебаний через нуль) не изменяется. Мощность (дисперсия) фазовых флюктуации как квадрат величины Δφ_эф возрастает:

•  в 4 раза при удвоении частоты;

•  в п² раз при умножении частоты в п раз.

Глава 5

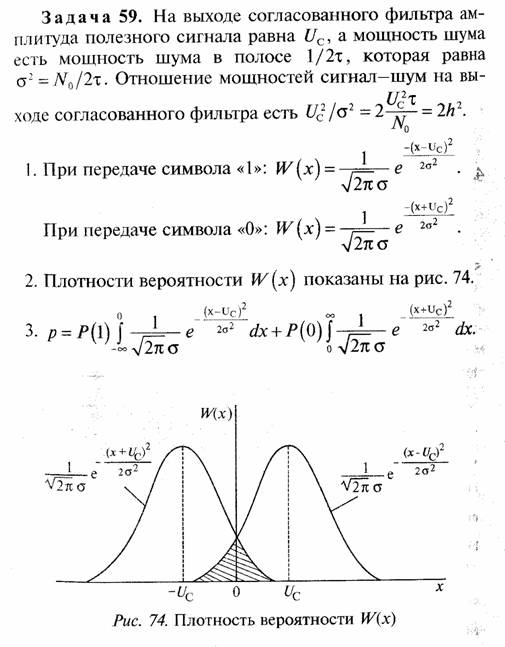
Задача 60. Передача сигналов по каналу связи без ошибок возможна. Шумы ограничивают скорость передачи информации согласно формуле Шеннона:

Вывод: в канале связи за счет идеального помехоустойчивого кодирования сообщений можно снизить требуемую величину h² с 10,5 дБ для канала без помехоустойчивого кодирования до величины —1,6 дБ. Таким образом, за счет помехоустойчивого кодирования потенциально можно получить выигрыш в энергетике канала связи до 10,5 + 1,6 = 12,1 дБ.

Задача 62. Находим вероятность того, что напряжение замирающего сигнала х будет больше величины х_п:

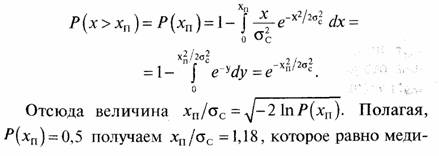
анному значению. По оси ординат будем откладывать глубину замираний в дБ относительно медианного значения напряжения, т.е. величину

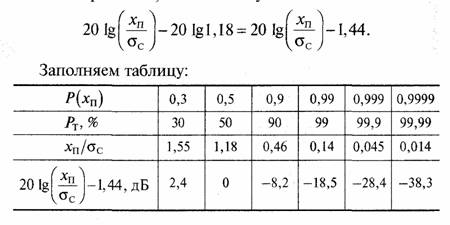
По данным таблицы строим график (рис. 76) глубины замираний сигнала относительно медианного значения в дБ в зависимости от процента времени Р_т, в течение которого глубина замираний меньше величины, отложенной по оси ординат.

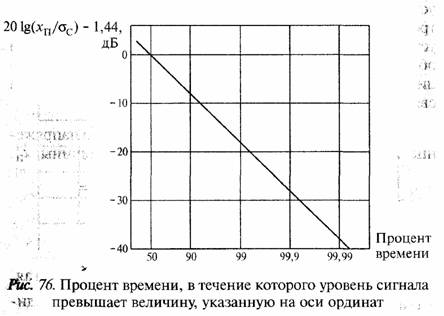
Из таблицы и приведенного графика определяем запас на замирания:

•  для мобильной связи (надежность связи 99%) — 18,5 дБ;

•  для   фиксированной   связи    (надежность   связи 99,99%)-38,3 дБ.

При разнесенном приеме вероятность того, что одновременно в двух приемниках напряжение будет меньше величины х_п равна [l-P(X_п)] ². Вероятность того, что напряжение в одном или двух приемниках будет больше х_п равна l-[l-P(x_п)] . Для мобильной связи должно обеспечиваться l-[l-Р(x_п)] ²= 0,99 откуда требуемая

величина Р(х_п) = 1 - √1-0,99 = 0,9 и требуемый запас на замирания составит 8,2 дБ. Таким образом, разнесенный прием дает энергетический выигрыш по отношению к одиночному приему 18,5 — 8,2 = 10,3 дБ.

Для   фиксированной   связи   аналогично   имеем 1-[1-Р(х_п)]² = 0,9999, откуда Р(х_п) = 0,99 и энергетический выигрыш от разнесенного приема равен 19,8 дБ.

Задача 63. Необходимый разнос частот между п несущими частотами для получения n-кратного частотно разнесенного приема равен ∆f= 1/τ_ЗАП.

3адача 64. На рис. 77 слева представлена векторная диаграмма двух лучей, отличающихся по частоте на ΔF_Д, а справа с помощью векторной диаграммы показана огибающая (кривая биений) двух лучей.

На рисунке интервал корреляции по времени τ_КОР определен как интервал времени, внутри которого значения огибающей биений еще близки друг к другу (τ_КОР в правой части рисунка кривой биений). Одновременно τ_кор определяет интервал времени, в течение которого огибающая изменяется от максимума до минимума.

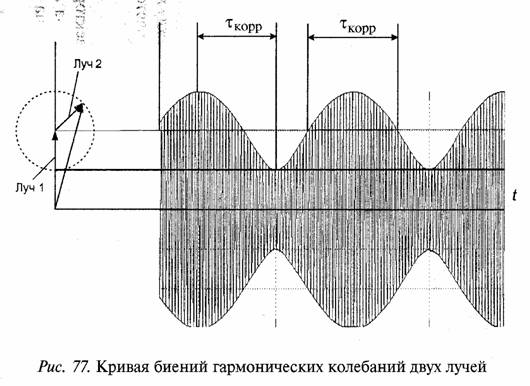
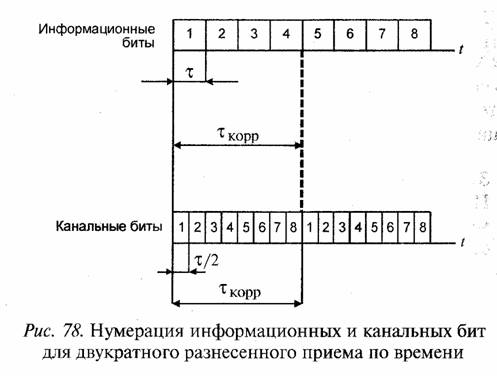
Период биений Т равен Т = 1/ΔF_д, а τ_КОР=Т/2 = 1/2 ΔFд. Для обеспечения разнесенного приема по времени символы сообщения должны быть разнесены на интервал корреляции τ_К0Р. Тогда если один символ попал в минимум кривой биений, то второй символ окажется в максимуме.

Отметим, что если число лучей велико с доплеровским рассеянием ±ΔFд, то обозначая интервал доплеров-ского рассеяния как ΔF_РАСС⁼2ΔFд, получим известный теоретический результат τ_К0РР = 1/2ΔF_д = 1/ΔF_PACC.

Для обеспечения сдвоенного разнесенного приема каждый информационной бит разбивается на два канальных символа длительностью τ/2 и формируется два повторяющихся кодовых слова на интервале времени 2 τ _{КОРР  ,}как это оказано на рис. 78.

Задача 65. Минимальный разнос частот для частотно-разнесенного приема сигналов равен Δf_p = 1/Δτ, где Δτ — интервал рассеяния сигнала по задержке. При Δτ = 3 мкс получаем Δƒ_р≥333 кГц.

Задача 66. Интервал корреляции тропосферного сигнала по частоте равен ΔF_К0РР =l/Δτ = l/0,25 мкс =  4 МГц. Для 4-кратного разнесенного приема необходимо полосу передаваемого тропосферного сигнала расширить (например, за счет псевдошумовой фазовой модуляции) до величины 4ΔF_K0PP = 16 МГц.

Задача 67

1. Пространственный разнос d между двумя антеннами мобильного терминала для пространственно-разнесенного приема сигналов определяется выражением:

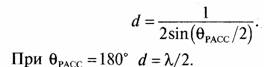
2.  Принимаемый сигнал изменяется от максимума до минимума при прохождении мобильным терминалом расстояния, равному интервалу пространственной корреляции сигнала d = λ/2 = 7,5 см.

3. При скорости движения мобильного терминала относительно базовой станции V= 60 км/ч = 17 м/с интервал временной когерентности сигнала есть τ_К0РР = = d/V = λ/2V = 4,4 мс.

4.  При скорости движения мобильного терминала V относительно базовой станции доплеровское рассеяние отраженных лучей лежит в пределах от нуля до ΔFд = V/λ. Согласно решению, полученному в задаче № 64, интервал корреляции по времени замирающего сигнала есть

Задача 68. Пространственный разнос между двумя приемными антеннами тропосферных станций в направлении перпендикулярном линии «Передатчик—приемник» для получения пространственно-разнесенного приема должен быть

и для  Ө_РАСС = 1⁰ = 0,0175 рад,   ƒ = 5,5 ГГц (λ = 5,45 см) получим d ≥ 3 м (между фазовыми центрами антенн).

Задача 69

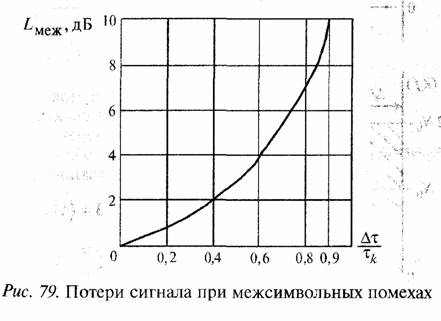
1. Потери в энергетике радиолинии за счет межеимвольной помехи в дБ:

Кривая энергетических потерь L_МЕЖ показана на рис. 79.

2. Если на передаче длительность канального символа τ_k уменьшается на величину Дт, то относительные потери в энергии символа составляют

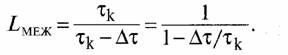
Эти потери равны потерям, рассмотренным в п. 1.

3. Из графика рис. 79 допустимым потерям в 1дБ соответствует величина Δτ/τ_k = 0,2, т.е. длительность канального символа τ_k = 5Дг =15 мкс. Отсюда скорость

передачи информации R при τ_k =15 мкс (R_k = l/τ_k =  67 кбит/с):

• при ФМ-2 R≤R_k = 67 кбит/с;

• при ФМ-4 R≤ R_k = 134 кбит/с;

• при ФМ-8 R ≤ 3R_k = 200 кбит/с;

• при КАМ-16 R ≤ 4R_k = 268 кбит/с.

4. Организация п параллельных каналов с разделением каналов по частоте или коду при допустимой канальной скорости R_k в одном канале.

Задача 70

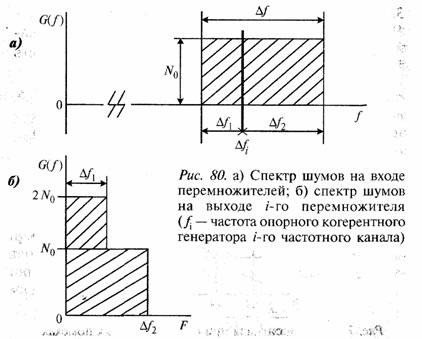
1. Представим напряжение шумов со спектральной плотностью N₀ в полосе частот Δƒ на входе схемы рис. 14 в виде U_Ш (t) = Σ_jU_j sin(2πƒ_jt+φ_j), где все  Uj одинаковы и U²_j/2= N_o (см. рис. 80).

На выходе i-го перемножителя напряжение шумов определяется выражением

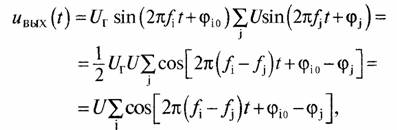
где опущены члены с суммарными частотами ƒi+ ƒj, поскольку они отфильтровываются интегратором с синхронным разрядом и где было положено U_Г/2 =1. Спектр шумов на выходе перемножителя в области видеочастот показан на рис. 80, б.

2. Интегратор с синхронным разрядом имеет амплитудно-частотную   характеристику

Мощность шума на выходе интегратора с синхронным разрядом равна

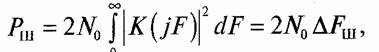
где шумовая полоса интегратора с синхронным разрядом есть;

Амплитуда сигнала на выходе интегратора с синхронным разрядом в конце интервала интегрирования равна:

Мощность сигнала на выходе интегратора с синхронным разрядом есть U²_C =2Р_С, где Р_с =U²_C /2 — мощность радиосигнала на выходе перемножителя и отношение мощностей сигнал—шум равно

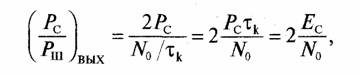
где Е_с = P_cτ_k есть энергия импульса сигнала длительностью τ_к на входе перемножителя.

Задача 71. Найдем напряжение помехи на выходе перемножителя k-го частотного канала, когда на его вход действует сигнал, передаваемый по i-му каналу.

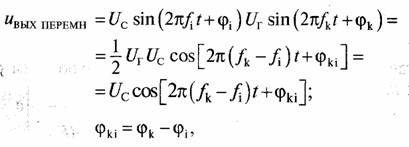
где было положено U_г/2 = 1 и опущен член с высокой частотой f_k+f_i, который отфильтровывается интегратором с синхронным разрядом.

На выходе интегратора с синхронным разрядом будем иметь напряжение помехи от одного сигнала

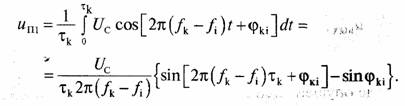
Напряжение помехи от всех п -1 ≈ п соседних каналов равно

Поскольку разность начальных фаз φ_ki есть случайная величина, то случайные независимые величины cosφ_ki суммируются по мощности (мощность случайной величины cos φ_ki равна 1/2). Тогда мощность результирующей помехи на выходе интегратора с синхронным разрядом k-го канала будет равна

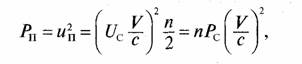
где P_C = U²_C /2 — мощность одного канального радиосигнала.

Так как амплитуда полезного сигнала на выходе интегратора с синхронным разрядом есть U_c, а мощность есть U²_C = 2Р_С, то отношение мощностей сигнала к помехе будет равно

Для наихудшего случая при п = 4096 каналов ОЧРК

и V= 300м/с получаем V/c = 10^-6и (P_c/P_п)_вых =5·10⁸ = =87 дБ. Отсюда следует вывод о возможности использования метода модуляции ОЧРК в мобильных сетях связи.

Глава 6

Задача 72. Следящая система по принципу работы есть система с отрицательной обратной связью, которая автоматически так подстраивает опорный управляемый сигнал (частоту и фазу ГУН на рис. 16), чтобы сигнал рассогласования (сигнал ошибки ε на рис. 16) на выходе фазового детектора (перемножителя) стремился к нулю.

В установившемся состоянии при входном сигнале U₀sin(ω_ct+τ_c) напряжение ГУНа должно равняться U_Гcos(ω_ct+τ_c).

Это следует из тригонометрического равенства

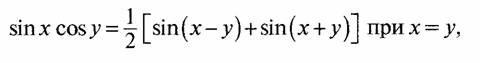
когда напряжение разностной частоты на входе перемножителя равно нулю, а член с удвоенной частотой подавляется фильтром нижних частот или самой схемой ФАП.

Задача 73. Изображение фазы ГУНа для системы ФАП без фильтра нижних частот есть

где опущен член с удвоенной частотой, который фильтровьтвается фильтром нижних частот.

В установившемся состоянии сигнал ошибки в системе ФАП с интегрирующим фильтром нижних частот равен нулю (в отличие от системы ФАП без фильтра нижних частот и системы ФАП с RC-фильтром нижних частот). При выключении входного сигнала частота и фаза ГУНа сохраняются, поскольку необходимое напряжение для управления частотой ГУНа запомнены интегратором фильтра нижних частот.

Задача 78. Изображение сигнала ошибки системы ФАП для фильтра нижних частот с интегратором при скачке частоты Δω найдено в задаче № 77

Знаменатель этого выражения преобразуем следующим образом:

По таблицам обратного преобразования Лапласа находим:

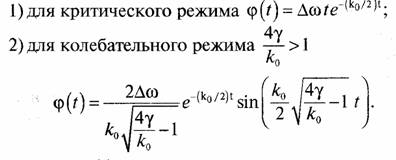
Кривые φ (t) показаны на рис. 81.

Для определения полосы захвата системы ФАП найдем максимум функции φ (t) для критического режима из уравнения

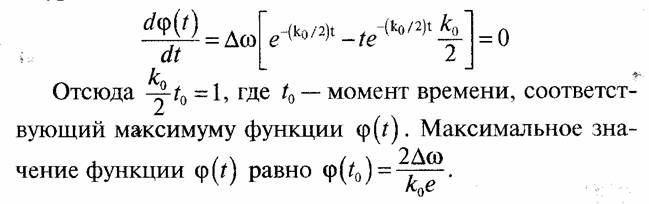
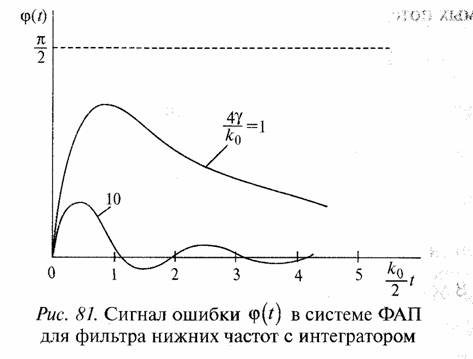
Полоса захвата Δω= Δω_ЗАХв определяется из уравнения

Задача 79. На входах когерентного детектора действует полезный сигнал U_csin(ω_ct+φ₀) и колебание когерентного генератора U_c sin (ω_с t+φ₀ + Δφ).

На выходе перемножителя получим колебание:

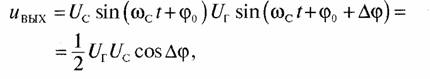
где член с удвоенной частотой опущен, поскольку он отфильтровывается последующим фильтром нижних частот.

Потери в амплитуде выходного сигнала по отношению к случаю Δφ = 0 равны 1/cos Δφ. Отсюда для допустимых потерь 0,3 дБ получаем уравнение

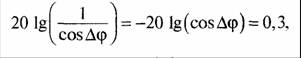
откуда cosΔφ = 0,966 и Δφ = 15°или Δφ = 0,26 радиан.

Задача 80. В теоретической части разд. 6.1 было получено выражение для сигнала ошибки слежения по фазе в системе ФАП без фильтра нижних частот

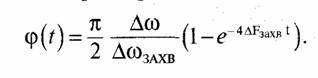
В установившемся режиме величина фазовой ошибки равна

При допустимой ошибке слежения рад получаем уравнение

При допустимой ошибке слежения рад получаем уравнение откуда величина  т. е. допустимая расстройка частоты радио-

сигнала составляет 13% от полосы захвата.

Задача 81. Время Т завершения процесса синхронизации в системе ФАП первого порядка определяется из уравнения 1 – е^{-4ΔFзахвТ} =0,95.

Отсюда 4ΔF_3AXBT = 3, Т = 0,75/ΔF_3AXB .

Время Т завершения процесса синхронизации, нормированное относительно величины 2/к₀, обозначим через    х = k₀Т/2.   Оно   определяется   из   уравнения

Последнее уравнение решается графически: х = 4,57. Отсюда Т = 9,14/k₀.

Используя уравнение Δω_ЗАХВ = 2πΔF_захв -= 8AF_3AXB /e, получим Т = 3,1/ΔF_ЗАхв.

Задача 83. Допустимая погрешность системы тактовой синхронизации Дт/т определяется из уравнения

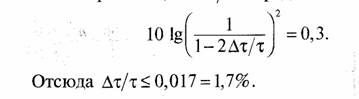
Задача 84. Обозначим тактовую частоту передаваемых символов сигнала через F_T=1/τ, где τ —длительность передаваемых символов сигнала. Аналогично обозначим тактовую частоту генератора тактовых импульсов в приемнике через 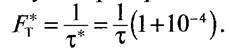Тогда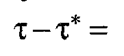

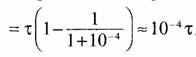
За некоторое число N передаваемых символов расхождение передаваемых символов относительно символов генератора тактовой частоты станет равным N(τ - τ*) = 10^-4Nτ = 0,01г. Отсюда N= 100.

Глава 7

Задача 91. Человек произносит в секунду 2—3 слова с общим числом букв в этих словах 10—15. Отсюда при слитной речи телефонный сигнал может быть передан по телеграфному каналу со скоростью 50—75 бит/с.

Задача 92

1. Общий диапазон уровней квантования должен составлять 15 + 8 = 23 дБ как для положительной полярности сигнала так и для отрицательных значений телефонного сигнала. Для этого потребуется число разрядов двоичного кода k= (23 + 3)/6 ≈ 4. Отсюда скорость передачи информации R = 8 кГц • 4 = 32 кбит/с.

2. Используя метод предсказания, можно иметь скорость передачи телефонного сигнала R= 16 кбит/с.

3. Считая, что пауза речи занимают 50% времени, телефонный сигнал можно передавать на скорости R = 8 кбит/с.

Задача 93. Для передачи 8—10 градаций яркости требуется оцифровка выборки телевизионного сигнала тремя-четырьмя битами. Коэффициент сжатия в этом случае будет равен 2—2,7 раза.

Глава 8

Задача 94. Напряжения на выходе интегратора подсчитывалось как

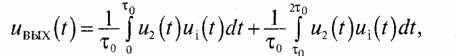
где i — 1,2,3. Из рис. 33 следует, что коэффициент корреляции между двумя разными сигналами равен cos 120° =

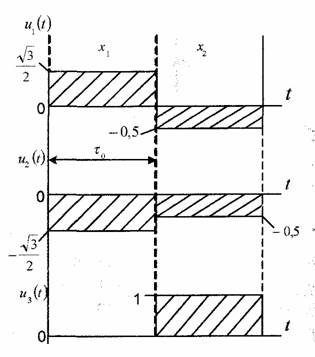
Рис. 83. Симплексные сигналы двумерного пространства сигналов как функции времени

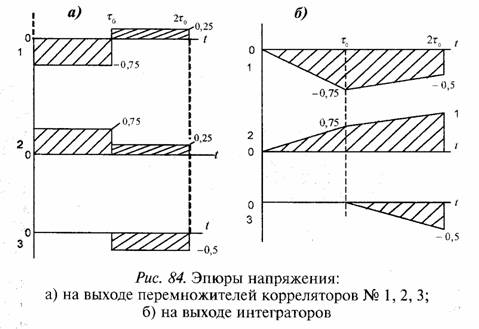
= -0,5, что совпадает со значением напряжений на выходе корреляторов, показанных на рис. 84, б.

Задача 95. Согласно рис.85 четыре симплексный сигнала записываются еле дующим образом:  

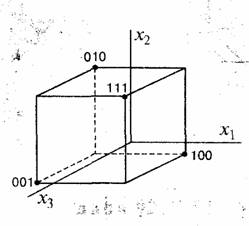
Рис. 85. Сигнальные точки симплексного кода в трехмерном пространстве

010

111

100

001

Добавим каждому кодовому слову справа по символу 1.

Получим следующий ансамбль двоичных ортогональных кодовых слов:

0101

1111

1001

0011

Каждая пара кодовых слов имеет ровно половину совпадающих символов и половину не совпадающих символов, что при перемножении напряжений двух кодовых слов и интегрирования (суммирования) полученного напряжения даст нуль (коэффициент корреляции р = 0).

Хэммингово расстояние между любой парой ортогонатных кодовых слов, полученных выше, равно двум.

Задача 96. Число кодовых слов троичного кода при фиксированном временном положении нулевого символа (рис. 86) равно 2² = 4. Число возможных положений нулевого символа есть число сочетаний из трех по одному С₃¹=3. Итого, число кодовых слов ансамбля равно М = 2²С¹₃ = 12.

На рис. 86, а показаны два ближайших кодовых слова. Радиус сферы, на поверхности которой лежат концы кодовых слов троичного кода, есть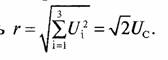

Из рис. 86, б расстояние между ближайшими сигналами d = √2 U_c и отношение d/r = 1. Коэффициент плотности укладки кодовых слов М (d/r)² =12.

Найдем величину d/r икосаэдра и сравним эту величину найденную для троичного кода.

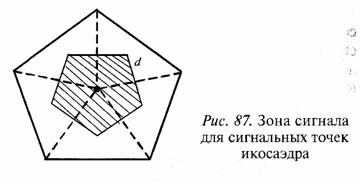
На рис. 87 показана зона сигнала для одной сигнальной точки икосаэдра. Заштрихованная площадь зоны сигнала равна S = 4πr²/12, где r—радиус сферы, на поверхности которой лежат сигнальные точки (вершины) икосаэдра.

Расстояние d между сигнальными точками найдем, заменив сферический пятиугольник плоским.

Получим

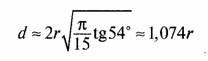
и d/r =1,074 ≈1, что совпадает с параметрами троичного кода.

На основании полученных результатов можно сделать заключение, что рассмотренный выше троичный код является оптимальным кодом поверхностно-сферической укладки трехмерного пространства.

Задача 97

1. Троичный код с одним нулевым символом имеет число  кодовых слов при п = 5   М = 2⁴  С¹₅ = 80.  

Два возможных ближайших кодовых слова показаны на рис. 88, а.

Аналогично показаны возможные ближайшие кодовые слова для троичного кода с двумя нулевыми символами (рис. 88,6) и тремя нулевыми символами (рис. 88, в). Для всех троичных кодов рис. 88 расстояние между ближайшими сигналами, как видно из рис. 88, равно d = √2U_C .

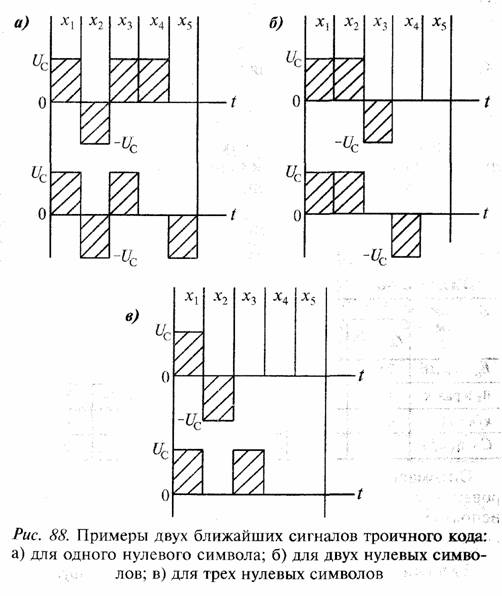
Для троичного кода с одним нулевым символом радиус сферы на поверхности которой лежат сигнальные точки кодовых слов, равен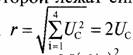 Тогда отношение d/r =1/√2 и величина M(d/r)² =40.

2. Для троичного кода с двумя нулевыми символами получим:

3. Для троичного кода с тремя нулевыми символами получим.;

4. Для полноты картины для троичного кода с четырьмя нулевыми символами получим:

Из рассмотренных троичных кодов при n = 5 с одним, двумя и тремя нулевыми символами при одном и том же расстоянии между ближайшими кодовыми словами наибольшее число возможных кодовых слов имеет троичный код с двумя нулевыми символами, который и следует считать оптимальным.

Оптимальный сверточный код имеет скорость кодирования r_к = 3/4. Оптимальный каскадный код должен использовать внутренний сверточный код со скоростью кодирования 3/4.

Задача 99. Оптимальный код БЧХ есть (64,45).

Глава 9

Задача 101. Образуем сферу с центром в точке расположения передающей антенны и радиусом r. Из закона сохранения энергии можно утверждать, что для свободного пространства без потерь мощность, проходящая через поверхность сферы площадью 4πr² равна излучаемой мощности Рп. Тогда плотность потока мощности, проходящая через площадку площадью 1 м² на расстоянии г от передающей антенны равна

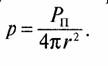
            Задача 103

1. Коэффициент усиления антенны ретранслятора КА с глобальным лучом 17°х17° равен 19,8 дБ.

2. Коэффициент антенны ретранслятора с шириной диаграммы направленности 5° х 11 °  равен 27 дБ.

3. Прямоугольная апертура 10 смх20 см на частоте 10 ГГц (λ = 3 см) создает диаграмму направленности 21⁰х10,5° и имеет коэффициент усиления 21 дБ.

Задача 104. Пусть на длине трассы l_z при распространении сигнала в зенит ослабление сигнала составило L_AZ дБ. Длина наклонной трассы распространения сигнала при угле места а будет равна l_z/sina и ослабление сигнала на наклонной трассе будет равно L_Az/sinα,дБ

Температура шумов атмосферы определяется выражением Т_А =275(1 -1/L_А), где L_A дается в разах. Для исходных данных задачи получим

Задача 106. Ответ: да, можно уменьшить диаметр апертуры антенны в √2 раз. Но при этом необходимо увеличить мощность передатчика наземной станции в 2 раза для сохранения той же самой ЭИИМ станции.

Задача 107. Для расчета энергетического потенциала радиолинии «Космос—Земля» и требуемых параметров наземной станции используем выражение

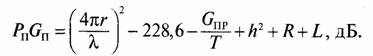
Из этого выражения необходимо определить требуемый коэффициент усиления приемной антенны и затем диаметр антенны.

Определим численные значения параметров, входящих в уравнение:

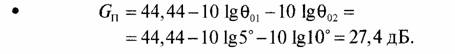
Это — коэффициент усиления антенны в максимуме в центре зоны обслуживания. Наша наземная станция находится на краю зоны обслуживания, где принимаем, что коэффициент усиления антенны КА на 3 дБ меньше и равен 24,4 дБ. Для одной станции на ее рабочей частоте выделяется излучаемая мощность 0,02 Вт = -17 дБВт. Тогда ЭИИМ

для угла места наземной станции 5° получаем дальность связи r = 40 000 км и для частоты радиолинии вниз 4 ГГц (λ= 7,5 см) получаем 

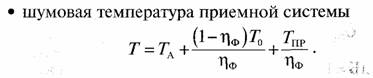
T_А —шумовая температура антенны, T_А=η_АT_я, где принимаем, что η_А =0,75, Т_я≈ Т_А, где шумы атмосферы Т_А при угле места 5° равны 30 К, космическими шумами можно пренебречь. Шумами Земли, принимаемыми боковыми лепестками диаграммы направленности, пренебрежем, считая уровень боковых лепестков малым. Тогда Т_А ≈ 23 К. Потери в фидере положим равными 0,3 дБ, что дает значение η_ф =0,93. Положим Т_о = 290К, Т_ПР = Т_мшу = 40К. Тогда

· для вероятности ошибки на бит 10 ⁶ и кода без избыточности h² =10,5дБ+Lд_ЕМ, где Lд_Eм — потери сигнала в демодуляторе приемника за счет шумов, вносимых системой синхронизации по несущей и фазовых шумов. Принимаем h² = 11 дБ;

· R = 64 кбит/с = 48 дБ;

· потери L в радиолинии складываются за счет переизлучения шумов радиолинии вверх (~ 1 дБ), перекрестных помех в ретрансляторе (~0,3 дБ для выбранного квазилинейного режима усилителя мощности ретранслятора), рассогласования поляризационных характеристик антенны ретранслятора и наземной станции (~0,25 дБ), неточности наведения антенны наземной станции на КА (~0,25 дБ). Итого, положим L = 1,8 дБ

Результат расчета:

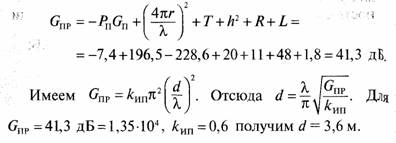
Задача 108. При всенаправленных передающих g приемных антеннах G_П = const и G_пp = const.

            Тогда Р_с = const • λ² и более выгодными энергетически будут более низкочастотные диапазоны частот, в частности метровой диапазон волн из числа перечисленных.

            Задача 109. В выражении (3) следует положить S_пр = const. Тогда Р_с = const • G_п, где коэффициент усиления передающей антенны при фиксированной апертуре растет с увеличением частоты как ƒ², т.е. Р_с = const·ƒ², т.е. наиболее выгодными энергетически оказывается наиболее высокочастотные диапазоны частот, т.е. оптический. Однако на частотах более 10 ГГц растет ослабление радиосигнала в дожде. Это ослабление растет быстрее чем Р, так что наиболее выгодными энергетически оказываются диапазоны частот 11—15 ГГц.

Задача 111. При связи с мобильным терминалом вектор отраженного сигнала все время вращается относительно вектора прямого луча. В наихудшем случае фаза отраженного сигнала сдвинута на 180° относительно фазы прямого луча. В этом случае амплитуда суммарного сигната составляет 30% от амплитуды прямого луча, что дает максимальные потери в мощности принимаемого сигнала

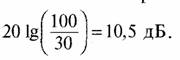
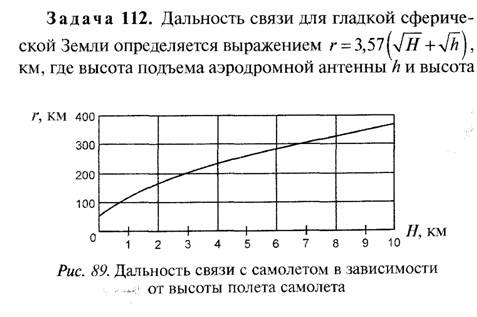
полета самолета H даны в метрах. Для h = 15 м график зависимости дальности связи с самолетом в зависимости от высоты его полета представлен на рис. 89.

Задача 113. Вначале определяем высоту подъема антенн h_x = h₂=h₀ для нулевого просвета трассы из уравнения 

Для r = 50 км получаем h₀ = 49 м ~≈50 м.                   

Радиус первой зоны Френеля F₁ = 25 м. Окончательно высоты подъема антенн должны быть

            Задача 114. Ослабление сигнала в дожде определяется выражением L_д = γ_дl_э. Определим γ_д =0,07/^1,07, где I= 30 мм/ч. Получим γ_д = 2,66 дБ/км.                      

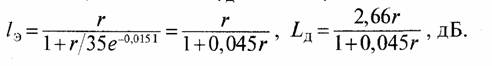
График величины L_д представлен на рис. 90. Из рис. 90 следует, что длина интервала между радиорелейными станциями не должна превышать 23 км.       

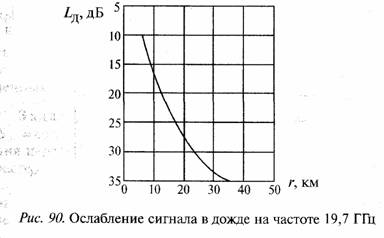
Задача 115. Находим удельное поглощение радиосигнала в дожде по формуле γ_д = аI^B, где для частоты 20 ГГц, а = 0,07, в = 1,07. Получим γ_д << 0,476 дБ/км.

Воспользуемся кривой эквивалентной длины трассы из рис.36, полагая I= 6 мм/ч = 5 мм/ч. Тогда получим требуемую зависимость поглощения радиосигнала от угла места наземной станции, показанную на рис. 91.

Задача 116. На максимальной дальности полета самолета следует принять угол места наземной станции равным нулю и воспользоваться кривыми эквивалентной длины трассы в дожде для спутниковых радиолиний (рис.36). Из решения задачи №115 берем значение γ_д =0,5 дБ/км и для l_э = 25 км получаем L_д = 12,5 дБ.

Глава 10

Задача 117. Число бит на периоде от последовательности равно N = 2^т -1 ≈ 2^т.

Длительность одного бита m-последовательности τ = 1/2,048-10⁶≈0,5мк

Тогда период m-последовательности будет равен

где было использовано соотношение 2^m = 10^mlg2 = 10^0,3m.

            Задача 118. Число избыточных бит г для каждой команды (или группы команд) определяется из уравнения (1/2)^r ≤10^-9 или 10^-0,3r =10^-9. Отсюда r= 30.

Для защиты командного приемника от приема ранее переданных команд, ретранслируемых противником, можно предложить нумерацию каждой команды со стиранием принятых команд с предыдущими номерами или с каждой командой передавать текущее время, если в радиолинии используется система единого времени.

Задача 119. Обеспечивать имитозащиту засекреченного телефонного сигнала не требуется, поскольку вероятность того, что случайная последовательность бит, сформированная противником, превратится в осмысленную речь ничтожно мала.

Задача 120. Время запаздывания ретранслированного сигнала составляет τ₃=Δr/с, где Δr = 30км, с — скорость света. Тогда τ₃ = 100 мкс и время передачи сигнала на одной частоте в режиме ППРЧ не должно превышать τ₃ = 100 мкс.

Задача 121. Коэффициент усиления антенны равен

G_nx = k_ипπ²(d/λ)² . Для коэффициента использования поверхности антенны k_ип=0,6 получим G_пх=50дБ. ЭИИМ станции помех P_пxG_пx = 90 дБВт.

Задача 122. Для условий задачи уравнение помехо-защиты запишется как P_CG_C = Р_пхG_пх +h² –B, дБ, где база псевдошумового сигнала

Тогда P_CG_C =90+ 8-41,8 = 56,2. Для излучаемой мощности сигнала Р_с = 50 Вт= 17 дБВт получим требуемый коэффициент усиления антенны G_c = 39,2 дБ.

Из выражения для коэффициента усиления антенны

Задача 123. При приеме ПШС совместно с мощными узкополосными помехами можно полосу приемника на промежуточной частоте разделить на 8—16 отдельных полос полосовыми фильтрами с большой прямоугольностью (резким спадом АЧХ вне полосы фильтра по уровню — 3 дБ) и выключать те фильтры, где находится мощная узкополосная помеха. Для этого должен быть предусмотрен измеритель среднего по всем фильтрам уровня напряжения, которое сравнивается с напряжением на выходе каждого фильтра.

Если на выходе фильтра напряжение превышает на заданную величину среднее по всем фильтрам напряжение, этот фильтр выключается.

Задача 124. Из уравнения к²(Р_с+Р_п) = Р_о при отсутствии помехи коэффициент усиления ствола ретранслятора по мощности есть k²₀ - Р_о /Р_с. При наличии помехи можно записать

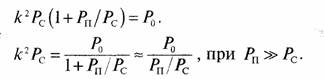
Для коэффициента усиления ретранслятора получим выражение

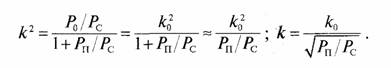
Задача 125. Используем выражение для времени скрытной работы

На основании исходных данных имеем:

Результат расчета:   T_0БН = 5,7 ∙ 10⁶ с ≈2 месяца.

При дополнительном уменьшении уровня боковых лепестков передающей антенны на 10 дБ в соответствии с выражением (5) и (6) время скрытной работы увеличивается в 100 раз.                                   

Задача 126. Время скрытной работы радиолинии определяется выражением:

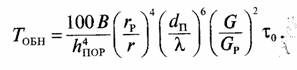
При дополнительном уменьшении уровня бокового излучения передающей антенны наземного терминала на 10дБ согласно выражениям (5) и (6) время скрытой работы радиолинии увеличивается в 100 раз и T_обн≈5,7 мин.

Задача 127. Рассмотрим спектр сигнала и шумов на выходе квадратичного детектора, показанный в решении задачи № 13 на рис. 67 в области удвоенной частоты. Из рис. 67 следует, что отношение мощностей сигнал—шум на выходе полосового фильтра с полосой Δƒ_у в области удвоенной частоты сигнала равно

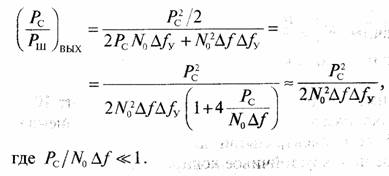
Из условия (Р_с/Рш)_вых = 50 находим:

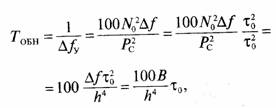
где было положено Р²_сτ²₀/N²₀= h⁴, где h² есть отношение энергии бита к спектральной плотности аддитивных шумов на входе приемника нашей радиолинии (и на входе разведывательного приемника); τ_o=1/R, где R — скорость передачи информации.

Также Δƒτ₀ = В есть база псевдошумового сигнала.

            Задача 128. Согласно исходным данным требуется обеспечить отношение спектральной плотности широкополосного стего-сигнала N_0cт к спектральной плотности аддитивных шумов приемника спутникового ретранслятора N_o, равное N_0CT/N₀ = 0,1.

Запишем: N_0СT =Р_СТ/Δƒ, где Р_ст —мощность стего-сигнала на выходе приемной антенны ретранслятора. Тогда

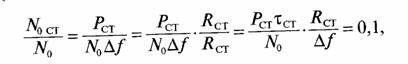
где R_CT = 1/τ_ст есть скорость передачи информации по стего-каналу.

Обозначим  отношение энергии бита к спектральной плотности аддитивных шумов в стего-канале.

            Положим, что для вероятности ошибки на бит 10 ^-6 в приемнике наземной станции требуется отношение энергии бита к спектральной плотности шумов 6дБ (сверточное помехоустойчивое кодирование).

            Тогда h²ст + Δ= 7дБ в радиолинии «Терминал—КА» и h²ст + Δ = 9 дБ в радиолинии «Базовая станция—терминал».

            Итак, имеем общее выражение для достижимой скорости передачи информации в спутниковой стего-радиолинии: