ПРЕДИСЛОВИЕ

Сборник задач с ответами и решениями по телекоммуникационным системам предназначен для закрепления знаний по базовым принципам и методам построения телекоммуникационных систем, излагаемых в курсах лекций «Основы построения телекоммуникационных систем и сетей», «Радиорелейные и спутниковые системы связи», «Проектирование телекоммуникационных систем», «Теоретические основы телекоммуникационных систем» (магистерский курс) и др.

Тематика задачника и сами задачи могут быть положены в основу государственного экзамена по совокупности телекоммуникационных дисциплин.

Способность решать предложенные задачи является прямым показателем понимания и усвоения студентом основополагающих принципов построения телекоммуникационных систем и его готовности к написанию дипломной работы или магистерской диссертации.

Сборник задач охватывает не весь спектр проблематики телекоммуникационных систем, который бесконечно широк, а только основной перечень фундаментальных проблем телекоммуникаций, которые должны быть успешно освоены студентом для подтверждения его высокой квалификации как современного специалиста.

Каждую тему предваряет краткое теоретическое введение, достаточное для решения предложенных задач, с тем, чтобы не обращаться к многочисленным литературным источникам, необходимы только калькулятор и «Справочник по математике для инженеров и студентов вузов» И.Н. Бронштейна и К.А. Семендяева («Физматгиз», любого года издания).

Необходимость издания такого сборника задач была инициирована заведующим кафедрой «Телекоммуникационные системы» МИЭТ профессором В.В. Бариновым, которому автор выражает глубокую признательность за помощь в работе. Также на написание сборника задач автор был вдохновлен своим успешным опытом использования материалов задачника при проведении семинарских занятий по читаемому им магистерскому курсу «Теоретические основы телекоммуникационных систем».

Профессор кафедры «Телекоммуникационные системы» МИЭТ,

докт. техн. наук КМ. ТЕПЛЯКОВ. Москва, 2008

ВВЕДЕНИЕ

Объединение компьютерных технологий и средств связи привело к созданию современных инфокоммуникационных систем. Инфокоммуникационную систему удобно разделить на две большие части: на так называемую первичную, или транспортную, сеть связи, назначение которой состоит в передаче и маршрутизации потоков информации, и на вторичную сеть — сеть информационных или телекоммуникационных услуг, в которой создаются многочисленные услуги такие, как услуги электронной почты, видеоконференцсвязи, доступа в Интернет и др.

Первичные или транспортные сети и системы называются телекоммуникационными сетями и системами. Создание телекоммуникационных систем требует больших материальных затрат и времени, вследствие чего они являются более консервативными по отношению к сетям информационных услуг. Основу вычислительных, или компьютерных, сетей и систем составляют различного рода протоколы: навигации в сети связи, поиска данных, доступа»к базам данных, протоколы обеспечения безопасности сети и данных и др., что следует отнести к области информационных услуг.

В данном учебном пособии рассматриваются только телекоммуникационные системы. Вся история развития телекоммуникационных систем, в первую очередь радиотехнических — это история борьбы с помехами: шумами, помехами от других радиосредств, искажениями сигналов в каналах передачи информации и др. Фундаментальную роль в создании высокоэффективных телекоммуникационных систем играют теория потенциальной помехоустойчивости В. А. Котельникова и теория информации К. Шэннона, а в более широком смысле — статистическая теория связи.

В сборник задач по телекоммуникационным системам включены все основные темы, составляющие фундамент проектирования телекоммуникационных систем:

спектры сигналов и шумов, критерии качества телекоммуникационных каналов и передаваемой информации, помехоустойчивость телекоммуникационных систем, оценка характеристик радиосигналов при их распространении, методы сжатия сообщений от источников информации, помехоустойчивое кодирование сообщений в каналах связи, методы синхронизации сигналов в радиолиниях, проблемы электромагнитной совместимости радиосистем, методы защиты информации и телекоммуникационных радиоканалов от организованных помех.

Решение задач сборника предполагает хорошую подготовку по всем дисциплинам телекоммуникационного профиля. Можно считать, что если студент решил все задачи сборника, то его уровень подготовки соответствует уровню магистра, если студент решил 100 задач, то он — бакалавр.

Сборник задач по совокупности телекоммуникационных дисциплин, по-видимому, является первым такого рода у нас в стране, поэтому автор с благодарностью ожидает предложения и критику от своих коллег-преподавателей по содержанию сборника.

ГЛАВА 1

ВЕКТОРНЫЕ И СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ И ШУМОВ

1.1. Векторное представление сигналов

Гармоническое колебание U_csin(ω_c+ φ) отображается на плоскости в виде вектора длиной, равной значению огибающей U_c, вращающегося на плоскости против часовой стрелки с угловой скоростью ω_с. Мгновенный угол вектора сигнала есть ω_сt+φ, где при t = 0 φ есть угол между направлением вектора сигнала и осью абсцисс.

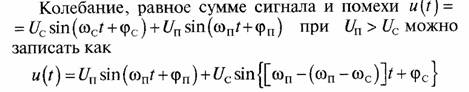
Задача 1. Для колебания, состоящего из суммы гармонических колебаний сигнала и помехи u(t) = U_c sin ω_c t + U_П sin ω_П t, показать на векторной диаграмме мгновенное значение огибающей u(t) и фазы вектора u(t) при U_П> U_С.

            Изобразить вид огибающей u(t) (кривую биений сигнала плюс помеха) как функцию времени, используя векторную диаграмму сигнала и помехи, для случаев: 1)U_П>>U_С; 2)U_П = U_С.

Задача 2. Для    суммы    гармонической    помехи: U_Пsinω_Пt и отрезка гармонического сигнала U_Сsinω _ct длительностью τ (τ — длительность радиоимпульса сигнала) для случаяизобразить вид огибающей помехи и огибающей колебания сигнал плюс помеха на некотором отрезке времени Т> т.

Задача 3. Заданы: гармоническая помеха U_Пsinω_Пt и фазоманипулированный на 180° сигнал U_Сsin [ω _сt+ φ (t)], где φ (t) поочередно имеет значения φ (t) = 0 и φ (t) = π, так что полезный сигнал проманипулирован по фазе на π меандровым сигналом с длительностью символа τ.

             Требуется:

•  изобразить векторную диаграмму фазоманипулированного сигнала U_c sin [ω _c t + φ (t¹)];

            •  изобразить векторную диаграмму суммы колебания помехи  и  фазоманипулированного  сигнала  при U_П>U_С;

            •  изобразить огибающую гармонической помехи и фазоманипулированного сигнала как функцию времени при U_П>U_С и 2 π (ω _п- ω _с) >> 1/ τ;

            •  полагая, что сумма гармонической помехи и фазоманипулированного сигнала поступают на вход радиоприемника и в тракте приемника или усилителя мощности ретранслятора происходит ограничение суммарного колебания сигнала плюс помеха, указать на входной огибающей суммы гармонической помехи и фазоманипулированного сигнала моменты времени, когда полезный сигнал будет подавлен помехой и пояснить почему. Принять U_П>U_C.

Задача 4. Задана радиолиния, работающая на длине волны λ = 50 см, со следующими параметрами:

            •  расстояние между неподвижным передатчиком и приемником r = 10 км;

            •  высоты поднятия передающей и приемной антенн радиолинии одинаковы и равны h = 10 м;

•  на вход приемной антенны поступает сигнал прямого луча и сигнал, отраженный от поверхности Земли. Фаза сигнала при отражении от Земли меняется на 180°. Коэффициент отражения сигнала от поверхности Земли равен 0,96.

Полагая поверхность Земли плоской в пределах действия радиолинии, определить:

•  амплитуду суммарного прямого и отраженного сигналов на выходе приемной антенны (используя векторное представление сигналов и запаздывание по фазе отраженного сигнала);

•  потери в энергетике радиолинии в дБ за счет вредного действия отраженного луча.

1.2. Спектры сигналов

Периодическая последовательность сигналов от t = - ∞ до t =+ ∞ может быть представлена в виде суммы гармонических сигналов с частотами к/Т_П (ряд Фурье), где k = 0,1,2,..., Т_П — период повторения сигналов. Амплитуды этих гармонических сигналов, отложенные по оси ординат как функция частоты, откладываемой по оси абсцисс, называются спектром периодического сигнала.

            Аналогично, непериодический сигнал может быть представлен суммой (интегралом) бесконечно близких частот, огибающая амплитуд которых является спектром (спектральной плотностью) непериодического сигнала. Если действительный (не комплексный) спектр сигнала есть U(F), то спектральная составляющая на частоте F может быть записана как dFU(F)cos(2πFt + φ). Сумма (интеграл) таких составляющих описывают непериодический сигнал во времени.

            Аналитически непериодический сигнал U(t) представим в форме  обратного преобразования Фурье

            Амплитудный спектр U(Ω.) или U(F) содержит как положительные, так и отрицательные частоты, которые появляются при представлении гармонических сигналов на комплексной плоскости.

            Из тождеств Эйлера

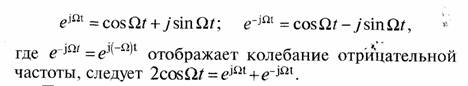
            Поскольку отрицательных частот в природе не существует, то для получения реального спектра амплитуд берут действительную часть комплексного спектра (положительные частоты) и умножают его на два. Таким образом, выражение для реального спектра амплитуд записывается как 2U(Ω)для положительных частот. Колебание на частоте Ω  равно 2U(Ω)cosΩt.

            Так как мощность гармонического колебания UcosΩt есть U²/2, то спектр мощности реального сигнала для положительных частот есть S(Ω) = 2U²(Ω) или S(F) =

= 2U²(F).

Задача 5. Вычислить спектр (интеграл Фурье) одиночного прямоугольного импульса U_c(t), изображенного на рис. 1.

            Найти спектр радиоимпульса U_c(t)sin2πf₀t с прямоугольной огибающей, показанной на

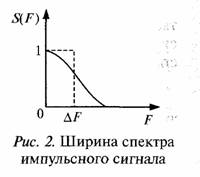
Задача 6. Ширина спектра импульсного сигнала определяется как ширина ΔF прямоугольника, равного площади нормированного спектра S(F), как это показано на рис. 2.

            Определить ширину спектра прямоугольного импульса сигнала с параметрами, показанными на рис. 1.

Определить произведение длительности импульса сигнала на ширину его спектра τ*ΔF (соотношение неопределенности). Найти соотношение неопределенности для радиоимпульса U_C(t)sin2πf₀t с прямоугольной огибающей и длительностью радиоимпульса τ.

Полагая, что амплитудно-частотная характеристика приемного устройства повторяет спектр радиоимпульса (линейная часть приемника представляет собой согласованный фильтр) определить требуемую ширину полосы пропускания приемного устройства.

Задача 7. Зная спектр одиночного прямоугольного импульса длительностью τ (рис. 1), изобразить спектр бесконечной периодической последовательности прямоугольных импульсов длительностью τ с периодом повторения Т_П:

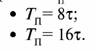
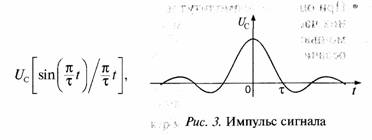
Задача  8. Для одиночного импульса вида показанного на рис. 3, найти его спектр.

Задача 9. Для гармонической несущей частоты f₀, манипулированной по фазе на 180° меандровым сигналом с длительностью импульсов τ, изобразить ее спектр.

Задача 10. Для передачи речевого сигнала по каналу связи используется полосный вокодер.

            Вокодер на передаче состоит из 10 параллельных фильтров с полосой каждого фильтра 300 Гц, которые перекрывают всю полосу частот речевого сигнала от 300 Гц до 3300 Гц. На выходе каждого фильтра стоит амплитудный детектор и фильтр нижних частот с полосой порядка 30 Гц (время интегрирования фильтра нижних частот порядка 30 мс равно длительности слога речевого сигнала).

            Таким образом, на передающем конце канала связи каждые 30 мс формируются коэффициенты Фурье амплитудного спектра речевого сигнала (фазы спектральных составляющих спектра речи не измеряются, поскольку фазовые искажения речевого сигнала не влияют на разборчивость речи).

            По каналу связи вместо речевого сигнала передаются каждые 30 мс коэффициенты Фурье спектра речевого сигнала.

            Требуется:

            •  Изобразить функциональную схему восстановления речевого сигнала на приемном конце канала связи при передаче звонких звуков, имеющих квазидискретный спектр.

            •  При оцифровке амплитуд на выходах фильтров нижних частот на передающем конце канала связи с помощью трехразрядного АЦП определить скорость передачи речевого сигнала по каналу связи с помощью вокодера. Определить во сколько раз скорость передачи речевого вокодерного сигнала меньше стандартной  скорости  передачи телефонного  сигнала 64 кбит/с при ИКМ

1.3. Спектральное представление шумов

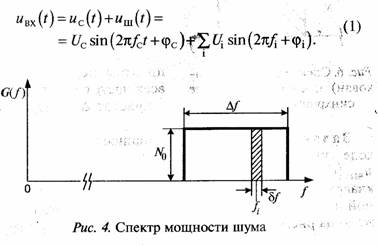
Гауссовский шум с равномерным спектром мощности в некоторой полосе частот Δf (см. рис. 4) можно аппроксимировать суммой большого числа гармонических колебаний равной амплитуды со случайными начальными фазами поскольку известно, что сумма большого числа гармонических колебаний со случайными начальными фазами имеет гауссовское распределение плотности вероятностей.

Итак, напряжение шума можно выразить как

где U²₁ /2 есть мощность i-й компоненты шума. Из рис. 4 можно записать

где N_o — спектральная плотность шума, δf — некоторая узкая полоса частот в окрестности частоты fi. Удобно положить δf=1 Гц. Тогда U²i/2 = N₀ и все U_i одинаковы в полосе частот Δf.

Для суммы полезного сигнала и шума можно записать

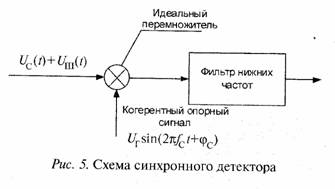
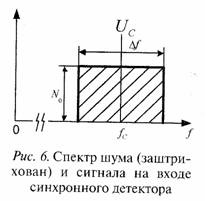
Задача 11. На входе синхронного детектора, показанного на рис. 5, действует сумма полезного сигнала и шума (см. выражение (1)). Спектр входного сигнала и шума показан на рис. 6. Положить амплитуду когерентного опорного сигнала U_Г/2 =1.

            Определить и нарисовать спектр шума на выходе перемножителя схемы рис. 5 и определить отношение мощностей сигнал—шум на выходе фильтра нижних частот с прямоугольной формой амплитудно-частотной характеристики с полосой от нуля до ΔF с коэффициентом передачи 1 для всех частот внутри полосы частот ΔF ≤ Δf/2.

Задача 12. Найти спектр мощности шумов на выходе квадратичного детектора с характеристикой u_вых(t) ⁼ u²_вх(t) в области видеочастот, если на входе квадратичного детектора действует шум со спектральной плотностью N₀ в полосе частот Δf, как это изображено на рис. 4.                           

Задача 13. Найти и нарисовать спектр сигнала и спектр мощности шумов на выходе квадратичного детектора в области видеочастот и на удвоенной частоте когда на входе квадратичного детектора с характеристикой и_вых(t) = u²_вх (t) действует гармонический сигнал и шум со спектральной плотностью N₀ в радиополосе Δf (выражение (1)), как показано на рис. 6.

Примечание. Удвоитель частоты часто используется как схема снятия фазовой манипуляции фазы сигнала на 180° для формирования в дальнейшем опорного когерентного колебания для синхронного детектора.

ГЛАВА 2

СКОРОСТЬ ПЕРЕДАЧИ ИНФОРМАЦИИ

В ОДНОКАНАЛЬНЫХ И МНОГОКАНАЛЬНЫХ

ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ

2.1. Скорость передачи информации в канале связи

На передающем конце канала связи скорость передачи в битах в секунду определяется выражением R= F_симв log₂ М, бит/с, где F_симв — частота следования канальных символов в Герцах, М— число возможных значений одного символа.                   

В одном направлении в полосе телефонного канала связи от 300 Гц до 3400 Гц на поднесущей (тональной) частоте 1800 Гц (полоса канала связи 3100 Гц) обеспечивается скорость передачи 2400 бит/с при использовании фазовой манипуляции сигнала на 180° (ФМ-2), т.е. F_симв =2400 Гц, М=2. Без расширения полосы частот передаваемых символов можно использовать большее число возможных значений фаз и амплитуд передаваемых символов М> 2, увеличив скорость передачи по каналу связи.

Задача 14. Найти скорость передачи R бит/с в канале тональной частоты для четырехфазной ФМ (ФМ-4) и восьмифазной ФМ (ФМ-8).

Заполнить таблицу:

Задача 15. При квадратурной амплитудно-фазовой модуляции (КАМ) используются 4 градации фазы сигнала, так что образуются два независимых канала связи, синфазный и квадратурный, в каждом из которых используется L амплитудных значений сигнала (L/2 положительной полярности и L/2 отрицательной полярности), итого М = L². При L = 2 получаем известную ФМ-4.

            Требуется определить скорость передачи в канале тональной частоты в соответствии с предлагаемой таблицей для модуляции сигнала методом КАМ.

Задача 16. При наличии в канале связи белого гауссовского шума возможна ли передача цифровых сообщений без ошибок? Если да, то с какой скоростью передачи информации?

2.2. Скорость передачи информации, необходимая для передачи аналоговых сообщений

            При передаче аналогового сообщения (телефонный сигнал, изображение, телеметрический сигнал и др.) по цифровому каналу связи при малой вероятности ошибки на бит (~10^-6) цифровой канал связи практически не вносит искажений в передаваемое аналоговое сообщение. Искажения аналогового сообщения возникают при преобразовании аналогового сообщения в цифровое при дискретизации аналогового сообщения во времени(формировании выборок аналогового сообщения) и квантовании (оцифровке) выборок по амплитуде. Эти отклонения переданного по каналу связи сигнала от исходного неискаженного аналогового сигнала вследствие случайного (стохастического) характера передаваемых аналоговых сообщений являются случайным процессом и в телеметрии, например, характеризуются среднеквадратической ошибкой дискретизации ε_д сообщения по времени и среднеквадратической ошибкой квантования ε_кв выборок по амплитуде. Величины ε_д и ε_кв являются независимыми и результирующая среднеквадратическая величина искажения аналогового сообщения при преобразовании  его  в  цифровое  сообщение  равна ε= √ε²д + ε²_кв. Среднеквадратические ошибки ε_кв, ε_д, ε вычисляются относительно максимального значения аналогового сигнала.

            Аналоговый сигнал с максимальной амплитудой ±U_C делится на L >>1 амплитудных уровней с шагом квантования Δ, который примем одинаковым для всех амплитудных уровней сигнала, так что при L >> 1 U_c = LΔ/2. Максимальная ошибка квантования не превышает величины Δ/2, а среднеквадратическое значение шумов квантования равно σ_кв = Δ/2√3. Отсюда, если все уровни квантования равновероятны,

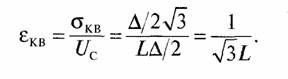
            Число уровней квантования L выбирается таким образом, чтобы оно было представимо двоичным кодом с числом информационных разрядов (бит) k, так, что L = 2^k. Оцифровка выборок осуществляется в АЦП.

Задача 17. Полагая, что шумы квантования описываются равновероятной плотностью распределения вероятностей внутри интервала квантования ±Δ/2, определить дисперсию шумов квантования σ²_кв.                      

            Задача 18. Отношение амплитуды сигнала к среднеквадратической ошибке квантования (отношение сигнал-шум квантования по амплитуде) есть

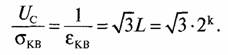
            На сколько дБ увеличится отношение сигнал—шум квантования при увеличении величины к на: а) один разряд; б) на два разряда?

            Задача 19. При передаче телеметрических сообщений требуется обеспечить погрешность измерений не хуже 1%. Полагая, что ошибка квантования ε_кв ≤ 0,5%, определить необходимое число разрядов АЦП при оцифровке выборок телеметрического сигнала.

Задача 20. При передаче вещательного телевизионного сигнала цифровым методом требуется обеспечить отношение сигнал—шум квантования не менее 50 дБ. Определить число разрядов АЦП, необходимых для оцифровки выборок телевизионного сигнала.

Дискретизация аналоговых сигналов по времени

            Передача оцифрованных выборок аналогового сигнала по цифровой линии связи называется передачей аналогового сигнала методом кодово-импульсной модуляции (КИМ), а для телефонного сигнала по традиции — методом импульсно-кодовой модуляции (ИКМ). В приемном устройстве оцифрованные выборки с помощью ЦАП преобразуются в амплитудные выборки — в сигнал с амплитудно-импульсной модуляцией (АИМ). Далее сигнал с АИМ поступает на устройство интерполяции или экстраполяции для восстановления значений аналогового сигнала в интервалах времени между выборками. Погрешность интерполяции (экстраполяции) и есть погрешность дискретизации аналогового сообщения

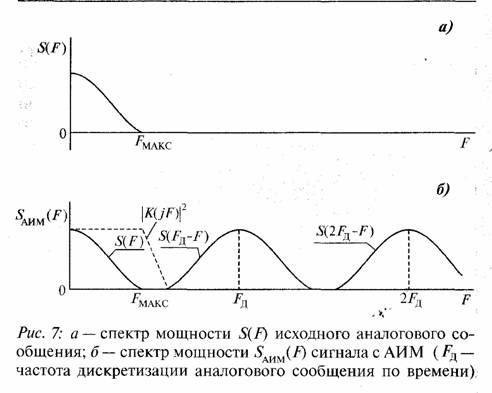
по времени. На рис. 7 показан спектр мощности сигнала с АИМ при дискретизации аналогового сигнала со спектром мощности S(F), который условно ограничен некоторой максимальной частотой F_MAKC, т.е. такой максимальной частотой, выше которой мощность аналогового сообщения может считаться пренебрежимо малой.

            На этом рисунке пунктиром показан квадрат амплитудно-частотной характеристики интерполирующего фильтра |К(jF)|² для выделения спектра S(F) из спектра

Из рис. 7 следует, что должно выполняться условие F_Д> 2F_MAKC. Однако, из-за конечной крутизны спада частотной характеристики фильтра в полосу фильтра

|K(jF)²|  попадают компоненты спектральной полосы S(F_Д -F), создавая помеху дискретизации. Для телефонного сигнала и вещательного телевизионного сигнала значения F_R выбираются экспериментально методами экспертной оценки качества воспроизводимого телефонного и телевизионного сигналов. Так для телефонного сигнала Международным союзом электросвязи установлена частота дискретизации F_Д=8 кГц, что при F_MAKC = 3400 Гц дает значение k_д =F_д/2F_MАКС ≈1,15. Для телевизионных сигналов с F_МАКС = 6 мГц выбирают k_д ≈1,15-1,25, так что частота дискретизации F_Д для сигнала яркости может быть взята не более 15 МГц (F_Д= 13,5 МГц стандарта «Секам»).

            Для телеметрических аналоговых сообщений частота дискретизации F_R может быть определена строго расчетным путем посредствам вычисления допустимой ошибки дискретизации за счет искажения спектра S(F) интерполирующим фильтром |K(jF)|² и попадания компонент спектра Sfa-F) в интерполирующий фильтр

|K(jF) |² . Если для интерполяции телеметрического сигнала между выборками используется ступенчатая экстраполяция или линейная интерполяция, то используется прямой метод вычисления ошибок ступенчатой экстраполяции или линейной интерполяции.

            Итак, скорость передачи аналоговых сообщений по цифровому канату связи можно определить выражением R=F_Дlog²L

            Задача 21. Определить скорость передачи телефонного сигнала методом ИКМ при следующих условиях:

•  F_д= 8 кГц:

•  шум амплитудного квантования не заметен на слух при отношении средней мощности телефонного сигнала к мощности шумов квантования 23 дБ;

•  пик-фактор телефонного сигнала равен 15 дБ;

•  средняя мощность телефонного сигнала (динамический диапазон) имеет разброс, равный 30 дБ, определяемый разбросом громкостей разговора различных

абонентов, разбросом коэффициентов передачи микрофонов, абонентских линий и др. Для уменьшения  динамического диапазона использовать компандер, м который уменьшает динамический диапазон среднего уровня телефонного сигнала с 30 до 10 дБ.

            Задача 22. a) Определить требуемую скорость передачи сигнала яркости телевизионного сигнала при следующих условиях:

• F_д-15МГц;

• динамический диапазон средней яркости сцен составляет 30 дБ;

•  человеческий глаз различает не более 10 градаций яркости в отдельной сцене.

б) Определить скорость передачи цветного ТВ сигнала при следующих условиях:

•  F_д= 13,5 МГц для сигналов как яркости, так и цветности;

•  динамический диапазон сигнала яркости 42 дБ;

•  динамический диапазон сигналов цветности (два цветовых сигнала) не более 24 дБ;

•  при передаче ТВ сигнала используется сжатие сигнала с коэффициентом сжатия 50.

            Задача 23. При передаче изображений земной поверхности качество изображения задается разрешающей способностью оптико-электронной системы наблюдения с параметрами:

            •  число пикселей (элементов разрешения) в одном кадре цифрового фотоаппарата равно 16 миллионов (разрешающая способность 16 Мегапикселей);

            •  число градаций яркости изображения должно быть не менее 256;

            •  число передаваемых кадров в секунду равно 5.

            Определить требуемую пропускную способность канала передачи изображений.

            Задача 24. При формировании изображения поверхности Земли на низколетящем космическом аппарате используется однострочное формирование оптического изображения с числом пикселей в строке 12 000.

            Развертка кадра осуществляется за счет движения космического аппарата по направлению вектора его скорости, однострочное формирование изображения производится в направлении, перпендикулярном вектору скорости. На борту космического аппарата одновременно производится запись изображения в трех строках для трех участков спектра — в видимом диапазоне длин волн, ближнем инфракрасном и дальнем инфракрасном диапазонах длин волн.

            Определить скорость создания информационного потока бит на борту космического аппарата при следующих исходных данных:

            •  скорость движения космического аппарата относительно поверхности Земли 8 км/с;

            •  требуемая разрешающая способность на поверхности Земли в продольном и поперечном направлениях равна: 1) 1 м; 2) 3 м; 3)10 м.

            Также определить для каждого значения разрешающей способности на поверхности Земли ширину полосы захвата на поверхности Земли, обеспечиваемую оптико-электронной системой космического аппарата.

2.3. Уплотнение и разделение каналов в многоканальных системах связи

            Теоретически возможны три метода уплотнения и разделения каналов в многоканальной линии связи: частотное (ЧРК — частотное разделение каналов), временное (ВРК) и кодовое (КРК). В существующих и перспективных телекоммуникационных линиях связи применяется только временное уплотнение и разделение цифровых каналов связи. Многоканальная линия связи (кабельная, радиорелейная, спутниковая) является некоторой магистральной линией связи, на вход которой подключаются п каналов связи, цифровых или аналоговых ( например аналоговые телефонные абонентские линии связи). Если по каждому каналу связи сообщения поступают непрерывно, например, в случае уплотнения телефонных или телевизионных каналов, то в многоканальной линии связи формируются кадры постоянной длительности и каждому каналу связи в кадре отводится фиксированный канальный интервал времени.

            Если же в каждом канале связи трафик сообщений является пульсирующим, когда в канале связи сообщения чередуются с длительными паузами, что характерно для компьютерного трафика и при передаче сообщений со сжатием информации, то используется кадр переменной длины без передачи кадрового синхросигнала. В этом случае пакет бит от каждого канала сопровождается адресом (заголовком) и пакеты от каждого каната записываются в общее буферное запоминающее устройство и передаются по очереди во времени при считывании их из буферного запоминающего устройства. В приемной части многоканальной линии связи разделение каналов производится на основе адресного признака пакетов сообщений.

            В многоканальных линиях связи с кадром фиксированной длины структуры кадров стандартизированы МСЭ и ГОСТ РФ для всех скоростей цифровой иерархии многоканальных линий связи. Основу цифрового многоканального сигнала составляет первичная система передачи Е-1, называемая в России также ИКМ-30. В этой системе длительность кадра составляет 125 мкс и частота повторения кадров 8 кГц соответствует стандартной частоте дискретизации по времени телефонного сигнала. За время одного кадра передается для каждого канала одна выборка телефонного сигнала, оцифрованная с помощью 8 бит. В кадре организуется 32 временных интервала для передачи сообщений по 30 каналам. Два временных интервала используются для передачи

сигналов синхронизации кадров, управляющих сигналов и организации служебных каналов связи. За время одного кадра передается 32x8 = 256 бит, так что скорость передачи информации составляет 256x8 кбит/с = 2,048 Мбит/с, а скорость передачи информации для одного канала равна 64 кбит/с. Скорость передачи для более высокой цифровой иерархии обеспечивают передачу числа информационных каналов в 4 раза больше числа информационных каналов системы передачи предыдущей иерархии. Так вторичная система передачи обеспечивает передачу 120 информационных каналов при той же частоте повторения кадров 8 кГц.

            Рассмотрим уплотнение п цифровых потоков информации, имеющих одинаковые номинальные скорости передачи информации и поступающие на устройство уплотнения линии связи по независимым каналам. Из-за неточности установки частоты опорных генераторов и независимого ухода их частоты из-за изменения температуры и других дестабилизирующих факторов частоты следования бит F_T в каналах будут немного отличаться друг от друга. При уплотнении цифровых каналов биты каждого канала записываются в свое буферное запоминающее устройство со своей тактовой частотой F_T, а считываются из запоминающего устройства с более высокой тактовой частотой F_T + δF_T ,где δF_т — максимальный уход тактовой частоты из-за неточности установки номинала тактовой частоты и ее дрейфа.

            За некоторое время T число бит записи в запоминающее устройство есть F_T T, а число бит, считываемых из запоминающего устройства, равно (F_T+δF_T)T. При некотором Т буферное запоминающее устройство полностью опустошится и при очередном тактовом импульсе считывания биты информации для передачи по каналу связи будут отсутствовать. Чтобы не нарушать непрерывность потока бит по каналу связи, по нему передается специальный стаффинг-бит, который должен обнаруживаться в приемнике для его удаления. Для этой цели передача стаффинг-бита должна сопровождаться передачей специальной стаффинг-команды по каналу управления.

Период появления T_ст стаффинг-бита определяется из условия (F_T+δF_T)T_CT — F_TT_CT= 1, откуда F_T = 1/δF_ct. Если относительная нестабильность тактовой частоты

есть δF_T/F_T,то T_CT

Задача 25. Определить период T_CT появления стаффинг-бита для канала связи со скоростью R = 64 кбит/с при относительной нестабильности частоты следования бит 10^-4.

            Задача 26. В многоканальном сигнале Е-1 с длительностью кадра или цикла Т_ц = 125 мкс для организации стаффинг-команд выделяется в каждом цикле один бит на фиксированной временной позиции в канале синхронизации и управления, предназначенного для формирования сигнала синхронизации сверхцикла из N циклов и формирования стаффинг-команд для каждого из п = 30 каналов.

Итак, за время сверхцикла будут переданы N бит для синхронизации сверхцикла и передачи п = 30 стаффинг-команд. Принять, что длина синхрослова сверхцикла равна k_сц = 32 бита, а длина стаффинг-команды равна k_сц = 11 бит, так что N = k_сц+пk_ст.

            Определить: 1) длительность сверхцикла NT_ц; 2) показать, что выполняется условие NT_ц < Т_ст, где Т_ст — период появления стаффинг-бита в канале со скоростью 64 кбит/с при относительной нестабильности частоты следования бит 10^-4.

            Задача 27. На вход мультиплексора многоканальной линии связи поступает пульсирующий трафик от п>>1 каналов. На выходе каждого канала сообщения появляются в виде пакетов, случайно появляющихся во времени. Пакеты от каждого канала записываются в буферное запоминающее устройство с большой памятью. Из буферного запоминающего устройства пакеты считываются с фиксированной частотой F_o. Средняя частота поступления пакетов в буферное запоминающее устройство от всех каналов есть F_т.

Если v = F_T/F₀ > 1, то буферное запоминающее устройство будет переполняться и часть пакетов будет потеряна. Если v < 1, то буферное запоминающее устройство будет опустошаться и в выходном потоке появятся пустые пакеты, которые необходимо удалять на приемном конце линии связи.

Считая, что емкость буферного запоминающего устройства очень велика:     1)определить при v >l процент потерянных пакетов

в линии связи;

2) определить при v < 1 процент пустых пакетов в линии

связи.

Задача 28. В спутниковой системе связи в одном стволе ретранслятора можно организовать п = 256 частотных или временных каналов связи (МДЧР или МДВР). Принимаем, что помехоустойчивость приема сигналов с МДЧР и МДВР одинакова при равных средних мощностях передатчиков и одинаковых антеннах наземных станций спутниковой связи.

1. Определить во сколько раз пиковая мощность передатчика наземной станции при МДВР должна быть больше мощности передатчика при МДЧР.

2. В стволе ретранслятора организуется 16 частотных канатов и на каждой из 16 несущих организуется 16 временных каналов (метод МДВР-МДЧР) с общим числом частотно-временных каналов п = 256. Определить во сколько раз пиковая мощность передатчиков наземных станций при МДВР-МДЧР должна быть больше мощности передатчика при МДЧР.

Задача 29. В сотовой наземной сети мобильной связи при приеме на базовой станции радиосигналов от мобильных терминалов при МДКР принимаем, что мощности принимаемых сигналов от мобильных терминалов Р_с в соте одинаковы, число одновременно работающих терминалов в соте равно п >>1. При асинхронной работе мобильных терминалов в приемнике базовой станции на входе демодулятора сигнала конкретного терминала (коррелятора) сигнал от другого работающего терминала можно заменить эквивалентной шумовой помехой в полосе Δƒ, занимаемой реальным радиосигналом, с равномерной спектральной плотностью шума

Энергия принятого информационного бита

где τ₀ — длительность информационного бита на входе канала связи, τ₀ = 1/R; R — скорость передачи информации.

Вероятность ошибки на бит определяется отношением энергии бита к спектральной плотности шума N₀+(n-1)P_C/ Δ f

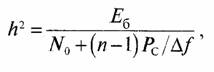
где  N_o — спектральная плотность собственных шумов приемника.

Для телефонных каналов связи, когда половину времени абонент говорит и половину времени слушает (в это время передатчик абонента выключается) спектральная плотность взаимных помех уменьшится в два раза. Обозначив B = τ₀ Δ f как базу широкополосного псевдошумового сигнала:

            1) определить при условии N₀<<(n-1)P_C/Δ f без учета помех от терминалов в соседних сотах максимально допустимое число одновременно работающих в соте терминалов п для h² = 13 дБ (кодирование без избыточности) и h² = 6 дБ (помехоустойчивое кодирование) для универсальных и телефонных каналов;

2) полученное число телефонных каналов связи для МДКР сравнить с максимальным числом каналов п для МДЧР в той же полосе частот Δƒ: п = τ ₀Δ f=B.

Задача 30. Используя расчеты для задачи 29 при h² = 6 дБ, провести сравнение наземной сотовой системы мобильной связи по числу возможных телефонных каналов при МДКР и МДЧР в направлении «Терминалы — базовая станция» при следующих исходных данных:

•  число смежных сот в кластере равно 7;

•  при полосе частот системы связи Δƒ, полоса частот, выделяемая одной соте при МДЧР, равна Δƒ, при МДКР полоса частот, выделяемая одной соте, равна Δƒ;

            •  при МДКР мобильные станции в смежных сотах создают помеху, эквивалентную увеличению числа мобильных терминалов в рассматриваемой соте в 1,5 раза;

•  при телефонной связи с МДКР мобильные терминалы в паузах речи выключают передатчик, уменьшая мощность взаимных помех на 50%.

Требуется определить допустимое число одновременно работающих мобильных терминалов в одной соте сотовой сети связи с МДКР и сравнить это число с допустимым числом мобильных терминалов в соте той же сети связи, но при МДЧР, которое принять равным п = τ ₀ Δƒ/7 = В/7.

ГЛАВА 3

КАЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ,

ТЕЛЕКОММУНИКАЦИОННЫХ

КАНАЛОВ И СИСТЕМ

3.1. Требования к качественным характеристикам телекоммуникационных каналов

Ранее каналы связи создавались как специализированные для передачи того или иного вида информации и требования к каналу связи определялись требованиями к качеству передаваемой специфической информации. Отдельные каналы связи создавались для передачи телеграфной информации (текста), телефонного сигнала (критерий разборчивости речи), телевизионных сигналов, сигналов телеуправления, телеметрии и др. В настоящее время подавляющее большинство телекоммуникационных сетей создаются на базе универсальных интегрированных цифровых каналов связи, предназначенных для передачи любых видов информации: текста, речевых сигналов, изображений, видео и др. (мультимедийные телекоммуникационные каналы). Требования, предъявляемые к характеристикам телекоммуникационных каналов, позволяют с запасом обеспечить высококачественную передачу всех основных сообщений.

Телекоммуникационный канал характеризуется величиной максимальной скорости передачи информации, помехоустойчивостью приема сигналов (вероятностью ошибки на бит) и надежностью функционирования канала связи (готовностью канала связи).

Качественные характеристики цифровых телекоммуникационных каналов задаются следующим образом. Для волоконно-оптических каналов связи частота появления ошибок BER (Bit error rate) или вероятность ошибки на бит информации р не должна превышать

величины р = 10^-9. Для телекоммуникационных каналов фиксированной связи длиной 2500 км, таких как медных кабельных каналов, спутниковых и радиорелейных линий связи величина BER не должна превышать:

•  10^-6—10^-7 в течение не менее 80% времени любого месяца;

            •  10^-4в течение не более 0,3% времени любого месяца;

            •  10^-3в течение не более 0,01% времени любого года.

Состояние канала связи при вероятности ошибки р > 10^-3 называется прерыванием канала связи и относится к так называемым кратковременным прерываниям, длительность которых не превышает 10 с.

Для этих же телекоммуникационных каналов готовность канала связи должна быть не менее 0,99—0,995. Эта величина определяется процентом времени появления долговременных прерываний (более 10 с) за счет неблагоприятных условий распространения радиосигналов, отказов аппаратуры, ошибок действия персонала и др.

Аналогичные, но менее жесткие требования по помехоустойчивости и готовности каналов связи предъявляются и к сетям мобильной связи.

Для отдельных видов сообщений, таких как сигналы управления и сигнализации сети связи, передача банковских данных, передача команд боевого управления в военных телекоммуникационных сетях и др. не допускается возникновение ложных или трансформированных сообщений, которые должны обнаруживаться и стираться. Высокая надежность приема таких сообщений достигается за счет переспроса и повторной передачи сообщений (метод кодирования ARQ — Automatic Repeat Request по международной классификации).

Основным методом обеспечения высокой достоверности и надежности передачи сообщений является использование кодирования передаваемых сообщений с обнаружением ошибок информационных бит при приеме, стирание недостоверных сообщений и повторной их передачей по каналу связи. Отметим, что использование классических помехоустойчивых кодов с исправлением ошибок не решает задачу стирания недостоверных сообщений и не гарантирует предотвращения появления ложных и трансформированных сообщений.

            Принимаем, что ошибки при приеме информационных бит являются независимыми, так что вероятность появления ровно i ошибочных бит в слове из п бит определяется выражением

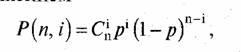
где р есть вероятность ошибки на бит в канале связи.

Код с обнаружением ошибок с минимальным хэмминговым расстоянием d_x обнаруживает все ошибки с кратностью t = d_x/2 и менее (d_x — четное число)

            Задача 31. Нарисовать функциональные схемы кодера и декодера, обнаруживающего ошибки, для циклического систематического (п; к) кода.

            Задача 32. Определить вероятность того, что в слове из п битбудут искажены не менее чем i бит Р_ош (t≥i), где t — число обнаруживаемых ошибочных бит. Ошибки независимы. Вероятность ошибки на бит р <<1.

            Задача 33. Для волоконно-оптического канала связи с вероятностью ошибки на бит р = 10^-9 определить минимальное хэммингово расстояние (п;k) кода с обнаружением ошибок, обеспечивающего вероятность необнаруженной ошибки 10^-12.

Задача 34. Для радиоканала с вероятностью ошибки на бит р≤ 10^-3 и длиной пакета из п = 64 бит определить минимальное хэммингово расстояние кода с обнаружением ошибок, обеспечивающего вероятность необнаруженной ошибки в пакете:

• 10^-6;

•10^-9.

Задача 35. Для радиоканала с вероятностью ошибки на бит р≤10^-4 и длиной пакета из п = 64 бит определить минимальное хэммингово расстояние кода, обнаруживающего ошибки и обеспечивающего вероятность необнаруженной ошибки в пакете, равной 10^-12.

Задача 36. В радиоканале при воздействии организованной шумовой помехи (или срыве синхронизации канала синхронизации слов) вероятность ошибки на бит р =0,5.

            Определить число избыточных бит г, которое необходимо добавить к пакету информационных бит к для обнаружения ошибок, чтобы за время передачи пакета вероятность формирования ложной команды не превышала величины Р_л= 10~⁹.

3.2. Надежность канала связи

            Готовность или коэффициент готовности канала связи определяется через относительное время (или через вероятность) безотказной работы канала связи:

где Т— требуемое время работы канала связи, Т_П — суммарное время перерывов связи.

            Зная требуемый коэффициент готовности, можно определить требования к надежности аппаратуры канала связи, которую характеризуют среднем временем безотказной работы Т₀.

            Для аппаратуры без ремонта (восстановления) во время выполнения задания (самолетная, ракетная, спутниковая аппаратура) надежность аппаратуры в соответствии с экспоненциальным законом надежности характеризуется вероятностью безотказной работы за время Т выполнения задания Р₀(Т) = е^-Т/То.

            Надежность аппаратуры с возможностью ее восстановления (ремонта или замены неисправного ТЭЗ-а —типового элемента замены) характеризуется коэффициентом готовности аппаратуры

где Т₀ — среднее время безотказной работы аппаратура, Т_В — время восстановления аппаратуры.

            Задача 37. В приемную антенну стационарной станции спутниковой связи, работающей с геостационарным КА, два раза в год шумы Солнца попадают в основной лепесток диаграммы направленности на время 30 мин в день в течении 5 дней подряд в дни как весеннего так и осеннего равноденствий. При этом прием сигналов с геостационарного КА становится невозможным.

Определить готовность (относительное время работоспособности) спутниковых линий связи, ограничиваемую воздействием шумов Солнца.

            Задача 38. Для самолетной аппаратуры принимаем, что за время полета самолета 5 часов вероятность безотказной работы должна быть не менее Р₀ (Т) = 0,999. Определить требования, предъявляемые к надежности самолетной аппаратуры (требуемое среднее время безотказной работы).

            Задача 39. Судовая станция морской спутниковой связи должна создаваться без резервирования аппаратуры. Время восстановления отказавшей аппаратуры по международным требованиям составляет не более четырех суток (время движения судна до ближайшего порта, куда могут быть доставлены ТЭЗ-ы для замены неисправных блоков). Для коэффициента готовности А_Г = 0,99 определить требования к надежности (Т₀) разрабатываемой аппаратуры станции спутниковой связи.

            Задача 40. Наземная станция спутниковой связи должна иметь коэффициент готовности  аппаратуры А_Г= 0,999. Время восстановления аппаратуры принять равным одним суткам (время доставки ТЭЗ-а самолетом).

            Определить требуемое среднее время безотказной работы, предъявляемое к разрабатываемой аппаратуре станции спутниковой связи.

3.3. Телекоммуникационный трафик

            Рассмотрим телекоммуникационную сеть с представлением каналов по требованию типа «звезда» с базовой станцией (или коммутатором АТС) с числом каналов п. В качестве базовой станции можно рассматривать и ретранслятор системы спутниковой связи с числом каналов п в стволе ретранслятора. Обозначим число абонентов сети через N.

            Принимаем, что статистические характеристики всех источников сообщений (абонентов) одинаковы.

            Обозначим через λ среднее число вызовов на связь от одного абонента в единицу времени, β — среднюю продолжительность сеанса связи одного абонента. Тогда λβТ есть чистое время работы абонента за время Т.

            Относительное время работы одного абонента за время Т, равное λβТ/Т=λβ = α, называется активностью абонента или нагрузкой на сеть от одного абонента. Величину а (безразмерную) принято измерять в Эрлангах

            Для мобильного абонента, работающего в сотовой сети связи или спутниковой сети связи, принимают нагрузку α = 0,01 Эрл, для стационарного телефонного абонента α = 0,1 Эрл в час наибольшей нагрузки (ЧНН).

            Нагрузка от N абонентов сети есть Nα Эрл. При большом числе абонентов N >>1 суммарный поток вызовов от всех абонентов в теории массового обслуживания называется простейшим без последствия и описывается распределением Пуассона. Тогда вероятность того, что в системе из п каналов будут заняты k каналов дается формулой Эрланга

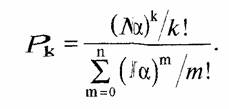
Вероятность того, что все n каналов будут заняты, так что будет дан отказ в связи любым другим абонентам (система массового обслуживания без постановки вызовов в очередь), равна

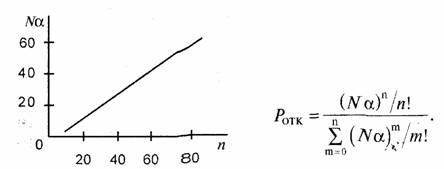
В соответствии с этим выражением допустимая нагрузка Nα системы из п каналов для Р_отк = 0,01 показана на рис. 8.

Эффективность    использования   телекоммуникационных каналов   (как бы коэффициент полезного

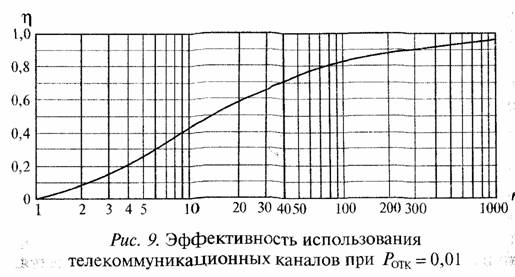
действия — КПД   телекоммуникационной   системы) есть

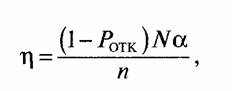
где (1- P_OTK)Na— обслуженная нагрузка. График величины ц представлен на рис. 9 для Р_отк = 0,01.

            Задача 41. 1. Определить эффективность (КПД) телекоммуникационной системы с закрепленными каналами (N = п) для мобильной связи с α = 0,01 Эрл и фиксированной связи с α = 0,1 Эрл.

            2. При числе каналов связи базовой станции 16 определить допустимое число мобильных терминалов сотовой сети связи, которое может обслужить базовая станция при Р_отк - 0,01 в системе с предоставлением каналов по требованию.

Задача 42. Оператор (владелец) космического сегмента спутниковой системы мобильной связи с предоставлением каналов связи по требованию имеет на геостационарном космическом аппарате ретранслятор емкостью 100 телефонных каналов.

Тариф за предоставление телефонного канала связи составляет 5 долларов за одну минуту. Затраты на запуск одного космического аппарата составляют 200 млн. долларов. Из каждых 5 долларов, получаемых от абонентов спутниковой системы связи, половина отчисляется оператору космического сегмента, половина операторам наземных базовых станций и владельцам наземной сети связи. Определить при Р_отк = 0,01, за сколько времени, доход оператора космического сегмента покроет первоначальные его затраты в сумме 200 млн. долларов.

Задача 43. Для телефонизации удаленного поселка и организации междугородной связи оператор приобрел за 50 тыс. долларов станцию фиксированной спутниковой связи VSAT с пропускной способностью 128 кбит/с для организации 12 телефонных каналов. Тариф за предоставление одного исходящего телефонного канала междугородной связи составляет 0,5 долл./мин. В сутки станция спутниковой связи эффективно работает 2,4 часа. Аренда всего ствола спутникового ретранслятора емкостью 200 каналов по 128 кбит/с составляет 2 млн. долл. в год.

            Принимая Р_отк = 0,01 и режим предоставления каналов по требованию, определить доход за год оператора наземной станции спутниковой связи и оценить сроки окупаемости приобретенной аппаратуры с учетом необходимого сценария эксплуатационных расходов.

Задача 44. Определить при Р_отк = 0,01 и α = 0,1 суммарную обслуживаемую нагрузку в Эрлангах для:

•  десяти 10-канальных коммутаторов;

•  одного 100-канального коммутатора. Определить какой вариант выгоднее и во сколько раз по величине обслуживаемой нагрузки.

3.4. Электромагнитная совместимость спутниковых телекоммуникационных систем

            Спутниковые системы фиксированной связи и спутникового вещательного телевидения с использованием КА на геостационарной орбите могут использовать одни и те же полосы рабочих частот независимо от местоположения наземных станций.

            Это оказывается возможным, если спутниковые телекоммуникационные системы используют КА в разных точках стояния на геостационарной орбите, с тем, чтобы сигналы от всех КА других спутниковых телекоммуникационных систем воздействовали на наземную станцию спутниковой связи по боковым лепесткам диаграммы направленности ее приемной антенны, а передающая антенна спутниковой наземной станции облучала все другие КА только боковыми лепестками своей диаграммы направленности. Диаметр апертуры антенны наземной станции определяется шириной диаграммы направленности основного лепестка антенны, которая, в свою очередь определяется величиной углового разноса соседних КА на геостационарной орбите.

            На сегодня минимальный диаметр антенны наземной станции спутниковой связи ограничивается не энергетическими характеристиками ретранслятора КА, а техническими требованиями по обеспечению электромагнитной совместимости спутниковых телекоммуникационных систем, работающих в одних и тех же полосах рабочих частот.

            Для спутниковых систем фиксированной связи должны выполняться два критерия:

            1. Уровень помех, создаваемой одной системой спутниковой связи, не должен увеличивать спектральную плотность шума N_o на выходе приемной антенны наземной станции другой системы спутниковой связи более чем на 4%. При этом мешающие сигналы от системы спутниковой связи рассматриваются как шумовые с равномерной спектральной плотностью в полосе излучаемых сигналов.

2. Огибающая боковых лепестков передающей и приемной антенн наземной станции спутниковой связи относительно изотропного излучателя не должна превышать следующих величин в дБ при d/X < 100:

где θ_m — граница основного лепестка диаграммы направленности, град. (θ_m~70λ/d), 8 есть угол в градусах, отчитываемый от направления максимума диаграммы направленности антенны, d — диаметр апертуры антенны, λ—длина волны.

            Рассмотрим первый критерий. Обозначим спектральную плотность помехи от другой системы спутниковой связи на выходе приемной антенны как N_on и мощность помехи в полосе сигнала ∆ƒ как Р_п = N_onAf.

Отношение мощности принимаемого полезного сигнала Р_с к мощности собственного шума и помехи в полосе принимаемого сигнала на выходе приемной антенны должно удовлетворять соотношению

где h²_пop — требуемое пороговое отношение сигнал-шум для обеспечения заданной вероятности ошибки на бит. Имеем следующие равенства:

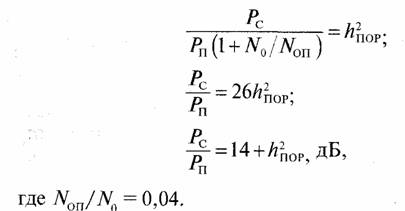
            Отсюда, принимая для вероятности ошибки на бит р= 10^-6и кодирования без избыточности h²_nov= 12 дБ, получим требование для расчета защитного отношения сигнал—помеха Р_с/Р_п>26дБ.

Для помехоустойчивого кодирования сообщений с h²_uov = 6 дБ получим требование Р_с/Р_п > 20 дБ.

            Задача 45. Рассматривается приемник наземной станции приема спутниковых телевизионных сигналов на частоте 12 ГГц. КА систем непосредственного телевизионного вещания располагаются на геостационарной орбите с угловым разносом 6⁰.

            Определить диаметры антенн наземного приемника с круглой апертурой, при которых все КА непосредственного ТВ вещания будут попадать в нули диаграммы направленности антенны приемника.

            Задача 46. Для однородных спутниковых систем фиксированной связи с идентичными наземными станциями спутниковой связи вывести выражение для защитного отношения сигнал—помеха в зависимости от коэффициента усиления приемных и передающих антенн наземных станций спутниковой связи при следующих условиях:

•  дальности связи от всех наземных станций до КА одинаковы;

•  среда распространения сигналов без потерь;

•  все КА разных систем спутниковой связи одинаковы и имеют угловой разнос на геостационарной орбите ∆φ.

            Определить минимальный диаметр антенны наземной станции с круглой апертурой при следующих условиях:

•  диапазон частот 11/14 ГГц;

•   ∆ φ = 2,5°;

•  требуемое   защитное   отношение   сигнал—помеха Р_с/Р_п ≥ 20дБ;

•  уровни боковых лепестков диаграммы направленности антенны соответствуют выражению (2).

При таких же условиях определить минимальный диаметр антенны наземной станции, работающей в диапазоне частот 20/30 ГГц.

ГЛАВА 4

РАДИОТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ

ТЕЛЕКОММУНИКАЦИОННЫХ

РАДИОКАНАЛОВ

4.1. Частота и длина волны электромагнитного колебания

Задача 47. Нарисуйте гармоническое колебание как функцию расстояния. Укажите длину волны колебания λ. Нарисуйте гармоническое колебание как функцию времени. Укажите период колебания Т. Установите связь между Т и λ, а также между λ и частотой гармонического колебания ƒ.

Выразите длину волны в сантиметрах через частоту гармонического колебания в ГГц. Заполните таблицу.

4.2. Доплеровское смещение частоты радиосигналов

            Задача 48. Выразите доплеровское смещение частоты ∆ƒ_д в зависимости от значения радиальной скорости V движения передатчика или приемника двумя способами:

• через частоту радиосигнала и отношение Vk скорости света; через отношение V/ λ, где λ — длина волны.

            Задача 49. Определить максимальный доплеровский сдвиг радиосигнала при авиационной радиосвязи на частоте 300 МГц и скорости самолета 800 км/ч.

            Задача 50. За счет малого перемещения геостационарного КА в направлении север—юг дальность связи до наземной станции меняется по синусоидальному закону с периодом 24 часа и амплитудой 100 км.

Определить максимальный доплеровский сдвиг и уравнение для доплеровского смещения частоты как функции времени. Определить доплеровский сдвиг на частоте радиосигнала 11 ГГц.

Задача 51. Нарисуйте примерный ход во времени относительного доплеровского смещения частоты для низколетящего КА при его прохождении в плоскости, проходящей через наземную космическую станцию при следующих исходных данных:

•  высота круговой орбиты КА 700 км;

•  скорость движения КА 8 км/с.

•  частота радиосигнала равна 2 ГГц

Задача 52. Определить максимальное доплеровское смещение частоты в тропосферной линии связи из-за перемещения отражающих неоднородностей тропосферы вдоль трассы распространения радиосигналов и поперек трассы при условиях:

•  частота радиосигнала 4,5 ГГц;

•  угловой размер отражающей области тропосферы 1 градус;

•  скорость перемещения неоднородностей тропосферы принять равной 100 м/с.

4.3. Нестабильность частоты генераторов

Все частоты в передающих и приемных устройствах получают из частоты одного опорного высокостабильного кварцевого генератора, так что номинал любой частоты радиостанции равен частоте кварцевого генератора, Умноженной на некоторое целое или дробное число. Частота опорного кварцевого генератора может уходить

от номинального значения, установленного на заводе-изготовителе, по трем основным причинам:

1. За счет процессов старения кварца, которые определяют долговременную нестабильность частоты кварцевого генератора (время старения кварца исчисляется годами).

2. За счет температурных изменений окружающего кварц пространства. Стандартный кварцевый резонатор имеет относительный уход частоты 1 (h⁶ на градус Цельсия.

3. За счет так называемых фазовых и, следовательно, частотных шумов кварцевого генератора. Эти шумы определяют кратковременную (за доли секунды) нестабильность частоты и фазы кварцевого генератора.

В паспорте опорного кварцевого генератора записывается гарантированная погрешность (нестабильность) кварцевого генератора за счет долговременных факторов (старение и температурные уходы частоты) и дается шаблон фазовых шумов генератора.

Задача 53. В аппаратуре заменили неисправный кварцевый резонатор на исправный, взятый из ЗИПа. На какую величину может отличаться частота кварцевого генератора с новым кварцем по сравнению с частотой кварцевого генератора с прежним (до замены) исправным кварцевым резонатором?

Задача 54. Бортовая самолетная аппаратура работает в интервале температур от —50 °С до +50 ⁰С. В аппаратуре используется кварцевый генератор без термостата. Какова его относительная нестабильность частоты в этих условиях?

            Задача 55. В демодуляторе приемника двоичных сигналов используется генератор тактовой частоты следования двоичных символов, который подстраивается под тактовую частоту принимаемых символов. При нарушении работы схемы слежения генератора тактовой частоты приемника, например, при передаче длинной последовательностей символов «ноль», генератор тактовой частоты приемника начинает работать в несинхронизированном режиме, так что его частота отличается от тактовой частоты передаваемых символов на величину, равную 10^-4 от значения тактовой частоты.

            Считая, что неправильная демодуляция символов происходит тогда, когда уход тактового импульса генератора тактовых импульсов приемника от середины принимаемого символа составляет более τ /2, где τ — длительность передаваемых символов, определить для скорости передачи информации 1 Мбит/с время, через которое начинается неправильная демодуляция символов.

            Задача 56. За счет фазовых шумов происходит случайный фазовый сдвиг синусоидального колебания (пунктир на рис. 10), который можно определить по отклонению точки пересечения оси времени t пунктирной кривой относительно сплошной кривой, которая представляет синусоидальное колебание в отсутствии фазовых шумов.

Случайному сдвигу ∆ τ соответствует сдвиг фазы ∆ φ = ω∆τ и среднеквадратическому значению временного сдвига точки пересечения оси t ∆τ _ЭФ соответствует среднеквадратическое значение случайного изменения

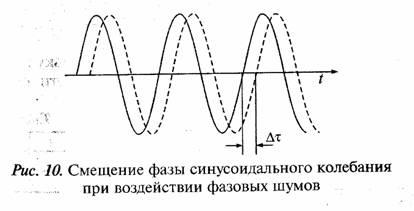
фазы ∆ φ _эф = ω ∆ τ _ЭФ, где ω — круговая частота радиосигнала.

            Определить, во сколько раз возрастает мощность фазовых флюктуации (∆φ _эф)² (фазовых шумов) при:

•  удвоении частоты генератора

•  при умножении в п раз частоты генератора.

4.4. Децибелы

            Очень большие и очень малые величины в радиотехнике принято выражать в децибелах. В децибелах отношение двух величин N= N₁/N₂, где N₁ и N₂ имеют одинаковую размерность, выражают следующим образом: N[дБ] = 10lgN.

Например, отношение мощностей сигнал-шум h² = Р_с/Р_ш в децибелах есть h² [дБ] = 10 lg(Р_С/Р_Ш). Для видеоимпульсов и шумов в видеотракте можно записать Рс/Рш =U²_c/U²_ш, где Р_с = U²_с на единичном сопротивлении, и_ш — эффективное напряжение шума. Тогда

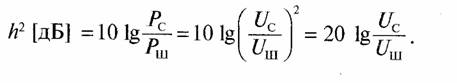
            Во многих случаях удобно положить в отношении двух величин N₁/N₂ величину N₂ = 1 (1 Вт, 1 градус и т. д.) Тогда, соответственно N [дБ] имеет размерность дБВт, дБград. и т.д. Если N₂ положить равной, например, одному милливатту, то размерность N [дБ] записывается как дБм (децибел милливатт).

Задача 57. Вычислить с помощью калькулятора значения в дБ чисел N= 1,2,3,10, округлить эти значения до целых чисел и записать в таблицу:

Используя представление N в виде произведения или частного отделения нескольких чисел, найти с помощью табл. 1 округленные значения N в дБ

Задача 58. 1. Выразить мощность излучаемого сигнала в дБВт и дБм для заданной излучаемой мощности Р, Вт, указанной в таблице.

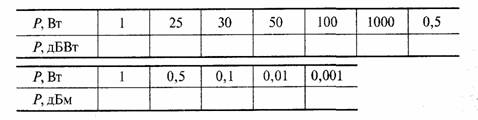
2. Выразить постоянную Больцмана в децибелах.

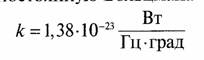
2. Пик-фактор телефонного сигнала у = 6 (отношение максимального значения амплитуды телефонного сигнала к среднеквадратичному значению амплитуды). Найти значение пик-фактора у в дБ.

ГЛАВА 5

ПОМЕХОУСТОЙЧИВОСТЬ РАДИОКАНАЛОВ СВЯЗИ С ГАУССОВСКИМИ ШУМАМИ

И МНОГОЛУЧЕВЫМ РАСПРОСТРАНЕНИЕМ СИГНАЛОВ

5.1. Помехоустойчивость передачи двоичных сигналов по каналу с гауссовским шумом

            Пусть по видеоканалу связи передаются импульсы прямоугольной формы с амплитудой U_c и длительностью τ. При передаче символа «1» передается импульс положительной полярности, при передаче символа «0» — импульс отрицательной полярности. В канале связи действует белый гауссовский шум со спектральной плотностью N_o. Примем, что на вход приемника сигналы и шумы приходят без искажений. Приемник состоит из согласованного фильтра и решающего устройства. Решающее устройство в момент времени, соответствующему максимуму сигнала на выходе согласованного фильтра, принимает решение: если мгновенное напряжение сигнал плюс шум имеет положительную полярность, то формируется символ «1», если мгновенное напряжение сигнал плюс шум имеет отрицательную полярность, то приемник формирует символ «0». Ошибка при приеме возникает, когда передавался символ «1», а мгновенное напряжение сигнал плюс шум имеет отрицательную полярность или если передавался символ «0», а мгновенное напряжение сигнал плюс шум на входе решающего устройства имеет положительную полярность.

            Спектр прямоугольного импульса амплитудой U_c и

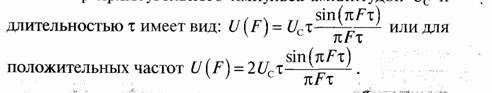
            Согласованный фильтр имеет амплитудно-частотную характеристику, повторяющую форму спектра импульса сигнала

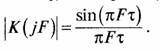
            Напряжение сигнала на выходе согласованного фильтра в момент окончания импульса сигнала равно

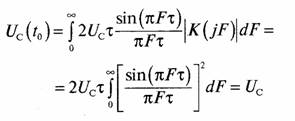
и мощность на единичном сопротивлении

            Мощность белого шума, прошедшего согласованный фильтр, есть

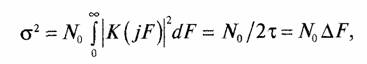
где   1/2t = AF есть ширина полосы согласованного фильтра.

            Отношение мощностей сигнал—шум на выходе согласованного фильтра есть

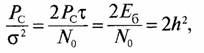
где энергия импульса есть отношение энергии бита к спектральной плотности шумов на входе приемника (согласованного фильтра).

            Реальный канал связи характеризуется помехоустойчивостью, которая определяется величиной ошибки на бит/? в функции величины /г², и пропускной способностью канала связи. Максимально-достижимая скорость передачи информации без ошибок при белом гауссовском шуме при некотором идеальном помехоустойчивом кодировании  передаваемых  сообщений  определяется выражением Шеннона, полоса канала связи, Р_ш — мощность шума в полосе частот AF.

            Для безызбыточного кодирования, когда по двоичному каналу связи передаются прямоугольные импульсы сигнала длительностью х, при большом отношении сигнал-шум, когда вероятностью ошибки на бит можно пренебречь, скорость передачи информации R =1/ τ = 2 ∆ F, что существенно отличается от выражения Шеннона для пропускной способности канала связи при идеальных методах кодирования сигналов.

            Задача 59. На входе приемника в видеополосе действует сигнал в виде прямоугольных импульсов с амплитудой U_c и длительностью т и белый гауссовский шум со спектральной плотностью N₀. 

            При передаче символа «1» на входе приемника присутствует импульс сигнала положительной полярности, при передаче символа «0» — импульс отрицательной полярности. Априорные вероятности передачи символов «1» и «0» одинаковы и равны P(1) - Р(0) = 0,5. Приемник состоит из согласованного фильтра и решающего устройства.

Требуется:

1. Написать выражение для плотности вероятности W(x) напряжения х, состоящего из суммы сигнала (максимальная амплитуда) и шума на входе решающего устройства при передаче символа «1» и при передаче символа «0».

2. Изобразить эти две плотности вероятности W(x) на общем рисунке, где по оси абсцисс откладывается величина х, а по оси ординат плотности вероятности W(x).

            3. Определить вероятность ошибки на бит р в зависимости от величины h

4. Пользуясь таблицами интеграла вероятности Ф(у) = а также представлением интеграла вероятности в виде асимптотического ряда при больших у

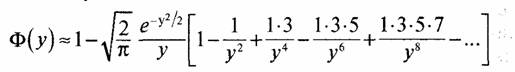
с точностью до первого отброшенного члена, построить кривую вероятности ошибки на бит в логарифмическом масштабе для р от р = 10^-1 до р=10^-6. Величину h² откладывать по оси абсцисс в дБ. 5, Определить величину h² в дБ, требуемую для получения вероятности ошибки р = 10^-6.

            Задача 60. Если сигнал передается по каналу связи с шумами, то возможна ли передача сообщений по этому каналу связи без ошибок? Если да, то какие параметры передачи ограничивают шумы канала связи.

            Задача 61. Пользуясь выражением Шеннона для пропускной способности канала связи R = ∆ Flog₂ (1 + Р_с/Р_ш) выразите отношение Р_с/Р_ш через отношение h² = E_б/N₀ и найдите выражение для h² как функцию отношения R/ ∆ F.

            Найдите минимально-возможное достижимое значение величины h² для канала связи. Выразите эту величину h² в дБ и сравните ее с величиной h² = 10,5 дБ, требуемой для получения вероятности ошибки на бит р = 10 ^-6 при передаче информации противоположными сигналами без избыточности. Какие заключения можно сделать в результате этого сравнения о возможностях помехоустойчивого кодирования в каналах связи

5.2. Надежность связи при замираниях сигнала

Мощность принимаемого сигнала в отсутствие замираний сигнала обозначим через Р_с. Пусть теперь сигнал замирает, так что плотность распределения вероятностей принимаемого радиосигнала является гауссовской с дисперсией σ ²_с, где σ²_c есть мощность принимаемого сигнала. Для сравнения надежности связи при замирающем сигнале по отношению к незамирающему сигналу положим σ ²_c= Р_с. Огибающая замирающего сигнала описывается релеевской плотностью распределения вероятностей с медианным значением х_м =

Вероятность того, что огибающая сигнала х будет больше некоторой пороговой величины х_п.(х>х_п), т.е. глубина замирания огибающей сигнала не превысит величины х_п равна

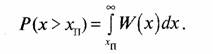
Интегральное распределение вероятностей определяется как

Кривые надежности связи строятся следующим образом. По оси ординат откладывается глубина замираний радиосигнала, которая не более величины х_п, и которая вычисляется относительно величины а_с (или медиального значения х_ы) в децибелах. Примем величину, откладываемую по оси ординат равную 20lg(x_n/ σ _c).По оси абсцисс принято откладывать процент времени Р₇ в течение которого глубина замираний 20lg(x_n/ σ _c) меньше величины, отложенной по оси ординат. Величина Р_г откладывается в специальном логарифмическом масштабе.

Величина 201g(x_n/ σ _c) с обратным знаком показывает, на сколько дБ нужно увеличить энергетический потенциал радиолинии при наличии замираний сигнала по отношению к радиолинии с незамирающим сигналом при заданной надежности связи Р_т.

Разметка оси абсцисс, на которой откладывается величина Р_T, производится следующим образом. Вначале по оси абсцисс откладывается вероятность F(x_П) в логарифмическом масштабе. Далее на оси абсцисс наносится разметка 1-F(x_n) и, окончательно, разметка Р_т как это показано на рисунке:

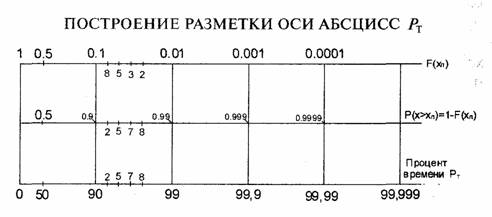
            Задача 62. Для огибающей замирающего сигнала, описываемой релеевской плотностью вероятности, вычислить и построить график процента времени, в течение которого глубина замираний сигнала в дБ меньше отложенной по оси ординат величины. Процент времени задается в пределах от 50% до 99,99%. Правильность расчетов проверить для медианного значения сигнала (Р_т=50%).

            Определить требуемый запас по энергетике радиолинии на замирания сигнала для надежности связи 99% (мобильная связь) и 99,99% (фиксированная связь). Оценить выигрыш в энергетике радиолинии при использовании сдвоенного пространственного разнесенного приема сигналов для мобильной и фиксированной связи.

5.3. Многолучевые каналы связи и характеристики замираний сигнала

            Многолучевой сигнал, приходящий в точку приема, характеризуется функциями рассеяния по задержке, доплеровским частотам и углам прихода, которые представляют собой спектры мощности по соответствующим

координатам. Преобразование Фурье этих спектров мощности дает корреляционную функцию, аргумент которой имеет размерность обратно пропорциональную размерности аргумента функции рассеяния (свойство преобразования Фурье).

            Ширина корреляционной функции определяет необходимый интервал разнесения сигналов соответственно по частоте, времени и пространству для организации разнесенного приема с целью существенного уменьшения влияния замираний сигнала на помехоустойчивость приема сигналов.

            Теория устанавливает следующие интервалы корреляции:

•  если ∆ τ есть интервал разброса задержек многолучевого сигнала, то интервал корреляции многолучевого сигнала по частоте есть ∆ F_K0РР=1 /∆τ. Спектральные компоненты сигнала, отстающие друг от друга на величину 1/Ах замирают независимо;

•  если ∆ F_д есть доплеровское рассеяние принимаемого сигнала (±∆ F_д/2) то, временной интервал корреляции сигнала есть τ _К0РР =1/ ∆F_д. Значения огибающей сигнала, отстающие по времени друг от друга на величину 1/∆F_д замирают независимо;

•  если θ _РАСС есть сектор углов, под которыми в точку приема приходят отраженные сигналы, то интервал пространственной корреляции сигнала (необходимый  пространственный  разнос  разнесенных  антенн) равен

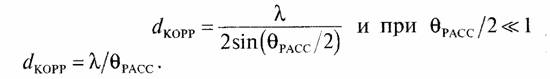
В инженерной практике также часто используется двухлучевая модель многолучевого канала связи, анализ характеристик которого имеет ясный физический смысл. Принимаемый сигнал с некоторой шириной спектра ∆, состоящий из двух одинаковых по амплитуде лучей с задержкой х одного луча относительно другого, можно

записать следующим образом:

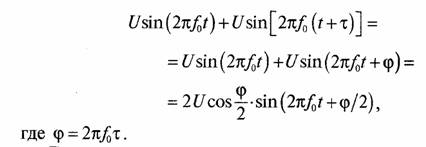
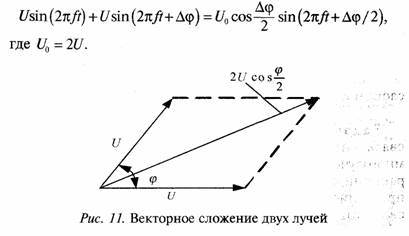
Последнее равенство следует из векторной диаграммы сложения двух лучей, показанной на рис. 11.

Для этих же двух лучей на частоте спектра сигнала

есть ширина спектра радиосигнала, аналогично запишем

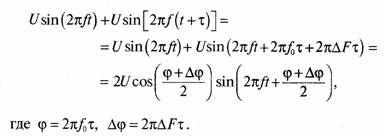
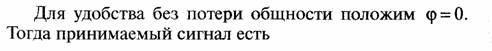
Таким образом поведение огибающей двух лучей одинаковой амплитуды описывается простым выражением U₀cos(Δφ/2), где Δφ = 2πΔFτ. Область корреляции огибающей U₀cos(Δφ/2) по частотной координате AF можно определить как те значения ±AF, которые лежат в пределах изменения Δφ от —π до π.

Таким образом ±ΔF =1/2τ или ΔF_KOPP = 2ΔF = 1/τ.

            Задача 63. Для двухлучевой модели канала связи для времени запаздывания одного луча по отношению к другому τ_ЗАП определить необходимый разнос частот между п несущими частотами, передаваемых одновременно для получения я-кратного разнесенного по частоте приема.

            Задача 64. Для двухлучевой модели канала связи, когда в точку приема приходят два луча, отличающиеся по частоте за счет разного доплеровского сдвига на величину ΔF_Л, изобразить графически поведение огибающей принимаемого двухлучевого сигнала во времени (кривая биений) и по кривой огибающей биений определить необходимый интервал разноса по времени повторения передаваемых символов сообщения для организации разнесенного по времени приема сигналов.

При длительности передаваемого информационного двоичного символа τ и интервалу временной корреляции замираний 4τ нарисовать структуру кодовых слов для организации сдвоенного временного разнесения принимаемых сигналов за счет повторения символов кодового слова и их перемежения.

            Задача 65. В городской сотовой сети мобильной связи интервал рассеяния по задержке принимаемого многолучевого сигнала равен 3 мкс. Для борьбы с замираниями сигнала каждый символ кодового слова с исправлением ошибок последовательно передается на своей отдельной частоте так, чтобы символы кодового

слова замирали независимо. Определить минимальный необходимый разнос между частотами.

Задача 66. В тропосферных линиях связи интервал рассеивания по задержке принимаемого сигнала составляет 0,25 мкс.

Оценить полосу частот, внутри которой необходимо передавать сигналы для организации в приемнике 4-кратного частотно-разнесенного приема сигналов.

            Задача 67. В городской сотовой сети мобильной связи, работающей в диапазоне частот/ = 2 ГГц (длина волны X = 15 см) мобильный терминал принимает отраженные от окружающих предметов сигналы базовой станции в угловом секторе по азимуту 180°.

Определить:

1) пространственный разнос между двумя антеннами мобильного терминала в горизонтальной плоскости для обеспечения двукратного пространственно-разнесенного приема;

2) какой путь должен пройти мобильный терминал, чтобы принимаемый сигнал изменился от некоторой максимальной амплитуды до минимальной;

3)при скорости движения мобильного терминала V = 60 км/ч определить интервал временной когерентности принимаемого сигнала как интервал времени, в котором огибающая сигнала сохраняет свою полярность относительно среднего значения замирающего сигнала;

            4) для сравнения определить интервал временной когерентности сигнала через интервал доплеровского рассеяния сигнала за счет движения мобильного терминала со скоростью V = 60 км/ч.

Задача 68. В тропосферной линии связи угловой размер эффективно отражающего объема тропосферы равен 1°. Для радиолинии, работающей в диапазоне

5,5 ГГц, определить расстояние между двумя антеннами приемной тропосферной станции для организации двухкратного пространственно-разнесенного приема.

5.4. Межсимвольные помехи в радиоканале связи с многолучевым распространением радиосигналов

Межсимвольные помехи резко ограничивают скорость передачи информации в канале связи. Для повышения скорости передачи информации приходится организовывать передачу информации по нескольким или даже многим параллельным каналам связи.

На рис. 12 показано взаимное положение сигналов нескольких лучей примерно равной мощности (прямой луч отсутствует) на входе приемника при поочередной передаче символов «1» и «0». Рассеяние лучей по задержке равно Δτ.

            Наиболее физически наглядно понять вредное воздействие межсимвольной помехи можно при передаче двоичных символов методом частотной манипуляции. Пусть при передаче символа «0» на частоте ƒ₀ на выходе частотного детектора приемника создается напряжение положительной полярности, а при передаче символа «1»

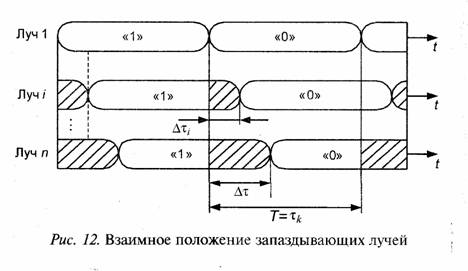
на частоте ƒ₁ — напряжение отрицательной полярности. На интервале времени Т =τk (рмс. 12) при передаче символа «0» заштрихованные части лучей будут создавать отрицательное напряжение на выходе частотного детектора (межсимвольную помеху). Например, при наличии всего двух лучей равной интенсивности и Δτ —> τ_k наглядно видно, что прием сообщений становится невозможным.

Рассмотрим передачу сигналов с фазовой манипуляцией на 180° с длительностью канальных символов τ_к. На интервале времени T заштрихованные участки сигналов каждого луча длительностью Δτ_i имеют фазу противоположную фазе последующего участка сигнала длительностью Т-Δτ_i. На выходе узкополосного фильтра (с полосой Δƒ≈ 1/τ_k) перед демодулятором отрезки сигнала каждого луча длиной Δτ_i (заштрихованная часть на рис. 56) будут компенсировать сигнал на последующем интервале времени Δτ_i имеющего противоположную фазу радиосигнала.

            В результате энергия канального импульса в луче уменьшится по сравнению со случаем Δτ_i<<τ_k на величину пропорциональную 2Δτ_i. Можно принять, что среднее значение интервала Δτ_i есть Δτ/2 и энергия многолучевого сигнала за счет межсимвольной помехи уменьшится и станет равной Р_с(τ_k-Δτ), где Р_с — мощность многолучевого сигнала.

Отношение принятой энергии символа на интервале времени Т к спектральной плотности шумов N_o будет равно

Потери в энергетике радиолинии по отношению к случаю отсутствия межсимвольных помех (Дт = 0) составляют величину

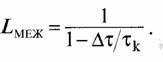
            Задача 69. Для многолучевого сигнала с рассеянием по задержке Дт и длительностью канального символа τ_k:

            1.  Построить кривую потерь в энергетике радиолинии за счет межсимвольной помехи L_МЕЖ в дБ в зависимости от отношения Дт/т_к.

2. Оценить влияние межсимвольной помехи и найти L_мвж для случая, когда на передаче длительность излучения канального символа уменьшается на величину Δτ , т. е. передатчик выключается на время Δτ перед излучением каждого следующего канального символа. Сравнить с ситуацией по п. 1 задачи с учетом статистики передаваемых последовательностей символов «1» и «0».

3. С учетом поведения кривой потерь L_МЕЖ по п. 1 задачи определить максимально-возможную скорость передачи канальных символов R_k - l/τ_k и скорость передачи информации R бит/с в одном канале для случаев:

• ФМ-2 (R = R_K);       • ФМ-8;

• ФМ-4;                   • КАМ-16,

если рассматривается сотовая сеть мобильной связи в городе с величиной рассеяния по задержке Δτ = 3 мкс и допустимая величина L_меж -1 дБ.

            4. Укажите возможные методы передачи сигналов, позволяющих на порядок и более увеличить скорость передачи информации в многолучевом канале с межсимвольными помехами.

5.5. Влияние эффекта Доплера на помехоустойчивость

приема сигналов с ортогональным частотным

разделением каналов (ОЧРК)

            Для устранения влияния межсимвольных помех в условиях многолучевого распространения сигнала используется синхронная параллельная передача информации по многим частотным каналам с уменьшением скорости

передачи информации в каждом частотном канале, так чтобы длительность канального символа в одном частотном канале была значительно больше интервала рассеяния сигнала по задержке.

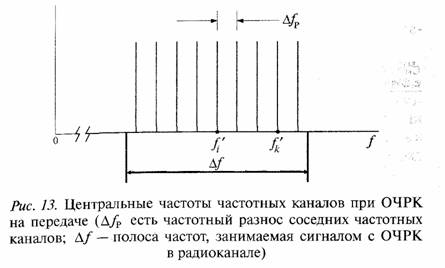
            На рис. 13 показаны центральные частоты парциальных каналов при ОЧРК при разносе соседних частот ΔF_P в радиоканале.

            Величина ΔF_P выбирается равной величине обратно пропорциональной длительности канального символа τ_k в парциальном канале, т. е. ΔF_P = 1/τ_k.

            В этом случае сигналы в отдельных частотных каналах выделяются в приемнике без взаимных помех.

            Однако, при использовании метода ОЧРК в мобильных сетях связи за счет доплеровского смещения частоты, разного для разных каналов, ортогональность принимаемых сигналов нарушается и возникают взаимные помехи между каналами, величину которых необходимо оценить.

Уровень междуканальных помех целесообразно определить для идеального приемного устройства, состоящего из п параллельных синхронных демодуляторов, где

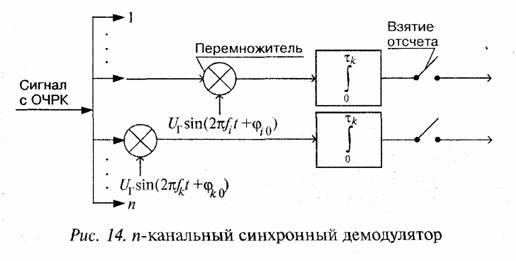
п — число частотных каналов при 04 РК, на выходе каждого из которых стоит интегратор с синхронным разрядом — согласованный фильтр для прямоугольных видеоимпульсов на выходе синхронного демодулятора.

            Функциональная схема приемного устройства показана на рис. 14.

Рассмотрим выделение и демодуляцию сигнала в одном частотном канале без учета влияния остальных каналов.

Принимаем, что в каждом частотном канале используется фазовая манипуляция радиосигнала на 180° (ФМ-2). На входе многоканального синхронного демодулятора действует сигнал

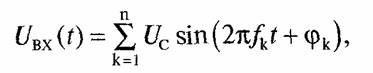
редаваемой частоты ƒ′_к, φ_к = φ_к(t) + φ_ko, где  φ _k(t) принимает значение 0 или π при манипуляции радиосигнала, φ_ко — некоторая начальная фаза радиосигнала в k-ом частотном канале.

Напряжения опорных когерентных генераторов в приемнике U_Гsin(2πf_kt + φ_ko) подстраиваются по частоте и фазе по приходящему в приемник радиосигналу. Аналогично генераторы тактовой частоты следования символов F_τ = 1/τk в каждом канале подстраиваются по частоте и фазе по принимаемому сигналу.

            Интегратор с синхронным разрядом производит интегрирование входного колебания с шумами за интервал времени х_к. В момент окончания символа с помощью узкого тактового импульса схемы тактовой синхронизации производится взятие отсчета для дальнейшей обработки принимаемых символов и их декодирования, и разряд выходного напряжения интегратора до нуля.

            Интегратор с синхронным разрядом является согласованным фильтром для прямоугольного импульса сигнала. Прямоугольный видеоимпульс сигнала с амплитудой U_c и длительностью т имеет спектр

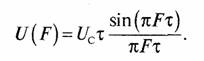
            Покажем, что амплитудно-частотная характеристика интегратора с синхронным разрядом также имеет форму типа U(F), т.е. является согласованным фильтром. Подадим на вход интегратора 5-импульс т.е. импульс бесконечно-короткий по длительности с площадью равной единице, так что интеграл от 6-импульса за бесконечно-короткий промежуток времени равен единице. Входной и выходной сигнал интегратора с синхронным разрядом показан на рис. 15.

            Так как спектр 5-импульса равномерен в бесконечно-широкой полосе частот, то спектр отклика интегратора с синхронным разрядом повторяет форму его АЧХ. Спектр выходного импульса единичной амплитуды длительностью т_к (АЧХ интегратора с синхронным разрядом) есть

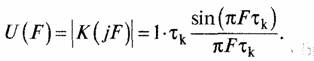
            Для анализа прохождения шумов через интегратор с синхронным разрядом удобно использовать нормированную форму его АЧХ.

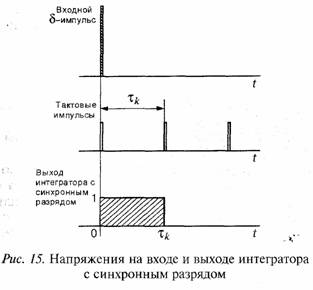
            Теперь можно определить, например, сигнал частотного канала ƒ_i в точках схемы рис. 14 на входе и выходе интегратора с синхронным разрядом.

Для компоненты входного сигнала с ОЧРК на частоте ƒ_i получим

Поскольку ƒ_i>>Δƒ, то второй член, содержащий колебание удвоенной частоты, будет отфильтрован (подавлен) интегратором с синхронным разрядом и мы его опустим для дальнейшего анализа. Также для удобства положим U_Г/2 = 1. Тогда с учетом сказанного для дальнейшего анализа запишем

Задача 70. На входе схемы рис. 14 в полосе частот Δƒ действует шум с равномерной спектральной плотностью N₀.

            1.  Покажите, что на входе интегратора с синхронным разрядом (например, для канала частоты ƒ_i) при U_Г/2 =1 спектральная плотность шумов в видеополосе будет равна 2 N_о. Нарисуйте график спектральной плотности шума на входе интегратора с синхронным разрядом.

            2. Определите полосу пропускания интегратора с синхронным разрядом для длительности канальных импульсов τ_к и найдите отношение мощностей сигнал-шум на выходе интегратора с синхронным разрядом через отношение энергии входного бита Р_сτ_к, (Р_с – U²_c /2,   U_c — амплитуда   входного   для   схемы рис. 14 радиосигнала на частоте ƒ_i), к спектральной плотности шумов N_o на входе схемы рис. 14.

Задача 71. При наличии эффекта Доплера при отсутствии нестабильности частот поднесущих ОЧРК определить эффективное значение и мощность перекрестных помех на выходе интегратора с синхронным разрядом частотного канала с центральной частотой ƒ_i от всех остальных (n — 1) каналов при следующих исходных данных:                                                                         

1. Число частотных каналов п:

• 256 для системы WiMax;

• 4096 для системы цифрового телевидения.

2. Скорости движения мобильных терминалов:            

•  V— 120 км/ч для автомобиля;

•  F= 300 км/ч для поезда;

•  V= 300 м/с для самолета.

При расчете принять, что ξ = соs(φ _к- φ _i) имеет по ансамблю случайную фазу φ _к - φ_i, равновероятную в интервале 0—2 π, так что дисперсия случайной величины ξ есть 0,5, а среднеквадратическое значение величины ξ, есть 1/ , аналогично тому как вычисляется мощность и эффективное значение косинусоидалъного колебания как средние значения за период гармонического колебания.

             В результате решения задачи сделать заключение о возможности или невозможности использования метода модуляции ОЧРК в мобильных сетях связи.

ГЛАВА 6

СИНХРОНИЗАЦИЯ СИГНАЛОВ В РАДИОЛИНИЯХ

Перед началом приема информации все необходимые устройства приемника: демодулятор, декодер, устройство разуплотнения сигналов, устройства свертки широкополосного сигнала, шифратор и др. должны быть синхронизированы по частоте, времени, фазе с приходящим радиосигналом. Также приемная антенна станции должна быть нацелена на передатчик корреспондирующего абонента. Первоначальная необходимая синхронизация приемного устройства осуществляется при приеме так называемой преамбулы, которая передается перед началом передачи пакета из информационных сообщений и затем поддерживается при приеме сообщений.

Если радиостанция работает в сети связи (спутниковой, наземной сотовой), то часть синхронизирующих функций приемника может быть реализована заранее (наведение антенны по сигналу маяка или сигналам общего канала управления трафиком сети, синхронизация по частоте, широкополосному сигналу и др.).

            Главное требование ко всем каналам синхронизации — это обеспечить прием всех сигналов синхронизации с помехоустойчивостью, существенно более высокой, чем помехоустойчивость приема информационных сигналов с учетом помехоустойчивого кодирования в информационном канале, поскольку потеря сигналов синхронизации приводит к потерям больших массивов информации. С другой стороны, энергетические и временные затраты на передачу сигналов синхронизации должны быть минимальными.

Устройства обнаружения и захвата сигналов синхронизации различны для каждого сигнала синхронизации, а все системы слежения (автосопровождения синхросигналов) строятся по единой концептуальной схеме следящих систем.

В качестве математического аппарата анализа следящих систем используется преобразование Лапласа для непрерывных сигналов синхронизации и аппарат z-пре-образований для импульсных следящих систем.

6.1. Синхронизация по несущей частоте

принимаемого сигнала

В подавляющем числе современных радиолиний используется когерентный прием радиосигналов с фазовой манипуляцией, при котором обеспечивается наибольшая помехоустойчивость приема сигналов. При использовании помехоустойчивых кодов когерентный прием ФМ сигналов обеспечивает выигрыш по энергетике радиолинии около 3 дБ по сравнению с некогерентным приемом тех же ФМ сигналов с таким же помежоустойчивым кодированием.

            Функциональная схема формирования когерентной опорной несущей в приемнике с помощью системы фазовой автоподстройки частоты (ФАП) показана на рис. 16. При приеме отрезка чистой несущей частоты в начале преамбулы схема снятия фазовой манипуляции не нужна и для анализа системы ФАП можно считать, что немодулированная несущая поступает на ограничитель с полосовым фильтром на его выходе (фильтр не показан на рис. 16). При приеме информационных фазоманипулированных сигналов схема снятия манипуляции, например, при ФМ-2 состоит из удвоителя частоты, на выходе которого появляется немодулированная несущая, полосового фильтра и делителя частоты на два. В итоге, на выходе схемы снятия фазовой манипуляции появляется чистая несущая U_c sin (ω_сt+ φ ₀).

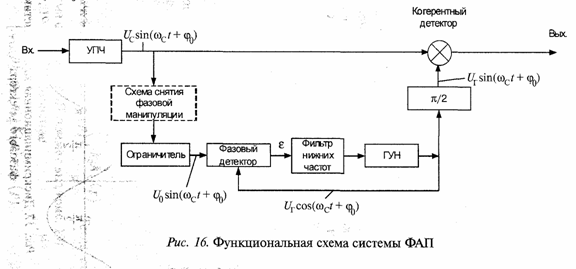
Фазовый детектор или фазовый дискриминатор является перемножителем двух входных колебаний: входного сигнала и напряжения ГУН-а. ГУН — генератор синусоидального сигнала, частота которого изменяется пропорционально управляющему напряжению (ГУН — генератор, управляемый напряжением). На выходе фазового детектора возникает сигнал рассогласования (управления), который, проходя фильтр нижних частот, управляет частотой и фазой ГУН-а таким образом, чтобы сигнал рассогласования стремился к нулю. В этом состоянии частота ГУН-а будет равна частоте входного сигнала, а фаза колебания ГУН-а будет отличаться от фазы входного сигнала на π /2.

            Определим передаточные функции элементов системы ФАП. Напряжение немодулированного .сигнала запишем как U₀sin((ω_ct+ φ ₀) = U₀sin φ _c, напряжение ГУН-а при разорванной цепи обратной связи — как U_гcos(ω_Гt+ φ _0Г) =U_Гcos φ_Г. На выходе фазового детектора напряжение сигнала ошибки (рассогласования)

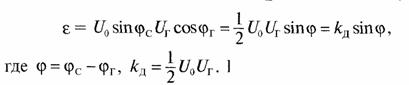
В выражении для ε опущена гармоническая составляющая на частоте ω_с+ω_г, которая подавляется фильтром нижних частот.

            Дискриминационная характеристика фазового детектора ε = k_дsinφ показана на рис. 17.

            Она является периодической с рабочей областью -π/2<φ<π/2. При разности фаз φ, попадающей в нерабочую область, отрицательная обратная связь в системе ФАП превращается в положительную и система ФАП переходит в режим биений (автогенерации) и становится неработоспособной.

            В режиме слежения сигнал ошибки ε мал, так что sinφ ≈φ и ε = k_дφ. В этом случае систему ФАП можно описать линейной следящей системой со структурной схемой, показанной на рис. 18.

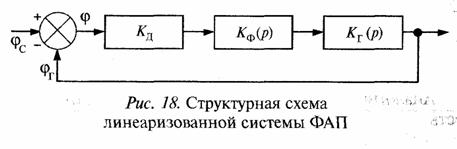
            Параметры φ _с, φ _г, φ, являющиеся функциями времени, в структурной схеме рис. 18 являются функциями оператора комплексной переменной p=jω, т.е.  φ_с =

= φс (р), φг = φг (Р) , φ = φ (р).                                       

Частота ГУН-а  ω_г=k_гU_BX. Частота и фаза ГУН-а связаны соотношениями ω _г(t) = dφ _г(t)/dt или φ_г(t) = ∫ω_г (t)dt.

            В операторной форме φ _г(p) = ω_г (a_r(p)/p = k_TU Передаточная функция ГУН-а равна

            Обозначим Тогда структурная схема системы ФАП примет вид (рис. 19). Из рис. 19 следует уравнение

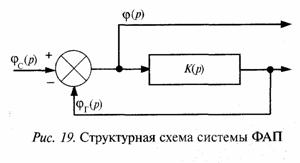
            Отсюда передаточная функция следящей системы

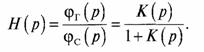
            Аналогично передаточная функция для частоты ГУН-а есть

            Для вычисления сигнала ошибки φ (р) (рис. 19) используем уравнение φ_c(p)- φ (p)K(p) = φ (p), откуда передаточная функция системы ФАП по ошибке равна

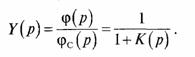
            Итак, изображение (преобразование Лапласа) частоты ГУН-а при изменении частоты сигнала есть:

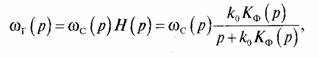
а изображение сигнала ошибки при изменении частота сигнала запишем следующим образом:                          

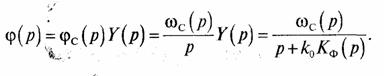
            Для получения выражений для частоты ГУН-а и сигнала ошибки как функций времени ω_г(t) и φ (t) необходимо перейти от изображений функций к обратному преобразованию Лапласа.

            Ниже в таблице приведены некоторые формулы преобразования Лапласа F(p)=F(t)dt.

Следящие системы исследуются на воздействия двух типов: единичного скачка и флкжтуационного воздействия в виде гауссовского шума.

Рассмотрим в качестве примера систему ФАП без фильтра нижних частот, т.е. положим К_ф(р) = 1. Пусть для моментов времени t < 0 разность частот входного сигнала и ГУН-а равна нулю, а для момента времени t > 0 частота входного сигнала изменилась скачком на величину Δω. Рассмотрим как частота ГУН-а будет отслеживать это изменение частоты входного сигнала. Положим ω_c(t)= Δω для   t≥0. Тогда

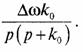
По таблицам обратного преобразования Лапласа найдем ω_г(t) =Δω (1 –e^-k0t), где величина k₀ — коэффициент усиления в петле обратной связи определяет быстродействие следящей системы.

Для сигнала ошибки при воздействии скачка частоты получим

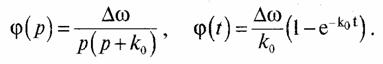
Система ФАП будет отслеживать изменения частоты и фазы входного сигнала, если сигнал ошибки (p(V) не будет выходить за пределы апертуры фазового детектора ±71/2.

При Δω/k₀>π/2 происходит срыв слежения. Величина Δω = Δω_захв, при которой выполняется условие Δω /k₀ < π /2, называется полосой захвата системы ФАП.

            Тогда для сигнала ошибки (разность фаз между фазой входного сигнала и фазой ГУН-а) можно записать

             Отсюда для задаваемой максимальной допустимой разности фаз φ (t) и величины Δω_захв можно определить допустимую расстройку Δω частоты входного сигнала от номинальной частоты ГУН-а.

            Линейную следящую систему как всякую линейную систему всегда можно представить в виде фильтра с некоторой полосой пропускания, называемой шумовой полосой следящей системы. Система ФАП есть узкополосный полосовой следящий фильтр с центральной частотой равной частоте входного сигнала.

            Увеличение коэффициента передачи к₀ петли обратной связи следящей системы увеличивает полосу захвата системы и ее быстродействие. При этом шумовая полоса частот следящей системы также растет, приводя к возрастанию шумовой ошибки следящей системы, которая может стать причиной срыва слежения. Без учета шумовых ошибок следящей системы выбор ее параметров бессмыслен.

            Шумовая полоса системы ФАП, как и другой системы синхронизации приемного устройства, определяется скоростью передачи информации в радиоканале и характеристиками помехоустойчивого кодирования.

            Помехоустойчивость системы ФАП и других систем синхронизации должна быть существенно выше, чем помехоустойчивость информационных каналов. С учетом использования помехоустойчивого кодирования в радиолинии шумовая полоса системы ФАП должна быть в 20—50 раз меньше скорости передачи информации по радиолинии.

Для системы ФАП необходимо найти флюктуационную ошибку ГУН-а. Эта ошибка влияет на качество когерентного детектирования радиосигнала (см. рис. 16) и определяет флюктационную разность фаз входного полезного сигнала и ГУН-а, которая не должна приводить к срыву слежения.

            Если на выходе УПЧ схемы рис. 16 действует гармонический сигнал мощностью Р_с и шум со спектральной плотностью N_o, то на входе фазового детектора линеаризованной схемы ФАП действует аддитивная смесь полезного сигнала φ_с(t) и шум с эквивалентной спектральной плотностью N_{0 Э}= N₀/P_C. Тогда дисперсия флюктуационной ошибки фазы ГУН-а есть σ²_φ, = N_oэΔF_ш  радиан², где ΔF_Ш — шумовая полоса следящей системы (видеополоса). Передаточная функция для фазы ГУН-а при воздействии фазы входного сигнала системы ФАП есть Н(р). Квадрат амплитудно-частотной характеристики следящей системы есть |H(jω) |² и шумовая полоса системы ФАП равна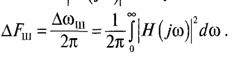

             Для системы ФАП без фильтра нижних частот получим

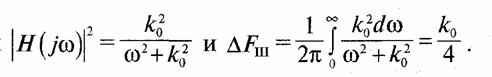
            Таким образом, шумовая полоса системы ФАП без фильтра нижних частот, называемой системой ФАП первого порядка (описывается дифференциальным уравнением первого порядка) или системой ФАП с первым порядком астатизма (с одним интегратором) равна полосе захвата ΔF_Ш - ΔF_3AXB.

Более высокие характеристики системы ФАП можно получить для систем ФАП второго порядка, оптимизируя характеристики фильтра нижних частот схемы рис. 16.

Задача 72. На схеме, изображенной на рис. 16, для установившегося режима частота ГУН-а равна частоте входного сигнала, а фаза колебания ГУН-а повернута на 90° по отношению к фазе входного сигнала. Объясните, по принципу действия ФАП как следящей системы, что это действительно так и должно быть.

Задача 73. Система ФАП без фильтра нижних частот в исходном состоянии находилась в установившемся режиме слежения за частотой и фазой радиосигнала. В момент времени t = 0 фаза входного сигнала изменилась скачком на величину φ (t) = Δφ₀ = const. Найти выражения для фазы ГУН-а φ_г(t) и сигнала ошибки φ (t) как функций времени.                                                    

Задача 74. В схеме, показанной на рис. 16, найти напряжение на выходе когерентного детектора, на один ,вход которого поступает фазоманипулированный сигнал U_Csin[ω_сt+φ₀ + φ (t)], где φ (t) = 0 при передаче символа «1» и φ (t) = π при передаче символа «О», а на другой вход когерентного детектора поступает опорное напряжение от ГУН-а U_г(ω_сt+φ₀).

Задача 75. В системе ФАП первого порядка изображение частоты ГУН-а ω_г (p) и сигнала ошибки φ (р) имеют вид при воздействии скачка частоты Δω на входе системы ФАП:

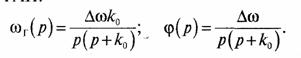
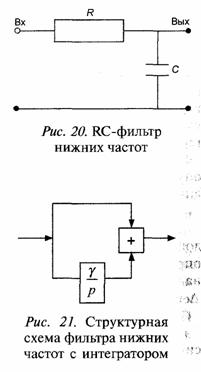            Найти установившиеся значения при / —> °° величин limω_г(t) и limφ (t).

t—>∞ t—>=о

Задача 76. Для системы ФАП с RC-фильтром нижних частот, показанного на рис. 20 найти передаточную функцию фильтра нижних частот К_ф(р) и изображение сигнала ошибки φ (p) системы ФАП, для скачка частоты входного сигнала Δω. Найти установившееся значение limφ (t).

                                               t—>∞

Задача 77. Для системы ФАП с интегрирующим фильтром нижних частот, показанного на рис. 21, написать выражение для передаточной характеристики фильтра    нижних    частот К_ф (р) и определить для скачка частоты входного сигнала Лео изображение сигнала ошибки φ (р). Найти установившееся значение limφ (t). Дать физическое толкование полученному установившемуся значению φ (t).    

Задача 78. Для системы ФАП с интегрирующим фильтром нижних частот (рис. 21) для скачка частоты входного сигнала Δω найти изображение сигнала ошибки φ (р). Привести это изображение к типовой форме вида, для которой имеются таблицы обратного преобразования Лапласа. Найти выражение для φ (t) при 4γ/k₀=1 (критический режим) и при 4у/к_о> 1 (колебательный режим). Построить кривые  φ (t)  для

этих режимов в функции аргумента .

            Для критического режима определить полосу захвата системы ФАП Δω_ЗАХВ из условия, что максимум функции φ (t) должен быть меньше или равен π/2 .

Задача 79. При когерентном детектировании радиосигнала (см. рис. 16) отклонение фазы ГУН-а от фазы принимаемого радиосигнала на некоторую величину Δφ уменьшает величину полезного сигнала на выходе когерентного детектора.                                                     

Для задаваемых допустимых потерь сигнала 0,З дБ определить допустимую величину Δφ в градусах и радианах.

            Задача 80. Для системы ФАП первого порядка для допустимой ошибки слежения по фазе не более 0,2 рад определить допустимую расстройку частоты радиосигнала Доз  относительно полосы захвата системы ФАП Δω_захв

Задача 81. Принимая, что процесс установления синхронизации ГУН-а по частоте и фазе практически завершен, когда значение ошибки φ (t) достигает величины 0,95 от установившегося значения, определить для системы ФАП первого порядка время (относительно величины 1/ΔF_m) окончания процесса синхронизации.

Задача 82. Для системы ФАП с двумя интеграторами (с интегрирующим фильтром нижних частот, показанном на рис. 21) для критического режима вычислить для входного скачка частоты радиосигнала Асо = А(О_ЗАХв изображение ошибки слежения ф(р) и его обратного преобразования Лапласа ф(^). Определить время синхронизации системы ФАП, считая, что синхронизация практически закончена, когда ошибка слежения становится равной или менее 0,2 рад.

6.2. Система тактовой синхронизации

            При приеме цифровых сигналов необходимо знать начало и конец каждого символа информации, что обеспечивается системой тактовой синхронизации. В приемном устройстве имеется генератор тактовой частоты (ГУН), который подстраивается по частоте и фазе по приходящему сигналу. При пакетной передаче сообщений в составе преамбулы после отрезка немодулированной несущей передается отрезок несущей, манипулированный меандром тактовой частоты для первоначальной синхронизации системы тактовой синхронизации приемника.

Функциональная схема автоподстройки частоты и фазы генератора тактовой частоты приемника по принимаемому сигналу не отличается от типовой схемы ФАП, рассмотренной ранее. Система тактовой синхронизации, выполняемая цифровыми устройствами или программным способом за счет высокой частоты дискретизации входного сигнала и многоразрядного АЦП сводится к непрерывному аналогу и рассчитывается как классическая система ФАП.

            Ошибки системы тактовой синхронизации приводят к уменьшению помехоустойчивости приема сигналов. Если на вход интегратора с синхронным разрядом поступают прямоугольные импульсы сигнала и система тактовой синхронизации выдает тактовые импульсы для разряда интегратора с ошибкой At по отношению к действительному положению фронтов импульса сигнала, то наличие ошибки Ах приводит к уменьшению амплитуды символа на выходе интегратора на величину 21/_с Дт., если перед (после) данным символом принимался символ другого знака.                                                          

При этом отношение мощностей сигнал—шум на, выходе интегратора с синхронным разрядом уменьшается в

            Задача 83. Система тактовой синхронизации не должна ухудшать отношение сигнал—шум на выходе интегратора с синхронным разрядом более чем на 0,3 дБ. Определить максимальную допустимую погрешность системы тактовой синхронизации Δτ в процентах по отношению к длительности символа τ .

            Задача 84. Задана нестабильность частоты генератора тактовой частоты приемника, равная 10^-4 относительно тактовой частоты принимаемых символов сигнала. После первоначального фазирования в приемнике тактовых импульсов с началом и концом принимаемых символов сигнала по преамбуле генератор тактовой частоты в приемнике не подстраивается по принимаемым информационным сигналам.

Определить через какое число принимаемых символов сигнала смещение тактовых импульсов системы синхронизации тактовой частоты относительно фронтов принимаемых символов достигнет допустимой величины в 1%.  

6.3. Прием стартового слова

            Наименьшую длину стартового слова обеспечивают корреляционные методы приема стартового слова или прием стартового слова на согласованный фильтр. В качестве стартового слова целесообразно выбрать m-последовательность, имеющей малые боковые лепестки автокорреляционной функции.

При приеме стартового слова возможны две ситуации: 1) часть меандра тактовой синхронизации преамбулы и часть стартового слова формируют сигнал синхронизации так, что происходит преждевременная ложная фиксация сигнала стартового слова. Также часть стартового слова и последующие символы информации или просто символы информации могут привести к ложной фиксации стартового слова. Вероятность ложного приема стартового слова обозначим через Р_л; 2) правильный прием стартового слова или неприем стартового слова. Вероятность правильного приема стартового слова обозначим через Р_пр, тогда вероятность неприема стартового слова есть 1 — Р_пр. Примем, что стартовое слово имеет длину из и канальных символов длительностью т. В канале передачи информации используется помехоустойчивое кодирование. При приеме каждого символа стартового слова в приемнике после когерентного детектора формируются символы с амплитудой +1 или — 1 в зависимости от фазы 0 или тс символов стартового слова. В отсутствие ошибок при приеме символов стартового слова на выходе согласованного фильтра в момент окончания стартового слова появится напряжение, равное +п.

            На рис. 22 показана схема согласованного фильтра для m-последовательности длиной п =71, состоящая из устройства задержки с отводами, фазовращателей и сумматора. Значок «—» фазовращателя означает изменение полярности сигнала, значок «+» означает, что полярность сигнала не меняется. На рис. 23 показаны эпюры сигналов на входе и выходе согласованного фильтра и результирующий импульс синхронизации на выходе порогового устройства.

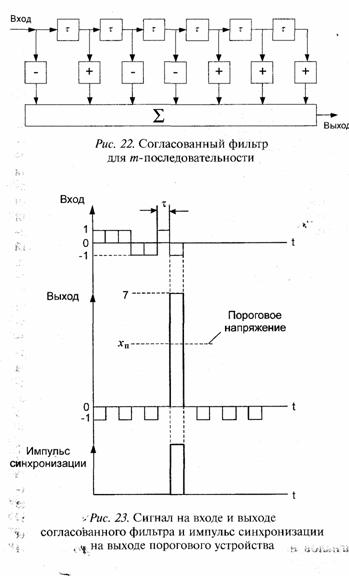
При наличии ошибок при приеме символов стартового слова распределение вероятностей напряжения на выходе согласованного фильтра (или коррелятора) в момент окончания стартового слова описывается биномиальным законом.

Вероятность того, что в блоке из п символов исказится ровно i символов, равна P(n,i) = Cⁱ_npⁱ{1-p)^n-1, где р — вероятность искажения одного символа. Среднее значение биномиального распределения вероятностей есть пр, а дисперсия равна пр(1-р). При единичной амплитуде символов стартового слова искажение одного символа приводит к уменьшению максимальной амплитуды сигнала на выходе согласованного фильтра на величину, равную 2.

Тогда среднее значение сигнала на выходе согласованного фильтра равно α = п-2пр = п(1-2р),а дисперсия будет равна σ² = 4пр(1-р), так как искажение одного символа дает амплитуду ошибки, равную 2.

Будем считать, что при формировании ложного сигнала стартового слова на входе согласованного фильтра присутствует случайная двоичная последовательность с вероятностью ошибки символа р = 1/2. Тогда среднее значение напряжения на выходе согласованного фильтра есть α = п(1-2р)= 0, а дисперсия σ²₀ =4пр(1- р) = п.

            При больших значениях п (п > 20) в соответствии с формулой Муавра—Лапласа теории вероятности биномиальное распределение вероятностей сходится к гауссовской плотности распределения вероятностей со средним значением ос и дисперсией Сто. Тогда вероятность ложного появления стартового слова равна

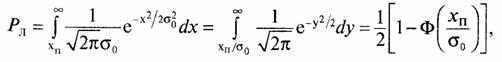
где х_п есть некоторое пороговое напряжение, которое выбирается исходя из заданной величины Р_л.     

В области малых значений Р_л (от 10 ³ до 10 ⁷) справедливо соотношение

Вероятность неприема стартового слова есть

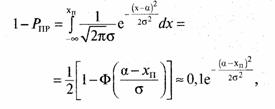
Помехоустойчивость приема стартового слова должна быть существенно выше помехоустойчивости приема информационных сообщений. Положим, что надежный прием стартового слова должен обеспечиваться при отношении сигнал—шум для одного канального символа равному единице (в канале передачи информационных сообщений используются мощные помехоустойчивые  коды). В этом случае следует положить р = 10^-1.

Задача 85. Построить зависимость вероятности неприема стартового слова 1 - Р_ПР от величины п (длина стартового слова) при вероятности ложного формирования стартового слова Р_л = 10^-6 для двух значений вероятности ошибки на символ стартового слова р = 10^-1 и р=10^-2. Для 1-Р_ПР= 10^-6 определить необходимую с длину стартового слова п при р = 10^-1 и р=10^-2.

ГЛАВА 7

КОДИРОВАНИЕ ИСТОЧНИКОВ СООБЩЕНИЙ

            Между кодером цифрового канала связи и источником сообщений включается кодер источника сообщений. Источник сообщения может быть цифровым (компьютер, магнитный или оптический диск) или аналоговым (телефонный, телевизионный, телеметрический сигналы). Задача кодера источника сообщения — представить передаваемое сообщение в цифровой форме для канала связи в наиболее экономном виде. Кодер источника сообщения также называют устройством сжатия сообщений. Если источник цифрового сообщения создает поток двоичных символов со скоростью R_и, то на выходе кодера сообщения появляется поток информационных бит со скоростью R<R_R. Отношение К_сж = R_и/R называется коэффициентом сжатия. Так для модема V.34 канала тональной частоты разработано устройство сжатия текстовой информации с коэффициентом сжатия К_сж=4. На выходе модема V.34 R = 32кбит/с при R_И= 128кбит/с.

            При передаче телефонного сигнала следует положить R_и = 64 кбит/с. При этой скорости передачи преобразование аналогового телефонного сигнала в цифровую форму с использованием командирования происходит без потери качества телефонного сигнала. Прослушивание бригадой экспертов телефонного сигнала после обратного преобразования цифрового телефонного сигнала в аналоговую форму показывает, что качество восстановленного сигнала не отличается от исходного. На сегодняшний день кодеры телефонного сигнала, называемые речепреобразующими устройствами, позволяют передавать телефонный сигнал с хорошим качеством на скорости до 2,4 кбит/е, т.е. обеспечивается получение коэффициента сжатия К_сж - 27.

            Для цветного телевизионного сигнала при цифровом его представлении без потери качества R_u ≈ 256 Мбит/с. Коэффициент сжатия телевизионного сигнала при коммерческом качестве телевизионного сигнала (качество принимаемого аналогового телевизионного сигнала стандарта «Секам») достигает величины К_сж = 50100.

            При обработке телеметрической информации от ракет и космических аппаратов достигается коэффициент сжатия порядка 100.                      

7.1. Кодеры стационарных цифровых источников информации

            Пусть источник информации имеет алфавит из п символов (букв) х₁…х₂...х_п с априорной вероятностью появления буквы х_i равной Р(х_i). Количество информации, s получаемое при появлении буквы х_i, есть логарифмическая мера отношения апостериорной вероятности появления х_i (которая равна 1 при появлении х_i) к априорной вероятности Р (х_i):

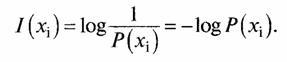
 Средняя информация источника цифровых сообщений на символ (букву) называется энтропией источника:

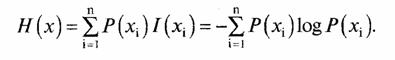
Если источник информации генерирует независимые буквы с некоторой электрической скоростью R_и букв за секунду, то скорость создания информации источником:

есть R = H(x)R_И и предельно-достижимый коэффициент сжатия равен К_СЖ = 1/H(x).

Рассмотрим источник двоичной информации, который выдает последовательность независимых символов «0» с вероятностью q и символов «1» с вероятностью 1 - q.

Энтропия такого источника на бит

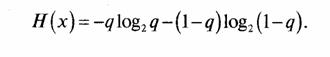
Задача 86. Определить максимально-достижимый коэффициент сжатия двоичных сообщений от источника независимых двоичных символов с вероятностью появления символов «О» Р(0) = 0,9 и символов «1» />(1)   01

Алгоритм кодирования Хаффмена

Алгоритм Хаффмена есть алгоритм кодирования с помощью кодовых слов переменной длины, в котором более вероятные буквы представляются более короткими кодовыми словами. При этом кодовые слова при приеме декодируются однозначно без каких-либо символов начала или конца кодового слова.

По методу Хаффмена буквы записываются в столбец сверху вниз по мере убывания их априорной вероятности Р(х_i) и строится кодовое дерево, как это иллюстрируется на рис. 24.

Процесс кодирования и построение кодового дерева начинаем с двух наименее вероятных символов (букв) х₈ и х₇. Эти два символа объединяем, как показано на рис. 24, причем верхнему ветвлению присваиваем символ «0», а нижнему «1». Вероятности этих двух ветвей складываются и общему узлу присваивается суммарная вероятность, как это показано на рис. 24. Далее опять объединяются ветви с наименьшими вероятностями и т.д. Кодовые слова получаются при движении от самого

правого узла дерева до крайнего левого узла. При движении вверх по дереву формируется символ «О», при движении вниз — символ «1», как это показано в таблице на рис. 24.

Задача 87

1. Определить максимально-достижимый коэффициент сжатия сообщений от источника независимых символов x₁...x₈ с априорными вероятностями, представленными в таблице рис. 24, если каждый символ ; х₁...x₈ от источника информации представлен трехразрядным двоичным кодовым словом.

2. Определить среднюю длину кодового слова в битах на букву п = Σ⁸_i=1 Р(х_i)n_i, где n_i — длина кодового слова х_i в таблице рис. 24. Определить эффективность (КПД) кодирования по методу Хаффмена, вычислив отношение п/Н(х).

7.2. Кодирование аналоговых источников сообщений

Количество информации, содержащееся в стационарном аналоговом сигнале в некотором интервале времени, дает теория информации, как и в случае цифровых источников информации.

Теоретически это количество информации равно бесконечности, если необходимо различать бесконечное число амплитудных уровней сигнала. Поэтому количество информации в аналоговом сигнале вычисляется при заданной допустимой величине искажения аналогового сигнала. Это количество информации и определяет величину до которой потенциально можно сжать стационарный аналоговый сигнал.

Количество информации, содержащемся в стационарном аналоговом гауссовском сигнале дается теорией е-энтропии А.Н. Колмогорова. Энтропия аналогового сигнала за время T—> ∞ равна, бит

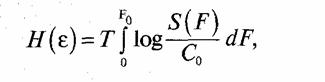
где S(F) — спектр мощности аналогового сигнала, С₀ — спектральная плотность мощности ошибки воспроизведения аналогового сигнала, равномерная в полосе частот от нуля до F₀, где интервал частот от нуля до F₀ есть интервал частот, где S(F) ≥ С₀, так как те частотные компоненты сигнала, для которой S(F)<C₀, воспроизводиться не должны, так как их воспроизведение с ошибкой  со  спектральной плотностью  С₀ даст большую

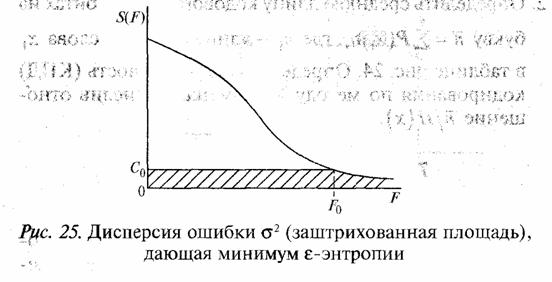
ошибку воспроизведения аналогового сигнала. Сказанное выше иллюстрируется рис. 25.

Минимально необходимая скорость передачи информации в бит/с от аналогового источника сообщений при максимальном сжатии сообщения будет равна

R=

определяется для заданной нормированной дисперсии ошибки воспроизведения аналогового сигнала из выражения (см. рис. 25)

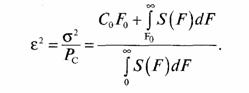
Для аналогового сигнала с равномерным спектром от нуля до некоторой максимальной частоты F₀ имеем

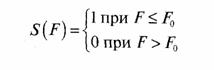
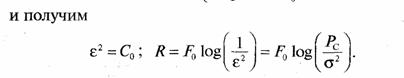
Из вышесказанного и рис. 25 следует метод сжатия аналоговых сигналов, называемых методом ортогональных преобразований, который является наиболее эффективным.

Спектр аналогового сигнала на интервале стационарности Т на основании обратной теоремы Котельникова представляется независимыми отсчетами, отстоящими по частоте на интервал 1/7⁷. Каждый отсчет характеризуется двумя координатами: амплитудой отсчета и его фазой или синусной и косинусной координатами. Для некоторых аналоговых сигналов, например, телефонного сигнала, необходимо знание только амплитуды сигнала, фаза частотного отсчета передаваться не должна, поскольку ухо человека не чувствительно к фазе гармонических составляющих спектра телефонного сигнала.

Для заданной спектральной плотности ошибки С₀ (см. рис. 25) все частотные отсчеты спектра аналогового сигнала, лежащие правее частоты F₀, отбрасываются. Оставшиеся отсчеты спектра оцифровываются, исходя из заданной дисперсии ошибки C/S(F_i) и передаются по каналу связи.

Для нестационарного процесса, у которого изменяется ширина спектра аналогового сигнала, при уменьшении ширины спектра сигнала на интервале стационарности T автоматически уменьшается величина F₀ и число отсчетов спектра сигнала, которое необходимо передавать по каналу связи, что и предопределяет возможность эффективного сжатия аналогового сигнала.

7.3. Сжатие аналоговых сигналов с помощью предсказателей

Рассмотрим аналоговые сигналы со спектрами мощности вида

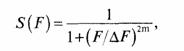
где ΔF есть ширина спектра сигнала по уровню половинной мощности, т— 1,2,...

При малых т частота дискретизации сигнала по времени F_д много больше ширины спектра сигнала ΔF, так что на интервале корреляции сигнала 1/ΔF укладывается большое число выборок сигнала. Это говорит о том, что соседние выборки сигнала сильно коррелированы и целесообразно по каналу связи передавать только разность между амплитудой текущей выборки сигнала и ее предсказанного значения.

Для спектра сигнала S(F) при т = 1 случайный аналоговый сигнал представляет собой марковский случайный процесс, у которого текущая выборка сигнала зависит только от одной предыдущей выборки сигнала.

Рассмотрим сжатие стационарного аналогового марковского случайного процесса при использовании предсказания амплитуды текущей выборки сигнала по значению предыдущей выборки. Обозначим текущее значение выборки сигнала через x(t), предыдущей выборки — через х(t-τ), мощность стационарного случайного сигнала — через σ²с. Среднее значение квадрата разности между текущей и предыдущей выборками есть

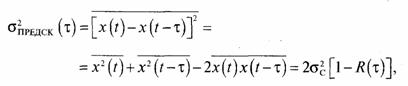
где горизонтальная черта означает операцию усреднения;

х² (t) = х² (7 - т) = σ_с есть мощность сигнала; R(τ) — коэффициент корреляции случайного процесса.

Обозначим квадрат нормированной ошибки предсказания как ε²_предск (τ) = σ²_прeдск (τ)/ σ²_C = 2[l - R(τ)] .

При расстоянии между соседними выборками сигнала Т_ОПР = 1/F_д, где Т_0ПР — интервал опроса, F_д —частота дискретизации аналогового сигнала по времени,

и τ = Т_опр получим ε²предск =2[l-R(T_oпp)].

Если при эффективном значении аналогового сигнала σ_с для квантования выборок по амплитуде используется равномерное квантование на L уровней, то для квантования предсказанного разностного сигнала потребуется    уровней квантования и требуемая скорость передачи аналогового сигнала методом предсказания составит величину R= F_д log(ε_предскL).

Выразим величины F_д и ε_ПРЕДСК через ε-результирующую среднеквадратичную погрешность передаваемого аналогового сигнала. Квадрат (дисперсия) результирующей погрешности передачи аналогового сигнала ε²=ε²_д+ε²_кв, где ε²_д-дисперсия ошибки дискретизации сигнала по времени при его восстановлении в приемнике, ε²_кв -дисперсия шумов амплитудного квантования (оцифровки) выборок сигнала, нормированная относительно мощности сигнала σ²_с.

Для восстановления значений марковского сигнала между соседними выборками сигнала можно использовать ступенчатую экстраполяцию или линейную интерполяцию между двумя соседними выборками.

Мы рассмотрим ступенчатую экстраполяцию в интервале времени Т_0ПР/2 вперед и назад по принимаемой выборке сигнала, как это показано на рис. 26.

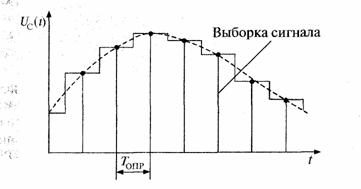
Для дисперсии ошибки дискретизации сигнала по времени при восстановлении его в приемнике с помощью ступенчатой экстраполяции можно записать

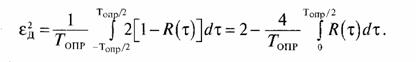
Задача 88. Для аналогового сигнала со спектром мощности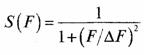

вычислить минимальную скорость передачи информации, даваемую теорией эпсилон-энтропии

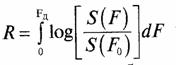
при задаваемой нормированной дисперсии ошибки воспроизведения аналогового сигнала е², которая связана с величиной F_o

соотношением

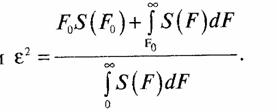
Сравнить полученное выражение для R с аналогичным выражением для метода предсказания. При вычислении R использовать значение неопределенного интеграла ∫ln(a² -x²)dx-=x ln(a²+ x²)-2x + 2aarctg из справочника Градштейн И.С. и Рыжик И.М. «Таблицы интегралов, сумм, рядов и произведений» («Физматгиз», 1962) и полагая ΔF/F₀ << 1.

            Задача 89. Оценить скорость передачи телефонного сигнала, даваемого теорией эпсилон-энтропии, R = 3,7ΔF/e², где ΔF ~ 700 Гц ширина спектра мощности телефонного сигнала по уровню половинной мощности согласно рис. 27, и приняв, что высокое качество речи обеспечивается при отношении средней мощности сигнала к мощности шума, равного 8 дБ.

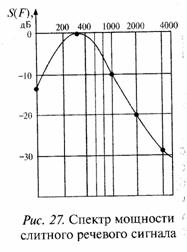
Задача 90. Оценить скорость передачи телефонного сигнала при методе его передачи с предсказанием,

приняв, что стационарный телефонный сигнал может быть аппроксимирован марковским случайным процес-

сом   со   спектром   мощности

где

 = 700 Гц и высокое качество телефонного сигнала обеспечивается при отношении средней мощности сигнала к мощности шумов дискретизации сигнала по времени и шумов квантования по амплитуде, равному 8 дБ.

Задача 91. Определить минимально достижимую скорость передачи телефонного сигнала по критерию разборчивости речи (узнаваемость голоса, тембр речи и др. не имеет значения) в следующей гипотетической линии связи. На передающей стороне канала связи стоит некий суперпроцессор, называемый в литературе пер-цептроном, который превращает речь в телеграфный текст, который и передается по каналу связи. На приемной стороне перцептрон превращает телеграфный текст в речевой сигнал, так что передача речи производится в реальном масштабе времени.

Принять, что телеграфный текст передается пятиразрядным кодовым словом для каждого телеграфного знака (буквы)

7.4. Сжатие нестационарных случайных процессов

Все реальные аналоговые сообщения, такие как телефонный, телевизионный сигналы и телеметрические сообщения, являются нестационарными. Вычисление требуемой скорости передачи аналогового сообщения методами эпсилон-энтропии и предсказания необходимо производить для каждого интервала стационарности сообщения или стационарного фрагмента передаваемого изображения. Для речи в качестве интервала стационарности может быть взята длительность звука, равная 25-30 мс.

Нестационарными также являются средние уровни сигнала на интервале (фрагменте) стационарности. Наличие пауз речи во временя разговора, также является признаком нестационарности.

Различают сжатие аналогового сигнала без потери качества исходного несжатого сигнала (например метод предсказания) и сжатие аналогового сигнала с ухудшением качества, например, до уровня коммерческого качества для телефонного и телевизионного сигналов. Уровни коммерческого качества определяются экспертным методом, например, по пятибалльной шкале для телефонного сигнала. Наибольший вклад в коэффициент сжатия аналогового сигнала вносит учет изменения ширины спектра аналогового сигнала при его передаче, поскольку требуемая скорость передачи информации прямо пропорциональна ширине спектра сигнала. Сжатие динамического диапазона по амплитуде передаваемого сигнала уменьшает скорость передачи информации только пропорционально логарифму уменьшения числа уровней квантования передаваемых сигналов.

Задача 92. Определить скорость передачи телефонного сигнала при сжатии телефонного сигнала без потери качества для каждого из следующих трех условий:

1. Средний уровень телефонного сигнала стабилизирован за счет схемы      автоматической регулировки среднего уровня сигнала (схемы АРУ), так что необходимо передавать сигнал с его естественным пик-фактором в 15 дБ. Принять что отношение средней мощности телефонного сигнала к мощности шумов квантования по амплитуде должно быть не менее 8 дБ. Частота дискретизации телефонного сигнала равна 8 кГц.

2. Дополнительно к условию 1 используется метод предсказания амплитуды           выборки по значению предающей выборки, что дает сжатие скорости передачи ин         формации в 2 раза.

            3. Дополнительно к условиям 1 и 2 в многоканальной системе в паузах речи одного          канала передаются выборки телефонных сигналов других каналов, так что в            многоканальном сигнале паузы отсутствуют.

Задача 93. При передаче телевизионного сигнала в существующей системе используется оцифровка сигнала яркости с помощью 8 бит, что учитывает динамический диапазон изменения среднего значения яркости на интервалах стационарности и число градаций яркости, различаемых человеком.

В предлагаемой в задаче системе сжатия телевизионных сигналов вычисляется средний уровень яркости сцены (кадра), который передается по отдельному низкоскоростному каналу (его учитывать в данный задаче не требуется).

Определить коэффициент сжатия канала яркости телевизионного сигнала, если принять, что человек различает не более 8—10 градаций яркости.

ГЛАВА 8

ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ В КАНАЛАХ СВЯЗИ

Помехоустойчивое кодирование сообщений в каналах связи используется в следующих целях:

•  для получения энергетического выигрыша в радиолиниях;

•  для передачи сообщений в более узкой полосе частот с целью экономии   занимаемой полосы частот и увеличения тем самым возможного числа каналов в телекоммуникационной системе;

            •  для получения квазибезошибочной передачи сообщений с вероятностью ошибки           на бит р≤10^-12 при существующей ошибке на бит в канале связи 10^-4  ÷10 ^-6;

•  для" контроля достоверности принимаемых сообщений путем обнаружения        ошибок в канале связи и стирания ошибочно принятых сообщений.

Получение     энергетического выигрыша в радиолиниях за счет помехоустойчивого кодирования             важно для спутниковых мобильных систем связи и авиационных высокоскоростных радиолиний. Энергетический выигрыш в радиолиниях позволяет существенно снизить мощности передатчиков или уменьшить габариты антенных систем приемо-передающих мобильных радиостанций и мощность передатчиков спутниковых ретрансляторов.

В наземных сотовых мультимедийных системах мобильной связи с кодовым многостанционным доступом повышение помехоустойчивости приема сигналов за счет кодирования позволяет уменьшить влияние внутрисистемных помех и за счет этого существенно увеличить число каналов связи в системе.

В наземных радиолиниях фиксированной связи, когда расстояния между передатчиком и приемником относительно невелики (десятки км) и мощности передатчиков имеют величины единицы милливатт (радиорелейные линии связи)получение энергетического выигрыша за счет кодирования не актуально и в таких радиолиниях помехоустойчивое кодирование, как правило, не используется.

Использование кодирования в канале связи с целью сокращения занимаемой полосы частот используется при создании высокоскоростных линий связи, в которых обеспечение необходимой энергетики каналов связи не вызывает затруднений. Такими каналами являются наземные каналы передачи вещательного цифрового телевидения, высокоскоростные радиосистемы типа WiMax, кабельные каналы связи «последней мили» и др. Экономия полосы канала связи (или возможность организации более высокоскоростных каналов связи) обеспечивается путем перехода от двоичного кодирования к кодированию с большим основанием кода, начиная с троичного кода и до квадратурно-амплитудной модуляции сигнала (КАМ-16, КАМ-64 и др.).

Достижение квазибезошибочного приема сообщений обеспечивается посредством обнаружения ошибок в принимаемом сообщении, стирании этого сообщения и повторной передачи стертого сообщения по каналу связи. Этот метод передачи называется методом передачи сообщений с переспросом и повторением и широко используется в кабельных каналах связи и спутниковых низкоскоростных каналах связи (передача сигналов электронной почты со скоростью 300 бит/с в системе INMARSAT).

Все командные радиолинии, авиационные и космические, также используют метод переспроса и повторения командных сообщений.

Помехоустойчивые коды обеспечивают энергетический выигрыш 5—7 дБ и более в радиоканалах без замираний сигнала и десятки дБ в каналах с замираниями s сигнала, если обеспечить независимость замираний символов кодового слова, например, разнесением символов во времени (метод перемежения символов) или передачи отдельных символов слова на разных частотах (частотное разнесение) на такой интервал частотного разнесения  при котором символы замирают независимо. При этом обеспечивается энергетический выигрыш, аналогичный выигрышу от d_x — кратного разнесенного приема символов, где d_x — минимальное Хэммингово расстояние ансамбля кодовых слов.                                                      

            При помехоустойчивом кодировании к информационным символам добавляются избыточные символы, пусть длительность одного двоичного символа на входе кодера равна х₀. Блок из k информационных бит будет передан за время Т = кτ₀. Если к k информационным битам добавляются r избыточных бит, так что кодовое слово содержит п=k + r бит, то эти п бит должны быть передать за время Т; при этом длительность канального бита х окажется равной  и полоса частот, занимаемая кодированным сигналом, увеличивается. Величина к/п называется скоростью кодирования r_к = k/п ≤1.                     Вторым основным параметром двоичного кода является минимальное Хэммингово расстояние d_x, которое равно минимальному числу символов, на которое отличаются любая пара кодовых слов.

8.1. Геометрические представления оптимальных кодов и энергетический выигрыш помехоустойчивого кода

Один кодовый символ (двоичный или АИМ) в виде прямоугольного видеоимпульса с амплитудой U_ci будем  характеризовать одной координатой с амплитудой U_ci в Евклидовом пространстве. Кодовое слово из п символов длительностью Т представляется в Евклидовом n-мерном пространстве вектором с длиной

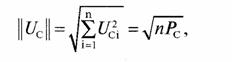
где Р_с — средняя мощность сигнала длительностью Т.

Аналогично, если мощность шума по одной координате есть а², то эффективная длина вектора шума ||U_ш||=√nσ. Так как все в мерном пространстве есть направления вектора шума в пространстве сигналов (Евклидовом пространстве) равновероятны, то шум в пространстве сигналов образует некоторое облако неопределенности сферической формы вокруг конца вектора принятого сигнала. Некоторый объем пространства сигналов можно разбить на М непересекающихся объемов (М— число кодовых слов ансамбля сигналов), расположенных около концов векторов сигнала. Этот объем называется зоной сигнала и определяет вероятность правильного приема этого сигнала, поскольку если вектор принятого сигнала плюс шум попадают в зону передаваемого сигнала, то сигнал считается принятым правильно.

Из-за сферической формы облака неопределенности шума при одном и том же объеме зоны сигнала наибольшая вероятность правильного приема сигнала будет соответствовать зоне сигнала, наиболее приближающейся к сфере. Концы векторов сигналов оптимального кода должны лежать в центрах гиперсфер при их плотнейшей укладке в объеме пространства сигналов, поэтому оптимальные коды называются кодами плотнейшей сферической укладки.

В двумерном пространстве задача плотнейшей сферической укладки сводится к задаче плотнейшей укладки кругов на плоскости и оптимальной формой зоны сигналов является правильный шестиугольник, как это показано на рис. 28.

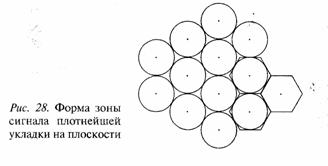
Если все кодовые слова имеют одинаковую среднюю мощность (одинаковую энергию), то концы векторов сигналов лежат на поверхности сферы одного и того же радиуса. Сигнальные точки оптимальных кодов в этом случае будут совпадать с центрами кругов плотнейшей укладки на поверхности гиперсферы. Такие оптимальные коды называются кодами поверхностно-сферической укладки.

Среди кодов с одинаковыми расстояниями между ближайшими сигналами коды плотнейшей укладки имеют максимальное количество кодовых слов, а среди кодов с одинаковым количеством кодовых слов коды плотнейшей укладки имеют наибольшее расстояние между ближайшими сигналами.

Максимальная средняя вероятность правильного приема кодовых слов ансамбля сигналов достигается, когда все области правильного приема сигналов или зоны сигналов одинаковы. Такие коды называются регулярными. Теория кодирования занимается построением регулярных кодов.

В трехмерном пространстве сигнальные точки регулярных кодов с равной энергией лежат на поверхности сферы и совпадают с вершинами правильных многогранников, которые показаны на рис. 29 с числом сигнальных точек М.

Если радиус сферы, на которой лежат сигнальные точки кодовых слов есть r, то площадь поверхности сферы зоны одного сигнала есть S₁ = 4πr²/M. Помехоустойчивость приема сигналов будет наибольшей для таких сигналов, для которых при одинаковой величине S₁ расстояние между соседними сигналами d будет наибольшим или для таких сигналов, для которых безразмерная величина d²/S_i будет наибольшей.

Запишем: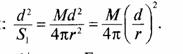

Величина d/r есть Евклидово расстояние между соседними сигналами на сфере единичного радиуса.

Итак, оптимальный код есть код, который обеспечивает максимум величины M(d/r)² . В таблице представлены значения величин M(d/r)² для сигнальных конструкций, представленных на рис. 29.

Из таблицы следует, что кодам плотнейшей поверхностно-сферической укладки соответствуют положения сигнальных точек в вершинах октаэдра и икосаэдра. Эти коды в трехмерном пространстве не являются двоичными. Для икосаэдра можно построить троичный код со значениями символов +1, — 1 и нуль.

Рассмотрим два сигнала в мерном пространстве. Расстояние между концами векторов сигнала есть d. Совместим отрезок d с одной из осей координат пространства сигналов (рис. 30). По координате х_х действует гауссовский шум с дисперсией σ². Ошибка при приеме кодового слова № 1 или № 2 произойдет, если мгновенное напряжение шума по координате х₁ превысит величину d/2. Вероятность этого события равна:

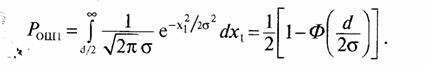
Найдем величину (d/2σ)² = , где σ ² = N₀, где τ — длительность одного символа передаваемого n-значного кодового слова.

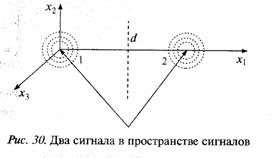
Вокруг каждого кодового слова находится M_БЛ ближайших кодовых слов. Принимая при малой вероятности ошибки, что принимаемое кодовое слово с наибольшей вероятностью перейдет в ближайшее кодовое слово, получим аддитивную границу (оценку сверху) вероятности ошибочного приема кодового слова Р_ош ≤ М_блР_ош1.

            Рассмотрим двоичные помехоустойчивые коды с одинаковыми энергиями кодовых слов и минимальным расстоянием Хэмминга d_x между словами. Хэммингово и Евклидово расстояния связаны соотношением d = 2√d_xP_c. Тогда

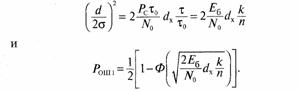
            При ошибочном приеме кодового слова с наибольшей вероятностью будет ошибочно восстановлено ближайшее кодовое слово, и число ошибочно принятых двоичных символов будет равно d_x. Доля ошибочных информационных бит равна d_x,a условная вероятность искажения одного информационного бита есть

Окончательно

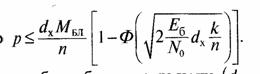
            По отношению к безызбыточному коду (d_x = l) при использовании помехоустойчивых кодов Евклидово расстояние между сигналами возрастает в  раз, а потенциальный энергетический выигрыш помехоустойчивого кода равен d_x раз.

            В таблице для р = 10 ^-6 и оптимального корреляционного декодера приведены некоторые характеристики помехоустойчивых кодов для п ≤ 128, когда аддитивная граница является еще достаточно точной; η_к— есть энергетический выигрыш кода по отношению к безызбыточному коду. Код БЧХ — код Боуза—Чоудхури-Хоквингема.

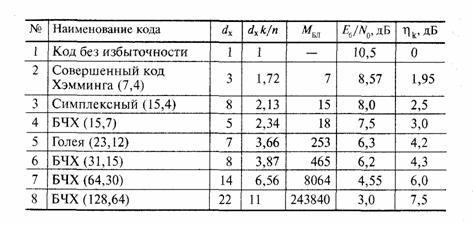
            Общая закономерность — энергетический выигрыш кода растет с увеличением длины кодового слова п (размерности пространства сигналов).

            Будем рассматривать кодовые слова с одинаковой энергией. Коэффициент корреляции между принятым сигналом u(t) и вектором сигнала u_i(t) есть

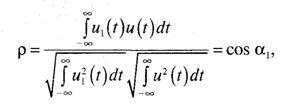
где а, есть угол между вектором принятого сигнала u(t) и вектором сигнала и,(/) (см. рис. 31).

Если передавался сигнал u₁(t), то он будет принят правильно, если проекция принятого сигнала u(t) на вектор u₁(t) будет больше проекции сигнала u(t) на

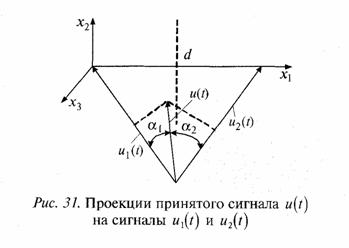
вектор u₂(t) (см. рис.31):  u(t)cosα₁ > u(t) cos α₂, или cos α₁> cos α₂.        

Вычислитель величин cos α₁, cos α₂ и т.д. есть вычислитель коэффициентов корреляции р принятого сигнала с опорными сигналами u₁(t), u₂(t) и т.д. и называется корреляционным декодером. Функциональная схема корреляционного декодера показана на рис. 32.

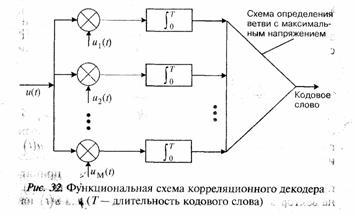
Задача 94. Для симплексного кода с M=3 в двумерном пространстве, показанного на рис. 33, изобразить три кодовых слова как функцию времени в виде прямоугольных видеоимпульсов длительностью т₀ по каждой координате. Длину вектора для каждого кодового слова принять равной единице.

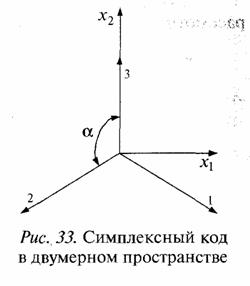
Для схемы корреляционного декодера (рис. 32), полагая, что входной сигнал u(t) = u₂(t) изобразить напряжения на выходах корреляторов (интеграторов со временем интегрирования Т = 2τ₀).

            Полученные значения напряжений в конце интервала интегрирования сравнить с величиной коэффициента корреляции p = cosα, получаемого из геометрии сигналов на рис. 33.

Задача 95. В трехмерном пространстве симплексный код с М = 4 (вершины тетраэдра) может быть двоичным. Из сигнальных точек куба с М= 8 отберите сигнальные точки, которые соответствуют симплексным сигналам. Запишите четыре симплексных сигнала в виде последовательностей из «единиц» и «нулей».

Добавьте к каждому двоичному кодовому слову слева или справа по одинаковому двоичному символу. Полученный ансамбль кодовых слов с М = 4 является ансамблем двоичных ортогональных кодовых слов.

Докажите это утверждение путем вычисления коэффициентов корреляции р каждой пары кодовых слов, которые должны быть равны нулю. Определите Хеммингово расстояние между словами двоичного ортогонального кода

Задача 96. Для трехмерного пространства сигналов рассмотреть троичный код, у которого на двух временных позициях могут находиться символы «1» или «—1», а на одной временной позиции нулевой сигнал (рис. 34).

Найти число кодовых слов М ансамбля сигналов. Определить расстояние между ближайшими сигналами на сфере единичного радиуса d/r и найти коэффициент плотности укладки кодовых слов M(d/r)².  Сравнить полученные характеристики кода с ансамблем сигнальных точек икосаэдра

.

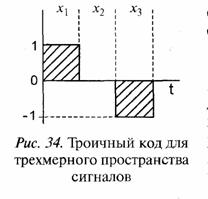
            Задача 97. Для кодовых слов, состоящих из 5 символов (п = 5) рассмотреть три варианта построения троичного кода:

1. На одной временной позиции располагается нулевой сигнал, на остальных         временных позициях располагаются символы «+1» и «—1».

2. На двух временных позициях располагаются нулевые сигналы, на остальных —             символы «+1» и «—1».

3.  На трех временных позициях находится нулевой сигнал, на остальных —           символы «+1» и «—1». Определить для каждого варианта кодов число сигнальных           точек М кодового ансамбля и коэффициенты плотности укладки кодовых слов M =    (d/r)². Определить наилучший вариант кода.

8.2. Стоимостной критерий оптимальности кода

Предлагается стоимостной критерий оптимальности кода по соотношению «эффективность—стоимость» телекоммуникационной системы.

Для систем фиксированной спутниковой службы введем величину                                       

C=

Доход системы Д пропорционален числу каналов ретранслятора КА и при помехоустойчивом двоичном кодировании Д~ T, где Т— время эксплуатации КА в годах.

            Затраты на создание космического сегмента определяются массой КА, которая в свою очередь определяется массой полезной нагрузки (ретранслятора). Обычно масса полезной нагрузки составляет 25% от массы КА. В свою очередь, масса связного ретранслятора пропорциональна мощности потребления электроэнергии от бортовой сети электропитания КА. Таким образом, можно записать, что масса КА и затраты на космический сегмент обратно пропорциональны энергетическому выигрышу кода Г)_к.

            Пренебрегая затратами на эксплуатацию космического сегмента (~1% в год от затрат на создание КА), получим,что удельный стоимостный доход системы (Т= 1)

C~η_k.  Итак,  принимаем, что оптимальный код —это код, который обеспечивает максимум стоимостной функции С~η_k

            Для сотовой мобильной сети связи с кодовым разделением каналов число каналов связи сети пропорционально η_к (влияние внутрисистемных помех уменьшается при увеличении η_к и пропорционально возрастает емкость сотовой сети связи) и также пропорционально скорости кодирования k/п, так что в итоге можно записать, что доходы от эксплуатации сети связи есть величина пропорциональная η_к.

            Так как η_к есть некоторая непрерывная возрастающая функция величины d_x , то η_k ~ d_x и более удобно принять за критерий оптимальности кода — получение максимума стоимостной функции

3адача 98. На рис. 35 представлены кривые вероятности ошибки на бит для кодов, широко используемых в системах спутниковой связи фиксированной службы: сверточных с декодированием по методу Витерби и каскадных кодов со сверточным декодированием внутреннего кода и внешним кодом Рида—Соломона (PC) (256,239).

Для вероятности ошибки на бит р = 10^-6 из кривых рис. 35 найти энергетический выигрыш кода η_к (в разах) по отношению к безызбыточному коду (E₆/N₀ =

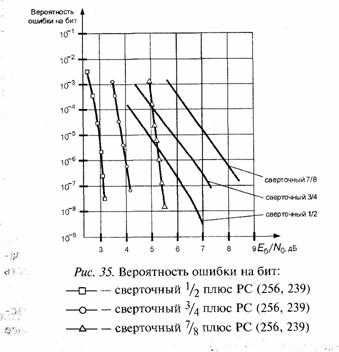
= 10,5 дБ) и величину С =η_к для всех кривых рис. 35. По критерию максимума величины С определить оптимальный сверточный код и оптимальный каскадный код.

Задача 99. Из таблицы параметров кода БЧХ длиной п = 64, приведенной ниже, определить оптимальный код по критерию максимума стоимостной функции -

к	7	10	16	18	24	30	36	39	45	51	57
dx	32	28	24	22	16	14	12	10	8	6	4

ГЛАВА 9

ЭНЕРГЕТИЧЕСКИЕ ПОТЕНЦИАЛЫ РАДИОЛИНИЙ

9.1. Основные параметры радиолиний, определяющие энергетические потенциалы

            Энергетический потенциал радиолинии определяется величиной отношения энергии бита Е_б к спектральной плотности шумов N₀ (h² =E₆/N₀) на выходе приемной антенны радиостанции в зависимости от параметров радиолинии: мощности излучения передающей станции, коэффициентов усиления передающей и приемной антенн, дальности радиосвязи, условий распространения радиосигнала, уровня шумов приемной системы, методов модуляции и кодирования.

            Если передающее устройство с изотропной антенной излучает в свободное пространство мощность Р_п, то в точке приема, находящейся на расстоянии r от передатчика, плотность потока мощности, проходящую через единичную площадку (вектор Умова—Пойнтинга) есть Р_о ⁼ Р_п/4πr². Если антенна передающей станции имеет коэффициент усиления G_П и максимум диаграммы направленности передающей антенны направлен на приемник, то p₀ = P_ПG_П/4πr², где P_ПG_П называется эквивалентной изотропно излучаемой мощностью (ЭИИМ).

            Мощность, перехватываемая приемной антенной, есть Р_с = p₀S_пр, где S_ПР — эффективная площадь приемной антенны, Р_с — мощность на выходе приемной антенны. Например, для параболической круглой приемной антенны с диаметром апертуры d эффективная площадь антенны есть S_пр –kипπd²/4, где k_ип— коэффициент использования поверхности (КИП) антенны (k_ип=0,55÷0,7). В общем случае S_np=(λ²/4π)G_ПP, где λ — длина волны, G_np — коэффициент усиления приемной антенны.

            Обозначим через L — коэффициент, характеризующий все потери в мощности сигнала на трассе распространения радиосигнала от антенны передатчика до выхода приемной антенны за счет поглощения радиосигнала в атмосфере Земли, рассогласования поляризационных характеристик передающей и приемной антенн, погрешностей наведения приемной и передающей антенн друг на друга, потерь при ослаблении сигнала при его замираниях и др. Тогда

            Спектральную плотность шумов, приведенную к выходу приемной антенны, обозначим через N₀, где N₀=kT, где к — постоянная Больцмана, Г—шумовая

температура приемной системы. Тогда -

            Умножим левую и правую часть равенства на τ₀ — длительность информационного бита, τ_о = 1/R, где R — скорость передачи информации.

            Умножим левую и правую часть равенства на τ₀ — длительность информационного бита, τ_о = 1/R где R — скорость передачи информации.

Соотношения между параметрами вышеполученного уравнения принято записывать в децибелах следующим образом

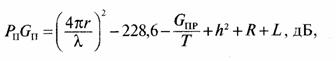
где (4πr/λ)² называется ослаблением сигнала в свободном пространстве для изотропных передающей и приемной антенн. Постоянная Больцмана 10 lgк = -228,6.

Параметр G_пр/T называется добротностью приемной системы.

            Шумовая температура приемной системы, приведенная к выходу приемной антенны, равна

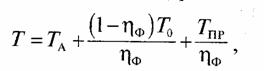
где Т_А — шумовая температура приемной антенны, η_ф — коэффициент передачи фидера, Т_о — температура окружающей фидер среды, Т_пр — шумовая температура приемника, которая фактически определяется шумами входного малошумящего усилителя (МШУ).

            Величина (1-η_ф)Т₀-Т_ф есть шумовая температура фидера, т.е. фидер на своем выходе создает мощность шумов в некоторой полосе частот Δƒ, равную кТ_фΔƒ. Потери мощности в фидере есть   L_ф = 1/η_ф   и   Т_ф = (1-1/L_ф)

            Шумы приемной антенны есть шумы принимаемых излучений внешних источников, таких как космические шумы (шумы звезд, планет и др.), шумы атмосферы и Земли. Внешние шумы характеризуют своей яркостной температурой Т_я, определяемой термодинамической температурой эквивалентного абсолютно черного тела.

            Шумовая температура в главном лепестке диаграммы направленности направленной приемной антенны есть Т_А = η _АТ_{я, где}  η _А(ηа = 0,7÷0,8) — доля мощности, излучаемой антенной в главном лепестке диаграммы направленности, как если бы приемная антенна использовалась в качестве передающей, Т_я — яркостная температура внешних излучений, принимаемых в главном лепестке диаграммы направленности антенны.

            Шумы атмосферы — это шумы трассы распространения радиосигнала, рассматриваемой как фидер. Тогда яркостная температура атмосферы есть Т_А = (l - 1/L_A) T_m, где Т_т = 275 К, L_A — потери сигнала в атмосфере за счет поглощения радиосигнала.

Потери радиосигнала в средах с поглощением или рассеянием сигнала

            Рассмотрим распространение радиосигнала в однородной среде вдоль пространственной координаты х. Обозначим плотность потока мощности при х = 0 как Р_со, а в точке х как Р_с. Уменьшение мощности сигнала вдоль оси х за счет его поглощения или рассеяния на малом отрезке пути dx есть -dP_c/dx. Тогда для однородной среды можно записать уравнение

где μ есть сечение процесса поглощения или рассеяния радиосигнала или удельный (погонный) коэффициент поглощения (μ=μ_п) или рассеяния (μ = μ_Р), показывающей долю поглощенного или рассеянного сигнала.

            Далее для простоты будем рассматривать только процесс поглощения радиосигнала. Величина 1/μ (как будет видно при решении задачи) имеет размерность длины и называется длиной свободного пробега излучения в среде  = 1/μ.

            Задача 100

            1.  Разделить в уравнении (4) переменные и проинтегрировать обе части уравнения. Решить уравнение и найти выражение для Р_с как функцию от Р_со , μ, и х.

            2. Определить в дБ ослабление радиосигнала L_п

и найти выражение для γ_П — удельного поглощения в дБ/км — (для х, выраженного в км) через ранее определенную величину μ.

Задача 101. Для изотропной передающей антенны, излучающей мощность Р_П и свободного пространства без потерь выведите формулу для плотности потока

мощности через единичную площадку на расстоянии r от передающей антенны.

            Задача 102. Определить коэффициент усиления круглой зеркальной антенны на частоте 6 ГГц при КПИ k_ип=0,6 для диаметров апертуры, указанных в таблице.

            Задача 103. Ширина диаграммы направленности по уровню половинной мощности в одной плоскости определяется выражением θ₀ = 70λ/d град, где λ — длина волны, d — размер апертуры в данной плоскости.

            Коэффициент усиления антенны, создающий эллиптический луч с шириной 6_0| и 0_О2 по главным осям эллипса, определяется согласно рекомендациям МСЭ выражением:

            Требуется определить:

            1. Коэффициент усиления антенны ретранслятора КА:

            а) с глобальным лучом θ₀ =17°;

             б) с эллиптическим лучом 5⁰ х 11⁰, покрывающим территорию России.

            2. Коэффициент усиления антенны с прямоугольной апертурой 10 см х 20 см на     частоте 10 ГГц.

            Задача 104. В справочниках приводятся таблицы и кривые ослабления (потерь) радиосигнала в атмосфере Земли для разных диапазонов частот при его распространении в зенит, L_AZ, дБ. Определить яркостную температуру атмосферы на частоте 11 ГГц с L_Аz = 0,06дБ для угла места спутниковой приемной антенны 5° и 10°.

Задача 105. Определить яркостную температуру трассы распространения радиосигнала в дожде, если

ослабление радиосигнала в дожде составляет: а) 10 дБ; б) 30 дБ.   

Задача 106. В существующей системе спутниковой связи используются наземные станции с зеркальной антенной с добротностью G_np/T. При модернизации наземной станции удалось уменьшить шумовую температуру приемной системы в два раза.

Можно ли теперь выпускать модернизированные станции с меньшим диаметром апертуры антенны? Если да, то во сколько раз можно уменьшить диаметр апертуры антенны? Во сколько раз в этом случае нужно увеличить мощность передатчика наземной станции?

Задача 107. Провести расчет энергетических потенциалов радиолиний «Ретранслятор КА—наземная станция» системы спутниковой связи с геостационарным КА и определить необходимый диаметр зеркальной приемной антенны стационарной наземной станции спутниковой связи при следующих условиях:

•  диапазон частот 4/6 ГГц;

•  угловая зона обслуживания КА 5°х 10°;

•  станция спутниковой связи находится на краю зоны обслуживания и работает при угле места 5°;

•  мощность ствола ретранслятора в квазилинейном режиме равна 8 Вт. Ствол предназначен для организации 800 каналов с МДЧР со скоростью 64 кбит/с в каждом канале. Изучаемая мощность для станций, находящихся на краю зоны обслуживания увеличивается по сравнению со станциями в середине зоны обслуживания. Принять, что для рассматриваемой наземной станции выделяется мощность ретранслятора 0,02 Вт;

•  наземная станция одноканальная и работает на прием (и передачу) со скоростью 64 кбит/с. Вид модуляции радиосигнала — четырехфазная относительная

фазовая манипуляция. Используется кодирование сигнала без избыточности. Требуемая вероятность ошибки на бит — не более 10^-6. Метод приема сигнала — когерентный.

Остальные необходимые параметры радиолинии рассчитать или задать при выполнении расчета энергетического потенциала радиолинии.

Задача 108. Для систем наземной радиосвязи с мобильными терминалами, которые характеризуются всенаправленными передающими и приемными антеннами базовой станции и терминалов (в азимутальной плоскости или во всей сфере), используя выражение (3) для мощности полезного сигнала на выходе приемной антенны, определить как при одинаковых Р_П, r и L будет изменяться принимаемая мощность сигнала при изменении диапазона частот радиолинии.

            Какие диапазоны частот: метровый, дециметровый, сантиметровый, миллиметровый или оптический являются наиболее выгодными при создании таких систем радиосвязи?

            Задача 109. Для систем радиосвязи «Точка—точка» (радиорелейные линии связи, межспутниковая связь) фиксируются диаметры апертур передающих и приемных антенн исходя из-за массогабаритных ограничений.

            Используя выражение (3) для мощности полезного сигнала на выходе приемной антенны, определить при одинаковых Р_п, r и L как будет изменяться мощность принимаемого сигнала Р_с при переходе от метрового диапазона длин волн к дециметровому, сантиметровому, миллиметровому и оптическому диапазонам волн.

Как изменятся результаты сравнения при учете быстрого увеличения потерь сигнала L в дожде на частотах выше 10 ГГц?

9.2. Учет особенностей распространения радиоволн при расчетах энергетических потенциалов радиолиний

Трассы распространения радиосигнала от передатчика к приемнику можно разделить на следующие основные классы.

1. Распространение радиосигнала по прямому лучу. Отраженные сигналы   отсутствуют, так как подавляются приемной антенной с высокой направленностью. Такой вид распространения радиосигнала характерен для систем спутниковой         связи со стационарными наземными станциями с направленными антеннами, когда            отраженные от Земли сигналы воздействуют только по боковым лепесткам      приемной антенны, уровень которых весьма мал. В каналах межспутниковой связи             распространение радиосигнала происходит также только по прямому лучу.

            2. На выходе приемной антенны в основном лепестке диаграммы  направленности           антенны наблюдается сигнал как прямого луча, так и отраженные лучи от       поверхности Земли или тропосферных неоднородноcтей атмосферы. Такие трассы        распространения радиосигнала характерны при радиорелейной связи, в       авиационных радиолиниях, при связи морских судов между собой и с береговыми   станциями, для спутниковых авиационных и морских радиолиний связи. Дальность             прямой геометрической видимости между передающей антенной с высотой  h_п и   приемной антенной с высотой h_пр относительно поверхности Земли в наземных,         авиационных и морских линиях связи определяется выражением r = 3,57(+             ) км, где h_п и h_ПР выражены в метрах.

            3.  В спутниковых системах связи с сухопутными мобильными терминалами при   углах места мобильноготерминала менее 30°— 40° на выходе приемной слабо    направленной антенны терминала присутствует сигнал прямого луча и отраженные          от Земли лучи. При этом прямой и отраженные лучи в отдельные моменты времени      могут экранироваться деревьями, холмами и другими местными предметами, в           результате чего связь прерывается. Таким образом, возникает прерывистый канал радиосвязи с замираниями сигнала.

 4. Прямой луч отсутствует все время или в большей части времени, так что            следует считать, что связь осуществляется за счет отраженных сигналов. К таким        каналам связи относятся радиолинии тропосферной связи и каналы сотовой     мобильной радиосвязи в городе, когда большую часть времени прямой           лучэкранируется зданиями.

Во всех каналах связи, где присутствует прямой луч, вначале определяется энергетический потенциал радиолиний для заданной дальности связи в условиях распространения радиосигнала в свободном пространстве. Для тропосферной радиолинии и радиоканалов сотовой мобильной связи в городе, когда прямой луч отсутствует, определяется для заданной дальности связи медианное значение сигнала по формулам и кривым, построенных на основе экспериментальных данных. Для тропосферной радиолинии вычисляется медианное значение сигнала для наихудшего месяца (зимы).

            Далее для всех радиолиний, работающих на частотах выше 8—10 ГГц определяется поглощение радиосигнала в дожде (радиорелейные линии связи, спутниковые радиолинии, высокоскоростные авиационные радиолинии) и производится увеличение ранее рассчитанного энергетического потенциала радиолинии на величину поглощений радиосигнала в дожде.

            Для каналов связи, в которых присутствует прямой и отраженные лучи, определяются характеристики отраженных лучей для наиболее тяжелых условий связи, обычно на максимальной дальности связи. При этом углы скольжения отраженных лучей являются весьма малыми и во многих случаях выполняются условия их зеркального отражения от поверхности Земли. При этом возможно использовать для расчетов двухлучевую модель распространения радиосигнала (прямой луч и один зеркальный отраженный луч).

            Для радиорелейной связи необходимо вычислить сумму прямого и отраженного от поверхности Земли луча с учетом фазы и коэффициента отражения зеркального луча. Эта сумма определяет мощность принимаемого сигнала, которая оказывается много меньше мощности прямого луча. Эти потери сигнала называются интерференционными и энергетический потенциал радиорелейной линии должен быть увеличен на величину этих потерь. Кроме этого в радиорелейной линии связи присутствуют отраженные от тропосферы лучи, которые вызывают быстрые замирания сигнала. Отраженные от тропосферы лучи образуют сигнал с гауссовским распределением вероятности и с огибающей, распределенной по закону Релея. Для компенсации уменьшения уровня сигнала при быстрых замираниях сигнала необходимо предусмотреть дополнительный запас по энергетике радиорелейной линии связи.

            Для авиационных радиолиний и спутниковых радиолиний связи с мобильными терминалами отраженные лучи будут иметь доплеровское смещение частоты, отличающееся от доплеровского смещения частоты прямого луча, так что вектор отраженного зеркального луча будет непрерывно вращаться относительно конца вектора прямого луча и среднее значение мощности сигнала будет равно мощности прямого луча. Для наихудшего случая, когда разность фаз прямого и отраженного сигнала равна 180°, необходимо вычислить разность амплитуд прямого и отраженного луча с учетом коэффициента отражения луча от поверхности Земли и характеристик направленности приемных антенн (для спутниковой связи с самолетами). Энергетический потенциал радиолиний должен быть увеличен на величину интерференционных потерь сигнала.

В радиолиниях, работающих на отраженных лучах, необходимо учесть медленные и быстрые замирания радиосигнала. Быстрые замирания сигнала создаются множеством отраженных лучей в приемной антенне, огибающая которых подчиняется релеевскому закону. Медленные замирания сигнала в тропосферных линиях связи возникают при медленной смене перемещающихся неоднородностей тропосферы в луче направленной антенны.

            В сотовой мобильной системе связи медленные изменения уровня сигнала возникают при перемещении мобильного терминала из одной локальной зоны диаметром 50—60 м в другую, приводящего к смене отражателей.

            Медленные замирания сигналов в тропосферных линиях связи и городской сотовой сети мобильной связи описываются логарифмически-нормальным законом распределения вероятностей. Для компенсации уменьшения уровня принимаемого сигнала за счет медленных и быстрых замираний радиосигнала энергетический потенциал радиолиний должен соответственно быть увеличен.

            Методика расчета ослабления радиосигнала в дожде состоит в следующем. Из допустимого процента времени кратковременных прерываний сигнала в радиолинии определяется допустимый процент времени кратковременных прерываний связи в течение года из-за дождя и интенсивность дождя, которая не превышается в этом проценте времени любого года. Для климатических зон России указанные выше проценты времени и интенсивность дождя, при которой необходимо обеспечить работу радиолиний, представлены в таблице.

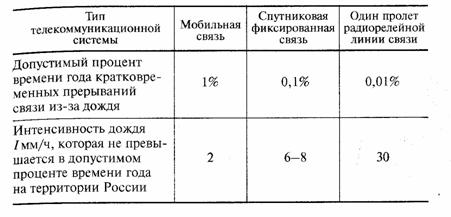
Поглощение радиосигнала в дожде в дБ вычисляется согласно выражению L_д = γ_дl_э, где γ_д — погонное ослабление сигнала в дожде в дБ/км, l_э — эквивалентная длина трассы распространения радиосигнала в дожде.

            Погонное ослабление радиосигнала есть l_д = аI^в, где I—интенсивность дождя, мм/ч, коэффициенты а и в определяют зависимость погонного поглощения радиосигнала от частоты и для вертикальной поляризации приведены в таблице.

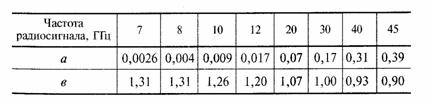
            Эквивалентная длина трассы сигнала в дожде l_э всегда меньше физической длины трассы распространения сигнала в дожде г ввиду неравномерности дождя по трассе. Ливневая составляющая дождя имеет протяженность 2—3 км, остальную часть трассы занимает более слабый фоновый дождь.

Для трассы распространения сигнала, пролегающей ниже высоты нулевой изотермы 4 км

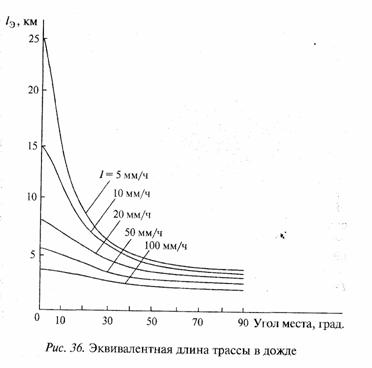
Для спутниковых радиолиний и авиационных радиолиний при высоте полета самолета (вертолета) выше 4 км величина l_э может определяться по экспериментальным кривым l_э МСЭ для климатических зон умеренного климата. Эти кривые l_э приведены на рис. 36.

            Задача 110. На рис. 37 изображена схема радиорелейной связи с параметрами: h = 10 м, дальность связи r = 20 км, длина волны радиолинии λ = 3 см (частота радиолинии 10 ГГц).

Определить разность хода Δr между отраженным и прямым лучом и разность фаз между отраженным и прямым лучом φ = 2πΔr/λ + π, считая, что при отражении

сигнала от поверхности гладкой Земли фаза отраженного сигнала меняется на 180°.

Принимая, что амплитуда отраженного сигнала равна амплитуде сигнала прямого луча, определить амплитуду суммарного прямого и отраженного сигналов и найти потери в мощности сигнала в дБ по сравнению со случаем отсутствия отраженного сигнала.

Задача 111. При самолетной радиосвязи сигнал, принимаемый от самолета, состоит из прямого луча и отраженного от Земли луча. Принимая, что амплитуда отраженного сигнала составляет 70% от амплитуды прямого луча, определить максимальные потери в энергетике радиолинии за счет мешающего отраженного луча.

Задача 112. Определить максимальную дальность связи с самолетами при высоте аэродромной антенны 15 м для высот полета самолета от 50 м до 10 км. Построить график дальности связи в зависимости от высоты полета самолета.

Задача 113. Определить необходимые высоты подъема антенн радиорелейной линии связи диапазона частот 6 ГГц для работы на дальности г = 50 км в условиях гладкой поверхности Земли с обеспечением просвета, равного радиусу первой зоны Френеля в середине трассы

F_l = , где λ — длина волны радиолинии.

            Задача 114. Для радиорелейной линии связи на частоте 19,7 ГГц построить кривую поглощения радиосигнала в дожде с интенсивностью / = 30 мм/ч в зависимости от расстояния между радиорелейными станциями. Полагая, что допустимое поглощение радиосигнала в дожде не должно превышать 30 дБ, определить максимальную длину интервала между радиорелейными станциями.

Задача 115. Для спутниковой радиолинии связи «Космос—Земля», работающей в диапазоне 20 ГГц, построить зависимость поглощения радиосигнала в дожде от угла места наземной станции для интенсивности дождя I = 6 мм/ч

Задача 116. Для авиационной телекоммуникационной радиолинии диапазона 10 ГГц определить поглощение радиосигнала в дожде с интенсивностью I = 6 мм/ч на максимальной дальности связи для высоты полета самолета 10 км.