Телекоммуникации и информационная безопасность телекоммуникационных систем являются в настоящее время одной из наиболее быстро развивающихся областей науки и техники. Жизнь современного общества уже невозможно представить без тех достижений, которые были сделаны в этих отраслях за последние годы. Непрерывно возрастает потребность общества в передаче различных потоков информации при сохранении ее конфиденциальности. Это обусловлено многими причинами и в первую очередь тем, что связь стала одним из самых мощных инструментов управления страной. Одновременно, претерпевая значительные изменения, становясь многосторонними и всеобъемлющими, системы электросвязи каждой страны все более интегрируются в мировое телекоммуникационное пространство.
В учебном пособии «Системы и сети передачи информации» систематизированы основные сведения о современном состоянии и перспективах развития систем телекоммуникаций: линиях связи, системах передачи и системах коммутации, представляющих физический уровень эталонной модели взаимодействия открытых систем Международной организации стандартизации.
Содержание учебного пособия «Системы и сети передачи информации» во многом соответствует дидактике телекоммуникационных дисциплин Государственных образовательных стандартов высшего профессионального образования по специальностям: «Криптография» (075100); «Компьютерная безопасность» (075200); «Комплексное обеспечение информационной безопасности автоматизированных систем» (075500); «Информационная безопасность телекоммуникационных систем» (075600).
Учебное пособие «Сети и системы передачи информации» основано на курсах лекций, читаемых авторами в Институте криптографии, связи и информатики (ИКСИ) Академии ФСБ РФ и Московском техническом университете связи и информатики (МТУСИ).
ОБЩИЕ ПОНЯТИЯ О ПЕРЕДАЧЕ ИНФОРМАЦИИ
Информация — это сведения о каких-либо процессах, событиях, фактах или предметах [8]. Известно, что 80...90% информации человек получает через органы зрения и 10...20% — через органы слуха. Другие органы чувств дают в сумме 1...2% информации. Физиологические возможности человека не позволяют обеспечить передачу больших объемов информации на значительные расстояния.
Связь — техническая база, обеспечивающая передачу и прием информации между удаленными друг от друга людьми или устройствами [3,5,8]. Аналогия между связью и информацией такая же, как у транспорта и перевозимого груза. Средства связи не нужны, если нет информации, как не нужны транспортные средства при отсутствии груза.
Сообщение — форма выражения (представления) информации, удобная для передачи на расстояние. Различают оптические (телеграмма, письмо, фотография) и звуковые (речь, музыка) со- общения. Документальные сообщения наносятся на определенные носители (чаще всего на бумагу) и там же хранятся. Сообщения, предназначенные для обработки в компьютерных информационных системах, принято называть данными.
Информационный параметр сообщения — параметр, в изменении которого «заложена» информация. Для звуковых сообщений информационным параметром является мгновенное значение звукового давления, для неподвижных изображений — коэффициент отражения, для подвижных — яркость свечения участков экрана.
По характеру изменения информационных параметров различают непрерывные и дискретные сообщения.
Сигнал — физический процесс, отображающий передаваемое сообщение. Отображение сообщения обеспечивается изменением какой-либо физической величины, характеризующей процесс. Эта величина является информационным параметром сигнала.
Сигналы, как и сообщения, могут быть непрерывными и дискретными. Информационный параметр непрерывного сигнала с течением времени может принимать любые мгновенные значения

в определенных пределах. Непрерывный сигнал часто называют аналоговым. Дискретный сигнал характеризуется конечным числом значений информационного параметра. Часто этот параметр принимает всего два значения. На рис.1.1 показаны виды непрерывного и дискретного сигналов.
В дальнейшем будем рассматривать принципы и средства связи, основанные на использовании электрической энергии в качестве переносчиков сообщений, т.е. электрических сигналов. Выбор электрических сигналов для переноса сообщений на расстояние обусловлен их высокой скоростью распространения (около 300 км/мс).
В технике связи наряду с абсолютными единицами измерения параметров электрических сигналов (мощности, напряжения и тока) широко используются относительные единицы [7].
Уровнем передачи сигнала в некоторой точке канала или тракта называют логарифмическое преобразование отношения значения энергетического параметра S (мощности, напряжения или тока) к эталонному значению S0 этого же параметра. Правило преобразования определяется формулой
Р = m loga(S/S0),
где т — масштабный коэффициент; а — основание логарифма;
Уровни передачи измеряются в децибелах, если справедливы соотношения:
для уровней по мощности: р, = 10 Ig (РIР,);
для уровней по напряжению: р„= 20 Ig (U/Up);
Уровень передачи называется абсолютным, если Р,=1мВт.
Если теперь задать R,, то легко получить соответствующие величины напряжения Up и тока в практических расчетах принимают округленные значения.
Измерительные уровни служат для определения уровней передачи с помощью измерительных приборов, называемых указателями уровня.
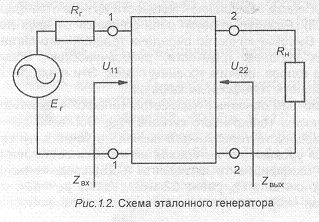
Для измерения уровня наиболее часто применяется схема эталонного генератора, показанная на рис.1.2. В этой схеме к входу исследуемого объекта, например некоторого четырехполюсника, подключается генератор испытательного сигнала с полностью определенными параметрами, т.е. должны быть известны его выходное сопротивление развиваемая ЭДС Е, (или напряжение на входе объекта U«), входное сопротивление объекта. К выходу объекта подключается указатель уровня с входным сопротивлением, равным номинальному значению сопротивления нагрузки RД; реальная нагрузка при этом отключается. В качестве испытательного при измерении уровней передачи чаще всего применяют одночастотный синусоидальный сигнал, частота которого также должна быть известна, а начальная фаза, как правило, не фиксируется.
Если генератор испытательного сигнала имеет внутреннее сопротивление 600 Ом и развиваемую ЭДС 1,55 В, то измеренный на сопротивлении уровень называется измерительным.
1.3. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ПЕРВИЧНЫХ СИГНАЛОВ
Описание сигналов электросвязи необходимо для их адекватной обработки в процессе передачи. Описанием сигнала может служить некоторая функция времени. Определив каким-либо образом данную функцию, определим и сигнал. Однако такое полное определение сигнала не всегда требуется. Достаточно описание в виде нескольких параметров, характеризующих основные свойства сигнала с точки зрения его передачи.
Основными первичными сигналами электросвязи являются [2,5,71: телефонный, звукового вещания, факсимильный, телевизионный, телеграфный, передачи данных.
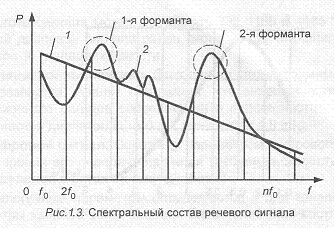
Телефонный (речевой) сигнал. Звуки речи образуются в результате прохождения воздушного потока из легких через голосовые связки и полости рта и носа. Существуют два основных типа звуков речи: вокализованные и невокализованные. Вокализованные звуки образуются в результате колебаний голосовых связок с так называемой частотой основного тона (f, на рис.1.3), значения которой лежат в пределах от 50...80 Гц (бас) до 200...250 Гц (женский и детский голоса). Импульсы основного тона содержат большое число гармоник (до 40) (2f,, ..., на рис.1.3), причем их амплитуды убывают с увеличением частоты со скоростью приблизительно 12 дБ на октаву (кривая 1 на рис.1.3). (Напомним, что октавой называется диапазон частот, верхняя частота которого в два раза выше нижней. Таким образом амплитуда гармоники 2f на 12 дБ больше амплитуды гармоники 4f, и т.д.). При разговоре частота основного тона f, меняется в значительных пределах.
Невокализованные звуки речи имеют шумовой характер.
В процессе прохождения воздушного потока из легких через голосовые связки и полости рта и носа образуются звуки речи, причем распределение мощности по спектру меняется (кривая 2 на рис.1.3). Области повышенной мощности называются формантами (см. рис.1.3). Различные звуки речи содержат от двух до четырех формант. Высокое качество передачи телефонного сигнала характеризуется уровнем громкости, разборчивостью, естественным звучанием голоса, низким уровнем помех. Эти факторы определяют требования к телефонным каналам.
Рассмотрим основные параметры телефонного сигнала. Мощность телефонного сигнала. Согласно данным ITU T средняя мощность телефонного сигнала в точке с нулевым измерительным уровнем на интервале активности составляет 88 мкВт. С учетом коэффициента активности (0,25) средняя мощность телефонного сигнала Р равна 22 мкВт. Кроме речевых сигналов в канал связи могут поступать сигналы управления, набора номера и
пр. С учетом этих сигналов среднюю мощность телефонного сиг- нала принимают равной 32 мкВт, т.е. средний уровень телефонного сигнала Р„=1019 (32 мкВт/1 мВт) = — 15 дБмО.
Коэффициент активности телефонного сообщения, т.е. от- ношение времени, в течение которого мощность сигнала на выходе канала превышает заданное пороговое значение, к общему времени занятия канала для разговора. При разговоре каждый из собеседников говорит приблизительно 50% времени. Кроме того, отдельные слова, фразы отделяются паузами. Поэтому коэффициент активности составляет 0,25...0,35.
Динамический диапазон телефонного сигнала определяется выраженным в децибелах отношением максимальной мощности сигнала минимальной: D,=10lg (Р,„/Р„;„); D,=35...40 дБ.
Пик-фактор речевого сигнала Q=10ig(Р,„/Р„)=14 дБ. При этом максимальная мощность, вероятность превышения которой исчезающие мала, равна 2220 мкВт (+3,5 дБмО).
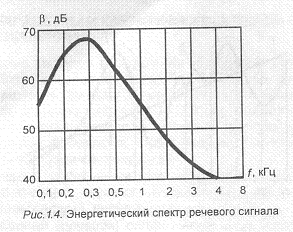
Энергетический спектр речевого сигнала — область частот, в которой сосредоточена основная энергия сигнала (рис.1.4): квадрата звукового давления; П,— порог слышимости (минимальное звуковое давление, которое начинает ощущаться человеком с нормальным слухом на частотах 600...800 Гц); Л(=1 Гц.
Речь представляет собой широкополосный процесс, частотный спектр которого простирается от 50...100 Гц до 8...10 кГц, а по некоторым данным и до 20 кГц. Установлено, однако, что качество речи получается вполне удовлетворительным при ограничении спектра частотами 300...3400 Гц. Эти частоты приняты ITU-Т в качестве границ эффективного спектра речи. При указанной полосе частот слоговая разборчивость составляет около 90%, разборчивость фраз — более 99 % и сохраняется удовлетворительная натуральность звучания.
Сигналы звукового вещания. Источником звука при передаче программ вещания обычно являются музыкальные инструменты или голос человека. Рассмотрим его основные параметры.
Динамический диапазон вещательной передачи: речь диктора 25...35 дБ, художественное чтение 40...50 дБ, вокальные и инструментальные ансамбли 45...55дБ, симфонический оркестр до 65дБ. При определении динамического диапазона максимальным считается уровень, вероятность превышения которого равна 2%, а минимальным — 98 %.
Средняя мощность сигнала вещания существенно зависит от интервала усреднения. В точке с нулевым измерительным уровнем средняя мощность составляет 923 мкВт при усреднении за час, 2230 мкВт — за минуту и 4500 мкВт-за секунду. Максимальная мощность сигнала вещания в точке с нулевым измерительным уровнем 8000 мкВт.
Частотный спектр сигнала вещания расположен в полосе час- тот 15...20000 Гц. При передаче как телефонного сигнала, так и сигналов вещания полоса частот ограничивается. Для достаточно высокого качества (каналы вещания первого класса) эффективная полоса частот должна составлять 0,05...10 кГц, для безукоризненного воспроизведения программ (каналы высшего класса) 0,03...15 кГц.
Факсимильный сигнал. Этот сигнал формируется методом построчной развертки. Частотный спектр первичного факсимильного сигнала определяется характером передаваемого изображения, скоростью развертки и размерами сканирующего пятна. Для параметров факсимильных аппаратов, рекомендованных ITU T, верхняя частота сигнала может составлять 732, 1100 и 1465 Гц. Динамический диапазон сигнала равен около 25дБ, пик-фактор равен 4,5 дБ при 16 градациях яркости.
Телевизионный сигнал. Этот сигнал также формируется методом развертки. Анализ показывает, что энергетический спектр телевизионного сигнала сосредоточен в полосе частот 0...6 МГц. Динамический диапазон 0,=40 дБ, пик-фактор 4,8 дБ.
Цифровой сигнал. Основным параметром цифрового сигнала с точки зрения его передачи является требуемая скорость передачи, выражаемая в битах на секунду (бит/с).
Аналогичные параметры определяются и для каналов связи. Параметры каналов связи должны быть не меньше соответствующих параметров сигналов.
Свести параметры аналоговых сигналов к единому параметру (скорости передачи) позволяет преобразование этих сигналов в цифровые.
1.4. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА СИСТЕМ ЭЛЕКТРОСВЯЗИ
Система электросвязи [6] — это совокупность технических средств и среды распространения, обеспечивающая передачу сообщений. Обобщенная структурная схема систем электросвязи показана на рис.1.5.
Сообщение с выхода источника сообщения (ИС) при помощи преобразователя сообщение — сигнал (Пр. С-С) преобразуется в первичный электрический сигнал, которые не всегда удобно (а иногда невозможно) непосредственно передавать по линии связи. Поэтому первичные сигналы при помощи передатчика (ПРД) преобразуются в так называемые вторичные сигналы, характеристики которых хорошо согласуются с характеристиками линии связи. С вызова линии связи сигналы поступают на вход приемника (ПРМ) и через (Пр. С-С) — потребителю сообщения (ПС).

Канал связи — совокупность технических устройств (преобразователей) и среды распространения, обеспечивающих передачу сигналов на расстояние.
Каналы и системы связи, использующие искусственную среду распространения (металлические провода, оптическое волокно), называются проводными, а каналы и системы связи, в которых сигналы передаются через открытое пространство — радиоканалами и радиосистемами.
1.5. КЛАССИФИКАЦИЯ ВИДОВ ЭЛЕКТРОСВЯЗИ
Условная классификация современных видов электросвязи показана на рис.1.6. Все виды электросвязи по типу передаваемых сообщений могут быть разделены на предназначенные для пере- дачи звуковых и оптических сообщений. В зависимости от назначения сообщений виды электросвязи могут быть классифицированы на предназначенные для передачи сообщений индивидуального и массового характера. В зависимости от временного режима доставки сообщений виды электросвязи могут быть разделены на предназначенные для работы в реальном времени и осуществляющие отложенную доставку сообщений.
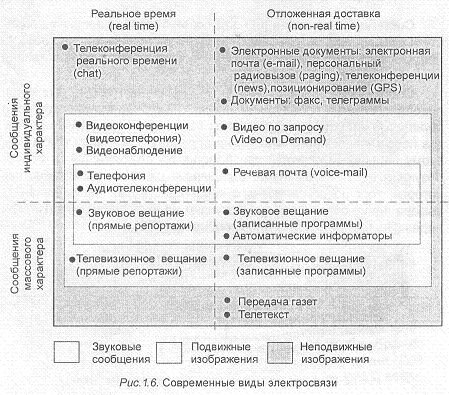
Приведенная на рис.1.6 классификация достаточно условна, поскольку в последнее время наметилась тенденция объединения видов электросвязи в единую интегральную систему на основе цифровых методов передачи и коммутации для передачи всех видов сообщений.
1.6. ОСНОВНЫЕ СВЕДЕНИЯ О СЕТЯХ ЭЛЕКТРОСВЯЗИ
Сеть связи — это совокупность технических средств, обеспечивающих передачу и распределение сообщений [2,3]. Принципы построения сетей связи зависят от вида передаваемых и распределяемых сообщений.
Существуют следующие принципы построения (топологии) сетей:
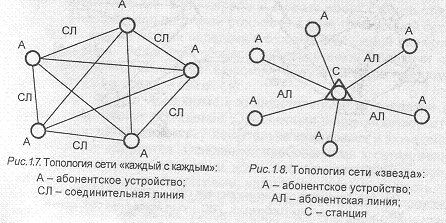
• «каждый с каждым» (рис.1.7); сеть надежна, отличается оперативностью и высоким качеством передачи сообщений, на практике применяется при небольшом числе абонентов;
• радиальный («звезда») (рис.1.8): используется при ограниченном числе абонентских пунктов, расположенных на небольшой территории;
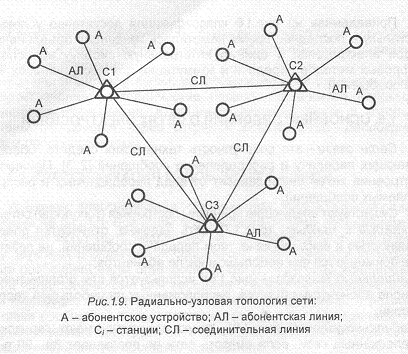
• радиально-узловой (рис.1.9): такую структуру имеют городские телефонные сети, если емкость сети не превышает 80...90 тыс. абонентов;
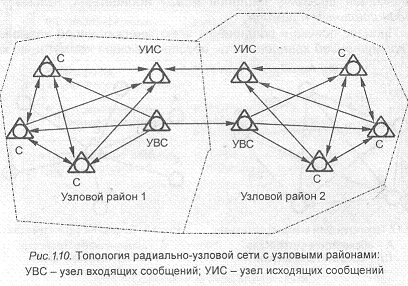
• радиально-узловой с узловыми районами (рис.1.10). Используется при построении телефонных сетей крупных городов.
Для обеспечения передачи индивидуальных сообщений необходимо связать (соединить) оконечные аппараты абонентов. Электрическая цепь (канал), состоящая из нескольких участков и обеспечивающая передачу сигналов между абонентами, называется соединительным трактом.
Процесс поиска и соединения электрических цепей называется коммутацией каналов. Сеть, обеспечивающая коммутацию каналов, называется сетью с коммутацией каналов (СКК). Узловые станции сети СКК называются станциями коммутации.
При передаче документальных сообщений кроме организации связи с коммутацией каналов возможно осуществлять поэтапную передачу сообщения от узла к узлу. Такой способ передачи получил название коммутации сообщений. Соответственно сеть, обеспечивающая коммутацию сообщений, называется сетью с коммутацией сообщении (СКС).
Разновидностью СКС является сеть с коммутацией пакетов (СКП). В этом случае полученное от передающего абонента сообщение разбивается на блоки (пакеты) фиксированной длины. Пакеты передаются по сети (необязательно по одному и тому же маршруту) и объединяются в сообщение перед выдачей принимающему абоненту. В свою очередь, СКП подразделяются на дейтаграммный (от англ. datagram) и сети виртуальных каналов. В дейтаграммных сетях каждый из пакетов рассматривается как независимый информационный блок, причем пакеты могут проходить через сеть по различным маршрутам. В сетях виртуальных каналов до передачи пакетов через сеть выбирается оптимальный в некотором смысле маршрут, по которому затем передаются пакеты. Последовательность узлов, входящих в выбранный маршрут, образуют собственно виртуальный канал.
Узловые станции СКС и СКП называются центрами коммутации сообщений (ЦКС) и пакетов (ЦКП) соответственно.
На практике наиболее широко применяются метод коммутации каналов и метод коммутации пакетов.
Телеграфные сети строятся по радиально-узловому принципу с учетом административно-территориального деления страны. Оконечными пунктами телеграфной сети являются либо отделения связи, либо телеграфные абоненты, обладающие телеграфной аппаратурой. Сеть имеет три уровня узловых пунктов: районные, областные и главные. Сеть передачи данных имеет схожую структуру. Сеть факсимильной связи строится на базе телефонной сети.
Важнейшими сетями передачи массовых сообщений являются сети вещания. Вещание — процесс одновременной передачи сообщений общего назначения широкому кругу абонентов при помощи технических средств связи.
Вещательная программа — последовательность передачи во времени различных сообщений. Организация вещания включает в себя две задачи: подготовку вещательных программ и доведение программ до абонентов. Основными требованиями к сетям вещания являются: охват вещанием
всего населения страны, высокое качество передаваемых программ, надежность и экономичность.
Распределение программ в ceти звукового вещания производится по каналам связи, разветвление — на специальных узлах.
Сеть каналов звукового вещания строится по радиально-узловому принципу. По способу доведения различают радиовещание и про- водное вещание (по специальным проводным линиям или линиям телефонной связи).
Распределение программ в ceти телевизионного вещания производится по каналам связи, разветвление — на специальных узлах. Сеть ТВ вещания строится по радиально-узловому принципу.
Используется два способа доведения ТВ программ: радиовещание с помощью радиотелевизионных передающих станций (РТПС) (эфирное ТВ) и проводное вещание (кабельное ТВ). Современной разновидностью эфирного ТВ является спутниковое телевизионное вещание с непосредственным приемом на установки, расположенные у абонентов. Закономерность распространения радиоволн метрового и дециметрового диапазона, которая будет рассмотрена ниже, ограничивает зону уверенного приема сигналов РПТС пределами оптической (прямой) видимости. Для увеличения зоны уверенного приема необходимо поднимать передающую и приемную антенны. Для типовых РТПС с опорами для антенн высотой 200...350 м радиус зоны обслуживания составляет 60...100 км. Останкинская телебашня при высоте 536 м обеспечивает радиус зоны обслуживания 120...130 км.
Передача газет в сети передачи газет обеспечивается факсимильным способом с использованием аналоговой аппаратуры «Газета-2», находящейся в эксплуатации более 20 лет. На территории России имеются 32 пункта приема газет, обычно расположенные непосредственно в типографиях. Пункт разветвления каналов находится на центральной междугородной телефонной станции, поскольку для передачи газет используются телефонные каналы. Газеты передаются ежедневно, по 4...5ч в сутки. В настоящее время происходит спад нагрузки на данную сеть, поскольку применение аналогового способа передачи не удовлетворяет в полной мере требования, предъявляемые полиграфистами. Рассматривается возможность модернизации сети, а также использование других сетей (Internet и т.п.) для передачи газет.
В историческом плане все виды электросвязи длительный период развивались независимо друг от друга, в результате чего сформировались несколько независимых сетей. Вместе с тем сети общего пользования (Минсвязи) не справлялись с объемами передачи сообщений, требуемых для нормального экономического развития страны, и поэтому ряд министерств и ведомств стали создавать свои сети для удовлетворения собственных нужд. Такая техническая политика привела к еще большему разобщению технических средств, а эффективность совокупности сетей в масштабах страны оставалась низкой.
Уже в начале 60-х годов ХХ века стало ясно, что перспективным направлением развития связи должно стать объединение сетей. Можно выделить следующие предпосылки для объединения сетей: унификация методов преобразования, необходимость передачи сигналов в совпадающих направлениях, сходство функций систем передачи и коммутации.
В 70-х годах было принято решение о создании Единой автоматизированной сети связи (ЕАСС) Союза ССР. Работа по созданию сети ЕАСС не была завершена и прекратилась в связи с развалом СССР. В настоящее время этот проект, отражая изменение геополитической ситуации и новые революционные достижения в области связи, называется Взаимоувязанной сетью связи России. (ВСС) [3). ВСС — это совокупность технически сопряженных сетей электросвязи общего пользования, ведомственных и других сетей электросвязи на территории России независимо от ведомственной принадлежности и форм собственности, обеспеченная общим централизованным управлением. Основными требованиями к ВСС являются надежность и экономичность.
Определенные технические средства ВСС участвуют в процессе передачи независимо от вида передаваемых сообщений. Совокупность этих элементов образует первичную сеть (ПС) ВСС (рис.1.11). В состав ПС входят сетевые узлы, сетевые станции и линии передачи.
Структура ПС учитывает административное деление страны. Территория страны поделена на зоны. Признак зоны — единая семизначная нумерация.
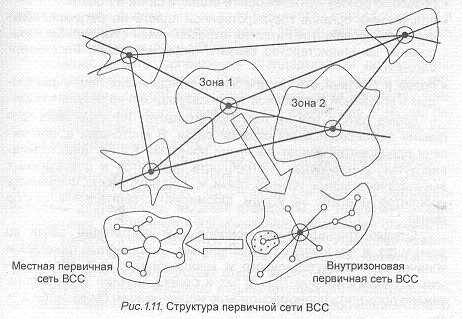
Как правило, зоны совпадают с территориями областей. В соответствии с этим делением ПС состоит из отдельных частей:
• местные ПС (МСП) ограничены территорией города или сельского района;
• внутрозоновые ПС (ВЗПС) охватывают территорию зоны и обеспечивают соединение местных сетей внутри зоны;
• магистральная ПС (СМП) соединяет зоновые сети. Каждая сеть связи, входящая в ВСС, помимо технических средств первичной сети, использует устройства, присущие этой сети. Вторичная сеть (ВС) ВСС — совокупность технических средств, обеспечивающих передачу сообщений определенного вида. В состав ВС входят: оконечные абонентские устройства, абонентские линии (АЛ), коммутационные устройства и каналы, выделенные из ПС для организации данной ВС.
До недавнего времени Минсвязи РФ являлось практически единственным оператором связи, предоставлявшим услуги организациям и населению. Ведомственные сети обеспечивали потребности самих организаций. Однако изменение экономической ситуации в стране и общемировая тенденция отхода от монопольно- го государственного или частного владения сетями и средствами связи привели к принятию Закона о связи, фактически определяющего основные принципы демонополизации отрасли связи.
Закон о связи был принят Государственной Думой в 1995 г. Этот закон определяет:
• правовую основу деятельности в области связи в России;
• полномочия органов государственной власти по регулированию функционирования и развития отрасли связи (эти функции возложены на Министерство связи и информатизации Российской Федерации;
• права и обязанности физических и юридических лиц, участвующих в указанной деятельности и пользующихся ее результатами.
Кроме того, в том же году Правительство РФ утвердило программу демонополизации отрасли связи. В настоящее время тысячи предприятий имеют лицензии Минсвязи РФ на предоставление услуг электросвязи. Потребность абонентов в современных высококачественных услугах связи и, соответственно, готовность абонентов платить за услуги формируют значительный сектор рынка.
Однако традиционным монопольным операторам связи во всем мире, в том числе и отечественным, отягощенным громадным количеством коммутационного и каналообразующего оборудования со значительными (до 20лет и более) сроками окупаемости, тяжело проводить полномасштабную модернизацию своих сетей для
соответствия современным потребностям в услугах связи. Демонополизация в отрасли связи приводит к появлению новых агрессивных операторов связи, которые стучат в двери буквально каждого потенциального клиента, завлекают его более низкими цена- ми, повышенным качеством и разнообразием услуг.
Операторы ведомственных сетей наряду с ростом услуг связи для собственных пользователей планируют предоставлять услуги своих сетей прочим пользователям. Уже сейчас наметился рост конкуренции между традиционными операторами и альтернативными поставщиками услуг связи на базе сетей энергосистем, газопроводов, железных дорог и метрополитенов.
Демонополизация отрасли связи и, как ее результат, конкуренция операторов будет выигрышна для абонентов, что на базе развития современных телекоммуникационных технологий выразится в расширении количества и повышении качества услуг связи при снижении их стоимости.
1.7. ОРГАНИЗАЦИИ СТАНДАРТИЗАЦИИ В ОБЛАСТИ ТЕЛЕКОММУНИКАЦИЙ
Цель деятельности организаций стандартизации в области телекоммуникаций заключается в создании единых международных стандартов. Отсутствие единых стандартов приводит к несовместимости оборудования различных производителей и, как следствие, невозможности организации международной связи. Организации стандартизации обеспечивают условия для обсуждения прогрессивных технологий, утверждают результаты этих обсуждений в виде официальных стандартов, а также обеспечивают распространение утвержденных стандартов.
Порядок работы организаций стандартизации по принятию стандартов может отличаться. Однако он схож в том, что производится несколько этапов разработки и обсуждения новых технологий, разработки проектов стандартов, голосования по всем или не- которым аспектам этих стандартов и, наконец, официального выпуска завершенных стандартов.
Наиболее известны следующие организации стандартизации. Международная организация стандартизации (МОС) (International Standard Organization — ISO) — автор стандартов в различных областях деятельности, включая стандарты по телекоммуникациям. Членами ISO являются национальные организации стандартизации. Участие в ISO является добровольным. Наиболее известным стандартом ISO в области телекоммуникаций является эталонная модель взаимодействия открытых систем.
Сектор стандартизации телекоммуникаций Международного союза электросвязи (MC3-T) (Telecommunication Standardization Sector of International Telecommunication Union — ITUT) — специализированный орган ООН, с 1993 г. преемник Международного консультативного комитета по телеграфии и телефонии (МККТТ) (Comite Consultatif International Telegraphique et Telephonique — CCITT) — международная организация, разрабатывающая стандарты в области связи. Стандарты ITU-Т называются Рекомендациями (Recommendation). Рекомендации объединены в серии, обозначаемые латинскими буквами. В пределах серии Рекомендации присваивается порядковый номер. Обозначение серии и номер Рекомендации отделяются друг от друга точкой, например V.90. Кроме ITU-Т, в состав ITU входят Сектор радиосвязи МСЭР (Radiocommunication Sector — ITU-R) и Сектор развития электросвязи (Telecommunication Development Sector — ITU-D). Стандарты ITU охватывают практически всю область телекоммуникаций.
Институт инженеров по электротехнике и электронике (Institute of Electrical and Electronic Engineers — IEEE) — профессиональная организация, разрабатывающая стандарты для сетей. Стандарты локальных сетей LAN являются наиболее известными стандартами IEEE по телекоммуникациям.
Европейский институт стандартизации электросвязи (European Telecommunications Standards Institute — ETSI). Определяет единую техническую политику в области телекоммуникаций для стран — членов Европейского сообщества. Наиболее известным стандартом ETSI является стандарт сотовой системы подвижной радиосвязи GSM.
Европейская конференция администраций почт и электро-: связи (Conference of European Posts and Telegraphs — СЕРТ).
Американский национальные институт стандартизации (American National Standard Institute — ANSI) — координирующий орган добровольных групп по стандартизации в пределах США. ANSI является членом ISO. Широко известен стандарт ANSI по коммуникациям FDDI.
Ассоциация телекоммуникационной промышленности (Telecommunication Industrial Association — TIA) — одна из групп ANSI, выпускающая стандарты по телекоммуникациям. Самым известным стандартом TIA является стандарт сотовой системы подвижной радиосвязи США IS-54.
Ассоциация электронной промышленности (Electronic Industrial Association — EIA) — одна из групп ANSI.
Федеральная комиссия по связи (Federal Communication Commission — FCC) США. Правительственная организация США, занимающаяся регулированием в отрасли связи, в том числе распределением спектра радиочастот.
Совет по регуляции работы Internet (Internet Activities Board — IAB). Определяет основную политику в области глобальной сети Internet. Включает в себя два подкомитета: исследовательский — IRTF (Internet Research Task Force) и стандартизации — IETF (Internet Engineering Task Force). Стандарты IAB называются «Request for Comments» (RFC) (Запрос для комментария).
Производители оборудования телекоммуникаций, заинтересованные в быстром продвижении некоторой конкретной технологии, также создают организации стандартизации в данной области. В качестве примера можно привести такие организации, как Форум АТМ, Форум Frame Relay, Альянс Gigabit Ethernet и пр.
В нашей стране работы по стандартизации и регулированию в области связи наряду с Государственным комитетом по стандартизации, метрологии и сертификации (Госстандартом) проводят Минсвязи РФ и его подразделения: Государственная комиссия по электросвязи (ГКЭС), Государственная комиссия по распределению частот (ГКРЧ) и Главгоссвязьнадзор.
МЕТОДЫ МОДУЛЯЦИИ
2.1. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ И ПОМЕХ ОСНОВНЫЕ СООТНОШЕНИЯ
Приведем основные аналитические соотношения, которые будем использовать в дальнейшем. При рассмотрении этих соотношений будем осуществлять временное и частотное представление функций времени (сигналов).
Для прямого преобразования Фурье (спектральной функции) сигнала s(t)
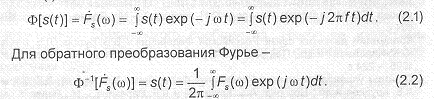
В ряде случаев для сокращения выкладок используется комплексное представление действительного сигнала s(t)
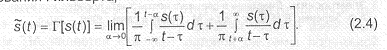
Представление s(t) в комплексной форме (2.3) называют представлением в аналитической форме или аналитическим сигналом.
Легко проверить, что I [cos cot] = sin cot, I [sin cot] = — cos cot. Следовательно, если имеется сигнал сложной формы
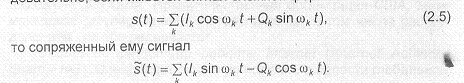
Таким образом, каждая гармоническая составляющая сопряженного сигнала s(t) повернута на угол относительно соответствующей составляющей исходного сигнала з(Ц.
Применив (2.2) к s(t), получим преобразование Фурье сопряженного сигнала

Следовательно, для получения спектральной функции комплексного сигнала необходимо удвоить спектральную функцию исходного сигнала s(t) при со>0 и приравнять ее нулю при со<0. Сигнал s(t), спектральная функция которого равна нулю за пределами некоторой полосы частот, так что
![]()
называется полосовым.
Для полосовых сигналов используется представление

Если W//со,<1, то сигнал (2.10) называют узкополосным тральном смысле. Его можно представить в комплексной (2.3) как

— комплексная огибающая (комплексная амплитуда) сигнала.
Узкополосный сигнал можно рассматривать в виде суммы двух квадратурных составляющих:

Между преобразованиями сигналов s(t) и S(t) имеет место соотношение
![]()
Представление узкополосных сигналов через комплексную огибающую можно распространить и на так называемые узкополосные системы. Узкополосными системами называются такие системы, отклик которых на произвольный входной сигнал s(t) является узкополосным сигналом.
Пусть линейная узкополосная система с постоянными параметрами имеет импульсную характеристику h(t) и частотную передаточную функцию H(03). Импульсную характеристику h(t) можно также представить в комплексной форме: h(t) =h(t)+josh(t). Ей соответствует частотная передаточная функция Н,(в)=2Н(в)У(в), где С/(в) согласно (2.7) есть частотная передаточная функция идеального фильтра верхних частот, пропускающего все «положительные» частоты.
Таким образом, отклик узкополосной системы в комплексной форме x(t) на входной сигнал s(t) может быть получен как выходной сигнал последовательно включенных.рассматриваемой узкополосной системы и фильтра верхних частот с частотной передаточной функцией 20(в). Поскольку все операции являются линейными, то порядок их выполнения может быть произвольным, как показано на рис.2.1.
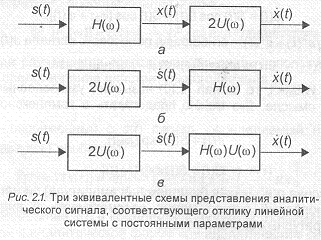
В варианте (рис.2.1,в) линейная система имеет комплексную импульсную характеристику h(t) I2, поэтому ее отклик на комплексный сигнал s(t) определяется выражением
![]()
Если h(t) и s(t) выразить через комплексные огибающие (2.13), то
![]()
Н(т) — комплексная огибающая импульсной характеристики.
Из (2.18) следует, что отклик узкополосной линейной системы с постоянными параметрами представляет собой узкополосный сиг- нал с комплексной огибающей
![]()
Таким образом, комплексная огибающая отклика узкополосной системы может быть найдена как результат обработки комплекс- ной огибающей входного сигнала эквивалентной низкочастотной линейной системой с комплексной импульсной характеристикой H(t) и частотной передаточной функцией Н(в+во)0(в+в,), как показано на рис.2.2.

Заметим, что если Н(в) симметрична относительно частоты в,, то низкочастотный эквивалент узкополосной линейной системы имеет действительную импульсную характеристику.
ДИСКРЕТНОЕ ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
Реальные сигналы, присутствующие в устройствах и системах связи, являются на определенных интервалах непрерывными функциями времени. Однако при анализе часто удобно использовать их представление в виде выборочных мгновенных значений, т.е, в виде рядов по системам ортонормальных функций, коэффициентами при которых являются выборочные значения.
Пусть имеется и независимых сигналов. Независимость сигналов означает, что ни один из этих сигналов не может быть представлен в виде линейной комбинации остальных (и — 1) сигналов, т.е. не существует постоянных (не равных нулю), таких, что
![]()
Эти сигналы образуют базис.
Предположим, что сигнал (t) может быть представлен в виде линейной комбинации и независимых сигналов
![]()
Если каждый сигнал может быть представлен в виде (2.21), то мы имеем и-мерное пространство сигналов. Множество сигналов называется ортонормальным, если выполняется условие
![]()
Для ортонормального множества коэффициенты s< в (2.21) определяются как
![]()
При выбранном множестве базисных сигналов сигнал s(t) может быть представлен набором чисел или точкой в и-мерном пространстве. Теперь сигнал s(t) может рассматриваться как вектор. Примером дискретного представления сигналов может служить представление в виде ряда В.А. Котельникова
s(t) = g s sine (2л В1 — k z), 2В
где sin c(x) =sinx(x), В — верхняя частота спектра сигнала s(t).
Здесь в качестве ортонормальных функций выбраны функции (2.24)
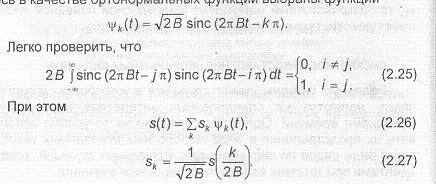
Таким образом, любой сигнал s(t) с ограниченным спектром может быть представлен точкой в пространстве сигналов с координатами значение отсчета, деленное на.
Рассмотрим теперь четыре сигнала:
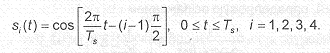

Таким образом, интеграл от произведения двух сигналов есть скалярное произведение векторов в пространстве сигналов, и взаимной ортогональности двух функций времени соответствует ортогональность векторов при их дискретном представлении.
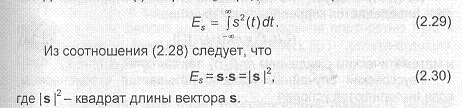
Следовательно, энергия сигнала равна квадрату длины соответствующего вектора в пространстве сигналов.
Итак, размерность пространства сигналов равна максимальному количеству независимых векторов в этом пространстве. В и-мерном пространстве может быть не более, чем и независимых векторов. Если найдено множество из и независимых векторов, то можно с помощью процедуры Грама — Шмидта построить другое множество из и независимых векторов, которые являются взаимно ортогональными и образуют координатную систему.
ГАУССОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС.
Случайный процесс ((t) называется гауссовским, если совокупность случайных величин определенных для моментов времени является совместно гауссовской, т.е. имеем совместную функцию плотности распределения вероятности (ФПРВ), определяемую выражением

— определитель матрицы — алгебраическое дополнение элемента в матрице. Заметим, что — дисперсия случайной величины Гауссовский случайный процесс не только представляет весьма удобную модель случайных процессов, которые встречаются в реальных ситуациях, но и обладает рядом свойств, позволяющих упростить получение некоторых математических, важных с практической точки зрения, результатов.
Из (2.31) следует, что гауссовский случайный процесс полностью определяется корреляционной функцией
![]()
и математическим ожиданием mg(Q(t)j так как Гауссовский случайный процесс называется стационарным, если выполняются условия
![]()
Условия (2.34) являются условиями стационарности в широком смысле, поэтому для гауссовского случайного процесса они являются условиями строгой стационарности. Для стационарного гауссовского случайного процесса ковариация определяется следующим выражением:
![]()
Другим важным свойством гауссовского случайного процесса является то, что отклик линейной системы на воздействие в виде гауссовского случайного процесса также гауссовский случайный процесс.
Пусть на входе линейной системы с импульсной характеристикой h(t) имеется гауссовский случайный процесс ((t). Тогда случайный процесс на выходе системы
![]()
Поскольку — гауссовский процесс, то все случайные вели- чины ((t — т) являются совместно гауссовскими (по определению). Следовательно, случайные величины п(4),q(t~),...,q(tД), определенные для моментов времени 1~,1~,...,1„, есть линейные комбинации совместно гауссовских случайных величин и также являются совместно гауссовскими. Таким образом, случайный процесс q(t) является гауссовским.
Если имеется полное множество ортонормальных базисных функций (yД(t)), то в пространстве сигналов реализация x(t) гауссовского случайного процесса может быть представлен в виде ряда
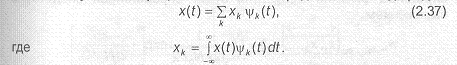
Заметим, что случайный процесс ~(Ц состоит из множества реализаций x(t). Поэтому для каждой реализации имеется собственный коэффициент. Отсюда следует, что значения коэффициентов— это значения случайных величин ((<,g>,...,EД), полученные для определенной реализации с функцией плотности распределения вероятности.
Рассмотрим в качестве примера гауссовский случайный процесс h(t) в виде белого шума со спектральной плотностью И,/2 и корреляционной функцией Я„(т) =(И,/2)5(т), 5(т) — дельта-функция.
Так как белый шум имеет неограниченную полосу, то размерность пространства сигналов также неограничена.
Покажем, что— независимые случайные величины с дисперсией И,/2. Действительно,
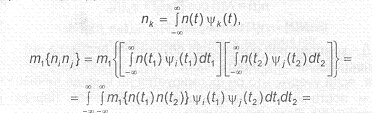
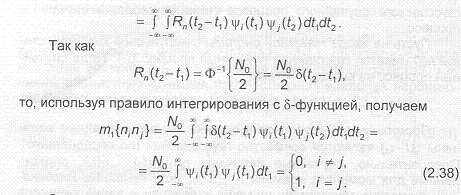
Следовательно случайные величины , некоррелированные, а поскольку они являются гауссовскими, то и независимы.
Если ограничиться представлением белого шума в виде конечного ряда, т.е. ограничить размерность пространства сигналов, то функция плотности распределения вероятности совокупности случайных величин будет определяться следующим выражением:
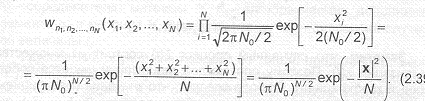
Из (2.39) следует, что ФПРВ белого гауссовского шума зависит только от длины шумового вектора х в пространстве сигналов и поэтому обладает свойством сферической симметрии.
УЗКОПОЛОСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
Рассмотрим теперь действительный, стационарный в широком смысле случайный процесс n(t) и комплексный процесс n(t)=n(t)+ +jn(t). Существуют следующие формы представления этих процессов:

где N(t) — комплексная огибающая случайного процесса n(t).
Спектральная плотность процесса ri(t) может быть легко определена, если учесть, что он формируется на выходе линейной системы и постоянными параметрами и частотной передаточной функцией 2U(f).
Из выражения (2.44) следует, что спектральная плотность комплексного процесса равна учетверенной односторонней спектральной плотности действительного процесса n(t).
Корреляционная функция комплексной огибающей N(t) равна
![]()
где (..) — символ комплексного сопряжения.
Следовательно, спектральная плотность
![]()
и совпадает со спектральной плотностью комплексного процесса, перенесенной в начало координат. Это отражено на рис.2.3.
Можно показать, что авто- и взаимно-корреляционные функции квадратурных составляющих удовлетворяют следующим соотношениям:
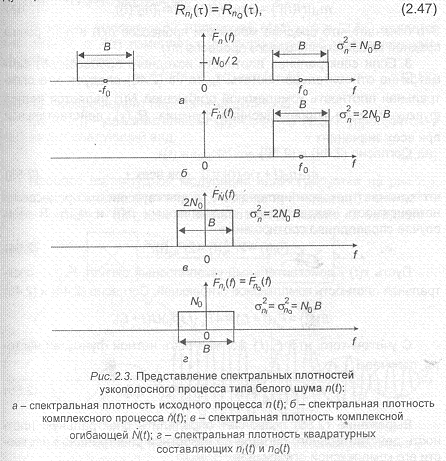
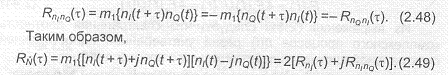
Из представленных результатов вытекают следующие выводы:
1. Так как есть действительная величина, то из (2.49) следует, что
![]()
Это означает, что для любого момента времени t процессы являются некоррелированными, а в случае гауссовского случайного процесса и статистически независимыми.
2. Из выражений (2.44), (2.45), (2.48), (2.49) следует, что
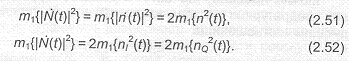
Это означает, что средние мощности процессов равны средней мощности исходного процесса n(t).
3. Если спектральная плотность исходного процесса n(t) симметрична относительно частоты (,, то из (2.46) следует, что спектральная плотность комплексной огибающей N(t) является четной функцией, а ее корреляционная функция (т) действительной при всех значениях т.
Согласно (2.49) и (2.50)
![]()
что означает некоррелированность, а для гауссовских процессов и
независимость квадратурных составляющих. В этом случае справедливо соотношение
![]()
Пусть x(t) — действительный узкополосный сигнал, F(f) — спектральная плотность комплексной огибающей. Согласно (2.44) и (2.46)
![]()
С учетом того, что FД(f) должна быть четной функцией частоты, получаем
![]()
Выражение (2.55) позволяет определить спектральную плотность действительного сигнала по известной спектральной плотности его комплексной огибающей.
2.2. АНАЛОГОВЫЕ МЕТОДЫ МОДУЛЯЦИИ
Модуляцией называется процесс, в результате которого происходит изменение параметра или параметров сигнала-переносчика пропорционально другому сигналу, сигналу сообщения. При аналоговой модуляции модулированный сигнал аналитически может быть представлен в комплексной форме:
![]()
где A(t) — изменяющаяся во времени амплитуда (огибающая), сор— частота несущей, q(t) — изменяющаяся во времени фаза.
Для узкополосных сигналов, удовлетворяющих условию W«o)o (W — ширина спектра), параметры АЯ и (p(t) изменяются достаточно медленно по сравнению с exp(jcopt).
АМПЛИТУДНАЯ МОДУЛЯЦИЯ
В случае амплитудной модуляции (АМ) (p(t) в (2.56) является постоянной, а A(t) изменяется пропорционально модулирующему сигналу сообщения c(t):
![]()
где — коэффициент передачи модулятора.
Если c(t) — действительная функция, то (2.57) упрощается и принимает следующий вид:
![]()
Процесс амплитудной модуляции иллюстрируется на рис.2.4. Заметим, что здесь изменение полярности (знака) c(t) приводит к изменению фазы несущей модулированного сигнала на радиан.
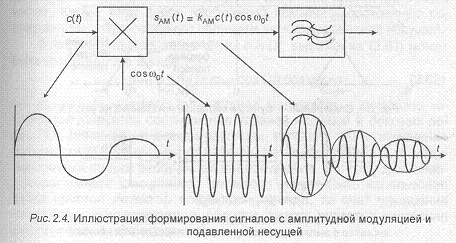
Спектральная функция АМ сигнала получается путем преобразования Фурье (2.58) и имеет следующий вид:
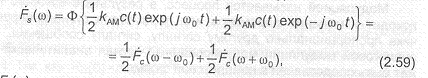
где Fc((o) — спектральная функция модулирующего сигнала. Заметим, что при таком выборе коэффициента в процессе амплитудной модуляции происходит перенос спектра модулирующего сигнала на частоты без его изменения. Эта разновидность амплитудной модуляции получила название амплитудной модуляции с двумя боковыми полосами и подавленной несущей (АМ-ДБП-ПН), поскольку спектр модулированного сигнала не со- держит несущей, а боковые полосы сосредоточены вокруг частот +co,. Если рассматривать только положительные частоты, имеющие физический смысл, то в результате амплитудной модуляции требуемая полоса частот увеличивается вдвое. Это показано на рис.2.5. Спектральные составляющие, расположенные выше частоты а,, образуют так называемую верхнюю боковую полосу, а спектральные составляющие, расположенные ниже частоты — нижнюю боковую полосу.
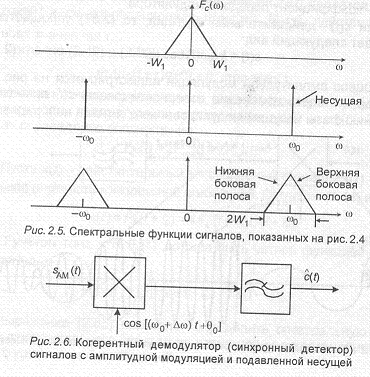
Демодуляция АМ-ДБП-ПН сигнала осуществляется путем его перемножения на опорный сигнал несущей и последующей низко- частотной фильтрации, как показано на рис.2.6.
![]()
Наличие фазовой ошибки О, в опорном сигнале несущей приводит только к уменьшению уровня демодулированного сигнала, частотная ошибка приводит к недопустимым мультипликативным искажениям. Поэтому для демодуляции АМ-ДБП-ПН сигнала необходимо использовать синхронный демодулятор (синхронный детектор).
Использование АМ-ДБП-ПН требует наличия в демодуляторе опорного сигнала несущей, совпадающего с несущей демодулированного сигнала с точностью до начальной фазы. А поскольку сиг- нал несущей в АМ-ДБП-ПН отсутствует, то для восстановления необходимо дополнительные средства. Это несколько усложняет схему демодулятора. Чтобы избежать этого, можно к АМ-ДБП-П Н сигналу добавить сигнал немодулированной несущей с таким уровнем, чтобы в нем отсутствовали скачки фазы на вызванные изменениями полярности модулирующего сигнала. В этом случае получим другую разновидность амплитудной модуляции, которая получила название амплитудной модуляции двумя боковыми полосами (АМ-ДБП), или просто АМ. Математически АМ-ДБП сигнал может быть представлен в следующем виде:
![]()
При соответствующем выборе значения амплитуда (огибающая) A(t) модулированного сигнала .будет пропорциональна c(t). Процесс демодуляции в этом случае упрощается и сводится к выделению огибающей с помощью диодного детектора и фильтра нижних частот. Кроме того, здесь необходимо исключить постоянную составляющую, обусловленную наличием немодулированной несущей.
В частном случае, когда, выражение (2.61) может быть представлено в виде
![]()
— индекс амплитудной модуляции, с помощью которого регулируется соотношение уровней несущей и боковых полос. При значениях индекса модуляции, меньших 100%, изменения полярности c(t) не вызывают скачков фазы несущей на л, и модулированный сигнал отображает эти изменения. Поэтому для демодуляции вместо синхронного детектора может быть использован более простой детектор огибающей, правда, за счет ухудшения частотной характеристики в области низких частот и снижения энергетической эффективности.
Если не ограничиваться рассмотрением в качестве модулирующих сигналов действительных функций времени, то согласно (2.57) получим
![]()
где /(Ц и q(t) — соответственно действительная и мнимая части модулирующего сигнала c(t). Используя известное тождество для комплексных величин
![]()
выражение (2.63) можно представить в следующем виде:
![]()
Сигнал (2.64) можно рассматривать как сумму двух АМ-ДБП-ПН сигналов находящихся в квадратуре (ортогональных сигналов). Поскольку i(t) и q(t) являются медленно изменяющимися функция- ми времени по сравнению с exp(Jm,t), то они могут быть разделены и демодулированы с помощью двух синхронных детекторов.
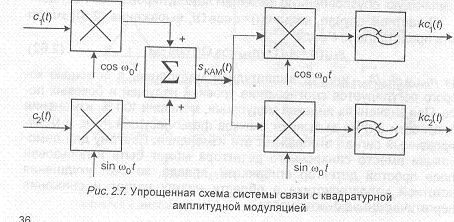
Разновидность амплитудной модуляции, описываемая (2.64), получила название квадратурной амплитудной модуляции (КАМ). Система связи с квадратурной амплитудной модуляцией в упрощенном виде показана на рис.2.7.
Рассмотренные разновидности амплитудной модуляции в лучшем случае требуют увеличения занимаемой полосы частот в два раза по сравнению с минимально необходимой для передачи сообщений с ограниченной полосой. Это их недостаток. Поэтому для экономии спектра желательно одну из боковых полос подавить. Принципиально подавление одной из боковых полос можно сделать с помощью фильтра одной боковой полосы (ОБП-фильтра). Однако требования, предъявляемые к подобному фильтру, оказываются достаточно жесткими. В идеальном случае он должен пропускать без искажений все спектральные составляющие одной боковой полосы и подавлять все спектральные составляющие другой.
Амплитудно-частотная характеристика низкочастотного эквивалента такого идеального ОБП-фильтра должна иметь следующий вид:

Ей соответствует комплексная частотная передаточная функция
![]()
Для выполнения условия нечетности фазово-частотной характеристики ОБП-фильтра необходимо, чтобы

Здесь знаки неравенства определены для ОБП-фильтра выделяющего верхнюю боковую полосу. Если выделяется нижняя боковая полоса, то знаки неравенств необходимо поменять местами.
Импульсная характеристика ОБП-фильтра имеет вид
![]()
Напомним, что C(sign(co))=( — /тИ). При воздействии на входе такого фильтра сигнала c(t) на его выходе будет формироваться отклик
![]()
где — символ операции свертки двух функций. Второе слагаемое в (2.69) представляет собой преобразование Гильберта функции с(Ц, которое обозначим с(1). Согласно выражению (2.67) все спектральные составляющие c(t) приобретают дополнительный фазовый сдвиг на л/2 по сравнению с аналогичными спектральными составляющими c(t), т.е. они находятся с ними в квадратуре.
Преобразование Гильберта не полностью определено при t=0, поэтому в точках, где c(t) претерпевает разрывы первого рода, возникают бесконечные скачки амплитуды. Поэтому амплитудную модуляцию с одной боковой полосой (АМ-ОБП) целесообразно использовать, когда модулирующий сигнал представляет собой «гладкую» функцию времени. В этом случае огибающая не будет иметь значительных выбросов.
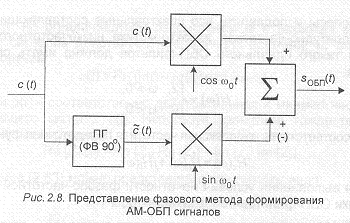
Комбинирование преобразования Гильберта и квадратурной амплитудной модуляции позволяет реализовать фазовый метод формирования АМ-ОБП сигнала, который представлен на рис.2.8.
Основной проблемой, которую необходимо решить при использовании фазового метода формирования АМ-ОБП сигнала, является построение фазовращателя, обеспечивающего фазовый сдвиг всех составляющих сигнала c(t) на л/2. С математической точки зрения фильтровой и фазовый методы формирования АМ-ОБП эквивалентны, поэтому в любом случае АМ-ОБП сигнал может быть записан следующим образом:
![]()
где знаки (+) соответствуют нижней и верхней выделяемым боковым полосам.
Если АМ-ОБП сигнал (2.70) подать на вход синхронного детектора, то на его выходе будет формироваться сигнал, который может быть представлен в виде
![]()
где — частотная и фазовая ошибки синхронизации.
Фазовые искажения, т.е. наложение c(t) на c(t) возникают, если. Кроме того, при имеет место частотный сдвиг всех составляющих.
При использовании синхронного детектора для демодуляции АМ-ОБП сигналов при наличии ошибок синхронизации происходит ухудшение качества демодуляции, но оно существенно меньше по сравнению с тем, которое обусловлено мультипликативными искажениями при демодуляции АМ-ДБП-ПН сигналов.
Таким образом АМ-ОБП позволяет за счет некоторого снижения качества передачи в два раза сократить требуемую полосу частот при передаче.
Существует еще одна разновидность амплитудной модуляции, получившая название амплитудной модуляции с частично-подавленной боковой полосой (АМ-ЧПБП). В этом случае обеспечивается компромисс между требуемой полосой передачи в случае АМ-ОБП и АМ-ДБП-ПН.
Модулятор сигналов АМ-ЧПБП содержит обычный АМ-ДБП-ПН модулятор и фильтр частично-подавленной боковой полосы (ЧПБП-фильтр) с амплитудно-частотной характеристикой НЧПБП((о).
Сигнал АМ-ЧПБП имеет спектральную плотность
![]()
При воздействии АМ-ЧПБП сигнала на вход синхронного детектора на его выходе формируется сигнал сообщения
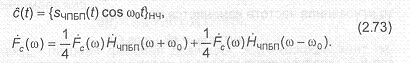
Таким образом, для неискаженного воспроизведения сигнала сообщения с(~) необходимо, чтобы выполнялось условие
![]()
где Q — верхняя частота спектра модулирующего сигнала. Если постоянную в (2.74) положить равной 2НЧПБП(а,), то можно убедиться, что амплитудно-частотная характеристика ЧПБП фильтра должна быть асимметричной относительно частоты несущей. Хотя при получении этого результата предполагалось использование синхронного детектора, он остается справедливым и в случае использования детектора огибающей, если «остаток» несущей имеет достаточный уровень.
Амплитудная модуляция с частично-подавленной боковой находит широкое применение в телевизионных системах для передачи сигналов изображения.
УГЛОВАЯ МОДУЛЯЦИЯ
В общем случае между фазой 0(t) и мгновенной частотой квазигармонического колебания имеют место следующие соотношения:

Это определение частоты, вообще говоря, отличается от того,
которое принято в спектральном анализе, где частоты не могут изменяться во времени.
При угловой модуляции в (2.56) мы полагаем постоянной амплитуду, и в соответствии с модулирующим сигналом c(t) изменяется фазовый угол. В случае прямой пропорциональности
![]()
и этот вид угловой модуляции носит название фазовой (ФМ).
Если прямо пропорционально модулирующему сигналу изменяется мгновенная частота:
![]()
то такой вид угловой модуляции носит название частотной (ЧМ). Если модуляция осуществляется гармоническим сигналом
![]()
то мгновенная частота изменяется по закону
![]()
где k« — коэффициент передачи частотного модулятора, имеющий размерность радиан на секунду-вольт [рад/(с В)].
Вводя новый параметр Am=ck«, так называемую пиковую частотную девиацию (частотное отклонение несущей), (2.80) можно представить в следующем виде:
![]()
Изменения фазы ЧМ сигнала при гармоническом модулирующем сигнале определяются выражением, которое следует из (2.75) и (2.81):
![]()
где — индекс частотной модуляции.
Согласно (2.56) ЧМ сигнал аналитически может быть представлен как
![]()
В (2.83) второй экспоненциальный сомножитель являет периодическую функцию (с основной частотой Q), поэтому он может быть представлен в виде ряда Фурье. В этом случае
![]()
где J(p) — функция Бесселя первого рода, порядка.
Используя свойства указанных функций Бесселя, можно получить следующее приближенное соотношение, определяющее ширину спектра или требуемую полосу частот ЧМ сигнала:
Согласно (2.85) ширина спектра ЧМ сигнала зависит от индекса частотной модуляции и при больших значениях существенно превышает ширину спектра АМ сигнала. Поэтому частотную модуляцию относят к видам модуляции с расширением спектра сиг- нала.
Демодуляцию ЧМ сигналов можно осуществить при помощи либо схем, обеспечивающих преобразование отклонений частоты от частоты несущей в изменения уровня, либо схем с обратной связью, примером которой может служить схема фазовой синхронизации. При использовании схем фазовой синхронизации качество демодуляции получается наиболее высоким, и при этом не требуется наличия резонансных элементов.
При фазовой модуляции гармоническим сигналом выражение (2.77) принимает вид
![]()
— пиковая фазовая девиация, — коэффициент передачи фазового модулятора, имеющий размерность радиан на вольт (рад/В).
Вычислив производную от (2.86) и сравнив полученный результат с (2.81), заметим, что в случае фазовой модуляции пиковая девиация частоты пропорциональна не только амплитуде модулирующего сигнала, но и его частоте, т.е.
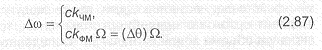
При представлении ФМ сигнала в виде ряда Фурье (2.84) численное значение индекса модуляции р равно пиковому значению фазовой девиации ЛО, поэтому ширина спектра ФМ сигнала определяется выражением (2.85), в котором вместо величины следует подставить величину ЛО.
2.3. ЦИФРОВЫЕ МЕТОДЫ МОДУЛЯЦИИ
ОСНОВНЫЕ ПАРАМЕТРЫ МОДУЛЯЦИИ
Рассмотрим некоторые виды модуляции, получившие широкое распространение в системах передачи дискретных сообщений и покажем, насколько эффективно каждый из рассматриваемых видов модуляции использует имеющиеся ресурсы системы связи: мощность, полосу частот, время — для обеспечения требуемой достоверности передачи, выражаемой в терминах частности или вероятности ошибки.
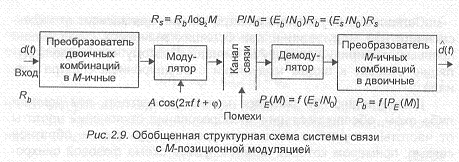
Обобщенная структурная схема системы связи приведена на рис.2.9. В системе используется многопозиционная модуляция, предполагающая переход от двоичного алфавита символов дискретного сообщения к М- ичному:

где т — длина преобразуемых последовательностей двоичных символов, М — объем алфавита.
Каждый символ из М-ичного алфавита модулирует один или несколько параметров гармонического колебания конечной длительности: амплитуду, частоту, фазу, время запаздывания. В некоторых случаях при многопозиционной модуляции производится предварительное преобразование (отображение) символов М- ичного алфавита в одну из кодовых последовательностей со специальными свойствами, позволяющими после модуляции сформировать алфавит ортогональных, биортогональных, трансортогональных сигналов объема М или сигнальных последовательностей конечной (или полубесконечной) длины с гарантированными дистанционными свойствами в сигнальном пространстве. Такое преобразование более корректно было бы назвать «кодированной модуляцией». Так как один из М символов или сигналов передается в течение времени Т равного его длительности, то скорость передачи (выражена в битах на секунду)
![]()
а длительность бита

При этом скорость передачи символов R, будет связана со скоростью передачи R|, следующим соотношением:

Спектральную эффективность различных видов модуляции принято оценивать удельной скоростью передачи:
![]()
где И/ — полоса частот, необходимая для передачи сигналов с выбранным видом модуляции.
Таким образом, чем меньше значение WT>1, тем выше спек- тральная эффективность рассматриваемого вида модуляции и системы передачи дискретных сообщений в целом. Виды модуляции с WTД<1 принято относить к классу спектрально-эффективных.
Энергетическую эффективность различных видов модуляции оценивают удельными энергетическими затратами:
![]()
т.е. отношением энергии, затрачиваемой на передачу одного бита сообщения, к спектральной плотности АБГШ, при заданном значении вероятности ошибки. Чем меньше эта величина, тем меньший энергетический потенциал радиолинии требуется для передачи сообщений с заданными скоростью и достоверностью. Виды модуляции с низкими значениями h принято относить к классу энергетически эффективных.
Напомним, что согласно теореме Шеннона предельное значение удельных энергетических затрат составляет — 1,6дБ. Отношение средней мощности сигнала к мощности шума (отношение сигнал/шум) может быть выражено через указанные показатели энергетической и спектральной эффективности видов модуляции следующим образом:
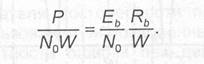
Из приведенного выражения следует, что спектрально-эффективные виды модуляции требуют при передаче сообщений больших значений отношения сигнал/шум и, наоборот, виды модуляции с низкой спектральной эффективностью — небольших значений этого отношения.
При определении показателя спектральной эффективности и отношения сигнал/шум необходимо знать полосу частот И/, занимаемую сигналом с заданным видом модуляции. К сожалению, однозначного определения этой величины нет. Рассмотрим некоторые наиболее употребительные определения полосы W на при- мере узкополосного сигнала с линейной модуляцией:
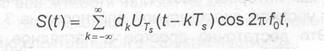
где стационарная последовательность случайных величин с нулевым математическим ожиданием и единичной дисперсией, U>(t) — прямоугольный импульс с единичной амплитудой и длительностью T, Спектральная плотность такого сигнала, вычисленная как преобразование Фурье корреляционной функции, определяется выражением [1]
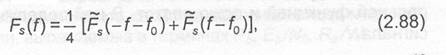

График функции F,(f) изображен на рис.2.10. Он состоит из главного и нескольких
боковых лепестков. Подобная структура спектра характерна для большинства
сигналов с дискретной модуляцией. Отметим, что ширина полосы частот, занимаемой
сигналом, определяется только для положительных частот спектра. На рисунке
обозначены:
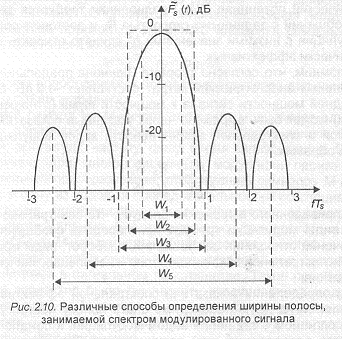
1. W1 — ширина полосы по уровню половинной мощности. Она определяется как интервал частот, граничные значения которого соответствуют уровням спектральной плотности на 3 дБ ниже максимального. Это достаточно простое и наглядное определение, позволяющее приближенно судить о степени расширения спектра.
2. W2— эффективная ширина полосы. Это определение ширины полосы частот аналогично определению эквивалентной шумовой полосы частот линейной системы и позволяет более точно судить о степени расширения спектра. По существу она равна основанию прямоугольника, равновеликого фигуре, образованной спектральной функцией и осью частот. В ней содержится вся мощность сигнала.
3. W3— ширина полосы по первым нулям спектра. Это определение ширины полосы частот является наиболее простым и широко распространенным. Оно исходит из предположения, что в пре- делах основного лепестка спектра сосредоточена значительная часть мощности сигнала. Поэтому она является достаточно грубой оценкой степени расширения спектра.
4. W4 — ширина полосы частот по доле мощности, содержащейся в ее пределах. При таком определении ширины полосы предполагается, что внутри полосы сосредоточена часть мощности сигнала, равная (1 — c), а за ее пределами только к.
5. W5-ширина полосы частот по выбранному уровню спектральной плотности. Подобное определение ширины полосы частот означает, что за ее пределами уровень спектральной плотности гарантированно будет ниже заданного и измеренного относительно максимального. Обычно заданные значения уровней спектральной плотности выбираются в пределах от — 35 до — 50 дБ.
Следует подчеркнуть, что целесообразность использования того или иного определения ширины полосы частот в значительной мере определяется спецификой решаемой задачи. В дальнейшем при сравнении различных видов модуляции будет использоваться определение ширины полосы частот по первым нулям спектральной функции.
В качестве показателя достоверности передачи дискретных сообщений при использовании М-позиционных видов модуляции можно принять вероятность ошибки при демодуляции М-ичного символа PE. Однако этот показатель не позволяет адекватно сравнивать различные виды модуляции при возможных вариантах выбора объема алфавита М. Поскольку потребителя обычно интересует достоверность передачи сообщения в виде последовательности двоичных символов, то в этой ситуации логичнее будет использование в качестве показателя достоверности передачи вероятность ошибки на бит Таким образом, выбор конкретного вида многопозиционной модуляции должен базироваться на трех параметрах: Тот или иной выбор вида многопозиционной модуляции направлен на достижение следующих основных целей:
• минимизацию вероятности ошибки на бит;
• минимизацию требуемого энергетического потенциала;
• максимизацию спектральной эффективности;
• минимизацию сложности аппаратуры формирования и обработки сигналов.
Интуитивно ясно, что сформулированные цели являются взаимо противоречивыми. Поэтому выбор конкретного вида многопозиционной модуляции предполагает компромиссное решение относительно значений указанных параметров. Для того чтобы не ошибиться в подобном выборе, необходимо знать свойства основных видов многопозиционной модуляции, выражаемые в терминах.
Амплитудная модуляция(ASK)
При амплитудной модуляции в соответствии с символами передаваемого сообщения изменяется амплитуда передаваемого сигнала, поэтому АМ сигнал можно записать в следующем виде:

случайные величины, принимающие значения из множества, элементы которого
![]()
М=2 — количество возможных двоичных последовательностей, создаваемых источником дискретных сообщений, длительностью и единичной энергией.
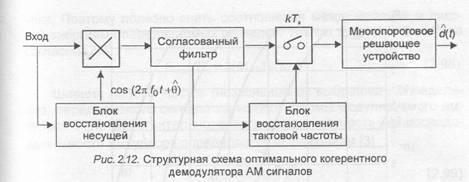
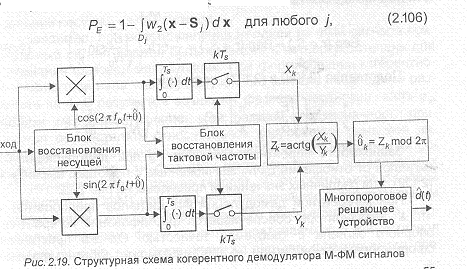
На рис.2.11 дана геометрическая иллюстрация формируемого ансамбля АМ сигналов для М=4, М=8, d=2. На рис.2.12 приведена структурная схема оптимального (в смысле минимальной средней вероятности ошибки при демодуляции) символа (элемента) сообщения когерентного демодулятора AM сигналов. Она содержит когерентный (синхронный) детектор, согласованный фильтр, дискретизатор, многопороговое решающее устройство. В многопороговом решающем устройстве производится сравнение текущего отсчета выходной сигнала согласованного фильтра с возможными значениями, соответствующими переданным символам, и выносится решение в пользу ближайшего. В демодулятор включены два вспомогательных элемента: блоки восстановления несущей и тактовой частоты. Первый служит для формирования опорного напряжения для когерентного (синхронного) детектора, второй — для формирования последовательности импульсов с частотой следования символов, моменты появления которых должны совпадать с моментами достижения максимального значения выходными сигналами согласованного фильтра, т.е. тактовыми моментами времени .

Вероятность ошибки при когерентной демодуляции AM сигналов определяется следующим выражением [2]:
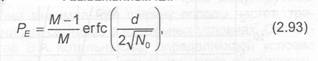
где
![]()
— функция ошибок, d-расстояние между соседними сигнальными точками.
Для того чтобы выразить PE через Е, определим среднюю энергию сигналов ансамбля:
![]()
Так как Е,=Е, log, М, то согласно (2.93) и (2.95) получим
![]()
Зависимости PE от Е,/И, при различных значениях М приведены на рис.2.13. Из них следует, что при увеличении М значения Е,/И,, требуемые для обеспечения заданной вероятности ошибки, возрастают. Так, при переходе от М=2 к М=4 оно возрастает при- мерно на 4 дБ, а при очень больших М его увеличение вдвое при- водит к возрастанию Е,/И, почти на 6 дБ.
Как было отмечено ранее, гораздо больший интерес представляет вероятность. Соотношение между этими вероятностями, вообще говоря, зависит от правила отображения последовательностей двоичных символов в М-ичные символы сообщения, и в общем виде его привести не представляется возможным. Поэтому приведем простые граничные соотношения, учитывающие тот факт, что ошибка в М-ичном символе может привести по крайней мере к одной или log М ошибкам в двоичных символах:
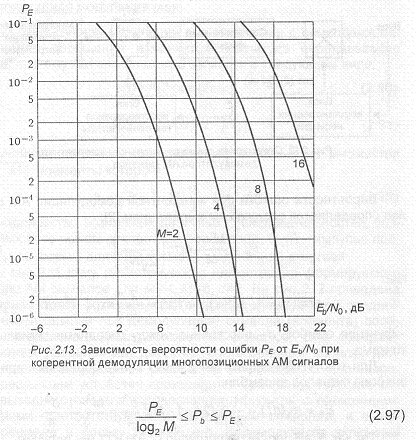
Наиболее часто на практике отображение последовательностей двоичных символов в М-ичные производят в соответствии с кодом Грея. В этом случае соседние сигнальные точки отображают двоичные последовательности, различающиеся только одним символом.
Зависимости, приведенные на рис.2.13, соответствуют именно этому правилу отображения. При больших значениях , весьма вероятно, что ошибки при демодуляции вызваны решения- ми в пользу сигнальных точек, расположенных по соседству с истинной точкой. Поэтому при отображении кодом Грея ошибки при демодуляции М-ичных символов будут с большой вероятностью вызывать одиночные ошибки в отображаемых последовательностях двоичных символов. Следовательно, вероятность ошибки на бит будет удовлетворять нижней границе (2.97).
Для АМ сигналов средняя энергия передаваемых сигналов отличается от пиковой (максимальной) которой обладает сигнал с максимальным уровнем (амплитудой). В некоторых реальных ситуациях вводится ограничение на пиковую мощность передатчика. Поэтому полезно знать соотношение между средней и пико- вой энергиями передаваемых сигналов. Так как
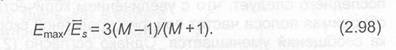
Ширина полосы частот (независимо от выбранного определения передаваемого сигнала зависит от формы модулируемого импульса ,(Ц. Действительно, спектральная плотность АМ последовательности импульсов определяется выражением [3]

где F>(f) — преобразование Фурье U~(t). Оставляя в стороне вопрос о выборе формы модулируемых импульсов, определим минимальную ширину полосы частот, требуемую для передачи АМ сигналов в идеальных условиях. Согласно теореме отсчетов В.А. Котельникова, определяющей условия восстановления сигнала, заданного отсчетами через фиксированные интервалы времени 7, и ограниченного по полосе И/, необходимая минимальная полоса частот идеального канала связи равна 1/(27). Хотя форма модулируемых импульсов при такой интерпретации имеет вид и соответствует функциям, не ограниченным временным интервалом она гарантирует отсутствие межсимвольной интерференции.
При передаче по полосовому каналу это же значение минимальной полосы может быть сохранено за счет использования однополосной (ОБП) либо квадратурной амплитудной модуляции (КАМ), когда исходная последовательность АМ импульсов разделяется на две последовательности и каждая из них передается с помощью одной из двух квадратурных несущих. Поэтому спектральная эффективность АМ модуляции будет определяться следующим выражением:
![]()
Однако на практике тяжело реализовать такую спектральную эффективность в силу определенных трудностей при формировании сигналов с минимальной полосой. Если UT(t) представляет собой импульс прямоугольной формы, то ширина полосы по первым нулям спектра будет равна 1/7,. Поэтому значения спектральной эффективности АМ модуляции, достигаемой в реальных системах. заключены в пределах
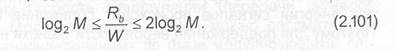
Сделаем несколько замечаний, касающихся рассматриваемо- го вида модуляции, на основании выражений (2.96) и (2.101). Из последнего следует, что с увеличением количества уровней М необходимая полоса частот при фиксированной скорости, источника сообщений уменьшается. Однако согласно (2.96) это увеличение спектральной эффективности достигается за счет увеличения удельных энергетических затрат, требуемых для обеспечения требуемой достоверности передачи.
В заключение отметим, что при демодуляции многопозиционных АМ сигналов можно использовать и некогерентный демодулятор. В этом случае блок восстановления несущей при обеспечении достаточной стабильности частот может быть исключен, согласованный фильтр должен быть настроен на промежуточную частоту, а на его выходе должен быть включен детектор огибающей.
ФАЗОВАЯ МОДУЛЯЦИЯ (PSK)
При фазовой модуляции в соответствии с символами передаваемого сообщения изменяется фаза гармонического колебания, поэтому передаваемый сигнал можно записать в следующем виде:
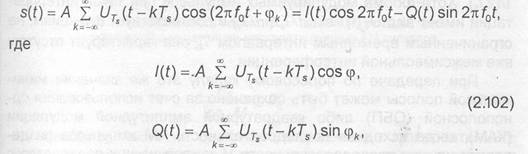
принимает значения из множества произвольная начальная фаза.
В результате передается последовательность сигналов конечной длительности Т, с постоянной огибающей и энергией
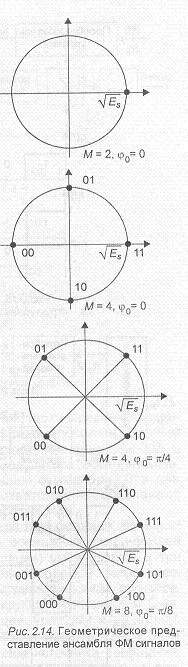
Геометрическая иллюстрация формируемого ансамбля ФМ сигналов изображена на рис.2.14. Здесь сигнальные точки лежат на окружности, радиус которой определяется энергией Е, сигналов. Можно заметить, что ФМ сигналы обладают некоторыми общими свойствами с АМ сигналами. Действительно, с увеличением M(M>2) размерность сигнального пространства не изменяется. А это означает, что с увеличением М возрастает спектральная эффективность. Но с другой стороны, с увеличением М при постоянной энергии сигналов происходит сближение сигнальных точек. Поэтому для поддержания вероятности ошибки на прежнем уровне приходится увеличивать энергию сигналов (увеличивать радиус окружности). Иначе говоря, здесь, как в случае АМ сигналов, увеличение спектральной эффективности достигается за счет снижения энергетической эффективности. Эти выводы, сделанные на основании геометрических представлений, в дальнейшем будут подтверждены аналитически.
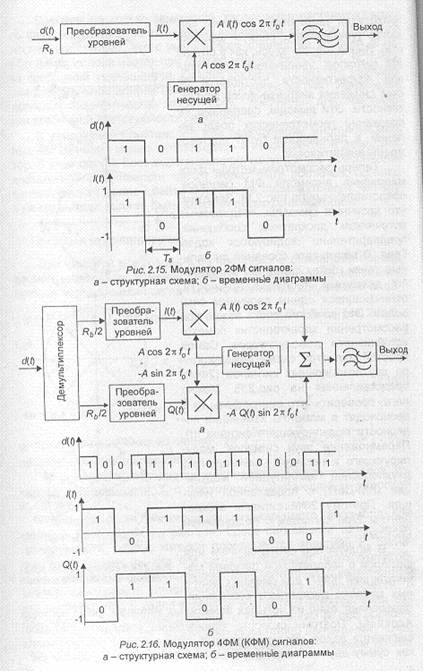
Теперь рассмотрим методы формирования ансамбля ФМ сигналов, представленных на рис.2.14. Заметим, что двоичные символы, создаваемые источником дискретных сообщений, предварительно кодируются кодом Грея. В результате соседние сигнальные точки (фазы сигналов) отображают двоичные последовательности, отличающиеся одним двоичным символом. Это свойство очень важно при рассмотрении характеристик помехоустойчивости демодуляторов. Самой простой является схема демодулятора двухпозиционных сигналов (2ФМ), представленная на рис.2.15. Можно легко проверить, что скачки фазы на и происходят в моменты изменения полярности модулирующего сигнала /(1). Перемножение двух сигналов: модулирующего и несущей — эквивалентно двухполосной амплитудной модуляции (АМ-ДБП) с подавленной несущей. Поэтому 2ФМ сигналы эквивалентны 2АМ сигналам с подавленной несущей.
В модуляторе сигналов 4ФМ или сигналов с квадратурной фазовой манипуляцией (КФМ) два смежных двоичных символа дискретного сообщения
определяют одно из четырех возможных значений фазы несущей Асов2л(ф Поэтому скорость манипуляции (передачи сигналов) снижается вдвое. Модулированный сигнал можно рассматривать как сумму двух манипулированных по фазе модулирующими сиг-
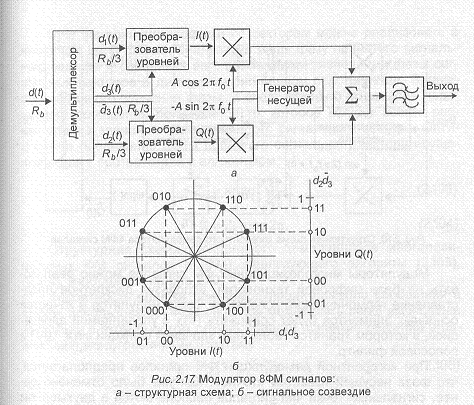
каналами /(t) и Q(t) гармонических колебаний, находящихся в квадратуре, т.е. отличающихся начальным фазовым сдвигом, равным .л/2. Схема модулятора 4ФМ сигналов приведена на рис.2.16 и представляет собой по существу два' модулятора 2ФМ сигналов, выходы которых объединены с помощью сумматора. Эти два квадратурных канала модулятора соответственно обозначают как /-канал (синфазный) и Q-канал (квадратурный).
В модуляторе 8ФМ сигналов группа из трех смежных двоичных символов определяет одну из восьми возможных фаз несущей Асоз2И,/. Скорость передачи (манипуляции) уменьшается в три раза. Схема модулятора, изображенная на рис.2.17, может рас- сматриваться как обобщение схемы модулятора 4ФМ сигналов. Четырехуровневые симметричные модулирующие сигналы /- и Q-каналов модулируют квадратурные несущие. Начальное значение фазы несущей выбрано равным. Каждый из трех смежных двоичных символов источника сообщений, разделяемых с помощью демультиплексора, используются следующим образом: первый определяет знак модулирующего сигнала в /-канале, второй — знак модулирующего сигнала в О- канале, третий — абсолютное значение уровня модулирующих сигналов в /- и О- каналах.
Модуляторы многопозиционных ФМ сигналов можно реализовать на базе цифровой технологии, используя дискретное представление гармонического колебания. Тогда модулятор в качестве основных элементов будет содержать ПЗУ с управляемой адресацией, в котором хранятся табличные значения функции sinx, ЦАП и полосовой фильтр.
При когерентной демодуляции ФМ сигналов предполагается, что фаза несущей известна «точно». Как уже было отмечено ранее, сигнальные точки ФМ сигналов располагаются в двухмерном сигнальном пространстве, поэтому при оптимальной когерентной демодуляции необходимо использовать только два согласованных фильтра для формирования достаточных статистик, с помощью которых выносятся решения относительно переданных символов сообщения.
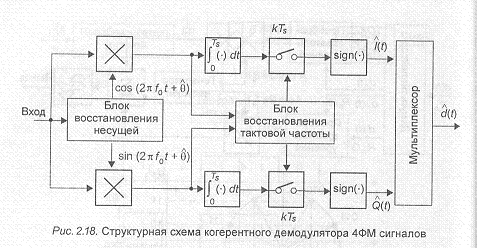
Структурная схема оптимального когерентного демодулятора 4ФМ сигналов (наиболее простого) изображена на рис.2.18. Демодулятор по существу представляет параллельное соединение 2-х когерентных демодуляторов 2ФМ сигналов, в которых решение относительно двоичных сигналов передаваемого сообщения выносятся независимо путем определения знака отсчетов квадратурных составляющих принимаемых сигналов. В общем случае решения относительно переданных символов сообщения на основе анализа отсчетов квадратурных составляющих принимаемых сигналов должны выноситься совместно. Вместо обычных знаковых компараторов необходимо использовать в каждом канале много пороговые решающие устройства и логическую схему, обеспечивающую однозначное восстановление исходных символов сообщения. С помощью этих элементов осуществляется разбиение двумерного сигнального пространства на. секторы шириной 2п/М и проверка на принадлежность принятого сигнального вектора тому или иному сектору.
Этот же принцип проверки по секторам можно реализовать в несколько иной форме, анализируя лишь фазу принятого сигналь- ного вектора и сравнивая ее с возможными значениями фазы сигнальных векторов в двумерном сигнальном пространстве. В качестве истинного значения фазы, а следовательно, и символа переданного сообщения принимается то, которое «ближе всего» расположено к значению фазы принятого сигнального вектора. Оптимальное оценивание фазы принятого сигнального вектора осуществляется в соответствии с алгоритмом

Структурная схема когерентного демодулятора многопозиционных ФМ сигналов (М-ФМ), реализующего алгоритм (2.103), (2.104), изображена на рис.2.19.
Вероятность ошибки при демодуляции символа сообщения в случае использования 4ФМ сигналов может быть легко вычислена,, поскольку в этом простом случае области принятия решения ограничены прямоугольниками. Поэтому

В общем случае вероятность ошибки при когерентной демодуляции М-ФМ сигналов с учетом симметрии сигнального созвездия определяется следующим выражением:

где О,— область принятия решения в пользу сигнала S;, изображенная на рис.2.20. Она представляет собой круговой сектор шириной 2н/М, внутри которого лежит сигнальная точка, соответствующая.
Можно получить выражения для точных верхней и нижней границ для вероятности ошибки с помощью геометрических представлений, изображенных на рис.2.21.
Вероятность того, что вектор r принятого сигнала окажется за пределами области D соответствующей сигналу S лежит в пределах
![]()
Вектор принятого сигнала r окажется в пределах полуплоскостей SД и S, тогда и только тогда, когда составляющая вектора шума, ортогональная разграничительной линии, будет больше расстояния между S и границей т.е. . Поэтому
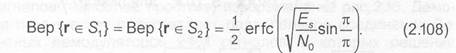
Подставляя (2.108) в (2.107), получаем
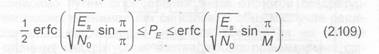
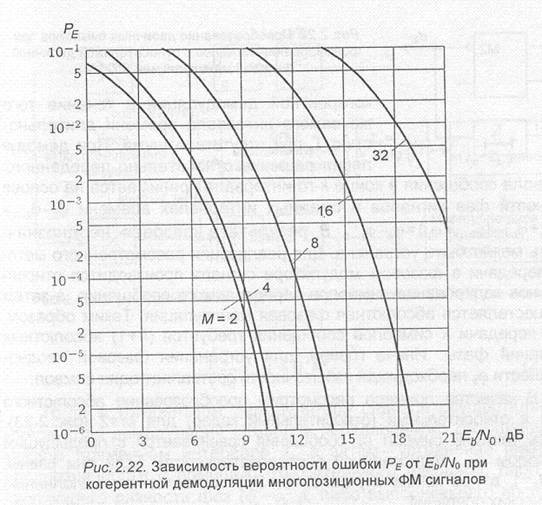
Зависимость вероятности ошибки PE при демодуляции ФМ сигналов от отношения вычисленные с помощью выражения (2.109), для различных значений М приведены на рис.2.22.
При когерентной демодуляции ФМ сигналов предполагается, что в демодуляторе обеспечивается формирование когерентного опорного сигнала с требуемой точностью. Однако практически сформировать такой сигнал не всегда возможно. Обычно фазовая
56 .
ошибка содержит две составляющие, обусловленные особенностями работы блока восстановления несущей из принимаемого сигнала: одна вызвана воздействием шума и представляет собой случайный процесс ,(0 другая — детерминированная составляющая и определяется возможной неоднозначностью при восстановлении несущей из ФМ сигнала.
Например, при восстановлении несущей из 4ФМ сигнала принимаемый сигнал должен быть возведен в четвертую степень для устранения фазовой манипуляции. При формировании когерентно- го опорного сигнала частоту полученного сигнала необходимо разделить на 4. В результате возникает фазовая неоднозначность кратная л/4. Для устранения этой фазовой неоднозначности приходится осуществлять относительное кодирование символов передаваемого сообщения так, чтобы необходимая информация содержалась в разности фаз двух последовательно передаваемых ФМ сигналов. В этом случае говорят об относительной фазовой манипуляции ОФМ) или фазовой манипуляции с относительным кодированием символов передаваемого сообщения. Пусть абсолютное значение фазы сигнала, передаваемого в интервал времени, и фаза опорного сигнала, формируемого для
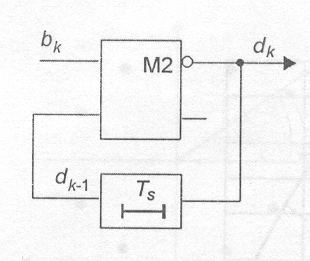
Рис. 2.23. Преобразование двоичных символов при формировании сигналов с относительной двоичной фазовой манипуляцией (20ФМ)
когерентной демодуляции в течение того же самого интервала времени длительностью Т, при отсутствии шума. При демодуляции решение относительно переданного
символа сообщения в конце интервала принимается на основе разности фаз сигналов в смежных интервалах времени. В результате фазовая неоднозначность может быть устранена. Для реализации рассмотренного метода передачи в фазовом модуляторе сигнала производится относительное кодирование символов передаваемого сообщения, а затем осуществляется абсолютная фазовая манипуляция. Таким образом, для передачи k символов сообщения требуется (k+1) абсолютных значений фазы. Иначе говоря, для устранения фазовой неоднозначности у необходимая избыточность составляет один символ.
В качестве примера рассмотрим преобразование абсолютного кода в относительный (относительный кодер) для М=2 (рис.2.23). Здесь текущий символ Ь„сообщения сравнивается с предыдущим символом кодированной последовательности. Если они равны, то в противном случае d»=0. Это соответствует выполнению логических операций
![]()
Здесь символ 9 означает сложение по mod 2, а черта сверху— логическую операцию дополнения.
В случае М=4 относительное кодирование осуществляется с помощью более сложного алгоритма. Исходная последовательность двоичных символов разделяется на две последовательности которые кодируются в последовательности с помощью логических функций (рис.2.24):
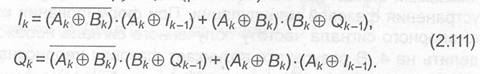
Предположим, что при когерентной демодуляции опорный сигнал, формируемый в блоке восстановления несущей когерентного демодулятора, имеет фазовую неоднозначность, т.е. принимает значения из множества
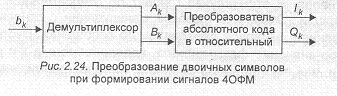
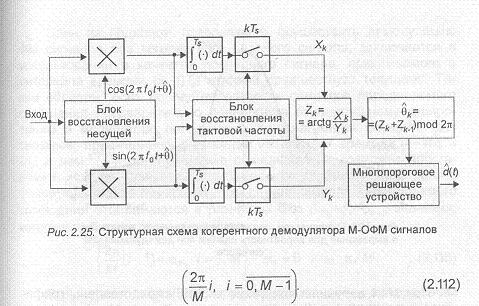
Тогда в когерентном демодуляторе сначала осуществляется демодуляция символов передаваемого сообщения на каждом временном интервале TД а затем — устранение фазовой неоднозначности с помощью относительного декодера, либо вычисляющего разность фаз либо выполняющего последовательность логических операций над двоичными символами. Структурная схема когерентного демодулятора сигналов с относительной фазовой модуляцией (М-ОФМ) изображена на рис.2.25. В случае М=2 оценки символов переданного сообщения могут быть восстановлены из оценок относительно кодированных символов с помощью следующей логической функции:
![]()
В случае М=4 логическая функция имеет следующий вид:
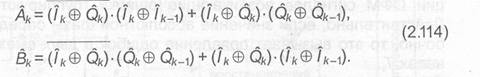
Вероятность ошибки при демодуляции М-ичного символа для ОФМ сигналов может быть вычислена по формуле
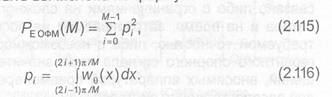
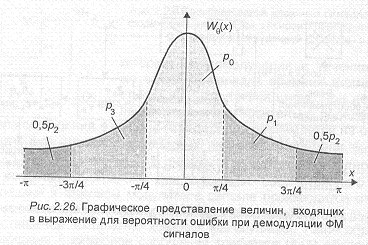
При М=4 величины, входящие в (2.115), представлены графически на рис.2.26.
Если учесть, что при когерентной демодуляции 2ФМ сигналов вероятность ошибки
то выражение для можно представить в следующем виде:
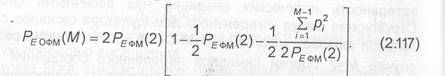
Из (2.117) следует, что при низких значениях вероятности относительное кодирование приводит, грубо говоря, к увеличению вероятности ошибки по отношению к вероятности ошибки при когерентной демодуляции вдвое. Это является платой за возможность устранения фазовой неоднозначности. Кроме того, при демодуляции ОФМ сигналов возникающие ошибки группируются в пары. Действительно, если значение абсолютной фазы определено ошибочно, то это вызывает появление ошибок в двух смежных интервалах Т,.
Иногда на практике возникает необходимость в демодуляции ФМ сигналов без когерентного опорного сигнала. Это прежде всего связано либо с ограничениями на сложность реализации демодулятора и на время, затрачиваемое на восстановление несущей с требуемой точностью, либо с невозможностью формирования когерентного опорного сигнала из-за значительных фазовых возмущений, вносимых аппаратурой приемопередающего тракта и средой распространения сигналов.
Один из подходов, позволяющих осуществить демодуляцию ФМ сигналов без когерентного опорного сигнала, заключается в использовании в качестве последнего сигнала, принимаемого в интервале времени (k — 1) который предшествует текущему. Таким образом, если последовательность символов передаваемого сообщения предварительно подвергнута относительному кодированию в модуляторе передатчика, то, анализируя разность фаз сигналов, принимаемых в смежных интервалах времени (k — 1)Т, и демодуляторе приемника принципиально возможно восстановить исходные символы передаваемого сообщения и устранить фазовую неоднозначность. В этом случае символы передаваемого сообщения отображаются в разностях фаз, значения, которых выбираются из множества
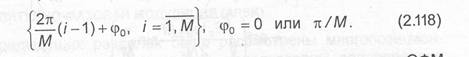
Структурная схема автокорреляционного демодулятора ОФМ сигналов для М=4 изображена на рис.2.27. Здесь фазовая неоднозначность д, может быть устранена, если она остается постоянной по крайней мере на протяжении двух смежных интервалов времени Т,. Эта схема реализует оптимальный по критерию максимального правдоподобия алгоритм оценивания разности фаз принимаемых сигналов на протяжении двух смежных интервалов времени Т,[5].
Традиционный метод вычисления вероятности ошибки при некогерентной демодуляции М-ОФМ сигналов заключается в нахождении функции плотности вероятности разности фаз принимаемых сигналов. Однако он, к сожалению, приводит к результатам, которые не могут быть представлены в компактной форме. Поэтому приведем выражение для верхней границы вероятности ошибки:
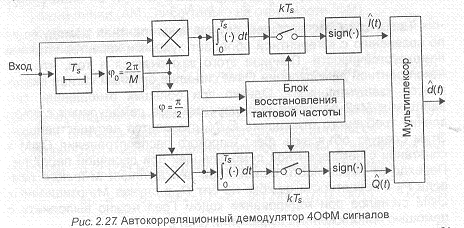

Сравнивая (2.120) с (2.109), можно заключить, что переход от когерентной демодуляции ОФМ сигналов к некогерентной сопровождается энергетическими потерями, асимптотическое значение которых составляет 3 дБ.
В частном случае М=2 неравенство обращается в равенство и вероятность ошибки при некогерентной демодуляции ОФМ сигналов определяется выражением
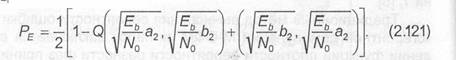
Но поскольку а,=2, Ь,=О, то с учетом того, что получаем следующий результат:

Таким образом, в общем случае некогерентная демодуляция по сравнению с когерентной обладает худшими характеристиками помехоустойчивости. Причина этого заключается в том, что при некогерентной демодуляции ОФМ сигналов опорный сигнал оказывается «зашумленным». Однако при больших отношениях сигнал/шум и различие этих двух методов демодуляции с точки зрения требуемого отношения, становится несущественным. Этим следует объяснить факт широкого распространения ОФМ в сочетании с некогерентной демодуляцией при двоичной передаче. Переход от вероятности ошибки при демодуляции М-ичного символа PE к вероятности ошибки на бит в случае М-позиционных ОФМ сигналов при кодировании кодом Грея можно выполнить с помощью приближенных выражений (2.97).
Минимально необходимая полоса частот при передаче сигналов с многопозиционной фазовой манипуляцией равна 1/Т,. Поэтому максимальное значение удельной скорости передачи, характеризующей спектральную эффективность многопозиционной фазовой манипуляции, равна
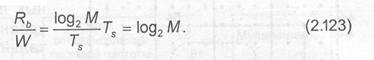
Из (2.123) следует, что с увеличением кратности манипуляции (числа позиций) спектральная эффективность возрастает. Однако за это приходится расплачиваться увеличением удельных энергетических затрат необходимых для обеспечения требуемого значения.
АМПЛИТУДНО-ФАЗОВАЯ МОДУЛЯЦИЯ (APSK)
В предыдущих разделах были рассмотрены многопозиционные АМ и ФМ, которые могут быть использованы для передачи битов информации с помощью одного сигнала. Оба вида модуляции позволяют обеспечить увеличение спектральной эффективности пропорционально log>M. Следует также отметить, что при больших значениях М за увеличение объема передаваемого сообщения на 1 бит при заданной вероятности ошибки PE приходится расплачиваться увеличением на 6 дБ требуемого отношения сигнал/шум. Лучшие результаты при том же самом значении спектральной эффективности можно получить, если для передачи сим- волов сообщения модулировать сразу два параметра: амплитуду и фазу. В этом случае сигнальные точки будут размещаться в двумерном сигнальном пространстве более рационально, поэтому увеличение спектральной эффективности не будет сопровождаться резким уменьшением минимального расстояния. Здесь снято ограничение на то, чтобы сигнальные точки располагались только на прямой линии (АМ), либо только на окружности (ФМ).
В общем виде сигнал с амплитудное фазовой модуляцией может быть представлен как
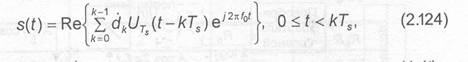
комплексные случайные величины, функция, описывающая форму модулируемых импульсов.
Если U>,(t) — импульс прямоугольной формы с единичной амплитудой, то (2.124) можно представить в следующем виде:


Из (2.125) следует, что передаваемый сигнал со- стоит из двух квадратурных несущих, модулированных по амплитуде много- уровневыми последовательностями импульсов. Такой вид модуляции принято называть комбинированной амплитудно-фазовой модуляцией (АМ-ФМ). Геометрически сигналы с этим видом модуляции могут быть представлены в виде двумерного сигнального созвездия точек в двумерном пространстве сигналов.
Следует подчеркнуть, что энергетический выигрыш, обеспечиваемый
АМ-ФМ сигналами по сравнению с ФМ сигналами возрастает с увеличением М. Поэтому было затрачено много усилий, направленных на поиски наилучших конфигураций сигнальных созвездий. Однако с точки зрения простоты технической реализации устройств модуляции и демодуляции наибольшей интерес представляют сигнальные созвездия прямоугольной конфигурации, изображенные на рис.2.28. Они образуются путем сложения двух квадратурных несущих, модулированных по амплитуде многоуровневыми последовательностями импульсов. Структурная схема модулятора сигналов с квадратурной амплитудной модуляцией (КАМ) изображена на рис.2.29, а структурная схема когерентного демодулятора — на рис.2.30. Здесь переданные символы сообщения восстанавливаются
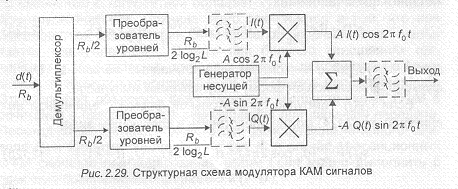
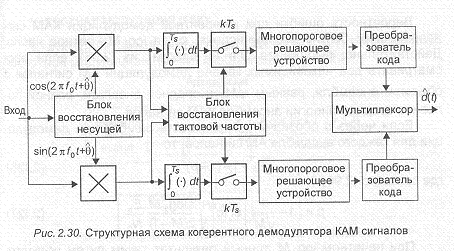
путем независимого сравнения выделенных квадратурных составляющих принимаемого сигнала с порогами в двух многопороговых решающих устройствах. Если log, М является четным числом, то структура демодулятора оптимальна в смысле критерия максимального правдоподобия. При нечетном количестве битов, приходящихся на символ сообщения, сигнальные созвездия пересекаются и их сигнальные точки могут принадлежать одной и той же прямоугольной сетке. Исключение составляет случай М=8.
Если сигнальные точки созвездий выбраны так, что минимальное расстояние между любой парой точек равно двум, то среднее значение энергии ансамбля сигналов различного объема приведены в табл.2.1. Здесь можно заметить, что каждый дополнительный бит информации требует увеличения средней энергии примерно на 3дБ для сохранения минимального расстояния неизменным.
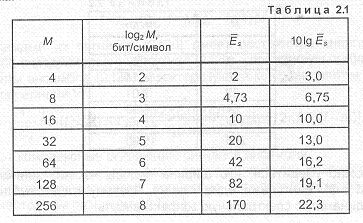
Вероятность ошибки при когерентной демодуляции КАМ сигналов может быть легко вычислена, когда четное число. Действительно, выражение для PE следует из (2.96), если рассматривать два независимых канала демодуляции АМ сигналов с объемом ансамбля, равным , и средней энергией, равной половине средней энергии ансамбля КАМ сигналов.
Если через р обозначить вероятность ошибки при демодуляции для каждого ансамбля АМ сигналов, то
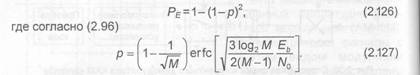
При нечетном log>M, точный результат таким путем получить не удается, поэтому приведем выражение для верхней границы вероятности ошибки:
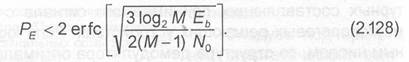
Интересно сравнить ансамбли ФМ и АМ-ФМ сигналов с точки зрения энергетических затрат. Чтобы минимальное расстояние между сигнальными точками было равно двум, как для сигнального созвездия, изображенного на рис.2.28, необходимая энергия ФМ сигналов должна быть равна. Согласно (2.41) тот же самый результат может быть получен с помощью ансамбля АМ-ФМ сигналов, если среднюю энергию ансамбля с ростом М увеличивать пропорционально 2(М-1)/3. В табл.2.2 приведены значения энергетического выигрыша (ЭВ), обеспечиваемого ансамблем АМ-ФМ сигналов по отношению к ансамблю ФМ сигналов, для различных значений М.
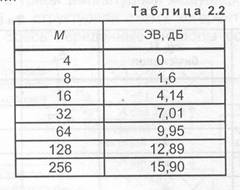
Можно убедиться, что ширина полосы частот, занимаемая АМ-ФМ и ФМ сигналами, одна и та же. Поэтому эти ансамбли имеют и одинаковую спектральную эффективность.
ЧАСТОТНАЯ МОДУЛЯЦИЯ (FSK)
Структурная схема модулятора сигналов с многопозиционной частотной модуляцией (М-ЧМ) изображена на рис.2.31.
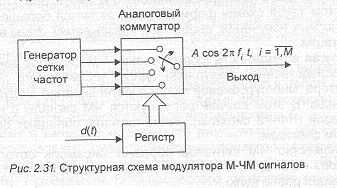
Здесь последовательность двоичных символов источника со- общений отображается в сдвиг частоты несущей сигнала. Последовательность, содержащая k таких сигналов, может быть представлена в следующем виде:
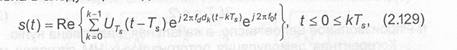
где случайная многоуровневая последовательность символов сообщения, принимающая значения из множества расстояние между соседними частотными позициями, функция, описывающая форму модулирующего импульса. Если От имеет постоянные амплитуду А и длительность Т то на интервале времени Т, реализации передаваемого сигнала могут быть записаны как
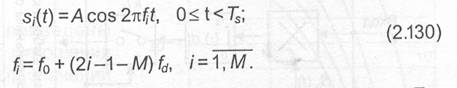
Каждый из сигналов (2.130) имеет постоянную энергию Е,= =А Т/2, а модулированный сигнал (2.129) — постоянную огибающую. Сигналы ансамбля (2.130) характеризуются коэффициентом взаимной корреляции
![]()
— комплексные огибающие сигналов ансамбля.
Таким образом, при фиксированной энергии евклидово расстояние между сигналами полностью определяется нормированным частотным разносом.
Как показано на рис.2.31, для формирования ЧМ сигналов может быть использован набор из М генераторов гармонических сигналов, настроенных на соответствующие частоты и подключаемых к выходу схемы с помощью аналогового коммутатора. Главным не- достатком такой схемы формирования является большой уровень внеполосных излучений, вызванных «разрывами» фазы в моменты коммутации.
Другая возможность формирования ЧМ сигналов заключается в непосредственной модуляции одного управляемого по частоте генератора многоуровневой последовательностью модулирующих импульсов. В этом случае формируются ЧМ сигналы с непрерывной фазой (НФЧМ сигналы). Такие сигналы обладают более компактным спектром.
Множество ЧМ сигналов образует ансамбль ортогональных сигналов, если действительная часть коэффициентов взаимной корреляции равна нулю
![]()
Это условие выполняется, если частотный разнос между соседними сигналами удовлетворяет соотношению
![]()
— произвольное целое число, а начальная фаза равна нулю.
Когерентная демодуляция ортогональных ЧМ сигналов может быть осуществлена с помощью многоканального корреляционного демодулятора. структурная схема которого изображена на рис.2.32.

Этот демодулятор является оптимальным в смысле критерия максимального правдоподобия. Каждый канал демодулятора представляет собой последовательное соединение перемножителя, осуществляющего перемножение входного сигнала на гармонический опорный сигнал s;(t)=Acos2xrft соответствующей частоты, и интегратор со сбросом, выполняющий интегрирование произведения в течение интервала времени Т,.
Фактически каждый канал представляет собой вычислитель коэффициента Фурье, а когерентный демодулятор в целом при выполнении условия (2.47) — анализатор Фурье, производящий Фурье- анализ реализаций входного сигнала длительностью Т,.
Поэтому в качестве когерентного демодулятора ЧМ сигналов южно использовать цифровой Фурье-процессор, реализующий один из алгоритмов быстрого преобразования Фурье (БПФ-процессор) [6]. Применение БПФ-процессора позволяет отчасти решить проблему сложности реализации многоканального когерентного демодулятора ортогональных ЧМ сигналов.
Выражение для вероятности ошибки при когерентной демодуляции ортогональных ЧМ сигналов в замкнутой форме получить не удается, поэтому приведем выражения для верхней и нижней границ [8]:
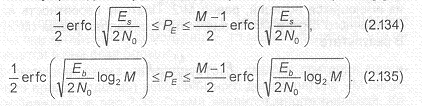
Заметим, что при М=2 верхняя и нижняя границы со- впадают и соответствуют точному результату.
На рис.2.33 приведены зависимости PE от отношения Е,IN, для различных значений М=2, полученные путем численного интегрирования [9]; на рис.2.34 — аналогичные зависимости, показывающие степень приближения граничных оценок вероятности PE к точным результатам. Из представленных кривых следует, что с увеличением М наблюдается увеличение вероятности ошибки при одних и тех же энергетических затратах.
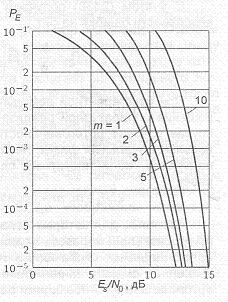
Puc.2.33. Зависимость вероятности ошибки PE от при когерентной демодуляции М-позиционных ЧМ сигналов
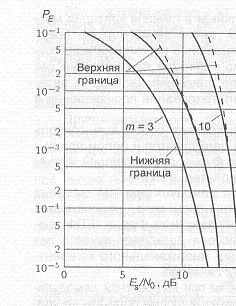
Puc.2.34. Зависимость вероятности ошибки PE от Е,/Ио при когерентной демодуляции М-позиционных ЧМ сигналов.
Для ансамбля ортогональных ЧМ сигналов может быть легко установлено соотношение между вероятностями PE и Р>. Действительно, для ортогональных сигналов ошибочная демодуляция М-ичного символа с равной вероятностью приводит к его трансформации в любой из (М — 1) оставшихся сим-
волов. Количество символов, содержащих ошибочный бит в любой из имеющихся позиций, равно М/2. Поэтому вероятность наличия ошибочного бита в (М — 1) ошибочных символах равна (/И/2)(М-1). В результате

С учетом (2.138) получаем выражение для верхней границы вероятности ошибки на бит:
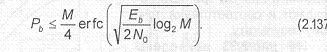
При некогерентной демодуляции ЧМ сигналов достигается упрощение аппаратурной реализации демодулятора. Однако в этом случае условие ортогональности должно выполняться при произвольных начальных фазах. Легко убедиться, что условие (2.131) выполняется, если частотный сдвиг между соседними сигналами равен
![]()
Сигналы, для которых условие ортогональности выполняется при произвольных фазовых сдвигах, называются также сигналами ( ортогональными огибающими или сигналами, ортогональными Е усиленном смысле. Минимальный частотный сдвиг для сигналов ( ортогональными огибающими равен
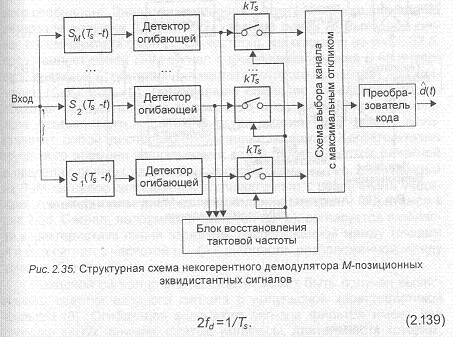
Если сравнивать это значение с минимальным частотным сдвигом при когерентной демодуляции, то можно убедиться, что он оказывается в два раза больше.
Структурная схема оптимального (в смысле критерия максимального правдоподобия) некогерентного демодулятора ЧМ сигналов изображена на рис.2.35. Схема является многоканальной. Каждый канал содержит полосовой согласованный фильтр, настроенный на соответствующую частоту, и детектор огибающей. Отсчеты огибающих в оптимальные моменты времени сравниваются между собой, и решение выносится в пользу того канала, на выходе которого огибающая в моменты отсчета достигает максимального значения. Некогерентный демодулятор ЧМ сигналов может быть также построен на базе цифрового Фурье-процессора или процессора использующего двойное ЛЧМ-преобразование [6,7].
Для пояснения основной идеи двойного ЛЧМ-преобразования воспользуемся случаем 2ЧМ. На рис.2.36 представлена структурная схема некогерентного демодулятора 2ЧМ сигналов с двойным ЛЧМ-преобразованием, а на рис.2.37 — временные диаграммы со- ответствующих сигналов. На рис.2.37,а изображены изменения частоты входного сигнала, происходящие в соответствии с символами передаваемого сообщения. Входной сигнал поступает на сигнальный вход перемножителя, а на опорный вход подается опорный сигнал с периодическим изменением частоты по линейному закону, синхронизированный по времени с символами передаваемого
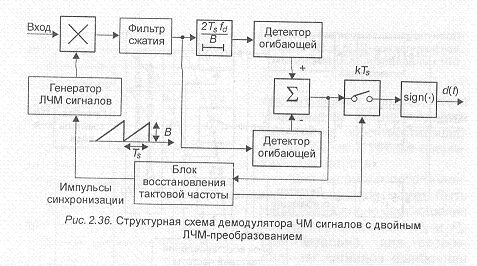
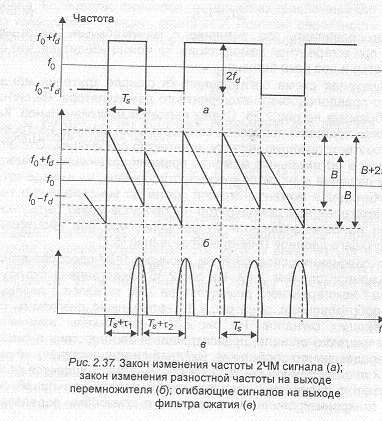
сообщения. Диапазон изменения частоты опорного сигнала на интервале времени Т, (диапазон качания) равен В. Выходной сиг- нал перемножителя (разностной частоты), как показано на рис.2.37, б, представляет собой ЛЧМ сигнал с диапазоном качания В на интервале времени Т центральная частота которого принимает два значения. Демодуляция символов передаваемого сообщения осуществляется с помощью второго ЛЧМ- преобразователя, реализуемого в форме фильтра сжатия. Этот фильтр представляет собой дисперсионную линию задержки. Характеристика группового времени запаздывания такой линии является линейной в пределах полосы частот В,21 и изображена на рис.2.38. Каждый из ЛЧМ сигналов оказывается согласованным с различными участками характеристики дисперсионной линии задержки. Обратимся к рис.2.38. Сигнал, например, с частотой согласуется в области характеристики линии задержки, расположенной между точками А и В, а сигнал с частотой (f,— f<) — в области, расположенной между точками С и О.
Выходной сигнал фильтра сжатия может быть получен вычислением свертки входного сигнала с импульсной характеристикой фильтра [8]. Огибающая выходного сигнала фильтра имеет вид функции sinx/x, причем, сжатые импульсы, длительность которых, измеренная по первым нулям, равна 2ЛТ, оказываются смещенными во времени на величину ЛТ. Иначе говоря, импульсы, соответствующие различным символам передаваемого сообщения появляются в различные моменты времени причем в указанные моменты присутствует лишь один импульс, определяемый значением символа передаваемого сообщения. На рис.2.37,в при- ведены огибающие основного лепестка сжатых импульсов, а также отмечено их временное положение. Решение относительно значения символа переданного сообщения выносятся в результате сравнения
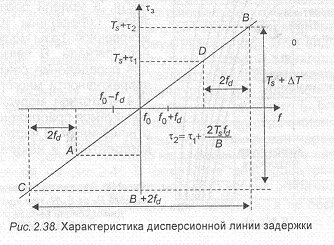
отсчетов огибающих в оптимальные моменты времени. Дополнительная линия задержки служит для приведения временного положения импульсов к одному и тому же моменту сравнения. Блок восстановления тактовой частоты необходим для формирования сигнала, определяющего моменты сравнения.
Описанный принцип можно распространить также на случай демодуляции М-позиционных ЧМ сигналов.
Вероятность ошибки при некогерентной демодуляции ЧМ сигналов определяется выражениями [8]:
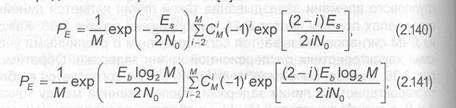
где CM' — биномиальные коэффициенты. Зависимости вероятности ошибки PE от отношения Е,IИ,, со- ответствующие выражению (2.140), приведены на рис.2.39. На рис.2.39 для сравнения приведены также кривые, соответствующие случаю когерентной модуляции ЧМ сигналов. Сравнив зависимости, можно заключить, что характеристики помехоустойчивости при некогерентной демодуляции оказываются несколько хуже, чем при когерентной. С увеличением М это различие становится менее заметным.
Вычисление спектральной плотности ЧМ сигналов представляет, вообще говоря, не простую задачу. Основная проблема COC-

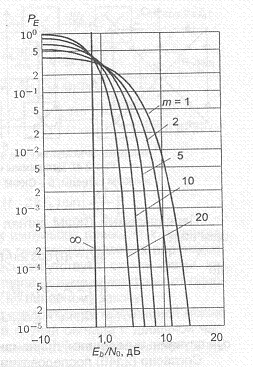
ортогональных ЧМ сигналов будем считать, что каждый сигнал занимает соответственно полосу 1/(2Т,) и 1/Т,. Поэтому имеем для когерентных сигналов

что при увеличении М спектральная эффективность частотной модуляции уменьшается. Учитывая поведение характеристик помехоустойчивости при увеличении М, приведенных
на рис.2.40, можно заключить, что свойства ЧМ сигналов противоположны свойствам АМ и ФМ сигналов. Действительно, при увеличении М для ЧМ сигналов требуемое значение EД/N, для обеспечения заданной вероятности P, уменьшается, но это уменьшение сопровождается снижением спектральной эффективности.
КВАДРАТУРНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ СО СДВИГОМ (OQPSK)
Уменьшить изменения огибающей сигнала с квадратурной фазовой модуляцией, вызванные ограничением полосы, можно введением задержки модулирующего сигнала в квадратурном (Q) канале по отношению к синфазному (/) каналу. Этот вид модуляции получил название квадратурной фазовой манипуляции со сдвигом (СКФМ) или офсетной квадратурной фазовой манипуляции (ОФКФМ), поскольку здесь квадратурные составляющие модулирующего сигнала смещены во времени на величину. Благодаря этому исключаются изменения фазы на сохраняются изменения фазы, причем, эти изменения происходят через каждые секунд. Это условно показано на диаграмме фазовых переходов, изображенной на рис.2.41. В результате для «фильтрованного» СКФМ сигнала отношение максимального уровня огибающей к минимальному оказывается равным примерно а не бесконечности, как у КФМ сигнала.
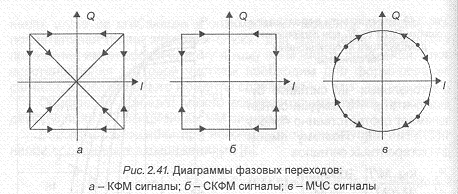
Передаваемый СКФМ сигнал может быть записан в следующем виде:
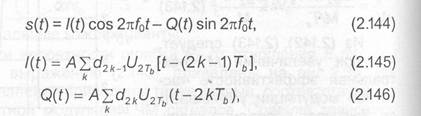
d,— случайные величины, принимающие значения ( — 1, +1). Согласно (2.146) последовательность символов передаваемого сообщения разделяется на две последовательности, содержащие нечетные , и четные б,» символы. Эти символы определяют полярность модулирующих сигналов в нечетные и четные 2kTg<t<(2k+2)Tg временные интервалы. В данном случае форма модулирующих сигналов определяется идеальным прямо- угольным импульсом длительности 2Т>. Когерентный демодулятор СКФМ сигналов аналогичен демодулятору КФМ сигналов, изображенному на рис.2.18, за исключением дополнительной линии задержки на Т введенной в квадратурный канал. Поэтому спектральные свойства и характеристики помехоустойчивости приема СКФМ и КФМ сигналов одинаковы.
ЧАСТОТНАЯ МОДУЛЯЦИЯ С МИНИМАЛЬНЫМ СДВИГОМ (MSK)
Этот вид модуляции можно трактовать как квадратурную фазовую модуляцию со сдвигом, в которой модулирующие импульсы вместо прямоугольной формы имеют синусоидальную, как показано на рис.2.42. В этом случае квадратурные составляющие передаваемого сигнала могут быть представлены следующим образом:

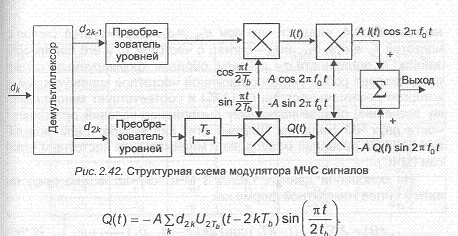
Такая форма модулирующих импульсов приводит к плавному изменению фазы, .как показано на диаграмме фазовых переходов, изображенной на рис.2.41,б. Здесь отсутствуют скачки фазы, характерные для КФМ и СКФМ сигналов, и изменения фазы от одного значения к другому происходят по линейному закону.
Эту разновидность сигнала с квадратурной модуляцией можно также рассматривать как частный случай сигнала с двоичной частотной манипуляцией, т.е. ЧМ сигнал. Действительно, определим величины (, и f2 следующим образом:
 ,
,
Тогда, используя известные тригонометрические тождества, из (2.147) получим
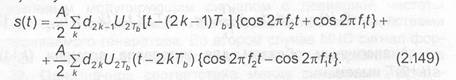
Таким образом, согласно (2.149) на интервале времени зависимости от комбинации пары символов » формируется сигнал на одной из двух частот.
В табл.2.3 представлена структура формируемого сигнала для каждой из возможных комбинаций символов. Из данных, приведенных

в табл.2.4, следует, что при И=И формируется сигнал с частотой сигнал с частотой и его полярность зависит от полярности. Таким образом формируемый сигнал представляет собой сигнал с двоичной частотной манипуляцией, у которого девиация частоты и соответствует минимальному значению, обеспечивающему выполнение условий ортогональности двух ЧМ сигналов. Поэтому этот вид квадратурной модуляции получил название модуляции с минимальным частотным сдвигом (МЧС).
На основании данных табл.2.3 МЧС сигнал можно представить в более компактной форме как

Условия, которым удовлетворяют значения гарантируют сохранение непрерывности фазы в моменты времени. Действительно, в интервале времени изменение фазы определяется следующим выражением:
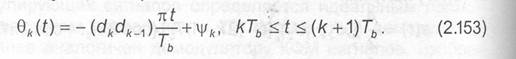
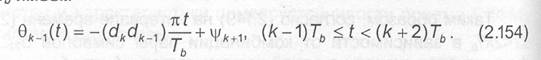
Вычислим значения этих фаз в моменты времени. Полагая k нечетным и используя условия (2.151), получаем значения для восьми возможных случаев. Эти значения приведены в табл.2.4.
В соответствии с данными, приведенными в табл.2.4, можно сделать два основных вывода. Фаза МЧС сигнала на границе смежных интервалов времени непрерывна и принимает только значения. Аналогичные выводы можно сделать, если рассмотреть изменения фазы при четном k. Однако в этом случае при t=(k+1)T, фаза может принимать значения 0 или л.

Наконец, если ввести случайную величину которая может принимать значения ( 1,1), то передаваемый сигнал можно представить в следующем виде:
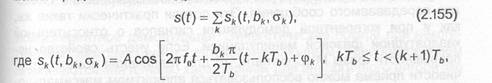
Формирование МЧС сигнала может быть осуществлено на основании его представлений в виде (2.155) или (2.147). В первом случае МЧС сигнал формируется путем управления частотой перестраиваемого по частоте генератора с номинальной частотой (, двухуровневым модулирующим сигналом с девиацией частоты f,=1/(4T)=R,/4. Непрерывность фазы обеспечивается свойствами перестраиваемого генератора. Во втором случае МЧС сигнал формируется с помощью квадратурной схемы, изображенной на рис.2.42. Однозначное соответствие между символами передаваемого сообщения и частотой сигнала может быть обеспечено с помощью схемы относительного кодирования, реализующей алгоритм (2.110).
Демодуляция МЧС сигнала может быть осуществлена с помощью когерентного демодулятора, изображенного на рис.2.43. Демодулятор содержит два квадратурных канала, состоящих из перемножителя, интегратора со сбросом и решающего устройства (знакового компаратора). Каждый канал, по существу, реализует оптимальный алгоритм приема двух противоположных сигналов синусоидальной формы. Время интегрирования в интеграторах равно 2Т. Характеристики помехоустойчивости при когерентной демодуляции МЧС сигналов и КФМ сигналов оказываются одинаковыми. Некоторые дополнительные энергетические потери могут возникать, если используется относительное кодирование символов передаваемого сообщения. Эти потери практически такие же, как и при когерентной демодуляции сигналов с относительной квадратурной фазовой манипуляцией. Если учесть свойство непрерывности фазы МЧС сигнала, то для увеличения помехоустойчивости приема можно воспользоваться алгоритмом максимального правдоподобия Витерби [13].
С другой стороны, если МЧС сигнал рассматривать как частный случай сигнала с двоичной частотной модуляцией, то можно использовать алгоритм когерентной демодуляции с посимвольными решениями через каждые секунд. В этом случае энергетические потери по сравнению с оптимальным алгоритмом когерентной демодуляции будут равны 3 дБ.
Поскольку МЧС сигнал относится к классу ЧМ сигналов, то для его демодуляции могут быть использованы некогерентные алгоритмы. Наиболее простой из них реализуется в виде последовательно включенных амплитудного ограничителя, частотного дискриминатора и интегратора со сбросом. Другие основаны на оценке набега фазы (или некоторой функции от набега фазы) за определенный интервал времени и сравнении с порогом. Длительность интервала анализа набега фазы, как правило, не превышает 27,. На рис.2.44 приведена структурная схема некогерентного де- модулятора МЧС сигнала с согласованными фильтрами (СФ), реализующего автокорреляционный алгоритм с задержкой на 27,. В этой схеме сигнал с выхода сумматора пропорционален и используется для восстановления символов передаваемого сообщения с помощью знакового компаратора.
Энергетические потери при демодуляции МЧС сигнала с помощью частотного дискриминатора составляют 3,6дБ по отношению к когерентной демодуляции и 6,6 дБ по отношению к оптимальной
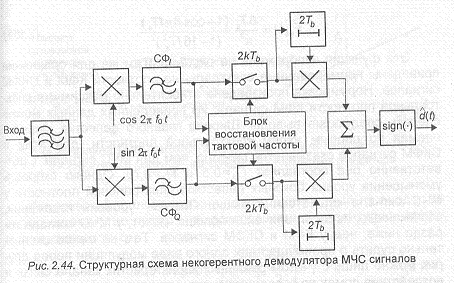
когерентной демодуляции. Энергетические потери при некогерентной демодуляции с автокорреляционным преобразованием оцениваются значением, характерным для аналогичного алгоритма демодуляции ОКОМ сигналов.
Повысить помехоустойчивость некогерентной демодуляции МЧС сигналов с автокорреляционным преобразованием можно за счет безызбыточного исправления ошибок при использовании автокорреляционных преобразователей: АП1, АП2 с задержкой на 7, и 27, соответственно [14].
Спектральная плотность МЧС сигнала определяется следующим выражением:
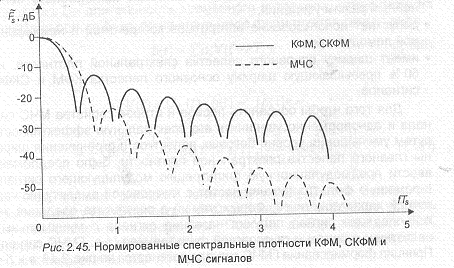
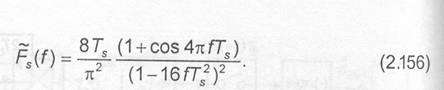
Эта функция изображена на рис.2.45. Там же для сравнения приведены нормированные спектральные плотности КФМ и СКФМ сигналов. Нормировка произведена относительно максимума спектральной плотности КФМ сигнала. Из приведенных данных можно сделать следующие выводы. Ширина главного лепестка, определяемая по первым нулям спектральной плотности, для КФМ и СКФМ сигналов оказывается меньше, чем для МЧС сигнала. Соответственно она составляет fT,=0,5 и fT,=0,75. Однако скорость уменьшения уровня боковых лепестков спектральной плотности у МЧС сигнала существенно выше. Поэтому уровень искажений, возникающих из-за ограничения полосы частот, у МЧС сигнала гораздо ниже, чем у КФМ и СКФМ сигналов. Тем не менее окончательно судить о преимуществах одного вида модуляции перед другим можно лишь с учетом реальных характеристик канала связи и воздействия помех по соседним каналам приема.
В заключение можно лишь отметить, что при заданных скорости передачи сообщений и характеристиках помехоустойчивости МЧС сигнал требует меньшей ширины полосы частот по сравнению с двоичным ФМ сигналом и меньшей мощности по сравнению с другими двоичными ЧМ сигналами.
ЧАСТОТНАЯ МОДУЛЯЦИЯ С МИНИМАЛЬНЫМ ЧАСТОТНЫМ СДВИГОМ И ГАУССОВСКОЙ ФИЛЬТРАЦИЕЙ (GMSK)
Рассмотренный МЧС сигнал обладает следующими свойствами:
• имеет постоянную огибающую и позволяет использовать нелинейный режим усиления;
• допускает использование алгоритмов когерентной и некогерентной демодуляции;
• имеет ширину основного лепестка спектральной плотности, на 50% превышающую ширину основного лепестка КФМ и СКФМ сигналов.
Для того чтобы сохранить первое и второе свойства МЧС сигнала и одновременно увеличить его спектральную эффективность путем уменьшения уровня боковых лепестков и ограничения ширины главного лепестка спектральной плотности, было предложено ввести предмодуляционную фильтрацию модулирующего сигнала с помощью фильтра нижних частот с гауссовской амплитудно-частотной характеристикой. Формируемый в результате введения та- кой операции сигнал получил название сигнала с минимальным частотным сдвигом и гауссовской фильтрацией (Т.е. ГМЧС сигнал). Принцип формирования ГМЧС сигнала поясняется на рис.2.46,а и б.

Гауссовский фильтр нижних частот, включенный на входе перестраиваемого по частоте генератора, имеет амплитудно-частотную характеристику

и импульсную характеристику
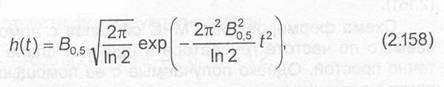
где В,5- полоса пропускания фильтра по уровню 3 дБ.
Если на вход такого фильтра поступает сигнал в виде двоичной последовательности импульсов прямоугольной формы
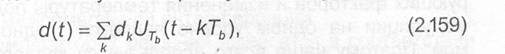
где dД=+1, T~ — длительность временного интервала, отводимого на передачу одного бита, то на его выходе формируется сигнал вида

Чем меньше значение произведения , тем более компактным получается спектр ГМЧС сигнала и тем больше уровень межсимвольной интерференции. Поэтому выбор значения E3„7b определяется из компромисса между спектральной эффективностью и энергетическими потерями.
Сигнал на выходе перестраиваемого по частоте генератора описывается следующим выражением:
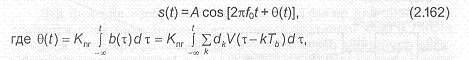
— крутизна характеристики управления перестраиваемого по частоте генератора.
В общем случае для сигналов с частотной модуляцией и гауссовской предмодуляционной фильтрацией (ГЧМ сигналов) индекс модуляции т в зависимости от назначения системы может выбираться в широких пределах, например 0,1<т(1. Для ГМЧС сигнала индекс модуляции должен быть равен 0,5. Поэтому при формировании ГМЧС сигнала К„должен выбираться из условия
![]()
где V(t) — реакция гауссовского фильтра при воздействии одного импульса прямоугольной формы, определяемая выражением (2.161).
Схема формирования ГМЧС сигналов с помощью перестраиваемого по частоте генератора в идейном плане является достаточно простой. Однако получаемые с ее помощью сигналы оказываются практически не пригодными для когерентной демодуляции, для которой необходимо, чтобы индекс модуляции т был строго равен 0,5. На практике из-за воздействия различных дестабилизирующих факторов и изменения температуры поддержание индекса модуляции на одном уровне является труднорешаемой проблемой. Поэтому чаще всего используется квадратурная схема формирования ГМЧС сигналов, изображенная на рис.2.47. Эта схема может быть реализована в цифровом виде, поэтому проблема стабилизации индекса модуляции решается сравнительно простыми средствами.
Квадратурная схема формирования ГМЧС сигналов основана на его квадратурном представлении:
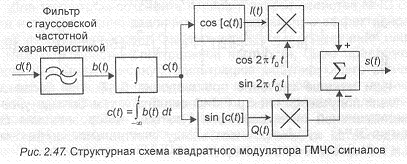

( [ — со
Для демодуляции ГМЧС сигнала могут быть использованы те же самые алгоритмы, что и для демодуляции МЧС сигнала: когерентные и некогерентные. При когерентной демодуляции может быть использована квадратурная схема, изображенная на рис.2.43, где интеграторы со сбросом заменяются квазисогласованными фильтрами нижних частот.
В результате перемножения принимаемого ГМЧС сигнала
![]()
с опорными и последующей низкочастотной фильтрации выделяются квадратурные составляющие

5 — составляющие межсимвольной интерференции.
В знаковых компараторах решения выносятся в соответствии со следующими правилами:

Поскольку в квадратурных составляющих Q(t) и l(t) демодулируемого сигнала уровень межсимвольной интерференции оказывается заметно ослабленным по сравнению с ее уровнем в модулирующем сигнале после предмодуляционной фильтрации, то алгоритмы когерентной демодуляции обеспечивают лучшие характеристики помехоустойчивости по сравнению с некогерентными.
При демодуляции ГМЧС сигнала с помощью частотного дискриминатора выделяется сигнал, пропорциональный производной фазы
![]()
Отсчеты обычно осуществляются в моменты времени, соответствующие максимальному раскрыв глазковой диаграммы. Обычно они выбираются в середине интервала времени. Поэтому
![]()
Из (2.171) следует, что демодулированный сигнал в момент отсчета содержит полезную составляющую и составляющие меж- символьной интерференции, причем соотношение их уровней не зависит от точности установки индекса модуляции. Это является одним из основных преимуществ алгоритма некогерентной демодуляции с помощью частотного дискриминатора.
ОТНОСИТЕЛЬНАЯ КВАДРАТУРНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ С ФАЗОВЫМ СДВИГОМ
Этот вид фазовой модуляции принят в качестве национального стандарта для цифровых сотовых систем радиосвязи с временным многостанционным доступом (TDMA) в США и Японии. Он занимает как бы промежуточное положение между квадратурной фазовой модуляцией и квадратурной фазовой модуляцией со сдвигом и для него изменения фазы происходят на +l/4, k 1, 2, 3.
Структурная схема модулятора л/4-ОКОМ сигналов изображена на рис.2.48, а диаграмма фазовых переходов — на рис.2.49. Здесь последовательность символов передаваемого сообщения разделяется с помощью демультиплексора на две последовательности , которые преобразуются в кодере в модулирующие сигналы в соответствии со следующим алгоритмом:
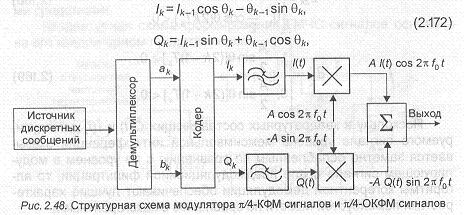
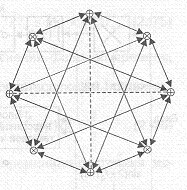
Рис.2.4k диаграмма фазовых переходов к/4-ОКОМ сигнала без фильтации. Знаком О+ показаны точки созвездия, соответствующие четным символам
сообщения, S — нечетным.
где / и О -текущие уровни модулирующих сигналов в синфазном и квадратурном каналах в интервале времени kT<t<(k+1)TД OД — текущее значение фазы, определяемые информационными символами в соответствии с табл.2.5. и Q< согласно (2.172) могут принимать значения О, +1, +1/12.
Предположим, что фильтры нижних частот отсутствуют, фаза несущей в интервале времени 0<t<T, равна нулю, т.е. /,=1, Q,=О. Пусть в момент времени t=T, символы сообщения принимают значения а„=1, Ь„~1; тогда О„=л/4. В соответствии с (2.172) имеем /,=1/12, О,=1/12, и фаза несущей скачком изменяется на л/4.
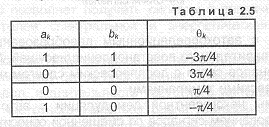
Согласно диаграмме фазовых переходов между двумя смежными элементами л/4-ОКФМ сигнала всегда происходят изменения фазы, причем эти изменения могут быть только на Одним из достоинств ~/4-ОКФМ сигнала является возможность достаточно простой реализации алгоритмов некогерентной
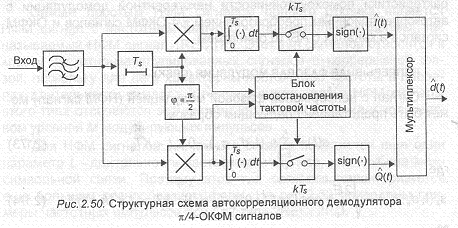
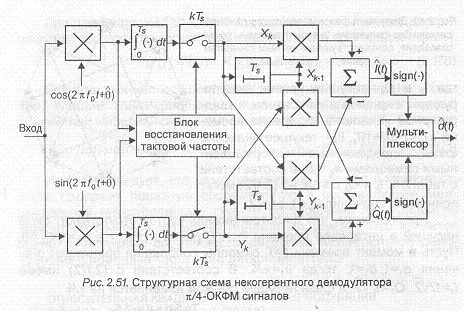
демодуляции с автокорреляционным преобразованием, не требующих предварительного восстановления несущей. Это особенно важно для каналов связи с допплеровским сдвигом частоты и быстрыми релеевскими замираниями.
Алгоритмы иекогерентной демодуляции с автокорреляционным преобразованием сигналов со смещенной относительной квадратурной манипуляцией реализуются сложнее.
Структурные схемы демодуляторов, реализующих алгоритмы некогерентной демодуляции л/4-ОКФМ сигналов изображены на рис.2.50, 2.51. Первая является чисто автокорреляционной, вторая — квадратурной с автокорреляционным преобразованием. Характеристики помехоустойчивости некогерентной демодуляции с автокорреляционным преобразованием ОКФМ сигналов и ОКФМ сигналов а каналах с АБГШ одинаковы.
НЕПРЕРЫВНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ (CPSK)
Сигнал с непрерывной фазовой модуляцией (НФМ сигнал) может быть представлен следующим образом:
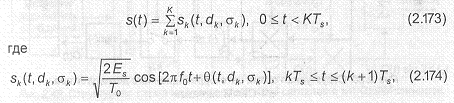

L-глубина межсимвольной свят, -переменная состояния модулятора, — начальная фаза.
Таким образом, НФМ сигнал представляет собой сигнал с постоянной огибающей и может рассматриваться как обобщение МЧС сигнала. Действительно,. в (2175) d; могут принимать значения из множества (+1;+3, ..., +(M — 1))Д x.е. последовательность символов передаваемого сообщения может быть многоуровневой. Кроме того, можно изменять форму частотных импульсов и их длительность. Все это позволяет получать сигналы с различными значениями показателей спектральной и энергетической эффективности.
Классификацию НФМ сигналов обычно осуществляют по двум признакам: количеству битов информации, приходящихся на передаваемый символ, и длительности частотного импульса g(t). Если длительность частотного импульса равна длительности символа сообщения, то НФМ сигнал носит название НФМ сигнала полного отклика. Если длительность частотного импульса не меньше двух длительностей символа сообщения, то НФМ сигнал носит название НФМ сигнала усеченного (парциального) отклика. На рис.2.52 приведены примеры функций, описывающих форму импульсов частотного отклика.
Самым простым НФМ сигналом полного отклика является НФМ сигнал с частотным импульсом прямоугольной формы, так называемый НФМ сигнал 1REC [15]. Этот тип сигналов относится кассу частотно-манипулированных сигналов с непрерывной фазой, поскольку для него характерны постоянство частоты в пределах длительности символа и непрерывность фазы. НФМ сигналы этого типа отличаются значениями индекса модуляции и количеством уровней М модулирующих импульсов.
Для НФМ сигналов усеченного отклика появляется еще один параметр L — длительность частотного импульса, или глубина меж символьной связи. Поэтому этот тип сигналов характеризуется еще большим разнообразием форм. На рис.2.52 приведены при- меры частотных импульсов при L=2 типа 2REC, 2RC.
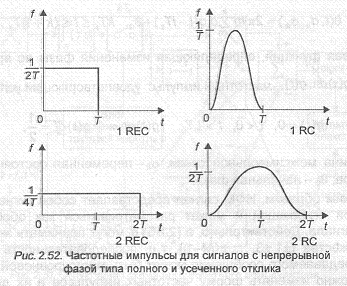
Вообще говоря, ширина главного лепестка спектральной плотности уменьшается с увеличением глубины межсимвольной связи L, а скорость уровня боковых лепестков увеличивается при выборе функции, описывающей форму частотного импульса, как много- кратно дифференцируемой функции.
Что касается квадрата евклидова расстояния d, определяющего помехоустойчивость, то для длинных импульсов g(t) оно увеличивается при увеличении индекса модуляции т. Для коротких импульсов д(1) оно увеличивается при уменьшении индекса модуляции. Таким образом, изменяя параметры НФМ сигналов усечен- ного отклика, можно получать большое разнообразие форм с различными показателями спектральной, энергетической эффективности и сложности реализации аппаратуры формирования и обработки.
2.4.СРАВНЕНИЕ РАЗЛИЧНЫХ ВИДОВ МОДУЛЯЦИИ.
При удачном выборе вида модуляции в определенной степени удается реализовать многие из указанных целей одновременно. Однако, как правило, в полной мере сделать это невозможно в силу их взаимной противоречивости и наличия ограничивающих факторов, среди которых следует указать:
• теоретически минимально возможную информационную. полосу, определяемую формулой Найквиста;
• пропускную способность канала связи, определяемую Теоремами Шеннона;
• выделенный радиочастотный диапазон;
• технологические и аппаратурные ограничения.
ДИАГРАММЫ ПОМЕХОУСТОЙЧИВОСТИ И СПЕКТРАЛЬНО- ЭНЕРГЕТИЧЕСКОЙ ЭФФЕКТИВНОСТИ
Рассмотрим некоторые подходы к решению задачи выбора вида манипуляции, результатом которых может быть установление компромиссного варианта. Воспользуемся диаграммами изображенными на рис.2.53. Верхняя диаграмма представляет собой семейство кривых помехоустойчивости, т.е. зависимостей вероятности ошибки на бит от отношения энергии, затрачиваемой на передачу бита информации, к спектральной плотности шума, правая — диаграмму спектрально-энергетической эффективности, т.е. семейство зависимостей удельной скорости передачи информации R,IИI от Е,IН,. Направления стрелок и соответствующие метки указывают общий эффект от перемещения рабочей точки по направлению, указанному стрелкой, при соответствующем выборе вида модуляции. Буквами 6, С, F соответственно обозначены следующие эффекты: выигрыш, плата, сохранение параметра неизменным. Взаимному размену подлежат параметры Р,, Я,/И/, Р (мощность или отношение сигнал/шум)'. На диаграммах указано минимальное значение удельных энергетических затрат, равное— 1,6 дБ и определяемое из формулы Шеннона для пропускной способности канала связи с ограниченной полосой И/, средней мощностью Р и помехой в виде аддитивного белого гауссовского шума.
На диаграмме спектрально-энергетической эффективности построена предельная кривая, определяемая выражением
![]()
Это выражение следует из формулы Шеннона при подстановке C=R,. Тогда для «идеального» вида модуляции рост энергетических., затрат при увеличении спектральной эффективности происходит по экспоненциальному закону. Минимально возможное значение удельных энергетических затрат определяется путем вычисления предела
![]()
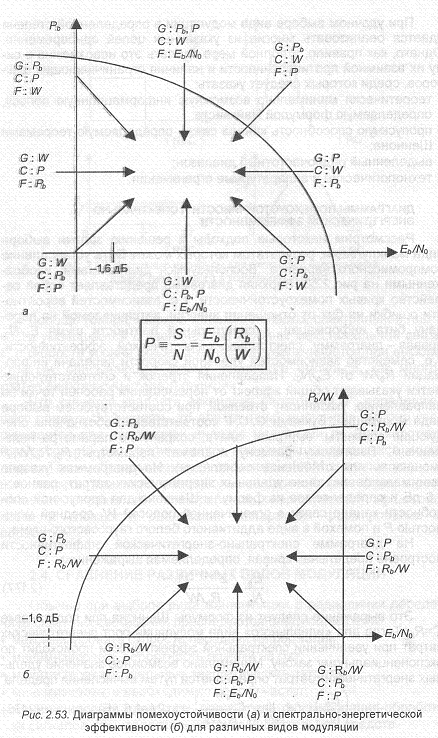
Двигаясь к пределу Шеннона на диаграмме рис.2.53,а, можно обеспечить снижение вероятности ошибки Р или удельных энергетических затрат за счет расширения полосы. Напротив, двигаясь к пределу Шеннона на диаграмме рис.2.53,б, можно повысить спектральную эффективность за счет увеличения удельных энергетических затрат или вероятности ошибки Р>. Поскольку обычно бывает заданным значение Р, то представляют интерес стрелки, отмеченные как (F: Р,). На рис.2.53 имеются четыре такие стрелки: две на диаграмме а и две на диаграмме b. Эти две диаграммы, иллюстрирующие возможность взаимного размена различных показателей вида модуляции лишь качественно иллюстрируют основные закономерности, проявляющиеся при подобном размене. Для получения более точных данных необходим детальный анализ.
Воспользуемся диаграммой спектрально-энергетической эффективности для сравнения различных видов модуляции. Результаты подобного сравнения приведены на рис.2.54. Здесь предполагается заданным значение Р, =10 . Из приведенных данных следует, что АМ, ФМ и ОФМ являются спектрально-эффективными видами модуляции, поскольку соответствующие точки располагаются выше разграничительной линии Я,/И/=1. Часть диаграммы, расположенная выше этой линии, соответствует ситуации, когда имеет место ограничение на имеющуюся полосу частот. Поэтому увеличение спектральной эффективности может быть достигнуто за счет увеличения числа позиций модуляции M. При заданной Р расплачиваться за это приходится увеличением удельных энергетических затрат.
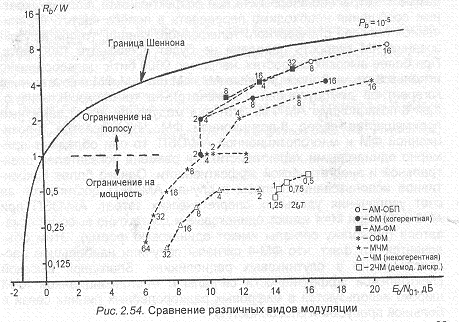
С другой стороны, при ЧМ неэффективно используется имеющаяся полоса, поскольку соответствующие ей точки располагаются ниже разграничительной линии RДIИ/=1. Для этого вида модуляции характерны повышенные значения показателя энергетической эффективности.
Следует отметить различный характер размена показателей спектральной и энергетической эффективности в областях, лежащих выше и ниже разграничительной линии. В соответствии с формой предельной кривой Шеннона в области, лежащей выше разграничительной линии, этот размен носит плавный характер. Поэтому за увеличение спектральной эффективности приходится расплачиваться существенным снижением энергетической эффективности. Напротив, в области, лежащей ниже разграничительной линии, небольшие потери энергетической эффективности приводят к заметному увеличению спектральной эффективности.
Из приведенных данных следует, что АМ/ОБП является асимптотически оптимальным видом модуляции для области диаграммы, характеризующейся ограничением на частотный ресурс системы. Ортогональная модуляция в сочетании с когерентной демодуляцией является асимптотически оптимальным видом модуляции для области диаграммы, характеризующейся ограничением на энергетический ресурс системы. При R~/ИГ-+О она позволяет обеспечить безошибочную передачу сообщений со скоростью Е,IN,~ — 1,6 дБ.
В заключение сделаем ряд замечаний практического характера, которые подтверждаются данными, приведенными на диаграмме спектрально-энергетической эффективности. Если дискретные сообщения необходимо передавать в полосе частот, ограниченной полосой стандартного телефонного канала, то при использовании ЧМ скорость передачи не будет превышать 1200 бит/с. При более высоких скоростях, например 9600 бит/с целесообразно использовать многопозиционные АМ, ФМ или АМ-ФМ в сочетании с когерентной демодуляцией. Примечательна точка, характеризующая 8-позиционную АМ-ФМ. Этот вид модуляции имеет заметные преимущества перед 8-позиционной ФМ. Что касается 8-позиционной ФМ и многопозиционной АМ/ОБП, то они обладают при- мерно одинаковыми характеристиками размена показателей спек- тральной и энергетической эффективности. Однако более эффективное использование полосы в случае АМ/ОБП достигается за счет увеличения удельных энергетических затрат. АМ/ОБП при М=2 и ФМ при М=4 имеют одинаковые и достаточно высокие показатели (поскольку сигналы имеют одинаковую форму). Этим объясняется тот факт, что ФМ-4 сигналы получили наибольшее распространение в спутниковых радиолиниях. Благодаря высокой спектральной эффективности сигналы с многопозиционной КАМ широко используются в цифровых радиорелейных линиях связи с большой пропускной способностью.