2.5. Частотно-эффективные методы модуляции

Фазовая и относительная фазовая модуляция. Высокая помехоустойчивость, энергетическая эффективность и экономное расходование полосы частот в современных цифровых системах связи и вещания достигаются в значительной степени благодаря рациональному выбору сигналов. При этом должна также учитываться сложность схемотехнической реализации модема.

Из теории сигналов известно, что максимальной (потенциальной) помехоустойчивостью, т.е. наименьшей вероятностью ошибочного приема, характеризуются так называемые противоположные (манипулированных по фазе на 180') сигналы ФМ-2 (PSK). Однако, несмотря на высокую помехоустойчивость,  по крайней мере, три причины, из-за которых часто отказываются от непосредственного применения противоположных сигналов. Это, во-первых, эффект "обратной работы" в когерентных демодуляторах, связанный с неоднозначностью фазы (ошибкой, кратной величине 2л) опорной несущей, выделяемой непосредственно из принимаемого сигнала. В результате передача сигналов ФМ-2 в каналах с неоднозначностью требует применения специальных мер. Именно по этой причине фазовая манипуляция, изобретенная известным американским ученым Г. Найквистом в 1928 г., долгое время не находила применения.

В качестве второй причины ограниченного применения сигналов ФМ-2 следует указать на весьма низкую эффективность использования спектра, определяемую отношением скорости передачи информации к занимаемой при этом полосе частот.

Третьим недостатком сигналов ФМ-2 являются большие искажения огибающей (провалы амплитуды до нуля), которые возникают в моменты скачков фазы колебания на 180' при прохождении последовательности сигналов через полосовые фильтры тракта. Такая паразитная АМ нежелательна, поскольку приводит к увеличению пик-фактора сигнала и, как следствие, к дополнительным искажениям спектра при нелинейных режимах усиления, например, в ЛБВ ретрансляторов ИСЗ.

С целью устранения первого из перечисленных недостатков сигналов ФМ-2 -"обратной работы" — и достижения, благодаря этому, системных преимуществ, связанных с серьезным упрощением и удешевлением ФМ- демодуляторов, чаще других (в том числе и в ряде систем ЦРВ) используют относительное кодирование передаваемого сообщения на стороне передачи (рис. 2.18а) и относительное декодирование — на приемной стороне (рис. 2.186). Перекодирование исходной цифровой последовательности осуществляется по правилу: b; = а; О+ b;, где а; — символ на входе относительного кодера; b; символ на его выходе; b

символ с выхода кодера, задержанный на такт, т.е. на длительность т, сигнала (времени, затрачиваемого на передачу одного бита информации); О+ — процедура сложения по модулю 2. Обратная перекодировка последовательности символов — оценок b;— осуществляется в приемнике по правилу: а; = b; О+ b; .

Относительную ФМ (ОФМ или DPSK) предложил в 1954 г. советский ученый Н.Т. Петрович. Такую модуляцию можно рассматривать как обычную ФМ, но при соответствующем дополнительном кодировании передаваемого сообщения. Поэтому сигналы ОФМ можно принимать так же, как и сигналы с ФМ, но с последующим декодированием в декодере, содержащем элемент памяти и сумматор по модулю 2 (рис. 2.186), реализующем правило b; = а; О+ b;.

При классической (противофазной) CM-2 определение фазы любой принятой посылки сигнала производится по отношению к некоторой фиксированной опорной фазе yД. При относительной ОФМ-2 началом отсчета фазы каждой очередной посылки является фаза предыдущей посылки: для передачи символа 0 начальная фаза передаваемого колебания сохраняется неизменной по отношению к начальной фазе колебания на интервале длительности предшествующего символа, а для передачи символа 1 начальная фаза излучаемого колебания изменяется на 180'.

Таким образом, при относительном методе передачи выбор сигнальной посылки зависит как от вида информационного символа (1 или О), так и от того, какой была предыдущая посылка (S или S). Часто этот вид кодирования называют дифференциальным, что точнее отражает принцип передачи разности элементов информации.

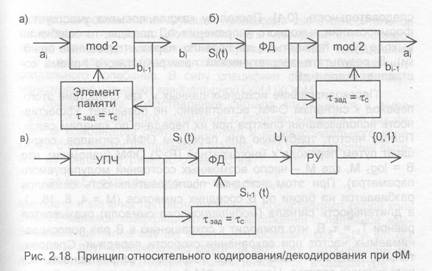
Применяются два оптимальных метода приема сигналов ОФМ; корреляционный (когерентный) и автокорреляционный (некогерентный). В первом методе прием осуществляется на оптимальный когерентный демодулятор ФМ сигналов, дополненный относительным декодером, включенным на выходе решающего устройства (рис. 2.186). Такой демодулятор содержит устройство формирования опорной несущей, что принципиально ограничивает возможности его применения в тяжелых приемных ситуациях и существенно усложняет реализацию.

Автокорреляционный метод приема применяют в каналах со сравнительно быстрыми флуктуациями фазы принимаемых сигналов, когда опорная несущая перестает достаточно точно следить за фазой сигнала и условие когерентности приема нарушается. При таком методе приема в качестве опорного напряжения используется предыдущая посылка сигнала, которая запоминается на время, равное ее длительности (рис. 2.18в). В фазовом детекторе (ФД) происходит сравнение фазы принятой посылки с фазой предыдущей (опорной) посылки. Реализуется это посредством выполнения в ФД операции перемножения сигналов S; (t) и 8;1 (1) с последующим интегрированием; в результате на выходе ФД вырабатывается напряжение Ц, поступающее на решающее устройство (РУ), на выходе которого формируется двоичная последовательность (0,1). Поскольку каждая посылка участвует в формировании выходного напряжения ФД дважды, то ошибки на выходе будут появляться, как правило, парами (сдвоенные ошибки). В результате энергетический проигрыш такого приема составляет около 1 дБ.

Перекодирование исходных данных и, как следствие этого, переход к сигналам ОФМ, естественно, не повышает эффективность использования спектра при их передаче по каналам связи. Полосу частот, требуемую для передачи ОФМ сигналов, сокращают путем перехода к многократной (В>2) ОФМ (напомним, что В = log, М, где М — число возможных состояний модулируемого параметра). При этом исходная последовательность символов разбивается на блоки по В соседних символов (М = 4, 8, 16,...), а длительность сигнала (модуляционного символа) оказывается равной Т, = т, В, что приводит к сокращению в В раз полосы занимаемых частот при сохранении скорости передачи. Следовательно, приблизительно в В раз возрастает эффективность использования спектра. Например, ФМ-4 имеет вдвое лучшую спек- тральную эффективность по сравнению с ФМ-2, поскольку в одном модуляционном символе передаются два бита информации.

Отображение или задание М информационных бит М=2 возможными фазами сигнала можно сделать различными способами. Наилучшим заданием является такое, при котором соседние фазы сигналов соответствуют информационным двоичным блокам, различающимся в одном разряде — в случае М=4 это 00, 01,11,10, а эквивалентный сдвиг фазы: О, л/2, л, -т/2. Такое отображение называется манипуляционным кодом Грея. Он важен при демодуляции сиг- нала, поскольку наиболее вероятные ошибки вызывают ошибочный выбор фазы, соседней по отношению к той, которая действительно передана. При М=4 при наиболее распространенных фазовых ошибках на н//2 использование такого кода приводит к ошибке только в одном двоичном символе, а в В- битовой информационной последовательности (т.е. в В- битовом модуляционном символе) возникает ошибка только в одном бите. В результате достигается максимальная помехоустойчивость передачи.

Один из широко используемых в ЦРВ методов формирования сигналов с двукратной (В=2, М=4) ОФМ-4 (DQPSK) состоит в следующем. Исходную кодовую последовательность делят на последовательности четных Х и нечетных Х(по порядку следования) символов, что эквивалентно передаче сообщения: x(t) = х(1) + х,(1).

При формировании этих функций производят также относительное кодирование исходного сообщения. Для передачи x(t) остается только осуществить фазовую манипуляцию на 180' сообщениями х(t) и х,(1) двух квадратурных составляющих одного и того же синусоидального колебания. В силу специфики формирования такую манипуляцию называют квадратурной ОФМ (КОФМ).

Квадратурное представление сигнала заключается в выражении синусоидального колебания с произвольной фазой как линейной комбинации синусоидального и косинусоидального колебаний с нулевыми начальными фазами. Это представление вытекает из тригонометрического равенства cos (t + q) = cos q cos t — sin y sin а,1,

где cos y и sin y на тактовом интервале представляют собой константы, являясь коэффициентами в выражении с линейной комбинацией сигналов cos а,1 и  ш,1. Поскольку Cos ы,1 и  а4 сдвинуты друг относительно друга на 90', они ортогональны на фазовой диаграмме (говорят, что они находятся "в квадратуре").

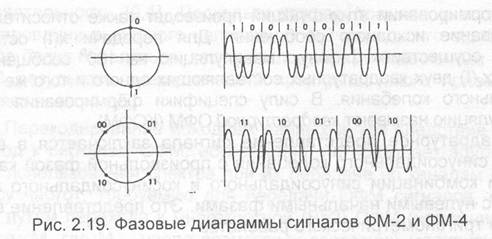
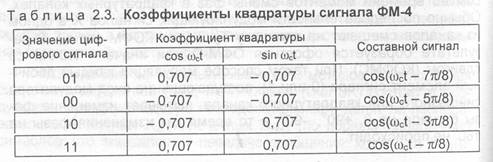
По существу, cos о,1 и sin со,1 представляют собой базовые векторы на двумерной фазовой диаграмме. В табл. 2.3 дан пример представления сигналов с ФМ-4, а на рис. 2.19 показаны диаграммы сигналов ФМ-2 и ФМ-4 для случая, когда скорость передачи символов сигнала в системе с ФМ-4 составляет точно поло- вину от скорости передачи символов при ФМ-2, так что получаются одинаковые скорости передачи двоичных сигналов. На этом же рисунке показаны фазовые диаграммы косинусоидального колебания, фазы которого соответствуют передаваемому сигналу. Возможны и другие расположения фаз.

При одновременной смене символов в каждом из квадратурных каналов модулятора в сигнале КОФМ происходит скачок фазы на л, т.е. сохраняется третий недостаток, присущий ФМ сигналам. Для снижения уровня паразитной АМ при КОФМ необходимо исключить скачки фазы на 180'. Достигается это разносом во времени моментов смены фаз в квадратурных каналах. Обычно последовательности модулирующих сигналов Х в одном из каналов смещают на величину Т,/2 (для КОФМ это т,). В результате образуется офсетная ОФМ-О или иначе — КОФМ со сдвигом (КОФМС). При таком способе модуляции каждый двоичный элемент сигнала (О или 1), поступающий на вход модулятора синфазного или квадратурного канала, вызывает изменение фазы сигнала на О, +90', — 90', в то время как изменения фазы на 180' не происходит.

            Таким образом, при переходе от двоичной ОФМ к КОФМ или КОФМС примерно вдвое сокращается полоса занимаемых частот без снижения помехоустойчивости приема, причем метод КОФМС обеспечивает снижение уровня паразитной АМ при прохождении сигналов через частотно-избирательные цепи. КОФМ и КОФМС характеризуются достаточно высокой эффективностью использования спектра, вследствие чего находят широкое применение. В частности, модификация КОФМ (н/4-shift DQPSK) применяется в современной версии ЦРВ Т-DAB и системах мобильной связи D-AMPS и PDC.

В тех применениях, когда необходимо обеспечить минимум помех в соседних по частоте каналах, прибегают к скруглению элементарных модулирующих сигналов. Одна из широко используемых форм скругления соответствует полупериоду косинусоиды. В результате линейного, а не мгновенного изменения фазы в процессе модуляции реализуется модуляция минимального частотного сдвига (ММС), которая значительно эффективнее КОФМ по полосе и имеет спектр ВПИ, убывающий как f. Однако это достигается ценой определенного усложнения аппаратуры.

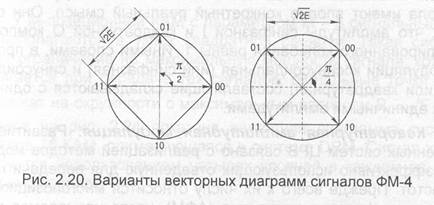
При исследовании свойств многопозиционных сигналов широко используется геометрическая теория сигналов. Сигналы отображаются точками, которые являются концами двумерных векторов на плоскости. Число сигналов обычно кратно 2, т.е. М = 2 (В=2,...7). В случае многопозиционной ФМ-М М сигнальных. точек располагаются на окружности с радиусом В, зависящим от мощности (или энергии посылки Е) сигнала, на равных расстояниях dM с угловым интервалом 21т/М радиан. Расстояние между сигнальными точками d является удобным параметром для качественного сопоставления различных систем сигналов.

      Векторные (фазовые) диаграммы для сигналов ФМ-4 показаны на рис. 2.20, где R= vE Е. Двукратная система ФМ сигналов представлена здесь в двух наиболее известных вариантах; в обоих случаях минимальное расстояние между вариантами сигнала 64= /2Е, что соответствует расстоянию между ортогональными сигналами. Эти сигналы являются наилучшими по помехоустойчивости из всех двумерных четырехпозиционных сигналов.

Сигналы, модулирующие несущую (точнее, синфазное и квадратурное колебания), при квадратурной модуляции многоуровневые, они описываются последовательностями модуляционных символов z. Модуляционные символы являются комплексными, их вещественная и мнимая части отображаются битами i0, у,. Для формирования таких символов входной последовательный поток битов (y0,у,) демультиплексируют на два субпотокасинфазный и квадратурный, в каждом из которых тактовая частота уменьшается вдвое. В способе ОФМ-4 модулирующий сигнал представляет собой последовательность четырехпозиционных символов, выбираемых из алфавита с четырьмя двухразрядными двоичными словами (00, 01, 10, 11), которые определяют фазу модулированного колебания. Соответствие между битами у, у, и модуляционными символами иллюстрирует диаграмма на рис. 2.21.

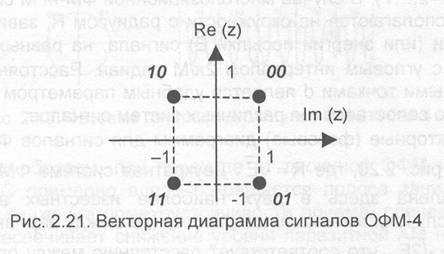
Здесь, например, значениям y,=0, у=0 соответствует комплексное число z = I + j (правая верхняя точка). Значения вещественной и мнимой частей этого комплексного модуляционного символа имеют вполне конкретный реальный смысл. Они означают, что амплитуды синфазной  и квадратурной Q компонент модулированного колебания равны 1. Иными словами, в процессе модуляции косинусоидальная (или синфазная) и синусоидальная (или квадратурная) составляющие складываются с одинаковыми единичными амплитудами.

Квадратурная амплитудная модуляция. Развитие современных систем ЦРВ связано с реализацией методов модуляции, эффективно использующих отведенную для передачи полосу частот. Прежде всего к их числу относится многопозиционная амплитудно-фазовая модуляция (АФМ), часто называемая в последнее время квадратурной АМ (КАМ). Известно, что при использовании КАМ (QAM) обмен мощности сигналов на полосу частот производится с меньшими энергетическими затратами, чем при использовании многопозиционной ФМ.

При квадратурной амплитудной модуляции представляющим параметром является комплексная амплитуда радиосигнала. При М = 4 КАМ (рис. 2.22) совпадает с ОФМ-4 (рис. 2.21), однако при М > 8 эффективность квадратурной амплитудной модуляции выше.

Отметим, что, в отличие от сигнала с ФМ, сигнал с КАМ, показанный на рис. 2.23, не имеет постоянной огибающей. При модуляции типа ФМ постоянная огибающая поддерживается за счет введения ограничений на комбинации уровней в квадратурных каналах. В системе с КАМ комбинации не ограничиваются, поскольку уровни в каждом канале выбираются независимо. В результате этого системы с КАМ в общем случае нельзя использовать с устройствами, которые могут входить в насыщение.

 Такая система имеет ограничение на максимальную мощность сигнала, которая достигается при передаче тех сигналов, сигнальные точки которых лежат на окружности с максимальным радиусом R = E Е. .Для примера на рис. 2.24 показана векторная диаграмма системы сигналов 16-КАМ, применяющаяся в системе DRM. Сигнал характеризуется использованием четырех уровней в каждом из квадратурных каналов.

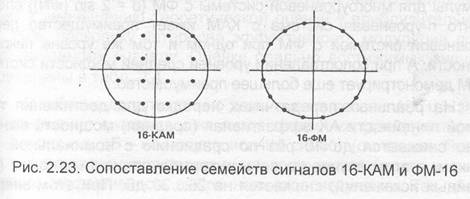
Обратим внимание на одну особенность сигналов с КАМ— искажения в нелинейном ретрансляторе (передатчике), существенно снижают их преимущества по сравнению с ФМ сигналами. Поэтому одним из основных требований к каналу с квадратурной АМ является его линейность, причем требования ужесточаются с увеличением кратности манипуляции — параметра В (или М).

Общее выражение для расстояния между соседними точками сигнала в системе с КАМ с пиковой амплитудой, равной единице, и L уровнями по каждой из осей имеет вид d = Г2/ (L — 1). Отсюда и из формулы для многоуровневой системы с ФМ (d = 2 sin (тт//N)} следует, что п- уровневая система с КАМ имеет преимущество перед п- уровневой системой с ФМ при одном и том же уровне пиковой мощности. А при сопоставлении уровней средней мощности система с КАМ демонстрирует еще большее преимущество.

На реальных передатчиках нередко для достижения требуемой линейности АХ эффективная (средняя) мощность вынужденно снижается до 10 раз по сравнению с номинальной. По оценкам, в этом случае уровень интермодуляционных помех (нелинейных искажений) снижается на 26...30 дБ. При этом энерго- потребление снижается приблизительно в 4 раза — при сохранении практически неизменной зоны обслуживания (по сравнению с АМ номинальным режимом), если реализуется цифровой прием. Недостаточная линейность АХ передатчика, помимо ухудшения качества радиоприема, приводит к увеличению уровня внеполосного излучения, что, в свою очередь, ухудшает характеристики ' ЭМС. Помимо требований к линейности АХ передатчика необходимо обеспечить надлежащую широкополосность его НЧ тракта. Частотная (спектральная) эффективность модулированных сигналов. Для оценки частотной (спектральной) эффективности модулированных сигналов обычно используют показатель:

Здесь: Rq, бит/с — скорость суммарного (т.е. учитывающего необходимость передачи всех дополнительных бит) цифрового потока (см. разд. 2.1); М, Гц — частотная полоса, занимаемая в эфире сигналом с данным видом модуляции при передаче цифрового потока Rq. Часто ширину полосы сигнала определяют как полосу, в пределах которой содержится 99% его мощности. Фактически величина у показывает, сколько бит в секунду информации можно передать в одном герце полосы. Учет дополнительных бит синхронизации и помехоустойчивого кодирования ведет к уменьшению теоретической оценки у приблизительно на 15...20%, поскольку интересна эффективность модуляции по информационному сигналу. Оценки реально достижимых значений у приведены в табл. 2.4.

В таблице дополнительно даны оценки полосы М, Гц и значения отношения сигнал/шум на входе приемника (демодулятора): h, дБ — на бит и q, дБ — на модуляционный символ (см. выше). Последние — параметры, характеризующие помехоустойчивость и энергетическую эффективность выбранного вида модуляции. Так, данные

показывают, что каждое удвоение кратности манипуляции приводит к необходимости удвоения излучаемой мощности.

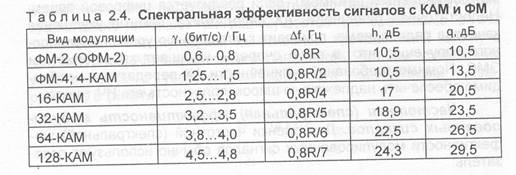
Величина спектральной эффективности сигналов зависит, в конечном счете, от компактности их спектра — относительной величины мощности, сосредоточенной в главном лепестке спектра, т.е. в полосе частот по первым "нулям" спектра, равной 2/т„где т, — длительность сигнала (время, затрачиваемое на передачу одного бита информации). В главном лепестке спектра сигнала после модуляции должно находиться не менее 94...97% всей энергии сигнала (в спектре широко распространенного сигнала ФМ-4 главный лепесток содержит порядка 87% энергии сигнала, в результате эффективность использования спектра не превосходит 1,5 бит/с/Гц).

Важным критерием, по которому оценивается компактность спектра систем нового поколения, следует также считать и увеличение скорости спадания внеполосного (ВПИ) — скорости убывания составляющих спектра при больших расстройках за пределами главного лепестка. Увеличение скорости спадания ВПИ обеспечивает непрерывность фазы сигнала в моменты перехода от символа к символу и максимально возможная линейность ее изменения без резких скачков. Для достижения этого производная изменения фазы не должна содержать точек разрыва (желательно обеспечить непрерывность по крайней мере второй производной, что гарантирует убывание внеполосных излучений по квадратичному закону). Другими словами: скорость спадания ВПИ зависит от числа непрерывных производных текущей фазы сигнала.

Системы сигналов с КАМ и ФМ имеют однотипные спектры, которые характеризуются ВПИ, убывающим пропорционально.

Из известных систем сигналов лишь модуляция ММС имеет спектр с ВПИ, убывающим пропорционально f '. Однако это достигается ценой значительного усложнения аппаратуры.

Абстрагируясь от вопросов практической реализации и ориентируясь на данные табл. 2.4, можно аргументировать выбор вида модуляции в конкретной системе ЦРВ. Так, для реализации системы Т-DAB оказалось достаточной иметь реальную частотную эффективность модуляции не хуже 1,3...1,5 бит/с/Гц, что обусловило применение квадратурной ФМ. В проекте консорциума DRM требования к эффективности модуляции были значительно выше, а именно: у > 4,5...5,0 бит/с/Гц. В результате стандартом DRM закреплено применение системы сигналов с КАМ: от 4- до 64-КАМ.

Известен также подход, связанный с оценкой спектральной эффективности (или эффективности использования полосы) системы, особенно распространенный при проектировании сотовых систем подвижной связи [98]. Это более полный и строгий подход, поскольку учитываются и характеристика формирующего (сглаживающего) фильтра на передаче и линейность амплитудной характеристики усилителя модулированного сигнала. В результате может быть получена оценка реально достижимой спектральной эффективности системы при обеспечении заданного уровня внеполосного излучения в соседнем канале.

2.6. Методы передачи аудиоданных. Сигналы с ортогональным частотным разделением (OFDM)

В цифровых системах связи и вещания применяются последовательный (односигнальный) и параллельный (многосигнальный) методы передачи аудиоданных (в англоязычной транскрипции это соответственно STD или TDM и FDM). Наиболее распространенным является последовательный метод, когда аудио- данные в общем (суммарном) потоке передаются посредством временного разделения каналов (ВРК) на единственной несущей с использованием той или иной цифровой модуляции (обычно это ФМ или ОФМ). Такой метод в спутниковой связи называют ВРК- ИКМ-ФМ. Вследствие использования одной несущей, системы вещания с последовательной передачей данных обладают серьезными достоинствами; ввиду небольшого пик-фактора и хорошей концентрации сигнала во времени они характеризуются хорошими энергетическими показателями, не требуют частотной избирательности для выделения различных программ, а также в таких системах не предъявляются повышенные требования к линейности тракта передачи.

Подавляющее большинство систем передачи сообщений строят, исходя из предположения, что длительность принимаемого сигнала равна длительности передаваемого, т.е. в канале отсутствует последействие (канал без памяти). В действительности только открытое космическое пространство может служить примером канала, не приводящего к рассеянию во времени посланного радиосигнала. В каналах наземных систем ЦРВ рассеяние сигнала как следствие его многолучевого распространения является решающим фактором, определяющим выбор метода передачи аудиоданных. К сожалению, от искажений сигнала, обусловленных рассеянием, нельзя избавиться простым увеличением мощности передатчика. В этом обстоятельстве — фактический приговор последовательному методу передачи. Действительно, при таком методе передачи при высоких скоростях цифровых потоков длительность элементарных сигналов (тактовых интервалов) т, весьма мала — доли микросекунд. В результате в высоко скоростном канале даже с незначительным рассеянием сигнала во времени последовательная передача сопровождается значительными межсимвольными искажениями (МСИ), что делает практически невозможным качественный прием цифровых данных на подвижном объекте, особенно в условиях пересеченной местности или в городе с многоэтажной застройкой. Обстоятельный анализ этого факта будет представлен в следующей главе.

Радикальным решением проблемы передачи больших потоков аудиоданных в каналах с рассеянием сигналов является распараллеливание передачи информации, т.е. использование большого числа частотно-разнесенных каналов (ЧРК) — несущих с низкими парциальными скоростями модуляции. В спутниковой связи такой метод передачи (при использовании ФМ) получил название ЧРК-ИКМ-ФМ, а при организации одного канала на каждой несущей — ОКН-ИКМ-ФМ.

Характерное для параллельного метода условие одновременной передачи через общий тракт сигналов предъявляет серьезные требования к ряду устройств системы и способам разделения этих сигналов. Из-за неидеальности характеристик реальных трактов (ограничения полосы частот, нелинейности амплитудных и фазовых характеристик и т.п.) неизбежно возникают взаимные помехи между сигналами, ухудшающие качество их разделения и приема. Наилучший метод разделения частотно-разнесенных сигналов должен обеспечить наиболее полное использование энергетических показателей радиопередатчика, а уровень взаимных помех между сигналами должен быть наименьшим, чтобы оказывать минимальное влияние на разделимость и помехоустойчивость приема каждого из сигналов.

В современных системах радио и телевизионного цифрового вещания принцип передачи ОКН-ИКМ-ФМ трансформировался в метод передачи широкополосных многочастотных сигналов, каждый из которых представляет собой ансамбль, состоящий из большого числа ортогональных частотно-разделенных несущих (отсюда и название OFDM). Таким образом, при параллельной передаче цифрового потока происходит частотное разнесение с использованием К несущих частот, когда сигнал одновременно передается на К несущих, причем на каждой из них скорость передачи уменьшается (следовательно, длительность тактового интервала т, увеличивается) в К раз.

"Ортогональная" часть в названии ОРОМ указывает на то, что существуют точные математические соотношения между несущих. В системах с ЧРК-ИКМ-ФМ несущие частоты расположены на таком расстоянии (друг от друга), которое можно позволить при применении (для расфильтровки) обычных фильтров и демодуляторов. В таких приемниках между несущими должны располагаться частотные защитные интервалы, введение которых в частотной области заметно снижает эффективность использования спектра.

Существует возможность расположить несущие так, чтобы боковые полосы соседних несущих перекрывались, однако при этом сохранялась возможность принимать информацию без их взаимного влияния. Для реализации этого несущие должны быть ортогональны. Лишь в этом случае может быть реализована плотная "упаковка" спектра многочастотного сигнала (рис. 2.25). Так, в стандарте Т-DAB частотный интервал (расстояние между соседними несущими — 5f) составляет в зависимости от режима передачи от 1 до 8 кГц. Несущие линейно независимы (т.е. ортогональны), если они расположены на расстоянии кратном  Т где Т— полезная часть ОРОМ- символа, равная длительности интервала обработки (интегрирования) сигнала. Ширина спектра сигнала с ортогональным ЧРК оценивается приближенным соотношением.

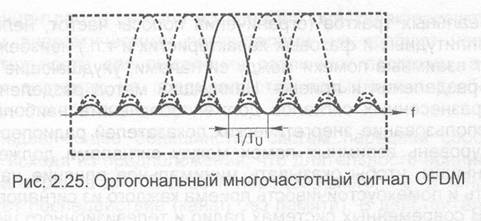
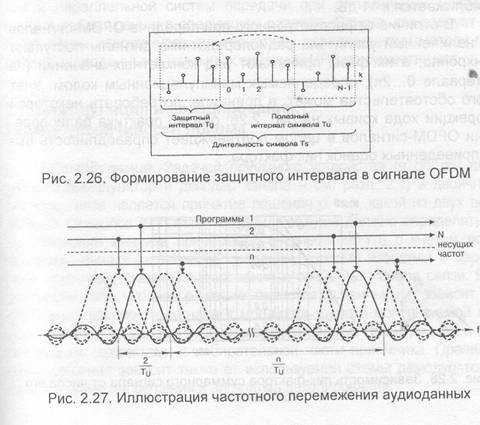
В технической литературе элементарный OFDM-сигнал именуют ОРОМ-символом. Каждый такой символ длительностью Т образуется путем модуляции К несущих. Интервал Т> состоит из двух компонентов: "полезного" интервала Т, во время которого собственно и передаются входные данные, т.е. полезная информация, и защитного интервала т(обозначаемого также Т,). Защитный интервал представляет собой копию, или циклическое повторение части полезного интервала, которая вставляется перед полезным (рис. 2.26) [12]. Так как ОРОМ- сигнал содержит много отдельно модулированных несущих, каждый ОРОМ- символ может, в свою очередь, рассматриваться как разделенный на ячейки, каждой из которых соответствует модуляция одной несущей в течение одного символа.

В традиционных системах с ЧРК используется фильтровый способ разделения несущих. В этом случае полоса занимаемых частот определяется характеристиками разделительных фильтров. Такой способ реализуется проще, однако расчеты показывают [51], что при т„< 0,3 т, система с ортогональным разделением сигналов занимает меньшую полосу частот, чем система с фильтровым разделением. При  = 0,1т, выигрыш достигает 35%. Таким образом, система с большим числом ортогональных несущих позволяет более экономно использовать полосу частот канала. Однако в этом случае, в отличие от ЧРК с фильтровым разделением, требуется обеспечить синхронность передачи по всем несущим, что возможно только при трансляции всех программ в одном "пакете" с помощью одного или нескольких синхронизированных передатчиков.

Уменьшение скорости передачи на каждой несущей, наряду с введением защитного интервала т, обеспечивает весьма высокий стандарт помехоустойчивости системы ОРОМ- сигналов в каналах с памятью. Помехоустойчивость передачи звуковых программ в системах с такими сигналами значительно возрастает также благодаря тому, что использование большого числа несущих позволяет осуществлять перемежение аудиоданных каждой программы по частоте. Это эквивалентно многократному разнесению сигналов по частоте, их многократному дублированию (повторению) в демодуляторе приемника.

В базовых предложениях Европейского союза радиовещания (EBU) 1988 г. [106] для спутникового ЦРВ предусматривалось использование К = 224 несущих, причем каждую из 16 стереофонических программ планировалось передавать одновременно на 14 несущих (рис. 2.27). В результате такого решения эффективная цифровая скорость передачи одной стереопрограммы, равная приблизительно 260 кбит/с, трансформируется в величину 18,8 кбит/с- скорость цифрового потока, передаваемого на каждой несущей. Здесь т, = 72 мкс, т = 8 мкс, а длительность полезной части принятого сигнала в демодуляторе составляет Т= 64 мкс, что многократно превышает величину возможной памяти канала — максимальной задержки сигнала при его многопутевом распространении.

Более обстоятельное изучение свойств ОРОМ- сигналов будет предпринято в следующей главе.

k

В заключение анализа общих характеристик методов передачи аудиоданных рассмотрим вопрос о пикфакторе суммарного многочастотного сигнала. Для этого воспользуемся результатами анализа многостанционного доступа с ЧРК (МДЧР) [92].

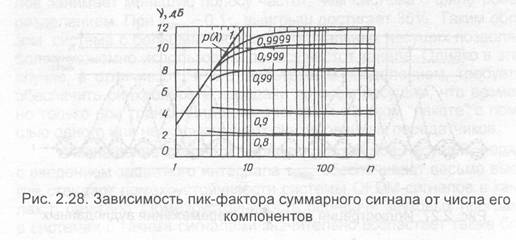
Важным параметром суммарного сигнала является функция распределения мгновенных значений, позволяющая оценить степень и вероятность превышения пиковым уровнем сигнала его среднеквадратического значения. При МДЧР на вход ретранслятора ИСЗ сигналы поступают асинхронно и со случайной фазой, значение которой считают распределенным равномерно на интервале 0...2л. В этом случае пикфактор суммарного сигнала определяется как отношение пиковой мощности Х этого сигнала, не превышаемой с вероятностью р(Х), к средней мощности суммы п гармонических колебаний: v = 2Х'/ п.

Кривые, характеризующие зависимость пик-фактора, определяемого по этой формуле, от числа сигналов, показаны на рис. 2.28. Отсюда следует, что для п»10 с вероятностью р = 0,99 пик- фактор суммарного сигнала не превышает 8 дБ, а при р = 0,999 приближается к 11 дБ.

В отличие от рассмотренного при передаче ОРОМ- сигналов на нелинейный усилитель радиопередатчика сигналы поступают синхронно, а их фазы принимают ряд конкретных значений (на интервале 0...2л), определяемых манипуляционным кодом. Учет этого обстоятельства может, в принципе, потребовать некоторой коррекции хода кривых на рис. 2.28, однако практика радиопередачи ОРОМ- сигналов в целом подтверждает справедливость вышеприведенных оценок пик-фактора.

Отсюда очевидны принципиальные недостатки, свойственные параллельным системам передачи аудиоданных:

- большой (порядка 10 дБ) пик-фактор многочастотного сигнала, зависящий от числа К используемых несущих. Поэтому на отдельную несущую приходится лишь часть пиковой мощности передатчика Р которая всегда меньше отношения Р/ К;

- в силу большого пик-фактора такая система передачи критична к нелинейным искажениям в канале, что ограничивает возможности использования нелинейных режимов усиления в мощных усилителях радиопередатчиков;

- из-за селективных по частоте замираний в многолучевых радиоканалах коэффициенты передачи по отдельным частотным каналам могут существенно различаться, что требует дублирования каналов для уменьшения вероятности потери передаваемой информации;

- аппаратурная реализация параллельного модема весьма сложна даже при использовании современной элементной базы.

О результатах сравнительных исследований последовательной и параллельной систем передачи при оптимальных методах приема пойдет речь и в следующем разделе. Однако, как следует из всего ранее изложенного, альтернативы параллельному методу передачи аудиоданных в наземных системах ЦРВ по существу нет.

2.7. Демодуляция и декодирование. Помехоустойчивость приема

Демодуляция. Задачей приемного устройства (в общем случае это демодулятор и декодер канала — см. разд. 2.1) в двоичной системе связи является принятие решения о том, какой из двух возможных символов (0,1} был передан. Решение должно определяться на основании анализа принимаемого колебания Y(t) с учетом всех предварительных (априорных) сведений, которые известны о характере источника, системе кодирования и свойствах канала связи. Вероятность того, что это решение окажется правильным, зависит от отношения мощности сигнала к мощности шума в используемой полосе частот и от искажений сигнала, вызываемых фильтрацией и не линейными эффектами в избирательной части приемника. Правильность решения зависит также от используемой схемы демодулятора, способа принятия решения и алгоритма декодирования.

Поскольку кодовая последовательность, порождаемая демодулятором, может содержать ошибки, декодер должен осуществлять отображение существенно более сложное, чем кодер — обнаруживать ошибки и исправлять их. Возможность выполнения этих функций связана с избыточностью, искусственно вносимой в передаваемый сигнал в процессе помехоустойчивого кодирования в кодере канала.

В системах с избыточным кодированием демодулятор часто выполняет еще одну функцию, состоящую в передаче декодеру информации о степени надежности оценки каждого символа. Эта информация может быть получена несколькими способами и используемый в каждом случае подход существенно зависит от природы помехи n(t) [41].

Анализируя принятую реализацию случайного процесса Y(t) в течение интервала времени  где т, — длительность элемента сигнала, приемник должен установить, какой из возможных сигналов (8( 1; Sp=-0) присутствует на его входе, и в соответствии с этим принять решение, какой элемент цифровой последовательности (1;О) был передан. Это классическая задача теории связи — задача различения двух сигналов, основным методом решения которой является метод проверки статистических гипотез.

Отсылая далее читателя к статистической теории радиоприема [31, 94, 97, 99 и др.], приведем здесь лишь базовые сведения, необходимые для понимания дальнейшего материала.

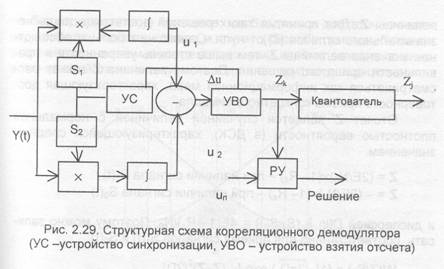
Процедура демодуляции реализуется в оптимальных схемах различения двух детерминированных сигналов либо с использованием корреляционного способа обработки колебания Y(t) (рис. 2.29), либо на основе оптимальной фильтрации с помощью линейных фильтров, согласованных с сигналами.

В обеих схемах результатом обработки в ветвях приема являются напряжения  которые подаются на вычитающее устройство. В результате работы демодулятора формируется множество т.е. последовательность отсчетов разностного напряжения которые в конце каждого интервала анализа т, сравниваются в решающем устройстве (РУ) со значением порога.

— коэффициент взаимной корреляции между сигналами

Величину Z часто называют статистикой, подчеркивая тем самым ее вероятностный характер, определяемый статистическими характеристиками процесса n(t); в рассматриваемом случае модели ДСК — это белый гауссовский шум.

Доказано, что при наблюдении процесса Y(t) отсчет Z содержит всю доступную информацию о сигнале S, необходимую для принятия решения, а функция Z(t) полностью определяет оптимальное (байесово) правило принятия решения в задаче различения двух детерминированных равновероятных сигналов, известных точно. Байесово правило выбора гипотез обеспечивает минимизацию ошибки при выборе решения в пользу того или иного сигнала. Согласно этому правилу, сравнение величины Z с нулем на k- ом интервале анализа (в дискретном симметричном канале) определяет однозначное (жесткое) решение:

 — справедлива гипотеза о приеме сигнала S,;

— справедлива гипотеза о приеме сигнала 8.

Назовем приемником с жестким решением (ПЖР) приемник, построенный в соответствии со схемой на рис. 2.29, где используется байесово правило выбора гипотез (2.11)

— по знаку величины Z. Для принятия таких решений достаточно лишь незначительного отличия Д от нуля. Однако чем больше абсолютное значение величины Z, тем выше степень уверенности в правильности принятого решения. Поэтому величина Z может рассматриваться как информационная мера, характеризующая достоверность приема конкретного символа.

Отсчет Z является случайной величиной с нормальной плотностью вероятности (в ДСК), характеризующейся средним значением:

и дисперсией D ln Х (1'So)] = 4Е(1 — В,)/No. Поэтому можно записать, соответственно для приема сигналов ,(t) и S,(t):

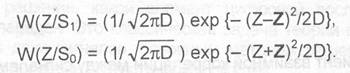
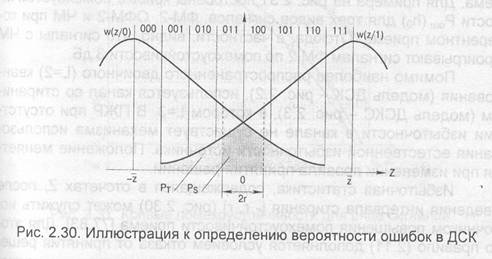
 Плотности вероятности W(Z/$,) и И/(2/,) представлены на рис. 2.30. Здесь левая полуплоскость соответствует области сигнала Sp(t), а правая — области сигнала (1); заштрихованное пространство под кривыми характеризует зону ошибок. Площадь этой зоны, численно равная вероятности ошибок в ПЖР при использовании модели ДСК, определяется соотношением:

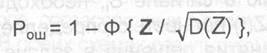
где Ф(*} — интеграл вероятностей (нормальная функция распределений). Отсюда легко получить: Р, = 1- Ф (h,(1 — R,)). Для канала с противоположными сигналами (ФМ-2), когда В = — 1, при использовании корреляционного демодулятора имеем:

Вычисляемая по этой формуле средняя вероятность проема элемента совпала fBER3 р. — основная характеристика помехоустойчивости цифровой системы связи и вещания. Такая характеристика носит групповой вид и показывает значение достоверности приема, среднее для всей информации, передаваемой по каналу за сеанс связи. Для ее вычисления в канале без кодирования, в принципе, необходимо и достаточно знать вид сигнала, модель  и схему (способ) приема. Помехоустойчивость систем с корректирующими кодами зависит помимо этого от свойств используемого кода и алгоритма декодирования.

Соотношение (2.12) показывает, что вероятность ошибок при передаче двоичной единицы информации по каналу с гауссовским шумом полностью определяется величиной энергетического отношения сигнал/шум (ОСШ). Если обозначить среднюю мощность сигнала на интервале времени т, через Рто Е = Р, х т,. Полагая далее, что шумовая полоса приемника М = М где М, — ширина спектра сигнала, получаем:

Здесь М, х т, — база сигнала, а (Р, / Р )— отношение средней мощности сигнала к средней мощности шума на входе приемника в полосе частот М,.

Если для передачи звуковых программ применяют простые (узкополосные) сигналы, база которых М, х т, = 1,0...1,2, то в этом случае (Р, / Р )= h,. В общем случае В- кратной модуляции: Т, = z, х В; Е = В х Е и следовательно, h, = В х h(, Здесь: т, — длительность (время передачи) двоичного символа (бита) с энергией Е б.

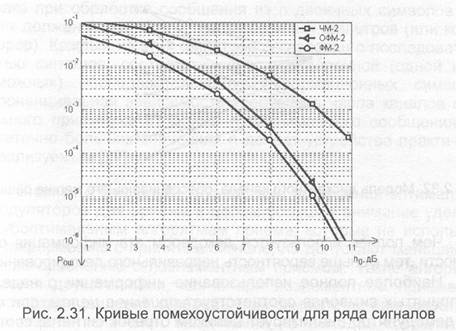
Значение ОСШ, необходимое для обеспечения заданной вероятности ошибки в цифровом канале, зависит от ряда факторов, важнейшие среди которых: методы (вид и кратность) модуляции и демодуляции цифрового сигнала, параметры корректирующего кода и алгоритм его декодирования, а также уровень энергетических потерь, определяемых как методом передачи цифрового сигнала, так и аппаратным запасом на реализацию модема. Для примера на рис. 2.31 построены кривые помехоустойчивости Р, (h p) для трех видов сигналов: ФМ-2, ОФМ-2 и ЧМ при когерентном приеме. Отсюда, в частности, видно, что сигналы с ЧМ проигрывают сигналам ФМ-2 по помехоустойчивости 3 дБ.

Помимо наиболее распространенного двоичного (L=2) квантования (модель ДСК — рис. 2.2), используется канал со стиранием (модель ДСКС — рис. 2.3), в котором L=3. В ПЖР при отсутствии избыточности в канале не существует механизма использования естественной избыточности источника. Положение меняется при изменении правила принятия решений.

Избыточная статистика, содержащаяся в отсчетах Z, после введения интервала стирания [ г, г] (рис. 2.30) может служить источником повышения помехоустойчивости приема [77,83]. Для этого правило (2.11) дополняется условием отказа от принятия решения на интервале — г < Z < г В таком канале со стиранием наименее надежные символы, для которых Д<I rl помечаются как стертые. Ошибки трансформации символов (вероятность их появления Р,) соответствуют пространству решений вне зоны стирания. Изменяя порог г в РУ демодулятора, можно уменьшить вероятность Р, за счет некоторого увеличения вероятности стирания Р.

Естественная избыточность источника может быть использована для повышения помехоустойчивости цифровой передачи сигналов 3B лишь при наличии механизма косвенного (например, нулевая зона) или кодового обнаружения ошибочных отсчетов. Реализуется это путем интерполяции таких отсчетов при незначительном, усложнении демодулятора. Проведенный в работе [83] анализ показал достаточно высокую энергетическую эффективность интерполяции в стирающих каналах без избыточности и с минимальной кодовой избыточностью (проверкой на четность) — выигрыш превышает 3,5 дБ. Введение в канал искусственной кодовой избыточности снижает возможность использования ресурса естественной избыточности источника для повышения помехоустойчивости канала. Однако существует приблизительное постоянство суммарной избыточности, реализуемой в канале для повышения помехоустойчивости, что может быть использовано при выборе методов кодирования для источника и канала и сочетания их объемов.

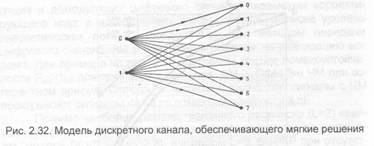
Для повышения помехоустойчивости цифровых каналов связи и вещания часто отказываются от жестких решений в демодуляторе, квантуя напряжение Z на L = 2" уровней при n > 2. Это обеспечивает реализацию мягких решений. В результативна выходе квантователя (рис. 2.29) образуется последовательность чисел 4 (j =1,...,L), которая является цифровым представлением множества (Е к). Если L велико, то этот метод, очевидно, не отличается от непрерывной обработки, т.е. аналогового декодирования. Однако с практической точки зрения желательно сделать квантование относительно грубым. Это уменьшает сложность и стоимость АЦП, а также число двоичных разрядов памяти, необходимых для представления в цифровом устройстве обработки каждого уровня квантования. В современных цифровых системах связи и вещания наиболее часто используют квантование на 4 или 8 уровней. Модель дискретного канала с L=8 приведена на рис. 2.32, а пример разбиения пространства решений на 8 зон показан на рис. 2.30.

Статистику Z называют коэффициентом надежности или сходства, поскольку она в полной мере характеризует надежность приема конкретного элемента сигнала, степень его сходства с образцами сигнала, имеющимися (генерируемыми) в приемнике.

Чем полнее используется декодером эта информация о надежности, тем меньше вероятность неправильного декодирования.

Наиболее полное использование информации о надежности принятых символов соответствует приему в целом, при котором демодулятор анализирует целиком отрезок сигнала, соответствующий, например, п- символьной кодовой комбинации. Такая кодовая комбинация характеризуется определенной избыточностью и, следовательно, взаимосвязями между символами, задаваемыми применяемым кодом. В этом случае принятое решение о приеме того или иного блока кода не может рассматриваться как простая сумма решений по каждому из принятых элементов сигнала. Поэтому при приеме в целом демодуляция и декодирование рассматриваются и оптимизируются как единый процесс, т.е. принятая совокупность элементов сигнала, соответствующая блоку кода, отождествляется с передаваемым отрезком сообщения непосредственно (на аналоговом уровне), минуя стадии по элементной демодуляции и последующего исправления ошибок. Это позволяет избежать потерь информации, возникающих в демодуляторе при регенерации дискретных символов, когда отбрасываются все сведения о величине Z, различных реализаций.

Заметим, что при кодировании без избыточности прием в целом не имеет никаких преимуществ перед поэлементным приемом, поскольку в общем случае здесь отсутствуют межсимвольные корреляционные связи, использование которых в процессе приема и способствует повышению помехоустойчивости.

Таким образом, в системах с избыточным кодированием можно повысить надежность приема, если отказаться от посимвольного приема и демодулировать кодовую комбинацию в целом. Такой метод приема единственно возможен в канале с МСИ.

Однако при обработке сообщения из п двоичных символов приемник должен содержать 2 согласованных фильтров (или корреляторов). Каждый из этих фильтров согласован с последовательностью сигналов, соответствующих определенной (одной из 2" возможных) последовательности информационных символов. Экспоненциальная зависимость требуемого числа каналов оптимального приемника от длины п принимаемого сообщения при достаточно больших значениях п делает устройство практически нереализуемым [77].

В связи с большими трудностями построения оптимальных демодуляторов для приема в целом большое внимание уделяется субоптимальным алгоритмам приема, которые не используют всю информацию о принятом сигнале, но допускают меньшие потери по сравнению с поэлементным приемом. Такие алгоритмы являются двухэтапными, как и при поэлементном приеме. На первом этапе решение о переданном символе не принимается, а запоминаются значения напряжений на выходах корреляторов (или согласованных фильтров), предназначенных для приема различных символов, из которых составляются кодовые комбинации. Эти напряжения несут информацию о степени соответствия принятого сигнала тому или иному символу. Их использование на втором этапе обработки (т.е. при декодировании) характеризует мягкие решения и позволяет получить лучшие результаты Ф о сравнению с поэлементным приемом. Так как выходное напряжение демодулятора обычно квантуется на L ) 2 уровней и представляется числами, то вместо оптимального аналогового обычно используется цифровое (субоптимальное) декодирование. Однако уже при L=8 цифровое декодирование может дать практически же результаты, что и аналоговое.

Среди субоптимальных методов приема, характеризуемых той или иной степенью использования информации о надежности решения и различающихся по помехоустойчивости, сложности реализации и области применения, наиболее известными являются: метод приема по наиболее надежным символам (метод Бородина), декодирование по принципу максимума правдоподобия (алгоритм Витерби), прием со стиранием и оценкой качества, а также ряд других. Среди перечисленных наиболее широко применяется декодирование по алгоритму Витерби с мягким решением, когда информация о надежности символов используется непосредственно. Отказ от жесткого декодирования позволяет в этом случае получить (при L=8) энергетический выигрыш около 2 дБ.

При некотором энергетическом проигрыше оптимальное устройство можно существенно упростить, переходя к поэлементному приему, когда решения принимаются последовательно о каждом очередном переданном символе. В этом случае достоверность приема можно повысить, если при принятии решения о k- ом (по порядку следования) символе х к учесть решения о ранее переданных символах х х ..., что позволяет устранять (компенсировать) помехи, вызванные ранее переданными сигналами. Такой метод называется приемом с обратной связью по решению. При достаточно хороших условиях (в реальных каналах при вероятностях ошибок 10' и менее) такой метод лишь незначительно уступает оптимальному приему в целом [77].

Последовательная (односигнальная) передача сообщений с тактовым интервалом т,/N могла бы снять недостатки параллельной системы (см. предыдущий раздел), но для этого должен быть найден метод (алгоритм) приема, обеспечивающий приемлемую помехоустойчивость при учете МСИ в канале с меняющимися параметрами. В принципе, такой алгоритм существует. Он был разработан Д.Д. Кловским и Б.И. Николаевым еще в конце 60-х гг. прошлого века, однако не получил широкого распространения [42, 60]. Сокращенно алгоритм называется ПЦППР — прием в целом на интервале многолучевости с поэлементным принятием решения. Его реализация основана на поэлементном адаптивном приеме с компенсацией эхо-сигналов от предшествующих посылок с помощью обратной связи по решению, а также на совместной демодуляции и декодировании (что характерно для приема в целом) и использовании системы с испытательным импульсом и предсказанием (СИИП). Алгоритм по своим характеристикам помехоустойчивости близок к алгоритму Витерби.

Сравнительные исследования последовательной и параллельной систем передачи при оптимальных методах приема и одинаковой скорости передачи подмазали [42], что в частотно- неселективном (однолучевом) канале системы энергетически эквивалентны, а в частотно-селективном (многолучевом) канале последовательная система передачи всегда энергетически выигрывает относительно параллельной системы. Так, в частотно- селективном стохастическом канале с релеевскими замираниями энергетический выигрыш последовательной системы передачи растет с уменьшением требуемой вероятности ошибки и с увеличением числа лучей: при Р=10 и числе лучей А=2 для ФМ-2 выигрыш равен 9,6 дБ, а при А=5 он возрастает до 12,8 дБ.

Однако, несмотря на столь убедительные преимущества последовательного способа передачи, последний в системах ЦРВ находит ограниченное применение. Это, видимо, связано с необходимостью больших затрат на доведение последовательного модема до практической реализации на современной элементной базе в высокоскоростных системах передачи, пригодных для эксплуатации в условиях интенсивных МСИ.

Из вышеизложенного ясно, что степень приближения к помехоустойчивости оптимального приема в целом определяется тем количеством информации, которое приемник способен извлечь из совокупности величин Z<, содержащей априорные сведения об источнике информации и апостериорные о свойствах канала. При этом канал без кодирования характеризуется минимальной помехоустойчивостью. В этом случае оптимальным методом приема, обеспечивающим минимальную вероятность ошибок (на бит в среднем), является поэлементный прием с жесткими решениями.

Декодирование. Как отмечалось выше, при приеме в целом число возможных последовательностей на входе двоичного канала растет пропорционально 2". В результате при больших п декодер становится очень сложным, а оптимальное декодирование — практически невозможным. Однако именно при больших п возможно значительное повышение надежности передачи, так как действие шума усредняется на длинной последовательности. Известны две группы методов (алгоритмов) декодирования, позволяющих снизить сложность декодера.

Алгебраические методы декодирования основаны на использовании алгебраических свойств кодовых последовательностей и отождествляются с поэлементным приемом, который по энергетической эффективности уступает приему в целом. Такие алгоритмы являются неоптимальными, поскольку предназначены для исправления конкретных конфигураций ошибок в канале.

Вероятностные методы декодирования значительно ближе к оптимальному приему в целом, так как в этом случае декодер оперирует с величинами, пропорциональными вероятностям, оценивает и сравнивает вероятности различных гипотез и на этой основе выносит решения о передаваемых символах. Как правило, вероятностные методы декодирования используют мягкие решения на выходе демодулятора, когда число уровней квантования каждого канального символа L)2. Обычно L=8, что соответствует

3-битовому квантованию двухполярного символа на входе квантователя на восемь уровней. Таким образом, при мягком решении выход квантователя более точно описывает величину отсчета сигнала с помехой. Это приводит к повышению помехоустойчивости декодирования.

Сверточные коды являются частным случаем блочных линейных кодов. Однако введение сверточной структуры наделяет эти коды рядом дополнительных свойств, которые существенно облегчают его декодирование. Как отмечалось в разд. 2.4, эти коды имеют древовидную (решетчатую) структуру. Каждому ребру древовидной структуры соответствует определенная последовательность, состоящая из m информационных символов. По принятой последовательности для каждого ребра может быть найден его вес — число, характеризующее расстояние от принятой последовательности. Для измерения этого расстояния может быть использована метрика Хэмминга, если в демодуляторе принимается жесткое решение, или евклидова метрика, если декодирование осуществляется по методу максимума правдоподобия [94]. Декодирование сверточных кодов состоит в прослеживании по кодовой решетке того пути, для которого расстояние от принятой последовательности символов имеет минимальное значение. Сверточная структура кода позволяет использовать рекуррентные алгоритмы, существенно упрощающие вычисления этого расстояния.

Типичным алгоритмом декодирования, основанным на использовании вероятностных характеристик принимаемых символов, является максимального правдоподобия (АМП). Декодирование по принципу максимума правдоподобия сводится к задаче отождествления принятой последовательности с одной из 2" возможных, где n — длина информационной последовательности. Решение принимается в пользу той кодовой последовательности, которая в меньшем числе позиций отличается от принятой. Другими словами: декодирование состоит в прослеживании по кодовой решетке (см. разд. 2.4, рис. 2.13) пути с максимальной апостериорной вероятностью.

При больших значениях п АМП практически не реализуем из-за необходимости перебора 2" возможных кодовых последовательностей. Пути уменьшения сложности приемных устройств, реализующих АМП, связаны с поиском соответствующих рекуррентных вычислительных процедур, позволяющих на каждом очередном этапе (при поступлении, например, очередного сигнала анализируемой последовательности), не производя большого объема вычислений, воспользоваться результатами обработки предшествующих сигналов. В частности, используя алгоритм Витерби, основанный на методе динамического программирования, не осуществляя перебора всех 2" последовательностей информационных символов, оказывается возможным к моменту окончания анализируемой последовательности сигналов принять решение сразу о всем переданном сообщении.

Такое приемное устройство может быть реализовано на основе сигнального процессора, функционирующего в реальном масштабе времени.

Ввиду широкого применения "декодера Витерби" во всех современных системах ЦРВ, кратко рассмотрим процедуру декодирования в соответствии с алгоритмом А. Витерби, ориентируясь прежде всего на монографию [41], широко цитируемую в отечественной научной и учебной литературе.

Итак, А. Витерби предложил существенное упрощение процедуры декодирования по АМП. Характерной особенностью его алгоритма является то, что на каждом шаге декодирования запоминается только 2 наиболее правдоподобных путей (здесь К — длина годового регистра сверточного кодера). Заметим, что часто величину К называют длиной кодового ограничения (см. разд. 2.4), хотя под ДКО понимают также и величину v = К-1[4,41].

Периодическая структура решетчатой диаграммы (рис. 2.13) существенно упрощает сравнение и выбор путей при реализации алгоритма Витерби. Из анализа диаграммы следует, что в любой  узел на любом j-  ом такте из начального состояния ведут несколько путей. Каждый из этих путей характеризуется собственной метрикой пути (МП) и каждому из них соответствует определенная кодовая последовательность. Метрика пути есть сумма метрик ветвей (МВ), образующих некоторый путь на решетчатой диаграмме. МВ равна расстоянию Хэмминга между символов на входе декодера и набором символов, соответствующих данной ветви на решетчатой диаграмме. Если, например, на вход декодера поступает пара символов 01, то возможные значения МВ для кода 1/2, К=З с решеткой, изображенной на рис. 2.13, будут МВ(00)=1, МВ(01)=0, МВ(11)=1 и МВ(10)=2.

Путь конечной длины оканчивается в определенном состоянии. Метрика состояния (МС) равна метрике пути, который заканчивается в данном состоянии. Согласно алгоритму Витерби, из всех возможных путей выбирается путь с Наименьшей метрикой. Такой путь называется выжившим. Ему соответствует кодовая последовательность (КП), отличающаяся от принятой в меньшем числе символов. В соответствии с алгоритмом Витерби сравнение и отбрасывание неоптимальных отрезков путей производится периодически на каждом шагу декодирования, а шаг декодирования состоит в обработке декодером принимаемых из канала данных в интервале между двумя соседними уровнями узлов.

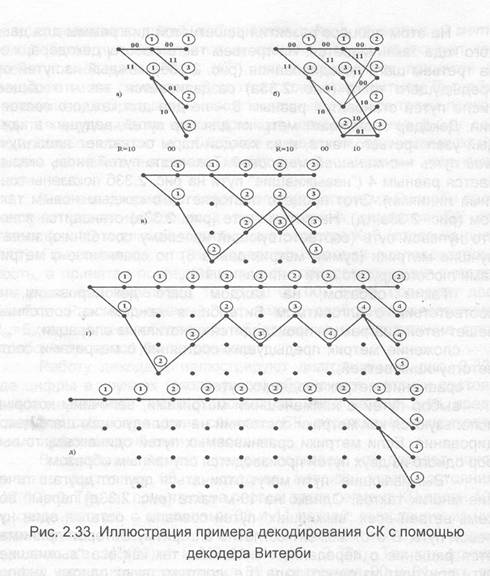
В качестве примера использования алгоритма Витерби рассмотрим развитие процесса декодирования символов СК со скоростью 1/2 и длиной кодирующего регистра К=З (кодер на рис. 2.12). Предположим, что передавалась нулевая последовательность, а принятая последовательность при демодуляции с жестким решением имеет вид 10 00 10 00 0 0 ..., т.е. содержит две ошибки. Рассматриваемый код имеет свободное расстояние dД=5, что должно обеспечить обнаружение и исправление этих ошибок в процессе декодирования.

Работу декодера иллюстрируют диаграммы на рис. 2.33, где цифры в кружках (около узлов) обозначают метрики состояний, а двузначные числа около ветвей, как и на рис. 2.13, представляют собой выходные символы СК, порождаемые приходящими информационными символами.

В начальный момент времени полагаем, что декодер находится в состоянии 00 и исходная метрика этого состояния МС(00)=0. Так как принятый на первом такте сегмент КП равен 10, то сравнивая его с символами 00 и 11 ветвей, выходящих из нулевого узла, определяем, что метрики этих ветвей будут равны единице, т.е. МВ(00)=1 и МВ(11)=1 (рис. 2.33а). Так как других ветвей, входящих из состояния 00 в состояния 00 и 01, нет, то метрики этих состояний принимаются равными метрикам входящих ветвей: МС(00)=1 и МС(01)=1.

Аналогичная картина имеет место и на следующем шаге декодирования, когда из канала (от демодулятора) поступает пара символов 00. Однако на втором такте необходимо рассматривать уже 4 узла, в которые ведут 4 ветви, метрики которых: МВ(00)=0, МВ(11)=2, МВ(01)=1 и МВ(10)=1. Метрики состояний на этом шаге демодуляции определяются теперь как суммы Метрик входящих ветвей с метриками предыдущих состояний: МС(00)=1+0=1, МС(01)=1+2=3, МС(10)=1+1=2 и МС(11)=1+1=2.

На этом процесс развития решетчатой диаграммы для данного кода заканчивается. На третьем такте работы декодера, т.е. на третьем шаге декодирования (рис. 2.336), каждый из путей от предыдущего такта (рис. 2.33а) раздваивается, так что общее число путей становится равным 8 — по два для каждого состояния. Декодер сравнивает метрики для пар путей, ведущих в каждый узел третьего такта, и из каждой пары оставляет лишь лучший путь — с меньшей. Так число путей вновь оказывается равным 4 ("невыжившие" пути на рис. 2.336 показаны тонкими линиями). Этот процесс повторяется с каждым новым тактом (рис. 2.33в,г,д). На пятом такте (рис. 2.33в) становится ясно, что нулевой путь (соответствующий нулевому состоянию) имеет лучшие метрики (сумма метрик равна 8) по сравнению с метриками любого другого пути (они равны 10).

Таким образом, на каждом шаге декодирования, в соответствии с алгоритмом Витерби, в каждом из состояний решетчатой диаграммы производятся однотипные операции:

- сложение метрик предыдущих состояний с метриками соответствующих ветвей;

- сравнение Метрик входящих путей;

- выбор путей с наименьшими метриками, величины которых используются как метрики состояний на последующем шаге декодирования. Если метрики сравниваемых путей одинаковы, то Выбор одного из двух путей производится случайным образом.

"Выживающие" пути могут отличаться друг от друга в течение многих тактов. Однако на 10-м такте (рис. 2.33д) первые восемь ветвей всех "выживших" путей совпали — остался один нулевой путь. В этот момент согласно алгоритму Витерби принимается решение о переданных символах, так как все "выжившие" пути приходят из одного узла (т.е. соответствуют одному информационному символу). Старший бит на пути с наименьшей метрикой является выходным битом декодера. В рассматриваемом примере "выживший" нулевой путь свидетельствует о том, что передавалась нулевая последовательность символов. Таким образом, декодер прослеживает по кодовой решетке путь, имеющий минимальное расстояние от пути, который порождает кодер, т.е. максимально правдоподобный путь. Состояния кодера, через которые проходит этот путь, и определяют последовательность информационных символов.

Мягкое декодирование представляет собой простую модификацию только что изложенной процедуры. Нужно лишь заменить метрику Хэмминга на метрику мягкого решения. Все остальные этапы декодирования не меняются. Таким образом, сложность реализации декодера с мягким решением не сильно отличается от сложности реализации декодера с жестким решением, хотя применение восьми- уровневого квантования выхода демодулятора, как известно, дает выигрыш по сравнению с двухуровневым порядка 2 дБ. Это является важным преимуществом алгоритма Витерби.

Основные трудности при реализации алгоритма возникают из- за того, что сложность декодера экспоненциально растет с ростом величины ДКО, так как число состояний кодера (узлов решетчатой диаграммы) равно 2 . Поэтому значения К, однозначно определяющие ДКО (при заданной скорости кода), должны быть сравнительно небольшими — как правило К < 10, и это приводит к необходимости оптимизации СК.

В начале 70-х гг. прошлого века американскими учеными Е. Велдоном и Д. Чейзом и для блочных кодов были предложены алгоритмы декодирования, использующие мягкое решение демодулятора и позволяющие приблизиться по эффективности к решению по максимуму правдоподобия.

Помехоустойчивость приема и энергетический выигрыш кодирования. Применительно к системам ЦРВ, помехоустойчивость характеризует способность доставить потребителю звуковые программы с субъективно высоким качеством (т.е. без заметных на слух искажений), а также передать без видимых искажений сопутствующие данные, по каналу с высоким уровнем аддитивных и мультипликативных помех. Поэтому должен быть установлен приемлемый уровень ошибок на бит информации, иначе — допустимая остаточная вероятность ошибок после декодирования (Р, )не приводящая к заметным на слух искажениям на аналоговом выходе. Как показано в разд. 2.4, величина (Р )определяется критерием щелчка, чему в канале без кодирования соответствует выполнение условия (2.10).

Уменьшение ОСШ (при заданной величине (Р), достигнутое благодаря кодированию канала, характеризует энергетический выигрыш кодирования q (ЭВК). В конечном счете целью применения кодирования является достижение максимального ЭВК. "Платой" за это является увеличение цифровой скорости передачи RД (2.1) — ввиду необходимости передачи поверочных символов корректирующего кода.

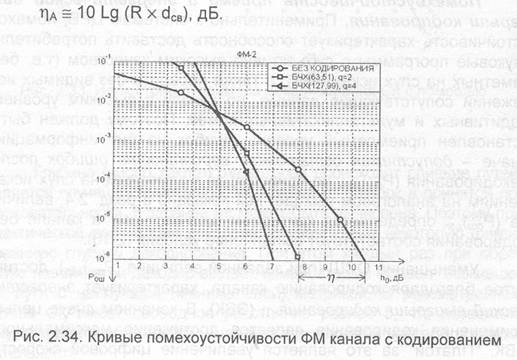
При применении конкретного кода величина ЭВК легко определяется по кривым помехоустойчивости Р, (h p). В качестве примера на рис. 2.34 такие кривые построены для двух вариантов кода БЧХ в канале с ФМ-2 при использовании жестких решений в корреляционном демодуляторе. Определение ЭВК осуществляется относительно кривой помехоустойчивости для ФМ канала без кодирования (R=1), поскольку ЭВК — это разность значений h p при заданной величине (Р ), с учетом кодирования и без него. Из построений следует, что при (Р), =1х10 (63,51)-код, обнаруживающий и исправляющий двукратные (ч=2) ошибки, обеспечивает ЭВК «) = 2,5 дБ, а (127,99) —- код при q=4 — выигрыш q = 3,5 дБ.

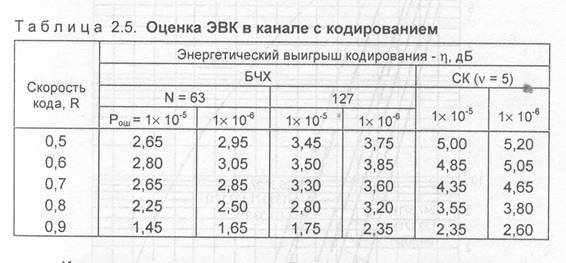
Знание параметров n, k, d блокового корректирующего кода позволяет определить асимптотический выигрыш от кодирования (АЭВК) достигаемый при и обеспечиваемый кодом [41]: Реальный ЭВК (при умеренных значениях ОСШ) составляет приблизительно половину от этой величины. В системах со сверточном кодированием АЭВК может быть найден по формуле [4]:

В качестве примера в табл. 2.5 приведены ориентировочные значения ЭВК, реализуемого в каналах с кодированием, для типовых значений Р, = (Р, )— в предположении использования двух наиболее часто применяемых разновидностей кодов: БЧХ с алгебраическим декодированием и сверточных с декодированием по алгоритму Витерби с мягким решением [79]. Более полные сведения об эффективности кодирования канала с использованием различных кодов можно найти, в частности, в работах [31, 68, 74, 94].

Помехоустойчивость декодирования сверточных кодов. При декодирований в соответствии с АМП ближайшим к передаваемому пути (определяемому информационной КП и структурой кодера СК) будет путь, который отстоит от него на величину, равную d Д. Если в канале передачи произойдут ошибки, кратность которых превысит исправляющую способность кода, декодер АМП выберет ошибочный путь. Это приведет к ошибкам в одном либо нескольких информационных символах на выходе декодера.

Как указывалось выше, свободное расстояние б„является мерой различия двух наиболее близких КП бесконечной длины на выходе кодера и в значительной мере определяет помехоустойчивость системы со сверточным кодированием. Другой важной характеристикой, определяющей помехоустойчивость СК, является спектр его весов — он показывает суммарное количество ошибок на выходе декодера АМП, когда вместо передаваемого пути по решетчатой диаграмме выбираются ошибочные пути, отстающие от него на величину веса d = m [4]. В справочных таблицах СК, помимо свободного расстояния и генераторных полиномов, приводятся спектры весов кодов с различными скоростями. Ясно, что код тем лучше, чем больше у него значение dД, а при одинаковых свободных расстояниях — чем меньше значения соответствующих коэффициентов спектра.

На рис. 2.35 приведены кривые помехоустойчивости для СК со скоростями 1/2, 2/3 и 3/4 в канале с ФМ-2 [4]. Коды заданы порождающими многочленами в восьмеричной форме записи. Наличие кривой помехоустойчивости для ФМ -канала без кодирования (R=1) позволяет легко определить ЭВК по разности требуемых затрат Е/Np при Р, = const. Видно, что при использовании кода (133,171) величина ЭВК достигает 5,4 дБ. Это означает, что в этом случае в канале с ФМ-2 скорость передачи информации понизится в два раза (скорость кода R=1/2), а отношение сигнал/шум, требуемое для достижения Р, = 10, может быть уменьшено на 5,4 дБ.

Анализ кривых помехоустойчивости для коротких СК, декодируемых по алгоритму Витерби с мягким решением (при квантовании выхода демодулятора на восемь уровней), позволяет получить оценку для ЭВК 4...6 дБ. Квантование на четыре уровня снижает ЭВК на 0,7...0,8 дБ, а переход к жесткому решению уменьшает ЭВК примерно на 2 дБ.

Декодирование по критерию максимума правдоподобия с использованием алгоритма Витерби позволяет существенно упростить основное оборудование, реализуя при этом в полной мере высокую помехоустойчивость. Декодирование по методу Витерби особенно перспективно в каналах с независимыми ошибками, а также в системах, где определяющим фактором в большей степени является ограничение мощности, а не полосы частот.

3. ОСНОВЫ ТЕХНОЛОГИИ ЦИФРОВОГО РАДИОВЕЩАНИЯ

Мысль А. Эйнштейна не так уж и парадоксальна. Достаточно ознакомиться с историей появления "примы" современной технологии ЦРВ — системы сигналов СОРОМ. "Связь времен" так же легко обнаружить, переходя к анализу основных технических решений, лежащих в основе технологии современных систем ЦРВ.

Ключевым моментом здесь является правильный выбор модели физического (непрерывного) канала, несмотря на то, что «...большинство моделей основаны на факторе веры» (Р.А. Уилсон). Тем не менее, модель канала — это обязательный атрибут расчета и проектирования любой системы. Важно, чтобы модель максимально точно описывала физические процессы, происходящие в системе при предоставлении услуг ЦРВ в соответствии с их номенклатурой и декларированным качеством. В противном случае при реализации системы не будут достигнуты в полной мере заявленные качественные показатели.

Модель — это всегда упрощение реального мира; применительно к описанию систем ЦРВ, к таким упрощающим допущениям отнесем следующие утверждения:

- приемное устройство считается неискажающим, т.е. при отсутствии помех информация принимается безошибочно;

- система синхронизации в приемном устройстве работает идеально, т.е. позволяет точно устанавливать начало и конец элемента сигнала в принятой последовательности;

- аддитивная помеха, действующая в канале, представляет собой белый гауссовский шум с односторонней спектральной плотностью мощности И,.

3.1. Варианты технической реализации цифрового радиовещания

Высокие потребительские характеристики сети многопрограммного высококачественного цифрового радиовещания определяют сложность реализации таких систем. В частности, это связано с:

- необходимостью обеспечить надежный высококачественный прием не только стационарными, но и мобильными (переносными и установленными на подвижном объекте) приемниками в условиях интенсивной городской застройки и горной местности, т.е. в многолучевом канале с МСИ и частотно-селективными замираниями;

- стремлением обеспечить высокую удельную скорость передачи информации, т.е. высокую эффективность использования отведенной полосы частот;

- ограниченными энергетическими ресурсами, особенно при использовании спутниковых ретрансляторов;

- жесткими ограничениями на сложность и стоимость бытового цифрового приемника.

Данные табл. 3.1 иллюстрируют теоретически возможные варианты технической реализации системы ЦРВ. Каждый из указанных здесь вариантов решения той или иной проблемы цифрового радиовещания имеет свои достоинства и недостатки. Выбор в пользу конкретного технологического решения может быть сделан только на основе анализа технико-экономических показателей с учетом высоких потребительских требований к сети много- программного высококачественного цифрового радиовещания.

Возможно использование разных методов передачи и приема, кодирования сигнала и канала, вариантов организации вещательной сети, других частных решений отдельных подсистем и элементов системы. Однако возможность реализации всех известных систем ЦРВ однозначно определяется достигнутым уровнем частотной (спектральной) и энергетической эффективности радиосистемы передачи (РСП) звукового вещательного сигнала. В свою очередь, частотно-энергетическая эффективность РСП определяется:

- эффективностью процедуры компактного представления звукового вещательного сигнала;

- эффективностью модуляции;

3.2. Разновидности цифровых систем эфирного радиовещания и их сравнительный анализ

Принципиально возможны следующие цифровые системы эфирного радиовещания с приемом как на стационарные, так и на мобильные цифровые радиоприемники:

• системы наземного ЦРВ, подразделяющиеся на системы, работающие на частотах ниже 30 МГц и в диапазонах ОВЧ и УВЧ;

• системы непосредственного (т.е, прямого спутникового) ЦРВ (НЦРВ) с приемом сигнала на бытовой радиоприемник;

• комбинированные системы ЦРВ, содержащие технические средства первых двух систем. В этом случае система ЦРВ может быть реализована так смешанная (гибридная) наземно-спутниковая система (НСС), в которой используется маломощная распределительная сеть для увеличения зоны обслуживания ИСЗ. НСС, как правило, предполагает использование одного и того же частотного диапазона спутниковыми и наземными службами.

В табл. 3.2 представлены сведения об известных в настоящее время (декабрь 2002 г.) системах ЦРВ разных частотных диапазонов и вариантов построения.

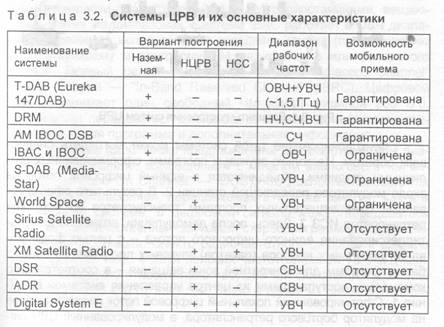
Архитектура системы ЦРВ (в общем случае, комбинированной) представлена на рис. 3.1. Здесь: 1- центр управления системой вещания, 2 — основная станция передачи программ на ИСЗ, 3 — бортовой ретранслятор ИСЗ, 4 — мобильная приемная установка, 5— стационарная приемная установка, 6 — антенны дополнительной наземной сети, где осуществляется переизлучение сигналов ИСЗ.

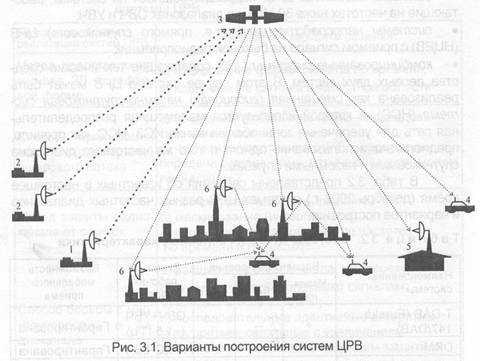
Функционирование такой системы может выглядеть следующим образом. Несколько звуковых программ, сформированных различными студиями, объединяются в единый цифровой поток на входе модулятора передающей станции 2. В результате сформированный банк вещательных программ транслируется на бортовой ретранслятор ИСЗ 3. Здесь, после демодуляции, возможно демультиплексирование единого цифрового потока — с целью формирования локальных наборов (пакетов) звуковых программ из общего банка программ для конкретной зоны вещания — в соответствии с командами, поступающими из центра управления системой вещания 1. Сформированный локальный цифровой поток поступает далее на модулятор бортового ретранслятора, а модулированный СВЧ сигнал излучается затем антенной системой (как вариант — многолучевой) ИСЗ в сторону Земли.

В принципе, любые системы радиовещания можно разделить на две категории:

— системы, требующие для функционирования выделения отдельного частотного диапазона, свободного от других радио- служб;

— системы, для работы которых это не является необходимым условием.

Наиболее совершенной из разработанных ныне систем ЦРВ, относящейся к первой категории, является Eureka 147/ОАВ. Для функционирования этой системы требуется выделение в диапазоне частот от 30 МГц до 3 ГГц полосы частот шириной не менее 1,54 МГц на один комплексный сигнал ЦРВ (так называемый "DAB- блок" или "ансамбль"), который может содержать, например, шесть высококачественных стереофонических программ и различную дополнительную информацию.

Которому категории относятся системы ЦРВ IBAC и IBOC, разработанные в США. Они предназначены для работы в диапазонах ОВЧ 88... 108 МГц и СЧ 525... 1608 кГц — одновременно с существующими аналоговыми ЧМ и АМ радиостанциями, вещающими в этих же диапазонах. Система IBAC работает в ОВЧ диапазоне в режимах использования соседнего канала (по  действующему аналоговому ЧМ радиоканалу) или резервного канала. Первый режим называется "In-Band Adjacent Channel" (IBAC), второй — "In-Band Reserved Channel" (IBRC). Цифровой сигнал занимает один свободный ЧМ канал шириной 200 кГц. В нем могут передаваться с высоким качеством одна звуковая стереофоническая программа и дополнительная информация.

Система IBOC также предназначена для работы в ОВЧ диапазоне, но в канале, совмещенном с каналом аналогового ЧМ вещания ("In-Band On Channel" — IBOC), что дословно переводится как "внутридиапазонная, передаваемая в том же канале". Как и в предыдущей системе, в цифровом сигнале может передаваться одна высококачественная звуковая стереопрограмма и дополнительная информация. Спектр радиочастотного цифрового сигнала располагается либо в двух полосах частот шириной 73,5 кГц каждая, симметрично относительно несущей ЧМ сигнала (на удалении от 126,5 до 200 кГц от несущей), либо в одной из боковых полос— верхней или нижней.

Система ЦРВ АМ IBOC DSB, предназначенная для радиовещательных диапазонов, где традиционно используется амплитудная модуляция, по утверждению разработчиков, гарантирует передачу стереофонических программ с качеством, близким к качеству звучания компакт-диска. При этом используется АМ радиопередатчик, передача ведется в одном канале с такой же аналоговой монофонической программой, причем уровень цифрового сигнала устанавливается на 25 дБ ниже уровня передачи аналогового сигнала.

С целью проведения сравнительного анализа технических возможностей и характеристик различных систем ЦРВ в 1995- 1996 гг. в США под эгидой Ассоциации электронной промышленности были проведены их лабораторные и полевые испытания.

Испытаниям были подвергнуты системы ЦРВ четырех типов, разработанные в течение последних нескольких лет: Eureka 147/DAB, IBAC,ВОС, а также система VOA/JPL (ITU-R System В), предназначенная для непосредственного спутникового вещания в диапазоне частот 2310...2360 МГц (эта система не включена в табл. 3.2, поскольку она так и не вышла из стадии испытаний). При тестировании оценивались: совместимость с другими (цифровыми и аналоговыми) системами, устойчивость приема сигналов в разных приемных ситуациях, качество звуковоспроизведения и возможность передачи данных. По результатам проведенных испытаний были сделаны следующие общие выводы.

1. Системы типа IBOC обладают рядом фундаментальных недостатков:

• отсутствие устойчивости к помехам, вызванным многолучевым распространением сигналов (что делает эти системы непригодными для пользователей на подвижных объектах или в любых других местах, где возможен прием отраженных сигналов);

• неприемлемое ухудшение параметров сигнала ведущей ЧМ радиостанции, что приводит к несовместимости данной системы с существующими радиовещательными ЧМ приемниками (а их общее число у потребителей достигает десятков миллионов единиц).

Общим недостатком для систем IBOC и IBAC является наличие взаимных помех между цифровыми и аналоговыми сигналами, передаваемыми в пределах ОВЧ диапазона 88... 108 МГц в одних и тех же или близко расположенных каналах. Это приводит к невозможности для указанных систем удовлетворительно работать при существующем распределении частот, а также усугубляет их несовместимость с ЧМ приемниками. Учитывая эти недостатки, комиссия сделала вывод о непригодности систем для организации высококачественного цифрового звукового вещания.

2. Система непосредственного спутникового вещания VOA/JPL также обладает низкой устойчивостью к помехам, вызванным многолучевым распространением сигналов. Кроме того, эта система не обеспечивает возможность приема сигналов в отсутствии прямой видимости между приемной антенной пользователя и ИСЗ при наличии блокирующих препятствий (зданий, деревьев, холмов и т.д.). Эти недостатки обусловливают непригодность данной системы для обслуживания пользователей, находящихся, например, в движущихся автомобилях в городских условиях, в лесу или в горах.

3. На основании проведенных испытаний экспертная комиссия сделала следующий общий вывод: из всех тестируемых систем только "Eureka 147/DAB" обеспечивает те параметры качества звучания и устойчивости приема сигналов, которые радиослушатели ожидают от новой службы цифрового звукового радиовещания. Эта система не имеет достойных конкурентов, завоевала широкое признание и внедряется не только в европейских, но и во многих других странах мира.

3.3. Типовая функциональная схема системы ЦРВ

Несмотря на разнообразие возможных вариантов построения систем ЦРВ (спутниковые, наземные, кабельные), можно выделить типовую структуру трактов формирования, передачи и приема сигналов ЗВ (рис. 3.2: а — передающая часть системы; б- приемная часть). В зависимости от варианта построения системы, используемого диапазона частот и количества передаваемых в одном блоке звуковых программ меняются методы преобразования, кодирования и модуляции сигналов. Рассматриваемая здесь типовая схема будет в дальнейшем (главы 4 и 5) уточнена на примерах конкретных систем.

Сигналы ЗВ, поступающие в тракт формирования в аналоговой форме, подвергаются аналого-цифровому преобразованию (АЦП). Звуковые программы, поступающие в тракт формирования в цифровой форме, как правило, имеют частоту дискретизации (ЧД)

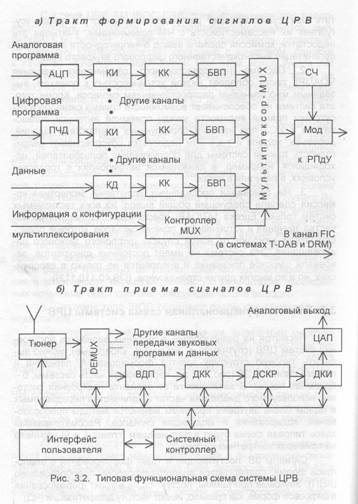
48 или 44,1 кГц. Частота 48 кГц является стандартной для цифровой студийной аппаратуры, используемой при подготовке программ ЗВ. Если же используются CD-фонограммы, то ЧД, равная 44,1 кГц, преобразуется в преобразователе частоты дискретизации (ПЧД) к номинальному значению, принятому в конкретном варианте построения системы ЦРВ.

Далее цифровые сигналы звуковых программ и данные подвергаются индивидуальному кодированию соответственно в кодерах источника (КИ) и кодере данных (КД). В современных версиях систем ЦРВ используются кодеки источника с устранением избыточности. Высокоэффективные алгоритмы сжатия таких кодеков (в частности, система MUSICAM) обеспечивают многократное сжатие звуковой информации при сохранении субъективно высокого качества передачи звука (см. разд. 2.2).

Следующим этапом обработки компактно представленных сигналов звуковых программ и данных является их канальное преобразование: скремблирование, помехоустойчивое кодирование и перемещение по времени. Хотя различные схемы кодеров канала (КК) очень непохожи друг на друга, все они характеризуются использованием значительного объема дополнительных, или избыточных, символов. Кодеру канала в системах ЦРВ всегда сопутствует блок временного перемежения (БВП), предназначенный для преобразования пакетов ошибок (декорреляции ошибок) в канале с замираниями в одиночные ошибки. Канальное кодирование предваряет скремблирование индивидуальных цифровых потоков. Основная цель этой процедуры — превратив цифровой сигнал в квазислучайный, облегчить решение задач синхронизации (см. разд. 2.4).

Полученные в результате индивидуального кодирования цифровые потоки звуковых программ и данных подвергаются третьему этапу обработки, включающему мультиплексирование, а также системную организацию и управление. Так, чтобы обеспечить синхронизацию приемника, парциальные цифровые потоки, поступающие на главный служебный мультиплексор (MUX), собираются в циклы определенной длительности (фреймы) с определенной последовательностью составных частей. Каждой звуковой программе, передаваемой по каналу передачи звуковых сигналов, или информации, передаваемой по каналу данных, соответствует свой временной интервал во фрейме.

Работой мультиплексора управляет контроллер MUX, причем режим мультиплексирования может при необходимости изменяться в соответствии с заданной программой. В системах

Т-DAB и DRM, чтобы обеспечить минимальную задержку доступа к передаваемым сигналам при их приеме, точная информация о текущем режиме мультиплексирования (например, данные для выбора требуемой программы) передается по каналу быстрой информации (FIC). В этом канале данные не подвергаются перемежению и потому не претерпевают задержки.

Следующим этапом является формирование сигнала ЦРВ, предназначенного для последующей передачи в эфир. В самом общем случае для этого необходимы модулятор (Мод) и синтезатор частоты (СЧ). Как уже отмечалось, в перспективных наземных системах ЦРВ применяется уплотнение с ортогональным частотным разделением кодированных сигналов — модем СОРОМ.

В системах НЦРВ, не использующих модем СОРОМ, сформированный из звуковых программ и дополнительной информации групповой поток поступает непосредственно на модулятор. Как правило, в таких системах используется дифференциальная квадратурная ФМ (ОФМ-4). Поэтому фазовую модуляцию должна предварять процедура перекодирования (дифференциального Кодирования) цифрового потока (см. разд. 2.5).

С выхода модулятора сигналы ЦРВ поступают в тракт радиопередающего устройства (РПдУ), где усиливаются по мощности и излучаются в эфир в выделенной для вещания полосе частот.

В тракте приема сигналов ЦРВ (рис. 3.26) выполняются операции обратные тем, которые выполнялись в тракте передачи. Сигнал, принятый антенной, поступает на вход тюнера, который обеспечивает выделение сигналов определенного диапазона частот, их усиление, преобразование по частоте и фазовую и дифференциальную демодуляцию суммарного потока. С выхода демодулятора тюнера цифровой поток демультиплексируется (DEMUX) на ряд компонентных потоков, каждый из которых последовательно претерпевает временное деперемежении (ВДП), коррекцию ошибок в декодере канала (ДКК) и дескремблирование (ДСКР). Данные с выхода этого блока обрабатываются в декодере источника (ДКИ), а в канале данных — в декодере данных. Восстановленные ИКМ- отсчеты передаваемой программы поступают далее на цифроаналоговый преобразователь (ЦАП) для преобразования в звуковые монофонические или стереофонические сигналы.

Приемник обеспечивает одновременное декодирование более чем одной канальной компоненты многопрограммного группового цифрового потока, например, звуковой программы параллельно с сервисной информацией.

Системным контроллер приемника взаимодействует с интерфейсом пользователя и управляет приемником в соответствии с командами пользователя и информацией, сопутствующей передаче звуковых программ, или поступающей по каналу FIC (в системах Т-DAB и DRM). [4,17,19,44,49,57,84,113-115]

3.4. Условия приема сигнала, характерные для разных систем ЦРВ

Проанализируем условия приема сигналов от радиопередатчика ЦРВ в конкретных пунктах зоны обслуживания. Вне зависимости от того размещается передатчик на ИСЗ или на Земле, можно выделить три характерных варианта приемных ситуаций, возникающих, в том числе, и при приеме на подвижном объекте (ПО). Их различие определяется способом формирования электромагнитного поля (ЭМП) в точке приема, а именно:

• вариант А — непосредственный прием (в условиях прямой видимости при отсутствии отраженных лучей) от спутникового или наземного ретранслятора либо от обоих одновременно. Такие условия приема характерны для относительно ровной открытой местности (схематично это показано на рис. 3.1) — при приеме на стационарную (направленную) антенну или слабонаправленную, установленную на ПО;

• вариант Б - непосредственным прием в условиях многолучевости — при наличии прямого луча (хотя бы от одного из ретрансляторов) — рис. 3.3а. Здесь и далее подразумевается прием на антенну с круговой диаграммой направленности;

• вариант В — прием в поле отраженных лучей — в условиях экранировки прямых лучей препятствиями. Такая ситуация сложилась для автомобильного приемника на рис. 3.36 — по отношению к спутниковому ретранслятору. Здесь же показан дополнительный ретранслятор "подсветки", ретранслирующий спутниковый сигнал для локальной микрозоны и обеспечивающий в ее границах прием по варианту А или Б.

Здесь уместна следующая иллюстрация. Некий ПО движется по открытой местности, затем въезжает в малоэтажный пригород и, наконец, попадает в район города с многоэтажной застройкой. В соответствии с этой схемой на первом участке условия приема благоприятные — прием типа А, на втором участие слабая многолучевость при наличии прямого луча — как правило, прием типа Б, на третьем участке интенсивная многолучевость — преимущественно прием типа В. Заметим, что искусство планирования наземной сети вещания проявляется, в частности, в том, чтобы свести к минимуму участки, характеризующиеся приемом типа В.

Возможности реализации варианта НЦРВ, предполагающего непосредственный прием спутникового сигнала наземным приемником, ограничены условием прямой видимости ИСЗ в течение всего времени приема (т.е. пользования услугой ЦРВ). Очевидно, что условия распространения радиоволн в месте нахождения приемника зависят, прежде всего, от углового расположения приемника относительно ИСЗ и от характера окружающей среды, в которой работает приемник. Так, потери, возникающие при прохождении радиоволн внутрь здания, могут быть решающим фактором, поскольку затухание может превышать 20 дБ. Ослабление сигнала листвой деревьев достигает 12 дБ (рис. 3.4). Поэтому может оказаться экономически неэффективным решение создать удовлетворительное отношение несущая/шум и, следовательно, обеспечить высокое качество услуги непосредственно в спутниковой системе.

Таким образом, требование обеспечения высокого качества радиоприема на мобильном объекте 4 (рис. 3.1) в системе НЦРВ трудно достижимо, что объясняется низкой надежностью приема при отсутствии видимости спутника и затенении в городских условиях, на пересеченной и лесистой местности, а также при расположении приемника в высоких широтах (для значительной части России). В то же время прием на стационарную установку 5 (рис. 3.1) или на направленную антенну наземного ретранслятора А A (рис. 3.36) не вызывает никаких трудностей и давно реализован (системы цифрового радио DSR, ADR и другие — см. табл. 3.2).

Ясно, что обеспечить надлежащее качество услуги в полной мере возможно лишь в рамках комбинированной НСС ЦРВ, т.е. если использовать определенное количество маломощных наземных ретрансляторов, которые необходимо дополнительно установить для обеспечения приема сигналов ЦРВ в местах сильного затенения ИСЗ и слушателям в многоэтажных жилых домах. Именно по такому пути пошли американские и японские специалисты, разворачивая системы Sirius Satellite Radio и ХМ Satellite Radio и соответственно Digital System Е. Компания World Space, организовав спутниковое вещание в L-диапазоне (1,5 ГГц), обеспечила некоторые возможности непосредственного приема сигнала на ПО.

3.5. Радиоканалы и их модели в системах ЦРВ

Наибольший интерес при анализе работы любой радиосистемы передачи информации представляет непрерывный (физический) канал (рис. 2.1), включающий в свой состав технические средства, расположенные между выходом модулятора (т. Б) и входом демодулятора (т. В). Проходя по непрерывному каналу связи, сигнал претерпевает ряд изменений. Эти изменения сводятся к ослаблению, искажению сигнала и наложению на него помех. Искажения сигналов и помехи в реальных каналах связи весьма многообразны. Тем не менее математическая модель канала должна по возможности точно описывать основные особенности реального канала и в то же время быть достаточно простой для получения конечных результатов при анализе и синтезе систем передачи. Рассмотрим модели каналов, наиболее пригодные для расчета и проектирования различных вариантов систем ЦРВ.

Идеальный канал без помех вносит детерминированные искажения, связанные с изменением амплитуды (коэффициента передачи р) и временного положения (запаздывания т) сигнала. Переданный по такому каналу сигнал может быть полностью восстановлен на приемной стороне в новом временном отсчете.

Канал с аддитивным белым гауссовском шумом (АБГШ) представляет собой идеальный канал, в котором на сигнал накладывается помеха:

Y(t) = p(t)S(t — x) + n(t).

Коэффициент передачи ц и запаздывание т постоянны и известны в точке приема. Такая модель, например, соответствует радиоканалам, работающим в пределах прямой видимости. Очевидно, что именно такой моделью следует пользоваться при расчетах спутниковых систем вещания — систем НЦРВ, когда прием осуществляется на направленную (стационарную) антенну.

Гауссовский канал с неопределенной фазой сигнала отличается от предыдущего тем, что фаза несущего колебания в точке приема предполагается случайной с плотностью распределения в(0) в интервале л < О < л. Эта неопределенность вызвана

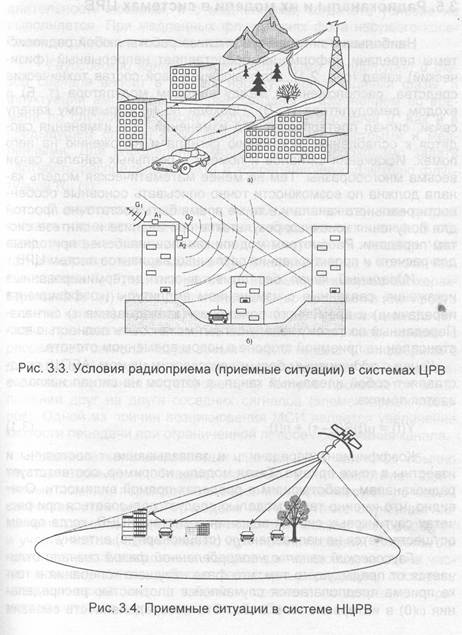
либо отсутствием устройств оценки и предсказания фазы, либо ошибками в оценке фазы при их работе. Важно знать скорость флуктуации фазы. В дискретных системах различают каналы с быстрыми флуктуациями, когда интервал их корреляции меньше длительности посылки, и с медленными, когда это условие не выполняется. При медленных флуктуациях фаза несущего колебания за длительность посылки практически не изменяется.

Гауссовской канал с неопределенными амплитудой и фазой сигнала вносит в сигнал, наряду с флуктуациями фазы, и флуктуации амплитуды, которые связаны с изменением во времени по случайному закону коэффициента передачи р. Как и в предыдущем случае, флуктуации могут быть быстрыми и медленными. Для определения модели канала необходимо задать плотность распределения а(ц) и корреляционную функцию флуктуации Rp, (т).

В гауссовском канале с линейными искажениями форма сигнала изменяется из-за наличия избирательных цепей. В общем случае линейные искажения носят случайный характер. Частотная характеристика канала К(со, t) неравномерна в полосе частот сигнала F,=F, и изменяется во времени, а импульсная характеристика h (t) имеет длительность т(время памяти или просто память канала), превышающую величину 1/F,. Такая модель полезна при анализе систем, использующих, например, каналы с рассеянием сигнала. Когда время памяти канала т соизмеримо с длительностью сигнала т. (а тем более превышает ее), имеет место межсимвольная интерференция, которая проявляется в наложении друг на друга соседних сигналов (элементарных посылок). Одной из причин возникновения МСИ является увеличение скорости передачи при ограниченной полосе пропускания канала.

Реальные каналы наземных систем ЦРВ являются обычно нестационарными и обладают памятью. В них действуют аддитивные помехи, порождаемые внешними источниками, по своим свойствам отличаемые от модели АБГШ, а также случайные искажения сигнала. Виды помех и искажений весьма разнообразны, и учесть все их одновременно при проектировании системы не представляется возможным. Однако для каждого диапазона частот можно указать наиболее характерные ситуации, составить математическую модель канала и провести оптимизацию параметров сигналов и алгоритмов их обработки.

Характер принимаемого радиосигнала (и, следовательно, качество радиоприема) определяется пространственной cmpyкmypoй уровней электромагнитного поля в точке приема. В свою очередь структура ЭМП зависит от трассы, по которой распространяются радиоволны от антенны передатчика к антенне приемника (см. разд. 3.3).

Реальные радиоканалы можно условно разделить на две группы: каналы с прямой волной, когда существует прямая видимость между передатчиком и приемником, и каналы с отраженно-рассеянной волной, когда прямая видимость отсутствует и связь обеспечивается за счет рассеивания и переизлучения энергии сигнала в среде распространения. Каналы второй группы являются каналами со случайными параметрами. В зависимости от условий работы (город, горная или равнинная, открытая или лесистая местность) и параметров линии передачи (состояние среды, дальность связи, характеристики антенн и т.д.) каналы первой группы иногда ближе к каналам с постоянными параметрами, а при мобильном приеме — к типичным каналам со случайными параметрами. В последнем случае пространственная структура уровней ЭМП при наличии объектов, препятствующих свободному распространению радиоволн, может, в первом приближении, рассматриваться в виде совокупности мокроструктуры и макроструктуры. Наличие этих структур проявляется в изменении условии проема в процессе перемещения мобильного приемника, что приводит к случайным изменениям уровня сигнала на его входе. При определенных условиях сигнал на входе приемника испытывает глубокие (до 40 дБ и более) замирания (фединг), вследствие чего на некоторых интервалах времени качество приема может резко ухудшиться.

Хотя практически все каналы обладают свойством рассеивать во времени передаваемый сигнал, во многих случаях этим свойством можно пренебречь. Борьба с последствиями временного рассеяния вырастает в реальную проблему в том случае, когда они начинают сказываться на качестве демодуляции [60].

Упрощенно модели каналов с учетом среды и условий приема можно представить в виде последовательно- параллельного соединения пассивных линейных четырехполюсников (рис. 3.5), учитывающих разные стороны процесса распространения радиоволн в общем случае мобильного приема радио- сигналов.

Первый четырехполюсник определяет ослабление сигнала при свободном распространении в идеальной среде. Его можно рассматривать как последовательное соединение аттенюатора и линейного фильтра с равномерной частотной и линейной фазовой характеристиками на вceх частотах. Ослабление сигнала здесь зависит только от дальности связи и характеристик приемной и передающей антенн. Форма сигнала на выходе этого четырехполюсника остается такой же, как и на его входе, меняется только уровень сигнала. Учтя действие аддитивных помех, которые, как правило, аппроксимируются белым шумом, приходим к модели канала с АБГШ, описываемого уравнением (3.1).

Второй четырехполюсник отражает макроструктуру уровней ЭМП, учитывая медленные колебания уровня прямого сигнала из-за ослабления листвой деревьев и небольшими сооружениями. Следствием такого ослабления является медленное изменение среднего уровня мощности принимаемого сигнала, которое может быть аппроксимировано логарифмически-нормальным распределением. Модель канала, включающая первый и второй четырехполюсники, достаточно полно характеризует условия мобильного приема сигнала спутникового ретранслятора на открытой местности с одноэтажными строениями и углом возвышения спутника не менее 20... 30'.

Параллельные четырехполюсники в рассматриваемой упрощенной модели учитывают сравнительно быстрые случайные изменения (флуктуации) принимаемого сигнала, что приводит к соответствующим замираниям сигнала на входе приемника. Эти явления свойственны микроструктуре уровней ЭМП. Они характеризуют условия приема в городах с различной интенсивностью застройки, этажностью зданий и рельефом местности и связаны с многолучевым распространением и рассеянием радиоволн на неоднородностях среды распространения.

Вследствие разности хода лучей, приходящих от передатчика к приемнику, сигнал в приемной антенне представляет собой сумму отдельных колебаний с различными фазами и амплитудами. Интерференция этих колебаний в условиях, когда разности хода лучей не остаются постоянными, и является основной причиной флуктуации как амплитуд, так фаз составляющих сигнала. Для количественной оценки многолучевого распространения используется понятие памяти канала (т, — интервал рассеяния сигнала во времени — см. выше). Обычно память канала определяется максимальным временем взаимного запаздывания лучей. Средние значения памяти канала составляют для города 1,5...2 мкс (хотя для ряда городов-мегаполисов эта оценка возрастает в 5...8 раз), для пригорода — 0,5 мкс, для сельской местности (при слабом затенении деревьями) — порядка 0,2 мкс.

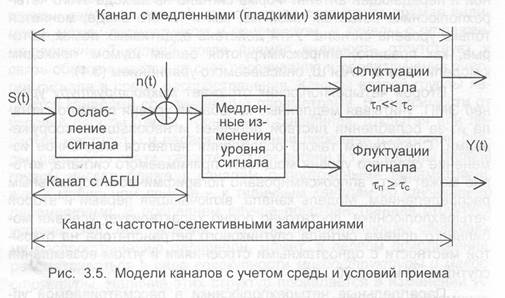
Приходящий сигнал отличается от переданного случайным коэффициентом передачи ц и случайным сдвигом фазы О. Изменения ц и О во времени можно характеризовать коэффициентом корреляции, который обычно определяется экспериментально. Используют понятие времени корреляции (средний период замираний) т. В зависимости от соотношения между длительностью элемента сигнала т памятью канала временем корреляции коэффициентов передачи т, могут быть три типичных случая [99]:

• медленные замирания с короткой памятью.

• медленные замирания с длинной памятью

• быстрые замирания с короткой памятью

В большинстве случаев реальных радиоканалов (исключение составляет мобильный прием в городах с интенсивной многоэтажной застройкой и в горной местности) имеют место медленные замирания, когда выполняется неравенство. Медленные замирания с короткой памятью обычно обусловлены относительно небольшими изменениями рельефа местности на пути распространения. Как правило, они не изменяют форму посылок сигнала. Такой канал называют каналом с общими (или гладкими) замираниями (см. рис. 3.5).

Для анализа условий передачи информации в канале с замираниями нужно знать распределение вероятностей случайных величин, и и О. Многочисленные экспериментальные данные показали, что коэффициент передачи, и достаточно точно подчиняется обобщенному распределению Релея (распределению Райса) с одномерной плотностью

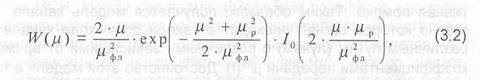
где  — регулярная составляющая коэффициента передачи, — среднее значение квадрата флуктуирующей части коэффициента распространения и, — среднее квадратичное значение коэффициента передачи и,, — функция Бесселя первого рода нулевого порядка. Сдвиг фазы в этом случае распределен неравномерно. Его плотность вероятности имеет максимум при 0 равном 0.  Обычно используется характеристический параметр распределения Райса, вводимый соотношением а =и

Плотность распределения амплитуд сигнала в антенне мобильного приемника в сильной степени зависит от соотношения регулярной и случайной составляющих, т.е. от величины параметра а. При большой амплитуде регулярной составляющей (а'>10), т.е. в условиях распространения прямой волны в пределах прямой видимости, плотность распределения амплитуд стремится к нормальному закону (а модель канала — к каналу с АБГШ), а при а —  0 (при затенении приемных антенн строениями и деревьями)— к распределению Релея, соответствующему предельному случаю наиболее глубоких флуктуаций:

Сдвиг фазы имеет равномерную плотность вероятности на интервале от 0 до 2л. Такие замирания называются релеевскими.

При мобильном приеме канал, как правило, характеризуется длинной памятью. Такой канал называют каналом с частотно-селективными замираниями (рис. 3.5). Одной из возможных моделей канала с частотно-селективными замираниями является модель многолучевого распространения (рис. 3.6). Она содержит линию задержки с ограниченной полосой пропускания на время т с отводами через т. Напряжения, снимаемые с отводов, умножаются на v(1), затем суммируются и к ним добавляется аддитивная помеха. Таким образом, получается модель канала, согласно которой сигнал проходит от входа до выхода канала по различным путям (лучам) с различными зависящими от времени коэффициентами передачи р(0 Достоинство этой модели в том, что в каждом отдельном луче коэффициент передачи зависит только от времени, а не от частоты. Частотная зависимость возникает здесь лишь в результате интерференции при суммировании лучей.

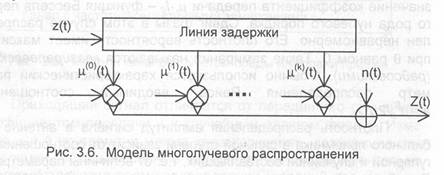
3.6. Характерные искажения сигналов в радиоканалах систем ЦРВ

Характер искажений сигнала в реальном радиоканале зависит от стабильности параметров канала и от соотношения параметров сигнала и канала. Для сигналов такими параметрами являются несущая частота f Д, ширина спектра F, и длительность посылки т а для канала — вид рассеяния сигнала, память т и скорость изменения параметров. В свою очередь параметры канала зависят от условий приема.

Типичным для распространения радиоволн метрового (ОВЧ) и дециметрового (УВЧ) диапазонов является тот факт, что радиоволны попадают на приемник несколькими путями (лучами) — не только по прямой, но и в виде отраженных лучей с запаздыванием по времени (рис. 3.3а). На прохождение радиоволн влияет окружающая приемник местность, наличие на трассе препятствий, ослабляющих и (или) изменяющих направление распространения радиоволн. Наличие этих препятствий проявляется в изменении условий приема вследствие интерференции прямого и отраженных лучей, что в определенных условиях проявляется в виде МСИ. Между сигналами, имеющими различные задержки, возможно возникновение корреляции, если сигналы недостаточно разделены по частоте. В результате замирания становятся частотно-зависимыми ( селективными). Разнос частот, при котором может проявиться такая корреляция, получил название полосы когерентности или полосы корреляции В,. Полоса корреляции сильно зависит от особенностей среды в месте приема. Измерения в городе дают для В, величину порядка 1 МГц.

Качественный прием в канале с частотно-селективными замираниями представляет собой основную проблему мобильного приема сигналов ЦРВ. Некоторого улучшения здесь можно достигнуть, используя хорошую антенну, но учитывая тенденцию  простым антеннам для всех типов приемников, это не привлекательно с коммерческой точки зрения.

Радиоканал, работающий в условиях прямой видимости (прием типа А), характеризуется тем, что коэффициент передачи канала и запаздывание сигнала в нем постоянны и известны в точке приема (см. разд. 3.4). В этом случае цифровому каналу соответствует модель ДСК и он полностью описывается средней вероятностью ошибок на информационный символ Р,, которая является функцией ОСШ на входе демодулятора приемника.

О памяти канала и, следовательно, о возможности возникновения МСИ имеет смысл говорить лишь тогда, когда память канала т, соизмерима с длительностью посылки т,. В противном случае (т.е. в ДСК) канал искажений не вносит, так как все рассеянные во времени сигналы складываются без относительных задержек практически синфазно.

Таким образом, при т, межсимвольными искажениями можно пренебречь, а характер искажений дискретных сигналов, передаваемых по такому каналу, будет определяться значением произведения F т а именно: для простых (узкополосных) сигналов (напомним, что сигнал является узкополосным, если F= 1/т,) будем иметь однолучевый канал с общими (относительно медленными) замираниями, а для сложных (широкополосных) сигналов, когда— многолучевый канал с селективными замираниями, при которых спектр сигнала изменяется. Как правило, канал с общими замираниями — это канал с АБГШ с неопределенной амплитудой и фазой сигнала. Хотя скорость изменения коэффициента передачи такого канала мала по сравнению со скоростью передачи посылок, но тем не менее достоверность принимаемых символов меняется во времени в зависимости от коэффициента передачи канала. Глубина замираний зависит от приемной ситуации: при приеме типа Б (см. разд. 3.3) характер замираний описывается законом Райса, а в приемной ситуации типа В — законом Репея. Поэтому наиболее глубокие и интенсивные замирания называют репеевскими.

При частотно-селективных замираниях амплитуда сигнала на некоторых частотах увеличивается, в то время как на других— уменьшается. Интенсивность этих изменений сигнала существенно зависит от того, перемещается ли приемник, или он неподвижен относительно источника излучения, а степень искажения сигнала от частотно-селективных замираний определяется его полосой. Так, если передаваемый сигнал и относится к части диапазона частот, который подвергается существенным ослаблениям, то это будет проявляться так спады и подъемы амплитуды сигнала на частотной характеристике вокруг наблюдаемой частоты. Также будут наблюдаться значительные изменения в фазовом отклике, которые затронут все системы, использующие фазовую модуляцию. Таким образом, если полоса сигнала F, < В, то существует вероятность, что сигнал будет подвержен в некоторых случаях сильному частотно-зависимому ослаблению.

Широкополосным сигнал, занимающий полосу частот большую, чем полоса корреляции, будет подвержен большим искажениям. Однако суммарная мощность сигнала будет подвержена меньшим изменениям — даже в условиях многолучевого распространения. Следовательно, трудности приема в многолучевом канале с селективными замираниями могут быть в значительной степени преодолены при использовании системы широкополосной модуляции.

Для выполнения конкретных расчетов помехоустойчивости цифровых каналов звукового вещания необходимо располагать статистикой группирования ошибок в реальном канале. Для получения количественных оценок нередко используют модель ДКП (см. разд. 2.1), в которой распределение длительности пакета подчиняется закону Пуассона:

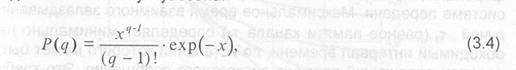
где q — кратность ошибок в канале; х — параметр распределения. Анализируя особенности прохождения сигналов в реальных радиоканалах, обратим внимание еще на два возможных источника появления искажений. Первый связан с фактом изменения плоскости поляризации радиоволн при их отражении: если передатчик излучает волны с определенной поляризацией (линейной или круговой), то в условиях интерференционных замираний приходящая к приемнику волна оказывается неполяризованной или частично поляризованной; если излучаемая волна не поляризована, то принимаемая волна также, как правило, оказывается неполяризованной.

Другой источник искажений радиосигнала связан с мобильным приемом, в процессе которого возможно доплеровское смещение частоты принимаемого сигнала, пропорциональное скорости V перемещения подвижного объекта. В многолучевом канале спектр принятого сигнала отличается от спектра переданногo и в результате эффекта Доплера каждая спектральная составляющая приобретает случайные изменения, что эквивалентно ее «размыванию» в области частот 1//Л, где Л — длина волны, соответствующая несущей частоте. Эффект Доплера возникает при достаточно быстрых перемещениях приемника (или объектов, от которых возможны отражения радиоволн в точку приема), вызывая небольшой частотный сдвиг, что может привести к временной интерференции.

Искажения сигнала, обусловленные всеми видами рассеяния, часто называют мультипликативными, имея в виду, что коэффициент передачи p(t) канала выступает в (3.1) как сомножитель передаваемого сигнала. От этих искажений нельзя избавиться увеличением мощности передатчика, причем в таких каналах ошибки при передаче сообщений возможны даже при отсутствии аддитивных помех. Это явление характеризуют несократимой вероятностью ошибки, т.е. вероятностью, которую нельзя уменьшить путем увеличения отношения сигнал/шум.

В разд. 2.6 указывалось на еще один возможный вид искажений сигнала в узкополосных каналах — межсимвольную интерференцию, которая является внутренним источником ошибок в системе передачи. Максимальное время взаимного запаздывания лучей т, (равное памяти канала т) определяет минимально необходимый интервал времени, по истечении которого может быть передан следующий элемент дискретного сообщения. Это требует снижения скорости передачи информации (т.е. увеличения длительности сигнала т,) для предотвращения МСИ. Оценим предельную скорость передачи информации R, при использовании односигнального (последовательного) метода передачи цифровых сигналов.

Вероятность появления ошибок в канале с МСИ зависит от относительного уровня таких искажений, т.е. от отношения т,/т, На рис. 3.7 показано [106], что в канале с релеевскими замираниями при конечном т,/т, вероятность ошибок с ростом ОСШ Eg N уменьшается лишь до некоторого ненулевого асимптотического предела — несократимой вероятности ошибки. Как отмечалось выше, этот предел, увеличивающийся с ростом отношения т,/т, не может быть улучшен за счет повышения мощности передатчика. Приняв для определенности т,/т, = 0,05, для города со средне- этажной застройкой (т, = 1,0 мкс) минимально-допустимая длительность посылки сигнала должна составлять т, = 20 мкс, чему соответствует R, = 50 кбит/с. Отсюда следует, что в цифровом вещательном канале с глубокими замираниями при последовательной передаче узкополосных сигналов можно без заметных искажений, в лучшем случае, передать одну монофоническую звуковую программу репортажного качества.

Тем не менее, последовательный способ передачи находит широкое применение в относительно узкополосных системах подвижной радиосвязи (СПРС). Здесь для уменьшения влияния МСИ используют эквалайзеры — специальные адаптивные фильтры — выравниватели. Однако такой метод является работоспособным в каналах с относительно низким уровнем шума и незначительными искажениями АЧХ и ФЧХ. При этом не следует забывать, что в радиоканале СПРС организуется передача лишь одного речевого сигнала невысокого класса качества.

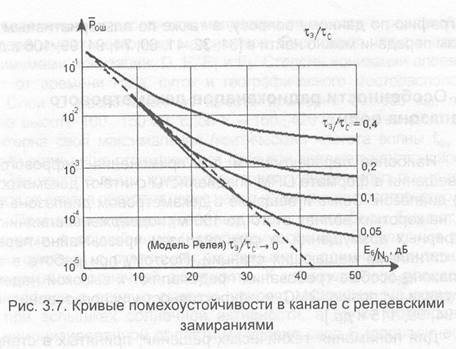
Заметим, что среди систем ЦРВ только в упоминавшейся в разд. 3.2 системе VOA/JPL предусмотрены методы повышения помехоустойчивости в каналах с МСИ, а именно:

временное разнесение (повторная передача данных, когда задержанная версия потока данных объединяется с данными и передается на той же несущей);

разнесенный прием (разнесение антенн/приемников, когда две физически разделенные пары антенна/приемник принимают и обрабатывают один и тот же сигнал);

разнесенная передача (разнесение спутников/передатчиков, когда один и тот же поток данных передается двумя физически разделенными передатчиками на разных частотах, принимается одной и той же антенной и затем независимо обрабатывается);

ретрансляторы в совмещенном канале (одночастотная сеть, когда один и тот же поток данных передается двумя или более физически разделенными передатчиками на одной и той же частоте, затем суммарный принятый сигнал обрабатывается специальным корректором).

С ростом информационных объемов использование одно- частотного канала передачи требует оптимизации процедур модуляции и демодуляции (в части решающего правила демодулятора) при малых априорных сведениях о канале. Обширную библиографию по данному вопросу, а также по альтернативным способам передачи можно найти в [31, 32, 41, 60, 74, 94, 99, 106 и др.].

3.7. Особенности радиоканалов декаметрового диапазона волн

Наиболее перспективным для применения цифрового радиовещания в формате DRM специалисты считают декаметровый (КВ) диапазон. Связь и вещание в декаметровом диапазоне волн (т.е. на коротких волнах от 10 до 100 м) подвержены влиянию ионосферных возмущений, а сам диапазон чрезвычайно перегружен сигналами мешающих станций. Поэтому при работе в этом диапазоне особые требования предъявляют к высокой надежности связи, условию ЭМС и эффективности использования РЧС [13, 94, 99, 115 и др.].

Для понимания технических решений, принятых в стандарте DRM, требуются знания об особенностях распространения КВ радиоволн, о характеристиках и моделях КВ каналов, об искажениях сигналов, передаваемых по таким каналам. Остановимся на этих вопросах, ориентируясь в основном на монографию [13].

Известно, что информацию на коротких волнах можно передавать с помощью земной или ионосферной волны. Земные волны распространяются параллельно поверхности Земли, дальность их распространения зависит от мощности передатчика, высот передающей и приемной антенн, характера и проводящих свойств поверхности Земли. Обычно с помощью земной волны осуществляют связь на расстоянии не более десятков километров.

Для радиосвязи на большие расстояния используют ионосферные КВ волны, отражающиеся от ионосферы в процессе распространения. Ионосферные волны позволяют устанавливать сверхдальнюю связь при относительно небольших мощностях передатчиков. Однако случайность свойств отражающей поверхности — ионосферы — делают связь в декаметровом диапазоне неустойчивой.

Ионосферой обычно называют ионизированную область атмосферы на высотах от 60 ... 80 до 1000 ... 1200 км. Основным источником ионизации атмосферы является Солнце. Помимо постоянных существуют нерегулярные источники ионизации атмосферы, такие, как мощные солнечные вспышки, потоки метеоров и т. д.

Распределение интенсивности ионизации по высоте в реальной атмосфере имеет несколько максимумов. Различают четыре слоя с максимумами ионизации: D, Е, F, и Fq. Степень ионизации слоев зависит от времени года, суток и географического месторасположения. Слой D расположен на высоте примерно 60...100 км, слой Е — на высоте 100...150 км, слой F — 160...420 км. Для каждого слоя' характерна своя максимальная (критическая) частота волны 1  при которой волны еще отражаются от слоя при вертикальном зондировании. При частоте выше критической зондирующие импульсы не отражаются от слоя, а проходят через него в космическое пространство.

Процессы в ионизированных слоях атмосферы бывают регулярными и случайными (непериодическими). Регулярные процессы связаны с суточными, сезонными и одиннадцатилетними изменениями солнечной активности. К нерегулярным процессам в ионосфере в первую очередь относят ионосферные возмущения при вспышках солнечной активности, а также образование сильно ионизированной области на уровне слоя Е (спорадический слой Е,).

Электромагнитные волны при движении в ионизированном слое испытывают, помимо поглощения, искривления своей траектории, а при некоторых условиях меняют свое направление, т.е. отражаются. Это связано с тем, что при движении волны в неоднородной по электронной плотности ионосфере траектория волны преломляется от слоя к слою и становится криволинейной. Участок, лежащий между передающей антенной и точкой возвращения луча к земле, называют скачком. Длина скачка зависит от угла наклона излучения и колеблется в пределах 500 ... 3500 км. При определенных условиях луч, пришедший к земле, может отразиться от нее и тогда формируется второй скачок.

При распространении коротких волн часть энергии теряется из-за их поглощения в ионизированных слоях и рассеяния энергии при отражении (т.е. образования лучей, которые никогда не достигают приемной антенны). Поглощение энергии радиоволн в ионизированном слое зависит от степени его ионизации и длины пути радиоволн в нем, а длина пути в основном определяется величиной угла, под которым луч входит в ионосферу. Если плотность ионизации слоя невелика или велик угол падения, то луч может пронизать слой и уйти в космическое пространство. В этом случае будет практически полная потеря энергии коротких волн. При меньших углах падения может иметь место наиболее общий случай, когда луч в слое разделяется на два, один из которых отражается к земле, другой пронизывает слой и может уйти в пространство или отразиться к земле от следующего слоя. Часть лучей, пронизывающих слой или отразившихся от верхних областей слоев, не может достичь приемника. Энергия этих лучей в конечном счете рассеивается и составляет вторую часть потерь.

Таким образом, передача радиоволны в заданную зону обслуживания (приема) возможна по целому ряду траекторий волны, основные из которых показаны на рис. 3.8. На рис. 3.8,а-в показаны соответственно одно, двух и трехскачковые трассы с отражением от слоя F. На рис. 3.8,г-и показаны трассы с отражением либо от слоя Е, либо от слоев Е и F. Заметим, что слой Е наблюдается только днем.

При удалении зоны приема на расстояния менее 3000 км днем имеет место либо односкачковая, либо двухскачковая трассы с отражением от слоя F; при удалении до 2000 км — односкачковая трасса с отражением от слоя Е, на частотах примерно до 8 МГц — трех- и двухскачковые трассы с отражением от слоя F.

Поглощение коротких волн в слоях D и Е примерно в 100 раз больше, чем в слое F. Электронная концентрация слоев D и Е недостаточна для отражения радиоволн, поэтому они являются поглощающими, а слой F — отражающим.

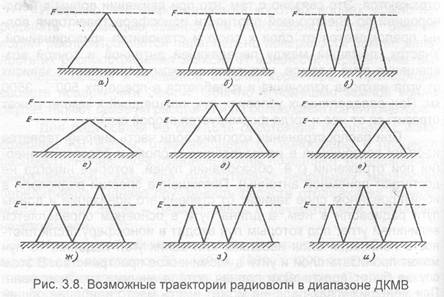
Для обеспечения устойчивого прохождения коротких волн необходимо знать предельно высокую частоту, которая, отражаясь от ионосферы, обеспечивает работу радиолинии.

Такую частоту называют максимально применимой (МПЧ). Поскольку слой F,, от которого в основном происходит отражение радиоволн, наиболее часто подвержен ионосферным возмущениям, в процессе вещания могут изменяться значения МПЧ. Если значение частоты радиоволны, на которой осуществлялось вещание до начала возмущений, было достаточно близко к МПЧ, то снижение электронной плотности слоя F, может привести к практическому пропаданию сигнала на приеме. Для возобновления радиоприема необходимо перейти к более низким рабочим частотам. Наименьшую частоту, при которой надежность оказывается минимально допустимой, называют наименьшей acmomou (НПЧ).

Результаты наблюдений показывают, что при спокойном состоянии ионосферы радиосвязь и вещание в диапазоне ДКМВ в течение 90% времени можно обеспечить на частотах f < 0,85fДД для слоя Fg и f — 0,951„„для слоя F„. Частоту f, при которой обеспечивается связь по условиям отражения в течение 90% времени за месяц, называют оптимальной рабочей частотой (ОРЧ). Точное определение ОРЧ для разных географических широт и часов суток ведется по данным о флуктуациях МПЧ и номограммам, приводимым в месячных прогнозах распространения радиоволн.

Физически в радиоканале сигнал распространяется по нескольким путям. Во-первых, в пункте приема обнаруживаются лучи, которые распространяются путем многократного или однократного отражения. Во-вторых, передающая антенна излучает волны в пределах более или менее широкого угла, поэтому можно считать, что на ионосферу падает не один луч, а как бы пучок подлучей. Подлучи отражаются при различной глубине проникновения в ионизированный слой и достигают поверхности Земли в различных точках. В-третьих, неизбежные неоднородности в ионосфере приводят к тому, что вместо зеркального отражения лучей от ионосферы возникают частично диффузионные отражения, где падающий на нижнюю границу один луч по выходе из ионосферы представляется в виде пучка подлучей, содержащего множество элементарных лучей. Угловой раствор пучка достигает нескольких градусов. Таким образом в место приема попадает множество лучей, относящихся к различным пучкам.

Вследствие многолучевого распространения и разностей хода подлучей при прохождении сигнала от передатчика к приемнику сигнал в приемной антенне представляет сумму отдельных колебаний с разными фазами и амплитудами. Каждому колебанию соответствует свое время распространения и свой коэффициент передачи, что и обусловливает флуктуации как амплитуд, так и фаз составляющих. Интерференция этих лучей — сигналов в антенне — в условиях непрерывного изменения их фаз является одной из причин появления замираний.

Итак, характерным для ДКМ радиоканала является замирание сигнала на входе радиоприемника. Под замирающим сигналом в КВ радиолиниях подразумевают сигнал с флуктуирующими параметрами, которые вызываются случайным изменением коэффициента передачи радиоканала.

В реальных каналах время распространения каждого подлуча и его коэффициент передачи изменяются относительно медленно. Если на протяжении длительности передачи одного элемента сообщения их можно считать неизменными [99], то такие замирания называют медленными (гладкими по времени), поскольку соотношения между амплитудами и фазами составляющих сигнала не изменяются. Как было показано в разд. 3.5, коэффициент передачи р канала с общими (или гладкими) замираниями достаточно точно подчиняется обобщенному распределению Релея (распределению Райса) с одномерной плотностью (3.2). Такие, квазирелеевские, замирания имеют место не только при наличии стационарной составляющей сигнала на входе приемника, но и при выполнении условия, когда разность времени распространения лучей во много раз меньше периода средней частоты сигнала. В частности, это условие часто выполняется в средневолновом и в нижнем участке ДКМ диапазона при отражении волн от ионосферы [99]. Согласно эксплуатационным данным, в ДКМ диапазоне также достаточно характерны и релеевские замирания, подчиняющиеся распределению (3.3). Таким образом, все, что выше (в разд. 3.5) было сказано о моделях радиоканалов, организованных на частотах выше 30 МГц (т.е. в метровом и дециметровом диапазонах волн), в значительной степени применимо и для диапазона частот ниже 30 МГц. Однако физические процессы, определяющие распространение радиоволн в этих диапазонах, различаются принципиально. В результате этого будут существенно отличаться и модуляционные параметры ОРОМ- сигналов, применяющихся в обоих случаях.

Процесс замираний радиосигналов характеризуется обычно двумя величинами — глубиной и скоростью. Под скоростью замираний понимают средний промежуток времени между двумя последовательными минимумами или максимумами. По скорости замирания разделяют на быстрые и медленные. По эксплуатационным данным в ионосферных ДКМ радиоканалах средний период замираний принимает значение от 0,1 с на длинных трассах до 2 с на коротких. Такой же медленный характер носят изменения фазы (примерно 1' в 1 • 10 с). Уровень сигнала из-за замираний может меняться на несколько порядков.

Условия отражения для частотных составляющих спектра электромагнитного колебания в ДКМ радиоканале оказываются различными. Это определяет частотно-селективный характер быстрых замираний, что обусловливает, в свою очередь, амплитудно-частотные искажения передаваемого сигнала.

При приеме сигналов в декаметровом диапазона также следует считаться и с эффектом Доплера. Дело в том, что ионные образования в ионосфере не являются застывшими, неподвижными. Они передвигаются, и скорость их передвижения может быть настолько большой, что сдвиг частот, отраженных от таких образований, из-за эффекта Доплера может быть уже заметным. Результаты измерений на частоте 30 МГц показали, что доплеровский сдвиг не превосходит 2...3 Гц.

3.8. Оптимизация процедур кодирования канала и модуляции

Как отмечалось ранее, применение кодирования канала повышает энергетическую эффективность радиосистемы передачи. Количественной мерой такого повышения может служить ЭВК. Для того чтобы получить одновременно наилучшую энергетическую и частотную эффективность, используется кодированная модуляция (решетчатая кодовая модуляция [6]) или в другой терминологии — используются определенные сигнально кодовые конструкции (СКК) [94]. СКК — это сигнальные последовательности, точки которых в многомерном пространстве плотно упакованы (чтобы обеспечить высокую частотную эффективность) и достаточно разнесены (чтобы обеспечить достаточно высокую энергетическую эффективность). Такими свойствами сигнальные последовательности обладают благодаря сочетанию многопозиционных сигналов и корректирующих кодов

в единой конструкции [32]. В качестве помехоустойчивых кодов в СКК обычно используются сверточные и каскадные коды, а в качестве многопозиционных сигналов — чаще всего сигналы ФМ и АФМ (КАМ).

Достижения в этой области в полной мере используются в современных системах ЦРВ, вследствие чего кратко рассмотрим основные принципы построения таких конструкций.

практической реализации СКК речь пойдет ниже — при описании конкретных систем ЦРВ.

Устройство, реализующее СКК, состоит из кодека, модема и согласующих устройств. Фрагмент модели двоичного канала связи (рис. 2.1), иллюстрирующий объект внимания, приведен на рис. 3.9. Обратим внимание, что понятия кодера и декодера СКК связаны здесь с каналом дискретного времени, эквивалентным непрерывному каналу с АБГШ (см. разд. 2.1 и 3.5).

Общую идею метода построения СКК иллюстрирует рис. 3.10, где кодер СК со скоростью R = m/n представлен в виде параллельного набора m регистров сдвига с различными длинами кодовых ограничений К; (см. разд. 2.4), так что К = ,'г. К,; на рисунке символ 

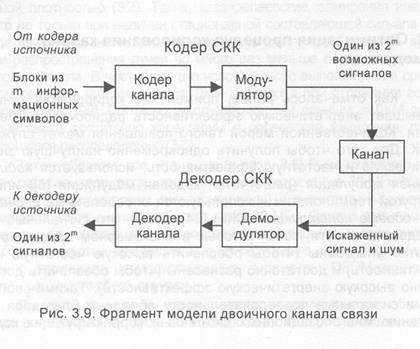
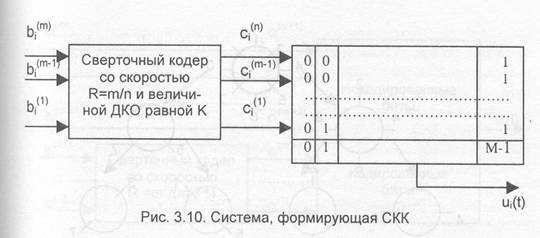
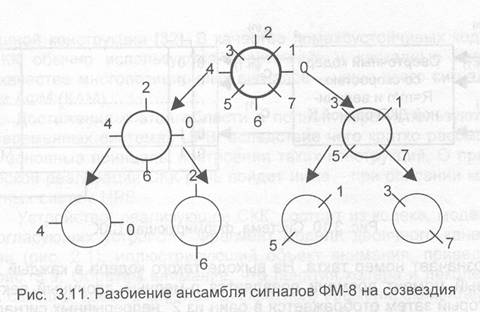
обозначает номер такта. На выходе такого кодера в каждый тактовый момент времени появляется п- мерный двоичный вектор, который затем отображается в один из 2" непрерывных сигналов, передаваемых в канал связи. Другими словами: происходит отображение двоичных п- последовательностей на множество сигналов (u< u<...,u< ). Для систем с ограниченной полосой (в том числе и для систем ЦРВ) типичным является использование сигналов с многократной (В > 2, где В = Log М) фазовой или ампли- фазовой модуляцией, причем ключевым моментом здесь является разбиение множества сигналов на созвездия (иначе— вложенные подансамбли) [4, 32, 94 и др.]. 

Пример такого разбиения для ансамбля сигналов восьмеричной (М=8) ФМ-8 показан на рис. 3.11. Созвездия находятся в нижнем ряду рисунка. Построение вложенных ансамблей сигналов составляет основу СКК, причем для двумерных сигналов (к ним относятся ансамбли сигналов ФМ-М и М-КАМ) нахождение вложенных ансамблей трудностей не представляет [32]. При этом важна нумерация подансамблей. Нумерация часто называется манипуляционным кодом и выбирается из разных соображений, в том числе для минимизации вероятности ошибки. Наиболее часто применяемым манипуляционным кодом является код Грея (см. разд. 2.5).

Благодаря такому кодированию, большему расстоянию по Хэммингу между блоками кодовых символов соответствует большее расстояние по Евклиду между соответствующими им сигналами [94]. Код Грэя, включенный между помехоустойчивым кодеком и модемом, преобразует М- позиционный канал без памяти в двоичный канал с памятью длиной В = Log М символов. Однако код Грея не является оптимальным.

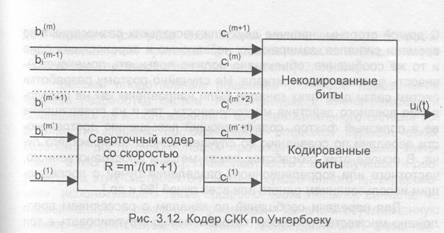
сигнал в созвездии, а кодированные — определяют выбор созвездия, т.е. вложенного подансамбля сигналов. Так, для схемы разбиения ансамбля сигналов ФМ-8 на рис. 3.11 кодер Унгербоека будет иметь параметры: m = 2, m' = 1, R = 1/2.

Поскольку, как видно из рис. 3.11, сигналы в каждом из созвездий удалены на значительное евклидово расстояние, а минимальное евклидово расстояние между сигналами различных созвездий может быть мало, то использование рассмотренного принципа позволяет максимизировать евклидово расстояние между последовательностями кодированных сигналов при сохранении высокой спектральной эффективности.

Разработана специальная техника, позволяющая объединить СК и квадратурную амплитудную модуляцию сигнала для обеспечения высокой энергетической и спектральной эффективности. В частности, такое решение применяется в системе DRM [115].