1. ОБЩИЕ СВЕДЕНИЯ

1.1. Элементы систем цифровой связи

Основной задачей помехоустойчивого кодирования является решение проблемы обеспечения высокой достоверности передаваемых данных за счет применения устройств кодирования/декодирования в составе системы передачи цифровой информации, структурная схема которой представлена на рис. 1.1 [15]. Данная схема широко используется в теории помехоустойчивого кодирования, поскольку она охватывает большинство ситуаций, которые встречаются на практике.

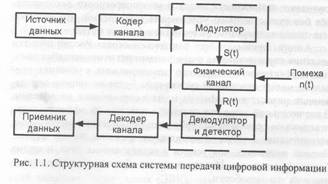
            Рассмотрим основные принципы работы представлю схемы. Сначала источник данных порождает данные в вид ячных символов. Обычно предполагают, что «нули» и «единицы» появляются независимо друг от друга и с одинаковым вероятностями. Затем кодер канала вносит в принятую инфоционную последовательность некоторую избыточность (да процесс называется кодированием), которую декодер см использовать для исправления возникающих при передаче ных по каналу связи ошибок.

Закодированные данные с выхода кодера поступают на модулятор, который с помощью какого-либо метода модуляции реализует их отображение в аналоговый сигнал S(t). Модулятор может просто отобразить каждый двоичный символ в один из М=2 возможных сигналов s_o(t) u s₁(t) (в этом случае говорят о двоичной модуляции), а может передавать q-битовые блоки (q>1) при помощи М=2^q возможных сигналов (М-позиционная модуляция).

В физическом канале сигнал S(t) подвергается воздействию шума n(t). Для количественной оценки степени влияния шума n(t) на сигнал S(t) обычно используют отношение сигнал-шум Е_s N_o, определяемое как отношение мощности сигнала Рс к мощности шума Рш. Часто данное отношение выражается в децибелах, т.е. Е_s/No=10 lg(P_c/Рш). Заметим, что на всех приводимых в справочнике графиках отношение сигнал-шум выражено в децибелах, а во всех формулах используется безразмерная величина Е_s/N_o=Рс/Рш. Далее демодулятор преобразует принятый из канала сигнал R(t) в последовательность чисел, представляющих оценку переданных данных. После этого детектор квантует выход демодулятора на Q-уровней. В случае если Q=M, то говорят, что детектор выносит жесткое решение относительно переданных символов, если же Q>M, то детектор выносит мягкие решения.

Затем квантованный выход детектора поступает на декодер канала, который, используя внесенную кодером избыточность, определяет переданное источником сообщение (данный процесс называется декодированием).

1.2. Модели каналов связи

Наиболее важной частью структурной схемы системы передачи цифровой информации для кодера и декодера является составной или дискретный канал, заключенный на рис. 1.1 в штриховую рамку. Рассмотрим наиболее часто встречающиеся математические модели данного канала.

Самой простой является модель двоичного симметричного канала (ДСК), представляемая графом на рис. 1.2 и соответствующая случаю использования двоичной модуляции в канале с аддитивным шумом (т.е. каналу, в котором выходной сигнал L R(t) равен сумме входного сигнала S(t) и шума n(t)) и жесткого

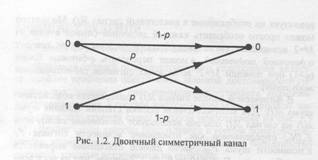
решения демодулятора. Входом и выходом данного канала являются наборы Х=(0, 1} и 7={0,1) из двух возможных двоичных символов. ДСК также характеризуется набором переходных вероятностей P(Y(X), определяющих вероятность приема из канала символа Y при передаче символа Х. Для ДСК переходные вероятности задаются выражениями:

            Как следует из представленного описания, основной характеристикой ДСК является вероятность искажения символа р. Запишем выражение, связывающее данную величину с ранее упоминавшимся отношением сигнал-шум Е_s,/И₀ для случая использования двух противоположных сигналов So(t) = — S₁(t)

Более общей моделью канала является дискретный канал без памяти (ДКВП). Входом данного канала являются q-ичные символы Х={х₀, х₁, ..., х_q-1 }, а выходом — Q-ичные символы Y={у_о, у₁, ...,у_q }. Термин «без памяти» означает, что выходной символ канала зависит только от текущего входного символа. ДКБП характеризуется набором из qQ переходных вероятностей

P(у_i,|x_i)=P(Y=у_i X=х_i), 

где i.=0, 1, ..., Q — 1 и j=О, 1, ..., q — 1. Для ДКВП переходные вероятности постоянны во времени и переходы различных символов независимы. Графическое представление данной модели канала показано на рис. 1.3.

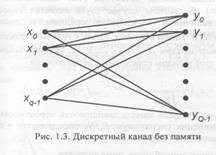
Частным случаем ДКБП является q-ичный симметричный канал, называемый далее qCK. Данный канал, получающийся при использовании модулятором q ортогональных сигналов и вынесении жесткого решения демодулятором, характеризуется дискретным входом Х= (х₀, х₁, ..., х_q-1 }, дискретным выходом У={у_о, y₁, ..., у_q-1 } и набором переходных вероятностей

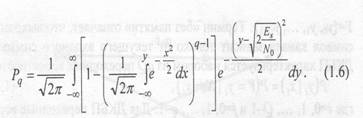
Последней рассматриваемой в справочнике моделью канала является канал с аддитивным белым гауссовским шумом (АБГШ), получающийся из ДКБП при бесконечном числе уровней квантования выхода детектора (т.е. квантование отсутствует, Q=1). В данном случае шум является гауссовской случайной величиной с нулевым средним и дисперсией   Таким образом, канал с АБГШ характеризуется дискретным входом непрерывным выходом  и рядом переходных вероятностей

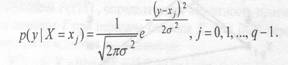
Для данной модели канала зависимость вероятности ошибки р от отношения сигнал-шум Е_s.|N₀ определяется в соответствии с выражением (1.2).

1.3. Пропускная способность канала связи

Одной из основных характеристик канала является его пропускная способность С, которая определяется как максимальная средняя взаимная информация 1(Х;У) между входом Х и выходом Y канала. Важность этого понятия основана на теореме о кодировании для канала с шумами [25], которая утверждает, что если скорость передачи двоичных сообщений (или кодовая скорость r, определяемая в разделе 1.4) меньше пропускной способности канала С, то с помощью правильно выбранных кодера и декодера можно вести передачу по каналу с шумом со сколь угодно малой вероятностью ошибки.

Для ДКБП пропускная способность вычисляется следующим образом:

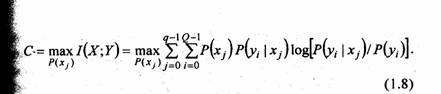
Здесь максимизация осуществляется по всем возможным наборам вероятностей входных символов Р(x_j). В том случае, если канал является симметричным, максимизация достигается при равновероятных входных символах, т.е. при Р(х_j,)=1/q

j=0,1, ..., q-1.

Для ДСК пропускная способность равна

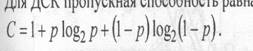
            Графики зависимости пропускной способности ДСК от вероятности ошибки р и от отношения сигнал-шум на символ Е_s,/N₀ в канале связи представлены на рис. 1.4 и 1.5.

Для канала с АБГШ пропускная способность С определяется так:

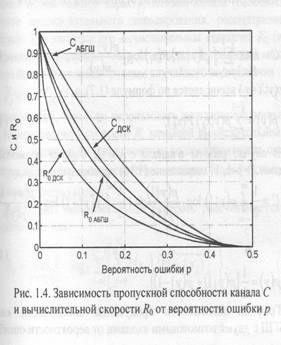
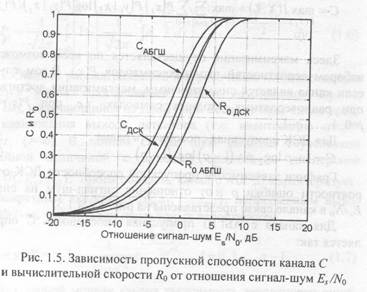
и от отношения сигнал-шум Е_s/N₀ в канале связи также представлены на рис. 1.4 и 1.5. Отметим, что одинаковой пропускной способности с ДСК канал с АБГШ достигает при отношении сигнал-шум примерно на 2 дБ меньшем, что показывает существенное преимущество использования мягких решений демодулятора.

Для q-ичного симметричного канала пропускная способность вычисляется следующим образом:

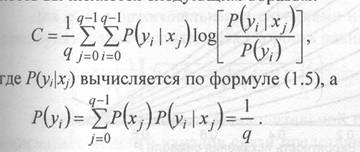
Графики зависимости пропускной способности qCK от вероятности символьной ошибки Рq и отношения сигнал-шум Е_sIN₀ представлены на рис. 1.6 и 1.7 соответственно.

Еще одной важной характеристикой канала (особенно для методов последовательного декодирования, рассматриваемых в разделе 3.2) является его вычислительная скорость Ro (иначе называемая параметром экспоненциальной границы), используемая при определении границы случайного кодирования

показывающей, что если использовать достаточно длинные коды, то при кодовой скорости R, меньшей вычислительной скорости R₀, среднюю по всевозможным кодам вероятность ошибки Р, при использовании достаточно длинных кодов можно сделать сколь угодно малой.

Для ДКВП вычислительная скорость рассчитывается следующим образом:

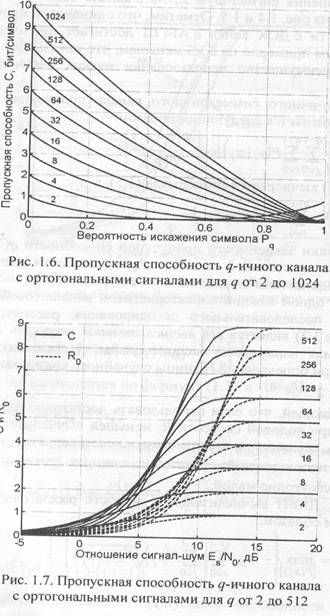
Графики зависимости вычислительной скорости для вышеописанных моделей каналов связи представлены на рис. 1.4, 1.5 и 1.7 кривыми R_o.

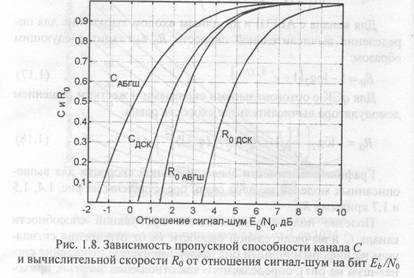
Полезно получить зависимости пропускной способности канала  С и вычислительной скорости R₀ от отношения сигнал- шум на информационный бит (далее именуемое отношение сигнал-шум на бит), определяемого как отношение энергии, приходящейся на один информационный символ к спектральной мощности шума Е_B Np. Для этого сначала необходимо нормализовать зависимость С(Е,. Np) делением на N/2 (здесь N — размерность пространства, используемого для передачи символов)

Аналогично можно получить зависимость вычислительной скорости R_o от отношения сигнал-шум на бит. Для примера на рис.1.8 представлены графики зависимости

для ДСК и канала с АБГШ.

Более детальную информацию о расчете пропускной способности и вычислительной скорости различных моделей каналов связи можно найти в книге Дж. Прокиса [20]..

1.4. Помехоустойчивые коды

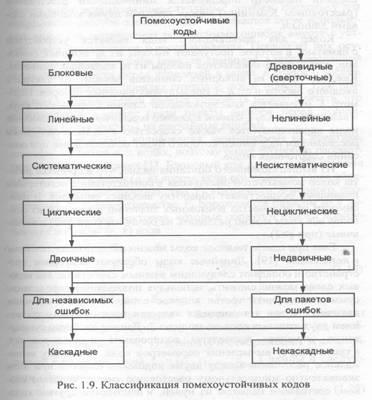
На сегодняшний день известно много различных классов помехоустойчивых кодов, отличающихся друг от друга структурой, функциональным назначением, энергетической эффективностью, алгоритмами кодирования и декодирования и многими другими параметрами. Рассмотрим основные подходы классификации данных кодов, представленные на рис. 1.9.

При одном подходе коды можно разбить на две группы: блоковые [19], в которых кодирование и декодирование производится в пределах кодовой комбинации или блока, и древовидные [18], в которых обработка символов производится непрерывно, без разделения на блоки. Кодер для блокового кода является устройством без памяти, отображающим последовательности из k входных символов в последовательности из и выходных символов. Термин «без памяти» указывает, что каждый

 выходной блок из и символов зависит только от соответствующего входного блока из k символов и не зависит от других блоков. Основными параметрами блокового кода являются длина кода и, длина информационной последовательности k скорость кода r=kln и минимальное кодовое расстояние d_min. Последний параметр определяется минимальным расстоянием (расстоянием Хэмминга) между любыми двумя кодовыми словами длины и.

Кодер для древовидного кода является устройством с памятью, в которое поступают наборы из k₀ входных символов, а на выходе появляются наборы из n₀ выходных символов. Каждый набор n₀ выходных символов зависит от текущего входного набора и от К — 1 предыдущих входных наборов. Параметр К называется конструктивной длиной сверточного кода, а величину r=k₀ /п_о — длиной кодового ограничения. Древовидные коды характеризуются также скоростью r=k₀/ n₀ и свободным расстоянием d_freeсмысл которого будет пояснен далее при описании сверточных кодов.

Из вышеизложенного описания видно, что в процессе работы кодер помехоустойчивого кода в соответствии с некоторыми правилами осуществляет обработку входных символов. В зависимости от количества возможных значений q каждого из символов все коды можно разделить на двоичные (при q=2) и недвоичные (при q>2).

Еще при одном подходе коды можно разделить на линейные и нелинейные [19]. Линейные коды образуют векторное пространство и обладают следующим важным свойством: два кодовых слова можно сложить, используя подходящее определение суммы, и получить третье кодовое слово. В случае обычных двоичных кодов эта операция является посимвольным сложением двух кодовых слов по модулю 2. Данное свойство существенно упрощает процедуры кодирования и декодирования, а также задачу вычисления параметров кода, поскольку минимальное расстояние между двумя кодовыми словами при этом эквивалентно минимальному расстоянию между кодовым словом, состоящим целиком из нулей, и некоторым другим кодовым словом. Кроме того, при вычислении характеристик линейного кода достаточно рассмотреть, что происходит при передаче кодового слова, состоящего целиком из нулей. Линейные древовидные коды обычно называют сверхточными.

Помехоустойчивые коды также можно разбить на коды, исправляющие случайные или независимые ошибки, и коды, исправляющие пакеты ошибок. На практике, в основном, применяются коды, исправляющие случайные ошибки, поскольку для исправления пакетов ошибок часто оказывается легче использовать коды для исправления независимых ошибок вместе с устройствами перемежения и восстановления. Первое из них осуществляет перемешивание порядка символов в закодированной последовательности перед передачей в канал, а второе — восстановление исходного порядка символов после приема. При правильном проектировании данных устройств можно считать, что образующиеся в канале связи пакеты ошибок перед декодированием будут разбиты на случайные ошибки.

Почти все схемы кодирования, применяемые на практике, основаны на линейных кодах, поэтому более подробно рассмотрим способ их описания [1]. Блоковый код длины и с 2^k словами называется линейным (n, k) кодом, если его кодовые слова образуют k- мерное подпространство V векторного и мерного пространства V_k. Подпространство V_n порождается базисом из k линейно независимых векторов, которые образуют строки порождающей матрицы (и, k) кода

Процесс кодирования блокового кода состоит в разбиении информационной последовательности на сообщения Ū =(u_0, u₁,..., и_k-1) длины k и отображении этих сообщений в кодовые слова С = (с_о, c₁, ..., с_n-1) длины п следующим образом:

َС =Ū G.

Часто кодовые слова лучше представлять в систематической форме С = (Ū, V), образуя отдельно информационную часть U из k символов и проверочную часть V из m=k символов. Порождающая матрица такого систематического кода будет иметь вид

В данном случае матрица G содержит единичную матрицу 1_k размером kxk, формирующую информационную часть слова,  и матрицу Р размером kx(n— k), определяющую проверочные  символы.

С порождающей матрицей тесно связано понятие проверочной матрицы Н, пространство строк которой ортогонально пространству строк порождающей матрицы, т.е.

символов синдрома Ŝ определяют их местоположение. Данный принцип лежит в основе методов синдромного декодирования.

Важный подкласс линейных кодов составляют циклические коды, обладающие циклическими свойствами: если C= (с_о, с₁, ..., с_n-1) — кодовое слово циклического кода, тогда и С=(с₁, с₂, ..., C_n-1 C_O) полученное циклическим сдвигом элементов С, также является кодовым словом. Эти коды обладают большим количеством структурных особенностей, которые значительно упрощают реализацию операций кодирования и декодирования.

Порождающую матрицу циклического кода можно записать в виде

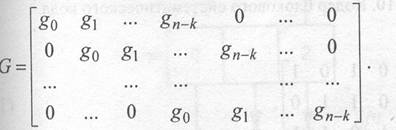
Для компактной записи циклического (n, k) кода часто используется порождающий или образующий полином g(x) степени n-k_- с коэффициентами из поля GF(q) (для двоичных кодов g_i={0,1})

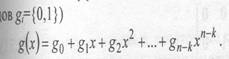
Если в виде полинома записать информационное сообщение U(x) и кодовое слово С(х), то кодовые слова кода образуются путем умножения сообщения на порождающий полином

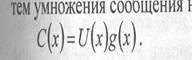
Обычно для удобства записи коэффициенты образующих полиномов объединяют в двоичное слово и представляют восьмеричной системе счисления. Также образующие полиномы можно записывать путем перечисления степеней с ненулевыми коэффициентами. Например, запись g(х)=1+х+х⁴ +х⁶ равносильна следующим: g=1010011₂=123₈ ;g=(0 1, 4, 6).

Для примера на рис. 1.10 показан кодер систематического блокового кода, соответствующий порождающей матрице вида

Получившийся код характеризуется следующими параметрами: количество кодовых символов n=6, количество информационных символов k=3, кодовая скорость r=1/2, минимальное кодовое расстояние d_min=3.

Далее рассмотрим способы описания сверточных кодов. Для построения кодера сверточного кода необходимо k регистров сдвига, связи между элементами которых определяются набором образующих полиномов g_(ij)(х), где i=0, 1, ...,k_0-1— номер входного потока, aj=0, 1, ..., n₀ — 1 — номер выходного потока. Поскольку на практике чаще используются коды с единственным входным потоком (k₀=1), индекс  обычно опускается. Еще одной характеристикой сверточного кода является его конструктивная длина К, влияющая на сложность его декодирования и равная длине самого длинного регистра сдвига.

Для примера на рис. 1.11 представлен кодер несистематического сверточного кода, заданный образующими полиномами g₀(х)=1+х² и g₁(х)=1+х+х² . Данный код характеризуется  следующими параметрами: количество информационных ветвей к₀=1, число проверочных ветвей n₀=2, кодовая скорость r=1/2, длина кодового ограничения n_a=6, конструктивная длина кода К=3.

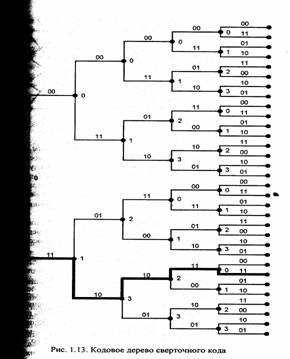
Так же как и блоковые, сверточные коды можно представить в систематической форме, частным случаем которой являются рекурсивные систематические сверточные (Recursive  Systematic Convolutional RSC) коды. Характерной особенностью кодеров данных кодов является наличие обратной связи. В качестве примера на рис. 1.12 представлен RSC кодер, заданный полиномом обратной связи (feedback polynomial) g₀(х)=1+х+х² и выходным полиномом (feedforward polynomial) g₁ (х) =1+ х² . Удобным способом представления процесса функционирования кодера сверточных кодов является кодовое дерево. Пример кодового дерева для кодера с рис. 1.11 показан на рис. 1.13. Как видно из рисунка, кодовое дерево состоит из узлов, связанных между собой ребрами. При этом каждому узлу соответствует од-

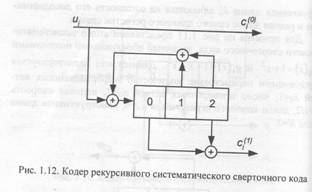
но из 2^(k-1)k₀ состояний кодера (в данном случае 4), определяемое содержимым всех, кроме самых правых, ячеек регистров сдвига кодера (десятичное представление содержимого этих ячеек показано на рисунке в виде меток О, 1, 2 и 3), а каждое ребро характеризуется входной и выходной последовательностью (верхнему ребру соответствует входной символ О, нижнему- 1, а выходная последовательность представлена метками 00, 01, 10 и 11). Результате любая входная последовательность задает некоторый путь на дереве, по которому можно определить выходную последовательность. Например, входной последовательности 11001 соответствует путь, показанный на рис. 1.13 жирной линией и задающий выходную последовательность 11 10101111,

Недостатком данного представления сверточных кодов является экспоненциальный рост числа ветвей с ростом длины входной последовательности. Поэтому часто кодовое дерево изображают в виде кодовой решетки, при построении которой учитывается конечное число возможных состояний кодера, что дает возможность отождествлять вершины дерева, характеризуемые одинаковыми состояниями. Изображение кодовой решетки для вышеприведенного примера путь, соответствующий входной последовательности 11001, показаны на рис. 1.14.

Используя решетчатое представление, определим ранее встречавшееся понятие минимального свободного расстояния сверточного кода d_free как минимальное расстояние между двумя различными путями по кодовой решетке, начинающимися и заканчивающимися в одном состоянии. Например, из рис. 1.14 следует, что минимальное свободное расстояние рассматриваемого кода равно 5 (общий вес пути 0→1→2→0, заданного вершинами на диаграмме).

Заметим, что далее, в случае применимости выводов, формул и т.д. как к сверточным, так и блоковым кодам, вместо минимального кодового расстояния d_min и свободного расстояния d_free используется общий термин кодовое расстояние d.

Теперь рассмотрим основные характеристики помехоустойчивости линейных кодов и методы их оценки.

1.5. Основные характеристики методов коррекции ошибок

Для оценки помехоустойчивости системы связи часто используют среднюю вероятность ошибки в информационном бите Р_b или последовательности бит (кодовом блоке) Р_в при определенном отношении сигнал-шум в канале связи. Данные вероятности ошибки могут быть определены как по точным или приближенным формулам, так и получены с помощью статистического моделирования системы связи на ЭВМ.

Для оценки вероятностей ошибки в бите Р_b и блоке Р_в линейного блокового кода длиной n, декодируемого с помощью декодера максимального правдоподобия (т.е. декодера, nвыбирающего из всех возможных кодовых слов то, которое находится на минимальном расстоянии от принятой из канала последовательности), можно воспользоваться аддитивной оценкой [14], характеризующейся достаточной точностью при большом отношении сигнал-шум

где р — вероятность битовой ошибки на входе декодера (т.е. в канале); Е_s,/И₀ — отношение сигнал-шум в канале; Q(x) — функция, определяемая формулой (1.3).

Недостатком данных оценок вероятности ошибки является их неточность при малом отношении сигнал-шум и необходимость определения спектра кода, что часто является достаточно трудной задачей. Поэтому для некоторых кодов при их описании будут рассмотрены более простые и точные границы вероятностей ошибки.

Еще одной, не менее важной характеристикой, является энергетический выигрыш кодирования (ЭВК), показывающий величину снижения энергии, необходимой для передачи одного бита данных при некоторой выбранной средней вероятности ошибки на бит P_b в случае использования тех или иных алгоритмов кодирования и декодирования, по сравнению со случаем, когда кодирования нет. Зарубежные специалисты оценивали каждый децибел ЭВК в миллионы долларов более 20 лет назад [2). Сейчас ценность ЭВК еще более возросла, поскольку он позволяет уменьшать размеры очень дорогих антенн, повышать дальность связи, увеличивать скорость передачи, снижать необходимую мощность передатчика и улучшать другие важные свойства систем связи.

При оценке эффективности алгоритмов декодирования различных кодов полезно знать предельные (или асимптотические) для малого шума характеристики данных кодов.

Асимптотический ЭВК зависит только от скорости кода r и кодового расстояния d, и для системы с двоичной фазовой модуляцией при приеме без квантования он равен

Ga = 101g(Rd). 

В случае использования двоичного симметричного канала

Ga =10 1g(R(t+1)), 

где t — максимальное целое, меньшее, чем d/2, определяющее число исправляемых кодом ошибок. Из сопоставления выражений (1.34) и(1.35) видно, что при приеме в целом в пределе обеспечивается на 3 дБ больший ЭВК, чем при использовании жестких решений демодулятора. Однако при реальных отношениях сигнал-шум и умеренных значениях d разница обычно близка к 1...2 дБ. Использование же мягкого модема с квантованием выходного значения на 8 и 16 уровней уменьшает ЭВК по сравнению с приемом в целом примерно на 0,25 и 0,1 дБ соответственно.

Среди других характеристик алгоритмов декодирования выделим сложность их реализации (как программной, так и аппаратной). Данная характеристика имеет чрезвычайно большое значение, так как применяя очень сложные методы декодирования можно получить весьма высокие значения ЭВК, но при этом практическое использование данных алгоритмов будет невозможно.

В следующих главах рассмотрим наиболее важные с точки зрения авторов коды и методы их декодирования.

2. БЛОКОВЫЕ КОДЫ И МЕТОДЫ ИХ ДЕКОДИРОВАНИЯ

2.1. Коды Хэмминга

Одними из самых простых являются коды Хэмминга, представленные Хэммингом в 1950 г. [44]. К данным кодам относятся линейные блоковые коды с параметрами (n,k) вида (2^m— 1, 2^m -т — 1), где т=п — число проверочных символов кода. Коды Хэмминга обладают кодовым расстоянием d_min=3 и поэтому способны исправлять только одну или обнаружить две ошибки.

Для задания кодов Хэмминга обычно используется проверочная матрица Н, содержащая и строк и 2^m -1 столбцов, причем столбцами являются все возможные ненулевые двоичные векторы длины m.

Знание спектра кода, как было показано в разделе 1.5, может оказаться полезным при получении границ его эффективности.

Кроме описанных кодов Хэмминга существуют так называемые укороченные и расширенные коды Хэмминга. Укороченные коды Хэмминга получаются при исключении какой-либо проверки (т.е. удалении одной строки проверочной матрицы). Расширенные коды Хэмминга получаются путем введения дополнительной проверки на четность всех символов кодового слова. В результате их минимальное расстояние увеличивается до D_min=4, что позволяет данным кодам исправлять одну обнаруживать две или только обнаруживать три ошибки. Проверочная матрица Н расширенного кода Хэмминга, заданного матрицей (2.1), имеет вид

Далее рассмотрим характеристики кодов Хэмминга. На с.2.1 и 2.2 представлены экспериментальные зависимости вероятности битовой ошибки Р_b от вероятности ошибки в канале р и от отношения сигнал-шум на бит Е_b / N₀ для кодов Хэмминга с т=З — 7 при работе в ДСК, декодируемых с помешаю

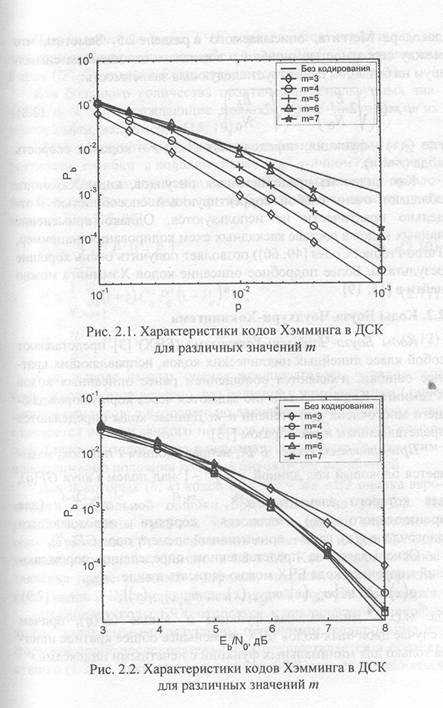
декодера Меггита, описываемого вразделе2.5. Заметим, что между вероятностью ошибки р в канале и отношением сигнал- шум на бит Е_b/N₀ существует следующая зависимость:

/

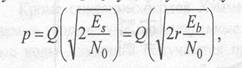
где Q(x) — функция, определенная (1.3); r — кодовая скорость кода (r=kln).

Как видно из представленных рисунков, коды Хэмминга обладают очень слабой корректирующей способность и  отдельно практически не используются. Однако применение данных кодов в составе каскадных схем кодирования (например, Turbo Product Codes [49, 60]) позволяет получить очень хорошие результаты. Более подробное описание кодов Хэмминга можно найти в [15, 19].

2.2. Коды Роуза-Чоудхури-Хоквингема

Коды Боуза-Чоудхури-Хоквингема (БЧХ) [3] представляют собой класс линейных циклических кодов, исправляющих кратные ошибки, и являются обобщением ранее описанных кодов Хэмминга. Коды БЧХ обычно задаются через корни порождающего многочлена g(x) степени n-k. Данные коды определяются представленным ниже образом

Примитивным кодом БЧХ, исправляющим t ошибок, называется блоковый код длиной n = q^m — 1 над полем Галуа GF(q), для которого элементы  α^m0_, α^m0+1,…,α^mo+2t-1 (для

произвольного m₀) являются корнями порождающего многочлена g(x), где а — примитивный элемент поля GF(q ).

Основываясь на представленном определении порождающий многочлен кода БЧХ можно записать в виде

g(x)=HOK(m_mo(x),m_mo+1 (x),…,m_mo+2t-1(x)),  2.9

где m_c(х) — минимальная функция а^c' в поле GF(q), причем в случае двоичных кодов БЧХ наименьшее общее кратное ищется только для минимальных функций с нечетными индексами.

Непримитивные коды БЧХ определяются аналогично, но примитивный элемент а заменяется не примитивным элементом β поля GF(q^m ), и длина блока становится равной порядку р.

Для большого количества практически используемых значений п, к и t порождающие полиномы уже получены, и их можно найти, например, в [15, 19].

Можно получить асимптотические оценки зависимости вероятности ошибки в кодовом блоке Рв,

q-ичном символе Р_s, и бите P_b при декодировании кодов БЧХ по максимуму правдоподобия. Данные оценки не требуют знания спектра кода и имеют вид [15, 20]

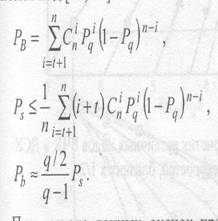
При выводе данных оценок предполагалось, что кодовый блок декодируется неверно при наличии в нем более чем t ошибочных символов, а неправильно декодированное кодовое слово отличается от переданного не более чем в (i+t) q-ичных символах. Также считалось, что в неправильно декодированном символе примерно половина кодовых битов будет ошибочной.

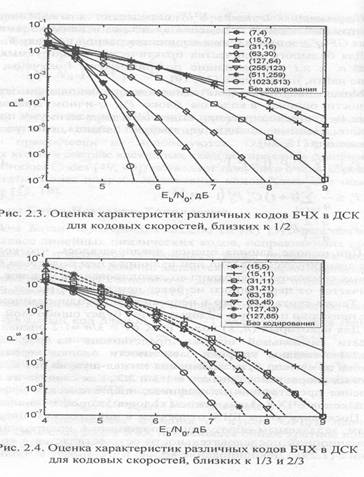
Для некоторых (n, k) кодов БЧХ с r = k/n =1/2 оценка вероятности символьной ошибки представлена на рис. 2.3. На рис.2.4 показаны графики зависимости оценки вероятности ошибки на символ Р_s, от отношения сигнал-шум на бит Е_b/N₀ для кодовых скоростей r, близких к 1/3 и 2/3. Как следует из сопоставления представленных графиков, энергетическая эффективность кодов БЧХ с уменьшением кодовой скорости понижается.

Поскольку коды БЧХ относятся к циклическим блоковым кодам, задаваемым образующим полиномом, кодирование информационной последовательности осуществляется в соответствии с (1.29). Декодирование кодов БЧХ может выполняться

с помощью алгебраических методов, достаточно подробно описанных в [15, 19].

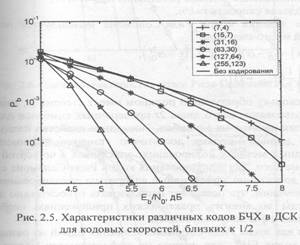
На рис. 2.5 представлены экспериментальные зависимости вероятности ошибки на бит Р~ от отношения сигнал-шум на бит ЕЩ для кодов БЧХ с кодовой скоростью r=l/2 при работе в ДСК. Из сопоставления данного рисунка с рис. 2.3 (для двоичных кодов вероятность ошибки на бит Pb и на символ P, совпадают) видно, что аналитическая зависимость вероятности ошибки (2.12) вполне подходит для оценивания сверху ее реального значения.

Как видно из представленных характеристики, коды БЧХ обладают существенно лучшей эффективностью по сравнению с кодами Хэмминга, однако эти характеристики все еще очень далеки от предельных значений (см. рис. 1.8). Кроме того, сложность декодирования данных кодов при большом значении и очень велика. Поэтому коды БЧХ небольшой длины, так же как и коды Хэмминга, в основном применяются в качестве составляющих элементов более эффективных каскадных кодов.

2.3. Коды Рида-Соломона

Важный подкласс кодов БЧХ составляют коды Рида- Соломона [21], для которых т=т₀= 1. Эти недвоичные коды характеризуются следующими параметрами:

- длина блока n=q — 1, выраженная числом q-ичных символов;

- количество информационных символов k от 1 до n-1;

- минимальное кодовое расстояние d_min=n-k+1;

- кодовая скорость r=k/n.

Для задания кодов Рида-Соломона используется порождающий многочлен вида

_{g(x)=(x-α)(x-α}²_)…(x-α^2t_),

_где t=[(d_min-1) ]

Поскольку образующий полином имеет степень 2t, возможно использование всего лишь 2t проверочных символов для исправления пакетов из t ошибок. Последнее свойство позволило найти данным кодам достаточно широкое применение в каскадных методах кодирования, описанных в четвертой главе. Кроме того, для декодирования кодов Рида-Соломона существуют достаточно эффективные алгоритмы декодирования жестких решений, что позволяет использовать относительно длинные коды во многих практических приложениях, особенно в системах с q-ичной модуляцией.

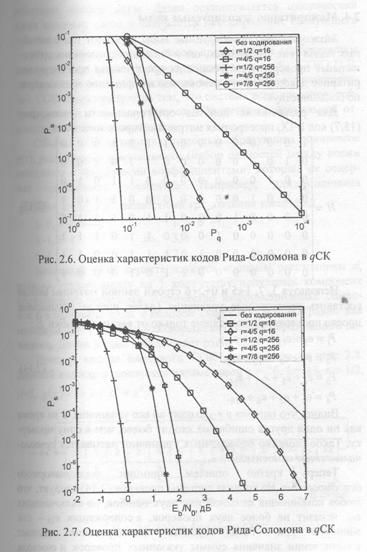
Так как коды Рида-Соломона являются одной из разновидностей кодов БЧХ, для оценки их эффективности можно воспользоваться формулами (2.10) — (2.12). Для примера на рис. 2.6 представлены зависимости оценки вероятности символьной ошибки Р_q от вероятности ошибки Р_s в q-ичном симметричном канале qCK для различных значений q и кодовых скоростей г. Кривые на рис. 2.7 отражают зависимость оценок Р_s для тех же кодов от отношения сигнал-шум F_b/N₀ на информационный бит.

2.4. Мажоритарно декодируемые коды

Мажоритарно декодируемые коды образуют класс линейных кодов (как сверточных, так и блоковых), имеющих ортогональные проверки и допускающих чрезвычайно простое мажоритарное декодирование, основанное на принципе «голосования по большинству».

Для разъяснения понятия ортогональности рассмотрим (15,7) код БЧХ, проверочная матрица которого имеет вид

Используя 3, 7, 1+5 и 0+2+6 строки данной матрицы можно составить проверочные уравнения (далее иногда называемые просто проверками), зависящие только от вектора ошибки Е:

Видно, что ошибка в е₁₄ входит во все уравнения, в то время как ни одна другая ошибка не входит более, чем в одну проверку. Такое свойство проверочных уравнений называется ортогональностью относительно е₁₄.

Теперь кратко опишем принцип мажоритарного декодирования. Из анализа системы проверок (2.14) следует, что любая комбинация из одной или двух ошибок, не включающих е₁₄, исказит не более двух проверок, а содержащих e₁₄ — как минимум три. Тогда процесс декодирования состоит в вычислении значения суммы указанных проверок и символа в позиции 14 в случае превышения данной суммой пороговой

Блоковый СОК характеризуются кодовым расстоянием d, равным увеличенному на 1 количеству ненулевых компонент образующего полинома. Количество информационных символов k в блоковом СОК с кодовой скоростью r = 1/2 равно как минимум 2т+1, где т — максимальная степень образующего полинома. Длина и такого кода будет равна 2k.

Пример кодера блокового СОК представлен на рис. 2.8.

Данный код характеризуется параметрами

n=26, k=13, r=1/2, d=5,g(x)=1+x+x⁴+x⁶.

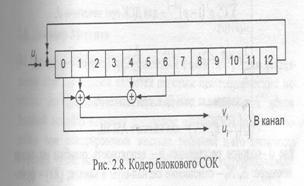
Зная порождающий полином g(x) систематического блокового СОК, можно определить его проверочную матрицу H=[P^TI_k], причем строками матрицы Р^T будут всевозможные циклические сдвиги коэффициентов образующего полинома. Например, для полинома g(x) = 1+ x+ x⁴ + x⁶ проверочная матрица будет иметь вид

Для оценки вероятности ошибки на бит Р_b при оптимальном декодировании блокового СОК, можно воспользоваться следующей формулой

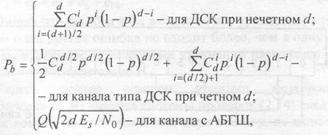
где d-кодовое расстояние; р — вероятность ошибки на входе декодера; Е_s/N₀ — отношение сигнал-шум в канале; Q(x) — функция, определяемая выражением (1.3).

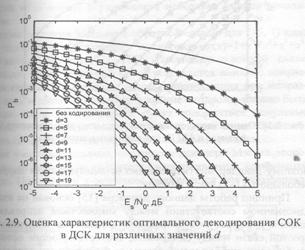
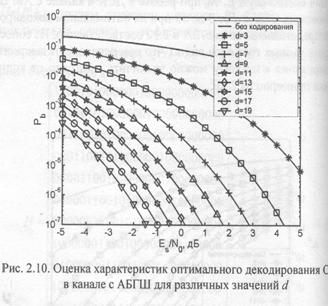
Графики зависимости оценки вероятности ошибки Pb от отношения сигнал-шум Е,INp при работе в ДСК и канале с АБГШ для блоковых СОК с d от 3 до 19 при их оптимальном декодировании представлены на рис. 2.9 и 2.10 соответственно. Из сопоставления данных графиков видно, что при переходе от жесткого декодирования к мягкому можно увеличить выигрыш от кодирования примерно на 2 дБ.

2.5. Декодер Меггита

Декодер Меггита предложенный еще в 1961 г. для исправления пакетов ошибок является простым неалгебраическим методом декодирования систематических циклических кодов. Данный декодер является декодером максимального правдоподобия при декодировании жестких решений и его сложность с ростом числа исправляемых ошибок растет экспоненциально.

Поэтому декодер Меггита обычно используется для коррекции небольшого (1 — 3) числа ошибок.

Принцип работы данного декодера [15] основан на взаимно однозначном соответствии между множеством исправляемых ошибок и множеством синдромов, а также на наличии очень простой связи между синдромом, соответствующим некоторой комбинации ошибок и синдромом ее циклического сдвига: если синдром S(x) соответствует вектору ошибок E(x), то синдром S'(х)= хS(х) mod g(x) соответствует комбинации ошибок x', равной хЕ(х) mod

(хⁿ —1).

Из последнего свойства следует, что все возможные синдромы можно разбить на непересекающиеся множества, каждое из которых соответствует циклическому сдвигу одной и той же комбинации ошибок. Таким образом, необходимо запомнить только синдромы, представляющие исправляемые комбинации ошибок, имеющие единицу в старшем разряде. В результате, процесс декодирования кодового блока можно разбить на и шагов, на каждом из которых текущий синдром сравнивается с запомненными, и, в случае совпадения, изменяется старший бит кодового блока. После этого содержимое синдрома сдвигается с помощью регистра с обратными связями и начинается следующий шаг декодирования.

Декодер Меггита также существует в несколько усовершенствованном варианте, в котором используется обратная связь для удаления из регистра синдрома выявленных ошибок. В этом случае для более полного использования корректирующей способности кода можно осуществлять несколько циклов декодирования.

Схема декодера Меггита с обратной связью для (15, 7) кода БЧХ, заданного образующим полиномом g(x)=1+x+⁴ +x⁶+x⁷+x⁸,  , представлена на рис. 2.11 [15]. Поскольку в данной схеме с помощью цепей обратной связи устраняется влияние исправленных ошибок на синдром, после декодирования при исправлении всех возможных ошибок значение синдрома должно быть нулевым. Если же в синдроме будут содержаться ненулевые символы, то выданное пользователю кодовое слово будет содержать обнаруживаемые, но не исправляемые ошибки.

Как уже было сказано, сложность декодера Мэгита экспоненциально зависит от количества распознаваемых комбинаций ошибок. Поэтому он в основном применяется для декодирования

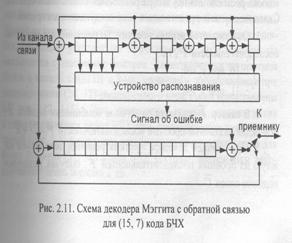
кодов с небольшим кодовым расстоянием d (т.е. кодов Хэмминга, коротких кодов БЧХ и т.д.). Например, при декодировании кодов Хэмминга необходимо запомнить всего одно значение синдрома, поскольку с их помощью возможно исправление только одной ошибки.

2.6. Мягкое декодирование блоковых кодов

В разделе 1.3 было показано, что использование при декодировании мягких решений относительно принятых из канал символов может улучшить эффективность декодирования при мерно на 2 дБ. К сожалению, многие методы декодировании такие как декодер Мэггита, алгебраические методы декодирования кодов БЧХ, очень трудно обобщить на случай использования мягких решений. Поэтому при переходе к работе в канал с АБГШ часто применяют методы декодирования, использующие при работе декодеры жестких решений. Одними из наиболее эффективных алгоритмов данного класса являются алгоритмы декодирования Чейза [15, 32], рассматриваемые в данном разделе.

Принцип работы алгоритмов Чейза основан на жестком де. кодировании нескольких пробных последовательностей, полученных внесением в вектор жестких решений относительно мягких решений демодулятора различных комбинаций ошибок, Сказанное можно представить в виде следующего алгоритма.

1. Определяется вектор жестких D решений для принятой последовательности У, т.е.       2. В вектор D вводятся различные комбинации ошибок Е, порождая различные пробные последовательности F= D+ Е .

3. При помощи декодера жестких решений декодируем каждую из пробных последовательностей F, получая различные кодовые слова С .

4. В качестве решения выбираем кодовое слово С_о, находящееся на наименьшем евклидовом расстоянии от принятой последовательности мягких решений У, т.е.

В работе [32] Чейз предложил три варианта данного алгоритма, отличающиеся методом выбора вносимых комбинаций ошибок. В первом методе в качестве векторов Е выбираются нулевой вектор и все комбинации ошибок веса Ldi2]. Второй метод предполагает выбор множества векторов, имеющих всевозможные символы на Cd)2J наименее достоверных позициях (т.е. позициях с наименьшим значением [у;!) и нулевые на остальных. И, наконец, в третьем методе множество векторов Е имеет единицы на i наименее достоверных позициях и нулевые символы на остальных. Для последнего метода i=0, 2, 4, ..., d — 1 при нечетном dи i=0, 1, 3, ..., d — 1 при четном d.

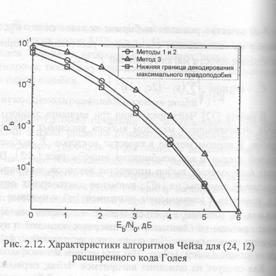
Как следует из описания алгоритмов Чейза, первый метод приводит к наибольшему числу комбинаций ошибок и, соответственно, показывает наилучшие характеристики. Второй метод, практически не уступая по эффективности первому, характеризуется значительно меньшим числом вводимых комбинаций ошибок, что положительно сказывается на его быстродействии. Третий метод, используя очень небольшое число векторов ошибок, несколько уступает по эффективности двум первым, но оказывается существенно быстрее. Характеристики алгоритмов Чейза в канале с АБГШ с 8-ми уровневым квантованием при декодировании (24, 12) расширенного кода Голеи представлены на рис. 2.12 [15]. При сравнении данных характеристик с характеристиками кодов БЧХ при декодировании жестких решений (рис. 2.5) видно, что алгебраические декодеры даже для более длинных (31, 15) кодов БЧХ уступают алгоритмам декодирования Чейза порядка 2 дБ.

2.7. Пороговое декодирование

Пороговое или мажоритарное декодирование [17] является очень простым алгоритмом декодирования, применимым к мажоритарно декодируемым кодам, представленным в разделе 2.4. Данный метод может использоваться для декодирования как двоичных, так и недвоичных кодов.

Рассмотрим работу порогового декодера (ПД) в ДСК ни примере двоичного блокового кода, кодер которого был изображен на рис. 2.8. На первом шаге работы ПД (см. рис. 2.13) с помощью входящего в его состав кодера, вычисляет проверочные элементы для принятых из канала информационных символов и (предположим, что данные символы уже находятся в информационном регистре) и складывает их по модулю 2 с принятыми проверочными v (при этом ключи К2 и К3 находятся в положении 1, а ключ K1 — в положении 2). В результате в синдромом регистре сформируется синдром. После заполнения

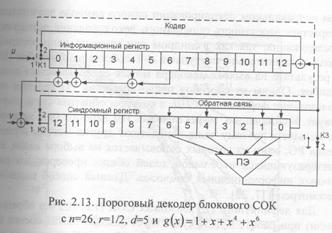
синдромного регистра ключи К2 и КЗ переводятся в положение 2 и осуществляется декодирование информационного символа с номером 12, для чего в пороговом элементе 1ПЭ) осуществляется сравнение суммы элементов синдромного регистра, соответствующих декодируемому символу (в данном случае элементов с номерами О, 1, 4 и 6), с некоторым пороговым значением. В случае если указанная сумма окажется больше порога, выход ПЭ устанавливается равным 1, что приводит к изменению информационного символа и связанных с ним проверок. В противном случае на выходе ПЭ будет О. Затем осуществляется циклический сдвиг содержимого регистров, после чего приступают к декодированию следующего информационного символа.

Рассмотренный ПД является ПД с обратной связью, поскольку исправленная в информационном регистре ошибка за счет обратной связи удаляется и из синдромного регистра. Использование обратной связи с одной стороны значительно улучшает эффективность работы ПД при небольшой вероятности ошибки в канале, а c другой — может привести к высокому уровню размножения ошибок (РО), заключающемуся в том, что при неправильном декодировании одного символа значительно возрастает вероятность ошибочного декодирования нескольких последующих, так как в синдром при этом по цепи обратной связи дополнительно поступают d — 1 собственных ошибок ПД. В результате на выходе декодера может сформироваться пачка ошибок. Одним из способов предотвращения РО является использование дефицитного ПД, в котором обратная связь отсутствует. К сожалению, эффективность ПД данного типа несколько меньше и поэтому чаще используют другие методы ограничения РО, один из которых основывается на выборе кодов, характеризующихся небольшой долей общих проверок для различных информационных символов. Данный способ подробно рассмотрен в [7, 22].

Для дефинитного ПД блоковых СОК (т.е. ПД без обратной связи) при работе в ДСК существует аналитическая оценка вероятности ошибки в информационном бите [17], задаваемая выражением

где р — вероятность искажения бита в канале связи; J число слагаемых образующего полинома; равное J=d-1(d-кодовое расстояние);расстояние

Графики зависимости оценки (2.17) от отношения сигнал шум в канале Е_s/N₀ для кодов с минимальным кодовым расстоянием d=3 — 11 представлены на рис. 2.14. Заметим, что выражение (2.17) подходит и для оценки вероятности ошибки дефинитного ПД сверточных СОК, описываемых в разделе 3.3.

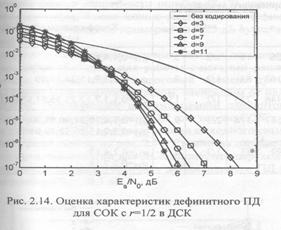
Из анализа представленных графиков следует, что с ростом d дополнительный выигрыш от его дальнейшего повышения уменьшается. А поскольку сложность ПД, как будет показано далее, пропорциональна кодовому расстоянию, то достаточно быстро увеличение d оказывается невыгодным. Еще одно свойство ПД состоит в том, что при фиксированном значении кодового расстояния d лучшими характеристиками при переходе к отношению сигнал-шум на бит E_b/N₀ будут обладать коды с большей кодовой скоростью г.

Результаты моделирования дефинитного ПД и ПД с обратной связью в случае работы в ДСК представлены на рис.2.15. Номера кривых на данном рисунке соответствуют номерам СОК в табл. 2.1. В данной таблице образующие полиномы заданы перечислением степеней с ненулевыми коэффициентами.

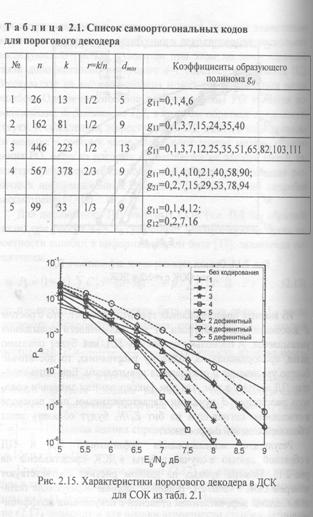
            Из сопоставления данного рисунка с рис.2.14 видно, что пиитическая оценка вероятности ошибки (2.17) дефинитного ПД достаточно точна. Также можно заметить, что дефинитные ПД при P_b=10^-5 оказываются примерно на 0,25 дБ хуже, чем ПД обратной связью.

В отличие от ранее рассмотренных методов декодирования,  можно легко обобщить для работы с мягкими решениями модулятора. В этом случае пороговый элемент суммирует элементы синдрома с некоторым весом, зависящим от надежно и символов, участвующих в формировании элементов синдрома. Результаты моделирования ПД для тех же СОК в случае боты в канале с АБГШ при квантовании выходного сигнала на уровней представлены на рис. 2.16. Сравнивая данные графики с ранее представленными для ДСК видно, что переход к мягким решениям позволяет увеличить эффективность ПД блокового кода всего на 0,2...0,3 дБ.

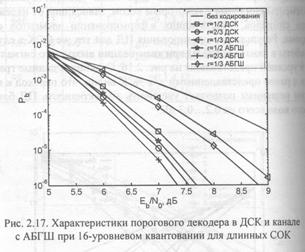
Еще немного увеличить выигрыш от кодирования можно использованием более длинных кодов при сохранении минимального кодового расстояния. Характеристики кодов с длиной до нескольких тысяч символов с d_min=9 для кодовых скоростей r=l/2, 2/3 и 1/3 при использовании как жестких, так и мягких решений демодулятора представлены на рис. 2.17.

Анализируя сложность программной реализации ПД можно заметить, что при декодирования одного информационного битв требуется d — 1 операций сложения целых чисел для подсчета суммы на ПЭ, 1 операция сравнения с порогом и, в случае необходимости коррекции информационного символа и связанных с ним проверок, d операций сложения по модулю 2 (в канале с АБГШ вместо сложения по модулю 2 выполняется инверсия). Кроме того, при вычислении синдрома выполняются д — 1 операций сложения по модулю 2. Поскольку коррекция выполняется с вероятностью р≤0,1 (р — вероятность ошибки в канале) и обычно ПД применяется для декодирования кодов с  небольшим значением d среднее количество операций Nпд, требуемых для декодирования одного информационного символ, будет примерно равно N_ПД ≈d+1+d-1=2d. Здесь предполагается, что операции сложения, сравнения, сложения по модулю 2 и инверсии имеют примерно одинаковую сложность. При аппаратной реализации ПД можно считать, что скорость его работы V_ПД в основном будет определяться скоростью продвижения данных V_p по регистрам сдвига, т.е. V_ПД≈ V_Р.

2.8 Многопороговых декодер

Многопороговых декодер (МПД) самоортогональных кодов [12, 22, 46, 62] является развитием простейшего порогового декодера Месси  и позволяет декодировать очень длинные коды с линейной от длины кода сложностью исполнения. В основе работы МПД лежит итеративное декодирование, что позволяет вплотную приблизиться к решению оптимального декодера в достаточно широком диапазоне кодовых скоростей и уровней шума в канале. При этом МПД сохраняет простоту и быстродействие обычного порогового декодера, что делает его очень привлекательным для применения в существующих и вишь создаваемых высокоскоростных системах связи.

Рассмотрим принцип работы МПД (рис. 2.18). Пусть задан двоичный линейный систематический блоковый или сверточный самоортогональных код, который используется для передачи сообщения из k двоичных символов. После кодирования общее число кодовых символов равно и, n>k.

В результате передачи по двоичному симметричному каналу (обобщение на канал с АБГШ будет проведено далее) декодер получает вместо кодового словаС₀ искаженное шумами сообщение Y длины n. Сначала, как и в обычном пороговом декодере, вычисляется синдром S = YH^T принятого из сообщения, и для каждого информационного символа i_j, 1≤j≤k выделяется множество {S_jk}  элементов синдрома с номерами {j_k}, называемых проверками относительно символа u_j и содержащих в качестве слагаемого ошибку е_j в этом символе.

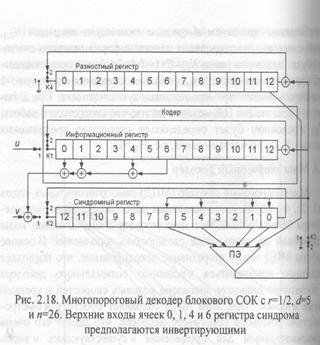
Дополнительно вводится двоичный вектор D длины k, называемый разностным, первоначально равный нулю. В данном регистре будут отмечаться измененные информационные символы для того, чтобы декодер «помнил» принятое из канала сообщение и всегда мог вычислить разность между этим сообщением и кодовым словом, находящимся в информационном регистре.

Основной шаг декодирования заключается в том, что для произвольно взятого символа и, вычисляется функция правдоподобия Lj, зависящая от относящихся к нему проверок S_jk и j-ro элемента вектора D:

L_j= _jk+d_j.

Общее число слагаемых в (2.18) равно минимальному кодовому расстоянию d. Если Lj>T, где T=(d-1)/2 — пороговое значении, то символ u_j все проверки {S_jk} и символ d_j, и инвертируются, после чего выбирается другой символ и_m, m≠j, для него снова вычисляется сумма L_m и т.д. Если же L_j≤Т, то сразу о осуществляется переход к очередному символу и_m.

При выполнении основного шага декодирования все k информационных символов сообщения могут перебираться многократно и в любом порядке. При этом часть решений декодера на каких-то символах может быть ошибочной. Некоторые из этих ошибок будут исправлены при следующих попытках декодирования тех же символов (т.е. на следующих итерациях).

Основным свойством МПД является постоянная сходимость его решения к решению оптимального (по максимуму правдоподобия) декодера (ОД), поскольку при каждом i-м изменении декодируемых символов суммарный вес синдрома S и разностного вектора D уменьшается, т.е. происходит переход к кодовому слову С_i которое более правдоподобно, чем кодовое слово С_i-1, находившееся в МПД в предыдущий момент времени. Переходя от одного слова С_i к другому, МПД может получить наиболее правдоподобное словo С_ОД, которое, собственно, и является решением ОД. Однако нельзя утверждать, что МПД обязательно достигнет решения ОД, так как во многих кодах, допускающих мажоритарное декодирование, МПД на некоторых конфигурациях ошибок веса несколько большего, чем d/2, прекратит изменять информационные символы раньше, чем достигнет решения ОД.

Отметим, что МПД сохраняет свое основное свойство в некотором диапазоне значений порогов Т, что позволяет осуществлять настройку декодера для минимизации вероятности ошибки. Например, на первых итерациях декодирования лучше увеличивать порог. При этом ПЭ этих итераций вносят меньшее количество собственных ошибок в сообщение, передаваемое следующим итерациям, что значительно повышает общую эффективность данной схемы.

Кроме того, МПД, как и обычный ПД, легко модифицируется для суммирования проверок в(2.18) с некоторыми коэффициентами, в частности, при работе с квантованными на несколько уровней решениями мягкого модема (т.е. при работе в канапе с АБГШ), дополнительные выходные биты которого определяют надежность выносимого им решения. Использование мягких решений демодулятора позволяет достигать результатов на 1,4...1,7 дБ лучших, чем при использовании только жестких демодулятора. При этом выражение (2.1S) для вычисления функции правдоподобия L_j принимает вид

где w_i— коэффициент, отражающий надежность проверки S_jk; w_j — коэффициент, отражающий надежность принятого символа и_j.

Как уже было сказано, в процессе работы МПД может прекратить изменение информационных символов, еще не достигнув решения ОД. Одной из основных причин этого является значительная подверженность пороговых декодеров, являющихся составной частью МПД, эффекту размножения ошибок (PO). В результате вторая и последующие итерации декодировании вынуждены работать в основном с потоками пакетов ошибок от декодеров предыдущих итераций, что существенно уменьшает эффективность всего декодера. Следовательно, основным способом приближения решения МПД крашению ОД является уменьшение эффекта РО. Для уменьшения РО необходим тщательный выбор кодов, характеризующихся малой степенью пересечения множеств ошибок, входящих в проверки относительно разных информационных символов, а также настройка параметров декодера (например, величины порогов на разных итерациях). Методика оценки качества кодов в соответствии с указанным выше критерием подробно изложена в [7, 22].

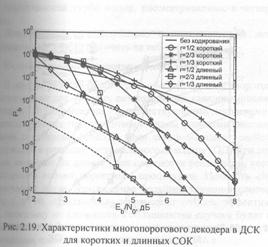
Для примера на рис.2.19 представлены характеристики МПД в ДСК для коротких кодов из табл. 2.1 с d=9 и длинных кодов, в малой степени подверженных РО (те же коды, что и для рис. 2.17). При получении данных графиков использовалось от 5 до 15 итераций декодирования. Как следует из представленных графиков, применение МПД для декодирования плохо выбранных кодов позволяет добиться лишь небольшого улучшения

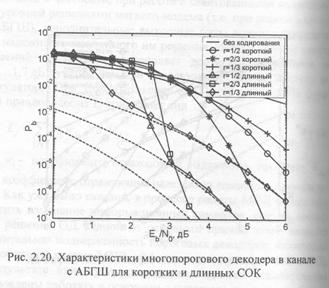
Характеристики МПД в канале с АБГШ при использовании квантования на 16 уровней для тех же кодов представлены на рис.2.20. При использовании длинных кодов и в данном случае практически достигается эффективность декодера максимального правдоподобия. Заметим, что переход к мягким решениям демодулятора позволяет увеличить ЭВК на 1,5...2 дБ по сравнению с применением только жестких решений.

Теперь рассмотрим вопросы сложности реализации МПД. Из сопоставления схемы МПД (рис. 2.18) со схемой ПД (рис.2.13) видно, что они отличаются только наличием разностного регистра, т.е. при работе МПД в случае его программной реализации добавляется всего одна операция сложения при вычислении суммы на ПЭ и одна операция сложения по модулю 2 (или инверсии) при необходимости коррекции информационного символа.

Таким образом, количество операций N_МПД, требуемых для декодирования одного информационного бита, примерно равно N_МПД≈I(d+2)d1≈(I+1)(d+2), где I — количество, итераций декодирования, а слагаемое d-1 соответствует вычислению синдрома, выполняемому только на первой итерации  декодирования. Заметим, что в большинстве случаев при незначительной потере в эффективности (около 0,1 дБ) удается, снимая общее число операций до величины N_МПД≈4d+3I. В случае аппаратной реализации блокового МПД скорость его работы Ряб также определяется скоростью продвижения данных в регистрах сдвига V_p, т.е. V_МПД ≈k₀V_p/I, где k₀ — количество информационных ветвей. В результате МПД при аппаратной реализации оказывается на два-три порядка быстрее [13, 51] сопоставимых по эффективности турбо кодов, рассматриваемых в четвертой главе.

Дополнительную информацию о многопороговом методе декодирования можно получить на веб-сайте [46].

2.9. Недвоичные многопороговые декодеры

В данном разделе рассмотрим обобщение многопорогового декодирования для q-ичных симметричных каналов, описанных в разделе 1.2. По аналогии с соответствующими декодерами для двоичных данных эти алгоритмы названы q-ичными  многопороговыми декодерами (дМПД). Они также обладают свойством сходимости к решению оптимального декодера (ОД) при сохранении линейной от длины кода сложности реализации, которая свойственна только пороговым процедурам. Ценность д МПД заключается в том, что в случае больших значений основания кода q, q>10, практически невозможно создать эффективные ОД, поскольку их сложность в большинстве случаев будет пропорциональна q^k, где k — длина информационной части кода, выраженная числом q-ичных символов.

Далее изложим основные принципы работы дМПД. Пуст, задан q-ичный (q>2) симметричный канал (qCK) с вероятностью ошибки Р_q >О такой, что при передаче любой исходный символ кода переходит в один из оставшихся q — 1 символов случайно, независимо и равновероятно. Для этого канала решением ОД будет такое, может быть единственное, кодовое слово из q^k возможных, которое отличается от принятого из канала сообщения в минимальном числе кодовых символов.

Рассмотрим линейный недвоичный код, проверочная матрица которого имеет такой же вид, как и в двоичном случае, т.е. состоит только из нулей и единиц. Пусть эта матрица соответствует самоортогональному систематическому блоковому коду. Поскольку проверочные (а значит, и порождающие) матрицы кода содержат только нули и единицы, то для выполнения операций кодирования и декодирования принятого сообщения достаточно использовать операции сложения и вычитания по модулю q. Таким образом, для кодирования и декодирования не требуется наличие недвоичного поля, а достаточно создать только группу чисел, что существенно упрощает все процедуры кодирования и декодирования. Пусть декодер типа дМПД (рис. 2.21) устроен так, что после вычисления обычным образом вектора синдрома S принятого сообщения начинается процедура декодирования, заключающаяся в том, что для очередного контролируемого недвоичным пороговым элементом информационного символа кода , происходит подсчет количества и определение значений двух относящихся к нему и наиболее часто встречающихся проверок кода, например, b₁ и b₂, причем b₁ встречается т₁ раз, b₂ — m₂ раз (т₁>т₂), а остальные значения проверок для декодируемого символа u_j, встречаются не более т₂ раз. Тогда на выходе дПЭ будет значение b₁ и дМПД при каждом изменении символа и, будет переходить к  все более правдоподобным решениям [5, 8], так как при этом число различий между кодовым словом, соответствующим текущему содержимому информационного регистра, и принятой

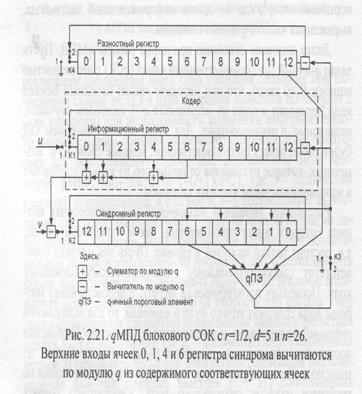
            из канала последовательностью будет уменьшаться. Если окажется, что два наиболее часто встречающихся значения проверок таковы, что т₁=т₂, то выход qПЭ устанавливается равным нулю, т.е. символ и, не изменяется, и делается попытка декодирования любого другого информационного символа кода. Наиболее существенным обстоятельством, повышающим корректирующие возможности описанного qМПД, является возможность принимать безошибочные решения при больших значениях q всего при двух правильных проверках относительно и_j из d-1 возможных, что происходит в том случае, когда все неправильные проверки относительно декодируемого символа и, имеют различные значения.

Теперь рассмотрим процесс вычисления нижней оценки вероятности ошибки при оптимальном декодировании кода, задаваемого описанным выше способом. При этом необходимо выявить наиболее часто встречающиеся условия того, что вектор ошибки будет иметь расстояние Лемминга до ближайшего кодового слова меньшее, чем его собственный вес. В силу линейности кода этого достаточно для вынесения неправильного решения даже оптимальным переборным алгоритмом. Рассматривая такой вектор ошибки, будем учитывать, что нужно анализировать только те символы этого вектора, которые соответствуют позициям проверок относительно очередного декодируемого символа и,. Выпишем вероятности таких наиболее частых событий, которые приводят к ошибкам оптимального декодера. К искомым векторам ошибки относятся такие, что [5, 8]:

- все проверочные символы и декодируемый символ и, ошибочны:

P₁ =P_q^j+1

где J- число проверок кода, определяющее минимальное кодовое расстояние СОК (d=j+1);

- все проверочные символы ошибочны, но два из них одинаковы, а u_j принят верно:

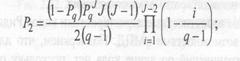
Заметим, что если кодовое расстояние d<7, то последний случай рассматривать не следует, так как он предполагает наличие J=6 проверок в коде, тогда как для СОК d=J+1. Таким образом, нижняя оценка вероятности символьной ошибки оптимального декодирования определяется суммой найденных выше вероятностей P_s=∑P_i,  i=1-6.

Перечисленных событий вполне достаточно, чтобы для большинства реальных условий применения кодов получать удовлетворительные по точности вероятностные оценки потенциальной помехоустойчивости кода. А поскольку qМПД на каждом шаге стремится к решению ОД, то можно ожидать, что при некотором достаточно высоком уровне шума он в большинстве случаев достигнет искомого оптимального решения.

Теперь сравним вероятностные характеристики кодов Рида- Соломона (РС) с возможностями qМПД. Подчеркнем, что для qМПД никаких ограничений по длине кода нет, поскольку он выполняет только операции сложения и сравнения в группе целых чисел. Очевидно, что недвоичный пороговый элемент, рассмотренный выше при описании операций в qМПД, — простейшее устройство или подпрограмма с числом операций N сложения и сравнения небольших целых чисел N=IO — 50 для всех тех значений минимального кодового расстояния d(d<15), которое следует применять в таком декодере.

На рис. 2.22 представлены характеристики qМПД для блоковых СОК с кодовыми скоростями 1/2 (код с d=9) в qCK при q=16 и 256. По горизонтальной оси отложены вероятности искажения символа Р_q в указанном канале, а по оси ординат— средние вероятности ошибки на символ Р_s после декодирования. На данном рисунке графики с пометкой «длинный» соответствуют кодам в наименьшей степени подверженных размножению ошибок, а без нее — кодам с длиной блока и порядка 400. Для достижения решения, обычно совпадающего с оптимальным или близкого нему (кривая ОД для кода с R=l/2, d=9 при q=256,

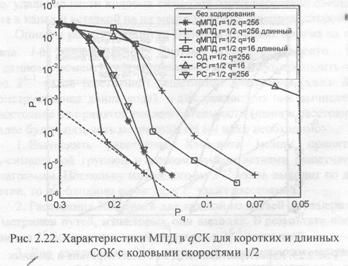
            полученная ранее описанным способом), qМПД требовалось от 5 до 20 итераций декодирования принятого сообщения. Для более удобного сравнения на рис. 2.22 также показаны оценки характеристик кодов Рида-Соломона с теми же параметрами. Как следует из вида графиков зависимостей средней вероятности ошибки декодирования на символ Р_s от вероятности ошибки Р_q канала qCK на входе декодеров, простейший по своему устройству qМПД обеспечивает гораздо более высокие характеристики, чем декодеры для кода РС (особенно при небольших значениях q), благодаря несколько большей длине и используемых кодов и хорошей сходимости решений qМПД крещению ОД. Заметим, что в настоящее время неизвестны другие алгоритмы декодирования с приемлемой сложностью реализации, которые могут обеспечить такие же характеристики.

На рис. 2.23 представлены характеристики qМПД для блоковых СОК с кодовыми скоростями 4/5 и 7/8 в qCK при q=256. Видно, что и в данном случае qМПД показывает сопоставимые с РС или лучшие характеристики.

3. СВЕРТОЧНЫЕ КОДЫ И МЕТОДЫ ИХ ДЕКОДИРОВАНИЯ

3.1. Алгоритм декодирования Витерби

Алгоритм декодирования Витерби [4] предназначен для декодирования сверточных кодов, описанных в разделе 1.4, и является оптимальным в смысле минимизации вероятности ошибки последовательности. Основная идея алгоритма Витерби состоит в пошаговом сравнении всех путей по кодовой решетке с принятой из канала последовательностью Y и отбрасывании тех из них, которые точно будут находиться на большем расстоянии, чем другие пути. В случае работы в ДСК под расстоянием между двумя последовательностями понимается расстояние Хэмминга. В дальнейшем будем рассматривать алгоритм Витерби применительно к сверточным кодам со скоростью r=1/n₀, так как сложность декодера с ростом k₀ значительно увеличивается. При необходимости использовать коды с кодовой скоростью вида r=k₀ /n₀ (k₀>1), можно применять выкалывание, т.е. удаление части кодовых символов перед передачей сообщения в канал и вставкой на их место нулей на приемной стороне.

Опишем работу алгоритма Витерби во время приема из канала i-й n₀-символьной группы последовательности Y . К данному моменту рассматриваемые пути могут проходить через 2^k-1 узлов (состояний) решетчатой диаграммы (здесь К— конструктивная длина кода), и для каждого из них вычислено расстояние от принятой последовательности (данное расстояние далее будем называть метрикой). На i-м шаге необходимо:

1. Вычислить расстояние Хэмминга между принятой n₀-символьной группой и всевозможными ветвями решетчатой диаграммы. Поскольку из каждого из 2^K-1 узлов выходит по две  ветви, то необходимо вычислить 2^K таких расстояний.

2. Расстояния Хэмминга для каждой из ветвей добавляются к метрикам путей, из которых они выходят. В результате получаются 2^K возможных путей, ведущих в 2^K-1 состояний.

3.Для каждого из 2^K-1 состояний сравниваются метрики двух входящих в него путей и путь с меньшей метрикой, т.е. находящийся на меньшем расстоянии от входной последовательности, становится выжившим. Путь с большей метрикой отбрасывается и не участвует в дальнейших вычислениях.

4. Запомнить все 2^K-1 выживших путей вместе с их метриками и перейти к выполнению (i+1)го шага.

Теперь рассмотрим работу декодера Витерби кода со скоростью r=l/2, заданного образующими полиномами g₀(х)=1+ х² и g₁(x)=1+x+x², на простом примере. Пусть в канал передавалась нулевая кодовая последовательность С =(0000...), а из канала принято сообщение Y =(1001000000...). Поскольку свободное расстояние кода d_free, равно 5, две полученные ошибки должны исправиться. Проследим за работой алгоритма Витерби при декодировании данной последовательности.

Первые два шага работы алгоритма тривиальны (рис. 3.1). На первом шаге из состояния 00 выходят два пути: в состояние 00 с расстоянием Хэмминга до принятой из канала n₀-символьной последовательности (далее именуемого метрикой), равным 1 и в состояние 10 с метрикой 1. На втором шаге формируются уже четыре пути, причем метрики состояний 00, 10, 01 и 11 становятся равными 2, 2, 1 и 3 соответственно.

Третий шаг работы является ключевым для понимания всего алгоритма. Рассмотрим состояние 00. В данное состояние можно прийти по двум различным путям: из состояния 00 и из состояния 01. Первый из них будет иметь метрику 2, поскольку метрика ветви (00→00) равна нулю и предыдущее значение метрики пути равно 2, а второй — 3, так как метрика ветви (01→00) равна 2 и предыдущая метрика пути равна 1. Сравнение метрик этих двух путей позволяет выбрать выживший путь (путь из состояния 00, так как он имеет меньшую метрику). Таким же образом выбираются выжившие пути для остальных узлов решетки.

Шаги 4, 5 и 6 полностью аналогичны третьему шагу. Особенностью шага 7 является равенство метрик конкурирующих путей, входящих в одно состояние (состояние 01). Простейшим способом разрешения данной неопределенности является случайный выбор выжившего пути. После выполнения 11 шага

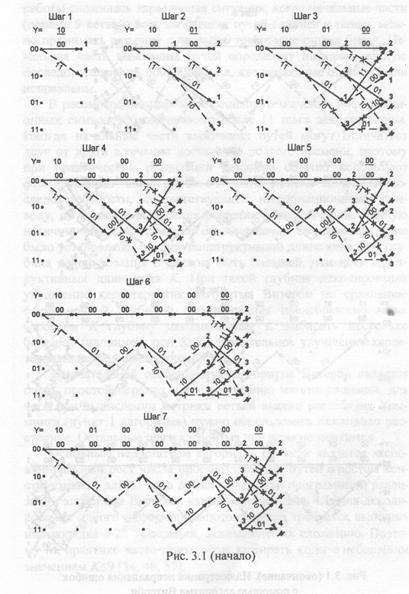
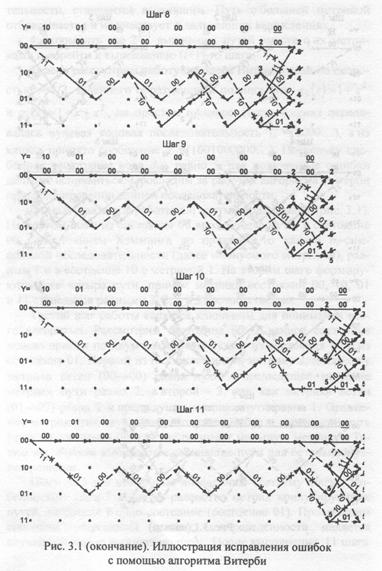
работы сложилась характерная ситуация, когда начальные части (первые 9 ветвей) всех выживших путей слились и теперь можно принимать решение о первых 9 информационных битах. Начальная часть выживших путей определяет информационную последовательность 000000000, т.е. две канальные ошибки были исправлены.

В рассмотренном примере решение о значении информационных символов было принято после 11 шага декодирования. Иногда начальные части выживших путей могут отличаться друг от друга в течение достаточно долгого времени, поэтому при практической реализации декодера обычно используют фиксированное число шагов с момента приема канальной последовательности, соответствующей информационному символу, до момента вынесения решения о его значении. Данную величину называют глубиной декодирования. Экспериментально было установлено, что при конструктивной длине кода К≤9 глубина декодирования L должна быть большей, чем пять конструктивных длин кода К. При такой глубине декодирования ухудшение характеристик алгоритма Витерби по сравнению с бесконечной глубиной декодирования пренебрежимо мало. С ростом К глубину декодирования L выбирать несколько большей (например, при К=12 значительное улучшение характеристик прекращается при L>9K).

Замечательной особенностью алгоритма Витерби является очень простой переход к декодированию мягких решений, для чего при вычислении метрики ветвей вместо расстояния Хэмминга (пункт 1 алгоритма) нужно использовать Евклидово расстояние. Остальные шаги алгоритма при этом не меняются.

Основным недостатком алгоритма Витерби является экспоненциальный рост числа просматриваемых путей с ростом конструктивной длины кода К. Например, при программной реализации алгоритма Витерби, как показано в табл. 4.1, для декодирования одного информационного символа требуется выполнение порядка 3*2^K-1 операций, эквивалентных сложению. Поэтому на практике часто приходится выбирать коды с небольшим значением K≤9 [34, 40, 57].

Далее рассмотрим характеристики алгоритма Витерби. Для сверточных кодов можно получить аддитивную границу вероятности битовой ошибки, имеющей вид

            где w_j — полный информационный вес всех путей веса j; Р_s — вероятность выбрать неправильный путь, отличающийся от правильного в позициях.

Для часто используемых кодов известны несколько первых ненулевых значений w_j, представленные в табл. 3.1 — 3.3 [15, 41]. Заметим, что в данных таблицах порождающие многочлены заданы в восьмеричной системе счисления. Вероятность Р, в выражении (3.1) можно определить по формуле (1.33).

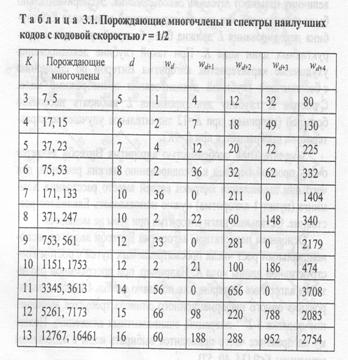
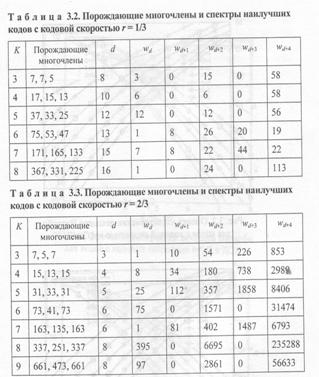
Аддитивная граница вероятности ошибки для представленных в таблицах кодов в случае работы в ДСК и канале с АБГШ показана на рис. 3.2 — 3.7. Из данных графиков следует, что с повышением конструктивной длины кода К на единицу выигрыш от кодирования увеличивается примерно на:0,3...0,5дБ, а при одинаковых значениях К лучшими характеристиками обладают коды с меньшей кодовой скоростью. Также отметим, что переход от декодирования жестких решений к мягким позволяет увеличить эффективность на 2...2,2 дБ.

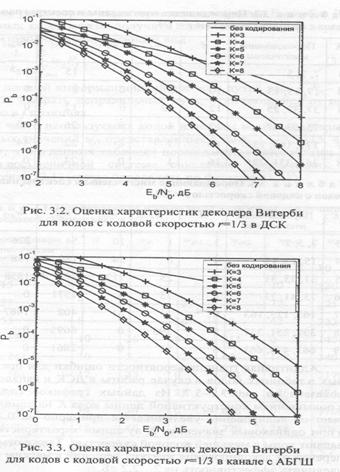
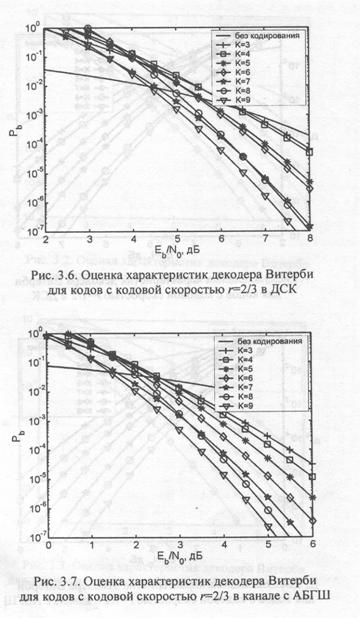
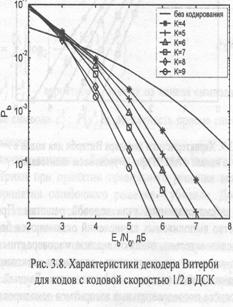
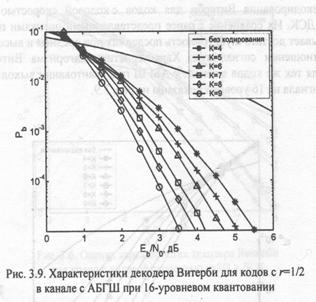
На рис. З.S отражены результаты моделирования алгоритма декодирования Витерби для кодов с кодовой скоростью 1/2 в ДСК. Их сравнение с ранее представленными оценками показывает достаточную точность последних при среднем и высоком отношении сигнал-шум. Характеристики алгоритма Витерби для тех же кодов в канале с АБГШ при квантовании выходного сигнала на 16 уровней показаны на рис. 3.9.

3.2. Последовательные алгоритмы декодирования

Другим методом декодирования сверточных кодов является алгоритм последовательного декодирования, впервые предложенный Возенкрафтом, а затем усовершенствованный Фано. На сегодняшний день известно еще несколько модификаций последовательного декодирования [15]. В данном разделе будет рассматриваться алгоритм, предложенный Фано.

Основным недостатком рассмотренного выше алгоритма Витерби является необходимость анализа всех путей, выходящих

из рассматриваемого узла кодовой решетки. При этом большинство выполняемых вычислений оказываются бесполезными и, следовательно, отказ от анализа маловероятных путей позволит кардинально уменьшить сложность декодирования при незначительных потерях в эффективности. Данный подход лежит в основе последовательных алгоритмов декодирования.

В процессе работы последовательный алгоритм декодирования, в отличие от алгоритма Витерби, осуществляет обработку лишь наиболее вероятного пути по кодовой решетке. Если декодер на каком-либо шаге декодирования совершит ошибку, расстояние между текущим путем и принятой последовательностью начнет быстро увеличиваться. Заметив это, декодер возвращается на один или несколько шагов назад и пытается найти более правильное решение. Для быстрого обнаружения неправильного пути и его быстрого исправления необходимо очень тщательно выбирать параметры декодера.

При поиске правильного пути на i-м шаге декодирования последовательный декодер стремится выбрать ветвь с максимальным значением функции правдоподобия L_i (также называемой далее метрикой пути), т.е. находящуюся на минимальном расстоянии от принятой n₀-символьной последовательности. При этом функция правдоподобия вычисляется следующим образом:

Величину смещения В обычно выбирают так, чтобы значение метрики при принятии правильного решения возрастало, а при принятии ошибочного решения — убывало. Достаточно хорошо указанным требованиям удовлетворяет выбор B=r, где r кодовая скорость.

Несмотря на то, что метрика правильного пути на достаточно больших интервалах имеет тенденцию к возрастанию, из-за всплесков шума в канале метрика какого-либо неправильного пути может оказаться больше функции правдоподобия для правильного пути. При снижении шума метрика неправильного пути начинает уменьшаться, и задачей алгоритма декодирования становится выявление такой ситуации и поиск пути с возрастающей метрикой. Для этого метрика текущего пути L_i сравнивается с некоторым переменным порогом Т, и, если L_i <T, то рассматриваемый путь является плохим и необходимо начать поиск лучшего пути. Отметим, что в процессе работы алгоритма значение порога может меняться.

Главным преимуществом последовательного алгоритма декодирования по сравнению с алгоритмом Витерби является меньшая зависимость сложности декодера от конструктивной длины кода. В результате с помощью данного метода можно декодировать более длинные коды, обладающие большим свободным расстоянием, а, соответственно, и лучшей эффективностью. Однако при практической реализации алгоритма последовательного декодирования сталкиваются с рядом трудностей, вызванных тем, что требуемое для декодирования одного информационного бита количество операций является случайной величиной и быстро растет с ухудшением канала передачи данных. Из-за этого возникает необходимость в наличии большого количества буферной памяти, предназначенной для хранения поступившей, но еще не обработанной канальной последовательности. Причем, так как объем данной памяти конечен, всегда существует вероятность ее переполнения, что приведет к стиранию потерянных символов.

Важной характеристикой канала для последовательных алгоритмов декодирования является вычислительная скорость R₀, рассмотренная в разделе 1.3. Данная величина определяет предельную скорость работы последовательного декодера, т.е. условием нормальной работы является r≤R_o. Если же r>R_o, то в декодере будут возникать вычислительные проблемы, вызванные частым переполнением буфера. Анализируя графики зависимости R₀(E_bN₀) можно определить наименьшее значение отношения сигнал-шум ЕЩ, при котором возможна работа последовательного декодера. Например, из графиков на рис. 1.8 следует, что для ДСК и канала с АБГШ в случае использования кодов с r=1/2 требуемые значения Е_b/И₀ равны соответственно 4,6дБ и 2,5дБ, что существенно ниже теоретически достижимых границ, определяемых пропускной способностью канала С.

Теперь рассмотрим характеристики данного метода. На рис. 3.10 представлены графики зависимости вероятности битовой ошибки Р_b от отношения сигнал-шум на бит E_b/N₀ для последовательного декодера кода с конструктивной длиной К=41 в канале с АБГШ [20]. Для сравнения здесь также представлены оценки характеристик сверточного кода с К=7, декодируемого с помощью декодера Витерби. Как следует из данного рисунка, последовательные декодеры за счет применения кодов с большим

К оказываются значительно эффективнее декодера Витерби при малых вероятностях ошибки декодирования Pb. К сожалению, практическая реализация последовательных алгоритмов декодирования все равно остается громоздкой, поскольку декодер проектируется в расчете на выполнение наибольшего количества операций, которое может понадобиться для декодирования сильно зашумленной последовательности.

Более подробную информацию о последовательных алгоритмах декодирования можно найти в книге [15].

3.3. Пороговый декодер

Перед описанием порогового декодера (ПД) сверточных кодов кратко рассмотрим способы задания сверточных самоортогональных кодов. Эти коды, так же как и ранее описанные блоковые СОК, обычно определяются с помощью образующих полиномов, разностные треугольники которых не содержат одинаковых элементов. Для примера на рис. 3.11 представлена схема кодера сверточного самоортогонального кода, заданного образующим полиномом g(x) = 1+ x+ х + х . Проверочная матрица данного кода определяется так:

Данный код является самоортогональных, поскольку множество компонент s_i синдрома S, содержащих в качестве слагаемых ошибку е0 в первом информационном символе

s₀ = e₀ + e_0v;

s₁=e₀+e₁+e_1v;

s₄=e₀+e₃+e₄+e_4v;

s₆=e₀+e₂+e5+e₆e_6v;

само является ортогональным относительно ошибки е₀. В выражении (3.5) ошибка е, определяет ошибку в i-м информационном символе, а е_iv- в i-м проверочном.

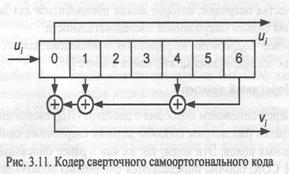
            Так же как и к блоковым, к сверточным с амоортогональным кодам применимо пороговое декодирование. Схема порогового декодера сверточного СОК, кодер которого представлен на рис. 3.11, показана на рис. 3.12. Как видно из рисунка, декодер состоит из кодера, синдромного регистра и порогового элемента. Процедура исправления ошибок данным декодером в целом совпадает с работой порогового декодера блокового СОК, за тем исключением, что при переходе к декодированию следующего информационного символа осуществляется обычный, а не циклический сдвиг составляющих регистров.

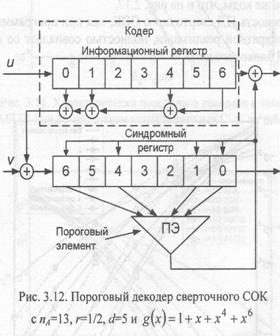
Для оценки вероятности ошибки дефинитного ПД сверточного СОК можно воспользоваться выражением (2.17). В случае ПД с обратной связью возможна оценка лишь вероятности первой ошибки, совпадающая с вероятностью ошибки оптимального декодера и определяемая по формуле (2.16).

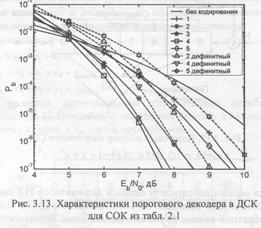
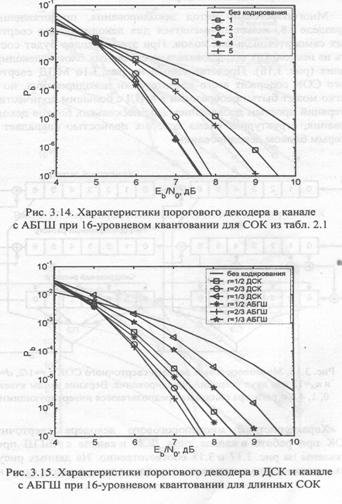
Результаты моделирования ПД с обратной связью и дефинитного ПД для коротких СОК из табл. 2.1 представлены на рис. 3.13 и 3.14. При сравнении характеристик ПД блоковых и сверточных кодов последние по эффективности оказываются лучше на 0,3...0,5 дБ, а соотношение между дефицитными ПД и ПД c обратной связью, между пороговыми декодерами для СОК с разной кодовой скоростью и свободным расстоянием остаются прежними. При переходе к более длинным кодам, характеристики которых представлены на рис. 3.15, не заметно значительного улучшения эффективности. В данном случае использовались те же коды, что и на рис. 2.17.

Сложность ПД сверточного СОК, как при программной, так и при аппаратной реализации, полностью совпадает со сложностью ПД блокового кода.

3.4. Многопороговых декодер

Многопороговых метод декодирования, представленный в разделе 2.8, может применяться для декодирования сверточных самоортогональных кодов. При этом декодер будет состоять из нескольких последовательно связанных блоков декодирования (рис. 3.16). Представленный на рис. 3.16 МПД сверточного СОК содержит всего две итерации декодирования, но он легко может быть преобразован в МПД с большим количеством итераций простым добавлением еще нескольких блоков декодирования, структурная схема которых полностью совпадает со вторым блоком декодировании.

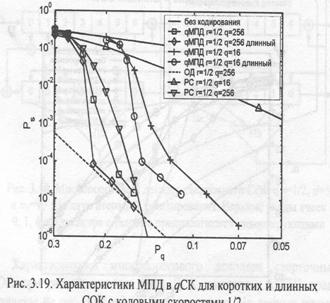
Характеристики многопорогового декодера сверточных СОК при работе в канале типа ДСК и канале с АБГШ представлены на рис. 3.17 и 3.18 соответственно. На данных рисунках отражены результаты моделирования тех же кодов, что и на

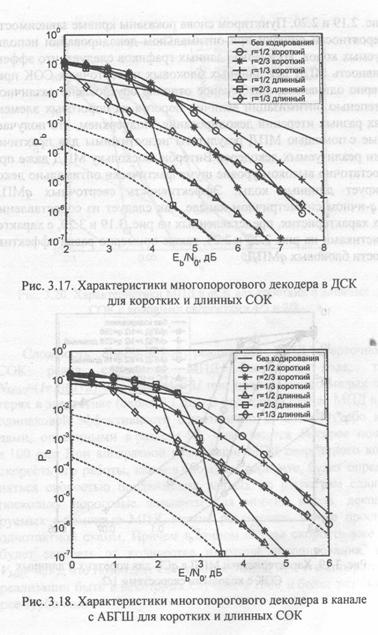
            рис. 2.19 и 2.20. Пунктиром снова показаны кривые зависимости вероятности ошибки при оптимальном декодировании используемых кодов. Из анализа данных графиков следует, что эффективность МПД для длинных блоковых и сверточных СОК примерно одинакова, а небольшое отличие обусловлено различной степенью оптимизации величин порогов на пороговых элементах разных итераций декодирования. Подчеркнем, что получаемые с помощью МПД результаты недостижимы для практически реализуемых декодеров Витерби, поскольку МПД даже при достаточно высоком уровне шума фактически оптимально декодирует длинные коды. Эффективность сверточных дМПД в q-ичном симметричном канале, как следует из сопоставления их характеристик, представленных на рис. 3.19 и 3.20, с характеристиками на рис. 2.22 и 2.23, также примерно равна эффективности блоковых дМПД.

Сложность программной реализации МПД сверточного СОК равна сложности МПД блокового кода, т.е. N_МПД≈(I+1)(d+2) или N_МПД≈4d+3I при пренебрежимо малых потерях в энергетике (около 0,1 дБ). В последнем случае МПД при одинаковой эффективности с достаточно мощными турбо кодами, описанными вразделе4.4, оказываются быстрее почти в 100 раз. При аппаратной реализации МПД сверточного кода скорость его работы, как и в блоковом варианте, будет определяться скоростью продвижения данных по регистрам сдвига, поскольку пороговые элементы для многих кодов, декодируемых с помощью МПД, можно реализовать в виде простой однотактной схемы. Причем в данном случае скорость уже не будет зависеть от количества итераций декодирования, т.е. V_МПД≈k_o V_p, что позволяет сверточному МПД при его аппаратной реализации быть в некоторых случаях в 1000 и более раз быстрее турбо кодов.

4. КАСКАДНЫЕ СХЕМЫ КОДИРОВАНИЯ

Важным этапом в развитии теории кодирования является появление каскадных кодов [24], в основе построения которых лежит идея совместного использования нескольких составляющих кодов. Данный подход позволил существенно повысить эффективность применения кодирования по сравнению с базовыми некаскадными методами.

Пример использования каскадного кода, состоящего из двух составляющих кодов, показан на рис. 4.1. Здесь данные источника сначала кодируются внешним (n₁, k₁) кодом. В качестве внешнего кода часто используются недвоичные коды, например, коды Рида-Соломона. Затем закодированные символы внешнего кода кодируются кодером внутреннего (n₂, k₂) кода. Общая длина кодового слова каскадного кода оказывается равной N=n₁n₂ двоичных символов, причем K=k₁k₂ из них являются информационными. Следовательно, кодовая скорость полученного каскадного кода оказывается равной

где r₁, r₂ — кодовые скорости составляющих кодеров.

Также отметим, что минимальное расстояние сформированного каскадного кода будет равно D=d₁d₂, где d₁ и d₂ — минимальные расстояния составляющих кодов.

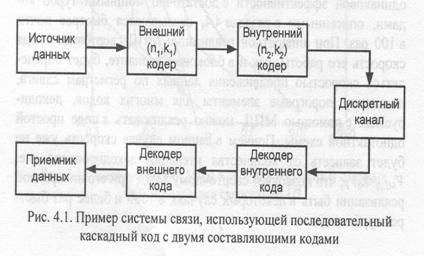
            Декодирование каскадного кода осуществляется в обратном порядке, т.е. принятая из

канала последовательность сначала декодируется декодером внутреннего кода, а затем полученная последовательность декодируется декодером внешнего кода. Подчеркнем, что хотя общая длина кода равна N, структура каскадного кода позволяет применять для декодирования два декодера кодов с длинами всего лишь n₁ и n₂ соответственно. Данное свойство позволяет существенно снизить сложность декодирования по сравнению с сопоставимыми по эффективности декодерами некаскадных блоковых или сверточных кодов.

4.1. Каскадные коды, построенные с использованием кода Рида-Соломона

Наиболее широкое распространение в реальных системах связи нашла каскадная схема, в которой внешним кодом является код Рида-Соломона, а внутренним — сверточный код, обычно декодируемый с помощью оптимального алгоритма Витерби. Часто в данной схеме между внешним и внутренним кодером/декодером включаются устройства перемежения и восстановления (деперемежения), осуществляющие псевдослучайную перестановку символов внешнего кода и восстановление исходного порядка символов соответственно. Рассмотренные устройства предназначены для разбиения пакетов ошибок, появляющихся при декодировании принятого из канала сообщения с помощью декодера внутреннего кода (алгоритма Витерби), что позволяет существенно улучшить эффективность всей каскадной конструкции.

Для оценки вероятности ошибки каскадного кода, состоящего из кода Рида-Соломона и сверточного кода, можно воспользоваться формулами (2.10)-(2.12), но в данном случае вместо вероятности ошибки в канале P_q необходимо использовать оценку вероятности ошибки декодирования сверточного кода (3.1). Полученные оценки будут точны только при независимом характере ошибок на входе декодера кода Рида-Соломона, что справедливо лишь при очень большой длине перемежителя. На рис,4.2 и4.3 представлены вычисленные вышеописанным образом оценки вероятности битовой ошибки Р_b от отношения

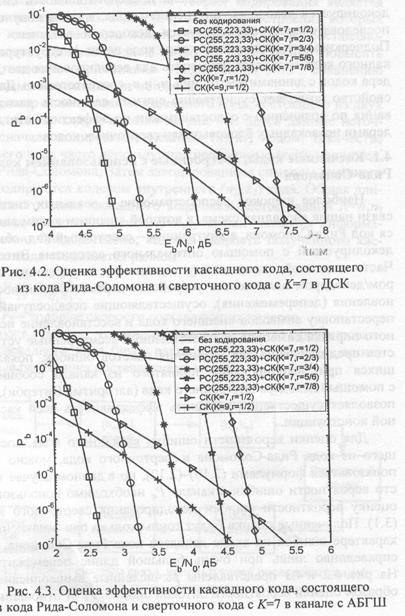
сигнал-шум на бит Е_b/N ₀ для каскадного кода, состоящего из кода Рида-Соломона (255, 223, 33) и сверточного кода с конструктивной длиной  К=7 в ДСК и канале с АБГШ. На этих рисунках параметры кода Рида-Соломона записаны в виде (n, k, d), . где и — общее число q-ичных символов в кодовом блоке, к — число информационных q-ичных символов в кодовом блоке, d — минимальное расстояние кода, а параметрами сверточного кода являются кодовая скорость r и конструктивная длина К. Из сопоставления данных графиков с оценкой характеристик сверточного кода с К=9, также приведенных на рисунках, следует, что уже при P_b<4 *10^-5' каскадная схема оказывается более эффективной, чем более сложный сверточный код, и с уменьшением P_b преимущество каскадной схемы становится все более очевидным.

Результаты моделирования каскадного кода, состоящего из кода Рида-Соломона (255, 223, 33) и сверточного кода с К=7 и r=l/2, при разной глубине перемещения I представлены на рис. 4.4. При получении данных графиков использовался обычный прямоугольный перемежитель, представляющий собой массив, состоящий из 1 строк (определяющих глубину перемежения) по 255 q-ичных символов (в каждом символе содержится 8 бит, поскольку q=256). В процессе кодирования кодовые слова кода Рида-Соломона построчно записывались в массив перемежителя, а затем считывались по столбцам и кодировались с помощью кодера сверточного кода. При декодировании принятая последовательность сначала обрабатывалась декодером внутреннего кода (декодером Витерби). Далее информация с выхода декодера Витерби группировалась в q-ичные символы и по столбцам записывалась в массив деперемежителя (т.е. первый символ записывается в первый столбец первой строки, второй — в первый столбец второй строки и т.д.), а затем построчно считывалась декодером кода Рида-Соломона и декодировалась. Анализируя данные графики можно заметить, что оценка эффективности рассматриваемого каскадного кода оказывается несколько завышенной. Это можно объяснить неточностью границы для характеристик сверточного кода при очень высоком уровне шума.

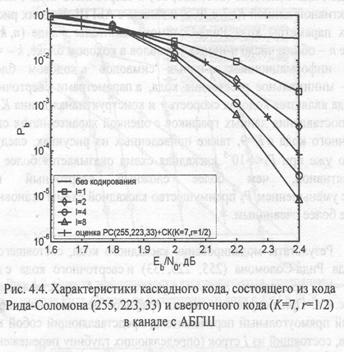
4.2. Каскадные коды, декодируемые с использованием многопорогового декодера

Высокие характеристики МПД способствуют его широкому применению в составе различных кодовых конструкций, поскольку эффективность последних непосредственно связана с эффективностью их составных элементов.

Среди возможных подходов к улучшению характеристик МПД следует выделить такие схемы кодирования, как параллельные коды [9], коды с неравномерной энергетикой и коды с выделенными ветвями. Хотя отдельное использование каждого из данных подходов приводит лишь к незначительному (0,3...0,7 дБ) повышению эффективности по сравнению с обычным МПД, совместное применение этих схем позволяет добиться превосходных результатов.

Особое место среди кодовых схем на базе МПД занимает каскадирование с кодами контроля по четности (ККЧ) [11, 12] использование которых также позволяет повысить эффективность применения кодирования. Особенность данной схемы заключается в том, что такое каскадирование практически не требует дополнительных затрат на оборудование (в схему кодирования требуется добавить лишь один сумматор по модулю 2), тогда как использование в каскадном коде, например, кодов Рида-Соломона несравненно труднее.

Кратко опишем принцип работы декодера каскадного кода, внешним кодом которого является ККЧ, а внутренним — СОК, декодируемый с помощью МПД. При этом длину п₁ ККЧ необходимо выбирать достаточно большой (25 — 100) для того, чтобы потери в энергетике из-за уменьшения кодовой скорости были незначительными.

На первом этапе, как в любом каскадном коде, осуществляется декодирование принятой из канала последовательности с помощью декодера внутреннего кода, т.е. МПД. Пусть после последней итерации МПД помнит все суммы проверок относительно всех декодированных символов. Тогда для исправления одиночных ошибок с помощью ККЧ для всех п₁ символов блока данного кода вычисляется достоверность решения ∆_i=|m_i-T|,  где т_i — сумма проверок относительно i-го символа, Т- значение порога на пороговом элементе последней итерации декодирования, i=1..n₁. Затем, в случае обнаружения с помощью ККЧ ошибки (т.е. в случае отличия от нуля суммы элементов блока ККЧ по модулю 2), исправляется символ, достоверность ∆_i, которого минимальна. Если есть несколько символов с минимальной достоверностью, то изменение символов не производится.

Рассмотрим методику оценки вероятности ошибки данной схемы при работе в ДСК. При вычислениях предполагаем, что на последней итерации декодирования вероятность ошибки МПД Р_МПД равна вероятности ошибки оптимального декодера (данное предположение, как было показано в разделах 2.8 и 3.4,

вполне обосновано), т.е.

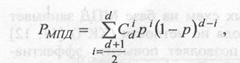
где р — вероятность ошибки в канале связи.

Ошибка при использовании ККЧ может произойти в следующих случаях:

1. В блоке ККЧ длиной n₁ находятся две ошибки. Вероятность такого события (ошибки предполагаются независимыми) равна

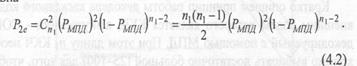
2. В блоке ККЧ длиной п1 находится одна ошибка, но достоверность одного или нескольких других символов меньше либо равна достоверности ошибочного символа, т.е. в проверочных символах относительно какого-либо правильно принятого символа не меньше ошибок, чем безошибочных проверок относительно ошибочно принятого символа. Вероятность данного события оценивается сверху, как

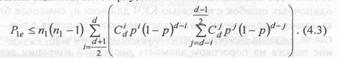
Другими сочетаниями ошибок канала при работе в области оптимального декодирования МПД можно пренебречь.

Так как в данных случаях количество ошибок либо остается прежним, либо увеличивается, вероятность ошибки декодирования каскадной схемы будет не больше, чем

На рис. 4.5 представлены верхние оценки вероятностей ошибки для СОК с d=7, 9, 11 (здесь и далее считается, что данные СОК декодируются с помощью МПД) и каскадной схемы на его основе (длина ККЧ n(=25). На этом же рисунке показаны результаты моделирования каскадного кода на базе СОК с r=1 /2,

Rasm-4.5

            d=7 и d=9. Заметим, что использование простейшего ККЧ совместно с СОК позволяет получить дополнительный энергетический выигрыш около 1...1,5 дБ при вероятности ошибки на выходе декодера P_b=10 ^-5.

Эффективность работы каскадной схемы, состоящей из тех же СОК, что и на рис. 4.5 и ККЧ с n₁=50, для канала с АБГШ отражена на рис. 4.6. Как видно из рисунков, и в данном случае каскадный код оказывается значительно лучше некаскадного. Следует отметить, что при получении представленных графиков ККЧ использовался на нескольких итерациях декодирования, тем самым как бы «помогая» МПД при декодировании внутреннего СОК. Также отметим, что каскадный код, состоящий из кода Рида-Соломона (255, 223, 33) и сверточного кода с кодовой скоростью 1/2 и длиной кодового ограничения К=7, декодируемый с помощью оптимального алгоритма Витерби, даже при меньшей общей кодовой скорости (R≈0,437) сильно уступает

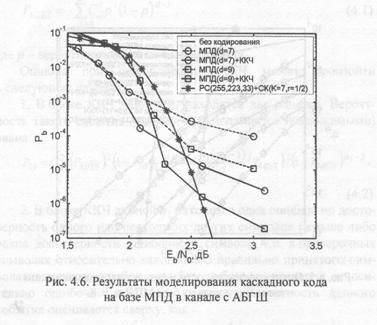
каскадной схеме на базе МПД при P_b>10^-6 . К сожалению, рассмотренный способ каскадирования позволяет улучшить характеристики МПД только в области его эффективной работы.

Сложность декодирования рассмотренной каскадной схемы по сравнению со сложностью обычного МПД увеличивается на сложность декодера ККЧ. Из описания принципа работы данного декодера ясно, что при декодировании блока ККЧ, длиной п₁ символов, требуется выполнить n₁ — 1 сложений по модулю 2 и 1 сравнение при определении наличия ошибки в блоке, n₁- 1 операций выбора максимума из двух чисел для определения символа с минимальной достоверностью и d+1 операций сложения по модулю 2 (инверсий) в случае необходимости коррекции информационного символа (также корректируются элементы разностного и синдромного регистров). Причем, так как коррекция осуществляется с вероятностью Р_МПД <<1, при определении общей сложности ей можно пренебречь. В результате при декодировании одного информационного бита декодером ККЧ в среднем требуется всего операции, эквивалентных сложению.

4.3. Применение многопорогового декодера в схемах с параллельным кодированием

Для приближения границы эффективной работы МПД к пропускной способности канала возможно его применение в ранее упомянутых схемах параллельного кодирования [9]. В основе построения данных схем лежит выделение в СОК C₀ с кодовым расстоянием d₀ и кодовой скоростью r₀ некоторого составляющего кода С₁ с кодовой скоростью r₁>r₀, тоже являющегося СОК. Кодовое расстояние d₁ выделенного кода выбирается значительно меньшим d₀, и, следовательно, область его эффективной работы будет ближе к границе Шеннона. При декодировании параллельного кода сначала выполняются несколько итераций декодирования составляющего кода С₁, позволяющие примерно на порядок снизить вероятность ошибки в принятой из канала информационной последовательности, после Юго в процесс декодирования включается оставшаяся часть кода С_о. Отличительной особенностью данной схемы кодирования является то, что здесь внешний код работает с кодовой скоростью r₀, вто время как в обычных каскадных кодах кодовая скорость внешнего кода близка к единице. Данное свойство обеспечивает существенное преимущество МПД перед другими каскадными конструкциями.

Для примера на рис. 4.7 и 4.8 представлены результаты моделирования схем с параллельным кодированием в ДСК и канале с АБГШ для СОК c r₀=6/12, d₀=13 и r_o=5/10, d₀=l5. В параллельном коде с d₀,=13 в данном случае был выделен внешний код с r₁=6/11, d₁=7., а в коде с d₀=15 был выделен код с r₁=5/9, d₁=9. Кривые «составляющий» на рисунках отражают вероятность ошибки на выходе выделенных кодов параллельной схемы. Пунктирными линиями без маркеров на данных рисунках показаны вероятности ошибки оптимального декодирования

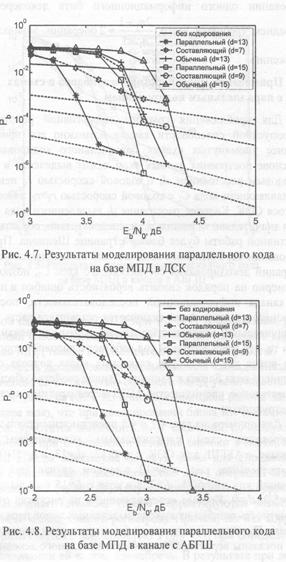
кодов с d=7, 9, 11, 13 и 15. Для сравнения на рис. 4.7 и 4.8 также показаны характеристики декодируемых с помощью МПД обычных СОК с аналогичными d и r.

Как следует из анализа представленных графиков, применение параллельного кодирования позволяет приблизить границу эффективной работы МПД к пропускной способности канала примерно на 0,5 дБ.

Сложность МПД при параллельном кодировании (в смысле количества выполняемых операций) оказывается даже меньше сложности обычного МПД, поскольку в данном случае на первых итерациях декодирования некоторые элементы синдромного регистра просто не участвуют в процессе вычисления суммы на пороговом элементе.

4.4. Турбо коды

Турбо коды [30] образуются при параллельном каскадировании двух или более составляющих систематических кодов. Рассмотрим общую схему кодера турбо кода, изображенную на рис. 4.9. Как показано на рисунке, передаваемые данные перед кодированием каждым из составляющих кодов перемешиваются с помощью входящих в состав кодера перемежителе. Поскольку систематические выходы каждого из кодеров с учетом перемежения идентичны, в канал можно передавать только исходную последовательность и проверочные выходы каждого из кодеров.

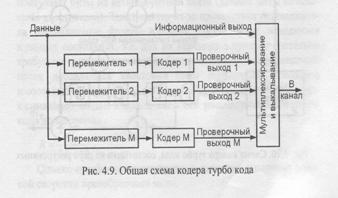
В результате общая кодовая скорость турбо кода при использовании составляющих кодов со скоростью 1/2 оказывается равной R=1/(М+1), где М — количество составляющих кодеров. Затем систематические и проверочные биты от всех составляющих кодеров объединяются в одно кодовое слово, передаваемое по каналу связи.

Обычно при построении турбо кодера используются два одинаковых рекурсивных систематических сверточных (RSC) кодера без перемежения в первой ветви. Применение таких составляющих кодов совместно с перемежителе позволяет уменьшить число кодовых слов низкого веса, определяющих эффективность турбо кода при большом уровне шума в канале связи [53].

Рассмотрим турбо код, кодер которого представлен на рис. 4.10. Данный код является стандартным турбо кодом с кодовой скоростью 1/3, включенным в стандарты систем мобильной          

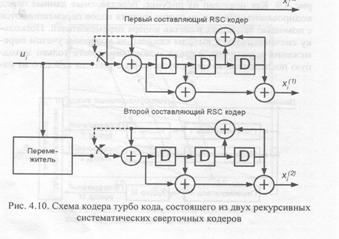
связи третьего поколения [40, 57]. Для построения указанного кода используются два одинаковых RSC кода с конструктивной длиной К=4, заданных образующими полиномами g₀=13, g₁=15. Как видно из рис. 4.10, выходом турбо кодера является последовательность, состоящая из систематических и проверочных бит первого кодера и проверочных бит второго кодера. Таким образом, общая кодовая скорость турбо кода равна R=l/3. При необходимости использования более высоких кодовых скоростей обычно применяют выкалывание, при котором часть проверочных символов не передается в канал. В этом случае перед декодированием вместо пропущенных проверочных символов вставляются нули.

В начале кодирования информационного блока, длина которого определяется размером L используемого перемежителя, оба составляющих кодера находятся в нулевом состоянии, т.е. их регистры сдвига заполнены нулями, После кодирования последнего информационного бита в блоке каждый декодер может оказаться в любом из 2^K-1 (в данном случае 8) состояний. Однако эффективность декодера будет значительно лучше, если идет известно не только начальное, но и конечное состояния кодеров. Поэтому в турбо кодер добавляется схема перевода составляющих кодеров в нулевое состояние, при работе которой (т.е. при переводе ключей в нижние позиции) на вход каждого из кодеров поступают биты из ветви обратной связи (данные биты называются хвостовыми). Заметим, что из-за присутствия перемежителя составляющие кодеры в общем случае будут находиться в разных состояниях, т.е. для их перевода в нулевое состояние требуются разные хвостовые биты. Поэтому в передаваемый поток добавляются хвостовые биты каждого из декодеров и соответствующие им проверочные биты, что приводит к снижению общей кодовой скорости рассматриваемого турбо кода до величины

Однако при больших значениях L данное уменьшение кодовой скорости пренебрежимо мало.

Для декодирования турбо кода с рис. 4.10 можно использовать декодер, изображенный на рис.4.11 [61]. Декодер представляет собой каскадное соединение двух элементарных декодеров, двух перемежителей, идентичных используемым в кодере, и двух деперемежителей, осуществляющих восстановление исходного (до перемежения) порядка символов. Как видно из рисунка, декодер каждого составляющего кода имеет три входа: принятые из канала информационные биты, канальные проверочные биты от соответствующего кодера и информация от другого декодера, оценивающая значение информационных бит (данная информация называется априорной). Единственным выходом компонентного декодера являются мягкие решения относительно декодируемых бит, причем для представления мягких решений обычно используется логарифм отношения правдоподобия, знак которого определяет значение декодированного бита (отрицательное значение соответствует нулю, положительное— единице), а модуль — надежность этого значения.

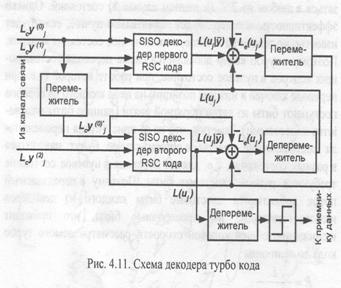
Логарифм отношения правдоподобия L(u_k) для информационного символа u_k, как следует из его названия, определяется следующим образом:

Принцип работы декодера турбо кода заключается в выполнении нескольких итераций декодирования, для первой из которых на входе декодера первого составляющего кода отсутствует априорная информация, т.е. он формирует оценку информационных бит, используя только принятую из канала последовательность. Далее из полученной оценки выделяется так называемая внешняя информация, определяемая исключением из оценки декодируемых символов априорной информации (на первой итерации априорная информация равна нулю) и принятых из канала систематических символов:

Затем декодер второго кода использует эту внешнюю Информацию в качестве априорной для получения своей оценки информационных бит.

На второй итерации первый декодер снова обрабатывает принятую из канала последовательность, но уже с учетом априорной информации, сформированной из оценки второго декодера на первой итерации. Эта дополнительная информация позволяет первому декодеру получить более точную оценку декодируемых бит, используемую затем вторым декодером в качестве априорной.

Далее декодер турбо кода выполняет еще несколько итераций декодирования, на каждой из которых осуществляется уточнение оценки информационной последовательности (т.е. средняя вероятность ошибки декодирования постепенно уменьшается). К сожалению, с каждой новой итерацией улучшение от ее применения становится все меньше. Поэтому, для снижения сложности декодера, итеративный процесс прекращается после выполнения некоторого небольшого (10 — 20) количества итераций. Также для завершения декодирования можно использовать некоторый критерий, определяющий целесообразность применения дополнительной итерации, что часто позволяет существенно сократить среднее число итераций и сложность декодера при незначительных потерях в эффективности. После выполнения заданного количества итераций или вынесения решения о нецелесообразности продолжения итеративного процесса жесткое решение о восстановленной после перемежения оценке второго декодера будет определять результат декодирования.

В качестве декодеров составляющих кодов турбо кода, применяемых в описанной схеме, можно использовать такие алгоритмы как MAP (Maximum А Posteriori) [27], Log-MAP [51], Мах-Log-MAP [4S, 39], SOVA (Soft Output Viterby Algorithm) [42]. Сложность реализации последних трех методов в смысле количества выполняемых операций для декодирования одного информационного символа представлена в табл.4.1. MAP алгоритм значительно превосходит остальные по сложности при одинаковой с Log-MAP алгоритмом эффективностью

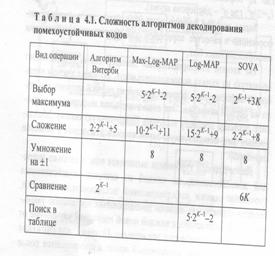
и поэтому на практике обычно не используется. Зная сложность реализации методов декодирования составляющих кодов NД, можно оценить сложность декодирования всего турбо кода:

N_mрубо=IN_cocmM,

где 1 — число итераций декодирования; М — число составляющих кодов.

Для аналитической оценки эффективности турбо кодов можно воспользоваться выражением для аддитивной границы вероятности битовой ошибки блокового кода

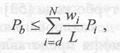
где N — длина кодового блока; L — количество информационных символов блока; d-минимальное кодовое расстояние; w_i — общий информационный вес всех кодовых слов веса i; Р_i — вероятность выбрать неправильное кодовое слово, отличающееся от правильного в i позициях, определяемая по формуле (1.33).

Для турбо кода с кодовой скоростью R=1/2, состоящего из двух одинаковых кодеров с конструктивной длиной К и перемежителя длиной L, длина кодового блока будет равна N=2(L+K — 1). Учитывая, что общий информационный вес w_i всех кодовых слов веса i равен w_i = ŵ_iN_i(ŵ_i— средний информационный вес кодовых слов веса i; N, — общее число кодовых слов веса i), перепишем выражение (4.6) следующим образом:

При вычислении границы (4.8) часто ограничиваются только первым слагаемым, хорошо аппроксимирующим вероятность битовой ошибки при средних и высоких значениях отношения сигнал-шум, и называемым асимптотой кодового расстояния:

Для примера рассмотрим оценку эффективности турбо кода с кодовой скоростью R=1/2, полученного из двух одинаковых составляющих RSC кодов с образующими полиномами g₀=37₈ и g₁=21₈и псевдослучайного перемежителя длиной L=65536 бит.

Данный код, используемый в работе [30], в дальнейшем будем обозначать как (37, 21, 65536). Поскольку для (37, 21, 65536) турбо кода d=6, w_d — — 2, N_d=3 [53], выражение (4.8) для канала с АБГШ принимает вид

График зависимости оценки вероятности ошибки от отношения сигнал-шум на бит E_b/N_O, полученный по формуле (4.10) и результаты моделирования (37, 21, 65536) турбо кода [53] для случая использования Log-МАР алгоритма декодирования составляющих кодов и 18 итераций декодирования представлены на рис. 4.12. Превосходные характеристики турбо кода в области, больших шумов объясняются очень малым отношением w_iN_i /Lдля кодовых слов низкого веса, вызванного использованием  

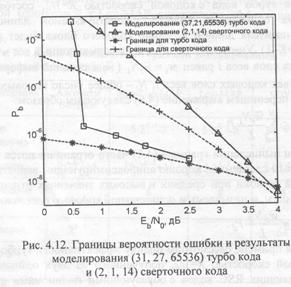
рекурсивных составляющих кодеров, часто позволяющих получить для информационных последовательностей низкого веса проверочные последовательности с высоким весом, и наличием перемежителя, с высокой вероятностью отображающего проверочные последовательности низкого веса первого составляющего кода в проверочные последовательности высокого веса второго составляющего кода [53].

Из рисунка следует, что асимптота кодового расстояния при умеренных и высоких значениях отношения сигнал-шум хорошо подходит для нижней оценки характеристик турбо кода. На рис.4.12 также можно наблюдать проявление свойственного турбо кодам эффекта насыщения вероятности ошибки, заключающегося в уменьшении угла наклона кривой характеристик турбо кода после достижения некоторого значения вероятности ошибки на выходе декодера. Данный эффект, как следует из анализа выражения (4.10), возникает из-за относительно небольшой величины кодового расстояния турбо кода, поскольку указанная величина влияет на наклон графика асимптоты. Кроме кодового расстояния на область насыщения вероятности ошибки большое влияние оказывает коэффициент w_dN_d/L, поскольку его увеличение поднимает асимптоту кодового расстояния, а уменьшение — понижает. Таким образом, для увеличения эффективности турбо кода в области средних и малых шумов можно увеличивать кодовое расстояние d или длину используемого перемежителя L.

На рис. 4.12 также представлена граница вероятности ошибки и результаты моделирования (2, 1, 14) сверточного кода с кодовой скоростью r=1/2 и конструктивной длиной кода К=14, декодируемого с помощью алгоритма Витерби. Сложность декодера Витерби для данного кода сопоставима со сложностью декодера (31, 27, 65536) турбо кода. При вычислении границы сверточного кода также использовалось только первое ненулевое слагаемое в (3.1), которое для данного кода принимает вид

Сравнение асимптот рассмотренных кодов показывает, что из-за большего кодового расстояния угол наклона асимптоты сверточного кода значительно больше, чем асимптота турбо кода. Однако, так как количество кодовых слов низкого веса для турбо кода гораздо меньше, чем для сверточного, две асимптоты не пересекаются до отношения сигнал-шум порядка 3,5 дБ. При этом вероятность ошибки при декодировании рассматриваемых кодов оказывается ниже 10 ', что меньше требуемой вероятности ошибки для многих реальных систем связи. Следовательно, несмотря на то, что при сопоставимой сложности сверточные коды асимптотически лучше турбо кодов, во многих практических случаях целесообразно использовать именно турбо коды.

Большое значение при разработке турбо кодов уделяют выбору типа перемежителя, поскольку он оказывает огромное влияние на минимальное расстояние и количество кодовых слов низкого веса, определяющих эффективность турбо кода. Все типы перемежителе в зависимости от способа построения можно условно разделить на два класса: псевдослучайные (например, S-random [38]) и регулярные (блоковый, циклический, диагональный и т.д. [28, 33, 35, 45, 56]). Зависимость позиций битов в перемеженном блоке от их позиций в исходном блоке для регулярных перемежителе имеет ярко выраженную структуру (рис.4.13). При использовании псевдослучайных перемежителе биты исходного блока в перемеженном блоке располагаются в псевдослучайном порядке (рис. 4.14), что положительно сказывается на общей эффективности турбо кода.

Представим результаты моделирования турбо кода в канале с АБГШ при использовании двоичной фазовой модуляции. Как следует из описания кодера и декодера турбо кодов, на их эффективность оказывают влияние много параметров, основными из которых являются алгоритм декодирования составляющих кодов, количество итераций декодирования, тип и длина перемежителя, составляющие коды. Далее рассмотрим характеристики турбо кодов, по умолчанию имеющих следующие параметры: кодовая скорость R=1/2, конструктивная длина составляющих рекурсивных систематических сверточных кодов К=4,

образукнцие полиномы составляющих кодеров go=13 и р=15, псевдослучайный перемежитель длиной L=1146 бит, Мах-Log- MAP алгоритм декодирования составляющих кодов, 8 итераций декодирования.

Влияние количества итераций декодирования на эффективность турбо кода показано на рис. 4.15. Как видно из рисунка, характеристики турбо кода уже после одной итерации декодирования сопоставимы с характеристиками составляющего сверточного кода с K=4, и с увеличением их числа вероятность ошибки постепенно уменьшается. Отметим, что уже после восьми итераций это уменьшение становится незначительным. Поэтому для всех далее приводимых результатов по умолчанию предполагается использование восьми итераций декодирования.

На рис. 4.16 представлены результаты моделирования турбо кода со стандартными параметрами при использовании различных алгоритмов декодирования. Заметим, что МАР и Log-МАР алгоритмы обладают одинаковыми характеристиками, а Мах-

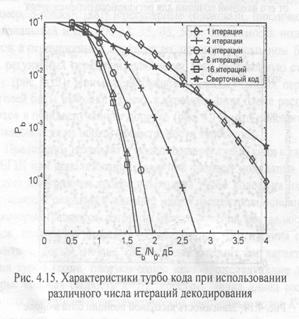
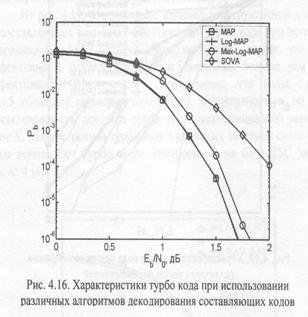
            Log-MAP и SOYA алгоритмы уступают при вероятности ошибки Pb=10 им примерно 0,1 и 0,6 дБ соответственно.

На рис. 4.17 показаны характеристики турбо кода для нескольких типов перемежителе различной длины. Видно, что при небольших длинах кодов эффективность перемежителе рассмотренных типов примерно одинакова, а с увеличением длины значительно лучшие результаты показывают псевдослучайные перемежителе.

Влияние длины перемежителя на эффективность турбо кода показано на рис. 4.18. Для сравнения на данном рисунке также представлены характеристики сверточного кода с K=l l, декодируемого с помощью алгоритма Витерби. Данный код был выбран потому, что К=11 является наименьшей конструктивной длиной, при которой сложность декодирования сверточного кода, исходя из табл. 4.1, становится больше сложности декодирования рассматриваемого турбо кода. Как видно из рисунка, турбо код с длиной блока всего 190 бит по эффективности соответствует

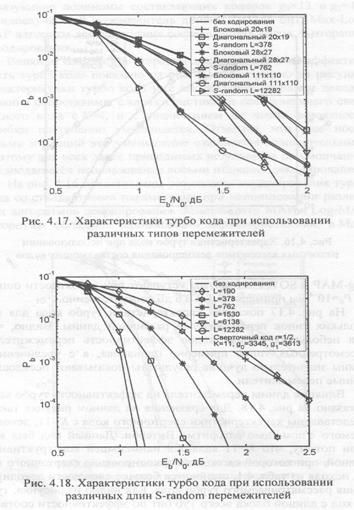
сверточному коду с К=11, а с ростом длины перемежителя характеристики турбо кода значительно улучшаются.

Из рис. 4.19, отражающего влияние конструктивной длины составляющих кодов на эффективность турбо кода при использовании Log-МАР алгоритма декодирования, следует, что эффективность турбо кодов с К=4 и 5 несколько больше, чем эффективность кодов с К=3. Также видно, что коды с К=4 и 5 обладают примерно одинаковой эффективностью, но так как сложность декодера турбо кода экспоненциально зависит от К для построения турбо кода в реальных системах связи часто используют турбо коды, построенные на базе RSC кодов с К=4 [40, 57].

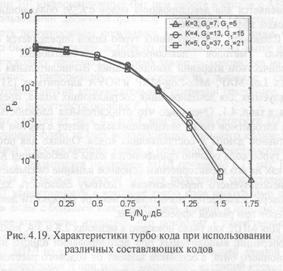
4.5. Сравнение сложности реализации эффективных методов декодирования помехоустойчивых кодов

В данном разделе проведем сравнение сложности практической реализации [13] нескольких наиболее эффективных методов декодирования, таких как алгоритм декодирования Витерби [4], методы декодирования турбо кодов [30] и многопороговых алгоритм декодирования (МПД) [12, 22]. Под сложностью реализации здесь будем понимать количество арифметических операций, требуемых для декодирования одного информационного бита.

Из табл. 4.1 видно, что сложность оптимального алгоритма Витерби растет экспоненциально с ростом конструктивной длины кода К в связи с чем на практике данный метод обычно применяется для декодирования кодов с К<9, обладающих невысокой эффективностью.

Сложность декодирования турбо кодов определяется сложностью методов декодирования составляющих кодов и количеством итераций декодирования. Вычислительная сложность Log-MAP,  Мах-Log-MAP и SOVA алгоритмов [51], используемых для декодирования составляющих кодов, представлена в табл.4.1. Очевидно, что относительная сложность данных алгоритмов также экспоненциально растет с ростом конструктивной длины К составляющих кодов. Однако для построения турбо кода обычно применяются коды с небольшим К=3 — 5, так как на его характеристики основное влияние оказывает длина используемого перемежителя. Поэтому сложность данного декодера оказывается значительно меньше сложности декодера Витерби при равной эффективности.

Для МПД, как было показано в разделах 2.8 и 3.4, количество операций,  выполняемых при декодировании одного информационного бита, в основном зависит от кодового расстояния d используемого кода и количества итераций декодирования I, т.е. N_МПД ≈(I+1)(d+2). Поскольку МПД обычно применяется для декодирования кодов с d=7 — 15 при 1<20, его сложность оказывается примерно на порядок меньше сложности сопоставимого по эффективности декодера турбо кода. Кроме того, небольшая модификация МПД при пренебрежимо малых потерях в энергетике (около 0,1 дБ) позволяет снизить суммарное количество операций, выполняемых на всех итерациях декодирования, до величины порядка N_МПД ≈4d+3I. В результате данных изменений сложность МПД при высоком уровне шума становится в десятки раз меньшей сложности всех других методов коррекции ошибок.

Для примера в табл. 4.2 и 4.3 приведены результаты исследования скорости работы декодера турбо кода и «быстрого» многопорогового декодера для кодовых скоростей 1/2 и 3/4. В последней строке табл. 4.2 представлены результаты для каскадного кода, состоящего из СОК, декодируемого с помощью МПД и кода с контролем четности. Данные результаты были получены на компьютере с процессором Athlon 850 при декодировании 10 информационных бит при работе в канале с АБГШ и использовании двоичной фазовой модуляции. Отметим, что скорость декодирования получилась в несколько раз ниже, чем можно было бы ожидать исходя из представленных выше формул, поскольку процессорное время также расходовалось на кодирование информации, ее искажение в канале связи и некоторые другие вспомогательные операции (например, определение вероятности ошибки P_b).

Как следует из табл. 4.2 и 4.3, при кодовой скорости 1/2 более мощный турбо за счет использования меньшего количества итераций и составляющих кодов с небольшой конструктивной длиной К оказывается медленнее МПД примерно в 13 раз. При переходе с кодовой скорости 3/4 для получения сопоставимой с МПД эффективности в декодере турбо кода необходимо применять коды с большей конструктивной длиной и использовать большее количество итераций, что приводит к существенному замедлению процесса декодирования, в то время как скорость работы МПД из-за использования кодов с меньшей длиной кодового расстояния d при том же количестве итераций несколько возрастает. В результате МПД оказывается быстрее декодера турбо кода в 40 и более раз.

Заключение

Представленный вниманию специалистов справочник является фактически первой попыткой в нашей стране систематически и кратко описать обширные возможности современных методов помехоустойчивого кодирования для систем связи самого широкого назначения.

Он выходит в свет в то время, когда динамичный конкурс между несколькими наиболее известными алгоритмами декодирования по критериям эффективности и сложности реализации становится особенно напряженным. В этой ситуации становится особенно важным, насколько реально полезными для создателей систем современной связи окажутся те алгоритмы, которые в настоящее время демонстрируют наиболее обнадеживающие характеристики.

Хотелось бы надеяться, что настоящий справочник поможет специалистам, создающим аппаратуру и программное обеспечение для систем и сетей связи, выбрать наиболее соответствующие их потребностям алгоритмы декодирования для будущих высококачественных и очень надежных систем телекоммуникаций и информатики. В этом случае авторы справочника будут считать, что свою задачу ускорения продвижения самых последних идей теории и достижений технологии кодирования в системы связи они выполнили.

Список сокращений, принятых в книге

АБГШ             аддитивный белый гауссовский шум

БЧХ                код Боуза-Чоудхури-Хоквингема

ДКВП             дискретный канал без памяти

ДСК               двоичный симметричный канал

ККЧ                канал код с контролем по четности

МПД               многопороговый декодер (алгоритм декодирования)

ОД                  оптимальный декодер

ПД                  пороговый декодер

ПЭ                  пороговый элемент

РО                  размножение ошибок

РС                   код Рида-Соломона

СК                  сверточный код

СОК               самоортогональный код

ЭВК                энергетический выигрыш кодирования

МАР               maximum а posteriori

RSC                recursive systematic convolutional (рекурсивный систематический сверточный)

qмпд               q-ичный многопороговый декодер

qПЭ                q-ичный пороговый элемент

qСК q-ичный симметричный канал

SISO               soft in soft out

SOVA             soft-output Viterby algorithm