ГЛАВА 19. ДИСКРЕТНЫЕ СИГНАЛЫ И ЦЕПИ

19.1. Дискретные сигналы

Дискретизация аналоговых сигналов. Сигнал — это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.

Существуют аналоговые, дискретные п цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией x(t), которая может принимать любые значения в определенном интервале (рис. 19.1, а); дискретные сигналы x_Т(t) представ ля ют собой последовательности или отсчеты функции x(t), взятые в определенные дискретные моменты времени kT (рис. 19.1, б); цифровыми являются сигналы, которые в дискретные моменты времени kT принимают конечные дискретные значения — уровни квантования (рис. 19.1, в), которые затем кодируются двоичными числами. (На рис. 19.1, в, Δ — шаг квантования).

Если в цепь микрофона (рис. 19.1), где ток i(t) является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не

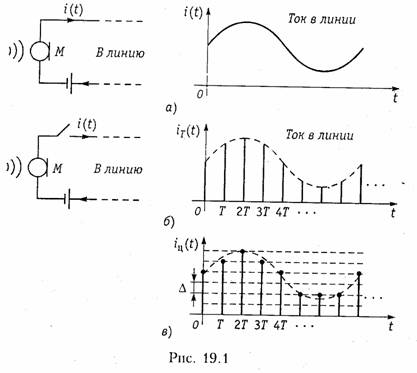
что иное, как дискретный сигнал. Причем, во всех этих записях k — целое число, принимающее как положительные, так и отрицательные значения.

В отличие от непрерывного сигнала i(t) дискретный сигнал можно обозначить i_Т(t). Так, на рис. 19.1 при k < О дискретный сигнал i_Т(t) = 0. При k = 0 значение i_Т(ОТ) равно значению сигнала i(t) в момент времени t = 0. При k > 0 отсчеты i(kT) повторяют форму сигнала i(t), т. к. их амплитуды равны значениям непрерывного сигнала в моменты времени kT.

Дискретные сигналы можно задавать графиками, как это показано на рис. 19.1, формулами, например, i_T( t) = sin(2πfkT), в виде таблиц дискретных значений или другими способами.

Цифровые сигналы будут рассмотрены в § 19.7.

Математическая модель дискретного сигнала. Аналитически дискретный сигнал x_Т(t) удобно представлять с помощью дискретизирующей последовательности δ-функций:

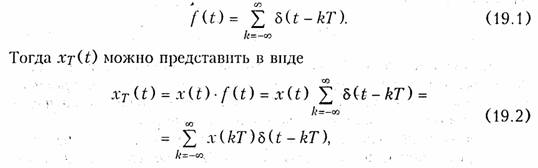
т. е. дискретный сигнал х_Т(t) с помощью (19.2) представляется в виде последовательности δ-функций с весовыми коэффициентами, равными отсчетам x(kT) аналогового сигнала x(t) в точках kT. На рис. 19.2 изображена схема, иллюстрирующая процедуру формирования дискретного сигнала согласно формулы (19.2).

Рассмотрим  примеры  некоторых  дискретных  сигналов,   полученных из типовых аналоговых сигналов.

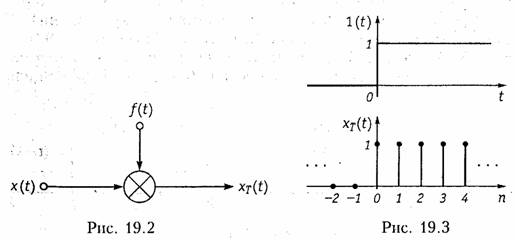
Пример. Единичный ступенчатый аналоговый сигнал 1(t) приведен на рис. 19.3.

Соответствующий ему дискретный сигнал x_Т(t) называется ступенчатой последовательностью. Он определяется следующим образом:

Такая последовательность приведена на рис. 19.3.

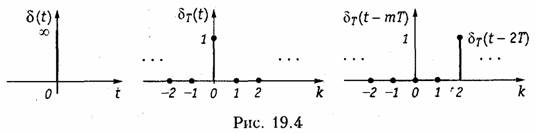
Пример. Импульс Дирака или δ-функция в аналоговой области приведена на рис. 19.4.

Дельта-последовательность или дискретная 5-фуикцня определяется выражжением

Последовательность δ_т(t), приведенная на рис. 19.4, принимает единственное значение, равное 1, при k = 0. Этот сигнал можно сдвинуть на т интервалов (рис. 19.4):

Интервал времени Т, через который отсчитываются значения непрерывного сигнала i(t), называется интервалом дискретизации. Обратная величина 1/Т (обозначим ее f_д) называется частотой взятия отсчетов или частотой дискретизации.

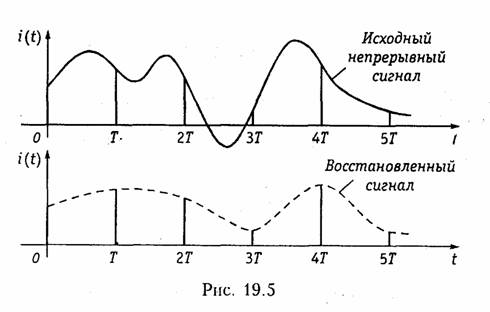
Отсчеты непрерывного сигнала следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного (рис. 19.5). Если обратиться к схеме рис. 19.1, то это означает, что звук на приеме будет восприниматься с искажениями.

Для сигналов с ограниченным спектром, т. е. сигналов, у которых спектр ограничен некоторой верхней частотой ω_в = 2πF_B существует теорема Котельникова, определяющая выбор интервала дискретизации Т (или, что то же, частоты дискретизации). Эта теорема впервые была доказана В.А. Котельниковым в 1933 г. в работе «О пропускной способности «эфира» и проволоки в электросвязи» ставшей основополагающей в теории и технике цифровой связи.

Теорема Котельникова. Если функция х(t) имеет спектр, ограниченный верхней частотой F_B, то x(t) полностью определяется последовательностью своих значений {.отсчетов) в моменты времени, отстоящие друг от друга на период Т ≤1/2F_B.

Математически теорема Котельникова записывается следующим образом

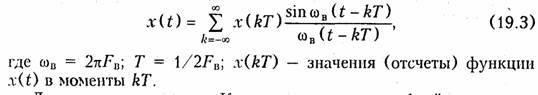
Доказательство теоремы Котельникова дается в общей теории связи. Здесь же отметим, что функция вида sinω_Bt'/ω_Bt' (t’ = t — kT) известна нам как функция отсчетов (см. § 5.3), поэтому теорему Котельннкова иногда называют еще теоремой отсчетов.

Физический смысл теоремы Котельникова (19.3) заключается в том, что непрерывная функция x(t) с ограниченным спектром F_B полностью может быть восстановлена, если известны ее отсчеты, взятые через интервал Т ≤ 1/2F_B. Эта теорема играет очень большую роль в теории связи, т. к. позволяет передачу аналоговых сигналов заменить передачей дискретных или цифровых сигналов, что позволяет существенно повысить эффективность систем связи.

19.2. Спектр дискретного сигнала

Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jω) аналогового сигнала х(t) и спектром Xт(jω) дискретного сигнала x_T(t), определенного моделью (19.2). Учитывая, что х_T(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала

Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства δ-функцни окончательно получим

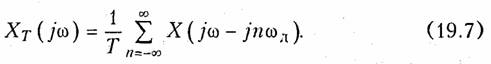
Из (19.7) следует важный вывод: спектр дискретного сигнала x_T(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных, на оси частот через одинаковые интервалы.

Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2).

Если же использовать вместо дискретнзирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр x_T(jω), энергия которого убывает с ростом ω («копни» X(jω) с ростом ω уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.

Спектр дискретного сигнала Х_T(jω) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t ≥ 0).

На практике в формулах (19.8), (19.9) часто вместо зависимости Х_T(jω) рассматривают зависимости X_T(jf), которые легко можно получить путем замены ω = 2πf.

Пример. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета x_T(t) =[а; 0; 0; 0; ...].

Воспользуемся формулой (19.8), в которую подставим значения x_t(t)заданного сигнала

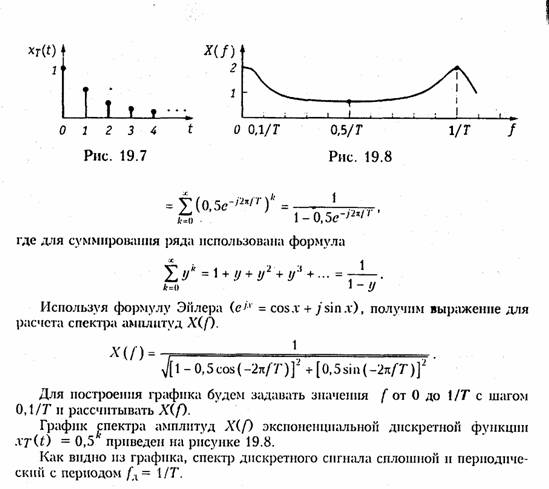
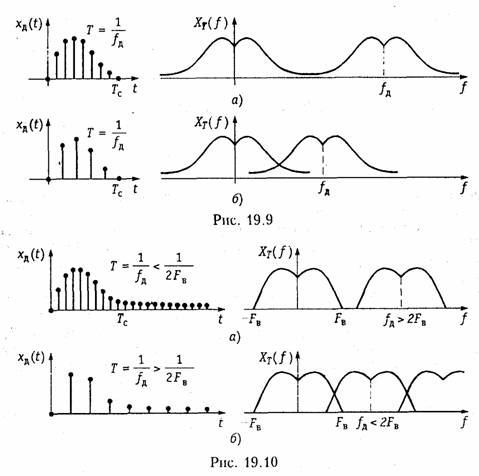
Следует отметить, что если не выполняется условие теоремы Котельникова: f_Д ≥ 2f_B, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала Х_T(f)при изменении частоты дискретизации сигнала x_T(t), ограниченного во времени интервалом Т_с (рис. 19.9) н неограниченного во времени (рис. 19.10).

Как следует из представленных графиков увеличение периода дискретизации Т >1/2F_B; F_Д < 2F_B приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра Х_T(f).Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до F_Д ≥ 2F_B.

Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.

Из условия задачи следует, что граничная частота спектра F_В равна 100 кГц. Тогда и соответствии с теоремой Котельникова имеем интервал дискретизации

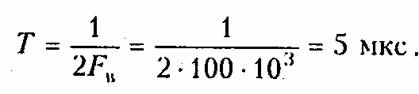
Минимально допустимая частота дискретизации fд = 2Fb = 2-100 = 200 кГц.

Пример. Определим дискретные отсчеты сигнала длительностью t_и = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра F_В принять значение З/t_и, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.

Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих F_В, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.

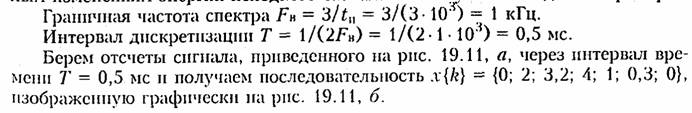
Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого   Этот вывод хорошо иллюстрирует рис. 19.10,

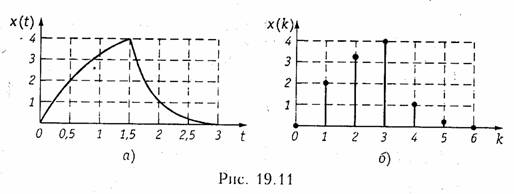
а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t).

Дискретное преобразования Фурье. Как следует из формулы (19.7) Х_T(jω) имеет периодическую структуру с ω_д = 2π/Т. Причем, как и спектр аналогового сигнала X(jω) спектр дискретного сигнала Х_T(jω) является сплошным (см. рис. 19.6, 6). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области.

Для сигнала x(t) ограниченного во времени интервалом Т_с (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем замены

С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену ω= nΔω. Тогда получим

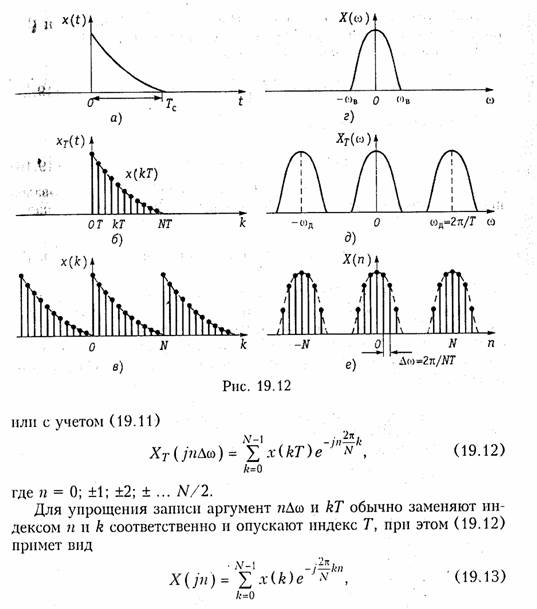
которое определяет прямое ДПФ.

С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).

Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:

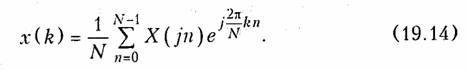
При  k  < О  обратное преобразование  Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).

Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства (см. § 9.2).

В частности, свойство линейности

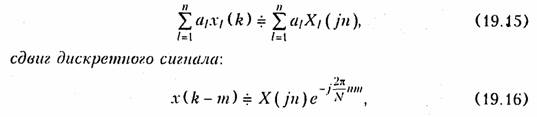
т.  е.  сдвиг последовательности отсчетов сигнала на т интервалов приводит лишь к изменению фазового спектра дискретного сигнала.

Теорема свертки:

Аналогично можно записать н другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3).

Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами x{k} = {0; 1; 2}.

Для расчета воспользуемся формулой ДПФ (19.13).

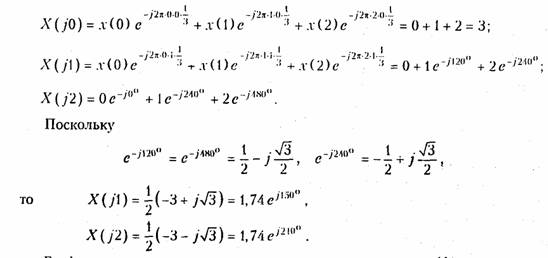
Графики заданного дискретного периодического сигнала x(k) н рассчитанного дискретного периодического спектра амплитуд Х(п) приведены на рис. 19.13.

Пример. Рассчитаем значения дискретного сигнала x(k), ДПФ которого имеет вид Х[п] = {0; 1; 0; 1}.

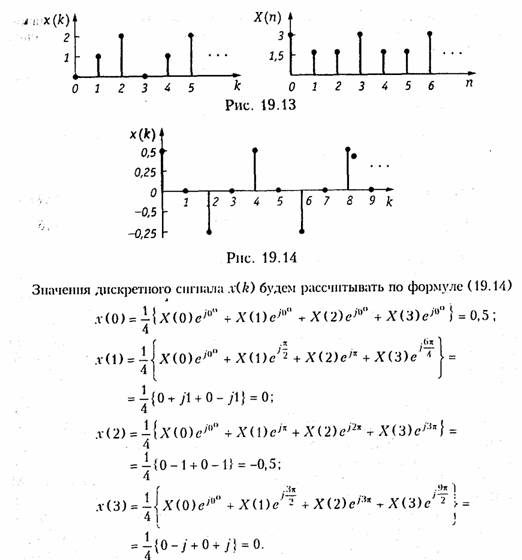
График   последовательности   x{k)   =   {0,5;   0;   —0,5;   0}   приведен   на рис. 19.14. Сигнал х{k) дискретный и периодический.

Пример. Определить с помощью ДПФ спектр аналогового сигнала, изображенного на рис. 19.15, а.

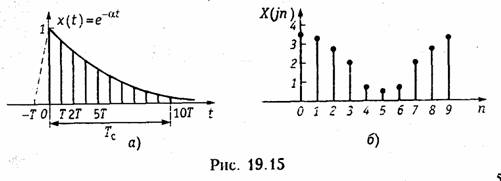
и т.д.

В таблице приведены результаты расчета спектра,

п	0	1	2	3	4	5	6	7	8	9
X(jn)	3.4	3.3	2.8	1.6	0.6	0.4	0.6	1.6	2.8	3.3

а на рис. 19.15, б спектр сигнала X(jn). Следует отметить, что с увеличением Т (уменьшение числа отсчетов N) погрешность аппроксимации x(t) увеличивается (см. рис. 19.5, а).

Как следует из вышеприведенных примеров и формул (19.13), (19.14), для вычисления ДПФ содержащих N отсчетов необходимо осуществить в общем случае N²операций с комплексными числами. Если длина обрабатываемых массивов достаточно велика, то вычисление ДПФ даже на современных быстродействующих ЭВМ занимает достаточно много времени. Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ. Здесь мы рассмотрим один алгоритм, основанный на прореживании по времени.

Быстрое преобразование Фурье. Положим, что число отсчетов N = 2^q, где q — целое число. Разобьем дискретную последователь-

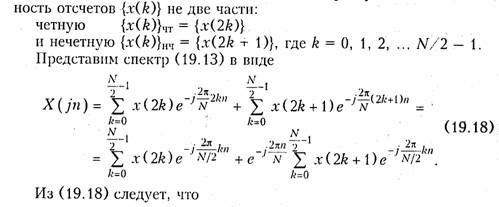
Формула (19.19) п (19.20) лежит в основе БПФ. Как следует из этих формул для вычисления X_чт(jn) и X_нч(jn) требуется (N/2)² операций и для выполнения операции умножения на ехр{·} — N операций:

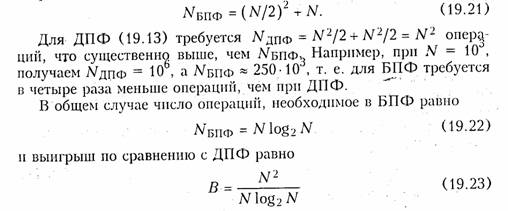
и  может достигать  сотен  и  тысяч  раз  при  достаточно  больших входных массивах N.

В заключении отметим, что сам процесс вычисления по формулам (19.18), (19.19) производят по итерационному принципу: последовательность отсчетов с четными и нечетными номерами снова разбивают на две части п т. д. Процесс разбиения продолжается до тех пор, пока не получится последовательность, состоящая из одного элемента (исходного ДПФ). Более подробно с алгоритмами БПФ можно ознакомиться в специальной литературе (см. например, Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М. «Радио и связь. 1990).

19.3. Z-преобразование и его свойства

При анализе и синтезе дискретных и цифровых цепей широко применяют так называемое z-преобразование. Это преобразование играет такую же основополагающую роль по отношению к дискретным сигналам, как преобразование Лапласа по отношению к аналоговым сигналам.

Z-преобразование дискретного сигнала. Заменим б уравнении (19.8) jω на комплексную переменную р:

где   интегрирование  осуществляется   по  окружности   с   радиусом │z│=1

Доказать справедливость (19.29) можно следующим образом. Пусть X(z) — функция комплексной переменной z, аналитическая в области |z| > r_о. Рас кроем ряд (19.28):

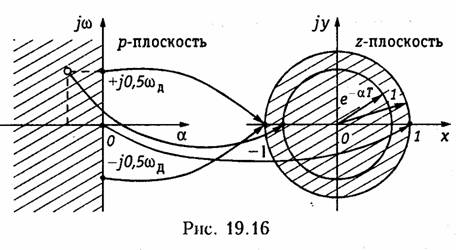
Установим связь между точками на комплексной плоскости р = α+jω и z-плоскости z= х + jу (рис. 19.16).

Если положить α = 0, то мы будем перемещаться по оси jω в плоскости р. При переходе в z-плоскость точки мнимой оси jω будут располагаться на единичной окружности z = е ^{jω T} . Причем, точка j0 на р- плоскости переходит в точку z = +1 на вещественной оси 2-плоскостн, а точки ±j0,5 ω _д — в точку z = — 1. Это означает, что точки отрезка (-j0,5 ω _д ÷j0,5 ω _д) р- плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция z = е^{± jω T} периодическая, то последующие отрезки оси jω на р -плоскости такой же длины будут вновь проектироваться на единичную окружность.

Точкам левой р- полуплоскости соответствуют точки внутри единичной окружности z-плоскости, а точкам правой р- полуплоскости — точки вне этой окружности.

Пример. Рассчитаем z- преобразование дискретного сигнала x(k), имеющего вид

Z-преобразование X(z) дискретного сигнала х(п) определено только для области z, в которой степенной ряд (19.28) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z - плоскости, радиус которого r₀ называется радиусом сходимости (рис. 19.17), т. е. при r₀ <| z |<∞ ряд сходится. В области сходимости существует взаимно однозначное соответствие между X(z) и x(k), т. е. каждому х(k) соответствует одно и только одно X(z), определенное для |z| > r₀  и наоборот.

Пример. Определим радиус сходимости для г-преобразовання сигнала, заданного в предыдущем примере.

Как уже было установлено, z- преобразование сигнала x(k) = е^-αkT имеет вид

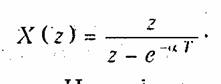
Нуль функции X(z) будет в точке z₀ =0, полюс — в точке z_k = с^-αT . Следовательно, радиус сходимости r₀ = e^-αT а функция Х(z) сходится при |z| > e^-αT.

Окружность, имеющая радиус сходимости r₀ = e^-αT , приведена на рис. 19.16, Область сходимости находится за пределами этой окружности.

Пример. Найдем z - преобразование сигнала x(k) = Аа^k,  k ≥ 0.  Этот дискретный сигнал

показан на рис. 19.18 для трех различных значений а: а = 0,8; а = 1; а = —0,8.

В  соответствии  с (19.28) z -преобразованпе такого дискретного  сигнала равно

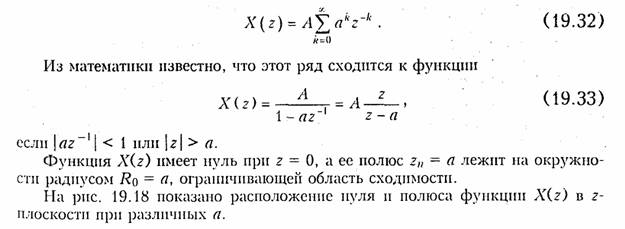
Нахождение дискретного сигнала по его г-изображению. Для этого можно воспользоваться обратным  z -преобразованием (19.29).

Другой способ заключается в том, чтобы разложить функцию X(z) в степенной ряд по степеням z^-1. Тогда коэффициенты при степенях z^-1 будут, в соответствии с формулой (19.28), отсчетами дискретного сигнала x(k).

Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе X(z), не слишком сложные.

Более эффективным способом нахождения x(k) по известному Х(z) является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.

Пример. Найдем общин член x_k дискретного сигнала x(k), которому соответствует z- изображение, заданное в предыдущем примере

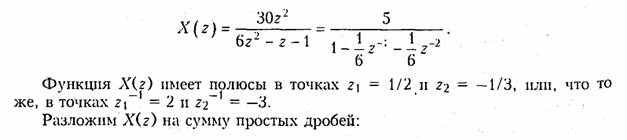
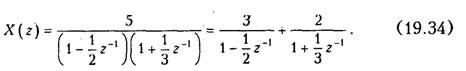
Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления z(p) реактивных двухполюсников при синтезе их по схеме Фостера:

Свойства z-преобразования. Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z-преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.

Теорема линейности (суперпозиции). Сумме дискретных сигналов соответствует сумма их z-изображений. Если дискретным сигналам x(k) и y(k) соответствуют г-изображения Х(z) и Y(z), то

где а и Ь — некоторые числа.

Доказательство теоремы выполните самостоятельно, используя выражение (19.28) для расчета z-изображения дискретного сигнала.

Теорема опережающего сдвига. Если дискретному сигналу x(k) соответствует одностороннее z-преобразование X(z), то сигналу, вдвинутому на один интервал дискретизации, x(k + 1) соответствует z-преобразование z(X(z) — х(0)).

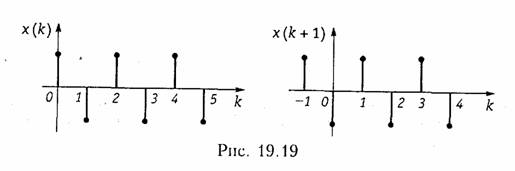
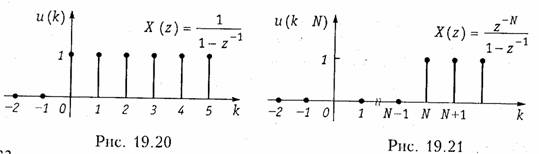
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т. е. при п < N. Из теоремы задержки в частности следует, что сдвиг дискретного сигнала на один интервал дискретизации Т соответствует умножению z-преобразования на оператор z^-1 , поэтому часто z^-1 называют оператором единичной задержки в z-области.

Теорема  умножения   на  а^k.   Математическая  запись  теоремы имеет вид

Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в специальной литературе.

Пример. Найдем z- преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.

Найдем z-преобразование дискретного δ-импульса δ(k) (рис. 19.4), используя выражение (19.28)

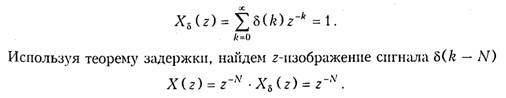
На рисунке 19.4 приведен также график задержанной функции единичного отсчета для частного случая N = 2.

В   табл.   19.1   дана   сводка   z- преобразованной   наиболее   часто встречающихся  дискретных  последовательностей.   Эти  табличные сведения также могут быть использованы для расчета z-преобразований сигналов и перехода от z-преобразований к дискретным сигналам.

Пример. Найдем общий член дискретного сигнала x(k), которому соответствует z-изображение

19.4. Дискретные цепи

Дискретная свертка. В предыдущих разделах этой главы бала установлена определенная аналогия между соотношениями, существующими для аналоговых и дискретных сигналов. Подобная аналогия существует и между методами анализа и синтеза аналоговых и дискретных цепей.

Под дискретной цепью понимают любое устройство, которое преобразует одну последовательность x{k} в другую y{k) (рис. 19.24).

Линейной дискретной цепью называют цепь подчиняющуюся принципу суперпозиции.

Связь между входным дискретным сигналом х{ k} (воздействием) и выходным сигналом y{k) (отсчетом) определяется дискретной сверткой (сравни с (8.12)):

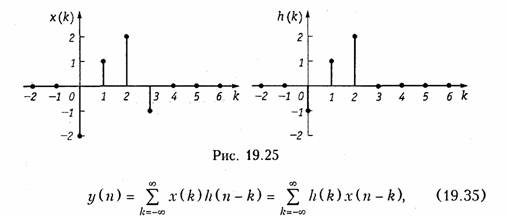
где h(k) — импульсная характеристика дискретной цепи. Она определяется как отклик дискретной цепи на воздействие в виде единичного импульса (δ-функция, рис. 19.4).

Иногда свертку (19.35) записывают символически: y(k) = x(k)_* h(k) (см. теорему свертки, § 19.3).

Линейная дискретная цепь, будет устойчива, если выполняется условие

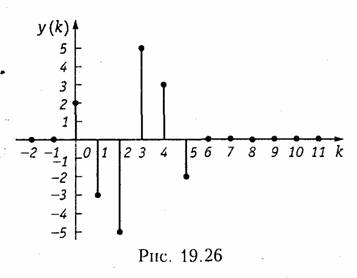
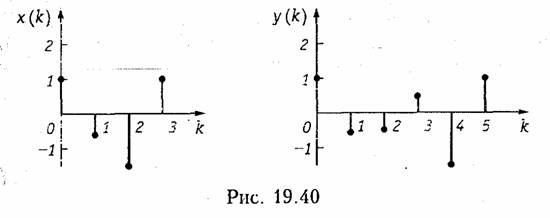
График дискретного сигнала y(k) приведен на рис. 19.26.

Вычисления по формуле (19.35) можно выполнить также с помощью простого устройства. Запишем последовательности чисел x(k) и h(—k) на отдельных полосках бумаги, как показано на рис. 19.27. На обеих полосках пометим маленькими стрелочками точки k = 0. Обратим внимание на то, что h(—k) является обратной последовательностью относительно h(k), так что она строится в обратном направлении от k = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность y(k).

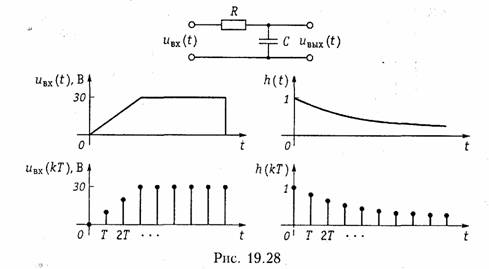
Проведя дискретизацию импульсной характеристики аналоговой цепи можно описать ее дискретной математической моделью. Если, например, для RC-цепи, изображенной на рис. 19.28 взять дискретные значения импульсной характеристики:

то получим дискретную математическую модель RC цепи, выходную реакцию которой можно найти с помощью (19.35). При этом, естественно входной сигнал также должен быть дискретизирован (рис. 19.28). Точно также можно получить дискретные модели

других аналоговых цепей. Таким образом формула дискретной свертки (19.35) является достаточно универсальной, пригодной для описания как аналоговых, так и дискретных цепей.

Пример. На вход цепи поступает сигнал в виде дискретной δ-функции. Рассчитаем выходные последовательности y(k) цепей, имеющих дискретные импульсные характеристики

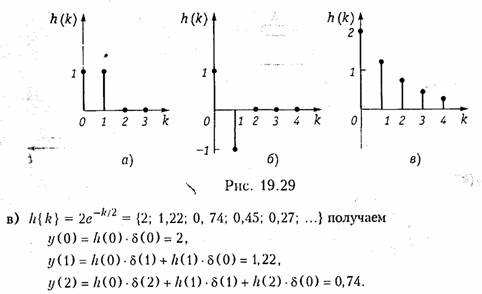
Все остальные отсчеты выходной последовательности у {k} повторяют соответствующие отсчеты дискретной импульсной характеристики h(k), также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т. к. импульсная характеристика — это реакция цепи на 5-импульс.

Графики y(k) будут такими же, как графики h(k) на рис. 19.29, что является очевидным, т. к. h(k) по определению есть реакция цепи на δ-функцию.

Элементы дискретных цепей. Как следует из уравнения (19.35) при вычислении реакции дискретной цепи на заданное воздействие выполняется всего три операции: умножение, задержка и сложение.

На рис. 19.30 эти действия представлены в виде элементов структурной схемы. Операцию умножения дискретного сигнала x(k) на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал y(k) = K·x(k). Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета x(k - 1) = x(kT - Т) из x(k) = x(kT) можно связать с задержкой последнего на время T, т. е. на один «такт». Действие элемента задержки поясняется на рис. 19.30.

Таким образом, алгоритм вычислений дискретного сигнала y(k), описываемый выражением (19.35), можно представить в виде структурной схемы.

Пример. Составим структурную схему цепи, дискретная импульсная характеристика которой дана в предыдущей задаче, т. е. h{k) = {—1; 1; 2} (рис. 19.25).

В соответствии с алгоритмом (19.35) и с учетом заданных значений характеристики Л(/г) структурная схема цепи приведена на рис. 19.32. По этой схеме несложно определить выражение для выходной последовательности

Как следует из рис. 19.30 и рис. 19.31 общим свойством элементов дискретных цепей является их однонаправленное действие, показанное на рисунках стрелками. С точки зрения топологии, элементы дискретных цепей представляют собой двухполюсные (элемент задержки, умножитель) или многополюсные элементы (сумматор).

Общее уравнение дискретных цепей. Из уравнения (19.35), рассмотренных примеров и рис. 19.32 отклик дискретной цепи y(k) на воздействие x(k) можно записать в виде следующего уравнения

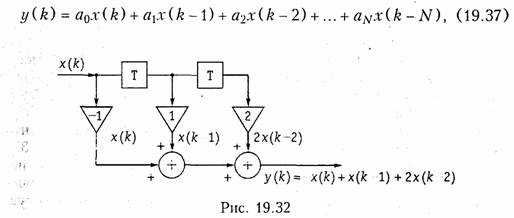
где a_0,a_1,a_2,…a_N  -некоторые числа (веса) представляющие собой по сути отсчеты импульсной характеристики цепи.

Уравнению (19.37) соответствует дискретная цепь, изображенная на рис. 19.33. В литературе эту цепь называют иногда транс-версальным фильтром.

Как следует из (19.37) для получения k-го отсчета выходного сигнала подвергаются обработке (k — N) отсчетов входного сигнала с соответствующими весовыми коэффициентами.

Следует однако отметит», что уравнением (19.37) не исчерпываются все возможные алгоритмы работы дискретных цепей. В частности, этот алгоритм может включать обработку не только отсчетов входного, но и отсчетов выходного сигнала, сдвинутого на определенное число тактов. Поэтому наиболее общее уравнение дискретной цепи имеет следующий вид

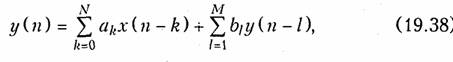
где b₁ — весовые коэффициенты.

На рис. 19.34 изображена схема дискретной цепи, соответствующей алгоритму (19.38).

Принципиальным отличием схемы, изображенной на рис. 19.34 от схемы на рис. 19.33 является наличие цепи обратной связи, поэтому схемы, описываемые уравнением (19.38), получили название рекурсивных, а цепи, описываемые (19.37), — нерекурсивных.

Для нахождения реакции дискретной цепи необходимо решить разностные уравнения (19.37) и (19.38). Если решение (19.37) обычно не представляет особого труда, то для решения (19.38) необходимо использовать специальные методы. По аналогии с решением   дифференциальных   уравнений,   описывающих   аналоговую

цепь, решение разностных уравнении можно осуществить как классическим, так и операторным методом. Обычно для решения разностных уравнений в теории дискретных цепей используется операторный метод, причем вместо преобразования Лапласа используют z-преобразование.

Передаточные функции. При анализе и синтезе дискретных систем важнейшую роль играют передаточные или системные функции цепей.

Применим к уравнению (19.38) прямое z-преобразование и учтя основные свойства z- преобразования (см. § 19.3), получим

Сравнение (19.41) и (19.42) показывает, что роль коэффициентов а_k играют отсчеты импульсной характеристики /i(k). Нетрудно также видеть, что импульсная характеристика нерекурсивной цепи согласно (19.37) является конечной, а рекурсивной согласно (19.38) бесконечной, поэтому иногда нерекурсивные дискретные цепи называют цепями с конечной импульсной характеристикой (КИХ), а рекурсивные — с бесконечной импульсной характеристикой (БИХ).

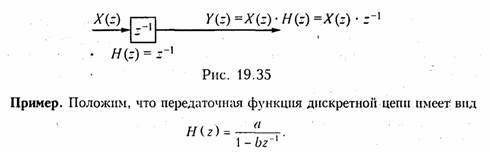
При а = 1; b= 0 получаем идеальный интегратор с импульсной характеристикой h{k) = {1, 1, ..., 1, ...}. По нерекурсивной схеме такую импульсную характеристику реализовать нельзя.

Анализ (19.40) показывает, что передаточная функция рекурсивной цепи имеет структуру, аналогичную типичной передаточной функции цепи с ОС (см. гл. 14). H(z) является дробно-рациональной функцией относительно z^-1 :

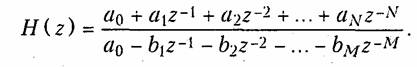
Из (19.40) и (19.41) также следует, что H(z) из (19.40) имеет полюса (нули полинома знаменателя), которые могут располагаться в любой точке z-плоскости, а H(z) из (19.41) только полюс кратности N в начале координат.

Пример. Найдем передаточную функцию элемента задержки. Сигнал на его выходе описывается уравнением

Пример. Найдем импульсную характеристику и передаточную функцию дискретной цепи (рис. 19.36), выходная последовательность которой задана выражением y(k) = 4x(k) — 1,5x(k — 1).

Отсчеты дискретной импульсной характеристики h(k) — это отсчеты y(k), рассчитанные при условии, что на вход цепи подается дискретная δ-функция.

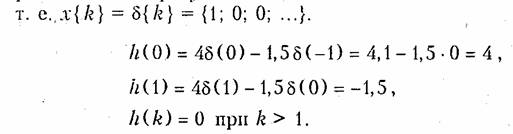
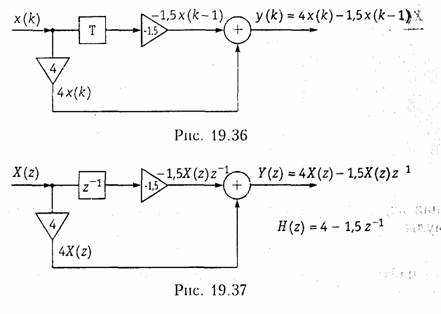
Таким образом, отсчеты дискретной импульсной характеристики h{k}  = {4; —1,5} соответствуют коэффициентам усиления усилителей в схеме (рис. 19.36).

Для нахождения передаточной функции Я(г) воспользуемся формулой (19.42):

Зная передаточную функцию дискретной цепи H(z) с помощью формулы

Y(z) = X(z)H(z) (19.43)

можно найти z- изображение выходного сигнала Y(z) по z-изображению входного Y(z).

Для нахождения отсчетов выходного сигнала y(k) по его 2-нзображеншо Y(z) можно точно также как и для аналоговых цепей использовать теорему разложения (см. § 7.2), которая применительно к дискретным цепям для правильной дробно-рациональной функции Y(z) = P(z)/Q(z) (где P(z), Q(z) — полиномы) имеет вид

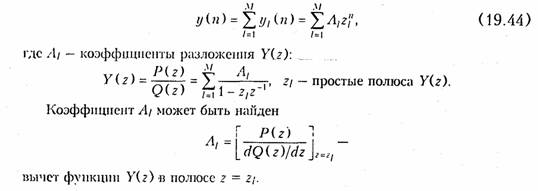
Следует отметить, что отсчеты y(k) для нерекурсивной цепи могут быть найдены как коэффициенты при отрицательных степенях z в уравнении для Y(z).

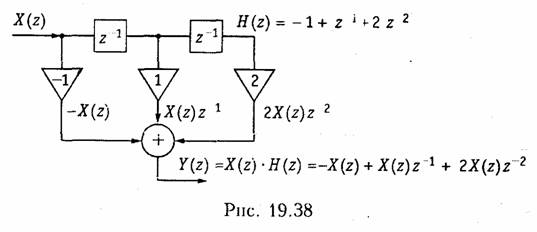
Пример. Найдем отсчеты выходного сигнала y(k) дискретной цепи, 2-нзоб-раженпе которой приведено на рис. 19.38, а входной сигнал x{k) = {—2; 1; 2; —1}.

Найдем z- изображение входного сигнала х(k):

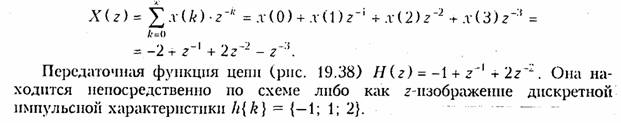
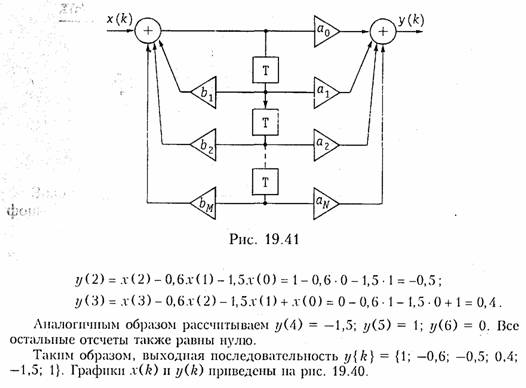
Из рис. 19.34 следует, что для реализации алгоритмов рекурсивной обработки сигнала дискретная цепь должна иметь большое количество ячеек памяти, что существенно усложняет схему. Для упрощения дискретной цепи используют, так называемую каноническую схему. Каноническая схема может быть получена из (19.40), если представить Y(z) в виде:

Тогда согласно (19.45) алгоритм дискретной обработки сигнала заключается в том, что вначале реализуется рекурсивное преобразование (19.46), а затем нерекурсивное (рис. 19.41).

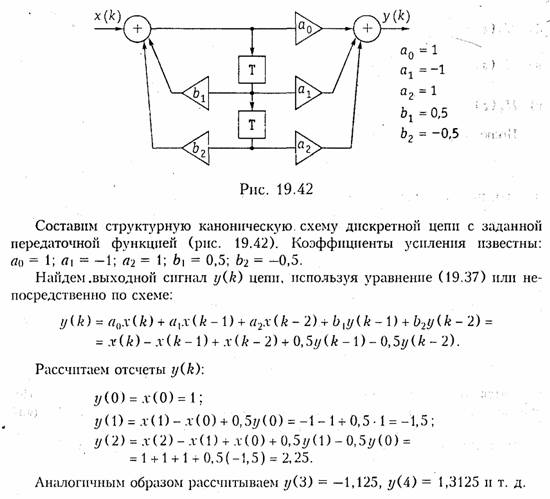
Устойчивость рекурсивных цепей. Дискретная цепь считается неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на ее выходе бесконечно нарастающий отклик. Наоборот, дискретная цепь устойчива, когда отклик на ограниченное воздействие также ограничен.

Известно, что у устойчивой аналоговой цепи полюсы передаточной функции располагаются в левой полуплоскости переменной р. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа z-преобразованием точки левой полуплоскости p-плоскости переходят в точки, лежащие внутри единичной окружности z-плоскости (рис. 19.16). Таким образом, полюсы передаточной функции устойчивой дискретной цепи располагаются внутри единичной окружности z-плоскости.

Нерекурсивные цепи всегда устойчивы.

Пример. Определим устойчивость цепей, имеющих передаточные функции:

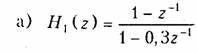
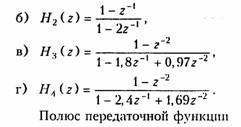
Частотные характеристики. Для перехода от передаточной функции H(z) к частотной характеристике H(jf) необходимо про извести замену

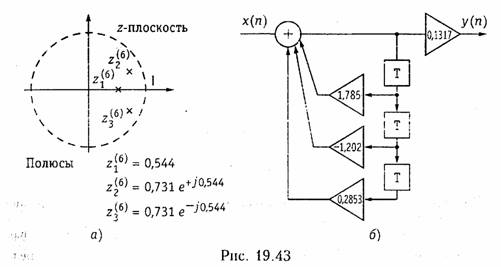
Из (19.47) легко получить амплитудно-частотную и фазо - частотную характеристики дискретной цепи. В частности, амплитудно-частотная характеристика будет представлена выражением

На рис. 19.44 изображен график АЧХ Н(Ω) цепи. Из рисунка видно, что АЧХ с передаточной функцией (19.49) соответствует ФНЧ Баттерворта. Как и следовало ожидать, амплитудно-частотная характеристика дискретной цепи является периодической функцией (так как H(jΩ) есть преобразование Фурье от Дискретной импульсной реакции). Ее период равен f_д =1/Т или Ω = f_д·T = 1. Поэтому она используется в диапазоне частот от 0 до 0,5 f_д (или до Ω = 0,5). Цепь устойчива.

Пример. Изменим коэффициенты усиления в предыдущем примере. Выберем a_c= a₂ = 1, а₁ = — 2. Вновь найдем выражение Н(Ω) и построим график его амплитудно-частотной характеристики.

Заменим в формуле для H(Ω), полученной в предыдущем примере, значения коэффициентов a_0, a₁ и a_2. Получим

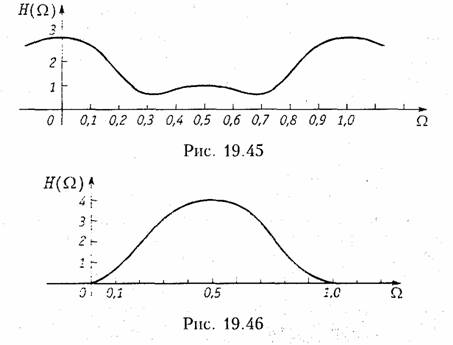
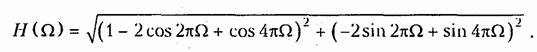
График АЧХ изображен на рис. 19.46. Из графика видно, что нерекурсивная цепь с такими значениями коэффициентов усиления — это режекторный фильтр.

19.5. Типовые звенья дискретных цепей

Звенья 1-го и 2-го порядков. В литературе типовыми звеньями дискретных цепей считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры рис. 19.41, если оставить в ней только один либо два элемента задержки.

На рис. 19.47, а показано звено 1-го порядка с передаточной функцией

Пример. Построим график АЧХ звена первого порядка, у которого a₀= 1. a₁ = 0.

Передаточная функция такого звена первого порядка

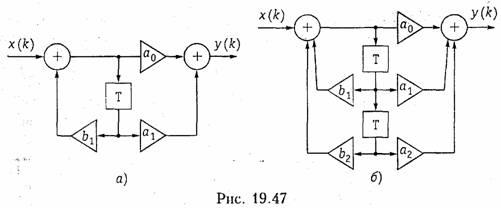
Как указывалось ранее, рекурсивную цепь с прямыми и обратными связями можно представить как каскадное соединение рекурсивного фильтра с передаточной функцией Н₁(z) нерекурсивного фильтра с передаточной функцией H₂(z). В нашем случае, для звена второго порядка,

Соединение типовых звеньев. Типовые звенья могут соединяться каскадно (рис.  19.50, а); при этом их передаточные функции

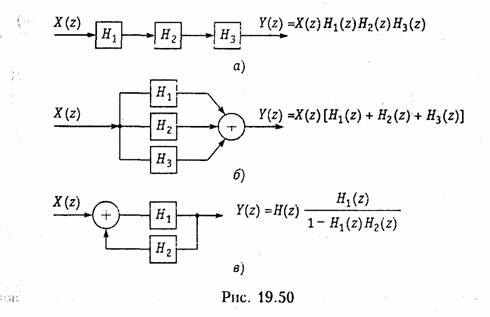
перемножаются:

Следует иметь в виду, что все соединения, изображенные на рис. 19.50, справедливы не только для типовых звеньев, но и для любых других структур.

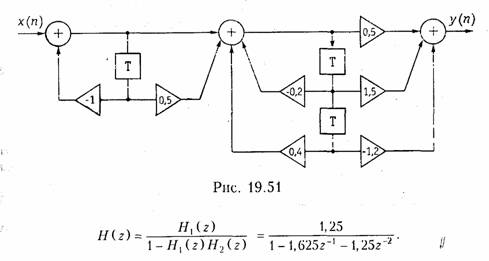
Пример. Найдем передаточную функцию дискретной цепи, изображенной на рис. 19.51.

Цепь, приведенная па рис. 19.51, представляет собой каскадное соединение типовых звеньев 1-го и 2-го порядков. Передаточная функция соединения имеет вид

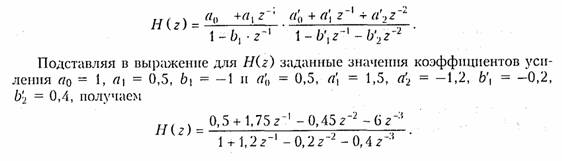
19.6. Дискретные фильтры и их синтез

Постановка задачи и этапы синтеза. Дискретная цепь может осуществлять любые операции: фильтрацию сигнала, корректирование характеристик и т. п., т. е. выполнять функции любой аналоговой цепи.

В частности, при синтезе дискретных частотных фильтров нужно найти такие коэффициенты передаточной функции (19.40), или (19.41), частотная характеристика которой удовлетворяла бы нормам ослабления фильтра в полосах пропускания и непропускания (рис. 19.52, а). Определение коэффициентов - это задача аппроксимации. Известен целый ряд методов ее решения. Наиболее распространенным является следующий метод. Сначала рассчитывают аналоговый НЧ- прототип и получают его передаточную функцию Н(р), затем путем замены комплексной переменной р = Ф{z} переходят от Н(р) к передаточной функции дискретной цепи H(z).

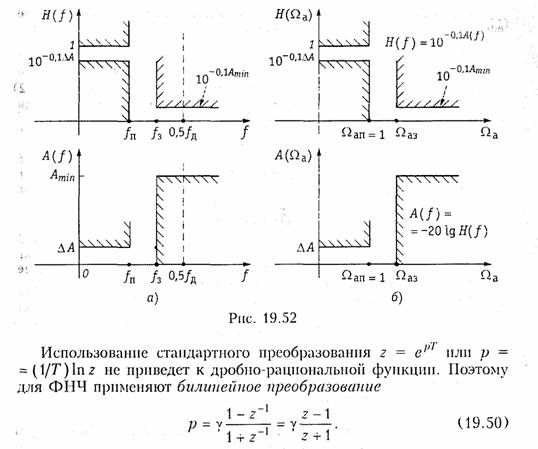
(у — некоторый постоянный множитель), которое является первый приближением стандартного преобразования при разложении его в ряд Тейлора:

Из разложения (19.51) следует, что необходимо выбирать γ = 2/Т. Однако, далее мы покажем, что удобнее брать другие значения коэффициента γ  .

Билинейное преобразование (19.50) переводит все точки из левой полуплоскости переменной р в точки на единичной окружности плоскости z. Так что, если была устойчива аналоговая цепь, будет устойчивой и дискретная. Подтвердим эти утверждения па примере.

Пример. Найдем положения точек на z-плоскости, соответствующих следующим значениям переменной р: р₁ = —2; р₂ = —2 + j2, р₃ = j2.

Из формулы (19.50) найдем выражение для расчета z:

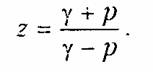
Модуль z равен 1, т. е. точка р =j2, лежащая на мнимой осп плоскости р, переходит в точку на единичной окружности плоскости z при использовании билинейного преобразования.

Переход к аналоговому прототипу применяется обычно для дискретных фильтров, имеющих бесконечную импульсную характеристику h(k), принимающую ненулевые значения на бесконечном множестве значений k = 0, 1.....

Дискретные цепи с конечной импульсной характеристикой, принимающей ненулевые значения лишь при k = 0, 1, ..., N — 1, не имеют аналогов среди пассивных электрических фильтров, поэтому для их расчета применяются другие методы.

Нерекурсивные фильтры с передаточной функцией (19.42) всегда имеют конечные импульсные характеристики. Рекурсивные фильтры с передаточной функцией (19.40) могут иметь как конечные, так и бесконечные импульсные характеристики.

Пример. Найдем дискретные импульсные характеристики фильтров, имеющих передаточные функции

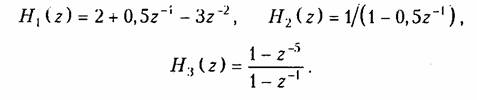
Дискретная   импульсная   характеристика   h(k)   связана   с   передаточной функцией обратным z-преобразованием (см. формулу (19.29)):

Требования к аналоговому фильтру-прототипу. Следует иметь в виду, что частотная характеристика аналогового фильтра определена на всей положительной полуоси частот, в то время как у дискретного фильтра она имеет тот же смысл только до частоты 0,5f_д, затем она периодически повторяется (рис. 19.44). Ясно, что шкала частот дискретного фильтра оказывается деформированной относительно шкалы частот аналогового фильтра. Соответствие этих шкал легко установить из билинейного преобразования (19.50). Перепишем его в виде:

Обозначим, во избежание путаницы, нормированную частоту для аналогового фильтра-прототипа Ω _a, обычную (т. е. ненормированную) частоту для дискретного фильтра будем, как и ранее, обозначать буквой f, а нормированную — буквой Ω. Теперь заменим в (19.53) комплексную переменную р на jΩ _a, а комплексную переменную z на е^j2πfT = е^{j2πf Ω} и установим соответствие между частотами f (пли Ω) и Ω_a:

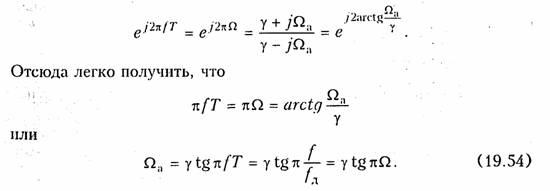
При изменении частоты fот 0 до 0,5f_д, или нормированной частоты Ω от 0 до 0,5, нормированная частота Ω _a в шкале аналогового прототипа будет пробегать значения от 0 до бесконечности (рис. 19.52).

Во многих справочниках по расчет фильтров граничная частота полосы пропускания принимается равной Ω _ап = 1. Чтобы частота f_и (или Ω _и) дискретного фильтра пересчитывалась в Ω _ап ⁼ 1 (рис. 19.52, б), из (19.54) ясно, что коэффициент у нужно взять равным:

Тем самым, произведен пересчет требований, предъявленных к дискретному фильтру (рис. 19.52, а) в требования к аналоговому НЧ- прототипу (рис. 19.52, 6).

Расчет аналогового НЧ- прототипа. Исходными данными для расчета являются требования к НЧ- пототипу (рис. 19.52, б). По ним, пользуясь любым справочником, рассчитывают передаточную функцию фильтра-прототипа.

Реализация рекурсивного фильтра. Для перехода от аналогового фильтра к дискретному воспользуемся заменой переменных (19.50)

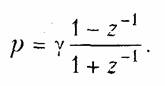
В результате получаем Н(z) в виде дробно-рациональной функции, которая может быть реализована.

Пример.   От передаточной функции (19.56) аналогового фильтра-прототипа перейдем к передаточной функции Н(z) дискретного фильтра.

Подставим в выражение (19.56) значение

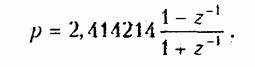
Получим

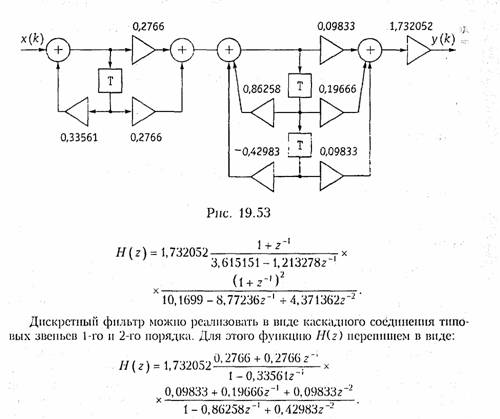
Схема фильтра, имеющего такую передаточную функцию, приведена на рис. 19.53. Амплитудно-частотная характеристика A(Ω) = 20lgH(Ω), рассчитанная па основании формул для АЧХ типовых звеньев, показана па рис. 19.54 (кривая 1).

Аналогичным образом производится расчет фильтров со всплесками ослабления (нулями передачи).

Пример. Найдем передаточную функцию дискретного фильтра НЧ с АЧХ, равноволновой в полосе пропускания и со всплеском ослабления в полосе за-

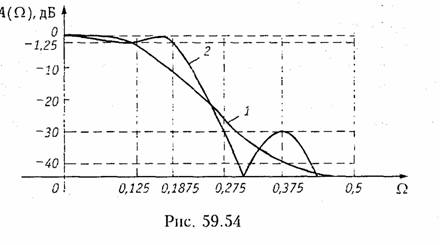
Амплитудно-частотная характеристика А(Ω) = 201gtН(Ω) такого фильтра показана на рис. 19.54 (кривая 2).

Синтез фильтров с конечной импульсной характеристикой. Если известна передаточная функция H(z) дискретного фильтра, то для реализации фильтра с конечной импульсной характеристикой h(k), равной нулю везде кроме 0 ≤ k≤ N-1, поступают следующим образом. Амплитудно-частотную характеристику H(Ω) фильтра дискретизируют, разбивая частотный интервал Ω = 0 ÷ 1 на N равных интервалов. В результате получают последовательность отсчетов АЧХ на N частотах Ω = n/N , т. е. H(n/N), 0 ≤n ≤ N - 1. Поскольку H(n/N) = N· Н(п), то, подставляя эту последовательность в формулу обратного дискретного преобразования Фурье (19.14), получаем выражение для дискретной импульсной характеристики h(k) фильтра

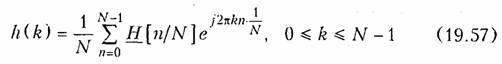
Как известно, конечную импульсную характеристику имеют нерекурсивные фильтры. Это значит, что полученные отсчеты дискретной импульсной характеристики h(k) являются коэффициентами усиления α_0,α_2,…, α _N-1 в схеме нерекурсивного фильтра, приведенной на рис. 19.33.

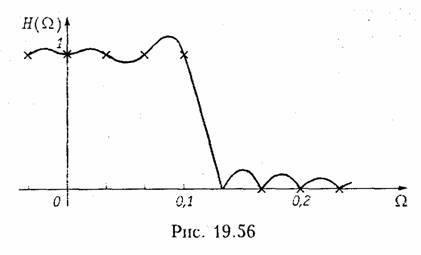
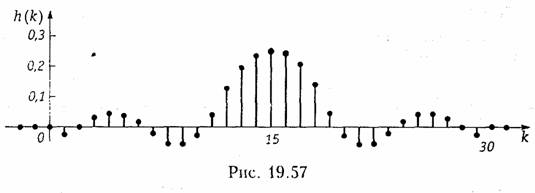
Пример. Найдем импульсную характеристику h(k) фильтра нижних частот, имеющего граничную частоту полосы пропускания Ω = 0,1, и АЧХ, приведенную на рис. 19.55. Импульсную характеристику будем рассчитывать для значения N = 30.

График конечной импульсной характеристики h(k) изображен на рис. 19.57.

Для реализации фильтра с такой импульсной характеристикой по схеме рис. 19.33 потребуется 30 усилителей и 29 элементов задержки, т. е. схема довольно громоздкая. Схема с обратными связями, реализующая АЧХ, изображенную на рис. 19.55, будет иметь гораздо меньше элементов. Однако достоинством нерекурсивных фильтров с конечной импульсной характеристикой является то, что они всегда устойчивы и, кроме того, обеспечивают линейные фазовые характеристики.

Синтез дискретных фильтров верхних частот, полосовых и режекторных. Требования к любому типу фильтра преобразуются

в требования к аналоговому ФНЧ-прототнпу. Затем рассчитывается аналоговый прототип, как это показано выше, п с помощью замены переменных переходят от Н(р) к Н(z).

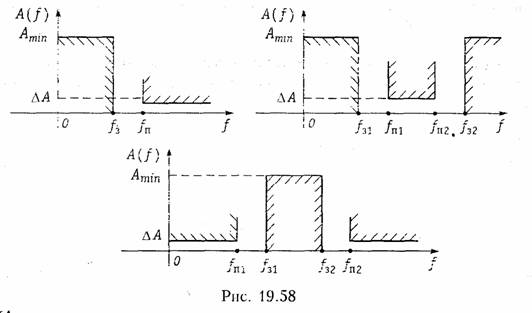
Конечно, формулы замены переменных уже не такие, как для ФНЧ. Они приведены для разных типов фильтров в табл. 19.2. Требования к дискретным фильтрам графически изображены на рис. 19.59.

19.7. Цифровые фильтры

Функциональная схема цифрового фильтра. В отличие от дискретных фильтров в цифровом фильтре (ЦФ) осуществляется обработка цифровых сигналов (рис. 19.1, в). На рис. 19.60 изображена функциональная схема цифровой обработки аналоговых сигналов. Аналоговый сигнал x(t) подается на аналого-цифровой преобразователь (АЦП), где осуществляется дискретизация, квантование непрерывного сигнала и его кодирование. В результате на выходе АЦП формируется цифровой сигнал, представляющий собой

последовательность двоичных чисел с фиксированным количеством разрядов.

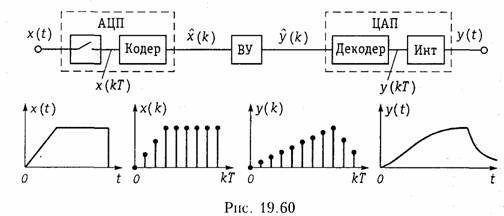
Например, если отсчет имеет величину 30 В, то запись числа в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на выходе кодера АЦП на рисунке обозначены x(k). Далее двоичная последовательность поступает на вычислительное устройство (ВУ), которое представляет собой универсальную или специализированную микро ЭВМ, микропроцессорное или любое другое вычислительное устройство. Главное состоит в том, что в памяти ВУ должна быть записана программа вычисления, например, выражение (19.35), и отсчеты импульсной реакции, заданной цепи. Следовательно, в результате работы программы ВУ будет выдавать закодированные в двоичном коде отсчеты y(k). Далее двоичная выходная последовательность поступает на вход цифро-аналогового преобразователя (ЦАП), содержащий декодер и интерполятор. В ЦАП осуществляется декодирование сигнала, в результате формируется дискретный выходной сигнал y(kT) и после интерполяции на выходе ЦАП получаем выходной аналоговый сигнал y(t).

Как видим, ВУ может сыграть роль реальной цепи. И хотя самой физической цепи в наличии может и не быть, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будет наблюдать на выходе описанной системы такое же выходное напряжение y(t), как и на выходе реальной цеписледует отметить, что при цифровой обработке ЦАП может и отсутствовать, если выходной сигнал надо получить в цифровой форме.

Аналогово-цифровое преобразование сигналов. Как следует из рис. 19.60 АЦП осуществляет дискретизацию аналогового сигнала, его квантование по уровню с шагом Δ (рис. 19.1, в) и кодирование. Обычно процесс квантования осуществляется одновременно с его

кодированием, в результате на выходе АЦП получаем сигнал, представленный в некотором цифровом коде.

Одним из основных параметров кода является его основание, соответствующее выбранной системе счисления. Близко к оптимальным реализуются двоичные или бинарные коды, которые нашли наибольшее распространение в связи.

Известно большое количество различных устройств преобразования непрерывного сообщения в бинарный код. Все их можно разбить на три основные группы: преобразователи последовательного счета, поразрядного кодирования и преобразователи считывания. Наибольшее применение в связи нашли преобразователи первых двух типов.

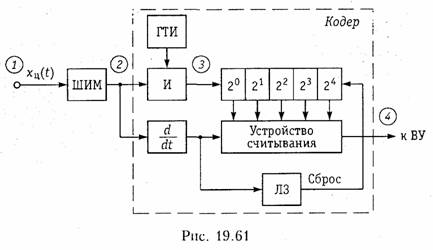
Принцип действия преобразователя последовательного счета с временным преобразованием иллюстрируется схемой изображенной на рис. 19.61 и временными диаграммами на рис. 19.62.

Кодирование в данной схеме осуществляется следующим образом. Аналоговый сигнал после дискретизации и квантования х_ц(t) поступает на вход широтно-импульсного модулятора (ШИМ), на выходе которого формируются прямоугольные импульсы ширина которых пропорциональна отсчету сигнала x_ц(t) в моменты kT (рис. 19.62). Далее этот ШИМ- сигнал подается на схему* «И», на второй вход которой поступают импульсы с генератора тактовой частоты (ГТИ). На выходе схемы «И» формируются импульсы, число которых в «пачке» пропорционально ширине импульса. Эти импульсы поступают в двоичный счетчик, где число их фиксируется в двоичной системе счисления. Задним фронтом ШИМ- импульса запускается устройство считывания результата, с выхода которого кодовая комбинация поступает в ВУ. Считывание может осуществляться последовательно или параллельно (последовательный пли параллельный код).

На рис. 19.62 приведен вид кодовой группы на выходе при последовательном считывании. Для возвращения двоичного счетчика в исходное состояние на него через линию задержки ЛЗ с τ₃ = τ _счит подается сигнал сброса, формируемый задним фронтом ШИМ- импульса. С приходом следующего измерительного импульса работа кодера повторяется.

Аналогичным образом можно кодировать и амплитудно - модулированную импульсную последовательность (кодер последовательного счета с частотным преобразованием). Для этого АИМ- сигнал подается на ЧМ- генератор (мультивибратор), и осуществляется счет импульсов этого генератора за фиксированные промежутки времени по рассмотренной выше схеме.

В преобразователях поразрядного кодирования производится последовательное сравнение выходного сигнала с набором эталонных напряжений, каждое из которых соответствует определенному разряду кода. В качестве эталонных напряжений используется геометрическая прогрессия вида

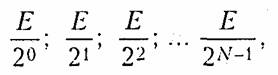
где N — число разрядов в бинарном коде. Причем Е > u_mах, где u_тах — максимально возможное значение кодирующего сигнала.

При поразрядном кодировании вначале формируется старший разряд кода путем сравнения u(t) с Е/2 (например, если u(t)≥ E/2, то формируется символ «1», в противном случае — «0»). Одновременно на выходе схемы сравнения образуется напряжение u(t)-E/2 при u(t)≥E/2 или u(t) при u(t)<E/2. Затем указанная процедура повторяется с полученным напряжением для эталонного напряжения Е/4 и т. д. В результате N сравнений получается символ самого младшего разряда.

Шумы квантования. При квантовании сигнала минимальный шаг квантования Δ (расстояние между смежными разрешенными уровнями) соответствует единице младшего двоичного разряда. Причем, поскольку при квантовании происходит округление значений сигнала до ближайшего дискретного уровня, то появляются ошибки округления   │ε│≤Δ/2. Если x(t) известен неточно, то ε -является случайной величиной и при малом Δ распределено по равномерному   закону.   Последовательность   значений   ошибки  ε_,

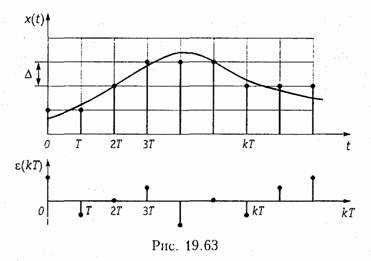
возникающей при квантовании дискретного сигнала x(kT) образует дискретный случайный процесс ε(kT) называемый шумом квантования (рис. 19.63).

Дисперсия  шума  квантования определяется для равномерного закона распределения р(ε) формулой

Если шаг квантования Д мал, то соседние значения ε(kT) можно считать некоррелированными.

Шум квантования является одним из главных источников погрешности цифровой обработки сигнала. Шум на выходе цифрового фильтра ζ(kТ) при условии некоррелированности отсчетов ε(kT) можно определить согласно (19.35)

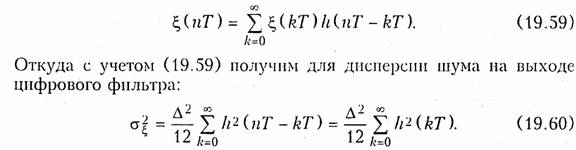
Поскольку для ЦФ обычно выполняется условие (19.36),то дисперсия шума квантования на выходе  всегда конечна.

Ошибки округления. При обработке цифрового сигнала в ВУ возникают дополнительные ошибки округления (усечения). Действительно, если при использовании в ВУ чисел с фиксированной запятой сложение чисел не приводит к увеличению разрядов, то при  умножении  число  разрядов  возрастает  и  возникает  необходимость

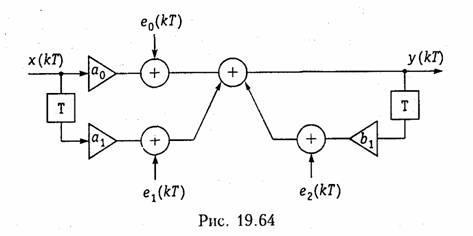
округления результата, что естественно приводит к ошибкам называемым ошибками округления. По своему характеру эти ошибки аналогичны шуму квантования. Для их учета обычно в схему ЦФ дополнительно вводят источники шума e_i(kT), число которых равно числу умножителей. На рис. 19.64 изображена схема рекурсивного ЦФ звена 1-го порядка с учетом источников шума округления. Источники шума e(kT) имеют одинаковую дисперсию σ² = Δ²/12, где Δ определяется числом используемых разрядов. Если принять, что источники e_o(kT), e₁(kT) н е₂(kT) независимы, то дисперсия суммарного шума округления будет равна

Для другой схемы реализации ЦФ результирующая   вычисляется в зависимости от того, куда будет подключен источник шума e(kT) и в общем случае может быть найден по формуле (19.60) или с учетом равенства Парсеваля

Кроме ошибок квантования и округления при синтезе ЦФ возникают ошибки, вызванные неточными значениями параметров фильтра. Эти ошибки особенно опасны в рекурсивных фильтрах высокого порядка, т. к. могут привести к потере устойчивости ЦФ, поэтому обычно используют звенья 1-го и 2-го порядков (см. § 19.5). Кроме рассмотренных выше при синтезе ЦФ возникают еще ряд дополнительных явлений, приводящих к погрешности цифровой фильтрации. К ним, например, относятся так называемые предельные циклы низкого уровня, представляющие собой периодические колебания, возникающие на выходе ЦФ при низком входном сигнале и обусловленные округлением результатов вычисления. Все эти явления и ошибки подробно исследуются в специальной литературе.

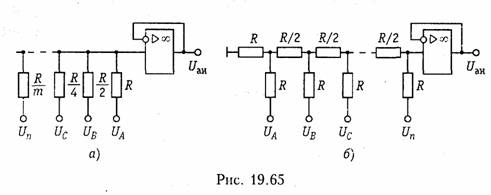
Цифро-аналоговое преобразование. Преобразование цифровых сигналов в аналоговый осуществляется с помощью различных цифро-аналоговых преобразователей (ЦАП). В основе простейшего ЦАП лежит принцип двоично-взвешенного суммирования напряжений или токов. На рис. 19.65 изображены схемы простейших ЦАП на базе резистивных цепей.

В ЦАП с двоично-весовыми резисторами (рис. 19.65, а) требуется меньшее число резисторов, однако при этом необходим целый ряд номиналов прецизионных сопротивлений. Аналоговое выходное напряжение U_ан ЦАП определяется как функция двухуровневых входных напряжений:

где п — число разрядов ЦАП; т — коэффициент, зависящий от числа разрядов ЦАП.

Для обеспечения высокой точности работы резистивные цепи ЦАП должны работать на высокоомную нагрузку. Чтобы согласовать резистивные цепи с низкоомной нагрузкой, используют буферные усилители на основе операционных усилителей, показанные на рис. 19.65, а, б.

Интерполяторы. На выходе ЦАП сигнал обычно имеет форму последовательности импульсов модулированных по амплитуде (АИМ- сигнал). Для восстановления (демодуляции) из АИМ- последовательности аналогового сигнала достаточно использовать ФНЧ с частотой среза ω_с = 2π/Т, где Т — частота дискретизации АИМ-   сигнала. Существуют и более сложные интерполирующие устройства, которые описаны в специальной литературе.

В заключении следует отметить, что в связи с бурным развитием вычислительной, микропроцессорной техники цифровые методы обработки сигналов получают все большее распространение. Они имеют более широкие возможности реализации сложных и эффективных алгоритмов обработки сигналов, которые в большинстве своем недоступны для реализации аналоговыми цепями.

Вопросы и задания для самопроверки

1.  Почему нельзя произвольно выбирать интервал дискретизации?

2.  Найдите спектр дискретного сигнала, состоящего из одного отсчета x{k} = {2}.

3.  Каким должно быть соотношение между интервалом дискретизации спектра по частоте ΔF и периодом повторения Т_с сигнала?

4.  Найдите частоту дискретизации и интервал дискретизации сигнала, имеющего спектр, ограниченный частотой F_B = 10 кГц.

ПРЕДМЕТНЫЙ  УКАЗАТЕЛЬ

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. —М.: Радио и связь, 1998.—444 с.

2.  Белецкий А.Ф. Теория линейных электрических цепей. —М.: Радио и связь 1986.-544 с.

3.  Воробиенко П.П. Теория линейных электрических цепей. Сб. задач и упражнений.-М.: Радио и связь, 1989.-328 с.

4.  Шебес М,Р., Каблукова М.В. Задачник по теории линейных электрических  цепей:   Учеб.   пособие для  вузов.-4-е изд.,  перераб.   и доп. —М.: Высшая школа, 1990,—544 с.

Дополнительная

5.  Андреев Б.С. Теория нелинейных электрических цепей. —М.: Радио и связь 1982.-280 с.

6.  Бакалов В.П., Игнатов А.Н., Крук Б.И. Основа теории электрических цепей и электроники. —М.: Радио и связь, 1989. —528 с.

7.  Гоноровский И.С, Демин М.П. Радиотехнические цепи и сигналы: [Учеб. пособие для вузов по направлению «Радиотехника»].—5-е изд., перераб. и доп. —М.: Радио и связь, 1994,— 481 с.

8.  Добротворский  И.Н.   Теория  электрических  цепей. —М.:   Радио  и связь, 1989.-472 с.

9.  Карташкин А.С. Линейные цифровые фильтры. Вопросы и задачи: Учеб. пособие. — М.: Радио и связь, 1995.-133 с.

10.  Сборник задач по теоретическим основам электротехники: Учеб. пособие /Под. ред. Л.А. Бессонова. —М.: Высшая школа, 2000.

11.  Яцкевич В.В. Теория линейных электрических цепей: Справ, пособие. — М.: Высшая школа, 1990.-264 с.