ГЛАВА 16. ПРОБЛЕМА СИНТЕЗА ЛИНЕЙНЫХ         

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

16.1. Постановка задачи синтеза

Линейные устройства систем передачи информации. Предыдущие главы посвящены в основном проблеме анализа электрических цепей. В них рассматривались методы анализа и на их основе изучались свойства электрических цепей. Другой проблемой является создание устройств и систем, обладающих заданными свойствами, что составляет содержание задачи синтеза электрических цепей-В последующих главах речь пойдет о синтезе конкретных линейных устройств, являющихся составной частью систем передачи информации.

Электрические фильтры это четырехполюсники, которые с пренебрежимо малым ослаблением пропускают колебания в определенном диапазоне (диапазонах) частот и практически не пропускают колебаний в других диапазонах.

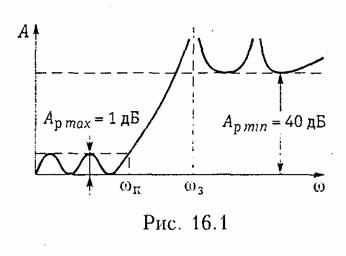
На рис. 16.1 приведена типичная характеристика рабочего ослабления ФНЧ. Для данного примера ослабление в полосе частот 0 ... ω_п не превышает 1 дБ, а в полосе частот ω₃ ... ∞ ослабление превышает 40 дБ Полоса частот, в которой ослабление относительно мало, называется полосой пропускания; полоса частот, в которой ослабление относительно велико, называется полосой задерживания. Между полосами пропускания и задерживания находится полоса расфильтровки (переходная полоса). В этой полосе требования на ослабление не задаются. Электрические фильтры служат для выделения колебаний в необходимой полосе частот. Например, в антенне существуют колебания, вызванные работой многих радиостанций. Каждая радиостанция работает в своей полосе частот. Радиоприемник с помощью фильтров выделяет колебания в желаемом диапазоне частот. Для того , чтобы была возможность последовательно принимать различные радиостанции, фильтр необходимо перестраивать. Вращение ручки настройки радиоприемника приводит к смещению полос пропускания и задерживания. Та же идея положена в основу разделения телефонных каналов в аналоговых многоканальных системах передачи. Фильтрами можно формировать сигналы сложной формы, уменьшать пульсации напряжения или тока в источниках питания.

Корректоры линейных искажений или просто корректоры — это четырехполюсники, служащие для компенсации линейных искажений. В § 9.6 приведены условия безыскаженной передачи. На практике эти условия выполняются далеко не всегда, вследствие чего возникают амплитудно-частотные и фазо-частотные искажения. Для того чтобы обеспечить условия безыскаженной передачи и применяются корректоры. Линейные искажения часто корректируются раздельно. Амплитудными корректорами компенсируются амплитудно-частотные искажения, а фазовыми — фазо-частотные. Корректоры могут быть постоянными, когда их характеристики не меняются в процессе работы или автоматическими (адаптивными), когда при изменении параметров среды Передачи (например линий) характеристики корректора автоматически также изменяются.

Линии задержки — это четырехполюсники, которые в некотором диапазоне частот имеют с заданной степенью точности линейную  фазо-частотную   характеристику  или  постоянное  групповое время пробега. Линии задержки применяются как элемент устройств, например, гармонических корректоров.

Требования к цепи, этапы синтеза. Требования к электрической цепи можно разделить на основные и дополнительные. Основные требования определяют целевое назначение синтезируемой цепи. Электрические свойства линейной цепи полностью описываются во временной области переходной g(t) или импульсной h(t) характеристиками, а в частотной области — амплитудно- и фазо-частотными характеристиками. Поэтому основные требования предъявляются либо к частотным, либо к временным характеристикам будущей цепи.

Дополнительные требования зависят от условий работы создаваемых устройств. К ним относятся ограничения на массу и габариты, чувствительность характеристик к изменению элементов, температурную нестабильность, элементный базис (например, в ряде случаев нежелательно применение катушек индуктивности), а также требования простоты процесса настройки в условиях производства и т. д. Часть дополнительных требований носит обязательный характер, а часть подлежат оптимизации (минимизации или максимизации) при прочих равных условиях. Так, возможен случай, когда требования по чувствительности должны выполняться безусловно, а габариты и масса минимизируются.

В классической постановке задача синтеза разбивается на два этапа: задачу аппроксимации и задачу реализации.

Решение задачи аппроксимации заключается в нахождении такой функции, которая, с одной стороны, удовлетворяет поставленным требованиям, а с другой — удовлетворяет условиям физической реализуемости характеристик (временных или частотных) электрических цепей.

Решение задачи реализации заключается в нахождении электрической цепи, временная или частотная характеристика которой совпадает с функцией, найденной в результате решения задачи аппроксимации.

16.2. Условия физической реализуемости

Синтез электрических цепей можно выполнить во временной области, когда требования задаются к переходной или импульсной характеристике, и в частотной области, когда требования задаются к амплитудно-частотной характеристике (АЧХ) и ФЧХ цепи. При этом требования часто задаются только к АЧХ цепи, а ФЧХ не контролируется. Очевидно, не любая вещественная функция может быть реализована в виде временной характеристики цепи и не любая комплексная функция может быть реализована в виде входной или передаточной функции.

Условия, при выполнении которых заданная функция может быть реализована как характеристика цепи, называются условиями физической реализуемости (УФР). Данные условия зависят от того, из каких элементов предполагается синтезировать цепь, т. е. УФР зависят от элементного базиса. Ниже будут рассматриваться линейные активные и пассивные -RLC-цепи с сосредоточенными и независящими от времени параметрами. Рассмотрим УФР данных цепей.

Условия физической реализуемости передаточных функций. В гл. 7 показано, что входные или передаточные функции являются дробно-рациональными функциями с вещественными коэффициентами (7.41):

Для того, чтобы дробно-рациональная функция с вещественными коэффициентами являлась с точностью до постоянного множителя передаточной функцией четырехполюсника, необходимо и достаточно, чтобы она удовлетворяла условиям, описанным в § 7.4:

1)  полином знаменателя должен быть полиномом Гурвица;

2)  степень полинома числителя не должна превышать степени полинома знаменателя.

В терминах нулей и полюсов эти два условия могут быть сформулированы следующим образом:

1)  полюсы передаточной функции должны находиться в левой полуплоскости;

2) отсутствуют полюсы в нуле и бесконечности.

На положение нулей никаких ограничений не накладывается. Эти два условия определяют условия устойчивой цепи.

Если некоторая дробно-рациональная функция удовлетворяет приведенным условиям, то говорят, что она удовлетворяет условиям физической реализуемости.

Структура четырехполюсника может накладывать дополнительные ограничения. Так часто представляют интерес четырехполюсники, не содержащие взаимных пидуктивностей и имеющие общий провод между входным и выходным зажимами, т. е. трехполюсники или неуравновешенные четырехолюсники. Такие цепи должны Дополнительно удовлетворять условиям Фиалкова — Герста, формулируемым следующим образом: для трехполюсных цепей без взаимной индуктивности коэффициенты числителя передаточной функции не отрицательны и не превышают соответствующих коэффициентов знаменателя. Это означает, что отсутствуют нули на положительной вещественной полуоси.

Дальнейшие ограничения, накладываемые на структуру четырехполюсника, приводят к дополнительным ограничениям на положение нулей. Так, нули лестничных схем могут находиться только в левой полуплоскости комплексной переменной р. Ограничения на свойства передаточных функций вызываются также видом элементов. Так, в RC-цепях полюсы могут располагаться только на отрицательной вещественной полуоси. В лестничных RC-цепях на отрицательной вещественной полуоси располагаются как полюсы

так и нули.

Условия физической реализуемости модуля и аргумента комплексной передаточной функции. Если переменная р принимает только мнимые значения р =jω, то операторные функции превращаются в комплексные функции вида:

(16.6)

В синтезе цепей часто пользуются понятием квадрата ыацу№ передаточной функции  Это позволяет избавиться от иррациональных функций. На основании формул (16.1) —(16.4) легко показать, что квадрат модуля передаточной функции в общем виде может быть представлен следующим образом (7.45):

Функция D(ω) называется функцией угла или тангенс-функцией. УФР тангенс-функции следует из УФР операторных функций. Тангенс-функция должна удовлетворять следующим условиям:

1) D(ω) — нечетная дробно-рациональная функция;

2) коэффициенты D(ω) должны быть вещественными.

Условия физической реализуемости временных функций цепи.

Как уже отмечалось, в зависимости от конкретно решаемой задачи, электрические цепи удобно описывать либо частотными характеристиками, либо временными. Так, при построении многоканальных систем передачи с частотным разделением каналов удобно пользоваться частотными характеристиками, а в цифровых системах связи, где применяется временное разделение каналов, удобно описывать электрические цепи временными характеристиками. К временным характеристикам относятся (см. § 8.1) переходная g(t) и импульсная h(t) характеристики. Напомним, что переходная характеристика численно равна отклику (реакции) цепи на единичное воздействие 1(t), в качестве которого может быть либо ток, либо напряжение. Отклик также может быть либо током, либо напряжением, поэтому, как и в случае передаточных функций существует

четыре типа переходных характеристик (гл. 8) g_u(t), g_i(t), g_Y(t) g_z(t). Первые две характеристики являются безразмерными, третья имеет размерность проводимости,  а четвертая — сопротивления .

Импульсная характеристика численно равна отклику цепи на Функцию. Существует также четыре типа импульсных характеристик (гл. 8): Как показано в гл. » импульсная и переходная характеристики выражаются одна через другую, поэтому они не являются независимыми (см § 8.1). Для описания цепи достаточно знать одну из них. Применение того или другого описания цепи зависит от конкретной задачи.

Условия физической реализуемости данных характеристик следует из свойств операторных передаточных функций. Действительно, так как изображение по Лапласу переходной и импульсной характеристик имеет соответственно вид

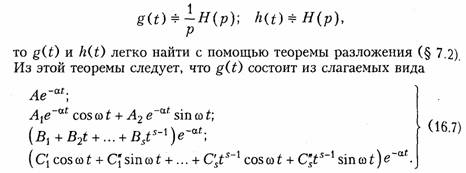
Функция h(t), кроме перечисленных слагаемых, может содержать слагаемое δ(t) (см. (8.3)).

Слагаемое, приведенное в первой строке (16.7) соответствует простым вещественным, во второй строке — простым комплексно-сопряженным, в третьей кратным вещественным, а в четвертой -кратным комплексно-сопряженным полюсам передаточной функции H(p).

На основании изложенного легко сформулировать УФР переходных и импульсных характеристик: если h(t) и g(t) могут быть представлены в виде суммы перечисленных выше слагаемых и при этом все коэффициенты являются вещественными, а α > 0, то h(t) и g(t) будут удовлетворять УФР.

Условия физической реализуемости входных функций (входных сопротивлений Zip) и проводимостей Y(p)).

Возникает вопрос: всякому ли выражению Z(p) можно сопоставить реальный, т. е. физически осуществимый двухполюсник. Очевидно, если синтезируется реактивный двухполюсник то функция Z(p) должна отвечать свойствам входного сопротивления реактивных двухполюсников: быть дробно-рациональной с вещественными коэффициентами и степенями числителя » знаменателя, отличающимися не более чем на единицу; нули и полюсы этой функции должны чередоваться на мнимой оси плоскости р (см. § 4.5).

При синтезе RLC-двухполюсников функция Z(p) должна обладать свойствами входного  сопротивления этих двухполюсников. Входные  функции таких четырехполюсников относятся к классу называемых положительных вещественных функций (ПБФ),которые  удовлетворяют   следующему  дополнительному  условию:

Re[Z(p)]≥0 или Re[Y(p)]≥0 при α>0.

Можно показать, что положительные вещественные функции всегда представляют собой отношение двух полиномов Гурвица, пени которых отличаются не более, чем на единицу, т. е. нули и полюсы расположены в левой полуплоскости. Кроме того, если ПВФ имеет полюсы или нули на мнимой оси (включая р = 0 и p = ∞), то эти полюсы и нули являются вещественными и положительными.

Часто рассматриваются цепи, содержащие элементы только двух видов: LC-, RC- и .RL-цепи. Ограничения на вид используемых элементов накладывают дополнительные ограничения на входные функции. Так, нули и полюсы входных функций LC-цепей находятся на мнимой оси и чередуются. Аналогичным свойством обладают входные функции RC- и RL-цепей с той лишь разницей, что их нули и полюсы находятся на отрицательной вещественной полуоси.

16.3. Нормирование элементов и частоты

В синтезе электрических цепей часто прибегают к нормированию элементов и частоты. Нормирование частоты уже встречалось ранее, когда рассматривались частотные характеристики колебательных контуров (гл. 4). Целесообразность применения нормирования ясна из следующего примера. Пусть необходимо рассчитать частотную характеристику сопротивления последовательного RLC-контура с параметрами элементов L = 10^-5 Гн, С = 10^-9 Ф, R =  5 Ом. Данный контур имеет добротность Q = 20, характеристическое сопротивление ρ = 100 Ом и резонансную частоту ω_p = 10⁷c^-1. При расчете сопротивления данного контура приходится оперировать с величинами от 10^-9 до 10⁷, что не всегда удобно. Выполним нормирование сопротивлений и частоты. Для этого запишем выражение сопротивления данного контура:

Разделим левую и правую часть равенства на некоторое норми-у^^{1466 значение} сопротивления R_H, а второе и третье слагаемое умножим и разделим на некоторое нормирующее значение частоты ω_н:

— нормированное резистивное сопротивление. Величины ω_н и R_H, вообще говоря, можно выбирать произвольно. В данном случае удобно положить ω_н =ω _р и R_н = ρ. Тогда параметры нормированных элементов принимают следующие значения:

Выполнение расчетов с такими числовыми значениями удобней, чем с ненормированными величинами.

Существует вторая, более важная причина, по которой применяют нормирование. Она проявляется в синтезе цепей. Допустим, что в результате сложных процедур получена некоторая цепь с нормированными значениями элементов. Истинные значения элементов определяются из формул (16.8) —(16.10) следующим образом:

Изменяя ω_н и R_H можно без выполнения сложных процедур получить схемы устройств, работающих в различных диапазонах частот и при различных нагрузках. Введение нормирования позволило создать каталоги фильтров, что во многих случаях сводит сложную проблему синтеза фильтра к элементарным действиям.

16.4. Чувствительность характеристик электрических цепей

Предположим, что каким-то образом синтезирован четырехполюсник. Его характеристики (частотные, или временные) выражаются через его элементы. Например, на рис. 16.2 показана простейшая схема фильтра. Его операторная передаточная функция имеет вид

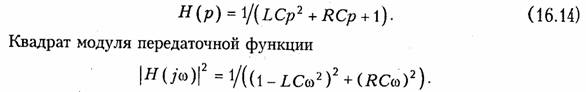
Как видно, характеристики цепи зависят от параметров ее элементов. В процессе производства и эксплуатации радиоэлектронных устройств значения параметров элементов неизбежно отличаются от расчетных значений, что приводит к изменению их характеристик. Изменения характеристик должны быть такими, при которых работа устройства не нарушается. Поэтому, чем меньше изменения характеристик при одном и том же отклонении величин параметров элементов, тем лучше это устройство. Для оценки влияния изменений характеристик устройств к изменению параметров элементов вводится понятие чувствительности. Пусть х_i i-й элемент (параметр) цепи, a F(х_i) — характеристика, зависящая от этого элемента. Чувствительностью некоторой характеристики F(х_i)  к изменению некоторого параметра х_i называется предел отношения относительного изменения функции к относительному изменению параметра:

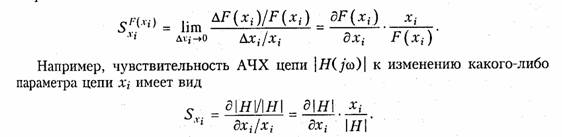
Кроме чувствительности временных и частотных характеристик в теории цепей рассматриваются также чувствительность полюса и добротности полюса к изменению (параметров) элементов. Для операторной передаточной функции (16.14) полюсы определяются выражением

Здесь предполагается, что полюсы являются комплексно-сопряженными числами. На рис. 16.3 показано положение этих полюсов на комплексной плоскости.

Добротностью полюса называют отношение его модуля (расстояние от полюса до начала координат) к удвоенной вещественной части:

Интересно, что добротность полюса совпадает с добротностью контура на резонансной частоте (см. (4.25)). В предельных случаях, когда полюс находится на мнимой оси, то Q = ∞, а когда на вещественной оси — Q = 0,5.

Чувствительность k-го полюса определяется как

где p_k — полюс передаточной функции цепи. Эта чувствительность показывает приращение полюса при изменении параметров элементов цепи.   В данном случае S — это не функция, а комплексное число.

Чувствительность добротности полюса вычисляется по формуле

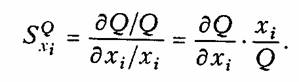
Исследование чувствительности при синтезе цепей помогает создать цепь характеристики которой наименее, подвержены воздействию различных дестабилизирующих факторов (например, температуры, влажности, старения элементов и др.).

16.5. Задача аппроксимации в синтезе электрических цепей

Аппроксимация функций является одним из разделов математики и широко используется в различных областях знаний. В § 10.2 мы сталкивались с аппроксимацией В АХ нелинейных элементов. И в данном случае подход к решению задачи остается прежним. Прежде всего это касается критериев близости функций. Напомним, что наиболее распространенными являются два критерия. Во-первых, это среднеквадратический критерий, когда минимизируется интеграл от квадрата модуля разности функций. Другим критерием является минимаксный критерий, когда минимизируется максимум модуля разности двух функций. Если достигается такой минимум, то говорят, что аппроксимация выполнена по Чебышеву или оптимально равномерно. Однако в решении задачи аппроксимации при синтезе цепей имеются и отличия. Во-первых, существуют ограничения на вид аппроксимирующих функций и, во-вторых, должны контролироваться УФР.

Действительно, если выполняется аппроксимация квадрата модуля передаточной функции, то в качестве аппроксимирующей необходимо выбрать дробно-рациональную функцию, которая представляет собой отношение двух четных полиномов с вещественными коэффициентами. При этом степень полинома числителя не должна превышать степени полинома знаменателя и свободный член полинома знаменателя не может равняться нулю. Таким выбором аппроксимирующей функции удовлетворяются первые два УФР квадрата модуля передаточной функции. Третье условие должно контролироваться в процессе решения аппроксимационной задачи.

Когда рассматриваются временные характеристики, то выбору  аппроксимирующей функции осуществляется в соответствии с выражениями (16.7).

Различные аппроксимации (приближения одной функции к другой) отличаются, прежде всего, понятиями «близости» двух функций. Наиболее широкое распространение в радиотехнике и связи получили такие методы аппроксимации, как интерполяция, приближение по Тейлору, приближение по Чебышеву, среднеквадратическое приближение.

При приближении функции F(x) и ζ(х) методом интерполяции наилучшей «близостью» этих функций считается совпадение их значений в выбранных точках — узлах интерполяции — х₁, х₂, ..., х_N, т. е.

Решение этой системы уравнений позволяет найти искомые значения коэффициентов ось α₁, α₂ ,…α_N.

Решение задачи аппроксимации данным методом (см. § 10.2) имеет следующие недостатки:

1.   Отсутствует процедура выбора точек интерполяции и первоначального порядка функции и поэтому время, необходимое для отыскания оптимального решения, зависит от квалификации и интуиции разработчика.

2.  В процессе решения не контролируются УФР.

Несмотря на отмеченные недостатки, метод интерполяции применяется довольно широко на практике, например, при синтезе амплитудных корректоров.

Данный метод аппроксимации применяется довольно часто ввиду его простоты, однако он не гарантирует получения физически реализуемой функции F(x).

Приближение функций по Тейлору предполагает, что наилучшая «близость» (Fx) и ζ(х) достигается при совпадении в выбранной точке x₀ значений самих функций и их (N— 1) производных. Таким образом,

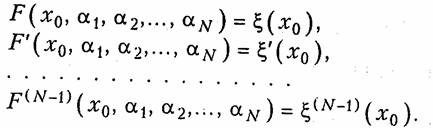
В основе этой системы уравнений лежит разложение функций F(x) и ζ(х)  в ряды Тейлора и приравнивание первых N коэффициентов соответствующих рядов. Приближение по Тейлору нашло применение, в частности, при синтезе электрических фильтров. По имени автора, впервые предложившего такой вид аппроксимации в теории фильтров, она называется аппроксимацией по Баттерворту (см. § 7.2).

Наилучшее приближение функции F(x) к ζ(х)  при аппроксимации по Чебышеву определяется из условия

Этот критерий «близости» функций следует понимать так: коэффициенты α₁, α₂ ,…α_N функции F(x) должны быть выбраны такими, чтобы самое наибольшее отклонение F(x) от ζ(х) в любой точке х рассматриваемого диапазона сделать минимально возможным.

Задача чебышевских приближений решена аналитически для электрических фильтров (см. § 17.2).

При использовании Чебышевского критерия близости полезной является теорема Чебышева, которая формулируется следующим образом.

Теорема Чебышева. Если рациональная функция F(x, α₁, α₂ ,…α_N) с п коэффициентами аппроксимирует вещественную функцию на данном интервале по Чебышеву, то все максимумы отклонения равны между собой, а также равны величинам отклонений на границах интервала и достигаются не менее, чем в N + 1 точках, причем знаки отклонений чередуются.

Эта теорема отвечает на вопрос: данная аппроксимация выполнена оптимально или нет.

При   среднеквадратическом   приближении   наилучшая   «близость» двух функций достигается при выполнении условиям

т.е. при таких значениях коэффициентов α₁, α₂ ,…α_N, при которых сумма квадратов отклонений F(x) от ζ(х) в точках х₁, х₂, ..., х_M (M>N)является минимально возможной.

Минимизация достигается путем составления и решения системы алгебраических уравнений:

Отметим, что заданная и аппроксимирующие функции могут быть не только вещественными, но и комплексными, что позволяет одновременно аппроксимировать как АЧХ, так и ФЧХ.

При решении задач среднеквадратических приближений разработано большое количество численных методов, предназначенных для использования их на ЭВМ.

Заметим, что не существует четких рекомендаций по применению того или иного метода аппроксимации. Зачастую выбор метода зависит от сложности решения задачи аппроксимации (аналитического или численного), от конкретного применения синтезированной цепи и т. п.

16.6. Задача реализации в синтезе электрических цепей. Синтез реактивных двухполюсников

Идея любого метода синтеза двухполюсников заключается в том, что находится способ разложения заданной операторной функции на более простые функции, по которым уже легко восстановить схему. Например, пусть входное сопротивление выражается формулой

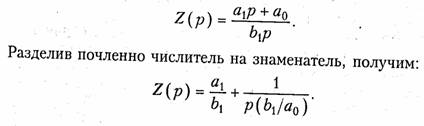
Из этой записи очевидно, что соответствующая схема состоит из последовательного соединения резистора а₁/b₁ в емкости b₁/ а₀.

Напомним общие свойства реактивных двухполюсников (см. § 4.5). Эти свойства вытекают из того факта, что LС-двухполюсники не могут рассеивать энергию, поэтому при р = jω вещественная часть функции сопротивления и проводимости равна нулю

Таким образом, сопротивление (проводимость) двухполюсника является мнимой функцией частоты, а нули и полюсы соответствующей операторной функции лежат на мнимой оси, чередуются и являются простыми, а вычеты в полюсах — положительными. Так как коэффициенты операторной входной функции являются вещественными, то нули и полюсы составляют комплексно-сопряженные пары. Учитывая сказанное, операторное сопротивление реактивного двухполюсника можно записать в виде

Если заданная функция Zip) обладает свойствами входного сопротивления реактивных двухполюсников, то говорят, что она удовлетворяет условиям физической реализуемости. Это означает, что существуют схемы двухполюсников с реальными значениями элементов, входное сопротивление которых описывается заданной функцией Z(p).

В результате синтеза часто получают двухполюсники в виде канонических схем Фостера или Кауэра (подобные схемы существуют и для -RLC-двухполюсников).

Для иллюстрации идеи синтеза ограничимся рассмотрением только реактивных двухполюсников.

Метод Фостера. Рассмотрим метод синтеза LC-двухполюсников, предложенный Фостером. Согласно этому методу функцию сопротивления либо функцию проводимости, как любую дробно-рациональную функцию, можно представить в виде суммы дробей (вспомним, например, теорему разложения).

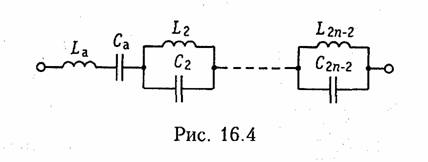
Для двухполюсников, построенных по первой форме Фостера, наиболее общей является схема, изображенная на рис. 16.4. Остальные схемы могут быть получены из нее путем «удаления» соответствующих элементов L_a и С_а.

Можно составить выражение для входного сопротивления Z(p), отражающее структуру рис. 16.4:

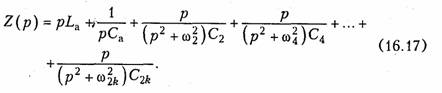
Первые два слагаемые соответствуют последовательному соединению элементов L_a и С_а, остальные — последовательному соединению параллельных контуров с элементами L₂ и С₂, L₄ и С₄ и т. п. Существуют формулы для расчета элементов этой схемы. Приведем их без доказательства:

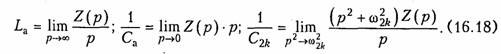
Процедура синтеза двухполюсников по первой форме Фостера сводится, таким образом, к представлению заданной рациональной дроби Z(p) в виде (16.17) и расчету элементов по формулам (16.18). Заметим, что первое слагаемое будет существовать в выражении (16.17) тогда, когда заданная дробь Z(p) неправильная, т. е. степень числителя будет на единицу превышать степень знаменателя. Число элементов двухполюсника соответствует наивысшей из степеней числителя и знаменателя заданной дроби Z(p). При четных степенях знаменателя из (16.17) исчезает второе слагаемое 1/(pС_а).

Пример. Дано выражение

Осуществим синтез двухполюсника по первой форме Фостера. Можно показать, что заданная функция Z(p) является физически реализуемой. Представим Z(p) в виде (16.17):

Аналогичным образом осуществляется синтез двухполюсников по второй форме Фостера. В этом случае наиболее общей является схема на рис. 16.5. Входная проводимость Y(p) такого двухполюсника представляется суммой слагаемых, описывающих проводимости последовательных контуров и элементов L_б и С_б. При синтезе двухполюсников заданная проводимость Y(p) раскладывается на сумму указанных слагаемых.

Метод Кауэра. В теории электрических фильтров (см. гл. 17) находит применение синтез реактивных двухполюсников по схемам Кауэра. Наиболее общими являются схемы на рис. 16.6. Из них получаются остальные разновидности двухполюсников. Выражения входных сопротивлений для этих схем можно записать в виде так называемых лестничных дробей. Так, в первой схеме Кауэра (левая схема на рис. 16.7, а) катушка индуктивности L₁соединена последовательно с остальной частью схемы, поэтому Z(p) – pL₁ + Z₂(р). Оставшаяся справа от катушки часть схемы представляет собой параллельное соединение конденсатора и части схемы правее точек а —b. Поэтому Y₂(p) =1/Z₂(p) = рС₂ + Yз(р). Рассуждая подобным образом, можно прийти в итоге к следующей записи:

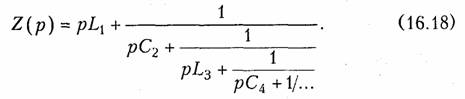
Дробь вида (8.19) называется лестничной. Синтез двухполюсников по первой схеме Кауэра состоит в разложении заданной функции Z{p) в лестничную дробь (16.18). Коэффициенты при р являются значениями элементов схемы.

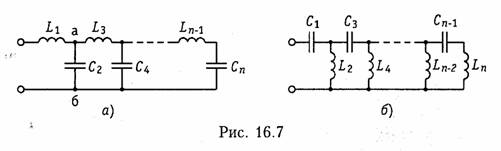
В виде лестничной дроби можно представить и входное сопротивление второй схемы Кауэра (правая схема на рис. 16.7, б). В этой дроби первый и остальные элементы будут следующего вида:

Пример. Осуществим синтез двухполюсника по выражению Zip) из предыдущего примера в виде первой схемы Кауэра. Заданная дробь имеет четвертый порядок (наивысшая из степеней числителя и знаменателя равна 4). Разложение ее в цепную дробь осуществляется последовательным делением полинома знаменателя на полином числителя*, последнего — на остаток от первого деления, остатка от первого деления — на остаток от второго деления и т.д.:

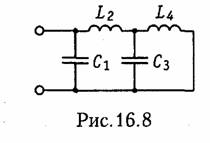
Этой дроби соответствует реактивный двухполюсник, схема которого приведена на рис. 16.8; она содержит четыре элемента С₁ = 1,0 мкФ; L₂ = 20 мГн; С₃ = 1,04 мкф; L₄ =9,4 мГн.

Пример. Найти лестничную схему, рассчитать значения параметров элементов, если ее нормированное сопротивление равно

Продолжая данную процедуру, в конечном итоге получаем следующее выражение:

г

Первое слагаемое представляет собой сопротивление индуктивности с L₁ = 1, второе — проводимость емкости с С₂= 1, третье — сопротивление индуктивности с Lз = 2, четвертое — сопротивление емкости с С₄ = 2 и пятое — сопротивление индуктивности с L₅ = 1. Подстановка данных элементов в схему рис. 16.6 дает окончательный результат синтеза двухполюсника (рис. 16.9).

Пример. По функции нормированного сопротивления

синтезировать схему двухполюсника в виде лестничной структуры. Будем осуществлять деление относительно р^-1 т. е. на каждом шаге исключать слагаемое минимальной степени. Процесс деления покажем в компактном виде:

Соответствующая данному разложению схема показана на рис. 16.10.

Таким образом, согласно методу Кауэра можно синтезировать два вида лестничных схем:

1)  с индуктивностями в продольных и с емкостями в поперечных ветвях (первая схема Кауэра);

2)  с емкостями в продольных и с индуктивностями в поперечных ветвях (вторая схема Кауэра).

Представляют определенный интерес двухполюсники, состоящие из элементов R и С, а также из элементов R и L. Подход к синтезу таких двухполюсников остается такой же, как и в случае

реактивных двухполюсников. Конечно, имеются свои особенности, но вид канонических схем остается прежним. Так RL-двухполюсники получаются из реактивных   канонических   схем  путем замены емкостей на резиcторы, а RC-двухполюсники — путем замены индуктивностей на резисторы. Одна из возможных канонических схем RС-двухполюсников показана на рис. 16.11.

16.7. Задача реализации в синтезе электрических цепей. Синтез четырехполюсников

Полученная в результате аппроксимации функция цепи F(x) подлежит в дальнейшем реализации в виде конкретной схемы. Существует большое число методов реализации цепи по функции квадрата АЧХ |Hjω)|², ФЧХ φ(ω) или характеристике ГВП t_гр(ω), по переходной g(t) и импульсной h(t) характеристикам. Даже краткое упоминание обо всех методах привело бы к чрезмерному увеличению объема книги. В § 17.4 приведены примеры реализации электрических фильтров по функции квадрата АЧХ в виде пассивных лестничных LC-схем и активных RC-cxeм.

Существуют общие методы синтеза операторных передаточных функций. Остановимся лишь на методах, имеющих в настоящее время практическое значение:

1)  синтез скрещенных (мостовых) схем с постоянным входным сопротивлением;

2)  синтез симметричных Т-перекрытых схем с постоянным характеристическим сопротивлением;

3)  синтез реактивных лестничных четырехполюсников,   нагруженных резистивным сопротивлением;

4)  синтез ARC-цeпeй.

Нахождение операторной передаточной функции по квадрату модуля комплексной передаточной функции. Предположим, что в результате решения задачи аппроксимации найден квадрат модуля комплексной передаточной функции (квадрат АЧХ). Далее необходимо знать операторную передаточную функцию. Определение квадрата модуля комплексной передаточной функции по соответствующей операторной функции осуществляется при помощи замены переменной р на  jω , и решается однозначно, т. е. операторной передаточной функции соответствует только один квадрат модуля комплексной передаточной функции.

Обратная задача решается несколько сложнее и неоднозначно. Вначале сформулируем теорему о квадрате модуля передаточной функции.

Теорема. Квадрат модуля комплексной передаточной функции не изменится, если изменить знак у всех или у некоторой части нулей и полюсов соответствующей операторной передаточной функции, а также если у комплексных нулей и полюсов знак изменяется одновременно у каждой комплексно сопряженной пары.

Докажем утверждение, что если в формуле для квадрата модуля выполнить обратную подстановку ω = —jp, то полученная функция обладает следующими свойствами:

1)  функция |Н(р)|² содержит в 2 раза больше нулей и полюсов, чем функция Н(р);

2) если функция Н(р) имеет нуль, равный р_0i, то |Н(р)|², кроме р_0i, имеет нуль — р_0i Это означает, что при наличии нуля Н(р) в левой полуплоскости, в |Н(р)|² появляется дополнительный нуль в правой полуплоскости и наоборот. Сказанное полностью относится к полюсам. Действительно, квадрат модуля передаточной функции представим в виде

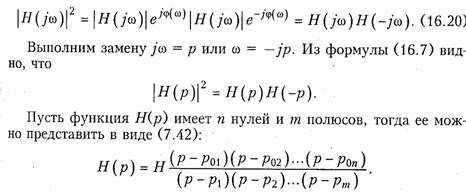
т. е. Н(—р) содержит все нули и полюсы, что и Н(р), но с противоположными знаками. Это и требовалось доказать.

Проведенный анализ позволяет сформулировать порядок определения операторной передаточной функции по квадрату ее модуля:

1.  В выражении для |H(jω)|² выполняем замену ω = —jр.

2.  Находим все нули и полюсы функции |Н(р)|² , половина из которых принадлежит функции Н(р). Полюсы, лежащие в левой полуплоскости относим к Н(р). Они составляют как раз половину всех полюсов. Остальные полюсы относятся к Н(—р). Такое распределение полюсов вызвано необходимостью получения устойчивых цепей (см. гл. 14). Таким образом, выбор полюсов передаточной функции осуществляется однозначно.

3.  Распределение нулей функции |Н(р)|² между Н(р) и Н(—р) не может быть выполнено однозначно. Согласно теореме о квадрате модуля передаточной функции здесь имеется определенная свобода в выборе числителя передаточной функции.  Если на ФЧХ никаких ограничений не накладывается, то обычно и нули выбирают в левой полуплоскости.

4. Постоянный  множитель  функции  Н(р)  равен  квадратному корню из постоянного множителя функции |Н(р)|² .

Пример. Определить операторную передаточную функцию, если квадрат ее модуля имеет вид

Рассмотрим перечисленные выше методы синтеза передаточных функций.

Синтез скрещенных (мостовых) схем с постоянным входным сопротивлением. Этот метод является общим, т. е. любую операторную функцию, удовлетворяющую УФР, можно с точностью до постоянного множителя реализовать мостовой схемой с постоянным входным сопротивлением. Метод имеет важное теоретическое значение, так как доказывает достаточность УФР. В практическом плане этот метод применяется при синтезе фазовых корректоров и линий задержки. Мостовая схема четырехполюсника, нагруженная с обеих сторон на сопротивление Ro показана на рис. 16.12. Если двухполюсники Z_a и Z_b являются обратными, т. е. Z_aZ_b = Ro²,то передаточная функция имеет вид

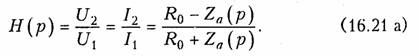
Пусть задана передаточная функция Н(р), удовлетворяющая УФР. Тогда для ее реализации мостовой схемой необходимо синтезировать двухполюсники с входными функциями:

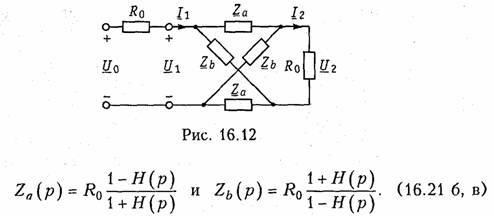
Синтез таких двухполюсников возможен, если доказать, что функции (16.21 б, в) являются ПВФ (на самом деле достаточно доказать, что ПВФ является Z_a, тогда функция сопротивления обратного двухполюсника также является ПВФ). Чтобы это доказать, вспомним, что ПВФ — это дробно-рациональная функция, вещественная часть которой неотрицательная в правой полуплоскости. То что Z_a является дробно-рациональной, вытекает из того, что Н(р) — дробно-рациональная функция. Для определения условий, при которых Re[Z_a(p)] ≥ 0, представим операторную передаточную функцию в виде суммы вещественной и мнимой частей:

Вещественная часть Z_a будет неотрицательной, если х² + у² = |Н(р)|² ≤ 1. Данное неравенство и является условием того, что Z_a(p) — ПВФ, а значит и условием физической реализуемости операторных передаточных функций в виде мостовой схемы с постоянным входным сопротивлением. Так как Н(р) удовлетворяет УФР, то она аналитическая (отсутствуют полюсы) в правой полуплоскости комплексной переменной р, а значит и ограничена по модулю |H(p)| ≤ М. Выбрав постоянный множитель Н = 1/М, получим функцию, реализуемую с точностью до постоянного множителя в виде мостовой схемы. Таким образом, реализация передаточной функции сводится к синтезу двухполюсников Z_a и Z_b. Отметим, что на практике заданную передаточную функцию реализуют не в виде одной сложной мостовой схемы, а в виде каскадного соединения более простых мостовых схем. Для этого заданную функцию представляют в виде произведения более простых функций:

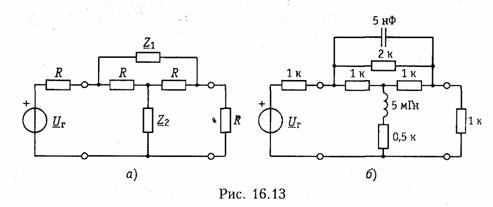
Каждая функция реализуется в виде мостовой схемы. Если сопротивление выбрано для всех схем одинаковым, то получается каскадное соединение согласованных четырехполюсников, и переданная функция каскадного соединения как раз и является произведением передаточных функций четырехполюсников, составляющих это каскадное соединение.

Синтез симметричных Т- перекрытых схем с постоянным характеристическим сопротивлением. Для симметричного Т- перекрытого четырехполюсника, показанного на рис. 16.13, а, характеристические сопротивления

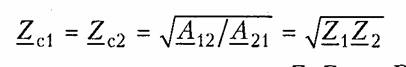
при взаимно-обратных двухполюсниках Z₁Z₂ = R² равны R, т. е. четырехполюсник включен согласованно. Следовательно, его собственная постоянная передачи непосредственно связана с рабочей передаточной функцией е^-Гс = Н_р или

Левая часть данного уравнения представляет собой квадрат модуля рабочей передаточной функции (12.44), а числитель правой части можно представить следующим образом:

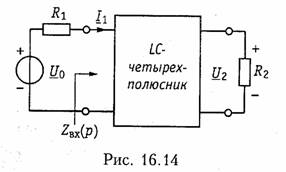
Убедиться в справедливости' уравнения (16.23) можно путем элементарных преобразований его правой части. С учетом сказанного уравнения (16,23) преобразуется к виду:

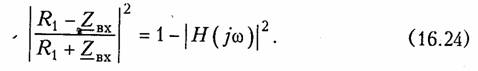
Из последней формулы можно найти операторное входное сопротивление Z_BX(p)- Реализуя Z_BX(p) в виде лестничной структуры, получаем цепь с заданной передаточной функцией Н(р). При этом, конечно, нужно следить, чтобы реализовывались нули передаточной функции. Обозначая

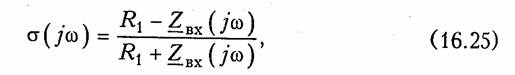
где а — коэффициент отражения мощности на входе четырехполюсника, получим из (16.24) связь между квадратом частотной характеристики коэффициента отражения и квадратом АЧХ четырехполюсника:

Практические аспекты применения данного метода будут рассмотрены при синтезе фильтров.

Синтез ARC-цепей. Активные RC-цепи возникли как альтернатива RLC-цепям. Дело в том, что катушки индуктивности, а значит и в целом .RLC-цепи плохо поддаются микроминиатюризации и обладают значительной массой и габаритами. Активные ЛС-цепи в принципе допускают микроминиатюризацию, что является их явным достоинством. Существенным же недостатком ARC-цепей является их относительно низкая стабильность, относительно высокий уровень собственных шумов и нелинейных искажений. Поэтому ARC-u.envi применяются в основном в области низких частот приблизительно до ШЙ кГц. На более высоких частотах применяются ARC-цепи невысоких порядков. Ниже кратко описаны методы синтеза ARC-цепей, которые нашли применение на практике.

Имитация в RLC-цепях индуктивностей их электронными эквивалентами. Существуют активные многополюсники, называемые обобщенными преобразователями сопротивлений, которые, будучи нагруженными на емкости или резисторы, реализуют на своих входных зажимах некоторую цепь, состоящую из индуктивностей. В простейшем случае индуктивность можно реализовать нагруженным на емкость гиратором (см. § 3.11). Данный метод синтеза ARC-цепи сводится к синтезу пассивной RLC-цепи с последующей заменой всех индуктивностей их электронными эквивалентами.

Синтез ARC-цепей по моделям. Этот метод заключается в том, что рассматривается ARC-схема, состоящая из одного или нескольких активных элементов и некоторого .RC-многополюсника. Методами анализа электрических цепей находится операторная передаточная функция, выраженная через параметры .RC-многополюс-ника и активного элемента. Сравнивая заданную передаточную функцию с полученной, определяют параметры синтезируемой схемы (метод выравнивания коэффициентов). Чаще всего в качестве активного элемента выбирают ОУ с бесконечным коэффициентом усиления и задаются структурой многополюсника.

Анализ цепей с ОУ рассмотрен ранее (п. 14.1) и основывается на замене О У зависимым источником. Согласно этому методу сформулируем алгоритм нахождения операторных передаточных функций цепей с ОУ. Он состоит из следующих шагов:

1.  Ко входу цепи подключить какой-либо источник.

2.  Заменить все ОУ их схемами замещения (зависимыми источниками) с конечным коэффициентом усиления Ну.

3.   Любым методом анализа цепей определить изображение по Лапласу входных (U\(p) или 1\(р)) и выходных ((/гСр) или /г(р)) напряжений и токов.

4.   Взять отношение найденных изображений и в этом отношении сделать предельный переход при Ну -» оо.

Пример. Зададимся моделью, показанной на рис. 16.15. При коэффициенте усиления ОУ, стремящемся к бесконечности, операторная передаточная функция примет вид (см. § 3.11 и гл. 14):

Полученная система из трех уравнений содержит шесть неизвестных. Она имеет множество решений. Наложим дополнительные ограничения на неизвестные. Пусть G₁ = G₂ = G₃ = G₄ = G, тогда система уравнений преобразуется к виду

Отсюда следует, что С₅,   = 3G/α, Сз = а/Зβ, Н = β. Задавшись конкретным значением G, найдем Сз и C_5.

Если проводимостям исходной схемы приписать другие значения, то можно реализовать множество различных функций.

Каскадная реализация заключается в представлении заданной передаточной функции в виде произведения множителей обычно второго, а иногда первого порядков. Такие функции в силу их простоты несложно реализовать в виде активной схемы, которую называют звеном. Затем полученные четырехполюсники включают каскадно, причем так, чтобы взаимное влияние звеньев было пренебрежимо мало. Это достигается двумя способами: либо включением между звеньями специальных буферных (развязывающих) активных четырехполюсников (например, повторителей напряжений), или таким выбором звеньев, при котором отношение выходного и входного сопротивлений звеньев в месте соединения стремилось либо к нулю, либо к бесконечности. Другими словами, данные сопротивления должны резко отличаться друг от друга. Например, если выходное сопротивление предыдущего звена стремится к нулю, то входное сопротивление последующего звена должно стремиться к бесконечности и наоборот.

Вопросы и задания для самопроверки

1.  Из каких этапов состоит синтез электрических цепей?

2.  Сформулируйте условия физической реализуемости передаточных функций, АЧХ и ФЧХ,  временных  функций и входных функций электрических цепей.

3.  В чем состоит отличие методов аппроксимации по различным критериям близости: интерполяции, по Тейлору, по Чебышеву и среднеквадратической аппроксимации?

4.  Аппроксимировать методом интерполяции зависимость ζ{х) = — е^-0,5х на  интервале   0,5 ≤ х≤ 2   полиномом  второй  степени

F(x) = x² + a₁x + α₂. Оценить точность аппроксимации для различных узлов интерполяции.

5.  Какой из вариантов аппроксимации (рис. 16.16, а — е) заданной на интервале (х₁, х₂) функции ζ(x) полиномом пятой   степени F(x) соответствует наилучшему приближению по критерию Чебышева?

Ответ:   д).

6. Какие из перечисленных функций удовлетворяют условиям физической реализуемости операторных передаточных функций и почему:

8. Найти схему и величины элементов мостового четырехполюсника постоянного характеристического сопротивления, реализующего передаточную функцию (при R = 1)

13.  Какими  свойствами  обладают входные функции  реактивных двухполюсников ?

14.  Опишите процедуры синтеза реактивных двухполюсников по методам Фостера и Кауэра.

ГЛАВА 17. ФИЛЬТРУЮЩИЕ ЦЕПИ И ИХ СИНТЕЗ

17.1. Классификация фильтров

Электрический фильтр — это устройство, которое практически не ослабляет спектральные составляющие сигнала в заданной полосе частот и значительно ослабляет (подавляет) все спектральные составляющие вне этой полосы.

Полоса частот, в которой ослабление мало, называется полосой пропускания. Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания). Между этими полосами находится переходная область.

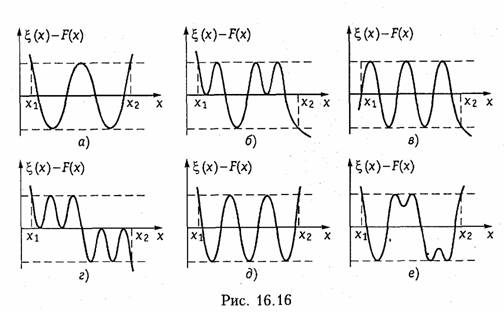
По расположению полосы пропускания на шкале частот различают следующие фильтры:

нижних частот (ФНЧ), в которых полоса пропускания располагается на шкале частот от ω = 0 до некоторой граничной частоты ω = ω _п, а полоса непропускания (задерживания) — от частоты ω = ω₃ до бесконечно больших частот (рис. 17.1, а);

верхних частот (ФВЧ) с полосой пропускания от частоты ω = ω_п до бесконечно больших частот и полосой непропускания от частоты  ω= 0 до ω= ω_з (рис. 17.1, б);

полосовые (ПФ), в которых полоса пропускания ω_п1...ω_п2 располагается между полосами непропускания О...ω₃₁ и ω₃₂...∞ (рис. 17.1, в);

заграждающие (режекторные) (ЗФ или РФ), в которых между полосами пропускания О...ω_п1 и ω_П2…∞ находится полоса непропускания ω₃₁...ω₃₂ (рис. 17.1, г);

многополосные, имеющие несколько полос пропускания.

На рис. 17.1, а — г показаны также условные обозначения фильтров каждого типа в соответствии с ГОСТ.

В соответствии с используемой элементной базой к настоящему моменту выделились несколько классов фильтров. Исторически первыми (и все еще широко применяемыми) являются пассивные фильтры, содержащие элементы L и С. Они носят название LC-фильтров.

Во многих случаях на практике требовалась крайне высокая избирательность (различие ослаблений в полосах пропускания и непропускания в десятки тысяч раз). Это привело к появлению фильтров с механическими резонаторами: кварцевых, магнитострикционных, электромеханических.

По-видимому, самые значительные достижения в области теории и проектирования фильтров связаны с успехами микроэлектроники. Требования микроминиатюризации радиоэлектронной аппаратуры заставили отказаться от использования индуктивностей, которые имеют большие габаритные размеры, особенно на низких частотах, и не поддаются исполнению в микроминиатюрном виде. Появились активные .RC-фильтры, состоящие из резисторов, конденсаторов и активных приборов (например, транзисторов). Эти фильтры могут быть выполнены в виде микромодульной конструкции или интегральной схемы. Применение активных .RC-фильтров ограничивается пока сравнительно небольшим диапазоном частот до десятков (иногда сотен) килогерц.

Разработка цифровых систем связи и достижения в области цифровых вычислительных машин стимулировали создание фильтров на базе элементов цифровой и вычислительной техники — цифровых фильтров. В силу специфики элементной базы цифровых фильтров не будем далее упоминать о них, хотя расчет таких фильтров производится методами теории электрических цепей. Заинтересованные читатели могут обратиться к специальной литературе по цифровым фильтрам.

В идеальном случае (идеальный фильтр) характеристика рабочего ослабления, например для ФНЧ, имеет вид, показанный на рис.  17.2, а. С рабочим ослаблением связана рабочая амплитудно-частотная характеристика (АЧХ):  На рис. 17.2, б изображена АЧХ идеального фильтра нижних частот.

Реальные фильтры (т. е. фильтры, состоящие из реальных  элементов)  имеют  характеристики рабочего ослабления и амплитудно-частотную,

отличные от идеальных.

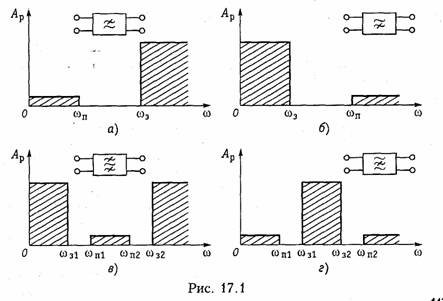
Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик. Так, рабочее ослабление в полосе пропускания не должно превышать некоторого максимального допустимого значения А_{р тах}, а в полосе непропускания не должно быть ниже некоторого минимально допустимого значения А_{р тix}. Нетрудно изобразить эти требования графически, как это сделано на рис. 17.3, а для ФНЧ. На этом рисунке ω_п и ω₃ — граничные частоты полос пропускания и непропускания.

Зная требования к Ар, можно пересчитать их в требования к АЧХ или, как это принято в теории фильтров, в требования к квадрату АЧХ (рис. 17.3, б):

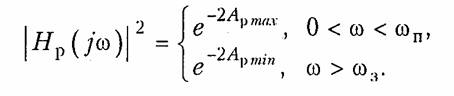
Характеристики проектируемых фильтров должны «укладываться» в эти требования (рис. 17.3, а и б).

Помимо требований к частотной зависимости рабочего ослабления (а значит, и к АЧХ) могут задаваться также требования к фазочастотной характеристике фильтра (скажем, допустимые отклонения от линейного закона) и величине нелинейных искажений (обусловленных, например, наличием железа в катушках индуктивности). Могут предъявляться требования и к другим характеристикам и параметрам фильтра. Ниже будем учитывать только требования к рабочему ослаблению и АЧХ.

Идеальные частотные характеристики фильтра (см. рис. 17.2, а) заведомо нереализуемы. Частотные характеристики реальных фильтров могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра.

17.2. Аппроксимация характеристик фильтров нижних частот

Функция фильтрации.В общем виде электрические фильтры описываются передаточной функцией вида:

могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов d_k удовлетворить заданным требования (см. рис. 17.3).

В теории фильтров принято иметь дело не с обычной угловой частотой ω, а с нормированной частотой Ω = ω/ω_н, где ω_н — нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания ω_п, так что

В теории электрических фильтров вместо формул (17.2) и (17.3) используют другие, также универсальные для любого типа фильтра:

Функция ψ²(Ω) называется функцией фильтрации, a ε — коэффициентом неравномерности ослабления. В общем случае ψ(Ω) — это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: —1 ≤ | ψ(Ω) | ≤1 в полосе пропускания и | у (Q )| » 1 в полосе непропускания фильтра.

В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если ψ(Ω) — дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.

Следует отметить, что имеет смысл подробно изучать только фильтры нижних частот, т. к. другие типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную Ω, нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ А_р(Ω) и |Нp(jΩ)|² преобразовались в характеристики соответствующего фильтра. Подобная замена переменной Ω называется преобразованием частоты, а исходный ФНЧ — фильтром НЧ-прототипа.

Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтров верхних частот, полосового или заграждающего, а также преобразовать схему ФНЧ в схемы ФВЧ, ПФ или ЗФ. Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в § 17.5.

Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта  (по имени автора, предложившего использовать их для «конструирования» частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.

Из формул (17.4) и (17.5) следует, что для фильтров Баттерворта на частоте Ω = 0 значение квадрата АЧХ равно единице, а рабочего ослабления — нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.

Чтобы эти характеристики «вписывались» в предъявляемые к фильтру требования (см. рис. 17.3), необходимо иметь рабочее ослабление (17.5) в полосе пропускания меньшее А_ртах, а в полосе непропускания большее А_{р min}. Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания (Ω = 1) выполнения равенства Ap(Ω)_Ω=1⁼ А_ртах или Отсюда с учетом (17.5) или (17.4) имеем Вычисленный таким способом коэффициент е:

называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.

В формуле (17.6) величина А_ртах имеет размерность непер. Если воспользоваться значениями А_ртах в децибелах, то

С учетом введенных обозначений квадрат АЧХ фильтра Баттер-ворта запишется в виде

Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.

Рабочее ослабление фильтра Баттерворта:

Половина полюсов функции Нр(р)Нр(—р) лежит в левой полуплоскости комплексной переменной р и может быть отнесена к передаточной функции реализуемого фильтра Нр(р). Другая половина полюсов, являясь зеркальным отражением первой, располагается в правой полуплоскости и относится к Нр(—р).

Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (17.1):

Используя введенное ранее обозначение B_m(Ω) = Ω'" полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме:

Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 17.4, а).

Полиномиальные фильтры Чебышева. Если в качестве функции фильтрации в (17.4) и (17.5) использовать полином Чебышева, обозначаемый то формулы (17.14) примут вид:

где T_m(Ω) — полином Чебышева степени (порядка) т; ε — коэффициент неравномерности, определяемый (17.6) или (17.7).

Фильтры с частотными характеристиками (17.15) называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов T_m(Ω). Ниже приведены шесть первых полиномов Чебышева:

Анализ поведения полиномов Чебышева показывает, что в интервале —1 ≤Ω ≤1 угол Θ = arccosΩ изменяется от —π (приΩ = —1) до 0 (при Ω = 1), поэтому полином T_m(Ω) = cosmΘ ровно т раз принимает значения, равные нулю, и  т +1 раз достигает значений, равных +1 пли —1 и чередующихся друг с другом. Вне интервала —1 ≤Ω≤ 1 полином Тm(Ω) согласно формуле (17.16 в) монотонно возрастает.

В качестве примера на рис. 17.6, а изображен график полинома Чебышева T₄(Ω), т. е. полинома четвертого порядка.

В соответствии с (17.15) рабочее ослабление А_р(Ω.) фильтра Чебышева на тех частотах Ω, где полином Т_m(Ω) обращается в нуль, также обращается в нуль. На частотах, на которых T_m(Ω) равен ±1, рабочее ослабление достигает величины:

С ростом значений полинома Т_m(Ω) на частотах Ω > 1 рабочее ослабление А_Р(Ω) также монотонно растет. На рис. 17.6, 6 приведен   график   рабочего   ослабления фильтра Чебышева четвертого порядка.

Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.

На рис. 17.7 показаны частотные зависимости квадрата АЧХ фильтра Чебышева для различных значений т, полученные для |Hp(jΩ)|² из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.

Чтобы характеристики фильтра отвечали требованиям в полосе непропускання, необходимо выбрать порядок фильтра т. из условия

Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полипомами наилучшего приближения. Это означает, что при одинаковом значении т из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают A_pmax, наибольшие значения ослабления в полосе непропускання имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе испропускания может превышать (п весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях т и А_pmax. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов.

Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.

Для получения передаточной функции фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта. Заменим оператор jΩ на оператор р и перейдем от функции  к функции:

В заключение отметим, что для полиномиальных фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов передаточных функций для различных величии A_pmax и т. Порядок же фильтров т определяется по специальным графикам, исходя из заданных величин _{Ар max}, A_pmin и Ω₃₎.

Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева). Частотные характеристики полиномиальных фильтров, описываемые выражениями (17.1) —(17.3), имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания (рис. 17.4, а и 17.6, б).

При «жестких» требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра т может получиться очень большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к излишнему «расходу» элементов.

В таких случаях целесообразно применять фильтры со всплесками рабочего ослабления в полосе непропускания (рис. 17.8, а). На частотах всплеска Ω_∞1, Ω_∞2 и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно AЧХ фильтра на частотах Ω_∞1, Ω_∞2 и т. д. будет обращаться в нуль (рис. 17.8, б).

Для выполнения указанных условий в выражениях (17.2) — (17.3) используют рациональные дроби вида:

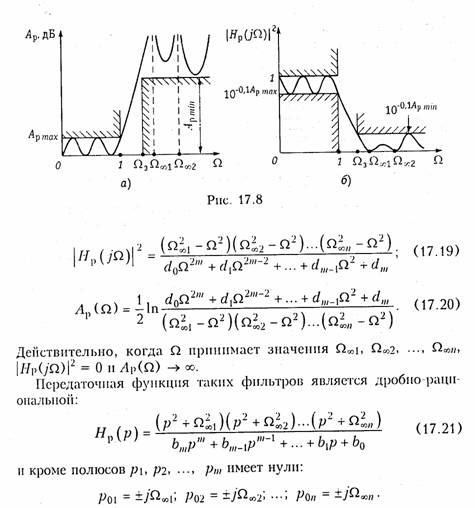
Фильтры со всплесками рабочего ослабления называют еще фильтрами с нулями передачи.

Среди фильтров со всплесками ослабления наиболее широкое распространение получили фильтры, построенные на основе дробен Чебышева и Золотарева. Чтобы получить частотные характеристики фильтра на основе дробей Чебышева, нужно в формулах (17.14) пли (17.15) использовать в качестве функции фильтрации дробь Чебышева. Обозначая ее Ф_m(Ω), получим:

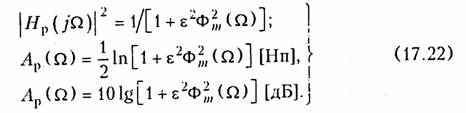
Очевидно, что подстановка этой дроби в (17.22) приведет после некоторых преобразований к выражениям общего вида (17.19) и (17.20).

В полосе пропускания дробь Чебышева ведет себя так же, как и полином Чебышева, т. с. рабочее ослабление фильтра носит равноволновый характер. На частотах всплеска Ω_∞1 и Ω_∞1 дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.

Следует отметить, что дробь Чебышева является дробью наилучшего приближения. Это означает, что фильтр на основе дроби Чебышева на любой частоте полосы непропускания имеет большее значение рабочего ослабления по сравнению с фильтрами на основе других дробей (и полиномов, как частных случаев дробей) при прочих равных условиях (при одинаковых порядках т, при таком же количестве и расположении частот всплеска и тех же величинах Артах).

Частным случаем дробей Чебышева являются дроби Золотарева:

Из формул (17.23) и (17.24) следует, что нули функции А_р>(Ω) совпадают с пулями дроби Золотарева, а всплески функции А_р>(Ω)  — с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать, однако обычно их определяют но каталогам для операторных передаточных функций ФНЧ. На рис. 17.9 показан график А_р>(Ω) для фильтра Золотарева пятого порядка.

Дроби Золотарева так же, как и полиномы Чебышева, дают равноволновую характеристику рабочего ослабления фильтра в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения всех минимумов рабочего ослабления оказываются одинаковыми и равными значению рабочего ослабления на частоте Ω₃.  Такие фильтры называются также фильтрами с изоэкстре малъиыми характеристиками рабочего ослабления.

Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выравнены, а число всплесков — максимально возможное при выбранном значении т.

17.3. Реализация фильтров нижних частот

Лестничные полиномиальные LС-фильтры. Любые из рассмотренных выше фильтров, как полиномиальные, так и со всплесками ослабления могут быть реализованы в виде пассивных LC-цепей.

Пассивные LC-фильтры обычно представляют собой реактивный лестничный четырехполюсник, включенный между генератором с активным внутренним сопротивление R_HHH п нагрузкой с активным сопротивлением R_Г (рис. 17.10). Входное сопротивление реактивного четырехполюсника, нагруженного па сопротивление R_H, обозначено па рисунке Z_BX1(p).

Если фильтр со стороны зажимов 1 — 1' рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой R_H, то, зная выражение 2_вх1(р), можно реализовать данный двухполюсник одним из известных в теории цепей методов синтеза двухполюсников. Таким образом, задача реализации фильтра сводится к реализации двухполюсника по его заданному входному сопротивлению. Идея данного подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом Дарлингтона.

На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения (16.25)

Из (17.27) следует, что знаменатель у σ(р) такой же, как и у Н_р(р): им является полином v(p). Остается найти нули правой части выражения (17.7) и половину из них «приписать» полиному числителя σ(р). Последний формируется из нулей по теореме Виета.

Пример. Реализовать фильтр нижних частот Баттерворта второго порядка нз примера (стр. 450) в виде пассивной LC-схемы. Внутреннее сопротивление генератора 1 кОм.

В примере была получена передаточная функция Баттерворта второго порядка для нормированных значений частоты Реализация нормированной передаточной функции приведет к схеме с нормированными значениями реактивных элементов (обозначим их L, С), которые затем необходимо де-нормнровать для получения реальных значений.

В соответствии с (17.27)

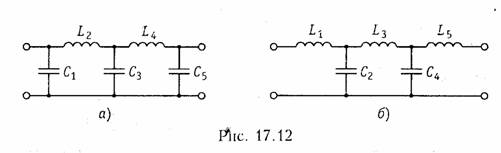
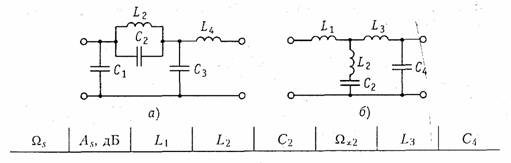
Аналогично рассмотренному примеру решается задача реализации фильтра любого порядка. Например, полиномиальный ФНЧ пятого порядка {т = 5) реализуется в виде одной из двух схем, показанных на рис. 17.12, а и б. Количество реактивных элементов определяется порядком фильтра т. Отличие фильтра Баттерворта от фильтра Чебышева будет заключаться в этом случае только в разных значениях реактивных элементов, получаемых в процессе реализации соответствующих передаточных функций.

Лестничные фильтры со всплесками ослабления. По подобной схеме осуществляется и реализация передаточных функций фильтров со всплесками ослабления (Чебышева пли Золотарева). Разложение входного сопротивления таких фильтров в цепную дробь приведет к схемам, содержащим резонансные контуры, в которых резонансы происходят на частотах Ω_∞1 ,Ω_∞1,.... Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах всплеска.

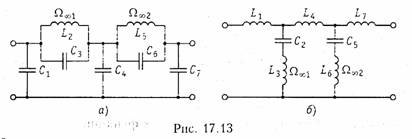
Так, ФНЧ пятого порядка со всплесками ослабления на частотах Ω_∞1 и Ω_∞2 реализуется в виде одной из схем, приведенных на рис. 17.13, а и б. И в первой и во второй схемах контуры рассчитаны на резонансные частоты Ω_∞1 и Ω_∞2. В первой схеме в параллельных контурах происходят резонансы токов; сопротивления контуров принимают бесконечно большие значения. В результате на частотах резонансов Ω_∞1 и Ω_∞2 наблюдается «обрыв» продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает, т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных контурах происходят резонансы напряжений; сопротивления контуров обращаются в нуль. Таким образом, здесь на частотах Ω_∞1 и Ω_∞2 поперечные ветви «закорачивают» нагрузку и сигнал па выход фильтра не поступает. Таким образом, имеет место бесконечно большое ослабление.

Реализация лестничных фильтров по каталогам. Из изложенного следует, что синтез фильтров представляет собой сложную процедуру, поэтому разработчики фильтров пытались облегчить ее. В результате были созданы обширные каталоги фильтров, применение которых значительно облегчает процедуру синтеза ФНЧ. Табл.   17.1   представляет собой  страницу из такого каталога,  где

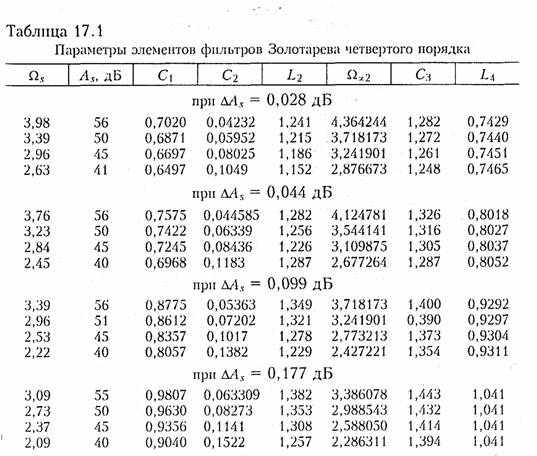
приведены нормированные элементы фильтра Золотарева четвертого порядка. В этой таблице Ω_s, A_s, ∆As — нормированная граничная частота полосы задерживания, минимальное ослабление в полосе задерживания, максимальное ослабление в полосе пропускания соответственно. Аналогичные каталоги существуют и для фильтров Баттерворта и Чебышева.

Процедура синтеза ФНЧ с помощью каталогов может выглядеть следующим образом:

1. По формуле (17.17 а) определяем порядок фильтра т. Если число т четное, то в числитель данной формулы добавляем слагаемое в соответствии с выражением (17.40) и уточняем порядок фильтра.

2.  Из каталога фильтров выбираем таблицы,  соответствующие данному порядку.

3.  Из данных таблиц выбираем строку, для которой с минимально возможным отклонением выполняются неравенства

Нормированные элементы данной строки и будут нормированными элементами фильтра, схема которого приведена на рисунке к данной таблице. При этом, обозначения элементов вверху таблицы относятся к схеме а, а внизу — к схеме 6. Истинные значения элементов получаются путем денормирования.

Активные RC-фильтры. Фильтры, представляющие собой комбинацию пассивной RС-цепи и активного элемента, называются активными RC-фильтрами. В качестве активного элемента чаще всего используются операционные усилители с двумя входами: инвертирующим и неинвертирующим.

Реализация передаточных функций фильтров на активных RC-цепях осуществляется следующим образом. Заданную функцию Н_p(р) порядка т разбивают на произведение передаточных функций не выше второго порядка, т. е. Н_р(р) = Нр₁(р)Н_р2(р) ... H_pk(p). Каждую передаточную функцию H_pi(p) реализуют в виде ARC-звена первого или второго порядка. Схему АRС-фильтра получают путем каскадного соединения звеньев.

Пример. Пусть задана передаточная функция полиномиального фильтра Чебышева пятого порядка.

Таким образом, фильтр Чебышева пятого порядка может быть реализован двумя звеньями с передаточными функциями второго порядка и одним звеном с передаточной функцией первого порядка.

В практике проектирования активных RC-фильтров используется большое число схем, реализующих передаточные функции первого и второго порядка.

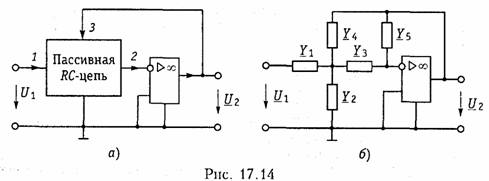
Один из способов построения таких схем показан на рис. 17.14, а. Пассивная часть схемы представлена в виде цепи из элементов R и С. Между зажимами 2 и 3 включен операционный усилитель, в котором использован инвертирующий вход. Примером пассивной RС- цепи является схема, приведенная на рис. 17.14, 6. Передаточная функция изображенной на рис. 17.14, б активной RC-цепи была получена ранее (см. § 3.11) и имеет вид:

Сопоставление коэффициентов при р в соответствующих степенях и свободных членов из (17.30), выраженных через элементы фильтра,  с заданными числовыми значениями коэффициентов при р и свободных членов из (17.29) позволяет определить значения элементов фильтра.

Пример. Реализовать фильтр нижних частот Баттерворта второго порядка из примера в виде активной RC-цепи..

Передаточная функция НЧ фильтра Баттерворта второго порядка была полу- чсна ранее (см. пример на стр. 450)  Для сопоставления с ней передаточной функции (17.30) представим последнюю в виде, когда коэффициент при р² равен 1:

Реализация фильтров со всплесками ослабления, передаточные функции которых описываются выражением (17.21), осуществляется так же, как и реализация полиномиальных фильтров. Передаточная функция (17.21) разбивается на произведение простейших (первого и второго порядков) передаточных функции; последние реализуются в виде фильтровых RС-звеньев первого и второго порядков, соединяемых каскадно в общую схему фильтра.

Для реализации передаточных функций второго порядка с нулем передачи  используются специальные фильтровые ARC-звенья.

Более подробно методику синтеза активных RC фильтров со всплесками ослабления можно изучить, обратившись к специальной литературе.

17.4. Переход от фильтров нижних частот

 к другим типам фильтров

Преобразование шкалы частот ФНЧ. Для синтеза фильтров верхних частот (полосовых или заграждающих) и, в частности, для нахождения их передаточных функций, можно было бы заново повторить все преобразования, примененные к фильтрам нижних частот. Однако такой подход нерационален. Обычно для расчета ФВЧ, ПФ пли ЗФ используют преобразование шкалы частот Ф Н Ч - прототипа.

На рис. 17.16 приведены характеристики ослабления фильтров: нижних частот (а), верхних частот (б) полосового (в) и заграждающего (г).

Для ФНЧ эта характеристика построена как для положительных, так и для отрицательных частот. Шкала частот для каждого фильтра помечена для удобства буквенными обозначениями: «нч», «вч», «пф», «зф».

Из рис. 17.16, а я б видно, что характеристика ослабления ФНЧ в отрицательной области частот повторяет характеристику ФВЧ. Преобразовать характеристику ФНЧ в характеристику ФВЧ можно с помощью замены переменной:

где ω_п — граничная частота полосы пропускания ФНЧ и ФВЧ.

График зависимости (17.31) представляет собой нижнюю ветвь гиперболы. На рис. 17.17 приведены характеристика ослабления ФНЧ, график преобразующей функции (17.31) и характеристика ослабления ФВЧ. Действительно, такое преобразование частоты приводит к соответствию: частоты ω_в._ч = — ∞ частоте ω_в._ч = 0; частоты ω_в._ч = —ω_п частоте ω_в._ч = ω_п; частоты ω_в._ч = 0 частоте ω_в._ч = ∞.

Чтобы из характеристики ФНЧ получить характеристику ПФ (рис. 17.16, в), необходима замена переменной:

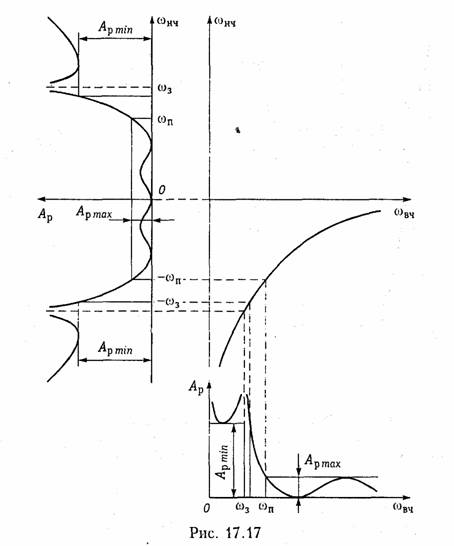
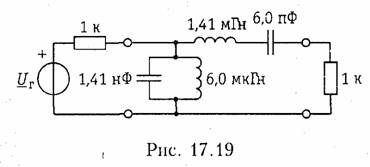
Преобразование схем пассивных LC-фильтров. Замена переменных (2.31) и (2.32) в выражении для квадрата АЧХ фильтра нижних частот приводит при реализации этой функции к преобразованию схемы ФНЧ в схемы ФВЧ и ПФ. Индуктивное сопротивление ФНЧ jω_н.ч L_н.ч переходит при преобразовании частот (17.31) в сопротивление:

переходит в индуктивную проводимость фильтра ВЧ с индуктивностью L_в.ч = 1/ω_п² С_н._ч.

Преобразование частоты (17.32) приводит к замене индуктивного сопротивления ФНЧ:

Нетрудно убедиться также, что индуктивный элемент ФНЧ преобразуется в ЗФ в параллельный колебательный контур с резонансной частотой ω_о, а емкость ФНЧ — в последовательный колебательный контур с той же резонансной частотой.

Преобразование передаточных функций активных RC-фильтров. В активных .RC-фильтрах для того, чтобы перейти от передаточной функции ФНЧ- прототипа к передаточным функциям ФВЧ и ПФ, следует осуществить замену комплексной переменном р. Из (17.31) получаем для ФВЧ

ARC-звена ФВЧ второго порядка, схема которого дана па рис. 17.20. Значения элементов схемы будут найдены, если приравнять коэффициенты из (17.37) и (17.38) при соответствующих степенях р.

Для перехода от НЧ- прототипа к полосовому фильтру воспользуемся (17.33):

Видим, что при переходе к ПФ порядок передаточной функции удваивается. Передаточную функцию (17.41) можно разбить на произведение передаточных функций второго порядка и каждую из них реализовать отдельной АRС-схемой.

Запишем передаточную функцию ПФ второго порядка:

Элементы схемы фильтра (рис. 17.21) определяются сопоставлением (17.42) и (17.43).

Порядок синтеза ФВЧ, ПФ и ЗФ. С помощью преобразования частоты был осуществлен переход от ФЫЧ к другим типам фильтра. Однако для их синтеза этого недостаточно, так как исходными при синтезе ФВЧ, ПФ п ЗФ являются требования не к ФЫЧ, а к данным фильтрам. Поэтому вначале требуется выполнять обратный переход. Сформулируем порядок синтеза ФВЧ, ПФ, ЗФ:

1)  по заданным требованиям к ФВЧ, ПФ и ЗФ необходимо определить требования к ФЫЧ;

2)  решить задачу аппроксимации для ФНЧ (получить квадрат АЧХ пли операторную передаточную функцию);

3)  реализовать квадрат АЧХ в виде лестничного ФНЧ и перейти с помощью преобразования частоты к схеме требуемого типа фильтра (если выбрана пассивная схема фильтра);

4)  используя соответствующее преобразование частоты, перейти от операторной передаточной функции ФНЧ к операторной передаточной  функции  искомого  фильтра  и  реализовать  его  в  виде АRС -схемы (если выбран активный RС фильтр).

Рассмотрим более подробно первый пункт.

Пусть заданы требования к ФВЧ, т. е. заданы ω _{п в}._{ч ,} ω _{з в}._ч А_{р max} и А_{р mix} (см. рис. 17.17). Определим требования к ФНЧ. Если в выражение (17.31) вместо ω_в._ч подставить ω_{п в}._ч ,то согласно рис. 17.17 получим

Величины А_ртах и A_pmin остаются для ФНЧ такими же как и для ФВЧ. Таким образом получены требования к ФНЧ. По найденным требованиям к ФНЧ решаем задачу аппроксимации одним из методов, изложенных выше.

Пусть заданы требования к ПФ, т. е. известны ω_з1, ω_п1 , ω_п2 , ω_з2 а также ослабление в полосе пропускания А_{р max}  и в полосе задерживания A_{p min} (см. рис. 17.18). Подставим в выражение (17.32) последовательно граничные частоты полос пропускания и задерживания полосового фильтра. Как видно из рис. 17.18, в результате такой подстановки получим:

Требования по ослаблению к ФНЧ- прототипу остаются такими же, как и к ПФ. Следовательно, имеются все исходные данные для решения задачи аппроксимации ФНЧ.

Аналогично решается задача для ЗФ. Граничные частоты для ПП и ПЗ фильтров рассчитываются по формулам

17.5. Резонаторные фильтры

В многоканальных системах передачи разделение каналов по частоте осуществляется с помощью полосовых фильтров. Чтобы сигналы одного канала не попадали в другой, ПФ должны иметь высокую избирательность. Добротность резонансных контуров таких фильтров Так, для фильтра с fо  = 62 кГц и полосой пропускания , в то же время для фильтра  

В радиосвязи используются еще более высокие частоты (десятки и сотни мегагерц) и для построения избирательных фильтров нужны резонаторы с добротностью в тысячи и десятки тысяч единиц. Такие значения добротности никогда не обеспечиваются в LC-резонаторах (их добротность не превышает сотен единиц), поэтому в фильтрах применяют высокодобротные механические резонаторы, пьезоэлектрические, магнитострикционные и электромеханические.

В пьезоэлектрических фильтрах роль резонатора выполняет пластинка, вырезанная специальным образом из материала, обладающего пьезоэлектрическим эффектом (например, из кристалла кварца). Пьезоэффект кварцевой пластинки заключается в появлении на ее поверхностях электрических зарядов при механическом воздействии на пластинку. Существует и обратный пьезоэффект — возникновение механических колебаний пьезопластинки при помещении ее в переменное электрическое поле.

Если пьезопластинку поместить между металлическими обкладками и подать на обкладки переменное напряжение, то пластинка начнет совершать механические колебания. На поверхностях пластинки возникнут электрические заряды и во внешней цепи потечет ток. При совпадении частоты переменного напряжения и частоты собственных колебаний пластинки возникает механический резонанс; амплитуда колебаний достигнет максимума и ток во внешнем цепи будет максимальным. Таким образом, механический резонанс в кварцевой пластине подобен резонансу напряжений в последовательном колебательном контуре.

Эквивалентная схема пьезоэлектрического (в частности, кварцевого) резонатора (рис.  17.22) помимо эквивалентных индуктивности L и емкости С резонатора

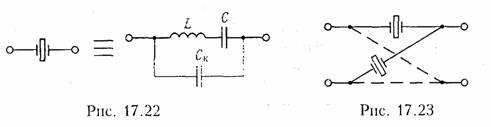
содержит емкость кварцедержателя С_к, т. е. обкладок, между которыми помещена кварцевая пластинка.

Пьезоэлектрические фильтры с кварцевыми резонаторами называют кварцевыми. Добротность кварцевых резонаторов достигает 10 ... 20 тыс. ед. Кварцевые фильтры могут быть построены по мостовой схеме (рис. 17.23).

Магнитострикционные фильтры строятся на основе резонаторов из ферромагнитного материала, обладающего магнитострикционный эффектом (например, из сплава никеля с кобальтом). Магнитострикционный эффект состоит в том, что стержень из ферромагнетика, помещенный в переменное магнитное поле, изменяет свои геометрические размеры. Обратный эффект — изменение магнитной проницаемости стержня при механическом воздействии па него. Если, например, никель-кобальтовый стержень поместить внутрь катушки индуктивности, создающей переменное магнитное поле, его геометрические размеры начнут меняться. При этом будет меняться и его магнитная проницаемость. В катушке индуктивности наведется ЭДС, направленная против ЭДС генератора и уменьшающая ток во внешней цепи. При механическом резонансе амплитуда колебаний стержня будет максимальной, а ток во внешней цепи — минимальный. Таким образом, механический резонанс магнитострикционного стержня подобен резонансу токов параллельного колебательного контура.

Эквивалентная схема резонатора приведена на рис. 17.24 и включает в себя элементы L_M и С_м эквивалентного резонатору контура, а также индуктивность L₀, учитывающую рассеяние магнитного потока при замыкании его через воздух.

Добротность манитострикционных резонаторов ниже, чем кварцевых, и составляет 5 ... 10 тыс. ед. Магнитострикционные фильтры строятся по мостовой схеме (рис. 17.25).

В электромеханических фильтрах резонаторами являются металлические тела (диски, шарики, стержни, пластинки), соединенные металлическими связками. На рис. 17.26 изображен трехрезонаторный стержневой электромеханический фильтр. Возбуждаются

колебания в фильтре с помощью входного магнитострикционного преобразователя (МСП); снимаются колебания с выхода фильтра с помощью выходного МСП. Электромеханические фильтры являются также высокодобротными.

Кроме рассмотренных существуют и другие типы фильтров: фильтры с переключаемыми конденсаторами, кварцевые фильтры на поверхностных акустических волнах (ПАВ) и др. С некоторыми из них можно ознакомиться в [2] и специальной литературе.

Вопросы и задания для самопроверки

1.  Что такое электрический фильтр? Какие типы фильтров существуют?

2.  Характеристика  рабочего  ослабления  фильтра  изображена  на рис. 17.3. Определить тип фильтра.

Ответ:     ФНЧ Чебышева 5 порядка.

3.  Какой вид имеют функции фильтрации фильтров Баттерворта, Чебышева, Золотарева?

4.  Привести графики Ap(Ω) ФНЧ третьего порядка Баттерворта, Чебышева и Золотарева.

5.  Рассчитать коэффициент неравномерности ослабления в полосе пропускания и порядок фильтра Баттерворта,  удовлетворяющего требованиям: А_{р max} = 2 дБ; A_pmin = 25 дБ; f_П = 15 кГц; f₃ = 26 кГц.

Ответ:   ε= 0,765; т = 6.

6.  Найти выражение для передаточной функции ФНЧ Баттерворта, удовлетворяющего требованиям, приведенным в задаче 5.

8.  Привести LC-схемы фильтров,  имеющих характеристики,  изображенные на рис. 17.4.

9.  Привести LC-схему фильтра,  характеристика которого изображена на рис. 17.3.

10.  Привести LC-схему фильтра НЧ Золотарева, а также график зависимости его рабочего ослабления от частоты.

11.  Каков алгоритм расчета фильтров методом Дарлингтона?

12.  Реализовать   ФНЧ   Баттерворта  третьего   порядка,   имеющего передаточную  функцию   Н_р (р) = 1/(р³ + 2р² + 2р + 1),   в  виде пассивной   LC-схемы.   Внутреннее   сопротивление   генератора R_Г = 1. V

Ответ:  

13.  Какие фильтры называются активными RС-фильтрами?

14.  Какие передаточные функции  имеют RС-фильтровые  звенья первого   и   второго   порядков?   Как   получить   передаточную функцию фильтра более высокого порядка?

15.  Реализовать   активный   .RC-фильтр,    имеющий   передаточную функцию, приведенную в задаче 12.

16.  Как осуществить переход от ФНЧ к ФВЧ, ПФ, ЗФ?

17.  Доказать,   что  при  переходе  от  ФНЧ   к   ЗФ   индуктивность фильтра-прототипа   преобразуется   в   параллельный   контур   в ЗФ, а емкость — в последовательный контур?

18.  Привести    схемы    LC-фильтров,    имеющих    характеристики, изображенные на рис. 17.16, б, в, г.

19.  Рассчитать ФВЧ с максимально плоской характеристикой ослабления, удовлетворяющий требованиям: А_рmаx =1,5 дБ: A_рmin = 20 дБ; ω₃ = 10⁶ с^-1; ω_п = 2·10^б   с^-1.

20.  Как осуществляется переход от схемы НЧ - прототипа к схемам ФВЧ и ПФ в активных .RC-фильтрах?

21.  Какие высокодобротные механические резонаторы используются для построения фильтров?

ГЛАВА 18. КОРРЕКТИРУЮЩИЕ

 ЦЕПИ И ИХ СИНТЕЗ

18.1. Принцип корректирования искажений

Корректирование амплитудно-частотных искажений. Рассмотрим некоторую электрическую цепь — четырехполюсник (рис. 18.1), имеющую амплитудно-частотную характеристику (АЧХ), изображенную на рис. 18.2, а, а ослабление — на рис. 18.2, 6. Пусть для упрощения входной сигнал u_BX(t) состоит из суммы всего двух гармоник с частотами ω₁ и 2ω₁ (рис. 18.3, а). Форма входного сигнала показана на этом рисунке жирной линией.

Из анализа графиков АЧХ и ослабления цепи следует, что амплитуда первой гармоники при прохождении сигнала через цепь останется практически неизменной, а амплитуда второй гармоники уменьшится в несколько раз.

Результат сложения гармоник па выходе цепи дает форму сигнала, отличающуюся от входной (рис. 18.3, б).

Изменение формы сигнала на выходе цепи по сравнению с формой сигнала на се входе называется искажением сигнала. Когда искажения формы сигнала связаны с непостоянством амплитудно-частотной характеристики цепи, они носят название амплитудно-частотпых искажений.

Таким образом, условием отсутствия амплитудно-частотных искажений в цепи следует считать постоянство ее АЧХ (ослабления) на всех частотах (см. § 9.9):

На практике условие (18.1) часто не выполняется, т, е. АЧХ и ослабление ценен аппаратуры и линий связи не являются постоянными. Эти цепи практически всегда вносят амплитудно-частотные искажения в передаваемый сигнал. Устранить подобные искажения полностью не удается, по их можно уменьшить до величин, допустимых соответствующими нормами. Для этих цепей применяются амплитудные корректоры.

Амплитудный корректор — это четырехполюсник, который включается каскадно с цепью. Его задача заключается в том, чтобы

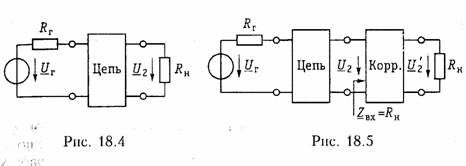
дополнить АЧХ цепи или ее рабочее ослабление до постоянной величины на всех частотах рабочего диапазона. Вне рабочего диапазона АЧХ цепи может иметь любую форму.

На рис. 18.4 изображена цепь, работающая между генератором с внутренним сопротивлением R_r и нагрузкой R_н. Рабочий коэффициент передачи этой цепи в соответствии с (12.44) равен:

Для достижения условий безискаженной передачи между цепью и нагрузкой включен корректор (рис. 18.5). Чтобы режим работы цепи не нарушался, входное сопротивление корректора должно равняться сопротивлению нагрузки. Очевидно, только при этом условии напряжение на выходе цепи будет равно U₂, как и в схеме рис. 18.4 до включения корректора.

Если обозначить напряжение на выходе каскадного соединения цепи и корректора U₂^’, то рабочий коэффициент передачи такого соединения запишется в виде

вычисляется путем сложения ослаблений цепи п корректора.

Из рис. 18.6 видно, что корректор должен вносить ослабление, дополняющее ослабление цепи в рабочей полосе частот ω_н ÷ω_в до постоянной величины А_о.

Корректирование фазочастотных искажений. Рассмотрим электрическую цепь — четырехполюсник (рис. 18.7), имеющую рабочую фазовую постоянную В(ω) изображенную на рис. 18.8, а, и характеристику группового времени прохождения (ГВП) t_гp(ω), являющуюся производной от рабочей фазовой постоянной, — на рис. 18.8, б. Входной сигнал u_ВX(t) состоит из суммы двух гармоник с частотами ω ₁и 2ω₁ (рис. 18.9, а). Форма входного сигнала изображена на этом рисунке жирной линией.

Анализ графиков B(ω) и t_гр(ω) цепи показывает, что фаза первой гармоники почти не меняется при прохождении сигнала через цепь, а фаза второй гармоники существенно увеличивается.

В результате сложения гармоник на выходе цепи получается сигнал, форма которого отличается от входной (рис. 18.9, б).

Искажения формы сигнала при прохождении его по цепи, обусловленные нелинейностью фазо-частотной характеристики цепи или непостоянством группового времени прохождения, называются фазо-частотпыми искажениями.

Условием отсутствия фазо-частотных искажений в цепи следует считать линейность рабочей фазовой постоянной B(ω) п ФЧХ цепи (рис. 18.10, а):

Производная от фазо-частотной характеристики — это групповое время прохождения, которое для неискажающей цепи:

должна быть постоянной на всех частотах (рис. 18.10, б).

В реальных цепях условия (18.2) и (18.3) обычно не выполняются, т. е. ФЧХ не является линейной, а ГВП — не постоянно. Такие цепи вносят фазо-частотные искажения в передаваемый сигнал. Для уменьшения подобных искажений до допустимых значений применяют фазовые корректоры.

Фазовый корректор — это четырехполюсник, включаемый каскадно с цепью и дополняющий фазовую характеристику цепи до линейной. Вместо корректирования частотной характеристики фазы можно выравнивать характеристику группового времени прохождения так, чтобы она была постоянной на всех частотах рабочего диапазона. Фазовый корректор не должен искажать АЧХ цепи.

На рис. 18.11 для достижения условий безискаженной передачи между генератором и нагрузкой включено каскадное соединение цепи с ФЧХ, подлежащей коррекции, и корректора. Входное сопротивление фазового корректора должно равняться сопротивлению нагрузки, чтобы условия работы цепи не изменялись по сравнению с теми, в которых находится цепь, включенная между генератором и нагрузкой в отсутствие корректора.

Передаточная функция цепи, изображенной на рис. 18.11:

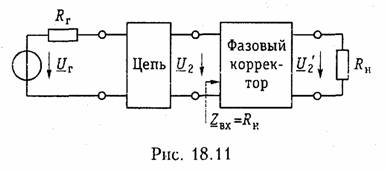
Умножим и разделим это выражение на U₂ и представим его в виде произведения передаточных функций цепи Н_ц(jω) и корректора H_к(jω):

вычисляется как сумма ФЧХ цепи и корректора.

Из рис. 18.12 видно, что фазовый корректор должен дополнять ФЧХ цепи в рабочей полосе частот ω_н÷ω _в до линейной зависимости (рис. 18.12, а) либо дополнять групповое время прохождения цепи до постоянной величины to в том же рабочем диапазоне частот (рис. 18.12, б). За пределами рабочего диапазона ФЧХ и ГВП могут иметь любую форму.

Корректоры бывают постоянными и непостоянными (регулируемыми). Характеристики постоянных корректоров не меняются при изменении характеристик цепи. Существуют корректоры, характеристики которых можно изменить в зависимости от изменения параметров цепи. Изменение параметров цепи возможно, во-первых, при изменении показателей окружающей среды, прежде всего температуры. Во-вторых, в технике связи распространены коммутируемые сети, когда канал связи между двумя пользователями устанавливается случайным образом на время сеанса связи и заранее неизвестно, из каких участков он будет составлен. Погрешности в АЧХ и ФЧХ, вносимые каждым участком могут складываться неудачно, так что общая погрешность будет больше допустимых величин. В этом случае включают так называемые «подчисточные» корректоры. Настройку регулируемых корректоров производят либо вручную, либо автоматически.

18.2. Амплитудные корректоры

Пассивные корректоры. Пассивные амплитудные корректоры строят, как правило, в виде симметричной Т- перекрытой схемы.

Симметричный Т- перекрытый четырехполюсник приведен на рис. 18.13. Сопротивления Z₁ и Z₂ выбираются обратными, т. е. Z₁  · Z ₂= R₀².Если такой четырехполюсник нагрузить на сопротивление Ro, то его входное сопротивление окажется равным также R₀.

Комплексная передаточная функция по напряжению схемы рис. 18.13 может быть вычислена по формуле:

Пример. Схема двухполюсника Z₁ в продольном плече корректора изображена на рис. 18.14, а. Построить график частотной зависимости ослабления корректора A_к(ω).

Построим вначале график частотной зависимости сопротивления реактивного двухполюсника Х₁(ω), образованного элементами L₁, C₂, L₃ и Сз. На нулевой частоте индуктивное сопротивление равно нулю, а емкостное — бесконечности, поэтому Х₁(0) → — ∞. Двухполюсник имеет три резонанса, причем первый — резонанс напряжений, на частоте ω₁, второй — резонанс токов на частоте ω₂, третий — снова резонанс напряжений на частоте ω₃. Это значит, что  При ω→∞ сопротивление Х₁(ω) также бесконечно большое (рис. 18.14, б).

Сопротивление Z₁, стоящее в продольном плече корректора, содержит помимо реактивных элементов активное сопротивление R₁ (рис. 18.14, а). Поэтому на частотах, равных 0, ω₂ и ∞, на которых реактивное сопротивление Х₁(ω) стремится к да, полное сопротивление │Z₁│двухплюсннка ограничено величиной R\ (рис. 18.14, в).

Ослабление корректора A_к(ω) рассчитывается по формуле (18.6) и зависит от значений |Z₁|(ω)|. График А_к(ω) повторяет по форме график |Z₁|(ω)|.  На частоте резонанса токов ω₂, а также на частотах ω = 0 и ω→∞ да ослабление корректора А_к(ω) достигает своего максимального значения:

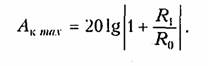
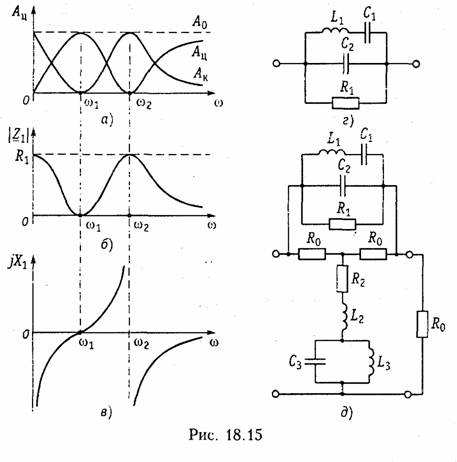
На частотах резонанса напряжений ω₁ и ω₃ значение А_к(ω) равно 0 (рис. 18.14, г).

Пример. Задано ослабление А_ц(ω) цепи, подлежащей коррекции (рис. 18.15, а). Привести схему корректора, выравнивающего характеристику этой цепи до значения А_0.

Находим требуемую характеристику ослабления А_к(ω) корректора из условия  График А_к(ω) приведен на этом же рис. 18.15, а.

По характеристике А_к(ω)  строим графики частотной зависимости полного сопротивления |Z₁|(ω)|и реактивного сопротивления Х₁(ω) продольного плеча корректора (рис. 18.15, б и 18.15, в).

Из графиков рис. 18.15, в и 18.15, б следует, что двухполюсник Z₁ имеет три реактивных элемента и одно активное сопротивление. В схеме два резонанса: первым наступает резонанс напряжений на частоте ω₁, вторым — резонанс токов на частоте ω₂. Таким условиям удовлетворяет двухполюсник Z₁, изображенный на рис. 18.15, г. Двухполюсник Z₂ в поперечном плече корректора является обратным двухполюснику Z₁.

Схема корректора приведена на рис. 18.15, д.

На практике широко используются типовые звенья пассивных корректоров 1-го и 2-го порядков. Звенья 1-го порядка содержат по одному реактивному элементу в двухполюсниках Z₁ и Z_2. На рис. 18.16, а изображено такое звено с двухполюсником Z₁, состоящим из параллельного соединения элементов R₁ и С₁.

Операторное сопротивление двухполюсника Z₁:

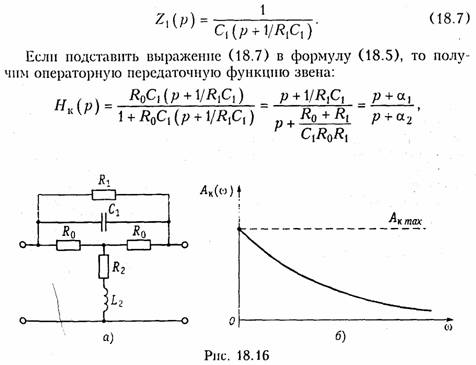
показана на рис. 18.16, б.

На рис. 18.17, а изображено звено 1-го порядка с двухполюсником Z₁, состоящим из параллельного соединения R₁ п L₁. Операторная передаточная функция этого звена:

Звенья 2-го порядка содержат по два реактивных элемента в двухполюсниках Z₁ и Z_2. На рис. 18.18, а изображено звено, содержащее последовательный колебательный контур и сопротивление R₁ в продольно ветви корректора. 

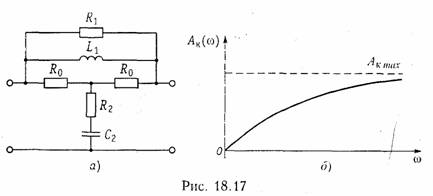
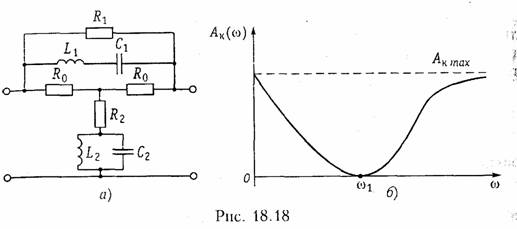
Операторная передаточная функция такого звена:

показана на рис. 18.18, б.

Максимальное значение А _{к mах} по-прежнему рассчитывается по формуле (18.9).

На рис.   13.19,  а изображено еще одно звено 2-го порядка с двухполюсником Z₁, представляющим собой параллельный колебательный контур. Операторная передаточная функция звена и частотная характеристика ослабления (рис. 3.19, б) имеют вид:

Значения A_к(ω) рассчитываем по формуле (18.8) или по общей формуле (18.6), применимой для корректора любого типа. Например, на частоте f= 0 получаем

Остальные значения А_к(f) рассчитываются аналогично. По результатам расчета простроен график А_к(f), изображенный на рис. 18.20.

Помимо Т-перекрытой схемы корректора (рис. 18.19) применяются также другие схемы, изображенные на рис. 18.21.

Передаточные функции, которые реализуются Т-перекрытым корректором, можно реализовать и элементарными четырехполюсниками, схемы которых приведены на рис. 18.22. Например, для четырехполюсника па рис. 18.22, а операторная передаточная функция       

рассчитывается также, как и для корректора, построенного по Т- перекрытой схеме (см. формулу (18.5)). Цепи с элементарными четырехполюсниками применяются в случаях, когда не требуется согласование между генератором, корректором и нагрузкой.

В табл. 18.1 приведены характеристики и расчетные формулы звеньев пассивных амплитудных корректоров.

Активные корректоры. Кроме пассивных схем амплитудных корректоров применяют активные схемы. Активные амплитудные корректоры строятся в общем случае с применением RC- и RLC-элементов, которые называют ARZ-цепями. Существует большое количество разновидностей активных звеньев эквивалентных по передаточной функции пассивным амплитудным корректорам. Две схемы таких активных звеньев на операционных усилителях изображены па рис. 18.23. Их передаточные функции выражаются соответствующими формулами:

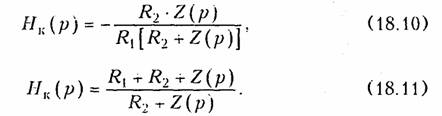
Если в схеме рис. 18.23, а в качестве двухполюсника Z выбрать последовательное соединение резистора R и емкости С, то передаточная функция (18.10) звена принимает вид:

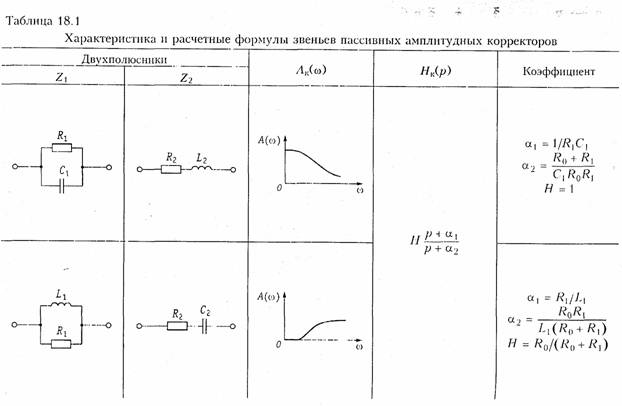
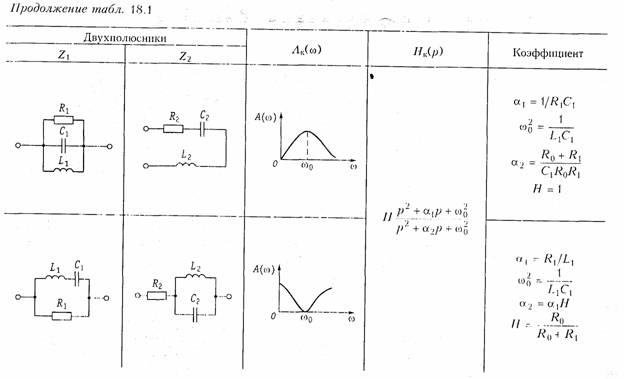
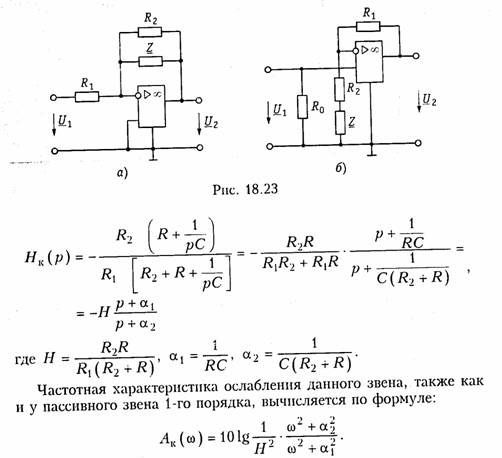
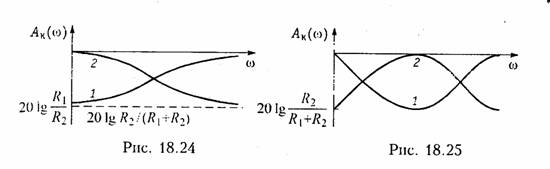
При увеличении частоты данная функция имеет монотонно убывающий характер от  (рис. 18.24, кривая 2).

Если в качестве двухполюсника Z выбрать последовательный LC-контур, то частотная характеристика ослабления будет иметь вид, показанный на рис. 18.25, кривая 1. При выборе в качестве двухполюсника Z параллельного LC-контура частотная характеристика ослабления будет иметь обратный характер, как показано на рис. 18.25, кривая 2.

Несмотря па то, что рассмотренные схемы могут содержать индуктивности, они имеют ряд преимуществ по сравнению с пассивными амплитудными корректорами. Так, число реактивных элементов вдвое меньше, а ослабление, вносимое каскадным соединением цепи и корректора, близко к нулю. Последнее важно также потому, что дополнительное ослабление за счет применения пассивного корректора, как правило, приходится компенсировать с помощью усилителя, т. е. общая схема все равно оказывается активной.

Пример. Определить передаточную функцию амплитудного корректора, построенного по схеме рис. 18.23, б, в которой в качестве двухполюсника Z выбран последовательный колебательный LC-контур. Рассчитать и построить частотную характеристику ослабления А_к(f) корректора в диапазоне частот от

Операционный усилитель в схеме рис. 18.23, 6 включен по неинвертирующей схеме, поэтому передаточная функция корректора определяется по формуле (18.11), в которой

Синтез амплитудных корректоров. При синтезе пассивного амплитудного корректора исходными данными являются: частотная характеристика ослабления цепи А_ц(ω), подлежащая коррекции в диапазоне частот ω_н ... ω_в; точность коррекции ∆А в этом же диапазоне частот; сопротивление нагрузки Ro_.

Вначале определяют частотную характеристику амплитудного корректора А_к(ω). Для этого необходимо задать характеристику ослабления А_о каскадного соединения цепи и корректора. Эта характеристика должна быть постоянной, не зависящей от частоты, причем ее величину принимают несколько большей, чем максимальное ослабление цепи:

На рис. 18.6 в качестве примера показаны характеристики ослабления цепи А_ц(ω), ослабления  А_о каскадного соединения цепи п корректора, а также ослабления А_к(ω) корректора.

Следующим этапом расчета амплитудного корректора является выбор схемы корректора. Выбирают такую схему, которая в диапазоне частот ω_н ... ω_в имеет нужный характер частотной зависимости ослабления. Например, для реализации частотной зависимости А_к(ω), приведенной на рис. 18.6, можно использовать амплитудный корректор, в котором двухполюсник Z₁ состоит из параллельного соединения емкости С₁ и резистора R₁ (рис. 18.16).

Выбрав схему корректора, приступают к ее расчету. При этом часто используется метод интерполирования. Согласно этому методу  задаемся  числом  точек   интерполирования,   равным  числу элементов в двухполюснике Z₁. С учетом формулы (18.6) составляется система уравнений вида:

где х₁ ... х_n значения параметров элементов двухполюсника Z₁. Решение данной системы и дает значения х₁ ... х_n которые являются параметрами индуктпвностей, емкостей и резисторов.

Особенностями расчета является то, что, во-первых, параметры элементов могут быть отрицательными, а во-вторых — точность коррекции может не удовлетворять заданным требованиям. Обычно приходится данный расчет повторять. Если параметры элементов получились отрицательными, то следует либо изменить величину A₁ в формуле (18.12), либо положение точек интерполяции. Если параметры элементов получились в конце концов положительными, то проверяется точность аппроксимации (коррекции). Для этого по формуле (18.6) рассчитывается ослабление корректора A_кр(ω) и проверяется выполнение неравенства:

При выполнении неравенства расчет на этом заканчивается. В противном случае необходимо снова повторить расчет, меняя точки интерполяции, до получения равноволиовой характеристики погрешности. Если при равноволновом характере погрешности требования к точности не выполняются, то необходимо либо увеличить число элементов в двухполюснике, либо поделить А_к(ω) пополам и построить корректор в виде каскадного соединения двух четырехполюсников.

Методика синтеза активных ARZ-корректоров такая же, как и описанная выше методика расчета пассивных амплитудных корректоров.

Отличие заключается в том, что характеристика ослабления Ао каскадного соединения цепи и корректора выбирается близкой к нулю.

Пример. В таблице 18.2 задана частотная характеристика ослабления цепи А_ц(f). Рассчитать элементы амплитудного корректора, если А_о  = 12 дБ и R₀ = = 200 Ом.

Воспользуемся формулой (18.13) и рассчитаем ослабление корректора в диапазоне частот от 0 до 50 кГц.

Результаты расчета А_к(f) приведены в таблице 18.3, а на рисунке 18.27 изображены графики ослаблений

Частотная характеристика ослабления А_r(f).  на рис. 18.27 может быть получена с помощью корректора, реализованного по схеме рис. 18.19, в которой двухполюсник Z₁ состоит из параллельного соединения элементов L₁ и R₁.

Найдем R₁ из формулы (18.9):

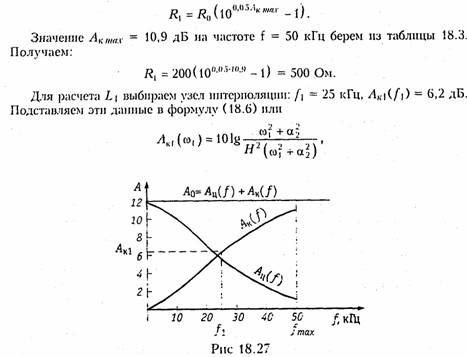
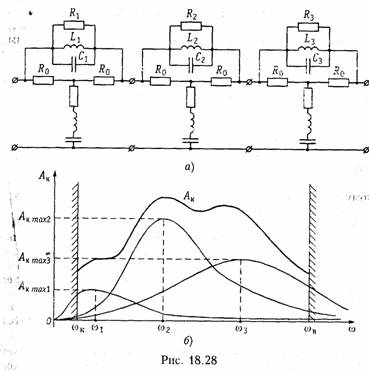
Используя каскадное соединение различных типовых звеньев корректоров, можно получить частотные зависимости ослабления А_к(ω)  любой сложности. На рис. 18.28 изображена схема сложного корректора, построенного на основе типовых схем (рис. 18.19), и его рабочее ослабление. Изменением характеристик типовых схем добиваются получения требуемой характеристики амплитудного корректора.

18.3. Фазовые корректоры

Пассивные корректоры. Фазовые корректоры должны иметь постоянное входное сопротивление п постоянное ослабление, которые не зависят от частоты. Таким условиям удовлетворяют симметричные мостовые четырехполюсники (рис. 18.29), у которых сопротивления Z₁ и Z₂ реактивные и взаимообратные, т. е.:

Такие четырехполюсники имеют с обеих сторон одинаковые характеристические сопротивления:

поэтому их легко согласовывать с внутренним сопротивлением генератора и сопротивлением нагрузки.

Рабочее ослабление мостового симметричного согласованно включенного четырехполюсника с взаимно-обратными сопротивлениями Z₁ и Z₂ равно нулю на всех частотах: А(ω) = 0, т. е. эта схема не вносит никакого дополнительного ослабления сигнала.

Операторная передаточная функция по напряжению схемы рис. 18.29 имеет вид:

Комплексная передаточная функция по напряжению схемы рис. 18.29, в которой Z₁и Z₂ — реактивные двухполюсники, может быть вычислена по формуле:

Нетрудно видеть, что модуль передаточной функции (18.15) равен 1, а аргумент п ГВП вычисляются по формулам:

Формулы (18.16), (18.17.) и (18.18) показывают, что фазочастотная характеристика, фазовая постоянная и характеристика группового времени запаздывания корректора зависят только от вида двухполюсника Х₁.

На практике используются типовые звенья пассивных фазовых корректоров первого н второго порядков.

На рис. 18.30, а изображена схема фазового корректора 1-го порядка, в котором двухполюсником Z₁ является индуктивность Z₁ (p) ⁼ pL, а двухполюсником Z₂ — емкость Z₂(p) =1/(pC).

Операторная передаточная функция этого корректора в соответствии с (18.14) имеет вид:

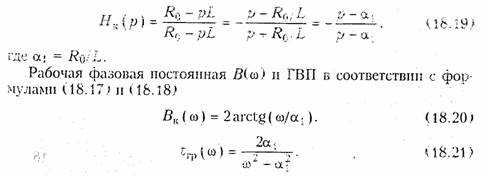
Графическое изображение данных характеристик показано на рис. 18.30. 6 и в.

На рис. 18.31, а изображена схема фазового корректора 2-го порядка, с двухполюсником Z₁, состоящим из последовательного соединения элементов

Операторная передаточная функция такого корректора в соответствии с (18.14) имеет вид:

Графики зависимостей В(ω) и tгp(ω) фазового корректора 2-го порядка приведены на рис. 18.31. б и в.

Если известны коэффициенты передаточной функции ω₀, Q_П и на грузка Ro, то параметры элементов корректора рассчитываются по формулам

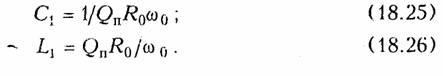
Пример. Фазовый корректор (рис. 18.30. л) имеет элементы L₁ = 100 мГн, R₀ — 500 Ом. Рассчитать и построить графики частотных зависимостей фазовой постоянной В_К(f) группового времени прохождения t_гp(f) is диапазоне частот от 0 до 10 кГц.

Фазовая характеристика В(ω) рассчитывается по формуле (18.20), по этому :

Подставляя знамения ω₀² и Q _нв выражения для расчета B_K(f) и t_гp(f), рассчитываем эти характеристики в диапазоне частот от 0 до 10 кГц и заносим результаты расчета в таблицу 18.5 для случая 1) и в таблицу 18.6 для случая 2).

Поскольку график tгp(ω) имеет максимум (рис. 18.31, в), то для определения частоты этого максимума берем производную dt_гр(ω), приравняв ее к нулю, находим:

Графики   зависимостей   В_к(ω)   и   t_гр(ω)   _для   двух   случаев   приведены   на рис. 18.33 (обозначены цифрами 1 и 2).

Мостовая схема не всегда удобна в реализации, так как является уравновешенной. Существует ряд эквивалентных схем в виде неуравновешенной схемы, как показано на рис. 18.34. Заметим, что на практике добротность полюса больше единицы и поэтому-чаще используется схема рис. 18.34, а, что удобно, так как она не содержит связанных индуктивностей с заданным коэффициентом связи. Неуравновешенные схемы по сравнению с мостовыми содержат вдвое меньше элементов.

Активные корректоры. Помимо пассивных фазовых корректоров применяют активные фазовые корректоры. Кроме пассивных RC или RLС-элементов схемы активных корректоров содержат операционные усилители. Существуют активные фазовые звенья 1-го и 2-го порядков. На рис. 18.35 приведена схема фильтрового звена на операционном усилителе. Передаточная функция этого звена вычисляется по формуле:

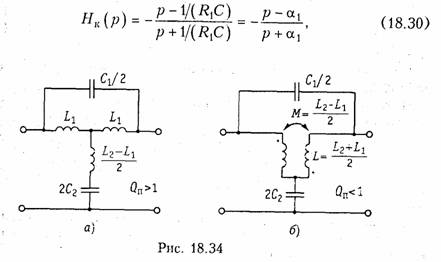
где α₁ = l/R₁C.

Выражение (18.30) аналогично формуле для расчета передаточной функции пассивного фазового корректора (18.19), т. е. схема, приведенная на рис. 18.35, — это активный корректор 1-го порядка.

Фазовые характеристики B(ω) и ГВП данного звена, также как у пассивного корректора 1-го порядка, вычисляются по формулам

т. е. схема на рис. 18.37 — это схема фазового корректора 1-го порядка.

Когда в качестве двухполюсника Z используется последовательный L С-контур, то получается передаточная функция фазового корректора 2-го порядка:

Хотя активные ARZ-фазовые корректоры имеют индуктивность, но преимуществом их по сравнению с пассивными корректорами является меньшее количество элементов при том же порядке передаточных функций.

Пример. Определить передаточную функцию фазового корректора, построенного по схеме рис. 18.35, в которой в качестве двухполюсника Z используется параллельный LC-контур. Рассчитать и построить качественно частотную характеристику ГВП t_гp(f) корректора в диапазоне частот от 0 до 5 кГц для элементов цепи R₁ = 37,5 Ом, L = 36 мГн, С = 1,6 мкФ.

Найдем сопротивление Z(p) параллельного LC-контура:

Синтез фазовых корректоров. При синтезе фазовых корректоров задаются характеристика ГВП корректируемой цепи, сопротивление нагрузки Ro, точность коррекции и диапазон частот ω_н ... ω_в, в котором осуществляется коррекция. Вначале определяют требуемую характеристику фазового корректора. Для этого задают постоянное значение ГВП t_o, которое должно быть несколько больше максимального значения ГВП цепи (рис. 18.12, б):

Затем любым способом определяют площадь S_K под характеристикой требуемого ГВП корректора, например, площадь можно рассчитать по формуле:

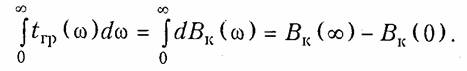
После этого приближенно можно определить число фазовых звеньев второго порядка, необходимых для коррекции, так как площадь под кривой группового времени фазового звена второго порядка равна 2π:

n = 1,1S_к/2π.

В данной формуле коэффициентом 1.1 учитывается то, что не вся площадь под характеристикой фазового звена попадает в диапазон/ коррекции. Зная число звеньев, задаемся в первом приближении их пара метрами Для начала частоты распределяют-

ся равномерно, добротность определяют из условия требуемой величины группового времени звена на частоте ω_maxk. Эта величина выбирается на 10 ... 20% меньше, чем требуемое групповое время корректора на этой частоте. Из сказанного и формулы (18.27) следует:

где т = 0,8 ... 0,9.

На рис. 18.40 показаны характеристики ГВП четырех фазовых звеньев, требуемая и реальная характеристики ГВП корректора.

Далее с применением компьютерных программ решается оптимизационная задача в общей постановке:

Если полученный минимум меньше или равен требуемой точности коррекции, то по заданным Q_Пk, ω_0k и R₀ рассчитывают элементы L_1k н С_1k мостовой схемы фазового звена (рис. 18.31, а). Остальные элементы находят из условия, что двухполюсники Z_a, и Z_b обратные:

Если полученная точность коррекции не удовлетворяет требованиям, то увеличивают число звеньев и повторяют расчет также с помощью компьютера.

С синтезом активных фазовых корректоров можно познакомиться в специальной литературе.

18.4. Гармонические корректоры

Линии задержки. Одним из элементов гармонических корректоров являются так называемые линии задержки (ЛЗ). Идеальная линия задержки осуществляет задержку колебания на постоянную величину ∆t, не изменяя энергии этого колебания. Очевидно, модуль передаточной функции (АЧХ) ЛЗ равен 1, а угол (ФЧХ) φ(ω) = —ω·∆t. Таким образом, передаточная функция линии задержки

( 18.32)

Однако данная функция не удовлетворяет УФР, так как φ(ω) не является тангенс-функцией. В реальной линии задержки ГВП является постоянным только с определенной степенью точности в заданном диапазоне частот.  Будем рассматривать низкочастотные ЛЗ, рабочий частотный диапазон которых простирается от нуля до частоты ω. Совершенно очевидно, что ЛЗ являются частным случаем фазового корректора (ФК). Отличие состоит в том, что от ФК требуется воспроизвести частотную характеристику ГВП, вообще говоря, произвольной формы, в то время как ЛЗ обладает только постоянным, с заданной степенью точности, групповым временем. В связи с этим есть возможность заранее рассчитать набор ЛЗ для различных значений ГВП и различной точности его воспроизведения и оформить результаты в виде каталогов. Как и в случае аппроксимации характеристик фильтров, применяется как равноволновая аппроксимация, так и аппроксимация монотонными характеристиками.

Определим далее общий вид операторной передаточной функции ЛЗ. Во-первых, знаменатель любой передаточной функции должен быть полином Гурвица v(p). Во-вторых, непосредственной подстановкой легко убедиться, что модуль комплексной передаточной функции равен единице, если в числителе находится полином, сопряженный полиному знаменателя. Поэтому в самом общем виде комплексная передаточная функция ФК или ЛЗ имеет вид

Мы уже убедились, что при построении каталогов удобно применять нормированные величины. В данном случае это нормированная частота  и нормированное ГВП t_гр = ω_нt_гр. При синтезе ЛЗ частота нормирования ω_н находится из условия, что на нулевой частоте нормированная функция φ'(0) = 1, а ГВП равно 2, т. е.

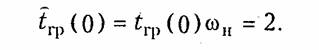
Отсюда

Аппроксимация  ГВП  гладкими функциями осуществляется  на основе полиномов Бесселя, которые имеют следующий вид:

Графики нормированной функции  показаны на рис. 18.41.

Задача аппроксимации максимально-гладкими функциями решена аналитически с помощью рядов Тейлора. Задаваясь погрешностью аппроксимации ∆, легко получить нормированные граничные частоты рабочей полосы линии задержки. На рис. 18.41 проведена линия на уровне 0,9, что отвечает 10% погрешности. Существуют справочники, в которых приведены таблицы, содержащие граничные нормированные частоты при различных порядках полинома Бесселя п и различных погрешностях.

Зная полином Бесселя нетрудно численно найти координаты его корней, которые являются полюсами передаточной функции. Напомним, что в соответствии с (18.33) каждому полюсу в левой полуплоскости соответствует нуль в правой, т. е. р_0k = —pk.1``1 Координаты корней полиномов Бесселя приведены в справочниках.

Рассмотрим порядок синтеза ЛЗ с максимально-плоской характеристикой группового времени. При синтезе заданными величинами являются групповое время t₃, рабочий диапазон частот 0 ... ω_1, погрешность аппроксимации ∆. Согласно (18.34) находим частоту нормирования ω_н при условии, что t_гp(O) = t_э. Зная ω_н рассчитываем нормированную граничную частоту ω₁/ω_н =Ω_1. Пользуясь графиками или таблицами, находим минимальный порядок передаточной функции ЛЗ, при которой граничная частота рабочей полосы частот равна или превышает Ω₁. Найденному порядку соответствует полином Бесселя v_Б(p). Таким образом, получена передаточная функция в виде

Зная координаты корней полинома Бесселя, передаточную функцию можно представить в виде произведений функций второго порядка и каждую функцию реализовать фазовым звеном, как это было рассмотрено ранее. Напомним, что при нечетном порядке т одна из функций будет первого порядка.

Решить задачу равноволновой аппроксимации аналитически трудно, поэтому она решается численными методами и в справочниках приведены такие же таблицы, как и в случае аппроксимации максимально гладкими функциями. Поэтому порядок синтеза ЛЗ с равноволновымн характеристиками группового времени остается прежним, как и в случае монотонных характеристик.

Гармонические корректоры. Как уже отмечалось, параметры тракта передачи нуждаются в окончательной коррекции. Для этой цели применяются регулируемые корректоры, которые, как правило, настраиваются автоматически. Теория таких корректоров заключается в том, что передаточную функцию корректора, которая является с точностью до постоянной обратно пропорциональной по отношению к линии передачи, раскладывают в ряд по системе ортогональных функций:

Сделаем важные замечания: 1. Ряд Фурье применяется для разложения периодических функций. Поэтому АЧХ и ФЧХ такого корректора также будут периодическими. Интервал [-ω_c,ω_c] является рабочим. 2. Так как АЧХ линии передачи является четной функцией, а ФЧХ — нечетной, то коэффициенты (18.36) в разложении ряда Фурье (18.35) являются вещественными числами. 3. Для ускорения сходимости ряда из фазочастотной характеристики линии вычитают линейную составляющую, что устраняет разрывы ФЧХ на границах интервала.

Попытаемся реализовать передаточную функцию (18.35). Из данного ряда следует, что передаточная функция корректора получается путем умножения передаточных функций линии задержки на вещественные числа с последующим суммированием. Однако, точная реализация функции (18.35) невозможна, так как требует бесконечного числа ЛЗ, поэтому ее реализуют приближенно, ограничиваясь конечными числами слагаемых с отрицательными (т) и положительными (п) индексами

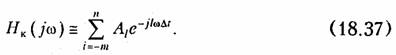
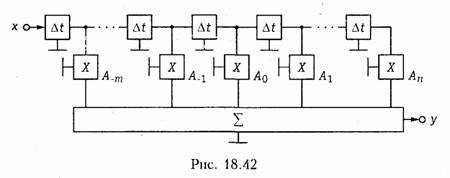
Даже после усечения ряда, передаточная функция остается нереализуемой. Во-первых, передаточная функция ЛЗ не удовлетворяет УФР. Во-вторых, при отрицательных значениях l ФЧХ линии задержки равна |l|∆tω, а ее групповое время .В данном случае это означает, что нарушается причинно-следственная связь и колебание на выходе появляется раньше, чем на входе. Данная трудность легко преодолевается, если допустить что корректор вносит постоянную задержку  С учетом сказанного, функциональную схему корректора представляют в виде, показанном на рис. 18.42.

Колебание х, поступающее на вход корректора, задерживается первой ЛЗ па время ∆t и поступает па входы умножителя и следующей ЛЗ. Колебание, поступившее на вход второй ЛЗ, задерживается дополнительно на время ∆t так, что общая задержка составляет 2∆t, Задержанное на эту величину колебание поступает на вход третьей ЛЗ и вход второго умножителя и т. д. Задержанные па величины ∆t, 2∆t, З∆t ... колебания суммируются, образуя колебание у. Таким образом, получается с точностью до множителя передаточная функция (18.37). Умножитель в простейшем случае представляет собой делитель напряжения. Регулировка (настройка) корректора осуществляется с помощью изменения коэффициентов A_l. На практике изменяется коэффициент деления делителя. Для упрощения изображения схемы гармонического корректора каскадное соединение линии задержки заменяют одной ЛЗ с отводами, а умножители —переменным сопротивлением (кроме этого не показывают заземленных проводов). Соответствующая данным упрощениям схема гармонического корректора показана на рис. 18.43. Частным случаем гармонического корректора является косинусный корректор. Он получается когда число отводов слева и справа от нулевого одинаково и соответствующие коэффициенты с положительными и отрицательными индексами равны между собой, т. е. A_-1 = А_l. Тогда попарные суммы дают косинусоидальную функцию

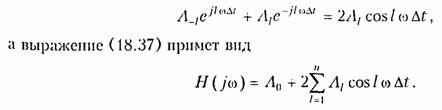
Полученная функция является вещественной, а значит может применяться только для коррекции АЧХ.

В данном параграфе изложены только основы построения гармонических корректоров в диапазоне частот 0 ... ω₁. Здесь не рассмотрены полосовые корректоры,

алгоритмы автоматической настройки корректоров, а также корректоры с обратными связями и ряд других вопросов, которые изучаются в специальных курсах.

Вопросы и задания для самопроверки

1.  Почему происходят искажения сигнала на выходе цепи?

2.  Сформулировать условие отсутствия амплитудно-частотных искажений в цепи.

3.  Каким образом корректируются частотные характеристики ценен?

4.  По  какой  схеме  можно  построить  пассивный  амплитудный корректор?

5.  Как рассчитывается передаточная функция Т-перекрытого корректора н вносимое им ослабление?

6.  Схема двухполюсника Z₂ в корректоре приведена на рис. 18.14, а. Получить схему двухполюсника Z₁. Построить график частотной зависимости ослабления A_к(ω) корректора.

7.  Какие  схемы  типовых   звеньев   пассивных  корректоров  известны?  Какой вид имеют частотные характеристики вносимого ими ослабления?

8.  Доказать, что частотная характеристика ослабления A_к(ω) звена, изображенного на рис. 18.16, имеет вид (18.8), а максимальное значение   ослабления   рассчитывается   по   формуле   А_кmax =

9.  Доказать, что операторная передаточная функция элементарного четырехполюсника, изображенного на рис.  18.22, б, соответствует передаточной функции корректора (формула (18.5)).

10. Какие амплитудные корректоры называются активными?

11. Получить передаточную функцию и частотную характеристику ; ослабления   активного   звена   корректора,   изображенного   на рис. 18.23, б,  в котором в качестве двухполюсника Z выбран параллельный  LC-контур.   Подтвердить,  что график  рабочего ослабления   A_к(ω) такого   корректора   —   это   кривая   2   на рис. 18.25.

12. Каков порядок расчета пассивного амплитудного корректора?

13. Рассчитать элементы, образующие двухполюсник Z₁ амплитудного корректора, частотная зависимость ослабления A_к(f) которого приведена в таблице, а значение Rо = 200 Ом.

Ответ:  R₁ = 1 кОм,    С₁= 51 нФ.

14. Зачем   применяют   каскадное   соединение   типовых   звеньев корректоров?

15. Сформулировать условия безискаженной передачи сигнала.

16. Почему происходят фазо-частотные искажения?

17. Что такое групповое время прохождения?

18. По рис. 18.12 пояснить, как работает фазовый корректор.

19. Каким образом строятся пассивные фазовые корректоры?

20. Как  рассчитываются  передаточные  функции  Н_к(р),   фазовые характеристики В_к (ω) и ГВП t_гp(ω) мостовых фазовых корректоров 1-го и 2-го порядков?

21. Как изменится график t_гp(ω) на рис. 18.32, б, если индуктивность L₁ уменьшить в 2 раза.

22. Определить параметры элементов фазового корректора 2-го порядка (рис.  18.32) по заданным коэффициентам передаточной функции ω₀ = 0,416 • 10⁴ с ^-1, Qn = 0,25 и R_o = 600 Ом.

Ответ:   L₁ = 36 мГн; C₁= 1,6 мкФ;

L₂ = 0,58 Гн; С₂ = 0,1 мкФ.

23. Каким образом строятся активные фазовые корректоры?

24. Доказать,  что операторная передаточная функция Н_к(р) корректора, изображенного на рис. 18.35, имеет вид (18.30).

25. Каким образом на основе схемы рис. 18.37 получить фазовые корректоры 1-го и 2-го порядков?

26. Как изменится график t_гp(f) на рис. 18.39, если сопротивление R₁: 1) увеличить в 4 раза; 2) увеличить в 10 раз; 3) уменьшить в 2 раза?

27. Каков алгоритм расчета фазовых корректоров?