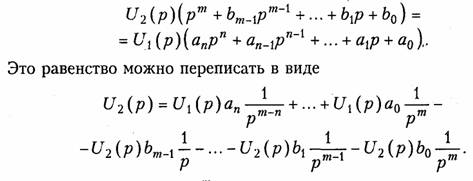ГЛАВА 14. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

 14.1. Определение и классификация обратных связей

В большинстве цепей с зависимыми источниками имеется по крайней мере два пути прохождения сигнала: прямой (от входа к выходу) и обратный (с выхода на вход). Обратный путь прохождения сигнала реализуется с помощью специальной цепи обратной связи (ОС). Таких путей, а значит, и цепей ОС может быть несколько. Наличие в цепях с зависимыми источниками ОС придает им новые ценные качества, которыми не обладают цепи без ОС. Например, с помощью цепей ОС можно осуществить температурную стабилизацию режима работы цепи, уменьшить нелинейные искажения, возникающие в цепях с нелинейными элементами, улучшить технические параметры усилителей и т. д.

Введение ОС позволяет создавать цепи, генерирующие колебания различной формы (гл. 15), моделирующие различные функции (суммирование, интегрирование, дифференцирование и др. (гл. 2, 3)).

Кроме положительных, ОС могут оказывать и отрицательные последствия на цепь. Так, ОС могут образовываться за счет различных «паразитных» связей, возникающих в результате неудачного монтажа элементов цепи или при нерациональном формировании элементов в подложке микросхемы и др. Подобные ОС могут возникать на высоких частотах за счет различных «паразитных» емкостей создающих цепи обратной связи с выхода на вход. «Паразитные» ОС могут оказывать неконтролируемые воздействия на работу цепи и поэтому должны учитываться в необходимых случаях при расчетах. Все вышеизложенное свидетельствует о важности изучения цепей с ОС.

Обратные связи могут быть классифицированы по различных признакам: по характеру связи — положительной (ПОС), отрицательной (ООС) и комплексной; по структуре — внешней и внутренней; по характеру реализующих ее элементов — активной и пассивной, линейной и нелинейной, частотно зависимой и частотно независимой и т. д.

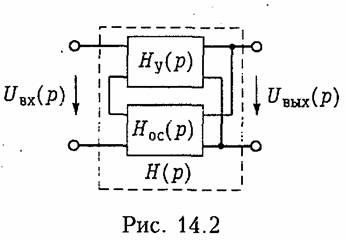
С точки зрения анализа важным являются способы соединения четырехполюсников прямой передачи и цепи ОС. На рис. 14.1 представлены основные схемы соединения четырехполюсника каналов прямого усиления с передаточной функцией Н_у(р) и четырехполюсника цепи ОС с передаточной функцией Н_ос(р). Причем, в качестве четырехполюсника с Н_у(р) обычно используют активные цепи (усилитель), а в качестве цепи ОС с передаточной функцией H_ос(р) пассивный четырехполюсник. В дальнейшем ограничимся случаем, когда усилитель и цепь ОС являются линейными четырехполюсниками.

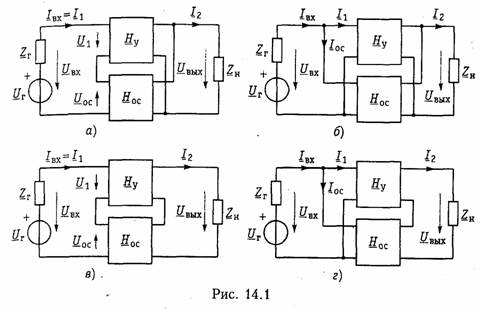
Данные схемы соответствуют последовательно-параллельному (a), параллельному (б), последовательному (в) и параллельно-последовательному (г) соединению четырехполюсников (см. § 12.3). В соответствии с этим для анализа подобных сложных четырехполюсников могут использоваться Н, Y, Z, F-параметры соответственно, поэтому в литературе иногда эти структуры называют ОС Н, Y, Z и F-типа соответственно.

В соответствии со структурными схемами (рис. 14.1) различают следующие виды ОС: последовательной по напряжению (рис. 14.1, а), т. к. U_оc зависит от U_вых; параллельной по напряжению (рис. 14.1, б), поскольку ток I_ос является функцией выходного напряжения U₂; последовательной по току (рис. 14.1, в), т. к. U_oc в этой схеме зависит от выходного тока I₂; параллельной по току (рис. 14.1, г), потому что I_ос будет зависеть от выходного тока I₂.

Для определения типа ОС (по току или напряжению) необходимо помнить, что ОС по напряжению будет максимальной при XX на выходе и минимальной при КЗ на выходе, а ОС по току будет максимальной при КЗ на выходе и минимальной (равной нулю) при XX на выходе.

14.2. Передаточная функция цепи с обратной связью

1.Передаточная функция цепи по напряжению.

Определим передаточную функцию по напряжению цепи с обратной связью на примере схемы, изображенной на рис. 14.1 а, и

проанализируем влияние ОС на основные параметры усилителя с ОС  цепи  как сложного четырехполюсника.

Для этого типа ОС можно записать следующее равенство согласно ЗНК в операторной форме (рис. 14.1, a):

Переходя в (14.3) от оператора р к оператору jω, получаем комплексную передаточную функцию

(14.4)

Таким образом, частотные свойства цепи в равной мере зависят как от Ну(jω) канала прямого усиления, так и от H_Oc(jω)  цепи обратной связи. Поэтому можно, оставляя неизменным основной элемент системы, в широких пределах изменять частотную характеристику всей цепи, изменяя лишь параметры цепи обратной связи.

Произведение 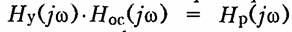представляет собой комплексную передаточную функцию усилителя и цепи обратной связи при условии, что обратная связь разорвана (рис. 14.3, а). Функцию Hp(jω) называют передаточной функцией по петле ОС или петлевым усилением,. Введем понятия положительной и отрицательной обратной связи. Эти понятия играют заметную роль в теории цепей с обратной связью.

Предположим вначале, что передаточные функции Н_у, H_ос, Н_p не зависят от частоты и являются вещественными числами. Такая ситуация возможна, когда в цепи отсутствуют LC-элементы. При этом Н_p может быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз между входным и выходным напряжениями, или другими словами, сдвиг фаз по петле обратной связи равен нулю или 2_kπ, k = О, 1, 2, ... Во втором случае, когда Н_p < 0, сдвиг фаз по этой петле равен ±π или ±(2k — 1)π. (Заметим, что сдвиг фаз на ±π можно легко получить путем перекрещивания проводов, например так, как показано на рис. 14.3, б).

Если в цепи с обратной связью сдвиг фаз по петле равен нулю, то обратная связь называется положительной, если же сдвиг фаз равен ±π, то такая обратная связь называется отрицательной.

Передаточную функцию H_P(jω) можно изобразить в виде векторов и показать их на комплексной плоскости. При положительной обратной связи вектор H_P(jω)  находится на положительной вещественной полуоси, а при отрицательной обратной связи — на отрицательной вещественной полуоси.

В § 4.1 было введено понятие годографа передаточной функции. Напомним, что годографом называется кривая, которую описывает конец вектора H_P(jω)  при изменении частоты со (рис. 4.3, в и 14.4).

Представление H_P(jω) в виде годографа позволяет определить вид обратной связи в случае частотнозависимой обратной связи. Обратная связь называется положительной, если годограф H_P(jω) лежит в правой, и отрицательной — если в левой полуплоскости комплексной плоскости. Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления паразитных сигналов, коррекции частотных характеристик; положительная ОС может являться причиной неустойчивости цепи. Поясним это. Пусть Н_ос и Н_у — положительные вещественные числа. Тогда при Н_у ·Н_ос = 1, т. е. когда Н_ос = 1/H_у, значение передаточной функции (14.4) стремится к бесконечности. Это означает, что даже при бесконечно малых значениях амплитуды входного напряжения u_BX(t) амплитуда выходного напряжения u_Вых(О будет неограниченно возрастать. Говорят, что в этом случае наступает самовозбуждение цепи с ОС. Поэтому при проектировании цепей с обратной связью одной из основных задач является исследование их устойчивости. Таким образом, термины неустойчивость и самовозбуждение являются синонимами.

2. Влияние ОС на параметры усилителя.

Обратная связь существенно влияет на результирующие параметры цепи с ОС; в частности ее входное и выходное сопротивления и коэффициенты передачи. Рассмотрим влияние ОС на параметры усилителя на примере схемы, изображенной на рис. 14.2.

На рис. 14.5 изображена эквивалентная схема с зависимым источником напряжения с Н-параметрами при отсутствии внутренней ОС (H₁₂ = 0);     

Поскольку в данной схеме (рис. 14.5) ОС предназначена для получения на выходе четырехполюсника определенного напряжения U_OC, то основное значение на свойство усилителя должен играть коэффициент H_12oc. Учитывая, что цепь ОС отбирает часть полезной энергии из нагрузки необходимо стремиться, чтобы H_22oc << H_22. Кроме того, для уменьшения потерь входного сигнала на входном сопротивлении цепи с ОС, необходимо выполнение условия H₁₁ >> H_11oc .Если при этом учесть, что обычно H_21oc >> H_21oc и для пассивной цепи H_12oc<1, то окончательно матрица Н-параметров сложного четырехполюсника с цепью ОС примет вид

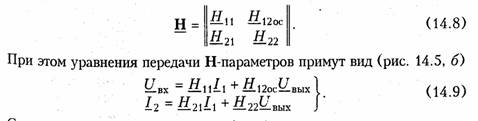
С помощью системы уравнений (14.9) можно определить искомые зависимости токов и напряжений от параметров цепи ОС. Можно, в частности показать, что отрицательная ОС (ООС) уменьшает коэффициент передачи по напряжению усилителя в k-раз, а входное сопротивление увеличивает в k-раз, где

Так как рассмотренный тип ОС (последовательной по напряжению) ведет к увеличению входного и уменьшению выходного сопротивлений усилителя, то это позволяет осуществить трансформацию сопротивлений, что используется для согласования отдельных каскадов усилителя.

Следует также отметить, что коэффициент передачи ОУ с после довательной ОС по напряжению при бесконечно большом коэффициенте усиления является функцией только параметров элементов цепи ОС.

В заключении рассмотрим влияние ОС на стабильность коэффициента усиления, как основного показателя усилителя.

Для отрицательной и вещественной ОС согласно уравнению (14.4) для коэффициента усиления усилителя можно записать

Аналогичным образом можно найти коэффициент передачи и исследовать влияние ОС на параметры других схем с ОС (см. рис. 14.1 б) —г)). При этом надо иметь ввиду, что в соответствующих выражениях будут фигурировать не только комплексные коэффициенты передачи по напряжению, но и по току, а также перепаточные комплексные сопротивления и проводимости. Кроме того уравнения передачи соответствующих четырехполюсников в зависимости от типа соединения должны быть записаны в Z или F-параметрах (см. § 12.2).

14.3. Примеры цепей с обратной связью

Масштабный усилитель с неинвертирующим входом. На рис. 14.6, а изображена цепь на ОУ, предназначенная для масштабирования напряжения, а на рис. 14.6, б - ее схема замещения с зависимым источником типа ИНУН. В гл. 2 данная схема анализировалась методом узловых потенциалов. Получим передаточную функцию этой цепи как цепи с обратной связью, используя формулу (14.4).

Цепью обратной связи на схеме рис. 14.6 служит Г-образный делитель напряжения, составленный из резистивных сопротивлений R₀ и R₁. Выходное напряжение усилителя U₂ поступает на вход цепи ОС (узлы 2 — 4); напряжение ОС U₃ снимается с резистора R₁ (узлы 3 — 4). Передаточная функция по напряжению цепи ОС

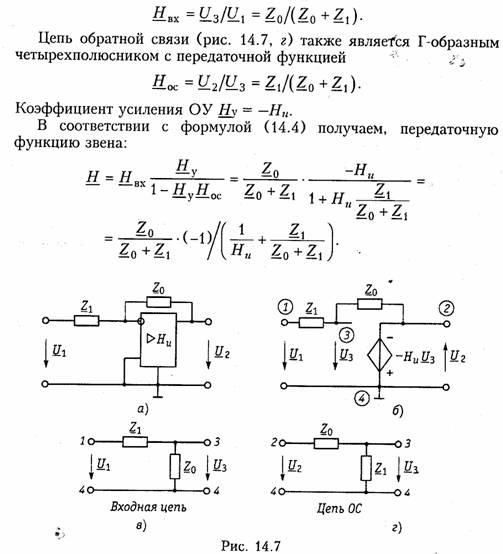
Звено на ОУ с частотно-зависимой ОС. Звено такого вида представлено на рис. 14.7, а, а его схема замещения — на рис. 14.7, б. Чтобы проанализировать прямой путь прохождения сигнала и путь прохождения сигнала ОС, необходимо воспользоваться методом наложения (см. § 2.3). Для этого следует поочередно исключать источники входного напряжения и напряжения обратной связи, заменяя их внутренним сопротивлением. В случае идеальных источников напряжения (рис. 14.17, 6) их внутреннее сопротивление равно нулю. Из схемы замещения следует, что напряжение U₁, приложенное к звену, ослабляется входной цепью, представляющей собой Г-образный делитель напряжения с сопротивлениями Z₁ и Z_o в плечах (рис. 14.7, в). Передаточная функция по напряжению такого делителя равна

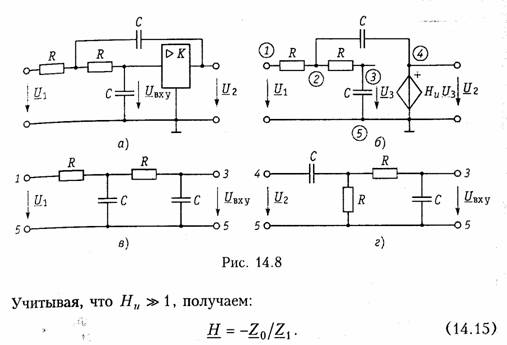
Звено второго порядка с регулируемым коэффициентом усиления. Схема звена показана на рис. 14.8, а. Усилитель с регулируемым коэффициентом усиления К может быть выполнен либо на транзисторных каскадах, либо на ОУ по схеме рис. 14.6, а, либо на других активных элементах. В схеме замещения на рис. 14.8, б он представлен идеальным ИНУН.

Анализ прохождения входного сигнала и сигнала в цепи ОС показывает, что звено имеет входную цепь, изображенную на рис. 14.8, в и цепь ОС, показанную на рис. 14.8, г. Передаточные функции этих цепей можно получить матричным методом (см. гл. 12), например, рассматривая каждую цепь как каскадное соединение соответствующих Г-образных четырехполюсников.

Для входной цепи (см. § 3.11)

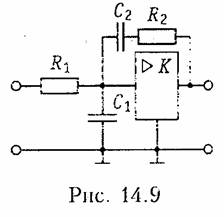
Так как операции 1/р^т соответствует m-кратное интегрирование, то последнему уравнению соответствует структурная схема, изображенная на рис. 14.9.

Таким образом, с помощью интеграторов, сумматоров, масштабных усилителей, умножителей может быть реализована передаточная функция Н(р) достаточно общего вида.

14.4. Устойчивость цепи с обратной связью

Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов (гл. 6, 7) следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.

Это и есть характеристическое уравнение цепи.

Заметим еще раз, что точно такое же уравнение мы бы получили, составляя дифференциальное уравнение по законам Кирхгофа, как мы это делали при изучении переходных процессов.

Корни уравнения (14.23) в общем случае являются комплексными величинами

Чтобы напряжение u_вых(t) не возрастало безгранично, всем корням p₁, p₂, ... , р_т. характеристического уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны располагаться в левой полуплоскости комплексной переменной р = α + jω . Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.

При исследовании цепей с обратной связью могут возникать две проблемы. Если проектируемая цепь должна быть устойчивой, то необходимо располагать критерием, который по виду функций Н_у(р) и Н_ос(р) позволял бы судить об отсутствии корней характеристического уравнения в правой полуплоскости р. Если обратная связь используется для создания неустойчивой автоколебательной цепи, то следует убедиться, что корни уравнения (14.23) расположены, наоборот, в правой полуплоскости. При этом необходимо иметь такое расположение корней, при котором самовозбуждение происходило бы на требуемой частоте.

Рассмотрим критерии устойчивости цепи с обратной связью.

Критерий устойчивости Рауса — Гурвица. Он относится к алгебраическим критериям устойчивости и позволяет по значениям коэффициентов Ь_т, Ъ_т-₁, ..., b_o характеристического уравнения (14.23), без определения его корней, узнать является ли исследуемая цепь устойчивой.

Критерий формулируется следующим образом: цепь с обратной связью является устойчивой, если полином характеристического уравнения, является полиномом Гурвица. При этом используется основное свойство полинома Гурвица: все его корни находятся в левой полуплоскости комплексной переменной р.

Для того, чтобы многочлен Ь_тр^т +b_m-1p^m-1 + ... + b₁p + b₀ являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительными определитель Рауса —Гурвица:

и все главные миноры этого определителя.

При составлении определителя Гурвица можно руководствоваться следующим правилом. В первой строке записываются коэффициенты полинома Гурвица через один, начиная со второго. Во второй строке записываются коэффициенты полинома через один, начиная с первого. Вторая пара строк формируется путем смещения первой пары строк на одну позицию. Третья пара — смещением второй пары строк еще на одну вправо и т. д.

Пример. Проверим с помощью критерия Рауса — Гурвица устойчивость цепи с обратной связью, характеристическое уравнение которой имеет вид

Критерий устойчивости Найквиста. Критерий Найквиста позволяет судить об устойчивости цепи с обратной связью по свойствам разомкнутой цепи (рис. 14.3, а).

Передаточная функция разомкнутой цепи, или петлевое усиление, входит в характеристическое уравнение (14.21):

Если найдется такая частота со, для которой конец вектора H_P(jω) попадает в точку с координатами (1,j0), то это будет означать, что выполняется условие (14.25), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит, по годографу можно определить, устойчива цепь или нет. Для этого используется критерий Найквиста, который формулируется следующим образом: если годограф передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0), то при замкнутой цепи обратной связи цепь является устойчивой. В том случае, когда годограф H_Р(ω) охватывает точку (1, j0), цепь неустойчива. На рис. 14.4 показаны годографы трех цепей с положительной обратной связью (цифра 1 соответствует годографу устойчив вой цепи).

Пользуясь критерием Найквиста, легко получить условия само-! возбуждения цепи с ОС. Запишем выражение для H_P(jω) в виде    

Выполнение неравенства соответствует режиму возникновения:; колебаний  с нарастающей  амплитудой,   что  характерно для  начального этапа самовозбуждения.  Выполнение равенства H_у(ω)х H_oc(ω)= 1  соответствует режиму генерации гармонического напряжения на частоте ω с постоянной амплитудой и носит название баланса амплитуд.

Как будет показано ниже, уравнение баланса фаз позволяет определить частоту, на которой происходит самовозбуждение цепи с ОС, а уравнение баланса амплитуд дает возможность определить величину амплитуды u_вых (t)генерируемого колебания в стационарном режиме.       

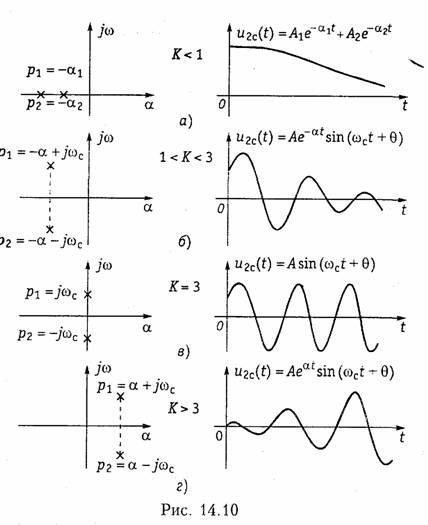
Пример. Исследуем устойчивость цепи, изображенной на рис. 14.8, а, В " можно выделить усилительный элемент с передаточной функцией Ну = К  и цепь обратной связи (рис. 14.8, г) с передаточной функцией (14.17)

зависят от коэффициента усиления усилителя К. Расположение корней р₁ и р₂ на плоскости комплексного переменного р для разных коэффициентов усиления и соответствующие этому графики свободных колебаний в цепи показаны на рис. 14.10.

Устойчивость данной  цепи  можно исследовать и с  помощью  критерия Найквиста. Комплексная передаточная функция разомкнутой цепи равна

Критерий устойчивости Михайлова. Этот простой и эффективный критерий был предложен в 1938 г. А.В. Михайловым и базируется он на характере поведения аргументов полинома Гурвица Ц/га) при изменении частоты со от нуля до бесконечности.

Положим, что полином Гурвица степени т

имеет l пар комплексно-сопряженных корней с отрицательной вещественной частью pk=-ak±jω_k. Остальные т —21 корней — вещественные отрицательные числа: p_s = -a_s. Если учесть при этом, что произведение линейных множителей двух комплексно-сопряженных корней равно

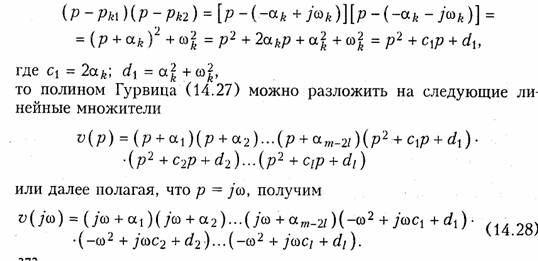
Как комплексную величину (14.28) можно представить в показательной форме        

Как следует из (14.29), (14.30), (14.31) с увеличением ω от 0 до ∞φ_у(ω) монотонно возрастает от 0 до тπ/2. Это свойство аргумента полинома Гурвица и лежит в основе критерия Михайлова, который формулируется следующим образом: если при изменении частоты ω от 0 до ∞ аргумент полинома Гурвица φ_v(ω) возрастает на угол тπ/2 (где т — степень полинома), то цепь будет устойчивой.

Действительно, если среди корней v(p) есть хотя бы один вещественный положительный корень, то в слагаемом типа (14.30) появится слагаемое φ_k(ω) < 0 и поэтому согласно (14.30) φ_у(ω) < тπ/2.

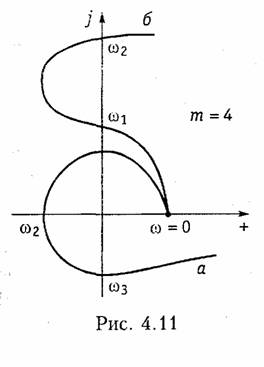
Критерий Михайлова имеет простой геометрический смысл: годограф v(jω) устойчивой цепи при изменении ω от 0 до ∞ будет последовательно обходить в положительном направлении (против; часовой стрелки) т квадрантов комплексной плоскости. На рис. 14.11 получены годографы устойчивой — а и неустойчивой — б цепи 4-го порядка:

В первом случае годограф v(jω) обходит 4 квадранта монотонно (последовательно) против часовой стрелки, при этом аргумент возрастает до величины

Во втором случае неустойчивой цепи φ_у(ω) изменяется скачком от 2-го квадранта в 4-й, при этом φ_k(ω) < 2π .

Вопросы и задания "для самопроверки

1.  Как рассчитывается передаточная функция цепи с обратной связью?

2.  Записать   уравнение   передачи   для   цепи,   изображенной   на рис. 14.1, в.

3.  Доказать,   что  операторная  передаточная функция дифференциатора на операционном усилителе равна (—pRC).  Построить график АЧХ такого дифференциатора.

4.  Определить передаточную функцию цепи, изображенной на рис. 14.9.

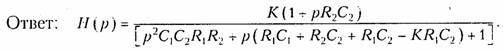
5.  Что такое годограф петлевого усиления? Как по годографу определить тип обратной связи?

6.  Как формулируется критерий устойчивости Найквиста? Для каких цепей он используется?

7.  Сформулируйте критерий устойчивости Рауса-Гурвица. Как составить определитель Гурвица? Приведите примеры.

8.  Определить комплексную передаточную функцию Нр(jω) цепи па рис.  14.9 разомкнутой обратной связью. Исследуйте зависимость устойчивости цени от величины коэффициента усиления К.

ГЛАВА 15. АВТОКОЛЕБАТЕЛЬНЫЕ ЦЕПИ

15.1. Физические процессы в автоколебательных цепях

Автоколебательными называются активные электрические цепи, в которых без посторонних воздействий самостоятельно возникают электрические колебания. Такие колебания называются автоколебаниями, а сами электрические цени, в которых возникают автоколебания, - автогенераторами (или, чаще, генераторами).

Автогенераторы используются в радиотехнике связи для получения электромагнитных колебаний. В зависимости от формы вырабатываемых колебаний различают генераторы гармонических и негармонических колебаний. По принципу работы генераторы делятся на генераторы с внешней обратной связью и с внутренней обратной связью, т. е. с отрицательным сопротивлением. Наконец, различие в элементной базе пассивной части схемы генератора позволяет вести речь об LC-генераторах или о RC-генераторах. В качестве активных элементов в генераторах применяются электронные лампы, биполярные и полевые транзисторы, туннельные диоды и др.

В данной главе наибольшее внимание будет уделено LC генераторам гармонических колебаний с внешней ОС, использующим в качестве активного элемента биполярные транзисторы. Однако следует указать, что, хотя изучение свойств автогенераторов производится па примере конкретных схем, результаты исследования носят достаточно общий характер.

Затем будут рассмотрены особенности построения RC-генераторов и генераторов с внутренней ОС.

Физические процессы в автоколебательных цепях. На рис. 15.1, а показан параллельный колебательный контур,  состоящий из элементов L,  С и G.  Если контуру сообщить некоторое количество энергии, то в нем возникнут свободные колебания, По первому закону Кирхгофа (ЗТК):

i_C + i_G + i_L = 0

Дифференцируя данное уравнение по времени и деля обе части на С, получаем

(15.1)

Напомним, что при сопротивлении контура R =1/G > 2p или G < l/(2p) переходный процесс имеет колебательный характер.

Величина a = G/(2C) является коэффициентом затухания контура, а величина  - резонансной частотой контура. В этих обозначениях (15.1) перепишется в виде

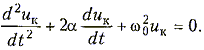
(15.2)

Дифференциальное уравнение (15.2) имеет следующее решение:

u_k(t) = U_mke^-atsin(w_ct + q),

(15.3)

где U_mk - начальная амплитуда напряжения на контуре, зависящая от введенной в контур энергии; - частота  собственных колебаний;  q - начальная фаза.

Так.как a= G/(2C) > 0, то колебание (15.3) имеют затухающий характер (см. рис. 15.1, 6, при q = 0), что объясняется потерями в контуре из-за наличия резистивной проводимости G. Чтобы превратить такой генератор в генератор незатухающих колебаний, нужно возмещать в нем потери, т. е. пополнять контур энергией.

Причем, если энергии в контур вводится ровно столько, сколько необходимо для компенсации потерь, то это эквивалентно внесению в контур отрицательной проводимости G_BH, при этом результирующая проводимость контура обращается в нуль. Тогда a= 0 и в контуре возникают незатухающие колебания.

В случае же, когда энергии в контур вводится больше, чем это необходимо для компенсации потерь (т. е. отрицательная проводимость G _BH  больше G и, следовательно, G_BH + G < 0), в контуре возникают нарастающие по амплитуде колебания, так как коэффициент затухания становится отрицательным.

Энергию в контуре можно пополнять, например, за счет собственных колебаний, снятых с контура и усиленных усилителем. Работающая на таком принципе схема автогенератора показана на рис. 15.2.

Рассмотрим процесс возникновения колебаний в автогенераторе, или механизм самовозбуждения генератора, и установление колебаний определенной амплитуды, т. е. стационарный режим работы генератора.

Причиной возникновения колебаний в автогенераторе являются флуктуации (случайные возмущения) тока в элементах реальной схемы (за счет теплового движения электронов в активных элементах и резисторах, дробового эффекта и т. д.), а также за счет внешних помех. Флуктуации тока i_К, протекающего через контур, вызывают флуктуации напряжения на контуре u_К .Спектр этих случайных возмущений весьма широк и содержит составляющие всех частот.

Составляющие напряжения u_К с частотами, близкими к резонансной частоте контура w₀, имеют наибольшую амплитуду, так как модуль комплексного эквивалентного сопротивления контура является наибольшим и равным R_Oэ именно на резонансной частоте w₀. Выделенное на контуре гармоническое с частотой w₀ напряжение через цепь ОС, образованную вторичной обмоткой трансформатора, передается на вход транзистора, создавая напряжение u_К. Это напряжение вызовет увеличение коллекторного тока i_К. что, в свою очередь, приведет к увеличению напряжения на контуре u_К. Как следствие этого увеличатся напряжение обратной связи u_ос и напряжение u_К и, значит, вновь увеличатся коллекторный ток и напряжение на контуре u_К и т. д. Таким образом, в замкнутой системе автогенератора самовозбуждаются колебания частоты, близкой к резонансной частоте контура w₀.

Очевидно, важным условием возникновения колебаний является то, что фаза напряжения u_БЭ должна быть такой, при которой увеличение напряжения u_К вызывает увеличение коллекторного тока i_К и, тем самым, порождает новое увеличение u_К. Данное условие и есть условие баланса фаз. Баланс фаз достигается правильным включением вторичной обмотки трансформатора. При другом ее включении возрастание напряжения на контуре u_К приведет к уменьшению коллекторного тока, т. е, баланс фаз нарушится и самовозбуждения не произойдет.

Обратная связь, при которой выполняется баланс фаз, является положительной ОС. В противном случае ОС отрицательная. Самовозбуждение автогенератора возможно только при наличии положительной ОС.

Процесс самовозбуждения колебаний в контуре с энергетической точки зрения объясняется тем, что от источника питания с помощью транзистора в контур за один период колебания поступает энергии больше, чем расходуется ее в резистивном сопротивлении контура. Это эквивалентно, как уже отмечалось ранее, внесению в контур отрицательной проводимости G_ВН, превышающей по величине эквивалентную проводимость контура G, что приводит к отрицательному значению коэффициента затухания контура a и, следовательно, к возникновению в контуре нарастающих колебаний.

Пока амплитуда напряжения u_БЭ, была мала, работа происходила на линейном участке ВЛХ транзистора. С увеличением амплитуды колебании в контуре возрастает напряжение ОС u_ос - и, следовательно, входное напряжение транзистора u_БЭ.При этом вес сильнее сказывается нелинейность ВАХ транзистора. Наконец, при достаточно больших амплитудах колебаний ток коллектора   i_К перестает увеличиваться, значения напряжения на контуре u_К, обратной связи u_ос и входное u_БЭ   стабилизируются, в автогенераторе установится стационарный динамический режим с постоянной амплитудой колебаний и частотой генерации, близкой к резонансной частоте колебательного контура w₀. Таким образом, стационарные колебания в автогенераторе устанавливаются только благодаря наличию нелинейности ВЛХ транзистора.

В стационарном режиме энергия, поступающая в контур, вся рассеивается в эквивалентной резистивной проводимости контура, т. е. вносимая в контур отрицательная проводимость G_ВН оказывается равной эквивалентной проводимости G и полностью компенсируют ее; коэффициент затухания контура a обращается в нуль. В контуре существуют незатухающие гармонические колебания.

15.2. Обобщенная схема автогенератора

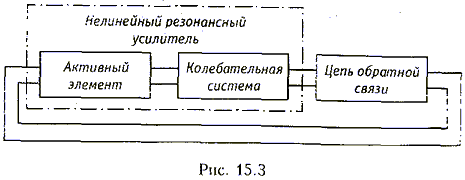
Из предыдущего рассмотрения следует, что схема автогенератора должна содержать активный элемент с нелинейной вольт-амперной характеристикой, колебательную систему (в данном случае контур), внешнюю цепь положительной ОС, по которой колебание с выхода колебательной системы подается на вход активного элемента. Такие автогенераторы являются генераторами с внешней ОС; структурная схема построения таких генераторов приведена на рис. 15.3.

Заметим, что нелинейный активный элемент с колебательной системой образуют нелинейный резонансный усилитель. Поэтому можно представить обобщенную структурную схему автогенератора с разомкнутой цепью обратной связи (рис. 14.17, а). Комплексная передаточная функция всей цепи

H_p(jw) = U_ос(jw)/U_вх(jw) = H_у(jw)H_ос(jw).

Для того, чтобы в генераторе происходило самовозбуждение колебаний, необходимо, чтобы модуль комплексного напряжения  | U_ос(jw)| на выходе схемы был больше модуля комплексного напряжения | U_вх(jw)| на входе схемы, откуда

   | H_p(jw)| =  | H_p(jw)| ^. | H_ос(jw)| > 1. 

При приближении к стационарному режиму модуль комплексного коэффициента передачи усилителя  | H_p(jw)| за счет влияния нелинейности начинает уменьшаться до тех пор, пока не наступит динамическое равновесие (см. § 14.3):

 | H_p(jw)| =  | H_p(jw)| ^. | H_ос(jw)| = 1. 

Это условие соответствует стационарному режиму и известно под названием баланса амплитуд. Учитывая, что

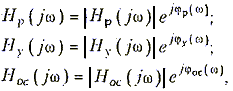
получаем фазовый сдвиг в разомкнутой цепи автогенератора

j_p(w) = j_p(w) + j_ос(w).

Баланс фаз, т. е. совпадение фаз напряжений на входе и выходе схемы рис. 14.17, а, наступает приj_p(w) = 2p. Таким образом, сдвиг фаз в цепи обратной связи зависит от сдвига фаз в усилителе п дополняет его до 2p. Если на частоте генерируемых колебаний усилитель вносит сдвиг фаз  j_у =2p (как, например, в схеме рпс. 15.2), то цепь обратной связи должна на этой же частоте вносить сдвиг фаз j_ос(w) = p. В схеме автогенератора рпс. 15.2 поворот фазы напряженияu_ос(t) на 180° достигается, как ранее отмечалось, соответствующим включением обмоток катушки индуктивности L_ос.

15.3. LC-генератор с трансформаторной обратной связью.

Классический метод анализа

Дифференциальное уравнение генератора. Обратимся вновь к схеме рис. 15.2. По первому закону Кирхгофа

i_C + i_G + i_L = i_K

или

(15.4)

Эти уравнения отличаются от соответствующих уравнений одиночного колебательного контура, полученных в § 15.1, тем, что в правой части записан коллекторный ток i_К.

Вольт-амперная характеристика транзистора i_К = F(u_БЭ - U₀) в окрестности рабочей точки U₀ является, вообще говоря, нелинейной, так как ток коллектора i_К   нелинейно зависит от напряжения OC. Из рис. 15.2 следует, что напряжение ОС, снимаемое с катушки индуктивности обратной связи L_oc, равноu_ос = u_БЭ - U₀, поэтому в дальнейшем удобно рассматривать ВАХ i_К = F(u_oc)= i_К(u_ос).

Заметим далее, что напряжение ОС u_ос   вычисляется через коэффициент взаимной индуктивности М и ток в катушке L (см. §3.7)

u_ос= -Мdi_L/dt.

В свою очередь, ток в катушке i_L и напряжение на ней u_К связаны соотношениемu_К = Ldi_L/dt , поэтому напряжение ОС u_ос , можно выразить через напряжение на контуре u_К:

u_ос= -Мu_К/L.

 (15.5)

Вернемся к уравнению (15.4). Продифференцируем его по времени и разделим обе части на С:

(15.6)

В отличие от уравнения (15.1) для одиночного колебательного контура в правой части уравнения (15.6) присутствует вынуждающая составляющая di_K(u_ос)/dt. Производную функции i_К(u_ос) будем искать как производную сложной функции:

(15.7)

где  S(u_ос) = di_K(u_ос)/du_ос  - дифференциальная крутизна ВАХ транзистора, нелинейно зависящая от напряжения u_ос .При дифференцировании напряжения u_ос по времени учтено соотношение (15.5).

Подставив (15.7) в (15.6), получим дифференциальное уравнение автогенератора

(15.8)

где - резонансная частота контура.

Это дифференциальное уравнение является нелинейным, так как коэффициент при первой производной напряженияu_К, в который входит крутизна S(u_ос). нелинейно зависит от напряжения обратной связиu_ос (или, что то же, от искомой переменной - напряжения на контуре). Уравнение (15.8) определяет все свойства автогенератора и позволяет установить условия самовозбуждения колебаний, особенности стационарного режима и характер переходных процессов в автогенераторе.

Условие возникновения колебаний. При определении условий самовозбуждения следует учесть, что амплитуда нарастающих колебаний в автогенераторе достаточно мала и работа автогенератора происходит на линейном участке ВАХ транзистора i_К = F(u_oc) . Иными словами, для малых амплитуд колебаний ВАХ можно аппроксимировать линейно-ломаной функцией, крутизна которой в рабочем диапазоне амплитуд напряжения является постоянной, не зависящей от напряжения u_oc, т. е.S(u_ос) = S. В этом случае дифференциальное уравнение автогенератора (15.8) становится линейным:

Перепишем его в виде

(15.9)

где - эквивалентный коэффициент затухания колебательного контура, включенного в цепь коллектора транзистора.

Сопоставление уравнения (15.9) с уравнением (15.2) для одиночного колебательного контура показывает, что при включении колебательного контура в коллекторную цепь транзистора коэффициент затухания контура a_э уменьшится на величину SM/2LC, зависящую от взаимоиндукции М, т. е. от ОС:

где a = G/2C - коэффициент затухания свободных колебаний контура.

Чтобы в контуре возникли нарастающие по амплитуде колебания, необходимо сделать коэффициент a_э< 0. Это возможно при условии SM/LC > G/C. Отсюда получаем значение коэффициента взаимной индукции М при котором в колебательном контуре возникнут нарастающие по амплитуде колебания:

М > LG/S.                             

(15.10)

Условие (15.10) называется условием самовозбуждения LC-aвтогенератора. Величина М_кр = LG/S называется критическим коэффициентом взаимной индукции. Колебания в автогенераторе могут возникнуть только при обратной связи с М > М_кр. При М < М_кр коэффициент затухания контура a_э> 0 и колебание в контуре становится затухающим. Коэффициент a_э в (15.9) можно представить в следующем виде:

a_э= (G + G_BH)/2C,                               

(15.11)

где G_BH = - (SM/L) -проводимость, вносимая в контур за счет действия обратной связи. Знак коэффициента М может меняться в зависимости от направления включения (согласно или встречно) вторичной обмотки трансформатора. При М > 0 вносимая проводимость оказывается отрицательной и если ее величина |G_вн| > G . что имеет место при М > М_кр, то a_э < 0 и в контуре возникнут нарастающие по амплитуде колебания. Положительные значения М соответствуют положительной ОС, отрицательные - отрицательной ОС.

Эквивалентная схема колебательного контура, соответствующая уравнению (15.9) с a_э из (15.11), приведена на рис. 15.4. Отрицательная общая проводимость контура G + G_BH < 0 при М > М_кр свидетельствует о том, что в контур поступает энергии больше, чем расходуется ее на активной проводимости контура G.

Стационарный режим работы. При больших амплитудах сигнала нелинейностью ВАХ транзистора i_К = F(u_oc) пренебречь уже нельзя: в общем случае она должна аппроксимироваться степенным полиномом высокого порядка.

Ток в цепи коллектора в стационарном режиме будет из-за нелинейности ВАХ несинусоидальной периодической функцией времени и может быть представлен рядом Фурье

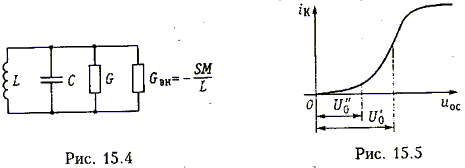
i_К = I₀ + I_m1cosw₀t + I_m2cos2w₀t +...

Падение напряжения u_К на колебательном контуре, настроенном на частоту w₀, определяется в основном первой гармоникой коллекторного тока, так как сопротивление контура для тока этой гармоники является наибольшим (равным R₀₃ = 1/G), а для остальных гармоник - достаточно малым. Напряжение ОС u_ос, определяемое (15.5), вследствие этого также будет гармоническим; его можно записать в виде

u_ос= U_moccosw₀t.

Введем понятие средней крутизны ВАХ

S_ср(U_moc) = I_m1/U_moc

Она определяется отношением амплитуды  I_m1 первой гармоники тока i_К, протекающего через нелинейный элемент, к амплитудеU_moc, действующего на нелинейный элемент напряжения u_ос.Среднюю крутизну часто поэтому называют крутизной ВАХ по первой гармонике. Средняя крутизна S_ср(U_moc) зависит от амплитуды напряжения обратной связи U_moc и от положения рабочей точкиU₀ . На рис. 15.5 показана типичная ВАХ транзистора i_К = F(u_oc). Пусть рабочая точка выбрана на середине линейного участка характеристики ( U0 = U₀') . При увеличении амплитуды напряжения U_moc   средняя крутизна, пока мы находимся в пределах линейного участка характеристики, остается неизменной. Затем средняя крутизна ВАХ падает (рис. 15.6, и). Если выбрать рабочую точку (U₀ = U₀'') на нижнем загибе характеристики i_К = F(u_oc), где средняя крутизна мала, то по мере увеличения амплитуды U_moc будут охватываться участки характеристики с большей крутизной и, следовательно, S_ср(U_moc) станет расти. После прохождения участка с наибольшей крутизной дальнейшее увеличение U_moc приводит к уменьшению средней крутизны (рис. 15.6, 6).

Дифференциальное уравнение (15.8) при работе генератора в режиме больших амплитуд является, вообще говоря, нелинейным, поскольку в коэффициент при du_K/dt входит средняя крутизнаS_ср(U_moc), зависящая от амплитуды U_moc напряжения ОС.

Однако  в стационарном режиме, когда гармоническое напряжение на контуре u_K   характеризуется установившейся (стационарной) амплитудой U_{м к}, гармоническое напряжение обратной связи u_oc также описывается установившейся (стационарной) амплитудой U_moc. При этом средняя крутизна S_ср(U_moc) является постоянной величиной и дифференциальное уравнение (15.8) можно считать линейным:

(15.12)

В стационарном режиме генерируются незатухающие гармонические колебания. Это имеет место, когда

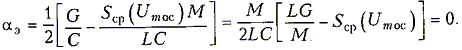
Отсюда установившееся (стационарное) значение средней крутизны равно

С учетом этого обозначения  коэффициент затухания контура перепишем в виде

(15.13)

Из формулы (15.13) при a_э = 0 можно определить стационарную амплитуду , которая соответствует точке пересечения кривой S_ср(U_moc)  и прямой линии Рис. 15.7 иллюстрирует процесс нахождения стационарной амплитуды для двух зависимостей средней крутизны, соответствующих различным положениям рабочей точки на ВАХ (см. рис. 15.5).

Частота генерируемых колебаний, определяемая как    w_г = , в стационарном режиме при a_э = 0 совпадает с резонансной частотой колебательного контура w₀ .

Устойчивость стационарного режима. Стационарный режим называется устойчивым, если отклонение DU_moc от стационарной амплитуды с течением времени будет уменьшаться.

Рассмотрим стационарный режим в точке А на рис. 15.7, а. Отклонение DU_moc  амплитуды приведет к S_ср(U_moc) и, в соответствии с (15.13), кa_э < 0, т, е. амплитуда колебаний будет увеличиваться и приближаться к стационарному значению. При отклонении +DU_moc средняя крутизна S_ср(U_moc) < , т. е. коэффициент затуханияa_э , станет положительным и амплитуда уменьшится, вновь приближаясь к стационарной. Таким образом, точка А соответствует устойчивому стационарному режиму.

Точка В на рис. 15.7, б соответствует неустойчивому режиму, так как отклонение амплитуды U_moc от стационарного значения в сторону уменьшения ведет к S_ср(U_moc) < и a_э ^> 0, т. е. к дальнейшему уменьшению амплитуды U_{m oc}, а отклонение амплитуды U_{m oc} от стационарной в сторону увеличения вызовет дальнейший ее рост и переход в следующее стационарное состояние, отмеченное точкой С.

Стационарное состояние в точке С является устойчивым, в чем легко убедиться с помощью рассуждений, аналогичных приведенным выше.

Можно заметить, что справедливо следующее утверждение: пересечение прямой линии с кривой средней крутизны S_ср(U_moc) дает устойчивые значения стационарной амплитуды если на этом участке dS_ср(U_{m oc})/dU_{m oc} < 0 и неустойчивые значения - если, dS_ср (U_{m oc})/dU_{m oc}> 0. Поэтому условие dS_ср (U_{m oc})/dU_{m oc}< < 0 можно считать условием устойчивости стационарного режима.

Режим самовозбуждения. Будем менять коэффициент взаимной индукции М и наблюдать за процессом возникновения колебаний.

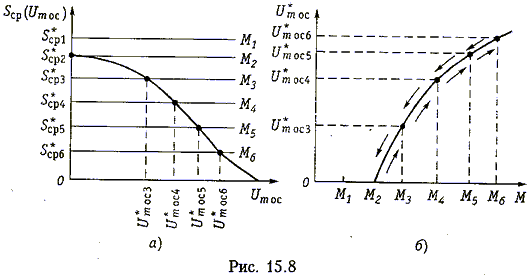
Этот процесс зависит также от выбора рабочей точки на ВАХ (напряжения смещения U₀).

Выбору рабоче точки в области наибольшей крутизны (напряжение смещения U₀' на рис. 15.5) соответствует график средней крутизны S_ср (U_{m oc}), показанный на рис. 15.8, а.

При изменении параметра M меняется значение средней крутизны ⁼ LG/M. На рис. 15.8, а изображены несколько прямых , соответствующих различным М,

При М = М₁ колебания в автогснераторе возникнуть не могут, поскольку > S_ср (U_{m oc}) и коэффициент затухания контураa_э > 0. значит, любые случайные флуктуации напряжения U_{m oc} будут быстро затухать.

Увеличение М до значения М₂ приводит к   = S_ср (U_{m oc}) и  a_э = 0. Дальнейший рост М снижает значение ; коэффициент a_э становится отрицательным, т. е.  a_э < 0. Таким образом, начиная с М³М₂ , и автогенераторе возникают незатухающие колебания с соответствующим и стационарными амплитудами С увеличением М стационарная амплитуда колебании плавно нарастает. Уменьшение М вызовет плавное уменьшение значений стационарной амплитуды . График зависимости  стационарной амплитуды генерируемых в автогенераторе колебании от коэффициента взаимной индукции М приведен на рис. 15.8, 6. Такой режим самовозбуждения генератора, при котором амплитуда колебаний плавно нарастает с увеличением М, называется мягким режимом симовозбужденпя.

Если рабочую точку выбрать на нижнем загибе ВАХ, как это показано на рис. 15.5 при U₀=U_0", то график средней крутизны S_ср (U_{m oc}) имеет вид. показанный на рисунке 15.9, а.

При М, равном М₁,М₂ и М₃, наличие малых флуктуации напряжения U_{m oc} не приведет к установлению стационарной амплитуды, поскольку при значениях , равных , , коэффициент затухания контура a_э,   будет положительным.

Только начиная с М = М₄ когда S_ср (U_{m oc}) = иa_э= 0, малые флуктуации амплитуды напряжения обратной связи начинают быстро расти, пока не установится устойчивое стационарное значение амплитуды . Дальнейшее  увеличение   М  ведет   к плавному росту стационарной амплитуды.

При плавном уменьшении обратной связи (коэффициентаМ  стационарная амплитуда будет также плавно уменьшаться. Колебания сорвутся при значении М = М₂, меньшем М₄, когда перестанет выполняться условие стационарности S_ср (U_{m oc}) = На рис. 15,9. 6 дан график изменения амплитуды  в зависимости от М. Такой режим, когда колебания возбуждаются при большем значении М, а срываются при меньшем значении М, называется жестким режимом, самовозбуждения.

Достоинством мягкого режима самовозбуждения является плавное изменение амплитуды при изменении коэффициента М; достоинством жесткого режима является высокий КПД за счет работы с отсечкой коллекторного тока.

Можно объединить достоинства мягкого и жесткого режимов самовозбуждения, если ввести в автогенератор цепь автоматического смешения R_Б С_Б (рис. 15.10, а). Исходное смещение U₀ выбирают таким, при котором рабочая точка находится на участке наибольшей крутизны ВАХ, что соответствует мягкому режиму. При нарастании амплитуды колебании u_oc в цепи базы за счет нелинейности ВАХ  i_Б = F(u_БЭ) произойдет детектирование колебаний. Возрастание постоянной составляющей тока базы I_БО, которая на резистнвном сопротивлении R_Б создает напряжение I_БО ^. R_Б, к уменьшению результирующего напряжения смещения  U_o - I_БО ^. R_Б и, как результат, к сдвигу рабочей точки влево (рис. 15.10, б) к нижнему загибу ВАХ i_К = F(u_БЭ). Переходный процесс заканчивается (при соответствующем значении R_Б) установлением жесткого стационарного режима с более высоким КПД.

15.4. .LC-генератор с трансформаторной обратной связью. Операторный и частотный методы анализа

Характеристическое уравнение. Операторный метод анализа автогенератора состоит в исследовании характеристического уравнения (14.11) цепи с ОС и выявлении из этого уравнения условий самовозбуждения. Записать характеристическое уравнение генератора можно было бы непосредственно по дифференциальному уравнению (15.9), однако это можно сделать и не прибегая к составлению дифференциального уравнения. Генератор как цепь с ОС описывается характеристическим уравнением ( см. гл. 14)

1 - H_y(p) H_oc(p) = 0.    

 (15.14)

Схема замещения усилителя на транзисторе дана на рис. 15.11 (см. § 3.11). Здесь R_BX и R_вых - входное и выходное сопротивления транзистора;    Z_к- комплексное сопротивление параллельного контура.

Операторная передаточная функция такого усилителя равна:

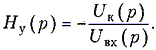
В свою очередь, из рис. 15.11 следует, что

Поэтому

На практике в качестве усилительного элемента используют такой транзистор, у которого R_вых достаточно велико. В этом случае

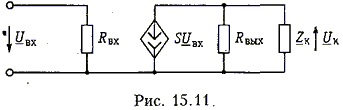
H_y(p) = - SZ_к(p).  

(15.15)

Учитывая, что сопротивление паралельного контура

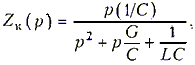
получаем окончательное выражение передаточной функции усилителя

Передаточную функцию цепи OC легко найти, если вспомнить ( см. 15.5), что

или для изображений по Лапласу

Отсюда

После того, как получены выражения для H_y(p) и H_oc(p), характеристическое уравнение (15.14) можно записать в следующем виде:

После простейших преобразований получим:

(15.16)

или

В режиме самовозбуждения рабочая точка располагается на линейнном участке ВАХ и, следовательно, крутизна S является постоянной величиной .

Корни характеристического уравнения (15.16)

p_1,2 = - a_э ± jw_c,

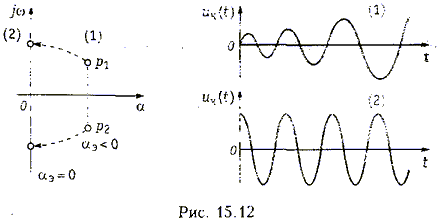
где - частота свободных колебаний в контуре.

Чтобы в генераторе возникли незатухающие колебания корни должны лежать в правой полуплоскости комплексной переменной р (рис. 15.12, случай 1), т. е.a_э< 0. Таким образом, условие самовозбуждения примет вид М > LG/S, что совпадает с выражением (15.10).

В стационарном режиме работы генератора корпи перемещаются на мнимую ось комплексной плоскости р (рис. 15.12, случай 2). Из условия a_э = 0 можно найти стационарное значение средней крутизны:

= LG/М.

Анализ в частотной области. Заменяя в выражениях для операторных передаточных функций оператор р на оператор jw;. запишем передаточную функцию цепи с разомкнутой ОС:

Из условия баланса фаз на частоте генерации

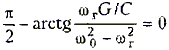
убеждаемся, что генератор возбуждается на частоте w_г= w₀.

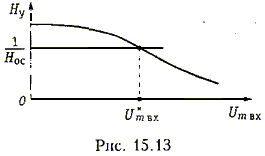
H_y( w_г)H_oc( w_г) = SM/GL > 1.

Из условия баланса амплитуд, которое должно выполняться на частоте генерации  находим, что самовозбуждение происходит при М > LG/S, что совпадает с полученными ранее результатами.

Баланс амплитуд па частоте генерации H_y( w_г)H_oc( w_г) =1 позволяет определить стационарное значение средней крутизны

= LG/M.

Можно построить зависимость H_y на частоте генерации от стационарной амплитуды колебании U_{m вх} (рис. 15.13). Функцию H_y( U_{m вх}) легко получить из формулы (15.15), зная среднюю крутизну S_ср( U_{m вх}) и сопротивление контура па частоте генерации Z_K(w_г)= 1/G:

H_y(U_{m вх}w_г) = S_ср( U_{m вх})/G.

В стационарном режиме выполняется условие

Воспользовавшись этим условием, можно найти стационарную амплитуду колебании на входе усилителя, как это сделано на рис. 15.13. Стационарная амплитуда колебаний на выходе генератора определяется по формуле

15.5. Трехточечные схемы генераторов

Индуктивная трехточка. Недостатком схем L/С-генераторов с трансформаторной обратной связью является наличие двух индуктивно связанных катушек. Поэтому на практике чаще используют схемы LC-генераторов с автотрансформаторной ОС, в которых напряжение ОС снимается с части колебательного контура. Такая схема изображена на рис. 15.14, а. Она известна также под названием схемы индуктивной трехтонки. Элементы С, L₁ и L₂ образуют колебательный контур; резистор R_Б является элементом цепи

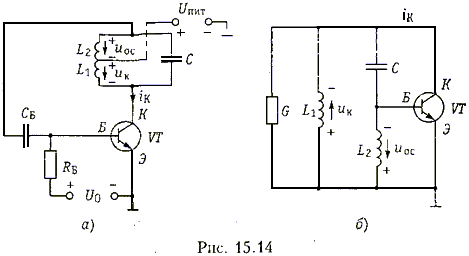
автоматического смещения, через который протекает постоянная составляющая тока базы; конденсатор С_Б предотвращает попадание напряжения питания U_ПИТ на базу и влияет на постоянную времени цепи автосмещения. На рис. 15.14, б приведена эквивалентная схема индуктивной трехточки по переменному току. т. е. цепи пи тания и смещения па рисунке не показаны.

Обычно полагают, что входное сопротивление транзистора настолько велико, что током базы можно пренебречь. В этом случае, как видно пз рис. 15.14, б, элементы С,L₁ и L₂ образуют трехэлементный реактивный двухполюсник, в котором сначала происходит резонанс токов, а затем резонанс напряжений в контуре CL2. Частотные характеристики реактивного и полного сопротивлении колебательного контура показаны па рис. 15.15, а п б.

Генерация колебаний происходит на частоте резонанса токов

Сопротивление контура на этой частоте является чисто резистивным и принимает максимальное значение, равное 1/G.

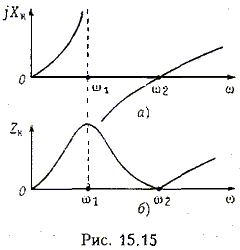
Цепью ОС в этой схеме служит делитель напряжения, образованный емкостью С и индуктивностью L₂. Действительно, напряжение, снимаемое с выхода усилительного элемента ( транзистора), приложено к колебательному контуру или, что то же, к ветви СL₂. Напряжение ОС снимается с индуктивности L₂ и подается на вход усилительного элемента. Усилительный каскад на одном транзисторе поворачивает фазу сигнала на 180°. Для соблюдения баланса фаз цепь обратной связи также должна вносить фазовый сдвиг 180°. Это п происходит в действительности. Ток в ветви СL₂ из-за емкостного характера ее сопротивления опережает напряжение на контуре u_К(t) на 90°. В свою очередь, напряжение u_oc(t) на индуктивности L₂ опережает этот ток еще на 90°. Таким образом, сдвиг фаз между напряжениям u_К(t) и u_oc(t) составляет 180°.

Перейдем к анализу работы генератора. Для определения условии самовозбуждения составим х а р а к т е р и с т и ч е с к о е  у р а в н е н и е   г е н е р а т о р а:

1 - H_y(p) H_oc(p) = 0.

   (15.17)

Передаточная функция усилителя, как и в случае LC-генератора с трансформаторной обратной связью, равна

H_y(p) = - SZ_к(p),

(15.18)

где Z_к(p)- операторное сопротивление контура:

После несложных преобразований выражения для Z_к(p) и подстановки его в (15.18) получим

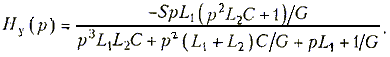
Передаточная функция цепи ОС имеет вид

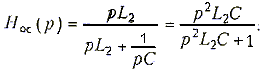
Запишим передаточную функцию цепи с разомкнутой ОС

Теперь легко получить характеристическое уравнение. С учетом (15.17) имеем

p³L₁L₂C(1 - S/G) + p²(L₁ + L₂)C/G + pL₁ + 1/G = 0

(15.19)

Заметим легко получить характеристическое уравнению соответствуют дифференциальное уравнение генератора - индуктивной трехточки

Для анализа устойчивости воспользуемся критерием Рауса - Гурвица и составим определитель Гурвица (см. гл. 14):

Цепь будет неустойчивой и в генераторе произойдет самовозбуждение, если хотя бы один минон определителя является отрицательным, например

Раскрывая определитель, получаем

L₁(L₁ + L₂)C/G - L₁L₂C(1 - S/G)G < 0

или

L₁ + L₂ <  L₂ + L₂S/G.

Отсюда условие самовозбуждения имеет вид

L₁/L₂< S/G.  

 (15.20)

Для анализа работы генератора в частотной области необходимо использовать соотношения баланса амплитуд и баланса фаз

H_y(w_г)H_oc(w_г)³1  и    j_y(w_г) + j_oc(w_г) = 2p

Поскольку на частоте генерации w_г сопротивления контура Z_k(w) = 1/G, комплексная передаточная функция усилителя принимает в соответствии с (15.18) простой вид

H_y(w_г) = - S/G =(S/G)e^jp.

Комплексная передаточная функция цепи ОС

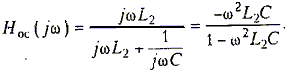
после подстановки значения частоты генерации она будет иметь вид

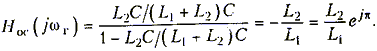
В режиме самовозбуждения, т.е когда

H_y(w_г)H_oc(w_г)>1,

имеем:

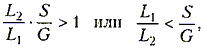
что совпадает с выражением (15.20).

Для стационарного режима, когда выполняется баланс амплитуд

H_y(w_г)H_oc(w_г) = 1,

можно определить стационарное значение средней крутизны:

.

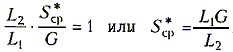Из анализа выражений H_y(jw_г) и  H_oc(jw_г) видно, что j_y (w_г) + j_о(w_г) = 2p

Емкостная трехточка. Если в предыдущей схеме использовать реактивный двухполюсник с обратной частотной зависимостью сопротивления, то полученная схема будет называться емкостной трехтонкой (рис. 15.16). Генерация колебании в этой схеме будет происходить на частоте резонанса токов

когда сопротивление колебательного контура будет активным Z_K(w)- 1/G  и максимальным по величине.

Анализ дайной схемы практически ничем не отличается от анализа индуктивной трехточкп. Для иллюстрации проведем анализ в частотной области. Исследование характеристического уравнения генератора предлагаем провести самостоятельно.

Комплексная передаточная функция усилителя на частоте генерации была получена ранее:

H_y(w_г) = (S/G)e^jp.

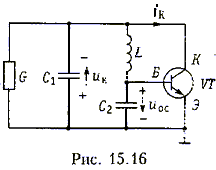
Цепь обратной связи представляет собой делитель напряжения. образованный индуктивностью L и емкостью С₂. Комплексная передаточная функция цепи обратной связи

па частоте генерации w_г  принимает вид

Из неравенства H_y(w_г)H_oc(w_г)>1 определим условия самовозбуждения емкостной трехточки

Из баланса амплитуд определяется стационарное значение средней крутизны

15.6. RC- генераторы

КС-генератор с мостом Вина. На сравнительно низких частотах, где реализация RC-контуров становится затруднительной из-за больших габаритов и массы, низкой добротности и невозможности перестройки, используют RC-автогеператоры. Они представляют собой комбинацию активных четырехполюсников (усилителей) и пассивных RC-цепей для создания ОС.

На рис. 15.17, а показана одна из таких схем (RC-генератор с мостом Вина), которая представляет собой усилитель с коэффициентом передачи К, между входом и выходом которого включена RC-цепъ. Усилитель с заданным коэффициентом передачи можно реализовать на ОУ (см. рис. 2.17) по схеме неинвертирующего масштабного усилителя.

Для составления характеристического уравнения (15.14) достаточно найти H_oc(p), так как H_y(p) =К. Схема генератора с разомкнутой ОС приведена па рис. 15.17. 6. Передаточную функцию цепи ОС. являющейся Г-образным четырехполюсником, будем искать в виде

( 15.21)

где Z₁(p) - операторное сопротивление последовательно соединенных емкости C₁ и сопротивления R₁:

Z₂(p) - операторное сопротивление соеденненыхпараллельно емкости C₂ и  сопротивления R₂

После подстановки в формулу (15.21) выражений Z₁(p) и Z₂(p) получим

(15.22)

Характеристическое уравнение (15.14) примет вид:

p²R₁C₁R₂C₂ + p[R₁C₁ + R₂C₂ + (1 - K)R₂C₁] + 1 = 0

 (15.23)

или

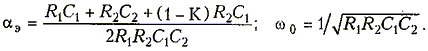
Режиму самовозбуждения соответствует расположение корней характеристического уравнения (15.14) в правой полуплоскости, что имеет место при a_э < 0, т. е. при

R₁C₁  + R₂C₂   + (1 - K)R₂C₁< 0.

Из данного условия следует,  что самовозбуждение генератора наступает при коэффициенте передачи усилителя

или

Если выбрать R₁= R₂ и C₁ = C₂, то колебания на выходе генератора появятся при К > 3.

В стационарном режиме a_э = 0. Характеристическое уравнение (15. 14) в этом случае принимает вид

p²R₁R₂C₁C₂+ 1 = 0

Его корни лежат на мнимой оси плоскости р и равны

Таким образом, генерация происходит па частоте w_г = w₀ .

Анализ работы RC- генератора с мостом Вина можно пронести также в частотной области. Про усилитель известно, что H_y(w) = K и j_y (w) = 0 на всех частотах. Комплексную передаточную функцию цепи H_oc(jw) получим из (15.22) заменой оператора р на jw преобразовав предварительно (15.22) к виду

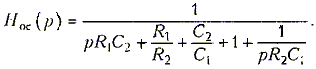
Откуда после замены р на jw, имеем

Поскольку усилитель не вносит фазового сдвига, для выполнения баланса фаз требуется обеспечить условие  j_oc(w_г) = 0. Оно выполняется тогда, когда передаточная функция цепи ОС является вещественной, т. е. ее мнимая часть обращается в пуль. Таким образом, па частоте генерации

Из этого условия определяется частота генерации

Значение передаточной функции на этой частоте

H_oc(w_г) = 1/(1 + R₁/R₂ + C₂/C₁).

Из условия самовозбуждения H_у(w_г) H_oc(w_г) > 1 находим коэффициент усиления К, при котором на выходе генератора возникают незатухающие гармонические колебания:

Стационарное значение коэффициента усиления усилителя определяется балансом амплитуд:

RC-генератор    с   лестничной   схемой   обратной   связи.    На рис 15.18, а показана схема такого генератора, представляющая собой одпокаскадный транзисторный усилитель, между входом п выходом которого включен лестничный пассивный RC четырехполюсник (для упрощения рисунка цепь смещения на нем не приведена)

Для возникновения генерации колебании необходимо, чтобы напряжение обратной связи, подаваемое на вход генератора, непрерывно возрастало. Это возможно только тогда, когда усиление усилительного каскада больше ослабления, вносимого цепью обратной связи. Кроме того, должно выполняться условие баланса фаз. Последнее означает, что поскольку один каскад транзисторного усилителя вносит сдвиг фаз, равный 180°, то цепь обратной связи также должна вносить сдвиг фаз 180°, чтобы общий сдвиг фаз равнялся 0° (или 360°)

Однако простейшее RС- звено вносит сдвиг фаз, не превышающий 90°. Поэтому необходимо взять число звеньев пе меньше трех. Зависимость сдвига фаз от частоты RС- цепи из трех звеньев показана на рис. 15.18, 6. Элементы RС- цепи рассчитывают так, что бы на частоте генерации получить сдвиг фаз 180".

И стационарном режиме, кроме баланса фаз, выполняется также п баланс амплитуд.  При  этом усиление усилительного каскада становится равным ослаблению цепи ОС, амплитуда напряжения цепи обратной связи, а значит и выходного, остаемся постоянной.

Если выбрать сопротивление коллекторной цепи транзистора R_К<<R,  чтобы избежать влияния на работу транзистора цепи ОС,

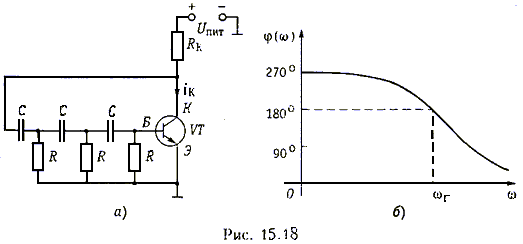
то операторная передаточная функция усилительного каскада определится, как и в LG-генераторах, следующей формулой:

H_y(p) = - SR_K.

Операторную передаточную функцию лестничной цепи обратной связи, нагруженной на транзистор с большим входным сопротивлением, т. е. работающей практически на холостом ходу, получим из условия Н(р) = 1/А₁₁. Параметр А₁₁ лестничной схемы найдем, воспользовавшись матричным методом расчета четырехполюсников (гл. 12). Представим лестничную схему как каскадное соединение Т-образного и П-образного четырехполюсников.

Тогда матрица А лестничной схемы запишется в виде

A = || A ||_T ´ || A ||_П

Предлагаем читателям самостоятельно получить элементы А-матриц четырехполюсников. Они имеют вид:

При этом нет необходимости осуществлять полностью перемножение матриц. Для получения коэффициента А₁₁ результирующей А-матрицы лестничной цепи ОС достаточно перемножить первую строку и первый столбец данных матриц. В итоге будем иметь

А₁₁(р) = ( 1 + pRC)² + pRC(2 + pRC)²

^и

Н_OC(p) = 1/A₁₁ = 1/(p³R³C³ + 5p²R²C² + 6pRC + 1).

(15.24)

Для нахождения условий возникновения генерации исследуем характеристическое уравнение генератора

1 - Н_у(р)Н_ос (р) = 0.

После подстановки в него Н_у(р) иН_ос (р) получим следующее уравнение:

p³R³C³ + 5p²R²C² + 6pRC + 1 + SR_K = 0

Цепь является неустойчивой, если

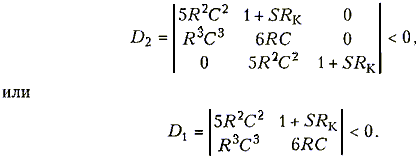
Раскрывая определитель D₁, придем к неравенству

30R³C³ - R³C³ - SR_KR³C³ < 0,

или SR_K > 29. Поскольку произведение SR_K есть ни что иное как усиление транзисторного усилительного каскада, то это условие означает, что для самовозбуждения генератора усиление транзисторного каскада должно превышать 29 едениц.

Переход из комплексной плоскости p в частотную область осуществляется заменой p на jw.

Усилитель имеет комплексную передаточную функцию

H_y(jw) = - SR_K = SR_Kе^jp.

Цепь обратной связи описывается комплексной передаточной функцией H_oc(jw), полученной из (15.24):

H_oc(jw) = 1/(1 - 5w²R²C² + jwRC(6 - w²R²C²)).

Из баланса фаз j_у(w_г) + j_ос(w_г) = 2p следует, что  j_ос(w_г) = p. Это будет иметь место при

6 - w_гR²C² = 0,

откуда находится частота генерации

Передаточная функция  H_oc(jw) равна

или

H_oc(jw) = 1/29;   j_ос(w_г) = p

Подстановка полученных значений H_y(w_г ) и H_oc(w_г )  в условие амплитуд

H_y(w_г )H_oc(w_г ) > 1.

даст SR_K> 29, что совпадает с полученным ранее результатом.

В стационарном режиме можно рассчитать средней крутизны

= 29/R_K

Недостатком RС-генераторов является то, что в стационарном режиме за счет нелинейности ВАХ (благодаря которой и устанавливается амплитуда колебаний) происходит искажение формы тока i_K в цепи коллектора. Выходное напряжение в RС -автогенераторе снимается с резистора R_K и имеет ту же форму, что и ток i_K, т. е. является несинусоидальным.

Для получения формы колебаний, близкой к синусоидальной, нужно, чтобы колебания не выходили за пределы линейного участ ка ВАХ

Поэтому на практике рост колебании ограничивается не нелинейностью транзистора, а специальным нелинейным элементом (НЭ), в качестве которого используются полупроводниковые или металлические терморезисторы.

15.7. Автогенераторы с внутренней обратной связью

Ранее была получена одна из форм дифференциального уравнения автогенератора с внешней ОС (15.9)

с коэффициентом a_э, определяемым формулой (15.11):

Здесь G_ВН- проводимость, вносимая в колебательный контур за счет действия внешней ОС.

Стационарному режиму соответствует равенство G_ВН = - G. Условие возникновения колебаний удовлетворяется при G_вн < 0 и |G_вн| > G.

Сравнение данного дифференциального уравнения с дифференциальным уравнением одиночного колебательного контура (15.2) позволяет составить эквивалентную схему генератора. Она дана на рис. 15.4 п отличается от схемы обычного контура наличием в ней отрицательной проводимости.

Отрицательную проводимость можно получать не только за счет действия внешней ОС, но н с помощью НЭ с ВАХ, имеющей падающий участок. Электронные приборы, являющиеся резистивными нелинейными элементами с падающими участками i= F(u), называются приборами с отрицательным сопротивлением. В частности, таким прибором является туннельный диод.

Генераторы, построенные на приборах с отрицательным сопротивлением, не содержат внешней цепи ОС н называются поэтому генераторами с внутренней ОС.

На рис. 15.19, а приведена ВАХ туннельного диода. На участке a - б дифференциальная проводимость G(u) = di/du < 0

Эквивалентная схема туннельного диода, соответствующая падающему участку характеристики, представляет собой параллельное соединение нелинейной отрицательной проводимости диода G(u), зависящей от приложенного к нему напряжения u, и емкости С_Д p-n  перехода (рис. 15.19, б).

Схема генератора с внутренней ОС, выполненного на туннельном диоде, изображена на рис. 15.20, а. При помощи напряжения смещения U₀ рабочая точка устанавливается примерно в середине падающего участка ВАХ диода. Блокировочная емкость С_бл образует путь для переменного тока генерируемой частоты. Заменив туннельный диод параллельным соединением отрицательной проводимости G(u) и емкости С_д перейдем к эквивалентной схеме генератора по переменному току. Она дана на рис. 15.20, б. Емкость эквивалентной схемы С = С_к + С_д. Данная эквивалентная схема полностью удовлетворяет приведенному в начале раздела дифференциальному уравнению.

Генератор на туннельном диоде является генератором почти гармонических колебаний, и анализ его работы можно провести так же, как и анализ работы генератора с внешней ОС.

Введем понятие средней проводимости НЭ G_cp(Um1) < 0 по первой гармонике с амплитудой U_m1. Графики зависимостей,|G_ср(Um1)| от амплитуды U_m1при различных напряжениях смещения U₀ приведены на рис. 15.21. На нем же показаны различные значения эквивалентной проводимости контура С.

Возбуждаются колебания при |G_ср(Um1)|. Стационарные амплитуды колебаний устанавливаются при |G_ср(Um1)|= G.

Проводя анализ зависимостей рис. 15.21 (подобный анализ зависимостей выполнен с помощью рис. 15.8 и 15.9 для генераторов с внешней ОС), можно убедиться, что в генераторах с внутренней ОС возможны мягкий и жесткий режимы самовозбуждения (рис. 15.22).

Мягкий режим самовозбуждения происходит при напряжениях смещения 0,15 В < U₀ < 0,3 В, жесткий режим - при U₀ > 0,3 В. На рис. 15.21 па кривой средней проводимости |G_ср(Um1)| полученной при U₀ = 0,4 В показаны стационарные точки А', А", А"'. Колебания возникают при значении эквивалентной проводимости контураG' (точка А').

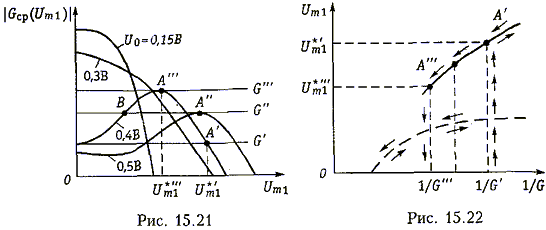
Амплитуда колебаний равна . При увеличении проводимости G  стационарная амплитуда уменьшается, срыв колебаний происходит при G'''(точка А'''). Поэтому жесткому режиму самовозбуждения соответствует сплошная кривая на рис. 15.22. Мягкому режиму возбуждения соответствует пунктирная кривая, полученная для средней проводимости при U₀= 0,3 В.

15.8. Анализ переходных процессов в автогенераторе методом

 медленно меняющихся амплитуд

При исследовании условий самовозбуждения и стационарного режима работы автогенератора принимались во внимание следующие обстоятельства. При самовозбуждении амплитуда нарастающих колебаний в автогенераторе мала и работа генератора происходит на линейном участке ВАХ транзистора i_к = F(u_K), на котором крутизна транзистора S(u_oc) = di_K(u_oc)/du_oc является постоянной величиной, не зависящей от напряженияи u_ос , т. е. S(u_ос) = S. В этом случае дифференциальное уравнение автогенератора (15.8) становится линейным.

В стационарном режиме, когда амплитуды гармонического колебания на контуре автогенератора U_{m к} и гармонического колебания обратной связи U_{m oc} являются установившимися, средняя крутизна S_ср(u_oc)в уравнении (15,8) является также постоянной величиной и дифференциальное уравнение автогенератора снова можно считать линейным:

Из решения этого уравнения определялись условия самовозбуждения, амплитуда и частота генерируемых колебаний

При анализе переходного режима автогенератора, когда амплитуды колебаний напряжения на контуре и напряжения обратной связи изменяются от очень малых величин U_{m к}(0)  и U_{m oc} (0), вызванных флуктуационными процессами в автогенераторе, до установившихся значении, считать крутизну S(u_oc) постоянной уже невозможно; дифференциальное уравнение автогенератора (15.8) является нелинейным. Поскольку способов точного аналитического решения нелинейного дифференциального уравнения второго порядка не существует воспользуемся для его решения приближенным методом медленно меняющихся амплитуд (ММА).

Метод ММА применяется для решения нелинейных дифференциальных уравнений с малым параметром. Этот метод введен в радиотехнику впервые Ван-дер-Полем, который рассмотрел ряд задач, связанных с установлением колебаний в ламповых генераторах и других колебательных системах. В дальнейшем этот метод получил обоснование в работах академиков Л.И. Мандельштама, Н.Д. Папалекси, А.А. Андронова и их учеников. Особо следует отметить работы академиков Н.Н. Боголюбова, Н.М. Крылова, а также Ю.A. Митропольского, посвященные развитию и метода ММА (или, как он часто называется, метода укороченных уравнений).

Поскольку в автогенераторах для повышения стабильности частоты генерируемых колебаний и подавления высших гармоник тока коллектора, являющихся продуктом нелинейности ВАХ транзистора, используется высокодобротный контур (Q >>1), то амплитуда напряжения на контуре, а также амплитуда напряжения обратной связи, изменяются так медленно, что их приращениеDU_m за время периода колебании Т много меньше самой амплитуды колебаний DU_m<< U_m ,. Это условие «малости» изменения амплитуды колебаний п будет использовано для анализа переходных процессов в автогенераторе.

Покажем, что указанное условие «малости» изменения амплитуды колебаний в автогенераторе, DU_m<< U_m, действительно выполняется при больших добротностях контура Q. Напряжение на колебательном контуре автогенератора изменяется по закону

u_k(t) = U₀e ^-atsinw₀t,

где a = G/2C-коэффициент затухания контура; U₀ - начальное значение амплитуды колебаний,  вызванное флуктуациями тока в транзисторе; w₀ - частота свободных колебаний в контуре. Введем обозначение

      U_mK(t) = U₀e ^-at

(15.25)

п перепишем выражение для u(t):

u_K(t) = U_mK(t)sinw₀t,

где U_m(t) - описывает закон изменения амплитуды автоколебаний во времени.

Продифференцировав (15.25),  найдем скорость изменения амплитуды

(15.26)

Перепишем (15.26) в приращениях

DU_{m к}(t) = -aU_{m к}(t)Dt

.(15.27)

Пусть отрезок времени Dt = Т, тогда DU_{m к}(t) = -aТU_{m к}(t) . Если aТ <<1, то условие DU_m<<U_m выполняется. Чтобы убедиться в этом, выразим декремент затухания aТ параллельного контура через добротность Q:

.(15.28)

где Q = l/(Gr) - добротность контура; r - характеристическое сопротивление контура.

Для контура высокой добротности (Q >>1) декремент затухания aТ << 1, поэтому

DU_{m к}<<U_{m к}

.(15.29)

Воспользуется условием (15.29) для перехода от полного дифференциального уравнения автогенератора (15.8) к укороченному.

Перепишем (15.29), разделив правую и левую части неравенства на период колебаний

Перейдем снова к бесконечно малым приращениям амплитуды колебаний, полагая, что период колебаний достаточно мал по сравнению со временем изменения амплитуды

(15.30)

Неравенство (15.30) еще более усилится, если правую часть умножим на 2p:

.                              (15.31)

Продифференцировав  (15.31),   получим   неравенство  для   2-ой производной

                            (15.32)

Воспользуемся (15.31) п (15.32) для перехода от дифференциального уравнения автогенератора (15,8), составленного относительно напряжения на контуре u_K(t). к дифференциальному уравнению, составленному относительно огибающей амплитуды этого напряжения U_{m к}(t). Тем самым удастся понизить порядок дифференциального уравнения.

Вычислим первую и вторую производные выражения u_к(t) =U_mк(t)sinw₀t учтем неравенства (15.31) и (15.32):

Подставим (15.33) и (15.34) в уравнение автогенератора (15.8):

После преобразования этого выражения имеем окончательно:

(15.35)

Получили так называемое «укороченное» нелинейное дифференциальное уравнение 1-го порядка для медленно меняющейся амплитуды колебаний, или уравнение Ван-дер-Поля.

Таким образом, использование условии медленности изменения амплитуды позволило перейти от мгновенных значений напряжения на контуре u_к к амплитудным U_{m к} и понизить порядок уравнения. Заметим, что уравнение (15.35) по-прежнему остается нелинейным, так как в него входят мгновенная крутизна ВAХ, зависящая от мгновенного напряжения и_0С. Однако, от мгновенной крутизны можно перейти к средней крутизне в силу того, что в высокодобротном контуре можно пренебречь высшими гармониками. Тогда уравнения (15.35) можно переписать в виде

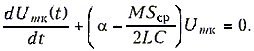
(15.36)

Это уравнение, строго говоря, также является нелинейным (так как средняя крутизна зависит от амплитуды); однако в таком уравнении первого порядка можно разделить переменные и получить его решение.

Для решения уравнения (15.36) прежде всего нужно выбрать выражение для средней крутизны. Если аппроксимировать ВАХ транзистора полиномом

i_k = a₀ + a₁(u_oc - U₀) + a₂(u_oc - U₀)² + ...

п считать, что  u_oc =U₀ + U_moccoswt, то можно найти амплитуду первой гармоники тока

п среднюю крутизну по первой гармонике

Это общее выражение для средней крутизны пригодно для расчета переходных процессов в автогенераторе как в мягком, так и в жестком режимах, по сложность расчетов при этом резко возрастает. Поэтому для практических расчетов используют не полиномиальную аппроксимацию, а аппроксимацию гиперболическим тангенсом.

Среднюю крутизну транзистора для мягкого режима самовозбуждения с достаточной для практических расчетов степенью точности можно аппроксимировать функцией

(15.37)

S₀ - начальное значение  крутизны S(0); a = S/I_H,  S - значение крутизны в рабочей точке, I_H - ток насыщения транзистора.

Подставив выражение для крутизны (15.37) в укороченное уравнение для огибающей амплитуды колебаний автогенератора (15.36) п вынося коэффициент затухания a за скобки, получим:

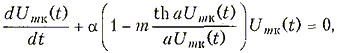
(15.38)

где m = M/M_кр;  M_кр = LG/S₀.

Получим решение уравнения (15.38) для двух отрезков времени: 0 £ t £ t- режим малых амплитуд, когда аргумент aU_mк£0,5. В это случае th aU_mк »aU_mк и уравнение (15.38) будет линейным однородным дифференциальным уравнением 1-го порядка:

(15.39)

t₁ £ t £ t_уст - режим больших амплитудa U_mк ³ 1,5, тогда th aU_mк » 1 и ( 15.38) будет линейным неоднородным дифференциальным уравнением 1-го порядка

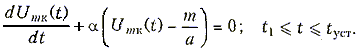
(15.40)

Решение уравнение (15.39) имеет вид:

U_mк(t) = U_mк(0)е^{- -a(t -m)t};       0£t£t₁,     

 (15.41)

где U_mк(0) - начальное значение амплитуды колебаний в момент t = 0 (на первом интервале времени 0£t£t₁), обусловленное флуктуациями в транзисторе. Из (15.41) видно, что амплитуда колебаний будет увеличиваться, m > 1, т.е. M>M_КР или M_КР/L > G/S.

Для решения (15.40) проведем разделение переменных и проинтегрируем

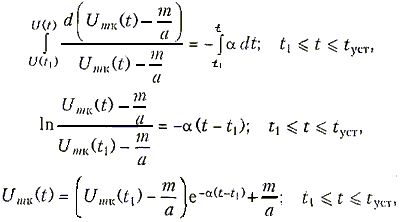
( 15.42)

где U_mк(t₁) - начальное значение амплитуды колебаний на втором интервале t₁ £ t £ t_уст, равное конечному значению амплитуды на первом интервале U_mк(t₁)  = U_mк(0)е ^{-a(t -m)t}

При t ® ¥ получим установившееся решение для амплитуды колебаний

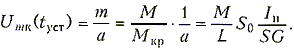
(15.43)

Из (15.43) видно. что установившееся колебание U_mк(t_уст) не зависит от начальных условий, а зависит от величины обратной связи M/L, проводимости контура G и характеристик транзистора.

Время установления колебаний в автогенераторе находится из условия, что амплитуда колебаний изменяется отU_mк(0) до 0,95 от установившегося решения, т. е. U_mк(t_уст) = 0,95m/a. Откуда имеем

(15.44)

Начальное значение амплитуды колебаний U_mк(t₁) найдем из выражения средней крутизны на первом интервале S_ср = SS_ср = S/(аU_mк(t₁)) и на втором интервале S_ср = S/(аU_mк(t₁)).Отсюда:

(15.45)

Из (15.45) находим

(15.46)

Подставив (15.46) в (15.44), получим

Откуда находим

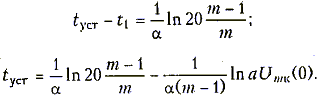
(15.47)

Из (15.47) видно, что длительность установления колебаний  t_уст  зависит от начальной амплитуды U_mк(0), коэффициента затухания а, величины обратной связи т и параметра транзистора а. С увеличением начальной амплитуды колебаний U_mк(0) время установления уменьшается.

Пример. Рассчитать время установления колебании в автогенераторе для следующих условий; величина взаимной индукции в два раза больше критической m = M/M_кр = 2; начальное значение амплитуды колебании в 300 раз меньше амплитуды колебаний и середине переходного процесса U_mк(0) = 0,01/а, добротность контура Q = 100.

Выразим в (15.47) коэффициент затухания a контура через добротность Q: a = w₀/(2Q) , тогда из (15.47) получим

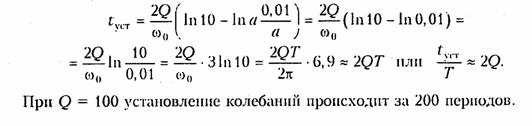
Вопросы и задания для самопроверки

1. Каким образом в автогенераторе (рис.  15.2) возникают стационарные гармонические колебания?

2. Пояснить принцип работы автогенератора по рис. 15.3.

3. Какие типы автогенераторов существуют? Как работают эти генераторы?

4. Сформулировать    условия    самовозбуждения    автогенераторов: а) с трансформаторной обратной связью; б) индуктивной трех точки;  в) .RC-генератора с лестничной цепью обратной связи; г) КС-генератора с мостом Вина.

5. Проверить,    произойдет   ли    самовозбуждение    автогенератора (рис.  15.2), если L = 200 мкГн, М = 50 мкГн, R_P = 10 кОм, S_ср = 1 мА/В.

Ответ:   да.

6.  Является   ли   цепь   на   рис.    15.4,    6   автогенератором,    если H_у = 2,5; L₁ = 30 мкГн; L₂ = 10 мкГн?

Ответ:   нет.

7.  Рассчитать значение крутизны характеристики транзистора, при котором произойдет самовозбуждение .RC-автогенератора с лестничной цепью обратной связи, если R_К = 0,5 кОм.

Ответ:   S_ср > 58 мА/В.

8. Как рассчитывается частота генерируемых колебаний в автогенераторах разных типов?

9. Рассчитать частоту генерации колебании в RС- генераторе с мостом Вина, если С₁ = С₂= 7 нФ, R₁ = R₂ = 10 кОм.

Ответ:  f_г = 2,27 кГц,

10.  Какими будут графики зависимости средней крутизны (или коэффициента передачи усилителя) от амплитуды напряжения  на  входе  усилителя  при  разных  положениях  рабочей точки на ВАХ (в середине линейного участка и на нижнем  загибе)?

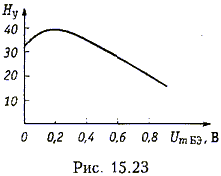
11. Сформулировать условия  баланса амплитуд  и баланса фаз  в установившемся режиме.

12. Каким образом по колебательной характеристике (рис.  15.13) определяется амплитуда стационарных колебаний?

13. Определить амплитуду стационарного колебания на выходе RС- генератора   с   лестничной   цепью   обратной   связи,   если S_ср = 14,5 мА/В, R_k = 2 кОм, колебательная характеристика  изображена на рис. 15.23.

Ответ:    U_{m вых} = 11,6 В.

14. При  каких условиях режим самовозбуждения автогенератора  является мягким (жестким)?

15. В чем отличие мягкого режима самовозбуждения автогенератора от жесткого режима?   Пояснить по графикам рис.   15.8 и рис. 15.9.

16. Каким  образом  объединить достоинства  мягкого  и  жесткого режимов самовозбуждения