3.7. Электрические цепи с индуктивными связями

В предыдущих параграфах этой главы рассматривались цепи без учета явления взаимной индукции. В то же время, при протекании тока i₁ в катушке индуктивности с параметром L₁ в окружающем пространстве согласно закону электромагнитной индукции создается магнитный поток Ф₁₁ (рис. 3.17, а). Если какая-либо часть этого потока Ф₁₂ пронизывает витки другой катушки с L₂, то в последней наводится ЭДС взаимной индукции, определяемая законом Максвелла —Фарадея:

где коэффициент М\2 носит название взаимной индуктивности катушек L₁ и L₂. Единица измерения взаимной индуктивности — М генри (Гн).

Знак «—» в уравнении (3.66) определяется согласно правилу Ленца направлением индукционного тока, который имеет такую ориентацию, чтобы создаваемый им магнитный поток препятствовал тому изменению магнитного потока Ф₁₂, которое этот ток вызывает. Напряжение взаимоиндукции на зажимах катушки индуктивности L2:

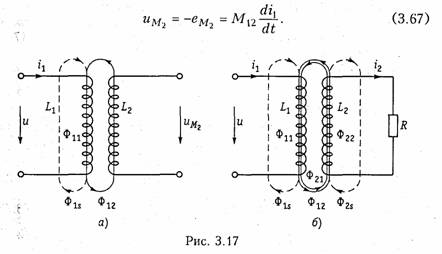
Если напряжение и приложено к катушке индуктивности Li, то под действием тока i₂ в катушке L₁ также будет наведена ЭДС взаимной индукции:

В соответствии с принципом взаимности (см. § 1.7) для линейных цепей М₁₂ = М_21.

Рассмотренная ниже индуктивная связь носит односторонний характер: ток i₁ вызывает ЭДС взаимоиндукции ем_2, или ток i₂ — ЭДС ем_1. В случае замыкания катушки L₂ на конечное сопротивление R (рис. 3.17, б) в последней под воздействием um₂ потечет индукционный ток i₂, который в свою очередь, вызовет в первой катушке L₁ ЭДС взаимоиндукции ем₁ (3.68). Таким образом, установится двухсторонняя индуктивная связь катушек L₁ и L₂. При этом каждая из катушек L₁ и L₂будет пронизываться двумя магнитными потоками: самоиндукции, вызванным собственным током, и взаимоиндукции, вызванным током другой катушки. Следовательно, в катушке L ₁ индуцируется ЭДС

Взаимное направление потоков само- и взаимоиндукции зависит как от направления токов в катушках, так и от их взаимного расположения.

Если катушки включаются таким образом, что потоки само- и взаимоиндукции складываются, то такое включение называется согласным. Если же потоки само- и взаимоиндукции вычитаются, то такое включение принято называть встречным. На рис. 3.17, б показан случай согласного включения.

Степень связи между L\ и Z-2 оценивается коэффициентом связи

Значение k изменяется в пределах от 0 (отсутствие связи) до 1 (жесткая или полная связь). Индуктивная связь существенным образом зависит от потоков рассеяния Ф_1s и Ф_2s, поэтому степень связи иногда характеризуют коэффициентом рассеяния σ² = 1 — k². Для компактности и удобства изображения схем электрических цепей с взаимной индуктивностью вводят понятие одноименных зажимов. Последними принято называть узлы, относительно которых одинаково ориентированные токи создают складывающиеся потоки само- и взаимоиндукции. На рис. 3.18 схематично изображены одноименные зажимы для случая согласного и встречного включений катушек L₁ и L_2.Следовательно, для определения вида включения L₁ и L₂на схеме достаточно определить, как ориентированы токи i₁ и i₂ относительно одноименных зажимов (на рис. 3.18 обозначены точкой): при одинаковой ориентации имеем согласное (рис. 3.18, а), а при разной — встречное включение (рис. 3.18, б),

Учет взаимной индуктивности существенно влияет на результаты анализа электрических цепей. Рассмотрим последовательное и параллельное соединение индуктивно-связанных катушек с индуктивностями L₁ и L₂и потерями R₁ и R₂, находящихся под действием гармонического напряжения:

Последовательное соединение. Для согласного включения катушек (см. рис. 3.19, а) в соответствии с ЗНК и уравнениями (3.66) и (3.67) можно записать:

— эквивалентная индуктивность цепи при встречном включении катушек индуктивности.

Как следует из (3.78) и (3.87) эквивалентная индуктивность при согласном включении больше на 2М, а при встречном меньше на 2М суммарной индуктивности L₁ + L_2.

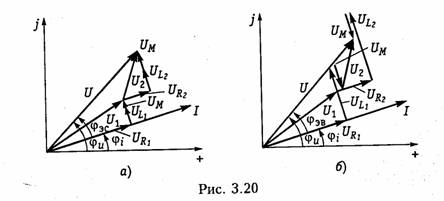
Уравнения для тока I, фазового сдвига φ_ЭB и напряжений U₁, U₂ аналогичны (3.80)-(3.83):

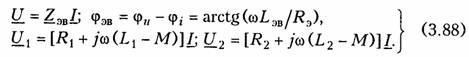
На рис. 3.20, б изображена векторно-топографическая диаграмма напряжений для случая встречного включения. При встречном включении катушек может наблюдаться «емкостный эффект», когда фазовый сдвиг между током и напряжением одной из катушек будет отрицательный. Это может иметь место при выполнении условия Li < М. В этом случае U_L2 < Um и

и напряжение U2 будет отставать от тока I. Однако вся цепь всегда будет носить индуктивный характер, так как при любых значениях параметров L₁, L₂ и М справедливо условие

Уравнения (3.79) и (3.87) можно положить в основу экспериментального определения взаимной индуктивности М. Для этого достаточно определить ток I, напряжение U, мощность Р в цепи при согласном и встречном включениях катушек и найти

где индексы «с» и «в» относятся к согласному и встречному включениям.

Реактивные составляющие комплексных сопротивлений при согласном и встречном включениях можно определить как

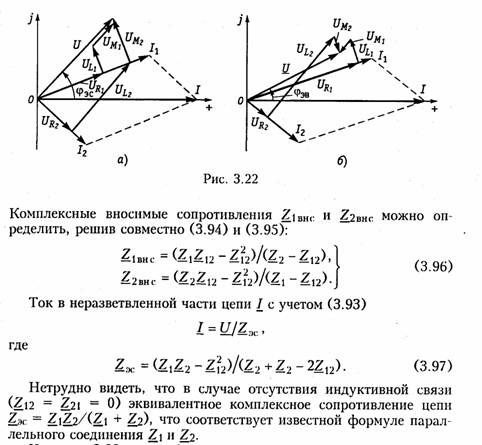
На рис. 3.22, а изображена векторно-топографическая диаграмма для случая согласного включения L₁ и L_2.Аналогичным образом можно получить соответствующие уравнения для встречного включения катушек (см. рис. 3.21, б). При этом необходимо учесть, что в уравнениях перед слагаемыми с Z₁₂ и Z₂₁ необходимо заменить знак на противоположный. Так, уравнения (3.94), (3.96), (3.97) принимают вид

На рис. 3.22, 6 изображена векторно-топографическая диаграмма для случая встречного включения.

Из уравнений (3.94), (3.98) нетрудно найти эквивалентные индуктивности ветвей:

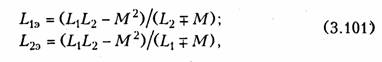
где знак «—» относится к согласному, а «+» — к встречному включению индуктивно связанных элементов.

3.8. Особенности анализа индуктивно связанных цепей

При расчете индуктивно связанных цепей обычно используют законы Кирхгофа и метод контурных токов. Другие методы либо нецелесообразно использовать из-за громоздкости решения, либо нельзя применять вследствие наличия индуктивной связи (методы узловых потенциалов, эквивалентного генератора). Для того чтобы можно было использовать все рассмотренные ранее методы расчета, применяют «развязку» индуктивных связей. Рассмотрим сущность этих методов на примере цепи, схема которой изображена на рис. 3.23.

Расчет по законам Кирхгофа. Составим уравнения по ЗТК и ЗНК, в комплексной форме:

При составлении уравнений по ЗНК необходимо пользоваться следующим правилом знаков: напряжение взаимоиндукции, создаваемое в k-й ветви от тока, протекающего в l-й ветви, берется со знаком «+», если направление обхода k-й ветви и положительное направление тока в l-й ветви одинаково ориентировано относительно одноименных зажимов. В противном случае берется знак «—».

Решая систему (3.102), получаем искомые токи I₁ и I₂ и I_3.

Метод контурных токов. В соответствии с этим методом (см. § 2.4) и правилом знаков уравнения для контурных токов I_К1 ,и I_КI₂ (см. рис. 3.23) принимают вид

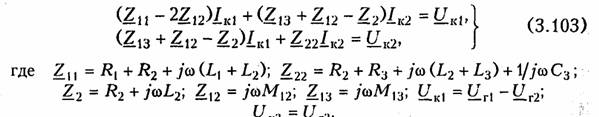
Решая систему (3.103), находим контурные токи I_К1 и I_К2, а затем токи ветвей I₁ = I_К1; I₂= I_К1- I_К2; I₃= I_К2.

Рассмотренные методы можно обобщить на схемы произвольной конфигурации.

Развязка индуктивных связей. Расчет индуктивно связанных цепей существенно упрощается, если использовать эквивалентные схемы, не содержащие в явном виде индуктивные связи. Составление подобных эквивалентных схем и составляет сущность метода «развязки» индуктивных связей. При этом эквивалентные связи учитываются в эквивалентных индуктивностях развязанных схем. Примером подобной развязки могут служить эквивалентные индуктивности, определяемые уравнениями (3.79), (3,87), (3.101).

В общем случае развязку любых двух индуктивно связанных элементов L₁ и L₂, соединенных в одном узле (рис. 3.24, а) можно осуществить с помощью схемы, изображенной на рис. 3.24, б для случая, когда элементы L₁ и L₂ соединены в узле 0' одноименными зажимами (•) и с помощью схемы на рис. 3.24, в для соединения L₁ и L₂ в узле 0' разноименными зажимами (Δ). Для доказательства эквивалентности этих схем достаточно составить уравнения по законам Кирхгофа для каждой из них и доказать их идентичность. Действительно, для случая включения одноименными зажимами для схемы на рис. 3.24, а имеем:

Учитывая, что после подстановки I₁ и I₂в (3.104) получаем уравнения, аналогичные (3.105). Подобным же образом доказывается эквивалентность и второй схемы при включении L₁ и L₂ разноименными зажимами.

В качестве примера на рис. 3.25 изображена схема с развязанными   индуктивными   связями,   эквивалентная   изображенной   на рис. 3.23. После развязки индуктивных связей расчет полученной эквивалентной схемы может быть осуществлен любым из известных методов.

Наличие индуктивных связей приводит к изменению матрицы сопротивления Z_B и проводимости Y_B. Из диагональных матриц они превращены в квадратные матрицы, по диагонали которых записываются собственные комплексные сопротивления или проводимости ветвей, а на пересечении k-й строки и l-го столбца записываются сопротивления или проводимости взаимной связи между k-й и l-й ветвями со знаком «+» при согласном включении и со знаком «—» при встречном.

Если цепь удовлетворяет условию взаимности (см. § 2.4), то Z_kl = Z_lk, Y_kl =Y_lk и матрица будет симметрична относительно главной диагонали.

Например, матрица сопротивлений цепи, изображенной на рис. 3.23, имеет вид

3.9. Трансформатор

Трансформатором называется статическое устройство, предназначенное для преобразования значений переменных напряжений и токов. Простейший трансформатор состоит из двух индуктивно связанных катушек с индуктивностями L₁и L₂, расположенных на общем сердечнике. Катушка, к которой подключается источник, называют первичной, а к которой подключают нагрузку — вторичной. Сердечник может быть выполнен из ферромагнитного или неферромагнитного материала. Примером трансформатора последнего типа является воздушный трансформатор, находящий широкое применение в технике связи, измерительных приборах, различных радиотехнических устройствах.

Воздушный      трансформатор.

На рис. 3.26 изображена схема простейшего воздушного трансформатора с потерями в первичной R₁ и вторичной R₂ катушках (обмотках), нагруженного на комплексное сопротивление Z_H = R_н + jХ_н.

Составим уравнение трансформатора по ЗНК для I и II контуров:

Уравнениям (3.110) соответствуют одноконтурные схемы замещения воздушного трансформатора, изображенные на рис. 3.27. Значения величин R_1BH и X_1BH, R₂вн и Х_2ВН определяются из (3.109) с учетом (3.107):

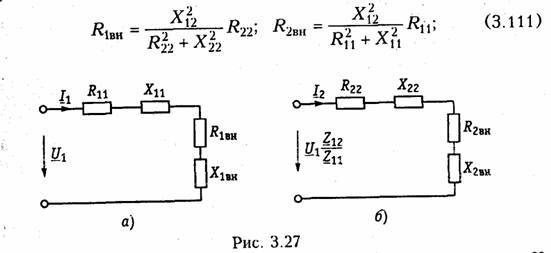
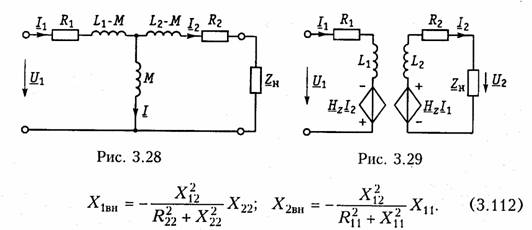
Знак «—» в уравнениях (3.112) свидетельствует о размагничивающем действии вторичной обмотки на первичную.

С физической точки зрения R_1вн и R_2вн представляют собой эквивалентные резистивные сопротивления, вносимые за счет взаимной индуктивности соответственно в контуры I и II.

При этом на Rвн при протекании тока I₁ рассеивается та же мощность, что и на R₂ при протекании тока I₂ и соответственно на R_2вн при протекании I₂ рассеивается та же мощность, что и на R₁ при протекании I₁.

Воздушный трансформатор может быть представлен двухконтурной схемой замещения, изображенной на рис. 3.28. Эта схема получается непосредственно из схемы, изображенной на рис. 3.26 после объединения в один узел одноименных зажимов и развязки индуктивных связей согласно рис. 3.24. Таким, образом, для определения токов в воздушном трансформаторе могут быть использованы одно- либо двухконтурные эквивалентные схемы замещения.

Если в уравнениях (3.107) обозначить то воздушный трансформатор можно представить схемой замещения с зависимыми источниками (рис. 3.29).

Из общих уравнений для комплексных токов I₁ и I₂ с учетом (3.106), (3.107) можно найти отношение комплексных токов и напряжений в воздушном трансформаторе:

где k_ТР = L₁/M — коэффициент трансформации. Как видно, в данном случае отношение напряжений не зависит от нагрузки, а отношение токов зависит от Z_h. Такой трансформатор называют совершенным. Для него коэффициент связи k = 1, а коэффициент рассеяния = 0.    

Существует     еще     понятие идеального трансформатора, у которого потери равны нулю, индуктивности катушек бесконечно велики, а их отношение равно коэффициенту трансформации ω₂— число витков первичной и вторичной катушек. В идеальном трансформаторе отношение как токов, так и напряжений не зависит от нагрузки и определяются только коэффициентом трансформации k_тр.

Трансформатор с ферромагнитным сердечником. Ферромагнитный сердечник применяется для увеличения магнитного потока и связи между катушками, что приводит к росту мощности, отдаваемой во вторичную цепь трансформатора. При этом по своим свойствам он приближается к идеальному трансформатору, но становится в общем случае нелинейным устройством вследствие появления дополнительных потерь на гистерезис и вихревые токи. Однако на практике трансформатор с ферромагнитным сердечником стараются конструировать таким образом, чтобы нелинейность была мала и ею можно было пренебречь. Тогда расчет подобного трансформатора можно осуществить на основе двухконтурной схемы замещения, изображенной на рис. 3.30 с параметрами, приведенными к параметрам первичной обмотки. Данная схема может быть получена по аналогии со схемой рис. 3.28 с учетом потерь в стали Go и намагничивания Во. Приведенные значения X'_S2, I'2 определяются согласно равенствам:

3.10. Баланс мощности

Представим пассивную электрическую цепь, находящуюся под воздействием источника гармонического напряжения, в форме двухполюсника (см. рис. 1.1). Под воздействием напряжения и_nb = = U_msinωt в цепи протекает ток i = I_msin(ωt — φ). Отдаваемая источником в цепь за период Т средняя мощность

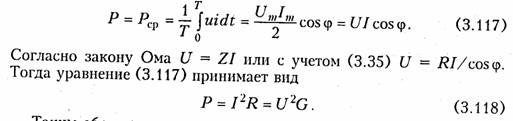
Таким образом, средняя за период мощность Р равна мощности, рассеиваемой на резистивном сопротивлении (проводимости) цепи. В этой связи мощность Р носит название активной и измеряется в ваттах (Вт).

Кроме активной мощности Р в цепях гармонического тока используют понятие реактивной мощности

Это отношение в энергетике называется коэффициентом мощности (косинусом φ) и является важной характеристикой электрических машин и линий электропередачи.  Чем выше cos φ,  тем

меньше потери энергии в линии и выше степень использования электрических машин и аппаратов. Максимальное значение cos φ = 1, при этом Р = S, Q = 0, т. е. цепь носит чисто активный характер и сдвиг фаз между током i и напряжением и равен нулю. Условие передачи максимальной мощности от генератора в нагрузку можно найти из условия

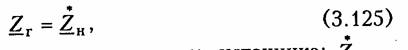
где Zj — комплексное внутреннее сопротивление источника; Z_H — комплексно-сопряженное сопротивление нагрузки. Это условие следует непосредственно из рассмотрения эквивалентной схемы, приведенной на рис. 3.31. Ток в данной цепи достигает максимума при Х_г = — Х_H и выполнении условия R_Г = R_H (см. § 2.6), что и доказывает равенство (3.125). При этом мощность в нагрузке будет определяться уравнением

По аналогии с треугольниками токов и напряжений, сопротивлений и проводимостей (§§ 3.4 и 3.5) можно ввести треугольники мощностей. Так согласно (3.121) и (3.122) треугольник мощностей для цепи, носящий индуктивный характер будет иметь вид, изображенный на рис. 3.32, а, а для цепи с емкостным характером — на рис. 3.32, б.

Рассмотрим условие баланса мощности в цепях при гармоническом воздействии. В силу справедливости первого и второго законов Кирхгофа для комплексных действующих значений тока I и напряжений U_в каждой из ветвей рассматриваемой цепи можно записать теорему Телледжена (1.35) в комплексной форме:

Однако поскольку ЗТК справедлив и по отношению к сопряженным токам то уравнение (3.127) можно записать в виде

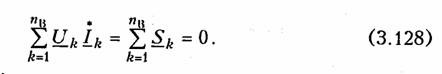
Уравнение (3.128) отражает баланс комплексной мощности, согласно которому сумма комплексных мощностей, потребляемых всеми ветвями цепи, равна нулю. Баланс комплексной мощности можно сформулировать и в другой форме: сумма комплексных мощностей, отдаваемых независимыми источниками, равна сумме комплексных мощностей, потребляемых остальными ветвями электрической цепи:

Условие баланса активных мощностей непосредственно вытекает из закона сохранения энергии.

3.11. Модели электрических цепей

с зависимыми источниками

Интегрирующие и дифференцирующие цепи. Интегрирующие и дифференцирующие цепи находят широкое применение в различных устройствах импульсной и вычислительной техники для формирования линейно изменяющихся напряжений и токов, селекции сигналов, линейного преобразования различных импульсов и т. д. Интегрирующая цепь описывается уравнением

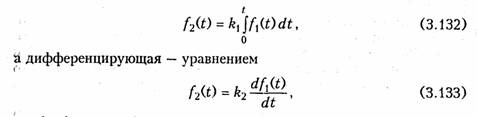
где k₁, k₂ — коэффициенты пропорциональности.

Простейшая интегрирующая и дифференцирующая цепи могут быть реализованы на базе RС-цепочки (рис. 3.33, 3.34). Действительно, если параметры интегрирующей цепочки (рис. 3.33) тако-

вы, что где t_И длительность входного сигнала, то на выходе такой цепи имеем

Однако точность интегрирования и дифференцирования такой пассивной цепи невысока. Поэтому на практике операции (3.132) и (3.133) реализуют с помощью активных цепей с зависимыми источниками, например на базе ОУ.

На рис. 3.35, а изображена схема интегратора, а на рис. 3.36, а — дифференциатора на ОУ. Определим комплексное действующее напряжение на выходе интегратора. Для этого воспользуемся эквивалентной схемой замещения ОУ в виде ИНУНа (рис. 3.35, б).

Приняв потенциал базисного узла V₄ = О составим уравнение равновесия узловых потенциалов:

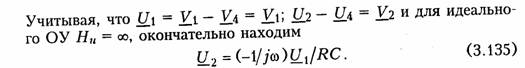
А так как деление U₁ на jω соответствует операции интегрирования входного сигнала u₁(t) (см. § 3.6), то схема, изображенная на рис. 3.34 является моделью идеального интегратора.

Аналогично можно получить для идеального дифференциатора (см. рис. 3.36):

т. е. u₁(t) и u₂(t) связаны между собой зависимостью, аналогичной (3.134). Знак «—» в уравнении (3.135) и (3.136) обусловлен поворотом на угол я фазы входного сигнала поданного на инвертирующий вход ОУ.

ARC-цепь второго порядка. На рис. 3.37 изображена активная RС-цепь (ARC-цепь) второго порядка, которая находит широкое применение в качестве типового звена различных устройств: фильтров, корректоров и др. (см.гл.14, 17, 18).

Приняв потенциал узла V₅ = 0 (базисный узел) составим для узлов 3 и 4 уравнения по методу узловых потенциалов (рис. 3.37, б):

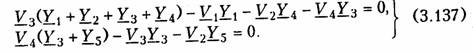
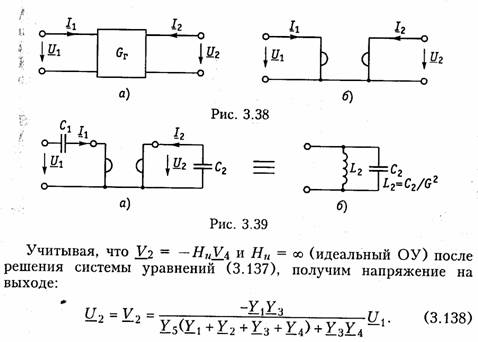
Гиратор. Гиратором называют необратимый четырехполюник (рис. 3.38, а), описываемый уравнениями где G_r проводимость гиратора.

Условное изображение гиратора показано на рис. 3.38, б. Нагрузим гиратор сопротивлением нагрузки Z₂. Входное сопротивление гиратора

т. е. обратно сопротивлению нагрузки, поэтому гиратор часто называют инвертором положительного сопротивления. Свойство (3.139) является очень важным, поскольку позволяет имитировать индуктивность с помощью емкости. Действительно, если

 — эквивалентная индуктивность. Это свойство гираторов является очень ценным для микроэлектроники, поскольку изготовление индуктивностей по интегральной технологии представляет сложную задачу. Использование же гираторов с малым значением G_r позволяет из небольших емкостей С моделировать большие значения индуктивности L.

Существуют и другие многочисленные применения гиратора: преобразование напряжения и тока, моделирование Т- и П- образных звеньев с катушками индуктивности, трансформаторов, резонансных контуров. В качестве примера на рис. 3.39 изображена Модель параллельного колебательного контура (рис. 3.39, б) на базе гиратора (3.39, а).

Важным свойством гиратора является то, что он не вносит энергии в цепь и не потребляет ее из цепи, т. е. ведет себя как пассивный элемент без потерь. Это следует непосредственно из уравнений

гиратора.

Реализация гиратора осуществляется с использованием активных элементов. Например, ОУ (на базе двух источников ИТУН: на базе ИТУН и ООС; на основе двух ПОС и др.). На рис. 3.40 изображена схема гиратора с двумя ИТУН, выполненными на базе ОУ.

Вопросы и задания для самопроверки

1.  В чем различие между мгновенным значением синусоидального тока и его действующим значением?

2.  Какой формулой связаны между собой активная, реактивная составляющие и комплексное напряжение?

3.  Как ориентированы между собой векторы тока и напряжения на индуктивности (емкости)?

4.  Может ли напряжение на индуктивности (емкости) в цепочке из последовательно соединенных RLC превышать уровень приложенного напряжения?

5.  Две индуктивности L₁ = 5 мГн и L₂ — 15 мГн включены последовательно.   Определить   их  эквивалентное   сопротивление  на частоте f — 1000 Гц.

Ответ:   Xl = 125,6 Ом.

6.  В схеме, изображенной на рис. 3.7, U = 10 В, падение напряжения на индуктивности u_l = 5 В, на емкости и_c = 11 В. Определить падение напряжения на резисторе u_r.

Ответ:   ur = 8 В.

7.  Вычислить  эквивалентное   сопротивление  двух   конденсаторов С₁ = 5 мкФ и С₂ = 15 мкФ, включенных параллельно на частоте f = 5 кГц.

Ответ:   Х_с = 1,59 Ом.

8.  Амперметр, включенный в ветвь с резистором R на рис. 3.10, показывает i_R = 3 А, включенный в цепь с индуктивностью — i_L — 3 А, а включенный последовательно с емкостью — ic — 7 А. Какую величину тока покажет амперметр, включенный на входе схемы?

Ответ:   i = 5 А.

9.   Вычислить входные сопротивления схемы рис. 3.10 на частоте f=10 кГц, если R = 100 Ом, L = 1 мГн, С = 1 мкФ.

Ответ    Z = 4,4 - j20,5 Ом.

10.  Чему равны максимальное и минимальное значения коэффициента связи между катушками?

11.  В каких единицах измеряется взаимная индуктивность?

12.  Может ли суммарная индуктивность двух индуктивно связанных катушек быть равной 0?

13.  К схеме рис. 3.19 приложено напряжение U = 10 В. Сопротивление резисторов R₁ = R₂ = 40 Ом. Индуктивные сопротивления катушек Xl₁ = 100 Ом, X_L2 — 50 Ом. Коэффициент связи между ними К = 0,6. Определить разность потенциалов между одноименными зажимами этих катушек.

Ответ    U = 4+j4,88 В.

14.  В схеме на рисунке 3.21  (б) сопротивление резисторов R₁ = = 20 Ом,  R₂ ⁼  0  Ом,  сопротивление индуктивностей X_L1 = = X_l2 = 30 Ом, коэффициент связи между катушками К = 0,5. Определить эквивалентное входное сопротивление цепи.

Ответ:   Zb_X = 4,76 + j7,56 Ом.

15.  Каковы особенности расчета цепей с индуктивными связями?

16.  Какое устройство называется трансформатором?  Какие виды трансформаторов известны?

17.  Составить уравнения баланса мощности для схемы, изображенной на рис. 3.15.

18.  В схеме, изображенной на рис. 3.7, U = 10 В, u_l = 5 В, и_с =  11 В, сопротивление резистора R — 40 Ом. Определить комплексную мощность, потребленную цепью.

Ответ:  S_ПОтр = 1,6 — j1,2.

19.  Каким образом можно уменьшить реактивную составляющую мощности потребляемую предприятием из сети?

20.  Каковы схемы интегрирующих и дифференцирующих цепей на операционном усилителе?

ГЛАВА 4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

 ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

4.1. Комплексные передаточные функции линейных

электрических цепей

Важнейшей характеристикой линейной электрической цепи является комплексная передаточная функция H(jω). При этом электрическую цепь удобно изображать в виде четырехполюсника (рис. 4.1), на входные зажимы (1 — 1’) которого подается сигнал в виде напряжения с комплексной амплитудой Uт₁, или тока с комплексной амплитудой I_m1, а реакция снимается с выходных зажимов (2 — 2') также в виде напряжения или тока с комплексными амплитудами U_m2, I_m2. Комплексная передаточная функция (КПФ) определяется как отношение комплексной амплитуды реакции цепи к комплексной амплитуде входного воздействия.

В зависимости от типов входного воздействия и реакции цепи различают следующие виды КПФ:

1. Комплексная передаточная функция по напряжению

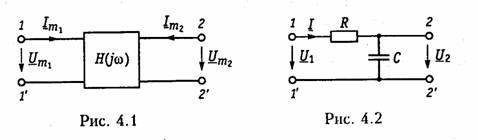
Комплексные передаточные функции определяются на частоте со сигнала воздействия и зависят только от параметров цепи.

Как всякую комплексную величину H(jω) можно представить в показательной, тригонометрической и алгебраической форме:

есть   вещественная   и   мнимая   части   комплексной   передаточной функции цепи.

Из (4.5) —(4.8) нетрудно получить соотношения, связывающие АЧХ и ФЧХ с вещественными и мнимыми частями комплексной передаточной функции

АЧХ и ФЧХ являются наиболее фундаментальными понятиями теории цепей и широко используются на практике. Важность этих характеристик для систем электрической связи, радиовещания и телевидения объясняется самой природой передачи сигналов определенного спектрального состава по каналам связи. Требования к АЧХ и ФЧХ различных устройств являются определяющими при проектировании любой аппаратуры связи, так как от степени их выполнения во многом зависит качество передачи информации.

Пример. Определить КПФ по напряжению H_u(jω), АЧХ и ФЧХ цепи, изображенной на рис. 4.2. Согласно (4.1) запишем:

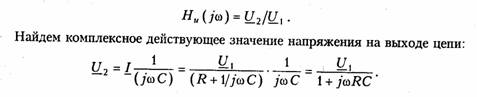
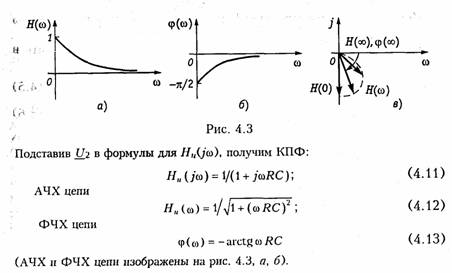
АЧХ и ФЧХ цепи можно представить единым графиком, если построить зависимость КПФ H(jω) от частоты со на комплексной плоскости. При этом конец вектора H(jω)  опишет некоторую кривую, которая называется годографом комплексной передаточной функции (рис. 4.3, в).

В ряде случаев частотные характеристики цепи могут изменяться в очень широких пределах, поэтому более удобно их оценивать в логарифмическом масштабе. С этой целью для оценки АЧХ вводят понятие логарифмической амплитудно-частотной характеристики (ЛАХ):

Оценивается ЛАХ согласно (4.14) в децибелах (дБ). В активных цепях К называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления оперируют ослаблением цепи:

которое также оценивается в децибелах.

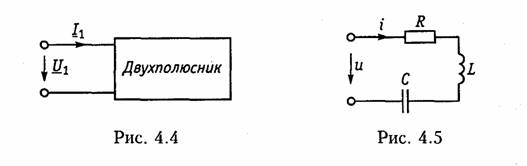
Наряду с передаточными функциями (4.1) —(4.4) в ряде случаев (см. гл. 16, 17,18) находят применение комплексные функции, определяющиеся отношением комплексной реакции к комплексному воздействию на входных зажимах электрической цепи (рис. 4.4)

Функции вида (4.16) носят название комплексных входных функций цепей.

4.2. Частотные характеристики последовательного колебательного контура

В радиотехнике и электросвязи большое значение имеет явление резонанса. Резонансом называют такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением равен нулю. Цепи, в которых возникает явление резонанса, называют колебательными контурами, или резонансными цепями.

Колебательные контуры и явления резонанса находят широкое применение в радиотехнике и электросвязи. Резонансные цепи являются составной частью многих радиотехнических устройств: избирательные цепи в радиоприемниках и усилителях, частотно-зависимые элементы автогенераторов, фильтров, корректоров, других устройств. Для получения высоких технико-экономических показателей (избирательности, полосы пропускания, коэффициента прямоугольности, равномерности и т. д.) резонансные цепи должны иметь достаточно сложную структуру (многоконтурные связанные цепи, активные резонансные системы и др.). Некоторые из этих систем будут рассмотрены в гл. 15, 17. В настоящей главе изучим основные особенности работы цепей в режиме резонанса на примере простейших колебательных контуров.

Простейший колебательный контур содержит индуктивный и емкостный элементы, соединенные последовательно {последовательный контур) или параллельно (.параллельный контур). В последнее время широкое распространение получили резонансные цепи на базе операционных усилителей (ОУ). Различают два типа резонансов: напряжений и токов. В последовательном контуре возникает резонанс напряжений, а в параллельном — резонанс токов.

Частоту, на которой наблюдается явление резонанса, называют резонансной.

На рис. 4.5 изображена схема последовательного контура с реактивными элементами L и С и резистивным сопротивлением R, характеризующим потери в контуре. Приложим к контуру гармоническое напряжение  с частотой ω.   Комплексное  входное сопротивление контура на данной частоте определяется согласно уравнению

На резонансной частоте комплексное сопротивление носит чисто активный характер, т. е. Z = R, ток совпадает по фазе с приложенным напряжением и достигает максимального значения Iо =  U/R. Реактивные сопротивления контура на резонансной частоте ω₀ равны друг другу:

Величина ρ носит название характеристического сопротивления контура.

Резонансные свойства контура характеризуются добротностью контура, которая в общем случае определяется величиной

где W_p — максимальные значения реактивной энергии, запасенной в контуре при резонансе; W_t — активная энергия, поглощаемая в контуре за период Т. Величина, обратная добротности, называется затуханием контура и обозначается d:

Величина Q безразмерна и обычно колеблется для реальных контуров от 10 до 100 и выше. Для выяснения физического смысла параметра Q исследуем энергетические соотношения в контуре при резонансе. Положим, например, что при резонансе ток в цепи Определим согласно (1.10) и (1.13) сумму энергий электрического и магнитного полей:

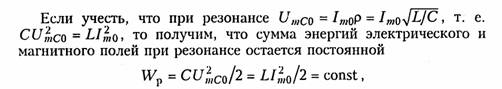
так как уменьшение Wl сопровождается увеличением We и наоборот. Таким образом,

происходит периодический обмен энергией между элементами I и С без участия источника. Энергия источника расходуется только на покрытие тепловых потерь в элементе активного сопротивления R; реактивная мощность при резонансе не потребляется.

Активная энергия, рассеиваемая в контуре за период Т, равна

Таким образом, добротность Q показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение. Отсюда следует и термин «резонанс напряжений». Это свойство контура «усиливать» приложенное напряжение резонансной частоты широко используется на практике.

Величины ρ,  ω_о,  Q,  d являются вторичными параметрами контура в отличие от величин R, L, С называемых первичными.

Анализируя характер уравнений напряжений и токов в RLC-цепи, фазовых сдвигов между ними при гармоническом воздействии нетрудно видеть, что они являются частотно-зависимыми. Эта зависимость вытекает непосредственно из зависимости реактивных   элементов  Xl и  Хс  .от

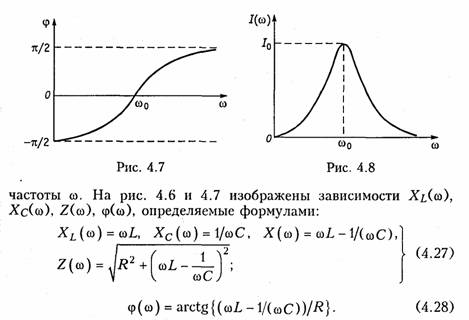
Из представленных характеристик следует, что при ω <ω₀ цепь имеет емкостный характер (Х<0; φ <0)и ток опережает по фазе приложенное напряжение при ω >ω₀ характер цепи индуктивный (X > 0; φ > 0) и ток отстает по фазе от приложенного напряжения; при со = соо наступает резонанс напряжений (X = 0; φ = 0) и ток совпадает по фазе с приложенным напряжением. Полное сопротивление цепи принимает при этом минимальное значение Z = R.

Зависимость действующего значения тока от частоты можно найти из уравнения (4.18)*:

Зависимости I(ω), Ul(ω), U_c(ω) называются резонансными характеристиками тока и напряжений. Анализ зависимости I(ω) показывает, что она достигает максимума при резонансе ω =ω₀

Выходное напряжение обычно снимается с емкостного или индуктивного элемента контура. В соответствии с этим представляет наибольший практический интерес КПФ по напряжению относительно элементов С и L:

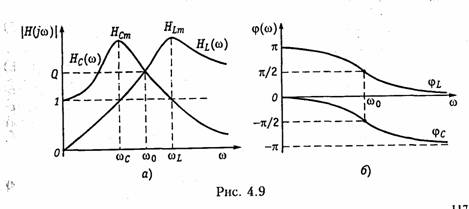
Анализ полученных зависимостей показывает, что с увеличением добротности Q (уменьшением затухания d) частоты ωс и ω_L сближаются с резонансной частотой ω_о.При этом C_Cт и H_Lm возрастают.

Степень отклонения режима колебательного контура от резонанса принято оценивать абсолютной, относительной и обобщенной расстройками.  Отклонение от резонансного режима может происходить в результате изменения частоты; задающего генератора или вариации параметров контура.

Расстройки определяются следующим образом:

абсолютная

\

Наиболее широко в теоретических исследованиях применяется обобщенная расстройка ζ, так как ее использование существенно упрощает расчет. Например, модуль входной проводимости можно записать через обобщенную расстройку ζ, в форме

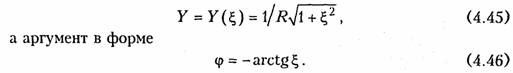
Важной характеристикой колебательного контура является полоса пропускания. В общем случае абсолютной полосой пропускания называют диапазон частот в пределах которого коэффициент передачи уменьшается в √2 раз по сравнению с максимальным*. Абсолютная полоса пропускания равна

Уравнения (4.50) могут быть положены в основу экспериментального определения добротности по резонансной кривой тока I(ω). Формула (4.50) показывает, что чем выше добротность Q, тем меньше полоса пропускания и наоборот. Причем, поскольку с увеличением потерь R добротность контура падает, то подключение к контуру сопротивления нагрузки или источника с внутренним сопротивлением приводит к расширению полосы пропускания.

Пример. Определить полосу пропускания контура, нагруженного на резистивное сопротивление R_н (рис. 4.11, й).

Преобразуем параллельный участок С и R_H в эквивалентный последовательный с помощью формул (3.56):

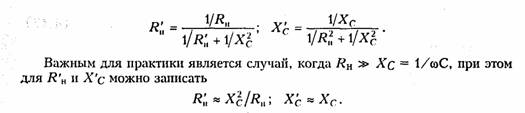
т. е. при подключении высокоомной нагрузки к контуру его резонансная частота не изменяется, но увеличиваются потери в контуре (рис. 4.11, б). При этом уменьшается добротность Q' = p/(R +R_H’) и увеличивается полоса пропускания контура (4.10).

В заключение следует отметить, что на практике обычно используются высокодобротные контуры, причем низкоомные нагрузки подключаются к контурам через различные согласующие устройства (трансформаторы, повторители и др.). Для получения высоких качественных характеристик (большого входного и низкого выходного сопротивлений, высокой добротности, малой чувствительности резонансной частоты и выходного сигнала от нагрузки) применяют электронные аналоги колебательных контуров, реализуемых на базе зависимых источников. На рис. 4.12 изображена схема колебательного контура, реализованного на базе ARC-звена, второго порядка (рис. 3.37, а), где принято Y₁ = G₁; Y₂ =jωC₂; Y₃ ⁼ Gз; Y₄ = G₄; Y₅ = jωC₅. При этом комплексная передаточная функция цепи с учетом (3.138)

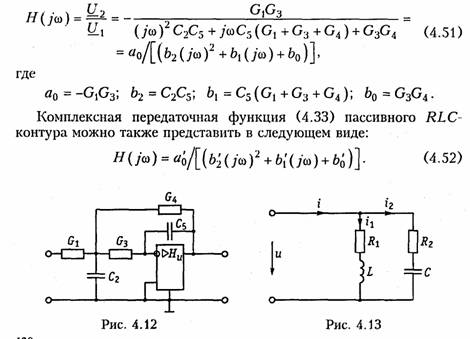
где т. е. (4.52) совпадает с (4.51) с точностью до постоянных множителей.

Таким образом, с помощью рассмотренной активной цепи можно получить электронный аналог колебательного контура. На базе активных элементов можно реализовать и другие схемы электронных аналогов колебательных контуров, важным преимуществом которых является отсутствие индуктивностей, высокое значение добротности, слабо зависящей от нагрузки, легкость перестройки.

4.3. Частотные характеристики параллельного

 колебательного контура

Простейший параллельный колебательный контур с потерями в ветвях R ₁и R₂ имеет вид, изображенный на рис. 4.13. Комплексная входная проводимость такого контура

Из уравнения (4.56) следует, что резонанс в параллельном контуре возможен лишь в случае неотрицательности подкоренного выражения (т. е. при R₁ < ρ и R₂< ρ или R₁> ρ и R₂ > ρ).

Реактивные составляющие токов в ветвях при резонансе равны друг другу:

При этом ток в неразветвленной части цепи определяется из уравнения

где активное сопротивление Яоэ, называют эквивалентным резонансным сопротивлением параллельного контура. Как следует из уравнения (4.58), входной ток контура совпадает по фазе с приложенным напряжением. Величину R₀₃ можно найти из условия резонанса токов. Так как при резонансе токов В = 0, то согласно (4.53) и (4.54) полная эквивалентная проводимость контура

Наибольший теоретический и практический интерес представляют резонанс токов в контурах без потерь и с малыми потерями.

Контур без потерь. Для контура без потерь (R₁= R₂ = 0) уравнение резонансной частоты (4.56) принимает вид

т. е. совпадает с выражением (4.21) для последовательного контура. Эквивалентное сопротивление контура без потерь R_0Э = ∞ и входной ток равен нулю, а добротность обращается в бесконечность. Комплексы действующих значений токов в ветвях

т. е. ток в индуктивности отстает от приложенного напряжения на π/2, а в емкости опережает на π/2. На рис. 4.14, а изображена векторная диаграмма токов для этого случая при U = Ue^]0 = U.

Сумма энергий электрического и магнитного полей для параллельного контура без потерь, как и для последовательного контура

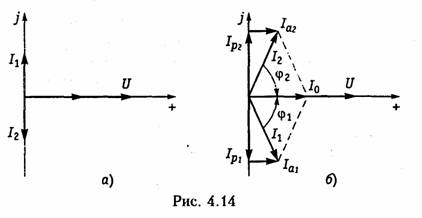
остается неизменной, т. е. энергетические процессы протекают аналогично процессам в последовательном контуре.

Частотные  зависимости  характеристик  параллельного  контура от частоты имеют вид

т. е. является зеркальным отображением модуля реактивной проводимости |В(ω)| (на рис. 4.15 показано штриховой линией).

Контур с малыми потерями  Резонансная частота для этого случая будет приближенно совпадать с частотой шо. Для контура с малыми потерями можно принять, что ρ>> R₁ R₂, тогда

Из уравнений (4.67) и (4.69) следует, что отношение токов в ветвях к току в неразветвленной части цепи равно добротности контура:

т. е. ток в реактивных элементах L и С при резонансе в Q раз больше тока на входе контура (отсюда термин «резонанс токов»). На рис. 4.14, б изображена векторная диаграмма токов для этого

случая. В контуре с потерями сумма энергий электрического и магнитного полей не остается постоянной с течением времени.

Интересен случай R₁ = R2 = ρ. Как; следует из уравнения (4.56), для ω_р получаем неопределенность, при этом входное сопротивление контура имеет чисто резистивный характер на любой частоте (случай безразличного резонанса).

Рассмотрим частотные характеристики контура с малыми потерями. Комплексное эквивалентное сопротивление контура можно определить уравнением

На рис. 4.16, а изображены нормированные относительно i?₀» частотные характеристики R_a/Ro_Э, X_Э/Ro_Э, и Z_Э/Ro_Э как функции обобщенной расстройки ζ. Фазочастотная характеристика цепи оп ределится уравнением (рис. 4.16. б):

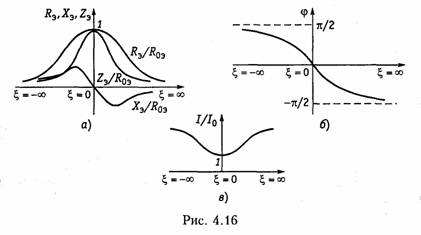
Анализ полученных зависимостей показывает, что по своему виду частотные характеристики контура с потерями существенно отличаются от характеристик контура без потерь. Это отличие касается прежде всего зависимости реактивного сопротивления контура от частоты: для контура с потерями при резонансе оно оказывается равным нулю (см. рис. 4.16, а), а в контуре без потерь терпит разрыв (см. рис. 4.15).

Зависимость комплексного входного тока от частоты определяется из уравнения

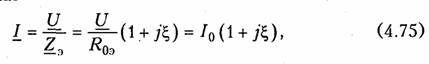
т. е. при резонансе (ζ = 0) ток принимает минимальное значение, определяемое формулой (4.58) (рис. 4.16, в).

Частотная зависимость токов I₁(ω) и I₂(ω) в ветвях определяется согласно закону Ома:

Сравнение формул (4.32) —(4.38) с формулами (4.78) —(4.81) показывает, что КПФ по току параллельного контура дуально соответствует КПФ по напряжению для последовательного контура.

Рассмотрим, как влияет на резонансные свойства параллельного контура подключение его к источнику с задающим напряжением U_r внутренним сопротивлением R_r. При этом выходное напряжение снимается с контура (рис. 4.17). Нетрудно видеть, что комплексное напряжение на контуре

На рис. 4.18 показан характер этих зависимостей при различных сопротивлениях R_r источника.

Полоса пропускания параллельного контура определяется как полоса частот, на границе которой напряжение на контуре уменьшается в √2 раз относительно U_Kp (см. рис. 4.18):

Сравнение уравнении (4.50) с уравнениями (4.91) и (4.92) показывает, что параллельный контур в общем случае имеет более широкую полосу пропускания, чем последовательный с такой же добротностью. И только при R_r =∞ (см. рис. 4.18) их полосы пропускания равны.

Таким образом, для улучшения избирательных свойств параллельного контура его необходимо возбуждать источником тока. Из уравнения (4.84) также следует, что параллельный контур нельзя использовать для усиления напряжения, если использовать независимый источник, так как при этом U_Kp < U_r.

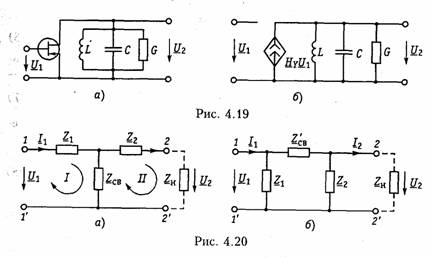
Поэтому для усиления напряжения и получения высокой добротности параллельного контура используют активные цепи с зависимыми источниками тока. На рис. 4.19 приведен пример подобной схемы на базе полевого транзистора и его эквивалентная схема замещения.

4.4. Частотные характеристики связанных

 колебательных контуров

В ряде радиотехнических устройств (входные цепи радиоприемников, усилители, фильтры сосредоточенной селекции, выходные каскады радиопередатчиков и др.) применяются системы связанных колебательных контуров. Отличительной особенностью связанных контуров является лучшая избирательность*АЧХ по сравнению с одиночными контурами. Это позволяет лучше отфильтровать частоты за границами полосы пропускания, обеспечить большую равномерность, а, следовательно, меньшие частотные искажения сигнала в полосе пропускания. На рис. 4.20 приведена обобщенная схема двух связанных колебательных контуров: с внутренней связью (рис. 4.20, а) и внешней связью (рис. 4.20, б), где Z₁, Z₂ — комплексное сопротивление первого и второго контуров, Z_CB — комплексное сопротивление связи между контурами, Z_H — сопротивление нагрузки.

Переход от схемы, изображенной на рис. 4.20, а к схеме рис. 4.20, б можно осуществить с помощью формул преобразования «звезда —треугольник» (см. § 2.2).

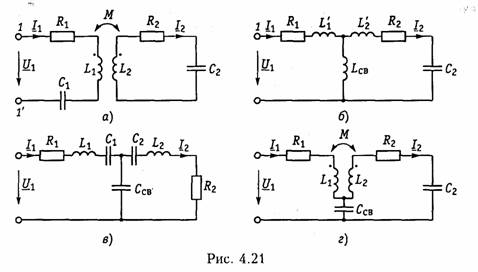
В зависимости от вида связи различают контуры с трансформаторной связью (рис. 4.21, а), автотрансформаторной связью (рис. 4.21, б), емкостной связью (внутренней) (рис. 4.21, в), комбинированной связью (рис. 4.21, г) и др. Важнейшей характеристикой связанных контуров является коэффициент связи. Для контура с трансформаторной связью коэффициент связи определяется известной формулой (3.74). Для других видов связи коэффициент k можно найти с помощью формулы

где Х_CB — реактивная составляющая комплексного сопротивления связи Z_CB; X₁, X₂ — реактивные сопротивления первого и второго контуров того же знака, что и реактивное сопротивление связи Х_CB. Например, для контура с индуктивной автотрансформаторной связью (рис. 4.21, б) коэффициент связи

Исследование частотных характеристик связанных колебательных контуров удобно вести с помощью одноконтурных схем замещения (рис. 4.22), которые могут быть получены для обобщенной схемы (рис. 4.20, а) аналогично уравнениям трансформатора (3.106):

Резонанс в системе связанных контуров достигается соответствующей их настройкой и подбором оптимальной связи между ними. В зависимости от видов настройки различают:

1. Первый частный резонанс, который обеспечивает максимум тока и достигается настройкой первого контура до обеспечения условия: Х₁₁ = —X_1BH (см. рис. 4.22, а).

2.  Второй частный резонанс, обеспечивающий максимум тока и который достигается настройкой до обеспечения условия Х₂₂ = —X₂вн (см. рис. 4.22, в).

3.  Сложный резонанс — осуществляется путем настройки каждого контура на частный резонанс и подбором оптимального сопротивления связи

Нетрудно видеть, что настройка I контура в первый частный резонанс и подбор связи (4.100) эквивалентен условию  аналогично второй частный резонанс совместно с условием (4.100)

эквивалентен условию

4. Полный резонанс — достигается настройкой каждого контура в индивидуальный резонанс (Х₁₁ = 0; Х₂₂ = 0) и подбором оптимальной связи:

При этом ток /2 определяется также формулой (4.101).

Уравнение сопротивления связи (4.100) может быть получено из уравнения  при условиях где I₂ определяется из (4.99). Аналогично уравнение (4.102) получаем из решения уравнения

Сравнение сложного и полного резонансов показывает, что в последнем случае _I2maxmax. достигается при меньшем сопротивлении связи.

Связанные контуры обычно используются в режиме передачи максимальной мощности во вторичный контур: P₂ —I²₂ R₂₂, поэтому среди частотных характеристик наибольший интерес представляет зависимость I₂(ω).

Выразим сопротивление контуров Z₁₁ и Z₂₂ (см. рис. 4.20, а) через обобщенную расстройку ζ:

Анализ формулы (4.107) показывает, что в зависимости от соотношения между коэффициентом связи k и затуханием контура d = 1/Q могут иметь место три основных случая:

1)  k < d — слабая связь (А < 1);

2)  k > d — сильная связь (A > 1);

3)  k = d — критическая связь (А = 1).

В зависимости от характера связи существенно изменяется вид АЧХ. Так, при слабой связи АЧХ имеет вид резонансной кривой (рис. 4.23), аналогичной одиночному колебательному контуру с максимумом при ζ = 0, при этом I_1тaх зависит от величины k: с увеличением k (или фактора связи A) I_2max растет, достигая I_2maxmax при k = d (A = 1) (критический случай).

С увеличением k > d (A > 1) характер зависимости тока I₂ от частоты существенно изменяется: АЧХ приобретает двугорбый характер (рис. 4.24). На частоте ζ = 0 образуется минимум тока, а на частотах

максимум I_2maxmax .

С учетом (4.47) из (4.108) можно найти уравнение частот со| и шн, на которых достигается максимум тока:

Полоса пропускания связанных контуров определяется из условия I₂ /I_2maxmax  =1/√2откуда с учетом (4.107)  получаем уравнение обобщенной расстройки,  соответствующей полосе пропускания:

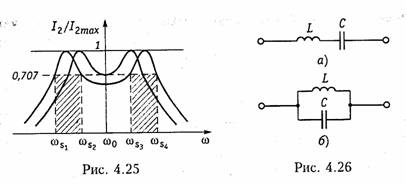
Из этого выражения видно, что при А > 1 полоса пропускания распадается на две (рис. 4.25) с граничными частотами ω_S1, ω_S2, ω_S3, ω_S4.Чтобы полоса пропускания не распадалась,на две, необходимо выполнить условие

где  I_2рез — значение тока I₂ на резонансной частоте (ζ= 0). Отсюда следует необходимое значение фактора связи А = 2,41. При этом максимальная относительная полоса пропускания связанных контуров δf_0max = 3,ld, т. е. в 3 раза больше, чем одиночного контура при той же добротности цепи (сравните с (4.50)).

При критической связи k = d, δf₀= 1,41d, т. е. относительная полоса шире, чем для одиночного контура.

Для случая слабой связи необходимо нормировать величину 1г относительно I₂рез:

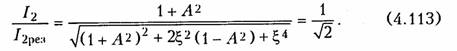
Далее находим обобщенную расстройку, соответствующую полосе пропускания

и относительную полосу пропускания связанных контуров:

Если связь очень слабая (A→0) то из (4.114) нетрудно видеть, что δf₀≈0,64d, т. е. существенно ниже полосы пропускания одиночного контура. Поэтому на практике связанные контуры при слабой связи обычно не используются. Фазочастотная характеристика связанных контуров может быть получена обычным способом из уравнения (4.104).

4.5. Частотные характеристики реактивных двухполюсников

Общие свойства реактивных двухполюсников. Наряду с комплексными передаточными функциями цепей, АЧХ и ФЧХ в задачах анализа и синтеза важно знать частотные зависимости входных функций цепи: входного сопротивления Z(jω) и входной проводимости Y(jω). При этом электрическая цепь рассматривается в виде двухполюсника с двумя парами зажимов, через которые они обмениваются энергией с внешними цепями (см. рис. 4.4). Существуют различные типы двухполюсников: активные и пассивные, линейные и нелинейные, реактивные (L, С) и двухполюсники общего вида (R, L, С). Из всего многообразия двухполюсников наибольший интерес представляют пассивные реактивные двухполюсники, состоящие только из иидуктивностей и емкостей. Важность этих двухполюсников объясняется тем, что они широко применяются в различных радиотехнических устройствах (LC-фильтры, корректоры, автогенераторы и др.). Кроме того свойства реактивных двухполюсников лежат в основе синтеза линейных электрических цепей (см. гл. 16, 17).

Простейшим реактивным двухполюсником является элемент индуктивности и емкости (одноэлементный двухполюсник). К двухэлементному двухполюснику относятся последовательный (4.26. а) и параллельный контуры без потерь (рис. 4.26, б). Функции входного сопротивления и проводимости этих двухполюсников равны:

На рис. 4.27 изображена зависимость функций входных сопротивлений двухполюсника (4.115) от частоты:

Двухполюсники называются эквивалентными, если они обладают одинаковыми входными функциями.

Двухполюсники называют обратными , если они удовлетворяют условию:

где R — некоторое постоянное сопротивление.

Рассматриваемые двухполюсники Z_a(jω) и Z₆(jω) являются потенциально обратными, так как условие (4.116) для них выполняется при

Из трех реактивных элементов можно составить уже четыре схемы двухполюсников. На рис. 4.28 приведены две возможные схемы. Их функции входных сопротивлений будут:

На рис. 4.29 изображены частотные характеристики (4.118) и (4.119).

Анализируя приведенные схемы и графики, можно сформулировать основные свойства реактивных двухполюсников:

1.   Входное сопротивление растет с ростом частоты (dZ (jω)/ dω > 0).

2.   Количество резонансных частот на единицу меньше числа элементов.

3.  Резонансы токов (полюса Z(jω)) и напряжений (нули Z(jω)) чередуются, причем, если входное сопротивление двухполюсника на нулевой частоте равна нулю, то первым наступает резонанс токов.

4.  В числителе функции входного сопротивления стоит множитель с частотами резонанса напряжения, а в знаменателе — резонанс токов.

5.  Множитель jω в уравнении Z(jω) стоит либо в числителе, если первым наступает резонанс токов,  либо в знаменателе,  если первый резонанс напряжений.

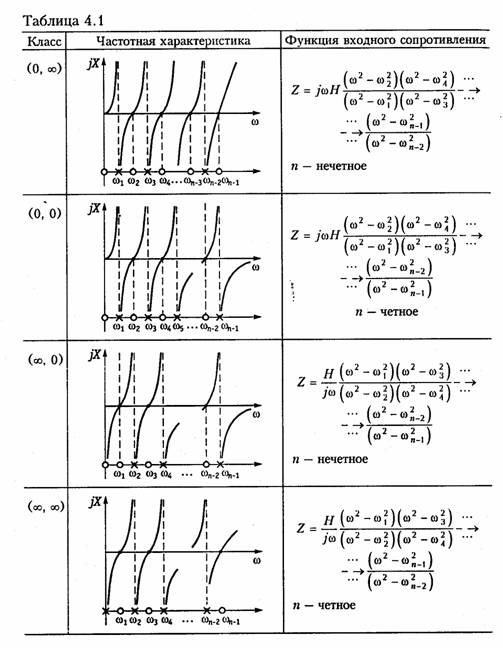
В зависимости от характера зависимой функции входного сопротивления на частоте ω = 0 и частоте ω = ∞ различают четыре класса реактивных двухполюсников: (0; ∞), (0; 0), (∞; 0), (∞; ∞). В табл. 4.1 приведены частотные характеристики двухполюсников различных классов и их функции входных сопротивлений. Внизу частотных характеристик показана полюсно-нулевая диаграмма, показывающая расположение полюсов — X и нулей — 0 по оси частот.

Канонические схемы реактивных двухполюсников. Наиболее распространенными в теории цепей являются канонические схемы, построенные по правилу (канону) Фостера и Кауэра.

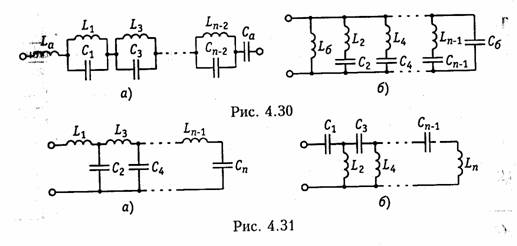
В схемах Фостера двухполюсник представляется либо в виде последовательного соединения параллельных колебательных контуров (первая схема Фостера) (рис. 4.30, а), либо в виде параллельно соединенных последовательных контуров (вторая схема Фостера") (рис. 4.30, б).

Коэффициент Н в  формулах (см. табл. 4.1) определяется как

 Например, для первой схемы Фостера класса (∞, ∞)

Н = L_a, для второй схемы Фостера класса (0, 0) Н = 1/С_б и т. д.

В схемах Кауэра двухполюсники представлены в виде цепочечных (лестничных) схем, в продольных ветвях которых находятся индуктивности, а в поперечных емкости (первая схема Кауэра, рис. 4.31, а), либо наоборот — в продольных емкости, а в    поперечных    —    индуктивности    (вторая    схема    Кауэра,рис. 4.31, б).

В зависимости от класса канонические схемы Фостера и Кауэра имеют частотные характеристики входных функций, изображенные

в табл. 4.1.

Положительной особенностью канонических схем Фостера и Кауэра является то, что нз всех эквивалентных двухполюсников с заданной частотной характеристикой, они имеют минимальное число элементов. При решении задач синтеза обычно входные функции в схемах Фостера представляются в виде разложения на простые дроби, а в схемах Кауэра — на цепные дроби (см. гл. 16).

4.6. Машинные методы анализа частотных характеристик электрических цепей

При расчете частотных характеристик цепи машинными методами представляют КПФ в виде отношений двух полиномов:

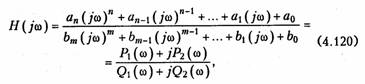
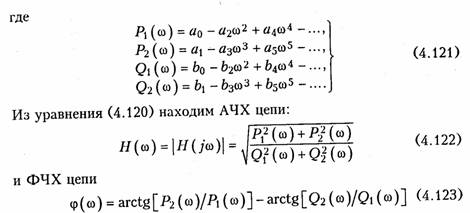
Для построения АЧХ и ФЧХ задаются равномерной либо логарифмической шкалой частот от f_min до f_max- Очередное значение частоты определяется из соотношения f_k+1 = c₂fk + с₁, где с₂, с₁ — коэффициенты, определяющие шаг по логарифмической и линейной шкале частот соответственно.

Затем на каждой из частот вычисляется АЧХ и ФЧХ цепи согласно формул (4.122) и (4.123). На рис. 4.32 приведена схема алгоритма расчета АЧХ и ФЧХ.

Если диапазон частот f_min и f_max, где расположены частотные характеристики цепи, заранее неизвестен, то положив с₁ = 0 и с₂ = = 0, можно в логарифмическом масштабе с большим шагом рас-

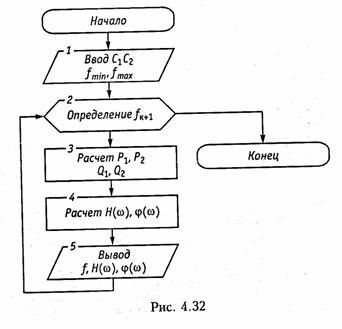
считать значение АЧХ в широком частотном диапазоне. После этого произвести более подробный расчет частотных характеристик цепи в выбранном диапазоне уже с равномерной шкалой частот с более мелким шагом.

Расчет частотных характеристик можно произвести и в базисе узловых потенциалов. Для этого уравнение равновесия (3.64) записывается в частотной области:

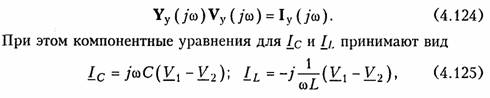
где V₁— V₂ — разность потенциалов на реактивном элементе.

Для решения (4.124) может использоваться как и для (3.64) либо стандартная программа обращения матрицы Yy(fω), либо решение системы линейных уравнений с комплексными коэффициентами по методу Гаусса. Полагая спектр входного сигнала, равный единице, с помощью решения для каждой из частот со уравнения (4.124) можно получить АЧХ и ФЧХ соответствующего узлового напряжения. Так, если, например, принять, что выходное напряжение снимается с k-го узла V_k, то после определения V_y(fω ) из решения системы (4.124) из вектора

Пример. Рассчитать передаточную функцию, АЧХ и ФЧХ цепи, изображенной на рис. 4.33

1. Задание схемы в ЭВМ. Для расчета на ЭВМ характеристик цепи необходимо схему цепи ввести в ЭВМ.

Одним из наиболее простых и удобных способов задания схемы в ЭВМ является табличный способ ее описания в виде соединения узел - ветвь. Для задания схемы в программах анализа все ее ветви и узлы нумеруются (используются простые узлы). Каждый элемент цепи характеризуется типом (R, L, С); узлами, между которыми он включен и численным значением.

R₁ = 100 Ом; L₁ = 0,1 мГн; R₂ = 200 Ом.

Схема, изображенная на рис. 4.33 полностью описывается следующей таблицей соединений:

R₁       1,2;      100

L₁ 2,3;     0.0001

R₂;      3,0;     200

Первый символ указывает тип (R, L, С) и порядковый номер элемента ветви. Вторая и третья цифры в спецификации указывают номера узлов, между которыми включен элемент. Последняя цифра характеризует значение параметра.

2. Расчет передаточной функции цепи. Приведем последовательность расчета передаточной функции цепи с использованием метода узловых напряжений:

-   По введенной в ЭВМ схеме определяется структурная матрица .

-   Формируются матрицы эдс источников напряжения  и проводимостей ветвей

-   Формируется матрица узловых проводимостей

-   Формируется матрица узловых токов

-   Определяется матрица узловых напряжений:

-   Положив U_BX=1B, определяется матрица комплексной передаточной функции

-   Рассчитываются и строятся графики АЧХ (H(f)) и ФЧХ (φ_н (f))

- Структурная матрица

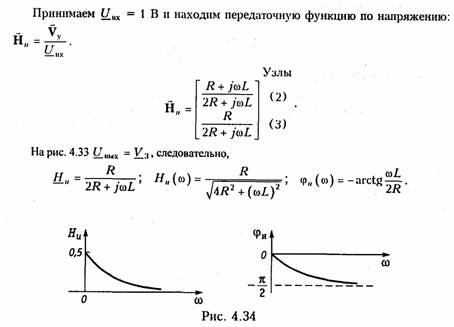
На рис. 4.34 приведены графики АЧХ- H_H (ω) и ФЧХ- φ_u (ω).

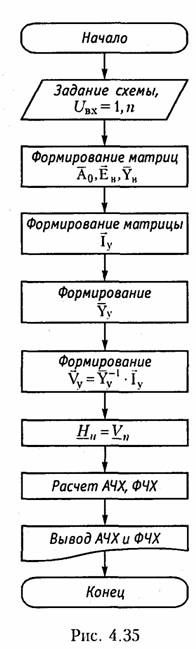
3. Алгоритм расчета АЧХ и ФЧХ. На рис. 4.35 приведен алгоритм расчета АЧХ и ФЧХ цепи на основе метода узловых напряжений.

Вопросы и задания для самопроверки

1.  Что такое АЧХ и ФЧХ цепи, если рассматривается ее комплексная передаточная функция по напряжению?

2.  Почему резонанс в последовательном колебательном контуре называется резонансом напряжений?

3.  Что такое добротность колебательного контура?

4.  Что такое полоса пропускания колебательного контура?

5.  Почему резонанс в параллельном колебательном контуре называется резонансом токов?

6.  Каковы эквивалентные схемы последовательного и параллельного контуров на резонансной частоте?

7.  Почему последовательный контур должен работать с источником сигнала,  имеющим малое внутреннее сопротивление,  а параллельный контур — с источником, имеющим большое внутреннее сопротивление?

8.  В чем заключается достоинство связанных колебательных контуров по сравнению с одиночным?

9.  Каковы основные свойства реактивных двухполюсников?

10.  Качественно построить АЧХ цепей, получаемых на рисунке 4.36.

11.  Последовательный    колебательный    контур,    имеющий    L  = 100 мкГн, С= 2,5 нФ, R = 6 Ом, работает с источником сигнала, у которого R_г = 2 Ом. Какова будет полоса пропускания системы до и после подключения нагрузки к емкостному элементу с сопротивлением R_H = 10 кОм?

Ответ:   Δf_a =12,7 кГц — ненагруженного и

Δf_a = 19,1 кГц — нагруженного контуров.

ГЛАВА 5. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ В

РЕЖИМЕ ПЕРИОДИЧЕСКИХ НЕГАРМОНИЧЕСКИХ

ВОЗДЕЙСТВИЙ

5.1. Негармонические периодические сигналы.

 Разложение в ряд Фурье

При передаче информации по каналам связи в процессе преобразования сигналов в различных устройствах, как правило, используют негармонические колебания, поскольку чисто гармонические колебания не могут являться носителями информации. Для передачи сообщений осуществляют модуляцию гармонического колебания по амплитуде — амплитудная модуляция (AM), частоте —частотная модуляция (ЧМ) или фазе — фазовая модуляция (ФМ), либо используют импульсные сигналы, модулируемые по амплитуде — амплитудно-импульсная модуляция (АИМ), ширине — широтно-импульсная модуляция (ШИМ), временному положению — время-импульсная модуляция (ВИМ). Существуют и другие, более сложные сигналы, формируемые по специальным законам. Отличительной чертой указанных сигналов является сложный негармонический характер. Несинусоидальный вид имеют токи и напряжения, формируемые в различных импульсных и цифровых устройствах (гл. 19), несинусоидальный характер приобретают гармонические сигналы, проходящие через различные нелинейные устройства (гл. 11) и т. д. Все это приводит к необходимости разработки специальных методов анализа и синтеза электрических цепей, находящихся под воздействием периодических несинусоидальных и непериодических токов и напряжений. В основе этих методов лежат спектральные представления несинусоидальных воздействий, базирующиеся на разложении в ряд или интеграл Фурье.

Из математического анализа известно, что периодическая негармоническая функция f(t) удовлетворяющая условиям Дирихле*, может быть разложена в ряд Фурье:

Уравнение (5.3) есть тригонометрическая форма ряда Фурье. При анализе цепей часто удобней пользоваться комплексной формой ряда Фурье, которая может быть получена из (5.3) с помощью формул Эйлера:

Совокупность амплитуд 0,5А_k = 0,5A-k в разложении (5.6), отложенных против соответствующих положительных и отрицательных частот*, образует симметричный относительно оси координат (вследствие четности коэффициентов а_k) линейчатый амплитудный спектр.

Совокупность ординат φ_k = — φ__k из (5.7), входящих в разложение (5.6) и отложенных против соответствующих положительных и отрицательных частот, образует симметричный относительно начала оси координат (вследствие нечетности коэффициентов b_k) линейчатый фазовый спектр.

Разложение (5.3) можно представить и в другой форме. Если учесть, что a_k = A_kcosφ_k и bk = A_ksinφ_k, то после подстановки в (5.3) получим:

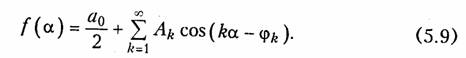
Если рассматривать постоянную составляющую α_о/2 как нулевую гармонику с начальной фазой φ₀ = 0, то разложение (5.9) примет вид

В частном случае, когда функция Да) симметрична относительно оси ординат (рис. 5.1, а), в разложении (5.3) окажутся только четные (косинусоидальные) гармоники:

а   при   симметричности   /"(а)   относительно   начала   координат (рис. 5.1, б) нечетные гармоники

При сдвиге начала отсчета функции f(α) ее амплитудный спектр не изменяется, а меняется только фазовый спектр. Действительно, сдвинем функцию f(α)  по оси времени влево на t_o и обозначим

Тогда разложение (5.9) примет вид

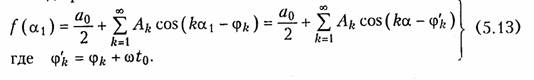
Пример. Разложить в ряд Фурье прямоугольные колебания (рис. 5.1, б). Учитывая, что f(α)  симметрична относительно начала координат в разложении (5.3) останутся только синусоидальные гармоники (5.12), где b_k определится согласно (5.4):         

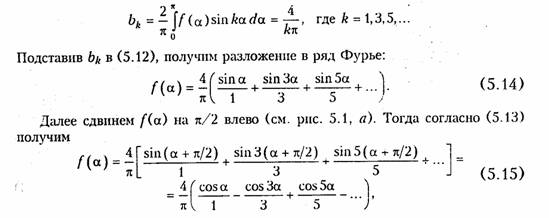
т. е. получили разложение по косинусоидальным составляющим как и должно быть для симметричного относительно оси ординат сигнала.

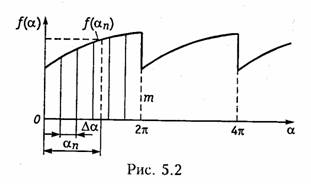
В ряде случаев, когда периодичная функция f(α)  задана графически и имеет сложную форму, ее разложение в ряд Фурье можно осуществить графоаналитическим способом. Его суть заключается в том, что период сигнала Т (рис. 5.2) разбивают на m интервалов, равных Δ α = 2π/т, причем точки разрыва f(α)  не должны попадать на середину участков разбиения; определяют значение сигнала f(α_n) в середине каждого участка разбиения.

Находят коэффициенты разложения а_k и b_k путем замены интеграла в (5.2) конечной суммой                

Уравнение (5.16) легко программируется и при вычислении a_k и b_k, может использоваться ЭВМ.

5.2. Действующее, среднее значение и мощность периодического негармонического сигнала

Для определенности положим, что f(t) имеет смысл тока i(t). Тогда действующее значение периодического негармонического тока определяется согласно (3.5), где i(t) определяется уравнением (5.10):

т. е. действующее значение периодического негармонического тока I полностью определяется действующими значениями его гармоник Ik и не зависит от их начальных фаз φ_k.

Аналогичным образом находим действующее значение периодического несинусоидального напряжения:

Среднее значение тока определяется согласно общему выражению (3.9). Причем обычно берут среднее значение i(t) по абсолютной величине

Аналогично определяется U_cp(2).

С точки зрения теории цепей, большой интерес представляет средняя активная мощность негармонического сигнала и распределение ее между отдельными гармониками.

Средняя активная мощность периодического несинусоидального сигнала

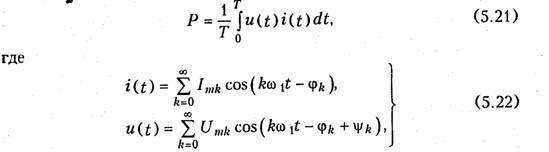
ψ_k — фазовый сдвиг между током и напряжением k-й гармоники. Подставляя значения i(t) и u(t) из (5.22) в уравнение (5.21), после интегрирования получаем:

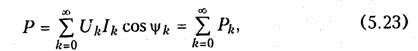
т, е. средняя за период активная мощность периодического негармонического сигнала равна сумме мощностей отдельных гармоник. Формула (5.23) является одной из форм широко известного равенства Парсеваля.

Аналогично находим реактивную мощность

Следует подчеркнуть, что в отличие от гармонических сигналов (см. (3.121)) для негармонических сигналов

5.3. Спектры периодических негармонических сигналов

Рассмотрим последовательность прямбугольных импульсов, изображенную на рис. 5.3, а. Сигналы подобной формы находят очень широкое применение в радиотехнике и электросвязи: телеграфия, цифровые системы передачи, системы многоканальной связи с временным разделением каналов, различные импульсные и цифровые устройства и др. (см. гл. 19). Импульсная последовательность характеризуется следующими основными параметрами: амплитудой импульса A_и*, его длительностью t_u и периодом следования Т. Отношение периода Т к длительности t_и называется скважностью импульсов и обозначается через q = Т/t_И. Обычно значения скважности импульсов лежат в пределах от нескольких единиц (в измерительной технике, устройствах дискретной передачи и обработки информации), до нескольких сотен или тысяч (в радиолокации).

Для нахождения спектра последовательности прямоугольных импульсов воспользуемся рядом Фурье в комплексной форме (5.6).

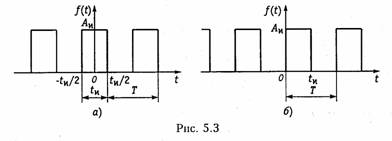
Комплексная амплитуда k-й гармоники равна согласно (5.8) после возвращения к исходной переменной t.

На рис. 5.4 изображен спектр комплексных амплитуд для q = 2 и q = А. Как видно из рисунка, спектр последовательности прямоугольных импульсов представляет собой дискретный спектр с огибающей (штриховая линия на рис. 5.4), которая описывается функцией

носящей название функции отсчетов (см. гл. 19). Число спектральных линий между началом отсчета по оси частот и первым нулем огибающей равно q —1. Постоянная составляющая сигнала (среднее значение) a_о/2 = A_и/q, а действующее значение А — A_u/√q, т. е. чем больше скважность, тем меньше уровень постоянной составляющей и действующее значение сигнала. С увеличением скважности q число дискретных составляющих увеличивается — спектр становится гуще (см. рис. 5.4, б), и амплитуда гармоник убывает медленнее. Следует подчеркнуть, что в соответствии с (5.27) спектр рассматриваемой последовательности прямоугольных

импульсов вещественный.

Из спектра комплексных амплитуд (5.27) можно выделить амплитудный A_k =|A_k|и фазовый спектр φ_k = argA_k, изображенный на рис. 5.5 для случая q = 4. Из рисунков видно, что амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Причем, фазы отдельных гармоник принимают либо нулевое значение между

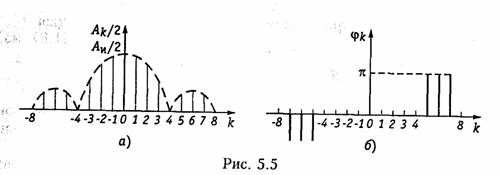
узлами, где синус положительный, либо ±π, где синус отрицательный (рис. 5.5, б)

На  основании  формулы  (5.28)  получим тригонометрическую форму разложения в ряд Фурье по четным гармоникам (сравни с (5.15))

В случае, когда периодическая последовательность имеет разно-полярную форму (см. рис. 5.1), в спектре будет отсутствовать постоянная составляющая (сравните (5.30) и (5.31) с (5.14) и (5.15)).

Аналогичным образом можно исследовать спектральный состав периодических негармонических сигналов другой формы. В табл. 5.1 приведено разложение в ряд Фурье некоторых наиболее распространенных сигналов.

5.4. Расчет цепей при периодических

 негармонических воздействиях

В основе расчета линейных электрических цепей, находящихся под воздействием периодических негармонических сигналов, лежит принцип наложения (см. § 1.6). Его суть применительно к негармоническим воздействиям заключается в разложении негармонического периодического сигнала в одну из форм ряда Фурье (см. § 5.1) и определении реакции цепи от каждой гармоники в отдельности. Результирующая реакция находится путем суперпозиции (наложения) полученных частичных реакций. Таким образом, расчет цепей при периодических негармонических воздействиях включает в себя задачу анализа спектрального состава сигнала (разложение его в ряд Фурье), расчет цепи от каждой гармонической составляющей и задачу

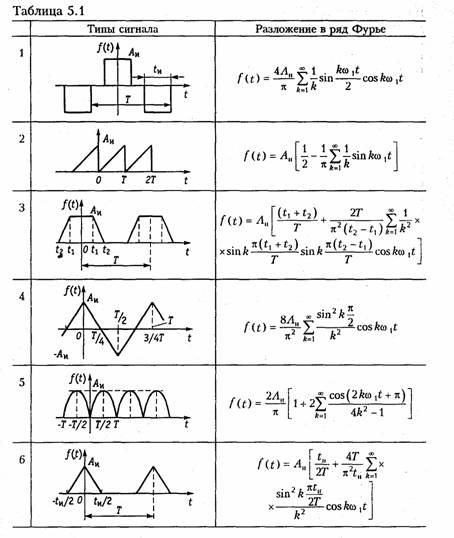
синтеза, в результате которого определяется результирующий выходной сигнал как функция времени (частоты) или его действующее (амплитудное значение).

При решении задачи анализа обычно пользуются тригонометрической (5.3) или комплексной (5.6) формой ряда Фурье с ограниченным числом членов разложения, что приводит к некоторой погрешности аппроксимации истинного сигнала. Коэффициенты разложения а_k и b_k в (5.3) или А_k и φ_k в (5.6) определяются с помощью уравнений (5.4), (5.7) и (5.8). При этом входной сигнал f(а) должен быть задан аналитически. В случае, если сигнал задается графически, например в виде осциллограммы, то для нахождения коэффициентов разложения а_k, и b_k можно использовать графоаналитический метод (см. (5.16)).

Расчет цепи от отдельных гармоник ведется обычно символическим методом (см. гл. 3). При этом необходимо иметь в виду, что на k-й гармонике индуктивное сопротивление Х_L(k) = kωL, a емкостное сопротивление Xc(k) = 1/(_kω_С), т. е. на k-й гармонике индуктивное сопротивление в k раз больше, а емкостное в k раз меньше, чем на первой гармонике. Этим в частности объясняется то обстоятельство, что высокие гармоники в емкости выражены сильнее, а в индуктивности слабее, чем в приложенном к ним напряжении. Активное сопротивление R на низких и средних частотах можно считать не зависящим от частоты.

После определения искомых токов и напряжений от отдельных гармоник методом наложения находят результирующую реакцию цепи на негармоническое периодическое воздействие. При этом либо определяют мгновенное значение результирующего сигнала на основании расчета амплитуд и фаз отдельных гармоник, либо его амплитудные или действующие значения согласно уравнениям (5.18), (5.19). При определении результирующей реакции необходимо помнить, что в соответствии с представлением периодических негармонических колебаний на комплексной плоскости (см. § 3.2) векторы различных гармоник вращаются с различной угловой частотой.

Пример. К цепи, изображенной па рис. 5.6, приложено напряжение u(t) в форме прямоугольных импульсов с периодом повторения Т = 2t_u и амплитудой А_u = 1В (см. рис. 5.3, б). Определить мгновенное и действующее значения напряжения на емкости.

Разложение данного напряжения в ряд Фурье определяется по формуле (5.31). Ограничимся первыми тремя членами разложения (5.31):

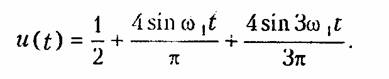
Таким образом, приложенное напряжение содержит постоянную составляющую U₀= 1/2, первую U₁ = 4/π и третью Uз = 4/(Зπ) гармоники с нулевыми начальными фазами. Найдем напряжение на емкости от постоянной составляющей приложенного напряжения U₀:

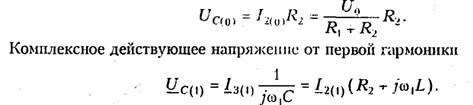
Токи I₂₍₁₎ или I₃₍₁₎  можно найти по формуле разброса (см.§ 2.2). Например, для I₃₍₁₎  имеем:

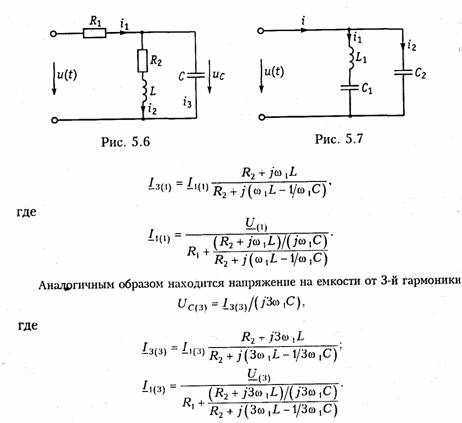
После нахождения комплексных действующих значений напряжений на емкости отдельных гармоник и выделения в них модулей Uc_(1),Uc₍₃₎ и фаз записывает мгновенное значение напряжения на емкости в форме суммы (ряда):

При анализе резонансных явлений в электрических цепях при периодических несинусоидальных воздействиях следует иметь в виду, что резонанс напряжений и токов может достигаться на разных гармониках. При этом, как и ранее, резонансом на k-й гармонике называется такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением k-x гармоник равен нулю. Явление резонанса может быть использовано для выделения отдельных гармоник из периодического несинусоидальнего сигнала. Следует подчеркнуть, что в цепи может одновременно быть достигнут резонанс токов на одной частоте и резонанс напряжений на другой.

Пример. Для цепи, изображенной на рис. 5.7, при заданной ω_1,L1 найти значение С₁и C₂, при которых одновременно возникает резонанс напряжений на 1-й и резонанс токов на 5-й гармонике. Из условия резонанса напряжений находим, что входное реактивное сопротивление цепи на первой гармонике должно равняться нулю:

Вопросы и задания для самопроверки

1.   Какова математическая модель спектра периодического несинусоидального сигнала?

2.   Какой вид имеет спектр периодического негармонического сигнала?

3.   Как изменяется спектр периодического негармонического сигнала при сдвиге начала отсчета заданной функции?

4.   Как определить спектр периодической функции, заданной графически?

5.   Как определяется средняя за период активная мощность периодического негармонического сигнала?

6.   Как определяется и что характеризует мощность искажений?

7.   Как рассчитывается спектр комплексных амплитуд последовательности прямоугольных импульсов?

8.  Как влияет скважность импульсов на спектр сигнала?

9.   Рассчитать  и  построить  спектр  амплитуд  последовательности прямоугольных импульсов с параметрами: U_m = ЗВ, f = 0,5 кГц для двух случаев (q = 2, q = 5).

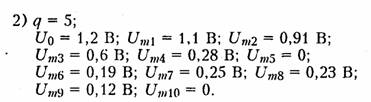
10. Каков алгоритм расчета линейных электрических цепей, находящихся под воздействием периодических негармонических сигналов?

11. На вход цепи, изображенной на рис. 5.8, поступает периодический негармонический сигнал u(t) = Uo + + U_m1sinω1t + U_m3sin(3_ω1t + φ₃): Uo = 30 В; U_m1 = 100 В; U_m3 = 40 В; φ_З = 20°. Параметры элементов цепи на основной частоте известны: ω₁L = 12 Ом; l/(ω₁C) = 30 Ом; R₁ = 6 Ом; R₂ = 5 Ом; Rз = 20 Ом. Рассчитать:

1) ток в неразветвленной части схемы и записать его мгновенное значение; 2) действующие значения всех токов; 3) активную мощность, потребляемую цепью.

12.  Резонансные явления в линейных электрических цепях при негармонических периодических воздействиях.

13.  Для цепи изображенной на рис. 5.7, найти значения С₁ и С₂, при которых одновременно возникает резонанс напряжений на 1-ой гармонике и резонанс токов на 5-ой гармонике, если заданы L₁ = 10 мГн; ω_l = 5∙10³ рад/с.

Ответ:   С₁ = 4 мкФ; С₂ = 0,167 мкФ.