ПРЕДИСЛОВИЕ

Дисциплина «Теория электрических цепей» (ТЭЦ)* является базовым курсом при подготовке бакалавров, магистров по направлениям «Телекоммуникации», «Радиотехника», а также инженеров по специальностям связи.

Несмотря на то, что курс ТЭЦ имеет сложившуюся структуру и уже значительную историю, бурное развитие телекоммуникаций и информатики потребовало внести в его содержание и методику изложения целый ряд изменений, которые нашли отражение во втором издании настоящего учебника. Это касается в первую очередь расширения разделов, посвященных теории активных цепей и цепей с обратной связью. Дополнены и переработаны разделы, посвященные машинным методам анализа и синтеза электрических цепей. Существенно переработаны и дополнены главы, в которых изучаются нелинейные и автоколебательные цепи, в частности, включен материал, посвященный анализу автогенераторов методом медленно меняющихся амплитуд.

Учитывая все большее применение цифровых методов обработки сигналов, полностью переработана и расширена глава, посвященная дискретным цепям и цифровым фильтрам.

С целью лучшего усвоения материала большинство теоретических положений проиллюстрировано примерами. В отличие от предыдущего издания каждая глава дополнена перечнем контрольных вопросов и задач с ответами, позволяющих закрепить изученный материал. Для удобства пользования учебник снабжен предметным указателем.

В конце учебника приведен список основной и дополнительной литературы, которая может быть использована при изучении курса теории электрических цепей. Кроме того, по тексту изложения материала сделаны дополнительные ссылки на литературу, где более подробно освещены некоторые специальные вопросы.

В подготовке данного издания учебника большую помощь оказали авторам сотрудники кафедр ТЭЦ Сибирского государственного университета телекоммуникаций и информатики (Сиб-ГУТИ) и Санкт-Петербургского государственного университета телекоммуникаций им. М.А. Бонч-Бруевича (СпГУТ), которым авторы выражают глубокую благодарность.

Мы также признательны своим коллегам из Московского технического университета связи и информатики (зав. кафедрой ТЭЦ проф. Урядников Ю.Ф.), Поволжской академии телекоммуникаций и информатики (зав. кафедрой ТЭЦ проф. Дубинин А.Е.) за их замечания, способствующие улучшению содержания учебника

Отв. редактор, д.т.н., проф. В.П. Бакалов

Введение

Одной из главных тенденций развития человеческого общества на рубеже XX и XXI столетняя явился стремительный рост потоков разнообразной информации, обеспечивающей его жизнедеятельность. Мировое сообщество вступает в новую эру — эру информатизации. Эффективное управление государством, экономикой, удовлетворение потребностей населения, развитие пауки, культуры, здравоохранения требует постоянного развития и совершенствования системы информационного обеспечения.

Техническую базу информатизации составляет связь и вычислительная техника, грань между которыми все больше стирается. Сети связи являются транспортной средой для информационных систем. В основе развития систем связи лежат современные достижения многих паук п в первую очередь электротехники, радиотехники и электроники. Общим для этих наук является изучение электромагнитных процессов в пассивных и активных электрических цепях с целью создания различных устройств для преобразования, передачи, обработки и хранения информации. На основе достижений в области радиотехники и электроники развиваются средства связи, автоматика и вычислительная техника, телеметрия, радиолокация и навигация, системы управления технологическими процессами и др.

Основными задачами электротехники являются генерирование, передача и преобразование электрической энергии в другие виды энергии (механическую, тепловую, световую, химическую п т. д.).

Одна из главных задач радиотехники — передача, преобразование информации и осуществление связи на расстоянии с использованием электромагнитных волн.

Зарождение пауки об электричестве относится к XVI в., когда английский ученый У. Гильберт (1544 — 1603) написал свой знаменитый трактат «О магните, магнитных телах и большом магните — «Земле». В XVII- XV1I1 вв. были проведены многочисленные опыты, позволившие установить существование электрических зарядов двух типов — положительных п отрицательных, изобрести первый конденсатор (Ж. Полис, 1745), разработать первую последовательную теорию электрических явлений (Б. Франклин).

Во второй половине XVIII в. началось «количественное изучение» электрических и магнитных явлений, появились первые измерительные приборы — электроскопы. В 1756 г. петербургский физик Ф. Эпинус (1724 — 1802) изобрел воздушный конденсатор, с помощью которого показал, что стекло в «лейденской» банке обладает свойством накапливать электричество, открыл явление электризации некоторых тел (турмалин) при нагревании (пироэлектричество). В работе Ф. Эпинуса впервые предпринята систематическая попытка подойти к изучению электрических явлений не только с качественной, но и с количественной стороны. В частности, им было установлено, что сила взаимодействия между зарядами пропорциональна величине этих зарядов. И хотя он не установил, как эта сила зависит от расстояния, однако значение его работы очень велико, так как она дала определенное направление дальнейшим исследованиям. Наконец, в 1784 г. французский 48-летний военный инженер Ш. Кулон (1736—1806) открывает закон, согласно которого сила взаимодействия между электрическими зарядами обратно пропорциональна квадрату расстояния между ними. С помощью созданных им крутильных весов, а также ряда оригинальных методов (методы колебаний) этот человек, никогда специально не занимавшийся электричеством и магнетизмом, проводя в качестве побочного занятия свои исследования, заложил ос-: новы количественной электростатики.

21 июля 1820 г. появилась небольшая заметка датского физика Г. Эрстеда (1777 — 1851), в которой он доказал, что ток в прямолинейном проводнике, идущем вдоль меридиана, отклоняет от него магнитную иглу. Это сообщение произвело большое впечатление на ученый мир, так как из опыта Эрстеда явствовало, что сила, действовавшая между элементом тока и магнитным полюсом, направлена не по соединяющей их прямой, а по нормали к ней. Эта работа вызвала первую трещину в ньютоновской модели мира.

Особое значение в развитии теории электрических явлений сыграли открытия законов Ома (1826) и Кирхгофа (1847), а также открытие М. Фарадеем (1831) явления электромагнитной индукции. В 1833 г. русский ученый Э. Ленц (1804 — 1865) открыл закон, устанавливающий связь между направлением индукционных токов и их электромагнитными взаимодействиями. Таким образом, к концу XIX в. было установлено единство электромагнитных явлений, получивших свое логическое завершение в работах Дж. Максвелла, сформулировавшего в 1873 г. фундаментальные уравнения классической электродинамики.

В конце XIX — начале XX веков с открытий дискретного характера зарядов (Дж. Томсон, 1897 г.) начался новый этап в развитии науки об электричестве. В этот период были заложены основы электронной теории строения вещества как совокупности электрически заряженных частиц, создана квантовая теория электромагнитных процессов, что привело к рождению электроники как науки о взаимодействии электронов с электромагнитными полями и о методах создания электронных приборов и устройств.

Со второй половины XIX в. началось широкое использование электрических и магнитных явлений в технике: построены электродвигатели и генераторы тока, появились первые электромагниты, массовое распространение получило электрическое освещение, начало которому положило изобретение электрической свечи русским ученым П.П. Яблочковым. Начало применения электрической энергии для технологических целей положили работы Б.С. Якоби (1838 г.), предложившего использовать электрический ток для нанесения различных металлических покрытий. Электроэнергию стали использовать при получении алюминия, меди, цинка, для резки и сварки металлов, упрочения деталей и в других технологических процессах; начинается применение электроэнергии на транспорте. Большое значение для развития электротехники имели изобретения русского инженера М.О. Доливо-Добровольского, разработавшего к концу 90-х гг. ряд промышленных конструкций трехфазных асинхронных двигателей, трансформаторов и построившего трехфазную линию электропередачи Лауфен — Франкфурт длиной 175 км, положившей начало современному развитию электротехники.

Подлинную революцию в электросвязи произвел П.Л. Шиллинг (1786 — 1837) в 1832 г. в России, который построил первый в мире электромагнитный телеграф и осуществил связь между Зимним дворцом и Министерством путей сообщений. Дальнейшее развитие эта идея получила в 1835 г., когда американцем С. Морзе (1791 — 1872) был разработан специальный алфавит и создана модель телеграфа в Нью-йоркском университете. Это были первые практические применения науки об электричестве в электросвязи. А уже в 1866 г. вступило в строй первое величайшее сооружение того времени — линия трансатлантической кабельной связи между Европой и Америкой. К 1870 г. в России было создано свыше 700 телеграфных станций и введена в эксплуатацию 91 тыс. км телеграфных линий, в том числе линия Москва—Владивосток протяженностью 12 тыс. км.

Качественно новый этап в развитии электросвязи возник после изобретения в 1876 г. А. Беллом телефона. Существенный вклад в развитие телефонной связи внес русский физик Л.М. Голубицкий, в 1882 — 1883 г. были построены первые телефонные станции в Москве и С.-Петербурге.

Особенно важное значение имело изобретение А.С. Поповым (1895) радио, открывшее новую страницу в развитии научно-технического прогресса. Значительную роль в практической реализации радио в телеграфии сыграл итальянский радиотехник и предприниматель Г. Маркони (1874 — 1937).

Открытие радио привело к рождению радиотехники как области науки и техники, занимающейся вопросами изучения и применения электромагнитных колебаний и волн радиодиапазонов для передачи   информации — и радиосвязи,   радиовещании и телевидении  в радиолокации   и   радионавигации,   в   радиотелеметрии   п   радиоуправлении, при контроле за различными технологическими процессами и механизмами, в научных исследованиях п др.                 

В XX в. начинается бурное развитие электроники — обширной области пауки, техники и производства, охватывающей исследование и разработку электронных приборов п принципов их использования, в частности, в электросвязи. В истории развития электроники можно выделить четыре основных этапа: электронных ламп, транзисторов, интегральных схем и функциональных устройств.

Первый этап начался в 1904 г., когда английским ученым Д.Л. Флемингом была изготовлена первая электронная лампа — диод. Прототипом электронной лампы явилась лампа накаливания, созданная русским электротехником Л. 11. Лодыгиным в 1872 г. В 1907 г. была предложена электронная лампа с управляющим электродом — триод, способная усиливать и генерировать электрические сигналы. В последующие годы, наряду с совершенствованием электронных ламп, разрабатывались п другие электронные приборы: электронно-лучевые, ионные, фотоэлектронные.

Начало второго этапа развития электроники связано с открытием в конце 1947 г. американскими учеными У. Браттсйпом, Дж. Бардиным п У. Шоткп транзисторного эффекта. В 1948 г. были изготовлены первые промышленные образцы биполярных транзисторов, а в 1952 г. — нолевые транзисторы. В транзисторах были реализованы идеи, которые впервые были сформулированы русским ученым О.В. Лосевым в 1922 г.

Непрерывное расширение функций электронной аппаратуры и се усложнение привели в 1958 г. к началу третьего этапа — возникновению микроэлектроники. В настоящее время разработаны сверхбольшие интегральные схемы (БИС), содержащие более 10⁵ элементов. Однако сейчас уже становится ясным, что увеличение степени интеграции не может быть беспредельным.

Научно-техническое направление, связанное с отказом от компонентной структуры микроэлектронных изделий п основанное на использовании объемных эффектов в твердом теле, является началом четвертого этапа развития электроники, получившего название функциональной микроэлектроники.

Крупный вклад в развитие электротехники, радиотехники и электроники внесли русские ученые. Фундаментальные исследования в области физики и технологии электронных и полупроводниковых приборов выполнили М.Л. Бонч-Бруевич, Л.И. Мандельштам, А.Ф. Иоффе, СИ. Вавилов, Л.Л. Чернышев; но проблемам возбуждения и преобразования электрических колебаний, распространения и приема радиоволн - Б.А. Введенский, В.О. Калмыков, М.В. Шулейкин, А.А. Расплетин и др.

Современные системы и сети связи являются сложнейшими техническими   сооружениями,   сконцентрировавшими   все   самые   последние достижения научно-технической революции в области радиотехники, электроники и вычислительной техники. В последнее время разработаны и эксплуатируются в ряде стран мира разнообразные федеральные и международные телекоммуникационные сети, оснащенные цифровыми автоматическими коммутационными станциями, цифровыми системами передачи, волоконно-оптическими линиями связи, спутниковыми системами связи и др.

В России разработана государственная концепция в области связи, предусматривающая построение подобной телекоммуникационной сети общего пользования (TCP). На базе TCP будут созданы интеллектуальные сети России (ИСР), которые должны предоставлять абонентам широкий круг различных услуг; российская сеть передачи данных (РСПД); цифровая сеть связи с интеграцией служб (ЦСИС) (многофункциональный телефон, факс, телекс, видеотекс и др.); сотовые мобильные и персональные сети связи (СМПС), широкополосные цифровые сети с интеграцией услуг и др.

Создание и эксплуатация подобных сетей потребует подготовки качественно новых специалистов. Среди дисциплин, составляющих основу базовой подготовки специалистов в области связи, важнейшее место отводится курсу «Теория электрических цепей» (ТЭЦ). Одним из основоположников курса теории электрических цепей был доктор технических наук, профессор А.Ф. Белецкий, внесший большой вклад в ее становление как самостоятельной дисциплины.

Содержание этой дисциплины составляют задачи анализа и синтеза линейных и нелинейных электрических цепей, изучение как с качественной, так и количественной стороны установившихся и переходных процессов, протекающих в различных электронных приборах и устройствах. ТЭЦ базируется на курсах математики, физики, технической электроники, вычислительной техники и является базовым для изучения последующих общетехнических и специальных дисциплин.

Данный учебник соответствует программе курса «Теория электрических цепей» по специальностям «Сети связи и системы коммутации» (200900); «Многоканальные телекоммуникационные системы» (201000); «Радиосвязь, радиовещание и телевидение» (201100); «Средства связи с подвижными объектами» (201200); «Аудиовизуальная техника» (201400); «Физика и техника оптической связи» (071700) п по направлению бакалавриата и магистратуры по специальности «Телекоммуникации» (550400). Он может быть использован также для родственных специальностей.

Проф. В.П. Бакаловым написано введение, гл. 1—9, 14; проф. В.Ф. Дмитриковым — гл. 10, И; проф. Круком Б.И. — гл. 12 — 13, H; —18; гл. 15 — написана совместно В.Ф. Дмитриковым и Б.И. Круком; гл. 19 — написана совместно Бакаловым В.П. и Круком В.И. Общее редактирование учебника выполнил проф. В.П. Бакалов.

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

1.1. Ток, напряжение, мощность

Понятия электрического тока и напряжения являются одними из основных в теории электрических цепей. Электрический ток в проводящей среде есть упорядоченное движение электрических зарядов под воздействием электрического поля (ток проводимости в металлах, электролитах, газах; ток переноса в электровакуумных

приборах и др.).

Количественно электрический ток в каждый момент времени характеризуется скалярной величиной i = i (t) — мгновенным значением тока, характеризующим скорость изменения заряда q во времени:

где Δq — электрический заряд, прошедший за время Δt через поперечное сечение проводника. В системе СИ заряд измеряется в кулонах (Кл), время — в секундах (с), ток — в амперах (А). В дальнейшем для краткости электрические токи и напряжения будем просто называть токами и напряжениями.

В соответствии с приведенным выше определением понятие «ток» может использоваться в двух смыслах: ток как физический процесс и ток как количественная характеристика (вместо «силы

тока»).

Как функция времени ток i (t) может принимать положительные и отрицательные значения. Принято считать значение тока i (t) положительным, если движение положительно заряженных частиц совпадает с заранее выбранным направлением отсчета тока и отрицательным — в противном случае. Выбор направления отсчета тока

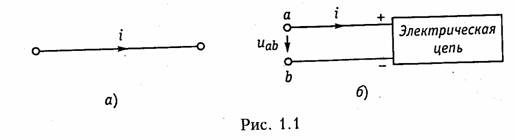
произволен, положительное направление отсчета тока показывается стрелкой (рис. 1.1).

Электрическое напряжение между двумя точками электрической цепи определяется количеством энергии, затрачиваемой на перемещение единичного заряда из одной точки в другую:

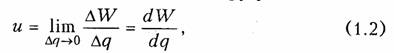
где W — энергия электрического поля. Единица измерения напряжения в системе СИ — вольт (В), энергии — джоуль (Дж).

В потенциальном электрическом поле напряжение между двумя точками совпадает по значению с разностью потенциалов между ними. Например, напряжение между точками а и b цепи, показанной на рис. 1.1, б,

где V_a и Vb — потенциалы точек а и b.

Значение напряжения в любой заданный момент t называется мгновенным и обозначается и = и (t). Являясь скалярной величиной, u(t) может принимать как положительные, так и отрицательные значения. Для однозначного определения знака напряжения выбирают положительное направление его отсчета, которое показывается стрелкой (рис. 1.1, б), направленной от одной точки электрической цепи к другой. Для определенности будем считать, что положительное направление отсчета совпадает с направлением стрелки от более высокого потенциала, т. е. «+», к более низкому, т. е. «—» (рис. 1.1, б). При этом положительные направления отсчета напряжения и тока будут между собой согласованы, так как положительное направление отсчета напряжения и₍,ь соответствует направлению перемещения положительно заряженных частиц от более высокого потенциала V_a(+) к более низкому V_b(-). Очевидно, что u_ab = — u_ba.Применительно к напряжению на участке цепи, по которому протекает ток, часто используют термин «падение напряжения».

Электрическая энергия, затраченная на перемещение единичного положительного заряда между двумя точками участка цепи с напряжением и (разностью потенциалов) к моменту времени t определится согласно (1.1) и (1.2) уравнением

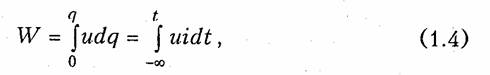
где принято W=0 при t = — ∞.

Производная энергии по времени определяет мгновенную мощность, потребляемую элементами, входящими в участок цепи:

Мощность измеряется в ваттах (Вт). Знак мощности р определяется знаком напряжения и тока. Если р>0, мощность потребляется элементами участка цепи, а при р<0 — отдается.

По характеру изменения во времени различают постоянные, гармонические, периодические несинусоидальные, непериодические токи и. напряжения. В ряде случаев (например, в цепях с распределенными параметрами) токи и напряжения могут быть не только функциями времени, но и функциями пространственных координат. В технике связи токи и напряжения как материальные носители сообщений называют сигналами.

1.2. Электрическая цепь, ее элементы и модели

Электрической цепью называют совокупность устройств, предназначенных для прохождения тока п описываемых с помощью понятий тока п напряжения. Электрическая пень состоит из источников (генераторов) и приемников электрической энергии.

Источником называют устройство, создающее (генерирующее) токи п напряжения. В качестве источников могут выступать как первичные устройства, преобразующие различные виды энергии в электрическую (аккумуляторы, электромашинные генераторы, термоэлементы, пьезодатчики п т. д.), так и устройства, преобразующие электрическую энергию первичных источников в энергию электрических колебаний требуемой формы.

Приемником называют устройство, потребляющее (запасающее) пли преобразующее электрическую энергию в другие виды энергии (тепловую, механическую, световую и т. д.). Физическими элементами реальной электрической цепи являются резисторы, катушки индуктивности, конденсаторы, трансформаторы, транзисторы, электронные лампы и другие компоненты электроники. При этом электрическая цепь может конструктивно выполняться либо из указанных выше дискретных компонентов, либо изготовляться в едином технологическом цикле (интегральные схемы). Электрические цени, содержащие как интегральные, так и дискретные компоненты, получили наименование гибридных.

В основе теории электрических цепей лежит принцип моделирования. При этом реальные электрические цепи заменяются некоторой идеализированной моделью, состоящей из взаимосвязанных идеализированных элементов. Последние представляют собой простые модели, используемые для аппроксимации (приближения) свойств простых физических элементов или физических явлений. В зависимости от точности приближения одна и та же физическая электрическая цепь может быть представлена различными моделями, причем, чем точнее модель, тем она сложнее. На практике обычно ограничиваются  наиболее простыми  моделями,  обеспечивающими решение задач

анализа и синтеза реальной цепи с заданной точностью. Важно иметь в виду, что если физические элементы и явления могут быть описаны лишь приближенно, то идеализированные элементы определяются точно. К простейшим идеализированным элементам модели электрической цепи относятся независимые и зависимые источники (активные элементы) и элементы резистивного сопротивления, индуктивности и емкости (пассивные элементы).

Систему уравнений, описывающую модель электрической цепи, называют математической моделью цепи. В теории электрических цепей изучаются общие свойства моделей цепей, поэтому в дальнейшем под электрической цепью будем понимать ее модель, свойства которой близки к свойствам реальной физической цепи.

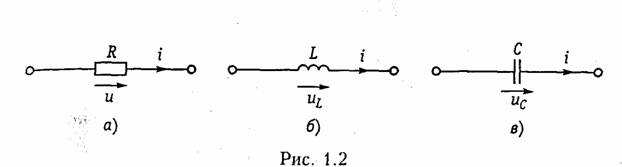
Пассивные элементы. Резистивным сопротивлением называют идеализированный элемент, обладающий только свойством необратимого рассеивания энергии. Условное обозначение резистивного сопротивления показано на рис. 1.2, а. Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:

Коэффициенты пропорциональности R и G в формулах (1.6) называются соответственно сопротивлением и проводимостью элемента и являются его количественной характеристикой, причем при согласованных направлениях тока и напряжения R и G положительны и связаны обратной зависимостью R = 1/G. Измеряют в системе СИ сопротивление R в омах (Ом), а проводимость G — в сименсах (См).

Уравнение (1.6) определяет зависимость напряжения от тока и носит название вольт-амперной характеристики (ВАХ) резистивного сопротивления. Если R постоянно, то ВАХ линейна (рис. 1.3, а) и соответствует линейному резистивному элементу. Если же R зависит от протекающего через него тока или приложенного к нему напряжения, то ВАХ становится нелинейной (рис. 1.3, б) и соответствует нелинейному резистивному сопротивлению.

Мощность в резистивном сопротивлении можно определить согласно уравнению (1.5):

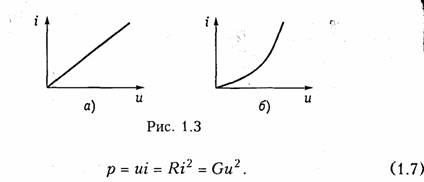
Мощность в резистивном сопротивлении всегда больше нуля, так как оно только потребляет энергию, преобразуя ее в тепло или другие виды энергии.

Индуктивным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное обозначение индуктивного элемента изображено на рис. 1.2, б.

Математическая модель, описывающая свойства индуктивного элемента определяется соотношением

где ψ — потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку:

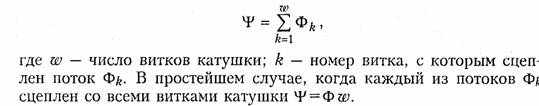
Коэффициент пропорциональности L в формуле (1.8) называется индуктивностью. Он имеет положительное значение и является количественной характеристикой индуктивного элемента. Измеряется индуктивность L в генри (Гн), а магнитный поток Ф — в веберах (Вб). Если величина L постоянна, то зависимость (1.8); {вебер-амперная характеристика} линейна и соответствует линейному индуктивному элементу. Если же L зависит от электрического режима (тока или напряжения), то зависимость (1.8) нелинейна и соответствует нелинейному элементу индуктивности.           

Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением      

т. е. напряжение на индуктивном элементе пропорционально скорости  изменения протекающего через  него тока.   Следовательно, при протекании через L постоянного тока u = 0 и свойства индуктивного элемента эквивалентны коротко замкнутому (КЗ) участку (_См. рис. 1.1, а).

Мгновенная мощность электрических колебаний в индуктивном элементе

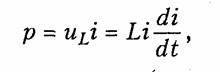
т.е. может быть как положительной (при совпадении направлений и и i), так и отрицательной (при несовпадении направлений и и i). Причем в первом случае (р>0) магнитная энергия запасается индуктивным элементом, а во втором (р<0) — отдается во внешнюю цепь.

Энергия, запасенная в индуктивном элементе к моменту t, определится согласно (1.4)

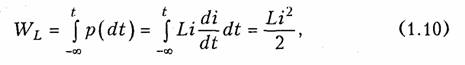
т. е. всегда полoжительна.

Емкостным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.2, в.

Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулонной характеристикой

q = Cu_c.                                     (1.11)

Коэффициент пропорциональности С в формуле (1.11) называется емкостью и является количественной характеристикой емкостного элемента. При согласованных направлениях тока и напряжения величина С всегда положительна. Измеряется С в фарадах (Ф).

Если величина С постоянная, то вольт-кулонная характеристика (1.11) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то характеристика (1.11) нелинейна и соответствует нелинейному элементу.

Между током и напряжением на емкостном элементе существует связь, определяемая согласно (1.1) и (1.11) равенством

т. е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. При постоянном напряжении и=const, i = 0 и емкостной элемент по своим свойствам эквивалентен разрыву цепи.

Мощность электрических колебаний в емкостном элементе

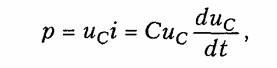
т. е. может быть как положительной, так и отрицательной в зависимости от направлений тока и напряжения. При р>0 энергия электрического поля запасается емкостным элементом, а при р<0 — отдается во внешнюю цепь.

Энергия, запасенная в емкостном элементе к моменту t,

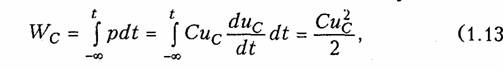
т. е. всегда положительна.

В инженерной практике резистивное сопротивление, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя, по существу, элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумениям, также будем пользоваться этой терминологией.   

Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями резисторов, высококачественных' катушек индуктивностей с малыми потерями и электрических конденсаторов с высокими диэлектрическими свойствами в области низких и средних частот. В области высоких, а особенно сверхвысоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными.Так, на высоких частотах резисторы уже нельзя с достаточной точностью описать идеальным резистивным элементом (1.6) из-за влияния различных «паразитных» емкостей.  Более точной здесь будет модель

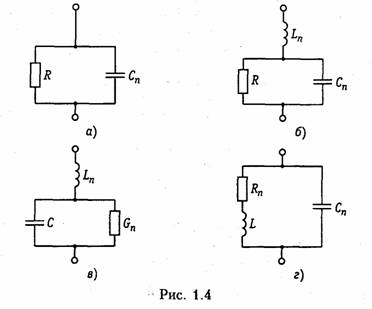
параллельного соединения R и С_П, изображенная на рис. 1.4, а. В некоторых случаях возникает необходимость учета, «паразитной» индуктивности L_П, учитывающей эффект накопления энергии магнитного поля в элементах резистора (рис. 1.4, б).

На высоких и сверхвысоких частотах также начинает проявляться поверхностный эффект, выражающийся в неравномерном распределении тока по сечению проводника {скип-эффект). В результате этого сопротивление R проводника начинает расти с увеличением частоты. Причем, чем толще проводник, тем при меньших частотах начинает проявляться скип-эффект. На сверхвысоких частотах зависимость сопротивления круглого медного проводника от частоты f можно выразить эмпирической формулой

где Ro — сопротивление проводника постоянному току, Ом; d — диаметр сечения проводника, мм; f — частота, МГц.

Модель конденсатора, кроме емкостного элемента С, может содержать параллельную проводимость G_П, учитывающую потерн , энергии в диэлектрике, и последовательную индуктивность L_П, учитывающую эффект запасения энергии магнитного поля в конструктивных элементах конденсатора (рис. 1.4, в).

Модель катушки индуктивности может учитывать потери энергии в проводе и энергию электрического поля, запасаемую между витками катушки путем дополнительного включения сопротивления потерн R_П и «паразитной» емкости С_П (рис. 1.4, г).

В зависимости от условий применения и конструктивных особенностей, требований к точности анализа могут использоваться и более сложные модели резисторов, катушек индуктивностей и конденсаторов.

В зависимости от соотношения между длинами цепи l и волны тока п напряжения λ различают цепи с сосредоточенными и распределенными параметрами. При l<λ можно считать, что параметры R, L, С сосредоточены в резисторах, катушках индуктивности и конденсаторах; при l>> λ необходимо пользоваться моделью цепи с распределенными параметрами (см. гл. 13).

Рассмотренные выше резистивные индуктивные и емкостные элементы относятся к двухполюсным, так как содержат только два зажима (полюса, вывода). Однако кроме двухполюсных элементов в теории цепей и электронике широко используются трехполюсные, четырехполюсные и многополюсные элементы. Например, свойства трансформатора как физического устройства, содержащего две индуктивно связанные катушки, не могут быть описаны моделью только двухполюсных элементов с индуктивностями L₁ и L₂. Для его моделирования необходимо введение еще одного параметра  —  взаимной   индуктивности  М;   при  этом  моделью

трансформатора  будет  являться  четырехполюсный  элемент  (см. гл. 3).

Активные элементы. Активными элементами электрической цепи являются зависимые и независимые источники электрической энергии. К зависимым источникам относятся электронные лампы, транзисторы, операционные усилители и другие, к независимым источникам — аккумуляторы, электрогенераторы, термоэлементы, пьезодатчики и другие преобразователи. Независимые источники можно представить в виде двух моделей: источника напряжения и источника тока.

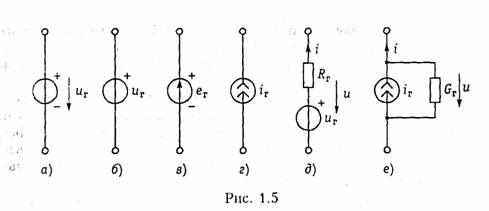
Независимым источником напряжения называют идеализированный двухполюсный элемент, напряжение на зажимах которого не зависит от протекающего через него тока. Условное обозначение источника напряжения показано на рис. 1.5, а.

Источник напряжения полностью характеризуется своим задающим напряжением щ, или электродвижущей силой (ЭДС) е_Г(рис. 1.5, в). Внутреннее сопротивление источника напряжения равно нулю н иногда при изображении источника напряжения обозначают знаком «+>> только один из зажимов и не показывают стрелкой положительное направление е_Г имея в виду, что оно действует от «+» к «—» (рис. 1.5, б). Часто при анализе цепей ограничиваются изображением только зажимов источника напряжения, как показано на рис. 1.1, б.

Вольт-амперная характеристика идеального источника напряжения представляет собой прямую, параллельную оси токов (рис. 1.6. а). Такой идеализированный источник способен отдавать во внешнюю цепь бесконечно большую мощность. Ясно, что физически такой источник реализовать нельзя. Однако в определенных пределах изменения тока он достаточно близко отражает реальные свойства независимых источников.

Независимым источником тока называют идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах.  Условное обозначение источника тока показано на рис.  1.5,  г.  Источник тока полностью характеризуется своим задающим током i_Г. Внутренняя проводимость источника тока равна нулю (внутреннее сопротивление бесконечно велико) и ВАХ представляет собой прямую, параллельную осп напряжений (рис. 1.6, б). Такой источник также способен отдавать во внешнюю цепь бесконечно большую мощность и является идеализацией реальных независимых источников.

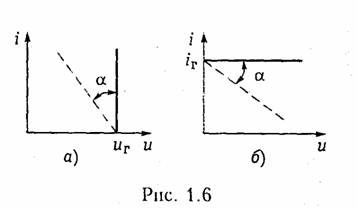
Свойства реальных источников с конечным внутренним сопротивлением R_T можно моделировать с помощью независимых источников напряжения и тока с дополнительно включенными резистивными сопротивлениями R_Г или проводимостью G_Г (см. рис. 1.5, д, е). Напряжение и и отдаваемый ток i этих источников зависят от параметров подключаемой к ним цепи, а их В АХ имеет тангенс угла наклона α, пропорциональный R_Г и G_Г соответственно (штриховые линии па рис. 1.6).

Однако свойства целого ряда электронных устройств нельзя описать моделью соединенных между собой указанных выше независимых источников и пассивных двухполюсных элементов. К числу таких устройств относятся электронные лампы, транзисторы, операционные усилители и другие электронные приборы. Это так называемые зависимые пли управляемые источники.

Зависимый источник представляет собой четырехполюспый элемент (рис. 1.7) с двумя парами зажимов — входных (/, /') н выходных (2, 2'). Входные ток i₁ и напряжение и₁ являются управляющими. Различают следующие разновидности зависимых источников:     источник  напряжения,   управляемый  напряжением

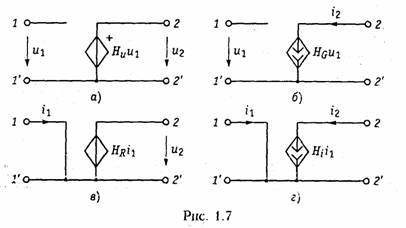
(ИНУН); источник тока, управляемый напряжением (ИТУН); источник напряжения, управляемый током (ИНУТ); источник тока управляемый током (ИТУТ). На рис. 1.7 показаны условные обозначения зависимых источников различного типа.

В ИНУН (рис. 1.7, а) входное сопротивление бесконечно велико, входной ток i₁= 0, а выходное напряжение и₂ связано со входным и₁ равенством и₂ — H_uu₁, где Н и — коэффициент, характеризующий усиление по напряжению зависимого источника. Источник типа ИНУН является идеальным усилителем напряжения.

 ИТУН (см. рис. 1.7, б) выходной ток i₂ управляется входным напряжением u₁ причем i₁= 0 и ток i₂ связан с и₁ равенством где Н_G — коэффициент, имеющий размерность проводимости.

В ИНУТ (рис. 1.7, е) входным током i₁ управляется выходное напряжение i₂, входная проводимость бесконечно велика: u₁=0, i₂ =H_i i_{2 1}, где Hi— коэффициент, имеющий размерность сопротивления.

В ИТУТ (рис. 1.7, г) управляющим током является i₁, а управляемым i₂. Входная проводимость ИТУТ, как и ИНУТ, бесконечно велика, где Hi — коэффициент, характеризующий усиление по току. Источник типа ИТУТ является идеальным усилителем тока. Коэффициенты Н_u Н_G, Hr, Hi, представляют собой вещественные положительные или отрицательные числа и полностью характеризуют соответствующий источник.

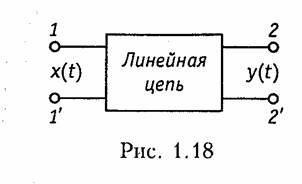
Примером зависимого источника является операционный усилитель (ОУ). Выпускаемые в виде отдельной микросхемы (рис. 1.8, а) ОУ широко применяются в качестве активных элементов электрической цепи.

Операционный усилитель имеет два входа: 1 — неинвертирующий и 2 — инвертирующий. При подаче напряжения и₁ на вход 1 — выходное напряжение u₂ имеет ту же полярность, что и u₂ а

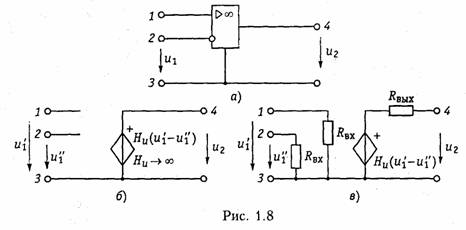
при подаче u₂на вход 2 напряжение u₂ меняет свою полярность па противоположную.

Идеальный ОУ (рис. 1.8, б) представляет собой ИНУН с бесконечно большим коэффициентом усиления (Ни→∞), бесконечно большими входным сопротивлением и выходной проводимостью (выходное сопротивление равно нулю).

Реальный ОУ можно представить в виде ИНУНа с конечными входным R_BX и выходным R_вых сопротивлениями (рис. 1.8, в).

Кроме ОУ в качестве активных элементов электрических цепей широко используются различные электронные и полупроводниковые приборы: электронные лампы, биполярные и полевые транзисторы и др.

На рис. 1.9, а приведена электронная лампа (триод) и ее модели (эквивалентные схемы замещения) в форме ИТУН (рис. 1.9, б) и ИНУН (рис. 1.9, в), где обозначены Gi = 1/Ri, — внутренняя проводимость лампы, S = di₂/du — крутизна; μ = SRi, — коэффициент усиления лампы. Параметры G i, S, μ обычно приводятся в справочниках. Эти эквивалентные схемы являются линейными и могут использоваться в области низких частот. В нелинейном режиме работы активного элемента используются более сложные модели (см. гл. 10, 11). В области высоких частот в моделях активных элементов появляются кроме резисторов, реактивные элементы — обычно емкость (см. табл. 1.1).

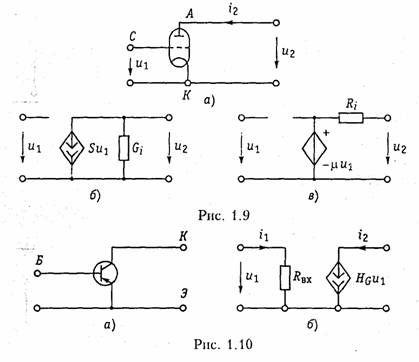
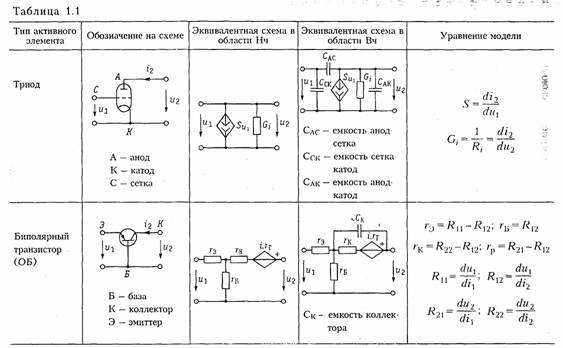
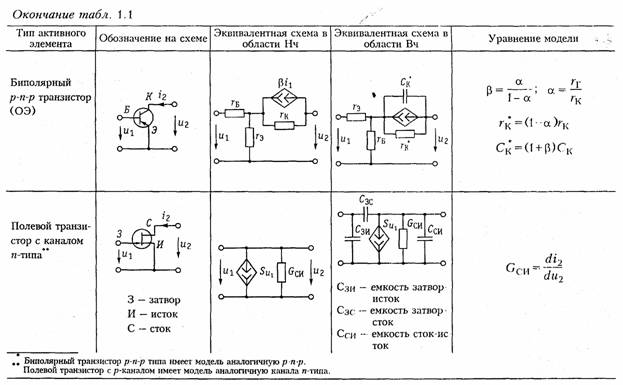
Транзисторы, как правило, имеют более сложную структуру, чем лампы и описываются в зависимости от решаемых задач более сложными моделями [2]. Наиболее распространенными для биполярных транзисторов являются образные и /7-образные эквивалентные схемы замещения, причем, последние можно получить из первых методами преобразования «звезда — треугольник» (см. § 1.5). В табл. 1.1 приведены образные схемы замещения биполярных транзисторов, включенных по схеме с общей базой (ОБ) и общим эмиттером (ОЭ) в области низких и высоких частот и основные соотношения, описывающие их модели.

Иногда для анализа цепей с биполярными транзисторами используются модель ИТУН с конечным входным сопротивлением (рис. 1.10). Для полевых транзисторов обычно используется модель в форме ИТУН (табл. 1.1).

Кроме рассмотренных эквивалентных схем нередко (особенно в справочной литературе) электронные лампы и транзисторы рассматриваются как бесструктурные четырехполюсники с той или иной системой параметров (см. гл. 12).

Отличительной особенностью зависимых источников является их необратимость, т. е. цепи с этими источниками имеют четко выраженный вход и выход. Таким образом, для цепей с зависимыми источниками различают путь прямого прохождения сигнала (от входа к выходу) и обратного прохождения (с выхода на вход), реализуемого с помощью специальных цепей обратной связи (ОС) (гл. 14). Необходимость введения в активные цепи ОС объясняется рядом важных качеств, которыми эти цепи обладают: возможностью моделирования различных функций (см. § 2.7) (суммирование, интегрирование, дифференцирование и др.), генерированием и усилением колебаний, моделированием пассивных элементов типа R, L, С и их преобразованием (например, С и L), перемещение нулей и полюсов функции цепи (см. гл. 14, 15) и др.

1.3.Электрическая схема, топология электрической цепи

Кроме понятия электрической цепи в инженерной практике широкое распространение нашел термин «электрическая схема». В теории цепей схемой называют графическое изображение электрической цепи. Элементам схемы соответствуют активные и пассивные элементы электрической цепи.

В микроэлектронике понятие электрической цепи и электронной схемы часто отождествляют между собой. Так, микросхемой (интегральной схемой) называют интегральную электрическую цепь, содержащую сотни и тысячи простейших активных и пассивных элементов. Чтобы не ломать сложившуюся традицию, будем использовать термин «электрическая схема» или просто «схема» применительно

к графическому изображению электрической цепи или электронной схемы и термины «электрическая цепь» или «электронная (микроэлектронная, интегральная) схема» применительно к моделям реальных физических электрических или электронных устройств.

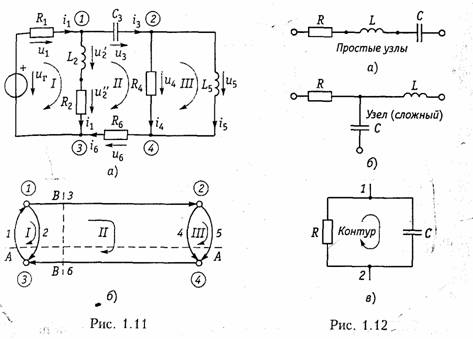
Для анализа электрических цепей в последнее время все большее распространение находят матрично-топологические методы. В их основе лежит представление электрической схемы с помощью графа цепи. Графом цепи называют геометрическую систему линий (ветвей), соединяющих заданные точки (узлы). Если ветви графа ориентированы по направлению токов ветвей, то граф называется ориентированным (направленным). На рис. 1.11, а изображена электрическая схема и ее ориентированный (рис. 1.11, б) граф. Граф содержит всю информацию о геометрической структуре схемы.

Простым узлом называют место соединения зажимов двух элементов (рис. 1.12, «), а сложным — место соединения зажимов трех и более элементов (рис. 1.12, б).

Ветвью называют часть цепи, включенной между двумя узлами, через которые она обменивается энергией с остальной цепью. Ветви, подсоединенные к одной паре узлов, образуют параллельное соединение (рис. 1.12, в).

Последовательно соединенные ветви, связывающие два заданиях узла образуют простой путь, если в нем нет повторяющих Узлов. Например, между узлами 1 и 4 (рис. 1.11, б) простой путь

образуется ветвями 3, 5 или 3, 4 и т. д. Замкнутый путь называется контуром (рис. 1.12, в).

Подграфом называют часть графа. Подграф является связным, если любые его два узла связаны, т. е. соединены ветвями.

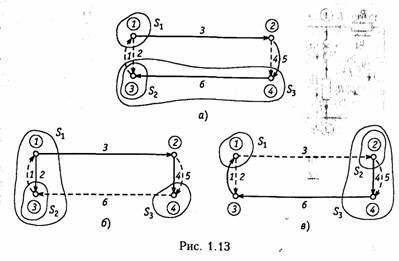
Деревом графа называют связный подграф, содержащий все узлы, но не содержащий ни одного контура (рис. 1.13). Ветви дерева называют ребрами (на рис. 1.13 показаны сплошными линиями).

В теории графов доказывается, что число ветвей дерева, содержащего «у узлов, определяется уравнением

Совокупность ветвей не входящих в состав дерева, образует его дополнение (на рис. 1.13 помечено штриховыми линиями). Ветви дополнения называют хордами. Можно показать, что число хорд

где п_в — общее число ветвей исходного графа.

Сечением графа называют минимальное множество ветвей, удаление которых разбивает граф на две несвязанных части (подграфы). На рис. 1.11, 6 показан пример двух сечений, образованных ветвями 1, 2, 4, 5 (по линии А—А) и 3, 6 (по линии В—В). Добавление любой из ветвей сечения делает граф связным. Обычно сечение изображают в виде замкнутой линии, рассекающей граф цепи на несвязанные компоненты. Сечение, «рассекающее» только одну ветвь дерева, называют главным сечением. Причем, каждому

дереву соответствует своя совокупность главных сечений (рис. 1.13, сечения S₁, S₂, S₃). Число главных сечений равно числу ветвей дерева (1.14).

Аналитически граф можно описать с помощью структурной матрицы А_с (матрицы соединений, инциденций), представляющей собой прямоугольную таблицу с числом столбцов, равным числу ветвей, и числом строк, равным числу узлов. Если положительное направление тока в ветви l выбрать от узла k, то элементы структурной матрицы аи определяются из условия:

Анализ матрицы Ас: показывает, что сумма элементов каждого ее столбца равна нулю. Это является следствием зависимости одной из строк, поэтому ее можно исключить из А_c. Узел, строка которого исключается, называют базисным, а матрица А_o, образующаяся при этом, редуцированная.

Кроме матрицы Ас при анализе электрических цепей используется матрица сечений С, представляющая собой таблицу со строками, соответствующими сечениям графа и столбцами — его ветвями.  Если за положительное направление принять направление ветви внутрь области, охваченной сечением, то элементы Матрицы сечений сы определяются следующим образом:

Матрицей контуров В называют таблицу, с числом строк равным числу независимых контуров, и числом столбцов равным числу ветвей. Элементы матрицы контуров определяются по правилу

Число независимых контуров определяется числом хорд графа , (1.15).

1.4. Законы Кирхгофа

В теории цепей различают два типа задач: задачи анализа и синтеза электрических цепей. К задаче анализа относятся все задачи, связанные с определением токов, напряжений или мощностей в элементах цепи, конфигурация и параметры которой известны. В задачах синтеза, напротив — известны токи и напряжения в отдельных элементах и требуется определить вид цепи и ее параметры, т. е. синтез является обратной задачей по отношению к анализу. Следует отметить, что задача синтеза существенно сложнее задачи анализа и будет рассмотрена в гл. 16.

В основе методов анализа электрических цепей лежат законы Кирхгофа.

Первый закон - закон токов Кирхгофа (ЗТК) формулируется по отношению к узлам электрической цепи и отражает тот факт, что в узлах не могут накапливаться заряды. Он гласит: алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Формально это записывается так:

где т -число ветвей, сходящихся в узле.

В уравнении (1.16) токи, одинаково ориентированные относительно узла, имеют одинаковые знаки. Условимся знаки выходящих токов считать положительными, а входящих - отрицательными .Тогда,    например,   для   узла    1   схемы,    изображенной на рис. 1.11, a, согласно ЗТК — i₁ + i₁ + iз = 0. Число независимых уравнений, составляемых по ЗТК, равно числу независимых узлов электрической цепи и определяется уравнением (1.14).

Закон токов справедлив и по отношению к сечениям электрической цепи. Покажем это на примере сечения Sз (рис. 1.13, а). Запишем ЗТК для узлов 1 и 2:

для узла 1: — i₁ + i₂+ iз ⁼ 0;

для узла 2: — iз + i₄ + i₅ = 0.

Сложив между собой эти уравнения, получим ЗТК для сечения 5з:

— i₁ + i₂ + i₄ + i₅ =0.

Второй закон — закон напряжений Кирхгофа (ЗНК) формулируется по отношению к контурам и гласит: алгебраическая сумма напряжений ветвей в любом контуре равна нулю:

где п - число ветвей, входящих в контур.

В уравнении (1.17) напряжения, совпадающие с направлением обхода контура, записываются со знаком «+», а не совпадающие — со знаком «—».

Составим, например, уравнение по ЗНК для цепи, изображенной на рис. 1.11, а. В соответствии с направлением для контура I:

Общее число линейно-независимых уравнений, составляемых по ЗНК, определяется числом независимых контуров, равных числу хорд (см. (1.15)).

Уравнение ЗТК и ЗНК можно записать в матричной форме, используя редуцированную структурную матрицу Ао и контурную матрицу В.

Закон токов получается путем перемножения матрицы Ао на матрицу-столбец токов ветвей:

l.5. Принцип эквивалентности.

Преобразования электрических схем

В основе различных методов преобразования электрических схем лежит принцип эквивалентности, согласно которому напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными. Преобразования электрических схем применяются для упрощения расчетов. Рассмотрим наиболее типичные преобразования, основанные на принципе эквивалентности.

Последовательное соединение элементов. Согласно ЗТК при последовательном соединении элементов через них протекает один и тот же ток (рис. 1.14). Согласно ЗНК напряжение, приложенное ко всей цепи,

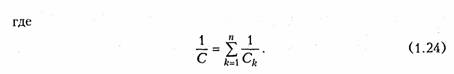
Таким образом, цепь из п последовательно соединенных резистивных, индуктивных или емкостных элементов может быть заменена одним эквивалентным резистивным, индуктивным или емкостным элементом с параметрами, определяемыми формулами (1.22) —(1.24). Причем, при нахождении эквивалентного сопротивления или эквивалентной индуктивности необходимо суммировать сопротивления и индуктивности отдельных резистивных и индуктивных элементов, а для нахождения эквивалентной обратной емкости — суммировать величины, обратные емкости отдельных емкостных элементов. В частности, при п = 2

C = C₁C₂/(C₁ + C₂). (1.25)

При последовательном соединении независимых источников напряжения они заменяются одним эквивалентным источником напряжения с задающим напряжением м_г, равным алгебраической сумме задающих напряжений отдельных источников. Причем со знаком «+» берутся задающие напряжения, совпадающие с задающим напряжением эквивалентного источника, а со знаком «—» — несовпадающие (рис. 1.15).

Параллельное соединение элементов. При параллельном соединении элементов согласно ЗНК к ним будет приложено одно и то же напряжение (рис. 1.16). Согласно ЗТК для тока каждой из схем, изображенных на рис. 1.16, можно записать

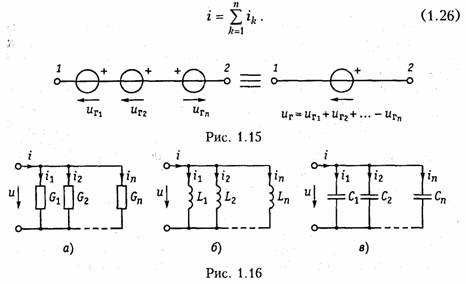
На основании этого,  уравнения с учетом формул (1.6),  (1.9) и (1.12) получаем:

для параллельного соединения резистивных элементов

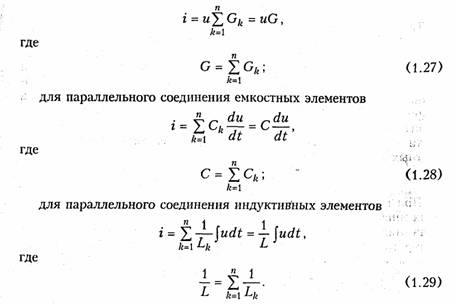
Следовательно, цепь из п параллельно соединенных резистивных, индуктивных или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом с параметрами, определяемыми формулами (1.27) — (1.29).

Таким образом, при параллельном соединении резистивных, емкостных и индуктивных элементов для нахождения эквивалентных проводимостей и емкости цепи проводимости или емкости отдельных элементов складываются. Эквивалентная обратная индуктивность цепи находится суммированием обратных индуктивностей отдельных индуктивных элементов. В частности, при п = 2

Параллельно соединенные независимые источники тока можно заменить одним эквивалентным источником тока с задающим током, равным алгебраической сумме задающих токов отдельных источников. Причем со знаком «+» берутся задающие токи, совпадающие по направлению с задающим током эквивалентного источника, а со знаком «—» — не совпадающие (рис. 1.17).

При расчете электрических цепей часто возникает необходимость преобразования источника напряжения с параметрами и_Г и R_Г (см. рис. 1.5, д) в эквивалентный источник

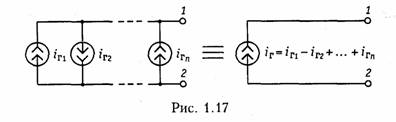
тока с параметрами i_г и G_r (см. рис. 1.5, е), или наоборот — преобразование источника тока в эквивалентный источник напряжения. Эти преобразования осуществляются в соответствии с формулами

которые  могут  быть  получены  из   ЗНК  и   ЗТК для  схемы  на рис. 1.5, д, е и принципа эквивалентности.

1.6. Принцип наложения

Принцип наложения (суперпозиции) имеет важнейшее значение в теории линейных электрических цепей. Подавляющее число методов анализа линейных цепей базируется на этом принципе. Если рассматривать напряжения и токи источников как задающие воздействия, а напряжение и токи в отдельных ветвях цепи как реакцию (отклик) цепи на эти воздействия, то принцип наложения можно сформулировать следующим образом: реакция линейной цепи на сумму воздействий равна сумме реакций от каждого воздействия в отдельности.

Принцип наложения можно использовать для нахождения реакции в линейной цепи, находящейся как под воздействием нескольких источников, так и при сложном произвольном воздействии одного источника.

Рассмотрим вначале случай, когда в линейной цепи действует несколько источников. В соответствии с принципом наложения для нахождения тока i или напряжения и в заданной ветви осуществим поочередное воздействие каждым источником и найдем соответствующие частные реакции i_k и и_k на эти воздействия. Тогда результирующая реакция в соответствии с принципом наложения определится как

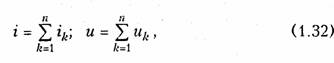
где п — общее число источников.

Если в линейной цепи приложено напряжение сложной формы, применение принципа наложения позволяет после разложения это-

го воздействия на сумму простейших найти реакцию цепи на каждое из них в отдельности с последующим наложением полученных результатов. Следует отметить, что принцип наложения является следствием линейности уравнений, которые описывают цепь,  поэтому его можно применить к любым физическим величинам, которые связаны между собой линейной зависимостью (например, ток и напряжение). В то же время этот принцип нельзя использовать при вычислении мощности, так как она связана с напряжением и током квадратичной зависимостью (1.7).

Принцип наложения лежит в основе большинства временных и частотных методов расчета линейных цепей, которые рассматриваются в последующих главах. В отличие от линейных для нелинейных цепей принцип суперпозиции неприменим — и это обстоятельство часто служит критерием оценки линейности или нелинейности электрической цепи.

Для оценки линейности электрической цепи подадим на ее вход воздействие x(t) в виде напряжения или тока (рис. 1.18) и будем наблюдать реакцию y(t) на выходе. Если при воздействии kx(t) (где k — вещественное число) реакция равна ky(t), то данная цепь будет линейной. Если такой пропорциональности нет, то цепь является нелинейной.

Многие нелинейные цепи в режиме малых сигналов также могут считаться линейными и к ним может быть применен принцип суперпозиции. Все это свидетельствует о чрезвычайно важном месте, который занимает принцип наложения в теории электрических цепей.

Большая часть радиотехнических устройств и систем относится к классу линейных цепей: это усилители, фильтры, корректоры, интеграторы, дифференциаторы, другие цепи, предназначенные для линейной обработки сигналов. В то же время имеется значительное количество устройств, которые нельзя отнести к классу линейных цепей и для их анализа необходимо использовать специальные методы (см. гл. 10, 11, 15).

1.7. Теорема замещения

При обосновании некоторых методов анализа электрических цепей используется теорема замещения, которую можно сформулировать следующим образом: значение всех токов и напряжений в цепи не изменится, если любую ветвь цепи с напряжением и и током i (рис. 1.19, а) заменить источником напряжения с задающим напряжением u_Г— и (рис. 1.19, 6) или источником тока с задающим током i_г (рис. 1.19, в).

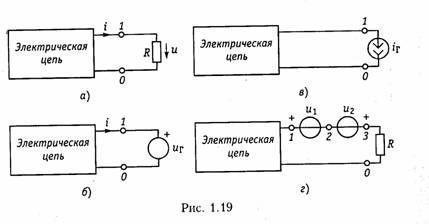
Докажем эту теорему на примере источника напряжения (рис. 1.19, б). Для этого включим в ветвь с R (рис. 1.19, а) два источника напряжения с задающим напряжением и направленные навстречу друг другу (рис. 1.19, г).

Приняв потенциал узла Vo ⁼ 0,найдем потенциалы узлов Vз> V₂,V₁:

V₃ = Ri, V₂ = V₃-u₂ = Ri-Ri = 0; V_x = V₂ + u₁ = Ri.

Таким образом, потенциал узла I в схеме рис. 1.19, а и в схеме рис. 1.19, г оказывается одинаковым. А так как V₂ = 0 и Vo = 0, то закорачивая их между собой, приходим к схеме рис. 1.19, б, что и доказывает теорему. Аналогично доказывается и теорема замещения источником тока (рис. 1.19, в).

Теорема замещения справедлива как по отношению к линейным, так и нелинейным цепям, так как при ее доказательстве не накладывается на выделенную ветвь никаких ограничений, кроме того, что она обменивается энергией с остальной частью цепи только через зажимы 1—0 с помощью тока i.

1.8. Теорема об активном двухполюснике

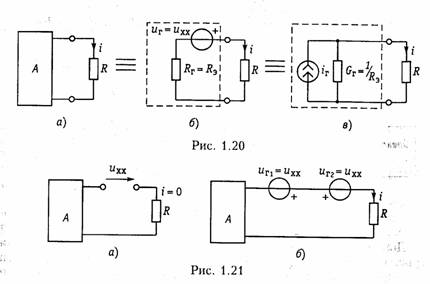
Теорема об активном двухполюснике используется обычно в случае, когда надо найти реакцию цепи (ток или напряжение) в одной ветви. При этом удобно всю остальную часть цепи, к которой подключена данная ветвь, рассматривать в виде двухполюсника (на рис. 1.20, а) показана резистивная ветвь). Двухполюсник называют активным, если он содержит источники электрической энергии, и пассивным — в противном случае. На рисунках активный двухполюсник будем обозначать буквой А, а пассивный — П. Более подробно определение и общая теория двухполюсников излагается в гл. 4.

Различают две модификации теоремы об активном двухполюснике: теорема об эквивалентном источнике напряжения (теорема Тевенина) и теорема об эквивалентном источнике тока (теорема Нортона).

Теорема об эквивалентном источнике напряжения. Согласно теореме Тевенина ток в любой ветви линейной электрической цени не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения с задающим напряжением, равным напряжению холостого хода на зажимах разомкнутой ветви и внутренним сопротивлением, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви (рис. 1.20, б).

Для доказательства этой теоремы предположим, что цепь не содержит зависимых источников. Тогда, разомкнув ветвь с элементом R, определим расчетным или экспериментальным путем напряжение холостого хода u_хх (рис. 1.21, а). Затем включим в эту ветвь навстречу друг другу два источника напряжения с задающим напряжением u_Г = м_Хх (рис. 1.21, б). Ток в ветви с R при этом (рис. 1.21, б) не изменится по сравнению с током i в исходной схеме (рис. 1.20, а). Результирующий ток в выделенной ветви найдем в соответствии с принципом наложения: i = i_А + i₁+ i₂, где i_А — частичный ток, обусловленный активным двухполюсником; i₁ — ток, обусловленный действием источника u_Г1 ;1₂ — ток, обусловленный действием источника и_Г2. Однако напряжение активного двухполюсника и задающее u_Г2 действует навстречу друг другу, поэтому i_А + i₂= 0.Следовательно, ток в цепи i = i₁ будет обусловлен только действием источника с u_Г1= u_Хх (см. рис. 1.20, б). Частичный ток i₁ может быть найден, если положить все задающие напряжения и токи активного двухполюсника равными нулю. Получившийся при этом пассивный двухполюсник полностью характеризуется своим эквивалентным сопротивлением R_э = R_г относительно выделенных зажимов. Таким образом, приходим к схеме, изображенной на рис. 1.20, б и теорема доказана.

Теорема об эквивалентном источнике тока (теорема Нортона): ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с задающим током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви (см. рис. 1.20, в).

Доказательство этой теоремы проще всего осуществить путем преобразования эквивалентного источника напряжения (см. рис. 1.20, б) в эквивалентный источник тока (рис. 1.20, в) с параметрами,

где i_Кз — ток короткого замыкания рассматриваемой ветви.

Из (1.33) следует формула, которую можно положить в основу экспериментального определения параметров пассивного двухполюсника:

Теорема об активном двухполюснике существенно упрощает расчет сложной цепи, так как позволяет ее представить в виде простейшей схемы эквивалентного источника напряжения или тока с конечным внутренним сопротивлением R_Г или внутренней проводимостью G_Г. В отличие от идеальных источников напряжения и тока (см. § 1.2) напряжение и ток этих источников зависят от сопротивления R ветви.

Теорема об активном двухполюснике справедлива и для случая, когда последний содержит зависимые источники с ограниченными задающими напряжениями и токами. При этом при нахождении параметров эквивалентного генератора следует положить равными нулю задающие напряжения и токи лишь независимых источников.

1.9. Принцип дуальности

Анализ уравнений для напряжений и токов, полученных в предыдущих разделах, позволяет сформулировать важный принцип теории электрических цепей — принцип дуальности (двойственности). Этот принцип гласит: если для данной электрической цепи

справедливы некоторые законы, уравнения или соотношения, то они будут справедливы и для дуальных величин в дуальной цепи. Этот принцип проявляется, например, в сходстве законов изменения напряжения в одной цепи и законов изменения токов в другой цепи (дуальной). Табл. 1.2 иллюстрирует двойственный характер основных законов и соотношений в электрических цепях.

Использование принципа дуальности в ряде случаев позволяет существенно упростить расчет. Так, если найдены уравнения для одной цепи, то используя дуальные соотношения можно сразу записать законы изменения дуальных величин в дуальной цепи.

1.10. Теорема Телледжена . Баланс мощности

Теорема Телледжена является одной из наиболее общих теорем теории электрических цепей. Рассмотрим граф произвольной электрической цепи, содержащей n_В ветвей и п_у узлов. Для согласованных направлений напряжений и токов ветвей теорема Телледжена гласит: сумма произведений напряжений u_k и токов i_k всех ветвей графа, удовлетворяющих законам Кирхгофа, равна нулю.

так как выражения, стоящие в скобках, равны нулю согласно ЗТК, что и доказывает теорему. Необходимо подчеркнуть, что поскольку теорема Телледжена следует непосредственно из законов Кирхгофа, то она справедлива для любых электрических цепей: линейных и нелинейных, активных и пассивных; цепей, параметры которых изменяются во времени {параметрических цепей). В общем случае эта теорема справедлива и для случая попарных произведений и_k и i_l разных ветвей, если для них выполняются ЗНК и ЗТК.

Из теоремы Телледжена вытекает ряд следствий, важнейшим из которых является баланс мощности. Действительно, произведение Ukik согласно формуле (1.5) представляет собой мгновенную мощность p_k k-ветви, поэтому в соответствии с (1.35) алгебраическая сумма мощностей всех ветвей цепи равняется нулю. Если в (1.35) выделить ветви с независимыми источниками, то баланс мощности можно сформулировать следующим образом: алгебраическая сумма мощностей, отдаваемых независимыми источниками, равняется алгебраической сумме мощностей, потребляемых остальными ветвями электрической цепи.

Пример. Составить баланс мощности для цепи, изображенной на рис. 1.23. Алгебраическая сумма мгновенных мощностей, развиваемых источниками на-

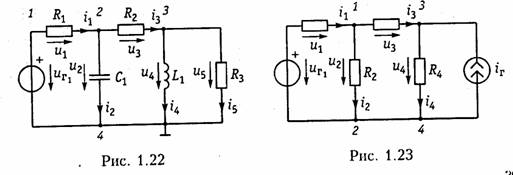
пряжения и тока Потребляемая мощность с учетом закона Ома

В соответствии с балансом мощностей

Следует отметить, что при определении р_псТ произведение щг берется со знаком «+», если направления задающего напряжения и_Т и тока i направлены навстречу друг другу, и со знаком «—» в противном случае. Аналогичное правило знаков для источников тока: если напряжение на зажимах источника направлено навстречу задающему току г_г, берется знак «+», а если напряжение совпадает с током — знак «—». Баланс мощности выражает не что иное, как закон сохранения энергии в электрической цепи.

Вопросы и задания для самопроверки

1.  Что называется электрическим током, напряжением, мощностью, энергией?

2.  Дать определения активных и пассивных элементов электрической цепи.

3.  Дать определения зависимых и независимых источников электрической энергии и привести примеры тех и других.

4.  В чем суть принципа суперпозиции? Для каких электрических цепей он применим?

5.  В чем суть теоремы замещения? Для каких цепей она применима?

6.  В чем суть теоремы об активном двухполюснике? Какие величины являются параметрами эквивалентного источника напряжения, эквивалентного источника тока?

7.  Что отражает баланс мощностей в электрической цепи? Могут ли не совпадать значения мощностей, отдаваемых источниками в цепь и потребляемых элементами цепи?

8.  Дать определения графа, узла, ветви, дерева, контура электрической цепи.

9.  Дать определения I и II законов Кирхгофа для электрической цепи. Как они записываются в матричной форме?

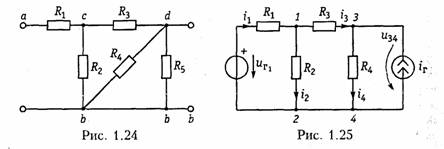
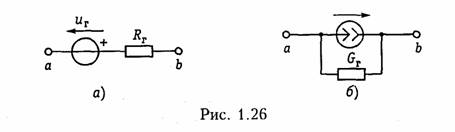
10.  Определить эквивалентное сопротивление цепи, изображенной на рис. 1.24, относительно точек ab, cd, db, ad.

ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ В РЕЖИМЕ ПОСТОЯННОГО ТОКА

2.1. Метод законов Кирхгофа

В электрических цепях, содержащих активные элементы (электронные лампы, транзисторы, операционные усилители и другие зависимые источники) важным режимом работы является статический. В статическом режиме на электроды активного элемента подаются постоянные токи и напряжения, обеспечивающие заданные условия работы того или иного устройства. Статический режим характеризуется зависимостями между постоянными токами и напряжениями в отдельных частях электрической цепи и является одним из основных режимов работы любого электрического устройства. Поэтому анализ цепей в режиме постоянного тока играет важную роль в общей теории электрической связи.

Как отмечалось в § 1.2 при постоянном токе и напряжении индуктивность эквивалентна короткозамкнутому участку (рис. 1.1, а), емкость — разрыву цепи. Таким образом, в режиме постоянного тока в модели цепи будут отсутствовать реактивные элементы, и она приобретет чисто резистивный характер. Линейные резистивные цепи полностью описываются системой линейных алгебраических уравнений, составляемых на основании закона Кирхгофа. В этой главе рассмотрим основные методы анализа линейных резистивных цепей, находящихся под воздействием постоянных токов и напряжений. Постоянные токи и напряжения в дальнейшем будем обозначать прописными буквами I и U соответственно.

Метод расчета электрических цепей, основанный на законах Кирхгофа, в которых независимыми переменными являются токи в ветвях, называют методом токов ветвей. В соответствии с этим методом для нахождения токов или напряжений ветвей составляются (п_у — 1) уравнений (1.16) по ЗТК и (n_B — n_у + 1) уравнений (1.17) по ЗНК. В результате получаем систему из (n_у — 1) + (n_B —  n_у + 1) = n_B линейно-независимых уравнений, число которых равно числу токов ветвей. Совместное решение этой системы позволяет найти все токи.

При выборе независимых контуров необходимо руководствоваться топологией электрической цепи (§ 1.3): составить граф цепи, выбрать дерево, дополнить его хордой, при этом образуется контур. Путем последовательного дополнения хордами дерева до исходного графа получаем (n_B — п_у +1) независимых контуров.

Пример. Рассчитать токн ветвей схемы резнстнвноп цепи, изображенной на рис. 2.1. а по методу уравнений Кирхгофа.

Построим граф цепи (рис. 2.1, б) и выберем дерево (рис. 2.1, в). Дополним дерево хордами 2, 5, 6 (на рис. 2.1, в показано пунктиром). В результате образуется три независимых контура I, II, III (рис. 2.1, я). Составим уравнение по ЗТК и ЗНК.

Схема имеет n_y = 4 узла, п_B = 6 ветвей. Выберем узел 4 в качестве базисного и составим n_у = 3 уравнения по ЗТК:

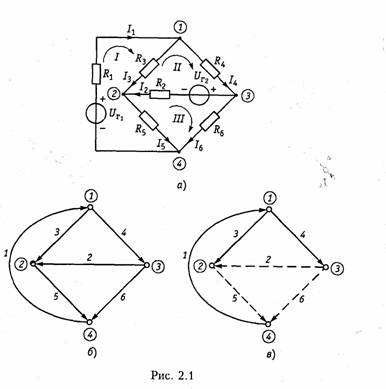
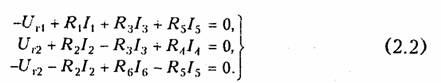
Решая совместно системы уравнений (2.1) и (2.2), найдем искомые токи.

При использовании законов Кирхгофа в качестве независимых переменных можно было взять напряжения ветвей (метод напряжения ветвей) или токи одних ветвей и напряжения других (гибридный метод).

В случае, если в цепи имеется ветвь с источником тока, то неизвестным параметром в этой ветви является напряжение на зажимах источника, которое можно найти методом напряжения ветвей.

2.2. Преобразование резистивных электрических цепей

В случае, когда на цепь воздействует один источник постоянного напряжения или тока, наиболее эффективным является метод преобразования электрических цепей. Суть этого метода заключается в нахождении эквивалентного сопротивления цепи относительно зажимов (полюсов) источника.

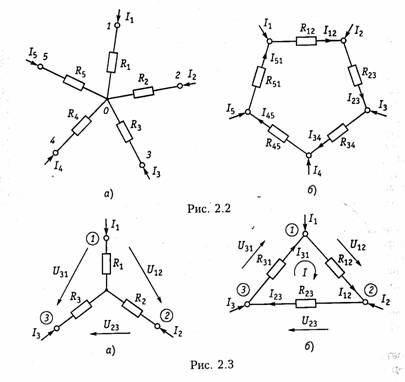
В § 1.5 были рассмотрены простейшие методы преобразования последовательного и параллельного соединенных пассивных элементов (см. формулы (1.22) —(1.24) и (1.27) —(1.29)). Однако на практике встречаются более сложные соединения элементов, которые нельзя свести только к последовательному или параллельному. Примером подобного соединения являются соединения многолучевой звездой (рис. 2.2, а) и многоугольником (рис. 2.2, б).

Характерной особенностью этих соединений является наличие внутреннего узла 0 в звезде и внутреннего контура в многоугольнике. Наиболее часто встречаются случаи трехлучевой звезды и треугольника (рис. 2.3, а, б).

Найдем формулы преобразования соединения «треугольника» в «звезду». Запишем для схемы «треугольник» уравнения по ЗТК и ЗНК (рис. 2.3, б):

Уравнения (2.6) и (2.7) позволяют осуществить переход от соединения резистивных элементов «треугольник» к соединению «звезда». Обратный переход можно получить по формулам

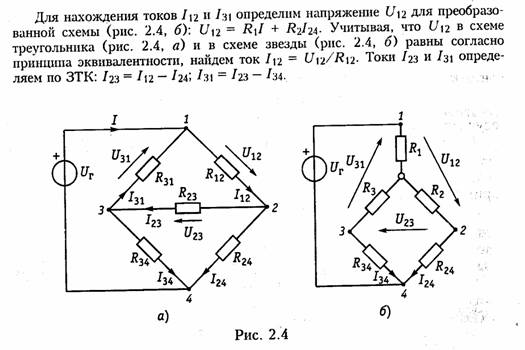
Пример. Рассчитать токи ветвей схемы резистивной цепи, изображенной на рис. 2.4, а. Данная схема может служить моделью измерительного моста, который находит широкое применение в различных измерительных приборах, в частности для измерения сопротивлений. Принцип работы моста основан на выполнении условий баланса его плечей.

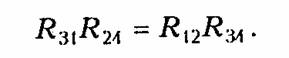
При этом потенциалы узлов 2 и 3 оказываются одинаковыми и в диагонали моста R₂₃ ток будет равен нулю. Таким образом, если включить в диагональ моста вместо R₂₃ измерительный прибор — амперметр, то путем изменения одного из сопротивлений плеча (например, R₂₄ с помощью магазина сопротивлений), можно найти сопротивление другого (например R_3l). Для случая, когда R₁₂ ⁼ Rm₃₁⁼ R, условие баланса достигается при R₃₄ = R₂₄.

Преобразуем треугольник R_12, R_23, R₁₃ в звезду с лучами R₁, R_2, R₃ (рис. 2.4, б), где R₁, R₂, R₃ определяются формулами (2.6) и (2.7). Тогда эквивалентное сопротивление цепи относительно зажимов источника (узлы 1 и 4)

Аналогично формуле (2.9) можно получить формулы преобразования n-лучевой звезды в полный многоугольник с числом ветвей равным п_в = п(п — 1)/2:

Следует отметить, что обратная задача преобразования многоугольника в эквивалентную n-лучевую звезду при n>3 не имеет решения, так как при этом оказывается число уравнений п(п — 1)/2 превышает число неизвестных.

2.3. Метод наложения

В основе метода наложения лежит принцип суперпозиции (наложения), линейных электрических цепей (§ 1.6). Этот метод применяется в случае, когда в цепи действует несколько источников напряжения или тока. При этом в соответствии с этим принципом находят частичные токи и напряжения, а результирующие реакции определяются путем алгебраического суммирования частичных токов и напряжений.

Проиллюстрируем принцип наложения на примере резистивной цепи, изображенной на рис. 2.5, а, содержащей идеальные источники напряжения. Найдем ток в резистивном элементе R3. Положим вначале, что в цепи действует только один источник U_T\; второй источник напряжения исключается и зажимы его закорачиваются. При этом получаем частичную схему, изображенную на рис. 2.5, 6. Определим ток Iз' от воздействия напряжения U_Г1'.

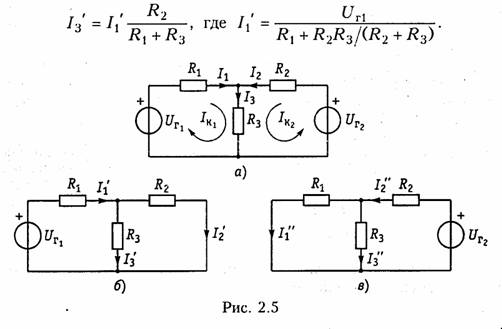
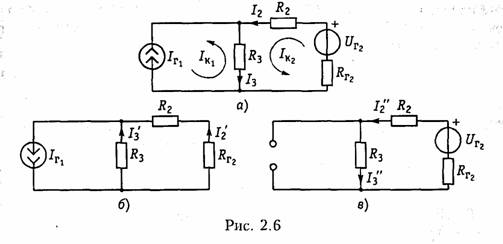
Теперь полагаем, что в цепи действует только источник U_Г2- Исключив источник U_Г1, получим вторую частичную схему (рис. 2.5, в). Ток Iз" от воздействия U_Г2 определится как

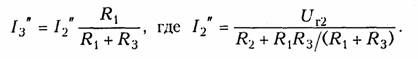
Результирующий ток Iз найдем как алгебраическую сумму частичных токов Iз ' и Iз ": Iз = Iз’ + Iз ". При определении результирующих токов знак «+» берут у частичных токов, совпадающих с выбранным положительным направлением результирующего тока, и знак «—» — у несовпадающих. Как следует из рассмотренного примера, при составлении частичных электрических схем исключаемые идеальные источники напряжения закорачиваются. В случае, если в цепи действуют источники напряжения с внутренними сопротивлениями R_Г, при их исключении они заменяются своими внутренними сопротивлениями R_Г.

При наличии идеальных источников тока соответствующие ветви исключаемых источников размыкаются, а при наличии реальных источников они заменяются своими внутренними проводимостями G_r.

Пример. Определить ток /з в цепи, изображенной на рис. 2.6, а. Составляем две частные схемы (рис. 2.6, б, в), для которых находим частичные токи:

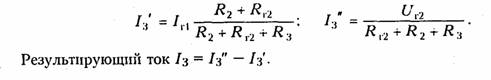
При наличии в цепи зависимых источников они остаются в частичных схемах неизменными.

2.4. Метод контурных токов

При определении токов и напряжений в отдельных ветвях цепи с n_{B -}ветями по законам Кирхгофа в общем случае необходимо решить систему из п_в уравнений. Для снижения числа решаемых уравнений и упрощения расчетов используют методы контурных токов и узловых напряжений.

Метод контурных токов позволяет снизить число решаемых уравнений до числа независимых контуров, определяемых равенством (1.15). В его основе лежит введение в каждый контур условного контурного тока Ik, направление которого обычно выбирают совпадающим с направлением обхода контура. При этом для контурного тока будут справедливы ЗТК и ЗНК. В частности, для каждого из выделенных контуров можно составить уравнения по ЗНК. Поясним суть метода контурных токов на примере резистивной цепи, схема которой изображена на рис. 2.5, а. Для контурных токов Iк₁ и I_К2 этой схемы можно записать уравнения по ЗНК в виде

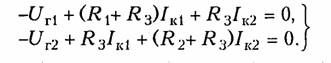
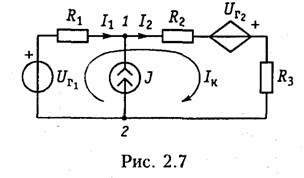
Перенесем U_T\ и U_r2 в правую часть системы и получим так называемую каноническую форму записи уравнений по методу контурных токов:

Слагаемые в уравнении (2.11) берутся со знаком «+», если ток I_кl и I_кп обтекают Rl_n в одном направлении и со знаком «—» в противном случае. Контурное задающее напряжение U_K равно алгебраической сумме задающих напряжений источников, входящих в каждый контур. Со знаком «+» суммируются источники, задающее напряжение которых направлено навстречу контурному току, и со знаком «—», если направление напряжения и контурного тока совпадают.

Решая систему уравнений (2.11), найдем значения контурных токов

Как следует из уравнений (2.14) и (2.15), контурный ток может быть получен алгебраическим суммированием частичных токов от воздействия каждого контурного задающего напряжения в отдельности. Таким образом, полученный результат отражает рассмотренный в § 1.6 принцип наложения.

Если в схеме кроме источников напряжения содержится п-ветвей с источниками тока, то независимые контуры выбираются так, чтобы источник тока входил только в один контур. Это можно сделать, если выбрать дерево графа цепи таким, чтобы источник тока   входил   в   одну   из   хорд.

Число контурных уравнений при этом уменьшается до

Напряжения от задающих токов этих источников учитываются в левой части системы (2.11) на взаимных сопротивлениях, которые эти токи обтекают. Например, для схемы, изображенной на рис. 2.6, а, составляется только одно уравнение для II контура:

Сформулированные выше правила составления уравнений по методу контурных токов справедливы и в случае зависимых источников напряжения ИНУН и ИНУТ.

Пример. Найдем токн в цепи содержащей ИНУТ с задающим напряжением U_г2 =  HrI₁ (рис. 2.7) по методу контурных токов.

Учитывая, что цепь содержит ветвь с идеальным независимым источником тока J согласно (2.15) составим всего одно уравнение для контурного тока I_к. При этом задающий ток источника тока J замыкаем по ветви с R₁ и U_Г1, в результате получим

где I_К — матрица-столбец контурных токов. Подставляя (2.19) в (2.18), получаем:

BR_BB^TI_K =BU_ГB. (2.21)

Если учесть, что

BR_BB^T=R_K,   Ви_ГВ=U_к, (2.22)

где R_K — квадратная матрица контурных сопротивлений; U_K — матрица-столбец контурных задающих напряжений, то в соответствии с (2.20) получим матричное уравнение контурных токов

R_KI_K=U_K. (2.23)

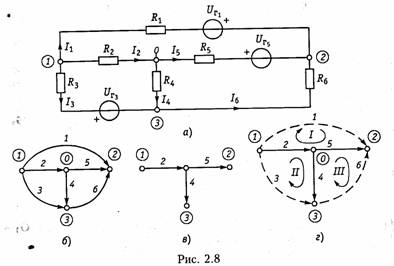
Пример. Рассмотрим схему, изображенную на рис. 2.8, а. В соответствии с направлением токов строим направленный граф цепи (рис. 2.8, б) и дерево графа (рис. 2.8, в). Подсоединяя к дереву хорды (на рис. 2.8, г обозначены пунктиром), получаем три независимых контура. Выбрав направление обхода контуров I, II и III, в соответствии с правилом, изложенным в § 1,3, строим контурную матрицу

Для линейных электрических цепей важную роль играет принцип взаимности (теорема обратимости). Он гласит: если источник напряжения, помещенный в какую-либо ветвь I пассивной линейной электрической цепи, вызывает в другой ветви k ток определенного значения, то этот же источник, будучи помещенный в ветвь k, вызывает в ветви l ток с тем же значением. Справедливость этого принципа следует непосредственно из уравнений (2.14) и (2.15) с учетом того, чтоΔlk = Δkl.

2.5. Метод узловых потенциалов

Метод узловых потенциалов (узловых напряжений) является наиболее общим и широко применяется для расчета электрических цепей, в частности, в различных программах автоматизированного проектирования электронных схем.

Метод узловых потенциалов базируется на ЗТК и законе Ома. Он позволяет снизить число решаемых уравнений до величины, определяемой равенством (1.14). В основе этого метода лежит расчет напряжений в (n_у — 1)-м узле цепи относительно базисного узла. После этого на основании закона Ома находятся токи или напряжения в соответствующих ветвях. Рассмотрим сущность метода узловых потенциалов на примере резистивной цепи, изображенной на рис. 2.9, а. Примем потенциал Vз ⁼ 0 (базисный узел) и с помощью (1.31) преобразуем источники напряжения в эквивалентные источники тока

Проводимости G₁₁ и G₂₂ представляют собой арифметическую сумму проводимостей всех ветвей, подсоединенных соответственно к узлам 1 и 2; они называются собственными проводимостями узлов 1 и 2. Проводимости G₁₂ = G₂₁ равны арифметической сумме проводимостей всех ветвей, включенных между узлами 1 и 2, и называются взаимными проводимостями узлов 1 и 2. Алгебраическую сумму задающих токов I_y1и I_У2 источников тока подключенных соответственно к узлам 1 и 2 называют задающими узловыми токами узлов 1 и 2. Задающие токи источников в алгебраической сумме берутся со знаком «+», если положительное направление задающего тока источника ориентировано к соответствующему узлу, и «—», если от узла. Например, для узлового тока I_y1 со знаком «+» берется ток I_Г1 так как ориентирован по направлению к узлу 1, и знак «—» берется для I_Г2, так как он ориентирован от узла 1.

Решив систему (2.26) относительно V₁ и V₂ определим узловые потенциалы цепи. Искомые токн находим по закону Ома.

Полученный результат можно обобщить на произвольную резистивную схему с п узлами. Если принять п-й узел за базисный, то система уравнений по методу узловых потенциалов приобретает вид

Из уравнений (2.29) так же как из уравнений (2.14), следует, что   узловые   потенциалы   определяются   алгебраической   суммой

частичных узловых потенциалов, обусловленных действием каждого задающего узлового тока в отдельности, т. е. как и в методе контурных токов уравнения (2.29) отражают принцип наложения, характерный для линейных электрических цепей.

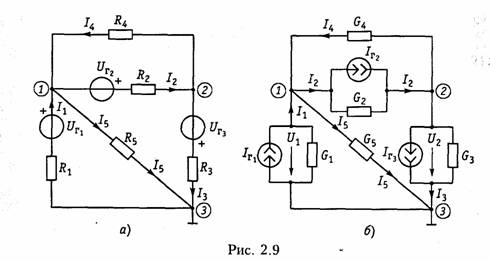
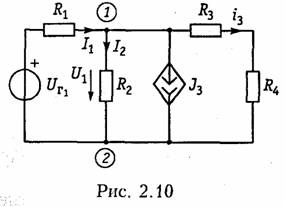
Рассмотренный   метод   составления узловых напряжений справедлив и при наличии в цепи зависимых источников типа ИТУТ и ИТУН. В цепи, изображенной на рис. 2.10, содержится кроме независимого источника напряжения U_Г1 зависимый ИТУН с задающим током Jз = = HgU₁. Определим токи в цепи методом узловых потенциалов.

В соответствии с вышеизложенным 'методом примем за базисный узел V₂ = 0. Тогда для узла / получим

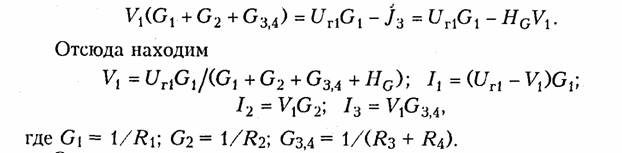
Запишем уравнение по метолу узловых потенциалов в матричной форме. Умножим элементы редуцированной структурной матрицы Ао на потенциалы V соответствующих узлов, в результате получим матрицу напряжения ветвей:

Умножим левую и правую часть матричного уравнения (2.17) на матрицу Ао и учитывая ЗТК в матричной форме (1.18) и равенство (2.30), получим

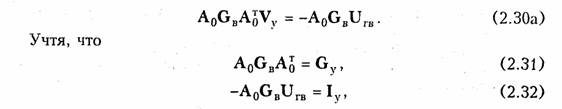
получим матричную форму уравнений равновесия узловых потенциалов:

где Gy — квадратная матрица узловых проводимостей, I_у — матрица-столбец узловых токов.

Пример. Составим уравнение узловых потенциалов в матричной форме для схемы, изображенной на рис. 2.8, а. Примем за базис нулевой узел Vo ⁼ 0. Структурная матрица Ао в этой цепи в соответствии с правилом, изложенным в § 1.3, имеет вид

Подставив G_y и I_У в (2.33), получим уравнение узловых потенциалов в матричной форме. После определения матрицы узловых потенциалов V_y найдем матрицу напряжений ветвей согласно (2.30) и токи ветвей по закону Ома (2.17).

Для решения матричных уравнений в (2.23) или (2.33) обычно используют ЭВМ (см. § 2.7).

2.6. Метод эквивалентного генератора

Метод эквивалентного генератора базируется на теореме об активном двухполюснике (см. § 1.8) и позволяет упростить решение многих задач, связанных с передачей сигналов и электрической энергии от источника к приемнику. При этом обычно источник рассматривается как активный двухполюсник с известными задающими напряжениями U_Г или током I_г и внутренними сопротивлением R_Г или проводимостью G_Г, а приемник — как пассивный

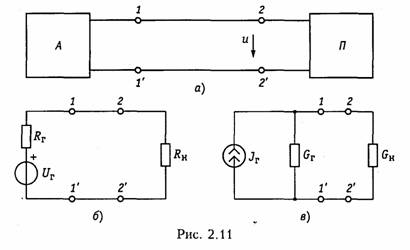
двухполюсник с внутренним сопротивлением нагрузки R_H или проводимостью G_H (рис. 2.11).

            Таким образом, система передачи, изображенная на рис. 2.11, а может быть представлена в виде двух эквивалентных схем: с источником напряжения (рис. 2.11, б) и с источником тока (рис. 2.11, в).

В соответствии с теоремами Тевенина и Нортона (см. § 1.8) задающее напряжение генератора определяется как напряжение холостого хода на разомкнутых зажимах активного двухполюсника U_Г =Uxx, а задающий ток — как ток короткого замыкания J_г  = I_КЗ. Внутреннее сопротивление активного двухполюсника R_Г или его проводимость G_г находятся как эквивалентные входные сопротивления или проводимость относительно разомкнутых зажимов пассивного двухполюсника, который получается после исключения из схемы всех источников напряжения и тока. При этом идеальные источники напряжения заворачиваются, а тока — размыкаются; реальные же источники заменяются своими внутренними сопротивлениями или проводимостями.

Параметры U_хх, Iкз, R_Г, G_Г можно найти как экспериментальным, так и расчетным путем. После нахождения параметров эквивалентного генератора напряжения или тока, ток I и напряжение U в нагрузке можно найти для схемы, изображенной на рис. 2.9, б, по формуле

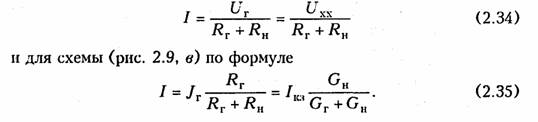
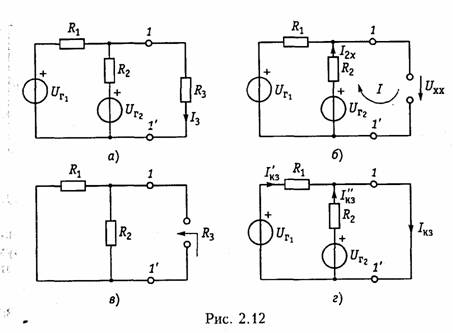
Пример. Найти ток в сопротивлении R₃ (рис. 2.12, а) методом эквивалентного источника напряжения.

Разомкнем ветвь с R₃ и определим U_хх (рис. 2.12, б) по ЗНК для I контура:

Очевидно, методы эквивалентного источника как напряжения так и тока дают один и тот же результат. Применение того или

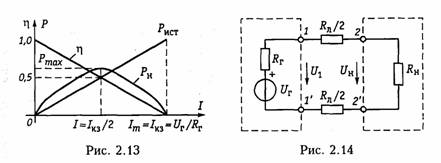
иного метода определяется удобством и простотой нахождения U_Xx или I_кз.

Одной из важнейших практических задач является оптимальная передача электрической энергии от активного к пассивному двухполюснику. Оптимум обычно понимается в смысле получения максимальной мощности в нагрузке Р_H. Мощность Р_н определим как

Из (2.37) видно, что сопротивление линии существенно снижает мощность, отдаваемую в нагрузку, за счет потерь в линии.

2.7. Примеры применения резистивных цепей

Аттенюатор. В технике связи широкое применение находят высокоточные делители напряжения (аттенюаторы), реализуемые с помощью Т-образных резистивных перекрытых схем (рис. 2.15).

Характерной особенностью этой схемы является то, что если выбрать сопротивление R₁ и R₂ из условия

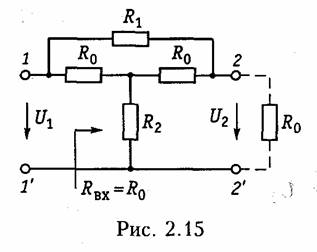
то при включении к точкам 2—2' или /—/' резистивного элемента с сопротивлением Ro, входное сопротивление цепи со стороны входа 1— 1' и выхода 2—2' будет одинаково и равно Ro- В этом можно легко убедиться, если свернуть схему к точкам 1—1' или 2—2' соответственно. Отношение выходного напряжения ко входному такого аттенюатора

т. е. полностью определится отношением сопротивления делителя R_ouR\.

Для получения высокоточного деления аттенюатор обычно выполняют в виде нескольких звеньев, включенных каскадно друг за другом (рис. 2.16).

При этом коэффициент деления

т. е. много меньше единицы.

Масштабный усилитель. В тех случаях, когда надо получить К ≥1, применяют обычно масштабные усилители, представляющие собой резистивную цепь, содержащую активный элемент. На рис. 2.17, а показана схема масштабного усилителя на операционном усилителе (ОУ), включенном по инвертирующей схеме. Заменим ОУ эквивалентной моделью ИНУН с определенными входным R_BX и выходным R_Вых сопротивлениями (рис. 2.17, б). Составим для нее уравнение равновесия по методу узловых потенциалов, приняв потенциал Vз = 0:

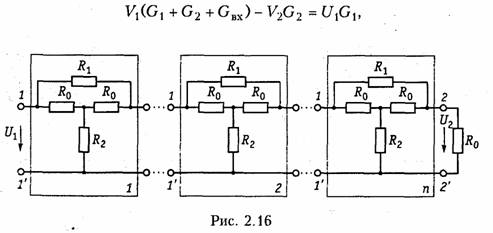
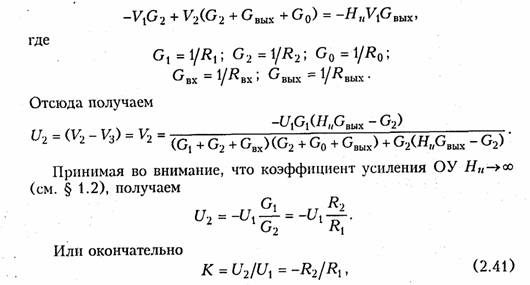
т. е. коэффициент усиления масштабного усилителя полностью определяется соотношением сопротивлений R₂ и R₁. Знак «—» в равенстве (2.41) свидетельствует об инвертировании полярности U2 по отношению к U₁.

Входное сопротивление масштабного усилителя

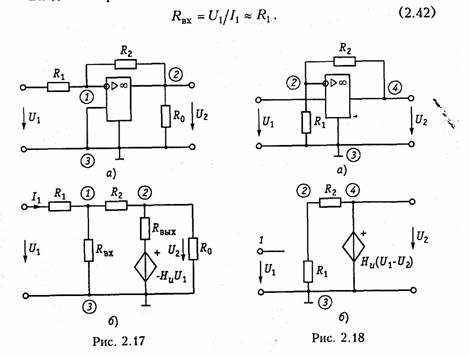
Усилитель,     включенный     по     неинвертирующей     схеме

(рис. 2.18, а), Используем идеальную модель ОУ, изображенного на рис. 2.18, 6. Приняв потенциал Vз ⁼ О, запишем уравнение равновесия по методу узловых потенциалов:

также не зависит от параметров ОУ.

Усилитель с неинвертирующим входом может использоваться как повторитель напряжения, если положить R₂ = О R₁ = ∞ (рис 2.19). Коэффициент усиления такой схемы равен К — 1, входное сопротивление очень велико, а выходное очень мало (см. § 1.2), что используется для согласования входных сопротивлений различных устройств.

Сумматор. Это устройство используется для выполнения арифметической операции взвешенного суммирования различных напряжений. На рис. 2.20 изображена схема активного сумматора двух напряжений U₁ и U₂, выполненного на базе ОУ, включенного по инвертирующей схеме.

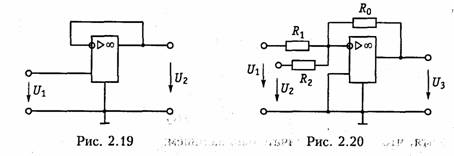
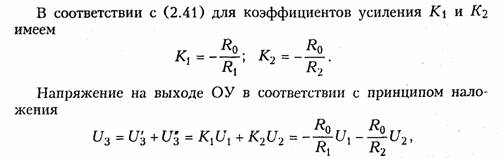
т. е. равно взвешенной с коэффициентами К₁ и К₂ арифметической сумме входных напряжений. Аналогичным образом можно построить активный сумматор на произвольное число п входных напряжений:

Отличительной чертой сумматора этого типа является хорошая «развязка» входных цепей, что обусловило его широкое применение в технике связи.

Конвертор отрицательного сопротивления (КОС). Конверторами отрицательного сопротивления называют активную резистивную цепь_; входное сопротивление которой равно сопротивлению нагрузки с отрицательным знаком. Одна из возможных схем КОС изображена на рис. 2.21, а.

Составим для эквивалентной схемы КОС (рис. 2.21, б) уравнение по методу узловых потенциалов для узла 1, приняв V3 = О (базисный узел) и учтя, что U₁ =V₁, U₂ =V₂, получим

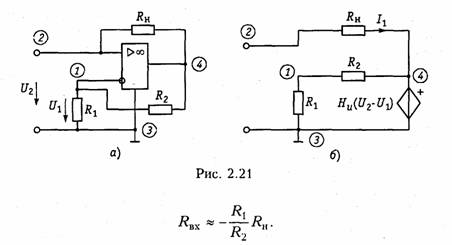
Если сопротивление R₁ = R₂, то получаем R_BX = —R_H> т. е. КОС позволяет получать отрицательное сопротивление, что широко используется на практике для компенсации потерь в различных цепях.

2.8. Алгоритмы анализа линейных резистивных цепей на ЭВМ

В основе машинных методов анализа электрических цепей лежат математические модели, задаваемые с помощью системы уравнений, которые описывают связь между токами и напряжениями на ее отдельных элементах (компонентах). Эти уравнения имеют название компонентных уравнений электрической цепи.

К числу подобных компонентных уравнений относятся уравнения (1.6), (1.9) и (1.12), связывающие токи и напряжения на резистивных, индуктивных и емкостных элементах. Сложные многополюсные элементы (электронные лампы, транзисторы, операционные усилители и др.) описываются моделями из нескольких компонентных уравнений.

Кроме компонентных уравнений математические модели цепей включают в себя топологические уравнения, которые вытекают из топологии цепи и записываются на основании законов Кирхгофа (1.18) и (1.20).

Для формирования математической модели могут использоваться различные базисы, наиболее распространенным из которых для резистивных цепей является метод узловых потенциалов. При использовании метода узловых потенциалов исходным является составление уравнения равновесия цепи в форме (2.33):

Последовательность формирования уравнения (2.45) на основании ЗТК (1.18), уравнения связи (2.30) и компонентных уравнений на базе закона Ома (2.17) рассмотрены в §§ 2.4, 2.5.

После формирования уравнения узловых потенциалов в форме (2.45) осуществляется его решение тем или иным способом. Таким образом, суть машинных методов анализа линейных резистивных цепей заключается в формировании и решении матричного уравнения состояния цепи в форме узловых потенциалов (2.45). Рассмотрим последовательность реализации обоих этих этапов на ЭВМ.

Формирование уравнения узловых потенциалов. В качестве первого шага осуществляется ввод в ЭВМ данных о топологии и параметрах цепи. Для этого выбираете базисный узел, потенциал которого принимается равным нулю. Затем осуществляется нумерация остальных узлов от 1 до (п_у — 1), а также нумерация ветвей от 1 до п_в. После этого на основании правила, изложенного в § 1.3, формируется структурная матрица цепи Ао.

Учитывая, что в матрице Ао обычно содержится много нулевых элементов (разряженная матрица), ее удобно вводить в память ЭВМ не в виде двумерного массива, а с помощью одномерного массива тройки целых чисел (l, k, m), характеризующих номер ветви — l,номер узла — k, из которого ветвь выходит, и номер узла — т, в который она входит.

После формирования таким образом ненулевых элементов матрицы Ао осуществляется ввод в ЭВМ параметров ветвей. При этом каждая одноэлементная ветвь характеризуется номером ветви; номерами узлов, из которых она выходит и в который входит; типом элемента (резистор, независимые источники напряжения и тока); параметром элемента (сопротивлением резистора, задающим напряжением U _г источника напряжения, задающим током I_г источника тока).

Далее в соответствии с алгоритмом, изложенным в § 2.5, формируется матрица узловых проводимостей G_y и матрица узловых токов I_у. При этом используются стандартные подпрограммы перемножения матриц AoG_B, Ао^т.

Методы решения уравнений узловых потенциалов. Уравнение (2.45) относится к классу линейных уравнений типа

Ax=B (2.46)

Решение уравнения типа (2.46) является самостоятельной задачей в методе узловых потенциалов. Кроме того, решение таких уравнений составляет одну из наиболее распространенных процедур при решении других задач, например, при анализе нелинейных цепей (см. гл. 11). Численным методам решения системы (2.46) посвящена обширная литература; все их можно разделить на две большие группы: прямые и итерационные. В большинстве машинных программ используются прямые методы, обеспечивающие получение решения за конечное число шагов.

Основные проблемы, с которыми приходится сталкиваться при использовании прямых методов — это большая разреженность матрицы G_y, приводящая к большим затратам машинного времени и быстрое возрастание ошибок округления промежуточных результатов, приводящих к большим погрешностям.

Для решения этих проблем используют различные модификации прямых методов, которые можно разбить на три группы: обращения матрицы Gy, разложения матрицы G_y на сомножители и методы для матриц G_y специального вида. Основным методом первой группы является метод Гаусса и его разновидности.

 Число арифметических операций по методу Гаусса

Таким образом, для сложной схемы число операций может оказаться очень большим. Для повышения эффективности метода Гаусса используют метод разряженных матриц.

Методы обращения матрицы G_y применяются, как правило, для сравнительно простых схем, так как для вычисления параметра Gy^-1 требуется больше операций, чем для решения системы (2.46) методами первой группы. Кроме того, при прямом обращении матрицы быстро возрастает ее разреженность, что существенно снижает эффективность этого метода.

Методы третьей группы применяются для матриц узловой проводимости специального вида: ленточного, блочно-диагонального и др. Матрицу Gy ленточного типа имеют, например, электронные схемы каскадной структуры без обратных связей (см. гл. 12).

Метод Гаусса. Алгоритм Гаусса состоит из прямого и обратного ходов. Прямой ход включает последовательное исключение неизвестных х из системы уравнений (2.46). При этом на первом шаге получаем явное выражение для х_1.

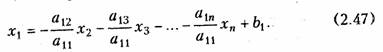
Подставив х₁ во все оставшиеся уравнения, исключаем из них переменную х₁, что приводит к изменению коэффициента a_ij в этих уравнениях.

На втором шаге определяется в явной форме x₂ после чего оно исключается из третьего и последующих уравнений и т. д. Причем, исключение переменной приводит к пересчету коэффициентов по формуле

Процедура исключения производится для всех токов i. В результате прямого хода матрица А преобразуется к треугольному виду.

Обратный ход позволяет вычислить составляющие искомого вектора х, начиная с последнего элемента. Действительно, в результате прямого хода в последнем n-м уравнении осталась единственная переменная После нахождения х_п определяется из (n — 1) уравнения х_п-1 и т. д. На рис. 2.22 изображена схема алгоритма расчета по методу Гаусса.

Метод разряженных матриц. Идея этого метода состоит в том, что если при прямом ходе Гаусса, хотя бы один коэффициент (a_ik или a_kj,) равен нулю, то коэффициент по формуле (2.48) можно не пересчитывать, что при высокой степени разреженности матрицы А может существенно сократить объем вычислений. При этом также отпадает необходимость хранить в памяти ЭВМ нулевые коэффициенты, что уменьшает затраты машинной памяти.

Для реализации этой идеи используются различные методы упорядочения матриц, обеспечивающие минимальный объем вычислений. Простейшим из них является следующий: строки с меньшим числом ненулевых элементов должны располагаться выше строк с большим числом ненулевых элементов.

Пусть строки и столбцы матрицы узловых проводимостей G_y располагаются в порядке возрастания номеров соответствующих им узлов. Тогда для минимизации объема вычислений нумерацию узлов необходимо производить в порядке возрастания количества ненулевых элементов в строке. При этом объем вычислений будет равен:

т. е. является линейной функцией числа узлов п = пу в эквивалентной схеме цепи.

Методы обращения матрицы узловой проводимости. С помощью этих методов решение системы (2.46) ищется в виде

На рис. 2.23 изображена схема алгоритма расчета электрической цепи по методу обращения узловой проводимости.

Кроме моделей индуктивных и емкостных элементов в виде (1.8) и (1.11) в последнее время в программах машинного анализа электрических цепей нашли применение дискретные модели L- и С-элементов, основанные на неявных методах численного интегрирования [1]. Так, значения производной х_п + 1 в соответствии с неявной формулой Эйлера можно зависать как

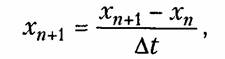
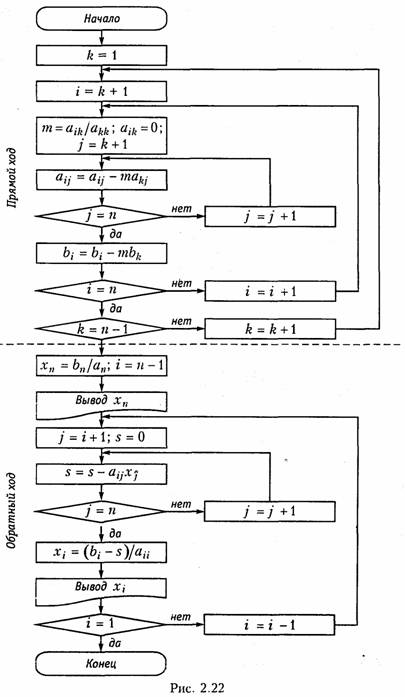
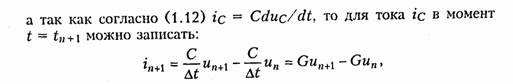
где Δt = t_n+₁ - t_n, что соответствует резистивной схеме замещения емкостного элемента, изображенной на рис. 2.23, а, где G=C/Δt; i_г = Gu_n.

Аналогично можно получить дискретную модель для элемента индуктивности:

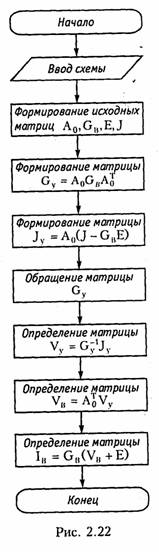
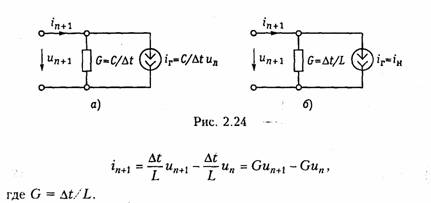
На рис. 2.24, б показана эквивалентная дискретная схема замещения L-элемента.

Использование дискретных моделей элементов позволяет свести RLC-цепь к соответствующей резистивной цепи, что существенно упростит их машинный анализ.

Вопросы и задания для самопроверки

1.  Принцип составления уравнений методом законов Кирхгофа.

2.  Какие токи и напряжения остаются неизменными при переходе от соединения «треугольника» в «звезду» и обратно?

3.  Чем определяется количество частичных схем при расчете токов в цепи методом наложения?

4.  Какие законы Кирхгофа используются при составлении уравнений по методам контурных токов и узловых напряжений?

5.  Рассчитать токи ветвей в цепи рис. 2.26 методами наложения законов Кирхгофа, контурных токов, узловых напряжений, если известно, что: U_г1 = 5 В; U_г3 = 10 В; J = 0,5 A; R₁ = R₂ = Rз =  10 Ом.

Ответ:   I₁ = 0,5 А;    I₂ = 0 А;    I₃ = 1 А.

6.  Какие теоремы используются при определении тока в отдельно взятой ветви методом эквивалентного генератора?

7.  Методом эквивалентного генератора в цепи рис. 2.24 определить сопротивление R₅,   когда  в  нем  выделяется  максимальная мощность, если U = 3 В; J = 0,5 A; R₁ = R₂ = Rз = R₄ =  2 Ом.

Ответ:   R₅ = 3,33 Ом;    Р = 216 мВт.

8.  В согласованном или несогласованном режиме работают высокоточные аттенюаторы и почему?

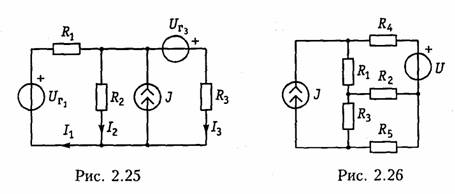
9.  Определить в аттенюаторе, изображенном на рис. 2.15, резисторы R₁ и R₂, если известно что R₀ = 50 Ом; К = 0,1.

Ответ:   R₁ = 450 Ом;    R₂ = 5,55 Ом.

10.  Чем определяются коэффициенты передачи масштабных усилителей,   включенных  по   инвертирующей   и   неинвертирующей схемам?

11.  Для конвертора отрицательного сопротивления, изображенного на рис. 2.21, определить R₁, если R_BX = 1 кОм; R_н = 50 Ом; R₂ = 500 Ом.

Ответ:   R₁ = 25 Ом.

12.  В чем особенности алгоритмов анализа линейных резистивных цепей на ЭВМ методом узловых потенциалов?

ГЛАВА 3. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ В РЕЖИМЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ

3.1. Гармонические колебания. Основные понятия и определения

Электрические цепи могут находиться под воздействием постоянных или переменных напряжений и токов. Среди этих воздействий важнейшую роль играют гармонические колебания. Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного сигнала. Исследование режима гармонических колебаний важно и с методической точки зрения, поскольку анализ электрических цепей при негармонических воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармонических воздействиях можно распространить и на цепи при периодических несинусоидальных, а также непериодических воздействиях (см. гл. 5, 9).

Гармоническое колебание i(t) (рис. 3.1) характеризуется следующими основными параметрами: амплитудой I_т; угловой частотой ω, начальной фазой φ_i. Амплитудой называют максимальное абсолютное значение тока i(t). Аналитически гармоническое колебание можно записать в виде

где  — называется текущей фазой (или просто фазой) гармонического колебания, так как она растет линейно во времени с угловой скоростью Вместо формулы (3.1) гармоническое колебание можно выразить и в косинусоидальной форме:

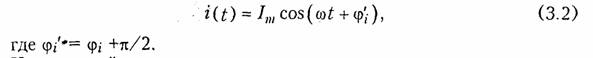
Наименьший промежуток времени, по истечении которого значения функции i(t) повторяются, называется периодом Т. Между периодом Т и угловой частотой ω существует простая связь:

Величину,   обратную периоду,   называют циклической частотой: f = 1/Т. Из вышеизложенного следует, что ω = 2πf. Единицей ■ измерения частоты f является герц (Гц), угловой частоты ω — радиан в секунду (рад/с). Так как радиан — величина безразмерная, то [ω] измеряется в 1/с или с^-1.

В радиотехнике и электросвязи используют гармонические сигналы от долей герц (инфранизкие частоты) до десятков и сотен гигагерц (сверхвысокие частоты).

Для питания различных электроэнергетических установок в России и ряде других стран принята промышленная частота f = 50 Гц. В качестве источников гармонических колебаний промышленной частоты используются электромашинные генераторы различного типа. Принцип работы простейшего электромашинного генератора иллюстрирует рис. 3.2. В состав генератора входят: статор, создающий магнитное поле с магнитной индукцией В, и ротор, вращающийся в этом магнитном поле с угловой частотой ω. При пересечении витками катушки ротора магнитного потока Ф в них согласно закону электромагнитной индукции наводится ЭДС

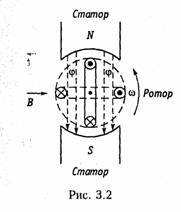
где  ψ= wФ— потокосцепление катушки с магнитными потоками; w — число витков катушки. При постоянной скорости вращения ротора для получения ЭДС синусоидальной формы применяются полюса специальной формы. Частота на выходе генератора

где р_п — число пар полюсов ротора; v — частота вращения ротора, об/мин.

Электромашинные генераторы используются для получения гармонических напряжений и токов не выше 5...8 кГц. Для получения гармонических сигналов более высоких частот обычно используются ламповые и полупроводниковые генераторы (см. гл. 15).

Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значение гармонического тока

Действующие  значения токов  и  напряжений  называют еще  их среднеквадратическими значениями.

Определим тепловую энергию, которая выделяется гармоническим колебанием  i(t) за период Т в резистивном элементе с сопротивлением R:

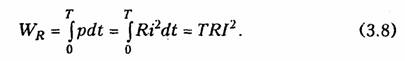
Таким образом, действующее значение тока численно равно такому постоянному току, который за период Т на том же сопротивлении выделяет то же количество тепла, что и гармонический ток.

Среднее значение гармонического тока

Подставив значение i из (3.6) в (3.9), находим, что I_ср = 0. Этот результат вполне понятен, если учесть, что уравнение (3.9) определяет площадь, ограниченную кривой i(t) за период Т (см. рис. 3.1). Если значение тока определено за полпериода, то можно записать:

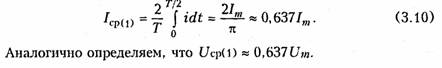
3.2. Способы представления гармонических колебаний

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы) (см. рис. 3.1); вращающимися векторами (векторные диаграммы); комплексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических преобразований. Более удобно векторное представление гармонических колебаний, при котором каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. В качестве примера на рис. 3.3 показано векторное представление двух колебаний токов i ₁ и i₂:

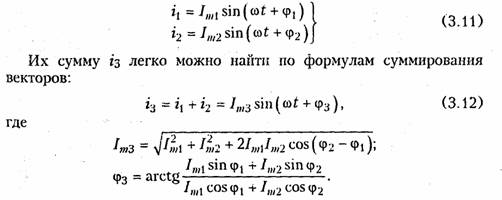
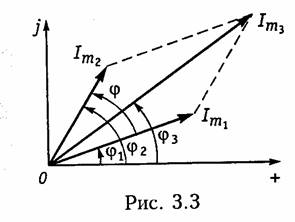
Величина φ= φ₂ —φ₁ называется фазовым сдвигом между колебаниями i ₁ и i₂. Он определяется только начальными фазами φ₂ и φ₁ и не зависит от начала отсчета времени. Нетрудно видеть, что суммирование (наложение) любого числа гармонических колебаний с частотой со приводит к гармоническому колебанию той же частоты со.

Совокупность   векторов,   изображающих гармонические колебания в электрической цепи, называют векторной диаграммой. Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и напряжений.

Наиболее распространенными являются представления гармонических колебаний с помощью комплексных чисел. Эти представления лежат в основе символического метода расчета электрических цепей — метода комплексных амплитуд. Представим ток i, определяемый формулой (3.6), на комплексной плоскости. Для этого изобразим вектор I_т на комплексной плоскости с учетом начальной фазы φ_i (рис. 3.4, а). Знаком «+» обозначено положительное направление вещественной оси, а j = √-1 — положительное направление мнимой оси. Будем вращать этот вектор в положительном направлении (против часовой стрелки) с угловой частотой со. Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармоническим колебанием):

Первая часть слагаемого (3.13) отражает проекцию вращающегося вектора на вещественную ось, а вторая часть — на мнимую ось. Сравнив второе слагаемое в (3.13) с (3.6), приходим к выводу: синусоидальный ток i на комплексной плоскости представляется

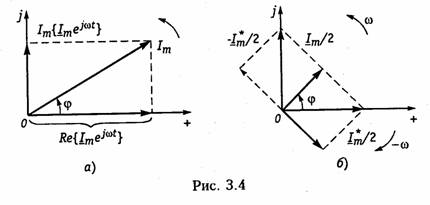
в форме проекции иа мнимую ось вращающегося вектора (3.13)

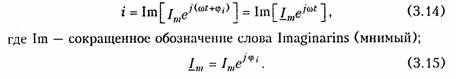
Величина I_т носит название комплексной амплитуды тока.

Важным свойством комплексной амплитуды является то, что она полностью определяет гармоническое колебание заданной частоты ω, так как содержит информацию об его амплитуде и начальной фазе.

Если гармоническое колебание задается в форме косинусоиды, например

где -сопряжение комплексная амплитуда тока.

Таким образом, ток i из (3.6) согласно (3.19) можно представить как геометрическую разность векторов  вращающихся в противоположных направлениях с угловой частотой со, а ток из (3.16) — как геометрическую сумму этих векторов (рис. 3.4, б). В первом случае i располагается на мнимой, а во втором случае — на действительной осях. Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.

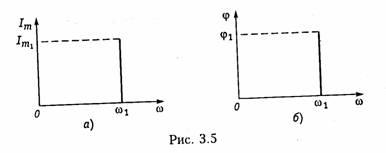
Спектральное (частотное) представление гармонических колебаний состоит в задании амплитудного и фазового спектров колебания (рис. 3.5). Более подробно спектральное представление и методы анализа цепей, основанные на этом, представлении, рассмотрены в гл. 5, 9.

3.3. Гармонические колебания в резистивных, индуктивных и емкостных элементах

Резистивные цепи. Пусть к резистивному элементу R приложено гармоническое напряжение

При последовательном или параллельном соединениях нескольких резистивных элементов ток в цепи определяется уравнением, аналогичным (3.22), где R определяется согласно (1.22) для последовательного и (1.27) для параллельного соединений элементов. При этом фазовый сдвиг между током и приложенным напряжением остается равным нулю.

Индуктивные цепи. Под действием напряжения (3.21) в индуктивном элементе будет протекать ток согласно (1.9):

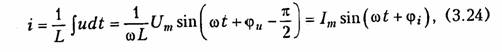
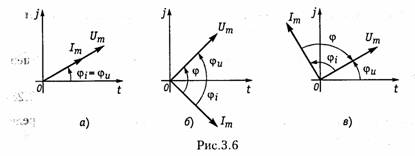
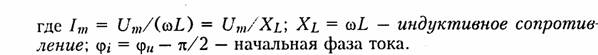
Величину, обратную X_L, называют индуктивной проводимостью Bl = l/(ωL). Как следует из полученных выражений, ток в индуктивности отстает от приложенного напряжения на π/2, т. е. фазовый сдвиг между током i и напряжением и (рис. 3.6, б)

На векторной диаграмме фазовый сдвиг φ откладывается от вектора тока к вектору напряжения. Нетрудно видеть, что средняя за период мощность в индуктивном элементе равна нулю.

При последовательном и параллельном соединениях индуктивных элементов ток в цепи определяется уравнением, аналогичным (3.24), где L находится согласно (1.23) для последовательного и (1.29) для параллельного соединений.

Емкостные цепи. Для емкостного элемента согласно уравнению (1.12) имеем:

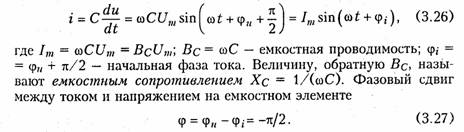
Из приведенных уравнений следует, что ток в емкости опережает приложенное напряжение на угол π/2 (рис. 3.6, в), причем знак «—>> свидетельствует об отставании напряжения и от тока i. Средняя за период мощность в емкостной цепи также равна нулю.

При последовательном и параллельном соединениях емкостных элементов ток в цепи определяется согласно (3.26), где С находится из (1.24) для последовательного и (1.28) для параллельного соединений.

3.4. Гармонические колебания в цепи при последовательном соединении R, L, С-элементов

Допустим, что в цепи, содержащей последовательно соединенные элементы R, L, С (рис. 3.7), протекает ток

На рис. 3.8 изображена векторная диаграмма напряжений, описываемых уравнений (3.30).

Напряжение U_mr на резистивном сопротивлении R называется активной составляющей приложенного напряжения и обозначается  разность напряжений называется реактивной составляющей. Согласно этому определению и формулам (3.31) имеем:

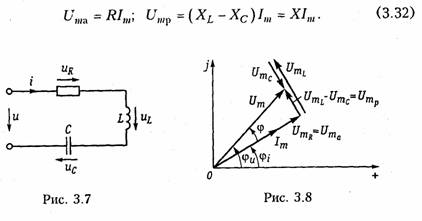
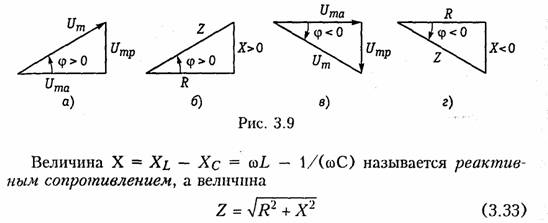
— полным сопротивлением цепи.

Треугольник на векторной диаграмме, образованный напряжениями U_ma, U_mp, U_m называют треугольником напряжений. Если U_mL > U_mc (Xl > Xc), то цепь носит индуктивный характер (приложенное напряжение опережает ток) и треугольник напряжений имеет вид, изображенный на рис. 3.9, а; если U_mL < U_mc (Xl < Хс), то цепь носит емкостный характер (приложенное напряжение отстает от тока) и треугольник напряжений принимает вид, изображенный на рис. 3.9, в. Треугольник со сторонами R, X, Z подобный треугольнику напряжений, называется треугольником сопротивлений (рис. 3.9, б, г). Из треугольников сопротивлений и напряжений следует:

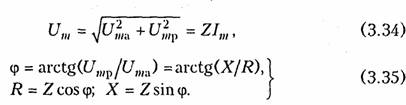
Треугольники напряжений и сопротивлений позволяют упростить анализ электрической цепи.

3.5. Гармонические колебания в цепи при параллельном

 соединении R, L, С-элементов

Приложим к цепи, содержащей параллельно соединенные элементы R, L, С (рис. 3.10), напряжение

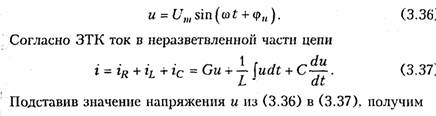
На рис. 3.11 изображена векторная диаграмма токов, описываемых уравнением (3.39).

Ток в резистивном сопротивлении I_тr называют активной составляющей тока I_та, а разность тока I_тр = I_тL — 1_тс — реактивной составляющей тока. Для I_тa и I_тр справедливы соотношения

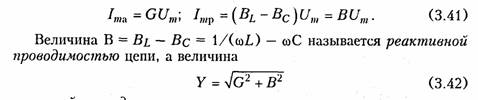
— полной проводимостью цепи.

По аналогии с треугольником напряжений и сопротивлений при параллельном соединении элементов можно ввести треугольники токов и проводимостей (рис. 3.12, а, б). Как следует из этих ри-

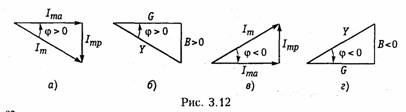
сунков, при I_тl > ImC (B_L > B_C) цепь носит индуктивный характер (общий ток отстает от приложенного напряжения) и при I_тl < I_mc (B_L < B_C) — емкостный характер (ток опережает приложенное напряжение). Из треугольников токов и проводимостей следует:

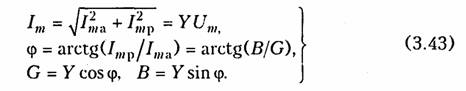
Сравнение треугольников токов и проводимостей с треугольниками напряжений и сопротивлений показывает их дуальный характер. Дуальны также и все соотношения, описывающие цепи при последовательном и параллельном соединении элементов, дуальны и сами цепи.

3.6. Символический метод расчета разветвленных цепей

Расчет разветвленных цепей при смешанном соединении элементов в режиме гармонических колебаний обычно осуществляется символическим методом. Это объясняется тем, что классический метод расчета приводит к громоздким интегрально-дифференциальным уравнениям и требует большого объема тригонометрических преобразований. Символический метод позволяет тригонометрические операции над гармоническими колебаниями и геометрические операции над векторами свести к алгебраическим операциям над комплексными числами, что существенно упрощает расчет. При этом могут быть использованы все методы преобразований и анализа, изложенные в гл. 1, 2. Допустимость использования символического метода объясняется тем, что в линейных цепях в режиме гармонических воздействий в цепи устанавливаются гармонические колебания тон же частоты. Таким образом, неизвестными параметрами токов и напряжений будут лишь амплитуды и фазы, определяемые однозначно их комплексными амплитудами. Запишем основные законы электрических цепей в символической форме.

Для резистивного элемента R связь между комплексными амплитудами тока I_т и напряжения U_т можно определить согласно закону Ома (1.6) путем замены мгновенных значений токов i и напряжений и их комплексными амплитудами:

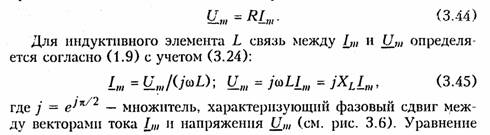
(3.45) отражает закон Ома для индуктивных элементов. Сравнение (3.45) с (1.9) показывает, что операция дифференцирования d/dt соответствует в комплексной форме умножению на jω.

Для емкостного элемента С на основании (1.12) можно записать:

т. е. операция интегрирования соответствует в комплексной форме делению на/со. Полученные уравнения (3.44) —(3.46) справедливы и для комплексных действующих значений токов и напряжений:

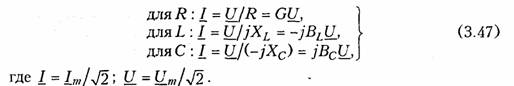
Аналогично можно получить уравнения законов Кирхгофа в комплексной форме. Так, для ЗТК (1.16) заменив мгновенные значения токов i_k их комплексными амплитудами I_mk, получим

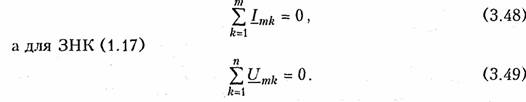
Полученные уравнения законов Ома и Кирхгофа в комплексной форме лежат в основе символического метода расчета линейных цепей при гармонических воздействиях. Причем, как показывает анализ уравнений (3.24), (3.26). (3.45) и (3.46), при переходе к комплексной записи операции дифференцирования заменяются умножением на jω, операции интегрирования — делением на jω. В результате вместо системы интегрально-дифференциальных уравнений получаем систему алгебраических уравнений, решение которой определяет амплитуды и начальные фазы искомых токов и напряжений.

Применим символический метод к анализу гармонических колебаний в цепи при последовательном (см. § 3.4) и параллельном (см. § 3.5) соединениях элементов R, L, С. Для последовательного

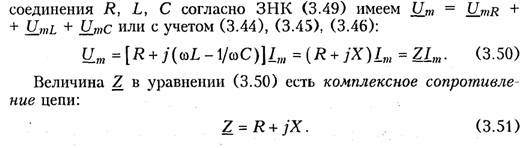
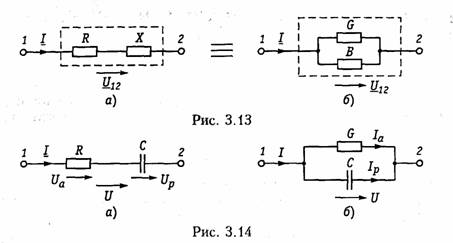
Комплексное сопротивление Z можно выразить в показательной или тригонометрической форме:

Таким образом, рассмотренное ранее полное сопротивление цепи (3.33) представляет собой модуль комплексного сопротивления:

а фазовый сдвиг φ — аргумент (arg) комплексного сопротивления:

Аналогичным образом можно получить уравнения токов и напряжений в комплексной форме для параллельного соединения элементов R, L, С (см. § 3.5). Так уравнение (3.39) в комплексной форме примет вид

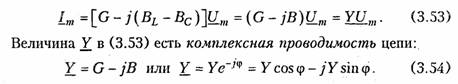
Следовательно, полная проводимость цепи Y равна модулю комплексной проводимости Y = | Y|, а фазовый сдвиг φ — аргументу комплексной проводимости φ = arg Y = arctg(B/G).

При анализе различных электрических цепей часто возникает необходимость преобразования схемы последовательно соединенных элементов в эквивалентное параллельное соединение и наоборот (рис. 3.13). В основе подобных преобразований лежит принцип эквивалентности (см. § 1.5). Согласно этому принципу ток I и напряжение U₁₂ в исходной (рис. 3.13, а) и преобразованной (рис. 3.13, б) схемах должны остаться неизменными. Для первой

Преобразование (3.56) и (3.57) можно положить в основу разложения тока в последовательном участке и напряжения в параллельном на активную и реактивную составляющие.

Пример. Преобразовать последовательный RC-участок (рис 3.14, я) в эквивалентный параллельный (рис. 3.14, б). Определить активные и реактивные составляющие токов и напряжений на обоих участках.

В соответствии с уравнением (3.57) получаем

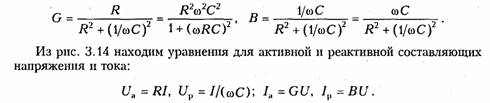
Символический метод особенно эффективен при анализе сложных разветвленных цепей. Причем поскольку все методы расчета подобных цепей (метод контурных токов, узловых потенциалов, наложения и др.) базируются на законах Ома и Кирхгофа, то эти методы могут использоваться и при комплексной форме с заменой соответствующих величин (токов, напряжений, сопротивлений, проводимостей) их комплексными значениями.

Пример. Проиллюстрируем это на примере расчета цепи, изображенной на рис. 3.15 различными методами в комплексной форме. Заменим элементы ветвей в исходной схеме их комплексными сопротивлениями, а источники напряжения и токи их комплексными значениями (рис. 3.16):

Рассчитаем теперь эту цепь различными методами в символической форме, используя комплексы действующих значений токов и напряжений.

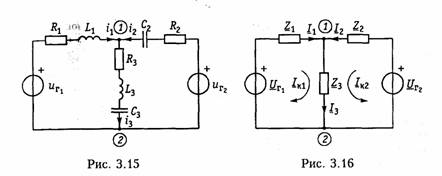
1. Метод наложения.   Сравнение схем,   изображенных  на рис.   3.16  и рис. 2.5. а показывает их одинаковую топологию. Таким образом, путем перехода от R к Z, от U_r к U_r и от I к I можно сразу получить соответствующие уравнения для токов I _1, I _2, I ₃(см. § 2.3).

2.  Метод контурных токов. В соответствии с § 2.4 составляем систему из двух уравнений для контуров I и II:

писать уравнения для мгновенных значений i и и. Так, если угловая частота задающих источников синусоидальных колебаний u_r1 и u_r2 равна ω, то мгновенное   значение   тока   

Аналогичным образом осуществляется преобразование электрических цепей, содержащих комплексные сопротивления. Комплексные сопротивления, соединенные звездой преобразуются в треугольник путем замены в формулах (2.6)—(2.9) параметров R и G на соответствующие комплексы Z и Y. Точно также осуществляется обратное преобразование треугольник-звезда.

Например, с учетом уравнений (1.9) и (1.12) можно получить формулы преобразования «звезда—треугольник» индуктивных и емкостных элементов. Так, для емкостных элементов при преобразовании «треугольник—звезда» имеем:

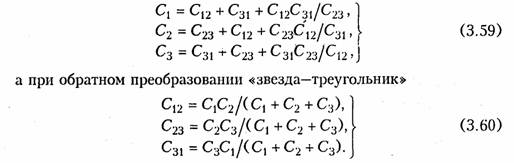
Преобразование «треугольник—звезда» и обратно для индуктивных элементов осуществляется по формулам, аналогичным (2.6)-(2.8).

Подобным же образом преобразуются матрично-топологические уравнения цепей в комплексную форму. Например, матричные уравнения (1.18), (1.20), (2.17) в комплексной форме принимают следующий вид:

где Y_B, Y_y — матрицы комплексной проводимости ветвей и комплексной узловой проводимости.

Z_B, Z_K — матрица комплексного сопротивления ветви и матрица комплексного контурного сопротивления.

Uгв, Jгb, Uв — матрицы-столбцы комплексных задающих напряжений и токов ветви и напряжений ветвей.