ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ

ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ. КЛАССИЧЕСКИЙ

МЕТОД АНАЛИЗА

6.1. Переходный режим электрических цепей.

Законы коммутации

В предыдущих главах рассматривались процессы в электрических цепях и методы их расчета в установившемся режиме, т. е. в режиме, при котором напряжения и токи в цепях либо не зависят от времени, либо являются периодическими функциями времени в зависимости от вида приложенного воздействия. Установившийся режим в цепи достигается обычно через определенный промежуток времени после начала воздействия, поэтому рассмотренные ранее методы анализа не охватывают так называемый переходный режим от начала воздействия до установившегося состояния цепи. Переходной режим работы цепи обусловлен наличием в ней реактивных элементов (индуктивности, емкости), в которых накапливается энергия магнитного и электрического полей. При различного рода воздействиях (подключении к цепи или исключении источников электрической энергии, изменении параметров цепи) изменяется энергетический режим работы цепи, причем эти изменения не могут осуществляться мгновенно в силу непрерывности изменения энергии электрического и магнитного полей (принцип непрерывности), что и приводит к возникновению переходных процессов. Следует подчеркнуть, что переходные процессы во многих устройствах и системах связи являются составной «нормальной» частью режима их работы. В то же время в ряде случаев переходные процессы могут приводить к таким нежелательным явлениям, как возникновение сверхтоков и перенапряжений. Все это определяет важность рассмотрения методов анализа переходных процессов в электрических цепях.

В основе методов расчета переходных процессов лежат законы коммутации. Коммутацией принято называть любое изменение параметров цепи, ее конфигурации, подключение или отключение источников, приводящее к возникновению переходных процессов. Коммутацию будем считать мгновенной, однако переходный процесс, как было отмечено выше, будет протекать определенное время. Теоретически для завершения переходного процесса требуется бесконечно большое время, но на практике его принимают конечным, зависящим от параметров цепи. Будем считать, что коммутация осуществляется с помощью идеального ключа К (рис. 6.1), сопротивление которого в разомкнутом состоянии бесконечно велико, а в замкнутом равно нулю. Направление замыкания или размыкания ключа будем показывать стрелкой. Будем также считать, если не оговорено иное, что коммутация осуществляется в момент t = 0.

Различают первый и второй законы коммутации. Первый закон коммутации связан с непрерывностью изменения магнитного поля катушки индуктивности W_L = Li² /2 и гласит: в начальный момент t = 0₊ непосредственно после коммутации ток в индуктивности имеет то же значение, что и в момент t = 0_ до коммутации и с этого момента плавно изменяется*

Второй закон коммутации связан с непрерывностью изменения электрического поля емкости W_c = Си ²/2; в начальный момент t = 0₊ непосредственно после коммутации напряжение на емкости имеет то же значение, что и в момент: t = 0_ до коммутации и с этого момента плавно изменяется:

В отличие от тока в индуктивности i_L и напряжения на емкости ис напряжение на индуктивности ui и ток в емкости i_с могут изменяться скачком, так как согласно (1.9) и (1.12) они являются производными от i_L и и_с и с ними непосредственно не связана энергия магнитного и электрического полей. Значения токов в индуктивности i_L(О₊) и напряжений на емкостях и_с(0+) образуют начальные условия задачи. В зависимости от начального энергетического состояния цепи различают два типа задач расчета переходных процессов: задачи с нулевыми начальными условиями, когда непосредственно после коммутации

Нулевые и ненулевые значения начальных условий для ii и ис называются независимыми, а начальные условия остальных токов и напряжений зависимыми. Независимые начальные условия определяются с помощью законов коммутации (6.1) и (6.2).

6.2. Классический метод расчета переходных процессов

В основе классического метода расчета переходных процессов в электрических цепях лежит составление интегрально-дифференциальных уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются на основе законов Кирхгофа, методов контурных токов, узловых напряжений и могут содержать как независимые, так и зависимые переменные. Для удобства решения обычно принято составлять дифференциальные уравнения относительно независимой переменной, в качестве которой может служить i_L или и_с .Решение полученных дифференциальных уравнений относительно выбранной переменной и составляет сущность классического метода.

Учитывая, что в ряде случаев решение дифференциальных уравнений проще интегрально-дифференциальных, полученную систему сводят к одному дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной i_L или и_с. Порядок дифференциального уравнения определяется числом независимых накопителей энергии электрического и магнитного полей.

Обозначим независимую переменную (i_L) или u_c) через х = x(t).

Дифференциальное уравнение m-го порядка, описывающее переходный процесс в электрической цепи, находящейся под воздействием источника w(t), описывается уравнением:

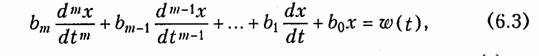
где bo, b₁, ..., b_m-₁, b_m — коэффициенты параметров цепи; w(t) — функция, описывающая характер воздействия на цепь.

Цепь, параметры которой bo, b₁, ..., b_m-₁, b_m— неизменны, называют цепью с постоянными параметрами. Если же какой-либо из коэффициентов bo, b₁, ..., b_m-₁, b_m — переменен, то цепь называют параметрической. В дальнейшем будем рассматривать цепи с постоянными параметрами.

Дифференциальное уравнение (6.3) относится к линейным неоднородным уравнениям m-го порядка. Как известно, его решение находится как сумма общего решения х_св однородного дифференциального уравнения т-г порядка:

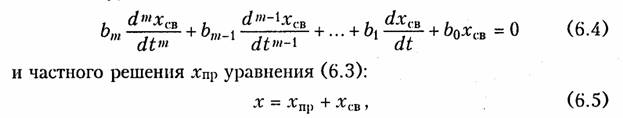
где х_св и x_Пр — общее и частное решения. Общее решение х_CB определяет свободные процессы, которые протекают в цепи без участия источника w(t) (отсюда индекс «cв»). Частное решение х_пр определяет принудительный процесс (отсюда индекс «пр»), который протекает в цепи под влиянием w(t). В теории цепей х_пр обычно находят одним из ранее рассмотренных методов расчета цепей в установившемся режиме.

Свободная составляющая переходного процесса х_CB будет зависеть от характера корней характеристического уравнения:

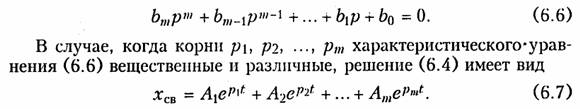
где А₁, А₂, ..., А_m — постоянные интегрирования, которые находятся из начальных условий.

В случае, когда корни уравнения (6.6) вещественные и равные, т. е. p₁ = р₂ — ... = р_т=p, свободная составляющая определяется уравнением

Представляет практический интерес и случай, когда корни попарно комплексно-сопряженные p_k,k-₁ ⁼ — α ± jω_с. При этом в формуле (6.7) соответствующая пара корней p_k,k-1 заменяется слагаемыми вида

где А,θ  —  постоянные интегрирования, определяемые также из начальных условий.

6.3. Переходные процессы в цепях первого порядка

Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка

Примером цепей первого порядка являются простейшие RL и

RC цепи.

Переходные процессы в RL-цепях. Рассмотрим включение RL-цепи к источнику напряжения u(t) (рис. 6.1). Из рис. 6.1 следует, что до коммутации ключ К разомкнут, поэтому ток i_l(0_) = 0 и цепь находится при нулевых начальных условиях. В момент t = О ключом К замыкаем (осуществим коммутацию) цепь, подключив ее к источнику напряжения u(t). После замыкания ключа К в цепи начнется переходный процесс. Для его математического описания выберем в качестве независимой переменной i_L = i и составим относительно нее дифференциальное уравнение по ЗНК:

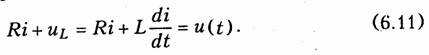
Уравнение (6.11) относится к линейным неоднородным дифференциальным уравнениям первого порядка типа (6.3), решение которого можно записать согласно (6.5) в форме

где i_CB — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t);i_np — принужденная составляющая тока, обусловленная действием источника напряжения u(t).

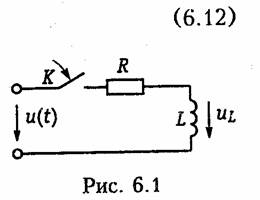
Свободная  составляющая  тока  i_св есть  общее  решение  однородного дифференциального уравнения

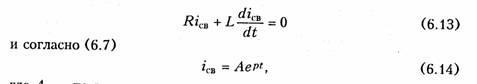
где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6);

Отсюда р =   —R/L.  Величина  1/|p| носит название постоянной времени цепи. В неразветвленной RL-цепп τ = L/R.

Принужденная составляющая i_Пр может быть определена как частное решение уравнения (6.11). Однако, как было указано выше, i_пр можно найти более просто методами расчета установившегося режима цепи. Рассмотрим два частных случая:

В первом случае принужденная составляющая может быть определена из установившегося режима: i_np = U/R. Для нахождения постоянной интегрирования А перепишем (6.12) в форме i = Ae^-t/τ + U/R и учтем начальные условия для i, а также первый закон коммутации (6.1):

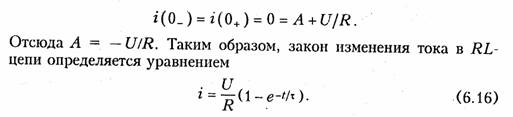
Напряжение на индуктивности согласно (1.9)

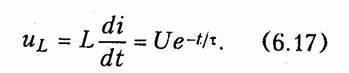
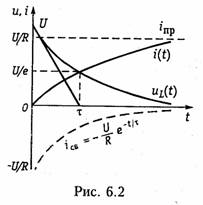
На рис. 6.2 изображены графики зависимости i(t) и u_L(t). Анализ полученных уравнений (6.16) и (6.17) показывает, что чем больше постоянная времени цепи τ, тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3... 5)τ, при t — Зτ ток достигает 95% своего установившегося значения, а при t = 5τ — более 99%. Графически постоянная времени τ может определиться как интервал времени на оси t от t — О до точки пересечения касательной к u_L (рис. 6.2), в указанный момент напряжение на u_L уменьшается в е раз но сравнению с начальным.

Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t = 0₊ индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t =∞ как бесконечно малое сопротивление (короткое замыкание цепи).

Для второго случая принужденная составляющая тока согласно

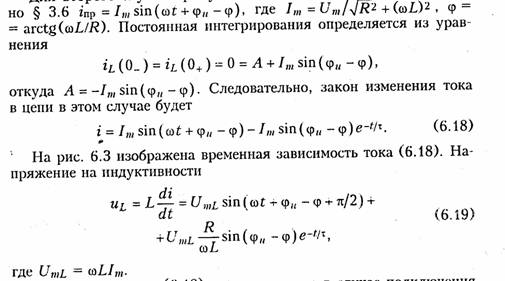
Анализ уравнения (6.18) показывает, что в случае подключения цепи к источнику u(t) в момент, когда  в последней могут возникать сверхтоки. Если постоянная времени цепи т достаточно велика, то скачок тока в начальный период может достигать i_max ≈ 2I_т. Напротив, при включении цепи в момент, когда φ_u = φ, в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).

В качестве второго примера расчета рассмотрим случай ненулевых начальных условий в RL-цепи (рис. 6.4). К моменту коммутации в данной цепи была запасена энергия магнитного поля, равная После коммутации в .RL-цепи возникает переходный процесс, описываемый уравнением:

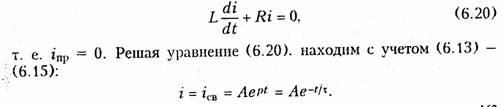
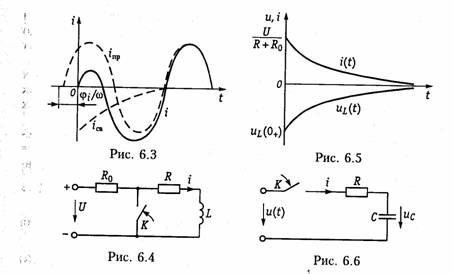
Постоянную А находим из начального условия i(0_) и закона коммутации (6.1):

Окончательно закон изменения тока в переходном режиме описывается уравнением

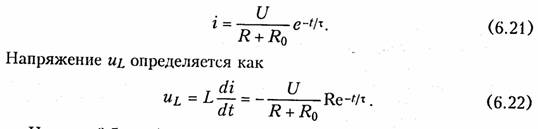
На рис. 6.5 изображены графики i и u_l- Следует отметить, что вся энергия Wl, запасенная в индуктивности с течением времени, расходуется на тепловые потери в R. При ненулевых начальных условиях L ведет себя как источник тока.

Переходные процессы в .RC-цепях. При расчете переходных процессов в .RC-цепях в качестве независимой переменной выбирают u_c. Затем также составляют дифференциальное уравнение для заданной RC-цепн, решение которого с учетом начальных условий для и_с(0) и определяет закон изменения напряжения на емкости.

Рассмотрим вначале RС-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику постоянного u(t) = U или синусоидального u(t) = U_msin((ωt + φ_u) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением

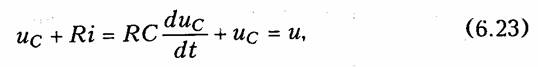
решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие:

Свободная составляющая является решением однородного дифференциального уравнения

На рис. 6.7 изображены графические зависимости u_c(t) и i(t).

Анализ   полученных   результатов   показывает,   что   в   момент t = 0₊ емкость С (при нулевых начальных условиях) ведет себя

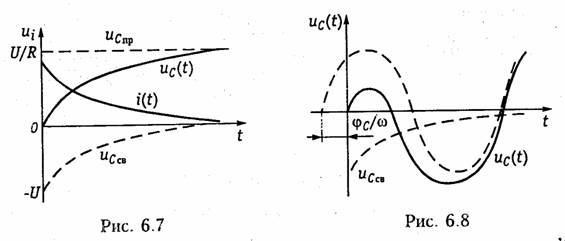
как короткозамкнутый участок. Напротив, при t = ∞ емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).

Рассмотрим случай гармонического воздействия. Нетрудно видеть что при этом

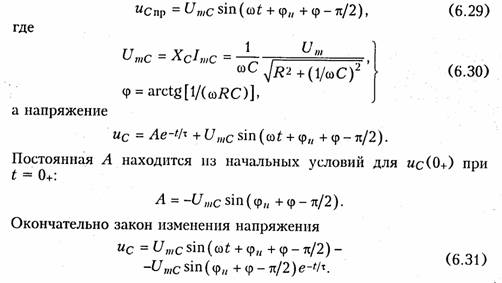
На рис. 6.8 изображен график зависимости u_c(t). Анализ уравнения (6.31) показывает, что в случае неудачного включения при φ_u = π - φ и большой τ в цепи могут возникать перенапряжения, достигающие на емкости величины ис_тах  ≈2U_mc. В случае удачного включения, когда φ_и = π/2 — φ, в цепи сразу наступает установившийся режим.

Ток в цепи

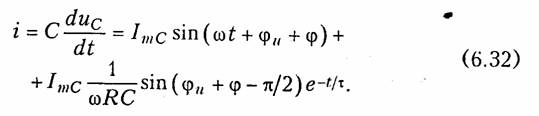
Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на сопротивление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия Wc= С U ²1/2. После коммутации возникает переходный процесс, определяемый уравнением

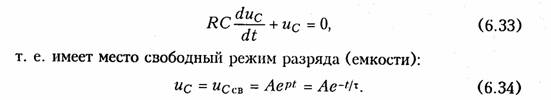
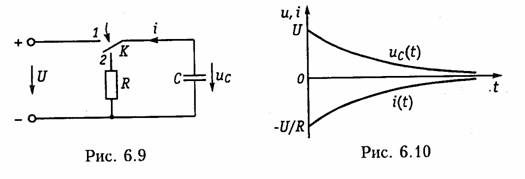
Постоянную интегрирования А находим из начального условия для uc(0₊) = U и

закона коммутации (6.2):

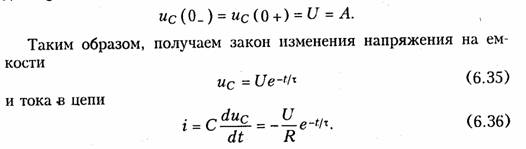
Знак «—» в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения и_с в емкости (см. § 1.2). На рис. 6.10 приведены графики изменения напряжения и_с(t) и тока i(t) данной .RC-цепи. Следует подчеркнуть, что вся запасенная энергия We емкости с течением времени преобразуется в элементе R в тепло. При ненулевых начальных условиях С ведет себя как источник напряжения.

6.4. Переходные процессы в цепях второго порядка

Ранее рассматривались переходные процессы в RL- и RС-цепях, которые относятся к цепям первого порядка, так как описываются дифференциальными уравнениями первого порядка (6.11), (6.23). При наличии в цепи двух независимых накопителей энергии переходные процессы в них описываются уравнением второго  порядка.   Простейшим  примером такой цепи является последовательный колебательный контур (рис. 6.11). Для этого контура можно по аналогии с RL- и RC-цепью составить дифференциальное уравнение второго порядка, выбрав в качестве независимой переменной напряжение на емкости

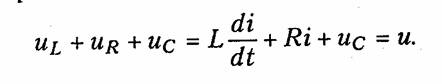
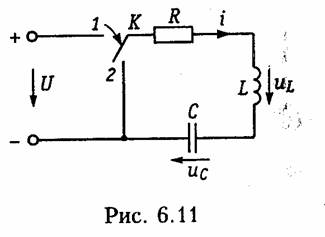
Характер переходного процесса существенным образом зависит от вида корней p₁, p₂, которые могут быть:

1) вещественными и различными (при R > 2р);

2) комплексно-сопряженными (при R < 2р);

3)  вещественными и равными (при R = 2р).

Здесь ρ = √L/C — характеристическое сопротивление контура (см. формулу (4.22)).

Разряд емкости на .RL-цепь. Для исследования характера переходного процесса во всех этих случаях рассмотрим разряд емкости С на цепь RL (см. рис. 6.11). Так как до коммутации емкость С была заряжена до напряжения U, то имеем ненулевые начальные условия:

u_c(0_) = U;   W_c(0_) = CU²/2.

После коммутации (переключение ключа К из положения 1 в положение 2 емкость начнет разряжаться и в цепи возникнет свободный переходный процесс. Найдем закон изменения тока и напряжений на отдельных элементах цепи для случая 1) — 3).

В первом случае, когда R > 2р корни р₁ и р₂ в (6.41) будут вещественными и различными, и решение уравнения определится согласно (6.7):.

Из уравнений (6.46) —(6.48) следует, что каждая из найденных величин ис, i, u_L состоит из двух слагаемых, затухающих по экспоненте с коэффициентами р₁ < О и р₂ < 0. На рис. 6.12 показан характер зависимостей (6.46) —(6.48). Момент времени t₁, соответствующий точке перегиба и_с, максимуму |i| и нулевому значению u_L определяется из решения уравнения di/dt = 0, а момент t₂ из решения уравнения du_L/dt = 0:

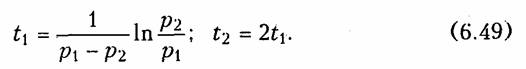
Анализ полученных кривых показывает, что в рассматриваемом случае происходит апериодический разряд емкости С, причем в интервале от 0 до ti энергия  Wc расходуется на покрытие тепловых потерь в резистивном

сопротивлении R и создание магнитного поля в индуктивности (рс = и_с i < 0; р_L = u_l i > 0). В дальнейшем (при t > t₁) как энергия электрического поля емкости Wc, так и запасенная к моменту t = t₁ магнитная энергия индуктивности Wl расходуется на покрытие тепловых потерь в сопротивлении R. Отрицательное значение тока свидетельствует о противоположном направлении тока разряда относительно опорного направления.

Во втором случае при R < 2ρ, когда корни р₁ и р₂ носят комплексно-сопряженный характер,

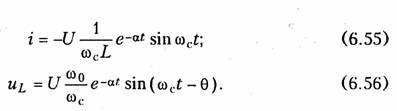
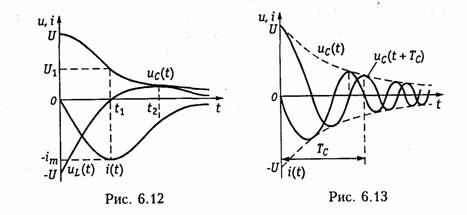
Полученные уравнения показывают, что в данном случае имеет место колебательный разряд емкости с частотой ω_с, зависящей только от параметров R, L, С цепи. Интервал времени T_с = 2π/ω_c носит название квазипериода. На рис. 6.13 изображены графики зависимостей uс(t) и i(t) определяемых уравнениями (6.54) и (6.55). Скорость затухания периодического процесса принято характеризовать декрементом- затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака (см. рис. 6.13):

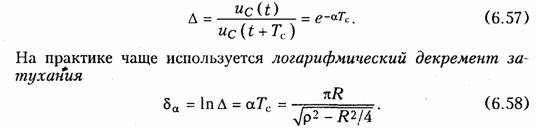
Из уравнений (6.57) и (6.58) следует, что затухание тем больше, чем больше R. При R = 2р колебания прекращаются и переходной процесс становится апериодическим. При R = 0 оказываются незатухающие гармонические колебания с частотой ω_с = ω₀ = 1/√LC. Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости (свободных колебаний в .RLC-контуре) имеет место попеременное запасание энергии W_c в электрическом поле емкости и магнитном поле индуктивности Wl. в начале энергия W_c расходуется на создание магнитного поля Wl индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия Wl, расходуется на перезаряд емкости и покрытие потерь в и т. д. до полного перехода первоначальной энергии W_c(0) в тепловые потери в резисторе R.

Третий случай R = 2ρ является пограничным между колебательным и апериодическим и соответствует критическому разряду емкости. Решение уравнения (6.39) при этом имеет вид (6.8)

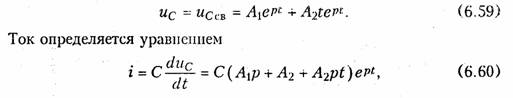
где pi=p2 = p=—α — корни характеристического уравнения (6.40); А₁, А₂ — постоянные интегрирования, определяемые из начальных условий для ис и i и законов коммутации (6.1), (6.2):

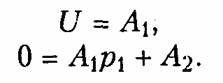
Отсюда A₂ = αU. Окончательные выражения для напряжения и тока принимают вид

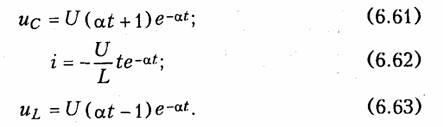
По своей форме графики зависимостей (6..61) —(6.63) аналогичны кривым, изображенным на рис. 6.12 с той лишь разницей, что их скорость изменения больше, чем при R > 2р. Значение R = 2р носит название критического сопротивления контура.

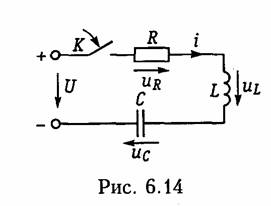
6.5. Включение .RLC-контура на постоянное и

гармоническое напряжение

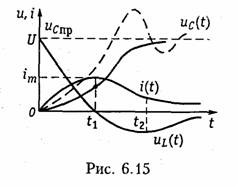
Включение RLC-контура на постоянное напряжение. Рассмотрим случай нулевых начальных условий u_с(0_{_}) ⁼ 0, i(0_) = 0, когда RLC-контур включается на постоянное напряжение (рис. 6.14). Отличие данного случая от рассмотренного выше заключается в нулевых начальных условиях и наличии принужденной составляю щей u_спр = U. Свободная составляющая u_CCB определяется, как и ранее, уравнениями (6.43), (6.51) или (6.59) в зависимости от вида корней р₁ и р₂. Постоянные интегрирования А₁ и А₂находятся при этом из начальных условий i(0_) = 0, u_с(0_) = 0 и законов коммутации для i и и_с. Определим, например, закон изменения и_с, i и u_L в случае, когда корни р₁ и р₂ — вещественные и различные. При этом и_CCB определяются уравнением (6.43), а напряжение и_с и ток i имеют следующий вид:

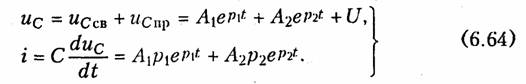
Для нахождения коэффициентов А₁ и А₂ используем начальные условия u_с(0_) = 0 и i(0_) = 0, а также законы коммутации, определяемые выражениями (6.1),(6.2):

На рис. 6.15 изображены графики зависимостей (6.67) —(6.69), где моменты времени t₁ и t₂ определяются уравнениями (6.49). Сравнение формул (6.67) —(6.69) с (6.46) —(6.48) показывает, что ток i и напряжение u_L отличаются только знаком, а напряжение и_с — наличием постоянной составляющей U.

Аналогичным можно найти уравнения напряжений и тока для случая R < 2ρ:

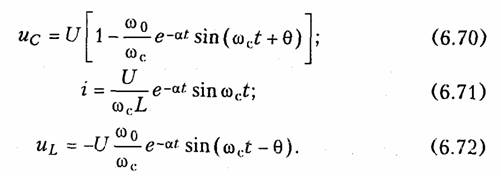
На рис. 6.15 штриховой линией показана зависимость (6.70), которая свидетельствует о колебательном характере заряда емкости. Таким же образом можно получить уравнения для и_с, i и u_L для случая критического заряда емкости С при R = 2ρ.

Включение RLC-контура на гармоническое напряжение. При включении RLG-контура на гармоническое напряжение и - U_msin(ωt + φ_u) принужденная составляющая напряжения на емкости

где φс =φ_u + φ — π/2. Здесь фазовый сдвиг между током в контуре и приложенным напряжением

а амплитуда принужденного напряжения на емкости

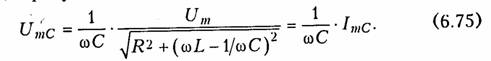
Учитывая, что колебательный контур в радиотехнических устройствах, как правило имеет высокую добротность, т. е. выполняется условие R <<2ρ, то свободная составляющая u_ссв определяется уравнением (6.51), и закон изменения напряжения на емкости будет иметь вид

Анализ уравнений (6.81), (6.82) показывает, что в случае, когда частота приложенного напряжения ω существенно превышает резонансную частоту контура ω₀ при φ_с ≈ 0 в цепи могут возникнуть сверхнапряжения, а в случае ω<<ω₀ и φ_c≈π/2— сверхтоки.

Если частота задающего напряжения ω= ω_о, то при этом в цепи возникают явления изохронизма, когда напряжение на емкости и ток в контуре плавно изменяется в соответствии с уравнениями:

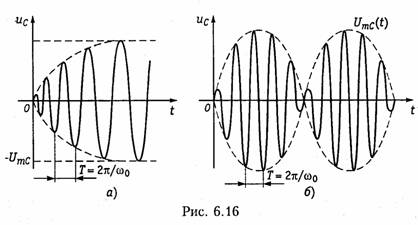
При этом переходный процесс протекает без перенапряжений и сверхтоков (рис. 6.16, а).

В случае, когда частота заданного напряжения ω и резонансная частота контура ω_о близки между собой, то в контуре возникают явления биений. Положим, что α = 0, тогда

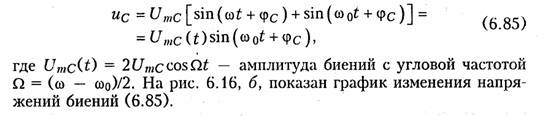
6.6. Переходные процессы в разветвленных цепях

При расчете переходных процессов в разветвленных цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений по ЗТК и ЗНК. Затем полученная система сводится к дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной (и_с или i_L.). После этого полученное уравнение решается по аналогии с уравнениями, рассмотренными в § 6.2 — 6.5.

В качестве примера рассмотрим разветвленную цепь второго порядка, изображенную на рис. 6.17. Для данной цепи имеем ненулевые    начальные    условия:

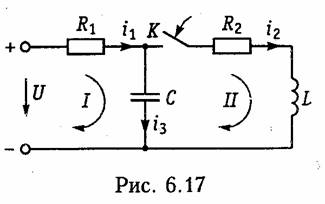
u_с(О_) = U; i_l(O_) = 0. Составим для нее систему уравнений по законам Кирхгофа:

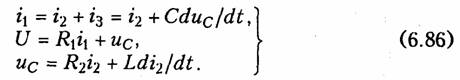
Постоянные интегрирования определяются из начальных условий и законов коммутации, причем для нахождения и_с используется система уравнений (6.86). Например, для случая вещественных и различных корней при R₁ = R₂ = R получим

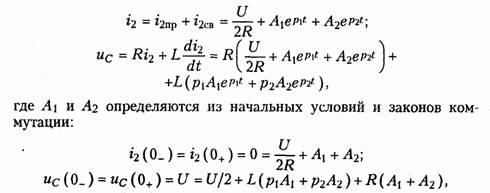
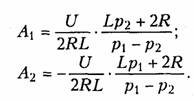
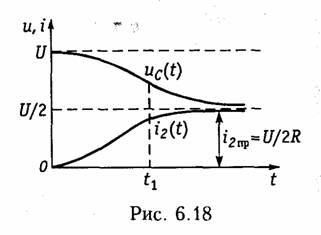
На рис. 6.18 изображены графики u_c(t) и i2(t).

Как следует из вышеуказанного, для определения характера переходного процесса и записи уравнения свободной составляющей независимой переменной необходимо располагать характеристическим уравнением цепи. Это уравнение может быть получено из соответствующего дифференциального уравнения цепи или из анализа ее операторного сопротивления (см. § 7.3). Последнее может быть получено, если в уравнении для комплексного сопротивления цепи Z = Z(jω) заменить оператор jω на р и приравнять его к нулю:

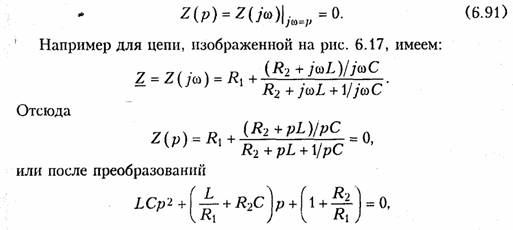
что полностью совпадает с (6.90).

Таким образом, отпадает необходимость преобразовывать систему уравнений к одному уравнению для выбранной независимой переменной.

В заключение следует отметить, что применение классического метода расчета к цепям более высокого порядка встречает определенные трудности. Главное из них резко возрастающий объем необходимых вычислений, связанных с решением задач уравнений высокого порядка. В этой связи в последнее время все большее применение находят другие методы расчета переходных процессов: метод переменных состояний, операторный и частотные методы, которые будут рассмотрены ниже.

6.7. Метод переменных состояния

В настоящее время для анализа переходных процессов в цепях широкое применение находит метод переменных состояния, позволяющий при расчетах эффективно использовать ЭВМ. Суть метода заключается в том, что переходный процесс в цепи рассматривается как траектория в m-мерном пространстве (где т — порядок цепи) с начальной точкой при t = 0 (начальное состояние) и конечной при t =∞. Например, переходный процесс в последовательном RLC-контуре (см. § 6.4, апериодический разряд и рис. 6.12) можно в пространстве состояний представить кривой, изображенной на рис. 6.19, где i_l(0) = 0 и и_с(0) = U характеризуют начальное состояние цепи, a i_L(t) и u_c(t) определяют состояние цепи в любой заданный момент времени. Достоинства этого метода — наглядность, простота, удобство программирования на ЭВМ, возможность анализа как линейных, так и нелинейных цепей, а также цепей с переменными параметрами.

Поясним сущность данного метода на примере цепи, находящейся при ненулевых начальных условиях: i_L (0)=i_0,u_c(0)=u₀(рис. 6.20). Для этой цепи при t ≥ 0 можно записать:

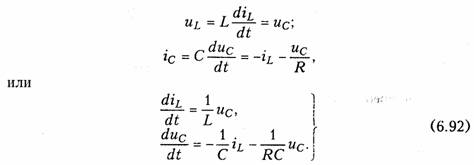
Уравнения (6.92) называются уравнениями состояния цепи, a i_L и  u_c- переменными состояния. Начальные условия i_L(0) = i₀ и u_c(0)=u₀ определяют с помощью (6.92) состояния цепи в любой момент t ≥ 0. Величины i_L и и_с можно считать компонентами вектора состояния х:

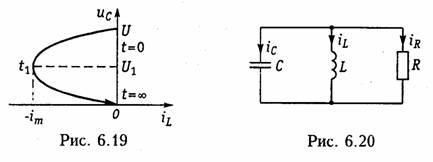
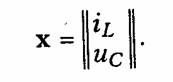
Зная состояние цепи х(t), реакцию цепи y(t) (токи и напряжения в любой ветви) можно найти как линейную комбинацию векторов состояния х(t) и входных воздействий w(t):

где у(t) — вектор искомых реакций цепи; С, D — матрицы, зависящие только от параметров цепи. Уравнение (6.95) называют уравнением реакции цепи.

Так, если в качестве компонентов вектора у(t) в предыдущем примере .RLC-контура взять u_r и u_l, то искомые реакции цепи (u_r и u_l) определяются согласно системе уравнений:

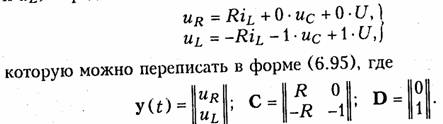
Следует подчеркнуть, что уравнения (6.93) —(6.95) справедливы для линейных цепей с постоянными параметрами (матрицы А, В, С, D не зависят от t). Для цепей с переменными параметрами (параметрические цепи) матрицы A(t). B(t), C(t), D(t) являются функциями времени.

Уравнения (6.94), (6.95) — основные в методе переменных состояний. Для решения уравнений состояния могут использоваться как аналитические, так и численные методы. Аналитически уравнение (6.94) может быть решено в области как действительного переменного t, так и комплексного переменного р (см. § 7.3). Рассмотрим некоторые основные методы решения уравнения состояния.

Метод матричных экспонент.   Решение этим методом ищут в форме

где е^At —   матричная экспонента (матрица перехода).  Из (6.96) следует, что решение уравнения состояния содержит два слагаемых: первое —  реакция цепи при нулевом входном сигнале; второе—реакция цепи при нулевом начальном состоянии. Для вычисления е^At обычно используют разложение

Таким образом, матрица перехода представляет собой квадратную матрицу порядка n с элементами в форме рядов от t. Подставив значение е^At в уравнение (6.96), можно определить после интегрирования искомое решение x(t).

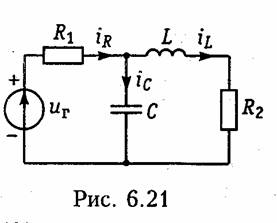
Следует, однако, отметить, что ряд (6.97) сходится медленно и использование уравнения (6.96) требует большого объема вычислений, поэтому вместо (6.96) обычно используют итерационную процедуру для дискретных моментов времени t_n = nΔt = nh, где h = Δt достаточно малый шаг:

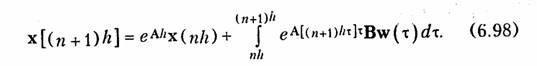
Интеграл в (6.98) вычисляется численными методами (методом прямоугольников, трапеций, Симпсона и др.). Так, при использовании метода прямоугольников алгоритм (6.98) приобретает вид

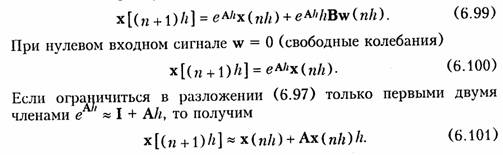
Алгоритм (6.101) легко программируется на ЭВМ и имеет ясный физический смысл. Он определяет положение точки в пространстве состояний на (п + 1)-м шаге, исходя из ее состояния на n-м шаге при аппроксимации траектории на участке h прямолинейным отрезком с постоянной скоростью x(h).

Пример. Рассчитать траекторию состояний, изображенную на рис. 6.19, используя аппроксимацию ее на каждом из т участков величины h в форме прямолинейных отрезков. Скорость изменения состояния х(h) на каждом из выделенных участков остается постоянной.

На основании уравнения состояния (6.93) имеем:

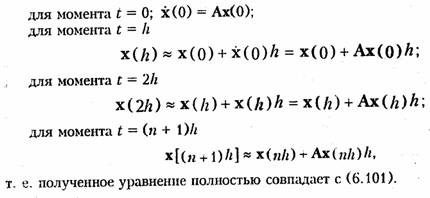
Метод Рунге—Кутта — метод численного решения уравнения состояния (6.94), при котором интервал 0...t разбивается на т малых участков Δt = h, на каждом из которых значение переменной х определяется с помощью линейной комбинации некоторых вспомогательных функций k_i(h) с постоянными коэффициентами. В зависимости от способа выбора коэффициентов и требуемой точности решения существуют различные модификации алгоритмов Рунге — Кутта.

Проиллюстрируем суть метода Рунге —Кутта на примере скалярного уравнения состояния

Как следует из (6.103), для определения х необходимо вычислить f(t, х) в четырех точках.

Аналогично записывается алгоритм Рунге —Кутта для системы уравнений типа (6.102). Например, для случая системы из двух уравнений

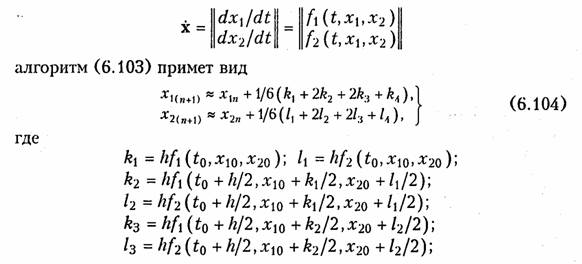
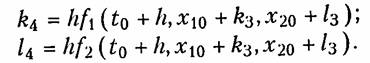
Частным случаем метода Рунге —Кутта является прямой алгоритм Эйлера (при k₂= k₃= k₄=0). Однако он имеет малую точность и не нашел широкого применения.

Разностные методы. Существенным недостатком метода Рунге—Кутта является то, что для получения каждого значения решения х необходимо вычислять правую часть уравнения (6.94) в нескольких точках (для алгоритма (6.103) — в четырех точках). Это приводит к большому объему вычислений, особенно для сложной правой части. Применение разностных методов позволяет существенно сократить объем вычислений и затраты машинного времени, так как на каждом шаге правая часть вычисляется только один раз.

В основе разностных методов лежит использование различных интерполяционных алгебраических многочленов (многочлены Ньютона, Стерлинга, Эрмита и др.). При этом решение х на (n + 1) шаге определяется алгоритмом

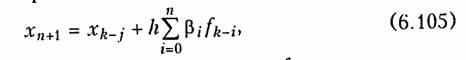
где h — шаг; β_i — постоянные коэффициенты; f_k — значение алгебраического многочлена в точке k. Как следует из (6.105) для определения решения x_k+j; необходимо знать значения х₁, x₂, …, x_j — они находятся обычно либо аналитически, либо методом Рунге—Кутта.

Вопросы и задания для самопроверки

1.  Каковы причины возникновения переходных процессов?

2.  Сформулировать законы коммутации.

3.  Дать понятия переходного, установившегося и свободного режимов в электрических цепях.

4.  Что такое нулевые и ненулевые начальные условия?

5.  Какой вид имеет свободная составляющая переходных колебаний в цепях первого порядка?

6.  Что представляет собой принужденная составляющая?

7.  Как рассчитываются постоянные интегрирования в цепях первого порядка?

8.  Что такое постоянная времени цепи?

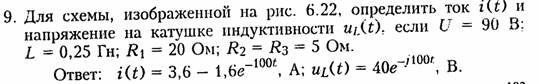
11.  Как зависит характер свободных колебаний в RLС-контуре от расположения на комплексной плоскости корней характеристического уравнения?

12.  Как определяются частота и период свободных колебаний?

13.  Что такое логарифмический декремент затухания?

14.  Какова последовательность анализа переходных процессов  в разветвленных цепях второго порядка?

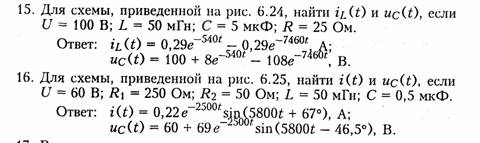
17.  В чем заключается суть метода переменных состояния?  Что понимают под переменными состояния?

18.  Что такое уравнения состояния цепи?  Какова его матричная форма записи?

19.  В чем сущность метода матричных экспонент?

20.  Суть метода Рунге-Кутта.

21.  Что лежит в основе методов решения уравнения состояния цепи?

ГЛАВА 7. ОПЕРАТОРНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

7.1. Преобразование Лапласа и его свойства

Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.

В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:

При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.

Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.

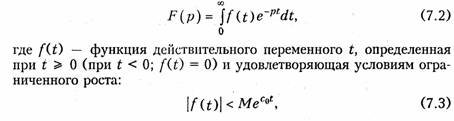
где множитель М и показатель роста с₀ — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).

Обратное  преобразование Лапласа  определяют  из  решения (7.2):

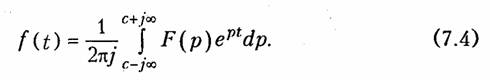
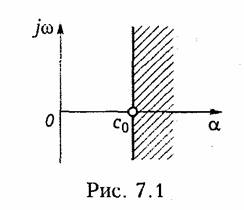
Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного f(t) и комплексного F(p) переменного, связанных преобразованием Лапласа. Для сокращенной   записи   преобразований   (7.2), (7.4) используют следующую символику:

где L — оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия

Рассмотрим основные свойства преобразований Лапласа.

Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме

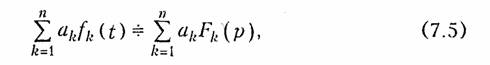
где a_k — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).

Дифференцирование оригинала. При ненулевых начальных условиях: f(0_) ≠ 0 дифференцирование оригинала соответствует следующему условию

Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).

Изменение масштаба независимого переменного (теорема подобия)

где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной τ = at в прямом преобразовании Лапласа (7.2).

Смещение в области действительного переменного (теорема запаздывания):

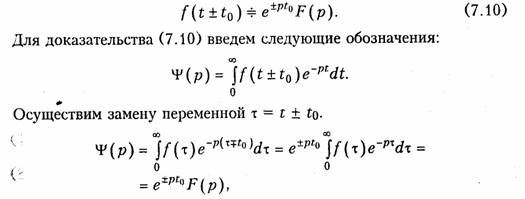
что и требовалось доказать.

Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t_o соответствует умножению изображения на е±^pt0.

Смешения в области комплексного переменного (теорема смещения):

Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить e^±λtf(t). Причем X может быть как действительной, так и комплексной величиной.

Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности):

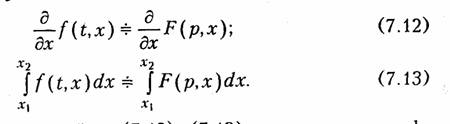
Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.

Данное свойство доказывается аналогично (7.15). В заключение приведем предельные соотношения для оригинала и изображения:

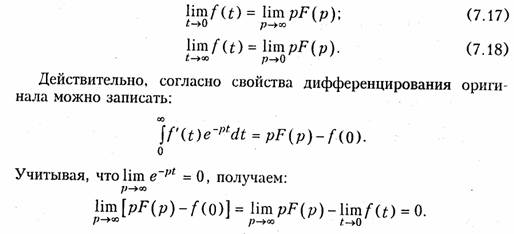
Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).

В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам

связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(0 и единичной импульсной функции 5(0 (функция Дирака).

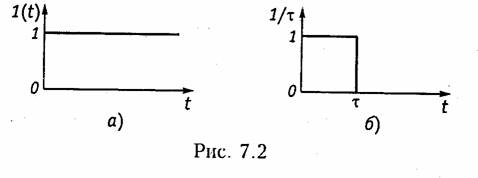
Единичная функция. Единичная функция задается уравнением (рис. 7.2, а)

Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при τ → 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:

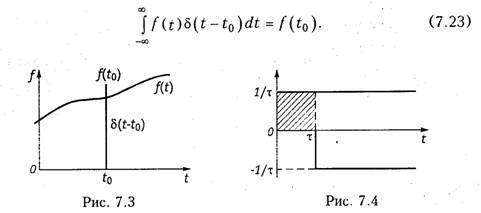
Одним из интересных свойств функции 5(0 является ее фильтрующее свойство, определяемое равенством (рис. 7.3):

Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на τ (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:

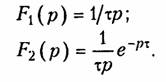
Для результирующего изображения с учетом свойства линейности получим

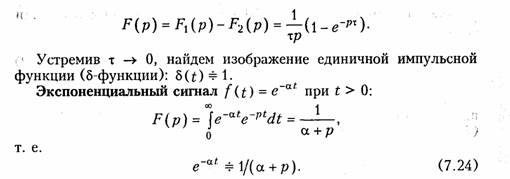
Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.

7.2. Теорема разложения

Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (7.4). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (7.4) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:

Формулу (7.31) можно получить, если подставить в (7.30) вместо F₂(p) значение pF₃( p) и осуществить операцию дифференцирования. Если среди корней уравнения (7.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни р_k и р_k+1, то в формуле (7.30) достаточно взять р_k, а для р_k+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом действительности f(t) будет равна

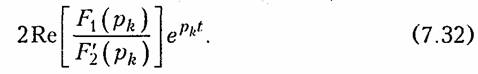
При этом в уравнении для f(t) появятся составляющие типа (6.9): Ae^-αtsin(ω_ct +θ).

Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (7.25) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).

Учитывая, что среди корней характеристического уравнения F₂(p) = О имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим

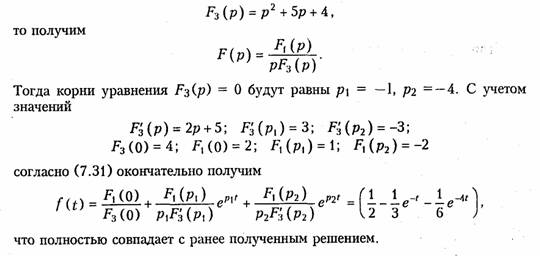
7.3. Расчет переходных процессов операторным методом

Пользуясь основными свойствами преобразования Лапласа, можно получить основные законы теории цепей в операторной форме. Рассмотрим, например, последовательный .RLC-контур (см. рис. 6.14), находящийся при ненулевых начальных условиях u_с(0_) ≠ 0; i_L(0_) ≠ 0. Для этого контура уравнение по ЗНК имеет вид:

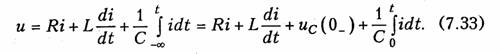
Применив к (7.33) прямое преобразование Лапласа и принимая во внимание свойства линейности, дифференцирования и интегрирования оригинала получим:

где Uo(p) = U(p) + Li(0) — и_с(0)/р носит название операторного напряжения; Z(p) = R + pL +\1рС — операторного сопротивления цепи. Если в Z(p) заменить р на jω, то получим комплексное сопротивление цепи. Величины Li0() и u_с(0)/р называют расчетными напряжениями. Они характеризуют энергию магнитного и электрического полей, запасенную в L и С к моменту коммутации. Величина, обратная Z(p) называется операторной проводимостью цепи:

Таким образом, закон Ома и законы Кирхгофа в операторной форме аналогичным этим же законам в комплексной форме (см. (3.48) —(3.50)) с той лишь разницей, что в (7.37) в каждой из п ветвей при наличии ненулевых начальных условий действуют дополнительные расчетные источники L_ki_k(0) и — u_ck0()/p, положительное направление которых совпадает с выбранным положительным направлением тока в этой ветви.

Используя законы Ома и Кирхгофа в операторной форме, можно найти изображения искомых токов и напряжений в цепи. Для определения  оригиналов  токов  и  напряжений  можно  воспользоваться либо таблицами оригиналов и изображений, либо применить теорему разложения.

Для иллюстрации основных теоретических положений найдем операторным методом закон изменения тока в последовательном RL С-контуре при включении его на источник постоянного напряжения (см. § 6.5). Уравнение для изображения тока можно найти по закону Ома для нулевых начальных условий (7.35) с учетом изображения постоянного напряжения U(p) = U/p:

что   полностью   совпадает   с   ранее   полученным   уравнением

(6.68).

Из рассмотренного примера хорошо видны преимущества операторного метода: простота, отсутствие громоздких операций по определению постоянных интегрирования. Следует подчеркнуть, что базируясь на законах Ома и Кирхгофа в операторной форме, можно рассчитать переходный процесс любым из ранее рассмотренных методов: контурных токов, узловых напряжений и др. При этом удобно пользоваться эквивалентными операторными схемами. При составлении эквивалентных операторных схем источники тока и напряжений i(t) и u(t) заменяются соответствующими изображениями I(р) и U(p), индуктивность L заменяется на pL, а емкость С — на 1/рС при нулевых начальных условиях. Если начальные условия ненулевые, то последовательно с pL добавляется источник напряжения Li(0), а с С — источник

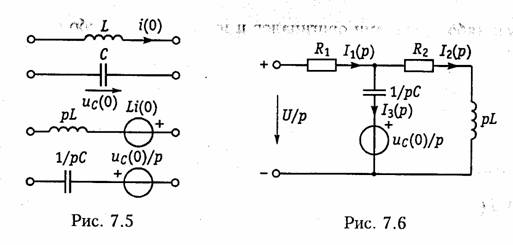
напряжения — u_с(0)/р (рис. 7.5)*. Например, эквивалентная операторная схема для цепи, изображенной на рис. 6.17, будет иметь вид (рис. 7.6). Составив для этой схемы уравнения по законам Кирхгофа в операторной форме, получим систему алгебраических уравнений, решение которых существенно проще системы (6.86).

Операторный метод можно использовать и для решения уравнения состояния цепи (см. § 6.7). При этом уравнение состояния (6.94) с учетом свойств дифференцирования оригинала и линейности преобразования Лапласа примет вид:

7.4. Операторные передаточные функции

Важную роль в методах анализа и синтеза электрических цепей при нулевых начальных условиях играют операторные передаточные функции, которые определяются как отношение изображения выходной реакции цепи к изображению входного воздействия. В соответствии с этим определением различают четыре вида передаточных функций:

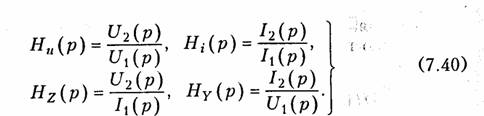
где Н_и(р), H_i(p) имеют смысл операторных передаточных функций по напряжению и току; H_L(p); Hγ(p) —операторные передаточные сопротивление и проводимость соответственно.

Если в (7.40) заменить оператор р на jω, то получим уравнение комплексных передаточных функций H(jω), которые были рассмотрены в § 4.1 и широко используются при частотных методах анализа электрических цепей (см. § 4.2 — 4.4, 9.5).

Зная передаточную функцию цепи Н(р), с помощью (7.40) нетрудно найти изображение реакции цепи, а следовательно, и саму реакцию на заданное воздействие.

Операторную передаточную функцию Н(р) для пассивной цепи можно представить как дробно-рациональную функцию с вещественными коэффициентами:

Учитывая, что согласно (7.43) |H(jω)| является иррациональной, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:

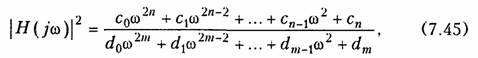
где коэффициенты C_k и d_k получаются путем объединения коэффициентов при одинаковых степенях переменной ω.

Перечислим    основные    свойства   операторных    передаточных функций и квадрата АЧХ пассивных цепей:

1.  Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.

2.  Полюсы передаточной функции располагаются  в левой полуплоскости комплексной переменной р.  На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции   Н_и(р) = U₂(p)/U₁(p).    Выберем    входное   воздействие u₁(t) = δ(t) или в операторной форме U(p) = 1. Изображение выходного напряжения U₂(p) = U₁ (p)H_u(p)   в этом случае численно равно Н_н(р), т. е.

В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (7.46) вещественные части полюсов p_i должны быть отрицательными (α_i < 0). т. е. полюсы должны находиться в левой полуплоскости переменной р.

3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. п < т. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.

4.  Квадрат АЧХ является четной рациональной функцией переменной ω с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.

5.  Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при ω > 0. Неотрицательности |H(jω)|²-следует из свойств квадрата модуля комплексной величины.  Конечность значений АЧХ на реальных частотах объясняется так же, как и в свойстве 3.

Вопросы и задания для самопроверки

1.  В чем заключается сущность операторного метода расчета цепи?

2.  Что такое операторное сопротивление цепи?

3.  Что такое операторные схемы замещения при составлении эквивалентной операторной схемы?

4.  Чем заменяются индуктивности и емкости в операторной   схеме замещения?

5.  Как учитываются независимые начальные условия?

6.  Записать закон Ома и законы Кирхгофа в операторной форме.

7.  Что такое единичная функция и 5-функция?

8.  Что понимается под операторной передаточной функцией? Каковы ее свойства?

9.  Каким образом можно перейти от изображения к оригиналу?

10.  Для схемы, изображенной на рис. 7.7, операторным методом определить напряжение на конденсаторе uc(t). U = 20 В; R₁=

13. Для схемы, изображенной на рис. 7.9, определить:

1) операторную передаточную функцию Н_и(р);

2) найти АЧХ цепи.

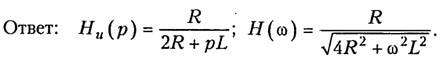
ГЛАВА 8. ВРЕМЕННОЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1. Переходные и импульсные характеристики электрических цепей

В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (δ-функции) (7.21). Обозначается импульсная характеристика h g(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи*. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.

Использование понятий переходной и импульсной характеристик цени позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции δ(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1 (t)  или δ(t).

Между переходной g(t) и импульсной h(t)характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/τ, сдвинутых друг относительно друга на время τ (см. рис. 7.4):

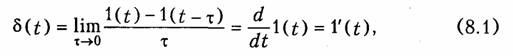
т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи

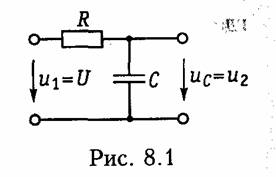
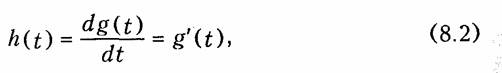
т. е. импульсная характеристика является производной от переходной характеристики цепи.

Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальные условия для цепи). Если же g g(0)≠0, то представив g(t) в виде g(t) = g₁(t)+ g(0)1(t), где g₁(0) = 0, получим уравнение связи для этого случая:

Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы.Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной δ(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.

Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно g_u(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t = О к источнику напряжения U₁ = 1 В:

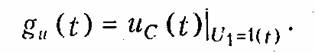
Закон изменения напряжения uc(t) определяется уравнением (6.27), где необходимо положить U = 1 В:

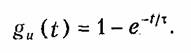
При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), δ(t) и методикой расчета переходных процессов, изложенных в гл. 7.

Пример. Определим операторным методом переходную характеристику g_u(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:

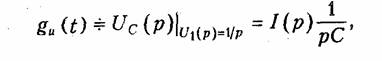
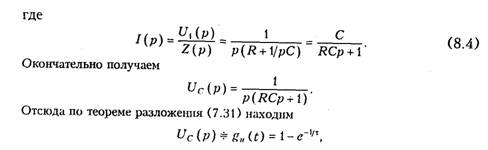
т. е. то же значение, что и полученное классическим методом.

Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи

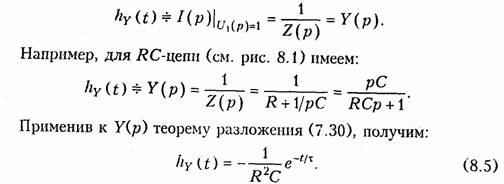
Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > О присутствует импульсное слагаемое, отображающее воздействие при t = О единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.0 переходная характеристика по tokv при U = 1(t) согласно (6.28) будет

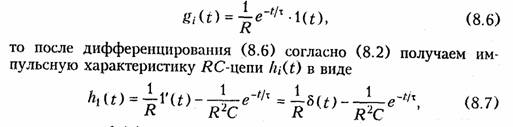
т. е. реакция h_i(t) содержит два слагаемых — импульсное и экспоненциальное.

Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения

δ(t)зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0_ до 0₊ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t > О и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t > О δ(t) = 0, что равносильно КЗ входа) с постоянной времени τ = RC. Из этого следует, что при 5(0-импульсном воздействии на RC-цепъ нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде δ(t).

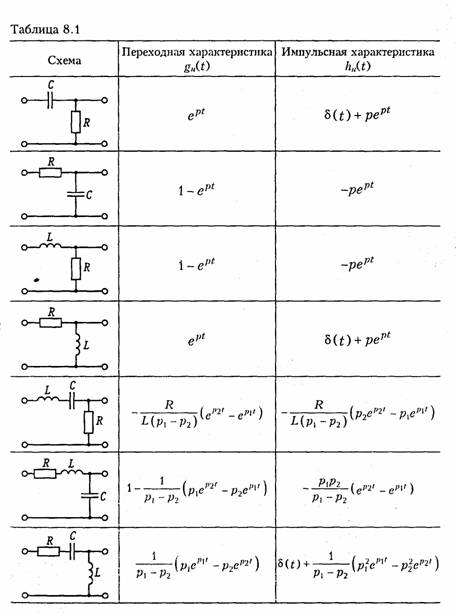
В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.

8.2. Интеграл Дюамеля

Интеграл Дюамеля может быть получен, если аппроксимировать приложенное воздействие f₁(t) с помощью единичных функций, сдвинутых относительно друг друга на время Δτ (рис. 8.2).

Реакция цепи на каждое ступенчатое воздействие определится как

Результирующая реакция цепи на систему ступенчатых воздействий найдется, исходя из принципа наложения:

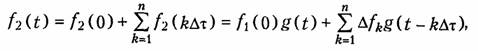
где п — число аппроксимирующих участков, на которые разбит интервал 0 ... t. Домножив и разделив выражение, стоящее под знаком суммы, на Δτ и перейдя к пределу с учетом того, что при Δτ→0k Δτ→τ, получим одну из форм интеграла Дюамеля:

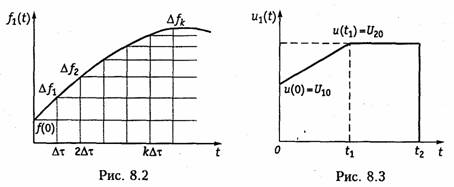
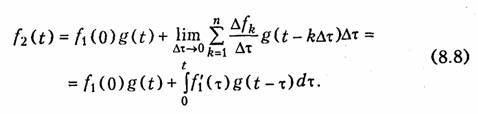
Уравнение (8.8) отражает реакцию цепи на заданное воздействие, поскольку при Δτ→ 0 аппроксимирующая функция стремится к исходной.

Вторая форма интеграла Дюамеля может быть получена с помощью теоремы свертки (см. § 7.1):

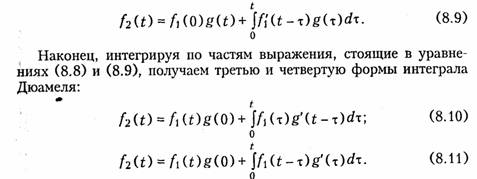
Применение той или иной формы интеграла Дюамеля диктуется удобством и простотой вычисления подынтегральных выражений.

Пример. Запишем реакцию цепи (см. рис. 8.1) на напряжение, изображенное на рис. 8.3 с помощью интеграла Дюамеля (8.8). Переходная характеристика данной цепи имеет вид

После нахождения переходной функции определяем число участков интегрирования, где функция непрерывна и дифференцируема. Определяем значение и’₁(τ) (т) на этих участках. Для рассматриваемого воздействия таких участков будет три:  Необходимость включения третьего участка объясняется тем обстоятельством, что несмотря на прекращение входного воздействия в силу переходных процессов (см. гл. 6) в цепи будет наблюдаться остаточная реакция. Для каждого из выделенных участков запишем уравнение (8.8) с учетом реакций предыдущих участков:

на участке 0 ≤ t < t₁

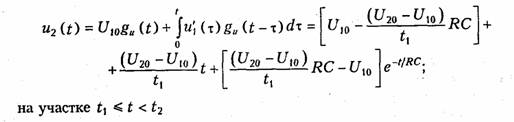
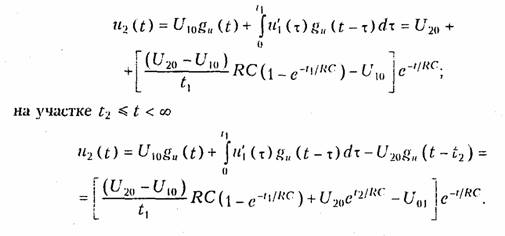
В случае, когда воздействие прикладывается к активной цепи (рис. 8.4, а), расчет переходных процессов можно вести методом наложения. При этом вначале расчет ведется с помощью интеграла Дюамеля для пассивной цепи (рис. 8.4, б), затем определяется классическим или операторным методом реакция цепи при включении рассматриваемой ветви к активному двухполюснику (рис. 8.4, в). Результирующая реакция находится как сумма реакций:

8.3. Интеграл наложения

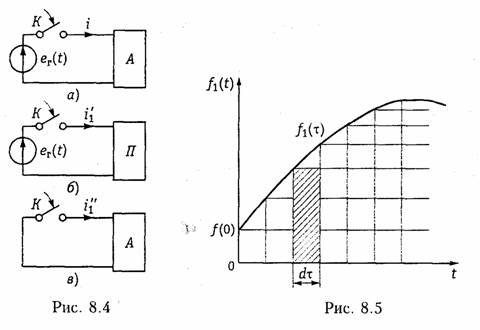
При нахождении реакции цепи с помощью интеграла наложения используется импульсная характеристика цепи h(t). Для получения общего выражения интеграла наложения аппроксимируем входной сигнал f₁(t) с помощью системы единичных импульсов длительности d_τ, амплитуды f₁(τ) и площади f₁(τ)dτ (рис.  8.5).  Выходная реакция цепи на каждый из единичных импульсов

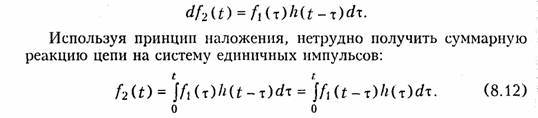
Интеграл (8.12) носит название интеграла наложения . Между интегралами наложения и Дюамеля существует простая связь, определяемая связью (8.3) между импульсной h (t) и переходной g(t) характеристиками цепи. Подставив, например, значение h(t) из (8.3) в формулу (8.12) с учетом фильтрующего свойства δ-функции (7.23), получим интеграл Дюамеля в форме (8.11).

Пример. На вход RC-цепи (см. рис. 8.1) подается скачок напряжения U₁. Определись реакцию цепи на выходе с использованием интегралов наложения (8.12) и Дюамеля (8.11).

Интегралы наложения (8.12) и (8.13) представляют собой свертку входного сигнала с импульсной характеристикой цепи и широко применяются в теории электрических цепей и теории передачи сигналов. Ее физический смысл заключается в том, что вход ной сигнал f₁(τ)как бы взвешивается с помощью функции h(t — τ): чем медленнее убывает со временем h(t), тем большее влияние на выходной сигнал оказывает более удаленные от момента наблюдения значение входного воздействия.

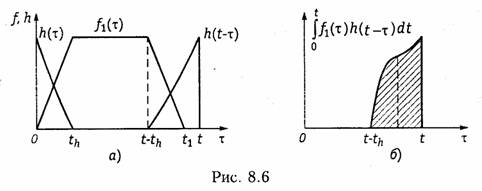
На рис. 8.6, а показан сигнал f₁(τ) и импульсная характеристика h(t — τ), являющаяся зеркальным отображением h(τ), а на рис. 8.6, б приведена свертка сигнала f₁(τ) с функцией h(t — τ) (заштрихованная часть), численно равная реакции цепи в момент t.

Из рис. 8.6 видно, что отклик на выходе цепи не может быть короче суммарной длительности сигнала t₁ и импульсной характеристики t_h. Таким образом, для того чтобы выходной сигнал не искажался импульсная характеристика цепи должна стремиться к δ-функции.

Очевидно также, что в физически реализуемой цепи реакция не может возникнуть раньше воздействия. А это означает, что импульсная характеристика физически реализуемой цепи должна удовлетворять условию

Для физически реализуемой устойчивой цепи кроме того должно выполняться условие абсолютной интегрируемости импульсной характеристики:

Если входное воздействие имеет сложную форму или задается графически, то для вычисления реакции цепи вместо интеграла свертки (8.12) применяют графоаналитические способы.

Вопросы и задания для самопроверки

1.   Дать определения переходной и импульсной характеристик цепи.

2.   Указать связь между импульсной и переходной характеристиками.

3.   Как определить переходную и импульсную характеристику цепи?

4.   В чем отличие переходных характеристик g_u(t), g_i(t), g_z(t), g_y(t), объяснить их физический смысл.

5.   Как определить, какую из четырех разновидностей переходных или импульсных характеристик необходимо применить в каждом конкретном случае при расчете реакции цепи?

6.   В чем заключается сущность расчета переходных процессов с использованием g(t) и h(t)?

7.   Как определить реакцию цепи, если воздействие имеет сложную форму?

8.   Каким условиям должна удовлетворять цепь при использовании интеграла Дюамеля?

9.   Приведите другую форму интеграла наложения, отличную от (8.12).

10. Расчет реакции цепи с использованием интегралов Дюамеля и наложения приводит к одинаковым результатам или разным?

11. Определить переходную проводимость цепи, образованной сопротивлением и индуктивностью, включенными последовательно.

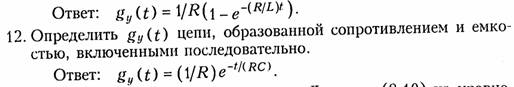
13. Полупить третью форму интеграла Дюамеля (8.10) из уравнения свертки (8.10).

ГЛАВА 9. ЧАСТОТНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

9.1. Интеграл Фурье

Для анализа переходных процессов при воздействии на цепь сигналов произвольной формы наряду с временным и операторным методом широко используется частотный метод анализа, базирующийся на спектральных представлениях сигнала.

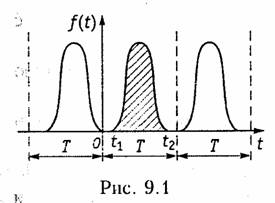
Для непериодических сигналов используются спектральные представления, основанные на паре преобразований Фурье. Преобразование Фурье может быть получено предельным переходом от ряда Фурье (5.6). Для этого зададим непериодический сигнал f(t), удовлетворяющий условию абсолютной интегрируемости в бесконечных пределах  (рис. 9.1):   С физической точки зрения, это означает, что задается реализуемый сигнал с конечной энергией; при этом

где М, с_о — положительные постоянные величины.

Условие (9.1) означает, что модуль │f(τ)│ имеет ограниченный показатель роста. Превратим мысленно этот сигнал в периодический повторением его через период Т (см. рис. 9.1). К полученному таким образом сигналу применимо разложение (5.6), которое после перехода к переменной t можно записать в виде

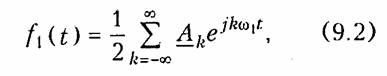
где

Уравнения (9.6) и (9.7) являются основными в теории спектрального анализа, причем (9.6) называется прямым, а (9.7) — обратным преобразованием Фурье. По аналогии с А_k спектр F(jω) является в общем случае комплексной функцией частоты и может быть записан в алгебраической форме

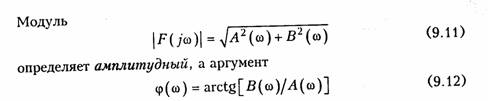
— фазовый спектр сигнала. Причем, как и для периодического сигнала, амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Физический смысл преобразования Фурье лучше всего проявляется при представлении обратного преобразования (9.7) в тригонометрической форме. Если подставить вместо F(jω) в (9.7) его значение из (9.9), то получим

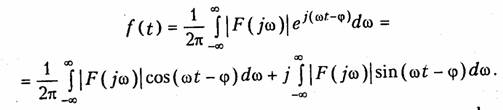
Учитывая, что |F(jω)| — четная, а синус — нечетная функция частоты интеграл от второго слагаемого равен нулю. Следовательно, принимая во внимание четность подынтегрального выражения в первом слагаемом, обратное преобразование Фурье имеет вид

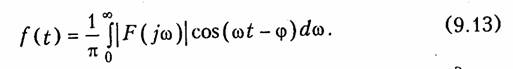
Из (9.13) следует важнейший вывод о том, что непериодический сигнал может быть представлен пределом суммы {интеграл) бесконечно большого числа бесконечно малых гармонических колебаний с амплитудами (1/π)| F(jω)| и начальными фазами φ = φ(ω), причем, учитывая, что разность частот соседних гармоник бесконечно мала Δω = dω, то F(jω) в уравнении (9.13) представляет непрерывный сплошной спектр в отличии от спектра периодического сигнала, который является дискретным (линейчатым) (см, гл. 5). Поэтому F(jω) называют комплексной спектральной плотностью, a | F(jω)| — спектральной плотностью амплитуд непериодического сигнала.

Смысл комплексного спектра F(jω) следует из связи между спектрами периодических и непериодических сигналов. Сравнение уравнений (9.3) с (9.6) позволяет установить эту связь между спектрами: при Т →∞;ω_k=kω₁→ω

и спектр комплексных амплитуд А_k обращается в комплексную спектральную плотность F(jω).

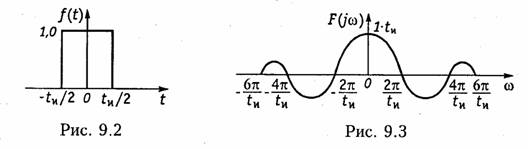
Из (9.14) следует и другой важный вывод: модуль спектральной плотности непериодического сигнала и огибающая линейчатого спектра периодического сигнала, полученного повторением с периодом Т непериодического сигнала, совпадают по форме и отличаются только масштабом. Это наглядно можно проиллюстрировать на примере периодической последовательности прямоугольных импульсов (см. рис. 5.3, а): с увеличением периода (скважности q) спектр становится гуще (см. рис. 5.4, б) и в пределе при Т = ∞ периодический сигнал превращается в непериодический (рис. 9.2), а дискретный спектр обращается в сплошной (рис. 9.3). При этом огибающая как линейчатого, так и сплошного спектра описывается функцией отсчетов (5.29): sinx/x:.

Рассмотрим некоторые основные свойства преобразования Фурье. Если сигнал f(t) является четной функцией времени, то, его спектр F(jω) — вещественный. Действительно, согласно (9.6) для F(jω) можно записать:

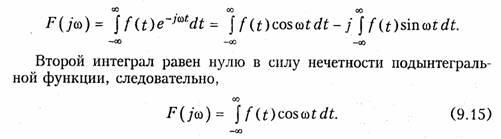
Аналогично при нечетности сигнала f(t) спектр F(jω) является чисто мнимым.

Важным свойством преобразования Фурье является взаимозаменяемость переменных t и ω. Для четного сигнала f(t) и вещественного спектра F(jω) можем заменить в преобразовании (9.6) знаки перед jωt:

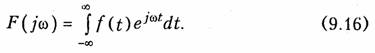
Тогда сравнивая (9.16) и (9.7) видим их подобие. Взаимозаменяемость переменных в преобразовании Фурье позволяет установить связь между частотными и временными характеристиками сигнала (см. § 9.5).

В соответствии с (9.8) и (9.9) сигнал может быть задан либо с помощью своего амплитудного | F(jω)| и фазового спектра φ(ω), либо с помощью вещественной A(ω) и мнимой частей B(ω) спектра сигнала. Причем, все они взаимосвязаны между собой согласно (9.11) —(9.12), т. е. нельзя задавать независимо амплитудный │F(jω)│ и фазовый спектр φ(ω), или вещественную А(ω) и мнимую часть спектраB(ω).

Наиболее ясно эта связь проявляется для сигнала, заданного на положительной полуоси времени t:

т. е. будет равен площади, ограниченной сигналом f(t). Формула (9.23) позволяет в ряде случаев оценить спектр сигнала по виду функции f(t).

Следует подчеркнуть, что временное и спектральное представление является просто двумя формами (моделями) представления реального физического процесса, и они лежат в основе временных и частотных методов анализа электрических цепей.

В заключение установим связь между преобразованием Фурье и преобразованием Лапласа. Если положить, что fit) удовлетворяет условию (9.17), то прямое преобразование Фурье принимает вид

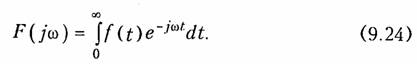
Соотношение (9.24) носит название одностороннего преобразования Фурье, так как оно определяется на положительной полуоси t. Если принять в качестве частного случая в формуле (7.1) α = 0, то р = jω, и прямое преобразование Лапласа (7.2)

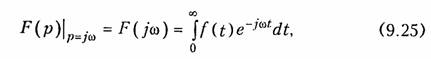
т. е. полностью совпадает с односторонним преобразованием Фурье (9.24).

Аналогично получим для обратного преобразования Лапласа (7.4) с учетом того, что dp = jdω:

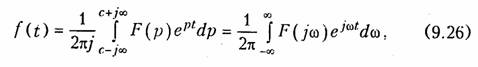
что полностью совпадает с (9.7).

Таким образом, преобразование Фурье есть частный случай преобразования Лапласа при α = 0. Следует подчеркнуть, что преобразование Фурье имеет более узкую область применения, чем преобразование Лапласа, так как условие (9.1), которым должны удовлетворять функции, преобразуемые по Фурье более жесткое, чем условие (7.3). Всякая функция, для которой применимо преобразование Фурье (9.6) всегда может быть преобразована по Лапласу, но не наоборот. В этой связи изображение F(p) можно трактовать как своего рода обобщенный спектр сигнала f(t).

9.2. Основные теоремы спектрального анализа

Как было установлено выше, между сигналом и его спектром существует однозначная связь, определяемая прямым преобразованием Фурье. Поскольку в процессе передачи сигнала он подвергается различным преобразованиям, очень важно установить как при этом изменяется спектр сигнала. Это имеет большое значение с точки зрения выбора оптимальных методов передачи, приема, требований к параметрам канала связи.

Рассмотрим основные теоремы о спектрах, имеющих практическое применение в электросвязи. Учитывая связь между преобразованием Фурье и Лапласа и имея в виду доказательства основных теорем, данных в § 7.1, остановимся только на физической интерпретации основных теорем спектрального анализа.

Спектр суммы сигналов (mеорема линейности) равен сумме спектров этих сигналов. Это свойство является следствием линейности преобразования Фурье. В более общем виде оно может быть записало следующим образом:

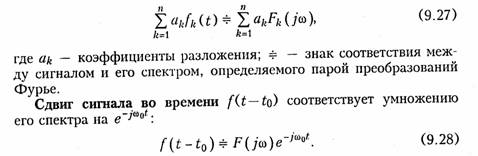
Из (9.28) следует важный вывод о том, что при сдвиге сигнала во времени его амплитудный спектр не изменяется, а фазовый изменяется пропорционально ωt_0. Эта теорема имеет большое значение, так как в процессе обработки сигналов часто возникает необходимость осуществлять задержку сигнала (см. гл. 18, 19).

Изменение масштаба независимого переменного (сжатие сигнала) описывается выражением

Из (9.29) следует, что сжатие сигнала во времени (а > 1) приводит к расширению спектра сигнала и напротив — растяжение сигнала (a< 1) — к сужению спектра.

Перемножение двух сигналов (теорема свертки). Спектр произведения двух функций f₁(t) и f₂(t)  соответствует свертке их спектров f₁(jω) и f₂(jω):

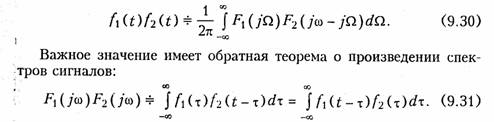
Свертка функций широко использовалась ранее во временных методах анализа электрических цепей (см. гл. 8).

Дифференцирование и интегрирование сигнала. При дифференцировании сигнала его спектр умножается на оператор jω:

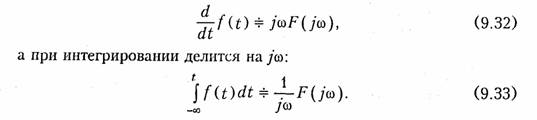
Доказательство (9.32) —(9.33) следует непосредственно из прямого и обратного преобразований Фурье. Следует подчеркнуть, что (9.33) справедливо для сигналов, удовлетворяющих условию F(0) = 0.

Смещение спектра сигнала на частоту  соответствует умножению сигнала на оператор e^±jΩt:

Теорема смещения (9.34) позволяет определить спектр модулированного сигнала и имеет большое значение в теории электрической связи.

9.3. Распределение энергии в спектре

 непериодического сигнала

Определим энергию сигнала f(t) по его спектральной характеристике f(jω). Предположим, что f(t) представляет собой напряжение или ток, протекающий в единичном сопротивлении R = 1 Ом. Тогда согласно (1.4) энергия выделяемая f(t) будет равна

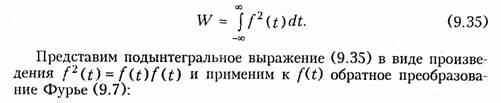
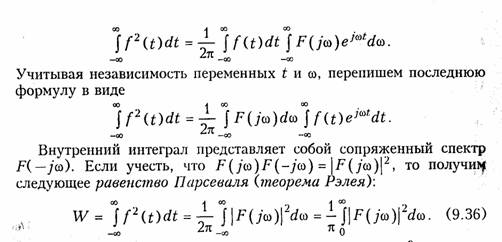
Из уравнения (9.36) следует, что величина |F(jω)|² представляет собой энергию сигнала, приходящуюся на 1 с^-1 текущей частоты со, поэтому квадрат модуля спектра |F(jω)| ²называют спектральной плотностью энергии сигнала. Вид модуля |F(jω)| позволяет судить о распределении энергии в спектре непериодического сигнала. Равенство Парсеваля широко используется в теории цепей и сигналов при выборе полосы пропускания канала связи, обеспечивающей наилучшее использование энергии сигнала.

Следует отметить, что в отличие от формулы (5.23), где рассматривалась средняя за период Т мощность периодического несинусоидального сигнала, для непериодического сигнала такое усреднение невозможно . Общим для обеих случаев является

то, что мощность и энергия сигналов не зависят от фаз спектральных составляющих.

9.4. Спектры типовых сигналов

Определим спектры наиболее распространенных типов электрических сигналов.

Единичная функция задается уравнением (7.19) (см. рис. 7.2, а). Строго говоря, функция (7.19) не удовлетворяет условию абсолютной интегрируемости (см. § 9.1), поэтому воспользуемся следующим приемом: умножим lit) на «гасящий» множитель е^сt (с = const). При этом можно использовать прямое преобразование Фурье (9.6):

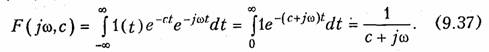
Преобразование F(jω, с) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:

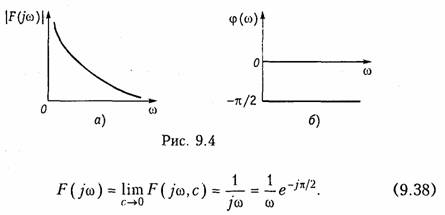
Из уравнения (9.38) получаем амплитудный |F(jω)| = 1/ω (рис. 9.4, а) и фазовый спектр функции φ(ω) (рис. 9.4, б): φ(ω) = = —π/2, т. е. амплитудный спектр при ω = 0 обращается в бесконечность, что свидетельствует о наличии в исходной функции 1(t) скачка при t = 0 (см. рис. 7.2, а). Для образования этого скачка в соответствии с (9.38) при t = 0 осуществляется суммирование бесконечно большого. числа синусоидальных составляющих. Спектр (9.38) может быть получен и с помощью изображения единичной функции (7.20):

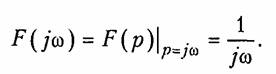
Единичная импульсная функция. Функция δ(t) задается аналитически условиями (7.21). Для нахождения спектра δ-функции воспользуемся прямым преобразованием Фурье (9.6), которое с учетом (9.8) — (9.10) можно записать в виде

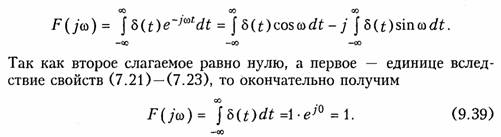
Таким образом, δ-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие δ-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.

Следует отметить, что сдвиг δ-функции на время т приводит согласно свойствам преобразования Фурье (см. § 9.2) к спектру F(jω) = 1 • e^-jωτ, т. е. амплитудный спектр функции δ(t-τ) остается прежним, а фазовый изменяется пропорционально ωτ.

Таким образом, спектр постоянной составляющей равен нулю на всех частотах, кроме ω = 0, где F(jω) обращается в бесконечность, то есть имеем на частоте ω = 0 дискретную составляющую частоты в форме 8-функции.

Спектр гармонического колебания. Проиллюстрируем методику использования прямого преобразования Фурье при определении спектра гармонического колебания

т. е. гармоническое колебание имеет дискретный спектр, состоящий из двух спектральных линий на частотах ±ω_0.

Спектр одиночного прямоугольного импульса (см. рис. 9.2) можно найти как непосредственно из прямого преобразования Фурье (9.6), так и путем предельного перехода при q →∞ (T→∞) в разложении (5.27). В результате получим

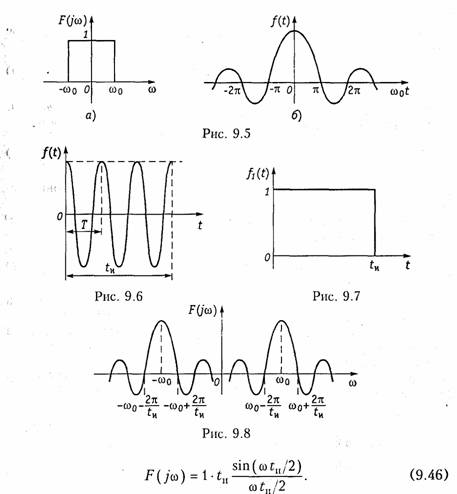
На рис. 9.3 изображен спектр одиночного импульса. Сравнение рис. 9.3 и рис. 5.4 показывает, что по своей форме спектр одиночного импульса совпадает с огибающей дискретного спектра последовательности периодических импульсов, однако спектр одиночного импульса является сплошным.

Из условия взаимосвязи между частотными и временными характеристиками сигнала следует, что сигнал с ограниченным по частоте ±ω₀ спектром прямоугольной формы (рис. 9.5, а) имеет бесконечную протяженность и форму, аналогичную спектру прямоугольного импульса (рис. 9.5, б).

Спектр радиоимпульса (рис. 9.6) можно найти как произведение видеоимпульса прямоугольной формы (рис. 9.7) и гармонического колебания (9.43). Тогда, воспользовавшись теоремой свертки (9.30), получим:

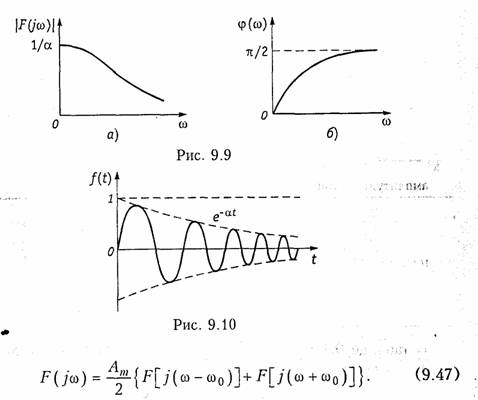
На рис. 9.8 показан вид спектра радиоимпульса.

Аналогичным образом можно найти спектр сигналов и более сложной формы.

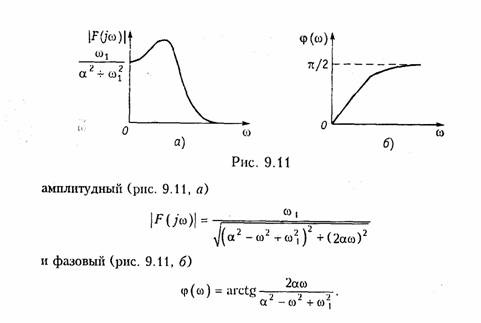
В таблице 9.1 приведены спектры некоторых наиболее распространенных сигналов.

9.5. Частотный анализ линейных электрических цепей при непериодических воздействиях

Представление непериодических сигналов в форме интеграла Фурье (9.6) и (9.7) позволяет применить к бесконечно малым гармоникам, составляющим его спектр, частотные методы анализа рассмотрены в гл. 3 и 4. В частности, если цепь находится при нулевых начальных условиях (т. е. до начала входного воздействия в реактивных элементах цепи не была накоплена энергия электрического и магнитного полей), то по аналогии с (3.46), (3.48) и (3.49) можно записать законы Ома и Кирхгофа для спектров:

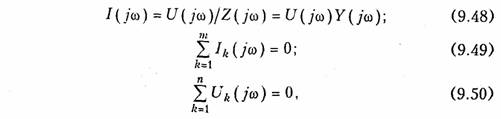
где I(jω), U(jω) — спектры токов и напряжений ветвей соответственно; Z₁(jω) и Y(jω) имеют смысл комплексных сопротивлений и  проводимостей  ветвей*. Законы  Ома и Кирхгофа для спектров

позволяют распространить рассмотренные ранее частотные методы анализа цепей при гармонических и периодических несинусоидальных воздействиях на непериодические сигналы.

В случае, если необходимо найти выходную реакцию цепи в виде четырехполюсника при воздействии на входе непериодического сигнала, используют комплексную передаточную функцию цепи (см. § 4.1). При этом спектр выходной реакции согласно (4.1) и (4.2)

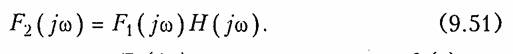
После определения спектра F₂(jω) выходная реакция f₂(t) может быть найдена с помощью обратного преобразования Фурье (9.7) или по таблицам.

Пример. Рассчитать спектральную плотность выходного сигнала в цепи (рис. 9.12), если па вход действует единичный импульс (рис. 9.7) с амплитудой U₁= 4 В.

Для заданного входного сигнала (3.15) преобразование Фурье дает выражение

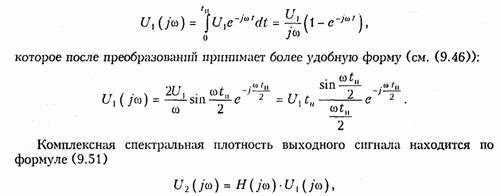
где H (jω) — комплексная передаточная функция цепи по напряжению. Функция Н (jω) находится как отношение комплексного значения гармонического напряжения U₂ на выходе цепи к комплексному значения гармонического напряжения U₁ той же частоты, приложенному ко входу цепи:

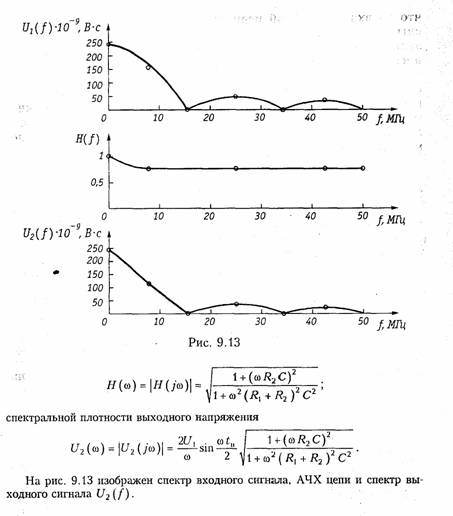
9.6. Условия безыскаженной передачи сигналов

через линейную цепь

Частотный метод является достаточно эффективным и наглядным при анализе передачи сигналов через линейную систему. Он позволяет оценить частотные искажения в канале связи, требования к характеристикам электрической цепи. Особенно важно определить требования к АЧХ и ФЧХ цепи с точки зрения искажения формы сигнала. Определим условия неискажаемой передачи сигнала через линейную систему.  Предположим, что на входе линейной цепи, как четырехполюсника действует сигнал /i(O определенной формы (рис. 9.12). На выходе в результате прохождения сигнала через четырехполюсник с комплексной передаточной функцией Ж/со) амплитуда сигнала может измениться (на рис. 9.12 уменьшилась), и сигнал вследствие конечности скорости его распространения может запаздывать относительно входного воздействия на to- Однако важно, чтобы при этом не изменилась форма сигнала. Таким образом, условие безыскаженной передачи можно сформулировать с помощью равенства

где k — некоторая вещественная постоянная; to — время задержки (запаздывания) выходного сигнала относительно входного. Применив к (9.52) прямое преобразование Фурье и учтя свойство линейности и теорему запаздывания (см. § 9.2), перепишем условие (9.52) в частотной области:

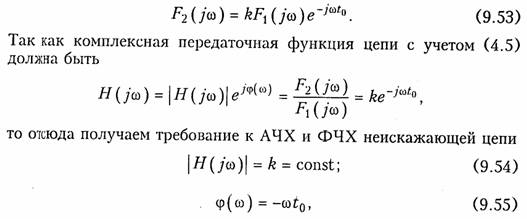
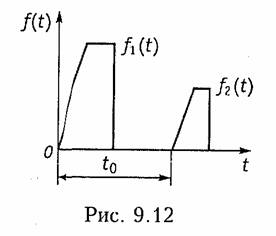
т. е. для того, чтобы линейная цепь не искажала форму сигнала ее АЧХ должна быть равномерной (рис. 9.13, а), а ФЧХ — линейной (рис. 9.13, б).

Условие безыскаженной передачи во всем частотном диапазоне можно выполнить лишь для резистив-ных цепей*. В цепях с реактивными элементами условия (9.54) и (9.55) можно обеспечить лишь в ограниченном частотном диапазоне соо (на рис. 9.13 показано пунктиром).

В этой связи представляет практический интерес вопрос о влиянии на форму сигнала   отклонения   АЧХ   и   ФЧХ   от

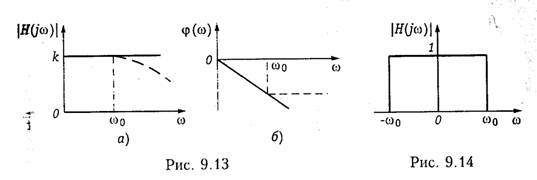
идеальной. Рассмотрим в качестве примера прохождение сигнала в форме единичной функции, в форме единичного импульса и импульса прямоугольной формы через цепь с АЧХ, изображенной на рис. 9.14. Эта цепь соответствует идеальному ФНЧ (см. гл. 17) и задается условием

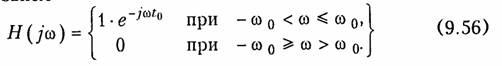
Фильтр нижних частот пропускает без искажений все частотные составляющие от 0 до ω₀ и задерживает составляющие больше ω₀.

Единичный импульс. Рассмотрим вначале входной сигнал f₁(t) в форме единичного импульса (рис. 7.2, б). Так как для единичного импульса F₁(jω), то с учетом (9.56) и обратного преобразования Фурье (9.7), получим:

На рис. 9.15 изображена форма выходного сигнала f₂(t), определяемая функцией (9.57). Из рисунка видно, что форма выходного сигнала существенно отличается от входного импульса f₁(t): он искажается по форме и растягивается во времени (теоретически на бесконечность), что отражает установленное ранее соотношение между длительностью сигнала и шириной его спектра: сигнал ограниченный по частоте — бесконечен во времени и наоборот (см. § 9.4). Запаздывание выходного сигнала t_o определяется крутизной ФЧХ: t_o = — dφ/dω). С увеличением ω₀ (с расширением полосы пропускания фильтра) ширина главного лепестка импульса

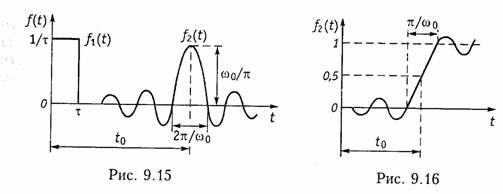
равная 2π/ ω₀ — сужается, задержка to уменьшается, амплитуда импульса увеличивается. Важно отметить, что теоретически согласно (9.57) сигнал f₂(t) существует и при t < О, т. е. до воздействия входного сигнала, что конечно, противоречит условию физической реализуемости и является следствием идеализации АЧХ ФНЧ.

Единичный сигнал. Рассмотрим теперь прохождение сигнала в форме единичной функции (рис. 7.2, а) через ФНЧ с характеристикой (9.56). Запишем уравнение единичной функции 1(t) в интегральной форме*:

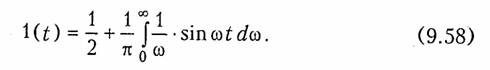
Интеграл в (9.58) можно рассматривать как вещественную форму обратного преобразования Фурье (9.7) для нечетной функции f(t) = 1(t) — 1/2, спектр которой равен 1/ω. Тогда на основании (9.58) и с учетом условий (9.52) и (9.56), для выходного сигнала можно записать:

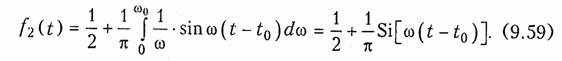
Интеграл в (9.59) табулирован и носит название интегрального синуса: Si[ω(t — to)]. На рис. 9.16 приведен график сигнала на выходе идеального ФНЧ, определяемой функцией (9.59).

Как следует из представленного графика, чем уже полоса пропускания ФНЧ (меньше ω₀), тем меньше крутизна фронта нарастания импульса: df₂/dt = ω₀/π. Таким образом, как и в случае единичного импульса для уменьшения искажений выходного сигнала необходимо расширять полосу пропускания ФНЧ. Выбросы в выходном сигнале обусловлены теми же причинами, что и в случае, изображенном на рис. 9.15 (идеализация АЧХ ФНЧ).

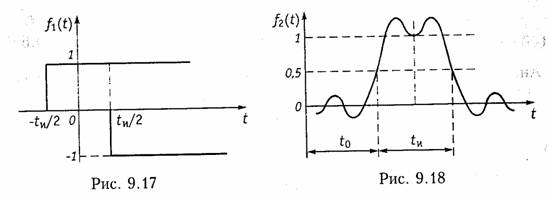
Прямоугольный импульс можно рассматривать как разность двух единичных функций сдвинутых относительно друг друга на t_и/2 (рис. 9.17). Тогда учитывая линейность цепи и равенство (9.59) получим уравнение выходного сигнала для этого случая:

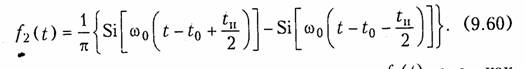
На рис. 9.18 изображен вид выходного сигнала f₂(t) , т. е., как и в предыдущих случаях, длительность фронта нарастания и спада импульса обратно пропорциональна полосе пропускания цепи ω₀. Чем уже полоса, тем более затянут фронт импульса; чем меньше длительность импульса, тем шире должна быть полоса пропускания цепи. Обычно на практике полосу пропускания выбирают из условия: S_A = 2/t_И.

9.7. Связь между временными и частотными характеристиками электрических цепей

Рассмотренные в гл. 8 и 9 временной и частотный методы анализа переходных процессов базируются на двух взаимосвязанных характеристиках электрических цепей: импульсной или переходной, с одной стороны, и комплексной передаточной функции, с другой. Между этими характеристиками существует однозначное соответствие. Определим эту связь. Допустим, что на вход пассивной электрической цепи с комплексной передаточной функцией Н(jω) приложено воздействие в виде единичной импульсной функции. Тогда с учетом того, что спектр единичного импульсного сигнала равен единице (см. (9.39)), спектр выходного сигнала согласно (9.51) будет:

Обратное преобразование (9.7).определит выходной сигнал f₂(t), который численно равен импульсной характеристике цепи:

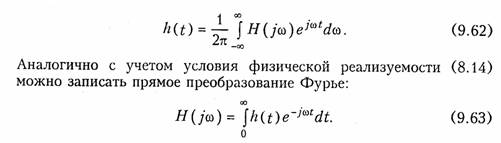
Таким образом, приходим к важному выводу: импульсная и комплексная передаточные функции пассивной электрической цепи связаны между собой парой преобразования Фурье (9.62) и (9.63). А это, в свою очередь, означает, что импульсная характеристика однозначным образом определяет комплексную -передаточную функцию цепи и наоборот. Причем, для hit) и Ж/со) справедливы все свойства и теоремы, рассмотренные в § 9.2. В частности, из теоремы изменения масштаба независимого переменного следует, что чем более растянута во времени импульсная характеристика цепи, тем уже ее АЧХ и наоборот. В § 9.6 было показано, что для неискажающей линейной цепи АЧХ должна быть равномерна, а это соответствует согласно (9.40) импульсной характеристике цепи в виде 5-функции, что полностью подтвер-.    ждает изложенное.

Связь комплексной передаточной функции с переходной характеристикой также определяется однозначно, поскольку последняя связана соотношением (8.2) с импульсной характеристикой цепи. Для установления этой связи можно воспользоваться интегральным представлением единичной функции (9.58):

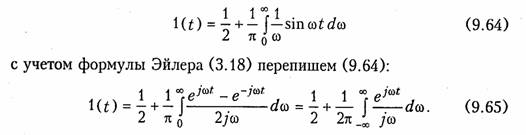
Если ко входу электрической цепи с передаточной функцией Ж/со) = | Я(усо )|е^{/<р и} приложена единичная функция (9.65), то сигнал на выходе цепи будет численно равен переходной характеристики git), спектр которой определяется согласно (9.51), где F\ (7^ю) ⁼ VJ® • Тогда после применения обратного преобразования Фурье с учетом (9.65) получим:

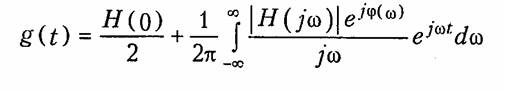
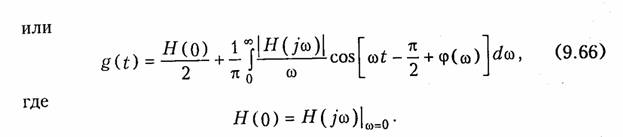
Таким образом, зная Ж/со), можно найти с помощью (9.66) также и g(t). Важно отметить предельное соотношение между git) и Ж/со), вытекающее непосредственно из свойств (7.17) —(7.18) и связи между преобразованием Фурье и Лапласа:

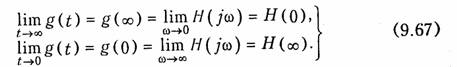
Эти соотношения означают, что реакция на выходе цепи от единичного воздействия в установившемся режиме будет отлична от нуля, если передаточная функция на нулевой частоте не равна нулю (ести* путь постоянной составляющей). И напротив, в начальный момент при t = 0 (момент коммутации) реакция на выходе будет изменяться скачком, если Жсо) — не равна нулю, т. е. цепь имеет бесконечно большую полосу пропускания. Рассмотренные соотношения хорошо иллюстрируются условиями пропускания сигнала через линейную цепь (см. § 9.6).

В заключение рассмотрим связь между вещественной H\ia) и мнимой #2(со) частями комплексной передаточной функции (4.7). Перепишем (9.62) в форме

Таким образом, для нахождения импульсной характеристики цепи достаточно воспользоваться частотной зависимостью только вещественной или мнимой частей H(jω). Из (9.71) следует также важный вывод о том, что нельзя независимо выбирать вещественную и мнимую части передаточной функции или, что то же самое, нельзя произвольно выбирать АЧХ и ФЧХ цепи, так как они связаны между собой определенной зависимостью (4.9), (4.10).

Вопросы и задания для самопроверки

1.  Какие существуют методы определения сигнала по спектру?

2.  Каким  образом  можно  определить  постоянную  составляющую единичной функции, если известна спектральная плотность единичной функции?

3.  Чем отличаются сигналы с дискретным и сплошным спектрами?

4.  В каких случаях используется теорема свертки?

5.  Каким образом и зачем определяют полюсы спектральной функции?

6.  Что понимают под спектральной плотностью энергии сигнала?

7.  Зависит ли спектральная плотность энергии сигнала от формы (вида) сигнала и фазы спектральных составляющих?

8.  Как можно  получить уравнение  единичной  функции  в  интегральной форме

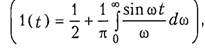    если известно обобщенное преобразование Фурье единичной функции?

9.  Как связаны между собой импульсная, переходная и комплексная передаточная функции пассивной электрической цепи?

10.  В чем сущность частотного анализа линейных электрических цепей при негармонических воздействиях?

11.  Можно ли создать электрическую цепь для безыскаженной передачи сигнала во всем частотном диапазоне?

12.  Как связаны между собой комплексная амплитуда и комплексная спектральная плотность?

13.  В каких случаях при анализе сигналов применяются интеграл Фурье и ряд Фурье?

14.  Каким условиям должен удовлетворять сигнал, подвергаемый преобразованию Фурье?

15.  Пояснить физический смысл основных теорем спектрального анализа?

16.  Связь между преобразованиями Фурье и Лапласа.

17.  Что представляет собой «обобщенный спектр сигнала»?