Предисловие

Переход к цифровому телевидению дает значительное увеличение числа телевизионных каналов, повышение качества изображения и звука, расширение функциональных возможностей телевизионных систем. Цифровое телевидение в течение первого десятилетия нового века займет ведущее положение в телевизионном вещании развитых стран. В то же время, в отечественной учебной литературе эта отрасль науки и техники пока освещена слабо, и чтобы ознакомиться с ней читатель вынужден искать информацию в журналах и в Интернет, что доступно не всем, и к тому же качество этой информации не всегда высокое.

Настоящее учебное пособие предназначено для студентов специальности "Радиотехника" и других специальностей, изучающих телевидение, и должно служить дополнением для имеющихся учебников по данному предмету, например, прекрасной книги "Телевидение" под редакцией В.Е. Джаконии. Цель, стоявшая перед автором, ознакомить студентов с принципами построения полностью цифровых систем телевидения, созданных в последние годы. Книга может быть полезной также преподавателям вузов, аспирантам и инженерам, желающим получить первое представление о цифровом телевидении и основу для дальнейшего изучения этой области по специальной литературе и стандартам.

В данном учебном пособии рассматриваются принципы построения и работы наиболее важных частей цифровой телевизионной системы. Материал в последующих главах расположен в следующем порядке:

В гл.1 сформулировано представление о цифровом телевидении кратко изложена история его возникновения и развития

В гл. 2 даны основные сведения о преобразовании одномерных и двумерных сигналов в цифровую форму, и описаны свойства цифрового телевизионного сигнала. Приведены основные параметры цифрового представления телевизионных сигналов в соответствии с Рекомендацией ITU-R ВТ 601 и некоторыми другими стандартами.

В гл. 3 приведены рассмотрены некоторые методы цифровой обработки и кодирования сигналов и изображений, используемые в цифровом телевидении. Это дискретное преобразование Фурье и дискретное косинусное преобразование, цифровая фильтрация, кодирование в частотных поддиапазонах и вэйвлетпреобразование, оценка и компенсация движения, кодирование с предсказанием, векторное квантование.

В гл. 4 описаны стандарт кодирования неподвижных изображений JPEG, стандарты кодирования движущихся изображений и звукового сопровождения MPEG-1, MPEG-2 и MPEG-4, а также стандарты кодирования, применяемые в видеосвязи.

В гл. 5 рассмотрены методы канального кодирования и модуляции, используемые для передачи сигналов цифрового телевидения по каналам связи.

В гл. 6 даны сведения о практической реализации цифровых телевизионных систем, а также об элементной базе и о приемной аппаратуре цифрового телевидения. Рассмотрены вопросы взаимодействия телевидения и компьютерных технологий, а также перспективные направления развития цифрового телевидения.

Первые два издания данного учебного пособия вышли в МИРЭА в 1995 и 1999 годах. В настоящем издании в основном сохранена структура предыдущего, но большинство разделов расширены за счет более подробного изложения и введения материалов, отражающих развитие цифрового телевидения за последние годы. Введен словарь терминов и сокращений, который одновременно выполняет функции предметного указателя. Изложение сверено с текстами Международных Стандартов и Рекомендаций. Исправлены ошибки и неточности, обнаруженные во втором издании.

Автор выражает глубокую признательность заведующему кафедрой радиоприборов МИРЭА профессору В.И. Нефедову, который оказывал всестороннюю поддержку работе над пособием. Автор также благодарит всех друзей и коллег, помогавших ему словом и делом. Особую благодарность автор испытывает к студентам факультета Радиотехнических систем МИРЭА, которые своим интересом к предмету стимулировали работу над новым изданием пособия.

1. ЭТАПЫ РАЗВИТИЯ ЦИФРОВОГО ТЕЛЕВИДЕНИЯ

Цифровое телевидение — это отрасль телевизионной техники, в которой передача, обработка и хранение телевизионного сигнала осуществляются в цифровой форме.

Применение методов и средств цифрового телевидения - это новая ступень развития телевизионной техники, обеспечивающая ряд преимуществ по сравнению с аналоговым телевидением:

-  повышение помехоустойчивости трактов передачи и записи телевизионных сигналов;

- уменьшение мощности передатчиков ТВ-вещания;

-  существенное увеличение числа телевизионных программ, передаваемых в том же частотном диапазоне;

- повышение качества изображения и звука в телевизионных приемниках с обычным стандартом разложения;

-   создание телевизионных систем  с новыми  стандартами разложения изображения (телевидение высокой четкости - ТВЧ);

- расширение функциональных возможностей студийной аппаратуры, используемой при подготовке и проведении телевизионных передач;

-   передача в телевизионном сигнале различной дополнительной   информации,   превращение  телевизионного   приемника в многофункциональную информационную систему;

-  создание интерактивных телевизионных систем, при пользовании которыми зритель получает возможность воздействовать на передаваемую программу.

Эти преимущества обусловлены как самими принципами, присущими цифровому телевидению, так и наличием разнообразных алгоритмов, схемных решений и мощной технологической базы для создания соответствующих устройств.

В своем развитии цифровое телевидение прошло ряд этапов. На каждом этапе сначала выполнялись научно-исследовательские и опытно-конструкторские работы, создавались экспериментальные устройства и системы, а затем принимались стандарты, как правило, международные, которые должны выполняться всеми организациями, ведущими телевизионное вещание и выпускающими видеопрограммы, и всеми фирмами-производителями аппаратуры. Принятие стандартов - важнейшая составляющая развития любой технологии, в том числе и телевидения.

Международные стандарты принимаются в первую очередь Международной организацией по стандартизации (ISO - International Organization for Standartization), созданной в 1947 г. Для разработки стандартов в какой-либо области техники ISO создает рабочие группы. Пример такой группы - MPEG (Motion Picture Expert Group), занимающаяся стандартами для цифрового телевидения. Члены рабочих групп большую часть времени работают в своих странах и по мере надобности проводят встречи, на которых обсуждают и подготавливают к утверждению материалы стандартов.

Другая организация, играющая важную роль в стандартизации - Международный Союз Электросвязи (ITU - International Communication Union). Документы, принимаемые ITU, называются Рекомендациями, и могут быть преобразованы в Международные стандарты решениями ISO, или в национальные стандарты решениями национальных органов стандартизации.

Первый этап развития цифрового телевидения - использование цифровой техники в отдельных частях телевизионной системы при сохранении обычного стандарта разложения и аналоговых каналов связи. Наиболее важным достижением данного этапа было создание полностью цифрового студийного оборудования. На современных телестудиях сигналы с передающих камер преобразуются в цифровую форму, и вся дальнейшая их обработка и хранение в пределах телецентра осуществляются цифровыми средствами. Это позволяет в значительной степени реализовать указанные выше преимущества цифрового телевидения. На выходе студийного оборудования телевизионный сигнал преобразуется в аналоговую форму и передается по обычным каналам связи.

Результаты работы специалистов разных стран были закреплены в документе, который называется Рекомендация ITU-R ВТ 601 (ITU-R - International Telecommunication Union, Radio, или в русском переводе - Сектор радиосвязи Международного Союза Электросвязи - МСЭ-Р). Старое название этого стандарта -Рекомендация 601 Международного консультативного комитета по радио (МККР). Данный стандарт был принят в 1982 г. и определяет основные параметры цифровой студийной аппаратуры [1].

Другое направление использования цифровой техники, характерное для первого этапа развития цифрового телевидения -

введение цифровых блоков в телевизионные приемники с целью повышения качества изображения или расширения функциональных возможностей. Примерами таких блоков могут служить цифровые фильтры для разделения яркостного и цветоразностных сигналов, для уменьшения влияния шумов на изображение и для подавления эхо-сигналов, возникающих при отражении радиоволн от поверхности Земли и различных объектов, то есть при наличии многолучевого приема. Широко известны также устройства для перехода от чересстрочной развертки к квазипрогрессивной, реализации функций "стоп-кадр" и "кадр в кадре", декодирования и воспроизведения на экране дополнительной информации, передаваемой по системе "Телетекст" и т. д. [1,2].

Все эти усовершенствования не затрагивали стандарт разложения и принципы передачи телевизионного сигнала по каналу связи.

Второй этап развития цифрового телевидения - создание гибридных аналого-цифровых телевизионных систем с параметрами, отличающимися от принятых в обычных стандартах телевидения. Можно выделить два основных направления изменений телевизионного стандарта: переход от одновременной передачи яркостного и цветоразностных сигналов к последовательной их передаче и увеличение числа строк в кадре и элементов изображения в строке. Реализация второго направления связана с необходимостью сжатия спектра телевизионных сигналов для обеспечения возможности его передачи по каналам связи с приемлемой полосой частот.

Примерами гибридных телевизионных систем могут служить японская система телевидения высокой четкости MUSE и западноевропейские системы семейства MAC [3]. В передающей и приемной частях всех этих систем сигналы обрабатываются цифровыми средствами, а в канале связи сигналы передаются в аналоговой форме. Системы ТВЧ MUSE и HD-MAC имеют формат изображения 16:9, число строк в кадре 1125 и 1250, частоту кадров 30 и 25 Гц, соответственно. С помощью цифрового кодирования исходная полоса частот сигналов этих систем, превышающая 20 МГц, сжимается примерно до 8 МГц. Это позволяет передавать эти сигналы с частотной модуляцией (ЧМ) по спутниковым каналам связи, имеющим ширину полосы 27 МГц. В то же время, широко развитая сеть наземного телевизионного вещания, включающая УКВ-передатчики, кабельную сеть и другую технику, не позволяет передавать и принимать сигналы указанных систем телевидения, так как рассчитана на ширину полосы частот одного канала, равную 6...8 МГц.

Третьим этапом развития цифрового телевидения можно считать создание полностью цифровых телевизионных систем.

После появления в Японии и Европе упомянутых выше систем телевидения высокого разрешения MUSE и HD-MAC, в США в 1987 г. был объявлен конкурс на лучший проект системы телевидения высокого разрешения для утверждения в качестве национального стандарта. В первые годы на этот конкурс были выдвинуты различные аналоговые системы. Система MUSE и другие системы, предусматривающие передачу только по спутниковым каналам, вскоре были сняты с рассмотрения. Это объяснялось тем, что в США около 1400 компаний осуществляют наземное телевизионное вещание, и очень широко развита сеть кабельных линий. Вся эта инфраструктура рассчитана на ширину полосы частот телевизионного канала 6 МГц.

Рассматривались проекты аналоговых телевизионных систем высокого разрешения, в которых по одному стандартному каналу передается обычный сигнал NTSC, а по другому - дополнительный сигнал, который в приемнике с соответствующим декодером позволяет получить изображение с большим количеством строк и элементов разложения в строке. В то время никто не мог предположить, что уже через несколько лет удастся по стандартному каналу с шириной полосы 6 или 8 МГц передавать сигналы полностью цифровой системы телевидения как обычного, так и ТВЧ.

Первые предложения по полностью цифровым системам телевидения появились в 1990 г. В основе этих проектов лежали достижения в методах и технике эффективного кодирования и сжатия изображений. Работы в этой области проводились не только с целью создания цифровых телевизионных систем, но и для таких применений, как видеотелефон и видеоконференции, запись видеопрограмм на цифровые лазерные компакт-диски, компьютерная графика, видеосредства мультимедиа и др.

С каждым годом возрастало количество проектов цифровых телевизионных систем и улучшались их характеристики. В начале 1993 г. последние аналоговые системы были сняты с рассмотрения. В мае 1993 г. четыре группы компаний и исследовательских

организаций, представлявших близкие по существу проекты, объединились в "Grand Alliance" и в дальнейшем представляли единый проект, который и стал основой стандарта полностью цифровой телевизионной системы в США. В числе создателей новой системы Массачусетский Технологический Институт, корпорации Zenith, AT&T, General Instruments, американские отделения Philips и Thomson и др.

Результаты работ нашли отражение в нескольких стандартах. Для сжатия неподвижных изображений широко используется стандарт JPEG (Joint Picture Expert Group) [4]. Методы сжатия движущихся изображений и сигналов звукового сопровождения описаны в стандартах MPEG-1 и MPEG-2 (MPEG - Motion Picture Expert Group). Стандарт MPEG-1, ориентированный в основном на запись кинофильмов и видеопрограмм на компьютерные лазерные диски с возможностью воспроизведения изображения и звука с помощью обычного персонального компьютера, был окончательно утвержден к декабрю 1993 г. [5-7]. Стандарт MPEG-2, предназначенный для систем телевизионного вещания как с обычным стандартом разложения, так и с увеличенным числом строк (ТВЧ), был утвержден в ноябре 1994 г. [8-10].

В настоящее время системы цифрового телевидения, основанные на сжатии телевизионных сигналов по стандарту MPEG-2, быстро распространяются во многих странах. При этом в первую очередь решается задача значительного увеличения количества передаваемых программ телевидения обычного разрешения, так как это дает быстрый коммерческий эффект.

В Европе уже в 1993 г., как только стало ясно, что за цифровыми телевизионными системами будущее, был принят проект DVB (Digital Video Broadcasting - Цифровое Видео Вещание), в работах по которому приняло участие более 130 фирм и научно-исследовательских организаций разных стран [11]. В 1997 г. через искусственные спутники Земли (ИЗС) на европейские страны передавалось 170 каналов цифрового ТВ, а к концу 1998 г. число таких каналов превысило 1000. Одновременно распространяются цифровое телевизионное вещание по кабельным линиям, цифровая видеозапись, цифровые видеодиски.

В развитых странах поставлен вопрос о прекращении в первом десятилетии XXI века аналогового телевизионного вещания. Главными особенностями нового поколения телевизионных систем являются:

1.  Существенное сужение полосы частот цифрового телевизионного сигнала, достигаемое с помощью эффективного кодирования, то есть сокращения избыточности изображений, и позволяющее передавать 4 и более программ телевидения обычной четкости или 1-2 программы ТВЧ по стандартному телевизионному каналу с шириной полосы частот 6...8 МГц.

2. Единый подход к кодированию и передаче телевизионных сигналов   с   различной   четкостью изображения:   видеотелефон и другие системы с уменьшенной четкостью, телевидение обычной четкости, ТВЧ.

3.  Интеграция с другими видами информации при передаче по цифровым сетям связи.

4.  Обеспечение защиты передаваемых телевизионных программ и другой информации от несанкционированного доступа, что дает возможность создавать системы платного ТВ-вещания.

Структурная схема цифровой телевизионной системы показана на рис. 1.1. Кратко рассмотрим назначение основных частей системы.

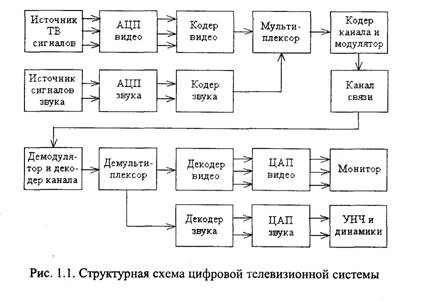
Источник аналоговых телевизионных сигналов формирует яркостный сигнал Е΄ _Y, и цветоразностные сигналы E΄_Y, E΄_B-Y, которые поступают на АЦП, где преобразуются в цифровую форму. В следующей части системы, называемой кодером изображения или кодером видео, осуществляется эффективное кодирование видеоинформации с целью уменьшения скорости передачи двоичных символов в канале связи. Как будет показано далее, эта операция является одной из наиболее важных, так как без эффективного кодирования невозможно обеспечить передачу сигналов цифрового телевидения по стандартным каналам связи.

Сигналы звукового сопровождения также преобразуются в цифровую форму. Звуковая информация сжимается в кодере звука. Кодированные данные-изображения и звука, а также различная дополнительная информация объединяются в мультиплексоре в единый поток данных. В кодере канала выполняется еще одно кодирование передаваемых данных, имеющее целью повышение помехоустойчивости. Полученным в результате цифровым сигналом модулируют несущую используемого канала связи.

В приемной части системы осуществляется демодуляция принятого высокочастотного сигнала и декодирование канального кодирования. Затем в демультиплексоре поток данных разделяется на данные изображения, звука и дополнительную информацию. После этого выполняется декодирование данных. В результате на выходе декодера изображения получаются яркостный и цветоразностные сигналы в цифровой форме, которые преобразуются в аналоговую форму в ЦАП и подаются на монитор, на экране которого воспроизводится изображение. На выходе декодера звука получаются сигналы звукового сопровождения, также преобразуемые в аналоговую форму. Эти сигналы поступают на усилители звуковой частоты и далее на динамики.

Помимо систем телевизионного вещания, методы и средства цифрового телевидения являются основой современных систем видеосвязи, к которым относятся видеоконференции и видеотелефон. Методы кодирования сигналов в системах видеосвязи описаны в специальных стандартах, таких как Н.261 [12], Н.262 [13], Н.263 [14] и др. В конце 1998 года был принят стандарт MPEG-4, в котором содержатся методы кодирования изображений и звука, обеспечивающие передачу видеоинформации со звуковым сопровождением по узкополосным каналам связи [15]. Контрольные вопросы

1. Что такое цифровое телевидение?

2. Какие преимущества может обеспечить цифровое телевидение?                    

3. Назовите основные этапы развития цифрового телевидения.

4.  Какие международные организации утверждают стандарты и рекомендации в области телевидения?

5. Что означают аббревиатуры "JPEG" и "MPEG"?                                            

6.   Каковы назначения кодера источника и кодера канала в цифровой телевизионной системе?

2. ЦИФРОВОЙ ТЕЛЕВИЗИОННЫЙ СИГНАЛ

2.1. Преобразование аналогового телевизионного сигнала в цифровой

Цифровой телевизионный сигнал получается из аналогового телевизионного сигнала путем преобразования его в цифровую форму. Это преобразование включает следующие три операции:

1.  Дискретизацию во времени, т. е. замену непрерывного аналогового сигнала последовательностью его значений в дискретные моменты времени - отсчетов или выборок.

2.   Квантование по уровню, заключающееся в округлении значения каждого отсчета до ближайшего уровня квантования.

3. Кодирование (оцифровку), в результате которого значение отсчета представляется в виде числа, соответствующего номеру полученного уровня квантования.

Все три операции выполняются в одном узле - аналого-цифровом преобразователе (АЦП). В современной аппаратуре АЦП реализуется в виде одной БИС. На входы АЦП (рис. 2.1,а) подаются аналоговый сигнал u(t) и тактовые импульсы CV, синхронизирующие моменты выборок. Выходные сигналы d₁...d_n образуют параллельный n-разрядный двоичный код, представляющий получающееся в результате аналого-цифрового преобразования число. Число двоичных разрядов для примера взято равным 4 (рис. 2.1,6).

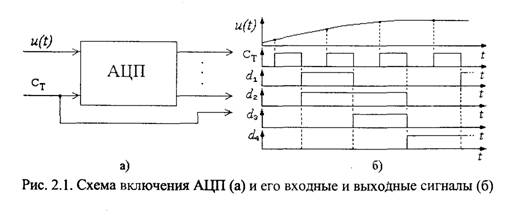
Преобразование очередного отсчета начинается по фронту тактового импульса, а результат появляется на выходах АЦП по срезу тактового импульса, поэтому сигналы d₁...d_n изменяются в моменты перехода сигнала С_T из высокого уровня (логическая 1) в низкий (логический 0).

ДИСКРЕТИЗАЦИЯ

Перейдем к анализу параметров аналого-цифрового преобразования. Первым из них является частота дискретизации ƒ_д. В соответствии с теоремой Котельникова должно выполняться условие ƒ_д > 2ƒ_в, где ƒ_в - верхняя граничная частота спектра преобразуемого в цифровую форму сигнала. Отсюда следует, в частности, что частота дискретизации телевизионного сигнала, используемого в нашей стране (ƒ_в = 6 МГц), должна быть не менее 12 МГц.

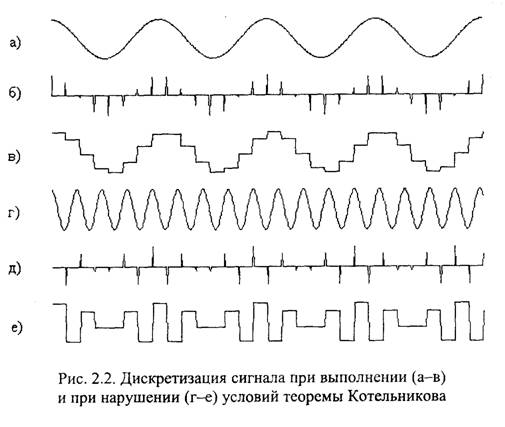
Рассмотрим примеры дискретизации сигналов. В результате дискретизации непрерывного синусоидального сигнала (рис. 2.2,а) получается дискретный сигнал, показанный на рис. 2.2,6. Обратное преобразование этого сигнала в непрерывный осуществляется с помощью операции, называемой интерполяцией. На рис. 2.2,в показана наиболее простая и часто применяемая ступенчатая интерполяция. В данном примере условия теоремы Котельникова на частоту дискретизации выполнены, поэтому дискретный сигнал имеет такую же частоту, как и исходный непрерывный сигнал, но форма его отличается из-за грубой интерполяции. Чтобы полностью выполнить условия Котельникова, надо при интерполяции пропустить дискретный сигнал через идеальный фильтр низких частот (ФНЧ) с частотой среза, равной половине частоты дискретизации, и тогда интерполированный сигнал не будет иметь искажений формы по сравнению с исходным сигналом.

На рис. 2.2,г-е показан пример дискретизации и интерполяции в случае нарушения условий теоремы Котельникова. Частота исходного синусоидального сигнала больше, чем половина частоты дискретизации. В результате в дискретном сигнале появилась ложная составляющая с частотой более низкой, чем частота исходного непрерывного сигнала. В англоязычной технической литературе это явление называется aliasing (от alias - вымышленное имя). Такое искажение необратимо, так как не может быть устранено никаким фильтром.

Анализ дискретизации и условий возникновения искажений возможен также с использованием спектрального подхода.

На рис. 2.3,а показан спектр дискретизированного сигнала в случае, если ƒ_д>2ƒ_в. Спектр исходного сигнала занимает полосу частот от 0 до ƒ_в . Модуль комплексного преобразования Фурье сигнала имеет симметричную относительно нуля форму, т. е. занимает полосу от -f_B до ƒ_в. В результате дискретизации в спектре возникают новые составляющие, огибающие которых совпадают по форме с огибающей исходного спектра, а точки, соответствующие точке ƒ= 0 в исходном спектре, находятся на частотах f_Д, 2f_Д, ... Если условие теоремы Котельникова выполнено, и ƒ_в < ƒ_д /2, то новые составляющие спектра не перекрываются с исходным спектром. Поэтому, с помощью идеального ФНЧ, имеющего частоту среза, равную ƒ_д/2, можно выделить частотные составляющие исходного сигнала, полностью подавив частотные составляющие, возникшие в результате дискретизации. Это означает, что исходный сигнал, передаваемый с использованием дискретизации, может быть восстановлен без искажений.

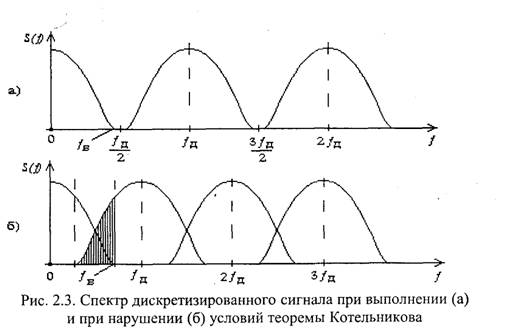
На рис. 2.3,6 показан спектр дискретизированного сигнала в случае, когда требования теоремы Котельникова не выполняются, т.е. ƒ_д<2 ƒ_в. При этом спектр исходного сигнала и спектр составляющих, возникших при дискретизации, перекрываются. Если пытаться выделить исходный сигнал с помощь идеального ФНЧ с частотой среза ƒ_вили ƒ_д/2, то на выходе ФНЧ помимо исходного сигнала окажутся дополнительные составляющие, т.е. возникнут искажения исходного сигнала.

Чтобы избежать возникновения необратимых искажений при дискретизации необходимо или выбирать достаточно большую частоту дискретизации, или ограничивать верхнюю граничную частоту дискретизируемого сигнала так, чтобы условия теоремы Котельникова выполнялись.

Перейдем к дискретизации телевизионных изображений, представляющих собой двумерные сигналы. Телевизионное изображение по вертикальной координате уже является дискретным вследствие разложения на строки. Поэтому для получения двумерной дискретизации достаточно выполнить одномерную дискретизацию телевизионного сигнала во времени.

При дискретизации изображения отсчеты образуют определенную структуру в его плоскости. На рис. 2.4,а показана наиболее широко применяемая ортогональная (прямоугольная) структура отсчетов, а на рис. 2.4,6 - шахматная структура. На рис. 2.4,в,г по-казаны варианты расположения отсчетов яркостного и цветоразностных сигналов при дискретизации цветных телевизионных изображений. Пояснения к этим рисункам будут даны позже.

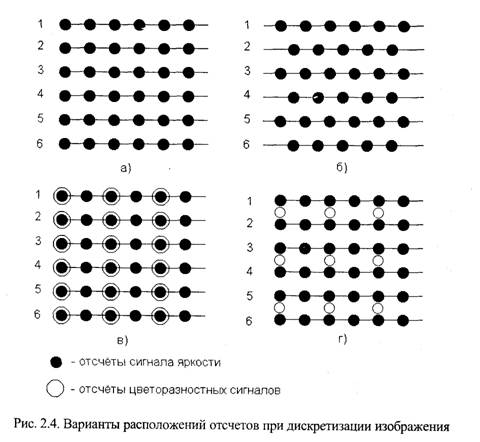
Процесс дискретизации изображения и его последующего воспроизведения иллюстрируется также в виде трехмерных графиков на рис. 2.5, где горизонтальные координаты X и Y соответствуют пространственным координатам в плоскости изображения, а вертикальная координата Z показывает величину яркости в каждой точке изображения. На рис. 2.5,а показано исходное аналоговое (непрерывное) изображение. На рис. 2.5,6 представлен результат дискретизации этого изображения, причем отсчеты или точки дискретизации расположены в виде ортогональной решетки. На рис. 2.5,в показана  двумерная функция функция яркости, получающаяся

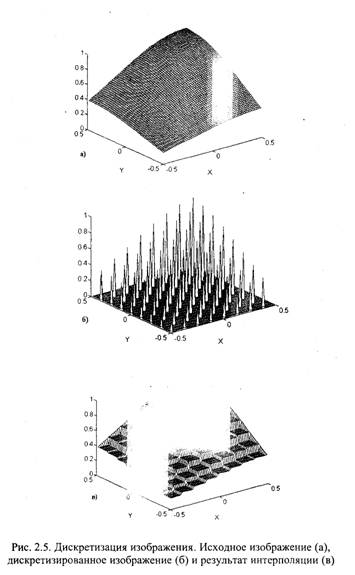
при воспроизведении дискретизированного изображения на экране с использованием двумерной ступенчатой интерполяции. Здесь изображение состоит из элементов, называемых пикселами (pixel -picture element). Яркость в пределах любого пиксела приблизительно постоянна и равна яркости исходного изображения в соответствующей точке дискретизации или в более общем случае средней яркости по некоторой площади в пределах пиксела. Размеры пикселов должны быть настолько малыми, чтобы зритель при нормальных условиях наблюдения воспринимал воспроизводимое изображение как непрерывное.

Как и в случае одномерного сигнала, можно рассмотреть дискретизацию со спектральной точки зрения. Для этого сначала введем понятия пространственных частот и пространственного спектра для непрерывного изображения.

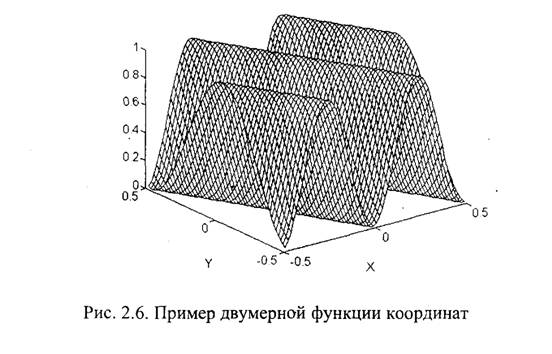
По аналогии с периодом одномерного периодического сигнала, являющегося функцией времени, назовем пространственным периодом Т_х по координате X пространственный интервал, через который значения двумерного сигнала b(х,у) повторяются. Тогда пространственной частотой этого сигнала по координате X будет величина обратная пространственному периоду f_x = 1/T_х. Аналогично вводятся пространственный период и пространственная частота по координате Y.

Для получения комплексного пространственного спектра изображения применяется двумерное преобразование Фурье

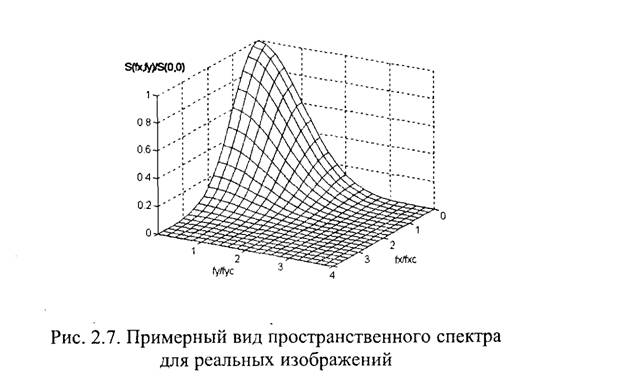
Низкие пространственные частоты соответствуют медленным изменениям яркости изображения по пространственным координатам, а высокие пространственные частоты — быстрым изменениям яркости, т. е. мелким деталям изображения и резким перепадам яркости на границах объектов. На рис. 2.7 показан примерный вид модуля S(f_x,f_y) комплексного спектра S(f_x, f_y) для реального изображения, в котором преобладают низкие пространственные частоты. По горизонтальным осям отложены величины отношений пространственных частот к значениям пространственных частот по соответствующим координатам, для которых модуль спектра убывает в е раз по отношению к постоянной составляющей 5(0,0). По вертикальной оси график нормирован по отношению к значению постоянной составляющей яркости изображения.

Преобразование пространственного спектра изображения при двумерной дискретизации показано на рис. 2.8. Пространственный спектр исходного изображения предполагается ограниченным в плоскости пространственных частот, т. е. вне некоторой замкнутой кривой все частотные составляющие можно считать равными нулю. Как и в случае дискретизации одномерных сигналов, при двумерной дискретизации появляются побочные спектры, сдвинутые относительно исходного спектра по горизонтали и по вертикали на величины пространственных частот дискретизации ƒ_ду и f_дх, соответственно.

На рис. 2.8,а показан случай, когда в результате дискретизации побочные спектры не пересекаются с основным. Такой случай достигается при достаточно больших пространственных частотах дискретизации по обеим координатам. В таком случае возможно восстановление исходного изображения по дискретизированному с применением пространственного фильтра, выделяющего спектр исходного изображения из спектра дискретизированного изображения. Это является обобщением теоремы Котельникова на двумерные сигналы.

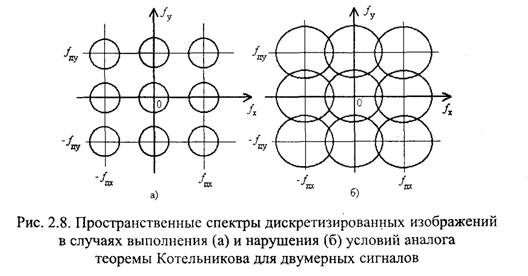
На рис. 2.8,6 показан случай, когда побочные спектры перекрываются со спектром исходного изображения, что является следствием недостаточно больших частот дискретизации по пространственным координатам. В этом случае восстановление исходного изображения по дискретизированному без искажений невозможно.

Конкретный вид искажений в изображении зависит от форм составляющих его объектов и особенностей его пространственного спектра. При наличии в исходном изображении хорошо выраженных периодических составляющих искажения могут проявиться в виде появления новых периодических составляющих, часто имеющих вид муара. Пример таких искажений приведен на рис. 2.9 слева. Это изображение получено при дискретизации изображения испытательной телевизионной таблицы. Муар в виде криволинейных полос наблюдается на участке таблицы, содержавшем периодическую структуру из тонких линий, предназначенную для визуальной оценки четкости на экране телевизора.

Другой распространенный вид искажений, создаваемых дискретизацией, показан на рис. 2.9 справа вверху. Если исходное изображение содержит наклонные линии, то в результате дискретизации края этих линий становятся зубчатыми. Из рисунка видно, что размеры зубцов зависят от наклона линии.

На рис. 2.8,6 показан случай, когда побочные спектры перекрываются со спектром исходного изображения, что является следствием недостаточно больших частот дискретизации по пространственным координатам. В этом случае восстановление исходного изображения по дискретизированному без искажений невозможно.

Конкретный вид искажений в изображении зависит от форм составляющих его объектов и особенностей его пространственного спектра. При наличии в исходном изображении хорошо выраженных периодических составляющих искажения могут проявиться в виде появления новых периодических составляющих, часто имеющих вид муара. Пример таких искажений приведен на рис. 2.9 слева. Это изображение получено при дискретизации изображения испытательной телевизионной таблицы. Муар в виде криволинейных полос наблюдается на участке таблицы, содержавшем периодическую структуру из тонких линий, предназначенную для визуальной оценки четкости на экране телевизора.

Другой распространенный вид искажений, создаваемых дискретизацией, показан на рис. 2.9 справа вверху. Если исходное изображение содержит наклонные линии, то в результате дискретизации края этих линий становятся зубчатыми. Из рисунка видно, что размеры зубцов зависят от наклона линии.

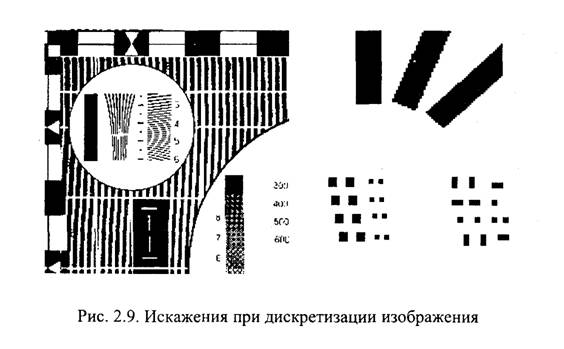
Искажения, возникающие при дискретизации, часто зависят от положения объекта относительно сетки точек дискретизации (сетки отсчетов), т. е. являются случайными. Этот факт иллюстрируется рис. 2.9 справа внизу, где показаны искажения тест-объектов различных размеров, постепенно смещаемых относительно сетки отсчетов (сама сетка отсчетов на рисунке не показана), причем пространственный период дискретизации меньше размеров более крупных квадратиков, но больше размеров меньших квадратиков. Слева показаны исходные изображения тест-объектов, а справа - изображения после дискретизации и интерполяции как на рис. 2.5. Видно, что размеры и формы тест-объектов изменяются в разных случаях по-разному, а для тест-объектов меньших, чем период дискретизации, наблюдается даже пропадание одного из квадратиков.

Отмеченные виды искажений наблюдаются и при дискретизации реальных изображений. На рис. 2.10,а приведено известное тестовое изображение "Лена", содержащее 256x256 элементов (пикселов) с числом градаций яркости 256. Это изображение уже является дискретным, но в том масштабе, который дан на иллюстрации, дискретность не заметна.

На рис. 2.10,6 приведено то же тестовое изображение, но с числом пикселов 128x128. На этом изображении можно видеть различные виды искажений, возникающих вследствие дискретизации. На перьях, украшающих шляпку, видны искажения типа муара. На контуре плеча и на краях шляпки отчетливо видна зубчатость. Искажения и пропадание мелких деталей изображения можно видеть на примере ресниц.

Чтобы искажений не возникало, необходимо выбирать достаточно большие пространственные частоты дискретизации по обеим координатам. Однако в телевидении эти пространственные частоты фактически предопределены параметрами, задаваемыми в используемом стандарте разложения, т. е. количеством строк и количеством элементов в каждой строке. Для согласования пространственного спектра изображения с указанными параметрами во многих случаях приходится ограничивать верхние граничные пространственные частоты изображения перед дискретизацией. Эта операция выполняется с помощью специальных оптических рассеивающих элементов, располагаемых перед ПЗС-матрицей, или просто путем небольшой расфокусировки объектива в телевизионной камере.

Как уже отмечалось, при передаче изображения в цифровой телевизионной системе осуществляется двумерная дискретизация. При этом дискретизация по вертикальной координате выполняется уже в оптико-электронном преобразователе путем разложения передаваемого кадра на строки. Эта операция имеется уже в обычном аналоговом телевидении. Дискретизация по горизонтальной координате выполняется путем дискретизации видеосигнала во времени.

Из курса "Основы телевидения" известно, что верхняя граничная частота видеосигнала определяется по формуле

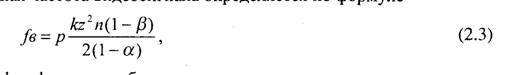
где k- формат изображения на экране; т. е. отношение ширины изображения к его высоте; z - полное число строк в кадре; п - частота кадров; α и β- коэффициенты, показывающие доли неактивных участков в периодах, соответственно, строчной и кадровой разверток; р - экспериментально определяемый коэффициент, равный 0,75...0,85.

Данная формула получена, исходя из условия одинаковой разрешающей способности телевизионной системы по горизонтали и по вертикали, что соответствует квадратной форме наименьших передаваемых элементов изображения. Поэтому при задании частоты дискретизации телевизионного сигнала по его верхней граничной частоте (обычной, а не пространственной) в соответствии с одномерным критерием, даваемым теоремой Котельникова, будет удовлетворяться и двумерное условие отсутствия искажений изображения из-за перекрытия пространственных спектров при дискретизации.

КВАНТОВАНИЕ

Следующий важнейший параметр аналого-цифрового преобразования - число уровней квантования N_KB, определяемое числом двоичных разрядов АЦП п в соответствии с соотношением

Выбор значения N_kb осуществляется так, чтобы влияние квантования на изображение не было заметно для получателя информации.

Рассмотрим пример квантования одномерного сигнала. На рис. 2.11,а показан дискретный сигнал, содержащий 256 отсчетов (отдельные отсчеты в этом масштабе не различимы), значения уровня сигнала измеряются в Вольтах и изменяются непрерывно, т. е. квантования нет. На рис. 2.11,6 показан тот же сигнал после квантования с числом двоичных разрядов, равным 4, т. е. имеющий 16 уровней квантования. Шаг квантования h = 0,1. Масштаб шкалы по вертикальной оси координат такой же, как на предыдущем рисунке.

На рис. 2.11,в показаны значения ошибки Δи, вносимой в сигнал операцией квантования. При этом предполагается, что квантование осуществляется путем округления значения сигнала до  ближайшего  снизу  уровня  квантования.   Величина  ошибки квантования Дм изменяется в пределах от 0 до h. Если ввести постоянную поправку, равную h/2, то величина Δи будет изменяться в диапазоне от -h/2 до h/2.

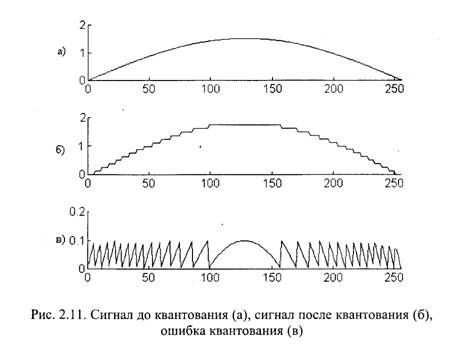
Ошибка квантования является случайной величиной, поэтому ее часто называют шумом квантования. В случае равномерного распределения вероятностей значений сигнала распределение величины ошибки квантования также равномерное. Дисперсия шума квантования  при  равномерном  квантовании  и  равновероятных

значениях  среднее квадратическое значение напряжения шума квантования.

На изображении шум квантования может проявляться различным образом в зависимости от изменений яркости или цвета данного участка изображения. На участках, состоящих из мелких деталей, квантование приведет к случайным изменениям их яркости или цвета. На участках изображения с плавным изменением уровня видеосигнала квантование может привести к возникновению ложных контуров по тем линиям, на которых уровень видеосигнала пересекает границу двух смежных интервалов квантования.

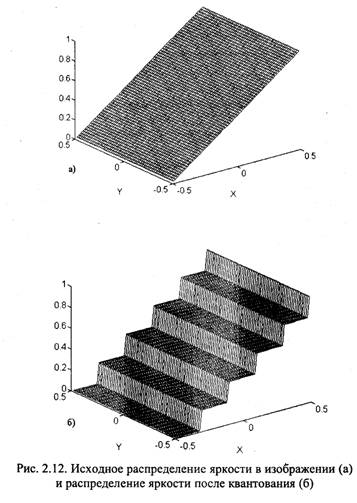
Это явление иллюстрируется рис. 2.12, на котором показаны плавная функция изменения яркости на каком-то участке изображения до квантования (рис. 2.12,а) и ступенчатая функция изменения яркости после квантования (рис. 2.12,6). Если перепады яркости на ступеньках достаточно большие, т. е. уровней квантования мало, то на изображении возникнут ложные контуры. Заметность ложных контуров существенно уменьшается при случайных смещениях значений яркости элементов изображения или положений уровней квантования. Поэтому в некоторых случаях перед квантованием в изображение вводится аддитивный шум.

На рис. 2.13 приведено тестовое изображение "Лена", прошедшее квантование с числом уровней равным 8. Ложные контуры особенно хорошо заметны на плече и на лице. В то же время на мелкоструктурных частях изображения, например, на перьях шляпки, искажения, создаваемые квантованием, практически незаметны. Следовательно, мелкие детали, текстуру изображения можно квантовать более грубо, чем участки с плавными изменениями яркости. Этот факт используется во многих методах сжатия изображений.

Равномерное квантование телевизионного сигнала, вообще говоря, не является наилучшим. Это обусловлено в первую очередь свойствами зрительного аппарата человека. Как известно, пороговое превышение яркости Δ в_пор объекта над фоном, при котором объект различается наблюдателем, подчиняется в первом приближении закону Вебера-Фехнера

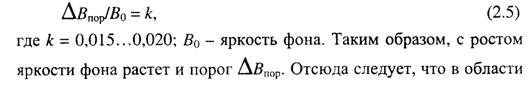
значений телевизионного сигнала, близких к уровню черного, шаг квантования должен быть меньше, чем в области, близкой к уровню белого.

Однако техническая реализация неравномерного квантования существенно сложнее, чем равномерного. Вместо использования переменного шага квантования обычно выполняют предварительное нелинейное преобразование видеосигнала - гамма-коррекцию. При этом решается одновременно две задачи. Во-первых, корректируется нелинейность передаточной характеристики кинескопа и обеспечивается оптимальная форма передаточной характеристики всего тракта телевизионной системы "от света до света". Во вторых, уменьшается влияние ошибок квантования при малых уровнях яркости изображения.

Передаточная характеристика гамма-корректора описывается соотношением

где U_вх и U_вых - напряжения сигналов на входе и на выходе гамма-корректора, соответственно; U_вхм и U_выхм - максимальные значения диапазонов напряжений сигналов на входе и на выходе гамма-корректора, соответственно; γ = 0,42...0,48 - показатель гамма-коррекции. График передаточной характеристики гамма-корректора для случая у- 0,45 приведен на рис. 2.14.

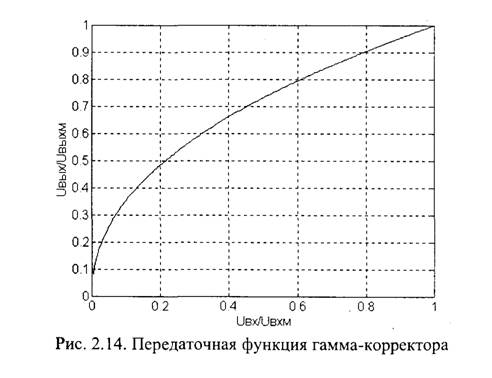
В системах цифрового телевидения, как правило, применяется равномерное квантование прошедших гамма-коррекцию сигналов с числом двоичных разрядов АЦП п = 8, что дает число уровней квантования N_KВ = 256. При этих условиях шум квантования на изображении практически незаметен.

На выходе АЦП полученный номер уровня квантования представляется в виде двоичного числа, т.е. кодируется (оцифровывается). Обычно используется прямой двоичный код. Значения цифрового сигнала представляются числами от 00000000 до 11111111 в порядке нарастания их величины.

2.2. Цифровые телевизионные сигналы согласно Рекомендации ITU-R ВТ 601

Рассмотрим требования Рекомендации ITU-R ВТ 601, определяющие единый международный стандарт цифрового кодирования телевизионного сигнала для студийной аппаратуры. Этот стандарт применяется и в современных полностью цифровых телевизионных системах при цифровом представлении телевизионных сигналов обычной четкости. В данном стандарте предусмотрено раздельное цифровое кодирование яркостного и двух цвето-разностных сигналов [1].

ДИСКРЕТИЗАЦИЯ

Установлено одно значение частоты дискретизации сигнала яркости, равное 13,5 МГц, для обоих стандартов развертки -25 Гц, 625 строк и 30 Гц, 525 строк. Каждый цветоразностный сигнал дискретизируется с вдвое меньшей частотой 6,75 МГц. В соответствии с принятыми обозначениями, данный стандарт цифрового кодирования телевизиоaнных сигналов обозначается 4:2:2. Это означает, что частота дискретизации цветоразностных сигналов в два раза меньше, чем частота дискретизации яркостного сигнала, определенная на основании теоремы Котельникова, причем в каждой строке присутствуют оба цветоразностных сигнала. Взаимное расположение отсчетов яркостного и цветоразностных сигналов было показано на рис. 2.4,в.

Полное число отсчетов яркости в строке равно 864, а число отсчетов каждого цветоразностного сигнала - 432. За время активного участка строки формируется 720 отсчетов сигнала яркости и 360 отсчетов каждого цветоразностного сигнала. Эти количества отсчетов являются промежуточными между значениями, необходимыми для получения квадратных пикселов в указанных стандартах развертки. Таким образом, при разработке Рекомендации 601 был достигнут компромисс. Число активных строк в кадре для стандарта 625 строк равно 576. Полное число передаваемых в каждом кадре элементов изображения равно 414720.

Предусмотрены и другие форматы преобразования телевизионных сигналов в цифровую форму. Например, при использовании формата 4:2:0 каждый цветоразностный сигнал имеет частоту дискретизации в 2 раза ниже частоты дискретизации яркостного сигнала и передается в каждой второй строке. Расположение отсчетов яркостного и цветоразностных сигналов в плоскости изображения для этого варианта было показано на рис. 2.4,г. Отсчеты цветоразностных сигналов показаны между строками отсчетов яр-костных сигналов и для каждого из этих сигналов образуют матрицу 360x288 элементов.

При формате 4:1:1 оба цветоразностных сигнала передаются в каждой строке, но их частоты дискретизации в четыре раза меньше частоты дискретизации сигнала яркости, т. е. равны 3,375 МГц. Число элементов каждого цветоразностного сигнала в кадре в этом случае такое же, как для формата 4:2:0.

Наконец, при формате 4:4:4 оба цветоразностных сигнала передаются в каждой строке и дискретизируются с той же частотой, что и яркостный сигнал.

КВАНТОВАНИЕ

В Рекомендации 601 для всех сигналов предусмотрено число разрядов квантования п = 8, что дает число уровней квантования N_KB = 256. При этом уровню черного сигнала яркости соответствует 16-й уровень квантования, а номинальному уровню белого -235-й уровень квантования. 16 уровней квантования снизу и 20 уровней квантования сверху образуют резервные зоны на случай выхода значений аналогового сигнала яркости за пределы номинального диапазона. Особые назначения имеют 0-й и 255-й уровни квантования. С помощью соответствующих им кодов передаются сигналы синхронизации.

где Е'у - аналоговый сигнал яркости, изменяющийся в диапазоне от 0 до 1 В (штрих, как это принято в технической литературе по телевидению, означает, что сигнал прошел гамма-коррекцию), Y - цифровой сигнал яркости, изменяющийся в диапазоне от 16 до 235.

При квантовании цветоразностных сигналов также предусматриваются резервные зоны - по 16 уровней квантования сверху и снизу. На АЦП поступают не сами цветоразностные сигналы Е´_R-_Y, E´_B-Y, а компрессированные цветоразностные сигналы, формируемые в соответствии с соотношениями

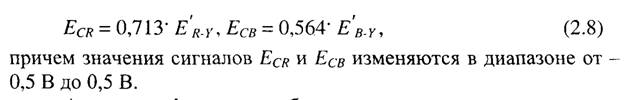
Аналого-цифровые преобразования цветоразностных сигналов, в результате которых получаются цифровые цветоразностные сигналы Cr и Сд, выполняются в соответствии со следующими соотношениями

Так как цветоразностные сигналы являются двуполярными. и максимальные отклонения от нулевого значения в положительную и отрицательную сторону примерно одинаковы, 128-й уровень квантования должен соответствовать нулевому значению этих сигналов. На рис. 2.15 показано соответствие между уровнями аналоговых телевизионных сигналов и уровнями квантования для обычного тестового изображения в виде восьми цветных полос.

В последние годы все шире применяется квантование яркостного и цветоразностных сигналов с помощью 10-разрядных АЦП, что дает 1024 уровня квантования.

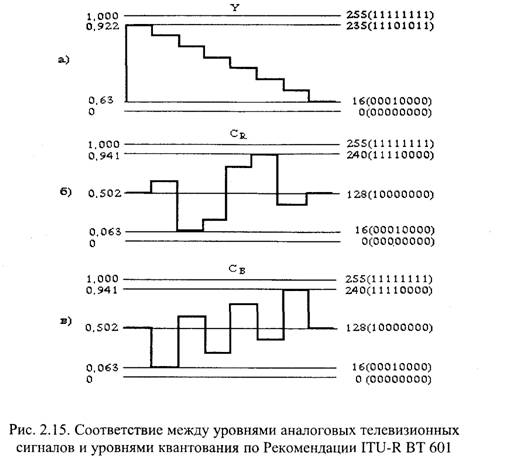
В состав цифрового телевизионного сигнала согласно Рекомендации ITU-R ВТ 601 входят синхросигналы. Перед началом активного участка каждой строки в конце строчного гасящего импульса передается синхросигнал начала активной строки (НАС), а после окончания активного участка каждой строки в начале строчного гасящего импульса передается синхросигнал конца активной строки (КАС).

Каждый из синхросигналов НАС и КАС содержит 4 байта. Первый байт состоит из восьми двоичных единиц, что соответствует десятичному числу 255 (в шестнадцатеричной записи FF). Следующие два байта равны 0. Последний четвертый байт содержит информацию о том, какое передается поле (четное или нечетное), какой именно это синхросигнал, а также обеспечивает защиту от ошибок. При использовании 10-разрядного квантования вместо числа 255 используется число 1023.

Большая часть длительности строчного гасящего импульса между синхросигналами НАС и КАС остается свободной, и во время ее можно передавать различную информацию, например, преобразованные в цифровую форму сигналы звукового сопровождения.

ФОРМИРОВАТЕЛИ ЦИФРОВЫХ ТЕЛЕВИЗИОННЫХ СИГНАЛОВ

Рассмотрим два варианта структурной схемы формирователя цифрового телевизионного сигнала в соответствии с Рекомендацией ITU-R ВТ 601. В устройстве, показанном на рис. 2.16,а, сигналы основных цветов E_R, E_G, Е_В с источника телевизионных сигналов (телекамеры) вначале поступают на гамма-корректоры (ГК), сформированные в которых сигналы E'_R, E'_G, E'_B в кодирующей матрице (КМ) по известным соотношениям преобразуются в сигнал яркости Е'у и цветоразностные сигналы E'_R-_Y и Е'_в._у. Далее эти сигналы преобразуются в АЦП в цифровые сигналы Y, C_R и С_в, соответственно. На входах АЦП имеются дополнительные аналоговые узлы, выполняющие масштабирование и сдвиг сигналов в соответствии с (2.8), (2.9) и (2.10). Число разрядов каждого АЦП, как правило, равно 8.

Синхроимпульсы развертки источника телевизионных сигналов поступают на формирователь цифровых синхроимпульсов (ФЦСИ), вырабатывающий синхросигналы НАС и КАС. Кроме того, синхроимпульсы используются для синхронизации генератора тактовых импульсов (ГТИ), который вырабатывает импульсы с частотами 27, 13,5 и 6,75 МГц, поступающие на другие узлы устройства. ГТИ содержит схему фазовой автоподстройки частоты (ФАПЧ), с помощью которой обеспечивается требуемое число периодов тактовых импульсов за период строчной развертки источника телевизионных сигналов.

Мультиплексор (MS) в заданной последовательности передает на выход цифровые сигналы Y, C_R и С_в и цифровые синхросигналы. В результате на выходе устройства оказывается сформированным цифровой телевизионный сигнал (ЦТС).

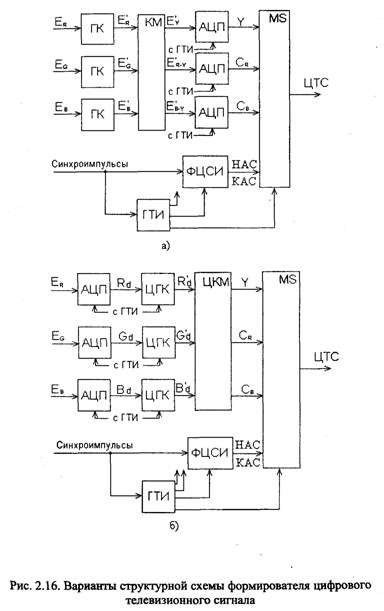
В другом варианте устройства (рис. 2.16,6) сигналы основных цветов E_R, Е_с, Е_в сразу преобразуются в цифровые сигналы R_d,G_d, B_d. При этом каждый АЦП должен иметь по меньшей мере 10, а лучше 12 двоичных разрядов. Далее цифровые сигналы R_d, Gd, B_d поступают на цифровые гамма-корректоры (ЦГК), в которых выполняются нелинейные преобразования. Число двоичных разрядов прошедших гамма-коррекцию цифровых сигналов R'_(!, G'_d, B'_d равно 8. Затем сигналы R'_d, G'_d, B'_dB цифровой кодирующей матрице (ЦКМ) преобразуются в цифровой сигнал яркости Y и цифровые цветоразностные сигналы C_R и С_в.

Формирование синхросигналов и тактовых импульсов и работа мультиплексора осуществляются аналогично первому варианту устройства. Выполнение гамма-коррекции цифровыми средствами обеспечивает более точное задание требуемой функции преобразования, но при этом требуются имеющие больше двоичных разрядов и, следовательно, более дорогие АЦП.

ПАРАЛЛЕЛЬНЫЙ ВИДЕОСТЫК

Перейдем к передаче цифрового телевизионного сигнала. Рекомендацией ITU-R ВТ 656 предусмотрены два варианта интерфейса для этой цели: параллельный видеостык и последовательный видеостык [1].

Стандарт на параллельный видеостык предусматривает передачу цифрового телевизионного сигнала в виде параллельного цифрового кода, как было показано на рис. 2.1. Для этого требуется 8 (или 10) линий связи для параллельной передачи 8 (или 10) двоичных разрядов и еще одна линия для передачи тактовых импульсов. Линии связи обычно выполняются в виде витых пар проводов. Из-за больших потерь и наводок таким способом можно передавать цифровой телевизионный сигнал внутри блоков и устройств или между устройствами на небольшие расстояния (до 50 м).

Передача значений отсчетов яркостного Y и цветоразностных C_R, С_в сигналов происходит по одним и тем же линиям в следующем порядке: Y, C_R, Y, Св, Y, ... . Частота тактовых импульсов при этом равна ƒ_т= 13,5 + 6,75 + 6,75 = 27 МГц. Сигналы синхронизации телевизионной развертки, представляемые, как указывалось ранее, кодами 00000000 и 11111111, передаются в общем потоке данных.

Произведение частоты дискретизации ƒ_д и числа разрядов квантования п называется скоростью передачи двоичных символов цифрового сигнала - Q [бит/с]. Для цифровой студийной аппаратуры, удовлетворяющей требованиям рассматриваемых Рекомендаций, получаются следующие значения этого параметра:

- для яркостного сигнала: Q_Y = 13,5 * 8 = 108 Мбит/с;

- для цветоразностного сигнала: Qc =6,75 * 8 = 54 Мбит/с.

Суммарная скорость передачи двоичных символов преобразованного в цифровую форму полного цветного телевизионного сигнала (ПЦТС) для параллельного видеостыка определяется следующим равенством

Qs = Qy + 2Q_c = 2l6 Мбит/с.

ПОСЛЕДОВАТЕЛЬНЫЙ ВИДЕОСТЫК

Передача цифрового телевизионного сигнала на большие расстояния осуществляется в последовательной форме. В этом случае двоичные разряды или биты каждого элемента изображения передаются один за другим по одной линии, в качестве которой можно использовать коаксиальный или волоконно-оптический кабель. Импульсы тактовой частоты отдельно не передаются. Тактовая частота восстанавливается в приемном устройстве по самому передаваемому сигналу.

Один из простейших способов синхронизации при приеме цифрового сигнала, передаваемого по последовательному каналу, иллюстрируется структурной схемой, показанной на рис. 2.17 сверху, и временными диаграммами, представленными на том же рисунке снизу (точки структурной схемы и соответствующие им временные диаграммы отмечены одинаковыми буквами).

Принимаемый цифровой сигнал (рис. 2.17,а), состоящий из последовательности "единичных" и "нулевых" уровней, поступает на формирователь импульсов, вырабатывающий короткие импульсы на каждый положительный и отрицательный перепад напряжения в сигнале (рис. 2.17,6). Расширитель импульсов преобразует короткие импульсы в импульсы, длительность которых равна половине периода тактовой частоты (рис. 2.17,в). Эти импульсы поступают на узкополосный фильтр, настроенный на тактовую частоту. На выходе фильтра выделяется синусоидальный сигнал тактовой частоты (рис. 2.17,г), который затем преобразуется в прямоугольные импульсы (рис. 2.17,д), используемые для тактирования принимаемого сигнала.

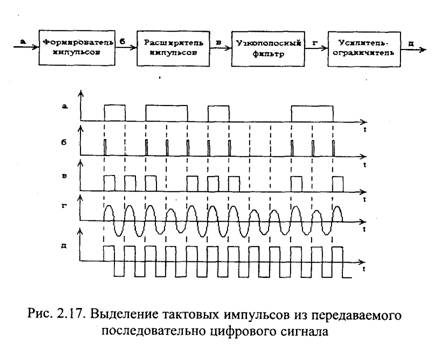
Как видно из временных диаграмм, в случае, если в принимаемом цифровом сигнале подряд идут несколько битов с одинаковыми значениями, импульсы на выходе формирователя отсутствуют, и выходные тактовые импульсы продолжают формироваться за счет наличия затухающего гармонического колебания на выходе узкополосного фильтра. Это накладывает ограничения на передаваемый сигнал, так как передача достаточно длинных последовательностей нулей или единиц приведет к прекращению формирования тактовых импульсов. Кроме того, в начале передачи цифрового сигнала амплитуда колебаний на выходе узкополосного фильтра нарастает постепенно, поэтому имеет место некоторая задержка до появления тактовых импульсов на выходе устройства синхронизации.

Для преодоления указанных трудностей в системах передачи цифровых сигналов по последовательным каналам связи выполняется дополнительное преобразование передаваемых данных, в результате которого число передаваемых подряд нулей или единиц ограничивается.

Рассмотрим построение последовательного видеостыка, соответствующего Рекомендации ITU-R ВТ 656. В таком видеостыке предусмотрена передача каждого 8-разрядного кода отсчета яркостного или цветоразностного сигнала с помощью 9-битовой посылки. В результате получается скорость передачи двоичных символов 243 Мбит/с. Таким образом, для передачи используется избыточный код. Это позволяет надежно осуществлять синхронизацию и избегать накопления ошибок передачи. Структурная схема последовательного видеостыка приведена на рис. 2.18.

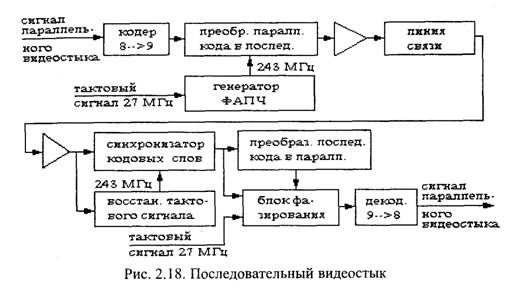
В передающей части из 8-разрядного параллельного кода формируется 9-разрядный параллельный код, который затем преобразуется в последовательный код. Тактовая частота 243 МГц формируется с помощью ФАПЧ из тактовой частоты 27 МГц параллельного видеостыка. В приемной части по принятому сигналу осуществляется восстановление тактовой частоты 243 МГц. Блок синхронизации кодовых слов по синхрослову, содержащемуся в каждой телевизионной строке, определяет начальные моменты параллельных кодовых слов. Преобразователь последовательного кода в параллельный формирует 9-разрядные слова, выдача которых синхронизируется в блоке фазирования тактовой частотой 27 МГц. Наконец, в декодере 9-разрядный параллельный код преобразуется в 8-разрядный.

2.3. Другие стандарты цифровых телевизионных сигналов

Рассмотренная выше Рекомендация 601 предназначена для телевизионного вещания. Параметры цифровых телевизионных сигналов для систем компьютерной видеосвязи установлены в Рекомендации ITU-T H.263.

В табл. 2.1 даны количества элементов изображения в кадре в соответствии с этой Рекомендацией для формата CIF (Common Interchange Format) и производных от него форматов QCIF (Quarter Common Interchange Format), SQCIF (sub-Quarter Common Interchange Format), 4CIF, 16CIF.

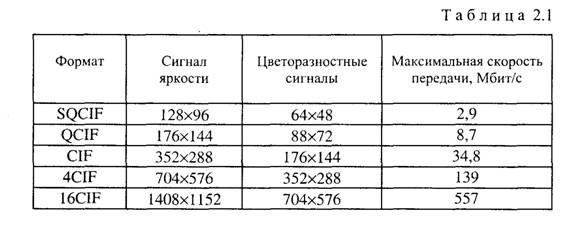
В последнем столбце таблицы даны значения максимальной скорости передачи двоичных символов для каждого формата. При этом частота передачи кадров принята равной 30 Гц. Следует отметить, что в цифровых системах видеосвязи частота передачи кадров по каналу связи может быть меньше максимального значения 30 Гц и, в зависимости от передаваемого сюжета, обычно составляет 5... 15 Гц. В то же время частота кадров на экране монитора будет существенно выше (обычно не менее 60 Гц), так как в приемной и декодирующей аппаратуре выполняются запоминание принятых и декодированных кадров и их многократное воспроизведение. Понижение частоты кадров в канале связи даст пропорциональное уменьшение требуемой скорости передачи двоичных символов.

При записи кинофильмов и видеопрограмм на компьютерные компакт-диски со сжатием по стандарту MPEG-1 (см. § 4.2) используется формат SIF (Source Input Format - входной формат источника), в соответствии с которым кадр содержит 360x240 или 360x288 элементов сигнала яркости, формат дискретизации 4:2:0, частота кадров 30 Гц, развертка прогрессивная. Если в формате SIF уменьшить количества элементов по горизонтали и по вертикали в два раза, получится формат QSIF (180x120 или 180x144 элементов).

Особые стандарты на цифровые телевизионные сигналы требуются для систем телевидения высокой четкости. Об одном из таких стандартов пойдет речь в § 6.5.

Рассмотренные выше методы цифрового представления цветного телевизионного сигнала называются компонентными (или раздельными), так как яркостный и цветоразностные сигналы преобразуются в цифровую форму раздельно, а затем полученные цифровые сигналы объединяются в единый поток данных. Компонентное кодирование хорошо приспособлено для студийной аппаратуры, в которой сигнал цветного телевидения разделен на компоненты. В некоторых случаях необходимо преобразовывать в цифровую форму полный сигнал одной из систем цветного телевидения (NTSC, PAL или SECAM). Такой вариант цифрового представления, называемый также композитным кодированием, применяется в некоторых системах цифровой записи телевизионных сигналов на магнитный носитель, в цифровых преобразователях телевизионных стандартов и в блоках цифровой обработки сигналов в телевизионных приемниках.

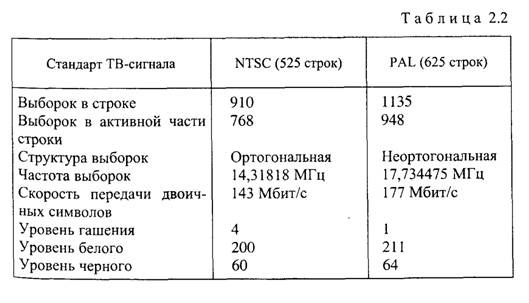
В табл. 2.2 приведены основные параметры преобразования в цифровую форму полных телевизионных сигналов стандартов NTSC и PAL. Квантование сигналов осуществляется на 256 уровней (8 бит). В последнее время используется и 10-разрядное квантование.

Для обоих стандартов частота дискретизации ƒ_д = 4 ƒ_подн, где ƒ_подн - частота цветовой поднесущей в данном стандарте. Уровни гашения, белого и черного в таблице записаны в виде номеров соответствующих уровней квантования. Необходимость цифрового кодирования фронтов и срезов синхроимпульсов композитного аналогового сигнала приводит к тому, что для диапазона от номинальной величины черного до номинального белого выделяется примерно на 30% меньше уровней квантования, чем для сигнала в компонентной форме.

Следует отметить, что, так как в системе PAL частота цветовой поднесущей не равна частоте строчной развертки, умноженной на целое число, то длительность цифровой строки принята не равной длительности аналоговой строки. В результате все строки поля за исключением двух содержат по 1135 отсчетов, а две - по 1137 отсчетов.

2.4. Передача цифровых телевизионных сигналов по каналам связи. Задача сжатия видеоинформации

Цифровой телевизионный сигнал в последовательной форме может непосредственно передаваться по каналам связи, предназначенным специально для передачи дискретных сигналов, например, по широкополосным многоканальным линиям телеграфной связи с временным разделением каналов. В последние годы все шире используются широкополосные цифровые линии связи. Для цифрового телевизионного вещания могут использоваться и каналы связи с модуляцией несущего колебания.

Возможность точной передачи цифрового сигнала в первую очередь определяется отношением Сигнал/Помеха (С/П) в канале связи. Возникновение ошибок иллюстрируется на рис. 2.19.

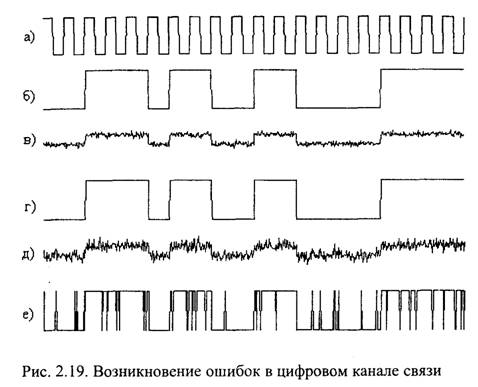
Импульсы тактовой частоты (рис. 2.19,а) не передаются и показаны, чтобы можно было судить о положении отдельных битов в передаваемом сигнале (рис. 2.19,6). В первом варианте канала связи отношение С/П равно 6 (рис. 2.19,в). В приемнике обработка сигнала выполняется пороговым устройством с порогом, расположенным посередине между верхним и нижним уровнями принятого сигнала. В результате обеспечивается безошибочный прием (рис. 2.19,г).

Во втором варианте канала связи отношение С/П равно 3 (рис. 2.19,д). В этом случае после пороговой обработки в принятом сигнале имеется много ошибок, имеющих вид ложных переходов с верхнего уровня на нижний и обратно. Из-за этого невозможно обеспечить правильное выделение тактовой частоты из принятого сигнала и правильное определение значений передаваемых двоичных символов.

Оценим ширину полосы частот цифрового сигнала в последовательной форме и требуемую для его передачи ширину полосы частот канала связи. Рассмотрим периодическую последовательность прямоугольных импульсов, имеющих период Т=2Т_и. Спектр такого сигнала содержит постоянную составляющую, основную гармонику частоты 1/Т и постепенно убывающие нечетные гармоники этой частоты. Следовательно, спектр идеального импульсного сигнала неограничен.

Если ограничить полосу частот такого сигнала с помощью ФНЧ с достаточно крутым срезом АЧХ, форма импульсов будет искажена (рис. 2.20), так как часть частотных составляющих спектра окажется подавленной. Искажения проявятся в виде увеличения длительности нарастания и спада импульса и возникновения колебательного переходного процесса. Это будет причиной ограничения допустимой частоты передаваемого импульсного сигнала, т. е. ограничения скорости передачи двоичных символов по каналу связи.

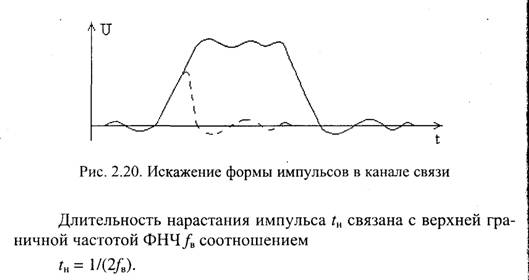
Если длительность входного импульса меньше t_н, амплитуда импульса на выходе ФНЧ станет уменьшаться. Этот случай показан на рис. 2.20. штриховой линией. При достаточно малой длительности импульсов, их амплитуда на выходе канала связи станет сравнимой с уровнем помех, что приведет к ошибкам работы приемного устройства.

Выбросы и колебательные переходные процессы, возникающие при передаче импульсов, также ограничивают частоту передаваемых по каналу связи импульсов. Если эта частота слишком велика, колебательный переходный процесс, созданный одним импульсом, будет накладываться на следующий импульс. Возникает помеха, называемая интерференционной, которая может привести к ошибкам приема.

Изложенные причины приводят к известному еще с ранних работ по теории связи условию: по каналу связи с шириной полосы пропускания ΔF можно передавать в виде двухуровневых импульсов 2 ΔF бит информации за 1 с. То есть эффективность использования полосы частот канала связи составляет 2 (бит/с)/Гц. Следовательно, для передачи в последовательной форме цифрового телевизионного сигнала со скоростью передачи двоичных символов 243 Мбит/с необходим канал связи с шириной полосы частот 121,5 МГц. Ясно, что ни стандартный канал наземного телевизионного вещания, имеющий ширину полосы 8 МГц, ни спутниковый канал связи, имеющий ширину полосы 27 МГц, непригодны для передачи цифрового телевизионного сигнала. Это относится и к цифровым телевизионным сигналам стандартов, применяемых в видеосвязи (см. табл. 2.1) даже при пониженной частоте кадров. А для передачи телевизионных сигналов высокой четкости необходима еще более широкая полоса частот.

Поэтому одной из важнейших задач в области цифрового телевидения была задача сокращения скорости передачи двоичных символов и, соответственно, требуемой полосы частот канала связи. Эта задача может быть решена путем уменьшения избыточности информации, передаваемой в телевизионном сигнале. Уменьшение избыточности обеспечивает также уменьшение требуемого объема ЗУ при записи телевизионных программ или отдельных изображений. В соответствии с установившейся в технической литературе терминологией уменьшение объема передаваемой информации в ряде случаев будем называть сжатием видеоинформации, а также сжатием изображений, сжатием звуковых сигналов, сжатием речи и т.д. Обратную операцию будем называть расширением, хотя это звучит не привычно. В англоязычной литературе используется термин compression, а для обратной операции -decompression. Русское произношение этих терминов компрессия и декомпрессия также используется в ряде случаев в этой книге.

Избыточность телевизионного сигнала разделяется на структурную, статистическую и психофизиологическую.

Структурная избыточность связана с. наличием в обычном телевизионном сигнале гасящих импульсов, во время которых информация об изображении не передается. Структурная избыточность телевизионного сигнала может быть уменьшена путем пере-дачи во время гасящих импульсов какой-либо полезной информацией, например - звукового сопровождения, однако большого выигрыша это не дает.

Статистическая избыточность вызывается наличием корреляционных связей между значениями сигнала в соседних элементах одной строки, в соседних строках и в соседних кадрах. Сокращение статистической избыточности достигается путем устранения указанных корреляционных связей. Одним из наиболее известных методов сокращения статистической избыточности является кодирование с предсказанием или дифференциальная импульсно-кодовая модуляция (ДИКМ), основанная на передаче приращений значений сигнала.

Психофизиологическая избыточность телевизионного сигнала определяется той информацией в нем, которая не воспринимается человеком и, следовательно, могла бы и не передаваться. Психофизиологическая избыточность сокращается за счет удаления из передаваемого сигнала информации, отсутствие которой не влияет существенно на восприятие изображения человеком.

Примером метода сокращения психофизиологической избыточности может служить способ кодирования Кретцмера, в соответствии с которым при передаче крупных деталей изображения количество градаций яркости увеличивается, а при передаче мелких деталей - уменьшается. Этот способ основан на использовании обратно пропорциональной зависимости между геометрическим и градационным разрешением зрительного аппарата человека. При восприятии мелких деталей ухудшается различие градаций яркости. В других методах используется ухудшение геометрического и градационного разрешения зрения при наблюдении движущихся объектов. Общая основа всех этих методов - ограниченность пропускной способности зрения как системы передачи и обработки информации.

Применение различных способов сжатия информации, заключенной в телевизионном изображении, позволяет не только передавать цифровой телевизионный сигнал обычной четкости по стандартным каналам телевизионного вещания, но и добиться возможности передачи по этим каналам одновременно нескольких программ телевидения обычной четкости, сигналов новых систем телевидения высокой четкости, а также передачи цифровых телевизионных сигналов по каналам связи с более узкой полосой частот, чем стандартные вещательные каналы. Соотношение потоков информации и требуемых значений ширины полосы пропускания каналов связи иллюстрируется рис. 2.21.

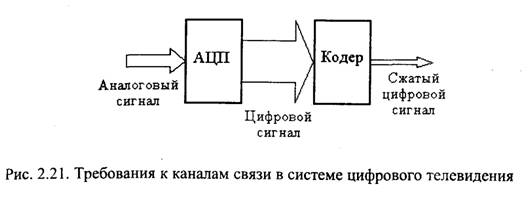
Методы сжатия изображений можно разделить на два класса: методы сжатия без потерь информации и методы сжатия с частичной потерей информации. При сжатии без потерь после декодирования получается изображение, идентичное исходному. Примерами таких методов могут служить различные алгоритмы архивирования изображений, применяемые в вычислительной технике и основанные на уменьшении статистической избыточности. Возможности сжатия реальных цветных или полутоновых черно-белых изображений без потерь весьма ограничены. Так путем преобразования записанного в компьютере изображения в формат GIF, являющийся одним из наиболее компактных и эффективных, объем информации сокращается в среднем в 2-3 раза, что явно недостаточно для решения задач, стоящих в области цифрового телевидения.

Гораздо большего эффекта позволяют достичь методы сжатия с частичной потерей информации. Как будет показано далее, с помощью метода JPEG можно уменьшить объем информации реального неподвижного изображения в 5-10 раз без заметного ухудшения визуально воспринимаемого качества декодированных изображений. Возможно и еще большее сжатие, но при этом уже начинают наблюдаться заметные искажения изображения. Получение минимального объема передаваемой или запоминаемой информации при сохранении достаточно высокого качества изображения является одной из главных задач при поиске новых алгоритмов сжатия.

Контрольные вопросы

1. Что такое дискретизация и интерполяция?

2.  В чем проявляются искажения одномерного сигнала, создаваемые дискретизацией, в случае нарушений условий теоремы Котельникова?

3. Что такое пространственная частота? В каких единицах она измеряется (в случае непрерывных изображений)?

4.  Как преобразуется пространственный спектр непрерывного изображения при дискретизации в случаях выполнения и нарушения условий двумерного аналога теоремы Котельникова?

5.  Укажите основные виды искажений изображения, создаваемых дискретизацией.

6. Что такое квантование?

7.  Почему ошибка квантования является случайной? Каков характер распределения этой случайной величины?

8.  Зачем перед квантованием выполняют гамма-коррекцию телевизионных сигналов?

9. Что является входным и выходными сигналами АЦП?

10.  Что означают записи "4:2:2" и "4:2:0", характеризующая формат дискретизации телевизионных сигналов?

11.  Как производится квантование яркостного и цветоразностных сигналов соответствии с Рекомендацией 601 ?

12.  Как передаются синхроимпульсы в цифровом телевизионном сигнале по Рекомендации 601 ?

13. Что такое параллельный видеостык?

14.  Вычислите скорость передачи двоичных символов для цифровых телевизионных сигналов при различных форматах дискретизации.

15. Что такое последовательный видеостык?

16. Чем различаются стандарты CIF и SIF?

17.  Что такое психофизиологическая избыточность телевизионного изображения?

Контрольные вопросы

1. Что такое дискретизация и интерполяция?

2.  В чем проявляются искажения одномерного сигнала, создаваемые дискретизацией, в случае нарушений условий теоремы Котельникова?

3. Что такое пространственная частота? В каких единицах она измеряется (в случае непрерывных изображений)?

4.  Как преобразуется пространственный спектр непрерывного изображения при дискретизации в случаях выполнения и нарушения условий двумерного аналога теоремы Котельникова?

5.  Укажите основные виды искажений изображения, создаваемых дискретизацией.

6. Что такое квантование?

7.  Почему ошибка квантования является случайной? Каков характер распределения этой случайной величины?

8.  Зачем перед квантованием выполняют гамма-коррекцию телевизионных сигналов?

9. Что является входным и выходными сигналами АЦП?

10.  Что означают записи "4:2:2" и "4:2:0", характеризующая формат дискретизации телевизионных сигналов?

11.  Как производится квантование яркостного и цветоразностных сигналов соответствии с Рекомендацией 601 ?

12.  Как передаются синхроимпульсы в цифровом телевизионном сигнале по Рекомендации 601 ?

13. Что такое параллельный видеостык?

14.  Вычислите скорость передачи двоичных символов для цифровых телевизионных сигналов при различных форматах дискретизации.

15. Что такое последовательный видеостык?

16. Чем различаются стандарты CIF и SIF?

17.  Что такое психофизиологическая избыточность телевизионного изображения?

3 НЕКОТОРЫЕ МЕТОДЫ ЦИФРОВОЙ ОБРАБОТКИ И КОДИРОВАНИЯ ТЕЛЕВИЗИОННЫХ СИГНАЛОВ И ИЗОБРАЖЕНИЙ

3.1. Дискретное преобразование Фурье и дискретное косинусное преобразование

Одними из наиболее распространенных средств обработки как одномерных, так и многомерных сигналов, в том числе и изображений, являются ортогональные преобразования. Особенно велика роль ортогональных преобразований в решении задачи уменьшения скорости передачи двоичных символов в цифровом телевидении и, следовательно, уменьшении требуемой полосы частот каналов связи. Сущность ортогональных преобразований заключается в представлении исходного сигнала в виде суммы ортогональных базисных функций.

Напомним, что функции x(t) и y{t) называются ортогональными на отрезке (г_ь /₂), если их скалярное произведение равно гулю

Это определение может быть распространено на дискретные сигналы, представляемые последовательностями чисел. Дискретные сигналы х(п) и у(п), имеющие по N отсчетов, называются ортогональными, если выполняется условие

В ряд Фурье может быть разложен не только периодический сигнал, имеющий период Т, но и сигнал, отличный от 0 только на интервале времени (-Т/2, Т/2). В этом случае используется периодическое продолжение сигнала на всю ось времени с периодом Т.

Рассмотрим дискретный сигнал х(п), отличный от 0 при я = 0,1, ..., N-1. Для такого сигнала также можно ввести разложение по базису синусоидальных функций. Так как частотный спектр дискретизируемого сигнала должен быть ограничен сверху в соответствии с условием теоремы Котельникова, в разложении дискретного сигнала остается конечное число частотных составляющих, представляющих собой дискретные комплексные гармонические   функции.    Такое   разложение,    называемое   дискретным преобразованием Фурье (ДПФ), имеет вид

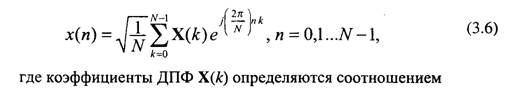
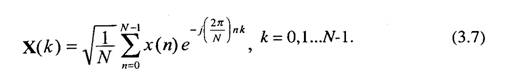
Следует отметить, что нахождение коэффициентов Х(к) по (3.7) обычно называют прямым ДПФ, а получение сигнала по этим коэффициентам в соответствии с (3.6) - обратным ДПФ.

В этих соотношениях вместо интегралов появились суммы, так как исходный сигнал не непрерывный, а дискретный. Частоте kω₀, используемой в разложении аналоговых сигналов и имеющей размерность рад/с, в ДПФ соответствует безразмерная величина

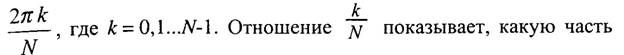частоты дискретизации  составляет частота данной дискретной гармоники.

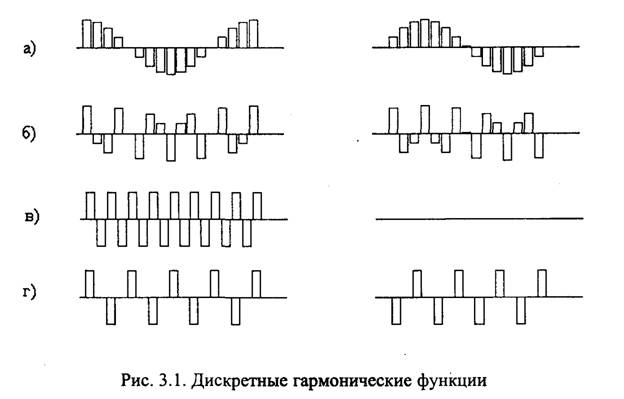
На рис. 3.1 показаны действительные (слева) и мнимые (справа) составляющие дискретных гармонических функций для N= 16 и разных значений к: а) k = 1; б) k = 5; в) k = 8; г) k = 12. В последнем случае частота дискретной гармонической функции превышает половину частоты дискретизации (k/N = 3/4), и реальная частота действительной и мнимой составляющих этой функции на временных диаграммах оказывается такой же, как для k = 4.

Рассмотрим пример ДПФ одномерного сигнала. На рис. 3.2,г показан отрезок дискретного сигнала, содержащий N = 256 отсчетов (отдельные отсчеты в масштабе рисунка неразличимы). Этот сигнал представляет собой сумму синусоидальных сигналов с дискретными частотами ƒ ₁ = 0,0625 (k =16), ƒ ₂ = 0,0664 (k =17) и ƒ₃ = 0,1680 (k = 43) и некоррелированного шума с гауссовым распределением значений. На рис. 3.2,6 показан график значений модулей коэффициентов ДПФ этого сигнала. По горизонтальной оси отложены значения частоты, выраженные в долях частоты дискретизации. Значение ƒ = 0,5 соответствует k = 128.                           

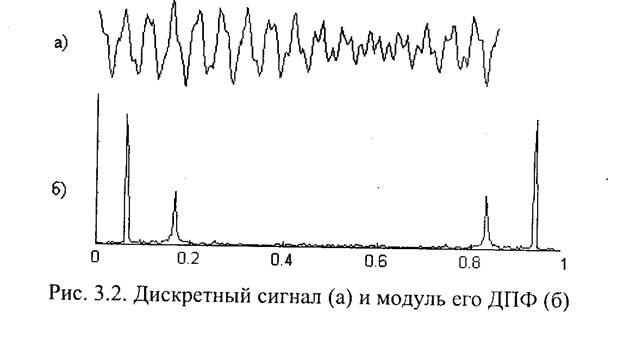
Составляющие с близкими частотами f и ƒ ₂ на графике cливаются в один пик. Шум дает равномерное распределение по всем частотам.

Как видно из рисунка, график значений модулей коэффициентов ДПФ симметричен относительно значения частоты ƒ = 0,5.  Поэтому для того, чтобы получить полную информацию о модулях коэффициентов ДПФ, достаточно взять первые N/2 этих коэффициентов. Однако для точного восстановления сигнала с помощью обратного ДПФ необходимы все N коэффициентов, чтобы учесть фазы всех гармоник.

Коэффициенты ДПФ Х(k) и экспоненциальные множители в (3.6), (3.7) являются комплексными числами. Каждое комплексное число запоминается в цифровом ЗУ в виде пары действительных чисел, представляющих его действительную и мнимую части. Сложение двух комплексных чисел требует выполнения двух операций сложения действительных чисел - отдельно складываются действительные и мнимые части. Умножение двух комплексных чисел требует выполнения четырех операций умножения и двух операций сложения действительных чисел. Таким образом, выполнение ДПФ в комплексной форме приводит к существенному увеличению необходимого объема ЗУ и времени вычислений.

Чтобы иметь дело только с действительными числами, обычно используют разложение с помощью дискретного косинусного преобразования (ДКП), описываемого соотношением [1]

Как и в случае ДПФ, нахождение коэффициентов С(k) по (3.9) называется прямым ДКП, а представление сигнала в виде (3.8) называется обратным ДКП.

Аналогично можно записать соотношения для прямого и обратного ДПФ и ДКП в двумерном случае. Двумерный дискретный сигнал, например, отдельный кадр цифрового телевизионного сигнала, представляется матрицей значений х(т,п), где т = О ... М— 1 — номер отсчета в строке, п = 0 .., N-1 - номер строки в кадре.

Прямое двумерное ДПФ имеет вид

венными частотами, по горизонтальной и вертикальной координатам, соответственно, которые выражаются безразмерными величинами, имеющими такой же смысл, как и дискретная частота в одномерном случае. Каждая дискретная пространственная частота пропорциональна отношению пространственного периода дискретизации по данной координате к пространственному периоду этой частотной составляющей. Пространственные периоды при этом измеряются в единицах расстояния.

На рис. 3.3 показаны в виде полутоновых картинок базисные функции двумерного ДКП для М = 8, N = 8. Светлые участки соответствуют положительным значениям, а темные - отрицательным. Показаны примеры:

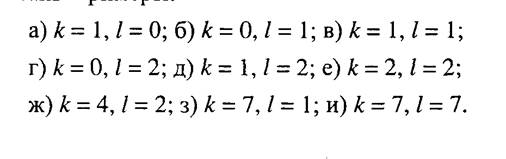
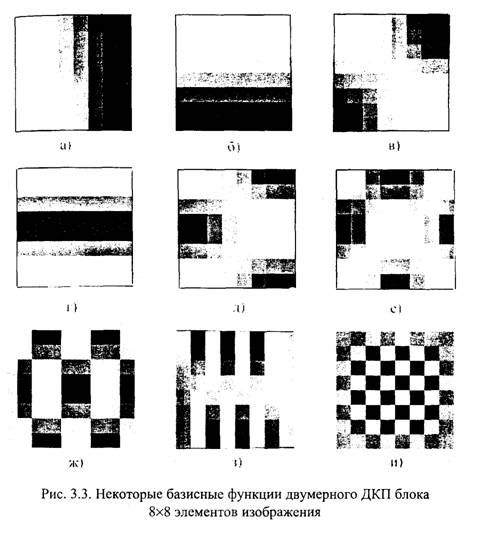
Следует иметь в виду, что в различных литературных источниках запись соотношений для ДПФ и ДКП может быть различной. В соотношениях (3.6)—(3.13) нормирующие множители вида

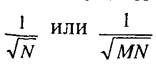 введены и в прямое, и в обратное преобразования.

В то же время в (3.3)—(3.5) нормирующий множитель имеется только в выражениях для прямого преобразования, как обычно Делается в справочниках по высшей математике. В технической литературе встречаются оба варианта записи для ДПФ и ДКП.

Оценим количество операций, необходимых для вычисления ДПФ в соответствии с (3.7). Для этого преобразуем (3.7), выделив в нем операции над действительными и мнимыми частями чисел

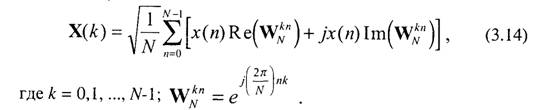
При этом учитывается, что значения сигнала х(п) являются действительными числами.

Из (3.14) видно, что для вычисления одного значения Х(k) необходимо выполнить приблизительно 2N умножений и (2N-2) сложений действительных чисел. Для вычисления всех N значений Х(k) надо выполнить 2N² умножений и N(2N-2) сложений действительных чисел. Кроме того, требуется ЗУ для хранения значений х(п), Х(k) и W^kn_N .

Выполнение обратного ДПФ потребует в два раза больше операций, так как значения Х(k) являются комплексными числами и число слагаемых увеличится вдвое.

В целом можно оценить затраты вычислительных ресурсов при выполнении прямого и обратного ДПФ, как пропорциональные N². Аналогично можно показать, что вычисление двумерных прямого и обратного ДПФ требует выполнения количества операций, пропорционального N² М².

Например, вычисление ДПФ для квадратного блока изображения, содержащего 8x8 элементов (пикселов), потребует выполнения примерно 16*10³ операций умножения и сложения. А вычисление ДПФ черно-белого телевизионного кадра обычного стандарта    разложения,    содержащего    720x576    пикселов,    потребует выполнения около 8*10¹¹ операций. Если вычисления производятся на компьютере, выполняющим 10⁶ операций над действительными числами в секунду, время вычисления ДПФ составит 8*10⁵с или более 200 ч. Очевидно, что для вычисления ДПФ телевизионных изображений в реальном времени, т. е. за период кадровой развертки, необходимо искать пути сокращения количества требуемых операций.

Наиболее радикальный способ уменьшения объема вычислений заключается в применении открытых в 60-е годы быстрых алгоритмов ДПФ, называемых алгоритмами быстрого преобразования Фурье (БПФ). Подход основан на использовании периодич-

ности экспоненциальных функций типа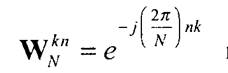  

симметрии относительно перестановки множителей п, к . В наиболее простом случае, когда N = 2^r , где r - натуральное число, вычисление значения Х(к) одномерного ДПФ разбивается на г шагов. На первом шаге отсчеты исходного сигнала х(п) разбиваются на пары и для каждой пары вычисляются коэффициенты ДПФ при N= 2. На втором шаге по результатам первого шага находят коэффициенты ДПФ с N = 4 для групп по четыре элемента и т.д. Аналогично выполняется вычисление обратного ДПФ.

На каждом шаге необходимо N комплексных сложений и N комплексных умножений. Число же шагов равно log₂NТаким образом, число операций, которые необходимо выполнить для вычисления прямого или обратного ДПФ, оказывается пропорциональным N log₂ N.

Подробно быстрые алгоритмы вычисления ДПФ описаны во многих литературных источниках, например, в [1].

Двумерное БПФ может быть разложено на последовательность одномерных. Число требуемых операций оказывается пропорциональным NMlog₂(NM). Для приведенного выше примера телевизионного кадра, состоящего из 720x576 пикселов, это значение оказывается равным примерно 8*10^б , что в 10⁵ раз меньше, чем число операций, требуемое для непосредственного вычисления ДПФ.

Существуют также быстрые алгоритмы вычисления ДКП. Как будет видно из дальнейшего, в цифровом телевидении главную роль играет ДКП блоков 8x8 пикселов, при выполнении которого используется алгоритм быстрого вычисления одномерного ДКП отрезка цифрового сигнала, содержащего восемь элементов. При этом сначала вычисляются ДКП для каждого столбца блока элементов изображения, а затем в полученной матрице 8x8 чисел вычисляются ДКП для каждой строки.

В современной аппаратуре, в том числе и для цифрового телевидения, ДПФ и ДКП как правило, выполняются в реальномвремени с применением цифровых процессоров обработки сигналов (ЦПОС) или специальных аппаратных средств, например, параллельных вычислительных устройств.

ДКП лежит в основе наиболее широко используемых в настоящее время методов кодирования JPEG, MPEG-1, MPEG-2, описание которых будет дано в гл. 4.

3.2. Цифровая фильтрация

Цифровая фильтрация - один из важнейших методов обработки одномерных и многомерных цифровых сигналов. С помощью цифровой фильтрации в телевидении решаются задачи уменьшения влияния шумов и помех, разделения сигналов яркости и цветности, повышения субъективного качества изображения и т. д. При этом используется как одномерная фильтрация, при которой обрабатывается телевизионный сигнал, так и двумерная {пространственная) фильтрация.

В  одномерном  случае цифровая  фильтрация  заключается в преобразовании последовательности отсчетов x(i) входного сигнала в последовательность отсчетов y(i) выходного сигнала по общей формуле y(i) = a_ox(i) + a_{x(i-l) +... + a_mx(i-m) + b_xy{i-\) + ... + b_ny{i-n). (3.15)

Значения т и п могут быть любыми натуральными числами, а коэффициенты а_j, b_j могут быть любыми действительными числами - как положительными так и отрицательными. Часть этих коэффициентов может быть равна нулю.

Если хотя бы один из коэффициентов b_j не равен нулю, цифровой фильтр называется рекурсивным, так как на текущее значение выходного сигнала влияют не только значения входного сигнала, но и более ранние значения выходного сигнала. Такие фильтры называют еще фильтрами с бесконечной импульсной характеристикой (БИХ-фильтрами), так как они "помнят" все предыдущие значения входного и выходного сигналов. Если же все коэффициенты b_j= 0, цифровой фильтр называется нерекурсивным или фильтром с конечной импульсной характеристикой (КИХ-фильтром).

На рис. 3.4 показана структурная схема цифрового фильтра, имеющего как рекурсивную, так и нерекурсивную части. Блоки z^-l выполняют задержку сигнала на один отсчет. Возможны и другие апианты структуры фильтра с таким же набором коэффициентов.

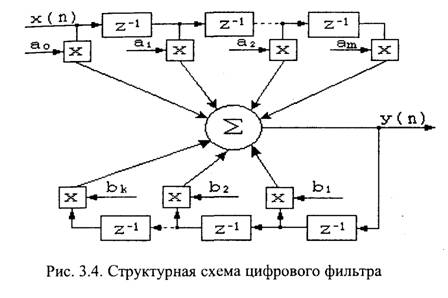
Цифровые фильтры, действие которых описывается формулой (3.15), являются линейными системами для цифровых сигналов, поскольку выполняется принцип суперпозиции. Поэтому по аналогии с аналоговыми фильтрами действие цифрового фильтра на сигнал можно описать комплексной частотной характеристикой Н(/ш). Если исходный аналоговый сигнал представляется в виде комплексной синусоиды е'^т, то получающийся из него при дискретизации цифровой сигнал будет иметь вид комплексной последовательности х(п) = е^jωt, где Т - период следования отсчетов, т. е. период дискретизации, п = 0, 1, 2,... . Сигнал на выходе цифрового фильтра в этом случае будет иметь вид у(п) = х(п) H(j ω).

Число уровней квантования при таком подходе к анализу цифровых фильтров считается настолько большим, что ошибкой квантования можно пренебречь.

Как и в случае аналоговых фильтров, модуль функции Н(j ω) - функция H(ω) - называется амплитудно-частотной характеристикой (АЧХ) цифрового фильтра, показывающей, как изменяется амплитуда синусоидальной последовательности отсчетов при прохождении через цифровой фильтр. При частотном анализе цифровых фильтров следует учитывать, что должно выполняться условие ω ≤ π/Т, вытекающее из теоремы Котельникова.

Рассмотрим несколько примеров АЧХ цифровых фильтров (рис. 3.5). По горизонтали отложена частота сигнала, выраженная в долях частоты дискретизации и изменяющаяся от 0 до 0,5.

На рис. 3.5,а представлена АЧХ нерекурсивного ФНЧ, у которого

a₀=a₁=a₂=a₃=a₄=1

а все остальные коэффициенты равны нулю. Такой фильтр выполняет сглаживание путем усреднения в "скользящем" окне размером пять отсчетов сигнала. Характеристика этого ФНЧ далека от идеальной.

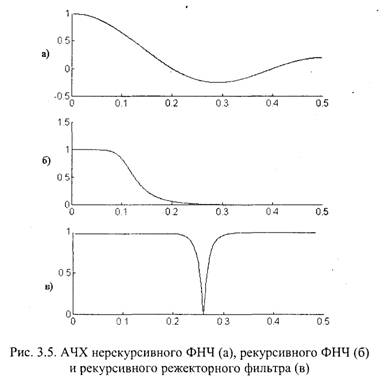
На рис. 3.5,6 представлена АЧХ рекурсивного ФНЧ Баттерворта четвертого порядка. Такой фильтр представляет собой последовательное соединение двух рекурсивных фильтров второго порядка, структурная схема каждого из которых соответствует рис. 3.4.

Первый из этих фильтров имеет коэффициенты

а₀ = 0,0722; а, = 0,1444; а₂ = 0,0722; b₁ = 0,9699; b₂ = -0,2587.

Второй фильтр имеет коэффициенты

а₀ = 0,0922; а₁ = 0,1845; а₂ = 0,0922; b₁ = 1,2388; b₂ = -0,6078.

Остальные коэффициенты обоих фильтров равны нулю. АЧХ полученного фильтра четвертого порядка имеет частоту среза равную 0,1 частоты дискретизации. Повышение порядка фильтра дает возможность увеличивать крутизну среза АЧХ.

На рис. 3.5,в представлена АЧХ рекурсивного режекторного фильтра второго порядка, имеющего коэффициенты

a₀ = 0,9243; а₁ = 0,1165; а₂ = 0,9243; b₁ = -0,1165; b₂ = -0,8487.

Этот фильтр имеет частоту режекции, равную 0,27 частоты дискретизации, и добротность, равную 10.

Рассмотренные цифровые фильтры являются одномерными, так как отсчеты входного и выходного сигналов образуют одномерные последовательности. В цифровой обработке изображений большую роль играют двумерные (или пространственные) фильтры. При выполнении пространственной фильтрации выполняется операция свертки входного изображения, представленного в виде матрицы элементов, с матрицей двумерного фильтра.

Пусть x(ij) - исходное изображение, y(ij) - изображение, получающееся в результате фильтрации, а(т,п) - матрица, задающая двумерный фильтр и имеющая размеры М по горизонтали и N по вертикали, причем М и N должны быть нечетными числами. Действие двумерного нерекурсивного фильтра может быть описано следующей формулой

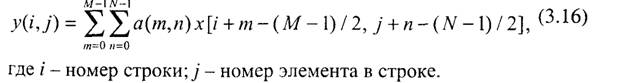
Как видно из этой формулы, каждый элемент выходного изображения представляется суммой элементов входного изображения, умноженных на заданные в матрице фильтра коэффициенты. Число учитываемых соседних элементов входного изображения определяется размером матрицы фильтра.

Простейшие двумерные фильтры имеют матрицу 3x3. Ниже приведено несколько примеров фильтров такого типа.

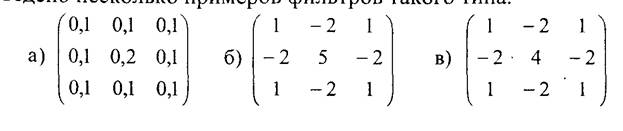
Пространственно-частотная характеристика (двумерный аналог АЧХ) для таких фильтров в случае, когда матрица фильтра симметрична как относительно среднего столбца и средней строки, так и относительно обеих главных диагоналей, рассчитывается по формуле

Первый фильтр (а) является фильтром низких пространственных частот. Значение яркости каждого элемента выходного изображения определяется путем усреднения значений яркости ближайших к нему соседних элементов исходного изображения. Сумма всех коэффициентов матрицы равна 1, что необходимо для сохранения среднего значения яркости изображения при фильтрации. Пространственно-частотная характеристика этого фильтра показана на рис. 3.6,а. Пространственные частоты ƒ_х иƒ_у измеряются в долях пространственной частоты дискретизации (т. е. величины, обратной расстоянию между соседними отсчетами) по соответствующей координате, и каждая из них изменяется в диапазоне от 0 до 0,5.

Такой фильтр уменьшает заметность шума на изображении, но при этом сглаживаются резкие перепады яркости, ухудшается передача границ объектов, могут пропадать мелкие детали изображения. Действие фильтра нижних пространственных частот на тестовое изображение "Лена" показано на рис. 3.7,а (исходное изображение можно видеть на рис. 2.10,а).

Второй фильтр (б) является фильтром высоких пространственных частот. Значения соседних элементов вычитаются из центрального элемента изображения. Сумма всех коэффициентов равна 1. В результате фильтрации подчеркиваются границы объектов, повышается резкость изображения, но одновременно становится более заметным шум. Пространственно-частотная характеристика этого фильтра показана на рис. 3.6,6, а действие фильтра на тестовое изображение продемонстрировано на рис. 3.7,6.

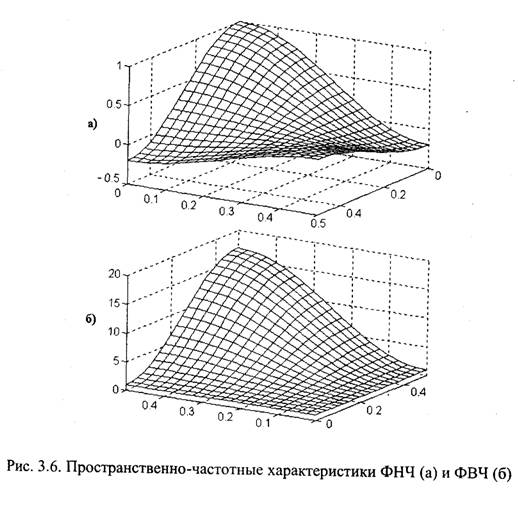
Третий фильтр (в) относится к так называемым операторам Лапласа. Сумма коэффициентов в отличие от предыдущих фильтров равна 0, вследствие чего средний уровень яркости изображения при фильтрации не сохраняется. Назначение фильтров, реализующих оператор Лапласа - выделять только границы объектов, т. е. линии, по которым происходит резкое изменение яркости. Области с постоянной или медленно меняющейся яркостью такой фильтр преобразует в темные участки изображения (рис. 3.7,в).

Наконец, на рис. 3.7,г показан результат обработки тестового изображения фильтром Собеля, который также выделяет контура и мелкие детали изображения.

Двумерная фильтрация широко используется при обработке изображений на компьютере. При этом отдельный кадр телевизионного изображения или изображение, полученное каким-либо другим способом, вводится в компьютер и подвергается фильтрации с целью сглаживания шумов, выделения границ объектов, повышения четкости и т.д. Двумерная фильтрация в реальном времени со скоростью телевизионной развертки часто реализуется помощью параллельных вычислительных устройств, специальных процессоров свертки и других аппаратных средств.

Помимо выполнения фильтрации путем свертки цифрового сигнала с матрицей, задающей фильтр, возможно выполнение фильтрации в частотной области. Для этого выполняется ДПФ исходного сигнала, полученный набор коэффициентов ДПФ почленно умножается на набор чисел, представляющих частотную характеристику фильтра, после чего выполняется обратное ДПФ. Такой вариант выполнения фильтрации во многих случаях позволяет добиться лучших результатов, чем свертка, но требует значительно большего объема вычислений.

Как уже указывалось, фильтры, заданные формулами (3.15) и (3.16), являются линейными. Большое значение имеют и нелинейные фильтры, для которых не выполняется принцип суперпозиции.

Одним из наиболее известных видов нелинейных фильтров являются медианные фильтры. Кратко принцип действия такого фильтра можно пояснить следующим образом. Для получения каждого элемента выходного сигнала берется соответствующий элемент входного сигнала и некоторое количество предшествующих ему и следующим за ним элементов входного сигнала. Значения этих элементов упорядочиваются по возрастанию или по убыванию. Далее берется центральный по порядку член полученной последовательности, и его значение присваивается элементу выходного сигнала. Например, если взято 3 предыдущих и 3 последующих элемента входного сигнала, то в последовательности будет 7 членов, и после упорядочивания элементу выходного сигнала присваивается значение 4-го члена последовательности.

При фильтрации изображений применяются двумерные медианные фильтры. При этом учитываются соседи не только по горизонтали, но и по вертикали. Медианный фильтр хорошо устраняет точечные помехи и шумы, сохраняя при этом резкие перепады яркости на границах объектов. Однако такой фильтр может подавить в изображении мелкие детали, размеры которых меньше размеров маски фильтра, определяющей учитываемые соседние элементы.

3.3. Обработка и передача сигналов с разложением на частотные поддиапазоны или на поддиапазоны по разрешающей способности. Вэйвлет-преобразование

Разложение сигнала на частотные поддиапазоны используется при решении многих задач, встречающихся в телевидении, в частности, при кодировании сигналов звукового сопровождения для передачи или записи в запоминающее устройство. Аналоговые системы передачи звуковых сигналов с разложением на частотные поддиапазоны, например, вокодеры, известны достаточно давно. В настоящее время подобные системы реализуются на основе цифровых средств.

Структурная схема системы передачи одномерного цифрового сигнала с разложением на М частотных поддиапазонов показана на рис. 3.8. Входной цифровой сигнал х(п), занимающий полосу частот от 0 до ƒ_в (где ƒ_в равна половине частоты дискретизации ƒд)> поступает на входы анализирующих фильтров АФ₁ АФ₂, ..., АФм, каждый из которых является полосовым фильтром, т. е. выделяет сигнал в заданном частотном поддиапазоне.

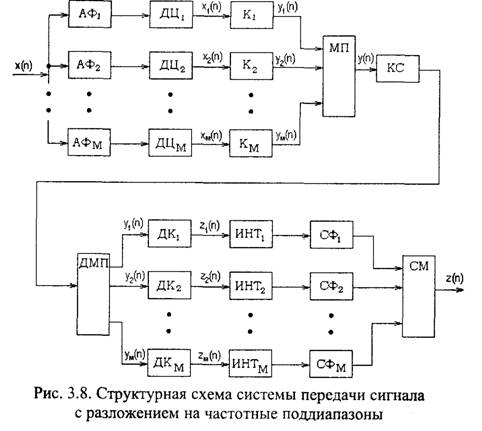
Затем сигналы, полученные на выходах анализирующих фильтров, переносятся с центральных частот соответствующих _поддиапазонов в область низких частот. При этом верхняя граничная частота ƒ_{в j}, j = 1...M, каждого из этих сигналов оказывается существенно меньше, чем верхняя граничная частота исходного сигнала х(п). Например, если весь диапазон частот исходного сигнала делится на М равных по ширине поддиапазонов, то верхняя граничная частота сигнала каждого поддиапазона оказывается в М раз меньше, чем у исходного сигнала. При этом частота дискретизации в каждом поддиапазоне может быть уменьшена в М раз по сравнению с частотой дискретизации исходного сигнала х(п).

Для уменьшения частоты дискретизации в М раз в сигнале каждого поддиапазона оставляют каждый М-й отсчет, отбрасывая остальные отсчеты. Эта операция, называемая децимацией или прореживанием, выполняется в Дециматорах Дц_{1 и} Дц ₂, ..., Дц _м, на выходах которых получаются цифровые сигналы x_M{п), х₂(п), ..., х_м(п). Суммарное число отсчетов в этих сигналах за некоторый интервал времени равно количеству отсчетов исходного сигнала x(п) за тот же интервал времени. Функции анализирующего фильтра и дециматора могут объединяться в одном функциональном узле.

Далее сигналы х₁п), х₂(п), ..., х₃(п) проходят кодирующие устройства (кодеры) К₁ К₂, ..., К_M , на выходах которых получаются кодированные сигналы частотных поддиапазонов у₁(п), y₂(п), ..., y_м(п). В случае передачи звуковой информации кодирование в поддиапазонах может заключаться, например, в выполнении более грубого квантования в тех частотных поддиапазонах, искажения в которых мало заметны для слушателя. Количество двоичных символов, используемых для передачи сигналов таких поддиапазонов, сокращается. Если сигнал в каком-либо частотном поддиапазоне настолько мал, что не оказывает влияния на слуховое восприятие, то он может вообще не передаваться. В результате уменьшается общая скорость передачи двоичных символов.

Затем сигналы у₁(п), y₂(n), ..., у_м(п) объединяются в мультиплексоре Мп в один кодированный цифровой сигнал у(п), который передается по каналу связи КС. Как уже отмечалось, скорость пе-оедачи двоичных символов, необходимая для передачи сигнала у(n), меньше, чем для передачи исходного сигнала х(п), причем уменьшение может быть весьма значительным. Вместо канала связи в системе может присутствовать носитель информации, на который осуществляется запись сигнала у{п).

После прохождения канала связи кодированный сигнал у(п) в демультиплексоре ДМп разделяется на кодированные сигналы частотных поддиапазонов у₁(п), у₂{п), ..., у_м(п). Каждый из этих сигналов декодируется в соответствующем блоке декодирования (декодере) Дk₁ Дk₂, ..., Дк_м. В процессе декодирования восстанавливается количество двоичных разрядов в данных (такая операция называется деквантованием). Так как при кодировании могли возникнуть необратимые потери информации, то декодированные сигналы поддиапазонов z₁₍n), z₂(n), ..., z_м(п) могут отличаться от исходных сигналов поддиапазонов x₁(п), x₂(п), ..., х_м(п).

Далее выполняется восстановление количества отсчетов в сигналах поддиапазонов. Эта операция, называемая интерполяцией, выполняется в интерполяторах Инт₁ Инт₂ ... Инт_м и заключается в том, что между каждыми двумя отсчетами каждого из сигналов z₁(n), z₂(n), ..., z_м(п) вставляют МЛ нулей. После этого сигналы обрабатываются синтезирующими фильтрами СФ_Ь СФ₂, ..., СФм и объединяются в сумматоре См. В результате формируется выходной сигнал z(n), имеющий такую же частоту дискретизации и занимающий такую же полосу частот, как исходный сигнал х{п).

Описанный метод используется, например, для кодирования сигналов звукового сопровождения в стандартах MPEG-1 и MPEG-2, которые будут подробно рассмотрены далее.

Эффективным средством разделения исходного сигнала на частотные поддиапазоны и синтеза выходного сигнала из сигналов частотных поддиапазонов являются квадратурные зеркальные фильтры (КЗФ) (quadrature mirror filter - QMF). Структурная схема системы, в которой используются такие фильтры, показана на рис. 3.9,а, положения получающихся частотных поддиапазонов - на рис. 3.9,6. Обозначения сигналов такие же, как на рис. 3.8. Кодеры, канал связи и декодеры не показаны.

Пара КЗФ состоит из цифрового нерекурсивного ФНЧ, обозначаемого G, и цифрового нерекурсивного ФВЧ, обозначаемого Н. Передаточные характеристики этих фильтров, полученные в результате г-преобразования, - G(z) и H(z), соответственно. Обратные фильтры, обозначенные на схеме G^-1 и Н^-1, имеют передаточные характеристики G(z^-1) и H(z^-1). Коэффициенты фильтра G^-1 получаются перестановкой коэффициентов фильтра G в обратном порядке. Аналогично коэффициенты фильтра Н^-1 получаются перестановкой коэффициентов фильтра Н.

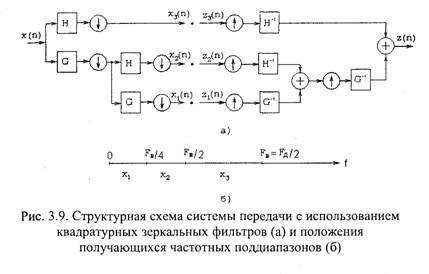
Особенность КЗФ состоит в том, что АЧХ фильтра Н получается зеркальным отображением АЧХ фильтра G, причем ось зеркальной симметрии обычно находится на частоте, равной, 1/4 частоты дискретизации. Пара КЗФ позволяет разделить исходный цифровой сигнал х(п) на два сигнала частотных поддиапазонов, соответствующих нижней и верхней половинам его полосы частот, а пара обратных фильтров позволяет восстановить исходный сигнал по двум сигналам частотных поддиапазонов.

Чтобы КЗФ обладали указанными свойствами, их передаточные характеристики должны удовлетворять условиям

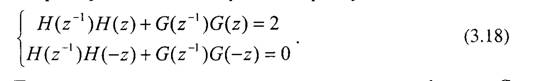
При разложении на поддиапазоны после каждого фильтра G или Н выполняется децимация, при которой отбрасывается каждый второй отсчет. Это соответствует тому, что пара КЗФ делит полосу частот входного сигнала на две равные части. Дециматоры на структурной схеме обозначены кружками со стрелками, направленными вниз. В процессе синтеза сигнала из сигналов частотных поддиапазонов перед каждым обратным фильтром G^-1 или Н^-1 выполняется интерполяция, при которой между каждыми двумя отсчетами вставляется нуль. Интерполяторы обозначены кружками со стрелками, направленными вверх. Объединение сигналов осуществляется сумматорами, обозначенными кружками со знаком "плюс" внутри.

Для разложения исходного сигнала х(п) на частотные поддиапазоны, число которых больше двух, используют древовидную структуру. После прохождения фильтра Н в первой паре КЗФ и соответствующего дециматора формируется сигнал х_з(п), соответствующий верхней половине частотного диапазона. Сигнал, соответствующий нижней половине частотного диапазона, получаемый после фильтра G в первой паре КЗФ, поступает на следующую пару КЗФ, которая делит нижний частотный поддиапазон еще раз. В результате получаются сигналы x₁(n) и х₂(п).

При синтезе выходного сигнала сначала интерполируются, фильтруются и объединяются сигналы z₁(n) и z₂(n), а затем результат объединяется с интерполированным и обработанным фильтром сигналом z₃(n).

Достоинством КЗФ является то, что при их использовании не возникает искажений, связанных с перекрытием частотных спектров сигналов смежных поддиапазонов из-за неидеальности АЧХ фильтров. Кроме того, на всех ступенях разложения и синтеза сигнала используются фильтры с одинаковыми наборами коэффициентов, что позволяет упростить реализацию.

Другой подход к обработке и передаче сигналов основан на разложении сигнала на составляющие по разрешающей способности. Такой подход оказывается особенно продуктивен для передачи изображений. Как известно, изображение состоит из крупных деталей, составляющих основу его содержания, и мелкой структуры. Во многих случаях полезно разделить указанные составляющие, чтобы передавать их раздельно, а в приемной части системы объединить эти составляющие в полное изображение.

Для решения этой задачи в последние годы все большую популярность получает подход, основанный на применении ортогонального вэйвлет - преобразования (Wavelet-Transform - WT). Термин wavelet дословно переводится как "маленькая волна". В отличие от гармонических ортогональных функций, которые периодически изменяются на всем интервале изменения аргумента, базисные функции вэйвлет-преобразования отличны от нуля только на ограниченном отрезке этого интервала. Полный набор таких функций, составляющих базис преобразования, покрывает весь интервал изменения аргумента.

Результатом вэйвлет-преобразованием является набор коэффициентов. Восстановление сигнала по этим коэффициентам называется обратным вэйвлет-преобразованием (Inverse Wavelet Transform - IWT).

Простым примером вэйвлет-преобразования является разложение сигнала по базису Хаара (Нааг). Базисная функция преобразования Хаара, показанная на рис. 3.10,а, называется scale-function или scaling-function. Ортогональный базис Хаара получается путем сдвига базисной функции с шагом равным единице во все возможные положения по оси абсцисс.

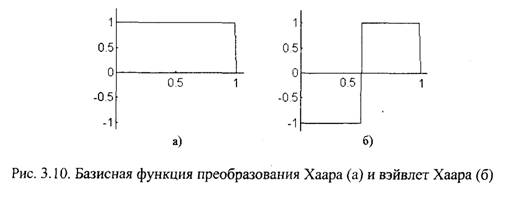
Функция, показанная на рис. 3.10,6, называется вэйвлетом Хаара (Haar Wavelet). Вэйвлеты Хаара, сдвигаемые по оси абсцисс, также образуют ортогональный базис для пространства сигналов деталей, о которых будет сказано ниже.

Другие типы вэйвлет-преобразования также имеют базисные функции (scaling-functions) и вэйвлеты, но более сложных форм.

Пусть есть исходный цифровой сигнал х(п), п = 0, 1, ..., N-1. В результате преобразования Хаара он преобразуется в два цифровых сигнала x₁(т) и х₂(т), т = 0, 1, ..., N/2-1 (N предполагается четным), в соответствии с соотношениями

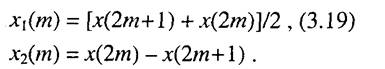
Отсчеты сигнала x₁(т) получаются путем усреднения пар смежных отсчетов исходного сигнала х(п). Поэтому сигнал x₁(т) содержит информацию с уменьшенной в два раза разрешающей способностью. В то же время сигнал x₂(m), отсчеты которого равны разностям значений смежных отсчетов исходного сигнала, содержит информацию о мелких деталях исходного сигнала. Именно для сигнала x₂(m) ортогональным базисом являются вэйвлеты Хаара. Каждый из сигналов x₁(т) и х₂(т) содержит N/2 отсчетов, и вместе они несут всю информацию, имеющуюся в исходном сигнале.

Обратное    преобразование    Хаара    определяется    соотношениями, получающимися из (3.19), где первое соотношение позволяет восстановить нечетные отсчеты исходного сигнала, а второе — четные,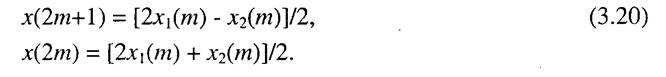

Далее преобразование Хаара может быть применено к сигналу x₁(т), который при этом будет разложен на сигнал x₁₁(k), соответствующий   еще   более   низкой  разрешающей   способности, и сигнал x₁₂(k), содержащий детали, необходимые для восстановления сигнала x₁(т). Сигналы x₁₁(k) и x₁₂(k) содержат по N/4 отсчетов.: Затем преобразование Хаара может быть применено к сигналу x₁₁(k) и т.  д.  Соответствующими обратными  преобразованиями могут быть последовательно восстановлены сигналы с более высокими разрешающими способностями, вплоть до исходного сигнала.

Важно отметить, что при выполнении прямого преобразования Хаара (как и прямого вэйвлет-преобразования другого типа) число отсчетов в получаемых сигналах на каждой ступени преобразования уменьшается в два раза, а количество самих сигналов i возрастает. При этом суммарное число отсчетов во всех получен-!: ных сигналах всегда равно N. При выполнении обратного преобра-1 зования количество отсчетов в восстанавливаемых сигналах на; каждой ступени увеличивается в два раза.                                        

Вэйвлет-преобразование изображения осуществляется путем; последовательного выполнения вэйвлет-преобразований по двум координатам (рис. 3.11). Исходное изображение представляет собой матрицу А, имеющую размер NxN и содержащую N ² элементов. В блоках WTx и WTy выполняются вэйвлет-преобразования одномерных цифровых сигналов, например, преобразования Хаара. В блоках IWTx и IWTy выполняются соответствующие обратные преобразования.

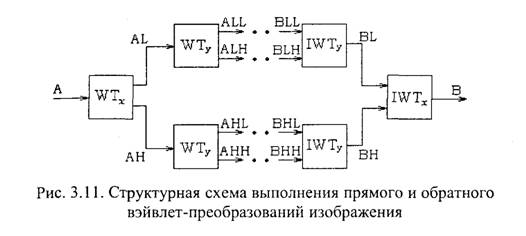
На первом этапе выполняется вэйвлет-преобразование по горизонтальной координате х (WTx). При этом элементы изображения А, расположенные в каждой строке матрицы, последовательно поступают на блок WTx, причем одна строка обрабатывается за другой. В результате формируются два изображения AL и АН, каждое из которых представляет собой матрицу, содержащую N/2 элементов по горизонтали и N элементов по вертикали. Суммарное количество элементов в этих изображениях остается равным N². В изображении AL разрешающая способность по горизонтали уменьшена в два раза. Изображение АН содержит информацию о деталях изображения, имеющих малые размеры по координате х.

Затем каждое из изображений AL и АН подвергается вэйвлет-преобразованию по вертикальной координате у. При этом на блоки WTy последовательно поступают элементы изображения, расположенные в столбцах соответствующих матриц. В результате получаются четыре матрицы, каждая из которых содержит (N/2)x(N/2) элементов. Суммарное число элементов по-прежнему равно N².

Матрица ALL соответствует изображению, подобному исходному, но с уменьшенными в два раза разрешающими способностями по обеим координатам. Матрица ALH содержит детали исходного изображения, имеющие относительно большие размеры ю горизонтали, но с минимальными размерами по вертикали. Матрица AHL содержит детали изображения, крупноразмерные по вертикали, но с минимальными размерами по горизонтали. Наконец, матрица АНН содержит детали изображения, имеющие малые оазмеры по обеим координатам. На рис. 3.12 показан результат двумерного преобразования Хаара тестового изображения "Лена". Левый верхний квадрант изображения образует матрица ALL, правый верхний квадрант -матрица ALH, нижний левый квадрант - матрица AHL и, наконец, правый нижний квадрант - матрица АНН.

Разложение на поддиапазоны по разрешающей способности позволяет анализировать или передавать изображение с разными степенями детальности. Для получения наиболее грубого представления об изображении достаточно использовать только информацию, содержащуюся в матрице ALL. Добавление других поддиапазонов увеличивает точность представления изображения.

Как и для одномерных сигналов, число ступеней двумерного вэйвлет-преобразования может быть увеличено. Матрица ALL может быть преобразована в четыре матрицы размером (N/4)x(N/4) элементов. Та из этих матриц, которая содержит изображение с уменьшенными в четыре раза пространственными разрешениями по обеим координатам, преобразована в четыре матрицы размером (N/8)х(N/8) элементов и т.д.

После разложения исходного изображения А на поддиапазоны по разрешающей способности может выполняться обработка д_Ля каждого из этих поддиапазонов. В результате матрица ALL преобразуется в матрицу BLL и т. д. Обратные вэйвлет-преобразования выполняются в обратном порядке (см. рис. 3.11). В результате формируется изображение В размером NxN элементов.

Обработка в поддиапазонах часто имеет целью сжатие изображения для его передачи по каналу связи или для записи на носитель информации. Как правило, для представления данных, содержащихся в матрицах ALH, AHL и АНН, может использоваться меньшее число двоичных разрядов, т. е. более грубое квантование, чем для исходного изображения. Это обусловлено тем, что сигналы малоразмерных деталей имеют меньший размах, а создаваемые квантованием искажения на мелких деталях менее заметны для зрителя. Данные из всех матриц после квантования объединяются в общий поток данных. В приемной части восстанавливается исходное количество двоичных разрядов.

Вэйвлет-преобразование обеспечивает более высокий коэффициент сжатия неподвижных изображений при сохранении их приемлемого качества, чем широко используемый стандарт JPEG. Однако для этого необходимо использовать не описанное здесь преобразование Хаара, а другие типы вэйвлет-преобразования, в которых используются базисные функции и вэйвлеты более сложных форм.

Важным преимуществом вэйвлет-преобразования перед ДПФ и ДКП является раздельное выполнение преобразований по двум координатам. Общее число вычислительных операций при вэйвлет-преобразовании изображения, содержащего NxN элементов, пропорционально N ², т. е. существенно меньше, чем для ДПФ и ДКП, даже в случаях применения для их реализации быстрых алгоритмов.

3.4. Оценка и компенсация движения

Одной из важных и часто встречающихся задач обработки изображений является оценка движения различных объектов, присутствующих в изображении. Выполнение такой оценки необходимо при сжатии движущихся изображений, для коррекции смазывания изображения из-за колебаний видеокамеры в руках опера-тора, для совмещения изображений объекта в двух смежных полях одного кадра при чересстрочной развертке, для обнаружения движущихся объектов в системах охранного ТВ и т. д.

Простейший вид движения объекта в кадре — плоскопараллельное движение, когда объект не приближается, не удаляется и не поворачивается. Более сложные виды движения - приближение или удаление объекта, в результате чего изменяются его размеры в кадре, поворот объекта, взаимное перекрытие объектов, деформация, появление или исчезновение объектов в кадре.

В цифровом телевидении широко применяется метод оценки движения в некотором кадре (далее для определенности называемом первым кадром) относительно какого-либо другого кадра (далее - второго кадра), называемый соответствием блоков (block matching). Во времени первый кадр может следовать как после второго кадра, так и до него. В простейшем варианте этого метода первый кадр разделяется на прямоугольные блоки одинаковых размеров. Отметим, что в стандартах MPEG, о которых пойдет речь ниже, эти блоки называются макроблоками, чтобы не путать с блоками, используемыми в дискретном косинусном преобразовании.

Для каждого блока первого кадра осуществляется поиск наиболее похожей на него прямоугольной области таких же размеров во втором кадре. При этом последовательно перебираются векторы движения (или векторы смещения) (Δп, Δ т), где Δп, Δ т - приращения координат по горизонтали и по вертикали, принимающие значения в некоторых заданных интервалах. Для каждого вектора движения берется область во втором кадре, смещенная на этот вектор относительно анализируемого блока первого кадра (см. рис. 3.13, где тонкими линиями показаны границы блоков первого кадра, а толстыми - положение смещенной области во втором кадре), и рассчитывается сумма S(Δ п, Δ т) абсолютных значений разностей элементов блока первого кадра и смещенной области второго кадра

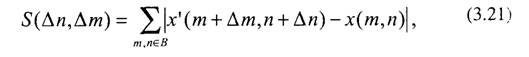
где х(т,п) - элемент первого кадра; х'(т,п) - элемент второго кадра; т, п - дискретные координаты по вертикали и по горизонтали, отсчитываемые, например, от левого верхнего угла блока первого кадра. Суммирование производится по всем элементам блока.

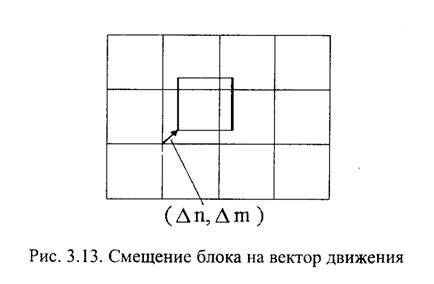
Из всех проверенных векторов (Δ п, Δ т) выбирается тот, который обеспечивает наименьшее значение суммы в (3.21). Этот вектор и считается далее вектором движения для данного блока. В некоторых случаях вместо суммы абсолютных значений используется корень из суммы квадратов разностей, однако его расчет требует большего объема вычислений.

Полный перебор возможных смещений в заданном диапазоне обеспечивает нахождение абсолютного минимума суммы в (3.21), но требует выполнения (2W+1)² расчетов по этой формуле, где W - максимальное смещение по какой-либо координате, выраженное в количестве пикселов. Существуют различные алгоритмы (или стратегии) поиска соответствия блоков с уменьшенным объемом вычислений. Например, сначала выполняется поиск с большим шагом смещения (в несколько пикселов) по всему диапазону смещений, а затем в зоне, где обнаружен минимум, производится поиск с шагом 1 или даже 1/2 пиксела для точного определения вектора движения.

После определения векторов движения для каждого блока текущего кадра может быть выполнена компенсация движения. Каждый блок первого кадра заменяется найденной для него соответствующей областью второго кадра, которая смещается на место этого блока. Величины смещений по горизонтали и по вертикали определяются вектором движения. В результате из элементов второго кадра формируется оценка первого кадра или предсказанный первый кадр. Компенсация движения является одной из основ методов сжатия движущихся изображений MPEG-1 и MPEG-2, о которых речь пойдет далее.

Разбиение кадра на прямоугольные блоки фиксированных размеров в большинстве случаев не позволяет точно описать и скомпенсировать движение объектов в изображении. Поэтом, в последние годы большое внимание уделяется разработке большое внимание уделяется разработке более совершенных методов. В их числе методы, в которых используются блоки с переменными размерами и формами, а также градиенные методы оценки движения, позволяющие определить вектор движения для каждого элемента изображения, и методы, основа -ные на анализе трехмерного спектра движущегося изображения (две пространственные координаты и время).

3.5. Дифференциальная импульсно-кодовая модуляция. Кодирование с предсказанием   

В простейшем варианте передачи цифровой информации по каналу связи передаются значения цифрового кода каждого отсчета сигнала в виде последовательности импульсов. Такой способ называется передачей с использованием импульсио-кодовой моду ляции (ИКМ), в англоязычной технической литературе называемой PCM (Pulse Code Modulation).

В случае применения кодирования с предсказанием или дифференциальной импульсно-кодовойa модуляции (ДИКМ) по ка налу связи передается разность между действительным значением текущего отсчета сигнала и значением этого же отсчета, предсказанным по предыдущим отсчетам. Структурная схема системы передачи информации с ДИКМ приведена на рис. 3.14.

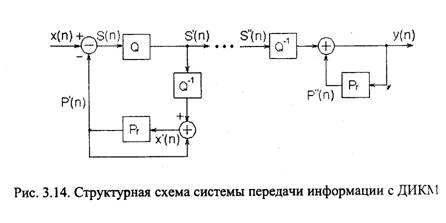
Система содержит кодирующую часть (кодер) и декодирующую часть (декодер), между которыми может быть канал связи или устройство записи информации на какой-либо носитель. На вход кодера поступает последовательность отсчетов входного сигнала х(п). В предсказателе Pr (predictor) формируются предсказанные значения сигнала р'(п). В вычитающем устройстве определяется разность действительного х(п) и предсказанного р'(п) значений сигнала, равная S(n) =х(п) - р'(п), называемая ошибкой предсказания. Затем сигнал S(n) поступает в квантователь Q. Уменьшение скорости передачи двоичных символов достигается за счет уменьшения в квантователем количества двоичных разрядов величины S(n), в результате чего получается передаваемый по каналу связи сигнал S'(n).

На вход декодера поступает сигнал S"(n), прошедший канал связи. В деквантователе Q^-1 восстанавливается исходное число двоичных разрядов. В сумматоре происходит формирование выходного сигнала у(п) в соответствии с соотношением у(п) =р"(п) + S"(n), где p"(п) - предсказанное по предыдущим значениям выходного сигнала его текущее значение.

Рассмотрим формирование в кодере предсказанных значений сигнала р'(п). Важно отметить, что предсказатели в кодере и декодере работают по идентичным алгоритмам. Квантованный сигнал ошибки предсказания S"(n) поступает во входящий в состав кодера деквантователь Q^-1, в котором восстанавливается исходное число двоичных разрядов. Выходной сигнал деквантователя в сумматоре складывается с предсказанным значением p'(п), в результате чего формируется сигнал х'(п), получающийся в результате выполнения таких же операций, что и выходной сигнал декодера у{п).

В общем случае предсказанные значения р'(п) вычисляются по формуле

где а_к, к= 1...К- коэффициенты, характеризующие метод предсказания. Такой метод называется линейным предсказанием (Linear Prediction), так как предсказываемые значения сигнала формируются в виде линейных комбинаций нескольких предыдущих значений.

Простейший вариант ДИКМ реализуется в случае, когда ai = 1, а все остальные коэффициенты равны нулю. В таком вари анте в качестве предсказанного значения берется предыдущее значение сигнала. При передаче телевизионного изображения дл предсказания значения отсчета можно использовать корреляцион ные связи между отсчетами одной строки, соседних строк и еле дующих друг за другом кадров. При этом в предсказателях в код© ре и декодере должны быть запоминающие устройства на несколько элементов, на несколько строк или на несколько кадров соответственно.

Перейдем к вопросу о помехоустойчивости систем с ДИКМ.

Как уже отмечалось, сумматор в кодере выполняет накоплю ние поступающих на него квантованных значений ошибки пред сказания подобно сумматору в декодере и формирует сигнал х'(п аналогичный выходному сигналу у(п). Поэтому в формируемы предсказанные значения р'(п) войдут ошибки, создаваемые квантователем. Эти ошибки затем вычитаются из входного сигнал. Благодаря этому не происходит накопления ошибок квантовании в выходном сигнале.

Рассмотрим следующий пример. Пусть квантование осуществляется путем уменьшения количества разрядов с 8 до 5, причем старший разряд используется как знаковый, так как разностно значение может быть как положительным, так и отрицательный. Тогда величина S'(n) может принимать значения от -15 до 15. Пусть в качестве предсказанного значения используется предыдущее значение сигнала на входе блока предсказателя. Для сигналов в кодере можно записать следующие соотношения:

т. е. ошибка компенсировалась. Так как в декодере сигнал у(п) формируется по тому же алгоритму, что и сигнал х'(п) в кодере, то компенсация ошибки будет иметь место и на выходе системы с ДИКМ.

В случае, если сразу ошибка не компенсируется, происходит постепенная коррекция ошибки путем передачи увеличенных значений разности S'(n) в нескольких следующих периодах дискретизации. Резкие перепады в передаваемом сигнале в такой системе могут несколько сглаживаться, но накопление ошибки не происходит. Начальные значения jc(O) и v(0) могут быть установлены равными между собой. В этом случае выходной и входной сигналы будут различаться между собой на сумму ошибок, вносимых квантователем за все время передачи сигнала.

Постепенная коррекция ошибки квантователя иллюстрируется табл. 3.1. Из приведенных данных видно, что ошибка, возникшая из-за перегрузки квантователя в такте 6, компенсируется за два такта, а ошибка, возникшая в такте 9 - за один такт.

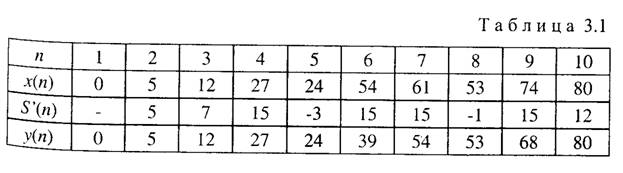
При наличии помех в канале связи в выходном сигнале декодера будут возникать ошибки, распространяющиеся на все последующие значения этого сигнала. Один из наиболее универсальных методов коррекции ошибок, возникших в канале связи, это использование обратной связи, охватывающей этот канал. В такой системе требуются два канала связи: прямой и обратный. В телевизионном вещании такой подход сопряжен со значительными трудностями и не применяется.

Еще один распространенный способ повышения помехоустойчивости систем с ДИКМ при наличии ошибок в канале связи -передача с определенной периодичностью опорных отсчетов с использованием обычной ИКМ. После приема каждого такого отсчета в декодере формирование выходного сигнала по принимаемым разностным значениям начинается заново. Все накопившиеся к этому моменту ошибки аннулируются. В телевидении этот метод согласуется с необходимостью периодически передавать опорный кадр без межкадрового предсказания, чтобы можно было начинать прием передачи в любой момент. Конкретная реализация такого подхода в системах цифрового телевидения будет рассмотрена позже.

Развитием метода ДИКМ является адаптивная импульсно-кодовая модуляция АДИКМ (Adaptive Differential Pulse Code Modulation - ADPCM). В соответствии с этим методом параметры квантователя Q и предсказателей Рr (рис. 3.14) изменяются в зависимости от параметров передаваемого сигнала. Например, если средняя за определенный интервал времени скорость изменения входного сигнала х(п) увеличилась, шаг квантования также увеличивается, чтобы не возникало перегрузок в квантователе. Наоборот, если средняя скорость изменения входного сигнала уменьшилась, шаг квантования также уменьшается, чтобы уменьшить влияние шума квантования на передаваемую информацию.

АДИКМ применяется в некоторых цифровых системах передачи речевой информации, например, в мобильных телефонах, и позволяет уменьшить скорость передачи двоичных символов в несколько раз.

3.6. Векторное квантование. Фрактальное кодирование

Квантование можно определить как замену реального значения сигнала на ближайшее к нему по некоторому критерию эталонное значение сигнала. Обычное квантование (см. § 2.1), состоящее в округлении до ближайшего уровня квантования, называют скалярным, так как отдельные отсчеты сигнала квантуются независимо друг от друга.

Более общей операцией является векторное квантование, при котором одновременно квантуется (кодируется) группа из N отсчетов цифрового сигнала, называемая Nмерным вектором [16]. В случае одномерного сигнала векторами могут быть группы по N последовательных отсчетов. В случае изображения векторами могут быть блоки из нескольких смежных по горизонтали и по вертикали элементов изображения. На рис. 3.15 представлена структурная схема системы передачи информации, в которой используется векторное квантование.

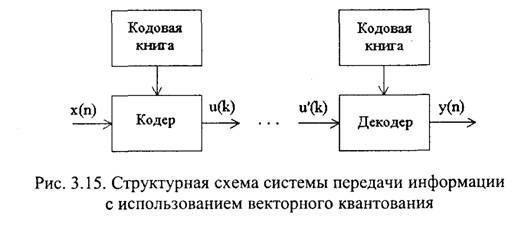
Множество всех встречающихся в сигнале N-мерных векторов разбивается на L подмножеств так, что входящие в каждое подмножества векторы мало отличаются друг от друга. В каждом подмножестве выбирается один эталонный вектор, представляющий все векторы этого подмножества. Все эталонные векторы записываются в кодовую книгу (Code Book), и каждому из них присваивается определенное кодовое слово.

Входной цифровой сигнал х(п) поступает на вход кодера. Процедура кодирования заключается в том, что для каждого N-мерного вектора в кодовой книге находится наиболее близкий к нему эталонный вектор, код которого поступает на выход коде-

pa. Таким образом, для каждой группы из TV отсчетов входного сигнала х(п) передается одно кодовое слово и(к).

В декодере в соответствии с принятым кодовым словом и'(к) (где штрих показывает, что информация прошла канал связи) из кодовой книги считывается эталонный вектор, преобразуемый в группу из N отсчетов выходного сигнала у(п).

Кодовая книга может изменяться в зависимости от свойств кодируемого сигнала. Построение кодовой книги является составной частью процесса кодирования, а ее содержание должно пересылаться в приемную часть системы вместе с кодовыми словами и(к). Наиболее известным алгоритмом построения кодовой книги для кодирования изображений является алгоритм LGB (по первым буквам фамилий его авторов Linde, Buzo, Gray). Задачей, решаемой с помощью этого и подобных ему алгоритмов, является построение кодовой книги минимального объема, позволяющей закодировать некоторое изображение, не превышая при этом установленный предел вносимых при кодировании искажений.

Векторное квантование относится к методам сжатия с потерями, так как реальные группы из N отсчетов входного сигнала х(п) в выходном сигнале у(п) заменяются эталонными N-мерными векторами. Одним из достоинств векторного квантования является простота декодера, в котором выполняется только операция считывания эталонного вектора из кодовой книги.

В то же время, осуществляемый в кодере поиск эталонного вектора, наиболее близкого к кодируемому вектору, требует выполнения большого объема вычислений. Обычно понятие "наиболее близкий эталонный вектор" означает, что для этого эталонного) вектора достигается минимальное значение квадратичной ошибки: квантования е, определяемой как

где aj - элементы входного вектора; bj - элементы эталонного вектора. Поиск минимума ошибки для каждого входного вектора осуществляется путем вычисления значений ошибки его квантования для всех эталонных векторов.                                                   

Близким по сущности к векторному квантованию является фрактальное кодирование изображений, при котором в качестве элементов кодовой книги используются блоки, вырезанные из самого исходного изображения.

Как известно, фракталами называются рисунки, обладающие свойством самоподобия. При этом часть рисунка подобна всему рисунку в целом, но в меньшем масштабе. В этой части есть подобная ей часть еще меньших размеров и т.д. Пример фрактала показан на рис. 3.16.

При фрактальном кодировании используется свойство подобия деталей разного масштаба, встречающееся в реальных изображениях. Допускаются преобразования блоков кодируемого изображения, позволяющие добиться подобия этих блоков эталонным блокам (повороты, зеркальные отражения). Как и при векторном квантовании, кодирование занимает намного больше времени и вычислительных ресурсов, чем декодирование.

Векторное квантование и фрактальное кодирование могут использоваться для кодирования звуковых сигналов и изображений, обеспечивая значительное сжатие информации. Однако большой объем вычислений, выполняемых при кодировании, пока что препятствует практическому применению этих методов в системах цифрового телевидения.

Контрольные вопросы

1. Почему ДПФ содержит конечное число частотных составляющих?

2. Почему ДКП во многих случаях удобнее применять, чем ДПФ?

3.  Нарисуйте структурные схемы нерекурсивного и рекурсивного цифровых фильтров.

4.  Напишите формулу, описывающую действие двумерного нерекурсивного цифрового фильтра.

5.  Чем различаются матрицы двумерного фильтра верхних частот и двумерного фильтра Лапласа и воздействия указанных фильтров на изображение?

6.  Почему при разложении сигнала на частотные поддиапазоны количество отсчетов в каждом поддиапазоне может быть уменьшено?

7.  Каковы свойства квадратурных зеркальных фильтров?

8.     Что    происходит    с    изображением    при    выполнении    вэйвлет-преобразования?

9.  За счет чего может быть достигнуто сжатие изображения с помощью вэйвлет-преобразования?

10. В чем состоит оценка движения методом соответствия блоков?

11. Что такое линейное предсказание?

12.  Почему использование ДИКМ позволяет уменьшить скорость передачи двоичных символов в канале связи?

13.  Какими средствами может быть обеспечена помехоустойчивость передачи информации с использованием ДИКМ?

14.  Как выполняются кодирование и декодирование в системах передачи с векторным квантованием?

4. МЕТОДЫ СЖАТИЯ ИЗОБРАЖЕНИЙ И ЗВУКОВЫХ СИГНАЛОВ

4.1. Сжатие неподвижных изображений по стандарту JPEG

ОБЩИЕ ПОЛОЖЕНИЯ

Один из наиболее эффективных и употребительных методов сжатия неподвижных изображений изложен в принятом Международной организацией стандартизации ISO стандарте JPEG (Joint Photographic Experts Group) [4]. Данный стандарт определяет последовательность и параметры операций при кодировании и декодировании неподвижных изображений.

JPEG относится к методам сжатия изображений с потерями и используется в основном при записи неподвижных изображений с целью экономии объема ЗУ.

Для большинства реальных полутоновых и цветных изображений этот метод позволяет уменьшить объем информации в 5-10 раз без заметного ухудшения визуально воспринимаемого качества. JPEG не предназначен для сжатия рисунков, чертежей и других изображений, имеющих два уровня яркости.

Последовательность операций при кодировании, поясняемая структурной схемой на рис. 4.1, включает:

- разбиение изображения на блоки 8x8 пикселов;

- выполнение быстрого ДКП (БДКП) в каждом блоке;

-  квантование полученных коэффициентов ДКП с использованием таблицы коэффициентов квантования (таблица Q);

-   энтропийное кодирование квантованных коэффициентов ДКП каждого блока изображения.

Последняя операция выполняется кодером Хаффмена с использованием таблицы кодирования (таблица кодов). Вместо кодера Хаффмена может использоваться арифметический кодер.

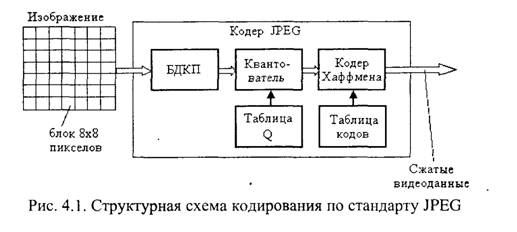
В результате кодирования исходное изображение преобразуется в сжатые видеоданные, записываемые в файл.

Последовательность операций при декодировании, поясняемая структурной схемой на рис. 4.2, включает:

- декодирование энтропийного кода (декодер Хаффмена);

- деквантование коэффициентов ДКП для каждого блока 8x8 пикселов;

- обратное БДКП для каждого блока;

- объединение блоков в декодированное изображение.

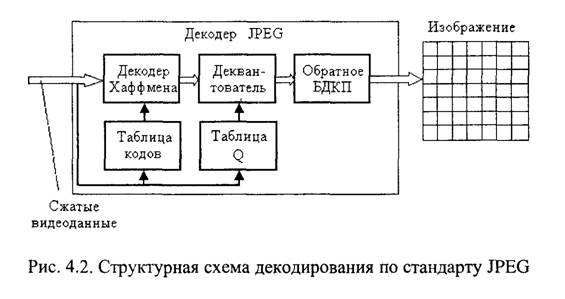
При декодировании энтропийного кода и при деквантовании используются таблицы  кодирования  и  таблицы  коэффициентов квантования, которые могут содержаться в одном файле со сжатым изображением.

Далее более подробно рассмотрены операции, выполняемые при кодировании, и соответствующие им обратные операции, выполняемые при декодировании.

РАЗБИЕНИЕ ИЗОБРАЖЕНИЯ НА БЛОКИ

Полутоновое монохромное (черно-белое) изображение разбивается на блоки 8x8 пикселов. Эти блоки далее кодируются один за другим. Порядок кодирования блоков слева направо, один горизонтальный ряд блоков за другим.

Цветное изображение может быть представлено в формате RGB, когда для каждого пиксела задаются значения трех основных цветов. В этом случае каждый блок 8x8 пикселов представляется тремя блоками 8x8 чисел. Кодирование данных каждого из трех цветов выполняется также, как для полутонового монохромного изображения.

Предпочтительнее представление цветного изображения в формате YC_BC_R, где для каждого пиксела задаются значения яркости и цветоразностных сигналов. В этом случае возможно уменьшение число блоков для информации о цвете. Например, если уменьшить число отсчетов цветоразностных сигналов по вертикали и по горизонтали в два раза, что соответствует формату 4:2:0, то на каждые четыре блока элементов сигнала яркости Y будет приходиться один блок элементов сигнала С_в и один блок элементов сигнала C_R. По сравнению с форматом RGB полное число кодируемых блоков уменьшится в два раза, но заметного ухудшения качества изображения при этом не произойдет, так как зрительный аппарат человека не воспринимает искажения цвета мелких деталей изображения.

Возможны два варианта последовательности кодирования блоков цветного изображения. Согласно первому варианту, называемому последовательным (sequential), сначала кодируются все блоки элементов сигнала Y, затем - все блоки элементов сигнала С_в, затем - все блоки сигнала C_R. Второй вариант предусматривает перемежение (interleaved) блоков разных составляющих. Например, в случае формата дискретизации 4:2:0, сначала кодируются четыре блока Y, образующие матрицу 2x2, затем соответствующий им один блок С_в, затем - один блок C_R, затем следующие четыре блока и т.д.

При объединении блоков в декодированное изображение количество элементов С_в и С_R восстанавливается с помощью интерполяции.

ДИСКРЕТНОЕ КОСИНУСНОЕ ПРЕОБРАЗОВАНИЕ

Исходные данные для ДКП имеют вид блоков или матриц 8x8 элементов сигналов Y, С_в или С_R, выражаемых 8-разрядными целыми положительными двоичными числами. Перед выполнением ДКП значение каждого элемента блока сдвигается путем вычитания числа 128, в результате чего элементы блоков выражаются целыми числами со знаком.

После этого в кодере JPEG выполняется ДКП в соответствии с формулами (3.12) при N = М =8. Обратное ДКП в декодере JPEG выполняется в соответствии с формулой (3.13). После него выполняется обратный сдвиг уровня каждого элемента путем прибавления числа 128. Как правило, при вычислениях используются алгоритмы быстрого ДКП.

В результате выполнении ДКП квадратной матрицы из 8x8 чисел получается квадратная матрица из 8x8 коэффициентов ДКП, которые могут быть как положительными, так и отрицательными целыми числами из диапазона -2047...2047. Эта операция сама по себе не изменяет количества передаваемой информации и является обратимой, так как после выполнения обратного ДКП в каждом блоке и объединения блоков получается изображение, идентичное исходному. Единственным источником необратимых потерь информации могут быть ошибки округления при вычислениях, однако эти ошибки могут быть сделаны достаточно малыми за счет выбора разрядности вычислительных средств.

Тем не менее, именно ДКП создает основу для последующего значительного уменьшения объема передаваемой информации. Рассмотрим, как это получается.

В первую очередь необходимо отметить, что каждый коэффициент ДКП содержит информацию не об одном каком-то элементе из матрицы элементов изображения, а о всех 64 элементах. Пусть {х(т,п)}, т,п = 0...7 - квадратная матрица элементов изображения представляющая собой один из его блоков, (С(k,1)}, k, I = 0 ...7 - квадратная матрица коэффициентов двумерного ДКП. Коэффициент С(0,0), как следует из (3.12), пропорционален постоянной составляющей, т. е. среднему значению величин

х(т,п) блока изображения. Коэффициент С(0,1) показывает величину пространственно-частотной составляющей, имеющей нулевую пространственную частоту по горизонтальной координате и пространственную частоту, равную 1/N, по вертикальной координате и т. д. (Понятие безразмерной дискретной частоты пояснялось в § 3.1).

При выполнении обратного ДКП в соответствии с (3.13), изображение формируется в виде суперпозиции составляющих, каждая из которых имеет определенную пространственную частоту. Как известно, наибольший вклад при формировании большинства реальных изображений вносят низкочастотные составляющие, определяющие формы и яркости основных объектов и фона. Высокочастотные составляющие создают резкие границы и контуры, а также мелкую структуру (текстуру) изображения.

Возможность уменьшения скорости передачи двоичных символов при помощи ДКП (как и при помощи ДПФ) основана на указанных свойствах пространственно-частотного спектра реальных изображений и на ограниченной способности человеческого зрения воспринимать изменения и искажения мелкой структуры изображения. Количество передаваемой информации уменьшается путем более грубого квантования части или всех передаваемых коэффициентов C(k,l), в результате которого уменьшается число двоичных разрядов, используемых для представления этих коэффициентов, а многие из коэффициентов становятся равными 0.

Как видим, уменьшение скорости передачи двоичных символов достигается за счет отбрасывания части информации. Поэтому изображение, получаемое с помощью обратного ДКП в приемной части системы, не будет идентично исходному передаваемому изображению. Следовательно, данный метод кодирования относится к методам кодирования с частичной потерей информации. Однако отбрасываемая информация оказывается несущественной для зрительного восприятия, а возникающие изменения и искажения изображения не снижают или почти не снижают его субъективно воспринимаемого качества. Поэтому рассмотренный метод кодирования является методом сокращения психофизиологической избыточности телевизионного сигнала.

Остановимся на последнем утверждении. Как уже указывалось, для реальных изображений наибольшую величину имеет низкочастотные составляющие, которые, естественно, должны передаваться с достаточно высокой точностью. Высокочастотные составляющие, имеющие относительно большой уровень, создают резкие границы и контуры, а также высококонтрастные малоразмерные детали. Эта информация также должна передаваться, хотя, может быть, и с меньшей точностью, чем низкочастотные составляющие. Остальные высокочастотные составляющие, величины которых малы и в результате квантования оказываются равными 0, создают слабо различимую мелкую структуру, текстуру отдельных участков изображения и незначительные особенности контуров объектов.

Потеря этой информации изменяет изображение, но во многих случаях эти изменения не существенны для получателя информации - зрителя. В случае же, когда получателем информации является система автоматического распознавания образов (например, в медицинской диагностике или при обнаружении целей), описанный подход может оказаться неприемлемым, так как именно теряемая информация может быть принципиально важной для распознавания.

Для сравнения можно отметить, что переход к более грубому квантованию исходного изображения приводит к возникновению заметных искажений в виде ложных контуров. В то же время ошибка квантования, возникающая при грубом квантовании коэффициентов ДКП, "размазывается" по всем элементам блока, и возникающие при этом искажения оказываются менее заметными.

Таким образом, использование ДКП в сочетании с последующим квантованием коэффициентов ДКП обеспечивает уменьшение количества передаваемой информации и, следовательно, требуемой ширины полосы частот канала связи.

КВАНТОВАНИЕ КОЭФФИЦИЕНТОВ ДКП

Квантование коэффициентов ДКП С(к,1) выполняется в соответствии с формулой

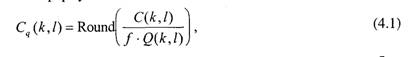
где Q(k,l) - коэффициенты квантования, задаваемые в виде таблицы из 8x8 целых чисел (таблица Q на рис. 4.1); ƒ параметр, определяющий степень сжатия изображения, Round() - операция округления до ближайшего целого значения; C_q(k,l) - полученные в

результате данной операции квантованные коэффициенты ДКП, которые могут быть как положительными, так и отрицательными.

Важно отметить, что для квантования сигнала яркости и цветоразностных сигналов используются разные таблицы. Примеры таблиц квантования для сигнала яркости и для цветоразностных сигналов приведены в табл. 4.1 и в табл. 4.2, соответственно. В результате выполнения операций деления и округления многие коэффициенты ДКП становятся равными нулю. Именно квантование создает возможность уменьшения числа двоичных символов, необходимых для представления информации о коэффициентах ДКП, т. е. сжатия изображения. В то же время именно квантование является источником необратимых потерь информации при сжатии.

Выбор конкретной таблицы квантования в стандарте JPEG оставлен на усмотрение пользователей, но таблицы квантования сигналов яркости и цветности должны быть одни и те же для всех блоков данного изображения.

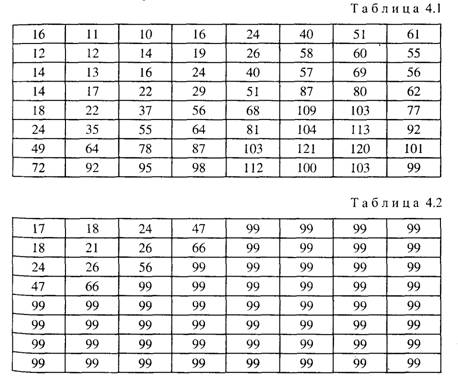
Операция деквантования, выполняемая в декодере JPEG, заключается в умножении коэффициентов C_q(k,l) на соответствующие коэффициенты Q(k,l) из таблиц квантования. Если таблицы, использованные при кодировании, не помещены в файл со сжатыми видеоданными, то при декодировании используются стандартные таблицы квантования "по умолчанию".

ЭНТРОПИЙНОЕ КОДИРОВАНИЕ

В первую очередь необходимо отметить, что для кодирования постоянных составляющих C_q(0,0) используется особый метод. Если остальные 63 коэффициента ДКП в каждом блоке кодируются независимо от соответствующих коэффициентов в других блоках, то коэффициенты Q(0,0) всех блоков каждой составляющей изображения предварительно кодируются с предсказанием. При этом коэффициент C_q(0,0) в каждом блоке заменяется на величину DIFF = С₉(0,0) - PRED, где PRED - значение коэффициента Q(0,0) в предыдущем по порядку кодирования блоке этой же составляющей. Для первого кодируемого блока берется PRED = 0. Для дальнейшего кодирования значения DIFF в каждом блоке преобразуются в двоичные числа с переменным числом бит, так что значения с малыми абсолютными величинами представляются более короткими последовательностями двоичных символов, а значения с большими абсолютными величинами - более длинными. Подробно правила выполнения этой операции здесь не рассматриваются.

В результате этих операций сокращается число двоичных символов, требуемых для представления информации о коэффициентах C_q(0,0) всех блоков.

Перед выполнением энтропийного кодирования остальных 63 квантованных коэффициентов ДКП в каждом блоке выполняется следующая подготовительная операция. Двумерная матрица коэффициентов преобразуется в одномерную последовательность путем считывания ее элементов в зигзагообразном порядке, как показано в табл. 4.3. По вертикали и по горизонтали показаны значения индексов к,1 коэффициентов C_q(k,l). В клетках таблицы показаны номера, которые получают эти коэффициенты в одномерной последовательности. Номер "0" в клетке, соответствующей C_q(0,0), показывает, что этот коэффициент в данной операции не участвует.

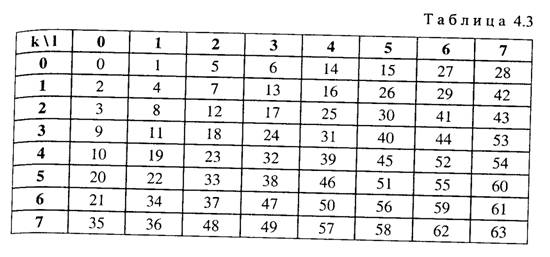
Как видно из табл. 4.3, первым следует коэффициент C_q(0,l), соответствующий самой низкочастотной составляющей по горизонтали, затем - C_q(l,0), а затем все более и более высокочастотные составляющие. Последовательность завершается специальным символом ЕОВ (end of block - конец блока).

Как отмечалось выше, в результате квантования многие из коэффициентов ДКП становятся равными 0, поэтому в получаемой одномерной последовательности этих коэффициентов оказывается большое число нулевых элементов. Каждый отличный от нуля коэффициент ДКП представляется в виде пары чисел. Первое из этих чисел показывает, сколько нулевых значений подряд прошло в последовательности перед данным ненулевым коэффициентом. Второе число в паре показывает значение самого квантованного коэффициента, преобразованное в число с переменным количеством бит. Правила этого преобразования аналогичны используемым при кодировании постоянных составляющих, т. е. коэффициенты с малыми абсолютными величинами представляются более короткими последовательностями   двоичных    символов,    а    коэффициенты с большими абсолютными величинами - более длинными.

Если в результате квантования получилось много нулевых и малых по абсолютной величине коэффициентов, кодирование по такому методу, называемому runlength coding ("кодирование с бегущей длиной"), дает значительный выигрыш, так как, во-первых, уменьшается общее количество чисел, представляющих кодируемый блок, а во-вторых, уменьшается число двоичных символов для представления большинства чисел.

Таким образом, для каждого блока 8x8 пикселов матрица квантованных коэффициентов ДКП оказалась преобразованной в последовательность двоичных чисел (называемых в соответствии с терминологией теории кодирования символами), которые затем подвергаются энтропийному кодированию.

Чаще всего применяется кодирование по методу Хаффмена, который заключается в построении такого кода с переменной длиной кодового слова, что чаще встречающимся (т. е. более вероятным) символам ставятся в соответствие более короткие кодовые слова, а реже встречающимся (менее вероятным) символам - более длинные кодовые слова. Это дает дополнительный выигрыш в сжатии информации.

Кодирование по Хаффмену выполняется с помощью таблицы кодов, в которой каждому символу кодируемой последовательности ставится в соответствие кодовое слово. Стандарт JPEG предусматривает возможность использования стандартной таблицы кодов "по умолчанию". Возможно и построение таблицы кодов, наиболее эффективной для данного изображения. В этом случае таблица кодов должна быть записана в файл, чтобы ее можно было использовать при декодировании.

В процессе декодирования кода Хаффмена кодовые слова, считываемые из файла сжатых видеоданных, преобразуются обратно в последовательность чисел, по которым восстанавливаются значения квантованных коэффициентов ДКП. Все операции, выполняемые при подготовке к энтропийному кодированию, и само это кодирование являются полностью обратимыми и не создают потерь информации, а достигаемое при них сжатие является следствием ранее выполненного квантования.

Вместо кодирования по Хаффмену может использоваться другой вид энтропийного кодирования, называемый арифметическим кодированием.                                                                          

ФОРМАТ ФАЙЛА JPEG

Сжатые видеоданные записываются в файл определенной структуры с расширением .jpg, о которой здесь даются только самые общие сведения.                                                                        

Файл начинается с заголовка, содержащего различные сведения о файле. Затем следует область данных об изображении, начинающаяся с маркера SOI (Start of Image). За этим маркером могут быть записаны таблицы квантования и таблица кодов для кодирования по Хаффмену. Затем следует заголовок изображения, в котором содержатся сведения о размерах изображения (в количестве пикселов), о характере изображения (черно-белое или цветное), о формате дискретизации и др. После этого следуют сами сжатые видеоданные. Область данных завершается маркером EOI (End of Image).

РЕАЛИЗАЦИЯ И РАЗЛИЧНЫЕ ВАРИАНТЫ JPEG

Метод JPEG реализуется, как правило, программными средствами на компьютерах. Основные области его применения: архивирование изображений на магнитных и оптических дисках, передача неподвижных изображений по каналам связи, запись отснятых кадров в электронных фотокамерах и др.

Многие графические программы, например популярная программа Adobe Photoshop, могут сжимать изображения методом JPEG, создавая файлы *.jpg, и декодировать такие изображения. Однако следует иметь в виду, что не все программы дают совместимые между собой форматы файлов.

На четвертой странице обложки для примера приведено изображение, верхний левый сектор которого взят из несжатого изображения. Правый верхний сектор взят из изображения, сжатого в восемь раз. Искажения практически не заметны. Правый нижний сектор взят из изображения, сжатого в 18 раз. Немного заметна блочная структура. Левый нижний сектор взят из изображения, сжатого в 25 раз. Блочная структура сильно заметна. Таким образом, по мере увеличения степени сжатия возрастает заметность блочной структуры, увеличиваются искажения яркости и цветности. Некоторые программы при декодировании и воспроизведении сжатых по стандарту JPEG изображений выполняют дополнительную фильтрацию (сглаживание) на границах блоков, чтобы уменьшить заметность блочной структуры.

JPEG может использоваться и для сжатия движущихся изображений. При этом каждый кадр кодируется независимо от других кадров. Такой метод, называемый Motion JPEG, может быть полезен для видеозаписи и в студийной аппаратуре, но он не дает достаточной степени сжатия видеоинформации для телевизионного вещания.

Существует также стандарт JPEG без потерь информации (Loseless JPEG), основанный на использовании кодирования с предсказанием по соседним элементам изображения. С описанным в настоящем разделе "обычным" стандартом JPEG его связывает лишь то, что он разработан той же организацией.

Стандарт JPEG развивается. Среди новых его возможностей следует отметить вариант с иерархическим кодированием, которое позволяет получить сначала, изображение с низким разрешением, используя небольшой объем сжатых видеоданных, а потом постепенно улучшать разрешение, добавляя дополнительные данные.

Операции, содержащиеся в стандарте JPEG, используются и в стандартах сжатия движущихся изображений MPEG, о которых пойдет речь в следующих разделах.

4.2. Стандарты сжатия движущихся изображений и звукового сопровождения MPEG-1 и MPEG-2

Стандарты сжатия движущихся изображений MPEG (Motion Picture Experts Group) вырабатываются и принимаются имеющей такое же название группой экспертов при Международной организации стандартизации ISO. Стандарт MPEG-1, используемый в основном при записи видеопрограмм на компакт-диски, был окончательно утвержден в 1993 г. [5-7], а стандарт MPEG-2, предназначенный в первую очередь для телевизионного вещания, был принят в ноябре 1994 г. [8-10].

Стандарты MPEG-1 и MPEG-2 имеют много общего, но между ними есть и различия. В данном разделе в основном излагается содержание стандарта MPEG-2, и указываются его отличия от MPEG-1.

4.2.1. Кодирование и декодирование движущихся изображений

Метод кодирования движущихся изображений, используемый в стандартах MPEG-1 и MPEG-2, называется гибридным, так как в нем сочетаются внутрикадровое (intraframe) кодирование,* направленное на уменьшение в основном психофизиологической избыточности в отдельных кадрах, и межкадровое (interframe) ко-дирование, с помощью которого уменьшается избыточность, обусловленная межкадровой корреляцией [6, 9]. Использование межкадрового кодирования позволяет получить существенно большую степень сжатия движущегося изображения, чем при раздельном сжатии отдельных кадров по методу JPEG.

Внутрикадровое кодирование содержит операции, аналогичные используемым в методе JPEG, т. е. поблочное дискретное косинусное преобразование, квантование и кодирование с переменной длиной кодовых слов. Межкадровое кодирование содержит операции оценки и компенсации движения и кодирования с предсказанием. Сущность этих операций, взятых по отдельности, была изложена в § 3.4 и 3.5.

Целые кадры и фрагменты кадров могут кодироваться с применением совместно межкадрового и внутрикадрового кодирования (для краткости этот случай далее называется просто межкадровым кодированием) или только с применением внутрикадрового кодирования.

ГРУППЫ ИЗОБРАЖЕНИЙ

Изображением (picture) в стандартах MPEG-1, MPEG-2 может быть как целый кадр, так и одно из полей кадра. Далее для упрощения изложения термин "кадр" используется вместо термина "изображение" везде за исключением подраздела, в котором специально говорится о кадровом и полевом режимах кодирования.

Последовательность кадров делится на группы, называемые GOP (group of pictire). В группе есть кадры трех типов:

- I-кадры (Intraframe - внутрикадровые), которые передаются только с внутрикадровым кодированием и являются опорными для декодирования остальных кадров группы, обеспечивая возможность начала декодирования и воспроизведения принятого ТВ-сигнала практически в любой момент времени;

- Р-кадры (Predictive - предсказанные), при передаче которых используется межкадровое кодирование путем предсказания с компенсацией движения по ближайшему предшествующему 1-кадру или Р-кадру (как будет пояснено далее, некоторые фрагменты Р-кадра могут кодироваться без предсказания с помощью внутри-кадрового кодирования);

-  В-кадры (Bidirectional - двунаправленные), которые передаются с межкадровым кодированием путем предсказания с компенсацией движения по ближайшим к ним как спереди, так и сзади I-кадрам и Р-кадрам, а сами не могут использоваться для предска-зания других кадров (некоторые фрагменты В-кадра могут кодироваться внутрикадровым методом).

Рассмотрим пример последовательности кадров.

Здесь кадры с 1 по 15 образуют группу кадров. Число кадров в группе может быть и другим, но она всегда начинается с 1-кадра. Р-кадр 4 предсказывается по 1-кадру 1, Р-кадр 7 - по Р-кадру 4, Р-кадр 10 - по Р-кадру 7 и т.д. 1-кадр 16 передается с внутрикадро-вым кодированием независимо от всех предшествующих ему кадров. В-кадры 2 и 3 предсказываются по 1-кадру 1 и по Р-кадру 4, В-кадры 5 и 6 - по Р-кадрам 4 и 7 и т.д. В-кадры 14 и 15 предсказываются по 1-кадру 16 и по Р-кадру 13. Перед кодированием порядок следования кадров изменяется, так как каждый В-кадр должен идти после обоих кадров, по которым он предсказывается.

В таком порядке кадры кодируются и передаются, а в процессе декодирования восстанавливается исходный порядок кадров.