ГЛАВА 5

ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА

МОДЕЛИРОВАНИЯ СИСТЕМ

Успех или неудача проведения имитационных экспериментов с моделями сложных систем существенным образом зависит от инструментальных средств, используемых  для   моделирования,   т.   е.   набора   аппаратно-программных средств, представляемых пользователю-разработчику или пользователю-исследователю машинной модели. В настоящее время существует большое количество языков имитационного моделирования — специальных языков программирования имитационных моделей на ЭВМ — и перед разработчиком машинной модели возникает проблема выбора языка, наиболее эффективного для целей моделирования конкретной системы. Языки моделирования заслуживают пристального внимания, так как, во-первых, число существующих языков и систем моделирования превышает несколько сотен и необходимо научиться ориентироваться в них, а во-вторых, почти каждый новый язык моделирования не только является средством, облегчающим доведение концептуальной модели до готовой машинной моделирующей программы, но и представляет собой новый способ «видения мира», т. е. построения моделей реальных систем. Необходимость эффективной реализации имитационных моделей предъявляет все более высокие требования как к инструментальным ЭВМ, так и к средствам организации информации в ЭВМ при моделировании. Поэтому с учетом использования новой информационной технологии в процессе моделирования следует учитывать особенности построения баз знаний и банков данных и систем управления ими.

5.1. ОСНОВЫ СИСТЕМАТИЗАЦИИ ЯЗЫКОВ ИМИТАЦИОННОГО          МОДЕЛИРОВАНИЯ

Использование современных ЭВМ и вычислительных комплексов и сетей является мощным средством реализации имитационных моделей и исследования с их помощью характеристик процесса функционирования систем S. В ряде случаев в зависимости от сложности объекта моделирования, т. е. системы S, рационально использование персональных ЭВМ (ПЭВМ) или локальных вычислительных сетей (ЛВС). В любом случае эффективность исследования системы S на программно-реализуемой модели М_ы прежде всего зависит от правильности схемы моделирующего алгоритма, совершенства программы и только косвенным образом зависит от технических характеристик ЭВМ, применяемой для моделирования. Большое значение при реализации модели на ЭВМ имеет вопрос правильного выбора языка моделирования.

Моделирование систем и языки программирования. Алгоритмические языки при моделировании систем служат вспомогательным аппаратом разработки, машинной реализации и анализа характеристик моделей. Каждый язык моделирования должен отражать определенную структуру понятий для описания широкого класса явлений. Выбрав для решения задачи моделирования процесса функционирования системы конкретный язык, исследователь получает в распоряжение тщательно разработанную систему абстракций, предоставляющих ему основу для формализации процесса функционирования исследуемой системы 5. Высокий уровень проблемной ориентации языка моделирования значительно упрощает программирование моделей, а специально предусмотренные в нем возможности сбора, обработки и вывода результатов моделирования позволяют быстро и подробно анализировать возможные исходы имитационного эксперимента с моделью М_м.

Основными моментами, характеризующими качество языков моделирования, являются: удобство описания процесса функционирования системы S, удобство ввода исходных данных моделирования и варьирования структуры, алгоритмов и параметров модели, реализуемость статистического моделирования, эффективность анализа и вывода результатов моделирования, простота отладки и контроля работы моделирующей программы, доступность восприятия и использования языка. Будущее языков моделирования определяется прогрессом в области создания мультимедийных систем машинной имитации, а также проблемно-ориентированных на цели моделирования информационно-вычислительных систем [17, 31, 41,46].

Рассмотрим основные понятия, связанные с алгоритмическими языками и их реализацией на ЭВМ вообще и языками моделирования в частности.

Язык программирования представляет собой набор символов, распознаваемых ЭВМ и обозначающих операции, которые можно реализовать на ЭВМ. На низшем уровне находится основной язык машины, программа на котором пишется в кодах, непосредственно соответствующих элементарным машинным действиям (сложение, запоминание, пересылка по заданному адресу и т. д.). Следующий уровень занимает автокод (язык АССЕМБЛЕРА) вычислительной машины. Программа на автокоде составляется из мнемонических символов, преобразуемых в машинные коды специальной программой — ассемблером.

Компилятором называется программа, принимающая инструкции, написанные на алгоритмическом языке высокого уровня, и преобразующая их в программы на основном языке машины или на автокоде, которые в последнем случае транслируются еще раз с помощью ассемблера.

Интерпретатором называется программа, которая, принимая инструкции входного языка, сразу выполняет соответствующие oneрации в отличие от компилятора, преобразующего эти инструкции в запоминающиеся цепочки команд. Трансляция происходит в течение всего времени работы программы, написанной на языке интерпретатора. В отличие от этого компиляция и ассемблирование представляют собой однократные акты перевода текста с входного языка на объектный язык машины после чего полученные программы выполняются без повторных обращений к транслятору.

Программа, составленная в машинных кодах или на языке АССЕМБЛЕРА, всегда отражает специфику конкретной ЭВМ. Инструкции такой программы соответствуют определенным машинным операциям и, следовательно, имеют смысл только в той ЭВМ, для которой они предназначены, поэтому такие языки называются машинно-ориентированными языками.

Большинство языков интерпретаторов и компиляторов можно классифицировать как процедурно-ориентированные языки. Эти языки качественно отличаются от машинно-ориентированных языков, описывающих элементарные действия ЭВМ и не обладающих проблемной ориентацией. Все процедурно-ориентированные языки предназначены для определенного класса задач, включают в себя инструкции, удобные для формулировки способов решения типичных задач этого класса. Соответствующие алгоритмы программируются в обозначениях, не связанных ни с какой ЭВМ.

Язык моделирования представляет собой процедурно-ориентированный язык, обладающий специфическими чертами. Основные языки моделирования разрабатывались в качестве программного обеспечения имитационного подхода к изучению процесса функционирования определенного класса систем [31].

Особенности использования алгоритмических языков. Рассмотрим преимущества и недостатки использования для моделирования процесса функционирования систем языков имитационного моделирования (ЯИМ) и языков общего назначения (ЯОН), т. е. универсальных и процедурно-ориентированных алгоритмических языков. Целесообразность использования ЯИМ вытекает из двух основных причин: 1) удобство программирования модели системы, играющее существенную роль при машинной реализации моделирующих алгоритмов; 2) концептуальная направленность языка на класс систем, необходимая на этапе построения модели системы и выборе общего направления исследований в планируемом машинном эксперименте. Практика моделирования систем показывает, что именно использование ЯИМ во многом определило успех имитации как метода экспериментального исследования сложных реальных объектов.

Языки моделирования позволяют описывать моделируемые системы в терминах, разработанных на базе основных понятий имитации. До того как эти понятия были четко определены и формализованы в ЯИМ, не существовало единых способов описания имитационных задач, а без них не было связи между различными- разработками в области постановки имитационных экспериментов. Высокоуровневые языки моделирования являются удобным средством общения заказчика и разработчика машинной модели М_м.

Несмотря на перечисленные преимущества ЯИМ, в настоящее время выдвигаются основательные аргументы как технического, так и эксплуатационного характера против полного отказа при моделировании от универсальных и процедурно-ориентированных языков. Технические возражения против использования ЯИМ: вопросы эффективности рабочих программ, возможности их отладки и т. п. В качестве эксплуатационных недостатков упоминается нехватка документации по существующим ЯИМ, сугубо индивидуальный характер соответствующих трансляторов, усложняющий их реализацию на различных ЭВМ, и трудности исправления ошибок. Снижение эффективности ЯИМ проявляется при моделировании задач более разнообразных, чем те, на которые рассчитан конкретный язык моделирования. Но здесь следует отметить, что в настоящее время не существует и ЯОН, который был бы эффективен при решении задач любого класса.

Серьезные недостатки ЯИМ проявляются в том, что в отличие от широко применяемых ЯОН, трансляторы с которых включены в поставляемое изготовителем математическое обеспечение всех современных ЭВМ, языки моделирования, за небольшим исключением, разрабатывались отдельными организациями для своих достаточно узко специализированных потребностей. Соответствующие трансляторы плохо описаны и приспособлены для эксплуатации при решении задач моделирования систем, поэтому, несмотря на достоинства ЯИМ, приходится отказываться от их практического применения в ряде конкретных случаев.

При создании системы моделирования на базе любого языка необходимо решить вопрос о синхронизации процессов в модели, так как в каждый момент времени, протекающего в системе (системного времени), может потребоваться обработка нескольких событий, т. е. требуется псевдопараллельная организация имитируемых процессов в машинной модели М_м. Это является основной задачей монитора моделирования, который выполняет следующие функции: управление процессами (согласование системного и машинного времени) и управление ресурсами (выбор и распределение в модели ограниченных средств моделирующей системы).

Подходы к разработке языков моделирования. К настоящему времени сложились два различных подхода к разработке языков моделирования: непрерывный и дискретный — отражающие основные особенности исследуемых методом моделирования систем [35, 43, 46]. Поэтому ЯИМ делятся на две самостоятельные группы, которые соответствуют двум видам имитации, развивавшимся независимо друг от друга: для имитации непрерывных и дискретных процессов.

Для моделирования непрерывных процессов могут быть использованы не только АВМ, но и ЭВМ, последние при соответствующем программировании имитируют различные непрерывные процессы. При этом ЭВМ обладают большей надежностью в эксплуатации и позволяют получить высокую точность результатов, что привело к разработке языков моделирований, отображающих модель в виде блоков таких типов, которые играют роль стандартных блоков АВМ (усилителей, интеграторов, генераторов функций и т. п.). Заданная схема моделирующего алгоритма преобразуется в систему совместно рассматриваемых дифференциальных уравнений. Моделирование в этом случае сводится, по сути дела, к отысканию численных решений этих уравнений при использовании некоторого стандартного пошагового метода.

Примером языка моделирования непрерывных систем на ЭВМ путем представления моделируемой системы в виде уравнений в конечных разностях является язык DYNAMO, для которого уравнения устанавливают соотношения между значениями функций в моменты времени t и t+dt и между значениями их производных в момент времени t+dt/2. И в этом случае моделирование, по существу, представляет собой пошаговое решение заданной системы дифференциальных уравнений [46].

Универсальная ЭВМ — устройство дискретного типа, а поэтому должна обеспечивать дискретную аппроксимацию процесса функционирования исследуемой системы S. Непрерывные изменения в процессе функционирования реальной системы отображаются в дискретной модели М_м, реализуемой на ЭВМ, некоторой последовательностью дискретных событий, и такие модели называются моделями дискретных событий. Отдельные события, отражаемые в дискретной модели, могут определяться с большой степенью приближения к действительности, что обеспечивает адекватность таких дискретных моделей реальным процессам, протекающим в системах S.

Архитектура языков моделирования. Архитектуру ЯИМ, т. е. концепцию взаимосвязей элементов языка как сложной системы, и технологию перехода от системы S к ее машинной модели М_ы можно представить следующим образом: 1) объекты моделирования (системы S) описываются (отображаются в языке) с помощью некоторых атрибутов языка; 2) атрибуты взаимодействуют с процессами, адекватными реально протекающим явлениям в моделируемой системе S; 3) процессы требуют конкретных условий, определяющих логическую основу и последовательность взаимодействия этих процессов во времени; 4) условия влияют на события, имеющие место внутри объекта моделирования (системы 5) и при взаимодействии с внешней средой Е; 5) события изменяют состояния модели системы М в пространстве и во времени.

    Типовая схема архитектуры ЯИМ и технология его использования при моделировании систем показана на рис. 5.1.

В большинстве случаев с помощью машинных моделей исследуются характеристики и поведение системы S на определенном отрезке времени, поэтому одной из наиболее важных задач при создании модели системы и выборе языка программирования модели является реализация двух функций: 1) корректировка временной координаты состояния системы («продвижение» времени, организация «часов»); 2) обеспечение согласованности различных блоков и событий в системе (синхронизация во времени, координация

с другими блоками).

Таким образом, функционирование модели М_м должно протекать в искусственном (не в реальном и не в машинном) времени, обеспечивая появление событий в требуемом логикой работы исследуемой системы порядке и с надлежащими временными интервалами между ними. При этом надо учитывать, что элементы реальной системы S функционируют одновременно (параллельно), а компоненты машинной модели М_м действуют последовательно, так как реализуются с помощью ЭВМ последовательного действия. Поскольку в различных частях объекта моделирования события могут возникать одновременно, то для сохранения адекватности причинно-следственных временных связей необходимо в ЯИМ создать «механизм» задания времени для синхронизации действий элементов модели системы [17, 46].

Задание времени в машинной модели. Как уже отмечалось в гл. 3, существует два основных подхода к заданию времени: с помощью постоянных и переменных интервалов времени, которым соответствуют два принципа реализации моделирующих алгоритмов, т. е. "принцип Δt" и "принцип δz".

Рассмотрим соответствующие спрособы управления временем в модели системы M(S) на примере, показанном на рис. 5.2, где по оси реального времени отложена последовательность событий в системе {s_i} во времени, причем события s₄ и s₅ происходят одновременно (рис. 5.2, а). Под действием событий s_i изменяются состояния модели z_i в момент времени t_zi, причем такое изменение происходит скачком δz.

В модели, построенной по "принципу Δt" (рис. 5.2, б), моменты системного времени будут последовательно принимать значения t ^'₁ = Δt , t ^'₂ = 2Δt , t ^'₃ = 3Δt, t ^'₄ = 4Δt, t ^'₅ = 5Δt. Эти моменты системного времени t ^'_j (Δt) никак не связаны с моментами появления событий s_i, которые имитируются в модели системы. Системное время при этом получает постоянное приращение, выбираемое в задаваемое перед началом имитационного эксперимента.

В модели, построенной по "принципу δz" (рис. 5.2, в), изменение времени наступает в момент смены состояния системы, и последовательность моментов системного времени имеет вид t^''₁ = t_z1, t^''₂ = t_z2, t^''₃ = t_z3, t^''₄ = t_z4, t^''₅ = t_z5, т. е. моменты системного времени t^''_k (δz), непосредственно связаны с моментами появления событий в системе s_i.

У каждого из этих методов есть свои преимущества с точки зрения адекватного отражения реальных событий в системе S и затрат машинных ресурсов на моделирование. При использовании «принципа δz» события обрабатываются последовательно и время смещается каждый раз вперед до начала следующего события. В модели, построенной по «принципу Δt», обработка событий происходит по группам, пакетам или множествам событий. При этом выбор Δt оказывает существенное влияние на ход процесса и результаты моделирования, и если Δt задана неправильно, то результаты могут получиться недостоверными, так как все события появляются в точке, соответствующей верхней границе каждого интервала моделирования. При применении «принципа δz» одновременная обработка событий в модели имеет место только тогда, когда эти события появляются одновременно и в реальной системе. Это позволяет избежать необходимости искусственного введения ранжирования событий при их обработке в конце интервала At.

При моделировании по «принципу Δt» можно добиться хорошей аппроксимации: для этого Δt должно быть малым, чтобы два неодновременных события не попали в один и тот же временной интервал. Но уменьшение Δt приводит к увеличению затрат машинного времени на моделирование, так как значительная часть тратится на корректировку «часов» и отслеживание событий, которых в большинстве интервалов может и не быть. При этом даже при сильном «сжатии» Δt два неодновременных события могут попасть в один и тот же временной интервал Δt , что создает ложное представление об их одновременности.

Для выбора принципа построения машинной модели М_м и соответственно ЯИМ необходимо знать: цель и назначение модели; требуемую точность результатов моделирования; затраты машинного времени при использовании того или иного принципа; необходимый объем машинной памяти для реализации модели, построенной по принципу Δt и δz; трудоемкость программирования модели и ее отладки.

Требования к языкам имитационного моделирования. Таким образом, при разработке моделей систем возникает целый ряд специфических трудностей, поэтому в ЯИМ должен быть предусмотрен набор таких программных средств и понятий, которые не встречаются в обычных ЯОН.

Совмещение. Параллельно протекающие в реальных системах S процессы представляются с помощью последовательно работающей ЭВМ. Языки моделирования позволяют обойти эту трудность путем введения понятия системного времени, используемого для представления упорядоченных во времени событий.

Размер. Большинство моделируемых систем имеет сложную структуру и алгоритмы поведения, а их модели велики по объему. Поэтому используют динамическое распределение памяти, когда компоненты модели системы М_м появляются в оперативной памяти ЭВМ или покидают ее в зависимости от текущего состояния. Важным аспектом реализуемости модели М_м на ЭВМ в этом случае является блочность ее конструкции, т. е. возможность разбиения модели на блоки, подблоки и т. д.

Изменения. Динамические системы связаны с движением и характеризуются развитием процесса, вследствие чего пространственная конфигурация этих систем претерпевает изменения по времени. Поэтому во всех ЯИМ предусматривают обработку списков, отражающих изменения состояний процесса функционирования моделируемой системы S.

Взаимосвязанность. Условия, необходимые для свершения различных событий в модели М_м процесса функционирования системы S, могут оказаться весьма сложными из-за наличия большого количества взаимных связей между компонентами модели. Для разрешения связанных с этим вопросом трудностей в большинство ЯИМ включают соответствующие логические возможности и понятия теории множеств.

Стохастичность. Для моделирования случайных событий и процессов используют специальные программы генерации последовательностей псевдослучайных чисел, квазиравномерно распределенных на заданном интервале, на основе которых можно получить стохастические воздействия на модель М_м, имитируемые случайными величинами с соответствующим законом распределения.

Анализ. Для получения наглядного и удобного в практическом отношении ответа на вопросы, решаемые методом машинного моделирования, необходимо получать статистические характеристики процесса функционирования модели системы M(S). Поэтому предусматривают в языках моделирования способы статистической обработки и анализа результатов моделирования.

Перечисленным требованиям при исследовании и проектировании различных систем S отвечают такие наиболее известные языка моделирования дискретных событий, как SIMULA, SIMSCRIPT, GPSS, SOL, CSL и др.

5.2. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЯЗЫКОВ

ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

За сравнительно небольшой срок в области машинного моделирования систем произошел скачок, который был обусловлен потребностью в принципиально новом методе исследования и развитием средств вычислительной техники и который в первую очередь выразился в увеличении количества специализированных ЯИМ, причем этот процесс имеет лавинообразный характер. К настоящему времени насчитывается несколько сотен развитых ЯИМ, поэтому очень важно разобраться в этом многообразии ЯИМ и выбрать для моделирования конкретной системы S наиболее эффективный язык [17, 31, 37, 46].

Основы классификации языков моделирования. Как уже отмечалось, для машинного моделирования системы S пригодны три способа проведения вычислений, в основе которых лежит применение цифровой, аналоговой и гибридной вычислительной техники. Рассмотрим методы моделирования систем с точки зрения использования языков программирования. При этом в данном параграфе опустим рассмотрение чисто аналоговых способов вычислений, так как они реализуются не программно, а путем составления электрических цепей, т. е. когда язык программирования не требуется (не обсуждая вопросы программирования АВМ). По этой же причине не будем рассматривать использование ЯИМ при гибридных методах вычислений. Тогда классификация языков для программирования моделей систем имеет вид, приведенный на рис. 5.3.

Для моделирования систем используются как универсальные и процедурно-ориентированные ЯОН, так и специализированные ЯИМ. При этом ЯОН предоставляют программисту-разработчику модели М_м больше возможностей в смысле гибкости разработки, отладки и использования модели. Но гибкость приобретается ценой больших усилий, затрачиваемых на программирование модели, так как организация выполнения операций, отсчет системного времени и контроль хода вычислений существенно усложняются.

Имеющиеся ЯИМ можно разбить на три основные группы, соответствующие трем типам математических схем: непрерывные, дискретные и комбинированные. Языки каждой группы предназначены для соответствующего представления системы S при создании ее машинной модели М_м.

В основе рассматриваемой классификации в некоторых ЯИМ лежит   принцип   формирования   системного   времени.   Так   как

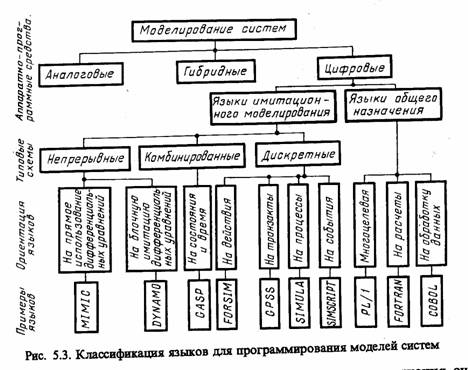
«системные часы» предназначены не только для продвижения системного времени в модели М_м, но также для синхронизации различных событий и операций в модели системы S, то при отнесении того или иного конкретного языка моделирования к определенному типу нельзя не считаться с типом механизма «системных часов».

Непрерывное представление системы S сводится к составлению уравнений, с помощью которых устанавливается связь между эндогенными и экзогенными переменными модели. Примером такого непрерывного подхода является использование дифференциальных уравнений. Причем в дальнейшем дифференциальные уравнения могут быть применены для непосредственного получения характеристик системы, это, например, реализовано в языке MIMIC. А в том случае, когда экзогенные переменные модели принимают дискретные значения, уравнения являются разностными. Такой подход реализован, например, в языке DYNAMO.

Представление системы 5 в виде типовой схемы, в которой участвуют как непрерывные, так и дискретные величины, называется комбинированным. Примером языка, реализующего комбинированный подход,  является GASP, построенный на базе языка FORTRAN. Язык GASP включает в себя набор программ, с помощью которых моделируемая система S представляется в следующем виде. Состояние модели системы M(S) описывается набором  переменных, некоторые из которых меняются во времени непрерывно. Законы изменения непрерывных компонент заложены в структуру, объединяющую дифференциальные уравнения и условия относительно переменных.. Предполагается, что в системе могут наступать события двух типов: 1) события, зависящие от состояния:, 2) события, зависящие от времени ,. События первого типа настушвают в результате выполнения условий, относящихся к законам изменения непрерывных переменных. Для событий второго типа процесс^; моделирования состоит в продвижении системного времени от момента наступления события до следующего аналогичного момента, События приводят к изменениям состояния модели системы и законов изменения непрерывных компонент. При использовании язын GASP на пользователя возлагается работа по составлению на язык FORTRAN подпрограмм, в которых он описывает условия наступления событий, зависящих от процесса функционирования системы S, законы изменения непрерывных переменных, а также правила перехода из одного состояния в другое.

Языки моделирования дискретных систем. В рамках дискретном подхода можно  выделить  несколько  принципиально разлита групп ЯИМ. Первая группа ЯИМ подразумевает наличие списка событий, отличающих моменты начала выполнения операций, Продвижение времени осуществляется по событиям, в момента наступления которых производятся необходимые операции, включая операции пополнения списка событий. Примером языка событий является язык SIMSCRIPT. Разработчики языка SIMSCR1FJ исходили из того, что каждая модель М_м состоит из элементов, с которыми происходят события, представляющие собой последовательность предложений, изменяющих состояния моделируемой системы в различные моменты времени. Моделирование с помощью языка SIMSCRIPT включает в себя следующие этапы: а) элементы моделируемой системы S описываются и вводятся с помощью карт определений; б) вводятся начальные условия; в) фиксируются и вводятся исходные значения временных параметров; г) составляются подпрограммы для каждого события; д) составляете  перечень событий и указывается время свершения каждого эндогенного события. Команды языка SIMSCRIPT группируются следующим образом: операции над временными объектами, арифметические и логические операции и команды управления, команды ввода-вывода, специальные команды обработки результатов. К центральным понятиям языка SIMSCRIPT относятся обработка списков с компонентами, определяемыми пользователем, и последовательность событий в системном времени. При этом имеются специальные языковые средства для работы с множествами.

При использовании ЯИМ второй группы после пересчета системного времени, в отличие от схемы языка событий, просмотр действий с целью проверки выполнения условий начала или окончания какого-либо действия производится непрерывно. Просмотр действий определяет очередность появления событий. Языки данного типа имеют в своей основе поисковый алгоритм, и динамика

-системы S описывается в терминах действий. Примером языка действий (работ) является ЯИМ FORSIM, представляющий собой пакет прикладных программ, который позволяет оперировать только фиксированными массивами данных, описывающих объекты моделируемой системы. С его помощью нельзя имитировать системы переменного состава. При этом размеры массивов устанавливаются либо во время компиляции программы, либо в самом начале ее работы.

Язык FORSIM удобен для описания систем с большим числом разнообразных ресурсов, так как он позволяет записывать условия их доступности в компактной форме. Конкретный способ формализации модели на языке действий в достаточной степени произволен и остается на усмотрение программиста, что требует его достаточно высокой квалификации. Полное описание динамики модели М_м можно получить с помощью разных наборов подпрограмм

Третья группа ЯИМ описывает системы, поведение которых определяется процессами. В данном случае под процессом понимается последовательность событий, связь между которыми устанавливается с помощью набора специальных отношений. Динамика заложена в независимо управляемых программах, которые в совокупности составляют программу процесса. Пример языка процессов — язык SIMULA, в котором осуществляется блочное представление моделируемой системы 5 с использованием понятия процесса для формализации элементов, на которые разбивается моделируемая система. Процесс задается набором признаков, характеризующих его структуру, и программой функционирования. Функционирование каждого процесса разбивается на этапы, протекающие в системном времени.

Главная роль в языке SIMULA отводится понятию параллельного оперирования с процессами в системном времени, а также универсальной обработке списков с процессами в роли компонент. Специальные языковые средства предусмотрены для манипуляций с упорядоченными множествами процессов.

В отдельную группу могут быть выделены ЯИМ типа GPSS, хотя принципиально их можно отнести к группе языков процессов. Язык GPSS представляет собой интерпретирующую языковую систему, применяющуюся для описания пространственного движения объектов. Такие динамические объекты в языке GPSS называются транзактами и представляют собой элементы потока. В процессе имитации транзакты «создаются» и «уничтожаются». Функцию каждого из них можно представить как движение через модель М_м с поочередным воздействием на ее блоки.       Функциональный аппарат языка образуют блоки, описывающие логику модели, сообщая транзактам, куда двигаться и что делать дальше. Данные для ЭВМ подготавливаются в виде пакета управляющих и определяющих карт, который составляется по схеме модели, набранной из стандартных символов. Созданная GPSS-nporpmm, работая в режиме интерпретации, генерирует и передает транзакты из блока в блок в соответствии с правилами, устанавливаемыми блоками. Каждый переход транзакта приписывается к определенному моменту системного времени.

Сравнение эффективности языков. При анализе эффективности использования для моделирования конкретной системы S того или иного ЯИМ (или ЯОН) выделяют несколько важных свойств языков: возможность описания структуры и алгоритмов поведения исследуемой системы S в терминах языка; простота применения для построения модели М, ее машинной реализации и обработки результатов моделирования; предпочтение пользователя, обычно отдаваемое языку, который ему более знаком или который обладает большей степенью универсальности, и т. д. При этом, естественно, большее количество команд ЯИМ обеспечивает лучшие возможности при написании программы моделирования. Однако вместе с увеличением числа команд возрастают трудности использования ЯИМ, поэтому пользователь обычно отдает предпочтение языкам, обладающим большей гибкостью при минимальном количестве команд.

Исходя из этих соображений, приводились экспертные оценки для сравнения различных языков при моделировании широкого класса систем. Результаты оценок сведены в табл. 5.1. Языки даны в порядке уменьшения их эффективности.

Перечисленные особенности ЯИМ во многом определяют возможности выбора того или иного языка для целей проведения имитационного эксперимента с моделью системы S, причем в каждом конкретном случае на выбор языка моделирования оказывают влияние многие факторы его практической реализации. Задачи выбора ЯИМ должны рассматриваться как одна из комплекса задач, решаемых при автоматизации процесса моделирования систем с использованием современных ЭВМ [7, 12, 25, 34].

Выбор языка моделирования системы. Основываясь на классификации языков (рис. 5.3) и исходя из оценки эффективности (табл. 5.1), можно рассмотреть подход к выбору языка для решения задачи машинного моделирования конкретной системы S. Такой подход можно представить в виде дерева решений с соответствующими комментариями (рис. 5.4). Перед тем как пользоваться деревом

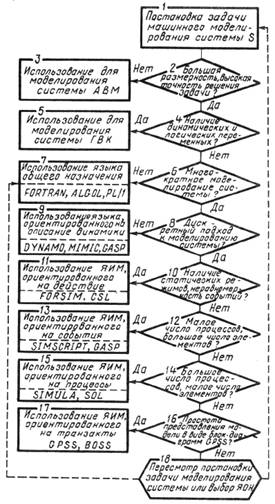
Рис. 5.4. Дерево решений выбора языка для моделирования системы

решений, разработчику машинной модели М_м необходимо выполнить все подэтапы первого этапа (построение концептуальной модели системы и ее формализация), а также предшествующие данному 6-му подэтапу подэтапы 2-го этапа (алгоритмизация модели и ее машинная реализация) (см. рис. 3.1). Приход в тот или иной конечный (нечетный) блок схемы дерева решений (рис. 5.4) означает рекомендацию более подробно рассмотреть указанные в нем технические средства или языки (ЯИМ и ЯОН), причем здесь для иллюстрации приведены лишь примеры основных языков, употребляемых наиболее часто при моделировании систем.

Исходя из постановки задачи машинного моделирования конкретной системы S, поставленных целей, выбранных критериев оценки эффективности и заданных ограничений (блок 1), можно сделать вывод о размерности задачи моделирования и требуемой точности и достоверности ее решения (блок 2). Для задач большой размерности моделирования на АВМ (блок 3) позволяет получить достаточно высокую точность. При этом АВМ позволит наглядно выявить компромисс между сложностью и точностью модели М, проиллюстрирует влияние изменения параметров и переменных на характеристики модели системы и т. п. Если в модели М при моделировании системы S имеют место как непрерывные, так и дискретные переменные, отражающие динамику системы и логику ее поведения (блок 4), то рекомендуется использовать для моделирования ГВК (блок 5). Подробно особенности и возможности применения гибридных (аналого-цифровых) моделирующих комплексов рассмотрены в § 5.5.

Если моделирование конкретной системы S представляет собой единичный акт (блок б), то, вероятно, в ущерб концептуальной выразительности модели М_х и отладочным средствам для проверки логики машинной модели М_м следует выбрать более распространенные и более гибкие ЯОН (блок 7). Очевидно, на выбор конкретного языка существенно повлияют специфика модели М (особенности процесса функционирования системы S) и квалификация пользователя в программировании на конкретном языке.

Если при моделировании на универсальной ЭВМ выбран непрерывный подход (блок 8), то следует остановить выбор на одном из языков, позволяющих отразить динамику системы при наличии обратных связей (блок 9). При этом могут быть приняты языки непрерывного типа DYNAMO, MIMIC либо комбинированные (дискретно-непрерывные) — GASP.

Если в основу модели М положена дискретная математическая схема и в ней при построении моделирующего алгоритма используется «принцип Δt » (постоянный шаг во времени) или «принцип δz» (переменный шаг во времени, задаваемый сменой состояний), причем имитируются взаимодействующие элементы статической природы при неравномерности событий во времени (блок 10), то рационально воспользоваться ЯИМ, ориентированным на действия, например FORSIM, CSL.

Если в модели М описывается малое число взаимодействующих процессов и имеется большое число элементов (блок 12), то целесообразно выбрать для построения моделирующих алгоритмов «принцип At» и остановиться на ЯИМ событий (блок 13), например SIMSCRIPT. GASP и т. п.

Если для программирования модели более эффективен ЯИМ, позволяющий описать большое число взаимодействующих процессов (блок 14), то следует использовать языки процессов (блок 15), которые не связаны с использованием блоков только определенных типов, например в транзактных языках. Наиболее распространенными языками описания процессов являются языки SIMULA и SOL.

И наконец, если предпочтение отдается блочной конструкции модели М при наличии минимального опыта в программировании (блок 16), то следует выбирать ЯИМ транзактов типа GPSS, BOSS (блок 17), но при этом надо помнить, что они негибки и требуют большого объема памяти и затрат машинного времени на прогон программ моделирования.

Если перечисленные средства по той или иной причине не подходят для целей моделирования конкретной системы S (блок 18), то надо снова провести модификацию модели М либо попытаться решить задачу с использованием ЯОН на универсальной ЭВМ.

5.3. ПАКЕТЫ ПРИКЛАДНЫХ ПРОГРАММ МОДЕЛИРОВАНИЯ

СИСТЕМ

Метод машинного моделирования все глубже входит в практику решения конкретных задач исследования и проектирования систем, ходит свое применение для широкого круга проблем в различных сферах (автоматизированные системы управления, системы автоматизации научных исследований и экспериментов, информационно-вычислительные системы и сети коллективного пользования, системы автоматизированного проектирования и т. д.). В решение этих задач вовлекается все большее количество специалистов разных квалификаций, часто далеких от использования средств вычислительной техники. Поэтому для таких пользователей должны быть разработаны специальные средства подготовки и общения с ЭВМ, позволяющие автоматизировать этот трудоемкий процесс [17,37].

Таким образом, возникает вопрос о создании автоматизированной системы моделирования (АСМ), которая должна повысить эффективность выполнения пользователем следующей совокупности процедур: преобразование к типовым математическим схемам элементов моделируемой системы S и построение схем сопряжения; обработка и анализ результатов моделирования системы S; реализация интерактивного режима с пользователем в процессе моделирования системы S.

Понятие пакета прикладных программ. Создание проблемно-ориентированных комплексов, в том числе и АСМ, называемых пакетами прикладных программ, является важным направлением работ в современной вычислительной математике. При создании пакетов прикладных программ моделирования (ППМ) помимо разработки и отбора моделирующих алгоритмов и программ существенное место занимают работы по соответствующему системному обеспечению. Быстрота и удобство решения задач моделирования конкретных классов систем S при использовании ППМ достигаются сочетанием в единой архитектуре функционального наполнения, состоящего из модулей и покрывающего предметную область моделирования, и специализированных средств системного обеспечения, позволяющих сравнительно легко реализовать различные задания и обеспечивающих пользователя разнообразным сервисом при подготовке задач моделирования и проведении машинных экспериментов с моделью М_м.

Характерно, что в ходе разработки и машинного эксперимента модель объекта претерпевает многочисленные изменения, которые неизбежно влекут за собой изменения соответствующих рабочих программ. В настоящее время ППМ является практически единственной приемлемой формой организации программ моделирования, позволяющей «удержаться на плаву» в безбрежном море версий и вариантов исходной концептуальной модели. Кроме того, пакетная организация программ машинного эксперимента с моделью с лью М_м дает возможность систематизировать выполнение исследований, используя теорию планирования экспериментов и способствуя тем самым повышению достоверности получаемых результата моделирования конкретной системы S.

Одной из важных проблем в области использования вычислительной техники для моделирования систем является проблема общения человека с ЭВМ при разработке модели и ее эксплуатации Для повышения эффективности такого общения требуются соответствующие алгоритмы и программные средства. Здесь можно выдылить три направления работ: 1) создание программных среден обеспечивающих пользователя различными инструментами для аи томатизации разработки  программ;   2)  создание программш средств, упрощающих процесс эксплуатации сетей ЭВМ инженера диспетчерским персоналом, а также обеспечивающих эффективна использование всех вычислительных ресурсов; 3) создание программных средств, предоставляющих пользователям разнообрау ные услуги при решении прикладных задач. Эти три направлена сводятся соответственно к повышению уровня инструментальном исполнительной и тематической квалификации вычислительной машины.

Таким образом, пакеты прикладных программ являются одна из основных форм специализированного программного обеспечения. НИМ — это комплекс взаимосвязанных программ моделирования и средств системного обеспечения (программных и языювых), предназначенных для автоматизации решения задач моделирования. Весь круг работ, связанных с разработкой алгоритма и программ моделирования, а также с подготовкой и проведением машинных экспериментов, называется автоматизацией моделирования и реализуется в виде конкретных АСМ.

В структуре НИМ можно выделить три основных компонент функциональное наполнение, язык заданий и системное наполнение

Функциональное наполнение пакета. Функциональное наполнен» ППМ отражает специфику предметной области применительно к конкретному объекту моделирования, т. е. системе S, и представляет собой совокупность модулей. Под модулем здесь понимаете конструктивный элемент, используемый на различных стадиях функционирования пакета. Язык (языки), на котором записываются модули функционального наполнения, будем называть базовым языком ППМ. Состав функционального наполнения пакета, его мощность или полнота охвата им предметной области отражают объем прикладных знаний, заложенных в ППМ, т. е. потенциальный уровень тематической квалификации пакета.

Одной из ключевых проблем разработки ППМ является модуляризация, т. е. разбиение функционального наполнения пакета на модули. Тщательно выполненный анализ объекта моделирования и проведенная на его основе модуляризация позволяют сократить  объем работ по реализации ППМ, повышают его надежность и облегчают дальнейшую эволюцию пакета.

Число разнообразных форм модулей, используемых в пакетах, весьма велико. Прежде всего следует выделить программные модули, модули данных и модули документации. Для программных модулей известны, например, такие формы, как подпрограмма; конструкция алгоритмического языка, допускающая автономную трансляцию; макроопределение; файл, содержащий такой текст фрагмента программы, который рассматривается как самостоятельный объект для изучения или редактирования; набор указаний, задающих способ построения конкретной версии программы; реализация абстрактного типа данных и др.

Уточним, что понимается под конструктивностью модуля. Прежде всего имеется в виду алгоритмическая конструктивность, так как модуль представляет собой элемент полученного в результате модульного анализа предметной области алгоритмического базиса, служащего основой для построения программ моделирования. Кроме того, на алгоритмическую конструктивность модулей влияют структуры типичных вычислительных алгоритмов, связи между элементами алгоритмического базиса, используемые в этих структурах, информационные потоки.

Помимо алгоритмической следует выделить и технологическую конструктивность модулей, определяемую дисциплиной работы в конкретной машинной модели М_м и системной средой, на базе которой разрабатывается и эксплуатируется ППМ. На технологическую конструктивность воздействуют такие факторы:

— формы представления программных модулей М_м;

— виды управляющих связей между отдельными частями программных комплексов (открытые и закрытые подпрограммы);

— методы разработки (сверху вниз, снизу вверх и др.) программных комплексов, применяемые при работе с моделирующим алгоритмом системы S;

— базовый язык или языки программирования, используемые при подготовке программ моделирования;

— ограничения на размеры программ моделирования;

— возможности штатных системных средств, обеспечивающих редактирование связей, загрузку и сегментацию программных комплексов, редактирование текстов.

Требования, вытекающие из алгоритмической и технологической конструктивности, составляют в совокупности регламент модуляризации, т. е. принятую разработчиками пакета форму представления материала в функциональном наполнении, а также способы его создания и эволюции. Если описание языка заданий рассматривать как спецификацию сопряжения пользователя с пакетом, то посредством регламента модуляризации определяется сопряжение с пакетом (точнее, с функциональным наполнением пакета) его разработчиков.

 Язык заданий пакета. Язык заданий ППМ является средством общения пользователя (разработчика или исследователя машинной модели М_ы процесса функционирования системы S) с пакетом . Он позволяет описывать последовательность выполнения различных операций, обеспечивающих решение задачи моделирования, или постановку задачи моделирования, которой эта последовательность строится автоматически. Архитектура ППМ, т. е. предоставляющийся пользователю внешний вид АСМ, определяется тем, какие задачи система может решать и какие возможности дает она пользователю. Язык заданий отражает основные архитектурные решения, принятые разработчиками ППМ, стремившимися повысить уровень квалификации вычислительной системы в определенной прикладной области. Именно через язык заданий пользователь воспринимает и оценивает, какие «вычислительные услуги» предоставляет АСМ и насколько удобно их использование, т. е., другими словами, каков фактический уровень тематической квалификации системы.

Общая структура и стиль языка заданий ППМ в значительной степени зависят от дисциплины работы, принятой в обслуживаемой пакетом предметной области. Можно выделить две основные (в определенном смысле противоположные) дисциплины проведения моделирования:

— активную дисциплину, предусматривающую при создании конкретных рабочих программ модели М_м модификацию и настройку имеющихся модулей функционального наполнения, а также разработку новых модулей;

— пассивную дисциплину, предусматривающую проведение машинных экспериментов с моделью М_м без модификации функционального наполнения ППМ.

Активная дисциплина работы свойственна специалистам, создающим программное обеспечение АСМ, а пассивная дисциплина характерна для деятельности так называемых конечных пользователей, т. е. специалистов, которые не обязательно имеют высокий уровень подготовки в области программирования. Такое выделение двух дисциплин работы достаточно условно и преследует цель подчеркнуть контрастность системных подходов, используемых при автоматизации процесса моделирования.

Так, характерной особенностью языков заданий пакетов, обслуживающих проведение моделирования в режиме активной дисциплины, является их направленность на описание схем программ решения конкретных задач моделирования процессов, причем центральное место в таких языках (их обычно называют языками сборки) занимают не средства описания данных и манипулирования ими, что свойственно универсальным процедурно-ориентированным языкам программирования, а средства:

— конструирования схем программ, в которых указывается порядок выполнения и взаимодействия модулей при моделировании конкретной системы S;

— развития или модификации  функционального наполнения

ППМ;

— управления процессами генерации и исполнения рабочей программы, реализующей задание пользователя.

Главная цель разработки языка заданий ППМ, обеспечивающего решение задач моделирования в режиме пассивной дисциплины, заключается в том, чтобы «спрятать» от конечного пользователя основную массу алгоритмических подробностей моделирования его конкретной системы S, или, другими словами, повысить уровень непроцедурное™ языка. Такие языки, называемые языками запросов, ориентированы обычно на формулирование содержательных постановок задач, т. е. запросов, указывающих, «что необходимо получить», без явного задания того, «как это получить». Пользователь тем самым избавляется от необходимости конкретизировать способы и средства решения его задачи моделирования конкретной системы S, что позволяет понизить порог требований к уровню его программистской подготовки.

Язык заданий ППМ может быть реализован как в форме самостоятельного языка, так и в форме встроенного языка, т. е. расширения существующего языка программирования. Независимо от формы реализации разработчик языка должен стремиться к тому, чтобы лексика, синтаксис и семантика языка заданий были как можно ближе к пользовательскому восприятию решаемых задач моделирования, т. е. чтобы языковые конструкции приближались к концептуальной модели М_х.

Системное наполнение пакета. Системное наполнение ППМ представляет собой совокупность программ, которые обеспечивают выполнение заданий и взаимодействие пользователя с пакетом, адекватное дисциплине работы в данной прикладной деятельности. Можно сказать, что системное наполнение организует использование потенциала знаний, заложенных в функциональном наполнении, в соответствии с возможностями, предусмотренными в языке заданий ППМ. Реализация функций системного наполнения ППМ осуществляется на основе согласованного использования:

— штатных общецелевых средств системного обеспечения;

— средств системного наполнения, расширяющих и сопрягающих возможности компонентов штатного обеспечения;

— специальных средств системного наполнения, выполняющих управляющие, архивные и обрабатывающие процедуры с учетом специфики моделирования процесса функционирования системы S.

Язык (языки), на котором пишутся программы системного наполнения пакета, называется инструментальным языком ППМ.

Можно выделить такие ставшие уже традиционными составляющие системного наполнения пакета:

— резидентный    монитор,    осуществляющий   интерфейс   какмежду отдельными компонентами  системного  наполнения, так и между ними и штатным программным обеспечением;

— транслятор  входных  заданий,  формирующий  внутреннее представление заданий и реализуемый обычно в виде макрогенератора или препроцессора;

— интерпретатор внутреннего представления задания;

— архив функционального наполнения (подсистема хранения программного материала);

— банк данных об объекте моделирования и машинном эксперименте;

— монитор организации процесса машинного моделирования (взаимодействия модулей по данным и управлению);

— планировщик процесса машинного моделирования, который определяет последовательность выполнения модулей, реализующую задание ППМ;

— монитор    организации    интерактивного    взаимодействия с пользователем (исследователем системы S).

Программные средства АСМ. Напомним, что под ППМ, ориентированным на решение задач машинного моделирования систем, понимается комплекс программных средств и документов, предназначенных для реализации функционального завершенного алгоритма моделирования процесса функционирования системы 5 и обеспечивающих автоматизацию управления ведением эксперимента с моделью М_м на ЭВМ [17, 37].

Сущность такого определения состоит в том, что ППМ не является набором готовых программ для проведения машинных экспериментов с моделью М_м, а представляет собой набор средств для разработки конкретных, удовлетворяющих требованиям пользователя рабочих программ моделирования, служащих для автоматизации определенных функций при построении модели, машинном эксперименте и обработке результатов моделирования системы S.

К программным средствам ППМ относится набор программных модулей (тело пакета), из которых в соответствии с требованиями пользователя по заданному алгоритму набирается конкретная рабочая программа моделирования заданного объекта. В состав ППМ также входят управляющая программа, представляющая собой аналог супервизора ЭВМ; средства генерации рабочих программ для конкретного применения при решении задач моделирования систем. Специальная программа (монитор) принимает от пользователя информацию о требуемой модификации программ, формирует из набора стандартных модулей законченные рабочие программы, готовые к реализации машинного эксперимента с моделью М_м. Такой процесс генерации (настройки) ППМ на конкретные условия его использования создает значительную гибкость при решении задач автоматизации моделирования различных объектов.

  между отдельными компонентами  системного  наполнения, так и между ними и штатным программным обеспечением;

— транслятор  входных  заданий,  формирующий  внутреннее представление заданий и реализуемый обычно в виде макрогенератора или препроцессора;

— интерпретатор внутреннего представления задания;

— архив функционального наполнения (подсистема хранения программного материала);

— банк данных об объекте моделирования и машинном эксперименте;

— монитор организации процесса машинного моделирования (взаимодействия модулей по данным и управлению);

— планировщик процесса машинного моделирования, который определяет последовательность выполнения модулей, реализующую задание ППМ;

— монитор    организации    интерактивного    взаимодействия с пользователем (исследователем системы S).

Программные средства АСМ. Напомним, что под ППМ, ориентированным на решение задач машинного моделирования систем, понимается комплекс программных средств и документов, предназначенных для реализации функционального завершенного алгоритма моделирования процесса функционирования системы  S  и обеспечивающих автоматизацию управления ведением эксперимента с моделью М_м на ЭВМ [17, 37].

Сущность такого определения состоит в том, что ППМ не является набором готовых программ для проведения машинных экспериментов с моделью М_м, а представляет собой набор средств для разработки конкретных, удовлетворяющих требованиям пользователя рабочих программ моделирования, служащих для автоматизации определенных функций при построении модели, машинном эксперименте и обработке результатов моделирования системы S.

К программным средствам ППМ относится набор программных модулей (тело пакета), из которых в соответствии с требованиями пользователя по заданному алгоритму набирается конкретная рабочая программа моделирования заданного объекта. В состав ППМ также входят управляющая программа, представляющая собой аналог супервизора ЭВМ; средства генерации рабочих программ для конкретного применения при решении задач моделирования систем. Специальная программа (монитор) принимает от пользователя информацию о требуемой модификации программ, формирует из набора стандартных модулей законченные рабочие программы, готовые к реализации машинного эксперимента с моделью М_м. Такой процесс генерации (настройки) ППМ на конкретные условия его использования создает значительную гибкость при решении задач автоматизации моделирования различных объектов.

Различают две разновидности генерации рабочих программ моделирования: статическую и динамическую.

При статической генерации из отдельных модулей формируется рабочая программа моделирования, необходимая пользователю при исследовании конкретного объекта. При этом определяются необходимые устройства ввода-вывода информации, описываются на специальном языке генерации необходимые свойства разрабатываемой программы. Созданная таким образом программа моделирования является одновариантной и при необходимости внесения изменений в процессе моделирования системы S требуется проведение новой генерации.

При динамической генерации заранее оговариваются все варианты рабочей программы моделирования системы S, которые могут потребоваться пользователю при машинном эксперименте с моделью М_м. При решении конкретной задачи моделирования, т. е. перед каждым новым прогоном программы в ходе машинного эксперимента, вводится специальная параметрическая карта, определяющая требуемый на этом прогоне вариант программы. Монитор пакета собирает необходимые модули и помещает их в оперативную память ЭВМ для решения задачи моделирования. Условия проведения машинного эксперимента при динамической генерации являются более гибкими, но при этом увеличиваются затраты машинных ресурсов на моделирование (увеличивается необходимый объем памяти и время моделирования каждого варианта модели системы S).

Кроме использования программных модулей, входящих в тело ППМ, пользователь имеет возможность подключать свои собственные программы моделирования в точках пользователя. Имеется также возможность замены имеющихся модулей ППМ на собственные, что еще больше расширяет возможности моделирования различных вариантов систем.

Таким образом, программные средства ППМ объединяют в себе три главных качества: 1) содержат алгоритмические решения по проведению моделирования и обработке результатов моделирования систем, доведенные до законченной машинной реализации; 2) имеют механизм автоматической настройки на параметры конкретных машинных экспериментов, задаваемые пользователем пакета на этапе генерации рабочих программ моделирования; 3) позволяют дополнять генерируемые ППМ рабочие программы моделирования пользовательскими блоками, расширяющими возможности проведения машинных экспериментов с конкретными объектами моделирования из заданного класса.

Кроме программных средств ППМ содержит комплект документов, т. е. ППМ является хорошо документированной системой для разработки рабочих программ. Без наличия этой документации использование ППМ становится неэффективным. В состав комплекта документов ППМ входят проектная документация, являющаяся

документацией разработчиков пакета, и пользовательская, необходимая для эксплуатации пакета при решении конкретных задан моделирования.

Существенный момент подготовки к генерации рабочих программ моделирования — обеспечение необходимой технической базы, т. е. выбор необходимой для реализации функциональных возможностей ППМ конфигурации технических средств. Это не только выбор типа ЭВМ и используемой версии операционной системы, но и выбор объема памяти, средств сбора, преобразования и представления информации. В описании каждого пакета указывается минимальная конфигурация технических средств, необходимая для его работы. При этом определяющими параметрами являются объем оперативной памяти ЭВМ, количество накопителей, необходимый набор средств ввода-вывода информации. Минимальная конфигурация технических средств обеспечивает удовлетворительную работу ППМ. Некоторое увеличение оперативной и промежуточной памяти, а также использование дополнительных периферийных средств повышает оперативность и расширяет возможности моделирования. Но при этом увеличиваются затраты на технические средства АСМ.

Структурно АСМ можно разбить на следующие комплексы программ: формирования базы данных об объекте моделирования (БДО); формирования базы данных о машинном эксперименте (БДЭ); моделирования процесса функционирования объекта; расширения возможностей ППМ; организации различных режимов работы ППМ.

Комплекс программ формирования БДО реализует все работы по созданию в АСМ сведений о моделируемом объекте, т. е. системе S. Причем в БДО эти сведения хранятся в стандартной форме, принятой в АСМ. Информация об объекте может корректироваться по мере получения новых сведений в процессе машинного моделирования. Для формирования БДО требуются следующие программы: ввода данных об объекте (сведения об элементах системы, типовых математических схемах и операторах их сопряжения); корректировки введенной информации; перевода в стандартную форму; диспетчеризации процедур ввода; формирования БДО (расположения информации во внешней памяти).

В результате работы комплекса программ формирования БДЭ в АСМ формируется база данных, т. е. сведения, достаточные для проведения конкретных экспериментов с машинной моделью объекта М_м. Информация для проведения машинного эксперимента переписывается из БДО и дополняется в соответствии с планом эксперимента факторами, реакциями, критериями оценки и т. п. Для формирования БДЭ необходимы следующие программы: ввода       данных о планируемом эксперименте (сведений о факторах, реакциях, начальных состояниях и т. п.); формирования БДЭ (выделения сведений из БДО, необходимых и достаточных для реализации конкретного машинного эксперимента с моделью М_м); корректировки введенной информации о машинном эксперименте; расположения информации в архивах во внешней и оперативной памяти ЭВМ.

Комплекс программ моделирования процесса функционирования объекта непосредственно осуществляет решение постановленной задачи моделирования, т. е. реализует план ведения машинных экспериментов, их организацию на ЭВМ и обработку промежуточных данных и результатов эксперимента, взаимодействие с пользователем. Для решения задачи моделирования требуются следующие программы: управления машинным экспериментом, реализации стратегии эксперимента и его диспетчеризация; машинной имитации, включая организацию вычислений и взаимосвязь модулей модели М_ы; обработки и выдачи результатов моделирования системы 5 в различных режимах взаимодействия с пользователем.

Комплекс программ расширения возможностей ППМ призван обеспечить пользователя средствами генерации новых программ моделирования при различных перестройках (объекта моделирования, машинного эксперимента, обработки результатов и т. п.), возникающих при решении различных задач моделирования. При этом в качестве базового языка пакета может быть выбран либо алгоритмический язык общего назначения, либо язык имитационного моделирования {SIMSCRIPT, SIMULA, GPSS и т. д.).

Комплекс программ организации различных режимов работы ППМ кроме основной работы по диспетчеризации процесса функционирования ППМ призван организовать его работу в режиме диалога с пользователем как на этапе ввода данных об объекте моделирования и эксперименте, корректировки БДО и БДЭ, так и непосредственно в ходе машинного эксперимента с моделью М_н использования мультимедиа технологий. Необходимо также обеспечить режим коллективного пользования пакетом, что существенно расширяет возможности и эффективность АСМ.

Обучение методам программной имитации систем. Специализированные языки и системы моделирования являются одним из базовых средств современной информационной технологии [35]. В последнее время наблюдается широкое развитие данных средств, совершенствование их возможностей и пользовательского интерфейса. Имеются программные пакеты GSPT, Vissim, SIMEX, GPSS/H, Stella, SimPack, DOBSim, Mosis, QSIM, SIMPLORER, Modsim и десятки других [2,48]. Реализация систем моделирования на персональных компьютерах расширила сферу их использования в качестве  простого и эффективного средства поддержки этапа проектирования сложных объектов и систем.  

Анализ рынка средств моделирования показывает, что наибольшую популярность получили транзактно-ориентированные языки класса GPSS. Это пакеты GPSSI World, GPSS/H, GPSS/PC, MicroGRSS. Языки данного класса хорошо согласуются с удобным описанием модели системы в форме Q-схемы (системы массового обслуживания).

Система моделирования GPSS/PC, отличающаяся возможностью установки на персональные компьютеры разного класса, была выбрана в качестве базовой для обучения методам программной имитации сложных систем. Пакет функционирует на персональных компьютерах моделей с i386 и выше, имеет более 70 типов блоков и команд, а также около 50 системных параметров. В процессе прогона имитационной модели обеспечивается возможность постоянного наблюдения в шести интерактивных графических окнах (машинная мультипликация, работа одноканальных и многоканальных устройств, функционирование блоков, отображение таблиц и матриц). Система выдает отчет о результатах моделирования, содержащий широкий спектр параметров блоков, устройств, очередей, таблиц, пользовательских списков.

В процессе лабораторного практикума и курсового проектирования обучающиеся приобретают навыки построения концептуальной модели исследуемой системы и ее формализации, алгоритмизации и машинной реализации модели, интерпретации результатов моделирования.

Широкие возможности GPSS/PC позволили создать на ее базе практикум по курсу "Моделирование систем", состоящий из лабораторного практикума и комплекса, поддерживающего курсовое проектирование [38, 39, 40, 51].

Особенности GPSS. Особенности построения и использования в процессе моделирования GPSS целесообразно рассмотреть на конкретном примере такого пакета, который получил широкое распространение в практике моделирования дискретных систем.

Пример 5.1. Рассмотрим пакет прикладных программ моделирования и исследования на ЭВМ дискретных систем [33, 38, 40]. Этот пакет реализован на базе языка GPSS. Для ПЭВМ имеется версия языка GPSS/PC.Основное достоинство этого пакета - наличие необходимого набора типовых элементов (устройств, накопителей, переключателей и т. п.), соответствующих компонентам реальных систем (например, формализуемых в виде Q-схем), и программная реализация алгоритмов их функционирования, позволяющая строить сложные модели, сохраняя привычную для исследователя или разработчика систем S запись.

В пакете GPSS для представления моделируемой системы S в виде машинной модели М_м используется язык блок-диаграмм. Блок-диаграммой в пакете GPSS называется графическое представление операций, происходящих в моделируемой системе S. В этом случае блок-диаграмма описывает взаимодействия, происходящие внутри моделируемой системы S в процессе ее функционирования.

Для пакета GPSS были введены некоторые условности н общие представления о моделируемых системах. Введение таких обобщений позволило создать язык блок-диаграмм, в котором блоки соответствуют некоторым действиям, встречающимся в системах исследуемого класса. Вводимый набор блоков для блок-диаграмм однозначно определяет наборы операторов языка, осуществляющих описание структуры моделируемой системы S, и логических правил, определяющих ее функционирование.

В блок-диаграммах GPSS блоки представляют собой выполняемые над динамическими объектами операции, а стрелки между блоками отражают маршруты передвижения данных объектов по системе. Альтернативные ситуации отражаются более чем одной стрелкой, выходящей из блока.

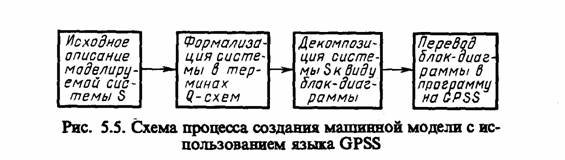
Таким образом, процесс создания модели М_м на языке блок-диаграмм GPSS сводится к декомпозиции исходной системы 5 до уровня элементарных операций, используемых в пакете GPSS, формированию фиксированной схемы, отражающей последовательность элементарных операций, выполняемых над динамическими объектами, и определению набора логико-вероятностных правил продвижения потоков объектов по имеющейся схеме.

Построение блок-диаграмм GPSS предполагает знакомство программиста с набором операторов пакета GPSS. Набор операторов языка однозначно соответствует набору блоков для описания блок-диаграмм, поэтому построение блок-диаграммы не является самоцелью, а лишь промежуточным этапом при построении имитационной модели исследуемой системы S с использованием операторов пакета GPSS. При этом процесс создания машинной модели М_м можно изобразить в виде схемы, показанной на рис. 5.5.

Условные обозначения, используемые на блок-диаграммах GPSS, представлены в табл. 5.2.

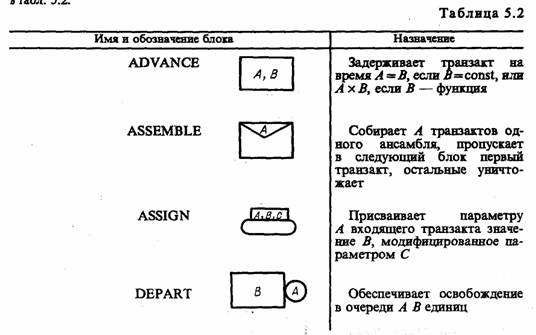
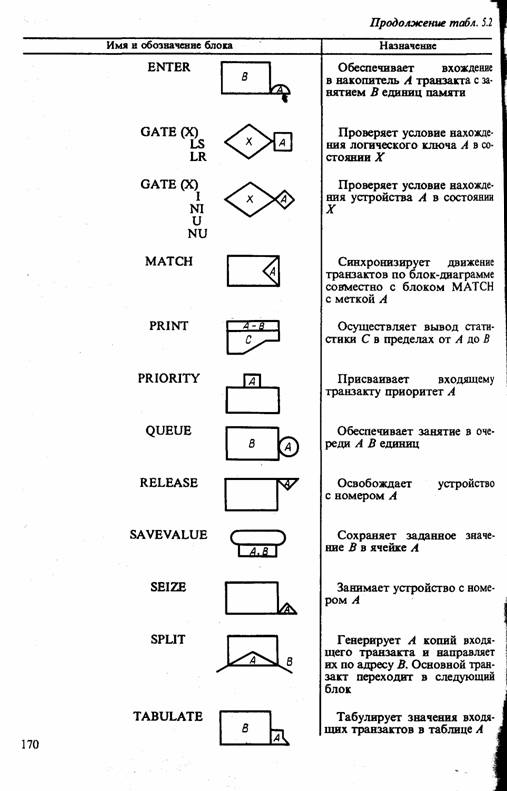
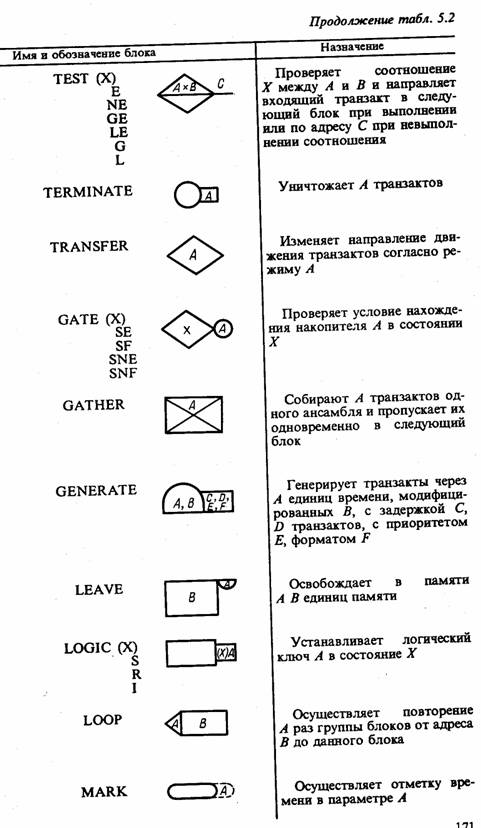
Особенности использования НИМ GPSS для моделирования систем, формализуемых в виде Q-схем, рассмотрены в гл. 8, там же приводятся примеры программ, генерированных пакетом GPSS.

Создание НИМ является крупным достижением в автоматизации моделирования больших систем. Однако любой НИМ, созданный на базе ЯИМ, характеризуется Некоторой узостью представлений, диктуемой особенностями языка, что является одним из слабых мест традиционных способов имитационного моделирования. В настоящее время проводится много работ по созданию систем моделирования для целых классов объектов, в основу которых положены идеи типизации способов описания структуры и динамики моделируемой системы S. Например, широко распространенной типовой математической схемой, используемой при моделировании организационно-производственных и информационно-вычислительных процессов, является Q-схема. Для создания машинных программ моделирования таких процессов могут быть привлечены такие ЯИМ, как GPSS, SIMSCRIPT u т. д. Тем не менее существуют (и продолжают разрабатываться) НИМ, в основу которых положены алгоритмические языки общего назначения, позволяющие детально и адекватно описать специфику процесса функционирования определенного класса систем и создать более эффективные программы моделирования, причем такие НИМ, ориентированные на определенный класс объектов, способные успешно конкурировать с известными ЯИМ при решении задач моделирования конкретного класса систем.

     Примеры дискретных, непрерывных и комбинированных ЯИМ приведены в табл. 5.3.

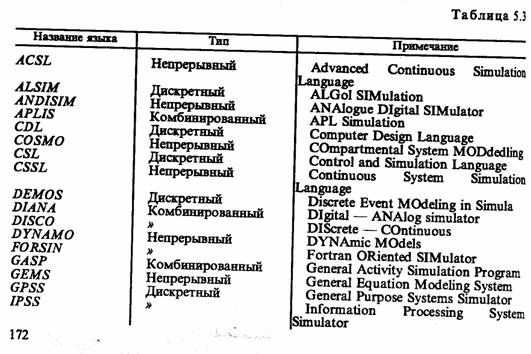
      Наиболее эффективно использование НИМ при исследовании и разработке систем на основе метода машинного моделирования    при реализации диалоговых процедур и концепции базы данных моделирования.

5.4. БАЗЫ ДАННЫХ МОДЕЛИРОВАНИЯ

Расширение возможностей моделирования различных классов систем S неразрывно связано с совершенствованием средств вычислительной техники и техники связи. Перспективным направлением является использование для целей моделирования иерархических многомашинных информационно-вычислительных систем и связанных с ними телекоммуникационными сетями удаленных персональных ЭВМ, работающих в режиме телеобработки.

При создании больших систем S их компоненты разрабатываются различными коллективами, которые используют средства моделирования при анализе и синтезе отдельных подсистем. При этом разработчикам необходим доступ как к коллективным, так и индивидуальным средствам моделирования, а также оперативный обмен результатами моделирования отдельных взаимодействующих подсистем. Таким образом, появляется необходимость в создании диалоговых систем моделирования коллективного пользования, для которых характерны следующие особенности: возможность одновременной работы многих пользователей, занятых разработкой одной системы S; доступ пользователей к программно-техническим ресурсам системы моделирования, включая распределенные банки данных и пакеты прикладных программ моделирования; обеспечение диалогового режима работы с различными вычислительными машинами и устройствами, включая цифровые и аналоговые вычислительные машины, установки физического моделирования, элементы реальных систем и т. п.; диспетчирование работ в автоматизированных системах моделирования (АСМ) и оказание различных услуг пользователям, включая обучение работе с диалоговой системой моделирования; использование сетевых технологий.

Рассмотрим основные моменты связанные с разработкой распределенной базы данных моделирования (РБДМ).

Ключевые аспекты разработки баз данных. Технология баз данных (БД) относится к числу основных компьютерных технологий и представляет собой совокупность методов и средств определения и манипулирования интегрированными в базу данными [2, 14, 16]. Важной целью применения технологии БД является создание разделяемого между функционально связанными приложениями информационного ресурса с обеспечением независимости внешнего, логического представления БД от способов ее внутренней, физической организации в памяти компьютера. Для достижения поставленной цели технология БД использует соответствующий набор технологических инструментов.

Современное представление технологии БД определяется тем, что в основу этой технологии положено применение реляционной модели данных (РМД), базирующейся на строгом аппарате реляционной алгебры и математической логики. Технологические операции определения и манипулирования БД выполняются с использованием систем реляционного исчисления. Реляционный подход в целом рассматривается в качестве идеологии создания баз данных и баз знаний [2, 14, 52]. Такой подход является наиболее эффективным при решении многих задач моделирования сложных систем S.

С одной стороны, широкое применение РМД позволило разрешить одну из серьезнейших проблем достижения модельной однородности баз данных, создаваемых в средах различных систем управления базами данных (СУБД), поскольку практически все современные СУБД используют модели, приводимые к реляционной. С другой стороны, опора на реляционную модель существенно ограничивает возможности определения данных в БД и, тем самым, предопределяет соответствующие границы применения всей технологии БД.

Такой подход, безусловно, оправдан при проектировании БД в тех случаях, когда администратор БД владеет схемой соответствия множества данных в реляционной модели с множеством данных о реальном мире. В тоже время, интеграционные тенденции, характерные для современного этапа развития компьютеризированных технологий (в том числе и в моделировании систем), ставят на повестку дня проблему построения интегрированных распределенных баз данных (ИРБД), для которых обеспечение схемной однородности на основе РМД в силу целого ряда причин оказывается недостаточно. Это не означает требования революционных изменений принципов реляционного подхода при проектировании БД в условиях построения ИРБД. Это означает только то, что при определении и построении ИРБД реляционный подход должен применяться с учетом классической схемы проектирования баз данных [2, 52], согласно которой необходимо знать, каким образом был выполнен полный цикл этапов моделирования заданной предметной области в виде реляционных схем интегрируемых БД. Очевидно, что расширение границ применения реляционного подхода, при этом, позволит проектировать новые БД уже с учетом возможности их будущей интеграции и ИРБД. Характерным примером реализации расширения реляционного подхода для разработки распределенных приложений на основе интегрированных реляционных баз данных стало создание методов и средств CASE-технологий [15].

С учетом сказанного, все основные понятия и определения технологии баз данных будут формулироваться именно с ориентацией на реализацию расширенного реляционного подхода для достижения цели методологического определния ИРБД. Полная технологическая схема определения и манипулирования интегрированными в базу данными представлена на рис. 5.6.

База данных. База данных составляет ключевое понятие технологии БД и стержневой объект управления в системах баз данных. Определение базы данных в качестве разделяемого информационного ресурса компьютеризированных технологий требует уточнения самих понятий данные и информация. Иногда база данных трактуется в качестве "подобия электронной картотеки", "хранилища для некоторого набора занесенных в компьютер файлов данных", подразумевая под термином файл "абстракный набор данных, не обязательно совпадающий с физическим дисковым файлом". Очевидно, что при таком взгляде данные и информация рассматриваются в качестве синонимов. Как следствие, истинным становится утверждение о том, что в этом случае любые данные, извлеченные любым способом из БД, являются информацией.

Классическое определение "база данных это - данные и связи между ними" представляется более точным и уместным с учетом высказанных выше соображений. Тогда данные, извлеченные из БД на основе установленных связей, являются информацией. В противном случае извлеченные из БД данные требуют интерпретации. Безусловно, хранящиеся в БД фрагменты связанных данных также соответствуют понятию информации. Вне связей данные являются информацией только в том случае, если они типизированы, или классифицированы, и известна примененная классификационная схема. С учетом применения реляционного подхода связи между данными можно разделить на связи совметности (совместность атрибутивных значений табличного определения прикладного объекта) и связи соответствия (совместность атрибутивных значений межтабличного определения прикладного объекта).

Таким образом, в дальнейшем под термином база данных будем понимать совокупность связанных данных, с одной стороны, являющихся информацией, и с другой стороны, составляющих основу для получения информации, как произвольных комбинаций

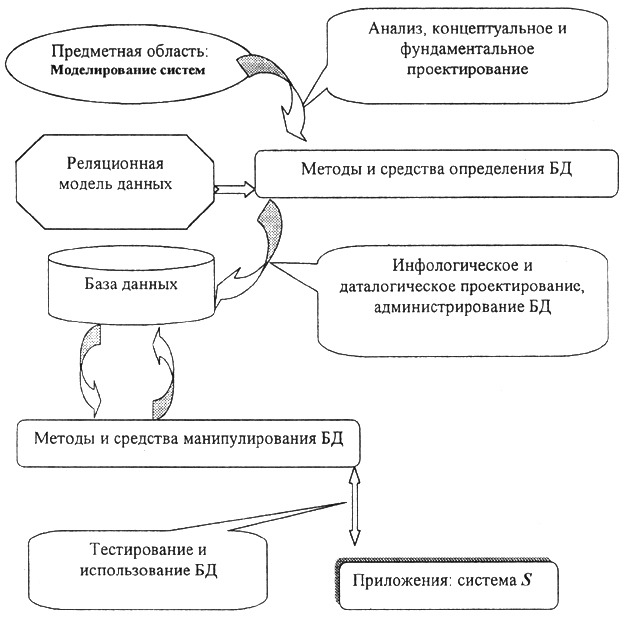
Рис. 5.6. Полная технологическая схема реализация БДМ

хранящихся связанных данных. Тогда данные БД и информация по определению оказываются синонимами.

Методы и средства определения и манипулирования БД. В технологии БД определены две основные группы механизмов определения и манипулирования БД.

К первой группе относится совокупность методов и средств определения связанных данных, включающая формальное описание структур данных, а также администрирование БД. Методы и средства определения данных реализуют ту или иную степень информативности хранящихся в базе данных в зависимости от возможностей и ограничений принятой модели данных. Определение данных выполняется статически, поскольку информативные связи между данными сохраняются и заносятся в БД наряду с собственно данными. На начальных этапах развития технологии БД именно разработка мощного языка определения данных (ЯОД) составляла главное направление развития. Хорошо известна многолетняя деятельность рабочей группы CODASYL [2] по созданию развитого ЯОД. Однако вывести языки определения данных на уровень общих языков программирования не удалось по целому ряду причин [3].

Вторую группу составляют методы и средства манипулирования данными, реализующие информативное связывание данных в динамике, в процессе доступа в БД. На начальных этапах языки манипулирования данными (ЯМД) сводились к определению простого СALL-интерфейса, однако на рубеже 80-х годов тенденция развития ЯМД практически перекрыла направление разработки ЯОД. Благодаря широкому применению реляционной модели языки манипулирования смогли пройти путь становления до уровня общих языков программирования. Наиболее известным представителем семейства ЯМД на сегодняшний день является язык SQL (Structured Query Language) [2], составляющий основу и являющийся сам международным стандартом ЯМД.

У многих пользователей зачастую складывается впечатление, что независимо от типа спроектированной БД посредством языка SQL можно получить доступ к любой информации на основе хранящихся данных в БД. На самом деле это далеко не так. Язык SQL действительно обеспечивает произвольный доступ к таблицам БД в любых сочетаниях и комбинациях. Но получение информации из БД при этом ограничивается возможностями связей между данными, хранящимися в БД. При отсутствии этих связей обычной практикой является встраивание обработки связей между данными в программный код приложений. Тогда можно выделить два основных компонента манипулирования БД:

 - собственно язык манипулирования как инструмент;

- процедуры связывания данных и управления извлечением информации из БД, реализованные средствами ЯМД.

Для реляционного подхода наиболее распространен процедурный способ управления извлечением информации из БД. При этом возможны три основных метода реализации этого способа:

1) модули связывания и манипулирования данными встраиваются в приложения путем программирования в профессиональных средах (MS Visual Studio, C+ + Builder, Dlphi);

2) модули связывания и манипулирования разрабатываются на языках SQL-cepверов и хранятся непосредственно в серверной БД, становясь также разделяемыми информационными ресурсами;

3) модули связывания и манипулирования оформляются в виде системных динамических загружаемых библиотек DLL, формируя таким образом доступ в БД в виде системного Windows-ресурса.

Построение модулей связывания и манипулирования БД в виде разделяемых информационных ресурсов в среде SQL-cepверов или в виде системных DLL-библиотек существенно приближает совокупное содержание таких БД к классическому определению. Характерно, что получаемая таким образом реализация БД по полной технологической схеме рис. 5.6 остается в границах реляционного подхода.

Разновидности систем баз данных. В зависимости от способов определения и манипулирования связанными данными системы БД можно разделить на следующие основные разновидности.

Системы с файловыми базами данных в качестве БД используют простые структурированные файлы в форматах dbf, bd и др., а все информативные связи определяются и обрабатываются в приложениях, использующих такие БД. Эффективность организации структурированных файлов обычно повышается путем построения индексов и других систем указателей, что, вообще говоря, характерно при создании картотек. Индексируются, как правило, ключевые поля структур с целью убыстрения доступа (за счет сортировки индексов), обеспечения уникальности значений полей, запрета на существование неопределенных значений и т. п. К числу наиболее существенных недостатков систем файловых БД (только в смысле их использования) можно отнести полную зависимость от приложений. Доступ к информации файловых БД возможен только посредством содержащего программные связи приложения. Очевидно, что как разделяемый информационный ресурс файловые БД могут существовать только в симбиозе с обеспечивающими связывание данных приложениями. Программная реализация связей на SQL-серверах или в виде DLL -библиотек естественно придает файловым БД совершенно новое качество реально разделяемого информационного ресурса.

К противоположной разновидности относятся такие системы БД, в которых все связи между данными определены как данные и хранятся в БД. Такие системы можно назвать системами с предметными базами данных. Суть названия предметная БД заключается в достижении полной независимости предметных баз данных от приложений. Предметные БД являются полноценными, самостоятельными ресурсами компьютеризированных технологий, что составляет главное преимущество их применения. В тоже время, полное определение всех связей между данными порождает существенную сложность проектирования таких БД.

Промежуточные варианты организации баз данных, при которых связи распределяются между приложениями и БД, определяют разновидность систем с прикладными базами данных. Суть названия отражает слабо или сильно выраженную ориентацию организации прикладной БД на потребности использующих ее приложений. Очевидно, что как компромиссный вариант, прикладные БД могут выступать в качестве оптимизируемого информационного ресурса компьютеризированных технологий. Прикладные базы данных находят широкое применение при моделировании на ЭВМ конкретных систем S.

Предметная область. Первичным источником связанных данных при проектировании баз данных любых разновидностей является соответствующая предметная область, которая будет рассматриваться как совокупность знаний и данных об объектах и процессах, подлежащих проектированию и хранению в БД. В данном случае в качестве предметной области рассматривается проблема имитационного моделирования сложных систем на ЭВМ.

Знания о предметной области, как это уже отмечалось в п. 3.1, посвященном методике разработки и машинной реализации моделей систем S, могут быть получены из разнообразных источников, таких, как:

- фундаментальные законы и устойчивые закономерности, теоретические знания прикладных наук о процессах в моделируемой системе S;

- эвристические знания в виде принятых правил, соглашений и обозначений, характерных для систем S;

- экспертные знания и экспертные оценки специалистов в области моделирования конкретных систем S;

- существующие базы данных, компьютеризированные системы, технологии и проекты.

Перечисленные источники знаний о предметной области "моделирование систем" не являются источниками собственно данных, а определяют методологические принципы выделения прикладных объектов и процессов, а также методы приобретения и связывания данных о выделенных объектах и процессах. Источники знаний о предметной области определяют выбор классификационной схемы формализованного описания объектов и процессов, которая в процессе проектирования БД отображается в результирующей реляционной схеме.

Таким образом, процесс проектирования базы данных по полной технологической схеме есть процесс пошагового отображения исходной классификационной схемы предметной области в реляционную схему реализации базы данных. Выбор той или иной методологической основы процесса проектирования БД определяет вид реализованных в БД связей между данными и характеризует интеграционные возможности построенной БД.

Важным методологическим признаком проектируемой БД и ее интеграционных возможностей является естественная или искусственная природа выделения прикладных объектов и процессов, связанные данные о которых будут храниться в проектируемой БД. Особое значение это обстоятельство приобретает при применении объектно-ориентированного подхода к проектированию баз данных и построению ИРБД.

В практике моделирования сложных систем S при проектировании локальных баз данных (Л БД) применение классификационных схем зачастую осуществляется интуитивно, с твердым убеждением в том, что выбранный способ определения данных БД естествен для решения данной задачи. На самом деле, проектировщик ЛБД просто принимает одну из существующих классификационных схем (например, традиционную схему построения базы данных "система S - концептуальная модель M_к - машинная модель М_м" из литературы). В тоже время, отсутствие знаний о правилах формирования и связывания атрибутивных значений даже в такой БД может привести к искажению и ошибкам в трактовке извлекаемых из БД данных как информации.

Концептуальный анализ и проектирование баз данных. Выбор или конструирование классификационной схемы выделения объектов и процессов составляет суть анализа предметной области (в данном случае это "моделирование сложных систем S"). Отображение классификационной схемы в результирующую реляционную схему определяет многошаговый процесс проектирования Б ДМ.

Прежде всего, под формализованным представлением предметной области будет пониматься классификационное выделение объектов и процессов, что в терминах объектно-ориентированного подхода соответствует классификационному определению абстракций сущностей и поведения [2,16]. Классифицирование может выполняться путем классической категоризации, концептуальной кластеризации или с применением методов теории прототипов. Абстракции сущностей определяют классы объектов предметной области и выражаются через совокупности характерных свойств объектов данного класса, в тоже время, отличающих объекты данного класса от объектов других классов. Абстракции поведения выражают правила взаимодействия объектов через общие или связанные свойства.

Таким образом, выбранная или сконструированная классификационная схема с применением той или иной классификационной методологии определяет систему формирования универсума проектируемой БД. Принципиально важным для технологии баз данных является принцип отделения классификационной схемы в виде совокупности элементов моделирования представлений данных от собственно системы классифицированных данных БД. Именно реализация этого принципа способна привести к разрешению проблемы построения определенной категории объектно-ориентированных баз данных. Элементы моделирования представлений данных также включаются в состав универсума.

Проектирование концентуального представления системы классифицирования предметной области на основе выбранной классификационной схемы называется концептуальным проектированием предметной области, в результате которого строится концептуальная модель семейства концептуально однородных баз данных. Очевидно, что выбор готовых проектных решений относит проектируемую базу данных к семейству БД с однородным концептуальным представлением. Например, типизация классификации данных о модели системы S (концептуальная модель, типовая математическая схема - см. гл. 3) практически исключает необходимость концептуального проектирования подобного фрагмента предметной области. Все базы данных, включающие описания моделей системы S, согласно принятой классификационной схеме определения математической схемы, в этом фрагменте БД концептуально однородны. Отметим, что такая классификационная схема имеет искусственную природу построения, в основе которой находится система эвристик.

Совершенно иначе обстоит дело, если проектируется фрагмент БД, посвященный описанию свойств материальных объектов (например, объектов моделирования, т. е. систем S). Классификационная схема для этого случая будет опираться на методологию классической категоризации, а знания о соответствующей предметной области будут носить фундаментальный характер. В этом случае, концептуальное проектирование окажется связанным с необходимостью проведения серьезной научно-методической работы по абстрагированию системы знаний, обычно описанной документально в словарях, справочниках, тезаурусах. Достижение концептуальной однородности, а, следовательно, и достаточных интеграционных возможностей семейства подобных баз данных становится крайне сложной проблемой. Таким образом, концептуальное моделирование предметной области включает выполнение следующих операций:

- определение природы источника знаний о предметной области (фундаментальной, эвристической, экспертной, существующего компьютеризированного решения в области моделирования конкретных систем S);

- выбор или конструирование классификационной схемы на основе классификационной методологии (классической категоризации, концептуальной кластеризации, теории прототипов);

- выделение абстракций объектов и процессов (взаимодействия объектов) через определение их свойств;

- построение структуры (иерархии) базовых классов предметной области и формализиция представления такой структуры.

В результате концептуального моделирования определяются следующие концептуальные компоненты:

- совокупность типизированных абстрактных представлений сущностей предметной области, определяющих систему правили ограничений на формирование атрибутивных значений свойств объектов;

- совокупность типизированных абстрактных представлений взаимодействия сущностей предметной области;

Классификационные правила формирования атрибутивных значений свойств объектов, а также правила взаимодействия объектов посредством их конкретных свойств образуют концептуальную семантику предметной области в базисе выбранной классификационной схемы. Абстракции в целом и отдельные их свойства, выделенные на основе фундаментальных знаний о предметной области, образуют фундаментальную семантику, сфера действия которой выходит за границы данной предметной области. Фундаментальная семантика является основой глобальной интеграции БД по определению. Концептуальная семантика является основой построения прототипов схем индексирования и установки ограничений элементов реляционных схем БД. Другими словами, построение или владение концептуальной семантикой предопределяет способность извлечения информации из реализованной БД. В значительной мере, концептуальная семантика управляет процедурами нормализации и упорядочения реляционных схем.

Концептуальная модель предметной области является основой проектирования (и интеграции) семейства концептуально однородных БДМ. Присутствие фундаментальной семантики способно принципиально повысить интеграционные возможности соответствующих БДМ. Концептуальная модель формирует заголовочные разделы универсума, определяет интерфейс семейства концептуально однородных баз данных, выражает множество концептуальных компонентов (абстракций, свойств связей), на основе которых путем комбинирования можно осуществлять варианты инфологического проектирования баз данных.

Мифологический анализ и проектирование БДМ. Мифологическое проектирование выполняется в базисе концептуальных компонентов и учитывает возможности и ограничения модели данных реализации БДМ. Для инфологического проектирования характерны следующие операции:

- расширение интерфейсов описания абстракций концептуально не классифицированными свойствами (например, дополнение к определению математической схемы свойства - примечание для записи произвольных дополнительных сведений о модели системы S); атрибутивные значения таких свойств носят характер сопутствующей информации и не могут использоваться в качестве критерия доступа к информации до проведения их концептуального моделирования, для реляционного подхода выполнение таких операций определяет процедуры инфологического проектирования связей совместности свойств объектов, т. е., прототипов таблиц;

- построение инфологических структур реализации концептуальной модели, в качестве структур могут использоваться любые структуры определения структурных абстракций [2, 16, 25]; для реляционного подхода выполнение таких операций определяет процедуры инфологического проектирования связей соответствия, т. е.прототипов межтабличных отношений.

Инфологическая модель, как интерпретация концептуальной модели, расширяет содержимое универсума. Инфологическая модель учитывает специфику проектируемой БД (например, различные моделирующие алгоритмы для реализации Q-схем при использовании статистического моделирования), сохраняя концептуальную однородность семейства подобных БДМ (например, единая система обозначений для типовых математических схем - см. гл. 2). Мифологическая модель является основой определения источников, накопителей и получателей информации и определения информационных потоков. И если своеобразным аналогом элементов концептуального проектирования в существующих CASE-технологиях является моделирование сущностей-связей, то аналогом инфологического проектирования в СASЕ-технологиях может рассматриваться моделирования процессов прикладных областей [2, 26, 30].

Совокупность правил построения инфологической модели образует мифологическую семантику проектируемой БД, состоящую из определений связей совместности и соответствия. Инфологическая семантика полностью определяет пути доступа к информации данной инфологической реализации БД. Мифологическими компонентами являются логические объекты и связи, представляющие собой логические обобщения концептуальных компонентов. Образно говоря, концептуальные компоненты являются символами, а инфологически компоненты соответствуют логическим словам и выражениям, построенным с использованием концептуальных символов.

Даталогнческнй анализ и проектирование БДМ. Даталогическое проектирование баз данных выполняется с учетом среды конкретной выбранной СУБД. Строго говоря, именно даталогическая схема БД является реляционной схемой. Даталогическое проектирование выполняется на основе принятой инфологической схемы и заключается в выполнении следующих операций:

- выделение таблиц для реализации схем логических объектов;

- определение физических форматов атрибутивного описания свойств логических объектов на основе типов соответствующих концептуальных символов;

- выделение внешних, первичных и потенциальных ключей таблиц;

- определение индексируемых полей и полей реализации логических связей между таблицами;

- проектирование представлений для организации хранимых результатов промежуточного доступа в БД;

- определение процедур обработки изменений атрибутивных значений по связям между таблицами и т. д.

Таким образом, даталогическое проектирование выполняет разложение логических слов и выражений на схемные элементы, которыми оперирует реляционная схема. Другими словами, на этапе даталогического проектирования логические выражения кодируются в терминах языка реляционной модели. Даталогичесское проектирование окончательно формирует универсум.

Важнейшей процедурой на этапе даталогического проектирования считается нормализация реляционных схем [3, 19, 23]. Однако, если рассматривать полный технологический цикл проектирования БД, то окажется, что нормализация есть ни что иное, как постклассифицирование представления данных предметной области в БДМ. Рассмотрим основные операции, выполняемые при нормализации схем БД.

Администрирование БДМ. Реляционная модель в значительной степени является идеалом, поскольку практически все современные СУБД работают в моделях, приводимых к реляционной. Поэтому чисто математическое моделирование и тестирование схем БДМ, как правило, неприменимо на практике. В тоже время, реализация расширенного реляционного подхода и проектирование или определение БДМ по полной технологической схеме создает необходимые предпосылки построения систем анализа и тестирования проектов БД.

Традиционное администрирование баз данных включает множество операций по сопровождению БД и описано в литературе [16, 52]. К числу решаемых в процессе администрирования БД задач обычно относятся:

- обеспечение физической целостности БД (разработка и реализация плана архивации физических файлов, обеспечение ведения журнала изменений, формирование точек отката);

- обеспечение безопасности данных, включая процедуры санкционирования доступа и другие средства защиты;

- обеспечение целостности, достоверности и многие другие функции администрирования.

Администрирование БДМ должно осуществляться путем организации соответствующей службы, в состав которой должны входить специалисты в области моделирования систем S, специалисты в области управления данными, системные программисты и операторы. Статус администратора БДМ должен соответствовать уровню полномочий руководителя проекта по моделированию сложного объекта, т. е. системы S, для возможности принятия легитимных решений.

Представление баз данных по полной технологической схеме расширенного реляционного подхода порождает иной взгляд на функции и состав служб администрирования БДМ. В частности, к числу задач администрирования БД можно отнести:

- администрирование фундаментальной семантики, естественно, что подобная служба должна быть организована для множества семейств фундаментально однородных             БДМ, администратор фундаментальной семантики должен возглавлять научно-методическую службу ведения и актуализации фундаментальной семантики;

- администрирование концептуальной семантики для семейства концептуально однородных БДМ, администратор концептуальной семантики должен профессионально владеть классификационной схемой формализации представления предметной области, смысловым содержанием данных о классифицированных объектах и процессах;

-администрирование инфологических представлений БДМ; соответствующий администратор должен обладать знаниями профессионала прикладника и осуществлять сопровождение БДМ как разделяемого информационного ресурса компьютеризированных систем; также администратору данного уровня необходимо владеть механизмами представлений логических структур данных, знать основы примененных моделей данных;

- администрирование компьютерной реализации БДМ, на этом уровне администрирования требуются знания системного программиста и владение методами и средствами СУБД;

- администрирование физической целостности и защиты БДМ; набор задач на этом уровне администрирования традиционен.

Рассмотренные уровни администрирования баз данных, спроектированных или представленных по полной технологической схеме, формируют прообраз службы администрирования интегрированными БДМ. В распределенной информационной среде служба администрирования БДМ также окажется распределенной в соответствии с рассмотренной схемой уровней и задач администрирования баз данных.

Использование БДМ при моделировании систем. Возможности использования баз данных в качестве источника информации, как следует из вышеизложенного, определяются знанием модельного представления связанных данных на всех уровнях проектирования БДМ. С другой стороны, разновидность конкретной БДМ, выбранный способ классификации предметной области, наличие фундаментальной семантики, особенности концептуальной семантики и многое другое предопределяют требуемый профессиональный уровень пользователей и возможный масштаб применения такой БДМ. Использование баз данных должно быть адекватно реализованному проектному решению, и только в этом случае извлекаемые из БДМ выборки данных могут действительно рассматриваться в качестве информации для целей моделирования системы S.

Вопросы использования баз данных должны предусматриваться в виде стратегических целей проектирования БДМ. Особенно формулирование стратегических целей важно в условиях проектирования, построения и использования интегрированных распределенных баз данных при моделировании сложных систем.

Реляционная модель данных. Такая модель обладает, по меньшей мере, двум принципиальными преимуществами по сравнению с другими моделями данных (древовидной, сетевой). Во-первых, РМД обеспечивает представление БД в виде повседневно встречающихся и привычных человеку двумерных таблиц независимо от способов компьютерной реализации БД. Таким образом, реляционная модель удобна и наглядна. Во-вторых, реляционная БД с математической точки зрения представляется конечным набором конечных отношений различной арности. Над отношениями модели можно осуществлять алгебраические операции. Можно сказать, что тем самым теория реляционных баз данных становится областью приложений математической логики и современной алгебры и опирается на точный математический формализм. Другими словами, вторым преимуществом реляционной модели является математическая строгость ее определения.

Реляционная модель однородна, поскольку все данные хранятся (представляются) в таблицах с фиксированным форматом строк, соответствующих данным об объектах и процессах предметной области. Очевидно, что однородность реляционной модели не распространяется на сущности хранимых в строках таблиц данных, конечно, если БД не была спроектирована по полной технологической схеме расширенного реляционного подхода. Математический формализм реляционной модели базируется на использовании аппарата современной реляционной алгебры.

Теоретические основы построения систем реляционного исчисления обычно скрыты за относительно простыми и понятными пользователям (разработчикам машинной модели М_м систем S) синтаксическими конструкциями формулирования запросов к БДМ. В тоже время, точное классифицирование того или иного языка манипулирования, а, следовательно, его возможностей и ограничений, особенно в условиях применения расширенного реляционного подхода, зачастую потребует учета заложенных в основу такого языка теоретических принципов и механизмов.

Объектно-ориентированный подход и БДМ. В современном представлении объектно-ориентированный подход (ОП - объектный подход) составляет основу методологий построения сложных систем. Объектно-ориентированный подход связан с представлением предметной области в виде классов и объектов, которые в зависимости от предназначения методологии могут иметь различную природу. Отображение предметной области моделирования систем S в виде совокупностей классов и объектов означает реализацию объектной модели представления систем, которая является ключевым понятием ОП. Таким образом, объектно-ориентированный подход, по сути, является методологией построения методологий объектного моделирования систем.Возможность применения ОП определяется способностью представить предмет моделирования (предметную область "моделирование систем S) в виде объектной модели.

На сегодняшний день сформировано несколько методологий, использующих ОП. В первую очередь, к ним относится методология объектно-ориентированного программирования (ООП), реализация которой привела к построению ряда систем ООП, таких, как Visual C + +, C + + Builder, Delphi. Успешность и высокая результативность разработки систем ООП в значительной степени объясняется тем, что классифицируемые объекты предметных областей систем программирования по своей природе носят искусственный характер, обладают конечным числом известных свойств и хорошо поддаются абстрагированию в соответствии с понятными классификационными схемами. Реализация принципиально новой технологии программирования с использованием систем ООП оказалась настолько эффектной и, что, зачастую, собственно объектно-ориентированный подход стал отождествляться с объектно-ориентированным программированием. На самом деле это далеко не так, хотя отсутствие хороших результатов применения ОП для реализации других методологий способствует формированию такого мнения.

Особое значение ОП приобретает при разработке методологии построения объектно-ориентированных баз данных (ООБД). В отличие от систем программирования, системы баз данных характеризуются принципиально иной, естественной природой классов и объектов предметных областей. Объектное представление какой-либо предметной области БДМ вызывает серьезные проблемы. Поэтому раздел информатики, посвященный вопросам построения ООБД, на сегодняшний день находится в начальной стадии становления, а многие работы в этой области ограничиваются уровнем предположений и гипотез. Представляется, что именно ОП может оказаться требуемым способом не только построения методологии ООБД, но и разработки методологии объектно-ориентированной интеграции распределенных баз данных (ООРБД). Очевидно, что центральной проблемой при этом становится проблема композиции объектно-ориентированного и реляционного подходов, способной привести к реализации расширенного реляционного подхода по полной технологической схеме (см. рис. 5.6).

Методология классифицирования предметной области. В основе механизмов выделения классов и объектов предметной области лежит применение выбранной классификационной схемы. К числу основных классификационных методологий относятся методология классической категоризации, методология концептуальной кластериазации и теория прототипов [16, 35].

Таким образом, говоря о классифицированных объектах и процессах предметной области, всегда будем иметь в виду выделенные классы - категории объектов, классы - кластеры объектов и классы - прототипы процессов. Для удобства, в дальнейшем все разновидности классов объектов и процессов будут называться просто классы объектов. Все классы объектов при применении объектно-ориентированного подхода определяются в виде абстракций, а представление предметной области с позиции классов объектов при применении ОП соответствует представлению предметной области "моделирование систем S" в объектной модели.

Основные совйства объектной модели. Рассмотрение свойств объектной модели часто выполняется с ориентацией на системы объектно-ориентированного программирования. Поэтому, некоторые, уже ставшие привычными трактовки понятий и определений объектной модели потребуют уточнения. Например, вряд ли стоит доказывать необходимость обеспечения свойства сохраняемости для классов объектов систем объектно-ориентированных баз данных.

Абстрагирование реализует свойство концентрации внимания на внешних особенностях объектов и позволяет отделить самые существенные особенности поведения от несущественных. Минимизацию связей, когда интерфейс объектов содержит только существенные аспекты поведения, реализует принцип барьера абстракции. Таким образом, абстракция выражается через свойства, присущие всем объектам заданного абстракцией класса и, в тоже время, отличающие объекты заданного ей класса от объектов других классов. Определение понятия абстракция, таким образом, содержит конфликтное условие, которое порождает многие классификационные проблемы. Суть такого конфликта заключается в необходимости совмещения в абстракции элементов общности и исключительности существенных свойств. Очевидно, что естественная природа выделения классов объектов предметной области обостряет указанный конфликт, доводя его до состояния неразрешимых противоречий. Именно с этим аспектом связаны главные трудности построения систем объектно-ориентированных баз данных.

Применение механизмов абстрагирования в рамках объектно-ориентированного подхода формулирует главное правило - представление предметной области в объектной модели. Классификационная схема, основанная на той или иной системе знаний о предметной области и классификационной методологии, обеспечивает выделение классов объектов. Заголовочное определение классов описывается в виде абстракций, интерфейсные свойства которых обладают качествами существенности, общности для данного класса и различимости для отделения объектов других классов.

Отметим, что совокупность классифицированных абстракций предметной области "моделирование систем S" в общем случае состоит из абстракций двух типов:

- абстракции определения объектов данных предметной области, которые называются абстракциями данных;

- абстракции определения модельных элементов представления данных, которые называются абстракциями моделей или модельными абстракциями.

Для систем объектно-ориентированного программирования абстракции данных определяют классы объектов программирования оконного интерфейса, работы с Internet, доступа в БД, связывания и внедрения объектов ActiveX и т. д. Абстракции моделей для систем ООП соответствуют структурным абстракциям. Для обоих типов абстракций систем ООП характерным является то, что определяемые абстракциями объекты выступают одновременно и в роли данных, и в роли инструментов управления такими данными. Например, стандартное окно системы Windows является объектом соответствующих классов (кнопка, панель, окно редактирования и т. п.).

Инкапсуляция реализует свойство объектной модели, связанное с абстрагированием и обеспечивающее разделение описания класса на интерфейс и реализацию. В интерфейсной части описания класса содержится суть определения классифицированной абстракции, т. е. то, что присуще всем объектам задаваемого абстракцией класса. Через интерфейс объекты взаимодействуют, и именно интерфейс является предметом интеграционной отладки при разработке проектируемой системы. Таким образом, интерфейс представляет собой формальное описание абстракции средствами реализации проектируемой системы. Реализация класса точно соответствует названию, и содержит детали реализации интерфейса (т. е. абстракции) при построении объектов данного класса.

Разделение на интерфейс и реализацию соответствует определению внешнего (логического) и внутреннего (физического) устройства объектов. Принцип инкапсуляции соответствует сути вещей, интерфейс при этом играет роль определения степени интереса и полезности знания такой сути. Объединение инкапсуляции с абстрагированием обеспечивает формирование видимости единой сущности множества физически различных объектов. Так, в технологии БД, табличная форма представления данных является интерфейсом, в то время как реализация таблиц в разных СУБД физически различна (начиная с различий форматов файлов - аb, dbf и др.).

Интерфейс и реализация исполняются в среде разработки проектируемой системы, поэтому можно построить следующую логическую цепочку взаимосвязи понятий: интерфейс есть исполнение абстракции, а реализация есть исполнение интерфейса. Например, в системах ООП интерфейс и реализация исполняются на языках C + +, Object Pascal и др. Для систем объектно-ориентированных БД смысл инкапсуляции, в первую очередь, связан с разделением модельных представлений абстракций данных и реализации объектов данных одного классификационного раздела в различном схемном исполнении. Логическая последовательность взаимосвязи понятий в этом случае следующая.

Модельные абстрагирование и инкапсуляция исполняют концептуальные, фундаментальные, инфологические и даталогические представления БД в реляционной модели, а абстрагирование и инкапсуляция данных предметной области исполняют собственно реализацию объектно-ориентированной базы данных с применением расширенного реляционного подхода. Таким образом, объектная модель ООБД многослойна и включает ирархию объектных представлений моделей и данных с реализацией всех уровней объектной модели БД в реляционной модели данных.

Иерархия реализует свойство объектной модели упорядочения и расположения по уровням выделенных абстракций предметной области. Основным свойством и преимуществом иерархической организации объектной модели является наследование свойств и других элементов определения объектов по схеме "родитель-потомок", при этом наследование касается только интерфейсных определений. О наследовании говорят, как об иерархии "обобщение-специализация", что в значительной степени напоминает определение родовидовых зависимостей. И если в системах объектно-ориентированного программирования иерархии классов отностильно просты и понятны (например, иерархии классов библиотеки MFC языка Visual C + +, или библиотеки VCL системы Delphi), то для систем объектно-ориентированных баз данных иерархии классов оказываются многомерными.

Одной из главных целей применения иерархической организации объектной модели является обеспечение возможностей синтеза и декомпозиции сложных объектов через простые объекты более низких уровней. Преимущества такого подхода очевидны, и особенно важным представляется реализация свойства иерархии в ООБД. Даже интуитивно понятия синтеза, декомпозиции, зависимостей ассоциируются с аспектами рассмотрения теории реляционных баз данных и модельными представлениями БД по полной технологической схеме. Свойство иерархии позволяет реализовать протокольный принцип организации информационной среды, что особенно важно при построении интегрированных РБД.

Свойство типизации дополняет свойства абстрагирования, инкапсуляции и иерархии определением типов сущностей классифицированных объектов предметной области. Типизация трактуется двояко: помимо типизации сущности объектов данного класса, это свойство обеспечивает защиту при использовании объектов, определенного рода различимость объектов разных классов. В системах ООП типизация осуществляется посредством объявления традиционных типов данных (integer, float, character и др.). Для объектно-ориентированных БД многомерность объектной модели порождает существование различных видов типизации объектов модельных классов и классов данных. Так, типизация объектов даталогических моделей похожа на типизацию языков программирования (типы атрибутов в столбцах таблиц соответствуют языковым типам данных). Типизация объектов инфологических, концептуальных и фундаментальных моделей, а, также объектов данных существенно иная. Различают сильную и слабую типизацию, что в первую очередь, связано с возможностями преобразования типов и объявлением объектов множественных типов (полиморфизм). Для объектно-ориентированных БД преобразования модельных типов будет играть ключевую роль при решении интеграционных задач.

Свойство модульности достаточно очевидно и должно быть реализовано в любой программной разработке. Модульность реализует абстрагирование не на уровне классов объектов, а на уровне программных единиц разрабатываемой системы. В этом смысле модуль можно уподобить классу с описанием интерфейса и реализации, содержащему один объект в виде программной единицы (unit в языке Object Pascal). При разработке модулей следует придерживаться правила их типизации (модуль должен управлять однотипными объектами), что зачастую приводит к реализации модулей в виде объектов какого-то класса (например, диалоговые модули "открыть файл", "сохранить файл", "открыть графический файл" и другие реализованы в системе Delphi в виде объектных компонентов). Модульная организация системы является необходимым требованием, а сама суть модульности тесно переплетена с сутью других свойств объектной модели. Для объектно-ориентированных БД свойство модульности должно быть обеспечено на уровне манипулирования объектами БД (например, модульный принцип построения программ SQL-сервера, на языке SQL).

Рассмотрим свойства параллелизма и сохраняемости. Для систем ООБД параллелизм особенно важен при построении или интеграции баз данных по полной технологической схеме. В любом случае БД в качестве разделяемого информационного ресурса должна функционировать в архитектуре "клиент-сервер", даже в локальном исполнении. Сохраняемость естественна для объектов данных БД. В тоже время, расширенный реляционный подход распространяет свойство сохраняемости не только на объекты данных, но и на объекты модельных классов, и это является принципиальной особенностью реализации полной технологической схемы построения БД в объектной модели.

Рассмотренные свойства объектной модели иллюстрирует рис. 5.7. В системах объектно-ориентированного программирования иерархия выделенных в предметной области классов обычно реализуется в виде библиотек базовых классов (например, библиотека MFC). Для систем ООБД реализация должна быть несколько иной. Иерархия классов данных выражает информативное связывание данных. Собственно данные организуются в табличном формате, связи реализуются либо в виде данных, либо в виде процедур связывания данных. Модельные абстракции должны исполняться либо в виде определения данных, либо путем построения библиотек базовых классов в среде SQL-серверов или в составе DLL-библиотек.

Мифологическое проектирование баз данных. К числу основных задач этапа инфологического проектирования баз данных (рис. 5.8) относятся следующие три задачи:

1. Проектирование логических объектов.

2. Проектирование логических структур данных.

3. Проектирование информационных связей (потоков) между логическими объектами.

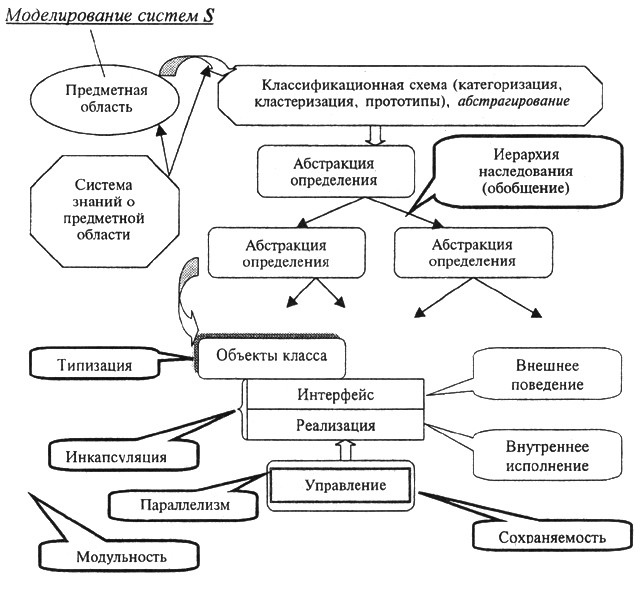
Рис. 5.7. Свойства объектной модели БДМ системы S

Для решения поставленных задач в качестве исходных условий для выполнения инфологического проектирования базы данных требуется обеспечить:

- реализацию концептуальной модели БД;

- выбор модели данных для реализации БД.

Модель и логические структуры данных. Существует множество типовых структур организации данных [2]. На сегодняшнем этапе развития компьютерных технологий типовые структуры важно рассматривать, с одной стороны, как основу построения абстракций при создании библиотек базовых классов объектно-ориентированных систем программирования, с другой стороны, как основу объектно-ориентированной ориентации моделирования баз данных.

Инфологическая модель БДМ. Мифологическая модель базы данных с ориентацией на ее реализацию в РМД представлена на рис. 5.9.

Логические объекты выделяются из концептуального представления базы данных на основе принятой классификационной схемы

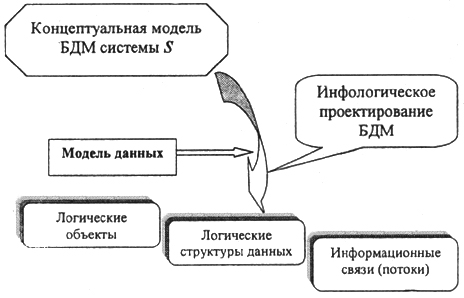
Рис. 5.8. Инфологическое проектирование БДМ

БД. Логические объекты порождаются на основе идентификационных совокупностей свойств концептуальных абстракций объектов и абстракций концептуальных связей. С точки зрения проектировщика базы данных, логические объекты соответствуют объектам прикладных данных, понятны по своему определению (например, абстракция "пользователь компьютерных систем" логически разделима на объекты "пользователь" и "компьютерная система" при условии соответственно построенной концептуальной модели). В любом случае, выделение логических объектов для каждой идентифицирующей группы свойств концептуальной модели БД является важным методологическим принципом мифологического проектирования БДМ.

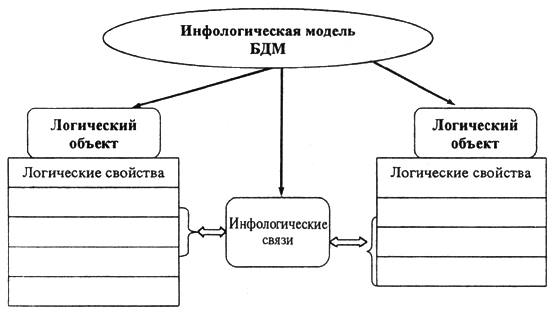
Рис. 5.9. Мифологическая модель БДМ с ориентацией на ее реализацию в РМД

Интеграция распределенных БДМ. В практике моделирования сложных систем приходится иметь дело с многомашинными комплексами и сетевыми структурами, что требует решить проблему интеграции БД. Основные понятия и определения формируемой интеграционной методологии представлены на рис. 5.10.

Сформированная таким образом архитектура интеграционной методологии позволяет сформулировать и определить ключевые понятия и принципы построения объектов компьютерных технологий класса интегрированных распределенных баз данных (ИРБД) [41, 52, 54].

Классы баз данных, распределенных баз данных и интегрированных распределенных баз данных образуют иерархию "обобщение-специализация", поэтому для определения интегрированной РБД можно использовать наследование существенных свойств объектов порождающих классов.

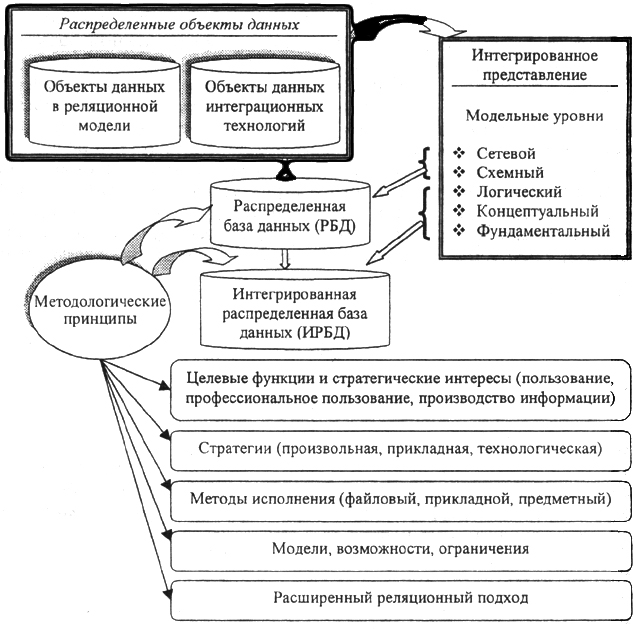
Рис. 5.10. Основные понятия и определения интеграционной методологии

Любая база данных определяется через совокупность связанных (интегрированных в базу) данных и является разделяемым информационным ресурсом компьютеризированных технологий. Тогда любая распределенная база данных также является разделяемым информационным ресурсом (совокупностью локальных информационных ресурсов) в виде связанных распределенных данных. Очевидно, что для определения понятия "интегрированная распределенная база данных" в первую очередь необходимо уточнить суть понятия "распределенные данные".

Распределенные БДМ. В обобщенном виде, классификационное определение распределенной базы данных следует из определения БД и формулируется в виде: распределенная база данных это распределенные данные и связи между ними. Локальная связанность распределенных данных присуща определениям локальных БДМ. Для распределенной БДМ ключевым объектом определения становятся связи между распределенными данными, т. е. теперь необходимо сформулировать условия, при которых распределенная информационная среда приобретает статус распределенной базы данных.

Одним из главных преимуществ применения реляционной модели является обеспечение однородности табличного представления любых БД. В терминах расширенного реляционного подхода такая однородность трактуется как даталогическая однородность реляционных БД. Именно это обстоятельство сопровождается сегодня формированием стандарта доступа в БД на основе языка SQL. Специфика СУБД, проявляющаяся, в том числе, и в существовании диалектов языка SQL нивелируется путем применения средств логического соединения с БД посредсвом механизма псевдонимов.

Реляционная модель обеспечивает однородность представления распределенных данных. Механизм псевдонимов обеспечивает однородность среды манипулирования распределенными данными (например, система драйверов БД DAO использует приложение Microsoft Jet Database Engine для однородного манипулирования базами данных Microsoft Access, а также FoxPro и Excel). В совокупности, таким образом, реализуется однородная среда определения и манипулирования распределенными данными. Назовем представление такой среды схемным модельным уровнем интегрированного представления совокупности распределенных распределенных данных, учитывая общепринятое понимание реализации реляционных БД в виде реляционных схем.

Тогда можно сказать, что реализация представления совокупности (интегрированного представления) распределенных данных на уровне схемной модели обеспечивает удовлетворение представленной таким образом совокупности распределенных данных требованиям реляционной модели. Совокупность распределенных данных становится при этом реляционной БД, и именно такая реляционная БД и будет называться распределенной базой данных. Учитывая интеграционный характер объединения распределенных данных в совокупность, схемную однородность РБД будем называть схемной интеграцией.Тогда определение распределенной БД формулируется следующим образом распределенная база данных это, по меньшей мере, схемно интегрированная совокупность распределенных данных.

По сути дела, такое определение распределенной БДМ означает построение совокупности локальных информационных ресурсов в виде однороной среды распределенных данных, причем однородность рассматривается с точки зрения определения и манипулирования распределенными данными в границах реляционного подхода, или на уровне даталогических схем локальных элементов БДМ. Обобщенная даталогическая схема РБД в принципе доступна для выполнения стандартных операций обобщенной нормализации, однако, при этом необходимо учитывать цели построения РБД, которую далеко не всегда целесообразно и возможно сформировать в виде единой реляционной БДМ.

Расширение реляционного подхода предусматривает представление баз данных по полной технологической схеме, т. е. включая формализованные описания инфологической, концептуальной и фундаментальной моделей БД. Распределенные объекты данных на этих уровнях представления разнородны по определению, содержательно, а не технически, в силу их построения в интересах локальных систем и приложений. Определим инфологический, концептуальный и фундаментальный уровни семантическими уровнями представления РБД. И если для локальных баз данных семантическая интеграция выполняется явно или интуитивно проектировщиком БДМ, то для распределенных БДМ достижение семантической однородности становится существенной проблемой. Декларируя факт возможности достижения семантической однородности распределенных БДМ, можно сформулировать следующее определение: интегрированная распределенная база данных - это семантически интегрированная распределенная база данных.

Другими словами, при интеграции РБД подразумевается семантическая интеграция, достижимая в рамках расширенного реляционного подхода. Схемная интеграция РБД однозначна (табличное представление распределенных данных независимо от специфики их реализации). Семантическая интеграция многозначна и допускает множество вариантов реализации. Это означает, что определение класса интегрированных РБД постулирует существование разновидностей ИРБД, объединенных существенным свойством семантической однородности (логической, концептуальной или фундаментальной) [2, 16].

5 .5. ГИБРИДНЫЕ МОДЕЛИРУЮЩИЕ КОМПЛЕКСЫ

В практике машинного моделирования сложных систем используется вычислительная техника трех типов: ЭВМ, АВМ и ГВК. При этом ГВК, обеспечение которых ориентировано на решение задач машинного моделирования (например, по составу программного обеспечения, наличию операционной системы реального времени и диалога, интерфейсу с натурными блоками моделируемой системы S и т. д.), называются гибридными или аналого-цифровыми моделирующими комплексами (АЦМК). Преимущества каждого типа вычислительных средств в первую очередь определяются спецификой основных свойств цифровых и аналоговых ЭВМ, используемых для моделирования конкретной системы S.

Рассмотрим достоинства и недостатки этих трех типов вычислительных средств (АВМ, ЭВМ и ГВК) применительно к машинному моделированию систем [52]. В общем случае с любой задачей, которую решает АВМ, может справиться и достаточно мощная универсальная ЭВМ. Но на АВМ можно решать задачи моделирования систем быстрее и эффективнее.

Основные черты, характерные для АВМ:

1) зависимые переменные модели системы S представляютсяв непрерывном виде;

2) точность результатов моделирования определяется качеством компонентов электрических схем АВМ;

3) возможно одновременное выполнение параллельных вычислительных операций, что особенно важно при моделировании сложных систем;

4) возможно выполнение операций в реальном или ускоренном масштабе времени (скорость вычислений ограничена главным образом частотными характеристиками элементов, а не сложностью решаемой задачи моделирования системы S);

5) операции сложения, вычитания, умножения, дифференцирования, интегрирования, генерирования непрерывных функций выполняются весьма эффективно, но имеются ограниченные возможности выполнения логических действий, накопления цифровых данных, обеспечения длительных задержек, обработки информации, которые весьма характерны для моделирования систем;

6) технология программирования состоит в основном в замещении элементами АВМ (такими, как операционные усилители, интеграторы и т. п.) соответствующих элементов моделируемой системы S;

7) к АВМ можно подключить блоки реальной системы S при комбинированном моделировании; пользователь имеет возможность в ходе машинного эксперимента на АВМ изменять значения установок, т. е. коэффициентов, устанавливаемых на АВМ, что обеспечивает более наглядное проведение эксперимента с моделью системы S.

Характерные черты ЭВМ:

1) вся обработка промежуточной и результирующей информации в процессе моделирования системы S реализуется в дискретном виде;

2) все операции по работе с машинной моделью М_м выполняются последовательно;

3) точность результатов моделирования системы S определяется главным образом выбранными численными методами решения задачи и формой представления чисел;

4) время решения определяется сложностью задачи моделирования системы S, т. е. числом операций, необходимых для получения результатов моделирования;

5) наличие компромисса между временем решения и точностью результатов моделирования системы S;

6) применяется ограниченное число арифметических операций(сложение, вычитание, умножение и деление), но с помощью численных методов можно в модели на базе этих исходных операций реализовать и более сложные, например дифференцирование, интегрирование и т. д.;

7) для выполнения логических операций и принятия решений в процессе моделирования используются как цифровые, так и нецифровые данные;

8) предусматриваются операции с плавающей запятой, что устраняет трудности масштабирования модели;

9) методы программирования базируются как на ЯОН (часто не имеющих непосредственного отношения к задаче моделирования), так и на ЯИМ.

Современные ГВК представляют собой попытку объединить все лучшее, присущее цифровой и аналоговой технике, и избежать их недостатков. Некоторые задачи требуют для своего решения усиления цифровой части комплекса аналоговой частью для увеличения скорости вычислений и распараллеливания процессов. При этом цифровая часть ГВК дает возможность:

1) управлять аналоговой частью машинной модели М_м при высоком быстродействии;

2) использовать устройства запоминания и хранения данных моделирования;

3) обеспечивать более высокую точность вычислений и применения логических операций при моделировании системы S.

Преимущества ГВК:

1) сочетает быстродействие АВМ и точность ЭВМ, что позволяет расширить класс моделируемых объектов;

2) в процессе машинного моделирования позволяет использовать реальные технические средства и части исследуемой конкретной системы S;

3) обеспечивает гибкость аналогового моделирования благодаря использованию логики и памяти ЭВМ;

4) увеличивает быстродействие ЭВМ за счет использования аналоговых подпрограмм;

5) делает возможной обработку входной информации о модели системы S, представленной частично в дискретной и непрерывной формах.

Говорить о преимуществах и недостатках ГВК можно применительно к машинному моделированию конкретного класса систем S. Для некоторых объектов использование при реализации модели системы ГВК аналогично их практической реализуемости.

В зависимости от специфики исследуемых объектов в ряде случаев эффективной оказывается ориентация при моделировании систем на ЭВМ. При этом надо иметь в виду, что АВМ значительно уступают ЭВМ по точности и логинеским возможностям, но по быстродействию, схемной простоте, сопрягаемости с датчиками внешней информации превосходят или, по крайней мере, не уступают им.

Для сложных динамических объектов перспективным является моделирование на базе ГВК, которые реализуют преимущества цифрового и аналогового моделирования и позволяют наиболее эффективно использовать ресурсы ЭВМ и АВМ в составе единого комплекса. При использовании ГВК существенно упрощаются вопросы взаимодействия с датчиками, установленными на реальных объектах, что позволяет, в свою очередь, проводить комбинированное моделирование с использованием аналого-цифровой части модели и натурной части объекта. Такие гибридные моделирующие комплексы могут входить в состав многомашинного информационно-вычислительного комплекса коллективного пользования, что еще больше расширяет его возможности с точки зрения моделируемых классов больших систем.

Состав и структура технического обеспечения АЦМК определяется множеством задач, на решение которых он ориентирован. В общем виде структура технических средств представлена на рис. 5.11. Здесь приняты следующие обозначения: АВМ - аналоговая вычислительная машина; ЭВМ - цифровая электронная вычислительная машина; АЦП - аналого-цифровой преобразователь; ЦАП - цифро-аналоговый преобразователь; БУС - блок управляющих связей; РА - реальная аппаратура; ПОп - пульт оператора.

Возможны различные варианты построения многомашинных комплексов, в которых используется по несколько АВМ и ЭВМ. Такие варианты обычно выбираются в случаях, когда не хватает производительности одного вычислителя или есть необходимость разделить средства выполнения отдельных задач моделирования системы S из-за ее функциональных или структурных особенностей.

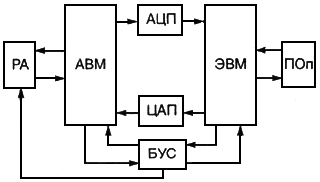
Рис. 5.11. Структура технических средств аналого-цифрового моделирующего комплекса

Преобразователи АЦП и ЦАП являются средствами организации информационных связей между АВМ и ЭВМ, т. е. средствами для обмена информацией между цифровой и аналоговой частями модели системы S.

Подготовка, запуск, останов и синхронизация элементов АЦМК в процессе решения задачи моделирования, как правило, осуществляются ЭВМ. Для реализации этих функций применяются специальные управляющие шины и аппаратура стыковки АВМ и ЭВМ по управлению, которые объединены на рассматриваемой схеме в БУС. Наряду с цифровой и аналоговой частями модели исследования на АЦМК могут использоваться реальные элементы исследуемой системы S. Исследования такого типа называются полунатурным моделированием.

Оператор управляет процессом моделирования с помощью средств, номенклатура которых определяется задачами, решаемыми на АЦМК. В состав ПОп могут входить печатающие устройства различного типа, дисплеи, графопостроители, самописцы и т. д., может иметь место специализированная клавиатура для передачи управляющих команд типа "Запуск", "Останов" и т. п. Таким образом, ПОп в АЦМК представляет собой набор технических средств для организации диалога "оператор - машинный эксперимент".

При распределении задачи моделирования системы S по средствам, входящим в состав АЦМК, могут быть выделены три типа комплексов.

Аналого-ориентированные комплексы используются в тех случаях, когда не требуется высокая точность результатов и когда моделируемая система S реализуема аналоговыми средствами. Системы такого класса исследуются на АЦМК, в которых цифровые средства необходимы на этапе подготовки модели для автоматизации набора задачи, накопления и обработки результатов моделирования. Сама же модель системы S реализуется исключительно на аналоговом вычислителе (аналоговое моделирование). Наряду с указанными функциями ЭВМ может выполнять задачи управления АВМ в процессе реализации модели. АЦМК с цифровым управлением и цифровой логикой способны воспроизводить более сложные модели по сравнению со стандартными АВМ. К аналого-ориентированным АЦМК относятся также комплексы, в которых ЦВМ применяются в качестве периферийного оборудования. В таких АЦМК малая ЭВМ используется с мощной АВМ для решения 170 специальных задач моделирования, решение которых было бы трудно или невозможно с помощью аналоговой аппаратуры.

К цифро-ориентированным комплексам можно отнести универсальные ЭВМ, где для отображения и регистрации результатов используются аналоговые средства - осциллографы, самописцы и т. д. В таких АЦМК модель М_м полностью реализуется цифровыми методами. Возможны варианты построения АЦМК для полунатурного моделирования, когда реальная аппаратура стыкуется с ЭВМ через аналоговый вычислитель. В цифро-ориентированных АЦМК может иметь место распараллеливание отдельных вычислительных процедур в процессе работы с цифровой моделью М_м за счет реализации их аналоговыми средствами.

Сбалансированные (универсальные) комплексы являются самым мощным средством для решения задач аналого-цифрового моделирования. В их состав входят средства, с помощью которых могут эффективно решаться не только аналого-цифровые задачи, но и задачи аналоговые с цифровым управлением, а также задачи цифрового моделирования. На комплексах такого типа широко используется диалог "оператор - машинный эксперимент", т. е. могут запоминаться, отображаться и регистрироваться результаты решений, оперативно вноситься изменения в модель М_м и осуществляться ее запуск. Другими словами, имеется возможность реализовать итеративный процесс исследования, сходящийся к получению искомого результата, что особенно важно при автоматизации проектирования системы S на базе машинного моделирования.

Задача построения технического обеспечения АЦМК в настоящее время сводится к выбору стандартной аппаратуры, разработке информационных и управляющих связей, реализуемых программно. Такой подход стал возможным благодаря тому, что сейчас промышленность выпускает широкий перечень ЭВМ, в которых предусмотрена возможность неавтономной работы. Это условие важно для построения АЦМК, так как в противном случае необходимы доработки универсальных вычислителей, создание нестандартного оборудования, что, как правило, делать нежелательно. При создании АЦМК должна быть возможность стыковки с периферийными устройствами широких функциональных возможностей: аналого-цифровые и цифро-аналоговые преобразователи, коммутаторы, регистры и т. д.

Современные АВМ, как правило, позволяют осуществлять цифровое управление. Принципиальных трудностей в построении технического обеспечения АЦМК нет. Однако, несмотря на широкие возможности, открывающиеся с выпуском большой номенклатуры цифровых и аналоговых вычислительных устройств, задача выбора комплекса технических средств АЦМК представляет собой сложную проблему, при решении которой необходимо ответить на следующие вопросы [36].

Прежде всего нужно обосновать преимущества гибридного моделирования системы перед аналоговым или цифровым. При этом задачи, для которых проектируется АЦМК, должны быть достаточно важными, чтобы оправдать затраты на его создание. Решая вопрос о том, должен ли комплекс быть аналого-ориентированным, цифро-ориентированным или сбалансированным, необходимо провести выбор ЭВМ средней, малой или большой мощности. При достаточно высоких требованиях к скорости реализации цифровой части модели системы можно пойти по пути создания многопроцессорного комплекса. Необходимо рассмотреть требования к архитектурным особенностям ЭВМ: длине слова, возможностям системы прерывания, наличию аппаратных средств для работы с плавающей запятой, организации памяти и т. д. При выборе АВМ необходимо учитывать полосу пропускания, эффективность управления от ЭВМ, возможности автоматического набора, точностные характеристики.

Следует ответить на вопросы: требуется ли работа в реальном масштабе времени, какие устройства должны быть включены в гибридный вычислительный контур, какие функции по управлению должны быть возложены на ЭВМ. При определении технологии проведения исследований на АЦМК выбирается номенклатура устройств отображения и регистрации, средств ведения диалога, находятся конфигурация системы связи, алгоритмы обмена и синхронизации работы отдельных устройств. Важными моментами при построении АЦМК являются выбор АЦП и ЦАП, количество каналов информационных связей, требования к точности и быстродействию.

Сложность перечисленных вопросов заключается в том, что большинство из них взаимосвязаны. От правильности их решения зависит эффективность моделирования систем на АЦМК, точность и достоверность результатов моделирования конкретной системы S.

Процедура компоновки технического обеспечения АЦМК представляет собой достаточно сложный неформальный процесс, в котором качество созданного комплекса в значительной степени зависит от интуиции, опыта и способностей его разработчиков. Данная процедура включает в себя этап логической, конструктивной и электрической компоновки.

Логическая компоновка подразумевает выбор минимального состава устройств, агрегатов и модулей из номенклатуры определенных семейств вычислительной техники, обеспечивающих выполнение функциональных задач, стоящих перед АЦМК, а также объединение их в единый комплекс, работающий под управлением общего программного обеспечения. При конструктивной компоновке решаются вопросы размещения устройств в типовых конструктивных элементах. Электрическая компоновка предполагает выбор линий связи для конструктивно скомпонованных элементов и порядок их соединений. Исходным материалом для логической компоновки являются агрегаты и модули технического обеспечения.

Опишем вариант построения АЦМК для решения задачи моделирования системы S на базе управляющей ЭВМ, которая имеет развитый интерфейс "Общая шина" (ОШ), т. е. на них могут быть возложены функции управления. Возможности расширения памяти и быстродействия позволяют достаточно эффективно использовать управляющие ЭВМ для реализации расчетных процедур в процессе моделирования различных систем. Мощная операционная система этих ЭВМ позволяет на базе стандартных средств реализовать процедуры генерации модели М_м на этапе ее подготовки [12].

Рассмотрим особенности компоновки устройств организации информационных и управляющих связей между ЭВМ и АВМ. Вариант использования ЭВМ в качестве цифровой части АЦМК состоит в применении для этих целей измерительно-вычислительных комплексов (ИВК). Развитие персональных и микроЭВМ, модульных программно-аппаратных средств, построенных на их базе для целей автоматизации научных исследований, создало благоприятные технико-экономические условия для компоновки модульных информационно-измерительных систем и ЭВМ в единые ИВК.

В общем случае ИВК - это автоматизированное средство измерения и обработки информации, предназначенное для исследования, контроля и испытаний сложных объектов и представляющее собой совокупность программно-управляемых технических средств, имеющих блочно-модульную структуру, определенную организацию и связи, обеспечивающие получение, преобразование, накопление, обработку и выдачу измерительной, командной и другой информации в соответствующей форме, в том числе для воздействия на объект исследования. При построении АЦМК на базе ИВК реальная аппаратура и АВМ выступают в качестве управляемого исследуемого объекта.

Пример 5.2. Рассмотрим возможности построения технического обеспечения АЦМК на базе ИВК (рис. 5.12). В данной структуре через интерфейс ОШ объединены следующие устройства: П - процессор, ОЗУ - оперативное запоминающее устройство, Д - дисплей, ПР - принтер, Н - накопители. Совокупность данных устройств представляет собой вычислительный комплекс. Связь с АВМ осуществляется через два крейта: устройство управления - КК1 - контролер крейта № 1, АЦП - аналого-цифровой преобразователь, К - коммутатор, ЦАШ и ЦАП2 - цифро-аналоговые преобразователи, РВИС - регистр ввода инициативных сигналов. В данном варианте стыковки с АВМ аппаратура крейта № 2 - КК2, входящего в состав ИВК, не используется, за исключением ЦАП2, перенесенного в крейт № 1. Управление процессом моделирования на АЦМК осуществляется с пульта управления ПУ.

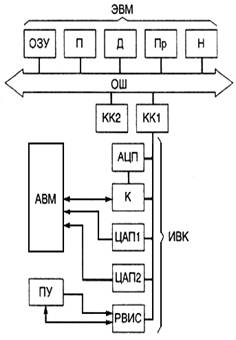
Рис. 5.12. Структура технического обеспечения АЦМК на базе ИВК

Развитая операционная система современных ЭВМ позволяет реализовать на их основе процедуры генерации цифровой части модели М_м, организовать диалоговые режимы на этапе подготовки машинного эксперимента и обработки его результатов. В то же время свойства ИВК как управляющего комплекса дают возможность управлять процессом моделирования системы S, осуществлять сбор, накопление и обработку результатов моделирования.

При рассмотрении приведенных примеров структур комплексов (рис. 5.11 и 5.12) не ставилась цель показать процесс проектирования технического обеспечения АЦМК. Данные структуры приводились как возможные варианты реализации АЦМК для моделирования систем.

Программное обеспечение (ПО) АЦМК (рис. 5.13) строится по модульному принципу и включает в себя комплексы программ: планирования машинных экспериментов, построения модели системы, проведения машинных экспериментов, обработки результатов моделирования. Наиболее перспективной формой реализации ПО АЦМК является построение его в виде набора пакетов прикладных программ (ППП), снабженных развитыми средствами генерации, модификации и расширения.

Функциональное разбиение ПО может быть произведено с привязкой его к составным частям АЦМК. В этом случае в ПО включаются ППП пользователей, ПО аппаратуры КАМАК, ППП управления АВМ, проблемно-ориентированное ПО ЭВМ.

Пример 5.3. Рассмотрим состав ПО АЦМК. В зависимости от вида модели конкретной системы S ППП пользователя включает в себя следующие программы:

STATE - программа, содержащая соотношения между переменными и параметрами и задающая описание непрерывной части модели системы;

SCOND - программа слежения за значениями дискретных переменных и определения наступления событий в модели системы;

SSAVE - программа сбора информации о состояниях моделируемой системы;

EVNTS - программа реализации событий, содержащая алгоритмы обработки событий в модели системы;

USINT - программа определения начальных значений переменных модели (может также переопределять значения переменных в процессе моделирования);

USOUT - программа вывода результатов моделирования, не предусмотренных системой моделирования;

PLNEX - ППП, позволяющий планировать эксперимент, собирать и обрабатывать статистическую информацию о результатах моделирования системы. Решая

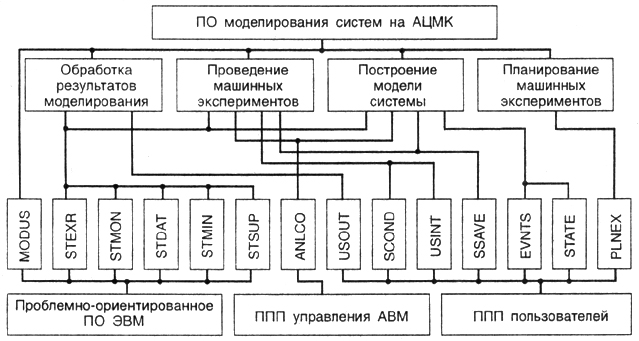
Рис. 5.13. Распределение задач моделирования по средствам АЦМК

задачу моделирования конкретной системы S, пользователь может отказаться от использования тех или иных программ.

MONIT - программа-монитор, которая представляет собой совокупность программ, решающих общие задачи управления аппаратурой и обработки прерываний в программах, написанных на языке ЯОН. В состав программы-монитора входят управляющая программа, предназначенная для организации работы с прерываниями от аппаратуры и блочного обмена данными в рамках операционной системы, и пакет программ, обеспечивающих выполнение основных функций из программ, написанных на ЯОН.

Программное обеспечение АВМ представляется в виде ППП ANLCO, позволяющего проводить автоматическую настройку блоков АВМ, имитирующих непрерывную часть в модели системы и управление этой настройкой и обменом информацией с другими составляющими АЦМК.

Наиболее сложная часть ПО - комплекс программных средств ЭВМ. Не останавливаясь на рассмотрении операционной системы MODOS, в рамках которой реализуется модель системы S, рассмотрим состав проблемно-ориентированного ПО ЭВМ, позволяющего управлять процессом моделирования и обеспечивающего при этом взаимодействие пользователя с моделью. В его состав входят:

STSUP - супервизор комплекса, осуществляющий управление процессами моделирования системы по командам пользователя;

STMIN - интерактивный монитор комплекса, позволяющий в процессе моделирования системы в режиме дружественного интерфейса выполнять отображение объектов модели, изменение содержимого модели системы в процессе моделирования и т. п.;

STDAT - модуль, выполняющий инициализацию объектов системы моделирования;

STMON - программный монитор комплекса, обеспечивающий реализацию системных функций в программном режиме по запросам программ модели;

STEXR - управляющий модуль комплекса, осуществляющий контроль за процессом моделирования.

Использование модульной структуры и организации ПО моделирования позволяет в режиме генерации создавать ППМ конкретной системы S, ориентированный на режим гибридного моделирования и конкретную конфигурацию комплекса технических средств АЦМК.

Контрольные вопросы

5.1. Чем отличаются языки имитационного моделирования от языков общего назначения?

5.2. как можно представить архитектуру языка имитационного моделирования?

5.3. Какие основные требования предъявляются к языкам имитационного моделирования?

5.4.Ккакие имеются группы языков моделирования дискретных систем?

5.5. Какие основные идеи положены в основу построения дерева решений по выбору языка для моделирования системы?

5.6. Что называется пакетом прикладных программ моелирования систем?

5.7. Что является функциональным и системным наполнением пакета прикладных программ моделирования?

5.8. Каковы функции языка заданий пакета прикладных программ моделирования?

5.9. Какие существуют моделирующие комплексы?

ГЛАВА 6

ПЛАНИРОВАНИЕ МАШИННЫХ ЭКСПЕРИМЕНТОВ

С МОДЕЛЯМИ СИСТЕМ

Имитационное моделирование является по своей сути машинным экспериментом с моделью исследуемой или проектируемой системы. План имитационного эксперимента на ЭВМ представляет собой метод получения с помощью эксперимента необходимой пользователю информации. Эффективность использования экспериментальных ресурсов существенным образом зависит от выбора плана эксперимента. Основная цель экспериментальных исследований с помощью имитационных моделей состоит в наиболее глубоком изучении поведения моделируемой системы. Для этого необходимо планировать и проектировать не только саму модель, но и процесс ее использования, т. е. проведение с ней экспериментов на ЭВМ. Весь комплекс вопросов планирования экспериментов с имитационными моделями для их успешного решения рационально разбить на стратегическое и тактическое планирование.

6.1. МЕТОДЫ ТЕОРИИ ПЛАНИРОВАНИЯ

ЭКСПЕРИМЕНТОВ

Машинный эксперимент с моделью системы S при ее исследовании и проектировании проводится с целью получения информации о характеристиках процесса функционирования рассматриваемого объекта. Эта информация может быть получена как для анализа характеристик, так и для их оптимизации при заданных ограничениях, т. е. для синтеза структуры, алгоритмов и параметров системы S. В зависимости от поставленных целей моделирования системы 5 на ЭВМ имеются различные подходы к организации имитационного эксперимента с машинной моделью М_м. Основная задача планирования машинных экспериментов — получение необходимой информации об исследуемой системе S при ограничениях на ресурсы (затраты машинного времени, памяти и т. п.). К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, увеличения точности и достоверности результатов моделирования, проверки адекватности модели и т. д.

       Машинный эксперимент. Эффективность машинных экспериментов с моделями М_м существенно зависит от выбора плана эксперимента, так как именно план определяет объем и порядок проведения вычислений на ЭВМ, приемы накопления и статистической обработки результатов моделирования системы S. Поэтому основная задача планирования машинных экспериментов с моделью М_м формулируется следующим образом: необходимо получить информацию об объекте моделирования, заданном в виде моделирующего алгоритма (программы), при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования.

Таким образом, при машинном моделировании рационально планировать и проектировать не только саму модель М_м системы S, но и процесс ее использования, т. е. проведение с ней экспериментов с использованием инструментальной ЭВМ.

К настоящему времени в физике, биологии и т. д. сложилась теория планирования экспериментов, в которой разработаны достаточно мощные математические методы, позволяющие повысить эффективность таких экспериментов [10, 18,21, 33J. Но перенос этих результатов на область машинных экспериментов с моделями М_м может иметь место только с учетом специфики моделирования систем на ЭВМ. Несмотря на то что цели экспериментального моделирования на ЭВМ и проведения натурных экспериментов совпадают, между этими двумя видами экспериментов существуют различия, поэтому для планирования эксперимента наиболее важное значение имеет следующее: 1) простота повторения условий эксперимента на ЭВМ с моделью М_м системы S; 2) возможность управления экспериментом с моделью М_м, включая его прерывание и возобновление; 3) легкость варьирования условий проведения эксперимента (воздействий внешней среды Е); 4) наличие корреляции между последовательностью точек в процессе моделирования; 5) трудности, связанные с определением интервала моделирования (0,7).

Преимуществом машинных экспериментов перед натурным является возможность полного воспроизведения условий эксперимента с моделью исследуемой системы 5". Сравнивать две альтернативы возможно при одинаковых условиях, что достигается, например, выбором одной и той же последовательности случайных чисел для каждой из альтернатив. Существенным достоинством перед натурными является простота прерывания и возобновления машинных экспериментов, что позволяет применять последовательные и эвристические приемы планирования, которые могут оказаться нереализуемыми в экспериментах с реальными объектами. При работе с машинной моделью М_м всегда возможно прерывание эксперимента на время,  необходимое для  анализа результатов и принятия решений об его дальнейшем ходе (например, о необходимости изменения значений параметров модели М_м).

Недостатком машинных экспериментов является то, что часто возникают трудности, связанные с наличием корреляции в выходных последовательностях, т. е. результаты одних наблюдений зависят от результатов одного или нескольких предыдущих, и поэтому вних содержится меньше информации, чем в независимых наблюдениях. Так как в большинстве существующих методов планирования экспериментов предполагается независимость наблюдений, то многие из этих методов нельзя непосредственно применять для машинных экспериментов при наличии корреляции [18, 21, 29, 46, 53].

Основные понятия планирования экспериментов. Рассмотрим основные понятия теории планирования экспериментов. В связи с тем что математические методы планирования экспериментов основаны на кибернетическом представлении процесса проведения эксперимента, наиболее подходящей моделью последнего является абстрактная схема, называемая «черным ящиком». При таком кибернетическом подходе различают входные и выходные переменные: x₁ x₂, ... ..., х_к; у₁ у₂,..., у_i В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место только две переменные: х и у. Тогда если цель эксперимента — изучение влияния переменной х на переменную у, то х — фактор, а у — реакция. В экспериментах с машинными моделями М_м системы S фактор является экзогенной или управляемой (входной) переменной, а реакция — эндогенной (выходной) переменной. Например, в агрегативной системе (А-схеме) факторами будут входные и управляющие сообщения, а реакциями — выходные.

Каждый фактор x_h i=l, к, может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.

Каждому фиксированному набору уровней факторов соответствует определенная точка в многомерном пространстве, называемом факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как, например, это показано для случая двух факторов х_х и х₂ на рис. 6.1 (плоскость х₁0₁х₂)

Существует вполне определенная связь между уровнями факторов и реакцией (откликом) системы, которую можно представить в виде соотношения

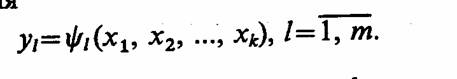
Функцию ψi связывающую реакцию с факторами   называют функцией реакции, а геометрический образ, соответствующий функции реакции,— поверхностью реакции. Исследователю заранее не известен вид зависимостей ψi,, 1=1, т, поэтому используют приближенные соотношения:

            Зависимости φ₁ находятся по данным эксперимента. Последний необходимо поставить так, чтобы при минимальных затратах ресурсов (например, минимальном числе испытаний), варьируя по специально сформулированным правилам значения входных переменных, построить математическую модель системы и оценить ее характеристики.

При планировании экспериментов необходимо определить основные свойства факторов. Факторы при проведении экспериментов могут быть управляемыми и неуправляемыми, наблюдаемыми и ненаблюдаемыми, изучаемыми и неизучаемыми, количественными и качественными, фиксированными и случайными.

Фактор называется управляемым, если его уровни целенаправленно выбираются исследователем в процессе эксперимента. При машинной реализации модели М_м исследователь принимает решения, управляя изменением в допустимых пределах различных факторов.

Фактор называется наблюдаемым, если его значения наблюдаются и регистрируются. Обычно в машинном эксперименте с моделью М_м наблюдаемые факторы совпадают с управляемыми, так как нерационально управлять фактором, не наблюдая его. Но неуправляемый фактор также можно наблюдать. Например, на этапе проектирования конкретной системы S нельзя управлять заданными воздействиями внешней среды Е, но можно наблюдать их в машинном эксперименте. Наблюдаемые неуправляемые факторы получили название сопутствующих. Обычно при машинном эксперименте с моделью М_м число сопутствующих факторов велико, поэтому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на интересующую исследователя реакцию.

Фактор относится к изучаемым, если он включен в модель М_м для изучения свойств системы S, а не для вспомогательных целей, например для увеличения точности эксперимента.

Фактор будет количественным, если его значения - числовые величины, влияющие на реакцию, а в противном случае фактор называется качественным. Например, в модели системы, формализуемой в виде схемы массового обслуживания (Q-схемы), количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, емкости накопителей, количество обслуживающих каналов и т. д., а качественными факторами - дисциплины постановки в очередь, выбора из очереди, обслуживания заявок каналами и т. д. Качественным факторам в отличие от количественных не соответствует числовая шкала. Однако и для них можно построить условную порядковую шкалу, с помощью которой производится кодирование, устанавливая соответствие между условиями качественного фактора и числами натурального ряда.

Фактор называется фиксированным, если в эксперименте исследуются все интересующие экспериментатора значения фактора, а если экспериментатор исследует только некоторую случайную выборку из совокупности интересующих значений факторов, то фактор называется случайным. На основании случайных факторов могут быть сделаны вероятностные выводы и о тех значениях факторов, которые в эксперименте не исследовались.

В машинных экспериментах с моделями М_м не бывает неуправляемых или ненаблюдаемых факторов применительно к исследуемой системе S. В качестве воздействий внешней среды Е, т. е. неуправляемых и ненаблюдаемых факторов, в машинной имитационной модели выступают стохастические экзогенные переменные. Если имитационная модель сформулирована, то все факторы определены и нельзя во время проведения данного эксперимента (испытания) с моделью М_м вводить дополнительные факторы.

Как уже отмечалось, каждый фактор может принимать в испытании одно или несколько значений, называемых уровнями, причем фактор будет управляемым, если его уровни целенаправленно выбираются экспериментатором. Для полного определения фактора необходимо указать последовательность операций, с помощью которых устанавливаются его конкретные уровни. Такое определение фактора называется операциональным и обеспечивает однозначность понимания фактора.

Основными требованиями, предъявляемыми к факторам, являются требование управляемости фактора и требование непосредственного воздействия на объект. Под управляемостью фактора понимается возможность установки и поддержания выбранного нужного уровня фактора постоянным в течение всего испытания или изменяющимся в соответствии с заданной программой. Требование непосредственного воздействия на объект имеет большое значение в связи с тем, что трудно управлять фактором, если он является функцией других факторов.

При планировании эксперимента обычно одновременно изменяются несколько факторов. Определим требования, которые предъявляются к совокупности факторов. Основные из них - совместимость и независимость. Совместимость факторов означает, что все их комбинации осуществимы, а независимость соответствует возможности установления фактора на любом уровне независимо от уровней других.

При проведении машинного эксперимента с моделью М_м для оценки некоторых характеристик процесса функционирования исследуемой системы S экспериментатор стремится создать такие условия, которые способствуют выявлению влияния факторов, находящихся в функциональной связи с искомой характеристикой.

Для этого необходимо: отобрать факторы х_i, i = 1, k, влияющие на искомую характеристику, и описать функциональную зависимость;

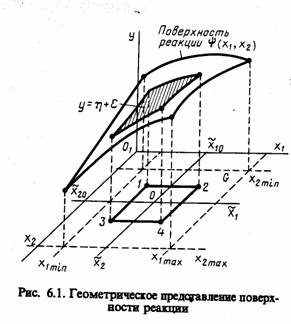
Свойства объекта исследования, т. е. процесса машинного моделирования системы S, можно описывать с помощью различных методов (моделей планирования). Для выбора конкретной модели необходимо сформулировать такие ее особенности, как адекватность, содержательность, простота и т. д. Под содержательностью модели планирования понимается ее способность объяснять множество уже известных фактов, выявлять новые и предсказывать их дальнейшее развитие. Простота - одно из главных достоинств модели планирования, выражающееся в реализуемости эксперимента на ЭВМ, но при этом имеет место противоречие с требованиями адекватности и содержательности.

Для экстремального планирования экспериментов наибольшее применение нашли модели в виде алгебраических полиномов. Предполагаем, что изучается влияние k количественных факторов x_i, i = 1, k, на некоторую реакцию η в отведенной для экспериментирования локальной области факторного пространства G, ограниченной х_{i min} ÷ x_{i max}, i = 1, k (рис. 6.1 для случая k = 2). Допустим, что функцию реакции ψ (х₁, х₂, ..., х_k) можно с некоторой степенью точности представить в виде полинома степени d от k переменных

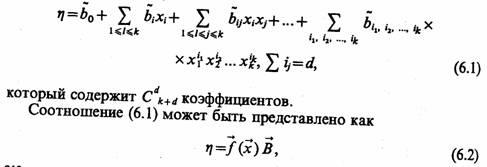
Для оценки коэффициентов в (6.3) можно применить методы линейной регрессии [10, 18, 21, 22].

Пример 6.1. Аппроксимация полиномов второго порядка функции реакции в однофакторной    модели    планирования    может    быть    представлена    в    виде

Более сложные объекты требуют применения полиномиальных моделей планирования большего порядка. Так, модель второго порядка в k-факторном эксперименте будет иметь вид η = b̃₀ + b̃₁ x₁ + b̃₁².

             Более сложные объекты требуют применения полиномиальных моделей планирования большего порядка. Так, модель второго порядка в ^-факторном эксперименте будет иметь вид

На практике часто стремятся к использованию линейной модели планирования, преобразуя исходные полиномиальные модели. Например, модель второго порядка

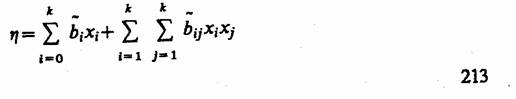
может быть преобразована к линейному виду путем введения фиктивных переменных x_tj=x_ix_j Тогда в результате получается модель множественной линейной регрессии

 вида

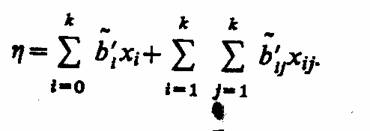
Функция реакции может иметь и более сложную зависимость от факторов. В этом случае некоторые из них удается привести к линейному виду. Такими моделями являются мультипликативная, регрессионная, экспоненциальная и др. [18, 21, 46].

Если выбрана модель планирования, т. е. выбран вид функции η=φ (.x₁, х₂,..., х_к) и записано ее уравнение, то остается в отведенной для исследования области факторного пространства G спланировать и провести эксперимент для оценки числовых значений констант (коэффициентов) этого уравнения.

        Так как полином (6.2) или (6.3) содержит G^d_k+d   коэффициентов, подлежащих определению, то план эксперимента D должен содержать по крайней мере N≥ С k+t различных экспериментальных точек:

где x_iu — значения, которые принимает i-я переменная в м-м испытании, i=1, к, и=1, N.

          Реализовав испытания в N точках области факторного пространства, отведенной для экспериментирования, получим вектор наблюдений, имеющий следующий вил

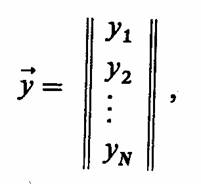
где у_и — реакция, соответствующая м-й точке плана х_и= \\x_iu, x_2u,...,x_ku\\,u=1,N

При незначительном влиянии неуправляемых входных переменных и параметров по сравнению с вводимыми возмущениями управляемых переменных в планировании эксперимента предполагается верной следующая модель:

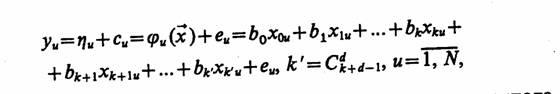
где е_и — ошибка (шум, флуктуация) испытания, которая предполается независимой нормально распределенной случайной величиной математическим   ожиданием       М(_еu).=0 и постоянной дисперсией D_(eu)σ²=const

         Выписав   аналогичные   соотношения для всех точек плана u=1, N, получим матрицу планирования

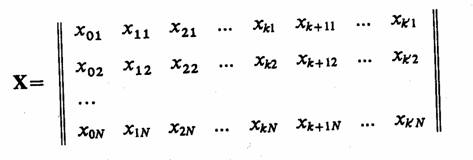
размерностью N х (к' +1).

Рассмотрим особенности планирования эксперимента для линейного приближения поверхности реакции, причем построению плана предшествует проведение ряда неформализованных действий (принятие решений), направленных на выбор локальной области факторного пространства G (рис. 6.1).

Вначале следует выбрать границы x_imin и х_imax области определения факторов, задаваемые исходя из свойств исследуемого объекта, т. е. на основе анализа априорной информации о системе S и внешней среде Е. Например, такая переменная, как температура, при термобарических экспериментах принципиально не может быть ниже абсолютного нуля и выше температуры плавления материала, из которого изготовлена термобарокамера.

После определения области G необходимо найти локальную подобласть для планирования эксперимента путем выбора основного (нулевого) уровня x_i0 и интервалов варьирования Δt, i=l, к. В качестве исходной точки x_i0 выбирают такую, которая соответствует наилучшим условиям, определенным на основе анализа априорной информации о системе 5, причем эта точка не должна лежать   близко    к   границам   области   определения   факторов x_imin и x_imax. На выбор интервала варьирования Δх, накладываются естественные ограничения снизу (интервал не может быть меньше ошибки фиксирования уровня фактора, так как в противном случае верхний и нижний уровни  окажутся неразличимыми) и сверху (верхний и нижний уровни не должны выходить за область определения G).

В рамках выбранной модели планирования в виде алгебраических полиномов строится план эксперимента путем варьирования каждого из факторов х_i, i = 1, k, на нескольких уровнях q относительно исходной точки x_i0, представляющей центр эксперимента.

Виды планов экспериментов. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Если выбранная модель планирования включает в себя только линейные члены полинома и их произведения, то для оценки коэффициентов модели используется план эксперимента с варьированием всех к факторов на двух уровнях, т. е. q=2. Такие планы называются планами типа 2, где N=2 — число всех возможных испытаний.

        Начальный этап планирования эксперимента для получения коэффициентов линейной модели основан на варьировании факторов на двух уровнях: нижнем x_in и верхнем x_iB,— симметрично расположенных относительно основного уровня  x_io, i= 1, к. Геометрическая интерпретация показана на рис. 6.2, а. Так как каждый фактор принимает лишь два значения x_is=x_i0—Δ_xi , и x_iB=x_i0+Δxi, то для стандартизации и упрощения записи условий каждого испытания и обработки выборочных данных эксперимента масштабы по осям факторов выбираются так, чтобы нижний уровень соответствовал — 1, верхний- +1   а основной — нулю. Это легко достигается с помощью преобразования вида

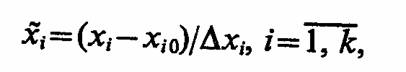
где _Xj — кодированное значение i-го фактора xi — натуральное значение фактора; х₁₀ — нулевой уровень; Δxi,=(х,_в —хi_Н)/2 — интервал варьирования фактора.

Пример 6.2. Пусть в качестве г-го фактора выступает такая переменная, как температура Т, °С, т. е. х, = Т', причем выбраны основной уровень х,о=100°С и интервал варьирования Ах,=20 "С. Тогда кодированные значения Х_i по уровням соответственно будут (80—100)/20 = — 1 для нижнего, (120-100)/20= +1 для верхнего, (100—100)/20=0 для основного.

         Расположение точек для ПФЭ типа 2² показано на рис. 6.1, а также на рис. 6.2, б. Выписывая комбинации уровней факторов для каждой экспериментальной точки квадрата, получим план D полного факторного эксперимента типа 2²:

При этом планы можно записывать сокращенно с помощью условных буквенных обозначений строк. Для этого порядковый номер фактора ставится в соответствие строчной букве латинского алфавита: х₁→а, х_г→b и т. д.

          Затем для каждой строки плана выписываются латинские буквы только для факторов, находящихся на верхних уровнях; испытание со всеми факторами на нижних уровнях обозначается как (1). Запись плана в буквенных обозначениях показана в последней строчке.

Полный факторный эксперимент дает возможность определить не только коэффициенты регрессии, соответствующие линейным эффектам, но и коэффициенты регрессии, соответствующие всем эффектам взаимодействия. Эффект взаимодействия двух (или более) факторов появляется при одновременном варьировании этих факторов, когда действие каждого из них на выход зависит от уровня, на которых находятся другие факторы.

       Для оценки свободного члена b_о и определения эффектов взаимодействия b₁₂, b₁₃,..., b₁₂₃,... план эксперимента D расширяют до матрицы планирования X путем добавления соответствующей «фиктивной переменной»: единичного столбца х₀ и столбцов произведений x₁ x_2,x₁ x₂ ..., x₁ x₂x₃,..., как показано, например, для ПФЭ типа 2³ в табл. 6.1.

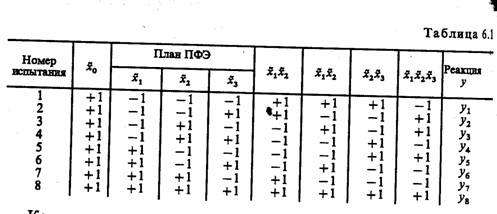
Как видно из рассмотренных планов экспериментов типов 2^г и 2³, количество испытаний в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели плана эксперимента, т. е. ПФЭ обладает большой избыточностью и поэтому возникает проблема сокращения их количества.

        Рассмотрим построение планов так называемого дробного факторного эксперимента. Пусть имеется простейший полный факторный эксперимент типа 2². Используя матрицу планирования, приведенную в табл. 6.2, можно вычислить коэффициенты и представить результаты в виде уравнения

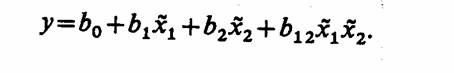
            Если в выбранных интервалах варьирования уровня процесс можно описать линейной моделью, то достаточно определить три коэффициента: b₀, b₁ и b₂. Таким образом, остается одна степень свободы, которую можно использовать для минимизации числа испытаний. При линейном приближении b₁₂ → 0 и вектор-столбец x̃₁x̃₂ (табл. 6.2) можно использовать для нового фактора x̃₃. Поставим в табл. 6.2 этот фактор в скобках над взаимодействием x̃₁x̃₂.В этом случае раздельных оценок, которые имели место в ПФЭ типа 2^k, уже не будет и оценки смещаются следующим образом: b̃₁ → β₁ + β₂₃, b̃₂ → β₂ + β₁₃, b̃₃ → β₃ + β₁₂.

При постулировании линейной модели все парные взаимодействия не учитывают. Таким образом, вместо восьми испытаний в полном факторном эксперименте типа 2³ необходимо провести только четыре. Правило проведения дробного факторного эксперимента формулируется так: для сокращения числа испытаний новому фактору присваивается значение вектор-столбца матрицы, принадлежащего взаимодействию, которым можно пренебречь.

При проведении эксперимента из четырех испытаний для оценки влияния трех факторов пользуются половиной ПФЭ типа 2³, так называемой "полурепликой". Если приравнять х₃ и - x₁x₂, то можно получить вторую "полуреплику". Для обозначения дробных реплик, в которых d линейных эффектов приравнены к эффектам взаимодействия, пользуются условным обозначением 2^{k - d}. Например, "полуреплика" от 2⁶ записывается в виде 2^{6 - 1}, а "четверть-реплика" - 2^{6 - 2}.

Пример 6.4. При построении "полурешшки" 2^3-1 х̃₃ можно приравнять к х̃₁х̃₂ или - х̃₁х̃₂. Две "полуреплики" 2^3-1 показаны в табл. 6.3. Для произведения трех столбцов левой матрицы выполняется соотношение + 1 = x̃₁ x̃₂ x̃₃, а правой матрицы - 1 = x̃₁ x̃₂ x̃₃, т. е. все знаки столбцов произведений одинаковы и в первом случае равны + 1, а во втором - 1.

Кроме симметричных двухуровневых планов типа 2^k при планировании экспериментов применяют также многоуровневые планы, в которых факторы варьируются на 3, 4, ..., т-м уровнях и обозначаются соответственно как 3^k, 4^k , ..., т^k-планы. Многоуровневые несимметричные планы, в которых факторы варьируются на различных уровнях, строятся различными способами: комбинированием полных и дробных факторных планов типа 2^k, методом преобразования симметричных планов в несимметричные и т. д. Рассмотренные планы носят название планов регрессионного анализа для многофакторного эксперимента [10, 22].

Когда модель планирования анализируется методами дисперсионного анализа, применяют планы дисперсионного анализа. Если при постановке эксперимента реализуются все возможные совокупности условий, то говорят о полных классификациях дисперсионного анализа. Если проводится сокращение перебора вариантов — это неполная классификация дисперсионного анализа. Сокращение перебора может проводиться случайным образом (без ограничения на рандомизацию) или в соответствии с некоторыми правилами (с ограничениями на рандомизацию). Чаще всего в качестве таких   планов используют блочные планы и планы типа латинского квадрата [10, 18, 21].

Перейдем далее к рассмотрению вопросов, связанных непосредственно с планированием экспериментов с машинной моделью М_м конкретной системы S.

6.2. СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕМАШИННЫХ

ЭКСПЕРИМЕНТОВ С МОДЕЛЯМИ СИСТЕМ

Применяя системный подход к проблеме планирования машинных экспериментов с моделями систем, можно выделить две составляющие планирования: стратегическое и тактическое планирование [46].

Стратегическое планирование ставит своей целью решение задачи получения необходимой информации о системе S с помощью модели М_м, реализованной на ЭВМ, с учетом ограничений на ресурсы, имеющиеся в распоряжении экспериментатора. По своей сути стратегическое планирование аналогично внешнему проектированию при создании системы S, только здесь в качестве объекта выступает процесс моделирования системы.

Тактическое планирование представляет собой определение способа проведения каждой серии испытаний машинной модели М_м, предусмотренных планом эксперимента. Для тактического планирования также имеется аналогия с внутренним проектированием системы S, но опять в качестве объекта рассматривается процесс работы с моделью М_ы.

Проблемы стратегического планирования. При стратегическом планировании машинных экспериментов с моделями систем возникает целый ряд проблем, взаимно связанных как с особенностями функционирования моделируемого объекта (системы S), так и с особенностями машинной реализации модели М_ы и обработки результатов эксперимента. В первую очередь к таким относятся проблемы построения плана машинного эксперимента; наличия большого количества факторов; многокомпонентной функции реакции; стохастической сходимости результатов машинного эксперимента; ограниченности машинных ресурсов на проведение эксперимента.

          Рассмотрим существо этих проблем, возникающих при стратегическом планировании машинных экспериментов, и возможные методы их решения. При построении плана эксперимента необходимо помнить, что целями проведения машинных экспериментов с моделью М_м системы S являются либо получение зависимости реакции от факторов для выявления особенностей изучаемого процесса функционирования системы S, либо нахождение такой комбинации значений факторов, которая обеспечивает экстремальное значение реакции. Другими словами, экспериментатору на базе машинной одели М_m необходимо решить либо задачу анализа, либо задачу синтеза системы S [7, 17, 33, 46].

Очевидно, что при реализации полного факторного плана различия между машинными экспериментами для достижения той или иной цели стираются, так как оптимальный синтез сводится к выбору одного из вариантов, полученного при полном факторном анализе. Но полный факторный эксперимент эквивалентен в этом случае полному перебору вариантов, что нерационально с точки зрения затрат машинных ресурсов. Для более эффективного (с точки зрения затрат машинного времени и памяти на моделирование) нахождения оптимальной комбинации уровней факторов можно воспользоваться выборочным методом определения оптимума поверхности реакции (систематическая или случайная выборка), методы систематической выборки включают в себя, факторный (метод равномерной сетки), одного фактора, предельного анализа, наискорейшего спуска. Выбор того или иного метода рационально проводить на основе априорной информации о моделируемой системе S.

Другая специфическая проблема стратегического планирования машинных экспериментов — наличие большого количества факторов. Это одна из основных проблем реализации имитационных моделей на ЭВМ, так как известно, что в факторном анализе количество комбинаций факторов равно произведению числа значений всех факторов эксперимента. Например, если число факторов к-10 и имеется два значения каждого фактора, т. е. q_t=2, то полный факторный анализ потребует моделирования 2^k=2¹⁰ = 1024 комбинаций. Если факторы х_i i=1, к, являются количественными, а реакция у связана с факторами некоторой функцией ф, то в качестве метода обработки результатов эксперимента может быть выбран регрессионный анализ. Когда при моделировании требуется полный факторный анализ, то проблема большого количества факторов может не иметь решения. Достоинством полных факторных планов является то, что они дают возможность отобразить всю поверхность реакции системы, если количество факторов невелико. Эффективность этого метода существенно зависит от природы поверхности реакции.

         Так как полные факторные планы изучения даже достаточно простых моделей приводят к большим затратам машинного времени, то приходится строить неполные факторные планы, требующие меньшего числа точек, приводя при этом к потере допустимого количества информации о характере функции реакции. В этом случае рациональный подход — построение плана эксперимента исходя из поверхности реакции (план поверхности реакции), что позволяет по сравнению с факторными планами уменьшить объем эксперимента без соответствующих потерь количества получаемой информации. Методы поверхности реакции    позволяют    сделать    некоторые    выводы    из    самых первых экспериментов с машинной моделью М_м. Если дальнейшее проведение машинного эксперимента оказывается неэкономичным, то его можно закончить в любой момент. Наконец, эти методы используются на начальном этапе постановки эксперимента для определения оптимальных условий моделирования исследуемой системы S.

Следующей проблемой стратегического планирования машинных экспериментов является многокомпонентная функция реакции. В имитационном эксперименте с вариантами модели системы S на этапе ее проектирования часто возникает задача, связанная с необходимостью изучения большого числа переменных реакции. Эту трудность в ряде случаев можно обойти, рассматривая имитационный эксперимент с моделью по определению многих реакций как несколько имитационных экспериментов, в каждом из которых исследуется (наблюдается) только одна реакция. Кроме того, при исследовании системы 5 часто требуется иметь переменные реакции, связанные друг с другом, что практически приводит к усложнению планирования имитационного эксперимента. В этом случае рационально использовать интегральные оценки нескольких реакций, построенные с использованием весовых функций, функций полезности и т. д. [10, 18, 21, 46].

Существенное место при планировании экспериментов с имитационными моделями, реализуемыми методом статистического моделирования на ЭВМ, занимает проблема стохастической сходимости результатов машинного эксперимента. Эта проблема возникает вследствие того, что целью проведения конкретного машинного эксперимента при исследовании и проектировании системы S является получение на ЭВМ количественных характеристик процесса функционирования системы S с помощью машинной модели М_ы. В качестве таких характеристик наиболее часто выступают средние некоторых распределений, для оценки которых применяют выборочные средние, найденные путем многократных прогонов модели на ЭВМ, причем, чем больше выборка, тем больше вероятность того, что выборочные средние приближаются к средним распределений. Сходимость выборочных средних с ростом объема выборки называется стохастической сходимостью.

Основной трудностью при определении интересующих характеристик процесса функционирования системы S является медленная стохастическая сходимость. Известно, что мерой флуктуации случайной величины служит ее нестандартное отклонение. Если а — стандартное отклонение одного наблюдения, то стандартное отклонение среднего N наблюдений будет равно σ/√N. Таким образом, для уменьшения случайной ошибки в К раз требуется увеличить объем выборки в К² раз, т. е. для получения заданной точности оценки может оказаться, что объем необходимой выборки нельзя получить на ЭВМ из-за ограничения ресурса времени и памяти.

Медленная стохастическая сходимость в машинных имитационных экспериментах с заданной моделью М_м требует разработки специальных методов решения этой проблемы. Необходимо учитывать, что в машинном эксперименте после того, как модель сформулирована, включение дополнительных факторов для повышения точности невозможно, так как это потребует изменения конструкции модели М_ы. Основная идея ускорения сходимости в машинных экспериментах со стохастическими моделями состоит в использовании априорной информации о структуре и поведении системы S, свойствах распределения входных переменных и наблюдаемых случайных воздействий внешней среды Е. К методам ускорения сходимости относятся методы регрессионной выборки, дополняющей переменной, расслоенной выборки, значимой выборки [10, 18, 21,

Переходя к рассмотрению проблемы ограниченности машинных ресурсов на проведение экспериментов с моделью системы S, необходимо помнить о том, что построение плана эксперимента с использованием различных подходов, рассмотренных в § 6.1, позволяет решить проблему стратегического планирования только с теоретической точки зрения. Но при планировании машинных экспериментов на практическую реализуемость плана существенное влияние оказывают имеющиеся в распоряжении экспериментатора ресурсы. Поэтому планирование машинного эксперимента представляет собой итерационный процесс, когда выбранная модель плана эксперимента проверяется на реализуемость, а затем, если это необходимо, вносятся соответствующие коррективы в исходную модель [46].

Этапы стратегического планирования. Применяя системный подход к проблеме стратегического планирования машинных экспериментов, можно выделить следующие этапы: 1) построение структурной модели; 2) построение функциональной модели. При этом структурная модель выбирается исходя из того, что должно быть сделано, а функциональная — из того, что может быть сделано.

Структурная модель плана эксперимента характеризуется числом факторов и числом уровней для каждого фактора. Число элементов эксперимента

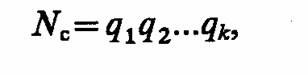
где к — число факторов эксперимента; q_i — число уровней i-го фактора, i=l, k. При этом под элементом понимается структурный блок эксперимента, определяемый как простейший эксперимент в случае одного фактора и одного уровня, т. е. к= 1, q= 1, N_c= 1.

Вопрос о виде и числе необходимых факторов следует рассматривать с различных точек зрения, причем основной является цель проводимого машинного эксперимента, т. е. в первую очередь решается вопрос о тех реакциях, которые надо оценить в результате эксперимента с машинной моделью М_ы системы S. При этом надо  найти наиболее существенные факторы, так как из опыта известно, что для большинства систем 20% факторов определяют 80% свойств системы S, а остальные 80% факторов определяют лишь 20% ее свойств [46].

Следующий шаг в конструировании структурной модели плана состоит в определении уровней, на которых следует устанавливать и измерять каждый фактор, причем минимальное число уровней фактора, не являющегося постоянным, равно двум. Число уровней следует выбирать минимальным, но достаточным для достижения цели машинного эксперимента. При этом надо помнить, что каждый дополнительный уровень увеличивает затраты ресурсов на реализацию эксперимента на ЭВМ.

Анализ результатов существенно упрощается, если уровни равноотстоят друг от друга, т. е. ортогональное разбиение упрощает определение коэффициентов аппроксимации. Можно получить значительные аналитические упрощения, если принять число уровней всех факторов одинаковым. Тогда структурная модель будет симметричной и примет вид N_c=q , где q=qi, i— 1, k.

Функциональная модель плана эксперимента определяет количество элементов структурной модели N_ф, т. е. необходимое число различных информационных точек. При этом функциональная модель может быть полной и неполной. Функциональная модель называется полной, если в оценке реакции участвуют все элементы, т. е. N_ф = N_c, и неполной, если число реакций меньше числа элементов, т. е. N_ф < N_c. Основная цель построения функциональной модели - нахождение компромисса между необходимыми действиями при машинном эксперименте (исходя из структурной модели) и ограниченными ресурсами на решение задачи методом моделирования.

Для более быстрого нахождения компромиссного решения можно при предварительном планировании машинного эксперимента использовать номограмму, построенную при варьировании числа факторов k, числа уровней факторов q, повторений эксперимента р, а также затрат времени на прогон модели τ и стоимости машинного времени с. Вид такой номограммы показан на рис. 6.4, причем при ее построении предполагалось, что полное число прогонов, необходимых при симметрично повторяемом эксперименте,

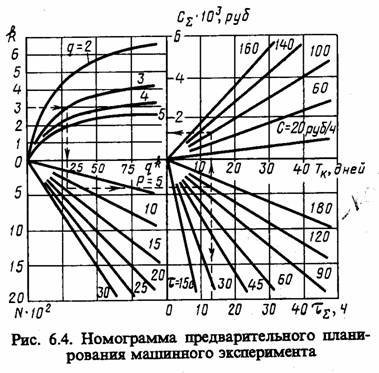
Рассмотрим особенности пользования такой номограммой на Mepe.

примере.

Пример 6.5. Пусть необходимо спланировать машинный эксперимент при наличии трех факторов k = 3, каждый из которых имеет три уровня q = 3, причем требуется р = 15 повторений с затратами τ = 120 с машинного времени на один прогон при стоимости 1 ч машинного времени с = 100 руб. Кроме того, предполагается, что в день на моделирование данной системы S выделяется 60 мин машинного времени, т. е. на моделирование требуется k = Nτ/3600 дней. Такой машинный эксперимент потребует около 400 прогонов, затрат примерно τ_∑ = 13 ч машинного времени, около T_k = 13 дней на получение результатов моделирования и 1304 руб. для оплаты машинного времени.

Сравним случай, рассмотренный в примере, при условии, что число уровней факторов уменьшено до двух, т. е. q = 2. Такой машинный эксперимент потребует только 135 прогонов; 4,5 ч машинного времени; 4,5 дня на получение результатов и всего 450 руб. затрат для оплаты машинного времени, т. е. имеет место сокращение затрат на 265%.

Такая номограмма (рис. 6.4) может быть использована и для других входов, например при фиксированной величине денежных средств, отводимых на машинный эксперимент.

Для более детального анализа имеющихся у экспериментатора возможностей при планировании эксперимента рассмотрим попарно относительное влияние числа факторов k, числа уровней q и числа повторений р на количество необходимых машинных прогонов модели N. Предполагая эти величины непрерывными, проанализируем, какая из трех величин дает наибольшее сокращение полного количества прогонов. Для этого продифференцируем уравнение (6.4):

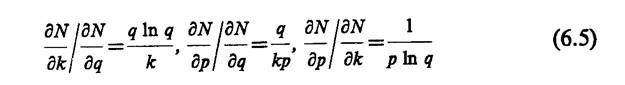
Из этих уравнений видно, что: 1) если kp > q и k > q ln q, то доминирует (оказывает наибольшее влияние на число машинных прогонов N) изменение числа уровней q; 2) если kp > q и k > q ln q, то доминирует число факторов k; 3) если p < q и p ln q < 1, то доминирует число повторений р.

Такой анализ позволяет дать наглядную графическую интерпретацию определения доминирующей для данного машинного эксперимента с моделью системы S переменной: k, q или р. Графически изобразим уравнения (6.5). На рис. 6.5, а приведен график отношения (q ln q)/k как функции числа уровней q при изменении числа факторов k от 1 до 5. Если отношение (q ln q)/k > 1 при данных k и q, то доминирует число факторов k. Если это отношение меньше 1, то доминирует число уровней q.

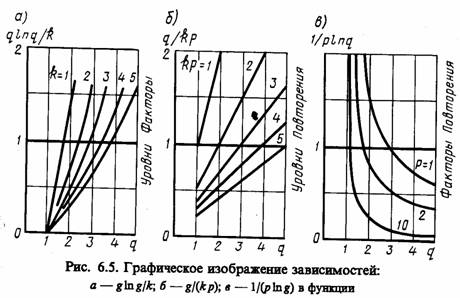
            На рис. 6.5, б приведен график зависимости отношения q/(kp) от числа уровней q для величин произведений kp в пределах от 1 до 5. Если в данном случае q/(kp) > 1, то доминирует число повторений р, а если q/(kp) < 1, то доминирует число уровней q.

На рис. 6.5, в показан график зависимости отношений 1/(p ln q) от числа уровней q для числа повторений р, изменяющихся в пределах от 1 до 10. Если 1/(р ln q) > 1, то доминирует число повторений р, а если 1/(p ln q) < 1, то доминирует число факторов k.

Пример 6.6.Пусть при составлении плана машинного эксперимента требуется оценить, какая переменная играет доминирующую роль в сокращении полного числа машинных прогонов модели N при k = 4, q = 3, p = 3. Воспользуемся рис. 6.5, а: для q = 3 и k = 4 отношение (q ln q) k < 1, т. е. число уровней q доминирует над числом факторов k. Исходя из рис. 6.5, б, для q = 3, kp = 8 имеем q/(kp) < 1, т. е. число уровней q доминирует над числом повторений р. И наконец, воспользовавшись рис. 6.5, в, видим, что для q = 3 и р = 2 отношение 1/(р ln q) < 1, т. е. число факторов k доминирует над числом повторений р.

Таким образом, использование при стратегическом планировании машинных экспериментов с М_м структурных и функциональных моделей плана позволяет решить вопрос о практической реализуемости модели на ЭВМ исходя из допустимых затрат ресурсов на моделирование системы S.