2.7. КОМБИНИРОВАННЫЕ МОДЕЛИ (A-СХЕМЫ)
Наиболее известным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Н. П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т. е. по сравнению с рассмотренными является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ. aggregate system), представляющей собой формальную схему общего вида, которую будем называть А-схемой
Основные соотношения. Анализ существующих средств моделирования систем и задач, решаемых с помощью метода моделирования на ЭВМ, неизбежно приводит к выводу, что комплексное решение проблем, возникающих в процессе создания и машинной реализации модели, возможно лишь в случае, если моделирующие системы имеют в своей основе единую формальную математическую схему, т. е. А-схему. Такая схема должна одновременно выполнять несколько функций: являться адекватным математическим описанием объекта моделирования, т. е. системы S, служить основой для построения алгоритмов и программ при машинной реализации модели М, позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования.
Приведенные требования в определенной степени противоречивы. Тем не менее в рамках обобщенного подхода на основе А-схем удается найти между ними некоторый компромисс.
По традиции, установившейся в математике вообще и в прикладной математике в частности, при агрегативном подходе сначала дается формальное определение объекта моделирования — агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс
их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней [35].
В качестве элемента А-схемы выступает агрегат, а связь между агрегатами (внутри системы S и с внешней средой Е) осуществляется с помощью оператора сопряжения R. Очевидно, что агрегат сам может рассматриваться как А-схема, т. е. может разбиваться на элементы (агрегаты) следующего уровня.
Любой агрегат характеризуется следующими множествами: моментов времени Т, входных X и выходных Y сигналов, состояний Z в каждый момент времени t. Состояние агрегата в момент времени t εT обозначается как z(t) εZ, а входные и выходные сигналы — как x(t) ε X и y(t)ε Y соответственно [4].
Будем полагать, что переход агрегата из состояния z (tj) в состояние z(t2)≠ z(t1) происходит за малый интервал времени, т. е. имеет место скачок Sz. Переходы агрегата из состояния z(t1) в z(t2) определяются собственными (внутренними) параметрами самого агрегата h (t) εH и входными сигналами x(t) εX.
В начальный момент времени t0 состояния z имеют значения, равные z°, т. е. z°=z(t0), задаваемые законом распределения процесса z(t) в момент времени t0, а именно L [z(t0)]. Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала хn описывается случайным оператором V. Тогда в момент поступления в агрегат tn εT входного сигнала хn можно определить состояние
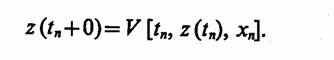
Обозначим полуинтервал времени t1<t≤ t2 как (t1t2) а полуинтервал tl≤ t<t2 — как
(tlt t2). Если интервал времени (t n tn+l) не содержит ни одного момента поступления сигналов, то для t ε(tn, tn+i) состояние агрегата определяется случайным оператором U в соответствии с соотношением
![]()
Совокупность случайных операторов Vи U рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний z в моменты поступления входных сигналов х (оператор V) и изменений состояний между этими моментами tn и tn+1 (оператор U). На оператор U не накладывается никаких ограничений, поэтому допустимы скачки состояний δz в моменты времени, не являющиеся моментами поступления входных сигналов х. В дальнейшем моменты скачков δz будем называть особыми моментами времени tδ,
а состояния z (ts) — особыми состояниями А-схемы. Для описания скачков состояний δz в особые моменты времени U будем использовать случайный оператор W, представляющий собой частный случай оператора U, т. е.
![]()
В множестве состояний Z выделяется такое подмножество Z(y), что если z(tδ) достигает Z (Y), то это состояние является моментом выдачи выходного сигнала, определяемого оператором выходов
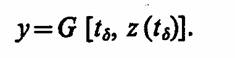
Таким образом, под агрегатом будем понимать любой объект, определяемый упорядоченной совокупностью рассмотренных множеств Т, X, Y, Z, Z(y), H и случайных операторов V, U, W, G.
Последовательность входных сигналов, расположенных в порядке их поступления в А-схему, будем называть входным сообщением или x-сообщением. Последовательность выходных сигналов, упорядоченную относительно времени выдачи, назовем выходным сообщением или у-сообщением.
Возможные приложения. Существует класс больших систем, которые ввиду их сложности не могут быть формализованы в виде математических схем одиночных агрегатов, поэтому их формализуют некоторой конструкцией из отдельных агрегатов Аn n=1, NA, которую назовем агрегативный системой или А-схемой. Для описания некоторой реальной системы S в виде А-схемы необходимо иметь описание как отдельных агрегатов Аn так и связей между ними.
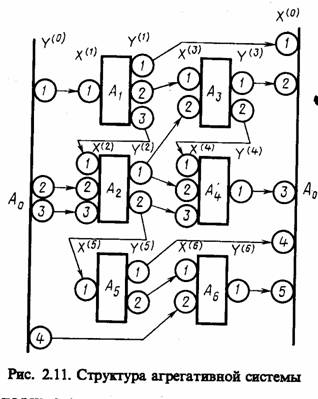
Пример 2.10. Рассмотрим А-схему, структура которой приведена на рис. 2.11. Функционирование А-схемы связано с переработкой информации, передача последней на схеме показана стрелками. Вся информация, циркулирующая в А-схеме, делится на внешнюю и внутреннюю. Внешняя информация поступает от внешних объектов, не являющихся элементами рассматриваемой схемы, а внутренняя информация вырабатывается агрегатами самой А-схемы. Обмен информацией между А-схемой и внешней средой Е происходит через агрегаты, которые называются полюсами А-схемы. При этом различают входные полюсы А-схемы, представляющие собой агрегаты, на которые поступают х-сообщения (агрегаты А1, А2, А6), и выходные полюсы А-схемы, выходная информация которых является y- сообщениями (агрегаты А1 А3, А4, А5, А6). Агрегаты, не являющиеся полюсами, называются внутренними.
Каждый n-й агрегат А-схемы Аn имеет входные контакты, на которые поступает совокупность элементарных сигналов xt(t),
i= 1, In одновременно возникающих на входе элемента, и выходные контакты, с которых снимается совокупность элементарных сигналов yj(t), j=1, Jn. Таким образом, каждый агрегат Л-схемы Аn имеет In входных и Jn выходных контактов.
Описание отдельного агрегата уже рассмотрено, поэтому для построения формального понятия А-схемы остается выбрать
достаточно удобные способы математического описания взаимодействия между агрегатами. Для этого введем ряд предположений о закономерностях функционирования А-схем, хорошо согласующихся с опытом исследования реальных сложных систем [4]: 1) взаимодействие между А-схемой и внешней средой Е, а также между отдельными агрегатами внутри системы S осуществляется при передаче сигналов, причем взаимные влияния, имеющие место вне механизма обмена сигналами, не учитываются; 2) для описания сигнала достаточно некоторого конечного набора характеристик; 3) элементарные сигналы мгновенно передаются в А-схеме независимо друг от друга по элементарным каналам; 4) к входному контакту любого элемента А-схемы подключается не более чем один элементарный канал, к выходному контакту — любое конечное число элементарных каналов при условии, что ко входу одного и того же элемента Л-схемы направляется не более чем один из упомянутых элементарных каналов.
Взаимодействие А-схемы с внешней средой Е рассматривается как обмен сигналами между внешней средой Е и элементами А-схемы. В соответствии с этим внешнюю среду Е можно представить в виде фиктивного элемента системы Ао, вход которого содержит Iо входных контактов Х (o) i= 1, Io а выход —J0 выходных контактов
Уi (0), i=l, J0. Сигнал, выдаваемый А-схемой во внешнюю среду Е, принимается элементом Ао как входной сигнал, состоящий из элементарных сигналов x 1(o) (t), y2(0) t ..., x io (О)(t) Сигнал, поступающий в А-схему из внешней среды Е, является выходным сигналом элемента Ао и состоит из элементарных сигналов y1(O)(t) y2 (o)(t) …, yi(O) I0t
Таким образом, каждый А„ (в том числе и Ао) как элемент А-схемы в рамках принятых предположений о механизме обмена сигналами достаточно охарактеризовать множеством входных контактов Х1(n) , X2(n), ..., Xn (n), которое обозначим {Xtn)}, и множеством выходных контактов Y1(n) , У2(n), ..., Y(n)j которое обозначим {У j,(n)},
где n=0, NA. Полученная пара множеств {Хi (n) }, {Уj (n) } является математической моделью элемента А„, используемого для формального описания сопряжения его с прочими элементами А-схемы и внешней средой Е. В силу предположения о независимости передачи сигналов каждому входному контакту
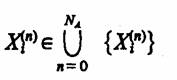
соответствует не более чем один выходной контакт
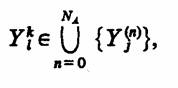
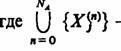 —
множество входных контактов всех элементов А-- схемы и внешней среды
—
множество входных контактов всех элементов А-- схемы и внешней среды  —
множество выходных контактов всех элементов А-схемы и внешней среды Е,
с которыми она связана элементарным каналом; k, n=0, NA.
—
множество выходных контактов всех элементов А-схемы и внешней среды Е,
с которыми она связана элементарным каналом; k, n=0, NA.
Поэтому можно ввести однозначный оператор 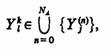 c областью
определения в множестве
c областью
определения в множестве  и областью
значений в множестве сопоставляющий входному контакту Хin выходной контакт У,(n) связанный с ним элементарным каналом. Если в А-схеме к
контакту Х( n ) не подключен никакой элементарный канал, то оператор R не определен на этом контакте Xin
. Оператор R называется
оператором сопряжения элементов (агрегатов) в А-схему. Совокупность
множеств {Xn}, { У1k } и оператор R образуют схему сопряжения элементов в систему S.
и областью
значений в множестве сопоставляющий входному контакту Хin выходной контакт У,(n) связанный с ним элементарным каналом. Если в А-схеме к
контакту Х( n ) не подключен никакой элементарный канал, то оператор R не определен на этом контакте Xin
. Оператор R называется
оператором сопряжения элементов (агрегатов) в А-схему. Совокупность
множеств {Xn}, { У1k } и оператор R образуют схему сопряжения элементов в систему S.
Рассмотрим, оператор сопряжения для А-схемы, структура которой показана на рис. 2.11. Оператор сопряжения R можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов) п и столбцов с номерами контактов располагаются пары чисел к, I, указывающие номер элемента k и номер контакта, l с которым соединен контакт X i(n) (табл. 2.7).
Если столбцы и строки такой таблицы пронумеровать двойными индексами п, i и k, I соответственно и на пересечении помещать для контактов п, i и k, l, соединенных элементарным каналом и 0 в противном случае, то получим матрицу смежности ориентированного графа, вершинами которого являются контакты агрегатов, а дугами — элементарные каналы А-схемы.
Рассмотренная схема сопряжения агрегатов в А-схему, заданная совокупностью множеств {Xi (n)}, {Уj (n)} и оператором R, является одноуровневой схемой сопряжения. В более сложных случаях могут быть использованы многоуровневые иерархические схемы сопряжения. Схема сопряжения агрегата, определяемая оператором R, может быть использована для описания весьма широкого класса объектов. Однако взаимодействие элементов реальных систем даже в рамках механизма обмена сигналами не сводится к одному лишь сопряжению. Помимо сопряжения контактов серьезную роль играют также согласование совокупности элементарных сигналов, поступающих в элементарный канал от выходных контактов и воспринимаемых входными, а также влияние реальных средств передачи сигналов на их содержание. Кроме того, оказываются полезными некоторые дополнительные ограничения на структуру сопряжения агрегатов системы S с внешней средой Е. Поэтому с практической точки зрения представляет интерес понятие А-схемы как типовой математической, отражающей наши представления о взаимодействии реальных объектов в рамках механизмов обмена сигналами.

Упорядоченную совокупность конечного числа агрегатов Аn n=1,NA системы S, агрегата Ао, характеризующего внешнюю среду Е, и оператора R, реализующего отображение
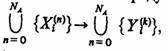 будем
называть Л-схемой при следующих условиях:
будем
называть Л-схемой при следующих условиях:
1) для любых ![]() в данной А-схеме
в данной А-схеме
2) если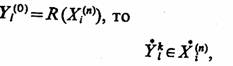 2.18
2.18
где Y\k) — соответствующие множества элементарных сигналов; для любого момента t' выдачи непустого элементарного сигнала
Yk(t) eYk 2.19
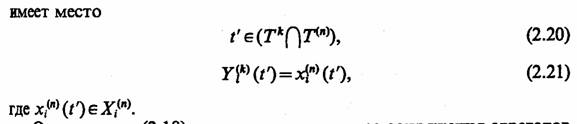
Ограничение (2.18) относится к структуре сопряжения агрегатов А-схемы системы S с внешней средой Е и требует, чтобы каждый элементарный канал, передающий сигналы во внешнюю среду, начинался в одном из выходных контактов одного из агрегатов системы, каждый элементарный канал, передающий сигналы из внешней среды, заканчивался на одном из входных контактов А-схемы. Ограничение (2.19) предусматривает, что сигналы в А-схеме передаются непосредственно от одного агрегата к другому без устройств, способных отсеивать сигналы по каким-либо признакам. Ограничение (2.20) относится к согласованию функционирования агрегатов А-схемы во времени. Ограничение (2.21) предусматривает, что сигналы между агрегатами А-схемы передаются мгновенно, без искажений и перекодирования, изменяющего структуру сигнала. Для многих реальных систем ограничения (2.19) и (2.21) оказываются несправедливыми. Для того чтобы А-схема была адекватной моделью реального объекта, достаточно описать селектирующие устройства, реальные средства передачи сигналов и всевозможные вспомогательные устройства как самостоятельные агрегаты, связи между которыми удовлетворяют перечисленным ограничениям.
Пример 2.11. Рассмотрим представление некоторой системы в виде отдельного агрегата [4]. Для того чтобы упростить описание объекта моделирования и проследить связи с уже рассмотренными схемами, воспользуемся в качестве объекта такого моделирования схемой массового обслуживания (Q-схемой) и представим ее в виде агрегата (А-схемы). Для определенности полагаем, что имеется однофазная одноканальная система SQ, показанная на рис. 2.6. В моменты времени tj, образующие однородный поток случайных событий, в прибор (Я) поступают заявки, каждая из которых характеризуется случайным параметром ej ,. Если обслуживающий канал (К) занят, то заявка поступает в накопитель (Я) и может ждать там не более чем y=φ (ej h), где h— параметр, характеризующий производительность системы обслуживания. Если к моменту (tj+yj) заявка не будет принята к обслуживанию, то она теряется. Время обслуживания заявки τj=ψ (ej, h).
При представлении этой Q-схемы в виде А-схемы опишем ее состояния вектором Z{t)eZ со следующими компонентами: zx(t) — время, оставшееся до окончания обслуживания заявки, которая находится в канале (К); г2 (t) — количество заявок в приборе (П); zm(t)—ek, где е^ — параметр к-й заявки в накопителе (H); ze(t) — оставшееся время ожидания к-й заявки в накопителе (Н) до момента, когда она
получит отказ, т=1+2к, l-2+lk, к=1, z2(t)-l.
Входные сигналы (заявки) поступают в А-схему в моменты tj и принимают значения Х/=е,-. Рассмотрим случайные операторы V, U и G, описывающие такой агрегат. Пусть в момент tj поступает новая заявка. Тогда оператор V можно записать следующим образом:
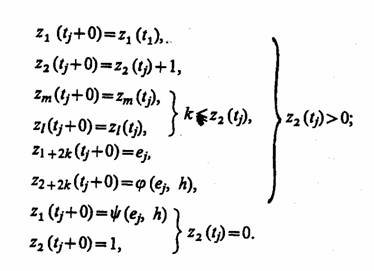
Пусть t=tst, т. е. обслуживание очередной заявки окончено. Этот момент является особым, так как в этот момент г (t) достигает 201, т. е. z1 (t)=0. Поэтому скачок состояний z (tsj определяется оператором W вида
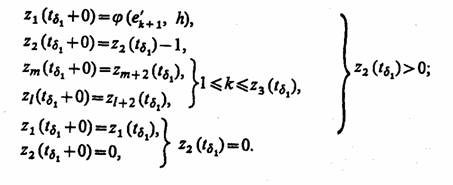
Рассмотрим еще один особый момент времени tδг, не являющийся моментом поступления входного сигнала. В момент ts2, когда истекает время ожидания одной из заявок, например i-й, число заявок в системе уменьшается на 1. Состояние А-схемы z2 (tδ2+0) определяется оператором W" вида
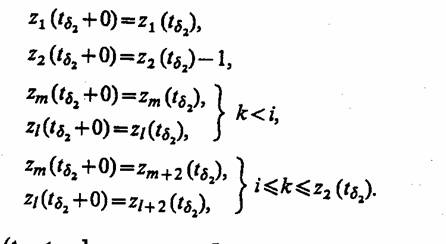
В полуинтервалах (tn tn„+1) между особыми моментами времени tn и tn+1 к которым относятся моменты поступления в А-схему входных сигналов и выдачи выходных сигналов, состояния А-схемы изменяются по закону, задаваемому оператором U, который можно записать так:

Выходными сигналами A-схемы будем считать сведения о заявках, покидающих прибор (Я). Пусть у (у1, у2), где у1 — признак (у1 = 1, если заявки обслужены; у1 =0, если заявки не обслужены); у2 — совокупность сведений о заявке, например у = (еj, h, tδ), т. е. заявки поступили в систему обслуживания с параметром ej, обслуживались при значении параметра системы Л, покинули систему в момент tg. Таким образом, действия оператора G сводятся к выбору признака у1 и формированию сведений о заявке у2. Для моментов tδ1 и tδ2 выходной сигнал у определяется параметром G и может быть записан в следующем виде:
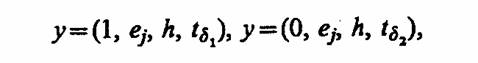
где tδ1 находят из z1 (t δ 1)=0, a t δ — из z1(t δ2 )=0.
На основании состояний системы Sa можно оценить ее вероятностно-временные характеристики, например вероятность нахождения в обслуживающем приборе (H) заданного числа заявок, среднее время ожидания заявок в накопителе (H) и т. д.
Таким образом, дальнейшее использование обобщенной типовой математической схемы моделирования, т. е. А-схемы, в принципе не отличается от рассмотренных ранее D-, F-, Р-, N-, Q-схем. Для частного случая, а именно для кусочно-линейных агрегатов, результаты могут быть получены аналитическим методом. В более сложных случаях, когда применение аналитических методов неэффективно или невозможно, прибегают к имитационному методу, причем представление объекта моделирования в виде А-схемы может являться тем фундаментом, на котором базируется построение имитационной системы и ее внешнего и внутреннего математического обеспечения. Стандартная форма представления исследуемого объекта в виде А-схемы приводит к унификации не только алгоритмов имитации, но и к возможности применять стандартные методы обработки и анализа результатов моделирования системы S.
Рассмотренные примеры использования типовых математических схем (D-, F-, Р-, Q-, N-, А-схем) позволяют формализовать достаточно широкий класс больших систем, с которыми приходится иметь дело в практике исследования и проектирования сложных систем. Особенности и возможности применения типовых схем при разработке машинных моделей систем рассмотрены в гл. 8 и 10.
Контрольные вопросы:
2.1. Что называется математической схемой?
2.2. Что является экзогенными и эндогенными переменными в модели объекта?
2.3. Что называется законом функционирования системы?
2.4. Что понимается под алгоритмом функционирования?
2.5. Что называется статистической и динамической моделями объекта?
2.6. Какие типовые схемы используются при моделировании сложных систем и их элементов?
2.7. Каковы условия и особенности использования при разработке моделей систем различных типовых схем?
ФОРМАЛИЗАЦИЯ И АЛГОРИТМИЗАЦИЯ ПРОЦЕССОВ ФУНКЦИОНИРОВАНИЯ СИСТЕМ
Несмотря на многообразие классов моделируемых систем и наличие широких возможностей реализации машинных моделей на современных ЭВМ, можно выделить основные закономерности перехода от построения концептуальной модели объекта моделирования до проведения машинного эксперимента с моделью системы, которые для целей эффективного решения пользователем практических задач моделирования рационально оформить в виде методики разработки и машинной реализации моделей. При этом наиболее существенным фактором, который следует учитывать уже при формализации и алгоритмизации моделей, является использование в качестве инструмента исследования аппаратно-программных средств вычислительной техники. В основе выделения этапов моделирования сложной системы лежит также необходимость привлечения для выполнения этой трудоемкой работы коллективов разработчиков различных специальностей (системщиков, алгоритмистов, программистов).
3.1. МЕТОДИКА РАЗРАБОТКИ И МАШИННОЙ
РЕАЛИЗАЦИИ МОДЕЛЕЙ СИСТЕМ
С развитием вычислительной техники наиболее эффективным методом исследования больших систем стало машинное моделирование, без которого невозможно решение многих крупных народнохозяйственных проблем. Поэтому одной из актуальных задач подготовки специалистов является освоение теории и методов математического моделирования с учетом требований системности, позволяющих не только строить модели изучаемых объектов, анализировать их динамику и возможность управления машинным экспериментом с моделью, но и судить в известной мере об адекватности создаваемых моделей исследуемым системам, о границах применимости и правильно организовать моделирование систем на современных средствах вычислительной техники [35, 43, 46].
Методологические аспекты моделирования. Прежде чем рассматривать математические, алгоритмические, программные и прикладные аспекты машинного моделирования, необходимо изучить общие методологические аспекты для широкого класса математических моделей объектов, реализуемых на средствах вычислительной техники. Моделирование с использованием средств вычислительной техники (ЭВМ, АВМ, ГВК) позволяет исследовать механизм явлений, протекающих в реальном объекте с большими или малыми скоростями, когда в натурных экспериментах с объектом трудно (или невозможно) проследить за изменениями, происходящими в течение короткого времени, или когда получение достоверных результатов сопряжено с длительным экспериментом. При необходимости машинная модель дает возможность как бы «растягивать» или «сжимать» реальное время, так как машинное моделирование связано с понятием системного времени, отличного от реального. Кроме того, с помощью машинного моделирования в диалоговой системе можно обучать персонал АСОИУ принятию решений в управлении объектом, например при организации деловой игры, что позволяет выработать необходимые практические навыки реализации процесса управления [12, 29, 46, 53].
Сущность машинного моделирования системы состоит в проведении на вычислительной машине эксперимента с моделью, которая представляет собой некоторый программный комплекс, описывающий формально и (или) алгоритмически поведение элементов системы S в процессе ее функционирования, т. е. в их взаимодействии друг с другом и внешней средой Е. Машинное моделирование с успехом применяют в тех случаях, когда трудно четко сформулировать критерий оценки качества функционирования системы и цель ее не поддается полной формализации, поскольку позволяет сочетать программно-технические возможности ЭВМ со способностями человека мыслить неформальными категориями. В дальнейшем основное внимание будет уделено моделированию систем на универсальных ЭВМ как наиболее эффективному инструменту исследования и разработки АСОИУ различных уровней, а случаи использования АВМ и ГВК будут специально оговариваться.
Требования пользователя к модели. Сформулируем основные требования, предъявляемые к модели М процесса функционирования системы S.
1. Полнота модели должна предоставлять пользователю возможность получения необходимого набора оценок характеристик системы с требуемой точностью и достоверностью.
2. Гибкость модели должна давать возможность воспроизведения различных ситуаций при варьировании структуры, алгоритмов и параметров системы.
3. Длительность разработки и реализации модели большой системы должна быть по возможности минимальной при учете ограничений на имеющиеся ресурсы.
4. Структура модели должна быть блочной, т. е. допускать возможность замены, добавления и исключения некоторых частей без переделки всей модели.
5. Информационное обеспечение должно предоставлять возможность эффективной работы модели с базой данных систем определенного класса.
6. Программные и технические средства должны обеспечивать
эффективную (по быстродействию и памяти) машинную реализацию модели и удобное общение с ней пользователя.
7. Должно быть реализовано проведение целенаправленных (планируемых) машинных экспериментов с моделью системы с использованием аналитико -имитационного подхода при наличии ограниченных вычислительных ресурсов.
С учетом этих требований рассмотрим основные положения, которые справедливы при моделировании на ЭВМ систем S, а также их подсистем и элементов. При машинном моделировании системы S характеристики процесса ее функционирования определяются на основе модели М, построенной исходя из имеющейся исходной информации об объекте моделирования. При получении новой информации об объекте его модель пересматривается и уточняется с учетом новой информации, т. е. процесс моделирования, включая разработку и машинную реализацию модели, является итерационным. Этот итерационный процесс продолжается до тех пор, пока не будет получена модель М, которую можно считать адекватной в рамках решения поставленной задачи исследования и проектирования системы S.
Моделирование систем с помощью ЭВМ можно использовать в следующих случаях [5, 29, 41]: а) для исследования системы S до того, как она спроектирована, с целью определения чувствительности характеристики к изменениям структуры, алгоритмов и параметров объекта моделирования и внешней среды; б) на этапе проектирования системы S для анализа и синтеза различных вариантов системы и выбора среди конкурирующих такого варианта, который удовлетворял бы заданному критерию оценки эффективности системы при принятых ограничениях; в) после завершения проектирования и внедрения системы, т. е. при ее эксплуатации, для получения информации, дополняющей результаты натурных испытаний (эксплуатации) реальной системы, и для получения прогнозов эволюции (развития) системы во времени.
Существуют общие положения, применяемые ко всем перечисленным случаям машинного моделирования. Даже в тех случаях, когда конкретные способы моделирования отличаются друг от друга и имеются различные модификации моделей, например в области машинной реализации моделирующих алгоритмов с использованием конкретных программно-технических средств, в практике моделирования систем можно сформулировать общие принципы, которые могут быть положены в основу методологии машинного моделирования [29, 35, 46].
Этапы моделирования систем. Рассмотрим основные этапы моделирования системы S, к числу которых относятся: построение концептуальной модели системы и ее формализация; алгоритмизация модели системы и ее машинная реализация; получение и интерпретация результатов моделирования системы.
Взаимосвязь перечисленных этапов моделирования систем и их составляющих (подэтапов) может быть представлена в виде сетевого
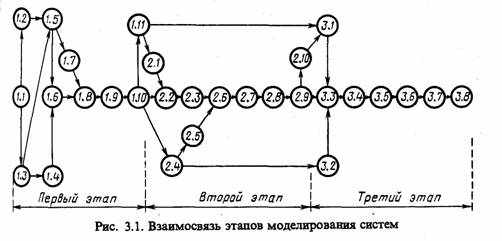
графика, показанного на рис. 3.1. Перечислим эти подэтапы:
1.1 — постановка задачи машинного моделирования системы;
1.2 — анализ задачи моделирования системы; 1.3 —определение требований к исходной информации об объекте моделирования и организация ее сбора; 1.4 — выдвижение гипотез и принятие предположений; 1.5 — определение параметров и переменных модели; 1.6 — установление основного содержания модели; 1.7 — обоснование критериев оценки эффективности системы; 1.8 — определение процедур аппроксимации; 1.9 — описание концептуальной модели системы; 1.10 — проверка достоверности концептуальной модели; 1,11 — составление технической документации по первому этапу; 2.1 — построение логической схемы модели; 2.2 — получение математических соотношений; 2.3 — проверка достоверности модели системы; 2.4 — выбор инструментальных средств для моделирования; 2.5 — составление плана выполнения работ по программированию; 2.6 —спецификация и построение схемы программы;
2.7 — верификация и проверка достоверности схемы программы;
2.8 — проведение программирования модели; 2.9 — проверка достоверности программы; 2.10 — составление технической документации по второму этапу; 3.1 — планирование машинного эксперимента с моделью системы; 3.2 — определение требований к вычислительным средствам; 3.3 — проведение рабочих расчетов; 3.4 — анализ результатов моделирования системы; 3.5 — представление результатов моделирования; 3.6 — интерпретация результатов моделирования; 3.7 — подведение итогов моделирования и выдача рекомендаций; 3.8 — составление технической документации по третьему этапу.
Таким образом, процесс моделирования системы S сводится к выполнению перечисленных подэтапов, сгруппированных в виде трех этапов. На этапе построения концептуальной модели Мх и ее формализации проводится исследование моделируемого объекта с точки зрения выделения основных составляющих процесса его-функционирования, определяются необходимые аппроксимации и получается обобщенная схема модели системы S, которая преобразуется в машинную модель Мм на втором этапе моделирования путем последовательной алгоритмизации и программирования модели. Последний третий этап моделирования системы сводится к проведению согласно полученному плану рабочих расчетов на ЭВМ с использованием выбранных программно-технических средств, получению и интерпретации результатов моделирования системы S с учетом воздействия внешней среды Е. Очевидно, что при построении модели и ее машинной реализации при получении новой информации возможен пересмотр ранее принятых решений, т. е. процесс моделирования является итерационным. Рассмотрим содержание каждого из этапов более подробно.
3.2. ПОСТРОЕНИЕ КОНЦЕПТУАЛЬНЫХ МОДЕЛЕЙ СИСТЕМ И ИХ ФОРМАЛИЗАЦИЯ
На первом этапе машинного моделирования — построения концептуальной модели Мх системы S и ее формализации — формулируется модель и строится ее формальная схема, т. е. основным назначением этого этапа является переход от содержательного описания объекта к его математической модели, другими словами, процесс формализации. Моделирование систем на ЭВМ в настоящее время — наиболее универсальный и эффективный метод оценки характеристик больших систем. Наиболее ответственными и наименее формализованными моментами в этой работе являются проведение границы между системой S и внешней средой Е, упрощение описания системы и построение сначала концептуальной, а затем формальной модели системы. Модель должна быть адекватной, иначе невозможно получить положительные результаты моделирования, т. е. исследование процесса функционирования системы на неадекватной модели вообще теряет смысл. Под адекватной моделью будем понимать модель, которая с определенной степенью приближения на уровне понимания моделируемой системы S разработчиком модели отражает процесс ее функционирования во внешней среде Е.
Переход от описания к блочной модели. Наиболее рационально строить модель функционирования системы по блочному принципу. При этом могут быть выделены три автономные группы блоков такой модели. Блоки первой группы представляют собой имитатор воздействий внешней среды Е на систему S; блоки второй группы являются собственно моделью процесса функционирования исследуемой системы S; блоки третьей группы — вспомогательными и служат для машинной реализации блоков двух первых групп, а также для фиксации и обработки результатов моделирования.
Рассмотрим механизм перехода от описания процесса функционирования некоторой гипотетической системы к модели этого процесса [29, 35]. Для наглядности введем представление об описании свойств процесса функционирования системы S, т. е. об ее концептуальной модели Мт как совокупности некоторых элементов, условно изображенных квадратами так, как показано на рис. 3.2, а. Эти квадраты представляют собой описание некоторых подпроцессов исследуемого процесса функционирования системы S, воздействия внешней среды Е и т. д. Переход от описания системы к ее модели в этой интерпретации сводится к исключению из рассмотрения некоторых второстепенных элементов описания (элементы 5 — 8,39 — 41,43 — 47).
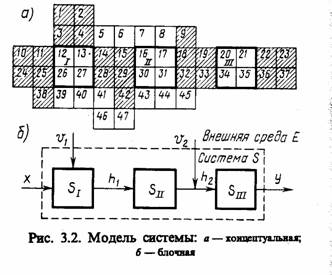
Предполагается, что они не оказывают существенного влияния на ход процессов, исследуемых с помощью модели. Часть элементов (14, 15, 28, 29, 42) заменяется пассивными связями hl3 отражающими внутренние свойства системы (рис. 3.2, б). Некоторая часть элементов (1 — 4, 10, 11, 24, 25) заменяется входными факторами х и воздействиями внешней среды v1. Возможны и комбинированные замены: элементы 9, 18, 19, 32, 33 заменены пассивной связью h2 и воздействием внешней среды Е. Элементы 22, 23,36,37 отражают воздействие системы на внешнюю среду у.
Оставшиеся элементы системы S группируются в блоки 5t, Sa, Sm, отражающие процесс функционирования исследуемой системы. Каждый из этих блоков достаточно автономен, что выражается в минимальном количестве связей между ними. Поведение этих блоков должно быть хорошо изучено и для каждого из них построена математическая модель, которая в свою очередь может содержать ряд подблоков. Построенная блочная модель процесса функционирования исследуемой системы 5 предназначена для анализа характеристик этого процесса, который может быть проведен при машинной реализации полученной модели.
Математические модели процессов. После перехода от описания моделируемой системы 5 к ее модели М„ построенной по блочному принципу, необходимо построить математические модели процессов, происходящих в различных блоках. Математическая модель представляет собой совокупность соотношений (например, уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы S в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды Е, начальных условий и времени. Математическая модель является результатом формализации процесса функционирования исследуемой системы, т. е. построения формального (математического) описания процесса с необходимой в рамках проводимого исследования степенью приближения к действительности [4, 35, 37].
Для иллюстрации возможностей формализации рассмотрим процесс функционирования некоторой гипотетической системы S, которую можно разбить на т подсистем с характеристиками у2 (t), … yhy(t )с параметрами h1 h2, ...,hnh при наличии входных воздействии х1г х2,..., хnx и воздействий внешней среды v1 v2,..., vny. Тогда математической моделью процесса может служить система соотношений вида
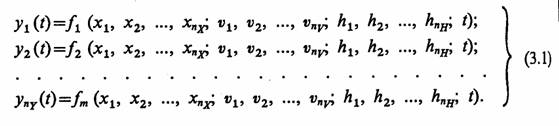
Если бы функции, ƒ1 ƒ 2, …, fm были известны, то соотношения (3.1) оказались бы идеальной математической моделью процесса функционирования системы S. Однако на практике получение модели достаточно простого вида для больших систем чаще всего невозможно, поэтому обычно процесс функционирования системы S разбивают на ряд элементарных подпроцессов. При этом необходимо так проводить разбиение на подпроцессы, чтобы построение моделей отдельных подпроцессов было элементарно и не вызывало трудностей при формализации. Таким образом, на этой стадии сущность формализации подпроцессов будет состоять в подборе типовых математических схем. Например, для стохастических процессов это могут быть схемы вероятностных автоматов (Р-схемы), схемы массового обслуживания (Q-схемы) и т. д., которые достаточно точно описывают основные особенности реальных явлений, составляющих подпроцессы, с точки зрения решаемых прикладных задач.
Таким образом, формализации процесса функционирования любой системы 5 должно предшествовать изучение составляющих его явлений. В результате появляется содержательное описание процесса, которое представляет собой первую попытку четко изложить закономерности, характерные для исследуемого процесса, и постановку прикладной задачи. Содержательное описание является исходным материалом для последующих этапов формализации: построения формализованной схемы процесса функционирования системы и математической модели этого процесса. Для моделирования процесса функционирования системы на ЭВМ необходимо преобразовать математическую модель процесса в соответствующий моделирующий алгоритм и машинную программу.
Подэтапы первого этапа моделирования. Рассмотрим более подробно основные подэтапы построения концептуальной модели М, системы и ее формализации (см. рис. 3.1).
1.1. Постановка задачи машинного моделирования системы. Дается четкая формулировка задачи исследования конкретной системы 5 и основное внимание уделяется таким вопросам, как: а) признание существования задачи и необходимости машинного моделирования; б) выбор методики решения задачи с учетом имеющихся ресурсов; в) определение масштаба задачи и возможности разбиения ее на подзадачи.
Необходимо также ответить на вопрос о приоритетности решения различных подзадач, оценить эффективность возможных математических методов и программно-технических средств их решения. Тщательная проработка этих вопросов позволяет сформулировать задачу исследования и приступить к ее реализации. При этом возможен пересмотр начальной постановки задачи в процессе моделирования.
1.2. Анализ задачи моделирования системы. Проведение анализа задачи способствует преодолению возникающих в дальнейшем трудностей при ее решении методом моделирования. На рассматриваемом втором этапе основная работа сводится именно к проведению анализа, включая: а) выбор критериев оценки эффективности процесса функционирования системы S; б) определение эндогенных и экзогенных переменных модели М; в) выбор возможных методов идентификации; г) выполнение предварительного анализа содержания второго этапа алгоритмизации модели системы и ее машинной реализации; д) выполнение предварительного анализа содержания третьего этапа получения и интерпретации результатов моделирования системы.
1.3. Определение требований к исходной информации об объекте моделирования и организация ее сбора. После постановки задачи моделирования системы S определяются требования к информации, из которой получают качественные и количественные исходные данные, необходимые для решения этой задачи. Эти данные помогают глубоко разобраться в сущности задачи, методах ее решения. Таким образом, на этом подэтапе проводится: а) выбор необходимой информации о системе S и внешней среде Е; б) подготовка априорных данных; в) анализ имеющихся экспериментальных данных; г) выбор методов и средств предварительной обработки информации о системе.
При этом необходимо помнить, что именно от качества исходной информации об объекте моделирования существенно зависят как адекватность модели, так и достоверность результатов моделирования.
1.4. Выдвижение гипотез и принятие предположений. Гипотезы при построении модели системы S служат для заполнения «пробелов» в понимании задачи исследователем. Выдвигаются также гипотезы относительно возможных результатов моделирования системы S справедливость, которых проверяется при проведении машинного эксперимента. Предположения предусматривают, что некоторые данные неизвестны или их нельзя получить. Предположения могут выдвигаться относительно известнйгх данных, которые не отвечают требованиям решения поставленной задачи. Предположения дают возможность провести упрощения модели в соответствии с выбранным уровнем моделирования. При выдвижении гипотез и принятия предположений учитываются следующие факторы: а) объем имеющейся информации для решения задач; б) подзадачи, для которых информация недостаточна; в) ограничения на ресурсы времени для решения задачи; г) ожидаемые результаты моделирования.
Таким образом, в процессе работы с моделью системы S возможно многократное возвращение к этому под этапу в зависимости от полученных результатов моделирования и новой информации об объекте.
1.5. Определение
параметров и переменных модели. Прежде чем перейти к описанию
математической модели, необходимо определить параметры системы hk,
к= 1nh, входные и выходные
переменные ![]() воздействия
внешней среды vh 1=1, nv. Конечной целью этого
подэтапа является подготовка к построению математической модели системы S, функционирующей во внешней среде Е, для чего
необходимо рассмотрение всех параметров и переменных модели и оценка степени
их влияния на процесс функционирования системы в целом. Описание каждого
параметра и переменной должно даваться в следующей форме: а) определение
и краткая характеристика; б) символ обозначения и единица измерения; в)
диапазон изменения; г) место применения в модели.
воздействия
внешней среды vh 1=1, nv. Конечной целью этого
подэтапа является подготовка к построению математической модели системы S, функционирующей во внешней среде Е, для чего
необходимо рассмотрение всех параметров и переменных модели и оценка степени
их влияния на процесс функционирования системы в целом. Описание каждого
параметра и переменной должно даваться в следующей форме: а) определение
и краткая характеристика; б) символ обозначения и единица измерения; в)
диапазон изменения; г) место применения в модели.
1.6. Установление основного содержания модели. На этом подэтапе определяется основное содержание модели и выбирается метод построения модели системы, которые разрабатываются на основе принятых гипотез и предположений. При этом учитываются следующие особенности: а) формулировка задачи моделирования системы; б) структура системы S и алгоритмы ее поведения, воздействия внешней среды Е; в) возможные методы и средства решения задачи моделирования.
1.7. Обоснование критериев оценки эффективности системы. Для оценки качества процесса функционирования моделируемой системы S необходимо выбрать некоторую совокупность критериев оценки эффективности, т. е. в математической постановке задача сводится к получению соотношения для оценки эффективности как функции параметров и переменных системы. Эта функция представляет собой поверхность отклика в исследуемой области изменения параметров и переменных и позволяет определить реакцию системы. Эффективность системы S можно оценить с помощью интегральных или частных критериев, выбор которых зависит от рассматриваемой задачи.
1.8. Определение процедур аппроксимации. Для аппроксимации реальных процессов, протекающих в системе 5, обычно используются три вида процедур: а) детерминированную; б) вероятностную; в) определения средних значений.
При детерминированной процедуре результаты моделирования однозначно определяются по данной совокупности входных воздействий, параметров и переменных системы S. В этом случае отсутствуют случайные элементы, влияющие на результаты моделирования. Вероятностная (рандомизированная) процедура применяется в том случае, когда случайные элементы, включая воздействия внешней среды Е, влияют на характеристики процесса функционирования системы S и когда необходимо получить информацию о законах распределения выходных переменных. Процедура определения средних значений используется тогда, когда при моделировании системы интерес представляют средние значения выходных переменных при наличии случайных элементов.
1.9. Описание концептуальной модели системы. На этом подэтапе построения модели системы: а) описывается концептуальная модель Мх в абстрактных терминах и понятиях; б) дается описание модели с использованием типовых математических схем; в) принимаются окончательно гипотезы и предположения; г) обосновывается выбор процедуры аппроксимации реальных процессов при построении модели. Таким образом, на этом подэтапе проводится подробный анализ задачи, рассматриваются возможные методы ее решения и дается детальное описание концептуальной модели Мk, которая затем используется на втором этапе моделирования.
1.10. Проверка достоверности концептуальной модели. После того как концептуальная модель Мх описана, необходимо проверить достоверность некоторых концепций модели перед тем, как перейти к следующему этапу моделирования системы S. Проверять достоверность концептуальной модели достаточно сложно, так как процесс ее построения является эвристическим и такая модель описывается в абстрактных терминах и понятиях. Один из методов проверки модели Мх — применение операций обратного перехода, позволяющий проанализировать модель, вернуться к принятым аппроксимациям и, наконец, рассмотреть снова реальные процессы, протекающие в моделируемой системе S. Проверка достоверности концептуальной модели Мт должна включать: а) проверку замысла модели; б) оценку достоверности исходной информации; в) рассмотрение постановки задачи моделирования; г) анализ принятых аппроксимаций; д) исследование гипотез и предположений.
Только после тщательной проверки концептуальной модели М, следует переходить к этапу машинной реализации модели, так как ошибки в модели Мk не позволяют получить достоверные результаты моделирования.
реальных или частных критериев, выбор которых зависит от рассматриваемой задачи.
1.8. Определение процедур аппроксимации. Для аппроксимации реальных процессов, протекающих в системе S, обычно используются три вида процедур: а) детерминированную; б) вероятностную; в) определения средних значений.
При детерминированной процедуре результаты моделирования однозначно определяются по данной совокупности входных воздействий, параметров и переменных системы S. В этом случае отсутствуют случайные элементы, влияющие на результаты моделирования. Вероятностная (рандомизированная) процедура применяется в том случае, когда случайные элементы, включая воздействия внешней среды Е, влияют на характеристики процесса функционирования системы S и когда необходимо получить информацию о законах распределения выходных переменных. Процедура определения средних значений используется тогда, когда при моделировании системы интерес представляют средние значения выходных переменных при наличии случайных элементов.
1.9. Описание концептуальной модели системы. На этом подэтапе построения модели системы: а) описывается концептуальная модель Мх в абстрактных терминах и понятиях; б) дается описание модели с использованием типовых математических схем; в) принимаются окончательно гипотезы и предположения; г) обосновывается выбор процедуры аппроксимации реальных процессов при построении модели. Таким образом, на этом подэтапе проводится подробный анализ задачи, рассматриваются возможные методы ее решения, и дается детальное описание концептуальной модели Мк которая затем используется на втором этапе моделирования.
1.10. Проверка достоверности концептуальной модели. После того как концептуальная модель М, описана, необходимо проверить достоверность некоторых концепций модели перед тем, как перейти к следующему этапу моделирования системы S. Проверять достоверность концептуальной модели достаточно сложно, так как процесс ее построения является эвристическим, и такая модель описывается в абстрактных терминах и понятиях. Один из методов проверки модели Мх — применение операций обратного перехода, позволяющий проанализировать модель, вернуться к принятым аппроксимациям и, наконец, рассмотреть снова реальные процессы, протекающие в моделируемой системе S. Проверка достоверности концептуальной модели Мх должна включать: а) проверку замысла модели; б) оценку достоверности исходной информации; в) рассмотрение постановки задачи моделирования; г) анализ принятых аппроксимаций; д) исследование гипотез и предположений.
Только после тщательной проверки концептуальной модели Ms следует переходить к этапу машинной реализации модели, так как ошибки в модели Мх не позволяют получить достоверные результаты моделирования.
1.11. Составление технической документации по первому этапу. В конце этапа построения концептуальной модели Мм и ее формализации составляется технический отчет по этапу, который включает в себя: а) подробную постановку задачи моделирования системы S; б) анализ задачи моделирования системы; в) критерии оценки эффективности системы; г) параметры и переменные модели системы; д) гипотезы и предположения, принятые при построении модели; е) описание модели в абстрактных терминах и понятиях; ж) описание ожидаемых результатов моделирования системы S.
Составление технической документации — обязательное условие успешного проведения моделирования системы S, так как в процессе разработки модели большой системы и ее машинной реализации принимают участие на различных этапах коллективы специалистов разных профилей (начиная от постановщиков задач и кончая программистами) и документация является средством обеспечения их эффективного взаимодействия при решении поставленной задачи методом моделирования.
3.3. АЛГОРИТМИЗАЦИЯ МОДЕЛЕЙ СИСТЕМ И ИХ МАШИННАЯ
РЕАЛИЗАЦИЯ
На втором этапе моделирования — этапе алгоритмизации модели и ее машинной реализации — математическая модель, сформированная на первом этапе, воплощается в конкретную машинную модель. Этот этап представляет собой этап практической деятельности, направленной на реализацию идей и математических схем в виде машинной модели Мы процесса функционирования системы S. Прежде чем рассматривать подэтапы алгоритмизации и машинной реализации модели, остановимся на основных принципах построения моделирующих алгоритмов и формах их представления [4, 36, 37, 53].
Принципы построения моделирующих алгоритмов. Процесс функционирования системы S можно рассматривать как последовательную смену ее состояний z=z(z1(t), z2(t), ..., zk(t)) в k-мерном пространстве. Очевидно, что задачей моделирования процесса функционирования исследуемой системы S является построение функций z, на основе которых можно провести вычисление интересующих характеристик процесса функционирования системы. Для этого должны иметься соотношения, связывающие функции z с переменными, параметрами и временем, а также начальные условия zo=z(z1(to), z2(t0), ..., zk(t0)) в момент времени t = t0.
Рассмотрим процесс функционирования некоторой детерминированной системы SD, в которой отсутствуют случайные факторы, т. е. вектор состояний такой системы можно определить из (2.3) как z =Ф(z°, х, t). Тогда состояние процесса в момент времени to+jΔt может быть однозначно определено из соотношений математической модели по известным начальным условиям. Это позволяет строить моделирующий алгоритм процесса функционирования системы. Для этого преобразуем соотношения модели Z к такому виду, чтобы сделать удобным вычисление z( t+Δt), z2(t+Δt), ..., zk(t+Δt) по значениям zi,(τ), i=1, к, где t≤t. Организуем, счетчик системного времени, который в начальный момент показывает время t0. Для этого момента zi(t0)=z°. Прибавим интервал времени At, тогда счетчик будет показывать t1 = t0+∆t. Вычислим значения г, (t0 + Δt). Затем перейдем к моменту времени t2 = t1+Δt и т. д. Если шаг Δt достаточно мал, то таким путем можно получить приближенные значения z.
Рассмотрим процесс функционирования стохастической системы SR, т. е. системы, на которую оказывают воздействия случайные факторы, т. е. вектор состояний определяется соотношением (2.3). Для такой системы функция состояний процесса z в момент времени T≤t и соотношения модели определяют лишь распределение вероятностей для zt(t+Δt) в момент времени t+Δt. В общем случае и начальные условия z° могут быть случайными, задаваемыми соответствующим распределением вероятностей. При этом структура моделирующего алгоритма для стохастических систем в основном остается прежней. Только вместо состояния z, (t+Δt) теперь необходимо вычислить распределение вероятностей для возможных состояний. Пусть счетчик системного времени показывает время t0. В соответствии с заданным распределением вероятностей выбирается z,°. Далее, исходя из распределения, получается состояние zi(t0+Δt) и т. д., пока не будет построена одна из возможных реализаций случайного многомерного процесса z,(/) в заданном интервале времени [9, 37].
Рассмотренный принцип построения моделирующих алгоритмов называется принципом Δt. Это наиболее универсальный принцип, позволяющий определить последовательные состояния процесса функционирования системы S через заданные интервалы времени Δt. Но с точки зрения затрат машинного времени он иногда оказывается неэкономичным.
При рассмотрении процессов функционирования некоторых систем можно обнаружить, что для них характерны два типа состояний: 1) особые, присущие процессу функционирования системы только в некоторые моменты времени (моменты поступления входных или управляющих воздействий, возмущений внешней среды и т. п.); 2) неособые, в которых процесс находится все остальное время. Особые состояния характерны еще и тем обстоятельством, что функции состояний Zi(t) в эти моменты времени изменяются скачком, а между особыми состояниями изменение координат z,(i) происходит плавно и непрерывно или не происходит совсем. Таким образом, следя при моделировании системы S только за ее особыми состояниями в те моменты времени, когда эти состояния имеют место, можно получить информацию, необходимую для построения функций Zi{t). Очевидно, для описанного типа систем могут быть построены моделирующие алгоритмы по «принципу особых состояний». Обозначим скачкообразное (релейное) изменение состояния z как δz, а «принцип особых состояний» — как принцип δz.
Например, для системы массового обслуживания (Q-схемы) в качестве особых состояний могут быть выбраны состояния в моменты поступления заявок на обслуживание в прибор П и в моменты окончания обслуживания заявок каналами К, когда состояние системы, оцениваемое числом находящихся в ней заявок, меняется скачком.
Отметим, что характеристики процесса функционирования таких систем с особыми состояниями оцениваются по информации об особых состояниях, а неособые состояния при моделировании не рассматриваются. «Принцип 6z» дает возможность для ряда систем существенно уменьшить затраты машинного времени на реализацию моделирующих алгоритмов по сравнению с «принципом Δt». Логика построения моделирующего алгоритма, реализующего «принцип Sz», отличается от рассмотренной для «принципа Δt» только тем, что включает в себя процедуру определения момента времени ts, соответствующего следующему особому состоянию системы S. Для исследования процесса функционирования больших систем рационально использование комбинированного принципа построения моделирующих алгоритмов, сочетающего в себе преимущества каждого из рассмотренных принципов.
Формы представления моделирующих алгоритмов. Удобной формой представления логической структуры моделей процессов функционирования систем и машинных программ является схема. На различных этапах моделирования составляются обобщенные и детальные логические схемы моделирующих алгоритмов, а также схемы программ.
Обобщенная (укрупненная) схема моделирующего алгоритма задает общий порядок действий при моделировании системы без каких-либо уточняющих деталей. Обобщенная схема показывает, что необходимо выполнить на очередном шаге моделирования, например обратиться к датчику случайных чисел.
Детальная схема моделирующего алгоритма содержит уточнения, отсутствующие в обобщенной схеме. Детальная схема показывает не только, что следует выполнить на очередном шаге моделирования системы, но и как это выполнить.
Логическая схема моделирующего алгоритма представляет собой логическую структуру модели процесса функционирования системы S. Логическая схема указывает упорядоченную во времени последовательность логических операций, связанных с решением задачи моделирования.
Схема программы отображает порядок программной реализации моделирующего алгоритма с использованием конкретного математического обеспечения. Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма разработчиком программы на базе конкретного алгоритмического языка. Различие между этими схемами заключается в том, что логическая схема отражает логическую структуру модели процесса функционирования системы, а схема программы — логику машинной реализации модели с использованием конкретных программно-технических средств моделирования.
Логическая схема алгоритма и схема программы могут быть выполнены как в укрупненной, так и в детальной форме. Для начертания этих схем используется набор символов, определяемых ГОСТ 19.701 — 90 (ИСО 5807 — 85) «Единая система программной документации.
Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения». Некоторые наиболее употребительные в практике моделирования на ЭВМ символы показаны на рис. 3.3, где изображены основные, специфические и специальные символы процесса. К ним относятся: основной символ: а — процесс — символ отображает функцию обработки данных любого вида (выполнение определенной операции или группы операций, приводящее к изменению значения, формы или размещения информации или к определению, по которому из нескольких направлений потока следует двигаться); специфические символы процесса: б — решение — символ отображает решение или функцию переключательного типа, имеющую один вход и ряд альтернативных выходов, один и только один из которых может быть активизирован после вычисления условий, определенных внутри этого символа (соответствующие результаты вычисления могут быть записаны по соседству с линиями, отображающими эти пути); в — подготовка — символ отображает модификацию команды или группы команд с целью воздействия на некоторую последующую функцию (установка переключателя, модификация индексного регистра или инициализация программы); г — предопределенный процесс — символ отображает предопределенный процесс, состоящий из одной или нескольких операций или шагов программы, которые определены в другом месте (в подпрограмме, модуле); д — ручная операция — символ отображает любой процесс, выполняемый человеком; специальные символы: е — соединитель — символ отображает выход в часть схемы и вход из другой части этой схемы и используется для обрыва линии и продолжения ее в другом месте (соответствующие символы-соединители должны содержать одно и то же уникальное обозначение); ж — терминатор — символ отображает выход во внешнюю среду и вход из внешней среды (начало или конец схемы алгоритма, внешнее использование или пункт назначения

Пример изображения схемы моделирующего алгоритма показан на рис. 3.3, з.
Обычно схема является наиболее удобной формой представления структуры моделирующих алгоритмов. В ряде случаев используются и другие формы представления моделирующих алгоритмов, например форма граф-схем (рис. 3.3, и). Здесь Hi— начало, Ki— конец, Bi — вычисление, Фi, — формирование, Пi— проверка условия, Сi — счетчик, Рi, — выдача результата, i=l, g, где g — общее число операторов моделирующего алгоритма. В качестве пояснения к граф-схеме алгоритма в тексте дается раскрытие содержания операторов, что позволяет упростить представление алгоритма, но усложняет работу с ним.
Моделирующие алгоритмы могут быть также представлены в виде операторных схем [4]. Обозначения операторов на такой схеме соответствуют обозначениям для граф-схем. Для рассмотренного примера операторная схема алгоритма имеет вид
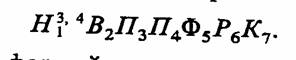
Более подробно с формой представления логической структуры моделирующих алгоритмов и машинных программ познакомимся при рассмотрении имитационных моделей процессов функционирования различных систем и способов их реализации на ЭВМ.
Подэтапы второго этапа моделирования. Рассмотрим подэтапы, выполненные при алгоритмизации модели системы и ее машинной реализации, обращая основное внимание на задачи каждого подэтапе и методы их решения.
2.1. Построение логической схемы модели. Рекомендуется строить модель по блочному принципу, т. е. в виде некоторой совокупности стандартных блоков. Построение модели систем S из таких блоков обеспечивает необходимую гибкость в процессе ее эксплуатации, особенно на стадии машинной отладки. При построении блочной модели проводится разбиение процесса функционирования системы на отдельные достаточно автономные подпроцессы. Таким образом, модель функционально подразделяется на подмодели, каждая из которых в свою очередь может быть разбита на еще более мелкие элементы. Блоки такой модели бывают двух типов: основные и вспомогательные. Каждый основной блок соответствует некоторому реальному подпроцессу, имеющему место в моделируемой системе S, а вспомогательные блоки представляют собой лишь составную часть машинной модели, они не отражают функции моделируемой системы и необходимы лишь для машинной реализации, фиксации и обработки результатов моделирования.
2.2. Получение математических соотношений. Одновременно с выполнением подэтапа построения логической схемы модели необходимо получить, если это возможно, математические соотношения в виде явных функций, т. е. построить аналитические модели. Этот подэтап соответствует неявному заданию возможных математических соотношений на этапе построения концептуальной модели. При выполнении первого этапа еще не может иметься информации о конкретном виде таких математических соотношений, а на втором этапе уже необходимо получить эти соотношения. Схема машинной модели Мм должна представлять собой полное отражение заложенной в модели концепции и иметь: а) описание всех блоков модели с их наименованиями; б) единую систему обозначений и нумерацию блоков; в) отражение логики модели процесса функционирования системы; г) задание математических соотношений в явном виде.
Таким образом, в общем случае построенная машинная модель Mm системы будет иметь комбинированный характер, т. е. отражать аналитико-имитационный подход, когда часть процесса в системе описана аналитически, а другая часть имитируется соответствующими алгоритмами.
2.3. Проверка достоверности модели системы. Эта проверка является первой из проверок, выполняемых на этапе реализации модели. Так как модель представляет собой приближенное описание процесса функционирования реальной системы 5, то до тех пор, пока не доказана достоверность модели Мм, нельзя утверждать, что с ее помощью будут получены результаты, совпадающие с теми, которые могли бы быть получены при проведении натурного эксперимента с реальной системой S. Поэтому определение достоверности модели можно считать наиболее важной проблемой при моделировании систем. От решения этой проблемы зависит степень доверия к результатам, полученным методом моделирования. Проверка модели на рассматриваемом подэтапе должна дать ответ на вопрос, насколько логическая схема модели системы и используемые математические соотношения отражают замысел модели, сформированный на первом этапе. При этом проверяются: а) возможность т решения поставленной задачи; б) точность отражения замысла в логической схеме; в) полнота логической схемы модели; г) правили ность используемых математических соотношений.
Только после того, как разработчик убеждается путем соответствующей проверки в правильности всех этих положений, можно считать, что имеется логическая схема модели системы S, пригодная для дальнейшей работы по реализации модели на ЭВМ.
2.4. Выбор инструментальных средств для моделирования. На этом подэтапе необходимо окончательно решить вопрос о том, какую вычислительную машину (ЭВМ, АВМ, ГВК) и какое программное обеспечение целесообразно использовать для реализации модели системы S. Вообще, выбор вычислительных средств может быть проведен и на предыдущих подэтапах, но рассматриваемый подэтап является последним, когда этот выбор должен быть сделан окончательно, так как в противном случае возникнут трудности в проведении дальнейших работ по реализации модели. Вопрос о выборе ЭВМ сводится к обеспечению следующих требований: а) наличие необходимых программных и технических средств; б) [ доступность выбранной ЭВМ для разработчика модели; в) обеспечение всех этапов реализации модели; г) возможность своевременного получения результатов.
2.5. Составление плана выполнения работ по программированию. Такой план должен помочь при программировании модели, учитывая оценки объема программы и трудозатрат на ее составление, План при использовании универсальной ЭВМ должен включать в себя: а) выбор языка (системы) программирования модели; б) указание типа ЭВМ и необходимых для моделирования устройств; в) оценку примерного объема необходимой оперативной и внешней памяти; г) ориентировочные затраты машинного времени на моделирование; д) предполагаемые затраты времени на программирование и отладку программы на ЭВМ.
2.6. Спецификация и построение схемы программы. Спецификация программы — формализованное представление требований, предъявляемых к программе, которые должны быть удовлетворены при ее разработке, а также описание задачи, условия и эффекта действия без указания способа его достижения. Наличие логической блок-схемы модели позволяет построить схему программы, которая должна отражать: а) разбиение модели на блоки, подблоки и т. д.; б) особенности программирования модели; в) проведение необходимых изменений; г) возможности тестирования программы; д) оценку затрат машинного времени; е) форму представления входных и выходных данных.
Построение схемы программы представляет собой одну из основных задач на этапе машинной реализации модели. При этом особое внимание должно быть уделено особенностям выбранного для реализации модели языка: алгоритмического языка общего назначения или языка моделирования (например, SIMULA, SIMSCRIPT, GPSS).
2.7. Верификация и проверка достоверности схемы программы.
Верификация программы — доказательство того, что поведение программы соответствует спецификации на программу. Эта проверка является второй на этапе машинной реализации модели системы. Очевидно, что нет смысла продолжать работу по реализации модели, если нет уверенности в том, что в схеме программы, по которой будет вестись дальнейшее программирование, допущены ошибки, которые делают ее неадекватной логической схеме модели, а следовательно, и неадекватной самому объекту моделирования. При этом проводится проверка соответствия каждой операции, представленной в схеме программы, аналогичной ей операции в логической схеме модели.
2.8. Проведение программирования модели. При достаточно подробной схеме программы, которая отражает все операции логической схемы модели, можно приступить к программированию модели. Если имеется адекватная схема программы, то программирование представляет собой работу только для программиста без участия и помощи со стороны разработчика модели. При использовании пакетов прикладных программ моделирования проводится непосредственная генерация рабочих программ для моделирования конкретного объекта, т. е. программирование модели реализуется в автоматизированном режиме.
2.9. Проверка достоверности программы. Эта последняя проверка на этапе машинной реализации модели, которую необходимо проводить: а) обратным переводом программы в исходную схему; б) проверкой отдельных частей программы при решении различных тестовых задач; в) объединением всех частей программы и проверкой ее в целом на контрольном примере моделирования варианта системы S.
На этом подэтапе необходимо также проверить оценки затрат машинного времени на моделирование. Полезно также получить достаточно простую аналитическую аппроксимацию зависимости затрат машинного времени от количества реализаций, что позволит разработчику модели (заказчику) правильно сформулировать требования к точности и достоверности результатов моделирования.
2.10. Составление технической документации по второму этапу. Для завершения этапа машинной реализации модели Мм необходимо составить техническую документацию, содержащую: а) логическую схему модели и ее описание; б) адекватную схему программы и принятые обозначения; в) полный текст программы; г) перечень входных и выходных величин с пояснениями; д) инструкцию по работе с программой; е) оценку затрат машинного времени на моделирование с указанием требуемых ресурсов ЭВМ.
Таким образом, на этом этапе разрабатывается схема модели системы S, проводится ее алгоритмизация и программирование
с использованием конкретных программно-технических средств, т. е. строится машинная модель Мм, с которой предстоит работать для получения необходимых результатов моделирования по оценке характеристик процесса функционирования системы S (задача анализа) или для поиска оптимальных структур, алгоритмов и параметров системы S (задача синтеза).
3.4. ПОЛУЧЕНИЕ И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ
МОДЕЛИРОВАНИЯ СИСТЕМ
На третьем этапе моделирования — этапе получения и интерпретации результатов моделирования — ЭВМ используется для проведения рабочих расчетов по составленной и отлаженной программе. Результаты этих расчетов позволяют проанализировать и сформулировать выводы о характеристиках процесса функционирования моделируемой системы S.
Особенности получения результатов моделирования. При реализации моделирующих алгоритмов на ЭВМ вырабатывается информация о состояниях процесса функционирования исследуемых систем z(t)eZ. Эта информация является исходным материалом для определения приближенных оценок искомых характеристик, получаемых в результате машинного эксперимента, т. е. критериев оценки. Критерием оценки будем называть любой количественный показатель, по которому можно судить о результатах моделирования системы. Критериями оценки могут служить показатели, получаемые на основе процессов, действительно протекающих в системе, или получаемых на основе специально сформированных функций этих процессов [4, 29, 35].
В ходе машинного эксперимента изучается поведение исследуемой модели М процесса функционирования системы S на заданном интервале времени [0, 7]. Поэтому критерий оценки является в общем случае векторной случайной функцией, заданной на этом же интервале:
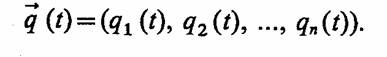
Часто используют более простые критерии оценки, например вероятность определенного состояния системы в заданный момент времени t* ε[0, 7], отсутствие отказов и сбоев в системе на интервале [0, 7] и т. д. При интерпретации результатов моделирования вычисляются различные статистические характеристики закона распределения критерия оценки.
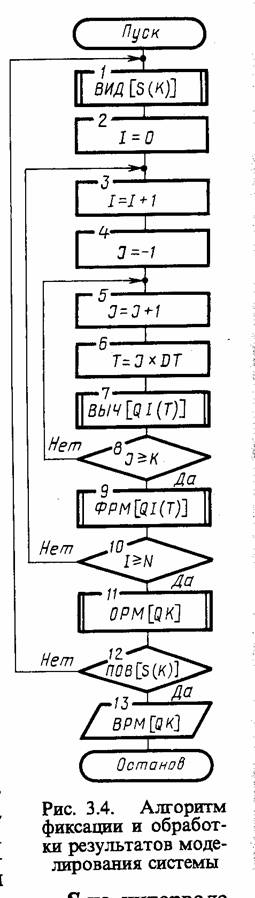
Рассмотрим общую схему фиксации и обработки результатов моделирования системы, которая приведена на рис. 3.4. Будем рассматривать гипотетическую модель М, предназначенную для исследования поведения системы S на интервале времени [0, T]. В общем случае критерием интерпретации результатов моделирования является нестационарный случайный n-мерный процес q (t), O ≤t≤T. Полагаем для определенности, что состояние моделируемой системы S проверяется каждые А* временных единиц, т. е, используется «принцип At». При этом вычисляют значения q (jAt), j=Q, к, критерия q (/). Таким образом, о свойствах случайного процесса q (i) судят по свойствам случайной последовательности q (j'Ai), j=0, к, или, иначе говоря, по свойствам /«-мерного вектора вида

Процесс функционирования системы S на интервале [0, T] моделируется N-кратно с получением независимых реализаций qt, z'= I, N, вектора q. Работа модели на интервале [0, T] называется прогоном модели.
На схеме, изображенной на рис. 3.4, обозначено: I≡i; J≡j; К≡к; N≡N; T≡t; DT≡Δt;
В общем случае алгоритмы фиксации и статистической обработки данных моделирования содержат три цикла. Полагаем, что имеется машинная модель Мм системы S.
Внутренний цикл (блоки 5 — 8) позволяет получить последовательность qi(t) = q (jΔt), j=0,k в моменты времени t=0, Δt, 2Δt, kΔt = Т. Основной блок 7 реализует процедуру вычисления последовательности qt(t): ВЫЧ [QI(T)]. Именно в этом блоке имитируется процесс функционирования моделируемой системы S на интервале времени [0, T ].
Промежуточный цикл (блоки 3 — 10), в котором организуется N-кратное повторение прогона модели, позволяющее после соответствующей статистической обработки результатов судить об оценках характеристик моделируемого варианта системы. Окончание моделирования варианта системы S может определяться не только заданным числом реализаций (блок 10), как это показано на схеме, но и заданной точностью результатов моделирования. В этом цикле содержится блок 9, реализующий процедуру фиксации
результатов моделирования по i-му прогону модели qt(t): ФРМ
Внешний цикл (блоки 1 —12) охватывает оба предшествующих цикла и дополнительно включает блоки 1, 2,11, 12, управляющие последовательностью моделирования вариантов системы S. Здесь организуется поиск оптимальных структур, алгоритмов и параметров системы S, т. е. блок 11 обрабатывает результаты моделирования исследуемого к-ro варианта системы ОРМ [QK\, блок 12 проверяет удовлетворительность полученных оценок характеристик процесса функционирования системы q^(t) требуемым (ведет поиск оптимального варианта системы ПОВ [S(K)]), блок 1 изменяет структуру, алгоритмы и параметры системы S на уровне ввода исходных данных для очередного к-го варианта системы ВИД [S(K)]. Блок 13 реализует функцию выдачи результатов моделирования по каждому k-му варианту модели системы Sk т. е. ВРМ ГОТ
Рассмотренная схема позволяет вести статистическую обработку результатов моделирования в наиболее общем случае при нестационарном критерии q (t). В частных случаях можно ограничиться более простыми схемами [22, 29, 37].
Если свойства моделируемой системы S определяются значением критерия q (t) в некоторый заданный момент времени, например в конце периода функционирования модели t=kΔt=T, то обработка сводится к оценке распределения n -мерного вектора q(t) по
независимым реализациям tji(t), i=1, N, полученным в результате N прогонов модели.
Если в моделируемой системе S по истечению некоторого времени с начала работы to = koΔt установится стационарный режим, то о нем можно судить по одной, достаточно длинной реализации qt (t) критерия q (t), стационарного и эргодического на интервале [t0T]. Для рассмотренной схемы это означает, что исключается средний цикл (n= 1) и добавляется оператор, позволяющий начать обработку значений q1(jΔt) при j≥k0.
Другая особенность применяемых на практике методов статистической обработки результатов моделирования связана с исследованием процесса функционирования систем с помощью моделей блочной конструкции. В этом случае часто приходится применять раздельное моделирование отдельных блоков модели, когда имитация входных воздействий для одного блока проводится на основе оценок критериев, полученных предварительно на другом блоке модели. При раздельном моделировании может иметь место либо непосредственная запись в накопителе реализаций критериев, либо их аппроксимация, полученная на основе статистической обработки результатов моделирования с последующим использованием генераторов случайных чисел для имитации этих воздействий.
Подэтапы третьего этапа моделирования. Прежде чем приступить к последнему, третьему, этапу моделирования системы, необходимо для его успешного проведения иметь четкий план действий, сводящийся к выполнению следующих основных подэтапов.
3.1. Планирование машинного эксперимента с моделью системы. Перед выполнением рабочих расчетов на ЭВМ должен быть составлен план проведения эксперимента с указанием комбинаций переменных и параметров, для которых должно проводиться моделирование системы S. Планирование машинного эксперимента призвано дать в итоге максимальный объем необходимой информации об объекте моделирования при минимальных затратах машинных ресурсов. При этом различают стратегическое и тактическое планирование машинного эксперимента. При стратегическом планировании эксперимента ставится задача построения оптимального плана эксперимента для достижения цели, поставленной перед моделированием (например, оптимизация структуры, алгоритмов и параметров системы S, исследуемой методом моделирования на ЭВМ). Тактическое планирование машинного эксперимента преследует частные цели оптимальной реализации каждого конкретного эксперимента из множества необходимых, заданных при стратегическом планировании (например, решение задачи выбора оптимальных правил остановки при статистическом моделировании системы S на ЭВМ). Для получения наиболее эффективного плана машинного эксперимента необходимо использовать статистические методы [10, 18, 21].
3.2. Определение требований к вычислительным средствам. Необходимо сформулировать требования по времени использования вычислительных средств, т. е. составить график работы на одной или нескольких ЭВМ, а также указать те внешние устройства ЭВМ, которые потребуются при моделировании. При этом также рационально оценить, исходя из требуемых ресурсов, возможность использования для реализации конкретной модели персональной ЭВМ или локальной вычислительной сети.
3.3. Проведение рабочих расчетов. После составления программы модели и плана проведения машинного эксперимента с моделью системы S можно приступить к рабочим расчетам на ЭВМ, которые обычно включают в себя: а) подготовку наборов исходных данных для ввода в ЭВМ; б) проверку исходных данных, подготовленных для ввода; в) проведение расчетов на ЭВМ; г) получение выходных данных, т. е. результатов моделирования.
Проведение машинного моделирования рационально выполнять в два этапа: контрольные, а затем рабочие расчеты. Причем контрольные расчеты выполняются для проверки машинной модели Мм и определения чувствительности результатов к изменению исходных данных.
3.4. Анализ результатов моделирования системы. Чтобы эффективно проанализировать выходные данные, полученные в результате расчетов на ЭВМ, необходимо знать, что делать с результатами рабочих расчетов и как их интерпретировать. Эти задачи могут быть решены на основании предварительного анализа на двух первых этапах моделирования системы S. Планирование машинного эксперимента с моделью Мм позволяет вывести необходимое количество выходных данных и определить метод их анализа. При этом необходимо, чтобы на печать выдавались только те результаты, которые нужны для дальнейшего анализа. Также необходимо полнее использовать возможности ЭВМ с точки зрения обработки результатов моделирования и представления этих результатов в наиболее наглядном виде. Вычисление статистических характеристик перед выводом результатов из ЭВМ повышает эффективность применения машины и сводит к минимуму обработку выходной информации после ее вывода из ЭВМ.
3.5. Представление результатов моделирования. Как уже отмечалось, необходимо на третьем этапе моделирования уделить внимание форме представления окончательных результатов моделирования в виде таблиц, графиков, диаграмм, схем и т. п. Целесообразно в каждом конкретном случае выбрать наиболее подходящую форму, так как это существенно влияет на эффективность их дальнейшего употребления заказчиком. В большинстве случаев наиболее простой формой считаются таблицы, хотя графики более наглядно иллюстрируют результаты моделирования системы S. При диалоговых режимах моделирования наиболее рациональными средствами оперативного отображения результатов моделирования являются средства мультимедиа технологии.
3.6. Интерпретация результатов моделирования. Получив и проанализировав результаты моделирования, их нужно интерпретировать по отношению к моделируемому объекту, т. е. системе S. Основное содержание этого подэтапа — переход от информации, полученной в результате машинного эксперимента с моделью Ми, к информации применительно к объекту моделирования, на основании которой и будут делаться выводы относительно характеристик процесса функционирования исследуемой системы S.
3.7. Подведение итогов моделирования и выдача рекомендаций. Проведение этого подэтапа тесно связано с предыдущим вторым этапом (см. п. 3.3). При подведении итогов моделирования должны быть отмечены главные особенности, полученные в соответствии с планом эксперимента над моделью Мм результатов, проведена проверка гипотез и предположений и сделаны выводы на основании этих результатов. Все это позволяет сформулировать рекомендации по практическому использованию результатов моделирования, например на этапе проектирования системы S.
3.8. Составление технической документации по третьему этапу. Эта документация должна включать в себя: а) план проведения машинного эксперимента; б) наборы исходных данных для моделирования; в) результаты моделирования системы; г) анализ и оценку результатов моделирования; д) выводы по полученным результатам моделирования; указание путей дальнейшего совершенствования машинной модели и возможных областей ее приложения.
Полный комплект документации по моделированию конкретной системы S на ЭВМ должен содержать техническую документацию по каждому из трех рассмотренных этапов.
Таким образом, процесс моделирования системы S сводится к выполнению перечисленных этапов моделирования. На этапе построения концептуальной модели Мж проводится исследование моделируемого объекта, определяются необходимые аппроксимации и строится обобщенная схема модели, которая преобразуется в машинную модель Мм на втором этапе моделирования путем последовательного построения логической схемы модели и схемы программы. На последнем этапе моделирования проводят рабочие расчеты на ЭВМ, получают и интерпретируют результаты моделирования системы S.
Рассмотренная последовательность этапов и подэтапов отражает наиболее общий подход к построению и реализации модели системы S. В дальнейшем остановимся на наиболее важных составляющих процесса моделирования.
Контрольные вопросы
3.1. В чем суть методики машинного моделирования систем?
3.2. Какие требования пользователь предъявляет к машинной модели системы?
3.3. Что называется концептуальной модель системы?
3.4. Какие группы блоков выделяются при построении блочной конструкции модели системы?
3.5. Каковы основные принципы построения моделирующих алгоритмов процессов функционирования систем ?
3.6. Какие схемы используются при разработке алгоритмического и программного обеспечения машинного моделирования?
3.7. Какие циклы можно выделить в моделирующем алгоритме?
3.8. Что называется прогоном модели?
3.9. Какая техническая документация оформляется по каждому этапу моделирования системы?
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
СИСТЕМ НА ЭВМ
В практикемоделирования систем информатики наиболее часто приходится
иметь дело с объектами, которые в процессе своего функционирования содержат элементы стохастичности или подвергаются стохастическим воздействиям внешней среды. Поэтому основным методом получения результатов с помощью имитационных моделей таких стохастических систем является метод статистического моделирования на ЭВМ, использующий в качестве теоретической базы предельные теоремы теории вероятностей. Возможность получения пользователем модели результатов статистического моделирования сложных систем в условиях ограниченности машинных ресурсов существенно зависит от эффективности процедур генерации псевдослучайных последовательностей на ЭВМ, положенных в основу имитации воздействий на элементы моделируемой системы.
4.1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДА СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
На этапе исследования и проектирования систем при построении и реализации машинных моделей (аналитических и имитационных) широко используется метод статистических испытаний (Монте-Карло), который базируется на использовании случайных чисел, т. е. возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес оценок характеристик моделируемой системы S с учетом воздействий внешней среды Е статистические данные обрабатываются и классифицируются с использованием методов математической статистики [10, 13, 18].
Сущность метода статистического моделирования. Таким образом, сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды Е, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.
Различают две области применения метода статистического моделирования: 1) для изучения стохастических систем; 2) для решения детерминированных задач. Основной идеей, которая используется для решения детерминированных задач методом статистического моделирования, является замена детерминированной задачи эквивалентной схемой некоторой стохастической системы, выходные характеристики последней совпадают с результатом решения детерминированной задачи. Естественно, что при такой замене вместо точного решения задачи получается приближенное решение и погрешность уменьшается с увеличением числа испытаний (реализаций
моделирующего алгоритма) N.
В результате статистического моделирования системы S получается серия частных значений искомых величин или функций, статистическая обработка которых позволяет получить сведения о поведении реального объекта или процесса в произвольные моменты времени. Если количество реализаций N достаточно велико, то полученные результаты моделирования системы приобретают статистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функционирования системы S.
Теоретической основой метода статистического моделирования систем на ЭВМ являются предельные теоремы теории вероятностей [2, 13]. Множества случайных явлений (событий, величин) подчиняются определенным закономерностям, позволяющим не только прогнозировать их поведение, но и количественно оценить некоторые средние их характеристики, проявляющие определенную устойчивость. Характерные закономерности наблюдаются также в распределениях случайных величин, которые образуются при сложении множества воздействий. Выражением этих закономерностей и устойчивости средних показателей являются так называемые предельные теоремы теории вероятностей, часть из которых приводится ниже в пригодной для практического использования при статистическом моделировании формулировке. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний (реализаций) N. Практически приемлемые при статистическом моделировании количественные оценки характеристик систем часто могут быть получены уже при сравнительно небольших (при использовании ЭВМ) N.
Неравенство Чебышева. Для неотрицательной функции g (ζ) случайной величины ζ и любого К> 0 выполняется неравенство
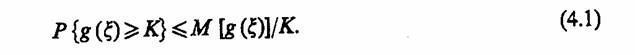
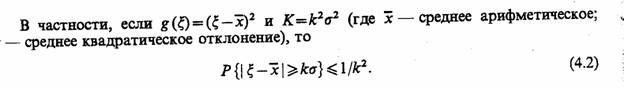
Теорема Бернулли. Если проводится N независимых испытаний, в каждом из которых некоторое событие А осуществляется с вероятностью р, то относительная частота появления события m/'N при N→oo сходится по вероятности к р, т. е. при любом ε >0
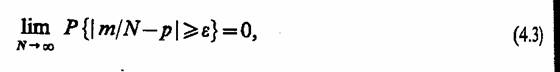
где т — число положительных исходов испытания.
Теорема Пуассона. Если проводится N независимых испытаний н вероятность осуществления события А в i-м испытании равна pi,-, то относительная частота появления события m/N при N-→ оо сходится по вероятности к среднему из вероятностей pi т. е. при любом ε >0
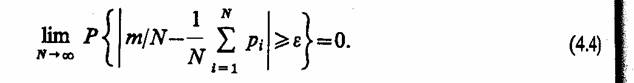
Теорема Чебышева. Если в N независимых испытаниях наблюдаются значения xlt .... хк случайной величины ζ, то при N-→co среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию а, т. е. при любом ε>0
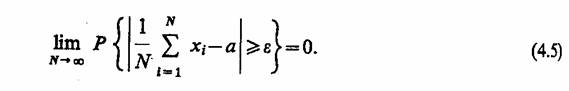
Обобщенная теорема Чебышева. Еслиζ1, ..., ζn— независимые случайные величины с математическими ожиданиями а1г ..., aN и дисперсиями. σ1., σn, ограниченными сверху одним и тем же числом, то при N→00 среднее арифметическое значений случайной величины сходится по вероятности к среднему арифметическому их математических ожиданий:

Теорема Маркова. Выражение (4.6) справедливо и для зависимых случайных величин ζ1,..., ζn если только
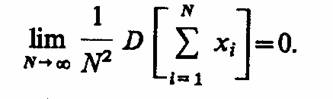
Совокупность теорем, устанавливающих устойчивость средних показателей, принято называть законом больших чисел.
Центральная предельная теорема. Если ζ,1 ..., ζ н— независимые одинаково распределенные случайные величины, имеющие математическое ожидание а и дисперсию
σ2, то при N-»оо закон
распределения суммы 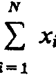 неограниченно
приближается к нормальному:
неограниченно
приближается к нормальному:
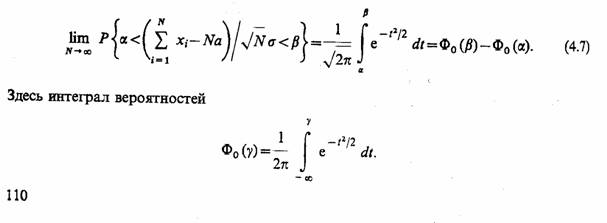
Теорема Лапласа. Бели в каждом из N независимых испытаний событие А появляется с вероятностью р, то

Примеры статистического моделирования, Статистическое моделирование систем на ЭВМ требует формирования значений случайных величин, что реализуется с помощью датчиков (генераторов) случайных чисел. Не останавливаясь пока на способах их реализации для целей моделирования на ЭВМ, поясним сущность метода статистического моделирования следующими примерами.
Пример 4.1. Необходимо методом статистического моделирования найти оценки выходных характеристик некоторой стохастической системы SR, функционирование которой описывается следующими соотношениями: х=1 — е -n— входное воздействие, v=l—e воздействие внешней среды, где λ и φ-случайные величины, для которых известны их функции распределения. Целью моделирования является оценка математического ожидания М]у] величины у. Зависимость последней от входного воздействия х и воздействия внешней среды
и имеет вид у=![]()

В качестве оценки математического ожидания М [у], как следует из приведенных теорем теории вероятностей, может выступать среднее арифметическое, вычисленное по формуле
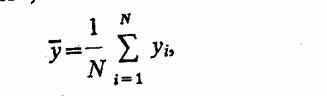
где yi — случайное значение величины у; N — число реализаций, необходимое для статистической устойчивости результатов.
Структурная схема системы SR показана на рис. 4.1.
Здесь элементы выполняют следующие функции:
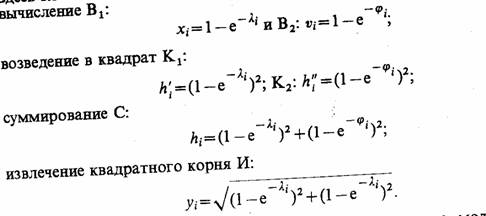
Схема алгоритма, реализующего метод статистического моделирования для оценки М[у] системы 5К, приведена на рис. 4.2. Здесь LA и FI — функции распределения случайных величин λ иφ; N — заданное число реализаций;I=i - номер текущей реализации; LAT= λiFII=φi
EXP=e MYsM]y![]() суммирующая ячейка; ВИД [...], ГЕН [4 ВРМ[...] — процедуры
ввода исходных данных, генерации псевдослучайных последовательностей и выдачи
результатов моделирования соответственно.
суммирующая ячейка; ВИД [...], ГЕН [4 ВРМ[...] — процедуры
ввода исходных данных, генерации псевдослучайных последовательностей и выдачи
результатов моделирования соответственно.
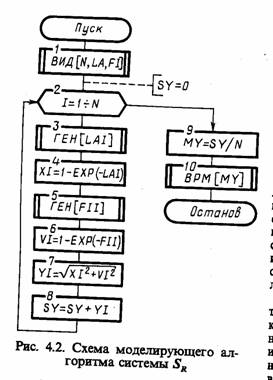
Таким образом, данная модель позволяет получить методом статистического моделирования на ЭВМ статистическую оценку математического ожидания выходной характеристики М\у] рассмотренной стохастической системы SR. Точность и достоверность результатов взаимодействия в основном будут определяться числом реализаций N.
Пример 4.2. Необходимо методом статистического моделирования найти оценку площади фигуры (рис. 4.3), ограниченной осями координат, ординатой а=1 и кривой у=/ƒ(а); при этом для определенности предполагается, что 0</(а)<1 для всех а, 0<а<1.
Таким образом, данная задача является чисто детерминированной и ее аналитическое решение сводится к вычислению определенного интеграла, т. е. искомая площадь фигуры
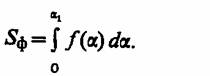
Для решения этой детерминированной задачи методом статистического моделирования необходимо предварительно построить адекватную по выходным характеристикам стохастическую систему 5D, оценки характеристик которой будут совпадать с искомыми в данной детерминированной задаче. Вариант структурной схемы такой системы SD показан на рис. 4.4, где элементы выполняют .следующие функции:
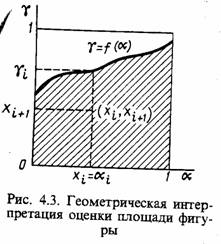

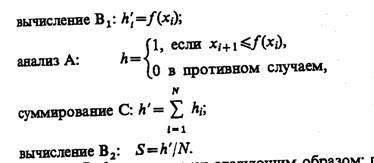
Система SD функционирует следующим образом: получается пара независимых случайных чисел интервала (0,1), определяется координата точки (х„ xi+i), показанной на рис. 4.3, вычисляется ордината у,-=ƒ (xi;) и проводится сравнение величин ;, γi и xi+1 причем если точка (х;i, хi,+1) попала в площадь фигуры (в том числе и на кривую ƒ (х)), то исход испытания считается положительным,hi= 1 ив итоге можно получить статистическую оценку площади фигуры 5ф по заданному числу реализаций N.
Логическая схема моделирующего алгоритма вероятностной системы SD представлена на рис. 4.5. Здесь У=у= ƒ (ά) — заданная функция (табличная кривая); N— заданное число реализаций I≡i — номер текущей реализации; XI≡xi
XIl≡xi+l; HI=hi{, S≡ s; SH≡h'= ∑ hi,- суммирующая ячейка.
Таким образом, построение некоторой стохастической системы SD позволяет методом статистического моделирования получить оценки для детерминированной
задачи.
Пример 4.3. Необходимо методом статистического моделирования решить следующую задачу. Проводится s= 10 независимых выстрелов но мишени, причем вероятность попадания при одном выстреле задана и равна р. Требуется оценить вероятность того, что число попаданий в мишень будет четным, т. е. 0, 2, 4, 6,
8,10.
Данная задача является вероятностной, причем существуетее аналитическое решение:

В качестве объекта статистического моделирования можно рассмотреть следующую вероятностную систему Sr, структура которой представлена на рис. 4.6, где элементы выполняют такие функции: анализ А±:

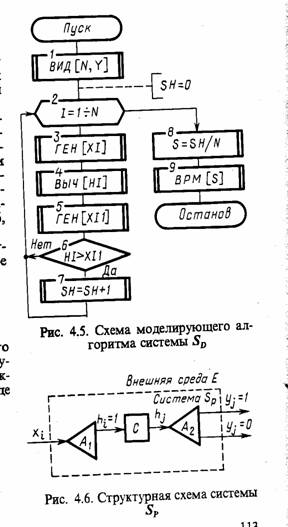
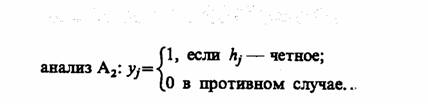
Выходным воздействием в данной системе SF является событие четного числа попаданий в мишень в серии из десяти выстрелов. В качестве оценки выходной характеристики необходимо при числе испытаний (серий выстрелов), равном Лг,
найти вероятность четного числа попаданий:
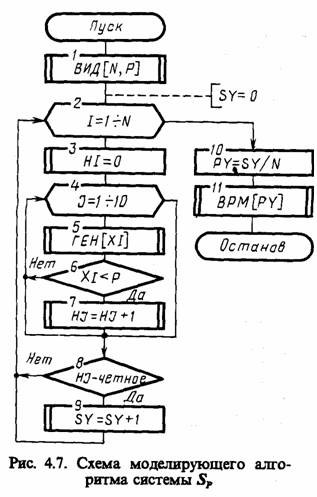
..
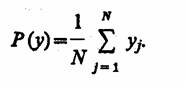
Логическая схема алгоритма статистического моделирования для оценки искомой характеристики такой системы Р(у) приведена на рис. 4.7. Здесь Р=р — заданная вероятность попадания в мишень при одном выстреле;
N — заданное число реализаций;
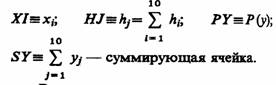
В данном моделирующем алгоритме после ввода исходных данных и реализации операторов цикла происходит обращение к генератору случайных чисел, т. е. получаются значения xt случайной величины, равномерно распределенной в интервале (0, 1). Вероятность попадания случайной величины в интервал (0, р), где р < 1, равна длине этого отрезка, т. е. Р {Xi<p} =p. Поэтому при каждом моделировании выстрела полученное случайное число х\ сравнивается с заданной вероятностью р и при Xj<p регистрируется «попадание в мишень», а в противном случае — «промах». Далее моделируются серии из десяти испытаний каждая, подсчитывается четное число «попаданий» в каждой серии и находится статистическая оценка искомой характеристики Р(у).
Таким образом, подход при использовании статистического моделирования независимо от природы объекта исследования (будет ли он детерминированным или стохастическим) является общим, причем при статистическом моделировании детерминированных систем (система SD в примере 4.2) необходимо предварительно построить стохастическую систему, выходные характеристики которой позволяют оценить искомые.
Отметим, что во всех рассмотренных примерах не требуется запоминания всего множества генерируемых случайных чисел, используемых при статистическом моделировании системы S. Запоминается только накопленная сумма исходов и общее число реализаций. Это немаловажное обстоятельство вообще является характерным при реализации имитационных моделей методом статистического моделирования на ЭВМ.
4.2. ПСЕВДОСЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ПРОЦЕДУРЫ
ИХ МАШИННОЙ ГЕНЕРАЦИИ
При статистическом моделировании систем одним из основных вопросов является учет стохастических воздействий. Количество случайных чисел, используемых для получения статистически устойчивой оценки характеристики процесса функционирования системы S при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно и большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества исходных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования, последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования систем [31, 37, 46].
Рассмотрим возможности и особенности получения последовательностей случайных чисел при статистическом моделировании систем на ЭВМ. На практике используются три основных способа генерации случайных чисел: аппаратный (физический), табличный (файловый) и алгоритмический (программный).
Аппаратный способ. При этом способе генерации случайные числа вырабатываются специальной электронной приставкой — генератором (датчиком) случайных чисел,— служащей в качестве одного из внешних устройств ЭВМ. Таким образом, реализация этого способа генерации не требует дополнительных вычислительных операций ЭВМ по выработке случайных чисел, а необходима только операция обращения к внешнему устройству (датчику). В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т. д.Рассмотрим принцип получения случайных чисел от приставки, основанный, например, на эффекте шума в полупроводниковых приборах.
Структурная схема аппаратного генератора случайных чисел приведена на рис. 4.8, а. Здесь ИШ — источник шума; КС — ключевая схема; ФИ — формирователь импульсов; ПС — пересчетная , схема. При усилении шумов на выходе ИШ получается напряжение
Иш, (t), которое является случайным процессом, показанным на временной диаграмме рис. 4.8, б. Причем отрезок шумовой реализации ux(t), сформированный на интервале времени (О, Т) с помощью КС, содержит случайное число выбросов Сравнение напряжения, м, (/) с пороговым Un позволяет сформировать на выходе ФИ серию импульсов Мф(/). Тогда на выходе ПС может быть получена последовательность случайных чисел Xi(f).). Например, если провести масштабирование и принять длину интервала (0,Т∆) за единицу, то значения интервалов времени ∆ti =t1+ — ti между соседними импульсами иф(/) будут случайными числами ;x,ε (0, 1). Возможны и другие схемные решения аппаратных генераторов случайных чисел [29, 37]. Однако аппаратный способ получения случайных чисел не позволяет гарантировать качество последовательности непосредственно во время моделирования системы S на ЭВМ, а также повторно получать при моделировании одинаковые последовательности чисел.
Табличный способ. Если случайные числа, оформленные в виде таблицы, помещать во внешнюю или оперативную память ЭВМ, предварительно сформировав из них соответствующий файл (массив чисел), то такой способ будет называться табличным. Однако этот способ получения случайных чисел при моделировании систем на ЭВМ обычно рационально использовать при сравнительно небольшом объеме таблицы и соответственно файла чисел, когда для хранения можно применять оперативную память. Хранение файла во внешней памяти при частном обращении в процессе статистического моделирования не рационально, так как вызывает увеличение затрат машинного времени при моделировании системы S из-за необходимости обращения к внешнему накопителю. Возможны промежуточные способы организации файла, когда он переписывается в оперативную память периодически по частям. Это уменьшает время на обращение к внешней памяти, но сокращает объем оперативной памяти, который можно использовать для моделирования процесса функционирования системы S.
 Алгоритмический способ.
Способ получения последовательностей случайных чисел основан на формировании
случайных чисел в ЭВМ с помощью специальных алгоритмов и реализующих их
программ,
Алгоритмический способ.
Способ получения последовательностей случайных чисел основан на формировании
случайных чисел в ЭВМ с помощью специальных алгоритмов и реализующих их
программ,
Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ.

Достоинства и недостатки трех перечисленных способов получения случайных чисел для сравнения представлены в табл. 4.1. Из этой таблицы видно, что алгоритмический способ получения случайных чисел наиболее рационален на практике при моделировании систем на универсальных ЭВМ.
Генерация базовой последовательности. При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Вообще говоря, в качестве базового может быть принят любой удобный в случае моделирования конкретной системы 5 процесс (например, пуассоновский поток при моделировании Q-схемы). Однако при дискретном моделировании базовым процессом является последовательность чисел {х,}=х0, хи ..., xs, представляющих собой реализации независимых, равномерно распределенных на интервале (0, 1) случайных величин {ζ,} = ζ 0> ζ i, ζ n, или — в статистических терминах — повторную выборку из равномерно распределенной на (0, 1) генеральной совокупности значений величиныI [29, 37, 46].
Непрерывная случайная величина ζ имеет равномерное распределение в интервале (а, b), если ее функции плотности
(рис. 4.9, а) и распределения (рис. 4.9, б) соответственно примут вид
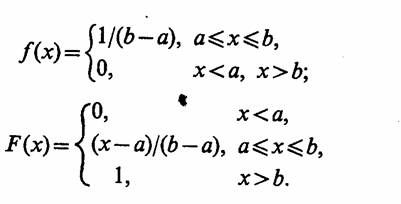
Определим числовые характеристики случайной величины ζ, принимающей значения х,— математическое ожидание, дисперсию и среднее квадратическое отклонение соответственно:
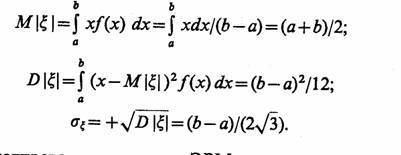
При моделировании систем на ЭВМ приходится иметь дело со случайными числами интервала (0, 1), когда границы интервала, а=0 и b = 1. Поэтому рассмотрим частный случай равномерного распределения, когда функция плотности и функция распределения соответственно имеют вид
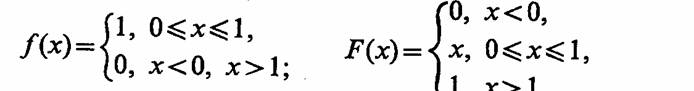
Такое распределение имеет математическое ожидание.M[ζ] =12
и дисперсию D [ζ] = 1/12.
Это распределение требуется получить на ЭВМ. Но получить его на цифровой ЭВМ невозможно, так как машина оперирует с п- разрядными числами. Поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0, 1) используют дискретную последовательность 2" случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.
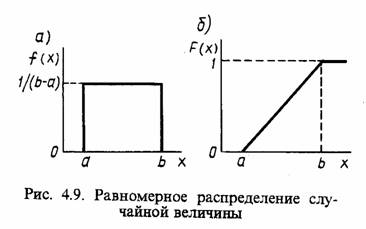
Случайная величина ζ, имеющая квазиравномерное распределение в интервале (0, 1), принимает значения х,= //(2п —1) с вероятностями pi= 1/2", f=0, 2"—1.
Математическое ожидание и дисперсия квазиравномерной случайной величины соответственно имеют вид
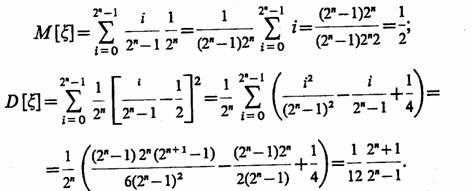
Таким образом, математическое ожидание квазиравномерной случайной величины совпадает с математическим ожиданием равномерной случайной последовательности интервала (0, 1), а дисперсия отличается только множителем (2П+1)/(2п — 1), который при достаточно больших п близок к единице.
На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины £ используются формулы (алгоритмы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными [4, 29].
Требования к генератору случайных чисел. Прежде чем перейти к описанию конкретных алгоритмов получения на ЭВМ последовательностей псевдослучайных чисел, сформулируем набор требований, которым должен удовлетворять идеальный генератор. Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.
Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных чисел находят алгаритимы вида

представляющие собой рекуррентные соотношения первого порядка, для которых начальное число х0 и постоянные параметры заданы [36, 37].
Определим качественно требования к виду функции Ф. Например, легко показать, что функция вида (4.9), изображенная на рис. 4.10, а, не может породить хорошую последовательность псевдослучайных чисел х1г х2, ... Действительно, если построить точки с координатами (x1 x2), (x3, x4) по случайным числам, полученным, например, из таблицы случайных чисел (табл. 4.2), то они будут равномерно распределены в единичном квадрате 0≤хi,+1≤ 1. Соответствующие же точки, построенные по числам (х1, Ф(x2)), (xз, Ф(x4)), …, располагаются в площади, ограниченной кривой jeI+1 = Ф (х,).
Хорошую последовательность случайных чисел может породить только такая функция xi+l = Ф (х(), график которой достаточно плотно заполняет единичный квадрат. Примером такой функции может служить Х1+1=Д(Ах,) при больших целых положительных А, где Д(и)=и—Ц(и) — дробная часть числа и; Ц(и) — целая часть числа и, т. е. наибольшее целое число, не превосходящее и. Пусть для примера А = 10, тогда функция х1+1=Ф(х,) будет иметь вид, показанный на рис. 4.10, б. Приведенные условия являются только необходимыми, но не достаточными для того, чтобы соотношение (4.9) порождало хорошие последовательности псевдослучайных чисел.
Рассмотрим некоторые процедуры получения последовательностей псевдослучайных квазиравномерно распределенных чисел, которые нашли применение в практике статистического моделирования систем на ЭВМ.
Одной из исторически первых процедур получения псевдослучайных чисел была процедура, получившая название метода серединных квадратов. Пусть имеется 2n-разрядное число, меньшее 1:xi,=0, a1 аг ...а2n. Возведем его в квадрат: xi,-2 = 0, b1 b2 ... b4n а затем отберем средние 2n разрядов х1+1 =0, bn+i bn+2 … Ь3„, которые и будут являться очередным числом псевдослучайной последовательности. Например, если начальное число хо = 0,2152, то (хо)2 = 0,04631104, т. е. x1 =0,6311, затем (xl)2 = 0,39828721, т. е. х2 = 0,8287, и т. д.
Недостаток этого метода — наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать. Например, если х0 — 0,4500, то (лг0)2 = 0,20250000, xt = 0,2500, (х1)2 = 0,06250000, х2 = 0,2500, (х2)2 = 0,06250000, х3 = 0,2500 и т. д. Кроме того, при некоторых вообще может наблюдаться вырождение последовательности, т. е. л:, = 0 при Это существенно ограничивает
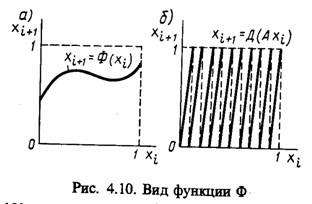
возможности использования метода серединных квадратов.
Конгруэнтные процедуры генерации. Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности. Два целых числа а и β конгруэнтны (сравнимы) по модулю т, где т — целое число, тогда и только тогда, когда существует такое целое число к, что a— β =km, т. е. если разность а— β делится на т и если числа α и β дают одинаковые остатки от деления на абсолютную величину числа т. Например, 1984=4 (mod 10), 5008 = 8 (mod 103) и т. д.
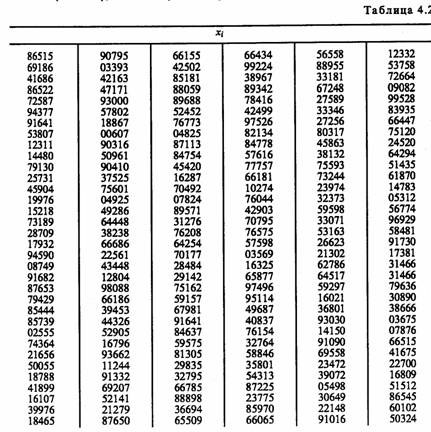
Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения, когда функция (4.9) имеет вид
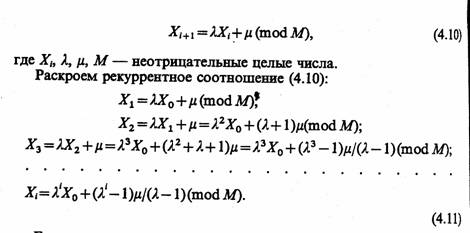
Если заданы начальное значение Х0, множитель λ и аддитивная константа μ, то (4.11) однозначно определяет последовательность целых чисел {Xi}, составленную из остатков от деления на М членов последовательности {λiX0 + μ(λi - 1)/(λ - 1)}. Таким образом, для любого i ≥ 1 справедливо неравенство Xi < M. По целым числам последовательности {Xi} можно построить последовательность {хi} = {Xi/M} рациональных чисел из единичного интервала (0, 1).
Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.
Мультипликативный метод. Задает последовательность неотрицательных целых чисел {Xi}, не превосходящих М, по формуле
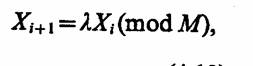
т. е. это частный случай соотношения (4.10) при μ= 0.
В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т. е. выполнение операции, которая быстро реализуется современными ЭВМ.
Для машинной реализации наиболее удобна версия М = рg, где р - число цифр в системе счисления, принятой в ЭВМ (р = 2 для двоичной и р = 10 для десятичной машины); g - число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Хi в рациональную дробь из интервала хi ∈ (0, 1) осуществляется подстановкой слева от Xi, двоичной или десятичной запятой.
Алгоритм построения последовательности для двоичной машины М = 2g сводится к выполнению таких операций [31, 36, 46]:
1. Выбрать в качестве Х0 произвольное нечетное число.
2. Вычислить коэффициент λ = 8t ± 3, где t - любое целое положительное число.
3. Найти произведение λХ0, содержащее не более 2g значащих разрядов.
4. Взять g младших разрядов в качестве первого члена последовательности X1, а остальные отбросить.
5. Определить дробь х1 = Х1/2g из интервала (0, 1).
6. Присвоить Х0 = Х1.
7. Вернуться к п. 3.
Пример 4.4. Необходимо получить числа последовательности для случая g = 4, используя приведенный алгоритм мультипликативного метода. Для этого выполняем следующие действия: 1. Выбираем Х010 = 7 (в десятичной системе счисления) или Х0 = 0111 (в двоичной системе счисления). 2. Найдем t = 1, тогда λ10 = 11 или 5; пусть λ10 = 5, λ = 0101. 3. Рассчитываем произведение λХ0, берем g младших разрядов, вычисляем Х1 и присваиваем Х0 = Х1, т. е. выполняем п. 3 - 7 алгоритма:
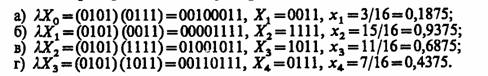
Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {Хi}, не превосходящих М, по формуле
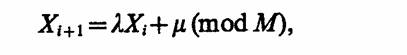
т. е. в отличие от мультипликативного метода μ ≠ 0 вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.
Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.
В настоящее время почти все пакеты прикладных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре [17, 38, 40].
4.3. ПРОВЕРКА И УЛУЧШЕНИЕ КАЧЕСТВА
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
Эффективность статистического моделирования систем на ЭВМ и достоверность получаемых результатов существенным образом зависят от качества исходных (базовых) последовательностей псевдослучайных чисел, которые являются основой для получения стохастических воздействий на элементы моделируемой системы. Поэтому, прежде чем приступать к реализации моделирующих алгоритмов на ЭВМ, необходимо убедиться в том, что исходная последовательность псевдослучайных чисел удовлетворяет предъявляемым к ней требованиям, так как в противном случае даже при наличии абсолютно правильного алгоритма моделирования процесса функционирования системы S по результатам моделирования нельзя достоверно судить о характеристиках системы [29, 37].
Проверка качества последовательностей. Результаты анализа системы S, полученные методом статистического моделирования на ЭВМ, существенно зависят от качества используемых псевдослучайных квазиравномерных последовательностей чисел. Поэтому все применяемые генераторы случайных чисел должны перед моделированием системы пройти тщательное предварительное тестирование, которое представляет собой комплекс проверок по различным статистическим критериям, включая в качестве основных проверки (тесты) на равномерность, стохастичность и независимость. Рассмотрим возможные методы проведения таких проверок, наиболее часто используемые в практике статистического моделирования систем.
|
m |
|
Σ |
|
j = 1 |
Проверка равномерности последовательностей псевдослучайных квазиравномерно распределенных чисел {хi} может быть выполнена по гистограмме с использованием косвенных признаков [4, 26]. Суть проверки по гистограмме сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел в интервале (0, 1). Затем интервал (0, 1) разбивается на m равных частей, тогда при генерации последовательности {хi} каждое из чисел х с вероятностью pj = 1/m, j = 1, т, попадает в один из подынтервалов. Всего в каждый j-й подынтервал попадает Nj чисел последовательности {хi}, i = 1, N, причем N =
Nj. Относительная частота попадания случайных чисел последовательности {хi} в каждый из подынтервалов будет равна Nj/N. Вид соответствующей гистограммы для примера показан на рис. 4.11, а, где пунктирная линия соответствует теоретическому значению pj, а сплошная - экспериментальному Nj/N. Очевидно, что если числа хi - принадлежат псевдослучайной квазиравномерно распределенной последовательности, то при достаточно больших N экспериментальная гистограмма (ломаная линия на рис. 4.11, а) приблизится к теоретической прямой 1/т.
Оценка степени приближения, т. е. равномерности последовательности {хi}, может быть проведена с использованием критериев согласия. На практике обычно принимается т = 20 ÷ 50, N = (102 ÷ 103)m.
Суть проверки равномерности по косвенным признакам сводится к следующему. Генерируемая последовательность чисел {хi} разбивается на две последовательности:
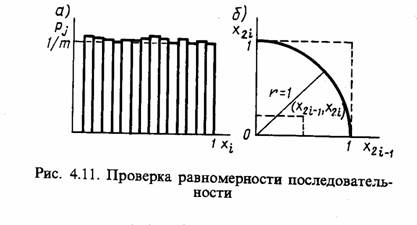
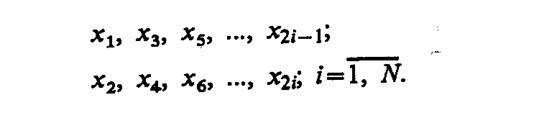
Затем проводится следующий эксперимент. Если выполняется условие
![]()
то фиксируется наступление некоторого события и в счетчик событий добавляется единица. После N/2 опытов, когда генерировано N число, в счетчике будет некоторое число k ≤ N/2.
Геометрически условие (4.13) означает, что точка (х2i - 1, х2i) = 1, N, находится внутри четверги круга радиусом r = 1, что иллюстрируется рис. 4.11, б. В общем случае точка (х2i - 1, х2i) всегда попадает внутрь единичного квадрата. Тогда теоретически вероятность попадания этой точки в четверть круга
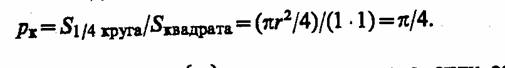
Если числа последовательности {хi} равномерны, то в силу закона больших чисел теории вероятностей при больших N относительная частота 2k/N → π/4.
Проверка стохастичности последовательностей псевдослучайных чисел {хi} наиболее часто проводится методами комбинаций и серий [7, 11, 25]. Сущность метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в n-разрядном двоичном числе Xi. На практике длину последовательности N берут достаточно большой и проверяют все п разрядов или только l старших разрядов числа Xi.
Теоретически закон появления j единиц в l разрядах двоичного числа Xi описывается исходя из независимости отдельных разрядов биномиальным законом распределения:
![]()
где P (j, l) - вероятность появления j единиц в l разрядах числа Хi; p(1) = p(0) = 0,5 - вероятность появления единицы (нуля) в любом разряде числа Хi; Cjl = l!/[j!/(l - j)!].
Тогда при фиксированной длине выборки N теоретически ожидаемое число появления случайных чисел Хi с j единицами в проверяемых l разрядах будет равно nj = NCjl pl (1).
После нахождения теоретических и экспериментальных вероятностей P (j, l) или чисел nj при различных значениях l ≤ n гипотеза о стохастичности проверяется с использованием критериев согласия [7, 11, 18, 21].
При анализе стохастичности последовательности чисел {хi} методом серий последовательность разбивается на элементы первого и второго рода (а и b), т. е.
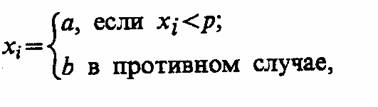
где 0 < р < .
Серией называется любой отрезок последовательности, состоящий из идущих друг за другом элементов одного и того же рода, причем число элементов в отрезке (а или b) называется длиной серии.
После разбиения последовательности {хi} на серии первого и второго рода будем иметь, например, последовательность вида
...aabbbbaaabaaaabbbab... .
Так как случайные числа а и b в данной последовательности независимы и принадлежат последовательности {хi}, равномерно распределенной на интервале (0, 1), то теоретическая вероятность появления серии длиной j в последовательности длиной l в N опытах (под опытом здесь понимается генерация числа хi и проверка условия хi < p) определится формулой Бернулли:
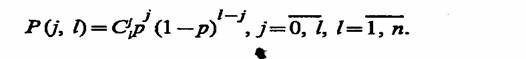
В случае экспериментальной проверки оцениваются частоты появления серий длиной j. В результате получаются теоретическая и экспериментальная зависимости P(j, l), сходимость которых проверяется по известным критериям согласия, причем проверку целесообразно проводить при различных значениях р, 0 < р < 1 и l.
Проверка независимости элементов последовательности псевдослучайных квазиравномерно распределенных чисел проводится на основе вычисления корреляционного момента [4].
Случайные величины ξ и η называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Таким образом, независимость элементов последовательности {хi} может быть проверена путем введения в рассмотрение последовательности {yj} = {xi+τ}, где τ - величина сдвига последовательностей.
В общем случае корреляционный момент дискретных случайных величин ξ и τ с возможными значениями хi и yj определяется по формуле
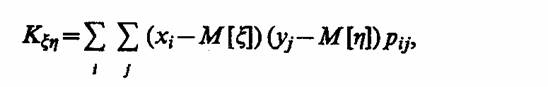
где pij - вероятность того, что (ξ, η) примет значение (хi, yj).
Корреляционный момент характеризует рассеивание случайных величин ξ и η и их зависимость. Если случайные числа независимы, то Kξη = 0. Коэффициент корреляции

где σх—σy— средние квадратические отклонения величин ξ и η.
При проведении оценок коэффициента корреляции на ЭВМ удобно для вычисления использовать следующее выражение

При любом τ ≠ 0 для достаточно больших N с доверительной вероятностью β справедливо соотношение
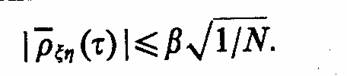
Если найденное эмпирическое значение Р ζητ (τ) находится в указанных пределах, то с вероятностью β можно утверждать, что полученная последовательность чисел {х,) удовлетворяет гипотезе корреляционной независимости.
Характеристики качества генераторов. При статистическом моделировании системы S с использованием программных генераторов псевдослучайных квазиравномерных последовательностей важными характеристиками качества генератора является длина периода Р и длина отрезка апериодичности L. Длина отрезка апериодичности L псевдослучайной последовательности {хi}, заданной уравнением
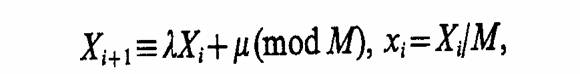
есть наибольшее целое число, такое, что при 0 ≤ j < i ≤ L, событие P{хi = хj} не имеет места. Это означает, что все числа хi в пределах отрезка апериодичности не повторяются.
Очевидно, что использование при моделировании систем последовательности чисел {хi}, длина которой больше отрезка апериодичности L, может привести к повторению испытаний в тех же условиях, что и раньше, т. е. увеличение числа реализаций не дает новых статистических результатов.
Способ экспериментального определения длины периода Р и длины отрезка апериодичности L сводится к следующему [29]. Запускается программа генерации последовательности {хi} с начальным значением x0 и генерируется V чисел хi. В большинстве практических случаев можно полагать V = (1 ÷ 5) 106. Генерируются числа последовательности {хi} и фиксируется число хV
Затем программа запускается повторно с начальным числом х0 и при генерации очередного числа проверяется истинность события P' {хi = хV}. Если это событие истинно: i = i1 и i = i2 (i1 < i2 < V), то вычисляется длина периода последовательности P = i2 - i1. Проводится запуск программы генерации с начальными числами х0 и xP. При этом
Рис. 4.12. Экспериментальное определение длины периода и длины отрезка
апериодичности:
a - вариант 1; б - вариант 2
фиксируется минимальный номер i = i3, при котором истинно событие Р’’ {хi = хP + i и вычисляется длина отрезка апериодичности L = i3 + P (рис. 4.12, а). Если Р' оказывается истинным лишь для i = V, то L > V (рис. 4.12, б).
В некоторых случаях достаточно громоздкий эксперимент по определению длин периода и отрезка апериодичности можно заменить аналитическим расчетом, как это показано в следующем примере.
Пример 4.5. Необходимо показать, что в последовательности чисел {хi}, описываемой уравнением
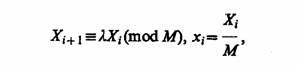
при простом модуле M можно так выбрать коэффициент λ, что при любом Х0, взаимно простом с М, длина отрезка апериодичности, совпадающая в этом случае с длиной периода Р, будет L = P = M - 1. Иначе говоря, надо найти, при каких условиях равенство

справедливо при минимальном значении s = M - 1.
Можно записать [см. (4.11)], что Xi + s ≡ λsXi (mod M), поэтому (4.14) имеет место при
![]()
(здесь существенно, что Х0 взаимно просто с М).
По условию требуется, что наименьший показатель степени s = PM(A), удовлетворяющий (4.15) и называемый показателем А по модулю М, был равен М - 1. Для любого простого модуля М существует φ (М - 1) значений λ (первообразных корней), удовлетворяющих уравнению (4.15) при РM(А) = φ(М), где φ(M) - функция Эйлера, определяемая как число натуральных чисел т ≤ М, взаимно простых с М. Для простого модуля М имеем φ(M) = М - 1.
Таким образом, доказано существование многих λ, при которых повторение элементов последовательности {хi} наступит на (М - 1)-м числе хM - 1, т. е. L = P = M - 1, что и требовалось доказать.
Для алгоритмов получения последовательностей чисел {хi} общего вида (4.10) экспериментальная проверка является сложной (из-за наличия больших Р и L), а расчетные соотношения в явном виде не получены. Поэтому в таких случаях целесообразно провести теоретическую оценку длины отрезка апериодичности последовательности L. Для этого воспользуемся элементарной вероятностной моделью, рассмотренной в следующем примере [4, 36, 37].
Пример 4.6. Пусть имеется конечное множество, содержащее N различных чисел. Проведем последовательность независимых опытов, в каждом из которых из этого множества извлекается и записывается одно число. Вероятность извлечения любого числа в каждом из опытов равна 1/N, так как выборка чисел проводится с возвратом. Обозначим через L случайную величину - номер опыта, в котором впервые будет снова извлечено уже записанное ранее число. Можно доказать, что в данной вероятностной модели для любого х > 0 имеем

Так как математическое ожидание случайной величины с такой функцией распределения равно √π/2, то при N → ∞ получим M[L] = √πN/2. Такая оценка длины отрезка апериодичности "груба", но полезна на практике для предварительного определения L с целью дальнейшего уточнения экспериментальным путем.
Рассмотрим некоторые особенности статистической проверки стохастичности псевдослучайных последовательностей. Для такой проверки могут быть использованы различные статистические критерии оценки, например критерии Колмогорова, Пирсона и т. д. Но в практике моделирования чаще всего пользуются более простыми приближенными способами проверки [29, 37].
Для проверки равномерности базовой последовательности случайных чисел хi , i = 1, N, можно воспользоваться такими оценками:
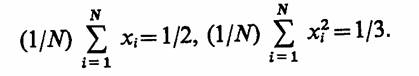
Для проверки таблиц случайных цифр обычно применяют различные тесты, в каждом из которых цифры классифицируются по некоторому признаку и эмпирические частоты сравниваются с их математическими ожиданиями с помощью критерия Пирсона [29, 46].
Для проверки аппаратных генераторов случайных чисел можно использовать те же приемы, что и для проверки последовательностей псевдослучайных чисел, полученных программным способом. Особенностью такой проверки будет то, что проверяются не те числа, которые потом будут необходимы для моделирования системы S. Поэтому кроме проверки качества выдаваемых генератором случайных чисел должна еще гарантироваться устойчивая работа генератора на время проведения машинного эксперимента с моделью Mм.
Улучшение качества последовательностей. В силу рассмотренных преимуществ основное применение в практике имитационного моделирования систем находят различные программные способы получения чисел. Поэтому рассмотрим возможные методы улучшения качества последовательностей псевдослучайных чисел. Одним из наиболее употребительных методов такого улучшения является употребление вместо формул вида (4.9). представляющих собой рекуррентные формулы первого порядка, рекуррентных формул порядка r, т. е.

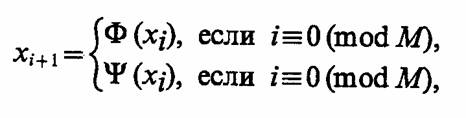
где функции Ф(и) и Ψ(и) различны.
В этом случае в основном используется формула xi+l=ф(xi). и только когда i кратно М, последовательность «возмущаете» т. е. реализуется переход к формуле xi+l = Ψ (xi). Целое число ¥ называется периодом возмущения.
Все рассмотренные критерии проверки последовательностей псевдослучайных чисел являются необходимыми при постановке имитационных экспериментов на ЭВМ с моделью Ммы, но об их достаточности можно говорить лишь при рассмотрении задачи моделирования конкретной системы.S
4.4. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ
НА СИСТЕМЫ
При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Для их формализации используются случайные события, дискретные и непрерывные величины, векторы, процессы. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преобразованию последовательностей случайных чисел. Вопросы генерации базовых последовательностей псевдослучайных чисел {хi}, имеющих равномерное распределение в интервале (0, 1), были рассмотрены в § 4.2, поэтому остановимся на вопросах преобразования последовательностей случайных чисел {хi} в последовательность {yi} для имитации воздействий на моделируемую систему S.
Эти задачи очень важны в практике имитационного моделирования систем на ЭВМ, так как существенное количество операций, а значит, и временных ресурсов ЭВМ расходуется на действия со случайными числами. Таким образом, наличие эффективных методов, алгоритмов и программ формирования, необходимых для моделирования конкретных систем последовательностей случайных чисел {yi}, во многом определяет возможности практического использования машинной имитации для исследования и проектирования систем [37, 46].
Моделирование случайных событий. Простейшими случайными объектами при статистическом моделировании систем являются случайные события. Рассмотрим особенности их моделирования [4].
Пусть имеются случайные числа хi, т. е. возможные значения случайной величины ξ, равномерно распределенной в интервале (0, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение хi случайной величины ξ удовлетворяет неравенству

Тогда вероятность события А будет Р(А)=∫Po dx=p. Противопо
ложное событие А состоит в том, что хi>р. Тогда Р(А)=1 —р.
Процедура моделирования в этом случае состоит в выборе значений xi и сравнении их с р. При этом, если условие (4.16) выполняется, исходом испытания является событие А.
Таким же образом можно рассмотреть группу событий. Пусть A1, A2, ..., As - полная группа событий, наступающих с вероятностями р1, р2, ..., рs соответственно. Определим Аm как событие, состоящее в том, что выбранное значение хi случайной величины ξ, удовлетворяет неравенству
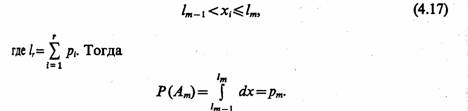
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел хi со значениями lr. Исходом испытания оказывается событие Аm, если выполняется условие (4.17). Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p1, p2, ..., ps.
Эти процедуры моделирования были рассмотрены в предположении, что для испытаний применяются случайные числа хi, имеющие равномерное распределение в интервале (0, 1). При моделировании на ЭВМ используются псевдослучайные числа с квазиравномерным распределением, что приводит к некоторой ошибке. Оценим ее.
Пример 4.7. Пусть имеются n-разрядные случайные числа с возможными значениями xkl = i/(2n - 1), i = 0,2n - 1. Подставив в (4.16) вместо хi число хi*, определим А* как событие, состоящее в том, что хi* ≤ р.
Вероятность наступления события А* может быть определена как Р(A*) = m/2n, где т - количество случайных чисел, меньших или равных р. Отсюда следует, что использование числа хi* вместо хi приводит к ошибке в определении вероятности события Δр = m/2n - р.
Очевидно, что максимальное значение ошибки не превосходит величины 1/(2n - 1). Таким образом, для уменьшения влияния ошибок можно воспользоваться увеличением разрядности случайных чисел.
При моделировании систем часто необходимо осуществить такие испытания, при которых искомый результат является сложным событием, зависящим от двух (и более) простых событий. Пусть, например, независимые события А и В имеют вероятности наступления рA и рB. Возможными исходами совместных испытаний в этом случае будут события АВ, АВ, АВ, АВ с вероятностями рA рB, (1 - рA) рB, рA (1 - рB), (1 - рA) (1 - рB).
Для моделирования совместных испытаний можно использовать два варианта процедуры: 1) последовательную проверку условия (4.16); 2) определение одного из исходов АВ, АВ, АВ, АВ по жребию с соответствующими вероятностями, т. е. аналогия (4.17). Первый вариант требует двух чисел хi и сравнений для проверки условия (4.16). При втором варианте можно обойтись одним числом хi, но сравнений может потребоваться больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и памяти ЭВМ более предпочтителен первый вариант.
Рассмотрим теперь случай, когда события А и В являются зависимыми и наступают с вероятностями рA и рB. Обозначим через Р(В/А) условную вероятность наступления события В при условии, что событие А произошло. При этом считаем, что условная вероятность Р(В/А) задана.
Рассмотрим один из вариантов построения модели. Из последовательности случайных чисел {хi} извлекается очередное число хm и проверяется справедливость неравенства хm < рA. Если это неравенство справедливо, то наступило событие А. Для испытания, связанного с событием В, используется вероятность P(B/A). Из совокупности чисел {хi} берется очередное число хm + 1 и проверяется условие хm + 1 ≤ P(B/A). В зависимости от того, выполняется или нет это неравенство, исходом испытания являются АВ или АВ.
Если неравенство хm < рA не выполняется, то наступило событие А. Поэтому для испытания, связанного с событием В, необходимо определить вероятность

Выберем из совокупности {хi} число хm + 1 и проверим справедливость неравенства хm + 1 ≤ P(B/A). В зависимости от того, выполняется оно или нет, получим исходы испытания АВ или АВ.
Логическая схема алгоритма для реализации этого варианта модели показана на рис. 4.13. Здесь ВИД [...] - процедура ввода исходных данных; ГЕН [...] - генератор равномерно распределенных случайных чисел; ХМ ≡ хm; ХМI ≡ хm + 1; РА ≡ рA; РВ ≡ рB; РВА ≡ Р(В/А); PBNA ≡ P(B/A); КА, KNA, КАВ, KANB, KNAB, KNANB - число событий А, A, АВ, АB, АВ, АВ соответственно; ВРМ [...] - процедура выдачи результатов моделирования.
Рассмотрим особенности моделирования на ЭВМ марковских цепей, служащих, например, для формализации процессов в Р-схемах (см. § 2.4). Простая однородная марковская цепь определяется матрицей переходов
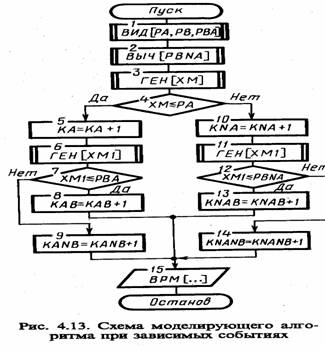
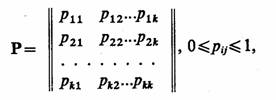
где pij— вероятность перехода из состояния zt в состояние zj.
Матрица переходов Р полностью описывает марковский процесс. Такая матрица является стохастической, т. е. сумма элементов
каждой строки равна единице: ∑kpij= 1; i= 1,k.
Обозначим через , pi(n), i=1, k, вероятности того, что система будет находиться в состоянии zi, после п переходов. По определению, ∑k pi(n)=1.
Используя событийный подход, можно подойти к моделированию марковской цепи следующим образом. Пусть возможными исходами испытаний являются события A1, A2, .., Ak. Вероятность pij - это условная вероятность наступления события Аj - в данном испытании при условии, что исходом предыдущего испытания было событие Ai. Моделирование такой цепи Маркова состоит в последовательном выборе событий Aj по жребию с вероятностями pij.
Сначала выбирается начальное состояние z0, задаваемое начальными вероятностями р1(0), р2(0), ..., pk(0). Для этого из последовательности чисел {хi} выбирается число хm и сравнивается с lr из (4.17), где в качестве pi используются значения р1(0), р2(0), ..., pk(0). Таким образом, выбирается номер т0, для которого оказывается справедливым неравенство (4.17). Тогда начальным событием данной реализации цепи будет событие Аm0. Затем выбирается следующее случайное число хm + 1, которое сравнивается с lr, где в качестве pi используются рm0j. Определяется номер m1 и следующим событием данной реализации цепи будет событие Am1 и т. д. Очевидно, что каждый номер mi, определяет не только очередное событие Ami формируемой реализации, но и распределение вероятностей рmi1, pmi2, ..., pmik для выбора очередного номера mi + 1 причем для эргодических марковских цепей влияние начальных вероятностей быстро уменьшается с ростом номера испытаний. Эргодическим называется всякий марковский процесс, для которого предельное распределение вероятностей рi (п), i = 1, k, не зависит от начальных условий pi(0). Поэтому при моделировании можно принимать, что Эргодическим называетевсякий марковский процесс, для которого предельное распределенье вероятностей pi(п), /=1, к, не зависит от начальных условий pi(0)
Поэтому при моделировании можно принимать, что
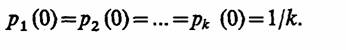
Аналогично можно построить и более сложные алгоритмы, например для моделирования неоднородных марковских цепей [29].
Рассмотренные способы моделирования реализаций случайных объектов дают общее представление о наиболее типичных процедурах формирования реализаций в моделях процессов функционирования стохастических систем, но не исчерпывают всех приемов, используемых в практике статистического моделирования на ЭВМ.
Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат базовые последовательности случайных чисел {хi}, имеющие равномерное распределение в интервале (0, 1). Другими словами, случайные числа х, как возможные значения случайной величины ξ, имеющей равномерное распределение в интервале (0, 1), могут быть преобразованы в возможные значения yj случайной величины η, закон распределения которой задан [4].
Моделирование дискретных случайных величин. Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина η принимает значения у1 ≤ у2 ≤ ... yj ≤ ... с вероятностями р1, р2, ..., pj, ..., составляющими дифференциальное распределение вероятностей
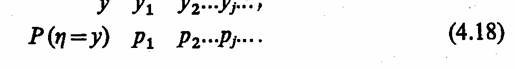
При этом интегральная функция распределения
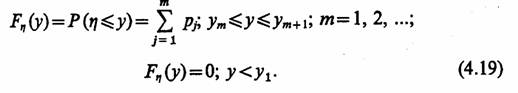
Для получения дискретных случайных величин можно использовать метод обратной функции [10, 29, 53]. Если ζ, — равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина η получается с помощью преобразования

Пример 4.8. Необходимо методом обратной функции на основании базовой последовательности случайных чисел {х,}, равномерно распределенных в интервале (0,1), получить последовательность чисел {yj}, имеющих биномиальное распределение, задающее вероятность у удачных исходов в N реализациях некоторого эксперимента:


Например, получив из равномерного распределения число хi = 0,85393 и проведя сравнения по алгоритму (4.21), найдем, что хi = 0,85393 0,89063, т. е. yj = 4.
При этом среднее число циклов сравнения μ = 1 · 0,01562 + 2 · 0,09375 + 3 · 0,23438 + 4 · 0,31250 + 5 · 0,23438 + 6 (0,09375 + 0,01562) ≈ 3,98.
Пример 4.9. Необходимо проверить стохастичность последовательности из N случайных чисел {yj}, полученных при имитации биномиального распределения при заданных параметрах п и р. Простейшим способом проверки является оценка выполнения условий
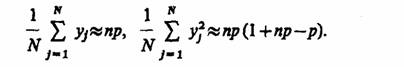
Проверим на соответствие биномиальному распределению с параметрами п = 5 и р = 0,1 такой последовательности случайных чисел: {yj} = 0, 0, 1, 0, 1, 0, 2, 0, 1, 0; N = 10.
Вычислим пр = 0,5; np (1 + np - p) = 0,7;

Как видно из оценок, данная последовательность чисел {yj] хорошо в условиих данного примера представляет биномиальное распределение с заданными параметрамии-
Можно привести и другие примеры алгоритмов и программ получения дискретных случайных величин с заданным законом распределения, которые находят применение в практике моделирования систем на ЭВМ.
Моделирование непрерывных случайных величин. Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина г\ задана интегральной функцией распределения
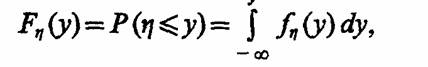
где fη, (у) — плотность вероятностей.
Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Взаимно однозначная монотонная функция η=F~lri(ζ), полученная решением относительно у уравнения Fn(y) = ζ преобразует равномерно распределенную на интервале (0, 1) величину ζ в η с требуемой плотностью fη, (у).Действительно, если случайная величина η имеет плотность распределения fη, (у). то распределение случайной величины
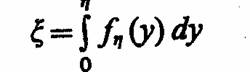
явлется равномерным в интервале (0,1) [4, 29]. На основании этого можно сделать следующий вывод. Чтобы получить число, принадлежащее последовательности случайных чисел {yj} имеющих функцию плотности fη (у), необходимо разрешить относительно уj уравнение

Рассмотрим некоторые примеры получения методом обратной функции непрерывных случайных величин с заданным законом распределения на основе случайных чисел, имеющих равномерное распределение в интервале (0, 1).
Пример 4.10. Необходимо получить случайные числа с показательным законом распределения

Можно привести и другие примеры использования соотношения (4.22). Но этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения в практике моделирования систем на ЭВМ, что объясняется следующими обстоятельствами: 1) для многих законов распределения, встречающихся в практических задачах моделирования, интеграл
(4.22) не берется, т. е. приходится прибегать к численным методам решения, что увеличивает затраты машинного времени на получение каждого случайного числа; 2) даже для случаев, когда интеграл (4.22) берется в конечном виде, получаются формулы, содержащие действия логарифмирования, извлечения корня и т. д., которые выполняются с помощью стандартных подпрограмм ЭВМ, содержащих много исходных операций (сложения, умножения и т. п.), что также резко увеличивает затраты машинного времени на получение каждого случайного числа.
Поэтому в практике моделирования систем часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом: а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения [4, 46].
Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности. Пусть требуется получить последовательность случайных чисел {yj} с функцией плотности fη(y), возможные значения которой лежат в интервале (а, b). Представим fη(y) в виде кусочно-постоянной функции, т. е. разобьем интервал (а, b) на т интервалов, как это показано на рис. 4.14, и будем считать fη(y) на каждом интервале постоянной. Тогда случайную величину η можно представить в виде η = ak + ηk*, где ak - абсцисса левой границы k-гo интервала; ηk* - случайная величина, возможные значения которой располагаются равномерно внутри k-гo интервала, т. е. на каждом участке аk ÷ ak+1 величина ηk* считается распределенной равномерно. Чтобы аппроксимировать fη(y) наиболее удобным для практических целей способом, целесообразно разбить (а, b) на интервалы так, чтобы вероятность попадания случайной величины η в любой интервал (ak, ak+1) была постоянной, т. е. не зависела от номера интервала k. Таким образом, для вычисления ak воспользуемся следующим соотношением:
 Алгоритм
машинной реализации этого способа получения случайных чисел сводится к
последовательному выполнению следующих действий: 1) генерируется случайное
равномерно распределенное число xi из интервала (0, 1); 2)
с помощью этого числа
Алгоритм
машинной реализации этого способа получения случайных чисел сводится к
последовательному выполнению следующих действий: 1) генерируется случайное
равномерно распределенное число xi из интервала (0, 1); 2)
с помощью этого числа
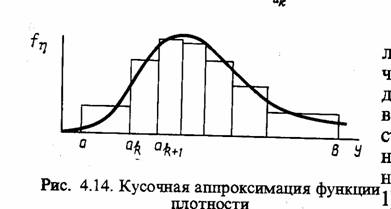
случайным образом выбирается интервал (ak, ak + 1); 3) генерируется число хi + 1 и масштабируется с целью приведения его к интервалу (ak, ak + 1), т. е. домножается на коэффициент (ak + 1 - ak) хi + 1; 4) вычисляется случайное число yj = (ak + 1 - ak) хi + 1 с требуемым законом распределения.
Рассмотрим более подробно процесс выборки интервала (ak, ak + 1) с помощью случайного числа xi. Целесообразно для этой цели построить таблицу (сформировать массив), в которую предварительно поместить номера интервалов k и значения коэффициента масштабирования, определенные из соотношения (4.23) для приведения числа к интервалу (а, b). Получив из генератора случайное число xh с помощью этой таблицы сразу определяем абсциссу левой границы ak и коэффициент масштабирования (ak + 1 - ak).
Достоинства этого приближенного способа преобразования случайных чисел: при реализации на ЭВМ требуется небольшое количество операций для получения каждого случайного числа, так как операция масштабирования (4.23) выполняется только один раз перед моделированием, и количество операций не зависит от точности аппроксимации, т. е. от количества интервалов т.
Рассмотрим способы преобразования последовательности равномерно распределенных случайных чисел {xi} в последовательность с заданным законом распределения {yj} на основе предельных теорем теории вероятностей. Такие способы ориентированы на получение последовательностей чисел с конкретным законом распределения, т. е. не являются универсальными [29, 43]. Поясним сказанное примерами.
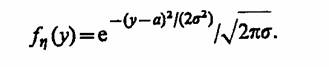
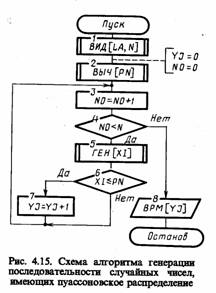 Будем формировать случайные числа уj в виде сумм последовательностей
случайных чисел {xi}, имеющих равномерное
распределение в интервале (0, 1). Так как исходной (базовой)
последовательностью случайных чисел {хi} при суммировании
является последовательность чисел, имеющих равномерное распределение в интервале
(0, 1), то можно воспользоваться центральной предельной теоремой для одинаково
распределенных случайных величин (см. § 4.1): если независимые одинаково
распределенные случайные величины х1г..., xN имеют каждая
математическое ожидание ах и среднее квадратическое
отклонение аи то сумма
Будем формировать случайные числа уj в виде сумм последовательностей
случайных чисел {xi}, имеющих равномерное
распределение в интервале (0, 1). Так как исходной (базовой)
последовательностью случайных чисел {хi} при суммировании
является последовательность чисел, имеющих равномерное распределение в интервале
(0, 1), то можно воспользоваться центральной предельной теоремой для одинаково
распределенных случайных величин (см. § 4.1): если независимые одинаково
распределенные случайные величины х1г..., xN имеют каждая
математическое ожидание ах и среднее квадратическое
отклонение аи то сумма 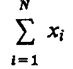 асимптотически нормальна с математическим
ожиданием a^Na^ и средним
квадратическим отклонением
асимптотически нормальна с математическим
ожиданием a^Na^ и средним
квадратическим отклонением ![]() Kак показывают
расчеты, сумма
Kак показывают
расчеты, сумма 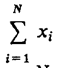 имеет
распределение, близкое к нормальному, уже при сравнительно небольших N. Практически
для получения последовательности нормально распределенных случайных чисел можно
пользоваться значениями N=S ÷ 12, а в простейших случаях — меньшими значениями N, например N=4+5 [4].
имеет
распределение, близкое к нормальному, уже при сравнительно небольших N. Практически
для получения последовательности нормально распределенных случайных чисел можно
пользоваться значениями N=S ÷ 12, а в простейших случаях — меньшими значениями N, например N=4+5 [4].
Пример 4.13. Пусть необходимо получить случайные числа, имеющие закон распределения Пуассона:
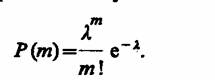
Для этого воспользуемся предельной теоремой Пуассона (см. § 4.1): если Р - вероятность наступления события А при одном испытании, то вероятность наступления т событий в N независимых испытаниях при N → ∞, р → 0, Np = λ асимптотически равна P(m).
Выберем достаточно большое N, такое, чтобы р = λ/N < 1, будем проводить серии по N независимых испытаний, в каждом из которых событие А происходит с вероятностью р, и будем подсчитывать число случаев yj - фактического наступления события А в серии с номером j. Числа yj будут приближенно следовать закону Пуассона, причем тем точнее, чем больше N. Практически N должно выбираться таким образом, чтобы р ≤ 0,1 ÷ 0,2 [4].
Алгоритм генерации последовательности случайных чисел yj, имеющих пуассоновское распределение, с использованием данного способа показан на рис. 4.15. Здесь LA ≡ λ; N ≡ N; PN ≡ p; XI ≡ xi - случайные числа последовательности, равномерно распределенной в интервале (0, 1); YJ ≡ yj; NO - вспомогательная переменная; ВИД [...] - процедура ввода исходных данных; ВЫЧ [...] - процедура вычисления; ГЕН [...] - процедура генерации случайных чисел; ВРМ [...] - процедура выдачи результатов моделирования.
Моделирование случайных векторов. При решении задач исследования характеристик процессов функционирования систем методом статистического моделирования на ЭВМ возникает необходимость в формировании реализаций случайных векторов, обладающих заданными вероятностными характеристиками. Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, описываемыми совместным законом распределения. В простейшем случае, когда рассматриваемый случайный вектор расположен на плоскости х0у, он может быть задан совместным законом распределения его проекций ξ и η на оси 0х и 0у [4].
Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (ξ, η) является дискретной и ее составляющая ξ принимает возможные значения x1, x1, ..., хn, а составляющая η - значения y1, y1, ..., yn, причем каждой паре (xi, yj) соответствует вероятность pij. Тогда каждому возможному
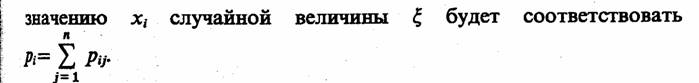
Тогда в соответствии с этим распределением вероятностей можно определить конкретное значение xt случайной величины ξ, (по правилам, рассмотренным ранее) и из всех значений ptj выбрать последовательность
![]()
которая описывает условное распределение величины η при условии, что ξ = xi. Затем по тем же правилам определяем конкретное значение yi1 случайной величины η в соответствии с распределением вероятностей (4.24). Полученная пара (xi1, yi1) будет первой реализацией моделируемого случайного вектора. Далее аналогичным образом определяем возможные значения xi2, выбираем последовательность

и находим yi2 в соответствии с распределением (4.25). Это дает реализацию вектора (xi2, yi2) и т. д.
Рассмотрим моделирование непрерывного случайного вектора с составляющими ξ и η. B этом случае двухмерная случайная величина (ξ, η) описывается совместной функцией плотности f(х, у). Эта функция может быть использована для определения функции плотности случайной величины ξ как
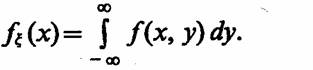
Имея функцию плотности fξ(x), можно найти случайное число xi, а затем при условии, что ξ = xi определить условное распределение случайной величины η:
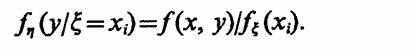
В соответствии с этой функцией плотности можно определить случайное число yi. Тогда пара чисел (yi, xi) будет являться искомой реализацией вектора (ξ, η).
Рассмотренный способ формирования реализаций двухмерных векторов можно обобщить и на случай многомерных случайных векторов. Однако при больших размерностях этих векторов объем вычислений существенно увеличивается, что создает препятствия к использованию этого способа в практике моделирования систем.
В пространстве с числом измерений более двух практически доступным оказывается формирование случайных векторов, заданных в рамках корреляционной теории. Рассмотрим случайный вектор с математическими ожиданиями а1, а2, ..., an и корреляционной матрицей

![]()
Пример 4.14. Для определенности остановимся на трехмерном случае n = 3. Пусть требуется сформировать реализации трехмерного случайного вектора (ξ, η, ψ), имеющего нормальное распределение с математическими ожиданиями M[ξ] = а1; M[η] = a2, М[ψ] = а3 и корреляционной матрицей К, элементы которой k11, k22 и k33 являются дисперсиями случайных величин ξ, η и ψ соответственно, а элементы k12 = k21, k13 = k31, k23 = k32 представляют собой корреляционные моменты ξ и η, ξ и ψ, η и ψ соответственно.
Пусть имеется последовательность некорреляционных случайных чисел {νi}, имеющих одномерное нормальное распределение с параметрами а и σ. Выберем три числа ν1, ν2, ν3 и преобразуем их так, чтобы они имели характеристики a1, a2, a3 и К. Искомые составляющие случайного вектора (ξ, η, ψ) обозначим как х, у, z и представим в виде линейного преобразования случайных величин νi:
![]()
где cij - некоторые коэффициенты (пока не известные). Для вычисления этих коэффициентов воспользуемся элементами корреляционной матрицы К. Так как случайные величины ν1, ν2, ν3 независимы между собой, то М [(νi - A) (νj - а)] = 0 при i ≈ j.
В итоге имеем:

Вычислив коэффициенты сij, легко три последовательных случайных числа νi, i = 1, 2, 3, преобразовать в составляющие случайного вектора (xi, yi, zi), используя соотношения, приведенные выше [4].
При таком формировании реализаций случайного вектора требуется хранить в памяти ЭВМ п(п+1)/2 корреляционных моментов kij и п математических ожиданий аi. При больших п в связи с этим могут встречаться затруднения при использовании полученных таким способом многомерных случайных векторов для моделирования систем.
Конкретные алгоритмы имитации стохастических воздействий в процессе машинного эксперимента рассмотрим далее применительно к случаям использования для формализации процесса функционирования системы S типовых математических схем (см. гл. 8).
Контрольные вопросы
4.1. В чем сущность метода статистического моделирования систем на ЭВМ?
4.2. Какие способы генерации последовательностей случайных чисел используются при моделировании на ЭВМ?
4.3. Какая последовательность случайных чисел используется в качестве базовой при статистическом моделировании на ЭВМ?
4.4. Почему генерируемые на ЭВМ последовательности чисел называются псевдослучайными?
4.5. Что собой представляют конгруэнтные процедуры генерации последовательностей?
4.6. Какие существуют методы проверки (тестирования) качества генераторов случайных чисел?
4.7. Что собой представляет процедура определения исхода испытаний по жребию?
4.8. Какие существуют способы генерации последовательностей случайных чисел с заданным законом распределения на ЭВМ?