Современный этап развития человечества отличается тем, что на; смену века энергетики приходит век информатики. Происходит интенсивное внедрение новых информационных технологий во все сферы человеческой деятельности. Встает реальная проблема перехода в информационное общество, для которого приоритетным должно стать развитие образования. Изменяется и структура знаний в обществе. Все большее значение для практической жизни приобретают фундаментальные знания, способствующие творческому развитию личности. Важна и конструктивность приобретаемых знаний, умение их структурировать в соответствии с поставленной целью. На базе знаний формируются новые информационные ресурсы общества. Формирование и получение новых знаний должно базироваться на строгой методологии системного подхода, в рамках которого особое место занимает модельный подход. Возможности модельного подхода крайне многообразны как по используемым формальным моделям, так и по способам реализации методов моделирования. Физическое моделирование позволяет получить достоверные результаты для достаточно простых систем.
Сложные по внутренним связям и большие по количеству элементов системы экономически трудно поддаются прямым способам моделирования и зачастую для построения и изучения переходят к имитационным методам. Появление новейших информационных технологий увеличивает не только возможности моделирующих систем, но и позволяет применять большее многообразие моделей способов их реализации. Совершенствование вычислительной; и телекоммуникационной техники привело к дальнейшему развитию методов машинного моделирования, без которых невозможно изучение процессов и явлений, а также построение больших и сложных систем. Поэтому дисциплина «Моделирование систем» сталан базовой в структуре подготовки бакалавров и специалистов по ряду направлений высшего профессионального образования. Среди этих направлений, прежде всего, следует отметить 654600 — «Информатика и вычислительная техника», 654700 — «Информационные системы», а также ряд специальностей, среди которых 654602 — «Автоматизированные системы обработки информации и управления» (АСОИУ), 654701 — «Информационные системы в технике и технологиях» (ИС) и др.
Материал предлагаемого учебника является третьим, дополненным и переработанным изданием и соответствует программам дисциплины «Моделирование систем» учебного плана подготовки инженеров по специальностям 654602 — АСОИУ и 654701 — ИС. При подготовке третьего издания использована новая отечественная и зарубежная литература по моделированию систем различных классов, опыт разработки реальных систем, а также результаты использования ранее выпущенных учебников «Моделирование систем» в учебном процессе на кафедре Автоматизированных систем обработки информации и управления Санкт-Петербургского государственного электротехнического университета ЛЭТИ.
Автору благодарны д.т.н., профессору О. С. Чугрееву за ценные замечания, сделанные при рецензировании рукописи.
Пожелания по содержанию книги просим направлять по адресу: 127994, Москва, ГСП-4, Неглинная ул., 29/14, издательство «Высшая школа».
Авторы
СОВРЕМЕННОЕ СОСТОЯНИЕ ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ
СИСТЕМ
Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, используемым для принятия решений в различных сферах инженерной деятельности. Существующие и проектируемые системы можно эффективно исследовать с помощью математических моделей (аналитических и имитационных), реализуемых на современных ЭВМ, которые в этом случае выступают в качестве инструмента экспериментатора с моделью системы.
В.1. МОДЕЛИРОВАНИЕ КАК МЕТОД НАУЧНОГО ПОЗНАНИЯ
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации. Остановимся на философских аспектах моделирования, а точнее общей теории моделирования [35, 37, 43].
Методологическая основа моделирования. Все то, на что направлена человеческая деятельность, называется объектом (лат. objection — предмет). Выработка методологии направлена на упорядочение получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.
В научных исследованиях большую роль играют гипотезы, т. е. определенные предсказания, основывающиеся на небольшом количестве опытных данных, наблюдений, догадок. Быстрая и полная проверка выдвигаемых гипотез может быть проведена в ходе специально поставленного эксперимента. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения имеет аналогия.
Аналогией называют суждение о каком-либо частном сходстве. Двух объектов, причем такое сходство может быть существенным и несущественным. Необходимо отметить, что понятия существенности и несущественности сходства или различия объектов условны и относительны. Существенность сходства (различия) зависит от уровня абстрагирования и в общем случае определяется конечной целью проводимого исследования. Современная научная гипотеза создается, как правило, по аналогии с проверенными на практике научными положениями. Таким образом, аналогия связывает гипотезу с экспериментом.
Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам; такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами, модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
Определение моделирования. Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием. Таким образом, моделирование может быть определено как пейредставление объекта моделью для получения информации об этом объекте путем проведения экспериментов с его моделью. Теория замещения одних объектов (оригиналов) другими объектами (моделями) и исследования свойств объектов на их моделях называется теорией моделирования [5, 36, 46].
Определяя гносеологическую роль теории моделирования, т. е. ее значение в процессе познания, необходимо, прежде всего, отвлечься от имеющегося в науке и технике многообразия моделей и выделить то общее, что присуще моделям различных по своей природе объектов реального мира. Это общее заключается в наличии некоторой структуры (статической или динамической, материальной или мысленной), которая подобна структуре данного объекта. В процессе изучения модель выступает в роли относительного самостоятельного квазиобъекта, позволяющего получить при исследовании некоторые знания о самом объекте.
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев.
Обобщенно моделирование можно определить как метод опосредованного познания, при котором изучаемый объект-оригинал находится в некотором соответствии с другим объектом-моделью, причем модель способна в том или ином отношении замещать оригинал на некоторых стадиях познавательного процесса. Стадии познания, на которых происходит такая замена, а также формы соответствия модели и оригинала могут быть различными:
1) моделирование как познавательный процесс, содержащий переработку информации, поступающей из внешней среды, о происходящих в ней явлениях, в результате чего в сознании появляются образы, соответствующие объектам;
2) моделирование, заключающееся в построении некоторой системы-модели (второй системы), связанной определенными соотношениями подобия с системой-оригиналом (первой системой), причем в этом случае отображение одной системы в другую является средством выявления зависимостей между двумя системами, отраженными в соотношениях подобия, а не результатом непосредственного изучения поступающей информации.
Следует отметить, что с точки зрения философии моделирование — эффективное средство познания природы. Процесс моделирования предполагает наличие объекта исследования; исследователя, перед которым поставлена конкретная задача; модели, создаваемой для получения информации об объекте и необходимой для решения поставленной задачи. Причем по отношению к модели исследователь является, по сути дела, экспериментатором, только в данном случае эксперимент проводится не с реальным объектом, а с его моделью. Такой эксперимент для инженера есть инструмент непосредственного решения организационно-технических задач.
Надо иметь в виду, что любой эксперимент может иметь существенное значение в конкретной области науки только при специальной его обработке и обобщении. Единичный эксперимент никогда не может быть решающим для подтверждения гипотезы, проверки теории. Поэтому инженеры (исследователи и практики) должны быть знакомы с элементами современной методологии теории познания и, в частности, не должны забывать основного положения материалистической философии, что именно экспериментальное исследование, опыт, практика являются критерием истины.
В.2. ИСПОЛЬЗОВАНИЕ МОДЕЛИРОВАНИЯ
ПРИ ИССЛЕДОВАНИИ И ПРОЕКТИРОВАНИИ
СЛОЖНЫХ СИСТЕМ
Одна из проблем современной науки и техники — разработка и внедрение в практику проектирования новейших методов исследования характеристик сложных информационно-управляющих и информационно-вычислительных систем различных уровней (например, автоматизированных систем научных исследований и комплексных испытаний, систем автоматизации проектирования, АСУ технологическими процессами, а также интегрированных АСУ, вычислительных систем, комплексов и сетей, информационное систем, цифровых сетей интегрального обслуживания и т. Д). При проектировании сложных систем и их подсистем возникают Многочисленные задачи, требующие оценки количественных и качественных закономерностей процессов функционирования такихсистем, проведения структурного алгоритмического и параметрического их синтеза [4,11, 37, 45].
Особенности разработки систем. Рассматриваемые в данном учебнике системы информатики и вычислительной техники, автоматизированные системы обработки информации и управления, информационные системы относятся к классу больших систем, этапы проектирования, внедрения, эксплуатации и эволюции которых в настоящее время невозможны без использования различных видов моделирования. На всех перечисленных этапах для сложных видов различных уровней необходимо учитывать следующие особенности: сложность структуры и стохастичность связей между элементами, неоднозначность алгоритмов поведения при различных условиях, большое количество параметров и переменных, неполноту и недетерминированность исходной информации, разнообразие и вероятностный характер воздействий внешней среды и т. д. Ограниченность возможностей экспериментального исследования больших систем делает актуальной разработку методики их моделирования, которая позволила бы в соответствующей форме представить процессы функционирования систем, описание протекания этих процессов с помощью математических моделей, получение результатов экспериментов с моделями по оценке характеристики исследуемых объектов. Причем на разных этапах создания и использования перечисленных систем для всего многообразия входящих, в них подсистем применив метода моделирования преследует конкретные цели, а эффективность метода зависит от того, насколько грамотно разработчик использует возможности моделирования [34].
Независимо от разбиения конкретной сложной системы на подсистемы при проектировании каждой из них необходимо выполнить внешнее проектирование (макропроектирование) и внутреннее проектирование (микропроектирование). Так как на этих стадиях разработчик преследует различные цели, то и используемые при этом методы и средства моделирования могут существенно отличаться.
На стадии макропроектирования должна быть разработана обобщенная модель процесса функционирования сложной системы, позволяющая разработчику получить ответы на вопросы об эффективности различных стратегий управления объектом при его взаимодействии с внешней средой. Стадию внешнего проектирования можно разбить на анализ и синтез. При анализе изучают объект управления, строят модель воздействий внешней среды, определяют критерии оценки эффективности, имеющиеся ресурсы, необходимые ограничения. Конечная цель стадии анализа — построение модели объекта управления для оценки его характеристик. При синтезе на этапе внешнего проектирования решаются задачи выбора стратегии управления на основе модели объекта моделирования, т. е. сложной системы.
На стадии микропроектирования разрабатывают модели с целью создания эффективных подсистем. Причем используемые методы и средства моделирования зависят от того, какие конкретно обсспенивающие подсистемы разрабатываются: информационные, математические, технические, программные и т. д.
Особенное использования моделей. Выбор метода моделировая и необходимая детализация моделей существенно зависят от этапа разработки сложной системы [34, 37, 46]. На этапах обследования объекта управления, например промышленного предприятия, я разработки технического задания на проектирование автоматизированной системы управления модели в основном носят описательный характер и преследуют цель наиболее полно представить в компактной форме информацию об объекте, необходимую разработчику системы.
На этапах разработки технического и рабочего проектов систем, модели отдельных подсистем детализируются, и моделирование служит для решения конкретных задач проектирования, т. е. выбора оптимального по определенному критерию при заданных ограничениях варианта из множества допустимых. Поэтому в основном на этих этапах проектирования сложных систем используются модели для целей синтеза [10, 18, 37].
Целевое назначение моделирования на этапе внедрения и эксплуатации сложных систем — это проигрывание возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом. Моделирование (имитацию) также широко применяют при обучении и тренировке персонала автоматизированных систем управления, вычислительных комплексов и сетей, информационных систем в различных сферах. В этом случае моделирование носит характер деловых игр. Модель, реализуемая обычно на ЭВМ, воспроизводит поведение управляемого объекта и внешней среды, а люди в определенные моменты времени принимают решения по управлению объектом.
АСОИУ являются системами, которые развиваются по мере эволюции объекта управления, появления новых средств управления и т.-д. Поэтому при прогнозировании развития сложных систем роль моделирования очень высока, так как это единственная возможность ответить на многочисленные вопросы о путях дальнейшего эффективного развития системы и выбора из них наиболее оптимального.
В.З. ПЕРСПЕКТИВЫ РАЗВИТИЯ МЕТОДОВ
И СРЕДСТВ МОДЕЛИРОВАНИЯ СИСТЕМ
В СВЕТЕ НОВЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
В последние годы основные достижения в различных областях науки и техники неразрывно связаны с процессом совершенствования ЭВМ. Сфера эксплуатации ЭВМ — бурно развивающаясяотрасль человеческой практики, стимулирующая развитие новых теоретических и прикладных направлений [35]. Ресурсы современной информационно-вычислительной техники дают возможность ставить и решать математические задачи такой сложности, которые в недавнем прошлом казались нереализуемыми, например моделирование больших систем.
Аналитические и имитационные методы. Исторически первым сложился аналитический подход к исследованию систем, когда ЭВМ использовалась в качестве вычислителя по аналитическим зависимостям. Анализ характеристик процессов функционирования больших систем с помощью только аналитических методов исследования наталкивается обычно на значительные трудности, приводящие к необходимости существенного упрощения моделей либо на этапе их построения, либо в процессе работы с моделью, что может привести к получению недостоверных результатов.
Поэтому в настоящее время наряду с построением аналитических моделей большое внимание уделяется задачам оценки характеристик больших систем на основе имитационных моделей, реализованных на современных ЭВМ с высоким быстродействием и большим объемом оперативной памяти. Причем перспективность имитационного моделирования как метода исследования характеристик процесса функционирования больших систем возрастает с повышением быстродействия и оперативной памяти ЭВМ, с развитием математического обеспечения, совершенствованием банков данных и периферийных устройств для организации диалоговых систем моделирования. Это, в свою очередь, способствует появлению новых «чисто машинных» методов решения задач исследования больших систем на основе организации имитационных экспериментов с их моделями. Причем ориентация на автоматизированные рабочие места на базе персональных ЭВМ для реализации экспериментов с имитационными моделями больших систем позволяет проводить не только анализ их характеристик, но и решать задачи структурного, алгоритмического и параметрического синтеза таких систем при заданных критериях оценки эффективности и ограничениях [4, 9, 18, 23].
Достигнутые успехи в использовании средств вычислительной техники для целей моделирования часто создают иллюзию, что применение современной ЭВМ гарантирует возможность исследования системы любой сложности. При этом игнорируется тот факт, что в основу любой модели положено трудоемкое по затратам времени и материальных ресурсов предварительное изучение явлений, имеющих место в объекте-оригинале. И от того, насколько детально изучены реальные явления, насколько правильно проведена их формализация и алгоритмизация, зависит в конечном итоге успех моделирования конкретного объекта.
Средства моделирования систем. Расширение возможностей моделирования различных классов больших систем неразрывно связано с совершенствованием средств вычислительной техники и техники связи. Перспективным направлением является создание для клей моделирования иерархических многомашинных вычислительных систем и сетей [2, 7, 12, 25, 41].
При создании больших систем их компоненты разрабатываются различными коллективами, которые используют средства моделирования при анализе и синтезе отдельных подсистем. При этом разработчикам необходимы оперативный доступ к программно-техническим средствам моделирования, а также оперативный обмен результатами моделирования отдельных взаимодействующих подсистем. Таким образом, появляется необходимость в создании диалоговых систем моделирования, для которых характерны следующие особенности: возможность одновременной работы многих пользователей, занятых разработкой одной или нескольких систем, доступ пользователей к программно-техническим ресурсам системы моделирования, включая, базы данных и знаний, пакеты прикладных программ моделирования, обеспечение диалогового режима работы с различными вычислительными машинами и устройствами, включая цифровые и аналоговые вычислительные машины, установки натурного и физического моделирования, элементы реальных систем и т. п., диспетчирование работ в системе моделирования и оказание различных услуг пользователям, включая обучение работе с диалоговой системой моделирования при обеспечении дружественного интерфейса,
В зависимости от специфики исследуемых объектов в ряде случаев эффективным оказывается моделирование на аналоговых вычислительных машинах (АВМ). При этом надо иметь в виду, что АВМ значительно уступают ЭВМ по точности и логическим возможностям, но по быстродействию, схемной простоте реализации, сопрягаемости с датчиками внешней информации АВМ превосходят ЭВМ или, по крайней мере, не уступают им.
Для сложных динамических объектов перспективным является моделирование на базе гибридных (аналого-цифровых) вычислительных комплексов. Такие комплексы реализуют преимущества цифрового и аналогового моделирования и позволяют наиболее эффективно использовать ресурсы ЭВМ и АВМ в составе единого комплекса. При использовании гибридных моделирующих комплексов упрощаются вопросы взаимодействия с датчиками, установленными на реальных объектах, что позволяет, в свою очередь, проводить комбинированное моделирование с использованием аналого-цифровой части модели и натурной части объекта [11, 19]. Такие гибридные моделирующие комплексы могут входить в состав многомашинного вычислительного комплекса, что еще больше расширяет его возможности с точки зрения моделируемых классов больших систем.
Информационные технологии в обществе XXI века. Конец XX столетия ознаменовался интенсивным развитием и внедрением во все сферы жизни общества информатики. Это проявилось в интенсивном совершенствовании средств вычислительной техники и техники связи, в появлении новых и в дальнейшем развитии существующих информационных технологий, а также в реализации прикладных информационных систем. Достижения информатики заняли достойное место в организационном управлении, в промышленности, в проведении научных исследований и в автоматизированном проектировании. Информатизация охватила и социальную сферу: образование, науку, культуру, здравоохранение.
Переход страны к рыночной экономике потребовал развития соответствующего информационного обеспечения. Постепенно в России формировался рынок, в котором информация начинала выступать как ресурс, имеющий коммерческий характер. Наряду с производством систем и средств информатики большое место в настоящее время занимают и информационные услуги, на базе самоокупаемости интенсивно развивается отрасль связи. Телефония, радиовещание, телевидение работают с использованием различных типов каналов связи. Компьютерная техника прочно вошла в быт и используется как в образовании, так и в воспитании подрастающего поколения.
Домашний компьютер стал естественным для многих семей. В образовании значительная доля нагрузки в учебном процессе переносится на самостоятельные задания, выполняемые на домашнем компьютере. По своему качеству домашний компьютер в настоящее время часто оказывается намного выше компьютера, используемого в школе или в ВУЗе. Характерно, что в последние годы, покупая домашний компьютер, пользователь начал обращать внимание на место сборки, конфигурацию и перспективные возможности техники. Приобретается и значительное количество программных средств, в том числе записанных на CD-ROM, огромное число абонентов подключается к Интернет, значительное число пользователей работает с использованием сотовой и других сетей. Все это подтверждает, что процесс информатизации интенсифицируется, завершается этап неуправляемой информатизации. Управляемая составляющая, которая реализовывалась в основном в образовании, в промышленности и в административном управлении оказалась явно недостаточной из-за малых финансовых средств, но в целом современный уровень информатизации позволяет констатировать, что начало следующего века, станет точкой перехода из века энергетики в век информатики, как это прогнозировал Норберт Винер [8, 35].
Информатизация как процесс перехода от индустриального общества к информационному характеризуется резким перераспределением трудовых ресурсов в материальное производство и в сферу информации. Это соотношение изменяется от 3:1 к 1:3. В ряде стран суммарные расходы на компьютерную технику, телекоммуникации, электронику превысили расходы на энергетику, а поэтому, рассматривая проблему перспектив развития образования, нам необходимо исходить из будущего, поскольку только логически разработанная картина будущего может помочь познать настоящее. Проблема становления информационного общества и составляющая ее проблема информатизации образования должна рассматриваться в тесной взаимосвязи с проблемой будущего устойчивого развития цивилизации
Модель образовательной системы должна быть сформирована с учетом адаптации образования к модели устойчивого развития цивилизации, а отсюда вытекает проблема опережающего развития образовательной системы, которая должна удовлетворять потребностям будущего информационного общества.
Для информационного общества характерно полное удовлетворение информационных потребностей населения при завершении формирования единой информационной среды, определяющей новую культуру как общества в целом, так и каждого человека в отдельности. Информационная культура как составляющая и базис информационного общества должна закладываться уже в настоящее время. Переход от консервативной образовательной системы к опережающей мог бы базироваться на опережающем формировании информационного пространства Российского образования. Только образование может служить фундаментом новой информационной культуры.
Информационная культура, конечно, не ограничивается системой знаний в области информационных процессов, технологий и должна включать активно преобразовательный аспект отношения к миру. По сути информационная культура может рассматриваться как свод правил поведения в информационном обществе, в коммуникационной среде, в человеко-машинных системах, вписывающихся в мировую гуманистическую культуру человечества. Уже в настоящее время вхождение пользователя в мировую сеть позволяет получить огромные объемы информации, которая может быть предназначена и для идеологической обработки.
Необходимо воспитывать корректное отношение к получаемой информации. Информационное пространство Российского образования должно отвечать национальным интересам и базироваться на традициях отечественной культуры. Повсеместное использование зарубежной компьютерной техники сопровождается планомерным информационным идеологическим воздействием на пользователей. Можно пойти по пути защиты от чуждой нам информации, создавая соответствующие методы и средства, но особое внимание нужно обратить на информационную культуру педагога, воспитателя, учителя школы и преподавателя ВУЗа.
Уровень информационной подготовки учителя нередко отстает от уровня ученика, работающего на домашнем компьютере, подключенном к сети. Проблема развития интеллекта учащихся не может быть решена только средствами информатики, но проблема развития науки об образовании должна разрешаться с учетом перехода в информационное общество, в котором будет сформирована инфоноосфера личности, а поэтому развитие интеллектуальных способностей личности даже в настоящее время тесно смыкается с проблемой информатизации образования. Возможности информатизации образования определяются современными достижениями информатики и методологией их использования в образовании.
Можно выделить три уровня информатики:
— физический — программно-аппаратные средства вычислительной техники и техники связи;
— логический — информационные технологии;
— прикладной — пользовательские информационные системы. Для физического уровня характерно, что компьютерная техника
и техника связи практически вся разработана за рубежом и в лучшем случае наблюдается лишь ее сборка на отечественном производстве.
Информатизация города, региона, области базируется на создании единой телекоммуникационной среды. Отличительными особенностями перспективных сетей являются интеграция услуг, предоставляемых пользователю, цифровизация, комплексное использование проводных, радио - и космических каналов связи, переход к цифровым сетям интегрального обслуживания [35]. Использование волоконно-оптических линий и сетей кабельного телевидения позволяет на одной и той же базе обеспечить передачу речи, видеосигнала, данных, служебной информации и тем самым обеспечить вхождение каждого пользователя как в Российское, так и в мировое информационное пространство.
Происходит формирование единой информационной среды на основе объединения банков данных и баз знаний, проектируются конкретные информационные системы в различных областях человеческой деятельности. Совершенствование технической базы сопровождается продвижением современных операционных систем в пользовательскую среду, развиваются открытые системы.
Модели базовых информационных технологий в образовании. Для логического уровня информатики характерно совершенствование существующих, создание и развитие новых информационных технологий. Получили развитие как теория, так и практика информационных технологий [1, 8, 35]. Развивается методология, совершенствуются средства информационных технологий. Уже в настоящее время могут быть выделены базовые информационные процессы и информационные технологии.
В рамках базовых технологий получают развитие конкретные технологии, решающие задачи в выбранных предметных областях. Переход к информационному обществу заставляет задуматься о готовности выпускников учебных заведений к жизни и к труду в обществе XXI века. Учитывая, что уже в настоящее время скорости преобразования технологий производства стали опережать темпы смены поколений, оказывается необходимым не только совершенствование и дополнительная подготовка, но и неоднократное освоение новых видов деятельности в течение трудовой жизни.
Поэтому в информационном обществе встает проблема обучения, и непрерывное образование становится составной частью жизни каждого человека. В этих условиях информатизация означает изменение всей образовательной системы с ее ориентацией на новую информационную культуру. Освоение новой информационной культуры может в значительной степени реализовываться за счет внедрения в учебный процесс, управление образованием и в повседневную жизнь перспективных информационных технологий.
Прежде всего, следует обратить особое внимание на проблему обеспечения сферы образования теорией и методикой, как разработки, так и эффективного применения новых средств информационных технологий. Теория информационных технологий должна определить модели базовых информационных процессов, связанных с получением, сбором, передачей, обработкой, хранением, накоплением и представлением информации. Особое место занимают модели формализации и представления знаний.
Весьма актуальным представляется выделение базовых информационных технологий, к которым уже в настоящее время можно отнести технологии распределенного хранения и обработки, офисные технологии, мультимедиа технологии, геоинформационные технологии, технологии защиты информации, CASE-технологии, телекоммуникационные технологии [15, 35]. На основе базовых разрабатываются прикладные информационные технологии по областям применения, позволяющие получать конкретные продукты соответствующего назначения в виде средств, систем, сред.
В рамках указанных технологий в образовании уже в настоящее время получили широкое применение:
1) компьютерные программы и обучающие системы, представляющие собой электронные учебники, учебные пособия, тренажеры, лабораторные практикумы, системы тестирования знаний и квалификации, выполненные на различных типах машинных носителей;
2) системы на базе мультимедиа-технологии, построенные с применением видеотехники, накопителей на CD-ROM и реализуемые на ПЭВМ;
3) интеллектуальные обучающие экспертные системы, которые специализируются по конкретным областям применения и имеют практическое значение как в процессе обучения, так и в учебных исследованиях;
4) информационные среды на основе баз данных и знаний, позволяющие осуществить как прямой, так и удаленный доступ к информационным ресурсам;
5) телекоммуникационные системы, реализующие электронную почту, телеконференции и т. д. и позволяющие осуществить выход в мировые коммуникационные сети;
6) электронные настольные типографии, позволяющие в индивидуальном режиме с высокой скоростью осуществить производство учебных пособий и документов на различных носителях;
7) электронные библиотеки как распределенного, так и централизованного характера, позволяющие по-новому реализовать доступ учащихся к мировым информационным ресурсам;
8) геоинформационные системы, которые базируются на технологии объединения компьютерной картографии и систем управления базами данных. В итоге удается создать многослойные электронные карты, опорный слой которых описывает базовые явления или ситуации, а каждый последующий — задает один из аспектов, процессов или явлений;
9) системы защиты информации различной ориентации (от несанкционированного доступа при хранении информации, от искажений при передаче информации, от подслушивания и т. д.).
Перспективы применения информационных технологий. Методически новые информационные технологии в образовании должны быть проработаны с ориентацией на конкретное применение. Часть технологий может поддерживать учебный процесс (лекционные и практические занятия), другие технологии способны эффективно поддержать разработку новых учебников и учебных пособий. Информационные технологии помогут также эффективно организовать проведение экспериментально-исследовательских работ, как в школе, так и в ВУЗе. Особую значимость информационные технологии приобретают при самостоятельной работе учащихся на домашнем компьютере с использованием современных методов моделирования.
Какие же новые возможности открываются при внедрении современных информационных технологий в образование? На основе мультимедиа технологии появляется возможность создавать учебники, учебные пособия и другие методические материалы на машинном носителе, которые могут быть разделены на некоторые группы:
1. Учебники, представляющие собой текстовое изложение материала с большим количеством иллюстраций, которые могут быть установлены на сервире и переданы через сеть на домашний компьютер. При ограниченном количестве материала такой учебник может быть реализован в прямом доступе пользователя к серверу.
2. Учебники с высокой динамикой иллюстративного материала, выполненные на CD-ROM. Наряду с основным материалом они содержат средства интерактивного доступа, средства анимации и мультипликации, а также видеоизображения, в динамике демонстрирующие принципы и способы реализации отдельных процессовявлений.
Такие учебники могут иметь не только образовательное, но и художественное назначение. Огромный объем памяти носителя информации позволяет реализовывать на одном оптическом диске
энциклопедию, справочник, путеводитель и т. д.
3. Современные компьютерные обучающие системы для проведения учебно-исследовательских работ. Они реализовывают моделирование, как процессов, так и явлений, т. е. создают новую учебную компьютерную среду, в которой обучаемый является активным, и может сам вести учебный процесс.
4. Системы виртуальной реальности, в которых учащийся становятся участником компьютерной модели, отображающей окружающий мир. Для грамотного использования мультимедиа продуктов этого типа крайне важно изучение их психологических особенностей и негативных воздействий на обучаемого.
5. Системы дистанционного обучения. В сложных социально-экономических условиях дистанционное образование становится особенно актуальным для отдаленных регионов, для людей с малой подвижностью, а также при самообразовании и самостоятельной работе учащихся. Эффективная реализация дистанционного обучения возможна лишь при целенаправленной программе создания высококачественных мультимедиа продуктов учебного назначения по фундаментальным, естественнонаучным, общепрофессиональным и специальным дисциплинам.
К сожалению, это требует значительных финансовых средств и пока не окупается на коммерческой основе, необходимы существенные бюджетные ассигнования в эту область. Реализация такой программы позволит по-новому организовать учебных процесс, увеличив нагрузку на самостоятельную работу обучаемого.
Формирование новой информационной культуры должно базироваться, прежде всего на определенном уровне обучения в школе, а поэтому особое внимание следует уделить содержанию программы базового курса информатики, который, с одной стороны, должен быть согласован по содержанию с последующим обучением в ВУЗе, а с другой, должен поддерживать и остальные предметы школьного образования. В курс информатики уже в настоящее время закладываются сведения по моделирования процессов и явлений, по методологии формирования информационных моделей окружающего мира. У учащихся должна возникать в процессе познания информационная картина мира. Это невозможно без формирования информационной культуры населения. В основу создания информационной культуры нового общества должна быть положена идея компьютерной поддержки каждого изучаемого предмета, нельзя подменить это изучением единственного курса информатики.
Весьма важным является принцип непрерывности информационной подготовки учащихся, который должен соблюдаться как на стадии школьного, так и при переходе от школьного к Вузовскому уровню. В структуре Вузовского образования информатика является фундаментальной дисциплиной. Наряду с информатикой в учебном плане специальностей может предусматриваться ряд курсов информационной подготовки даже для нетехнических ВУЗов, которые должны совершенствоваться, чтобы компьютер стал естественным орудием труда в любой предметной области деятельности выпускника ВУЗа. К информационной подготовке можно отнести обучение методологии и средствам моделирования. Создание oпeрежающей информационной среды непрерывного Российского образования требует и решения ряда методических и организационных проблем, в том числе следующие:
1. Принятие единой системы программно и аппаратно совместимых средств вычислительной техники и техники связи, используемой в непрерывном учебном процессе. Это требует сертификации используемых средств учебного назначения и реализации программы по созданию сертификационных центров и эффективному их использованию.
2. Подключение образовательных организаций к единой цифровой сети в последующим выходом в Интернет. Решение этой задачи в значительной степени реализуется в настоящее время в высшем образовании и сдерживается в школьном образовании по финансовым причинам, а также и по сложностям выполнения для отдаленных районов.
3. Формирование единой информационной среды непрерывного образования с созданием баз данных по направлениям и специальностям подготовки, которые бы включали в себя методические документы, энциклопедии, справочники, учебники и учебные пособия, а также дополнительные средства, поддерживающие учебный процесс. Актуальным является представление в международной сети наших достижений и возможностей. Необходима организация обмена информационными ресурсами Российской образовательной системы с международной.
4. Необходимо совершенствование инструментальных средств непрерывного образования, ориентированных на ускоренное освоение материала и приобретение устойчивых навыков обучаемых, а также преследующих цели индивидуального обучения. Сюда можно отнести перспективные программные оболочки по разработке компьютерных учебников и методических материалов, программные и аппаратные средства создания компьютерных обучающих систем, средства технологии разработки мультимедиа продуктов, геоинформационных систем и т. д.
5. Необходима организация инфраструктуры информатизации образования как составной части информатизации общества в целом. Эта структура должна обеспечить создание новых, тиражирование и внедрение существующих информационных технологий в непрерывное образование.
Идеологически при инфарматизатзици образования необходимо учитывать ряд принципиальных позиций
• Эволюционное развитие сложившейся методологии образования за счет явных преимуществ новых информационных технологий, а именно, возможность наглядного, динамичного представления информатизации с использованием видеоизображений и звука, применения удаленного доступа для ознакомления с внешним и внесения собственного информационного ресурса в образовании.
• Непрерывность и преемственность компьютерного образования на всех уровнях обучения от дошкольного до послевузовского.
•Непрерывность может быть обеспечена компьютерной поддержкой всех предметов и дисциплин учебного процесса.
• Обеспечение свободы выбора методики, стиля и средств обучения с целью выявления творческих индивидуальных способностей обучаемого в сочетании с возможностью их коллективной деятельности на основе информационных технологий и телекоммуникационных систем.
• Создание научно и методически основанной системы базового образования на основе компьютерных технологий. Одним из реальных путей решения проблемы в целом является формирование и реализация региональных научно-технических программ с долевым федеральным и местным бюджетным финансированием при (дополнительном использовании внебюджетных средств. Предметом специальных исследований коллективов Высшей школы должны стать содержание, методы и средства развития образования как опережающей системы в будущем информационном обществе. При этом фундаментальное место занимают методы и средства моделирования, на основе которых можно предсказать будущее. Только при устойчивом развитии цивилизации мы можем надеяться на последовательное становление ноосферы как сферы разума. Будущее развитие человечества должно быть управляемым и в этом аспекте, несомненно, управляемым должно быть и развитие образования.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МОДЕЛИРОВАНИЯ
СИСТЕМ
Моделирование начинается с формирования предмета исследований — системы понятий, отражающей существенные для моделирования характеристики объекта. Эта задача является достаточно сложной, что подтверждается различной интерпретацией в научно-технической литературе таких фундаментальных понятий, как система, модель, моделирование. Подобная неоднозначность не говорит об ошибочности одних и правильности других терминов, а отражает зависимость предмета исследований (моделирования) как от рассматриваемого объекта, так и от целей исследователя. Отличительной особенностью моделирования сложных систем является его многофункциональность и многообразие способов использования; оно становится неотъемлемой частью всего жизненного цикла системы. Объясняется это в первую очередь технологичностью моделей, реализованных на базе средств вычислительной техники: достаточно высокой скоростью получения результатов моделирования и их сравнительно невысокой себестоимостью.
1.1. ПРИНЦИПЫ СИСТЕМНОГО ПОДХОДА В МОДЕЛИРОВАНИИ
СИСТЕМ
В настоящее время при анализе и синтезе сложных (больших) систем получил развитие системный подход, который отличается от классического (или индуктивного) подхода. Последний рассматривает систему путем перехода от частного к общему и синтезирует (конструирует) систему путем слияния ее компонент, разрабатываемых раздельно. В отличие от этого системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды.
Объект моделирования. Специалисты по проектированию и эксплуатации сложных систем имеют дело с системами управления различных уровней, обладающими общим свойством — стремлением достичь некоторой цели. Эту особенность учтем в следующих определениях системы. Система S — целенаправленное множество взаимосвязанных элементов любой природы. Внешняя среда Е — множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием .
В зависимости от цели исследования могут рассматриватьсяразные соотношения между самим объектом S и внешней средой Е.
Таким образом, в зависимости от уровня, на котором находится наблюдатель объект исследования может выделяться по-разному и могут иметь место различные взаимодействия этого объекта с внешней средой.
С развитием науки и техники сам объект непрерывно усложняется и уже сейчас говорят об объекте исследования как о некоторой сложной системе, которая состоит из различных компонент, взаимосвязанных друг с другом. Поэтому, рассматривая системный подход как основу для построения больших систем и как базу создания методики их анализа и синтеза, прежде всего необходимо определить само понятие системного подхода.
Системный подход — это элемент учения об общих законах развития природы и одно из выражений диалектического учения. Можно привести разные определения системного подхода, но наиболее правильно то, которое позволяет оценить познавательную сущность этого подхода при таком методе исследования систем, как моделирование. Поэтому весьма важны выделение самой системы S и внешней среды Е из объективно существующей реальности и описание системы исходя из общесистемных позиций.
При системном подходе к моделированию систем необходимо прежде всего четко определить цель моделирования. Поскольку невозможно полностью смоделировать реально функционирующую систему (систему-оригинал, или первую систему), создается модель (система-модель, или вторая система) под поставленную проблему. Таким образом, применительно к вопросам моделирования цель возникает из требуемых задач моделирования, что позволяет подойти к выбору критерия и оценить, какие элементы войдут в создаваемую модель М., Поэтому необходимо иметь критерий отбора отдельных элементов в создаваемую модель.
Подходы к исследованию систем. Важным для системного подхода является определение структуры системы — совокупности связей между элементами системы, отражающих их взаимодействие. Структура системы может изучаться извне с точки зрения состава отдельных подсистем и отношений между ними, а также изнутри, когда анализируются отдельные свойства, позволяющие системе достигать заданной цели, т. е. когда изучаются функции системы. В соответствии с этим наметился ряд подходов к исследованию структуры системы с ее свойствами, к которым следует прежде всего отнести структурный и функциональный.
При структурном подходе выявляются состав выделенных элементов системы S и связи между ними. Совокупность элементов связей между ними позволяет судить о структуре системы. Последняя в зависимости от цели исследования может быть описана на. разных уровнях рассмотрения. Наиболее общее описание структуры — это топологическое описание, позволяющее определить в самых общих понятиях составные части системы и хорошо формализуемое на базе теории графов.
Менее общим является функциональное описание, когда рассматриваются отдельные функции, т. е. алгоритмы поведения системы, и реализуется функциональный подход, оценивающий функции которые выполняет система, причем под функцией понимается свойство, приводящее к достижению цели. Поскольку функция отображает свойство, а свойство отображает взаимодействие систему S с внешней средой Е, то свойства могут быть выражены в виде либо некоторых характеристик элементов S;W и подсистем St системы, либо системы S в целом.
При наличии некоторого эталона сравнения можно ввести количественные и качественные характеристики систем. Для количественной характеристики вводятся числа, выражающие отношения между данной характеристикой и эталоном. Качественные характеристики системы находятся, например, с помощью метода экспертных оценок.
Проявление функций системы во времени S(t), т. е. функционирование системы, означает переход системы из одного состояния в другое, т. е. движение в пространстве состояний Z. При эксплуатации системы S весьма важно качество ее функционирования, определяемое показателем эффективности и являющееся значением критерия оценки эффективности. Существуют различные подходы к выбору критериев оценки эффективности. Система S может оцениваться либо совокупностью частных критериев, либо некоторым общим интегральным критерием.
Следует отметить, что создаваемая модель М с точки зрения системного подхода также является системой, т. е. S' = S'(M), и может рассматриваться по отношению к внешней среде Е. Наиболее просты по представлению модели, в которых сохраняется прямая аналогия явления. Применяют также модели в которых нет прямой аналогии, а сохраняются лишь законы и общие закономерности поведения элементов системы S. Правильное понимание взаимосвязей как внутри самой модели М, так и взаимодействия ее с внешней средой Е в значительной степени определяется тем, на каком уровне находится наблюдатель.
Простой подход к изучению взаимосвязей между отдельными частями модели предусматривает рассмотрение их как отражение связей между отдельными подсистемами объекта. Такой классический подход может быть использован при создании достаточно простых моделей. Процесс синтеза модели М на основе классического (индуктивного) подхода представлен на рис. 1.1, а. Реальный объект, подлежащий моделированию, разбивается на отдельные подсистемы, т. е. выбираются исходные данные Д для
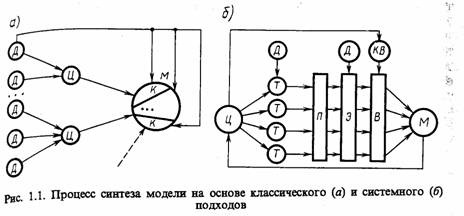
моделирования и ставятся цели Ц, отображающие отдельные стороны процесса моделирования. По отдельной совокупности исходных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некоторая компонента К будущей модели. Совокупность компонент объединяется в модель М.
Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно независимое рассмотрение отдельных сторон функционирования реального объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличительные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возникновение нового системного эффекта.
С усложнением объектов моделирования возникла необходимость наблюдения их с более высокого уровня. В этом случае наблюдатель (разработчик) рассматривает данную систему как некоторую подсистему какой-то метасистемы, т. е. системы более высокого ранга, и вынужден перейти на позиции нового системного подхода, который позволит ему построить не только исследуемую систему, решающую совокупность задачи создавать систему, являющуюся составной частью метасистемы. Например, если ставится задача проектирования АСУ предпятием, то с позиции системного подхода нельзя забывать том, что эта система является составной частью АСУ объедением.
Системный подход получил применение в системотехнике в связи с необходимостью исследования больших реальных систем, когда сказалась недостаточность, а иногда ошибочность принятая каких-либо частных решений. На возникновение системного подхода повлияли увеличивающееся количество исходных данных праазработке, необходимость учета сложных стохастических связей I в системе и воздействий внешней среды Е. Все это заставило исследователей изучать сложный объект не изолированно, а во взаимодействии с внешней средой, а также в совокупности с другими системами некоторой метасистемы.
Системный подход позволяет решить проблему построения сложной системы с учетом всех факторов и возможностей, пропорциональных их значимости, на всех этапах исследования системы S и построения модели М. Системный подход означает, что каждая система S является интегрированным целым даже тогда, когда она состоит из отдельных разобщенных подсистем. Таким образом, в основе системного подхода лежит рассмотрение системы как интегрированного целого, причем это рассмотрение при разработке начинается с главного — формулировки цели функционирования. Процесс синтеза модели М на базе системного подхода условно представлен на рис. 1.1, б. На основе исходных данных Д, которые известны из анализа внешней системы, тех ограничений, которые накладываются на систему сверху либо, исходя из возможностей ее реализации, и на основе цели функционирования формулируются исходные требования Т к модели системы S. На базе этих требований формируются ориентировочно некоторые подсистемы П, элементы Э и осуществляется наиболее сложный этап синтеза — выбор В составляющих системы, для чего используются специальные критерии выбора КВ.
При моделировании необходимо обеспечить максимальную эффективность модели системы. Эффективное» обычно определяется как некоторая разность между какими-то показателями ценности результатов, полученных в итоге эксплуатации модели, и теми затратами, которые были вложены в ее разработку и создание.
Стадии разработки моделей. На базе системного подхода может быть предложена и некоторая последовательность разработки моделей, когда выделяют две основные стадии проектирования: макропроектирование и микропроектирование.
На стадии макропроектирования на основе данных о pеальной системе S и внешней среде Е строится модель внешней среды, выявляются ресурсы и ограничения для построения модели системы, выбирается модель системы и критерии, позволяют оценить адекватность модели М реальной системы S. Построив модель системы и модель внешней среды, на основе критерия эффективности функционирования системы в процессе моделирования выбирают оптимальную стратегию управления, что позволяет реализовать возможности модели по воспроизведению отдельных сторон функционирования реальной системы S.
Стадия микропроектирования в значительной степени зависит от конкретного типа выбранной модели. В случае имитационной модели необходимо обеспечить создание информационного, математического,технического и программного обеспечений системного моделирования. На этой стадии можно установить основные характеристики созданной модели, оценить время работы с ней я затраты ресурсов для получения заданного качества соответствия модели процессу функционирования системы S.
Независимо от типа используемой модели М при ее построении необходимо руководствоваться рядом принципов системного подхода: 1) пропорционально-последовательное продвижение по этапам и направлениям создания модели; 2) согласование информационных, ресурсных, надежностных и других характеристик; 3) правильное соотношение отдельных уровней иерархии в системе моделирования; 4) целостность отдельных обособленных стадий построения модели.
Модель М должна отвечать заданной цели ее создания, поэтому отдельные части должны компоноваться взаимно, исходя из единой системной задачи. Цель может быть сформулирована качественно, тогда она будет обладать большей содержательностью и длительное время может отображать объективные возможности данной системы моделирования. При количественной формулировке цели возникает целевая функция, которая точно отображает наиболее существенные факторы, влияющие на достижение цели.
Построение модели относится к числу системных задач, при решении которых синтезируют решения на базе огромного числа исходных данных, на основе предложений больших коллективов специалистов. Использование системного подхода в этих условиях позволяет не только построить модель реального объекта, но и на базе этой модели выбрать необходимое количество управляющей информации в реальной системе, оценить показатели ее функционирования и тем самым на базе моделирования найти наиболее эффективный вариант построения и выгодный режим функционирования реальной системы S.
1.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРОБЛЕМЫ
МОДЕЛИРОВАНИЯ СИСТЕМ
С развитием системных исследований, с расширением экспериментальных методов изучения реальных явлений все большее значение приобретают абстрактные методы, появляются новые научные дисциплины, автоматизируются элементы умственного труда. Важное значение при создании реальных систем S имеют математические методы анализа и синтеза, целый ряд открытий базируется на чисто теоретических изысканиях. Однако было бы неправильно забывать о том, что основным критерием любой теории является практика, и даже сугубо математические, отвлеченные науки базируются в своей основе на фундаменте практических знаний.
Экспериментальные исследования систем. Одновременно с развитием теоретических методов анализа и синтеза совершенствуются и методы экспериментального изучения реальных объектов, появляются новые средства исследования. Однако эксперимент был и остается одним из основных и существенных инструментов познания Подобие и моделирование позволяют по-новому описать реальный процесс и упростить экспериментальное его изучение. Совершенствуется и само понятие моделирования. Если раньше моделирование означало реальный физический эксперимент либо построение макета, имитирующего реальный процесс, то в настоящее время появились новые виды моделирования, в основе которых лежит постановка не только физических, но также и математических экспериментов.
Познание реальной действительности является длительным и сложным процессом. Определение качества функционирования большой системы, выбор оптимальной структуры и алгоритмов поведения, построение системы S в соответствии с поставленной перед нею целью — основная проблема при проектировании современных систем, поэтому моделирование можно рассматривать как один из методов, используемых при проектировании и исследовании больших систем.
Моделирование базируется на некоторой аналогии реального и мысленного эксперимента. Аналогия — основа для объяснения изучаемого явления, однако критерием истины может служить только практика, только опыт. Хотя современные научные гипотезы могут создаться чисто теоретическим путем, но, по сути, базируются на широких практических знаниях. Для, объяснения реальных процессов выдвигаются гипотезы, для подтверждения которых ставится эксперимент либо проводятся такие теоретические рассуждения, которые логически подтверждают их правильность. В широком смысле под экспериментом можно понимать некоторую процедуру организации и наблюдения каких-то явлений, которые осуществляют в условиях, близких к естественным, либо имитируют их.
Различают пассивный эксперимент, когда исследователь наблюдает протекающий процесс, и активный, когда наблюдатель вмешивается и организует протекание процесса. В последнее время распространен активный эксперимент, поскольку именно на его основе удается выявить критические ситуации, получить наиболее интересные закономерности, обеспечить возможность повторения эксперимента в различных точках и т. д.
В основе любого вида моделирования лежит некоторая модель, имеющая соответствие, базирующееся на некотором общем качестве характеризует реальный объект. Объективно реальный объект обладает некоторой формальной структурой, поэтому для любой модели характерно наличие некоторой структуры, соответствующей формальной структуре реального объекта, либо изучали стороне этого объекта.
В основе моделирования лежат информационные процессы, поскольку само создание модели М базируется на информации о реальном объекте. В процессе реализации модели получается информация о данном объекте, одновременно в процессе эксперимента с моделью вводится управляющая информация, существенное место занимает обработка полученных результатов, т. е. информация лежит в основе всего процесса моделирования [36,37].
Характеристики моделей систем. В качестве объекта моделирования выступают сложные организационно-технические системы, которые можно отнести к классу больших систем. Более того, по своему содержанию и созданная модель М также становится системой S{M) и тоже может быть отнесена к классу больших систем, для которых характерно следующее [35, 37].
1. Цель функционирования, которая определяет степень целенаправленности поведения модели М. В этом случае модели могут (быть разделены на одноцелевые, предназначенные для решения (одной задачи, и многоцелевые, позволяющие разрешить или рассмотреть ряд сторон функционирования реального объекта.
2. Сложность, которую, учитывая, что модель М является совокупностью отдельных элементов и связей между ними, можно оценить по общему числу элементов в системе и связей между ними. По разнообразию элементов можно выделить ряд уровней иерархии, отдельные функциональные подсистемы в модели М, ряд входов и выходов и т. д., т. е. понятие сложности может быть идентифицировано по целому ряду признаков.
3. Целостность, указывающая на то, что создаваемая модель М является одной целостной системой S(M), включает в себя большое. количество составных частей (элементов), находящихся I в сложной взаимосвязи друг с другом.
4. Неопределенность, которая проявляется в системе: по состоянию системы, возможности достижения поставленной цели, методам решения задач, достоверности исходной информации и т. д. Основной характеристикой неопределенности служит такая мера информации, как энтропия, позволяющая в ряде случаев оценить количество управляющей информации, необходимой для достижения заданного состояния системы. При моделировании основная цель — получение требуемого соответствия модели реальному объекту и в этом смысле количество управляющей информации в модели можно также оценить с помощью энтропии и найти предельное минимальное количество, которое необходимо для получения требуемого результата с заданной достоверностью. таким образом, понятие неопределенности, характеризующее большую систему, применимо к модели М и является одним из ее основных признаков [35].
5. Поведенческая страта, которая позволяет оценить эффективность достижения системой поставленной цели. В зависимости от наличия случайных воздействий можно различать детерминированные и стохастические системы, по своему поведению — непрерывные и дискретные и т. д. Поведенческая страта рассмотрения системы S позволяет применительно к модели М оценить эффективность построенной модели, а также точность и достоверность полученных при этом результатов. Очевидно, что поведение модели М не обязательно совпадает с поведением реального объекта, причем часто моделирование может быть реализовано на базе иного материального носителя [44].
6. Адаптивность, которая является свойством высокоорганизованной системы. Благодаря адаптивности удается приспособиться к различным внешним возмущающим факторам в широком диапазоне изменения воздействий внешней среды. Применительно в модели существенна возможность ее адаптации в широком спектре возмущающих воздействий, а также изучение поведения модели в изменяющихся условиях, близких к реальным. Надо отметить, что существенным может оказаться вопрос устойчивости модели к различным возмущающим воздействиям. Поскольку модель М—сложная система, весьма важны вопросы, связанные с ее существованием, т. е. вопросы живучести, надежности и т. д. [50, 54].
7. Организационная структура системы моделирования, которая во многом зависит от сложности модели и степени совершенства средств моделирования. Одним из последних достижений в области моделирования можно считать возможность использования имитационных моделей для проведения машинных экспериментов. Необходимы оптимальная организационная структура комплекса технических средств, информационного, математического и программного обеспечений системы моделирования S'(M), оптимальная организация процесса моделирования, поскольку следует обращать особое внимание на время моделирования и точность получаемых результатов.
8. Управляемость модели, вытекающая из необходимости обеспечивать управление со стороны экспериментаторов для получения возможности рассмотрения протекания процесса в различных условиях, имитирующих реальные. В этом смысле наличие многих управляемых параметров и переменных модели в реализованной системе моделирования дает возможность поставить широкий эксперимент и получить обширный спектр результатов [16, 45]. Управляемость системы тесно связана и со степенью автоматизации моделирования. В настоящее время получили применение системы моделирования, отличающиеся высокой степенью автоматизации процесса моделирования, когда наряду с программными средствами управления машинным моделированием используется возможность мултимедийного общения исследователя с процессом моделирования.
9.Возможность развития модели, которая исходя из современного науки и техники позволяет создавать мощные системы моделирования S(M) для исследования многих сторон функционирования реального объекта. Однако нельзя при создании системы моделелирования ограничиваться только задачами сегодняшнего дня. Не обходимо предусматривать возможность развития системы молдилирования как по горизонтали в смысле расширения спектра и3учаемых функций, так и по вертикали в смысле расширения числа подсистем, т. е. созданная система моделирования должна позволять применять новые современные методы и средства. Естественно, что интеллектуальная система моделирования может функционировать только совместно с коллективом людей, поэтому к ней предъявляют эргономические требования [45, 50, 54].
Цели моделирования систем. Одним из наиболее важных аспектов построения систем моделирования является проблема цели. Любую модель строят в зависимости от цели, которую ставит перед ней исследователь, поэтому одна из основных проблем при моделировании — это проблема целевого назначения. Подобие процесса, протекающего в модели М, реальному процессу является не целью, а условием правильного функционирования модели, и поэтому в качестве цели должна быть поставлена задача изучения какой-либо стороны функционирования объекта.
Для упрощения модели М цели делят на подцели и создают более эффективные виды моделей в зависимости от полученных подцелей моделирования. Можно указать целый ряд примеров целей моделирования в области сложных систем. Например, для АСУ предприятием весьма существенно изучение процессов оперативного управления производством, оперативно-календарного планирования, перспективного планирования и здесь также могут быть успешно использованы методы моделирования [11, 35, 37].
Если цель моделирования ясна, то возникает следующая проблема, а именно проблема построения модели М. Построение модели оказывается возможным, если имеется информация или выдвинуты гипотезы относительно структуры, алгоритмов и параметров исследуемого объекта. На основании их изучения осуществляется
интификация объекта. В настоящее время широко применяют различные способы оценки параметров: по методу наименьших квадратов, по методу максимального правдоподобия, байесовские, Марковские оценки [10, 13, 18, 22].
Если модель М построена, то следующей проблемой можно считать проблему работы с ней, т. е. реализацию модели, основные задачи которой — минимизация времени получения конечных результатов и обеспечение их достоверности.
Для правильно построенной модели М характерным является то, что она выявляет лишь те закономерности, которые нужны исследователю, и не рассматривает свойства системы S, не существенные для данного исследования. Следует отметить, что оригинал и модель должны быть одновременно сходны по одним признакам и различны по другим, что позволяет выделить наиболее важные изучаемые свойства. В этом смысле модель выступает как некоторый «заместитель» оригинала, обеспечивающий фиксацию и изучение лишь некоторых свойств реального объекта.
Таким образом, характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических проблем, к основным из которых можно отнести следующие: идентификацию реальных объектов, выбор вида моделей, построение моделей и их машинную реализацию, взаимодействие исследователя с моделью в ходе машинного эксперимента, проверку правильности полученных в ходе моделирования результатов, выявление основных закономерностей, исследованных в процессе моделирования. В зависимости от объекта моделирования и вида используемой модели эти проблемы могут иметь разную значимость.
В одних случаях наиболее сложной оказывается идентификация, в других — проблема построения формальной структуры объекта. Возможны трудности и при реализации модели, особенно в случае имитационного моделирования больших систем. При этом следует подчеркнуть роль исследователя в процессе моделирования. Постановка задачи, построение содержательной модели реального объекта во многом представляют собой творческий процесс и базируются на эвристике. И в этом смысле нет формальных путей выбора оптимального вида модели. Часто отсутствуют формальные методы, позволяющие достаточно точно Описать реальный процесс. Поэтому выбор той или иной аналогии, выбор того или иного математического аппарата моделирования полностью основывается на имеющемся опыте исследователя и ошибка исследователя может привести к ошибочным результатам моделирования [37, 46].
Средства вычислительной техники, которые в настоящее время широко используются либо для вычислений при аналитическом моделировании, либо для реализации имитационной модели системы, могут лишь помочь с точки зрения эффективности реализации сложной модели, но не позволяют подтвердить правильность той или иной модели. Только на основе обработанных данных, опыта исследователя можно с достоверностью оценить адекватность модели по отношению к реальному процессу.
Если в ходе моделирования существенное место занимает реальный физический эксперимент, то здесь весьма важна и надежность используемых инструментальных средств, поскольку сбои и отказы программно-технических средств могут приводить к искаженным значениям выходных данных, отображающих протекание процесса. И в этом смысле при проведении физических экспериментов необходимы специальная аппаратура, специально разработанное математическое и информационное обеспечение, которые позволяют реализовать диагностику средств моделирования, чтобы отсеять те ошибки в выходной информации, которые вызваны неисправностями функционирующей аппаратуры. В ходе машинного эксперимента могут иметь место и ошибочные действия человека-оператора. В этих условиях серьезные задачи стоят в области эргономического обеспечения процесса моделирования.
1.3. КЛАССИФИКАЦИЯ ВИДОВ МОДЕЛИРОВАНИЯ
СИСТЕМ
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же [5]. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.
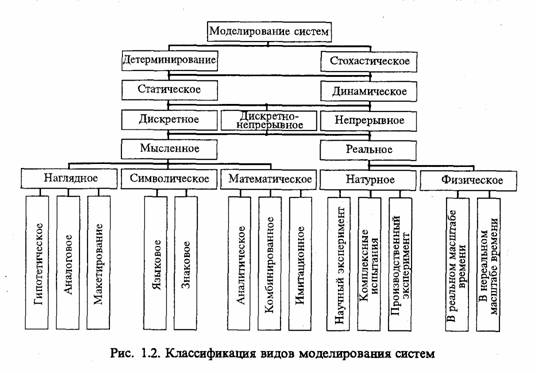
Классификационные признаки. В качестве одного из первых признаков классификации видов моделирования можно выбрать степень полноты модели и разделить модели в соответствии с этим признаком на полные, неполные и приближенные. В основе полного моделирования лежит полное подобие, которое проявляется как во времени, так и в пространстве. Для неполного моделирования характерно неполное подобие модели изучаемому объекту. В основе приближенного моделирования лежит приближенное подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем [5, 36, 37]. Классификация видов моделирования систем S приведена на рис. 1.2.
В зависимости от характера изучаемых процессов в системе S все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает детерминированные процессы, т. е. процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса, и оцениваются средние характеристики, т. е. набор однородных реализаций. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, а динамическое моделирование отражает поведение
объекта во времени. Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.
В зависимости от формы представления объекта (системы S) можно выделить мысленное и реальное моделирование.
Мысленное моделирование часто является единственным способом моделирования объектов, которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания. Например, на базе мысленного моделирования могут быть проанализированы многие ситуации микромира, которые не поддаются физическому эксперименту. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического.
При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте. В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.
Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта.
Существенное место при мысленном наглядном моделировании занимает макетирование. Мысленный макет может применяться в случаях, когда протекающие в реальном объекте процессы не поддаются физическому моделированию, либо может предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, однако обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте. Если ввести условное обозначение отдельных понятий, т. е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий — составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.
В основе языкового моделирования лежит некоторый тезаурус. Последний образуется из набора входящих понятий, причем этот набор должен быть фиксированным. Следует отметить, что между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус — словарь, который очищен от неоднозначности, т. е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову могут соответствовать несколько понятий.
Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков или символов.
Математическое моделирование. Для исследования характеристик процесса функционирования любой системы S математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т. е. построена математическая модель.
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.
Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегродифференциальных, конечно-разностных и т. п.) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы S. Однако такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности, которые часто бывают непреодолимыми. Поэтому, желая использовать аналитический метод, в этом случае идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Такое исследование на упрощенной модели аналитическим методом помогает получить ориентировочные результаты для определения более точных оценок другими методами. Численный метод позволяет исследовать по сравнению с аналитическим методом более широкий класс систем, но при этом полученные решения носят частный характер. Численный метод особенно эффективен при использовании ЭВМ.
В отдельных случаях исследования системы могут удовлетворить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Такие качественные методы широко используются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.
В настоящее время распространены методы машинной реализации исследования характеристик процесса функционирования больших систем. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм.
При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы S во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы S.
Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование — наиболее эффективный метод исследования больших систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования [4, 11, 31, 37, 46].
Когда результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы S, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой информации и целесообразно в качестве метода машинной реализации имитационной модели использовать метод статистического моделирования. Первоначально был разработан метод статистических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название метода Монте-Карло). Затем этот прием стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т. е. появился метод статистического моделирования [4, 10, 18, 29, 37]. Таким образом, методом статистического моделирования будем в дальнейшем называть метод машинной реализации имитационной модели, а методом статистических испытаний (Монте-Карло) — численный, метод решения аналитической задачи.
Метод имитационного моделирования позволяет решать задачи анализа больших систем S, включая задачи оценки: вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть положено также в основу структурного, алгоритмического и параметрического синтеза больших систем, когда требуется создать систему, с заданными характеристиками при определенных ограничениях, которая является оптимальной по некоторым критериям оценки эффективности.
При решении задач машинного синтеза систем на основе их имитационных моделей помимо разработки моделирующих алгоритмов для анализа фиксированной системы необходимо также разработать алгоритмы поиска оптимального варианта системы. Далее в методологии машинного моделирования будем различать два основных раздела: статику и динамику,— основным содержанием которых являются соответственно вопросы анализа и синтеза систем, заданных моделирующими алгоритмами [29, 37].
Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие под процессы и для тех из них, где это, возможно, используются аналитические модели, а для остальных под процессов строятся имитационные модели. Такой комбинированный подход позволяет охватить качественно новые классы систем, которые не могут быть исследованы с использованием только аналитического и имитационного моделирования в отдельности.
Другие виды моделирования. При реальном моделировании используется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части. Такие исследования могут проводиться как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т. д.). Реальное моделирование является наиболее адекватным, но при этом его возможности с учетом особенностей реальных объектов ограничены. Например, проведение реального моделирования АСУ предприятием потребует, во-первых, создания такой АСУ, а во-вторых, проведения экспериментов с управляемым объектом, т. е. предприятием, что в большинстве случаев невозможно. Рассмотрим разновидности реального моделирования.
Натурным моделированием называют проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. При функционировании объекта в соответствии с поставленной целью удается выявить закономерности протекания реального процесса. Надо отметить, что такие разновидности натурного эксперимента, как производственный эксперимент и комплексные испытания, обладают высокой степенью достоверности.
С развитием техники и проникновением в глубь процессов, протекающих в реальных системах, возрастает техническая оснащенность современного научного эксперимента. Он характеризуется широким использованием средств автоматизации проведения, применением весьма разнообразных средств обработки информации, возможностью вмешательства человека в процесс проведения эксперимента, и в соответствии с этим появилось новое научное направление — автоматизация научных экспериментов [12, 34, 40].
Отличие эксперимента от реального протекания процесса заключается в том, что в нем могут появиться отдельные критические ситуации и определяться границы устойчивости процесса. В ходе эксперимента вводятся новые факторы и возмущающие воздействия в процессе функционирования объекта. Одна из разновидностей эксперимента — комплексные испытания, которые также можно отнести к натурному моделированию, когда вследствие повторения испытаний изделий выявляются общие закономерности о надежности этих изделий, о характеристиках качества и т. д. В этом случае моделирование осуществляется путем обработки и обобщения сведений, проходящих в группе однородных явлений. Наряду со специально организованными испытаниями возможна реализация натурного моделирования путем обобщения опыта, накопленного в ходе производственного процесса, т. е. можно говорить о производственном эксперименте. Здесь на базе теории подобия обрабатывают статистический материал по производственному процессу и получают его обобщенные характеристики.
Другим видом реального моделирования является физическое, отличающееся от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени, а также может рассматриваться без учета времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, которые фиксируются в некоторый момент времени. Наибольшие сложность и интерес с точки зрения верности получаемых результатов представляет физическое моделирование в реальном масштабе времени.
С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные). Под аналоговой моделью понимается модель, которая описывается уравнениями, связывающими непрерывные величины. Под цифровой понимают модель, которая описывается уравнениями, связывающими дискретные величины, представленные в цифровом виде. Под аналого-цифровой понимается модель, которая может быть описана уравнениями, связывающими непрерывные и дискретные величины.
Особое место в моделировании занимает кибернетическое моделирование, в котором отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируют некоторые связи между выходами и входами. Чаще всего при использовании кибернетических моделей проводят анализ поведенческой стороны объекта при различных воздействиях внешней среды [11, 25, 27, 44]. Таким образом, в основе кибернетических моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения имитационной модели в этом случае необходимо выделить исследуемую функцию реального объекта, допытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести на имитационной модели данную функцию, причем на базе совершенно иных математических соотношений и, естественно, иной физической реализации процесса.
1.4. ВОЗМОЖНОСТИ И ЭФФЕКТИВНОСТЬ МОДЕЛИРОВАНИЯ
СИСТЕМ НА ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Обеспечение требуемых показателей качества функционирования больших систем, связанное с необходимостью изучения протекания стохастических процессов в исследуемых и проектируемых системах S, позволяет проводить комплекс теоретических и экспериментальных исследований, взаимно дополняющих друг друга. Эффективность экспериментальных исследований сложных систем оказывается крайне низкой, поскольку проведение натурных экспериментов с реальной системой либо требует больших материальных затрат и значительного времени, либо вообще практически невозможно (например, на этапе проектирования, когда реальная система отсутствует). Эффективность теоретических исследований с практической точки зрения в полной мере проявляется лишь тогда, когда их результаты с требуемой степенью точности и достоверности могут быть представлены в виде аналитических соотношений или моделирующих алгоритмов, пригодных для получения соответствующих характеристик процесса функционирования исследуемых систем.
Средства моделирования систем. Появление современных ЭВМ было решающим условием широкого внедрения аналитических методов в исследование сложных систем. Стало казаться, что модели и методы, например, математического программирования, станут практическим инструментом решения задач управления в больших системах. Действительно, были достигнуты значительные успехи в создании новых математических методов решения этих задач, однако математическое программирование так и не стало практическим инструментом исследования процесса функционирования сложных систем, так как модели математического программирования оказались слишком грубыми и несовершенными для их эффективного использования. Необходимость учета стохастических свойств системы, недетерминированности исходной информации, наличия корреляционных связей между большим числом переменных и параметров, характеризующих процессы в системах, приводят к построению сложных математических моделей, которые немогут быть применены в инженерной практике при исследовании таких систем аналитическим методом. Пригодные для практических расчетов аналитические соотношения удается получить лишь при упрощающих предположениях, обычно существенно искажающих фактическую картину исследуемого процесса. Поэтому в последнее время все ощутимее потребность в разработке методов, которые дали бы возможность уже на этапе проектирования систем исследовать более адекватные модели. Указанные обстоятельства приводят к тому, что при исследовании больших систем все шире применяют методы имитационного моделирования [8, 11, 19, 25, 41, 54].
Наиболее конструктивным средством решения инженерных задач на базе моделирования в настоящее время стали ЭВМ. Современные ЭВМ можно разделить на две группы: универсальные, прежде всего предназначенные для выполнения расчетных работ, и управляющие, позволяющие проводить не только расчетные работы, но прежде всего приспособленные для управления объектами в реальном масштабе времени. Управляющие ЭВМ могут быть использованы как для управления технологическим процессом, экспериментом, так и для реализации различных имитационных моделей. В зависимости от того, удается ли построить достаточно точную математическую модель реального процесса, или вследствие сложности объекта не удается проникнуть в глубь функциональных связей реального объекта и описать их какими-то аналитическими соотношениями, можно рассматривать два основных пути использования ЭВМ: как средства расчета по полученным аналитическим моделям и как средства имитационного моделирования.
Для известной аналитической модели, полагая, что она достаточно точно отображает исследуемую сторону функционирования; реального физического объекта, перед вычислительной машиной стоит задача расчета характеристик системы по каким-либо математическим соотношениям при подстановке числовых значений. В этом направлении вычислительные машины обладают возможностями, практически зависящими от порядка решаемого уравнения и от требований к скорости решения, причем могут быть использованы как ЭВМ, так и АВМ.
При использовании ЭВМ разрабатывается алгоритм расчета характеристик, в соответствии с которым составляются программы (либо генерируются с помощью пакета прикладных программ) дающие возможность осуществлять расчеты по требуемым аналитическим соотношениям. Основная задача исследователя заключается в том, чтобы попытаться описать поведение реального объекта одной из известных математических моделей.
Использование АВМ, с одной стороны, ускоряет для достаточно простых случаев процесс решения задачи, с другой стороны, могут возникать погрешности, обусловленные наличием дрейфа параметр ров отдельных блоков, входящих в АВМ, ограниченной точностью с которой могут быть заданы параметры, вводимые в машину, а также неисправностями технических средств и т. д.
Перспективно сочетание ЭВМ и АВМ, т. е. использование гибридных средств вычислительной техники — гибридных вычислительных комплексов (ГВК), что в ряде случаев значительно ускоряет процесс исследования [12, 20, 37, 49].
В ГВК удается сочетать выcокую скорость функционирования аналоговых средств и высокую точность расчетов на базе цифровых средств вычислительной техники. Одновременно удается за счет наличия цифровых устройств обеспечить контроль проведения операций. Опыт использования вычислительной техники в задачах моделирования показывает, что с усложнением объекта большую эффективность по скорости решения и по стоимости выполнения операций дает использование гибридной техники.
Конкретным техническим средством воплощения имитационной модели могут быть ЭВМ, АВМ и ГВК. Если использование аналоговой техники ускоряет получение конечных результатов, сохраняя некоторую наглядность протекания реального процесса, то применение средств цифровой техники позволяет осуществить контроль за реализацией модели, создать программы по обработке и хранению результатов моделирования, обеспечить эффективный диалог исследователя с моделью.
Обычно модель строится по иерархическому принципу, когда последовательно анализируются отдельные стороны функционирования объекта и при перемещении центра внимания исследователя, рассмотренные ранее подсистемы переходят во внешнюю среду. Иерархическая структура моделей может раскрывать и ту последовательность, в которой изучается реальный объект, а именно последовательность перехода от структурного (топологического) уровня к функциональному (алгоритмическому) и от функционального к параметрическому.
Результат моделирования в значительной степени зависит от адекватности исходной концептуальной (описательной) модели, от полученной степени подобия описания реального объекта, числа реализаций модели и многих других факторов. В ряде случаев сложность объекта не позволяет не только построить математическую модель объекта, но и дать достаточно близкое кибернетическое описание, и перспективным здесь является выделение наиболее трудно поддающейся математическому описанию части объекта и включение этой реальной части физического объекта в имитационную модель. Тогда модель реализуется, с одной стороны, на базе средств вычислительной техники, а с другой — имеется реальная часть объекта. Это значительно расширяет возможности и повышает достоверность результатов моделирования.
Имитационная система реализуется на ЭВМ и позволяет исследовать имитационную модель М, задаваемую в виде определенной совокупности отдельных блочных моделей и связей между ними в их взаимодействии в пространстве и времени при реализации какого-либо процесса. Можно выделить три основные группы блоков: блоки, характеризующие моделируемый процесс функционирования системы S; блоки, отображающие внешнюю среду Е и ее воздействие на реализуемый процесс; блоки, играющие служебную вспомогательную роль, обеспечивая взаимодействие первых двух, а также выполняющие дополнительные функции по получению и обработке результатов моделирования. Кроме того, имитационная система характеризуется набором переменных, с помощью которых удается управлять изучаемым процессом, и набором начальных условий, когда можно изменять условия проведения машинного эксперимента.
Таким образом, имитационная система есть средство проведения машинного эксперимента, причем эксперимент может ставиться многократно, заранее планироваться, могут определяться условия его проведения. Необходимо при этом выбрать методику оценки адекватности получаемых результатов и автоматизировать как процессы получения, так и процессы обработки результатов в ходе машинного эксперимента.
Обеспечение моделирования. Эксперимент с имитационной моделью требует серьезной подготовки, поэтому имитационная система характеризуется наличием математического, программного, информационного, технического, эргономического и других видов обеспечения,
Математическое обеспечение имитационной системы включает в себя совокупность математических соотношений, описывающих поведение реального объекта, совокупность алгоритмов, обеспечивающих как подготовку, так и работу с моделью. Сюда могут быть отнесены алгоритмы ввода исходных данных, имитации, вывода, обработки.
Программное обеспечение по своему содержанию включает в себя совокупность программ: планирования эксперимента, имитационной модели, проведения эксперимента, обработки и интерпретации результатов. Кроме того, программное обеспечение имитационной системы должно обеспечивать синхронизацию процессов в модели, т. е. необходим блок, организующий псевдопараллельное выполнение процессов в модели. Машинные эксперименты с имитационными моделями не могут проходить без хорошо разработанного и реализованного информационного обеспечения.
Информационное обеспечение включает в себя средства и технологию организации и реорганизации базы данных моделирования, методы логической и физической организации массивов, формы документов, описывающих процесс моделирования и его результаты. Информационное обеспечение имитационной системы является наименее разработанной частью, поскольку только в настоящее время наблюдается переход к созданию сложных имитационных моделей и разрабатывается методология их использования при анализе и синтезе сложных систем с использованием концепции базы данных и знаний.
Техническое обеспечение имитационной системы включает в себя прежде всего средства вычислительной техники, связи и обмена между оператором и сетью ЭВМ, ввода и вывода информации, управления проведением эксперимента. К техническому обеспечению предъявляются весьма серьезные требования по надежности функционирования, так как сбои и отказы технических средств, ошибки оператора ЭВМ могут резко увеличить время работы с имитационной моделью и даже привести к неверным конечным результатам.
Эргономическое обеспечение имитационной системы представляет собой совокупность научных и прикладных методик и методов, а также нормативно-технических и организационно-методических документов, используемых на всех этапах взаимодействия человека-экспериментатора с инструментальными средствами (ЭВМ, гибридными комплексами и т. д.). Эти документы, используемые на всех стадиях разработки и эксплуатации имитационных систем и их элементов, предназначены для формирования и поддержания эргономического качества путем обоснования и выбора организационно-проектных решений, которые создают оптимальные условия для высокоэффективной деятельности человека во взаимодействии с моделирующим комплексом.
Таким образом, имитационная система может рассматриваться как машинный аналог сложного реального процесса. Позволяет заменить эксперимент с реальным процессом функционирования системы экспериментом с математической моделью этого процесса в ЭВМ. В настоящее время имитационные эксперименты широко используют в практике проектирования сложных систем, когда реальный эксперимент невозможен.
Возможности машинного моделирования. Несмотря на то что имитационное моделирование на ЭВМ является мощным инструментом исследования систем, его применение рационально не во всех случаях. Известно множество задач, решаемых более эффективно другими методами. Вместе с тем для большого класса задач исследования и проектирования систем метод имитационного моделирования наиболее приемлем. Правильное его употребление возможно лишь в случае четкого понимания сущности метода имитационного моделирования и условий его использования в практике исследования реальных систем при учете особенностей конкретных систем и возможностей их исследования различными методами.
В качестве основных критериев целесообразности применения метода имитационного моделирования на ЭВМ можно указать следующие: отсутствие или неприемлемость аналитических, численных и качественных методов решения поставленной задачи; наличие достаточного количества исходной информации о моделируемой системе S для обеспечения возможности построения адекватной имитационной модели; необходимость проведения на базе других возможных методов решения очень большого количества вычислений, трудно реализуемых даже с использованием ЭВМ; возможность поиска оптимального варианта системы при ее моделировании на ЭВМ.
Имитационное моделирование на ЭВМ, как и любой метод исследований, имеет достоинства и недостатки, проявляющиеся в конкретных приложениях [37, 43, 46]. К числу основных достоинств метода имитационного моделирования при исследовании сложных систем можно отнести следующие: машинный эксперимент с имитационной моделью дает возможность исследовать особенности процесса функционирования системы S в любых условиях; применение ЭВМ в имитационном эксперименте существенно сокращает продолжительность испытаний по сравнению с натурным экспериментом; имитационная модель позволяет включать результаты натурных испытаний реальной системы или ее частей для проведения дальнейших исследований; имитационная модель обладает известной гибкостью варьирования структуры, алгоритмов и параметров моделируемой системы, что важно с точки зрения поиска оптимального варианта системы; имитационное моделирование сложных систем часто является единственным практически реализуемым методом исследования процесса функционирования таких систем на этапе их проектирования.
Основным недостатком, проявляющимся при машинной реализации метода имитационного моделирования, является то, что решение, полученное при анализе имитационной модели М, всегда носит частный характер, так как оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы S, начальных условий и воздействий внешней среды Е. Поэтому для полного анализа характеристик процесса функционирования систем, а не получения только отдельной точки приходится многократно воспроизводить имитационный эксперимент, варьируя исходные данные задачи. При этом, как следствие, возникает увеличение затрат машинного времени на проведение эксперимента с имитационной моделью процесса функционирования исследуемой системы S.
Эффективность машинного моделирования. При имитационном моделировании, так же как и при любом другом методе анализа и синтеза системы S, весьма существен вопрос его эффективности. Эффективность имитационного моделирования может оцениваться рядом критериев, в том числе точностью и достоверностью результатов моделирования, временем построения и работы с моделью М, затратами машинных ресурсов (времени и памяти), стоимостью разработки и эксплуатации модели. Очевидно, наилучшей оценкой эффективности является сравнение получаемых результатов с реальным исследованием, т. е. с моделированием на реальном объекте при проведении натурного эксперимента. Поскольку это не всегда удается сделать, статистический подход позволяет с определенной степенью точности при повторяемости машинного эксперимента получить какие-то усредненные характеристики поведения системы, Существенное влияние на точность моделирования оказывает число реализаций, и в зависимости от требуемой достоверности можно оценить необходимое число реализаций воспроизводимого случайного процесса.
Существенным показателем эффективности являются затраты машинного времени. В связи с использованием ЭВМ различного типа суммарные затраты складываются из времени по вводу и выводу данных по каждому алгоритму моделирования, времени на проведение вычислительных операций, с учетом обращения к оперативной памяти и внешним устройствам, а также сложности каждого моделирующего алгоритма. Расчеты затрат машинного времени являются приближенными и могут уточняться по мере отладки программ и накопления опыта у исследователя при работе с имитационной моделью. Большое влияние на затраты машинного времени при проведении имитационных экспериментов оказывает рациональное планирование таких экспериментов. Определенное влияние на затраты машинного времени могут оказать процедуры обработки результатов моделирования, а также форма их представления.
Построение имитационных моделей больших систем и проведение машинных экспериментов с этими моделями представляют собой достаточно трудоемкий процесс, в котором в настоящее время много неизученного. Однако специалисты в области проектирования, исследования и эксплуатации больших систем должны в совершенстве знать методологию машинного моделирования, сложившуюся к настоящему времени, чтобы быть готовыми к появлению ЭВМ следующих поколений, которые позволят сделать еще один существенный шаг в автоматизации построения моделей и использования имитационного моделирования систем.
МАТЕМАТИЧЕСКИЕ СХЕМЫ МОДЕЛИРОВАНИЯ
СИСТЕМ
Наибольшие затруднения и наиболее серьезные ошибки при моделировании возникают при переходе от содержательного к формальному описанию объектов исследования, что объясняется участием в этом творческом процессе коллективов разных специальностей: специалистов в области систем, которые требуется моделировать (заказчиков), и специалистов в области машинного моделирования (исполнителей). Эффективным средством для нахождения взаимопонимания между этими группами специалистов является язык математических схем, позволяющий во главу угла поставить вопрос об адекватности перехода от содержательного описания системы к ее математической схеме, а лишь затем решать вопрос о конкретном методе получения результатов с использованием ЭВМ: аналитическом или имитационном, а возможно, и комбинированном, т. е. аналитико-имитационном. Применительно к конкретному объекту моделирования, т. е. к сложной системе, разработчику модели должны помочь конкретные, уже прошедшие апробацию для данного класса систем математические схемы, показавшие свою эффективность в прикладных исследованиях на ЭВМ и получившие название типовых математических схем.
2.1. ОСНОВНЫЕ ПОДХОДЫ К ПОСТРОЕНИЮ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СИСТЕМ
Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы 5. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Причем уровень абстрагирования зависит от круга тех вопросов, на которые исследователь системы хочет получить ответ с помощью модели, и в какой-то степени определяет выбор математической, схемы [4,13, 29, 37, 42, 48].
Математические схемы. Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Например, представление процесса функционирования информационно-вычислительной системы коллективного пользования в виде сети схем массового обслуживания дает возможность хорошо описать процессы, происходящие в системе, но при сложных законах распределения входящих потоков и потоков обслуживания не дает возможности получения результатов в явном виде [13, 21, 30, 33, 37, 41].
Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель — математическая схема — математическая [аналитическая или (и) имитационная] модель».
Каждая конкретная система Охарактеризуется набором свойств, под которыми понимаются величины, отражающие поведение моделируемого объекта (реальной системы) и учитывающие условия ее функционирования во взаимодействии с внешней средой (системой) Е. При построении математической модели системы необходимо решить вопрос об ее полноте. Полнота модели регулируется в основном выбором границы «система S—среда Е». Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства .системы, отбросив второстепенные. Причем отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы (например, анализ вероятностно-временных характеристик процесса функционирования системы, синтез структуры системы и т. д.).
Формальная модель объекта. Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
совокупность входных воздействий на систему -
![]()
совокупность воздействий внешней среды
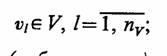
совокупность внутренних (собственных) параметров системы
![]()
' Ш1'
совокупность выходных характеристик системы
![]()
При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае xh vh hk, yj являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.
При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид x(t) = (x1(t), xz(t), ..., xnX(t));
v (t) = (v1 (t), v2 (t) (t)=h (t)= (h1(t),h2 (t)…,hnн а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
![]()
![]()
Процесс функционирования системы S описывается во времени оператором Fs, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида
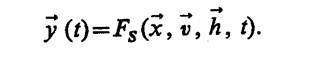
(2.1)
Совокупность зависимостей выходных характеристик системы от
времени yj(t) для всех видов j=1, nY называется выходной
траекторией ![]() Зависимость
(2.1) называется законом функционирования системы S и обозначается Fs. В общем случае закон функционирования системы Fs может быт задан в виде функции, функционала, логических
условий, в алгоритмической и табличной формах или в виде словесного правила
соответствия.
Зависимость
(2.1) называется законом функционирования системы S и обозначается Fs. В общем случае закон функционирования системы Fs может быт задан в виде функции, функционала, логических
условий, в алгоритмической и табличной формах или в виде словесного правила
соответствия.
Весьма важным для описания и исследования
системы S является
понятие алгоритма функционирования As, под которым понимается
метод получения выходных характеристик с учетом входных воздействий ![]() воздействий внешней среды
воздействий внешней среды ![]() и собственных параметров
системы
и собственных параметров
системы ![]() Очевидно,
что один и тот же закон функционирования Fs системы S может быть реализован различными способами, т. е. с
помощью множества различных алгоритмов функционирования As.
Очевидно,
что один и тот же закон функционирования Fs системы S может быть реализован различными способами, т. е. с
помощью множества различных алгоритмов функционирования As.
Соотношения (2.1) являются математическим описанием поведения объекта (системы) моделирования во времени t, т. е. отражают его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами) [4,11, 43, 44].
Для статических моделей математическая модель (2.1) представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, Н}, что в векторной форме может быть записано как
(2.2)
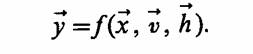
Соотношения (2.1) и (2.2) могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т. д. Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторами
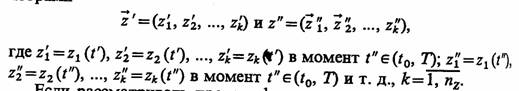
Если рассматривать процесс функционирования системы S как последовательную смену состояний z1 (t), z2(t), ..., zk(t), то они могут быть интерпретированы как координаты точки в k -мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний { z } называется пространством состояний объекта моделирования Z, причем zk€Z.
Состояния системы S в момент времени t0 < t* < Т полностью определяются начальными условиями z° = (z°1,. z20, ..., z°k) [где z°1=zl(t0), z°2=z2(t0), ..., z°k=zk(t0)], входными воздействиями x (t), внутренними параметрами h (t) и воздействиями внешней среды v (t), которые имели место за промежуток времени t* —10, с помощью двух векторных уравнений
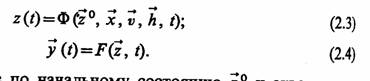
Первое уравнение по начальному состоянию z° и экзогенным переменным x,v,h определяет вектор-функцию z(t), а второе по полученному значению состояний z (t) — эндогенные переменные на выходе системы у (t). Таким образом, цепочка уравнений объекта «вход — состояния — выход» позволяет определить характеристики системы
![]()
В общем случае время в модели системы S может рассматриваться на интервале моделирования (О, Т) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной At временных
единиц каждый, когда T=m∆t, где m=l, mT — число интервалов дискретизации.
Таким образом, под математической моделью объекта (реальной системы) понимают конечное подмножество переменных {х (t), v (t), h (t)} вместе с математическими связями между ними и характеристиками у (t) [4, 9, 10, 35].
Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т. е. если можно считать, что в этом случае стохастические воздействия внешней среды v (t) и стохастические внутренние параметры h (t) отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

Очевидно, что детерминированная модель является частным случаем стохастической модели.
Типовые схемы. Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т. д.
Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения. В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени,— конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем — системы массового обслуживания и т. д.
Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших информационно-управляющих системах. Для таких систем в ряде случаев более перспективным является применение агрегативных моделей [4, 37]. Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.
Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный (например, дифференциальные уравнения); дискретно-детерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный, или универсальный (агрегативные системы).
Математические схемы, рассматриваемые в последующих параграфах данной главы, должны помочь оперировать различным подходами в практической работе при моделировании конкретных систем.
2.2. НЕПРЕРЫВНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
(D-СХЕМЫ)
Рассмотрим особенности непрерывно-детерминированного подхода на примере использования в качестве математических моделей дифференциальных уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями.
Основные соотношения. Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем (2.6) в общем виде будет
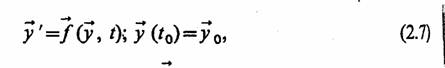
![]()
векторы;f(у, t) — вектор-функция, которая определена на некотором (n+ 1)-мерном (у, t) множестве и является непрерывной.
Так как математические схемы такого вида отражают динамику изучаемой системы, т. е. ее поведение во времени, то они называются D-схемами (англ. dynamic) [4, 37].
В простейшем случае обыкновенное дифференциальное уравнение имеет вид
![]()
Наиболее важно для системотехники приложение D-схем в качестве математического аппарата в теории автоматического управления. Для иллюстрации особенностей построения и применения D-схем рассмотрим простейший пример формализации процесса функционирования двух элементарных систем различной физической природы: механической SM (колебания маятника, рис. 2.1, а) и электрической 5, (колебательный контур, рис. 2.1, б).
Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением
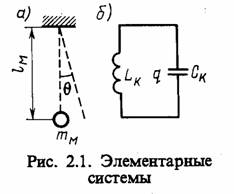
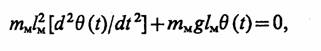
где mm lM — масса и длина подвеса маятника; g — ускорение свободного падения; θ (t) — угол отклонения маятника в момент времени t.
Из этого уравнения свободного колебания маятника можно найти оценки интересующих характеристик. Например, период колебания маятника
![]()
Аналогично, процессы в электрическом колебательном контуре описываются обыкновенным дифференциальным уравнением
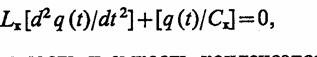
где LK, CK — индуктивность и емкость конденсатора; q (t) — заряд конденсатора в момент времени t.
Из этого уравнения можно получить различные оценки характеристик процесса в колебательном контуре. Например, период характеристических колебаний
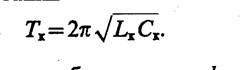
Очевидно, что, введя обозначения ho=mMl2M=Lx, h1 = 0, h2=mMglm = 1/Сk θ(t) = q (t)=z (t), получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение этой замкнутой системы:
![]()
где h0, hlt h2 — параметры системы; z(t) — состояние системы в момент времени t.
Таким образом, поведение этих двух объектов может быть исследовано на основе общей математической модели (2.9). Кроме того, необходимо отметить, что поведение одной из систем может быть проанализировано с помощью другой. Например, поведение маятника (системы SM) может быть изучено с помощью электрического колебательного контура (системы 5Х).
Если изучаемая система S, т. е. маятник или контур, взаимодействует с внешней средой Е, то появляется входное воздействие x(t) (внешняя сила для маятника и источник энергии для контура) и непрерывно-детерминированная модель такой системы будет иметь вид
![]()
С точки зрения общей схемы математической модели (см. § 2.1) x(t) является входным (управлявшим) воздействием, а состояние системы S в данном случае можно рассматривать как выходную ; характеристику, т. е. полагать, что выходная переменная совпадает с состоянием системы в данный момент времени y=z.
Возможные приложения. При решении задач системотехники важное значение имеют проблемы управления большими системами. Следует обратить внимание на системы автоматического управления — частный случай динамических систем, описываемых D-схемами и выделенных в отдельный класс моделей в силу их практической специфики [24, 43].
Описывая процессы автоматического управления, придерживаются обычно представления реального объекта в виде двух систем: управляющей и управляемой (объекта управления). Структура многомерной системы автоматического управления общего вида представлена на рис. 2.2, где обозначены эндогенные переменные: х (t) — вектор входных (задающих) воздействий; v (t) — вектор возмущающих воздействий; h'(t) — вектор сигналов ошибки; h "(t) — вектор управляющих воздействий; экзогенные переменные: z (0 — вектор состояний системы S; у (t) — вектор выходных
переменных, обычно у (t)=z (t).
Современная управляющая система — это совокупность программно-технических средств, обеспечивающих достижение объектом управления определенной цели. Насколько точно объект управления достигает заданной цели, можно судить для одномерной системы по координате состояния y(t). Разность между заданным Узад (t) и действительным y(t) законами изменения управляемой величины есть ошибка управления
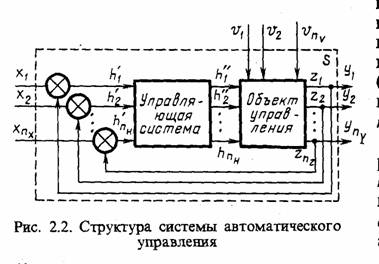
h'(t)=y3aд(t)—y(t). Если предписанный закон изменения управляемой величины соответствует закону изменения входного (задающего) воздействия, т. е. x(t)=yзад(t), то h'(t)=x(t)-y(t).
Системы, для которых ошибки управления h'(t) = O во все моменты времени, называются идеальными. На практике реализация идеальных систем невозможна. Таким образом, ошибка h’ (t) — необходимый субстрат автоматического управления, основанного на принципе отрицательной обратной связи, так как для приведения в соответствие выходной переменной у (t) ее заданному значению используется информация об отклонении между ними. Задачей системы автоматического управления является изменение переменной у (t) согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы S, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной y(t) в переходном процессе, время переходного процесса и т. п. Выводы о свойствах систем автоматического управления различных классов можно сделать по виду дифференциальных уравнений, приближенно описывающих процессы в системах. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы S.
Пример 2.1. Рассмотрим одноканальную систему автоматического управления SA, которая описывается D-схемой общего вида
![]()
где хm и уn — производные по времени т-го и n-ro порядков от функции х и у соответственно. Пусть система SA, описываемая уравнением (2.10), работает в некотором режиме, характеризуемом функциями х0 (г) и у0 (t). Обозначим малые отклонения х (t) от хо(t) через ∆x(t), a y(t) от yo{t) через ∆y (t), т. е. x(t)=xo(t)+∆x(t),
y(t)=yо(t)+∆у(t)
Тогда уравнение (2.10) можно линеаризовать, разложив функцию F(yn , уn-1 ,...,
у, х , х , ..., х) в ряд Тейлора и ограничившись его линейными членами относительно приращений ∆ х и ∆у, т. е.
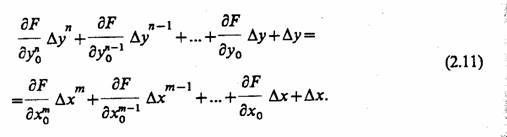
Так как полученное уравнение (2.11) приближенно описывает рассматриваемый процесс, то производные вычисляют при некоторых фиксированных значениях входящих в него переменных, т. е. получается система с постоянными коэффициентами. Кроме того, уравнения получаются линейными относительно Δх, Δу и их производных. Это весьма существенно, так как методы решения и исследования линейных систем значительно проще, чем систем общего вида, и более детально разработаны.
Таким образом, для линейных систем автоматического управления, т. е. для систем, описываемых линейными дифференциальными уравнениями, можно записать
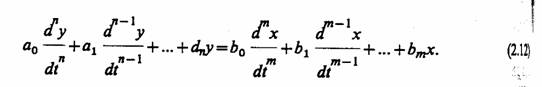
В уравнении (2.12) для простоты предполагается, что точки приложения возмущающих воздействий совпадают с входом системы. Для решения (2.12) мот воспользоваться, например, операторным методом, заменяя дифференциальное уравнение алгебраическим.
Таким образом, использование D-схем позволяет формализовать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход, реализованный в виде соответствующего языка для моделирования непрерывных систем или использующий аналоговые и гибридные средства вычислительной техники.
2.3. ДИСКРЕТНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
(F-СХЕМЫ)
Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата теории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени, Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности.
Основные соотношения. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами.
Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством X входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z0, z0 е Z; функцией переходов ср (г, х); функцией выходов ψ(z, х). Автомат, задаваемый F-схемой: F=(Z, X, Y, φ, ψ zо>,— функционирует в дискретном автоматном времени, моментами которого являются такты, т. е, примыкающие друг
к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-му такту при t=0, 1, 2, ..., через z(t) x(t), y(t). При этом, по условию, z(0)=zo, a z(t) ε Z, x(t)εX,
Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t = 0, 1, 2, ... дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=zo. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t) ε X и выдать на выходном канале сигнал y(t) = ψ[z (t), x (/)], переходя в состояние z (t+1) = φ[z (t), x (t)], z(t)εZ, y(t)εY. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, подавать в некоторой последовательности буквы входного алфавита y(0), y(1), х(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), у(1), у{2),..., образуя выходное слово.
Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t+1) я выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили,
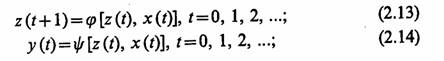
для F-автомата второго рода
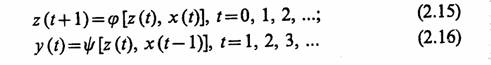
Автомат второго рода, для которого
![]()
т. е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.
Таким образом, уравнения (2.13) — (2.17), полностью задающие F-автомат, являются частным случаем уравнений (2.3) и (2.4), когда система S детерминированная и на ее единственный вход поступает дискретный сигнал X.
По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом, согласно (2.14), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный выходной сигнал у (0, т. е. реализует логическую функцию вида
![]()
Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов хну, состоят из двух букв.
По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-aemo- матах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с уравнениями (2.13) — (2.17) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может, как следует из (2.13) — (2.17), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.
Возможные приложения. Чтобы задать конечный F-автомат, необходимо описать все элементы множества F= <Z, X, Y, φ, ψ, z0>, т. е. входной, внутренний и выходной алфавиты, л также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние z0, в котором автомат находился в момент времени t=0. Существует несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графический и матричный.
Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы — его состояниям. При этом обычно первый слева столбец соответствует начальному состоянию z0. На пересечений i- й строги и k-го столбца таблицы переходов помещается соответствующее значение ψ(zk, xi) функции переходов, а в таблице выходов — соответствующее значение ψ(zк,хi,) функции выходов. Для F-автомата Мура обе таблицы можно совместить, получив так называемую отмеченную таблицу переходов, в которой над каждым состоянием zk автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно (2.17), выходной сигнал ψ (zi).
Описание работы F-автомата Мили таблицами переходов φ и выходов ψ иллюстрируется табл. 2.1, а описание F-автомата Мура — таблицей переходов (табл. 2.2).
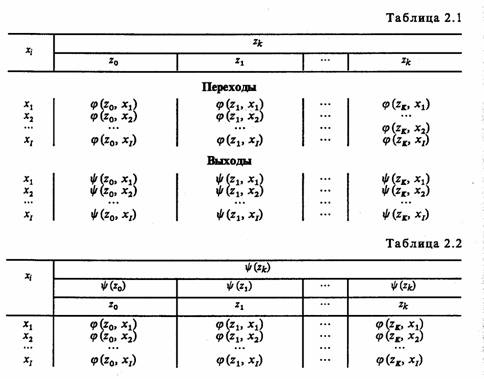
Примеры табличного способа задания F-автомата Мили F1 с тремя состояниями, двумя входными и двумя выходными сигналами приведены в табл. 2.3, а для F-автомата Мура F2 — в табл. 2.4.
При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал хк вызывает переход из состояния zi, в состояние Zi, то на графе автомата дуга, соединяющая вершину zi с вершиной zj обозначается хк. Для того чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производится так: если входной сигнал хк действует на состояние zi, то, согласно сказанному, получается дуга, исходящая из zi и помеченная хк; эту дугу дополнительно отмечают выходной сигналом у=ψ(zь хк). Для автомата Мура аналогичная разметка графа такова: если входной сигнал хк, действуя на некоторое состояние автомата, вызывает переход в состояние Zj, то дугу, направленную в Zj и помеченную хк. дополнительно отмечают выходным сигналом у=ψ (zj, xk).

На рис. 2.3, а, б приведены заданные ранее таблицами F-автоматы Мили F1 и Мура F2 соответственно.
При решении задач моделирования систем часто
более удобной формой является матричное задание конечного автомата. При этом
матрица соединений автомата есть квадратная матрица ![]() строки которой соответствуют исходным
состояниям, а столбцы -состояниям перехода. Элемент сij= xk/ys, стоящий на пересечении i-й строки и j-го столбца, в случае автомата Мили соответствует входному
сигналу хk, вызывающему переход
из состояния zj, в состояние zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили F1, рассмотренного выше, матрица соединений имеет вид
строки которой соответствуют исходным
состояниям, а столбцы -состояниям перехода. Элемент сij= xk/ys, стоящий на пересечении i-й строки и j-го столбца, в случае автомата Мили соответствует входному
сигналу хk, вызывающему переход
из состояния zj, в состояние zj, и выходному сигналу ys, выдаваемому при этом переходе. Для автомата Мили F1, рассмотренного выше, матрица соединений имеет вид
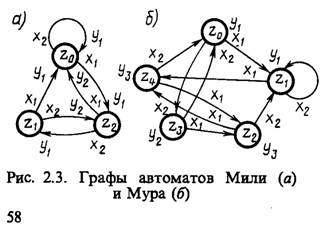
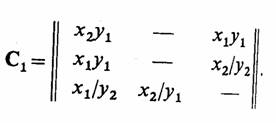
Если переход из состояния zi в состояние zj происходит под действием нескольких сигналов, элемент матрицы сij представляет собой множество пар «вход-выход» для этого перехода, соединенных знаком дизъюнкции.
Для F-автомата Мура элемент cij равен множеству входных сигналов на переходе (zh Zj), а выход описывается вектором выходов
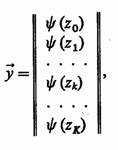 г
г
i-я компонента которого — выходной сигнал, отмечающий состояние Z,.
Пример 2.2. Для рассмотренного выше F-автомата Мура F2 запишем матрицу соединений и вектор выходов:
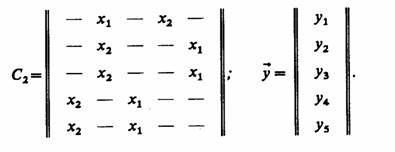
Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания F-автомата это означает, что в графе автомата из любой вершины не могут выходить два ребра и более, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.
Рассмотрим вид таблицы переходов и графа асинхронного конечного автомата. Для F-автомата состояние zk называется устойчивым, если для любого входа хiε Х, для которого φ{zk, xi)=zk, имеет место ψ(zк, хi)=ук. Таким образом, .F-автомат называется асинхронным, если каждое его состояние zkεZ устойчиво.
Необходимо отметить, что вообще на практике автоматы всегда являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например введением сигналов синхронизации. Однако на уровне абстрактной теории, когда конечный автомат выступает в виде математической схемы для формализации конкретных объектов без учета ряда второстепенных особенностей, часто удобно оказывается оперировать с синхронными конечными автоматами.
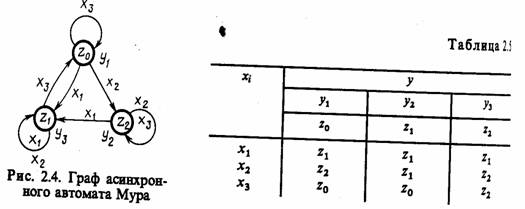
Пример 2.3. Рассмотрим асинхронный F-автомат Мура, который описан табл. 2.5 и приведен на ряс. 2.4. Очевидно, что если в таблице переходов асинхронного автомата некоторое состояние zk стоит на пересечении строки хi- и столбца zs (z≠k), то это состояние zk обязательно должно встретиться в этой же строке в столбце zk. В графе асинхронного автомата, если в некоторое состояние имеются переходы в других состояний под действием каких-то сигналов, то в вершине zk должна быть петля, отмеченная символами тех же входных сигналов. Анализ табл. 2.3 и 2.4 или рис. 2.3, б и 2.4 показывает, что представленные там F-автоматы Fl и F2 являют синхронными.
Таким образом, понятие F-автомата в дискретно-детерминированном подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах обработки информации и управления. В качестве таких объектов в первую очередь следует назвать элементы и узлы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией и т. д. Для всех перечисленных объектов характерно наличие дискретных состояний и дискретный характер работы во времени, т. е. их описание с помощью F-схем является эффективным. Но широта их применения не означает универсальности этих математических схем. Например, этот подход непригоден для описания процессов принятия решений, процессов в динамических системах с наличием переходных процессов и стохастических элементов.
2.4. ДИСКРЕТНО-СТОХАСГИЧЕОСИЕ МОДЕЛИ
(Р-СХЕМЫ)
Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе к формализации процесса функционирования исследуемой системы S. Так как сущность дискретизации времени при этом подходе остается аналогичной рассмотренным в § 2.3 конечным автоматам, то влияние фактора стохастичности проследим также на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.
Основные соотношения. В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.
Применение схем вероятностных автоматов (Р-схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.
Введем математическое понятие Р-автомата, используя понятия, введенные для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (хi„ zs,), где xi и zs, — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции φ и ψ, то с их помощью осуществляются отображения G→Z и G→Y, то говорят, что F = <Z, X, Y, φ>, ψ определяет автомат детерминированного типа.
Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида (zk, yj), где уj — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:
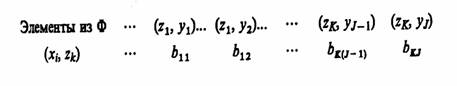
При этом ![]() вероятности перехода автомата в
состояние zk и
появления на выходе сигнала yj если он
был в состоянии zs и на его
вход в этот момент времени поступил сигнал Xj. Число таких распределений, представленных в виде таблиц,
равно числу элементов множества G. Обозначим множество
этих таблиц через В. Тогда четверка элементов P=(Z, X, Y, В) называется вероятностным автоматом (Р-автоматом).
вероятности перехода автомата в
состояние zk и
появления на выходе сигнала yj если он
был в состоянии zs и на его
вход в этот момент времени поступил сигнал Xj. Число таких распределений, представленных в виде таблиц,
равно числу элементов множества G. Обозначим множество
этих таблиц через В. Тогда четверка элементов P=(Z, X, Y, В) называется вероятностным автоматом (Р-автоматом).
Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

При этом ![]() вероятности перехода Р-автомата в
состояние zk и
появления выходного сигнала ук при условии, что yk-автомат
находился в состоянии zs и на его вход
поступил входной сигнал xi.
вероятности перехода Р-автомата в
состояние zk и
появления выходного сигнала ук при условии, что yk-автомат
находился в состоянии zs и на его вход
поступил входной сигнал xi.
Если для всех к и j имеет место соотношение qkzi=bkj, то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.
Пусть теперь определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющее следующий вид:
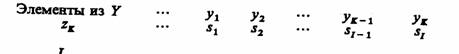
Здесь 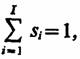 где si — вероятность появления выходного сигнала yt при условии, что Р-автомат
находился в состоянии zk
где si — вероятность появления выходного сигнала yt при условии, что Р-автомат
находился в состоянии zk
Возможные приложения. Если для всех k и i имеет место соотношение zksi=bki, то такой Р-автомат называется вероятностным автоматом Мура. Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом, задаваемым F= ‹Z, X, Y, φ,ψ› . Частным случаем Р-автомата, задаваемого как P=‹Z, X, Y, В›, являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминирование . Если выходной сигнал Р-автомата определяется детерминировано, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.
Пример 2.4. Рассмотрим У-детерминированный Р-автомат, который задан таблицей переходов (табл. 2.6) и таблицей выходов:
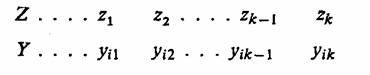
В этих
таблицах рij —
вероятность перехода Р-автомата из состояния z, в состояние zj. При этом, как и ранее, ![]()
Первую из этих таблиц можно представить в виде квадратной матрицы размерности К х К, которую будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае такая матрица переходов имеет вид
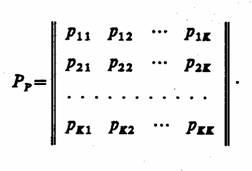
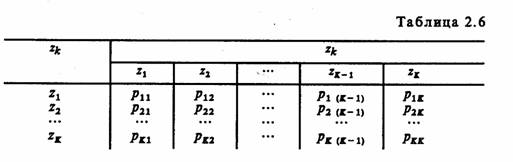
Для описания Υ-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида
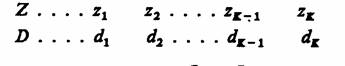
Здесь dK —
вероятность того, что в начале работы Р-автомат находится в состоянии к.к.
При этом 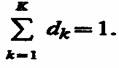
Будем считать, что до начала работы (до нулевого такта времени) Р-автомат всегда находится в состоянии г0 и в нулевой такт времени меняет состояние в соответствии с распределением D. Дальнейшая смена состояний Р-автомата определяется матрицей переходов Рp. Информацию о начальном состоянии Р-автомата удобно внести в матрицу Pp увеличив ее размерность до (K+1) х (К+1). При этом первая строка такой матрицы, сопоставляемая состоянию z0, будет иметь вид (0, dl, d2, ... ..., dK), а первый столбец будет нулевым.
Описанный У-детерминированный Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода рij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями.
Пример 2.5. Пусть задан Ү-детерминированный Р-автомат

На рис. 2.5 показан граф переходов этого автомата. Требуется оценить суммарные финальные вероятности пребывания этого Р-автомата в состояниях z2 и z3.
При использовании аналитического подхода можно записать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей. При этом начальное состояние z0 можно не учитывать, так. как начальное распределение не оказывает влияния на значения финальных вероятностей. Тогда имеем

где сk — финальная вероятность пребывания Р-автомата в состоянии zk.
Получаем систему уравнений
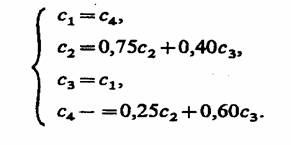
Добавим к этим уравнениям условие нормировки с1+с2 + с3 + с4, — 1. Тогда, решая систему уравнений, получим с1 = 5/23, c2=8/23, с3 = 5/23, с4 = 5/23. Таким образом , с2+с3 = 13/23=0,5652. Другими словами, при бесконечной работе заданного в этом примере У-детерминированного Р- автомата на его выходе формируется двоичная последовательность с вероятностью появления единицы, равной 0,5652.
Подобные Р-автоматы могут использоваться как генераторы марковских • последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е.
Для оценки различных характеристик исследуемых систем, представляемых в виде Р-схем, кроме рассмотренного случая аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.
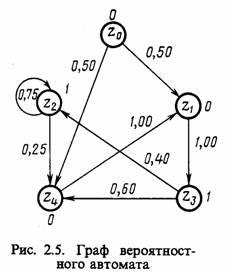
.
2.5. НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ
(Q-СХЕМЫ)
Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ. queuing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания [6, 13, 33, 37, 51].
Основные соотношения. В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т. д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирования. Остановимся на основных понятиях массового обслуживания, необходимых для использования Q-схем, как при аналитическом, так и при имитационном.
В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого г-го прибора обслуживания Пi(рис. 2.6), состоящего из накопителя заявок Hh в котором может одновременно находиться li,=0, LiH заявок, где LfH — емкость г-го накопителя, и канала обслуживания заявок (или просто канала) Kt. На каждый элемент прибора обслуживания Д поступают потоки событий: в накопитель Hi — поток заявок,wi на канал Ki — поток обслуживании.
Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью {tn„} = {0≤ t1≤t2…≤tn≤… }, где tn — момент наступления n-го события — неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между n-м и (n—1)-м событиями {τn}, которая однозначно связана с последовательностью вызывающих моментов {tn}, где τn= tn -tn -tn -1,1 to =0 Т.Е τ =t1.
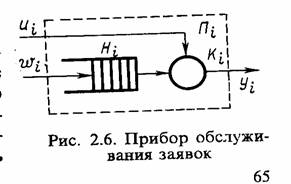
Потоком неоднородных событий называется последовательность {tn,ƒn), где tn -вызывающие моменты; tn — набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок могуть быть заданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т. п.
Рассмотрим поток, в котором события разделены интервалами времени τ1„ τ 2,... ..., которые вообще являются случайными величинами. Пусть интервалы τ 1; τ 2,... независимы между собой. Тогда поток событий называется потоком с ограниченным последействием.
Пример потока событий приведен на рис. 2.7, где обозначено Tj — интервал между событиями (случайная величина); Ти — время наблюдения, Тс — момент совершения события.
Интенсивность потока можно рассчитать экспериментально по формуле
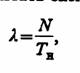
где N— число событий, произошедших за время наблюдения Ти. Если Тj =const или определено какой-либо формулой Tj=ƒ(Tj -1), то поток называется детерминированным. Иначе поток называется случайным
Случайные потоки бывают:
— ординарными, когда вероятность одновременного появления 2-х и более событий равна нулю;
— стационарными, когда частота появления событий постоянная;
— без последействия, когда вероятность не зависит от момента совершения предыдущих событий.
Поток событий называется ординарным, если вероятность того, что на малый интервал времени Δt, примыкающий к моменту времени t, попадает больше одного события Р>1 (I, Δt), пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени Δt попадает ровно одно событие Р1 (t, Δt), т. е. Р1 (t, Δt)»P>t1 (t, Δt). Если для любого интервала Δt событие
![]()
как сумма вероятностей событий, образующих полную группу и несовместных, то дня ординарного потока событий
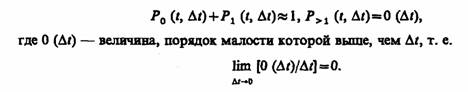
Стационарным потоком событий называется поток, для которого вероятность появления того или иного числа событий на интервале времени τ зависит лишь от длины этого участка и не зависит от того, где на оси времени 0t взят этот участок.
Рассмотрим на оси времени 0t ординарный поток событий и найдем среднее число событий, наступающих на интервале времени Δt, примыкающем к моменту времени t. Получим
![]()
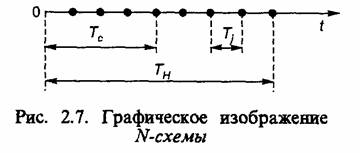
Тогда среднее число событий, наступающих на
участке времени Δt в единицу
времени, составит [Pt (t, Δt)]/Δt. Рассмотрим предел
этого выражения при Δt→0. Если этот
предел существует, то она называется интенсивностью (плотностью) ординарного
потока событий![]()
![]()
Интенсивность потока может быть любой неотрицательной функцией времени, имеющей размерность, обратную размерности времени. Для стационарного потока его интенсивность не зависит от времени и представляет собой постоянное значение, равное среднему числу событий, наступающих в единицу времени
Возможные приложения. Обычно в приложениях при моделировании различных систем применительно к элементарному каналу обслуживания Кi можно считать, что поток заявок w,e W, т. е. интервалы времени между моментами появления заявок (вызывающие моменты) на входе Ki образует подмножество неуправляемых переменных, а поток обслуживания, u i€ Uт. е. интервалы времени между началом и окончанием обслуживания заявки, образует подмножество управляемых переменных.
Заявки, обслуженные каналом Кi и заявки, покинувшие прибор Пi по различным причинам необслуженными (например, из-за переполнения накопителя Пi), образуют выходной поток y>,e Y, т. е. интервалы времени между моментами выхода заявок образуют подмножество выходных переменных.
Процесс функционирования прибора обслуживания Пiможно представить как процесс изменения состояний его элементов во времени zi(t). Переход в новое состояние для Пi означает изменение количества заявок, которые в нем находятся (в канале Ki и в накопителе Нi .Таким образом, вектор состояний для Пi имеет вид z,= (z,H, ZiK), где z,н — состояние накопителя Нi (z; =0 — накопитель пуст, z,н=1 — в накопителе имеется одна заявка, ..., zн=Lн — емкость накопитель полностью заполнен); Li — емкость накопителя Hh измеряемая числом заявок, которые в нем могут поместиться; ztK — состояние канала Ki(zk =0— канал свободен, zik =1—канал занят и т. д.).
В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания Пi(сети массового обслуживания). Если каналы Kt различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы Пi и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.
Связи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.
Собственными (внутренними) параметрами Q-схемы будут являться количество фаз Lф, количество каналов в
каждой фазе Lkp ![]() ,
количество накопителей каждой фазы
,
количество накопителей каждой фазы ![]() емкость i-го накопителя
емкость i-го накопителя
![]() Следует отметить, что
в теории массового обслуживания в зависимости от емкости накопителя применяют
следующую терминологию для систем массового обслуживания: системы с потерями
Следует отметить, что
в теории массового обслуживания в зависимости от емкости накопителя применяют
следующую терминологию для систем массового обслуживания: системы с потерями
(Li н=0, т. е. накопитель в приборе Пi отсутствует, а имеется только канал обслуживания Ki), системы с ожиданием (LiH→oo, т. е. накопительПi, имеет бесконечную емкость и очередь заявок не ограничивается) и системы смешанного типа (с ограниченной емкостью накопителя Нi. Всю совокупность собственных параметров Q-схемы обозначим как подмножество Н.
Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Ht и обслуживания заявок каналом Kt каждого элементарного обслуживающего прибора Пi Q-схемы. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов.
В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т. е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя на обслуживание каналом Kh можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Нi ожидает окончания обслуживания предшествующей заявки каналом Ki и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н;, прерывает обслуживание каналом Ki, заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из Kt заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Нi.
При рассмотрении алгоритмов функционирования приборов обслуживания Пi(каналов Ki и накопителей Нi ) необходимо также задать набор правил, по которым заявки покидают Нi, и Кi{. для Hi — либо правила переполнения, по которым заявки в зависимости от заполнения Нi покидают систему, либо правила ухода, связанные с истечением времени ожидания заявки в Hi для Ki — правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале Кi или не допускаются до обслуживания каналом Ki т. е. правила блокировок канала. При этом различают блокировки Кi по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q-схеме, регулирующих поток заявок в зависимости от состояний Q-схемы. Весь набор возможных алгоритмов поведения заявок в Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.
Таким образом, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается в виде Q=(W, U, H, Z, R, А).
При ряде упрощающих предположений относительно подмножеств входящих потоков W и потоков обслуживания U(выполнение условий стационарности, ординарности и ограниченного последействия) оператора сопряжения элементов структуры R (однофазное одноканальное обслуживание в разомкнутой системе), подмножества собственных параметров Н (обслуживание с бесконечной емкостью накопителя), оператора алгоритмов обслуживания заявок А (бесприоритетное обслуживание без прерываний и блокировок) для оценки вероятностно-временных характеристик можно использовать аналитический аппарат, разработанный в теории массового обслуживания. При принятых предположениях в обозначениях Д. Кендалла будет иметь место классическая система обслуживания типа М/М/1 (одноканальная система с марковским входящим потоком заявок и марковским потоком обслуживания). Рассмотрим на примере основные аналитические соотношения для такой элементарной Q-схемы [6, 24, 37].
Пример 2.6. Допустим, что процесс обслуживания начинается при отсутствии заявок в накопителе. Тогда состояния системы массового обслуживания описываются следующей системой уравнений:
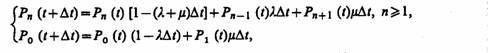
где Рп (t) — вероятность нахождения системы в состоянии zn (t)€Z в момент времени t, т. е. когда в ней имеется п заявок.
Эти уравнения следуют из того, что вероятность нахождения в системе л заявок в момент времени (t+∆t) равна вероятности нахождения в системе л заявок в момент t, умноженной на вероятность того, что за время ∆t в систему не поступит ни одной заявки и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе (n— 1) заявок в момент t, умноженная на вероятность того, что за время ∆t поступит одна заявка и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе (n+ 1) заявок в момент t, умноженная на вероятность того, что за время ∆t одна заявка покинет систему и не поступит ни одной заявки. Вероятность того, что за время ∆t не поступит ни одной заявки и ни одна заявка не покинет систему, равна (1 —λ∆t)(1+ µ∆t). Член, содержащий (∆t)2, при составлении дифференциального уравнения опускается. Следовательно, можно записать 1— (λ+μ)∆t. Относительно остальных двух членов первого уравнения заметим, что
![]()
Перенеся Рn (t) влево и устремив ∆t к нулю, получим систему дифференциальных уравнений
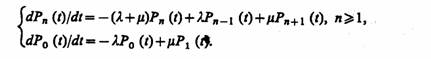
Найдем выражение для математического ожидания числа заявок, находящихся в накопителе, и среднего времени ожидания заявок в накопителе для стационарного состояния р= λ / µ <1. Приравняв нулю производные по времени и исключив, таким образом, время t из уравнений, получим систему алгебраических уравнений
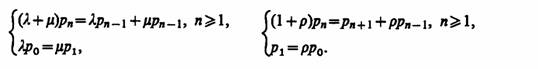
Пусть в первом уравнении и=1. Тогда (1+p)P1=P2+PP0- Подставив сюда
значение, из второго уравнения, находим р2=р2Ро- Повторяя эти операции,получаем рn=р2р0,
причем ![]() так как это сумма вероятностей того, что в
системе нет ни одной заявки, имеется одна заявка, две заявки и т. д. Сумма этих
вероятностей должна быть равна единице, так как рассматриваются все возможные состояния
системы. Поэтому
так как это сумма вероятностей того, что в
системе нет ни одной заявки, имеется одна заявка, две заявки и т. д. Сумма этих
вероятностей должна быть равна единице, так как рассматриваются все возможные состояния
системы. Поэтому 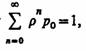
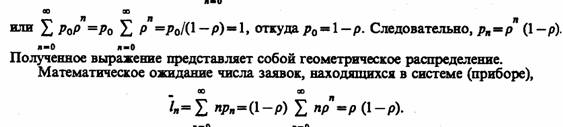
Отметим, что ln — среднее значение и возможны колебания числа заявок, ожидающих обслуживания, что можно оценить с помощью дисперсии:
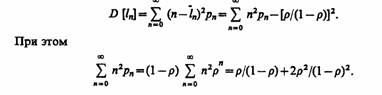
![]()
Математическое ожидание числа заявок, находящихся в
накопителе,
777777777777777777777777777777777777777777777777777
Среднее время ожидания заявок в накопителе
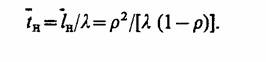
Возможности оценки характеристик с использованием аналитических моделей теории массового обслуживания являются весьма ограниченными по сравнению с требованиями практики исследования и проектирования систем, формализуемых в виде Q-схем. Несравненно большими возможностями обладают имитационные модели, позволяющие исследовать Q-схему, задаваемую Q—(W, U,H, Z, Y, R, А), без ограничений. На работу с Q-схемами при машинной реализации моделей ориентированы многие языки имитационного моделирования, например SIMULA, SIMSCRIPT, GPSS и др. Детально вопросы, связанные с имитационным моделированием Q-схем, будут рассмотрены далее.
2.6. СЕТЕВЫЕ МОДЕЛИ (N-СХЕМЫ)
В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри [28, 30].
Основные соотношения. Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное программирование, дискретные динамические системы и т. д.).
Формально сеть Петри (N-схема) задается четверкой вида
![]()
где В — конечное множество символов, называемых позициями, В ≠Ø; D — конечное множество символов, называемых переходами, D≠Ø, В ∩D ≠Ø ; I—входная функция (прямая функция инцидентности), I: ВхD→-{0, 1}; О — выходная функция (обратная функция инцидентности), О : D х В→ {0,1}. Таким образом, входная функция отображает переход dj в множество входных позиций bi € I(dj), а выходная функция О отображает переход dj в множество выходных позиций bi € D(dj). Для каждого перехода
di€ D можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О(dj) как
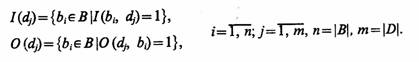
Аналогично, для каждого перехода bi€В вводятся определения множества входных переходов позиции I(bi) и множества выходных переходов позиции I(bi):
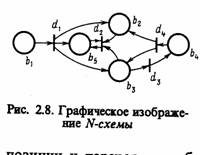
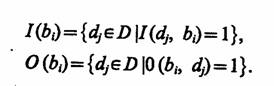
Графически N-схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходовние N-схемы (рис. 2.8). Как видно из этого рисунка ,граф N-схемы имеет два типа узлов :позиции и переходы, изображаемые 0 и 1 соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или перехода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.
Пример 2.7. Представим формально N-схему, показанную в виде графа на рис. 2.7:
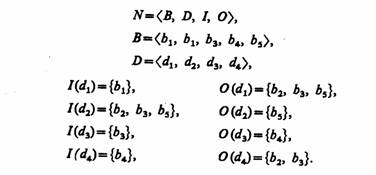
Возможные приложения. Приведенное представление N-схемы может использоваться только для отражения статики моделируемой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки) М: В→{О, 1, 2, ...}. Маркировка М есть присвоение неких абстрактных объектов, называемых метками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графическом задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры).
Маркированная (размеченная) N-схема может быть описана в виде пятерки NM = ‹B, D, I, О, М› и является совокупностью сети Петри и маркировки М [28, 30].
Функционирование N-схемы отражается путем перехода от разметки к разметке. Начальная разметка обозначается как Мо : В→ {0, 1, 2, ...}. Смена разметок происходит в результате срабатывания
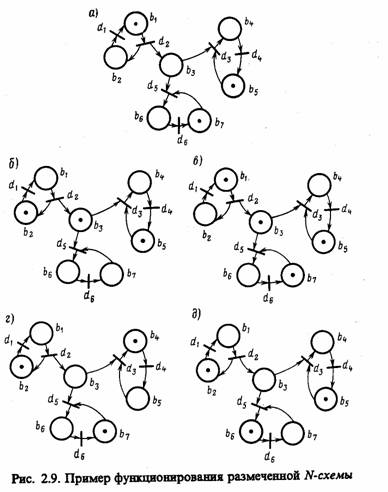
одного из переходов dj εD сети. Необходимым условием срабатывания перехода dj является btel(dj) {M(bi)^l}, где M{bt} — разметка позиции Ьг. Переход dh для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход.
Срабатывание перехода dj изменяет разметку сети М(b) = =(M(b1), M(b2), ..., M(bn))2 на разметку М'(b) по следующему правилу:
![]()
т. е. переход dj изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций. Для изображения смены разметки М на М' применяют обозначение М |dj_М'.
Пример 2.8. Рассмотрим размеченную N-схему с начальной разметкой Мо={1, 0, 0, 0, 1, 0, 1}, которая приведена на рис. 2.9, а. При такой начальной разметке N-схемы единственным готовым к срабатыванию является переход d2, срабатывание
которого ведет к смене разметки Мо |-2 М1, где M1 = {0, 1, 1, 0, 1, 0, 1} (рис. 2.9, б). При разметке М1 возможно срабатывание переходов d1, d3 и d5. В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок (рис. 2.9, в, г. д). Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.
Таким образом, N-схема выполняется путем запусков переходов под управлением количества меток и их распределения в сети. Переход запускается удалением меток из его входных позиций и образованием новых меток, помещаемых в выходные позиции. Переход может запускаться только тогда, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число меток, по крайней мере равное числу дуг из позиции в переход.
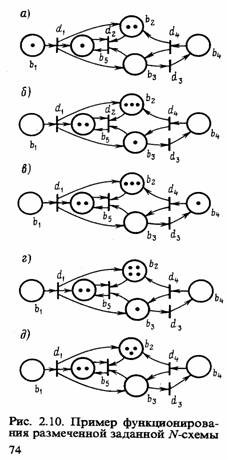
Пример 2.9. Для некоторой заданной размеченной N-схемы (ряс. 2.8) с начальной маркировкой Мо = {1, 2, О, 0, 1} (рис. 2.10, а) разрешенным является только переход d1, а остальные переходы d2, d3 и d4 — запрещенные. В результате выполнения этого перехода получим новую размеченную N-схему (рис. 2.10, б). Теперь разрешены переходы d2 и d%; в результате их запуска получим новую размеченную N-схему. Переходы d2 и d3 находятся в конфликте, так как запущен, может быть только один из них. Например, при запуске d3 получим сеть, показанную на рис. 210, в. Теперь разрешен только переход d4. и получим новую размеченную сеть (рис. 2.10, г). Теперь разрешено два перехода: d2 и d3 (в конфликте). Запустим переход d2 (рис. 2.10, д). Теперь ни один переход не может быть запущен и выполнение сети прекращается.
Важной особенностью "моделей процесса функционирования систем с использованием типовых N-схем является простота построения иерархических конструкций модели. С одной стороны, каждая N-схема может рассматриваться как макропереход или макропозиция модели более высокого уровня. С другой стороны, переход, или позиция N-схемы, может детализироваться в форме отдельной подсети для более углубленного исследования процессов в моделируемой системе. Отсюда вытекает возможность эффективного использования N-схем для моделирования параллельных и конкурирующих процессов в различных системах.
Типовые N-схемы на основе обычных размеченных сетей Петри пригодны для описания в моделируемой системе S событий произвольной длительности. В этом случае модель, построенная с использованием таких N-схем, отражает только порядок наступления событий в исследуемой системе S. Для отражения временных параметров процесса функционирования моделируемой системы S на базе N-схем используется расширение аппарата сетей Петри: временные сети, ii-сети, сети Мерлина и т. д. [19]. Детально вопросы, связанные с имитационным моделированием с использованием N-схем, будут рассмотрены далее.