Измерения
4.1. Результат измерения и его характеристики
4.2. Элементы теории вероятностей и характеристики распределения случайных величин
4.3. Виды измерений. Основное уравнение измерений
4.4. Общие требования к проведению измерений
4.5. Методики выполнения измерений
4.6. Обработка результатов прямых однократных измерений
4.7. Обработка результатов прямых многократных измерений
4.8. Обработка результатов косвенных измерений
4.1. Результат измерения и его характеристики
♦ Измерение — это совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения данной величины. ♦
Результат измерения представляет собой конечный продукт некоего производственного процесса, имеющего, как и любая другая продукция, свои показатели качества. Среди них важнейшим с учетом того, что речь идет об измерительном процессе, показателем качества является точность полученного результата.
Под точностью результата измерений понимают одну из его характеристик, отражающую близость к нулю погрешности.
Погрешность результата измерения — это отклонение результата измерения от истинного значения измеряемой величины. Так как истинное значение может быть получено только в результате бесконечного процесса измерений и требует непрерывного совершенствования методов и средств измерений, то оно всегда остается неизвестным. В практических целях вместо ис-тинного значения используется действительное значение измеряемой величины, т.е. значение, полученное экспериментальным путем и настолько близкое к истинному, что в рамках поставленной измерительной задачи может быть использовано вместо него. Таким образом, погрешность измерения может быть выражена зависимостью:

Значение АХ получило название абсолютной погрешности измерения. Абсолютная погрешность измерения выражена в единицах измеряемой величины. К сожалению, судить по значению абсолютной погрешности о качестве измерения нельзя. Действительно, если известно, что погрешность измерения составляет ± 1 мм, то оценить его качество затруднительно. Необходимо сопоставить значение абсолютной погрешности и значение измеренной величины. Эта задача решается введением понятия относительной погрешности измерения. Относительная погрешность измерения рассчитывается как отношение абсолютной погрешности к действительному (или измеренному) значению величины. Относительную погрешность выражают в долях единицы или в процентах в соответствии с зависимостью:

По закономернорти появления погрешности делятся на систематические и случайные. При этом, как правило, самостоятельного значения они не имеют, а рассматриваются в качестве составляющих собственно погрешности измерения.
♦ Систематической погрешностью измерения называется составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. ♦
Рекомендациями МИ 1317—04 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов и контроле их параметров» установлено, что в качестве характеристик систематической погрешности измерения целесообразно использовать среднее квадратическое отклонение неисключенной систематической составляющей или границы, в которых неисключенная систематическая составляющая находится с заданной вероятностью (в том числе и с вероятностью, равной единице). Первая характеристика получила название точечной; вторая — интервальной. При проведении измерений принято вводить поправки в результаты и исключать систематическую составляющую. Однако всегда остаются погрешности вычисления и погрешности в определении значения самих поправок, а также систематические составляющие, ввести поправки на величину которых не представляется возможным ввиду их малости. Поэтому считается, что результат всегда содержит систематическую составляющую погрешности измерения, которую называют неисключенной.
♦ Случайной погрешностью измерения называется составляющая погрешности, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью. ♦
В качестве характеристик случайной составляющей погрешности используются ее среднее квадратическое отклонение и (при необходимости) нормализованная автокорреляционная функция.
Для характеристики погрешности измерений кроме характеристик случайной и систематической составляющих используются среднее квадратическое отклонение и границы, в пределах которых погрешность измерений находится с заданной вероятностью. Точечные характеристики рекомендуется использовать в случаях, когда результаты измерений (испытаний) используются совместно с другими результатами измерений, а также при расчетах погрешностей величин, функционально связанных с результатами измерений (например, результатов косвенных измерений). Интервальные характеристики используются для решения определенных технических задач. Если интервал ограничен наибольшим и наименьшим значениями погрешности измерений, а истинное значение погрешности находится внутри него с заданной вероятностью, то этот интервал называется доверительным интервалом, а вероятность — доверительной вероятностью.
В связи с тем, что истинное значение и измеряемой величины, и погрешности результата измерения неизвестны, а измерениям подвергаются все больше величин, для которых само определение «физическая величина» неприменимо, в последнее
время для оценки качества измерительной информации все чаще используется понятие «неопределенность измерений».
• Неопределенность измерений — параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине. ♦
Этим параметром может быть среднее квадратическое отклонение (стандартное отклонение), число, кратное ему, или половина доверительного интервала. Неопределенность состоит, как правило, из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментально определенными средними квадратическими отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются на данных эксперимента или другой информации. Структурно неопределенность результата измерения обычно состоит из нескольких составляющих, которые могут быть вызваны следующими причинами:
• неполным описанием (неточным определением) измеряемой величины;
• несовершенной реализацией описания (несовершенством выбранного метода измерения);
• неполным учетом влияющих величин и несовершенством методов их измерения;
• субъективными погрешностями оператора;
• конечной величиной разрешающей способности примененных средств измерений;
• неточными значениями констант и других параметров, полученных от внешних источников и используемых в алгоритме обработки результатов эксперимента, и др.
Эти составляющие определяют также и погрешность измерения. Еще раз отметим, что основное различие между неопределенностью и погрешностью состоит в представлении о существовании истинного значения. Если в начальный постулат заложено существование истинного значения, то это неизбежно приводит к определению погрешности измерения. Если существование истинного значения отрицается, то следствием является представление о неопределенности результата измерения.
Составляющие неопределенности по способу получения их численных значений подразделяются на две категории: А и В.
К категории А относят составляющие, численные значения которых получены на основе статистического анализа экспериментальных данных. Это стандартные отклонения (средние квадратические отклонения). При достаточно большом числе наблюдений данные оценки (среднее арифметическое значение и стандартное отклонение) являются наилучшими. Составляющие, относимые к категории В, оцениваются любым другим способом, кроме статистического анализа. Для их оценки используется аппарат субъективной теории вероятностей на основе априорной информации — справочных материалов, экспертных оценок, данных предварительных измерений и т.д.
4.2. Элементы теории вероятностей
и характеристики распределения случайных величин
Для оценки составляющих погрешности и неопределенности результата измерения используются такие характеристики, как среднее арифметическое значение, среднее квадратическое отклонение и др. Для лучшего понимания предлагаемого материала рассмотрим некоторые понятия и определения теории вероятностей и математической статистики, применяемых в метрологии.
Наличие случайной составляющей погрешности измерения приводит к тому, что для получения результата измерения целесообразно рассматривать измеряемые величины как случайные. Кроме того, сами случайные погрешности могут быть определены только с привлечением аппарата теории вероятностей, которая представляет собой науку, изучающую закономерности случайных явлений. Теория вероятностей устанавливает закономерности только для массовых явлений, т.е. таких явлений, которые могут повторяться многократно при одних и тех же условиях. В метрологии массовыми являются измерения, проводимые с помощью одного и того же средства измерений, характеристики множества средств измерений одного типа и др.
Для того чтобы охарактеризовать случайную погрешность измерения, обратимся к определению случайного события и его вероятности.
Случайным называется событие, которое в данном опыте может произойти или не произойти. Каждый опыт может быть охарактеризован множеством событий. Например, при игре в кости один и тот же опыт может быть представлен следующими событиями: «выпало 1»; «выпало 2»; «выпало 3»; «выпало 4»; «выпало 5»; «выпало 6». Точное определение ожидаемого исхода опыта — установление случайного события — имеет важнейшее значение. Обозначим случайное событие А и будем иметь в виду, что большинство событий в метрологии понимаются как выполнение соотношения

Каждое из событий в опыте обладает какой-то степенью возможности: одни — большей, другие — меньшей. Для количественного сравнения случайных событий по степени их возможности используется количественная характеристика каждого случайного события, которая выражается числом тем большим, чем более возможно данное событие. Эту характеристику называют вероятностью случайного события и обозначают, как правило, Р. Таким образом, вероятность случайного события является численной мерой объективной возможности этого события и определяется по формуле:

Назначение события оказывает прямое влияние на значение вероятности. Так, если речь идет об игре в кости и первый из играющих имеет результат 4, то ожидаемых событий для второго играющего — два: выигрыш или поражение. Для выигрыша необходимо получить 5 и 6. Таким образом, в этом случае вероятность выигрыша для него составит Р(5,6) = 2/6 = 1/3. Вероятность будет совсем другой, если в качестве события А рассматривать вероятность проигрыша или если первый из играющих набрал, например, два очка.
Определение числа п — числа всех возможных исходов опыта — часто весьма затруднительно, но самое главное, что в метрологии попросту невозможно ввиду ограниченной возможности повторения опытов. Число т — количество раз, когда событие А в результате опыта наступило, в метрологии также определяется на основе ограниченного числа опытов. Поэтому в практике метрологических работ вместо вероятности используют частоту появления случайного события А:

Частоту Р*(А) ввиду ее использования в роли вероятности в практике метрологических работ называют статистической вероятностью.
Свойства случайной величины исчерпывающе описываются законом распределения случайной величины, который представляет собой соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Случайные величины можно разделить на дискретные и непрерывные. Значения дискретной случайной величины могут быть перечислены. Значения непрерывной случайной величины непрерывно заполняют некоторый интервал. Случайные погрешности измерений относятся к непрерывным случайным величинам, но проявляются часто в виде некоторого набора значений, т.е. дискретно. Поэтому к ним применимы понятия и непрерывных, и дискретных случайных величин.
Для дискретной случайной величины удобной формой описания закона распределения является ряд распределения — таблица, в которой перечислены возможные значения случайной величины х, и соответствующие им значения вероятности />,-(табл. 4.1).
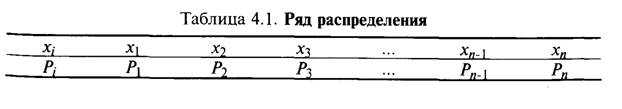
Еще одной, более удобной, универсальной и часто применяемой на практике формой описания закона распределения случайной величины является функция распределения F(x), которая определяет вероятность того, что случайная величина X будет принимать значения, меньшие некоторого ограничения х:


Рис. 4.2. График функции распределения дискретной случайной величины
Так как функция распределения непрерывной случайной величины (см. рис. 4.1) является непрерывно дифференцируемой, то для ее описания часто пользуются первой производной
 или
плотностью распределения. Плотность распределения представляет собой
одну из форм описания закона распределения, применяемых для непрерывных
случайных величин. Плотность распределения обозначается, как правило, F'(x) или f(x). График плотности
распределения представлен на рис. 4.3.
или
плотностью распределения. Плотность распределения представляет собой
одну из форм описания закона распределения, применяемых для непрерывных
случайных величин. Плотность распределения обозначается, как правило, F'(x) или f(x). График плотности
распределения представлен на рис. 4.3.

Рис. 4.3. График плотности распределения непрерывной случайной величины
Взаимосвязь между функцией распределения и плотностью распределения случайной непрерывной величины имеет вид:


Законы распределения позволяют решать любые практические задачи, связанные со случайными величинами, и в этом их безусловное достоинство. Однако использование законов распределения для решения практических метрологических задач связано также и с определенными проблемами. Прежде всего, чтобы определить закон распределения, необходимо провести достаточно трудоемкое исследование (требуются специальные оборудование и методика, многократные измерения, качественный анализ и т.д.), что не всегда возможно. Наибольшее удобство для практического использования предоставляют числовые характеристики случайной величины — математическое ожидание и дисперсия случайной величины, которые характеризуют значение случайной величины и ее разброс соответственно. Числовые характеристики связаны с законами распределения, поэтому иногда используют и другие показатели, но математическое ожидание и дисперсия — наиболее употребляемые, основные числовые характеристики случайной величины.
Математическим ожиданием случайной величины называется число, определяемое для непрерывных случайных величин по зависимости:

Из формулы (4.12) следует, что значение случайной величины х может быть определено величиной среднего арифметического значения X, полученного по результатам многократных наблюдений этой величины. Среднее арифметическое значение может сильно отличаться от действительного значения измеряемой величины за счет:
• наличия систематических составляющих погрешности измерения, поэтому для его получения категорически необходимо введение поправки на величину систематической составляющей погрешности;
• возможности появления грубой погрешности измерения, для устранения которой проводят минимум три измерения;
• несоответствия среднего арифметического значения закону распределения случайной величины, в связи с чем обработка результатов измерений всегда должна начинаться с определения (указания) принятого закона распределения.
Итак, после определения среднего арифметического значения случайной величины на числовой оси можно отложить ее значение — среднее арифметическое. Легко представить случай, когда для двух рядов измерений средние арифметические значения равны. Значит, одного этого значения недостаточно, чтобы охарактеризовать случайную величину. Необходима характеристика разброса. В качестве ее можно принять разность значений xmax — xmшn, полученных при измерениях результатов. Эта характеристика получила название размаха значений, случайной величины.
Однако при равенстве и средних арифметических значений, и размахов два ряда измерений будут отличаться степенью группирования (концентрации) полученных результатов, например, относительно среднего арифметического значения. Подходящей характеристикой, позволяющей индивидуализировать разброс результатов многократных измерений, является суммирование величины их отклонений от среднего арифметического значения. Эта характеристика получила название дисперсии случайной величины D(x). По определению дисперсия случайной величины — это математическое ожидание квадрата соответствующего отклонения случайной величины х от ее математического ожидания т(х):

В формулах (4.13)—(4.15) рассматривается квадрат отклонений значений случайной величины от ее математического ожидания, что позволяет устранить взаимную компенсацию положительных и отрицательных значений отклонений при их суммировании. Дисперсия случайной величины имеет размерность квадрата размерности собственно величины, что затрудняет использование дисперсии в практике метрологических работ. Поэтому в метрологии чаще используется понятие «среднее квадра-тическое отклонение» S(x), которое принимается равным положительному корню квадратному из значения дисперсии:


Корректировка знаменателя в зависимости (4.17) позволяет компенсировать приведенные выше допущения за счет увеличения значения S(x). При очень большом числе измерений (п > 15) корректировка знаменателя не сказывается на величине S(x); при малом — имеет большое значение, причем тем больше, чем меньше п.
Форма кривой плотности распределения (см. рис. 4.3) отражает вид функции f(х). Во многих характерных случаях эти функции исследованы и результатами этих исследований пользуются на практике. Среди наиболее часто употребляемых распределений прежде всего необходимо выделить так называемое нормальное распределение, или распределение Гаусса. Это обусловлено тем, что если случайная величина представляет собой сумму трех и более составляющих, то ее распределение, независимо от формы распределения слагаемых, описывается уравнением:

График функции нормального распределения представлен на рис. 4.4.

В связи с тем, что большинство процессов измерения характеризуются большим числом составляющих погрешности измерения и это предоставляет право без проведения каких бы то ни было исследований принять для случайной погрешности нормальное распределение, нормальный закон стандартизован и является одной из двух установленных в нормативной документации форм законов распределения, применяемых при обработке результатов многократных измерений.
Если результаты наблюдений имеют нормальное распределение, то средние арифметические значения (результаты измерения) также распределены по нормальному закону. Это дает возможность оценить разброс результатов измерений, проводимых сериями (например, при проведении операций допускового контроля), по формуле:

В соответствии с зависимостями (4.6) и (4.18) функция распределения F(x), распределенной по нормальному закону, имеет вид:

Второй установленной в нормативной документации формой закона распределения является равномерное распределение. Равномерное распределение используется для описания таких величин, как вариация показаний средств измерений, неисключенная систематическая погрешность, погрешность округления. Равномерное распределение описывается уравнениями:

Равномерное распределение обладает наибольшей неопределенностью для всех случайных величин в выбранном интервале и может рассматриваться как худший случай.
Для количественной оценки погрешности измерения часто пользуются так называемыми доверительными интервалами и соответствующими им доверительными вероятностями. Доверительные интервалы позволяют оценить диапазон значений величины, в котором с принятой вероятностью находится неизвестное истинное значение измеряемой величины. Пусть при измерении физической величины с истинным значением ХИ получен результат измерения X. Задаваясь значением вероятности РД того, что случайная погрешность измерения находится внутри некоторого интервала ∆гр = ± ε, необходимо найти граничные значения этого интервала, удовлетворяющие условию:

4.3. Виды измерений.
Основное уравнение измерений
Искомое значение получают, как правило, в виде числа, показывающего, во сколько раз измеряемая величина больше или меньше однородной с ней величины, размер которой принят за единицу, т.е. результат измерений всегда выражается в единицах, которые хранят и воспроизводят средства измерений. Уравнение измерения, таким образом, имеет вид:

Представленное уравнение описывает физический смысл измерения, но не учитывает всего многообразия преобразований, которые измеряемая величина претерпевает в процессе измерения. Действительно, совсем необязательно получение на выходе числового значения величины, однородной с измеряемой (например, измерение объема жидкости по результатам измерения ее массы). В этом случае уравнение измерения может быть представлено в виде:

Результат измерения представляет собой конечный продукт производственного процесса, имеющего свои показатели качества как измерительного процесса и, конечно, важнейший из них — точность полученного результата. Под точностью результата измерений понимают одну из его характеристик, отражающую близость к нулю погрешности. Из сопоставления формул (4.28) и (4.29) видно, что первая, очевидная, составляющая погрешности измерения величины Q, — это погрешность примененного средства измерений, включая погрешность отсчета его показаний. Однако, применив другую модель процесса измерений, мы получаем другую (более простую или более сложную) структуру его погрешности, куда входит, как это следует из зависимости (4.29) дополнительно по отношению к зависимости (4.28), погрешность, вносимая функцией преобразования F.
Уравнение измерения является основным признаком, по которому измерения классифицируются с целью разделения методов обработки экспериментальных данных и получения характеристик погрешности результата. Известно достаточно много классификаций измерений (по виду измеряемой величины, по виду представления измерительной информации и др.). По виду уравнения измерения, связывающего измеряемую и непосредственно наблюдаемую величины, измерения подразделяются на прямые, косвенные, совместные и совокупные [20].
♦ Прямыми называются измерения, при которых искомое значение физической величины получают непосредственно (например, измерение массы на весах). ♦
Прямые измерения характеризуются уравнением измерения (4.28), которое соответствует преобразованию вида:

где Q — значение измеренной величины;
с — коэффициент (постоянный или переменный);
X — непосредственно наблюдаемая величина.
♦ Косвенными называются измерения, при которых определение искомого значения физической величины производится на основании результатов прямых измерений других физических величин, функционально связанных с искомой (например, определение объема тела по результатам его трех измерений). ♦
Уравнение косвенных измерений характеризуется зависимостью (4.29), а преобразования имеют вид:

♦ Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними (например, измерение температуры и плотности вещества). ♦

♦ Совокупными принято называть проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемой в результате измерений этих величин в различных сочетаниях (например, определение массы отдельных гирь из набора при известном значении лишь одной из них). ♦
При проведении совокупных измерений реализуется метод измерения сумм или разностей искомых значений этой величины в различных сочетаниях [8], т.е. уравнение измерения имеет вид:

Вторым важным классификационным признаком, определяющим качество результатов измерений и технологию их получения, является разделение измерений на однократные и многократные. Напомним, что однократным измерением называется измерение, выполненное один раз, а многократным — измерение, результат которого получен из нескольких, следующих друг за другом, измерений (т.е. состоящее из ряда однократных измерений).
4.4. Общие требования к проведению измерений
Общие требования к проведению измерений установлены рекомендациями МИ 2091—90 «ГСИ. Измерения величин. Общие требования» и должны применяться при разработке нормативных документов, регламентирующих правила выполнения как однократных, так и многократных измерений.
При подготовке к измерениям Необходимо учитывать соблюдение некоторых общепринятых и установленных в нормативно-технической документации правил:
• результаты измерений должны выражаться в единицах величин, соответствующих требованиям ГОСТ 8.417;
• измерения должны выполняться средствами измерении, прошедшими испытания и поверку (калибровку);
• правила выполнения наиболее ответственных, повторяющихся и сложных измерений (прямых многократных, косвенных, совокупных, совместных, имеющих существенные методические составляющие, требующих обработки измерительной информации и др.) рекомендуется регламентировать методиками выполнения измерения;
• при планировании измерений необходимо проанализировать правильность постановки измерительной задачи, установить требования к погрешности измерений, числу измерений, квалификации оператора, форме представления результатов измерений и предусмотреть мероприятия, обеспечивающие их выполнение.
Анализ правильности постановки измерительной задачи включает:
• выбор модели, которая соответствует свойствам объекта. Выбор модели следует производить таким образом, чтобы погрешности из-за несоответствия выбранной модели объекту измерений и из-за нестабильности измеряемых физических величин в течение времени, необходимого для проведения измерения, не превышали 10% от предела допускаемой погрешности измерений каждая;
• определение номенклатуры измеряемых параметров;
• оценку предполагаемой точности результата измерений и формы его представления. Требования к погрешности результата измерений должны соответствовать цели измерительной задачи. Эту погрешность целесообразно оценить предварительно с учетом ее предполагаемых источников. Предварительную оценку погрешности измерений производят путем суммирования всех составляющих погрешностей, возникновение которых предполагается при выполнении измерений. Если ожидаемая погрешность не соответствует требованиям точности измерительной задачи, следует проанализировать предполагаемые источники погрешности и осуществить мероприятия по их уменьшению (выбрать более точное средство измерений, изменить метод измерений, поручить измерения более квалифицированному оператору, уточнить влияющие величины и уменьшить их воздействие);
• проведение (при необходимости) предварительных измерений.
Результат измерений обычно сопровождается указанием погрешности, с которой выполнено измерение. В зависимости от цели измерительной задачи погрешность результата измерений может быть представлена своими составляющими или суммарной погрешностью с указанием доверительной вероятности. Выбор характеристик погрешности измерений, форм их представления и способов использования должны соответствовать МИ 1317.
Обеспечение точности измерений Точные измерения отличаются отсутствием промахов (результатов, не соответствующих свойствам измеряемого объекта, а являющихся следствием действия посторонних, кратковременных причин, как-то: сбой в системе энергопитания, ошибка оператора и т.п.) и малостью систематических и случайных погрешностей.
Спрогнозировать промахи невозможно. Их наличие определяется в процессе проведения измерений при обработке результатов. Промахи исключают из результатов измерений.
При однократных измерениях обнаружить промах очень трудно, так как отсутствует сама возможность его диагностики. В этом случае главное — профилактика (стабилизация источников питания и других условий функционирования средств измерений и т.д.). Самое надежное средство от промахов — повторить измерения два-три раза, а за результат измерений принять среднее арифметическое полученных отсчетов.
При многократных измерениях для обнаружения промахов используют статистические критерии. Предварительно должно быть проверено, какому виду распределений соответствует распределение результатов измерений. Для результатов измерений, распределенных нормально, наибольшее (наименьшее) значение из полученных отсчетов является промахом, если удовлетворяется неравенство:

Наряду с промахами из результатов измерений путем введения поправок должны быть устранены обнаруженные систематические погрешности. Неисключенные остатки систематических погрешностей, границы которых обозначим Θ, оцениваются нестатистическими методами в соответствии с требованиями ГОСТ 8.207.
Постоянно возрастающую или постоянно убывающую систематическую погрешность можно обнаружить по одной группе результатов измерений с помощью критерия Аббе.
Неизменяющуюся в процессе измерений систематическую погрешность по одной группе многократных измерений обнаружить невозможно. При наличии двух и более групп результатов измерений одной и той же физической величины, полученных различными методами, средствами измерений и операторами либо отличающихся условиями или методикой выполнения измерений, неизменяющуюся систематическую погрешность или различия систематических погрешностей в группах обнаружить можно. Для этого используют специальные статистические критерии.
При наличии двух групп результатов измерений
одной и той же физической величины, имеющих нормальное распределение с
однородными  средними
квадратическими отклонениями, неизменяющуюся систематическую погрешность или
различия систематических погрешностей в группах можно обнаружить при помощи
критерия Стьюдента. Считается, что систематическая погрешность присутствует в
одной из групп или значения систематической погрешности различны в группах,
если выполняется неравенство:
средними
квадратическими отклонениями, неизменяющуюся систематическую погрешность или
различия систематических погрешностей в группах можно обнаружить при помощи
критерия Стьюдента. Считается, что систематическая погрешность присутствует в
одной из групп или значения систематической погрешности различны в группах,
если выполняется неравенство:


При неизвестном законе распределения результатов измерений для обнаружения систематической погрешности или различия систематических погрешностей в группах применяют статистический критерий Вилкоксона.
По значениям случайных погрешностей измерений могут оцениваться сходимость измерений, т.е. близость друг к другу результатов измерений, выполняемых в одинаковых условиях, и воспроизводимость измерений, т.е. близость друг к другу результатов измерений, выполненных в различное время, в разных местах, разными методами и средствами измерений, но приведенных к одним и тем же условиям: температура, давление, влажность и т.д.
Сходимость группы результатов измерений характеризуют средним квадратическим отклонением результата группы или его доверительной случайной погрешностью.
Воспроизводимость нескольких групп результатов измерений характеризуют близостью результатов измерений групп и характеристик их случайных погрешностей.
При нормальном распределении результатов измерений для проверки их сходимости используются статистические критерии Аббе и Фишера (4.40).
Воспроизводимость результатов измерений оценивается допустимостью различия средних квадратических отклонений групп результатов измерений (близостью средних квадратических отклонений). Для нормального распределения и числа групп L = 2 используют критерий Фишера, а для числа групп L > 2 — критерий Бартлетта.
Согласно критерию Фишера различие средних квадратических отклонений S1 и S2 двух групп результатов с числом измерений п 1 и n 2 допустимо, если выполняется неравенство:


При неизвестном распределении результатов измерений для проверки близости результатов измерений групп применяют статистический критерий Вилкоксона, а для проверки допустимости различия средних квадратических отклонений — критерий Сиджела — Тьюки.
Причины, вызывающие систематические погрешности, различны по своей природе, поэтому трудно установить единые правила по их обнаружению и исключению. Все же существуют общие (не исчерпывающие) правила проведения работ по выявлению и устранению этих погрешностей:
• поверка применяемых СИ с целью определения действительного значения их погрешностей;
• предварительный анализ методической погрешности с целью введения поправок;
• проведение измерений влияющих величин;
• поддержание стабильности условий измерений;
• использование метода замещения;
• устранение влияния вариации;
• исключение погрешности от мертвого хода (люфта);
• измерение одной величины несколькими независимыми методами и несколькими СИ и т.п.
Точность полученных при измерении отсчетов и последующих вычислений при их обработке должна соответствовать требуемой точности результата измерений. Число разрядов при отсчете и в промежуточных вычислениях должно быть на единицу или две больше, чем в окончательном результате.
Условия выполнения измерений В зависимости от требований измерительной задачи измерения могут выполняться как в нормальных, так и в рабочих условиях.
При выполнении измерений в нормальных условиях должно быть выделено рабочее пространство (рабочее место, комната, лаборатория, цех), действием влияющих величин внутри которого можно пренебречь. При выборе номинальных значений и
пределов допускаемых отклонений влияющих величин для нормальных условий следует руководствоваться ГОСТ 8.395.
Если действием влияющих величин внутри рабочего пространства пренебречь нельзя, их измеряют с целью расчета и последующего введения поправок в результаты измерений или с целью расчета дополнительных погрешностей.
Погрешность средств измерений, применяемых для контроля влияющих величин, должна составлять не более 25% от изменения влияющей величины.
Для обеспечения возможности сопоставления результатов измерений они должны выполняться в одинаковых условиях или их результаты должны приводиться к одинаковым условиям, чаще всего к нормальным.
Выбор метода и средства измерений осуществляется исходя из условия выполнения измерительной задачи. Главное требование — обеспечить требуемую измерительной задачей точность измерений в данных условиях измерений.
При выборе средства измерений прежде всего учитывают принцип его действия, приемы применения, метрологические характеристики, характеристики надежности, стойкость к внешним воздействиям и др. Рекомендации по выбору методов и средств измерений с учетом факторов, характерных для технических измерений, изложены в МИ 1967.
Метод измерений должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу систематических погрешностей в разряд случайных (рандомизация систематических погрешностей). Например, с целью исключения систематических погрешностей из-за неадекватности модели измеряемому объекту намечают выполнение измерений в нескольких точках; для исключения систематических погрешностей от вариации, гистерезиса, мертвого хода измерения выполняют при подходе к определенной точке шкалы слева и справа.
В соответствии с выбранным методом и средством измерений целесообразно предварительно оценить погрешность измерений ∆Σ, включающую погрешность средств измерений, метода, оператора и погрешности, обусловленные внешними воздействиями, и сравнить ее с пределом допускаемой погрешности измерений ∆р. Если ∆Σ < ∆р, то выбранные метод и средства измерений обеспечивают получение результата с заданным уровнем погрешности. В противном случае уточняют правильность выбранного метода, условий выполнения измерений или выбирают более точное средство измерений. Для выполнения однократных измерений предпочтительны средства измерений с возможно меньшей случайной погрешностью.
Так как диапазоны значений нормальных условий применения средств измерений устанавливаются исходя из допустимости изменения основной погрешности на величину до 35% от установленного значения (ГОСТ 8.395), то, следовательно, погрешность выбираемого средства измерений Леи должна быть

Определение требуемого числа измерений Принципиально число измерений п может быть произвольным, однако если существует возможность проведения многократных измерений, то за счет их количества можно минимизировать случайную составляющую погрешности измерения. Таким образом, многократные измерения имеют смысл при сопоставимости значений систематической и случайной составляющих погрешности результата или при преобладающем значении случайной погрешности. Исходя из этой предпосылки максимальное значение случайной составляющей может быть равно допускаемой погрешности измерения (систематическая составляющая равна нулю). При появлении и росте значения систематической составляющей соответственно должна уменьшаться случайная составляющая погрешности измерения. В этом случае число измерений должно удовлетворять неравенству:
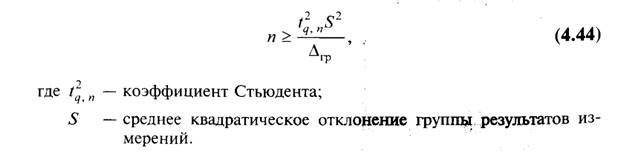
Число измерений может быть увеличено при наличии существенных систематических погрешностей (метода, средства измерений, оператора) с целью их перевода в случайные (рандомизация систематических погрешностей).
При наличии в результате измерений случайных (среднее квадратическое отклонение S) и неисключенных систематических погрешностей (Θ) число измерений п определяется их соотношением Θ/S и требованиями к точности результата измерений. На графике (рис. 4.6) приведена зависимость числа измерений п от значений соотношения Θ/S и относительного изменения погрешности результата измерений γ (n) при увеличении числа измерений.

Рис. 4.6. График зависимости погрешности измерений от числа измерений
Требования к оператору при проведении измерений Перед проведением измерений оператор должен изучить методику выполнения измерений и убедиться в том, что основные и вспомогательные средства измерений имеют действующие свидетельства о поверке или калибровке.
При использовании автоматизированных средств измерений их тестируют и сопоставляют результат, полученный на выходе, с ожидаемым результатом.
Для уменьшения субъективных погрешностей оператора наиболее ответственные, высокоточные измерения допускается выполнять несколькими операторами, а за результат измерений принять среднее арифметическое их показаний. Автоматизация измерений позволяет исключить возможность появления подобных погрешностей.
Погрешность округления при снятии отсчетов оператором не должна влиять на последнюю значащую цифру погрешности окончательного результата измерения, т.е. она не должна превышать 10% от предела допускаемой погрешности результата измерений. Если это условие не выполняется, число отсчетов необходимо увеличить или учесть эту составляющую погрешности результата измерений.
Обработка и представление результатов измерений Обработке результатов измерений предшествует этап их анализа.
Если при анализе процесса измерений удалось установить источник появления промахов (неверное действие оператора, падение напряжения в электрической сети, магнитные бури и другие причины), то их исключают перед обработкой результатов измерений. Если причины появления промахов неизвестны, то для решения вопроса о возможности их исключения используют статистические критерии.
Обнаруженные систематические погрешности измерения (систематические погрешности средств измерений, метода, оператора, воздействия влияющих факторов) исключают из результатов измерений внесением поправок, а неисключенные систематические и случайные погрешности составляют погрешность результата измерений.
Обработка прямых однократных измерений проводится в соответствии с Р 50.2.038—04, прямых многократных измерений — в соответствии с ГОСТ 8.207, косвенных измерений — в соответствии с МИ 2083. Обработка результатов сличений при совокупных измерениях изложена в МИ 1832.
Результаты измерений в зависимости от цели измерительной задачи могут быть представлены числом, в виде таблицы, графика или в другом виде.
Формы представления результатов измерений и их погрешностей должны соответствовать МИ 1317.
Погрешность результата измерений выражают, как правило, одной значащей цифрой. Две значащие цифры в погрешности результата измерения сохраняют:
• при точных измерениях;
• если первая значащая цифра не более трех;
• если предел допускаемой погрешности задан двумя значащими цифрами.
4.5. Методики выполнения измерений
Для обеспечения единства измерений недостаточно иметь поверенные средства измерений, так как погрешность измерений может содержать в качестве составляющих погрешности метода, оператора, условий применения средств измерений и др. Нередки случаи, когда погрешность средства измерений в общей погрешности измерений составляет всего 10—20%.
Получение результатов измерений с известной погрешностью или с погрешностью, не превышающей допускаемых пределов (норм точности измерений), — одно из важнейших условий обеспечения единства измерений. Именно с этой целью в статье 9 Закона РФ «Об обеспечении единства измерений» установлено, что измерения должны осуществляться в соответствии с аттестованными методиками. Данное требование относится к измерениям, выполняемым в сферах, определенных статьей 13 Закона.
Постановлением Госстандарта РФ от 23 мая 1996 г. № 329 утвержден и введен в действие ГОСТ 8.563—96 «ГСИ. Методики выполнения измерений».
• Согласно этому стандарту методика выполнения измерений
(МВИ) — совокупность операций и правил, выполнение которых обеспечивает получение результатов измерений с известной погрешностью. ♦
Из определения видно, что МВИ — это технологический процесс измерений. Его не следует смешивать с документом на МВИ. Не все МВИ описываются или регламентируются документами. Для измерений величин с помощью простых средств измерений документированные МВИ не требуются. Достаточно лишь указаний в конструкторской или технологической документации типов и основных метрологических характеристик средств измерений. Если разработка МВИ необходима, то она Должна иметь следующую структуру и примерное содержание (табл. 4.2).

♦ Аттестация МВИ — это процедура установления и подтверждения соответствия МВИ предъявляемым к ней требованиям. ♦
Следует отличать аттестацию от метрологических исследований МВИ. В результате метрологических исследований устанавливаются метрологические характеристики, а при аттестации на основе результатов исследований делается вывод о соответствии МВИ заданным требованиям или приписанным характеристикам (регламентированным в документе на МВИ). Аттестации должны подвергаться МВИ, применяемые в сферах распространения государственного контроля и надзора. Ее проводят Государственные научные метрологические центры (ГНМЦ), территориальные структуры Ростехрегулирования (ЦСМ) и другие метрологические службы (МС), аккредитованные на право проведения аттестации МВИ.
Аттестация МВИ, применяемых вне сфер распространения государственного контроля и надзора, проводится в порядке, установленном ведомством или предприятием. Ее проводят ГНМЦ, ЦСМ, МС предприятий, разрабатывающих или применяющих МВИ. Если МС выполняет аттестацию МВИ для других предприятий, то она должна быть аккредитована на право проведения аттестации МВИ в соответствии с ПР 50.2.013—94 «ГСИ. Порядок аккредитации метрологических служб юридических лиц на право проведения аттестации МВИ».
Основная цель аттестации МВИ — подтверждение возможности измерений по данной методике с погрешностью, не превышающей указанную в документе на МВИ. На аттестацию МВИ представляют:
• исходные данные на разработку МВИ;
• документ (его проект), регламентирующий МВИ;
• программу и результаты экспериментального или расчетного оценивания характеристик погрешности МВИ, если оно проводилось.
Аттестация МВИ осуществляется путем метрологической экспертизы документации, теоретических или экспериментальных исследований МВИ.
При экспертизе документа на МВИ устанавливают соответствие назначения МВИ и измеряемой величины задаче контроля и контролируемому параметру, полнота и четкость требований к условиям измерений и метрологическим характеристикам средств измерений, проверяется утверждение типов средств измерений, анализируются факторы, влияющие на погрешность измерений и корректность ее оценивания. Теоретические и экспериментальные исследования МВИ заключаются в оценивании погрешности измерений. При положительных результатах аттестации на МВИ оформляется свидетельство, форма которого приведена в ГОСТ 8.563-96.
4.6. Обработка результатов прямых однократных измерений
Методика получения результата при проведении однократных прямых измерений установлена рекомендацией Р 50.2.038—2004 «ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений». В соответствии с рекомендацией за результат однократного прямого измерения принимается значение величины (обозначим Л), полученное при измерении. Рассматриваемая методика построена таким образом, чтобы имелась возможность определения и погрешности, и неопределенности измерения.
Исходные данные:
(1) составляющие погрешности результата измерения известны (перечислены) до начала проведения измерения;
(2) известные систематические погрешности исключены (внесены поправки на все известные источники неопределенности, имеющие систематический характер);
(3) распределение случайных погрешностей не противоречит нормальному распределению;
(4) неисключенные систематические погрешности представлены заданными границами ± Θ и распределены равномерно;
(5) распределение вероятностей возможных значений измеряемой величины не противоречит нормальному распределению;
(6) для количественного выражения неопределенности результата измерения, представленной в виде границ отклонения значения величины от ее оценки | — Θ; + Θ| (неполное знание о значении величины), принимают, что распределение возможных значений измеряемой величины в указанных границах не противоречит равномерному распределению;
(7) проведение однократных измерений обосновано следующими факторами:
• производственной необходимостью (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.);
• возможностью пренебрежения случайными погрешностями.
Случайные погрешности считаются пренебрежимо малыми по сравнению с неисключенными систематическими, если выполняется условие:

• случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерений;
• стандартная неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность не превышает заданного предела.
Определение доверительных границ погрешности или расширенной неопределенности При определении доверительных границ погрешности или расширенной неопределенности U принимают вероятность не ниже 0,95.
♦ Расширенная неопределенность — это границы интервала, в пределах которого находится большая часть распределения значений, которые могли бы быть приписаны измеряемой величине. ♦
Правила округления при вычислениях должны соответствовать требованиям МИ 1317. Доверительные границы погрешности (характеристики погрешности) и расширенная неопределенность (расширенная неопределенность для уровня доверия Р) результата измерения должны быть представлены не более чем двумя значащими цифрами.
Значащей в записи числа считается любая цифра, если ее предельная погрешность не превышает половины разряда, в котором эта цифра записана.
Составляющие погрешности и неопределенности результата измерения К составляющим погрешности результата однократного измерения относят погрешности средства измерений, метода измерений, оператора, а также погрешности, обусловленные изменением условий измерения. Погрешность средства измерений должна быть указана в технической документации на него или определена в соответствии с рассмотренными выше рекомендациями [10]. Погрешности метода и оператора определяются на этапе разработки и аттестации методики выполнения измерений, о чем будет сказано далее.
В качестве погрешности результата однократного измерения, как правило, представляют
• неисключенную систематическую погрешность, выраженную или границами ±Θ(P= 1), или доверительными (Р < 1)
и границами ±Θ(P);
• случайную погрешность, выраженную или средним квад-ратическим отклонением S, или доверительными границами ±ε(Р).
Неопределенность результата однократного измерения может быть представлена стандартными неопределенностями UA (4.47) и UB{4A%).
Определение неисключенной систематической погрешности и стандартной неопределенности UB результата измерения Неисключенную систематическую погрешность результата измерения выражают границами погрешности ±Θ, если среди составляющих погрешности результата измерения в наличии только одна НСП. В этом случае стандартная неопределенность UB, обусловленная неисключенной систематической погрешностью, оценивается по формуле (4.48).
Доверительные границы ±Θ (Р) результата измерения вычисляются следующим образом.
При наличии нескольких неисключенных систематических погрешностей, заданных своими границами ±Θj, доверительную границу ±Θ (Р) (без учета знака) вычисляют по формуле:


Если случайные погрешности представлены доверительными границами εi (P), соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле:

Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, то сначала определяют СКО результата измерения по формуле:
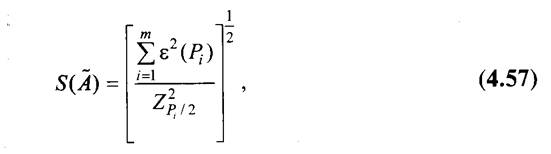
а затем вычисляют доверительные границы случайной погрешности результата измерения по формуле (4.55).
Определение погрешности и расширенной неопределенности результата измерения Выходное значение погрешности или расширенная неопределенность результата измерения рассчитываются в зависимости от соотношения составляющих погрешности (неопределенности) .
Если погрешности метода измерения и оператора не превышают 15% погрешности СИ, то за погрешность результата измерения принимают погрешность используемых СИ.
Если [Θ/S(A)] < 0,8, то НСП или стандартной неопределенностью, оцениваемой по типу В, пренебрегают и принимают в качестве погрешности или неопределенности результата измерения доверительные границы случайных погрешностей или расширенную неопределенность для уровня доверия Р, вычисляемую по формуле:


Значение результата измерения должно оканчиваться цифрами того же разряда, что и значение погрешности или расширенной неопределенности.
Пример. Пример расчета погрешности однократного измерения рассмотрим для измерения напряжения показывающим прибором на участке электрической цепи сопротивлением R = 4 Ом.
Априорные данные об исследуемом объекте. Участок электрической цепи представляет собой соединение нескольких резисторов, имеющих стабильное сопротивление. Ток в цепи постоянный. Измерение выполняют в сухом отапливаемом помещении при температуре окружающего воздуха до 30°С и напряженности магнитного поля до 400 А/м. Предполагаемое падение напряжения на участке цепи, не превышающее 1,5 В, постоянно. Для измерения используется вольтметр класса точности 0,5 по ГОСТ 8711 (приведенная погрешность — 0,5%) с верхним пределом диапазона измерений Uпp = 1,5 В. Вольтметр имеет магнитный экран. Некоторый запас по точности средства измерений необходим из-за возможного наличия дополнительных погрешностей, погрешности метода и т.д. Инструментальная составляющая погрешности определяется основной и дополнительной погрешностями.
Основная погрешность прибора указана в приведенной форме. Тогда предел допускаемой основной погрешности вольтметра составит:

Дополнительная погрешность из-за влияния магнитного поля не превышает 1,5% нормирующего значения прибора и равна ±0,0225 В (0,015∙ 1,5).
Дополнительная температурная погрешность, обусловленная отклонением температуры на 10°С от нормальной (20°С), не превышает 60% предела допускаемой основной погрешности, она равна ±0,0045 В (0,0075∙0,6).
Оценивание погрешности результата измерения. Погрешность метода определяется соотношением между сопротивлением участка цепи R и сопротивлением вольтметра RV. «„Сопротивление вольтметра известно: RV = 1000 Ом. Напряжение в цепи после подсоединения вольтметра может быть рассчитано по формуле

Методическая погрешность является систематической составляющей погрешности измерений и должна быть внесена в результат измерения в виде поправки V = +0,004 В. Тогда результат измерения А с учетом поправки на систематическую погрешность будет равен:

Так как основная и дополнительные погрешности средства измерений заданы границами, следует рассматривать эти погрешности как не исключенные систематические. Воспользовавшись формулой (4.49), находят доверительную границу неисключенной систематической погрешности результата измерения, которая при доверительной вероятности Р = 0,95 составит:

4.7. Обработка результатов прямых многократных измерений
Методика получения результатов при проведении многократных прямых измерений установлена ГОСТ 8.207—76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдения. Основные положения». Перед рассмотрением методики напомним, что ГОСТ 8.207 разработан и утвержден в период действия ныне отмененных ГОСТ 16263 на термины и определения в области метрологии, ГОСТ ов серии «П.», устанавливающих правила математической статистики при определении закона распределения, и отсутствия каких бы то ни было представлений о неопределенности результатов измерений.
Основные операции и их последовательность Методика обработки результатов прямых многократных измерений включает в себя следующие операции:
• определение наличия грубых погрешностей и исключение промахов;
• исключение известных систематических погрешностей из результатов наблюдений;
• вычисление среднего арифметического исправленных результатов наблюдений, принимаемого за результат измерения;
• вычисление оценки среднего квадратического отклонения результата наблюдений;
• вычисление оценки среднего квадратического отклонения результата измерения;
• проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению. Проверку гипотезы о том, что результаты наблюдений принадлежат
нормальному распределению, следует проводить с уровнем значимости q от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений;
• вычисление доверительных границ случайной погрешности (случайной составляющей погрешности) результата измерения;
• вычисление границ неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;
• вычисление доверительных границ погрешности результата измерения. Для определения доверительных границ погрешности результата измерения доверительную вероятность Р, как правило, принимают равной 0,95. В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99. В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р = 0,99 принимать более высокую доверительную вероятность.
Подготовка результатов наблюдений к обработке Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений. Важное значение при определении наличия грубых погрешностей имеет вопрос о законе распределения результатов измерений. Как правило, результаты измерений считают принадлежащими к нормальному распределению. Для нормального распределения разработано несколько критериев оценки наличия грубых погрешностей. В целом их действие основано на представлении о том, что измеряемая величина может характеризоваться большим количеством измерительной информации (генеральной выборкой) и ее ограниченным количеством (выборкой). Результаты обработки будут тем точнее, чем на больший объем информации они опираются. Поэтому критерии отнесения погрешностей к грубым можно разделить на критерии сопоставления имеющихся результатов с характеристиками генеральной выборки и характеристиками распределения собственно полученных результатов.
Если известны характеристики генеральной выборки (среднее квадратическое отклонение) или они могут быть получены в результате обработки предшествующих опытов, то следует пользоваться критериями, основанными на известном генеральном среднем квадратическом отклонении, и только когда оно неизвестно и нет возможности его получить, следует пользоваться критериями, основанными на использовании выборочного среднего квадратического отклонения. Так как грубые погрешности способны заметно повлиять на результат измерения, рассмотрим некоторые, наиболее употребляемые из известных критериев.
1. Значение генерального среднего квадратического отклонения неизвестно.
В таком случае имеются результаты наблюдений, составляющие упорядоченную выборку, которую можно представить в виде:
![]()
Сомнению могут быть подвергнуты, естественно, результаты, заметно отличающиеся по величине от остальных, т.е. либо наименьший (x1), либо наибольший (хn).
Среднее арифметическое значение выборки [хи хп] составит:

Принадлежность х1 или хп к данной выборке, распределенной по нормальному закону, определяется по значению соотношений:
ношений:

Если значения Un или U1 превысят критические значения р, приведенные в табл. 4.3, то соответствующий результат не принадлежит нормальному распределению и из результатов измерений должен быть исключен.

2. Значение генерального среднего квадратического отклонения известно. Значение генерального среднего арифметического неизвестно.
Практика измерений столь обширна, что довольно часто встречается ситуация, когда из предшествующих опытов значение генерального среднего квадратического (обозначим его а Для различия со средним квадратическим выборки S) известно, а генеральное среднее арифметическое — нет. В этом случае составляют упорядоченную выборку (4.62) и подсчитывают среднее арифметическое (4.63). По полученным данным подсчитывают значения коэффициентов:

Если полученные значения превысят критические значения β, приведенные в табл. 4.4, то соответствующие результаты анормальны и из полученного ряда измерений должны быть исключены.
Таблица 4.4. Предельные значения р для случая известного значения
генерального среднего квадратического отклонения и неизвестного
значения генерального среднего арифметического

3. Значение генерального среднего квадратического отклонения известно. Значение генерального среднего арифметического известно.
Этот случай довольно часто встречается на практике при контроле постоянно протекающих процессов (транспортировка газа, жидкости и т.п.). Проверка принадлежности к нормальному распределению для этих условий возможна даже для выборки, состоящей из одного члена. Предположим, что выборка упорядочена и представлена в виде (4.62). Значение генерального среднего арифметического обозначим а. Рассчитаем значения:

Если какое-то значение, полученное по зависимостям (4.67), будет больше критических значений β, приведенных в табл. 4.5, то соответствующий результат должен быть исключен.
Таблица 4.5. Предельные значения р для, случая известных значений генерального среднего арифметического и генерального
среднего квадратического

После оценки наличия грубых погрешностей и исключения содержащих их результатов производят оценку наличия систематических погрешностей и внесение поправок в результаты измерений. Если во всех результатах содержится постоянная систематическая погрешность, то допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.
Определение результата измерения и оценка его среднего квадратического отклонения За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей.
Несмещенной оценкой генерального среднего арифметического значения исправленных результатов наблюдений (а) нормального распределения является выборочное среднее X, определяемое по формуле (4.63). Несмещенная оценка (Si) для генерального среднего квадратического отклонения (α) определяется по зависимости:

Зависимости (4.68) и (4.69) позволяют оценить среднее квадратическое отклонение результата наблюдения.
Среднее квадратическое отклонение S(A) результата измерения оценивают по формуле:

Доверительные границы случайной погрешности результата измерения ГОСТ 8.207 установил методику оценки доверительных границ случайной погрешности результата измерения для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, то методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
Принадлежность результатов наблюдений к нормальному распределению проверяют с помощью специальных критериев.
Если число результатов наблюдений п > 50, то для проверки принадлежности их к нормальному распределению предпочтительно использовать один из критериев: χ2 Пирсона или ω2 Мизеса — Смирнова.
- Критерий χ2 Пирсона. Результаты наблюдений случайной величины xi располагают в порядке возрастания (4.62) и вычисляют размах хп — х1. Размах разбивают на г равных интервалов шириной h:

Число интервалов r выбирают в зависимости от объема выборки п. При п = 200 r = 18—20, при п = 400 r = 25—30, при п = 1000 r=— 35—40. Стандарт не рекомендует использовать критерий Пирсона при числе наблюдений меньше 200, допуская в исключительных случаях его применение при 100 < п < 200 с количеством интервалов r = 15—18. Однако в работе [10] приводятся несколько иные рекомендации. Так, при числе наблюдений 50 < п≤ 100 рекомендуемое число интервалов r = 7—9, при 100 < п ≤ 500 r = 8—12, при 500 < n ≤1000 r = 10—16 и при 1000 < п ≤ 10 000 r = 12—22.
Результаты наблюдений группируют по полученным интервалам и подсчитывают частоты mj попадания результатов наблюдений в j-е интервалы.
Затем вычисляются среднее арифметическое значение X и среднее квадратическое отклонение S:

Задаются значением доверительной вероятности того, что величина χ2, полученная вследствие случайных отклонений частостей опытного распределения от соответствующих вероятностей теоретического распределения, будет меньше значения
(χ *)2, установленного для значения доверительной вероятности γ. Для доверительной вероятности γ и числа степеней свободы k = r — 1 находят величину (χ*)2/k, вычисляют (χ*)2 и сравнивают с ним вычисленную величину χ2. Если χ2 окажется меньше (χ*)2, то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределений принимается, в противном случае — отвергается.
2. Критерий ω2 Мизеса — Смирнова. Критерий ω2 является более мощным, чем критерий χ2, но его применение требует выполнения большого количества вычислительных операций. Критерий ω2 может быть применен, если число наблюдений превышает 50. Его применение является обязательным, если число наблюдений меньше 200; если число наблюдений более 200, то его применение рекомендуется в случаях, когда результаты проверки по другим критериям не позволяют сделать безусловный вывод о согласии опытного и теоретического распределений. Например, если при проверке согласия по критерию χ2 гипотеза принята при уровне значимости 0,1 и отвергнута при уровне значимости 0,05, то следует дополнительно применить критерий ω2.
Вычисление по критерию ω2 проводят в следующем порядке.
Вычисляют значение величины ![]() по формуле:
по формуле:

Если число результатов наблюдений 50 > п > 15, то для проверки принадлежности их к нормальному распределению предпочтительно использовать составной критерий.
- Составной критерий. Критерий 1. Вычисляют отношение d по формуле:

Значения Р определяются из табл. 4.8 по выбранному уровню значимости q* и числа результатов наблюдений п.
При уровне значимости, отличном от представленных в табл. 4.8, значение Р находят путем линейной интерполяции.
В случае если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q, а для критерия 2 — уровень значимости q*, то результирующий уровень значимости составного критерия qΣ<q + q* .
В случае если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Если число результатов наблюдений n≤ 15, то принадлежность их к нормальному распределению не проверяют. Нахождение доверительных границ случайной погрешности результата измерения по рассматриваемой нами методике возможно только в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.
Доверительные границы ε (без учета знака) случайной погрешности результата измерения находят по формуле:

Значения коэффициента Стьюдента в зависимости от задаваемых значений доверительной вероятности Р и числа результатов наблюдений п приведены в табл. 4.9.
Таблица 4.9. Значения коэффициента tp,n для случайной величины, имеющей распределение Стьюдента с n - 1 степенями свободы

Доверительные границы неисключенной систематической погрешности результата измерения Не исключенная систематическая погрешность результата измерения образуется из составляющих, в качестве которых могут быть рассмотрены неисключенные систематические погрешности метода измерения, средств измерений или вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.
При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.
Границы неисключенной систематической погрешности 0 результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода измерения и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле:

При трех или четырех слагаемых Θi в качестве значения Θ1 принимают составляющую, по числовому значению наиболее отличающуюся от других, а в качестве Θ2 — ближайшую по значению к Θ1 составляющую.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной погрешности результата измерения.

Граница погрешности результата измерения Методика оценки границ погрешности результата измерения зависит от соотношения значений случайной и неисключенной систематической составляющих, рассмотренных нами выше. Выделяют три возможных случая.
1. Неисключенной систематической составляющей погрешности результата измерения можно пренебречь. Необходимым условием для этого является соблюдение неравенства:

На основе (4.83) принимают, что граница погрешности результата измерения ∆ = ε.
2. Случайной составляющей погрешности результата измерения можно пренебречь. Необходимым условием для этого является соблюдение неравенства:

На основе (4.84) принимают, что граница погрешности результата измерения ∆= Θ.
При выполнении условий 1 и 2 погрешность оценки величины ∆ за счет пренебрежения значением случайной или неисключенной систематической составляющих не превышает 15%.
3. В случае если неравенства (4.83) или (4.84) не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисклю-ченных систематических погрешностей, рассматриваемых в данном случае. Если доверительные границы случайных погрешностей найдены в соответствии с (4.80), то допускается границы погрешности результата измерения ∆ (без учета знака) вычислять по формуле:

Форма записи результатов измерений При оформлении результатов измерений следует пользоваться рекомендациями МИ 1317.
Если доверительные границы погрешности результата измерения симметричны, то результаты измерений представляют в форме:

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности ∆ .
Если данные о виде функций распределений составляющих погрешности результата измерения и необходимость в дальнейшей обработке результатов или анализе погрешностей отсутствуют, результаты измерений представляют в форме:

В случае если границы неисключенной систематической погрешности 0 вычислены в соответствии с (4.81), следует дополнительно указывать доверительную вероятность Р. Значения S(A) и Θ могут быть выражены в абсолютной и относительной формах.
4.8. Обработка результатов косвенных измерений
Косвенные измерения представляют собой специфический вид измерений, в котором искомая величина не подвергается инструментальному измерению, а оценивается расчетным путем по зависимости между ней и измеряемыми величинами. Методика обработки результатов косвенных измерений установлена в рекомендации МИ 2083—90 «ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей». Важным обстоятельством для рассматриваемой методики является требование, чтобы аргументы, от которых зависит оцениваемая величина, являлись постоянными величинами; известные систематические погрешности результатов измерений аргументов были исключены, а неисключенные систематические погрешности распределены равномерно внутри заданных границ ± Θ.
Искомое значение величины А в результате
косвенных измерений находят на основании результатов измерений аргументов ![]() связанных с искомой
величиной зависимостью:
связанных с искомой
величиной зависимостью:
![]()
Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.
Результаты измерений аргументов ![]() и оценки их погрешностей
могут быть получены из прямых однократных или многократных, косвенных,
совокупных или совместных измерений. Сведения об аргументах могут быть также
взяты из справочной литературы и технической документации.
и оценки их погрешностей
могут быть получены из прямых однократных или многократных, косвенных,
совокупных или совместных измерений. Сведения об аргументах могут быть также
взяты из справочной литературы и технической документации.
При оценивании доверительных границ погрешностей результата косвенных измерений обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.
МИ 2083 устанавливают методику обработки результатов косвенных измерений для трех характерных случаев:
(1) функция f линейная, корреляция между погрешностями измерений аргументов отсутствует;
(2) функция f нелинейная, корреляция между погрешностями измерений аргументов отсутствует;
(3) функция f представляет собой ряды отдельных значений измеряемых аргументов, погрешности измерений аргументов коррелированы между собой.
1. Оценка результата измерения и характеристик погрешности при косвенных измерениях с линейной зависимостью между оцениваемой величиной и измеряемыми аргументами и отсутствием корреляции между погрешностями аргументов проводится следующим образом.


![]()
Доверительные границы неисключенной систематической погрешности результата косвенных измерений вычисляют следующим образом.
Если неисключенные систематические погрешности результатов измерений аргументов заданы границами 0„ то доверительные границы неисключенной систематической погрешности результата косвенных измерений Θ(Р) без учета знака при вероятности Р вычисляют по формуле:

где k — поправочный коэффициент, определяемый принятой доверительной вероятностью Р и m -числом составляющих Θi.
Значения коэффициента к определяются так, как это указано в пояснениях к зависимостям (4.81) и (4.82) и на графике (рис. 4.7). Для нахождения к с помощью графика гра-


Отклонения ∆ai, при этом должны быть взяты из полученных значений погрешностей такими, чтобы они максимизировали выражение для остаточного члена R.
Результат измерений А вычисляют по формуле:

Доверительные границы случайной погрешности результата косвенных измерений при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют в соответствии с (4.90).
Границы неисключенной систематической
погрешности результата косвенных измерений вычисляют в соответствии с (4.92) и
(4.93), подставляя вместо коэффициентов bi,
соответствующие первые производные ![]() . Погрешность результата косвенных
измерений оценивают в соответствии с методикой (4.96).
. Погрешность результата косвенных
измерений оценивают в соответствии с методикой (4.96).
3. Оценка результата измерения и характеристик погрешности при косвенных измерениях в случае, когда функция / представляет собой ряды отдельных значений измеряемых аргументов, а погрешности измерений аргументов коррелированы между собой, проводится следующим образом.
При наличии корреляции между погрешностями измерений аргументов для определения результатов и погрешности косвенных измерений используют метод приведения, который предполагает наличие ряда отдельных значений измеряемых аргументов, полученных в результате многократных измерений. Этот метод можно также применять при неизвестных распределениях погрешностей измерений аргументов.
Метод основан на приведении ряда отдельных значений косвенно измеряемой величины к ряду прямых измерений. Получаемые сочетания отдельных результатов измерений аргументов подставляют в формулу (4.88) и вычисляют отдельные значения измеряемой величины Аj. A1, ..., АL.

где Т — коэффициент, зависящий от вида распределения отдельных значений измеряемой величины А и выбранной доверительной вероятности.
При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей вычисляют в соответствии с ГОСТ 8.207.
Границы неисключенной систематической погрешности результата косвенных измерений рассчитывают в соответствии с (4.94) и (4.95), доверительные границы погрешности результата косвенного измерения — в соответствии с (4.96).
Формы представления результата измерений должны соответствовать МИ 1317 (см. выше).
