Типичный сценарий для PayWord — каждый элемент микроплатежной цепочки выполни оплату в пределах очень незначительной суммы, например одного цента. Механизм платежей действует так, что аутентичность обязательства гарантирует продавцу аутентичность самой микроплатежной цепочки. Безопасность и гибкость механизма позволяют платежи произвольного объема. Особенность PayWord — отсутствие информации об объекте платежа (за что платит покупатель) в самом элементе цепочки. Следовательно, продав может обмануть покупателя.— отказать или обеспечить не' тем товаром, который был оплачен. Таким образом, существует риск потери выплаченных денег. Можно переложить риск на продавца, оплачивая товар после его доставки. Если покупатель отказывается оплачивать товар, продавец уведомляет посредника и тот аннулирует сертификат покупателя. Однако точки зрения микроплатежной схемы указанный риск можно игнорировать.
Одна из целей, достигнутых при разработке PayWord, — минимальное число on-line транзакций при взаимодействии с посредником. Продавцу не нужно взаимодействовать с посредником ни при первом контакте с покупателем, ни при последующей серии платежей. При транзакциях объем информации при передаче элемента цепочки не превышает 30 6sO- тов. Кроме того, продавец передает посреднику не всю микроплатежную цепочку, а только ее элемент с наибольшим индексом. Наиболее эффективно PayWord работает в случае серии запросов для фиксированной пары «покупатель — продавец».
Участники PayWord выполняют следующие функции:
• посредник выдает сертификаты (подписывает открытый ключ покупателя и другую информацию на своем секретном ключе), проверяет цифровую подпись каждого обязательства, а также платежи, рекурсивно вычисляя значения хэш-функции. Все указанные операции выполняются в режиме off-line. Кроме того, посредник хранит свой секретный ключ, копии сертификатов покупателей и управляет счетами покупателей и продавцов;
• покупатель проверят цифровую подпись сертификатов, полученных от посредника, подписывает каждое обязательство, вычисляет значение хэш-функции для каждого элемента микроплатежной цепочки. Только подпись обязательства из указанных операций выполняется в режиме on-line. Покупатель хранит свой секретный ключ, активные обязательства, связанные с ними цепочки и текущую позицию в каждой цепочке;
• продавец проверяет цифровые подписи всех полученных сертификатов и обязательств, вычисляет (или пропускает вычисление) значение хэш-функции для каждого элемента цепочки. Все операции выполняются в режиме on-line. В течение рабочего периода продавец хранит все обязательства и соответствующие элементы микроплатежные цепочек с наибольшим индексом.
MicroMint — допечатный станок» электронных наличных. Основное экономическое свойство MicroMint — стоимость выпуска электронных денег обратно пропорциональна объему денежной массы (из расчета на одну денежную единицу). На начальном этапе выпуск электронных наличных требует значительных инвестиций, однако затраты на все последующие выпуски прогрессивно убывают. Выпущенные электронные деньги действуют в пределах установленного срока (например, одного месяца). Посредник, отвечающий за выпуск электронных наличных, инвестирует средства в создание компьютера заданной мощности, способного выполнить необходимый объем вычислений. Отметим, что возможность подделки электронных наличных зависит от доступности вычислительных ресурсов. Для выпуска денежной массы требуется непрерывная работа компьютера в течение месяца. Выпущенные в начале каждого месяца электронные наличные передаются покупателям, те перечисляют их продавцам в качестве платы за товар, продавцы в соответствии с установленными правилами возвращают деньги посредникам для погашения.
5.1. Электронные наличные как коллизии хэш-функции
Деньги в MicroMint представляются коллизиями некоторой хэш-функции h, отображающей m-битную последовательность x в n-битную последовательность у. k-коллизией называют множество k различных значений (х1, х2,..., хk,), удовлетворяющих заданному значению у, то есть у = h(xi) для всех 1 ≤ i ≤ k. Оценим вычислительную трудоемкость нахождения коллизии. Предположим, что входные значения хэш-функции выбираются случайно и независимо, тогда для нахождения .коллизии понадобится проверить приблизительно 2n(k-1)/k выходных значений. Однако, если осуществлять проверку в течение некоторого времени с, 1 < с < 2n/k, можно с достаточно высокой вероятностью найти сk k-коллизий. Таким образом, эффективность процедуры возрастает по мере нахождения коллизий. При возрастании параметра k возникает двойной эффект — увеличение задержки при поиске первой коллизии и ускорение поиска всех последующих.
Пусть денежная единица представляется k-коллизией (х1,х2,...,xk). Тогда денежную единицу можно легко проверить, убедившись, что различные xi для некоторой n-битной последовательности у удовлетворяют следующему равенству:
![]()
5.2. Процедура выпуска электронных наличных
Процедура вычисления h(x) = у аналогична случайному бросанию шара х в одну из 2nячеек. Ячейка, в которую, попадает шар х, имеет индекс у. Таким образом, денежную единицу можно интерпретировать как множество из k шаров, попавших в ячейку с индексом у. Для получения k шаров в одной ячейке в результате случайного бросания необходимо использовать не менее k2n шаров. Тогда процедура выпуска электронных наличных своди следующему: посредник выбирает k2n шаров и случайно бросает их в 2n ячеек. В качестве денежной единицы выбирается ячейка с индексом у, содержащая не менее k шаров. Основная проблема — высокая стоимость хранения информации. Для минимизации объема памяти воспользуемся следующим методом: разобьем n-битную последовательность y = h(х) на две части: старшую, состоящую из t бит, и младшую — из и бит, n = t + и. Далее, если старшие t бит у равны некоторому наперед заданному посредником значению z, то младшие u бит у задают индекс ячейки для шара x. Выбор параметра t позволяет сбалансировать объем памяти и вычислительные ресурсы компьютера. Описанный метод замедляет процедуру в 2t раз. Таким образом, посредник выполняет случайное бросание k2n шаров, запоминает 2u шаров, попавших в 2u ячеек, и затем использует их для генерации (1/2) × 2u денежных единиц.
Рассмотрим стратегию посредника при выборе параметров (k, и, t, n). Предположим, что средник, взимая с продавцов 10% комиссионных за услуги, получает один млн. долл. чистой прибыли в месяц. Для этого он должен ежемесячно выпускать приблизительно 230 (биллион) денежных единиц (при условии, что в среднем каждый покупатель ежемесячно получает 2500 денежных знаков, или 25 долл.).
Посредник сначала выбирает k = 4, то есть денежная единица будет интерпретироваться как 4-коллизия. Затем выбирает и = 31 (создает 231 ячеек) — такой выбор позволяет выпустить около (1/2) × 231 = 230 денежных единиц в месяц.
Предположим, что в качестве хэш-функции h(x) посредник выбирает криптоалгоритм DES, выполняя шифрование некоторого фиксированного значения v на переменном ключе х. Предположим также, что для реализации DES применяется технология FPGA (Р Programmable Gate Array). Стоимость одного FPGA-чипа при производительности 225 DES- шифрований в секунду составляет 400 долл. Инвестиции в размере 100 тыс. долл. (28 FP чипов) обеспечат производительность порядка 254 DES-шифрований в месяц. Если k=4, и = 31, то n = 52 и t = 21. Тогда стоимость хранения всех пар (х, h(x)) — не боле байт 237 байтов памяти — при использовании стандартной технологии магнитной записи не яре 400 тыс. долл. Таким образом, общая стоимость оборудования не превысит 150 тыс. долл. - менее 15% месячной прибыли посредника. В начале каждого месяца посредник объявляет новую хэш-функцию h или меняет значение z. Платежный механизм может быть ко дебетовым, так и кредитным, поскольку полученные при погашении электронные наличные контролируются посредником. Посредник сохраняет информацию о денежных единицах, переданных покупателю. Неиспользованные электронные наличные возвращаются к посреднику в конце каждого месяца. При оплате товара покупатель передает продавцу денежную единицу (x1,x2,...,хk). Продавец убеждается, что принятая от покупателя денежная единица удовлетворяет k-коллизии, или y = h(x,) для всех 1 ≤ i ≤ k. В конце рабочего периода продавец передает посреднику накопленные денежные единицы. Если электронные наличные не были использованы ранее, посредник выплачивает продавцу один цент (за выч комиссионных) за каждую денежную единицу.
MicroMint не исключает возможности обмана со стороны как покупателей, так и продавцов с целью получения нескольких лишних центов. Однако в целом уровень безопасности валяет осуществлять катастрофических по своим последствиям атак. Проанализируем возможные атаки.
Подлог. Может ли злоумышленник с выгодой для себя подделывать электронные наличные? Во-первых, вычислительная трудоемкость процедуры выпуска денег требует значительных инвестиций в оборудование. При указанных выше параметрах и использовании стандартной рабочей станции понадобится не менее 80 лет для получения первой денежной единицы. Во-вторых, даже в случае подделки последствия крупномасштабных атак легко обнаруживаются. Выпущенные электронные наличные действительны в течение одного месяца. Новая хэш-функция объявляется в начале каждого месяца. Например, в течение мая посредник занимается выпуском наличных на июнь. Злоумышленник может начать исследования новой хэш-функции только в начале июня. По этой причине он всегда отстает от выпуска наличных. Дополнительная мера противодействия — «скрытые» проверки электронных наличных. Проверки раскрываются : только в случае обнаружения подделки. Например, отдельные биты подлинных денежных единиц могут быть функционально связаны. Таким образом фальшивые деньги легко обнаружить.
Повторное использование. Анонимные платежи в MicroMint не предусмотрены — посредник сохраняет полную информацию о прохождении денег. Повторное использование в пределах незначительных сумм не представляет принципиальной опасности. Механизмы безопасности MicroMint позволяют легко обнаруживать подобные злоупотребления.
Обман со стороны продавца. Как поступить, если продавец передает копии денежных единиц своему сообщнику? Посредник может обнаружить дублирование денежных единиц при погашении накопленных продавцами сумм. При помощи покупателей посредники могут установить факт первого платежа и таким образом раскрыть злоумышленника.
Воровство электронных наличных. Это проблема начального распределения и погашения платежей. Решение проблемы — передача денежных единиц в зашифрованном виде. Поскольку отношения покупателей и. продавцов с посредниками стабильны во времени, допустимо использование долговременных ключей для симметричного шифрования.
Дополнительные защитные меры подробно описаны в статье [99].
Рассмотренная схема микроплатежей и парадигма электронных денег [99] отличаются высокой эффективностью с точки зрения операций двухключевой криптографии. Взаимодействие с посредниками осуществляется в режиме off-line.
В настоящее время исследования в области микроплатежных механизмов приобрели особую актуальность. Целый ряд исследователей предложили свои варианты схем: Millicent [97], NetBill [95], NetCsrd [94], VarietyCash [437], кредитная схема Педерсена (Pedersen) [98], а также схемы на базе протокола iKP [96].
Подробный анализ преимуществ и недостатков различных решений в области микроплатежных механизмов изложен в статье [99].
Депонирование ключей
В апреле 1993 г. правительство США анонсировало новый метод криптографической за ты информации, обеспечивающий высокий уровень безопасности при передаче по открыты каналам связи, с одной стороны, и отвечающий требованиям национальной безопасное с другой. Метод основан на применении шифрующей /дешифрующей микросхемы Clipper, разработанной по специальной, препятствующей считыванию информации с помощью вне него воздействия технологии TEMPEST и процедуры депонирования ключа, определяют дисциплину раскрытия уникального ключа микросхемы. Раскрытый ключ используется затем для дешифрования перехваченной информации. Генерация и запись ключа выполняют до встраивания микросхемы в конечное устройство. Не существует способа, позволяющего непосредственно прочитать ключ как во время, так и по завершении технологического процесса производства и программирования микросхемы. Ключ разбивается на два компонента каждый из которых шифруется и затем передается на хранение доверенным агентам депозитной службы. Агенты представляют собой правительственные организации, обеспечивающие надежное хранение ключевых компонентов в течение срока их действия. Агенты выдают ключевые компоненты только тогда, когда соответствующий запрос подтвержден решением федерального суда. Полученные компоненты позволяют восстановить уникальный ключ выполнить дешифрование.
Технологию разделения ключа можно описать следующим образом. Пусть имеются первичный секретный ключ и два участника, образующих легальную коалицию для получения доступа к секретной информации. Последнее означает, что ни один из участников не знает первичного секретного ключа и только объединение вторичных ключей, которыми располагают участники, позволяет восстановить первичный ключ и выполнить дешифрование. Практическая реализация идеи основана на свойствах арифметики по модулю 2.
Рассмотрим первичный ключ как последовательность двоичных символов (бит) дли n. Тогда вторичный ключ первого участника вычисляется путем суммирования первично ключа и шумовой последовательности двоичных символов длины n. Та же шумовая последовательность используется в качестве вторичного ключа другого участника. Следовательно первичный ключ может быть вычислен суммированием (по модулю 2) вторичных ключ участников. Схема обладает абсолютной секретностью — оценка трудоемкости раскрытия первичного ключа каждым из участников составляет 2n попыток дешифрования в худшем случае и 2n-1 в среднем. Данная схема является частным случаем классического метода разделения секрета, впервые описанного и изученного в работах [29,67].
В микросхеме Clipper реализован секретный симметричный (одноключевой) алгоритм криптографического преобразования Skipjack с 80-битным ключом и 64-битным размером входного и выходного блоков. Другой долговременный проект правительства США, действующего на основании закона о компьютерной безопасности (Computer Security Act) от 1987 г., связан с разработкой микросхемы Capstone. Поддержка проекта осуществляется Национальным институтом стандартов и технологии (National Institute of Standards and Technology, NIST) и Агентством национальной безопасности (National Security Agency, NSA).
В микросхеме Capstone помимо стандартных компонентов микросхемы Clipper реализованы алгоритм обмена открытыми ключами КЕА (Кеу Exchange Algorithm), цифровая подпись А (Digital Signature Algorithm [368]), хэш-функция SHA (Secure Hashing Algorithm [53]), алгоритм быстрого экспоненцирования (модульное возведение в степень) общего назначения и генератор псевдослучайных чисел на основе источника чистого шума. Все криптоалгоритмы микросхемы Capstone имеют 80-битный секретный ключ.
Основная область применения микросхемы Capstone — безопасность электронных сделок и платежей, а также ряд других сфер в рамках национальной информационной инфраструктуры. Одна из первых реализаций Capstone в виде PCMCIA-карты была использована в правительственной системе Mosaic для обеспечения безопасности электронной почты.
2. Депонирование ключей — стандарт EES
Ряд правительственных организаций принял участие в разработке и обеспечении стандарта EES. Департамент юстиции (Department of Justice, DOJ) выступил в качестве спонсора проекта, Национальный институт стандартов и технологии (National Institute of Standards lad Technology, NIST) и Отдел автоматизированных систем Министерства финансов США 9epartment of the Treasury Automated Systems Division) выполняют функции доверенных агентов депозитной службы, Агентство национальной безопасности отвечает за разработку, за Федеральным Бюро Расследования (Federal Bureau of Investigation, F.В.I.) закреплено право получать ключевые компоненты (при наличии санкции федерального суда). В качестве внешних наблюдателей в проекте участвуют пять независимых экспертов, в том числе известный специалист, доктор Д. Деннинг (D.Е. Denning) из Джорджтаунского университета [55]. Управление осуществляется Национальным менеджером программы (Кеу Escrow Ьо8тат Manager) из NIST.
Стандарт EES специфицирует алгоритм криптографического преобразования Skipjack с 80-битным ключом и метод вычисления специального поля доступа LEAF (Law Enforcement ccess Field), позволяющего впоследствии раскрывать секретный ключ в целях контроля над ) соблюдением законности. Предполагается, что алгоритм Skipjack и метод вычисления поля LEAF должны быть реализованы на базе микросхемы Clipper или другой аналогичной технологии [54]. Стандарт вводит также спецификацию уникального идентификатора (серийного номера) микросхемы UID (Device Unique Identifier), уникального ключа KU (Device Unique Кеу) и общего для семейства микросхем ключа KF (Family Кеу). Вся эта информация записывается в микросхему после ее производства, но до встраивания в конкретное устройство. Хотя ключ KU не используется для шифрования информационных потоков между отправителем и получателем, объединение его с LEAF и ключом KF позволяет восстановить сеансовый ключ и выполнить дешифрование. Детали алгоритма Skipjack и метода вычисления LEAF засекречены и составляют государственную тайную1.
Экспорт криптографических устройств с депонированием ключа не ограничен, однако в ряде случаев может потребоваться специальное разрешение [56].
Криптоалгоритм Skipjack преобразует 64-битный входной блок в 64-битный выходной блок помощью 80-битного секретного ключа. Поскольку один и тот же ключ используется для шифрования и дешифрования, алгоритм относится к классу одноключевых, или симметричных криптосистем (в отличие от двухключевых, или асимметричных криптосистем, где шифрования и дешифрования применяются различные ключи). Отметим, что размер блока в алгоритме Skipjack тот же, что и в DES (Data Encryption Standard), но при этом используя более длинный ключ (80 бит против 56). Алгоритм Skipjack может функционировать в одном из четырех режимов, введенных FIPS 81 [23] для стандарта DES: ЕСВ, СВС, 64-битного OF и CFB для 1, 8, 16-, 32- или 64-битных блоков.
Skipjack был разработан Агентством национальной безопасности и засекречен с целью исключения возможности разработки программной или аппаратной реализации отдельно от процедуры депонирования ключа. Секретность не позволяет подвергнуть алгоритм всестороннему исследованию (в отличие от DES) и продемонстрировать (или опровергнуть) его криптостойкость. По приглашению Правительства США группа независимых экспертовкриптографов выполнила исследование алгоритма Skipjack. Результаты, приведенные в отчете [57], свидетельствуют о практической криптостойкости алгоритма.
Поле LEAF передается получателю в начале каждого сеанса связи и содержит секретны сеансовый ключ шифрования/дешифрования (Session Кеу, KS), причем только официальные лица, имеющие соответствующее разрешение, могут получить KS и дешифровать в ранее зашифрованные на нем сообщения. Хотя ключ KS передается в поле LEAF, последнее используется исключительно для контроля над соблюдением законности и не предназначу для распределения ключей. Микросхема Clipper, установленная в принимающем устройстве, не позволяет извлечь ключ KS из информации в поле LEAF.
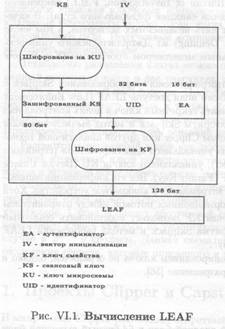
Поле LEAF вычисляется как функция от сеансового ключа KS, вектора инициализации IV (Initialization Vector), идентификатора UID и ключа KU. LEAF состоит из ключа KS, зашифрованного на KU (80 бит), идентификатора UID (32 бита) и 16-битного аутентификатора EA (Escrow Authenticator). Формирование поля завершается шифрованием указанной информации на ключе KF. Таким образом, ключ KS закрыт двойным шифрованием и может быть получен в результате последовательное)
дешифрования на ключах KF и KU (рис. VI.1). Детали алгоритма засекречены, включая
режим шифрования алгоритма Skipjack и метод вычисления аутентификатора ЕА.
Аутентификатор ЕА позволяет контролировать целостность и защищает от навязывании ложной информации в поле LEAF. Основное внимание уделяется ситуации, в которой злоумышленник может разработать специальное нелегальное приложение, взаимодействующее с легальным и передающее фиктивный LEAF получателю сообщений. При этом принимающее устройство не проверяет целостность LEAF, однако с точки зрения контроля над соблюдением законности эта информация будет бесполезной.
Воспользовавшись программным интерфейсом к криптографическому устройству Tessera, разработанного на базе PCMCIA-карты и микросхемы Capstone (Skipjack и другие необходимые функции стандарта EES), Блэйз (М. Blaze) продемонстрировал возможность создания нелегального приложения (например, е-mail), передающего фиктивный LEAF при взаимодействии с удаленным легальным приложением [58].
Атака заключается в подборе такого LEAF (путем формирования запросов для PCMCIA- карты), фиктивность которого не может быть обнаружена проверкой ЕА. Для осуществления атаки потребовалось 216 попыток (размер ЕА — 16 бит), задержка составила 42 минуты.
Однако описанная атака непрактична для существующих разработок в области секретной афонии, например устройства защиты телефонных переговоров (3600 Telephone Security Device) компании АТ&Т. Данное устройство не имеет внешнего интерфейса, необходимого для тестирования LEAF, кроме того, в случае если валидный LEAF не принят в течение короткого интервала времени, устройство переводится в режим ожидания (time out). Для PCMCIA-карт в настоящее время разработана специальная стратегия, позволяющая подсчитывать отказы при проверке LEAF и блокировать устройство (или переводить в режим ожидания) в случае превышения порогового значения.
Для защиты телефонных переговоров каждый из абонентов должен иметь специальное криптографическое устройство, содержащее Clipper, Capstone или любую другую аналогичную микросхему. В устройстве должен быть реализован протокол, позволяющий абонентам обмениваться секретным сеансовым ключом KS, например, с помощью известного метода цифрового конверта. Данный метод применяется в устройстве защиты телефонных переговоров TED (3600 Telephone Security Device), разработанном компанией АТЛЕТ. Устройство TSD подключается встык между телефонной трубкой и основным блоком и активизируется нажатием кнопки.
После установления ключевого синхронизма KS вместе с вектором инициализации IV подается на вход микросхемы для вычисления LEAF. Затем LEAF вместе с IV передается принимающей стороне для проверки и синхронизации микросхем на передающем и приемном концах. После синхронизации микросхем KS используется для шифрования и дешифрования данных (речь предварительно оцифровывается) в обоих направлениях.
В дуплексном и полудуплексном режимах связи каждое криптографическое устройство передает свою уникальную пару IV и LEAF. При этом оба устройства используют один и тот же сеансовый ключ KS для шифрования и дешифрования. Первая партия микросхем для криптографических устройств с депонированием ключа была изготовлена компанией VLSI Technology, Inc. и запрограммирована компанией Mykotronx. В устройстве TSD используется микросхема MYK-78Т (Mykotronx) с быстродействием 21 Мбит/с.
Рассмотрим процедуру генерации ключей и программирования микросхемы Clipper. В процедуре участвуют Национальный менеджер программы, два агента депозитной службы, два агента, отвечающие за формирование и хранение ключа семейства KF, представитель службы программирования (Programming Facility) микросхем, Департамент юстиции, а также некоторые правительственные подразделения, отвечающие за соблюдение законности. Участие всех сторон в процедуре генерации строго обязательно.
До начала генерации уникального ключа микросхемы и соответствующих ему ключевых компонентов необходимо сгенерировать некоторые вспомогательные ключи и случайные числа (Random Seeds). В процедуре генерации используется специальная интеллектуальная карточка (Smart Card), разработанная и рекомендованная NIST для криптографических приложений. Ввод информации выполняется с помощью считывающего устройства, подключенного к последовательному порту персонального компьютера. В Smart Card в соответствии со стандартом Х9.17 (FIPS 171) [59] реализован генератор псевдослучайных чисел. Начальное значение генератора формируется как результат вычисления хэш-функции [53] от последовательности случайных символов, введенных с клавиатуры, временных интервалов между нажатиями при вводе символов с клавиатуры и текущего времени суток.
Описанная выше процедура используется агентами депозитной службы для генерации ключевых чисел KN1, KN2 и случайных чисел RS1, RS2. Агенты, отвечающие за формирование ключа семейства (агенты KF-службы), генерируют компоненты KFC1 и KFC2. Назначение вспомогательных ключей и случайных чисел будет описано в следующих параграф
2.4.1. Компоненты ключа семейства
Каждый агент KF-службы генерирует свой компонент на отдельном операционном пункте. Четыре копии (по две копии каждого компонента) записываются на магнитные носители. Каждый магнитный носитель помещается в специальный пронумерованный контейнер. Копия каждого компонента (магнитный носитель в контейнере) помещается в отдельный сейф. Протокол генерации записывается в специальный файл.
2.4.2. Ключевые и случайные числа
Каждый агент депозитной службы генерирует и записывает на магнитные носители чет ре копии ключевых чисел. Каждый магнитный носитель помещается в специальный пронумерованный контейнер, копия каждого компонента (магнитный носитель в контейнере) помещается в отдельный сейф, установленный на операционном пункте агента.
Каждый агент генерирует и записывает на магнитный носитель одно случайное число. Магнитный носитель в контейнере помещается в сейф.
Каждый офицер депозитной службы (представитель агента) доставляет в службу программирования микросхем две копии ключевого числа (KN1 или KN2) и одну копию случайного числа (RS1 или RS2).
2.5. Программирование микросхемы
Программирование микросхемы происходит внутри специального бокса SCIF (Sensiti Compartmented Information Facility). Операция программирования выполняется с санкции Национального менеджера программы и требует участия офицеров депозитной службы (по одному от каждого агента), двух офицеров, представляющих агентов KF-службы (далее офицеров KF-службы), и представителя службы программирования микросхем. Служба программирования использует автоматизированное рабочее место (под управлением ОС. UNIX™) для генерации ключа микросхемы KU и его компонентов КС1 и КС2, персональный компьютер для контроля процесса программирования и само устройство программирования микросхем IMS (Integrated Measurement System) с производительностью порядка 1ф микросхем в час.
Служба программирования имеет также сверхнадежный сейф с двойным замком для хранения данных. Для отпирания сейфа требуется участие двух офицеров депозитной службы, по одному от каждого агента. В сейфе находится контейнер, содержащий компоненты KFCI я KFC2. Вскрытие контейнера контролируется агентами KF-службы, полученные компоненты передаются затем представителю службы программирования. ]
Как минимум один офицер депозитной службы от каждого агента должен находиться внутри SCIF во время генерации ключа KU и программирования микросхемы. Бокс авто» магически блокируется, если кто-либо покидает его во время выполнения процедуры. Для отпирания SCIF требуется участие двух офицеров депозитной службы, по одному от каждого агента.
Подготовительные действия перед каждой процедурой включают передачу (секретной почтой) по одной копии каждого компонента ключа семейства в службу программирования.

Две другие копии доставляются офицерами KF-службы. Контейнеры с магнитными носителями помещаются в сейф с двойным замком, сейф запирается представителем службы программирования. По завершении процедуры передачи ключевой информации офицеры KF-службы возвращаются на свои операционные пункты. Офицеры депозитной службы доставляют в службу программирования свои контейнеры с ключевой информацией (KN1, KN2, RS1, RS2). Далее два офицера депозитной службы (по одному от каждого агента) отпирают сейф. Представитель службы программирования, действующий по доверенности от агентов KF-службы, извлекает магнитные носители с компонентами KFC1 и KFC2.
Следуя установленной процедуре, магнитные носители с компонентами KFC1 и KFC2 вставляются в считывающее устройство автоматизированного рабочего места. Ключ семейства KF вычисляется путем побитного сложения (по модулю 2, XOR) компонентов KFCl и KFC2. Затем офицеры депозитной службы вводят KN1, KN2, RS1, RS2 и произвольные последовательности символов AI1 и AI2 с клавиатуры. Ключевые числа KN1 и KN2 побитно суммируются (по модулю 2, XOR) для вычисления ключа шифрования КСК (Кеу Component Enciphering Кеу). Назначение ключа КСК — шифрование компонентов КС1 и КС2. Офицеры депозитной службы вводят также начальный серийный номер (Stert UID) для формирования уникального идентификатора микросхемы UID. Процедура генерации ключа и программирования микросхемы показана на рис. VI.2.
Случайные числа RS1, RS2 и произвольные последовательности символов AI1, AI2 используются для вычисления пары значений. Одно из значений используется для формирования ключа KU, а другое для формирования компонента КС1. Далее ключ KU и компонент КЯ побитно суммируются (по модулю 2, XOR) для вычисления компонента КС2. Таким образом, ключ KU может быть вычислен как сумма компонентов КС1 и КС2. Затем КС1 и КС3 шифруются на ключе КСК.
Пара KU/UID подается на вход устройства программирования IMS и вместе с ключом KF записывается в микросхему. Зашифрованные компоненты КС1 и КС2 (ЕКС1, ЕКС2) вместе с UID записываются на четыре магнитных носителя (по две копии каждого компоненты упаковываются в пронумерованные контейнеры и помещаются в сейф с двойным замком момента завершения процедуры программирования микросхемы.
2.5.3. Уничтожение и транспортировка ключей
В обязанности офицеров входит активизация специальной программы, стирающей ключевую информацию с магнитных накопителей и оперативной памяти. По завершении процедуры каждый из двух офицеров депозитной службы независимо доставляет в депозитарий первого агента контейнер с магнитным носителем, содержащим компоненту ЕКС1 и UID. Аналогично выполняется доставка компонента ЕКС2 и UID в депозитарий второго агента.
До того как покинуть SCIF, офицеры депозитной службы регистрируют свои действия в специальном журнале. Копия журнала регистрации записывается на магнитный носитель и помещается в сейф с двойным замком. Оригинал журнала регистрации доставляется агентам депозитной службы.
2.6. Обслуживание ключей
Агенты депозитной службы помещают копии ключевых компонентов в отдельные сейфы с двойным замком. Для отпирания сейфа требуется участие двух лиц. Таким образом, надежность депозитария обеспечивается за счет двойного контроля, физической безопасности, криптографии и избыточности.
После доставки ключевых компонентов в депозитарий каждый из двух офицеров проверяет целостность контейнеров и их номеров. Если контейнеры не были скомпрометированы, офицеры выполняют их регистрацию и помещают копию регистрационной записи вместе с контейнерами в сейф. Контейнеры хранятся в сейфах до тех пор, пока не будет получены санкция на их извлечение.
2.6.1. Процедура выдачи ключевых компонентов
Ключевые компоненты выдаются только с санкции федерального суда и в соответствии с процедурой, установленной генеральным прокурором. Процедура предполагает формирование специальных запросов и представление их агентам депозитной службы. Назначение запроса заключается в установлении факта легальности расследования со стороны запрашивающего, законности самого расследования, определении сроков и т.д. Запрос включает также идентификатор UID и серийный номер дешифрующего процессора (Кеу Escrow Decryption Processor).
В случае если запрос принят, агенты депозитной службы выдают ключевые компоненты, соответствующие заданному UID. Должна быть обеспечена гарантия того, что по истечении срока расследования ключевые компоненты не смогут быть повторно использованы в тех же целях.
Департамент юстиции США устанавливает дисциплину использования ключевых компонент и осуществляет надзор за соблюдением законности на всех этапах расследования.
2.6.2. Извлечение и транспортировка ключевого компонента
Получив официальное разрешение на выдачу ключевого компонента, соответствующего одному или более UID, агент депозитной службы дает указание офицерам открыть один из сейфов и извлечь ключевой компонент. Поскольку сейф имеет двойной замок, для его отпирания необходимо участие двух офицеров. Помимо ключевого компонента из сейфа извлекаются ключевые числа (KN1, KN2), необходимые для формирования ключа дешифрования КСК. Факт извлечения ключевого компонента регистрируется в журнале.
Далее офицеры извлекают магнитные носители из контейнеров и в соответствии с за просом программы извлечения ключа (Кеу Extract Program) вставляют их в считывающее устройство персонального компьютера. Программа идентифицирует ключевой компонент по заданному UID и копирует его на отдельный магнитный носитель. По завершении процесса копирования все магнитные носители убираются в контейнеры. Все контейнеры, кроме контейнеров с копией зашифрованного ключевого компонента и ключевым числом, помещаются в сейф.
В итоге два офицера от каждого агента депозитной службы доставляют контейнеры с копией зашифрованного ключевого компонента и ключевыми числами на специальный операционный пункт службы дешифрования. Права доступа на операционный пункт службы дешифрования подтверждаются процедурой авторизации.
Поставщики телекоммуникационных услуг обязаны предоставлять доступ к каналам связи в том случае, если необходимость этого подтверждена соответствующим судебным решением. Обычной практикой является предоставление выделенной линии связи для передачи перехваченных шифротекстов на операционный пункт службы дешифрования. Дешифрующий процессор, установленный на операционном пункте, представляет собой персональный компьютер со специально разработанной платой. Для обработки речевой информации необходимо дополнительное оборудование для преобразования цифрового сигнала в аналоговый (ЦАП). Запуск персонального компьютера выполняется только после ввода ключа с Touch Memory. Этот же ключ используется для дешифрования программного обеспечения компьютера. Дешифрующий процессор узкоспециализирован, функционально ограничен и предназначен для решения конкретных задач дешифрования.
2.7.1. Инициализация дешифрующего процессора
Перед тем как дешифрующий процессор будет использован по назначению, необходимо выполнить его инициализацию — ввести ключ семейства KF. Для этого два офицера от каждого агента KF-службы доставляют компоненты ключа семейства на операционный пункт службы дешифрования. Далее компоненты KFC1 и KFC2 вводятся в дешифрующий процессор для формирования (сумма по модулю 2, XOR) ключа KF.
Дешифрующий процессор выделяет LEAF отправителя и получателя из зашифрованного информационного потока и затем выполняет его дешифрование на ключе семейства KF с целью получения UID. Pис. VI.З иллюстрирует процедуру дешифрования информации отправителя.
Несмотря на то что дешифрующий процессор выделяет два, возможно, различных UID микросхем на приемном и передающем концах, ключ KS используется для шифрования/дешифрования в обоих направлениях. Полученный в результате дешифрования UID вместе с запросом передается агенту депозитной службы с целью получения ключевого компонента.

2.7.3. Загрузка ключевых компонентов и чисел
После доставки магнитных носителей с ключевыми числами (KN1, KN2) и копий зашифрованного ключевого компонента (ЕКС1, ЕКС2) офицеры депозитной службы проверяют соответствие серийного номера дешифрующего процессора номеру, указанному в запрос (см. параграф 2.6.1). Если номера идентичны, офицеры извлекают магнитные носители из контейнеров и в соответствии с процедурой вставляют их в считывающее устройство дешифрующего процессора. Кроме того в дешифрующий процессор вводится информация о временном интервале, в течение которого ключевой материал может быть использован на законном основании (срок действия). Дешифрующий процессор выполняет суммирование ключевых чисел KN1 и KN2 для вычисления ключа КСК. После дешифрования ЕКС1 и ЕКС2 на ключе КСК и получения компонентов КС1 и КС2, последние суммируются ля получения ключа KU. По завершении процедуры копия диска с ключевым компонентом, доставленная офицером депозитной службы, уничтожается, контейнер с ключевыми числами (KN1, KN2) доставляется обратно в депозитарий агента.
2.7.4. Дешифрование
Раскрытие ключа KU конкретной микросхемы позволяет дешифровать любой шифротекст, полученный с помощью этой микросхемы. Для этого достаточно перехватить LEAF, передаваемый в начале каждого сеанса связи, затем дешифровать LEAF, на KF, получить UID и зашифрованный сеансовый ключ KS. Следующее действие заключается в раскрытии KS (дешифрованием на KU) и проверке аутентификатора ЕА. Валидность ЕА свидетельствует о том, что ключ KS восстановлен правильно и может быть использован для дешифрования информации в обоих направлениях. Полученные в результате дешифрования речевые данные в цифровой форме преобразуются в сигнал тональной частоты с помощью цифро-аналогового преобразователя (ЦАП). Ранее перехваченная зашифрованная информация (до раскрытия KU) также может быть дешифрована. Если KU известен, быстродействие аппаратуры позволяет осуществлять прослушивание телефонных переговоров в реальном масштабе времени.
2.8. Завершающая фаза
По истечении установленного срока действия выдается команда на уничтожение ключа KU, хранящегося в памяти дешифрующего процессора. Эта операция может быть выполнена до или в момент истечения срока. Уничтожение ключа подтверждается аутентичным сообщением, посылаемым каждому агенту депозитной службы. Таким образом, применение ключа после истечения срока действия будет обнаружено в результате аудиторской проверки. Специальная служба Департамента юстиции отвечает за проведение расследования в случае, если агенты депозитной службы не получают уведомления об уничтожении ключа по истечении срока его действия.
Многоуровневая криптография
Начнем с рассмотрения классического решения для экспортной криптографии: ограничения длины ключа. Стандартный подход заключается в использовании криптосистемы с фиксированной (например, DES) или переменной длиной ключа (такой, как RC2 RC4 или RC5 и RC6), удовлетворяющей установленным экспортным ограничениям. Типичным является ограничение длины ключа до 40 бит. Известно, что подобное ограничение делает криптосистему уязвимой.
Таким образом, если 40 бит ключа недостаточно для обеспечения требуемого уровня криптостойкости, какова должна быть «правильная» длина ключа для криптосистемы с экспортными ограничениями? Под «правильной» подразумевается длина ключа, одновременно удовлетворяющая противоречивым требованиям как национальной, так и коммерческой без опасности. Ответ на поставленный вопрос чрезвычайно сложен. С одной стороны, транснациональные корпорации выдвигают законные требования по обеспечению высокого уровня секретности при осуществлении электронных платежей и проведении сделок. С другой стороны, возможности разведывательных служб по раскрытию секретной информации не должны существенно зависеть от незначительных изменений длины ключа.
Важное обстоятельство заключается в понимании существенной разницы в затратах при атаке на конкретный, отдельно взятый шифротекст и множество различных шифротекстов (при условии, что шифрование выполняется на различных ключах). Известно, что такие крупные разведывательные службы, как Агентство национальной безопасности США, обл. дают достаточным потенциалом для успешного проведения силовой атаки на большом ключевом пространстве (например, при длине ключа 64 бита). При этом все существующие ресурсы будут задействованы для решения одной конкретной задачи. Очевидно также, что основное назначение АНБ заключается в сборе и обработке большого количества информации. Тогда, например, силовая атака каждого из миллиона шифротекстов, полученных в течение дня, приведет к неприемлемым затратам даже для столь неограниченного бюджета, которым располагает АНБ. Следовательно, разница между пиковой и средней вычислительными 1 возможностями является важным обстоятельством при выборе длины ключа.
Требования коммерческой безопасности устанавливают такую длину ключа, при которой затраты на силовую атаку приближаются к пиковым возможностям АНБ, тогда как требования самого Агентства направлены на ограничение ключевого пространства с целью минимизации необходимых затрат.
1. Принципы многоуровневой криптографии
Задача может быть решена путем разработки криптосистем, обладающих специальными свойствами. Идея [62] заключается в том, что затраты на силовую атаку при раскрытии первого (произвольного) ключа и всех последующих различаются. С вычислительной точки зрения объем перебора (первый уровень сложности), который необходимо выполнить для раскрытия первого ключа, должен превышать объем перебора (второй уровень сложности), необходимый для раскрытия любого следующего ключа. При этом неважно, какой ключ атакуется первым: любой ключ из заданного ключевого пространства должен удовлетворять первому уровню сложности. Раскрытие первого ключа дает криптоаналитику дополнительную информацию о структуре ключевого пространства, и все последующие ключи могут быть раскрыты с меньшими затратами. Для примера рассмотрим многоуровневую криптосистему 68/48, где поиск первого ключа требует «просеивания» всевозможных ключей из пространства 268, однако поиск последующих ограничен пространством 248. В данной ситуации коммерческий пользователь должен быть удовлетворен, так как для успешной атаки на подобную криптосистему потребуются значительные начальные инвестиции. С другой стороны, АНБ также должно согласиться с таким методом, поскольку значительные затраты потребуются только на начальном этапе и усредненные затраты на атаку криптосистемы будут вполне приемлемыми.
Таким образом, предлагаемый подход отличается от ранее используемых методов, игнорировавших существенную разницу в затратах при атаке на единичный шифротекст и множество шифротекстов.
Конструктивная особенность криптосистемы заключается в специальном, структурированном методе построения ключей. Так, произвольно выбрав начальный ключ некоторой длины, пользователь ограничивается в выборе всех последующих ключей. Такой принцип построения позволяет ввести зависимость на некотором подмножестве ключей из полного пространства. При этом каждый отдельный ключ из подмножества (при условии, что другие ключи подмножества неизвестны) обеспечивает заданную криптостойкость (устойчивость криптосистемы к силовой атаке).
Разработка параметрических криптосистем является одним из возможных путей развития методов многоуровневой криптографии. Например, параметры могут быть выбраны таким образом, что для раскрытия ключей второго уровня сложности понадобится раскрыть не один, а несколько ключей первого уровня сложности. Возможен также вариант криптосистемы с большим числом уровней сложности.
Отметим, что в случае применения многоуровневой криптосистемы внутри группы пользователей раскрытие ключа первого уровня сложности одного из пользователей не позволяет раскрыть ключи второго уровня сложности других пользователей данной группы. Последнее означает, что криптосистема содержит множество секретных параметров, выбираемых пользователями на начальном этапе. Выбранный однажды параметр не может быть заменен впоследствии. Таким образом, раскрытие одного или нескольких ключей первого уровня сложности позволяет установить секретный параметр пользователя. Очевидно, что любая атака сводится к раскрытию уникального ключа (ключей) первого уровня сложности конкретного пользователя, поскольку ключи построены с применением различных (уникальных) секретных параметров многоуровневой криптосистемы. В данном контексте термин «пользователь» может означать корпорацию или любую другую организацию в пределах установленной зоны безопасности, отдельную рабочую станцию, часть криптографического оборудования.
Необходимо случайным образом выбрать начальный секретный ключ К:
К = (К0, К1).
Компоненты К0 и К1 представляют собой последовательности n0 и n1 двоичных символов (бит) соответственно. Обозначим через n = n0 + n1 общую длину ключа К. Все последующие ключи выбираются аналогично, однако их построение должно быть согласовано с компонентом К1. Таким образом, выбрав первый ключ, пользователь устанавливает жесткую зависимость всех последующих ключей от К1, то есть n1 последних бит нового ключа будут содержать компонент К1 (при условии, что ключ К представляет собой конкатенацию компонентов К0 и К1). Назовем введенное ограничение многоуровневым ограничением (multi-grade constraint). Выбирая n = 68 и n0 = 48 (n1 = 20 соответственно), пользователь задает параметры многоуровневой 68/48 криптосистемы, рассматривавшейся ранее. Назовем компонент К0 кратковременным ключом (short-term key) (точнее, кратковременным ключевым сегментом), а К1 — долговременным ключом (long-term key) (или долговременным ключевым сегментом). Соответственно ключ К состоит из кратковременного и долговременного ключевых сегментов. Отметим, что компонент К1 не является открытым, а представляет собой фиксированный секретный параметр, выбираемый пользователем. Объем перебора при силовой атаке составляет 2n ключей, так как для раскрытия ключа первого уровня сложности криптоаналитик противника должен раскрыть оба ключевых сегмента K0 и К1. Трудоемкость (объем перебора) раскрытия последующих ключей второго уровня сложности будет составлять 2n0, так как усилия криптоаналитика сводятся к определению кратковременного ключевого сегмента K0. С точки зрения коммерческого пользователя, многоуровневую n/n0 криптосистему можно рассматривать как некоторое усовершенствование последовательное (одноуровневой) n-битной криптосистемы. Необходимость раскрытия долговременного ключа K1 в дополнение к кратковременному ключу К0, позволяет пользователю устанавливать нижнюю границу сложности атаки (объема перебора) со стороны криптоаналитика противника. В то же время с точки зрения АНБ данный метод открывает путь для достижения компромисса при согласовании требований коммерческой и национальной безопасности. Выбор двух параметров (n и n0) в отличие от одного позволяет принимать гибкие решения и удовлетворять противоречивые требования всех сторон. Хотя Агентству понадобится предпринять значительные усилия по раскрытию n-битного ключа, основная работа сведется к поиску no-битного ключа.
3. Соблюдение многоуровневых ограничений
Для рассматриваемых криптосистем необходим контроль соблюдения многоуровневых ограничений. Ряд важных свойств многоуровневой криптографии может быть утерян, если разрешить пользователю выбирать подходящий n-битный ключ произвольным образом и тем самым влиять на многоуровневое ограничение. Криптосистема должна быть устроена так, чтобы первый и-битный ключ мог выбираться произвольным образом, выбор же всех последующих ключей должен подчиняться жесткой дисциплине, вынуждающей пользователей включать компонент К1 в каждый ключ второго уровня сложности. Таким образом, криптосистема, не имеющая надежного механизма установки и соблюдения многоуровневых ограничений, не сможет, по-видимому, рассчитывать на доверие со стороны федеральных служб и не будет принята для экспорта. Данное обстоятельство является мотивировкой для создания надежных методов установки и соблюдения многоуровневых ограничений со стороны разработчиков многоуровневых криптосистем. Некоторые возможные решения рассмотрены в [62].
Один из методов основан на применении цифровой подписи. Смысл метода заключается в том, что криптосистема адекватно воспринимает только подписанные копии долговременных ключей (и других секретных параметров). Подпись параметров выполняется либо производителем криптосистемы, либо соответствующим подразделением экспортной службы. Для проверки подписи необходимо иметь копию открытого ключа службы, подписавшей параметры криптосистемы. Таким образом, режим функционирования будет определяться наличием подписи под долговременным ключом К1 (если ключ не подписан, выдается предупреждение или устанавливается К1 = 0).
Пользователь должен обратиться к специальной службе с целью получения заверенного, цифровой подписью ключа К1.
Подписанный долговременный ключ инсталлируется затем в программное или аппаратное обеспечение и устанавливает многоуровневое ограничение в криптосистеме пользователя.
Важное требование многоуровневой криптографии заключается в том, что служба, выполняющая подпись долговременного ключа, не должна знать, что она noдnucываem. Существует два стандартных метода такой подписи:
хэш-функция. Пользователь передает службе значение H(R), где Н — подходящая хэш- функция (например, MD5 или SHA), а R — случайное число. Служба подписывает значение НЩ и возвращает пользователю. Для выявления подлога необходимо проверить подлинность полученного от службы значения H(R) — заново вычислить значение хэш-функции от R, сравнить результаты и затем проверить подпись. В случае удачного завершения всех проверок в качестве долговременного ключа К1 пользователь выбирает n1 младших бит из случайного числа R;
«слепая» RSA-подпись. Как и в первом случае, выбирается подходящая хэш-функция. Затем пользователь случайно выбирает «ослепляющий» параметр — число b — и передает службе на подпись результат вычисления Н(В)be(mod n), где (n, е) — открытый RSA-ключ службы. В ответ пользователь получает подпись (H(R)be mod n)d ,где d- парный секретный ключ. Выполняя деление принятого значения на b, пользователь получает подпись (H(R)d). В качестве долговременного ключа выбирается п1 младших бит из случайного числа R [63].
Обратная задача получения В из H(R) и Н(R) из H(R)be mod n является вычислительно-трудоемкой и требует экспоненциального объема вычислений.
Вычисление значения хэш-функции в «слепом» методе может быть опущено, то есть вместо H(R) можно непосредственно подписывать ключ К1. Однако подписанное значение хэш-функции в отличие от секретного ключа может храниться в незащищенной памяти.
Дополнительная особенность метода на основе подписи заключается в том, что подписывающая служба может контролировать число используемых ключей К1 (несмотря на то, что сами ключи неизвестны), а также устанавливать их принадлежность. Например, служба может скрепить подписью (авторизовать) несколько долговременных ключей для некоторой организации, отдельного криптографического устройства или программного обеспечения.
Отметим, что служба может выполнять авторизацию долговременных ключей с различными значениями длины n1 для различных пользователей. Например, служба может авторизовать 20-битный долговременный ключ для крупной финансовой организации и 6-битный ключ для индивидуального пользователя. Длина долговременного ключа будет зависеть от различных обстоятельств, таких, например, как период времени, в течение которого ключ будет использоваться, количество шифруемых на ключе сообщений и т.д.
При авторизации долговременных ключей переменной длины служба может подписывать (метод на базе хэш-функции) пару значений (n1, H(R)) вместо H(R). Авторизация методом «слепой» подписи связана с некоторыми трудностями — для каждой новой длины потребуется новый открытый RSA-ключ.
Таким образом, для авторизации ключей переменной длины предлагается использовать метод на базе хэш-функции с последующим использованием стандартных (не «слепых») методов цифровой подписи для заверения (n1, H(R)).
Преимущество многоуровневой криптографии увеличивается с ростом числа используемых ключей. Секретный параметр длиной 1gd бит может использоваться в d различных ключах одного пользователя без существенного увеличения средней рабочей нагрузки со стороны федерального агентства. Так, например, для пользователя, работающего с одним миллионом ключей, длина компонента К1 может составлять 20 бит. Преимущество схемы 68/48 по сравнению с простым ограничением ключа до 48 бит для такого пользователя будет очевидным.
Одно из требований может заключаться в необходимости решения t1 сложных n-битных проблем до того, как решение всех последующих станет существенно более простым. Например, применение 6416/48 криптосистемы потребует в начале решения t1= 16 проблем с объемом перебора 264. Суммарная сложность (объем перебора) раскрытия 6416/48 криптон системы эквивалентна сложности раскрытия 68/48 криптосистемы.
Для реализации описанной схемы необходимо установить функциональную зависимость между К1 и К0:
K1 = fu(К0).
Функция fu случайно выбирается пользователем (один раз) в начальный момент времени из некоторого известного класса функций F. Тогда раскрываемая в процессе атаки пара ключей (К0, К1) дает дополнительную информацию об аргументе и значении неизвестном функции fu. Функции из класса F, восстанавливаемые по определенному числу входных и выходных значений, хорошо известны. Так, например, если функция fu задается в виде многочлена степени (t1 — 1) над некоторым конечным полем, то для восстановления функции потребуется t1 значений. Секретный параметр криптосистемы будет определяться коэффициентами восстановленного многочлена.
Другой естественный подход заключается в увеличении числа сегментов ключа. Для до ступа к 40-битному ключу в 701/6432/40 многоуровневой криптосистеме потребуется раскрыть один 70-битный и 25 64-битных ключа. Подобную иерархию ключей организовать несложно, хотя общий метод построения пока неизвестен. Основная идея сводится к тому, что каждый новый секретный параметр некоторого вложенного уровня сложности может быть получен только в результате раскрытия секретного параметра (параметров) объемлющего уровня.
В качестве вариации основной идеи рассмотрим ключ-триплет (К0, К1,К2), где ключу К0 разрешено меняться ежедневно, К1 — ежемесячно, К2 — ежегодно. Пользователь может удостовериться, что ключи текущего года не зависят от ключей прошлых лет, при этом агентство будет знать, что смена ключа пользователем потребует серьезных усилий по раскрытию ключа один раз в течение года.
Наиболее эффективно описанные методы работают в случае, если ключи применяются для шифрования файлов или сообщений внутри некоторого сообщества, например одном организации, — тогда получатель и отправитель разделяют общий долговременный ключ, Когда Алиса и Боб принадлежат к различным организациям и хотят установить безопасным режим взаимодействия, им необходимо позаботиться о том, чтобы их долговременные ключи не были раскрыты в процессе согласования общего сеансового ключа. Рассмотрим следующим метод. Обозначим через KA многоуровневый ключ Алисы (включающий ее долговременный ключ), а через КB — многоуровневый ключ Боба. Алиса и Боб вырабатывают общий сеансовый ключ КS (например, по схеме экспоненциального ключевого обмена Диффи — Хеллмана) и затем обмениваются значениями ЕKA (КS) и EKB (KS) По смыслу эти значения аналогичны LEAF в алгоритме Clipper. При известном КA или КB можно вычислить KS. Алгоритм шифрования должен быть устроен так, чтобы случайное или преднамеренное изменение этих параметров делало шифротекст бесполезным для получателя.
Новые идеи в криптографии
1. Криптография с временным раскрытием
Криптографическая задача шифрования сообщения рассматривается таким образом, чтобы бы полученная криптограмма могла быть дешифрована, в том числе и самим отправителем сообщения, по истечении заданного интервала времени. Атака на подобную криптосистему считается успешной, если удается дешифровать сообщение существенно ранее установленного срока. Такой способ защиты, с возможностью раскрытия секретной информации по истечении определенного времени, называется криптографией с временным раскрытием (timed-release crypto). Криптосистема с временным раскрытием, предложенная Ривестом (В. Rivest), Шамиром (А. Shamir) и Вагнером (D. А. Wagner) [60], получила название «шарады» с временным замком (time-lock puzzles). Практическая обоснованность такого подхода к защите информации связана прежде всего с проблемами, возникающими при «посылке» секретного сообщения в будущее. Специфика заключается в том, что в отличие от традиционных криптографических методов, предполагающих наличие у получателя сообщения секретного ключа отправителя (в симметричных криптосистемах) или у отправителя сообщения аутентичного (подлинного) открытого ключа получателя (в асимметричных криптосистемах), секретный ключ уничтожается сразу после шифрования и неизвестен ни отправителю, ни получателю сообщения/Мэй (Т. Мау) был первым, кто обратился к сообществу Internet c предложением рассмотреть подобную задачу в связи с потребностями людей, пользующихся услугами криогенных депозитариев (cryonic suspension). Современные технологии позволяют «замораживать» тело человека до уровня поддержания минимальных функций жизнедеятельности организма и надежно хранить в течение определенного времени. Услуги такого рода в ряде случаев являются единственной надеждой людей, страдающих тяжелыми заболеваниями. Очевидно, что «замороженный» человек не является дееспособным и не может отвечать за какую-либо секретную информацию. Вместе с тем он должен иметь возможность оставить некоторые распоряжения (например, установить дату «размораживания»), которые были бы гарантированно выполнены по истечении заданного срока. Таким образом,
криптографические методы обеспечения конфиденциальности и целостности при заданном времени дешифрования сообщения и неизвестном ключе позволяют решить данную задачу. Известны также и некоторые другие практические приложения криптографии с временным раскрытием:
• участник торгов может пожелать «запечатать» предложение цены с тем, чтобы оно( было «распечатано» по завершении торговой сессии;
• домовладелец хочет предоставить держателю закладной возможность осуществлять платежи с использованием зашифрованных электронных наличных с различными датами дешифрования, так чтобы оплата выполнялась в начале каждого следующего месяца;
• частное лицо может пожелать зашифровать свой дневник, так чтобы он мог быть дешифрован по истечении определенного срока.
Схема шифрования с депонированием ключей (key-escrow scheme) может быть реализована на базе «шарад» с временным замком, с тем чтобы правительственные организации могли получить ключи для расшифровки сообщения лишь по истечении определенного периода времени. В настоящее время существует два основных метода построения криптосистем с временным раскрытием:
• «шарады» с временным замком на базе вычислительных проблем с существенно последовательными алгоритмами решения;
• использование доверенных агентов, принимающих на себя обязательство не раскрывать информацию в течение заданного интервала времени.
Очевидно, что при использовании доверенных агентов возникает проблема надежности, которая частично может быть решена за счет применения криптографической техники разделения секрета. Процессорное время, необходимое для решения «шарады», зависит от количества и вида применяемого аппаратного обеспечения, а также достижений в области распараллеливания вычислений. Далее будут рассмотрены оба метода. (Отметим, что Мэй предложил метод построения с использованием доверенных агентов.)
1.1. «Шарады» с временным замком
Идея заключается в том, что решение «шарады» позволяет получить секретный ключ для дешифрования ранее зашифрованного сообщения. Как было отмечено выше, сложность (вред мя) решения «шарады» существенно зависит от количества вычислительных ресурсов. Таким образом, основная задача при построении любой «шарады» сводится к выбору алгоритма доказуемо-последовательной природы, то есть алгоритма, который не может быть распараллелен в принципе и эффективность (сложность) которого существенно не зависит от вложенных в аппаратуру и программное обеспечение средств. Использование нескольких, работающих параллельно компьютеров не позволяет ускорить решение «шарады» (в некоторая смысле это аналогично вынашиванию ребенка: две различные женщины не могут выносить одного и того же ребенка за 4,5 месяца). Однако такой подход к построению «шарад» не позволяет точно определить время решения, так как использование различных технологических элементов (например, на базе арсенида галлия или кремния) приводит к. разбросу производительности конечных аппаратных реализаций. Метод, основанный на использовании доверенных агентов, является более предпочтительным в случае, когда решение должно быть предъявлено точно в указанный срок.
Необходимо подчеркнуть, что предлагаемый метод построения «шарад» не позволяет автоматически получать решение через определенное время, а требует непрерывной работы компьютера в течение заданного срока. Например, решение, рассчитанное на 10 лет, требуют непрерывных вычислений в течение 10 лет. Очевидно, что решение не будет получено через 10 лет, если вычислительный процесс был запущен через пять лет после того, как сообщение было зашифровано. Таким образом, по сравнению с использованием доверенных агентов метод последовательных вычислений требует большего количества ресурсов (для выполнения непрерывных вычислений) и может эффективно применяться для решения простых «шарад» (например, со сроком раскрытия в течение месяца).
Для пояснения задачи рассмотрим следующий пример. Обозначим через М сообщение, которое должно быть зашифровано, а через S — производительность (дешифрований в секунду) компьютера. Для шифрования сообщения М так, чтобы оно могло быть дешифровано по истечении Т секунд, выберем симметричную криптосистему (например, RC5) и выполним шифрование сообщения на ключе длиной т = 1g(2ST) бит. Сохраним криптограмму и уничтожим ключ. При помощи силовой атаки (исчерпывающего перебора в ключевом пространстве) можно найти ключ в среднем за Т секунд.
Отметим, что Меркль (R.C. Merkle) [61] был первым, кто предложил данный метод построения «шарад» и определил направление исследований в области криптографии с открыл ключом.
В связи с описанным выше методом построения возникает две проблемы:
●силовая атака допускает тривиальное распараллеливание, так что применение N компьютеров позволяет получить результат в N раз быстрее:
• время Т является ожидаемым временем дешифрования; на практике это время может быть существенно большим или меньшим, в зависимости от того, в каком порядке проверяются ключи.
1.2. Построение «шарад» с временным замком
Рассмотрим метод построения «шарад», предложенный в работе [60] и основанный на последовательном применении операции возведения в квадрат.
Предположим, что Алиса желает зашифровать сообщение М с применением «шарады» зэк, чтобы расшифровать его через Т секунд. Для этого Алиса
• генерирует составной модуль
![]()
как произведение двух простых, случайно выбранных чисел р и q и вычисляет
![]()
• Затем вычисляет (VIII.2)
![]()
где S — производительность (число возведений в квадрат по модулю и в секунду) компьютера, предназначенного для решения «шарады». Генерирует случайный ключ К для симметричной криптосистемы, например RC5. Ключ должен быть достаточно длинным (например, 160 бит), для того чтобы предотвратить возможность силовой атаки (с учетом развития технологии за время существования «шарады»).
●Применяет RC5 для шифрования М на ключе К
![]()
●Случайным образом выбирает а по модулю и (1 < а <nи) и шифрует ключ К
![]()
Для этого сначала вычисляет
![]()
и затем
![]()
• Объявляет «шараду» в виде набора параметров (и, а, g, СК, СМ) и стирает переменные (такие как р и q), созданные в процессе вычислений.
По построению ключ К не может быть найден при помощи силовой атаки. Поэтому самый быстрый способ решения «шарады» — это вычисление
![]()
При известном φ(n) можно быстро вычислить е по формуле VIII.6 и затем b по формуле VIII.7. Однако известно, что вычисление φ(n) столь же трудоемкая задача, что и разложение n на множители. Таким образом, единственный известный в настоящее время способ вычисления b (при правильно выбранных параметрах а, р, q) сводится к последовательному возведению а в квадрат (t аз), причем каждый раз в квадрат возводится предыдущая результат.
Хотя попытка разложения и на множители представляет собой альтернативный метод рения, при достаточно больших р и q такой подход менее эффективен, чем последовательное возведение в квадрат.
Число возведений в квадрат t может контролироваться с точностью до операции, следовательно, имеется возможность построения «шарад» с различными уровнями сложности решения.
Более важное обстоятельство заключается в том, что алгоритм вычисления b по формуле VIII.8 является доказуемо-последовательным (в теории сложности подобная задача известна под названием дискретной логарифмической проблемы). Иными словами, алгоритм параллельного вычисления b по формуле VIII.8 в настоящее время не известен (справедливости ради, необходимо отметить, что некоторая возможность распараллеливания существует для отдельной операции возведения в квадрат). Таким образом, число компьютеров, применяемых для решения, в данной ситуации значения не имеет.
Создание секретного канала — принципиальная проблема технологии защиты информации. По сути, секретный канал — это физическая среда распространения, гарантирующая с определенной вероятностью невозможность считывания и изменения информации во время ее передачи. Абсолютно надежный и высокоскоростной секретный канал позволил бы решить проблему конфиденциальности без применения криптографии. К сожалению, традиционные каналы связи не обеспечивают секретности в силу своей физической природы. Однако невозможно полностью исключить использование секретного канала при передаче, хранении я обработке конфиденциальной информации. Один из основных подходов к развитию криптографии заключается в создании адекватных методов защиты при минимальном количестве и загрузке секретных каналов. Несмотря на появление алгоритмов двухключевой криптографии, позволивших существенно снять остроту проблемы, зависимость от секретного канала сохраняется на этапе распределения открытых ключей.
С появлением квантовой криптографии, основанной на фундаментальных принципах квантовой механики, наметился новый путь решения проблемы секретного канала. Квантовомеханический подход необходимо рассматривать как одну из первых попыток построения канала со строгим теоретическим обоснованием его секретности.
2.1. Рождение квантовой криптографии
Отцом квантовой криптографии по праву считают физика С. Уиснера (S. Wiesner), автора основополагающей работы под названием «Сопряженное кодирование» (Conjugate Coding). По всей видимости, в конце 60-х годов идеи Уиснера выглядели слишком «сумасшедшими», и поэтому статья была опубликована только в 1983 г. [105]. В ней Уиснер объяснял, как принципы квантовой физики могут применяться для создания денежных знаков — квантовых банкнот, которые невозможно подделать. Другая идея, изложенная в статье Уиснера и относящаяся к области криптографических протоколов, спустя десять лет была заново открыта Рабином (М. О. Rabin) и получила название забывающая передача1 (oblivious transfer) [92].
Рождение квантовой криптографии состоялось благодаря Беннетту (С. Н. Bennett), лично знавшему Уиснера, и Брассару (G. Brassard), которые сформулировали и опубликовали основные положения нового научного направления в трудах симпозиума, организованного Институтом инженеров по электротехнике и радиоэлектронике США в октябре 1979 г. Широкое обсуждение идей Уиснера привело к публикации его статьи в журнале Sigact News.
Вначале квантово-механический подход к защите информации воспринимался как нечто, имеющее отношение к научной фантастике; уровень технологий не допускал практической реализации идеи (например, для создания квантовой банкноты необходимо хранить поляризованный фотон или частицу со спином — в течение длительного времени без поглощения или потери поляризации).
Советский математик А. С. Холево первым осознал, что фотон может использоваться не для хранения, а для передачи информации [102 — 104] (необходимо отметить, что в работе Уиснера подобная возможность также рассматривалась). Первая попытка «проращивания» идеи на криптографической почве привела к появлению некоторой модификации шифра Вернама (или так называемого одноразового блокнота) многократного использования [106]. Позднее Беннетт разработал квантовый протокол распределения ключей, а Брассар предложил квантовый протокол подбрасывания монеты2 [107, 108]. В настоящее время квантовая криптография интенсивно развивается. Разработан квантовый вариант протокола, известного под названием доказательство с нулевым знанием [109, 110]. Экерт (А. Ekert) предложил альтернативный вариант квантового протокола распре, деления ключей на основе эффекта Эйнштейна — Подольского — Розена (EPR effect) и теоремы Белла. Упрощенный, однако не менее криптостойкий вариант протокола Экерта, как показано в работе [112], эквивалентен протоколу, предложенному ранее Беннеттом и Брассаром [108]. Протоколы, рассчитанные на практическую реализацию, описаны в статье [113]. Вариант протокола распределения ключей, построенный на фундаментальном соотношении неопределенности для энергии-времени предложен в статье [115]. Перечень библиографических ссылок по квантовой криптографии можно найти в Internet по адресу http://www.cs.mcgill.ca/crepeau/CRYPTO/Biblio-QC.html.
С момента первых достижений в области практической реализации идей квантовой криптографии [101] были получены впечатляющие результаты [114, 116].
2.2. Элементарное введение в квантовую физику
Объектом изучения квантовой физики являются фотоны — мельчайшие частицы, или кванты, света, представляющие собой микроскопическое переменное электромагнитное поле. Явление поляризации — изменение направления электромагнитного поля — хорошо изучено в современной физике. В квантово-механической системе существуют фотоны с различной поляризацией. Так, если обычный свет пропустить через поглощающий поляризационный фильтр, то через него смогут пройти фотоны, имеющие определенную поляризацию. Разделить фотоны без поглощения можно при помощи кристалла с двойным лучепреломлением, например кальцита. При поляризации, перпендикулярной оптической оси, входящий в кристалл фотон будет детерминированно направлен по сдвинутому пути, при поляризации вдоль оптической оси — по прямому пути. Известно также, что процесс измерения в
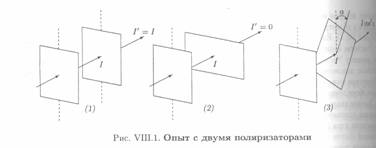
Рис. VIII.1. Опыт с двумя поляризаторами
квантово-механической системе в отличие от классической физики является неотъемлемой частью самой системы. При некоторых условиях акт измерения фотона приводит к его переполяризации, причем результат имеет вероятностный характер. Это фундаментальное свойство квантово-механической системы известно как принцип неопределенности Гейзенберга. Например, если поляризация фотона отличается от перпендикулярной или продольной (состояний поляризации фотона бесконечно много), то выходной фотон с некоторой вероятностью будет направлен по одному из двух возможных путей. Несмотря на то что с момента, рождения теории прошло 70 лет, точный физический смысл понятия «состояние» квантовой, системы продолжает обсуждаться. Бесспорно одно: состояние квантовой системы до взаимодействия с некоторым классическим измерителем (детектором) может быть использовано для предсказания вероятностей возможных результатов, которые будут зафиксированы данным детектором. Подобный подход известен также под названием копенгагенской uнmepnpетации и принадлежит Нильсу Вору, одному из основоположников квантовой теории.
Вероятностные свойства квантово-механической системы можно проиллюстрировать на примере физического опыта, хорошо известного в классической оптике (рис. VIII.1).
Пропустим пучок света через поляризатор, например кристалл турмалина. Из кристалла выйдет линейно поляризованный световой пучок; его направление поляризации совпадает с направлением оси поляризатора. Обозначим интенсивность линейно поляризованного пучка через 1. Поместим на пути выходного пучка второй поляризатор и рассмотрим три случая:
(1) ось второго поляризатора параллельна оси первого;
(2) ось второго поляризатора перпендикулярна оси первого;
(3) ось второго поляризатора составляет угол а с осью первого.
Далее будем измерять интенсивность света I' на выходе второго поляризатора. В случае (1) получим I' = I, в случае (2) — I' = 0 и в случае (3) – I1 = I cos2 α. Будем уменьшать интенсивность светового пучка до тех пор, пока через поляризаторы не пойдут одиночные фотоны. Рассмотрим проиллюстрированные на рисунке случаи в применении к одиночным фотонам. Исходные фотоны (на выходе первого поляризатора) будут иметь линейную поляризацию в направлении оптической оси поляризатора. В случае (1) исходный фотон всегда проходит через второй поляризатор; в случае (2), напротив, никогда не проходит. Иными словами, в первом случае «ворота» для фотона открыты (оптические оси параллельны), во втором «ворота» закрыты (оптические оси перпендикулярны). В случае же (3) фотон может пройти через второй поляризатор, но может и не пройти. Нельзя предсказать, какая именно из двух альтернатив (прошел или не прошел) будет реализована конкретным фотоном. Если окажется, что фотон прошел, его поляризация изменится — теперь он будет поляризован в направлении оси второго поляризатора. Таким образом, судьба исходного фотона (на выходе первого поляризатора) в принципе непредсказуема — он может «исчезнуть» или появиться в новом качестве.
Пусть имеется N исходных фотонов. Если N достаточно велико, то число прошедших фавнов можно предсказать с хорошей точностью — оно близко к N cos2α. Иными словами, неопределенность в отношении поведения отдельного фотона сочетается с предсказуемостью поведения множества фотонов. Существует определенная вероятность прохождения исходного фотона через второй поляризатор; она равна соs2α.
Несколько усложним опыт: добавим третий поляризатор, ось которого ориентируем перпендикулярно оси первого поляризатора (рис. VIII.2).

Пусть имеется N фотонов на выходе первого поляризатора. Как отмечено выше, на выходе второго поляризатора имеется N cos2α фотонов, поляризованных по оси второго поляризатора. Рассуждая далее аналогичным образом, заключаем, что после третьего поляризатора имеется N cos2α sin2 α фотонов, причем их поляризация должна совпадать с направлением оси третьего поляризатора.
Если убрать средний поляризатор, то после третьего поляризатора не будет обнаружено никаких фотонов. На первый взгляд, убирая средний поляризатор, мы улучшаем условия прохождения фотонов, однако в результате добиваемся противоположного эффекта.
Известно, что поведение фотонов подчиняется принципу суперпозиции состояний Произвольное состояние квантовой системы может быть получено как линейная комбинация, или суперпозиция, базисных состояний. Так, состояние поляризации после первого поляризатора на рис. VШ.2 можно рассматривать как суперпозицию двух базисных состояний, отвечающих двум независимым поляризациям фотона — соответственно вдоль (состояние 1 с вероятностью cos2 а) и поперек (состояние 2) оси второго поляризатора. Перед вторым поляризатором фотон находится как бы частично в первом и частично во втором состоянии (отметим, что слово «частично» нельзя воспринимать буквально, более точная интерпретация вытекает из математического обоснования теории). При взаимодействии фотона с поляризатором происходит реализация фотона либо в состоянии 1, и тогда он проходит через поляризатор, либо в состоянии 2, и тогда он не проходит. Для конкретного фотона нельзя предсказать, какое именно состояние будет реализовано, поэтому нельзя предсказать, пройдет или не пройдет через поляризатор данный фотон. Аналогичное рассуждение справедливо и для третьего поляризатора, пропускающего фотоны в первом состоянии с вероятностью sin2α. Таким образом, если убрать второй поляризатор, то ни одно из базисных состояний фотона после первого поляризатора не может быть реализовано при его взаимодействии с третьим поляризатором.
Пребывание фотона в суперпозиционном состоянии соответствует ситуации, когда фотон обладает определенным набором потенциальных возможностей. В результате взаимодействия фотона с детектором суперпозиция потенциально возможных альтернатив, разрушаясь, заменяется одной реализованной альтернативой. Причем акт этого разрешения носит характер необратимого и неконтролируемого скачка.