10.1.3. Генерация простых чисел

Леистра и Чабер указали, что при использовании некоторых модулей существует эффективная атака на DSA [370]. Если заставить абонентов криптосети использовать один из слабых модулей, то их подписи не сложно подделать. Однако такие модули легко обнаружить, и они настолько редко встречаются, что вероятность случайной генерации подобного модуля пренебрежимо мала (меньше, чем вероятность генерации составного числа).

В [368] рекомендован конкретный метод генерации двух простых чисел, р и q, где q является делителем р — 1. Длина простого числа р — между 512 и 1024 битами и кратна 64 битам.

Пусть L — 1 = 160n + b, где L — длина р, а n и b — произвольные числа, причем b < 160. Процедура генерации простых чисел состоит из следующих этапов.

(1) Построить произвольную двоичную последовательность S (не менее 160 битов). Пусть g — длина S в битах.

(2) Вычислить

где SHA — хэш-функция стандарта SHS.

(3) Образовать q, установив наибольший и наименьший значащие биты U в 1.

 (4) Проверить q на простоту.

(5) Если q не является простым, .вернуться к этапу (1).

 (6) Пусть С=0 и  N=2.

(7) Вычислить V_k = SHA((S+ N + k) mod 2^g) для k = 0, 1,..., n.

(8) Пусть W — целое число и

W=V₀ +2¹⁶⁰ V₁+…+2^160(n-1)V_n-1+2¹⁶⁰(V_n mod 2^b),

и пусть Х = W+ 2^L-1. Отметим, что Х — L-битовое число.

(9) Пусть р = Х — ((Х mod 2q) — 1). Отметим, что р конгруэнтно 1 mod 2q.

(10) Если р ( 2ь ~, то перейти к этапу (13).

(11) Проверить р на простоту.

(12) Если р — простое, перейти к этапу (15.

 (13) Пусть С = С + 1 и N = N +n+ 1.

(14) Если С = 4096, вернуться к этапу (1), иначе перейти к этапу (7).

 (15) Сохранить значения S и С, использованные, для генерации р и q.

Для всех практических применений этот метод позволяет избежать слабых значений р и q. Зная S и С, можно убедиться, что числа р и q получены при помощи описанной выше процедуры. Использование хэш-функции (в стандарте используется SHA) не позволяет получил S и С по значениям p и q. Отметим, что в RSA возможность контроля не предусмотрена— злоумышленник может сгенерировать число, форма которого упрощает разложение на мну жители. Не зная секретного ключа, проверить это невозможно. В DSA, даже если секретный ключ неизвестен, можно убедиться, что р и q генерировались случайным образом.

10.1.4. Шифрование по алгоритму ЭльГамаля

Можно использовать вызов функции DSA для шифрования криптосистемой ЭльГамаля. Пусть алгоритм реализован как вызов одной функции

Задав входные значения р, q, g,k, x и h,можно получить параметры подписи: r и s.

Для шифрования сообщения m по алгоритму ЭльГамаля при помощи открытого ключа у необходимо выбрать случайное число k и вызвать функцию

Возвращенное значение т будет эквивалентно а из схемы ЭльГамаля. Следующий вызов функции

Затем следует переименовать значение r в и u снова вызвать функцию

Возвращенное значение s будет эквивалентно 6 из схеме ЭльГамаля. Таким образом, а и b— шифротекст.

Для дешифрования необходимо, используя секретный ключ s и шифротекст а и b, вызвать функцию

Обозначим r = а^x mod р через е. Затем необходимо вызвать функцию

В результате значение а будет открытым текстом сообщения m. Этот способ работает не со всеми реализациями DSA — в некоторых могут быть зафиксированы значения р и q или длины других параметров. Однако если реализация является достаточно общей, то можно выполнить шифрование, не используя ничего, кроме функции цифровой подписи.

10.1.5. Шифрование по алгоритму RSA

Для шифрования по алгоритму RSA при заданных модуле и, сообщении m и открытом ключе е необходимо вызвать функцию

Возвращенное значение т и есть шифротекст.

Дешифрование по алгоритму RSA является точно таким же. Если d — секретный ключ, то после вызова функции

открытый текст возвращается как значение r.

10.1.6. Атака на основе фиксированного k

Для каждой подписи нужно новое значение k₁, которое должно выбираться случайным образом. Если злоумышленник узнает k₁, то, воспользовавшись некоторыми свойствами генератора случайных чисел, при помощи которого генерируется Й, он сможет раскрыть секретный ключ х. Если злоумышленник получит два сообщения, подписанных с помощью одного и того же k, то, даже не зная значения k, он сможет раскрыть x. Зная x, можно подделать подпись. В любой реализации DSA для обеспечения адекватной криптостойкости очень важен хороший генератор случайных чисел [371].

10.1.7. Опасность скрытого канала

Симмонс (G. Simmons) открыл в DSA скрытый канал [371,372]. Этот канал позволяет встраивать в подпись тайное сообщение, которое может быть прочитано только тем, у кого есть ключ. Таким образом, скрытый канал, например, позволяет при недобросовестной реализация DSS передавать с каждой подписью часть секретного ключа.

10.1.8. Варианты оптимизации

Существует вариант оптимизации, упрощающий вычисление подписи [373]. Все используемые параметры — такие же, как в DSA. Для вычисления подписи для сообщения т Алиса [ генерирует два случайных числа k и d, меньшие q. Процедура вычисления подписи выглядит следующим образом:

Боб проверяет подпись, вычисляя

Если r = ((g^u1∙y^u2) mод р) тоd q. то подпись правильна.

Следующий вариант упрощает вычисления при проверке подписи [374,375]. Все используемые параметры — такие же, как в DSA. Для подписи сообщения m Алиса генерирует случайное число k, меньшее q. Процедура вычисления подписи выглядит следующим образом:

Боб проверяет подпись, вычисляя

Если r = ((g^u1∙ y^u2) mod р) mod q, то подпись правильна.

10.2. Стандарт России — ГОСТ Р 34.10-94

ГОСТ Р 34.10-94 — российский стандарт цифровой подписи [16]. Алгоритм очень похож DSA и использует следующие параметры: р — простое число, длина которого находится диапазоне либо от 509 до 512 бит, либо от 1020 до 1024 бит, q — простое число (делитель р-1) длиной от 254 до 256 бит, а — произвольное число, меньшее р — 1, для которого а^q mod р =1 х — число, меньшее q:

Этот алгоритм также использует однонаправленную хэш-функцию H(x) из стандарта ГОСТ Р 34.11-94 [17], основанную на симметричном криптоалгоритме ГОСТ 28147-89 [10].

Первые три параметра р, q и а, открыты и могут использоваться совместно абонентами криптосети. Секретным ключом служит x, а открытым — у. Чтобы подписать сообщение m,

(1) Алиса генерирует случайное число k, меньшее q;

(2) затем Алиса вычисляет

Если H(m) mod q = 0, то значение хэш-функции устанавливается равным 1. Если r =0 то генерируется другое k и вычисления выполняются заново. Подписью служат два числа: r mod 2²⁵⁶ и s mod 2²⁵⁶ — Алиса посылает их Бобу;

(3)Боб проверяет подпись, вычисляя

Если и =r, то подпись правильна.

Различие между этой схемой и DSA заключается в том, что в DSA s = (k^-1 (Н(m) + xr)) mod q, что дает другое уравнение проверки. Отметим, что длина q равна 256 битая, Большинство западных криптографов считают, что для q достаточно 160 бит. Стандарт введен в действие с начала 1995 г.

Глава Ш

Управление ключами

Управление ключами представляет собой самую трудную часть криптографии. Проектировать криптографические алгоритмы и протоколы не просто, однако можно воспользоваться результатами теоретических исследований. Сохранить в секрете ключи намного труднее. Криптоаналитики часто атакуют симметричные и асимметричные криптосистемы, используя недостатки схемы распределения ключей. Иногда украсть ключ стоит намного дешевле, чем построить суперкомпьютер или нанять криптоаналитика. Известно, что некоторые коммерческие продукты не обеспечивают надежного хранения ключей. Например, программа DiskLock для Macintosh (версия 2.1) претендует на криптостойкое шифрование файлов по алгоритму DES. Реализация алгоритма соответствует стандарту. Однако DiskLock сохранят ключ DES вместе с зашифрованным файлом. Если известно, где искать ключ, то очень просто восстановить ключ из зашифрованного файла и затем расшифровывать его. В следующих параграфах обсуждаются некоторые задачи управления ключами и возможные пути их решения. Дополнительные сведения, касающиеся управления ключами, можно найти в ]244-248].

1. Генерация ключей

Безопасность криптосистемы сосредоточена в ключе. Если используется криптографически уязвимый процесс генерации ключей, то криптосистема в целом уязвима. Криптоаналитику не нужно заниматься криптоанализом алгоритма криптографического преобразования, достаточно проанализировать алгоритм генерации ключей.

1.1 . Ограниченное пространство ключей

DES использует 56-битовый ключ. Любая правильно заданная последовательность из 56 бит может быть ключом, существует 2⁵⁶ (10¹⁶) возможных ключей. Norton Discreet для MS-DOS (версии 8.0 и более ранние) разрешает вводить ключи в ASCII-коде, обнуляя старший бит каждого байта. Программа также преобразует символы нижнего регистра в верхний регистр. В результате преобразования пятый бит каждого байта является инверсией шестого бита, а младший разряд каждого байта игнорируется. Все эти ограничения приводят к тому, что программа использует для шифрования 40-битный ключ вместо 56-битного. В табл. Ш.1 приводится число возможных ключей для различных ограничений на размер ключевого пространства. В табл. III.2 приведено время, необходимое для осуществления силовой атаки при производительности один миллион ключей в секунду.При такой производительности возможно раскрыть ключи, состоящие из цифр и символов нижнего регистра длиной до 8 байтов, алфавитно-цифровые ключи — до 7 байтов, ключи из печатаемых символов и ASCII-символов — до 6 байтов и ключи из 8-битовых ASCII-символов — длиной до 5 байтов.

1.1. Случайные ключи

Хорошими ключами являются последовательности случайных битов, созданные некоторым автоматическим процессом. Если длина ключа составляет 64 бита, то все возможные ключи из пространства 2а4 должны быть равновероятны. Для генерации ключей важно использовать хороший генератор случайных чисел, но гораздо важнее использовать надежные процедуры управления и проверки ключей. Некоторые алгоритмы шифрования имеют ключи, обладающие рядом специфических свойств, облегчающих их раскрытие. Если эти ключи известны, необходимо выполнять их проверку в процессе генерации. В случае обнаружении слабого ключа генерируется новый ключ. У 0Е$16 слабых ключей на 2аа возможных, так что вероятность получения такого ключа достаточно мала. Генерация ключей для асимметричных криптосистем сложнее; часто ключи должны обладать определенными математически. ми свойствами (возможно, они должны быть простыми числами, квадратичными вычетами и т.д.). Стартовые последовательности для генераторов ключей должны быть случайными.

1.3.  Генерация ключей по стандарту ANSI Х9.17

 Стандарт ANSI Х9.17 определяет способ генерации ключей (рис. Ш.1) [249]. Способ подходит для генерации сеансовых ключей или псевдослучайных чисел. Дли генерации ключей используется DES, но он может быть легко заменен любым  другим крипто

алгоритмом.

Пусть E_K(X) — это Х, зашифрованное на специальном ключе К, предусмотренном для генерации секретных ключей. V₀— секретная 64-битовая стартовая последовательность. Т — метка времени. Для генерации случайного ключа R_i необходимо выполнить следующие вычисления:

Для генерации V_i+1 необходимо вычислить:

Для превращения R_i в ключ DES необходимо удалить каждый восьмой бит. Более длинный ключ получается путем конкатенации нескольких коротких ключей. Так, например, для получения 128-битового ключа необходимо сначала сгенерировать пару ключей, а потом выполнить их конкатенацию.

2.Неравносильные ключи

Иногда необходимо (например, если криптографическое устройство попадает в руки к противнику), чтобы криптоалгоритм обеспечивал адекватную криптостойкость только с секретными ключами некоторого специального вида (легальные ключи), а со всеми остальными ключами (нелегальными) для шифрования использовался бы менее криптостойкий алгоритм. Можно сделать так, чтобы вероятность случайной генерации легального ключа была пренебрежимо мала. Простой способ заключается в генерации ключа, состоящего из двух частей: непосредственно ключа и некоторой вспомогательной фиксированной последовательности бит, зашифрованной на этом ключе. Перед шифрованием блока данных расшифровывается вспомогательная последовательность. Если результатом оказывается фиксированная последовательность бит, то применяется криптостойкий алгоритм шифрования, если нет, то-менее криптостойкий алгоритм. Если алгоритм имеет 128-битный ключ и 64-битный размер блока, то длина полного ключа — 192 бита. Таким образом, существует 2¹²⁸ различных легальных ключей, однако вероятность случайного выбора легального ключа — 2^-64.

3. Распределение ключей

Стандарт ANSI Х9.17 [249] определяет два типа ключей: ключи шифрования ключей и ключи данных. На ключах шифрования ключей шифруются ключи данных при передаче по открытым каналам. На ключах данных шифруются сами сообщения. Ключи шифрования ключей должны распределяться вручную и меняются достаточно редко. Смена ключей данных происходит гораздо чаще. Подробности можно найти в [250]. Другим решением проблемы распределения является разбиение ключа на несколько различных частей и передача, их по различным каналам. Если противник соберет все части, кроме одной, он все равно, не сможет раскрыть ключ (при условии, что трудоемкость силовой атаки при восстановлении недостающей части ключа достаточно велика). Как только и у Алисы и у Боба будет ключ шифрования ключей, Алиса сможет посылать Бобу ключи данных по открытому каналу, шифруя при этом каждый ключ данных ключом шифрования ключей. Так как трафик, шифруемый ключом шифрования ключей, незначителен, то этот ключ часто менять не нужно. Однако необходимо помнить, что при компрометации ключа шифрования ключей будут 1 скомпрометированы все зашифрованные на нем ключи данных.

Ключи шифрования ключей, общие для пары пользователей, удобно использовать в сетях с небольшим числом абонентов, однако с ростом числа абонентов такая схема быстро  становится громоздкой. Так как каждая пара абонентов должна обменяться ключами, общее число обменов ключами в сети из и абонентов равно n(n — 1)/2. В сети с шестью пользователями потребуется 15 обменов ключами. В сети из 1000 пользователей понадобится уже около 500 000 обменов ключами. В этом случае распределение ключей осуществляется при помощи центрального сервера.

Известный способ организации доверенных ЦРК на базе симметричных криптосистем (симметричная схема управления ключами) имеет ряд недостатков. Существенный недостаток заключается в том, что для получения секретного ключа абонента необходимо обратиться в ЦРК с соответствующим запросом, то есть центр должен обрабатывать потоки запросов в режиме on-line. Очевидно, что нагрузка на ЦРК в сети с большим числом абонентов может быть весьма велика.

3.1. Централизованное управление

Современный подход к решению проблемы основан на свойствах асимметричных криптосистем (асимметричная схема управления ключами) и применении специальных сертификатов, выдаваемых доверенным Центром Сертификации (ЦС). Сертификат состоит из открытого ключа абонента и уникальной идентифицирующей информации, скрепленных цифровой подписью ЦС. Абоненты обмениваются сертификатами, полученными от ЦС, при установлении защищенного режима обмена или помещают их в общедоступные сетевые справочник Перед использованием открытого ключа получателя для шифрования адресованного ему сообщения отправитель может убедиться в его подлинности, проверив цифровую подпись сертификата получателя с помощью известного открытого ключа ЦС. Аналогичная пропер открытого ключа отправителя выполняется перед проверкой цифровой подписи принять получателем сообщения.

Компрометация ЦС, так же как и в случае ЦРК, приводит к компрометации всей с однако предлагаемая асимметричная схема позволяет снять нагрузку с ЦС, так как кол честно запросов на получение сертификатов существенно меньше, чем количество запросов на установление защищенного режима обмена информацией на уровне абонентов. Для получения сертификата в начальный момент времени требуется организация секретного как для передачи в ЦС открытого ключа и идентифицирующей информации. При замене открытого ключа необходимая для получения сертификата информация подписывается на стар секретном ключе (предполагается, что ключ не скомпрометирован) и передается в ЦС по крытому каналу. Результат проверки подписи является критерием для принятия решения смене открытого ключа и выдаче нового сертификата. Подробнее процедура взаимодействия с ЦС описана в документе [18].

Открытые ключи с истекшим сроком действия помещаются в специальный Список аннулированных сертификатов (САС). Существует несколько причин, по которым ключи должны удаляться и помещаться в САС. Например, ключи могут принадлежать некоторым потерявшим доверие сотрудникам компании. Следовательно, должен существовать механик позволяющий исключить возможность использования скомпрометированных ключей. Для этих целей и служит САС. Таким образом, перед проверкой подписи принятого сообщения и после верификации сертификата (проверки подписи сертификата на открытом ключ ЦС) необходимо установить, входит ли данный сертификат в САС. Если факт вхождения установлен, принятое сообщение отвергается. САС формируется специальной службой ЦС и содержит информацию о сертификатах, выданных данным ЦС. Отметим, что список держит не сами отмененные сертификаты, а только информацию, позволяющую установить что сертификат был отменен. Способы распространения САС могут быть различными: непосредственной рассылки пользователям криптосети до организации в сети специальных узлов.

3.2. Распределенное управление

В некоторых случаях способ централизованного управления ключами работать не будет. Возможно, не существует такого ЦС, которому доверяли бы Алиса и Боб. Возможно, Алиса и Боб доверяют только своим друзьям или вообще никому не доверяют. Распределенное управление ключами, используемое в PGP, решает эту проблему с помощью поручителей. Поручители это абоненты криптосети, которые подписывают открытые ключи своих друзей. Например когда Боб создает свой открытый ключ, он передает копии ключа своим друзьям. Они знают Боба, поэтому каждый из них подписывает ключ Боба и выдает Бобу копию своей подписи, Теперь, когда Боб предъявляет свой ключ чужому человеку, например Алисе, он предо являет его вместе с подписями этих двух поручителей. Если Алиса также знает одного их поручителей (или обоих) и доверяет ему, у нее появляется основание для доверия Бобу. Если Алиса не знает поручителей, то у нее нет причин доверять ключу Боба. Спустя какое-то время Боб соберет подписи большего числа поручителей. Если Алиса и Боб имеют общих знакомых, то с большой вероятностью Алиса будет знать одного из поручителей Боба. Для

предотвращения подмены ключа, прежде чем подписывать, поручитель должен быть уверен, что ключ принадлежит именно Бобу. Возможно, поручитель потребует передачи ключа при личной встрече. Выгода этого механизма — отсутствие ЦС, которому каждый должен доверять. А отрицательной стороной является отсутствие гарантий того, что Алиса, получившая открытый ключ Боба, знает кого-то из поручителей, и, следовательно, нет гарантий, что она поверит в подлинность ключа.

3.3. Атаки на ЦС

Поскольку ЦС играет ведущую роль в инфраструктуре криптосети, рассмотрим некоторые простые атаки на ЦС на примере асимметричной схемы управления ключами.

Предположим, Боб желает выдать себя за Алису. Если Боб умеет подписывать сообщения от лица Алисы, он может, например, распорядиться о снятии определенной денежной суммы со счета Алисы в банке. Для этого Боб генерирует пару ключей (открытый и секретный) и посылает открытый ключ (по секретному каналу) в ЦС с утверждением, что он является Алисой. Боб достигнет цели, если ему удастся обмануть ЦС и получить сертификат на имя Аписы. Для предотвращения подобной атаки необходимо точно идентифицировать личность спрашивающего. ЦС может, например, потребовать личного присутствия и/или предъявления удостоверения личности. Каждый ЦС может иметь свою процедуру аутентификации, а также методы хранения копий сертификатов пользователей. Очевидно, что надежная организация служб ЦС определяет надежность криптосети в целом.

Злоумышленник, раскрывший секретный ключ ЦС, может подделывать сертификаты. Для предотвращения утечки секретной информации ЦС должен хранить свой секретный ключ, а также подписанные на нем сертификаты в специальном сверхнадежном, ударопрочном, защищенном от электромагнитных излучений, электронном приборе с энергонезависимой памятью, так называемом Устройстве Подписи Сертификатов (УПС).

Известно, что силовая атака на криптосистему RSA, введенную рядом стандартов и широко используемую для шифрования и аутентификации, сводится к задаче разложения большого двусоставного модуля на простые сомножители. Причем модуль известен и входит в открытый ключ ЦС. Данное обстоятельство вынуждает ЦС использовать сверхдлинные ключи (от 1000 бит и более) и регулярно их обновлять. Периодичность процедуры обновления ключей в иерархической структуре ЦС [18] увеличивается в направлении от верхних уровней иерархии к нижним. Иными словами, частая смена ключей в ЦС верхнего уровня может быть непрактична, так как влечет за собой смену ключей у большого числа пользователей криптосети.

Другая модель атаки рассматривает возможность подкупа Боба со стороны Алисы. В этой ситуации Боб является сотрудником ЦС, и цель подкупа заключается в получении Алисой сертификата на имя Фреда. Получив сертификат, Алиса сможет посылать сообщения от имени Фреда, и все эти сообщения, в силу легальности выданного сертификата, будут адекватно восприниматься другими пользователями криптосети. Таким образом, для достижения цели необходимо объединение двух или более злоумышленников (коллаборативная атака). Учитывая возможность подобной атаки на ЦС, применяется специальный метод разграничения доступа к УПС, основанный на известной криптографической технике разделения секрета [29]. Так, например, для доступа к УПС может потребоваться участие нескольких сотрудников ЦС. Процедура предполагает предъявление специальных секретных ключей (так называемых теней основного ключа доступа), проверку их аутентичности и разрешение доступа в том случае, если число предъявленных теней не меньше заданного порогового значения. Необходимо, однако, помнить, что если поток запросов на выдачу сертификатов контролируется ' одним человеком, то описанная выше атака может быть успешной.

Другая атака заключается в подделке старых документов. Алиса осуществляет силовую Атаку модуля, входящего в состав открытого ключа ЦС. В результате по истечении определенного времени (например 15 лет) ей удается разложить модуль и восстановить старый секретный ключ ЦС. Срок действия этого секретного ключа уже истек, однако Алиса может подделать сертификат 15-летней давности, заверяющий ложный открытый ключ Боба.

В результате Алиса может подделать любой документ с подписью Боба 15-летней давности, Обычно после истечения определенного срока, например двух лет с момента подписи, электронный документ становится недоступным. Однако существует ряд ситуаций, в которых электронные документы должны надежно храниться длительное время (долгосрочные коня тракты и т.д.), при этом должна быть обеспечена возможность проверки их аутентичности и целостности. Один из способов заключается в использовании помимо обычных ключей специального сверхдолговременного ключа. Такие ключи имеют существенно больший моду и хранятся надежнее, чем все остальные. Если действие сверхдолговременного ключа истекает через 50 лет, то все подписанные на нем документы должны иметь такой же срок действия. При этом возникает проблема, связанная с неограниченным ростом САС, поскольку сверхдолговременные ключи, так же, как и все остальные, могут быть скомпрометирована и должны храниться в течение срока их действия. Для устранения указанного недостатки предлагается регистрировать сверхдолговременные ключи с помощью стандартной процедуры для обычных ключей, например со сроком действия в течение двух лет. По истечении двухгодичного периода сверхдолговременные ключи, если они не были скомпрометированы, должны быть ресертифицированы на следующие два года. Теперь скомпрометированный сверхдолговременные ключ должен храниться в САС в течение двух, а не пятидесяти лк При этом, однако, злоумышленник может добиться своего, вмешиваясь в работу служба единого времени с целью изменения периодичности процедуры ресертификации. Проблема может быть решена введением специальной Службы временных мешок (СВМ). Для этого все долговременные электронные документы должны регистрироваться со специальными цифровыми мешками, выдаваемыми СВМ. Цифровые метки позволяют удостовериться в тон, что срок действия ключа (ключей), на котором был подписан долговременный документ, не истек. Кроме того, цифровые метки позволяют устанавливать законность долговременных электронных документов даже в том случае, когда секретный ключ был скомпрометирован после того, как документ был подписан.

Предположим, Алиса желает проставить цифровую метку на подписанном ею электронном документе. Для этого Алиса хэширует нужный документ (вычисляет значение хэш. функции) и посылает полученное значение в СВМ. В ответ Алиса получает заверенную подписью СВМ цифровую метку, состоящую из полученного от нее значения хэш-функции, времени и даты, проставленных СВМ. Хэширование позволяет не раскрывать содержимое документа (хэш-функцию невозможно обратить) в процессе взаимодействия с СВМ. Очевидно, что передача информации между пользователем и СВМ осуществляется с учетами требований безопасности и может быть проконтролирована на целостность и аутентичность, В дальнейшем для доказательства даты и времени подписи документа Алиса предоставляю сам документ и цифровую метку. Проверяющий вычисляет значение хэш-функции представ ленного документа, сравнивает полученное значение с тем, которое хранится в цифровой метке, и затем проверяет заверяющую цифровую метку подпись СВМ. Доказательство будет принято при совпадении значений хэш-функции и валидности цифровой подписи СВМ.

4. Проверка ключей

Как Боб, получив ключ, узнает, что ключ передан именно Алисой, а не кем-либо другим, кто выдает себя за Алису? Если Алиса посылает свой ключ через доверенного курьера, то курьеру должен доверять также и Боб. Если ключ зашифрован ключом шифрования ключей, m Боб должен быть уверен, что этот ключ есть только у Алисы. Если используется электронная цифровая подпись, Боб при проверке подписи должен доверять открытому ключу. Он также должен быть уверен, что парный секретный ключ Алисы не скомпрометирован. Если Центр распределения ключей (ЦРК) подписывает открытый ключ Алисы, Боб должен быть уверен в аутентичности открытого ключа ЦРК. Асимметричная криптография, применяемая вместе с электронными цифровыми подписями и надежными ЦРК, сильно усложняет подмену одного ключа другим. Боб никогда не может быть абсолютно уверен в том, что злоумышленник его не контролирует, однако Боб может знать наверняка, что подмена ключа потребует гораздо больше ресурсов, чем по силам заполучить реальному злоумышленнику.

 Иногда ключи искажаются при передаче. Использование искаженного ключа при дешифровании не позволяет получить открытый текст, соответствующий принятому шифротексту. Все ключи должны передаваться с обнаружением или исправлением ошибок. Одним из наиболее широко используемых методов является шифрование ключом некоторой константы и передача первых нескольких байтов полученного шифротекста вместе с ключом. Получатель якает константу и выполняет аналогичные действия — шифрует константу на полученном ключе. Если принятый шифротекст совпадает с результатом шифрования получателя, то ключ был передан без ошибок. Вероятность ошибки находится в диапазоне от 2^-16 то до 2^-32.

5. Использование ключей

Исполнение криптографических программ под управлением многозадачных ОС связано с некоторым риском. Невозможно сказать, когда операционная система остановит работающую программу, запишет все промежуточные данные на жесткий диск и передаст ресурсы другой задаче. Возвращая управление прерванной программе и считывая при этом всю необходимую информацию с жесткого диска, операционная система не очищает память накопителя. Очевидно, что, если исполнялась программа шифрования помимо самой программы, на жесткий диск будут записаны некоторые данные, в том числе и секретный ключ. Секретный ключ будет храниться на диске до тех пор, пока не будет выполнена запись в эту же область памяти. В приоритетной, многозадачной среде для снижения риска можно установить высокий приоритет выполнения задачи. Но даже в этом случае надежность системы в целом будет невысокой. Аппаратные реализации надежнее. Многие из устройств шифрования разработаны так, что любое вмешательство приводит к уничтожению ключа. Некоторые устройства, например телефонные шифраторы, используют сеансовые ключи. Сеансовым называется ключ, который используется только для одного сеанса связи — единственного телефонного разговора — и затем уничтожается. Нет смысла хранить ключ после того, как он был использован.

В некоторых приложениях необходим контроль процесса использования сеансового ключа. Некоторым пользователям сеансовые ключи нужны только для шифрования или только для дешифрования. Сеансовые ключи могут быть разрешены к использованию только на определенной машине или только в определенное время. О

дна из схем управления подобными ограничениями предполагает добавление к ключу специального вектора контроля [251,252]. Значение хэш-функции вектора контроля суммируется (XOR) с главным ключом. Результат используется как ключ для шифрования сеансового ключа. Полученный шифротекст затем хранится вместе с вектором контроля. Для восстановления сеансового ключа нужно  вычислить значение хэш-функции вектора контроля и просуммировать результат с главным  ключом. Полученный ключ используется для дешифрования и восстановления сеансового ключа.

 Преимущество этой схемы состоит в том, что длина вектора контроля может быть произвольной и что он всегда хранится в открытом виде вместе с зашифрованным ключом. Такой способ не выдвигает требований относительно защищенности аппаратуры и предполагает отсутствие непосредственного доступа пользователей к ключам.

6. Обновление ключей

Распределение ключей при частой их замене — сложная практическая задача. Более простое решение — генерировать новый ключ из старого. Иногда такую схему называют схемой обновления ключа. Для этого необходима хэш-функция, известная и Алисе и Бобу. Если Алиса и Боб применят к общему ключу одну и ту же хэш-функцию, они получат одинаковый результат. Затем они могут выбрать из результата нужные им биты и создать новый ключ. Необходимо, однако, помнить, что секретность нового ключа определяется секретностью старого. Если злоумышленнику удалось раскрыть старый ключ, он сможет выполни обновление ключей самостоятельно.

7. Хранение ключей

Можно хранить ключ в памяти пользователя. Однако это не слишком надежно. Другое решение — хранение ключа в виде карточки с магнитной полосой, пластикового ключа с встроенной микросхемой или интеллектуальной карточки [253,254,257]. Пользователь может ввести свой ключ в систему, вставив физический носитель в считывающее устройство, встроенною автономное шифрующее/дешифрующее устройство или подключенное к компьютеру. Хотя пользователь может использовать ключ, он не знает его и не может его скомпрометировать. Он может использовать его только тем способом и только для тех целей, которые определены вектором контроля. Практически любой способен осознать, что такое физический ключ, каково его значение и как его защитить. Придание криптографическому ключу некоторой физической формы делает хранение и защиту такого ключа интуитивно понятными, Разумный способ заключается в разделении ключа на две половины, одна из которых храни

в терминале, а вторая записана в память портативного носителя. Потеря носителя не приводит к компрометации криптографического ключа. Компрометация также невозможна при несанкционированном доступе к терминалу. Следовательно, компрометация носителя ил терминала ничего не дает — для компрометации ключа необходимо заполучить обе его част Ключи, которые трудно запомнить, можно хранить зашифрованными. Например, секретный ключ RSA может быть зашифрован ключом DES и записан на жесткий диск. Для восстановления RSA-ключа пользователь должен выполнить DES-дешифрование. В идеале ключ никогда не должен оказываться вне шифрующего/дешифрующего устройства в открытом виде. Эта цель не всегда достижима, но к этому нужно стремиться.

8. Резервные ключи

Если ключ шифрования по какой-либо причине будет потерян, будет потеряна и вся зашифрованная на нем информация. Дублирование ключей увеличивает риск их компрометации. Лучшим решением является использование схемы разделения секрета (см. раздел IV). Когда Алиса генерирует ключ, она одновременно делит его на несколько частей и затем посыл эти части в зашифрованном виде различным уполномоченным лицам. Ни одна из этих част сама по себе не является ключом, но, собрав их вместе, можно восстановить ключ. Согласно идеологии разделения секрета, ключ может быть восстановлен даже при потере одно или нескольких частей. Можно просто хранить разные части, зашифрованные открытыми ключами соответствующих доверенных лиц, на своем жестком диске. Таким образом, никто не участвует в управлении ключами, пока это не станет необходимым. Другая схема резервирования [255] использует интеллектуальные карточки для временного вручения ключей Алиса может записать ключ, которым зашифрован ее жесткий диск, на интеллектуальную карточку и передать ее Бобу. Боб может использовать карточку для доступа к жестковат диску Алисы, но, так как ключ хранится на карточке, Боб не сможет его раскрыть. Кроме того, такой способ допускает двусторонний контроль: Боб может удостовериться в том, что ключ открывает диск Алисы, а Алиса всегда может проверить, был ли использован ключ.

9. Скомпрометированные ключи

Все протоколы, методы и алгоритмы современной криптографии имеют смысл только в тюк случае, если ключ хранится в секрете. Однако ключ Алисы может быть украден, потеря» или скомпрометирован иным способом. Если скомпрометированный ключ использовался в или симметричной криптосистеме, Алисе придется заменить ключ и надеяться, что ущерб минимален. Если это секретный ключ асимметричной криптосистемы, то все осложняется, так как парный открытый ключ может храниться на многих серверах в сети. Если злоумышленник получил доступ к секретному ключу Алисы, он может выдать себя за нее и, как следствие, 'читать адресованные ей сообщения и подписываться за нее. Очень важно, чтобы известие о компрометации секретного ключа быстро распространилось по криптосети. Нужно немедленно известить все серверы, управляющие базами данных открытых ключей, о случившейся компрометации, чтобы ничего не подозревающий абонент криптосети не зашифровал сообщение скомпрометированным парным открытым ключом. Хорошо, если Алиса знает, когда был скомпрометирован ее ключ. Если ключ распределяет ЦРК, то Алиса обязана сообщить ему с факте компрометации. Если ЦРК не используется, то ей следует известить всех абонентов, которые могут получать от нее сообщения. Соответствующая служба криптосети должна обнародовать тот факт, что любое сообщение, полученное после компрометации ключа, является подозрительным и что никто не должен посылать сообщения Алисе, используя соответствующий открытый ключ. Механизм временных меток позволяет абонентам определить, некие сообщения законны, а какие подозрительны. Дополнительные осложнения возникают, если Алиса не знает точно, когда ее ключ был скомпрометирован. Например, Алиса может пожелать отказаться от контракта, так как он был подписан вместо нее человеком, укравшим у нее ключ. Если такой отказ возможен, то кто угодно сможет отказаться от контракта, утверждая, что его ключ был скомпрометирован до подписания контракта. Для решения подобных вопросов необходимо привлечение независимого арбитра. Этот пример показывает, как опасно иметь один-единственный ключ (точнее, одну-единственную пару ключей). Лучше, чтобы у Алисы были различные ключи (пары ключей) для различных приложений— точно так же, как для различных замков нужны различные физические ключи. Другие решения проблемы включают биометрическую аутентификацию, ограничение на использование ключа, временную задержку и дополнительную подпись.

10. Время жизни ключей

Ни один ключ шифрования нельзя использовать бесконечно. Время его действия должно истекать автоматически, подобно паспортам и лицензиям. Причины этого в следующем:

— чем дольше используется ключ, тем больше вероятность его компрометации. Если ключ используется в течение года, то вероятность его компрометации гораздо выше, чем если бы его использовали только один день;

— чем дольше используется ключ, тем больше потери при компрометации ключа. Если ключ используется для шифрования одного документа, то потеря ключа означает компрометацию только этого документа. Если тот же самый ключ используется для шифрования больших объемов информации, то его компрометация приводит к значительным потерям;

-чем дольше используется ключ, тем больше соблазн приложить необходимые усилия для его раскрытия. Раскрытие ключа, используемого в течение суток, позволит прочитать все сообщения, переданные в течение суток. Раскрытие ключа, используемого в течение года, позволит злоумышленнику получить доступ к секретной информации, переданной в течение года;

-в ряде случаев трудоемкость криптоанализа определяется количеством шифротекстов, полученных в результате шифрования на одном ключе.

Для любого криптографического приложения необходима стратегия, определяющая допустимое время жизни ключа. У различных ключей могут быть различные времена жизни. Например, для криптографического телефона имеет смысл использовать ключ только в течение телефонного разговора, а для нового разговора — использовать новый ключ. У ключей должно быть относительно короткое время жизни, в зависимости от значимости и количества данных, зашифрованных в течение заданного периода. Ключ для канала связи со скоростью передачи 1 Гбит/с, возможно, придется менять гораздо чаще, чем для модемного канала скоростью 9600 бит/с. Если существует эффективный метод передачи новых ключей, ceaнсовые ключи должны меняться ежедневно. Ключи шифрования ключей так часто менять не нужно. При этом шифротекста для криптоаналитика образуется немного, а соответствующий открытый текст (случайные ключи) невозможно угадать. Однако, если ключ шифрования ключей скомпрометирован, потенциальные потери катастрофичны. В некоторых приложениях ключи шифрования ключей заменяются только раз в месяц или даже раз в год' Необходимо сбалансировать риски, связанные с заменой ключа или использованием фиксированного ключа. Ключи шифрования, используемые при шифровании данных длительно хранения, нельзя менять часто. Ежедневное дешифрование и повторное шифрование на новом ключе может привести к отрицательным последствиям — подобная процедура приводит к накоплению криптоаналитиком рабочего материала для последующей атаки. Решением может послужить шифрование данных на некотором уникальном ключе (или ключах) с по следующим его шифрованием на ключе шифрования ключей. Ключ шифрования ключи должен храниться в безопасном месте. Конечно же, потеря этого ключа означает потерю всех ключей, которые были на нем зашифрованы. Время жизни секретных ключей асимметричной криптографии зависит от приложений. Секретные ключи для цифровых подписей могут использоваться годами (даже в течение человеческой жизни). Во многих криптосетях срок действия секретных ключей ограничен двумя годами. Старый ключ тем не менее должен храниться в секрете на случай подтверждения подписи, сделанной во время действия старого ключа. Но для подписания новых документов должен использоваться новый ключ, Такой подход позволяет уменьшить количество материала, которое криптоаналитик сможет использовать для раскрытия ключа.

11. Уничтожение ключей

Принимая во внимание, что ключи должны регулярно меняться, старые ключи необходимо уничтожать. Старые ключи имеют определенное значение, даже если они никогда больше не используются. С их помощью можно прочитать старые сообщения [256]. Ключи должны уничтожаться надежно. Если ключ записан в EEPROM-память, то для его уничтожения нужно многократно перезаписать память. Если ключ записан в память EPROM или РВОМ, то он должен быть уничтожен вместе с микросхемой памяти. Если ключ хранится на жесткими диске компьютера, данные соответствующего участка накопителя должны быть многократно перезаписаны. Серьезная проблема заключается в том, что в компьютере ключи могут бы размножены и сохранены в различных областях жесткого диска. Любая ОС, реализующая какую-либо схему управления памятью, постоянно выгружает программы из оперативно памяти на жесткий диск и загружает их обратно. Для уничтожения ключей необходима использовать специальную программу, которая сначала выполняет поиск копий ключа на физическом уровне, даже в неиспользуемых блоках, а затем стирает их.

Глава IV

Разделение секрета

Криптографические схемы разделения секрета были независимо открыты Шамиром (А. Shamir) [68] и Блэкли (G. R. Blakley) [67]. Основное назначение схем — управление ключами. Во многих практических приложениях доступность информации зависит от одного-единственного секретного ключа. Если ключ каким-либо образом утерян (потерян носитель с записанным ключом, разрушена память, в которой хранится ключ, и т.д.), доступ к информации блокируется. Схемы разделения секрета позволяют решить сформулированную проблему. Идея заключается в разделении секретного ключа на компоненты с последующим их распределением среди легального сообщества участников. Восстановление ключа возможно только в том случае, если некоторая легальная коалиция участников объединит свои ключевые компоненты. Отметим, что первая постановка задачи была сформулирована в виде следующей комбинаторной проблемы [79].

Рассмотрим ситуацию, в которой одиннадцать ученых работают над секретным проектом. Рабочие документы проекта заперты в сейфе. Условие задачи — только шесть и более ученых, объединившись и предъявив ключи, могут отпереть сейф и получить доступ к документам. Постановка задачи сводится к оценке наименьшего числа замков сейфа и наименьшего числа ключей у каждого из ученых. В качестве решения предлагается следующее рассуждение. По условию существует как минимум один замок, который не может быть открыт ни одним ученым из произвольной пятерки. Таким образом, каждый из шести оставшихся ученых имеет ключ от этого замка. Причем нет необходимости в более чем одном подобном замке для коалиции из пяти ученых. Таким образом, минимальное число замков и ключей оценивается как число сочетаний () = 462 и () = 252 соответственно. Очевидно, что предлагаемое комбинаторное решение неприемлемо с практической точки зрения.

Криптографические схемы разделения секрета предлагают иное решение проблемы. Рассматриваемые схемы известны также под названием т-из-п-схем или (т, n)-пороговых схем для некоторого 1≤ т ≤ n. Предполагается, что схема разделения секрета включает n участников и управляется авторизованным дилером. Основная функция дилера — разделение секрета на n компонентов (теней) и распределение их среди участников так, что любые т (и более) участников, собравшись вместе и предъявив тени, могут восстановить секретный ключ. Причем любые (т — 1) (и менее) участников не могут этого сделать. Компромисс между криптостойкостью и гибкостью схемы регулируется выбором параметров т и n. Схема разделения секрета называется совершенной, если произвольная коалиция либо полностью раскрывает секрет, либо в результате не получает о нем никакой апостериорной информации. Рассмотрим простейший вариант совершенной схемы. Пусть имеется первичный секретный ключ и два участника, образующих легальную коалицию для получения доступа к секретной информации. Ни один из участников не знает первичного секретного ключа, и только объединение теней, которыми располагают участники, позволяет восстановить первичный ключ и выполнить дешифрование. Практическая реализация идеи основана на свойствах арифметики по модулю 2.

Рассмотрим первичный ключ как последовательность двоичных символов (бит) длины n.Тогда тень первого участника вычисляется путем побитного суммирования первичного ключа и шумовой последовательности двоичных символов длины п. Та же шумовая последовательность используется в качестве тени другого участника. Следовательно, первичный ключ может быть вычислен суммированием (по модулю 2) теней участников. Оценка трудоемкое раскрытия первичного ключа для каждого из участников, так же, как и для нелегально злоумышленника, составляет 2ⁿ попыток дешифрования в худшем случае и 2^n-1 — в среднем. Дополнительные сведения о схемах разделения секрета изложены в книге [69], а так в статьях [73-78].

1. Схема Шамира

Схема разделения секрета, предложенная Шамиром [68], построена по принципу полиномиальной интерполяции. Пусть задан многочлен степени (т — 1) над конечным полем GF(q) из q элементов

Секретный ключ задается свободным членом а₀, все остальные коэффициенты многочлена — случайные элементы паля. Поле GF(q) известно всем участникам. Каждая из n теней представляет собой точку (x_i, у_i,) кривой, описываемой многочленом F(x), х_i ≠ 0  Воспользовавшись интерполяционной формулой Лагранжа, можно восстановить исходный многочлен (и, следовательно, секрет а₀) по любым m точкам (теням). При этом вероятность раскрытия секрета в случае произвольных (m — 1) теней оценивается как q^-1, то есть в результате интерполяции по (т — 1) точке секретом может быть любой элемент поля с равной вероятностью. Следовательно, схема Шамира является совершенной.

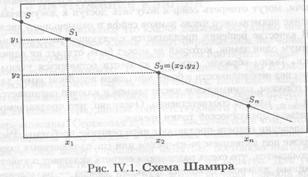
На рис. IV.1 представлен специальный случай для m = 2 (для восстановления секрета необходимо две тени). Таким образом, двучлен описывает некоторую прямую, пересекающуюся с осью у в точке s (секрет). Каждая тень — точка на прямой. Следовательно, секрет может быть восстановлен по двум произвольным теням, так как для однозначного определения прямой достаточно двух произвольных точек. В случае задания одной тени в качестве искомого секрета может быть выбрана любая точка на оси у, так как через одну точку можно провести множество различных прямых, пересекающихся с осью у в произвольных точках.

2. Схемы на основе кодов Рида — Соломона

Схема Шамира тесно связана с кодами Рида — Соломона¹, широко известными в теории помехоустойчивого кодирования [72]. Обозначим через список ненулевых элементов конечного поля GF(q). Последовательность входных символов а = (а₀, a₁,...,а_k-1), а_i € GF(q) кодируется в кодовое слово D = (D₁, D₂,..., D_q-1), где D_i =Σ a_j,  — примитивный элемент поля. Секрет задается как а₀ = - Σ D_i, в качестве теней выбираются D_i. Предположим, t из s теней содержат ошибки (ошибки, например, могли возникнуть при передаче теней по каналу связи). Согласно существующей модели, ошибки, возникающие в канале связи, рассматриваются как сумма по модулю 2 ошибочного значения и символа кодового слова. Таким образом, суть процедуры декодирования с исправлением ошибок заключается в определении позиции и значения ошибки (для кода Рида — Соломона и то и другое — элементы поля). Помимо ошибок различают стирания. В отличие от ошибок при исправлении стираний позиции известны. Применяя алгоритм декодирования с исправлением ошибок и стираний, можно гарантированно восстановить D и а, а следовательно, и а₀, пря условии что s — 2t ≥ k. Схема Шамира представляет собой специальный случай кода Рида-Соломона, где q простое число, а_i = i и t = 0. Рассмотрим ситуацию, в которой злоумышленник препятствует получению секрета легальными пользователями. Для этого он искажает тени D_i. Однако секрет будет восстановлен при условии, что кроме t искаженных легальные пользователи предоставят k неискаженных теней. В общем случае для блокирования работы (k,n) пороговой схемы злоумышленник должен исказить более |(n — k)/2| теней. Алгоритм декодирования полезен для борьбы с ошибками, возникающими вследствие несовершенства носителей (магнитных дисков, лент и т.д.) и устройств хранения информации. Применение декодирования не приводит к существенному возрастанию вычислительной сложности схемы Шамира. Вычислительная сложность алгоритма декодирования с исправлением ошибок и стираний (алгоритм Берлекэмпа — Мэсси в модификации Форни) оценивается как О(n²) (известен и более эффективный алгоритм со сложностью O(nlog² n)).

3. Схема Блэкли

Схема разделения секрета Блэкли [67] имеет геометрическую природу. Секрет представляет собой точку в т-мерном пространстве. Отметим, что для случая т > 2 все геометрические построения выполняются над конечным полем GE(q). Основы теории конечных геометрий изложены в книге [86].

Каждая из n теней задается как гиперплоскость в т-мерном пространстве.

Определение секрета сводится к нахождению точки пересечения т гиперплоскостей. В исходном виде схема является совершенной. Вариант совершенной схемы описан в [69].

На рис. IV.2 представлен специальный случай схемы Блэкли. Для восстановления секрета необходимо иметь две тени. Секрет задается как точка на плоскости. Каждая тень — прямая, проходящая через эту точку. Таким образом, секрет может быт получен по двум теням (как точка пересечения двух прямых).

4. Метод «расслаивания» изображения

Наор (Иа1ог) и Шамир [70] разработали оригинальный вариант схемы разделения секрета. Авторы схемы предложили следующую постановку задачи. Пусть имеется секретное изображение (в некотором графическом формате), которое необходимо распределить среди n участников. Для этого изображение «расслаивается» на n составляющих (теней) таким образом, что объединение любых т из них позволяет восстановить изображение. Очевидно, что ни одна из теней не дает представления об исходном изображении. Более того, никакие (m — 1) и менее теней не позволяют восстановить исходное изображение. Возможный вариант  конструктивной реализации схемы заключается в «расслаивании» изображения на черные и белые пикселы с последующей их обработкой (см. подробное изложение метода в статье [7ol]) Схема является совершенной и проста в реализации. Дополнительная модификация позволяет получать в качестве теней не «шумовые», а вполне содержательные изображения (например, изображение пейзажа или здания и т.д.), что позволяет скрыть сам факт разделения секрета.

5. Верифицируемые схемы разделения секрета

Верифицируемые схемы разделения секрета позволяют решать следующую практическую задачу: каждый из участников может убедиться в том, что полученная им тень (или тени), объединенная с тенями других участников, позволяет гарантированно восстановить раза» ленный секрет. Постановка задачи и ее решение изложены в статьях [80,81].

Для примера рассмотрим схему Шамира и ситуацию, в которой коалиция из k участников пытается восстановить секрет s при условии, что один из участников обманщик и предоставляет «ложную» тень (не ту, что была получена в результате разделения секрета). Подобною действие приведет к тому, что секрет не будет правильно восстановлен. При этом невозможно определить, кто из участников коалиции виноват в этом. В худшем случае участники просто не обнаружат, что восстановленный секрет не соответствует исходному разделенному секрету. Возможное решение заключается в применении протокола доказательства с нулевым знанием² [92], позволяющего одному участнику доказать корректность выполненных им вычислений и знание тени, полученной в результате разделения секрета, другому участнику схемы, не раскрывая при этом самой тени.

Основная проблема верифицируемого разделения секрета заключается в следующем. Дилер распределяет секрет среди n > = 2t+ 1 участников, причем предполагается, что 1 из них являются обманщиками. Сам дилер тоже может быть обманщиком. Предполагается также, что дилер является участником схемы и, соответственно, обладает некоторой тенью (тенями) разделенного секрета. Если же дилер честный, нечестные участники не смогут восстановить секрет s. Известное решение основано на протоколе с фиксированным числом транзакций и невысокой вычислительной сложностью для каждого из участников (≈ O(n^t)). Для реализации протокола необходим один широковещательный канал и по одному секретному каналу для каждой пары участников.

Некоторые дополнительные идеи относительно верифицируемых схем разделения секрета изложены в статье [71]. Схемы разделения секрета для криптосистемы RSA, а также для стандарта цифровой подписи DSS описаны в статьях [85,91] и [84,90] соответственно.

6. Разделение секрета в системах с пролонгированной безопасностью

Идея пролонгированной безопасности (proactive security) возникла в результате осознания угрозы долговременной атаки, когда злоумышленник, располагая достаточным ресурсом времени, может «взламывать» отдельные компоненты (например, последовательно преодолевать парольную защиту серверов сети) и в конечном счете скомпрометировать безопасность системы в целом. Гарантия пролонгированной безопасности важна для центров сертификации, а также для ряда криптографических приложений в тех случаях, когда восстановление режима безопасного взаимодействия сопряжено с дополнительными трудностями (например, организация секретного канала для связи с удаленными космическими станциями). Механизм пролонгированной безопасности [89] позволяет минимизировать угрозу долговременной атаки. Пролонгированная безопасность построена на принципах распределенности и периодического обновления секрета.

Пролонгированная безопасность = Распределенности + Периодическое обновление

Таким образом, криптографические функции распределяются среди компонентов системы, например секретный ключ по схеме разделения секрета распределяется среди серверов криптосети. Периодически вырабатывается новый секретный ключ, его тени распределяются среди серверов с помощью специального протокола и используются для замены теней «старого» секрета. Отметим, что подобный подход к безопасности позволяет автоматически устранять последствия успешных, своевременно не обнаруженных атак — секретная информация, раскрытая злоумышленником в некоторый момент времени, становится бесполезной после обновления.

Островский (Ostrovsky) и Юнг (Yung) предложили вариант схемы разделения секрета для систем с пролонгированной безопасностью [82]. Схема построена исходя из предположения о том, что злоумышленник может захватить отдельного участника, получить доступ к его тени и затем продолжить экспансию. Причем за один раз злоумышленник может захватить не более (k — 1) участников. Тем не менее в результате долговременной активности злоумышленника все участники будут захвачены и все тени раскрыты. Описанная стратегия характерна для некоторых разновидностей сетевых вирусов.

Для противодействия описанной выше долговременной атаке необходимо периодически (например, каждый день) обновлять тени секрета. При этом новые тени не должны зависеть от старых. Однако все тени (как старые, так и новые) должны позволять однозначно восстанавливать один и тот же секрет. Например, для схемы Шамира, где в качестве секрета s выбирается некоторое целое число из диапазона [0...р — 1], р — простое число, процедура периодического обновления теней сводится к следующему [82,83]. Дилер генерирует t случайных чисел а₁,..., а_t modulo р. Затем дилер передает серверу i тень s_i, = f(i) mod р, вычисленную для многочлена f (X) = s+ а_t Х^t . Таким образом, (t + 1) серверов могут восстановить секрет s, тогда как t серверов не могут этого сделать. Процедура обновления предполагает выполнение следующих действий. Каждый сервер i случайно разыгрывает коэффициенты многочлена f_i(X) степени t, такого, что f_i(0) =0. Затем сервер» посылает серверу j значение s_ij = f_i,(j) mod р. Сервер j вычисляет новую тень s_j:

s_j= s_j+s_1j+…+s_nj mod p

и затем стирает старую. Легко видеть, что новые тени удовлетворяют многочлену f(X) = f(X) + f₁(Х) +... + f_n(X) степени t с секретом s в качестве свободного члена. Процедура гарантирует эффективное противодействие атакам со стороны пассивного злоумышленника, имеющего доступ к памяти сервера, но не способного влиять на его работу. Противодействие активному злоумышленнику реализовано в верифицируемых схемах разделения секрета [80]. Схема Фельдмана (Feldman) [81] обладает рядом дополнительных свойств, позволяющих восстанавливать утраченные или искаженные тени и осуществлять их реинсталляцию. Более подробно упомянутые схемы описаны в статье [83]. В течение последних лет было предложено несколько схем разделения секрета для систем с пролонгированной безопасностью, включая схемы для различных видов цифровой подписи [84] и RSA [85].

7. Некоторые практические приложения

Сертификат представляет собой цифровое удостоверение личности, устанавливающее связь между открытым ключом и его владельцем, — точно так же, как водительские права устанавливают связь фотографии владельца с его именем и датой рождения. Управление сертификатами (выдача, замена и отмена) осуществляется доверенными центрами сертификации. Сертификат состоит из открытого ключа абонента и уникальной идентифицирующей информации, скрепленных цифровой подписью ЦС.

Злоумышленник, раскрывший секретный ключ ЦС, может подделать любой сертификат, что приводит к компрометации всей криптосети. Для предотвращения утечки секретной информации ЦС должен хранить свой секретный ключ, а также подписанные на нем сертификаты, в специальном сверхнадежном, ударопрочном, защищенном от электромагнитных излучений, электронном приборе с энергонезависимой памятью — устройстве подписи ceртификатов (YПC).

Существует теоретическая возможность подкупа сотрудника ЦС со стороны злоумышленника. Без помощи сотрудника ЦС доступ к информации в УПС невозможен. Цель лодку заключается в получении злоумышленником сертификата на фиктивное лицо. Получив сертификат, злоумышленник сможет посылать сообщения от имени фиктивного лица, и все эти сообщения, в силу легальности выданного сертификата, будут адекватно восприниматься другими пользователями криптосети. Таким образом, для достижения цели необходимо объединение злоумышленника и сотрудника (сотрудников) ЦС. Учитывая возможность подобной атаки, применяется специальный метод разграничения доступа к УПС, основанный на криптографической технике разделения секрета. Так, например, для доступа к УПС может потребоваться участие нескольких сотрудников ЦС. Процедура предполагает предъявления специальных секретных ключей — теней основного ключа доступа, проверку их аутентичности и разрешение доступа в том случае, если число предъявленных теней не меньше заданного порогового значения.

Так, для доступа к УПС BBN SafeКеуреr^TM, применяемого компанией VeriSign (ЦС, обеспечивающий безопасность коммерческой и финансовой деятельности в Internet), используются специальные пластиковые ключи (DataKey) — один длинный и несколько коротких. Datakey содержат чипы памяти, позволяющие запоминать криптографические ключи (ил» их части). Каждому отдельному сертификату соответствует свой набор ключей. Оператор использует длинный ключ для создания архивной копии секретного RSA-ключа. Короткий ключи распределяются среди доверенных лиц компании, получившей сертификат. Доступ к секретной информации УПС можно получить, представив один длинный и некоторое количество коротких ключей. При формировании запроса задается пороговый номер — числю коротких ключей, открывающее доступ в УПС. Например, компания, получив сертификат, может раздать короткие ключи восьми доверенным лицам при установленном пороговом номере четыре. Последнее означает, что любые четверо из восьми доверенных лиц, предоставив свои короткие ключи, могут получить доступ к УПС (при наличии одного длинного ключа),

Глава V

Финансовая криптография

В феврале 1996 г. крупнейшее консалтинговое агентство США Воок Allen й Hamilton опупликовало аналитический обзор, посвященный банковской активности в Internet. Результаты исследования указывают на высокий уровень конкурентной борьбы между банками, воспринимающими Internet как новую возможность для предоставления широкого спектра банковских услуг. По прогнозам агентства, число банковских Web-узлов возрастет с 285 (начало 1995 г.) до 900 (1999 г.) — 2000 (2000 г.). Таким образом, почти 20% банков, будут представлены в Internet. Ожидается, что к 2000 г. Internet захватит около 40% депозитных ресурсов всех банков, или более шестнадцати миллионов вкладчиков. Причем банковские услуги в Internet — это не только информационно-справочные системы на базе Web-технологии. Предполагается, что 50% всех работающих в Internet банков предоставят своим клиентам доступ к счетам в реальном масштабе времени, обеспечат возможность электронных сделок и платежей. В настоящее время подобные услуги предоставляются большинством банков США и Западной Европы.

1. Основные принципы

С наличными деньгами связано множество различных проблем практического свойствах. Чеки и кредитные карточки уменьшили количество наличных денег. При этом чеки и кредитные карточки не гарантируют анонимности — всегда можно проследить, что, когда и где покупалось. Однако электронные платежи не должны быть дополнительным способом контроля за движением денег. Человек должен иметь возможность охранять свои личные тайны; по этой причине электронные платежные системы должны гарантировать анонимность платежей.

Известный протокол на основе анонимных кредитных карточек для защиты личности клиента использует несколько различных банков [436]. Каждый клиент имеет счет в двух различных банках. Первый банк, которому известна личность человека, может зачислять деньги на его счет. Второй банк знает клиента только под псевдонимом (подобно номерному счету в швейцарском банке). Клиент может брать деньги из второго банка, доказывая, что он является владельцем счета. Но этот банк не знает личности человека и не может зачислять деньги на его счет. Первый банк знает клиента и перечисляет деньги во второй банк, не зная псевдонима. Затем клиент анонимно тратит эти деньги. В конце месяца второй банк выставляет счет первому банку, веря, что тот его оплатит. Первый банк передает счет клиенту, веря, что тот его оплатит. Когда клиент оплачивает счет, первый банк перечисляет дополнительные деньги во второй банк. Все транзакции проводятся через посредника, который действует подобно электронному Федеральному Резерву: оплачивает банковские счета, регистрирует сообщения и создает контрольный след. Если все они не сговорятся против клиента, его анонимность гарантирована. Протокол позволяет клиентам пользоваться преимуществами кредитных карточек, не раскрывая своей личности. Однако это не электронные наличные; банк слишком легко может мошенничать.

Требование анонимности платежей приводит к постановке следующей криптографической задачи (проблема «ужинающих криптографов), впервые сформулированной Чаумом (D. Chaum) в статье [430].

Предположим, что двое ваших друзей приглашают вас в ресторан на ужин. После ужин» официант подходит к столу и заявляет, что за ужин уже заплачено, но при этом не говорит, кто конкретно из сидящих за столом это сделал. Возникает следующая задача: если за ужин заплатили вы, то ваши друзья хотели бы знать об этом, так как они вас пригласили. Однако, если заплатил кто-то их них, они хотели бы знать, кто именно, но при этом не хотели бы, чтобы вы узнали об этом. Очевидно, что обсуждение возможно только за столом и при общем участии.

Чаум предложил простое решение задачи.

Ваши друзья отгораживаются от вас меню и подбрасывают монету так, чтобы вы не могли видеть результат. Затем они объявляют результат — «орел» или «решка», предварительно договорившись, что тот, кто заплатил, называет «решку», если выпал «орел», и наоборот а тот, кто не платил, всегда объявляет истинное событие. Очевидно, что если оба ваших друга называют одно и то же, то всем ясно, что заплатили вы. Однако если ваши друзья объявляют разные события, то вы знаете, что заплатил кто-то из них, но не знаете, кто именно. Поскольку оба ваших друга знают истинный результат бросания, они также знают, кто из них заплатил за ужин.

На практике решение задачи просто реализуется при помощи арифметики по модулю 2.Предположим, что возможные исходы бросания монеты — «орел» и «решка» — соответствуют двоичным нулю и единице. При этом единица также означает положительный ответ на вопрос об оплате, а ноль — отрицательный. Обозначим результат бросания монеты как k. Тогда после бросания монеты тот, кто заплатил, объявляет k Θ1, а тот, кто не платил, — просто k. Очевидно, что приглашенный всегда может выяснить, что за него заплатили, выполни суммирование объявленных результатов 1 = (k Θ 1) Θ k. Если заплатил приглашенный, об, этом также станет известно, так как 0 = (k Θ 0) Θ k.

Чаум отметил, что решение гарантирует безусловную неотслеживаемость (uncondition untraceability), или анонимность, так как основано на применении безусловно секретно шифра Вернама.

Рассмотренная постановка возникает в ряде практических задач. Например, группа абонентов сети может воспользоваться предложенным решением для отправки анонимных широковещательных сообщений (одно сообщение для многих абонентов).

(1) Участвующие упорядочиваются по кругу.

(2) Через регулярные интервалы времени соседние пары бросают между собой монету.

(3) После каждого бросания монеты объявляется результат — либо «орел», либо «решка» Если Алиса хочет передать широковещательное сообщение, она объявляет событие обратное произошедшему в тех раундах, которые соответствуют единице в двоичном представлении сообщения. Предположим, что ее сообщение — 1001. Если в результате бросаний были получены «орел», «решка», «решка», «решка», то Алиса будет объявлять «решка», «решка», «решка», «орел». Если Алиса замечает, что результат не cooтветствует сообщению, которое она пробует посылать, она понимает, что в это же время кто-то еще пытается посылать сообщение. Тогда она прекращает передачу сообщение и выжидает случайное количество раундов перед очередной попыткой.

Полученные таким образом сообщения могут быть зашифрованы открытым ключом того, кому они адресованы. В этом случае только определенный получатель, воспользовавшись парным секретным ключом, сможет расшифровать и прочесть сообщение. Никто другю3 ничего не узнает об отправителе сообщения и не сможет определить получателя.

 Альтернативой бросанию монет между соседними сторонами могло бы стать использование файла с заранее сгенерированной случайной двоичной последовательностью. Возможны и другие варианты, например, один член пары мог бы генерировать случайную последовательность и посылать ее другой стороне в зашифрованном виде. Или же участники могли бы договориться о совместном использовании генератора псевдослучайных чисел, и каждый из них имел бы возможность получить фиксированную псевдослучайную последовательность.

 Проблема заключается в том, что мошенник может незаметно все испортить, постоянно совершая обман на этапе (3). Известна модификация рассмотренного решения, позволяющая обнаруживать факт обмана [438,439].

2. Финансовые протоколы

Существуют протоколы, разрешающие использование заверенных, но неотслеживаемых (анонимных) сообщений. Так, Алиса может передать электронные наличные Бобу так, чтобы злоумышленник ничего не узнал об Алисе. Боб может затем перевести эти электронные наличные на свой банковский счет, даже если банк не имеет об Алисе никакого представления. Однако банк может установить факт повторной оплаты теми же электронными наличными. Если Боб переведет эти электронные деньги на два различных счета, это также будет: обнаружено, но анонимность Боба и Алисы при этом гарантируется.

Рассмотрим несколько подобных протоколов [430].

Следующий протокол для анонимных денежных чеков является упрощенным физическим аналогом криптографического протокола на базе «слепой» подписи, введенной Чаумом.

Протпокол 1.

(1) Алиса готовит сто анонимных денежных чеков по 1000 долл. каждый.

(2) Алиса вкладывает каждый чек вместе с листком копировальной бумаги (сначала чек и затем поверх него копировальную бумагу) в сто различных конвертов и отсылает все конверты в банк.

(3) Банк открывает девяносто девять выбранных наугад конвертов и убеждается в том что каждый чек выписан на 1000 долл.

(4) Банк подписывает единственный оставшийся нераспечатанным конверт. С помощью копировальной бумаги подпись переводится на чек. Банк возвращает нераспечатанный конверт Алисе и списывает 1000 долл. с ее счета — по существу, банк открывает анонимный счет, на который переводятся суммы, указанные на чеках.

 (5) Алиса вскрывает конверт и передает чек продавцу.

(6) Продавец проверяет банковскую подпись, убеждаясь в законности чека.

7) Продавец отсылает денежный чек в банк.

(8) Банк проверяет свою подпись и начисляет (переводит с анонимного счета) 1000  на счет продавца.

Прокомментируем рассмотренный протокол.

Может возникнуть вопрос: почему бы банку не подписать чек вместо конверта, ведь после того как вскрыты девяносто девять конвертов, он знает содержимое единственного нераспечатанного конверта с вероятностью, близкой к единице? Во-первых, банк не может вскрыть все конверты по условию: если Алиса получит подписанный чек без конверта, она заблокирует платеж. Во-вторых, банк не может сам вскрывать конверты, об этом надо просит» Алису (почему это так, станет ясно из описания свойств «слепой» RSA-подписи). Следовательно, Алиса всегда может проконтролировать то, что вскрыты девяносто девять из ста конвертов. И наконец, в-третьих, подпись непосредственно чека открывает возможности для злоупотреблений со стороны банка. Например, банк может пометить чек и таким образами отследить платеж. В этой ситуации конверт и копирка имеют принципиальное значение.

Конечно, банк не будет подписывать любой конверт. Для этого Алиса должна доказать свою подлинность. Вся необходимая для аутентификации Алисы информация должна бы указана на конверте. Однако чек должен содержать только ту информацию, которая необходима для осуществления банковских платежей, — сумму, банковские реквизиты (не раскрывающие личность плательщика) и т.д. Выполнив полный цикл аутентификации Алисы и убедившись, что она является законным владельцем счета, банк заверяет чек. Однако, получив впоследствии заверенный чек от продавца, банк не может гарантированно установить, что он принадлежит именно Алисе. Действительно, банк точно знает, что Алиса заверила чек на 1000 долл. Когда этот чек попадет к продавцу, банк не знает. Очевидно, что банк обслуживает множество клиентов и каждый их них может заверить чек на 1000 долл. Например, если Боб является законным клиентом банка, он тоже может заверить чек на эту сумму. Чеки Алисы и Боба ничем не будут различаться. Поэтому, получив чек от продавца, банк не может достоверно установить плательщика.

Банк убеждается в законности чека путем проверки подписи. Поскольку банк проверяет девяносто девять из ста конвертов, то вероятность обмана со стороны Алисы не превышает одного процента.

Рассмотрим криптографический эквивалент описанного выше протокола с использованием «слепой» RSA-подписи.

(1) Алиса генерирует сто чеков т, по 1000 долл. каждый.

(2) Затем Алиса «вкладывает» все сто чеков в «конверты». Для этого она генерирует сто случайных маскирующих множителей r_i, и вычисляет с_i =

m_i. r (mod n), где (n,е) — открытый ключ банка и 1 ≤ i ≤ 100. Полученные «конверты» отсылаются в банк.

(3) Банк случайным образом выбирает девяносто девять «конвертов» и просит Алису прислать маскирующий множитель r_i для каждого из них. Сняв маскировку («вскрыв конверты») — m_l —— с_l/r (mod n), банк убеждается, что все чеки правильно оформлены. Банк подписывает последний «нераспечатанный конверт» — с^d = т^d . r^d( mod n) = т^d. r( mod n), где d — секретный ключ банка, и возвращает его Алисе, списав с ее счета 1000 долл.

(4) Алиса сначала проверяет подпись банка. Подлинность подписи подтверждается равенством (с^d)^e =^?с. Затем Алиса «вскрывает» подписанный «конверт» — с^d/r = m^d(mod n) и передает чек продавцу.

(5) Продавец проверяет банковскую подпись — (с^d/r)^e =^? m( mod n) и отсылает чек в банк.

(6) Банк проверяет свою подпись аналогичным образом и начисляет 1000 долл. на счет продавца.

Для того чтобы «вскрыть конверт», банк должен получить от Алисы маскирующий множитель г. Тогда m = с/r^e(mod n). Задача получения т при неизвестном r столь же трудоемка, как и атака на криптосистему RSA при неизвестных р и q. Может показаться, что достаточно «вскрыть» один «конверт», получить т_i и затем «вскрыть» все остальные, не зная маскирующего множителя. Действительно, если m_i = m_j при i ≠ j, то r_j = (с_j /т_i)^d (mod n). Однако очень просто сделать так, чтобы все чеки были различными. Например, можно сгенерировать необходимое количество уникальных случайных чисел s_i, и вычислить h_i =m_i Θ s_i) ║s_i, где через ║ обозначена конкатенация. Всегда можно получить m_i из h_i и = т_i= при i ≠ j, но h_i ≠ h_j при i = j. Следовательно, если с_i = h_i . r(mоd n), то r_j ≠  (с_j/h_i)^d(mod n).

«Слепые» подписи обладают следующими свойствами:

• подпись банка под документом правильна и служит доказательством того, что именно он подписал этот документ. Подпись убедит банк в том, что он заверил этот документ, когда впоследствии документ будет ему предъявлен. Подпись также обладает всеми известными свойствами электронных цифровых подписей;

• банк не может связать заверенный им документ с моментом его подписания. Даже если банк регистрирует все «слепые» подписи, он не сможет определить, когда был подписан конкретный документ.

Рассмотренный протокол не позволяет Алисе написать чек на сумму, отличную от заявленной, но он не мешает ей скопировать чек и использовать его дважды. Для разрешения проблемы повторной оплаты предлагается следующая модификация протокола. Для наглядности изложения протокола опять воспользуемся аналогией с конвертом и копиркой.

Протокол 2.

(1) Алиса готовит сто анонимных денежных чеков по 1000 долл. каждый. К каждому денежному чеку она добавляет уникальный идентификатор Х, выбранный случайным образом и достаточно длинный, чтобы вероятность появления двух одинаковых идентификаторов была пренебрежимо мала.

(2) Алиса вкладывает каждый чек вместе с листком копировальной бумаги в сто различных конвертов и отсылает все конверты в банк.

(3) Банк открывает девяносто девять конвертов и убеждается, что каждый чек выписан на 1000 долл.

(4) Банк подписывает единственный оставшийся нераспечатанным конверт. С помощью копировальной бумаги подпись переводится на чек. Банк возвращает нераспечатанный конверт Алисе и списывает 1000 долл. с ее счета.

(5) Алиса вскрывает конверт и передает чек продавцу.

(6) Продавец проверяет банковскую подпись, убеждаясь в законности чека.

(7) Продавец отсылает чек в банк.

(8) Банк проверяет свою подпись и по своей базе данных убеждается, что денежный чек с идентификатором Х ранее не депонировался. Если это так, банк начисляет 1000 долл. на счет продавца и заносит Х в свою базу данных.

(9) Если денежный чек уже был депонирован ранее (идентификатор Х обнаружен в базе данных), банк отказывается принять его.

Теперь, если Алиса попытается расплатиться копией денежного чека или продавец попытается депонировать денежный чек повторно, используя копию, то банк обнаружит факт мошенничества.

Предыдущий протокол позволяет защитится от мошенников, но не дает возможности установить их личность. Банк не знает, попытался ли получатель заверенного банком чека обмануть продавца или продавец предпринял попытку обмануть банк. Эта неоднозначность исправляется следующим протоколом.

Протокол 3

.

(1) Алиса готовит сто анонимных денежных чеков по 1000 долл. каждый. К каждому чеку она добавляет уникальный идентификатор Х, выбранный случайным образом и достаточно длинный, чтобы вероятность появления двух одинаковых идентификаторов б пренебрежимо мала.

(2) Алиса вкладывает каждый чек и листок копировальной бумаги в сто различных конвертов и отсылает все конверты в банк.

(3) Банк открывает девяносто девять конвертов и убеждается, что каждый чек выписан на 1000 долл. и что идентификаторы всех девяноста девяти чеков различны.

(4) Банк подписывает единственный оставшийся нераспечатанным конверт. С помощь копировальной бумаги подпись переводится на чек. Банк возвращает нераспечатанный конверт Алисе и списывает 1000 долл. с ее счета.

(5) Алиса вскрывает конверт и передает денежный чек продавцу.

(6) Продавец проверяет банковскую подпись, убеждаясь в законности денежного чека.

(7) Продавец просит Алису написать случайный идентификатор Y на чеке³.

 (8) Алиса выполняет требование продавца.

(9) Продавец отсылает денежный чек в банк.

(10) Банк проверяет подпись и по своей базе данных убеждается, что денежный чек и идентификатором Х ранее не депонировался. Если это так, банк начисляет 1000 долл. счет продавца и заносит идентификаторы Х и Y в базу данных.

(11) Если идентификатор Х обнаружен в базе данных, банк отказывается принять денежный чек и сравнивает идентификатор У на чеке с аналогичным идентификатором базы данных. Если они совпадают, банк заключает, что копия была снята с чека продавцом. В противном случае банк знает, что чек был скопирован тем, кто его выписал.

В этом протоколе предполагается, что продавец не может изменить идентификатор Y после того, как Алиса напишет его на чеке. Однако проблема не решается полностью — Али может потратить копию денежного чека во второй раз, написав тот же самый идентификатор на этапе (7). Если продавец не сохраняет полученные денежные чеки и идентификаторы своей базе данных, он будет введен в заблуждение. Эту проблему устраняет следующий протокол. Если установлено, что тот, кто выписал банковский чек, попытался обмануть продавца, банк может захотеть идентифицировать злоумышленника. Для этого можно воспользоваться известной криптографической техникой разделения секрета.

Протокол 4.

(1) Алиса готовит сто анонимных денежных чеков по 1000 долл. Каждый из чеков держит уникальный идентификатор Х, полученный случайным образом и достаток длинный, чтобы вероятность появления двух одинаковых идентификаторов была пренебрежимо мала. Имеется также n вспомогательных идентификаторов, I₁,I₂,...,I₃. Каждый вспомогательный идентификатор генерируется следующим образом: Алиса создает двоичную последовательность р, содержащую ее имя, адрес и прочие сведения. Затем она генерирует и случайных двоичных последовательностей s_j и вычисляет s_j Θ p и I_j = (s_j, s_j Θ р). Алиса легко может быть идентифицирована при наличии пары s_j и s_j Θ р, так как р = s_j Θ (s_j Θ р). Далее Алиса генерирует и случайных пар r_j,₁ и r_j,2. Компоненты каждого вспомогательного идентификатора маскируются («вкладываются в конверты»): h_j,1= s_j∙ r,₁(mod n) и h_j,2 = (s_j Θ p)∙r_,2(mod n), где (n,е)— открытый ключ банка. В результате Алиса получает и замаскированных вспомогательных идентификаторов Н_i = (h_j,1, h_j,2), 1 ≤ j ≤ n. Каждый чек m выглядит следующим образом:

Сумма

Уникальный идентификатор Х

Замаскированные вспомогательные идентификаторы

Н₁ = (h₁,₁, h_1,2), Н₂ = (h_2,1, h_2,2) , Н_п = (h_n,1, h_n,2)

(2) Алиса «вкладывает» все сто чеков в «конверты» и отсылает их в банк. Для этого она генерирует сто случайных маскирующих множителей k_i и вычисляет c_i = т_i∙ k(mod n), где (n, e) — открытый ключ банка и 1≤ i ≤ 100.

(3) Банк случайным образом выбирает девяносто девять «конвертов» и просит Алису прислать маскирующий множитель k_i для каждого из них. Сняв маскировку (вскрыв конверты») т_l= с_l/k(mod n) банк убеждается, что все чеки правильно оформлены. Для этого банк проверяет сумму и устанавливает уникальность идентификатора Х. Затем банк убеждается, что вспомогательные идентификаторы принадлежат Алисе. Для этого он просит Алису прислать все маскирующие множители r_j,1 и r_j,2 для каждого из девяносто девяти чеков. Сняв маскировку (вскрыв конверты»)— (h_j,1)/r(mod n) = s_j и (h_j,2)/г,'~(mod n) = s_jΘ р, банк устанавливает подлинность Алисы, так как р = s_jΘ (s_jΘp).

(4) Если банк не обнаружил попыток мошенничества, он подписывает оставшийся «конверт» с^d = m^d ∙k^ed(mod n) = т^d∙ k(mod n), где d — секретный ключ банка, и возвращает его Алисе, списав с ее счета 1000 долл.

(5) Алиса сначала проверяет подпись банка. Подлинность подписи подтверждается равенством (с^d)^e =^?с. Затем Алиса «вскрывает» подписанный «конверт» — с^d/k = m^d (mod n) и передает подписанный чек продавцу.

(6) Продавец проверяет банковскую подпись — (с^d /k)^e = m(mod n) и убеждается в законности чека.

(7) Продавец просит Алису раскрыть либо г_j,1, либо r_j,2 для каждого из n замаскированных вспомогательных идентификаторов Н_j = (h_j,1,h_j,2). Для этого продавец выдает Алисе случайную и-битовую последовательность-селектор b₁, b_a,..., b_n„. Если b_j = 1, то раскрывается г_j,1, а если b_j =0, то раскрывается г_j,2.

(8) Алиса выполняет требование продавца

(9) Продавец «вскрывает конверты». Если для j-го замаскированного вспомогательного идентификатора Алиса раскрыла r_j,1, то продавец получит Н= (s_j, h_j,₂~), а если г_j,2,то Н_j' = (h_j,1,(s_j Θ p)). Затем продавец отсылает чек и полученные

Н_j' в банк.

(10) Банк проверяет подпись и по своей базе данных убеждается, что денежный чек с идентификатором Х ранее не депонировался. Если это так, банк переводит сумму, указанную на чеке, на счет продавца, Затем банк заносит Х и полученные на этапе (9) компоненты вспомогательных идентификаторов в базу данных. Банк всегда может проверить, что Н_j' получено из заверенного его подписью Н_j . Например, если на этапе (8) для j-й позиции Алиса раскрыла r_j.1,банк получит h_j,1 = s_j∙ r(mod n) и s_j и может выполнить проверку h_j,1 =^? (h открытый, а d — секретный  ключ банка.

(11) Если идентификатор Х обнаружен в базе данных, банк отказывается принять денежный чек и сравнивает компоненты вспомогательных идентификаторов, полученные продавца, с аналогичными компонентами из базы данных. Если они совпадают, то 6 убеждается, что чек был скопирован продавцом. Если компоненты различны, то 6 знает, что чек был скопирован тем, кто его выписал. Так как каждый продавец выдает Алисе уникальную последовательность-селектор, банк обнаружит, что для какой- из позиций Алиса раскрыла s_j одному продавцу, а s_j Θ р — другому. Тогда, вычислив р = s_j Θ s_j Θ р, банк установит личность Алисы.

Прокомментируем рассмотренный протокол. Может ли Алиса мошенничать? Ее электронные наличные представляют собой просто последовательность битов, которую она легко и может скопировать. Продавец выдаст ей на этапе (7) случайный n-битовый селектор и в результате получит либо s_j, либо s_jΘр для каждого Н_j, на этапе (9). На этапе (10) банк запишет эти данные в свою базу данных. Когда Алиса попытается использовать те же электронные I наличные повторно, продавец (тот же или иной) выдаст ей на этапе (7) другой случайный n-битовый селектор. Алиса должна выполнить этап (8), ее отказ немедленно встревожит продавца. Теперь банк немедленно заметит, что денежный чек с идентификатором Х уже был депонирован. Банк сравнивает компоненты вспомогательных идентификаторов. Вероятность совпадения двух случайных селекторов оценивается как 2^-n. Теперь банк находит пару, которой s_j было раскрыто на предыдущих сеансах, а s_j Θ р — на последующих, выполняет суммирование по модулю 2 (операция XOR) и извлекает имя Алисы. Так банк узнает, к попытался воспользоваться чеком дважды. Отметим, что этот протокол не мешает Алисе и мошенничать, но ее мошенничество почти наверняка будет обнаружено. Смошенничав, Али не сможет сохранить в тайне свою личность. Она не может изменить ни Х, ни какие-либо иные данные чека, иначе не сойдется банковская подпись, и продавец немедленно замет это на этапе (6). Алиса могла бы попытаться передать банку ложный денежный чек, такой на котором вспомогательные идентификаторы не раскрывают ее имени или, еще лучше, раскрывают имя кого-то еще. Очевидно, что вероятность успеха Алисы можно минимизировать, увеличив число чеков и мошенничество будет обнаружено на этапе (3).

Может ли смошенничать продавец? Его шансы даже хуже. Он не может депонировать денежный чек дважды: банк заметит повторное использование селектора. Он не сможет и мошенничать, обвиняя Алису, — только она может открыть любой идентификатор. Не помог обмануть банк и любой сговор между Алисой и продавцом. Если банк подписал денежный чек с уникальным идентификатором Х, он может быть уверен в том, что этот чек будет оплачен только один раз.

Возникает еще один вопрос. Может ли банк определить, что чек, полученный от продавца, и есть тот самый чек, который был подписан для Алисы на этапе (4)? На этапах

второго по пятый Алиса защищена «слепой» подписью. Банк не сможет установить соответствие между Алисой и чеком, даже если он сохраняет информацию о каждой транзакции. Более того, даже объединившись, банк и продавец не смогут установить личность Алисы. Однако если злоумышленник может перехватывать и читать сообщения Алисы и продавца имеет выигрыш во времени, то сможет первым депонировать чек. Банк примет его, и, когда продавец попытается депонировать свой чек, он будет обвинен в мошенничестве. Если злоумышленник украдет электронные наличные Алисы и успеет потратить их прежде Алисы, то в мошенничестве будет обвинена Алиса. Не существует способа помешать этому, и это является прямым следствием анонимности. И Алиса, и продавец должны защищать свои 6и. ты так, как они защищали бы свои деньги. И Алиса, и продавец доверяют банку в том, что касается денег, но Алиса не должна доверять банку сведения о своих покупках.

Конечно, необходима гарантия того, что банк не сможет получить доступ к компонентам вспомогательных идентификаторов, если чек с идентификатором Х ранее не депонировался.

В общем случае электронные наличные не слишком удобны для преступников. Проблема в том, что анонимность имеет односторонний характер — покупатель анонимен, а продавец нет. Более того, продавец не сможет скрыть факт получения наличных. Электронные наличные помогут налоговой службе определить, сколько денег заработано, но установить, как они тратятся, невозможно.

В [431] Окамото (Т. Okamoto) и Охта (К. Ohta) перечислили шесть свойств идеальной системы электронных наличных:

Независимость. Безопасность электронных наличных не зависит от местонахождения. Наличные могут быть переданы по компьютерным сетям;

Безопасность. Электронные наличные нельзя скопировать и повторно использовать;

Анонимность (Неотслеживаемость). Тайна личности пользователя защищена; связь между пользователем и его покупками установить невозможно;

Автономность платежей. Когда пользователь расплачивается за покупку электронными наличными, протокол между пользователем и продавцом выполняется автономно. То есть магазину не нужно соединяться с центральным компьютером для обработки платежа пользователя;

Перемещаемость. Наличные могут передаваться другим пользователям;

Делимость. Заданная сумма электронных наличных может быть поделена на части. (Конечно, общая сумма в конце должна сойтись.)

Ранее приведенные протоколы удовлетворяют всем требованиям, кроме перемещаемости и делимости. Ряд диалоговых систем электронных наличных не удовлетворяют требованию автономности [430,432;433]. Первая система, удовлетворяющая требованиям независимости, безопасности, анонимности и автономности, была предложена в [434]. Окамото и Охта предложили систему, удовлетворяющую всем требованиям, однако объем данных для одного платежа составил приблизительно 200 Мбайт. Другая автономная система электронных наличных с возможностью деления описана в [435]. Схема, предложенная теми же авторами [431], удовлетворяет всем требованиям и исключает при этом необходимость памяти для хранения большого объема данных. Общий объем данных для одного электронного платежа составляет около 20 Кбайт, и протокол может быть выполнен за несколько секунд. Авторы рассматривают эту схему как первую идеальную систему неотслеживаемых электронных наличных.

В последующих параграфах разъясняются методы, составляющие суть механизма электронных платежей и электронных наличных, на примере систем PayWord и MicroMint, предложенных в 1996 г. известными специалистами в области криптографии Шамиром (А. Shamir) и Ривестом (В. Rivest).

3. Системы PayWord и MicroMint

В течение последних лет было предложено несколько различных схем электронных платежей, обеспечивающих безопасность транзакций при сетевом взаимодействии. Микроплатежная схема — вариант для приложений с малыми объемами одноразовых платежей. В таких схемах стоимость самого платежного механизма не должна превышать общего объема платежей, в противном случае система не будет рентабельной. PayWord и

MicroMint относятся к простым микроплатежным схемам. Каждая схема предполагает три категории участников: посредники, потребители и торговцы. Посредники выполняют авторизацию платежей потребителей и погашение накопленных торговцами сумм (см. схему на рис. V.1). Причем отношения

между посредниками и потребителями, а также между посредниками и торговцами имеют долговременный характер, а между потребителями и торговцами — кратковременный.

Пусть честный останется честным — таков основной принцип микроплатежной схемы нового поколения, предложенной Шамиром и Ривестом [93]. С учетом специфических особенностей микроплатежных схем авторы сформулировали следующие целевые задачи разработки:

● применять хэш-функции (там, где это возможно) вместо двухключевых криптоалгоритмов (по приблизительным оценкам, число операций для вычисления хэш-функции в 100 и 10 000 раз меньше, чем при проверке и генерации подписи по алгоритму RSA);

• минимизировать информационные потоки с посредниками, в первую очередь в режиме on-line. Вычислительная нагрузка ограниченного числа посредников, обслуживаю транснациональные платежные запросы в режиме off-line, не должна быть чрезмерной;

• обеспечить эффективность транзакций, в особенности для потоков одноразовых микроплатежей.

PayWord — кредитная платежная схема, оптимизированная для потоков одноразов микроплатежей. Схема обладает достаточной надежностью и гибкостью для осуществлен платежей произвольного объема.

MicroMint представляет собой новую парадигму электронных наличных. Особенность MicroMint — отсутствие алгоритмов двухключевой криптографии. При этом обеспечиваю достаточный уровень безопасности и высокая экономическая эффективность.

4. PayWord

В общих чертах работа PayWord может быть представлена следующим образом:

1) покупатель открывает счет у посредника и получает сертификат, что подтверждает легальность осуществляемых им платежей;

2) перед непосредственным контактом с продавцом покупатель создает специальную, ориентированную на продавца микроплатежную цепочку;

3) покупатель заверяет микроплатежную цепочку электронной цифровой подписью и затем последовательно раскрывает элементы цепочки для осуществления каждого микроплатежа;

4) посредники погашают суммы, накопленные продавцами в результате платежей покупателей.

4.1. Микроплатежные цепочки

В конструкции микроплатежной цепочки авторы PayWord воспользовались хэш-функции MD5 [20]. Хэш-функция h — преобразование последовательности бит переменной длины x в последовательность бит фиксированной длины y.

Напомним, что хэш-функция должна отвечать следующим требованиям:

• прямое вычисление у = h(х) не должно быть вычислительно-трудоемким;

• обратное вычисление (или обращение) х = h^-1(у) (восстановление входной последовательности по выходной) должно быть вычислительно-трудоемким;

• задача нахождение двух (и более) различных последовательностей бит с одинаковыми результатами преобразования h(x_i) = h(x_j ), x_i ≠ x_j (коллизия) должна быть вычислитель но-трудоемкой.

Покупатель создает цепочку вида w₀,w₁,w₂,...,w_n, случайно выбирая значение w_n и рекурсивно вычисляя промежуточные значения по правилу w_i = h(w_i+1), начиная с w_n. Твоим образом устанавливается функциональная связь i-го элемента с предшествующими (n — i) элементами цепочки. Финальный результат рекурсивного хэширования w₀ называют корнем» цепочки:

При заданном w₀ никто, кроме покупателя, не сможет восстановить как полную цепочку, так и отдельные ее элементы, — для этого потребуется обратить хэш-функцию. Однако по раскрытому w₀ можно выяснить принадлежность цепочки и установить покупателя, отвечающего за проведение микроплатежей.

Отметим, что микроплатежная цепочка концептуально аналогична схеме одноразовых паролей S-Кеу, предложенной в качестве Internet-стандарта [100].

4.2. Отношения Покупатель — Посредник

Отношения между покупателем и посредником начинаются с открытия счета и получения сертификата. Для этого покупатель передает посреднику по конфиденциальному и аутентичному каналу связи следующую информацию: номер кредитной карты, открытый ключ РК_U и адрес доставки (например, IP-адрес). Посредник, в свою очередь, создает сертификат и передает его покупателю. Получение сертификата подтверждает право покупателя осуществлять микроплатежные операции в течение установленного срока действия, гарантирует доставку товара по указанному адресу.

Сертификат покупателя С_U имеет следующий вид:

где информационный блок (последовательность бит) {∙}, подписанный на секретном ключе посредника SK_B, обозначен {∙}_SKB∙

Сертификат С_U — гарантия посредника в том, что все микроплатежи исходят от легального покупателя и осуществляются в течение установленного срока действия.

4.3. Отношения Покупатель — Продавец

Когда покупатель намеревается вступить в деловые отношения с продавцом, он генерирует новую микроплатежную цепочку w₀, w₁,w₂,…,w_n. Параметр и выбирается покупателем и зависит от объема платежа. Затем покупатель генерирует платежное обязательство вида:

Обязательство М, подписанное на секретном ключе покупателя SK_U, санкционирует погашение посредником сумм, полученных продавцом в результате последовательности микроплатежей по цепочке w₁,w₂,..., w_n. Отметим, что микроплатежная цепочка связывает конкретную пару покупатель-продавец и не имеет отношения к другим продавцам и покупателям. После получения обязательства М продавец сначала проверяет его подпись, а также подпись сертификата С_U (передается вместе с M) и затем срок действия сертификата. Платежное действие заключается в передаче продавцу элемента микроплатежной цепочки и его индекса: (w_i,i). При этом элементы цепочки не заверяются цифровой подписью покупателя. Платежи выполняются в следующей последовательности: сначала (w₁,1), затем (w₂,2) и т.д. Предположим, покупатель приобретает информацию с Web-сервера, получая ее постранично. Если каждый элемент цепочки обеспечивает проплату одного цента и стоимость одной страницы информации составляет один цент — покупатель передает продавцу (w_i,i) при покупке i-й страницы.

Суть платежной дисциплины PayWord состоит в том, что для каждого обязательства продавцу будет погашено l центов, где (w_l,l) — полученный продавцом элемент цепочки с наибольшим индексом. Продавец легко может проверить, что l-й платеж исходит от пеку покупателя, подлинность которого установлена ранее с помощью обязательства М. Для это продавец выполняет следующие рекурсивные вычисления:

W₀=h(h(…h(h(w_l))…))

Равенство w₀= w₀ свидетельствует о легальности платежа. Продавец может сократить объем вычислений, воспользовавшись последним проверенным платежом w_i:

W_i=h(h(…h(h(w_l)…).

При w_i = w_i платеж принимается, в противном случае — отвергается. Очевидно, что передачи посреднику необходимо сохранять элемент цепочки с наибольшим индексом.

4.4. Отношения Продавец-Посредник

Никакого предварительного взаимодействия между продавцом и посредником в рамках платежной схемы не требуется. Однако продавец должен иметь аутентичный открытый ключ для проверки сертификатов, подписанных посредником. Важным элементом в отношения «продавец-посредник» является механизм погашения накопленных сумм. В конце каждого рабочего периода продавец посылает посреднику специальный запрос, содержащий обязательство М и последний платеж P = (w_l, l) для каждого покупателя, выполнявшего платежи в течение этого периода. Посредник, в свою очередь, сначала проверяет цифровую подписи обязательства и затем каждый платеж (w_l, ), рекурсивно вычисляя значения хэш-функции, В случае успешного завершения проверок посредник удовлетворяет все запросы на погашение сумм.