8.1.9. Практическая криптостойкость RSA: оценки и прогнозы

Известно, что практическая криптостойкость RSA зависит от вычислительной трудоемкости задачи факторизации — разложения двусоставного модуля (произведение двух простых чисел) на сомножители. Факторизация модуля позволяет раскрыть секретный ключ и, как следствие, дешифровать любое сообщение, подделать цифровую подпись. Чем больше число, тем выше вычислительная трудоемкость факторизации. Необходимо отметить, что повышение производительности компьютеров положительно сказалось на успехах в области факторизации, но криптостойкость RSA при этом также возросла. Эффект объясняется различиями в вычислительной трудоемкости процедур факторизации и шифрования/дешифрования: в результате очередного скачка производительности число, поддающееся факторизации, увеличивается два разряда, тогда как RSA-модуль, без потери вычислительной эффективности,- на двенадцать разрядов. Однако факторизация возможна в случае, если рост производительности не учитывается при периодичности смены ключей.

Каким должен быть модуль RSA? Точный ответ вряд ли возможен — развитие методов численной факторизации с трудом поддается прогнозированию. При этом нельзя полностью исключить возможность атак на основе иных, отличных от факторизации методов. Kpoме того, вычислительная трудоемкость модульного возведения в степень (основной операции при шифровании/дешифровании) возрастает с увеличением разрядности модуля. Основная задача при выборе модуля RSA — одновременное обеспечение криптостойкости и вычислительной эффективности процедуры шифрования/дешифрования. Таким образом, при выборе модуля необходимо исходить из реальных оценок роста производительности компьютеров в области вычислительной теории чисел. Согласно оценкам [139], для обеспечения адекватного уровня практической криптостойкости разрядность модуля RSA должна быть увеличена в ущерб вычислительной эффективности. Однако идея разбаланса RSA, предложенная Шамиром [141], позволяет этого избежать. 

В настоящее время криптосистема RSA с модулем 512 бит, реализованная во многих криптографических приложениях, не гарантирует объявленной криптостойкости. Отметим отличие от строгого обоснования низкой криптостойкости RSA с модулем 512 бит прогнозы на будущее менее конкретны; пока анализируются лишь тенденции роста производительности компьютеров и возможные пути развития вычислительной теории чисел. О опираются на предположение о последовательной природе криптографических алгоритмов и использовании стандартной технологии СВИС при их реализации. Ситуация мо измениться, если исследования в области квантовых [125] и молекулярных [142-146] вычислений перейдут в практическую фазу.

В большинстве работ при оценке производительности используется единица МY(Mips/- Year). Данная единица измерения может быть истолкована следующим образом: компьютер с производительностью один миллион целочисленных инструкций в секунду (million instructions per second, mips) эквивалентен DEC VAX 11/780, тогда год работы VАХ 11/780. Для разрядности десятичных чисел введем обозначение число_ десятичных_ разрядов. Например, 43D — целое число из 43 десятичных разрядов.

 Задача факторизации всегда привлекала внимание математиков. Фундаментальность проблемы впервые была отмечена Гауссом. Одна из первых попыток (1874 г.) ее практической постановки и оценки трудоемкости принадлежит английскому экономисту и логику су (W.S. Jevons) [152], предполагавшему, что никому, кроме него, не удастся разя множители число 8 616 460 799 (10D). Однако в 1925 г. число было факторизовано

8 616 460 799 = 96079 х 89681.

В 1967 г. факторизация числа 25D считалась практически нереализуемой [148]. В 1 новый метод факторизации Моррисона — Бриллхарта (Morrison — Brillhart) позволил р седьмое число Ферма F₇ = 2¹²⁸ + 1 (39D). Барьер 80D, установленный в 1976 г. [151] преодолен через пару лет. В 1977 г. профессор Ривест из Массачусетского технологического университета привел убедительные аргументы в пользу выбора в качестве RS числа 129D [150]. Ривест предполагал, что для факторизации

 понадобится более 40 квадрильонов (4 х 10|в) лет работы самого быстрого компьютера. Однако факторизация числа была выполнена в 1994 г. по алгоритму квадратичного решета (КР) [147].

В целях развития математических методов факторизации корпорация RSA Data Inc. объявила открытый конкурс на факторизацию RSA-модулей и учредила специальную денежную премию. В 1996 г. число RSA-130 (130D) было факторизовано при помощи ритма обобщенного числового решета (ОЧР). За счет применения алгоритма ОЧР эффективность факторизации RSA-130 возросла на порядок по сравнению с факторизацией RSA-129.

Проект RSA-130 был коллективным, вклад каждого из участников проекта приведен табл. П.24.

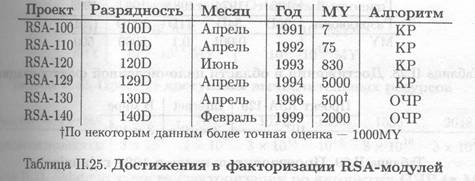
К моменту факторизации RSA-130 четыре из объявленных ранее модулей были факторизованы при помощи алгоритма КР (табл. Н.25).

Таким образом, возможность успешной атаки на криптосистему RSA с 512-битным модулем (=160D) подтверждается результатами, приведенными в табл. II.25. В настоящее время рекомендуемая минимальная длина RSA-модуля — 768 бит (= 230D). Исходя из оценки трудоемкости проекта RSA-130, производительность компьютера для эффективной факторизации числа 230D должна быть не меньше 10⁸ MY.

В феврале 1999 г. методом ОЧР был факторизован модуль RSA-140. Данный проект, и RSA-130, был коллективным (табл. II.26).

Суммарная производительность проекта RSA-140 достигла 2000МY, а объем оперативной памяти (на одной рабочей станции) при реализации ключевого этапа алгоритма ОЧР составил 800 Мбайт.

Данные о трудоемкости проекта RSA-140 позволяют построить прогноз относительно количества ресурсов, необходимых для факторизации модулей с разрядностью 512, 768, 1024 . бит ( П.27).

В табл.П.28 приведены сведения о достижениях в области целочисленной факторизации е тридцать лет, а также указана производительность компьютера, достаточная ой факторизации чисел заданной разрядности.

Отметим, что для эффективной факторизации RSA-129 по алгоритму ОЧР потребуется 1000 MY вместо 5000 МY при факторизации по алгоритму КР [149]. Существенный скачок в производительности компьютеров в период между 1984 и 1994 годами обусловлен интенсивным развитием компьютерных сетей и, как следствие, практической реализацией метода распределенных вычислений. Идея использования свободного времени рабочих станций сети для факторизации принадлежит Силверману (В. Silverman). (К сожалению, более ранняя попытка Шреппеля (R. Schroeppel) использовать сетевые ресурсы

для факторизации восьмого числа Ферма F₈ = 2²⁵⁶ + 1 не привлекла внимания специалистов.) Дальнейшее развитие идея распределенных вычислений получила в исследованиях  Ленстры (А. Lenstra) и Мэнэсса (M. Manasse). В проекте RSA-129 было задействовано 1600 рабочих станций в течение восьми месяцев. В отличие от традиционного по для эффективной силовой атаки необходимо построить специальный компьютер.[156,158], атака идеи распределенных вычислений не требует значительных ин технических ресурсов на основе.

Другой прогноз относительно будущего целочисленной факторизации предлагает

(В. Rivest) [157]. В основе прогноза — оценка инвестиций для производства специального факторизующего компьютера.

Отметим, что участники проекта RSA-129 без значительных усилий получил 0,03% вычислительных ресурсов Internet. По их собственным оценкам, в проекте и задействовано около 3% вычислительных ресурсов сети [147].

Помимо сети Internet существует ряд локальных организаций (фирм, корпораций консорциумов), обладающих достаточными вычислительными ресурсами. Например, компания Silicon Graphics имеет около 5000 сотрудников и .10 000 рабочих станций с общей производительностью 10⁵ mips — в десять раз больше производительности проекта RSA-129. Воспользовавшись алгоритмом ОЧР, компания, в частности, может легко факторизовать число 160D (512-битный RSA-модуль) в течение одного года.

Известно, что вычислительные ресурсы рабочих станций Internet могут использоваться незаметно для их владельцев. Недавно в результате несанкционированного использования вычислительных ресурсов общей производительностью 400 MY был факторизован 384-битный RSA-модуль [154].

Обратимся к прогнозу роста производительности. Закон Мура утверждает, что производительность компьютеров удваивается каждые 18 месяцев. Таким образом, за 10 лет она возрастет приблизительно в 100 раз и в 2004 г. составит 10³ mips, а в 2014 — 10⁴-10⁵ mips [139].

В настоящее время в мире существует около 10⁸ компьютеров, в 2004 году менее 2 х 10⁹, в 2014 г. — 10¹⁰— 10¹¹ [139]. Прогноз основан на оценке роста населения, которое в 2014 г. составит около 10¹⁰ человек. Предполагается, что на каждого 2014 году будет приходиться около 10 компьютеров — это вполне реально с учетом большого числа встроенных микропроцессоров (smart card, бытовое оборудование и т.д.).(Отметим, что в проекте RSA-129 использовались две факс-машины.) Не приходится сомневаться и в том, что практически все компьютеры будут связаны в единую сеть. Однако вопрос компьютеров, доступных для решения задач факторизации, остается открытым.

Рассмотрим два сценария.

• Открытый проект — широко объявленная атака на известную криптосистему. Вполне очевидно, что при этом может быть задействовано не менее 0,1% мирового тельного ресурса в течение одного года. (Напомним о 3% вычислительных' Internet-проекта RSA-129.) Принимая во внимание фактор роста сети, суммарная производительность в 2004 г. составит 2 х 10⁹ MY и 10¹¹ — 10¹³ MY в 2014 г. [139].

• Скрытая атака, предпринятая локальной группой участников, университетом

порацией. Организаторы атаки могут получить в свое распоряжение 10⁵ компьютеров в 2004г. и 10¹⁰-10¹¹ в 2014-м. Таким образом, суммарная производительность составит в 2004г. 10⁸ МY, в 2014 г. 10¹⁰— 10¹¹ MY [139].

Приведенные выше оценки представлены в табл. П.30.

            Известные алгоритмы факторизации можно разделить на два типа: алгоритмы, время зависит от разрядности простых делителей, и алгоритмы, время работы которых зависит исключительно от разрядности факторизуемого числа n. Ранние алгоритмы

.поиск наименьшего простого делителя р числа n и относились к первому типу. Время работы современных алгоритмов не зависит от разрядности простых делителей модуля.

Самым быстрым алгоритмом факторизации первого типа считается метод эллиптических кривых . Асимптотическая оценка времени работы этого алгоритма ехр(0((1п(р))^1/2.(In In(p))^1/2)).Основной практический недостаток — вычислительная трудоемкость базовых операций. Наибольшее число, факторизованное этим методом, имело 145 двоичных разрядов. Маловероятно, что в ближайшем будущем при помощи этого алгоритма будет выполнена факторизация 512-битного модуля RSA. Алгоритмы второго типа существенно быстрее. Наилучшим считается алгоритм ОЧР. Асимптотическая оценка времени работы ОЧР

Ехр(о((In(n))^1/2.(In In(n))^2/3)). Алгоритм позволяет факторизовать 512-битный модуль при производительности от 10 000 до 15 000 MY. Отметим, что алгоритмы факторизации второго типа применялись во всех успешных атаках на криптосистему RSA. Таким образом, логично предположить, что тенденция сохранится в будущем.

Алгоритм ОЧР удобен для практической реализации, максимальный выигрыш наблюдается при факторизации чисел порядка 115D и более. Прогноз производительности, необходимой для факторизации чисел различной разрядности по алгоритму ОЧР (см. табл. П.31), построен исходя прецедента факторизации числа 130D при производительности 500 MY [139].

Данные табл. 11.30 и П.31 позволяют заключить, что 1280-битный RSA-модуль гарантирует адекватный уровень практической криптостойкости в течение ближайших 20 лет. Однако в прогнозу представленному в табл. П.З1 и основанному на предположении о превосходстве алгоритма ОЧР, необходимо относиться осторожно — не исключена возможность появления более эффективных методов целочисленной факторизации.

Отметим, что факторизация 512-битного модуля реальна уже сегодня. Не нужно открывать алгоритмы факторизации, нет необходимости в увеличении числа компьютеров

Или в более производительных компьютерах — достаточно найти нужное количество участников и воспользоваться свободным временем их рабочих станций для факторизации. Например, лишь компьютеры компании Silicon Graphics могут факторизовать 512-битный модуль при условии, что будут свободны две трети рабочего времени.

Для факторизации чисел Ферма (F_n = 2²ⁿ+ 1) разработан алгоритм специального числового решета (СЧР). Рекорд факторизации по алгоритму СЧР — число 162D при производительности 200 MY. Прогноз производительности, необходимой для факторизации чисел различной разрядности по алгоритму СЧР, представлен в табл. П.32 [139].

При сохранении тенденции (число F₇ факторизовано в 1970 г., F₈ в 1980 и F₉ в 1990) логично предположить, что в 2000 г. будет факторизовано число F₁₀ = 2¹⁰²⁴+1.

Возможно ли появление универсальных методов целочисленной факторизации, столь же эффективных, как алгоритм СЧР для чисел Ферма? Специалисты в области вычислительной теории чисел полагают, что возможно [139]. Прогресс в целочисленной факторизации имеет устойчивый характер. Считалось, например, что методы линейной алгебры, играющие ключевую роль в большинстве алгоритмов факторизации и плохо поддающиеся распараллеливанию, ограничат применение распределенных вычислений. Однако факт новых алгоритмов опроверг сложившееся мнение.

Для факторизации числа 129D по сравнению с факторизацией числа 45D по методу непрерывных дробей в 1970 г. понадобилось бы в 6 ´ 10¹¹ раз больше производительности и в 5´10⁶ раз больше — при использовании быстрого алгоритма.

Таким образом, развитие алгоритмической базы сравнимо (по логарифмической шкале ростом производительности компьютеров. При условии сохранения отмеченной тенденции в 2004 г. скрытая атака позволит факторизовать 1024-битные числа (современные алгоритмы позволяют факторизовать 768-битные числа). В 2014 г. разрядность факторизуемых возрастет до 1500 бит и более.

Рассмотрим эвристические оценки времени работы алгоритмов. Отметим, что приведенные ниже оценки не имеют строгого математического доказательства и вытекают из экспериментальных данных [139].

Зададим общую формулу эвристической оценки времени работы упомянутых выше алгоритмов:

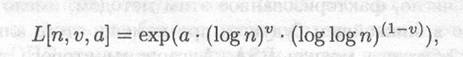
где через log n обозначен натуральный логарифм n.

Тогда время работы алгоритма ОЧР при факторизации числа n оценивается как

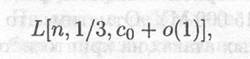
где с_о = (64/9)^1/3 = 1.9229...

Другой вариант оценки [153, 155] предполагает замену константы с₀ на константу с₁= 1.9018...

Алгоритм СЧР позволяет факторизовать целые числа вида а^k± b, где а и b малые, а k большое. Время работы СЧР оценивается как:

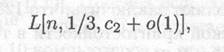
где с₂ = (32/9)^1/3=1. 5262

Время работы различных вариантов алгоритма КР:

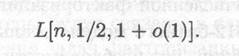
Метод непрерывных дробей, широко распространенный в 70-е годы, имеет следующую

 оценку:

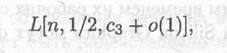
где с₃ = 2^1/2=1. 4142

Поскольку при точном вычислении асимптотической оценки о(1) возникают определенные сложности, можно воспользоваться следующим методом.. Для оценки асимптотического времени работы L[n, v, а+o(1)] некоторого алгоритма при факторизации числа n необх мерить время работы Х при факторизации числа т и затем вычислить Х L[n,v,a]/L[m,v,a].

Для многих криптографических приложений приведенный прогноз не представляет серьезной угрозы. Например, механизм временных меток Хабера — Сторнетты (Haber- Stornetta) [159[ обеспечивает действие цифровой подписи даже в случае факторизации модуля некоторых приложений недостаточно и 20-летней гарантии криптостойкости. Для исключительно секретной информации представляется разумным выбор RSA-модуля с

порядка 5000 бит.

Основная причина стремительного роста разрядности надежного модуля заключается в субэкспоненцальной оценке времени работы современных алгоритмов факторизации. Для сравнения трудоемкость силовой атаки на симметричную криптосистему, например DES, объемом ключевого пространства (2ⁿ— в худшем случае и 2^n-1 — в среднем, при n-разрядном ключе).

8.1.10. Разбалансированная RSA

Тенденция к увеличению размера модуля криптосистемы RSA вполне обоснованна — атака на факторизации представляет реальную угрозу. Тем более, когда речь идет о хранении долговременных секретов (например, долговременных долговых обязательств, закладных и о с увеличением разрядности модуля сложность вычислений возрастает кубически. Таким образом, выбор разрядности модуля представляет собой компромисс между ной эффективностью и криптостойкостью.

Как было отмечено в предыдущем параграфе, трудоемкость современных алгоритмов факторизации (например, ОЧР) не зависит от разрядности делителей модуля: для нахождения простого делителя из одной и из пятидесяти десятичных цифр требуется одинаковое время. Поскольку основные достижения в области факторизации получены в результате алгоритма ОЧР или аналогичных ему, можно предположить, что эта тенденция и впредь.

Шамир (А. Shamir) предложил новый подход к решению проблемы RSA-модуля [141].Криптосистема с модулем, построенным методом Шамира, получила название «разбалансированной- RSA». В такой криптосистеме — разрядность модуля n = pq увеличена в десять раз (до 5000 бит), а разрядность делителя р в два раза (до 500 бит). Соответственно на делитель q приходится 4500 бит. Название криптосистемы отражает диспропорцию в разрядности делителей n. Такой выбор делителей, по мнению Шамира, учитывает тенденции развития методов целочисленной факторизации и обеспечит адекватную криптостойкость в течение десятилетия [141].

Основная проблема заключается в том, что при таком модуле быстродействие реализации в 1000 раз ниже: теперь задержка на одну операцию модульного возведения в степень пеной секунды (при микропроцессорной реализации и 500-битном модуле) составит 16 минут - что неприемлемо.

При использовании ВЯА в процедуре установления ключевого синхронизма (метод цифрового конверта) шифруемые сообщения (сеансовые ключи), как правило, не превышают размера модуля р: даже при использовании режима трехкратного DES-шифрования (EDE) на трех  независимых ключах размер сообщения не превышает 168 бить. Таким образом, можно предположить, что шифруемый блок открытого текста в числовом отображении находится в интервале [0,р — 1]. При этом чрезмерно короткие блоки могут искусственно дополняться помощи известной техники «набивки».

Широко распространенный способ повышения вычислительной эффективности RSA при шифровании с = m^e(mod n) заключается в выборе малого e. Однако при заданных делителях выбор е < 10 не обеспечивает приведения по модулю в процессе шифрования, так как длина сообщения т составляет десятую часть от длины модуля n. При е » 20 разрядность m^e приблизительно в два раза превышает разрядность модуля n, что обеспечивает по модулю в процессе шифрования. Отметим, что при таком е и вычислении

т^e (mod n) методом последовательного возведения в квадрат [380[ большинство промежуточных произведений не приводится по модулю и только последняя операция квадрат является модульной. Таким образом, при 20 < е < 100 быстродействие при 5000-битном модуле сравнимо с быстродействием дешифрования при 500-битном модуле (менее одной секунды).

Рассмотрим процедуру дешифрования т = с^d (mod n) при условии, что с, n и d- 500- битные числа. Воспользовавшись Китайской теоремой об остатках [380], можно эффективно вычислить т₁= с^d (mod р) для 500-битного модуля р, предварительно приведя р и d по модулю (р — 1). Однако вычисление m₂ = с^d (mod q) при 4500-битном модуле q требует в 9³ = 729 раз больше операций.

Шамир выдвинул простое рассуждение, из которого следует, что выполнение этих сложных вычислений не является обязательным. Действительно, по определению m¹(mod р). При этом известно, что открытый текст m меньше р и, следовательно, m (mod p)= т. Это, в свою очередь, означает, что т₁= т и приведение т₂ по модулю q приведет к тому же самому результату.

Несмотря на то, что разбалансированная и стандартная криптосистемы RSA. сравнимую вычислительную трудоемкость, затраты памяти для хранения открытых разбалансированной RSA возрастают в десять раз. Для устранения этого недостатка было предложено несколько методов [141].

Рассмотрим последствия увеличения размера памяти с произвольным доступом(RAM) для различных приложений. Для персонального компьютера десятикратное увеличение памяти для хранения ключей не приводит к серьезным последствиям. (Если в памяти компьютера хранится 100 000 ключей по 5000 бит, то необходимый объем памяти для составит 60 Мбайт.) Однако для интеллектуальных карточек (Smart Card) их стоимость прямо пропорциональна объему памяти. Кроме того, многие интеллектуальных карточек уже реализовали специализированный RSA-процессор на базе 512-битного модуля. По этой причине можно ожидать, что их реакция на увеличение размера модуля будет негативной. В ряде практических приложений интеллектуальные карточки используются совместно с мощными персональными компьютерами. Таким образом открывается возможность выбора технологической базы (персональный компьютер или интеллектуальная карточка) для реализации процедур шифрования/дешифрования. Например персональный компьютер может генерировать и шифровать первичный сеансовый к шифротекст подается на вход последовательного интерфейса карточки и в тек (по мере поступления бит шифротекста) приводится по модулю р; в ходе вычислений пользуются 512-битные регистры RSA-процессором интеллектуальной карточки. Преимущество описанного метода заключается в возможности использования вычислительных ресурсов современных интеллектуальных карточек боте с модулем переменной длины без их замены.

Еще один потенциальный недостаток связан с десятикратным увеличением памяти справочника открытых ключей. Однако разбалансированность открытых ключей устранить и эту проблему. Обозначим через G генератор псевдослучайных последовательностей, применяемый для отображения идентификационной информации и (им электронной почты и т.д.) в уникальную 5000-битную псевдослучайную последовательность t.Предполагается, что G всем известно. Каждый пользователь генерирует 500-битное простое число р, затем генерирует q — простое число из интервала [а, a+ 2⁵⁰], где а наименьшее целое, большее или равное t/р. Поскольку простых чисел достаточно много, такое q почти всегда существует. В результате разница в разрядности модуля n = pq и t не будет превышать 550 бит. Каждый пользователь и может опубликовать число s = n — t своего открытого ключа. Тогда каждый абонент-отправитель криптосети может 5000-битный открытый ключ абонента-получателя, вычислив G(u)+s. Необходимо отметить что описанный метод не облегчает задачу факторизации модуля n: единственное заключается в том, что стартовая точка в процедуре генерации q не просто выбирается чайным образом, а задается как отношение случайного и простого числа. Поскольку закон распределения простых чисел отличается от равномерного⁷, число а также не является равномерно распределенным. Для сглаживания побочных эффектов неравномерности граница м выбирается q, задается как а + 2⁵⁰. Таким образом, представление модуля n в виде s ничем не хуже, и тот факт, что t не является истинно случайным числом, не влияет на его криптостойкость.

Необходимо также отметить, что разбалансированность может использоваться для удвоения производительности существующих в настоящее время реализаций RSA, в которых одинаковый размер. Причем для МА-подписи такая оптимизация проверяющему неизвестен делитель р. Кроме того, способ, при котором опубликованный короткий открытый ключ на самом деле является длинным, является м при ограничениях на размер модуля, аналогичных экспортным ограничениям на длину ключа для симметричных криптосистем.

Гилберт (Н.Gilbert), Гупта (D. Gupta), Одлыжко (А. Odlyzko) и Квискватер (J.J Quisquater) показали, что разбалансированная RSA может быть успешно атакована при помощи специального протокола взаимодействия между отправителем и получателем [409].

Предположим что и и е — открытый ключ Боба. Задача Алисы — раскрытие р и q.

шифрует сообщение т > р и посылает Бобу шифротекст m^e mod п. Боб дешифрует шифротекст и получает m. Так как m > р, то m # m. Предположим теперь, что Алиса каким-либо образом получила доступ к сообщению т, тогда она может проверить, что p½(m-m). При соблюдении ограничений 0 < т, m < n и т # т из Китайской теоремы , что q † (т — т). Следовательно, Алиса может восстановить р, вычислив НОД (m-m,n).

Отметим при определенных обстоятельствах Боб может раскрыть Алисе m ( например в сообщениях типа «Что за “мусор” ты мне прислала?»). В статье [410] описывается ряд сценариев, для которых это возможно. Дополнительные возможности появляются интеллектуальных карточек (Smart Card), которые могут автоматически выдавать m в качестве криптографического ключа.

Очевидный способ противодействия заключается во введении избыточности в сообщение некоторой специальной идентификационной последовательности.

Однако в статье [409] показано, что этого недостаточно. Рассмотрим пример, в котором сообщение типа «Переведите на счет Боба сумму в размере 101,74 долл. с моего счета 123 в банке г. Замухрышина». Сообщение «набивается» до нужной длины (исходя из размера делителя р) и заверяется цифровой подписью Алисы. Если m > р, сообщение т будет отвергнуто. Если m < р и m = m, сообщение будет принято и денежный перевод инициирован. Факт денежного перевода позволит Алисе узнать, что m < р. Подобная стратегия позволяет раскрывать биты р. Стоимость раскрытия одного бита р можно уменьшить, даже при условии что сумма в 100 долл. является минимальной для инициирования денежного перевода. Предположим, что Алиса сумела установить границы р, например, 6´2^k < р < 7´2^k. Тогда с помощью бинарного поиска Алиса могла бы приблизительно оценить m как 13 ´2^k-1, Однако Алиса может попытаться раскрыть биты р методом последовательных приближений:

Сначала опробовав m как 111 ´2^k-4, затем, если р < 111´2^k-4, как 110 ´2^k-4 и так далее.

Метод позволяет раскрыть четыре бита р вместо одного при той же стоимости. Отметим, что метод требует большого числа попыток; соответственно, возросшая активность может вызвать подозрение и взаимодействие будет заблокировано.

Возможно, приведенная выше атака выглядит несколько надуманно, однако она вполне реальна в ситуациях, когда по косвенным признакам можно принять решение о соотношении m и p. Например, если разбалансированная RSA используется для передачи сеансового ключа от отправителя (Алисы) к получателю (Бобу), атака может заключаться в передаче Бобу т^e mod п с последующей проверкой факта использования ключа m для шифрования  сообщений сеанса.

Необходимо отметить, что данная атака не приводит к полной компрометации разбалансированной RSA, но свидетельствует о необходимости введения избыточности в открытый текст, а также гарантий того, что в ходе взаимодействия получатель никогда дешифрованные сообщения.

8.1.11. Пакетная RSA

Пакетная RSA (411] (batch RSA) представляет собой метод, позволяющий выполнять множество RSA-дешифрований (порядка п/log²(n), где n — секретный параметр логарифм берется по основанию 2) с вычислительной эффективностью одиночного RSA-дешифрования. При этом предполагается, что используется единый модуль, но различные и попарно взаимно простые экспоненты шифрования е. Проблема вычислительной эффективности в ряде криптографических приложений с централизованным управлением. Так, например,  некоторые схемы цифровой подписи предполагают наличие депозитарно-распределительного центра, генерирующего заверенные цифровой подписью квитанции для каждой транзакции. В других распространенных приложениях центральный компьютер должен ток запросов в режиме on-line, например при управлении ключами в сетях со звездообразной топологией. Таким образом, пакетная RSA позволяет минимизировать вычислительную нагрузку центра.

Рассмотрим пакетную RSA подробнее. Пусть N = р q, р — 1 = 2р', q — 1 = 2q¹ где p,q,p¹, q¹ - простые. Предположим, что необходимо вычислить m^1/ei mod N для i = 0,1,2,…, b- 1, где b — размер пакета и числа е_i, сравнительно невелики в отличие от обратных, 1/e_i mod λ (N),где λ(N) = (р — 1). (q — 1)/2. Основной цикл вычислений состоит из трех этапов. На первом этапе при помощи специальной бинарной структуры данных, смысл которой будет пояснен далее, вычисляется с =mod N, где p= На втором этапе вычисляется m = с^1/p mod N — полноценная операция модульного возведения в степень. Однако вычислительная эффективность такой операции выше и определяется суммарной эффективностью b операций на первой фазе. На последнем этапе т = mod N разбивается на b компонентов mod N, i = 0,1,2,...,b — 1, что и является конечным результатом. Отметим, что разбивка на последнем этапе выполняется при помощи той же бинарной структуры, что и на первом этапе.

Поясним смысл бинарной структуры данных, необходимой для вычислений на первом и последнем этапах. Для простоты предположим, что b = 2^k для некоторого k. полное бинарное дерево⁸ и пометим все его листья т₀, m₁, т₂,..., т_b-1.Путь в дереве определим как соответствующую двоичную последовательность € Σ, Σ={0,1}.Воспользуемся символом е для обозначения двоичной последовательности нулевой длины. Пусть правые сыновья ассоциируются с 1, а левые — с 0. Путь в дереве и η € Σ^k, k' <k задает ребро глубины k¹ и соответствует обходу дерева от корня по пути η. Если η имеет длину k, то он приводит к листу т_i. Таким образом, путь η соответствует двоичному представлению i.Пусть х € Σ.Обозначим через ηx конкатенацию (справа от η) последовательностей η и х. Через х обозначим двоичное дополнение х. Каждое ребро η имеет метку l(η). Ребра в дереве помечаются снизу вверх по правилу:

Процедура разметки дерева зависит не от сообщения т_i, а только от показателя степени. Следовательно, такая процедура может быть выполнена предварительно и однократно (показатели степени фиксированы). Узлы дерева содержат данные, которые зависят от сообщений степени. Пусть каждый узел определяется путем, который в него приводит. Данный узла η обозначим d(η). Изначально содержимое каждого листа i соответствует некоторому сообщению m_i.Тогда содержимое каждого узла дерева вычисляется при движении вверх, после того как вычислены сыновья d(η) ≡ d(η0)^1(η0) .d(η1)^1(η0) mod N. Таким образом вычисляется содержимое корня дерева d(ε) ≡ mod N. На этом заканчивается первый этап вычислений.

После вычисления М ≡ d(ε)^1/p ≡ mod N на втором этапе бинарное дерево используется для разбивки М на составные компоненты. Это делается при помощи следующей рекурсивной процедуры.

Пусть 0,1,…, r — 1 — листья, ассоциированные с левым сыном корня, а r, r+1,...,

b-1— . Заметим, что l(0) = , l(1) = и р = l(0) . 1(1). Воспользовавшись Китайской теоремой об остатках, можно вычислить Х, такое, что Х ≡ 0 mod l(0) и X ≡ 1 mod l(1), следовательно,сущестуют X₁ и X_0, такие что Х = 1(1) . Х₁+1и =Х=l(0).X_0. Обозначим М₀ ≡ mod N и M₁ ≡ mod N. Для удобства воспользуемся

обозначениями l₀, l_1, d₀, d₁ вместо l(0), l(1),.... Поскольку M₀ = mod N и М₁= mod N, имеем d₁ = mod N и d₀ = mod N. Можно легко проверить, что М₀ ≡ М^Х/() mod N. Эти вычисления выполняются на третьем этапе при движении от корня к левому сыну. Для правого сына М₁≡ М/M₀ mod N. Все d вычисляются на первом этапе и сохраняются в узлах. Числа Х не зависят от сообщения и могут быть вычислены заранее. Процедура повторяется рекурсивно до тех пор, пока не будет получен конечный

результат для каждого листа.

8.1.12. Итоги

На основании перечисленных атак можно сформулировать следующие ограничения при использовании RSA [300, 301]:

- звание одной пары показателей шифрования/дешифрования для данного модуля позволяет злоумышленнику разложить модуль на множители;

- знание одной пары показателей шифрования/дешифрования для данного модуля позволяет злоумышленнику вычислить другие пары показателей, не раскладывая модуль на множители;

- в криптографических протоколах с использованием RSA общий модуль использоваться не должен. (Это является очевидным следствием предыдущих двух пунктов.);

-для предотвращения раскрытия малого показателя шифрования сообщения должны быт дополнены («набитыми) случайными значениями;

-показатель дешифрования должен быть большим.

Отметим, что недостаточно использовать криптостойкий алгоритм; безопасной должна быт вся криптосистема, включая криптографический протокол. Слабое место любого из этих компонентов сделает небезопасной всю систему.

8.2. Криптосистема ЭльГамаля

Криптосистему, предложенную ЭльГамалем (Т. E1Gamal) в 1985 г. [302,303], можно использовать как для цифровых подписей, так и для шифрования. Криптостойкость  определяется трудоемкостью вычисления дискретного логарифма в конечном поле. Криптоалгоритм  патентован, но попадает под действие патента на метод экспоненциального ключевого обмена Диффи — Хеллмана [304].

Для генерации пары ключей сначала выбираются простое число р и два случайных числа, g и x; оба этих числа должны быть меньше р. Затем вычисляется

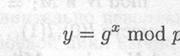
Открытым ключом являются у, g и р. И g, и р можно сделать общими для группы пользователей. Секретным ключом является x.

8.2.1. Вычисление и проверка подписи

Чтобы подписать сообщение М, сначала выбирается случайное число k, взаимно простое е р — 1. Затем вычисляется а = g^k mod р, и с помощью расширенного алгоритма Евклида из уравнения

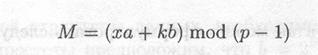
находится b. Подписью является пара чисел: а и b. Случайное значение k должно храниться в секрете. Для проверки подписи необходимо убедиться, что

Каждая новая подпись требует нового значения k, и это значение должно выбираться случайным образом. Если злоумышленник раскроет k, используемое Алисой, он смоет секретный ключ Алисы x. Если злоумышленник сможет получить два сообщения, подписанные при помощи одного и того же k, он сможет раскрыть х, даже не зная k.Параметры криптосистемы, а также процедуры вычисления и проверки подписи сведены в табл. II.33.

Рассмотрим простой пример. Выберем р = 11 и g = 2. Пусть секретный ключ x=8. Вычислим

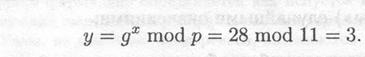
Открытым ключом являются у = 3, g = 2 и р = 11. Чтобы подписать М = 5, сначала выберем случайное число k = 9. Убедимся, что gcd (9, 10) = 1. Далее вычислим

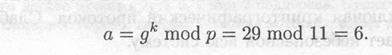
и затем с помощью расширенного алгоритма Евклида найдем b из уравнения М = (xa+ кb) mod (р — 1):

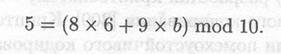
Решение; b = 3, а подпись представляет собой пару: а = 6 и b = 3. Для проверки подписи убедимся, что у^a а^b mod р = g^м mod р:

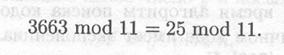
 Вариант криптосистемы, используемый для подписей, описан в [305]. Другой вариант, подходящий для доказательства подлинности, описан в [306]. Существуют варианты для проверки подлинности пароля [307] и для обмена ключами [308].

8.2.2. Шифрование/дешифрование

Некоторая модификация позволяет использовать криптосистему для шифрования/дешифрования сообщений .

Для шифрования сообщения М сначала выбирается случайное число k, взаимно-простое с р — 1. Затем вычисляются

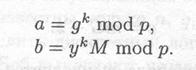
Пара (а, b) является шифротекстом. Отметим, что шифротекст в два раза длиннее открытого текста.

Для дешифрования (а, Ь) вычисляется

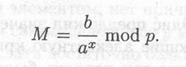
Преобразование обратимо, так как

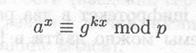
И

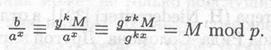
По сути описанное преобразование — это то же самое, что и экспоненциальный ключевой обмен по Диффи — Хеллману, за исключением того, что у — это часть ключа, а при шифровании сообщение умножается на у^k. Параметры криптосистемы, а также процедуры шифрования и дешифрования сведены в табл. П.34.

8.2.3. Эффективность реализации

Некоторые примеры скорости работы программных реализаций криптосистемы при 160- битовом показателе степени и различной разрядности модуля приведены в табл. II.35[286].

8.3. Криптосистемы МакЭлиса и Нидеррайтера

В 1978 г. МакЭлис (R. McEliece) разработал криптосистему с открытыми ключ методов теории помехоустойчивого кодирования [309]. Криптосистема использует корректирующий код, известный в теории помехоустойчивого кодирования как код Гоппы. Основная идея заключается в том, чтобы построить код Гоппы и замаскировать его под линейный код без определенной структуры. Существует быстрый алгоритм декодирования однако известный в настоящее время алгоритм поиска кодового слова по заданному весу в произвольном линейном двоичном коде имеет экспоненциальную трудоемкость. Хорошее описание криптосистемы дано в [310]. Коротко суть криптографического преобразования заключается в следующем.

Обозначим через d_н(х,y) расстояние Хэмминга между двоичными последовательностями x и у. Числа n,k и t являются параметрами криптосистемы. Секретный ключ состоит из трех частей: G' — порождающая матрица кода Гоппы, исправляющего t ошибок. Р- матрица перестановок размером n × n. S — невырожденная матрица размером k × k.Открытым ключом служит матрица G размером k × n: G = SG'Р. Открытый текст представляет собой строку k битов в виде k-элементного вектора над полем GF(2). Для шифрования сообщения случайным образом выбирается n-элементный вектор z над полем GF(2), для которого расстояние Хэмминга меньше или равно t, и вычисляется:

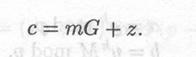
Для дешифрования сообщения сначала вычисляется с' = Ср^-1'. Затем с помощью алгоритма декодирования для кодов Гоппы находится т', для которого d_н(х, у) меньше или равно t. Наконец вычисляется

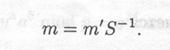
В своей оригинальной работе МакЭлис предложил значения n = 1024, t = 50 и k=524.Это минимальные значения, гарантирующие адекватную криптостойкость. Известный реализации криптосистемы МакЭлиса на два-три порядка быстрее, чем RSA. Однако с и ряд недостатков. Во-первых, длина открытого ключа — 219 бит. Во-вторых, но увеличивается объем данных — шифротекст в два раза длиннее открытого текста. Ряд попыток криптоанализа этой системы можно найти в [311 — 314]. Некоторые модификации криптосистемы изложены в [317 — 320].

В криптосистеме Нидеррайтера (Н. Niederreiter) [321], в отличие от криптосистемы МакЭлиса, используется обобщенный код Рида — Соломона. Другой алгоритм, используемый для цифровой подписи, основан на процедуре синдромного декодирования линейного кода [322](пояснения см. в [312]). Алгоритм [323], использующий коды, исправляющие ошибки, небезопасен [324 — 328]. Атака российских криптоаналитиков на криптосистему Нидеррайтера описана в [315]. Другая криптосистема на основе двоичных кодов описана в [316].

8.4.Метод экспоненциального ключевого обмена Диффи — Хеллмана

Метод экспоненциального ключевого обмена Диффи-Хеллмана — первая криптосистема с клинком — был изобретен Диффи (W. Diffie) и Хеллманом (М. Hellman) в 1976 году [161]. Криптостойкость метода определяется трудоемкостью вычисления дискретного логарифма. Метод может быть использован для распределения ключей — Алиса и Боб могут воспользоваться им для генерации общего секретного ключа, но его нельзя использовать для и дешифрования сообщений. Метод запатентован в США [304] и Канаде [329].Группа, называющаяся Public Key Partners (PKP), вместе с другими патентами в области криптографии с открытыми ключами получила лицензию и на этот патент. Срок действия истек 29 апреля 1997 г.

Сначала Алиса и Боб вместе выбирают большие простые числа n и g, так, чтобы g было примитивным элементом в конечном поле GF(n). Эти два целых числа хранить в секрете необязательно, Алиса и Боб могут договориться об их использовании по несекретному каналу. Эти числа могут даже совместно использоваться группой пользователей. Затем реализуется следующий протокол:

(1) Алиса выбирает случайное большое целое число х и посылает Бобу

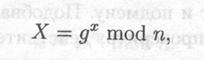
(2) Боб выбирает случайное большое целое число у и посылает Алисе

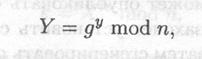
(3) Алиса вычисляет

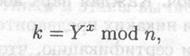
(4) Боб вычисляет

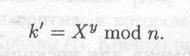
И k, и k¹ равны g^xy mod n. Никто из прослушивающих этот канал злоумышленников не сможет вычислить это значение, им известны только n, g, Х и Y, и не известны x и у. Для получения x и y необходимо вычислить дискретный логарифм. Таким образом, k — это секретный ключ, который Алиса и Боб вычисляют независимо. Выбор g и n может заметно влиять на криптостойкость. Отметим, что (n — 1)/2 также должно быть простым [160]. Кроме того,n должно быть обязательно большим числом: криптостойкость зависит также от трудоемкости разложения на множители чисел того же размера, что и n. Можно выбирать любое g, являющееся примитивным элементом; нет причин, по которым нельзя было бы выбрать наименьшее возможное g. (На самом деле число g может даже и не быть примитивным элементом, оно лишь должно порождать достаточно большую подгруппу мультипликативной группы в GF(n).)

Без дополнительных мер безопасности (введения сертификатов открытых ключей) описанный метод ключевого обмена уязвим с точки зрения атаки, известной под названием человек посередине» (man-ш-the-middle attack).

Предположим, злоумышленник может не только подслушивать сообщения Алисы и Боба, но и изменять удалять сообщения, а также создавать совершенно новые ложные сообщения, а также создавать совершенно новые ложные сообщения. Тогда злоумышленник может выдавать себя за Боба, сообщающего что-то Алисе, или за Алису  сообщающую что-то Бобу. Атака состоит из следующих действий:

(1) Алиса посылает Бобу свой открытый ключ. Злоумышленник перехватывает  его и посылает Бобу свой собственный открытый ключ;

(2) Боб посылает Алисе свой открытый ключ. Злоумышленник перехваты лает Алисе свой собственный открытый ключ;

(3) когда Алиса посылает сообщение Бобу, зашифрованное на его открытом ключе, злоумышленник его перехватывает. Так как сообщение в действительности зашифровано на открытом ключе злоумышленника, он расшифровывает его, снова за на открытом ключе Боба и посылает Бобу;

(4) когда Боб посылает сообщение Алисе, зашифрованное на ее открытом ключе злоумышленник его перехватывает. Так как сообщение в действительности зашил крытом ключе злоумышленника, он расшифровывает его и затем снова зашифровывает на открытом ключе Алисы и посылает Алисе.

Атака возможна, даже если открытые ключи Алисы и Боба хранятся в базе данных. Злоумышленник может перехватить запрос Алисы к базе данных и подмени ключ Боба своим собственным. То же самое он может сделать и с открытым ключом Алисы. Злоумышленник может атаковать базу данных и подменить открытые ключи Боба и Алисы своими собственными. Затем, дождавшись, когда Алиса и Боб начнут обмениваться сообщениями, он выполняет перехват и подмену. Подобная атака весьма эффективно Алисы и Боба нет возможности проверить, действительно ли они общаются я другом. Если вмешательство злоумышленника не приводит к заметным задержкам при передаче сообщений, абоненты не смогут обнаружить, что кто-то, расположенный читает все их секретные сообщения.

Каждый абонент криптосети может опубликовать свой открытый ключ Х=g^x mod n в общей базе данных. Если Алиса захочет установить связь с Бобом, ей понадобится только получить открытый ключ Боба и затем сгенерировать общий секретный ключ. Она может зашифровать сообщение этим ключом и послать его Бобу. Боб извлечет открытый ключ Алисы и вычислит общий секретный ключ. Каждая пара абонентов может использовать уникальный секретный ключ; не требуется никаких предварительных обменов данными Открытые ключи должны пройти сертификацию, чтобы предотвратить атаки, подменой ключей (в первую очередь для противодействия атаке «человек посередине), и должны регулярно меняться.

8.4.1. Протокол ключевого обмена для нескольких участников

Описанный выше протокол ключевого обмена легко можно расширить для более участников. В приводимом ниже примере Алиса, Боб и Кэрол вместе генерируют общий секретный ключ.

(1) Алиса выбирает случайное большое целое число х и вычисляет

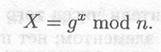
 (2) Боб выбирает случайное большое целое число у и посылает Кэрол

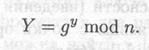
(3) Кэрол выбирает случайное большое целое число z и посылает Алисе

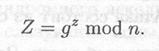
(4) Алиса посылает Бобу

(5) Боб посылает Кэрол

(6) Кэрол посылает Алисе

(7) Алиса вычисляет

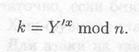
(8) Боб вычисляет

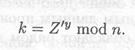
(9) Кэрол вычисляет

Секретный ключ k равен g^xyz mod n, и никто из подслушивающих каналы злоумышленников не сможет вычислить это значение. Протокол можно легко расширить для четырех и более участников, просто добавляются участники и этапы вычислений.

8.4.2. Некоторые модификации метода

Метод работает в коммутативных кольцах [160]. Шмули (Z. Shmuley) и МакКерли (K. McCurley) изучили вариант алгоритма, в котором модуль является составным числом [330, 331]. Миллер (V.S. Miller) и Коблиц (N. Koblitz) перенесли этот метод на эллиптические кривые [332,333.]. ЭльГамаль (Т. E1Gamal) использовал метод в качестве основополагающей идеи для разработки своей криптосистемы. В ряде реализаций используется конечное поле GF(2ⁿ) [334-336], так как вычисления в таком поле выполняются намного быстрее (по сравнению с GF(n)). Однако криптоаналитические атаки в таком поле также намного эффективнее, поэтому важно тщательно выбирать поле, достаточно большое, чтобы обеспечить нужную криптостойкость.

8.4.3. Односторонняя генерация ключа

Этот вариант метода Диффи — Хеллмана позволяет Алисе сгенерировать ключ и послать его Бобу [337].

(1) Алиса выбирает случайное большое целое число x и генерирует

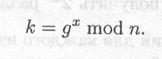
(2) Боб выбирает случайное большое целое число у и посылает Алисе

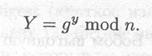
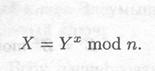
 (3) Алиса посылает Бобу

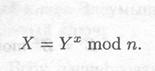
 (4) Боб вычисляет

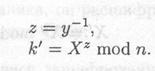
Если все выполнено правильно, то k = k'. Преимуществом этого метода состоит в том, что k можно вычислить заранее, до взаимодействия, и Алиса может шифровать сообщения с

помощью k задолго до установления соединения с Бобом. Она может послать сразу множеству абонентов, а передать ключ позднее — каждому в отдельности.

9. Хэш-функции

Односторонняя функция Н применяется к сообщению произвольной длины М и значение h = H(M) фиксированной длины т. Многие функции позволяют вычислять значение фиксированной длины по входным данным произвольной длины, но однонаправленные (или односторонние) хэш-функции обладают рядом дополнительных свойств [338:

• зная М, легко вычислить h;

1

• при заданном Ь задача нахождения M, для которого Н(М) = h, должна быть вычеслительно-трудоемкой;

• при заданном M задача нахождения другого сообщения М', для которого

 Н(М) =H(M'), должна быть вычислительно-трудоемкой.

Смысл применения однонаправленных хэш-функций и состоит в обеспечении М уникального значения — «отпечатка пальца» сообщения. Если Алиса подписала М цифровой подписью с использованием хэш-функции Н(М), а Боб может создать другое с отличное от М¹, отличное от М для которого H(M) = Н(М'), то Боб сможет утверждать, что Алиса подписала сообщение M'. В некоторых приложениях необходимо выполнение дополнительного требования, называемого устойчивостью к коллизиям. Смысл данного требования заключается в том, что задача нахождения двух случайных сообщений M и М', для которых H(M) = Н(М'), должна быть вычислительно-трудоемкой (с экспоненциальный перебора).

Следующий протокол, впервые описанный Ювалом (G. Yuval) [339], показывает, как Алиса может воспользоваться коллизиями для обмана Боба.

(1) Алиса готовит две версии контракта: одну, выгодную для Боба, и другую, приводящую его к банкротству.

(2) Алиса вносит несколько незначительных изменений в каждый документ и хэш-функции. (Этими изменениями могут быть действия, подобные следующим: замена одного пробела комбинацией пробелов, вставка одного-двух пробелов перед возвратом каретки и так далее. Производя или не производя по одному изменению в каждой из 32 строк, Алиса может легко получить 2³² различных документов.)

(3) Алиса сравнивает хэш-значения для каждого изменения в каждом из двух документов, разыскивая пару, для которой эти значения совпадают. (Если выходом

хэш-функции является 64-битное значение, Алиса, как правило, сможет найти совпадающую пару выполнив 2³² сравнений.) Таким образом, она получает два документа, дающих одинаковое значение хэш-функции.

(4) Алиса получает подписанную Бобом выгодную для него версию контракта, протокол, в котором он подписывает только значение хэш-функции.

(5) Спустя некоторого время Алиса подменяет контракт подписанный Бобом другим которого он не подписывал. Теперь она может убедить арбитра в том, что Боб подписал другой контракт.

Отметим, что могут применяться и другие атаки. Например, противник может посылать системе автоматического контроля (может быть, спутниковой) случайные сообщения со случайными цифровыми подписями. В конце концов подпись под одним из этих случайных общений окажется правильной. Противник не сможет узнать, к чему приведет эта команда, но если его единственной целью является вмешательство в работу спутника, он своего добьется.

Хэш-функции с 64-битным выходным значением не могут противостоять описанной выше атаке. Хэш-функции, выдающие 128-битовые значения, имеют определенное преимущество. Для того чтобы найти коллизию, придется вычислить значение хэш-функции для 2⁶⁴ случайных документов, чего, впрочем, недостаточно, если безопасность должна обеспечиваться в учение длительного периода времени. Хэш-функция стандарта SHS (Secure Hash Standard) имеет 160-битовое выходное значение. Для атаки на такую хэш-функцию понадобится вычислить хэш-значения для 2⁸⁰ случайных документов. Для удлинения значений, выдаваемых конкретной хэш-функцией, был предложен следующий метод.

(1) Для заданного сообщения с помощью одной из однонаправленных хэш-функций генерируется хэш-значения.

(2) Выполняется конкатенация вычисленного значения хэш-функции и исходного сообщения.

(3) Вычисляется значение хэш-функции от конкатенации сообщения и значения хэш-функции первого этапа.

(4) Выполняется конкатенация значений хэш-функции первого и третьего этапа.

(5) Этапы с первого по четвертый повторяются нужное количество раз для обеспечения, результата требуемой длины.

Как правило, при построении однонаправленных хэш-функций используется функция сжатия. Такая однонаправленная функция выдает значение длины n при заданных входных данных большей длины т [340,341]. Входами функции сжатия являются блок сообщения и выход функции на предыдущем шаге. Выход представляет собой хэш-значения всех блоков до текущего момента. То есть хэш-значения блока М_i равно h_i = f(M_i, h_i-1). Это хэш-значения вместе со следующим блоком сообщения становится входом функции сжатия. Конечным результатом является хэш-значения последнего блока.

Хэшируемый вход должен каким-то образом содержать бинарное представление длины всего сообщения. Таким путем исключается потенциальная проблема, связанная с тем, что сообщения различной длины могут приводить к одному и тому же значению хэш-функции [340, 341]. Различные исследователи выдвигали предположения, что метод хеширования на основе криптостойкой функции сжатия также будет криптостойким, однако это не было доказано [341-343]. Более подробную информацию о проектировании хэш-функций можно найти в [66, 340, 341,343-349].

9.1. MD4

MD4 — это однонаправленная хэш-функция, разработанная Ривестом [350,351]. Аббревиатура «MD» обозначает Message Digest (краткое изложение сообщения, или дайджест); алгоритм для входного сообщения выдает 128-битное значение-результат.

В [351] Ривест сформулировал цели, которые он преследовал при разработке алгоритма.

Безопасность. Малая вероятность коллизии. Нахождение коллизии (поиск различных сообщений с одинаковым значением хэш-функции) должно быть вычислительно- трудоемким. Безопасность MD4 не должна основываться на каких-либо допущениях, предположении о трудоемкости факторизации.

Эффективность реализации. Для высокоскоростной программной реализация должен состоять из набора простых операций с 32-битовыми операндами.

Простота и компактность. Алгоритм должен быть максимально прост и не сложных структур данных или программных модулей.

Унифицированность архитектуры. Алгоритм должен легко оптимизироваться для произвольной микропроцессорной архитектуры (в первую очередь для микрон Intel).

Босселэрс (А. Bosselaers) и ден Бур (В. den Boer) добились успеха в криптоанализе последних двух из трех этапов алгоритма [352]. Бихам (Е. Biham) применил метод дифференциального криптоанализа против первых двух этапов MD4 [353]. Хотя все эти атаки не были распространены на полный алгоритм, Ривест усилил свою разработку. В результате появилась хэш-функция MD5.

9.2. MD5

MD5 — это улучшенная версия MD4 [20,354]. Хотя она сложнее MD4, их схемы похожи, и результатом MD5 также является 128-битовое значение.

9.5.1. Описание MD5

MD5 обрабатывает входной текст 512-битовыми блоками, разбитыми на шестнадцать 32- битовых подблоков. Выходом алгоритма является набор из четырех 32-битовых блоков которые объединяются в единое 128-битовое значение. Вначале сообщение дополняется так, чтобы его длина была на 64 бита короче числа, кратного 512. Этим дополнением является 1, за которой вплоть до конца сообщения следует необходимое количество нулей. Затем к результату добавляется 64-битовое представление длины сообщения.

Эти действия необходимы для того, чтобы длина сообщения была кратна 512 также для гарантии того, что разные сообщения будут различаться после обработки. Инициализируются четыре переменные:

Теперь перейдем к основному циклу алгоритма. Этот цикл продолжается, пока не исчерпаются 512-битовые блоки сообщения. Четыре переменные копируются во вспомогательные переменные: А → а, В→b, С → с и D →d. Главный цикл состоит из четырех идентичных этапов (у MD4 было только три этапа).

На каждом этапе 16 раз используются различные операции. Каждая операция представляет собой нелинейную функцию над некоторыми тремя из четырех переменных а,b,c и d. Затем результат суммируется с четвертой переменной, подблоком текста и константой Далее результат циклически сдвигается вправо на переменное число бит и суммируется с одной из переменных а, b, с и d. И наконец, заменяет одну из переменных а, b, с и d (рис. П.30 и рис. II.31).

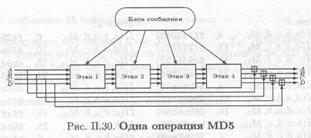
Существует четыре нелинейные функции. На каждом этапе используется своя функция:

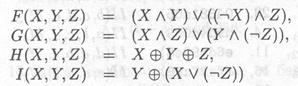
(Θ — это XOR, А — AND, V — OR, а⌐ — NOT).

Эти функции спроектированы так, что если соответствующие биты Х, Y и Z независимы, то каждый бит результата также будет независимым. Функция F — это побитовое условие: если Х, то У, иначе Z. Функция F — это побитовое условие если Х, то Y, иначе Z. Функция Н- побитовая операция проверки четности. Если М_j обозначает j-й подблок сообщения (от 0 до 15), а < << в обозначает циклический сдвиг влево на s битов, то используются следующие четыре операции:

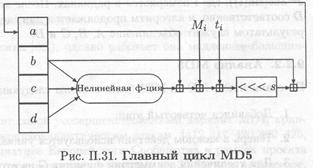
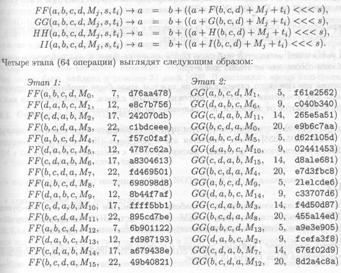
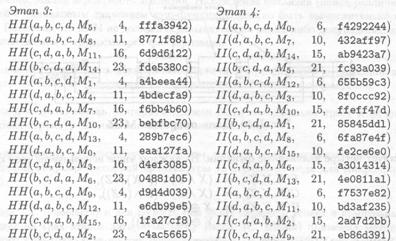
Константы t_i выбирались следующим образом: на i-м этапе t_i является целой частью 2³² abs (sin (i)), где i измеряется в радианах. После этого а, b, с и d суммируются с А, В, С и D соответственно, и алгоритм продолжается для следующего блока данных. Окончательным результатом служит объединение А, В, С и D.

9.5.2. Анализ MD5

По сравнению с MD4 в MD5 были внесены следующие изменения [20]:

1. Добавился четвертый этап;

2. Теперь в каждом действии используется уникальная аддитивная константа;

3. Для увеличения асимметрии функция G на втором этапе с ((Х ^ Y) v(Х ^ Z)

 v(Y^ Z)) была заменена на (Х ^ Z) v (Y^ (- Z));

4. Теперь результат каждой операции суммируется с результатом предыдущего этапа, что обеспечивает нарастание лавинного эффекта;

5. Для увеличения несходства шаблонов был изменен порядок, в котором использовались подблоки сообщения на этапах два и три;

6. Значения циклического сдвига влево на каждом этапе были приближенно оптимизированы для ускорения лавинного эффекта. Четыре сдвига, используемые на каждой этапе, отличаются от значений, используемых на других этапах.

Берсон (Т. Berson) безуспешно попытался применить дифференциальный криптоанализ к одному этапу MD5 [355]. Более успешная атака дев Бура (В. den Boer) и Босселэрса (А. Bosselaers), использующая функцию сжатия, привела к обнаружению коллизий в MD5 [356 — 358].

9.3. MD2

MD2 — это 128-битовая хэш-функция, разработанная Ривестом [19,359]. Эта хэш-функция вместе с MD5 используется в стандарте РЕМ. Безопасность MD2 определяется случайной перестановкой байтов. Чтобы выполнить хеширование сообщения М, нужно:

(1) дополнить сообщение i байтами; значение i должно быть таким, чтобы длина полученного сообщения была кратна 16 байтам;

(2) добавить к сообщению 16 байтов контрольной суммы;

(3) проинициализировать 48-байтовый блок: Х_о, Х₁, Х₂,..., Х₄₇. Заполнить первые 16 байтов блока Х нулями, во вторые 16 байтов блока Х скопировать первые 16 байтов сообщения, а третьи 16 байтов блока Х должны быть равны сумме по модулю 2 первых и вторых 16 байтов блока Х;

(4) сжатие выполняется при помощи следующей процедуры:

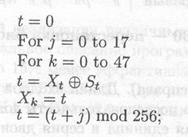
(5) скопировать вторые 16 байтов сообщения во вторые 16 байтов блока Х, а третьи 16 байтов блока Х должны быть равны XOR (сумме по модулю 2) первых и вторых 16 байтов блока Х. Выполнить этап (4). Повторять этапы (5) и (4) по очереди для каждых 16 байтов сообщения;

(6) выходом являются первые 16 байтов блока Х.

Хэш-функция MD2 достаточна надежна [66]), однако работает она медленнее большинства известных хэш-функций.

9.4. RIPEMD-160

Хеш-функция RIPEMD-160 представляет собой усовершенствованный вариант MD4, криптостойкий по отношению к известным криптоаналитическим атакам [412, 417 — 420, 422 — 425, 429].RIPEMD-160 разработана по инициативе Европейского Сообщества в рамках проекта RAСЕ [427] и допускает эффективную программную реализацию на 32-битном процессоре. Как следует из названия, хэш-функция выдает 160-битный результат. Предполагается, что EMD-160 обладает гарантированной криптостойкостью (по отношению к силовой атаке) десятилетний период. Первоначальный вариант — RIPEMD-128 — выдавал 128-битный результат и допускал более эффективную реализацию. Переход к 160-битному варианту обусловлен возможностью силовой атаки на 128-битную хэш-функцию. Винер (М.J. Wiener) и ван Ооршот (P. van Oorschot) показали, что при инвестициях порядка 10 млн. долл. коллизия может быть найдена в течение 24 дней [428]. В настоящее время хэш-функции SHA, RIPEMD-160 и RIPEMD-128 включены в международный стандарт ISO/IEC 10118-3 [426].

9.4.1. Описание RIPEMD-160

Как и все подобные MD4 хэш-функции, RIPEMD-160 оперирует с 32-битными словами. Используется следующий набор операций:

• циклический левый сдвиг слов;

• поразрядные булевы операции (AND, NOT, OR, XOR) над словами;

 • суммирование слов по модулю 2³².

Входная последовательность двоичных символов разбивается на блоки по 512 бит каждый. Каждый блок разбивается на шестнадцать подпоследовательностей по 4 байта, и каждая такая подпоследовательность преобразуется в 32-битное слово с крайним левым наименьшим значащим разрядом. Отметим, что в MD4, MD5 и RIPEMD используется один и тот же способ  преобразования (в SHA применяется иной способ — в результате конвертации наименьший

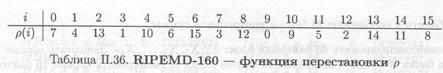
значащий разряд расположен справа). Длина входной двоичной последовательности должна быть кратна 512. Для этого последовательность дополняется по следующему правилу: конец приписываются двоичная единица и серия двоичных нулей переменной длины (от до 511). Последние 64 бита входной последовательности содержат двоичное представлением длины (наименьший значащий бит расположен слева).

Результат работы RIPEMD-160 — пять 32 битных слов, которые преобразуются в 160-битную двоичную последовательность.

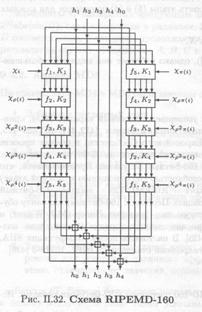
Начальное состояние задается пятью 32-битными словами-константами. Основу RIPEMD-160 составляет функция сжатия, состоящая из пяти параллельных и независимых циклов, каждый цикл состоит из шестнадцати шагов. Общее число шагов – 5 × 16 × 2 = 160. Для сравнения — число шагов для MD4 и MD5 — 3 × 16 = 48 и 4 × 16 = 64 соответственно. На начальном этапе набор из пяти 32-битных констант h₀, h_1, h_2, h_3, h₄ реплицируется и подается на, входы параллельных циклов — правого и левого. Обработка выполняется независимо и параллельно. На каждом цикле обработки задействовано пять 32-битных регистров — А, В, С, D, Е (на параллельном цикле — А', В'; С', D', Е'). В общем виде преобразование на каждом шаге выглядит следующим образом: А:= (А+ j(B,С,D)+х+К)<<< s+E, С:= С <<< 10, где <<< s — циклический сдвиг на s двоичных позиций влево, К— вспомогательная константа, а χ — 32-битный блок входной последовательности. Схема RIPEMD-160 представлена на рис. П.32.

Выбор входных блоков для левого цикла осуществляется в соответствии с функцией перестановки р, заданной в табличном виде (табл. П.36).

Выбор входных блоков в правом цикле преобразования зависит от дополнительной перестановки π, где π (i) = 9i+ 5(mod 16). Для n-кратной перестановки относительно позиции i вводится обозначение рⁿ (i). Перестановка блоков в параллельных правом и левом циклах представлена в табл. П.37.

Криптостойкость RIPEMD-160 определяется выбором параметров, порядком перестановки входных блоков и набором булевых функций на каждом цикле.

Операции с регистром А аналогичны операциям в MD5 (с тем отличием, что используется пять различных 32-битных регистров); сдвиг регистра С позволяет предотвратить атаку, описанную в [418]. Отметим, что циклические сдвиги также применяются в хэш-функции SHA. Поскольку сдвига на десять позиций в ходе преобразования не возникает (см. табл П.43), это число выбрано в качестве параметра циклического сдвига регистра С. Перестановка π гарантирует, что пары входных блоков в левом и правом цикле будут максимально разнесены. Набор булевых функций RIPEMD-160 аналогичен набору в MD5. Порядок применения 6улевых функции в правом цикле обратен порядку их применения в левом.

9.4.2. Эффективность реализации

Оценки эффективности программной реализации различных хэш-функций для Pentium 90 МГц представлены в табл. П.38. Детальное описание программной реализации дано в [413, 416,416]. Реализация RIPEMD-160 на 15% менее эффективна, чем SHA. Реализация MD4 в четыре раза эффективнее реализации RIPEMD-160. При использовании языка Си эффективность реализации хэш-функций SHA и MD4 в 2,2 и 2,6 раз выше аналогичной реализации RIP EMD-160.

Псевдокод RIPEMD-160 представлен на табл. П.39. После дополнения сообщение состоит из t блоков по шестнадцать слов, обозначенных как X_i [j], где 0 ≤ i ≤ t — 1 и 0≤ j ≤ 15. Суммирование по модулю 2зг обозначено 83. Циклический сдвиг влево на s позиций обозначен rol_s. Результат состоит из конкатенации значений h₀, h₁, h₂, h₃ и h₄ после их конвертации в 4-байтные блоки.

Порядок выбора булевых функций, вспомогательных констант, набор 32-битных констант и входных блоков приведены в табл. П.40 П.41 и II.42. Циклический сдвиг влево как функция номера позиции приведен в табл. П.43.

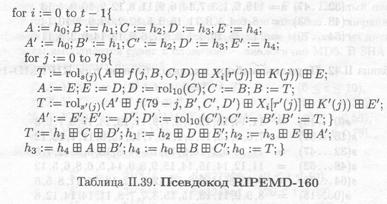
9.5. Федеральный стандарт США — SHS (алгоритм SHA)

Национальный Институт Стандартов США при участии АНБ разработал алгоритм вычисления хэш-функции SHA (Secure Hash Algorithm), используемый в алгоритме цифровой подписи DSA (Digital Signature Algorithm) стандарта DSS (Digital Signature Standard) [368]. Алгоритм SHA описан в стандарте SHS (Secure Hash Standard) [53].

Для любого входного сообщения длиной меньше 2в4 битов SHA выдает 160-битовый «дайджест» сообщения. Далее «дайджест» подается на вход DSA, который вычисляет подпись для сообщения. Подписывание «дайджеста» вместо сообщения часто повышает эффективность процесса, так как «дайджест» намного меньше, чем само сообщение. Тот же «дайджест» сообщения должен быть получен тем, кто проверяет подпись. При использовании SHA задача поиска сообщения, соответствующего данному «дайджесту», или двух различных сообщений с одинаковым «дайджестом» является вычислительно-трудоемкой. Любые изменения сообщения, произошедшие во время передачи, с очень высокой вероятностью приведут к изменению «дайджеста», и подпись не пройдет проверку. Принципы, лежащие в основе SHA, аналогичны принципам, которые использовались при разработке MD4 [351]. SHA выдает 160-битовое хэш-значения, более длинное, чем у MD5.

9.5.1. Описание SHA

 Вначале сообщение дополняется так, чтобы его длина была кратной 512 битам. Используется то же дополнение, что и в MD5: сначала добавляется 1, а затем нули, так чтобы длина полученного сообщения была на 64 бита меньше числа, кратного 512, а затем добавляется 64-. битовое представление длины оригинального сообщения. Инициализируется пять 32-битовых переменных (в MD5 используется четыре переменных, но рассматриваемый алгоритм должен выдавать 160-битовое хэш-значения):

 Затем начинается главный цикл алгоритма. Сообщения обрабатываются 512-битовыми блоками до тех пор, пока не исчерпаются все блоки. Сначала пять переменных копируются во вспомогательные переменные: А в а, В в b, С в с, D в d и Е в е. Главный цикл состоит из четырех этапов по 20 операций в каждом (в MD5 четыре этапа по 16 операций в каждом). Каждая операция представляет собой нелинейную функцию над тремя из пяти переменных а, b, с, d и е, затем выполняется сдвиг и сложение — аналогично MD5. В SHA используется следующий набор нелинейных функций:

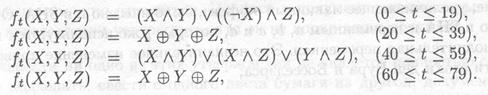
 В алгоритме используется следующие четыре константы:

Блок сообщения превращается из шестнадцати 32-битовых слов (М_о по М₁₅) в 32-битовых слов (W₀ по W₇₉) с помощью следующего алгоритма:

 Отметим, что в первоначальной спецификации SHA не было циклически сдвига влево. Если t — номер операции(1≤ t ≤ 80), W_t, t-й подблок расширенного сообщения, а <<< s — циклический сдвиг влево на s битов, то главный цикл выглядит следующим образом:

На рис. П.ЗЗ показана одна операция. Сдвиг переменных выполняет ту же функцию, что использование в различных местах различных переменных на разных этапах преобразован (как в MD5). После этого а, b, с, d и е суммируются с А, В, С, D и Е соответственно и алгоритм переходит к следующему блоку данных. Окончательным результатом служи объединение А, В, С, D и Е.

9.5.2. Анализ SНА

Алгоритм SHA очень похож на MD4, но выдает 160-битовое хэш-значения. Главным изменением являются введение расширяющего преобразования и суммирование выходного значения предыдущего шага с последующим с целью более быстрого нарастания лавинного эффекта

Сравним изменения, внесенные в MD5 относительно MD4, с SHA:

1. В SHA также добавился четвертый этап. Однако в SHA на четвертом этапе используется та же функция f, что и на втором этапе;

2. SHA придерживается схемы MD4, повторно используя константы;

3. В SHA используется версия функции из MD4: (Х A Y) V (X A Z) V (Y Л z);

4. Изменение, увеличивающее лавинный эффект, было внесено и в SHA. Отличие состоит в том, что в SHA к переменным а, b, с и d, которые уже используются в f_t, добавлю пятая дополнительная переменная. Это незначительное изменение приводит к несостоятельности атаки ден Бура и Босселэрса;

5. SHA в этом месте совершенно отличается, так как использует циклический код исправления ошибок;

6. SHA на каждом этапе использует постоянное значение сдвига. Это значение — число взаимно-простое с размером слова, также как и в MD4.

Можно заключить, что SHA — это MD4 с добавлением расширяющего преобразования, дополнительного этапа и улучшенным лавинным эффектом. MD5 — это MD4 с улучшенным битовым хешированием, дополнительным этапом и улучшенным лавинным эффектом. Сведения об успешных атаках на SHA отсутствуют. Так как хэш-функция выдает 160-значени она в большей степени способна противостоять силовой атаке, чем 128-битовые хэш-функции рассматриваемые в этой главе.

9.6. Стандарт России — ГОСТ Р 34.11-94

Разработанная российскими криптографами хэш-функция описана в стандарте ГОСТ Р 34.11-94 [17]. В ней используется блочный шифр ГОСТа 28147-89, хотя теоретически может использоваться любой блочный шифр с 64-битным блоком и 256-битным ключом. Хэш-функция выдает 256-битное значение.

Функция сжатия Н; = f (M,, Н, q) (оба операнда — 256-битовые двоичные последовательности) определяется следующим образом:

(1) при помощи линейного смешивания М_i, Н_i-1, и некоторых констант генерируются четыре ключа шифрования ГОСТ;

(2) каждый ключ используется для шифрования отличных 64 битов Н_i-1 в режиме ЕСВ. Полученные 256 битов сохраняются во вспомогательной переменной S;

(3) Н_i является сложной, хотя и линейной функцией S, M_i, и Hi — 1.

Хэш-значения последнего блока сообщения не является его окончательным хэш-значением. На деле используется три переменные: Н_n- это хэш-значения последнего блока, Z— это XOR всех блоков сообщения, а L — длина сообщения. С использованием этих переменных дополненного последнего блока М' окончательное значение хэш-функции будет равно:

10. Цифровая подпись

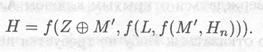
Рукописные подписи издавна используются как доказательство авторства документа или, по крайней мере, согласия с ним. Подпись обладает следующими свойствами:

1. Подпись достоверна. Она убеждает получателя документа в том, что подписавший сознательно подписал документ;

2. Подпись неподдельна. Она доказывает, что именно подписавший, и никто иной, сознательно подписал документ;

3. Подпись не может быть использована повторно. Она является частью документа, злоумышленник не сможет перенести подпись на другой документ;

4. Подписанный документ нельзя изменить;

5. От подписи невозможно отказаться. Подпись и документ материальны. Подписавший не сможет впоследствии утверждать, что он не подписывал документ.

В действительности ни одно из этих утверждений не является полностью справедливым. Подпись можно подделать, свести с одного листа бумаги на другой, документ может быть изменен после подписания и так далее. Аналогичные проблемы существуют в мире электронных документов.

Существуют алгоритмы с открытыми ключами, которые можно использовать для цифровых подписей. В некоторых алгоритмах — примером является RSA — для шифрования может быть использован или открытый, или секретный ключ. При шифровании документа па секретном ключе можно получить надежную цифровую подпись. В других случаях— примером является DSA — для цифровых подписей используется отдельный алгоритм, который невозможно использовать для шифрования. Основополагающая идея впервые была предложена Биффи и Хеллманом [161] и в дальнейшем была расширена и углублена в других исследованиях [44,274,360 — 362]. Хороший обзор приведен в [363]. Основной протокол прост:

(1) Алиса шифрует документ своим секретным ключом, таким образом подписывая его;

(2) Алиса посылает подписанный документ Бобу;

(3) Боб расшифровывает документ, используя открытый ключ Алисы, таким образом л проверяя подпись.

Отметим, что нотариус не нужен ни для подписи, ни для ее проверки. (Он нужен для подтверждения, что открытый ключ принадлежит именно Алисе.) Если на третьем этапе подпись не сошлась, то становится ясно, что документ был подписан кем-то другим или б искажен до того, как попал к Бобу. Такая подпись соответствует всем требованиям:

1. Эта подпись достоверна. Когда Боб расшифровывает сообщение с помощью открыть ключа Алисы, он знает, что она подписала это сообщение;

2. Эту подпись нельзя подделать. Только Алиса знает свой секретный ключ;

3. Эту подпись нельзя использовать повторно. Подпись является функцией документа не может быть перенесена на другой документ;

4. Подписанный документ нельзя изменить. После любого изменения документа подпись не сможет больше подтверждаться открытым ключом Алисы;

5. От подписи невозможно отказаться. Бобу не требуется помощь Алисы при проверке подписи.

На самом деле при определенных условиях Боб сможет смошенничать. Он может повторно использовать подписанный документ. Это не имеет значения, если Алиса подписали контракт (одной копией подписанного контракта больше, одной меньше), но что если Алиса поставила цифровую подпись под чеком? Предположим, что Алиса послала Бобу подписанный чек на 100 долл. Боб отнес чек в банк, который проверил подпись и перевел деньги одного счета на другой. Боб, выступающий в роли злоумышленника, сохранил копию злак тронного чека. На следующей неделе он снова отнес его в тот же самый или в другой банк, Банк подтвердил подпись и перевел деньги с одного счета на другой. Если Алиса не проверяет свою чековую книжку, Боб сможет проделывать это годами. Поэтому в цифровые подписи часто включают метки времени. Дата и время подписания документа добавляются к документу и подписываются вместе с сообщением. Банк сохраняет эту метку времени базе данных. Теперь, если Боб попытается получить наличные по чеку Алисы во второй р банк проверит метку времени по своей базе данных и обнаружит злоумышленника.

На практике алгоритмы с открытыми ключами часто недостаточно эффективны для подписи больших документов. Для экономии времени протоколы цифровой подписи нередко используют вместе с однонаправленными хэш-функциями [364,365]. Алиса подписывает не документ, а значение хэш-функции для данного документа. В этом протоколе хэш-функции и алгоритм цифровой подписи согласовываются заранее.

(1) Алиса вычисляет значение хэш-функции для документа.

(2) Алиса вычисляет подпись — шифрует значение хэш-функции на своем секретном ключе.

(3) Алиса посылает Бобу документ и зашифрованное значение хэш-функции.

(4) Боб получает значение хэш-функции для документа, присланного Алисой.

Затем, используя алгоритм цифровой подписи, он расшифровывает подписанное значение хеш-функции с помощью открытого ключа Алисы. Если подписанное значение хэш-функции совпадает с рассчитанным, подпись правильна.

При таком подходе эффективность реализации заметно возрастает, кроме того, вероятность получения одинакового 160-битного хэш-значения для двух различных документов превышает 2^-160. Основное требование заключается в использовании однонаправленной хеш-функции. Существуют и другие преимущества. Во-первых, подпись может быть отдела от документа. Во-вторых, значительно уменьшаются требования к объему памяти для хранения документов и подписей. Архивная система может использовать этот протокол для подтверждения существования документов, не сохраняя самих документов. В центральной базе данных могут храниться лишь значения хэш-функций. Пользователи помещают свои гения хэш-функции в базу данных, а база данных хранит эти значения, помечая их временем получения документа. Если в будущем возникнет какое-либо разногласие по поводу авторства и времени создания документа, база данных сможет разрешить его при помощи хранящихся в ней хэш-значения. Подобная система имеет большое значение при хранении секретной информации: Алиса может подписать документ и сохранить его в секрете. Ей надобится опубликовать документ, только если она захочет доказать свое авторство.

Как Алисе и Бобу одновременно подписать один и тот же документ? Алиса и Боб могут подписать различные копии одного и того же документа. Либо сначала Алиса подписывает документ, а затем Боб подписывает подпись Алисы. Однако проверить подпись Алисы, не проверяя при этом подписи Боба, невозможно. С помощью механизма хэш-функций можно реализовать несколько подписей:

(1) Алиса подписывает значение хэш-функции документа;

(2) Боб подписывает значение хэш-функции документа;

(3) Боб посылает свою подпись Алисе;

(4) Алиса посылает доверенному лицу документ, свою подпись и подпись Боба;

 (5) доверенное лицо проверяет подписи Алисы и Боба.

Алиса и Боб могут выполнить первый и второй этапы или параллельно, или последовательно. На пятом этапе доверенное лицо может проверить любую подпись независимо от другой.

 Алиса может мошенничать с цифровыми подписями. Например, она может подписать документ и затем утверждать, что она этого не делала. Для этого Алиса, как обычно, подписывает документ. Затем она анонимно раскрывает свой секретный ключ (например, теряет его, так чтобы он непременно был найден). Теперь Алиса утверждает, что ее подпись была скомпрометирована и использована кем-то другим, выдающим себя за нее. Она дезавуирует свою подпись под всеми документами, подписанными с помощью этого секретного ключа. Метки времени позволяют снизить эффект такого мошенничества, но Алиса всегда может заявить, что ее ключ был скомпрометирован раньше. Если Алиса правильно рассчитает время, она сможет подписать документ и затем дезавуировать свою подпись. Хотя с подобным злоупотреблением бороться трудно, можно предпринять некоторые действия, гарантирующие, что старые подписи не будут признаны недостоверными из-за разногласий по новым подписям. (Например, Алиса может «потерять свой ключ, чтобы не платить Бобу, и в результате сделает свой банковский счет недействительным.) Необходимо проставлять метки времени для полученных документов [366]. Общая схема протокола приведена в [311[:

(1) Алиса подписывает документ;

(2) Алиса создает уникальный идентификатор и присоединяет его к подписанному документу, затем подписывает все вместе и посылает полученное сообщение нотариусу;

(3) нотариус проверяет внешнюю подпись и уникальность идентификатора. Затем он добавляет метку времени к сообщению Алисы и подписывает "все вместе и посылает полученное сообщение Алисе и Бобу;

(4) Боб проверяет подпись нотариуса, идентификатор и подпись Алисы;

(5) Алиса проверяет сообщение, которое нотариус послал Бобу, и делает заявление, если признает своего авторства.

В другой схеме нотариус используется в качестве арбитра [367]. Получив подписанное общение, Боб посылает копию нотариусу для проверки. Нотариус может подтвердить подпись Алисы.

10.1. Федеральный стандарт США — DSS (алгоритм DSA)

В августе 1991 г. Национальный Институт Стандартов США предложил для использования в своем стандарте цифровой подписи DSS (Digital Signature Standard) алгоритм цифровой подписи DSA (Digital Signature Algorithm) [368]. В DSS используется открытый ключ проверки целостности полученных данных и подлинности источника сообщения. DSS также может быть использован третьей стороной для проверки легальности подписи и связанных с ней данных.

При разработке стандарта учитывались следующие факторы: уровень криптостойкости, простота аппаратной и программной реализации, возможность экспорта за пределы С требования национальной безопасности, вычислительная эффективность.

Окончательный вариант стандарта был выпущен 19 мая 1994 года [368].

10.1.1. Описание DSA

DSA представляет собой вариант алгоритма цифровой подписи ЭльГамаля в модификации Шнорра (Schnorr). Алгоритм использует следующие параметры: р — простое число длиной L битов, где L принимает значение, кратное 64, в диапазоне от 512 до 1024 (в первоначальном стандарте размер р был фиксирован и равен 512 битам [369]), q — 160-битовое простое число делитель р — 1.

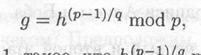
где b — любое число, меньшее р — 1, такое, что h^(p-1)/q mod p > 1.

где х < q. В алгоритме также используется однонаправленная хэш-функция Н(т) стандарта  SHS.

Первые три параметра р, q и g открыты и могут быть общими для абонентов криптосети Секретным ключом является x, а открытым — у. Чтобы подписать сообщение m,

(1) Алиса генерирует случайное число k < q,

(2) затем Алиса вычисляет

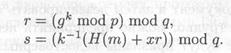
Подписью служат числа r и s.

(3)Боб проверяет подпись, вычисляя

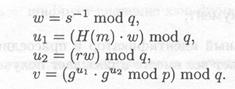
Если v = r, то подпись правильна.

Доказательства математических соотношений можно найти в [368]. Краткое описание алгоритма приводится в табл. П.44.

10.1.2. Эффективность реализации

В табл. II.45 приведена производительность программной реализации DSA для различной разрядности модуля и 160-битного показателя степени [286].

Практические реализации DSA часто можно ускорить с помощью предварительных вычислений. Отметим, что значение r не зависит от сообщения. Можно задать последовательность случайных значений k и затем рассчитать значение r для каждого из них. Можно также вычислить k^-1 для каждого из этих значений. Затем для сообщения можно вычислить s  при заданных r и k^-1. Эти предварительные вычисления заметно ускоряют DSA.