Метод линейного криптоанализа
впервые, был применен для атаки блочного FEAL [376] и затем DES [377]. Данный
метод использует линейные приближения. Это означает, что, если выполнить
операцию XOR над некоторыми битами открытого текста, затем над некоторыми
битами шифротекста, а затем выполнить XOR результатов предыдущего суммирования,
можно получить бит, который равен сумме некоторых бит ключа. Это называется
линейным приближением, которое может быть верным с некоторой вероятностью p. Если р ![]() 1/2, то этот факт можно
использовать для раскрытия бит ключа.
1/2, то этот факт можно
использовать для раскрытия бит ключа.
Рассмотрим данный метод подробнее. Пусть в общем виде линейное выражение уравнением:

где i1,
i2,….,ia,
jb и
l1,l2,….,lc — позиции некоторых бит открытого текста Р,
шифротекста С и ключа К. (Напомним, что суммирования в (II.1)
выполняется по модулю. Для случайно выбранного открытого текста Р и
соответствующего шифротекста с уравнение (П.1) выполняется с
вероятностью р![]() 1/2. Величина р — 1/2[ определяет эффективность уравнения (II.1).
1/2. Величина р — 1/2[ определяет эффективность уравнения (II.1).
Таким образом, при заданном эффективном линейном выражении можно оп один бит ключа К, воспользовавшись следующим алгоритмом максимума правдоподобия
Алгоритм 1.
Шаг 1. Пусть Т задает число открытых текстов, таких, что левая часть уравнения равна нулю.
Шаг 2. Тогда, если Т > N/2 (N — общее число открытых текстов),
угадываем
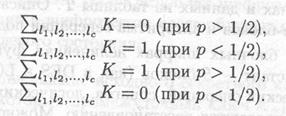
или угадываем
Вероятность успеха увеличивается с ростом N или [р — ½].
Рассмотрим криптоалгоритм DES с n-циклами криптографического преобразования учетом 48-битного ключа Kn и F-функции линейное выражение принимает следующий вид:

где через СR обозначена правая половина блока шифротекста.
Оценивая
эффективность уравнения (II.2) при подстановке различных кандидатов, можно
восстановить Кn и ![]()
![]()
![]() Для этого следует
воспользоваться следующим алгоритмом максимального правдоподобия:
Для этого следует
воспользоваться следующим алгоритмом максимального правдоподобия:
Алгоритм 2.
Шаг 1. Пусть Т задает число открытых текстов,
таких, что левая часть уравнения равна нулю для каждого кандидата ![]()
Шаг 2. Обозначим
через Т и Тmin максимальное
и минимальное значения среди ![]() ,
,
Тогда,
если ½Tmах — N/2½ >½Tmin — N/2½,
воспользовавшись кандидатом для Tmax угадываем

если ½Т — N/2½ <½Тmin — N/2½,
воспользовавшись кандидатом для Тmin угадываем
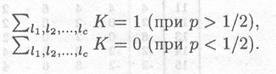
Рассмотрим линейные приближения для S-блоков. Задача заключается в исследовании вероятности того, что некоторый бит на входе S-блока равняется некоторому биту на выходе. Однако в более общем случае полезно рассмотреть зависимости сумм бит на некоторых выходных и выходных позициях.
Для заданного S-блока S,(а = 1,2,...,8) и чисел 1 £ а £ 63 и 1 £ b£ 15 определим NSa(a,b).— число выходных значений для 64 возможных значений на входе Sa, таких; что результат логической операции «И» суммы по модулю 2 некоторых бит значения на входе Sa и числа а равен результату логической операции «И» суммы по модулю 2 некоторых бит значения на выходе Sa, и числа b. Данное условие можно записать в виде:

Где Sa(x)t— t-й бит выходного значения Sa при заданном на входе значении х.
Если NSа(a,b) не равно 32, можно сделать вывод о корреляционной зависимости входных и выходных бит Sа. Например, уравнение И.4 показывает, что четвертый бит входных значений S5 равен сумме всех бит выходных значений с вероятностью 12/64 = 0, 19:
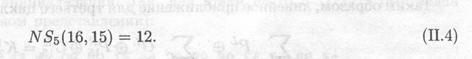
Следующее уравнение выполняется с вероятностью 0,19 для случайно выбранного Х и зафиксированного К (с учетом перестановки в Е- и Р-блоках):

В усеченной табл. II.19 представлены значения NS5(a,b) — 32 для всевозможных значений a (номер строки) и b (номер столбца). Исследование полной таблицы показывает, что (II.4) является наилучшим линейным приближением во всех S-блоках (то есть величина ½NS5(a,b)½ принимает максимальное значение). Следовательно, уравнение (II.4) является наилучшим линейным приближением для F-функции.
Из определения S-блоков вытекает, что

Рассмотрим криптоалгоритм DES с тремя циклами преобразования. Следующее уравнение выполняется для первого цикла с вероятностью 12/64:
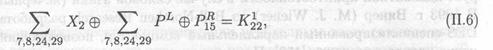
Где через РR и PL обозначены правая и левая половины открытого текста. Аналогичное уравнение выполняется для последнего третьего цикла преобразования:

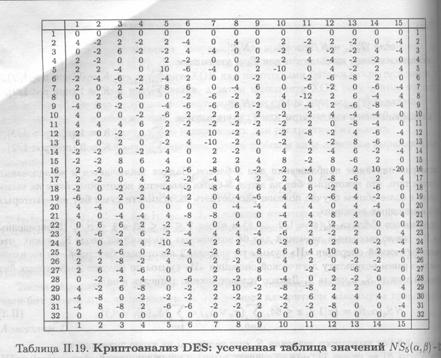
где через СR и СL обозначены правая и левая половины шифротекста.
Таким образом, линейное приближение для третьего цикла выглядит следующим образом:

Для случайно
выбранного открытого текста Р и соответствующего шифротекста C уравнение (II.8) выполняется с вероятностью (12/64)2
+ (1 — 12/64)2 = 0, 70. Поскольку уравнение (П.5) является наилучшим
линейным приближением F-функции, уравнение (II.8) является наилучшим
приближением для DES с тремя циклами. Теперь, воспользовавшись Алгоритмом 1,
можно решить уравнение (II.8) для того, чтобы получить значение К122
Å К![]()
Описанный метод можно обобщить на полный DES с шестнадцатью циклами криптографического преобразования.
4.6.4. Силовая атака на основе распределенных вычислений
В конце января 1997 г. компания RSA Data Security, Inc. анонсировала новый криптографический конкурс (табл. П.20). Цель конкурса — оценка криптостойкости федерального стандарта США DES [15] и симметричных криптосистем с переменной длиной ключа н8 криптоалгоритма RC5. Хорошо известно, что 56-битный ключ стандарта DES не гарантирует адекватной криптостойкости в случае силовой атаки (исчерпывающий перебор ключа). В 1993 г. Винер (М. J. Wiener) из Bell-Northen Research разработал для силовой атаки на DES специализированный параллельный компьютер, позволяющий раскрывать ключ в течение нескольких часов [158]. Попытки устранения основного недостатка DES, связанного с коротким ключом, привели к появлению различных DES-модификаций — метода DES-шифрования [138], метода DЕSХ, предложенного Ривестом (R. Rivest) [140], а также ряда альтернативных криптосистем, таких, как IDEA [164] и RC5 [162]. Известно также, что кроме криптостойкости существуют и другие факторы, оказывающие влияние на выбор

Длины ключа симметричной криптосистемы. Так, например, в соответствии с законодательством длина ключа для экспортируемых за пределы США и Канады криптографических приложений на основе симметричного криптоалгоритма ограничена 40 битами. Необходимость теоретических обоснований в данном случае отпадает, несостоятельность криптографии с 40-битным ключом убедительно продемонстрирована первыми результатами — криптосистема КС5-32/12/5 была «взломана» через 3,5 часа после объявления в Internet условий криптографического конкурса (см. табл. П.20). Параметры криптосистемы RC5 в табл. II.20 обозначаются как RC5-Х/Y/Z, где Х — разрядность блока в битах, Y — число циклов криптографического преобразования, Z — длина ключа в байтах (Z*8=разрядность в битах). Силовая атака сводится, по сути, к дешифрованию фиксированного шифротекста на различных на ключах при заданном векторе инициализации. Так, для атаки на RC5-32/12/5 был задан шифротекст
(в шестнадцатеричном представлении):

И вектор инициализации 8а 16 2f 69 е8 37 98.
Секретный ключ считается раскрытым, если результат дешифрования на текущем ключе приводит к содержательному тексту на английском языке. Условия конкурса, а также все необходимые исходные данные могут быть получены с Web-сервера компании RSA Data Secutky, Inc. по адресу http://www.rsa.com.
Отметим, что все результаты табл. II.20 в отличие от идеи Винера получены при помощи программной реализации криптоалгоритма и массированной параллельной атаки с привлечением десятков, а иногда и тысяч рабочих станций. Сеть Internet, пример практического приложения идеи распределенных вычислений, стала мощным инструментом силовой атаки в руках криптоаналитиков и хакеров. Силовая атака на основе распределенных вычислений имеет свою динамику, связанную с активностью сетевых пользователей. Проанализируем возможности распределенной силовой атаки на примере криптосистем RC5-З2/12/5 и RC/12/6 [137].
Для ранения ряда задач практической криптографии необходимы значительные вычислительные ресурсы. При этом некоторые из этих задач поддаются распараллеливанию. Таким образом, Internet, объединяющий многие тысячи рабочих станций, позволяет эффективно решать трудоемкие задачи путем координированной и одновременной работы большого числа компьютеров. Такой подход, реализующий возможности компьютерных сетей, известен названием метода распределенных вычислений. Одна из первых успешных попыток использования Internet для факторизации RSA-модуля из 129 десятичных разрядов предпринята в 1994 г. [147]. Объединенные усилия 600 человек и 1600 компьютеров, включая две факс-машины, координировались при помощи электронной почты. Недавняя факторизация RSA-модуля из 130 десятичных разрядов продемонстрировала исключительную эффективность решения, основанного на объединении метода распределенных вычислений, алгоритма обобщенного числового решета и координации работы компьютеров Web-технологии.
Проблема поиска ключа симметричной криптосистемы путем исчерпывающе, перебора относится к классу задач, допускающих распараллеливание. В настоящее время обладает достаточными ресурсами для успешной силовой атаки на DES (или любую другую криптосистему, сравнимую с DES по длине ключа) в течение нескольких недель. Таким образом, анализ потенциальных возможностей метода распределенных вычислений при криптографических задач интересен как для криптоаналитиков, так и для разработчиков криптографических приложений.
В 1992 г. Каронин (G. Caronni) и Алемсбергер (W. Alemsberger) разработали программное обеспечение для координации одновременной работы сетевых компьютеров «плохих» паролей локальных UNIX-серверов. Программа позволила решить поставленную задачу объединенными усилиями 350 рабочих станций. Объявленный в январе 1997 криптографический конкурс открыл новую область приложения для программного Каронни — Алемсбергер. В течение января программа была переработана под новую Программная реализация криптоалгоритма RC5, оптимизированная для компьютера Ultra 1/170, позволяла проверять миллион ключей криптосистемы RC5-32/12/5 за 6,15 с. За неделю до начала атаки организаторы разослали в ряд университетов США и Европы предложения об участии в проекте с просьбой привлечения всех заинтересованных лиц. За до начала атаки стало ясно, что объединенное общей целью сетевое сообщества, достаточным потенциалом для решения поставленной задачи. Запуск проекта с 18:07 по западноевропейскому времени (9:07 PST). Ошибки в работе программно обеспечения сервера, обнаруженные Шнайдером (С. Schneider) в 20:30, привели к перезапуску 40 серверов, участвовавших в проекте. Несмотря на сбои, задача была решена объединенными усилиями 800 компьютеров в Швейцарии, Германии, Норвегии и США. Секретный криптосистемы RC5-32/12/5 найден за 231 мин после проверки 51% всех ключей со средней производительностью 40 млн. ключей в секунду. Известно, что аналогичная атака, предпринятая ранее Голдбергом (I. Goldberg)
из Университета Беркли, успешно завершил перебора 31% ключей за 210 мин. Отметим, что с методологической точки зрения в организации атаки Каронни и Голдберга мало существенны. В проекте Голубе задействовано 259 компьютеров (287 процессоров):
• 97 UltraSPARC;
• 4 UltraSPARC (8 процессоров);
• 120 рабочих станций НР;
• 8 процессоров Pentium;
• 30 SPARCStation 20s.
Все ресурсы были полностью доступны к моменту запуска и оставались неизменными в период осуществления проекта. Средняя скорость проверки составляла 27 млн. ключей в секунду. Управление перебором ключей осуществлялось при помощи центрального cepвера получением очередной порции ключей для проверки клиент прогонял специальный оценивающий текущую производительность его компьютера, и сообщал результаты серверу.
Сервер, в свою очередь, передавал клиенту сегмент ключевого пространства, обеспечивающий 20-минутную загрузку с учетом текущей производительности компьютера После завершения проверки сегмента клиент извещал сервер о результатах, и цикл повторялся. При этом все проверенные, а также непроверенные и находящиеся в работе учитывались сервером при организации дальнейшей проверки.

Молниеносная «расправа» с криптосистемой RC5-32/12/5 стала безусловным стимулом для силовой атаки криптосистемы RC5-32/12/6 с 48-битным ключом (далее в тексте — проект RC5-32/12/6). Проект был запущен 29 января в 18:00 по западноевропейскому времени после переработки программного обеспечения и предварительного шестичасового тестирования. Существует два подхода к организации силовой атаки на основе метода распределенных вычислений. Первый — централизованное управление процессом поиска при помощи сервера. Второй — случайный и независимый выбор стартовой точки в ключевом пространстве каждым из участвующих в проекте компьютером и оповещение в случае раскрытия ключа. Первый подход более предпочтителен, но связан с определенными трудностями. Так, не исключена возможность перегрузки сервера потоком запросов со стороны клиентов. К тому же некоторые непреднамеренные действия клиентов могут привести к сбоям в работе центрального сервера. Не исключен также риск злонамеренного деструктивного воздействия. Для сведения к минимуму указанных рисков необходимы дополнительные меры. Известный метод обеспечения отказоустойчивости предполагает введение дополнительной избыточности. «серверов, а также принцип иерархии в проектировании структуры связей по устранить некоторые риски и ограничить последствия сбоев и отказов. Применение когда аутентификации гарантирует подлинность всех сообщений при передаче как от клиента к серверу, так и в обратном направлении. Ведение регистрационного журнала упрощает анализ и отслеживание последствий отказов.
Организаторы проекта намеренно предложили упрощенную схему взаимодействия по технологии «клиент-сервер» [137]. Для регистрации клиента и получения очередного задания от сервера использовался простейший протокол. Типичный протокол обмена между клиентом представлен на рис. П.23.
Запрос Регистрация включает номер версии, тип компьютера и другую необходимую для начала информацию. Запрос_ задания содержит сведения об объеме сегмента ключевого пространства и оценку времени перебора сегмента указанного объема. Клиент может от участия или приостановить выполнение задания. Факт отказа со стороны клиента устанавливается по нулевому объему сегмента в Запросе_ задания. Сервер подтверждает отказ клиента сообщением Сброс_ задания. В случае раскрытия ключа или возобновления работы клиент уведомляет сервер с помощью специально предусмотренных сообщений. Если сервер по каким-либо причинам завершает свою работу и вместо него включается новый, то в ответ на сообщение клиента Задание_ выполнено новый сервер отвечает сообщением Запрос_регистрации, чем инициирует регистрацию клиента на новом сервере. Для немедленной остановки работы клиентов предусмотрено сообщение Остановка. Сервер управляет сегментированием ключевого пространства, периодически записывая текущее состояние на диск, в целях оперативного восстановления программного обеспечения в случае перезагрузки операционной системы. Сервер динамически отслеживает время работы всех зарегистрированных у него клиентов. Если время перебора ключевого сегмента, клиентом в Запросе_ задания, истекает, сервер передает сегмент другому клиенту виртуальной сети. По завершении процедуры проверки текущего ключевого сегмента клиенту, по соответствующему запросу, передается новый сегмент.
Криптоалгоритм RC5 для программного обеспечения клиента был реализован на языке ассемблера для процессоров Intel и RS6000. Оптимизация на уровне компилятора языка С выполнялась для следующих операционных систем: AIX, FreeBSD, HPUX, IRIX, Linux, NEXTSXEP, NetBSD, OS2, OSF1, OpenBSD, SСО _SV, SunOS, ULTRIX, Windows (NT& 95),

AMIGA MacOS MIPS, Alpha, (Ultra) SPARC, 486/586 Intel, Pentium Pro, Paragons, ОС для компьютеров с параллельной архитектурой (до 16 000 процессоров).
Лавинообразное вовлечение участников в силовую атаку на криптосистему RC5-32/12/6 позволило задействовать значительные сетевые ресурсы. Отметим, что пиковая производительность тестирования ключей достигала 440 млн. ключей в секунду, а максимальное количество одновременно работающих компьютеров — 4500 единиц.
Рис. II.24 иллюстрирует закономерность роста производительности при проверке ключей. После медленного роста в течение первой недели производительность удвоилась за 2 дня - с 4 по 6 февраля. Следующее удвоение производительности произошло также через 2 дня - с 7 по 9 февраля.
Рост производительности в ходе силовой атаки на криптосистему RC5-32/12/6 сравним с производительностью атаки Гольдберга на криптосистему RC5-32/12/5 (27 млн. ключей в секунду), в которой было задействовано фиксированное число компьютеров.
На рис. II.25 представлена закономерность роста количества проверенных ключей в процентах от объема ключевого пространства.
Более подробную информацию о развитии проекта можно получить из различных сетевых источников. Например,
http://www.ee.ethz.ch/challenge/
http://www.klammeraffe.org/challenge/.
Рассматриваемая организация силовой атаки на основе метода распределенных вычислений порождает следующий вопрос. В состоянии ли один-единственный центральный сервер справиться с возрастающим потоком запросов, и в какой степени такой рост влияет на эффективность распределенных вычислений? Исходя из данных о пиковой нагрузке последних дней проекта можно предположить, что центральный сервер обслуживал 5000 клиентов каждые 30 мин. Это, в свою очередь, означает, что каждую секунду к серверу обращалось более двух клиентов. Производительность современных серверов позволяет легко справляться с подобной нагрузкой при интенсивности трафика порядка 300 байт в секунду. Так, сервер

проекта RC5-32/12/6, сконфигурированный на Sun Ultra 1/170, был загружен менее чем на 2%, при этом потребность в оперативной памяти составила менее 6 Мбайт. Таким образом, экспериментальные данные, полученные в ходе проекта, подтверждают, что один сервер без перегрузки может обслужить миллион клиентов. Отметим, что эффективность описанного подхода может быть невысокой из-за дополнительных задержек, возникающих в связи с низкой пропускной способностью каналов связи.
Оценим вычислительную производительность проекта. Поскольку для проверки одного ключа криптоалгоритму RC5 требуется порядка 2000 инструкций, то для нахождения методом силовой атаки понадобится 3.24 ´ 1017 инструкций. Так как принятая единица измерения вычислительной производительности в один миллион инструкций в секунду (MIPS/Year, MY) оценивается как 3.15 ´ 1013 инструкций, суммарная производительность составила 104 MY в течение 10 календарных дней. Это свидетельствует о росте вычислительной производительности Internet. Для сравнения: вычислительная производительности при факторизации 129-разрядного RSA-модуля в 1994 г. составила 5 ´ 103 MY за девять календарных месяцев.
По результатам проекта RC5-32/12/5 и RC5-32/12/6 в статье ]137] представлен прогноз будущего силовой атаки на основе распределенных вычислений. В первую очередь отметим, производительность проверки ключей, достигнутая в последние дни проекта RC5-32/12/6 (330 млн. ключей в с.), недостаточна для эффективной силовой атаки на криптосистему RC-332/12/7. Учитывая производительность проекта RC5-32/12/6, для силовой атаки криптосистемы RC5-32/12/7 по оценкам [137] потребуется около 255/330 ´ 220 секунду — приблизительно три с половиной года непрерывной работы. Однако экспериментальные данные (рис.II.24) свидетельствуют об удваивании производительности каждые три дня. Таким образом, ожидаемая производительность при сохранении тенденции может возрасти на порядок по сравнению с пиковой производительностью проекта RC5-32/12/6. В этом случае для осуществления атаки понадобится не более полугода.
При одинаковой длине ключа криптоалгоритм DES позволяет проверять ключи в 2 — 4 раза быстрее (в зависимости от реализации), чем RC5-32/12/7. Производительность некоторых программных реализаций составляет 500 тысяч ключей в секунду на процессоре Pentium 120. С учетом изложенных выше тенденций для поиска ключа DES методом исчерпывающего перебора понадобится не более нескольких месяцев. Отметим, что прогноз, представленный в статье [137], подтвердился недавно опубликованными результатами (см. табл. II.20).
Результаты распределенной силовой атаки на криптосистемы RC5-32/12/5 и RC3 32/12/6 продемонстрировали слабость 40- и 48-битных ключей. Известно, что в хо де обсуждения экспортного законодательства США было предложено ограничить длину ключа в экспортируемых криптографических приложениях 56 битами (см. http://www.bxa.doc.gov/encstart.htm). Однако, учитывая рост производительности компьютеров (удваивается каждые 18 месяцев по закону Мура) и динамику развития Internet, можно предположить, что 56-битный ключ также не гарантирует адекватной криптостойкости. По оценкам ведущих криптографов и специалистов по компьютерным технологиям, минимальная длина ключа симметричной криптосистемы, гарантирующая криптостойкость по отношению к силовой атаке, должна колебаться от 75 до 90 бит (см. отчет http://www.bsa.org/policy/encryption) Многие специалисты с консервативными взглядами придерживаются мнения, что длина ключа должна быть не менее 128 бит.
4.7. Другие известные блочные шифры
Криптоалгоритм RC2 представляет собой блочный шифр с ключом переменной длины Разработан Ривестом по заказу компании RSA Data Security, Inc. Аббревиатура «ВС» означает «код Рональда» (Ron's Code), или «шифр Ривеста» (Rivest's Cipher). Криптоалгоритм разрабатывался как альтернатива криптостандарта DES. RC2 работает с блоками по 64 бита, программная реализация криптоалгоритма приблизительно в два-три раза быстрее, чем DES. Переменная длина ключа позволяет добиваться адекватной криптостойкости с учетом том возможностей силовой атаки. Криптоалгоритм RC2 позволяет выполнять шифрование в различных режимах — ЕСВ, СВС, CFB. Правительство США не запрещает экспортировать аппаратные и программные реализации криптоалгоритмов RC2 и RC4 — при соблюдении ограничения на длину ключа (40 бит). Американские компании за пределами США и Канады могут использовать криптоалгоритмы с длиной ключа 65 бит. При шифрования по криптоалгоритму RC2 к секретному ключу методом конкатенации добавляется некоторый вспомогательный ключ от 40 до 88 бит. Для выполнения дешифрования вспомогательный ключ передается получателю зашифрованного сообщения в открытом виде.
Криптоалгоритм RC5 также разработан Ривестом по заказу компании RSA Data Security, Inc. Это блочный шифр с переменной длиной блока (32, 64 и 128 бит), ключа и числом циклов криптографического преобразования (от 0 до 255). Длина ключа варьируется от 0 до 2048 бит. Возможность параметризации позволяет гибко настраивать криптоалгоритм с учетом конкретных требований по криптостойкости и эффективности реализации. Криптоалгоритм RC5 состоит из трех основных процедур: расширения ключа, шифрования и дешифрования. В процедуре расширения ключа заданный секретный ключ подвергается специальному преобразованию с целью заполнения ключевой таблицы, причем размер таблицы зависит от числа циклов криптографического преобразования. Ключевая таблица используется затем для шифрования и дешифрования. Процедура шифрования состоит из трех основных операций: целочисленного суммирования, суммирования по модулю 2 (операция XOR) и циклического сдвига. Безусловное преимущество криптоалгоритма заключается в простоте реализации. Непредсказуемость результата операции циклического сдвига, зависящей от конкретных входных данных при шифровании, обеспечивает необходимый уровень криптостойкости. Исследования криптостойкости RC5 показали [163], что вариант криптоалгоритма с разрядностью блока 64 бита и двенадцатью (и более) циклами преобразования гарантирует адекватную криптостойкость по отношению к дифференциальному и линейному криптоанализу.
4.7.3 IDEA
Криптоалгоритм IDEA (International Data Encryption Algorithm) [164] представляет собой ого итеративного блочного шифра со 128-битным ключом и восемью циклами криптографического преобразования. IDEA не соответствует схеме Фейстеля, однако процедура дешифрования выполняется аналогично процедуре шифрования. Структура криптоалгоритма допускает простую программную и аппаратную реализацию. Секретность обеспечивается за счет трех различных типов арифметических операций над 16-битными словами. Эффективность программной реализации IDEA не уступает DES. Специфическая особенность IDEA — сравнительная простота анализа криптостойкости алгоритма по отношению к дифференциальному криптоанализу. Результаты успешного линейного также не известны. Исследования криптостойкости IDEA опубликованы в [165].В ходе исследования было установлено, что существует подмножество из 251 слабых ключей, которые могут быть раскрыты путем анализа процедуры шифрования на ключе из данного подмножества. Результат, однако, не оказывает существенного практическую криптостойкость, так как мощность подмножества «слабых» ключей мала по сравнению с мощностью всего ключевого пространства (2 128 различных ключей.)
Криптоалгоритм SAFER (Secure And Fast Encryption Routine) представляет собой блочный шифр, разработанный по заказу корпорации Cylink [166]. Длина секретного ключа в одной из версий 64 бита. Криптоалгоритм ориентирован на байтовую обработку блоков по 64 бита. Имеет переменное число циклов криптографического преобразования (до 10, 6). В отличие от большинства блочных шифров имеет различные процедуры и дешифрования. Первая версия SAFER с длиной ключа 64 бита известна под названием SAFER К-64. Вторая версия — ВАРЕВ К-128 имеет 128-битный ключ. Результаты криптоанализа [166] продемонстрировали криптостойкость SAFER К-64 по отношению к дифференциальному и линейному криптоанализу при соблюдении одного условия — число циклов преобразования должно быть больше шести. В результате исследования [167] было обнаружено слабое место в процедуре преобразования ключа. В новых модификациях SAFER SK-64 и SAFER SK-128 обнаруженный недостаток устранен. Модификация SAFER SК-40ййвт 40-битный ключ и пять циклов преобразования и требует большего объема вычислений при дифференциальном и линейном криптоанализе по сравнению с силовой атакой (всче1вййающим перебором на множестве ключей).
4.7.5. FEAL
Криптоалгоритм FEAL был разработан как альтернатива DES [168]. Оригинальный криптоалгоритм (FEAL-4) был рассчитан на программную реализацию и имел четыре цикла преобразования при обработке 64-битного блока и 64-битный секретный ключ. Криптоаналитические исследования продемонстрировали слабость криптоалгоритма — для раскрытия ключа при атаке на основе выборочного открытого текста достаточно 20 образцов [169]. Успехи в криптоанализе FEAL-8 (восемь циклов преобразования) привели к появлению модификации с переменным числом циклов преобразования FEAL-N. Опубликованы результаты успешного дифференциального криптоанализа FEAL-N при N ≤ 31. Для раскрытия секретного ключа FEAL-8 методом линейного криптоанализа достаточно 225 различных открытых текстов [172] и[171]
Криптоалгоритм Skipjack разработан Агентством национальной безопасности США и является неотъемлемой частью микросхемы Clipper. Рассчитан на обработку 64-битных входных блоков данных (32 цикла преобразования на каждый блок) и имеет 80-битный ключ. По-видимому, криптоалгоритм имеет высокую криптостойкость — для сравнения: DES имеет 56-битный ключ и 16 циклов преобразования на блок. Однако детали криптоалгоритма засекречены. Таким образом, открытые Криптоаналитические исследования Skipjack невозможны. По заказу правительства США независимая группа экспертов провела ограниченна исследование криптостойкости Skipjack и опубликовала результаты в отчете [57]. Программная реализация Skipjack невозможна по причине его секретности.
Криптоалгоритм Blowfish [173] — вариант шифра Фейстеля — рассчитан на обработку 64. битных входных блоков. Каждый цикл криптографического преобразования состоит из серии перестановок (зависят от ключа) и подстановок (зависят от ключа и входных данных). Процедура криптографического преобразования построена на операциях суммирования 32-разрядных чисел и суммирования по модулю 2 (операция XOR). Ключ имеет переменную длину (максимум 448 бит) и используется для построения нескольких вспомогательных ключевых таблиц. Криптоалгоритм разработан специально для 32-битных компьютеров. Пo эффективности программная реализация Blowfish значительно превосходит аналогичную реализацию DES. Известен ряд успешных атак на Blowfish с тремя циклами преобразовании. Исследования криптостойкости алгоритма продолжаются.
Feistel
Криптоалгоритм REDOC разработан для компании Cryptech, 1пс. [174,175]. В нем используются 20-байтовый (160-битный) ключ и 80-битный блок (по 10 циклов криптографического преобразования на каждый блок). REDOC ориентирован на байтовые операции и эффективен при программной реализации. REDOC использует меняющиеся табличные функции, В отличие от DES, имеющего фиксированный набор таблиц подстановок и перестановок, REDOC II использует зависимые от ключа и открытого текста наборы таблиц. Особенность криптоалгоритма — использование специальных масок — чисел полученных из ключей и необходимых для выбора табличных функций. С точки зрения силовой атаки REDOC очень надежен: для раскрытия ключа требуется 2160 попыток дешифрования. Используя дифференциальный криптоанализ, Бихам и Шамир достигли успеха в криптоанализе одного цикли криптографического преобразования REDOC с помощью 2300 выбранных открытых текстов [176]. Другая успешная попытка криптоанализа одного цикла преобразования описана в [175]. Попытки криптоанализа двух и более циклов преобразования закончились неудачей.
Криптоалгоритм LOKI был представлен в 1990 г. в качестве возможной альтернативы, DES [177]. В нем используются 64-битовый блок и 64-битовый ключ. Общая схема алгоритма описана в [178, 179] и [180]. По сравнению с силовой атакой метод дифференциального криптоанализа позволяет эффективнее раскрывать ключи LOKI с 11 циклами криптографического преобразования [176]. Криптоалгоритм обладает свойством комплементарности, что уменьшает трудоемкость силовой атаки в 256 раз [176,181, 182]. В исследовании [183, 184] показано, что LOKI с 14 и менее циклами чувствителен к дифференциальному криптоанализу.
Криптоалгоритм Khufu разработан Р. Мерклем (R. Merkl) и представляет собой 64-битный шифр с 512-битным ключом и переменным числом циклов криптографического преобразования. Автор криптоалгоритма отметил, что Khufu с 8 циклами менее криптостоек при атаке на основе выборочного открытого текста, чем вариант с 16, 24 или 32 циклами [192]. Известно, что Khufu устойчив к атаке методом дифференциального криптоанализа. Известен результат успешной атаки на Khufu с 16 циклами. Для осуществления атаки понадобилось 231. образцов выборочного открытого текста [193]. Результат, однако, не удалось распространить на большее число циклов преобразования. Силовая атака на Khufu безнадежна: 2512 попыток дешифрования — такой объем перебора не реализуем ни при каких условиях.
Khafre — еще один криптоалгоритм, предложенный Мерклем [192]. Khufu (Хуфу) и Khafre (Хафр) — имена египетских фараонов.) По конструкции этот алгоритм похож на Khufu. При реализации Khafre менее эффективен, чем Khufu, за счет использования 64- или 128-битных ключей и большего числа циклов преобразования. Атака на основе метода дифференциального криптоанализа позволила раскрыть ключ Khafre с 16 циклами после часа работы на персональном компьютере [176].
Прочные шифры преобразуют открытый текст в шифротекст по одному биту за операцию.
Генератор потока ключей (иногда называемый генератором с бегущим ключом) выдает поток 6итов: k1, k2, k3,..., ki,. Этот поток битов (иногда называемый бегущим ключом) и поток битов открытого текста, p1,р2,р3,...,рi, подвергаются операции ХОВ (сумма по модулю 2, исключающее ИЛИ»), и в результате получается поток битов шифротекста:

При дешифровании, для восстановления битов открытого текста, операция XOR выполняется над битами шифротекста и тем же самым потоком ключей:
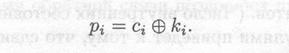
Отметим, что рi Θ сi= ki,. Безопасность системы полностью зависит от свойств генератора потока ключей. Если генератор потока ключей выдает бесконечную строку нулей, шифротекст будет совпадать с открытым текстом и преобразование будет бессмысленным. Если тор потока ключей выдает повторяющийся 16-битовый шаблон, криптостойкость будет пренебрежимо мала. В случае бесконечного потока случайных битов криптостойкость поточного шифра будет эквивалентна криптостойкости одноразового блокнота. Генератор потока ключей создает битовый поток, который похож на случайный, но в действительности детерминирован и может быть безошибочно воспроизведен при дешифровании. Чем ближе выход генератора потока ключей к случайному, тем выше трудоемкость криптоаналитической атаки.
Блочные и поточные шифры реализуются по-разному. Поточные шифры, дешифрующие данные по одному биту, не очень подходят для программных реализаций. Блочные шифры легче реализовывать программно, так как они позволяют избежать трудоемких манипуляций с битами и оперируют удобными для компьютера блоками данных. С другой стороны, поточные шифры больше подходят для аппаратной реализации.
5.1. Регистры сдвига с обратной связью
Большинство реальных поточных шифров основано на регистрах сдвига с обратной связью.
Регистр сдвига применяют для генерации ключевой последовательности. Регистр сдвига с обратной связью состоит из двух частей: регистра сдвига и функции обратной связи рис. П.26). Регистр сдвига представляет собой последовательность битов. (Количество битов определяется длиной сдвигового регистра. Если длина равна и битам, то регистр называется п-битовым регистром сдвига.) Всякий раз, когда нужно извлечь бит, все биты регистра сдвига сдвигаются вправо на 1 позицию. Новый крайний левый бит является функцией всех остальных битов регистра.
На выходе регистра оказывается один, обычно младший значащий бит. Периодом регистра называется длина получаемой последовательности до начала ее повторения.
Простейшим видом регистра сдвига с обратной связью является регистр "!"!" Г сдвига с линейной обратной связью (РСЛОС) (рис. П.27).
Обратная связь представляет собой XOR некоторых битов регистра; эти биты называются отводной последовательностью.

На рис. П.28 показан 4-битовый
РСЛОС с отводом от первого и четвертого битов. Если его проинициализировать значением 1111, то до повторения регистр будет принимать следующие внутренние состояния:
1111 0111 1011 0101 1010 1101 0110 0011 1001 0100 0010 0001 1000 1100 1110
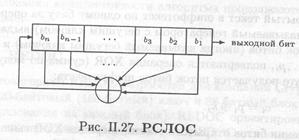
Выходной последовательностью будет строка младших значащих битов:
111101011001000 ...
РСЛОС (n-битовый) может находиться в одном из 2n— 1 внутренних состояний. Это означает, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом 2n — 1 битов. (Число внутренних состояний и период равны 2n — 1, потому что заполнение РСЛОС нулями приведет к тому, что сдвиговый регистр будет выдавать бесконечную последовательность нулей, что абсолютно бесполезно.) Только при определенных отводных последовательностях РСЛОС циклически пройдет через все 2n — 1 внутренних состояний. Такие РСЛОС имеют максимальный период. Получившийся результат называется М-последовательностью. Для того чтобы конкретный РСЛОС имел максимальный период,
многочлен, ассоциированный с отводной последовательностью, должен быть примитивным по модулю 2 — то есть не раскладываться на произведение двоичных многочленов меньшей степени. Соответствующую математическую теорию можно найти в [86].

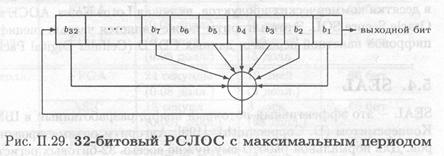
Например, многочлен х32 + х7 + х5 + х3 + х2+х+1 примитивен по модулю 2. Рассмотрим этот многочлен в терминах РСЛОС с максимальным периодом. Степень многочлена задает длину РСЛОС. Свободный член многочлена всегда равен 1, и его можно опустить. Степени формальной переменной многочлена, задает длину РСЛОС исключением 0-й, задают отводную последовательность, отсчитываемую от левого края сдвигового регистра. То есть члены многочлена с меньшей степенью соответствуют позициям, расположенным ближе к правому краю регистра. Тогда для взятого 32-битового сдвигового регистра новый бит генерируется с помощью XOR тридцать второго, седьмого, пятого, третьего, второго и первого битов (рис. П.29); получающийся РСЛОС будет иметь максимальную длину, циклически проходя до повторения через 232 — 1 различных значений.
Сами по себе РСЛОС являются хорошими генераторами псевдослучайных последовательностей, но они обладают некоторыми нежелательными неслучайными свойствами. Для РСЛОС длины n внутреннее состояние представляет собой предыдущие n выходных битов генератора.. Даже если схема обратной связи хранится в секрете, она может быть определена по 2n выходным битам генератора с помощью алгоритма Берлекэмпа — Мэсси [87).
Кроме того, большие случайные числа генерируемые с использованием идущих подряд бит этой последовательности, сильно коррелированны и для некоторых типов приложений вовсе не являются случайными. Несмотря на это, РСЛОС часто используются при разработке алгоритмов шифрования.
А5-это поточный шифр, используемый для шифрования GSM (Group Special Mobile),— европейского стандарта для цифровых сотовых мобильных телефонов. А5 состоит из трех РСЛОС длиной 19, 22 и 23. Выходом является XOR трех РСЛОС. В А5 используется изменяемое управление тактированием. Каждый регистр тактируется в зависимости от своего бита, затем выполняется XOR с обратной пороговой функцией средних битов всех трех регистров. Обычно на каждом этапе тактируется два РСЛОС. Существует тривиальная атака на открытом тексте, основанная на предположении о содержании первых двух РСЛОС и попытке определения третьего РСЛОС по ключевой последовательности. Тем не идеи, лежащие в основе А5, позволяют проектировать надежные поточные шифры. Алгоритм эффективен и удовлетворяет всем известным статистическим тестам, единственная его, слабость — короткие регистры. Варианты А5 с более длинными сдвиговыми регистрами и более плотными многочленами обратной связи позволяют противостоять силовой атаке.
RC4-это поточный шифр с переменным размером ключа, разработанный в 1987 г. Ривестом ) для RSA Data Security, Inc. Алгоритм работает в режиме OFB: поток ключей не
от открытого текста. Используется S-блок размером 8 × 8: S0, S1,..., S255. Элементы собой перестановку чисел от 0 до 255, а перестановка является функцией ключа переменной длины. В алгоритме применяются два счетчика, i и j, с нулевыми начальными и. Для генерации случайного байта выполняются следующие вычисления:

К используется в операции ХОВ с открытым текстом для получения шифротекста или в XOR с шифротекстом для получения открытого текста. Шифрование выполняется
примерно в 10 раз быстрее, чем в DES. 'Также несложна и инициализация S-блока. Сначала S-блок заполняется по правилу: S0 =0,S1 = 1,...,S255 =255. После этого ключ записывается в массив: К0, К1,..., К255. Затем при начальном значении j = 0 в цикле выполняются афф6щие вычисления:

Компания RSA Data Security, Inc. утверждает, что алгоритм устойчив к дифференциальному и линейному криптоанализу и что он в высокой степени нелинеен. S-блок медленно изменяется при использовании: i и j обеспечивают случайное изменение каждого элемента. Ш.4 входит в десятки коммерческих продуктов, включая Lotus Notes, АОСЕ компании Apple Computer и Oracle Secure SQL Этот алгоритм также является частью спецификации стандарта Сотовой цифровой пакетной передачи данных CDPD (Cellular Digital Packet Data) [198].
SEAL — это эффективный поточный шифр, разработанный в IBM Рогэвэем (P. Rogaway) и Копперсмитом (D. Coppersmith) [199]. Алгоритм оптимизирован для 32-битовых процессоров. Для нормальной работы ему нужно восемь 32-битовых регистров и память на несколько I килобайтов. В SEAL предусмотрен ряд предварительных действий с ключом с сохранением результатов в нескольких таблицах. Таблицы используются для ускорения процедур шифрования и дешифрования. Особенностью SEAL является то, что он в действительности является не традиционным поточным шифром, а представляет собой семейство псевдослучайных функций. При 160-битовом ключе k и 32-битовом регистре n SEAL растягивает и в L-битовую строку k(n). L может принимать любое значение, меньшее 64 Кбайт. SEAL использует следующее правило: если k выбирается случайным образом, то k(n) должно быть неотличимо от случайной L-битовой функции n. Практический эффект того, что SEAL является семейством псевдослучайных функций, состоит в том, что он удобен в ряде приложений, где неприменимы традиционные поточные шифры. При использовании большинства поточных шифров создается однонаправленная последовательность бит: единственным способом определить i-й бит (зная ключ и позицию i) является генерирование всех битов вплоть до i-гo. Отличие семейства псевдослучайных функций состоит в том, что можно легко получить доступ к любой позиции ключевой последовательности. Например, для шифрования жесткого диска, состоящего из множества 512-байтовых секторов, можно воспользоваться семейством псевдослучайных функций, подобных SEAL, и выполнить XOR каждого сектора с k(n). Это то же самое, как если бы была выполнена операция XOR всего диска с длинной псевдослучайной функцией, причем любая часть этой длинной последовательности бит может быть вычислена независимо. Семейство псевдослучайных функций также упрощает проблему синхронизации, встречающуюся в стандартных поточных шифрах, — можно зашифровать на ключи k n-e передаваемое сообщение, хn выполнив XOR xn и k(n). Получателю не нужно хранить состояние шифра для восстановления хn, ему не приходится беспокоиться и о потерянных сообщениях, влияющих на процесс дешифрования.
Оценим минимальную длину ключа симметричной криптосистемы, позволяющего противостоять силовой атаке. Минимальная длина ключа, установленная экспортным ограничением правительства США, составляет 40 бит. Мощность ключевого пространства для 40-битного ключа составляет 240. В среднем объем перебора при силовой атаке (перебор ключей при наличии пары «открытый текст/шифротекст) равен половине мощности пространства и со ставляет 239. Используя свободное время рабочих станций локальной сети, можно раскрыть 40-битный ключ в течение нескольких дней. Эффективность силовой атаки может быть повышена за счет применения технологии FPGA (Fild Programmable Gate Array). Технология FPGA позволяет создавать программируемые (перестраиваемые) аппаратные реализации и широко используется при разработке спецвычислителей и проектировании СВИС. Так, при стоимости 200 долл. АТ&Т ОRСА-чип способен выполнить 30 млн. DES-дешифрований в секунду. Это в тысячу раз быстрее стандартного PC — за одну десятую его стоимости. FPGA-~ чипы выпускаются в виде PCMCIA-карт и могут подсоединяться к персональному компьютеру. Часто широко распространенные криптографические алгоритмы, такие, как, например,, DES, реализуются в виде специализированных интегральных схем ASIC (Application-Specific Integrated Circuits).
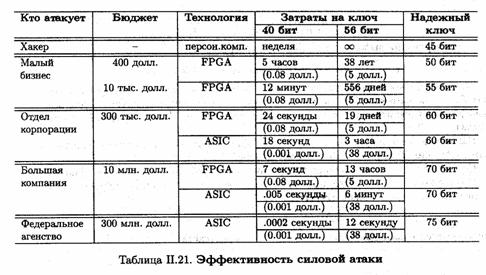
При более высоких начальных инвестициях и низкой конечной стоимости позволяют получить еще больший эффект по сравнению с FPGA. Так, ASIC чип стоимостью
10 долл. способен выполнить 200 млн. DES-дешифрований в секунду. Это в семь технологии FPGA — за одну двадцатую ее стоимости.
Таким образом, применение FPGA-чипа на PCMCIA-карте (стоимостью 400 долл.) позволяет раскрыть 40-битный ключ в среднем за 5 часов. При использовании чипа для силовой атаки в течение трех лет средняя стоимость в расчете на один ключ будет составлять восемь центов.
Подробно длина ключа симметричной криптосистемы, обеспечивающая адекватную коммерческую безопасность, обсуждается в [52]. Результат исследования представлен в табв.П.21.
7. Метод расширения ключевого пространства
Как было показано, размер ключа, а следовательно, и объем ключевого пространства может быть ограничен по ряду объективных причин, например вследствие экспортной политики государства. При определенных инвестициях такой ключ легко раскрывается методом силовой атаки. Возникает вопрос: существует ли способ противодействия силовой атаке при заданном коротком ключе?
Ривест (R. Rivest) из компании RSA Data Security, Inc. исследовал эту проблему и предложил универсальный, не зависящий от используемого шифра метод расширения ключевого пространства [402[.
7.1. Принцип несепарабельного шифрования
Основная проблема большинства известных режимов шифрования блочных шифров заключается, в том, что для раскрытия одного блока открытого текста достаточно дешифровать один блок шифротекста. Рассмотрим режим СВС. Обозначим 8 блоков открытого текста m1 ,m2,:.,ms,. Для шифрования необходим инициализирующий вектор IV и ключ К. Режим СВС продуцирует блоки шифротекста сi, 1 ≤ I ≤ s + 1, где
C1= IV
![]()
. При дешифровании выполняется обратное преобразование
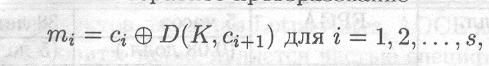
и любой из 8 блоков открытого текста может быть получен путем дешифрования только одного блока шифротекста. Это свойство облегчает задачу криптоаналитика — для реализации силовой атаки достаточно одного блока шифротекста (и соответствующего блока открытого текста).
Назовем режим шифрования блочного шифра сепарабельным, если он обладает указанным свойством. Так, режим СВС является сепарабельным.
Сформулируем общий принцип построения несепарабельного режима шифрования. Предположим, что в результате применения некоторого режима шифрования исходная последовательность s блоков открытого текста

преобразуется в последовательность t блоков шифротекста
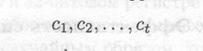
для некоторого t ≥ а Назовем режим шифрования строго несепарабельным, если для получения одного блока открытого текста т, необходимо дешифровать все t блоков шифротекста.
7.2. Метод построения несепарабельного режима шифрования
Ривест предложил следующий метод построения несепарабельного режима шифрования [402|:
— при помощи специального AoN-преобразования (All-or-Nothing, AoN) отобразить последовательность блоков открытого текста т1,|, m2,..., m8, в последовательность псевдоблоков т1, т2,..., т8+1 и затем
— получить последовательность блоков шифротекста с1, с2,..., сt, зашифровав псевдоблоки в режиме ЕСВ на секретном ключе К.
AoN-преобразование должно обладать некоторыми специальными свойствами. Преобразование f, отображающее последовательность блоков т1, m2,..., m8, в последовательность псевдоблоков т1 ,т2~,...,т8, называется AoN-преобразованием, если
- преобразование f обратимо: по заданной последовательности псевдоблоков можно восстановить исходную последовательность блоков открытого текста;
- вычислительная трудоемкость прямого и обратного преобразований (при наличии всех псевдоблоков) не должна быть экспоненциальной;
- вычислительная трудоемкость процедуры получения блока открытого текста, при условии отсутствия хотя бы одного из псевдоблоков, должна быть экспоненциальной.
Отметим, что AoN-преобразование также должно обладать свойством рандомизации. Это свойство необходимо для предотвращения атаки на основе выборочного или известного открытого текста.
Само по себе AoN- преобразование не является криптографическим, так как не использует никакой секретной информации. Шифрованию подвергаются псевдоблоки, полученные в результате применения AoN-преобразования. Кроме того, AoN-преобразование не является секретным — любой может им воспользоваться для получения последовательности псевдоблоков, или наоборот — исходной последовательности блоков открытого текста.
Описанный метод шифрования является строго несепарабельным, так как для получения всех псевдоблоков необходимо дешифровать все блоки шифротекста, и, следовательно, все блоки шифротекста должны быть дешифрованы для получения всех блоков открытого текста.
7.3.Схема шифрования с AoN-преобразованием
В статье[402] Ривест предложил конкретный вариант схемы несепарабельного шифрования. Схема обладает высокой вычислительной эффективностью: по сравнению с обычным режимом шифрования применение AoN-преобразования увеличивает задержку не более чем в три раза. Кроме того, схема допускает распараллеливание вычислений. Трудоемкость силовой атаки при этом возрастает в t раз, где t — число блоков шифротекста.
Рассмотрим пример, в котором схема используется для шифрования восьмимегабайтного сообщения в СВС-режиме на 40-битном ключе. Криптоаналитик противника перехватывает шифротекст и пытается раскрыть секретный ключ методом силовой атаки. Предполагается также, что криптоаналитик знает один или несколько блоков открытого текста соответствующих перехваченному шифротексту. Очевидно, что в случае применения AoN-преобразования для получения нужных блоков открытого текста криптоаналитик вынужден дешифровать весь шифротекст. Таким образом, проверка каждого 40-битного ключапретендена требует дешифрования всего шифротекста. Следовательно, по сравнению с обычным режимом СВС трудоемкость атаки возрастает в миллион раз (при 64-битном), что эквивалентно применению 60-битного ключа вместо 40-битного(106 = 220, = 260 =240 ×220). Для получения сообщения нужной длины можно искусственно дополнить текст псевдослучайным «мусором».
Блочный шифр, лежащий в основе AoN-преобразования схемы Ривеста, не обеспечивает и, так как его ключ легко определяется из последовательности псевдоблоков. шифр необязательно должен совпадать с внешним блочным шифром, обеспечивающим шифрование последовательности псевдоблоков. Основное требование заключается что размер несекретного ключа AoN-преобразования должен превышать размер ключа для внешнего шифрования. Так, при использовании блочного шифра с переменной длиной ключа, например RC5, можно установить 128-битный размер блока для AoN-преобразования и внешнего шифрования и различные ключи — 128-битный несекретный и 40-битный секретный для внешнего шифрования.
Рассмотрим схему Ривеста. Для простоты предположим, что секретный и несекретный имеют одинаковый размер. Предположим также, что длина несекретного ключа исключает возможность применения силовой атаки. Кроме случайного несекретного ключа в Ривеста используется фиксированный несекретный ключ Ко. Схема включает следу действия:
●имеется набор блоков открытого текста т1, т2,..., ms;
● для использования в AoN-преобразовании генерируется случайный ключ К',
●последовательность псевдоблоков т1 ,т2,...,тs, вычисляется при помощи преобразования;
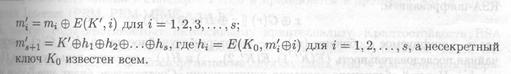
Ключевое пространство, которому принадлежит К', должно быть достаточно большим , К' может быть 128-битным ключом RC5).
Приведенная выше схема похожа на шифрование в режиме ЕСВ, за тем исключением, что ключ преобразования не фиксирован, а для каждого нового сообщения генерируется заново. Кроме того последний псевдоблок представляет собой сумму по модулю 2 (операция XOR) одноразового ключа и значений хэш-функции всех предыдущих псевдоблоков.
Значение i-й хэш-функции есть результат шифрования суммы по модулю 2 i-го псевдоблока с его номером i на некотором фиксированном несекретном ключе. Такое преобразование гарантирует, что любая модификация шифротекста со стороны злоумышленника, например перестановка или реплицирование блоков, эквивалентна замене ключа К'. Помимо ЕСВ в преобразовании может использоваться любой другой известный режим шифрования.
Легко показать, что описанное преобразование обратимо. Действительно:
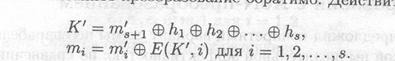
Отметим, что, если хотя бы один псевдоблок не известен, ключ К' получить невозможно и, следовательно, невозможно раскрыть исходный открытый текст.
7.4. Обсуждение метода
Некоторые методы обеспечения криптостойкости при ограниченном размере ключа изложены в [403] и [173]. AoN-преобразование лишено подобных недостатков подобных методов, s которых смена ключа приводит к значительной задержке, связанной с его предварительной обработкой.
Отметим, что описанное AoN-преобразование возможно только для сообщений конечной длины с заданной последовательностью блоков открытого текста, тогда как другие режимы шифрования, например СВС, позволяют шифровать неограниченные последовательности блоков открытого текста по мере их поступления на вход шифратора. AoN-преобразование и | внешнее шифрование могут выполняться поблочно — каждый новый полученный псевдоблок: может быть немедленно зашифрован, однако для дешифрования необходимо иметь полный I шифротекст, так как для получения ключа К' нужно дешифровать последний блок. При использовании режима ЕСВ в AoN-преобразование и для внешнего шифрования возможно эффективное распараллеливание вычислений. При достаточном количестве модулей шифрования сообщение длины s может быть зашифровано (или дешифровано) за время О(log s). I Очевидно, что криптоаналитик также может реализовать параллельную схему и эффективно дешифровать блоки шифротекста. Если предположить, что все передаваемые сообщении имеют фиксированную длину и криптоаналитик противника разработал специализированный параллельный компьютер для реализации силовой атаки, то стоимость такого проекта будет значительно превосходить стоимость аналогичного проекта при шифровании сообщений без предварительного AoN-преобразования. Расширение ключевого пространства всегда приводит либо к увеличению ресурса времени (при фиксированной стоимости аппаратуры), необходимого для реализации атаки, либо к возрастанию стоимости аппаратуры.
Радиомизирующие свойства AoN-преобразования сами по себе полезны, так как обеспечивают дополнительную криптостойкость по отношению к ряду атак на основе выборочного открытого текста (дифференциальный и линейный криптоанализ). Использование AoN-преобразования в схеме RSA-шифрования также позволяет поднять уровень криптостойкости [404].
AoN-преобразование можно рассматривать как специальный случай схемы «набивки», предложенной Беллэром (М. Веllаге) и Рогавеем (Р. Rogaway) [405] и выполняемой перед RSA-шифрованием:
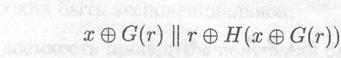
где х — шифруемое сообщение (т), r — некоторое случайное число (К'), G(r) — псевдослучайная последовательность (E(K 1), E(K 2),...) и Н(.) — значение хэш-функции (h1 Θ h2 Θ ...,hs). Через││ обозначена операция конкатенации. Соответствие будет еще более полным, если модифицировать AoN-преобразование следующим образом:

Существует много различных подходов к разработке AoN-преобразований. Можно, например, случайным образом выбрать хэш-функцию h из некоторого семейства функций и воспользоваться ею для продуцирования последовательности псевдоблоков. Еще один способ основан на использовании преобразования Фурье [406]. AoN-преобразование можно построить на основе схемы разделения секрета. Если воспользоваться пороговой схемой s- из-s, то при дешифровании менее а блоков невозможно получить никакой информации о блоках открытого текста. [407].
Другой подход был предложен Андерсоном (R. Anderson) и Бихамом (Е. Biham), разработавшими блочные шифры с переменной длиной блока (BEAR и LION), обладающие свойствами AoN-преобразования [408].
Отметим что схема шифрования с AoN-преобразованием приводит к размножению ошибок если произвольный блок шифротекста в процессе передачи по каналу с шумом исказится,
8. Асимметричные криптосистемы
Криптостема RSA, предложенная в 1977 г. Ривестом (R. Rivest), Шамиром (А. Shamir) (Ь. Adleman) [44], предназначена для шифрования и цифровой подписи. В
время RSA является наиболее распространенной криптосистемой — стандартом для многих криптографических приложений. Статус де-факто послужил причиной включения криптосистемы RSA в принятые ранее криптографические стандарты. Так, стандарт США ANSI Х9.30 предусматривал использование федерального стандарта цифровой подписи DSS. Выпущенная позднее версия стандарта ANSI Х9.31 была дополнена криптосистемой RSA. Последний является также частью многих официальных стандартов, в частности международных стандартов ISO 9796 и ITU-Т Х.509, SWIFT, французского финансового стандарта ЕТАВАС 5, австралийского стандарта управления ключами
6.5.3. Криптосистема RSA широко применяется в составе различных стандартов и Internet, включая PEM, S/MIME, РЕМ-MIME, S-НТТР и SSL.
Возможно ли использование RSA в России? С точки зрения правовых норм это исключено-RSA не входит ни в один из действующих на территории России криптографических стандартов. Отметим, что стандарты двухключевого шифрования и управления ключами в России также пока не приняты. Таким образом, разработчик криптографических приложений поставлен перед выбором: построить схему управления ключами по методу полной экспоненциального ключевого обмена Диффи — Хеллмана или воспользоваться методам цифрового конверта (шифрование сеансового ключа при помощи двухключевого криптоалгоритма).
Недостатки существующего не одно десятилетие метода полной матрицы хорошо известны Протокол Диффи — Хеллмана предполагает двусторонний обмен открытыми ключами и наличие сертификатов у отправителя и получателя сообщений. В случае односторонней аутентификации (сертификат имеется у одной из сторон) предпочтение отдается последнему методу. В этой ситуации выбор МА вполне оправдан — метод цифрового конверта на базе криптоалгоритма RSA описан в стандарте PKCS и применяется в протоколе SSL и других стандартах Internet (РЕМ, РЕМ-MIME и т.д.).
RSA многие годы противостоит интенсивному криптоанализу. Криптостойкость RSA основана на трудоемкости разложения на множители (факторизации) больших чисел. Открытый и секретный ключи являются функциями двух больших (100 200 двоичных разрядов или даже больше) простых чисел. Предполагается, что задача восстановления открытого текста по шифротексту и открытому ключу эквивалентна задаче факторизации.
Для генерации парных ключей используются два больших случайных простых числа, р и q. В целях максимальной криптостойкости р и q выбираются равной длины. Затем вычисляется пяоязведение:
N=pq
Далее случайным образом выбирается ключ шифрования е, такой, что е и ф(n) = (р — 1)
(q — 1) являются взаимно простыми числами. Наконец расширенный алгоритм Евклида используется для вычисления ключа дешифрования d, такого, что
![]()

Другими словами,
![]()
Заметим, что d и n — также взаимно простые числа. Числа е и n — открытый ключ, a d — секретный. Два простых числа р и q хранятся в секрете. Для шифрования сообщения т необходимо выполнить его разбивку на блоки, каждый из которых меньше n (для двоичных данных выбирается самая большая степень числа 2, меньшая и). То есть p и q — 100-разрядные простые числа, то и будет содержать около 200 разрядов и каждый блок сообщения mi должен иметь такое же число разрядов. (Если нужно зашифрованное число блоков, их можно дополнить несколькими нулями слева, чтобы
что блоки всегда будут меньше и.) Зашифрованное сообщение с будет состоять из блоков ci той же самой длины. Шифрование сводится к вычислению
![]()
При дешифровании для каждого зашифрованного блока сi вычисляется
![]()
Последнее справедливо так как
![]()
Все вычисления выполняются по mod n. Параметры криптосистемы и процедуры шифрования/дешифрования сведены в табл. П.22.
Отметим, что сообщение может быть зашифровано с помощью d, а дешифровано с помощью е, возможен любой выбор.
Рассмотрим короткий пример. Если

Ключ е не должен иметь общих множителей с

Выберем (случайно) е равным 79. В этом случае d = 79-1 mod 3220 = 1019. Опубликуем e и, сохранив в секрете d. Для шифрования сообщения
m = 6882326879666683
сначала разделим его на блоки. Для выбранных параметров ограничимся блоками десятичных разряда. Сообщение разбивается на шесть блоков mi.

Первый блок шифруется как 68879 mod 3337 = 1570 = с1. Выполняя те же операции для блоков, создадим шифротекст сообщения:
с = 15702756209122762423158.
Для дешифрования нужно выполнить возведение в степень, используя ключ дешифрования 1019;
![]()
Аналогично восстанавливается оставшаяся часть сообщения;
Описанные свойства RSA вытекают из теоремы Ферма — Эйлера: Пусть а и n положительные числа (НОД(а,n) = 1). Тогда
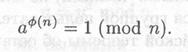
Поскольку ed =1 mod ф(n), то ed = 1+ К. ф(n) для некоторого целого К. Справедливость равенства
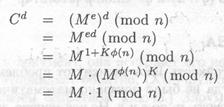
обеспечивается условием НОД(М,n)=1
Существует единственное исключение, для которого теорема Ферма — Эйлера справедлива при НОД(М,n) ≥ 1. По теореме Кармайкла
![]()
Где λ(n) — функция Кармайкла, которая при n = pq принимает вид:
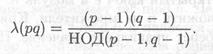
Отметим, что при составном и функция A(n) является делителем ф(n). Тогда для е и d справедливо
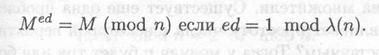
8.1.1 .Эффективность реализации
Существует много публикаций, затрагивающих тему аппаратных реализаций RSA [266-272,275-283].Хорошими обзорными статьями служат [284,285].
Быстродействие аппаратной реализации RSA примерно в 1000 раз ниже, чем быстродействие твой реализации DES. Быстродействие СВИС-реализации RSA с 512-битовым модулем— 64 Кбит/с [284]. Существуют также микросхемы RSA, которые оперируют с 1024-битовыми числами. В настоящее время разрабатываются микросхемы, которые, используя 512-битовый модуль, приблизятся к рубежу 1 Мбит/с. Производители также реализуют RЗА в интеллектуальных карточках, однако производительность этих реализаций невысока. Программная реализация DES примерно в 100 раз быстрее программной реализации 'Эти сценки могут незначительно меняться в зависимости от используемой технологии, 'никогда не достигнет производительности симметричных алгоритмов. В табл. П.23 примеры производительности программной реализации RSA для 8-битовой экспоненты шифрования и различной разрядности модуля [286].
Шифрование RSA выполняется намного эффективнее, если правильно выбрать значение всего используются 3, 17 или 65537 = 216 + 1 — двоичное представление этого числа только две единицы, поэтому для возведения в степень нужно выполнить лишь 17 умножений. Стандарт Х.509 рекомендует число 65537 [18], PEM — 3 [287], а РКСS #1—

3 или 65537 [27]. Использование в качестве е любого из указанных значений (при условии что сообщения дополняются случайными числами) не влияет на криптостойкость, одно и то же значение е используется группой пользователей. Операции с секретным можно ускорить при помощи Китайской теоремы об остатках [380], если сохранить р и q, а также заранее по секретному и открытому ключам вычислить вспомогательные
значения: d mod (р — 1), d mod (q — 1) и q-1 mod р [273,274].
Предполагается, что криптостойкость RSA зависит от проблемы разложения на больших чисел. Однако никогда не было доказано математически, что нужно разложить n
на множители, чтобы восстановить т по с и е. Не исключено, что может быть открыт совсем иной способ криптоанализа RSA. Однако, если этот новый способ позволит крип получить d, он также может быть использован для разложения на множители
сел. Также можно атаковать RSA, угадав значение (р — 1)(q — 1). Однако этот метод не проще разложения n на множители [288]. В [289] показано, что при использовании RSA ' даже нескольких битов информации по шифротексту не легче, чем дешифрования общения. Самой очевидной атакой на RSA является разложение и на множители. Любой противник сможет получить открытый ключ е и модуль n.Чтобы найти ключ дешифрования d, противник должен разложить и на множители. Криптоаналитик может все возможные d, пока не подберет правильное значение. Но подобная силовая а менее эффективна, чем попытка разложения n на множители. В 1993 г. был предложен криптоанализа, основанный на малой теореме Ферма [290]. К сожалению, этот метод медленнее разложения на множители. Существует еще одна проблема. Большинство принятых тестов устанавливает простоту числа с некоторой вероятностью. Что если р или q окажется составным? Тогда у модуля n будет три или более делителей, Соответственно некоторые делители будут меньше рекомендованной величины, что, в свою очередь открывает возможности для атаки путем факторизации модуля. Другая опасность заключается в генерации псевдопростых чисел (чисел Кармайкла), удовлетворяющих простоту, но при этом не являющихся простыми. Однако вероятность генерации пренебрежимо мала [291]. На практике, последовательно применяя набор различных тестов на простоту, можно свести вероятность генерации составного числа до необходимого минимума.
8.1.3. Атака на основе выборочного шифротекста
Некоторые атаки используют уязвимость криптографического протокола. Важно понимать, что само по себе использование RSA не обеспечивает требуемого уровня безопасности системы. Рассмотрим несколько сценариев.
Сценарий 1.
Злоумышленнику удалось перехватить сообщение с, зашифрованное с помощью того RSA-ключа Алисы. Он хочет прочитать сообщение. Для раскрытия т = сd он сначала выбирает первое случайное число r, меньшее и, и затем, воспользовавшись открытым ключом Алисы е, вычисляет
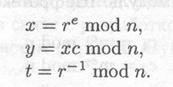
Если x=re mod n,то r=xd mod n.
Далее злоумышленник вынуждает Алису подписать сообщение у. Таким образом, процедура вычисления подписи на секретном ключе соответствует процедуре дешифрования сообщения у (Отметим, что Алиса должна подписать сообщение, а не значение хэш-функции.) Такой обман вполне реален, так как Алиса никогда раньше не видела y. Алиса посылает злоумышленнику

Теперь злоумышленник раскрывает т, вычисляя
![]()
![]()
Если Алиса хочет заверить документ, она посылает его нотариусу. Нотариус подписывает подписью и отправляет обратно. (Хэш-функции не используются, нотариус шифрует все сообщение на своем секретном ключе.) Злоумышленник хочет, чтобы нотариус подписал такое сообщение, которое в обычном случае тот никогда не подпишет. Это быть фальшивая временная метка, либо автором этого 'сообщения может являться другое лицо. Какой бы ни была причина, нотариус никогда не подпишет это сообщение, если у него будет возможность выбора. Назовем это сообщение т'. Сначала злоумышленник выбирает произвольное значение х и вычисляет у = хe mod и. Параметр е он может труда — это открытый ключ нотариуса, и должен быть опубликован для проверки подписи последнего. Теперь злоумышленник вычисляет т = ym' mod n и посылает m нотариусу на подпись. Нотариус возвращает тd mod n. Далее злоумышленник вычисляет (md mod n)x-1mod n, которое равно т'd mod n и является подписью m'. На самом деле у злоумышленника есть множество различных способов решения подобной задачи [292 — 294].Описанная атака основана на сохранении мультипликативной структуры арифметической операции возведения в степень:

Сценарий 3.
Злоумышленник хочет, чтобы Алиса подписала некое сообщение тз. Для этого он создает два сообщения, т1 и т2, такие, что тз = т1 m2 mod n. Если злоумышленник заставит Алису подписать m1 и m2, то сможет вычислить подпись для тз;
![]()
![]()

Отсюда вывод — никогда нельзя использовать RSA для подписи случайных документов. Применение хэш-функций в технологии RSA-подписи строго обязательно. Отметим, что специальный формат блоков стандарта ISO 9796 предотвращает подобную атаку.
8.1.4. Атака на основе общего RSA-модуля
При реализации RSA можно попробовать раздать всем абонентам криптосети одинаковый модуль n, но каждому — свои значения показателей степени е и d. При этом наиболее очевидная проблема заключается в том, что если одно и то же сообщение когда-нибудь шифровалось разными показателями степени (при фиксированном модуле) и эти два показателя— взаимно- простые числа (как обычно и бывает), то открытый текст может быть раскрыт даже при неизвестных ключах дешифрования [295]. Пусть заданы: m — открытый текст, e1 и e2- два ключа шифрования, n — общий модуль. Шифротекстами сообщения являются:

Криптоаналитик знает n, е1, е2, с1 и с2. Так как е1 и е2 — взаимно-простые числа, пользовавшись расширенным алгоритмом Евклида, можно найти такие числа r и s, что
.

Полагая r
отрицательным (или r, или s должно быть
отрицательным), можно снова воспользоваться расширенным алгоритмом Евклида для
вычисления ![]() Тогда
Тогда
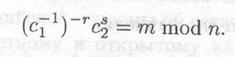
Существует два других, более тонких метода раскрытия подобного типа. Один вероятностный метод для разложения n на множители. Другой — детерминированный алгоритм вычисления какого-нибудь секретного ключа без разложения модуля на множители. Оба метода подробно описаны в [296]. Таким образом, использование общего пользователей параметра n может отрицательно сказаться на уровне безопасности криптосети.
8.1.5. Шифрование коротких сообщений
Известно, что криптосистема RSA oбладаeт низкой криптостойкостью при зашифрованном на малом е коротком сообщении. Действительно, при сe = тe< n открытый текст быть восстановлен по шифротексту с при помощи процедуры извлечения корня. Фактически подобная атака возможна и тогда, когда в процессе возведения в степень выполнялось некоторое количество приведений по модулю. При с> n трудоемкость такой атаки ниже кости исчерпывающего перебора для т. Однако меры противодействия также очей либо открытый ключ е должен быть достаточно большим, либо открытый текст быть коротким. Выбор малого е обусловлен соображениями вычислительной эффективности шифрования и проверки подписи [297]. Таким образом, разумный подход заключается в искусственном наращивании коротких открытых текстов («набивки»). При этом необходимо следить за тем, чтобы удлиненный открытый текст при числовом отображении не превращался в набор множителей некоторого известного числа Р, например Р = 21, что при дополнении открытого текста последовательностью нулей справа (со стороны разрядов).
8.1.6. Раскрытие малого показателя шифрования
Хэстед (J. Hasted) продемонстрировал уязвимость RSA при условии, если криптоаналитик может получить множество шифротекстов фиксированного сообщения т, зашифрованного при помощи криптосистемы RSA с различными секретными параметрами р и q, но пользовании фиксированного открытого ключа е [379]. При соблюдении сформулированных условий можно раскрыть сообщение т. Известен частный случай, когда при заданных l различных результатах шифрования тe mod n1,...
, тe mod n1 можно раскрыть m при Китайской теоремы об остатках [380]. В общем случае, при заданных t результатах шифрования

где ai и bi заданы и t > е(е+1)/2, можно раскрыть сообщение m,воспользовавшись из математическим методом. Еще раз отметим, что данная атака возможна только при условии что исходные сообщения получены известным криптоаналитику способом (фиксированное сообщение m является частным случаем).
Меры противодействия сводятся к использованию псевдослучайного контекста для «набивки перед их шифрованием. Метод «набивки» из стандарта PKCS #1 [27] в настоящее время пересматривается в связи с разработкой нового оптимального метода «набивки для асимметричных криптосистем (Optimal Asymmetric Encryption Padding) [381].
8.1.7. Раскрытие малого показателя дешифрования
Другая атака позволяет раскрывать d, когда d не превышает четверти размера n, а е< n [298].При случайном выборе е и d это маловероятно и никогда не произойдет, если значение е мало. Значение d должно быть большим.
При использовании RSA можно атаковать протокол, в котором сообщение шифруется, а затем подписывается [299]. Предположим, Алиса желает послать сообщение Бобу. Сначала она шифрует сообщение на открытом ключе Боба, а затем подписывает на своем секретном ключе Зашифрованное и подписанное сообщение выглядит следующим образом:

Однако Боб может доказать, что Алиса послала ему т', а не т. Так как Бобу известно разложение на множители nB (это его собственный модуль), он может вычислить дискретные логарифмы но основанию пв. Следовательно, ему остается найти х, для которого

Если он может опубликовать хев в качестве своего нового открытого показателя степени и свой прежний модуль пв, он сможет утверждать, что Алиса послала ему сообщение m' зашифрованное на хеВ. Заметим, что применение хэш-функции не позволяет решить проблему. Однако ее можно решить путем использования фиксированного показателя шифрования для каждого пользователя криптосети.