Наложение текстуры на многогранник
Рассмотрим наложение растровой текстуры на шар, аппроксимированный многогранником. В главе 3 мы с вами уже обсуждали способы вывода полигонов с наложением текстуры. Эти способы были представлены в обобщенном виде. Здесь мы разберемся с некоторыми особенностями наложения текстуры для шара.
Пусть в качестве текстуры будет карта, которую мы уже рассматривали выше. Кстати, во многих англоязычных графических пакетах программ файлы текстур так и называются "maps", хотя и не представляют собой продукцию картографии. Термин "карта" для текстур можно еще трактовать как "развертка".
В нашем случае каждая грань многогранника будет соответствовать одной прямоугольной клетке текстуры (рис. 5.12).
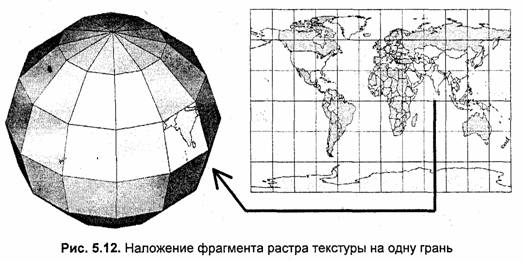
Для рисования каждой грани можно использовать алгоритм вывода полигонов, модифицированный следующим образом. Мы уже рассматривали выше в главе 3 один из алгоритмов вывода полигонов, который рисует полигон горизонталями заполнения внутренних точек. Операции по наложению текстуры удобно встроить в цикл рисования каждой такой горизонтали. При этом в ходе вывода пиксела горизонтали по известным текущим координатам пиксела в основном растре (X, Y) определяются соответствующие координаты (хТ, уТ) тексела в растре текстуры. Затем определяется цвет тексела, который и будет определять цвет пиксела в основном растре. Вычислить координаты (хТ, уТ) Для каждой точки грани можно следующим образом. Рассмотрим рис. 5.13.
Для определения искомых координат в точке горизонтали будем использовать линейную интерполяцию координат угловых точек. При этом до начала цикла вывода горизонтали определим текстурные координаты в точках А нВ — (хТА, уТА) и (хТВ, УТВ)- Это можно сделать, разделив отрезки (0-1) и (2-3) пропорционально Y.
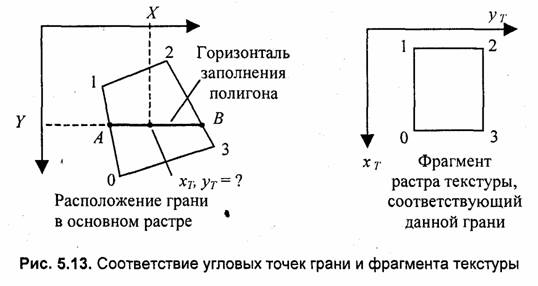

В ходе цикла вывода горизонтали вычисление координат (хТ, yТ), соответствующих текущим пикселам горизонтали, можно выполнять делением отрезка (А-В) пропорционально X:
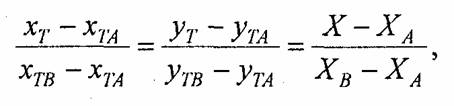
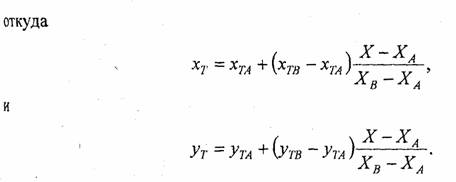
Следует учесть, что приведенные выше формулы отражают лишь отдельный эпизод в ходе заполнения полигона грани. Очевидно, что в другие моменты времени горизонталь заполнения будет пересекать иные ребра полигона (а им будут соответствовать свои индексы вершин). Это достаточно просто реализуется в алгоритмах заполнения полигонов — в том числе и в алгоритме, приведенном в главе 3 этой книги.
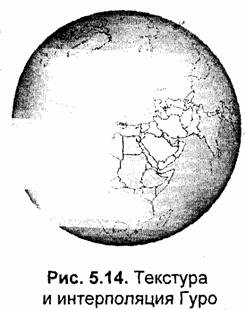
Как вы, наверное, уже заметили, интерполяция координат для такой текстурированной грани аналогична интерполяции интенсивностей отраженного света для метода Гуро. Кстати, если в цикл вывода горизонтали заполнения встроить и интерполяцию по методам Гуро или Фонга, то можно получить более реалистичное текстурированное изображение — с учетом отражения света (рис. 5.14).
Необходимо принимать во внимание, что линейная интерполяция текстурных координат вершин граней (хТI, УТI) вносит погрешность. Эта погрешугловых координат (B L) и (хТ, yТ) для текстуры карты мира нелинейно — а это так для многих проекций карты мира. В этом случае для уменьшения погрешности отображения целесообразно увеличивать число граней. Можно интерполировать не текстурные координаты, а широту и долготу (В L), и для них потом в каждой точке горизонталей заполнения находить соответствующие значения (хТ, уТ) — это уже чем-то напоминает метод Фонга, не так ли?
Давайте рассмотрим еще один способ наложения текстур на многогранник. В отличие от только что рассмотренного, здесь не используется интерполяция. При интерполяции требуется выполнять достаточно много операций, в том числе операции деления. Избавиться от достаточно медленной операции деления (в общем случае — над числами с плавающей точкой) можно, если
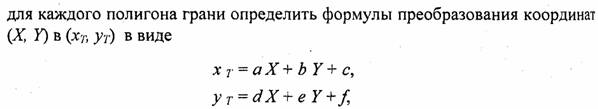
причем, коэффициенты а, b, с, d, e и ƒ являются константами в течение всего цикла вывода одной грани.
В общем случае для четырехугольной грани это невозможно.
Подобное аффинное преобразование нельзя построить по четырем точкам ; соответствия четырехугольников текстуры и четырехугольника грани, ориентированной произвольным образом. Преобразование формы прямоугольного фрагмента текстуры в форму четырехугольной грани многогранника значительно сложнее — попробуйте, например, выразить процесс интерполяции для рассмотренного выше способа в одной функциональной зависимости (хТ уТ) = F(X, Y) и вы увидите, что она является сложной, нелинейной.
Однако можно представить четырехугольник в виде двух треугольников (рис. 5.15), а каждый треугольник выводить отдельно. Для каждой треугольной грани перед циклом заполнения нужно определять свои коэффициенты преобразования координат. Сделать это можно по трем точкам вершин треугольника. Рассмотрим треугольник (0-1-2). Очевидно, должны выполняться следующие равенства:
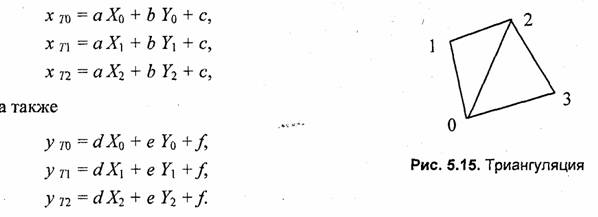
Рассматривая эти равенства как две системы линейных уравнений третьего порядка относительно (а, Ъ, с) и (d, e, f), можно найти искомые коэффициенты преобразования — подобно тому, как это сделано в разд. 3.7.
Следует заметить, что использовать такой способ триангуляции здесь следует только при большом числе граней, поскольку имеется значительная методическая погрешность. Преимуществом данного способа наложения текстуры является простота вычислительных операций в цикле вывода каждого полигона. В некоторых случаях это позволяет достичь высокой скорости графики.
Хотя теперь полигонов уже почти вдвое больше (грани, примыкающие к полюсам, и так были треугольными), но треугольники обычно выводятся быстрее четырехугольников. Для треугольников часто используют особые алгоритмы, оптимизированные по быстродействию. Кроме того, в цикле вывода грани можно использовать, в основном, целочисленные операции, если соответствующим образом применять коэффициенты аффинного преобразования координат.
Теперь сделаем замечания общего характера по текстурированию.
При наложении текстуры на отдельные грани шара совершенно необязательным является склеивание карты мира в один растр текстуры. Может оказаться удобном для каждой грани иметь отдельную текстуру. Это относится и к случаю, когда текстуры хранятся в файлах.
Для построения реалистичного изображения поверхности Земли в качестве текстуры лучше всего использовать космические снимки, трансформированные надлежащим образом.
Достоинством полигонального текстурирования поверхностей является универсальность метода, применимость его к самым разнообразным поверхностям, которые могут быть представлены многогранниками и полигональными сетями. Еще одним достоинством является высокая скорость графики. Базовые операции текстурирования граней в настоящее время аппаратно поддержаны многими графическими процессорами для видеоадаптеров.
Недостатком метода является погрешность отображения, которая, однако, стремится к нулю при увеличении числа граней.
Вариации формы шара
Обозначим через хш, уш, zш координаты точек поверхности шара. Будем, как и прежде, использовать параметрическую форму — функции угловых координат широты и долготы:
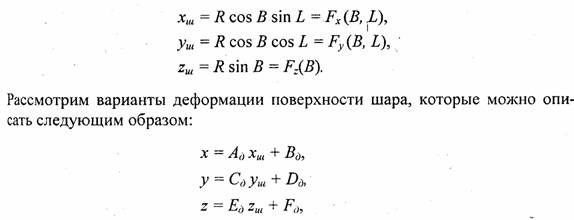


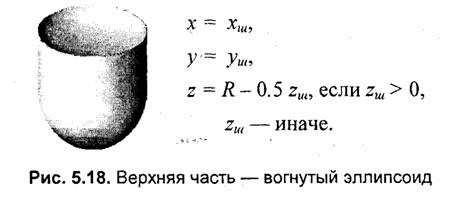
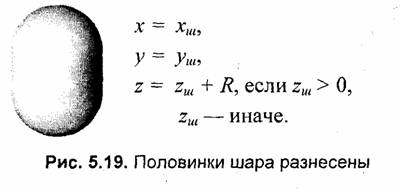
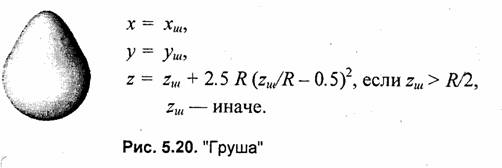
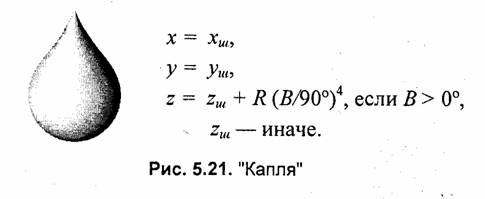
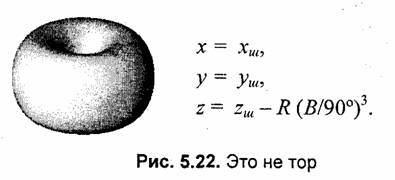
В рассмотренных выше примерах для деформации формы шара были использованы преобразования координат только по оси z. В нижеследующих примерах выполняются преобразования также и координат х, у (рис. 5.23—5.27).
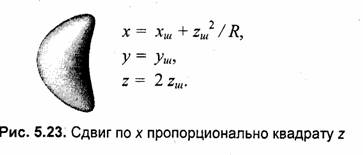
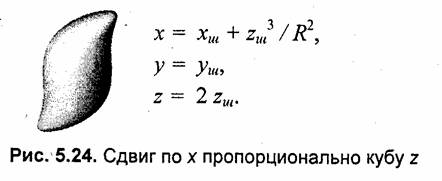
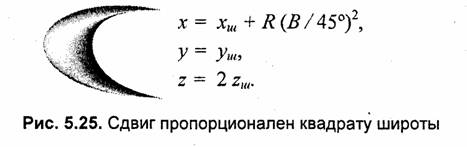
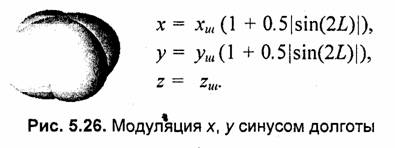
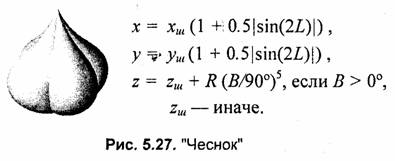
5.2. Цилиндр
Здесь мы будем использовать формулы параметрического описания поверхности цилиндра. В одной из возможных разновидностей такого описания применяются следующие параметры — долгота (l) и высота (h).
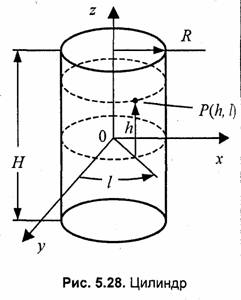
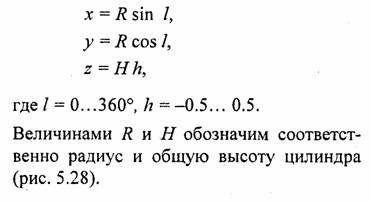
Каркасное изображение
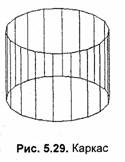
Построение каркасного изображения полностью аналогично рассмотренному выше способу для шара. Для цилиндра также рисуются меридианы (здесь это вертикальные линии) и параллели (эллипсы) На рис. 5.29 изображен каркас из прямых линий — ребер вписанного многогранника.
Одним из свойств каркасного изображения без удаления невидимых точек является иллюзия неопределенности ракурса. Непонятно — это вид сверху или вид ' снизу. Раньше вы, наверное, уже замечали подобный эффект, Например, когда мы рассматривали каркасное i изображение шара.
Удаление невидимых точек
На рис. 5.30 показано изображение цилиндра в двух вариантах— с верхней крышкой и без.
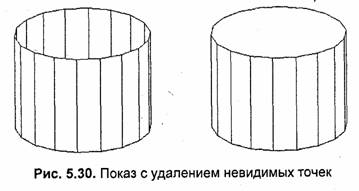
В обоих случаях для создания иллюзии объемности здесь выделены черным цветом видимые ребра аппроксимирующего многогранника. Для показа поверхности многогранника с крышкой достаточно показать ребра граней передней стороны и крышку. Задние грани являются невидимыми (рис. 5.31).
Если верхняя крышка отсутствует, то видимыми являются все грани. В этом случае следует рисовать объект, начиная с самых дальних граней задней стороны.
Грани можно выводить попарно, начиная с грани, соответствующей самой дальней точки, как показано на рис. 5.32.
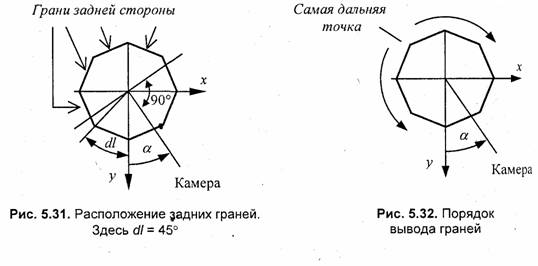
Долгота дальней точки определяется расположением камеры:
![]()
где [ ... ] — целая часть
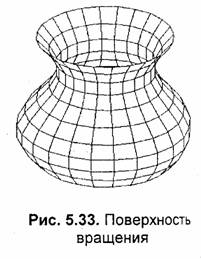
Такой метод сортировки граней молено использовать не только для цилиндра, но и для достаточно широкого класса поверхностей. На рис. 5.33 показан пример поверхности вращения, изображенной описанным выше методом. Такая поверхность подобна цилиндру. Единственное отличие здесь состоит в том, что боковая поверхность криволинейна по вертикали, поэтому для аппроксимации четырехугольными гранями следует использовать двойной цикл - как по долготе (l), так и по высоте (h). Подобные примеры мы рассмотрим несколько позже.
Здесь мы будем рассматривать изображение боковой поверхности цилиндра, аппроксимированного многогранником. Грани нужно изображать цветом в соответствии с выбранной моделью отражения. Мы будем рассматривать цилиндр без крышек. Это позволяет наглядно проиллюстрировать проблемы показа поверхностей, для которых могут быть видимыми обе стороны.
В чем суть проблемы? Проблема в выборе направления нормали к грани, В предыдущем разделе мы рассматривали шар, и вы, наверное, заметили, что и там мы аппроксимировали поверхность многогранником. Однако для шара указанной проблемы не существует, у него всегда видимой является внешняя сторона поверхности. Необходимое направление нормалей для всех граней легко обеспечить соответствующей нумерацией вершин каждой грани. Для цилиндра без крышек нельзя жестко зафиксировать направление векторов нормали, если предполагается показывать цилиндр с разных ракурсов (например, изменяя углы поворота камеры а и 0).
Для диффузного отражения цвет грани определяется значением косинуса угла между лучом источника света и нормалью к поверхности. Одним из вариантов решения проблемы является взятие модуля косинуса, если косинус отрицательный. Это можно делать, когда положение источника света совпадает с положением камеры. На рис. 5.34 показано несколько вариантов задания направления нормалей.
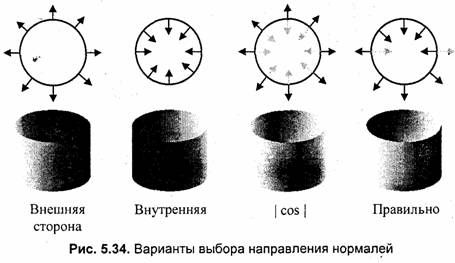
На рис. 5.35 изображена боковая поверхность многогранников, аппроксимирующих"11(йлиндр с различной точностью. Моделируется боковое расположение источника света.
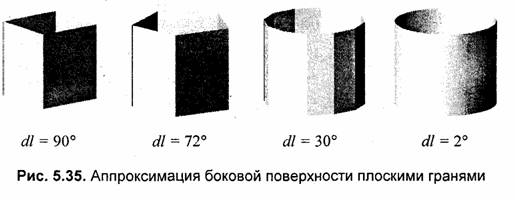
Рассмотрим один из алгоритмов изображения гладкой боковой поверхности цилиндра — рисование вертикальными линиями. На рис. 5.36 показаны: вид сверху (ось z мировых координат направлена на нас), полутоновое изображение поверхности в аксонометрической проекции и направление осей мировых координат (х, у, z). Положение камеры здесь задано одним углом β. Источник света располагается так же, как и камера. В этом случае цвет пикселов вертикали боковой поверхности определяется коэффициентом отражения
![]()
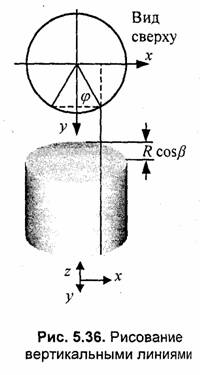
где R — радиус цилиндра. Вдоль любой вертикали боковой поверхности цвет пикселов здесь одинаков. Кроме того, при данном расположении источника света имеет место полная симметрия относительно центральной вертикали. Это позволяет построить достаточно быстрый алгоритм рисования. Крышки цилиндра можно также рисовать вертикалями, но это уже не принципиально.

В ходе работы этого алгоритма вычисляются координаты точек эллипса для одного квадранта. Вначале определяется координата у для круга, а затем она умножается на коэффициент сжатия эллипса (cosβ). Определение величины cosβ целесообразно вынести за цикл — вычислить ее один раз в начале работы. В теле цикла нужно вычислять квадратный корень и выполнять несколько операций умножения и деления. Хотя эти операции являются мед ленными, но они выполняются сразу для нескольких пикселов, расположенных посимметричным вертикалям. Чем длиннее вертикали, тем меньшую часть от общего времени вывода составляют такие операции (поэтому не I обязательно для вычисления точек эллипса использовать алгоритм Брезенхэма — хотя почему бы и нет?). Поскольку собственно вертикаль рисуется достаточно быстро, то данный алгоритм может успешно конкурировать по быстродействию с алгоритмами полигонального вывода. Еще одно полезное свойство — высокое качество рисования гладкой боковой поверхности. Недостатком данного алгоритма является показ только вертикального расположения цилиндра, в то время как полигональную форму можно свободно поворачивает в пространстве.
Следует учитывать, что данный алгоритм можно использовать для углов наклона камеры β от 0 до 90° (вид сверху). Этим и объясняется рисование только верхней крышки. Для вида снизу (β от 90 до 180°) необходимо показывать нижнюю крышку (верхнюю не нужно она становится невидимой). Алгоритм легко обобщить.
Если цилиндр является отдельным элементом некоторой сложной сцены, то при выводе, например, с использованием Z-буфера необходимо соответствующим образом построить цикл вывода вертикалей.
Теперь рассмотрим произвольное расположение источника света. Как и прежде, будем рассматривать только один точечный источник, расположенный в бесконечности. Пусть расположение источника описывается двумя углами наклона (ас и βс.). Положение камеры будем задавать двумя углами наклона — (а и β ). Для простоты вначале положим угол поворота камеры, а= 0.
На рис. 5.37 изображен цилиндр, освещенный сбоку. Здесь показана только боковая
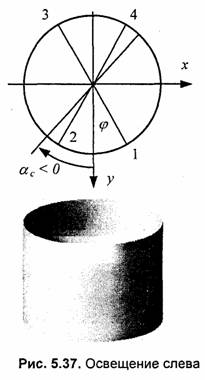
поверхность — без верхней и нижней крышек. Это более
сложный вариант показа, поскольку нужно рисовать и внутреннюю часть
поверхности. Рассмотрим четыре точки, расположенные симметрично на поверхности
цилиндра. Для первой точки угол между нормалью к боковой поверхности и лучом от
источника света составляет φ1 = φ — ас, Для
второй точки аналогичный угол равен φ2 = -φ - ас.
Поскольку точки 3 и 4 показываются с внутренней стороны поверхности, то их
нормали совпадают по направлению с нормалями соответственно в точках 1 и 2.
Поэтому φ3 = φ1 и φ4
= φ2
Изображаемая форма цилиндра не зависит от угла поворота камеры а. Этот угол обуславливает лишь закрашивание боковой поверхности (наряду с углами расположения источника света). Учесть угол а можно, если вычесть его из угла поворота источника света. Рассмотрим алгоритм графического вывода.

Здесь для упрощения записи алгоритма использована идеальная диффузная модель отражения света. Вначале определяются коэффициенты k1 и k2, которые затем можно использовать для вычисления цвета, например, в виде компонент R, G, В:
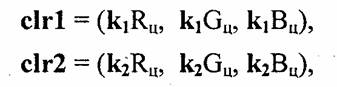
где Ru, Gu и Вц — компоненты описания цвета поверхности цилиндра.
Вертикали выводятся сначала для задней стороны боковой поверхности, а затем для передней. При использовании Z-буфера порядок вывода безразличен.
Данный алгоритм сложнее предыдущего. Здесь в теле цикла выполняется значительное количество медленных операций — кроме корня квадратного вычисляется также и арксинус. Это является недостатком алгоритма с позиций быстродействия. Положительной чертой алгоритма является вычисление угловой, координаты (φр), которую можно использовать для наложения текстуры-развертки (карты).
В некоторой степени, компьютерная графика — это создание иллюзий. Текстуры наглядно это демонстрируют (рис. 5.38). Разве бывают кирпичи округлой формы? Крайний справа цилиндр "выложен" именно такими кирпичами. При наложении текстуры плоская карта-развертка растрового образца текстуры плавно искривляется, следуя гладкой форме боковой поверхности.

Попробуйте подобрать текстуру, чтобы кирпичи выглядели действительно плоскими, как в реальной жизни. Однако тогда может оказаться заметным искривление в другом ракурсе. Текстура — это достаточно простой способ изображения сложных поверхностей, это начальный уровень имитации материалов. В самом деле, если строить модель каждого отдельного кирпича или углублений шероховатой поверхности, то эта модель будет намного сложнее цилиндра. Таким образом, для создания более или менее правдоподобного изображения, которое в отдельных случаях удается выдавать в качестве реалистичного, необходимо, в первую очередь, подобрать соответствующую текстуру.
Кроме того, и для текстурированных объектов очень важно соблюдать законы отражения. Если убрать градиентную закраску у четырех цилиндров, изображенных на рис. 5.38, то для первых трех (кроме "кирпичного") почти полностью исчезнет иллюзия объемности.
Поскольку текстура чаще всего представляет собой оцифрованный фотоснимок реальных объектов, сделанный с определенного ракурса съемки, то текстурирование дает удовлетворительный результат только для соответствующих ракурсов показа.
Рассмотрим, как наложить текстуру на боковую поверхность цилиндра. Способ наложения определяется типом алгоритма рисования. Если цилиндр рисуется как многогранник, то в этом случае текстурирование выполняется так, как нами уже было рассмотрено выше для многогранников, аппроксимирующих шар. Алгоритмы рисования объектов в виде многогранников и политональных сетей являются достаточно универсальными и могут быть использованы для широкого класса объектов.
Здесь мы рассмотрим один способ наложения текстуры, специально предназначенный для цилиндра. В его основе лежит способ рисования цилиндра вертикалями, рассмотренный выше. На рис. 5.39 показана одна из вертикалей закрашивания поверхности.
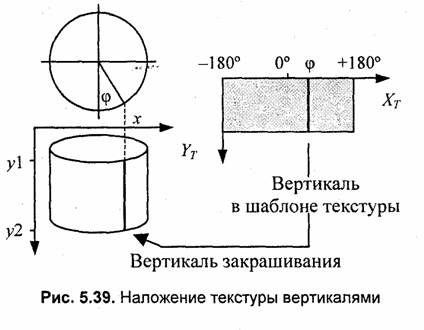
Общий цикл рисования боковой поверхности можно представить себе следующим образом. Вначале определяются координаты текущей вертикали закрашивания в экранной системе координат. Пусть эти координаты составляют (х, у1) - (х, у2). Необходимо также вычислить угловую координату этой вертикали (<р). По значению угла ^определяем координату Хт в шаблоне текстуры
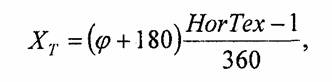
где НоrТех— горизонтальный размер шаблона текстуры. Угол φ измеряется в градусах.
Одна вертикаль закрашивания (х, у1)- (х, у2) соответствует вертикали с координатами (ХТ, 0) - (XТ, VertTex - 1) в шаблоне текстуры, где VertTex — размер текстуры по вертикали.
Рисование одной вертикали боковой поверхности можно представить как цикл, в ходе которого последовательно рисуются пикселы с координатами у от у1 доу2. Для пиксела в точке (х, у) определяются соответствующие координаты (Хт, Yr) в шаблоне текстуры, причем Хг нам уже известна, а координата YT вычисляется по формуле:
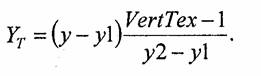
Затем в шаблоне текстуры определяется цвет точки (XТ, YT). После этого выбранным цветом рисуется пиксел с координатами (х, у) в основном растре.
Формулы вычисления координат можно преобразовать к следующему виду:
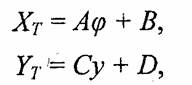
где А, В, С и D — константы для всех пикселов одной вертикали. Таким образом, для каждого пиксела вертикали приходится выполнять несколько операций умножения и сложения. Для ускорения текстурирования можно построить инкрементный алгоритм.
Данный способ наложения текстуры можно использовать только для простейших цилиндров, расположенных вертикально. При наложении текстур на более сложные поверхности (в том числе вариации формы цилиндра) следует применять полигональные методы.
Параметрические формулы цилиндра удобно использовать в качестве основы для описания поверхностей достаточно сложной формы. В исходных параметрических уравнениях цилиндра
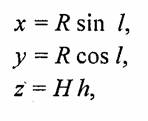
величины Н и R — это константы. Рассмотрим примеры поверхностей, когда радиус R является функцией параметров h и l, то есть R = R(h, l).
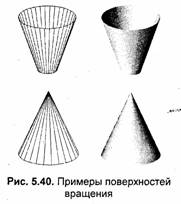
Если радиус зависит только от высоты, то есть R = R(h), то это соответствует поверхности вращения относительно оси z. Задание конкретной функции R(h) для описания какой-либо поверхности напоминает вытачивание цилиндрической заготовки на токарном станке. На рис. 5.40 приведены примеры поверхностей вращения (во всех случаях параметр h изменяется от -0.5 до +0.5).
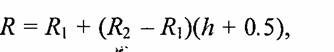
где R1 и R2 — радиусы нижней и верхней части соответственно. При R2 =0 получаем конус. Очевидно, что при аппроксимации многогранниками конус следует рисовать уже не четырехугольными, а треугольными гранями.
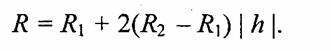
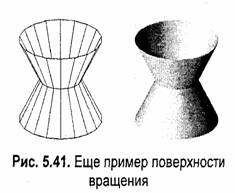
Для поверхности, изображенной на рис. 5.41, при вычислении координат вершин четырехугольных граней необходимо использовать уже два цикла — по l и по h.

В данном случае вдоль вертикали располагаются по две грани (dh = 0.5).
В следующих примерах для создания иллюзии гладкой поверхности нужно использовать большее число граней (рис. 5.42, 5.43).

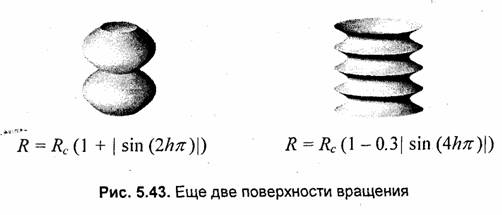
Следующую группу составляют такие вариации формы цилиндра, когда радиус зависит только от долготы, то есть R = R(l). Пример подобной поверхности показан на рис. 5.44.
И, наконец, последнюю разновидность вариаций данного типа, согласно нашей классификации, представляют поверхности R = R(h,l). Пример такой поверхности приведен на рис. 5.45.

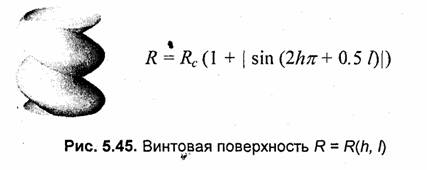
4
5.3. Top
Функции параметрического описания поверхности тора запишем в следующем виде
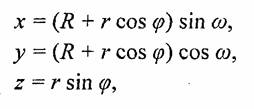
где R и r — большой и малый радиусы, φ и ω — широта и долгота. Для замкнутой поверхности углы φ и ω должны изменяться в полном круговом диапазоне, например, от 0 до 360° или от-180о до +180°.
На рис. 5.46, 5.47 показаны различные способы изображения тора.
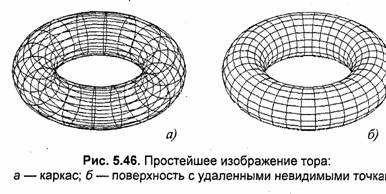
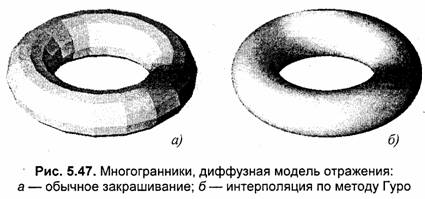
Рисование тора средствами компьютерной графики достаточно просто может быть выполнено на основе аппроксимации многогранником, подобно тому, что мы уже рассматривали для шара и цилиндра. Повторим запись алгоритма вывода многогранника четырехугольными гранями, видоизменив его для данного конкретного случая

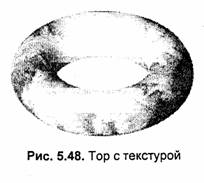
Очевидно, что чем меньше величины dω и dω, тем больше число граней у вписанного многогранника и тем лучше такой многогранник соответствует гладкой поверхности тора. При использовании такого полигонального метода получения изображения достаточно просто наложить текстуру. Полигональный способ наложения текстур для тора полностью аналогичен способу, рассмотренному выше для шара. Пример подобного текстурирования приведен на рис. 5.48.
Рассматривая в предыдущих разделах шар и цилиндр, мы наряду с полигональными способами пытались анализировать и другие способы изображения. Например, рисование цилиндра вертикальными линиями. Для тора изобрести эффективный специальный алгоритм графического вывода, вероятно, достаточно сложно. Во всяком случае, автору он неизвестен. Хотя во второй части этой книги есть пример программирования одного "неполигонального" способа рисования тора. Можно представить тор как след движения шара.
Если шар перемещается с достаточно малым шагом, то след получается весьма похожим на тор. Впрочем, данный пример рисования приведен в книге не как рекомендуемый способ изображения тора, а как пример изображения движущихся шариков. По быстродействию данный способ изображения тора весьма плох из-за того, что приходится многократно рисовать одни и те лее точки (подобные аспекты мы рассматривали в главе 3 при обсуждении алгоритмов рисования толстых линий).
На рис. 5.49 изображена поверхность многогранника, для которой параметрические формулы такие же, как и для тора. Единственное отличие здесь в том, что широта φ изменяется в диапазоне от -135° до +225° с шагом! d<p =90°.
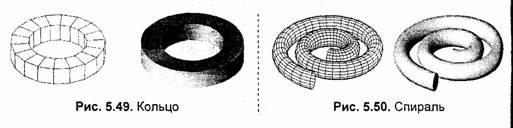
Если изменять радиус R пропорционально долготе, т. е. R = R(co), то получим спираль (рис. 5.50). Здесь больший диапазон изменения долготы: oт -360° до +360°, соответствует двум виткам спирали.
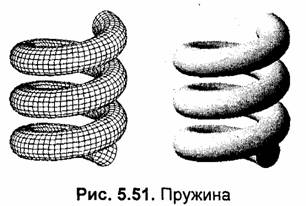
Для пружины (рис. 5.51) значения координат х и у такие же, как и для тора, а координата z тора суммируется с приращением, пропорциональным долготе:
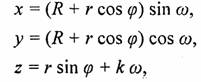
где k: — некоторая константа, определяющая шаг витков спирали по высоте. Долгота здесь изменяется в троекратном круговом диапазоне (соответствующем числу витков).
Если объединить спираль и пружину, то получим коническую спираль (рис. 5.52):-
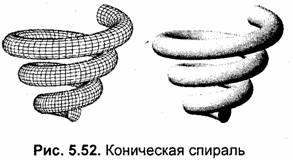
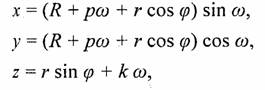
где константа р определяет увеличение большого радиуса пропорционально долготе, а к— задает шаг витков пружины по высоте;
5.4. Общие замечания
Мы рассмотрели шар, цилиндр и тор, а также их некоторые вариации. Очевидно, что это лишь малая часть всего многообразия трехмерных форм. Тем не менее, можно сделать некоторые обобщения.
Модель описания и способ отображения
Для описания формы поверхности мы использовали аналитическую модель — параметрические формулы
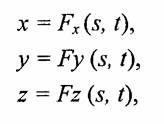
где s и t — параметры, непрерывно изменяющиеся в некотором диапазоне.
В качестве одного из возможных способов построения изображения поверхности мы рассматривали такой способ. В процессе рисования выполняется цикл


Таким образом, здесь вычисляются координаты узлов сетки с шагом ds и dt. Поверхность изображается в вид четырехугольных граней. Чем меньше шаг сетки, тем больше таких граней и тем лучше соответствие форме гладкой поверхности,
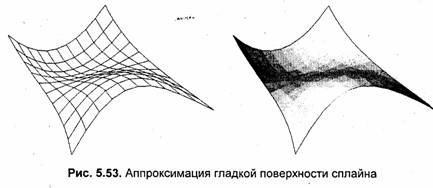
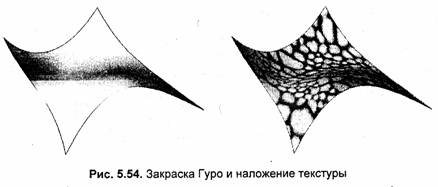
Является ли данный способ отображения поверхности наилучшим? Вряд ли. Здесь каждая точка поверхности вычисляется четырежды, что существенно замедляет процесс, если поверхность описана сложными формулами. Является ли данный способ самым простым? Вероятно. Можно также подчеркнуть его экономичность по затратам памяти, поскольку не нужны массивы для хранения координат граней —г координаты вычисляются "на ходу". Но главное, что следует подчеркнуть, — этот способ универсален. Его можно применить для отображения широкого класса поверхностей. Он может использоваться для произвольных поверхностей, для которых известны параметрические формулы, например для сплайнов. На рис. 5.53 и 5.54 показаны несколько вариантов изображения кубического сплайна Безье рассматриваемым способом.
В компьютерной графике важную роль играет быстродействие вывода. Повысить скорость рисования для рассматриваемого базового алгоритма можно следующим образом. Чтобы избежать повторного вычисления координат вершин граней, вначале следует вычислить узловые координаты всех точек поверхности и записать в массив. Затем можно в отдельный массив записать координаты векторов нормалей в вершинах. Потом преобразовать координаты и рисовать полигоны граней. Введение дополнительных массивов для вершин и нормалей обычно заметно увеличивает скорость, например, при закрашивании Гуро; поскольку исключаются повторные расчеты не только координат вершин, но и векторов нормалей к соседним граням.
Однако общий характер цикла отображения здесь сохраняется. Когда нужно
отобразить требуемый объект, то заново вычисляются все узловые координаты. А теперь представим себе, что некоторая трехмерная сцена содержит несколько таких объектов. Предположим, что многие объекты остаются неподвижными, а изменяется лишь ракурс показа. Зачем тогда всякий раз вычислять мировые (а точнее, некоторые локальные) координаты по параметрическим формулам? Их можно вычислить только один раз при инициализации сцены и записать координаты всех вершин (и нормалей, если необходимо) в массивы. А при расчете кадров производить только все необходимые преобразования координат и закрашивание. Более того, можно параметричдские формулы не вычислять вообще, если хранить описание координат вершин (и нормалей) в файлах соответствующего формата, которые загружаются при инициализации сцены. Так мы постепенно перешли от аналитической модели описания объектов к полигональной модели, которая также имеет свои плюсы и минусы.
Модель описания и способ отображения, вообще говоря, не обязательно со-
ответствуют друг другу.
"Квадратирование" и триангуляция
В качестве небольшого околонаучного развлечения давайте попрактикуемся в терминологии. Рассматриваемый здесь способ отображения поверхностей четырехугольными гранями можно назвать "квадратированием". Способ этот известен давно, а такое название мы с вами можем изобрести и сами. Оно кажется достаточно звучным и вполне соответствующим сути, а главное— может помочь застолбить "непоправимый вклад в науку" (последнее выражение в кавычках придумано не мною). А если говорить серьезно, то лучше все-таки следовать общему правилу — не засорять язык без крайней необходимости. Поэтому используем кавычки,
Применение четырехугольных граней для поверхностей общего вида, вообще говоря, это вопрос спорный. Почему именно четырехугольные грани? Для сравнения на рис. 5.55 и 5.56 приведены два варианта граней — четырехугольники и треугольники.
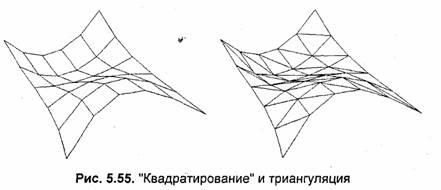
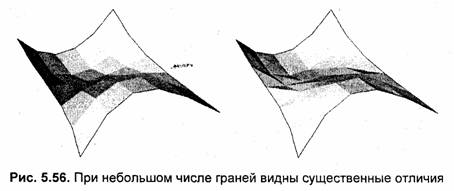
Здесь необходимо упомянуть следующие понятия. Грань называется плоском, если все ее вершины располагаются в одной плоскости трехмерного пространства. При отображении трехмерного объекта на плоскости пространственные грани (как плоские, так и неплоские) изображаются закрашенными многоугольниками — полигонами. Полигоны бывают выпуклыми и невыпуклыми. Выпуклый полигон — это фигура на плоскости, контур которой пересекается любой прямой линией только дважды. Если находится такая прямая линия, которая пересекает контур большее число раз, то это невыпуклый полигон. Это обуславливает особенности алгоритмов графического вывода. Алгоритмы вывода полигонов мы рассматривали в главе 3.
Очевидно, что любой треугольник всегда выпуклый. Таким образом, треугольная грань в пространстве всегда является плоской и отображается на плоскости выпуклым полигоном. Четырехугольная грань может быть как плоской, так и неплосйой. И та и другая четырехугольная грань может отображаться в проекции как выпуклым, так и невыпуклым полигоном. Любой четырехугольник можно изобразить в виде двух треугольников. Некоторые примеры таких полигонов приведены на рис. 5.57.
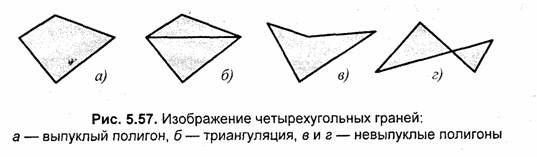
Для поверхностей вращения все четырехугольные грани являются плоскими (разумеется, если поверхность аппроксимировать так, как это сделано в предыдущих разделах — по меридианам и параллелям). Если форма — не поверхность вращения, то такие грани могут быть плоскими, а могут таковыми и не быть. Это можно отметить и для некоторых вариаций формы шара, цилиндра и тора, приведенных выше. Зачем нужны именно плоские грани? И когда необходимо применять триангуляцию? Для ответа на эти вопросы нужно учитывать многие аспекты.
Алгоритм отображения может вносить некоторую погрешность — в одних случаях заметную, а в некоторых случаях ею можно пренебречь. Триангуляция в этом плане является более корректной. В то же время, иногда изображение, построенное из треугольных граней, субъективно выглядит существенно хуже, чем при использовании четырехугольников.
С другой стороны, неплоские грани могут значительно затруднить процесс формирования изображения из-за ограничений используемой технологии. В разных графических системах в этом плане имеются существенные отличия. Так, например, при определенном ракурсе показа неплоская четырехугольная грань изображается невыпуклым полигоном. Это и приводит к проблемам. Например, в API библиотеки OpenGL в качестве графических примитивов предлагаются только выпуклые полигоны, а в API Windows полигон-примитив может быть и невыпуклым. Очевидно, что любой невыпуклый полигон может быть разрезан на треугольники (или другие выпуклые фигуры), но это усложняет алгоритм отображения.
Существенную роль играет быстродействие. Например, если в некоторой графической системе два треугольника выводятся быстрее, чем один четырехугольник, то при прочих равных условиях это может оказаться решающим фактором.
При аппроксимации поверхностей не обязательно использовать постоянный шаг сетки. Размеры и ориентация граней могут варьироваться в зависимости от кривизны участков поверхностей. Это позволяет достичь лучшего соотношения между точностью аппроксимации и количеством граней.
ЧАСТЬ II
Программирование компьютерной графики

глава 6
Разработка графических программ
для Windows
Для разработки разнообразных программ для операционной системы Windows существует много инструментальных средств. Различные средства могут воплощать в практику различные методологические подходы. Одну и ту же программу можно изготовить, как правило, несколькими способами.
В том числе и графическую программу.
Мы будем использовать язык программирования C++, а если говорить точнее, то преимущественно обычный С. Везде, где это возможно, будем обходиться простыми языковыми средствами. Такие элементы C++, как классы, будем использовать только там, где они действительно необходимы, и где без них трудно обойтись. Не следует считать это отказом от современных технологий, например, от объектно-ориентированного и компонентного программирования, визуальной технологии разработки программ. Я с большим уважением отношусь к этим действительно эффективным технологиям, но здесь они практически бесполезны (во всяком случае, последние две).
Для того чтобы сосредоточиться на особенностях программирования именно графики, при написании наших учебных программ мы не будем отвлекаться на другие аспекты программирования (например, разработку пользовательского интерфейса). Такое упрощение, как представляется, позволит детальнее ознакомиться с компьютерной графикой изнутри. Если не знать графику, то компоненты и визуальное программирование не помогут. Последнее утверждение может показаться явно спорным, однако, по-моему, это именно так— не следует писать программы, не понимая сути того, что программируешь.
Графическая программа, как конечный продукт, с одной стороны, воплощает некоторые обобщенные методы и алгоритмы. С другой стороны, эти методы и алгоритмы должны обязательно соответствовать архитектуре компьютера и операционной системы. Разумеется, можно писать программы, не зная, как устроен процессор и как работает память, однако это непрофессионально.
Важный аспект при разработке программ — это изучение особенностей операционной системы (ОС) — в нашем случае это будет Windows. Известно несколько библиотек, например MFC или OWL, которые прячут детали функционирования Windows, и может показаться, что успешно программировать можно без изучения операционной системы. Вместо этого изучается версия библиотеки, считающаяся на данный момент современной. Но библиотеки изменяются, некоторые из них вообще исчезают, и тогда необходимо изучать очередную библиотеку и инструментальную среду разработки.
Так рано или поздно приходит осознание того, что изучение самой операционной системы (которая существует значительно дольше, чем любая из библиотек и сред программирования для этой ОС) и архитектуры компьютера закладывает надежный фундамент для дальнейшего повышения квалификации, в том числе и для овладения новыми технологиями программирования.
Мы будем изучать использование функций API Windows без посредничества высокоуровневых библиотек общего назначения для разработки программ.
Потом рассмотрим графическую библиотеку OpenGL.
Из множества литературных источников, освещающих эту тему, можно порекомендовать в первую очередь документацию SDK для разработчиков Windows-программ [61] и прекрасную книгу [20].
6.1. Первый пример программы для Windows
Наша первая графическая программа названа StudEx. Она предназначена для работы в среде 32-битных ОС Windows различных версий, например, 95, 98, 2000, Millennium, NT. Программа написана на языке C++ (строго говоря, почти что на чистом С, если не считать комментариев) с использованием
функций API Windows. Текст программы состоит из трех файлов:
studex.cpp, studex.rc, studex.def.
Файл studex. cpp (это главный файл текста программы):




Приведенный выше текст программы — это только исходный текст. Его необходимо скомпилировать, чтобы получить выполняемый файл в машинных кодах. Для компиляции и отладки этой программы можно использовать разнообразные инструментальные средства программирования, например, Borland C++ 5.02, Borland C++ Builder, Microsoft Visual C++ 6.0 и другие. После создания проекта в среде системы программирования в результате компилирования получим выполняемый файл. Имя этого файла— studex.exe (или другое, что определяется при создании проекта). Запустите программу в среде Windows. После появления окна программы выберите пункт меню "Графика". На экране дисплея будет изображение, как на рис. 6.1.

6.2. Модульность программ
Приведенный выше текст первого Примера графической программы для ОС Windows достаточно объемный. Для того чтобы упростить тексты других примеров графических программ, необходимо спланировать наше дальнейшее программирование. Рассмотрим структуру главного файла (studex. срр):

Как видим, программа состоит из трех частей. Первая из них, содержащая функцию winMain, будет присутствовать во всех следующих примерах без всяких изменений. Это достаточно длинный текст, поэтому вместо того, что бы его каждый раз копировать во всех следующих примерах, создадим отдельный файл, на который будем ссылаться в дальнейшем, и назовем его winmain.срр:

В следующих примерах мы будем использовать различные варианты оконной функции wndProc. Тот вариант, что приведен для первого примера, будет часто использоваться— его также запишем в отдельный файл и назовем
winmai.nl. срр:
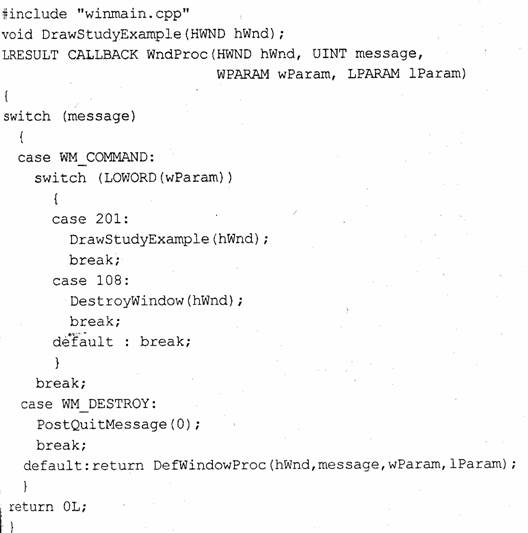
В файле winmaini.cpp содержится текст оконной функции, объявление функции DrawStudyExample И директива'#include "winmain.cpp", благодаря которой при компиляции используется текст функции winMain. Следовательно, текст первого примера программы можно трансформировать в такой:

Это значительно короче. Большой кусок программы, включающий функции создания и обслуживания окна, спрятан в отдельных файлах, ссылка на которые выполнена директивой #inciude. Такая модульность с использованием отдельных кусков текста, которые вначале собираются в единый текст и затем компилируются все вместе, может эффективно применяться лишь для небольших программ, которые мы и рассмотрим в качестве примеров. Для более сложных программ лучше использовать проекты из раздельно компилируемых модулей OBJ, а также библиотеки DLL и компоненты типа ActiveX.
6.3. Использование
графических функций API Windows
Операционная система Windows предоставляет программистам возможность использовать в своих программах сотни разнообразных функций, доступ к которым сделан в виде интерфейса API (Application Program Interface). При разработке программы на основе компьютерных языков, таких как С, C++, Pascal, в текст программы можно включать вызовы функций, которые входят в состав API Windows. После компиляции создается выполняемый файл (*.ехе), который можно запускать на разных компьютерах с различными версиями ОС Windows, и программа будет корректно выполняться. Поскольку сами функции располагаются в модулях операционной системы, а в нашей программе содержатся только вызовы функций (call), то код выполняемого файла имеет небольшой размер.
Необходимо заметить, что мы будем рассматривать программы согласно спецификации Win32 для ОС Windows версий 95, 98, частично для NT I и 2000. Существует несколько систем программирования, которые поддерживают разработку таких программ, например, Borland C++ [1 ], 59].
6.4. Контекст графического устройства
Графические функции из состава API Windows объединены в отдельную группу— подсистему GDI (Graphic Device Interface). Важная черта подсистемы GDI — аппаратная независимость многих функций от конкретного графического устройства.
Контекст графического устройства (Device Context) — это важный элемент графики в среде операционной системы Windows. Понятие контекста введено для описания того, где будет рисоваться изображение. Другими словами, контекст графического устройства указывает плоскость отображения, на которую делается графический вывод. В качестве контекста может быть окно программы на экране дисплея или страница принтера, или другое место, куда можно направить графический вывод.
Если ваша программа делает вызов графических функций API Windows,, таких как рисование точек, линий, фигур, текста и тому подобных, необходимо указывать идентификатор контекста (handle of device context) и координаты. Вызов необходимого драйвера — для экрана дисплея, принтера или другого устройства — делает уже сама Windows. Это в значительной мере освобождает программиста от второстепенных дел и облегчает разработку программ, однако желательно учитывать специфику работы конкретного устройства.
Идентификатор контекста графического устройства (hdc)— это числовое значение, знание которого дает возможность направить графический вывод в нужное место. Перед началом рисования необходимо получить это числовое значение. После рисования обычно нужно освободить, деактивизировать контекст. Несоблюдение этого требования чревато неприятными последствиями — от утечек памяти до прекращения нормальной работы программы. Корректноё использование контекста графического устройства осуществляется в такой последовательности:
1. Создание, активизация контекста, получение значения hdc.
2. Рисование с помощью графических функций API Windows.
3. Уничтожение, деактивизация контекста соответствующего hdc.
Контекст окна на экране дисплея
Для рисования в окне программы на экране дисплея можно использовать два I способа. Эти способы различаются как по особенностям получения значения I hdc, так и по возможностям рисования.
Первый способ основывается на использовании пары функций Get DC и

Функция Getoc получает hdc для. окна, заданного кодом hwnd. Например, для главного окна программы. Использование контекста графического выводя завершается вызовом функции Releaseoc. Другую функцию для освобождения контекста в этом случае использовать не следует. Такой способ работы с контекстом использован в приведенном выше примере программы. Вообще этот способ можно рекомендовать везде, за исключением рисования во время обработки сообщения wm_paint.
Второй способ. Используется исключительно в теле обработчика сообщения'
WM_PAINT оконной функции.

Во время обработки сообщения wm_paint функция BeginPaint обязательно должна вызываться первой, a EndPaint — последней.
Когда необходимо обрабатывать сообщения wm_paint? Это сообщение присылается любой программе тогда, когда повреждено изображение клиентской области окна этой программы. Повреждение изображения окна случаются довольно часто, например, при отображении на экране нескольких окон — когда на окно было наложено еще одно окно, а потом после закрытия последнего окна части изображения первого окна уже нет. Если в программе предусмотрена перерисовка изображения рабочей (клиентской) области окна путем программирования обработчика сообщения wm_paint, to это позволяет в большинстве случаев гарантировать корректное отображение окна.
Приведем пример программы, рисующей согласно второму способу.
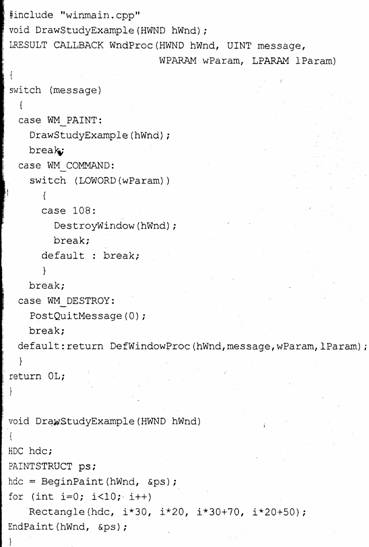
Рассмотрим, как можно нарисовать (а точнее, напечатать) что-то на принтере. Для этого также сначала необходимо получить значение hdc соответствующего графического устройства. Потом выполняется рисование. А затем контекст освобождается. Общая схема такая же. Пример программы:
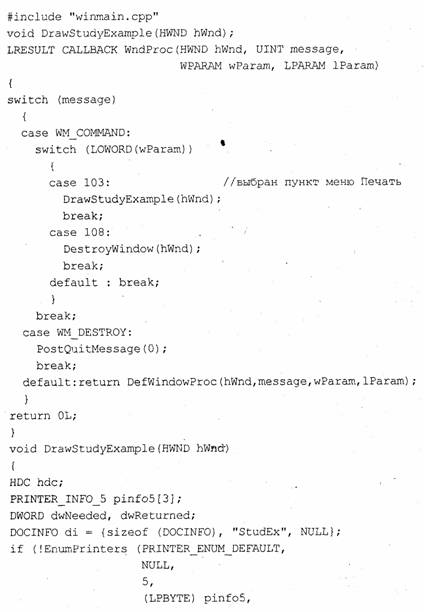
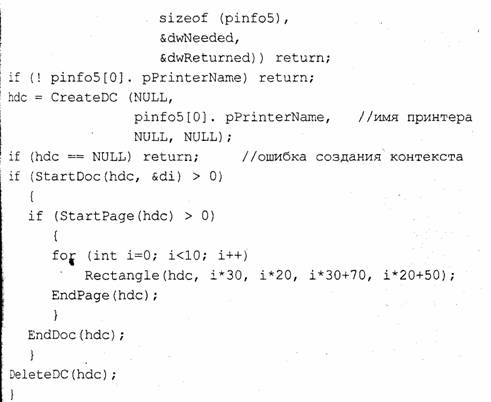
Для принтера значение hdc получить несколько сложнее. Сначала необходимо узнать имя принтера — здесь это делается с помощью функции EnumPrinters. Обратите внимание на то, что использована не одна структура, а массив из трех структур pinfo5 — это сделано согласно рекомендациям [20]. Потом создается контекст вывода с помощью функции CreateDC. Печать на принтере выполняется С ПОМОЩЬЮ функций StartDoc, Start Page, EndPage и EndDoc. После вызова функции EndDoc контекст принтера необходимо освободить С помощью функции DeleteDC.
Следует заметить, что приведенный пример предназначен для Windows 95, 98. Для Windows NT функцию DrawStudyExampie необходимо модифицировать — об этом можно узнать в документации Win32 SDK [61].
После печати на бумаге можно заметить отличия результата от изображения на экране. Прежде всего, это касается размера прямоугольников. Для лазерного принтера размеры значительно меньше, а для матричного размеры могут быть и больше. Это объясняется различными разрешающими способностями (dpi) принтеров и экрана дисплея. Кроме того, на матричном принтере рисунок может изменить пропорции — в случае, когда (dpi) по вертикали отличается от (dpi) по горизонтали. При вызове функции Rectangle мы использовали координаты в виде пикселов. Функции API Windows разрешают использовать и другие системы координат.
Контекст метафайла
Рассмотрим еще одну разновидность контекста — контекст метафайла. Здесь рисунок создается в виде файла на диске. Известны два формата метафайлов для Windows: WMF и EMF. Формат EMF более совершенный. В качестве примера приведем текст программы, записывающей рисунок в файл *.emf после выбора пункта меню "Записать Как".


Запустите программу и выберите меню "Файл \ Записать как". После определения имени файла и записи метафайла на диск в окне должно появиться следующее изображение (рис. 6.2).
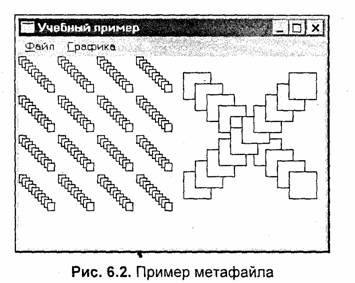
Метафайл описывает изображение в виде последовательности вызовов графических функций, использованных при создании изображения (в приведенном примере программы это 10 вызовов функции Rectangle). В метафайл записываются функции вместе со значениями аргументов-координат, границы рисунка и другая информация. Общие параметры рисунка можно узнать, если прочитать заголовок метафайла с помощью функции GetEnhMetaFileHeader.
Для отображения метафайла нужно задать границы вывода. Поскольку метафайл — векторное описание изображения, то это дает возможность при отображении плавно растягивать рисунок, причем намного лучше, чем растровые изображения. В нашей программе метафайл отображен 18 раз в контексте главного окна. Обратите внимание на крестик — здесь использовано зеркальное отображение.
В результате работы этой программы на диске должен появиться файл *.emf. Чтобы проверить содержимое файла, вызывайте любую программу, которая может читать файлы формата EMF — например, Word для Windows. Выполните вставку рисунка *.emf и вы увидите десять прямоугольников. Рисунок векторный, поэтому его можно свободно растягивать. Границы рисунка onределяются согласно диапазону координат всех элементов рисунка— apryментов вызова функции Rectangle.
Необходимо заметить, что нижний прямоугольник этого рисунка обычно выглядит поврежденным (как именно — это еще зависит от версии Word).
Этот прямоугольник рисуется согласно координатам при i = 9:
Rectangle (hdc, 9*30, 9*20, 9*30+70, 9*20+50). Координаты правого нижнего угла (э*зо+7О, 9*20+50) этого прямоугольника определяют правую и нижнюю границу всего рисунка. Границы рисунка записываются в метафайл в виде координат левого верхнего и правого нижнего углов. Чтобы узнать, какие границы определены для метафайла, можно использовать функцию

Эта функция заполняет поля структуры emh, имеющей тип enhmetaheader. Границы рисунка записываются в поля emh.rciBounds, и имеют такие значения:

Обратите внимание на то, что координаты правого нижнего угла имеют значения на единицу меньше, чем должны быть. Это — проявление особенностей функции Rectangle, рисующей правый нижний угол контура как раз на один пиксел ближе к левому верхнему углу. К тому можно привыкнуть, но почему Microsoft Word (версий 6.0 для 95 и 97-й) искажает рисунок (отрезает границы крайнего прямоугольника)? Средствами Word можно расширить границы этого рисунка, но для других файлов *. emf это может привести, например, к повреждению стиля линий. Поэтому попробуем расширить границы рисунка собственноручно, например, так:

Здесь мы сначала рисуем один белый пиксел с помощью функции setPixel, что никак не изменяет сам рисунок, но координаты его (х,у) = (9*30+70, 9*20+50) = (340, 230) будут учтены при определении границ рисунка. Запустите модифицированную программу, запишите метафайл, и попробуйте загрузить этот метафайл в редактор Word. Рисунок должен выглядеть неповрежденным.
Кроме того, в некоторых рисунках, которые записываются в метафайлы, необходимо учитывать толщину пера. В нашем случае используется перо по умолчанию, имеющее толщину в один пиксел. Если рисовать толстыми перьями, то это также может привести к ошибкам определения границ рисунка — не только для правого нижнего, а и левого верхнего углов. Рассмотрим такой пример:

В приведенном примере две функции SetPixel использованы для установления границ рисунка (-1, -1, 341, 231). Если выбросить эти две функции, то границы будут (0, 0, 339, 229), что может привести к проблемам с использованием метафайла в программе Word.
Необходимо отметить, что в нашей программе функция API piayEnhMetaFiie корректно отображает этот метафайл, поэтому к ней никаких претензий, а расширение границ с помощью функции SetPixel — это попытка исправить ошибки соответствующих прикладных программ.
Если при создании метафайла его имя отсутствует, напримерCreateEnhMetaFile (NULL, NULL, NULL, NULL), TO метафайл не будет записываться на диск, поверхность контекста будет существовать только в памяти компьютера. Такой метафайл также можно использовать, например, отображать в другом контексте помоощю функции PlayEnhMetaFile.
Контекст памяти
Рассмотрим контекст памяти (memory context), для которого поверхность рисования создается на основе битовой карты (bitmap).


Контекст в памяти создается вызовом функции createCompatibleDC. Здесь он создается по образцу контекста окна программы. Но в таком контексте отсутствует поверхность рисования. Эту поверхность создаем по образцу цветового формата поверхности окна экрана вызовом функций CreateCompatibleBitmap И SelectObject. Потом можно рисовать в соответствии с hdc. Сначала мы очищаем поверхность (закрашиваем белым цветом), а потом рисуем десять прямоугольников. Потом вызов функции BitBit, копирующей растровое изображение из контекста памяти (hdc) в контекст окна (hdcwin). После использования контекста памяти его необходимо закрыть и освободить выделенную память, которая была выделена. Здесь это сделано функциями DeleteDC и Delete Object.
Контекст памяти часто используется для "заэкранного" рисования — например, для анимации. Рассмотрим один из простейших примеров анимации — в цикле рисуется по десять прямоугольников, размеры которых изменяются от 5 до 300. Это мы сделаем на основе текста программы для предыдущих примеров.

Изображение кажется подвижным, но поскольку здесь все рисуется непосредственно в окне программы, то это воспринимается плохо. Сравните с работой следующего примера, где использован контекст памяти.
Изображение вначале рисуется в контексте памяти, а затем быстро копируется на экран с помощью функции BitBlt.
Программы КГ часто применяют подобный способ рисования — "за экраном". Этот способ называется двойной буферизацией (double buffering). Кроме анимации, использование двойной буферизации иногда позволяет ускорить рисование — если графические функции могут рисовать в контексте памяти быстрее, чем в окне на экране. Также полезно использование контекста памяти тогда, когда программа, например графический редактор, манипулирует изображением, которое по размерам больше, чем способен отобразить экран дисплея.
Параметры контекста графического устройства
Для рисования важно знать параметры графического устройства, такие как размеры области отображения, количество цветов. Для этого можно использовать функцию GetDeviceCaps:
![]()
Для того чтобы узнать необходимые параметры контекста hdc, нужно в ка-: честве аргумента index задавать соответствующие значения. Например:

Так можно узнать размеры в пикселах (сх, су), разрешающую способность (dpix, dpiY), количество бит на пиксел для цвета (bits) и много других параметров.
Такие параметры, как размеры изображения (сх, су) для окна можно получить и другими способами, например, вызовом функции GetClientRect:

Эта функция заполняет поля структуры гс типа rect. Поля rc.ieft и rc.top заполняются нулями, а поля re.right и re.bottom хранят координаты соответственно правого и нижнего края данного окна.
Графические примитивы
API Windows
Функция setPixel рисует один пиксел растра. Она имеет такие аргументы:
SetPixel (tide, х, у, clr)
где hdc— контекст, х,у — координаты, clr— цвет пиксела. Аргумент clr имеет тип 4-байтного colorref, причем три младших байта соответствуют компонентам Blue,Green,Red (в диапазоне от 0 до 255 каждая), а старший байт не используется. Цвет, кодируемый типом colorref, удобно задавать макросом RGB(r,g,b). Функция SetPixel сама имеет тип colorref— она возвращает значение цвета пиксела.
Кроме SetPixel в API Win32 есть функция Setpixeiv, работающая немного быстрее, поскольку не возвращает значения; а также предусмотрена функция для получения цвета любого пиксела растра — GetPixei.
С помощью таких функций, которые оперируют отдельными пикселами, очевидно, возможно создать любое растровое изображение. Рассмотрим, как нарисовать шар. Пусть источник света расположен далеко позади нас, а шар отражает свет согласно модели диффузного рассеяния пропорционально квадрату косинуса угла нормали. Рисование шара запрограммируем в виде t функции MySphere. Текст программы studexg. cpp.



Получим рисунок, подобный рис. 7.1. В особенности обратите внимание на то, что для качественного отображения такого рисунка необходимо установить, как минимум, 16-битный (а лучше 24- или 32-битный) видеорежим дисплея. Для 256-цветного видеорежима изображение будет плохим — много оттенков будет искажено.
Приведенный выше пример программы можно рассматривать как попытку имитации изображения объемных объектов. Эта программа имеет очень ограниченные возможности. Например, если мы попробуем сдвинуть шары, то получится так, как на рис. 7.2. Это тоже имитация объема — маленькие шары выглядят более близкими, поскольку мы их нарисовали в последнюю очередь. А как получить изображение шаров, которые частично входят вглубь один другого (рис. 7.3)?
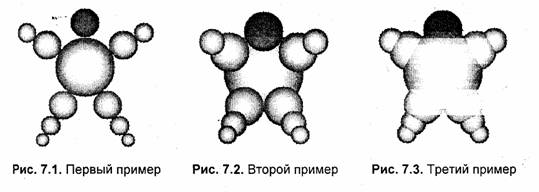
Любая последовательность рисования отдельных шаров не даст желаемого результата. Необходимо как-то отрезать части шаров. Для создания того, что нам нужно, используем универсальный метод — метод Z-буфера. Рассмотрим текст программы studex7. срр.



В этом примере для удаления невидимых точек реализован метод Z-буфера. Однако в качества меры дальности (глубины) используется не z, a z2 для упрощения вычислений — не нужно определять квадратный корень. Это вполне корректно, поскольку отрицательные значения z здесь не встречаются.
Удаление невидимых точек реализовано функцией setPixMyZ. Если текущее значение (z2) оказывается большим, чем содержимое Z-буфера, то пиксел рисуется в растре, а значение z2 записывается в Z-буфер. Необходимо заметить, что для уменьшения затрат памяти можно открывать Z-буфер не для всего окна, а только в границах рисунка.
Подвижные шары
В следующем примере использования функции SetPixel рассмотрим некоторые аспекты расчета трехмерных координат. В качестве пространственных объектов снова используем шары. Попробуем моделировать движение шаров, которые вращаются один вокруг другого (рис. 7.4).
Положение шаров зададим с помощью углов а и р. Эти углы описывают положения в локальных системах координат. Здесь определены три системы координат — две локальные для отдельных шаров и система координат (X, Y, Z) для окна программы. Для рисования шаров необходимо указывать , оконные координаты. Чтобы вычислять эти координаты, используются матрицы коэффициентов (в тексте программы матрицы имитируются одномерными массивами). Матрица matrixi отвечает преобразованию координат из системы (д;1, у1, z\) в (X, Y, Z). Матрица matrix2 — для преобразования (х2, у2, z2) в (X, Y, Z). Кроме того, указанные преобразования координат обеспечивают центрирование изображения в окне программы.
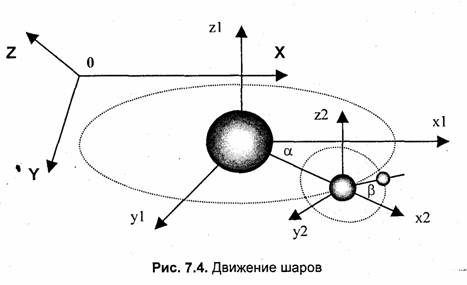
Для имитации движения использован цикл, в котором изменяются углы а и р. Цикл движения составляет один полный оборот среднего шара. Угол β изменяется быстрее, поэтому маленький шар делает несколько оборотов.
Рассмотрим текст программы studex8. срр

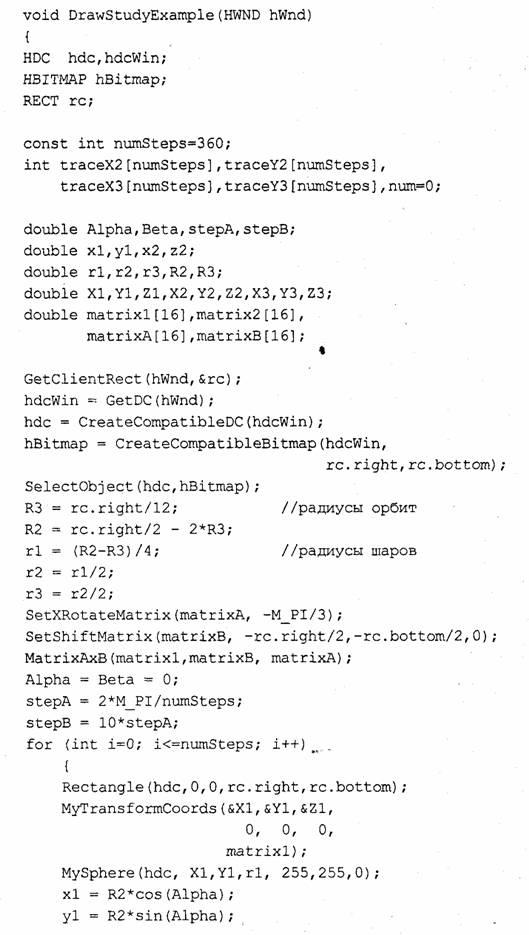



Запустите программу на выполнение, выберите пункт меню "Графика" и подождите, пока зеленый шар опишет один оборот. В результате получим изображение, как на рис. 7.5.
Необходимо заметить, что эту программу можно было бы упростить. Например, рисование эллипса трасы среднего шара лучше делать функцией Arc, a не использовать массивы для координат точек эллипса и рисовать каждую точку функцией SetPixel. Кроме того, не обязательно каждый раз рисовать центральный шар — это очень замедляет рисование (и вдобавок он — самый большой). Ускорить рисования можно, если рисование центрального шара вынести из общего цикла — нарисовать его лишь один раз, а в цикле стирать изображения только двух подвижных шаров.
Кроме того, в этом примере так подобран ракурс обзора, чтобы упростить программирование трехмерного показа. В первую очередь это касается удаления невидимых точек методом сортировки объектов по глубине (дальности). В программе использована простая сортировка по глубине для второго и третьего шаров путем сравнения координат Z центров шаров. Центральный шар здесь рисуется всегда первым — но будет ошибкой, если увеличить угол наклона плоскости проецирования. Для решения этой проблемы можно сделать сортировку по глубине более универсальной — для всех трех шаров
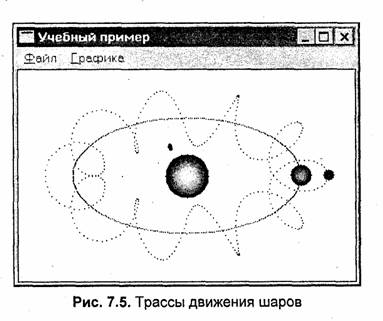
Интересный рисунок можно получить, если использовать основные идеи программы studexs и предыдущей программы studex7. Используем Z-буфер для рисования спирали (рис. 7.6).

Текст соответствующей программы (studex9) дадим только для тех функций, которые отличаются от соответствующих функций программ studex7,8.
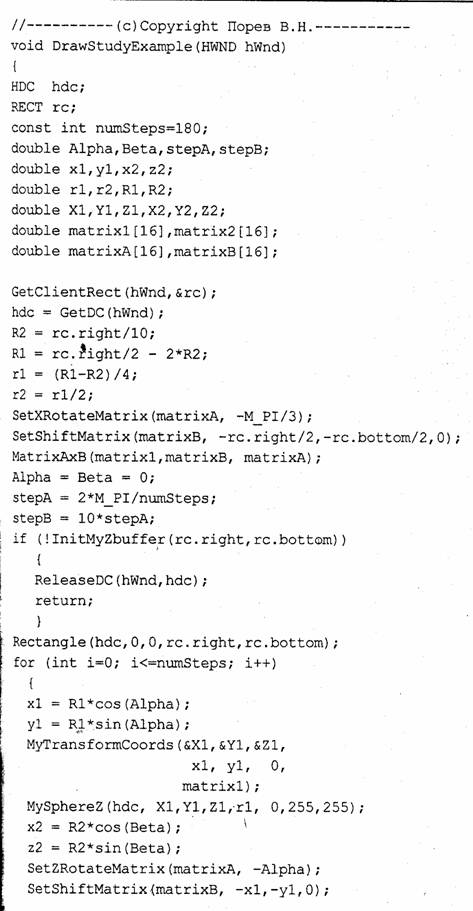


В приведенных выше примерах вызов функций setPixel — самое критичное место программы с точки зрения быстродействия. Можно усовершенствовать отдельные фрагменты этих примеров, но, как кажется, скорость увеличится не намного. Обычно, чем больше делается вызовов SetPixel, тем больше требуется времени на создание изображения. Необходимо искать возможности использовать функции, которые рисуют сразу много пикселов. Это можно считать общим правилом. Однако можно найти и исключения из этого правила— когда процесс расчета точек изображения длится дольше чем собственно рисование пикселов
.