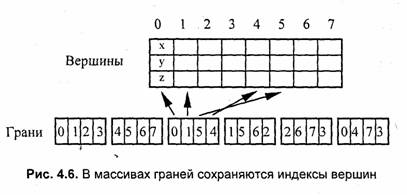
Второй способ описания. Для такого варианта координаты восьми вершин сохраняются без повторов. Вершины пронумерованы (рис. 4.5), а каждая грань дается в виде списка индексов вершин (указателей на вершины).

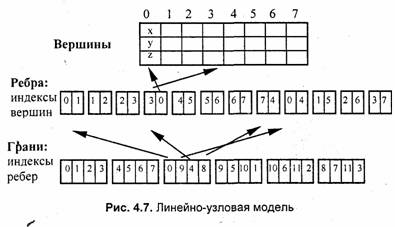
Для сравнения объемов памяти этих трех вариантов необходимо определиться с разрядностью данных. Предположим, что разрядность координат и индексов составляет четыре байта. Это соответствует, например, типу чисел с плавающей точкой float для координат и целому типу long для индексов (названия этих типов на компьютерном языке С, C++). Тогда затраты памяти в байтах составляют:

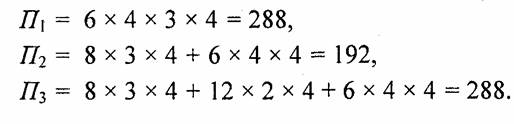
Пусть для координат отведено 8 байтов (тип с плавающей точкой double), a для индексов — 4 байта. Тогда:

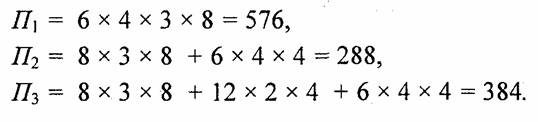
     Когда разрядность для координат больше, чем для индексов, то ощутимо преимущество второго и третьего вариантов. Наиболее экономичным можно считать второй вариант. Необходимо заметить, что такой вывод мы сделали для куба. Для других типов объектов соотношение вариантов может быть иным. Кроме того, необходимо учитывать такие варианты построения структур данных: использован ли единый массив для всех объектов, или же для каждого объекта предназначен отдельный массив (при объектно-ориентированном стиле программирования каждый объект можно сохранять в отдельном классе). Это может обуславливать разную необходимую разрядность для индексов.

А теперь сравним эти три разновидности векторной полигональной модели, учитывая другие аспекты.

Скорость вывода полигонов. Если для полигонов необходимо рисовать линию контура и точки заполнения, то первый и второй варианты близки по быстродействию — и контуры, и заполнения рисуются одинаково. Отличия в том, что для второго варианту сначала надо выбирать индекс вершины, что замедляет процесс вывода. В обоих случаях для смежных граней повторно  рисуется общая часть контура. Для третьего варианта можно предусмотреть более совершенный способ рисования контура— каждая линия будет рисоваться только один раз, если в массивах описания ребер предусмотреть бит, означающий, что это ребро уже* нарисовано. Это обуславливает преимущества третьего варианта по быстродействию.

Блокирование повторного рисования линий контуров смежных граней позволяет решить также проблему искажения стиля линий, если линии контуров не сплошные, а, например, пунктирные.

Топологический аспект. Представим, что имеется несколько смежных граней. Что будет, если изменить координаты одной вершины в структурах данных? Результат приведен на рис. 4.8.

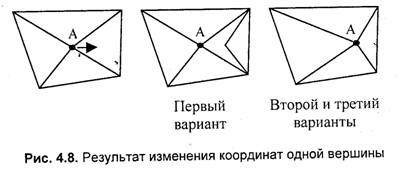
Поскольку для второго и третьего вариантов каждая вершина сохраняется в одном экземпляре, то изменение ее координат автоматически приводит к изменению всех граней, в описании которых сохраняется индекс этой вершины. Это полезно, например, в геоинформационных системах при описании соседних земельных участков или других смежных объектов. Следует заметить, что подобного результата можно достичь и при структуре данных, соответствующей первому варианту. Можно предусмотреть поиск других вершин, координаты которых совпадают с координатами точки А.-

Иначе говоря, поддержка такой операции может быть обеспечена как структурами данных, так и алгоритмически.

Однако когда нужно разъединить смежные грани, то для второго и третьего вариантов это сложнее, чем для первого — необходимо записать в массивы новую вершину, новые ребра и определить индексы в массивах граней. При разработке новой графической системы обычно приходится решать такой вопрос,: какие операции реализовывать только алгоритмически, а какие обеспечивать структурами данных? Ответ на это можно дать, проанализировав много других факторов. Здесь мы рассмотрели только малую часть из них.

Положительные черты векторной полигональной модели:

□ удобство масштабирования объектов. При увеличении или уменьшении объекты выглядят более качественно, чем при растровых моделях описания. Диапазон масштабирования определяется точностью аппроксимации и разрядностью чисел для представления координат вершин;

□  небольшой объем данных для описания простых поверхностей, которые адекватно аппроксимируются плоскими гранями;

□  необходимость вычислять только координаты вершин при преобразованиях систем координат или перемещении объектов;

□  аппаратная поддержка многих операций в современных графических видеосистемах, которая обуславливает достаточную скорость для анимации.

Недостатки полигональной модели:

□  сложные алгоритмы визуализации для создания реалистичных изображений; сложные алгоритмы выполнения топологических операций, таких, Например, как разрезы;

□ аппроксимация плоскими гранями приводит к погрешности моделирования. При моделировании поверхностей, которые имеют сложную фрактальную форму, обычно невозможно увеличивать количество граней из-за ограничений по быстродействию и объему памяти компьютера.

Воксельная модель

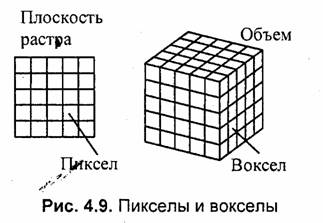
Вексельная модель -— это трехмерный растр. Подобно  тому, как пикселы . располагаются на плоскости 2О-изображения, так и вокселы образовывают трехмерные объекты в определенном объеме (рис. 4.9). Воксел — это элемент объема (voxel — volume element).

       Как мы знаем, каждый пиксел должен иметь свой цвет. Каждый воксел также имеет свой цвет, а, кроме того, прозрачность. Полная прозрачность воксела означает пустоту соответствующей точки объема. При моделировании объема каждый воксел представляет элемент объема определенного размера. Чем больше вокселов в определенном объеме и меньше размер вокселов, тем точнее моделируются трехмерные объекты — увеличивается разрешающая способность.

Для современной КГ вексельный метод считается одним из перспективных. Его используют в компьютерных системах для медицины. Например, при сканировании томографом (computer tomography) получаются изображения срезов объекта, которые потом объединяются в виде объемной модели для дальнейшего анализа [53]. Вексельный метод используется в геологии, сейсмологии, в компьютерных играх [50, 56]. Вокселы также используются для графических устройств отображения, которые создают действительно объемные изображения [37].

Положительные черты вексельной модели:

□ позволяет достаточно просто описывать сложные объекты и сцены; простая процедура отображения объемных сцен;

□ простое выполнение топологических операций над отдельными объектами и сценой в целом. Например, просто выполняется показ разреза — для этого соответствующие вокселы можно сделать прозрачными.

Недостатки вексельной модели:

□  большое количество информации, необходимой для представления объемных данных. Например, объем 256x256x256 имеет небольшую разрешающую способность, но требует свыше 16 миллионов вокселов;

□  значительные затраты памяти ограничивают разрешающую способность, точность моделирования; большое количество вокселов обусловливает малую скорость создания изображений объемных сцен;

           □  как и для любого растра,  возникают проблемы при увеличении или уменьшении изображения. Например, при увеличении ухудшается разрешающая способность изображения.

Равномерная сетка

Эта модель описывает координаты отдельных точек поверхности следующим способом (рис. 4.10). Каждому узлу сетки с индексами (i, j) приписывается значение высоты Z_ij. Индексам (i, j) отвечают определенные значения координат (х, у). Расстояние между узлами одинаковое— dx по оси х и dy по оси y

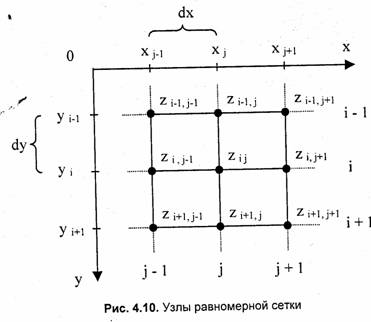
Фактически, такая модель — двумерный массив, растр, матрица, каждый элемент которой сохраняет значение высоты.

Не каждая поверхность может быть представлена этой моделью. Если в каждом узле записывается только одно значение высоты, то это означает, что поверхность описывается однозначной функцией z - f(x, у). Иначе говоря, это такая поверхность, которую любая вертикаль пересекает только один раз.

Не могут моделироваться также вертикальные грани. Необходимо заметить, что для сетки не обязательно использовать только декартовые координаты. Например, для того чтобы описать поверхность шара однозначной функцией, можно использовать полярные координаты. Равномерная сетка часто используется для описания рельефа земной поверхности.

Рассмотрим, как можно вычислить значения высоты для любой точки внутри границ сетки. Пусть ее координаты равны (х, у). Надо найти соответствующее значение z.  Решением такой задачи является интерполяция значений координат z ближайших узлов (рис. 4.11).

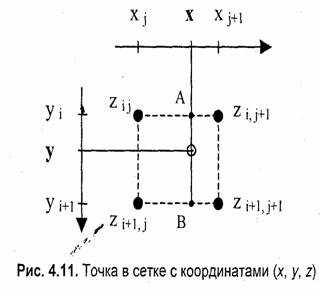
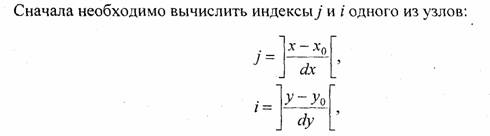
где ]а[ — целая часть числа а, то есть наибольшее целое, которое не превышает а.

          Далее используем, например, линейную интерполяцию. Для этого сначала найдем значения z в точках А и B. Из пропорции

 Положительные черты равномерной сетки:

□ простота описания поверхностей;

□ вазможность быстро узнать высоту любой точки поверхности простой интерполяцией.

Недостатки равномерной сетки:

□ поверхности, которые соответствуют неоднозначной функции высоты в   узлах сетки, не могут моделироваться;

□ для описания сложных поверхностей необходимо большое количество    узлов, которое может быть ограничено объемом памяти компьютера;

 □ описание отдельных типов поверхностей может быть сложнее, чем в других моделях. Например, многогранная поверхность требует избыточный объем данных для описания по сравнению с полигональной моделью

Неравномерная сетка. Изолинии

 Неравномерной сеткой назовем модель описания поверхности в виде множества отдельных точек {(х₀, у₀, z₀), (х₁, y₁ z₁), ..., (х_п-1  у_п-1, z_п-1)}, принадлежащих поверхности. Эти точки могут быть получены, например, в результате  измерений поверхности какого-нибудь объекта с помощью определенного  оборудования.

 Такую модель можно считать обобщением для некоторых рассмотренных нами моделей. Например, векторная полигональная модель и равномерная  сетка могут считаться разновидностями неравномерной сетки. Эти разновидности мы рассмотрели в отдельности, так как они играют важную роль для решения задач  КГ. А вообще, может существовать много вариантов классификации способов описания поверхностей. Следует учитывать определенную условность нашего перечня моделей поверхностей, последовательность перечисления таких моделей может быть и другой.

Рассмотрим модель поверхности в виде множества точечных значений, логически никак не связанных между собой. Неравномерность задания опор-

ных точек усложняет определение координат для других точек поверхности, которые не совпадают с опорными точками. Нужны специальные методы пространственной интерполяции. Так, например, можно поставить такую задачу — по известным координатам {х, у) вычислить значения координаты z. Для этого необходимо найти несколько самых близких точек, а потом вычислить искомое значение z, исходя из взаимного расположения этих точек в проекции (х, у). Как мы уже рассмотрели выше, для равномерной сетки это намного проще — поиска фактически нет, мы сразу рассчитываем индексы самых близких опорных точек. Еще одна задача— отобразить поверхность.

Эту задачу можно решать несколькими способами, в том числе триангуляцией. Процесс триангуляции можно представить себе так (рис. 4.12). Сначала находим первые три самые близкие друг другу точки — и получаем одну плоскую треугольную грань. Потом находим точку, ближайшую к этой грани, и образовываем смежную грань. И так далее, пока не останется ни одной отдельной точки. Это общая схема, в литературе описано много разных способов триангуляции. Довольно часты ссылки на триангуляцию Делоне [48].

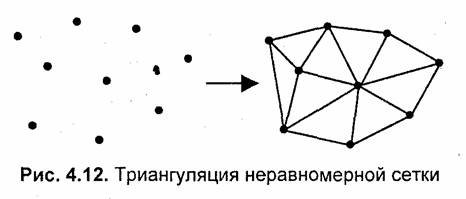
Описание поверхности треугольными гранями можно уже считать разновидностью векторной полигональной модели. В англоязычной литературе для  нее встречается такое название: TIN (Triangulated Irregular Network). После  триангуляции получаем полигональную поверхность, отображение которой  сделать уже достаточно просто.

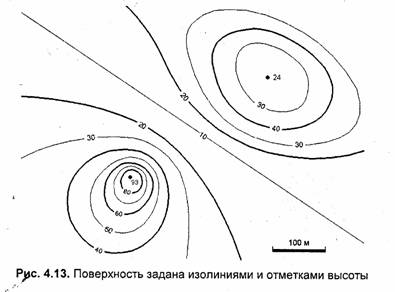
Рассмотрим еще один из вариантов описания поверхности — изолинии высоты. Любая изолиния состоит из точек, представляющих одно числовое  значение какого-то показателя, в данном случае—. значение высоты  (рис. 4.13, 4.14). Изолинии высоты также можно вообразить себе как контуры  разреза поверхности горизонтальными плоскостями (поэтому для изолиний  высоты часто применяется название "горизонтали").

Описание поверхности изолиниями высоты часто используется, например,  в картографии. По бумажной карте можно с определенной точностью рассчитать высоты в точках местности, углы наклона и прочие параметры рельефа. Необходимо заметить, что описание рельефа земной поверхности изолиниями высоты неправильно представлять как разрезы горизонтальными  плоскостями, ибо поверхность Земли не плоская. Если бы Земля была шаром,  то изолинии высоты можно было бы трактовать как изолинии радиусов. Однако Земля — это не шар, она имеет намного более сложную форму, названную геоидом. В геодезии и картографии геоид аппроксимируют с определенной точностью разнообразными эллипсоидами. Таким образом, здесь можно говорить об изолиниях некоторых условных высот в специальных системах координат.

Конечно, для описания поверхности можно использовать не только изолинии высоты, но и другие изолинии, например x- или y-изолинии.

В компьютерных системах изолинии часто описываются векторно —  полилиниями. Используются также изолинии в виде сплайновых кривых.

          Точки, которые составляют изолинии, и отдельные опорные точки располагаются неравномерно. Это усложняет расчет координат точек поверхности. В графических компьютерных системах для выполнения многих операций, и в первую очередь — для показа поверхности, обычно необходимо преобразовывать описание поверхности в другую форму. Преобразование изолиний в полигональную модель также выполняется методами триангуляции (здесь алгоритмы триангуляции сложнее, чем для триангуляции отдельных точек). Для преобразования неравномерной сетки в равномерную используют специальную интерполяцию.

       Положительные черты неравномерной сетки: использование отдельных опорных точек, наиболее важных для заданной формы поверхности, обуславливает меньший объем информации по сравнению с другими моделями, например, с равномерной сеткой; наглядность показа рельефа поверхности изолиниями на картах, планах.

Недостатки: невозможность или сложность выполнения многих операций над поверхностями; сложные алгоритмы преобразования в другие формы описания поверхностей.

Преобразование моделей описания поверхности

Рассмотрим, как можно выполнить преобразование моделей описания поверхности. Сделаем это на примере преобразования неравномерной сетки в равномерную. Задачу можно сформулировать так: поверхность описана в виде точечных значений, изолиний и площадных изообластей. Необходимо построить равномерную сетку так, чтобы она представляла эту поверхность с определенной точностью,

Для решения данной задачи ,можно использовать алгоритм, предложенный автором этой книги и реализованный в геоинформационной системе ГИС "ОКО" в 1996 году [57].

Сначала рассмотрим аспекты точности алгоритма и ограничения для его использования.

Равномерную сетку можно рассматривать как растр. Расстояние между узлами сетки в плоскости (хoу) обуславливает разрешающую способность такого растра и определяет точность моделирования по осям х и у. Конечно, чем меньше расстояние между узлами, тем больше точность моделирования, но это ведет к возрастанию количества узлов и соответственно увеличивает размеры растра. Таким образом, мы определили размер растра по горизонтали (с_х) и вертикали (с_у).     

Необходимо также учесть дискретность представления чисел в компьютере при хранении в памяти значений в узлах сетки. В современных цифровых компьютерах числа обычно представляются в форматах с разрядностью, кратной 8 (байт). Однобайтовые целые числа дают 256 градаций, двухбайтовые— 65 536 и так далее. Можно также использовать и форматы с плавающей точкой.

           Выбираем формат чисел для кодирования пикселов растра. Одной из основных особенностей предложенного алгоритма является то, что число 0 для каждого пиксела указывает на неопределенное значение высоты (пустоты до интерполяции). Это означает, что, например, для однобайтовых пикселов высота имеет не 256, а 255 градаций. Дискретность значений высоты = = диапазон значений /255.-

Разумеется, лучше использовать большую разрядность, чем 8 бит. Основное ограничение — объем памяти, необходимый для растра:

П = сх .  су  (байтов на пиксел).

Все это необходимо учитывать для построения равномерной сетки поверхности с необходимой точностью.

Общая схема алгоритма

            1. Открываются два массива для растров: А и В. Каждый растр имеет размер сх x су   пикселов.

2.  В растре А обнуляются все его пикселы.

3.  В растре А отображаются изообласти высот в виде точечных значений, изолицнй и заполненных фигур (полигонов). Для отображения этих элементов используем известный алгоритм растеризации для линий и полигонов (для точек это тривиально — отдельные пикселы). Каждый пиксел рабочего растра представляет значение высоты согласно выбраннрму способу кодирования. Нулевые пикселы растра (пустоты) отвечают неопределенности высоты.

4.  Заполняются пустоты. В процессе заполнения пикселы результата записываются в растр В. В ходе заполнения пустот вычисляется R_max.

5.  Если R_max < 2, то интерполяция закончена. Результат— равномерная сетка — находится в массивах растра В.

6.  Проводятся контуры на границах раздела областей заполнения. В процессе оконтуривания пикселы результата записываются в растр А.

7.   Переход к пункту 4.

В результате работы этого алгоритма мы получаем растр, в котором нет ни одного нулевого пиксела, то есть высоты определены для всех узлов сетки.

Продолжим описание алгоритма согласно приведенной выше общей схеме. В пункте 3 точечные, линейные и площадные изообласти высоты отображаются как обычные пикселы, линии и полигоны. При таком отображении существует проблема "одного пиксела". Она обусловлена тем, что некоторые алгоритмы растеризации могут различно располагать пикселы, например, для линии. Для линии необходимо использовать алгоритмы, способные отрабатывать нецелые координаты вершин. Это касается и полигонов. Конечно, использование таких алгоритмов приводит к уменьшению скорости, но главное здесь — точность. Точность растеризации в значительной степени предопределяет точность преобразования в равномерную сетку.

В ходе заполнения анализируются пикселы рабочего растра, и результаты записываются в другой растр. Для этого и предусмотрены два массива. Необходимо отметить, что пункт 4 алгоритма заполнения можно упростить, если при его выполнении не копировать ненулевые пикселы, а перед началом сканирования растра (п. 2) сразу скопировать весь рабочий растр в другой  массив. Это позволяет ускорить работу при условии, что групповое копирование блоков памяти выполняется быстрее.

Проведение контуров. Оконтуривание можно выполнить методами локальной фильтрации изображения растра. Например, таким способом:

В процессе оконтуривания в растре А появляются новые контуры на границе областей заполнения. Линии контуров образовываются пикселями, значение (цвет) которых равно полусумме пикселов областей заполнения, а располагаются новые контуры посредине старых, то есть, выполняется линейная интерполяция высоты. В растре Л также хранятся предыдущие линии контуров. Таким образом, с каждым циклом заполнения-оконтуривания количество контуров изолинии удваивается. Так длится до тех пор, пока контурные лишний не сомкнутся — нечего будет заполнять. Количество циклов интерполяции оценивается как двоичный логарифм расстояния между ненулевыми пикселами растра, на котором отображены исходные данные.

Поиск самого близкого ненулевого пиксела. Эта процедура использована в алгоритме заполнения. Для того чтобы найти пиксел, ближайший к точке 1(х,у), можно, казалось бы, сделать, так: последовательно увеличивать радиус, анализируя пикселы, располагающиеся на окружности. Однако в растре это делать нельзя. Если увеличивать радиус окружности, используя +1, то будет пропущено много точек растра, а если радиус окружности увеличивать шагами, меньшими 1, то много пикселов будет проанализировано повторно.

Быстро и просто этот поиск можно осуществить, если идти по контуру квадрата (рис. 4.15). Однако точки на периметре квадрата имеют различное расстояние до центра. Решение этой проблемы заключается в организации двухэтапного цикла поиска. Сначала последовательно увеличиваем размер квадрата с Центром в точке (х, у) до тех пор, пока на периметре не обнаружится ненулевой (значащий) пиксел растра. Рассчитываем расстояние R\ Если это расстояние больше, чем (размер квадрата + 1), то начинаем второй этап поиска. Для этого продолжаем увеличивать размер квадрата вплоть до значения R₁. Если при этом находятся новые точки с расстоянием R₂ < R₁, то поиск продолжается, но максимальный размер окрестности ограничиваем уже R₂. Здесь необходимо пояснить, что в качестве размера квадрата здесь считается половина его стороны.

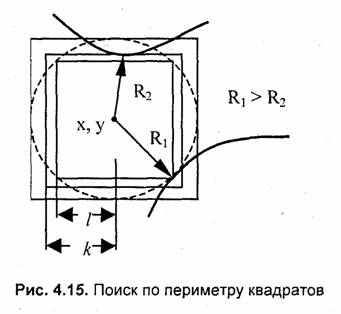
Процедура поиска пикселов по периметру квадрата названа здесь ППК(l, х_с, у_с, r), где l— половинный размер квадрата; х_с и у_с — координаты центра квадрата; r — расстояние для сравнения — если находится пиксел с большим расстоянием, то он не учитывается. В результате работы процедуры ППК определяется" цвет найденного пиксела (с) и рассчитывается расстояние до центра (R).

          Алгоритм для ППК может быть, например, таким:

Рассмотрим пример работы приведенного алгоритма преобразования неравномерной сетки в равномерную. На рис. 4.16 изображена модель некоторой i поверхности в виде изообластей высоты.

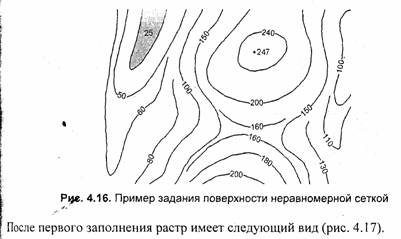
 Это уже равномерная сетка высоты. Однако поверхность будет негладкой,  иметь большие ступени. Необходимо продолжать интерполяцию дальше.

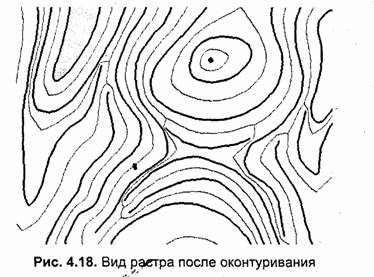
 Потом выполняется оконтуривание (рис. 4.18).

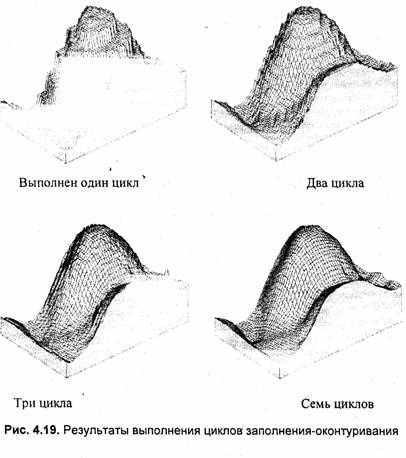
 И так далее — выполняются циклы заполнения-оконтуривания. Всего было  выполнено 7 циклов. После выполнения каждого цикла равномерная сетка  все более точно соответствует гладкой поверхности. Это изображено на  рис. 4.19.

4.2. Визуализация объемных изображений

Любой объект, в том числе и объемный, может быть изображен различными

 способами. В одном случае необходимо показать внутреннюю структуру объектов, в другом — внешнюю форму объекта, в третьем — имитировать

 реальную действительность, в четвертом — поразить воображение зрителя

 чем-то неизвестным. Условно разделим способы визуализации по характеру

 изображений и по степени сложности соответствующих алгоритмов на такие

 уровни:

1. Каркасная ("проволочная") модель.

2. Показ поверхностей в виде многогранников с плоскими гранями или

    сплайнов с удалением невидимых точек.

3. То же, что и для второго уровня,   плюс сложное закрашивание объектов    для имитации отражения света, затенения, прозрачности, использование    текстур.

        На рис. 4.20—'4.26 изображены различные способы показа трехмерных объектов в порядке усложнения используемых алгоритмов.

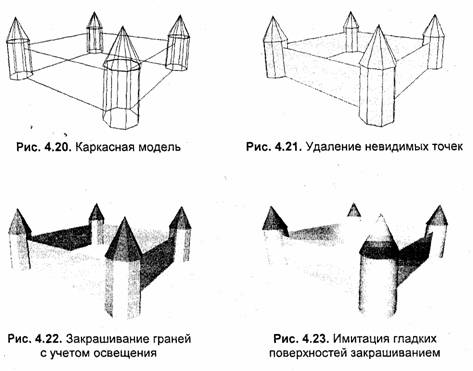
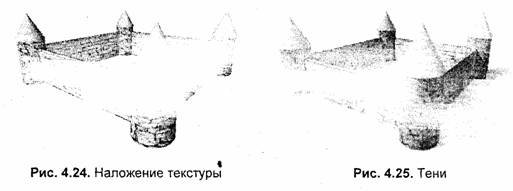
Простейшая каркасная модель часто применяется в процессе редактирования объемных объектов. Визуализация второго уровня используется для упрощенного показа объемных объектов. Например, для графиков функций z = f(x,y) (в виде рельефа поверхности) часто достаточно показать все грани сетки одним цветом, но зато необходимо обязательно удалить невидимые точки. Это более сложная процедура по сравнению с выводом каркасного изображения.

        Сложность процесса графического вывода возрастает по мере приближения к некоторому идеалу для компьютерной графики — создания полной иллюзии естественных, живых, реалистичных изображений. Усилия многих ученых и

инженеров во всем мире направлены на разработку методов и средств достижения этой цели. В этом плане наиболее полно ощущается связь компыотерной графики с естественными науками, с дисциплинами, посвященными изучению окружающего нас мира. Например, для создания реалистичных изображений необходимо учитывать законы оптики, описывающие свет и тень, отражение и преломление. Компьютерная графика находится на стыке многих дисциплин и разделов науки.

Каркасная визуализация

Каркас обычно состоит из отрезков прямых линий (соответствует многограннику), хотя можно строить каркас и на основе кривых, в частности сплайновых кривых Безье. Все ребра, показанные в окне вывода, видны — как ближние, так и дальние.

 Для построения каркасного изображения надо знать координаты всех вершин  в мировой системе координат. Потом преобразовать координаты каждой  вершины в экранные координаты в соответствии с выбранной проекцией.  Затем выполнить цикл вывода в плоскости экрана всех ребер как отрезков  прямых (или кривых), соединяющих вершины

.

Показ с удалением невидимых точек

 Здесь мы будем рассматривать поверхности в виде многогранников или полигональных сеток. Известны такие методы показа с удалением невидимых  точек: сортировка граней по глубине, метод плавающего горизонта, метод  Z-буфера [28, 32].

Сортировка граней по глубине. Это означает рисование полигонов граней в  порядке от самых дальних к самым близким. Этот метод не является универсальным, ибо иногда нельзя четко различить, какая грань ближе (рис. 4.27).  Известны модификации этого метода, которые позволяют корректно рисовать такие грани, они описаны в [28]. Метод сортировки по глубине эффективен для показа поверхностей, заданных функциями z =f(x,y) (рис. 4.28).

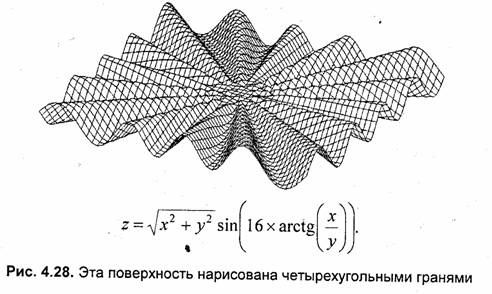
Метод плавающего горизонта. В отличие от предыдущего метода при методе плавающего горизонта грани выводятся в последовательности от ближайших к самым дальним. На каждом шаге границы граней образовывают две ломаные линии — верхний горизонт и нижний горизонт. Во время вывода каждой новой грани рисуется только то, что выше верхнего горизонта, и то, что ниже нижнего горизонта. Соответственно, каждая новая грань поднимает верхний и опускает нижний горизонты. Этот метод часто используют для показа поверхностей, которые описываются функциями z —f(x,y).

Метод Z-буфера. Метод основывается на использовании дополнительного массива, буфера в памяти, в котором сохраняются координаты Z для каждого пиксела растра. Координата Z отвечает расстоянию точек пространственных объектов до плоскости проецирования. Например, она может быть экранной координатой Z в системе экранных координат (X, Y,Z), если Z перпендикулярна плоскости экрана.

           Рассмотрим алгоритм рисования объектов согласно этому методу. Пусть, чем ближе точка в пространстве к плоскости проецирования, тем больше значение Z. Тогда сначала Z-буфер заполняется минимальными значениями. Потом начинается вывод всех объектов. Причем не имеет значение порядок вывода объектов. Для каждого объекта выводятся все его пикселы в любом порядке. Во время вывода каждого пиксела по его координатам (X, Y) находится текущее значение Z в Z-буфере. Если рисуемый пиксел имеет большее значение Z, чем значение в Z-буфере, то это означает, что эта точка ближе к объекту. В этом случае пиксел действительно рисуется, а его Z-координата записывается в Z-буфер. Таким образом, после рисования всех пикселов всех объектов растровое изображение будет состоять из пикселов, которые соответствуют точкам объектов с самыми большими значениями координат Z, то есть видимые точки — ближе всех к нам.

 Этот метод прост и эффективен благодаря тому, что не нужно ни сортировать  объекты, ни сортировать их точки. При рисовании объектов, которые описываются многогранниками или полигональными сетками, манипуляции со : значениями Z-буфера легко совместить с выводом пикселов заполнения полигонов плоских граней.

В настоящее время метод Z-буфера используется во многих графических 3 d- акселераторах, которые аппаратно реализуют этот метод. Наиболее целесообразно, когда акселератор имеет собственную память для Z-буфера, доступ  к которой осуществляется быстрее, чем к оперативной памяти компьютера.  Возможности аппаратной реализации используются разработчиками и пользователями компьютерной анимации, позволяя достичь большой скорости  прорисовки кадров.

4.3. Закрашивание поверхностей

В этом разделе мы рассмотрим методы, которые позволяют получить более- менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками. Эти методы достаточно подробно описаны в [9, 28, 32], а также в [58, 60].

Модели отражения света

Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.

Зеркальное отражение света. Угол между нормалью и падающим лучом (0)

  равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).

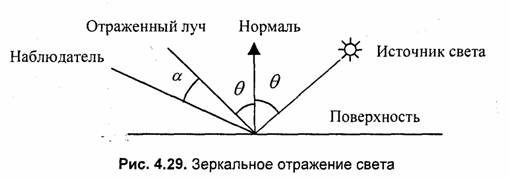
Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм*[30].

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов 9, близких к 90 градусам [13, 30].

Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cosay, где а — угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки [28]. Запишем это таким образом:

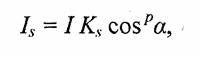
где I— интенсивность излучения источника, К_х— коэффициент пропорциональности.

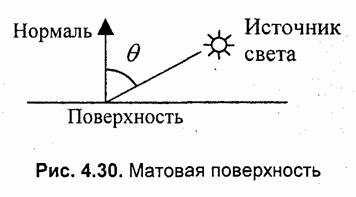
          Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка, бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отсаженного света поопопциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).

 где I— интенсивность источника света, K_d— коэффициент, который учитывает свойства материала поверхности. Значение Kj находится в диапазоне от

0 до 1 [28]. Интенсивность отраженного света не зависит от расположения наблюдателя.

Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых  поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:

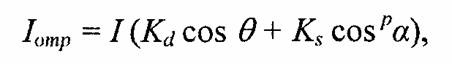
где константы K_d, K_s определяют отражательные свойства материала.

 Согласно этой формуле интенсивность отраженного света равна нулю для г некоторых углов в и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

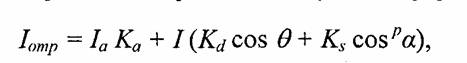
где 1_а — интенсивность рассеянного света, К_а — константа.

          Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на  практике часто реализуют модель, выражаемую эмпирической формулой [28]:

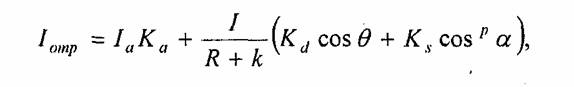
где R — расстояние от центра проекции до поверхности, к — константа.

Как определить цвет закрашивания точек объектов в соответствии с данной  моделью? Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит  дело с цветными источниками света, освещающими цветные поверхности.  Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициенты К_а и K_d различны для разных компонент — они выражают собственный цвет  поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент К_х будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.

Алгебра векторов

Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как |R| и вычисляется следующим образом:

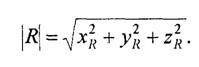
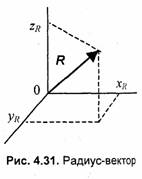
Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.

1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а<0 вектор X имеет противоположное направление вектору V. Если V— это радиус-вектор, то координаты вектора результата будут {a .х_v, а .у _v, a. z_v), то есть каждая координата вектора умножается на число а.

2.Сложение векторов С = А+В. Результат сложения — это вектор, соответствующий одной из диагоналей параллелограмма, сторонами которого являются векторы А и В (рис. 4.32). Все три вектора лежат в одной плоскости. Для радиус-векторов А и В координаты вектора результата определяются так:

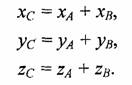
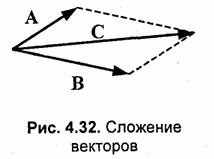
Разность двух векторов С = А - В можно определить через операцию сложения С = А + (-В). Вектор разности соответствует другой диагонали параллелограмма, изображенного на рис. 4.32. При вычитании радиус-векторов соответствующие координаты вычитаются:

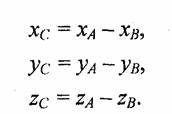
 3. Скалярное произведение векторов с =А'В. Результатом операции является  число (скаляр), которое равно произведению длин векторов на косинус  угла между ними:

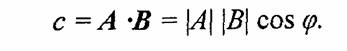
Если А и В — это радиус-векторы, то результат можно вычислить через координаты следующим образом:

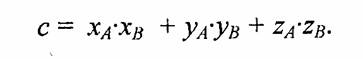
. Векторное произведение векторов С = АхВ. Результатом операции является вектор, перпендикулярный к плоскости параллелограмма, образованного сторонами векторов А и В, а длина вектора равна площади этого параллелограмма — подобно тому, как изображено на рис. 4.33.

В случае, когда векторы А и В являются радиус-векторами, координаты вектора результата С вычисляются по формулам:

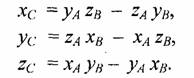
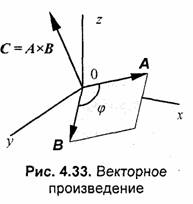
Обратите внимание на то, что АхВ = -ВхА.

          Иными словами, порядок сомножителей определяет   направление   вектора   результата.

В этом можно убедиться, если в формуле координат поменять местами координаты векторов A и В.                                                                                   

Кроме того, направление вектора результата операции АхВ зависит и от расположения   координатных   осей   (система   координат,   изображенная  на  рис. 4.33, называется левой [16]). Назовите ось у осью х, а ось х — осью у  (получится правая система), а также соответственно поменяйте местами координаты  x и у  векторов А и В в формуле векторного произведения. В результате такой перестановки координаты вектора С поменяют знак, то есть вектор будет иметь противоположное направление.

Вычисление нормалей и углов отражения

                    Вычисление координат вектора нормали. Рассматривая модели отражения света, вы, наверное, обратили внимание на то, что нормаль к поверхности  является важным элементом. Определение вектора нормали к поверхности в заданной точке может быть выполнено различными способами. В значительной степени это определяется типом модели описания поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных производных функций описания [19].  Например, если поверхность задана параметрическими функциями

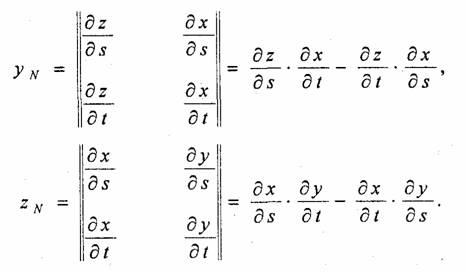
В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная поверхность. Рассмотрим одну ее плоскую грань в виде треугольника (рис. 4.34). Для вычисления  координат вектора нормали воспользуемся векторным произведением любых  двух векторов, лежащих в плоскости грани. В качестве таких векторов могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены нами только для радиус-векторов. Чтобы перейти к радиус-векторам, введем новую систему координат, центр которой совпадает с вершиной , а оси параллельны осям прежней системы. Координаты вершин в новой системе:

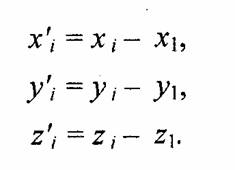
         Теперь назовем ребро (1-2) вектором А, а ребро (1-3) — вектором В, как показано на рис. 4.35. Таким образом, положение нормали к грани в пространстве будет описываться  радиус-вектором N.  Его координаты  в  системе f (x\ у', z') выразим формулами для векторного произведения:

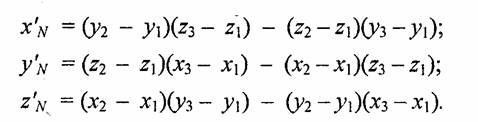
Здесь использованы координаты вершин грани до переноса.                         

Плоская грань может изображаться в различных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, соответствующее видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать в качестве нормали обратный вектор, то есть (-N).                                         

Если полигональная поверхность имеет не треугольные грани, а, например, плоские четырехугольные, то расчет нормали можно выполнять по любым трем вершинам грани.

Диффузное отражение. Определим косинус угла между вектором нормали и  направлением на источник света

Первый пример (возможно, самый простой). Источник света располагается на оси z в бесконечности. Если расчеты производятся для видовой системы координат, то это означает, что источник света располагается на одной оси с камерой.

Косинус угла нормали к грани с осью z равен отношению координаты г и длины радиус-вектора

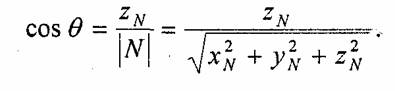
Второй пример. Источник сведа располагается в бесконечности и не лежит  на оси z. В этом случае существенным является способ задания направления  на источник света. Если расположение источника света описывать так же,  как и для камеры — двумя углами (а_с и Д), то можно сделать поворот координат так, чтобы ось z была направлена на источник света, и применить формулы для первого примера. Иными словами, необходимо преобразовать координаты вектора нормали. Здесь можно использовать тот факт, что длина  вектора при повороте не изменяется, поэтому достаточно вычислить координату z_N в повернутой системе координат.                                                          

         Если расположение источника света описывается вектором, направленным на  источник света, то косинус угла с вектором нормали можно вычислить следующим образом. Вначале необходимо определить радиус-вектор, направленный на источник света. Обозначим его как S. Затем, для вычисления косинуса угла между радиус-векторами S и N воспользуемся формулами скалярного произведения векторов. Так как

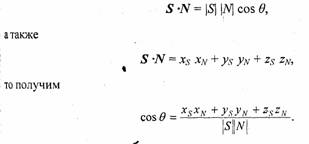
Очевидно, что для упрощения вычислений целесообразно использовать вектор S единичной длины, то есть \S\ = 1.

Третий пример. Источник света располагается в конечной точке пространства с координатами (х_с, у_с, z_c). Для определения косинуса угла с нормалью выполним сдвиг координат источника света так, чтобы вектор нормали в точке поверхности и вектор, направленный на источник света, выходили из общего центра. Выше мы уже рассматривали построение радиус-вектора нормали к треугольной грани путем сдвига (параллельного переноса) координат на (~x₁, -у₁, ~z₁). Радиус-вектор, который направлен на источник света и который можно использовать для расчетов, будет иметь координаты (х_с- х₁ у_{с -}y₁, z_c-z₁). Затем уже можно вычислить искомый косинус угла через скалярное произведение радиус-векторов, как в предыдущем примере.

Зеркальное отражение. Будем считать, что задан радиус-вектор S, направленный на источник света, а также известен радиус-вектор нормали N. Требуется найти косинус угла между отраженным лучом и направлением камеры.

           Вначале необходимо вычислить радиус-вектор отраженного луча. Обозначим  его как R. Выполним некоторые геометрические построения, как показано на рис. 4.36.-

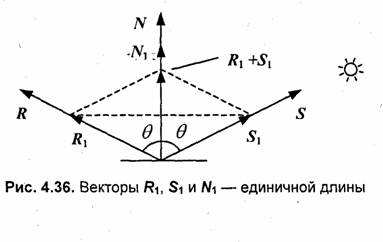
Для решения нашей задачи вначале рассмотрим единичные векторы R₁ S₁ и N i. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно записать R₁ + S₁ = N', где N' — это вектор, соответствующий диагонали ромба и совпадающий по направлению с нормалью. Длина вектора N' равна 2cos θ. Так как вектор N' по направлению совпадает с N₁ , то

Теперь осталось найти косинус угла между отраженным лучом и направлением камеры. Обозначим радиус-вектор, направленный на камеру, как К. Искомый косинус угла найдем, используя скалярное произведение векторов К и R:

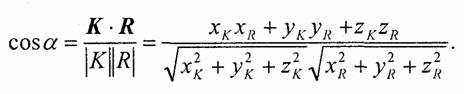
Очевидно, что для упрощения вычислений целесообразно задавать векторы S,N и K единичной длины (тогда и R будет единичным).

Метод Гуро

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней — такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации — чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа.

□  Вычисляются нормали к каждой грани.

□ Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 4.37).

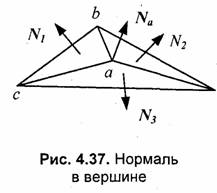
□    На основе нормалей в вершинах вычисляются значения интенсивностей в вершинах согласно выбранной модели отражения света.

             □ Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.

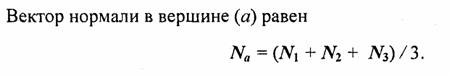
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 4.38).

Метод Фонга

Аналогичен методу Гуро, но при использовании метода Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей.

□ Определяются нормали к граням.

□ По нормалям к граням определяются нормали в вершинах. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали.

□ По направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света.

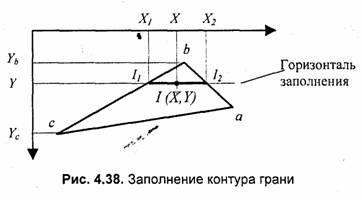
            Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'_a, N'_b и N'_c, исходящими из  центра координат плоскости проецирования и параллельными соответствующим нормалям N_a, N_b и N_c в вершинах a, b и с (рис. 4.39).

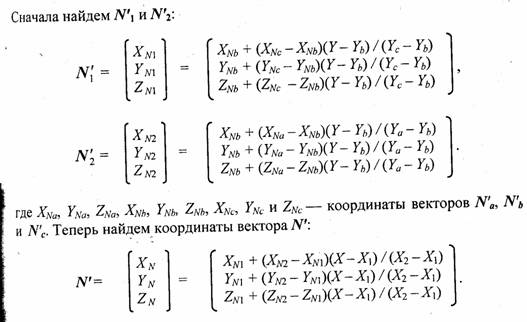
Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.

Метод Фонга сложнее, чем метод Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций, Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркальных поверхностей.

Общие черты и отличия методов Гуро и Фонга можно показать на примере цилиндрической поверхности, аппроксимированной многогранником (рис. 4.40). Пусть источник света находится позади нас. Проанализируем закрашивания боковых граней цилиндра.

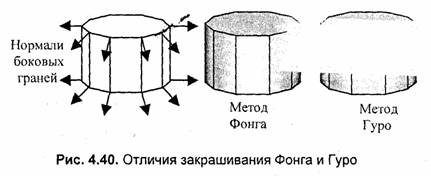
На рис. 4.40 на закрашенной поверхности показаны черным цветом ребра граней — это сделано для иллюстрации особенностей закрашивания, на самом деле после закрашивания никакого черного каркаса не будет, и поверхность выглядит гладкой.       

Основные отличия можно заметить для закрашивания передней грани. Она перпендикулярна направлению лучей света. Поэтому нормали в вершинах  этой грани располагаются симметрично — они образовывают попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обуславливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность одинакова (для линейной интерполяции). Это обуславливает единый  цвет закрашивания. Все точки передней грани имеют одинаковый цвет, что, очевидно, неправильно.

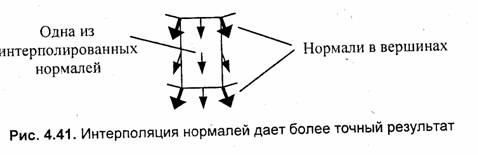
Метод Фонга дает правильное закрашивание.. Если интерполировать векторы нормалей передней грани, то по центру будут интерполированные нормали, параллельные лучам света (рис. 4.41).

           По методу Фонга центр передней грани будет светлее, чем края. Возможно, это не очень заметно на типографском отпечатке рисунка данной книги, однако это именно так.

Преломление света

Законы преломления света следует учитывать при построении изображений прозрачных объектов.

Модель идеального преломления. Согласно этой модели луч отклоняется на границе двух сред, причем падающий луч, преломленный луч и нормаль лежат в одной плоскости (в этой же плоскости лежит и зеркально отраженный луч). Обозначим угол между падающим лучом и нормалью как а₁ а угол между нормалью и преломленным лучом как a₂. Для этих углов известен закон Снеллиуса, согласно которому

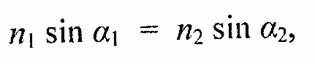
                   где n₁ и п₂— абсолютные показатели преломления соответствующих сред. На рис. 4.42 изображен пример отклонения луча при преломлении. В данном случае границами раздела сред являются две параллельные плоскости, например, при прохождении луча через толстое стекло. Очевидно, что угол а₁ равен углу , а₄  угол а₂ равен углу а_{3 .} Иными словами, после прохождения сквозь стекло луч параллельно смещается. Это смещение зависит от толщины стекла и соотношения показателей преломления сред. Возможно, это самый простой пример преломления. Вы наверняка уже наблюдали и более сложные объекты, например треугольную призму. Для нее границами сред

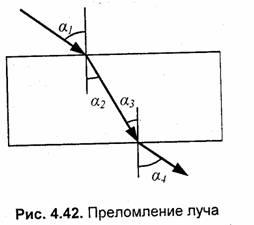
являются непараллельные плоскости (рис. 4.43). Прозрачные объекты могут иметь и криволинейные поверхности, например линзы в разнообразных оптических приборах.

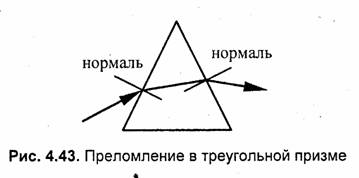
Принято считать, что для вакуума абсолютный показатель преломления равен единице. Для воздуха он составляет 1.00029, для воды — 1.33, для стекла разных сортов: 1.52 (легкий крон), 1.65 (тяжелый крон) [13]. Показатель преломления зависит от состояния вещества, например, от температуры. На практике обычно используют отнашение показателей преломления двух сред (n₁ I n₂), называемое относительным показателем преломления.

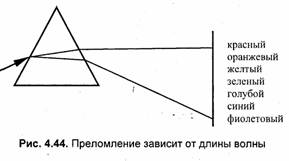
Еще одним важным аспектом преломления является зависимость отклонения луча от длины волны. Это наблюдалось еще И. Ньютоном в опытах по разложению белого света треугольной призмой (рис. 4.44).

Чем меньше длина волны, тем больше отклоняется луч при преломлении. Благодаря этому свойству преломления мы и наблюдаем радугу. Фиолетовый (λ.=0.4 мкм) луч отклоняется больше всего, а красный (λ,=0.7 мкм) — меньше всего. Например, для стекла показатель преломления в видимом спектре изменяется от 1.53 до 1.51 [13].

          Таким образом, каждый прозрачный материал описывается показателем преломления, зависящим от длины волны. Кроме того, необходимо учитывать, какая часть световой энергии отражается, а какая часть проходит через объект и описывается преломлением света.

Кроме идеального преломления в компьютерной графике (хотя и значительно реже, вследствие сложности реализации) используется диффузное преломлепие [32]. Согласно этой модели падающий луч преломляется во все стороны. Примером может служить молочное стекло, обледеневшее стекло.

Вычисление вектора преломленного луча

         Сформулируем задачу следующим образом. Заданы два единичных вектора: S₁ — это радиус-вектор, направленный на источник, и N₁ — радиус-вектор нормали к границе раздела двух сред. Также должны быть известны два коэффициента преломления для данных сред — n₁ и п₂ (или же их отношение).

         Требуется найти единичный радиус-вектор  преломленного луча Т₁. Для решения этой задачи выполним некоторые геометрические подстроения (рис. 4.45). Нанесем еще несколько радиус-векторов (далее мы их все для краткости будем называть векторами).

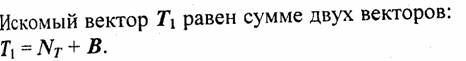
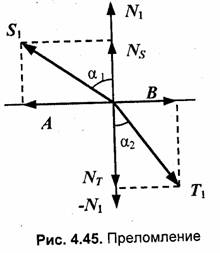
Найдем вначале вектор N_Т- Он противоположен по направлению вектору нормали, а его длина равна    |T₁| cos а₂ = cos a₂ (поскольку по условию задачи Т₁ — единичный). Таким образом, N_Т = -N₁ cos a₂. Необходимо определить cos а₂. Запишем закон преломления n₁ sin a₁ = n₂ sin а₂ в виде:

Если подкоренное выражение отрицательно, то преломленный луч не существует. Это соответствует так называемому полному внутреннему отражению [13, 30, 32].

Это решение задачи в векторном виде. Используя полученное выражение,] можно записать координаты вектора Ту. Сделайте это самостоятельно в качестве упражнения.

Трассировка лучей

Методы трассировки лучей на сегодняшний день считаются наиболее мощными и универсальными методами создания реалистичных изображений. Известно много примеров реализации алгоритмов трассировки для качественного отображения самых сложных трехмерных сцен. Можно отметить, что универсальность методов трассировки в значительной степени обусловлена тем, что в их основе лежат простые и ясные понятия, отражающие наш опыт восприятия окружающего мира.

Как мы видим окружающую нас реальность? Во-первых, нужно определиться с тем, что мы вообще способны видеть'. Это изучается в специальных дисциплинах, а в некоторой степени, это вопрос философский. Но здесь мы будем полагать, что окружающие нас объекты обладают по отношению к свету такими свойствами:

□  излучают;

            □  отражают и поглощают;

          □ пропускают сквозь себя.

Каждое из этих свойств можно описать некоторым набором характеристик.

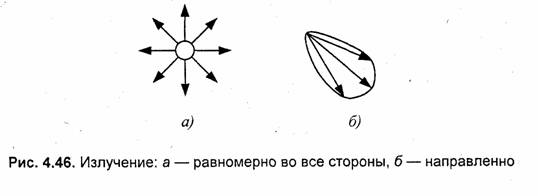
Например, излучение можно охарактеризовать интенсивностью, направленностыо, спектром. Излучение может исходить от условно точечного источника (далекая звезда) или протяженного (скажем, от извергающейся из кратера вулкана расплавленной лавы). Распространение излучения может осуществляться вдоль достаточно узкого луча (сфокусированный луч лазера),  конусом (прожектор), равномерно во все стороны (Солнце), либо еще как нибудь,. Свойство отражения (поглощения) можно описать характеристиками  диффузного рассеивания и зеркального отражения. Прозрачность можно  описать ослаблением интенсивности и преломлением.

Распределение световой энергии по возможным направлениям световых лучей можно отобразить с помощью векторных диаграмм, в которых длина                           векторов соответствует интенсивности (рис. 4.46—4.4.8).

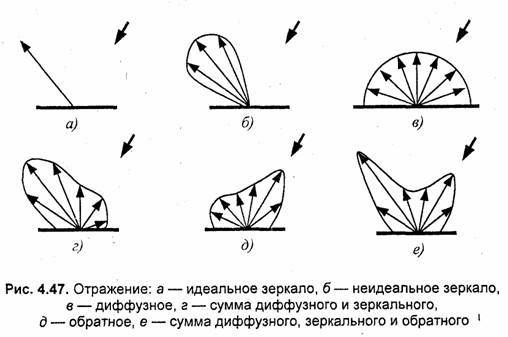
В предыдущих разделах мы с вами уже ознакомились с наиболее часто упоминаемыми видами отражения — зеркальным и диффузным. Реже в литературе упоминается обратное, антизеркальное отражение, у которого максимум интенсивности отражения соответствует направлению на источник. Обратным зеркальным отражением обладают некоторые виды растительности на поверхности Земли, наблюдаемые с высоты, например, рисовые поля [9].

Два крайних, идеализированных случая преломления изображены на рис. 4.48.

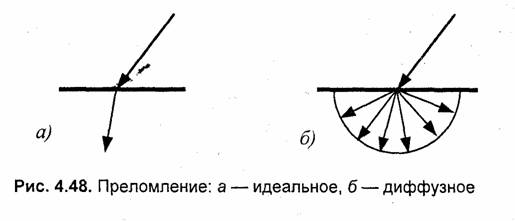
Некоторые реальные объекты преломляют лучи гораздо более сложным образом, например, обледеневшее стекло.

Один и тот же объект реальной действительности может восприниматься в виде источника света, а при ином рассмотрении может считаться предметом, только отражающим и пропускающим свет. Например, купол облачного неба в некоторой трехмерной сцене может моделироваться в виде протяженного (распределенного) источника света, а в других моделях это же небо выступает как полупрозрачная среда, освещенная со стороны Солнца.

В общем случае каждый объект описывается некоторым сочетанием перечисленных выше трех свойств. В качестве упражнения попробуйте привести пример объекта, который обладает одновременно тремя указанными свойствами — сам излучает свет и, в то же время, отражает, а также пропускает свет от других источников. Вероятно, ваше воображение подскажет иные примеры, нежели, скажем, докрасна раскаленное стекло.

         Теперь рассмотрим то, как формируется изображение некоторой сцены, включающей в себя несколько пространственных объектов. Будем полагать, что из точек поверхности (объема) излучающих объектов исходят лучи света. Можно назвать такие лучи первичными— они освещают все остальное. Важным моментом является предположение, что световой луч в свободном пространстве распространяется вдоль прямой линии (хотя в специальных разделах физики изучаются также и причины возможного искривления). Но в геометрической оптике полагают, что луч света распространяется прямолинейно до тех пор, пока не встретится отражающая поверхность или граница среды преломления. Так будем полагать и мы.

От источников излучения исходит по различным направлениям бесчисленное множество первичных лучей (даже луч лазера невозможно идеально сфокусировать — все равно свет будет распространяться не одной идеально тонкой линией, а конусом, пучком лучей). Некоторые лучи уходят в свободное пространство, а некоторые (их также бесчисленное множество) попадают на другие объекты. Если луч попадает в прозрачный объект, то, преломляясь, он идет дальше, при этом некоторая часть световой энергии поглощается. Подобно этому, если на пути луча встречается зеркально отражающая поверхность, то он также изменяет направление, а часть световой энергии поглощается. Если объект зеркальный и одновременно прозрачный (например, обычное стекй), то будет уже два луча— в этом случае говорят, что луч расщепляется.

Можно сказать, что в результате действия на объекты первичных лучей возникают вторичные лучи. Бесчисленное множество вторичных лучей уходит в свободное пространство, но некоторые из них попадают на другие объекты.  Так, многократно отражаясь и преломляясь, отдельные световые лучи приходят в точку наблюдения — глаз человека или оптическую систему камеры,  Очевидно, что в точку наблюдения может попасть и часть первичных лучей  непосредственно от источников излучения. Таким образом, изображение  сцены формируется некоторым множеством световых лучей.

Цвет отдельных точек изображения  определяется спектром и  интенсивностью первичных лучей источников излучения, а также поглощением световой энергии в объектах, встретившихся на пути соответствующих лучей.

Непосредственная реализация данной лучевой модели формирования изображения представляется затруднительной. Можно попробовать построить алгоритм построения изображения указанным способом. В таком алгоритме  необходимо предусмотреть перебор всех первичных лучей и определить те из них, которые попадают в объекты и в камеру. Затем выполнить перебор всех  вторичных лучей, и также учесть только те, которые попадают в объекты и в  камеру. И так далее. Можно назвать такой метод прямой трассировкой лучей.

 Практическая ценность такого метода вызывает сомнения. В самом деле, как  учитывать бесконечное множество лучей, идущих во все стороны? Очевидно,  что полный перебор бесконечного числа лучей в принципе невозможен. Даже  если каким-то образом свести это к конечному числу операций (например,  разделить всю сферу направлений на угловые секторы и оперировать уже не  бесконечно тонкими линиями, а секторами), все равно остается главный недостаток метода— много лишних операций, связанных с расчетом лучей, которые затем не используются. Так, во всяком случае, это представляется в настоящее время.

Метод обратной трассировки лучей позволяет значительно сократить перебор световых лучей. Метод разработан в 80-х годах, основополагающими считаются работы Уиттеда и Кэя [28]. Согласно этому методу отслеживание  лучей производится не от источников света, а в обратном направлении — от  точки наблюдения. Так учитываются только те лучи, которые вносят вклад в формирование изображения.

Рассмотрим, как можно получить растровое изображение некоторой трехмерной сцены методом обратной трассировки. Предположим, что плоскость  проецирования разбита на множество квадратиков— пикселов. Выберем центральную проекцию с центром схода на некотором расстоянии от плоскости проецирования. Проведем прямую линию из центра схода через середину  квадратика (пиксела) плоскости проецирования (рис. 4.49). Это будет первичный луч обратной трассировки. Если прямая линия этого луча попадает в j один или несколько объектов сцены, то выбираем ближайшую точку Пересечения. Для определения цвета пиксела изображения нужно учитывать свойства объекта, а также то, какое световое излучение приходится на соответствующую точку объекта.

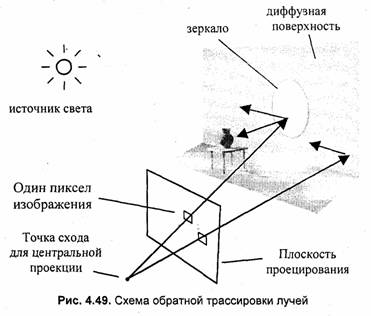
Если объект зеркальный (хотя бы частично), то строим вторичный луч — луч падения, считая лучом отражения предыдущий, первичный трассируемый луч. Выше мы рассматривали зеркальное отражение и получили формулы для вектора отраженного луча по заданным векторам нормали и луча падения. Но здесь нам известен вектор отраженного луча, а как найти вектор падающего луча? Для этого можно использовать ту же самую формулу зеркального отражения, но определяя необходимый вектор луча падения как отраженный луч. То есть отражение наоборот.

Для идеального зеркала достаточно затем проследить лишь очередную точку пересечения вторичного луча с некоторым объектом. Что означает термин "идеальное зеркало"? Будем полагать, что у такого зеркала идеально ровная отполированная поверхность, поэтому одному отраженному лучу соответствует только один падающий луч. Зеркало может быть затемненным, то есть поглощать часть световой энергии, но все равно остается правило: один луч падает — один отражается. Можно рассматривать также "неидеальное зеркало". Это будет означать, что поверхность неровная. Направлению отраженного луча будет соответствовать несколько падающих лучей (или наоборот, один падающий луч порождает несколько отраженных лучей), образующих некоторый конус, возможно, несимметричный, с осью вдоль линии Падающего луча идеального зеркала. Конус соответствует некоторому закону распределения интенсивностей, простейший из которых описывается моделью Фонга — косинус угла, возведенный в некоторую степень. Неидеальное зеркало резко усложняет трассировку — нужно проследить не один, а множество падающих лучей, учитывать вклад излучения от других видимых из данной точки объектов.

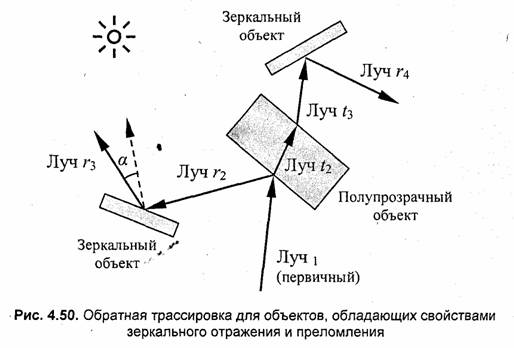
Если объект прозрачный, то необходимо построить новый луч, такой, который при преломлении давал бы предыдущий трассируемый луч. Здесь также можно воспользоваться обратимостью, которая справедлива и для преломления. Для расчета вектора искомого луча можно применить рассмотренные выше формулы для вектора луча преломления, считая, что преломление происходит в обратном направлении (рис. 4.50).

Если объект обладает свойствами диффузного отражения и преломления, то, в общем случае, как и для неидеального зеркала, необходимо трассировать лучи, приходящие от всех имеющихся объектов. Для диффузного отражения интенсивность отраженного света, как известно, пропорциональна косинусу угла между вектором луча от источника света и нормалью. Здесь источником света может выступать любой видимый из данной точки объект, способный передавать световую энергию.

           Когда выясняется, что текущий луч обратной трассировки не пересекает какой-либо объект, а уходит в свободное пространство, то на этом трассировка для этого луча заканчивается.

Обратная трассировка лучей в том виде, в каком мы ее здесь рассмотрели хоть и сокращает перебор, но не позволяет избавиться от бесконечного числа анализируемых лучей. В самом деле, данный метод позволяет сразу получить для каждой точки изображения единственный первичный луч обратной трассировки. Однако вторичных лучей отражения уже может быть бесконечное количество. Так, например, если объект может отражать свет от любого другого объекта, и если эти другие объекты имеют достаточно большие размеры, то какие именно точки излучающих объектов нужно учитывать для построения соответствующих лучей, например, при диффузном отражении? Очевидно, все точки.

При практической реализации метода обратной трассировки вводят ограничения. Некоторые их них необходимы, чтобы можно было в принципе решить задачу синтеза изображения, а некоторые ограничения позволяют значительно повысить быстродействие трассировки. Рассмотрим примеры такая ограничений [28, 32].

1.   Среди всех типов объектов выделим некоторые, которые назовем источниками света. Источники света могут только излучать свет, но не могут его отражать или преломлять. Будем рассматривать только точечные источники света.

            2.   Свойства отражающих поверхностей описываются суммой двух компонент  диффузной и зеркальной.

3. В свою очередь, зеркальность также описывается двумя составляющими. Первая {reflection) учитывает отражение от других объектов, не являющихся источниками света. Строится только один зеркально отраженный луч г для дальнейшей трассировки. Вторая компонента {specular) означает световые блики от источников света. Для этого направляются лучи на все источники света и определяются углы, образуемые этими лучами с зеркально отраженным лучом обратной трассировки (r). При зеркальном отражении цвет точки поверхности определяется цветом того, что отражается. В простейшем случае зеркало не имеет собственного цвета поверхности.

4. При диффузном отражении учитываются только лучи от источников света. Лучи от зеркально отражающих поверхностей игнорируются. Если луч,  направленный на данный источник света, закрывается другим объектом,  значит, данная точка объекта находится в тени. При диффузном отражении цвет освещенной точки поверхности определяется собственным цветом поверхности и цветом источников света.

5. Для прозрачных {transparent) объектов обычно не учитывается зависимость коэффициента преломления от длины волны. Иногда прозрачность  вообще моделируют без преломления, то есть направление преломленного   луча t совпадает с направлением падающего луча.

6. Для учета освещенности объектов светом, рассеиваемым другими объектами, вводится фоновая составляющая {ambient).

7. Для завершения трассировки вводят некоторое пороговое значение освещенности, которое уже не должно вносить вклад в результирующий цвет,    либо ограничивают количество итераций.

Согласно модели Уиттеда цвет некоторой точки объекта определяется суммарной интенсивностью

где р — показатель степени от единицы до нескольких сотен (согласно модели Фонга), а, — угол между отраженным лучам (обратной трассировки) и направлением на i-й источник света.

Интенсивности излучений, приходящих по отраженному лучу (I_r,.), а также по]преломленному лучу (I_t,), умножают на коэффициент, учитывающий ослабление интенсивности в зависимости от расстояния, пройденного лучом. Такой коэффициент записывается в виде е^βd , где d— пройденное расстояние, β- параметр ослабления, учитывающий свойства среды, в которой распространяется луч.

           На рис. 4.51 показан пример изображения трехмерной сцены.

Запишем базовую операцию обратной трассировки лучей в виде функции которую назовем ЛУЧ. Она вычисляет значение интенсивности для текущей трассируемого луча. Для описания функции используем псевдокод, близкий по синтаксису языку С.

      Функция ЛУЧ представлена здесь в схематичном и достаточно обобщенном виде (хотя и не в самом общем— например, здесь не предусмотрено диффузное преломление). Для правильного функционирования процесса обратной трассировки необходимо предусмотреть еще некоторые действия, которые не описаны в тексте функции. Сделайте это самостоятельно в виде упражнения. Так, например, необходимо предусмотреть, чтобы при трассировке первичного луча можно было бы получить изображение источников света, не заслоняемых другими объектами. Кроме того, когда выпускается прелом ленный луч от границы внутрь некоторого объекта, и далее, когда он достигнет внешней границы, то в этот момент можно заблокировать появление зеркального луча, направленного внутрь объекта (например, при моделировании стеклянной линзы, заданной в виде объема, ограниченного некоторой поверхностью). Также следует предусмотреть, чтобы зеркальный луч мог быть выпущен при трассировке преломленного луча, но только если луч пересекает иной объект, нежели тот, от границы объема которого началось преломление (например, при изображении рыбок в аквариуме). Для этого предусмотрены аргументы "тип луча" и "номер объекта". Для предотвращения "зацикливания" (например, при попадании луча внутрь пространства, ограниченного зеркальными стенками) предусмотрен аргумент "номер итерации". Этот же аргумент можно использовать для распознавания первичного луча.

Вы, наверное, уже заметили, что определение функции ЛУЧ является рекурсивным, то есть в теле функции присутствуют вызовы этой же функции. Таи можно достаточно просто моделировать все дерево лучей: сначала первичный луч, затем — порождающиеся вторичные, третичные и так далее. Веси процесс обратной трассировки для одной точки изображения представляется в виде единственной строчки.

Для первичного луча необходимо задать направление, соответствующее выбранной проекции. Если проекция центральная, то первичные лучи расходятся из общей точки, для параллельной проекции первичные лучи параллельны. Луч можно задать, например, координатами начальной и конечной точек отрезка, координатой начальной точки и направлением, или же еще как нибудь. Задание первичного луча полностью определяет "проекцию изображаемой сцены. В главе 2 мы рассматривали основные типы проекции и связанные с ними преобразования координат. А при обратной трассировке лучей какие-либо преобразования координат вообще не обязательны. Проекция получается автоматически — в том числе, не только плоская, но и, например,  цилиндрическая или сферическая. Это одно из проявлений универсальности метода трассировки.

В ходе трассировки лучей необходимо определять точки пересечения прямой линии луча с объектами. Способ определения точки пересечения зависит от того, какой это объект, и каким образом он представлен в некоторой графикой системе. Так, например, для объектов, представленных в виде многоинников и полигональных сеток, можно использовать известные методы рределения точки пересечения прямой и плоскости, рассматриваемые в аналитической геометрии [16]. Однако если ставится задача определения пересечения луча с гранью, то необходимо еще, чтобы найденная точка пересечения лежала бы внутри контура грани.

Известны несколько способов проверки произвольной точки на принадлежность полигону. Рассмотрим две разновидности, в сущности, одного и того же метода (рис. 4.52).

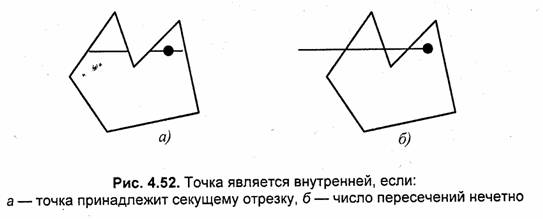
Первый способ. Находятся все точки пересечения контура горизонталью, соответствующей координате Y заданной точки. Точки пересечения сортируются по возрастанию значений координат X. Пары точек пересечения образуют отрезки. Если проверяемая точка принадлежит одному из отрезков (для этого сравниваются координаты X заданной точки и концов отрезков), то она является внутренней.

Второй способ. Определяется точка, лежащая на одной горизонтали с испытуемой точкой, причем требуется, чтобы она лежала вне контура полигона. Найденная внешняя точка и испытуемая являются концами горизонтального отрезка. Определяются точки пересечения данного отрезка с контуром полигона. Если количество пересечений нечетно, это значит, что испытуемая точка является внутренней [32, 33].

Если точек пересечения луча с объектами несколько, то выбирается ближайшая точка по направлению текущего луча.

В сложных сценах со многими объектами для нахождения ближайшей точки пересечения необходимо перебирать все объекты. Если каждый объект представляется многими гранями-полигонами, то нужно анализировать еще и каждую грань на предмет пересечения с лучом. Для ускорения этого процесса используется метод оболочек [28]. Суть данного метода в том, что припереборе объектов анализируются сначала не сами объекты, а более простые формы — оболочки. Оболочка должна удовлетворять следующим требованиям. Во-первых, она должна охватывать объект, который должен целиком умещаться в ней. Если луч не пересекает оболочку, значит, .этот же луч не пересечет объект. Во-вторых, процедура определения пересечения луча и оболочки должна быть как можно проще, а главное, наиболее быстрой.

 Использование оболочек позволяет в ходе перебора объектов сразу отбрасывать те, которые заведомо не пересекаются с лучом. Но если луч пересекает оболочку, тогда ищется точка пересечения луча с объектом. Очевидно, что если луч пересек оболочку, то не обязательно этот луч пересечет соответствующий объект — форма оболочки не совпадает с формой объекта.

В качестве оболочек можно исильзовать шар, параллелепипед, цилиндр и другие простые формы.

Если объектов достаточно много, то объекты (или оболочки) можно объединять в группы — для нескольких объектов одна оболочка. Таким образом, выстраивается уже иерархия оболочек: на нижнем уровне оболочки для одиночных объектов, на следующем уровне — оболочки оболочек и так далее.

 Такая древовидная структура может иметь несколько уровней. Это позволяет существенно ускорить процесс перебора, сделать время работы пропорциональным (теоретически) логарифму числа объектов.

Необходимо отметить, что метод оболочек можно применять не только для  трассировки лучей. Этот метод является достаточно универсальным методом  ускорения вычислительных процессов переборного типа. По крайней мере,  в алгоритмах компьютерной трафики он используется часто. Иногда метод оболочек называется по-другому, но от этого суть не меняются.

Для упрощения некоторых операций, выполняемых в ходе обратной трассировки, можно использовать следующий способ. Он разработан автором этой  книги и заключается в следующем. В ходе трассировки лучей с каждым лучом связывается локальная система координат. Центр этой трехмерной декартовой системы располагается в точке, из которой направляется текущий  луч трассировки. Ось Z направлена противоположно лучу, расположение  осей X и Y безразлично. Таким образом, координаты X и Y точки пересечения  луча с объектами всегда равны нулю. Это позволяет упростить нахождение  координат точки пересечения луча, поскольку направления луча всегда одно  и то же, и вычислять нужно только координату Z. Для плоских полигональных граней это можно сделать с помощью линейной интерполяции координат Z соответствующих вершин. Кроме того, упрощаются и некоторые другие операции. В частности, для отбора ближайшей точки пересечения достаточно анализировать только координату Z. Следует заметить, что упрощение отдельных операций достигается за счет усложнения других— например, необходимо вычислять коэффициенты преобразования координат для каждой локальной системы, а также выполнять преобразования координат объектов.

В главе 7 приведен пример графической программы (studexl3), реализующей данный способ, а здесь мы еще рассмотрим некоторые теоретические аспекты. На рис. 4.53 показаны локальные координаты.

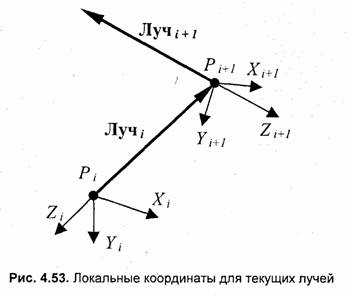
Пусть из точки Р_i выпущен i-й луч, который пересек ближайший объект в точке P_i+1  Координаты точки Р_i+1   в системе координат {Х_i Y_i Z_i) равны (О, 0, z_p). Предположим, что направление нового, (i+1)-го, луча определяется в виде параллельного ему радиус-вектора в этой же системе координат, то есть (Х_i Y_i, Z_i,). Обозначим координаты этого радиус-вектора через (х_r, у_r , z_r). Катсопределить новую систему координат, связанную с (i+1)-м лучом?

Эту систему координат можно получить следующим образом. Вначале сдвинуть систему (X_i, Y_i Z_i,) по оси Z, на величину z_p, а затем выполнить поворот так, чтобы ось Z_i+1 была бы направлена против нового луча. Запишем формулы преобразований в следующем виде:

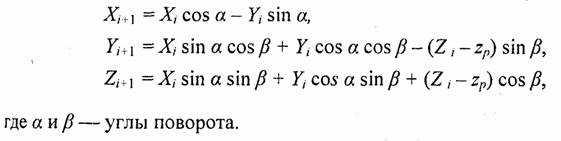
Выразим поворот не углами,,а через координаты радиус-вектора, который указывает новое направление оси Z. Рассмотрим рис. 4.54. Пусть радиус-вектор имеет координаты (х, у, z). Длина радиус-вектора равна R:

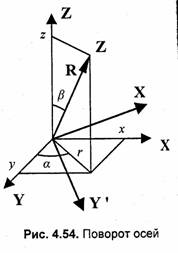
Подставим эти значения в формулы преобразования координат, учитывая, что радиус-вектор нового трассируемого луча направлен противоположно направлению оси Z,_i+1, то есть (х, у, z) - {-x_r, -y_r, ~z_r). Запишем формулы в следующем виде

:

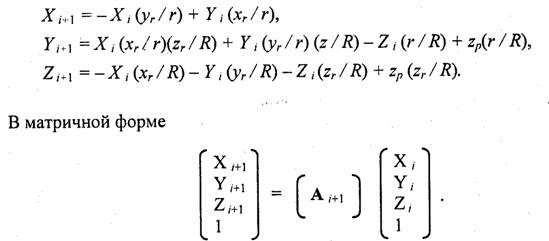
Матрица A,_i+1 соответствует аффинному преобразованию сдвига и поворота. В ходе трассировки лучей нам необходимо выполнять преобразования из мировой системы в систему координат текущего луча. Обозначим матрицу преобразований через М,_i+1:

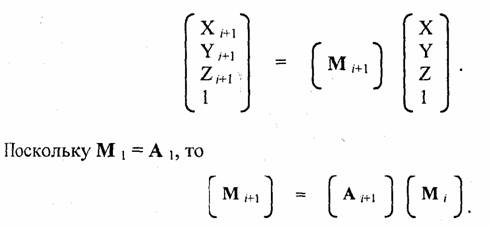
Таким образом, матрица для системы координат нового луча образуется умножением матрицы предыдущего луча на матрицу сдвига и поворота.

Важным моментом при расчетах отражения и преломления является определение нормали к видимой для текущего трассируемого луча стороны участка поверхности (рис. 4.55).

Введение локальной системы координат значительно упрощает такой выбор направления нормали. Можно руководствоваться следующим правилом — среди двух ротивоположно направленных векторов нормали (N и -N) выбирается тот, у которого соответствующий радиус-вектор в локальной системе координат {Х„ Yi, Z,) имеет положительную координату 2.

         Рассмотрим вычисление вектора зеркально отраженного луча (Луч ;₊₁). Для этого воспользуемся уже известной нам векторной формулой, которую здесь запишем для единичных векторов: R = 2 N (N • S) - S. Вычисляемый по этой формуле вектор R направлен так же, как искомый вектор Луч ,+i, а единичный вектор $ нацелен противоположно вектору падающего луча, то есть вектору Луч,-.

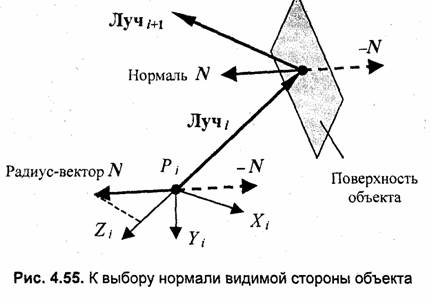
Еще раз подчеркнем, что речь здесь идет о лучах обратной трассировки, для которой падающий и отраженный лучи имеют противоположный смысл световым лучам, распространяемым в реальном случае.

Координаты вектора S составляют (0, 0, 1) в локальной системе. Обозначим координаты единичного вектора нормали N через (x_N, y_N, z_N). Найдем вначале скалярное произведение (N • S) = (0 • х_N+ 0 • y_N+ 1 • z_N) = z_N. Координаты вектора отраженного луча (R) составляют

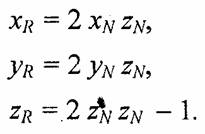
Очевидно, что направление вектора не изменится, если все его координаты разделить на два. Тогда можно записать для координат радиус-вектора отраженного луча (Луч _l+i = 0.5 R) такие формулы:

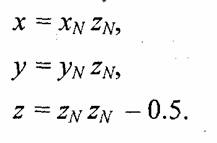
Если подкоренное выражение отрицательно, то преломленный луч не может быть построен.

          Использование локальной системы координат, ось Z которой совпадает с линией текущего трассируемого луча, позволяет упростить также определение пересечения с оболочкой объекта. Наиболее просто определяется пересечение луча с оболочкой-шаром. Поскольку в любой локальной системе координат, задаваемой линейными преобразованиями, проекция шара есть круг, то достаточно узнать локальные координаты центра круга (Хс и Yc) и проверить, выполняется ли следующее соотношение: (Хс)² + (Yс)² < (радиус оболочки)².

Если выполняется, то текущий луч пересекает оболочку.

    В качестве оболочки можно использовать и другую форму, например цилиндр или параллелепипед. Поскольку определение пересечения луча с произвольно повернутым цилиндром или параллелепипедом уже не столь простая задача, то здесь можно использовать следующее. Хотя расположение осей координат X, Y локальной системы ранее было нам безразлично (главное, чтобы  ось Z лежала бы на линии луча), но, оказывается, приведенные выше формулы преобразования координат для локальной системы обеспечивают сохранение одинаковой ориентации для вертикальных линий. Ранее мы уже отмечали это свойство выбранного способа поворота осей применительно к аксонометрической проекции. Поэтому возможно определить проекции оболочки для всех поворотов локальных систем координат в виде прямоугольника некоторых размеров в плоскости (X0Y). Определение пересечения  луча с оболочкой сводится к проверке, находится ли точка локальных координат (X_i Y_i,)= (0, 0) внутри прямоугольника, описывающего оболочку.

А теперь сделаем общие выводы по методу обратной трассировки лучей. Положительные черты:

1. Универсальность метода, его применимость для синтеза изображений достаточно сложных пространственных схем. Воплощает многие законы  геометрической оптики. Просто реализуются разнообразные проекции.

2. Даже усеченные варианты данного метода позволяют получить достаточно реалистичные изображения. Например, если ограничиться только первичными лучами (из точки проецирования), то это дает удаление невидимых точек. Трассировка уже одногодвух  вторичных лучей дает тени, зеркальность, прозрачность.

 3. Все преобразования координат (если таковые есть) линейны, поэтому достаточно просто работать с текстурами.

4.  Для одного пиксела растрового изображения можно трассировать несколько близко расположенных лучей, а потом усреднять их цвет для устранения эффекта ступенчатости (антиалиасинг).

5.  Поскольку расчет отдельной точки изображения выполняется независимо от других точек, то это может быть эффективно использовано при реализации данного метода в параллельных вычислительных системах, в которых лучи могут трассироваться одновременно.

Недостатки:

1.  Проблемы с моделированием диффузного отражения и преломления.

2.  Для каждой точки изображения необходимо выполнять много вычислительных операций. Трассировка лучей относится  к числу самых медленных алгоритмов синтеза изображений.

ГЛАВА 5

Примеры изображения

 трехмерных объектов

5.1. Шар

Каркасное изображение

Для каркасного изображения шара можно рисовать сетку меридианов и параллелей. Для этого удобно воспользоваться известными формулами параметрического описания. Координаты точек поверхности шара определяются как функции от двух переменных (параметров) — широты и долготы (рис. 5.1):

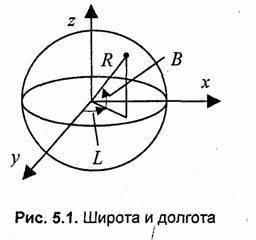
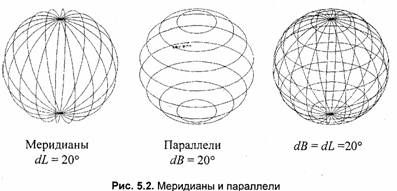
Здесь введены две величины — dL и dB. Значение dL определяет шаг меридианов по долготе, значение dB — это шаг по широте, который должен быть малым (единицы градусов) для изображения меридиана достаточно гладкой кривой. Преобразование координат производится по формулам, соответствующим выбранной проекции. Для аксонометрической проекции — это поворот мировых координат на углы йиДс последующим преобразованием видовых координат в экранные координаты (как было рассмотрено в главе 2).

Параллель — это линия, состоящая из точек с постоянной широтой. Для рисования каркаса из параллелей можно использовать такой цикл:

Удаление невидимых точек

Для изображения поверхности шара с удалением невидимых точек в аксонометрической проекции можно воспользоваться таким свойством: видимыми являются точки с неотрицательным значением координаты Z в системе видовых координат. При этом центр видовых координат (X, Y, Z) совпадает с центром шара, плоскость X0Y является плоскостью проецирования, а ось Z направлена на камеру (наблюдателя). На рис. 5.3 приведен простейший вариант показа поверхности шара с удалением невидимых точек меридианов и параллелей.

Приведенные выше изображения были построены на основе линий и являются схематичными, весьма далекими от реалистичного изображения поверхности шара. Значительно лучше можно нарисовать шар с помощью фигур с заполнением — закрашиванием поверхности разными цветами.

Многогранник с закрашиванием граней

Теперь нарисуем шар в виде многогранника, аппроксимирующего форму поверхности с заданной точностью. Известно большое число типов многогранников. Сведения о них имеются в многочисленных книгах по геометрии.

Мы будем рассматривать достаточно узкий класс многогранников. Отличительным признаком рассматриваемых многогранников является то, что у них ребра ориентированы вдоль меридианов и параллелей. Такие многогранники будем описывать двумя параметрами — шаг по широте (dB) и шаг по долготе (dL) в градусах. Кроме того, будем считать эти многогранники вписанными изнутри в шар, то есть вершины каждой грани лежат на поверхности шара. Очевидно, что с увеличением количества граней такие многогранники все больше приближаются к шару. Иными словами, чем меньше dB и dL, тем лучше поверхность многогранника аппроксимирует форму поверхности шара.

В табл. 5.1 приведены примеры таких многогранников.

Некоторые из этих многогранников достаточно интересны по форме, а многогранник с параметрами dB = 90°, dL = 90° называется октаэдром.

           Все грани, примыкающие к верхнему и нижнему полюсам, являются треугольными, а остальные грани — четырехугольными. С позиций компьютерной графики это выгодно отличает многогранники рассматриваемого типа  от других, например, правильных многогранников, у которых грани могут иметь значительно больше ребер, чем четыре.

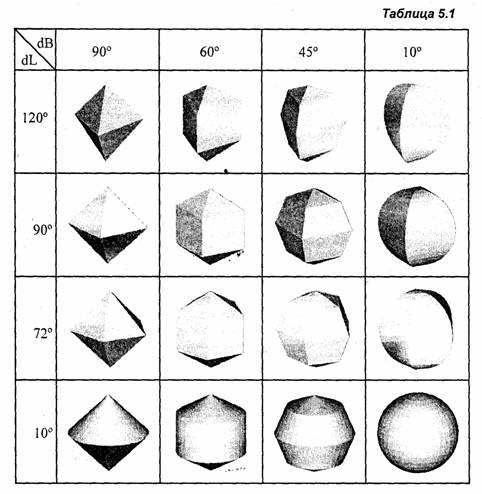
Для построения изображения многогранников будем рисовать каждую грань как полигон. Для вывода полигона требуется определить координаты всех его вершин и задать цвет заполнения.

Очевидно, что показ граней одним цветом дает неудовлетворительный результат — полностью теряется форма поверхности трехмерного объекта. Показ ребер (контуров полигонов граней) другим цветом немного улучшает восприятие (рис. 5.4).

Построим изображение так, чтобы грани были окрашены в соответствии с законами отражения света. Общую схему алгоритма можно изобразить таким образом:

Приведенную тут схему алгоритма не следует воспринимать как программу на языке С, а также сам алгоритм как оптимальный. В частности, здесь много лишних вычислений косинусов и синусов — количество таких операций обязательно нужно уменьшать, поскольку они выполняются в традиционных компьютерах очень медленно. Кроме того, здесь и далее мы будем рисовать все грани четырехугольниками, хотя, лишь незначительно усложнив данную схему, можно предусмотреть и отдельную ветвь для треугольных граней у полюсов.

Для удаления невидимых точек можно использовать Z-буфер, но можно перестроить цикл так, чтобы грани рисовались в таком порядке — начиная с самых дальних и заканчивая ближайшими.

Для определения цвета каждой грани нужно учесть взаимное расположение источника света и нормали грани. Как уже было показано выше для диффузной и зеркальной моделей отражения, важно определить координаты вектора нормали. Мы уже рассматривали общий способ вычисления координат нормали к произвольной плоской грани (см. разд. 4.3). Этот способ, на основе векторного произведения, можно применить, естественно, и в данном случае. Однако для таких многогранников как наши, нормали к граням можно вычислять значительно проще и быстрее. Поскольку радиус-вектор для каждой точки поверхности шара и есть вектор нормали, то координаты каждой точки поверхности шара являются координатами вектора нормали, если координаты центра шара равны (0, 0, 0). Такум образом, для вычисления координат вектора нормали к грани достаточно определить координаты точки поверхности шара, соответствующей центру грани. Или же можно взять сумму координат вершин грани и разделить на число вершин — это уже приближенный неточный способ.

На рис. 5.5 изображены многогранники с различным числом граней, причем источник освещения расположен сзади нас — на оси Z видовых координат.

Как видим, для создания иллюзии гладкой поверхности шара нужно очень большое число граней (очевидно, что это число возрастает с увеличением видимого радиуса шара). Если рассматривать рис. 5.5, то при dB = dL = 5° многогранник уже похож на шар — отдельные грани достаточно сложно различить на типографском отпечатке этой книги (здесь также сказывается то, что при печати используется дизеринг, который сглаживает изображение).

Однако на экране дисплея грани все еще заметны. Глаз человека подчеркивает границы.

Закрашивание граней методом Гуро

Метод Гуро дает хорошие результаты для создания иллюзии гладкой поверхности шара, изображаемого достаточно большим числом плоских граней. В соответствии с этим методом для каждой грани нужно определить векторы в вершинах, затем для каждой вершины вычислить значение интенсивности отраженного света и потом, при выводе полигона грани, интерполировать интенсивности вершин для вычисления интенсивности отраженного света в каждой точке внутри грани.

Значительным удобством при вычислении координат нормалей в вершинах граней в нашем случае является то, что координаты вектора нормали в любой вершине грани совпадают с координатами самих вершин — если центр шара имеет координаты (0, 0, 0).

Рассмотрим случай, когда точечный источник света расположен на оси Z видовых координат. Используем диффузную модель отражения. В этом случае рассчитать интенсивность отраженного света в вершине грани можно следующим образом. Косинус угла между осью Z и нормалью

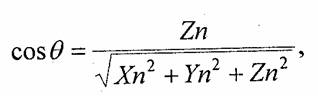
где Хп, Yn и Zn — видовые координаты вектора нормали. Поскольку координаты вектора нормали в вершине равны координатам вершин, а Сумма квадратов координат (в том числе и видовых) для любой точки поверхности шара равна квадрату его радиуса, то

Как видно на рис. 5.6, иллюзия гладкости поверхности достигается уже при достаточно малом числе граней. Так, например, при dB = dL = 20° в большей степени заметны неровности контура, чем погрешности закрашивания.

Учет расположения источника света

В приведенных выше примерах использовался точечный источник освещения, расположенный так же, как и камера — на оси Z видовых координат. Как получить изображение шара, освещенного сбоку?

           Рассмотрим для простоты диффузное рассеивание. Для расчета косинуса угла наклона нормали по отношению к направлению луча источника света удобно ввести еще одну систему координат. Эта система координат— обозначим ее как (Хс, Yc, Zc) — повернута в пространстве таким образом, чтобы источник света располагался на оси Zc. Здесь следует уточнить, что мы рассматриваем точечный источник света, расположенный снаружи шара на достаточно большом расстоянии, причем не учитываем зависимость освещенности точек поверхности от расстояния до источника света.

Ориентацию системы координат источника света (Хс, Yc, Zc) можно задать двумя углами поворота (а_с β_с) — подобно тому, как задается видовая система координат. На рис. 5.7 показано расположение осей.

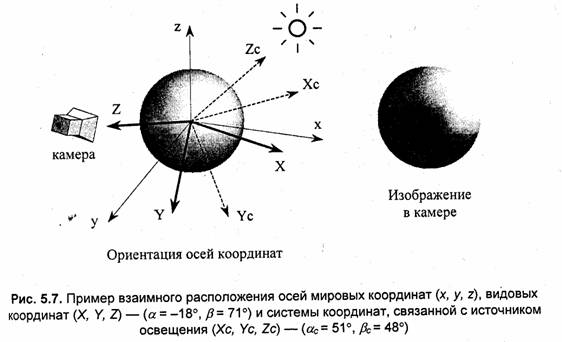
где Zc-. координата точки поверхности в системе координат источника света. Необходимо учесть, что нулевые и отрицательные значения косинуса соответствуют неосвещенным точкам поверхности.

Таким образом, для рисования поверхности с учетом произвольной ориентации источника света необходимо определять еще и значение координаты Zc. В остальном алгоритм рисования шара полностью аналогичен уже рассмотренным алгоритмам.

Градиентное закрашивание круга

           В предыдущем разделе мы пытались изобразить гладкую поверхность шара путем рисования многогранника с достаточно сложным закрашиванием полигонов отдельных граней. А нельзя ли рисовать шар как-нибудь попроще?

Если рассматривать общий контур шара— то это линия круга. Остается лишь каким-то образом закрасить внутренности круга, чтобы цвет пикселов более или менее соответствовал бы изображению объемного объекта. Нужно закрашивать так, чтобы цвет пикселов внутри круга плавно изменялся бы в соответствии с освещенностью поверхности шара. Для этого можно использовать градиентное закрашивание.

Для простоты будем полагать, что источник света расположен позади нас. В этом случае можно использовать радиальное градиентное закрашивание — наиболее яркие точки расположены в центре, яркость остальных точек убывает пропорционально расстоянию до центра круга.

Вашему вниманию предлагается следующий алгоритм закрашивания.

В этом алгоритме использована симметрия шара, освещенного указанным   образом. Поэтому вычисления производятся только для точек одного октанта   круга. Для определения цвета пикселов вычисляется значение (к), которое равно квадрату косинуса угла нормали по отношению к оси Z видовых координат.

Во второй части этой книги мы рассмотрим примеры программ, в которых использован данный алгоритм градиентного закрашивания.

Проанализируем алгоритм и попробуем оптимизировать его по быстродействию. В первую очередь отметим, что в данном алгоритме вычисляется квадрат косинуса нормали именно из соображений повышения быстродействия— для вычисления косинуса в первой степени необходимо вычислять квадратный корень из (к). Далее заметим, что во внутреннем цикле присутствуют операции деления и умножения. Как от них избавиться? Вначале рассмотрим вычисление величины г2 = х²+у². Поскольку во внутреннем цикле изменяется у, то рассмотрим г 2 как функцию от у. Обозначим ее как г2(у), и найдем разность значений этой функции для соседних шагов цикла:

Умножение на 2 компьютер может выполнять как сдвиг двоичного числа, что несколько быстрее обычного умножения. Попробуем еще улучшить цикл. Для этого рассмотрим разности второго порядка:

То, что вторая разность является константой, не зависящей от у, можно использовать для построения цикла, в теле которого присутствуют только операции сложения. Перестроим цикл следующим образом.

       Можно применить этот разностный метод (известный в математической литературе для организации итерационных вычислений) также и для вычисления величины к=1- r2K2. Вы можете это сделать в качестве упражнения.

Необходимо отметить, что подобная оптимизация может не дать существенного ускорения графического вывода, если время вычисления величин г² и к мало по сравнению с другими операциями. Так, например, в первую очередь необходимо обеспечивать быструю запись в память пикселов растра отображения. Хорошие возможности для ускорения тут дает симметрия круга по октантам.

Кроме иллюстрации возможностей ускорения, модифицированный алгоритм здесь приведен еще с одной целью. Оказывается, если заменить операцию (dr2 = drl + 2) на (dr2 = dr2 + D), где D является константой для всего цикла рисования, то можно получить довольно любопытные вариации формы круга. На рис. 5.8 приведена форма фигур, соответствующих некоторым значениям D.

Значение константы D может быть и дробным — форма фигуры плавно изменяется в зависимости от D.

Наложение текстуры на шар

До сих пор мы с вами рассматривали одноцветный шар. Однако, возможно, требуется построить изображение шара, раскрашенного более сложным образом. Часто бывает необходимо имитировать различные материалы, сложную структуру поверхности — например, пористую, с трещинами и тому подобное. Для этого могут быть использованы текстуры. Изображение текстуры как бы накладывается на поверхность объекта.

Давайте построим изображение поверхности шара, на который как резиновая оболочка "натянута" текстура — карта мира.

Из картографии известны многие способы изображения Земли в соответствии с различными проекциями. Выберем вертикальную цилиндрическую равнопромежуточную проекцию шара, для которой наиболее просто пересчитываются координаты — из угловых координат (широты, долготы) в пиксельные координаты текстуры (х_Т, Ут) и обратно (рис. 5.9).

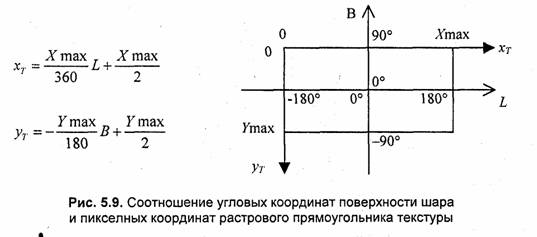
На рис. 5.10 приведен один из возможных вариантов карты мира в цилиндрической равнопромежуточной проекции.

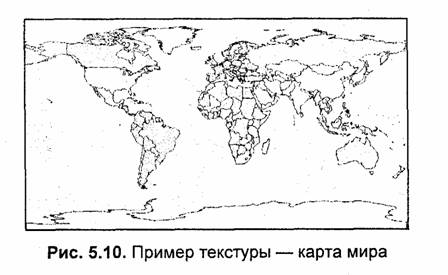
Как использовать текстуру для построения требуемого изображения шара? Это можно сделать несколькими способами. Разнообразие вариантов обуславливается, в том числе, и способом описания поверхности шара.

Рассмотрим вначале вариант, основывающийся на аналитической форме описания шара. Будем использовать формулу, связывающую координаты каждой точки поверхности шара в виде

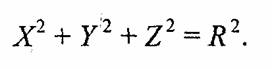
      Построение растрового изображения шара в аксонометрической проекции представим как двумерный цикл перебора всех пикселов квадрата, охватывающего круг на плоскости проецирования. При этом для каждого пиксела вначале пересчитываются координаты проекции в мировые координаты, а далее — в координаты точки в текстуре.

Рассмотрим данный алгоритм подробнее. Для простоты будем использовать аксонометрическую проекцию, которая строится как поворот исходной (мировой) системы координат (х, у, z) на углы а и β соответствующие положению камеры наблюдения. Поскольку в обеих системах координат — как в исходной (х, у, z), так и в повернутой системе (X, Y, Z) — для шара сохраняется равенство суммы квадратов координат квадрату его радиуса, то можно найти Z по известным двум координатам X и Y следующим образом:

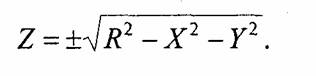
Поскольку мы строим изображение для передней стороны шара, то нужно брать значение Z со знаком "+". Вычисление координаты Z является ключевым моментом рассматриваемого алгоритма. Это достаточно уникальный случай простого определения трехмерных координат точек объекта по двумерным координатам проекции.

          Далее, координаты точки (х, у, г) можно вычислить, выполнив обратный поворот координат {X, Y, Z). Например, если считать, что плоскость проецирования повернута вокруг оси х на угол β то

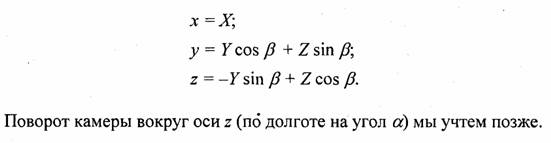
Приведенные выше формулы справедливы для случая, когда центр координат плоскости проецирования совпадает с точкой (0, 0) основного растра. При построении изображения в окне необходимо еще вычислять экранные координаты, что можно сделать путем масштабирования и сдвига осей координат.

По известным значениям широты (В) и долготы (L) определяем координаты точки в растре текстуры. Как уже указывалось выше, для текстуры в виде вертикальной равнопромежуточной цилиндрической проекции шара пересчет координат выполняется простейшим образом:

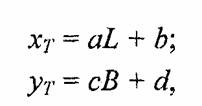
где a, b, c и d— константы, определяемые размерами растра текстуры.

На рис. 5.11 показаны несколько текстурированных изображений поверхности шара.

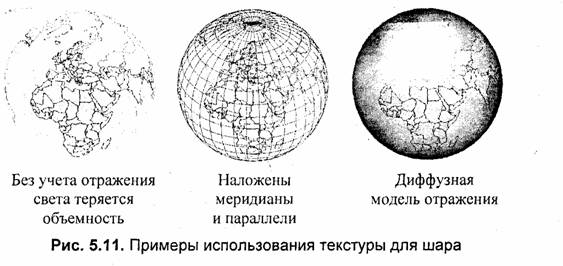
Данный способ построения текстурированного изображения имеет свои достоинства и недостатки. Положительной чертой способа можно считать высокую точность отображения— точность определяется разрешением растров текстуры и основного растра. Погрешность вычисления координат по формулам преобразований здесь незначительна при использовании стандартной разрядности чисел с плавающей точкой.

Недостатком рассмотренного способа является низкая скорость построения изображения, поскольку для каждого пиксела основного растра нужно выполнять несколько вычислительных операций, требующих много машинного времени — в первую очередь, это арксинус и арктангенс.

Разумеется, приведенный выше алгоритм можно усовершенствовать с целью повышения быстродействия. Так, например, можно использовать симметрию шара, что позволяет совместить вычисления для нескольких точек поверхности одновременно. Однако все равно приходится вычислять арксинусы и арктангенсы наряду с другими операциями с плавающей точкой.

Здесь мы рассмотрели подход, основной идеей которого было получение формул преобразования координат изображения в мировые координаты и далее— в текстурные. Формулы преобразования здесь достаточно просты с точки зрения математики, но не слишком удобны для быстрых вычислений. Необходимо отметить, что такие формулы мы получили для, возможно, простейшего объемного объекта — шара. Для других типов поверхностей, которые описываются значительно более сложными формулами, вероятно, и не существует решение в точном аналитическом виде такой задачи, как пересчет координат плоскости проецирования в мировые трехмерные. Сложность решения обуславливается сложностью формул аналитического описания поверхности. И не только. Например, для эллипсоида формулы описания поверхности не намного сложнее, чем для шара. Однако определение значения координаты Z по известным X и Yявляется гораздо более сложной задачей, поскольку видимые точки эллипсоида могут иметь как положительные, так и отрицательные значения координаты Z.

Значительно более универсальным и, как правило, более эффективным по быстродействию можно считать метод текстурирования, использующий представление поверхностей полигональными гранями.