2.3. Связь преобразований объектов
с преобразованиями координат
Когда пользователь графической системы видит на экране перемещающийся
объект, то, как вы считаете, что на самом деле происходит — перемещаются
объекты или система координат в обратном направлении? Например, если в кино вы видите объекты, вращающиеся на экране по часовой стрелке, то может в ействительности это камера поворачивается против часовой стрелки?
Преобразование объектов и преобразование систем координат тесно связаны между собой. Движение объектов можно рассматривать как движение в обратном направлении соответствующей системы координат.
Такая относительность для объектов отображения и систем координат дает разработчикам компьютерных систем дополнительные возможности для моделирования и визуализации пространственных объектов. С каждым объектом можно связывать как собственную локальную систему координат, так и единую для нескольких объектов. Это можно использовать, например, для моделирования подвижных объектов.
Обычно, того же самого эффекта можно добиться, если использовать различные подходы. Однако в одних случаях удобнее использовать преобразование координат, а в других — преобразование объектов. Не последнюю роль играет сложность обоснования какого-то способа, его понятность.
Рассмотрим пример комбинированного подхода. Пусть нам нужно получить i функцию расчета координат (X, Y) для поворота вокруг центра с координатами (х0,у0) (рис. 2.13).

Выше мы рассмотрели поворот относительно центра координат (0, 0). Для I решения нашей задачи введем новую систему координат (х',0',уг) с центром в точке (х0, уо):
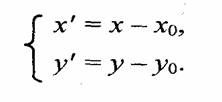

Рассмотрим второй пример. Нашей задачей будет вывод формул параметрического описания поверхности тора. Изобразим тор следующим образом (рис. 2.14).
Для произвольной точки Р, лежащей на поверхности тора, требуется выразить координаты (х, у, z) через константы, описывающие размеры фигуры, а также через некоторые параметры. Для поверхности в трехмерном пространстве необходимо использовать два параметра. В качестве таковых выберем угловые величины: φ (широта) и ω (долгота).

Непосредственное определение координат точки Р представляется сложным, поэтому искомые координаты будем искать несколькими шагами преобразований. Рассмотрим окружность, лежащую в плоскости z0y, центр этой окружности совпадает с центром координат. Координаты точки Р" с широтой φ составляют
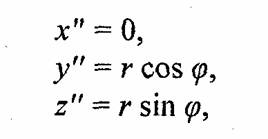
где r— малый радиус тора.
Теперь перенесем окружность на расстояние R (большой радиус тора) по оси у в той же плоскости z0y. Получим точку Р Ее координаты:
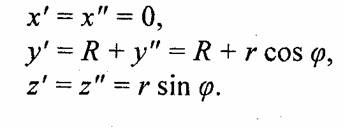
Окружность, которой принадлежит точка Р', является геометрическим местом точек тора с нулевой долготой и). Если точку Р' повернуть на угол а), то получим искомую точку Р поверхности тора с координатами

Эту задачу можно было бы решить, используя преобразование координат. Подобный случай мы рассмотрим ниже (пример studex8 в разделе программирования). Однако, как представляется, более ясным здесь выглядит использование операций перемещения точки (из положения Р" в Р', а затем в Р).
В настоящее время наиболее распространены устройства отображения, которые синтезируют изображения на плоскости— экране дисплея или бумаге. Устройства, которые создают истинно объемные изображения, пока достаточно редки. Но все чаще появляются сведения о таких разработках, например, об объемных дисплеях [37] или даже о трехмерных принтерах [45].
При использовании любых графических устройств обычно используют проекции. Проекция задает способ отображения объектов на графическом устройстве. Мы будем рассматривать только проекции на плоскость.
При отображении пространственных объектов на экране или на листе бумаги с помощью принтера необходимо знать координаты объектов. Мы рассмотрим две системы координат. Первая — мировые координаты, которые описывают истинное положение объектов в пространстве с заданной точностью. Другая — система координат устройства изображения, в котором осуществляется вывод изображения объектов в заданной проекции.
Пусть мировые координаты будут трехмерными декартовыми координатами. Где должен размещаться центр координат и какими будут единицы измерения вдоль каждой оси, пока для нас не очень важно. Важно то, что для отображения мы будем знать какие-то числовые значения координат отображаемых объектов.
Для получения изображения в определенной проекции необходимо рассчитать координаты проекции. Из них можно получить координаты для графического устройства— назовем их экранными координатами. Для синтеза изображения на плоскости достаточно двумерной системы координат. Однако в некоторых алгоритмах визуализации используются трехмерные экранные координаты, например, в алгоритме Z-буфера.
В компьютерной графике наиболее распространены параллельная и центральная проекции (рис. 2.15).
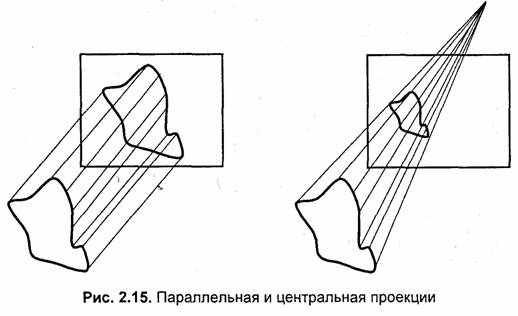
Для центральной проекции (также называемой перспективной) лучи проецирования исходят из одной точки, размещенной на конечном расстоянии от объектов и плоскости проецирования. Для параллельной проекции лучи проецирования параллельны.
Аксонометрическая проекция — разновидность параллельной проекции. Для нее все лучи проецирования располагаются под прямым углом к плоскости проецирования (рис. 2.16).
Зададим положения плоскости проецирования с помощью двух углов — а и β Расположим камеру так, чтобы проекция оси z на плоскости проецирования X0Y была бы вертикальной линией (параллельной оси 0Y).

Для того чтобы найти соотношения между координатами (х, у, z) и (X, Y, Z) для любой точки в трехмерном пространстве, рассмотрим преобразования системы координат (х, у, z) в систему (X, Y, Z). Зададим такое преобразование двумя шагами.
1-й шаг. Поворот системы координат относительно оси z на угол а. Такой поворот осей описывается матрицей
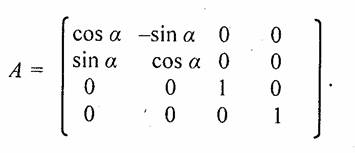
2-й шаг. Поворачиваем систему координат (V, у', z') относительно оси х' на угол β— получаем координаты (X, Y, Z). Матрица поворота
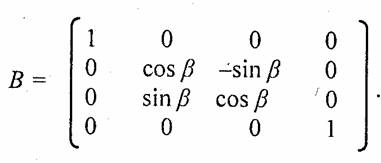

Как вы считаете, будет ли получена та же проекция, если описывать преобразования координат теми же двумя шагами, но в другой последовательности — сначала поворот системы координат относительно оси х на угол Д а потом поворот системы координат относительно оси z' на угол а? И будут ли вертикальные линии в системе координат (x,y,z) рисоваться также вертикалями в системе координат (X, Y, Z)? Иначе говоря, выполняется ли А x В = ВxА?
Обратное преобразование координат аксонометрической проекции. Для того, чтобы координаты проекции (X, Y, Z) преобразовать в мировые координаты (х, у, z), нужно проделать обратную последовательность поворотов. Вначале выполнить поворот на угол -Д а затем — поворот на угол -а. Запишем обратное преобразование в матричном виде
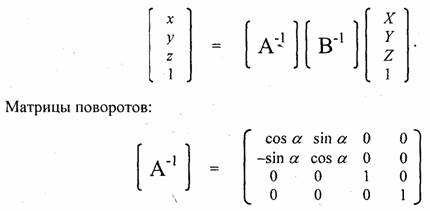

Перспективная проекция
Перспективную проекцию (рис. 2.17) сначала рассмотрим при вертикальном расположении камеры, когда а = β = 0. Такую проекцию можно себе представить как изображение на стекле, через которое смотрит наблюдатель, расположенный сверху в точке {х, у, z) = (0, 0, zk). Здесь плоскость проецирования параллельна плоскости (х 0 у).
Исходя из подобия треугольников, запишем такие пропорции:


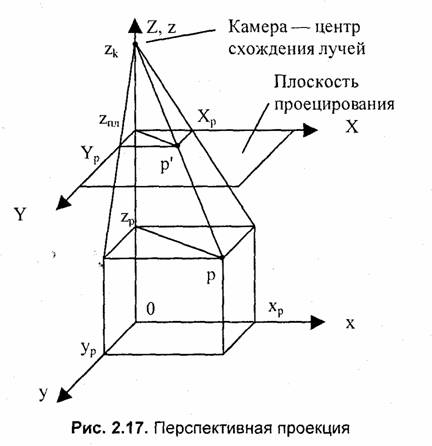
Обратите внимание на то, что здесь коэффициенты матрицы зависят от координаты z (в знаменателе дробей). Это означает, что преобразование координат является нелинейным (а точнее, дробно-линейным), оно относится к классу проективных преобразований.
Теперь рассмотрим общий случай — для произвольных углов наклона камеры (а и β) так же, как и для параллельной аксонометрической проекции. Пусть (х', у', z’) — координаты для системы координат, повернутой относительно начальной системы (х, у, z) на углы а и β.

Преобразование в целом нелинейное. Его нельзя описать одной матрицей коэффициентов-констант для всех объектов сцены (хотя для преобразования координат можно использовать и матричную форму).
Для такой перспективной проекции плоскость проецирования перпендикулярна лучу, исходящему из центра (х, у, z) = (0, 0, 0) и наклоненному под углом а, р. Если камеру отдалять от центра координат, то центральная проекция видоизменяется. Когда камера в бесконечности, центральная проекция вырождается в параллельную проекцию.
Укажем основные свойства перспективного преобразования. В центральной проекции:
□ не сохраняется отношение длин и площадей;
□ прямые линии изображаются прямыми линиями;
□ параллельные прямые изображаются сходящимися в одной точке.
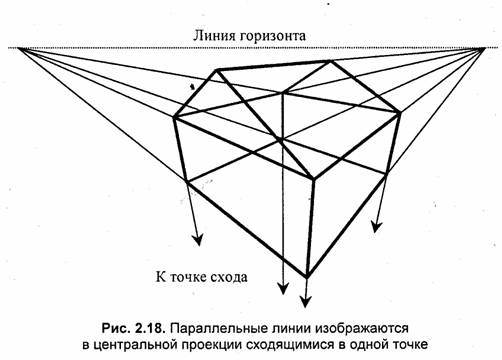
Последнее свойство широко используется в начертательной геометрии для ручного рисования на бумаге. Проиллюстрируем это на примере каркаса домика (рис. 2.18).
Существуют и другие перспективные проекции, которые различаются положением плоскости проецирования и местом точки схождения лучей проецирования. Кроме того, проецирование может осуществляться не на плоскость, а, например, на сферическую или цилиндрическую поверхность.
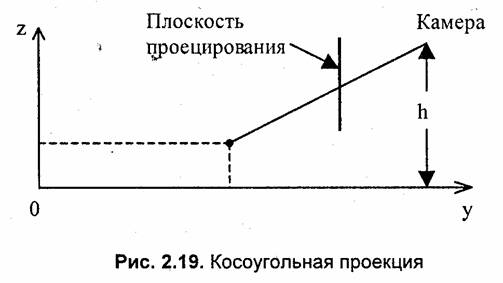
Рассмотрим косоугольную проекцию, для которой лучи проецирования не перпендикулярны плоскости проецирования. Основная идея такой проекции — камера поднята на высоту h с сохранением вертикального положения плоскости проектирования (рис. 2.19).
Получить такую проекцию можно следующим способом:
1. Выполняем поворот вокруг оси z на угол а.
2. Заменяем z'на-у', а у'на z'.
3. Выполняем сдвиг системы координат вверх на высоту камеры h.
4. В плоскости (х1, у', 0) строим перспективную проекцию уже рассмотренным выше способом (точка схода лучей на оси z).-
Преобразование координат может быть описано таким образом. Сначала определяются (х', у', z1).
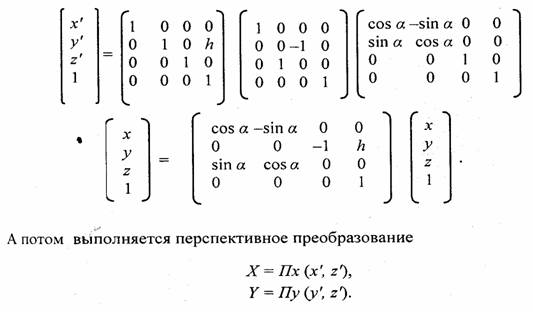
Преимущество такой проекции заключается в сохранении параллельности вертикальных линий, что иногда полезно при изображении домов в архитектурных компьютерных системах.
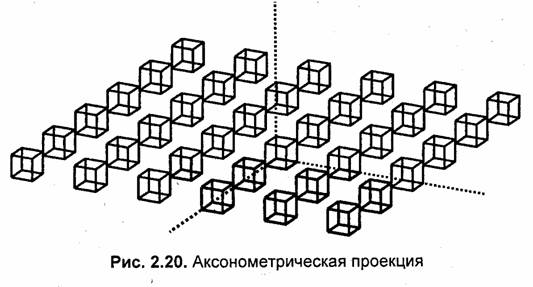
Примеры изображений в различных проекциях. Приведем примеры изображений одинаковых объектов в различных проекциях. В качестве объектов будут кубы одинакового размера. Положение камеры определим углами наклонна a = 27°,β = 70°. Пример аксонометрической проекции приведен на рис. 2.20.
Теперь рассмотрим примеры для перспективной проекции. В отличие от параллельной проекции, изображение в перспективной проекции существенно зависит от положения плоскости проецирования и расстояния до камеры.
В оптических системах известно понятие фокусного расстояния. Чем больше фокусное расстояние объектива, тем меньше восприятие перспективы (рис. 2.21), и наоборот, для короткофокусных объективов перспектива наибольшая (рис. 2.22). Данный эффект вы, наверное, уже замечали, если занимались съемками видеокамерой или фотоаппаратом. В наших примерах можно наблюдать некоторое соответствие величины расстояния от камеры до плоскости проецирования (zK – zпл) и фокусного расстояния объектива. Это соответствие, однако, условно, аналогия с оптическими системами здесь неполная.
Для приведенных ниже примеров (рис. 2.21, 2.22) zпл = 700. Углы наклона камеры а = 27°, β= 70°.
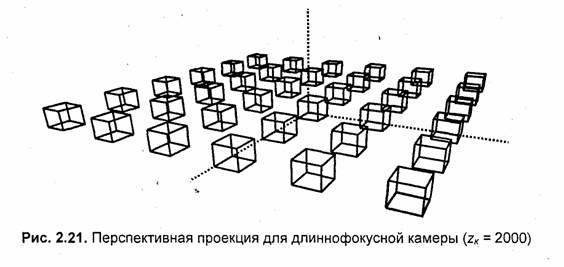
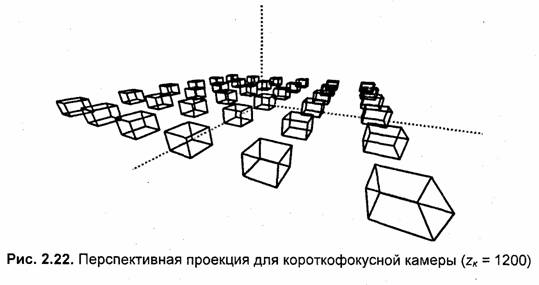
В случае короткофокусной камеры (zK = 1200) восприятие перспективы наиболее заметно для кубов, которые расположены ближе всего к камере. Вертикальные линии объектов не являются вертикалями на проекции (объекты "разваливаются").
Рассмотрим примеры косоугольной проекции (рис. 2.23, 2.24). Для нее вертикальные линии объектов сохраняют вертикальное расположение на проекции. Положение камеры (точки схождения лучей проецирования) описывается углом поворота а = 27° и высотой подъема h = 500. Плоскость проецирования параллельна плоскости (х'Оу') и располагается на расстоянии zпл = 700.
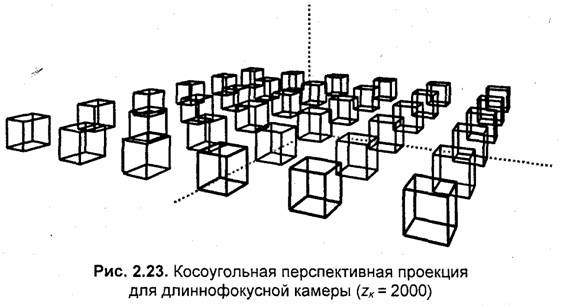
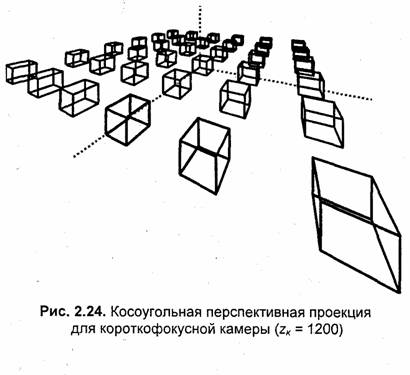
Рассмотрим еще один пример изображения в центральной проекции — текст в стиле фильма "Звездные войны":

Как мы уже рассмотрели выше, отображение на плоскость проецирования соответствует некоторому преобразованию координат. Это преобразование координат различно для разных типов проекции, но, так или иначе, осуществляется переход к новой системе координат — координатам проецирования. Координаты проецирования могут быть использованы для формирования изображения с помощью устройства графического вывода. Однако при этом могут понадобиться дополнительные преобразования, поскольку система координат в плоскости проецирования может не совпадать с системой координат устройства отображения. Например, должны отображаться объекты, измеряемые в километрах, а в растровом дисплее единицей измерения является пиксел. Как выразить километры в пикселах?
Кроме того, вы, наверное, видели, что на экране компьютера можно показывать увеличенное, уменьшенное изображение объектов, а также их перемещать. Как это делается?
Введем обозначения. Пусть (Хэ, YЭ, Zэ) — это экранные координаты объектов в графическом устройстве отображения. Заметим, что не следует воспринимать слово "экранные" так, будто речь идет только о дисплеях — все нижеследующее можно отнести и к любым другим устройствам, использующим декартову систему координат. Координаты проецирования обозначим здесь как {X, Y, Z).
Назовем окном прямоугольную область вывода с
экранными координатами![]() Обычно
приходится отображать в окне или всю сцену, или отдельную ее часть (рис. 2.25).
Обычно
приходится отображать в окне или всю сцену, или отдельную ее часть (рис. 2.25).
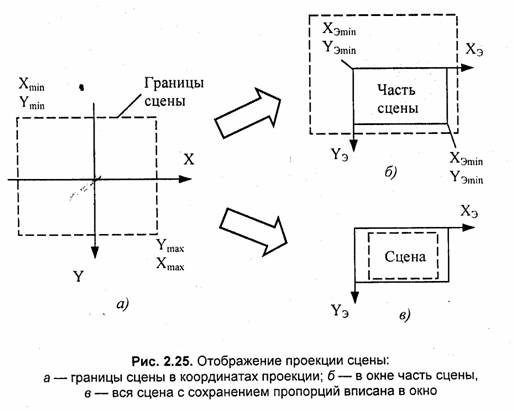
Преобразование координат проекции в экранные координаты можно задать как растяжение/сжатие и сдвиг:
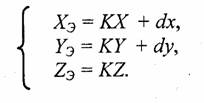
Такое преобразование сохраняет пропорции объектов благодаря одинаковому коэффициенту растяжения/сжатия (К) для всех координат. Заметим, что для плоского отображения можно отбросить координату Z.
Рассмотрим, как можно вычислить К, dx и dy. Например, необходимо вписать все изображение сцены в окно заданных размеров. Условие вписывания можно определить так:

Если значение Кх или значение Ку равно бесконечности, то его необходимо отбросить. Если оба — то значение Kmin можно задать равным единице. Для того чтобы изображение в окне имело наибольший размер, выберем К = Kmin. Теперь можно найти dx. Из неравенства (1):

При таких значениях dx и dy центр сцены будет в центре окна.
В других случаях, когда в окне необходимо показывать с соответствующим масштабом лишь часть сцены, можно прямо задавать числовые значения масштаба (К) и координаты сдвига (dx, dy). При проектировании интерфейса графической системы желательно ограничить выбор К, dx, dy диапазоном допустимых значений.
В графических системах используются разнообразные способы задания масштаба отображения и определения границ сцены для показа в окне просмотра. Например, для сдвига часто используют ползунки скроллинга. Также можно указывать курсором точку на сцене, и затем эта точка становится центральной точкой окна. Или можно очертить прямоугольник, выделяя границы фрагмента сцены, — тогда этот фрагмент затем будет вписан в окно.
И так далее. Все эти способы отображения основываются на растяжении/сжатии (масштабировании), а также сдвиге, и описываются аффинным преобразованием координат.
2.5. Выводы
Представим цепочку преобразований координат от мировых к экранным следующим образом (рис. 2.26):

Для аксонометрической (параллельной) проекции координаты проекции совпадают с видовыми координатами (хотя это и не обязательно). Преобразование координат можно описать одной матрицей, которая получается перемножением соответствующих матриц.
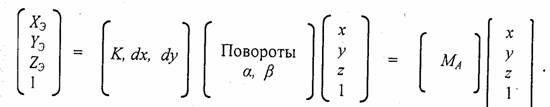
Важно то, что для аксонометрической проекции коэффициенты матрицы — это константы, одинаковые для всех точек трехмерного пространства. Это дает возможность свести к минимуму вычисления координат в цикле графического вывода. В этом плане можно отметить крайний случай, когда мировые координаты совпадают с экранными — вообще нет никаких преобразований координат. Например, координаты объектов задаются в пикселах экрана. Такое часто встречается, например, в двухмерной графике. Для перспективной (центральной) проекции коэффициенты матрицы проецирования на плоскость не являются константами — они зависят от Z. Это делает нецелесообразным запись цепочки преобразований в виде одной матрицы и, как следствие этого, усложняется расчет координат в сравнении с параллельной проекцией.

Для центральной проекции иногда используют матричную форму с применением обобщенных однородных нелинейных координат [28, 32]. В качестве мировых и экранных координат нами была использована трехмерная ортогональная система. В компьютерных графических системах также используются другие системы координат и иные проекции. В особенности это касается систем, которые моделируют объекты, располагающиеся на поверхности Земли. С этими вопросами можно ознакомиться в многочисленной литературе по геодезии и картографии, а также в работах, посвященных геоинформационным системам.
ГЛАВА 3
растровые алгоритмы
Сформировать растровое изображение можно по-разному. Для того чтобы создать изображение на растровом дисплее, можно просто скопировать готовый растр в видеопамять. Этот растр может быть получен, например, с помощью сканера или цифрового фотоаппарата. А можно создавать изображение объекта путем последовательного рисования отдельных простых элементов.
Простые элементы, из которых складываются сложные объекты, будем называть графическими примитивами. Их можно встретить повсюду. Например, для построения изображения используется некоторый набор примитивов, которые поддерживаются определенными графическими устройствами вывода. Графические примитивы также можно применять для описания пространственных объектов в базе данных компьютерной системы— модели объектов. Могут использоваться различные множества примитивов для модели и для Алгоритмов отображения. Удобно, когда эти множества совпадают, тогда упрощается процесс отображения.
Простейшим и, вместе с тем, наиболее универсальным растровым графическим примитивом является пиксел. Любое растровое изображение можно нарисовать по пикселем, но это сложно и долго. Необходимы больше сложные элементы, для которых рисуются сразу несколько пикселов.
Рассмотрим графические примитивы, которые используются наиболее часто : в современных графических системах, — это линии и фигуры.
3.1. Алгоритмы вывода прямой линии
Рассмотрим растровые алгоритмы для отрезков прямой линии. Предположим, что заданы координаты (x 1 ,y 1 - х2,у2) концов отрезка прямой. Для вывода линии необходимо закрасить в определенный цвет все пикселы вдоль линии. Для того чтобы закрасить каждый пиксел, необходимо знать его координаты.
Наиболее просто нарисовать отрезок горизонтальной линии:
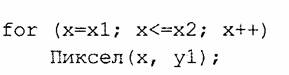
Вычисление текущих координат пиксела здесь выполняется как приращение по х (необходимо, чтобы х1 <-х2), а вывод пиксела обеспечивается функцией Пиксел(). Поскольку в языке С, C++ для названия функции нельзя использовать кириллицу, то будем дальше использовать ее как комментарий.
Аналогично рисуется отрезок вертикали:
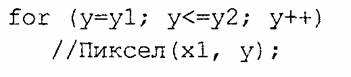
Как видим, в цикле выполняются простейшие операции над целыми числами — приращение на единицу и проверка на "< =". Поэтому операция рисования отрезка выполняется быстро и просто. Ее используют как базовую операцию для других операций, например, в алгоритмах заполнения плоскости полигонов.
Можно поставить такой вопрос: какая линия рисуется быстрее — горизонталь или вертикаль? На первый взгляд — одинаково быстро. Если учитывать только математические аспекты, то скорость должна быть одной и той же при одинаковой длине линий, поскольку в обоих случаях выполняется равное количество идентичных операций. Однако если кроме расчета координат анализировать также вывод пикселов, то могут быть отличия. В растровых системах рисование пиксела обычно означает запись одного или нескольких бит в память, где сохраняется растр. И здесь уже не все равно — по строкам или по столбцам заполняется растр. Необходимо учитывать логическую организацию памяти компьютера, в которой хранятся, биты или байты растра.
Даже для компьютеров одного типа (например, персональных компьютеров) для различных поколений процессоров и памяти скорость записи по соседним адресам может существенно отличаться от скорости записи по не соседним адресам [40]. В особенности это заметно, когда для растра используется виртуальная память с сохранением отдельных страниц на диске и (или) в оперативной памяти (RAM). При работе графических программ в среде операционной системы Windows часто случается так, что горизонтали рисуются быстрее вертикалей, поскольку в страницах памяти хранятся соседние байты. А может быть, что RAM достаточно, но скорости рисования все же различны.
Например, если используется черно-белый растр в формате один бит на пиксел, то для вертикали битовая маска одинакова для всех пикселов линии, а для горизонтали маску нужно изменять на каждом шаге. Здесь необходимо заметить, что рисование черно-белых горизонталей можно существенно ускорить, если записывать сразу восемь соседних пикселов — байт в памяти.
Горизонтали и вертикали представляют собой частный случай линий. Рассмотрим линию общего вида. Для нее также необходимо вычислять координат каждого пиксела. Известно несколько методов расчетов координат точек линии.
Пусть заданы координаты конечных точек отрезка прямой. Найдем координаты точки внутри отрезка (рис. 3.1).

В зависимости от угла наклона прямой выполняется цикл по оси х или по у
(рис. 3.2).
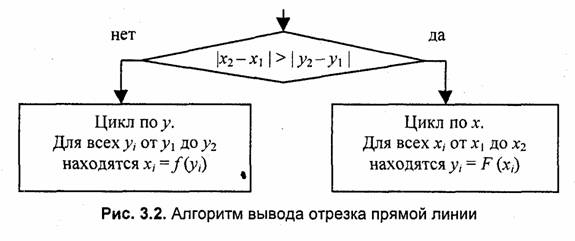
Приведем пример записи этого алгоритма на компьютерном языке программирования С, C++. Для сокращения текста рассмотрим фрагмент программы, где выполняется цикл по оси х, причем х1 <х2:
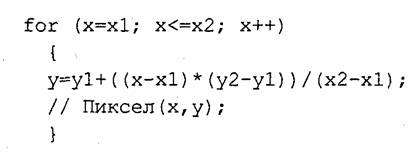
Здесь все операции выполняются над целыми числами. Двойные скобки необходимы для того, чтобы деление выполнялось после умножения. Недостатки такой программы — в цикле выполняется много лишних операций, присутствуют операции деления и умножения. Это обуславливает малую скорость работы. Относительно лишних операций в цикле. Можно вынести вычисление (у2 - у 1)/(х2 – х1) из цикла, поскольку это значение не изменяется. Однако для этого уже необходимо использовать операции с плавающей точкой:

Поскольку мы решили использовать операции с плавающей точкой, то попробуем еще уменьшить количество операций в цикле. Если раскрыть скобки в выражении у = у1 + (х – х1)-к; то получим у = у1 + х.к- х1 .к. Здесь значение (yl – х1.к) является константой— эти операции также вынесем из тела цикла.

В цикле выполняются только две арифметические операции и преобразование х из целого в форму с плавающей точкой.
Если рассматривать цикл вычисления у, по соответствующим значениям хi = х1, х1 +1, ... , х2 как итеративный процесс, то можно поставить такой вопрос: чему равна разность (уi+1 — уi)1 Она равна уi+1 —уi = xl + (хi+1 —xl)k-xl- (xi – х1) к = (хi+1 – xi) к = к; поскольку xi+1 – xi =1. Разность (yi+1 – уi) — константа, равная к. Исходя из этого, можно построить цикл таким образом:

В теле цикла есть только одна операция для вычисления координаты у (если не учитывать <= и ++).
Если сравнивать последний вариант с предыдущим, то последний лучше по быстродействию. Также существенно отличаются способы вычисления координаты у. В последнем варианте значение у вычисляется прибавлением приращения к на каждом шаге, и на последнем шаге цикла (когда х=х2) должно стать у=у2. Исходя из чисто математических соображений здесь все корректно, однако необходимо учесть, что в компьютере дробные числа представляются в формате с плавающей точкой не точно. Кроме погрешности представления чисел существует ошибка выполнения арифметических операций с плавающей точкой. Ошибка зависит от разрядности мантисс, и самая малая — для long double, но все равно не нулевая. С каждым шагом цикла ошибки накапливаются, и может так произойти, что у не равно у2 на последнем шаге. Это необходимо учитывать при использовании алгоритма.
Положительные черты прямого вычисления координат:
1. Простота, ясность построения алгоритма.
2. Возможность работы с нецелыми значениями координат отрезка. (Как вы считаете, какой вариант из четырех корректно вычисляет координаты пикселов, если х1, у1, х2 иу>2 — дробные?)
Недостатки:
1. Использование операций с плавающей точкой или целочисленных операций умножения и деления обуславливает малую скорость. Однако это зависит от процессора и для различных типов компьютеров может быть по-разному. В современных компьютерах, в которых процессоры используют эффективные способы ускорения (например, конвейер арифметических операций с плавающей точкой), время выполнения целочисленных операций уже не намного меньше. Для старых компьютеров разница могла быть в десятки раз, поэтому и старались разрабатывать алгоритмы только на основе целочисленных операций.
2. При вычислении координат путем добавления приращений может накапливаться ошибка вычислений координат.
Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа.
Брезенхэм предложил подход [54, 55], позволяющий разрабатывать так называемые инкрементные алгоритмы растеризации. Основной целью для разработки таких алгоритмов было построение циклов вычисления координат на основе только целочисленных операций сложения/вычитания без использования умножения и деления. Уже известны инкрементные алгоритмы не только для отрезков прямых, но и для кривых линий [33, 55].
Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат. Приращения рассчитываются на основе анализа функции погрешности. В цикле выполняются только целочисленные операции сравнения и сложения/вычитания. Достигается повышение быстродействия для вычислений каждого пиксела по сравнению с прямым способом. Один из вариантов алгоритма Брезенхэма:
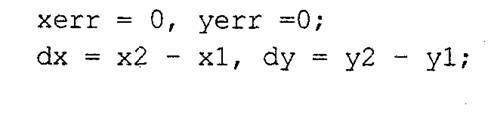

Рассмотрим пример работы приведенного выше алгоритма Брезенхэма для отрезка (х1у1 - х2у2) = (2,3 - 8,6). Этот алгоритм восьмисвязный, то есть при вычислении приращений координат для перехода к соседнему пикселу возможны восемь случаев (рис. 3.3).

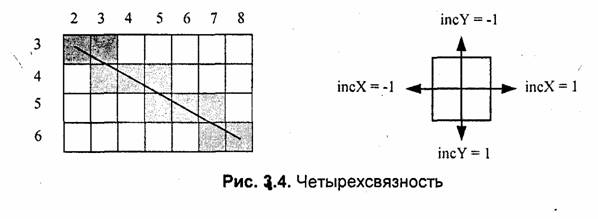
Известны также четырехсвязные алгоритмы (рис. 3.4).
Четырехсвязные алгоритмы проще, но они генерируют менее качественное
изображение линий за большее количество тактов роботы. Для приведенного
примера четырехсвязный алгоритм работает 10 тактов, а восьмисвязный —
только 7.
3.2. Алгоритм вывода окружности
Для вывода контура круга можно использовать соотношение между координатами X и Y для точек круга X2 + Y2 = R2 и построить алгоритм прямого вычисления координат. Однако тогда необходимо вычислять квадратный корень, а это в цифровом компьютере выполняется медленно.
Дадим запись инкрементного алгоритма Брезенхэма на языке C++:


В этом алгоритме использована симметрия круга — в основном цикле вычисляются координаты точек круга только для одного октанта и сразу рисуются восемь симметрично расположенных пикселов [33].
3.3. Алгоритм вывода эллипса
Инкрементный алгоритм для эллипса подобен алгоритму для круга, но более сложный.Этот алгоритм приведен в [33].


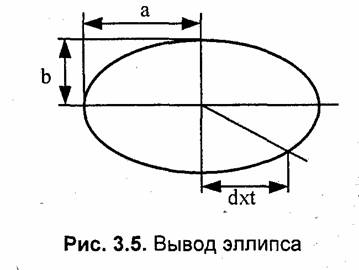
В этом алгоритме использована симметрия эллипса по квадрантам (рис. 3.5).
Алгоритм состоит из двух циклов. Сначала от х=0 до x=dxt, где
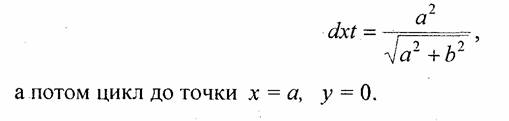
Разработана математиком Пьером Безъе. Кривые и поверхности Безье были ; использованы в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике.
Кривые Безье описываются в параметрической форме:
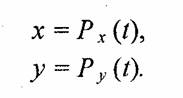
Значение t выступает как параметр, которому отвечают координаты отдельной точки линии. Параметрическая форма описания может быть более удобной для некоторых кривых, чем задание в виде функции y=f(x). Это потому, что функцияƒ(х) может быть намного сложнее, чем Px{f) и Py(t), кроме того, f(x) может быть неоднозначной.
Многочлены Безье для Р х и Ру имеют такой вид:
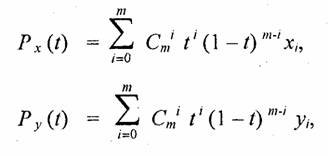


m = 3 (по четырем точкам, кубическая, рис. 3.8). Используется довольно часто, в особенности в сплайновых кривых.
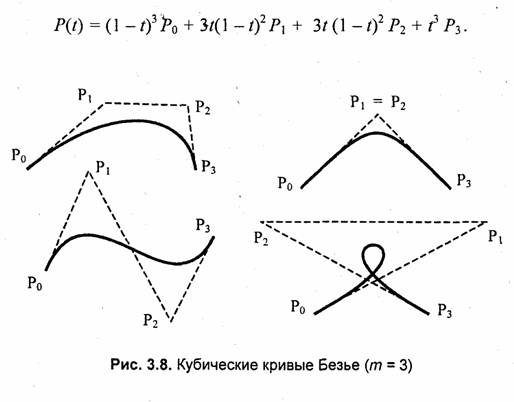
Геометрический алгоритм для кривой Безье
Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t. Алгоритм описан в [19].
1. Каждая сторона контура многоугольника, проходящего по точкам-ориентирам, делится пропорционально значению t.
2. Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предыдущего контура.
3. Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная "речка деления. Эта точка и будет точкой кривой Безье (рис. 3.9).

Результат работы алгоритма— координаты одной точки кривой Безье — записываются в R[0].
Фигурой здесь будем считать плоский геометрический объект, который состоит из линий контура и точек, которые содержатся внутри контура.
В общем случае линий контура может быть несколько — когда объект имеет внутри пустоты. В этом случае для описания таких фигур необходимы два и более контуров (рис. 3.10).
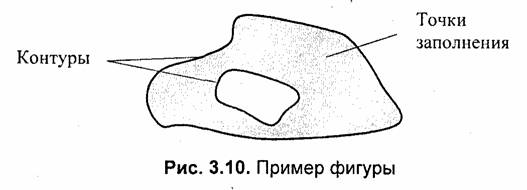
В некоторых графических системах одним объектом может считаться и более сложная многоконтурная фигура — совокупность островов с пустотами.
Графический вывод фигур разделяется на две задачи: вывод контура и вывод точек заполнения. Поскольку контур представляет собой линию, то вывод контура проводится на основе алгоритмов вывода линий. В зависимости от сложности контура, это могут быть отрезки прямых, кривых или произвольная последовательность соседних пикселов.
Для вывода точек заполнения известны методы, разделяющиеся в зависимости от использования контура на два типа— алгоритмы закрашивания от внутренней точки к границам произвольного контура и алгоритмы, которые используют математическое описание контура.
Рассмотрим алгоритмы закрашивания произвольного контура, который уже нарисован в растре. Сначала находится пиксел внутри контура фигуры. Цвет этого пиксела изменяем наружный цвет заполнения. Потом проводится анализ цветов всех соседних пикселов. Если цвет некоторого соседнего пиксела не равен цвету границы контура или цвету заполнения, то цвет этого пиксела изменяется на цвет заполнения. Потом анализируется цвет пикселов, соседних с предыдущими. И так далее, до тех пор, пока внутри контура все пикселы не перекрасятся в цвет заполнения.
Пикселы контура — это граница, за которую нельзя выходить в ходе последовательного перебора всех соседних пикселов. Соседними могут считаться только четыре пиксела (справа, слева, сверху и снизу — четырехсвязность), или все восемь пикселов (восьмисвязность). Не всякий контур может служить границей закрашивания (рис. 3.11).
Простейший алгоритм закрашивания. Для всех алгоритмов закрашивания нужно задавать начальную точку внутри контура с координатами xo, yo. Простейший алгоритм можно описать так [32]:
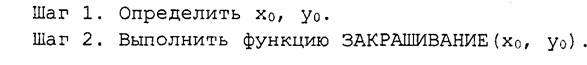

Такое определение функции является рекурсивным. Рекурсия позволяет „ упростить запись некоторых алгоритмов. Но для этого алгоритма рекурсия порождает существенные проблемы — рекурсивные вызовы функции закрашивание () делаются для каждого пиксела, что обычно приводит к переполнению стека в ходе выполнения компьютерной программы. Практика показывает, что этот алгоритм неприемлем для фигур площадью в тысячу и больше пикселов.
Можно построить подобный алгоритм и без рекурсии, если вместо стека компьютера использовать отдельные массивы. Тогда стек не переполняется.
Волновой алгоритм закрашивания. Алгоритм был разработан авторами работы [38] и предназначался для расчета центра тяжести объектов по соответствующим изображениям. Идея была навеяна волновым алгоритмом поиска трассы на графе, известным в САПР электронных схем. Суть подобных алгоритмов состоит в том, что для начальной точки (вершины на графе) находятся соседние точки (другие вершины), которые отвечают двум условиям: во-первых — эти вершины связаны с начальной; во-вторых — эти вершины еще не отмечены, то есть они рассматриваются впервые. Соседние вершины текущей итерации отмечаются в массиве описания вершин, и каждая из них становится текущей точкой для поиска новых соседних вершин в следующей итерации. Если в специальном массиве отмечать каждую вершину номером итерации, то когда будет достигнута конечная точка, можно совершить обратный цикл — от конечной точки к начальной по убыванию номеров итераций. В ходе обратного цикла и находятся все кратчайшие пути (если их несколько) между двумя заданными точками на графе. Подобный алгоритм можно также использовать, например, для поиска всех нужных файлов на диске. Относительно закрашивания растровых фигур, то здесь вершинами графа являются пикселы, а отметка пройденных пикселов делается прямо в растре цветом закрашивания. Как видим, это почти полностью повторяет идею предыдущего простейшего алгоритма, однако здесь мы не будем использовать рекурсию. Это обуславливает совсем другую последовательность обработки пикселов при закрашивании.
Запишем волновой алгоритм закрашивания на языке C++ с использованием графических функций API Windows.


Здесь цвет закрашивания и цвет контура — черный цвет (код 0). Пример работы алгоритма приведен на рис. 3.12.
От начальной точки распространяется волна пикселов закрашивания в виде ромба. В одном цикле onestep закрашиваются пикселы вдоль линии периметра ромба (или нескольких ромбов в зависимости от сложности фигуры).
В качестве рабочих массивов для текущего сохранения координат пикселов
фронтов волн использованы динамические массивы емкостью по 10 000 элементов. Максимальная емкость массивов обуславливается размерами контура и рассчитывается эмпирически.
Достаточно просто модифицировать приведенный алгоритм для случая отличающихся цветов контура и заполнения.
Необходимо заметить, что этот алгоритм не является самым быстрым из известных алгоритмов закрашивания, особенно если для его реализации использовать медленную функцию setPixel для рисования отдельных пикселов в программах для Windows. Большую скорость закрашивания обеспечивают алгоритмы, которые обрабатывают не отдельные пикселы, а сразу большие блоки из многих пикселов, которые образовывают прямоугольники или линии.

Алгоритм закрашивания линиями. Данный алгоритм получил широкое распространение в компьютерной графике. От приведенного ранее простейшего рекурсивного алгоритма он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселами контура. Алгоритм рекурсивный, но поскольку вызов функции осуществляется для линии, а не для каждого отдельного пиксела, то количество вложенных вызовов уменьшается пропорционально длине линии. Это уменьшает нагрузку на стековую память компьютера.
Приведем запись алгоритма на языке C++. Этот пример взят из [32], незначительно усовершенствован и переработан для использования в среде Windows.

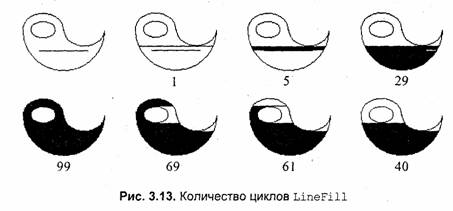
Так же, но немного быстрее, работает функция FioodFiii API Windows. Разница в быстродействии обусловлена тем, что для LineFiii мы использовали стандартные функции для интерфейса прикладных программ, a FioodFiii оптимизирована на системном уровне
Алгоритмы заполнения, которые используют
математическое описание контура
Математическим описанием контура фигуры может служить уравнение у = f(x) для окружности, эллипса или другой кривой. Для многоугольника (полигона) контур задается множеством координат вершин (х1 у1). Возможны и другие формы описания контура. В любом случае алгоритмы данного класса не предусматривают обязательное предварительное создание пикселов контура растра — контур может совсем не выводиться в растр. Рассмотрим некоторые из подобных алгоритмов заполнения.
Заполнение прямоугольников. Среди всех фигур прямоугольник заполнять наиболее просто. Если прямоугольник задан координатами противоположных углов, например, левого верхнего (х1 у1) и правого нижнего (х2 у2), тогда алгоритм может заключаться в последовательном рисовании горизонтальных линий заданного цвета (рис. 3.14).

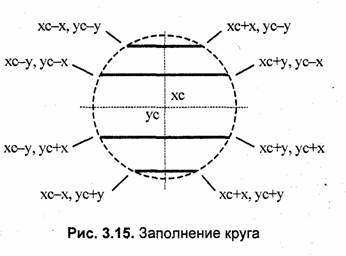
Заполнение круга. Для заполнения круга можно использовать алгоритм вывода контура, который мы уже рассмотрели в разд. 3.2. В процессе выполнения этого алгоритма последовательно вычисляются координаты пикселов контура в границах одного октанта. Для заполнения надлежит выводить горизонтали, которые соединяют пары точек на контуре, расположенные симметрично относительно оси у (рис. 3.15).
Так же может быть построен и алгоритм заполнения эллипса.
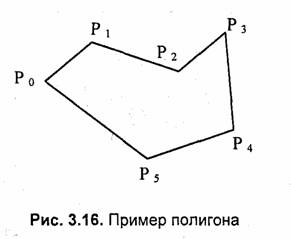
Заполнение полигонов. Контур полигона определяется вершинами, которые соединены отрезками прямых (рис. 3.16). Это— векторная форма задания фигуры.
Рассмотрим один из наиболее популярных алгоритмов заполнения полигона. Его основная идея — закрашивание фигуры отрезками прямых линий. Наиболее удобно использовать горизонтали. Алгоритм представляет собою цикл вдоль оси у, в ходе этого цикла выполняется поиск точек сечения линии контура с соответствующими горизонталями. Этот алгоритм получил название XY [33]:


В этом алгоритме использовано свойство топологии контура фигуры. Оно состоит в том, что любая прямая линия пересекает любой замкнутый контур четное количество раз (рис. 3.17). Для выпуклых фигур точек пересечения с любой прямой всегда две. Таким образом, на шаге 3 этого алгоритма в массив { xj} всегда должно записываться парное число точек сечения.
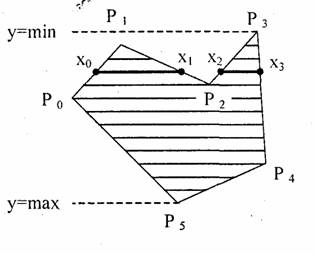
При нахождении точек пересечения горизонтали с контуром необходимо принимать во внимание особые точки. Если горизонталь имеет координату (у), совпадающую с уi вершины Рi тогда надлежит анализировать то, как горизонталь проходит через вершину. Если горизонталь при этом пересекает контур, как, например, в вершинах Рo или Р4 то в массив записывается одна точка сечения. Если горизонталь касается вершины контура (в этом случае вершина соответствует локальному минимуму или максимуму как, например, в вершинах Р1 Р2, Рз или Р5), тогда координата точки касания или не записывается, или записывается в массив два раза. Это условие четности количества точек пересечения, хранящихся в массиве {xj}.
Процедура определения точек пересечения контура с горизонтальной разверткой, учитывая анализ на локальный максимум, может быть достаточно сложной. Это замедляет работу. Радикальным решением для упрощения поиска точек сечения может быть смещение координат вершин контура или горизонталей заполнения таким образом, чтобы ни одна горизонталь не попала в вершину. Смещение можно выполнять различными способами, например, ввести в растр дробные координаты для горизонталей: утiп+ 0.5, ymin + 1.5, ..., ymax-0,5.
Но такое упрощение процедуры нахождения точек пересечения приводит к искажению формы полигона.
Для определения координат (х) точек пересечения для каждой горизонтали необходимо перебирать все п отрезков контура. Координата пересечения отрезка pi—рk с горизонталью у равна

где к— коэффициент пропорциональности, п — число вершин полигона.
Возможны модификации приведенного алгоритма для ускорения его работы. Например, можно принять во внимание то, что каждая горизонталь в большинстве случаев пересекает небольшое количество ребер контура. Поэтому если при поиске точек сечения делать предварительный отбор ребер, которые находятся вокруг каждой горизонтали, то можно добиться уменьшения количества тактов работы с Nгop = к. п до к .пр, где пр — число отобранных ребер. Например, разделим диапазон уmin - ymax пополам. Если для диапазона от ymin до уср составить список отрезков (или вершин), которые попадают в этот диапазон, то в этот список будет включено приблизительно вдвое меньшее р количество, чем для всего диапазона от ymin до утах. Почему приблизительно— ибо это зависит от формы полигона. Таким образом, при работе алгоритма для каждой горизонтали в диапазоне ymin до уср уже нужно не к.п тактов, а ~ к .п/2.
Аналогично для диапазона уср – ymax также можно составить список ребер, (который также будет почти вдвое меньшим. Если принять, что подсчеты для каждой горизонтали теперь выполняются за вдвое меньшее количество тактов, а именно за (Nгop/2), то общее число тактов:
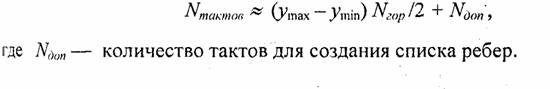
Такой способ повышения быстродействия эффективен для большого количества вершин. Контур можно делить не пополам, а на более мелкие части — соответственно повышается скорость.
Приведенные выше алгоритмы заполнения могут быть использованы не только для рисования фигур. На основе алгоритмов заполнения могут быть разработаны алгоритмы для других целей. Например, для определения площади фигуры, если считать плрщадь пропорциональной количеству пикселов заполнения. Или, например, алгоритм для поиска объектов по внутренней точке — эта операция часто используется в векторных графических редакторах.
Что общее и что разное у объектов, изображенных на рис. 3.18?
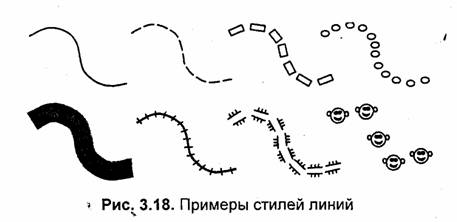
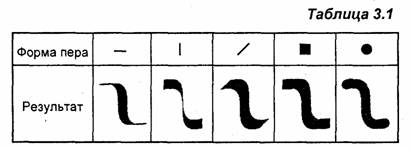
Общее — линия оси, описывающая каждый из восьми объектов. Разное — элементы вдоль линии оси. Для описания различных по виду изображений на основе линий используют термин стиль линий или перо. Термин перо иногда делает более понятной суть алгоритма вывода линий для некоторых стилей — в особенности для толстых линий. Например, если для тонкой непрерывной линии перо соответствует одному пикселу, то для толстых линий перо можно представить себе как фигуру или отрезок линии, который скользит вдоль оси линии, оставляя за собой след (табл. 3.1).
Алгоритмы вывода толстой линии
Взяв за основу любой алгоритм вывода обычных тонких линий (например, алгоритм Брезенхэма), запишем его в следующем обобщенном виде:

Можно представить себе такой алгоритм, как цикл, в котором определяются координаты (х,у) каждого пиксела. Этот алгоритм можно модифицировать для вывода толстой линии следующим образом:

Вместо вывода отдельного пиксела стоит вывод фигуры или линии, соответствующей перу — прямоугольник, круг, отрезок прямой.
Такой подход к разработке алгоритмов толстых линий имеет преимущества и недостатки. Преимущество— можно прямо использовать эффективные алгоритмы для вычисления координат точек линии оси, например, алгоритмы ррезенхэма. Недостаток — неэффективность для некоторых форм пера. Для перьев, которые соответствуют фигурам с заполнением, количество тактов работы алгоритма пропорционально квадрату толщины линии. При этом большинство пикселов многократно закрашивается в одних и тех же точках (рис. 3.19).

Такие алгоритмы более эффективны для перьев в виде отрезков линий. В этом случае каждый пиксел рисуется только один раз. Но здесь важным
является наклон изображаемой линии. Ширина пера зависит от наклона (рис. 3.20).
Очевидно, горизонтальное перо не может рисовать толстую горизонтальную линию.
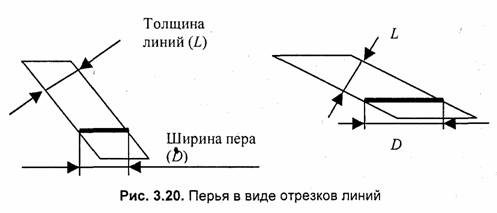
Для вывода толстых линий с помощью пера в качестве отрезка линии чаще всего используются отрезки горизонтальной или вертикальной линий, реже — диагональные отрезки под углом 45 градусов. Целесообразность использования такого способа определяется большой скоростью вывода горизонтальных и вертикальных отрезков прямой. Для того чтобы достигнуть минимального количества тактов вывода, толстые линии, которые по наклону ближе к вертикальным, рисуют горизонтальным пером, а пологие линии — вертикальным пером.
При выводе толстых линий с использованием пера-отрезка линии заметны разрывы в углах полилиний и плохие концы (рис. 3.21).
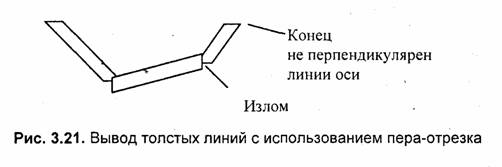
Для решения таких проблем иногда используют другие алгоритмы вывода толстых линий. Например, вывод толстой полигинии можно выполнить как рисование полигона с заполнением (рис. 3.22).
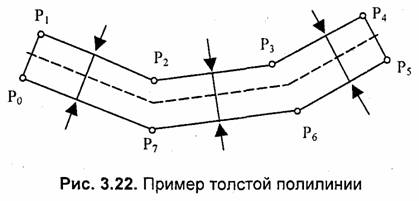
Очевидный недостаток такого подхода— меньшая скорость вывода, поскольку заполнение полигона — это существенно более трудоемкая задача, чем вывод линий, а кроме того, нужно еще определять координаты его вершин.
Третья разновидность алгоритмов вывода толстых линий — рисование толстой линии последовательным наложением нескольких тонких линий, смещенных одна относительно второй.
Алгоритмы вывода пунктирной линии
Алгоритм для рисования тонкой пунктирной линии можно получить из алгоритма вывода тонкой непрерывной линии

В, таком алгоритме используется новая переменная (С) — счетчик пикселов линии. Если значение С удовлетворяет некоторому логическому условию, то рисуется пиксел заданного цвета с текущими координатами (х, у). Логическое условие будет определять стиль линии. Например, если условием будет четность значения С, то получим линию из одиночных точек. Для рисования пунктирной линии можно анализировать остаток от деления С на S. Например, если рисовать пикселы линии только тогда, когда С mod S < S/2, то получим пунктирную линию с длиной штрихов S/2 и с шагом S.
При выводе полилиний, которые состоят из отрезков прямых, или сплайновых кривых, необходимо предотвратить обнуление значения счетчика в начале каждого отрезка и обеспечить продолжение непрерывного приращения вдоль всей сложной линии. Иначе будут нестыковки пунктира. Использование переменной-счетчика затруднено при генерации пунктирных линий в алгоритмах, которые используют симметрию, например, при выводе круга или эллипса. В этом случае будут нестыковки пунктира на границах октантов или квадрантов.
Алгоритм вывода толстой пунктирной линии
Объединив алгоритм для вывода толстой непрерывной линии и алгоритм для тонкой пунктирной линии, можно получить следующий алгоритм:

3.7. Стиль заполнения. Кисть. Текстура
При выводе фигур могут использоваться различные стили заполнения. Для обозначения стилей заполнения, отличных от сплошного стиля, используют такие понятия, как кисть и текстура. Их можно считать синонимами, однако понятие текстуры обычно используется применительно к трехмерным объектам, а кисть — для изображения двумерных объектов. Текстура — это стиль заполнения, закрашивание, которое имитирует сложную рельефную объемную поверхность, выполненную из какого-то материала. Для описания алгоритмов заполнения фигур с определенным стилем используем тот же способ, что и для описания алгоритмов рисования линий. Мы уже ранее рассмотрели некоторые алгоритмы заполнения, и вы, наверное, согласитесь, что описание всех разновидностей подобных алгоритмов можно дать с помощью такой обобщенной схемы:

Например, в алгоритме вывода полигонов пикселы заполнения рисуются в теле цикла горизонталей, а все другие операции предназначены для подсчета координат (х, у) этих пикселов. Сплошное заполнение означает, что цвет (С) всех пикселов одинаков, то есть C=const. Нам нужно как-то изменять цвет пикселов заполнения, чтобы получить определенный узор. Преобразуем алгоритм заполнения следующим образом:

Функция f(x,y) будет определять стиль заполнения. Аргументами функции цвета являются координаты текущего пиксела заполнения. Однако в отдельных случаях эти аргументы не нужны. Например, если цвет С вычислять как случайное значение в определенных границах: С = random (), то можно создать иллюзию шершавой матовой поверхности (рис. 3.23).

Другой стиль заполнения — штриховой (рис. 3.24). Для него функцию цвета также можно записать в аналитической форме:

Если не рисовать пикселы фона, то можно создать иллюзию полупрозрачной фигуры. Подобную функцию можно записать и для других типов штриховки. Аналитическая форма описания стиля заполнение позволяет достаточно просто изменять размеры штрихов при изменениях масштаба показа, например, для обеспечения режима WYSIWYG.
Зачастую при использовании кистей и текстур используется копирование небольших растровых изображений. Такой алгоритм заполнения можно описать вышеупомянутой общей схемой, если строку С =f(x, у) заменить двумя г другими строками:
Преобразование координат пиксела заполнения (х, у) в координаты внутри образца кисти можно выполнить таким образом:
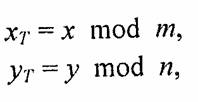
где т, п — размеры растра кисти соответственно по горизонтали и вертикали. При этом координаты (хТ, уТ) будут в диапазоне хТ= 0...m- 1, уТ =0...п - 1 при любых значениях х и у. Таким образом, обеспечивается циклическое копирование фрагментов кисти внутри области заполнения фигуры (рис. 3.25).
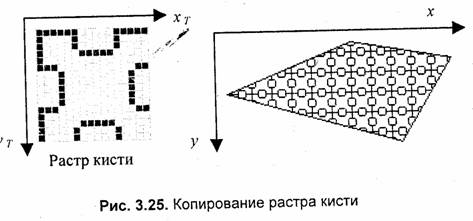
Удобно, когда размеры кисти равны степени двойки. В этом случае вместо операций взятия остатка (mod) можно использовать более быстродействующие для цифровых компьютеров поразрядные двоичные операции. Приведем пример вычисления остатка от деления на 16.

Здесь можно использовать поразрядную операцию & (И). Еще один пример. Если необходимо вычислить X mod 256, а значение X записано в регистре АХ микропроцессора (совместимого с 80x86), то в качестве результата достаточно взять содержимое младшей байтовой части этого регистра — AL.
Для пикселов текстур часто употребляется название тексел. Растровые текстуры и кисти широко используются в современной компьютерной графике, в том числе и в ЗD-графике. Для отображения трехмерных объектов часто используются полигональные поверхности, каждая грань отображается с наложенной текстурой. Поскольку объекты обычно показываются с разных ракурсов — повороты, изменения размеров и тому подобное, то необходимо соответственно трансформировать и каждую грань с текстурой. Для этого используются проективные текстуры.
Общая схема алгоритма заполнения контуров полигонов для проективных текстур такая же, как и приведенная выше. Однако растровый образец здесь представляет всю грань, а преобразование координат из (х, у) в (хг, уТ) более сложное, например, аффинное:
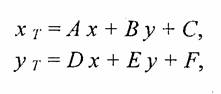
где коэффициенты А, В, ... , F —- константы при пересчете координат всех пикселов для отдельной текстурированной грани. Такое преобразование координат можно использовать, если привязать текстуру к грани по трем опорным точкам. Пример наложения проективной текстуры приведен на рис. 3.26.
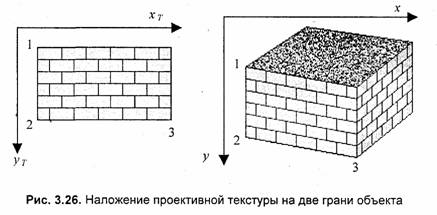
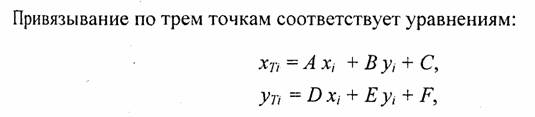
где i = 1, 2, 3. По, известным координатам (jt7y, Утд и (*/, Уд можно найти коэффициенты А, В, ... , F, если решить систему линейных уравнений. Эта система распадается на две независимые системы третьего порядка. Для упрощения записи заменим xTi наXi ayTi на У,:
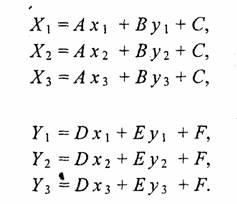
Для решения систем линейных уравнений известно множество способов. Используем способ, основанный на вычислении определителей. Решение первой системы для коэффициентов А, В и С можно записать в виде
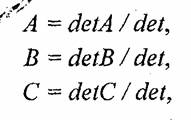

Если главный определитель равен нулю, то это означает, что решение системы невозможно. Это может быть, например, тогда, когда все три точки (х1 y1), (х2, у2) и (x3 x3) располагаются вдоль прямой линии (грань видна с торца). Однако в этом случае рисовать текстуру и не нужно. Вычислить определитель третьей степени можно, например, по "правилу Саррюса" [3]. Для этого справа нужно дописать первые два столбца, а затем сложить (вычесть) произведения по диагоналям:

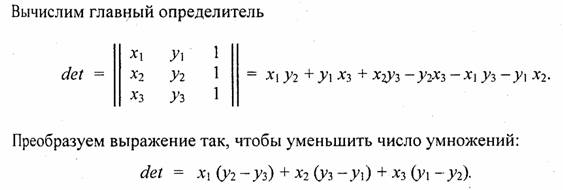
Аналогично вычисляются определители detA и detB. Определитель detC является самым сложным из всех. Но его вычислять не обязательно. Запишем решение системы в следующем виде:
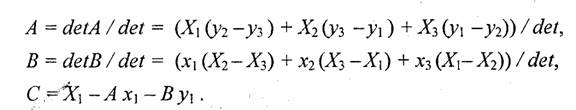
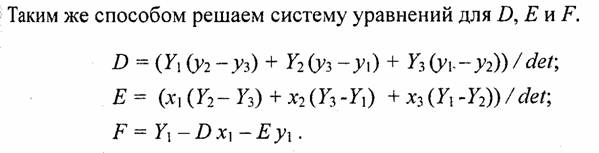
Заметьте, что здесь главный определитель det совпадает с определителем первой системы уравнений — для А, В я С.
Наложение текстур в перспективной проекции сложнее, чем для аксонометрической проекции. Рассмотрим рис. 3.27, на котором изображен текстурированный прямоугольник.
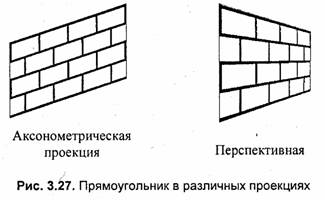
Прямоугольник в аксонометрической (параллельной) проекции всегда выглядит как параллелограмм, поскольку для этой проекции сохраняется параллельность прямых и отношение длин. В перспективной (центральной) проекции это уже не параллелограмм и не трапеция (в косоугольной — трапеция), поскольку параллельность и отношение длин здесь не сохраняются. А что сохраняется? Как изображать плоские грани?
В этой книге мы рассматриваем проекции на плоскость. Для таких проекций прямые линии остаются прямыми линиями, поэтому грани можно выводить как полигоны.
Здесь уместно вспомнить, как формируется изображение в некоторой проекции средствами компьютерной графики. Как уже нами было рассмотрено в главе 2, последовательность преобразований координат выглядит так:

Если считать, что точки текстуры должны соответствовать точкам на объекте, то координаты текстуры должны связываться с мировыми координатами. Однако поскольку для аксонометрической проекции в цепочке от мировых координат до экранных все преобразования линейны, то вполне допустимо связать координаты текстуры с экранными координатами одним аффинным преобразованием.
Для перспективной проекции так делать нельзя. Преобразование координат из видовых координат в координаты плоскости проецирования не линейно. Поэтому экранные координаты вначале следует преобразовать в такие, которые линейно связаны с мировыми — это могут быть, скажем, видовые. А затем видовые координаты (или непосредственно мировые) связать с координатами текстуры аффинным преобразованием, используя, например, метод трех точек.
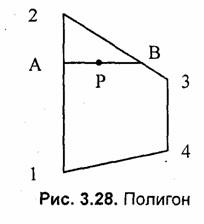
Рассмотрим, как можно выводить в перспективной проекции полигон с текстурой. Будем использовать алгоритм заполнения полигона горизонтальными линиями, уже рассмотренный нами. На рис. 3.28 изображена одна из горизонталей (АВ). Вершины полигона (1-2-3-4) здесь заданы экранными двумерными координатами. Для краткости изложения положим, что экранные координаты совпадают с координатами в плоскости проецирования. В ходе вывода полигона для связи с текстурой будем вычислять видовые координаты произвольной точки (Р) этого полигона. Для этого будем использовать в качестве базовой такую операцию: по известным видовым координатам концов отрезка находим видовые координаты точки отрезка, заданной координатами в плоскости проецирования.
Для определения видовых координат X, Y, Z точки А должны быть известны видовые координаты концов отрезка (1-2). Тогда справедливы соотношения:

после чего вычисляется X, например, по формуле Х= а + Zb. Для определения координаты Y достаточно заменить везде X на У. Здесь можно отметить, что вычисление видовых координат (X, Y, Z) соответствует обратному проективному преобразованию.-
Найдя видовые координаты точки А, мы можем точно так же вычислить видовые координаты и для точки В, лежащей на отрезке (3-4). Аналогично вычисляются видовые координаты точки Р.
Следует отметить, что, несмотря на то, что для преобразования координат необходимо вычислять дробно-линейные выражения, цикл вычислений можно сделать достаточно простым подобно инкрементным алгоритмам. Сделайте это самостоятельно в виде упражнения.
Для точного наложения текстур на поверхности используются и более сложные преобразования координат. Некоторые из них нами будут рассмотрены в главе 5.
Одна из проблем наложения текстур заключается в том, что преобразование растровых образцов (повороты, изменение размеров и тому подобное) приводят к ухудшению качества растров. Повороты растра добавляют ступенчатость (aliasing); увеличение размеров укрупняет пикселы, а уменьшение размеров растра приводит к потере многих пикселов образца текстуры, появляется муар. Для улучшения текстурованных изображений используют методы фильтрации (интерполяции) растров текстур [41, 47]. Также используются несколько образцов текстур для различных ракурсов показа (mipmaps) — компьютерная система во время отображения находит в памяти наиболее пригодный растровый образец.
Для использования текстур необходим достаточный объем памяти компьютера — количество растровых образцов может достигать десятков, сотен и более в зависимости от количества типов объектов и многообразия пространственных сцен. Чтобы как можно быстрее создавать изображение, необходимо сохранять текстуры в оперативной памяти.
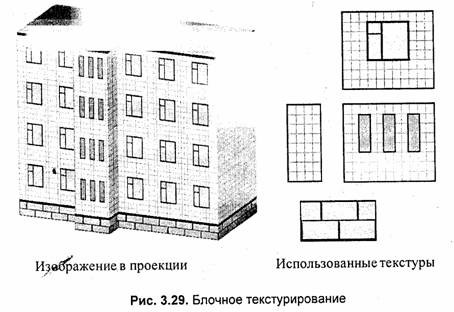
Для экономии памяти, выделяемой для текстур, можно использовать блочное текстурирование. Текстура здесь уже не представляет всю грань целиком, а лишь отдельный фрагмент, который циклически повторяется в грани. Это напоминает процесс размножения рисунка кисти при закрашивании полигонов, рассмотренный нами в этом разделе.
Разумеется, далеко не для всех объектов можно использовать такой способ отображения, однако, например, для образцов современной массовой "коробочной" архитектуры в этом плане имеются практически неограниченные возможности (рис. 3.29).
Современные видеоадаптеры оснащены графическими процессорами, которые аппаратно поддерживают операции с текстурами.
Фрактал можно определить как объект довольно сложной формы, получающийся в результате выполнения простого итерационного цикла. Итерационность, рекурсивность обуславливают такие свойства фракталов, как самоподобие— отдельные части похожи по форме на весь фрактал в целом. Латинское fractus означает "составленный из фрагментов". В 1975 году французский математик Бенуа Мандельброт издал книгу "The fractal Geometry of Nature". С того времени слово "фрактал" стало модным. Фракталом Мандельброта названа фигура, которая порождается очень простым циклом. Для создания этого фрактала необходимо для каждой точки изображения выполнить цикл итераций согласно формуле:
. 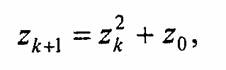
где к = 0, 1, ..., п. Величины zk — это комплексные числа, Zk - xк + i уk причем стартовые значения x0 и у0 — это координаты точки изображения. Для Каждой точки изображения итерации выполняются ограниченное количество раз (п) или до тех пор, пока модуль числа Zk не превышает 2. Модуль комплексного числа равен корню квадратному из х2+у2. Для вычисления квадрата величины zk можно воспользоваться формулой z = (х + iy) (x + iy) = (x2 -у2) + i (2у), поскольку i2 = -1. Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне: х = (от -2.2 до 1), у = (от -1.2 до 1.2). Для того чтобы получить изображение в растре, необходимо пересчитывать координаты этого диапазона в пиксельные. В главе 6 мы рассмотрим соответствующий пример программы, генерирующей изображения этого фрактала.
Фрактал Джулия внешне совсем не похож на фрактал Мандельброта, однако он определяется итерационным циклом, почти полностью тождественным с циклом генерации Мандельброта. Формула итераций для фрактала Джулия такая:
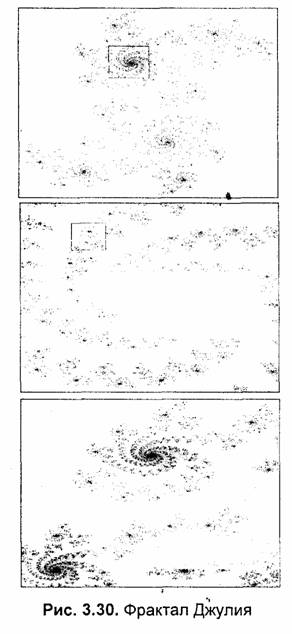
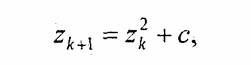
где с — комплексная константа. Условием завершения итераций является | z k | > 2 — гак же, как для фрактала Мандельброта.
На рис. 3.30 приведено несколько изображений фрактала Джулия для с = 0.36 + i 0.36, n=256. На верхнем образце картинка построена в границах х = (от -1 до 1), у = (от -1.2 до 1.2). На втором и третьем изображениях рис. 3.30 показаны увеличенные фрагменты фрактала. Как видим, фрактал самоподобный — при любом увеличении отдельные части напоминают формы целого. Самоподобие считается важным свойством фракталов. Это отличает их от других типов объектов сложной формы.
Рассмотрим следующий пример фрактала — фрактал Ньютон. Для него итерационная формула имеет такой вид:

где z — также комплексные числа, причем z0 = x + iy соответствует координатам точки изображения.
Условием прекращения цикла итераций для фрактала Ньютон есть приближение значений |z4- 1| к нулю. Например, изображение на рис. 3.31 было получено для |z4- 1|2> 0.001, границы расчетах = (от-1 до 1),у = (от-1 до 1).
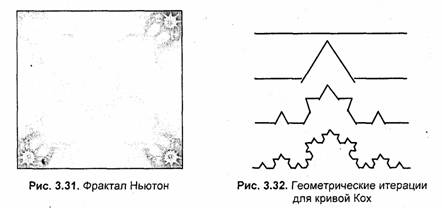
Рассмотрим еще одну разновидность фракталов. Такие фракталы названы геометрическими, поскольку их форма может быть описана как последовательность простых геометрических операций. Например, кривая Кох становится фракталом в результате бесконечного количества итераций, в ходе которых выполняется деление каждого отрезка прямой на три части. На рис. 3.32 показаны три итерации— постепенно линия становится похожей на снежинку.
Следующую группу составляют фракталы, которые генерируются согласно методу "систем итеративных функций" — IFS (Iterated Functions Systems). Этот метод может быть описан, как последовательный итеративный расчет координат новых точек в пространстве:
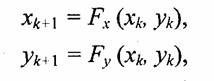
где Fx и Fy— функции преобразования координат, например, аффинного преобразования. Эти функции и определяют форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов.
Давайте попробуем создать фрактал, который бы выглядел как растение. Вообразим себе ствол, на котором много веточек. На каждой веточке много меньших веточек и так далее. Самые малые ветки можно считать листвой или колючками. Все элементы будем рисовать отрезками прямой. Каждый отрезок будет задаваться двумя конечными точками.
Для начала итераций необходимо задать стартовые координаты линии. Это будут точки 1, 2. На каждом шаге итераций будем рассчитывать координаты других точек.


Теперь зададим длину и угол наклона ветвей, которые выходят из точки 4. Сначала найдем координаты точки 5. Введем еще один параметр— к1, который будет определять соотношение длин отрезков 4-5 и 4-3, причем так же I 0<А:1<1. Координаты точки 5 равны:

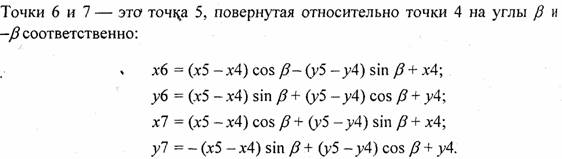
Кроме расчета опорных точек на каждом шаге будем рисовать один отрезок 1-4. В зависимости от номера итераций можно изменять цвет отрезка. Также можно устанавливать его толщину, например, пропорционально длине.
Таким образом, фрактал мы задали как последовательность аффинных преобразований координат точек. Величины а,β к, к1 — это параметры, которые описывают вид фрактала в целом. Они представляют собой константы на протяжении всего итеративного процесса. Это дает возможность в итерациях использовать только операции сложения, вычитания и умножения, если вычислить значения sin(), cos(), (I - к) и (1 – к1) только один раз перед началом итераций как коэффициенты-константы.
Дадим запись алгоритма в виде рекурсивной процедуры шаг ()

Для того чтобы нарисовать фрактал, необходимо вызывать процедуру шаг, установив соответствующие значения ее аргументов: шаг( х1 yl, х2, у2, о) . Обратите внимание на один из аргументов этой процедуры — num, который в начале работы равен 0. В теле процедуры есть три рекурсивных вызова с различными значениями этого аргумента:
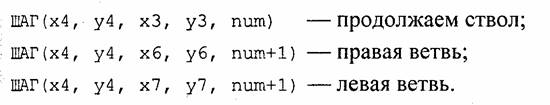
Значение num показывает степень детализации расчета дерева. Один цикл итераций содержит много шагов, соответствующих одному значению величины num. Числовое значение num можно использовать для прекращения итеративного процесса, а также для определения текущего цвета элементов "растения".
Завершение циклов итераций в нашем алгоритме происходит тогда, когда длина ветви становится меньше некоторой величины lmm, например, l min=1. Этот фрактал при а = 2°, β = 86°, к = 0.14, к1 = 0.3 похож на папоротник (рис. 3.34).
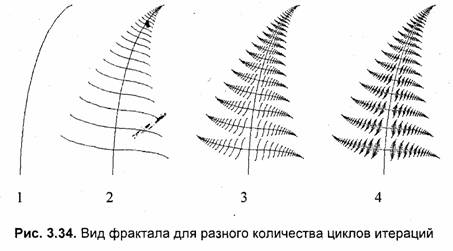
Метод IFS применяется не только для создания изображений. Его использовали Барнсли и Слоан для эффективного сжатия графических изображений при записи в файлы. Основная идея такая: поскольку фракталы могут представлять очень сложные изображения с помощью простых итераций, то описание этих итераций требует значительно меньшего объема информации, чем соответствующие растровые изображения. Для кодирования изображений необходимо решать обратную задачу — для изображения (или его фрагмента) подобрать соответствующие коэффициенты аффинного преобразования. Этот метод используется для записи цветных фотографий в файлы со сжатием в десятки и сотни раз без заметного ухудшения изображения. Формат таких графических файлов назван FIF (Fractal Image Format) и запатентован фирмой Iterated Systems [36].
ГЛАВА 4
Методы и алгоритмы трехмерной графики
Понятие ""трехмерная графика" в настоящее время можно считать наиболее Fраспространенным для обозначения темы, которую мы рассмотрим (в литературе название часто сокращается до "ЗD-графики"). Однако необходимо отметить, что такое название не совсем точно, ибо речь пойдет о создании изображения на плоскости, а не в объеме. Истинно трехмерные способы отображения пока что не достаточно широко распространены.
4.1. Модели описания поверхностей
Рассмотрим, как можно представлять форму трехмерных объектов в системах КГ. Для описания формы поверхностей могут использоваться разнообразные методы. Сделаем обзор некоторых из них.
Аналитической моделью будем называть описание поверхности математическими формулами. В КГ можно использовать много разновидностей такого описания. Например, в виде функции двух аргументов z =f(x, у). Можно использовать уравнение F (х, у, z) = .0.
Зачастую используется параметрическая форма описания поверхности. Запишем формулы для трехмерной декартовой системы координат (х, у, z):
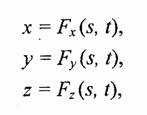
где s и t— параметры, которые изменяются в определенном диапазоне, а функции Fx, Fy и убудут определять форму поверхности.
Преимущества параметрического описания — легко описывать поверхности, которые отвечают неоднозначным функциям, замкнутые поверхности. Описание можно сделать таким образом, что формула не будет существенно изменяться при поворотах поверхности, масштабировании.
В качестве примера рассмотрим аналитическое описание поверхности шара. " Сначала как функцию двух1 аргументов:

Для описания сложных поверхностей часто используют сплайны. Сплайн — это специальная функция, более всего пригодная для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образовывают модель сложной поверхности. Другими словами, сплайн — эта тоже поверхность, но такая, для которой можно достаточно просто вычислять координаты ее точек. Обычно используют кубические сплайны. Почему именно кубические? Потому, что третья степень — наименьшая из степеней, позволяющих описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную — такая поверхность будет без изломов в местах стыка. Сплайны часто задают параметрически. Запишем формулу для компоненты x(s,t) кубического сплайна в виде многочлена третьей степени параметров s Ht:
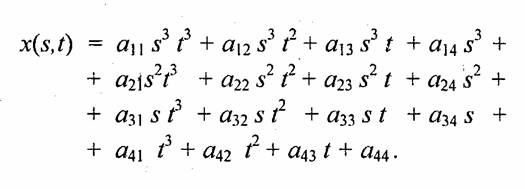
В математической литературе можно ознакомиться со способами определения коэффициентов ау для сплайнов, которые имеют заданные свойства. Примеры анализа и синтеза сплайнов в матричной форме приведены в [19, 28].


Характеризуя аналитическую модель в целом, можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхностей. С позиций КГ' можно указать такие положительные черты модели: легкая процедура расчета координат каждой точки поверхности, нормали; небольшой объем информации для описания достаточно сложных форм.
К недостаткам относятся следующие: сложные формулы описания с использованием функций, которые медленно вычисляются на компьютере, снижают скорость выполнения операций отображения; невозможность в большинстве случаев применения данной формы описания непосредственно для построения изображения поверхности. В таких случаях поверхность отображают как многогранник, используя формулы аналитического описания для расчета кординат вершин граней в процессе отображения, что уменьшает скорость сравнительно с полигональной моделью описания.
Векторная полигональная модель
Для описания пространственных объектов здесь используются такие элементы: вершины; отрезки прямых {векторы); полилинии, полигоны; полигональные поверхности (рис. 4.2). Элемент "вершина" (vertex) — главный элемент описания, все другие являются производными. При использовании трехмерной декартовой системы координаты вершин определяются как (хi уi zi,). Каждый объект однозначно определяется координатами собственных вершин.

Вершина может моделировать отдельный точечный объект, размер которого не имеет значения, а также может использоваться в качестве конечных точек для линейных объектов и полигонов. Двумя вершинами задается вектор. Несколько векторов составляют полилинию. Полилиния может моделировать отдельный линейный объект, толщина которого не учитывается, а также может представлять контур полигона. Полигон моделирует площадный объект. Один полигон может описывать плоскую грань объемного объекта. Несколько граней составляют объемный объект в виде полигональной поверхности— многогранник или незамкнутую поверхность (в литературе часто употребляется название "полигональная сетка").
Векторную полигональную модель можно считать наиболее распространенной в современных системах трехмерной КГ. Ее используют в системах автоматизированного проектирования, в компьютерных играх и тренажерах, в САПР, геоинформационных системах и тому подобное.
Обсудим структуры данных, которые используются в векторной полигональной модели. В качестве примера объекта будет куб. Рассмотрим, как можно организовать описание такого объекта в структурах данных.о-

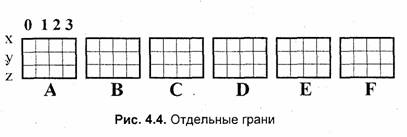
В компьютерной программе такой способ описания объекта можно реализовать разнообразно. Например, для каждой грани открыть в памяти отдельный массив. Можно все грани записывать в один массив-вектор. А можно использовать классы (языком C++) как для описания отдельных граней, так и объектов в целом. Можно создавать структуры, которые объединяют тройки (х, у, z), или сохранять координаты отдельно. В значительной мере это относится уже к компетенции программиста, зависит от его вкуса. Принципиально это мало что изменяет— так или иначе в памяти необходимо сохранять координаты вершин граней плюс некоторую информацию в качестве накладных затрат.
Рассчитаем объем памяти, необходимый для описания куба следующим образом:
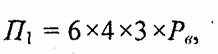
где Рв — разрядность чисел, необходимая для представления координат.
Шесть граней здесь описываются 24 вершинами. Такое представление избыточно — каждая вершина записана трижды. Не учитывается то, что у граней есть общие вершины.
