Предисловие

Целью написания этой книги было создать пособие по компьютерной графике для студентов, которые также изучают программирование. Занятие программированием облегчает восприятие компьютерных информационных технологий, это позволяет глубже заглянуть в мир компьютеров, получить ответы на многие вопросы типа "почему именно так". Оказалось полезным построить курс компьютерной графики с точки зрения программистов. Для лучшего восприятия этого курса желательно уже уметь, хотя бы немного, программировать на компьютерном языке C++ или С.

Материал данной книги в значительной мере соответствует курсу компьютерной графики, что читается мною в Киевском инженерно-техническом институте на протяжении последних нескольких лет. Также полезным для написания книги оказался опыт автора в качестве одного из разработчиков и программистов геоинформационной системы "ОКО" в фирме "Геобио-номика".

Я понимаю, что это безнадежное дело — охватить в довольно небольшой по объему книге огромный массив знаний, накопленный в области компьютерной графики. Тем более, что уже издано достаточное количество книг на эту тему, многие из них считаю непревзойденными. Однако компьютерная графика бурно развивается, поэтому есть потребность обобщить некоторые аспекты современного состояния, написать о них как можно более простым и ясным языком, четко и понятно объяснить суть вещей. Кроме того, надеюсь, и мой собственный опыт программирования графики может кому-то быть полезным.

В любом обществе можно встретить людей, которые не удовлетворяются только использованием результатов труда других. Эта книга в первую очередь для тех, кто хочет создавать что-то собственноручно и получать удовлетворение от процесса созидания. Компьютерная графика дает бесконечный простор для творчества. Кроме того, она возбуждает воображение человека — это один из факторов ее популярности.

Выражаю благодарность всем тем, кто, так или иначе, помогал мне в работе над книгой. Это сотрудники Киевского инженерно-технического и Киевского политехнического институтов, работники фирмы "Геобиономика". Особая благодарность жене Татьяне, без которой этой книги никогда бы не было.

Введение

Самая важная функция компьютера — обработка информации. Особо можно выделить обработку информации, связанную с изображениями. Она разделяется на три основные направления: компьютерная графика (КГ), обработка изображений и распознавание изображений [19].

Задача компьютерной графики — визуализация, то есть создание изображения. Визуализация выполняется исходя из описания (модели) того, что нужно отображать. Существует много методов и алгоритмов визуализации, которые различаются между собою в зависимости от того, что и как отображать. Например, отображение того, что может быть только в воображении человека— график функций, диаграмма, схема, карта. Или наоборот, имитация трехмерной реальности — изображения сцен в компьютерных развлечениях, художественных фильмах, тренажерах, в системах архитектурного проектирования. Важными и связанными между собою факторами здесь являются: скорость изменения кадров, насыщенность сцены объектами, качество изображения, учет особенностей графического устройства.

Обработка изображений — это преобразование изображений. То есть входными данными является изображение, и результат — тоже изображение. Примером обработки изображений могут служить: повышение контраста, четкости, коррекция цветов, редукция цветов, сглаживание, уменьшение шумов и так далее. В качестве материала для обработки могут быть космические снимки, отсканированные изображения, радиолокационные, инфракрасные изображения и тому подобное. Задачей обработки изображений может   

быть как улучшение в зависимости от определенного критерия (реставрация,

восстановление), так и специальное преобразование, кардинально изменяющее изображения. В последнем случае обработка изображений может быть промежуточным этапом для дальнейшего распознавания изображения. Например, перед распознаванием часто необходимо выделять контуры, создавать бинарное изображение, разделять по цветам. Методы обработки изображения могут существенно отличаться в зависимости от того, каким путем оно получено — синтезировано системой КГ, .либо это результат оцифровки черно-белой или цветной фотографии.

Для распознавания изображений основная задача— получение описания изображенных объектов. Методы и алгоритмы распознавания разрабатывались, прежде всего, для обеспечения зрения роботов и для систем специального назначения. Но в последнее время компьютерные системы распознавания изображений все чаще появляются в повседневной практике многих людей— например, офисные системы распознавания текстов или программы векторизации, создание трехмерных моделей человека.

Цель распознавания может формулироваться по-разному— выделение отдельных элементов (например, букв текста на изображении документа или условных знаков на изображении карты); классификация изображения в целом (например, проверка, изображен ли определенный воздушный аппарат, или установление персоны по отпечаткам пальцев).

Методы классификации и выделения отдельных элементов могут быть взаимосвязаны. Так, классификация может быть выполнена на основе структурного анализа отдельных элементов объекта. Или для выделения отдельных элементов можно использовать методы классификации. Задача распознавания является обратной по отношению к визуализации.

До недавнего времени достаточно популярным было словосочетание интерактивная компьютерная графика. Им подчеркивалась способность компьютерной системы создавать графику и вести диалог с человеком. Раньше системы работали в пакетном режиме — способы диалога были не развиты. В настоящее время почти любую программу можно считать системой интерактивной КГ.

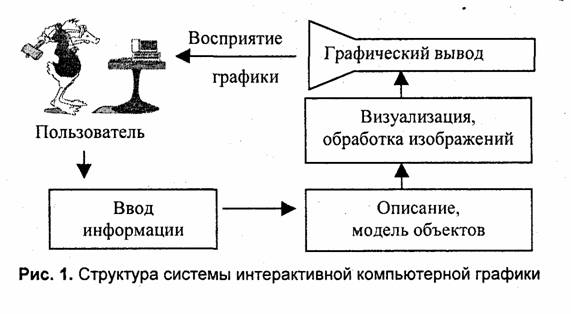
Исторически первыми интерактивными системами считаются системы автоматизированного проектирования (САПР), которые появились в 60-х годах [18, 19, 28]. Они представляют собой значительный этап в эволюции компьютеров и программного обеспечения. В системе интерактивной КГ пользователь воспринимает на дисплее изображение, представляющее некоторый сложный объект, и может вносить изменения в описание (модель) объекта (рис. 1). Такими изменениями могут быть как ввод и редактирование отдельных элементов, так и задание числовых значений для любых параметров, а также иные операции по вводу информации на основе восприятия изображений.

Системы типа САПР активно используются во многих областях, например в машиностроении и электронике. Одними из первых были созданы САПР для проектирования самолетов, автомобилей, системы для разработки микроэлектронных интегральных схем, архитектурные системы. Такие системы на первых порах функционировали на достаточно больших компьютерах. Потом распространилось использование быстродействующих компьютеров среднего класса с развитыми графическими возможностями — графических рабочих станций. С ростом мощностей персональных компьютеров все чаще САПР использовали на дешевых массовых компьютерах, которые сейчас имеют достаточные быстродействие и объемы памяти для решения Многих задач. Это привело к широкому распространению систем САПР

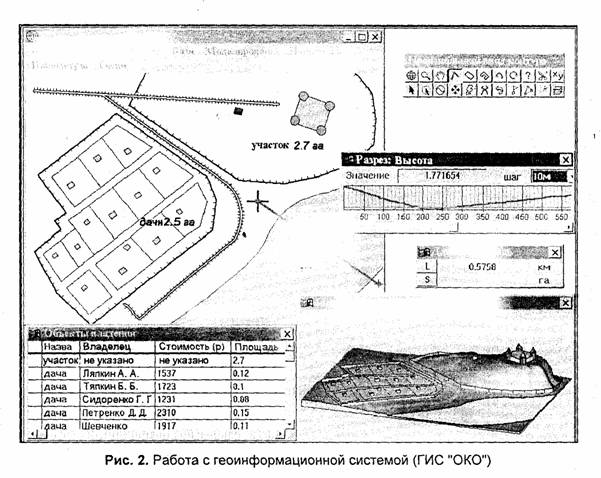
Ныне становятся все более популярными геоинформационные системы (ГИС). Это относительно новая для массовых пользователей разновидность систем интерактивной компьютерной графики. Они аккумулируют в себе методы и алгоритмы многих наук и информационных технологий. Такие системы используют последние достижения технологий баз данных, в них заложены многие методы и алгоритмы математики, физики, геодезии, топологии, картографии, навигации и, конечно же, компьютерной графики. Системы типа ГИС зачастую требуют значительных мощностей компьютера как в плане работы с базами данных, так и для визуализации объектов, которые находятся на поверхности Земли. Причем, визуализацию необходимо делать с различной степенью детализации — как для Земли в целом, так и в границах отдельных участков (рис. 2). В настоящее время заметно стремление разработчиков ГИС повысить реалистичность изображений пространственных объектов и территорий.

Типичными для любой ГИС являются такие операции — ввод и редактирование объектов с учетом их расположения на поверхности Земли, формирование разнообразных цифровых моделей, запись в базы данных, выполнение разнообразных запросов к базам данных. Важной операцией является анализ с учетом пространственных, топологических отношений множества объектов, расположенных на некоторой территории.

Важным этапом развития систем компьютерной графики являются так называемые

системы виртуальной реальности (virtual reality). Наращивание мощности компьютеров, повышение реалистичности трехмерной графики и совершенствование способов диалога с человеком позволяют создавать иллюзию вхождения человека в виртуальное пространство. Это пространство может быть моделью или существующего пространства, или выдуманного. Системы класса виртуальной реальности для диалога с компьютером обычно используют такие устройства, как шлем-дисплей, сенсоры на всем теле человека.

Образцы компьютерной графики известны уже каждому. Приобрели распространение, например, разнообразные компьютерные игры. Значительную роль в них играет анимация, реалистичность изображений, совершенство способов ввода-вывода информации. Здесь следует отметить, что во многих компьютерных играх реализованы идеи и методы, которые ранее были воплощены в профессиональных дорогостоящих системах, например, в тренажерах для летчиков.

Широко используется компьютерная графика в кино. Одним из первых известных фильмов был фильм "Звездные войны". Он был создан с помощью суперкомпьютера Cray. Этапы дальнейшего развития компьютерного кинематографа можно проследить по таким фильмам, как "Терминатор-2", "Вавилон 5", "Леке" и десяткам (если уже не сотням) других. До недавнего времени технологии компьютерной графики использовались для спецэффектов создания изображений экзотических чудовищ, имитации стихийных бедствии и других элементов, которые являлись лишь фоном для игры живых актеров. В 2001 году вышел на экраны полнометражный кинофильм "Финальная фантазия", в котором все, включая изображения людей, синтезировано компьютером — живые актеры только озвучили роли за кадром.

Важным событием в жизни общества стало появление глобальной сети Internet. Сейчас происходит бурное развитие этой сети. Наращиваются мощности каналов передачи данных, усовершенствуются способы обмена и обработки информации. Сеть Internet используют все больше людей во всех странах. Это способ общения людей, обмена информацией, сближения языков, распространения идей, новое пространство для бизнеса и тому подобное. Можно относиться к Internet по-разному — например, одни считают ее важным фактором демократизации, а другие ее называют орудием чьего-то мирового господства. Вероятно, оба эти мнения справедливы, как и многие другие. Одно несомненно — создание сети Internet является выдающимся достижением человечества. Важное место в Internet занимает компьютерная графика. Все больше совершенствуются способы передачи визуальной информации, разрабатываются более совершенные графические форматы, ощутимо желание использовать трехмерную графику, анимацию, весь спектр мультимедиа.

ЧАСТЬ 1

Основы

компьютерной графики

ГЛАВА 1

                                              1.1 . Визуализация изображений

Наиболее известны два способа визуализации: растровый и векторный. Первый способ ассоциируется с такими графическими устройствами, как дисплей, телевизор, принтер. Второй используется в векторных дисплеях, плоттерах.

Наиболее удобно, когда способ описания графического изображения соответствует способу визуализации. Иначе нужна конвертация. Например, изображение может храниться в растровом виде, а его необходимо вывести (визуализировать) на векторном устройстве. Для этого нужна предварительная векторизация — преобразование из растрового в векторное описание. Или наоборот, описание изображения может быть в векторном виде, а нужно визуализировать на растровом устройстве — необходима растеризация.

Растровая визуализация основывается на представлении изображения на экране или бумаге в виде совокупности отдельных точек (пикселов). Вместе пикселы образуют растр

Векторная визуализация основывается на формировании изображения на экране или бумаге рисованием линий (векторов) — прямых или кривых. Совокупность типов линий (графических примитивов), которые используются как базовые для векторной визуализации, зависит от определенного устройства. Типичная последовательность действий при векторной визуализации для плоттера или векторного дисплея такова: переместить перо в начальную точку (для дисплея — отклонить пучок электронов); опустить перо (увеличить яркость луча); переместить перо в конечную точку; поднять перо (уменьшить яркость луча).

Качество векторной визуализации для векторных устройств обуславливается точностью вывода и номенклатурой базовых графических примитивов — линий, дуг, кругов, эллипсов и других

Доминирующим сейчас является растровый способ визуализации. Это обусловлено большей распространенностью растровых дисплеев и принтеров. Недостаток растровых устройств — дискретность изображения. Недостатки векторных устройств — проблемы при сплошном заполнении фигур, меньшее количество цветов, меньшая скорость (в сравнении с растровыми устройствами).

1.2.Растровые изображения и их основные характеристики

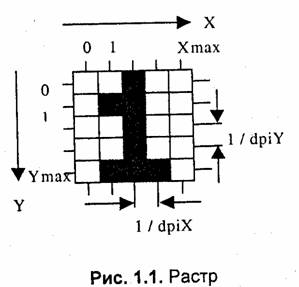
Растр — это матрица ячеек (пикселов). Каждый пиксел может иметь свой цвет. Совокупность пикселов различного цвета образует изображение. В зависимости от расположения пикселов в пространстве различают квадратный, прямоугольный, гексагональный или иные типы растра. Для описания расположения пикселов используют разнообразные системы координат. Общим для всех таких систем является то, что координаты пикселов образуют дискретный ряд значений (необязательно целые числа). Часто используется система целых координат — номеров пикселов с (0,0) в левом верхнем уголку.

Такую систему мы будем использовать и в дальнейшем, ибо она удобна для рассмотрения алгоритмов графического вывода.

Какие основные характеристики растровых изображений?

Геометрические характеристики растра 

Разрешающая способность. Она характеризует расстояние между соседними пикселами (рис. 1.1). Разрешающую способность измеряют количеством пикселов на единицу длины. Наиболее популярной единицей измерения является dpi (dots per inch)— количество пикселов в одном дюйме длины (2.54 см). Не следует отождествлять шаг с размерами пикселов — размер пикселов может быть равен шагу, а может быть как меньше, так и больше, чем шаг.

Размер растра обычно измеряется количеством пикселов по горизонтали и вертикали. Можно сказать, что для компьютерной графики зачастую наиболее удобен растр с одинаковым шагом для обеих осей, то есть dpiX = dpiY. Это удобно для многих алгоритмов вывода графических объектов. Иначе — проблемы. Например, при рисовании окружности на экране дисплея EGA (устаревшая модель компьютерной видеосистемы, ее растр — прямоугольный, пикселы растянуты по высоте, поэтому для изображения окружности необходимо генерировать эллипс).

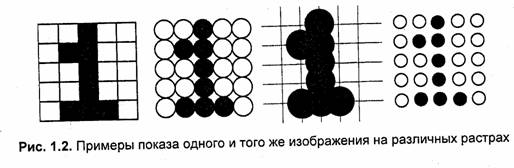
Форма пикселов растра определяется особенностями устройства графического вывода (рис. 1.2). Например, пикселы могут иметь форму прямоугольника или квадрата, которые по размерам равны шагу растра (дисплей на жидких кристаллах); пикселы круглой формы, которые по размерам могут и не равняться шагу растра (принтеры).

Количество цветов

Количество цветов (глубина цвета) — также одна из важнейших характеристик растра. Количество цветов является важной характеристикой для любого изображения, а не только растрового. Согласно психофизиологическим исследованиям глаз человека способен различать 350 000 цветов [28].

Классифицируем изображения следующим образом:

□  Двухцветные (бинарные) — 1 бит на пиксел. Среди двухцветных чаще всего встречаются черно-белые изображения.

□  Полутоновые — градации серого или иного цвета. Например, 256 градаций (1 байт на пиксел).

□  Цветные изображения. От 2 бит на пиксел и выше. Глубина цвета 16 бит на пиксел (65 536 цветов) получила название High Color, 24 бит на пиксел

(16,7 млн цветов)— True Color. В компьютерных графических системах используют и большую глубину цвета — 32, 48 и более бит на пиксел.

 В качестве примера рассмотрим растровый рисунок (рис. 1.3). Количество цветов — 256 градаций серого, разрешающая способность — примерно 100 dpi. Отметим, что в книге вы видите печатное изображение, поэтому о количестве цветов и разрешающей способности можно говорить лишь условно.

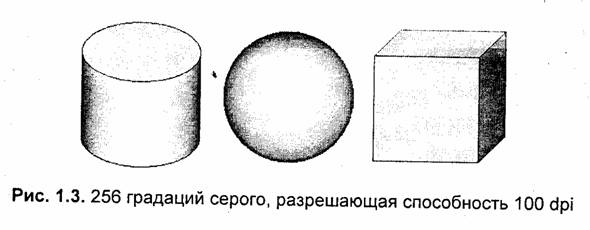
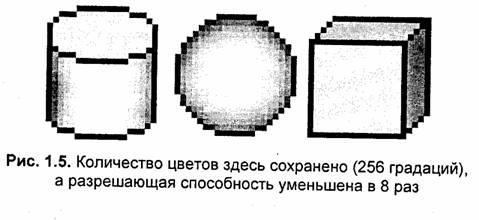
Изображения тех же объектов, но для иных параметров растра даны на рис. 1.4 и 1.5.

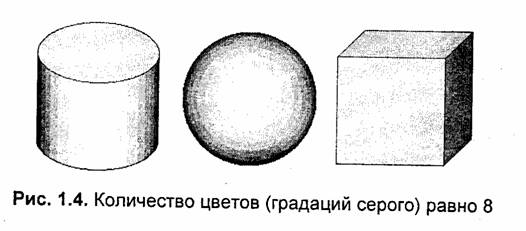
      Недостаточное количество цветов приводит к появлению лишних контуров на гладких поверхностях цилиндра и шара.

Оценка разрешающей способности растра

      Глаз человека с нормальным зрением может различать объекты с угловым размером около одной минуты. Если расстояние до объекта равно R, то можно приблизительно оценить этот размер (dP) как длину дуги, равную Ra (рис. 1.6). Можно предположить, что человек различает дискретность растра (шаг) также соответственно этому минимально различимому размеру.

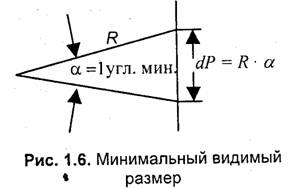
Иначе говоря, отдельные точки (пикселы), смещенные менее чем на dP, уже не воспринимаются смещенными. Тогда можно оценить разрешающую способность растра, который не воспринимается как растр, следующей величиной:

dpi = 25.4/dP [мм].

 Приведем несколько значений dpi для различных R (табл. 1.1).

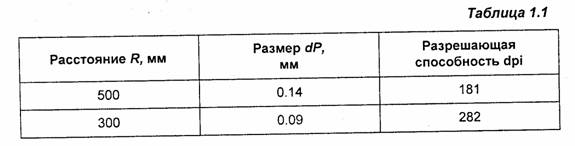
Если считать расстояние, с которого человек обычно разглядывает бумажные документы, равным 300 мм, то можно оценить минимальную разрешающую способность, при которой уже не заметны отдельные пикселы, как приблизительно 300 dpi (примерно 0,085 мм). Лазерные черно-белые принтеры полностью удовлетворяют такому требованию.

          Дисплеи обычно рекомендуется разглядывать с расстояния не ближе 0.5 м. В соответствии с приведенной выше оценкой минимальной разрешающей способности расстоянию 0,5 м соответствует около 200 dpi. В современных дисплеях минимальный размер пикселов (пятна) примерно 0,25 мм, что дает 100 dpi — это плохо, например, дисплей 15" по диагонали должен обеспечивать не 1024 на 768 пикселов, а вдвое больше. Но на современном уровне техники это пока что невозможно.

Примеры изображений

для некоторых растровых устройств

Для иллюстрации работы реальных растровых устройств рассмотрим результаты вывода одной и той же картинки. Поскольку в этой книге невозможно показать цветные изображения, то в качестве тестового образца выбран черно-белый рисунок, состоящий из текста и простейшей графики. Образец изображен на рис. 1.7 в натуральную величину. Текст ("Строчка текста") набран шрифтом TrueType Times New Roman, размер 8 пунктов. Графика — векторный рисунок из линий минимально возможной толщины. Тестовый образец изготовлен и выводился на устройства с помощью редактора Word 97.

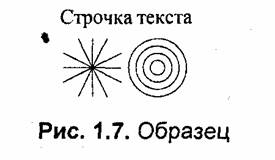
Почему именно такой образец? Для того чтобы оценить погрешности вывода, тест следует подобрать так, чтобы устройства работали в режиме, близкому к предельно возможному. Тогда и можно оценить их возможности. Однако задача усложняется тем, что проверяются устройства различного класса. Оказалось, что некоторые устройства почти не в состоянии удовлетворительно отобразить даже такой простой образец, а некоторые устройства продемонстрировали значительный запас точности — для них нужны другие тесты.

После вывода образца на графическом устройстве соответствующее растровое изображение оцифровывалось сканером с оптическим разрешением 600x600 dpi (2400x2400 в режиме интерполяции). Отсканированные изображения в увеличенном масштабе приведены ниже. Безусловно, погрешность сканера существенна для изображений, полученных устройствами, обладающих соизмеримым, а также более высоким разрешением. Однако полученные здесь результаты не следует рассматривать как точные измерения. Здесь ставилась иная цель — проиллюстрировать геометрические свойства растров (расположение, форму и размеры отдельных пикселов) для устройств различного типа, показать наиболее характерные особенности отображения.

Для сравнения были выбраны графические устройства, которые можно встретить практически в любом современном офисе, — это дисплеи и принтеры.

           Торговые марки устройств не приводятся. Приведенные образцы не следует рассматривать как тестирование или рекламу.

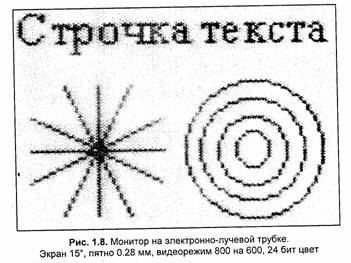
        Изображение, полученное на экране, было сфотографировано и оцифровано. Картинка имеет множество градаций серого цвета, которые здесь, к сожалению, не могут быть точно воспроизведены. Для печати иллюстраций на бумаге (в том числе и для этой книги) используется дизеринг — имитация оттенков серого цвета многими близко расположенными черными точками.

       Поэтому при просмотре с помощью лупы данная картинка "рассыпается" на отдельные мелкие точки. На рис. 1.9 показано увеличенное изображение фрагмента рис. 1.8. Здесь уже отчетливо видна шестиугольная структура растра, характерная для цветного кинескопа.

      Растровый характер изображения монитора на жидких кристаллах (рис. 1.10) выражен значительно четче, нежели монитора на электронно-лучевой трубке. Четкость отдельных пикселов обуславливает заметный лестничный эффект наклонных линий (рис. 1.11).

Качество печати для матричных принтеров определяется погрешностями механики и износом красящей ленты. Здесь красящая лента выработала свой ресурс наполовину, поэтому изображение получилось как бы "в градациях серого цвета". Кроме того, полутоновый характер изображение имеет и из-за того, что чернота уменьшается на краях впадин оттиска игл (рис. 1.13). Вообще говоря, матричные принтеры могут печатать и намного лучше. Даже испытуемый принтер может печатать с разрешением 240x216 dpi. Однако драйвер для Windows позволяет установить только 240x144 dpi, а качество практически не улучшается по сравнению с 120x144 dpi (вероятно из-за износа механики).

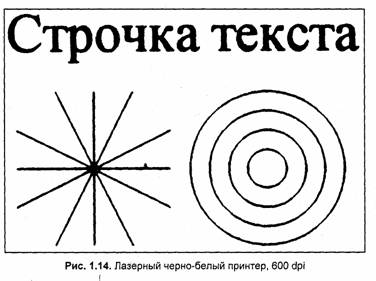
      Лазерные принтеры, как правило, безупречно отрабатывают свое паспортное разрешение. Немаловажным является то, что качество печати стабильно и практически не зависит от качества бумаги. Принтеры данного типа вне конкуренции (по крайней мере, в настоящее время) по быстродействию и качеству черно-белой печати среди других типов принтеров. Более дорогие модели лазерных принтеров обладают в несколько раз большим разрешением, при этом качество печати, как правило, возрастает соответственно паспортному разрешению. Оптического разрешения сканера в 600 dpi (2400 dpi интерполяция) уже не достаточно, чтобы точно отобразить фрагмент растра в мельчайших деталях (рис. 1.15).

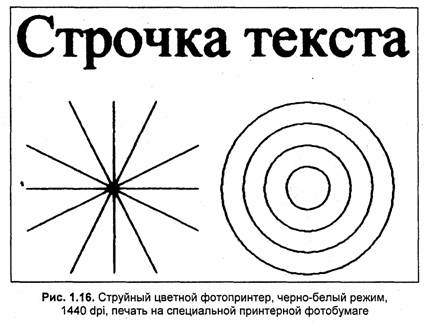
      Струйные принтеры достаточно редко соответствуют заявляемой паспортной разрешающей способности. Данная модель, возможно, исключение из общего правила. В черно-белом режиме здесь фактически продемонстрирована точность печати на уровне 600 dpi лазерного принтера (рис. 1.17). Многие другие струйные принтеры с рекламируемым разрешением более тысячи dpi работают еще хуже. И это при печати на специальной бумаге.

Достоинством струйных принтеров является то, что это относительно недорогое устройство для цветной печати. С приемлемым качеством для цветной фотографии работают струйные фотопринтеры. Технология струйной печати также используется и в достаточно популярных крупноформатных (АЗ-А1) цветных растровых принтерах.

1.3.Цвет

Для изучения способов представления цвета в компьютерных системах вначале рассмотрим некоторые общие аспекты.

Цвет— это один из факторов нашего восприятия светового излучения. Светом и цветом исследователи интересовались давно. Одним из первых выдающихся достижений в этой области являются опыты Исаака Ньютона в 1666 г. по разложению белово света на составляющие. Ранее считалось, что белый свет является простейшим. Ньютон опроверг это. Суть опытов Ньютона такова. Белый луч света (использовался солнечный свет) направлялся на стеклянную треугольную призму. Пройдя сквозь призму, луч преломлялся и, будучи  направленный  на  экран,  давал  в  результате  цветную  полосу — спектр. В спектре присутствовали все цвета радуги, плавно переходящие друг в друга. Эти цвета уже не раскладывались на составляющие. Ньютон разбил весь спектр на семь участков, соответствующих ярко выраженным различным цветам. Он считал эти семь цветов основными — красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый. Почему именно семь? Некоторые объясняют это убежденностью Ньютона в мистических свойствах семерки [10].

Вторая часть опытов Ньютона такова. Лучи, прошедшие сквозь призму, направлялись на вторую призму, с помощью которой удалось вновь получить белый свет. Таким образом, было доказано, что белый цвет является смесью множества различных цветов. Семь основных цветов Ньютон расположил по кругу (рис. 1.18).

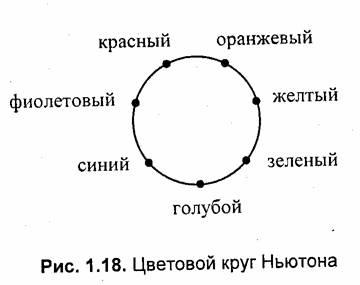
Ньютон предположил, что некоторый цвет образуется путем смешивания основных цветов, взятых в определенной пропорции. Если в точках на границе цветового круга, соответствующих основным цветам, расположить грузы, пропорциональные количеству каждого цвета в смеси, то суммарный цвет будет соответствовать точке центра тяжести. Белый цвет соответствует центру цветового круга [15].

Последующие исследования цвета выполняли Томас Юнг, Джемс Максвелл и другие ученые. Исследования человеческого световосприятия являлись достаточно важной задачей, но основные усилия были направлены на изучение объективных свойств света. В настоящее время физики полагают, что свет имеет двойственный характер. С одной стороны, свет представляется в виде потока частиц (еще Ньютон выдвинул так называемую корпускулярную теорию). С другой стороны, свету присущи волновые свойства. С помощью волновой теории, выдвинутой Христианам Гюйгенсом в 1678 году, были объяснены многие свойства света, в частности законы отражения и преломления [30].

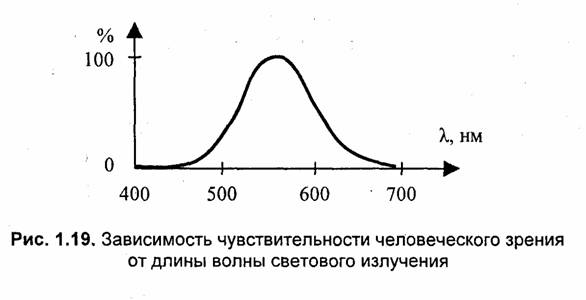
          Рассмотрим цвет с позиций волновых свойств. Одной из волновых характеристик света является длина волны — расстояние, которое проходит волна в течение одного периода колебания. Монохроматическим называется излучение, спектр которого состоит из единственной линии, соответствующей единственной длине волны. Радуга, полученная Ньютоном, состоит из бесчисленного множества монохроматических излучений (равно как и радуга, наблюдаемая нами после дождя). Достаточно качественным источником монохроматического излучения является лазер — именно поэтому его луч легко сфокусировать. Цвет монохроматического излучения определяется длиной волны. Диапазон длин волн для видимого света простирается от 380—400 нм (фиолетовый) до 700—780 нм (красный). В указанном диапазоне чувствительность человеческого зрения непостоянна. Наибольшая чувствительность наблюдается для длин волн, соответствующих зеленому цвету (рис. 1.19).

Как показал Ньютон, белый цвет можно представить смесью всех цветов радуги. Иными словами, спектр белого является непрерывным и равномерным — в нем присутствуют излучения всех длин волн видимого диапазона.

Для характеристики цвета используются следующие атрибуты:

□  Цветовой тон. Можно определить преобладающей длиной волны в спектре излучения. Цветовой тон позволяет отличать один цвет от другого — например, зеленый от красного, желтого и других.

□ Яркость. Определяется энергией, интенсивностью светового излучения. Выражает количество воспринимаемого света.

□  Насыщенность или чистота тона. Выражается долей присутствия белого цвета. В идеально чистом цвете примесь белого отсутствует. Если, например, к чистому красному цвету добавить в определенной пропорции белый цвет (у художников это называется разбелом), то получится светлый бледно-красный цвет.

Указанные три атрибута позволяют описать все цвета и оттенки. То, что атрибутов именно три, является одним из проявлений трехмерных свойств цвета. Как мы увидим далее, имеются и другие трехмерные системы описания цвета.

Мы попытались объяснить цвет с помощью длин волн и спектра. Как оказывается, это неполное представление о цвете, а вообще говоря, оно неправильно. Во-первых, глаз человека — это не спектроскоп. Зрительная система человека, скорее всего, регистрирует не длину волны и спектр, а формирует ощущения иным способом. Во-вторых, без учета особенностей человеческого восприятия невозможно объяснить смешение цветов. Например, белый цвет действительно можно представить равномерным спектром смеси бесконечного множества монохроматических цветов. Однако тот же белый цвет можно создать смесью всего двух специально подобранных монохроматических цветов (такие цвета называются взаимно дополнительными). Во всяком случае, человек воспринимает эту смесь как белый цвет. А можно получить белый цвет, смешав три или более монохроматических излучений. Излучения, различные по спектру, но дающие один и тот же цвет, называются метамврными [15].

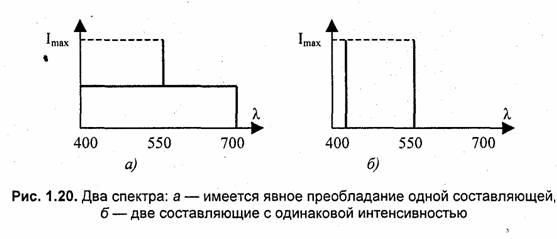
Необходимо также уточнить, что понимается под цветовым тоном. Рассмотрим два примера спектра (рис. 1.20).

Анализ спектра, изображенного на рис. 1.20 (а), позволяет утверждать, что излучение имеет светло-зеленый цвет, поскольку четко выделяется одна спектральная линия на фоне равномерного спектра белого. А какой цвет (цветовой тон) соответствует спектру варианта (б)? Здесь нельзя выделить в спектре преобладающую составляющую, поскольку присутствуют красная и зеленая линии одинаковой интенсивности. По законам смешения цветов это может дать оттенок желтого цвета, однако в спектре нет соответствующей линии монохроматического желтого. Поэтому под цветовым тоном следует понимать цвет монохроматического излучения, соответствующего суммарному цвету смеси. Впрочем, как именно "соответствующего" — это также требует уточнения.

Наука, которая изучает цвет и его измерения, называется колориметрией. Она описывает общие закономерности цветового восприятия света человеком [1,10, 15].

Одними из основных законов колориметрии являются законы смешивания цветов. Эти законы в наиболее полном виде были сформулированы в 1853 году немецким математиком Германом Грассманом:

1. Цвет трехмерен— для его описания необходимы три компоненты. Любые четыре цвета находятся в линейной зависимости, хотя существует неограниченное число линейно независимых совокупностей из трех цветов.

Иными словами, для любого заданного цвета (Ц) можно записать такое цветовое уравнение, выражающее линейную зависимость цветов:

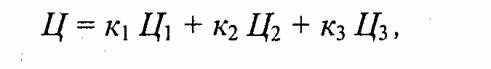
где Ц₁ Ц₂ Ц₃ — некоторые базисные, линейно независимые цвета, коэффициенты к₁, k₂ и к₃ указывают количество соответствующего смешиваемого цвета. Линейная независимость цветов Ц₁ Ц₂, Ц₃ означает, что ни один из них не может быть выражен взвешенной суммой (линейной комбинацией) двух других.

        Первый закон можно трактовать и в более широком смысле, а именно, в смысле трехмерности цвета. Необязательно для описания цвета применятьсмесь других цветов, можно использовать и другие величины — но их обязательно должно быть три.

2.   Если в смеси трех цветовых компонент одна меняется непрерывно, в то время, как две другие остаются постоянными, цвет смеси также изменяется непрерывно.

3.  Цвет смеси зависит только от цветов смешиваемых компонент и не зависит от их спектральных составов.

Смысл третьего закона становится более понятным, если учесть, что один и тот же цвет (в том числе и цвет смешиваемых компонент) может быть получен различными способами. Например, смешиваемая компонента может быть получена, в свою очередь, смешиванием других компонент.

Аддитивная цветовая модель RGB

Эта модель используется для описания цветов, которые получаются с помощью устройств, основанных на принципе излучения. В качестве основных цветов выбран красный (Red), зеленый (Green) и синий (Blue). Иные цвета и оттенки получаются смешиванием определенного количества указанных основных цветов.

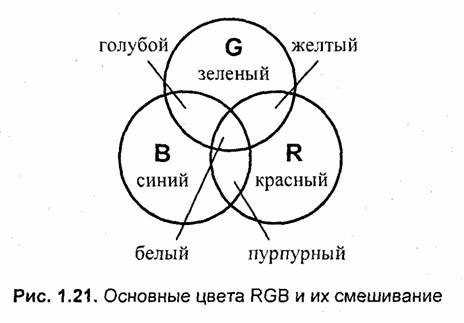
        Вкратце история системы RGB такова. Томас Юнг (1773—1829) взял три фонаря и приспособил к ним красный, зеленый и синий светофильтры. Так были получены источники света соответствующих цветов. Направив на белый экран свет этих трех источников, ученый получил такое изображение (рис. 1.21). На экране свет от источников давал цветные круги. В местах пересечения кругов наблюдалось смешивание цветов. Желтый цвет получался смешиванием красного и зеленого, голубой — смесь зеленого и синего, пурпурный — синего и красного, а белый цвет образовывался смешением всех

трех основных цветов. Некоторое время спустя, Джемс Максвелл (1831—1879) изготовил первый колориметр, с помощью которого человек мог зрительно сравнивать монохроматический цвет и цвет смешивания в заданной пропорции компонент RGB. Регулируя яркость каждой из смешиваемых компонент, можно добиться уравнивания цветов смеси и монохроматического излучения. Это описывается следующим образом:

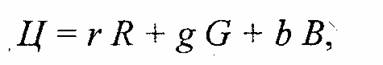
где r, g и b — количество соответствующих основных цветов.

Соотношение коэффициентов г, g и b Максвелл наглядно показал с помощью треугольника, впоследствии названного его именем [1]. Треугольник Максвелла является равносторонним, в его вершинах располагаются основные цвета— R, G и В (рис. 1.22). Из заданной точки проводятся линии, перпендикулярные сторонам треугольника. Длина каждой линии и показывает соответствующую величину коэффициента r, g или b. Одинаковые значения r=g=b имеют место в центре треугольника и соответствуют белому цвету. Следует также отметить, что некоторый цвет может изображаться как внутренней точкой такого треугольника, так и точкой, лежащей за его пределами. В последнем случае это соответствует отрицательному значению соответствующего цветового коэффициента. Сумма коэффициентов равна высоте треугольника, а при высоте, равной единице, — r+g+b = 1.

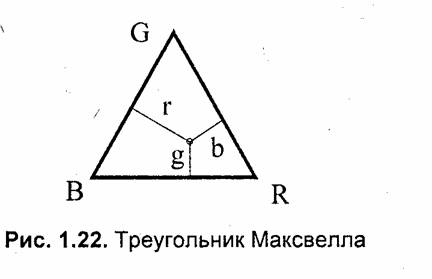
В качестве основных цветов Максвелл использовал излучения с такими длинами волн— 630, 528 и 457 нм.

К настоящему времени система RGB является официальным стандартом. • Решением Международной Комиссии по Освещению — МКО (CIE — Соmmision International de 1'Eclairage) в 1931 году были стандартизованы основные цвета, которые было рекомендовано использовать в качестве R, G и В. Это монохроматические цвета светового излучения с длинами волн соответственно:

R—700 нм; G — 546.1 нм; В — 435.8 нм.

Красный цвет получается с помощью лампы накаливания с фильтром. Для получения чистых зеленого и синего цветов используется ртутная лампа. Также стандартизировано значение светового потока для каждого основного цвета [ 1].

Еще одним важным параметром для системы RGB является цвет, получаемый смешением трех компонент в равных количествах. Это белый цвет. Оказывается, что для того, чтобы смешиванием компонент R, G и В получить белый цвет, яркости соответствующих источников не должны быть равны друг другу, а находиться в пропорции

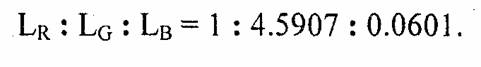
Если расчеты цвета производятся для источников излучения с одинаковой яркостью, то указанное соотношение яркостей можно учесть соответствующими масштабными коэффициентами [15].

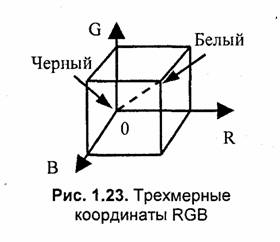
Теперь рассмотрим другие аспекты. Цвет, создаваемый смешиванием трех основных компонент, можно представить вектором в трехмерной системе координат R, G и В, изображенной на рис. 1.23. Черному цвету соответствует центр координат,— точка (0, 0, 0). Белый цвет выражается максимальным значением компонент. Пусть это максимальное значение вдоль каждой оси равно единице. Тогда белый цвет— это вектор (1, 1, 1). Точки, лежащие на диагонали куба от черного к белому, соответствуют равным значениям: R_i = G_i = В_i. Это градации серого — их можно считать белым цветом различной яркости. Вообще говоря, если все компоненты вектора (г, g, b) умножить на одинаковый коэффициент (к = 0...1), то цвет (кr, kg, kb) сохраняется, изменяется только яркость. Поэтому, для анализа цвета важно соотношение компонент. Если в цветовом уравнении

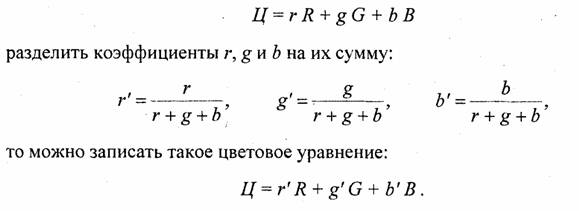
Это уравнение выражает векторы цвета (г^’, g^’ b^’), лежащие в единичной плоскости r'+g'+b' = 1. Иными словами, мы перешли от куба к треугольнику Максвелла.

          В ходе колориметрических экспериментов были определены коэффициенты (r', g', b^’), соответствующие чистым монохроматическим цветам. Простейший колориметр можно представить как призму из белого гипса, грани которой освещают источниками света. На левую грань направлен источник чистого монохроматического излучения, а правая грань освещается смесью трех источников RGB. Наблюдатель видит одновременно две грани, что позволяет фиксировать равенство цветов (рис. 1.24).

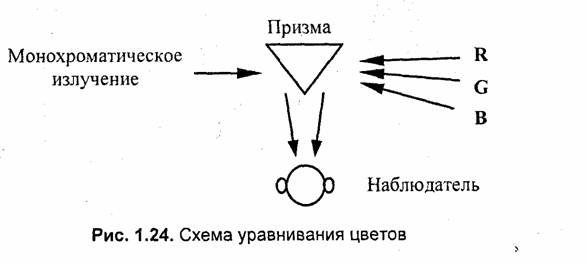
Результаты экспериментов можно изобразить графически (рис. 1.25).

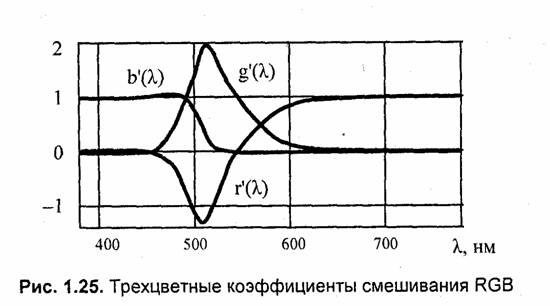
Как видим, коэффициенты г', g' и b' могут быть и положительными, и отрицательными. Что это означает? То, что некоторые монохроматические цвета не могут быть представлены суммой компонент R, G и В. Но как отнять то, чего нет? Для уравнивания цвета пришлось добавить к монохроматическому излучению одну из компонент R, G или В. Например, если монохроматическое излучение для некоторого значения Я разбавлялось красным, то это можно выразить так:

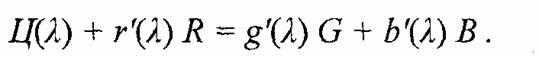
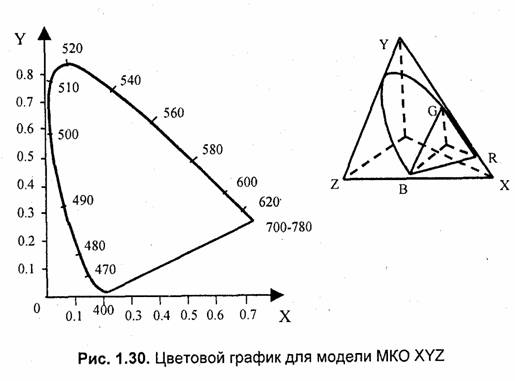
          Как оказалось, ни один цвет монохроматического излучения (за исключением самих цветов R, G и В) не может быть представлен только положительными значениями коэффициентов смешивания. Это наглядно можно изобразить с помощью цветового графика, построенного на основе треугольника Максвелла (рис. 1.26). Верхняя часть кривой линии соответствует чистым монохроматическим цветам, а нижняя линия— от 380 до 780 нм-— представляет так называемые пурпурные цвета (смесь синего и красного), которые не являются монохроматическими. Точки, лежащие внутри контура кривой, соответствуют реальным цветам, а вне этого контура— нереальным цветам. Точки внутри треугольника соответствуют неотрицательным значениям коэффициентов r^’ g' и b' и представляют цвета, которые можно получить смешиванием компонент RGB.

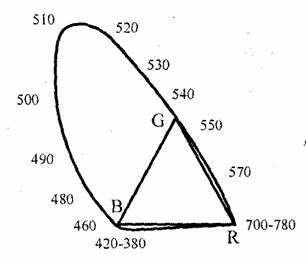
^R

Таким образом, система RGB имеет неполный цветовой охват— некоторые насыщенные цвета не могут быть представлены смесью указанных трех компонент. В первую очередь это цвета от зеленого до синего, включая все оттенки голубого — они соответствуют левой ветви кривой цветового графика. Еще раз подчеркнем, что речь здесь идет о насыщенных цветах, поскольку, например, ненасыщенные голубые цвета смешиванием компонент RGB получить можно. Несмотря на неполный охват, система RGB широко используется в настоящее время — в первую очередь, в цветных телевизорах и дисплеях компьютеров. Отсутствие некоторых оттенков цвета не слишком заметно.

Еще одним фактором, способствующим популярности системы RGB, является ее наглядность — основные цвета находятся в трех четко различимых участках видимого спектра.

           Кроме того, одной из гипотез, объясняющих цветовое зрение человека, является трехкомпоиентная теория, которая утверждает, что в зрительной системе человека есть три типа светочувствительных элементов. Один тип элементов реагирует на зеленый, другой тип — на красный, а третий тип — насиний цвет. Такая гипотеза высказывалась еще Ломоносовым [15], ее обоснованием занимались многие ученые, начиная с Т. Юнга. Впрочем, трехкомпонентная теория не является единственной теорией цветового зрения человека [1, 10, 15].

Цветовая модель CMY

Используется для описания цвета при получении изображений на устройствах, которые реализуют принцип поглощения (вычитания) цветов. В первую очередь она используется в устройствах, которые печатают на бумаге. Название данной модели составлено из названий основных субтрактивных цветов — голубого (Cyan), пурпурного (Magenta) и желтого (Yellow) (рис. 1.27).

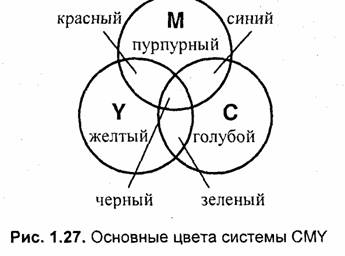
Для того чтобы разобраться с поглощением цветов, рассмотрим рис. 1.28.

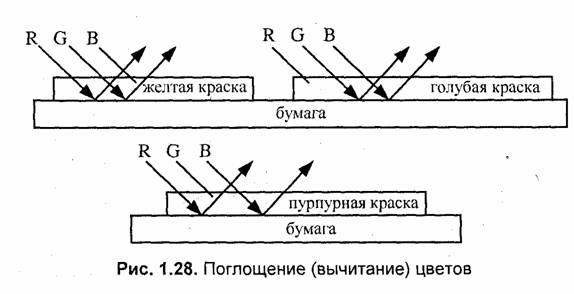
Нанесение желтой краски на белую бумагу означает, что поглощается отраженный синий цвет. Голубая краска поглощает красный цвет, пурпурная краска — зеленый.

Комбинирование красок позволяет получить цвета, которые остались — зеленый, красный, синий и черный. Черный цвет соответствует поглощению всех цветов при отражении (рис. 1.29).

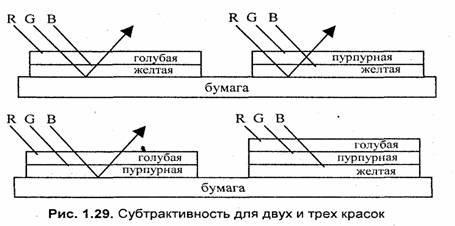
На практике добиться черного смешиванием сложно из-за неидеальности красок, поэтому в принтерах используют еще и краску черного цвета (blасК). Тогда модель называется CMYK.

Необходимо также отметить, что не всякие краски обеспечивают указанное выше вычитание цветов CMY. Подробнее об этом в [10].

В табл. 1.2 представлены некоторые цвета в моделях RGB и CMY.

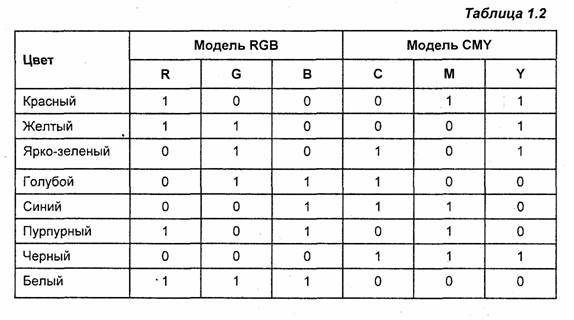
Здесь считается, что компоненты кодируются числами в диапазоне от 0 до 1. Для иного диапазона чисел можно записать соответствующие соотношения.

Другие цветовые модели

          Для решения проблемы отрицательных коэффициентов, которая имеет место для модели RGB, в 1931 году Международной Комиссией по Освещению (CIE) была принятая колориметрическая система XYZ (рис. 1.30). В системе МКО XYZ в качестве основных цветов были приняты также три цвета, однако они являются условными, нереальными [1,15].

         Рассмотренные выше цветовые модели так или иначе используют смешивание некоторых основных цветов. Теперь рассмотрим цветовую модель, которую можно отнести к иному, альтернативному типу.

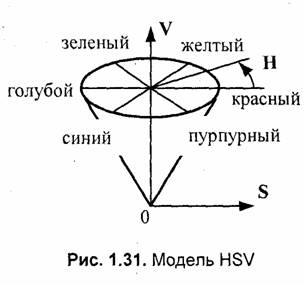
В модели HSV цвет описывается следующими параметрами — цветовой тон Н (hue), насыщенность S (saturation), яркость, светлота V (value). Значение Н измеряется в градусах от 0 до 360, поскольку здесь цвета радуги располагаются по кругу в таком порядке — красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый (известна поговорка "каждый охотник желает знать, где сидят фазаны"). Значения S и V находятся в диапазоне (0...1).

Приведем примеры кодирования цветов для модели HSV (рис. 1.31). При S=0 (то есть на оси V) — серые тона. Значение V=0 соответствует черному цвету. Белый цвет кодируется как S=0, V=l. Цвета, расположенные по кругу напротив друг друга, то есть отличающиеся по Н на 180 градусов, являются дополнительными [28]. Задание цвета с помощью параметров HSV достаточно часто используется в графических системах, причем обычно показывается развертка конуса.

Существуют и другие цветовые модели, построенные аналогично HSV, например, модель HLS (Hue, Lighting, Saturation) также использует цветовой конус.

В [42] есть сведения о цветовой модели CIE L*a*b*, которая была принятая МКО.

Все вышеперечисленные цветовые модели описывают цвет тремя параметрами. Они описывают цвет в достаточно широком диапазоне. Теперь рассмотрим цветовую модель, в которой цвет задается одним числом, но уже для ограниченного диапазона цветов (оттенков).

На практике часто используются черно-белые (серые) полутоновые изображения. Серые цвета в модели RGB описываются одинаковыми значениями компонентов, то есть r_i = g_i = b_i. Таким образом, для серых изображений нет необходимости использовать тройки чисел — достаточно и одного числа. Это позволяет упростить цветовую модель. Каждая градация определяетсяяркостью Y. Значение Y=0 соответствует черному цвету, максимальное значение Y — белому.

В качестве примера рассмотрим преобразование цветных изображений, представленных в системе RGB, в градации серого (подобно тому, как показываются цветные фильмы на черно-белом экране телевизора). Для этого можно воспользоваться соотношением

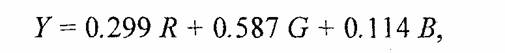
где коэффициенты при R, G и В учитывают различную чувствительность зрения к соответствующим цветам и, кроме того, их сумма равна единице. Очевидно, что обратное преобразование R=Y, G=Y, B=Y не даст никаких других цветов, кроме градаций серого.

Еще один пример использования различных цветовых моделей. При записи цветных фотографий в графический файл формата JPEG выполняется преобразование из модели RGB в модель (Y, Сb, Сr). Это используется для дальнейшего сжатия объемов информации растрового изображения. При чтении файлов JPEG выполняется обратное преобразование в RGB.

Разнообразие моделей обусловлено различными областями их использования. Каждая из цветовых моделей была разработана для эффективного выполнения отдельных операций: ввода изображений, визуализации на экране, печати на бумаге, обработки изображений, сохранения в файлах, колориметрических расчетов и измерений. Преобразование одной модели в другую может привести к искажению цветов изображения.

Кодирование цвета. Палитра

Для того чтобы компьютер имел возможность работать с цветными изображениями, необходимо представлять цвета в виде чисел — кодировать цвет. Способ кодирования зависит от цветовой модели и формата числовых данных в компьютере.

Для модели RGB каждая из компонент может представляться числами, ограниченными некоторым диапазоном — например, дробными числами от О до 1 либо целыми числами от 0 до некоторого максимального значения. В настоящее время достаточно распространенным является формат True Color, в котором каждая компонента представлена в виде байта, что дает 256 градаций для каждой компоненты: R=0...255, G = 0...255, В = 0...255. Количество цветов составляет 256x256x256 = 16.7 млн (2²⁴).

            Такой способ кодирования цветов можно назвать компонентным. В компьютере коды изображений True Color представляются в виде троек байтов, либо упаковываются в длинное целое (четырехбайтное) — 32 бита (так, например, сделано в API Windows):

С = 00000000 bbbbbbbb gggggggg rrrrrrrr.

При работе с изображениями в системах компьютерной графики часто приходится искать компромисс между качеством изображения (требуется как можно больше цветов) и ресурсами, необходимыми для хранения и воспроизведения изображения, исчисляемыми, например, объемом памяти (надо уменьшать количество бит на пиксел).

Кроме того, некоторое изображение само по себе может использовать ограниченное количество цветов. Например, для черчения может быть достаточно двух цветов, для человеческого лица важны оттенки розового, желтого, пурпурного, красного, зеленого; а для неба— оттенки голубого и серого. В этих случаях использование полноцветного кодирования цвета является избыточным.

При ограничении количества цветов используют палитру, представляющую набор цветов, важных для данного изображения. Палитру можно воспринимать как таблицу цветов. Палитра устанавливает взаимосвязь между кодом цвета и его компонентами в выбранной цветовой модели.

В качестве примера дадим стандартную палитру дисплейных 16-цветных видеорежимов EGA, VGA (табл. 1.3).

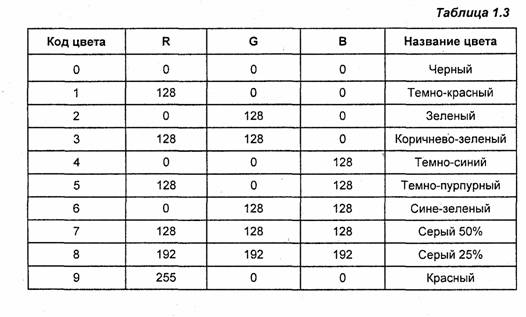
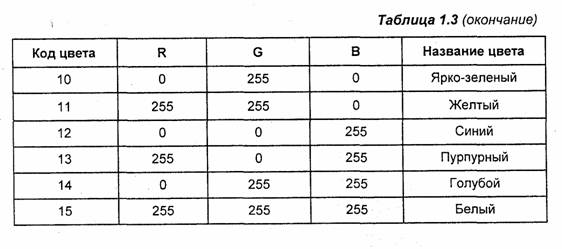
Недостатком такой палитры можно считать отсутствие одного из важных цветов— оранжевого. Существуют также иные стандартные палитры, например, 256-цветная для VGA. Компьютерные видеосистемы обычно предоставляют возможность программисту установить собственную палитру.

Каждый цвет изображения, использующего палитру, кодируется индексом, который будет определять номер строки в таблице палитры. Поэтому такой способ кодирования цвета называют индексным.                          

Формат файлов

для хранения растровых изображений

К настоящему времени известно много форматов файлов для растровых изображений. Здесь мы рассмотрим один из самых популярных форматов, который обязан своей распространенностью операционной системе Windows — формат BMP.

Общая структура BMP-файла такова:

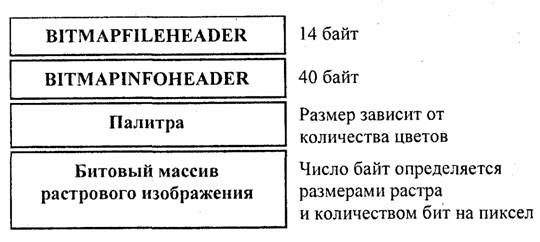
Количество записей RGBQUAD равно количеству используемых цветов. Палитра отсутствует, если число бит на пиксел равно 24. Также палитра не нужна и для некоторых цветовых форматов 16 и 32 бит на пиксел.

После палитры (если она есть) в файле BMP записывается растр в виде битового (а точнее, байтового массива). В битовом массиве последовательно записываются байты строк растра. Количество байт в строке должно быть кратно четырем, поэтому если количество пикселов по горизонтали не соответствует такому условию, то справа в каждую строку дописывается некоторое число битов (выравнивание строк на границу двойного слова).

Сжатие изображений в файлах BMP отсутствует, однако подобный формат (Device Independent Bitmap) описания растровых изображений также используется и для файлов типа DIB, где применяются простейшие алгоритмы сжатия RLE (Run Length Encoding) [61]. Алгоритмы RLE также используются и в других популярных растровых графических форматах, например PCX.

Описание других графических форматов можно найти в литературных источниках, например [2], а также в сети Internet.

1.4.Методы улучшения растровых изображений

Рассмотрим некоторые из существующих методов улучшения качества изображений, которые основываются на субъективном восприятии разрешающей способности и количества цветов. При одних и тех же значениях технических параметров устройства графического вывода можно создать иллюзию увеличения разрешающей способности или количества цветов. Причем субъективное улучшение одной характеристики происходит за счет ухудшения другой.

Устранение ступенчатого эффекта

В растровых системах при невысокой разрешающей способности (меньше 300 dpi) существует проблема ступенчатого эффекта (aliasing). Этот эффект особенно заметен для наклонных линий — при большом шаге сетки растра пиксель образуют как бы ступени лестницы.

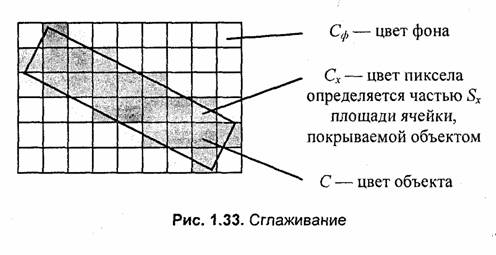
           Рассмотрим это на примере отрезка прямой линии. Вообще говоря, растровое изображение объекта определяется алгоритмом закрашивания пикселов, соответствующих площади изображаемого объекта. Различные алгоритмы могут дать существенно отличающиеся варианты растрового изображения одного и того же объекта. Можно сформулировать условие корректного закрашивания следующим образом — если в контур изображаемого объекта попадает больше половины площади ячейки сетки растра, то соответствующий пиксел закрашивается цветом объекта (С), иначе— пиксел сохраняет цвет фона (С_ф).

На рис. 1.32 показано растровое изображение толстой прямой линии, на которое для сравнения наложен идеальный контур исходной линии.

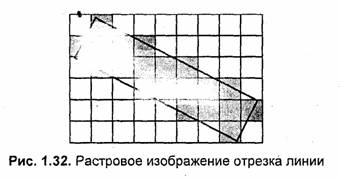
         Устранение ступенчатого эффекта называется по-английски antialiasing. Для того чтобы растровое изображение линии выглядело более гладким, можно цвет угловых пикселов "ступенек лестницы" заменить на некоторый оттенок, промежуточный между цветом объекта и цветом фона. Будем вычислять цвет пропорционально части площади ячейки растра, покрываемой идеальным контуром объекта. Если площадь всей ячейки обозначить как S, а часть площади, покрываемой контуром, — S_x, то искомый цвет равен

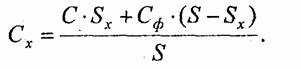
    На рис. 1.33 показано сглаженное растровое изображение, построенное указанным выше методом.

Методы получения сглаженных растровых изображений можно разделить на две группы. Первую группу составляют алгоритмы генерации сглаженных изображений отдельных простейших объектов — линий, фигур. Некоторые из таких алгоритмов описаны в [33].

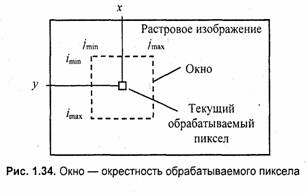
Другую группу методов сглаживания составляют методы обработки уже нарисованного изображения. Для сглаживания растровых изображений часто используют алгоритмы цифровой фильтрации. Один из таких алгоритмов — локальная фильтрация. Она осуществляется путем взвешенного суммирования яркостей пикселов, расположенных в некоторой окрестности текущего обрабатываемого пиксела. Можно представить себе, что в ходе обработки по растру скользит прямоугольное окно, которое выхватывает пикселы, используемые *для вычисления цвета некоторого текущего пиксела. Если окрестность симметрична, то текущий пиксел находится в центре окна (рис. 1.34).

Базовую операцию такого фильтра можно представить так:

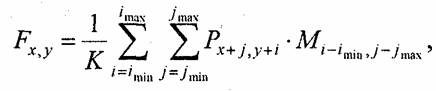
где Р— значение цвета текущего пиксела, F— новое значение цвета пиксела, К— нормирующий коэффициент, М— двумерный массив коэффициентов, который определяет свойства фильтра (обычно этот массив называют маской).

Размеры окна фильтра: (j_max- j_min +1) по горизонтали и (i_max – i_min+1)— по вертикали. При i_min , j_min⁼ -1 и i_max,j_max = +1 имеем фильтр с окном 3x3, который часто используется на практике.

            Для обработки всего растра необходимо произвести указанные выше вычисления для каждого пиксела. Если в ходе обработки новые значения цвета пикселов записываются в исходный растр и вовлекаются в вычисления для очередных пикселов, то такую фильтрацию называют рекурсивной. При нерекурсивной фильтрации в вычисления вовлекаются только прежние значения цвета пикселов. Нерекурсивность можно обеспечить, если новые значения записывать в отдельный массив.

На рис. 1.35 представлены результаты работы двух вариантов сглаживающего нерекурсивного фильтра с окном (маской) 3x3.

г.

Значение нормирующего коэффициента здесь выбрано равным сумме элементов маски. Этим обеспечивается сохранение масштаба яркости преобразованного растра. Заметьте, что маска — это не матрица, а массив коэффициентов, располагающихся соответственно пикселям окна. Средний фильтр можно задать и маской 2x2 — отбросить нулевые коэффициенты.

При сглаживании цветных изображений можно использовать модель RGB и производить фильтрацию по каждой компоненте.

С помощью локальной цифровой фильтрации можно выполнять достаточно разнообразную обработку изображений — повышение резкости, выделение контуров и многое другое [31, 34].

Дизеринг

Хорошо, когда растровое устройство отображения может прямо воссоздавать тысячи цветов для каждого пиксела. Не так давно это было проблемой даже для компьютерных дисплеев (а точнее — для видеоадаптеров). Современные

растровые, дисплеи достаточно качественно отображают миллионы цветов, благодаря чему без проблем можно отображать цветные фотографии. Но для растровых устройств, которые печатают на бумаге, положение совсем другое. Устройства печати обычно имеют высокую разрешающую способность (dpi), часто на порядок большую, чем дисплеи. Однако нельзя непосредственно воссоздать даже сотню градаций серого для пикселов черно-белых фотографий, не говоря уже о миллионах цветов. Вы можете возразить, что в любой газете или журнале мы видим иллюстрации. Возьмите лупу и посмотрите, например, на изображение любой напечатанной фотографии. В большинстве случаев можно увидеть, что оттенки цветов (для цветных изображений) или полутоновые градации (для черно-белых) имитируются комбинированием, Смесью точек. Чем качественнее полиграфическое оборудование, тем меньше отдельные точки и расстояние между ними.

Иногда отдельные точки на фотографии нельзя различить даже с помощью лупы, что может быть в таких случаях — или нам посчастливилось увидеть печать многими сотнями красок, или разрешающая способность устройства печати очень высокая. Оба варианта пока что не встречаются. Однако, безусловно, с течением времени будут изобретены способы печати если не многими тысячами красок (что маловероятно), то хотя бы красками, которые плавно изменяют свой цвет, или будет изобретена бумага с соответствующими свойствами [51].

Для устройств печати на бумаге проблема количества красок достаточно важна. В полиграфии для цветных изображений обычно используют три цветных краски и одну черную, что в смеси дает восемь цветов (включая черный и белый цвет бумаги). Встречаются образцы печати большим количеством красок — например, карты, напечатанные с использованием восьми красок, однако такая технология печати намного сложнее. Состояние дел с цветной печатью можно оценить также на примере относительно простых офисных принтеров. Недавно появились струйные принтеры с шестью цветными красками вместо трех. В таких принтерах в состав обычных CMYK-красок добавлены бледно-голубая, бледно-пурпурная и бледно-желтая краски (семицветные принтеры). В шестицветных принтерах отсутствует бледно-желтая краска [43]. Увеличение количества красок значительно улучшило качество печати, однако и этого пока явно мало.

Если графическое устройство не способно воссоздавать достаточное количество цветов, тогда используют растрирование — независимо от того, растровое это устройство или не растровое. В полиграфии растрирование известно давно [14, 21]. Оно использовалось несколько столетий тому назад для печати гравюр. В гравюрах изображение создается многими штрихами, причем полутоновые градации реализованы или штрихами различной толщины на одинаковом расстоянии, или штрихами одинаковой толщины с переменной густотою расположения. Такие способы используют особенности человеческого зрения и в первую очередь — пространственную интеграцию. Если достаточно близко расположить маленькие точки различных цветов, то они будут восприниматься как одна точка с некоторым усредненным цветом. Если на плоскости густо расположить много маленьких разноцветных точек, то будет создана визуальная иллюзия закрашивания плоскости некоторым усредненным цветом. Однако если увеличивать размеры точек и (или) расстояние между ними, то иллюзия сплошного закрашивания исчезает — включается другая система человеческого зрения, обеспечивающая нашу  способность различать отдельные объекты, подчеркивать контуры.

В компьютерных графических системах часто используют эти методы. Они позволяют увеличить количество оттенков цветов за счет снижения пространственного разрешения растрового изображения. Иначе говоря — это обмен разрешающей способности на количество цветов. В литературе по компьютерной графике такие методы растрирования получили название dithering (дрожание, разрежение).

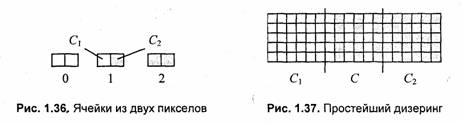
Простейшим вариантом дизеринга можно считать создание оттенка цвета парами соседних пикселов.

Если рассмотреть ячейки из двух пикселов (рис. 1.36), то ячейка номер 1 дает оттенок цвета

где С₁ и Сг — цвета, которые графическое устройство способно непосредственно воспроизвести для каждого пиксела. Числовые значения С, С₁ и С₂ можно рассчитать в полутоновых градациях или в модели RGB — отдельно для каждой компоненты.

Пример растра с использованием ячеек из двух пикселов приведен на рис. 1.37. Как видим, для создания промежуточного оттенка С ячейки образовывают вертикальные линии, которые очень заметны. Для того чтобы человек воспринял это как сплошной оттенок, необходимо, чтобы угловой размер ячеек был меньше одной угловой минуты. Можно изменять положения таких ячеек в растре, располагая их, например, по диагонали. Это несколько лучше, но не намного.

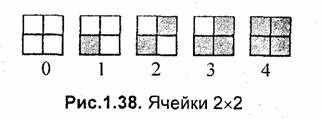
Чаще используют квадратные ячейки больших размеров. Дадим пример ячеек размером 2 x 2 (рис. 1.38).

Такие ячейки дают 5 градаций, из них три комбинации (1, 2, 3) образуют новые оттенки.

Расчет цвета, соответствующего одной из комбинаций пикселов в ячейке, можно выполнить таким образом. Если пикселы ячейки могут быть только двух цветов (С₁ и С₂), то необходимо подсчитать часть площади ячейки для пикселов каждого цвета. Цвет ячейки (С) можно оценить соотношением

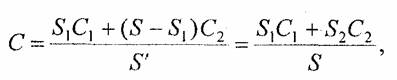
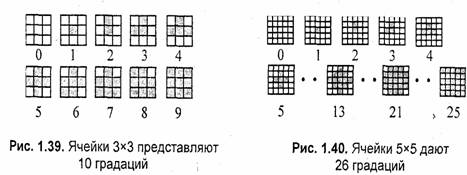
где S— общая площадь ячейки; Si и S₂ — части площади, занятых пикселями цветов С₁ и С₂ соответственно, причем S₁ + S₂ = S. Проще всего, когда пикселы квадратные, а их размер равен шагу размещения пикселов. Примем площадь одного пиксела за единицу. В этом случае площадь, занимаемая пикселями в ячейке, равна их количеству (рис. 1.41).

Для ячейки 5 x 5, изображенной на рис. 1.41, дадим расчет цвета С для некоторых цветов С₁ и С₂. Пусть С₁ — белый цвет (R₁ G₁ B ₁) = (255, 255, 255), а С₂ — черный (R₂ G₂ B₂) = (0, 0, 0), тогда

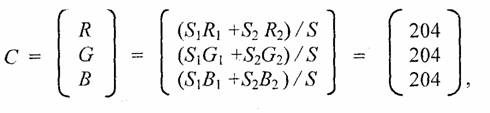
то есть мы получили светло-серый цвет.

Еще пример. Если С)— желтый (R ₁G ₁B₁ = (255, 255, 0), а С₂— красный (R₂G₂B₂) = (255, 0, 0), то С = (255, 204, 0). Это оттенок оранжевого цвета.

Следовательно, если в ячейке размерами п^x п использованы два цвета, то с помощью этой ячейки можно получить п²+₁ различных цветовых градаций. Две комбинации пикселов — когда все пикселы ячейки имеют цвет С₁ или С₂ — дают цвет ячейки соответственно С, или С₂. Все иные комбинации дают оттенки, промежуточные между С₁ и С₂.

Можно считать, что ячейки размером п^x п образовывают растр с разрешающей способностью в п раз меньшей, чем у исходного растра, а глубина цвета возрастает пропорционально и². Для характеристики изображений, которые создаются методом дизеринга, используют термин лшшатура растра. Линиатура вычисляется как количество линий (ячеек) на единицу длины — сантиметр, миллиметр, дюйм. В последнем случае единицей измерения для линиатуры является lpi (по аналогии с dpi).

Как реализовать метод дизеринга в графической системе? Рассмотрим примеры преобразования растрового изображения размером pxq с определенной глубиной цвета в другой растр, предназначенный для отображения с помощью графического устройства, в котором используется ограниченное количество основных цветов. В таком случае нужно выбрать размеры ячейки тxп, которые обеспечивают достаточное количество цветовых градаций. Затем каждый пиксел растра превращается в пиксел растра отображения. Это можно осуществить двумя способами.

Первый способ. Каждый пиксел заменяется ячейкой из m^п пикселов. Это самое точное преобразование по цветам, но размер растра увеличивается и равен mp x nq пикселов.

Второй способ. Размер растра в пикселях не изменяется, если пиксел растра отображения образовывается следующим образом:

1.   Определяем координаты пиксела (х, у) для преобразуемого растра.

2.   Находим цвет пиксела (х, у)

3.   По цвету пиксела находим номер (к) ячейки, наиболее адекватно представляющей этот цвет.

4.   По координатам (х,у) вычисляем координаты пиксела внутри ячейки: х_к = х mod т; у_k ⁼ у mod п.

5.  Находим цвет (С) пиксела ячейки с координатами (х_ky_k )

6.  Записываем в растр отображения пиксел (х,у) с цветом С.

Такой способ можно использовать не для любых вариантов расположения пикселов в ячейках. Конфигурации пикселов должны быть специально разработаны для таких преобразований. Одно из требований можно сформулировать так. Если ячейки разработаны на основе двух цветов, например, белого и черного, а градации изменяются пропорционально номеру ячейки, то необходимо, чтобы ячейка с номером (i) для более темной градации серого содержала бы все черные пикселы ячейки номер (i- 1).

Рассмотрим пример изображения, созданного на основе ячеек 5 ^Х5.

Для создания такого изображения специально была выбрана небольшая разрешающая способность, чтобы подчеркнуть структуру изображения. Ячейки образовывают достаточно заметный квадратный растр (рис. 1.42).

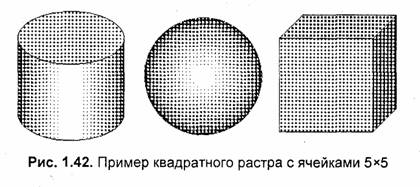
         Для улучшения восприятия изображения можно использовать иное расположение ячеек, например, диагональное (рис 1.43).

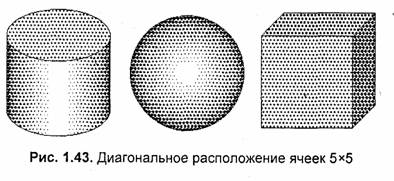
Диагональное расположение можно получить, если сдвигать четные строки

ячеек (рис. 1.44).

Координаты пикселов ячеек можно вычислять следующим образом:

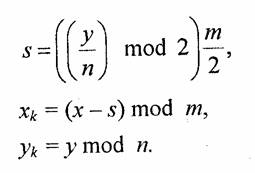
Для, того чтобы получить диагональную структуру растра подобную той, что используется для печати газет, можно использовать квадратное расположение ячеек другого типа (рис. 1.45).

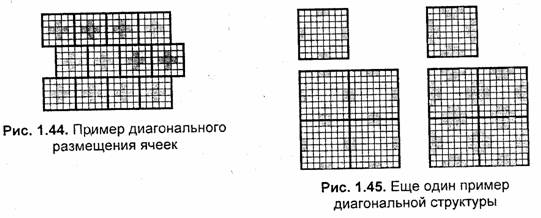
Вы, наверное, уже заметили, что для всех приведенных выше примеров дизеринга ячейки образовывают точки переменного размера с постоянным шагом. Однако часто используется иной подход— переменная густота расположения точек постоянного размера. Такой способ получил название частотной модуляции (ЧМ)'(рис. 1.46).

      Положительная черта способа ЧМ — меньшая заметность структуры растра. Однако его использование затруднено в случае, когда размер пикселов больше, чем их шаг. Начиная с определенной густоты, пикселы смыкаются. Кроме того, на дискретном растре невозможно обеспечить плавное изменение густоты (частоты), в особенности для ячеек небольшого размера. Рассмотрим пример ячеек 5x5, реализующих ЧМ-дизеринг (рис. 1.47).

Для изображений, созданных методом ЧМ-дизеринг, наблюдается меньшая заметность растровой структуры (рис. 1.48).

Однако при регулярном расположении одинаковых ячеек всегда образовывается текстура, муар, лишние контуры. Одна из важных задач— разработка таких вариантов ячеек, которые предопределяют наименее заметную растровую структуру (кроме тех случаев, когда, наоборот, такую структуру нужно подчеркнуть для создания изображения в стиле гравюры). Это довольно сложная задача.

Один из способов создания достаточно качественных изображений — это диффузный дизеринг (diffused dithering). Суть его в том, что ячейки создаются случайно (или псевдослучайно). Если для каждой градации создавать случайные ячейки, то даже для фрагмента растра пикселов с постоянным цветом не будут образовываться регулярные структуры. Это соответствует диффузному отражению света от матовой поверхности.

1.5.Эволюция компьютерных видеосистем

         Компьютерные видеосистемы рассмотрим на примере персональных компьютеров класса IBM PC. Первый персональный компьютер фирмы IBM появился в 1981 году. Сейчас уже можно сказать, что появление как раз этого компьютера привело к значительному распространению персональных компьютеров. Некоторые особенности архитектуры IBM PC сохранены и по сей день (рис. 1.49).

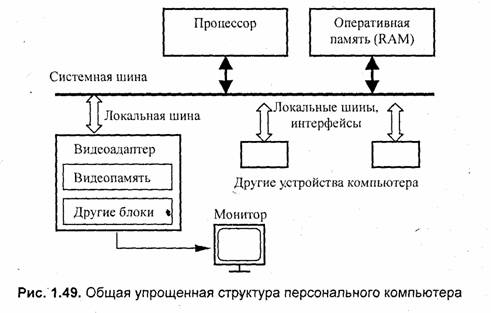
Одной из таких особенностей, которые выгодно отличали его от других персональных компьютеров, является открытость архитектуры. Это означает гибкие возможности подключения разнообразных устройств, простоту модернизации компьютера. Важным фактором была цена— для IBM PC она была меньшей, чем, например, для компьютеров Apple, которые были лучше по другим показателям (в первую очередь, по графическим возможностям). Кроме того, с самого начала пользователям компьютеров семейства IBM PC были доступны разнообразные средства программирования — миллионы пользователей получили возможность сами разрабатывать программное обеспечение. Все это привело к массовому распространению таких компьютеров, использованию в разнообразных областях.

Важная черта архитектуры персонального компьютера с позиций графики — то, что контроллер видеосистемы (видеоадаптер) расположен рядом с процессором и оперативной памятью, так как подключен к системной шине через скоростную локальную шину. Это дает возможность быстро вести обмен данными между оперативной памятью и видеопамятью. Для вывода графических изображений, в особенности в режиме анимации, нужна самая высокая скорость передачи данных. В отличие от этого в больших компьютерах (мэйнфреймах) данные к дисплеям передавались через интерфейс канала ввода-вывода, который работает намного медленнее, чем системная шина. Большие компьютеры, как правило, работают со многими дисплеями, расположенными на значительном расстоянии.

         Первый компьютер IBM PC был оснащен видеоадаптером MDA (Monochrome Display Adapter). Видеосистема была предназначена для работы в текстовом режиме — отображалось 25 строк по 80 символов в каждой строке.

Год спустя небольшая фирма Hercules выпустила видеоадаптер Hercules Graphic Card. Он поддерживал также и графический черно-белый режим

720x348.

Следующим шагом был видеоадаптер CGA (Color Graphic Adapter). Это первая цветная модель для IBM PC. Адаптер CGA позволял работать в цветном текстовом или графическом режимах. Далее мы будем рассматривать только графические режимы видеоадаптеров. Графических режимов для CGA было два: черно-белый 640x200 и цветной 320^х200. В цветном режиме можно было отображать только четыре цвета одновременно (2 бита на пиксел).

В 1984 году появился адаптер EGA (Enhanced Graphic Adapter). Это было значительное достижение для персональных компьютеров этого типа. Появился графический 16-цветный видеорежим 640^х350 пикселов. Цвета можно выбирать из палитры 64 цветов. В это время уже получили распространение компьютерные игры с более или менее качественной графикой и графические программы для работы. Однако шестнадцати цветов явно мало для показа изображений типа фотографий, а разрешающая способность недостаточна для графических пакетов типа САПР. Кроме того, видеорежим 640x350 имеет еще один недостаток — различная разрешающая способность по горизонтали и вертикали — "не квадратные пикселы".

В 1987 году появились видеоадаптеры MCGA (Multi-Color Graphic Array) и VGA (Video Graphic Array). Они обеспечивали уже 256-цветные видеорежимы.

Более совершенным был адаптер VGA — он стал наиболее популярным. Адаптер VGA имел 256-цветный графический видеорежим с размерами растра 320x200. Цвета можно выбирать из палитры в 256 тысяч цветов. Это дало возможность полностью удовлетворить потребности отображения полутоновых черно-белых фотографий. Цветные фотографии отображались достаточно качественно, однако 256 цветов мало, поэтому в компьютерных играх и графических пакетах активно использовался дизеринг. Кроме того, режим 320x200 тоже имеет различную разрешающую способность по горизонтали и вертикали. Для мониторов, которые используются в персональных компьютерах типа IBM PC, необходимо, чтобы количество пикселов по горизонтали и вертикали была в пропорции 4:3. То есть, не 320x200, а 320x240. Такого документированного видеорежима для VGA нет, однако в литературе [39] приведен пример, как создать 256-цветный видеорежим 320^х240 на видеосистеме VGA. Можно запрограммировать видеоадаптер, записав в его регистры, соответствующие значения, и получить видеорежим "X" (не путать с XGA). Несколько лет тому назад автор этой книги проверял сведения, приведенные в статье [39], и может подтвердить, что действительно, "X — видеорежим" 256 цветов 320x240 может быть установлен для любой видеосистемы VGA (во всяком случае, не было найдено ни одной, где этого делать  нельзя).             Видеоадаптер VGA также имеет 16-цветный видеорежим 640^х480. Это соответствует "квадратным пикселем". Рост разрешающей способности в сравнении с EGA не очень большой, но ощутимый, что дает новый толчок для развития графических программ на персональных компьютерах.

Дальнейшее развитие видеоадаптеров для компьютеров типа IBM PC связано   с повышением разрешающей способности и количества цветов. Можно отметить видеосистему ЮМ 8514, которая была предназначена для работы с пакетами САПР. Стали появляться видеоадаптеры различных фирм, которые обеспечивали на первых порах видеорежимы 800*600, а потом и 1024*768 цветов при 16-ти цветах, и видеорежимы 640x480, 800x600 и больше для 256 цветов. Эти видеоадаптеры стали называть SuperVGA. Чуть позже появился видеоадаптер IBM XGA.

Первой достигла глубины цвета в 24 бит фирма Targa с видеоадаптером Targa24, что позволило получить на персональных компьютерах IBM PC видеорежим True Color. Такое достижение можно считать началом профессиональной графики на персональных компьютерах этого типа. Там, где ранее использовались графические рабочие станции или персональные компьютеры Apple Macintosh, отныне постепенно переходили на более дешевые компьютеры IBM PC. Одной из таких областей является компьютерное настольное издательство.

Сейчас на компьютерах ЮМ PC с процессором Pentium используется много типов видеоадаптеров. Все видеосистемы растрового типа. Некоторые из них позволяют устанавливать глубину цвета 32 бит на пиксел при размерах растра 1600x1200 и более. Существуют стандарты на видеорежимы, установленные VESA (Video Electronic Standards Association).

Параметры отображения обусловливаются не только моделью видеоадаптера, но и объемом установленной видеопамяти. Видеопамять персонального компьютера (VRAM — Video RAM) хранит растровое изображение, которое показывается на экране монитора. Изображение на мониторе полностью соответствует текущему содержанию видеопамяти. Видеопамять постоянно сканируется с частотой кадров монитора. Запись новых данных в видеопамять немедленно изменяет изображение на мониторе. Необходимый объем видеопамяти вычисляется как площадь растра экрана в пикселях, умноженная на количество бит (или байтов) на пиксел. Например, для 24-битного видеорежима 1024x768 нужна видеопамять 24x1024x768 = 18 874 368 бит = = 2.25 Мбайт.

В видеоадаптерах первых образцов количество видеопамяти вычислялось в килобайтах, например, адаптер CGA имел 16 Кбайт [6, 29]. В современных видеоадаптерах счет идет на мегабайты. Как правило, объем видеопамяти кратен степени двойки-— 1, 2, 4, 8 Мбайт, встречаются также видеоадаптеры с 16 Мбайт и более. Наблюдается тенденция увеличения объемов видеопамяти — соответственно увеличению разрешающей способности и глубины цвета видеосистем. В видеопамяти могут храниться несколько кадров изображения — это может быть использовано при анимации. Кроме того, в некоторых видеоадаптерах предусмотрена возможность использования видеопамяти для хранения другой информации, например Z-буфера, растров текстур.

Адреса, по которым процессор обращается к видеопамяти, находятся в общем адресном пространстве. Например, для видеорежимов VGA 256 цветов 320 х200, 16 цветов 640 х480, а также для некоторых других, адрес первого байта видеопамяти равен А000:0000 (сегмент  смещение) или А0000 (абсолютный адрес) (рис. 1.50).

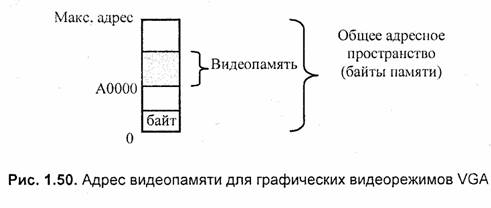
Для некоторых видеорежимов (старых образцов) используется другой адрес, например, В800:0000 для CGA 320x200. Современные видеоадаптеры обычно поддерживают видеорежимы, которые использовались ранее. Это делается для обеспечения возможности функционирования старых программ. Каждый видеорежим имеет собственный номер (код).

Кроме физической организации памяти компьютера— в виде одномерного вектора байтов в общем адресном пространстве, необходимо учитывать логическую организацию видеопамяти. Следует отметить, что названия "физическая" и "логическая" организация могут означать разные вещи для различных уровней рассмотрения. Например, если говорить о физической организации памяти, то она в микросхемах выглядит совсем не как одномерный вектор байтов, а как матрица бит. Логическая организация видеопамяти зависит от видеорежима. В качестве примера на рис. 1.51 приведен видеорежим VGA 256 цветов 320x200 (его код 13h).

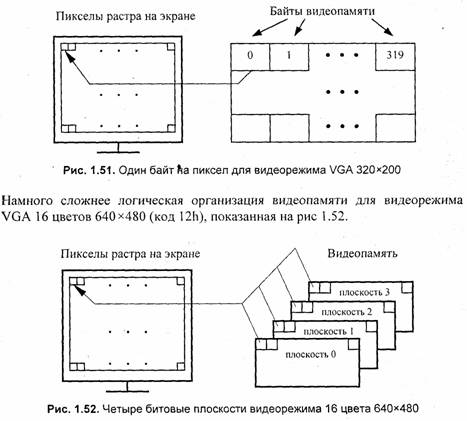
В этом видеорежимё используются четыре массива байтов памяти. Каждый массив назван битовой плоскостью, для каждого пиксела используются одинаковые биты данных различных плоскостей. Каждая битовая плоскость имеет 80 байтов в одной строке. Плоскости имеют одинаковый адрес в памяти, для доступа к отдельной плоскости необходимо устанавливать индекс плоскости в соответствующем регистре видеоадаптера. Подобный способ организации видеопамяти используется во многих других видеорежимах, он позволяет, например, быстро копировать массивы пикселов.

Для сохранения нескольких кадров изображения в некоторых видеорежимах предусматриваются отдельные страницы видеопамяти с одинаковой логической организацией. Тогда можно изменять стартовый адрес видеопамяти — это приводит к сдвигу изображения на экране. Во всех графических видео-режимах стартовый адрес видеопамяти соответствует левому верхнему пикселу на экране. Поэтому координатная система с центром координат (0,0) в левом верхнем углу растра часто используется в качестве основной (или устанавливается по умолчанию) во многих графических интерфейсах программирования, например, в API Windows.

Обмен данными по системной шине для видеосистемы обеспечивают процессор, видеоадаптер и контроллер локальной шины. До недавнего времени для подключения видеоадаптеров использовалась локальная шина PCI (Peripheral Component Interconnect local bus). Шина PCI предназначена не только для графики, она является стандартом подключения самых разнообразных устройств, например, модемов, сетевых контроллеров, контроллеров интерфейсов. Эта шина— 32-битная, работает на частоте 33 МГц, скорость обмена до 132 Мбайт/с.

В настоящее время видеоадаптеры подключаются через локальную шину AGP (Accelerated Graphics Port). Разрядность — 64 бит. На частоте 66 МГц обеспечивала скорость обмена 528 Мбайт/с. Сейчас AGP работает и на более высоких частотах. Шина AGP была разработана для повышения скорости обмена данными между видеоадаптером и оперативной памятью в сравнении с возможностями шины PCI. Это позволяет достичь большей частоты кадров при работе графических ЗD-акселераторов. Высокая скорость обмена с оперативной памятью также позволяет хранить в этой памяти растровые текстуры (ранее для этого часто использовалась видеопамять, однако она обычно имеет недостаточную для этого емкость). Наличие AGP-порта также приводит к возрастанию быстродействия компьютера в целом благодаря уменьшению нагрузки на шину PCI, что дает возможность эффективнее использовать последнюю для работы с сетью, мультимедиа.

Современные видеоадаптеры представляют собой сложные электронные устройства. Кроме видеопамяти, на плате видеоадаптера (сейчас его часто называют видеокартой) располагается мощный специализированный графический процессор, который по сложности уже приближается к центральному процессору. Кроме визуализации содержимого видеопамяти графический процессор видеоадаптера выполняет как относительно простые растровые операции — копирование массивов пикселов, манипуляции с цветами пикселов, так и более сложные. Там, где ранее использовался исключительно центральный процессор, в данное время все чаще применяется графический процессор видеоадаптера, например, для выполнения операций графического вывода линий, полигонов. Первые графические процессоры видеоадаптеров выполняли преимущественно операции рисования плоских элементов. Современные графические процессоры выполняют уже много базовых операций ЗD-графики, например, поддержку Z-буфера, наложение текстур и тому подобное. Видеоадаптер выполняет эти операции аппаратно, что позволяет намного ускорить их в сравнении с программной реализацией данных операций центральным процессором. Так появился термин графические акселераторы. Быстродействие таких видеоадаптеров часто измеряется в количестве графических элементов, которые рисуются за одну секунду. Современные графические акселераторы способны рисовать миллионы треугольников за секунду. Возможности графических акселераторов сейчас активно используются разработчиками компьютерных игр.

Широка номенклатура видеоадаптеров для персональных компьютеров. Несколько примеров. Видеоадаптеры Matrox (качественная двумерная графика), NVidia GeForce (игровые ЗD-акселераторы), 3Dlabs Wildcat (для профессионального ЗD-моделирования).

Использование программистами графических возможностей видеосистемы может осуществляться различно. Во-первых, простейшие операции, такие как определение графического видеорежима, вывод пиксела на экран и некоторые другие, поддерживаются BIOS. Во-вторых, можно использовать функции операционной системы. Различные операционные системы могут предоставлять различные возможности. Например, в MS-DOS графических функций почти не было, однако программисту был разрешен свободный доступ ко всем аппаратным ресурсам компьютера. В быстродействующих графических программах часто использовался непосредственный доступ к видеопамяти. В отличие от этого, операционная система Windows запрещает прикладным программам непосредственный доступ к аппаратным ресурсам, однако можно применять несколько сотен графических функций операционной системы — интерфейс API. В-третьих, можно использовать специализированные графические интерфейсы, которые поддерживают аппаратные возможности современных графических процессоров.

Одним из наиболее известных графических интерфейсов является OpenGL. Этот интерфейс в виде библиотеки графических функций был разработан Silicon Graphics, и поддерживается многими операционными системами (в том числе Windows) а также производителями графических акселераторов. Интерфейс OpenGL для графического отображения использует взаимодействие типа клиент-сервер [25, 61].

Другим известным графическим интерфейсом является DirectX с подсистемой трехмерной графики Direct3D, а также подсистемой Direct Draw, которая обеспечивает, в частности, непосредственный доступ к видеопамяти. Этот интерфейс разработан Microsoft и предназначен только для Windows [26].     

Известны также другие разработки графических интерфейсов для видеоадаптеров. Например, интерфейс GLide, разработанный 3Dfx для графических видеоадаптеров семейства Voodoo (впрочем, это уже история, поскольку фирма 3Dfx недавно прекратила свое существование как изготовитель видеоадаптеров).

ГЛАВА 2

Координатный метод

Координатный метод был введен в XVII веке французскими математикам Р. Декартом и П. Ферма. На этом методе зиждется аналитическая геометрия которую можно считать фундаментом компьютерной графики. В современной компьютерной графике широко используется координатный метод. Этому есть несколько причин.

Каждая точка на экране (или на бумаге при печати на принтере) задается координатами — например, пиксельными.

 Координаты используются для описания объектов, которые будут отображаться как пространственные. Например, объекты микромира, объекты на поверхности Земли, объекты космического пространства и тому подобное. Даже тогда, когда отображается нечто, не имеющее привязки к положению в пространстве (например, случайные цветовые пятна в каком-то видеоэффекте), то и здесь используются координаты для учета взаиморасположения отдельных элементов.

 При выполнении многих промежуточных действий отображения используют разные системы координат и преобразования из одной системы в другую.

2.1. Преобразование координат

      Сначала рассмотрим общие вопросы преобразования координат; Пусть задана и-мерная система координат в базисе (к₁, к₂, ..., к_п), описывающая положение точки в пространстве с помощью числовых значений к,. В компьютерной графике чаще всего используется двумерная (п=2) и трехмерная ( n=3) системы координат.

Если задать другую, N-мерную, систему координат в базисе {т₁, m₂, ..., m_N) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

Гдеƒ_i— функция пересчета i-й координаты, аргументы — координаты в системе к_i

Можно поставить и обратную задачу — по известным координатам (m_i, m_i, ..., m_N) определить координаты {к₁, к₂, .... к_n,). Решение обратной задачи запишем так:

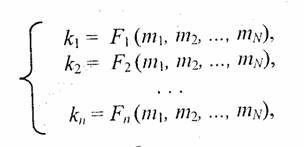
где F_i — функции обратного преобразования.

В случае, когда размерности систем координат не совпадают (п ≠ N), осуществить однозначное преобразование координат зачастую не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.

 Если размерности систем совпадают (n = .N), то также возможны случаи, когда нельзя однозначно решить прямую или обратную задачи.

 Преобразование координат классифицируют:

 по системам координат — например, преобразование из полярной системы в прямоугольную; □ по виду функций преобразования ƒ_i.

По виду функций преобразования различают линейные и нелинейные преобразования. Если при всех i = 1, 2, ..., N функцииƒ_i — линейные относительно аргументов (k₁,, к₂ ..., к_п), то есть

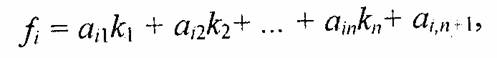
где a,j— константы, то такие преобразования называются линейными, а при п = N—- аффинными.

Если   хотя   бы   для   одного   i функция fi—   нелинейная   относительно (k₁ к₂, ..., к_n), тогда преобразование координат в целом не линейно.

нелинейное, так как в выражении для Y присутствует ху.

Тем, кто интересуется математическими аспектами, относящимся к системам

координат и преобразованиям систем координат, можно порекомендовать

такие книги, как [16, 23].

Линейные преобразования наглядно записываются в матричной форме:

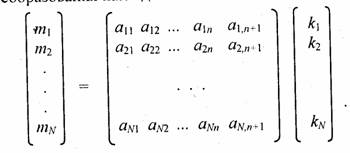
Здесь матрица коэффициентов (а_ij) умножается на матрицу-столбец (k_i) и в результате получается матрица-столбец (т_i).

       Мы и далее часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц А размером {т x п) и В размером (n х р):

Правило вычисления элементов матрицы С можно легко запомнить по названию "строка на столбец". И действительно, для вычисления любого элемента Су необходимо умножить элементы i-й строки матрицы А на элементы j-ro столбца матрицы В.

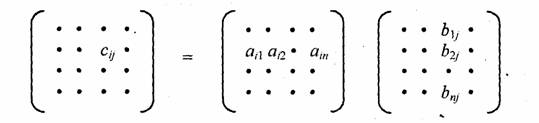
Произведение матриц определено только для случая,  когда количество столбцов матрицы А равно количеству строк матрицы В.

Подробнее с матрицами вы можете ознакомиться в специальной математической литературе, например в [S].

Ну а теперь вернемся к преобразованиям координат. Рассмотрим более подробно некоторые отдельные типы преобразований.

Аффинные преобразования на плоскости

Зададим некоторую двумерную систему координат (х, у). Аффинное преобразование координат (х, у) описывается формулами

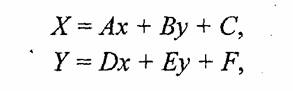
где A, В, ..., F — константы. Значения (X, Y) можно трактовать как координаты в новой системе координат.

Обратное преобразование (X, Y) в (х, у) также является аффинным:

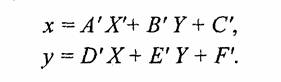
          Аффинное преобразование удобно записывать в матричном виде. Константы А, В, .... F образовывают матрицу преобразования, которая, будучи умноженная на матрицу-столбец координат {х, у), дает матрицу-столбец (X, Y). Однако для того, чтобы учесть константы С и F, необходимо перейти к так называемым однородным координатам — добавим строку с единицами в матрицах координат:

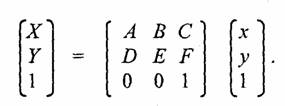
Матричная запись дает возможность наглядно описывать несколько преобразований, которые идут одно за другим. Например, если необходимо сначала выполнить преобразования

где матрица (С) равна произведению (В)(А).

^: Перемножение матриц выполняется так, как это принято в линейной алгебре. Рассмотрим частные случаи аффинного преобразования.

1. Параллельный сдвиг координат (рис. 2.1).

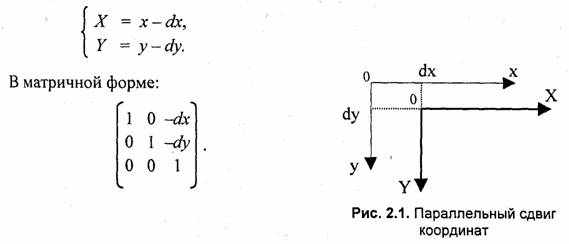
Коэффициенты к_х и к_у могут быть отрицательными. Например, к_х = -1 соответствует зеркальному отражению относительно оси у.

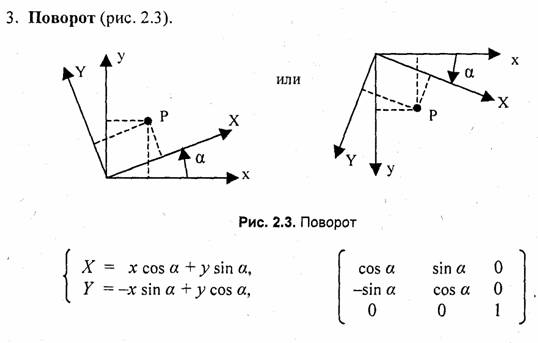
Свойства аффинного преобразования.

 Любое аффинное преобразование может быть представлено как последовательность операций из числа указанных простейших: сдвиг, растяжение сжатие и поворот.

 Сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Трехмерное аффинное преобразование

Запишем в виде формулы:

Для трехмерного пространства любое аффинное преобразование также может быть представлено последовательностью простейших операций. Рас-s смотрим их.

1. Сдвиг осей координат соответственно на dx, dy, dz:

2.2. Преобразование объектов

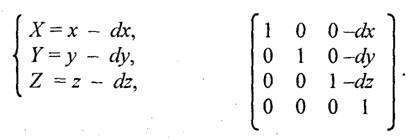
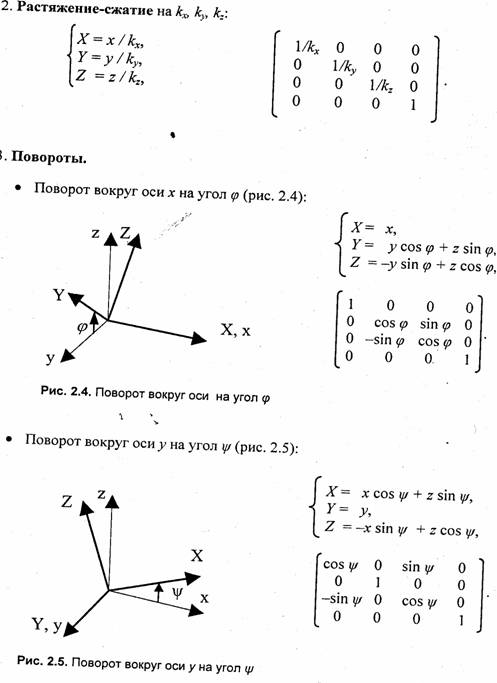
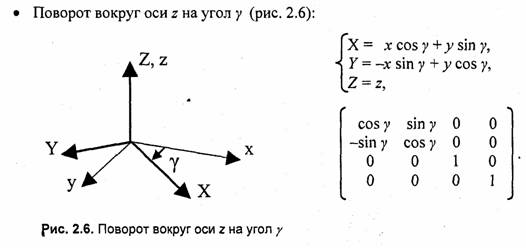
Преобразование объектов можно описать так. Пусть любая точка, которая принадлежит определенному объекту, имеет координаты (k₁ к₂ ..., к_n) в n-мерной системе координат. Тогда преобразование объекта можно определить как изменение положения точек объекта. Новое положение точки пространства отвечает новым значениям координат (т₁, m₂ ..., m_n).

Соотношение между старыми и новыми координатами для всех точек объекта (m₁ m₂ ..., m_n) = F(k₁, k₂ ..., к_n) и будет определять преобразование объекта, где F— функция преобразования.

Классифицировать преобразования объектов можно согласно типу функции преобразования и типу системы координат.

Например, преобразование объектов на плоскости можно определить так:

Аффинные преобразования объектов

на плоскости

Аффинные преобразования объектов на плоскости описываются так:

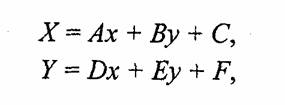
где А, В, ..., F — константы; x, у — координаты до преобразования; X,Y— новые координаты точек объектов.

        Рассмотрим частные случаи аффинного преобразования.

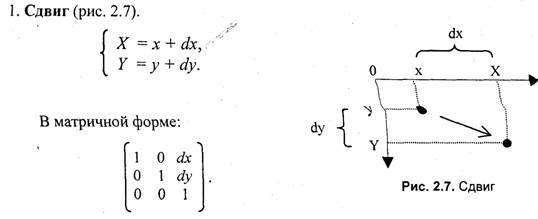
Обратное преобразование позволяет рассчитать старые координаты точек объектов по известным>новым координатам:

2. Растяжение-сжатие (рис. 2.8).

      Необходимо отметить, что это, вероятно, не очень удачное название, так как для некоторых типов объектов размеры и форма не изменяются — например, для точечных объектов. По-другому это преобразование можно назвать масштабированием.

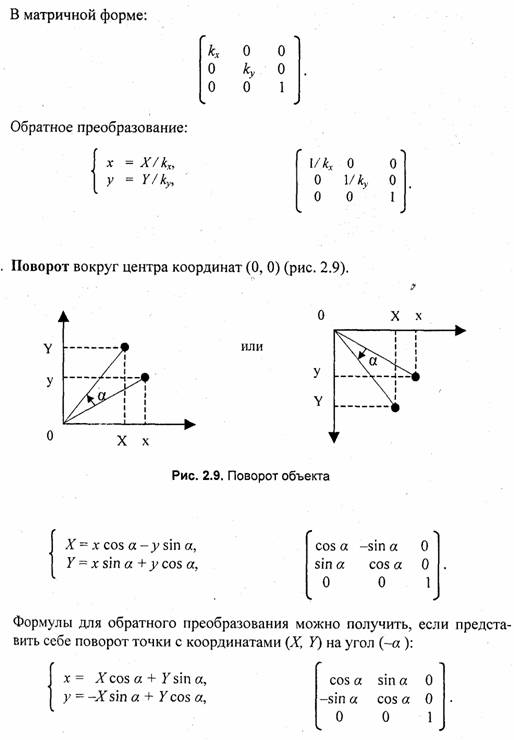
Трехмерное аффинное преобразование объектов

Приведем в виде формулы:

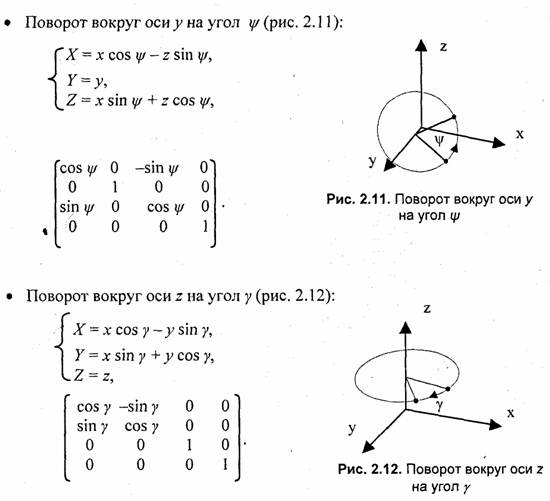
Формулы для обратных преобразований не приведены, но их несложно получить по аналогии с преобразованиями, которые рассмотрены выше.