Г л а в а    5

Преднамеренная энергетическая безопасность ТКС

5.1. Изменение параметров сигнала как мера повышения энергетической безопасности

Одним из основных методов повышения энергетической безопасности телекоммуникационных систем, как отмечалось в гл. 4, является изменение параметров сигнала, приводящее к снижению вероятности обнаружения сигнала благодаря уменьшению времени контакта средств РР и РТР противника с сигналом ТКС.

Необходимость защиты информации, передаваемой в дискретных каналах радиосвязи, привела к появлению широкополосных адресных систем передачи данных (ШАСПД), в которых используются сигналы, максимально защищенные от разведки и воздействия помех за счет их формирования двойной модуляцией несущей: передаваемым информационным сигналом и широкополосным кодирующим сигналом.

Широкополосный кодирующий сигнал определяет программу (алгоритм) перестройки рабочих параметров (ПРП) (или одного параметра) сигнала. Каждая линия (сеть) радиосвязи (ЛРС), организуемая в ШАСПД, работает по своей программе ПРП, известной только абонентам данной ЛРС, что существенно усложняет задачу стороннего наблюдателя по обнаружению, приему и обработке сигналов данной ЛРС.

Таким образом, широкополосный кодирующий сигнал выполняет функцию адреса конкретной ЛРС и может быть представлен некоторой несущей адресной последовательностью (НАП), определяющей изменение нулевых уровней параметров сигнала в рассматриваемой ЛРС. Несущая адресная последовательность представляет собой последовательность векторов {α(t)}, определяющих нулевой уровень параметров сигнала, и в общем виде может быть представлена выражением

где β(t) , γ (t),…v (t) - символы частных НАП, определяющие значения параметров сигнала в текущий момент времени t.

При синхронной перестройке параметров несущая адресная последовательность может быть представлена выражением

где α_i, — символ НАП; β_i, γ_i, … v_i— символы частных НАП на i-м шаге программы   ПРП.

Остановимся на последнем варианте, поскольку он проще для понимания и легче в реализации.

Максимальное количество НАП, которые могут быть сформированы,  определяется  Выражением          

При работе нескольких ЛРС, использующих различные программы ПРП (НАП), в общем пространстве сигналов, определяемом разрешенными интервалами изменения или фиксированными значениями параметров (частоты, амплитуды, фазы, времени), функция разделения сигналов различных ЛРС ложится на несущие адресные последовательности сигналов. Поэтому в ШАСПД могут применяться только ортогональные или квазиортогональные НАП. При этом их количество Q_a, как правило, много меньше максимального количества W_a, т.е. Q_α <<C W_α. .Совокупность используемых в ШАСПД несущих адресных последовательностей называют ансамблем, а величину Q_a — объемом ансамбля НАП.

Повысить количество ЛРС, использующих общее пространство сигналов, и обеспечить их высокую развед- и помехозащищенность можно при использовании несущих адресных последовательностей, формируемых из частных НАП, удовлетворяющих определенным требованиям, о которых речь пойдет ниже. Такие последовательности получили название псевдослучайных последовательностей (ПСП).

На сегодняшний день наиболее широкое распространение получили системы передачи данных, использующие сигналы с программной перестройкой одного параметра — частоты или фазы (сигналы с псевдослучайной перестройкой рабочей частоты (ППРЧ), дискретно-частотные (ДЧ) шумоподобные сигналы (ШПС), дискретно-фазовые (ДФ) ШПС или двух параметров — частоты и фазы (ППРЧ в сочетании с ДЧ-ШПС или ДФ-ШПС, дискретные составные (ДЧ-ДФ) ШПС). Наиболее сложными являются сигналы, используемые в системе «Джитидс», поскольку в них используется программная перестройка трех рабочих параметров — частоты, времени задержки излучения (джиттера) и фазы (ППРЧ в сочетании с ДФ-ШПС и перестройкой джиттера по псевдослучайному закону).

В зависимости от способов формирования сигналов, а также свойств используемых в них несущих адресных последовательностей сигналы с программной перестройкой рабочих параметров (ПрПРП) могут иметь схожие свойства, позволяющие осуществлять их обработку с использованием единого подхода. Классификация сигналов с программной перестройкой рабочих параметров, позволяющая разделить сигналы с ПрПРП на группы с общими свойствами, определяемыми программами перестройки рабочих параметров, может быть проведена по следующим  признакам:                                                                                                     

I.В зависимости от синхронности перестройки параметров, сигналы  ПрПРП  можно разделить  на:                                                                              

•  сигналы с асинхронной ПрПРП, т.е. сигналы с произвольными скоростями перестройки  параметров;

•  сигналы с кратной  ПрПРП,  т.е. сигналы,  для которых имеет место равенство m₁T_снап1 = т₂Т_снап2 = ... = т_kТ_спапk, ,где T_снапi -( i= 1,2,... ,к) — длительность символа частной НАП (шага программы перестройки) i-го параметра; k — количество программно-перестраиваемых   параметров;   m_i-   —  коэффициенты   пропорциональности,   принадлежащие   множеству   натуральных   чисел,   при этом, как правило, хотя бы один из коэффициентов равен единице и  выполняется принцип  «вложенности»,  т.е. для любой пары программно-перестраиваемых параметров существует коэффициент

пропорциональности, такой, что T_снапi = m_ij Tснап_j как разновидность сигналов с кратной ПрПРП можно выделить сигналы с синхронной ПрПРП, т.е. сигналы, для которых имеет место равенство T_снап1 = T_снап2=…= T_снапk ;

•  сигналы с комбинированной ПрПРП —сигналы с программной перестройкой нескольких параметров, в которых имеет место как кратная, так и асинхронная  ПрПРП.

II.  В зависимости от способа использования символов информационной последовательности (ИП) сигналы с ПрПРП можно разделить на:

•  сигналы с информационной  ПрПРП,  в которых информационная последовательность,   подлежащая  передаче  в радиоканале,  «суммируется» с несущей адресной последовательностью и модулирует  несущую;

• сигналы с неинформационной  ПрПРП,  в которых несущей адресной последовательностью модулируют несущую, после чего один из ее параметров (или несколько параметров) модулируют символами информационной последовательности.

III.  В зависимости от соотношения длительности используемой НАП (периода НАП) Т_нап и времени анализа сигнала средствами радиоразведки Т_а, сигналы с ПрПРП можно разделить на:

•  сигналы с локальной ПрПРП, для которых Т_нап < Т_а, представляющие собой последовательность фрагментов, внутри которых перестройка рабочих параметров осуществляется в соответствии с локальными НАП, имеющими сравнительно небольшой период,  что позволяет стороннему наблюдателю воспользоваться свойством периодичности сигналов при их обработке, при этом можно выделить:

-  сигналы с локально-информационной  ПрПРП (известные как ШПС), для которых Т_нап соизмеримо с длительностью информационного символа Т_сип, т.е. Т_нап, где m — количество символов информационной последовательности, переносимых одной частной локальной НАП, m≤logq _сип Q_α ; q_сип — значность символов ИП, Q_a —объем ансамбля несущих адресных последовательностей, используемых в системе связи;

-  сигналы с локально-структурной ПрПРП, для которых T_нап соизмеримо с каким-либо временным параметром системы связи, например равно длительности передаваемого пакета информации T_п,  т.е. Т_нап  =  Т_п;

• сигналы с глобальной ПрПРП, представляющие собой сигналы с перестройкой рабочих параметров по псевдослучайному закону (ППРП), при длительности периода несущей адресной последовательности, не позволяющей стороннему наблюдателю при обработке сигнала воспользоваться свойством ее периодичности, т.е. Т_нап ≥ Т_п. Наряду с известными сигналами с псевдослучайной перестройкой рабочей частоты (ППРЧ) и фазы (например, сигналы системы «Навстар»), возможно формирование сигналов с программной перестройкой других параметров. При этом в зависимости от соотношения длительностей символов информационной и несущей адресной последовательностей (T_сип и Т_снап соответственно) сигналы с ППРП можно разделить на:

-  сигналы с медленной ППРП, когда на очередном шаге программы перестройки параметров передается несколько (два и более) информационных символов, т.е. Т_сип ≤Т_снап;

-  сигналы с быстрой ППРП,  когда на передачу одного информационного символа задействуется несколько (в том числе и один) шагов программы перестройки параметров, т.е. Т_сип  ≥ T _снап.

IV. В зависимости от степени общности программ перестройки рабочих параметров можно выделить:

•  сигналы с индивидуальной  ПрПРП,  когда каждый активный абонент системы связи использует свою (индивидуальную) программу перестройки  рабочих параметров;

•  сигналы с групповой  ПрПРП,  когда несколько (группа) активных абонентов системы связи, например абоненты линии (сети) радиосвязи,   используют общую программу  перестройки  рабочих параметров;

•  сигналы с единой  ПрПРП,  когда все абоненты системы связи  используют общую программу перестройки рабочих параметров;

•  сигналы со смешанной общностью программ перестройки рабочих параметров, когда при ПрПРП нескольких параметров программы перестройки различных параметров имеют различную общность.

Аналитически сигнал с синхронной ПрПРП представляется выражением (5.4), в котором учтена возможность программного варьирования всей совокупностью рабочих параметров — частотой, фазой, амплитудой, временем задержки излучения и длительностью элементарного импульса (скоростью передачи информации) при информационной модуляции  частоты, фазы и амплитуды:

Аналитические выражения для сигналов с любым сочетанием программно-перестраиваемых параметров получаются из (5.4) при фиксации значений неперестраиваемых параметров и принятии ∆П_q = 0 для немодулируемых информационной последовательностью параметров.

Необходимо отметить, что при формировании сигналов с псевдослучайной перестройкой времени задержки излучения и длительности элементарного импульса возможны два варианта: 1) Т_ц = const; 2) Тц = var. Второй вариант сложнее с точки зрения реализации, но при нем существенно усложняется и задача стороннего наблюдателя по определению принадлежности излучения, выделению передаваемого сигнала, а также по созданию прицельной имитирующей помехи.

В принципе при формировании сигналов с программной перестройкой нескольких параметров возможны различные сочетания относительных скоростей перестройки, периодов и значностей символов частных НАП, определяющих значения различных рабочих параметров.

На сегодняшний день широкое распространение получили ШАСПД, использующие сигналы, в которых расширение спектра осуществляется за счет программной перестройки одного параметра. Это ДФ-ШПС, ДЧ-ШПС и ППРЧ-сигналы. Аналитическая запись таких сигналов может быть получена из выражения (5.4).   Так, для ДФ-ШПС

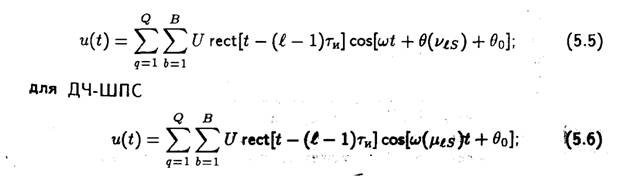
Если в результате ведения радиоразведки стороннему наблюдателю удастся обнаружить излучение, запеленговать источник, определить параметры сигнала с ПрПРП и обеспечить выделение используемой последовательности номиналов рабочих параметров, то может быть предпринята попытка НСД к передаваемой информации с использованием быстроперестраиваемых средств НСД или средств с ФНП.

Для осуществления эффективного прослушивания информации с использованием средств с ФНП может понадобиться до G_p каналов НСД

(приема). Для осуществления эффективного разрушения информации необходимо (при выполнении требований по мощности) обеспечить долю «накрытия» сигнала помехой не меньше заданной D_ТР, зависящей от типа сигнала, отношения сигнал/помеха, наличия избыточности кодирования и перемежения символов (например, для цифровых телефонных каналов D_ТР = 0,3-0,5). Поэтому для эффективного разрушения информации необходимо не менее D_ТРG_П каналов НСД (помех). Поскольку значение G_Р(П) как правило, велико, обеспечение эффективного прослушивания или разрушения информации с использованием средств с ФНП в большинстве случаев не представляется возможным. Подмена информации с использованием средств с ФНП без знания программы ПРП  невозможна.

При использовании для НСД быстроперестраиваемых средств, эффективные прослушивание и подмена информации не представляются возможными из-за потерь времени на определение параметров сигнала и настройку средств НСД. Осуществление эффективного разрушения информации в режиме индивидуальной погони (при отсутствии знания программы ПРП) возможно при обеспечении выполнения неравенства

где t_p — время реакции средств разрушения информации; t₁ (t₂) — время распространения сигнала от передающего устройства ШАСПД до приемного устройства ШАСПД (средства НСД); t₃ — время распространения помехи от средства НСД до приемного устройства ШАСПД.

Обеспечение требования (5.12) при высоких скоростях перестройки рабочих параметров сигнала становится проблематичным.

Осуществление эффективного НСД к информации при любых значениях параметров сигналов и скоростях их перестройки возможно при применении быстроперестраиваемых средств НСД после вскрытия алгоритма формирования сигнала, т.е. при выявлении дискретных значений параметров сигнала и построении несущей адресной последовательности, эквивалентной той, которую использует ЛРС-объект НСД.

В качестве параметра, характеризующего «невскрываемость» алгоритма формирования сигнала, может быть рассмотрен коэффициент эквивалентной линейной сложности l_s, равный минимальной длине Фрагмента НАП, необходимого для построения линейного алгоритма, позволяющего сформировать эквивалентную НАП. При псевдослучайной перестройке нескольких параметров П_i в общем случае для определения алгоритмов формирования частных несущих адресных последовательностей НАП потребуются различные длины фрагмента используемой «суммарной» НАП _Пi — l_si, определяемые их эквивалентной линейной сложностью. Эквивалентная линейная сложность «суммарной» НАП для случая синхронной  перестройки параметров сигнала определяется  следующим образом:

Анализ особенностей построения многоуровневых последовательностей, используемых в качестве несущих адресных последовательностей в ШАСПД, и изыскания возможностей построения эквивалентных последовательностей позволяют сделать вывод о возможности формирования трудновскрываемых несущих адресных последовательностей на основе нелинейных двоичных псевдослучайных последовательностей методом комбинационно-числового преобразования в режиме последовательных выборок или выборок с пропусками с последующей нелинейной перенумерацией символов формируемой последовательности. При этом задача построения алгоритма формирования эквивалентной НАП тем сложнее, чем больше значность и период (длина) исходной НАП.

Таким образом, применение широкополосных адресных систем передачи данных, использующих сигналы с программной (псевдослучайной) перестройкой нескольких рабочих параметров, позволит существенно усложнить задачу стороннего наблюдателя по обнаружению, пеленгованию, выявлению параметров, определению принадлежности источника радиоизлучения и осуществлению несанкционированного радиодоступа  к передаваемой  информации.

Далее в разделах 5.2 и 5.3 будут рассмотрены псевдослучайные последовательности, применяемые для формирования программ перестройки рабочих параметров в широкополосных адресных системах передачи информации, их разновидности, свойства и способы формирования. Разделы 5.4 и 5.5 посвящены рассмотрению широкополосных адресных систем передачи информации, использующих ШПС- и ППРЧ-сигналы  соответственно.     

5.2. Свойства числовых и периодических

последовательностей

5.2.1. Требования к используемым в ШСПД    

числовым последовательностям

К несущим адресным последовательностям, используемым в широкополосных адресных системах передачи информации, предъявляется ряд требований, обусловленных, с одной стороны, удобством пользователей, а с другой — необходимостью обеспечения высокой развед- и помехозащищенности этих систем.  К таким требованиям относятся:

•  простота аппаратной реализации генераторов последовательностей;

•  большой объем множества X генерируемых последовательностей;

•  необходимая длина используемых последовательностей х Є X;

•  высокая степень взаимного различия любой пары последовательностей  из генерируемого множества;

•  высокая степень отличия любой последовательности из генерируемого множества от своей сдвинутой по времени копии.

Простота реализации генераторов последовательностей обеспечивается ограничением,  которое (для  ШАСПД практически  всегда) выражается  в использовании  лишь периодических дискретных последовательностей   x(t):

В широкополосных адресных системах передачи информации при выделении последовательностей смены частот x(t) и y(t) различным радиолиниям параметр Θ характеризует уровень их взаимных помех.

Требование различимости в множестве генерируемых последовательностей с учетом их возможных связей во времени приводит к необходимости минимизации их автокорреляционной (5.17) и взаимнокорреляционной  (5.18) функций:

При этом в качестве обобщенных характеристик множества X обычно используется пиковое значение бокового лепестка автокорреляционной функции Θ_а и пиковое значение взаимно-корреляционной функции   Θ_С:

5.2.2. Определения и основные свойства

периодических числовых последовательностей

5.2.3. Корреляционные тождества и границы корреляционных функций

Рассмотрим несколько корреляционных тождеств, которые могут быть использованы при построении множества «адресных» последовательностей X для широкополосных адресных систем передачи данных.

Теорема 5.1. Пусть — вектора, а х, у, z, w — соответственно порождаемые ими последовательности. Тогда для их ВКФ справедливо соотношение

В качестве дополнения следует заметить, что в процессе преобразования было использовано свойство периодичности ВКФ и на его основе — возможность перехода от индекса j к индексу k в тех же пределах суммирования, что и завершает доказательство.

Положив в (5.39) w — z, а затем х = у, получим следующие соотношения, связывающие ВКФ трех (5.40) и соответственно двух (5.41) последовательностей:

При оценке объема множества генерируемых последовательностей X с целью выполнения требований к «адресным» последовательностям, используемым в ШАСПД, оказываются полезными граничные значения их авто- и взаимнокорреляционных функций, а также границ пикового значения взаимнокорреляционной функции Θ_с:

5.3. Псевдослучайные последовательности, применяемые для формирования программ перестройки рабочих параметров широкополосных систем связи

5.3.1. Линейные псевдослучайные последовательности

Для формирования программ перестройки рабочих параметров в ШАСПД возможно использование различных псевдослучайных последовательностей (ПСП). Наиболее известны линейные рекуррентные последовательности  (ЛРП).

Их нормированный и приведенный формирующие полиномы совпадают.

При этом всегда

Генераторы двоичных ЛРП обычно строятся на регистрах сдвига с линейными обратными связями (РСЛОС), роль умножителей на постоянные коэффициенты могут выполнять электронные ключи, которые либо замыкают (при = 1), либо размыкают (при = 0) связи соответствующих ячеек регистра сдвига с сумматором по модулю 2.

Рассмотрим наиболее распространенные типы ЛРП.

М-последовательности. Последовательность максимальной длины, или М-последовательность, формируемая n-разрядными РСЛОС, имеет период (длину) L = 2ⁿ — 1, что обеспечивается соответствующим выбором схемы обратной связи, которая полностью определяется характеристическим (порождающим) многочленом (5.54). В соответствии с теорией М-последовательностей порождающий многочлен должен быть неприводимым и примитивным относительно двучлена х^L — 1. Это означает, что характеристический многочлен не разложим на множители меньших степеней, делит без остатка двучлен x^L — 1 и не входит в разложение ни одного двучлена x^v — 1, степень V которого меньше L.

Максимальное число М-последовательностей заданного периода L находится  из  выражения

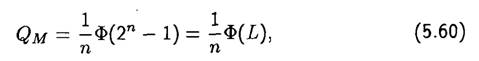
где Ф(L) — функция Эйлера, определяющая количество целых чисел, которые меньше данного положительного числа L и являются взамно  простыми  с  ним.

Для формирования М-последовательности может быть использована схема, приведенная на рис. 5.2. Конкретное устройство формирования М-последовательности может сформировать только одну М-последовательность, длина которой L = 2ⁿ-1, а характеристический многочлен которой определяет структуру обратной связи регистра сдвига. В зависимости от начального заполнения регистра сдвига, генерируемая М-последовательность может иметь L вариантов:   λ = 0,1,..., L — 1, где Т^λ — оператор левого циклического сдвига последовательности  М_i-  на λ позиций.

Если предполагается использовать несколько полиномов, необходимо предусмотреть возможность оперативного изменения схемы логической обратной связи (значений коэффициентов а_k).

Особенностью М-последовательности является то, что ее периодическая автокорреляционная функция (АКФ) принимает только два значения Я(0) = 1; Я(λ) = -1/λ, 1 ≤ λ ≤ L - 1.

Большой интерес представляют и взаимнокорреляционные свойства М-последовательностей. Среди всего множества М-последовательностей заданной длины L существуют пары, которые обеспечивают гарантированный малый уровень взаимной корреляции.  К ним в первую очередь относятся так называемые предпочтительные пары, обладающие трехуровневой  периодической  ВКФ:

В интересах связи больший интерес представляют не пары, а большие множества последовательностей с малым уровнем взаимной корреляции. Естественный способ расширения множества сигналов — использование всех М-последовательностей данного периода. Однако ансамбли таких множеств невелики (Q_m <<L) и взаимнокорреляционные свойства оказываются неудовлетворительными. Для L = 15-2047 максимальное значение ПВКФ обычно ограничено диапазоном V — (1,5...6)/L, но в некоторых случаях, особенно с ростом L, значение R существенно превышает эту оценку.

На основе М-последовательностей были получены системы последовательностей, обладающих хорошими корреляционными свойствами при существенно большем ансамбле сигналов. Среди таких последовательностей важное для практики место занимают последовательности Голда,  Касами и некоторые другие.

Последовательности Голда. Последовательность Голда представляет собой результат сложения по mod 2 символов двух исходных М-последовательностей с различными формирующими полиномами

f м _r(x) и fm _l(х), степени которых не кратны четырем, т.е.

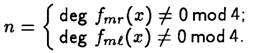
Формирующий полином последовательности Голда определяется как произведение полиномов М-последовательностей:

Все множество G(M _r,M_l) включает исходные последовательности М_r и M _l и результат сложения по mod 2 одной из них М _r с каждой из последовательностей T ^λM _l, получаемых при циклических сдвигах другой:

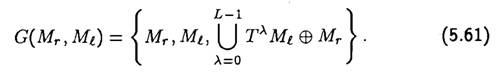
Множество G(M_r ,M _l) состоит, таким образом, из L + 2 =   2 ⁿ + 1 последовательностей длины  L.

Схема формирования последовательности Голда приведена на рис.   5.3.

Последовательности Голда являются линейными рекуррентными последовательностями немаксимальной длины, и их можно рассматривать как частный случай комбинированных последовательностей, когда функцией комбинирования является сложение по mod 2.

Рис. 5.3. Схема устройства формирования последовательности Голда

Достоинством последовательностей Голда является большое разнообразие сигналов с хорошими корреляционными свойствами. Известно, что набор значений, которые принимает ПВКФ последовательностей (M_r и M _l) и набор значений,  принимаемых корреляционными функциями последовательностей из множества G(M_r ,M _l), совпадают. Поэтому для образования множества G(M_r ,M _l), целесообразно выбирать М-последовательности с малой взаимной корреляцией. Этим требованиям удовлетворяют предпочтительные пары с трехуровневой ПВКФ со значениями —1; —1 ± 2^(n+2)/2, где п — степень исходных формирующих полиномов. Для построения множеств последовательностей Голда с малым уровнем взаимной корреляции наряду с предпочтительными парами с трехуровневыми ПВКФ могут быть использованы пары с четырехуровневыми ПВКФ и пары взаимно-обратных М-последовательностей. Объемы этих множеств также равны (L + 2), а максимальные значения ПВКФ такие же, как и у ПВКФ исходных пар М-последовательностей.

Использование множества последовательностей Голда, Касами и подобных им позволяют строить системы сигналов большого объема с достаточно малым уровнем взаимной корреляции. Однако для всех линейных последовательностей характерен один общий недостаток — это невысокая структурная скрытность.

Поскольку любая ЛРП имеет формирующий полином вида (5.52), может быть построена система из п уравнений:

5.3.2. Нелинейные псевдослучайные последовательности

К нелинейным ПСП относятся последовательности, которые не могут быть описаны рекуррентным правилом (5.52). В отличие от линейных, нелинейные ПСП обладают высокой структурной скрытностью,

что обуславливает их широкое применение в системах связи и управления. Предполагается, что все вновь создаваемые широкополосные системы будут использовать нелинейные ПСП для манипуляции как фазами в одночастотных псевдослучайных сигналах, так и частотами в сигналах с  ППРЧ.

В настоящее время известны и получили широкое распространение для различных приложений следующие нелинейные ПСП:

•  нелинейные последовательности, формируемые применением нелинейной внешней логики для комбинирования символов РСЛОС и имеющие период L = 2ⁿ — 1 (рис.  5.4,а);

•  составные нелинейные последовательности, формируемые путем чередования символов с выходов двух или более РСЛОС по определенному правилу (рис.  5.4,6);

•  нелинейные рекуррентные последовательности с периодом L = 2ⁿ (последовательности де Брейна),  генерируемые  PC с нелинейной обратной связью (РСНОС) (рис. 5.4,в).

Последовательности, формируемые нелинейной внешней логикой.    Одним  из способов получения   ПСП с высокой ЭЛС является нелинейное комбинирование символов М-последовательности.   Для этой  цели  на  выходе РСЛОС включают нелинейную внешнюю логику (рис.   5.4,а).

В качестве нелинейной функции комбинирования предложена бент-функция (БФ) (максимально-нелинейная функция), обладающая свойством равномерности спектра при ее разложении в дискретном базисе Уолша-Адамара. Получаемые ПСП назвали бент-последовательностями или последовательностями бент-функций (ПБФ).

Правило построения бент-последовательностей  может быть представлено   в  виде

При выбранной функции G(x) 2^n/2 различных значений векторе задают ансамбль из 2ⁿ/² бент-последовательностей с асимптотически оптимальными взаимнокорреляционными функциями. Изменение G(x] задает другой ансамбль из 2ⁿ/² бент-последовательностей, если изменение касается операций  умножения.

Логика выходной цепи РСЛОС, формирующего поле GF(2ⁿ) в степенном базисе, состоит из ряда линейных и нелинейных преобразователей,  которые обеспечивают следующие операции:

1)  преобразование степенного базиса поля GF(2ⁿ) к нормальному (след-ортогональному) базису GF(2ⁿ);

2)  преобразование пространства  поля GF(2ⁿ) в подпространстве GF(2ⁿl²);

3)  вычисление бент-функции.

На величину эквивалентной линейной сложности (ЭЛС) бент-после-Довательностей оказывает влияние число нелинейных операций в функции G(x).   ЭЛС определяется по формуле

так как G(x) определена на подпространстве GF(2^n/4). Например, при использовании 48-каскадного генератора могут быть получены бент-последовательности  с l_s   =   10¹¹.

Синтез бент-последовательностей   может быть произведен  только Для четных п, при этом оптимальные корреляционные свойства получаются при п ≡ 0 mod 4.   Период бент-последовательностей L = 2^n-1. Они сбалансированы по числу нулей и единиц и имеют трехуровневые

АКФ и ВКФ со значениями, не превышающими величины 2ⁿ/² + 1, что в 2 раза лучше,  чем у кодов Голда.

Аппаратная сложность генераторов бент-последовательностей приблизительно такая же, как и генераторов кодов Голда. Большим преимуществом бент-последовательностей является простота смены ПСП в ансамбле, а при небольшом усложнении аппаратуры один генератор может генерировать одновременно 2ⁿ/⁴ (или 2ⁿ/²) бент-последовательностей.

Составные нелинейные последовательности. Составными, или комбинированными называют последовательности, формируемые комбинированием (чередованием) символов с выходов нескольких PC. В простейшем случае такие ПСП можно сформировать перемножением символов с выходов РСЛОС, генерирующих ПСП с периодами Период результирующей ПСП при этом равен наименьшему общему кратному (L_1, L₂), а ЭЛС — l_s = n₁ n_{2 .}Однако операция умножения нарушает баланс нулей и единиц. Для сохранения балансности в составной ПСП предлагаются разные способы представления символов с выходов РСЛОС.

В качестве объединяющего элемента может быть использован JK-триггер. При этом получается периодическая, хорошо сбалансированная ПСП. Значение любого сегмента выходной ПСП не дает никакой информации о составляющих ПСП. Однако корреляционные свойства таких ПСП не контролируются, и боковые выбросы АКФ могут принимать произвольные значения в зависимости от исходного состояния PC

Наиболее известным способом формирования нелинейной составной ПСП является алгоритм Джеффа. Схема генератора, реализующего этот алгоритм представлена на рис. 5.5,а. При этом ЭЛС выходной ПСП определяется как l_s = mn + (n + 1)к, где т, п, k — число каскадов в РСЛОС 1, РСЛОС 2 и РСЛОС 3 соответственно. Если т, п, k взаимно простые, т.е. наибольший общий делитель (НОД) (т, п, k) =1  то период формируемой ПСП L = L₁L₂L₃ = (2^m-1)( 2^n-1)( 2^k-1). Достоинством такого построения генераторов является сбалансированная структура формируемой ПСП и практически неисчерпаемые возможности его модификации путем  варьирования структуры (рис.  5.5,6), на-

чального заполнения регистров, тактовой частоты, что позволяет формировать большие ансамбли сигналов.

Дженнингс предложил формировать ПСП чередованием символов РСЛОС таким образом, чтобы на выход в соответствии с определенным алгоритмом поступали символы генератора М-последовательности. На рис. 5.6 представлена схема генератора составной нелинейной ПСП Дженнингса. RG1 и RG2 — два РСЛОС с т и п каскадами соответственно, причем т и п — взаимно простые, т.е. (т, п) = 1. Алгоритм формирования составной ПСП следующий:

Известны алгоритмы формирования составных нелинейных ПСП, получаемых чередованием символов более коротких линейных ПСП. наибольший интерес представляют М-подобные и Касами-подобные последовательности, названные так по причине сходства их корреляционных функций с корреляционными функциями М-последовательностей и последовательностей малого множества Касами соответственно, но имеющие более высокую ЭЛС.

где Сⁱ — последовательности, относящиеся к i-му множеству и получаемые линейным комбинированием последовательности с различными сдвигами М-последовательности М_r. Таким образом, кодовые слова, принадлежащие к i-му множеству, получаются варьированием фазы j в дополнительной М-последовательности Т^j М_r.

Максимально достижимые значения ЭЛС Касами-подобных ПСП и бент-последовательностей приведены в табл. 5.1.

Таким образом, составные нелинейные последовательности по сравнению с последовательностями, получаемыми на выходе нелинейной внешней логики, обладают более высокой ЭЛС.

Последовательности де Брейна. Среди нелинейных ПСП особый интерес представляют последовательности де Брейна (ПБ). Характерной особенностью ПБ является то, что каждое n-ичное состояние регистра сдвига встречается на периоде ПСП только один раз. ПБ имеют длину L = 2ⁿ, где п — степень ПБ, сбалансированы по числу нулей и единиц в периоде и имеют нормальное распределение серий. Последовательности де Брейна имеют большую ЭЛС l_s, что определяет их высокую непредсказуемость. ЭЛС ПБ находятся в пределах  2^n-1+n≤l_s ≤ 2 ⁿ -1, причем половина всех последовательностей де Брейна имеет l_s  = 2ⁿ— 1.

Последовательности де Брейна можно рассматривать:

1)  как циклический обход всех вершин графа В_п с условием посещения каждой вершины за один цикл ровно по одному разу;

2)  как циклический обход всех дуг графа B_n-1 с аналогичным условием   на   дуги.

В первом случае имеем цикл Гамильтона в графе В_п, во втором — цикл  Эйлера  в  графе В_п-1.

В настоящее время неизвестны практически осуществимые алгоритмы, позволяющие генерировать весь ансамбль последовательностей де Брейна для произвольных значений  п.

Наиболее простым способом генерирования ПБ является использование генератора М-последовательности (РСЛОС), в котором искусственно создают состояние «все нули». Функция обратной связи такого генератора  будет иметь  вид

Известен класс лексикографических последовательностей де Брей-на, называемых последовательностями предпочтительных единиц, так как при их построении происходит группирование единиц в начале последовательности. Эти последовательности не могут быть получены линейными методами. Объем ансамбля таких последовательностей N   =   2^2n-5.

Периодическая АКФ ПБ обладает рядом важных свойств, позволяющих использовать их в широкополосных системах связи (в том числе и   для  синхронизации):

т.е. сумма положительных и отрицательных выбросов равна нулю. Таким образом,  можно отметить,  что:

•  максимальные значения боковых выбросов ПАКФ в основном сгруппированы в точках R(kn), k=  1,2,...;

•  минимальные значения максимального бокового выброса составляют R (τ) ≤ R (0)/ 4 для большинства последовательностей де Брейна;

•  для лексикографических ПБ значение R(n)возрастает с ростом п;

•  максимальное значение выбросов ПВКФ может достигать величины  R(0)/4 и  выше.

Последовательности де Брейна могут быть использованы в качестве «внутренних последовательностей» при построении PC с нелинейной внешней логикой, генерирующих последовательности с высокой непредсказуемостью и требуемыми корреляционными свойствами.

5.3.3. Многоуровневые числовые последовательности

При формировании сигналов с программной перестройкой рабочих параметров наряду с двоичными ПСП широко используют многоуровневые (многозначные) числовые последовательности (МЧП), имеющие значность q > 2, которые могут быть сформированы следующим  образом:

•  непосредственно с использованием регистров сдвига в числовых полях R (τ) ≤ R (0)/ 4  или в расширенных числовых полях GF(q^m);

•  на основе комбинационно-числового преобразования исходных, как правило,   двоичных ПСП;

•  на основе вычислений в конечных числовых полях. Недостатком непосредственного формирования МЧП с использованием регистров сдвига является сложность генераторов МЧП при необходимости обеспечения большой значности последовательностей.  Поэтому при формировании МЧП большого периода и большой значности, например для формирования программ ППРЧ, используют комбинационно-числовое преобразование (КЧП) ПСП малой значности.

Особенностью МЧП, формируемых на основе вычислений в конечных полях, является их небольшая длина (период), поэтому они нашли широкое применение при формировании дискретно-частотных шумоподобных сигналов.   Наиболее известными представителями таких последовательностей являются матричные последовательности.

Поскольку алгоритмы непосредственного формирования МЧП изложены в разделе 5.3.2, в данном разделе остановимся на вопросах формирования комбинационных и матричных МЧП.

Комбинационные многоуровневые числовые последовательности. Комбинационными многоуровневыми числовыми последовательностями называют последовательности, получаемые в результате комбинационно-числового преобразования (КЧП) символов исходной, как правило, двоичной псевдослучайной последовательности, заключающегося в выделении из исходной ПСП {x_i }_N комбинаций символов (фрагментов ПСП) длиною т-{х_i}_т или Х_т, которые, в свою очередь, являются элементами МЧП {г_i}, записанными в q-ичной системе счисления.   Значения элементов r_i определяются выражением

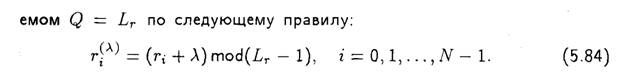
Любые две МЧП ансамбля обеспечивают не более одного совпадения за период при различных временных сдвигах между ними.

Большой практический интерес представляет МЧП при т < п. В этом случае на одном периоде МЧП любое его значение может встречаться многократно. Использование таких.гюследовательностей возможно для формирования сигналов с глобаль/ной перестройкой рабочих параметров (например сигналов с ППРЧ), поскольку при заданном количестве дискретных значений параметров могут быть сформированы МЧП, имеющие временной период,  измеряемый годами.

Матричные многоуровневые числовые последовательности. На основе использования элементов теории чисел и вычислений в конечных числовых полях могут быть построены МЧП, обеспечивающие формирование оптимальных и близких к оптимальным ансамблей сигналов с программной перестройкой рабочих параметров. Среди таких МЧП особое место занимают матричные МЧП, представляющие собой отдельные строки или столбцы матриц, рассчитываемых по определенным алгоритмам. Кроме этого, возможно построение матричных МЧП путем последовательного считывания всех строк (столбцов) матриц. Алгоритмы построения оптимальных и кваэиоптимальных систем дискретных сигналов приведены  в табл. 5.2.

5.4. Основы применения шумоподобных сигналов в системах связи

5.4.1. Определение шумоподобных сигналов и широкополосных систем связи

Одним из параметров дискретного сигнала является его база В, равная произведению длительности информационного символа Т (Т = Тсип см. разд. 5.1) на ширину спектра сигнала F:

В = FT.                                         (5.85)

Сигналы, у которых база много больше единицы (В>>1), называют шумоподобными сигналами (ШПС). Иногда их называют сложными, в отличие от простых сигналов с В =  1.

В системах связи с ШПС ширина спектра сигнала F всегда много больше ширины спектра передаваемого сообщения. В цифровых системах связи, передающих информацию в виде двоичных символов, длительность ШПС и скорость передачи информации Л связаны соотношением  Т =  1/R,  поэтому база  ШПС

В = F/R      (5.86)

характеризует расширение спектра ШПС относительно спектра сообщения. Именно поэтому системы связи с ШПС в зарубежной литературе получили название «системы связи с расширенным (или распределенным) спектром», а в отечественной литературе —«широкополосные системы связи». В дальнейшем термин «широкополосные системы связи» (ШСС) будет относиться только к системам связи с ШПС.

Расширение спектра в шумоподобных сигналах осуществляется на основе использования псевдослучайных последовательностей, имеющих период, кратный длительности информационного символа: Тпсп = = тТ, где m≤ log_q Q, q — значность символов информационной последовательности, Q — объем ансамбля ортогональных (квазиортогональных) ПСП, используемых для формирования ШПС.

В широкополосных сигналах очередной информационный символ или фрагмент определяет очередной фрагмент последовательности номиналов перестраиваемого параметра (ПНП), т.е.

где— i-й фрагмент ПНП сигнала; N— количество субпосылок, соответствующих информационному символу s_i, или фрагменту S_mi ; А_дп— алгоритм формирования ПНП, определяемый используемой расширяющей последовательностью.

Шумоподобные сигналы нашли применение в широкополосных системах связи в интересах защиты информации, так как они обеспечивают высокую развед- и помехозащищенность систем связи; позволяют бороться с искажениями сигнала из-за многолучевого распространения радиоволн; обеспечивают электромагнитную совместимость ШСС с узкополосными системами радиосвязи, а также радио- и телевизионного вещания; позволяют организовать одновременную работу многих абонентов в общей полосе частот при асинхронно-адресном принципе работы системы связи, основанном на кодовом разделении абонентов; обеспечивают лучшее использование спектра частот на ограниченной территории по сравнению с узкополосными системами связи.

При дальнейшем изложении материала в основном будем останавливаться на рассмотрении вопросов, существенных с точки зрения защиты  информации.

5.4.2. Основные типы шумоподобных сигналов

Известно большое число различных шумоподобных сигналов, используемых в системах цифровой радиосвязи, свойства которых описаны в многих книгах и статьях. В зависимости от перестраиваемого параметра шумоподобные сигналы можно классифицировать (см. разд. 5.1) на сигналы с дискретной перестройкой частоты (ДЧ-ШПС), фазы (ДФ-ШПС), времени  задержки   излучения  (ДВ-ШПС),  длительности  (ДД-ШПС) и амплитуды (ДА-ШПС) импульсов, а также на комбинированные сигналы с программной перестройкой нескольких параметров.

В настоящее время находят практическое применение ШПС с дискретной перестройкой фазы (их часто называют фазоманипулированными (ФМ-ШПС)) и с дискретной перестройкой частоты (их часто называют частотно-манипулированными (ЧМ-ШПС)), а также комбинированные — с программной перестройкой частоты и фазы (их часто называют дискретными составными частотными сигналами с фазовой манипуляцией (ДСЧ-ФМ-ШПС или ЧМ-ФМ-ШПС).

Фазоманипулированные сигналы (ДФ-ШПС или ФМ-ШПС) представляют собой последовательность радиоимпульсов, фазы которых изменяются по заданному закону. Обычно фаза принимает два значения (0 или π). При этом радиочастотному ФМ-сигналу соответствует видео ФМ-сигнал или расширяющая последовательность, состоящая из положительных и отрицательных импульсов. Если число импульсов равно N, то длительность одного импульса τ₁ = T/N, а ширина его спектра равна приближенно ширине спектра сигнала F₀ = 1/ τ = N/T. На частотно-временной плоскости (рис. 5.11,е) штриховой линией выделено распределение энергии одного элемента (импульса) ФМ-сигнала. Все элементы перекрывают выделенный квадрат со сторонами F и Т. База ФМ-сигнала

B = FT = Т/τ₀ = N,                               (5.88)

т.е. равна числу импульсов в расширяющей последовательности.

В качестве примера реализации ШСС с ФМ-ШПС (ДФ-ШПС) на рис. 5.11 представлена структурная схема линии радиосвязи цифровой широкополосной системы связи, предназначенной для передачи дискретных сообщений.

В передатчике (рис. 5.11,а) от источника информации ИИ последовательность информационных двоичных символов (1 и 0) со скоростью R = 1/Т (рис. 5.11,в) поступает на вход фазового модулятора ФМ. На второй вход ФМ поступает фазоманипулированный сигнал (рис. 5.11,г) от генератора ФМ-сигнала  ГФМ.

Фазоманипулированный сигнал имеет длительность Т и представляет собой последовательность видеоимпульсов 1 и 0 длительностью τ₀ = T/N, где N — число импульсов в расширяющей последовательности (несущей адресной последовательности). На рис. 5.11 N = 11. Работой ГФМ управляет синхронизатор С, который формирует необходимые сигналы управления. Последовательность ШПС в виде ФМ-сигналов, переносящая информационные символы (рис. 5.11,д), поступает в модулятор Мод, в котором осуществляется балансная модуляция колебания с несущей частотой ФМ-сигналом. Колебание с несущей частотой создается генератором несущей частоты ГНЧ. Усилитель мощности УМ усиливает фазоманипулированный сигнал, а затем через антенну сигнал излучается в пространство. В приемнике (рис. 5.11,6) сигнал проходит через смеситель См, переносится с помощью гетеродина Г на промежуточную частоту, усиливается в усилителе промежуточной частоты УПЧ

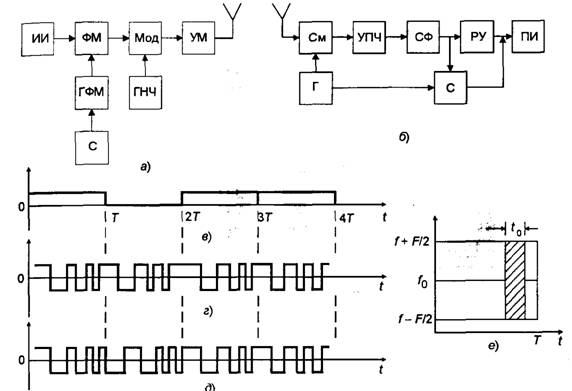
Рис. 5.11. Цифровая линия радиосвязи с ФМ-ШПС: а, 6— приемное устройство; в — информационная последовательность; г — расширяющаяся последовательность; д — ФМ-ШСП; е — частотно-временная плоскость ФМ-ШСП

и обрабатывается согласованным фильтром СФ. Сигнал с выхода СФ поступает на синхронизатор С и решающее устройство РУ. Синхронизатор осуществляет поиск ФМ-сигнала по частоте и по времени, накапливает сигнал для увеличения надежности синхронизации, управляет режимом работы решающего устройства. Для поиска ФМ-сигнала по частоте синхронизатор перестраивает гетеродин. После окончания поиска и вхождения в синхронизм на выходе решающего устройства появляется информационная последовательность в виде двоичных символов, которая передается получателю информации ПИ. Приемник, изображенный на (рис. 5.11,6), является наиболее простым. Вместе с тем необходимо отметить, что согласованный фильтр и синхронизатор, содержащий блоки поиска и синхронизации, являются при больших базах ШПС сложными устройствами. Кроме того, для поиска ШПС и поддержания синхронизма приемник охвачен петлей обратной связи. Реальный приемник ШПС может содержать несколько блоков поиска и слежения, в том числе блок поиска ШПС по времени и временной синхронизации, блок фазовой автоподстройки частоты ФАПЧ, которые охвачены собственными  или обратными связями.

Фазоманипулированные сигналы (ДФ-ШПС) позволяют широко использовать цифровые методы и технику формирования и обработки, при этом возможна  реализация таких сигналов с относительно большими

Рис. 5.12. Структурная схема цифровой телефонной линии радиосвязи с ФМ-

ШПС:  а — передающее устройство; б— приемное устройство; в — телефонный

сигнал; г— ШИМ-сигнал; д— расширяющая последовательность; е — ФМ-ШПС

базами. Поэтому ФМ-сигналы (ДФ-ШПС) являются одним из наиболее распространенных и перспективных видов ШПС.

На рис. 5.12 представлена структурная схема телефонной ЛРС с ФМ-ШПС.

В передатчике (рис. 5.12,а) телефонное сообщение (рис. 5.12,в) от источника информации ИИ поступает на вход широтно-импульсного модулятора ШИМ, с выхода которого ШИМ-сигнал (рис. 5.12,г) подается на вход фазового модулятора ФМ. На второй вход ФМ подается ФМ-ШПС (рис. 5.12,д), формируемый ГФМ. Фазоманипулированный сигнал с выхода фазового модулятора (рис. 5.12,е), содержащий информацию, поступает на вход модулятора Мод, в котором осуществляется балансная модуляция колебания с несущей частотой от ГНЧ. Затем усиленный по мощности в усилителе мощности УМ ФМ-сигнал через антенну излучается в пространство. Работой широтно-импульсного модулятора и генератора ФМ-сигнала управляет синхронизатор С, который вырабатывает необходимые частоты и управляющие сигналы. В приемнике (рис. 5.12,6) принятый сигнал в смесителе См с помощью гетеродина Г переносится на промежуточную частоту и после УПЧ поступает на коррелятор Кор. Коррелятор, как и согласованный фильтр, производит оптимальную обработку принятого сигнала. Хотя они отличаются по принципу работы, но обеспечивают одинаковую помехоустойчивость приема. Коррелятор состоит из перемножителя и интегратора. На второй вход коррелятора подается опорный сигнал в виде ФМ-ШПС (рис. 5.12,л). Напряжение на выходе коррелятора содержит телефонное сообщение в виде ШИМ-сигнала, который подается на вход демодулятора Дем, с выхода которого принятое телефонное сообщение передается получателю информации ПИ.  Работой приемника в целом и его отдельными блоками (Г, ГФМ, Кор, Дем) управляет синхронизатор С, который сначала осуществляет поиск ФМ-ШПС по времени и частоте, а затем поддерживает синхронизм. Все, что было ранее отмечено относительно синхронизатора приемника, изображенного на рис. 5.11,6, полностью относится как к синхронизатору данного приемника, так и приемников, изображенных на рис.  5.13,6 и 5.14,6.

Дискретные частотные (ДЧ) сигналы представляют собой последовательность радиоимпульсов, несущие частоты которых изменяются по заданному закону. На рис. 5.13 представлена структурная схема цифровой  ЛРС с ДЧ-ШПС.

Отличие передатчика и приемника, изображенных на рис. 5.13, от передатчика и приемника на рис. 5.11 сводится к следующему. В передатчике на рис. 5.13,а в модуляторе Мод1 производится модуляция ДЧ-ШПС дискретным сообщением. ДЧ-ШПС представляет собой сигнал, состоящий из М импульсов, несущие частоты которых принимают одно из возможных значений от f_min до  f_min + (М — 1)T с интервалом между соседними значениями ∆f = 1/Т. Всего используется М частот, и ни одна из них не применяется дважды в одном ШПС. ДЧ-ШПС формируется с помощью частотного манипулятора (ЧМ), у которого на один вход через шину подаются М частот от генератора сетки частот ГСЧ. На другой вход подается кодовая последовательность от генератора кодовой последовательности (ГЧМ), определяющая порядок изменения частот в ДЧ-ШПС. В модуляторе Мод2 производится перенос ДЧ-ШПС на несущую частоту. Работой ГСЧ, ГЧМ, ГНЧ управляет синхронизатор С. В приемнике (рис. 5.13,6) ДЧ-ШПС на промежуточной частоте поступает на смеситель (См2), в котором производится перенос всех частот сигнала на вторую промежуточную частоту с помощью опорного ДЧ-ШПС, поступающего от частотного манипулятора ЧМ. Назначение ГСЧ и ГЧМ такое же, как и в передатчике на рис. 5.13,а. С выхода УПЧ2 сигнал длительностью Г, не имеющий частотной манипуляции, поступает на СФ, а затем на РУ и С. Последний производит поиск ДЧ-ШПС по времени и частоте, затем поддерживает синхронизм и управляет работой  Г,  ГСЧ,  ГЧМ  и РУ.

На рис. 5.13,в изображен ДЧ-сигнал, при этом над каждым импульсом указана его несущая частота. На частотно-временной плоскости (рис. 5.13,д) штриховой линией выделены квадраты, в которых распределена энергия импульсов ДЧ-сигнала. Как видно из рис. 5.13.Д, . энергия ДЧ-сигнала распределена неравномерно на частотно-временной плоскости.

Если расширяющая последовательность ДЧ-сигнала содержит М импульсов, длительность импульса То = Т/М, ширина спектра F₀ = 1/Т =  М/Т,  то база сигнала

В = FT = MF₀MT₀ - M²F₀T₀ = М²,                 (5.89)

поскольку база импульса F ₀T₀ = 1. Из (5.89) следует, что для получения

необходимой базы В число каналов М =√В, т.е. значительно меньше, чем для ЧМ-сигналов. Именно это обстоятельство и обусловило внимание к таким сигналам и их применение в системах связи. Вместе с тем для больших баз (В = 10⁴-10⁶) использовать только ДЧ-сигналы нецелесообразно, так как число частотных каналов М = 10²-10³, что представляется чрезмерно большим.

Дискретные составные частотные (ДСЧ) сигналы являются ДЧ-сигналами, у которых каждый импульс заменен шумоподобным сигналом. На рис. 5.14,в изображен видеочастотный ФМ сигнал, отдельные части которого передаются на различных несущих частотах. Номера частот указаны над ФМ-сигналом. На рис. 5.14,г изображена частотно-временная плоскость, на которой штриховкой выделено распределение энергии ДСЧ-сигнала. Рис. 5.14,г по структуре не отличается от рис. 5.13,г, но для рис. 5.14,г площадь F₀T₀ = N_o равна числу импульсов ФМ-сигнала в одном частотном элементе ДСЧ-сигнала. База  ДСЧ-сигнала

B = FT= M²F₀T₀ = N₀M².                          (5.90)

Число импульсов полного ФМ-сигнала

N = N₀M.                                        (5.91)

Изображенный на рис. 5.14,в ДСЧ-сигнал содержит в качестве элементов ФМ сигналы. Поэтому такой сигнал сокращенно будем называть ДСЧ-ФМ-сигнал. На рис. 5.14 представлена структурная схема цифровой ЛРС с ДСЧ-ФМ-ШПС. Поскольку ДСЧ-ФМ-ШПС является объединением ФМ-ШПС и ЧМ-ШПС сигналов, то и схема передатчика (рис. 5.14,а), и схема приемника (рис. 5.14,6) являются, в свою очередь, объединением передатчиков (рис. 5.И,а и 5.13,а) и приемников (рис. 5.11,6 и 5.13,6). Для дополнительного повышения помехоустойчивости используются корректирующие коды, которые формируются в передатчике (рис. 5.14,а) с помощью кодера (К) и декодируются в приемнике (рис. 5.14,6) с помощью декодера (Д). В приемнике оптимальную фильтрацию осуществляет коррелятор (Кор). Назначение остальных блоков такое же, как и в предыдущих схемах.

В качестве элементов ДСЧ-сигнала можно использовать ДЧ-сигналы, но особых преимуществ такой сигнал перед ДЧ-сигналом не имеет, что ограничивает его применение.

5.4.3. Общая характеристика режима ШПС как

способа защиты информации в радиоканале

Помехозащищенность системы связи — это способность системы связи противостоять воздействию мощных помех. Помехозащищенность включает в себя скрытность системы связи и ее помехоустойчивость, так как для создания мощных помех необходимо сначала обнаружить систему связи и измерить основные параметры ее сигналов, а затем организовать мощную, наиболее сильно действующую помеху. Чем выше скрытность и помехоустойчивость, тем выше помехозащищенность системы  связи.

Помехоустойчивость ШСС определяется широко известным соотношением, связывающим отношение сигнал/помеха на выходе приемника (на выходе согласованного фильтра или коррелятора) q² с отношением сигнал/помеха на входе приемника р²:

q²=2Bp²,                                    (5.92)

где р² = Р_с/Р_п {Р_с, Р_п — мощности ШПС и помехи соответственно), q² = 2E/N_п, {E = Р_СТ — энергия ШПС, N_п = P_п/F — спектральная плотность мощности помехи в полосе ШПС); В — база ШПС. Отношение сигнал/помеха на выходе q² определяет рабочие характеристики приема ШПС, а отношение сигнал/помеха на входе р² — энергетику сигнала и помехи. Величина q² может быть получена согласно требованиям к системе (10-30 дБ) даже если р² << 1. Для этого достаточно выбрать ШПС с необходимой базой В, удовлетворяющей (5.92). Как видно из соотношения (5.92), прием ШПС согласованным фильтром или коррелятором сопровождается усилением сигнала (или подавлением помехи) в 2В раз.    Именно поэтому величину

Kшпс=q²/P²,                                (5.93)

называют коэффициентом усиления ШПС при обработке, или просто усилением обработки. Из (5.92), (5.93) следует, что усиление обработки Кшпс = 25. В ШСС прием информации характеризуется отношением сигнал/помеха  h²  =  q²/2,  т.е.

h² = Bp².                                        (5.94)

На рис. 5.15 представлены зависимости усиления обработки и базы ШПС В от отношения сигнал/помеха на входе р² = —40 дБ при значениях q² (сплошные линии) и h² (штриховые линии), равных 10, 20 и 30 дБ, построенные согласно (5.92) и (5.94). Например, если необходимо иметь h² = 20 дБ, а на входе приемника р² = —40 дБ, то требуемая база должна быть равна 60 дБ, т.е. В = 10⁶ .

Соотношения (5.92), (5.94) являются фундаментальными в теории систем связи с ШПС. Они получены для помехи в виде белого шума с равномерной спектральной плотностью мощности в пределах полосы частот, ширина которой равна ширине спектра ШПС. Вместе с тем эти соотношения справедливы для широкого круга помех (узкополосных, импульсных, структурных), что и определяет их фундаментальное значение.  В общем случае усиление обработки ШПС для произвольных помех

К_шпс≈ 2 В, (5.95)

где степень приближения зависит как от вида помех, так и от базы ШПС.

Рис. 5.15. Зависимость усиления обработки и базы ШПС от отношения сигнал/помеха на выходе приемника

Рис. 5.16. Помехоустойчивость систем связи с ШПС, ЧМ и AM

На рис. 5.16 приведены графики помехоустойчивости систем связи с ШПС, с частотной модуляцией (ЧМ) и с амплитудной модуляцией (AM). Для сравнения ЧМ и ШПС взяты одинаковые полосы частот, что соответствует В = 100. Помехоустойчивость системы связи с ШПС рассчитана согласно (5.92), причем положено, что информация передается с помощью широтно-импульсной модуляции (ШИМ). Известно, что ЧМ обладает высокой помехоустойчивостью и обеспечивает высокое качество воспроизведения информации при условии, что отношение сигнал/помеха на входе выше порогового значения  При уменьшении  p ²ниже порогового значения помехоустойчивость системы связи с ЧМ резко падает (см. рис. 5.16). Система с AM и эквивалентной базой B = 1 работает лишь при р² > 0 дБ, зависимость q² от р² линейная. Система связи с ШПС обеспечивает надежный прием информации и при р² < 0 дБ. Например, если положить q² = 10 дБ, то система связи будет работать при отношении сигнал/помеха на входе —13 дБ, т.е. р² = 0,05. Таким образом, одним из основных назначений системы связи с ШПС является обеспечение надежного приема информации при воздействии мощных помех, когда отношение сигнал/помеха на входе приемника р может быть много меньше единицы.

Необходимо еще раз отметить, что приведенные соотношения строго справедливы для помехи в виде гауссовского случайного процесса с равномерной спектральной плотностью мощности (белый шум).

Скрытность (разведзащищенность) системы связи — это способность противостоять обнаружению излучения и измерению параметров как самой системы связи, так и используемых сигналов. Поскольку обнаружение ШПС и измерение параметров возможны при различной первоначальной осведомленности (априорной определенности) о системе связи, то можно указать только основные соотношения, характеризующие скрытность. Когда известно, что в данном диапазоне частот может работать система связи, но параметры ее неизвестны, можно говорить об энергетической скрытности системы связи, так как ее обнаружение возможно с помощью анализа спектра (энергетическое обнаружение). Характеристика обнаружения (вероятности ложной тревоги и пропуска сигнала) полностью определяется отношением сигнал/помеха на входе приемника-анализатора р² = Р_с/Р_п, где помеха представляет собой собственный шум приемника Р_п = kT₀(N_ш — l)F; k— постоянная Больцмана; Т₀ — температура окружающей среды, N_ш — коэффициент шума приемника. Время обнаружения ШПС при условии р² << 1 приближенно определяется  как

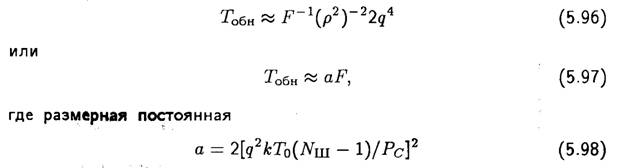
зависит как от шумовых свойств приемника и мощности сигнала на входе, так и от требуемого отношения сигнал/помеха на выходе q². Таким образом, чем шире спектр ШПС, тем больше время обнаружения и, следовательно, тем выше энергетическая скрытность системы связи.

Если ШПС системы связи воспроизводятся приемником-анализатором уверенно, то время анализа приближенно определяется соотношением, аналогичным по виду соотношению (5.97), но при этом

где b — постоянная величина. Чем шире спектр ШПС, тем больше и время анализа и, следовательно, тем выше параметрическая скрытность системы  связи.

Таким образом, чем шире спектр шумоподобного сигнала и чем больше его база, тем выше как энергетическая, так и параметрическая скрытность  ШПС.

В целях защиты информации от несанкционированного доступа в ШСС применяют смену ШПС (программы перестройки рабочего параметра). Интенсивность смены ШПС, их выбор из некоторого ансамбля (системы сигналов) зависят от многих требований к системе связи и не могут быть однозначно определены. Однако полагают, что число сигналов в системе (или объем системы сигналов) должно быть много больше базы ШПС. Можно предположить, что для помехозащищенных систем связи объем системы сигналов Q определяется степенным законом:

Q ~5^m,                                 (5.100)

где т — некоторое число, по крайней мере удовлетворяющее условию т ≥ 2, хотя для работы ШСС может использоваться гораздо меньшее  число   ШПС.

Таким образом, использование ШПС повышает развед- и помехозащищенность системы связи, что определяет целесообразность их применения в интересах защиты информации.

Кодовое разделение абонентов. С развитием асинхронных адресных систем связи стало возможным внедрение ШПС в системах массовой радиосвязи. Основу для этого представляет кодовое разделение абонентов за счет ШПС, отличающихся по форме.

При больших базах можно построить большое число различных ШПС. Например, пусть ШПС представляет собой фазоманипулированный сигнал, состоящий из радиоимпульсов, фазы которых равны 0 или тт. а число их равно В. Можно построить множество сигналов (так называемый полный код), число сигналов в котором равно 2^В, а сигналы между собой отличаются хотя бы в одном импульсе. Если положить В = 100, то имеем 2¹⁰⁰ ≈ 10³⁰ различных сигналов. Из такого большого множества можно отобрать систему сигналов так, чтобы каждому абоненту в системе связи выделить свои собственные сигналы. При этом все абоненты могут работать в общей полосе частот, а разделение их возможно за счет различия ШПС по форме. Такое разделение абонентов называется кодовым. При этом ШПС является по сути адресом абонента, и в этом случае принципиально нет необходимости в принудительной временной синхронизации абонентов. Поэтому подобные системы связи получили название асинхронных адресных систем связи (ААСС). Они основаны на применении ШПС и кодовом разделении абонентов.

В ААСС все абоненты работают в общей полосе частот. Поэтому при передаче информации ШПС различных абонентов перекрываются по времени и частоте и создают взаимные помехи. Однако при работе фиксированного количества абонентов в общей полосе частот уровень взаимных помех можно снизить до требуемого, обеспечивающего необходимое качество приема информации, увеличением базы ШПС. Если предположить, что на входе одного из приемников системы связи действуют п мешающих ШПС с одинаковыми мощностями, то отношение сигнал/помеха  на  выходе приемника

h² = В/п.                                    (5.101)

Таким образом, увеличивая базу ШПС, всегда можно добиться требуемого качества приема  информации.

На рис. 5.17 представлены зависимости базы ШПС от числа активных абонентов, построенные согласно (5.101). Графики рис. 5.17 позволяют определить помехоустойчивость ААСС.

Эффективность использования радиоспектра в ААСС. Поскольку повышение помехоустойчивости ААСС при заданном числе активных абонентов возможно только за счет увеличения базы ШПС (см. (5.101)), а при заданной скорости передачи информации увеличение базы приводит согласно (5.86) к пропорциональному расширению спектра ШПС, возникает вопрос об эффективности использования радиоспектра в системах связи с ШПС.

В   системах   связи   эффективность использования радиоспектра характеризуется удельной плотностью активных абонентов у, равной числу активных абонентов, приходящихся на  1  МГц полосы частот,  т.е.

γ = n/F,                                    (5.102)

где п — число активных абонентов, одновременно работающих в полосе частот шириной F.  Заменяя п в (5.102) согласно (5.101), имеем

γ = T/h².                                   (5.103)

Часто удельная плотность активных абонентов называется просто эффективностью систем связи. Из (5.103) следует, что эффективность ААСС тем меньше, чем больше требуемое отношение сигнал/помеха на выходе приемника. Таким образом, ААСС более перспективны в тех случаях, когда не требуется высокое качество передачи информации, что характерно для систем массовой радиосвязи. Для примера в радиотелефонной системе подвижной связи с частотным разделением каналов максимальная эффективность γ_max ⁼ 250 аб./МГц, так как минимальная ширина каждого канала (с учетом защитных интервалов) равна 4 кГц и в 1 МГц можно разместить 250 таких каналов, т.е. активных абонентов или линий (сетей) радиосвязи. Однако в реальных системах связи для повышения помехоустойчивости используется частотная модуляция (ЧМ) и соседние частотные каналы разнесены на 25 кГц. При этом в 1 МГц можно разместить 40 частотных каналов, т.е. γ_чм = 40 аб./МГц. Для оценки эффективности систем связи с ШПС в (5.103) положим Т = 1/4 кГц, Т = 250 мс, a h² = 10. В этом случае γ_шпс = 25 аб./МГц, т.е. в ШСС одновременно может работать на излучение до 25 абонентов с ШСС.   Если учесть,  что в ЛРС коэффициент загрузки

Рис. 5.18. Шумоподобный сигнал (а), автокорреляционная функция (б), разделение лучей (в)

К₃ меньше 1, то количество ЛРС с ШПС может быть увеличено, так для телефонных ЛРС Кз = 0,1-0,3, поэтому в таких ШСС загрузка частотного диапазона может достигать величины 80-250 аб./МГц, что больше,  чем в системах связи с ЧМ.

Борьба с многолучевостью. Применение ШПС в системах связи позволяет бороться с помехами, возникающими из-за многолучевости распространения радиоволн. Многолучевость возникает в том случае, когда радиоволны приходят в точку приема, отразившись от различных препятствий на пути распространения (слоев атмосферы, зданий, холмов и т.п.). Из-за различия в длине пути эти радиоволны приходят с различным запаздыванием. В результате, если сигналы, пришедшие по разным путям, перекрываются во времени, то между ними возникает интерференция, которая, в свою очередь, вызывает глубокие замирания результирующего сигнала. Обычно для компенсации замираний предусматривают увеличение мощности сигнала на 20 дБ. Иначе обстоит дело при использовании ШПС, поскольку при обработке ШПС согласованным фильтром происходит сжатие ШПС по времени, что иллюстрируется рис. 5.18. На рис. 5.18,а изображен ШПС с частотной модуляцией длительностью Т. На рис. 5.18,5 изображено напряжение на выходе согласованного фильтра — отклик фильтра на ШПС. Этот отклик представляет собой автокорреляционную функцию (АКФ) ШПС. Хотя АКФ имеет длительность 2Т, в ней можно выделить две резко отличающиеся структуры. В центре АКФ резкий выброс в виде узкого импульса, называемого центральным пиком.  Его амплитуда равна V, а длительность

τ₀ ≈ 1/F.                                       (5.104)

Чем шире спектр ШПС, тем короче центральный пик АКФ. Вторую область составляют боковые пики с максимальным значением V_max. Шумоподобные сигналы с большими базами обладают свойствами, которые записываются двумя соотношениями:,

Т/τ₀ ≈ В                                            (5.105)

V/V_max ≈√αB,                                 (5.106)

где α — некоторая постоянная, в общем случае зависящая от базы В.

Соотношение (5.105) определяет сжатие ШПС — отношение длительности ШПС Т к длительности центрального пика. Сжатие ШПС примерно равно базе. Поэтому при Т = const увеличение F приводит к уменьшению длительности центрального пика τ₀ и к увеличению  сжатия.

Соотношение (5.106) характеризует подавление боковых пиков. Оно равно отношению амплитуды центрального пика V к амплитуде максимального бокового пика V_max Чем больше база, тем больше подавление боковых пиков. И в пределе АКФ ШПС с ростом базы стремится к узкому дельта-импульсу. Такую АКФ имеет широкополосный шум, что и послужило причиной названия — «шумоподобные сигналы».

На рис. 5.18,в изображен отклик согласованного фильтра на несколько ШПС, пришедших по разным путям.

Если задержка между лучами At больше длительности центрального пика Го, то лучи разделяются и центральные пики различных лучей можно разделить один от другого, а затем их объединить, устранив задержку между ними. Такой принцип борьбы с многолучевостью был использован в одной из первых систем связи с ШПС RAKE. Таким образом, условие ∆t > τ₀ обеспечивает разделение лучей. Поскольку τ₀ и F связаны соотношением (5.104), то условие разделения лучей записывается следующим образом:

F∆t > 1.                                       (5.105)

Например, если при распространении радиоволн существуют два луча — прямой и отраженный от некоторого объекта, то задержка ∆t≈2d/Rc, где с — скорость света; R — расстояние между передатчиком и приемником; d — расстояние между отражающим объектом и прямым лучом. В этом случае необходимо использовать ШПС с  шириной  спектра

F ≥ Rc/2d²,                                     (5.108)

при этом чем больше d, тем меньше F. Может оказаться, что при малых d могут потребоваться ШПС с очень широкими спектрами, что не всегда можно реализовать  на  практике.

Электромагнитная совместимость. Существенным моментом с точки зрения защиты информации в канале радиосвязи является возможность функционирования ШСС в общем диапазоне частот с другими системами связи. Необходимо отметить, что шумоподобные сигналы обеспечивают хорошую электромагнитную совместимость (ЭМС)

ШСС с узкополосными системами радиосвязи и вещания. На рис. 5.19 изображены спектры ШСС с ШПС с шириной спектра F и узкополосной системы связи с шириной спектра сигнала F_y. Соответственно для ШПС спектральная плотность мощности N_шпс = P_шпс/F, для узкополосного сигнала N_y = P_y/F_y. Помехоустойчивость системы связи с ШПС определятся фундаментальным соотношением (5.92), в котором р² = Р_шпс/Р_у .Усиление обработки равно 2В. Если узкополосная система связи постоянно занимает определенный частотный интервал, то ее спектр можно полностью подавить, используя режекторный фильтр, настроенный на частоту узкополосной системы связи. Таким образом, воздействие узкополосной системы связи на широкополосную незначительно. В свою очередь, широкополосная система также слабо влияет на узкополосную систему связи. Мощность ШПС, проходящего на выход приемника, ЛГцшс-Fy = PumcF_y/F. Поэтому отношение сигнал/помеха на выходе узкополосного приемника будет определяться соотношением (5.92), в котором р² = Ршпс/Ру, s В = F/F_y. Поэтому чем больше отношение F/F_y, тем лучше фильтрация ШПС в узкополосной системе связи. Следовательно, чем больше база ШПС, тем выше ЭМС широкополосной и узкополосной систем связи.

Системы связи с ШПС можно совмещать и с радиотелевизионными системами. На рис. 5.20 изображен спектр телевизионного сигнала Ntb. Программы телевидения в одной территориальной зоне передаются по нескольким каналам с большими защитными частотными интервалами. Обычно в этих частотных защитных интервалах не допускается работа каких-либо радиотехнических систем, чтобы не создавать помех телевизионным передачам. Однако можно в этих частотных интервалах разместить системы связи с ШПС так, как это показано на рис. 5.20. Спектр ШПС расположен вблизи спектра телевизионного сигнала, там, где спектральная плотность последнего резко уменьшается. При этом взаимные помехи и той, и другой системе будут малыми. Следует отметить, что если вместо ШПС использовать сигналы с частотной модуляцией, то уровень взаимных помех возрастет, так как сигналы системы связи и телевидения относятся к одному классу и демодулируются  частотным  детектором.

Таким образом, системы связи с ШПС обладают хорошей ЭМС с системами радиосвязи, вещания и телевидения.  Ранее было упомянуто,что ШПС обеспечивает высокую эффективность использования радиоспектра. Если рассматривать действие систем связи в некотором замкнутом пространстве, то оказывается, что наилучшую ЭМС при ограниченном диапазоне частот обеспечивают ШПС, хотя сами по себе они требуют более широкой полосы, чем традиционные узкополосные системы.

Из рассмотрения основных свойств ШПС следует, что применение ШПС в системах связи позволяет обеспечивать высокую помехоустойчивость относительно мощных помех, скрытность, адресность, работоспособность в общей полосе частот, борьбу с многолучевостью, хорошую ЭМС со многими радиотехническими системами. Эти преимущества получаются за счет применения ШПС с большими базами, что приводит к резкому усложнению устройств формирования и обработки, увеличению их массы, объема, потребляемой мощности. В большинстве случаев переход к ШПС с большими базами требует резкого расширения полосы частот, что приводит к определенным трудностям в создании широкополосной элементной базы. Однако эти трудности преодолимы. И поэтому ШПС находят широкое применение в системах связи, особенно в системах массовой радиосвязи.

5.5. Системы передачи информации  

с псевдослучайной перестройкой рабочих частот

5.5.1. Определение и классификация сигналов

с псевдослучайной перестройкой рабочих частот

Сигналы с псевдослучайной перестройкой рабочей частоты (ППРЧ) — это сигналы, при использовании которых в течение передачи одного сообщения частота излучения дискретно изменяется во времени в соответствии с заранее определенным алгоритмом, задаваемым некоторой псевдослучайной последовательностью, в пределах адресной группы частот (АГЧ) линии радиосвязи. Формирование сигнала может быть представлено выражением

где i — порядковый номер единичного временного интервала излучения; N — множество натуральных чисел; f_i — частота излучения, используемая на i-м временном интервале; F = {fⁿ : п Є S= {0,1,..., K-1}} — адресная группа частот; К — объем АГЧ; А — алгоритм формирования частотной последовательности, задающий отображение множества натуральных чисел на множество используемых частот — АГЧ.

При этом можно выделить сигналы с неинформационной ППРЧ (НППРЧ-сигналы), в которых очередной номинал рабочей частоты определяется только символами  ПСП {x_t}, т.е.   

где Z_mi — кодовое слово, определяющее номинал рабочей частоты на i-м шаге программы, например состоящее из k элементов информационной последовательности и (т — к) элементов ПСП: Z_mi = X(_m__k)_i,US_ki (U — знак конкатенации (приписывания) символов последовательности)  или являющееся суммой фрагмента ПСП Х_mi, и фрагмента информаци- 1 онной последовательности S_ki(k ≤ т), т.е. Z_mi — Х_тi + S_ki mod q^m,  где q — значность символов ПСП {x_i}.                                                           

Используемый на практике принцип разделения ППРЧ на быструю и        медленную основан на оценке соотношения длительностей информационных символов (Тцс) и частотных элементов (субпосылок) (Тч).  При быстрой ППРЧ каждый информационный символ передается с использованием одного или нескольких частотных элементов (Т_Ч ≤ Т_ИС)- При медленной ППРЧ каждый частотный элемент переносит более одного информационного символа (Т_Ч > Т_ИС).

Неинформационные и информационные ППРЧ-сигналы могут применяться  как при быстрой, так и при медленной ППРЧ. Хотя наиболее вероятно, что в системах связи с быстрой ППРЧ широкое применение найдут ИППРЧ-сигналы, а в системах связи с медленной ППРЧ — НППРЧ-сигналы.

При использовании  НППРЧ-сигналов,  генератор псевдослучайной числовой последовательности определяет очередную рабочую частоту,     < которая модулируется при быстрой ППРЧ — очередным информационным символом, при медленной ППРЧ — фрагментом информационной

последовательности.

В режиме быстрой НППРЧ возможно применение только частотной манипуляции (ЧМ), а в режиме медленной НППРЧ — также од-ноканальных методов модуляции сигнала — амплитудной манипуляции (AM), фазовой манипуляции (ФМ), относительной ФМ (ОФМ), многопозиционной ФМ (М-ФМ), ЧМ с непрерывной фазой (ЧМ-НФ) и, как частный случай, ЧМ с минимальным сдвигом (ЧМ-МС).

При использовании режима быстрой ППРЧ с двоичной ЧМ последовательность частот, на которых осуществляется передача информационных символов, называется основным каналом. Последовательность частот, не используемых для передачи, т.е. последовательность инверсная информационной, называется дополнительным каналом.  При этом

Рис. 5.21. Структурная схема ЛРС с НППРЧ-сигналами (а) и диаграмма формирования НППРЧ-сигнала (б)

разность номиналов частот основного и дополнительного каналов будет постоянной величиной, равной разносу между частотами «нажатия»  и  «отжатия».

При использовании ИППРЧ-сигналов информационным параметром сигнала является номинал используемой частоты, поэтому сигнал в этом случае представляет собой последовательность радиоимпульсов с изменяющейся частотой заполнения (несущей частотой). Очередной номинал частоты ИППРЧ-сигнала определяется фрагментом числовой последовательности (кодовым словом), являющимся результатом объединения информационной и псевдослучайной последовательностей. В этом случае можно сказать, что генератор псевдослучайной числовой последовательности определяет группу рабочих частот, которые могут быть использованы в очередной момент времени. Всего таких непересекающихся групп может быть 2^т-k, по 2^k частот в каждой, а очередной номинал рабочей частоты из группы определяется передаваемым информационным символом (фрагментом).

Быстрая ИППРЧ предполагает смену группы рабочих частот с каждым частотным скачком. При медленной ИППРЧ на очередной группе рабочих частот передается несколько информационных символов, т.е. происходит несколько скачков частот одной группы.

При k = 1 ИППРЧ-сигнал представляет собой аналог НППРЧ-сигнала с двоичной ЧМ, но при этом разнос между частотами основного и дополнительного каналов в общем случае не будет постоянной величиной.

Упрощенные структурные схемы передатчиков и приемников линий радиосвязи с неинформационной и информационной псевдослучайной перестройкой рабочих частот, а также диаграммы формирования частотных последовательностей приведены на рис. 5.21 и 5.22 соответственно. Режим ППРЧ определяется соотношением скоростей передачи информации и генерирования псевдослучайных чисел. В соответствии со схемами, приведенными на рис. 5.21 и 5.22, на генератор псевдослучайной

Рис. 5.22. Структурная схема ЛРС с ИППРЧ-сигналами (а) и диаграмма формирования ИППРЧ-сигнала (т     =     3, к     =     1) (б)

числовой последовательности (ГЧП) возлагается задача формирования последовательности номеров частотных каналов (ПНК), в соответствии с которой синтезатор частот (СЧ) формирует последовательность номиналов частот (ПНЧ), используемую линией радиосвязи с ППРЧ.

Системы связи с ППРЧ принято относить к адресным системам связи.  При этом частотные последовательности, получившие название несущих адресных последовательностей,  формируются на основе многоуровневых (многозначных) числовых  последовательностей,  которые и определяют свойства линий  радиосвязи с ППРЧ.    Несущие адресные последовательности должны обеспечивать:  требуемую значность (объем АГЧ ЛРС с ППРЧ); большой объем ансамбля последовательностей; большую длину используемых последовательностей;   высокую степень взаимного различения  последовательностей,  используемых различными ЛРС с ППРЧ; высокую непредсказуемость;  простоту реализации и эксплуатации генераторов. Высокая степень взаимной различимости последовательностей,   используемых  различными  линиями  радиосвязи с ППРЧ, определяется их авто- и взаимно-корреляционными характеристиками и означает, что число совпадающих элементов между любыми двумя сдвигами одной или различных последовательностей из ансамбля не должно превышать заранее заданного значения, что обеспечит работу нескольких ЛРС с ППРЧ на одних частотах с требуемым качеством.   Большая значность (объем АГЧ ЛРС с ППРЧ), большой объем ансамбля последовательностей,  их большая длина (период) и высокая непредсказуемость дают высокую развед- и помехозащищенность систем  связи с  ППРЧ.

5.5.2. Структура алгоритмов формирования частотных

последовательностей, используемых в линиях радиосвязи с псевдослучайной перестройкой рабочих частот

Передача информационных сообщений в линиях радиосвязи, работающих в режиме ППРЧ, производится на частотах АГЧ, перестройка по которым осуществляется синхронно передатчиком и приемником ЛРС с ППРЧ в соответствии с заранее выбранной программой. Под ППРЧ понимается алгоритм формирования последовательности номиналов частот (ПНЧ) {f_i}, используемой при работе ЛРС с ППРЧ и по существу задающей отображение множества (ряда) натуральных чисел N({i}) на

Правило А₄ определяет тип используемой ДПСП и ее параметры, что, в свою очередь, однозначно определяет схему генератора ДПСП. В качестве ДПСП могут использоваться как линейные, так и нелинейные  последовательности.    Из линейных  возможно применение  М-последовательностей, последовательностей Голда, Касами и др. Достоинствами линейных ДПСП является простота формирующих генераторов и хорошие авто- и взаимнокорреляционные свойства. Недостаток линейных ДПСП — низкая эквивалентная линейная сложность, т.е. низкая непрогноэируемость. Из нелинейных последовательностей возможно применение составных нелинейных последовательностей, бент-последовательностей, последовательностей де Брейна и др. У нелинейных ДПСП по сравнению с линейными хуже корреляционные свойства, но при этом их эквивалентная линейная сложность (непрогнозируемость)  гораздо выше.

Правилом Аз, преобразующим ДПСП в МЧП, является комбинационно-числовое преобразование, схематическое представление которого при га = 3, с = 2 приведено на рис. 5.10. Параметрами КЧП являются параметр выборки т и параметр смещения с. В зависимости от их соотношения можно выделить три режима КЧП: 1) скользящий режим (с <m ); 2) режим последовательных выборок (с = m); 3) режим выборок с пропусками (с > m). Аналитически КЧП может быть представлено  в  виде

Полученная в результате комбинационно-числового преобразования МЧП с целью повышения разведзащищенности ЛРС с ППРЧ преобразуется (перенумеровывается) в соответствии с правилом А₂, задаваемым транзективной переменной ключа ЛРС. Наиболее легко реализуемыми представляются способы перенумерации, заключающиеся в инверсии отдельных символов элемента Х_тi или изменении порядка следования его весовых коэффициентов. Возможно совместное применение описанных выше способов перенумерации элементов МЧП. В этом случае элементы  ПНК определяются формулой

где l_k — 0 или 1. если k-й  символ не инвертируется или инвертируется, соответственно; Р_т(k) — k-й символ перестановки Р_т на множестве {0,1,..., т — 1};  — операция сложения по mod 2.

Возможны и другие способы перенумерации элементов МЧП (правило А₂), в том числе и способ, заключающийся в произвольном (табличном) соответствии элементов МЧП и ПНК.

Правило А₁ определяется порядком ввода в память радиостанций ЛРС с ППРЧ номиналов частот адресной группы, который в общем случае может быть произвольным, хотя известны регулярные способы закрепления номиналов частот за элементами ПНК в порядке их одновременного возрастания, что при равномерном распределении частот в

адресной группе ЛРС с ППРЧ может быть выражено формулой

где f° — минимальное значение частоты АГЧ ЛРС с ППРЧ; ∆f — минимальное приращение частоты (шаг сетки частот).

Кроме описанного выше алгоритма формирования ПНЧ (5.113) возможно использование алгоритма, имеющего структуру

предусматривающего непосредственное формирование МЧП, при этом возможно формирование МЧП как в простых GF(q), так и в расширенных GF(qⁿ) числовых полях, где q — основание; п — степень расширения   поля.

Значность МЧП определяет максимальный объем АГЧ ЛРС с ППРЧ. Для ПНЧ, формируемых на основе комбинационных МЧП, K_mах = 2ⁿ; на основе МЧП, формируемых в простых полях, К_тах = q в расширенных полях К_тах =  qⁿ.

В качестве дополнительных мер развед- и помехозащиты в современных ЛРС с ППРЧ предусматривается смена ключевых данных (смена правил А₁, А₂), транзективной переменной (правило A₂), текущего заполнения генераторов (пересинхронизация сети). Кроме этого, возможно оперативное изменение АГЧ (правило А₁), заключающееся в исключении или замене отдельных частот АГЧ, подверженных воздействию помех, или в смене всей АГЧ. Современный уровень развития техники позволяет сделать вывод о возможности оперативной смены в перспективных радиостанциях любого из правил формирования ПНЧ (А₁, А₂, A₃, A₄) как по отдельности, так и в любом сочетании.

В качестве примера рассмотрим возможные варианты схемной реализации алгоритма формирования ПНЧ для системы радиосвязи с объемом АГЧ К = 51. В этом случае при формировании ПНЧ возможно использование алгоритма, имеющего структуру (5.113), в основе которого лежит комбинационно-числовое преобразование с параметром выборки m = 6. Вариант структурной схемы, обеспечивающей формирование такой ПНЧ,  приведен  на рис. 5.23.

Устройство преобразования УПЗ реализует правило Аз и представляет собой преобразователь последовательного кода в параллельный (рис.   5.24).

Устройство преобразования УП2 обеспечивает перенумерацию элементов МЧП в соответствии с правилом А₂ и представление их в десятичном  виде (рис.  5.25).

Устройство преобразования УП1 обеспечивает формирование ПНК требуемой мощности (мощность адресной последовательности должна быть равна объему АГЧ ЛРС с ППРЧ) и преобразование ПНК в ПНЧ. При этом сокращение мощности ПНК возможно двумя способами:

Рис. 5.25. Устройство преобразования УП2 (вариант)

а) назначением запрещенных номеров и выбрасыванием их из последовательности (рис. 5.26,з). При этом для устранения пропусков в ПНЧ необходимо осуществление дополнительного такта (нескольких тактов) в генераторе ДПСП (ГДПСП) и дополнительного считывания в УПЗ;

б)  назначением  нескольким номерам одной частоты (рис. 5.26,6). При этом в ПНЧ рассматриваемой ЛРС с ППРЧ нарушается баланс частот, поскольку некоторые частоты оказываются более загруженными. Поэтому в системе связи для ЛРС с ППРЧ, работающих на тех же частотах,

Рис. 5.27. Структурная схема устройства, обеспечивающего формирование ПНЧ

(вариант)

в те же временные интервалы необходимо обеспечить несовпадение номиналов частот с повышенной загрузкой.

При формировании ПНЧ наряду с алгоритмом (5.113) возможно использование алгоритма (5.118). Вариант структурной схемы, обеспечивающий формирование ПНЧ для этого случая приведен на рис. 5.27.