ГЛАВА 4

                                                           Организация устройств ЭВМ

            4.1. Принцип микропрограммного управления

            Для выполнения операций над информацией используются операционные устройства — арифметико-логические, управления, контроллеры ВУ и т. п. Функцией операционного устройства является выполнение заданного множества операций F ={f₁, f₂, ..., f_k } над входными словами из множества D₁ с целью вычисления выходных слов из множества Do представляющих результаты операций D₀  = f_k (D₁).  k=1,…, K.

            Функциональная и структурная организация операционных устройств, определяющая порядок функционирования и структуру устройств, базируется на принципе микропрограммного управления, который состоит в следующем [7]:

            1. Любая операция f_k, реализуемая устройством, рассматривается как сложное действие, которое разделяется на последовательность элементарных действий над словами информации, называемых микрооперациями.

            2. Для управления порядком следования микроопераций используются логические условия, которые, в зависимости от значений слов, преобразуемых микрооперациями, принимают значения "истина" или "ложь" (1 или 0).

            3. Процесс выполнения операций в устройстве описывается в форме алгоритма, представляемого в терминах микроопераций и логических условий и называемого микропрограммой. Микропрограмма определяет порядок проверки значений логических условий и следования микроопераций, необходимый для получения требуемых результатов.

            4. Микропрограмма используется как форма представления функции устройства, на основе которой определяются структура и порядок функционирования устройства во времени.

            Сказанное можно рассматривать как содержательное описание принципы микропрограммного управления, из которого следует, что структура и порядок функционирования операционного устройства предопределяются алгоритмами выполнения операций из F .

4.2. Концепция операционного и управляющего автоматов

            В функциональном и структурном отношении операционное устройство, входящее в состав ЭВМ, удобно представить разделенным на две части: операционный и управляющий автоматы (рис. 4.1).

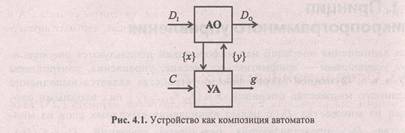
            Операционный автомат (ОА) служит для хранения слов информации, выполнения набора микроопераций и вычисления значений логических условий, т. е. операционный автомат является структурой, организованной для выполнения действий над информацией. На вход ОА подаются входные данные D₁ которые в соответствии с алгоритмом операции преобразуются в выходные данные D₀ . Кроме того, ОА вырабатывает множество {х} осведомительных сигналов (логических условий) для управляющего автомата.

            Управляющий автомат (УА) генерирует последовательность управляющих сигналов  {у}, обеспечивающую выполнение в операционном автомате заданной последовательности элементарных действий, которая реализует алгоритм выполняемой операции. Управляющая последовательность генерируется в соответствии с заданным алгоритмом и с учетом значений логических условий х, формируемых ОА.

            Часто операционное устройство может выполнять несколько различных операций (например, арифметико-логическое устройство может выполнять четыре арифметических действия и несколько логических операций над входными словами). В этом случае на вход УА поступает команда С, определяющая тип выполняемой операции. Кроме того, поскольку различные операции над различными данными выполняются за разное время, УА формирует сигнал g, отмечающий окончание операции и готовность выходных данных.

            Таким, образом, любое операционное устройство — процессор (который

обычно, в свою очередь, представляют состоящим из двух операционных устройств: АЛУ — арифметико-логического устройства и ЦУУ — центрального устройства управления), канал ввода/вывода, контроллер внешнего устройства — можно представить как композицию операционного и управляющего автоматов. Операционный автомат, реализуя действия над словами информации, является исполнительной частью устройства, работу которого организует управляющий автомат, генерирующий необходимые последовательности управляющих сигналов.

            Такой подход позволяет разработать эффективные процедуры синтеза ОА и УА, формализовать эти процедуры и, в некоторых случаях, автоматизировать процесс синтеза цифровых устройств.

            4.3. Операционный автомат

            Исходным для разработки структуры операционного автомата (ОА) являются:

            • описание входных и выходных слов ОА (множеств D₁ и D₀)'

            • список множества операций из F, которые должны выполняться над словами.

            Процесс разработки ОА, таким образом, следует начинать с определения форматов входных и выходных слов и разработки алгоритмов выполнения операций в терминах слов и стандартных действий над словами (сложение, копирование, инверсия, сдвиг и т.д.).            Разработанные алгоритмы удобно представить в форме граф-схемы алгоритма (ГСА).

           Далее необходимо разработать структуру ОА. Операционный автомат строится на базе операционных и логических элементов. Предложенные процедуры формального синтеза ОА [7] не получили широкого распространения; обычно используют т. н. "содержательный" метод синтеза.

            Разработать структуру — значит определить набор элементов, входящих в нее, и установить связи между этими элементами. Структура реализуется, исходя из разработанных на предыдущем этапе алгоритмов таким образом, чтобы обеспечить реализацию всех действий, предусмотренных в операторных вершинах ГСА.

            Действия в структуре ОА выполняются под управлением микроопераций, поэтому при разработке ОА следует определить полный список микро операций, наличие которых обеспечит выполнение в разработанной структуре всех предусмотренных в алгоритмах преобразований слов.

            Наконец, формирование последовательности микроопераций в управляющем автомате осуществляется с учетом значений логических условий, которые формируются в ОА. Поэтому при разработке ОА следует сформировать список логических условий, определяемый содержимым условных вершин ГСА, и предусмотреть в структуре ОА (если это необходимо) специальные элементы для формирования этих логических условий.

            Итак, процесс разработки ОА можно представить состоящим из следующих этапов:

            1. Определение форматов входных и выходных данных (слов).

            2. Разработка ГСА выполняемых операций.

            3. Разработка структуры ОА — выбор элементов и организация связей.

            4. Определения множества {у} микроопераций, выполняемых в ОА.

            5. Определения множества {x} логических условий, формируемых в ОА.

            4.3.1. Пример проектирования операционного автомата АЛУ

            В качестве примера рассмотрим разработку операционного автомата арифметического устройства, реализующего операцию деления чисел с фиксированной запятой, представленных в прямом коде.

            Определение форматов данных

            Будем считать, что в арифметической операции деления участвуют операнды А — делимое и В — делитель. Результат операции С — частное. Кроме того, устройство должно формировать признаки результата — двоичные переменные:

            • Z — признак нулевого результата;

            • S — признак отрицательного результата;

            • OV — признак переполнения.

            Алгоритм операции алгебраического деления разрабатываются для 16-разрядных двоичных чисел с фиксированной запятой, представленных в прямом коде. Знак числа кодируется в старшем (нулевом) разряде числа, запятая фиксирована после знакового разряда, таким образом, все числа могут быть только дробными (рис. 4.2).

            Разработка алгоритма деления

            В прямых кодах удобнее делить модули чисел. Знак результата не зависит от соотношения модулей делимого и делителя и определяется по выражению (4.1).

С₀ =a₀b₀ v a₀b₀

            Деление чисел с фиксированной запятой в заданном формате невозможно, если модуль делимого не меньше модуля делителя. Поэтому сначала следует проверить соотношение операндов путем вычитания делителя из делимого. Если разность окажется положительной, то можно формировать признак переполнения OV =1 и завершать операцию. В противном случае модуль частного оказывается меньше 1, т. е. переполнение отсутствует и деление возможно.

            Алгоритмы деления с восстановлением остатка и без восстановления остатка подробно рассмотрены в разд. 3.9. Учитывая приведенный там сравнительный анализ алгоритмов, выберем метод деления без восстановления остатка.

            ГСА деления без восстановления остатка представлена на рис. 4.3. Алгоритм предусматривает формирование знака результата согласно формуле (4.1) и сохранение его временно в переменной s После этого производится деление модулей чисел (знаки операндов обнуляются).

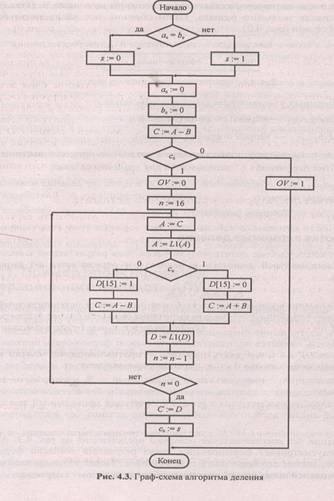
Сначала производится пробное вычитание делителя из делимого. Поскольку знаки операндов — О, то появление 1 в знаковом разряде разности означает, что А < В, и можно продолжать деление (целая часть частного равна 0).

            При с₀ = О деление невозможно — формируется признак переполнения.

В процессе получения цифр частного значение очередного остатка принимает переменная С. Независимо от знака остатка она копируется в переменную А, которая затем увеличивается вдвое путем сдвига влево на один разряд. В зависимости от знака переменной С (знака остатка) формируется очередная цифра переменной D (частного) и принимается решение о действии на следующем шаге — добавлять или вычитать делитель из сдвинутого остатка. После арифметической операции выполняется сдвиг влево частного D (освобождается место для очередной цифры частного), изменяется счетчик цифр частного и проверяется условие выхода из цикла — получение шестнадцати цифр частного, включая самую первую цифру — "0 целых", на место которой копируется знак частного из переменной s .

            Разработка структуры операционного автомата

            Анализ алгоритма деления (см. рис.4.3) позволяет разработать структуру операционного автомата. Учитывая действия, которые требуется выполнить для реализации алгоритма, включим в состав операционного автомата следующие элементы:

            • два шестнадцатиразрядных регистра Рг А и Рг В для хранения входных операндов и промежуточных результатов, причем регистр Рг А должен обеспечить возможность сдвига своего содержимого влево;

• шестнадцатиразрядный регистр Рг С для размещения результата арифметической операции сложения или вычитания (в нашем случае в этом регистре формируется остаток): в конце операции в нем будет размещен результат — частное;

• шестнадцатиразрядный регистр Pг D с возможностью левого сдвига кода для размещения частного в процессе его формирования;

• шестнадцатиразрядный двоичный параллельный сумматор/вычитатель Сум/Выч;

            • четырехразрядный вычитающий счетчик Сч и по модулю 16 для подсчета цифр частного;

            • триггер переполнения Тг ОV для хранения признака переполнения разрядной сетки;

• триггер знака Тг s для временного хранения знака частного;

• схема сравнения на "равно" знаковых разрядов исходных операндов;

•дешифратор DC "0" нулевой комбинации в разрядах C[1: 15], формирующий признак нулевого результата Z.

            Связи между перечисленными выше элементами, а также управляющие ими микрооперации показаны на рис. 4.4, а в табл. 4.1 приведен полный список микроопераций и логических условий.

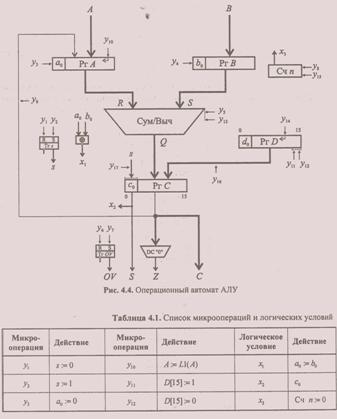
Внимательно посмотрим на рис. 4.4. Очевидно, любые действия, обозначенные в операторных вершинах алгоритма, приведенного на рис.4.3, могут быть реализованы на разработанной нами структуре (см. рис. 4.4).

            Теперь определим, какая последовательность микроопераций должна быть

реализована в разработанной структуре, чтобы выполнилась операция деления, предусмотренная алгоритмом рис.4.3. Простейшее решение — сохранить топологию графа алгоритма и заменить содержимое его операторных вершин на соответствующие микрооперации, а содержимое условных вершин — на соответствующие логические условия.

            Полученный таким образом граф принято называть микропрограммой и рассматривать в качестве исходных данных при проектировании управляющего (микропрограммного) автомата. При этом содержимое операторной вершины графа соответствует действиям, выполняемым устройством в один такт дискретного времени.

            При проектировании цифровых устройств обычно стремятся достичь максимальной скорости их работы. Один из путей достижения этой цели — параллельное (во времени) выполнение некоторых операций. Поэтому при преобразовании графа алгоритма в граф микропрограммы следует объединять в одной операторной вершине те микрооперации, которые могут быть в данной структуре выполнены одновременно с учетом реализуемого алгоритма. Совокупность микроопераций, выполняемых одновременно в один такт дискретного времени, называется микрокомандой

            Например, анализируя ГСА рис. 4.3, можно отметить, что операторы а_{0 =} 0; b_0;= 0 можно выполнить в структуре, изображенной на рис. 4.4, одновременно. То же можно сказать о паре операторов D:= Ll(D);  n:= n — 1 и некоторых других. В то же время, операторы А:= С, А:= Ll(A) нельзя выполнять

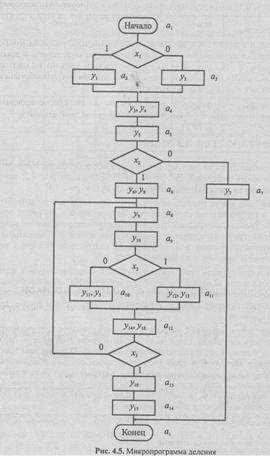
одновременно. (Для ускорения этой процедуры можно передавать информацию из С в А со сдвигом: С:= Ll(A), но это уже будет другая структура ОА.) Проанализировав с этой точки зрения исходный алгоритм, получим микропрограмму, приведенную на рис. 4.5.    Микропрограмма определяет, в какой последовательности и в зависимости от каких условий должны выдаваться микрокоманды, чтобы реализовалась операция деления на разработанной структуре (см. рис. 4.4) операционного автомата.

            Следующая задача — построить управляющий автомат, обеспечивающий выдачу микрокоманд в заданной микропрограммой последовательности.

            4.4. Управляющий автомат

            Исходным для проектирования управляющего автомата (УА) является микропрограмма, представленная, например, в форме ГСА. Различают два класса управляющих автоматов [2, 7]:

• с "жесткой" логикой:

• автомат Мура;

            • автомат Мили;

            • С-автомат;

• с программируемой логикой.

            4.4.1. Управляющий автомат с "жесткой" логикой

            Автоматы с "жесткой" логикой проектируются как обычные конечные структурные автоматы [2, 7, 8].

            Сначала необходимо перейти от ГСА микропрограммы к графу автомата, для чего следует:

            1. Разметить исходную микропрограмму.

            2. Построить по размеченной микропрограмме граф автомата.

            Далее реализуются стандартные процедуры синтеза структурного автомата, заданного графом:

            • кодирование алфавита входных и выходных символов автомата двоичными кодами;

            • кодирование внутренних состояний автомата;

            • выбор элемента памяти (типа триггера);

• построение автоматной таблицы переходов;

            • синтез комбинационной схемы, реализующей функцию переходов КСх 1;

            • синтез комбинационной схемы, реализующей функцию выходов КСх 2.

            Процедура разметки микропрограммы ставит в соответствие символам состояний автомата (а₁, a₂, ..., а_м,) некоторые объекты микропрограммы. Способы разметки микропрограмм различаются для автоматов различных типов.

            Для автомата Мура разметка выполняется по следующим правилам [2]:

            •символом а₁ отмечается начальная и конечная вершина ГСА;

            • различные операторные вершины отмечаются разными символами состояний;

            • все операторные вершины должны быть отмечены.

Для автомата Мили разметка выполняется по следующим правилам [2]:

• символом а₁ отмечается вход вершины, следующей за начальной, а также вход конечной вершины;

• входы всех вершин, следующих за операторными, должны быть отмечены

символами состояний;

             • если вход вершины отмечается, то лишь одним символом;

            • входы различных вершин, за исключением конечной, отмечаются различными символами.

Пример проектирования УАЖЛ

            Рассмотрим пример построения управляющего автомата Мура для устройства, реализующего операцию деления. Операционный автомат (см. рис. 4.4) и ГСА микропрограммы (см. рис.4.5) этого устройства были построены ранее.

            Шаг 1. Выполним разметку микропрограммы. Для этого сопоставим каждой операторной вершине ГСА в произвольном порядке (например, слева направо и сверху вниз) символ состояния автомата из множества {а₂ ,а₃, ..., а₁₄}. Начальную и конечную вершины сопоставим с начальным состоянием автомата а_1. Такая разметка показана на рис. 4.5.

            Шаг 2. Построим граф автомата, заданного размеченной микропрограммой, которую получили на предыдущем шаге. Для этого вершины графа сопоставим с состояниями автомата a₁, a₂, ..., а₁₄. Соединим ориентированными ребрами те пары вершин графа, между которыми на ГСА микропрограммы существуют переходы, причем пометим ребра графа соответствующими условиями перехода. Если переход между двумя операторными вер- шинами микропрограммы осуществляется безусловно, то условие перехода на ребре графа — константа 1.

            Построив таким образом граф, мы фактически задаем алфавиты внутренних состояний и входных символов и определяем функцию переходов. Для задания алфавита выходных символов и функции выходов (для автомата Мура функция выходов зависит только от его состояний) следует сопоставить каждой вершине автомата в качестве выходного символа содержимое соответствующей операторной вершины ГСА микропрограммы. Таким образом, получим граф микропрограммного автомата, который приведен на рис. 4.6.

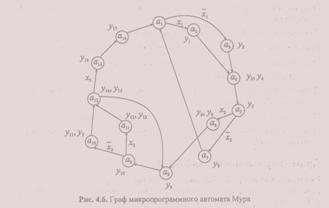
Шаг 3. Кодирование алфавитов входных и выходных символов автомата двоичными кодами. Алфавит входных символов составляет множество двоичных переменных Х = (х₁, х₂, х₃}, поэтому проблема кодирования входных символов двоичными переменными здесь не стоит. Что касается кодирования символов выходного алфавита, то отложим обсуждение этого вопроса до шага 8.

            Шаг 4. В процессе кодирования внутренних состояний автомата могут решаться проблемы исключения гонок в автомате, проблемы минимизации комбинационной схемы, обеспечивающей функцию переходов автомата. Для решения этих задач разработаны достаточно сложные алгоритмы, которые описаны в литературе, например, [2, 5]. Здесь мы не будем касаться этой стороны процедуры синтеза автомата.

            Следует отметить, что проблемы гонок могут быть полностью решены при использовании в автомате двухтактных элементов памяти, причем способ кодирования состояний в этом случае роли не играет. Правда, затраты оборудования при таком решении несколько возрастают, по сравнению с использованием метода противопоточного кодирования, но во-первых, эффективность метода заметно проявится лишь при достаточно большом числе состояний автомата (25 — 40), а во-вторых, большинство современных интегральных элементов памяти (триггеров) выпускаются именно двухтактными. Применение специальных методов кодирования "с учетом сложности комбинационных схем" [2] так же обеспечивает заметный эффект лишь для достаточно громоздких автоматов.

            В нашем примере воспользуемся простейшим методом кодирования состояний автомата, когда код состояния совпадает с двоичным числом, соответствующим номеру состояния. В рассматриваемом автомате насчитывается 14 состояний (см. рис. 4.6), поэтому для их кодирования требуется четырехразрядный двоичный код (24) 14; 2 (14) — табл. 4.2.

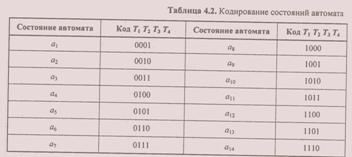
            Шаг 5. Выбор элемента памяти (типа триггера). При выборе элемента памяти следует учитывать простоту управления им. С этой точки зрения удобнее выбирать триггеры, управляемые по единственному информационному входу — к таким относятся D- и Т-триггеры. В нашем примере в качестве элемента памяти автомата выберем синхронный двухтактный D-триггер. Очевидно, для реализации нашего автомата понадобятся четыре D-триггера.

            Шаг 6. Построение автоматной таблицы переходов (табл. 4.3). Эта таблица практически описывает функцию переходов автомата, строится по графу автомата и определяет, какие значения необходимо подать на управляющие входы триггеров на каждом переходе автомата в новое состояние. Строка таблицы соответствует одному переходу автомата. Таким образом, автоматная таблица содержит столько строк, сколько ребер в графе автомата (включая и петли, если они имеются в графе).

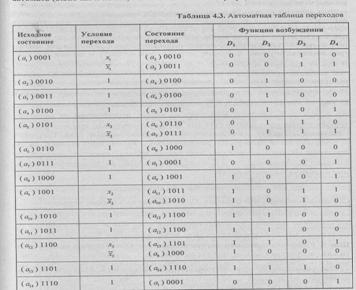
            Шаг 7. Синтез комбинационной схемы, реализующей функцию переходов автомата. Эта комбинационная схема в нашем случае реализует четыре булевы функции D₁, D₂, D₃, D₄, зависящие от четырехразрядного двоичного кода состояния автомата Т₁,Т₂ Т₃ Т₄ и трех битного вектора входных символов х₁х₂х₃. Комбинационная схема, описываемая системой четырех булевых функций от семи переменных, должна обеспечивать переходы автомата в соответствии с графом рис. 4.6

            Для построения этой схемы можно построить четыре карты Карно для D₁, D₂, D_{3 ,} D₄ по таблицам истинности, заданным соответствующими столбцами автоматной таблицы переходов, и минимизировать эти функции. Менее трудоемкий способ состоит в предварительной дешифрации состояний автомата (булевы функции четырех переменных) и записи функций возбуждения через значения а_i и x_k . Воспользуемся последним способом, тем более, что дешифрированные состояния автомата пригодятся нам и на следующем шаге при формировании функции выходов.

            Итак, предусмотрим дешифратор, на входы которого поступает двоичный код состояния автомата Т₁,Т₂Т₃Т₄, а на выходах формируется унитарный код ã_{1 …} ã_i-1 ã_i ã_i+1… ã₁₄.          Кстати, поскольку на входах дешифратора не могут появиться комбинации 0000 и 1111 (их мы не использовали при кодировании состояний), то схему дешифратора можно минимизировать. (Как? Попробуйте построить такой дешифратор самостоятельно.)      Рассмотрим столбец D> автоматной таблицы переходов, отметив те наборы входных переменных функции возбуждения (из {a} и {x}), на которых D₁ принимает единичные значения. Можно записать:

            Обратите внимание, что функция D₁ не зависит от входных переменных {х} (частный случай!). Действительно, переход, например, из состояния a₉ в зависимости от значения х₂ может произойти в а₁₀ или в а₁₁, но в обоих этих состояниях значение старшего разряда кодов одинаково. То же для D₁ можно сказать и обо всех остальных переходах, зависящих от входных символов (из

А₁, а₅, а12)).

            Теперь запишем булевы выражения для остальных функций возбуждения.

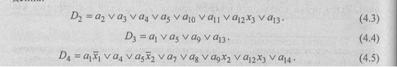
Шаг 8. Синтез комбинационной схемы, реализующей функцию выходов. Функция выходов автомата Мура зависит только от его внутреннего состояния и задана непосредственно на графе автомата (см. рис. 4.6). Выходами микропрограммного автомата являются микрооперации, поступающие в точки управления операционного автомата. Поэтому выходные символы микропрограммного автомата обычно не кодируют, а формируют на выходе значение вектора микроопераций. При большом числе микроопераций с целью уменьшения связности между ОА и УА на вход ОА передают не вектор микроопераций, а номер активной в данном такте микрооперации. Подробнее об этом — в следующем разделе.

            Из графа автомата (см. рис. 4.6) видно, что микрооперация у₂ должна вырабатываться автоматом, когда он находится в состоянии а₃, микрооперация y₅ — в состоянии а₅ и т. д. Микрооперация у₂ должна вырабатываться автоматом, находящимся в состоянии a₅ и a₁₀. Запишем функцию выходов автомата в виде системы булевых функций'.

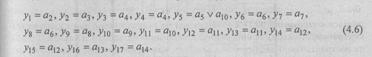
            Шаг 9. Теперь изобразим функциональную схему управляющего автомата, используя выражения (4.2) — (4.6) с учетом выбранного типа элемента памяти.

            Управляющий микропрограммный автомат с жесткой логикой (автомат Мура), изображенный на рис. 4.7, имеет три двоичных входа x₁, x₂, х₃, вход тактового сигнала СЬК и семнадцать двоичных выходов — микрооперации

У_1, У_{2,…………} У₁₇

            Память автомата представлена четырьмя двухтактными синхронными D-триггерами, объединенными общей цепью синхронизации (СБК). Выходы триггеров поступают на вход дешифратора DC "4→16", на выходах которого формируется унитарный код текущего состояния автомата. Поскольку проектируемый автомат является автоматом Мура, выходы дешифратора фактически являются выходами управляющего автомата (значениями микроопераций). Исключение составляет микрооперация у₅ которая формируется как

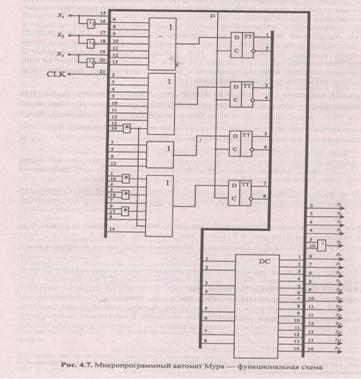
дизъюнкция двух различных состояний автомата, поскольку эта микрооперация присутствует в двух различных операторных вершинах исходной микропрограммы (см. рис. 4.5).

Функции возбуждения триггеров формируют значения D_i, i € {1,2,3,4} на выходах одно или двухуровневых схем, построенных согласно выражениям (4.2) — (4.5). Обратите внимание, что в выражениях (4.3) и (4.5) имеется одинаковый терм — а₁₂х₃. На функциональной схеме выход конъюнктура, реализующего этот терм, поступает на два входа различных дизъюнкторов, "обеспечивая" одновременно две функции возбуждения — D₂ и D_4.

            Схемы, реализующие функции возбуждения, можно построить иначе. Для примера рассмотрим выражение (4.4). Состояния автомата, входящие в это выражение, если выразить их через значения состояний триггеров, окажутся соседними и склеиваются. Действительно:

Очевидно, схема, реализованная по выражению (4.7), будет проще, чем схема (4.4). Проверьте, можно ли подобным образом минимизировать выражения остальных функций возбуждения.

Итак, мы построили микропрограммный автомат с "жесткой" логикой. Давайте представим, что нам понадобилось незначительно изменить исходную микропрограмму, например, добавить еще одну операторную вершину. Практически это приведет к необходимости полного перепроектирования всей схемы автомата. Это особенность автоматов с "жесткой" логикой является их серьезным недостатком.

Для того чтобы уменьшить зависимость структуры автомата от реализуемых им микропрограмм, используют управляющие автоматы с программируемой логикой.

4.4.2. Управляющий автомат с программируемой логикой

Принципы организации

Заметим, что функция любого управляющего автомата — генерирование последовательности управляющих слов (микрокоманд), определенной реализуемым алгоритмом с учетом значений осведомительных сигналов.

Если заранее разместить в запоминающем устройстве все необходимые для реализации заданного алгоритма (группы алгоритмов) микрокоманды, а потом выбирать их из памяти в порядке, предусмотренном алгоритмом (с учетом значения осведомительных сигналов), то получим управляющий автомат, структура которого слабо зависит от реализуемых алгоритмов, а поведение в основном определяется содержимым запоминающего устройства.

            При изменениях реализуемого алгоритма в достаточно широких пределах структура такого автомата не меняется, достаточно лишь изменить содержимое ячеек запоминающего устройства. Управляющий микропрограммный автомат, построенный по таким принципам, называется управляющим автоматом с программируемо логикой.

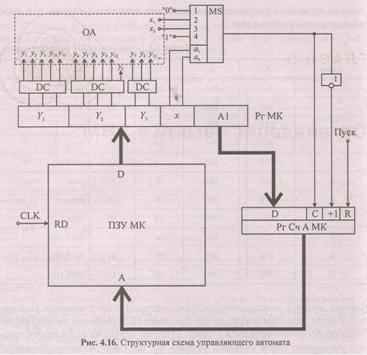
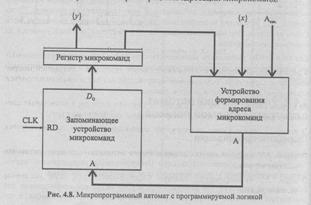
            Структурная схема такого автомата в самом общем виде приведена на рис. 4.8. Автомат включает в себя запоминающее устройство микрокоманд (обычно реализуемое как ПЗУ), регистр микрокоманд и устройство формирования адреса микрокоманды.

            В каждом такте дискретного времени из памяти микрокоманд считывается одна микрокоманда, которая помещается в регистр микрокоманд. Микрокоманда содержит два поля (две группы полей), одно из которых определяет набор микроопераций которые в данном такте поступают в операционный автомат, а другое содержит информацию для определения адреса следующей микрокоманды.

            При проектировании управляющего автомата с программируемой логикой (УАПЛ) необходимо выбрать формат (форматы) микрокоманд (микрокоманды), способы кодирования микроопераций и адресации микрокоманд.

            Адресация микрокоманд

            Исходными данными для проектирования УАПЛ является, как и для УАЖЛ (управляющий автомат с "жесткой" логикой), микропрограмма, представленная, например, в форме ГСА. Каждая операторная вершина должна реализоваться в один такт машинного времени, причем после операторной вершины в ГСА может следовать:

            • операторная вершина;

            • условная вершина, оба выхода которой или один из них соединены с операторными вершинами, например, как показано на рис. 4.9, и;

            • цепочка из двух или более условных вершин, выходы которых соединены с условными вершинами (рис. 4.9, б).

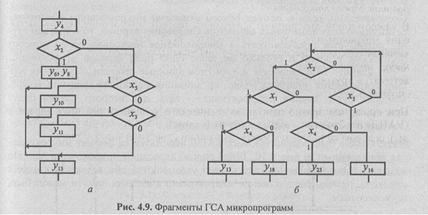
            В первом случае осуществляется безусловный переход к следующей микрокоманде, и адрес этой единственной микрокоманды (А1) должен размещаться в поле адреса выполняемой микрокоманды.

            Во втором случае необходимо сделать выбор одного из двух возможных следующих адресов. В поле адреса микрокоманды следует разместить:

            • номер х логического условия, по значению которого осуществляется выбор;

            • адрес А1 микрокоманды, которая будет выполняться, если указанное условие истинно;

            • адрес АО микрокоманды, которая будет выполняться, если указанное условие ложно.

            В третьем случае количество проверяемых в микрокоманде условий и адресов переходов может быть произвольным, в т. ч. и достаточно большим. В этом случае длина микрокоманды может быть весьма велика.

            При выборе формата микрокоманды нужно учитывать следующие обстоятельства:

            • следует эффективно использовать разряды поля, обеспечив по возможности его минимальную длину;

            • желательно ограничиться единственным форматом микрокоманды, в крайнем случае, выбирать минимально возможное разнообразие форматов.

            Справедливость первого требования очевидна. Относительно второй предпосылки можно заметить, что при большом числе форматов соответственно усложняется схема декодирования микрокоманды.

            Следовательно, если в рамках одного формата микрокоманды обеспечить реализацию всех возможных вариантов следования вершин, то в третьем случае потребуется предусмотреть в микрокоманде несколько полей номеров логических условий и столько же плюс одно поле адресов микрокоманд. Учитывая, что в большинстве алгоритмов длинные цепочки логических вершин встречаются довольно редко, организация подобного формата микрокоманды будет весьма неэффективна — ведь для второго случая будут использоваться только одно поле логического условия и два поля адреса, а для первого случая — только одно поле адреса.

            Чаще всего в быстродействующих УАПЛ используется формат микрокоманды, приведенный на рис. 4.10. Такой способ адресации микрокоманд принято называть принудительным, здесь явно указываются оба возможных адреса перехода, причем расположение микрокоманд в ячейках памяти может быть произвольным.

            Если в ГСА встречаются цепочки из  последовательных условных вершин, последняя из которых связана с операторной вершиной, то для их реализации в рамках формата микрокоманды, представленной на рис. 4.10, потребуется k микрокоманд (а следовательно, k тактов), в каждой из которых, кроме последней, поле микроопераций будет пустым. При выполнении таких микрокоманд в операционном автомате никаких действий не выполняется (он "простаивает"!), а управляющий автомат тратит k — 1 тактов на определение следующего адреса.

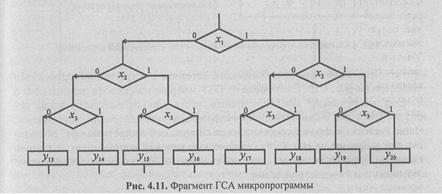
            Когда в ГСА встречается большое число таких цепочек, снижение производительности системы становится существенным. В этом случае используют другие подходы к формированию следующего адреса микрокоманды. Например, на рис. 4.11 представлен фрагмент ГСА, при реализации которого необходимо последовательно проверить три логических условия. Для быстрой реализации этого фрагмента достаточно выбрать некоторый базовый адрес (в данном случае он должен быть кратным 8), начиная с которого в ПЗУ микропрограмм расположить последовательно блок микрокоманд y₁₃ …у₂₀ Для определения адреса очередной микрокоманды достаточно к базовому адресу прибавить (приписать справа) значение вектора логических условий х₁х₂х₃. Адрес следующей микрокоманды определяется, таким образом, за один такт, но разработчик лишается возможности произвольного размещения микрокоманд в памяти.

            Если в ГСА имеется большое число линейных участков и, следовательно, безусловных переходов, то применение принудительной адресации ведет к неэффективному использованию памяти. Действительно, при безусловном переходе информативным является только поле адреса перехода А1, а поля х и АО — не используются.

            В целях уменьшения длины поля адреса микрокоманды можно использовать т. н. естественную адресацию (рис. 4.12), напоминающую механизм адресации команд в программе. В этом случае в состав устройства формирования адреса микрокоманды включают регистр-счетчик адреса микрокоманд, а в адресном поле микрокоманды — два поля: х и Al. Если заданное полем х условие истинно, то выполняется микрокоманда по адресу Al, иначе — микрокоманда по текущему значению счетчика адреса микрокоманд, предварительно увеличенному на единицу.

            Таким образом, УАПЛ с естественной адресацией работает с той же скоростью, что и УАПЛ с принудительной адресацией, при этом длина микрокоманды уменьшается на длину одного адресного поля, зато в структуре УФАМК необходимо дополнительно предусмотреть регистр-счетчик.

            Структурная схема микропрограммного автомата с естественной адресацией приведена на рис. 4.13. Считанные из ПЗУ микрокоманд слова помещаются в регистр микрокоманд (Рг МК), причем часть микрокомандного слова дешифрируется для выработки микроопераций, а поле адресации, естественно, используется для формирования адреса следующей микрокоманды. Мультиплексор выбирает из множества логических условий переменную, заданную полем х, а поле i позволяет при необходимости проинвертировать значение выбранного логического условия:

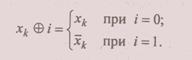
            Если значение выбранного логического условия истинно, то осуществляется переход по микропрограмме: при единичном значении на выходе сумматора по модулю два в регистр-счетчика адреса микрокоманды (Рг Сч А МК) загружается значение поля Al микрокоманды, содержащее адрес перехода. Если условие не выполняется (ложно), то загрузки нового адреса в Pг Сч А МК не производится, зато его прежнее значение увеличивается на единицу. В случае безусловного перехода (после операторной вновь следует операторная вершина) так же следует просто увеличить на единицу содержимое Рг Сч А МК. Для этого достаточно среди множества логических условий иметь константу 0 (тождественно ложное логическое условие) и именно ее номер указывать в поле х в случае безусловного перехода.

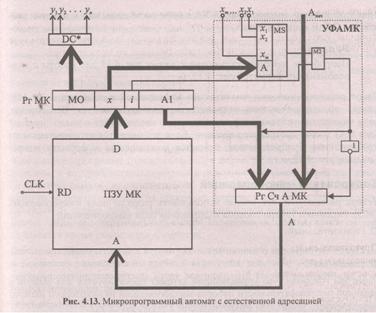
            Итак, для реализации формата микрокоманды с естественной адресацией (рис. 4.12, а) можно использовать структуру УА, показанную на рис. 4.13. Однако не всегда такой формат обеспечит оптимальные характеристики управляющего автомата.

            Действительно, на практике часто встречаются алгоритмы, содержащие в основном линейные участки и лишь изредка — условные вершины. Тогда для большинства микрокоманд (для тех, за которыми в ГСА следует операторная вершина) поля переадресации формата рис. 4.12, а использоваться не будут.

            В этом случае имеет смысл введение двух различных форматов микрокоманд, показанных на рис. 4.12, б. Один формат содержит только информацию о микрооперациях и после выполнения такой микрокоманды всегда добавляется единица к Рг Сч А МК — таким образом реализуется линейный участок.

            Команды другого формата применяются только в случае реализации условной вершины. Как обычно, проверяется значение заданного логического условия (или его инверсии), и если оно истинно — в Рг Сч А МК загружается значение поля Al микрокоманды, иначе к Рг Сч А МК добавляется единица.

            При этом никаких микроопераций УА в этом такте не выдает и никаких действий в ОА выполняется.

         Задание

            Попробуйте изменить структурную схему рис. 4.13 для работы с микрокомандами форматов рис. 4.12, б.

            Такое решение позволяет значительно эффективней использовать ЗУ МК, однако производительность устройства несколько снижается. Естественно, если количество условных вершин велико, то велико будет и число "пустых" (для ОА) тактов дискретного времени. Если это окажется неприемлемым по соображениям быстродействия, придется возвращаться к формату микрокоманды рис. 4.12, а.

         Кодирование микроопераций

            Теперь рассмотрим, как можно использовать разряды поля микроопераций (МО). Различают [2] три способа кодирования поля микроопераций: О горизонтальный; О вертикальный; CI смешанный.

            Ранее мы говорили, что управляющий автомат проектируется для выдачи в

заданной последовательности наборов микроопераций из некоторого наперед определенного множества микроопераций Y={y₁ ,…y_n}

            При горизонтальном способе кодирования каждой микрооперации Y_i E{y₁ ,…y_n }

ставится в соответствие разряд поля микроопераций микро- командного слова. В этом случае количество разрядов поля микроопераций N равно числу и различных микроопераций, вырабатываемых УА.

            Достоинствами горизонтального способа кодирования являются: CI возможность формирования произвольных микрокоманд из заданного набора микроопераций;

О простота реализации схем формирования микроопераций, фактических отсутствие, т. к. выход каждого разряда поля микроопераций регистра микрокоманд является выходной линией УА — соответствующей микрооперацией.

            Недостаток — чаще всего неэффективно используется память микрокоманд, Действительно, если число микроопераций УА составляет 80, а количество выполняемых в микрокоманде микроопераций — не более б (типичные характеристики для УА АЛУ), то в восьмидесяти разрядном поле микроопераций каждого микрокомандного слова будет не более б единиц.

            При вертикальном способе кодирования в поле микроопераций помещается номер выполняемой микрооперации. При этом количество разрядов N, которое следует предусмотреть в поле микроопераций, определяется выражением: N = k > log₂< и. Достоинство способа в экономном использовании памяти микрокоманд. Недостаток — в невозможности реализовать в микрокоманде более одной микрооперации.

Если реализуемые алгоритмы и структура ОА таковы, что в каждом такте дискретного времени выполняется не более одной микрооперации, то вертикальный способ кодирования — оптимальное решение. В иных случаях можно попытаться преобразовать исходную микропрограмму к такому виду, чтобы в каждом такте выполнялось не более одной микрооперации. Например, если в микропрограмме (представленной в форме ГСА) имеется операторная вершина, в которой устанавливаются в исходное состояние несколько ячеек (элементов) памяти (и, следовательно, она включает несколько микроопераций), то ее можно заменить на несколько вершин, в каждой из которых устанавливается только один элемент с помощью одной микрооперации. Теперь можно применить вертикальный способ кодирования, правда, при этом увеличивается время реализации алгоритма.

            Однако во многих случаях структура операционного автомата не допускает возможности разнесения во времени некоторых действий, управляемых различными микрооперациями. Тогда вертикальный способ кодирования поля микроопераций не применим.

            Вертикальный и горизонтальный способы кодирования — две крайности. Истина обычно лежит "посередине". Рассмотрим смешанный способ кодирования, идея которого состоит в следующем. Если во всех микропрограммах, реализуемых УА, нет микрокоманды с большим, чем s, числом микроопераций, то в поле микроопераций можно предусмотреть s подполей разрядностью k, в каждом из которых помещать номер нужной микрооперации. Такой способ позволяет в любой микрокоманде реализовать произвольную s-ку микроопераций, т. е. сохранить гибкость горизонтального кодирования, при возможном значительном сокращении разрядности поля микроопераций: N s· k=slog₂>n. Так, для приведенного выше примера (n=80, s=6) определим k = 7 ≥ log₂> 80, N 7 6 = 42 (тоже, конечно, немало), что позволит почти вдвое сократить разрядность поля микроопераций по сравнению с горизонтальным способом кодирования.

            Эффективность применения смешанного кодирования существенно зависит

от значения s, которое может лежать в диапазоне 1≤s≤n. При s =1 имеем случай вертикального кодирования, при s = n — горизонтального.

            Канонический способ смешанного кодирования, идея которого представлена выше, предполагает, что каждое из s подполей микроопераций содержит k разрядов, следовательно, в любом подполе можно закодировать любую микрооперацию у E Y. Возможно, например, построение микрокоманды, содержащей s одинаковых микроопераций у_i, у_i,...у_i, что является явно бессмысленным.

            С целью сокращения разрядности полей микроопераций множество микроопераций Y разбивается на подмножества У_i, Y₂, ..., У_p, такие, что

Каждое подполе поля микроопераций кодирует микрооперации только одного подмножества Y_i € Y. Поскольку, разрядность k_i каждого из подполей может быть меньше k . Очевидно, при "удачном" (пока скажем так) распределении микроопераций по подмножествам можно будет реализовать любую операторную вершину ГСА микропрограммы с помощью одной микрокоманды (т. е. достигнуть быстродействия, характерного для горизонтального способа кодирования), при этом значительно уменьшить разрядность поля микроопераций даже по сравнению с каноническим способом смешанного кодирования.

            "Удачное" разбиение исходного множества микроопераций связано с понятием совместимости (несовместимости) микроопераций [7]. Некоторые из используемых в микропрограмме микроопераций могут выполняться параллельно во времени, в то время как другие — только последовательно. Свойство совокупности микроопераций, гарантирующее возможность их одновременного выполнения, называется совместимостью. Микрооперации, не обладающие указанным свойством, называются несовместимыми.

            Рассматриваются два аспекта совместимости. Совместимость, обусловленная содержанием операторов, реализуемых под действием микроопераций, называется функциональной. Примером двух функционально несовместимых микроопераций могут служить следующая пара: (у₈ . Сч _n:= О) и (y₁₅  Сч n:= Сч n — 1) и вообще любые микрооперации, присваивающие различные значения одной и той же переменной.

            Если невозможность одновременного выполнения микроопераций связана с ограничениями возможностей структуры операционного автомата, то такая несовместимость называется структурной. Например, операторы (Рг С:= Рг А) и (Рг Р:= Рг В) функционально совместимы, но если в конкретной структуре ОА связь между этими регистрами осуществляется через общую магистраль (шину), то они структурно несовместимы.

            Вернемся к способам разбиения исходного множества микроопераций на подмножества. Очевидно, в каждое подмножество следует включать только взаимно несовместимые микрооперации. При проектировании УА возникает вопрос: какой тип совместимости микроопераций учитывать при разбиении исходного множества Y на подмножества?

            Если несовместимыми считать только те микрооперации, которые принципиально нельзя реализовать на заданной (спроектированной) структуре ОА, то таких пар окажется немного, большинство микроопераций будут попарно совместимыми, следовательно, их необходимо включать в разные подмножества. При этом число подмножеств р может превысить значение s и приближаться к n.

            Если рассматривать в качестве совместимых только те микрооперации, которые размещаются в одной операторной вершине реализуемых алгоритмов, а все остальные считать несовместимыми, даже если их можно выполнить одновременно в структуре ОА (но не требуется при реализации данных алгоритмов), то р→s, эффективность кодирования будет значительно выше. Правда, если потребуется модифицировать реализуемый алгоритм или добавить еще группу алгоритмов для реализации, и в одной операторной вершине окажутся микрооперации, включенные ранее в одно подмножество, придется заново перепроектировать УА.

            Разработано несколько формальных методов [7] разбиения множества микроопераций на подмножества. В простейшем случае можно воспользоваться методом "прямого включения". Рассмотрим пример проектирования УАПЛ по заданной микропрограмме.

            Пример проектирования УАПЛ

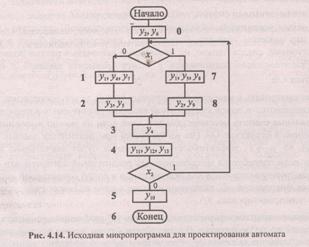
            Мы уже говорили, что исходным для проектирования УА является микропрограмма, представленная, например, в форме ГСА. На рис. 4.14 изображена некоторая микропрограмма, которую мы будем считать исходной для проектирования нашего автомата.

            Заметим, что на этапе проектирования управляющего автомата семантика ГСА не рассматривается: сейчас нас уже не интересует "правильность" микропрограммы относительно реализуемого алгоритма. Просто имеется синтаксически правильно построенная ГСА и требуется разработать устройство, реализующее это поведение.

            В качестве управляющего устройства будем проектировать управляющий микропрограммный автомат с программируемой логикой.

            Общая структура такого устройства представлена на рис. 4.8. Исходя из описанных выше вариантов организации адресации и способов кодирования поля микроопераций, выберем естественную адресацию и смешанный способ кодирования микроопераций. Ограничимся единственным форматом микрокоманды.

Определение формата микрокоманды

            На разрядность полей микрокоманды влияют следующие параметры:

            • количество различных микроопераций, формируемых УА, в конечном итоге определяет (с учетом выбранного способа кодирования) длину поля микроопераций;

            • количество различных логических условий определяет длину поля х;

            • количество вершин ГСА связано с общим числом микрокоманд, а следовательно, с объемом памяти микропрограмм и разрядностью поля адреса микрокоманды.

            Множество микроопераций У, используемых в заданной ГСА- Y = {у₁, у₂, ..., у₁₃}, мощность множества IYI = 13 При горизонтальном кодировании поле микроопераций будет занимать 13 разрядов. Вертикальный способ кодирования микроопераций к заданной ГСА неприменим, поскольку ГСА содержит вершины с двумя и тремя микрооперациями.      Попробуем реализовать разбиение множества Y на подмножества несовместимых микроопераций. Воспользуемся методом прямого включения, учитывая, что отношение совместимости задано на самой ГСА. Строго говоря, следовало бы построить матрицу совместимости микроопераций, но в рассматриваемом примере небольшой размер алгоритма позволяет определять отношение совместимости непосредственно по ГСА.

            На сколько подмножеств следует разбивать исходное множество? По меньшей мере, на s =3 в нашем случае. Образуем три подмножества — Y₁, Y₂ Y₃ и разместим в них микрооперации операторной вершины, имеющей s микроопераций. Если в ГСА таких вершин несколько — выберем любую из них.

            Теперь разместим по множествам микрооперации следующей вершины, содержащей (в нашем случае) три микрооперации:

            Заметим, что первая микрооперация второй рассматриваемой вершины совпадает с первой микрооперацией первой вершины. Она уже присутствует в множестве Y_i (у₁ € Y₁), поэтому не включается вторично. Наконец, разместим микрооперации третьей "тройной" вершины:

            Теперь нераспределенными остались микрооперации (некоторые) "двойных" и "одинарных" вершин. Вершина (y₂, у₆) — обе микрооперации несовместимы с уже распределенными, поэтому могут располагаться произвольно, лишь бы они находились в разных подмножествах:

Вершина (у₂, у₉) — y₉ нельзя помещать в Y₁ поскольку совместимая с ней у₂ E Y₁ Подмножества лучше заполнять равномерно, поэтому разместим Y₉ B Y₃:

            Остались две нераспределенные микрооперации — у₃ и у₁₀, первая из которых совместима с у₅, поэтому ее нельзя помещать в У₂, а вторая несовместима ни с какими другими и может размещаться произвольно. Поместим их в множество, имеющее пока наименьшую мощность — Y₁ ..

Все 13 микроопераций распределились по трем подмножествам, при этом выполняются условия (4.8) (т. е. имеет место разбиение исходного множества, Y₂), однако УА обычно должен вырабатывать еще одну микрооперацию, свидетельствующую об окончании выполнения алгоритма и предназначенную, для использования не в ОА, а в управляющем автомате верхнего уровня иерархии. Назовем эту микрооперацию у_k и включим в произвольное множество (например, в Y₂), поскольку она, естественно, несовместима ни с одной микрооперацией. Итак, имеем следующее распределение:

Для кодирования элементов каждого из трех подмножеств потребуется по три двоичных разряда. Может показаться, что для Уз хватит и двух, ведь

|Y₃| =4=2²  ,однако следует учесть, что в каждом подмножестве необходимо предусмотреть один код для случая отсутствия микрооперации из этого под множества в микрокоманде. Оптимальным разбиением исходного множества будет такое, когда  |= 2r-1, где r-натуральное число.

            В подмножестве Y₃, всего одна "лишняя" микрооперация, а среди кодов Y_i и Y₂ есть свободные. Попробуем перенести одну из микроопераций из Уз в другое подмножество, сохраняя, естественно, требование к попарной несовместимости всех микроопераций одного подмножества. Очевидно, первые три элемента подмножества Уз нельзя перенести в другое, т. к. они являются микрооперациями из "тройных" вершин. Зато микрооперация у₉ совместима только с у₉ поэтому у₉ можно перенести в У. Окончательно получим, предварительно упорядочив элементы подмножеств в порядке возрастания индексов:

Теперь мы можем определить размеры полей микрокоманды. Поле микроопераций будет состоять из трех подполей — Y₁, Y₂, Y₃ (назовем их по именам соответствующих подмножеств), размером в 3, 3 и 2 двоичных разрядов

соответственно.

            Поле номера условия х должно содержать номер одного из двух логических условий — x₁ , x₂ (один разряд?), однако для повышения гибкости процесса микропрограммирования удобно иметь возможность выбирать еще и тождественно истинное и тождественно ложное условия. Итак, поле х занимает два разряда.

            Наконец, поле адреса определяется объемом памяти микропрограмм. Если в нашем примере мы будем считать, что разрабатываем УА только для реализации микропрограммы рис. 4.14, а она содержит 8 вершин, не считая начальной, конечной и условных, количество микрокоманд (каждая микрокоманда — ячейка памяти, имеющая свой адрес), выдаваемых УА, будет никак не менее 8, а реально — (1,2, ..., 1,3) х 8, то для поля адреса в микрокоманде следует отвести 4 разряда (2 =16 >1,3 х 8 =11).

            В поле адреса будет располагаться адрес памяти — двоичный номер ячейки, а в паях У, и х — коды микроопераций и логических условий. Окончательно формат микрокоманды будет иметь вид, приведенный на рис. 4.15.

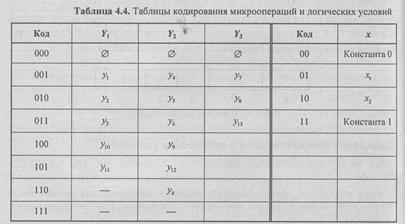
            Кодировка микроопераций и логических условий

            Здесь может осуществляться произвольно, например так, как показано в табл. 4.4.

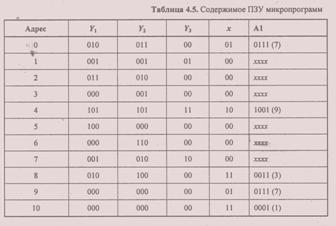
Выбрав кодировку, можно начинать писать микропрограмму в машинных микрокодах. Фактически мы формируем содержимое ПЗУ микропрограмм (табл. 4.5).

            Анализируя ГСА микропрограммы (см. рис. 4.14), увидим, что в первом такте работы автомата должны быть выданы микрооперации у₂ и у₅. Учитывая, что в начальном состоянии автомата Рг Сч АМК удобно установить в 0, микрокоманда, расположенная по нулевому адресу, должна сформировать микрооперации у₂ и у₆. Из табл. 4.4 следует, что у_{2 €} Y₁  имеет код 010, а у₆ € Y₂ (код 011). Микрооперации, включенные в множество в этой микрокоманде отсутствуют. Тогда поле микроопераций микрокоманды должно содержать следующий код: 010 011 00.

            После первой операторной вершины ГСА следует условная вершина, содержащая логическую переменную х_1. Следовательно, в микрокоманде должна анализироваться переменная х_1.  При x₁= 0 следующей должна выполняться микрокоманда (у_{1 ,} у₄, у₇) по адресу 1, иначе — микрокоманда (у₁, у₅, у₈) по неизвестному пока адресу. Заполним строку таблицы для нулевой ячейки памяти следующим кодом: 010 011 00 01????. К этой строке нам еще придется вернуться для заполнения поля адреса перехода.

            По адресу 1 должна располагаться микрокоманда, формирующая микрооперации (у₁, у₄, у₇) и безусловно передающая управление следующей микрокоманде (уз, у5). Заполняем строку таблицы для первой ячейки памяти: 001 001 01 00 хххх. В поле х этой микрокоманды код 00 указывает на тождественно ложное условие (константу 0) — к Рг Сч А МК будет добавлена 1, а содержимое поля адреса перехода не используется.

Действуя аналогичным образом, заполняем строки табл. 4.5, соответствующие адресам ПЗУ 3, 4, 5, 6 (на рис. 4.14 рядом с операторными вершинами обозначены адреса соответствующих микрокоманд). В микрокоманде по адресу 4 выполняется условный переход по переменной х₂, причем адрес перехода при х₂ =1 пока также неизвестен. По адресу 6 размещается микрокоманда, соответствующая конечной вершине ГСА, завершающая работу микропрограммы микрооперацией у_k. Таким образом, завершено микропрограммирование участка ГСА от начальной до конечной вершины, соответствующего нулевым значениям логических переменных.

            Теперь можно вернуться к логической вершине, размещенной после первой операторной. Микрокоманду, следующую за ее единичным выходом (y₁, y₅, у₈), можно разместить по следующему свободному (7) адресу. Поэтому в поле адреса перехода ячейки 0 теперь можно поместить код 0111. Сама микрокоманда по адресу 7 формирует три микрооперации и переходит к микрокоманде по адресу 8: 001 010 10 00 хххх.

            Микрокоманда по адресу 8 не связана с логической вершиной, но она должна передавать управление уже существующей (по адресу 3) микрокоманде. Поэтому ее поле

х = 11 адресует тождественно истинное условие, а в поле переадресации указан адрес 3.

            Наконец, остался неопределенным адрес перехода в микрокоманде по адресу 4. Сейчас уже всем операторным вершинам ГСА (включая конечную) соответствуют микрокоманды в ячейках ПЗУ. На какую из них следует передать управление после проверки условия x₂, если оно окажется истинным? Из ГСА видно, что тогда следует проверить условие х₁ — случай двух подряд расположенных условных вершин. Передать управление на адрес О, где проверяется это условие? Но тогда выполнятся и микрооперации у₁, у₄, у₇, а это микропрограммой не предусмотрено. Очевидно, в микропрограмму следует включить дополнительно микрокоманды (в нашем случае — по адресам 9 и 10), которые не формируют никаких микроопераций, а обеспечивают только передачу управления. Первая осуществляет условный переход по переменной х₁ на адрес 7, вторая (которая будет выполняться только при x₁ =0) — безусловно на адрес 1. Теперь код микропрограммы полностью сформирован.

            Осталось изобразить структурную схему разработанного управляющего автомата (рис. 4.16).