3.5. Обратный код и выполнение алгебраического сложения в нем

            При выполнении алгебраического сложения в прямом коде приходится, во-первых, не только складывать, но и вычитать двоичные коды; во-вторых, код знака результата формируется искусственно, т. е. знаковые разряды обрабатываются по правилам, отличным от правил обработки разрядов числа. Для устранения отмеченных недостатков в ЭВМ широко используются специальные представления двоичных чисел — т. н. обратный и дополнительный коды.

            Представление обратного кода определяется следующим соотношением:

Из (3.17) следует, что обратный код положительного числа равен самому числу! Для получения обратного кода отрицательного числа достаточно присвоить знаковому разряду значение 1 и про инвертировать все остальные разряды числа:

3.5.1. Алгебраическое сложение в обратном коде

            Очевидно, что при отсутствии переполнения возможны четыре случая сочетания знаков и модулей слагаемых [11]. 0 Случай 1.

Заметим, что в случаях 2 и 4 требуется одинаковая коррекция: — 2+ 2^-n, причем только в этих двух случаях возникает перенос из знакового разряда. Действительно, в случае 4 оба знаковых разряда равны 1, а в случае 2 знак результата — О, что при разных знаках слагаемых может получиться только при появлении переноса из первого разряда в нулевой (знаковый), а следовательно, обязательно будет перенос и из знакового разряда. Вес знакового разряда соответствует 2⁰, а вес переноса из него — 2¹ . Таким образом, игнорируя перенос 0 1 из знакового разряда, мы вычитаем из результата 2, что соответствует первому члену корректирующего выражения. Для учета второго члена следует добавить 1 к младшему разряду суммы, вес которого составляет 2^-n .

            В случаях 1 и 3 переноса из знакового разряда не возникает и коррекция результата не требуется.

            Таким образом, для выполнения алгебраического сложения двоичных чисел, представленных в обратном коде, достаточно, не анализируя соотношение знаков и модулей, произвести сложение чисел, включая знаковые разряды, по правилам двоичной арифметики, причем возникающий в знаковом разряде перенос должен быть добавлен к младшему разряду результата, осуществляя тем самым коррекцию предварительной суммы. Полученный код является алгебраической суммой слагаемых, представленной в обратном коде.

Приведенный пример соответствует рассмотренному выше случаю 2; перенос, возникающий в знаковом разряде, циклически передается в младший разряд предварительного результата.

Таким образом, ноль в обратном коде бывает "положительный" и "отрицательный" (обратите внимание на выражение (3.17)), причем добавление к числу "отрицательного" нуля, как и "положительного", дает в результате значение первого слагаемого.

Теперь рассмотрим случаи, когда |А +В| >1| , что соответствует переполнению разрядной сетки. Очевидно, учитывая, что |А| <1 и |В|  <1, переполнение возможно только при сложении чисел с одинаковыми знаками. Рассмотрим примеры.

Сложить два числа в обратном коде: 13/16+5/16=18/16. Результат — на рис. 3.9.

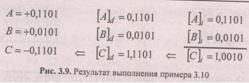
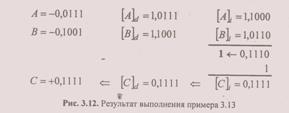
Переполнение в соответствии с (3.19) обнаруживается и в этих случаях.

            Итак, использование обратного кода в операциях алгебраического сложения/вычитания позволяет:

            • использовать только действие арифметического сложения двоичных кодов;

            • получать истинное значение знака результата, выполняя над знаковыми

разрядами операндов те же действия, что и над разрядами чисел;

            • обнаруживать переполнение разрядной сетки.

            Еще одним достоинством применения обратного кода можно считать простоту взаимного преобразования прямого и обратного кода. Однако использование обратного кода имеет один существенный недостаток — коррекция предварительной суммы требует добавления единицы к ее младшему разряду и может вызвать (в некоторых случаях) распространение переноса по всему числу, что, в свою. очередь, приводит к увеличению вдвое времени суммирования. Для преодоления этого недостатка можно использовать вместо обратного дополнительный код.

            3.6. Дополнительный код и арифметические операции в нем

            Связь между числом и его изображением в дополнительном коде определяется соотношениями  

Таким образом, и дополнительный код положительного числа равен самому числу (как обратный и прямой). Дополнительный код отрицательного числа дополняет исходное число до основания системы счисления.

            Дополнительный код отрицательного числа образуется в соответствии со следующим выражением:

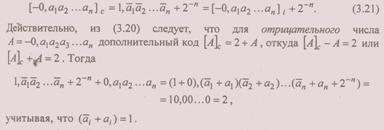
Таким образом, для преобразования отрицательного двоичного числа в дополнительный код следует преобразовать его сначала в обратный код (установив знаковый разряд в 1 и проинвертировав все остальные разряды числа) и добавить единицу к младшему разряду обратного кода.

            Другой способ перевода прямого кода отрицательного двоичного числа в дополнительный (приводящий, разумеется, к такому же результату) определяется следующим правилом: оставить без изменения все младшие нули и одну младшую единицу, остальные разряды (кроме знакового!) про инвертировать.

             3.6.1. Алгебраическое сложение в дополнительном коде                     

            Рассмотрим те же четыре случая сочетания знаков и модулей операндов, что и при рассмотрении сложения в обратном коде в разд. 3.5.1:

            Как и в обратном коде, коррекция требуется только в случаях 2 и 4, причем в дополнительном коде коррекция заключается просто в игнорировании переноса, возникающего из знакового разряда. Рассмотрим несколько примеров.

Из примера 3.18 видно, что "ноль" в дополнительном коде имеет единственное "положительное" представление.

            Теперь рассмотрим случаи, когда |А+ В| >1, что соответствует переполнению разрядной сетки.

Очевидно, для дополнительного кода, как и для обратного, справедливо выражение (3.19). Теперь рассмотрим случаи |А+В| =l. Для положительных слагаемых пример 3.12 может относиться как к обратным, так и к дополнительным кодам, но преобразование результата — дополнительного кода в прямой приведет к другому значению. Действительно,

Переполнение по признакам выражения (3.19) не обнаружено! Однако результат операции — "отрицательный ноль", который не может использоваться

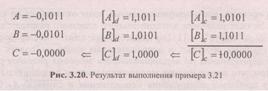
в дополнительном коде. Действительно, сложение в дополнительном коде  любого числа с "отрицательным нулем" 1,00...0 меняет знак этого числа. Итак, : при А <0, В<0, |А+В| =1 признаком переполнения служит не выражение (3.19), а код результата 1, 00...0. . Таким образом, значение признака переполнения в дополнительном коде можно получить в соответствии со следующим выражением:

 Подведем итоги. Применение дополнительного кода, по сравнению с обратным, имеет одно существенное преимущество — коррекция результата  сводится просто к отбрасыванию переноса из знакового разряда и не , требует дополнительных затрат времени. К недостаткам применения , дополнительного кода можно отнести, во-первых, более сложную процедуру взаимного преобразования ПК↔ДК, требующую дополнительных затрат времени, и, во-вторых, проблемы с обнаружением переполнения. Для того чтобы минимизировать влияние первого не  недостатка, данные в ' памяти часто хранят в дополнительном коде. В этом случае преобразования ПК↔ ДК выполняются относительно редко — только при вводе и выводе.

            3.6.2. Модифицированные обратный и дополнительный коды

            Для определения переполнения используют выражение (3.19) — булеву функцию трех переменных. С целью более удобного обнаружения переполнения в обратном и дополнительном кодах можно применить т. н. "модифицированные" их представления:

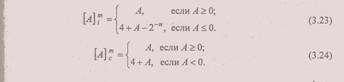
Нетрудно показать, что модифицированные коды отличаются от соответствующих обычных наличием дополнительного знакового разряда: "плюс" кодируется 00, а "минус" — 11. Эта своеобразная избыточность, сохраняя все качества обычных обратных и дополнительных кодов, позволяет фиксировать факт переполнения по неравнозначности знаковых разрядов результата. Заметим, что использование модифицированного дополнительного кода не решает проблемы обнаружения переполнения в случаях A<0, В<0, |А+ В| =1.

            3.7. Алгоритмы алгебраического сложения в обратном и дополнительном коде

В разд. 3.5.1 и 3.6 подробно обсуждалось, как выполнить операцию алгебраического сложения чисел, уже представленных соответственно в обратном или дополнительном коде. Для этого достаточно выполнить арифметическое сложение двоичных векторов, получив истинное значение результата в код с представления операндов. При операции в обратном коде возникающий из знакового разряда перенос следует добавить к младшему разряду суммы. Переполнение обнаруживается согласно выражению (3.19).

            В случае если слагаемые представлены в прямом коде, а операция выполняется в обратном или дополнительном, их следует сначала преобразовать в соответствующий код, затем выполнить сложение и сумму вновь преобразовать в прямой код — код результата всегда должен соответствовать коду исходных данных. На рис. 3.21 приведен пример алгоритма алгебраического сложения в обратном коде чисел, представленных в прямом коде, а на рис.3.22 — алгебраическое сложение/вычитание чисел в дополнительном коде.

            При рассмотрении алгоритмов использованы те же обозначения, которые были введены в разд. 3.4 для рис. 3.1. Дополнительно введем обозначения:

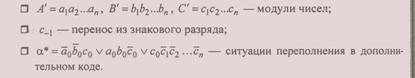
В алгоритме рис. 3.22 можно отметить один недостаток. При выполнении вычитания   ( f = 1) необходимо получить дополнение второго операнда: В':= В'+1, что является арифметической операцией и требует времени, достаточного для прохождения переноса по всем разрядам числа. Для исключения дополнительной арифметической операции можно в первой операторной

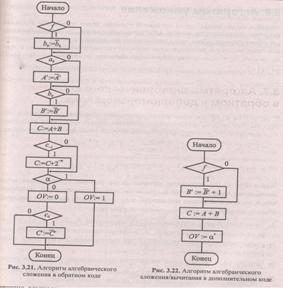
f вершине осуществить только инверсию (логическую операцию, которая выполняется быстро), а недостающую "единицу" к младшему разряду добавить,  если это необходимо, в качестве входного переноса младшего разряда в момент суммирования слагаемых. Таким образом, в двух первых операторных вершинах алгоритма рис. 3.22 следует поместить такие операторы:

3.8. Алгоритмы умножения .

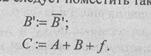
            Умножение двоичных чисел со знаком удобнее всего проводить в прямом коде. Действительно, знак произведения не зависит от соотношения величие модулей сомножителей, а зависит только от их знаков:

Выражение (3.26) определяет процесс формирования произведения путем вычисления частичных сумм и суммы частичных произведений. Напомним, что b_n — старший разряд множителя, а b_n младший. Вычисляя непосредственно по формуле (3.26), следует на каждом шаге:

            1. Проанализировать очередную цифру множителя b_i,. Если b_i, =1, то очередная частичная сумма равна А, и она добавляется к накопленной ранее сумме частичных произведений S (на первом шаге S = 0), иначе добавления не производится.

            2. Осуществить правый сдвиг частичного произведения S на один разряд. Умножение S∙2^-2 соответствует делению на 2, что в двоичной систем счисления равносильно сдвигу числа на один разряд вправо.

            3. Пункты 1 и 2 повторяются до тех пор, пока не будут исчерпаны все

цифры множителя.

            Очевидно, число шагов при использовании приведенного выше метода равно разрядности модуля множителя. Алгоритм умножения чисел, представленных в прямом коде, приведен на рис. 3.23.

            В изображенном на рис. 3.23 алгоритме, в отличие от алгоритмов сложения/вычитания, значение OV = 0 устанавливается безусловно. Действительно, А и В — дробные числа; очевидно при |А|<1 и |В|<1 всегда |А х В| <1.

            В результате вычисления по формуле (3.26) получается произведение разрядностью 2п. Если рассматривать сомножители как дроби, то младшие n разрядов можно просто отбросить (округление с недостатком) или округлить до n-разрядного модуля по правилам округления. Очевидно, из выражения (3.26) легко получить

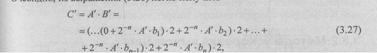
что позволяет производить умножение, начиная со старших разрядов множителя. При этом сдвиг суммы частичных произведений осуществляется влево на один разряд, чему соответствует умножение двоичного числа на 2.

3.8.1.Умножение в дополнительном коде

            Если числа поступают на обработку уже представленные в дополнительном коде, то для умножения их можно перевести в прямой код или умножать сразу в дополнительном коде. В последнем случае в умножении участвуют и знаковые разряды сомножителей, причем знак произведения получается в том же цикле, что и разряды модуля произведения. Однако в некоторых случаях требуется коррекция предварительного результата. Мы не будем рассматривать здесь случаи умножения в дополнительном коде. Любознательным рекомендуем соответствующую литературу, например [11].

            3.8.2.Методы ускорения умножения

            Методы ускорения умножения принято делить [8, 11] на аппаратные и логические. Как те, так и другие требуют дополнительных затрат оборудования, При использовании аппаратных методов дополнительные затраты оборудования прямо пропорциональны числу разрядов в операндах. Эти методы вызывают усложнение схемы операционного автомата АЛУ.

            Дополнительные затраты оборудования при реализации логических методов ускорения умножения не зависят от разрядности операндов. Усложняется в основном схема управления АЛУ. В ЭВМ для ускорения умножения часто используются комбинации этих методов.

            К аппаратным методам ускорения умножения относятся ускорение выполнения операций сложения и сдвига, введение дополнительных цепей сдвига, позволяющих за один такт производить сдвиг информации в регистрах сразу на несколько разрядов, совмещение во времени операций сложения и сдвига, построение комбинационных схем множительных устройств, реализующих "табличное" и "матричное" умножение.

           Пример реализации умножения с использованием n-входового сумматора показан на рис. 3.24.

            Здесь частичные произведения формируются на схемах n-разрядных конюъкторов одновременно и подаются на входы n-входового сумматора, причем в сумматоре за счет соответствующей коммутации цепей осуществляются сдвиги частичных произведений (как при выполнении умножения на бумаге "в столбик"). На выходе сумматора получается 2n-разрядное произведение.

            Метод табличного умножения (рис.3.25) позволяет получить произведение за один такт при условии, что вся таблица умножения (результаты умножения всевозможных пар n-разрядных сомножителей!) будет размещена в памяти. Очевидно, для этого понадобится запоминающее устройство объемом 2²ⁿ 2n-разрядных слов (точно таким же способом можно выполнять и другие "длинные" операции — деление, вычисление функций). Так, для организации 8-разрядного умножителя потребуется память объемом 2¹⁶ ×16 бит = = 128 Кбайт, что для современного уровня развития интегральной технологии не кажется чрезмерным.

            Однако для 16-разрядного АЛУ умножитель "потянет" уже на 2³² ×32 бит = = 16 Гбайт! Что касается современных 32-разрядных процессоров, то к расчету потребности в памяти для таких умножителей даже страшно приступать.

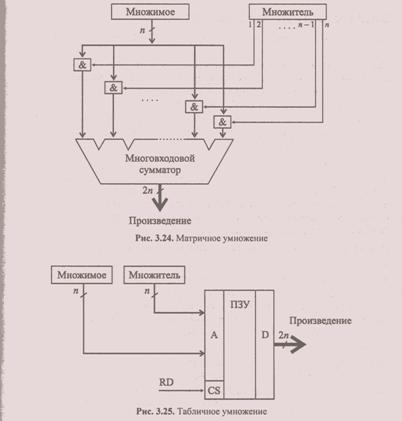
            В этом случае можно воспользоваться таблицей умножения меньшей разрядности, получая с ее помощью частичные произведения, а потом просуммировать их, предварительно сдвинув на соответствующее число разрядов.

            Рассмотрим этот способ умножения подробнее. Пусть n — четное. Тогда каждый из двух сомножителей можно представить конкатенацией двух полей одинаковой разрядности n/2: А = А_h А₁, В = В_h В₁. В этом случае произведение можно представить следующим выражением:

            Таким образом, располагая, например, таблицей умножения Зх8, можно получить произведение двух 16-разрядных сомножителей, сложив (с соответствующим сдвигом) всего 4 слагаемых. Проиллюстрируем этот метод на простом примере.

            Пусть требуется перемножать 4-разрядные числа без знака. Построим таблицу умножения 2 х 2 (при рассмотрении примера не будем включать в нее пары сомножителей, когда один из них равен нулю, а так же пары сомножителей, симметричные уже включенным) — рис. 3.26.

            Среди логических наиболее распространены в настоящее время методы, позволяющие за один шаг умножения обработать несколько разрядов множителя. Рассмотрим один из способов умножения на два разряда множителя, начиная с его младших разрядов. В зависимости от результата анализа пары разрядов множителя предусматриваются следующие действия (табл. 3.3).

            Таким образом, для умножения сразу на два разряда множителя достаточно:

            • при 00 просто произвести сдвиг на два разряда;

            • при 01 прибавить к сумме частичных произведений множимое и произвести сдвиг на два разряда;

            • при 10 прибавить к сумме частичных произведений удвоенное множимое и произвести сдвиг на два разряда;

            • при 11 вычесть из суммы частичных произведений множимое (или добавить обратный (дополнительный) код множимого), произвести сдвиг на два разряда и добавить 1 к следующей (старшей) паре цифр множителя.

            При классическом методе умножения двоичных n-разрядных чисел согласно выражению (3.26) потребуется и сдвигов суммы частичных произведений и n/2 (в среднем) сложений множимого с суммой частичных произведений, Один из методов ускорения операции умножения — анализ сразу двух разрядов множителя. Это позволит получить результат, применяя n/2 сдвигов и (в среднем) 3п/8 сложений/вычитаний.

            3.9. Алгоритмы деления

            Знак частного, как и знак произведения, не зависит от соотношения модулей операндов и определяется в зависимости от знаков операндов по выражению (3.25). Поэтому рассмотрим сначала процесс деления модулей двоичных чисел.

            Пусть А — делимое, В — делитель, С — частное, W — остаток.

            Очевидно, при представлении чисел с фиксированной запятой как дробных, должно соблюдаться условие

|А| <|В|,

иначе С≥ 1, что соответствует переполнению разрядной сетки.

            Процесс деления двоичных чисел может быть сведен к последовательности вычитаний и анализа знаков получающихся остатков. Сформулируем словесный алгоритм деления следующим образом:

            1. Вычитают из делимого делитель. Если знак разности 0, то деление невозможно в силу нарушения условия (3.29), и следует, установив OV =1, завершить операцию; иначе в разряд целой части частного записывают 0 (в конце операции в этот разряд помещается знак частного).

            2. Так как остаток (разность А — В) оказался отрицательным, восстанавливают остаток путем добавления делителя к остатку.

            3. Сдвигают восстановленный остаток влево на один разряд.

            4. Вычитают из сдвинутого остатка делитель; если полученная разность положительна, то очередной цифрой частного становится 1, и следует перейти к п. 3; иначе очередная цифра частного — 0 и переходят к п. 2.

            Пункты 2 — 4 повторяют столько раз, сколько цифр требуется получить в

частном.

            3.9.1. Деление без восстановления остатка

            Приведенный выше метод деления называется методом деления с восстановлением остатка. При получении отрицательного остатка на очередном шаге деления необходимо перед левым сдвигом восстановить остаток путем добавления к нему делителя. При этом для получения n-разрядного частного требуется в среднем 1,5n циклов сложения/вычитания.

            Существует алгоритм деления без восстановления остатка, позволяющий

корректировать отрицательные остатки без дополнительного цикла сложения. Рассмотрим действия, производимые с остатками в цикле деления в зависимости от полученного знака остатка (табл. 3.4).

            Видно, что если на очередном шаге остаток получился отрицательный, его можно не восстанавливать, но на следующем шаге в этом случае нужно вместо вычитания делителя из сдвинутого остатка добавить делитель к сдвинутому остатку.

            Действительно, если W- В< О, то следует восстановление остатка и сдвиг восстановленного остатка влево (его удвоение) 2 ·(W- В+В). На следующем шаге вычитаем делитель и получаем 2W— В. Тот же результат может быть получен, если сдвинуть не восстановленный остаток, но на следующем шаге вместо вычитания произвести добавление делителя:

2∙ (W — B)+B =2W — 2B+B = 2W+В.

            3.10. Арифметические операции с числами, представленными в формате с плавающей запятой

            В таком формате число определяется значениями мантиссы и порядка:

N= m∙q^p

где и — мантисса числа, р — порядок, q — основание. (3.30)

            Мантисса и порядок могут иметь свои знаки, причем знак мантиссы соответствует знаку числа. Основание q может не совпадать с основанием системы счисления. При операциях с двоичными числами часто для расширения диапазона представления чисел выбирают q = 2^k, например, q = 16.

            В машинном представлении формат числа с плавающей запятой (рис. 3.30)

задается двумя полями — полем мантиссы m и полем порядка р, причем каждое поле имеет свой разряд знака. Значение порядка в формате числа не указывается — оно подразумевается одинаковым для всех чисел.

            Мантисса и порядок представляются в формате с фиксированной запятой, причем обычно порядок — целое число со знаком (запятая фиксирована после младшего разряда), а мантисса — правильная дробь (запятая фиксирована между знаковым разрядом и старшим разрядом модуля). С целью увеличения точности представления числа в заданном формате мантиссу представляют в нормализованной форме, когда старший разряд модуля мантиссы — не ноль (для прямых кодов). Действительно, 0,2364 10 = 0,0024 10, однако в последнем случае мантисса не нормализована и точность представлений числа — всего два десятичных разряда.

Существуют и другие форматы представления чисел с плавающей запятой. Так, стандарт IEEE¹, который, кстати, поддерживают (со)процессоры семейства х86(87) предусматривает числа с одинарной и двойной точностью. Форматы представлены тремя полями:

            • s — знак числа;

            • е — характеристика;

            • т — мантисса.

Формат с одинарной точностью занимает 32-разрядное двоичное слово, причем знак s размещается в его старшем разряде, характеристика е — в следующих 8 разрядах и, наконец, 23 младших разряда занимает мантисса т .

            Порядок р, под который отводится один байт, может принимать значения в диапазоне ±127. Характеристика в стандарте IEEE получается как порядок с избытком 127: е = р + 127 . При этом характеристика всегда положительна, что упрощает выполнение арифметических операций.

            Мантисса числа в стандарте IEEE нормализована и лежит в диапазоне 1≤ m < 2. Целая часть мантиссы всегда равна 1, поэтому значение целой части не хранится в формате числа, а подразумевается (т. н. "скрытая единица"). Дробная часть мантиссы хранится в 23 младших разрядах формата.

            Формат с двойной точностью отличается длиной полей характеристики (11 битов с избытком 1023) и мантиссы (52 бита) и размещается в 64-разрядном двоичном слове.

Попробуйте самостоятельно оценить диапазон представления чисел в форматах IЕЕЕ. Подробности о выполнении операций с этими форматами можно посмотреть в [3, 12].

            3.10.1. Сложение и вычитание

            Ранее мы договорились, что алгебраическое вычитание легко свести к алгебраическому сложению путем замены знака второго операнда. Поэтому рассмотрим процесс алгебраического сложения. Для уяснения принципа выполнения сложения чисел с плавающей запятой рассмотрим пример в десятичной системе.

Обратите внимание, мантиссы чисел нормализованы. Очевидно, прежде чем складывать мантиссы, требуется преобразовать числа таким образом, чтобы они имели одинаковые порядки. Выравнивание порядков можно выполнить двумя способами — уменьшением большего порядка до меньшего или увеличением меньшего до большего (рис. 3.31).

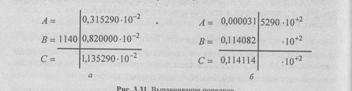
В первом случае за разрядную сетку выходят старшие разряды сдвигаемой мантиссы и результат сложения оказывается неверным. Во втором случае при сдвиге теряются младшие разряды мантиссы, что не влияет на точность результата. Поэтому при выравнивании порядков всегда следует увеличивать меньший порядок до большего при соответствующем уменьшении мантиссы.

            Для выравнивания порядков следует определить разность порядков слагаемых и сдвинуть мантиссу числа с меньшим порядком вправо на величину этой разности. Если разность порядков превышает разрядность поля мантиссы, то значение слагаемого с меньшим порядком может быть принята за 0, а результат суммирования будет равен слагаемому с большим порядком.

            После выравнивания порядков следует сложить мантиссы и определить в качестве порядка результата порядок любого из слагаемых (после выравнивания порядки слагаемых равны). Если при сложении мантисс возникает переполнение, то результат может быть исправлен путем сдвига мантиссы суммы на один разряд вправо и добавления единицы к порядку результата.

            Однако если в результате этого добавления произойдет переполнение разрядной сетки порядков, то результат окажется неверным — имеет место т. н. положительное переполнение: OV:= 1 (рис. 3.32).

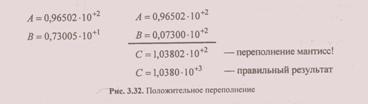
            В результате алгебраического сложения мантисс результат может оказаться ненормализованным. Для нормализации результата необходимо сдвигать мантиссу результата влево до тех нор, пока в старшем значащем разряде не окажется цифра, отличная от 0 (в двоичной системе это 1), сопровождая каждый сдвиг уменьшением на 1 порядка результата (рис. 3.33). Этот процесс называется нормализацией результата.

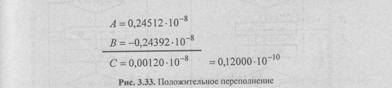
            В процессе уменьшения порядка при нормализации может оказаться, что модуль порядка превысил максимальную величину, размещаемую в поле порядка. Этот случай называют отрицательным переполнением. Его можно избежать, оставив результат ненормализованным, однако принято считать, что сохранять ненормализованный результат в памяти недопустимо. Поэтому в случае отрицательного переполнения результат принимает значение "машинный ноль".

            Итак, процедура алгебраического сложения чисел с плавающей запятой складывается из следующих этапов:

            1. Выравнивание порядков.

            2. Алгебраическое сложение мантисс как чисел с фиксированной запятой.

3. Нормализация результата.

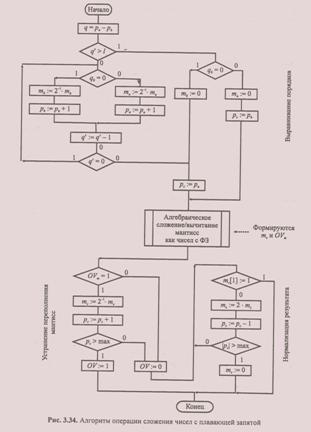
            Алгоритм операции сложения с плавающей запятой представлен на рис. 3.34.

            Первая часть алгоритма — выравнивание порядков, представлена достаточно подробно, хотя можно предложить несколько различных способов реализации этой процедуры (в зависимости от способа кодирования порядков, требования к быстродействию и экономичности арифметического устройства). Алгоритм алгебраического сложения мантисс (как чисел с фиксированной запятой) подробно обсуждался выше (см. разд. 3.4 — 3.6, рис. 3.3, 3.21, 3.22), поэтому в рассматриваемом алгоритме он представлен одним блоком. Нормализация результата приведена для случая представления чисел в прямом коде.

            3.10.2. Умножение и деление

            Положим

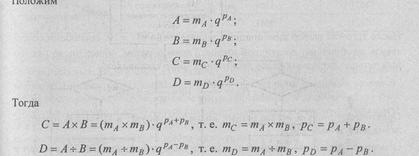
            Таким образом, умножение чисел с плавающей запятой сводится к двум операциям (умножение мантисс и сложение порядков) над числами с фиксированной запятой, а деление — к делению мантисс и вычитанию порядков— также к двум операциям с фиксированной запятой, которые были подробно рассмотрены выше.

3.11. Арифметические операции над десятичными числами

            3.11.1. Кодирование десятичных чисел

            При использовании в ЦВМ десятичные числа кодируются группой двоичных разрядов. Учитывая, что

Log₂ 10= 3,32, (3.31)

для представления одной десятичной цифры требуется не менее четырех двоичных разрядов. Соответствие между десятичной цифрой и ее двоичным представлением называют двоичным кодом десятичной цифры. Наиболее естественным представляется кодирование десятичных цифр позиционными двоичными кодами с естественными весами разрядов. Такой код принято называть кодом "8421".

            Ясно, что это далеко не единственный способ кодирования десятичных цифр. Используя только четырехразрядные двоичные коды, следует выбрать 10 из шестнадцати возможных комбинаций для представления цифр. Количество способов, которыми могут быть выбраны 10 комбинаций из 16, равно числу сочетаний из 16 по 10:

            После того как выбор комбинаций сделан, можно Р₁₀— 10! способами сопоставить комбинацию десятичной цифре. Таким образом, общее число различных четырехразрядных кодов десятичных цито составляет

            Практически лишь 5 — 6 различных кодов используют в ЦВМ для представления десятичных цифр.

            Основной недостаток кодирования десятичных цифр в коде "8421" состоит в несоответствии веса десятичного и шестнадцатеричного переносов. Действительно, перенос из тетради шестнадцатеричной цифры имеет вес 16, а десятичный перенос — 10.

            Для устранения этого противоречия можно выбрать другие способы кодирования десятичных цифр. Например, код "8421+3" (иногда его называют код с избытком три) позволяет при сложении получать сумму "с избытком 6", при этом вес переноса соответствует десятичному.

            Можно подобрать такие веса двоичных разрядов при кодировании десятичных цифр, чтобы их сумма равнялась 10. Например, код "5211" обладает именно таким свойством. При этом, однако, нарушается свойство функциональности соответствия десятичных цифр и их двоичного представления. Например, цифра 7 может быть представлена как 1100 или как 1011. Для преодоления этого недостатка достаточно договориться, чтобы в подобных ситуациях всегда сначала заполнялись младшие разряды кода.

            В табл. 3.5 приведены упомянутые двоичные коды десятичных цифр.

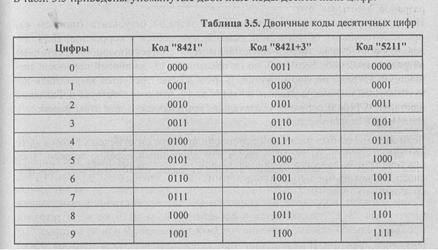
            Арифметические операции над десятичными числами можно выполнять как на специальных десятичных сумматорах (в этом случае можно применять любую кодировку десятичных цифр), так и на обычных двоичных сумматорах. В последнем случае десятичные числа обрабатываются по правилам двоичной арифметики, и десятичный результат операции, естественно, нуждается в коррекции. В этом случае сложность коррекции и длительность ее реализации существенно зависят от выбранного кода.

            3.11.2. Арифметические операции над десятичными числами

            Рассмотрим выполнение операции сложения десятичных чисел в коде "8421" по правилам двоичной арифметики.

            Из рассмотренного примера видно, что тетради результата (назовем его предварительным), обрамленные рамкой, нуждаются в коррекции. Действительно, если сумма тетрадь, представляющих соответствующие десятичные разряды слагаемых, больше 9, но не превышает 15, двоичный перенос в следующую тетрадку не формируется. В этом случае требуется выработать искусственный перенос и удалить из тетради 10, что соответствует добавлении шестерки (0110) и передаче обязательно возникающего при этом переноса в следующий старший разряд.

            Если из тетради был двоичный перенос (в примере он отмечен знаком ← ), то,: он "унес" из тетради 16, в то время как десятичный перенос должен "уносить" только 10. Следовательно, в такие тетради, из которых был перенос, следует добавить шестерку (0110).

            Таким образом, коррекция предварительной двоичной суммы при использовании кода "8421" заключается в добавлении кода 0110 ко всем тетрадям предварительной суммы, значение которых превышает 9 или из которых был двоичный перенос. Возникающие при коррекции переносы должны обязательно передаваться в следующую старшую тетрадку. Выполним операции примера 3.26 с учетом сформулированных правил коррекции.

Из примера 3.28 видно, что межтетрадные переносы, возникающие в процессе коррекции предварительной суммы, могут таким образом изменить старшие тетрады, что их также потребуется корректировать. В худшем случае количество последовательных коррекций будет равно разрядности слагаемых (рассмотрите пример сложения 9999+ 1 в коде "8421").

            На основании вышеизложенного можно отметить следующие недостатки применения кода "8421":

            • необходимо отслеживать не только переносы из тетрад, но и значения модулей тетрад предварительной суммы;

            • в общем случае невозможно произвести одновременно коррекцию во всех тетрадях, где может потребоваться коррекция.

            Для преодоления отмеченных выше недостатков можно использовать другие коды, например "8421+3". При кодировании с избытком три каждая десятичная цифра представляется как а_i,' = а_i, +0011, где а, — код "8421" цифры. Тогда при сложении

где с^h — предварительная сумма, в тетраде всегда будет формироваться истинное значение десятичного переноса — для всех комбинаций десятичных слагаемых, для которых а_i + b_i + p_i-₁ > 0, значение а₁'+ b_i + p_i-₁ > 15 . Однако если переноса из тетрады не было, то результат сформируется "с избытком 6", поэтому потребуется коррекция тетрады предварительной суммы — удаление из тетрады лишней тройки. Вычитание ( — 3 ) можно заменить сложением с дополнением до 3 — (+13 ). Обязательно возникающий при этом пере нос не передается в следующую тетраду. Потеря переноса равносильно потере 16, т. е. — 16+13 = — 3.

            Если перенос из тетрады был, то его вес равен 2⁴ =16, таким образом, из тетрады удаляется 16, а вес десятичного переноса — 10. Поэтому перенос из тетрады в коде "8421+3" уносит из тетрады лишнюю шестерку, которую и нужно добавить при коррекции. Но согласно (3.32) сложение тетрадь "с избытком 3" приводит к получению суммы "с избытком 6", поэтому вместо добавления шестерки достаточно добавить тройку.

            Итак, коррекции при сложении в коде "8421+3" подлежат все тетрады предварительной суммы, причем к тем тетрадам, из которых сформировался перенос, следует добавить константу 0011, а к тетрадам, из которых не было переноса, добавить константу 1101. Возникающие при коррекции межтетрадные переносы игнорируются!

            Таким образом, коррекция при сложении в коде "8421+3", во-первых, определяется только значениями переносов из тетрад предварительной суммы и, во-вторых, может проводиться параллельно во всех тетрадах,

            Еще одним достоинством кода "8421+3" является простой способ получения дополнения до 9 — достаточно просто про инвертировать разряды кода. Действительно, про инвертировав все разряды четырехразрядного двоичного числа а, мы получим его дополнение до 1111=15₁₀, что в коде "с избытком 3" соответствует 15-(а+ 3) = (9- а)+ 3.

            Это свойство позволяет довольно просто реализовать операцию вычитания через сложение в обратном или дополнительном коде.

            3.12. Машинная арифметика в остаточных классах

            Органическим недостатком любой позиционной системы счисления является наличие меж разрядных связей. Действительно, результат сложения в i-м разряде зависит не только от значений i -х разрядов слагаемых, но и от переноса из i — 1 разряда и, в конечном итоге — от значений всех младших разрядов слагаемых: i — 1, i-2, ..., 1, 0.      Поэтому вычисление разрядов суммы может проходить только последовательно (с учетом формирования переноса из предыдущего (младшего) разряда. Это обстоятельство препятствует распараллеливанию процесса вычисления и, естественно, снижает быстродействие процессора.

            В рамках позиционных систем счисления известно [2, 8, 11] несколько способов логического и схемотехнического ускорения арифметических операций — параллельный перенос, матричная и табличная арифметика и др., однако все они требуют весьма значительных аппаратных затрат.

            Поиск новых путей построения арифметических устройств ЭВМ, позволяющий исключить зависимость между разрядами при выполнении арифметических операций, привел к применению в машинной арифметике аппарата теории вычетов — одного из разделов теории чисел. В рамках этого аппарата разработана [1] непозиционная система счисления — система счисления в остаточных классах (СОК).

            3.12.1. Представление чисел в системе остаточных классов

            Будем говорить, что "а есть остаток числа А по модулю р" (иногда говорят, что "А сравнимо с а по модулю р "), если имеет место следующее равенство:

            3.12.2. Арифметические операции с положительными числами

            Рассмотрим правила выполнения операций сложения и умножения в СОК в случае, если оба операнда и результат операции находятся в диапазоне [0, Р).

            Операция вычитания в общем случае в СОК не определена, т. к. в СОК отсутствуют отрицательные числа. Однако в частных случаях, когда А, В, (А — В) € (0, Р), можно записать

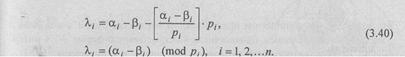
Операция вычитания в тех случаях, когда ее результат положителен, выполняется вычитанием соответствующих цифр разрядов по модулю соответствующего основания, т. е. если цифра уменьшаемого меньше соответствующей цифры вычитаемого, то к цифре уменьшаемого добавляется соответствующее основание.

            3.12.3. Арифметические операции , с отрицательными числами

            Если необходимо оперировать отрицательными числами, можно ввести т. н. [ искусственные формы представления чисел в СОК. Выражение (3.36) определяет диапазон представления чисел в СОК с основаниями р₁, p₂, ..., р_n.  Пусть одно из оснований системы равно 2, например, для определенности

Р₁ =2.

Обозначим через h величину

N'=h-|N|. Тогда при алгебраическом суммировании получим следующий вид представления положительных и отрицательных чисел:

N'=h+N.

            Это означает, что в принятом представлении мы всегда будем иметь дело с

положительными числами, однако числа в искусственной форме N' в интервале [0, h) будут отображать отрицательные числа, а в интервале [h, Р)— положительные.