Начальные сведения об ЭВМ
1.1. История развития вычислительной техники
С тех пор, как человечество осознало понятие количества, разрабатывались и применялись различные приспособления для отображения количественных эквивалентов и операций над величинами. Отбросив рассмотрение "доисторических" с точки зрения вычислительной техники средств (кучки камней, счеты и т. д.), рассмотрим кратко историю развития вычислительных машин.
Пожалуй, первой реально созданной машиной для выполнения арифметических действий в десятичной системе счисления можно считать счетную машину Паскаля. В 1642 г. Б. Паскаль продемонстрировал ее работу. Машина выполняла суммирование чисел (восьмиразрядных) с помощью колес, которые при добавлении единицы поворачивались на 36 и приводили в движение следующее по старшинству колесо всякий раз, когда цифра 9 должна была перейти в значение 10. Машина Паскаля получила известность во многих странах, было изготовлено более 50 экземпляров машины.
Впрочем, еще до Паскаля машину, механически выполняющую арифметические операции, изобразил в эскизах Леонардо да Винчи (1452 — 1519). Суммирующая машина по его эскизам выполнена в наши дни и доказала свою работоспособность.
В средние века (расцвет механики) было предложено и выполнено много различных вариантов арифметических машин: Морлэнд (1625 — 1695), К. Перро (1613 — 1688), Якобсон, Чебышев и др. Первую машину, с помощью которой можно было не только, складывать, но и умножать и делить, разработал Г. Лейбниц (1646 — 1716). Однако большинство подобных машин изготавливались авторами в единичных экземплярах. Удачное решение инженера В. Однера, разработавшего колесо с переменным числом зубьев, позволило почти век серийно выпускать арифмометры (например, "Феликс" Курского завода "Счетмaш"), являвшиеся основным средством вычислений вплоть до эпохи ПЭВМ и калькуляторов.
Все упомянутые выше механизмы обладали одной особенностью — могли автоматически выполнять только отдельные действия над числами, но не могли хранить промежуточные результаты и, следовательно, выполнять последовательность действий.
Первой вычислительной машиной, реализующей автоматическое выполнение последовательности действий, можно считать разностную машину Ч. Беббиджа (1792 — 1871). В 1819 г. он изготовил ее для расчета астрономических и морских таблиц. Машина обеспечивала хранение необходимых промежуточных значений и выполнение последовательности сложений для получения значения функции. В дальнейшем Беббидж предложил т. н. аналитическую машину, предназначенную для решения любых вычислительных задач. При желании в аналитической машине Беббиджа можно найти прообразы всех основных устройств современной ЭВМ: арифметическое устройство ("мельница"), память ("склад"), устройство управления (на перфокартах), позволяющее выбирать различные пути решения в зависимости от значений исходных данных и промежуточных результатов. Проект аналитической машины Беббиджа так и не был реализован — из-за несоответствия идеи и элементной базы.
Даже выпускаемые большими сериями электрические релейные машины Холлерита (1860 — 1929) — табуляторы — не произвели переворота в средствах обработки информации, хотя и широко использовались для обработки статистической информации вплоть до 70-х годов прошлого века.
Идеи аналитической машины Беббиджа были использованы в релейных машинах, выпускавшихся в 30 — 40-х годах ХХ века. Теоретической основой разработки релейно-контактных схем явился аппарат булевой алгебры, который в дальнейшем использовался для синтеза схем ЭЭВМ. Однако и электрические реле как элементная база вычислительной техники не удовлетворяли потребностям этой техники по всем основным параметрам (быстродействие, надежность, потребляемая мощность, стоимость, габариты и др.).
Только освоение электронных схем в качестве элементной базы положило начало действительно массовому внедрению сначала вычислительной, а потом и информационной техники во все сферы человеческой деятельности. Первые электронные цифровые вычислительные машины (ЭЭВМ) были разработаны и выпущены на рубеже 40 — 50-х годов прошлого века в США, Англии и чуть позднее — в СССР.
1.2. Цифровые и аналоговые вычислительные машины
Все приведенные выше факты относятся к истории т. н. цифровой вычислительной техники, в которой информация представлена в дискретной форме (в форме чисел, кодов, знаков). Однако большинство физических величин может принимать значение из непрерывного множества — континуума. Существуют вычислительные устройства, оперирующие непрерывной информацией (пример — логарифмическая линейка, где информация представлена отрезками длины). Существует и целый класс электронных вычислительных машин — т. н. аналоговые, информация в которых представляется непрерывными значениями электрического напряжения или тока. Принцип работы таких машин — в построении электрических цепей, процессы в которых описываются теми дифференциальными уравнениями, которые требуется решить.
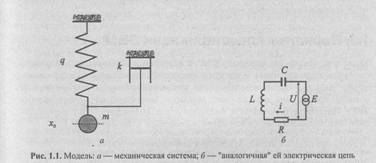
Классический пример такого подхода показан на рис. 1.1. Например, требуется изучить поведение механической колебательной системы, описываемой дифференциальным уравнением (1.1). Подберем электрическую цепь, процессы в которой описываются тем же дифференциальным уравнением с точностью до обозначений (1.2). Между механическими величинами (рис. 1.1, а) и электрическими (рис. 1.1, б) существует соответствие (сравните уравнения (1.1) и (1.2)).
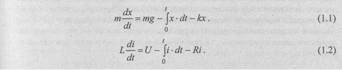
Принципы организации ЭВМ
Таким образом, для механического устройства можно подобрать электрическую цепь, процессы в которой описываются аналогичными дифференциальными уравнениями. Или, для заданного дифференциального уравнения (системы) построить электрическую цепь, которая описывается этим уравнением..
Существует хорошо отработанная методика синтеза таких цепей и наборы функциональных блоков (АВМ), позволяющие собирать и исследовать синтезированные цепи.
Достоинства АВМ: простота подготовки решения, высокая скорость решения.
Недостатки АВМ: не универсальность (предназначены только для решения дифференциальных уравнений) и низкая точность решения.
В настоящее время АВМ находят применение лишь в ограниченных областях технического моделирования. Поэтому в дальнейшем будем употреблять термин "ЭВМ", имея в виду только цифровые вычислительные машины, как это принято в современной терминологии.
1.3. Варианты классификации ЭВМ
За свою полувековую историю ЭВМ из единичных экземпляров инструментов ученых превратились в предмет массового потребления. Спектр применения ЭВМ в современном обществе чрезвычайно широк, причем именно область применения накладывает основной отпечаток на характеристики ЭВМ. Поэтому в большинстве подходов к классификации ЭВМ именно область применения является основным параметром классификации.
Изделия современной техники, особенно вычислительной, традиционно принято делить на поколения (табл. 1.1), причем основним признаком поколения ЭВМ считается ее элементная база. Следует помнить, что любая классификация не является абсолютной. Всегда можно отыскать объект классификации, который по одним параметрам относится к одному классу, а по другим к другому. Это в большой степени относится и к классификации поколений ЭВМ: некоторые авторы выделяют три поколения ЭВМ (дальнейшее развитие ЭВМ идет как бы вне поколений), другие насчитывают целых шесть.
В рамках первого поколения ЭВМ не возникала необходимость в классификации, т. к. машин были считанные единицы и использовались они, как правило, для выполнения научно-технических расчетов. Отдельные машины характеризовались быстродействием (числом выполняемых операций в секунду), объемом памяти, стоимостью, надежностью (наработка на отказ), габаритно- весовыми характеристиками, потребляемой мощностью и другими параметрами.
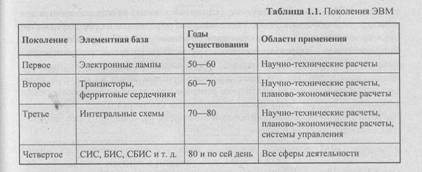
Использование транзисторов в качестве элементной базы второго поколения привело к улучшению примерно на порядок каждого из основных параметров ЭВМ. Это, в свою очередь, резко расширило сферу применения ЭВМ, причем в разных областях применения к ЭВМ предъявлялись различные требования. Так называемые "научно-технические расчеты" характеризовались относительно небольшим объемом входной и выходной информации, но очень большим числом сложных операций с высокой точностью над входной информацией, а "планово-экономические расчеты"' — наоборот, простейшими операциями (сложение, сравнение) над огромными объемами информации.
Соответственно в рамках второго поколения ЭВМ выделялись: CI ЭВМ для научно-технических расчетов, характеризующиеся мощным быстродействующим процессором с развитой системой команд (в т. ч. реализующей арифметику с плавающей запятой) и относительно небольшой внешней памятью и номенклатурой устройств ввода/вывода;
CI ЭВМ для планово-экономических расчетов, характеризующиеся, прежде всего, большой многоуровневой памятью, развитой номенклатурой устройств ввода/вывода (УВВ), но относительно простым и дешевым процессором, система команд которого включает простые арифметические команды (сложение, вычитание) с фиксированной запятой.
Характерно, что и языки программирования "второго поколения" так же разделялись на "математические" (FORTRAN) и "экономические" (COBOL).
Однако по мере расширения сферы применения ЭВМ, улучшения их основных характеристик, появления новых задач, границы между выделенными классами стали размываться. Уже в рамках второго поколения стали выделять т. н. ЭВМ общего назначения, одинаково хорошо приспособленные для решения разнообразных задач. Такие машины объединяли в себе достоинства "научно-технических" и "планово-экономических" ЭВМ: мощный процессор, большую память, широкую номенклатуру УВВ (в то время это уже можно было себе позволить). Такие машины могли решать задачи, недоступные предыдущим моделям. Но для, решения более простых задач их ресурсы являлись избыточными и, следовательно, решение этих задач — экономически не оправдано. Поэтому ЭВМ общего назначения (универсальные ЭВМ) стали выпускать различной вычислительной мощности (и, следовательно, стоимости): большие, средние и малые.
В рамках ЭВМ третьего поколения стал усиленно развиваться новый класс — управляющие ЭВМ. К ЭВМ, работающим в контуре управления объектом или технологическим процессом, предъявляются специфические требования: прежде всего, высокая надежность, способность работать в экстремальных внешних условиях (перепады температуры, давления, питающих напряжений, высокий уровень электромагнитных помех и т. п.), быстрая реакция на изменения состояния внешней среды, малые габариты и вес, простота обслуживания. В то же время к таким характеристикам, как быстродействие процессора, мощность системы команд, объем памяти, часто не предъявлялись слишком высоких требований, зато решающим становился фактор стоимости. Эти особенности привели к появлению класса т. н. мини-ЭВМ, а затем и микро ЭВМ хотя в дальнейшем и мини и микро ЭВМ использовались не только в качестве управляющих. Иногда эти классы объединяли понятием проблемно-ориентированные ЭВМ.
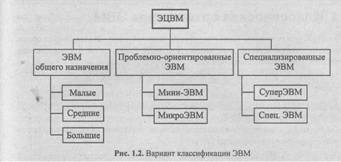
Наряду с упомянутыми классами ЭВМ широкого применения всегда выпускались машины, которые можно было считать специализированными. Это, во-первых, т. н. суперЭВМ, выпускаемые в единичных экземплярах и предназначенные для решения задач, недоступных для серийной вычислительной техники. Для ряда применений создавались специализированные ЭВМ, архитектура и структура которых оптимизировалась под решение конкретной задачи. Ту же задачу можно было решить и на универсальной ЭВМ подходящего класса, но со значительно более низкими показателями качества. В то же время решение других задач на специализированной ЭВМ было либо невозможно, либо крайне неэффективно. Одна из возможных классификаций ЭВМ на рубеже 3 — 4 поколений показана на рис. 1.2
Еще одним важным явлением, проявившимся при развитии третьего поколения ЭВМ, стало появление семейств ЭВМ. В рамках одного семейства, объединенного общими архитектурными, структурными, а иногда — и конструктивными решениями, выпускались несколько (иногда — более десятка) классов ЭВМ: малые, средние, "полусредние", большие, очень большие и т. д.
Общими для большинства семейств являются:
О внутренний язык, что позволяет осуществлять совместимость программ на уровне машинных кодов (IBM-360, ЕС ЭВМ) либо системы команд, обладающие совместимостью "снизу вверх" (PDP-11), когда старшие представители семейства реализуют все команды младших моделей плюс еще некоторые команды;
• форматы данных;
• форматы записи на внешний носитель;
• интерфейс, что позволяет иметь единую номенклатуру внешних устройств для всех представителей семейства;
• преемственность программного обеспечения (как правило, та же совместимость "снизу вверх").
Для решения конкретной задачи пользователь подбирал соответствующий экземпляр семейства, а по мере усложнения задачи осуществлялся переход на более старшие модели семейства, причем уже отлаженные на младших моделях программы, как правило, не требовали доработки.
Наиболее известными примерами семейств ЭВМ могут служить:
• семейство универсальных ЭВМ третьего поколения IBM-360 и его советский аналог — ЕС ЭВМ, включающее малые машины ЕС-1010 и ЕС-1020, средние ЕС-1022, ЕС-1030, ЕС-1035 и др., большие ЕС-1050, ЕС-1060, ЕС-1065;
• семейство мини-ЭВМ PDP-11 и его советский аналог — СМ ЭВМ (лишь часть представителей семейства — СМ-3, СМ-4, СМ-1420);
• семейство микро ЭВМ LXI-11 (Электроника-60 и ее модификации);
• семейство микропроцессоров i80x86.
1.4. Классическая архитектура ЭВМ
Считается, что основные идеи построения современных ЭВМ в 1945 г. с формулировал американский математик Дж. фон Нейман, определив их как принципы программного управления:
1. Информация кодируется двоичной форме и разделяется на единицы— слова.
2. Разнотипные по смыслу слова различаются по способу использования, но не по способу кодирования.
3. Слова информации размещаются в ячейках памяти и. идентифицируются номерами ячеек — адресами слов.
4. Алгоритм представляется в форме последовательности управляющих слов, называемых командами: Команда определяет наименование операции и слова информации, участвующие в ней. Алгоритм, записанный в виде последовательности команд, называется программой.
5. Выполнение вычислений, предписанных алгоритмом, сводится к последовательному выполнению команд в порядке, однозначно определенном программой.
По этому классическую архитектуру современных ЭВМ, представленную на рис. 1.3, часто называют "архитектурой фон Неймана".
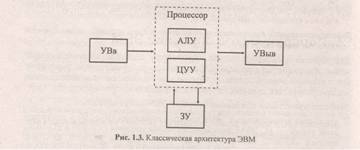
Программа вычислений (обработки информации) составляется в виде последовательности команд и загружается в память машины — запоминающее устройство (ЗУ). Там же хранятся исходные данные и промежуточные результаты обработки. Центральное устройство управления (ЦУУ) последовательно извлекает из памяти команды программы и организует их выполнение. Арифметико-логическое устройство (АЛУ) предназначено для реализации операций преобразования информации. Программа и исходные данные вводятся в память машины через устройства ввода (УВв), а результаты обработки предъявляются на устройства вывода (УВыв).
Характерной особенностью архитектуры фон Неймана является то, что память представляет собой единое адресное пространство, предназначенное для хранения как программ, так и данных.
Такой подход, с одной стороны, обеспечивает большую гибкость организации вычислений — возможность перераспределения памяти между программой и данными, возможность самомодификации программы в процессе ее . выполнения. С другой стороны, без принятия специальных мер защиты снижается надежность выполнения программы, что особенно недопустимо в управляющих системах.
Действительно, поскольку и команды программы, и данные кодируются в ЭВМ двоичными числами, теоретически возможно как разрушение программы (при обращении в область программы как к данным), так и попытка "выполнения" области данных как программы (при ошибочных переходах программы в область данных).
Альтернативной фон-неймановской является т. н. гарвардская архитектура.
ЭВМ, реализованные по этому принципу, имеют два непересекающихся адресных пространства — для программы и для данных, причем программу нельзя разместить в свободной области памяти данных и наоборот. Гарвардская архитектура применяется главным образом в управляющих ЭВМ.
1.5. Иерархическое описание ЭВМ
ЭВМ как сложная система может быть адекватно описана на нескольких уровнях с применением различных языков описания на каждом из уровней.
Принципы структурного описания предполагают введение следующих понятий:
• система — совокупность элементов, объединенных в одно целое для достижения определенных целей. Для полного описания системы следует определить ее функции и структуру;
• структура системы — фиксированная совокупность элементов системы и связей между ними;
• элемент — неделимая часть системы, структура которого не рассматривается, а определяются только его функции.
Функции системы стремятся описывать в математической форме, иногда в словесной (содержательной форме). Структура системы может быть задана в виде графа или эквивалентных ему математических форм (матриц). Инженерной формой задания структуры является схема (отличается от графа только формой). Различным уровням представления систем соответствуют различные виды схем.
Свойства системы не являются простой суммой свойств входящих в нее элементов; за счет организации связей между элементами приобретается новое качество, отсутствующее в элементах. Например, радиокомпоненты → логические элементы → сумматор.
Для сложных систем характерно, что функция, реализуемая системой, не может быть представлена как композиция функций, реализуемых наименьшими элементами системы (иначе говоря, функцию сложной системы нельзя адекватно описать на одном языке). Действительно, функционирование ЭВМ нельзя описать лишь на языке электрических процессов, в ней происходящих. Функции ЭВМ как системы выявляются лишь при рассмотрении информационных и логических аспектов ее работы.
По этому в описании сложных систем используют несколько форм описания (языков) функций и структуры — иерархию функций и структуры. Иерархический подход к описанию сложных систем предполагает, что на высшем уровне иерархии система рассматривается как один элемент, имеющий входы и выходы для связи с внешней средой. В этом случае функция не может быть задана подробно и представляется как отображение состояний входов на со- стояние выходов системы.
Чтобы раскрыть устройство и порядок функционирования системы, глобальная функция и сама система разделяются на части — функции и структурные элементы следующего более низкого уровня иерархии и т. д. до тех пор, пока функции и структура системы не будут раскрыты полностью, с необходимой степенью детализации.
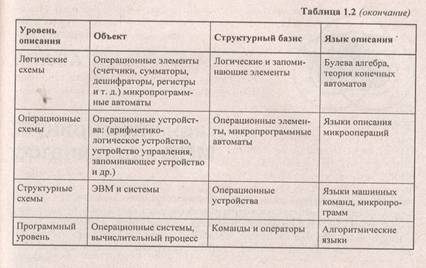
В этом случае элемент — это, прежде всего, удобное понятие, а не физическое свойство, т. к. один и тот же физический объект может рассматриваться как элемент на одном уровне иерархии и как система — на другом (более низком) уровне. В табл. 1.2 представлены основные уровни ЭВМ и языки описания этих уровней.

Функциональная организация ЭВМ
Термин "функциональная организация ЭВМ" часто используют в качестве синонима (в некотором смысле) более широкого термина — "архитектура ЭВМ", который, в свою очередь, трактуется разными авторами несколько в различных смыслах. Наиболее близким к трактовке автора может служить определение термина "архитектура ЭВМ", данное в [8]. Приведем это определение.
Архитектура ЭВМ — это абстрактное представление ЭВМ, которое отражает ее структурную, схемотехническую и логическую организацию. Понятие архитектуры ЭВМ является комплексным и включает в себя:
• структурную схему ЭВМ;
• средства и способы доступа к элементам структурной схемы
• организацию и разрядность интерфейсов ЭВМ;
• набор и доступность регистров;
• организацию и способы адресации памяти;
•способы представления и форматы данных ЭВМ;
• набор машинных команд ЭВМ;
• форматы машинных команд;
• обработку нештатных ситуаций (прерываний).
В рамках данной книги мы, в основном, будем рассматривать перечисленные
выше вопросы.
2.1. Командный цикл процессора
Командой называется элементарное действие, которое может выполнить процессор без дальнейшей детализации. Последовательность команд, выполнение которых приводит к достижению определенной цели, называется программой. Команды программы кодируются двоичными словами и размещаются в памяти ЭВМ. Вся работа ЭВМ состоит в последовательном выполнении команд программы. Действия по выбору из памяти и выполнению одной команды называются командным циклом.
В составе любого процессора имеется специальная ячейка, которая хранит адрес выполняемой команды — счетчик команд или программный счетчик. После выполнения очередной команды его значение увеличивается на единицу (если код одной команды занимает несколько ячеек памяти, то содержимое счетчика команд увеличивается на длину команды). Таким образом осуществляется выполнение последовательности команд. Существуют специальные команды (передачи управления), которые в процессе своего выполнения модифицируют содержимое программного счетчика, обеспечивая переходы по программе. Сама выполняемая команда помещается в регистр команд — специальную ячейку процессора.
Во время выполнения командного цикла процессор реализует следующую последовательность действий:
1. Извлечение из памяти содержимого ячейки, адрес которой хранится в программном счетчике, и размещение этого кода в регистре команд (чтение команды).
2. Увеличение содержимого программного счетчика на единицу.
3. Формирование адреса операндов.
4. Извлечение операндов из памяти.
5. Выполнение заданной в команде операции.
6. Размещение результата операции в памяти.
7. Переход к п. 1.
Пункты 1, 2 и 7 обязательно выполняются в каждом командном цикле, остальные могут не выполняться в некоторых командах. Если длина кода команды составляет несколько машинных слов, то 1 и 2 повторяются.
Фактически вся работа процессора заключается в циклическом выполнении пунктов 1 — 7 командного цикла. При запуске машины в счетчик команд аппаратно помещаешься фиксированное значение — начальный адрес программы (часто 0 или последний адрес памяти; встречаются и более экзотические способы загрузки начального адреса). В дальнейшем содержимое программного счетчика модифицируется в командном цикле. Прекращение выполнения командных циклов может произойти только при выполнении специальной команды "СТОП".
2.2. Система команд процессора
Разнообразие типов данных, форм их представления и действий, которые необходимы для обработки информации и управления ходом вычислений, порождает необходимость использования различных команд — набора команд. Каждый процессор имеет собственный вполне определенный набор команд, называемый системой команд процессора. Система команд должна обладать двумя свойствами — функциональной полнотой и эффективностью. Функциональная полнота — это достаточность системы команд для описания любого алгоритма. Требование функциональной полноты не является слишком жестким. Доказано, что свойством функциональной полноты обладает система, включающая всего три команды (система Поста): присвоение 0, присвоение 1, проверка на 0. Однако составление программ в такой системе команд крайне неэффективно.
Эффективность системы команд — степень соответствия системы команд назначению ЭВМ, т. е. классу алгоритмов, для выполнения которых предназначается ЭВМ, а также требованиям к производительности ЭВМ. Очевидно, что реализация развитой системы команд связана с большими затратами оборудования и, следовательно, с высокой стоимостью процессора. В то же время ограниченный набор команд приводит к снижению производительности и повышенным требованиям к памяти для размещения программы. Даже простые и дешевые современные микропроцессоры поддерживают систему команд, содержащую несколько десятков (а с модификациями — сотен) команд.
Система команд процессора характеризуется тремя аспектами: форматами, способами адресации и системой операций.
Под форматом команды следует понимать длину команды, количество, размер, положение, назначение и способ кодировки ее полей.
Команды, как и любая информация в ЭВМ, кодируются двоичными словами, которые должны содержать в себе следующие виды информации:
• тип операции, которую следует реализовать в данной команде (КОП);
• место в памяти, откуда следует взять первый операнд (Al);
• место в памяти, откуда следует взять второй операнд (А2);
• место в памяти, куда следует поместить результат (A3).
Каждому из этих видов информации соответствует своя часть двоичного слова — поле, а совокупность полей (их длины, расположение в командном слове, способ кодирования информации) называется форматом команды. В свою очередь, некоторые поля команды могут делиться на подполя. Формат команды, поля которого перечислены выше, называется трехадресным (рис. 2.1, а).
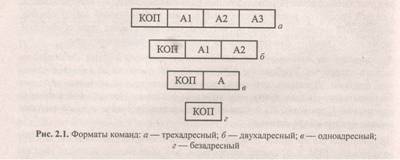
Команды трехадресного формата занимают много места в памяти, в то же время далеко не всегда поля адресов используются в командах эффективно. Действительно, наряду с двухместными операциями (сложение, деление, конъюнкция и др.) встречаются и одноместные (инверсия, сдвиг, инкремент и др.), для которых третий адрес не нужен. При выполнении цепочки вычислений часто результат предыдущей операции используется в качестве операнда для следующей. Более того, нередко встречаются команды, для которых операнды не определены (СТОП) или подразумеваются самим кодом операций (DAA, десятичная коррекция аккумулятора).
Поэтому в системах команд реальных ЭВМ трехадресные команды встречаются редко. Чаще используются двухадресные команды (рис. 2.1, б), в этом случае в бинарных операциях результат помещается на место одного из операндов.
Для реализации одноадресных форматов (рис. 2.1, в) в процессоре предусматривают специальную ячейку — аккумулятор. Первый операнд и результат всегда размещаются в аккумуляторе, а второй операнд адресуется полем А.
Реальная система команд обычно имеет команды нескольких форматов, причем тип формата определяется в поле КОП.
Способ адресации определяет, каким образом следует использовать информацию, размещенную в поле адреса команды.
Не следует думать, что во всех случаях в поле адреса команды помещается адрес операнда. Существует пять основных способов адресации операндов в командах.
• Прямая — в этом случае в адресном поле располагается адрес операнда. Разновидность — прямая регистровая адресация, адресующая не ячейку памяти, а РОН. Поле адреса регистра имеет в команде значительно меньшую длину, чем поле адреса памяти.
• Непосредственная — в поле адреса команды располагается не адрес операнда, а сам операнд. Такой способ удобно использовать в командах с константами.
• Косвенная — в поле адреса команды располагается адрес ячейки памяти, в которой хранится адрес операнда ("адрес адреса"). Такой способ позволяет оперировать адресами как данными, что облегчает организацию циклов, обработку массивов данных и др. Его основной недостаток — потеря времени на двойное обращение к памяти — сначала за адресом, потом — за операндом. Разновидность — косвенно-регистровая адресация, при которой в поле команды размещается адрес РОН, хранящего адрес операнда. Этот способ, помимо преимущества обычной косвенной адресации, позволяет обращаться к большой памяти с помощью коротких команд и не требует двойного обращения к памяти (обращение к регистру занимает гораздо меньше времени, чем к памяти).
• Относительная — адрес формируется как сумма двух слагаемых: базы, хранящейся в специальном регистре или в одном из РОН, и смещения, извлекаемого из поля адреса команды. Этот способ позволяет сократить длину команды (смещение может быть укороченным, правда в этом случае не вся память доступна в команде) и/или перемещать адресуемые массивы информации по памяти (изменяя базу). Разновидности — индексная и базово-индексная адресации. Индексная адресация предполагает наличие индексного регистра вместо базового. При каждом обращении содержимое индексного регистра автоматически модифицируется (обычно увеличивается или уменьшается на 1). Ббазово-ииндексная адресация формирует адрес операнда как сумму трех слагаемых: базы, индекса и смещения.
• Безадресная — поле адреса в команде отсутствует, а адрес операнда или не имеет смысла для данной команды, или подразумевается по умолчанию. Часто безадресные команды подразумевают действия над содержимым аккумулятора. Характерно, что безадресные команды нельзя применить к другим регистрам или ячейкам памяти.
Одной из разновидностей безадресного обращения является использование т. н. магазинной памяти или стека. Обращение к такой памяти напоминает обращение с магазином стрелкового оружия. Имеется фиксированная ячейка, называемая верхушкой стека. При чтении слово извлекается из верхушки, а все остальное содержимое "поднимается вверх" подобно патронам в магазине, так что в верхушке оказывается следующее по порядку слово. Одно слово нельзя прочитать из стека дважды. При записи новое слово помещается в верхушку стека, а все остальное содержимое "опускается вниз" на одну позицию. Таким образом, слово, помещенное в стек первым, будет прочитано последним. Говорят, что стек поддерживает дисциплину LIFO — Last In First Out (последний пришел — первый ушел). Реже используется безадресная память типа очередь с дисциплиной FIFO — First In First Out (первый пришел — первый ушел).
Все операции, выполняемые в командах ЭВМ, принято делить на пять классов. • Арифметико-логические и специальные — команды, в которых выполняется собственно преобразование информации. К ним относятся арифметические операции сложение, вычитание, умножение и деление (с фиксированной и плавающей занятой), команды десятичной арифметики, логические операции конъюнкции, дизъюнкции, инверсии и др., сдвиги, преобразование чисел из одной системы счисления в другую и такие экзотические, как извлечение корня, решение системы уравнений и др. Конечно, очень редко встречаются ЭВМ, система команд которых включает все эти команды.
• Пересылки и загрузки — обеспечивают передачу информации между процессором и памятью или между различными уровнями памяти (СОЗУ → ОЗУ). Разновидность — загрузка регистров и ячеек Контантами.
•Ввода/вывода — обеспечивают передачу информации между процессором и внешними устройствами. По структуре они очень похожи на команды предыдущего класса. В некоторых ЭВМ принципиально отсутствует различие между ячейками памяти и регистрами внешних устройств (единое адресное пространство) и класс команд ввода/вывода не выделяется, все обмены осуществляются в рамках команд пересылки и загрузки.
• Передачи управления — команды, которые изменяют естественный порядок выполнения команд программы. Эти команды меняют содержимое программного счетчика, обеспечивая переходы по программе. Существуют команды безусловной и условной передачи управления. В последнем случае передача управления происходит, если выполняется заданное в коде команды условие, иначе выполняется следующая по порядку команда.
В качестве условий обычно используются признаки результата предыдущей операции, которые хранятся в специальном регистре признаков (флажков). Чаще всего формируются и проверяются признаки нулевого результата, отрицательного результата, наличия переноса из старшего разряда, четности числа единиц в результате и др. Различают три разновидности команд передачи управления:
• переходы;
• вызовы подпрограмм;
• возвраты из подпрограмм.
Команды переходов помещают в программный счетчик содержимое своего адресного поля — адрес перехода. При этом старое значение программного счетчика теряется. В микро ЭВМ часто для экономии длины адресного поля команд условных переходов адрес перехода формируется как сумма текущего значения программного счетчика и относительно короткого знакового смещения, размещаемого в команде. В крайнем случае, в командах условных переходов можно и вовсе обойтись без адресной части — при выполнении условия команда "перепрыгивает" через следующую команду, которой обычно является безусловный переход.
Команда вызова подпрограммы работает подобно команде безусловного перехода, но старое значение программного счетчика предварительно сохраняется в специальном регистре или в стеке. Команда возврата передает содержимое верхушки стека или специального регистра в программный счетчик. Команды вызова и возврата работают "в паре". Подпрограмма, вызываемая командой вызова, должна заканчиваться командой возврата, что обеспечивает по окончании работы подпрограммы передачу управления в точку вызова. Хранение адресов возврата в стеке обеспечивает возможность реализации вложенных подпрограмм.
• Системные — команды, выполняющие управление процессом обработки информации и внутренними ресурсами процессора. К таким командам относятся команды управления подсистемой прерывания, команды установки и изменения параметров защиты памяти, команда останова программы и некоторые другие. В простых процессорах класс системных команд немногочисленный, а в сложных мультипрограммных системах предусматривается большое число системных команд.
Арифметические основы ЭВМ
Безусловно, одним из основных направлений применения компьютеров были и остаются разнообразные вычисления. Обработка числовой информации ведется и при решении задач, на первый взгляд не связанных с какими-то расчетами, например, при использовании компьютерной графики или звука.
В связи с этим встает вопрос о выборе оптимального представления чисел в компьютере. Безусловно, можно было бы использовать 8-битное (байтовое) кодирование отдельных цифр, а из них составлять числа. Однако такое кодирование не будет оптимальным, что легко увидеть из простого примера. Пусть имеется двузначное число 13. При 8-битном кодировании отдельных цифр в кодах ASCII его представление выглядит следующим образом: 0011000100110011, т. е. код имеет длину 16 битов; если же определять это число просто в двоичном коде, то получим 4-битную цепочку 1101.
Важно, что представление определяет не только способ записи данных (букв или чисел), но и допустимый набор операций над ними; в частности, буквы могут быть только помещены в некоторую последовательность (или исключены из нее) без изменения их самих; над числами же возможны операции, изменяющие само число, например, извлечение корня или сложение с другим числом.
Представление чисел в компьютере имеет две особенности:
• числа записываются в двоичной системе счисления (в отличие от привычной десятичной);
• для записи и обработки чисел отводится конечное количество разрядов (в «некомпьютерной» арифметике такое ограничение отсутствует).
Следствия, к которым приводят эти отличия, и рассматриваются в данной главе.
Начнем с некоторых общих замечаний относительно понятия число [12]. Можно считать, что любое число имеет значение (содержание) и форму представления.
Значение числа задает его отношение к значениям других чисел ("больше", "меньше", "равно") и, следовательно, порядок расположения чисел на числовой оси. Форма представления, как следует из названия, определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа является инвариантом, т. е. не зависит от способа его представления. Это означает также, что число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие между представлением числа и его значением.
В связи с этим возникают вопросы, во-первых, о формах представления чисел и, во-вторых, о возможности и способах перехода от одной формы к другой.
Способ представления числа определяется системой счисления.
Определение
Система счисления — это правило записи чисел с помощью заданного набора специальных знаков — цифр.
Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.
Унарная — это система счисления, в которой для записи чисел используется только один знак — (вертикальная черта, палочка). Следующее число получается из предыдущего добавлением новой палочки: их количество (сумма) равно самому числу. Унарная система важна в теоретическом отношении, поскольку в ней число представляется наиболее простым способом и, следовательно, просты операции с ним. Кроме того, именно унарная система определяет значение целого числа количеством содержащихся в нем единиц, которое, как было сказано, не зависит от формы представления.
Из непозиционных наиболее распространенной можно считать римскую систему счисления. В ней некоторые базовые числа обозначены заглавными латинскими буквами: 1 — I, 5 — V, 10 — Х, 50 — L, 100 — С, 500 — D, 1000 — М. Все другие числа строятся комбинаций базовых в соответствии со следующими правилами:
• если цифра меньшего значения стоит справа от большей цифры, то их значения суммируются; если слева — то меньшее значение вычитается из большего;
• цифры I Х, С и М могут следовать подряд не более трех раз каждая;
• цифры V, L и D могут использоваться в записи числа не более одного раза. Например, запись XIX соответствует числу 19, MDXLIX — числу 1549.
Запись чисел в такой системе громоздка и неудобна, но еще более неудобным оказывается выполнение в ней даже самых простых арифметических операций. Отсутствие нуля и знаков для чисел больше М не позволяют римскими цифрами записать любое число (хотя бы натуральное). По указанным причинам теперь римская система используется лишь для нумерации.
В настоящее время для представления чисел применяют, в основном, позиционные системы счисления.
Определение
Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
Наиболее распространенной и привычной является система счисления, в которой для записи чисел используется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число представляет собой краткую запись многочлена, в который входят степени некоторого другого числа — основания системы счисления. Например:
![]()
В данном числе цифра 5 встречается трижды, однако значение этих цифр различно и определяется их положением (позицией) в числе. Количество цифр для построения чисел, очевидно, равно основанию системы счисления. Также очевидно, что максимальная цифра на 1 меньше основания. Причина широкого распространения именно десятичной системы счисления понятна — она происходит от унарной системы с пальцами рук в качестве "пало- чек".
Однако в истории человечества имеются свидетельства использования и других систем счисления — пятеричной, шестеричной, двенадцатеричной, двадцатеричной и даже шестидесятеричной. Общим для унарной и римской систем счисления является то, что значение числа в них определяется посредством операций сложения и вычитания базисных цифр, из которых составлено число, независимо от их позиции в числе. Такие системы получили название аддитивных.
В отличие от них позиционное представление следует считать аддитивно- мультипликативным, поскольку значение числа определяется операциями умножения и сложения. Главной же особенностью позиционного представления является то, что в нем посредством конечного набора знаков (цифр, разделителя десятичных разрядов и обозначения знака числа) можно записать неограниченное количество различных чисел. Кроме того, в позиционных системах гораздо легче, чем в аддитивных, осуществляются операции умножения и деления. Именно эти обстоятельства обуславливают доминирование позиционных систем при обработке чисел как человеком, так и компьютером.
По принципу, положенному в основу десятичной системы счисления, очевидно, можно построить системы с иным основанием. Пусть р — основание системы счисления. Тогда любое число Z (пока ограничимся только целыми числами), удовлетворяющее условию Z ( рк ( к> 0, целое), может быть представлено в виде многочлена со степенями (при этом, очевидно, максимальный показатель степени будет равен к-1):
![]()
Из коэффициентов аj при степенях основания строится сокращенная запись числа:
![]()
Индекс р числа Z указывает, что оно записано в системе счисления с основанием р: общее число цифр числа равно k . Все коэффициенты аj — целые числа, удовлетворяющие условию: 0 < аj < р - 1.
Уместно задаться вопросом: каково минимальное значение р Очевидно, р =1 невозможно, поскольку тогда все а =0 и форма (3.1) теряет смысл. Первое допустимое значение р = 2 — оно и является минимальным для позиционных систем.
Система счисления с основанием 2 называется двоичной. Цифрами двоичной системы являются 0 и 1, а форма (3.1) строится по степеням 2. Интерес именно к этой системе счисления связан с тем, что, как указывалось выше, любая информация в компьютерах представляется с помощью двух состояний — 0 и 1, которые легко реализуются технически.
Наряду с двоичной в компьютерах используются восьмеричная и шестнадцатеричная системы счисления — причины будут рассмотрены далее.
3.2. Представление чисел в различных системах счисления
Очевидно, что значение целого числа, т. е. общее количество входящих в него единиц, не зависит от способа его представления и остается одинаковым во всех системах счисления; различаются только формы представления одного и того же количественного содержания числа.
Например: IIIII1=510=1012=516.
Поскольку одно и то же число может быть записано в различных системах счисления, встает вопрос о переводе представления числа из одной системы в другую.
3.2.1. Перевод целых чисел из одной системы счисления в другую
Обозначим преобразование числа Z, представленного в р -ричной системе счисления в представление в q -ричной системе как Zp→Zq . Теоретически возможно произвести его при любых q и р. Однако подобный прямой перевод будет затруднен тем, что придется выполнять операции по правилам арифметики недесятичных систем счисления (полагая в общем случае, что р,q≠10).
По этой причине более удобными с практической точки зрения оказываются варианты преобразования с промежуточным переводом Zp→Zp→Zq с основанием r, для которого арифметические операции выполнить легко.
Такими удобными основаниями являются r =1 и r =10, т. е. перевод осуществляется через унарную или десятичную систему счисления.
Преобразование Zp → Z1 →Zq
Идея алгоритма перевода предельно проста: положим начальное значение Zq:=0 из числа Zp вычтем 1 по правилам вычитания системы р, т. е. Zp:=Zp- 1, и добавим ее к Zq по правилам сложения системы q, т. е. Zq:= Zq +1. Будем повторять эту последовательность действий, пока не достигнем Zq= 0. Правила сложения с 1 (инкремента) и вычитания 1 (декремента) могут быть записаны так, как представлено в табл. 3.1.

Примечание: π — перенос в случае инкремента или заем в случае декремента.
Промежуточный переход к унарной системе счисления в данном случае осуществляется неявно — используется упоминавшееся выше свойство независимости значения числа от формы его представления. Рассмотренный алгоритм перевода может быть легко реализован программным путем.
Преобразование ZP→Zw→Zq
Очевидно, первая и вторая часть преобразования не связаны друг с другом, что дает основание рассматривать их по отдельности. Алгоритмы перевода Zw→ Zq вытекают из следующих соображений. Многочлен (3.1) для Zq может быть представлен в виде:

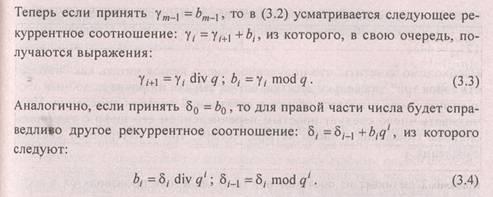
Из соотношений (3.3) и (3.4) непосредственно вытекают два способа перевода целых чисел из десятичной системы счисления в систему с произвольным основанием q.
Способ 1 является следствием соотношений (3.3), предполагающий следующий алгоритм перевода:
1. Цело численно разделить исходное число (Z>z) на основании новой системы счисления (q) и найти остаток от деления — это будет цифра 0-го разряда числа Zq.
2. Частное от деления снова цело численно разделить на q с выделением остатка; процедуру продолжать до тех нор, пока частное от деления не окажется меньше q.
3. Образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq .

Остатки от деления (3, 4) и результат последнего целочисленного деления (4) образуют обратный порядок цифр нового числа. Следовательно, 123)10 —— 4435.
Необходимо заметить, что полученное число нельзя читать как "четыреста сорок три", поскольку десятки, сотни, тысячи и прочие подобные обозначения чисел относятся только к десятичной системе счисления. Прочитывать число следует простым перечислением его цифр с указанием системы счисления ("число четыре, четыре, три в пятеричной системе счисления").
Способ 2 вытекает из соотношения (3.4), действия производятся в соответствии со следующим алгоритмом:
1. Определить и — 1 — максимальный показатель степени в представления числа по форме (3.1) для основания q.
2. Цело численно разделить исходное число (Z10) на основание новой системы счисления в степени т — 1 (т. е. qm-1) и найти остаток от деления; результат деления определит первую цифру числа 2 .
3. Остаток от деления цело численно разделить на g m-2, результат деления принять за вторую цифру нового числа; найти остаток; продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.
Продемонстрируем действие алгоритма на той же задаче, что была рассмотрена выше.

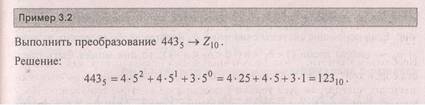
Необходимо еще раз подчеркнуть, что приведенными алгоритмами удобно пользоваться при переводе числа из десятичной системы в какую-то иную или наоборот. Они работают и для перевода между любыми иными системами счисления, однако преобразование будет затруднено тем, что все арифметические операции необходимо осуществлять по правилам исходной (в первых алгоритмах) или конечной(в последнем алгоритме) системы счисления.
По этой причине переход, например, Z3→Z8 проще осуществить через промежуточное преобразование к десятичной системе Z3→ Z10→ Z8. Ситуация, однако, значительно упрощается, если основания исходной и конечной систем счисления оказываются связанными соотношением р = qr, где r — целое число (естественно, большее 1) или r = 1/п (n >1, целое) — эти случаи будут рассмотрены далее.
3.2.2. Перевод дробных чисел из одной системы счисления в другую
Вещественное число, в общем случае содержащее целую и дробную часть, всегда можно представить в виде суммы целого числа и правильной дроби. Поскольку в предыдущем разделе проблема записи натуральных чисел в различных системах счисления уже была решена, можно ограничить рассмотрение только алгоритмами перевода правильных дробей.
Введем следующие обозначения: правильную дробь в исходной системе счисления р будем записывать в виде 0,Yp дробь в системе q — 0,Yq, а преобразование — в виде 0,Yp→ 0,Yq .
Последовательность рассуждений весьма напоминает проведенную ранее для
натуральных чисел. В частности, это касается рекомендации осуществлять преобразование через промежуточный переход к десятичной системе, чтобы избежать необходимости производить вычисления в "непривычных" системах счисления, т. е. 0,Yp→ 0,Y10→0,Yq .
Это, в свою очередь, разбивает задачу на две составляющие: преобразование 0,Yp→ 0,Y10 и 0,Y10→0,Yq, каждое из которых может рассматриваться независимо.

Если вновь позаимствовать в PASCAL обозначение функции — на этот раз trunc, производящей округление целого вещественного числа путем отбрасывания его дробной части, то следствием (3.6) будут соотношения, позволяющие находить цифры новой дроби:
![]()
Соотношения (3.7) задают алгоритм преобразования: 0, Y10→ 0,Yq:
1. Умножить исходную дробь в десятичной системе счисления на q, выделить целую часть — она будет первой (старшей) цифрой новой дроби; отбросить целую часть.
2. Для оставшейся дробной части операцию умножения с выделением целой и дробных частей повторять, пока в дробной части не окажется О или не будет достигнута желаемая точность конечного числа; появляющиеся при этом целые будут цифрами новой дроби.
3. Записать дробь в виде последовательности цифр после нуля с разделителем в порядке их появления в пп. 1 и 2.


Перевод 0,Yq→ 0,Y10 как и в случае натуральных чисел, сводится к вычислению значения формы (3.5) в десятичной системе счисления. Например:
![]()
Следует сознавать, что после перевода дроби, которая была конечной в исходной системе счисления, она может оказаться бесконечной в новой системе. Соответственно, рациональное число в исходной системе может после перехода превратиться в иррациональное. Справедливо и обратное утверждение: число иррациональное в исходной системе счисления в иной системе может оказаться рациональным.
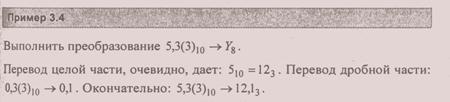
Как уже было сказано, значение целого числа не зависит от формы его представления и выражает количество входящих в него единиц. Простая дробь имеет смысл доли единицы, и это "дольное" содержание также не зависит от выбора способа представления. Другими словами, треть пирога остается третью в любой системе счисления.
3.2.3. Перевод чисел между системами счисления 2 ↔ 8 ↔ 16
Интерес к двоичной системе счисления вызван тем, что именно она используется для представления чисел в компьютере. Однако двоичная запись оказывается громоздкой, поскольку содержит много цифр и, кроме того, плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц). Поэтому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16. Выбор именно этих
систем счисления обусловлен тем, что переход от них к двоичной системе и обратно осуществляется, как будет показано далее, весьма простым образом.
Двоичная система счисления имеет основанием 2 и, соответственно, две цифры: 0 и 1.
Восьмеричная система счисления имеет основание 8 и цифры 0, 1, ..., 7. Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, ..., 9, А, В, С. D, Е, F. При этом знак А является шестнадцатеричной цифрой, соответствующей числу 10 в десятичной системе, В16=1110, C12= 121 , D16=1310 , E16=1410 и F16 = 1510. Другими словами, в данном случае А, ..., F — это не буквы латинского алфавита, а цифры шестнадцатеричной системы счисления.
Докажем две. теоремы [12].
Теорема 1. Для преобразования целого числа Zp→ Zq в том случае, если системы счисления связаны соотношением q = р r, где r — целое число, большее 1, достаточно Zp разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q .
Доказательство. Пусть максимальный показатель степени в записи числа р по форме (3.1) равен k -1, причем, 2r > k-1> r .
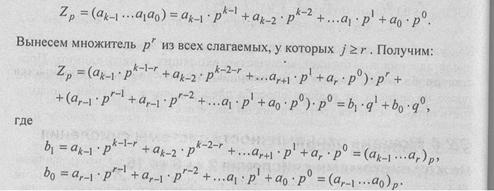
Таким образом, r-разрядные числа системы с основанием р оказываются записанными как цифры системы с основанием q. Этот результат можно обобщить на ситуацию произвольного k - 1 > r — в этом случае выделятся не две, а больше (и) цифр числа с основанием q. Очевидно, Zq= (bm…b0)q .
Теорема 2. Для преобразования целого числа Zp→Zq в том случае, если системы счисления связаны соотношением p=qr, где r — целое число, большее 1, достаточно каждую цифру Zr заменить соответствующим r -разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.
Доказательство. Пусть исходное число содержит две цифры, т. е.
Zr=(a1a0)p = a1· р1 + a0 · р0
Для каждой цифры справедливо: 0 < а, < р — 1 и поскольку р = qr, 0≤aj ≤q -1, то в представлении этих цифр в системе счисления q максимальная степень многочленов (3.1) будет не более r - 1 и эти многочлены будут содержать по r цифр:
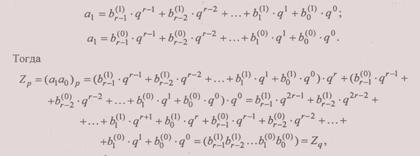
причем число Zq содержит 2r цифр. Доказательство легко обобщается на случай произвольного количества цифр в числе Zr.
3.2.4. Понятие экономичности системы счисления
Число в системе счисления с k разрядами, очевидно, будет иметь наибольшее значение в том случае, если все цифры числа окажутся максимальными, т. е. равными р — 1.
Тогда
(Zr)max =< р-1>...< р-1>= рk-1.
k цифр
Количество разрядов числа при переходе от одной системы счисления к другой в общем случае меняется.
Очевидно, если р = qσ (σ — не обязательно целое), то (Zp)max =рk-1=qσk -1
т. е. количество разрядов числа в системах счисления р и q будут различаться в σ раз, причем
lоg р
σ = —.
log q
.
При этом основание логарифма никакого значения не имеет, поскольку σ определяется отношением логарифмов. Сравним количество цифр в числе 9910 и его представлении в двоичной системе счисления: 9910 = 11000112 т. е. двоичная запись требует 7 цифр вместо 2 в десятичной, σ= log10/log2 = 3,322; следовательно, количество цифр в десятичном представлении нужно умножить на 3,322 и округлить в большую сторону: 2 3,322 = 6,644 = 7.
Введем понятие экономичности представления числа в данной системе счисления [12].
Определение
Под экономичностью системы счисления будем понимать то количество чисел, которое можно записать в данной системе с помощью определенного количества цифр.
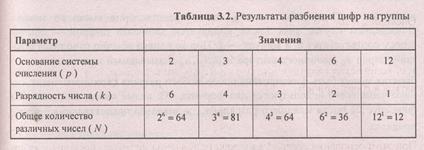
Речь в данном случае идет не о количестве разрядов, а об общем количестве сочетаний цифр, которые интерпретируются как различные числа. Поясним на примере: пусть в распоряжении имеется 12 цифр. Можно разбить их на 6 групп по 2 цифры ("0" и "1") и получить шестиразрядное двоичное число; общее количество таких чисел, как уже неоднократно обсуждалось, равно 26 . Можно разбить заданное количество цифр на 4 группы по три цифры и воспользоваться троичной системой счисления — в этом случае общее количество различных их сочетаний составит 3 . Аналогично можно произвести другие разбиения; при этом число групп определит разрядность числа, а количество цифр в группе — основание системы счисления. Результаты различных разбиений можно проиллюстрировать табл. 3.2.
Из приведенных оценок видно, что наиболее экономичной оказывается троичная система счисления, причем результат будет тем же, если исследовать случаи с другим исходным количеством сочетаний цифр.
Точное расположение максимума экономичности может быть установлено путем следующих рассуждений. Пусть имеется n знаков для записи чисел, а
основание системы cсчисления равно р. Тогда количество разрядов числа k=n/р, а общее количество чисел N, которые могут быть составлены, равно:
![]()
Если считать N(p) непрерывной функцией, то можно найти такое значение р, при котором N принимает максимальное значение. Для нахождения положения максимума нужно найти производную функции N(p), приравнять ее к нулю и решить полученное уравнение относительно р .
![]()
Приравнивая полученное выражение к нулю, получаем ln p =1, или рm = е, где е = 2,71828... — основание натурального логарифма. Ближайшее к е целое число, очевидно, 3 — по этой причине троичная система счисления оказывается самой экономичной для представления чисел, однако следующей по экономичности оказывается двоичная система счисления.
Таким образом, простота технических решений — не единственный аргумент в пользу применения двоичной системы в компьютерах.
3.3. Представление информации в ЭВМ. Прямой код
В современных ЭВМ используются, в основном, два способа представления двоичных чисел — с фиксированной и с плавающей запятой, причем в формате с фиксированной запятой (ФЗ) используется как беззнаковое представление чисел (" целое без знака"), так и представление чисел со знаком. В последнем случае знак также кодируется двоичной цифрой — обычно плюсу соответствует 0, а минусу — 1. Под код знака обычно отводится старший разряд а0 двоичного вектора а2 а1а2...а„, называемый знаковым.
Запятая может быть фиксирована после любого разряда двоичного числа, однако чаще всего используются два формата ФЗ: целые числа, когда запятая фиксируется после младшего разряда an, а диапазон представления лежит в пределах
![]()
и дробные числа — запятая фиксирована после а0, а диапазон
![]()
Далее, если не сделано специальных оговорок, будем рассматривать дробные двоичные числа со знаком, запятая в которых фиксирована после знакового разряда а1:
![]()
Очевидно, если двоичное число А = 0,а1 а2а3 ...аn > 0, то оно будет представлено в форме (3.14) как 0,а1 а2а3 ...аn а если О1,а1 а2а3 ...аn<0 то как 1,а1 а2а3 ...аn Приведенное кодирование дробных двоичных чисел со знаком принято называть прямым кодом числа (обозначается как [А]d). Итак

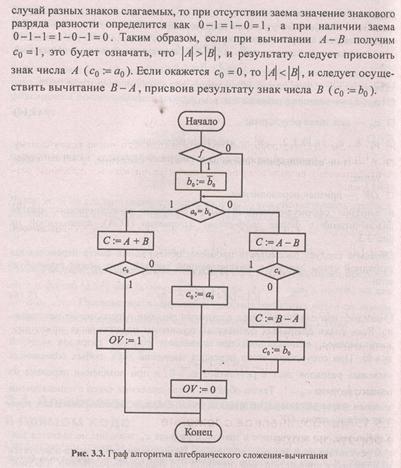
3.4. Алгебраическое сложение/вычитание в прямом коде
Сформулируем правила выполнения операций сложения и вычитания чисел со знаками (такие операции принято называть алгебраическими). Во-первых, алгебраическое вычитание всегда можно свести к алгебраическому сложению, изменив знак второго операнда. Далее следует сравнить знаки слагаемых. При одинаковых знаках складывают модули слагаемых и результату присваивают знак любого слагаемого (они одинаковые). Если знаки слагаемых разные, то из большего модуля слагаемого вычитают меньший модуль и присваивают результату знак слагаемого, имеющего больший модуль.

и выразим сформулированный выше алгоритм алгебраического сложения/вычитания в форме граф-схемы алгоритма (ГСА), приведенной на рис. 3.3.
Отдельно следует рассмотреть проблему обнаружения факта переполнения разрядной сетки данных с фиксированной запятой. Эго может произойти, если
![]()
Очевидно, при сложении чисел с разными знаками переполнение невозможно. Если знаки слагаемых одинаковы, признаком переполнения может служить перенос, возникающий при сложении старших разрядов модулей a1+b1. При отсутствии этого переноса сложение двух любых одинаковых знаковых разрядов даст в результате c0 =0, а при появлении переноса из первого разряда с0 = 1. Таким образом, после сложения чисел с одинаковыми знаками значение знакового разряда суммы можно рассматривать как признак переполнения ОV .
Характерно, что полученное в знаковом разряде с0 =1 значение не является знаком результата (алгебраической суммы). Истинное значение знака образуется не в процессе арифметической операции над знаковыми разрядами, а формируется искусственно.
Рассмотрим случай сложения чисел с разными знаками. Он сводится к вычитанию модулей слагаемых, причем уменьшаемым должен стать больший модуль. Чтобы избежать дополнительной модульной операции сравнения, можно произвести "наугад" вычитание А — В. Признаком того, что |А|> |В| будет отсутствие заема из нулевого в первый разряд. Поскольку рассматривается