1-МАЪРУЗА

ЎЗБЕКИСТОН РЕСПУБЛИКАСИ АХБОРОТ ТЕХНОЛОГИЯЛАРИ ВА КОММУНИКАЦИЯЛАРИНИ РИВОЖЛАНТИРИШ ВАЗИРЛИГИ

ТОШКЕНТ АХБОРОТ ТЕХНОЛОГИЯЛАР УНИВЕРСИТЕТИ

“ОПТИК ТОЛАЛИ ЛИНИЯЛАР ВА ЎЛЧОВ ТИЗИМЛАРИ” кафедраси

Электр занжирлар назарияси

Фани бўйича

Махсус факультет талабалари учун маърузалар тўплами

Тошкент 2016

Маърузалар тўплами ТАТУ Махсус факультетининг ишчи ўқув дастури ва ўқув режаларига мос холда ишлаб чиқилди.

Тузувчилар:

Парсиев С. С. - «Оптик толали линиялар ва ўлчов тизимлари»

кафедраси мудири, т.ф.н., доцент.

Тўлаганова В. А. – «Оптик толали линиялар ва ўлчов тизимлари»

кафедраси доценти.

Абдуллаев У. М. – «Оптик толали линиялар ва ўлчов тизимлари»

кафедраси ассистенти.

Тақризчилар:

Абдуллаев Б. А. – ТДТУ кафедраси доценти, т.ф.н.

Соатов Х. С. – “ТРЭТ” кафедраси мудири, т.ф.н., доцент

Маърузалар тўплами «Оптик толали линиялар ва ўлчов тизимлари» кафедрасининг 2016 йил ________даги йиғилишида мухокама қилинди ва факультет илмий услубий кенгашига муҳокама учун тавсия этилди. (Баённома №_____ 2016 йил _______).

Маърузалар тўплами «Телекоммуникация технологиялари» факультетининг 2016 йил _________ даги йиғилишида мухокама қилинди ва чоп этиш учун тавсия этилди. (Баённома №_______ 2016 йил_____).

“ К Е Л И Ш И Л Д И “

ТАТУ Махсус факультети бошлиғининг ўқув

ишлар бўйича муовини М. Ж. Қутлимуратов

Мундарижа

	Кириш........................................................................................................	1
1.	Зарядланган заррачалар. Зарядланган заррачаларнинг ўзаро ҳаракатлари. Электр майдон...................................................................	2
2.	Кучланиш. Электр потенциали ва потенциаллар фарқи. Электр юритувчи куч............................................................................................	8
3.	Электр занжири. Электр занжир элементлари. Элементларни кетма-кет ва параллел улаш....................................................................	13
4.	Электр занжирлар назариясининг асосий қонунлари. Кирхгоф қонунлари. Ом қонуни.............................................................................	21
5.	Доимий ток занжирларини ҳисоблаш. Электр схемаларини эквивалент усули билан алмаштириш (эквивалент алмаштириш усули).........................................................................................................	26
6.	Ўзгарувчан ток. Синусоидал ток. Синусоидал токни характерловчи миқдорлар..................................................................................................	34
7.	Синусоидал функцияларни вектор диаграммаси ва комплекс сонлар орқали ифодалаш........................................................................	41
8.	Комплекс ифодалар. Комплекс сонлар устида амаллар бажариш…..	48
9.	Комплекс қаршилик ва ўтказувчанлик. Кирхгоф ва Омқонунларини комплекс миқдорлар орқали ифодалаш……………….........................	55
10.	Гармоник ток занжирларида қувват…………………………………...	60
11.	Параллел тебраниш контури. Ток резонанси…………………………	65
12.	Даврий функцияларнинг гармоник таркибларга ёйилиши………….	71
13.	Иккиқутбли электр занжирлари. Таърифлари ва классификациялари .	78
14.	Чизиқли электр занжирларида ўтиш жараёнлари……………………	85
15.	Ўтиш жараёнларини оператор усулида ҳисоблаш…………………..	92
16.	Спектрал (частотавий) усул ёрдами билан ЧЭЗларни тахлил қилиш. Тўртқутбликлар (ТҚ)………………………………………………….	100
17.	Баттерворд, Чебышев ва Золотарёв филтрлари.....................................	114
18.	Ночизиқли электр занжирлари................................................................	121
19.	Магнитли занжирлар................................................................................	127
20.	Тескари боғланган электр занжирлари. Автогенераторлар.................	133

Кириш

Республикамизда “ТЕЛЕКОММУНИКАЦИЯ” тармоқларининг шиддат билан ривожланиб бориши, ИНТЕРНЕТ тармоғининг ҳаётимизга кириб келиши илм-фан ривожига катта таъсир қилди.

Барча ахборотлар ушбу тармоқлар орқали катта тезликларда узатилади, интернет тармоғи орқали барча ахборотларни қабул қилиш, узатиш ва ахборот алмашиш имконияти яратилди.

Ушбу телекоммуникация тармоқлари мураккаб қурилмалардан, узатувчилардан, қабул қилувчи ва ахборотларни қайта ишлаш, бошқа турларга айлантириш ускуналаридан ташкил топган. Ушбу мураккаб турдаги қурилмалар ҳар ҳил турдаги электротехник ва электрон схемалардан ташкил топган бўлади.

Телекоммуникация тармоқларининг техник қурилмаларини яратиш, ишлатиш учун ушбу техник воситалар орқали бораётган жараённи ўрганиш, уларни ташкил этган электр занжирларини тахлил қилиш, электр токи оқаётган жараён қайси қонунлар асосида амалга оширилишини билиш зарур бўлади. Ушбу қонунларнинг кўпчилиги “Электр занжирлар назарияси” (ЭЗН) фани орқали ўрганилади. ЭЗН фани ўтган асрнинг 60 йилларида алоҳида фан сифатида ташкил топган. Ўша йилгача умумий фан сифатида “Электротехника” фани ўрганилиб келинган Кейинчалик телекоммуникация тармоқларида фаолият олиб борувчи инженер техник ҳодимлар учун мураккаб электр занжирлар орқали оқиб ўтаётган ток ва кучланишнинг асосий параметрларини ҳисоблаш ва тахлил қилиш асосий ўрин эгаллади. Шунинг учун ҳам ҳозирги вақтда ушбу фан орқали техник қурилмаларда бўлаётган жараённи ўрганиб борилади. Техник қурилмаларни ташкил этувчиларини тахлил қилиш учун электр занжирлар назариясини ўрганиш керак бўлади.

Ушбу маърузалар тўпламидан Махсус факультет талабалари ва бошқа мутахассисликлар бўйича таълим олаётган талабалар фойдаланишлари мумкин.

1-МАЪРУЗА

ЗАРЯДЛАНГАН ЗАРАЧАЛАР. ЗАРЯДЛАНГАН ЗАРРАЧАЛАРНИНГ ЎЗАРО ҲАРАКАТЛАРИ. ЭЛЕКТР МАЙДОН.

1.1 ЭЛЕКТР ЗАРЯД ТУШУНЧАСИ

Физика фанидан маълумки бир бўлак ойна синиғини шойи матога ишқаланса, ойна синиғи майда қоғоз бўлакчаларини ўзига тортадиган бўлиб қолади. Лекин шойи матога ишқаланган икки ойна синиғи бир - бирини итариш хусусиятига эга бўлади. Эбонит материали мех материалига ишқланса ҳам худди шундай хусусиятга эга бўлади, икки эбонит материали эса бир бирини итариш хусусиятига эга бўлади.

Жисмларнинг бир бирини тортиши ва итариши одам кўзига кўринмайдиган майда ЗАРЯДЛАРНИНГ ПАЙДО бўлиши билан тушунтирилиши мумкин. Кейинчалик бу майда зарядлар ЭЛЕКТР ЗАРЯДЛАРИ деб номланди.

Зарядланган жисмлар бир бирларини тортишлари ва итаришлари орқали уларни ажратиш хусусияти пайдо бўлди. Масалан ойна синиғида ҳосил бўлган зарядлар тортиш, эбонитда эса бир биридан қочиш хусусиятига эга эканлиги аниқланди. Шу орқали ойна синиғида ҳосил бўлган зарядлар МУСБАТ, эбонитда ҳосил бўлган зарядлар МАНФИЙ деб номланадиган бўлди.

Зарядланган заррачаларни ўрганиш вақтида шу нарса аниқландики: бир хил зарядлар бир бирларидан қочишади, ҳар хил зарядлар эса бир бирини тортишади.

Кейинчалик маълум бўлдики, ҳар бир жисм АТОМЛАРДАН ташкил топган бўлиб, ҳар бир атом мусбат зарядланган ЯДРОДАН ва манфий зарядланган ЭЛЕКТРОНДАН ташкил топганлиги аниқланди. Агар мусбат зарядланган ядролар, манфий зарядланган электронларга тенг бўлса атом НЕЙТРАЛ холатда бўлади. Агар зарядланган электронлар кўпайса, манфий, агар камайса мусбат зарядлар ҳосил бўлади.

ДЕМАК ЭЛЕКТРОН ЗАРЯДИ – ТАБИАТДАГИ ЭНГ КИЧИК ЭЛЕКТР ЗАРЯДИ ҲИСОБЛАНАДИ.

Заряд бирлиги бир электрон заряди эмас, балки КУЛОН деб номланади ва қуйидаги миқдорга тенг деб белгиланади, яъни (Ш. О. КУЛОН электростатикага асос солган француз инженер физиги номига)

6 290 000 000 000 000 000

электрон зарядлар.

Демак электрон заряд.

1.1.1. ЗАРЯДЛАРНИНГ ЎЗАРО ҲАРАКАТЛАРИ

Зарядларга ўзаро таъсир этувчи куч зарядланган зарядлар кўпайтмасига тўғри пропорционал, улар орасидаги масофа квадратига тескари пропорционал.

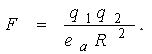
Юқоридаги формула зарядланган заррачаларнинг ўзаро таъсир кучларини ҳисоблаш формуласи ҳисобланади.

Бу формулада: F - зарядларнинг ўзаро таъсир кучи, ўлчов бирлиги Ньютон (Н), инглиз физики Исаак Ньютон (1643-1727) номи билан номланган;

q₁, q₂ –зарядлар , Кл;

R – зарядланган заррачалар орасидаги масофа, м;

еа – диэлектрик сингдрувчанлик;

еа= ео х еr;

е о - вакуумнинг диэлектрик сингдирувчанлик доимийлиги;

еr- муҳитнинг нисбий диэлектрик сингдирувчанлик доимийлиги (миқдорлари жадвал орқали берилади);

Юқоридаги ифодаларни инобатга оладиган бўлсак КУЛОН қонуни қуйидагича ёзилади:

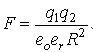, 1.1.

Тажриба йўллари билан аниқланганки вакуумнинг диэлектрик сингдирувчанлиги қуйидаги миқдорга тенг : , Ф.

Вакуумнинг диэлектрик сингдирувчанлигининг ўлчов бирлиги Инглиз физики Майкл Фарадей (1791 – 1867) номи билан номланган ва “Фарад” (Ф) деб белгиланади.

1.1.2. ЭЛЕКТР МАЙДОН

Зарядланган жисм атрофида бир бирини тортиш ва итариш кучларини намоён этувчи майдон бўлади. Бу майдон ЭЛЕКТРЛАНГАН майдон деб юритилади.

Электрланган майдон материянинг бир тури бўлиб, шу майдон орқали зарядланган заррачаларнинг ўзаро ҳаракатлари амалга оширилади.

Зарядлари ўзгармайдиган майдон ЭЛЕКТРОСТАТИК майдон деб юритилади.

Электр майдонининг ҳар бир нуқтаси электр майдонининг КУЧЛАНГАНЛИГИ E билан характерланади.

Кучланганлик 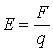формула орқали ифодаланади, бу ерда – F майдонда жойлашган q зарядга таъсир этувчи куч.

Зарядланган заррачаларга таъсир этувчи куч F НЬЮТОНДА (Н), заряд q эса КУЛОНДА (Кл), электр майдонининг кучланганлиги E эса (Н/Кл) да ўлчанади.

Электр майдон кучланганлиги деб, электр майдонининг кўрилаётган нуқтасига киритилган зарядланган қўзғолмас жисмга таъсир этаётган куч миқдорини шу заряд нолга интилгандаги миқдорига нисбатининг, жисмга таъсир этаётган мусбат куч йўналиши билан мос бўлган вектор миқдорига айтилади:

Электр майдонининг кучланганлиги вектор катталик ҳисобланади ва электр майдонини ва шу майдон орқали зарядланган заррачаларга таъсир этувчи кучни характерлайди.

Электр майдон майдоннинг кучланганлик чизиқлари билан тасвирланади. Майдон кучланганлигининг вектори майдоннинг ҳар бир нуқтасида бир ҳил бўлган майдон БИР ТУРДАГИ МАЙДОН деб аталади.

Электр кучланганлик чизиқлари ёпиқ чизиқлар бўлмасдан, мусбат зарядли жисмлардан бошланади ва манфий зарядланган жисмларда тугайди. Мисол тариқасида 1.1. ва 1.2 Расмлардаги шаклларни келтиришимиз мумкин. 1.3 Расмда иккита паралел жойлашган пластиналарнинг электр майдон кучланганлиги келтирилган.

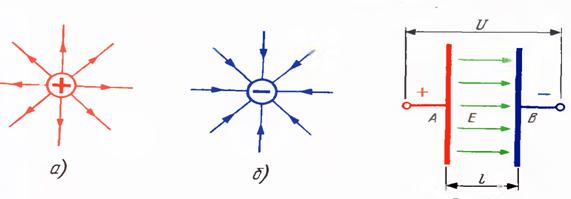
Расм 1.1. Мусбат ва манфий зарядларнинг кўриниши

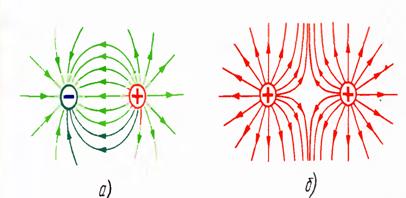
Расм 1.2. Зарядларнинг ўзаро тортишишлари ва қочишлари

1.2. ЭЛЕКТР ТОКИ

Ҳар қандай металл ўтказгичларда эркин ҳаракатланувчи ЭЛЕКТРОНЛАР мавжуд бўлади. Агар металл ўтказгич учларига (клеммаларига) ҳеч қандай кучланганлик уланмаса, электроннлар ҳар хил йўналишлар бўйича тартибсиз ҳаракатланади, электронларнинг ҳеч қандай тартибли ҳаракати кузатилмайди.

Агар металл ўтказгич учларига ҳар хил қийматларга эга бўлган кучланганлик уланса, у холда электронларни тартибли ҳаракатга келтирувчи ЭЛЕКТР МАЙДОН ҳосил бўлади.

Шу холатда ўтказгич кесимидан бир вақтнинг ўзида бир хил миқдордаги электр зарядлари кўчиб ўтиши кузатилади.Электронларнинг тартибли ҳаракати орқали зарядли заррачаларнинг ўтказгичнинг бир нуқтасидан иккинчи нуқтасига кўчиб ўтиши ЭЛЕКТР ТОКИ деб аталади, қисқача ТОК дейилади.

ТОКНИНГ ўлчов бирлиги француз физики Н. М. АМПЕР (1775-1836) номига атаб АМПЕР (А) деб белгиланади. Ток миқдорини аниқлаш учун маълум вақт оралиғида заряд ўзгаришини билиш керак бўлади.

Вакт ўртиши билан кийматини ўзгартирмайдиган ток ўзгармас ток деб аталади . Вакт утиши билан синусоидал (гармоник)конун бўйича ўзгарадиган ток ўзгарувчан ток деб аталади.

Ток худди кучланиш сингари i – оний , амплитуда I_m ва максимал I_p қийматларга эга бўлади. Ток миқдори бирор юза s орқали вақт бирлигида ўтаётган заряд миқдори q билан ўлчанади. Вақтнинг ихтиёрий онида ўтказувчанлик токи кўрилаётган s юзадан заряд ташувчилар билан кўчирилаётган электр зарядининг вақт бўйича ҳосиласига тенг, яъни

, 1.2.

Ўтказгичнинг барча нуқталарида тартибли ҳаракатланаётган зарядлардан ташқари, тартибсиз ҳаракатланаётган электроннлар ҳам мавжуд бўлади, оқибатда улар ўтказгич орқали ўтаётган токнинг тартибли ҳаракатига халақит беради.

Бу холат ўтказгичнинг ёки материалнинг ҚАРШИЛИГИ деб аталади.

Ўтказгич қаршилиги R ҳарфи билан, ёки r билан белгиланади. ҚАРШИЛИКнинг ўлчов бирлиги немис олими Георг ОМ (1787-1854) шарафига Ом деб белгиланади.

1.3. СОЛИШТИРМА ҚАРШИЛИК

Ўтказгичларнинг қаршилиги шу ўтказгич тайёрланган материалнинг хусусиятига боғлиқ бўлади. Шу материалларни бир бири билан таққослаш, хусусиятларини аниқлаш мақсадида СОЛИШТИРМА ҚАРШИЛИК тушунчаси киритилади ва (РЎ деб ўқилади) билан белгиланади.

Бир m² кесимга эга бўлган 1м узунликдаги ўтказгич қаршилиги СОЛИШТИРМА ҚАРШИЛИК деб аталади ва қуйидаги формула орқали ҳисобланади

Бу ерда: . 1.3.

R – ўтказгич қаршилиги, Ом;

S – ўтказгичнинг кесим юзаси, м²;

L - ўтказгич узунлиги, м .

1.4. ЎТКАЗГИЧНИНГ РЕЗИСТОР ҚАРШИЛИГИ

Бирор ўтказгич орқали ўтаётган электр токи бир қанча қаршиликларга учрайди, шу сабабли энергия йўқотилади. Одатда энергия йўқотилмайди, фақат бир турдан бошқа турга ўтади, бу холатда ЭЛЕКТР ЭНЕРГИЯСИ ИССИҚЛИК ЭНЕРГИЯСИГА ЎТАДИ. Электр қаршиликка эга бўлган ўтказгич орқали электр токи ўтса шу ўтказгичда ИССИҚЛИК ажралади.

Электр энергиясини иссиқлик энергиясига айлантириш хусусиятига эга бўлган ўтказгич РЕЗИСТОР ҚАРШИЛИГИ дейлади. Худди шундай хусусиятга эга бўлган жисм РЕЗИСТОР деб аталади.

Электр схемаларда резисторлар қуйидаги расмда кўрсатилгандек белгиланади:

Расм-1.3

Қаршиликка тескари бўлган физик катталик ЎТКАЗУВЧАНЛИК деб аталади.

Резисторли занжирларда ўтказувчанлик қуйидаги формула орқали ифодаланади. Ўтказувчанликнинг ўлчов бирлиги немис электротехники Э. В. Сименс (1816-1892) шарафига Сименс (См) да ўлчанади. Солиштирма қаршиликка тескари бўлган катталик СОЛИШТИРМА ЎТКАЗУВЧАНЛИК деб аталади ва формула орқали ифодаланади. Солиштирма ўтказувчанликнинг ўлчов бирлиги қуйидаги қиймат билан аниқланади.

ёки

1.5. МАНБАНИНГ ИЧКИ ҚАРШИЛИГИ

Ҳар қандай электр энергияси манбалари ички қаршиликка эга бўладилар ва электр схемаларида қуйидагича белгиланади

(ёки r)

Электр манбаларнинг ички қаршиликлари жуда муҳим аҳамиятга эга бўлган катталик ҳисобланади, чунки ички қаршилик орқали манбанинг баъзи хусусиятларини аниқлаш мумкин бўлади. Одатда манбанинг ички қаршилиги манбанинг ичида бўлади, фақат схемаларда алохида белгилар билан кўрсатилади, масалан:

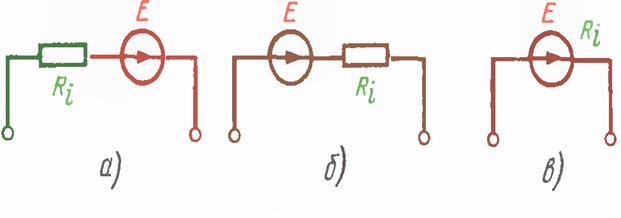
Расм-1.4

НАЗОРАТ САВОЛЛАРИ

1. Зарядланган зарачалар.

2 . Зарядланган заррачаларнинг ўзаро ҳаракатлари.

3. Электр майдон.

4. Электр майдон тушунчаси.

5. Электр токи тушунчаси.

6. Ўтказгич қаршилиги.

7. Солиштирма қаршилик.

8. Ўтказгичнинг резистор қаршилиги.

9. Ўтказувчанлик тушунчаси.

10. Солиштирма ўтказувчанлик.

11. Манбанинг ички қаршилиги.

2-МАЪРУЗА.

КУЧЛАНИШ. ЭЛЕКТР ПОТЕНЦИАЛИ ВА ПОТЕНЦИАЛЛАР ФАРҚИ. ЭЛЕКТР ЮРИТУВЧИ КУЧ.

2.1 КУЧЛАНИШ

Электр занжирининг бирон бир участкасидаги КУЧЛАНИШ деб шу участканинг чекка нуқталаридаги потенциаллар фарқига айтилади.

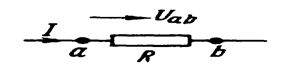
Расм-2.1

Ушбу рамсда электр занжирининг чекка нуқталари a ва b ҳарфлар билан белгиланган. Фараз қилайлик, I ток a нуқтадан b нуқтага, яъни потенциали юқори бўлган нуқтадан, потенциали кичик бўлган нуқтага қараб оқаяпти.

Кучланиш йўналиши потенциали юқори бўлган нуқтадан потенциали кичик бўлган нуқта томон йўналган бўлади. Демак “а“ нуқтанинг потенциали “b” нуқтанинг потенциалидан формулада келтирилган миқдордай катта ҳисобланади.

_a=_b+ IR , 2.1.

Демак “a” ва “b” нуқталар ўртасидаги КУЧЛАНИШ қуйидаги формула орқали аниқланади:

U_ab₌_a- _b_,2.2.

Шундан келиб чиқадики, КУЧЛАНИШ электр занжирининг қаршилиги орқали оқиб ўтаётган токнинг шу қаршилик миқдори кўпайтмасига тенг, яъни:

U_ab= IR, 2.3.

Электротехникада қаршиликнинг икки чекка нуқталаридаги потенциаллар фарқи кучланиш ПАСАЙИШИ (падение напряжение) деб аталади.

Занжирнинг бирон бир участкасида потенциалларнинг пасайиш йўналиши стрелка билан кўрсатилади, одатда ток йўналиши билан мос келади.

Энди электр занжирининг қаршилик уланган қисми эмас, балки ЭЛЕКТР ЮРИТУВЧИ КУЧ (ЭЮК) уланган қисмини кўриб чиқамиз.

Расмда кўрсатилган занжирнинг “a” ва “c” нуқталари учун потенциаллар фарқини аниқлаймиз:

U_ac=_a-_c , 2.4.

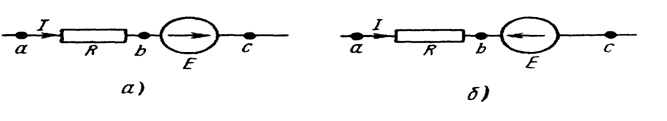
Расм-2.2

2.2 а расмда “c” нуқтадан “b” нуқтага қараб юрилса ЭЮК йўналишига тескари бўлади ва “b” нуқтанинг потенциали “c” нуқтанинг потенциалидан ЭЮК нинг қуйидаги миқдорича кам бўлади, яъни

_b= _c- E, 2.5.

Агар “b” нуқтадан “c” нуқтага қараб юрилса, ЭЮК йўналишига мос келади ва “c” нуқтанинг потенциали “b” нуқтанинг потенциалидан ЭЮКнинг қуйидаги миқдорича катта бўлади, яъни:

_b=_c+ E , 2.6.

Юқорида кўриб чиқилган электр занжирининг қисмларида, ЭЮК бўлмаган участкаларида, электр токи потенциал юқори бўлган нуқтадан потенциали паст бўлган нуқтага томон оқаётганини кўрамиз. 2.2 расмнинг иккаласида ҳам “a” нуқтанинг потенциали “b” нуқтанинг потенциалидан қаршиликнинг қуйидаги миқдорича юқори бўлади, яъни:

_a=_b+IR , 2.7 .

Шундай қилиб 2.2 а расм учун қуйидаги ифода тўғри келади:

_a=_c- E + IR, U_ac=_a-_c= IR - E, 2.8.

2.2. б расм учун эса қуйидаги ифода тўғри келади:

_a=_c+E+IR, U_ac=_a-_c=IR + E, 2.9.

U_ac кучланишнинг мусбат томонга йўналиши “a” нуқтадан “c” нуқта томон стрелка орқали кўрсатилган.

Қоидага кўра “a” ва “c” нуқталар кучланиши қуйидаги формула орқали ифодаланади_.

U_ca= _c- _a,2.10.

Шунинг учун ҳам U_ca= -U_ac яъни кучланиш ҳам мусбат, ҳам манфий қийматларга эга бўлиши мумкин. Кучланишнинг ўлчов бирлиги Италия физики Александро Вольт (1745 - 1827) шарафига Вольт (В) деб белгиланади. Электротехникада кучланишнинг қуйидаги ўлчов бирликлари ишлатилади:

Киловольт (кВ)=1000 В , 1кВ=10³В;

Милливольт (мВ)=0,001 В, 1В=1000 мВ, 1 мВ=10^-3 В;

Микровольт (мкВ) =0,000001 В=10^-6 В, 1В=10⁶ мкВ;

2.2. ПОТЕНЦИАЛ.
ПОТЕНЦИАЛЛАР ФАРҚИ.

Мусбат ишорали заряд “ Q “атрофида Электр майдон ҳосил бўлади, шу майдон нуқтасига яна “ q “ бир мусбат заряд киритамиз.

Бу икки (Q вa q) заряд бир ҳил номланган зарядга эга, яъни иккаласи ҳам (+) мусбат зарядланаган. Демак бу икки заряд бир бирини итариш “F” Кучига эга бўлади. Шу куч зарядларни бир биридан итариши оқибатида бирон “A” иш бажарилади.

Демак бирон бир зарядни электр майдонига олиб кириш учун “A” иш бажарилиш ҳисобига бирон энергия сарф қилинади. Электр майдонининг ҳар бир нуқтаси электр потенциали билан характерланади, ёки ПОТЕНЦИАЛ деб юритилади.

, 2.11.

Ушбу формула зарядланган зарядни бирон бир нуқтага кўчириш учун, бажарилган “A” иш ҳисобига, бирон бир энергия сарф қилинишини кўрсатади. Потенциалнинг ўлчов бирлиги (ВОЛЬТ, қисқача (В). ЭНЕРГИЯ иш каби инглиз физики ДЖЙМС ДЖОУЛ (1818 – 1889) шарафига ДЖОУЛ (Дж) ўлчов бирлиги билан ўлчанади. Бир метр йўл узунлигида бир НЬЮТОН куч бажарган иш бир ДЖОУЛ дейилади, яъни

[Дж] =Нм=кг м м/с²=кг м²/с²

1 Кл зарядни майдоннинг бир нуқтасидан иккинчи бир нуқтасига кўчириш учун сарфланадиган 1 Дж энергияга 1 В ПОТЕНЦИАЛ деб аталади.

Майдон кучланганлигини “E” потенциал “ ” орқали ифодалаймиз, яъни:

E= , 2.12.

Q=, W=A=F L, F-куч, L -масофа. Унда:

E= , 2.13 .

Демак электр майдоннинг ҳар бир нуқтаси ПОТЕНЦИАЛ билан характерланади.

ИККИ НУҚТАНИНГ ПОТЕНЦИАЛЛАР ФАРҚИ КУЧЛАНГАНЛИК ДЕЙИЛАДИ ва U билан белгиланади.

Икки “а” ва “в” нуқталарнинг потенциаллар фарқи қуйидаги формула орқали ифодаланади

2.3. ЭЛЕКТР ЮРИТУВЧИ КУЧ

Олдинги бўлимларда икки нуқтанинг потенциаллар фарқи КУЧЛАНИШ деб аталган эди.

Потенциаллари ҳар хил бўлган иккита майдонни олсак, улар ўртасида қуйидаги миқдордаги кучланиш ҳосил бўлади.

U=₁- ₂, 2.13 .

Бу ерда (₁ва₂) майдонлардаги ноэлектрик энергия ҳисобига ҳосил бўлган потенциаллар миқдори. Масалан химиявий элементлардан ташкил топган (кўмир, цинк, агломерат ва б.) элементни оламиз. Химиявий реакция ҳисобига энергия сарфланади ва майдонларда маълум бир сондаги электронлар пайдо бўлади, шунинг ҳисобига кўмир ва цинк элементларида ҳар ҳил потенциаллар пайдо бўлади. Шу химиявий элементлар чиқишларида КУЧЛАНИШ ҳосил бўлади.Ушбу кучланиш манбанинг очиқ клеммаларида ЭЛЕКТР ЮРИТУВЧИ КУЧ (ЭЮК) деб юритилади.

Демак ЭЮК ҳам ҳар ҳил кўринишдаги КУЧЛАНИШ ҳисобланади. ЭЮК ҳам кучланиш каби ВОЛЬТ (В) ўлчов бирлигида ўлчанади. Демак манбанинг ЭЛЕКТР ЮРИТУВЧИ КУЧИ шу манба ичидаги энергиянинг сарфланиши ҳисобига ҳосил бўладиган потенциаллар фарқига айтилади.

Ишлаб чиқаришда, электростанцияларда ЭЮК механик энергия ҳисобига ҳосил бўлади. ЭЮК нинг йўналиши ташқи майдон кучлари манба ичида мусбат зарядни мусбат йўналишдаги кўчиришга айтилади. Ташқи майдон йўналиши ҳам дейилади.

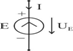
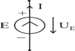
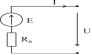
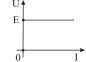
Расм-2.3

Юқоридаги расмларда ЭЮКнинг схемаларда белгиланиши, ЭЮК нинг электр занжирига уланиши ва Вольт Ампер характеристикаси (ВАХ) келтирилган.

ВАХ дан кўринадики ЭЮК (Е) занжирнинг кучланишига (U) тенг бўлади, ва занжир орқали оқаётган I токка боғлиқ бўлмайди.

НАЗОРАТ САВОЛЛАРИ

• 1. Кучланиш, таърифи.

• 2. Кучланишни ҳосил қилиш.

• 3. Кучланиш ўлчов бирлиги.

• 4. Потенциал, таърифи.

• 5. Потенциаллар фарқи.

• 6. Электр юритувчи куч, таърифи.

• 7. ЭЮК ўлчов бирлиги.

• 8. ЭЮКнинг электр схемаларида белгиланиши.

• 9. ДЖОУЛ деб нимага айтилади

3-МАЪРУЗА.

ЭЛЕКТР ЗАНЖИРИ. ЭЛЕКТР ЗАНЖИР ЭЛЕМЕНТЛАРИ. ЭЛЕМЕНТЛАРНИ КЕТМА КЕТ ВА ПАРАЛЕЛ УЛАШ.

3.1. ЭЛЕКТР ЗАНЖИРИ

ЭЛЕКТР ТОКИ УЧУН ЙЎЛ (ЙЎЛАК) ҲОСИЛ ҚИЛАДИГАН ЭЛЕМЕНТЛАР ВА ҚУРИЛМАЛАР ЙИҒИНДИСИГА ЭЛЕКТР ЗАНЖИРИ ДЕБ АТАЛАДИ.

Электр занжирини шартли белгилар билан тасвирлаш ЭЛЕКТР СХЕМАСИ дейилади. Ушбу расмда электр схемасининг бир кўриниши келтирилган.

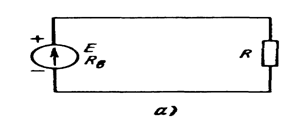
Расм-3.1

3.1.1. ЭЛЕКТР ЗАНЖИР ЭЛЕМЕНТЛАРИ

Электр занжирлар асосан ҚАРШИЛИК, ИНДУКТИВЛИК, КОНДЕНСАТОР (СИҒИМ), ЭЮК ва ТОК МАБАЛАРИДАН ташкил топган бўлади. Уларнинг ҳарактеристикаларини кўриб чиқамиз:

ҚАРШИЛИК ЭЛЕМЕНТИ электр энергиясининг иссиқлик энергиясига ўтишишини ифодалайди ва модда молекуласи ҳаракатланаётган зарядли зарядчалар қаршилигига учрайди.

Бу холатда электр энергияси иссиқлик энергиясига айланади, элементда сақланиб қолмайди. Ушбу расмларда қаршилик элементининг электр занжирларда белгиланиши ва чизиқли ва ночизиқли элементлар ва Вольт Ампер характеристикалари (ВАХ) келтирилган.

а)Чизиқли, б)Ночизиқли

Расм-3.2

ИНДУКТИВЛИК ЭЛЕМЕНТИ қурилмада магнит майдон борлигини ифодалайди ва ўзгармас ток бўйича қаршилик кўрсатади. Индуктив элементида магнит майдон энергияси сақланиб қолади. Ушбу расмларда чизиқли ва ночизиқли элементлар ва Вебер Ампер характеристикаси (ВебАХ) келтирилган.

а) Чизиқли. б) Ночизиқли.

Расм-3.3

Ф=LI , L= [L]=

КОНДЕНСАТОР (СИҒИМ) ЭЛЕМЕНТИ қурилмада электр майдон борлигини ифодалайди. Бунда зарядларнинг ҳаракат энергияси электр майдонининг потенциал энергиясига айланади.
Кейинчалик бу потенциал энергия элементда сақланиб қолади. Ушбу расмларда чизиқли ва ночизиқли элементлар ва мос холда улар характеристикалари келтирилган.

a) Чизиқли. b) Ночизиқли

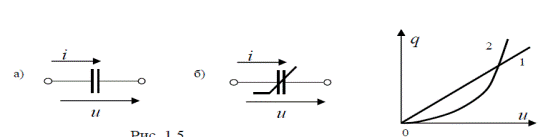
Расм-3.4

Юқорида кўриб чиқилган электр занжирининг элементлари (қаршилик, индуктивлик ва сиғим) ПАССИВ ЭЛЕМЕНТЛАР деб аталади, чунки занжирнинг бошқа қисмларидан олган энергиялари фақат мусбат бўлади, ёки нолга тенг бўлади, яъни ўзида қолади.

3.1.2. ЭЛЕКТР ЮРИТУВЧИ КУЧ (ЭЮК).

ЭЮК ва ТОК манбалари электр занжирининг АКТИВ ЭЛЕМЕНТЛАРИ ҳисобланади, чунки улар электр занжирига уланган элементларга энергияларини беради. Шунинг учун ҳам улар “истъемол” қиладиган ташқи энергия манфий ҳисобланади. Қуйида ЭЮК ва ТОК манбаларининг электр занжирларда белгиланиши, ВАХ лари келтирилган. ВАХ дан кўриниб турибдики ЭЮК занжирда ҳосил бўладиган кучланиш миқдорига тенг бўлади ва ток миқдорига боғлиқ бўлмайди.

r_вн 0, U U_xx=E

r_вн = 0; U = U_xx=E=const;

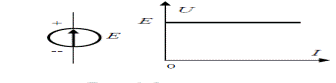
Расм-3.5

Ток манбасининг ички қаршилиги чексизликка интилади, занжирда қисқа туташув юз беради ва қисқа туташув ток миқдори ток манбаига тенг бўлади, ушбу холат ВАХ да яққол кўриниб турибди.

r_вн, I I_КЗ=J,

r_вн= , I=I_КЗ=J=const;

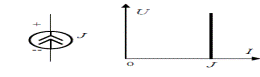
Расм-3.6

Мисол тариқасида қуйидаги электр занжирини кўриб чиқами: Фараз қилайлик, электромагнит энергияси иссиқлик энергиясига фақат а-b соҳадаги резистордагина ўтаяпти, яъни бу оралиқда занжирнинг барча қаршилиги r миқдорида мужассамланган; электр силжиш токлари фақат c-d оралиқда конденсатор қопламалари орасида мавжуд, яъни бу соҳада занжирнинг барча С сиғими мужассамланган; ниҳоят, ўзгарувчан магнит майдон ЭЮКни фақат h-j оралиқда мужассам-ланган ғалтакда индуктивлайди, яъни ушбу соҳада занжирнинг барча L индук-тивлиги йиғилган.

Расм-3.7

3.1.3.Тармоқланган ва тармоқланмаган занжирлар.

Барча турдаги электр занжирлари ТАРМОҚЛАНГАН ва ТАРМОҚЛАНМАГАН занжирларга бўлинади.

Электр занжир элементларидан ҳар хил миқдордаги токлар ўтса бундай электр занжири ТАРМОҚЛАНГАН электр занжири деб аталади (3.8. расм).

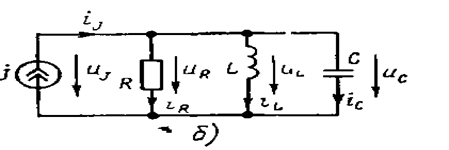
Расм-3.8

Электр занжир элементларидан бир хил миқдордаги токлар ўтса бундай электр занжири ТАРМОҚЛАНМАГАН электр занжири деб аталади (3.9 расм).

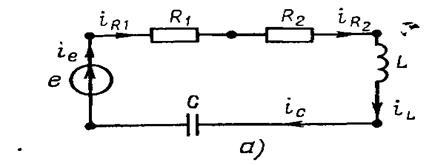
Расм-3.9

3.1.4. ЭЛЕКТР ЗАНЖИР ЭЛЕМЕНТЛАРИНИНГ ВОЛЬТ - АМПЕР ХАРАКТЕРИСТИКАЛАРИ.

Қаршилик орқали оқаётган токнинг шу қаршилик кучланишига боғлиқлик графиги ВОЛЬТ - АМПЕР ХАРАКТЕРИСТИКАЛАРИ (ВАХ) дейилади. Одатда графикда абцисса ўқига КУЧЛАНИШ, ордината ўқига эса ТОК миқдори қўйилади.

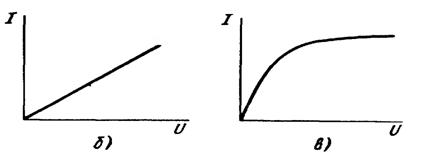
Расм-3.10

Чизиқли ВАХ га эга бўлган қаршилик ЧИЗИҚЛИ ҚАРШИЛИК деб аталади (а расм), фақат чизиқли қаршиликка эга бўлган электр занжирлар ЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРЛАР дейилади.

Ночизиқли ВАХ га эга бўлган қаршилик НОЧИЗИҚЛИ ҚАРШИЛИК деб аталади (в расм), фақат ночизиқли қаршиликка эга бўлган электр занжирлар НОЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРЛАР дейилади.

ТОК ва КУЧЛАНИШГА нисбатан праметрлари ўзгарадиган ЭЛЕМЕНТЛАР НОЧИЗИҚЛИ ЭЛЕМЕНТЛАР дейилади.

Қуйидаги расмларда Чизиқли қаршилик, чизиқли конденсатор ва чизиқли индуктивлик характеристикалари келтирилган.

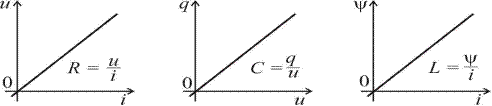
Расм-3.11

3.1.5.ЭЛЕКТР ЗАНЖИРЛАРНИНГ ТОПОЛОГИК ХАРАКТЕРИСТИКАЛАРИ.

Электр занжирлари умумий ҳолда ШОХОБЧАЛАР, ТУГУНЛАР ВА КОНТУРЛАРДАН иборат бўлади.

Электр занжири схемасининг ШОХОБЧАСИ деб занжирнинг шундай қисмига айтиладики, унинг ихтиёрий бўлагида токнинг миқдори доимо бир хил бўлади.

ШОХОБЧА таркибида ихтиёрий миқдордаги кетма-кет уланган қаршилик, конденсатор, индуктивлик элементлари, ЭЮК манбалари бўлиши мумкин. Бунга қуйидаги расмда келтирилган электр занжирини мисол тариқасида келтиришимиз мумкин.

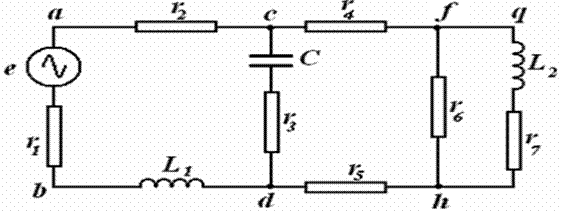
Расм-3.12

Унда схеманинг d нуқтасидан c нуқтасига L1, r1 , e ва r2 элементлари бўйлаб юрсак, шу элементларнинг ҳар биридан бир хил ТОК оқишини кўрамиз.

Демак, схеманинг d - L1 - r1 - e - r2 - с бўлаги шохобча ҳисобланади. Шу dс оралиқни с – C – r3 – d бўйлаб юрсак, яни бир шохобчани кўрамиз.

Ушбу схемада яна c – r4 – f, f -r6 - h, q - L2 - r7 – h ва d - r5 – h шохобчалар ҳам мавжуд. Демак, ҳар бир шохобчадаги элементлар ўзаро кетма-кет уланган экан.

Электр занжирининг ТУГУНЛАРИ деб шохобчаларнинг камида учтаси уланган нуқталарига айтилади. Тугун электр схемасида нуқта билан белгиланади. Мисол сифатида юқоридаги расмда кўришимиз мумкин. Ундаги c, d, f, ва h нуқталар тугун дейилади.

Мисол тариқасида ушбу расмларни келтиришимиз мумкин.

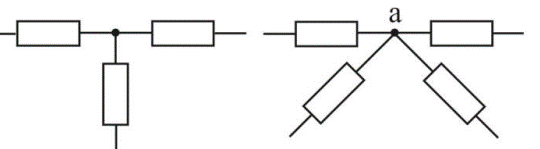
Расм-3.13

Электр занжирининг КОНТУРИ деб, бирнеча кетма кет шохобчалар орқали ўтган ихтиёрий берк йўлга айтилади. Бунга мисол қилиб юқоридаги расмдаги abdcа, cdhfс ва fqhf контурларни олишимиз мумкин.

3.1.6. ЗАНЖИРЛАРНИ КЕТМА-КЕТ ВА ПАРАЛЕЛ УЛАШ

Электр занжири қисмларининг КЕТМА-КЕТ улангани деб шундай уланишига айтиладики, унда занжир шу бўлагининг ҳар бир қисмидан оқаётган ток бир бирига тенг бўлади.

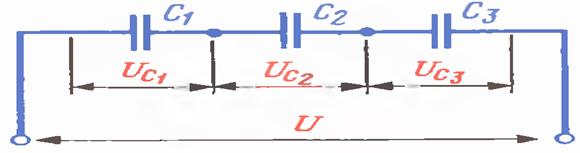
Расм-3.14

Кетма-кет уланган элементларга мисол сифатида расмда келтирилган схемаларни кўриб чиқайлик. Унда a – b оралиқда r1, C ва r2 элементлари кетма-кет уланган (а-расм); бунда уччала элементнинг токлари ir1 = iC = ir2 ўзаро тенг. Иккинчи шохобчада эса c ва d нуқталари орасида r ва L элементлари кетма-кет уланган ва ir = iL (б-расм).

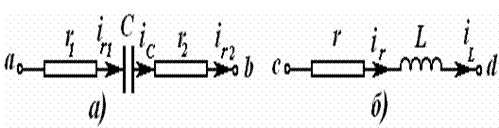
Расм-3.15

3.3.1

Электр занжири элементларининг ПАРАЛЛЕЛ уланиши деб шундай уланишга айтиладики, унда барча элементлар (шохобчалар) занжирнинг бир жуфт тугунларига уланади ва барча элементлардаги (шохобчалардаги) кучланишлар бир хил бўлади.

Параллел уланган шохобчаларга 3.16-расмда келтирилган схемалар мисол бўла олади.

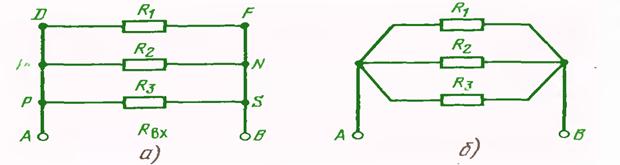
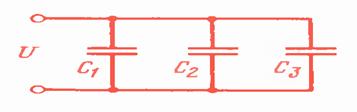
U_J=U_R=U_L=U_C 3.3.2

Расм-3.16

НАЗОРАТ САВОЛЛАРИ

1.Электр занжири, таърифи.

2. Электр занжир элементлари.

3. Тармоқланган ва тармоқланмаган электр занжирлари.

4. Элементларни кетма-кет ва паралел улаш.

5. Электр занжирининг топологик структураси (шохобча, тугун, контур) тушунчалари.

6. Актив ва пассив элементлар, характеристикалари.

7. Чизиқли ва ночизиқли занжир элементлари.

8. Элементларнинг Вольт-Ампер характеристикалари.

4-МАЪРУЗА

ЭЛЕКТР ЗАНЖИРЛАР НАЗАРИЯСИНИНГ АСОСИЙ ҚОНУНЛАРИ. КИРХГОФ ВА ОМ ҚОНУНЛАРИ.

Электр занжирлар назариясида Ом қонуни билан бирга шохобчалардаги ТОКЛАР ва ёпиқ занжирлардаги кучланишлар балансларини ифодалайдиган АСОСИЙ қонунлардан бири КИРХГОФ қонунлари ҳисобланади.

Электр занжирларида ТОК ва КУЧЛАНИШЛАРнинг занжир бўйича тақсимланиши КИРХГОФ қонунлари орқали ифодаланади.

4.1. КИРХГОФ ҚОНУНЛАРИ

Электр занжирлар элементларининг асосий параметрларини ҳисоблаш учун КИРХГОФ ВА ОМ қонунларидан фойдаланилади.

Немис физики Густав Роберт Кирхгоф электр занжирлар назариясида ўзининг биринчи ва иккинчи қонунларини яратган олимлардан ҳисобланади.

4.1.1. КИРХГОФНИНГ БИРИНЧИ ҚОНУНИ

Тугундаги токларнинг алгебраик йиғиндиси нолга тенг.

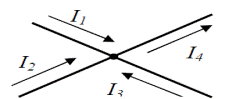
I=0 -I₁-I₂-I₃+I₄=0 4.1.1

Расм-4.1

КИРХГОФ ҚОНУНИНИНГ БОШҚАЧА ТАЛҚИНИ: Тугунга кириб келаётган токлар йиғиндиси тугундан чиқаётган токлар йиғиндисига тенг.

I₁+I₂+I₃=I₄

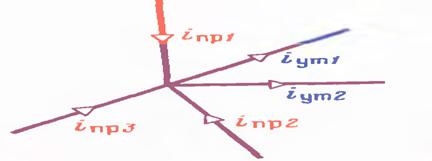
Расм-4.2

i_пр1+ i_пр2+ i_пр3- i_ут1-i _ут2=0 , 4.1.2.

Кирхгофнинг биринчи қонуни бўйича тенгламалар сони қуйидаги аниқланади: (у-1) , бу ерда у – занжирдаги тугунлар сони.

Тугунларга келаётган ва тугунлардан чиқаётган ТОКЛАР ЙИҒИНДИСИ кўриб чиқилаётган ТУГУНДАГИ барча шохобчалардаги ТОКЛАРГА тегишли бўлади. Тугунларга келаётган ва чиқаётган токларга БИР ХИЛ ишоралар қўйилади, яъни мусбат ва манфий.Мисол тариқасида юқоридаги расмларда кўрсатилган.

Кирхгофнинг биринчи қонунинг маъноси шундан иборатки, тугунларда электр зарядлари йиғилмайди ҳам, сарф ҳам қилинмайди, фақат маълум бир вақт оралиғида тугунга келаётган зарядлар йиғиндиси, тугундан чиқаётган зарядлар йиғиндисига тенг бўлади.

Кирхгофнинг биринчи қонуни фақат тугун учун эмас, балки бирон бир контур учун ҳам қўлланиши мумкин, мисол учун:

Расм-4.3

-i₁+i₂+i₃=0 , 4.1.3

4.1.2. КИРХГОФНИНГ ИККИНЧИ ҚОНУНИ

Занжир контуридаги элементлар кучланишларининг алгебраик йиғиндиси шу контурдаги эюк ларнинг алгебраик йиғиндисига тенг бўлади.

, , 4.1.4

Контур ичидаги ток йўналиши ихтиёрий йўналишда олинади, мисол учун соат стрелкаси йўналиши бўйича олиниши мумкин. Бу холатда ЭЮК ва КУЧЛАНИШЛАР учун қуйидаги қоидага риоя қилинади, яъни контурдаги ток йўналиши билан ЭЮК ва КУЧЛАНИШ йўналишлари мос келса БИР ХИЛ ишора билан олинади.

e₁ u₁

u₄ u₂

e₂ u₃ e₁-e₂=u₁+u₂+u₃-u_4, 4.1.5

Расм 4.4.

Кирхгофнинг ИККИНЧИ қонунини формула орқали ифодалаш учун қуйидаги электр занжирдан фойдаланамиз:

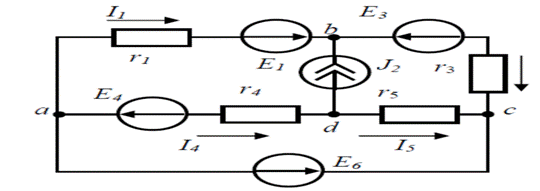
Расм-4.5

Мисол тариқасида: a тугун учун 1 шохобча, b тугун учун 3 шохобча, c тугун учун 5 шохобча, d тугун учун эса 4 шохобчаларга қуйидаги тенглама мос келади:

I₃ r₃ –I₅ r₅ –I₄ r₄ =E₁ – E₃ + E_{4 ,} 4.1.6

Кирхгофнинг иккинчи қонуни бўйича тузиладиган тенгламалар сони қуйидагича аниқланади: [в - (у-1)] , бу ерда : в – шохобчалар сони;

4.1.3. КИРХГОФ ҚОНУНЛАРИ АСОСИДА ЗАНЖИРЛАРНИ ҲИСОБЛАШ ТАРТИБИ

1. Барча шохобчаларда токлар йўналиши аниқланади.

2. Схемадаги тугунлар учун Кирхгофнинг биринчи қонуни учун тенглама тузилади.

3. Мустақил контурлар аниқланади (танланади).

4. Кирхгофнинг иккинчи қонуни учун тенглама тузилади.

5. Тузилган тенгламалар мустақил токлар учун ечилади.

6. Агар қуйидаги элементларнинг миқдорлари аниқ бўлса:

E₁, E₃, E₆, r₁, r₂, r₃, r₄, r₅, r₆

У холда қуйида келтирилган электр занжири учун КИРХГОФ қонунлари бўйича тенгламалар тузамиз.

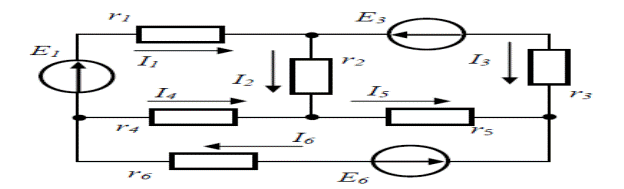
Расм-4.6

I₆-I₄-I₁=0, I₁r₁+I₂r₂-I₄r₄=E_1,

I₁-I₂-I₃=0, I₃r₃-I₅r₅-I₂r₂=-E_3,

I₃+I₅-I₆=0, I₄r₄+I₅r₅+I₆r₆=-E₆

4.2. ЭЛЕКТР ЗАНЖИРЛАР УЧУН ОМ ҚОНУНИ

Занжирнинг ЭЮК бўлмаган қисми учун ОМ ҚОНУНИ занжирнинг шу қисми учун ток ва кучланиш ўртасидаги боғланишни ифодалайди ва қуйидаги кўринишга эга бўлади.

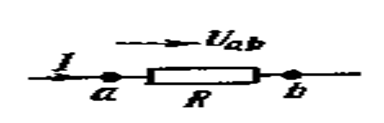
Расм-4.6

U_ab=IR, , 4.2.1

Занжирда ТОК ва КУЧЛАНИШ вақт бўйича ўзгармаслиги мумкин (доимий ток режими) у холда ток ва кучланишнинг оний қийматлари ҳам ўзгармас қийматга эга бўлади. Шу холат учун Ом қонуни қуйидагича ифодаланади ва таърифланади: занжирдан ўтаётган ТОК кучланишга тўғри пропорциогнал, қаршиликка тескари пропорционал

I= ёки U=RI , 4.2.2

Занжирнинг ЭЮК бўлган қисми учун ОМ қонуни қуйидагича ифодаланади:

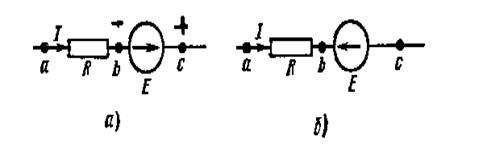
Расм-4.7

, , 4.2.3

Умумий холатда эса қуйидагича ифодаланади:

, 4.2.4

Электр занжирининг ЭЮК уланган қисми учун ОМ қонуни қуйидагича ифодаланади

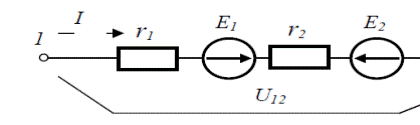
Расм-4.8

, 4.2.5

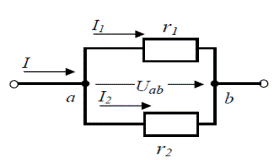
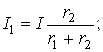
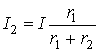, 4.2.6

Расм-4.9

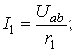
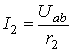; , 4.2.7

НАЗОРАТ САВОЛЛАРИ

1.Кирхгофнинг биринчи қонуни, таърифи.

2. Кирхгофнинг иккинчи қонуни, таърифи.

3. Занжирнинг ЭЮК бўлмаган қисми учун ОМ қонуни.

4. Занжирнинг ЭЮК мавжуд бўлган қисми учун ОМ қонуни.

5. Кирхгоф ва Ом қонунларини тадбиқ этувчи мисоллар ечиш.

5-МАЪРУЗА.

ДОИМИЙ ТОК ЗАНЖИРЛАРИНИ ҲИСОБЛАШ. ЭЛЕКТР СХЕМАЛАРИНИ ЭКВИВАЛЕНТ УСУЛИ БИЛАН АЛМАШТИРИШ (ЭКВИВАЛЕНТ АЛМАШТИРИШ УСУЛИ).

5.1. ЭКВИВАЛЕНТ АЛМАШТИРИШ УСУЛИ .

Эквивалент алмаштириш усулининг маъноси: занжирнинг бир нечта элементларини бир элемент билан, ёки электр схемасини бир бошқа схема билан алмаштириш, яъни соддалаштириш тушунилади.

Схеманинг киришидаги ток ва кучланишлар миқдори ўзгармай қолса алмаштириш эевивалент ҳисобланади.

Эквивалент алмаштиришнинг мақсади, электр схемаларини соддалаштириш ва тенгламалар сонини камайтириш ҳисобланади. Эквивалент алмаштиришлар учун қуйидаги мисолларни келтирамиз:

Қаршиликларни кетма кет улаш:

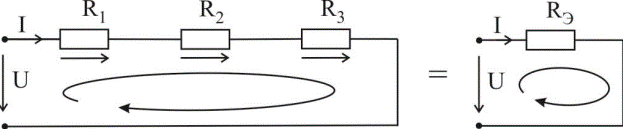
расм-5.1

Бу схемада эквивалент алмаштиришнинг негизи УМУМИЙ ТОК ҳисобланади.

Кирхгофнинг иккинчи қонунига асосан қуйидаги формула ҳосил бўлади:

U=IR₁+IR₂+IR₃=I(R₁+R₂+R₃)=IR_Э , 5.1.1

Ёки умумий холда қуйидаги кўринишда ёзилади:

U=_k=_k=I_k=IR_э , 5.1.2

Бу ерда: R_э=_k алмаштирилган схеманингг эквивалент қаршилиги ҳисобланади.

Қаршиликларнинг паралел уланган холда, бу ерда алмаштириш негизи ҳамма элементларда кучланишнинг бир ҳил бўлиши, яъни:

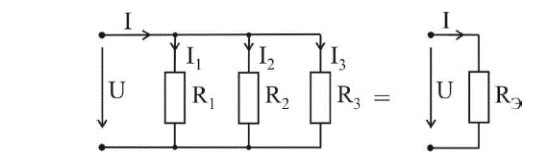
расм-5.2

Ёки умумий холда қуйидагича ёзилади:

I=_k=_k=U_k=Ug_э , 5.1.3

Бу ерда: g_э=_k эквивалент ўтказувчанлик дейилади.

R_э= - электр схеманинг эквивалент қаршилиги ҳисобланади.

АЙРИМ ХОЛАТЛАР УЧУН:

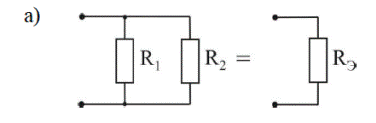
расм-5.3

R_э=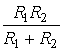 ; R₁=R₂=R ; R_э=, 5.1.4

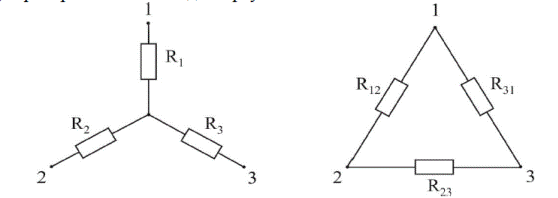
расм-5.4

R₁=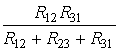; R₁₂=R₁+R₂+; 5.1.5

R₂=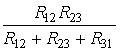; R₂₃=R₂+R₃+; 5.15.

R₃=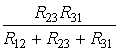 ; R₃₁=R₁+R₃+;

5.2. КОНТУР ТОКЛАР УСУЛИ

Контур токлар усули Кирхгофнинг 2 қонуни асосида контур учун тузилган тенгламаларни ечишга қаратилган бўлади. Бу усул орқали схемадаги тенгламалар сони Кирхгофнинг 2 қонуни тенгламаларигача қисқартириш имкониятини беради.

Кирхгофнинг биринчи ва иккинчи қонунларидан фойдаланган холда қуйидаги электр занжирини кўриб чиқамиз:

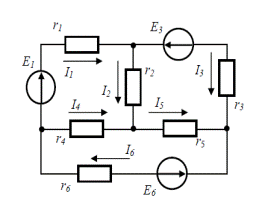
расм-5.6

Кирхгофнинг биринчи ва иккинчи қонунлари бўйича тенгламалар тузамиз:

I₆-I₄-I₁=0 I₁r₁+I₂r₂-I₄r₄=E₁

I₁-I₂-I₃=0 I₃r₃-I₅r₅-I₂r₂=-E₃

I₃+I₅-I₆=0 I₄r₄+I₅r₅+I₆r₆=-E₆5.1.9

Юқоридаги формулалардан қуйидаги токлар ифодаларини топамиз ва (2) тенгламага қўямиз

I₄=I₆-I₁, I₂=I₁-I₃, I₅=-I₃+I₆

5.1.10

5.1.11

(5.1.11) Тенглама контур токлар учун Кирхгофнинг 2 қонуни ҳисобланади. Тенгламанинг чап томони схемадаги элементлар орқали оқиб ўтган контур токидан ҳосил бўлган кучланишлар ва аралаш (қўшни) контурларнинг контур токларини ҳисобга олади. Тенгламанинг ўнг томони эса контурдаги ЭЮК ларни ҳисобга олади.

КТУ бўйича ҳисоблаш тартиби

1. Мустақил контурлар танлаб олинади.

2. Контур токлар киритилади ва улар йўналиши белгиланади.

3. Номаълум контур токлар учун тенгламалар тузилади (агар контурда ток манбаси бўлса, у контур учун тенглама тузилмайди).

4. Контур тенгламалар тизими ечилади ва контур токлар топилади.

5. Шохобчалардаги токлар йўналишлари аниқланади ва улар қиймати ҳисобланади (шохобчалардаги токлар контур токларга тенг бўлади).

5.3. ТУГУНЛАР ПОТЕНЦИАЛИ УСУЛИ

Ушбу усул тугунлар потенциалларини Кирхгофнинг 1 қонуни асосида аниқлашга ва шохобчалардаги токлар қиймати эса Ом қонуни асосида аниқлашга бағишланади. Бу усулда тенгламалар сони Кирхгофнинг 1 қонуни тенгламалари сонигача камайтириш имконини беради.

Шохобчалардаги токлар занжирдаги потенциаллар айирмасига боғлиқ бўлади, агар занжирдаги битта тугунни ерга уласак, у ҳолда унинг потенциали НОЛГА тенг бўлади, лекин схемада токлар ўзгармайди.

Расмдаги схемани кўриб чиқамиз ва d тугун потенциалини НОЛГА тенг деб оламиз

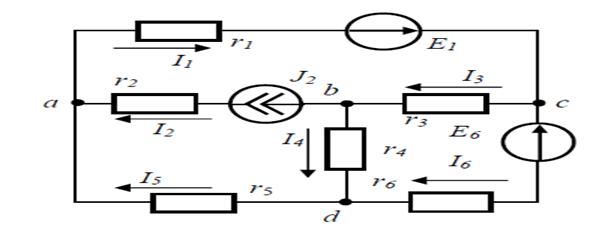
расм-5.7

Номаълум бўлган (a. b. c) тугунлар учун Кирхгофнинг 1 қонуни бўйича тенгламалар тузамиз:

Тугун <<a>>

Тугун <<b>> 5.3.1

Тугун <<c>>

Токлар йўналишларини аниқлаган холда Ом қонуни асосида шохобчалардаги токлар учун тенгламалар тузамиз

; ; ;

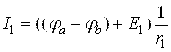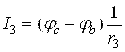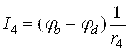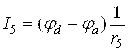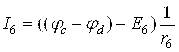; ; ; 5.3.2

5.3.2 тенгламани 5.3.1 тенгламага қўямиз:

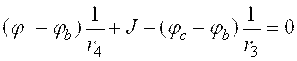
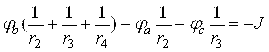
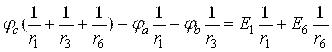
Бошқа шаклда қуйидагича ифодаланади:

Ушбу тенглама тугунлар тенгламаси дейилади.

Тугунлар потенциали усули бўйича ҳисоблаш тартиби

1. Схемадаги бирон бир тугун потенциали НОЛГА тенг деб олинади.

2. Номаълум бўлган тугунлар учун тугунлар тенгламалари ёзиб чиқилади.

3. Тенгламалар тизими ечилади ва номаълум тугунлар потенциали аниқланади.

4. Шохобчаларда токлар йўналиши аниқланади ва Ом қонунига асосан улар қийматлари аниқланади.

5. Агар схемада қаршиликсиз ЭЮК манбаси бўлса, у холда шу манба уланган бошқа шохобча тугунини НОЛГА тенг деб олинади ва бошқа шохобча тугунлари ҳисобланади, лекин бу шохобча учун тенглама тузилмайди.

5.4. ЎЗГАРМАС ТОК ЗАНЖИРИНИНГ ПОТЕНЦИАЛ ДИАГРАММАСИ

Ҳар қандай ЎЗГАРМАС ток занжири учун потенциаллар диаграммасини тузиш мумкин.

Ёпиқ контур ёки электр занжиринг бирон бир участкаси бўйлаб потенциаларнинг график тақсимотига потенциаллар диаграммаси дейилади. Графикнинг абсцисаа ўқига занжирнинг қаршилиги, ордината ўқига эса потенциал жойлаштирилади.

Электр занжирининг потенциалини аниқлаш учун занжирнинг бирон бир тугунини (нуқтасини) НОЛГА тенг деб оламиз.

Занжирнинг ушбу қисми учун Ом қонуни, яъни “a” нуқтанинг потенциали “b” нуқтанинг потенциалидан Uab миқдоргача катта. Демак ток потенциал катта бўлган нуқтадан потенциал кичик бўлган нуқта томонга оқади. Потенциал диаграмма тузиш вақтида айнан шу холат эътиборга олинади.

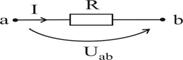
расм-5.8

; ; ;

Агар электр занжир қисмида ЭЮК бўлса, ток йўналиши ЭЮК йўналишига мос келса “a” “b” нуқталар потенциали ЭЮК миқдорича ошади, агар мос келмаса шу миқдорча камаяди.

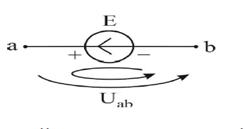
расм-5.9

5.10 расмда кўрсатилган бир контурли электр схемаси учун потенциал диаграммасини тузамиз.

расм-5.10

Потенциал диаграммада ордината ўқи бўича контурнинг потенциал нуқталари жойлашади, абсцисса ўқи бўйича нуқталар ўртасидаги қаршилик жойлашади. “a” нуқта потенциалини НОЛга тенг деб оламиз, яъни . У холда қолган нуқталар потенциали қуйидагича аниқланади:

ёки

Юқорида келтириган бир контурли схема учун Потенциал диаграммаси қуйидаги кўринишда бўлади:

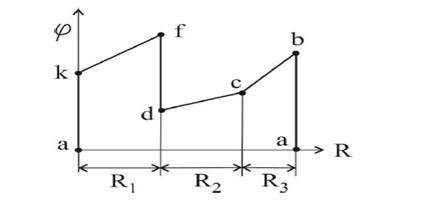
расм-5.11

НАЗОРАТ САВОЛЛАРИ

1. Электр схемаларини эквивалент усули билан алмаштириш.

2. Эквивалент усулини мисоллар билан тугунтириш.

3. Контур токлар усули, маъноси.

4. Контур токлар усулини бажариш тартиби.

5. Тугун потенциали усули, маъноси.

6. Тугун потенциали усулини бажариш тартиби.

7. Электр контури учун потенциал диаграммасини тузиш.

6 –МАЪРУЗА.

ЎЗГАРУВЧАН ТОК. СИНУСОИДАЛ ТОК.

СИНУСОИДАЛ ТОКНИ ХАРАКТЕРЛОВЧИ МИҚДОРЛАР

6.1. ЎЗГАРУВЧАН ТОК

Вақт бўйича ўзгарувчан ток миқдорига Ўзгарувчан ток деб аталади .

Ҳар қандай вақт оралиғидаги ток миқдори ОНИЙ ТОК деб аталади ва i ҳарфи билан белгиланади. Оний қийматлари аниқ вақт бирлигида ва бир ҳил кетма кетликда қайтариладиган токлар ДАВРИЙ деб аталади.

Электр занжирларининг Даврий жараёнларида синусоидал режим асосий ўрин тутади. Бу режимда ток ва кучланишлар бир хил частотали синусоидал функциялар ҳисобланади.

6.1. 2. СИНУСОИДАЛ ТОК

Қийматлари Синусоидал қонун асосида ўзгарувчан ток (кучланиш) ГАРМОНИК ТОК (КУЧЛАНИШ) деб аталади.

Гармоник сигналнинг асосий хусусиятларидан бири гармоник сигналнинг шакли фақат битта (бир хил) f=1/T частотадан ташкил топган бўлади.

Гармоник сигналлардан шакли бошқа бўлган сигналлар ҳар хил частоталардан ташкил топган бўлади. Гармоник сигналлар ёрдамида энергияни узатиш анча қулай, лекин гармоник сигналлар ёрдамида ахборотларни узатиб бўлмайди.

СИНУСОИДАЛ ТОК қуйидагича ифодаланади.(6.1 Расм).

I_msin()=I_msin()

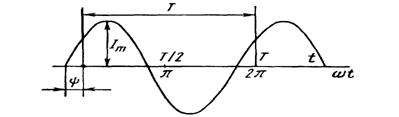
расм-6.1

Ҳар қандай синусоидал ТОК АМПЛИТУДА, БУРЧАК ЧАСТОТАСИ ва БОШЛАНҒИЧ ФАЗА орқали характерланади.

Синусоидал токлар частотасининг ишлатилиши жуда кенг (Гц дан то миллиард Гц гача).

Масалан барча МДҲ давлатларида ва европанинг баъзи мамлакатларида синусоидал ток частотаси 50 Гц деб олинади. АҚШ эса 60 Гц деб олинган.

Функциянинг максимал қийматига АМПЛИТУДА деб аталади.

ТОК Амплитудаси I_m белгиланади.

Вақт оралиғида битта тўлиқ тебраниш ДАВР деб аталади ва T билан белгиланади.

1 секунда тебранишлар сонига ЧАСТОТА деб аталади (частотанинг ўлчов бирлиги Гц (Герц) ёки Электр тармоғи кучланишининг стандарт частотаси 50 Гц.га шу кучланишнинг ҳар Т=0,02с.да бир марта ўзгариши мос келади.

2 миқдор фазанинг ўзгариш тезлигини ифодалайди ва билан белгиланади ва у бурчак частотаси дейилади;

, 6.1.1

Бурчак частотасининг ўлчов бирлиги: рад/c ёки с^-1

Синус аргументи () ФАЗА деб юритилади. Вақт t бирлигида тебранишлар холати ФАЗА деб аталади

Фаза вақт оралиғида ўсиб боради.Фаза 2 миқдоргача ўзгарганда токнинг ўзгариш цикли яна қайтарилади.

Бир давр T мобайнида фаза 2 миқдорга ошади.

Синусоидал ўзгаручан катталикларнинг ўртача қиймати деб уларнинг ярим давр ичидаги ўртача қийматларига айтилади.

Электр токининг ўртача қиймати қуйидаги формула орқали ифодаланади, яъни синусоидал токнинг ўртача қиймати ток амплитудасининг Қийматига тенг бўлади.

I_ср=_msin_m_,6.1.2.

Худди шундай ЭЮК ва кучланишларнинг ўртача қийматлари

E_ср=2E_m/; 6.1.3.

U_ср=2U_m/ 6.1.4.

6.2.1. ҚАРШИЛИК ОРҚАЛИ ГАРМОНИК ТОК ЎТИШИ

Агар қаршиликка кучланишни уласак, қаршилик орқали қуйидаги миқдордаги гармоник ток ўтади:

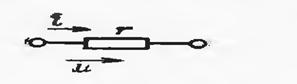
расм-6.2

I=U_m/r cos(_u)=I_mcos(_i) , 6.1.5.

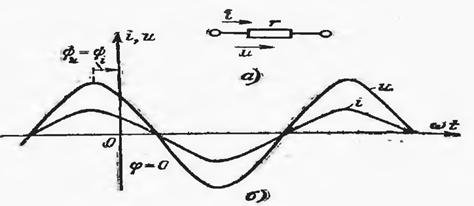
расм-6.3

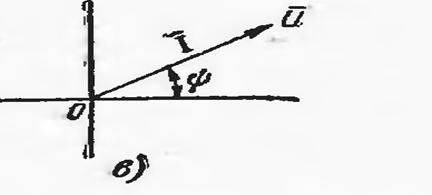
расм-6.4

Келтирилган графикдан шундай хулоса қилиш мумкинки, қаршилик орқали ўтаётган ток ва кучланишларнинг фазалари бир бирига мос келади ва бир пайтда максимум қийматга эришади. Фазалар бўйича мос келган ТОК ва КУЧЛАНИШ бир хил ишорага эга бўлади (мумсбат ёки манфий).

Бу холатда фазалар бўйича силжиш нолга тенг, яъни:

_u-_i=0 , 6.1.6.

Қаршилик орқали ток ва кучланиш ўтар экан Ом қонуни қуйидаги кўринишда бўлади:

U_m=rI_m; U=Ri , 6.1.7.

Ўтказувчанлик g=1/r орқали ифодаласак қуйидаги ифодани олмаиз:

I_m=gU_m; I=gU , 6.1.8.

Қувватнинг бир давр ичидаги ўртача қиймати АКТИВ ҚУВВАТ деб аталади.

P=_rdt , 6.1.9.

P=UI=rI²^,6.1.11.

Ўтказгичнинг қаршилиги ўзгарувчан токда доимий токдагига қараганда кўпроқ бўлади (ташқи таъсирлар оқибатида).

Ўзгарувчан токдаги ўтказгичнинг қаршилиги АКТИВ қаршилик деб аталади.

6.2.2. ИНДУКТИВЛИК ОРҚАЛИ ГАРМОНИК ТОК ЎТИШИ

Индуктивлик орқали қуйидаги гармоник ток ўтаётган бўлсин:

i=I_mcos() , 6.1.12.

Электр юритувчи куч қуйидагича ифодаланади:

e_L=-L_msin()=-U_mcos() , 6.1.13.

Индуктивликдаги кучланиш қуйидагича ифодаланади:

u_L=-e_L=U_mcos() , 6.1.14.

Олинган формуладан шундай хулоса қилиш мумкин: индуктивликдаги кучланиш бурчак миқдорида токдан илгарилаб кетмоқда.
= 6.1.15.

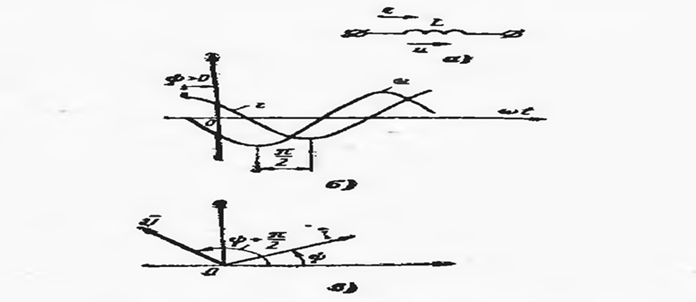
расм-6.5

Ушбу холат учун Ом қонуни қуйидагича аниқланади:

U_m=LI_m=x_LI_m; U=x_LI , 6.1.16.

x_L= L ушбу миқдор ИНДУКТИВ ҚАРШИЛИК деб аталади. Унга тескари бўлган миқдор эса индуктив ўтказувчанлик дейилади.

b_L= , 6.1.17.

Индуктивликдаги қувват миқдори қуйидагича аниқланади:

p_L=ui=-UIsin2() , 6.1.18.

Хулоса қилиб шуни айтиш мумкинки, индуктивлик орқали гармоник ток ўтганда, энергиянинг манба билан индуктивлик ўртасида тебраниши ҳосил бўлади, натижада ҚУВВАТ НОЛГА ТЕНГ БЎЛАДИ.

6.2.3. ГАРМОНИК ТОКНИНГ СИҒИМ ОРҚАЛИ ЎТИШИ

Сиғим орқали кучланиш миқдори қуйидагича бўлади:

, 6.1.19.

Гармоник ток эса:

, 6.1.20.

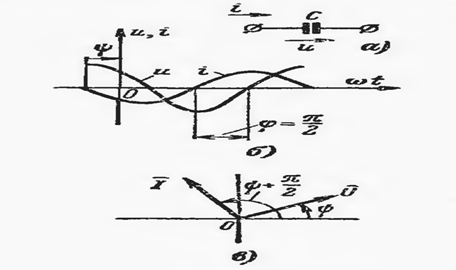
Расм-6.6

Конденсатор пластинкаларида электр зарядларнинг ўзгариши косинусоидал қоидага асосланади. Мусбат ва манфий зарядларнинг пластинкаларда йиғилиши гармоник ток миқдорининг ўтишига сабаб бўлади.

Гармоник токнинг миқдори конденсатордаги зарядларнинг ўзгариш тезлиги орқали аниқланади, яъни:

6.1.20 ифода шуни кўрсатадики, гармоник ток кучланишдан бурчакка илгарилаб кетган, демак токнинг НОЛЬ қийматига кучланишнинг МАКСИМАЛ қиймати МОС келади. Фазалар фарқи қуйидаги формула билан аниқланади:

, 6.1.21.

Ом қонунига асосан:

; ; , 6.1.22.

сиғим қаршилиги;

Бунга тескари бўлган қиймат Сиғим ўтказувчанлиги дейилади. Сиғим қуввати:

, 6.1.23.

Элемент

Умумий кўриниши

Гармоник ҳолатда

Оний қийматлар

Аниқ қийматлар

Қаршилик

Индуктивлик

Сиғим

НАЗОРАТ САВОЛЛАРИ

1. Ўзгарувчан ток, таърифи.

2. Синусоидал ток, таърифи.

3. Гармоник (ток), кучланиш, таърифи.

4. Синусоидал ток амплитудаси, бурчак частотаси.

5. Синусоидал ток графиги, бошланғич фаза.

6. Синусоидал ўзгарувчан катталиклар, ўртача қийматлари.

7. Қаршилик орқали гармоник ток ўтиши.

8. Индуктивлик орқали гармоник ток ўтиши.

9. Сиғим орқали гармоник ток ўтиши.

7–МАЪРУЗА

СИНУСОИДАЛ ФУНКЦИЯЛАРНИ ВЕКТОР ДИАГРАММАСИ ВА КОМПЛЕКС СОНЛАР ОРҚАЛИ ИФОДАЛАШ.

Ҳар қандай чизиқли электр занжирларида, элементлар қандай бўлишидан қатъий назар улар орқали ўтаётган гармоник КУЧЛАНИШ гармоник шаклдаги ТОКНИ ҳосил қилади. Ҳар қандай холатларда чизиқли электр занжирларига гармоник сигналлар таъсир этса улар ҳосил қилган сигналлар гармоник шаклида бўлади.

Шундай экан, ТОК ва КУЧЛАНИШЛАРнинг ОНИЙ қийматлари ҳам гармоник шаклда бўлади. Агар чизиқли электр занжири бир нечта элементлардан ташкил топган бўлса синусоидал графиклар сони кўпайиб кетади ва уларни тахлил қилиш мураккаблашади.

Шунинг учун мураккаблашган электр занжирларидаги гармоник сигналлар таъсирларини синусоидал графиклар орқали эмас, балки ВЕКТОР ДИАГРАММАЛАР орқали тахлил қилиш осонроқ бўлади.

Вектор диаграммасида вектор узунликлари, бурчак ва фазалар миқдорлари пропорционал равишда олинади. Бизга маълумки, Комплекс текисликда ҳар бир нуқта радиус, яъни вектор орқали аниқланади,

Векторнинг бошланиши координата ўқининг бошланиш нуқтасига тўғри келса, унинг охири эса координата учига, яъни комплекс миқдорга тўғри келади. Демак бир нечта чизилган синусоидал графиклар ўрнига ВЕКТОРЛАР йиғиндиси гармоник сигналларнинг электр занжирлар эдементларига таъсирини ифодалайди.

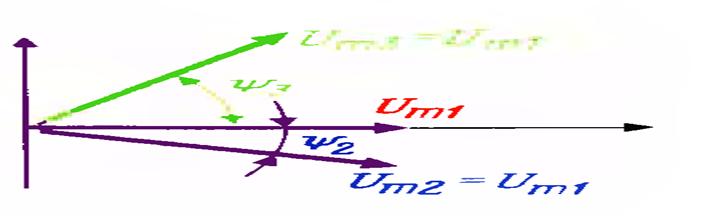расм-7.1

Вектор диаграммасида бирон бир бурчак бошланғич нуқтадан бирон бир бурчакка орқада қолаётган бўлса, у холда вектор соат стрелкаси йўналишига МОС ХОЛДА буралади, агар илгарилаб кетаётган бўлса соат стрелкасига ТЕСКАРИ йўналишда буралади.

ВЕКТОР ДИАГРАММАСИ ДЕБ – синусоидал ўзгарувчан, фазалар бўйича бир – бирига нисбатан тўғри жойлашган, частоталари бир хил қийматга эга бўлган комплекс текисликдаги векторлар йиғиндисига айтилади.

Юқорида келтирилган расмда учта ҳар хил фазадаги, лекин бир хил амплитудага эга бўлган диаграмма кўрсатилган.

Ушбу графикда биринчи кучланишнинг вектор қиймати координатанинг горизонтал ўқига мос келади, иккинчи кучланишнинг вектори бурчакка соат стрелкаси йўналиши бўйича бурилади, учинчи кучланишнинг вектор қиймати эса бурчакка соат стрелкаси йўналишига тескари томонга бурилган бўлади (7.1.) расм.

Вақт бўйича диаграмма гармоник функция қийматларини ҳар қандай вақтда қуйидаги тенглама орқали кўрсатади.

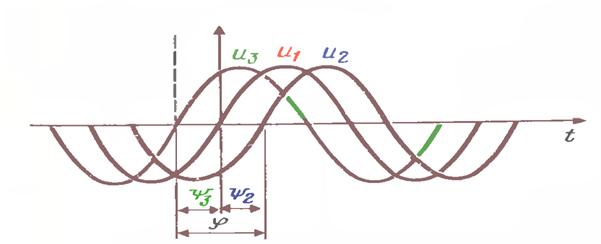
расм-7.2

Вектор диаграммаси орқали эса гармоник функция қийматларини

ифодалаш учун гармоник функцияни соат стрелкасига қарама қарши йўналишда бурчак частотаси билан айланаётган вектор орқали ифодаланади. Бунда айланаётган вектор проекциясини координатанинг вертикал ўқига нисбатан оламиз.

Ҳосил бўлган проекция худди вақт диаграммаси каби синусоидал функция орқали ифодаланади, яъни:

Бу холатда векторнинг соат стрелкаси йўналиши бўйича айланиши МУСБАТ, соат срелкасига қарама қарши йўналиши МАНФИЙ деб юритилади. Мисол тариқасида вектор диаграммаси орқали кучланишнинг оний қийматини аниқлаймиз. Графикнинг чап томонида вектор диаграмма, ўнг томонида вақт диаграммаси келтирилган.

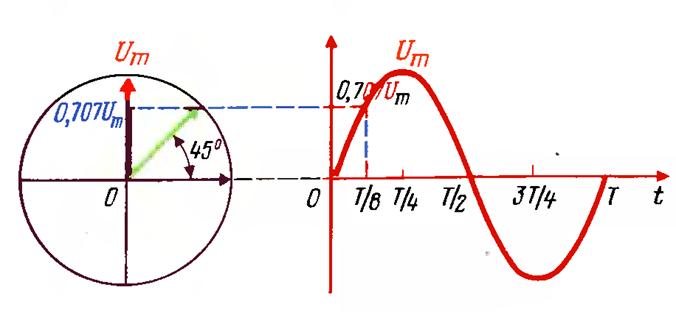
расм-7.3

Бошланғич фаза бурчаги НОЛГА тенг бўлсин.

Бу холатда t = 0 бўлганда кучланишнинг ОНИЙ қиймати ҳам НОЛГА тенг бўлади, вақт диаграммасига мос бўлган ВЕКТОР эса мусбат йўналишга эга бўлган абцисса ўқи йўналишига МОС ТУШАДИ. Шу векторнинг проекцияси координатанинг ВЕРТИКАЛ ўқида ҳам НОЛГА ТЕНГ бўлади, яъни вектор проекциясининг узунлиги синусоиданинг ОНИЙ қиймати билан МОС ТУШАДИ.

вақт ўтгандан кейин бурчак ФАЗАСИ 45 ГРАДУСГА тенг бўлади, кучланишнинг ОНИЙ қиймати эса қуйидаги қийматга тенг бўлади:

Шу вақт оралиғида ВЕКТОР ҲАМ 0.707U_m Қийматга тенг бўлади. Энди вақт ўтгандан кейин кучланишнинг ОНИЙ қиймати U_m га тенг бўлади, вектор эса 90 градусга БУРИЛАДИ.

Векторнинг вертикал ўққа нисбатан ПРОЕКЦИЯСИ векторнинг ўзига тенг бўлиб қолади, узунлиги эса кучланишнинг ОНИЙ қийматининг МАКСИМУМ қийматига тенг бўлади. Худди шундай асосда ҳар қандай вақт оралиғида кучланишнинг ОНИЙ қийматларини аниқлаш мумкин бўлади.

Хулоса қилиб шуни таъкидлаш лозимки: Синусоидал функциялар қийматларини аниқлаш вақтида уларнинг графиклари орқали эмас, балки уларнинг тасвирлари, яъни ВЕКТОРЛАРИ орқали АНИҚЛАНАДИ.

Мисол тариқасида қуйида келтирилган электр занжири ва унга мос бўлган вектор диаграммаси келтирилган (7.4. расм).

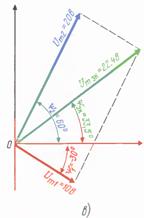
расм-7.4

Мисол учун: бир хил йўналишга эга бўлган векторларнинг натижавий вектори уларнинг арифметик йиғиндисига тенг бўлади. Агар битта координата ўқида жойлашиб тескари йўналишга эга бўлса улар йиғиндиси мусбат ва манфий ишоралар билан олинади. Бу холатлар координата бурчаклари 0 ёки 180 градус бўлган холатлар учун тўғри бўлади (7.5. расм).

расм-7.5

Бошқа холатлар учун қуйидаги вектор диаграммаси тўғри бўлади.

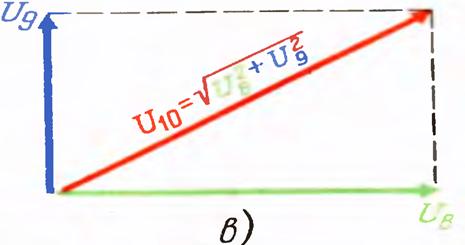
расм-7.6

Юқоридаги жараённи кўриб чиқадиган бўлсак қуйидаги ХУЛОСА ҚИЛИНАДИ: Гармоник функциянинг вақт диаграммаси вектор диаграммаси билан алмаштирилади ва уларнинг ҳар бири горизонтал ва вертикал ўқлар бўйича жойлаштирилади.

Векторнинг Горизонтал ва вертикал ўқлардаги қийматлари ҳисоблаб чиқилади ва НАТИЖАВИЙ вектор ва унинг бошланғич фазаси аниқланади.

Гармоник функциялар қийматини ҳисоблашнинг бундай йўли график усулга қараганда осон туюлади, лекин горизонтал ва вертикал ўқлардаги векторлар қийматини математик ифодалаларини ҳисоблаш анча мураккаб жараён ҳисобланади.

7.1. ВЕКТОРЛАР УСТИДА СИМВОЛИК УСУЛДА АМАЛЛАР БАЖАРИШ

Вектор бирликлар устида Символик усулда амаллар бажариш қуйидагича амалга оширилади: ҳар бир вектор иккита таркибда: бири абцисса ўқи бўйича горизонтал, иккинчиси эса ордината ўқи бўйича вертикал ўқларига жойлаштирилади. Бу холатда барча векторлар қийматларини горизонтал ва вертикал ўқлар бўйича алгебраик усулда қўшиши мумкин бўлади. Бундай холатда бир бири билан 90 градусли бурчак билан фарқ қилувчи иккита ташкил этувчи пайдо бўлади ГОРИЗОНТАЛ ва ВЕРТИКАЛ ташкил этувчилар.

Демак ташкил этувчилар катетлар ҳисобланиб уларнинг геометрик йиғиндиси гипотенуза ҳисобланади, яъни

Электр схемаси мураккаблашганда, яъни шохобчалар ва контурлар сони кўп бўлганда тригонометрик ва вектор диаграмма усуллари орқали гармоник функция параметрларини ҳисоблаш анча мураккаблашади.

Шунинг учун ҳам доимий ток занжирларини ҳисоблаш учун одиий усул керак бўлади, шундай усулни америкалик олимлар (1893-1894 йиллари А. Е. Кеннели ва П. Ч. Штейнметцомлар) томонидан КОМПЛЕКС АМПЛИТУДА УСУЛИ яратилди.

Ушбу усул гармоник функция ўз ўқи атрофида айланаётган векторнинг проекциясига асосланган бўлиб, айланаётган вектор аналитик ифода бўлиб КОМПЛЕКС ШАКЛДА ифодаланади. Комплекс сонларни тасвирловчи комплекс текисликда Комплекс сонлар ҲАҚИҚИЙ ва МАВҲУМ қисмларга бўлинади. Абсцисса ўқига ҲАҚИҚИЙ миқдорлар, ордината ўқига эса МАВҲУМ миқдорлар жойлаштирилади.

МАВҲУМ ва ҲАҚИҚИЙ қисмлардан ташкил топган сонлар КОМПЛЕКС СОНЛАР, улар устида бажариладиган ҳисоблаш УСУЛЛАРИ СИМВОЛИК УСУЛИ деб аталади.

Ҳақиқий миқдорлар ўқига +1, мавҳум миқдорлар ўқига эса катталиклар қўйилади.

Комплекс сонларни ифодаловчи Вектор диаграмма қуйидаги кўринишда бўлади.

расм-7.7

Математика курсидан бизга маълумки ЛЕОНАРДО ЭЙЛЕР (1707 – 1783) формуласи қуйидагича ифодаланади.

Бу формуладаги e^ja ифода комплекс текисликдаги вектор ҳисобланиб сон жиҳатдан бирга тенг бўлади ва ҲАҚИҚИЙ миқдорлар ўқи билан бурчак ҳосил қилади.

бурчак ҲАҚИҚИЙ миқдорлар ўқидан соат стрелкаси йўналишига тескари йўналиш бўйича ҳисобланади.

У холда функциянинг МОДУЛИ қуйидаги кўринишда бўлади:

e^ja -функциянинг ҲАҚИҚИЙ миқдорлар ўқидаги проекцияси га тенг бўлса, МАВҲУМ миқдорлар ўқидаги проекцияси га тенг бўлади.

Агар ўрнига қўйилса у холда қуйидаги ифода ҳосил бўлади:

НАЗОРАТ САВОЛЛАРИ

1. Гармоник функцияларни вақт диаграммаси орқали ифодалаш (тасвирлаш).

2. Гармоник функцияларни вектор диаграммаси орқали тасвирлаш.

3. Гармоник функциялар устида символик усулда амаллар бажариш.

4. Комплекс сонлар

8 –МАЪРУЗА

КОМПЛЕКС ИФОДАЛАР.

КОМПЛЕКС СОНЛАР УСТИДА АМАЛЛАР БАЖАРИШ.

Агар юқорида келтирилган формулада:

Тенг бўлса, у холда:

Ушбу формулада биринчи қўшилувчи функциянинг ҲАҚИҚИЙ қисми ҳисобланади ва R_e коэффицент билан белгиланади.

У холда қуйидаги формулани оламиз:

Иккинчи қўшилувчи эса функциянинг МАВҲУМ қисми ҳисобланади ва I_m ифода билан белгиланади.

У холда қуйидаги ифодани оламиз:

Демак синусоидал қонун асосида ўзгарадиган i токни кўринишда, ёки 3.3. расмда кўрсатилган айланма векторнинг МАВҲУМ координата ўқига тушган проекцияси кўринишида ифодалаш мумкин, яъни

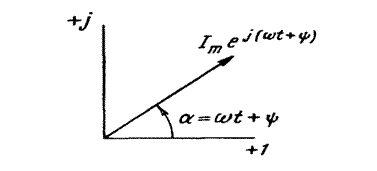расм-8.1

Комплекс сонларнинг
ҲАҚИҚИЙ ва МАВҲУМ ҚИСМЛАРИ

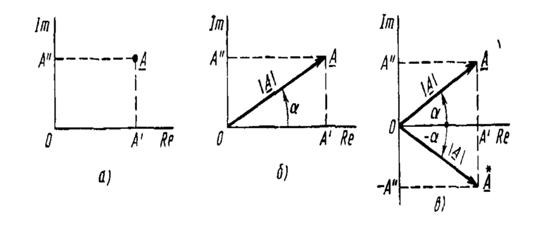
расм-8.2

Комплекс текисликда холат учун синусоидал қонун бўйича ўзгарадиган миқдорлар учун вектор қуйидаги кўринишда бўлади:

Бу формулада: модул жихатдан га тенг бўлган комплекс миқдор; комплекс текисликдаги ҲАҚИҚИЙ миқдорлар ўқига ўтказилган вектор бурчаги дейилади. ток миқдори нинг КОМПЛЕКС АМПЛИТУДАСИ деб аталади.

КОМПЛЕКС АМПЛИТУДА холат учун токнинг миқдорини комплекс текисликдаги тасвири ҳисобланади.

Кучланиш ва ток миқдорлари устига НУҚТА қўйилиши уларнинг вақт бўйича СИНУСОИДАЛ равишда ўзгаришларини билдиради. Демак, КОМПЛЕКС АМПЛИТУДА – бу, вақтга боғлиқ бўлмаган, модул ва аргументи гармоник функциянинг амплитудасига ва бошланғич фазасига тенг бўлган комплекс миқдор ҳисобланади. МИСОЛ ТАРИҚАСИДА ҚУЙИДАГИЛАРНИ КЎРИБ ЧИҚАМИЗ:

Агар КОМПЛЕКС АМПЛИТУДАДАН ОНИЙ ҚИЙМАТГА ўтиш керак бўлса, у холда:

Агар КОМПЛЕКС АМПЛИТУДА ҳолати учун ток миқдорини топиш керак бўлса:

КОМПЛЕКС ТОК ДЕБ КОМПЛЕКС ТОКНИНГ АМПЛИТУДА МИҚДОРИНИ га БЎЛИНГАНЛИК ИФОДАСИГА АЙТИЛАДИ, ЯЪНИ

КОМПЛЕКС СОНЛАР УСТИДА АМАЛЛАР БАЖАРИШ

КОМПЛЕКС СОНЛАРНИ ҚЎШИШ:

Мисол учун қуйидаги икки комплекс сонларни қўшиш керак бўлсин А ва В

МАВҲУМ ва ҲАҚИҚИЙ қисмларни эътиборга олсак:

КОМПЛЕКС СОНЛАРНИ АЙИРИШ

КОПЛЕКС СОНЛАРНИ КЎПАЙТИРИШ ВА БЎЛИШ

Модуллар кўпайтирилади, аргументлар эса қўшилади

Бўлишда модуллар бўлинади, аргументлар эса айирилади:

Мисол учун: икки комплекс сонларни кўпайтирамиз:

A=1 B=j1

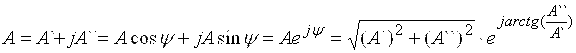
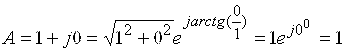
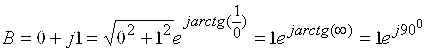
Агар j ва -j миқдорларни Векторга кўпайтирадиган бўлсак, у ҳолда қуйидаги ифодаларни оламиз:

ВЕКТОР ДИАГРАММАСИ

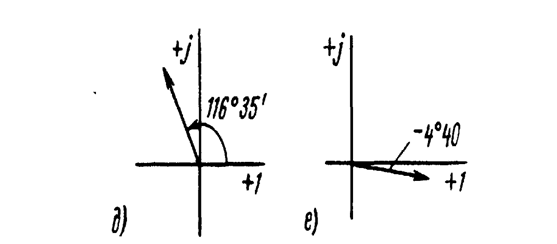
расм-8.3

ОДДИЙ ЭЛЕКТР ЗАНЖИРЛАРИНИ КОМПЛЕКС ИФОДАЛАР ОРҚАЛИ ҲИСОБЛАШ

R - ЗАНЖИРНИ ҲИСОБЛАШ

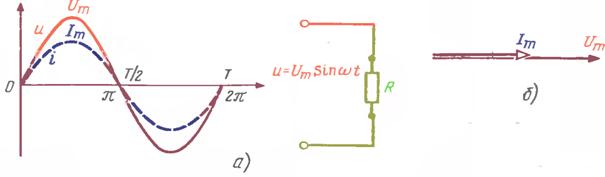
расм-8.4

Комплекс ток қиймати:

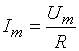
Токнинг ОНИЙ қиймати:

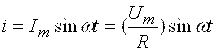
Комплекс токнинг максимал қиймати:

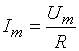
Максимал ток ва кучланиш қийматлари:

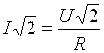
РЕЗИСТОР ОРҚАЛИ ЎТАЁТГАН ГАРМОНИК ТОКНИНГ КОМПЛЕКС КЎРИНИШДАГИ ИФОДАСИ:

I , U - ток ва кучланишларнинг комплекс миқдорлари.

L- ЗАНЖИРНИ ҲИСОБЛАШ

Занжир орқали ўтаётган ТОК КУЧЛАНИШДАН 90 ГРАДУСГА ОРҚАДА ҚОЛАДИ,

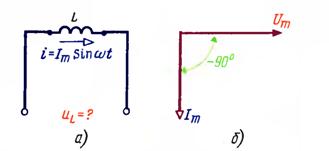
Расм-8.5

Индуктив ғалтакда Ток ва кучланишнинг ОНИЙ қийматлари қуйидагича боғланган:

Токнинг комплекс шаклдаги ифодаси қуйидаги кўринишда бўлади:

Кучланишнинг комплекс шаклдаги ифодаси эса қуйидаги кўринишда бўлади:

Индуктив элементнинг комплекс қаршилиги қуйидаги кўринишда бўлади:

Ток ва кучланишнинг комплекс шаклдаги ифодалари қуйидаги кўринишда бўлади:

C- ЗАНЖИРНИ ҲИСОБЛАШ Занжир орқали ўтаётган ТОК КУЧЛАНИШДАН 90 ГРАДУСГА ИЛГАРИЛАБ КЕТАДИ

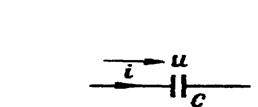
Расм-8.6

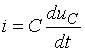
НАЗОРАТ САВОЛЛАРИ

1. Комплекс сонларнингҳақиқий ва мавҳус қисмлари.

2. Комплекс амплитуда, таърифи.

3. Комплекс қийматдан рний қийматга ўтиш.

4. Комплекс ТОК, таърифи.

5. Комплекс сонларни қўшиш.

6. Комплекс сонларни айириш.

7. Комплекс сонларни бўлиш ва даражага кўтариш.

8. Оддий электр занжирларини комплекс сонлар орқали ҳисоблаш.

9 –МАЪРУЗА

КОМПЛЕКС ҚАРШИЛИК ВА ЎТКАЗУВЧАНЛИК.

КИРХГОФ ВА ОМ ҚОНУНЛАРИНИ КОМПЛЕКС МИҚДОРЛАР ОРҚАЛИ ИФОДАЛАШ.

Гармоник сигнал таъсир этаётган оддий чизиқли электр занжирини кўриб чиқамиз.

расм-9.1

Схеманинг кириш қисмидаги гармоник ТОК ва КУЧЛАНИШ гармоник функциялар ҳисобланади

Пассив электр участкасининг КОМПЛЕКС ҚАРШИЛИГИ (КИРИШ ҚАРШИЛИГИ) деб комплекс амплитуда кучланишининг занжир учларидаги комплекс ток амплитудаси НИСБАТИГА АЙТИЛАДИ

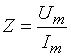
Бу формулада:

Комплекс ҚАРШИЛИК ТОК ва КУЧЛАНИШНИНГ ҳақиқий қийматларининг нисбати орқали ҳам ифодаланади:

Комплекс ҚАРШИЛИК кўрсаткичли функция орқали қуйидагича ифодаланади:

Алгебраик шаклда эса қуйидагича ифодаланади:

Ушбу ифода ва комплекс қаршиликнинг, мос холда, МОДУЛИ ва АРГУМЕНТИ ҳисобланади. Комплекс амплитуда ва ток ва кучланишнинг ҳақиқий қийматлари орқали ифодаланиши қуйидаги кўринишда бўлади:

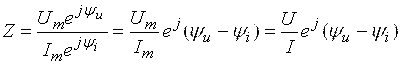
Юқорида келтирилган формулаларни эътиборга оладиган бўлсак ТЎЛИҚ КИРИШ ҚАРШИЛИК қуйидагича ифодаланади:

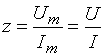
Аргумент эса ток ва кучланиш фазаларининг айирмасига тенг бўлади:

КОМПЛЕКС КИРИШ ҚАРШИЛИГИ комплекс текисликда жойлашган ВЕКТОР кўринишида ҳам тасвирланади:

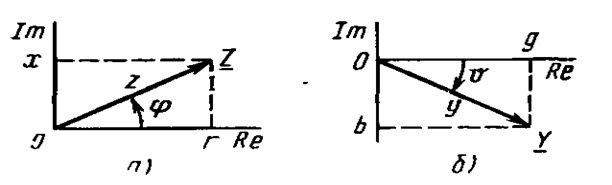
расм-9.2

МАВҲУМ ва ҲАҚИҚИЙ қисмларини эътиборга олсак:

Комплекс кириш қаршилигига тескари бўлган миқдор КОМПЛЕКС КИРИШ ЎТКАЗУВЧАНЛИК деб аталади ва қуйидагича ифодаланади:

Комплекс кириш ўтказувчанлиги кўрсаткичли функция орқали қуйидагича ифодаланади:

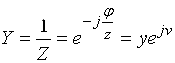
Ушбу ифода - комплекс кириш ўтказувчанлигининг модули ҳисобланади ва КОМПЛЕКС ТЎЛИҚ ЎТКАЗУВЧАНЛИК деб аталади ва қуйидагича ифодаланади:

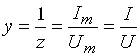
Кириш ўтказувчанлигининг аргументи

Занжирнинг комплекс ўтказувчанлиги алгебраик кўринишда қуйидагича ифодаланади:

Бу ерда юқоридаги расмга асосан:

КОМПЛЕКС ШАКЛДАГИ ОМ ВА КИРХГОФ ҚОНУНЛАРИ.

Занжир участкасининг комплекс қаршилиги ва ўтказувчанлиги занжир учларидаги комплекс ТОК ва КУЧЛАНИШЛАРнинг ўзаро боғланганлик ифодалари орқали аниқланади. Ўз ўрнида комплекс ҚАРШИЛИК ва ЎТКАЗУВЧАНЛИК амплитудага, ток ва кучланишнинг бошланғич фазаларига боғлиқ эмас ва уларнинг миқдорлари занжир элементлари орқали аниқланади.

Комплекс қаршиликни ва комплекс ўтказувчанликни билган холда, ҳамда занжир учларига қуйидаги ва Миқдордаги ТОК ва КУЧЛАНИШлар юклатилган бўлса, юқоридаги формулалардан фойдаланган холда шу занжир участкасининг номаълум бўлган ТОК ва КУЧЛАНИШларини топиш мумкин.

Худди шундай ТОК ва КУЧЛАНИШнинг комплекс миқдорларини топамиз:

2.56) ва (2.57) формулалар ТОК ва КУЧЛАНИШЛАРнинг оний қийматлари ўртасидаги ифодалар бўлиб, КОМПЛЕКС ШАКЛДАГИ ОМ ҚОНУНИ ҲИСОБЛАНАДИ.

КОМПЛЕКС ШАКЛДАГИ КИРХГОФНИНГ БИРИНЧИ ҚОНУНИ.

Комплекс шаклдаги КИРХГОФнинг биринчи қонуни кўрилаётган занжир тугунлардаги комплекс шаклдаги ТОКЛАР ўртасидаги боғланишни ифодалайди.

ТАЪРИФ: ЭЛЕКТР ЗАНЖИРДАГИ ТУГУНЛАРГА УЛАНГАН БАРЧА ШОХОБЧАЛАРДАГИ ТОКЛАРНИНГ КОМПЛЕКС АМПЛИТУДАЛАРИНИНГ АЛГЕБРАИК ЙИҒИНДИСИ НОЛГА ТЕНГ

к- кўрилаётган шохобчадаги тугун рақами.

КОМПЛЕКС ШАКЛДАГИ КИРХГОФНИНГ ИККИНЧИ ҚОНУНИ.

Комплекс шаклдаги КИРХГОФнинг иккинчи қонуни электр занжир контуридаги ШОХОБЧАЛАР КУЧЛАНИШЛАРИ ўртасидаги боғланишни ифодалайди.

ТАЪРИФ: ЭЛЕКТР КОНТУРИГА КИРУВЧИ БАРЧА ШОХОБЧАЛАРДАГИ КУЧЛАНИШЛАР КОМПЛЕКС АМПЛИТУДАЛАРИНИНГ АЛГЕБРАИК ЙИҒИНДИСИ НОЛГА ТЕНГ.

v - кўрилаётган контурга кирувчи шохобча рақами.

КОМПЛЕКС ШАКЛДАГИ КИРХГОФНИНГ ИККИНЧИ ҚОНУНИНИНГ БОШҚА ШАКЛДАГИ ТАЪРИФИ.

ТАЪРИФ: КОНТУРГА КИРУВЧИ ШОХОБЧАЛАРДАГИ КОМПЛЕКС КУЧЛАНИШЛАРНИНГ АЛГЕБРАИК ЙИҒИНДИСИ ШУ КОНТУРДАГИ КОМПЛЕКС ЭЮК ЛАРНИНГ АЛГАБРАИК ЙИҒИНДИСИГА ТЕНГ БЎЛАДИ:

- контурга кирувчи барча элементларнинг

комплекс миқдорлари.

- кўрилаётган контурдаги манбанинг комплекс

ЭЮК лар миқдорлари.

Юқорида келтирилган комплекс шаклдаги ОМ ва КИРХГОФ қонунлари ёрдамида ҳар қандай электр занжири параметрларини комплекс ифодаларини ҳисоблаш мумкин ва олинган ифодалар алгебраик ифодалар ҳисобланади.

ТОК ва КУЧЛАНИШНИНГ ОНИЙ қийматларини ушбу қонунлар орқали ҳисоблаш, дифференциал тенгламаларга қараганда, анча қулай ва осон ҳисобланади.

НАЗОРАТ САВОЛЛАРИ

1. Комплекс қаршилик, таърифи, формуласи.

2. Тўлиқ кириш қаршилиги, формуласи.

3. Комплекс кириш қаршилигининг вектор кўриниши.

4. Комплекс кириш ўтказувчпнлиги, таърифи, формуласи.

5. Клмплекс тўлиқ ўтказувчанлик.

6. Комплекс шаклдаги Ом қонуни, таърифи, формуласи.

7. Комплекс шаклдаги Кирхгофнинг БИРИНЧИ қонуни.

8. Комплекс шаклдаги Кирхгофнинг ИККИНЧИ қонуни.

10 –МАЪРУЗА

ГАРМОНИК ТОК ЗАНЖИРЛАРИДА ҚУВВАТ

ВАҚТ БИРЛИГИДА БАЖАРИЛГАН ИШГА ҚУВВАТ ДЕБ АТАЛАДИ.

Ўзгармас ток занжирларида ҚУВВАТ қуйидаги ифода орқали аниқланар эди:

ҚУВВАТ ўлчов бирлиги сифатида инглиз кашфиётчиси Д. Уатт шарафига ватт (Вт) деб қабул қилинган.

ҚУВВАТ ЎЛЧОВ БИРЛИКЛАРИ

мВт (милливатт = 10^-3 Вт)

кВт (киловатт = 10³ Вт)

МВт (мегаватт = 10⁶Вт)

Ҳар секунда 1 Дж иш бажариладиган ҚУВВАТ Ватт деб аталади.

Электр занжир қисмига ўзгарувчан гармоник сигнал таъсир этганда қуйидаги ҚУВВАТ турлари ҳосил бўлади:

- ОНИЙ ҚУВВАТ

- АКТИВ ҚУВВАТ (ҚУВВАТ)

- РЕАКТИВ ҚУВВАТ

- ТЎЛИҚ ҚУВВАТ

- КОМПЛЕКС ҚУВВАТ

Энди ҳар бир ҚУВВАТ турларини алоҳида кўриб чиқамиз:

Оний ҚУВВАТ ўзгарувчан миқдор бўлиб қуйидаги ифодага тенг бўлади:

p=ui

Мисол учун РЕЗИСТОР уланган занжир орқали ўтаётган гармоник ТОК ва КУЧЛАНИШ қуйидаги ифодаларга тенг бўлса

у холда ОНИЙ ҚУВВАТ қуйидаги ифодага тенг бўлади:

Агар электр занжирига фақат РЕАКТИВ элемент уланган бўлса (масалан индуктивлик L) ва занжир орқали қуйидаги миқдордаги гармоник ТОК ва КУЧЛАНИШ ўтаётган бўлса. У холда ОНИЙ ҚУВВАТ қуйидагича ифодаланади:

Агар электр занжири қаршилик ва индуктивликлардан ташкил топган бўлса (яъни R. L) ва занжир орқали қуйидаги миқдордаги гармоник ТОК ва КУЧЛАНИШ ўтаётган бўлса:

)

АКТИВ ҚУВВАТ (ҚУВВАТ):

Актив қувват деб бир давр Т мобайнидаги оний P қувватнинг ўртача қийматига айтилади ва қуйидагича ифодаланади:

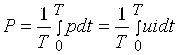
Агар занжир қисмидан қуйидаги миқдордаги ток ва кучланишлар ўтса

у холда актив қувват:

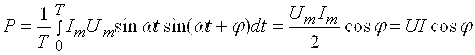
Актив қувват деганда бир вақт бирлигида қаршилик уланган электр занжирида узатиладиган иссиқлиқ энергиясини ифодалайди. Агар қуйидаги кўпайтмани эътиборга олсак

у холда:

Актив қувватнинг ўлчов бирлиги Вт ҳисобланади.

РЕАКТИВ ҚУВВАТ

РЕАКТИВ ҚУВВАТ ТОК ва КУЧЛАНИШЛАР, ҳамда улар ўртасидаги синус бурчаги кўпайтмасига тенг бўлади:

Реактив қувват ўлчов бирлиги (ВАр) ҳисобланади ва қуйидаги шарт бажарилади:

унда агар унда

ТЎЛИҚ ҚУВВАТ

Тўлиқ қувват ТОК ва КУЧЛАНИШЛАРНИНГ ҳақиқий қийматлари кўпайтмасига тенг бўлади ,

ўлчов бирлиги () ҳисобланади.АКТИВ, ТЎЛИҚ ва РЕКАТИВ ҚУВВАТ бирликлари ўзаро қуйидаги ифода орқали боҳланади:

График орқали боҳланиши эса қуйидаги кўринишга эга бўлади. Бу расмда АКТИВ ва ТЎЛИҚ қувватлар учбурчакнинг кателари хисобланса, РЕАКТИВ қувват учбурчакнинг гипотенузасига тўғри келади.

Расм-10.1

КОМПЛЕКС ҚУВВАТ

Занжирнинг Комплекс қуввати қуйидаги формула орқали ифодаланади:

Тригонометьрик шаклда қуйидагича ифодаланади:

Ушбу формуладан кўриниб турибдики, унинг ҲАҚИҚИЙ қисми АКТИВ ҚУВВАТ, МАВҲУМ қисми эса РЕАКТИВ қувватдан ташкил топган.

Демак КОМПЛЕКС ҚУВВАТ:

Энди юқоридаги формулаларни ҳисобга олган холда АКТИВ, РЕАКТИВ, ТЎЛИҚ ва КОМПЛЕКС қувватларни мисоллар орқали ҳисоблаймиз: Мисол учун қуйидаги миқдордаги ТОК ва КУЧЛАНИШ электр занжиридан ўтаётган бўлса:

ТОК, КУЧЛАНИШ ва ФАЗАЛАР миқдорлари берилган бўлса:

ҚУВВАТ МУВОЗАНАТИ

N та кучланиш манбасидан ва M та ток манбасидан, ҳамда H та пассив элементлардан ташкил топган электр занжирида ҚУВВАТ мувозанатини кўриб чиқамиз.

- к элементли занжирдаги ТОК ва КУЧЛАНИШ ҳисобланади. Энергиянинг сақланиш қонунига асосан вақт оралиғида барча элементларнинг оний қувватлари йиғиндиси НОЛГА ТЕНГ

Бир нечта ўзгартиришлардан кейин қуйидаги ифодани оламиз:

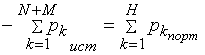
Ушбу формула ОНИЙ ҚУВВАТНИНГ МУВОЗАНАТ ТЕНГЛАМАСИ деб аталади. Ушбу формулада МИНУС ишораси энергиянинг бошқа элементларга узатилиш тезлигини билдиради. Демак: БАРЧА МАНБАЛАРДАН узатилаётган оний ҚУВВАТЛАР йиғиндиси бошқа МАНБАЛАР қабул қилаётган ОНИЙ ҚУВВАТЛАР йиғиндисига ТЕНГ. Худди шундай КОМПЛЕКС қувват мувозанати ифодаланади:

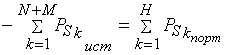
Ушбу ифода комплекс қувваттлар мувозанат ТЕНГЛАМАСИ деб аталади.

АКТИВ ЭЛЕМЕНТЛАР УЗАТАЁТГАН КОМПЛЕКС ҚУВВАТЛАР ЙИҒИНДИСИ, ПАССИВ ЭЛЕМЕНТЛАР КОМПЛЕКС ҚУВВАТЛАР ЙИҒИНДИСИГА ТЕНГ.

НАЗОРАТ САВОЛЛАРИ

• 1. Қувват таърифи, ўлчов бирлиги.

• 2. Қувват турлари.

• 3. Оний ва актив қувват, формуласи.

• 4. Тўлиқ ва реактив қувват, формуласи.

• 5. Комплекс қувват, формуласи.

• 6. Қувват мувозанати, формуласи, таърифи.

• 7. Комплекс қувват мувозанати, таърифи, формуласи.

11 –МАЪРУЗА

ПАРАЛЕЛ ТЕБРАНИШ КОНТУРИ. ТОК РЕЗОНАНСИ.

Энергия манбасига элементларнинг уланиш турига қараб тебраниш контурлари КЕТМА КЕТ (энергия манбаси индуктивлик ва сиғимга кетма кет уланган) ва ПАРАЛЕЛ тебраниш контурларига бўлинади (энергия манбаси реактив элементларга паралел уланган).

Ўз ўрнида ТОК РЕЗОНАНСИ индуктивлик ва сиғимлар паралел уланган электр занжирларида кузатилади.

Радиотехникада бундай контурлар ПАРАЛЕЛ ТЕБРАНИШ КОНТУРЛАРИ деб аталади.

ТОК резонанси холати электр занжирининг бир қисмидаги индуктив ўтказувчанлик занжирининг бошқа қисмидаги паралел уланган сиғим ўказувчанлиги билан қопланади (компенсируется).

Натижада занжирнинг учларидаги РЕАКТИВ Ўтказувчанлик ва РЕАКТИВ қувват НОЛГА тенг бўлади.

ТОК резонанси ходисасини Паралел уланган оддий тебраниш контури орқали тахлил қилинади:

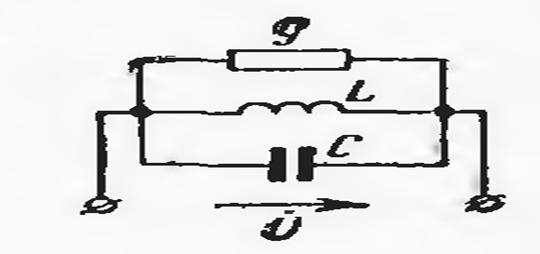
Расм-11.1.

Бундай схемада КОМПЛЕКС ҚАРШИЛИК қуйидагича ифодаланади:

РЕЗОНАНС частота эса қуйидагича ифодаланади:

Кўрилаётган контурнинг АСЛЛИЛИГИ кетма кет тебраниш контурининг миқдорига тесқари бўлган миқдор орқали ифодаланади.

РЕЗОНАНС холатида манбадан келаётган ТОК қуйидагича ифодаланади:

ТОК резонансида паралел тебраниш контурида контурнинг ТЎЛИҚ ЎТКАЗУВЧАНЛИГИ МИНИМУМ қийматга тенг бўлади, яъни КИРИШ ҚАРШИЛИГИ МАСИМАЛ қийматга тенг бўлади.

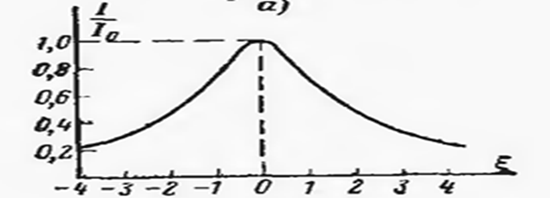
Расм-11.2.

Бу холатда манбадан келаётган ТОК кам миқдорга тенг бўлади, яъни

Индуктив ва сиғим элементларидаги ТОКлар миқдор жиҳатдан ТЕНГ, лекин ишоралари бир бирига қарама қарши ифодаланади.

Олинган охирги формуладан кўринадаки паралел тебраниш контурининг АСЛЛИЛИГИ индуктивлик ва сиғим элементларидаги токларга ва умумий (йиғинди) ток миқдорларига нисбатан КАРРАЛИ (бутун сонларга бўлинувчи) қийматга тенг бўлади.

Контурнинг асллилиги бирдан катта бўлса, яъни Q>1 контурдаги токлар миқдор жиҳатдан умумий ток миқдоридан ошиб кетади, шунинг учун ҳам паралел тебраниш контурларидаги резонанс холати ТОК РЕЗОНАНСИ деб юритилади.

ТОК резонанси холатида контурда индуктив ва сиғим элементлари ўртасида энергиянинг узлуксиз алмашинуви содир бўлади. Агар паралел тебраниш контури бир бирига паралел уланган индуктив ва сиғим элементларидан ташкил топган бўлса эди унинг кириш қаршилиги жкда катта миқдорга эга бўлар эди ва манбадан ТОК контурга келмай қолар эли.

Контурдаги Бирламчи энергия миқдори сарфланмас эди ва магнит ва электр майдонлари ўртасида навбат билан тақсимланиб борар эди. Манбани токдан узиб қўйилса контурдаги тебраниш холати чексиз давом этиб борган бўлар эди..

БУНДАЙ КОНТУР ИДЕАЛ КОНТУР деб аталади, чунки паралел уланган индуктивлик ва сиғим элементдаридаги энергия йўқотилишини эътиборга олмайди

ПАРАЛЕЛ ТЕБРАНИШ КОНТУР ТУРЛАРИ

Фараз қилайлик, паралел тебраниш контур шохобчаси паралел уланган иккита КОМПЛЕКС қаршиликлардан ташкил топган бўлсин

ва

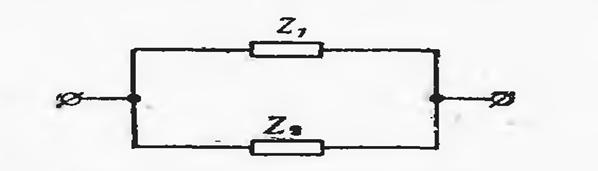
Расм-11.3.

Раектив қаршиликларнинг x₁ ва x₂ ўзгаришларига қараб 3(УЧ) хил ТУРДАГИ паралел ТЕБРАНИШ контурлари бўлади:

Биринчи турдаги тебраниш контури:

Контурнинг бир шохобчасида индуктивлик, иккинчи шохобчасида эса сиғим элементлари улангван тебраниш контури.

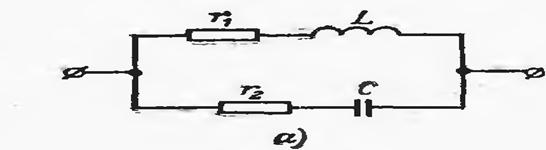
Расм-11.4.

Бундай холатда индуктивлик ва сиғим элементларида реактив қаршиликлар қуйидаги формулалар орқали ифодаланади:

Иккинчи турдаги паралел контурда бир шохобчада индуктивлик, иккинчи шохобчада эса индуктивлик ва сиғим элементлари уланган бўлади:

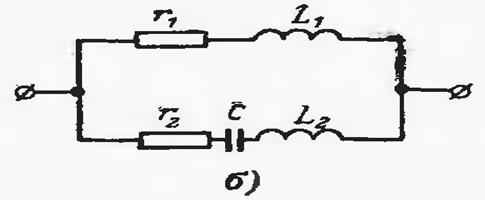
Расм-11.5.

Бу холатда реактив қаршиликлар қуйидагича ифодаланади:

Учинчи турдаги паралел тебраниш контурида эса, бир шохобчада сиғим элементи уланган бўлса, иккинчи шохобчада индуктивлик ва сиғим элеиентлари уланган бўлади.

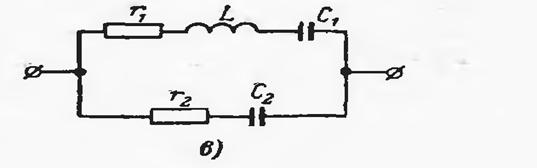
Расм-11.6.

Бундай холатда контурнинг реактив қаршиликлари қуйидагича ифодаланади:

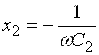
Паралел контурларда КИРИШ ЎТКАЗУВЧАНЛИГИ қуйидаги формула орқали ифодаланади:

Актив ўтказувчанлик эса қуйидагича ифодаланади:

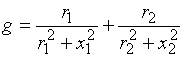
Реактив ўтказувчанлик эса қуйидагича ифодаланади:

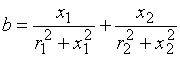
Резонанс шартига кўра: b=0 бўлса у холда:

Юқоридаги ифодаларни инобатга олган холда контурнинг резонанс ЎТКАЗУВЧАНЛИГИ

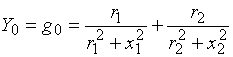
Юқоридаги формулага асосан:

Шунга асосан:

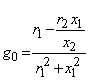
Резонансга яқин бўлган холатда:

ва

РЕЗОНАНС ШАРТИГА АСОСАН:

Ёки:

Юқоридаги тенгликка асосан

ХУЛОСА: ПАРАЛЕЛ ТЕБРАНИШ КОНТУРЛАРИДА ШОХОБЧАЛАРДАГИ РЕАКТИВ ҚАРШИЛИКЛАР АБСОЛЮТ МИҚДОР ЖИҲАТДАН БИР БИРЛАРИГА ТЕНГ ВА ИШОРАЛАРИ БИР БИРЛАРИГА ТЕСКАРИ БЎЛГАН ХОЛАТДАГИНА ТОК РЕЗОНАНСИ СОДИР БЎЛАДИ.

НАЗОРАТ САВОЛЛАРИ

1. Паралел тебраниш контурлари.

2. Ток резонанси.

3. Паралел тебраниш контурларида Контурнинг асллилиги.

4. Комплекс қаршилик ва резонанс частота формулалари.

5. Идуктив ва сиғим токлари, формулалари.

6.Паралел тебраниш контури асллилиги, формуласи.

7. Паралел тебраниш контури турлари.

8. Резонанс холати содир бўлиш шарти.

12 –МАЪРУЗА

ДАВРИЙ ФУНКЦИЯЛАРНИНГ ГАРМОНИК ТАРКИБЛАРГА ЁЙИЛИШИ.

АСОСИЙ ТУШУНЧАЛАР.

Гармоник сигналлардан фарқ қилувчи барча даврий сигналлар (ток ва кучланиш) НОГАРМОНИК СИГНАЛЛАР деб аталади. Ҳар қандай ногармоник сигналлар ўзларининг даври Т, ток ва кучланишларнинг шакли ва амплитудалар қийматлари

(Ua, Ia) билан фарқ қилади.

Ногармоник сигналларнинг бир нечта турлари мавжуд, уларни тахлил қилиш учун бир қанча усуллар ишлаб чиқилган.

Ногармоник сигналларнинг шаклидан қатьи назар гармоник сигналларнинг (синусоидал ва косинусоидал) шундай шакллари олинадики, уларнинг частоталари, бошланғич фазалари, амплитудаларининг ордината ўқидаги қийматларининг алгебраик йиғиндилари, ҳар қандай вақтда, чиқишдаги носинсуоидал сигналнинг ордината ўқидаги қийматига тенг бўлади.

Масалан 10.1 расмдаги 1 кучланишни 2 ва 3 кучланишлар билан алмаштириш мумкин, чунки U₁ ва U₂ кучланишларнинг оний қийматлари йиғиндиси U кучланишга тенг.

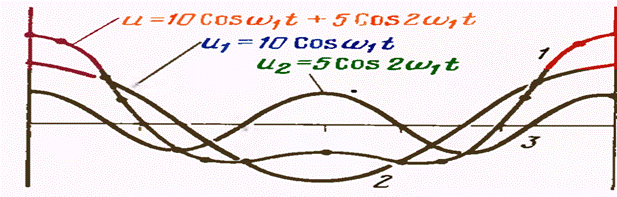
Расм-12.1.

Энди гармоник сигналнинг бошланғич фазасини, амплитудасини ва частотасини, қандай қилиб НОГАРМОНИК сигналга алмаштирилиш орқали аинқлашни кўриб чиқамиз.

Расмда кўрсатилган НОГАРМОНИК сигнал таркибини аниқлаш учун ҳар қандай кўринишдаги синусоидал сигналлар олинмайди, фақат ЧАСТОТАЛАРИ қуйидаги кўринишдаги қийматларга тенг бўлган сигналлар олинади, яъни КАРРАЛИ бўлган қийматлари:

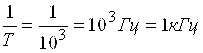
Гармоник сигнал даври Т ногармоник сигнал даврига тенг бўлса шу ногармоник сигналнинг БИРИНЧИ ёки АСОСИЙ гармоник таркиби деб аталади.

Қолган ҳамма гармоник таркиблар сигналларнинг ОЛИЙ ГАРМОНИКАЛАРИ деб юритилади.

Частотаси Асосий гармоникадан ИККИ марта катта бўлган гармоник сигналлар “ИККИНЧИ” гармоника, УЧ марта катта бўлса “УЧИНЧИ” гармоника деб юритилади.

Ҳар қайси гармоника бошланғич фазаси НОЛГА тенг бўлмаган частоталали гармоникадан, ёки бошланғич фазаси НОЛГА тенг бўлган синусоидал гармоникалардан ташкил топган бўлади.

Юқорида келтирилган фикрлар қуйидаги формулалар орқали ифодаланади:

Бу ифодада:

Амалиётда биринчи навбатда ҳар қайси гармоник сигналнинг синусоидал амплитудасини A`_m ва косинусоидал амплитудасини A``_m аниқлаб олинади.

Кейин эса Асосий гармоник сигналнинг УМУМИЙ сигнал амплитудаси ва бошланғич фазалари аниқланади, яъни

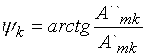
Синусоидал ва косинусоидал сигналларнинг амплитудалари таркибий қисмларини

A`_m A``_m

Математикадан аниқ бўлган ФУРЬЕ қаторлари коэффицентларини аниқлаш формуласи орқали аниқланади.

СИНУСОИДАЛ ва КОСИНУСОИДАЛ гармоник сигналлар ФУРЬЕ қаторлари орқали қуйидагича ифодаланиши:

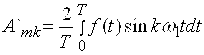
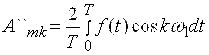
Бу ифодада:

k - гармоник қатор рақами;

f(t)- гармоник қатор аниқланадиган математик ифода;

T - ногармоник сигнал даври;

- ногармоник сигналнинг бирнчи гармоникасининг бурчак частотаси

Шундай қилиб, ҳар қандай даврий ногармоник сигналнинг оний қийматларини гармоникани ташкил этувчи доимий қийматлар йиғиндиларини ФУРЬЕ ҚАТОРЛАРИ ОРҚАЛИ МАТЕМАТИК ифодалаш мумкин.

Агар ногармоник сигналнинг оний кучланиши қуйидаги қийматга тенг бўлса: u(t) у холда бундай ногармоник кучланишни ФУРЬЕ қаторлари орқали қуйидагича ифодалаймиз:

Энди бир нечта сигналларнинг ФУРЬЕ қаторига ёйилганда хосил бўлган чизмаларини кўрамиз:

СИНУСОИДАЛ чизма, қаторга ёйилганда “ОЛИЙ ГАРМОНИК” сингнал амплитудаси НОЛГА ТЕНГ БЎЛАДИ:

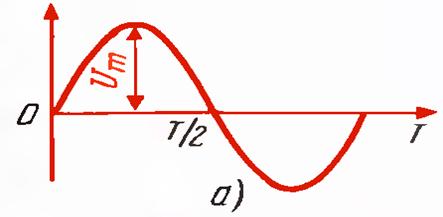
Расм-12.2.

СИГНАЛНИНГ УЧБУРЧАК ШАКЛИДАГИ ЧИЗМАСИ:

Расм-12.3.

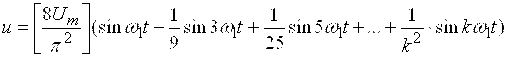
СИГНАЛНИНГ ТЎРТБУРЧАК ШАКЛИДАГИ ЧИЗМАСИ: бу ифодада k – бутун жуфт сон.

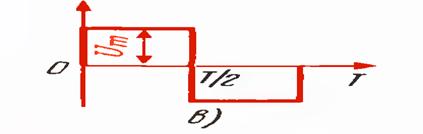
Расм-12.4.

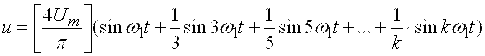
СИГНАЛНИНГ БИР ЯРИМ ДАВР ШАКЛДАГИ ЧИЗМАСИ:

Расм-12.5.

СИГНАЛНИНГ ИККИ ЯРИМ ДАВР ШАКЛДАГИ ЧИЗМАСИ:

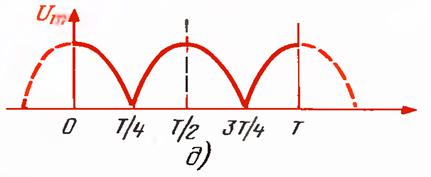
Расм-12.6.

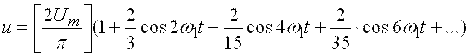
ДАВРИЙ НОГАРМОНИК СИГНАЛЛАРНИНГ СИММЕТРИК КЎРИНИШЛАРИ

СИГНАЛЛАРНИНГ ГОРИЗОНТАЛ ЎҚҚА НИСБАТАН СИММЕТРИЯ КЎРИНИШИ.

Ҳар қандай сигнал шакли учун қуйидаги шарт бажарилса, у сигнал горизонтал ўққа нисбатан СИММЕТРИК деб аталади.

Агар сигналнинг горизонтал ўқдаги ярим давр шаклини ўқнинг ярим қисмига ўтказилса, у холда сигнал шакли симметрик равишда олдинги холатини такрорлайди, яъни горизонтал ўққа нисбатан симметрик шакл хосил бўлади.
Бундай сигналлар жуфт гармоникалар коэффицентлари НОЛГА ТЕНГ бўлади.

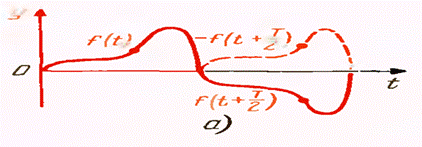
Расм-12.7.

Демак горизонтал ўққа нисбатан симметрик бўлган ҳар қандай ногармоник сигналнинг оний қийматларини ифодаловчи математик қаторлар фақат ТОҚ гармоникалардан ташкил топган бўлади.

ГОРИЗОНТАЛ ЎҚҚА НИСБАТАН СИММЕТРИК СИГНАЛ ШАКЛИ

Қуйидаги ифодага тўғри келадиган ногармоник сигнал горизонтал ўққа нисбатан СИММЕТРИК деб юритилади:

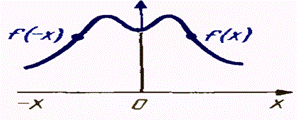
Расм-12.8.

Бундай сигналларда бошланғич фаза қиймати НОЛГА тенг бўлади.

НОГАРМОНИК СИГНАЛЛАРНИНГ КООРДИНАТА ЎҚИ БОШЛАНИШИГА НИСБАТАН СИММЕТРИК ШАКЛИ

Ҳар қандай ногармоник сигал қуйидаги

шартга тўғри келса у координата ўқи бошланиш ига нисбатан СИММЕТРИК ҳисобланади.

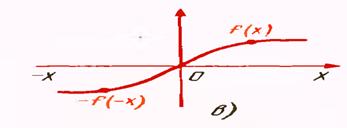
Расм-12.9.

Бундай сигналлар фақат НОЛГА тенг бўлган бошланғич фазалардан иборат бўлган сигналлардан ташкил топган бўлади.

НАЗОРАТ САВОЛЛАРИ

1. Ногармоник сигналлар, таърифи.

2. Ногармоник сигналларнинг қандай шакллари олинади.

3. Иккинчи ва учинчи гармоникалар деб нимага айтилади.

4. Даврий ногармоник сигнал амплитудалари қандай формула орқали ифодаланади.

5. Фурье қаторлари қайси формула орқали ифодаланади.

6. Даврий ногармоник сигналларнинг симметрик турлари (горизонтал ўққа, вертикал ўққа, координата ўқининг бошланишига нисбатан).

13 –МАЪРУЗА

ИККИ ҚУТБЛИ ЭЛЕКТР ЗАНЖИРЛАРИ.

ТАЪРИФЛАРИ ВА КЛАССИФИКАЦИЯЛАРИ.

Икки учли ҳар қандай электр занжирлари ИККИ ҚУТБЛИ электр занжирлари деб аталади. Икки қутбли электр занжирлари мураккаб ва ҳар хил тузилишларга эга бўлади.

Энг оддий икки қутбли жлектр занжирининг тузилиши қуйидагича белгиланади:

Расм 13.1

ИККИ қутбли электр занжирлари:

- чизиқли ва ночизиқли;

- бир, икки ва кўп элементли;

- реактив (индуктивлик ва сиғим уланган);

- энергия йўқотувчи (актив қаршилик уланган);

- актив ва пассив турларига бўлинади.

Электр энергияси ўзаро қопланмайдиган электр манбаси уланган икки қутбли электр занжирлари АКТИВ Икки қутбли электр занжирлари деб аталади, яхни электр энергияси фақат сарфланади, лекин ўзаро қопланмайди.

Электр манбаси уланмаган электр занжири ПАССИВ ИККИ қутбли электр занжири деб аталади.

Мисол учун қуйидаги электр занжири ПАССИВ икки қутбли электр занжири деб юритилади.

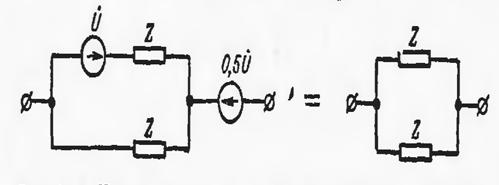
расм 13.2

Икки қутбли электр занжирларнинг ҚАРШИЛИГИ ва ЎТКАЗУВЧАНЛИГИ частотага боғлиқлиги ЧАСТОТАЛАЛИ ХАРАКТЕРИСТИКАЛАР деб аталади.

Бундай боғлиқлик икки қутбли электр занжирининг ТОК ва КУЧЛАНИШлар амплитудаси ва фазаси, частотага боғлиқлигини кўрсатади.

13.1 БИР ЭЛЕМЕНТЛИ РЕАКТИВ ИККИ ҚУТБЛИ ЭЛЕКТР ЗАНЖИРИ

Индуктивлик ва сиғим элементлари РЕАКТИВ икки қутбли электр занжирлари ҳисобланади, масалан:

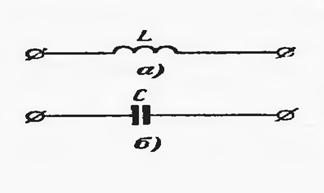
расм 13.3

Ушбу графикда индуктив ва сиғим элементларининг комплекс қаршилигининг частотага боғлиқлик графиги кўрсатилган. Графикда комплекс қаршилик бутун частота спектри бўйича МУСБАТ қийматга, комплекс ўтказувчанлик эса МАНФИЙ қийматга тенг бўлиб турибди.

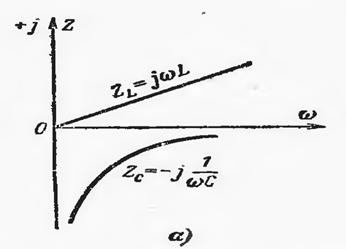
13.1.1

Расм 13.4

Сиғим элементида эса, комплекс қаршилик МАНФИЙ ишорага, комплекс ўтказувчанлик эса МУСБАТ ишорага тенг бўлиб турибди,

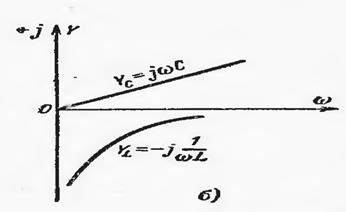
13.1.2 расм 13.5

Хулоса қилиб қуйидаги фикрларни келтиришимиз мумкин:

бир элементли реактив икки қутбли электр занжирларида индуктив элементнинг комплекс қаршилиги ва сиғим элементининг ўтказувчанлиги ТЎҒРИ ЧИЗИҚЛИ характеристикага, сиғим элементининг комплекс қаршилиги ва индуктив элементининг ўтказувчанлиги ГИПЕРБОЛА туридаги ЧАСТОТАЛИ характеристикаларга эга бўлади.

Демак:

Бир элементли икки қутбли РЕАКТИВ электр занжирларида частота ошган сари комплекс қаршилик ва ўтказувчанлик ўсиб боради, яъни ушбу ифода ўринли бўлади:

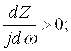
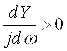13.1.3

13.2 ИККИ ЭЛЕМЕНТЛИ РЕАКТИВ ИККИ ҚУТБЛИ ЭЛЕКТР ЗАНЖИРИ

Икки элементли икки қутбли реактив электр занжири индуктив ва сиғим элементларининг кетма кет ва паралел уланишлари орқали ҳосил бўлади, мисол учун:

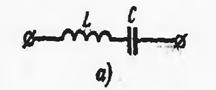
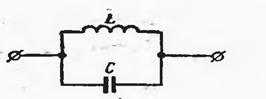
расм 13.6

Ушбу графикдан кўриниб турибдики, кетма кет уланган икки элементларнинг реактив қаршиликларининг алгебраик йиғиндисига тенг бўлади, яъни қалин чизиқ билан уларнинг частотали характеристикалари кўрсатилган.

расм 13.7

Бу қалин чизиқ координатанинг абсцисса ўқини резонанс частотанинг қуйидаги қийматига тенг бўлган қийматида, яъни

13.2.1

РЕЗОНАНС КУЧЛАНИШИ холатида кесиб ўтади (графикка қаранг).

Ўтказувчанликнинг частота характеристикаси қуйидаги графикда кўриниб турибди. Реактив жлементнинг ўтказувчанлиги қаршиликка тескари қийматга тенг бўлади, яъни

13.2.2

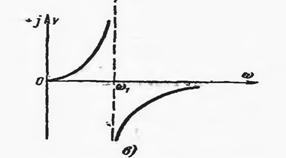
расм 13.8

Реактив қаршилик ва ўтказувчанликларнинг частота характеристикаларининг графиклари қуйидаги формулаларга мос келади, яъни:

13.2.3

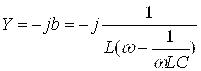
Агар қуйидаги ифодани эътиборга олсак,

13.2.4

у холда:

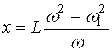
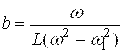13.2.5

Шундай қилиб, келтирилган графикдан хулоса қилиб қуйидагиларни келтирамиз:

Резонанс частотасидан кичик бўлган қийматда, яъни сиғим элементи қаршилиги абсолют миқдор сифатида индуктив элемент қаршили гидан катта бўлади, шунинг учун ҳам икки қутбли электр занжирининг натижавий қаршилиги СИҒИМ элементига яқин характеристикага тенг бўлади.

Агар частота резонанс частотасидан катта бўлса, яъни у холда сиғим элементи қаршилиги индуктив элементи қаршилигидан абсолют миқдор жихатдан кичик бўлади, шунинг учун ҳам икки қутбли электр занжирининг натижавий қаршилиги ИНДУКТИВ элементига яқин бўлган характеристикага тенг бўлади.

Сиғим ва индуктив элементлар паралел уланган икки қутбли реактив электр занжирларида элементларнинг КОМПЛЕКС ЎТКАЗУВЧАНЛИКЛАРИНИНГ алгебраик йиғиндисига тенг бўлади (графикда қалин чизиқ)

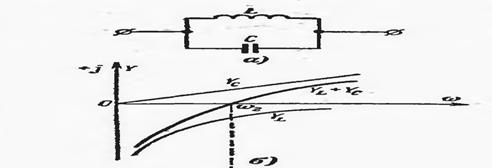
расм 13.9

Резонанс частотаси қуйидаги миқдорга тенг бўлган вақтда

13.2.6

натижавий ўтказувчанлик абсцисса ўқини кесиб ўтади, яъни ТОК РЕЗОНАНСИ ҳосил бўлади.

Худди шу икки қутбли электр занжирининг реактив қаршилик характеристикаси ўтказувчанликка тескари қийматга тенг бўлади, яъни:

13.2.7

Комплекс қаршиликнинг частотавий характеристикаси ушбу графикда кўрсатилган:

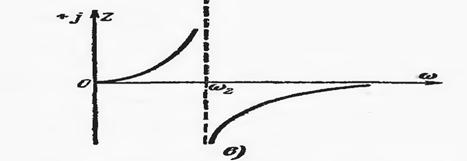
расм 13.10

Энди Юқорида келтирилган частотавий графиклар ҳосил бўлган формулаларни келтирамиз, яъни:

13.2.8

Агар қуйидаги ифодани эътиборга олсак, у холда:

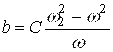13.2.9

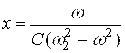
Юқоридаги формулалар орқали қуйидаги ча хулосалар қиламиз:

Частота қиймати резонанс частотаси қийматидан кичик бўлган вақтда, индуктив элементнинг ўтказувчанлиги, сиғим элементи ўтказувчанлигининг абсолют миқдоридан катта бўлади, шунинг учун икки қутбли электр занжирининг ҚАРШИЛИГИ индуктив характерга эга бўлади.

Агар частота резонанс частотасидан КАТТА бўлганда, икки қутбли электр занжирининг қаршилиги СИҒИМ элементи характерига эга бўлади.

ДЕМАК ИККИ ЭЛЕМЕНТЛИ РЕАКТИВ ИККИ ҚУТБЛИ ЭЛЕКТР ЗАНЖИРИ ЧАСТОТАГА БОҒЛИҚ ХОЛДА ИНДУКТИВ ЁКИ СИҒИМ ҚАРШИЛИКЛАРИГА ЭГА БЎЛАДИ.

НАЗОРАТ САВОЛЛАРИ

1. Икки қутбли электр занжирлар.

2. Икки қутбли электр занжирларининг турлари.

3. Актив ва пассив икки қутбли электр занжирлари.

4. Частота характеристикалари.

5. Бир элементли реактив икки қутбли электр занжирлари.

6. Реактив қаршилик ва ўтказувчанлик графиклари, формулалари.

7. Кетма кет уланган икки элементли икки қутбли реактив электр занжирлари, графиклари ва формулалари.

8. Паралел уланган икки қутбли реактив электр занжирлари, графиклари ва формулалари.

14 –МАЪРУЗА

ЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРЛАРИДА. ЎТИШ ЖАРАЁНЛАРИ.

Электр занжирининг бир турғун холатидан бошка бир турғун холатига ўтишини ифодаловчи жараён ЎТИШ ЖАРАЁНИ деб аталади.

Электр занжирининг асосий иш холати қуйидаги жараёнлар орқали ифодаланади: манбага уланиш ва ундан ажралиш, ишлаётган занжирга қўшимча манбаларнинг уланиши, занжир таркибий қисмларининг қисқа туташуви, занжирда юкламанинг кескин ортиши ва камайиши ва х.к.

Юқоридаги омиллар орқали занжир параметрлари ўзгариши мумкин.

Электр занжирининг иш холатларининг ўзгаришига олиб келувчи барча сабаблар оддий равишда КОММУТАЦИЯ ёки КОММУТАЦИОН жараён орқали содир бўлади. Мисол учун ушбу расмда коммутация жараёни кўрсатилган.

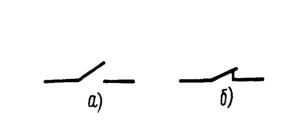
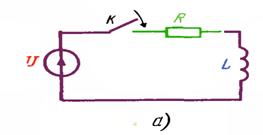
расм 14.1

Электр занжири элементларининг ва манбаларнинг уланиши, занжирдан узилиши ёки қайта уланиши – КОММУТАЦИЯ деб аталади. Электр занжирларида Коммутация қуйидаги кўринишда бўлади.

Муҳандислик ҳисобларида, электр занжиридаги ўрнатилган холат КОММУТАЦИЯ содир бўлган ондан (занжирга юклама улангандан ёки узилгандан) кейин бошланади деб тахмин қилинади. Бу тахмин фақат занжирда фақат актив қаршилик уланган бўлсагина тўғри бўлади. Агар занжирда индуктивлик ёки сиғим элементлари уланган бўлса, у холда бу тахмин нотўғри бўлади.

Индуктивлик ёки сиғим элементлари уланган занжирда турғун холатдан бошқа холатга ўтиши шу элементларнинг магнит ва электр майдонларида электромагнит энергиянинг миқдор жиҳатдан ўзгаришига боғлиқ бўлади.

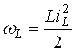
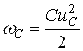
Энергиянинг сон жиҳатдан маълум бир миқдорга ўзгариши бир зумда содир бўлмайди, яъни занжирнинг турғун холатдан бошқа холатга ўтиши маълум бир вақтни талаб қилади.

Физик нуқтаи назардан қаралганда ЎТКИНЧИ жараён электр занжирининг коммутациягача бўлган энергетик холатидан коммутациядан кейинги энергетик холатига ўтиш жараёни тушунилади.

Шунинг учун ҳам электр занжирларининг ЎТКИНЧИ холати реактив элементларнинг (L ва C)

Хусусиятларидан келиб чиққан холда қуйидаги КОММУТАЦИЯ қонунлари орқали ифодаланади:

КОММУТАЦИЯНИНГ БИРИНЧИ ҚОНУНИ:

Ҳар қандай индуктивликка эга тармоқдаги ток ва магнит оқим КОММУТАЦИЯ пайтида (t = 0) ўзининг коммутацияга қадар бўлган қийматини сақлайди ва бундан кейин ана шу қийматларидан бошлаб ўзгаради.

КОММУТАЦИЯНИНГ ИККИНЧИ ҚОНУНИ:

Ҳар қандай тармоқда сиғимдаги кучланиш ва заряд КОММУТАЦИЯ пайтида (t = 0) ўзининг коммутацияга қадар бўлган қийматини сақлайди ва бундан сўнг ана шу қийматларидан бошлаб ўзгаради.

Электр занжирларида Ўтиш жараёнларини тахлил қилиш учун қуйидаги усуллардан фойдаланилади:

• 1. Классик усули.

• 2. Оператор усули.

• 3. Вақт усули.

• 4. Частотавий усул..

Юқорида келтирилган усулларни тахлил қилишдан олдин электр занжирларидаги ўтиш жараёнларини ифодаловчи бир нечта холатларни кўриб чиқамиз.

1. ТОК ва КУЧЛАНИШНИНГ ЭРКИН ВА МАЖБУРИЙ ТАШКИЛ ЭТУВЧИЛАРИ.

Юқорида кўрсатиб ўтилгандек электр занжирининг бир турғунлашган холатидан бошқа холатга ўтиши бир зумда содир бўлмайди, балки энергия манбаи билан занжирнинг энергия тўпловчи элементлари орасидаги энергиянинг тақсимланиш жараёнига кетган вақт қадар давом этади

Шундан келиб чиққан холда электр занжирлари учун дифференциал тенгламаларнинг бир жинсли ва бир жинсли бўлмаган ифодалари тузилади.

Бир жинсли дифференциал тенгламани ечишда хусусий ечими ва умумий ечимини топиш керак бўлади. Мисол учун ушбу электр занжирини кўриб чиқамиз:

расм 14.2

Юқорида келтирилган электр занжири учун қуйидаги тенглама ўринли бўлади:

U_L+U_R=U

бунда i -ўткинчи жараён токи, яъни ЎТКИНЧИ ТОК.

Ўткинчи токни иккита токлар йиғиндиси деб қараш мумкин: мажбурий ток i_мажб, у ўткинчи жараён тугугандан сўнг намоён бўлади ва эркин ток i_эрк, ўткинчи жараён давом этаётган вақтда содир бўлади, у индуктив ғалтакда тўпланган магнит майдон энергияси эвазига хосил бўлади:

Мажбурий ток (кучланиш) деганда занжирдаги ЭЮК орқали ҳосил бўладиган токни (кучланишни) тушуниш керак бўлади.

Эркин ток (кучланиш) кўрсатгичли функция орқали ифодаланади, улар экспоненциал қонун асосида сўнади ва вақт t ошган сари кўрсатгичли функция камайиб боради.

Ўткинчи жараёнларда электр занжирини участка ва элементларида ток ва кучланишларни хисоблаш электр холат тенгламалари бўйича амалга оширилади.

Бу тенгламалар ток ва кучланишларни оний қийматлари учун тузилади. R, L ва С параметрлари ўзгармас бўлган чизиқли электр занжирлари учун тенгламалар ўзгармас коэффицентлар орқали ифодаланади.

Бу тенгламаларни ечилиши ўткинчи жараёнлардаги ток ёки кучланишларни ўзгариш қонуниятини белгилайди (коммутация қонунлари орқали).

Мажбурий режим учун электр холат тенгламаси қуйидагича ёзилади:

• Ri_мажб=U

Эркин режим учун электр холат тенгламаси ўткинчи жараён тенгламасидан мажбурий режим тенгламасини айирмаси (йиғиндиси) орқали топилади:

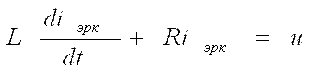
Математикадан маълумки, бу тенгламани ечими қуйидагича бўлади

i_эрк=Ае-т/t

бунда А-ўзгармас катталик, t= -вақт доимийси.

Ўзгармас А бошланғич шартлардан топилади: (t=0) қачонки i(0)=i_мажб(0)+i_эрк(0)

Индуктивлик занжири учун коммутация вақтида ўткинчи ток коммутациягача бўлган токка тенг, яъни i(0)=0.

Мажбурий режим учун : i_мажб(0)=t_мажб=U/R

Эркин режим учун i_эрк(0)=А ва, ундан келиб чиқиб

А=-

Ўткинчи жараёндаги ток

I=I_мажб+I_эрк =

Ўткинчи жараёнда индуктивликдаги кучланиш

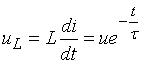
Ўтиш жараёнларида ток ва кучланишларнинг Эркин ташкил этувчилари ташқи таъсир этувчиларга боғлиқ бўлмасдан, фақат занжирнинг пассив элементлари параметрлари орқали аниқланади. Аниқланадиган параметрлар коммутациядан кейинги холат учун аниқланади.

Ўтиш жараёнларини тахли қилишда Тўлиқ , мажбурий ва эркин ТОК ва КУЧЛАНИШлари тахлил қилинди.

Амалда ТЎЛИҚ ТОК ва КУЧЛАНИШлардан фойдаланилади.

ЎТИШ ЖАРАЁНЛАРИНИ КЛАССИК УСУЛ ОРҚАЛИ ТАХЛИЛ ҚИЛИШ

1. Электр занжирининг коммутациягача бўлган холати t=0 тахлил қилинади, яъни занжирдаги калит холатига қараб унинг индуктив ва сиғим элеметлари орқали ўтаётган ток ва кучланишлар аниқланади.

2. Занжирнинг коммутациядан кейинги холати учун, яъни t холат учун, ўтиш жараёни тугагандан кейинги холат. Индуктив ва сиғим, қаршилик элеметларидан ўтган ток ва кучланишлар миқдори аниқланади.

Шу холатда занжирнинг характеристик тенгламаси тузилади, яъни занжирдаги манба узилади ва индуктив, сиғим элементларини ифодаловчи комплекс қаршиликлар орқали тенглама тузилади.

Илдизи иккига тенг бўлган тенглама ечилади. Бунда P - катталикнинг илдизи топилади. Бу катталик кўрсатгичли функциянинг бирлиги бўлиб, ўтиш жараёнида ток ва кучланишлар қийматларининг ўзгариш тезлигини аниқлайди.

Бундан ташқари ўтиш жараёнинг доимий вақтини ифодаловчи катталик, ҳамда ўтиш жараёнинг вақти аниқланади.

4. Коммутация қонунларига асосан Ток ва кучланишларнинг МАЖБУРИЙ ва ЭРКИН ташкил этувчилари топилади. Бу холатда А – доимий интеграл катталаги аниқланади. Шу босқичда электр занжир элементларининг ТОК ва КУЧЛАНИШларининг барча қийматлари аниқланади.

5. ТОК ва КУЧЛАНИШларнинг барча қийматлари учун вақтга боғлиқ бшлган графиклари чизилади.

Ўтиш жараёнини ифодаловчи график 4 (ТЎРТ) босқичдан иборат бўлади:

1. Коммутациягача бўлган холат. 2. Коммутациядан кейинги холат. 3. Коммутация вақтидаги холат. 4. Ўтиш жараёнини ифодаловчи холат.

Классик усул учун мисол

Коммутациягача электр занжири турғунлашган холатда эди. Қуйидаги қийматлар берилган бўлсин:

расм 14.3

C=100 мкФ E=150 В

1. Коммутациягача ва коммутациядан кейинги холатлар учун i₁ i₂ i₃

қийматларини топиш талаб этилади.

• 2. Вақт функцияси бўйича ток ва кучланишлар қийматларини топиш керак.

Мисолнинг биринчи қисми: Коммутациягача:

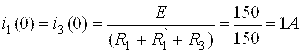
Конденсатордаги кучланиш:

Коммутациядан кейинги ТОК ва КУЧЛАНИШЛАР қийматини топамиз:

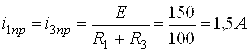
Кирхгофнинг иккинчи қонуни бўйича тенглама тузамиз: t=0 холат учун

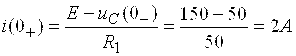
Кирхгофнинг БИРИНЧИ қонуни бўйича:

холат учун ток ва кучлвнишларнинг эркин ва мажбурий қийматларини топамиз:

Конденсаторда эркин ТОК

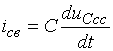
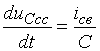
Мисолнинг 2 қисми

Коммутациядан кейинги холат учун тенглама қуйидаги кўринишда бўлади.

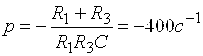
Электр занжиридаги ҳар бир ток мажбурий ва эркин ташкил этувчиларнинг йиғиндисига тенг бўлади:

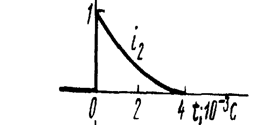
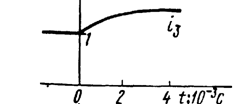
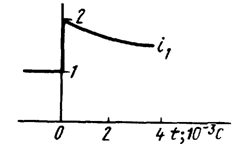
Расм 14.4

НАЗОРАТ САВОЛЛАРИ

1. Электр занжирларида Ўтиш жараёнлари.

2. Эдектр занжирларида коммутация деб нимага айтилади.

3. Коммутация қонунлари.

4. Ток ва кучланишнинг эркин ва мажбурий ташкил этувчилари.

5. Ўтиш жараёнларида Тўлиқ ток ва кучланишлар ифодалари.

6. Электр занжирининг классик усулда тахлил қилиш тартиби.

7. Комплекс қаршиликлар орқали дифференциал тенгламалар тузиш.

15 –МАЪРУЗА
ЎТИШ ЖАРАЁНЛАРИНИ ОПЕРАТОР УСУЛИДА ҲИСОБЛАШ.

Ўткинчи жараёнларда Электр занжирининг ток ва кучланишлар ОНИЙ қийматларини ҳисоблашда математик усул анча мураккаб ҳисобланади. Чунки ўтиш жараёнларини ёзишда дифференциал ва интеграллардан фойдаланилади. Шу билан бир қаторда электр занжирдаги индуктив ва сиғим элементлар орқали ўтаётган ток ва кучланишларнинг оний қийматлари қуйидаги формулалар орқали ифодаланади: L ва C занжирларда ТОК ва КУЧЛАНИШ:

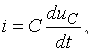
Ўтиш жараёнларида Электр занжирнинг ток ва кучланиш қийматларини оператор усулида ҳисоблашда улар ифодаларининг ТАСВИРЛАРИ орқали ифодаланади. ТОК ва КУЧЛАНИШларнинг интеграл орқали ифодалари алгебраик ифодаларга айланади ва уларнинг оний қийматларини ҳисоблаш мумкин бўлади.

Ўтиш жараёнларининг ОПРЕРАТОР усули ЛАПЛАС формуласига асосланади, яъни:

Француз математиги, физиги Пеър Симон ЛАПЛАС номи билан аталадиган ФОРМУЛА ОРҚАЛИ ҳисобланади (ЛАПЛАС ИНТЕГРАЛИ)

Бу формулада функция f (t) – функцияниннг оригинали, F (p) - функциянинг тасвири ҳисобланади.

Агар

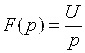
Тенг бўлса, у холда ЛАПЛАС ИНТЕГРАЛИ

Агар тенг бўлса, у холда ЛАПЛАС ИНТЕГРАЛИ:

Демак, функция = ифодага алмаштирилди.

Юқоридаги ЛАПЛАС формуласи орқали ҳар қандай функциянинг унинг тасвири ва оригинали орқали бўлинмалар билан ифодалаш имконини беради (ЖАЛВАЛ)

	Оператор кўриниши


	1

Бу ифодаларда p – ЛАПЛАС ОПЕРАТОРИ деб юритилади.

Опрератор усулида R. L. C занжирларида хосила d/dt p – ЛАПЛАС оператори билан, интеграл эса 1/p ифода билан АЛМАШТИРИЛАДИ,

Ҳар бир элементнинг ток ва кучланишларинии боғловчи Лаплас формуласидан фойдаланган холда электр занжирларининг оддий схемаларидан ОПЕРАТОР холатларига ўтиш усулини келтириш мумкин:

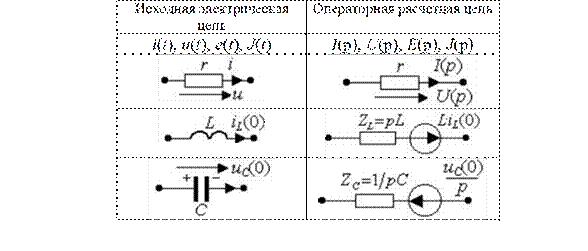
ОПЕРАТОР УСУЛИГА МИСОЛЛАР

Келтирилган электр занжири учун ОПЕРАТОР усулида чиқиш КУЧЛАНИШИНИ Ҳисоблаш талаб қилинса, ухолда

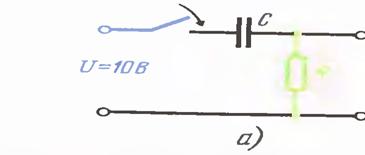
Расм-15.1

Келтирилган электр занжирини коммутациядан кейинги холат учун бошқатдан чизиб оламиз:

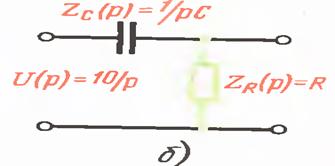
Расм-15.2

Ушбу схема учун ОПЕРАТОР ТОКИНИ АНИҚЛАЙМИЗ:

ЧИҚИШ КУЧЛАНИШИ ЭСА қуйидагича ифодаланади:

Юқоридаги келтирилган таблицадан фойдаланган холда

Электр занжирларида ОПЕРАТОР усулида ҳисоблаш учун ЭКВИВАЛЕНТ қуйидаги схемалар орқали ифодаланади.

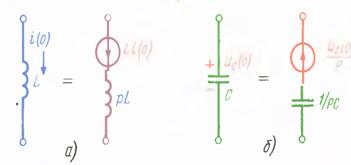
Расм-15.3

Қуйидаги электр занжир учун ОПЕРАТОР схемасини чизинг ва оператор токини ёзинг.

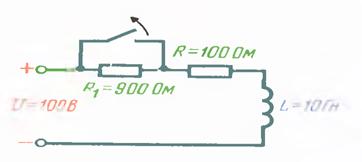
Расм-15.4

Юқоридаги электр занжири учун коммутациядан кейинги ОПЕРАТОР Схемасини чизамиз:

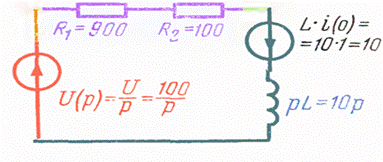
Расм-15.5

Коммутациядан кейин ТОК қуйидаги қийматга тенг бўлади

Оператор ТОКИНИ ҳисоблаймиз:

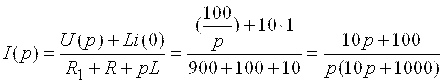
Баъзи қисқартиришлардан кейин

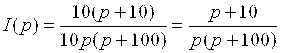
ЁЙИЛИШ ТЕОРЕМАСИ

Оператор умулида функция оригиналини ва тасвирини

Таблица орқали эмас, балки математик ифода орқали ҳам аниқлаш мумкин, бундай математик ифодага ЁЙИЛИШ ТЕОРЕМАСИ деб аталади:

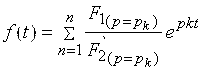
• Бу ифодада йиғинди, қуйидаги

• ифодани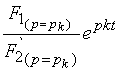

• нечта илдизга эга бўлса

• шунча марта қўшади.

ТОК ва КУЧЛАНИШЛАРНИНГ ОПЕРАТОР ШАКЛИДАГИ БАЛАНСИ, оператор қаршилиги ва оператор ўтказувчанликлар ифодалари қуйидаги кўринишда бўлади:

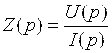
ПАССИВ ИККИ ҚУТБЛИ ЭЛЕКТР ЗАНЖИРЛАРИНИНГ ОПЕРАТОР ТЕНГЛАМАЛАРИ ВА ЭКВИВАЛЕНТ СХЕМАЛАРИНИ КЎРИБ ЧИҚАМИЗ

1. ҚАРШИЛИК

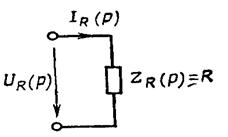
Расм-15.6

2. СИҒИМ

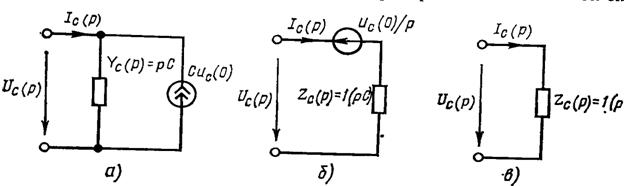
Расм-15.7

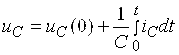
Оператор ТОК ва КУЧЛАНИШлар:

3. ИНДУКТИВЛИК

Расм-15.8

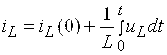
Оператор ТОК ва КУЧЛАНИШ ифодалари:

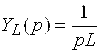
ХУЛОСА

Электр занжирларини ОПЕРАТОР усулида ҳисоблашда электр схемаларини эквивалент холатига келтрилади ва мураккаб бўлган математик ифодалар ўрнига алгебраик ифодалардан фойдаланиб занжир хисобланади.

НАЗОРАТ САВОЛЛАРИ

1. Лаплас интеграл формуласи, маъноси.

2. Функция тасвири ва оригинали, маъноси, формуласи.

3. Оператор усулининг маъноси.

4. Оператор умулини ифодаловчи жадвални ёзинг.

5. Оператор усулидан фойдаланган холда электр схемаларни чизинг.

6. Қаршилик элементининг оператор ТОК, кучланиш, ўтказувчанлик формулалари.

7. Сиғим элементининг оператор ТОК, кучланиш, ўтказувчанлик формулалари.

8. Индуктивлик элементининг оператор ТОК, кучланиш, ўтказувчанлик формулалари.

16 –МАЪРУЗА

Спектрал (частотавий) усул ёрдами билан ЧЕЗларни тахлил қилиш. Тўртқутбликлар(ТҚ)

Спектрал (частотавий) усул ёрдами билан ЧЕЗларни тахлил қилиш.

Электр занжирларини ЧАСТОТАВИЙ усулда тахлил қилишда занжир орқали ўтаётган сигналларнинг частотавий характеристикаларини ҳисоблашда қўлланилади. Сигнал энергиясини спектр бўйича тақсимланишини кузатиш мумкин. Шу хусусиятлари туфайли электр занжирлардаги ўтиш жараёларини тахлил қилишга имкон беради.

Шунинг учун ҳам ЧАСТОТАВИЙ усулда электр занжирлари орқали ўтаётган сигналларни математик усулда ифодалаш мумкин бўлади. Сингаллар спектрларини вақт функцияси орқали топиш гармоник ТАХЛИЛ , берилган спектр орқали вақт функциясини топиш гармоник СИНТЕЗ деб аталади.

Юқоридаги фикрларни эътиборга олган холда электр занжирлар параметрларини ЧАСТОТАВИЙ УСУЛДА ҳисоблаш тартибини кўриб чиқамиз.

Частотавий усул:

1) Ўткинчи жараённи турқунлашган режимлар ечимларининг йиғиндиси кўринишида бажариш имконини беради;

2) нодаврий якка функсияни (ток ёки кучланишни) синусоидал ташкил этувчилар ёрдамида тахлил қилиш имкониятини беради.

Эанжир орқали ўтаётган сигналларга частотавий усулни қўллаш учун қуйидаги келтирилган носинусоидал сигнални синусоиддал сигналга айлантирамиз.

а) сигнал спектри вақт оралиғида

б) сигнал спектри (синусоидал) шаклига мос келади.

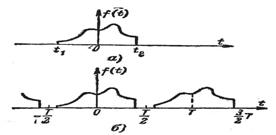
расм-16.1

Шу сабабли бу сигнал спектри ФУРЬЕ қаторлари орқали ифодаланиши мумкин. Келтирилган вақт ИНТЕРВАЛИ дан катта интервалларда сигнал спектрини ФУРЬЕ қатори орқали ифодалаб бўлмайди.

Фурье қаторининг комплекс шаклидаги ифодаси қуйидагича ёзилади,

Бу формулани қуйидаги шаклда ёзиб оламиз:

()

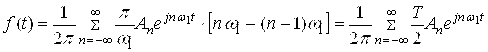Бу ифодада:

()=

Фурье қаторидаги частота интервали.

Агар тенг бўлса,

У холда:

Келтирилган формулада, агар

Бўлса, у холда ИНТЕГРАЛ чегараларидаги

T интилган бўлса НОДАВРИЙ ФУНКЦИЯНИНГ СПЕКТРИ деб аталади ва қуйидагича ифодаланади:

Агар “Т” ни чексиз равишда ошириб борсак у холда ифода қуйидаги функция холатига келади:

Юқорида келтирилган формула ФУРЬЕ функциясининг ИККИ томонлама алмаштириш функцияси, формула эса ФУРЬЕ функциясининг ТЕСКАРИ алмаштириш функцияси деб юритилади.

Фурье ИНТЕГРАЛИ бўйича қуйидаги ифодалар ва алмашттришлар ўринли бўлади:

F(jw)= f(t) e dt

f(t) = F (jw);

F(jw) = F(p)/p=jw

Частотавий (спектр) усули учун Ом ва Кирхгоф қонунлари

Ом ва Кирхгоф қонунлари

I(p)= → I(jω)=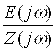

∑I_k(p)=0 → ∑I_k(jω)=0

∑E_k(jω) = ∑I_k(jω)

I(jω), E(jω) – спектрлар;

Z(jω) – комплекс қаршилик.

Тўртқутбликлар(ТҚ)

Электр занжирининг Исталган икки жуфт икки клеммаларига нисбатан қўриладиган электр занжир қисми тўртқутблик деб аталади.

Тўртқутбли занжир клеммаларига электр энергия манбаси уланса клеммалар КИРИШ, агар бирон бир ЮКЛАМА уланса ЧИҚИШ клеммалари деб аталади.

Ёки “КИРИШ” ва “ЧИҚИШ” деб ҳам юритилади.

Тўртқутбли занжирлар клеммаларига уланган узун линия, электр фильтрлари, трансформаторлар мисол бўла олади.

ТҚнинг киришдаги ва чиқишдаги комплекс токлар ва кучланишларни боғловчи муносабатлар ТҚнинг узатиш тенгламалари дейилади. Улар 6 та шаклда ифодаланади:

1) Z-шакл

Ủ₁ = Z ₁₁İ₁ + Z ₁₂İ₂′

Ủ₂ = Z ₂₁İ₁ + Z ₂₂İ₂′

2) Y- шакл

İ₁ =Y₁₁Ủ₁+ Y₁₂ Ủ₂

İ₂′=Y₂₁Ủ₁ + Y₂₂ Ủ₂

3) A- шакл

(тўғри узатиш)

4) B- шакл

(тескари узатиш)

5)H- shakli

Ủ₁ = H₁₁İ₁ + H₁₂ Ủ₂

İ₂′ = H₂₁İ₁ + H₂₂ Ủ₂

6)F- shakli

İ ₁= F₁₁ Ủ ₁ +F₁₂ İ`₂

Ủ ₂= F₂₁ Ủ ₁+F₂₂ İ`₂

Бу тенгламалардаги комплекс коэффицентлар ТҚнинг параметрлари дейилади. Улар хаммаси ўзаро боғланган.

ТҚ уланиш турлари

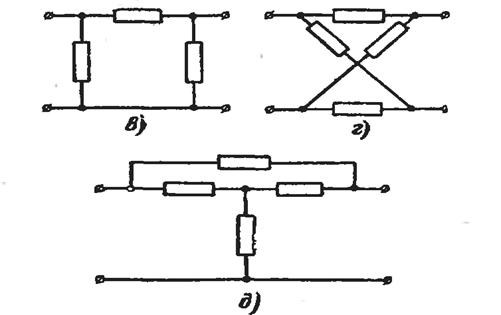
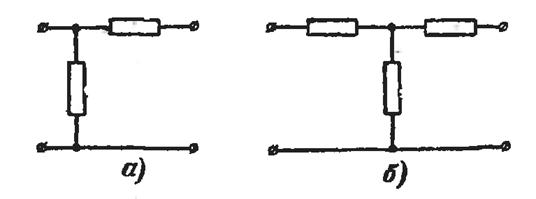
расм-16.2

Каскадли (ЗАНЖИРЛИ) уланиш

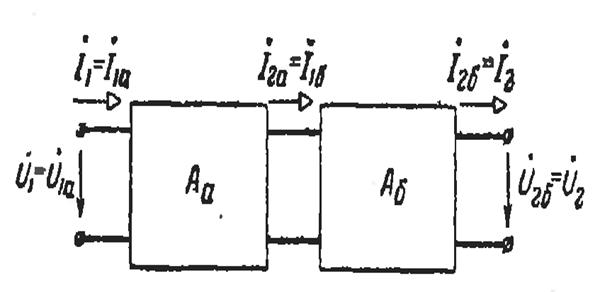
расм-16.3

КЕТМА КЕТ УЛАНИШ

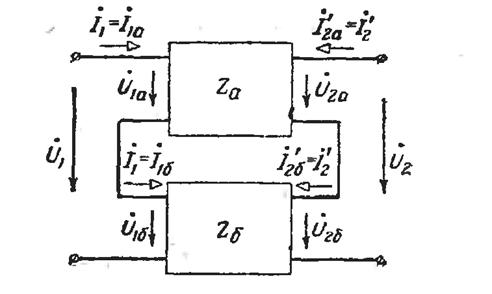
расм-16.4

ПАРАЛЕЛ УЛАНИШ

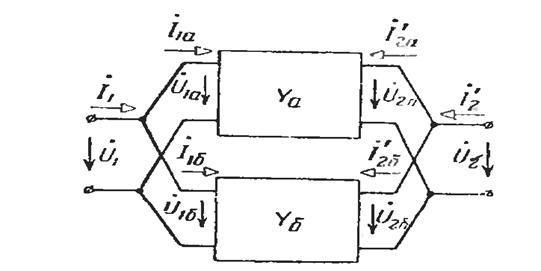
расм-16.5

НАЗОРАТ САВОЛЛАРИ

1. Частотавий усул маъноси.

2. Фурье қаторининг комплекс шаклидаги ифодаси.

3. Нодаврий функциянинг спектр формуласи.

4. ФУРЬЕ функциясининг ИККИ томонлама алмаштириш функцияси,

5. ФУРЬЕ функциясининг ТЕСКАРИ алмаштириш функцияси.

6. Частотавий усул учун Ом ва Кирхгоф қонунлари.

7. Тўртқубли электр занжирлари.

8.Тўртқутбли электр занжирларнинг узатиш тенгламалари.

9.Тўртқутбли электр занжирларнинг уланиш схемалари (кетма кет, паралел, каскадли).

17 –МАЪРУЗА

БАТТЕРВОРД, ЧЕБЫШЕВ ва ЗОЛОТАРЁВ ФИЛТРЛАРИ

Фильтрлар асосан индуктивлик ва сиғим элементларидан ташкил топган занжири хисобига ташкил топади. Шундай экан бизга маьлумки индукив қаршилиги частотага туғри пропорционал, сиғим қашилигига эса тескари пропорционал. Бундан ташқари индуктивликдаги ток миқдордаги бурчакка кучланишдан орқада қолади. Сиғимда эса ток кучланишдан бурчакка илгарилаб кетади.Келтирилган маълумотлар асосида ва ИНДУКТИВЛИК ва СИҒИМ элементлариниг бир бири билан боғланиш комбинациялари ҳисобига электр фильтрлари тузилади ва бир нечта турларга бўлинади.

Идеал фильтлар фақат реактив элементлардан тузилган бўлади.

Қуйида электр фильтрларининг бир нечта турларини кўриб чиамиз.

Электр филтрларини синтез қилишда С. БАТТЕРВОРД (электрик – муҳандис), П. Л. ЧЕБЫШЕВ ва Е. И. ЗОЛОТАРЁВ (йирик математик олимлар) номлари билан аталадиган электр филтрлари кенг тарқалган.

Юқоридаги фильтрларни кўриб чиқишдан олдин қуйидаги тушунчаларни келтирамиз:

Қуйи ва юқори частотали Филтрлардаги реактив элементлар сонига Фильтр тартиби ( n )деб аталади. Масалан ушбу схемаларда: 2 ва 7 тартибли фильтлар келтирилган

Расм-17.1

Демак филтр нечанчи тартибли бўлса филтр параметрларини ҳисоблашда оператор, комплекс ва дифференциал тенгламалар ҳам 2, 3 ва 7 тартибли холатда тузилади.

Электр филтрларининг горизонтал елкаларидаги қаршиликларини перпендикуляр елкаларидаги қаршилик қийматларига кўпайтмаси ФИЛТРНИНГ ХАРАКТЕРИСТИК ҚАРШИЛИГИ деб аталади:

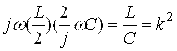
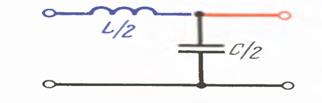
Расм-17.2

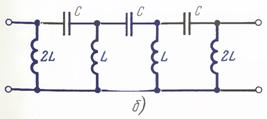Расм-17.3

Электр фильтрлари расмда кўрсатилгандек тўртқутбли электр занжирлари таркибига киради ва қуйи частотали фильтрлар K=√(L/C)(ҚЧФ)деб аталади.

Бундай фильтрларда индуктив элементларида қаршилик жуда кам бўлади, частота ошган сари горизонтал шохобчадаги қаршилик оша боради, перпендикуляр шохобчада эса узатиш коэффиценти камаяди.

Бу турдаги фильтрлада РЕЗОНАНС ЧАСТОТАСИ ҚИРҚИШ ЧАСТОТАСИ деб аталади ва қуйидагича ифодаланади:

Расм-17.4

Расм-22.3

Расм-17.5

Электр филтрларида НОРМАЛЛАШТИРИЛГАН (нормированный) катталик бу ўлчов бирликсиз катталик бўлиб қуйидагича ифодаланади: масалан нормаллаштирилган частота, частотанинг қирқиш частотаси нисбатига айтилади.

ёки

Баттерворд характеристикаларига эга бўлган филтрлар шундай филтрларки, ҚЧФ ларда частотата НОЛГА тенг бўлганда сигнал сўниши ҳам НОЛГА тенг бўлади, ўтказиш йўлакчасида эса сигнал сўниши монотон равишда ўсади ва чегаравий 3 дБ частотага тенг бўлади. Кейинчалик ушлаб қолиш (здерживания) йўлакчасида эса монотон равишда кескин ошади

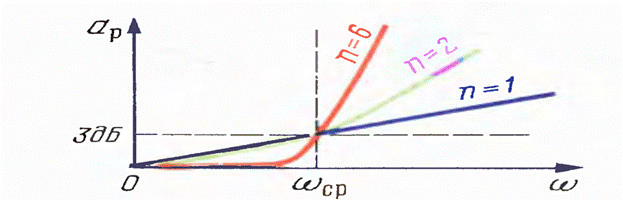
Расм-17.6

Бундай фильтрларда фильтр тартиби қанчалик катта бўлса, ушлаб қолиш йўлакчасида сигнал характеристикаси кескинлашади, ўтказиш йўлакчасида эса кучсизланади. Эътиборга олиш керакки Фильтр элементлари фақат реактив элементлар бўлганда шундай холат юз беради.

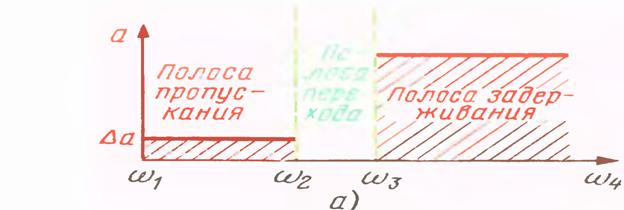Чебышев фильтрларида сигналнинг сўниш характеристикаси ўтказиш йўлакчасида амплитудаси 3 дБ дан ошмайдиган тебранма (колебательный) кўринишда бўлади, ушланиб қолиш йўлакчасида эса худди шундай тартибга эга бўлган БАТТЕРВОРД фильтларидан катта бўлган монотон равишда ўсиб борувчи характеристикага эга

бўлади.

Расм-17.7

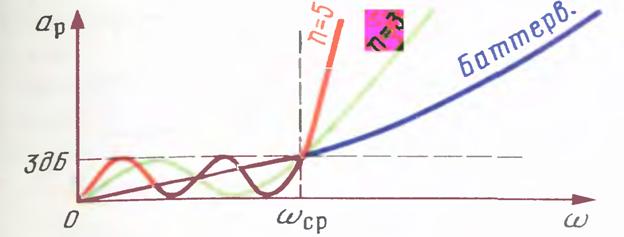
Расм-17.8

Ўтказиш йўлакчасида сигналнинг тебраниш амплитудаси қанчалик катта бўлса, филтрнинг ушланиб қолиш йўлакчасида сигнал характеристикасининг кескин ошиб кетиши кузатилади., ёки унинг тескариси, сигнал амплитудаси қанчалик кичик бўлса сигнал характеристикасининг ўсиши ҳам анча паст дарахада эканлиги кузатилади. Агар сигнал параметрларини шундай танлансаки ўтиш йўлакчасида сигнал амплитудаси нолга тенг бўлса (тугатилса) ЧЕБЫШЕВ фильтри БАТТЕРВОРТ филтрига айланади.

ЗОЛОТАРЁВ ФИЛЬТРЛАРИ

Бу турдаги фильтрларда ўтказиш йўлакчасида сигналлар тебранма характерга эга бўлади, ушланиб қолиш йўлакчасида эса монотон бўлмаган, кескин ўзгарувчан характерга эга бўлади. Қуйидаги расмларда Золотарёв фильтрлари келтирилган:

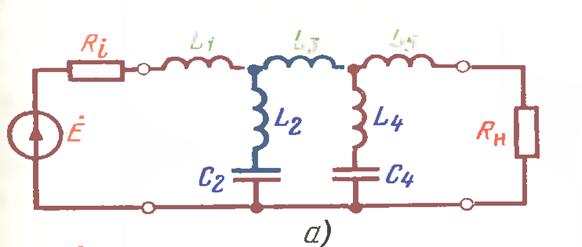Расм-17.9

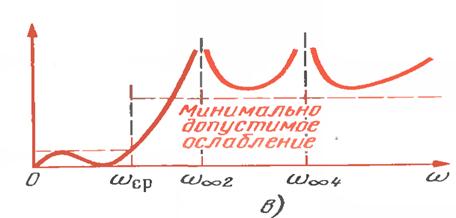
Расм-17.10

Бу турдаги фильтрлар шундай тузиладики, электр схемаларда бир нечта частота резонанси хосил бўлувчи занжирлардан тузилади (расмга қаранг), чунки кам частоталарда горизонтал шохобчаларда қаршилик кам бўлаиши, перпендикуляр шохобчаларда эса катта бўлиши кузатилади.

Энди катта миқдордаги частоталарда бунинг тескариси кузатилади.

ФИЛЬТРЛАРДА ЎТКИНЧИ ЖАРАЁН

Фильтрларда ўткинчи жараённларни кузатиш учун уларнинг кириш қисмига БИРЛИК функцияси узатилади ва фильтрнинг ЧИҚИШ қисмидаги сигнал шаклига қараб тахлил қилинади.

Юқорида кўриб чиқилган фильтрларда ўткинчи жараёнлар қуйидаги кўринишда бўлади:

Расм-17.11

Расмдан кўринадики сигнал шаклининг энг кам бузилиши БЕССЕЛ фильтрида кузатиган, сигнал шаклининг энг кўп бузилиши ЧЕБЫШЕВ фильтрида кузатилган.

Шуни таъкидлаш кераккки, БЕССЕЛ фильтрлари ўткинчи жараёнларда сигнал характеристикалари ёмон кўрсатгичларга эришади, ЧЕБЫШЕВ филтрлари эса бунинг тескариси бщлган характеристикаларга эга бщлади.

Яна шуни таъкидлаш керакки, фильтрлар тартиби ( n ) ошган сари БЕССЕЛ филтрлари характеристикалари яхшиланиб боради, БАТТЕРВОРД фильтрларида эса ёмонлашади.

Шундай қилиб кўриб чиқилган вариантлардан, БАТТЕРВОРД фильтрлари энг оптимал деб топилган ва шу фильтрлар электротехникада ишлатилиб келинмоқда.

ФИЛЬТР ПАРАМЕТРЛАРИНИ ҲИСОБЛАШ ТАРТИБИ

Фильтрлар параметрларини ҳисоблашда ҚЧФ лар асос қилиб олинади ва қолган фильтрларга тадбиқ этилади.

Фильтр параметрларини ҳисоблашда қуйидагилар асос қилиб олинади:

1. Фильтр туркуми (ЮЧФ, ҚЧФ, ЙФ, УҚФ ва х.)

2. Ўтказиш йўлакчаси учун частоталар диапазони (қиймати).

3. Ушланиб қолиш йўлакчасида частоталар диапазони (қиймати).

4. Ушланиб қолиш йўлакчасида, маълум бир частоталар учун, рухсат этилган сигналнинг сўниш қиймати.

5. Генератор ва схемадаги юкламалар учун қаршиликлар қиймати.

НАЗОРАТ САВОЛЛАРИ

1. Электр фильтр турлари.

2. Фильтрларни ташкил этувчи элементлар.

3. Фильтр тартиби қандай аниқланади.

4. Фильтрнинг характеристик қаршилиги нима.

5. Қирқиш частотаси, формуласи, графиги.

6. Баттерворд фильтрлари.

7. Чебышев фильтрлари.

8. Золотарёв фильтрлари.

9. Фильтрларда ўткинчи жараёнлар.

Фильтр параметрларини ҳисоблаш тартиби.

18 –МАЪРУЗА

НОЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРЛАРИ.

ЧИЗИҚЛИ занжирларнинг параметрлари, яъни қаршиликлари, индуктивликлари, бошқарувчи манбаларнинг сиғимлари - уларга уланган кучланишлар ёки улардан оқиб ўтаётган токларнинг қийматларига боғлиқ эмас эди.
Элемент қаршилиги шу қаршилик қутбларидаги кучланиш U нинг миқдори ва шу қаршиликдан оқиб ўтаётган ток I нинг миқдори қандайлигидан қатъий назар, унга нисбати доимо бир хил миқдорга тенг бўлган, яъни қаршиликнинг кучланиши ва токи орасидаги боғланиш U(I)=Ω·I=const доимо ўзгармас бўлган электр занжирлари ЧИЗИҚЛИ электр занжирлари деб аталади ва ТОК ва КУЧЛАНИШ шакллари қуйидагича бўлади.

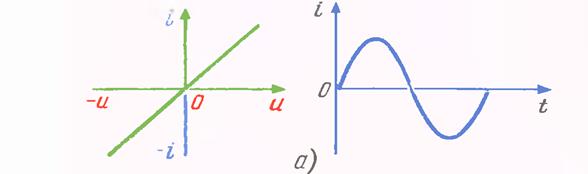
расм-18.1

Электр занжирининг қаршилиги ток кучига ва кучланишига боғлиқ бўлган занжир ночизиқли занжир деб аталади.

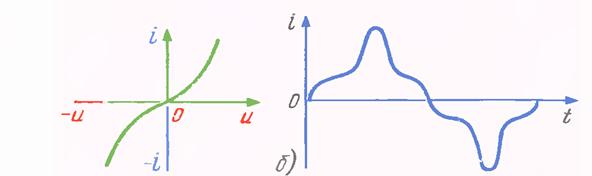
расм-18.2

Ночизиқли электр занжирлари ўзларининг характеристикаларига асосан икки турга бўлинади: СИММЕТРИК ва СИММЕТРИК БЎЛМАГАН;

Занжир қутбларидаги (на зажимах) ток ва кучланишлар йўналишлари Вольт ампер характеристикаларига боғлиқ бўлмаган ночизиқли элементларга СИММЕТРИК НОЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРЛАРИ деб аталади.

Бу турдаги электр занжирларига электр лампалари, бареттерлар (токни стабил холатга келтирувчи қурилма) терморезисторлар киради.

Занжир қутбларидаги ток ва кучланишлар йўналишлари ҳар хил бўлган вольт ампер характеристикали ночизиқли элементларга СИММЕТРИК бўлмаган электр занжирлари деб аталади.

Бундай турдаги электр занжирларига триодлар (лампали, яримўтказгичли) киради.

Ночизиқли занжирларга чўғланма лампалар, электрон лампалар, ион ва ярим ўтказгичли асбоблар мисол бўла олади.

Будай занжирларнинг қаршилиги доимий бўлмагани учун занжирдаги ток кучи унинг қутбларидаги (на зажимах) кучланишга пропорционал бўлмайди.

Ночиқли характеристикали элементларга актив ночизиқли қаршиликлар; термисторлар, ярим ўтказгичли диод, стабилизатор, яримўтказгичли термоқаршиликлар ва реактив ночизиқли қаршиликлар, тўйинган ферромагнит ўзакли дросселлар хамда ночизиқ диэлектрикли конденсаторлар киради.

Ночизиқли электр занжирлар параметрлари

Резистив қаршилик, индуктивлик ва сиғим уларнинг параметрлари мос равишда R, L ва C уз қийматларини сақлашмаса ва токка ёки кучланишга боғдиқ булса, улар ночизиқли дейилади.

Ударнинг характеристикаси: (волт-ампер u=iR, вебер-ампер Ψ=Li ва волт-кулон q=Cu ) эгри чизиқли линя орқали ифодаланади.

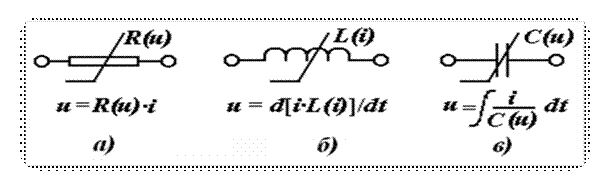
расм-18.3

Ҳар бир элемент учун қутбларида (клеммаларида) ҳосил бўладиган кучланиш ва шу элемент орқали ўтаётган ТОК ларни бир бирига боғлиқликларини кўрсатувчи ВОЛЬТ АМПЕР ХАРАКТЕРИСТИКАЛАРИ (ВАХ) мавжуд бўлади.

Ушбу графикда ЧИЗИҚЛИ ва НОЧИЗИҚЛИ элементларнинг ТОК ва КУЧЛАНИШЛАРГА боғлиқлик графиги келтирилган. Чизиқли элементларда КУЧЛАНИШ ошган сари ТОК ҳам ошиб боради, Ночизиқли элементларда эса ҳар бир нуқтада ток ва кучланиш қийматлари ҳар хил бўлади ва ўзгаришлар ҳам ҳар хил бўлади.

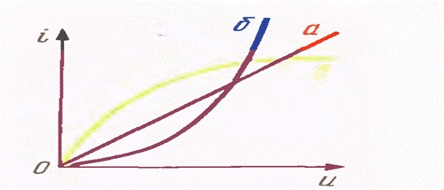
расм-18.4

БАРЕТТЕР нинг ВАХ келтирилган. Кучланишнинг Uн ва Uк оралиғида бареттердаги ТОК миқдори ўзгармайди, қаршилик эса R б ток ошган сари ошиб боради

ТЕРМОРЕЗИСТОР (кучланишлни нормал холатга келтирувчи қурилма) нинг ВАХ келтирилган. Ҳарорат ошган сари қаршилик камайиб боради. Бу қурилма электр занжирларда ҳароратни ўлчаш ва нормаллаштириш учун ишлатилади.

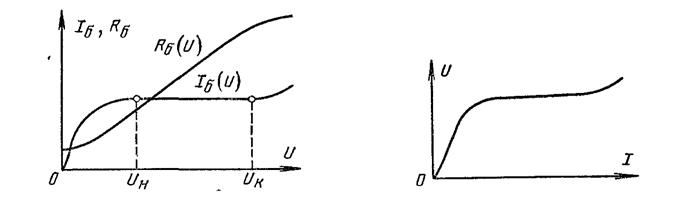
расм-18.5

Ночизиқли иккита паралел уланган элементлар ва уларнинг ВАХ қуйидагича берилган бўлса.

ва ва

Берилган занжир учун кучланишнинг токлар йиғиндисига (I1 + I2) боғлиқлик графигини чизиш керак бўлади.

Паралел уланган электр занжирларида шохобчалардаги кучланишлар бир бирига тенг бўлганлигини U₁ + U₂ = U ва I = I₁ + I₂ эътиборга олган холда, ордината ўқига токлар қийматини қўямиз (ОС нуқта), С нуқтадан тўғри чизиқ ( сd нуқта). Шу нуқтадан ордината ўқига паралел бўлган (da кесимини тушурамиз), натижада ad ва af масштабга тенг бўлган кесама оламиз.

Худди шундай йўл билан паралел уланган ҳар қандай нояизиқли электр занжир параметрларини график усулда ҳасоблаш мумкин.

Кетма – кет уланган ночизиқли элементлар уланганэлектр занжир график усулда ҳисоблаш

Кетма кет уланган ночизиқли Электр занжирларда ток I= I₁ +I₂, U=U₁+U₂ га тенг бўлади. Шу ифодаларни эътиборга олган холда, бир хил кучланишлар қийматида токлар йиғиндиси топилади (Графикда келтирилган).

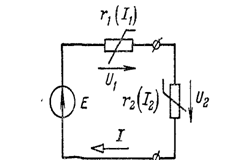
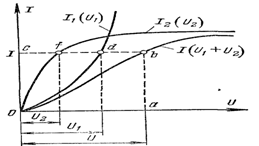
расм-18.6

Ночизиқли резистив элементи

Таркибида сиғим ва индуктивликлари, яъни энергияни заҳираловчи реактив элементлари бўлмаган электр занжирлари резистив занжирлар дейилади. Резистив элементнинг схемадаги шартли белгиси юқорида келтирилган.

НЧ резистив элементни аниқлашда албатта унинг Вольт-Ампер характеристикалари келтирилади:

Ночизиқли сиғим.

Ночизиқли сиғимнинг схемадаги шартли белгиланиши қуйида келтирилган.

Ундаги тўпланган заряд q=q(u) кучланишга u(t) ночизиқли боғланишда бўлади.

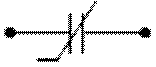
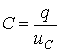
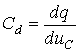
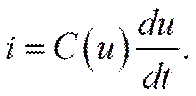
расм-18.7

Ночизиқли индуктивлик

Ночизиқли индуктивликнинг электр схемадаги шартли белгиси қуйида расмда келтирилган. Магнит илашувнинг токга ночизиқли боғланганлигини қуйидаги ифодаланади:

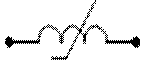
Реал элементларнинг НЧ резистив элементлар моделлари шаклидаги тавсифланишига диод, тиристор, динистор мисол бўла олади.

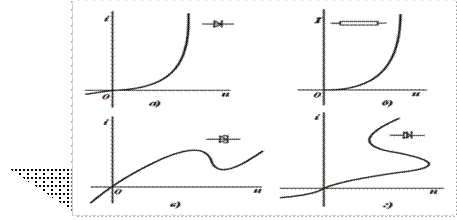
расм-18.8

Чизиқли электр занжир параметрлари Ом қонуни орқали ҳисобланса,

Ночизиқли ВАХ катта тартибдаги кўпҳадлар орқали ҳисобланади:

Бу формулада: - токнинг доимий ташкил этувчиси;

- ВАХ турига боғлиқ бўлган ва ўтказувчанлик ўлчов бирлигига эга бўлган доимий коэффицентлар.

Ночизиқли электр занжирлар ВАХлари қанчалик чизиқли электр занжирлар ВАХ ларидан фарқ қилса кўпҳадли формуладаги даража кўрсатгичлари шунчалик катта тартибга эга бўлиб бораверади, ва занжир қутбларига (клеммаларига) қўйилган кучланиш ўзгариб борган сари ТОК ҳам шунчалик ўзгариб бораверади.

Мисол учун

Агар кириш сигнали қуйидаги гармоник функция кўринишига эга бўлса

Ночизиқли Электр занжирининг ВАХси 2 тартибдаги кўпҳаддан ташкил топган бўлса ва қуйидаги тенглама билан ифодаланса

U кучланиш ўрнига ифодани қўямиз ва қуйидаги тенгламани оламиз:

Ва қуйидаги ифодани эътиборга олсак

У холда ночизиқли электр занжирида ТОК қуйидаги ифодага тенг бўлади

ХУЛОСА

ДЕМАК НОЧИЗИҚЛИ ЭЛЕКТР ЗАНЖИРИ:

кириш қисмига узатилган КУЧЛАНИШ частотали синусоидал сигналдан ташкил топган бўлади, ТОК эса доимий катталикдан

ва иккиланган частотали гармоник сигналдан ташкил топган

19 –МАЪРУЗА

МАГНИТЛИ ЗАНЖИРЛАР

МАГНИТ ОҚИМИ БОҒЛАНГАН ФЕРРОМАГНИТ МАТЕРИАЛЛАР ВА МАГНИТ ЮРИТУВЧИ КУЧЛАР ЙИҒИНДИСИГА МАГНИТ ЗАНЖИРЛАР ДЕБ АТАЛАДИ.

Магнит занжирлар тармоқланмаган ва тармоқланган турларига бўлинади.

Магнит кесим юзаларида магнит оқими бир хил бўлган магнит занжирига ТАРМОҚЛАНМАГАН магнит занжири деб аталади. ТАРМОҚЛАНМАГАН магнит занжирига қуйидаги расмдаги занжир мисол бўла олади. Тармоқланмаган магнит занжирида магнит ОҚИМИ бир хил бўлади, яъни:

расм-19.1

Φ=∫BdS=0

Магнит оқими магнит кесим юзаларида ҲАР ХИЛ бўлган магнит занжирлари ТАРМОҚЛАНГАН магнит занжири деб аталади.

Тармоқланган магнит занжирлари СИММЕТРИК ва НОСИММЕТРИК магнит занжирларига бўлинади. СИММЕТРИК магнит занжирига қуйидаги расмдаги занжир мисол бўлади.

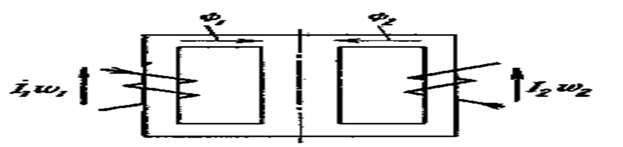
расм-19.2

Агар расмда кўрсатилган магнит занжирининг икки томонидаги магнит юритувчи кучлари

I₁ω₁=I₂ω₂

Ва МАГНИТ ОҚИМЛАРИ

Φ₁=Φ₂

бир бирига тенг бўлса бундай занжир СИММЕТРИК деб юритилади.

Агар МАГНИТ оқими ва магнит юритувчи кучлар бир бирига тенг бўлмаса , яъни

I₁ω₁≠I₂ω₂

Φ₁≠Φ₂

Бундай магнит занжири НОСИММЕТРИК магнит занжири деб юритилади.

Магнит занжирларида асосий катталиклар қуйидагилар ҳисобланади: МАГНИТ ИНДУКЦИЯСИ, МАГНИТЛАНИШ ва МАГНИТ МАЙДОН КУЧЛАНГАНЛИГИ.

МАГНИТ ИНДУКЦИЯСИ:

B=μ₀(H+J) 1T=1 B*c/м²=1 B б/м²

B=μ₀μH=μ_aH

H=B / μ₀≈0,8*10⁶B

МАГНИТЛАНИШ:

J=χH 1+χ=μ

Магнитланиш ва магнит майдон кучланганлиги ўлчов бирликлари: (А/м) ўлчов бирлиги билан ўлчанади.

МАГНИТ ОҚИМИ: ўлчов бирлиги (Вебер – Вб)

Φ=∫BdS

Магнит занжирлар параметрларини ҳисоблашда асосий қонунлардан бири бу ТЎЛИҚ ТОК ҚОНУНИ ҳисобланади ва қуйидагича ифодаланади:

ЁПИҚ МАГНИТ КОНТУРИ ОРҚАЛИ АЙЛАНАЁТГАН МАГНИТ МАЙДОН КУЧЛАНГАНЛИК ВЕКТОРИ ШУ КОНТУР ОРҚАЛИ ОҚАЁТГАН ТОКЛАРНИНГ АЛГЕБРАИК ЙИҒИНДИСИГА ТЕНГ БЎЛАДИ

Агар магнит катушкасидаги чўлғамлар сонини эътиборга олсак, у холда тўлиқ ток қонуни қуйидаги ифодага тенг бўлади.

Бу ерда F магнитланиш кучи, ёки магнит юритувчи куч деб юритилади, ўлчов бирлиги (ампер- витках).

Юқоридаги формулани эътиборга оладиган бўлсак, МАГНИТ ЗАНЖИР ҚОНУНИ қуйидагича ифодаланади:

Бу ифодада: l магнит индукцияси линиясининг ўртача узунлиги.

МАГНИТ ЗАНЖИРЛАРИ УЧУН КИРХГОФ ҚОНУНЛАРИ

КИРХГОФНИНГ БИРИНЧИ ҚОНУНИ:

Магнит занжирининг ҳар қандай тугунларидаги магнит оқимларнинг алгебраик йиғиндиси нолга тенг.

∑Ф=0

КИРХГОФНИНГ ИККИНЧИ ҚОНУНИ:

Ҳар қандай ёпиқ контурдаги магнит кучланганликлар тушумининг алгебраик йиғиндиси шу контурнинг магнит юритувчи кучларининг алгебраик йиғиндисига тенг

∑U=∑Iω

МАГНИТ ҚАРШИЛИГИ, МАГНИТ ЗАНЖИР УЧАСТКАСИНИНГ МАГНИТ ЎТКАЗУВЧАНЛИГИ. МАГНИТ ЗАНЖИРИ УЧУН ОМ қонуни

Қоидага кўра магнит кучланланганлик қуйидагича ифодаланади:

U=Hl

Бу ифодада:

H=B/( μμ₀)= Φ/(μμ₀S)

Ф - магнит оқими;

S- магнит участкасининг кўндаланг кесим юзаси;

Юқоридаги формулаларни инобатга олган холда МАГНИТ ЗАНЖИРИ УЧУН ОМ қонуни қуйидагича ифодаланади:

U=Φl/(μμ₀S)=ΦR

R=l/(μμ₀S)

Магнит занжири учун ОМ қануни магнит оқими билан магнит кучланганлик ўртасидаги боғланишни ифодалайди.

Бу ифодаларда қуйидаги формула МАГНИТ ЗАНЖИР УЧАСТКАСИНИНГ МАГНИТ ҚАРШИЛИГИ деб юритилади ва қуйидагича ифодаланади:

R=l/(μμ₀S)

Магнит участкасининг магнит қаршилиги миқдорига тескари бўлган ифода МАГНИТ ЎТКАЗУВЧАНЛИК деб аталади ва қуйидагича ифодаланадии:

G=1/R= μμ₀S/l

Магнит занжирлар кўпчилик машиналар, аппаратлар, электромагнит асбоблар ва ўлчаш техникаси хамда автоматика қурилмаларининг асосини ташкил қилади. Масалан, қуйидаги расмда кучли магнитавий майдон манбайи хисобланган ва тез-тез учраб турадиган ўзгармас ток электромагнити кўрсатилган.

расм-19.3

Бунда электромагнит энергия механик энергияга ва энергиянинг бошқа кўринишларига хамда тескарисига алмашинади.

Масалан, ўзгармас ток синхрон машинасининг ротори чулғамидан ток ўтганда ўзгармас“N-S”қутбли магнит майдони хосил бўлади.

Бу магнит майдоннинг куч чизиқлари ротор ва статорнинг (А.В.С. чулғамларини хам кесиб ўтиб) пўлат ўзаклари орқали туташади. Ротор маълум ω бурчак тезлик билан айлан ганда статорнинг чулғамларида ω частотали ўзгарувчан Э Ю К индукцияланади.

Ўзгармас токнинг электромагнитавий майдонидан пўлат буюм ва металл синиқла рини ташишда ишлатиладиган кўтаргич электромагнитлар қуришда фойдаланилиши ни мисол тариқасида кўрсатиш мумкин.

Магнит материаллар ёрдамида магнит оқими кескин кучайтирилади.

Магнит оқимидан паст кучланишли токларни юқори кучланишли токларга ёки электр энергиясини механик энергияга айлантиришда ва электр энергиясини шунга ўхшаш тарзда генерациялашда фойдаланилади.

Ташқи магнит майдони та`сирида магнитланиш хоссасига эга материаллар магнит материаллари деб аталади.

Асосий магнит материалларга никел, кобалт ва тоза темир асосидаги турли қотишмалар мисол бўлади.

Техника аҳамиятга эга магнит материалларига ферромагнит материаллар ва ферромагнит кимёвий бирикмалар (ферритлар) киради.

Материалларнинг магнит хоссалари электр зарядларининг ички ҳаракатига асосланган бўлиб, бунда зарядлар элементар айланма ток кўринишида ифодаланади. Бундай айланма токлар электронлпарнинг ўз ўқи атрофида айланиши (электрон спинлар) ҳамда уларнинг атом ичида орбита бўйлаб айланишидан ҳосил бўлади.

Ферромагнит ҳодисаси баъзи материалларнинг ички микроскопик қисмида кристалл структуралар ташкил қилиши билан боғлиқ бўлиб, бундай структуралар МАГНИТ ДОМЕНЛАРИ ДЕЙИЛАДИ.

Бунда электрон спинлар ўзаро параллел равишда бир томонга йўналган бўлади

Баъзи материаллар (қатлам чегаралари орасидаги қалинлик бир неча ўн-юз атом масофасига тенг бўлган) да доменларнинг ўлчами тахминан 0,001-10 мм³ оралиғида бўлади. Ўта тоза материалларда эса доменларнинг ўлчами юқорида келтирилган қийматдан ҳам каттароқ бўлади.

Ферромагнитнинг магнитланишида доменларда спонларнинг йўналиш олиши.

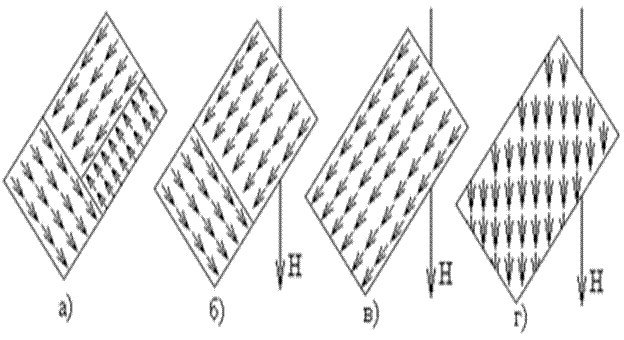
расм-19.4

Поликристалл магнетикларда анизотропия кескин ифодаланган ҳолларда ферромагнетик магнит текстурага эга бўлади.

Керакли магнит текстура олиш орқали материалда маълум йўналишда юқори магнит характеристикага эришиш мумкин.

Ташқи магнит майдони таъсирида ферромагнит материалнинг магнитланиш жараёни қуйидагича кечади:

1) магнит моменти майдон йўналиши билан кичик бурчак ҳосил қилган доменлар катталашади ва бошқа доменлар ўлчами кичраяди; 2) магнит моментлари майдон йўналиши узра бурилади ва бир хил йўналишга эга бўлади.

Магнит тўйиниши доменнинг катталишиши тўхтаганда ва ўз-ўзидан магнитланган барча монокристалл қисмларнинг магнит моменти майдон узра йўналганида содир бўлади. Доменлардаги спинлар йўналишининг ўзгариши расмда келтирилган.

Ферромагнит монокристаллари магнитланаётганда уларнинг чизиқли ўлчамлари ўзгаради. Бу ҳодиса магнит-стрикция дейилади. Темир монокристалининг магнит-стрикцияси кристаллнинг ҳар хил йўналишларида турлича бўлади.

Материалларнинг нисбий магнит сингдирувчанлиги магнит индукцияси (В) нинг магнит майдони кучланганлигига нисбати билан аниқланади:

r_р= B/μ₀H

Магнит материалларнинг магнит сингдирувчанлиги бирдан юқори m»1 (m_р=m₀×m, m=1,2566×10^-6 Гн/м) бўлади

Магнит сингдирувчанлик чулғамга магнит ўзак киритилганда магнит оқимининг кўпайишини билдиради. Бу юксалиш бир неча ўн минг мартагача ортади.

Узунлиги L, кесим юзаси S бўлган ўзакнинг магнит қаршилиги қуйидагича аниқланади:

Р_m=L/μS=L/μμ₀S

Шундай қилиб, ғалтакка ўзак киритилиши натижасида магнит қаршилиги m га боғлиқ равишда камаяди.

НАЗОРАТ САВОЛЛАРИ

1. Магнит занжирлар таърифи.

2. Магнит занжир турлари (тармоқланган ва тармоқланмаган МЗ).

3. Симметрик ва носимметрик МЗ.

4. Магнит занжирлар учун КИРХГОФ қонунлари.

5. МЗ тўлиқ ток қонуни.

6. МЗ тўлиқ мангнит қонуни.

7. МЗ учун ОМ қонуни.

8. МЗ тўлиқ магнит қаршилиги, магнит ўтказучанлик.

20 –МАЪРУЗА

Тескари боғланган электр занжирлари. Автогенераторлар.

ЧИҚИШИДАГИ СИГНАЛ ҚАЙТАДАН КИРИШИГА УЗАТИЛАДИГАН ЗАНЖИР ТЕСКАРИ БОҒЛАНИШЛИ (ТБ) ЗАНЖИР ДЕБ АТАЛАДИ.

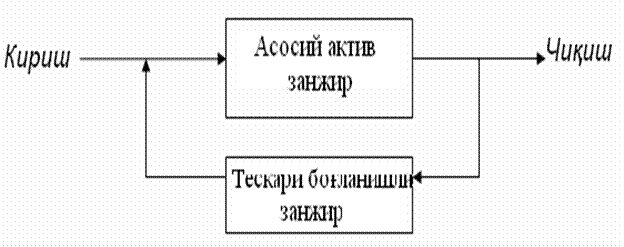
расм-20.1

Занжирга тескари боғланишни киритиш занжирнинг ишчи характеристикаларини ўзгартиради.

Масалан чиқишидаги сигналнинг бир қисми ТБ орқали киришга узатилса ҳамда, у киришдаги сигналдан айириб ташланса бундай ТБ манфий тескари боғланиш деб аталади. (манфий ТБ).

Агар чиқишдаги сигналнинг бир қисми киришга узатилса ҳамда у киришдаги сигналга қўшилса бундай тескари боғланиш мусбат тескари боғланиш (Мусбат ТБ) ёки регенератив тескари боғланиш дейилади.

Манфий тескари боғланиш кучайтириш коэффициентини камайтиради ва текислайди, унинг ўтказиш оралиғини кенгайтиради, шовқин ва бўзилишларни камайтиради. Кучайтиргичларда кўпроқ манфий ТБ қўлланади.

Мусбат тескари боғланиш кучайтириш коэффициентини орттиради, ўтказиш оралиғини кичрайтиради ва кучайтириш барқарорлигини камайтиради. Мусбат ТБ кўпинча генераторларда қўлланади.

Актив ночизиқли элементлардан ташкил топган электр занжирларда электр тебранишлар даврий таъсирсиз ўз ичидан ҳосил бўлиши мумкин.

Ўзгармас манбалар энергиясининг тебранишлар энергиясига алмашиш жараёни занжирдаги автотебранишлар деб аталади.

Автотебранишлар ҳосил бўладиган занжир тескари боғланишли занжирлар ҳисобланади.

Оператор узатиш функцияларини К(Р) ва β (Р) бўлган иккита тизим қуйидагича боғланган бўлсин

АСОСИЙ ТИЗИМ

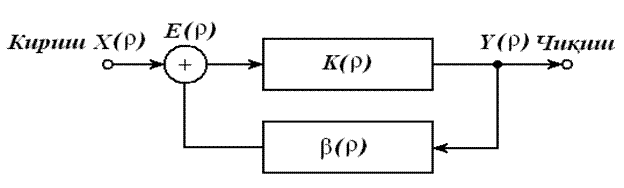
расм-20.2

ТЕСКАРИ ТИЗИМ

Бундай тизим тескари боғланишли тизим деб юритилади.

Агар Х (Р) ва Y (Р) мос равишда киришдаги ва чиқишдаги оператор сигналлар бўлса, у холда:

Тескари боғланган тизимнинг узатиш функциясини Н (Р) аниқлаймиз:

ва га тенг бўлса, у холда:

Демак:

Агар Р = jω бўлса, у холда бу ифода қуйидаги шаклда бўлади.

Бу формулда ушбу ифода

F(jω)=1-β(jω)·K (jω) - тескари боғланишнинг комплекс чуқурлиги деб юритилади.

Агар |1-β(jω)·K (jω)|>1 бўлса, тизимнинг узатиш коэффициенти модули ва унга мос равишда чиқишдаги сигнал амплитудаси камайгани сабабли тескари боғланиш манфий ТБ бўлади.

Агар |1-β(jω)·K(jω)|<1 бўлса, тескари боғланиш мусбат ТБ бўлади.

Масалан, Кучайтириш коэффициенти

K (jω)=1000 бўлса, тескари боғланишнинг узатиш коэффициенти в(jω)=-0,099 бўлса, у ҳолда тескари боғланишни ўз ичига олган кучайтиргичнинг умумий кучайтириш коэффициенти қуйидагига тенг балади

Манфий тескари боғланиш узатиш функциясининг барқарорлигини (кучайтиргич ишининг барқарорлигини) кўпайтиради;

Манфий тескари боғланиш деярли барча кучайтиргичларда ишлатилади.

Мусбат тескари боғланиш эса автогенераторларда ишлатилади.

Автогенераторлар

Ташқи таъсирсиз ҳосил бўладиган тебранишлар-автотебранишлар дейилади.

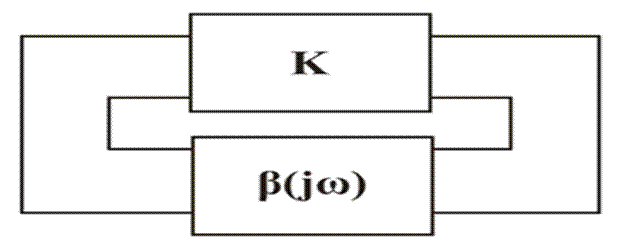
расм-20.3

Бу схемада:

K – кучайтиргич элементи;

β (ϳω) – тескари боғланган тўрқутбли элементи .

Ичида автотебранишлар ҳосил бўладиган махсус қурилма автогенератор деб аталади. (масалан: соат, юрак,ўпканинг ҳаракати ва ҳ.к. )

Автотебранишларнинг хусусиятлари:

1) ташқи таъсирлардан ҳосил бўлмайди, система ўзининг тебраниш хусусиятидан ҳосил бўлади;

2) тебраниш шакли, уларнинг амплитудаси ва частотаси системанинг ўз хусусиятидан аниқланади;

3) ҳосил бўлаётган автотебранишлар махсус энергияга эга (системада ўз манбаи бор).

Автогенераторнинг умумий схемасига кучайтиргич ва ТБ тўртқутблиги киради; уларнинг узатиш коэффициентлари шартини бажариладиган килиб танланади.

LC– автогенератор
Параллел тебраниш контурига асосан LC – автогенераторни ташкил этиш мумкин. Мисол учун қуйидаги электр занжирлари мисол бўлади.

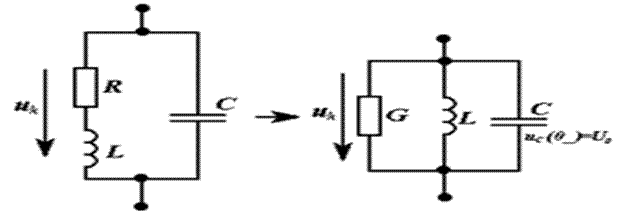
расм-20.4

Одатда тебраниш контури таъсир бўлмаган холда фақат сўнувчи тебранишлар хосил бўлади: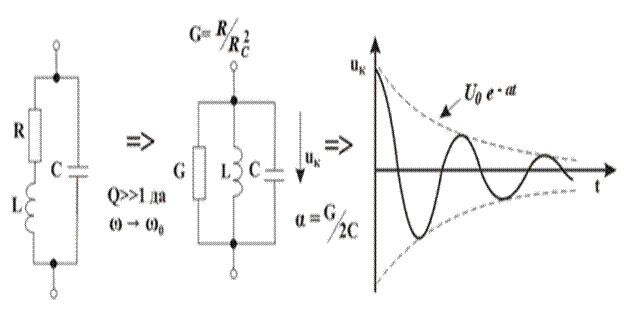

расм-20.5

Агар контурга тебраниш ҳосил қилувчи элементлар уланса, у холда тебранишлар ўсувчи бўлиб қолади

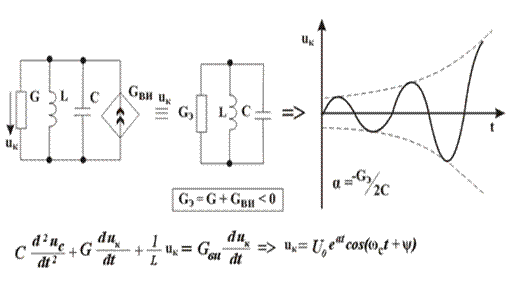
расм-20.6

Атогенератор дифференциал тенгламалари

Агар қуйидаги кўринишда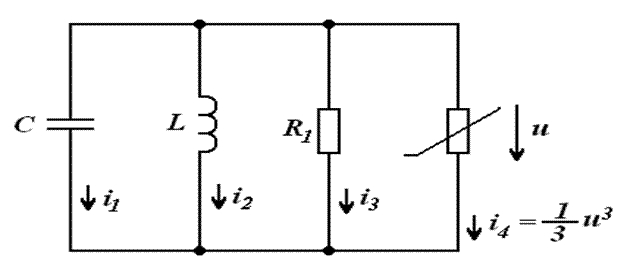

расм-20.7

ги автогенератор берилган бўлса, у холда

Қуйидаги тенгламалар ўринли бўлади:

Кирхгофнинг биринчи қонуни бўйича:

i₁+i₂+i₃+i₄=0

Юқоридаги занжир учун токлар қуйидагича ифодаланади:

Агар бир бирини ўрнига қўйсак, қуйидаги ифодани оламиз:

вақт бўйича дифференциаллаб қуйидагини оламиз

Юқоридаги формулаларни бир бирига қўйсак,

Ван – дер – Польнинг ночизиқли дифференциал тенгламасини оламиз.

Тебраниш контури бўлган автогенераторларнинг кўплаб тенгламалари Ван – дер – Поль тенгламаларига келтирилади.

Автогенераторлар парметрларини ҳисоблаганда қуйидаги харакктеристикаларни олишимиз мумкин:

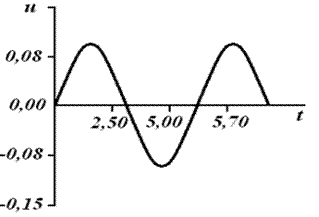
Расм-20.8

Келтирилган графиклар Автогенераторлар параметрларини ҳисоблашда кучланишнинг вақт бўйича ўзгаришини ҳар хил қийматлари орқали ифодалайди.

НАЗОРАТ САВОЛЛАРИ

1. Тескари боғланган занжирлар, таърифи, схемаси.

2. Манфий ва мусбат тескари боғланиш занжирлари.

3. Тескари боғланишнинг узатиш функцияси.

3. Автотебранишлар, таърифи.

4. Автогенераторлар,таърифи.

5. LC– автогенератор, схемаси.

6. Сўнувчи тебранишлар.

7. Ўсувчи тебранишлар.

8. Автогенераторлар дифференциал тенгламалари.