O’ZBEKISTON POCHTA VA TELEKOMMUNIKASIYALAR AGENTLIGI
TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
Oliy matematika kafedrasi
Oliy matematikadan
fanidan kunduzgi va sirtqi ta’lim talabalari uchun yozma ish variantlari va bajarishga doir uslubiy ko’rsatmalar
(1-qism)
(informasion texnologiyalar qo’llash asosida)
Toshkent 2005
So’zboshi
Sirtqi bo’lim talabalarining oliy matematika fani bo’limlari bo’yicha ko’p sonli so’rovnomalariga javoban TATU oliy matematika kafedrasi jamoasi oliy matematika fanining ba’zi mavzularini talabalarning talab darajasida o’zlashtirishlari uchun tajriba tariqasida zamonaviy informasion texnologiyalari asosida masofadan o’qitishni tashkil etish maqsadga muvofiq, deb hisoblaydi. Ana shu maqsadda mazkur qo’llanmada funksiyani to’la tekshirish mavzusi Maple 7.0 belgili matematika tizimi yordamida misollar bilan yoritilgan.
Maple 7.0 tizimining intellektual quvvati xozirgi davrda fan va texnikaning muhim masalalariyechilishini osonlashtirmoqda. Shu bilan birga, bu tizimning intellektual, grafik imkoniyatlari matematika fanini o’qitish (oliy, elementar) jarayonining samaradorligini oshirishga keng yo’l ochmoqda.
Funksiyani to’la tekshirish mavzui funksiyaning aniqlanish va o’zgarish sohalarini topish, juft yoki toqligini, uzluksizligini tekshirish, o’sish va kamayish oraliqlarini topish, shubhali nuqtalarini aniqlash va bu nuqtalarda ekstremum turlarini topish va xokazo bosqichlarni o’z ichiga oladi. Barcha sanab o’tilgan bosqichlarni bajarish uchun Maple 7.0 tizimining operatorlari mavjud. Mazkur mavzuning eng muhim tushunchalari va ba’zi bosqichlari uchun ishlatiladigan operatorlar va ularning qisqacha bayoni quyidagicha:
1.
Agar ![]() funksiya uchun
funksiya uchun ![]() shart
bajarilsa, funksiya juft;
shart
bajarilsa, funksiya juft; ![]() shart
bajarilsa, funksiya toq deyiladi.
shart
bajarilsa, funksiya toq deyiladi.
2.
![]() funksiyaning
aniqlanish sohasi deb erkli o’zgaruvchi x ning qabul qilishi mumkin
bo’lgan barcha qiymatlari to’plamiga aytiladi.
funksiyaning
aniqlanish sohasi deb erkli o’zgaruvchi x ning qabul qilishi mumkin
bo’lgan barcha qiymatlari to’plamiga aytiladi.
![]() funksiyaning o’zgarish
sohasi deb u-ning qabul qilishi mumkin bo’lgan barcha qiymatlari
to’plamiga aytiladi.
funksiyaning o’zgarish
sohasi deb u-ning qabul qilishi mumkin bo’lgan barcha qiymatlari
to’plamiga aytiladi.
Maple da funksiyaning uzluksizligini tekshirish uchun iscont operatori ishlatiladi:
iscont(expr. x - a .. b)
Bu operator x uzgaruvchining funksiyasi sifatida berilgan expr ifodaning uzluksizligini tekshiradi. Agar ifoda uzluksiz bo’lsa operator ishining natijasi true mantiqiy qiymatiga, aks holda false teng bo’ladi.
Masalan,![]() funksiyaning
uzluksizligini tekshiramiz.
funksiyaning
uzluksizligini tekshiramiz.
> iscont(1/(x-2),x=-3..3);
false
Demak, qaralayotgan oraliqda funksiya uzluksiz emas. Uzilish nuqtasini topish uchun discont(expr, x) operatoridan foydalanamiz. Yuqoridagi misol uchun:
> discont(l/(x-2).x);
{2}
Demak, qaralayotgan oraliqda x=2 nuqtada funksiya uzilishga ega.
Yana
bir misol, ![]() bo’lsin.
bo’lsin.
> discont(l/(x-l)+3/(x-2),x);
{1,2}
Funksiya uzilish nuqtalari atrofidagi holatini yaqqol ko’z oldimizga keltirish uchun uning grafigini chizish maqsadga muvofiq.
Ikki o’lchovli funksiyalar grafiklari plot operatori yordamida chiziladi. Bu operator quyidagicha ko’rinishga ega:
plot(f, h, v)
plot(f, h, v, o)
buyerda f - funksiyaning analitik ko’rinishi, h - o’zgaruvchi (aniqlanish sohasi ko’rsatiladi), v - o’zgaruvchi (ko’rsatilishi shart emas), o - grafikning xususiyatlarini (chiziklar qalinligi, rangi, belgilari va h.k.) ko’rsatuvchi parametr yoki parametrlar ro’yxati.
Masalan,
![]() funksiyaning
grafigini chizish talab qilinsin, buyerda
funksiyaning
grafigini chizish talab qilinsin, buyerda ![]() .
.
Maple 7.0 tizimida bu jarayon quyidagi buyruq satri orqali amalga oshiriladi:
> plot(x^4-5*x^2+6*x-2,x=-3..3, title=grafic1);
Natijada quyidagi ko’rinishda grafik hosil bo’ladi (1- rasm):
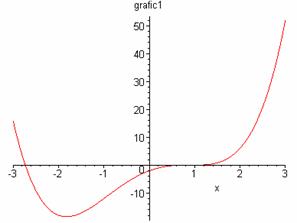
1-rasm. ![]() funksiya
grafigi.
funksiya
grafigi.
Plot
operatori funksiyaning uzilish nuqtalari atrofidagi holatini to’liq
ko’rsatishga imkon beradi. Masalan,  funksiya
grafigini Maple yordamida chizsak:
funksiya
grafigini Maple yordamida chizsak:
> plot({x^2/(x+1), x<>-1 }, x=-5..5, view=[-4..4,-10..5]);
Natijada quyidagi ko’rinishda grafik hosil bo’ladi (2-rasm):
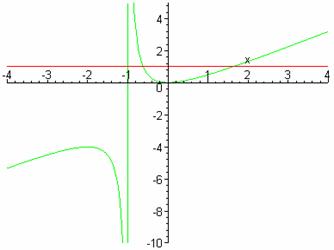
2-rasm.
 funksiya
grafigi (
funksiya
grafigi (![]() ikkinchi tur uzilish nuqtasi).
ikkinchi tur uzilish nuqtasi).
3. Funksiyaning o’sish va kamayish oraliqlari, ekstremumlarini topish uchun talabadan differensiallash qoidalarini bilish talab qilinadi. Quyida differensiallashning asosiy qoidalari qisqacha keltiriladi:
f(x) = u, g(x) = v - x nuqtada differensiallanuvchi funksiyalar bo’lsin.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3)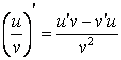 , agar v ¹ 0
, agar v ¹ 0
Bu qoidalar limitlar to’g’risidagi teoremalar asosida oson isbotlanadi.
Asosiy elementar funksiyalar xosilalari jadvali:
|
1) S¢ = 0; |
|
9) |
|
2) (xm)¢ = mxm-1; |
|
10) |
|
3) |
|
11) |
|
4) |
|
12) |
|
5) |
|
13) |
|
6) |
|
14) |
|
7) |
|
15) |
|
8) |
|
16) |
Murakkab funksiya xosilasi.
Agar y
= f(u); u = g(x), bo’lsa, u holda ![]() .
.
Logarifmik differensiallash.
Agar ![]() ko’rinishda bo’lsa, bu
ifoda avval logarifmlanadi va quyidagi ko’rinishga keltiriladi:
ko’rinishda bo’lsa, bu
ifoda avval logarifmlanadi va quyidagi ko’rinishga keltiriladi:
![]() ,
,
so’ngra bu ifodadan murakkab funksiya va ko’paytmadan xosila olish qoidalariga asosan:
 , yoki
, yoki 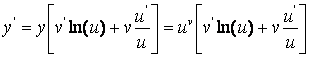
Teskari funksiya xosilasi.
u = f(x) funksiyaning teskarisi x = g(y) funksiya mavjud bo’lsin. U xolda agar g(y) – funksiya xosilasi mavjud va g¢(y) ¹ 0 bo’lsa:

Parametrik funksiya xosilasi.
Agar y ning x ga bog’likligi t parametr vositasida quyidagicha berilgan bo’lsa
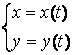 , u xolda
, u xolda  , va
, va 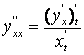
Endi differsiallash qoidalaridan foydalangan xolda funksiyaning o’sish va kamayish oraliklari va ekstremumlarini topish qoidalarini qisqacha keltiramiz.
1-ta’rif: agar ![]() bo’lsa,
funksiya o’suvchi yoki:
bo’lsa,
funksiya o’suvchi yoki:
![]() - funksiya
- funksiya![]() ;
;
agar ![]() bo’lsa, funksiya
kamayuvchi yoki:
bo’lsa, funksiya
kamayuvchi yoki:
![]() - funksiya
- funksiya![]() ;
;
Teorema: Agar [a,b]
oraliqda![]() bo’lsa
bo’lsa ![]()
![]() ,
,
agar [a,b] oraliqda![]() bo’lsa
bo’lsa ![]()
![]() .
.
2-ta’rif:![]() ;
;
![]() .
.
Ekstremumning zaruriy sharti
Agar ![]() shubhali nuqta bo’lsa, bu
nuqtada funksiyaning birinchi tartibli xosilasi 0 ga teng yoki mavjud emas:
shubhali nuqta bo’lsa, bu
nuqtada funksiyaning birinchi tartibli xosilasi 0 ga teng yoki mavjud emas: ![]() yoki
yoki ![]() yoki
yoki ![]() mavjud emas.
mavjud emas.
Ekstremumningyetarlilik sharti
Agar
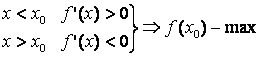 ;
;
agar
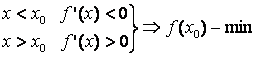 .
.
Ekstremumni tekshirishda ikkinchi tartibli xosiladan foydalanish
Agar ![]() nuqta shubhali nuqta
bo’lsa, u xolda:
nuqta shubhali nuqta
bo’lsa, u xolda:
![]()
![]()
Funksiya grafigining qavarik va botiqligi.
Agar (a,b)
oraliqda funksiya grafigi unga ixtiyoriy nuqtada o’tkazilgan urinmadan pastda
(yoki yuqorida) yotsa, ![]() differensiallanuvchi
funksiyaning grafigi qavariq (yoki botiq) deyiladi.
differensiallanuvchi
funksiyaning grafigi qavariq (yoki botiq) deyiladi.
 |
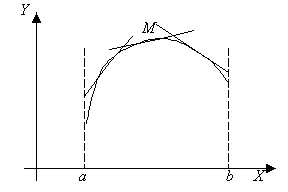 |
Botiq funksiya grafigi Qavariq funksiya grafigi
Agar ![]() oraliqning barcha
nuqtalari uchun
oraliqning barcha
nuqtalari uchun ![]() bo’lsa, u holda
bo’lsa, u holda ![]() funksiya
funksiya ![]() oraliqda qavariq
deyiladi; agar
oraliqda qavariq
deyiladi; agar ![]() oraliqning barcha
nuqtalari uchun
oraliqning barcha
nuqtalari uchun ![]() bo’lsa, u holda
bo’lsa, u holda ![]() funksiya
funksiya ![]() oraliqda botiq deyiladi.
oraliqda botiq deyiladi.
Agar ![]() bo’lsa,
bo’lsa, ![]() nuqta burilish nuqtasi
deyiladi. Burilish nuqtasi funksiya grafigining qavarik va botiq qismlarini
ajratib turadi.
nuqta burilish nuqtasi
deyiladi. Burilish nuqtasi funksiya grafigining qavarik va botiq qismlarini
ajratib turadi.
Funksiyaning grafigini
chizish uchun uning asimptotalarini aniqlash zarur. Funksiyaning og’ma
asimptotasi ![]() ko’rinishga ega, buyerda
ko’rinishga ega, buyerda ![]()
Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() - gorizontal assimptota.
- gorizontal assimptota.
Funksiyani to’lik tekshirish va grafiklarini chizish talabalarning differensial hisob kursini o’zlashtirishida muhim axamiyatga ega.
Mazkur o’quv-uslubiy qo’llanmadagi mustaqil vazifalar ikki qismdan iborat. Birinchi qism misollari differensial hisob qoidalari asosida turli funksiyalardan hosila olish amalini bajarishga muljallangan. Mazkur vazifani talaba mustaqil bajarish jarayonida differensial hisob kursi bo’yicha bilimlarini mukammallashtirish imkonini hosil qiladi. Ikkinchi qism vazifalari funksiyani differensial hisob usullari asosida to’la tekshirishga bag’ishlangan bo’lib, bu masalada informasion texnologiyalardan foydalanishni maqsadga muvofiq deb topildi va Maple 7.0 amaliy dasturidan foydalanib funksiyani to’la tekshirish uslubiyati yaratildi. Quyida ana shu uslub yordamida ba’zi funksiyalarni to’la tekshirish bo’yicha misollar ko’rildi.
1-misol.
![]() funksiya to’la
tekshirilsin va grafigi chizilsin.
funksiya to’la
tekshirilsin va grafigi chizilsin.
Maple 7.0 dan tuzilgan dastur quyidagi natijalarni berdi:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
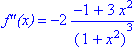
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
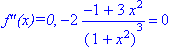
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
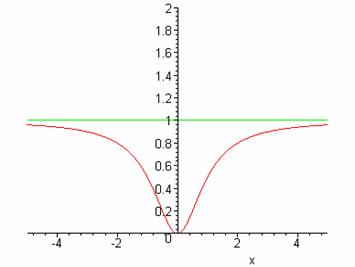
2-misol.
![]() funksiya to’la
tekshirilsin va grafigi chizilsin.
funksiya to’la
tekshirilsin va grafigi chizilsin.
Maple 7.0 dan tuzilgan dastur quyidagi natijalarni berdi:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
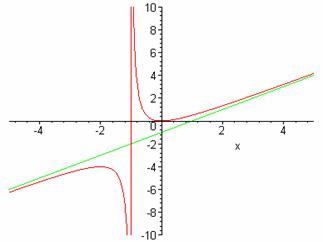
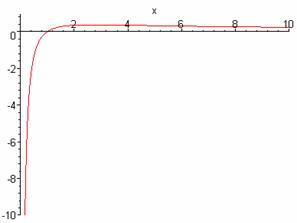
3-misol.
![]() funksiya to’la
tekshirilsin va grafigi chizilsin.
funksiya to’la
tekshirilsin va grafigi chizilsin.
Maple 7.0 dan tuzilgan dastur quyidagi natijalarni berdi:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mustaqil ishlar variantlari
Mustaqil ishlar ikki bosqichda bajariladi:
1. Differensiallash qoidalari asosida funksiyalar xosilalarini topish.
2. Funksiyani to’la tekshirishga doir misollarni kompüyuterda Maple 7.0 belgili matematik tizim yordamida bajarish.
3. Bajarilgan mustaqil ishlarni alohida daftarda rasmiylashtirish.
1.1-1.25. Quydagi funksiyalar xosilalarini toping.
1.1 a)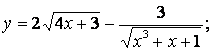
b) ![]()
![]() v)
v)![]()
g) ![]() d)
d) ![]()
1.2 a) ![]() b)
b)![]()
v) ![]() g)
g) ![]() ;
;
d) ![]() ;
;
1.3 a)  ; b)
; b) ![]() ;
;![]()
v) ![]() ; g)
; g) ![]()
d) ![]() ;
;
1.4 a) 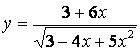 ;
b)
;
b)![]() ;
;
v) ![]() g)
g) ![]()
d) ![]()
1.5 a)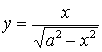 b)
b) 
v) ![]() g)
g) ![]()
d) ![]()
1.6 a)  b)
b) ![]()
v) ![]() g)
g) ![]()
d) ![]()
1.7 a)  b)
b)
![]()
v)  g)
g) ![]()
d) ![]()
![]()
1.8 a) ![]() b)
b)
![]()
v) 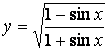 g)
g)
![]()
d) ![]()
1.9 a) 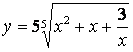 b)
b)
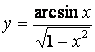
v) ![]() g)
g) ![]()
d) 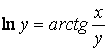
1.10 a) 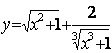 b)
b)
![]()
v) 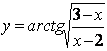 g)
g)
![]()
d) ![]()
1.11 a) ![]() b)
b) 
v) ![]()
![]() g)
g)![]()
d) ![]()
1.12 a) 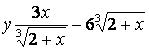 b)
b) ![]()
v) ![]() g)
g) ![]()
d) ![]()
1.13 a) 
![]() b)
b)![]()
v)![]() g)
g) ![]()
d) ![]()
1.14 a) ![]() b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
1.15 a) ![]() b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
1.16 a) b)
b) ![]()
v) ![]() g)
g)
![]()
d) ![]()
1.17 a) 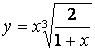 b)
b)
![]()
v)  g)
g)
![]()
d) ![]()
1.18 a) ![]() b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
1.19 a) 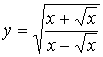 b)
b)
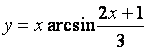
v)![]() g)
g) ![]()
d) ![]()
1.20 a) ![]() b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
1.21 a) 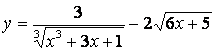 b)
b) ![]()
v) ![]() g)
g)
![]()
d) ![]()
1.22 a)  b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
1.23 a) b)
b) ![]()
v) ![]() g)
g) ![]()
d) ![]()
1.24 a) ![]() b)
b)
![]()
v) 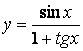 g)
g)
![]()
d) 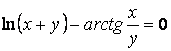
1.25 a)  b)
b)
![]()
v) ![]() g)
g)
![]()
d) ![]()
2.1-2.25 ![]() ;
; ![]() ni toping.
ni toping.
2.1 a)![]() b)
b) 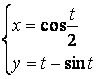
2.2 a) ![]() b)
b)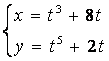
2.3 a) ![]() b)
b) 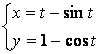
2.4 a) ![]() b)
b) 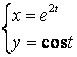
2.5 a) ![]() b)
b)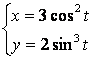
2.6 a) ![]() b)
b)
2.7 a) ![]() b)
b)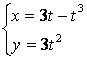
2.8 a) ![]() b)
b)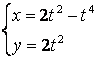
2.9 a)![]() b)
b)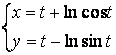
2.10 a)![]() b)
b)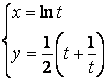
2.11 a) b)
b)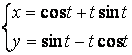
2.12 a)![]() b)
b)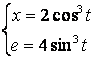
2.13 a) ![]() b)
b)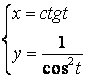
2.14 a) ![]() b)
b)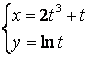
2.15 a) ![]() b)
b)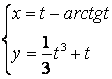
2.16 a) ![]() b)
b)
2.17 a) ![]() b)
b)
2.18 a)![]() b)
b)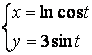
2.19 a)![]() b)
b)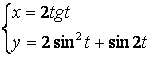
2.20 a)![]() b)
b)
2.21 a)![]() b)
b)
2.22 a)![]() b)
b)
2.23 a)![]() b)
b)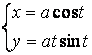
2.24 a)![]() b)
b)
2.25 a) b)
b)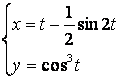
3.1-3.25
![]() funksiyaning
funksiyaning ![]() kesmada eng katta va eng
kichik qiymati topilsin.
kesmada eng katta va eng
kichik qiymati topilsin.
3.1 ![]()
![]()
3.2 ![]()
![]()
3.3 ![]()
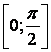
3.4 ![]()
![]()
3.5 ![]()
![]()
3.6 ![]()
![]()
3.7 ![]() ;
; 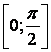
3.8 ![]() ;
; ![]()
3.9 ![]()
![]()
3.10 ![]()
![]()
3.11 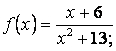
![]()
3.12 ![]()
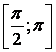
3.13 ![]()
![]()
3.14 ![]()
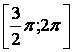
3.15 ![]()
![]()
3.16 ![]()
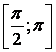
3.17 ![]()
![]()
3.18 ![]()
![]()
3.19 ![]()
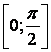
3.20 ![]()
![]()
3.21 ![]()
![]()
3.22 ![]()
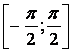
3.23 ![]()
![]()
3.24 ![]()
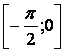
3.25 ![]()
![]()
4.1-4.25 Differensial hisob usullari va Maple 7.0 belgili matematik tizim yordamida quyidagi funksiyalar to’la tekshirilsin.
4.1 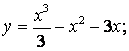 4.2
4.2 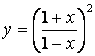
4.3 ![]() 4.4
4.4
![]()
4.5![]() 4.6
4.6 ![]()
4.7 ![]() 4.8
4.8
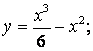
4.9 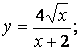 4.10
4.10
![]()
4.11 ![]() 4.12
4.12 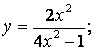
4.13 ![]() 4.14
4.14 ![]()
4.15 ![]() 4.16
4.16 ![]()
4.17 ![]() 4.18
4.18 
4.19 ![]() 4.20
4.20 
4.21 ![]() 4.22
4.22

4.23  4.24
4.24 ![]()
4.25 ![]()
Adabiyotlar:
1. Piskunov N.S. Differensial’noe i integral’noe ischislenie.
T.1. M.: Nauka, 1977-1985.
2.Shneyder V.Ye., Sluskiy A.I., Shumov A.S. Kratkiy kurs obshchey matematiki. T.1. M. : Nauka, 1978.
3. D’yakonov V. P. Maple-7. Uchebnûy kurs. Piter, 2001.
4. D’yakonov V.P. Komp’yuternaya matematika. Teoriya i praktika. Nolidj,
2000.
5.Matrosov A. Maple-6. Resheniya zadach vûsshey matematiki i mexanike.
Oliy matematika fanidan kunduzgi va
sirtqi bo’lim talabalari uchun yozma
ish variantlari va bajarishga doir
uslubiy ko’rsatmalar (informasion
texnologiyalar qo’llash asosida).
Oliy matematika kafedrasi majlisida ko’rildi va bosmadan chiqarishga tavsiya etildi (5.04.2004, 28-bayonnoma).
Tuzuvchilar: dosent Usmonov R.N.,
katta o’qituvchi Muxatdinov M.Ya.
Mas’ul muharrir: akademik Abutaliev F.B.
Muharrir: Parpieva Q.