ЎЗБЕКИСТОН ПОЧТА ВА ТЕЛЕКОММУНИКАЦИЯЛАР АГЕНТЛИГИ
ТОШКЕНТ АХБОРОТ ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ
Олий математика кафедраси
Олий математикадан
фанидан кундузги ва сиртқи таълим талабалари учун ёзма иш вариантлари ва бажаришга доир услубий курсатмалар
(1-кисм)
(информацион технологиялар қўллаш асосида)
Тошкент 2005
Сузбоши
Сиртқи бўлим талабаларининг олий математика фани бўлимлари бўйича кўп сонли сўровномаларига жавобан ТАТУ олий математика кафедраси жамоаси олий математика фанининг баъзи мавзуларини талабаларнинг талаб даражасида ўзлаштиришлари учун тажриба тариқасида замонавий информацион технологиялари асосида масофадан ўқитишни ташкил этиш мақсадга мувофиқ, деб ҳисоблайди. Ана шу мақсадда мазкур қўлланмада функцияни тўла текшириш мавзуси Maple 7.0 белгили математика тизими ёрдамида мисоллар билан ёритилган.
Maple 7.0 тизимининг интеллектуал қуввати хозирги даврда фан ва техниканинг муҳим масалалари ечилишини осонлаштирмоқда. Шу билан бирга, бу тизимнинг интеллектуал, график имкониятлари математика фанини ўқитиш (олий, элементар) жараёнининг самарадорлигини оширишга кенг йўл очмоқда.
Функцияни тўла текшириш мавзуи функциянинг аниқланиш ва ўзгариш соҳаларини топиш, жуфт ёки тоқлигини, узлуксизлигини текшириш, ўсиш ва камайиш оралиқларини топиш, шубҳали нуқталарини аниқлаш ва бу нуқталарда экстремум турларини топиш ва хоказо босқичларни ўз ичига олади. Барча санаб ўтилган босқичларни бажариш учун Maple 7.0 тизимининг операторлари мавжуд. Мазкур мавзунинг энг муҳим тушунчалари ва баъзи босқичлари учун ишлатиладиган операторлар ва уларнинг қисқача баёни қуйидагича:
1.
Агар ![]() функция учун
функция учун ![]() шарт
бажарилса, функция жуфт;
шарт
бажарилса, функция жуфт; ![]() шарт
бажарилса, функция тоқ дейилади.
шарт
бажарилса, функция тоқ дейилади.
2.
![]() функциянинг
аниқланиш соҳаси деб эркли ўзгарувчи х нинг қабул
қилиши мумкин бўлган барча қийматлари тўпламига айтилади.
функциянинг
аниқланиш соҳаси деб эркли ўзгарувчи х нинг қабул
қилиши мумкин бўлган барча қийматлари тўпламига айтилади.
![]() функциянинг ўзгариш
соҳаси деб у-нинг қабул қилиши мумкин бўлган барча
қийматлари тўпламига айтилади.
функциянинг ўзгариш
соҳаси деб у-нинг қабул қилиши мумкин бўлган барча
қийматлари тўпламига айтилади.
Maple 7.0 да функциянинг узлуксизлигини текшириш учун iscont оператори ишлатилади:
iscont(expr. х - а .. b)
Бу оператор х узгарувчининг функцияси сифатида берилган ехрr ифоданинг узлуксизлигини текширади. Агар ифода узлуксиз бўлса оператор ишининг натижаси true мантиқий қийматига, акс ҳолда false тенг бўлади.
Масалан,![]() функциянинг
узлуксизлигини текширамиз.
функциянинг
узлуксизлигини текширамиз.
> iscont(1/(x-2),x=-3..3);
false
Демак, қаралаётган оралиқда функция узлуксиз эмас. Узилиш нуқтасини топиш учун discont(expr, x) операторидан фойдаланамиз. Юқоридаги мисол учун:
> discont(l/(x-2).x);
{2}
Демак, қаралаётган оралиқда х=2 нуқтада функция узилишга эга.
Яна бир
мисол, ![]() бўлсин.
бўлсин.
> discont(l/(x-l)+3/(x-2),x);
{1,2}
Функция узилиш нуқталари атрофидаги ҳолатини яққол кўз олдимизга келтириш учун унинг графигини чизиш мақсадга мувофиқ.
Икки ўлчовли функциялар графиклари plot оператори ёрдамида чизилади. Бу оператор қуйидагича кўринишга эга:
plot(f, h, v)
plot(f, h, v, о)
бу ерда f - функциянинг аналитик кўриниши, h - ўзгарувчи (аниқланиш соҳаси кўрсатилади), v - ўзгарувчи (кўрсатилиши шарт эмас), о - графикнинг хусусиятларини (чизиклар қалинлиги, ранги, белгилари ва ҳ.к.) кўрсатувчи параметр ёки параметрлар рўйхати.
Масалан,
![]() функциянинг
графигини чизиш талаб қилинсин, бу ерда
функциянинг
графигини чизиш талаб қилинсин, бу ерда ![]() .
.
Maple 7.0 тизимида бу жараён қуйидаги буйруқ сатри орқали амалга оширилади:
> plot(x^4-5*x^2+6*x-2,x=-3..3, title=grafic1);
Натижада қуйидаги кўринишда график ҳосил бўлади (1- расм):
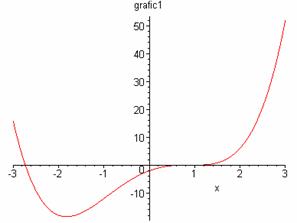
1-расм. ![]() функция графиги.
функция графиги.
Plot
оператори функциянинг узилиш нуқталари атрофидаги ҳолатини тўлиқ кўрсатишга имкон беради.
Масалан,
 функция графигини Maple7.0
ёрдамида чизсак:
функция графигини Maple7.0
ёрдамида чизсак:
> plot({x^2/(x+1), x<>-1 }, x=-5..5, view=[-4..4,-10..5]);
Натижада қуйидаги кўринишда график ҳосил бўлади (2- расм):
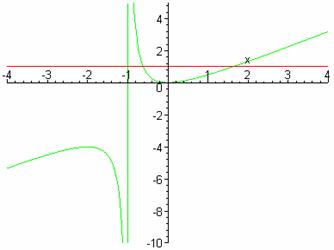
2-расм.
 функция графиги (
функция графиги (![]() иккинчи тур узилиш нуқтаси).
иккинчи тур узилиш нуқтаси).
3. Функциянинг ўсиш ва камайиш оралиқлари, экстремумларини топиш учун талабадан дифференциаллаш қоидаларини билиш талаб қилинади. Қуйида дифференциаллашнинг асосий қоидалари қисқача келтирилади:
f(x) = u, g(x) = v - х нуқтада дифференциалланувчи функциялар бўлсин.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3)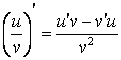 , агар v ¹ 0
, агар v ¹ 0
Бу қоидалар лимитлар тўғрисидаги теоремалар асосида осон исботланади.
Асосий элементар функциялар хосилалари жадвали:
|
1) С¢ = 0; |
|
9) |
|
2) (xm)¢ = mxm-1; |
|
10) |
|
3) |
|
11) |
|
4) |
|
12) |
|
5) |
|
13) |
|
6) |
|
14) |
|
7) |
|
15) |
|
8) |
|
16) |
Мураккаб функция хосиласи.
Агар y = f(u);
u = g(x),
бўлса, у ҳолда ![]() .
.
Логарифмик дифференциаллаш.
Агар ![]() кўринишда
бўлса, бу ифода аввал логарифмланади ва қуйидаги кўринишга келтирилади:
кўринишда
бўлса, бу ифода аввал логарифмланади ва қуйидаги кўринишга келтирилади:
![]() ,
,
сўнгра бу ифодадан мураккаб функция ва кўпайтмадан хосила олиш қоидаларига асосан:
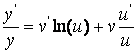 , ёки
, ёки 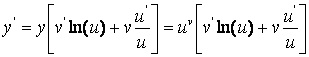
Тескари функция хосиласи.
у = f(x) функциянинг тескариси x = g(y) функция мавжуд бўлсин. У холда агар g(y) – функция хосиласи мавжуд ва g¢(y) ¹ 0 бўлса:

Параметрик функция хосиласи.
Агар y нинг x га боғликлиги t параметр воситасида қуйидагича берилган бўлса
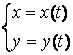 , у холда
, у холда  ,
ва
,
ва 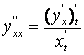
Энди дифферциаллаш қоидаларидан фойдаланган холда функциянинг ўсиш ва камайиш ораликлари ва экстремумларини топиш қоидаларини қисқача келтирамиз.
1-таъриф: агар ![]() бўлса, функция ўсувчи ёки:
бўлса, функция ўсувчи ёки:
![]() -
функция
-
функция![]() ;
;
агар ![]() бўлса,
функция камаювчи ёки:
бўлса,
функция камаювчи ёки:
![]() -
функция
-
функция![]() ;
;
Теорема: Агар [a,b]
оралиқда![]() бўлса
бўлса ![]()
![]() ,
,
агар [a,b] оралиқда![]() бўлса
бўлса ![]()
![]() .
.
2-таъриф:![]() ;
;
![]() .
.
Экстремумнинг зарурий шарти
Агар ![]() шубҳали
нуқта бўлса, бу нуқтада функциянинг биринчи тартибли хосиласи 0 га тенг ёки мавжуд эмас:
шубҳали
нуқта бўлса, бу нуқтада функциянинг биринчи тартибли хосиласи 0 га тенг ёки мавжуд эмас: ![]() ёки
ёки ![]() ёки
ёки
![]() мавжуд эмас.
мавжуд эмас.
Экстремумнинг етарлилик шарти
Агар
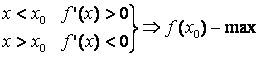 ;
;
агар
 .
.
Экстремумни текширишда иккинчи тартибли хосиладан фойдаланиш
Агар ![]() нуқта
шубҳали нуқта бўлса, у холда:
нуқта
шубҳали нуқта бўлса, у холда:
![]()
![]()
Функция графигининг қаварик ва ботиқлиги.
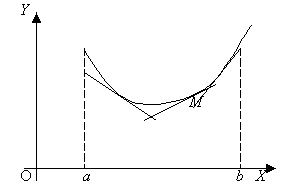
Агар (a,b)
оралиқда функция графиги унга ихтиёрий нуқтада ўтказилган
уринмадан пастда (ёки юқорида) ётса, ![]() дифференциалланувчи
функциянинг графиги қавариқ (ёки ботиқ) дейилади.
дифференциалланувчи
функциянинг графиги қавариқ (ёки ботиқ) дейилади.
 |
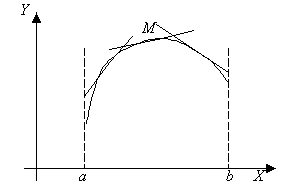 |
Ботиқ функция графиги Қавариқ функция графиги
Агар ![]() оралиқнинг барча
нуқталари учун
оралиқнинг барча
нуқталари учун ![]() бўлса, у ҳолда
бўлса, у ҳолда ![]() функция
функция ![]() оралиқда
қавариқ дейилади; агар
оралиқда
қавариқ дейилади; агар ![]() оралиқнинг барча
нуқталари учун
оралиқнинг барча
нуқталари учун ![]() бўлса, у ҳолда
бўлса, у ҳолда ![]() функция
функция ![]() оралиқда
ботиқ дейилади.
оралиқда
ботиқ дейилади.
Агар ![]() бўлса,
бўлса, ![]() нуқта
бурилиш нуқтаси дейилади. Бурилиш нуқтаси функция графигининг
қаварик ва ботиқ қисмларини ажратиб туради.
нуқта
бурилиш нуқтаси дейилади. Бурилиш нуқтаси функция графигининг
қаварик ва ботиқ қисмларини ажратиб туради.
Функциянинг графигини чизиш учун
унинг асимптоталарини аниқлаш зарур. Функциянинг оғма асимптотаси ![]() кўринишга
эга, бу ерда
кўринишга
эга, бу ерда ![]()
Агар ![]() бўлса, у
ҳолда
бўлса, у
ҳолда ![]() - горизонтал
ассимптота.
- горизонтал
ассимптота.
Функцияни тўлик текшириш ва графикларини чизиш талабаларнинг дифференциал ҳисоб курсини ўзлаштиришида муҳим ахамиятга эга.
Мазкур ўқув-услубий қўлланмадаги мустақил вазифалар икки қисмдан иборат. Биринчи қисм мисоллари дифференциал ҳисоб қоидалари асосида турли функциялардан ҳосила олиш амалини бажаришга мулжалланган. Мазкур вазифани талаба мустақил бажариш жараёнида дифференциал ҳисоб курси бўйича билимларини мукаммаллаштириш имконини ҳосил қилади. Иккинчи қисм вазифалари функцияни дифференциал хисоб усуллари асосида тўла текширишга бағишланган бўлиб, бу масалада информацион технологиялардан фойдаланишни мақсадга мувофиқ деб топилди ва Maple 7.0 амалий дастуридан фойдаланиб функцияни тўла текшириш услубияти яратилди. Қуйида ана шу услуб ёрдамида баъзи функцияларни тўла текшириш бўйича мисоллар кўрилди.
1-мисол.
![]() функция тўла
текширилсин ва графиги чизилсин.
функция тўла
текширилсин ва графиги чизилсин.
Maple 7.0 дан тузилган дастур қуйидаги натижаларни берди:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
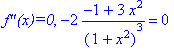
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
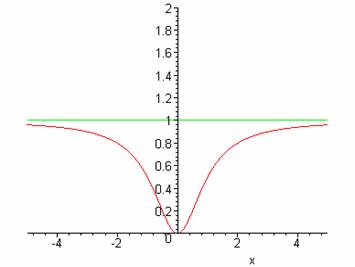
2-мисол.
![]() функция тўла
текширилсин ва графиги чизилсин.
функция тўла
текширилсин ва графиги чизилсин.
Maple 7.0 дан тузилган дастур қуйидаги натижаларни берди:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

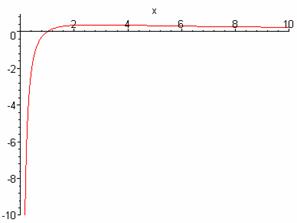
3-мисол.
![]() функция тўла
текширилсин ва графиги чизилсин.
функция тўла
текширилсин ва графиги чизилсин.
Maple 7.0 дан тузилган дастур қуйидаги натижаларни берди:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Мустақил ишлар вариантлари
Мустақил ишлар икки босқичда бажарилади:
1. Дифференциаллаш қоидалари асосида функциялар хосилаларини топиш.
2. Функцияни тўла текширишга доир мисолларни компьютерда Maple 7.0 белгили математик тизим ёрдамида бажариш.
3. Бажарилган мустақил ишларни алоҳида дафтарда расмийлаштириш.
1.1-1.25. Қуйидаги функциялар хосилаларини топинг.
1.1 a)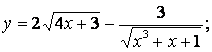
б) ![]()
![]() в)
в)![]()
г) ![]() д)
д) ![]()
1.2 а) ![]() б)
б)![]()
в) ![]() г)
г) ![]() ;
;
д) ![]() ;
;
1.3 a)  ;
б)
;
б) ![]() ;
;![]()
в) ![]() ; г)
; г) ![]()
д) ![]() ;
;
1.4 a)  ;
б)
;
б)![]() ;
;
в) ![]() г)
г)
![]()
д) ![]()
1.5 a)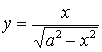 б)
б) 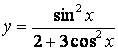
в) ![]() г)
г) ![]()
д) ![]()
1.6 a) 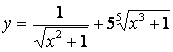 б)
б)
![]()
в) ![]() г)
г) ![]()
д) ![]()
1.7 a)  б)
б) ![]()
в)  г)
г) ![]()
д) ![]()
![]()
1.8 a) ![]() б)
б) ![]()
в) 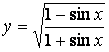 г)
г) ![]()
д) ![]()
1.9 а) 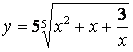 б)
б) 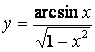
в) ![]() г)
г)
![]()
д) 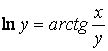
1.10 а) 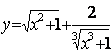 б)
б) ![]()
в)  г)
г)
![]()
д) ![]()
1.11 а) ![]() б)
б) 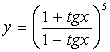
в) ![]()
![]() г)
г)![]()
д) ![]()
1.12 а) 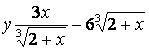 б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.13 а) 
![]() б)
б)![]()
в)![]() г)
г) ![]()
д) ![]()
1.14 а) ![]() б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.15 а) ![]() б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.16 а) б)
б) ![]()
в) ![]() г)
г)
![]()
д) ![]()
1.17 а) 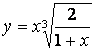 б)
б)
![]()
в)  г)
г)
![]()
д) ![]()
1.18 а) ![]() б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.19 а)  б)
б)
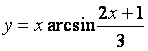
в)![]() г)
г) ![]()
д) ![]()
1.20 а) ![]() б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.21 а)  б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.22 а) 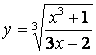 б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
1.23 а) б)
б) ![]()
в) ![]() г)
г)
![]()
д) ![]()
1.24 а) ![]() б)
б)
![]()
в) 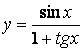 г)
г)
![]()
д) 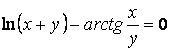
1.25 а)  б)
б)
![]()
в) ![]() г)
г)
![]()
д) ![]()
2.1-2.25 ![]() ;
; ![]() ни
топинг.
ни
топинг.
2.1 а)![]() б)
б) 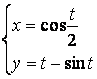
2.2 а) ![]() б)
б)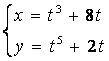
2.3 а) ![]() б)
б) 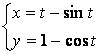
2.4 а) ![]() б)
б) 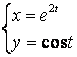
2.5 а) ![]() б)
б)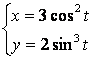
2.6 а) ![]() б)
б)
2.7 а) ![]() б)
б)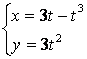
2.8 а) ![]() б)
б)
2.9 а)![]() б)
б)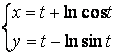
2.10 а)![]() б)
б)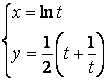
2.11 а) б)
б)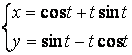
2.12 а)![]() б)
б)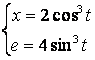
2.13 а) ![]() б)
б)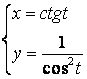
2.14 а) ![]() б)
б)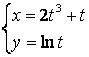
2.15 а) ![]() б)
б)
2.16 а) ![]() б)
б)
2.17 а) ![]() б)
б)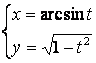
2.18 а)![]() б)
б)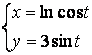
2.19 а)![]() б)
б)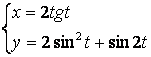
2.20 а)![]() б)
б)
2.21 а)![]() б)
б)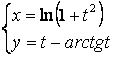
2.22 а)![]() б)
б)
2.23 а)![]() б)
б)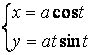
2.24 а)![]() б)
б)
2.25 а) б)
б)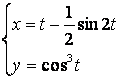
3.1-3.25
![]() функциянинг
функциянинг
![]() кесмада энг катта
ва энг кичик қиймати топилсин.
кесмада энг катта
ва энг кичик қиймати топилсин.
3.1 ![]()
![]()
3.2 ![]()
![]()
3.3 ![]()
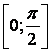
3.4 ![]()
![]()
3.5 ![]()
![]()
3.6 ![]()
![]()
3.7 ![]() ;
; 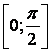
3.8 ![]() ;
; ![]()
3.9 ![]()
![]()
3.10 ![]()
![]()
3.11 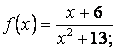
![]()
3.12 ![]()
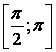
3.13 ![]()
![]()
3.14 ![]()
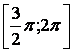
3.15 ![]()
![]()
3.16 ![]()
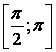
3.17 ![]()
![]()
3.18 ![]()
![]()
3.19 ![]()
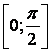
3.20 ![]()
![]()
3.21 ![]()
![]()
3.22 ![]()

3.23 ![]()
![]()
3.24 ![]()

3.25 ![]()
![]()
4.1-4.25 Дифференциал ҳисоб усуллари ва Maple 7.0 белгили математик тизим ёрдамида қуйидаги функциялар тўла текширилсин.
4.1 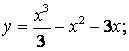 4.2
4.2
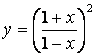
4.3 ![]() 4.4
4.4
![]()
4.5![]() 4.6
4.6 ![]()
4.7 ![]() 4.8
4.8
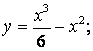
4.9 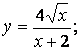 4.10
4.10
![]()
4.11 ![]() 4.12
4.12
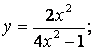
4.13 ![]() 4.14
4.14
![]()
4.15 ![]() 4.16
4.16
![]()
4.17 ![]() 4.18
4.18
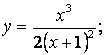
4.19 ![]() 4.20
4.20

4.21 ![]() 4.22
4.22
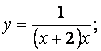
4.23 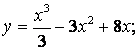 4.24
4.24 ![]()
4.25 ![]()
Адабиётлар:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т.1. М.: Наука, 1977-1985.
2.Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс общей математики. Т.1. М. : Наука, 1978.
3. Дьяконов В. П. Maple-7. Учебный курс. Питер, 2001.
4. Дьяконов В.П. Компьютерная математика. Теория и практика. Нолидж,
2000.
5.Матросов А. Maple-6. Решения задач высшей математики и механике.
Олий математика фанидан кундузги
ва сиртқи бўлим талабалари учун
ёзма иш вариантлари вабажаришга
доир услубий курсатмалар
(информацион технологиялар қўллаш асосида).
Олий математика кафедраси мажлисида кўрилди ва босмадан чиқаришга тавсия этилди (5.04.2004, 28-баённома).
Тузувчилар: доцент Усмонов Р.Н.,
катта ўкитувчи Мухатдинов М.Я.
Масъул муҳаррир: академик Абуталиев Ф.Б.
Муҳаррир: Парпиева Қ.